| ciphers | ||
| data_structures | ||
| dynamic_programming | ||
| File_Transfer_Protocol | ||
| Graphs | ||
| hashes | ||
| machine_learning | ||
| Neural_Network | ||
| other | ||
| Project Euler | ||
| searches | ||
| sorts | ||
| strings | ||
| traversals | ||
| .gitignore | ||
| License | ||
| Multi_Hueristic_Astar.py | ||
| README.md | ||
The Algorithms - Python
All algorithms implemented in Python (for education)
These are for demonstration purposes only. There are many implementations of sorts in the Python standard library that are much better for performance reasons.
Sort Algorithms
Bubble
From Wikipedia: Bubble sort, sometimes referred to as sinking sort, is a simple sorting algorithm that repeatedly steps through the list to be sorted, compares each pair of adjacent items and swaps them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which indicates that the list is sorted.
Properties
- Worst case performance O(n^2)
- Best case performance O(n)
- Average case performance O(n^2)
View the algorithm in action
Insertion
From Wikipedia: Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort.
Properties
- Worst case performance O(n^2)
- Best case performance O(n)
- Average case performance O(n^2)
View the algorithm in action
Merge
From Wikipedia: In computer science, merge sort (also commonly spelled mergesort) is an efficient, general-purpose, comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the implementation preserves the input order of equal elements in the sorted output. Mergesort is a divide and conquer algorithm that was invented by John von Neumann in 1945.
Properties
- Worst case performance O(n log n)
- Best case performance O(n)
- Average case performance O(n)
View the algorithm in action
Quick
From Wikipedia: Quicksort (sometimes called partition-exchange sort) is an efficient sorting algorithm, serving as a systematic method for placing the elements of an array in order.
Properties
- Worst case performance O(n^2)
- Best case performance O(n log n) or O(n) with three-way partition
- Average case performance O(n^2)
View the algorithm in action
Selection
From Wikipedia: The algorithm divides the input list into two parts: the sublist of items already sorted, which is built up from left to right at the front (left) of the list, and the sublist of items remaining to be sorted that occupy the rest of the list. Initially, the sorted sublist is empty and the unsorted sublist is the entire input list. The algorithm proceeds by finding the smallest (or largest, depending on sorting order) element in the unsorted sublist, exchanging (swapping) it with the leftmost unsorted element (putting it in sorted order), and moving the sublist boundaries one element to the right.
Properties
- Worst case performance O(n^2)
- Best case performance O(n^2)
- Average case performance O(n^2)
View the algorithm in action
Shell
From Wikipedia: Shellsort is a generalization of insertion sort that allows the exchange of items that are far apart. The idea is to arrange the list of elements so that, starting anywhere, considering every nth element gives a sorted list. Such a list is said to be h-sorted. Equivalently, it can be thought of as h interleaved lists, each individually sorted.
Properties
- Worst case performance O(nlog2 2n)
- Best case performance O(n log n)
- Average case performance depends on gap sequence
View the algorithm in action
Time-Compexity Graphs
Comparing the complexity of sorting algorithms (Bubble Sort, Insertion Sort, Selection Sort)
Search Algorithms
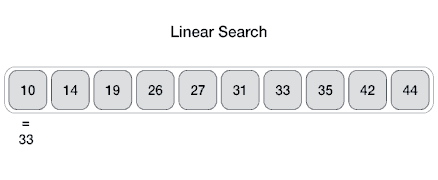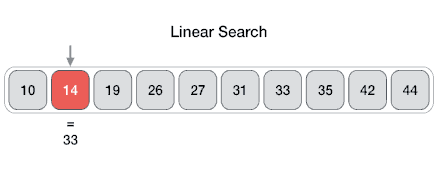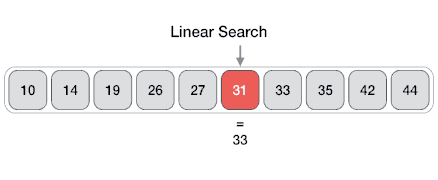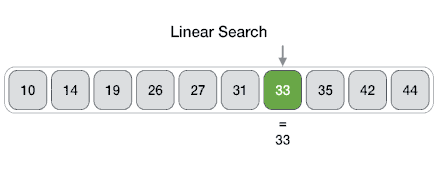
Linear
From Wikipedia: linear search or sequential search is a method for finding a target value within a list. It sequentially checks each element of the list for the target value until a match is found or until all the elements have been searched. Linear search runs in at worst linear time and makes at most n comparisons, where n is the length of the list.
Properties
- Worst case performance O(n)
- Best case performance O(1)
- Average case performance O(n)
- Worst case space complexity O(1) iterative
Binary
From Wikipedia: Binary search, also known as half-interval search or logarithmic search, is a search algorithm that finds the position of a target value within a sorted array. It compares the target value to the middle element of the array; if they are unequal, the half in which the target cannot lie is eliminated and the search continues on the remaining half until it is successful.
Properties
- Worst case performance O(log n)
- Best case performance O(1)
- Average case performance O(log n)
- Worst case space complexity O(1)
Ciphers
Caesar
In cryptography, a Caesar cipher, also known as Caesar's cipher, the shift cipher, Caesar's code or Caesar shift, is one of the simplest and most widely known encryption techniques.
It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet. For example, with a left shift of 3, D would be replaced by A, E would become B, and so on.
The method is named after Julius Caesar, who used it in his private correspondence.
The encryption step performed by a Caesar cipher is often incorporated as part of more complex schemes, such as the Vigenère cipher, and still has modern application in the ROT13 system. As with all single-alphabet substitution ciphers, the Caesar cipher is easily broken and in modern practice offers essentially no communication security.
Source: Wikipedia
Vigenère
The Vigenère cipher is a method of encrypting alphabetic text by using a series of interwoven Caesar ciphers based on the letters of a keyword. It is a form of polyalphabetic substitution.
The Vigenère cipher has been reinvented many times. The method was originally described by Giovan Battista Bellaso in his 1553 book La cifra del. Sig. Giovan Battista Bellaso; however, the scheme was later misattributed to Blaise de Vigenère in the 19th century, and is now widely known as the "Vigenère cipher".
Though the cipher is easy to understand and implement, for three centuries it resisted all attempts to break it; this earned it the description le chiffre indéchiffrable(French for 'the indecipherable cipher').
Many people have tried to implement encryption schemes that are essentially Vigenère ciphers. Friedrich Kasiski was the first to publish a general method of deciphering a Vigenère cipher in 1863.
Source: Wikipedia
Transposition
In cryptography, a transposition cipher is a method of encryption by which the positions held by units of plaintext (which are commonly characters or groups of characters) are shifted according to a regular system, so that the ciphertext constitutes a permutation of the plaintext. That is, the order of the units is changed (the plaintext is reordered).
Mathematically a bijective function is used on the characters' positions to encrypt and an inverse function to decrypt.