mirror of
https://github.com/rasbt/python_reference.git
synced 2024-12-19 00:30:19 +00:00
1255 lines
183 KiB
Plaintext
1255 lines
183 KiB
Plaintext
|
|
{
|
||
|
|
"metadata": {
|
||
|
|
"name": "",
|
||
|
|
"signature": "sha256:e0aeebc5816e30eb2937ee4b331a3885fbaf1583183823ad07fb79e368b90290"
|
||
|
|
},
|
||
|
|
"nbformat": 3,
|
||
|
|
"nbformat_minor": 0,
|
||
|
|
"worksheets": [
|
||
|
|
{
|
||
|
|
"cells": [
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"[Sebastian Raschka](www.sebastianraschka.com) \n",
|
||
|
|
"last updated: 05/04/2014\n",
|
||
|
|
"\n",
|
||
|
|
"- [Link to this IPython Notebook on GitHub](https://github.com/rasbt/python_reference/blob/master/not_so_obvious_python_stuff.ipynb) \n",
|
||
|
|
"- [Link to the GitHub repository](https://github.com/rasbt/python_reference)"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"#### All code was executed in Python 3.4"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<hr>\n",
|
||
|
|
"I am really looking forward to your comments and suggestions to improve and \n",
|
||
|
|
"extend this little collection! Just send me a quick note \n",
|
||
|
|
"via Twitter: [@rasbt](https://twitter.com/rasbt) \n",
|
||
|
|
"or Email: [bluewoodtree@gmail.com](mailto:bluewoodtree@gmail.com)\n",
|
||
|
|
"<hr>"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"# Implementing the least squares fit method for linear regression and speeding it up via Cython"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<a name=\"sections\"></a>\n",
|
||
|
|
"<br>\n",
|
||
|
|
"<br>\n"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"#Sections"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"- [Introduction](#introduction)\n",
|
||
|
|
"- [Least squares fit implementations](#implementations)\n",
|
||
|
|
"- [Generating sample data and benchmarking](#sample_data)\n",
|
||
|
|
"- [Compiling the Python code via Cython in the IPython notebook](#cython_nb)\n",
|
||
|
|
"- [Bonus: How to use Cython without the IPython magic](#cython_bonus)"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<a name=\"introduction\"></a>\n",
|
||
|
|
"<br>\n",
|
||
|
|
"<br>"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"## Introduction"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"[[back to top](#sections)]"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
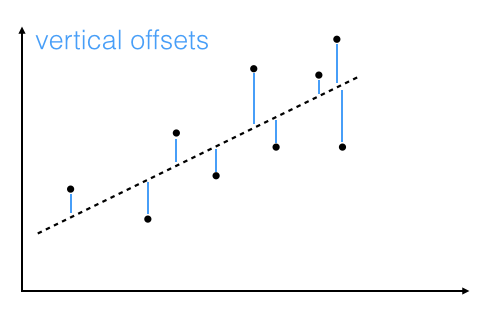
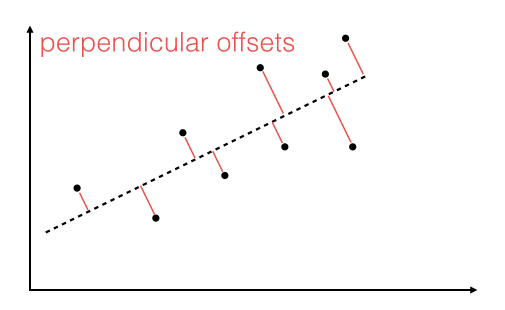
"Linear regression via the least squares method is the simplest approach to performing a regression analysis of a dependent and a explanatory variable. The objective is to find the best-fitting straight line through a set of points that minimizes the sum of the squared offsets from the line. \n",
|
||
|
|
"The offsets come in 2 different flavors: perpendicular and vertical - with respect to the line. \n",
|
||
|
|
" \n",
|
||
|
|
" \n",
|
||
|
|
"\n",
|
||
|
|
"Here, we will use the more common approach: minimizing the sum of the perpendicular offsets.\n"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"In more mathematical terms, our goal is to compute the best fit to *n* points $(x_i, y_i)$ with $i=1,2,...n,$ via linear equation of the form \n",
|
||
|
|
"$f(x) = a\\cdot x + b$. \n",
|
||
|
|
"Here, we assume that the y-component is functionally dependent on the x-component. \n",
|
||
|
|
"In a cartesian coordinate system, $b$ is the intercept of the straight line with the y-axis, and $a$ is the slope of this line."
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"In order to obtain the parameters for the linear regression line for a set of multiple points, we can re-write the problem as matrix equation \n",
|
||
|
|
"$\\pmb X \\; \\pmb a = \\pmb y$"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"$\\Rightarrow\\Bigg[ \\begin{array}{cc}\n",
|
||
|
|
"x_1 & 1 \\\\\n",
|
||
|
|
"... & 1 \\\\\n",
|
||
|
|
"x_n & 1 \\end{array} \\Bigg]$\n",
|
||
|
|
"$\\bigg[ \\begin{array}{c}\n",
|
||
|
|
"a \\\\\n",
|
||
|
|
"b \\end{array} \\bigg]$\n",
|
||
|
|
"$=\\Bigg[ \\begin{array}{c}\n",
|
||
|
|
"y_1 \\\\\n",
|
||
|
|
"... \\\\\n",
|
||
|
|
"y_n \\end{array} \\Bigg]$"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"With a little bit of calculus, we can rearrange the term in order to obtain the parameter vector $\\pmb a = [a\\;b]^T$"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"$\\Rightarrow \\pmb a = (\\pmb X^T \\; \\pmb X)^{-1} \\pmb X^T \\; \\pmb y$"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"The more classic approach to obtain the slope parameter $a$ and y-axis intercept $b$ would be:"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"$a = \\frac{S_{x,y}}{\\sigma_{x}^{2}}\\quad$ (slope)\n",
|
||
|
|
"\n",
|
||
|
|
"\n",
|
||
|
|
"$b = \\bar{y} - a\\bar{x}\\quad$ (y-axis intercept)"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"where \n",
|
||
|
|
"\n",
|
||
|
|
"\n",
|
||
|
|
"$S_{xy} = \\sum_{i=1}^{n} (x_i - \\bar{x})(y_i - \\bar{y})\\quad$ (covariance)\n",
|
||
|
|
"\n",
|
||
|
|
"\n",
|
||
|
|
"$\\sigma{_x}^{2} = \\sum_{i=1}^{n} (x_i - \\bar{x})^2\\quad$ (variance)"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<a name=\"implementations\"></a>\n",
|
||
|
|
"<br>\n",
|
||
|
|
"<br>"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"\n",
|
||
|
|
"## Least squares fit implementations"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"[[back to top](#sections)]"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"<br>"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"### 1. The matrix approach"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"First, let us implement the equation:"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"$\\pmb a = (\\pmb X^T \\; \\pmb X)^{-1} \\pmb X^T \\; \\pmb y$"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"which I will refer to as the \"matrix approach\"."
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"import numpy as np\n",
|
||
|
|
"\n",
|
||
|
|
"def lin_lstsqr_mat(x, y):\n",
|
||
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
||
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
||
|
|
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [],
|
||
|
|
"prompt_number": 1
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"<br>"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"### 2. The classic approach"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"Next, we will calculate the parameters separately, using only standard library functions in Python, which I will call the \"classic approach\"."
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"$a = \\frac{S_{x,y}}{\\sigma_{x}^{2}}\\quad$ (slope)\n",
|
||
|
|
"\n",
|
||
|
|
"\n",
|
||
|
|
"$b = \\bar{y} - a\\bar{x}\\quad$ (y-axis intercept)"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"def classic_lstsqr(x, y):\n",
|
||
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
||
|
|
" x_avg = sum(x)/len(x)\n",
|
||
|
|
" y_avg = sum(y)/len(y)\n",
|
||
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
||
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
||
|
|
" slope = cov_xy / var_x\n",
|
||
|
|
" y_interc = y_avg - slope*x_avg\n",
|
||
|
|
" return (slope, y_interc)"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [],
|
||
|
|
"prompt_number": 4
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"<br>"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"### 3. Using the lstsq numpy function"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"For our convenience, `numpy` has a function that can also compute the leat squares solution of a linear matrix equation. For more information, please refer to the [documentation](http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.lstsq.html)."
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"def numpy_lstsqr(x, y):\n",
|
||
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
||
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
||
|
|
" return np.linalg.lstsq(X,y)[0]"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [],
|
||
|
|
"prompt_number": 5
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"<br>"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"### 4. Using the linregress scipy function"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"The last approach is using `scipy.stats.linregress()`, which returns a tuple of 5 different attributes, where the 1st value in the tuple is the slope, and the second value is the y-axis intercept, respectively. The documentation for this function can be found [here](http://docs.scipy.org/doc/scipy-0.13.0/reference/generated/scipy.stats.linregress.html)."
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"import scipy.stats\n",
|
||
|
|
"\n",
|
||
|
|
"def scipy_lstsqr(x,y):\n",
|
||
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
||
|
|
" return scipy.stats.linregress(x, y)[0:2]"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [],
|
||
|
|
"prompt_number": 6
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<a name='sample_data'></a>\n",
|
||
|
|
"<br>\n",
|
||
|
|
"<br>"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"## Generating sample data and benchmarking"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"[[back to top](#sections)]"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"In order to test our different least squares fit implementation, we will generate some sample data:\n",
|
||
|
|
"- 500 sample points for the x-component within the range [0,500) \n",
|
||
|
|
"- 500 sample points for the y-component within the range [100,600) \n",
|
||
|
|
"\n",
|
||
|
|
"where each sample point is multiplied by a random value within\n",
|
||
|
|
"the range [0.8, 12)."
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"import random\n",
|
||
|
|
"random.seed(12345)\n",
|
||
|
|
"\n",
|
||
|
|
"x = [x_i*random.randrange(8,12)/10 for x_i in range(500)]\n",
|
||
|
|
"y = [y_i*random.randrange(8,12)/10 for y_i in range(100,600)]"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [],
|
||
|
|
"prompt_number": 7
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"<br>\n",
|
||
|
|
"#### Visualization"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"To check how our dataset is distributed, and how the straight line, which we obtain via the least square fit method, we will plot it in a scatter plot. \n",
|
||
|
|
"Note that we are using our \"matrix approach\" here for simplicity, but after plotting the data, we will check whether all of the four different implementations yield the same parameters."
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"%pylab inline\n",
|
||
|
|
"from matplotlib import pyplot as plt\n",
|
||
|
|
"\n",
|
||
|
|
"slope, intercept = lin_lstsqr_mat(x, y)\n",
|
||
|
|
"\n",
|
||
|
|
"line_x = [round(min(x)) - 1, round(max(x)) + 1]\n",
|
||
|
|
"line_y = [slope*x_i + intercept for x_i in line_x]\n",
|
||
|
|
"\n",
|
||
|
|
"plt.figure(figsize=(8,8))\n",
|
||
|
|
"plt.scatter(x,y)\n",
|
||
|
|
"plt.plot(line_x, line_y, color='red', lw='2')\n",
|
||
|
|
"\n",
|
||
|
|
"plt.ylabel('y')\n",
|
||
|
|
"plt.xlabel('x')\n",
|
||
|
|
"plt.title('Linear regression via least squares fit')\n",
|
||
|
|
"\n",
|
||
|
|
"ftext = 'y = ax + b = {:.3f} + {:.3f}x'\\\n",
|
||
|
|
" .format(slope, intercept)\n",
|
||
|
|
"plt.figtext(.15,.8, ftext, fontsize=11, ha='left')\n",
|
||
|
|
"\n",
|
||
|
|
"plt.show()"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"Populating the interactive namespace from numpy and matplotlib\n"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stderr",
|
||
|
|
"text": [
|
||
|
|
"WARNING: pylab import has clobbered these variables: ['random']\n",
|
||
|
|
"`%matplotlib` prevents importing * from pylab and numpy\n"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"metadata": {},
|
||
|
|
"output_type": "display_data",
|
||
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAfoAAAH4CAYAAACi3S9CAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdUVMfbwPHv0lm6giAgooBRbNi7GCv2EnvXWOPPnhg1\nGksSxRhjoiYaE0SNsb4xEY0Fe+zGmijGLkZARRERFljYnfeP1Y0ELJRlAedzDkf2lpln7q48e++d\nO6MQQggkSZIkSSqSTIwdgCRJkiRJhiMTvSRJkiQVYTLRS5IkSVIRJhO9JEmSJBVhMtFLkiRJUhEm\nE70kSZIkFWEy0UtGd+jQIcqXL2/sMAqtSpUq8fvvv+drnSNHjuTTTz/N0b7e3t7s3bs3jyN6s/3y\nyy+UKlUKe3t7zp07Z5TPhFRwKeRz9FJ+8fb2JiQkhGbNmhk7FMmIypQpQ0hICE2bNjVI+QcOHKBf\nv378888/Bim/IPLx8eGrr76iffv2mdbNnDmT69ev8+OPPxohMqkgkGf0Ur5RKBQoFApjh6Gn0Wjy\nZJvXJYRAfq+Wnsmrz5YQgtu3b+Pv758n5UlFj0z0ktEdOHCAUqVK6V97e3uzYMECqlatiqOjIz17\n9iQ1NVW/ftu2bQQEBODk5ESDBg3466+/9OuCg4Px9fXF3t6eihUr8uuvv+rXrVy5kgYNGjBhwgSc\nnZ2ZNWtWplhmzpxJ165d6devHw4ODqxatYrHjx/z7rvv4u7ujqenJ9OnT0er1QKg1WqZOHEiLi4u\nlC1bliVLlmBiYqJf36RJE6ZNm0aDBg2wsbHh5s2b/P3337Ro0YLixYtTvnx5Nm3apK9/+/btVKxY\nEXt7ezw9PVmwYAEADx48oF27djg5OVG8eHEaN26c4Xg9uxSemprKuHHj8PDwwMPDg/Hjx6NWq/XH\n2dPTky+//BJXV1fc3d1ZuXJllu/Jhg0bqFWrVoZlCxcupGPHjgAMHDiQ6dOnA/Do0SPatWtHiRIl\nKFasGO3btycqKirLcv9LCKF/z5ydnenRowePHj3Sr+/WrRslS5bE0dGRwMBAIiIiXnisvvzyS1Qq\nFa1btyY6Oho7Ozvs7e25e/dupnpfdJwB5s+fr3+vV6xYgYmJCTdu3AB072dISIh+25UrV9KoUSP9\n67Fjx+Ll5YWDgwM1a9bk8OHD+nXZ/Wxdu3aNwMBAHB0dcXFxoWfPnpnakZqaip2dHRqNhqpVq+Ln\n5wf8+5nYuXMnc+fOZcOGDdjZ2VGtWrXXel+kIkZIUj7x9vYWe/fuzbR8//79wtPTM8N2derUETEx\nMSIuLk5UqFBBLFu2TAghxJkzZ0SJEiXEyZMnhVarFatWrRLe3t5CrVYLIYTYtGmTiImJEUIIsWHD\nBmFjYyPu3r0rhBAiNDRUmJmZiSVLlgiNRiOSk5MzxTJjxgxhbm4utmzZIoQQIjk5WXTq1EmMGDFC\nqFQqcf/+fVG7dm3x3XffCSGEWLp0qfD39xdRUVHi0aNHolmzZsLExERoNBohhBCBgYGidOnSIiIi\nQmg0GhEfHy88PT3FypUrhUajEWfPnhXOzs7i0qVLQggh3NzcxOHDh4UQQsTHx4szZ84IIYSYPHmy\nGDFihEhPTxfp6en6bf57XKdPny7q1asnYmNjRWxsrKhfv76YPn26/jibmZmJGTNmiPT0dLF9+3ah\nVCpFfHx8puOgUqmEnZ2duHr1qn5ZzZo1xYYNG4QQQgwcOFBf7sOHD8XmzZtFcnKyePLkiejWrZvo\n1KlT1h+C/8T71VdfiXr16omoqCihVqvF8OHDRa9evfTbhoaGisTERKFWq8W4ceNEQECAft2LjtWB\nAwcyfJ6y8qJ9d+zYIVxdXcXFixdFUlKS6NWrl1AoFOL69etCCCGaNGkiQkJCMsTXsGFD/es1a9aI\nuLg4odFoxIIFC4Sbm5tITU0VQmT/s9WzZ08xZ84cIYQQqamp4siRIy9sz/Mx/vcYz5w5U/Tr1++l\nx0Mq2uQZvVQgjRkzBjc3N5ycnGjfvj3nzp0DYPny5QwfPpxatWqhUCjo378/lpaWHDt2DICuXbvi\n5uYGQPfu3fHz8+PEiRP6ct3d3Rk1ahQmJiZYWVllWXf9+vXp0KEDAI8fP2bHjh0sXLgQa2trXFxc\nGDduHOvXrwdg48aNjBs3Dnd3dxwdHZkyZUqGy/MKhYKBAwdSoUIFTExM2LlzJ2XKlGHAgAGYmJgQ\nEBBAly5d2LhxIwAWFhZcvHiRhIQEHBwc9GdgFhYWxMTEcOvWLUxNTWnQoEGWsa9du5aPP/4YZ2dn\nnJ2dmTFjRoZ7s+bm5nz88ceYmprSunVrbG1tuXz5cqZyrK2t6dixI+vWrQPg6tWrXL58WX9cAH07\nixUrRufOnbGyssLW1papU6dy8ODBrN/Y//juu+/49NNPcXd3x9zcnBkzZvB///d/+rPagQMHYmNj\no193/vx5njx58tJjJV7j9siL9t24cSODBw/G398fpVKZ5VWfl+nTpw9OTk6YmJgwYcIEUlNTMxzf\n7Hy2LCwsuHXrFlFRUVhYWFC/fv1sxfKMkLeM3ngy0UsF0rNkDbqkk5iYCEBkZCQLFizAyclJ/3Pn\nzh1iYmIAWL16NdWqVdOvu3DhAg8fPtSX9fwtghfx9PTU/x4ZGUlaWholS5bUlzlixAhiY2MBiImJ\nyVDm8/tmVWdkZCQnTpzIEP/atWu5d+8eAD///DPbt2/H29ubJk2acPz4cQA++OADfH19admyJT4+\nPsybNy/L2KOjoyldurT+tZeXF9HR0frXxYsXx8Tk3//2SqVSf2z/q3fv3vpEv3btWn0y/y+VSsXw\n4cPx9vbGwcGBwMBAHj9+/FrJ5datW3Tu3Fl/LPz9/TEzM+PevXtoNBomT56Mr68vDg4OlClTBoVC\nwYMHD156rF7Hi/b97/vp5eX12mUCfPHFF/j7++Po6IiTkxOPHz/WxwvZ+2x9/vnnCCGoXbs2lSpV\nIjQ0NFuxSNIzZsYOQJJex7NOfF5eXnz00UdMnTo10zaRkZEMGzaMffv2Ua9ePRQKBdWqVct0hv2q\nep7fplSpUlhaWvLw4cMMCfKZkiVLZujdnVVP7+fL8/LyIjAwkPDw8Czrr1mzJr/++isajYbFixfT\nvXt3bt++ja2tLV988QVffPEFFy9epGnTptSuXZu33347w/7u7u7cunWLChUqAHD79m3c3d1f2uYX\nad68ObGxsZw/f57169fz1VdfZdmuBQsWcOXKFU6ePEmJEiU4d+4c1atXRwjxyuPt5eVFaGgo9erV\ny7Tuxx9/JCwsjL1791K6dGni4+MpVqyY/v180bF6nQ6fL9q3ZMmS3L59W7/d878D2NjYkJSUpH/9\n/P3/Q4cOMX/+fPbt20fFihUBMsT7/DGDV3+2XF1dWb58OQBHjhyhefPmBAYGUrZs2Ve273kFqQOs\nZBzyjF7KV2q1mpSUFP3P6/Y8fvbHcujQoSxbtoyTJ08ihCApKYnffvuNxMREkpKSUCgUODs7o9Vq\nCQ0N5cKFC9mK779noSVLlqRly5ZMmDCBJ0+eoNVquX79uv4Z5e7du/P1118THR1NfHw88+bNy/SH\n9fky27Vrx5UrV1izZg1paWmkpaXxxx9/8Pfff5OWlsZPP/3E48ePMTU1xc7ODlNTU0DXAfHatWsI\nIbC3t8fU1DTL5NCrVy8+/fRTHjx4wIMHD5g9ezb9+vXL1jF4xtzcnG7duvH+++/z6NEjWrRokaFN\nz9qVmJiItbU1Dg4OxMXFZety94gRI5g6dao+ocbGxhIWFqYv19LSkmLFipGUlJThy93LjpWrqysP\nHz4kISEhyzpftm/37t1ZuXIlly5dQqVSZWpLQEAAmzdvJjk5mWvXrhESEqJ/v588eYKZmRnOzs6o\n1Wpmz579whjg1Z+tTZs2cefOHQAcHR1RKBRZvuev4ubmxq1bt+Tl+zeYTPRSvmrTpg1KpVL/M2vW\nrFc+dvf8+ho1avD999/zv//9
|
||
|
|
"text": [
|
||
|
|
"<matplotlib.figure.Figure at 0x105785f60>"
|
||
|
|
]
|
||
|
|
}
|
||
|
|
],
|
||
|
|
"prompt_number": 8
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"<br>\n",
|
||
|
|
"#### Comparing the results from the different implementations"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"As mentioned above, let us confirm that the different implementation computed the same parameters (i.e., slope and y-axis intercept) as solution for the linear equation."
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"import prettytable\n",
|
||
|
|
"\n",
|
||
|
|
"params = [appr(x,y) for appr in [lin_lstsqr_mat, classic_lstsqr, numpy_lstsqr, scipy_lstsqr]]\n",
|
||
|
|
"\n",
|
||
|
|
"print(params)\n",
|
||
|
|
"\n",
|
||
|
|
"fit_table = prettytable.PrettyTable([\"\", \"slope\", \"y-intercept\"])\n",
|
||
|
|
"fit_table.add_row([\"matrix approach\", params[0][0], params[0][1]])\n",
|
||
|
|
"fit_table.add_row([\"classic approach\", params[1][0], params[1][1]])\n",
|
||
|
|
"fit_table.add_row([\"numpy function\", params[2][0], params[2][1]])\n",
|
||
|
|
"fit_table.add_row([\"scipy function\", params[3][0], params[3][1]])\n",
|
||
|
|
"\n",
|
||
|
|
"print(fit_table)"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"[array([ 0.95181895, 107.01399744]), (0.95181895319126741, 107.01399744459181), array([ 0.95181895, 107.01399744]), (0.95181895319126764, 107.01399744459175)]\n",
|
||
|
|
"+------------------+----------------+---------------+\n",
|
||
|
|
"| | slope | y-intercept |\n",
|
||
|
|
"+------------------+----------------+---------------+\n",
|
||
|
|
"| matrix approach | 0.951818953191 | 107.013997445 |\n",
|
||
|
|
"| classic approach | 0.951818953191 | 107.013997445 |\n",
|
||
|
|
"| numpy function | 0.951818953191 | 107.013997445 |\n",
|
||
|
|
"| scipy function | 0.951818953191 | 107.013997445 |\n",
|
||
|
|
"+------------------+----------------+---------------+\n"
|
||
|
|
]
|
||
|
|
}
|
||
|
|
],
|
||
|
|
"prompt_number": 9
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"<br>\n",
|
||
|
|
"#### Initial performance comparison"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"For a first impression how the performances of the different least squares implementations compare against each other, let us do a quick benchmark using the `timeit` module via IPython's `%timeit` magic."
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"import timeit\n",
|
||
|
|
"\n",
|
||
|
|
"for lab,appr in zip([\"matrix approach\",\"classic approach\",\n",
|
||
|
|
" \"numpy function\",\"scipy function\"],\n",
|
||
|
|
" [lin_lstsqr_mat, classic_lstsqr, \n",
|
||
|
|
" numpy_lstsqr, scipy_lstsqr]):\n",
|
||
|
|
" print(\"\\n{}: \".format(lab), end=\"\")\n",
|
||
|
|
" %timeit appr(x, y)"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n",
|
||
|
|
"matrix approach: 1000 loops, best of 3: 270 \u00b5s per loop"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n",
|
||
|
|
"\n",
|
||
|
|
"classic approach: 100 loops, best of 3: 2.83 ms per loop"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n",
|
||
|
|
"\n",
|
||
|
|
"numpy function: 1000 loops, best of 3: 372 \u00b5s per loop"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n",
|
||
|
|
"\n",
|
||
|
|
"scipy function: 1000 loops, best of 3: 594 \u00b5s per loop"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n"
|
||
|
|
]
|
||
|
|
}
|
||
|
|
],
|
||
|
|
"prompt_number": 10
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"The timing above indicates, that the \"classic\" approach (Python's standard library functions only) is significantly worse in performance than the other implemenations - roughly by a magnitude of 10."
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"<br>\n",
|
||
|
|
"<a name=\"cython_nb\"></a>"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"## Compiling the Python code via Cython in the IPython notebook"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"[[back to top](#sections)]"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"Maybe we can speed things up a little bit via [Cython's C-extensions for Python](http://cython.org). Cython is basically a hybrid between C and Python and can be pictured as compiled Python code with type declarations. \n",
|
||
|
|
"Since we are working in an IPython notebook here, we can make use of the IPython magic: It will automatically convert it to C code, compile it, and load the function. \n",
|
||
|
|
"Just to be thorough, let us also compile the other functions, which already use numpy objects."
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"%load_ext cythonmagic"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [],
|
||
|
|
"prompt_number": 15
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"%%cython\n",
|
||
|
|
"import numpy as np\n",
|
||
|
|
"import scipy.stats\n",
|
||
|
|
"cimport numpy as np\n",
|
||
|
|
"\n",
|
||
|
|
"def cy_lin_lstsqr_mat(x, y):\n",
|
||
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
||
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
||
|
|
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)\n",
|
||
|
|
"\n",
|
||
|
|
"def cy_classic_lstsqr(x, y):\n",
|
||
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
||
|
|
" x_avg = sum(x)/len(x)\n",
|
||
|
|
" y_avg = sum(y)/len(y)\n",
|
||
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
||
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
||
|
|
" slope = cov_xy / var_x\n",
|
||
|
|
" y_interc = y_avg - slope*x_avg\n",
|
||
|
|
" return (slope, y_interc)\n",
|
||
|
|
"\n",
|
||
|
|
"def cy_numpy_lstsqr(x, y):\n",
|
||
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
||
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
||
|
|
" return np.linalg.lstsq(X,y)[0]\n",
|
||
|
|
"\n",
|
||
|
|
"def cy_scipy_lstsqr(x,y):\n",
|
||
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
||
|
|
" return scipy.stats.linregress(x, y)[0:2]"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [],
|
||
|
|
"prompt_number": 16
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"<br>"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"#### Comparing the compiled Cython code to the original Python code"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"import timeit\n",
|
||
|
|
"\n",
|
||
|
|
"for lab,appr in zip([\"matrix approach\",\"classic approach\",\n",
|
||
|
|
" \"numpy function\",\"scipy function\"],\n",
|
||
|
|
" [(lin_lstsqr_mat, cy_lin_lstsqr_mat), \n",
|
||
|
|
" (classic_lstsqr, cy_classic_lstsqr),\n",
|
||
|
|
" (numpy_lstsqr, cy_numpy_lstsqr),\n",
|
||
|
|
" (scipy_lstsqr, cy_scipy_lstsqr)]):\n",
|
||
|
|
" print(\"\\n\\n{}: \".format(lab))\n",
|
||
|
|
" %timeit appr[0](x, y)\n",
|
||
|
|
" %timeit appr[1](x, y)"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n",
|
||
|
|
"\n",
|
||
|
|
"matrix approach: \n",
|
||
|
|
"1000 loops, best of 3: 274 \u00b5s per loop"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n",
|
||
|
|
"1000 loops, best of 3: 260 \u00b5s per loop"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n",
|
||
|
|
"\n",
|
||
|
|
"\n",
|
||
|
|
"classic approach: \n",
|
||
|
|
"100 loops, best of 3: 2.82 ms per loop"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n",
|
||
|
|
"1000 loops, best of 3: 212 \u00b5s per loop"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n",
|
||
|
|
"\n",
|
||
|
|
"\n",
|
||
|
|
"numpy function: \n",
|
||
|
|
"1000 loops, best of 3: 379 \u00b5s per loop"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n",
|
||
|
|
"1000 loops, best of 3: 370 \u00b5s per loop"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n",
|
||
|
|
"\n",
|
||
|
|
"\n",
|
||
|
|
"scipy function: \n",
|
||
|
|
"1000 loops, best of 3: 608 \u00b5s per loop"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n",
|
||
|
|
"100 loops, best of 3: 613 \u00b5s per loop"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n"
|
||
|
|
]
|
||
|
|
}
|
||
|
|
],
|
||
|
|
"prompt_number": 17
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"<br>\n",
|
||
|
|
"As we've seen before, our \"classic\" implementation of the least square method is pretty slow compared to using numpy's functions. This is not surprising, since numpy is highly optmized and uses compiled C/C++ and Fortran code already. This explains why there is no significant difference if we used Cython to compile the numpy-objects-containing functions. \n",
|
||
|
|
"However, we were able to speed up the \"classic approach\" quite significantly, roughly by 1500%.\n",
|
||
|
|
"\n",
|
||
|
|
"The following 2 code blocks are just to visualize our results in a bar plot."
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"import timeit\n",
|
||
|
|
"\n",
|
||
|
|
"funcs = ['classic_lstsqr', 'cy_classic_lstsqr', \n",
|
||
|
|
" 'lin_lstsqr_mat', 'numpy_lstsqr', 'scipy_lstsqr']\n",
|
||
|
|
"labels = ['classic approach','classic approach (cython)', \n",
|
||
|
|
" 'matrix approach', 'numpy function', 'scipy function']\n",
|
||
|
|
"\n",
|
||
|
|
"times = [timeit.Timer('%s(x,y)' %f, \n",
|
||
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000)\n",
|
||
|
|
" for f in funcs]\n",
|
||
|
|
"\n",
|
||
|
|
"times_rel = [times[0]/times[i+1] for i in range(len(times[1:]))]"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [],
|
||
|
|
"prompt_number": 18
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"%pylab inline\n",
|
||
|
|
"import matplotlib.pyplot as plt\n",
|
||
|
|
"\n",
|
||
|
|
"x_pos = np.arange(len(funcs))\n",
|
||
|
|
"plt.bar(x_pos, times, align='center', alpha=0.5)\n",
|
||
|
|
"plt.xticks(x_pos, labels, rotation=45)\n",
|
||
|
|
"plt.ylabel('time in ms')\n",
|
||
|
|
"plt.title('Performance of different least square fit implementations')\n",
|
||
|
|
"plt.show()\n",
|
||
|
|
"\n",
|
||
|
|
"x_pos = np.arange(len(funcs[1:]))\n",
|
||
|
|
"plt.bar(x_pos, times_rel, align='center', alpha=0.5, color=\"green\")\n",
|
||
|
|
"plt.xticks(x_pos, labels[1:], rotation=45)\n",
|
||
|
|
"plt.ylabel('relative performance gain')\n",
|
||
|
|
"plt.title('Performance gain compared to the classic least square implementation')\n",
|
||
|
|
"plt.show()"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"Populating the interactive namespace from numpy and matplotlib\n"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"metadata": {},
|
||
|
|
"output_type": "display_data",
|
||
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAFhCAYAAABwNN3iAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdYFGfXB+DfLoiwVAEBXZpYEkBEbNgiS+yoSDS22Msr\nEjQaEyOmKCb2GhMTY4n62n01FkQwxrIalWI3kSCWgIC6ETtFYHfP9wcwH0sRMO4u6Lmvi4udnWdm\nzjPtzDxTVkREBMYYY288sb4DYIwxVj1wQmCMMQaAEwJjjLFCnBAYY4wB4ITAGGOsECcExhhjAF7z\nhKBQKNCpUydYWFhg2rRp+g5H73JyctCnTx9YWVlh0KBBFZaXy+VwcnISups2bYqTJ08CAIgIo0eP\nhrW1Ndq2bQsAWLVqFezt7WFhYYFHjx5ppxIvqWRdWOVdu3YNzZs3h4WFBb7//nuEhIRgzpw5lR6+\nquWrwtXVFUePHtXKuPVp69at6N69u+4nTNWMi4sLmZiYkJmZGdnb29OoUaMoMzPzpcb19ddfU//+\n/V9xhDXXpk2bqE2bNqRSqSpV/vjx4+To6Fhmv5MnT5KjoyNlZ2cTEVFeXh6ZmJjQH3/88crirQoX\nFxc6evRouf1fVJdXZeTIkfTll19qdRr6MGbMGJo6dWqZ/XQxX1/E1dX1hctdHzZs2EAdO3asdPm/\n//6bRCJRpbdLbap2ZwgikQiRkZF49uwZLly4gHPnzlX56IKIoFarkZKSAnd395eKQ6lUvtRw1VlK\nSgqaNGkCsfjfL/aUlBS4urrCxMQEAHDv3j08f/78pee3Wq3+V/GIRCIQP2NZoZdZr1NSUuDh4aGF\naFhx1WL91XNCKqVkxv/000+pd+/eREQUExND7dq1IysrK/L29ia5XC6U8/Pzoy+++II6dOhAJiYm\nNGzYMKpVqxYZGRmRmZkZHT16lHJzc2ny5MlUv359ql+/Pk2ZMoVyc3OJqOBIRyqV0sKFC8nBwYGG\nDx9O4eHh9P7779OwYcPI3NycvLy8KCkpiebNm0d2dnbk7OxMhw8fFmJYv349ubu7k7m5Obm5udHq\n1auFfkXjX7p0KdnZ2VG9evVow4YNQv/s7GyaOnUqubi4kKWlJXXs2JFycnIqrHdJCQkJ5OfnR1ZW\nVuTp6UkRERFERDRz5kwyMjKiWrVqkZmZGa1fv77UsNnZ2TRy5EiqU6cOeXh40KJFizSO/lxcXOjI\nkSO0bt06MjY2JgMDAzIzM6MhQ4aQqakpiUQiMjMzo86dOxMR0V9//UVdunQha2treuutt+h///uf\nMK6RI0fShAkTqGfPnmRqakpHjx6l9PR06tevH9WtW5caNGhA3333nVB+1qxZNGDAABoxYgSZm5uT\np6cnnTt3joiIhg0bRmKxWDizXLx4cam6lTySfdG04uLiqG3btmRlZUX16tWjiRMnUl5entB/ypQp\nZGdnRxYWFuTl5UV//vknrV69WmN9CwwMLHP5lDUsEVFGRgb16dOHLCwsqE2bNvTll18KR5llHUH6\n+fnRunXriIjoxo0b5O/vTzY2NmRra0tDhw6lx48fayy3hQsXkpeXFxkbG5NKpar0OuXv708GBgZk\nbGxM5ubmlJSUJJwJZWVlkbGxMYnFYjIzMyNzc3O6e/duqXEUP3Mq2g4WLVpEdevWpXr16tHevXvp\n4MGD1LhxY7K2tqb58+drLPf+/fvToEGDyNzcnFq0aEGXL18W+hffX6jVapo/fz41bNiQbGxsaODA\ngfTw4UONebhhwwZycnIia2trWrVqFcXHx5OXlxdZWVnRxIkTNeL++eefyd3dnerUqUPdu3enlJQU\noZ9IJKKffvqJGjduTFZWVhQaGkpEBdtf8W2jTp06REQUGRlJzZs3JwsLC3JycqLw8HBhXE5OTsK2\nY25uTjExMaXOMk6fPk2tWrUiS0tLat26NZ05c0ZjXfjqq6+oQ4cOZG5uTt26daOMjAwiIsrJyaGh\nQ4eSjY0NWVlZUevWrUmhUJS5rImIqmVCOHLkCBER3b59mzw9PWnmzJmUlpZGNjY2FB0dTUREv/32\nG9nY2AgV9/PzIxcXF0pISCCVSkX5+fk0atQo+uqrr4Rxf/XVV9SuXTu6f/8+3b9/n9q3by/0P378\nOBkaGlJYWBjl5eVRTk4OzZo1i4yNjenw4cOkVCppxIgR5OLiQvPmzSOlUklr166lBg0aCOM/ePAg\n3bp1i4iITpw4QRKJhC5cuKAx/lmzZpFSqaSoqCiSSCTChvvhhx+Sv78/3blzR9hgc3Nzy633/fv3\nS827vLw8atiwIc2fP5/y8/Pp2LFjZG5uTteuXSMiovDwcBo+fHi583769OnUqVMnevToEaWmppKn\npyc5OTlpLJuijW/jxo0aK2xycrLGTiszM5McHR1p48aNpFKp6OLFi2Rra0sJCQlEVLCTsLS0FFbs\n7OxsatGiBX3zzTeUn59Pt27dIjc3N/r111+JiIRlER0dTWq1mmbMmEFt27YtM7ayFE8IKpXqhdM6\nf/48xcXFkUqlouTkZHJ3d6dvv/2WiIgOHTpELVu2pCdPnhARUWJiorATLLm+lfSiYQcNGkSDBg2i\n7Oxs+vPPP0kqldI777xDRGUnBJlMRj///DMRFSSEI0eOUF5eHt2/f586depEU6ZMEcq6uLiQj48P\npaWl0fPnz6u0TpWcVsl6yuXyCpuMipcv2g6++eYbYRuysbGhDz74gDIzM+nq1atkYmJCycnJRFSw\n3GvVqkW//PILKZVKWrJkCTVo0ICUSiURaS73b7/9ltq1a0fp6emUl5dHwcHBNGTIEI15GBISQrm5\nuXT48GEyMjKioKAgun//PqWnp5OdnR2dOHGCiIj27dtHjRo1osTERFKpVDRnzhxq3769UCeRSER9\n+vShJ0+e0O3bt6lu3bp06NAhIiq9bRTNp6Lkf+XKFbK3t6d9+/YRUelth0iz2enBgwdkZWVFW7Zs\nIZVKRdu3b6c6deoIyc7Pz48aNWpE169fp5ycHJLJZBQWFkZERD/99BP16dOHcnJySK1W04ULF+jp\n06flLqtqlxBcXFzIzMyMrKysyMXFhUJDQyknJ4cWLFhQamfWvXt3+u9//0tEBSvtrFmzNPqPGjVK\no023YcOGwkZARPTrr7+Sq6srERWsqEZGRsIZA1HBytitWzehOyIigszMzEitVhMR0dOnT0kkEgkb\neElBQUG0YsUKYfwmJiYaC93Ozk7Y8ZiYmNCVK1dKjaOiehd38uRJcnBw0PhuyJAhwtHIrFmzaNiw\nYWXGSkQaO0UiojVr1mhs7MU3vpJHMCV3Wjt27BB2aEXGjx9Ps2fPJqKChDBy5EihX2xsLDk7O2uU\nnzdvHo0ePVqIvWvXrkK/oh1HWbGVpXhCqGhaJS1fvpzee+89IiI6evQoNWnShGJjY0u1+ZZc30o6\nduxYmcMqlUqqVauWkLiJiD7//PMXniGU3EkXt3fvXvLx8RG6XV1dNc5Gq7JOFU2r6GykZD0rcw2h\nZHkTE5NS21B8fLxQvmXLlrR//34iKlju7dq1E/qp1WqqV68enTp1Sqhb0XJ3d3fXWAfu3LlDtWrV\nIpVKJczDO3fuCP1tbGw0zlr79+8vbK89evTQmL8qlYokEgndvn2biAoSwunTp4X+AwcOpAULFhBR\n5a4hTJ48mT7++GMiKnv5Fh/Hpk2byNfXV2P4du3a0caNG4moYPnMnTtX6Pfjjz9Sjx49iKig1aJ9\n+/Zl7lvKYqjvJquSRCIR9u/fj3fffVfj+5SUFOzatQsHDhwQvlMqlRrlKrqL5M6dO3BxcRG6nZ2d\ncefOHaG7bt26MDIy0hjGzs5O+GxiYgJbW1uIRCKhGwAyMzNhYWGB6OhozJ49G9evX4darUZ2djaa\nNWsmDG9jY6PRfi+RSJCZmYmMjAw8f/4cDRs2LBVzZepdvH4l54GLiwvS09NfOF/KG97Z2blSw5Ul\nJSUFcXFxqFOnjvCdUqnEiBEj
|
||
|
|
"text": [
|
||
|
|
"<matplotlib.figure.Figure at 0x105a7fe10>"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"metadata": {},
|
||
|
|
"output_type": "display_data",
|
||
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAbwAAAFhCAYAAAALEB8uAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdYFNfXB/Dv0HvvSBFLbKhoVMQCBAt2xdiiGMXYEo2G\nFImxkGjsxhKNURNrLLEiYo0i6M+GGkuQCDZQkSKCUgV2Oe8fvjthAbvMIns+z+MjW+7cM3fKmTsz\nd1YgIgJjjDFWzWmoOgDGGGNMCpzwGGOMqQVOeIwxxtQCJzzGGGNqgRMeY4wxtcAJjzHGmFqQNOGl\npaWhffv2MDExwddffy1l1e+krl27YuPGjaoOo8pydXXF0aNHJatPQ0MDt27dqtQ6hg0bhqlTp1ba\n9I2NjZGYmPhKZaKiouDk5FQ5AVVzjRo1wvHjx9/6dBMTE6GhoYGSkpK3Pm1VGzt2LGbOnFkp09Z6\n0RdcXV2Rnp4OTU1NGBoaokuXLli2bBkMDQ1fubJVq1bBxsYG2dnZrxWsutm/f7+qQ6jSBEGAIAgV\nfjZs2DA4OTlhxowZrzVtHx8fBAYGYsSIEW8S4it73jy9DTk5OZU27TfxpsurqoqNjVV1CJJ61eW4\nbt06/P777zhx4oT43ooVKyorvBf38ARBQEREBHJycvD333/j/Pnzr5x9iQglJSVISkpC/fr1XytQ\nmUz2WuXYu6GqLd/KTDovws+CqJqq2jrKXgO9gKurKx09elR8/dVXX1H37t2JiOj06dPUunVrMjMz\noyZNmlBUVJT4PW9vb/ruu++oTZs2pK+vT0OGDCFtbW3S0dEhIyMjOnr0KBUWFtKECRPIwcGBHBwc\naOLEiVRYWEhERMeOHSNHR0eaO3cu2dnZUWBgIIWGhtKHH35IQ4YMIWNjY3J3d6eEhASaNWsW2djY\nkLOzMx0+fFiMYc2aNVS/fn0yNjYmNzc3WrlypfiZYvoLFy4kGxsbsre3p7Vr14qf5+fnU3BwMLm4\nuJCpqSm1bduWCgoKXjjfZV24cIGaNm1KxsbG1K9fP+rfvz9NmTKFiIgyMzOpW7duZG1tTebm5tS9\ne3e6d++eUhv+9ttvRES0du1aatOmDX311Vdkbm5ONWvWpAMHDjyz3jt37lCfPn3I2tqaLC0tady4\ncUREJJfLacaMGeTi4kI2NjY0dOhQevz4MRER3b59mwRBoLVr15KTkxNZWFjQihUrKCYmhtzd3cnM\nzEycjiImLy8vGjduHJmamlK9evWU1pWXaX/F8h06dCiVlJTQ7NmzqVatWmRpaUn9+/enzMxMscyG\nDRvI2dmZLC0t6ccffyy3biqsXLlSaV3r2bMnERHFxcWRt7c3mZmZUcOGDSk8PLzCtps8eTJpamqS\nnp4eGRkZ0fjx44mISBAE+vXXX6lOnTpkZmZGn332mVK533//nerXr0/m5ubUuXNnSkpKeubyOXHi\nhLgOOTk50fr164mIaNiwYS+9fqxdu5bc3NzI2NiYatasSZs2bSIiouvXr1P79u3J1NSUrKysaMCA\nAWIZQRDo5s2bRPT8dby0Y8eOUY0aNcTXycnJFBAQQNbW1lSzZk1aunSp+NnZs2fJ09OTzMzMyN7e\nnsaNG0dFRUXi5xMnTiQbGxsyMTEhd3d3io2NfebyKquiskREGRkZ1KNHDzIxMaGWLVvSlClTqG3b\ntkT03zotl8vF6ZTerm7cuEG+vr5kaWlJVlZWNHjwYHr06JH4XRcXF5o7dy65u7uTnp4eyeXyV9r+\nXVxcxHV0+vTpr7T/8vb2ppCQEGrZsiWZmJhQr169xO2h7Hw9evSIgoKCyN7enhwdHWnKlCniZ4rt\n9IsvviAzMzOqVasWnTx5ktasWUNOTk5kY2Mjrn9ERE+ePKEvv/ySnJ2dydbWlsaMGSOuF8/bbz5r\nOSq2aWNjY2rQoAHt3r2biJ5uj3p6eqSpqUlGRkZkbm5OREQff/yxuA0QEa1atYpq165NFhYW1LNn\nT7p//7742Yu2ybJeKuEdOXKEiJ7uRBs2bEjTpk2je/fukaWlpbjT/euvv8jS0pIyMjLEheXi4kJx\ncXEkl8upuLiYhg0bRlOnThWnPXXqVGrdujU9ePCAHjx4QF5eXuLnx44dIy0tLQoJCaGioiIqKCig\n6dOnk56eHh0+fJhkMhkNHTqUXFxcaNasWSSTyWj16tVUs2ZNcfr79u2jW7duERFRdHQ0GRgY0N9/\n/600/enTp5NMJqP9+/eTgYGBuLJ/+umn5OvrS/fv3xdX8sLCwmfO94MHD8q1XWFhITk7O9PSpUtJ\nJpPRrl27SEdHR5zHhw8f0q5du6igoIBycnKoX79+1Lt3b7G8j48P/f7770T0dKXV1tam3377jUpK\nSmjFihXk4OBQ4TKTyWTUuHFjCg4Opvz8fHry5AmdPHmSiJ7ulGvXrk23b9+m3NxcCggIoMDAQCL6\nbyMaO3YsFRYW0uHDh0lHR4d69+5NDx48oOTkZLKxsaHo6GgxJi0tLVq8eDHJZDL6888/ydTUVNwo\nX6b9Sy/fxYsXU+vWrSk5OZmKiopo9OjRNGjQICIiunr1KhkZGdGJEyeosLCQgoODSUtLq8KER0Tl\n1rWioiKqVasWzZ49m4qLiykyMpKMjY0pPj6+wvKl215BEATq0aMHPX78mO7cuUPW1tZ08OBBIiIK\nCwuj2rVr07Vr10gul9PMmTPJy8urwmknJiaSsbExbd26lWQyGT18+JAuXbokxq3Y2J+3fuTm5pKJ\niQklJCQQEVFqaipdvXqViIgGDhxIs2bNIqKn66Bi2SvmQZHwnrWOl1U64cnlcmrWrBnNmDGDiouL\n6datW+Tm5kaHDh0ioqcHeGfPniW5XE6JiYlUv359Wrx4MRERHTx4kJo3by4eYF27do1SUlIqXF5l\nPa/sgAEDaMCAAZSfn0+xsbHk6OhI7dq1I6KKE17pZXvjxg06cuQIFRUV0YMHD6h9+/Y0ceJE8bsu\nLi7k4eFB9+7doydPnrzS9k+k3GF41f2Xt7c3OTo60tWrVykvL4/69u1LQ4YMqXC+evfuTWPGjKH8\n/HxKT0+nli1bigeYiu103bp1VFJSQlOmTCFHR0fxYOTw4cNkbGxMeXl5RPT0wKJXr16UlZVFOTk5\n1KNHD/r222/FdeF5+82KluP27dvFZfXnn3+SoaEhpaamEhHRunXrxIMThdLTOHr0KFlZWdHFixep\nsLCQxo8fT+3btxe/+7xtsiIvTHguLi5kZGREZmZm5OLiQp999hkVFBTQnDlzxB2lQufOncUjBR8f\nH5o+fXq5GSmduWvVqqXUSzl06BC5uroS0dOG1dHRUdoAp0+fTp06dRJfh4eHk5GREZWUlBARUXZ2\nNgmCIG4UZfXu3ZuWLFkiTl9fX19pQ7CxsRE3Vn19fbpy5Uq5abxovkuLjo4mR0dHpffatm37zA37\n4sWL4lEOUfmEV7t2bfGzvLw8EgSB0tLSyk3n1KlTZG1trTRvCh988AGtWLFCfB0fH0/a2tokl8vF\njaj0EZSlpSVt27ZNfN23b19xB7Z27dpySbdly5a0cePGCuevbPuXXb7169dXSmD3798nbW1tkslk\n9P3334vJTzH/Ojo6z014pde148ePk52dndJ3Bg0aRKGhoRWW9/HxEXsBCoIgKCWP/v3709y5c4mI\nyN/fXylByuVyMjAwoDt37pSb9qxZsyggIOCl4i6t9PqRm5tLZmZmtHPnTsrPz1f63tChQ2nUqFFK\nvcHS83Dz5s3nruNllU54Z86cIWdn53LzM3z48ArLLlq0iPr06UNET3dedevWpTNnzpRbN58330RE\nkZGRFZaVyWSkra2tdOAyefLk5/bwKjqYUdi9ezd5eHiIr11dXZXO/LzK9q8oXzrhvcr+y8fHR0w0\nRE97RDo6OlRSUqI0X6mpqaSrq6vUO9+8eTP5+voS0dPttE6dOuJnV65cIUEQKD09XXzP0tKSLl++\nTCUlJWRoaCgeFBE93Z8oEvHz
|
||
|
|
"text": [
|
||
|
|
"<matplotlib.figure.Figure at 0x1066dcef0>"
|
||
|
|
]
|
||
|
|
}
|
||
|
|
],
|
||
|
|
"prompt_number": 19
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<a name=\"cython_bonus\"></a>\n",
|
||
|
|
"<br>\n",
|
||
|
|
"<br>"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"## Bonus: How to use Cython without the IPython magic"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"[[back to top](#sections)]"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"IPython's notebook is really great for explanatory analysis and documentation, but what if we want to compile our Python code via Cython without letting IPython's magic doing all the work? \n",
|
||
|
|
"These are the steps you would need."
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"<br>"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"#### 1. Creating a .pyx file containing the the desired code or function."
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"%%file ccy_classic_lstsqr.pyx\n",
|
||
|
|
"\n",
|
||
|
|
"def ccy_classic_lstsqr(x, y):\n",
|
||
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
||
|
|
" x_avg = sum(x)/len(x)\n",
|
||
|
|
" y_avg = sum(y)/len(y)\n",
|
||
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
||
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
||
|
|
" slope = cov_xy / var_x\n",
|
||
|
|
" y_interc = y_avg - slope*x_avg\n",
|
||
|
|
" return (slope, y_interc)"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"Writing ccy_classic_lstsqr.pyx\n"
|
||
|
|
]
|
||
|
|
}
|
||
|
|
],
|
||
|
|
"prompt_number": 11
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"<br>"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"#### 2. Creating a simple setup file"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"%%file setup.py\n",
|
||
|
|
"\n",
|
||
|
|
"from distutils.core import setup\n",
|
||
|
|
"from distutils.extension import Extension\n",
|
||
|
|
"from Cython.Distutils import build_ext\n",
|
||
|
|
"\n",
|
||
|
|
"setup(\n",
|
||
|
|
" cmdclass = {'build_ext': build_ext},\n",
|
||
|
|
" ext_modules = [Extension(\"ccy_classic_lstsqr\", [\"ccy_classic_lstsqr.pyx\"])]\n",
|
||
|
|
")"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"Writing setup.py\n"
|
||
|
|
]
|
||
|
|
}
|
||
|
|
],
|
||
|
|
"prompt_number": 12
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"<br>\n",
|
||
|
|
"<br>\n"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"####3. Building and Compiling"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"!python3 setup.py build_ext --inplace"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"running build_ext\r\n"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"cythoning ccy_classic_lstsqr.pyx to ccy_classic_lstsqr.c\r\n"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"building 'ccy_classic_lstsqr' extension\r\n",
|
||
|
|
"creating build\r\n",
|
||
|
|
"creating build/temp.macosx-10.6-intel-3.4\r\n",
|
||
|
|
"/usr/bin/clang -fno-strict-aliasing -Werror=declaration-after-statement -fno-common -dynamic -DNDEBUG -g -fwrapv -O3 -Wall -Wstrict-prototypes -arch i386 -arch x86_64 -g -I/Library/Frameworks/Python.framework/Versions/3.4/include/python3.4m -c ccy_classic_lstsqr.c -o build/temp.macosx-10.6-intel-3.4/ccy_classic_lstsqr.o\r\n"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\u001b[1mccy_classic_lstsqr.c:2040:28: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_AsString'\r\n",
|
||
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE char* __Pyx_PyObject_AsString(PyObject* o) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2037:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function\r\n",
|
||
|
|
" '__Pyx_PyUnicode_FromString' [-Wunused-function]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyUnicode_FromString(char* c_str) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2104:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_IsTrue'\r\n",
|
||
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE int __Pyx_PyObject_IsTrue(PyObject* x) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2159:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyIndex_AsSsize_t'\r\n",
|
||
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE Py_ssize_t __Pyx_PyIndex_AsSsize_t(PyObject* b) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2188:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_FromSize_t'\r\n",
|
||
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE PyObject * __Pyx_PyInt_FromSize_t(size_t ival) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1584:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_From_long'\r\n",
|
||
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyInt_From_long(long value) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1631:27: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_long' is not\r\n",
|
||
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE long __Pyx_PyInt_As_long(PyObject *x) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1731:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_int' is not\r\n",
|
||
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE int __Pyx_PyInt_As_int(PyObject *x) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"8 warnings generated.\r\n"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\u001b[1mccy_classic_lstsqr.c:2040:28: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_AsString'\r\n",
|
||
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE char* __Pyx_PyObject_AsString(PyObject* o) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2037:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function\r\n",
|
||
|
|
" '__Pyx_PyUnicode_FromString' [-Wunused-function]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyUnicode_FromString(char* c_str) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2104:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_IsTrue'\r\n",
|
||
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE int __Pyx_PyObject_IsTrue(PyObject* x) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2159:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyIndex_AsSsize_t'\r\n",
|
||
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE Py_ssize_t __Pyx_PyIndex_AsSsize_t(PyObject* b) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2188:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_FromSize_t'\r\n",
|
||
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE PyObject * __Pyx_PyInt_FromSize_t(size_t ival) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1584:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_From_long'\r\n",
|
||
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyInt_From_long(long value) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1631:27: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_long' is not\r\n",
|
||
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE long __Pyx_PyInt_As_long(PyObject *x) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1731:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_int' is not\r\n",
|
||
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
||
|
|
"static CYTHON_INLINE int __Pyx_PyInt_As_int(PyObject *x) {\r\n",
|
||
|
|
"\u001b[0;1;32m ^\r\n",
|
||
|
|
"\u001b[0m"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"8"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
" warnings generated.\r\n",
|
||
|
|
"/usr/bin/clang -bundle -undefined dynamic_lookup -arch i386 -arch x86_64 -g build/temp.macosx-10.6-intel-3.4/ccy_classic_lstsqr.o -o /Users/sebastian/Github/python_reference/benchmarks/ccy_classic_lstsqr.so\r\n"
|
||
|
|
]
|
||
|
|
}
|
||
|
|
],
|
||
|
|
"prompt_number": 13
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "markdown",
|
||
|
|
"metadata": {},
|
||
|
|
"source": [
|
||
|
|
"#### 4. Importing and running the code"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"cell_type": "code",
|
||
|
|
"collapsed": false,
|
||
|
|
"input": [
|
||
|
|
"import ccy_classic_lstsqr\n",
|
||
|
|
"\n",
|
||
|
|
"%timeit classic_lstsqr(x, y)\n",
|
||
|
|
"%timeit cy_classic_lstsqr(x, y)\n",
|
||
|
|
"%timeit ccy_classic_lstsqr.ccy_classic_lstsqr(x, y)"
|
||
|
|
],
|
||
|
|
"language": "python",
|
||
|
|
"metadata": {},
|
||
|
|
"outputs": [
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"100 loops, best of 3: 2.9 ms per loop\n",
|
||
|
|
"1000 loops, best of 3: 212 \u00b5s per loop"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n",
|
||
|
|
"1000 loops, best of 3: 207 \u00b5s per loop"
|
||
|
|
]
|
||
|
|
},
|
||
|
|
{
|
||
|
|
"output_type": "stream",
|
||
|
|
"stream": "stdout",
|
||
|
|
"text": [
|
||
|
|
"\n"
|
||
|
|
]
|
||
|
|
}
|
||
|
|
],
|
||
|
|
"prompt_number": 20
|
||
|
|
}
|
||
|
|
],
|
||
|
|
"metadata": {}
|
||
|
|
}
|
||
|
|
]
|
||
|
|
}
|