mirror of
https://github.com/rasbt/python_reference.git
synced 2024-11-30 15:31:12 +00:00
1151 lines
130 KiB
Plaintext
1151 lines
130 KiB
Plaintext
{
|
|
"metadata": {
|
|
"name": "",
|
|
"signature": "sha256:a96ed2f762cf56d93a4e5345428c7db5ec576916158ce54446dfdf837ec7e505"
|
|
},
|
|
"nbformat": 3,
|
|
"nbformat_minor": 0,
|
|
"worksheets": [
|
|
{
|
|
"cells": [
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[Sebastian Raschka](http://sebastianraschka.com) \n",
|
|
"\n",
|
|
"- [Open in IPython nbviewer](http://nbviewer.ipython.org/github/rasbt/python_reference/blob/master/tutorials/multiprocessing_intro.ipynb?create=1) \n",
|
|
"\n",
|
|
"- [Link to this IPython notebook on Github](https://github.com/rasbt/python_reference/blob/master/tutorials/multiprocessing_intro.ipynb) \n",
|
|
"\n",
|
|
"- [Link to the GitHub Repository python_reference](https://github.com/rasbt/python_reference)\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import time\n",
|
|
"print('Last updated: %s' %time.strftime('%d/%m/%Y'))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"Last updated: 20/06/2014\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 1
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<hr>\n",
|
|
"I would be happy to hear your comments and suggestions. \n",
|
|
"Please feel free to drop me a note via\n",
|
|
"[twitter](https://twitter.com/rasbt), [email](mailto:bluewoodtree@gmail.com), or [google+](https://plus.google.com/+SebastianRaschka).\n",
|
|
"<hr>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 1,
|
|
"metadata": {},
|
|
"source": [
|
|
"Parallel processing via the `multiprocessing` module"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"CPUs with multiple cores have become the standard in the recent development of modern computer architectures and we can not only find them in supercomputer facilities but also in our desktop machines at home, and our laptops; even Apple's iPhone 5S got a 1.3 Ghz Dual-core processor in 2013.\n",
|
|
"\n",
|
|
"However, the default Python interpreter was designed with simplicity in mind and has a thread-safe mechanism, the so-called \"GIL\" (Global Interpreter Lock). In order to prevent conflicts between threads, it executes only one statement at a time (so-called serial processing, or single-threading).\n",
|
|
"\n",
|
|
"In this introduction to Python's `multiprocessing` module, we will see how we can spawn multiple subprocesses to avoid some of the GIL's disadvantages."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 2,
|
|
"metadata": {},
|
|
"source": [
|
|
"Sections"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"- [An introduction to parallel programming using Python's `multiprocessing` module](#An-introduction-to-parallel-programming-using-Python's-`multiprocessing`-module)\n",
|
|
" - [Multi-Threading vs. Multi-Processing](#Multi-Threading-vs.-Multi-Processing)\n",
|
|
"- [Introduction to the `multiprocessing` module](#Introduction-to-the-multiprocessing-module)\n",
|
|
" - [The `Process` class](#The-Process-class)\n",
|
|
" - [How to retrieve results in a particular order](#How-to-retrieve-results-in-a-particular-order)\n",
|
|
" - [The `Pool` class](#The-Pool-class)\n",
|
|
"- [Kernel density estimation as benchmarking function](#Kernel-density-estimation-as-benchmarking-function)\n",
|
|
" - [The Parzen-window method in a nutshell](#The-Parzen-window-method-in-a-nutshell)\n",
|
|
" - [Sample data and `timeit` benchmarks](#Sample-data-and-timeit-benchmarks)\n",
|
|
" - [Benchmarking functions](#Benchmarking-functions)\n",
|
|
" - [Preparing the plotting of the results](#Preparing-the-plotting-of-the-results)\n",
|
|
"- [Results](#Results)\n",
|
|
"- [Conclusion](#Conclusion)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 3,
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"Multi-Threading vs. Multi-Processing\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Depending on the application, two common approaches in parallel programming are either to run code via threads or multiple processes, respectively. If we submit \"jobs\" to different threads, those jobs can be pictured as \"sub-tasks\" of a single process and those threads will usually have access to the same memory areas (i.e., shared memory). This approach can easily lead to conflicts in case of improper synchronization, for example, if processes are writing to the same memory location at the same time. \n",
|
|
"\n",
|
|
"A safer approach (although it comes with an additional overhead due to the communication overhead between separate processes) is to submit multiple processes to completely separate memory locations (i.e., distributed memory): Every process will run completely independent from each other.\n",
|
|
"\n",
|
|
"Here, we will take a look at Python's [`multiprocessing`](https://docs.python.org/dev/library/multiprocessing.html) module and how we can use it to submit multiple processes that can run independently from each other in order to make best use of our CPU cores."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
""
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 1,
|
|
"metadata": {},
|
|
"source": [
|
|
"Introduction to the `multiprocessing` module"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The [multiprocessing](https://docs.python.org/dev/library/multiprocessing.html) module in Python's Standard Library has a lot of powerful features. If you want to read about all the nitty-gritty tips, tricks, and details, I would recommend to use the [official documentation](https://docs.python.org/dev/library/multiprocessing.html) as an entry point. \n",
|
|
"\n",
|
|
"In the following sections, I want to provide a brief overview of different approaches to show how the `multiprocessing` module can be used for parallel programming."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 3,
|
|
"metadata": {},
|
|
"source": [
|
|
"The `Process` class"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The most basic approach is probably to use the `Process` class from the `multiprocessing` module. \n",
|
|
"Here, we will use a simple queue function to compute the cubes for the 6 numbers 1, 2, 3, 4, 5, and 6 in 6 parallel processes."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import multiprocessing as mp\n",
|
|
"import random\n",
|
|
"import string\n",
|
|
"\n",
|
|
"random.seed(123)\n",
|
|
"\n",
|
|
"# Define an output queue\n",
|
|
"output = mp.Queue()\n",
|
|
"\n",
|
|
"# define a example function\n",
|
|
"def rand_string(length, output):\n",
|
|
" \"\"\" Generates a random string of numbers, lower- and uppercase chars. \"\"\"\n",
|
|
" rand_str = ''.join(random.choice(\n",
|
|
" string.ascii_lowercase \n",
|
|
" + string.ascii_uppercase \n",
|
|
" + string.digits)\n",
|
|
" for i in range(length))\n",
|
|
" output.put(rand_str)\n",
|
|
"\n",
|
|
"# Setup a list of processes that we want to run\n",
|
|
"processes = [mp.Process(target=rand_string, args=(5, output)) for x in range(4)]\n",
|
|
"\n",
|
|
"# Run processes\n",
|
|
"for p in processes:\n",
|
|
" p.start()\n",
|
|
"\n",
|
|
"# Exit the completed processes\n",
|
|
"for p in processes:\n",
|
|
" p.join()\n",
|
|
"\n",
|
|
"# Get process results from the output queue\n",
|
|
"results = [output.get() for p in processes]\n",
|
|
"\n",
|
|
"print(results)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"['BJWNs', 'GOK0H', '7CTRJ', 'THDF3']\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 2
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 3,
|
|
"metadata": {},
|
|
"source": [
|
|
"How to retrieve results in a particular order "
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
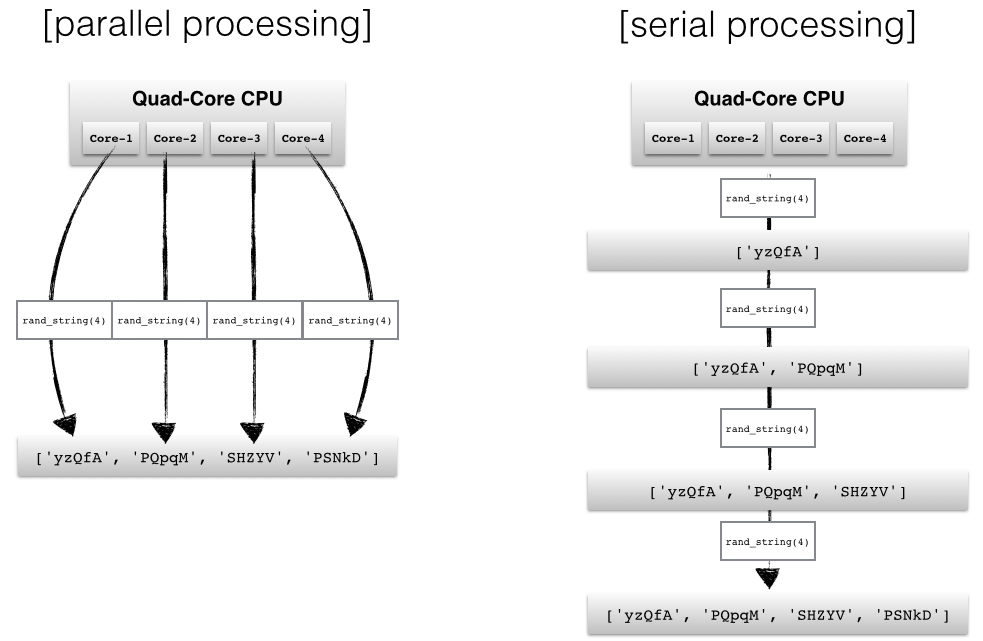
"The order of the obtained results does not necessarily have to match the order of the processes (in the `processes` list). Since we eventually use the `.get()` method to retrieve the results from the `Queue` sequentially, the order in which the processes finished determines the order of our results. \n",
|
|
"E.g., if the second process has finished just before the first process, the order of the strings in the `results` list could have also been\n",
|
|
"`['PQpqM', 'yzQfA', 'SHZYV', 'PSNkD']` instead of `['yzQfA', 'PQpqM', 'SHZYV', 'PSNkD']`\n",
|
|
"\n",
|
|
"If our application required us to retrieve results in a particular order, one possibility would be to refer to the processes' `._identity` attribute. In this case, we could also simply use the values from our `range` object as position argument. The modified code would be:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"# Define an output queue\n",
|
|
"output = mp.Queue()\n",
|
|
"\n",
|
|
"# define a example function\n",
|
|
"def rand_string(length, pos, output):\n",
|
|
" \"\"\" Generates a random string of numbers, lower- and uppercase chars. \"\"\"\n",
|
|
" rand_str = ''.join(random.choice(\n",
|
|
" string.ascii_lowercase \n",
|
|
" + string.ascii_uppercase \n",
|
|
" + string.digits)\n",
|
|
" for i in range(length))\n",
|
|
" output.put((pos, rand_str))\n",
|
|
"\n",
|
|
"# Setup a list of processes that we want to run\n",
|
|
"processes = [mp.Process(target=rand_string, args=(5, x, output)) for x in range(4)]\n",
|
|
"\n",
|
|
"# Run processes\n",
|
|
"for p in processes:\n",
|
|
" p.start()\n",
|
|
"\n",
|
|
"# Exit the completed processes\n",
|
|
"for p in processes:\n",
|
|
" p.join()\n",
|
|
"\n",
|
|
"# Get process results from the output queue\n",
|
|
"results = [output.get() for p in processes]\n",
|
|
"\n",
|
|
"print(results)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"[(0, 'h5hoV'), (1, 'fvdmN'), (2, 'rxGX4'), (3, '8hDJj')]\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 3
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"And the retrieved results would be tuples, for example, `[(0, 'KAQo6'), (1, '5lUya'), (2, 'nj6Q0'), (3, 'QQvLr')]` \n",
|
|
"or `[(1, '5lUya'), (3, 'QQvLr'), (0, 'KAQo6'), (2, 'nj6Q0')]`\n",
|
|
"\n",
|
|
"To make sure that we retrieved the results in order, we could simply sort the results and optionally get rid of the position argument:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"results.sort()\n",
|
|
"results = [r[1] for r in results]\n",
|
|
"print(results)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"['h5hoV', 'fvdmN', 'rxGX4', '8hDJj']\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 4
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"**A simpler way to to maintain an ordered list of results is to use the `Pool.apply` and `Pool.map` functions which we will discuss in the next section.**"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 3,
|
|
"metadata": {},
|
|
"source": [
|
|
"The `Pool` class"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Another and more convenient approach for simple parallel processing tasks is provided by the `Pool` class. \n",
|
|
"\n",
|
|
"There are four methods that are particularly interesing:\n",
|
|
"\n",
|
|
" - Pool.apply\n",
|
|
" \n",
|
|
" - Pool.map\n",
|
|
" \n",
|
|
" - Pool.apply_async\n",
|
|
" \n",
|
|
" - Pool.map_async\n",
|
|
" \n",
|
|
"The `Pool.apply` and `Pool.map` methods are basically equivalents to Python's in-built [`apply`](https://docs.python.org/2/library/functions.html#apply) and [`map`](https://docs.python.org/2/library/functions.html#map) functions."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Before we come to the `async` variants of the `Pool` methods, let us take a look at a simple example using `Pool.apply` and `Pool.map`. Here, we will set the number of processes to 4, which means that the `Pool` class will only allow 4 processes running at the same time."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def cube(x):\n",
|
|
" return x**3"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 5
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"pool = mp.Pool(processes=4)\n",
|
|
"results = [pool.apply(cube, args=(x,)) for x in range(1,7)]\n",
|
|
"print(results)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"[1, 8, 27, 64, 125, 216]\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 6
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"pool = mp.Pool(processes=4)\n",
|
|
"results = pool.map(cube, range(1,7))\n",
|
|
"print(results)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"[1, 8, 27, 64, 125, 216]\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 7
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The `Pool.map` and `Pool.apply` will lock the main program until all a process is finished, which is quite useful if we want to obtain resuls in a particular order for certain applications. \n",
|
|
"In contrast, the `async` variants will submit all processes at once and retrieve the results as soon as they are finished. \n",
|
|
"One more difference is that we need to use the `get` method after the `apply_async()` call in order to obtain the `return` values of the finished processes."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"pool = mp.Pool(processes=4)\n",
|
|
"results = [pool.apply_async(cube, args=(x,)) for x in range(1,7)]\n",
|
|
"output = [p.get() for p in results]\n",
|
|
"print(output)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"[1, 8, 27, 64, 125, 216]\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 8
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 1,
|
|
"metadata": {},
|
|
"source": [
|
|
"Kernel density estimation as benchmarking function"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In the following approach, I want to do a simple comparison of a serial vs. multiprocessing approach where I will use a slightly more complex function than the `cube` example, which he have been using above. \n",
|
|
"\n",
|
|
"Here, I define a function for performing a Kernel density estimation for probability density functions using the Parzen-window technique. \n",
|
|
"I don't want to go into much detail about the theory of this technique, since we are mostly interested to see how `multiprocessing` can be used for performance improvements, but you are welcome to read my more detailed article about the [Parzen-window method here](http://sebastianraschka.com/Articles/2014_parzen_density_est.html). "
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import numpy as np\n",
|
|
"\n",
|
|
"def parzen_estimation(x_samples, point_x, h):\n",
|
|
" \"\"\"\n",
|
|
" Implementation of a hypercube kernel for Parzen-window estimation.\n",
|
|
"\n",
|
|
" Keyword arguments:\n",
|
|
" x_sample:training sample, 'd x 1'-dimensional numpy array\n",
|
|
" x: point x for density estimation, 'd x 1'-dimensional numpy array\n",
|
|
" h: window width\n",
|
|
" \n",
|
|
" Returns the predicted pdf as float.\n",
|
|
"\n",
|
|
" \"\"\"\n",
|
|
" k_n = 0\n",
|
|
" for row in x_samples:\n",
|
|
" x_i = (point_x - row[:,np.newaxis]) / (h)\n",
|
|
" for row in x_i:\n",
|
|
" if np.abs(row) > (1/2):\n",
|
|
" break\n",
|
|
" else: # \"completion-else\"*\n",
|
|
" k_n += 1\n",
|
|
" return (k_n / len(x_samples)) / (h**point_x.shape[1])"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 9
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<hr>\n",
|
|
"**A quick note about the \"completion else**\n",
|
|
"\n",
|
|
"Sometimes I receive comments about whether I used this for-else combination intentionally or if it happened by mistake. That is a legitimate question, since this \"completion-else\" is rarely used (that's what I call it, I am not aware if there is an \"official\" name for this, if so, please let me know). \n",
|
|
"I have a more detailed explanation [here](http://sebastianraschka.com/Articles/2014_deep_python.html#else_clauses) in one of my blog-posts, but in a nutshell: In contrast to a conditional else (in combination with if-statements), the \"completion else\" is only executed if the preceding code block (here the `for`-loop) has finished.\n",
|
|
"<hr>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 3,
|
|
"metadata": {},
|
|
"source": [
|
|
"The Parzen-window method in a nutshell"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"So what this function does in a nutshell: It counts points in a defined region (the so-called window), and divides the number of those points inside by the number of total points to estimate the probability of a single point being in a certain region.\n",
|
|
"\n",
|
|
"Below is a simple example where our window is represented by a hypercube centered at the origin, and we want to get an estimate of the probability for a point being in the center of the plot based on the hypercube."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%matplotlib inline"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 10
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"from mpl_toolkits.mplot3d import Axes3D\n",
|
|
"import matplotlib.pyplot as plt\n",
|
|
"import numpy as np\n",
|
|
"from itertools import product, combinations\n",
|
|
"fig = plt.figure(figsize=(7,7))\n",
|
|
"ax = fig.gca(projection='3d')\n",
|
|
"ax.set_aspect(\"equal\")\n",
|
|
"\n",
|
|
"# Plot Points\n",
|
|
"\n",
|
|
"# samples within the cube\n",
|
|
"X_inside = np.array([[0,0,0],[0.2,0.2,0.2],[0.1, -0.1, -0.3]])\n",
|
|
"\n",
|
|
"X_outside = np.array([[-1.2,0.3,-0.3],[0.8,-0.82,-0.9],[1, 0.6, -0.7],\n",
|
|
" [0.8,0.7,0.2],[0.7,-0.8,-0.45],[-0.3, 0.6, 0.9],\n",
|
|
" [0.7,-0.6,-0.8]])\n",
|
|
"\n",
|
|
"for row in X_inside:\n",
|
|
" ax.scatter(row[0], row[1], row[2], color=\"r\", s=50, marker='^')\n",
|
|
"\n",
|
|
"for row in X_outside: \n",
|
|
" ax.scatter(row[0], row[1], row[2], color=\"k\", s=50)\n",
|
|
"\n",
|
|
"# Plot Cube\n",
|
|
"h = [-0.5, 0.5]\n",
|
|
"for s, e in combinations(np.array(list(product(h,h,h))), 2):\n",
|
|
" if np.sum(np.abs(s-e)) == h[1]-h[0]:\n",
|
|
" ax.plot3D(*zip(s,e), color=\"g\")\n",
|
|
" \n",
|
|
"ax.set_xlim(-1.5, 1.5)\n",
|
|
"ax.set_ylim(-1.5, 1.5)\n",
|
|
"ax.set_zlim(-1.5, 1.5)\n",
|
|
"\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAZQAAAGUCAYAAAASxdSgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXeUVOX9/9/3Tp/ZQpG6LCxNQUXEgCJIEVgWUIkRCwqK\nDdFEjTExNiwYG/zUX+QY2/fYYn5BiFEhAZYOFiKgIUG/iqgUkaZI2d2pt/3+WJ/rnbv3ztyZuW1m\nn9c5niO7s3eeO+V5P5/OSJIkgUKhUCiUAmGdXgCFQqFQSgMqKBQKhUIxBSooFAqFQjEFKigUCoVC\nMQUqKBQKhUIxBSooFAqFQjEFKigUCoVCMQUqKBQKhUIxBSooFAqFQjEFKigUCoVCMQUqKBQKhUIx\nBSooFAqFQjEFKigUCoVCMQUqKBQKhUIxBSooFAqFQjEFKigUCoVCMQUqKBQKhUIxBSooFAqFQjEF\nKigUCoVCMQUqKBQKhUIxBSooFAqFQjEFKigUCoVCMQUqKBQKhUIxBSooFAqFQjEFKigUCoVCMQUq\nKBQKhUIxBSooFAqFQjEFKigUCoVCMQUqKBQKhUIxBSooFAqFQjEFr9MLoFD0kCQJqVQKPM/D7/fD\n4/GAYRgwDOP00igUigaMJEmS04ugUNSIogiO4+T/iIiIoohAICALDMtSI5tCcQvUQqG4CkmSIAgC\nGhoa4Pf7wbKs/J8kSYjH42AYBhzHAQBYloXX64XP56MCQ6E4DBUUimuQJAkcx0EQBNnNpYRYKcT1\nRYzrVCqFVCoFgAoMheIkVFAorkAURaRSKUiSJMdJRFFEPB6HIAjwer3weDxpf6MUGKBZkEjchQoM\nhWI/NIZCcRTi4iJxEiISx44dgyRJspVCHicIAliWhcfjkf/TC9ITgVF+xFmWhc/nkwWKCgyFYh5U\nUCiOQawJURRlMSFxkkQigVAoBL/fD47j5I2/qakJgUCACgyF4kKoy4viCFouLkEQ0NTUlCYQahiG\nSdv4lcJCxElPYNQpx0RckskkkskkACowFEohUEGh2IokSeB5HjzPg2EYecNOpVKIRqMIBoMIBoNo\namoydD2GYeD1euH1euXrmykwHo9Hjr94vV5aA0OhZIAKCsU2SG2J2sUVi8XAcRzKy8tlYSDkuoEb\nFRilBZJJYERRRGNjIwDIwqK0YKjAUCg/QQWFYjnKwDvw08bN8zyi0Sg8Hg8qKyst2ZwzCUwymYQo\nimnWi5bAkP9YloUoikgkEvL1qcBQKD9BBYViKWoXF7FKEokE4vE4wuEw/H6/bRtxPgKj/FstC4YK\nDIXSDBUUimXo1ZZEo1GIooiKigrNwDvBjgREIwJDrBOSUZbNRUYFhtJaoYJCMR11bQk55XMch2g0\nCp/Ph7Kysoyba6bfWSk0WgKTSCTkYL0RF5lynVRgKK0JKigUU9GrLUkkEkgkEohEIi1aquSC3Rsw\nEUSGYeD3+yGKIkRRBM/z4DgOkiTlLDCkHxlABYZSWlBBoZgGyYiSJAnBYFB2cZEU4MrKyqKv6yCN\nKokFI4qi7CIzKjDKGhoqMJRSggoKpWCUgXdRFAE0b57q2pJS3ByJwPh8PgAtBYY8RikQRgVGEAT4\nfD74/X4qMJSigAoKpSC0XFyiKCIWiyGVSqGsrEzebPO5drGRSWBIw0p1kaWewKRSKVlYyGNIfIcK\nDMWNUEGh5A2JIwBIE5NUKgWv14uKioq8XVylslEWIjDAT0kCQMtkBwBpnZSpwFCchgoKJWe0aksA\nyC1LvF5v1iyu1opSYEirFz2BUVtoWi4yMjuGQATG6/WmxW8oFDuggkLJCb32KdFoFDzPIxgMynUn\nZlGqm6JSILQERhRFJJNJ8DxvuNCSCIwkSXIPMyowFLuggkIxhLp9CtnYeJ5HU1MTvF4vKisrkUwm\nIQiCk0stWtQCE4vF5IaUPM8jmUzK3ZZzFRjye2UMhgoMxWyooFCyohzNq7RKksmk3D4lEAjYup7W\nABEX4sYiWWBEJPIRGHXciwoMxUyooFAykmv7FCI2haJ3nda84SnFA0BGgdHKAqMCQ7EaKigUTfTm\nlpD2KX6/nwbeLSabMGcSGI7jkEgkMk6z1BOYeDwOAHLshQoMxShUUCgtyDSaN5lMFtw+JZ/1tNaN\nLJf7NktgyPvNMAw4jmthwZA0ZSowFDVUUChpaNWWCIKAaDQKIHv7FLNcXsrr0U0rP8wQGKU7k8TS\nqMBQ9KCCQgGgX1vSGtqnGKEUEgGMCgx5rNoyNCIwyj5kVGBaH1RQKHIDR5JRRDaTTKN5rcZsS4fS\nEj2BIW36o9FozhZMKpWSkwOUAkM+V1RgShsqKK0YZW1JKpWSJycKgoCmpiZ4PJ6C2qdQigulwBAx\nUFbxi6KYt8AAkOtrqMCULlRQWimZaktisRhCoRACgUDOX/hStCxK8Z6MoEwjBtKnWRYqMEoLhsRg\nqMAUP1RQWiFatSUA5JOkEy6uTLTmLC83YURg9GbBkL9XuteA5hgd6WGmbhVDBab4cM+uQbEcvdoS\nnuflDsHl5eWu+xKrN6XWaC24kUwCY2RcMoAWAkPa+JDHq7PIKO6GCkorIdtoXq/XK8dQCsHMSnky\nrItSHJghMADSxENtwVCBcTdUUFoByvG06vYpkiShoqICyWTSlSd/0t2YbiD2QToVF0o+AqP8W6Cl\nBUMFxt1QQSlhMrVPaWpqQiAQQCgUcp2LiyAIAhoaGsCyrFzrQKBB3OIjk8AkEglZNEh35GwuMmJ1\nKwVGXQdDsRcqKCWK3twS0j6lkNG8VkM2Cp7nUV5eLt+DKIpIJBLy3HUAuidcivtRCkwgEJBHRxNX\nrCRJGV1k6j5kJEtRK02Zfj7sgQpKiaGeW6Jsn0KKF7Xap1jdJdgopM2LKIrw+/3wer1pJ1CSCeT1\netMsMJKKSjYPOg63+CCC4ff7wbJs2rhk4rKlAuNuqKCUEFq1JUDxtE9RrpNhmLTRtmrI/ZEmlbn2\nqSoGWnu6tHJcMoAWAgOgxfubi8CQFGVq4ZoHFZQSQau2JNf2KU4F5bVcceRLbxS9NiIkJZoU4dE+\nU9lxMjkjk4hmEhhixeYiMMSFSlAWWpI6GEpuUEEpcjLVlkSjUXg8HlRWVmb9cjj15SF9xIDsnYxz\nQUtgjKawUopjkJlSYIgFUojAJBIJcBwnH7yURZbFaOE6ARWUIkavtkQ5mteM2pJcyCWGko8rLt8Y\njZEMI7Lx0Crt4oO8X7kIjF6assfj0bRgqMBkhwpKkSIIAmKxmOwmUtaWaI3mzYadFehuyDbTyjAi\nm486g8yN9TmliBVzdHIRGK2/V66NCkx2qKAUGUoXF/k3wzDyaF6fz+fq0by5uLjs3MgzuU+Ur7XS\ngqFYgxWvrZbAkEMEyRIkkPdZbcFQgckOFZQiIlNtSSKRsH00rxaZLB1SUGnExeXkl1G9+ZAuAizL\nyptPsWeQtXa0YmyxWCztPVY+hgqMMaigFAF6tSXKnxca0LbS5eUGF1chkI2glFOUlbRGFx/5TpHN\nX8uCydaqX0tg4vF4Wnym1AWGCorLyTaal2EYV3YIJliVxeUkmTLIjLRxLwacWK+b6m700tCNHiKU\nVq7y70tdYKiguBi92pJ4PI5UKoVwOJz2AXUTRAiLoWdYoWTKIKMpysVDJkGzWmDIcweDwaIWGCoo\nLkTpylJ+CJXtUyoqKkzPijGr9QoAU1xcxep6UQtMtgrvUrDaWhtmC4yyjxl53Pz583H//ffbf3MF\nQD/JLoPUlhAxIR+uZDKJhoYGBAIBlJWVyadct226ZIYJz/OorKzMW0wync7cds/ZIMH9YDCISCSC\nUCgEj8cjpyhHo1G5qI7OgHGOQlxuRGD8fj9CoRAikYg8QptkYJI0f57nNT/DyhgOy7JYuXJlobdk\nO9RCcRF6Lq5oNCp33rVyNG+hGzXJ4gIgi54ZqE92xSYoatQpynrBX5K+3FpwUwylUIzE2ZQWjPq+\nBUEoSsuVCooLyNQ+hYxE1WqfYubmWsgXWTn5MRKJIBqNmrKm1kAm1wnQ7Dq0O4OslDZ2o1gt3Jni\nbERggGZPxM6dO9G+fXuEQiFL12QFxSeBJYZy9ofSKkkkEmhsbEQoFCqKQkWSuux0HUyxo3SdAJDb\n5wA/ZfaRpAxBEFqVBWMHdn3PiMAEAgGEw+G0uqyHHnoIp512GrZv346HHnoI7777bsZmqddeey06\ndeqEAQMGaP5+/fr1qKysxKBBgzBo0CA8/PDDltwTQAXFMYhVQgZGETEhG3QymURFRQUCgYChaxVK\nPtYOx3FoaGiAx+NBeXm56SY63SxbbjyRSER2lSWTSSowJQTLsggEAliwYAFWrVqFvn37oqmpCb/9\n7W/RvXt32WpVc80116C+vj7jtUeNGoWtW7di69atmD17thXLB0BdXo6gV1tCgnd+v9+QVeKU1aJ2\ncVlhlbjVInMaPdcJz/PyECr1kLFieS1bo6tND5Zl0bNnT8ybNw9As+tTrzffiBEjsHv37ozXs+ug\nQS0UmyG1CWoXVywWQ1NTE8LhMMLhsGu/WEoXV0VFhaaYmB04p6dufYjAkAyycDiclkEWi8VoBpkB\nnBYz9fPHYjGEw2H534XEUxiGwcaNGzFw4EBMmjQJn332WUFrzQS1UGyCnCRJxlZZWRmAn0beAvlV\nkiuLogrBiAgoLahSLlQsZvSaXKr7UxVz8VxrIB6PIxKJmHKtM844A3v37kU4HMby5ctx4YUXYseO\nHaZcWw21UGxAXVtCSKVSaGhogM/nsyQGYRakOr8YLCjKTygbXJLaiGAwCJZlM9ZGOH1adwKn71n9\n/NFoNM1CKYTy8nL5WhMnTgTHcThy5Igp11ZDLRSL0aotIXNLOI4ruFmi1XUZhcxYobiLTCnKytoI\noNlyttuCcXpTdxNkQJ4ZHDp0CB07dgTDMNi8eTMkSUK7du1MubYaKigWoVdbQuack/YpbrFKtISJ\n1MEYTRLIdK1816OMMykFmVI4SoHx+/2yeyyRSJRMk8tiQf19ycXldfnll2PDhg04fPgwqqurMWfO\nHLnFz6xZs/Dmm2/iueeeg9frRTgcxhtvvGH6+glUUCxAbzRvKpWSC9UikYgpX04rLBQ7srgo7oME\n+IGfgsCtZUyyG6wjtcurU6dOhv5uwYIFGX//q1/9Cr/61a8KWptRqKCYDEnfBJB2oo7FYhAEAeFw\nGIlEwvEPrx5ktDB1cVGUKcrZxiSb0eTSDZu6W4jH40VZKU8FxST0akuI28jn86GiokK3OKnQ5y4U\nst7GxsaCxwiXQr+t1kqm9y3TmGT1jHY6Jjk3yERQQiwWkzNBiwkqKCagN5pXy21k9mZrxpeWVF0D\nza4OI9X5lNLGSFGtMoss1wmHbsNt1pGZQXk7oYJSAOrRvMrAezQahSRJtriNChEoZRYXANeM5yXC\nS2JPSv9+a4C8p27a5DJR6HyQ1k62wsZiofV8Q01GkiRwHAdBEFq0T8k0pdBNForSHVdWVoZjx46Z\nti4zkCQJDQ0N8v+TwjyGYeT23nRTcidG2rer4y9OWgluc9FSC6UVkWk0b6FTCu2AbM4kNdHsLC4z\nRJNYfWRIEYF0ZlaP1i21rKNSI1P7dvJeEheaU4cFNxU20hhKK0CvtkQ5mjdb+xQrLJRcrqfMOFO7\n49wQTFcKMwAEg8E08SZuk2AwaHnWEcU61AIjiiKSyaQcewTQwj3Wmg4L1OVV4mjVlgDNA3FisRiC\nwWDaTAMj17P7C6LOOHPbF5Q0ngSa20U0Nja2eIxS9LSyjojgF1tQuLVD3kuGYeD3+9MOC+oMMisO\nC04H5dXPb2YvLzuhgmIAskmpXVyxWAwcx+U0mtfsD60Rq0Lp4gqHw5ZnceVj6Sir8kn+fS7XIO8L\ncd9ptRWhVd/ZcTqOQYSitR8WOI4ryoJiKigZIB/iY8eOpc1I53ke0WgUHo9HczSv0Wvb8SUgM+m1\nXFxqnHB56cVzzGjdotVWROmzV3fdLbVNqVTIdFgolQwyrf2g2O4BoIKii7K2hBQjqk/6fr8/rzfd\nzA9KJhFwu4srF7ErFC2fPS3KK070UpR5nk9rckkOC0asUXVhodM4HcvMFyooKjLVlsTjcVNaklht\nCRTi4rLrg0wSGTweT1axs+L1ysWlUqxf7mIjX6s9U4qyOhvQje5O9eermD9vVFAU6NWWAM0tSXLt\numsH6s22kFO/WfeVTQBSqRSi0ahcle/066nnUlGeeMlj3LghUdLRS1FWjkl245Ax5TqK1QVLBeVH\n9GpLSJfVUChkWrM2qyyUYnBxxeNxpFIpw4kMTpzW1CdecspVfh6Uc9vd5CoplGI+HethxN1JHqec\nCWMXWpZZsb4PrV5QMs0tISmsxDXiVkgOP8ldzzeLy0pXHHk9GYYxNAfGTWJIPheBQKBF111l/MVt\nJ958Kfb1Z0PL3RmPx2VXNzlQOPV+8jxftF2+W7Wg6NWWEJcMqS1pbGx0tBgxGzzP2xLYzhfSjibX\nWh23ot6QSi3jyCmcSFkm33uGYRAIBMCyrO3vp3oviMViRVmDArRiQSEfGL3aEmX7FDdUkGvB87w8\nW8VNLi7yelkxqMtt74WRjKN8AsJOF9q1VvTeT/WYZGLBmBVPU7ddKcYqeaAVCoqR9ilWj+Y1Y1Mk\nLi6l6LlhXQRJktDU1NTqBnVlyjjSailSSvGXUsRoPZOZGWTFOlwLaGWCojW3BPhpc9bLOnLTqZhk\ncfE8j/Ly8rQUZ7dAXmc3ZsXZjTIg3BriL8WKUYtQL4NMS2CMNizVagxJXV4uRl1bonRxKTdnvawj\nswUl3+spazdIhT7JPnILyWQSqVQKPp+v4C+Fm4TcLIzGX0g7d7tx8vUuRjdfpgyyfBuWUpeXi9Gr\nLSEptl6vN+/2KfmSz0apzOLKt0LfinURlPEnN9SWFAOZ3GPk8BOPx20vyKPvXf4oDwxA5o4MenNg\nqKC4FL3aklyryJ08KWdrQumGU7w6/kTakFNyQ3naJWMGfD6fXJAH0PiLVVhlHelZpMqODMokFoZh\nilpQSvITSQLvZKYGedNILUQymURFRYVjLUmMioAgCGhoaIAkSaisrLRlBG6u98lxHBoaGuR4SWvb\n5FauXIna2lrU1NTgzDPPxOuvvy6PUy4UIjDBYBCRSAShUAgejweCICAWiyEajSKZTMqdsCnuhlik\npKN2JBKR9yBJkvD9999j3LhxWLp0KQ4cOCC7zPS49tpr0alTJwwYMED3Mbfeeiv69u2LgQMHYuvW\nrabejxYl9+0XRRGJREIuUCKnDrLxkd5RTrQkyYVkMomGhgYEAgFEIhHdNZhpoeRyn6QYrKmpCWVl\nZWnjjq2IOTmN1v3Mnz8fV111FTZt2oQjR45g+/btuOOOO3DttddassGTky4RGFLTw3EcotEoYrEY\nkskkBEEoSoFxKobi1GuldHl6vV60adMG9957LwRBwLJly9ChQweMHTsWr7zyiubfX3PNNaivr9e9\n/rJly/DVV1/hyy+/xIsvvoibbrrJqluRKSmXF6kYP3bsGNq2bStvbGQCYL61EMS6MYtMG26+c1bs\nRBRFRKNR2XKyyipxgzuPrEPNDz/8gIcfflhOBSbEYjHU19fjww8/xNlnn23pmoq5IaIbcer1IULq\n9/tx7rnnYseOHZg0aRIuuOACvPvuu3K3czUjRozA7t27da+7ZMkSzJgxAwBw1lln4dixYzh06BA6\ndepkxW0AKCFBUfflIT+LRqMAUPDGZ8fGppXFZSdGNnD1ICw3rtEOli1bpvt5isfjWLBggaWCoiZb\nQ0TAWPylGDOtSg0S362oqMD555+f93X27duH6upq+d/dunXDt99+SwXFCOQEpmyfks9oXi3M/oJp\nWTzZamEyXcuODVZvEJaTa3ISMspAC5KO7iR66axunXjYmtOV1bNYzKxDUb+uVt9nyQgKkL6RxePx\ntPYpZl3XbIrBxWXnIKxiYcSIEbpfzrKyMowfP97mFWXGSP2L1+uVs42cwmlhcwNmZXlVVVVh7969\n8r+//fZbVFVVFXzdTJRUUJ5kRQEwTUysgAgUWS9pT5KPmJgdlFdfS/maOikmbrN4+vfvj5EjRyIY\nDKb93OfzoX379rjwwgsdWll2tLKNSFsR0miUjBlwW+FsKaK2kIjLq1AmT56MP//5zwCADz/8EG3a\ntLHU3QWUkIUiSRIaGhoQCoUQj8dNPelYYaGQjdotQ6a0cHoQlttdZ6+//jp+//vf44033oDX6wXH\ncRg5ciSee+65vEcIEOx0wyjdYyzLgud5eL3egqq9iwmnXV5qiFs5G5dffjk2bNiAw4cPo7q6GnPm\nzJHjZbNmzcKkSZOwbNky9OnTB5FIRDdbzExKRlBYlkWbNm3AMIzphXVmN01MpVKy+6hQF5cVm65y\nEFY+lp7bhcAsgsEg5s+fj0cffRT79u3DCSecgPbt2zu9rIJhGAY+ny9tXojV8Re3bep2ov6uRKNR\nQ4KyYMGCrI955pln8l5XPpSMoABIa2Pgxg2NZHERl4Pb4iUkWaCxsREALO+6XCqUlZXhpJNOcnoZ\npqDe2Emii1b8RdnOnTS3pOnJ+WGFy8sJ3LWjmYRbmjkqUbqPWJZtUb9QKGac8EiQNhgMOpISrIfT\ngWLKTxht567snuyWz5EebrOOjLq83EhJCorZmNU0kWRxmdkqwyx3QzKZRDKZhMfjMeV0ZNb9ET++\nJEmOduGlaJOp265eM0RKOmpB4zjOtQlF2SgpQSEbv1tcXnYN7VLed64oU4JDoZAps1XMOu0RMSYB\nbrJZAc2plWZPzaMUjta8djLQLlP8xUkrwW0WClC86dMlJSgEN7i81HPp1X5ptwheY2MjvF4vKioq\nXDOoS5KaRweLoohwOAyfzweO4+Q6iWg0Cr/fr+tmoadgd0DcXaQIViv+ohQWN3wnnMCNgpYvVFBy\nwMgbr8yQsrNQsZD5KsQCcMOXWtknTNmrSk02NwsRFzdUgVOayRR/4ThO/u60poOB+vumHLVRjJSk\noJiN0TfXqIvLyW68dlTm53t/xGLy+XwIh8Nytlk2jFaB0yyk7DhV/+LxeJBMJuX6F3X8hYzTtQI3\nWAjK53f6UFcIJSUoVrVPV15T74OXycXlFsg8GIZhXJcSTF4/o0PP9DDShVdpvbjpNWjtkENBpmFU\nbuo/RmlJSQkKwex28wQtkcqnCNCJGA/HcWhqasooeE64vLK5CAtdT6YspGQyKf+eblLuQutgIIoi\neJ5vEX8pZsuzlDK8gBIWFCssFDWkPX6+J347TG0S4E4kEq7rb6aMl2i9fla8NnrusVLapEqRTJZn\nIpGAJEl5W55ucHkRiJVerJSUoFj5oVCLVCEuLiva4WsJKNmwSfNJuxo7FsNcFSBzkJgUnio3MIp1\n5LqpKy3PQCCgW/+iLLB0I1qNIUOhkIMrKoySEhSC1e3mC+lzRSikdsQIZMP2+XwoKysz9Dx2uby0\nMszcgN4mxXEcRFGUa1/scI9RAcsNI4kZxRB/KeYqeYAKSk7XFAQBsVjMdUFt9f26dcM2I6XazkI4\nskkBzQJNal/sco85semphz0VI7nGX0iihhOoP8dmzUJxCiooBiHptmZlcVm5xnxTgs1ak9Z18s0w\nc8tJXc89pjVi18oUV0ruGIm/kM+Z05l/NIbiIqz4EpNTNWlN4kb/JrGe4vE4WJZ1ZB59JvKNl7jp\nHtQo3WN2tXgvZZyqfwkEAojFYmBZ1pHCWKuGazlFSQkKwayTNjlVA82T+Mw8uZhpoYiiKHcJdlsN\nDHG/ZZtDX8yQyma1D1/LxUKsFze9R60d9eFAL/5iR984M+fJOwEVFB3UdRuxWMw17hcCSQnmeR6B\nQKBg68lMkSM9tziOKzjDrNg2Xy0Xi3K0LlAcGUitESOFsWbGzmgMpQgoZGMkLq5kMmlp3Uahm7ey\nhsPv9zs2610Lcl8kXbnYg7yFwjAtJyCS2IvdJ+BsuO3QZAeZ3G3qwthMsTMz4i9UUFyE+kORq19W\n6eKqrKxM+3BYFUTPB3VMIhaLmb6ufDc1YtkBMJyunG0tdvDRgY8Q42IY2X2kpc+j1YFX6wTsZKNO\np7LLisFSs7rzQjweL+ox0iUlKIR8PphkIySuI/U1nGzoSCCDsEiuOtmUzMzOyhfl2sLhsNxBwKn1\n5MLOYzvx87//HDEuhtM6noaxNWMxrsc4DOkyBD6PtZ0F9DYoUvsSjUape8zFGK1/0bM+aWFjkWC0\ncNCp1iS5ioByEJadVe9GIOnKPM/LLi7ijnP7Brjhmw24btl1GNV9FKrLq3F+n/OxZvca3LX+Luw6\nvgvndDsHo6tHY1TVKPQL9rN8PWSDYhgGqVQKgUCAdk62GLM+p7nEX/RSy2lQ3kVoqX8mMrm4tK5t\nRcNJI5C2+B6PBxUVFZZbT/msjbTst2ODM6PLgCRJ+J///g/mfTgPL096Gf/57j84GD2IEdUjMKJ6\nBB4c8SC+j32PtXvWYtXOVZi3aR7KA+UY22MsxtWMw4jqESjzl5l4Vy0xskGVSufkUiioVKMVf1En\nZwCQiytZli36GEppvYMKsm02HMfh+PHj8Hq9KC8vN/RhtrtDMNDcM6yhoQGBQACRSMTyDTsXceI4\nDg0NDfD7/abES+wiJaRw2+rb8PJ/X8aqqaswsvtIMGh53x3CHXBZ/8vw3Pjn8MnVn+DP5/8Z1RXV\nePbfz+LEF07EpEWT8OTmJ/GfQ/+BKFl/2CAbVCAQQDgcRjgchsfjkTs4RKNRJJNJ8DzfKoPr+WKX\nJU2SM4LBIMLhsOxaF0URy5cvx+DBg7Fjxw58/PHHhmYB1dfXo1+/fujbty/mzp3b4vfr169HZWUl\nBg0ahEGDBuHhhx+24rbSKCkLBcg+V17p4sqlNsLuzTKXNiV2W0/KeInbOhhn43DsMKb/YzraBNtg\n1eWrUO4vB/Dj5wb6mzDLsDit42k4reNpuG3IbYhyUby39z2s2b0G1y67FseTx3Fu93MxtmYsxvQY\ng06RTpbfSzb/fT7prVSI7IEkZxCRqaurQ8eOHTF37lz89a9/xT333INBgwZhzpw5GDNmTIu/FwQB\nN998M1YioTvAAAAgAElEQVSvXo2qqioMGTIEkydPRv/+/dMeN2rUKCxZssSu2yo9QSHotf8gvv1s\nLi4j1zN7fQSlK87utNts92k0lmOGW8rs1/yT7z/BFYuvwCX9L8HsYbPBMumvay7PFfFFMKHXBEzo\nNQEAsOf4HqzdsxZLv1qKO9fdieqKaoztMRZja8ZiaNehCHit7amWrb0IYDy9tVgszVLC6/ViyJAh\niEQiePnll9G2bVu899576Natm+bjN2/ejD59+qCmpgYAMHXqVCxevLiFoNh9QChZQQHSX0yO4xCN\nRgtql27Hm5Mt20wLu2Io2WI5bmbxjsW4bc1teGLME5hy0pQWv89moWSjR2UPXHPaNbjmtGvAizw+\nOvARVu9ejQfffxA7juzA2VVny/GXPm37GEoWKVSM9dq7u7E1jFMJHE5bZFqFjZFIBOFwGHV1dbp/\nt2/fPlRXV8v/7tatGzZt2pT2GIZhsHHjRgwcOBBVVVV44okncPLJJ5t/EwpKVlDIm5Svi0vvemah\nFgG9lGC3QIQuFAohEAjY/uXP9/lEScTcD+fi9U9fx1sXvYVBnQZpX18jhpIvXtaLoVVDMbRqKGYP\nn40j8SNY/816rNm9Bk9/9DS8rFe2XkZ1H4XKQKUpz5sJo4PFlI0SWxNOCyrBaFDeyHrPOOMM7N27\nF+FwGMuXL8eFF16IHTt2mLFMXUpOUJSuFuI6kiTJlPYfVs5YKTQl2Ky1aQmdWyc+ZqMp1YSbVtyE\nA00HsO6KdRnjGgys21DahdrhopMuwkUnXQRJkrD9h+1Ys2cNXt72Mm6svxGndDhFFpgzOp0BD2tt\nSrjSPabunEze71LJHnM7agtFEARDXcKrqqqwd+9e+d979+5t4R4rLy+X/3/ixIn45S9/iSNHjqBd\nu3YmrFybkhMUAglq5+I6shMieIIgoLGxET6fL283klX3VojQOZnKDDTHNC5ffDkGdhqIpZcsNRTD\nKMTlZRSGYdD/hP7of0J/3PyzmxHn4ti4byPW7FmDm1fejIPRgzi3+7kYXT0aI6tGolewly1rIu6x\nWCwmHxpaQ+dkt9VKGW0cOnjwYHz55ZfYvXs3unbtioULF2LBggVpjzl06BA6duwIhmGwefNmSJJk\nqZgAJSgoREg4joPf7zctp9uKDVIQBDQ0NLhuEBbgjnhJvq/5xm83YsbSGbhtyG345aBfuioOpSbk\nC2FsTbN1glHA/sb9zbUvu1bhwQ8eRMdIR9l6GV41HCGftVXUkiTJVomdnZPdtrHbhfK+c/n8eb1e\nPPPMM6irq4MgCLjuuuvQv39/vPDCCwCAWbNm4c0338Rzzz0Hr9eLcDiMN954w5J7UMJIJeYwPXr0\nKDiOk1sdmNXGQBRFHD9+HG3bti34WpIkobGxUa4sL3RaHMdxiMfjqKioKHhtDQ0N8Pl8SCQSBcVL\njh07hvLy8oLcjPF4HJIkIRgMguM4eR2xWAyBQEDz2q9uexV/2PgHvDjhxeZN2iAvbH0BXxz5Ak+N\nfarF7ziOgyAICAaDed9LrnAchxSXwufHP8eaPWuwZvcafPr9pziz65kYVzMOY3qMQf/2/U3fhKPR\nKEKhkK6bS+keEwQBgDmDxTK9p1ZCsuCcqk5vamqS68skScLEiRPxwQcfOLIWMyg5C4UMwSKT2NyG\nMq6jrKJ1A+Q0aka8xKwTP2nrkkqlZL++1nU5gcPdG+7Guj3rUH9ZPfq27Zv7em1weeWCh/VgcJfB\nGNxlMO4ceieOJ4/j3W/exZo9a/DC1hfAiRzG9BiDsTVjMbr7aLQPWd9UUOkeU3ZOVrvH3NA52ShO\nrdGN+1OhuGc3Mwmv1wtBEEwv9jNjg1TOWGFZVp4O54a1kRodURQRDoddEXyXJEkWklAoJLtelIFj\nr9eLY8ljuHrp1fB7/Fh7xdq8sqYYMHCZnrSgMlCJC/pegAv6XgBJkvDVsa+wZvcavPHZG7h11a3o\n27Zvc2PLmubGll7W2q+30c7JRtxjrdXlBaQLWrG/BiUnKFaTzwdfK1OK4zjXnFCUiQHkZOk0yhNv\nJBIBx3HweDzw+XyIRqOyf/+/B/6LGctn4Pze5+OB4Q/A78s/LdxtFkomGIZB37Z90bdtX9w46EYk\n+SQ27d+ENXvW4I61d+Cbhm8wonpEc3ymx1j0qOxhy5qy9a5yW+dkNwlZKpVyxUGuEEpOUMiHww3t\n5oHCqvONUsi9plIpRKNROTHASA8hqyFjg30+n+aplqS9rty9Er9c+Us8MvIRXHLiJXJPq3yyksys\nQ3GCgDeAkd1HYmT3kZgzYg4ORQ9h7Z61WLtnLR7Z+Agq/BVy8H9EN+sbWwItB4tptXbP5MYsddRi\nRr6HxUzJCQrBiqydXNuJkEFYPp8P4XC4hWnr5JdIr1eYWevK5zrqNSkDv+rHPbXlKby07SUsunAR\nhnQZAgBZi/YyWV9uOaWaRadIJ1x+8uW4/OTLIUoiPvn+E6zZvQbPfPQMrlt6Hc7ofAZ6VPTA0Kqh\nuPLUK+W/s+rEnq1zMtB8kFC25m9tkFlCxQwVlBwxek1yyrYjJTjXe1VaTW4Z0au1Jp7nWzwuxsVw\n05qbsKdhD9ZevhZdy7um/V6raE/tdtGbqFdMLq9cYBkWAzsOxMCOA3H7mbejKdWEl7e9jAffexD/\ne/h/0wTFLtTuMZKiTg4CgP77ZCZOurzUz00FpZVhtFtrLBYDx3GGmifaTSarySmUMZxMa9rXuA9X\nLLkCvSp6YeklS1EWyO62yeZ2kVuOiJItLejdwLo96/B/t/xfnNfnPAzsONDp5cgQF2c291ixZI/l\nCnV5uRCrYihGrqksBqysrLT1Q2/kXo1YTWa+bkbnvZDah0x1Hpv3b8ZV/7wKN51xE2aePBNBb+41\nIXpuF5L2yvN8WtsRJzctq07Of/r3nzB/y3y8ddFbeOuLtyzPBMuHbJ2TScp9sbeG0WoMSQXFpdjt\n8lJujEaKAc1cn5HOtUZnq5iFkTVl6xFGXqPXP3kd96y7B8/WPYsJvSbIBY9mrFHuyOsPgPU0N1BU\nn4pLoWGiIAq4e8PdWP/Neqy6fBW6V3THos8XwcO4Z5S0HlZ2TnZTlhdpDFvMUEHJ8ZpqlJt1LsWA\nVqxP68vh5GwVPYz2CONFHrPfm41V36zCskuWod8J1s10J7NRtGoqlLUvhVaEO0GMi+G6ZdehMdWI\nlZetRJtgGwCAIAlpnwenRJM8r9HX1GjnZLe7x2iWVytHLQJu2az1vjAkXpLLDBirYzuiKKKxsTFr\nj7CjiaOY9s40CKKAd698F2Ue6+e3K4PyylMxSRDweDxFVxH+XfQ7XPrOpTip/Ul47fzX4Pf8VKcj\niAK8TMstwK33ooVe52Sjg8XcZHmWQlDe+eOqyVgZQ1HC8zwaGhpymkmvhVVrTCaTaGxslGeP271J\naL3+HMfh+PHj8Pv9cv8iLXb8sAMj/zwSJ7U7CQsvWIh2IWs7pALZ29eT4H4oFEIkEpFjUMlkEtFo\nVG5Iauco5mx88cMXGPfGOIzvOR7P1z2fJiZAs4Vidat8uyEHgUAggEgkglAoJB8EYrEYYrEYksmk\nbHWSv3ECrRgKdXm5FGUHT7M+MKSdSyKRKHgQltkfYuUGTrLM8o2XWCFyRl+zFV+vwPVLr8dDox7C\nFf2uAMdxpq9FD6P3rQ4au3Ea4vt738eMpTPw0IiHMO2UaZqPEUShKGIohaDlHlN2TmYYBizLQhAE\nxy3NeDyODh06OPb8ZlCyggKYM9dcDSnCKnRgF2D++kRRRCwWA8MwebvgzLbsjKZRS5KEpzc/jae3\nPI2FFy3EsG7DkEwmbXNJFNJ6JdumZaSw0kwWfb4Id62/Cy+f9zJGdx+t+zhBElyR5WVXYFwre4wk\neKjdY3bEybQsFLO6ozuF858mk7HqQ0By4lmWde089cbGRlcNFCNt+rMJXIJP4Ff1v8Kn332KDVdu\nQPfK7gDsd0WYlTmm3rSMFlYWiiRJeGLzE3h126v45yX/xMknZJ4fzou8nIzQGiHWCREQpzsnx+Nx\nlJVZ3xLHSkpOUJSYddomKcFmn1zMWh/JzQ+HwwXP7CBuvUIhp79sAneg6QAue+syVFdUY+30tYj4\nnfEhZ7NQ8n2fjBZWFpqRxAkcfrPmN9j23Tasvnw1upR1yfo3glT6Li+jkJ5xyiw/Ymnm2jnZKJIk\npR2yaB2KS1G6kgrZsNX1G27qEAyku5NIzYQbSKVShiZmfnTgI1z21mW4/vTrcdewuxy1qjI1hzTz\nAKFXWEliRcrTslEakg246p9Xwct6sezSZYYbP6pdXk7VZLip/QnBiKVpdudkKigupxBBISnBSneN\n2QHiQtfX2NgIlmVRWVmJhoYGU9eWD0oBJq3w9Zj+znQs3rEYdw+7G78b+rucvpCW1BjB/vb1ytRk\nUjxJxIXM9CEbm571sq9xHy5++2IM7ToU/2fM/8kpJiKIpZflZRVqS1P5XpEi2FzdY7SXVytBOQgr\nGAympSK7IS1Ub31OdQkmz00mUVZUVGStZi/3l+Ok9idh6VdL8fSWpzG6x2jU9a5DXa86VJVXpV3X\nDpzqraZ8fqXLhbhZMgWMt323DZe9cxluHHQjbh18a86nZKuzvARBwBdffAGGYXDSSSe5oqhWTT7v\nuZZ7TGuwWK6dk2kMxeXkukko24Fopbeavenks75kMqmZfuuku4j0MPN6vXLNS7b1nNzhZIR9YTxZ\n+yS+i36HVbtWof7resxeNxtdy7tiQu8JGNt9LE5re5ot95CtDsVuSMA4EAiktRshPv0N+zbglrW3\nYN7oeZjSb0pe77+VWV6LFi3CnXfeKYthJBLBU089hcmTJ1vyfIVQ6HdHaWkC6WnkmTonq7/7tFLe\npeQTQyEnbFEUTUkJNkKu6zPSrsRuiLVktIcZwct6wUvN7ek7Rjpi2qnTMO3U5sr4LQe2oP7retyz\n4R58ffRrnFtzLsb1GIfamtoW7erNxE3t69XuEGVq8ivbXsEjGx/BqxNfxeCOgxGNRvNqlmhVltey\nZctwyy23yLEGoHmznDlzJsrKyjBmzJi0x7upn5YZ6LWG0eoRp6QUXF7us0FNxOiGzfM8jh8/LqcE\nu63lvCAIcoxEb31mrc3odYg119TUhLKysjTXmxE8jAeC2HJ4lof1YGjVUDw48kG8O/1dbLxiIy7o\newHW7VmHs18/G8P+PAx/+NcfsHHfRnCCeTGtQupQ7EKURMx5fw6e/uhp1F9Wj5E1I+VOCGSWiF41\nuBbqLC+zPtv33XdfmpgQ4vE4HnjgAVOewyysFjMSAyPtj4hngcRhEokE1qxZg1deeQXBYNDQQbG+\nvh79+vVD3759MXfuXM3H3Hrrrejbty8GDhyIrVu3mn1bupSkhZILuQ7CstvlpRcvcRKSXcbzfN4C\n52E9EKSWgqKmY7jZernkxEsgSAI+Pvgxln+5HLPfm409DXswqvsojO85HuNqxhlKldWDAQM360mS\nT+KmFTfhm4ZvsHrqapwQPkH+nZHCSi1/viiJLVxehX6+4vE4du7cqfv7bdu2lZxFkgtK9xjP8wgE\nAvB4PFi/fj02btyIU045BXV1dRg/fjzGjBnTogxAEATcfPPNWL16NaqqqjBkyBBMnjwZ/fv3lx+z\nbNkyfPXVV/jyyy+xadMm3HTTTfjwww9tub+StFCM9PMiLqR4PI7y8nJDYmLnl4BkTBELIFuxopnW\nU6brkOyyQl2DHsYDXmw5kTHTWrysF2d1PQt3nXUX1k5diy1Xb8GEXhOwZvcanPXaWRj++nA8+N6D\n2PjtRkPXVuK0hcJu2QLPu+9q/u5I/Ah+/vefgxd5/OPif6SJiRpyIg4EAgiHw4hEIvB6vXK6azQa\nla0XXuRND8qTIVl6+P3+VismWrAsi9GjR+PVV1/FwIED8frrr6NTp06YN28evvvuuxaP37x5M/r0\n6YOamhr4fD5MnToVixcvTnvMkiVLMGPGDADAWWedhWPHjuHQoUO23E9JWyh6mywJIhMXl1Gfs11B\neSfjJZm+7KR7cSAQKNha8rDaLi+jawGa56ZPO2Uapp0yDbzI46MDH2Hl7pW4c/2d2HN8D0Z3H43a\nnrWGrJdMdSiWI4oIXXMNEIsh+sUXgGIEwq5ju3Dx2xdjYq+JeGjkQznHPPQKK1OpFFJ8CjzXbMnk\nWvuih9frRW1tLVasWNEiI9Lj8eDnP/95i79xYx2KE8/NMAwGDx6MwYMH4+6779b8m3379qG6ulr+\nd7du3bBp06asj/n222/RqVMnk++gJSVpoSjR6njb0NAAv9+PsrIy16UyGomXaGF1fEfZvdhoa5dM\n6/GyXkMuL0K25/OyXgytGor7h9+P96a/hy1Xb0FdrzrZejnn9XMw5/05+Ne+f2laL05aKN4lS8D8\n8AOYeBy+v/5V/vnHBz9G3cI63DjoRjw86uGCA+hKf344HAYYIOBvziCLx+Nyymu22Es25s6dizZt\n2qRlIfr9frRr1w4PPfRQQfdQKmi9vka+U0bFT319u0Sz5C0UgjIlOJdBWOrrWWmh5Dr10QrUa1J3\nC9AqVvzmm2+wcuVKSJKE8ePHo0ePHlnXrheUz2eNWqitly0HtmDVrlX4/brfY8/xPTi3x7morWm2\nXjqXdXYubVgUEZg9G0w0CgDwz5kD7oorsHTnUvx23W/x7IRnMbHXREuemhd5+L1+BINBuVCPdDko\nZI57TU0N/vWvf2H+/PlYvHgxGIbBlClTcMstt7iqm64bul7kWkNWVVWFvXv3yv/eu3cvunXrlvEx\n3377LaqqqmAHJSko6hiKKIqIRqOQJAmVlZV5WyVWWQFuFDsAaa+blmtQkiTcfvvteOWVV+Takzvu\nuANXXXUVHn/88YzXztVCKQQv68XZVWfj7Kqzcf859+Ng00Gs3r0aq3avwj0b7kGPyh7oXtEdRxJH\nwIu8rR14iXVCYOJxvPfYTNzVaSMWTl6IM7udadlzi5Iox1DI+8cwDEKhUFqxXj6deLt06YLHHnsM\njz32WNZ1OB2kd0NMJ5VKGRqFMXjwYHz55ZfYvXs3unbtioULF2LBggVpj5k8eTKeeeYZTJ06FR9+\n+CHatGlji7sLKFFBIZDKduLicksXXgJZH6l/KUTszEYQBDQ2NsLn8+kO6Hr++efx2muvyRsO4S9/\n+Qtqamowa9Ys3esbDcoDP/VRItlMhdK5rDOmnzod00+dDl7ksXn/Zvzp33/CJ999gl7P9cKYHmPk\n2EuniIVfRJV1AgBMNIqznl+MZR9tRPcTelv33NAubFQexrTmuBfbxEq3otW63shwLa/Xi2eeeQZ1\ndXUQBAHXXXcd+vfvjxdeeAEAMGvWLEyaNAnLli1Dnz59EIlE8Morr1h2Hy3WZ9sz2YwkSeA4DjzP\no6ysLO9BWErMtgJEUZRPJmVlZaZ0Ly0UpQhnS6WeN28eYrFYi5/HYjH88Y9/xMyZM3X/1mhQXim4\n5P5IFbkZJ1sv68WwbsNwOH4YkiThybFPYvXu1VixcwXuXn83aiprMLbHWIyuGo3hNcNNtV7U1gmh\nrRSAf/lGpK60VlByyfJSpyarW43kU1jpNE5bRkpymYUyceJETJyY7gZVH96eeeYZ09aWCyUpKCRL\niswBN0NM1Ncv9IOYSqWQTCbh9XpNGftphtiR1i6SJKG8vDyj643neRw8eFD394cPH5bbTmhhxOUl\nCAIkSZLfQyIwyWQSgiCkjRQodCMjzSG7lHXBladeiStPvRKcwGHzgc1Y8fUK3PXeXdhfv1+OvdTW\n1KJjpGPezwcAgQceAGIxSCwLUWrOiGIZFkwsjsgjjyA1fXpB189GviOAM7UaccvESrejZaEUe5U8\nUKKCQjaySCSieYLOFzO+GMogdzAYNLXZZKGt+kmqMkk1zYTH40FZWRkaGxs1fx8KhTIKeTaXF0lQ\nYBgG4XAYqVRKzlIim5TP55Nbihe6kWllefk8PgzvNhxndT4Ld595N47yR7F692rU76zH3evvRs82\nPTGupnlm++DOg3PenFO3347D33yOv372V5zWYSBGdx8lr5kLBgGLN2Kzug3nW1hJcJOl4BRUUFxM\nMBgEy7JpbhKzUPYJyxV1kJvjONMEpZAvJKnLISJhpBU+wzCYOXMmnn322RYxlGAwiKuvvjrjmvQq\n5ZUNMMPhsGYLD+Ua1DUWuWxkadcyUIfStbwrrhpwFa4acBU4gcOm/Zuwavcq/Gb1b7Cvad9PsZce\n4wxZL+vG9MaMpQ/hodmPYfgp06BsJJNMJi3PO7NiwJZS9IH0OSKZGiU6gZtqUIzGUNxOSQoKkHs6\nXi7XzeeapChQGeR2qjeYEnVrl1zWc99992Hjxo349NNP0dTUBAAoKytD//79cd9992VuvaJhoahb\nuuSCeiPTc8PoBZFzrUPxeXw4p/ocnFN9DuaMmIP9jfuxevdqLPtqGe5cdyd6tenV7BrrWatpvSz8\nfCHuXn+37tx3SZIsj0Wo29dbscFmKqwkok/cmq3ZUqEWiotRZqq4gVz7heVDPuKUSCQ0W+EbvU4o\nFMKaNWuwatUqvPnmmxBFERdffLGcgZJMJnX/Vm2hqAeakXiJcpPJZcPRc8PoBZELrUPRsl5W7lqJ\n21bfhgNNB2TrZWyPsXjt09fw2ievGZr7biVWtq/XQin6pEEiEReSQGP2FES3ov4sl0KnYaBEBYVg\nhQWQyzWzFQU6ZaEQS4DjuIJbu3g8HkyYMAETJkxI+7kgZA64e1mv7O4jKcqZUruVr1Wur5ue9aJM\ngSXuRzNOyUrr5aGRD2Ff4z6s3r0a//zqn/jVil8h5Avh46s/RueyzgU9T6FY0csrF0hwn+f5tIaJ\nhRZWGsVNFhF1eRURZn9wjGxm5MQNIKd+YflidJPVGm3sxHqIy4sE36203tRopcAyDANBFNJmixgp\n4DNCVXkVZgyYgRkDZuAP7/8BxxLHHBcTIP8sLysgqeBaUxDzKawsNqLRKMrLy51eRsGUtKBY8aEz\nck0SL8lWTGm3hWJ0XYD1pzcP4wEncIhGo3l3BzADckr2+XxgWRbhcLiF9UJqXsx4TYK+ICqQW3zI\nKqweAVwIpV5Yqf4sJRIJdO7s/CGjUEpSUNQdPM3cHLOJgB3xknzWZdQSsOOLKUkSuCQHTijc5WYW\npA5Fy3oh7rBYLJZ2Sg7eeSe4Sy+FOHiw4eeRJMk144bdZKFkw4rCSre5vGgMpQiwywpQxiX0mig6\nsTYjzR3tRHa5gQEYZBQTOy04recip2RCIBBoniPC8xA++gjlL7wAZtMmRNeuNXxKliDBJXpiS5aX\nEXJ93lIorNQKytMYiotRWiZWzzApJC5h5trU15IkCU1NTbrNHfUww6rTep2UwfeKsgrbmkMagVgo\nmVD6+IM/Nj30fvEFhLVrkRg2zFCGktssFDuzvKwi38JKaqGYT/F/mgxgpaDkEpfQupaZ61JCihW9\nXq9uc0c7IfUuxOXmTXhznqpoJbm8Pux//wvvpk1gJAlSLIbKRx5BdO3atAwldQBZTn2GewTF6Swv\nK8ilsNLJGjB1nREVlCLByo2UxEvUdRxGscqlQzZvJ+eqKCH1Lsrgu9GZ8nZitLAxcN99wI+ZRwwA\nz/bt8G3cCPacc5qv86OPn+d5udKfiIubTsVuiaFY+ZpkK6wkYq8WfruhLi+XY6XLi7RQMaOOw+x1\naW3e+VzLjNdM2aRT/Trl0r7eDhgwMKIn7H//C8+P1olMLIbA7NmIrV/ffC2Fj1+5iXEch2QqCQ/r\nkcfuOrWJiZIIBkzBUyCLCXVhJUlHJhMrARhyW5oBbb1SpFhhBZAuwZWVlaY1jCz0OiStNZlMukbk\nRFGEKIpy5bsSD+uRO+xmQytYbmZTTXJNIxaK0jqR/xYAu307PO+/D+FHK0V5XaULxufzgQGTtok5\n0duKF3lXWCdOQsScVO0T95hdhZVKqMurFUI+aF6v15T5JWZ9QInFBEBz886VQkWYxG8A6L5OXtZr\naB6KXRhpDsns2gXv+vWQysshqnuBJRLwP/kk4ipBUSNBgpf1yn3TtHpb2eHf16pBcZM7zm6U4gJY\nX1ipVYdCBaUIMMNCUXbAJTUcZte15Hs9ZVIAqfh2EmWzyWQyqbse17m8DFgoUnU1YsuXA7z2ukXV\nbG/Na+Cn91qrtxUJIAuCIFt4VlgvbsrwcjJdWS/z0e7CSjuagdqBOz5RFqD80po1J6SiokI2id2A\nMinA5/O1aCNvN8r4jcfjybieXIPyVtekiKKIpKDfzBIA4PVCGD7csjUoA8ixWEyus8inHX82SjHD\ny0rMLqxUi2ipWIclKyiEQjYi5ZwQ4kridU6ndq5Pq1jR6lqbbOtRN5vMFuPwMu5JGxYlEX/c8kds\n3r8ZV/7jSozvOR61NbXW9NuSYChtmPS28nq9LawXM4r3BEloVQF5LfLdxM0urHR6hIWZlLyg5It6\nTohZFk+hqId0qU9Ddp908i3qdEvacJyL48YVNyIhJLBpxiZ8fPBjrNy1EvduuBc1lTUY33M8xnYf\niwHtBpjyfEqXVy5opb/mO0wMaBZRt7i8ip18CivV31MnU5bNpOQ/UblmBEmShEQigUQioZt665Q1\nQCrNlUO6lNexm0zryYaRoDxgrYAfjh3G1MVT0b2iO5ZcvARBbxD92vfDtFOmpc00+fWaX+P72PcY\n13Mc6nrWYUyPMWgXapfXc5pRKa/OHMt1mBjgriyvUnH3AMYLK8nv5ILXErFSSlZQ8rEo1PESrdRb\nKz74RtZntLmjGV9OI6+ZsngyGAzmfA2ng/JfHvkSU96egov7XYzZw2a3cP8oZ5rcP+x+7DyyE+8e\neBeLti/Cr1f/Gqd2OBXje45HXc86nHLCKYZf83wtlEzkOkwM0B7/WyqBYaPYIWR6liXQnCr8yiuv\nQBRF2a1pdD1HjhzBZZddhj179qCmpgaLFi1CmzZtWjyupqZG3st8Ph82b95s6v2pKflPj1FBEQRB\nnjZC2BQAACAASURBVKWeqY7DikLJTJB4CWnz7nSnYKA5+N7U1ISysjJNMTECy7CQIBmuRTGT9/e+\njwmLJuCOs+7A/cPvNxRLqC6vxvUDr8eiCxfhq1lf4Xdn/g4Hmg7giiVX4OT/ORm/XvVrLP1qKZpS\nTRmvY3UvL3JCDgQCCIfDCIfD8Hg84HkesVgMsVgMyWQSHM9Rl5fNkPeGpCZHIhH069cPX3zxBT76\n6CPU1NRg1qxZePvtt7N6VR5//HHU1tZix44dGDt2LB5//HHd51y/fj22bt1quZgAJWyh5AI5/TvR\nqiSTQCktpsrKSsdPj1rB93xhGAYexgNBFMB6cruvQkT9jc/ewD0b7sFLk17CuT3OzesaIV8ItT2b\n58VLkoQvj36JlbtW4vmtz2Pm8pkY0nUI6nrWYXzP8ejTtk/a39rdy0svOymWiIGRGLnvmFNdqEvF\n1ZMPDMOgtrYWgwYNwrFjxzBv3jzU19fj7bffxoUXXpjxb5csWYINGzYAAGbMmIHRo0frioqdr3HJ\nCooRl5eReInWde14g7QyzOxam9Z18p1AmcmMJ4F5H6wfriVJEuZ+OBd/+d+/YOklS9H/hP6mXJdh\nGJzY7kSc2O5E3Pyzm9GQbMD6b9Zj5a6V+OOWPyLiizS7xnrVYXjVcEfjBcrsJH/AD6/HK1svyWRz\nyjRxe9k9tMqpOhQ3PC+pku/fvz/69zf2uTx06BA6deoEAOjUqRMOHTqk+TiGYTBu3Dh4PB7MmjUL\nM2fOLPwGMlCygkLQ22RJa3dRFHM6/Vvh8lJfTy/DzCnyCb4beYzRavlCX++UkMKtq27F5z98jjWX\nr0GnSKeCrpeJikAFJvedjMl9J0OSJGz7fhtW7FyBRzc+iu0/bEf7UHsM6DAA+xr3oaq8yrJ1ZIMU\nNir9+6QVTGsYuesm9BpD1tbW4uDBgy1+/sgjj6T9O1OG2AcffIAuXbrg+++/R21tLfr164cRI0aY\ns3ANWqWgKFu7m9FCxUxIcWA+HYytsFCyBd8LIZfAvCiKeZ0ojyaOYvqS6agIVGDZpcsQ8dnXgI9h\nGAzsOBADOw7E74f+Hj/Ef8ANy2/AruO7MOz1YehW3k0O7A/uMtjWmIa6sJFsSmQcMgkeKyvD7epr\nZRdOudv0LBQ1q1at0r1Gp06dcPDgQXTu3BkHDhxAx44dNR/XpUsXAECHDh3wi1/8Aps3b7ZUUEo+\nKK8mlUqhoaEBgUAAkUgk5y+GVRYKiZckEglUVFTk1Q7fbMwIvmfCwxirRSExLhJU5nlefs0ysevY\nLtS+UYsBHQfgLxf8xVYx0aJ9qD1ObHcipvafiq9v/BpPjnkSDBj8du1v0fv53rhm6TV447M38EP8\nB8vXote6nnwfyDCxUCgkH26IizgWiyGRSMjvQyE4nTLsBmEk2Zu5MHnyZLz22msAgNdee00z5hKL\nxdDY2Cg/x8qVKzFggDn1VHqUrIWijqEQkz6ZTBbU2p1g5hdBkiQ0NjbmXByoxiyxkyRJLsoqJPie\nrU+Zl/VmFBSSZqlsnCeKYosZ71rtxrcc2IIrllyB3535O8waNCuv9VsBSRv2sl4MrRqKoVVDcf85\n92N/436s3LUSS75cgt+t/R36tu2L8T3HY2LviRjYcaDpG58gGu/llRZ7UVTtZxsmRtFG/Z2Ix+M5\nC8pdd92FSy+9FC+99JKcNgwA+/fvx8yZM7F06VIcPHgQF110EYDmnn/Tpk3D+PHjzbsRDUpWUAhk\nUyOjcAvNljL7y0JOfYFAIOeJj1agzJMvRNyM4GH1XV7EYgN+6lgsCEJaUVgwGNSsSP7nzn/i9rW3\n49m6ZzGx10TL1p8PeoLftbwrrj7talx92tVI8kms27kOa79di2uXXYumVBNqa2pR16sOo7uPRkWg\nouB18CKfV+sVIhjqrrxaw8TcOs8dcFd2WT7Dtdq1a4fVq1e3+HnXrl2xdOlSAECvXr3wn//8x5Q1\nGqXkBUUQmk/ALMuaNgo328nbKKlUCqlUSg52m7WufCHBd1KMZXWasl5QXhRFNDY2pvnriT+ftHYn\nva78fr98auY4DvM/mo8Xt72IBZMWYFDnQRAEwXU+/2xrCXgDGNltJGp712KeZx6+Pvo1Vu5aiZe3\nvYwb62/EGZ3PkNOST2x3Yl73JkqiKc0hldaL1kwRt1svbsjyysfl5VZKWlCI7x2AqXPVC924lc0d\n3TCiF0gPvpPRqFbDMmwLC4WIGvHfNzQ0yKJAxIS0dud5Xk5xFSQBd757Jz7c/yFWX74aXSNdNavF\nrchYYvbvh//pp5F8/HEgW6GqwTHDSnq37Y2b2t6Em864CVEuig3fbMDKXStx4d8vhM/jk62XEd1G\nIOQLGbqmFe3rjVgv6mFiTsdQ3EAsFkNlZaXTyzCFkhUUsmmXl5ejsbHRNR9cpfutoqICqVRKtqLM\nun6uqMcGx+Nxy+pZlKiD8kTUSHsZ8rfxeFxOb+U4DoIgwO/3y26wo7GjmLliJiRIWH7JcrQJNbeg\nUPe6UmcsmXVq9j/8MHx/+Qv4sWMhZPFRF1opH/FFMKn3JEzqPQmSJOGzw59hxa4VeGrzU7hm6TUY\nVjUMdb2arZfuFd11r6PVvt5sN5DaetEaJsayrCPuJyf3A/VzJxIJVFU5l0JuJiUrKCzLygWBdtSO\nGEGZrmymxaRcVy6YWfmeD17WK7deUYsacZ2EQiHZnUUKK5XWxrcN3+Lity7Gzzr/DHNHzoXP40Mq\nlZItF+V/ymrxTKfmXGC+/Ra+N98EAzTPla+tzWilmFkpzzAMTulwCk7pcApuP/N2HE0cxdo9a7Fi\n5wo8svERdAh3kF1jQ7sOhc/zUyJKtiwvs1E2TSQuSkEQwHGcHC9zYhSyG4jFYgiFjFmWbqdkBQWA\nfPqxoro91+vp1XPYVXmvRm0pabXBtxoP6wEncIjFYkilUrKoEZcWiZNIkiRbFqFQSO6qu+mbTbhm\nxTW44fQbcPtZt8tzWMjfkzYjANLiMdlOzbm0gfc/+ijwY98ldu9eeFatymilWHkybhtsiyknTcGU\nk6ZAEAX8+9C/sXLXSsx+dzZ2HduF0d1Ho65XHWprajVHANsJeR8Yprn9SzAYLOh9KCa06lByDcq7\nlZIWFKvIZUMgm6Hy9G3luow2wsxkKdkVa/IyXjRGG8EHeNmaVIoJwzByejDLsnK2l9frxbp963DD\n8hvwxLlP4Pye5yMajcrJBMr0VjJGVykuRFiUg5AyDbHSuw/ZOvmxLTkTjWa1Uuzq5eVhPRjSZQiG\ndBmCe4fdi0PRQ1i1axVW7FyBu9ffjTJfGTjJ+cmjpNWLkffBTOvFLS5wIL+0YbfSKgTFKZeXsrlj\npnb4dlooVla+54IoioDU7HopLy+Xf6bMyhIEAdFoFH6/Py154cWtL+Lxfz2Ov/3ibzir6iwALQPA\nkiTJlghxdSktEqBZWImwkOfUajVO3DKJRCItHVZpnRCyWSlWtK83QqdIJ0w/dTqmnzod7+99H5ct\nvgwjq0favg4j6L0PpWK9EBElUAulSFBmkdjtViKpr8pYjtVku08ygz6bpWT168XzfLOF5GluUgg0\nb+7ki8YwDDiOQzweRzAYlLOGBFHAvRvuxYqdK7DmijXo2aZn2pqJgASDQbkAklyHzINQurvIc2az\nXjwejxyXIemwvoMHUaawTuR1ZLNSDI4AtorlO5fjlyt+iT+f/2eMrRnr2DqMooy9APkNE9PCTXUo\neq1XipGSFhQldlooPM+jsbHRUHNHO8ROmabsRPBdiXJQmN/jhyAJ8sZO3FypVEqujieFjDEuhuuW\nXoejiaNYc8WarBMTWZZFIBCQs8VIHQtxjRHLRVk/QdxtAFrUr6jTYf0vvgjwPMSyMvz4AFkmPNu3\nw7NxI4Thw1usyykLBQD+3//+Pzzw3gNYdOEiDOkypMXvnXAD5fqc+QwT08NNLi9qoRQRVmRT6YkA\nsQLyae5oxbqyBd/tXI86k4tlWCS5pGyZEOHjeR6RSEQWvkPRQ7j07UvRt21fvHr+qwh49YeM6a2D\nuFCU1ksikZCr74m4sCybFtgn/082L7nQcuZMSMOHt3ClkXsR+vWD58fHKyk0bThf5n80Hy9sfQFL\nL1mKk9qfZPvzW4Ge9aJMD8/HerEaGpQvcuy2AsrLyw0PLLJybfmmKZu9Jq30ZEFozjISJVEWk1gs\nBkmSEIlE5I3488OfY8pbUzDtlGm4Z9g9BW8KWpsQiZMQ15hSYIjvnqyZiIanVy8IvXunCYYH6TPE\nkz8mEyg3NbstFEmScP9796N+Zz1WTF2BbuXdbHtuu9EbJqZV3OqmoHwikaBpw8WA0l1hpcsr3+FT\nZkOyooD04LuT1fhqC0mZyUUGbCkzuZTCt27POlz9z6vx6KhHMe3UaZasT92+hdRGEHGTJAl+vx/B\nYFDXNZYpsE82NTJjhOf5vFvx5wov8rhl1S3YcWQH6i+rR/tQe0ufz00oY2pAS+uFuFedaM2jfu/d\nJG6FUtKCosQqQcln+JTetczCSbebmlgsJs+dAdIzuTxMcx1KU1NTi0yu1z99HfdtuA+vX/A6Rna3\nJxtJuQklk0kkEgn4/X4IgoCGhoa0rDG1a0xd8wIgrSI/EAg0CwkjQRRERKPRtD5XZh9C4lwcVy+9\nGpzIYcnFSxxv3a+HXZup2npJpVLged41w8SooBQRVrmVlAHmQCA3vz7B7LWRzCYz2s4XAgmC+/1+\n2T+szuTyMB5EY9G0TC5JkvCHD/6AhZ8tRP3UevRr36+gdeQK2WzImAPyGpJqfeUJN1PNC9kolVlj\nLMvCw3oQ8DfP4slUsV/IRns0cRRTF09FdXk1nqt7Lq1CnpI+TIwIvZ3DxJTvbSlZJ0ArEhTiojAL\njuOQTCZzipdYCSmglKTCW/QXChFaUqgGQDOTCxLg9XvlxyT5JG6svxG7ju3Cumnr0DGiPYXOKkit\nCc/zKCsrS3sNSZaX0jWWT80LaTWTrWIfaBblXK2XA00HcNFbF2Fk9Ug8NvqxnFrUl9rmZhTi9gSg\n6aa0uh1/Kb3uzu+EFmJFDIWcYHOdRa+HGWsjwXeySZkhJvmsSdkVoLy8XN5seZ5Pa6OSSCTAcRwC\nvgBIwtMP8R9w+TuXo0O4A5Zfttxw11yzUCYFZBsLXUjNi1I4yAalrhQnMSXyOKMn5q+OfoWL3roI\nMwbMwO1Dbi+ZTcoK9D7fyvdWab2o2/EXYr2UkoCoKWlBUWKGoFixcReKMvgun/wLJN8vCRnPq3S3\nkRb9yrRgURQRiUTgZb3gRR5fH/0aU/4+Bef1OQ9/GPWHvAY/FYJeUoBRcql5YVgGPq9P7jsGQJ7z\nog7uk5iSkRPzfw79B5e+cynuHXYvZgyYYe4LZCFObq5GnlfLeiECAxRuvair5oudViEoZnxgycYd\nDAbBsqwpGzfw09ry+WKpg+9mrSlXlJlc5eXl8ibo8/lk9xexxDweD8LhsByU//yHz/Gb1b/BvcPv\nxfWnX2/72kWxOUDu8/lMyYbLVvPC8zwkUcpY86K+XrYT8wcHPsANK27A/Nr5OL/P+QWtn6KP2k1J\nDg+5DBNTH2xJN4hSoaQFxSyXFynIU27cTrZu0Kt8N8u1l8t11LUuwE+ZXORkzvO8bAGQFGufz4dP\nv/8Uy3cux6vnv4oL+l5Q8LpzhayLWBdmo1XzwrBM2kRKdcW+KIry50vpKlRaL8oT89tfvI3frfsd\nXhj3AoZ1GYZkMum6Qj43UqhlQAQjl2Fi6r8HSqvtClDigkLId6PVKsgj17NifUau62Tluxp1ixmg\nZSYX2bRJJpeyXUbXSFcwEoPrl16PYVXDcF6f8zCpzyR0Le9q+dpJvCMUClnaAVqJ0pVVUVHRouaF\nrIPjOIRCobR2/EDLmpdXPnkFc/81F+9MeQcDOgzQbUNiJBXWiQPSwYMH8f777yMcDmPMmDFFfVLP\nlmShF3ehgtJKICdphmFQWVmZ9iGwo/JeCyNt5+1aF3FlEatNGXhWZnKpe3IpT+3LLl8GURTxQ/QH\nrNy5Est3LseD7z2I7hXdMbH3RJzX5zwM6jzIdAHXWpddkPb16sI7EiPh+eaRyKTDMXGfKdOReZ7H\nk1uexILPF2DpxUvRq20vQ21IjAT27bBqeJ7HbbfdhoULF8Ln88mf26effhqXXHKJ5c9vNcr3Qp0V\nSNzSyWQSX3zxBQDkLCh/+9vf8OCDD2L79u3YsmULzjjjDM3H1dfX47bbboMgCLj++utx5513FnZj\nBmgVgpLrRku64ZK55lZ/yYysz87K90zrIVlaiURCTpnWy+RKpVJpPbm0YFkWHco7YNrAabjitCuQ\n5JJ4/5v3sXznclz9j6sR5aOY0HMCzut7Hs7tcW5B2V8kC43juKzrsgotS5TUuIiiKMegiG9eXfPC\neljcteEubNy3EfWX1qNDqIOua0yrDYldqbCZeOCBB/C3v/0NyWQSyWRS/vnNN9+M6upqDB061PI1\n2JkMoDw8KOuY5syZgw8//BBdu3bF888/j0mTJqF7d/2xzYQBAwbg7bffxqxZs3QfIwgCbr75Zqxe\nvRpVVVUYMmQIJk+ejP79+5t5ay0onfQCDfKJoaRSKTQ2NiIUCulm/JhtCWS7XjKZRFNTEyKRSMbu\nxVZbKMQFSGI3Xq9XPnkRq4TEd0gtRy6bNsMwCPqDGNdnHJ6ofQJbr9uKxb9YjJryGjz14VOo+VMN\nprw5BS/95yUcaDqQ89q1Gk/ajXrAlnpdyvYt4XAY5eXlcp+n403HcdU7V2Hbd9vwjyn/QLc23eQO\nA6QYkrjRSIsX4KcNLRAIIBwOIxQKya34o9Eo4vG4nLVkNbFYDC+99JIcZ1ASj8fx+OOP27IOp1DG\nXv7+97/jpZdewoknnogPPvgAP/vZzzB9+vSs1+jXrx9OPPHEjI/ZvHkz+vTpg5qaGvh8PkydOhWL\nFy826zZ0oRbKjygD3dmKFe1yLeWyJqtRugArKioAQHe6IsMwiEQiBZ0Aidvg1C6n4tQup+K3w36L\n75u+x4qvV6B+Zz3uf/d+1FTWYFLvSTivz3kY2Gmg7vMRIQRQ8LoKRdkc0si6iBgkxASuWXUNQt4Q\n/n7h3+GFFw0NDYbmvJDsOqUVowwmk2aWQPOGb2WH3j179mSM+23bts3U53Mb6n2DZVkMHjwY999/\nPwRBwHfffWfK8+zbtw/V1dXyv7t164ZNmzaZcu1MtApBIeiZuU4HurUEKp81WZXllSmTSzldkfTt\nyjYDJh9YlkWnik64atBVuPL0KxFPxvH+3vex/OvlmL54OpJiUnaNje4xGkFvUF5nNBq1bF25IknN\nFookNU/zZFk2q1v1cOwwprw1BaeccArmj58PL+uVr5XrnBee59NcYkp3Gs/zCAQCeQf2jdC2bduM\n1lDbtm0Lfg4juKX+RRmU93g86NKlCwCgtrYWBw8ebPG3jz76KC64IHtGpFP31ioEJdOLm0+Ld6st\nFLImj8eTtWrbakgmFxkZrDwB62VyWQ3DMAgHwxjfdzxq+9RCEAR89t1nWP71cszbOA9X//NqjOg2\nAhN7T8TIziPRrU03Rzsut0CC/JnLJnJ7G/bi53/7OS7oewEeHPFgi+SQfOe8qJtZks+zGYH9THTu\n3Bmnn346tmzZ0qIdUigUwg033JDzNYsZvSyvVatWFXTdqqoq7N27V/733r170a2b9aMLSlpQtDKz\nlD8rdL66WaccpUApCyjzOVGbKXTqwslMmVx2pt8qIafy07qehtO6noY7ht+B7xq/Q/3X9aj/uh6z\nN8xG77a9ZdfYgI4DHBUWURKRTCYNFVJ+fvhzXPjmhbhl8C24efDNGa+rleVFrBetOS/qZpZ67fgz\nBfYz1Vlk4oUXXsDYsWMRi8XkWEokEsHPfvYzXHvttYavUwhOWSjq543FYmjXLvP00WzX02Lw4MH4\n8ssvsXv3bnTt2hULFy7EggUL8n4eo5S0oChRbtrKnlPZ5qvrXcsKCm07b/a6YrGYKZlcdsKyLNqF\n2uGiPhdh2oBpSAkpvP/N+1j29TJMfWcqeJGXU5JHdh8pu8bsgOd58BwvWxSZ2LRvE6a+MxWPnfsY\npp48NefnyjbnhYiLz+eT3ZUkPRnQnvNC4jSk35i6zkJpvWSiV69e+Pe//43XXnsNy5YtQ3l5Oa66\n6iqcd955rmi0aickfT0X3n77bdx66604fPgwzjvvPAwaNAjLly/H/v37MXPmTCxduhRerxfPPPMM\n6urqIAgCrrvuOsszvACAkZws+bYBUnV87NgxlJeXg2VZRKNRCIKQcxaSkqNHj5rW1bexsREA5DXl\n+6WSJAlHjx5F27Zt8xYX4ttPpVLy/ZGTrDqTSxRFuY2KGyCNO5PJZAuRI5vqp999iuVfL8eKXSuw\n/eh2jKoehUl9JmFi74mWdjcmhZQ3rb0Jv+j3C1zc72Ldx67YuQI3LL8BL058EXW96kxfi7IfFXF7\neb1eOftLPfYYQIvAvhJlYJ/EaIwG9kmnArsPJNFoVL5fOyH7EenMMHfuXAwbNgyTJk2ydR1W0WqO\nAyRwTGITZHpgIdczQ4uVJ/9CEwIKtVCUmVzKn6nFhASAnc6YUkIsJq3W88BPrrHTu56O07uejjuH\n34lDjYew/KvlWLZjGe5adxdObHciJvWehEl9JuHUDqeadm/KQkqGYTLOlH/jszdw97q7sejCRTir\n6ixTnl+NsucUqbciSSDKIL1eYF+ZjPH/2zvz6KiqdO0/VZlIJZUAgmkI+RjES6AbIQFJd2OYp5AR\nQQkgImCMtBr0gihLWxBtnJDlvYJcR4aFBklCBiEJU0tkSoKCCkhE8KabQSIIZK6qVKW+P3L38eTk\nnKpTVWeq1P6t1auXUNTZOTlnP3vv932fl69LJbtinwiRms2r+FAzKM+mubmZVsp7K42NjW7HJuSA\n7V5MHHnVHAu78+Tt27fb1TGQtGAtZUwRSPqt3e7cep6g1+vRK7wXFo1YhIWxC9FkbsJX//oKJT+X\n4IFdbdXa5GgsPioeQf7ueX2R4j2yY3LUU37D1xvw7tfvYs/sPRjSY4hb1xMLSaQwGAzMkS/Xj4oc\njZHjMfIMsM0syWKIHah3FNjXorgoCVfIqKB4GTqdjsl66dKlC1MkJsX3erJDYftgkfNqKcflyvdx\nkxPIz2UymdqllMpppOgunlrPA233LKRLCBIGJWDaf0yDzWbD6ZrTKL5YjFcOv4Lzt85j3P8bh8SB\niZh611T0NPR0+p1COyaSNsz97OrDq1H0UxEOzD2AqLAovq+UDCEfM3acRGyfF3bGGDk+c1axzzZQ\nJN+hpJmllk75Scy0s9DpBaWxsZFxYJU64Ofug8kNvpPVtRoIZXIZDAam5zbZqZAgr1aQ2noe+H1S\njYmMQUxkDFbetxK/1P2C0oulKKwqxPJ/LsfgOwa3ZY3dnYjBdwzucF12jIlUvzN/x6mUt7ZakbUv\nC2eun8H+OfvRw9DD45/BEa74mInp88Jugcx3NCYU2CdCQqr0ye5FbGBfCtTK8mL/bNQc0ssglhNS\nT9ruPIxCle9S1rWI/S6ygma3MWbHc8iLDbSJTlBQEGw2G+rq6todg6h1TKfUjkmv1yOyayQWj1iM\nRbGL0GhqRNm/ylDycwnSctLgr/dHwoAEJN6diPui7kOAPsBh9Tt792iymtr8yloaUTy7GKGBobL9\nHEDH4zdXEKp5IQsSsTUv7N0LCfKT41MS2Cc1L3JW7GsFkmnaWej0gkKaEkldjOjq96ldjc8dC8l0\nI8kJXBsVIn42m43JjiP/lm1cSIrdiLgo8eKrYT0PtP3OQ4NDkRidiOmDpsNms+G7a9+h+EIxVpWt\nwsXaixgTOQZT+09FcnQyQnQdjzLIDqXWXIvZ+bMRERKBbSnbEOgn785PyhRvd2pe2LsXIqok/Zw8\nc3yBfS2YWUoJXx0KPfLyIsgvT47qdrHfx26oxBc0JsFOKXD2c/J5cjnK5OKOl/vi8/X0IDsYOV58\nNa3n2ZBd3Ig+IzCizwistK7Ev278CwcuHcDui7ux8vBK/LHHH5mjsUHdB7XdW9hRa67F1OypGN1n\nNN6a+JasLY+dZb9JgSs1L0RciGAAbQsErh0MESxHfd3dbcOtlQwvoE3otRST9JROX4dCttHEtFCq\noDzpOujsYeA2oeJ7kEnSgBQrldra2rZ+7TyTLcnkIrb8QEcxcTeTi0wSxOmWtABmZwh5AilGbWlp\ngcFg0EwhJdB2XxsbG9vFGxpMDfiy+kuU/lyK/f/ajyD/ICQMSMCRK0dQ01CDx2Iew3N/eU7WiU0L\n9ULcmhf2YoNMpmSnQnYvABzWvJDvZNfQuFKxT2I3auwMuHU3CQkJOHz4sGYEzlM6/Q6FoMaRl9jK\nd6nHxvddfJlcXBsVT+ISQscg3Awhd+IujoLcasPnY6bT6WAMNiJlcAqSo5NhtVrx7bVvUXyxGD/e\n+BET+k7AsnuXyTou7j1Ta8Ji7zTIcanFYmFideT5c8XM0llnRGeBfS3tUDobPiUoUh0rOUMo+K4E\nfC8KETZiM8MnJlLHJbjHIEINo5ytKkmNCaC+9TwXMfeM/Kz3Rt2Le6PuxQvxL8BmbZsASTBb6gQH\nrd4zMg6SRUgWMWJqXrhmltyjMbYdjJRmllLDFjMioJ2JTi8ocsVQhL6PxB9aW1sVt53nGwsRtrCw\nMMZVlpxdk6MGT7J/xMAXd+FOJERguFX6WiykBNyP5fj7+cPfz7/dit0doRWCPH9ibPGVhggw+565\nWvPiKGtMbJdKraGl35GnaO/uegl8IsAOvpNWrmqNiytsQplccgds+cbHLp5jryjZ6ad6vR5NTU1M\nR0KtvHREgKXImHJXaIXwBgEWumdia164gX0iLI5qXriBffJvLBaL24F9d+Eet2npdyQFPiMocu0C\nCGKC70qNjQibXq+H0Whk/owrJuRYRM2eK3zZPBaLpZ1fFDkbVxs5BVioSl3s0ZgcRZ5S4UxMV40U\noQAAIABJREFUuLhS80IckrldKoGOuxcS4yI7IRKcB9y34vcE4hDQmej0giLnkReJyXhqOw9IawfR\n3NyMoKAgyTO55Ia8XCQrCQBvN0I1ahHYQW4lBJhvxS50NEZ+n1qzxQE8K6YEXKt5IUe4YswsSUEl\nO4WZBPal7lJJ4L7jzc3NbvVh0jKdXlDYyCEozc3N7arN3f0uKSArr8DAQBgMBt7gOzvFNTAwUDNi\nYrfzW89zV6nuHgd5OjYpg9y1tbX4+eefERERgd69ezv9vKOjMa3a4gBgjgal3M25UvPCDewT4WDP\nA3yCJXdgn3xHZytqBHxIUKSedNirICls5z0VO5PJhObm5nbVyXJnckmFs6Mk9kvvznGQJxDzSXJt\nT54jk8mEZ555Bjt37kRgYCDMZjNGjBiBTz75BFFR4gwh2Udj/v7+zDFXa2urZmxx2DVDcqZ5s+8F\nAN54HFtgiFg0NzdDr9ejpaUFdnv7Pi9iA/tS7JKbmpokq4vTCj4lKFLtUFpbW2EymWC32xEeHq7q\nKp+byUXGJZTJpXaFORey+rfbXbOeZx8HkWJKqa1gpI5LPPzwwzh48CBMJhMzQVVUVGDcuHH4/vvv\nXVqtksUBu4hVjqwxV2EvDpSuGeKreWHfC+KaTQL1AESbWXLT392p2OezXelMxpCADwiK1DEUq9WK\nhoYG+Pv7S2Y77+7YuP5g5HssFku7YjGlM7nEIpX1PN8RSGNjIwAwq1NXJ1Ru9bunnD9/nhET7nXq\n6+uxY8cOLF68WNR3CaUs8x2NKXlMSJ414vqg5rPGvRdsy3yy2BJT88KNvZBjRfKdxIXDHTPLztYL\nBfABQSFIISgWiwWNjY3MOTp5QNWA6w9G/owcZZGdCvB//T40VmEup/U8N1OKTHJirWBI9buUR4PH\njx8XvP+NjY3Yu3evKEERG+R25ThIiudCK5X5QpjNZiYex95pOKt54ZpZsv9fqEulUGCfu0Mhc0ln\nwmcEheCO7QJZebGD79zgnie4KnZklxQUFMRkiZCHnzzEbBNInU6H+vr6DgFLtVDCel4oO8iZFQxf\n8Z0UOPLS0ul+N+oUgh2XcGenyT0OYh8Teno0pmUxIfVY7BgYd1fLrnkB0G7hIbbmRUxgn/ue0yMv\nL4R95OUO5IEkVu/tmiVJXNciRuzILslgMDCTg5hMLim9tTxBrcQAMVYw5LgwNDRU8rqXqVOnMkct\nXIKDg/HQQw8J/lup4xJCx4TuHI1p1eYFEFfo6WnNC/mdignskyQAk8mEiooK1NfXuywoOTk5WL16\nNaqqqnDixAnExsbyfq5fv36MO0ZAQAAqKytdv4Fu0OkFhQ1ZIYh96NnHSiRGwf4uKcclBpLJ5Y4n\nl5gJVe6eJlqynueer5vNZmblSSqopYw1hIWFYf369Vi+fDkzAQNtO5dp06Zh7NixvP9O7voXMUdj\n7MZZ3LGRn8XdGJhcuFNrJUXNi9VqbScu7PtLMsssFgvWrl2LM2fOoH///ggNDUViYiL69OnjdIxD\nhw5Ffn4+MjMznf4shw4dQvfu3UXcLenwCUFhbzXF7iq4x0rcB1LqQklHkBe3paVF0JMLgOhMLqHg\nLbuniZQFhNw0Ui1UvbMhx5dGo7GdwDibUF1lwYIFGDhwIN58802cOXMGEREReOKJJzBnzhze+6zG\n6l/oaMxkMrXLoNPpdEwwWmueYVLF5zyteeGaWZLvDAsLw969e/Hee+/h3//+N44cOYIXXngBzzzz\nDF544QWHY4qOjhY9fqXmJzY+ISgEsQ8WO/iuVLGY0O6JL5NLSk8u9gqKnBWTQDYJLnqSGcQ9X9dS\nYoBQyjJfYydu8NZdURw9ejQKCwtFjY04BKi1+hc6GmtqamJsQ7SUgg7IZ0EjtJPjq4UiR2PsjDHy\nP/KO6fV6WK1WjB8/HrNmzYLNZkNDQ4MkYyXjnTRpEvz8/JCZmYmMjAzJvtsR2noaZMbZroIv+O7u\nd0kxNqFMLj5PLlfqOByNgbvl5xYQurJa1/L5OpmwHaUs8x0TKmEFw06n1srqn/y85NiGHPtYLBY0\nNzdLupNzFyX9zMTUvAQEBLQTY4vFAj8/P0ZcfvvtNyapxs/PD+Hh4QCAyZMn49q1ax2uuXbtWiQn\nJ4sa39GjR9GrVy9cv34dkydPRnR0NOLj46W7AQJQQfk/HAXfHeFO1pgYHGVyETEhL5Cfn58sq1ih\nAkIxq3Wt+oUB7p+v8wVvpa7x8Ib7xnWAdhZrUOJnYIuJ0v5YfEfIbNdoIiKBgYHMs/Prr79i9+7d\nmDBhQofv279/v8dj6tWrFwCgZ8+emDFjBiorK6mgSIWzGIqj4Luj75RrjNwjN0eZXErZuztKteSm\nnQpNPFpAivvG3skJWcG4s1rXsmOwownbWayBXeMhx8+kpphw4dZCkRR5nU6H27dv45FHHkF8fDz2\n7t2LDz74AOPGjXP7WkKL46amJthsNhiNRjQ2NmLfvn1YtWqV29dxBe0caCsA38NstVpRV1eHwMBA\nl49l5AjMm0wmNDY2wmg0CooJqQR3xypfCoiABAcHw2g0Mn5Ezc3NqK+vR0NDgyYnRSKAUt83spML\nCQlBWFgYAgICmB1mQ0MDU1jp6FkhZ+hkFaul+8YdmyPIhBocHIzQ0FAmbmY2m1FXV4fGxkbG1VcK\ntCQmXIh5bGBgIIxGI7p3746MjAwcOXIEly5dwqJFi5CVlYWTJ0+K/s78/HxERUWhvLwciYmJSEhI\nAABcvXoViYmJAIBr164hPj4ew4cPR1xcHJKSkjBlyhRZfkYuOrsaqQAKQ3ofsCc6wPPg++3bt2E0\nGiXJWqqtrYVer2fSQz3N5FIDcp7OztcXW50uN2rUv7BX6y0tLQD4rWD4+tJrBbKjk2Js7CQHkl7r\nydEYdyesJfh2m7W1tUhPT8cLL7yAyZMn48yZM9i9ezf+9Kc/iY6NaB2fEhQSbwgKCmKC76GhoW5P\nzFIJit1ux+3bt5mGWCQ+IpTJZTAYNJV6SwoCuZYg3AlELSdcLdS/sDPorFYrk0FHVu+k3cAXX3yB\nH3/8EZGRkZgxY4bTCno5kVJMuLCPTdliK/ZojCwQtdgDhmRmssWkvr4ec+bMwfLlyzF9+nS1hygb\nPiEoxMSNZPWQLAuj0ejRxFZbW9vO7dUdyHGC3W5HcHAwAgMDHWZyObLwUAOxVdzsTBir1SqpK7Aj\nPG3wJBetra1MvxAAuHDhAu6//36YTCY0NDQwHk+ffvopJk+erPj45PAzE4IrtjabzWEcSutiwrV6\naWxsRHp6OrKyspCamqr2EGXF5wTFYrEgICBAkjTWuro6j144dtvglpYWBAUFMT5c7EwuraWQEthC\n58r95B4FyZGCyy2m1JIIA+3b4ra2tmLQoEGoqanp8DmDwcAUQSqFkmLCh6OjMQCa7U7JJyZNTU2Y\nO3cuMjMzMXPmTLWHKDvaestkhBQh6fV6TdREWCwW1NfXIyQkBMHBwczOiS0mZPdCgpxqj5kNOULU\n6XRuJTOQn8loNDIpzySoT1wB3F3rkGJKNXpyiMFsNrfrsX7w4MF2dixsbDYbPv74Y4/uhyuQ7CyD\nwaBaEzaSNUaSHEjaemNjIxoaGhireC2thfnEpLm5GfPnz8fixYt9QkwAH0kbJpM3CQxLWT3r6kNN\njohMJhNTPGm326HX65mjI7YFvRYDtVKmtwql4LprfaL1Yko+x+ALFy4wR19czGYzqqqqZLGC4SKX\n07InkIxCUkRJdiXclgRqFlTyiYnZbMaCBQvw0EMPYfbs2aqMSw208dTIjE6ng9FoZI6+pMQVQSGT\nndVq7eDJRfL4ST2DzWZjDOiIVYMWkNt6nl1M6ar1idaPB4ViTX379mVaAnMJCgpCdHQ0QkNDZbGC\nIWghcUEIclxNYowER/dDqYJKtuMCEROLxYJHHnkEs2bNwty5c2Ufg5bwiRgK20GVrA6lgJuG7Ah2\nfxJHNipkjMHBwe2q09nVuEq9LFzU7EnPDepziynJi63FCnOunxl3bC0tLbjrrrvw22+/dfi3wcHB\n+P7779G7d+8O38nOkvIkDsWO52gpcQEQn2km5f0QC1tMyAKmpaUFixYtwrRp0/Doo49q6jlUAm0t\nRWRGCf8tPtixENL/wFEmF3sFy3UElttHSgi1V7DO7C1IRbYWxcTZEVxAQAAKCwuRmJjYrvhSp9Ph\n448/7iAmQEcrGO79EGsFo9UsOMC1tGUhaxy2yamU9VDk98oWE6vVioyMDEyYMMEnxQTwkR0KebjI\nCluq3H72uakQJJMrODiYaT/K58kl9qiGnWJJArVy9gpn75q0Vv8C/F79TmJRWiqm5FvBOqKxsRG5\nubk4ffo0+vbti/T0dPTs2dPl67KfD0cpuJ1FTJzBlzXmyVEhEROdTtdOTB5//HHExcUhKyvLJ8UE\noILiEeyHig8lPLnIypRMHlJOpuyjGq3VvwD8R3BaKaYkiwR2oFYN2MemLS0t7VpEu9PuQAmULKh0\ndbfP3nGS7ESbzYYnn3wSQ4cOxbJly3xWTAAfExSymiU20Z5Cjhe4bTzZNvikEp8tJuQFltpyg28y\ndTcjiO/F0RJijuDUKqbUqskjuR/s7pRSN1PzFHYAXsmCSvZuX2hBxvdOtLa2YunSpRg4cCCef/55\nTdxDNaExFInhs8EnL7JOp2MmdjliElzXVz67eTErdS1bqJMjOIvF4vSohi/uInccikyIWiy8A37v\nTkkSQ+SMM7iKkmICCKesC2WNNTc3A2gvJsuWLUPfvn2pmPwfPrFDIV5Tra2tqK2tRbdu3ST5XpIL\nT2wyXM3kUiomIZQhxbdSV9oW3xXE2ryI+R454lByHtV4irNMM/YuXo2jQrWr87lw3xlyTM1Omnn+\n+efRtWtXvPLKKx69J4sWLcKePXtw55134vTp0x3+/tChQ0hNTcWAAQMAADNnzsSLL77o9vXkxKd2\nKFLD3vHYbDameNJRJpca7XDFrtTJ+LQ+IUrZmVKKYkpAexMiG2diAnRspsbtQChnyroW7x07LZ1k\nX/r5+WHz5s147bXXMGTIEHTv3h2vvvqqx/dj4cKFeOqpp/Dwww8Lfmbs2LEoKiry6DpK4FOCIteR\nV0tLCxoaGkRncqlZwU0EhBxnkcmUvDRkhU5WZFpA7up3McWUjlbqatbnOMOdeye0AJGjYZYWxYRA\nhJjtVbdkyRL88ssv+Omnn2A2mxEVFYW4uDhs2bIFffr0ces68fHxqK6udjoWb8AnBIU89OT/pZos\n2X5bzjK5mpqaNBekJTEdMh6DwcC44JLxqp1+q3T1O18feUcrdaliYS0tLfjmm29gt9sRGxsrSfxF\nisQK9gIEaF8k7KkVjDeICXtXZ7fb8dprr8FsNqOgoAB6vR4NDQ3Yv38/7rzzTtnGotPpcOzYMQwb\nNgyRkZFYt24dhgwZItv1PMEnBIWNVKtvEpchwXelMrmkhB2TYKeP8q3U5fSQEkLtbClnK3Vi6Olp\nC4NPP/0Uzz77LLOjtdvtWLNmDR577DG3v9PVGhixkKNCd6xx2GhdTEiiAltM1q1bh+vXr2PTpk3M\nOxAaGooZM2bIOp7Y2FhcunQJBoMBJSUlSEtLw/nz52W9prv4RFAeaMuqstvtuHXrFsLDwz2aFMnL\nSgLc4eHhTIdCsish19SqPxK3Mt9ZMSW3lkFsxpi7aDlbikw4xL3ak6B+aWkpHnroISaDiBAcHIz3\n3nsPDz74oFvjk0NMnF2TW9/BFhf2GIiYaPW9YCfbEDH57//+b1y4cAEffPCBLIk01dXVSE5O5g3K\nc+nfvz+++eYbdO/eXfJxeIq2KpoUwNM4SmtrK+rr65mJGADTsIsdfCeOwp6uXuXAVet5nU6HwMBA\nGAwGxk6cHPXV19eL6pnuCqReKDg4WJNiYjabYbVaYTQaYTQamZbNFovF5b7pq1at6iAmQFuN06pV\nq1y+p+zOpEoaZBIBIS0JSLEvtyUB2x5fa++FkJi89957OHfunGxi4oyamhrmOaisrITdbtekmAA+\nfOTlDiSTKzAwEMHBwcwkSpyBuZlcWqxC9vQYSe7aDi1aqBO4Ew753XIzpLj1P+x7wv2+s2fPCl7v\nypUraGpqYhYuzlD7iJAglPhBjpH8/PyYpBWtvB/c41/yLn/00Uf49ttvsXXrVtnEZM6cOSgrK8ON\nGzcQFRWFl19+mWmLnJmZidzcXGzatInxAtyxY4cs45ACnzvyqq2tdat5EF8mFzmWIX5J/v7+zDGI\nFqvL5bSel6K2Q8veUmJSb/n+jTObj549ewo21woICMD169dFPataERMh2Jlw7GQHtuCq5aLNrg0j\nCwW73Y7Nmzfj8OHD2L59u+biPFpFW0tAGfEkGE8yWkJDQ9utzMmxFwnQm0wmAG0r1paWFlWb/nCR\nO7WVW9vBzQZylDHGfaG1KCbupC2zd3NCjsCzZs1CdnY2syIl+Pn5ISkpSbSYaLXHOsC/62Rn0ZEj\nTrncC5zBJybbt2/Hl19+iezsbComLuAzO5SWlhYm/hEUFCQq44qsSi0WC4xGI9N3QyiTi3wvWaWz\nnU2VNidko3ZygCOPMZ1OJ0n1u1zIFeAm4vLLL79gypQp+O2335gFSVBQEMLDw3H06FFe63ru92g1\neQEQf4TJ3uFarVbGCkYuF22CyWTqICY7duxAUVERdu7cqcl7qmV8TlDENsVie3IZjUbo9XqHmVx8\nK38+c0KpOuyJQQ2bFzFjYmeMAWCSA7QwPjZKeZrdunULH374IXbu3AmbzYbU1FRkZmYiIiLCocBq\n2eoF8CwepoQVDFdMACA3Nxeff/458vLyHLaloPDjM4JC2v+K6WFChIdUtZM/4/PkEmNSCAinVcp1\ndsw+89ei9bzdbmd8z/R6vWa6UhLUikmI9V3Tcn0TIG1yhStedGJhv7vk3SgoKMC2bduQn58v2JKC\n4hgqKBy4mVyAY08udyZrdnaUs5x9d5CiQlpO+Fb+fPdEjfN0QDvHSOx7QgwKySRKjjC1eL5PxESO\nXafQPXHFCoZPTHbv3o0PP/wQBQUForPqKB3xOUFx1BSLZHIZDAYmBZRPTEgAUYrJmrwgZAVGXhB3\nJ1ItW88D4tyMpcgY83R8Wlv5k3tCjjABMM+J3PfEFeQUEy7knvA1mBNKiCGZhOyU/r1792LDhg0o\nKCiA0WiUdcydHZ8TFKGmWI4yudgGj3JO1p5OpFq2ngfcP6aRsysl3/i0aAcCtD9GIpmE7BiD0tY4\nXEg8Ua14mLNWv3xicvDgQbz99tsoLCyUrPGeL+MzgsJO2SS1BIB7mVxKHYNwe4M7WpF6y5m6p5O1\nlF0p+canxYJKwPH4hKxxlEr+ANQXEy7cuAv5sy5dujD3paysDK+99hoKCws97pHkrKcJAGRlZaGk\npAQGgwFbtmxBTEyMR9fUIj4nKOxKZxIYttvtzKrF1UwupeCKC5lIAwICmCpkrU6GcqUtS+UxpnZa\ntTNcmaxd8dRSY3xqYDabYTKZEBAQgFOnTmHevHm47777cO7cOezfv99t23k2hw8fRmhoKB5++GFe\nQSkuLsaGDRtQXFyMiooKLF26FOXl5R5fV2toK/VHAUgcpLW1FXV1ddDpdDAajYzNvCNPLjWPQYi9\nR2hoKIxGIyMkdXV1aG5uRmBgoOYyuYDfX2Y5PM2k8BiTc3xS4Opk7cxTq7m5mTlOVWN8SmOxWJhj\nLoPBgNGjR+O//uu/cOPGDfTo0QNDhgxBamoqjh8/7tF14uPjHe5yioqKsGDBAgBAXFwcbt++jZqa\nGo+uqUW09wbJDImF1NXVISgoiMn2EsrkstlsmvPkIvUsRPzIRFpfX6+JQkqgfQ2MEvfPVY8xpcfn\nDp5a0XA9tVxxLxCDN4gJd3wnTpzAu+++i/z8fERERODWrVsoLi7uEFOVmitXriAqKor57z59+uDy\n5cuIiIiQ9bpK4zOCws7fJ1XZYjK5PG03Kwds63myuyJ/zm4IpXQhJXt8arQ6JgiZE7ItT4joaFVM\nSNGdlONz1MvE1cJBrYsJOQZmj+/kyZN4/vnnsWvXLmYi79atG+bNm6fImLi7Qq3NK1LgM4ICtL2k\nZrOZeanUyOTyFHYHQ27asrNVuhJFg+76XskFn8dYU1MTYy1vMplU70rJhs+oUA4cdabU6/UODRu1\nbOIJ8Kcuf/fdd1i2bBl27dqFXr16KT6myMhIXLp0ifnvy5cvIzIyUvFxyI32lmYywV5RAeiQyaXT\n6WC1WtHQ0MAUNWphgmHDFjtn4yOrdPZZOtl5NTQ0oLm5mSkMk3p8UtXoSA2Jien1eoSFhcFoNMLf\n35+JRbnSx0TO8cktJlzIYsNgMMBoNDJu2o2NjUzchTwr7NRbbxGTs2fPYunSpdi5c6dqk3hKSgq2\nbdsGACgvL0fXrl073XEX4ENZXq2trcxkUV9fz6yeyaQntxuvp0iVtsxX6+JJISVB6zs7Z+4BUmWM\neTI+bnMnteE+K0RoSWq6FsbIhi+1+ty5c1iyZAk+//xz9O/fX7Zrs3uaREREdOhpAgBPPvkkSktL\nERISgs2bNyM2Nla28aiFzwgKWV2R4DU7vkAClVrfwsshdmy7E3cr0rViVSKEq47BcnhHObueq71W\nlIZkwwUFBTFFwloopiTwicn58+eRkZGB7OxsDBw4UNXx+Qo+Iyitra1MxzigbRK0WCxM0ROxnlf7\nxeCiZI2EK4WUBK0XVHq6c5LbY4yICXFv0KqYcL2vyI5OqCpdSfh61F+8eBGLFi3C9u3bMWjQIEXH\n48toa/aUkS+++AIpKSn46KOP8Ouvv6KxsRHLli1DfX09goODGYfhhoYGmM1m1c7RCeQIhOyclKiR\n4Na68PVJZ68/SH/w4OBgTYsJaXDlzmTNjUWRSZ/bK92ddRk7W0+rYmIymTqICfB7DVBISAhTA0Tu\nN6kBkjpGxwefmFRXV2PRokXYunUrFROF8Zkdit1ux40bN5Cfn4/s7GxUVVVh1KhReO2119C3b18m\nXZjbv0SoH7jcY9WS9Tyf3YlOp2OCx1osCFTiGM4TjzEiJsSoVKti4mqCgJDZqStuwGLhE5NLly5h\n/vz5+PjjjzF06FDJrkURh88ICuGbb75BSkoKHn/8cURGRiI/Px/19fWYOnUqUlNT24kLn8W83OLi\nDdbzZKIBoJlCSjZqHMO54jEmVxdIKZEq20wuY08+I8+rV69i7ty5+OCDDzB8+HC3v5viPj4lKHa7\nHcnJyVi8eDFmzJjB/HltbS2++OIL5OXl4caNG5gyZQpSU1Nx1113ORUXKYO03pApxW7XS1Kt1d7R\nsdGCY7CjjDEAaGpqYupitPg7lqsOhk903enCyPc7vnbtGubMmYP33nsPI0aMkGzMFNfwKUEBwBQx\nClFfX489e/YgLy8PV69excSJE5GWloZBgwY5FBdPzfe0bj3vLBNJKdF1hBYdg7nHqHa7nRETpRuH\nOUOpokpyLaHFiKPnhbwnbDH59ddfkZ6ejnfeeQd//vOfZRszxTk+Jyiu0NjYiJKSEuTl5aG6uhrj\nxo3DjBkzMGTIEOj1eslqOrSeKeXqMZxQVz05uy9q3QqEJH2w409qdqXkoqSY8F1bTCYdn5jcuHED\n6enpeOuttzB69GjFxkzhhwqKSJqbm7Fv3z7k5eXhxx9/xJgxYzBjxgzcc889HomL1q3T2VYv7pz3\ny1VIyUbrViDkKJPsPgF1u1Jy4R5lqm0qyndf/Pz8OrQ9vnnzJmbPno21a9di7Nixqo2Z8jtUUNzA\nYrHg4MGDyM3NxenTpzF69GikpaVhxIgRzMvILRjkTqJ2u52x1tb6RBgQECDZMRx759La2urRJKrm\nqlosYrPNlOpKyUVLYsIHaXtssVgAABcuXMDp06cxZswYLFmyBKtXr8bEiRMluVZpaSmefvpp2Gw2\nPProo3juuefa/f2hQ4eQmpqKAQMGAABmzpyJF198UZJrdxaooHhIS0sLysrKkJOTg1OnTmHUqFFI\nS0tDXFwcIxLsyYJMolp3u1Ui7ZavkNKVtFstT4SA+/3p5epKyUWLdi9c2PfQ398fX3/9Nd566y18\n+eWXGDhwIBYuXNhukvfkOoMGDcKBAwcQGRmJe++9F9nZ2Rg8eDDzmUOHDmH9+vUoKiry9MfqtGjv\nLfQyAgICMGnSJLz//vs4duwYZs2ahYKCAkyYMAHLli3DV199BbvdzhQMkt7WJLZA0jO1pOtWq5V5\nieW0UuEWUoo1atRyrxqCu2IC/O4ETIoGAwICYLVaUV9fL1nhrbeJCXGxGDx4MJqamrB9+3asXbsW\nZ8+exV/+8hccOHDAo2tVVlZi4MCB6NevHwICApCeno7CwsIOn9PSe6pFtHdo78X4+/tj3LhxGDdu\nHGw2G44fP47c3Fy89NJLuOeeezB58mS8/fbbmDVrFp544gkmvZTd8EiNM3Q2amVKce3Uyc6lubm5\nXdqtTqfTlD0+H1KmLpOKdD6beXcz6bxRTIC2JJm5c+di6dKlSEtLAwAkJSU57copBr4GWBUVFe0+\no9PpcOzYMQwbNgyRkZFYt24dhgwZ4tF1OxtUUGTCz88P9913H+677z60traisLAQjz76KAYPHowf\nfvgB+/btw7hx45gjJXL8Y7FY0NTU1K5nvFIvvFYypYQmUZPJBAC8vWC0gpx1MK52peTDG4woSeyO\nLSZNTU2YN28elixZwogJQYpnVcx9iI2NxaVLl2AwGFBSUoK0tDScP3/e42t3JrR3VtAJOXXqFJ54\n4gmsWbMGX331FZYuXYoTJ04gISEBGRkZ2L17N8xmM4KCghASEtKhZzyfj5aUcH3DtJQgQCbRLl26\nMLUKfn5+7TyjpFihSgHxNmNnIsmFOx5j3iImDQ0NjFkr0JZhOX/+fCxevBizZs2S5brcBliXLl1C\nnz592n2G3GcASEhIQEtLC27evCnLeLwVGpRXgLNnz+LChQtITU1t9+d2ux1nzpxBTk7Dwr5tAAAY\nl0lEQVQODhw4gD59+iAtLQ1TpkxhHlyuq6vUAVpvCG7zZZtpoZCSjZaKKoUyxojAaFlMuOnVZrMZ\n8+fPR3p6Oh566CHZrm21WjFo0CAcPHgQvXv3xqhRozoE5WtqanDnnXdCp9OhsrISDz74IKqrq2Ub\nkzdCBUUj2O12VFVVITc3F3v37sWdd96J1NRUTJs2DUajkfkMV1zcsa5gX5O43Wp1khGTbSZkSKhU\nwaBWjgr5IEepZrO5Q62LlhYPfGJisVjwyCOPIDU1FY888ojsv8eSkhImbXjx4sVYuXIl3n//fQBt\nTbI2btyITZs2wd/fHwaDAevXr6eV+RyooGgQu92OCxcuIC8vD8XFxejWrRuSk5Mxffp0dO3alfkM\nmUDd6TBIDAq12q4XcC9TSqiQUg63W0DbYgJ0dK62Wq2qdaUUgk9MWlpasGjRIkydOhUZGRmafD4p\nHaGConHsdjuqq6uRl5eHPXv2wGAwIDk5GUlJSejWrZug7b6jiULrJpSAdHY0fDVAUmXSab1C31Hz\nLqW7UgrB7VkDtP3uMzIyMGbMGPztb3/T5PNJ4YcKihdht9tx+fJl7Nq1C0VFRfD390dycjKSk5PR\no0cPUT1dbDYbk6KsRRNKQL6Wx9xCSk8y6YiYaLUOxpVOkHJ3pRSCT0xsNhsef/xxjBo1CllZWZp8\nPinCUEHxUux2O2pqarBr1y4UFhbCZrMhKSkJKSkpiIiIEAxct7a2IigoiHmBtYZSwW13q9G9we7F\nk546SnmM8SVa2Gw2PPnkk/jTn/6E5cuXUzHxQjqdoOTk5GD16tWoqqrCiRMnEBsby/u5fv36ISws\njDlHrqysVHik0sHuRllQUACTyYTp06cjJSUFkZGR0Ol0OH78OO666y6EhITAZrOpnhXFh1rxCG6y\ng1BswRsy4qRu0CaHx5jdbmecl8mRa2trK55++mkMGDAAK1eu1MTzSHGdTicoVVVV0Ov1yMzMxNtv\nvy0oKP3798c333yD7t27KzxC+bl58yYKCwuxa9cu1NXVITo6Gnl5eSgoKEBsbKzmUm4B7cQjhOJR\n/v7+sFgssNlsmmjLzIfc3T6l8BgjySDsBmOtra1Yvnw5evXqhZdeeomKiRfT6QSFMH78eKeC8vXX\nX+OOO+5QeGTK8uabb+L111/HxIkTce3aNcFulGql3Gr5CImbSQcAQUFBmtrVEeQWE77rCXWlFPod\nConJypUrERYWhldffVVT95TiOj5rvaLT6TBp0iT4+fkhMzMTGRkZag9JctavX4+PP/4YJ0+eRL9+\n/ZhulK+88gquXLmCSZMmMd0o/f3921nAkICunOLC9ZTSkpgAv1ejt7S0QK/Xo0uXLoxxplSdOqWA\niIlOp1OsR72rHmNCYvLSSy8hODgYr7zyChWTToBX7lAmT56Ma9eudfjztWvXIjk5GYDzHcovv/yC\nXr164fr165g8eTLeffddxMfHyzpupblw4QLCw8PRs2fPDn/X2NiI0tJS5Obm4n//938xfvz4dt0o\nAec9XTzBG2xAhFb9SjQNc3WMSoqJs/HwZYyR40NyH+12O9asWQOz2Yz169dLsphw1s8EALKyslBS\nUgKDwYAtW7YgJibG4+tSfscrBUUMzgSFzcsvv4zQ0FAsW7ZMgZFpD75ulGlpaRg2bFgHcZGqMZaS\nxzPuIHaManZeJKt+d7tpyg0RF+LGoNPpsG7dOsTFxeHUqVOora3Fu+++K4mYiOlnUlxcjA0bNqC4\nuBgVFRVYunQpysvLPb425Xe0dcYgMUJa2dTUhPr6egBtK/V9+/Zh6NChSg5NUwQHByM1NRXbtm3D\n4cOHMWHCBHzyySeYMGECXnjhBZw4cQI6nQ5dunRBaGhou74uQkaEQnhDhb4rY9TpdMwxjtFobHdv\n6urqXLo37oxRq2JCMJlM8Pf3R1hYGLp06YLw8HCsXbsW69evx40bN5CTk8O8i54gpp9JUVERFixY\nAACIi4vD7du3UVNT4/G1Kb/T6QQlPz8fUVFRKC8vR2JiIhISEgAAV69eRWJiIgDg2rVriI+Px/Dh\nwxEXF4ekpCRMmTJFzWFrhsDAQCQkJODjjz/G0aNHkZiYiM8++wzjx4/HihUrcOzYsXYNw1yZQImT\nrJ+fn2YnQU8nam7TMPa9kco12hvEhOzw2GMku7bhw4fj4sWLmDhxIrZu3YoHHnjA4+vx9TO5cuWK\n089cvnzZ42tTfqfTBeVnzJiBGTNmdPjz3r17Y8+ePQCAAQMG4Ntvv1V6aF4H6UY5adIkWK1WHDly\nBLm5uVi5ciVGjhyJ1NRU/PWvf+3Q04U0DGNXopNJUMsV+lJb0hBxIfeGBK6bm5vdNmn0JjFhx3Xs\ndjs2bdqEH374AVu2bIGfnx8ee+wxPPbYYx53nwTE9TMhY3Pn31HE0el2KGqQk5ODP/7xj/Dz88PJ\nkycFP1daWoro6GjcfffdeOONNxQcoeeQbpQbNmxAeXk55s2bh9LSUkycOBFZWVn45z//CZvN1m51\nzu7pUl9fDz8/P82LCbEBkXqMUrT19SYxAdBOTD766COcPHkSmzdv7lBnJEUMRUw/E+5nLl++jMjI\nSI+vTfkdKigSMHToUOTn52PMmDGCnyG2EqWlpfjhhx+QnZ2Nc+fOKThK6SDdKN955x1UVFQgIyMD\nZWVlmDx5MpYsWYK9e/eipaUFgYGBqKqqwrlz55hdirN+8Wogt5hwISm3BoMBYWFhCAoKgs1mQ0ND\nAxoaGphUajbstFtvEBN2NteWLVtw9OhRbN26VTY7nZEjR+Knn35CdXU1LBYLPv/8c6SkpLT7TEpK\nCrZt2wYAKC8vR9euXRERESHLeHyVTnfkpQbR0dFOP8MOGgJggobsLBRvRK/XIy4uDnFxcWhtbcV3\n332HnJwcvPHGG7jjjjtQUVHRrm8Et1+8pz1dPEVMvxU5cdbWlxyLkXulVXdokgYOtBeTTz/9FAcP\nHsSOHTtk7WLp7++PDRs2YOrUqUw/k8GDB7frZzJ9+nQUFxdj4MCBCAkJwebNm2Ubj69CBUUh+AKC\nFRUVKo5IevR6PWJiYhATE4M9e/Zg/vz5uP/++/E///M/2L17N9LS0jB58mSEhITw9otXuj+H2mLC\nhdRsEOFgiwvBZrOpXkjJRcjZeMeOHdi9ezdycnI8akEgloSEBCYJh5CZmdnuvzds2CD7OHwZKigi\nEVNM6QgtTQByc/ToUSxevBglJSWIi4tr141y48aNiIiIaNeNkqzO2dXWznq6eIo7zbuURKfTQa/X\nw2q1IiAgAIGBgbBarYo4GLiCkJjk5uZi165dyMvL04RYU5SBCopI9u/f79G/FxM07CyMGjUKR48e\nxV133QWgbXIcPHgw/v73v+PFF19kulE+8MADHbpROhIXYnPiKaR5l9T9VqSEL+OMu3MxmUySNw1z\nBSG3g4KCAnz22WfIz8/XbJsEijx02kp5NRg/fjzWrVuHESNGdPg7q9WKQYMG4eDBg+jduzdGjRrV\noZLX1xDbjVLIGdkdcfEmMRGTYs1tGkbujRJV+nxisnv3bnz44YcoKChASEiIbNenaBMqKBKQn5+P\nrKws3LhxA+Hh4YiJiUFJSQmuXr2KjIwMpv6lpKSE8RpavHgxVq5cqfLItYPYbpSe2O4r1bzLE1wR\nE75/S+xx2PbynvQu4YNr6km+e+/evXj33XdRWFgIo9Eo2fUo3gMVFIrm4OtGmZiYiNTUVIfdKB2J\nS2cXEy7cpmFSZdMJicnBgwfx9ttvo7CwEOHh4W5/P8W7oYJC0TRiulE66+lC4g3eIiZSxx24fV3c\nzaYTEpOysjKsXbsWRUVF6Natm6Rjp3gXVFC8mJs3b2L27Nn417/+hX79+mHnzp3o2rVrh891pnbH\n3G6U06ZNQ2pqKvr27cuICzuuQIonScxEi9l2cooJF76OlGTn4igmxW5/HBoaytzHI0eOYM2aNSgs\nLOz0zeoozqGC4sWsWLECPXr0wIoVK/DGG2/g1q1beP311zt8rrO2O66trcUXX3yBvLw8XL9+nelG\nOXDgQOh0OuTn52P06NEwGo2wWq2aSrclKCkmXMQeGwp11Tx+/Dj+/ve/o7CwkLfnDsX3oILixURH\nR6OsrAwRERG4du0axo0bh6qqqg6f84V2x6QbZV5eHlNEevz4cZSWljLuBFL2dJECIiaBgYGq12qw\nxYUrvuTP2GJy4sQJPP/88ygoKJDcvsQXd96dBSooXky3bt1w69YtAG0TQvfu3Zn/ZjNgwACEh4d3\n6nbHbF566SV89NFHGD9+PC5evMjbjZJ7LKa0uGhJTLiwjw2J3X5AQADOnTuHoUOH4uzZs1i2bBny\n8/PRq1cvya/v6ztvb0abEUoKg1CF/j/+8Y92/63T6QQnwqNHj7ZrdxwdHd3p2h0T3nrrLezatQsn\nT57EH/7wB6Yb5YYNGzp0oxSy3Ze7loP0hdGK5QsX0jSMHIMZDAa0tLTg2WefxY8//gij0YjVq1fL\nFoAvKipCWVkZAGDBggUYN24cr6AAwk30KOpAdyheTHR0NA4dOoQ//OEP+OWXXzB+/HjeIy82nb3d\n8YULF9C1a1f06NGjw99ZLBYcPHgQubm5OH36NEaPHo3U1FSMHDmSd+dis9kkr+XQupgQzGYzLBZL\nu2Ous2fPYsWKFRg7diwOHTqEb7/9FvPmzcPGjRslvTbdeXsvdIfixaSkpGDr1q147rnnsHXrVqSl\npXX4TFNTE2w2G4xGI9PueNWqVSqMVhkGDhwo+HekG2VCQgJaWlpQVlaG7OxsPPvss4iLi0NaWhri\n4uKcNsVyV1y0ZkYpBJ+YnDt3Dn/729/w+eefY8CAAQCAX3/91ekCRgi68+6c0B2KF3Pz5k08+OCD\n+Pe//90ueMmu0P/5559x//33A2izHZk3bx6t0OfA7kZZUVGBESNGIC0tDX/961+ZuhW+QkFXOi5q\n3YySYDabYTabERoayvxc58+fR0ZGBj777DPcfffdso+B7ry9FyooFAoLm82G48ePIzc3F0ePHsU9\n99yDtLQ0jBkzhvH+crUK3ZvF5OLFi1i0aBG2b9+OQYMGKTKOFStW4I477sBzzz2H119/Hbdv3+4Q\nQ+HuvKdMmYJVq1ZhypQpioyRwg8VFApFgNbWVpw4cQK5ubkoKyvD4MGDkZaWhnHjxjFHVs6q0L1F\nTCwWC0wmE0JCQpgCx+rqaixYsABbt27FkCFDFBsL3Xl7L1RQKKIpLS1lzC0fffRRPPfccx0+k5WV\nhZKSEhgMBmzZsgUxMTEqjFR62N0o//nPf2LAgAFIS0vDxIkTERwcDKCjuOj1erS2tiIoKEjTNu58\nYnL58mXMmzcPn3zyCYYOHaryCCneAhUUiihsNhsGDRqEAwcOIDIyEvfee28H+/3i4mJs2LABxcXF\nqKiowNKlS1FeXq7iqOXBbrfjzJkzyMnJwYEDB9CnTx+kpqZiypQpjGX7+fPncccddzDBfal7ukgF\nn5hcvXoVc+fOxfvvv99pFgQUZVC+iTfFK6msrMTAgQPRr18/BAQEID09HYWFhe0+U1RUhAULFgAA\n4uLicPv2bdTU1KgxXFnR6XQYOnQo1qxZg6NHj+Lll1/Gzz//jLS0NDz00EPYuHEjpk6diu+//x6h\noaEwGo3o0qULU8xYX1/PmCyqCZ+YXLt2DfPmzcN7771HxYTiMlRQKKIgdiaEPn364MqVK04/c/ny\nZcXGqAbsbpRHjhzBggULsGbNGgwfPhzvv/8+PvvsM9TW1sLf3x/BwcEwGo0IDg6G3W7vIC5KHhYQ\nB2a2mPz666+YO3cu3nnnHYwcOVKxsVA6D7QOhSIKsXUX3ElRCwaMSnHq1ClkZmZiy5YtuP/++5lu\nlPPmzWO6USYmJqJ79+4d2vk2Nja63DDMXUhdDVtMbty4gblz52LdunX4y1/+Ist1KZ0fKigUUURG\nRuLSpUvMf1+6dAl9+vRx+JnLly8jMjJSsTGqTVBQED744AOkpKQAaPOaWr58OZYtW8Z0o3zkkUeY\nbpRJSUno2bNnB3FpamqSzRmZT0xu3ryJuXPnYu3atbjvvvskuQ7FN6FBeYoorFYrBg0ahIMHD6J3\n794YNWqUw6B8eXk5nn766U4ZlPcEdjfKgoIC2Gw2JCUldehGybaAkUpc+LpW3r59G7Nnz8aqVasw\nadIkKX9Uig9CBYUimpKSEiZtePHixVi5ciXef/99AEBmZiYA4Mknn0RpaSlCQkKwefNmxMbGqjlk\nTcPXjTIhIQEpKSno06cPIxzsniXuigufmNTV1SE9PR3PP/88pk2bJtvPSfEdqKBQKBrBWTdKwL2e\nLlarFU1NTe3EpKGhAenp6fjP//xPJCUlKfYzUjo3VFAoFA3irBslIK6nC5+YNDY2Ys6cOXjiiScw\nY8YM1X5GSueDCgqFonG43SgnTpyItLQ0REdH84qLzWZjMsXMZjNCQkIYMWlqasLcuXORkZGBBx54\nQPKx5uTkYPXq1aiqqsKJEycEjzzFuC5QvA9ah0LxCkpLSxEdHY27774bb7zxRoe/P3ToEMLDwxET\nE4OYmBi8+uqrKoxSHoxGI9LT05GTk4P9+/dj+PDhWLduHSZOnIhXXnkFZ86cAdCWZUYKKYE2s0eg\nrY/Jjh07cP36dcyfPx8LFy6URUwAYOjQocjPz8eYMWMEP2Oz2ZhY2w8//IDs7GycO3dOlvFQlIWm\nDVM0D5mA2LYvKSkp7TLMAGDs2LEoKipSaZTKEBISgpkzZ2LmzJmC3SjNZjNWrFiBvXv3IigoCE1N\nTdi+fTueeuopDB48GDabDbW1tQgPD5d8fNHR0U4/w3ZdAMC4LnB/nxTvg+5QKJpHjO0L4HvtYIOD\ng5Gamopt27bh8OHDmDBhAt58802mC+Xp06cBACNGjEBYWBhef/11PPXUU9i5cyeioqKQnZ2tyrjF\nuC5QvBO6Q6FoHr4JqKKiot1ndDodjh07hmHDhiEyMhLr1q1T1HJdbQIDA9GrVy9UVFRgy5YtCA8P\nR3Z2NpYvX46GhgY888wzeOyxx6DT6bBgwQLU1dW57SUm1G1x7dq1SE5Odvrvfck9wdeggkLRPGIm\noNjYWFy6dAkGgwElJSVIS0vD+fPnFRiddvjHP/6BjRs3YubMmQCASZMmwWq1orS0FImJie3uY1hY\nmNvX2b9/v0fjFOO6QPFO6JEXRfOImYCMRiMMBgMAMD3jb968qeg41Wbnzp2MmBD8/f2RlJSkyq5A\n6Ahy5MiR+Omnn1BdXQ2LxYLPP/+csauheDdUUCiaR8wEVFNTw0xglZWVsNvt6N69uxrDVQ0tHCXl\n5+cjKioK5eXlSExMREJCAoC2HiuJiYkA2kRuw4YNmDp1KoYMGYLZs2fTgHwngdahULwCZ7YvGzdu\nxKZNm+Dv7w+DwYD169fjz3/+s8qjplB8CyooFAqFQpEEeuRFoVAoFEmggkKhOGHRokWIiIjA0KFD\nBT+TlZWFu+++G8OGDcOpU6cUHB2Foh2ooFAoTli4cCFKS0sF/764uBgXLlzATz/9hA8++ABLlixR\ncHQUinaggkKhOCE+Ph7dunUT/PuioiIsWLAAABAXF4fbt2+jpqZGqeFRKJqBCgqF4iF8lfyXL19W\ncUQUijpQQaFQJICbLKmFmhAKRWmooFAoHsKt5L98+TIiIyNVHBGFog5UUCgUD0lJScG2bdsAAOXl\n5ejatSsiIiJUHhWFojzUHJJCccKcOXNQVlaGGzduICoqCi+//DJaWloAtFXpT58+HcXFxRg4cCBC\nQkKwefNmlUfsHmK7Lfbr1w9hYWHw8/NDQEAAKisrFR4pRavQSnkKhQIAqKqqgl6vR2ZmJt5++21B\nQenfvz+++eYbn/NKoziH7lAoFAoAcd0WCXQdSuGDxlAoFA3jrEr/0KFDCA8PR0xMDGJiYvDqq6/K\nPiadTodJkyZh5MiR+PDDD2W/HsV7oDsUCkXDLFy4EE899RQefvhhwc+MHTsWRUVFor7P026LAHD0\n6FH06tUL169fx+TJkxEdHY34+HhR/5bSuaGCQqFomPj4eFRXVzv8jCvHT552WwSAXr16AQB69uyJ\nGTNmoLKykgoKBQA98qJQvBqdTodjx45h2LBhmD59On744QdJvldIpJqamlBfXw8AaGxsxL59+xya\nZlJ8CyooFIoXExsbi0uXLuG7777DU089hbS0NLe/S0y3xWvXriE+Ph7Dhw9HXFwckpKSMGXKFEl+\nFor3Q9OGKRSNU11djeTkZJw+fdrpZ2lKL0VN6A6FQvFiampqmOOpyspK2O12KiYU1aBBeQpFwzir\n0s/NzcWmTZvg7+8Pg8GAHTt2qDxiii9Dj7woFAqFIgn0yItCoVAokkAFhUKhUCiSQAWFQqFQKJJA\nBYVCoVAokkAFhUKhUCiSQAWFQqFQKJLw/wG01aU/LOMn1wAAAABJRU5ErkJggg==\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10905d0f0>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 11
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"point_x = np.array([[0],[0],[0]])\n",
|
|
"X_all = np.vstack((X_inside,X_outside))\n",
|
|
"\n",
|
|
"print('p(x) =', parzen_estimation(X_all, point_x, h=1))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"p(x) = 0.3\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 12
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 2,
|
|
"metadata": {},
|
|
"source": [
|
|
"Sample data and `timeit` benchmarks"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In the section below, we will create a random dataset from a bivariate Gaussian distribution with a mean vector centered at the origin and a identity matrix as covariance matrix. "
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import numpy as np\n",
|
|
"\n",
|
|
"np.random.seed(123)\n",
|
|
"\n",
|
|
"# Generate random 2D-patterns\n",
|
|
"mu_vec = np.array([0,0])\n",
|
|
"cov_mat = np.array([[1,0],[0,1]])\n",
|
|
"x_2Dgauss = np.random.multivariate_normal(mu_vec, cov_mat, 10000)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 13
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The expected probability of a point at the center of the distribution is ~ 0.15915 as we can see below. \n",
|
|
"And our goal is here to use the Parzen-window approach to predict this density based on the sample data set that we have created above. \n",
|
|
"\n",
|
|
"\n",
|
|
"In order to make a \"good\" prediction via the Parzen-window technique, it is - among other things - crucial to select an appropriate window with. Here, we will use multiple processes to predict the density at the center of the bivariate Gaussian distribution using different window widths."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"from scipy.stats import multivariate_normal\n",
|
|
"var = multivariate_normal(mean=[0,0], cov=[[1,0],[0,1]])\n",
|
|
"print('actual probability density:', var.pdf([0,0]))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"actual probability density: 0.159154943092\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 14
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 2,
|
|
"metadata": {},
|
|
"source": [
|
|
"Benchmarking functions"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Below, we will set up benchmarking functions for our serial and multiprocessing approach that we can pass to our `timeit` benchmark function. \n",
|
|
"We will be using the `Pool.apply_async` function to take advantage of firing up processes simultaneously: Here, we don't care about the order in which the results for the different window widths are computed, we just need to associate each result with the input window width. \n",
|
|
"Thus we add a little tweak to our Parzen-density-estimation function by returning a tuple of 2 values: window width and the estimated density, which will allow us to to sort our list of results later."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def parzen_estimation(x_samples, point_x, h):\n",
|
|
" k_n = 0\n",
|
|
" for row in x_samples:\n",
|
|
" x_i = (point_x - row[:,np.newaxis]) / (h)\n",
|
|
" for row in x_i:\n",
|
|
" if np.abs(row) > (1/2):\n",
|
|
" break\n",
|
|
" else: # \"completion-else\"*\n",
|
|
" k_n += 1\n",
|
|
" return (h, (k_n / len(x_samples)) / (h**point_x.shape[1]))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 15
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def serial(samples, x, widths):\n",
|
|
" return [parzen_estimation(samples, x, w) for w in widths]\n",
|
|
"\n",
|
|
"def multiprocess(processes, samples, x, widths):\n",
|
|
" pool = mp.Pool(processes=processes)\n",
|
|
" results = [pool.apply_async(parzen_estimation, args=(samples, x, w)) for w in widths]\n",
|
|
" results = [p.get() for p in results]\n",
|
|
" results.sort() # to sort the results by input window width\n",
|
|
" return results"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 16
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Just to get an idea what the results would look like (i.e., the predicted densities for different window widths):"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"widths = np.arange(0.1, 1.3, 0.1)\n",
|
|
"point_x = np.array([[0],[0]])\n",
|
|
"results = []\n",
|
|
"\n",
|
|
"results = multiprocess(4, x_2Dgauss, point_x, widths)\n",
|
|
"\n",
|
|
"for r in results:\n",
|
|
" print('h = %s, p(x) = %s' %(r[0], r[1]))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"h = 0.1, p(x) = 0.016\n",
|
|
"h = 0.2, p(x) = 0.0305\n",
|
|
"h = 0.3, p(x) = 0.045\n",
|
|
"h = 0.4, p(x) = 0.06175\n",
|
|
"h = 0.5, p(x) = 0.078\n",
|
|
"h = 0.6, p(x) = 0.0911666666667\n",
|
|
"h = 0.7, p(x) = 0.106\n",
|
|
"h = 0.8, p(x) = 0.117375\n",
|
|
"h = 0.9, p(x) = 0.132666666667\n",
|
|
"h = 1.0, p(x) = 0.1445\n",
|
|
"h = 1.1, p(x) = 0.157090909091\n",
|
|
"h = 1.2, p(x) = 0.1685\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 17
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Based on the results, we can say that the best window-width would be h=1.1, since the estimated result is close to the actual result ~0.15915. \n",
|
|
"Thus, for the benchmark, let us create 100 evenly spaced window width in the range of 1.0 to 1.2."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"widths = np.linspace(1.0, 1.2, 100)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 18
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"mu_vec = np.array([0,0])\n",
|
|
"cov_mat = np.array([[1,0],[0,1]])\n",
|
|
"n = 10000\n",
|
|
"\n",
|
|
"x_2Dgauss = np.random.multivariate_normal(mu_vec, cov_mat, n)\n",
|
|
"\n",
|
|
"benchmarks = []\n",
|
|
"\n",
|
|
"benchmarks.append(timeit.Timer('serial(x_2Dgauss, point_x, widths)', \n",
|
|
" 'from __main__ import serial, x_2Dgauss, point_x, widths').timeit(number=1))\n",
|
|
"\n",
|
|
"benchmarks.append(timeit.Timer('multiprocess(2, x_2Dgauss, point_x, widths)', \n",
|
|
" 'from __main__ import multiprocess, x_2Dgauss, point_x, widths').timeit(number=1))\n",
|
|
"\n",
|
|
"benchmarks.append(timeit.Timer('multiprocess(3, x_2Dgauss, point_x, widths)', \n",
|
|
" 'from __main__ import multiprocess, x_2Dgauss, point_x, widths').timeit(number=1))\n",
|
|
"\n",
|
|
"benchmarks.append(timeit.Timer('multiprocess(4, x_2Dgauss, point_x, widths)', \n",
|
|
" 'from __main__ import multiprocess, x_2Dgauss, point_x, widths').timeit(number=1))\n",
|
|
"\n",
|
|
"benchmarks.append(timeit.Timer('multiprocess(6, x_2Dgauss, point_x, widths)', \n",
|
|
" 'from __main__ import multiprocess, x_2Dgauss, point_x, widths').timeit(number=1))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 19
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 2,
|
|
"metadata": {},
|
|
"source": [
|
|
"Preparing the plotting of the results"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import platform\n",
|
|
"\n",
|
|
"def print_sysinfo():\n",
|
|
" \n",
|
|
" print('\\nPython version :', platform.python_version())\n",
|
|
" print('compiler :', platform.python_compiler())\n",
|
|
" \n",
|
|
" print('\\nsystem :', platform.system())\n",
|
|
" print('release :', platform.release())\n",
|
|
" print('machine :', platform.machine())\n",
|
|
" print('processor :', platform.processor())\n",
|
|
" print('CPU count :', mp.cpu_count())\n",
|
|
" print('interpreter:', platform.architecture()[0])\n",
|
|
" print('\\n\\n')"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 20
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"from matplotlib import pyplot as plt\n",
|
|
"import numpy as np\n",
|
|
"\n",
|
|
"def plot_results():\n",
|
|
" bar_labels = ['serial', '2', '3', '4', '6']\n",
|
|
"\n",
|
|
" fig = plt.figure(figsize=(10,8))\n",
|
|
"\n",
|
|
" # plot bars\n",
|
|
" y_pos = np.arange(len(benchmarks))\n",
|
|
" plt.yticks(y_pos, bar_labels, fontsize=16)\n",
|
|
" bars = plt.barh(y_pos, benchmarks,\n",
|
|
" align='center', alpha=0.4, color='g')\n",
|
|
"\n",
|
|
" # annotation and labels\n",
|
|
" \n",
|
|
" for ba,be in zip(bars, benchmarks):\n",
|
|
" plt.text(ba.get_width() + 2, ba.get_y() + ba.get_height()/2,\n",
|
|
" '{0:.2%}'.format(benchmarks[0]/be), \n",
|
|
" ha='center', va='bottom', fontsize=12)\n",
|
|
" \n",
|
|
" plt.xlabel('time in seconds for n=%s' %n, fontsize=14)\n",
|
|
" plt.ylabel('number of processes', fontsize=14)\n",
|
|
" t = plt.title('Serial vs. Multiprocessing via Parzen-window estimation', fontsize=18)\n",
|
|
" plt.ylim([-1,len(benchmarks)+0.5])\n",
|
|
" plt.xlim([0,max(benchmarks)*1.1])\n",
|
|
" plt.vlines(benchmarks[0], -1, len(benchmarks)+0.5, linestyles='dashed')\n",
|
|
" plt.grid()\n",
|
|
"\n",
|
|
" plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 25
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 1,
|
|
"metadata": {},
|
|
"source": [
|
|
"Results"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"plot_results()\n",
|
|
"print_sysinfo()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAowAAAIACAYAAAAIQT11AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl8TPf6B/DPmZBVElmERGWzFQlFaFGyqL3V2kKqIfYt\nqm7Rlt4mVAVxKbXUls3FrSD2NRJL0LpibWuXxBZLbElIJJHz+8NvzjVmJjPImJP4vF8vr3bOnDnn\nmfPM8uScZ75fQRRFEUREREREWiiMHQARERERyRsLRiIiIiIqEQtGIiIiIioRC0YiIiIiKhELRiIi\nIiIqEQtGIiIiIioRC0YCAOzduxcKhQKxsbGvvA2FQoEBAwaUYlRln5+fHzw8PPRePyQkBAoF35a6\npKenQ6FQYPLkycYORW/u7u7w9/c3dhikhaE+v8ria7U0lYXnHxMTA4VCgX379hk7FFnjN5MMXb58\nGUOHDsW7774LKysr2Nvbo379+ggJCcHevXsNtl9BECAIwmtvQ+6URZlCoUBqaqrGdebMmSOt8zpF\nNKB+TGJiYjB37lyt65aFYygXZelYGSq37u7u0mtVoVDAzMwMHh4eGDJkCK5du1bq+yvPDPl6Kkuv\n1ZeVnp6O8PBwnDx5Uus6xn7+e/fuxeTJk/Hw4UO1+5TvTWPHKHcVjB0AqTp69Ch8fX1hZmaGfv36\noUGDBsjLy8P58+exa9cu2NjYwM/Pr9T36+vri7y8PFSo8Pa8JMzNzREdHY2mTZuq3RcdHQ1zc3Pk\n5+eX+odITEwMMjIyMGbMGLX7li5disWLF5fq/sojd3d35Ofnw8TExNih6O38+fMG+0KqUaMGIiIi\nAAA5OTlITk5GVFQUtm3bhlOnTsHBwcEg+y1PytrrSU7S09MxZcoUeHp6olGjRir3yeW9unfvXkyZ\nMgUDBgyAra2tyn3BwcEICgpCxYoVjRRd2fD2VAdlxOTJk5Gfn4/ff/8d3t7eavffunWrVPeXk5MD\na2trCIIAU1PTUt223HXr1g2rV6/G7NmzVZ77f//7X/z555/4/PPPsWrVKoPsW1vhYKiCPTc3F5Uq\nVTLIto2lrL1eDfllZGtri88//1y6PWzYMDg5OWH+/PmIjo7GuHHjXnsfys+K8qqsvZ7kSNvEcXI6\ntppiVCgUsopRrnhJWmYuXLgABwcHjcUiAFStWlVtWWJiItq3bw87OztYWFigUaNGGs9SKXuojh8/\njg4dOqBy5crSX4OaehhFUcRPP/2ENm3awNnZGWZmZnBzc8PIkSNx7969V3p+Z86cgUKhwNdff63x\n/qCgIJiZmeHu3bsAgKtXr2LgwIFwc3ODubk5qlatilatWiEuLu6V9v+8AQMG4P79+9iwYYPK8ujo\naDg5OeHjjz9We4yy12X//v1q9+nTr+ju7o79+/dLfT3Kf8rtaephVC7LyspCv3794OjoiEqVKuGj\njz7C8ePHVdZ9vl/ot99+Q9OmTWFpaYnRo0dL6yxbtgxNmjSBpaUlKleujA4dOuDgwYMa401OTkaX\nLl3g4OAACwsL1KxZE4MHD5byo/Tbb7/hww8/hI2NDaysrPDBBx9g3bp1atvbunUrfH19UaVKFVha\nWsLNzQ09evTAhQsXpHX0ybmmvqjnl23ZsgXNmjWDhYUFXFxcMGHCBDx9+lQtnnXr1qFRo0awsLCA\nm5sbpkyZgsTERL1aEb755hsoFAqcPn1a7b6HDx/CwsIC3bp1k5Zp6mHctWsXevfuDU9PT1haWsLO\nzg4dOnTQ+Pp6We3btwcAXLp06aX3pXwtp6WloWfPnrC3t5fOyrx4Cfz5fy8+v6NHj6Jbt26oUqUK\nzM3N8e6772LatGlquVDuLzMzE0FBQbC3t4eVlRU6duyo8tooyYABA2BhYYEnT55Iyw4fPgyFQgEH\nBweVQmH79u1QKBSIj4+XlmnqYVQuO3z4MHx9fVGpUiU4OjpiyJAhePTokVoMKSkpaNWqFSwtLVGt\nWjWMHj0aubm5GuN99OgRvvvuO9SsWRPm5uZwdnZG//79ceXKFWmdJ0+ewMLCAiEhISqPHTZsGBQK\nBb766iuV5b1794atrS2Ki4t1Hq8LFy4gODhY+mz38PDAhAkT8PjxY5X1dL0fY2JiEBAQAOBZDl58\nLeh6r65duxbvvfceLC0tUatWLSxbtgwAkJGRgZ49e8LBwQE2NjYIDg5WO5Znz57FyJEj0aBBA+mz\nx8fHB8uXL1dZLyQkBFOmTAEAeHh4SDEql2n7XM/KysKoUaNQo0YNmJmZwdXVFaGhoWrff8rHJycn\nY9asWVJO69atWyrfVXLBM4wyU6tWLWzbtg0JCQkqXzbaLFmyBMOHD0fLli3x/fffw8rKCrt27cKI\nESNw6dIlzJw5U1pXEARcuXIFbdu2RWBgIHr16qX2Bnz+zNeTJ08wa9Ys9OzZE926dYOVlRWOHDmC\n5cuXIyUlBampqS991qRevXpo1qwZVq1ahcjISJXiKDs7Gxs3bkTnzp3h4OCAoqIitGvXDjdu3MCo\nUaNQp04dPHz4ECdPnkRKSgr69ev3Uvt+8Xk2btwY7733HqKiohAYGAjg2WWp1atXY9CgQa90RkjX\nJce5c+fiu+++Q1ZWFn7++Wdpeb169XRuo2PHjnBwcMDkyZORmZmJ+fPnw9fXF4cPH0aDBg1U1t2w\nYQOuXLmCkSNHYuTIkbCxsQHwrMiJjIzE+++/j4iICGRnZ2PJkiXw9/fHxo0b0alTJ2kbixcvxogR\nI1CjRg2MGjUKbm5uyMjIwJYtW3D9+nXpMuf333+PadOmoVOnTpg6dSoUCgXWr1+PXr16Yf78+Rg5\nciQAYN++fejatSsaNmyIiRMnonLlyrh+/Tr27NmDS5cuoXbt2i+dc03Hatu2bVi4cCFGjBiBwYMH\nY8OGDZg1axbs7Ozw3XffSev99ttvCAoKQu3atREeHg4TExPExsZi8+bNeuUyJCQEkZGRiIuLQ2Rk\npMp9a9aswZMnT1S+6DX1SMXGxuLBgwcICQnBO++8g2vXrmHZsmVo27YtkpOT8eGHH5YYQ0mUhZaj\no+NL70sQBOTm5sLX1xcffvghIiIicPv2bQDPXsMvFku///475s+fj2rVqknLtm7diu7du6NOnToY\nN24c7O3tcejQIfzwww84ceIE1qxZo7K/R48eoU2bNmjRogUiIiJw+fJlzJ07F59++in+/PNPnT8G\na9u2LWJjY3Hw4EGpgNmzZw8UCgUePHiA48ePo0mTJgCApKQkjQWuppyfOHECn3zyCQYOHIgvvvgC\nycnJWL58ORQKhcof5n/88Qc++ugj2Nra4ttvv4WtrS3+85//aPxjrLCwEB06dMChQ4fQq1cvjB8/\nHufPn8eiRYuwa9cuHD16FNWrV4eZmRlatWqF5ORklccrn1dSUpK0TBRF7N27F23atNF5rFJTUxEQ\nEAB7e3uMGDEC1atXx4kTJzBv3jwcPHgQ+/btQ4UKFfR6P/r6+mLixImYNm0ahg0bhtatWwNQP7mh\n6dhu2bIFv/76K0aNGgV7e3ssW7YMQ4cOhYmJCcLCwtCuXTtERETgyJEjiIqKgrm5OZYuXSo9ft++\nfThw4AC6du0KDw8PPHr0CGvWrMGQIUNw584dfPvttwCA4cOHIycnBwkJCfj555+l90TDhg21HqOH\nDx+iZcuWuHTpEgYNGoQmTZrg2LFjWLRoEZKSknDkyBG1qzYTJ05Efn4+RowYAVNTUyxatAghISGo\nVasWWrZsWWJOygSRZOXw4cOiqampKAiCWLt2bXHAgAHiokWLxDNnzqite+PGDdHMzEzs27ev2n1j\nxowRTUxMxMuXL0vL3NzcREEQxOXLl6utn5ycLAqCIMbGxqosz8/PV1t3+fLloiAI4po1a1SWC4Ig\nDhgwQOdzXLBggSgIgrht2zaV5cuWLRMFQRATEhJEURTFkydPioIgiJGRkTq3+TL69+8vCoIgZmVl\nib/88otoYmIiXrt2TRRFUVy5cqUoCIL4119/ifHx8WrHJDo6WhQEQdy3b5/adn19fUUPD49XWvZi\nbJqW9ejRQ2V5amqqqFAoxI4dO0rL0tLSREEQRFNTU/Hs2bMq6589e1YUBEFs3bq1WFhYKC2/ceOG\nWLlyZdHd3V18+vSpKIqiePXqVdHU1FRs0KCB+PDhQ7U4i4uLpRgEQRAnTZqkts5nn30m2tjYiLm5\nuaIoiuLYsWNFQRDEO3fuaHzuoqh/zpXPc/LkyWrLKlWqJGZkZKis7+XlJTo7O0u3CwsLRRcXF7Fa\ntWrigwcPpOW5ubmip6enxveCJs2aNRNdXFyk46b04YcfilWqVFE5zm5ubqK/v7/Keo8ePVLb5q1b\nt0RHR0exc+fOOvev3G69evXErKws8c6dO+Lly5fFqKgo0dbWVjQ1NRX/+uuvl96Xr6+vKAiC+M9/\n/lPn/tPS0kQnJyexdu3a4r1790RRFMW8vDyxatWqoq+vr9qxmTNnjigIgrh37161/b2Y98jISFEQ\nBHHnzp0647h27Zraa9Hf31/89NNPRRsbG3HmzJnS8iZNmogNGzZUebymzy9BEEQTExPxyJEjKsu7\ndOkiVqxYUeWYtmjRQjQzMxMvXLggLSsoKBCbN2+u9lpdsmSJKAiC+M0336hsd+vWraIgCGJwcLC0\nbOrUqaIgCNJ2MzIypHUEQRBv3boliqIonjp1ShQEQZw9e7bOY9WwYUOxXr160ntTKSEhQRQEQYyJ\niRFFUf/3o7bvD1HU/V69cuWKtPzOnTuiubm5KAiCOGfOHJXtdO/eXTQ1NVU55ppe08XFxaKfn59o\na2ur8v4LCwsTBUFQ+2wQRc2f6xMnThQFQRAXLVqksq7y++v594by8U2aNFHZ5/Xr10UzMzMxKChI\nbZ9lES9Jy8wHH3yA1NRU9O/fH9nZ2YiJicHIkSNRv359+Pr6Ii0tTVp37dq1KCgowMCBA5GVlaXy\n7+OPP0ZxcTESExNVtu/g4PBSQ0eYmZkBAJ4+fYoHDx4gKytL+qv8yJEjr/Qcg4KCYGpqqnaqPi4u\nDg4ODtKlYOUlsKSkJNy5c+eV9lUSQRDw+eefo2LFitLlx+joaDRv3hz169cv9f29rgkTJqjcbtKk\nCdq1a4fExES1y0hdunRB3bp1VZZt3LhR2s7zvZLOzs4YMGAAMjIycOLECQBAfHw8CgsLERYWJp2d\nfJ7ybMHKlSshCAL69eun9hr85JNPkJOTg8OHDwMAKleuDODZ67aoqEjjcyyNnH/22WdwdXVVWebn\n54ebN29Kxyk1NRWZmZkICQlRaYC3srLC8OHD9d5X//79kZmZid27d0vL0tLScOjQIQQFBensSbW0\ntJT+Pzc3F3fv3oVCoUDz5s3xxx9/6B3H2bNnUaVKFTg5OaFmzZoYNGgQnJycsHHjRum1/LL7EgRB\nZ+/jw4cP8fHHH6OoqAhbt26FnZ0dAGD37t24ffs2QkJCcO/ePZXXhfIs9q5du1S2ZWJigi+//FJl\nmfKz5uLFizqPQfXq1VGnTh3prJuyF7xjx47w9fXFnj17AAAPHjzAyZMnpbOQurRo0QLNmjVTi6uo\nqAjp6ekAgNu3b+P333/Hp59+ilq1aknrVaxYEWPHjlXbZkJCAkxMTFTOeANA586d0ahRI+m9Cjw7\ncwpAel5JSUmoUKECwsPDIQiCdPZR+V9dz+v06dM4ffo0goKCkJeXp5Ib5eV0ZW4M/Rn82WefoUaN\nGtJtR0dH1KlTBxUqVMCoUaNU1v3www9RWFgoHXNA9TWdn5+Pu3fv4u7du2jXrh2ys7Nx7ty5V44t\nISEBTk5OGDp0qMryYcOGoUqVKkhISFB7zMiRI1Xe8y4uLqhTp45er9+ygAWjDHl5eSE6Oho3b95E\neno6YmNj0bp1axw4cACffvopCgsLATzrBwSAjz76CE5OTir/2rdvD0EQpMtISjVr1nypX2quWbMG\n77//PiwtLWFvby99IQHA/fv3X+n52dnZ4eOPP8bGjRuRk5MD4FlPS0pKCvr06SO94dzc3DBp0iTs\n2rULzs7O8PHxwTfffIOjR4++0n41sbe3R9euXaVfLicnJ8t2LMnnL1s/v+zp06fIyMhQWV6nTh21\ndZV/bLx4+RqAVFRcvnwZwP8uZzZu3LjEmM6cOQNRFPHuu++qvQYHDx4MQRCkH2qFhoaicePGGDly\nJBwcHNClSxf88ssvyMrKkrZXGjn39PRUW6a8fK7svVQeixeLakDzsdNG0x8/cXFxEEVRr5aJS5cu\noU+fPrCzs4ONjY1U9G3fvh0PHjzQOw4PDw8kJiYiMTER+/fvx8WLF3H+/Hl07NjxlfdVpUoVjX8s\nKBUVFaFXr164ePEi1q1bh9q1a0v3KT+bBg4cqPa6qFevnsbPJhcXF7UfHryYt+LiYty8eVPlX3Z2\ntrS+v78/jh49itzcXBw6dAj5+fkICAiAv78/UlJSUFhYiL1796K4uFjvglGf15PyffPuu++qravp\nfZuWlgYXFxe1X+sCz96fOTk50vvCx8cH1tbWUkGYlJQEHx8feHp6wtvbWyqEk5KS4ODgoPYr5Rcp\ncxMWFqaWm6pVq+Lx48dSbgz9Gazp2NrZ2cHZ2VmtJUj5x8jz/dO5ubkYN24cXF1dYWlpKb2mv//+\newCv/h0FPMtR3bp11S7vm5iYoHbt2ionb0p6Pvb29mo932UVexhlztXVFcHBwQgODkbr1q1x8OBB\n/Pe//0XLli2lJu4VK1bA2dlZ4+Nf/BHG83+R6bJ+/Xr06dMH77//PubNm4caNWrA3NwcRUVF6Nix\no16N1dr069cP69evx5o1azBo0CCsWLECoiiif//+Kuv9+OOPGDhwILZu3YoDBw5g2bJliIyMxIQJ\nEzB9+vRX3v/zBg4ciE6dOmHIkCEwMzNDUFCQ1nVLKra1nTUzhpfJ8+sQRRGCIGDHjh1ah81QFqP2\n9vb473//iwMHDmD37t3Yv38/xo4di7CwMGzbtg0ffPABgNfPeUnDd4hafsX5quzt7dG5c2ds2LAB\njx49gpWVFVasWIH69etrHK7pebm5uWjTpg3y8vIwduxYeHt7w9raGgqFAtOmTVPrWyuJlZVViQXQ\nq+xL12to5MiRSExMxPLly9WG+lIe51mzZuG9997T+HgXFxeV2/rk7cqVK2pfyiEhIYiKigLw7Gzc\n4sWLsX//fhw6dEg665iXl4evv/4av//+O5KSkmBiYgJfX98Sn9/LxGVIFSpUQOvWrVUKRmVvrL+/\nPzZt2gRRFLFv3z589NFHOrenjHncuHEqf1A8T1mcAYb9DNZ2bPU95p9//jm2bt2KYcOGoU2bNnBw\ncICJiQm2bt2KOXPmvNZ31KvQFvebeJ28CSwYy5DmzZvj4MGDuH79OoD/nQlxcHDQ+6/ll7FixQpY\nWFggOTkZ5ubm0vKzZ8++9rY7d+4MR0dHrFixQioY69WrBx8fH7V1PTw8EBoaitDQUDx58gQdOnTA\nzJkzMW7cOKl5+XW0b98e77zzDhITE9G3b98Sz6rY29sDgMZfiaelpUmX8EvyqmPx/f3333j//ffV\nllWoUAFubm46H688M/znn3+q/SHx999/A/jfX8jKM2/Hjx9XucT2ojp16mDnzp2oUaOGxrMrL1Io\nFPD19ZW+rE+fPo2mTZti6tSp2LJli7SeoXPu7u4OQPNr+WUvY/Xv3x8bNmzAmjVrUKdOHVy+fBkz\nZszQ+bg9e/YgMzMT0dHRan8oTZw48aVieNP7ioyMxLJly/DNN99oPCOv/GyytLQs1c8mZ2dntTab\n5wtPPz8/CIKAPXv24PDhw9K+GzZsCEdHR+zZswfJyclo0qRJie/zl6V8PynP3j1P+d56nqenJ3bu\n3ImHDx+qnWX8+++/YWtrq/I6DwgIwLZt2xAfH48bN25Il6nbtm2LuXPnYt26dXj48KFex1qZG4VC\noXdudL0fjTHg9YMHD7Blyxb0798fCxcuVLnvxXYH4OU/dz09PXH27Fk8ffpUpRAsKirC+fPnNZ5N\nLO94SVpmdu/erXH4j7y8POzatQuCIEhnbAIDA2FmZoawsDDk5+erPebhw4coKCh45ViUb5Ln4xFF\nEVOnTn3lbSpVqFABn3/+OQ4cOIBVq1bh4sWLal9k2dnZ0uV3JTMzM6kwef5yw9mzZ6XLQi9LEAQs\nWLAA4eHh+Oabb0pcV/lh+3zPGgCsXr0amZmZeu2vUqVKJQ5LpO2D7flfvAPAsWPHkJiYiLZt2+p1\nRrFr164QBAGRkZEqZ0OVhYS7u7t0Cbpnz54wNTXF5MmTpbYBTYKDgwE8Kzo0/TX//Lihmi7L1K1b\nF+bm5lIuXybnr6NZs2ZwdnZGTEyMyuXY3Nxc/Prrry+1rS5dusDR0RFxcXGIi4uDQqHAF198ofNx\nyvfXi8dt165dr9wf/Cb2lZCQgG+//Rbdu3eXBgt/UYcOHeDk5ITp06drzFleXp7W4WZKYmZmhoCA\nAJV/z/+h4ujoCG9vb2zZsgVHjx6VCiJBEODv74/4+Hj8/fffpf4HdtWqVfHBBx9g48aNKsMAFRQU\nYM6cOWrrd+vWDcXFxWpn6LZv344TJ06ga9euKsuV8YaHh8Pc3BytWrUCALRp0wYmJiYIDw9XWa8k\njRs3hpeXF3799VeNl1WLiope+v2o/LXwm7z0amJiAkEQ1F7TmZmZWLZsmdrn6MvG2K1bN9y5c0ca\n5kdp6dKlyMrK0msUk/KGZxhlZuzYsbh37x66du0KLy8vWFpa4urVq1i1ahUuXLiA/v37Sz1o1atX\nx6JFizB48GDUq1cPwcHBcHV1xZ07d3D69Gls3LgRZ86cUfsBgL569eqF9evXIyAgAMHBwSgsLMSG\nDRuQl5dXKs+1f//+mDdvHkaMGAETExO1L9mkpCQMHToUPXv2RJ06dVCpUiWkpqZi+fLl+OCDD1R6\npurXrw83NzeNH4D6+OSTT/DJJ5/oXK9u3br46KOPsHjxYoiiiEaNGuHEiRPYsGEDatWqpfbhCqhf\njmjRogW2bt2K0NBQtGjRAiYmJmjbti2qVKmicX2lK1euoEOHDvjkk0+kYXWsrKzUhnTRpk6dOhg/\nfjxmzpyJNm3aIDAwEDk5OViyZAkeP36M1atXSx+y1atXx88//4xRo0bB29sb/fr1g6urK65fv45N\nmzYhKioKjRo1go+PD8LDwxEeHo733nsPvXr1grOzMzIzM5Gamort27dL4+INHjwY169fR/v27eHq\n6oq8vDz89ttvePTokdTv9zI5fx0mJiaYNWsW+vbti+bNm2PQoEEwMTFBTEwMHBwckJ6ervcZiQoV\nKiAoKAjz589Hamoq2rVrp7VF5HmtW7dGtWrV8PXXXyM9PV0a2uTf//43vL29NY7v+KpeZV+aXod3\n797FF198AUtLS3To0AH//ve/Ve6vVq0aPvroI1haWiIuLg6fffYZ6tati4EDB6JmzZp48OABzp49\ni4SEBGzYsAFt2rQpcX+vIiAgAD///DMEQVApoAICAqRxFw1xRWb27Nnw8/NDq1atMGrUKGlYHU0n\nAEJCQhAbG4sZM2YgPT0drVu3xsWLF7Fw4UJUq1YN06ZNU1n/vffeg52dHc6cOQN/f3+p19PGxgY+\nPj74448/4OLiorEnV5MVK1YgICAADRs2xMCBA1G/fn08fvwYFy9eREJCAqZPn45+/frp/X5s0KAB\nrK2tsXDhQlhaWsLW1hZVq1Z95bnT9XktWFtbo3379vj3v/8NCwsL+Pj4ICMjA0uWLIGnp6dan2WL\nFi0APBta7PPPP4e5uTm8vb019nQDz34cGB8fj1GjRuHYsWN47733cPz4cURFReHdd99V+xHi6z6f\nMuGN/iabdNq1a5c4atQosVGjRqKjo6NYoUIF0dHRUQwICBCjo6M1PubgwYNit27dRCcnJ9HU1FR0\ncXERAwICxNmzZ6sMi+Pu7q42rIdScnKyqFAo1IZFWLp0qVi/fn3R3NxcdHZ2FocNGybeu3dP6xAU\n+gyr8zxvb29RoVCI7du3V7svLS1NHD58uFivXj3RxsZGtLKyEuvXry+GhYWJ2dnZavvWNlTNi0JC\nQkSFQiHevXu3xPXi4+M1HpObN2+KvXr1Em1sbMRKlSqJnTt3Fs+ePSv6+fmpxaBp2ePHj8VBgwaJ\nVatWFU1MTESFQiEN56CM7Xn9+/cXFQqFmJWVJQYHB4sODg6ipaWl2LZtW/HYsWMq62oawuJFS5cu\nFRs3biyam5uLNjY2Yvv27cWUlBSN6+7atUts166daGtrK5qbm4s1a9YUhw4dqnbstm7dKnbo0EG0\nt7cXzczMRFdXV7Fz587i4sWLpXXWr18vdu3aVXznnXdEMzMzsUqVKqKfn5+4fv16lfj1yXlJQ3Vo\neu7h4eGiQqFQG1IjPj5ebNiwoRRzWFiYNLRIfHy81mP4IuXwQgqFQly1apXGdTS9/06dOiV27NhR\ntLOzE62trUV/f38xJSVF4+tAG3d3d9Hb21vnei+zL02vW1H83zFWKBSiIAhq/158fn/++af4xRdf\niNWrVxdNTU3FqlWriq1atRKnTp0qDcGjz/5Kej2/aPPmzaIgCGKtWrVUll+4cEEUBEE0MzMT8/Ly\n1B73Mp9p0dHRKu9bpf3794stW7YUzc3NxWrVqomhoaHin3/+qfE5PHr0SPzuu+9ET09P6dj069dP\nZZiZ5/Xo0UNUKBTi1KlTVZZPmjRJVCgU4hdffKH9oGiQkZEhDh8+XHR3dxdNTU1FBwcH0cfHR5w4\ncaI0zNjLfAZv27ZNbNKkiTQsjvK18LLvVW2vBU3HPCsrSxw8eLDo4uIimpubiw0bNhSXLVsmxsTE\naMzPzJkzRU9PT7FixYqiQqGQ9q8tn3fu3BFHjhwpvvPOO2LFihXFGjVqiKGhoWqff9oeX9LzKYsE\nUSwvpS9R+RQSEoK4uLg33sD9tvrXv/6F8ePH4/fff0fz5s2NHQ4RkSywh5GoDDBGU3l5V1hYqHa5\nMDc3FwsWLICjo6M0KwgREbGHkahM4IWA0nfp0iV06tQJQUFBcHd3R2ZmJmJjY5GRkYFFixbpHHSb\niOhtwk9xJtkgAAAgAElEQVREIpnTNAcxvT4nJye0aNECK1euxO3bt1GhQgU0bNgQM2fORM+ePY0d\nHhGRrLCHUYf33nsPJ0+eNHYYRERERDr5+vpi7969pb5dFow6CILAy4EyoxzGheSFeZEn5kWemBd5\nUX7Xl4e8GKpu4Y9eqMx5fvJ5kg/mRZ6YF3liXuSJedGOBSMRERG91cLCwowdguyxYKQyJyQkxNgh\nkAbMizwxL/LEvMiL8jI086Idexh1YA8jERERlRXsYST6f4b49Re9PuZFnpgXeWJe5Il50Y4FIxER\nERGViJekdeAlaSIiIioreEmaiIiIyADK+tiLbwILRipz2GMiT8yLPDEv8sS8yMvkyZMBMC8lYcFI\nRERERCViD6MO7GEkIiIq38rTdz17GImIiIjIKFgwUpnDHhN5Yl7kiXmRJ+ZFnpgX7VgwEhER0VuN\nc0nrxh5GHcpTXwMRERGVb+xhJCIiIiKjYMFIZQ57TOSJeZEn5kWemBd5Yl60Y8FIRERERCViD6MO\n7GEkIiKisoI9jEREREQGwLmkdWPBSGUOe0zkiXmRJ+ZFnpgXeeFc0rqxYCQiIiKiErGHUQf2MBIR\nEZVv5em7nj2MRERERGQULBipzGGPiTwxL/LEvMgT8yJPzIt2LBiJiIjorca5pHVjD6MO5amvgYiI\niMo39jASERERkVGwYKQyhz0m8sS8yBPzIk/MizwxL9qxYCQiIiKiErGHUQf2MBIREVFZwR5GIiIi\nIgPgXNK6sWCkMoc9JvLEvMgT8yJPzIu8cC5p3VgwEhEREVGJ2MOoA3sYiYiIyrfy9F3PHkYiIiIi\nMgoWjFTmsMdEnpgXeWJe5Il5kSfmRTsWjERERPRW41zSurGHUYfy1NdARERE5Rt7GImIiIjIKFgw\nUpnDHhN5Yl7kiXmRJ+ZFnpgX7VgwEhEREVGJ2MOoA3sYiYiIqKxgDyMRERGRAXAuad1YMFKZwx4T\neWJe5Il5kSfmRV44l7RuLBiJiIiIqETsYdSBPYxERETlW3n6rmcPIxEREREZBQtGKnPYYyJPzIs8\nMS/yxLzIE/OiHQtGIiIieqtxLmnd2MOoQ3nqayAiIqLyjT2MRERERGQULBipzGGPiTwxL/LEvMgT\n8yJPzIt2LBiJiIiIqETsYdSBPYxERERUVrCHkYiIiMgAOJe0biwYqcxhj4k8MS/yxLzIE/MiL5xL\nWjcWjERERERUIvYw6sAeRiIiovKtPH3Xs4eRiIiIiIyCBSOVOewxkSfmRZ6YF3liXuSJedGOBSMR\nERG91TiXtG7sYdShPPU1EBERUfnGHkYiIiIiMgoWjFTmsMdEnpgXeWJe5Il5kSfmRTsWjERERERU\nIvYw6sAeRiIiIior2MNIREREZACcS1o3FoxU5rDHRJ6YF3liXuSJeZEXziWtGwtGIiIiIioRexh1\nYA8jERFR+VaevuvZw0hERERERsGCkcoc9pjIE/MiT8yLPDEv8sS8aMeCkYiIiN5qnEtaN/Yw6iAI\nAibOmGjsMIjKBCcbJ4wZPsbYYRARvbUM1cNYodS3WA65tXUzdghEZULGngxjh0BERAbAS9JU5pw7\nes7YIZAGzIs8sSdLnpgXeWJetGPBSEREREQlYg+jDoIgYPHRxcYOg6hMyNiTgZ8m/GTsMIiI3loc\nh5GIiIjIADiXtG4sGKnMYa+cPDEv8sSeLHliXuSFc0nrxoKRiIiIiErEHkYd2MNIpD/2MBJRWcS5\npHXjGUYiIiIiKhELRipz2CsnT8yLPLEnS56YF3liXrRjwUhERERvNc4lrRt7GHVgDyOR/tjDSERk\nXOxhJCIiIiKjYMFIZQ575eSJeZEn9mTJE/MiT8yLdiwYiYiIiKhELBipzKnrU9fYIZAGr5uXgoIC\nDBo0CO7u7rCxsUHjxo2xY8cOtfWmTJkChUKBpKQkaVlRURFGjx4NZ2dnODg4oGvXrrhx44bG/fz+\n++9o164dHBwc4OTkhMDAQNy8eVOvbRUVFaFPnz6ws7NDp06dkJOTIz1u2rRpmDNnzmsdA0Pw8/Mz\ndgikAfMiT8yLdiwYiUgWioqK4Orqiv379yM7OxtTp05FYGAgMjIypHUuXbqEtWvXwsXFReWxCxcu\nxIEDB3Dq1CncuHEDdnZ2GD16tMb9PHjwAMOHD0dGRgYyMjJgbW2NAQMG6LWt9evXw8TEBHfv3oWt\nrS2WLFkCAEhLS8PmzZsxZsyY0j4sRPQGcC5p3VgwUpnDXjl5et28WFpaIiwsDK6urgCALl26wMPD\nA8eOHZPWCQ0NxYwZM1CxYkWVx/7111/o0KEDqlSpAjMzMwQGBuKvv/7SuJ+OHTuiR48eqFSpEiws\nLDBq1CgcPHhQr22lp6fD19cXCoUCfn5+uHz5MgDgyy+/xOzZs6FQyO8jlT1Z8sS8yAvnktZNfp9u\nREQAbt26hfPnz6NBgwYAgPj4eJibm6NTp05q67Zv3x7bt29HZmYmHj9+jJUrV6Jz58567Wf//v3w\n8vLSa1teXl5ISkrCkydPkJycDC8vLyQkJMDJyQktWrQohWdNRCRPFYwdANHLYg+jPNX1qYuMPRm6\nV9RDYWEh+vbti5CQENSpUwc5OTmYNGkSEhMTNa7fo0cPbNq0CdWrV4eJiQkaNmyIBQsW6NzPqVOn\n8OOPP2LTpk16batz5844cOAAmjdvjhYtWqB3795o27YtEhMTMWnSJKSkpMDLyws///yz2llQY2FP\nljwxL/LEvGj31p5h3LZtG9q0aQNra2vY2tqiWbNmSE5ONnZYRG+94uJiBAcHw9zcHPPnzwfwrL8o\nODhYulwNQGVg2nHjxiEnJwf37t3Do0eP0K1bN41nIp938eJFdO7cGfPmzUOrVq303lZERAROnjyJ\nX3/9FRERERgxYgT++OMPpKamYt++fSgoKEBUVFRpHQ4iIll4KwvGxYsX47PPPkOzZs2wYcMGxMfH\nIzAwEHl5ecYOjfTAHkZ5Ko28iKKIQYMG4c6dO1i3bh1MTEwAAElJSZg3bx6cnZ3h7OyMq1evIjAw\nEJGRkQCAHTt2YMCAAahcuTJMTU0RGhqKI0eO4N69exr3k5GRgXbt2uGHH35A3759Ve7Td1unT5/G\n4cOHMWTIEJw+fRpNmzYFAPj4+ODUqVOvfSxKC3uy5Il5kSfmRbu37pJ0eno6vvrqK8yaNQtffvml\ntLx9+/ZGjIqIAGDEiBE4e/YsEhMTYWZmJi3fs2cPioqKADwrKps1a4Y5c+ZIZ/4aNmyI2NhY+Pr6\nwsLCAgsXLkT16tVhb2+vto/r168jICAAoaGhGDp0qNr9+mxLFEWMHj0av/zyCwRBgKenJ+bPn4+C\nggLs27cPPj4+pX1oiMiAOJe0bm/dGcaoqChUqFABw4cPN3Yo9IrYwyhPr5uXjIwMLFmyBCdPnkS1\natVgbW0Na2trrF69Gvb29nBycoKTkxOqVq0KExMT2NnZwdLSEgAwZ84cKBQK1KxZE05OTtixYwcS\nEhKkbXt5eWH16tUAgGXLliEtLQ3h4eHSPmxsbKR1dW0LAGJiYuDt7Y3GjRsDALp37w4XFxc4OTnh\n/v37GgtRY2FPljwxL/KiHFaHedFOEA0xQ7WMBQQEIDs7G6Ghofjxxx9x5coVuLu7Y+zYsRg5cqTa\n+oIgYPHRxUaIlKjsydiTgZ8m/GTsMIiI3lqCIMAQpd1bd4bxxo0buHDhAiZMmICJEydi9+7daNeu\nHUJDQzFv3jxjh0d6YA+jPDEv8sSeLHliXuSJedHurethLC4uRk5ODmJjY/HZZ58BeHYKOj09HRER\nESp9jUrRYdFwdHEEAFhUskCNujWky2/KL0nefnO3r567Kqt4ePt/tzMuZWDv3r3SZR3lhy9vG+/2\niRMnZBUPb/O2nG+XxfeL8v/T09NhSG/dJekWLVrgyJEjyM7OhpWVlbR8zpw5+Prrr5GZmYmqVatK\ny3lJmkh/vCRNRGRcvCRdSho0aGCQA0lERERlE+eS1u2tKxi7d+8O4NlYa8/bsWMHatSooXJ2keSJ\nvXLyxLzI0/OXrUg+mBd54VzSur11PYydO3eGv78/hg0bhqysLHh4eCA+Ph67d+9GTEyMscMjIiIi\nkp23rocRAHJycvDdd99h7dq1uH//PurVq4dvv/0Wffr0UVuXPYxE+mMPIxGVRYbq+zMGQz2Xt+4M\nIwBYW1tj/vz50jy1RERERKTdW9fDSGUfe+XkiXmRJ/ZkyRPzIk/Mi3YsGImIiOitxrmkdXsrexhf\nBnsYifTHHkYiIuPiOIxEREREZBQsGKnMYa+cPDEv8sSeLHliXuSJedGOBSMRERERlYg9jDqwh5FI\nf+xhJCIyLvYwEhERERkA55LWjQUjlTnslZMn5kWe2JMlT8yLvHAuad1YMBIRERFRidjDqAN7GIn0\nxx5GIiqLOJe0bjzDSEREREQlYsFIZQ575eSJeZEn9mTJE/MiT8yLdiwYiYiI6K3GuaR1Yw+jDuxh\nJNIfexiJiIyLPYxEREREZBQsGKnMYa+cPDEv8sSeLHliXuSJedGOBSMRERERlYg9jDqwh5FIf+xh\nJCIyLvYwEhERERkA55LWjQUjlTnslZMn5kWe2JMlT8yLvHAuad0qGDuAsiBjT4axQ6Dn3Lp0C+YP\nzY0dBr3g1qVbaNa4mbHDICIiA2APow7laX5JIiIiUleevuvZw0hERERERsGCkcoc9pjIE/MiT8yL\nPDEv8sS8aMeCkYiIiN5qnEtaN/Yw6lCe+hqIiIiofGMPIxEREREZBQtGKnPYYyJPzIs8MS/yxLzI\nE/OiHQtGIiIiIioRexh1YA8jERERlRXsYSQiIiIyAM4lrRsLRipz2GMiT8yLPDEv8sS8yAvnktaN\nBSMRERERlYg9jDqwh5GIiKh8K0/f9YZ6LhVKfYvl0KSZk4wdAlGZ4GTjhDHDxxg7DCIiKmUsGPXg\n1tbN2CHQc84dPYe6PnWNHQa94NzRc7j98Laxw6AX7N27F35+fsYOg17AvMgT86IdexiJiIjorca5\npHVjD6MOgiBg8dHFxg6DqEzI2JOBnyb8ZOwwiIjeWhyHkYiIiIiMggUjlTnnjp4zdgikAfMiTxxX\nTp6YF3liXrRjwUhEREREJdKrh/Hp06cAABMTEwBAZmYmtm7dinr16qFVq1aGjdDI2MNIpD/2MBIR\nGZdRexi7dOmC+fPnAwByc3PRrFkzjB8/Hr6+voiNjS31oIiIiIjeFM4lrZteBWNqair8/f0BAOvX\nr4e1tTVu376NZcuW4V//+pdBAyR6EXvl5Il5kSf2ZMkT8yIvnEtaN70KxtzcXNjZ2QEAdu3ahW7d\nuqFixYrw9/fHxYsXDRogERERERmXXgVjjRo1kJKSgtzcXOzcuRPt2rUDANy7dw+WlpYGDZDoRZzl\nRZ6YF3nirBXyxLzIE/OinV5TA3799dfo168frKys4ObmhjZt2gAA9u/fj4YNGxo0QCIiIiIyLr3O\nMA4bNgyHDx9GVFQUDh48KP1aumbNmvjxxx8NGiDRi9grJ0/MizyxJ0uemBd5Yl600+sMIwD4+PjA\nx8dHZdnHH39c6gERERERvUmcS1o3vc4wiqKIBQsWoEGDBrCwsMDly5cBANOnT8eaNWsMGiDRi9gr\nJ0/MizyxJ0uemBd5UQ6rw7xop1fBOHfuXEydOhVDhgxRWe7i4iKNz0hE9DoKCgowaNAguLu7w8bG\nBo0bN8aOHTvU1psyZQoUCgX27NkjLevUqROsra2lf2ZmZlr7q1euXKmyrpWVFRQKBY4fPw7g2RdH\nxYoVpfttbGyQnp4OACgqKkKfPn1gZ2eHTp06IScnR9rutGnTMGfOnFI8IkRE8qFXwbho0SIsXboU\nX331FSpU+N9V7CZNmuDPP/80WHBEmrBXTp5eNy9FRUVwdXXF/v37kZ2djalTpyIwMBAZGRnSOpcu\nXcLatWvh4uICQRCk5du3b0dOTo70r2XLlggMDNS4n759+6qsu3DhQtSsWRONGzcG8GyWhKCgIOn+\n7OxsuLu7A3g2Dq2JiQnu3r0LW1tbLFmyBACQlpaGzZs3Y8yYMa91DAyBPVnyxLzIE/OinV4F45Ur\nV+Dt7a22vGLFisjLyyv1oIjo7WNpaYmwsDC4uroCeDbDlIeHB44dOyatExoaihkzZqBixYpat5Oe\nno4DBw6gX79+eu03JiZGZV1RFLVOq5Weng5fX18oFAr4+flJ7TlffvklZs+eDYVCr49UIqIyR69P\nNw8PD6Smpqot3759O+rXr1/qQRGVhL1y8lTaebl16xbOnz+PBg0aAADi4+Nhbm6OTp06lfi4uLg4\ntGnTRio8S5KRkaFWXAqCgM2bN8PBwQFeXl749ddfpfu8vLyQlJSEJ0+eIDk5GV5eXkhISICTkxNa\ntGjxis/UsNiTJU/MizwxL9rpVTCOHz8eoaGhWLlyJYqLi3Ho0CGEh4dj4sSJGD9+vKFjNKiOHTtC\noVDgn//8p7FDIaL/V1hYiL59+yIkJAR16tRBTk4OJk2ahLlz5+p8bFxcHEJCQvTaj7K4dHNzk5YF\nBgbi7NmzyMrKwtKlSzFlyhT85z//AQB07twZHh4eaN68Oezs7NC7d29MmTIFM2fOxKRJk+Dr64tR\no0ahsLDwlZ43ERkH55LWTa+CccCAAZg8eTK+++475OXloV+/fli2bBl++eUX9OnTx9AxGszq1atx\n6tQpAFDphyJ5Yw+jPJVWXoqLixEcHAxzc3PpR3Xh4eEIDg5WOWuo6bJxSkoKbt26hZ49e+q1r7i4\nOPTv319lWb169VCtWjUIgoAWLVpgzJgxWLt2rXR/REQETp48iV9//RUREREYMWIE/vjjD6SmpmLf\nvn0oKChAVFTUqzx1g2BPljwxL/LCuaR107vhZsiQIbhy5Qpu3bqFzMxMXLt2DYMGDTJkbAZ1//59\n/OMf/+CvGolkRBRFDBo0CHfu3MG6deukSQKSkpIwb948ODs7w9nZGVevXkVgYCAiIyNVHh8bG4se\nPXroNWXpwYMHkZmZqXdx+aLTp0/j8OHDGDJkCE6fPo2mTZsCeDZmrfIPUSKi8kKvgvHp06d4+vQp\nAKBKlSooLi7GsmXLcPDgQYMGZ0jffPMNvL290bt3b2OHQi+JPYzyVBp5GTFiBM6ePYtNmzbBzMxM\nWr5nzx789ddfOHnyJE6cOAEXFxcsWbIEI0eOlNbJy8tDfHy83pejY2Nj0bNnT1hZWaks37hxI+7f\nvw9RFHHkyBHMmzcPn376qco6oihi9OjR+OWXXyAIAjw9PZGSkoKCggLs27cPNWvWfPWDUMrYkyVP\nzIs8MS/a6VUwdunSRbo0lJubi2bNmmH8+PHw9fVFbGysQQM0hJSUFKxYsQILFiwwdihE9P8yMjKw\nZMkSnDx5EtWqVZPGQVy9ejXs7e3h5OQEJycnVK1aFSYmJrCzs1Mp9jZs2AA7OzuNH/heXl5YvXq1\ndDs/Px/x8fFql6MB4LfffkPt2rVhY2OD/v3747vvvkNwcLDKOjExMfD29paG4unevTtcXFzg5OSE\n+/fvY+jQoaV0VIiI5EEQtY0f8ZwqVapgz549aNiwIeLi4hAREYFTp05h5cqVmD17dpm6/FJQUIDG\njRujR48emDJlCgBAoVDg+++/l24/TxAELD66+E2HSSU4d/QczzLK0Lmj52D+0Bw/TfjJ2KHQc/bu\n3cuzJjLEvMiLIAgQRbFc5EX5XEqbXmcYc3NzYWdnBwDYtWsXunXrhooVK8Lf3x8XL14s9aAMaebM\nmXjy5AkmTZpk7FCIiIhIBjiXtG4VdK8C1KhRAykpKfjkk0+wc+dOaf7oe/fu6dVcLhdXrlzBTz/9\nhOXLlyMvL09l0PH8/Hw8fPgQ1tbWaoPvRodFw9HFEQBgUckCNerWkM5wKX8Zyttv9raSXOLh7bqo\n61MX+5fsV/kLXfmLQ9427m0lucTD237w8/OTVTxv++3w8PAy+35R/r9yClND0euS9OLFixEaGgor\nKyu4ubnh2LFjMDExwdy5c7Fx40YkJSUZNMjSsnfvXgQEBJS4zokTJ1TmoOUlaSL9ZezJ4CVpIiIj\nMuol6WHDhuHw4cOIiorCwYMHpaEuatasiR9//LHUgzKUxo0bY+/evSr/kpOTAQDBwcHYu3evrH7d\nSJpxHEZ5Yl7k6cWzJiQPzIs8MS/a6XVJGng2tpiPj490u7CwEB9//LFBgjIUW1tbtGnTRuN9bm5u\nWu8jIiIiepvpdYZx7ty5WLdunXR74MCBMDc3R506dXDuHM8q0JvFX0jLE/MiT8p+J5IX5kWemBft\n9CoY582bB0fHZz/62L9/P+Lj47Fq1So0btwYX3/9tUEDfBOKi4s1DqlDRERE5R/nktZNr4Lxxo0b\n8PT0BABs3rwZPXv2RO/evREeHo7Dhw8bNECiF7FXTp6YF3liT5Y8MS/ywrmkddOrYLSxscGtW7cA\nALt370bbtm0BABUqVEB+fr7hoiMiIiIio9PrRy/t27fHkCFD0KRJE1y8eBGdOnUCAPz999/w8PAw\naIBEL2KvnDzV9amLjD0Zxg6DXsCeLHliXuSJedFOrzOM8+fPx4cffoisrCysXbsWDg4OAIDU1FR8\n/vnnBg2QiIiIiIxLr4G732YcuFt+OJe0PHEuaXnaWw7mxi2PmBd54VzSuul1hhEAbt68icjISIwY\nMQJZWVkAgJSUFKSlpZV6UERERERvCueS1k2vM4ypqakICAiAp6cn/vzzT5w7dw6enp4ICwvDhQsX\nsGrVqjcRq1HwDCOR/jg1IBGRcRn1DOPXX3+NMWPG4Pjx4zA3N5eWd+zYESkpKaUeFBERERHJh14F\n47FjxxASEqK2vFq1atJwO0RvCsf7kyfmRZ44rpw8MS/yxLxop1fBaGFhgXv37qktP3fuHJycnEo9\nKCIiIiKSD70Kxk8//RSTJ09WGaQ7LS0NEyZMQI8ePQwWHJEm/IW0PDEv8lTWf/FZXjEv8sS8aKdX\nwRgZGYn79++jSpUqePz4MT788EPUqlULlStXxtSpUw0dIxEREZHBcC5p3fQqGG1tbXHgwAFs3LgR\n06dPx5gxY7Bz507s378flSpVMnSMRCrYKydPzIs8sSdLnpgXeeFc0rrpNTUg8Oxn2gEBAQgICDBk\nPEREREQkM3qdYQwJCcGcOXPUls+ePRuDBw8u9aCISsJeOXliXuSJPVnyxLzIE/OinV4F444dO+Dv\n76+2PCAgAFu3bi31oIiIiIhIPvQqGB88eKCxV9HS0lLjcDtEhsReOXliXuSJPVnyxLzIE/OinV4F\nY+3atbFlyxa15du2bUOtWrVKPSgiIiKiN4VzSeum11zSsbGxGD58OMaOHYu2bdsCABITE/Hzzz9j\nwYIFGDhwoMEDNRbOJU2kP84lTURkXIaaS1qvX0n3798f+fn5+PHHHzF9+nQAQPXq1TFnzpxyXSwS\nERERkZ6XpAFg2LBhuHbtGm7evImbN2/i6tWrGD58uCFjI9KIvXLyxLzIE3uy5Il5kSfmRTu9x2EE\ngMuXL+Pvv/+GIAioV68ePD09DRUXEREREcmEXj2M2dnZGDhwINavXw+F4tlJyeLiYvTo0QNRUVGw\ntrY2eKDGIggCJs6YaOwwiMoEJxsnjBk+xthhEBG9tQzVw6hXwThgwAAcOnQIS5YsQYsWLQAAhw4d\nwrBhw9CqVStERUWVemByYagDT0RERPIQHh5ebuaTNlTdolcP46ZNm7B06VL4+vrC1NQUpqam8PPz\nw9KlS7Fhw4ZSD4qoJOwxkSfmRZ6YF3liXuSFc0nrplfBmJeXBwcHB7Xl9vb2yM/PL/WgiIiIiEg+\n9Lok/dFHH8HGxgYrVqyAlZUVACA3Nxf9+vVDdnY2EhMTDR6osfCSNBERUflWnr7rjdrDePr0aXTo\n0AGPHz9Go0aNIIoiTp8+DUtLS+zcuRNeXl6lHphclKcXEREREakrT9/1Ru1h9Pb2xoULFxAZGYmm\nTZvCx8cHkZGRuHjxYrkuFkme2GMiT8yLPDEv8sS8yBPzop3OcRgLCgrg6uqKPXv2YMiQIW8iJiIi\nIqI3hnNJ66bXJel33nkHu3btQv369d9ETLJSnk5TExERUflm1EvSo0ePRkREBAoLC0s9ACIiIiKS\nN70KxpSUFGzcuBHvvPMO2rZti08++UT617VrV0PHSKSCPSbyxLzIE/MiT8yLPDEv2uk1l7SDgwO6\nd++u8T5BEEo1ICIiIiKSF716GN9m7GEkIiKissJQdYteZxiVLl26hDNnzgAA6tWrh5o1a5Z6QHI0\naeYkY4dAVG442ThhzPAxxg6DiEhSnuaSNhS9zjDevXsXAwcOxObNm6FQPGt7LC4uxscff4zo6GiN\n0waWF4IgYPHRxcYOg55z7ug51PWpa+ww6AX65iVjTwZ+mvDTG4iIgGc9WX5+fsYOg17AvMiL8qxc\neciLUX8lPXjwYFy6dAkHDhxAXl4e8vLycODAAaSlpWHw4MGlHhQRERERyYdeZxgtLS2RmJiIli1b\nqiw/fPgw2rZti8ePHxssQGPjGUai0sUzjEQkN+Xp9wpGPcPo6OgIKysrteWWlpZwdHQs9aCIiIiI\nSD70Khh/+OEHjB07FteuXZOWXbt2Df/4xz/www8/GCw4Ik3OHT1n7BBIA+ZFnjiunDwxL/LEvGin\n16+k586di/T0dLi7u6N69eoAgOvXr8PCwgK3b9/G3LlzATw7DXrq1CnDRUtERERUyjiXtG56FYw9\nevTQa2McxJveBP5CWp6YF3kq67/4LK+YF3lRDqnDvGinV8HIsYmIiIiI3l569TASyQl75eSJeZEn\n9mTJE/MiT8yLdiwYiYiIiKhEnEtaB47DSFS6OA4jEZHhGHUcRiIiIqLyir/V0E1rwWhiYoLbt28D\nAAYOHIjs7Ow3FhRRSdgrJ0/MizyxJ0uemBd5mTx5MgDmpSRaC0YLCwvk5OQAAGJiYpCfn//GgiIi\nIp2VIUAAACAASURBVCIi+dA6rE7Lli3RrVs3NGnSBAAwZswYWFhYqKwjiiIEQUBUVJRhoyR6Dsf7\nkyfmRZ44rpw8MS/yxLxop7VgjIuLw6xZs3Dx4kUAwN27d2FqaqoyOLeyYCQiIiKi8kvrJelq1aph\n1qxZ2LBhA1xdXbFq1Sps2bIFmzdvlv4pbxO9SeyVk6c3kZeCggIMGjQI7u7usLGxQePGjbFjxw4A\nwN9//w0fHx/Y29ujcuXKaNWqFVJSUqTHdurUCdbW1tI/MzMzNGzYUON+Vq5cqbKulZUVFAoFjh8/\nLq1z7NgxtGnTBtbW1qhWrRrmzZsHACgqKkKfPn1gZ2eHTp06Sa09ADBt2jTMmTPHEIdGK/ZkyRPz\nIk/Mi3Z6/Uo6PT0djo6Oho6FiKhERUVFcHV1xf79+5GdnY2pU6ciMDAQGRkZqF69OuLj43H37l3c\nv38fffr0Qc+ePaXHbt++HTk5OdK/li1bIjAwUON++vbtq7LuwoULUbNmTTRu3BgAkJWVhU6dOmHE\niBG4d+8eLl26hPbt2wMA1q9fDxMTE9y9exe2trZYsmQJACAtLQ2bN2/GmDFjDHyUiOhlcS5p3fQe\nVmfLli1o3bo1HBwc4OjoCF9fX2zdutWQsRFpxF45eXoTebG0tERYWBhcXV0BAF26dIGHhweOHTsG\nW1tbeHh4QBAEPH36FAqFAs7Ozhq3k56ejgMHDqBfv3567TcmJkZl3dmzZ6Njx44ICgpCxYoVYWVl\nhXfffVfatq+vLxQKBfz8/HD58mUAwJdffonZs2dDoXizo5mxJ0uemBd54VzSuun1ybVs2TJ0794d\ntWrVwowZMzB9+nR4eHigW7duWL58uaFjJCLS6NatWzh//jwaNGggLatcuTIsLCwwc+ZMrF27VuPj\n4uLi0KZNG6nwLElGRoZacfnHH3/Azs4OrVq1QtWqVdG1a1dcvXoVAODl5YWkpCQ8efIEycnJ8PLy\nQkJCApycnNCiRYvXfMZERMahV8E4Y8YMzJ49G9HR0Rg8eDAGDx6MmJgY/Otf/8KMGTMMHWOp2rlz\nJwICAuDs7Axzc3PUqFEDvXv3xpkzZ4wdGumJPYzy9KbzUlhYiL59+yIkJAR16tSRlj948AAPHz5E\nnz590KtXL40zHsTFxSEkJESv/SiLSzc3N2nZ1atXERsbi3nz5uHKlSvw8PBAUFAQAKBz587w8PBA\n8+bNYWdnh969e2PKlCmYOXMmJk2aBF9fX4waNQqFhYWvdwD0xJ4seWJe5Il50U6vgvHKlSvo2LGj\n2vKOHTsiPT29tGMyqPv376NZs2ZYsGABdu/ejYiICPz111/44IMPpDMERCRvxcXFCA4Ohrm5OebP\nn692v6WlJaZPn47z58/j9OnTKvelpKTg1q1bKv2NJYmLi0P//v3Vtt+9e3c0bdoUZmZmCAsLw6FD\nh6QfuERERODkyZP49ddfERERgREjRuCPP/5Aamoq9u3bh4KCAg5HRkRlil4FY40aNbBr1y615bt3\n71b5q7ss6NOnD2bMmIHu3bujdevW+OKLL7B+/Xrk5ORovXxF8sIeRnl6U3kRRRGDBg3CnTt3sG7d\nOpiYmGhc7+nTpyguLoalpaXK8tjYWPTo0UNtuSYHDx5EZmamWnGp7dfVLzp9+jQOHz6MIUOG4PTp\n02jatCkAwMfHB6dOndJrG6+LPVnyxLzIE/OinV4F4/jx4/HVV19h8ODBiI6ORnR0NAYNGoSvvvoK\n48aNM3SMBmdvbw8AWr94iEg+RowYgbNnz2LTpk0wMzOTlicmJuLEiRN4+vQpsrOz8Y9//AN169ZF\nrVq1pHXy8vIQHx+v9+Xo2NhY9OzZE1ZWVirLBwwYgISEBJw8eRKFhYX48ccf0bp1a1hbW0vriKKI\n0aNH45dffoEgCPD09ERKSgoKCgqwb98+1KxZ8/UOBBGVGs4lrZteBeOwYcPw22+/4cyZMxg3bhzG\njRuHc+fOIT4+HsOGDTN0jAbx9OlTFBQU4MKFCxg2bBiqVq2KPn36GDss0gN7GOXpTeQlIyMDS5Ys\nwcmTJ1GtWjVpnMRVq1bhwYMHCAoKQuXKlVG3bl3cuXMHmzZtUnn8hg0bYGdnp/EsgpeXF1avXi3d\nzs/PR3x8vNrlaADw9/fHtGnT0KVLF1StWhWXL1/GqlWrVNaJiYmBt7e3NBRP9+7d4eLiAicnJ9y/\nfx9Dhw4thSOiG3uy5Il5kRfOJa2bIGrqCH8L+Pj44NixYwAANzc3bN26FfXr11dbTxAELD66+E2H\nRyU4d/QcL0vL0P+1d+dxVdX5/8Bf5yoICAgpICAi4C6oCDlp7pOm5JKaS5qKmlt9zZrMMiaFHFya\nEXNpcsnUxiWdxFzGVFJBEZVwRQwtA1FUFGUUcGH7/P7oxx2vcBeNy/3ce1/Px4NHnOWe8768vfHm\nc97nfAzNy+X9lxE9I7oaIiLg91+AvMwmH+ZFLoqiQAhhEXkpfy9VflxrLRjT09ORn5+PS5cu4R//\n+AdycnKQmJhYoSeTBSNR1WLBSESyMVaRZQosGI3o7t27aNSoEYYPH44vv/xSY5uiKHjhlRdQz+v3\nmW7sHe3h08xHPZJSfhmOy1zmsmHLOSdzsH7FegD/u/xT/hc9l7nMZS6bYllRFBw8eFCaeJ5mufz7\n8qfWrFu3jgWjMZXPQfvk3eAcYZQPL0nLiZek5RRvAZfYLBHzIhdektaveueoklROTg7S09N51yIR\nEZEV4lzS+ukdYSwqKkLnzp3xzTffoFkz8x/VGThwIEJCQhAUFARnZ2dcvHgRixYtws2bN5GcnKzx\nCA6AI4xEVY0jjERExmOsEcaa+nawtbVFRkYGFEWp8pObQocOHbBlyxYsXLgQRUVF8PHxQffu3TFz\n5kyD5pUlIiIisjYGXZIePXo0Vq1aZexYqsWMGTOQkpKCvLw8FBYWIj09HV9++SWLRTPC5zDKiXmR\n0+ON8SQP5kVOzIt2ekcYAeD+/ftYv3494uLiEBISop71QAgBRVGwZMkSowZJRERERKZj0F3ST94x\nVH55urxgLL8V3RKxh5GoarGHkYjIeEzWwwhwiJaIiIgsV2RkJOeT1uOpHquTm5uL48eP4+HDh8aK\nh0gv9srJiXmRE//glxPzIhfOJa2fQQVjfn4+hgwZAnd3d3Ts2BHXrl0DAEyePJkVOREREZGFM6hg\n/PDDD5GdnY2TJ0/C3t5evb5v376IjY01WnBEleEsL3JiXuRk7rNWWCrmRU7Mi3YG9TDu2LEDsbGx\naNu2rcbzGJs3b47ffvvNaMERERERkekZNMKYl5eHunXrVlifn5+PGjVqVHlQRLqwV05OzIuc2JMl\nJ+ZFTsyLdgYVjKGhodixY0eF9StXrkTHjh2rPCgiIiKi6sK5pPUz6DmMSUlJePnllzFs2DCsX78e\nEyZMwLlz55CcnIxDhw4hJCSkOmI1CT6Hkahq8TmMRETGY6znMBo0wtixY0ckJSWhqKgIAQEB2L9/\nP7y9vXHs2DGLLhaJiIiI6CmewxgUFIRvvvkGaWlpOH/+PNavX4+goCBjxkZUKfbKyYl5kRN7suTE\nvMiJedHOoLukAeDBgwfYuHEjfv75ZwBAixYtMGLECI3H7BARERGR5TGoh/HkyZPo27cvHjx4gKCg\nIAghkJaWhlq1amHXrl0WfVmaPYxEVYs9jERExmPSHsaJEyeiU6dOuHr1Kg4dOoTDhw/jypUr6NKl\nCyZNmlTlQRERERFVF85ap59BBWNaWhpmz56N2rVrq9fVrl0bs2bNwrlz54wWHFFl2CsnJ+ZFTuzJ\nkhPzIhfOJa2fQQVjs2bN1PNHP+769eto1ozTgRERERFZMq09jHfu3FF/f/ToUUyfPh2zZs1Chw4d\n1Ouio6Mxf/589O3bt3qiNQH2MBJVLfYwEpFsjNX3ZwrGei9a75KuV69ehXUjR46ssG7AgAEoLS2t\n2qiIiIiISBpaC8YDBw5UZxxEBruQcgHNQtkKIRvmRU7x8fHo1q2bqcOgJzAvcmJetNNaMPIHRkRE\nRNaAc0nrZ9BzGAHg0aNHSEtLw82bN1FWVqaxLSwszCjByUBRFHy84GNTh0FkMdyd3TFt8jRTh0FE\nZJGM1cNoUMF44MABjBw5Ejk5OZVuf7KAtCSW1AhLREREls2kD+6eMmUKXnnlFWRkZKCwsBD379/X\n+CKqTnxOlpyYFzkxL3JiXuTEvGhn0FzS165dw8cffwxfX19jx0NEREREkjHokvTQoUPRv39/vPHG\nG9URk1R4SZqIiIjMhUl7GPPy8vD666+jefPmCAoKgo2Njcb20aNHV3lgsmDBSEREZNkiIyMtZj5p\nkxaMW7ZsQXh4OB4+fAgHBwcoiqKxPT8/v8oDkwULRvnwOVlyYl7kxLzIiXmRS/nvekvIi0lvepk+\nfTreeust5Ofno6CgAPn5+RpfRERERGS5DBphdHZ2xqlTpxAQEFAdMUmFI4xERESWzZJ+15t0hHHQ\noEGIi4ur8pMTERERkfwMeqxOQEAAIiIicPjwYbRu3brCTS9/+ctfjBIcUWUsocfEEjEvcmJe5MS8\nyIl50c6ggnH16tVwcnLCkSNHkJSUVGE7C0YiIiIyV5xLWj+D55K2VpbU10BERESWzaQ9jERERERk\nvQy6JD116tQKz1583JIlS6osIBlFfBZh6hDoMZcvXYZvAKeplA3zIqfqyIu7szumTZ5m1HNYGvbK\nyYl50c6ggjE1NVWjYCwqKkJ6ejpKS0sRHBxstOBk4ftn/hKUycM6D+EbypzIhnmRU3Xk5fL+y0Y9\nPhGZnkEFY3x8fIV1Dx8+xLhx49ClS5eqjolIp2ahzUwdAlWCeZET8yInjmLJiXnR7pl7GO3s7BAR\nEYHo6OiqjIeIiIioWlnKPNLG9IduesnNzeXUgFTtLqRcMHUIVAnmRU7Mi5wqu3JHphMVFQWAedHF\noEvSCxcu1OhhFELg2rVr2LBhA8LCwowWHBERERGZnkHPYWzUqJFGwahSqeDm5oYePXpg5syZcHJy\nMmqQpqQoClakrDB1GERE0rq8/zKiZ7A9icyXJT1z2VjvxaARxszMzCo/MRERERGZBz64m8wOe7Lk\nxLzIiXmRE3vl5MS8aGfQCKMQAps3b8b+/ftx8+ZNlJWVqbcpioIdO3YYLUAiIiIiY+Jc0voZ1MP4\nwQcf4PPPP0f37t3h6emp0c+oKArWrFlj1CBNiT2MRES6sYeRSB4m7WH85ptvsHHjRgwZMqTKAyAi\nIiIiuRnUw1hWVmYVUwCSeWBPlpyYFzkxL3Jir5ycmBftDCoYJ0yYgPXr1xs7FiIiIiKSkEGXpO/e\nvYsNGzYgLi4OrVu3ho2NDYDfb4ZRFAVLliwxapBEj+PcuHJiXuTEvMiJcxbLiXnRzqCCMS0tDW3b\ntgUApKenq9eXF4xERERE5ioyMpLzSeth0CXp+Ph49dfBgwfVX+XLRNWJPVlyYl7kJHteli1bhtDQ\nUNjZ2WHs2LHq9ZmZmVCpVHByclJ/RUf/707sRYsWISAgAM7OzvDw8MDYsWORn5+v9Tz379/HW2+9\nBTc3N7i4uKBr164a20+ePIkuXbrAyckJ9evXV185KykpwfDhw+Hq6oo+ffponGPu3LlYtGjRM71v\n9srJhXNJ68cHdxMRkcl4e3vjk08+wbhx4yrdfu/ePeTn5yM/Px8RERHq9QMGDEBKSgru3buH9PR0\nZGVlaRSUT5o4cSL++9//Ij09HXl5efj888/V23Jzc9GnTx9MmTIFd+7cwaVLl9CrVy8AQGxsLGrU\nqIHbt2+jTp06WLlyJQAgIyMDO3fuxLRp06rix0AkPYMuSRPJhD1ZcmJe5CR7XgYOHAgASElJwdWr\nVytsLysrQ40aNSqs9/f319hHpVLB09Oz0nOkp6dj586dyM7OhqOjIwBoPPkjJiYGvXv3xuuvvw4A\nsLGxQfPmzQH8PtLZtWtXqFQqdOvWDampqQCAd955BzExMVCpnm3chb1ycmJetOMIIxERmZy2Bw37\n+vrCx8cH48aNw+3btzW2bdy4EXXq1IGbmxvc3Ny0jvYlJyfD19cXs2bNgpubG1q3bo3Y2Fj19uPH\nj8PV1RUvvvgiPDw80L9/f1y5cgUAEBgYiAMHDuDRo0c4ePAgAgMDsW3bNri7u6NDhw5V9O6J5MeC\nkcyO7D1Z1op5kZO55OXJGyjd3NyQkpKCrKwsnDhxAvn5+Rg5cqTGPiNGjMDdu3dx8eJF/Pzzz1r7\nCa9evYpz587BxcUF169fx7JlyzBmzBhcuPD7z+bKlStYt24dlixZgqysLPj5+alHG8PCwuDn54f2\n7dvD1dUVw4YNw6efforPPvsMERER6Nq1K95++20UFxc/1ftlr5ycmBftrK5g/O677/Dqq6+iYcOG\ncHBwQPPmzfHxxx+joKDA1KEREVmtJ0cYa9eujXbt2kGlUsHd3R3Lli3Dvn37UFhYWOG1jRs3xkcf\nfYRvvvmm0mPb29vDxsYGf/3rX1GzZk106dIF3bt3x969ewEADg4OGDRoEEJCQlCrVi3Mnj0bSUlJ\n6htc5s2bhzNnzmD58uWYN28epkyZguPHj+PEiRNISEhAUVERvv766yr+iVB14lzS+lldwbhw4ULY\n2Nhg/vz52LNnD6ZMmYIvv/wSPXv2NMrci1T1ZO/JslbMi5zMJS+GPqKtrKys0vXFxcVwcHCodFvr\n1q0BVCxKy89Zvl2f1NRUHD16FBMmTEBqaipCQkIAAKGhoTh79qxBxyjHXjm5lD9Sh3nRzuoKxl27\nduHf//43RowYgS5dumDatGlYsmQJjh8/zqFoIqJqVlpaiocPH6KkpASlpaV49OgRSkpKkJycjAsX\nLqCsrAy3b9/GO++8g+7du8PJyQkA8NVXX+HWrVsAgPPnz2P+/PkYPHhwpefo2rUrGjZsiHnz5qGk\npARHjhxBfHw8Xn75ZQDA2LFjsW3bNpw5cwbFxcWYM2cOOnfurD4X8HuxOXXqVCxduhSKosDf3x+J\niYkoKipCQkICAgICjPyTIjItqysY69atW2FdaGgoAODatWvVHQ49A3PpybI2zIucZM/LnDlz4ODg\ngAULFmD9+vWwt7fH3Llz8dtvv6FPnz5wdnZGUFAQ7O3tsWnTJvXrkpKSEBQUBCcnJwwcOBCjR4/G\ne++9p94eGBio3r9mzZrYvn07du/eDRcXF0yaNAn/+te/0LRpUwBA9+7dMXfuXLzyyivw8PDAb7/9\nho0bN2rEuXbtWgQFBanvrh40aBC8vLzg7u6OvLw8TJw48aneNwco5MS8aKcIXofF8uXL8dZbbyEl\nJQXt2rXT2KYoClakrDBRZFSZCykXzOYymzVhXuRUHXm5vP8yomdofwYiVRQfH8/LnxKyhLwoimKU\nFjurLxizs7MRHByM4OBgdQP041gwEhHpxoKRSB7GKhit+sHdBQUFGDBgAGxtbbFmzRqt+62ZvQb1\nvOoBAOwd7eHTzEf9F3v55R4uc5nLXLbWZTvYAfjf5bzyERouc9lcliMjI9XrZYjnaZbLv8/MzIQx\nWe0I44MHDxAWFobU1FQkJCSgVatWle7HEUb58NKnnJgXOfGStJws4dKnJSkflbOEvHCEsQoVFxfj\ntddew8mTJxEXF6e1WCQiIiIiKywYy8rKMHLkSMTHx2PXrl1o3769qUOip8RRLDkxL3JiXuRk7qNY\nlop50c7qCsa3334b3333HSIiImBvb49jx46pt/n4+MDb29uE0RERERHJx+qew7hnzx4oioLo6Gh0\n7NhR42v16tWmDo8MIPtz5awV8yIn5kVOfN6fnJgX7axuhDEjI8PUIRAREZFEOJe0flZ7l7SheJc0\nEZFuvEuaSB7Gukva6i5JExEREdHTYcFIZoc9WXJiXuTEvMiJvXJyYl60Y8FIRERERDqxh1EP9jAS\nEenGHkYiebCHkYiIiMgIIiMjTR2C9FgwktlhT5acmBc5MS9yYq+cXKKiogAwL7qwYCQiIiIindjD\nqAd7GImIdGMPI5k7Y/X9mQJ7GImIiIjIJFgwktlhT5acmBc5MS9yYq+cnJgX7VgwEhERkVXjXNL6\nsYdRD/YwEhHpxh5GInmwh5GIiIiITIIFI5kd9mTJiXmRE/MiJ/bKyYl50Y4FIxERERHpxB5GPdjD\nSESkG3sYieTBHkYiIiIiI+Bc0vqxYCSzw54sOTEvcmJe5MReOblwLmn9WDASERERkU7sYdSDPYxE\nRLqxh5HMHeeS1q9mlR/RAl3ef9nUIRARScvd2d3UIRCRkXGEUQ9L+qvDUsTHx6Nbt26mDoOewLzI\niXmRE/Mil/Lf9ZaQF94lTURERGQEnEtaP44w6sERRiIiIjIXHGEkIiIiIpNgwUhmh8/JkhPzIifm\nRU7Mi5yYF+1YMBIRERGRTuxh1IM9jERERGQu2MNIREREZAScS1o/FoxkdthjIifmRU7Mi5yYF7lw\nLmn9WDASERERkU7sYdSDPYxERESWzZJ+17OHkYiIiIhMggUjmR32mMiJeZET8yIn5kVOzIt2NU0d\ngDmI+CzC1CHQYy5fuoy45DhTh0FPYF7kxLzIiXmRy8uvvGzqEKTHHkY9FEXBipQVpg6DiIiIjOTy\n/suInhFt6jCqBHsYiYiIiMgkWDCS2bmQcsHUIVAlmBc5MS9yYl7kxB5G7VgwEhEREZFOLBjJ7DQL\nbWbqEKgSzIucmBc5MS9y6tatm6lDkBYLRiIiIrJqh+IOmToE6bFgJLPD3h85MS9yYl7kxLzIJfHH\nRADsYdSFBSMRERER6cTnMOrB5zASERFZtkmhkziXtB4cYSQiIiIinVgwktlh74+cmBc5MS9yYl7k\nxB5G7VgwEhERkVXr9FInU4cgPfYw6sEeRiIiIsvGuaT14wgjEREREenEgpHMDnt/5MS8yIl5kRPz\nIif2MGrHgpGIiIjoGS1btgyhoaGws7PD2LFjNbbt378fzZs3R+3atdGjRw9kZWVpbP/www9Rr149\n1KtXDx999JHO8xh6LAAaxyopKcHw4cPh6uqKPn36ID8/X71t7ty5WLRokUHvkwUjmR3OwSon5kVO\nzIucmBc5Pctc0t7e3vjkk08wbtw4jfW5ubkYPHgwoqOjkZeXh9DQUAwbNky9fcWKFdi+fTvOnj2L\ns2fPYufOnVixovJ7Jp7mWAA0jhUbG4saNWrg9u3bqFOnDlauXAkAyMjIwM6dOzFt2jSD3icLRiIi\nIrJqf2Qu6YEDB2LAgAGoW7euxvrY2FgEBgZi8ODBsLW1RWRkJM6cOYOLFy8CANatW4fp06fDy8sL\nXl5emD59OtauXVvpOZ7mWAA0jpWZmYmuXbtCpVKhW7du+O233wAA77zzDmJiYqBSGVYKsmAks8Pe\nHzkxL3JiXuTEvMilKuaSfvLO5LS0NLRp00a97ODggMaNGyMtLQ0AcP78eY3trVu3Vm970h85VmBg\nIA4cOIBHjx7h4MGDCAwMxLZt2+Du7o4OHToY/P4sqmAMDw+Hn5/fU78uPj4eKpUKhw49+18YRERE\nZL0URdFYLiwshLOzs8Y6Z2dndQ9hQUEB6tSpo7GtoKCg0mP/kWOFhYXBz88P7du3h6urK4YNG4ZP\nP/0Un332GSIiItC1a1e8/fbbKC4u1vn+LKpgnDVrFr7//ntTh0FGxt4fOTEvcmJe5MS8yOlZehjL\nPTnC6OjoiHv37mmsu3v3LpycnCrdfvfuXTg6OlZ67D96rHnz5uHMmTNYvnw55s2bhylTpuD48eM4\nceIEEhISUFRUhK+//lrn+7OIgvHRo0cAAH9/f40hWSIiIqLq8OQIY6tWrXDmzBn1cmFhIS5duoRW\nrVqpt58+fVq9/cyZMwgMDKz02FV1rNTUVBw9ehQTJkxAamoqQkJCAAChoaHqG2a0qdaC8eLFixg4\ncCA8PDxgb28PX19fDB06FKWlpQCAW7duYfLkyWjQoAHs7OzQokULrFq1SuMYa9euhUqlwuHDhzFk\nyBC4urqqr8FXdkl69uzZaNeuHerUqQM3Nzf8+c9/xvHjx6vnDZNRsPdHTsyLnJgXOTEvcnqWHsbS\n0lI8fPgQJSUlKC0txaNHj1BaWoqBAwfi3LlziI2NxcOHDxEVFYW2bduiadOmAIDRo0cjJiYG165d\nQ3Z2NmJiYhAeHl7pOZ7mWAAqPZYQAlOnTsXSpUuhKAr8/f2RmJiIoqIiJCQkICAgQOf7rNaC8ZVX\nXsH169exfPly7Nu3D/Pnz4ednR2EELh37x46deqEPXv2ICoqCrt370a/fv0wZcoULFu2rMKxRo4c\niYCAAGzduhXz589Xr3+yws/Ozsa7776LHTt2YN26dXB3d0eXLl1w7tw5o79fIiIikt8fmUt6zpw5\ncHBwwIIFC7B+/XrY29sjOjoa9erVw9atWxEREYHnnnsOKSkp+Pbbb9WvmzRpEvr164egoCC0bt0a\n/fr1w8SJE9XbAwMDsWnTJgB4qmMBqHAs4PcBt6CgIAQHBwMABg0aBC8vL7i7uyMvL6/C/k+qtrmk\nc3Nz4e7ujh07dqBv374Vts+ZMwdz587FuXPnNKrciRMnYtu2bcjJyYFKpcLatWsxbtw4vPfee1i4\ncKHGMcLDw5GQkICMjIxKYygtLYUQAoGBgejduzc+//xzAL//RdGjRw/Ex8ejS5cuGq/hXNJERESW\njXNJ61dtI4z16tWDv78/PvzwQ3z11Vf45ZdfNLbv2bMHL7zwAho1aoSSkhL1V69evXD79m2cP39e\nY/+BAwcadN4ff/wR3bt3R7169WBjYwNbW1tcvHhR/ewiIiIiItKtZnWeLC4uDpGRkZg5cyZu374N\nPz8/fPDBB5g8eTJu3ryJS5cuwcbGpsLrFEXB7du3NdZ5enrqPd/JkycRFhaGPn364Ouvv4anpydU\nKhXefPNNPHz40OC418xeg3pev0+3Y+9oD59mPuo73Mr7ULhcfctXLlzBSyNfkiYeLv++/HhPgnjy\nNAAAFuBJREFUlgzxcJmfF5mX+XmRbzk+Ph6nT5/Gu+++q14G/nfntKzL5d9nZmbCmKrtkvSTzpw5\ng2XLlmH16tXYvXs3oqKiULNmTSxevLjS/Zs2bQpHR0f1Jelff/0V/v7+Gvs8eUk6IiICixcvxt27\nd1GjRg31fr6+vggICMCBAwcA8JK0ubmQcoGPpJAQ8yIn5kVOzItcyi9Jx8fH/6FH68jAWJekq3WE\n8XFt2rTBwoULsXr1aqSlpaF3795YunQpfHx84ObmViXnuH//foUpbw4cOIArV67ovRuI5MX/ycqJ\neZET8yIn5kVO5l4sGlO1FYxnz57FtGnTMHz4cAQEBKC0tBRr166FjY0NevTogYCAAGzevBmdO3fG\ne++9h6ZNm6KwsBDp6elITEx8pgdy9+nTB4sXL0Z4eDjCw8Nx8eJF/O1vf4O3t7dRqm8iIiIyP4fi\nDgEzTB2F3KrtphdPT0/4+voiJiYGAwYMwIgRI3Djxg3s2rULwcHBcHZ2RlJSEsLCwrBgwQL07t0b\n48ePx86dO9GjRw+NYz356JzH1z++rVevXliyZAmOHDmCfv36Ye3atfjXv/6Fxo0bVziGtmOSfB7v\n/SF5MC9yYl7kxLzIpSrmkrZ0JuthNBfsYZQPe3/kxLzIiXmRE/Mil0mhkyCEYA+jruOyYNSNBSMR\nEZFlKy8YLYHZP4eRiIiIiMwTC0YyO+z9kRPzIifmRU7Mi5zYw6gdC0YiIiKyan9kLmlrwR5GPdjD\nSEREZNk4l7R+HGEkIiIiIp1YMJLZYe+PnJgXOTEvcmJe5MQeRu1YMBIRERGRTiwYyezwYbdyYl7k\nxLzIiXmRk7k/tNuYWDASERGRVTsUd8jUIUiPBSOZHfb+yIl5kRPzIifmRS6cS1o/FoxEREREpBOf\nw6gHn8NIRERk2TiXtH4cYSQiIiIinVgwktlh74+cmBc5MS9yYl7kxB5G7VgwEhERkVXjXNL6sYdR\nD/YwEhERWTbOJa0fRxiJiIiISCcWjGR22PsjJ+ZFTsyLnJgXObGHUTsWjERERESkEwtGMjucg1VO\nzIucmBc5MS9y4lzS2rFgJCIiIqvGuaT1q2nqAMzB5f2XTR0CPebypcvwDfA1dRj0BOZFTsyLnJgX\nuTw+lzRHGSvHx+roYazb0+nZ8QMtJ+ZFTsyLnJgXuZT/rreEvBirbmHBqAcLRiIiIstmSb/r+RxG\nIiIiIjIJFoxkdvicLDkxL3JiXuTEvMiJedGOBSMRERFZtdmzZ5s6BOmxh1EPS+prICIiIsvGHkYi\nIiIiMgkWjGR22GMiJ+ZFTsyLnJgXOTEv2rFgJCIiIiKd2MOoB3sYiYiIyFywh5GIiIjICCIjI00d\ngvRYMJLZYY+JnJgXOTEvcmJe5BIVFQWAedGFBSMRERER6cQeRj3Yw0hERGTZLOl3PXsYiYiIiMgk\nWDCS2WGPiZyYFzkxL3JiXuTEvGjHgpGIiIisGueS1o89jHpYUl8DERERWTb2MBIRERGRSbBgJLPD\nHhM5MS9yYl7kxLzIiXnRjgUjEREREenEHkY92MNIRERE5oI9jERERERGwLmk9WPBSGaHPSZyYl7k\nxLzIiXmRC+eS1o8FIxERERHpxB5GPdjDSEREZNks6Xc9exiJiIiIyCRYMJLZYY+JnJgXOTEvcmJe\n5MS8aMeCkYiIiKwa55LWjz2MelhSXwMRERFZNvYwEhEREZFJsGAks8MeEzkxL3JiXuTEvMiJedGO\nBSMRERER6cQeRj3Yw0hERETmgj2MREREREbAuaT1Y8FIZoc9JnJiXuTEvMiJeZEL55LWjwUjmZ3T\np0+bOgSqBPMiJ+ZFTsyLnJgX7Vgwktn573//a+oQqBLMi5yYFzkxL3JiXrRjwUhEREREOrFgJLOT\nmZlp6hCoEsyLnJgXOTEvcmJetONjdfRo27Ytzpw5Y+owiIiIiPTq2rWrUW7eYcFIRERERDrxkjQR\nERER6cSCkYiIiIh0YsFIRERERDqxYNRiz549aN68OZo0aYIFCxaYOhz6/xo1aoTWrVsjODgY7du3\nN3U4VmvcuHHw8PBAUFCQet2dO3fQs2dPNG3aFL169eLzzEygsrxERkaiQYMGCA4ORnBwMPbs2WPC\nCK3PlStX0L17d7Rq1QqBgYFYsmQJAH5eTE1bXvh50Y43vVSitLQUzZo1w48//ghvb288//zz2LRp\nE1q0aGHq0Kyen58fTpw4geeee87UoVi1w4cPw9HREaNHj0ZqaioAYMaMGahXrx5mzJiBBQsWIC8v\nD/PnzzdxpNalsrxERUXByckJf/nLX0wcnXW6ceMGbty4gbZt26KgoAAhISH4/vvvsWbNGn5eTEhb\nXrZs2cLPixYcYaxEcnIyGjdujEaNGsHGxgbDhw/H9u3bTR0W/X/8G8f0OnfuDFdXV411O3bswJgx\nYwAAY8aMwffff2+K0KxaZXkB+Jkxpfr166Nt27YAAEdHR7Ro0QLZ2dn8vJiYtrwA/Lxow4KxEtnZ\n2fDx8VEvN2jQQP0PiUxLURS89NJLCA0NxapVq0wdDj0mJycHHh4eAAAPDw/k5OSYOCIqt3TpUrRp\n0wbjx4/npU8TyszMxKlTp/CnP/2JnxeJlOflhRdeAMDPizYsGCuhKIqpQyAtjhw5glOnTuGHH37A\nF198gcOHD5s6JKqEoij8HEliypQpyMjIwOnTp+Hp6Yn333/f1CFZpYKCAgwePBiLFy+Gk5OTxjZ+\nXkynoKAAr732GhYvXgxHR0d+XnRgwVgJb29vXLlyRb185coVNGjQwIQRUTlPT08AgJubGwYOHIjk\n5GQTR0TlPDw8cOPGDQDA9evX4e7ubuKICADc3d3VBcmbb77Jz4wJFBcXY/DgwRg1ahReffVVAPy8\nyKA8L2+88YY6L/y8aMeCsRKhoaH45ZdfkJmZiaKiImzevBn9+/c3dVhW7/79+8jPzwcAFBYWYt++\nfRp3g5Jp9e/fH+vWrQMArFu3Tv0/YDKt69evq7/ftm0bPzPVTAiB8ePHo2XLlnj33XfV6/l5MS1t\neeHnRTveJa3FDz/8gHfffRelpaUYP348Zs6caeqQrF5GRgYGDhwIACgpKcHIkSOZFxN5/fXXkZCQ\ngNzcXHh4eODTTz/FgAEDMHToUGRlZaFRo0bYsmULXFxcTB2qVXkyL1FRUYiPj8fp06ehKAr8/Pyw\nYsUKde8cGV9iYiK6dOmC1q1bqy87z5s3D+3bt+fnxYQqy8vcuXOxadMmfl60YMFIRERERDrxkjQR\nERER6cSCkYiIiIh0YsFIRERERDqxYCQiIiIinVgwEhEREZFOLBiJiIiISCcWjERWKjMzEyqVCidP\nnqz2c69du7bC9GjWIjc3FyqVCocOHXrmY2zfvh1NmjSBjY0Nxo0bV4XRERFVjgUjkRXo1q0bpk6d\nqrGuYcOGuHHjBtq0aVPt8QwfPhwZGRnVfl5LMX78eAwZMgRZWVlYvHixqcPRa+XKlejevTtcXFyg\nUqmQlZVVYZ+8vDyMGjUKLi4ucHFxwejRo3H37l2NfbKystCvXz84OjrCzc0N06ZNQ3FxscY+qamp\n6Nq1KxwcHNCgQQPMmTOnwrkSEhIQEhICe3t7BAQEYMWKFVX7hoksEAtGIiulUqng7u6OGjVqVPu5\n7ezsUK9evWo/ryXIy8vDnTt30KtXL3h6ej7zSG1RUVEVR6bdgwcP0Lt3b0RFRWndZ8SIETh9+jT2\n7t2LPXv24OTJkxg1apR6e2lpKV555RUUFhYiMTERmzZtwnfffYf3339fvc+9e/fQs2dPeHp6IiUl\nBYsXL8bf//53xMTEqPfJyMhAWFgYOnXqhNOnT2PmzJmYOnUqYmNjjfPmiSyFICKLNmbMGKEoisbX\n5cuXRUZGhlAURZw4cUIIIcTBgweFoijihx9+EMHBwcLe3l507txZXL16Vezfv18EBQUJR0dH0a9f\nP3Hnzh2Nc3z99deiRYsWws7OTjRt2lQsWrRIlJWVaY1pzZo1wtHRUb08e/ZsERgYKDZt2iT8/f2F\nk5OTePXVV0Vubq7O9xYVFSV8fX1FrVq1RP369cXo0aM1ti9YsEAEBAQIe3t7ERQUJNavX6+xPTs7\nW4wYMULUrVtXODg4iLZt24qDBw+qty9fvlwEBAQIW1tb0bhxY7Fq1SqN1yuKIlauXClee+01Ubt2\nbeHv71/hHMnJyaJdu3bCzs5OBAcHi127dglFUURCQoIQQoiioiIxdepU4eXlJWrVqiV8fHzERx99\nVOn7Lc/R41/lx9m6dasIDAxUHyM6Olrjtb6+viIyMlKMHTtWuLi4iKFDh1Z6jjFjxoi+ffuKzz//\nXHh7ewtXV1cxduxYcf/+fS1ZMNxPP/2k/vf3uPPnzwtFUURSUpJ6XWJiolAURVy8eFEIIcTu3buF\nSqUSV69eVe+zfv16YWdnJ/Lz84UQQvzzn/8UderUEQ8fPlTv87e//U14e3url2fMmCGaNm2qcf43\n33xTdOjQ4Q+/PyJLxoKRyMLdvXtXdOzYUYwfP17k5OSInJwcUVpaqrVg/NOf/iQSExPF2bNnRWBg\noOjYsaPo3r27SE5OFikpKcLPz09MmzZNffyVK1cKT09PsXXrVpGZmSl27twp6tevL5YtW6Y1psoK\nRkdHRzFo0CCRmpoqjh49Knx9fcWkSZO0HuO7774Tzs7OYvfu3eLKlSsiJSVFfPHFF+rtH3/8sWje\nvLnYu3evyMzMFBs3bhS1a9cW//nPf4QQQhQUFIjGjRuLTp06icTERJGRkSG2b9+uLhhjY2OFjY2N\n+OKLL8Qvv/wili5dKmxsbMTOnTvV51AURTRo0EBs2LBBXLp0ScycOVPY2tqKrKwsIYQQ+fn5ws3N\nTQwdOlSkpaWJvXv3iubNm2sUev/4xz+Ej4+POHz4sLhy5YpISkoSa9eurfQ9FxUVqYurbdu2iZyc\nHFFUVCRSUlJEjRo1RGRkpPjll1/Ehg0bhKOjo1i6dKn6tb6+vsLZ2Vn8/e9/F5cuXRK//vprpecY\nM2aMqFOnjpg4caJIT08X+/btEy4uLmLevHnqfaKjo4Wjo6POr8TExArH1lYwrl69Wjg5OWmsKysr\nE46OjuqfxSeffCICAwM19rl586ZQFEXEx8cLIYQYNWqU6Nu3r8Y+ycnJQlEUkZmZKYQQonPnzuL/\n/u//NPbZsmWLsLGxESUlJZX+TIiIBSORVejWrZuYOnWqxjptBeO+ffvU+yxbtkwoiiJOnTqlXhcZ\nGanxi9vHx6fCqNqiRYtEy5YttcZTWcFoZ2cn7t27p14XHR0tGjdurPUYCxcuFM2aNRPFxcUVthUU\nFAh7e/sKRcu0adNEWFiYEOL3QtfJyUncvn270uOXF9mPCw8PF506dVIvK4oiPv74Y/VySUmJcHBw\nEBs2bBBCCLFixQrh4uIiCgsL1fusX79eo2B85513xJ///Get7/NJt27d0ni9EEKMGDGiwjEiIyNF\ngwYN1Mu+vr6if//+eo8/ZswY0bBhQ40R4gkTJoiXXnpJvXznzh1x6dIlnV8PHjyocGxtBWN0dLTw\n9/evsL+/v7+YP3++OoYn32NZWZmoWbOm+Pbbb4UQQvTs2bNCzi5fviwURRHHjh0TQgjRtGlTMWfO\nHI19EhIShKIo4saNG3p/PkTWqqapL4kTkVxat26t/t7d3R0AEBQUpLHu5s2bAIBbt27h6tWrmDhx\nIiZPnqzep6Sk5KnP6+vrq9GP5+npqT5PZYYOHYolS5bAz88PL7/8Mnr37o3+/fvD1tYW58+fx8OH\nD/Hyyy9DURT1a4qLi+Hn5wcAOHXqFNq0aYPnnnuu0uOnp6fjzTff1Fj34osvYseOHRrrHv951ahR\nA25ubuq4f/75Z7Rp0wYODg7qfV544QWN14eHh6Nnz55o2rQpevXqhbCwMPTp00cjbn3S09PRt2/f\nCrFGRUWhoKAAjo6OUBQFoaGhBh2vZcuWGuf39PTE8ePH1cuurq5wdXU1OL6qIoTQuf1pfmZE9HRY\nMBKRBhsbG/X35b+AH78xRlEUlJWVAYD6vytWrEDHjh2r7LxPnqcyDRo0wIULF7B//378+OOPeP/9\n9xEVFYXjx4+rX7dr1y40bNhQ63n0FSCVebIo0Re3vnMEBwcjMzMTe/fuxf79+zFmzBi0adMGcXFx\nT1UAaTvP48eoXbu2QceqWVPzV8OT72nu3LmYN2+ezmPs2bMHL774okHnq1+/Pm7duqWxTgiBmzdv\non79+up9kpKSNPbJzc1FaWmpxj43btzQ2CcnJ0e9Tdc+NWvW5I1YRDrwLmkiK2Bra/tMo376eHh4\nwMvLC7/++iv8/f0rfBlbrVq1EBYWhpiYGPz0009IS0tDUlISWrVqhVq1aiEzM7NCTD4+PgCAdu3a\n4ezZs7h9+3alx27RogUSExM11iUmJqJVq1YGx9eyZUukpqbi/v376nXHjh2rsJ+joyMGDx6Mf/7z\nn/jPf/6DAwcO4NKlSwafp0WLFjhy5EiFWH18fAwuEh+nr1CdMmUKzpw5o/MrJCTE4PN16NABBQUF\nOHr0qHrd0aNHUVhYqP5DpGPHjvj555+RnZ2t3icuLg61atVSn6tDhw44fPgwHj16pLGPt7c3fH19\n1fvExcVpnD8uLg7PP/+8SZ4YQGQuOMJIZAUaNWqE5ORkXL58GbVr10bdunWr7NhRUVGYOnUqXFxc\n0KdPHxQXF+PkyZO4du0aPvrooyo7z5PWrl2L0tJStG/fHo6Ojti8eTNsbW3RpEkTODo6Yvr06Zg+\nfTqEEOjcuTMKCgpw7Ngx1KhRAxMmTMCIESMwf/58DBgwAPPnz4eXlxfOnTsHZ2dndOvWDR988AGG\nDBmCkJAQ9OzZE3v27MHGjRuxbds2g2McMWIEIiIiMG7cOMyaNQvZ2dmIjo7W2CcmJgZeXl5o06YN\nbGxssGHDBtSpUwcNGjQw+Dzvv/8+nn/+eURFReH111/HTz/9hJiYGL2jgNroGxV92kvSN27cwI0b\nN3Dx4kUAQFpaGu7cuQNfX1+4urqiRYsW6N27NyZNmoSVK1dCCIFJkyahX79+aNKkCQCgV69eaNWq\nFUaPHo2FCxciNzcXM2bMwMSJE+Ho6Ajg9593VFQUwsPD8de//hUXLlzAggULEBkZqY5l8uTJWLZs\nGd577z1MnDgRR44cwbp16/Dtt98+5U+JyMqYrn2SiKrLxYsXRYcOHYSDg4NQqVTqx+qoVCqNm15U\nKpXGTSD//ve/hUql0jjW8uXLhZubm8a6TZs2qR8d4+rqKjp37iw2b96sNZ41a9Zo3BUbGRkpgoKC\ndO7zpO+//1506NBBuLi4iNq1a4v27dur74Aut3TpUtGyZUtRq1Yt4ebmJnr16iV+/PFH9farV6+K\nYcOGCRcXF+Hg4CDatWuncTPJ8uXLRePGjYWNjY1o0qSJ+OqrrzSOryiK2Lp1q8a6Ro0aiYULF6qX\njx8/Ltq1aydq1aol2rZtK3bu3ClUKpX6PKtWrRLt2rUTTk5OwtnZWXTr1k0cPXpU6/u+deuWxuvL\nxcbGiqCgIGFraysaNmwo5s6dqzMubcLDw0W/fv001lWWn6cxe/Zs9WOAVCqV+r/r1q1T75OXlyfe\neOMN4ezsLJydncWoUaPE3bt3NY6TlZUl+vbtKxwcHETdunXFtGnTRFFRkcY+qampokuXLsLOzk54\neXmJTz/9tEI8CQkJ6pz4+/uLFStWPPN7I7IWihDP0MRDRERERFaDPYxEREREpBMLRiIiIiLSiQUj\nEREREenEgpGIiIiIdGLBSEREREQ6sWAkIiIiIp1YMBIRERGRTiwYiYiIiEin/wdr/eoLv1plMAAA\nAABJRU5ErkJggg==\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10f1dd160>"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"Python version : 3.4.1\n",
|
|
"compiler : GCC 4.2.1 (Apple Inc. build 5577)\n",
|
|
"\n",
|
|
"system : Darwin\n",
|
|
"release : 13.2.0\n",
|
|
"machine : x86_64\n",
|
|
"processor : i386\n",
|
|
"CPU count : 4\n",
|
|
"interpreter: 64bit\n",
|
|
"\n",
|
|
"\n",
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 26
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 1,
|
|
"metadata": {},
|
|
"source": [
|
|
"Conclusion"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"We can see that we could speed up the density estimations for our Parzen-window function if we submitted them in parallel. However, on my particular machine, the submission of 6 parallel 6 processes doesn't lead to a further performance improvement, which makes sense for a 4-core CPU. \n",
|
|
"We also notice that there was a significant performance increase when we were using 3 instead of only 2 processes in parallel. However, the performance increase was less significant when we moved up to 4 parallel processes, respectively. \n",
|
|
"This can be attributed to the fact that in this case, the CPU consists of only 4 cores, and system processes, such as the operating system, are also running in the background. Thus, the fourth core simply does not have enough capacity left to further increase the performance of the fourth process to a large extend. And we also have to keep in mind that every additional process comes with an additional overhead for inter-process communication. \n",
|
|
"\n",
|
|
"Also, an improvement due to parallel processing only makes sense if our tasks are \"CPU-bound\" where the majority of the task is spent in the CPU in contrast to I/O bound tasks, i.e., tasks that are processing data from a disk. "
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": []
|
|
}
|
|
],
|
|
"metadata": {}
|
|
}
|
|
]
|
|
} |