mirror of
https://github.com/rasbt/python_reference.git
synced 2024-11-24 04:21:15 +00:00
2475 lines
630 KiB
Plaintext
2475 lines
630 KiB
Plaintext
{
|
|
"metadata": {
|
|
"name": "",
|
|
"signature": "sha256:12829b0c696b932be7039bcfd54490f1918f4155c72cd73b7fcfe1b46387decb"
|
|
},
|
|
"nbformat": 3,
|
|
"nbformat_minor": 0,
|
|
"worksheets": [
|
|
{
|
|
"cells": [
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[Sebastian Raschka](http://www.sebastianraschka.com) \n",
|
|
"last updated: 05/06/2014\n",
|
|
"\n",
|
|
"- [Link to this IPython Notebook on GitHub](https://github.com/rasbt/python_reference/blob/master/benchmarks/cython_least_squares.ipynb) \n",
|
|
"- [Link to the GitHub repository](https://github.com/rasbt/python_reference)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### The code in this notebook was executed in Python 3.4.0"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<hr>\n",
|
|
"I am really looking forward to your comments and suggestions to improve and \n",
|
|
"extend this little collection! Just send me a quick note \n",
|
|
"via Twitter: [@rasbt](https://twitter.com/rasbt) \n",
|
|
"or Email: [bluewoodtree@gmail.com](mailto:bluewoodtree@gmail.com)\n",
|
|
"<hr>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"# Implementing the least squares fit method for linear regression and speeding it up via Cython"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"sections\"></a>\n",
|
|
"<br>\n",
|
|
"<br>\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#Sections"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"- [Introduction](#introduction)\n",
|
|
"- [Least squares fit implementations](#implementations)\n",
|
|
"- [Generating sample data and benchmarking](#sample_data)\n",
|
|
"- [Compiling the Python code via Cython in the IPython notebook](#cython_nb)\n",
|
|
"- [Performance growth rates for different sample sizes](#sample_sizes)\n",
|
|
"- [Bonus: How to use Cython without the IPython magic](#cython_bonus)\n",
|
|
"- [Appendix I: Cython vs. Numba](#numba)\n",
|
|
"- [Appendix II: Cython with and without type declarations](#type_declarations)\n",
|
|
"- [Appendix III: Cython performance after replacing list comprehensions by explicit for loops](#explicit_loops)\n",
|
|
"- [Final Comparison: Cython vs. NumPy vs. SciPy for least squares fitting](#showdown)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"introduction\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
" \n",
|
|
"(Note that this chart just reflects my rather objective thoughts after experimenting with Cython, and it is not based on real numbers or benchmarks.)\n",
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Introduction"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Linear regression via the least squares method is the simplest approach to performing a regression analysis of a dependent and a explanatory variable. The objective is to find the best-fitting straight line through a set of points that minimizes the sum of the squared offsets from the line. \n",
|
|
"The offsets come in 2 different flavors: perpendicular and vertical - with respect to the line. \n",
|
|
"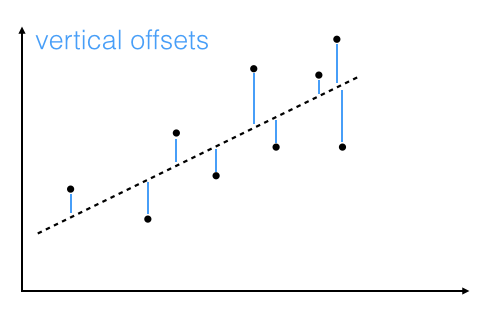 \n",
|
|
"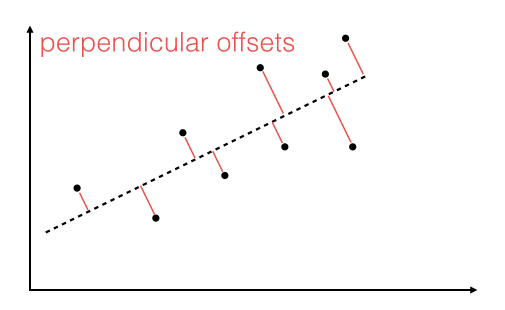 \n",
|
|
"\n",
|
|
"As Michael Burger summarizes it nicely in his article \"[Problems of Linear Least Square Regression - And Approaches to Handle Them](http://www.arsa-conf.com/archive/?vid=1&aid=2&kid=60101-220)\": \"the perpendicular offset method delivers a more precise result but is are more complicated to handle. Therefore normally the vertical offsets are used.\" \n",
|
|
"Here, we will also use the method of computing the vertical offsets.\n",
|
|
"\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In more mathematical terms, our goal is to compute the best fit to *n* points $(x_i, y_i)$ with $i=1,2,...n,$ via linear equation of the form \n",
|
|
"$f(x) = a\\cdot x + b$. \n",
|
|
"We further have to assume that the y-component is functionally dependent on the x-component. \n",
|
|
"In a cartesian coordinate system, $b$ is the intercept of the straight line with the y-axis, and $a$ is the slope of this line."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In order to obtain the parameters for the linear regression line for a set of multiple points, we can re-write the problem as matrix equation \n",
|
|
"$\\pmb X \\; \\pmb a = \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\Rightarrow\\Bigg[ \\begin{array}{cc}\n",
|
|
"x_1 & 1 \\\\\n",
|
|
"... & 1 \\\\\n",
|
|
"x_n & 1 \\end{array} \\Bigg]$\n",
|
|
"$\\bigg[ \\begin{array}{c}\n",
|
|
"a \\\\\n",
|
|
"b \\end{array} \\bigg]$\n",
|
|
"$=\\Bigg[ \\begin{array}{c}\n",
|
|
"y_1 \\\\\n",
|
|
"... \\\\\n",
|
|
"y_n \\end{array} \\Bigg]$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"With a little bit of calculus, we can rearrange the term in order to obtain the parameter vector $\\pmb a = [a\\;b]^T$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\Rightarrow \\pmb a = (\\pmb X^T \\; \\pmb X)^{-1} \\pmb X^T \\; \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"The more classic approach to obtain the slope parameter $a$ and y-axis intercept $b$ would be:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$a = \\frac{S_{x,y}}{\\sigma_{x}^{2}}\\quad$ (slope)\n",
|
|
"\n",
|
|
"\n",
|
|
"$b = \\bar{y} - a\\bar{x}\\quad$ (y-axis intercept)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"where \n",
|
|
"\n",
|
|
"\n",
|
|
"$S_{xy} = \\sum_{i=1}^{n} (x_i - \\bar{x})(y_i - \\bar{y})\\quad$ (covariance)\n",
|
|
"\n",
|
|
"\n",
|
|
"$\\sigma{_x}^{2} = \\sum_{i=1}^{n} (x_i - \\bar{x})^2\\quad$ (variance)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"implementations\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"## Least squares fit implementations"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 1. The matrix approach"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"First, let us implement the equation:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\pmb a = (\\pmb X^T \\; \\pmb X)^{-1} \\pmb X^T \\; \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"which I will refer to as the \"matrix approach\"."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import numpy as np\n",
|
|
"\n",
|
|
"def lin_lstsqr_mat(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 1
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 2. The classic approach"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Next, we will calculate the parameters separately, using standard library functions in Python only, which I will call the \"classic approach\"."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$a = \\frac{S_{x,y}}{\\sigma_{x}^{2}}\\quad$ (slope)\n",
|
|
"\n",
|
|
"\n",
|
|
"$b = \\bar{y} - a\\bar{x}\\quad$ (y-axis intercept)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 2
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 3. Using the lstsq numpy function"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"For our convenience, `numpy` has a function that can computes the least squares solution of a linear matrix equation. For more information, please refer to the [documentation](http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.lstsq.html)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def numpy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return np.linalg.lstsq(X,y)[0]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 3
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 4. Using the linregress scipy function"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Also scipy has a least squares function, `scipy.stats.linregress()`, which returns a tuple of 5 different attributes, where the 1st value in the tuple is the slope, and the second value is the y-axis intercept, respectively. \n",
|
|
"The documentation for this function can be found [here](http://docs.scipy.org/doc/scipy-0.13.0/reference/generated/scipy.stats.linregress.html)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import scipy.stats\n",
|
|
"\n",
|
|
"def scipy_lstsqr(x,y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" return scipy.stats.linregress(x, y)[0:2]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 4
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### Teaser"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"The following plot below should give you an impression of how the performance of the 4 different approaches will compare to each other at the end of this article.\n",
|
|
"\n",
|
|
"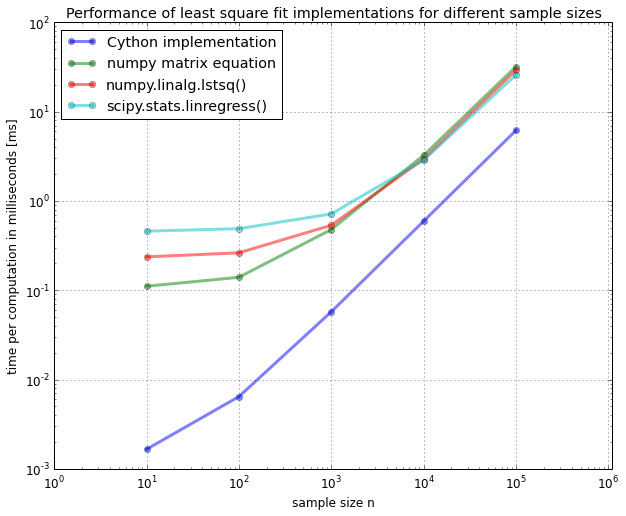\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name='sample_data'></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Generating sample data and benchmarking"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In order to test our different least squares fit implementations, we will generate some sample data: \n",
|
|
"- 500 sample points for the x-component within the range [0,500) \n",
|
|
"- 500 sample points for the y-component within the range [100,600) \n",
|
|
"\n",
|
|
"where each sample point is multiplied by a random value within\n",
|
|
"the range [0.8, 12) to simulate some scatter in our dataset."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"x = [x_i*random.randrange(8,12)/10 for x_i in range(500)]\n",
|
|
"y = [y_i*random.randrange(8,12)/10 for y_i in range(100,600)]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 5
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"#### Visualization"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"To check how our dataset is distributed, and how the least squares regression line looks like, we will plot the results in a scatter plot. \n",
|
|
"Note that we are only using our \"matrix approach\" to visualize the results - for simplicity. We expect all 4 approaches to produce similar results, which we will confirm after visualizing the data."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%pylab inline"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 7
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"from matplotlib import pyplot as plt\n",
|
|
"\n",
|
|
"slope, intercept = lin_lstsqr_mat(x, y)\n",
|
|
"\n",
|
|
"line_x = [round(min(x)) - 1, round(max(x)) + 1]\n",
|
|
"line_y = [slope*x_i + intercept for x_i in line_x]\n",
|
|
"\n",
|
|
"plt.figure(figsize=(8,8))\n",
|
|
"plt.scatter(x,y)\n",
|
|
"plt.plot(line_x, line_y, color='red', lw='2')\n",
|
|
"\n",
|
|
"plt.ylabel('y')\n",
|
|
"plt.xlabel('x')\n",
|
|
"plt.title('Linear regression via least squares fit')\n",
|
|
"\n",
|
|
"ftext = 'y = ax + b = {:.3f} + {:.3f}x'\\\n",
|
|
" .format(slope, intercept)\n",
|
|
"plt.figtext(.15,.8, ftext, fontsize=11, ha='left')\n",
|
|
"\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAfoAAAH4CAYAAACi3S9CAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdUVMfbwPHv0lm6giAgooBRbNi7GCv2EnvXWOPPnhg1\nGksSxRhjoiYaE0SNsb4xEY0Fe+zGmijGLkZARRERFljYnfeP1Y0ELJRlAedzDkf2lpln7q48e++d\nO6MQQggkSZIkSSqSTIwdgCRJkiRJhiMTvSRJkiQVYTLRS5IkSVIRJhO9JEmSJBVhMtFLkiRJUhEm\nE70kSZIkFWEy0UtGd+jQIcqXL2/sMAqtSpUq8fvvv+drnSNHjuTTTz/N0b7e3t7s3bs3jyN6s/3y\nyy+UKlUKe3t7zp07Z5TPhFRwKeRz9FJ+8fb2JiQkhGbNmhk7FMmIypQpQ0hICE2bNjVI+QcOHKBf\nv378888/Bim/IPLx8eGrr76iffv2mdbNnDmT69ev8+OPPxohMqkgkGf0Ur5RKBQoFApjh6Gn0Wjy\nZJvXJYRAfq+Wnsmrz5YQgtu3b+Pv758n5UlFj0z0ktEdOHCAUqVK6V97e3uzYMECqlatiqOjIz17\n9iQ1NVW/ftu2bQQEBODk5ESDBg3466+/9OuCg4Px9fXF3t6eihUr8uuvv+rXrVy5kgYNGjBhwgSc\nnZ2ZNWtWplhmzpxJ165d6devHw4ODqxatYrHjx/z7rvv4u7ujqenJ9OnT0er1QKg1WqZOHEiLi4u\nlC1bliVLlmBiYqJf36RJE6ZNm0aDBg2wsbHh5s2b/P3337Ro0YLixYtTvnx5Nm3apK9/+/btVKxY\nEXt7ezw9PVmwYAEADx48oF27djg5OVG8eHEaN26c4Xg9uxSemprKuHHj8PDwwMPDg/Hjx6NWq/XH\n2dPTky+//BJXV1fc3d1ZuXJllu/Jhg0bqFWrVoZlCxcupGPHjgAMHDiQ6dOnA/Do0SPatWtHiRIl\nKFasGO3btycqKirLcv9LCKF/z5ydnenRowePHj3Sr+/WrRslS5bE0dGRwMBAIiIiXnisvvzyS1Qq\nFa1btyY6Oho7Ozvs7e25e/dupnpfdJwB5s+fr3+vV6xYgYmJCTdu3AB072dISIh+25UrV9KoUSP9\n67Fjx+Ll5YWDgwM1a9bk8OHD+nXZ/Wxdu3aNwMBAHB0dcXFxoWfPnpnakZqaip2dHRqNhqpVq+Ln\n5wf8+5nYuXMnc+fOZcOGDdjZ2VGtWrXXel+kIkZIUj7x9vYWe/fuzbR8//79wtPTM8N2derUETEx\nMSIuLk5UqFBBLFu2TAghxJkzZ0SJEiXEyZMnhVarFatWrRLe3t5CrVYLIYTYtGmTiImJEUIIsWHD\nBmFjYyPu3r0rhBAiNDRUmJmZiSVLlgiNRiOSk5MzxTJjxgxhbm4utmzZIoQQIjk5WXTq1EmMGDFC\nqFQqcf/+fVG7dm3x3XffCSGEWLp0qfD39xdRUVHi0aNHolmzZsLExERoNBohhBCBgYGidOnSIiIi\nQmg0GhEfHy88PT3FypUrhUajEWfPnhXOzs7i0qVLQggh3NzcxOHDh4UQQsTHx4szZ84IIYSYPHmy\nGDFihEhPTxfp6en6bf57XKdPny7q1asnYmNjRWxsrKhfv76YPn26/jibmZmJGTNmiPT0dLF9+3ah\nVCpFfHx8puOgUqmEnZ2duHr1qn5ZzZo1xYYNG4QQQgwcOFBf7sOHD8XmzZtFcnKyePLkiejWrZvo\n1KlT1h+C/8T71VdfiXr16omoqCihVqvF8OHDRa9evfTbhoaGisTERKFWq8W4ceNEQECAft2LjtWB\nAwcyfJ6y8qJ9d+zYIVxdXcXFixdFUlKS6NWrl1AoFOL69etCCCGaNGkiQkJCMsTXsGFD/es1a9aI\nuLg4odFoxIIFC4Sbm5tITU0VQmT/s9WzZ08xZ84cIYQQqamp4siRIy9sz/Mx/vcYz5w5U/Tr1++l\nx0Mq2uQZvVQgjRkzBjc3N5ycnGjfvj3nzp0DYPny5QwfPpxatWqhUCjo378/lpaWHDt2DICuXbvi\n5uYGQPfu3fHz8+PEiRP6ct3d3Rk1ahQmJiZYWVllWXf9+vXp0KEDAI8fP2bHjh0sXLgQa2trXFxc\nGDduHOvXrwdg48aNjBs3Dnd3dxwdHZkyZUqGy/MKhYKBAwdSoUIFTExM2LlzJ2XKlGHAgAGYmJgQ\nEBBAly5d2LhxIwAWFhZcvHiRhIQEHBwc9GdgFhYWxMTEcOvWLUxNTWnQoEGWsa9du5aPP/4YZ2dn\nnJ2dmTFjRoZ7s+bm5nz88ceYmprSunVrbG1tuXz5cqZyrK2t6dixI+vWrQPg6tWrXL58WX9cAH07\nixUrRufOnbGyssLW1papU6dy8ODBrN/Y//juu+/49NNPcXd3x9zcnBkzZvB///d/+rPagQMHYmNj\no193/vx5njx58tJjJV7j9siL9t24cSODBw/G398fpVKZ5VWfl+nTpw9OTk6YmJgwYcIEUlNTMxzf\n7Hy2LCwsuHXrFlFRUVhYWFC/fv1sxfKMkLeM3ngy0UsF0rNkDbqkk5iYCEBkZCQLFizAyclJ/3Pn\nzh1iYmIAWL16NdWqVdOvu3DhAg8fPtSX9fwtghfx9PTU/x4ZGUlaWholS5bUlzlixAhiY2MBiImJ\nyVDm8/tmVWdkZCQnTpzIEP/atWu5d+8eAD///DPbt2/H29ubJk2acPz4cQA++OADfH19admyJT4+\nPsybNy/L2KOjoyldurT+tZeXF9HR0frXxYsXx8Tk3//2SqVSf2z/q3fv3vpEv3btWn0y/y+VSsXw\n4cPx9vbGwcGBwMBAHj9+/FrJ5datW3Tu3Fl/LPz9/TEzM+PevXtoNBomT56Mr68vDg4OlClTBoVC\nwYMHD156rF7Hi/b97/vp5eX12mUCfPHFF/j7++Po6IiTkxOPHz/WxwvZ+2x9/vnnCCGoXbs2lSpV\nIjQ0NFuxSNIzZsYOQJJex7NOfF5eXnz00UdMnTo10zaRkZEMGzaMffv2Ua9ePRQKBdWqVct0hv2q\nep7fplSpUlhaWvLw4cMMCfKZkiVLZujdnVVP7+fL8/LyIjAwkPDw8Czrr1mzJr/++isajYbFixfT\nvXt3bt++ja2tLV988QVffPEFFy9epGnTptSuXZu33347w/7u7u7cunWLChUqAHD79m3c3d1f2uYX\nad68ObGxsZw/f57169fz1VdfZdmuBQsWcOXKFU6ePEmJEiU4d+4c1atXRwjxyuPt5eVFaGgo9erV\ny7Tuxx9/JCwsjL1791K6dGni4+MpVqyY/v180bF6nQ6fL9q3ZMmS3L59W7/d878D2NjYkJSUpH/9\n/P3/Q4cOMX/+fPbt20fFihUBMsT7/DGDV3+2XF1dWb58OQBHjhyhefPmBAYGUrZs2Ve273kFqQOs\nZBzyjF7KV2q1mpSUFP3P6/Y8fvbHcujQoSxbtoyTJ08ihCApKYnffvuNxMREkpKSUCgUODs7o9Vq\nCQ0N5cKFC9mK779noSVLlqRly5ZMmDCBJ0+eoNVquX79uv4Z5e7du/P1118THR1NfHw88+bNy/SH\n9fky27Vrx5UrV1izZg1paWmkpaXxxx9/8Pfff5OWlsZPP/3E48ePMTU1xc7ODlNTU0DXAfHatWsI\nIbC3t8fU1DTL5NCrVy8+/fRTHjx4wIMHD5g9ezb9+vXL1jF4xtzcnG7duvH+++/z6NEjWrRokaFN\nz9qVmJiItbU1Dg4OxMXFZety94gRI5g6dao+ocbGxhIWFqYv19LSkmLFipGUlJThy93LjpWrqysP\nHz4kISEhyzpftm/37t1ZuXIlly5dQqVSZWpLQEAAmzdvJjk5mWvXrhESEqJ/v588eYKZmRnOzs6o\n1Wpmz579whjg1Z+tTZs2cefOHQAcHR1RKBRZvuev4ubmxq1bt+Tl+zeYTPRSvmrTpg1KpVL/M2vW\nrFc+dvf8+ho1avD999/zv//9j2LFiuHn58fq1asB8Pf3Z+LEidSrVw83NzcuXLhAw4YNsyzndep6\nZvXq1ajVavz9/SlWrBjdunXTn8kNHTqUli1bUqVKFWrUqEHbtm0zJeHny7O1tSU8PJz169fj4eFB\nyZIlmTJlir5n/Jo1ayhTpgwODg4sX76cn376CdD1wG7RogV2dnbUr1+fUaNGERgYmCn+adOmUbNm\nTapUqUKVKlWoWbMm06ZNyzKW19G7d2/27t1Lt27dMrXpWVnjxo0jOTkZZ2dn6tevT+vWrV+7nrFj\nx9KhQwdatmyJvb099erV4+TJkwD079+f0qVL4+HhQaVKlfRXaZ550bEqX748vXr1omzZshQrVizL\nXvcv2jcoKIhx48bRtGlTypUrl2nMh/Hjx2NhYYGrqyuDBg2ib9+++nVBQUEEBQVRrlw5vL29sba2\nznDpP7ufrVOnTlG3bl3s7Ozo2LEjixYtwtvbO8vj+LLj3a1bN0B326ZmzZov3E4qugw6YM7ly5cz\nPBJy48YNPvnkE/r27UuPHj2IjIzE29ubjRs34ujoCMDcuXNZsWIFpqamLFq0iJYtWxoqPEnKczt2\n7GDkyJHcunXL2KFIecTExIRr165l+5K5JBUUBj2jf+uttzh79ixnz57l9OnTKJVKOnfuTHBwMC1a\ntODKlSs0a9aM4OBgACIiItiwYQMRERHs3LmT9957T9/7VpIKopSUFLZv3056ejpRUVHMmjWLLl26\nGDssSZIkvXy7dL9nzx58fX0pVaoUYWFhDBgwAIABAwboBzXZsmULvXr1wtzcHG9vb3x9ffWX8SSp\nIBJCMHPmTIoVK0b16tWpWLEis2fPNnZYUh6Sndmkwi7fet2vX7+eXr16AXDv3j1cXV0BXceZZ48W\nRUdHU7duXf0+np6erz3CliQZg7W1tfwyWsTl5TDIkmQM+ZLo1Wo1W7duzfLZ39fpiPU8X19frl+/\nnucxSpIkSVJB5ePjw7Vr13K0b75cut+xYwc1atTAxcUF0J3FP+tZGhMTQ4kSJQDw8PDI8BzynTt3\n8PDwyFDW9evX9Y/2vIk/M2bMMHoMsv2y7bL9sv2y/fn7k5sT3HxJ9OvWrdNftgfo0KEDq1atAmDV\nqlV06tRJv3z9+vWo1Wpu3rzJ1atXqV27dn6EKEmSJElFksEv3SclJbFnzx6+//57/bLJkyfTvXt3\nQkJC9I/Xge456O7du+uHwfz2229lRxhJkiRJygWDJ3obG5sMYz2DbljIPXv2ZLn91KlTsxzeVNJp\n0qSJsUMwqje5/W9y20G2X7a/ibFDKLQMOmCOISgUCgpZyJIkSZKUK7nJfXIIXEmSJEkqwmSilyRJ\nkqQiTCZ6SZIkSSrCZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIkwmekmSJEkqwmSilyRJkqQiTCZ6\nSZIkSSrCZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIkwmekmSJEkqwmSilyRJkqQiTCZ6SZIkSSrC\nZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIszM2AFIkiRJWYuNjWXHjh2YmJjQtm1bnJycjB2SVAgp\nhBDC2EFkh0KhoJCFLEmSlG03btygdu1AUlLqAOnY2p7nzJkjuLu750v9f/75JzNnzichIYn+/bvQ\nv3/ffKlXylpucp88o5ckSSqAJk78mEePRqDVfgRAauqHTJv2KStWfGvwuv/880/q1GlCSso0wINj\nxz7m8eMERo9+z+B1S3lP3qOXJEkqgKKi7qHV1tC/Tk+vwe3bdw1e78OHDwkMbEVKyhBgAtADlWo1\n8+d/Y/C6AU6cOMHIkWMZO/Z9/v7773yps6iTiV6SJKkAatWqMUrlF8Bj4CFK5Ve0bh1o8HqnTp1N\nQoInYPrcUpN8uWW6f/9+mjZtz7JlJVm8WEmtWo25ePGiwest6mSilyRJKoA+/ngy77zjg6lpCczM\nPBgwoA7jx482eL2XLt1Aq+0P/AB8A/yCiUkPxo4dZvC6P/poHirVV8BkhJhNUtJ4Pv98scHrLepk\nopckSSqAzM3NWb36O1JTVaSkJPHttwsxMTH8n+yGDWtgbb0bCAMOYGLyPs2a+TNx4liD152cnAIU\n178WwpnExGSD1qlSqRg+fCzly9chKKgr169fN2h9xiA740mSJBVgpqamr94olx49esSOHTtQKBSM\nHTuSs2ffY//+NoCCRo0aERa2AYVCYfA4hgzpyaRJE1GpbAAVSuVsBg9eZtA6O3fuw++/W5CSspCr\nVw9Tp04Trlw5T7FixQxab36SiV6SJOkN9s8//1CzZiNUqiqAwMZmKqdOHcLc3BwhBK6urvmS5AHe\ne284arWab78dh5mZGR9/PJ+2bdsapK7k5GQ++mgWu3dvR4gngAVabX3U6gMcOHCALl26GKReY5DP\n0UuSJBnZX3/9RUxMDJUrV6ZkyZL5WnfPnoP5v//zRKOZDYCZ2VR69XrI6tXf5Wsc+UkIQZMmbTlx\nwoLU1J3APcABENjZNWbt2g9p166dkaPMKDe5T96jlyRJMqIxYyZRt24Q3bvPw8+vCrt3787X+v/5\n5y4aTS396/T0WkRGRudrDPnt+vXr/PHHeVJTNwHDgCBgBebmg3Fze0KzZs2MHGHekolekiTJSA4f\nPsyKFT+jUl3k8eO9JCX9TNeuffLlquW6devx9q7C+fOnMDObDyQAj1Eqv6Zly0YGr9+YhBAoFKbo\nUuBXQD9MTafRo4eCP/44iLW1tZEjzFsy0UuSJBnJjRs3UCjqAo5PlzRCpUokMTHRoPXu3buXd9+d\nSGTkIpKSdiNEJAqFM6amJejevQKTJ080aP3G5uPjg79/WSwt3wV2Y2FxET8/d0JCluHg4GDs8PKc\nTPSSJElGUqVKFTSafcDNp0vW4eLijq2trUHr3bhxC8nJE4AmQFU0mp/x8ipPcnIioaFL86WnvzGZ\nmJiwb99WBg1yombN+fTuLThyJBwLCwtjh2YQste9JEmSkQQEBDBv3sd88EFVzMycsLaG7du3GLyX\nu4ODLaamd9Boni25g52dHebm5gattyCxs7Nj6dKFxg4jX8he95IkSUaWkJBAbGwspUqVypezyjt3\n7lC1al0SEjqQnl4Ca+tv+eWXH2nVqpXB65ZyJje5TyZ6SZKkN1B0dDQ//BBCUlIyXbt2platWq/e\nSTIameglSZIkqQiTz9FLkiRJkpQlmeglSZIk6UWEgEWLIC7O2JHkmEz0kiRJkpQVrRZGj4axY6FD\nB93rQkg+XidJkiRJ/5WeDkOHwsqVYGEBkyZBPkwTbAgy0UuSJEnS89Rq6NsXNm0CpRK2bIHmzY0d\nVY4Vzq8nkiRJ0hsvKSmJLl36olQ64uzsxY8//pT7QlNS4J13dEne3h7Cwwt1kgf5eJ0kSZJUSPXo\nMYgtW1JITV0M3MTauiPh4Rtp2LBhzgpMTISOHWHfPiheHHbtgho18jTmnJKP10mSJElvnF27dpGa\nOg9wBmqRkjKY3bv35Kyw+Hho2VKX5N3c4ODBApPkc0smekmSJKlQcnAoBlzWv7a0vEzx4sWyX1Bs\nLDRtCseOgZcXHDoEFSvmXaBGJhN9Ieft7U1ERIRBytZoNIwaNQpfX1/8/PwICQl54bZz586lcuXK\nVKhQgYEDB6JWqwG4desWZmZmVKtWTf/z6NEjAI4ePUqDBg2oWLEiFStWZNKkSXkaf58+ffDw8MDE\nxASVSpVh3fHjx6latSpvvfUWrVq1IjY2Vh/T87F6eHhQ4wXf6lUqFT169MDPz48KFSrw22+/6det\nWbOGKlWqYG5uzjfffJPl/gcOHMDU1PSF6yVJermlSz9HqeyDufk4lMqOeHpeYdCgQdkrJDoaAgPh\n7Fnw89MleV9fwwRsLKKQKYQh50hoaKiYOXPmK7fz9vYWFy5cMEgMq1atEq1atRJCCBEbGys8PT3F\nrVu3Mm23a9cuUaVKFaFSqYQQQgwdOlQEBwcLIYS4efOmcHZ2zrL8CxcuiGvXrgkhhEhNTRUNGzYU\nP/744yvjGjBggDhw4MArt9u/f7+4f/++UCgUIikpSb9co9EIHx8fceTIESGEEJ9++qkYPHhwlmV0\n6tRJLFiwIMt1s2bNEsOGDRNCCHH16lXh5uYmEhMT9W2LiIgQ/fv3F998802mfRMSEkSdOnVE+/bt\nxZIlS17ZFkmSsnbu3Dnx+eefi++++048efIkezvfvClE2bJCgBCVKgkRE2OQGPNCbnLfG3VGP3/+\nfP73v//pX9+7dw83NzdSUlJyXfa9e/do2rQpNWvWpFKlSnz44Yf6dUOHDmXChAn67cqWLcuff/75\n0vKyM03lmjVrqFmzJn5+fnl6drhx40aGDRsGgLOzM506dWLTpk2Ztvvzzz9p1KgR1tbWAAQFBfHT\nT6/u/VqxYkV8fHwAsLCwICAggNu3b79yP4VC8VrHp0mTJri4uGRafvr0aaytralfvz4Aw4cPZ+PG\njZm2u3//PuHh4fTr1y/L8jdu3Mjw4cMB8PX1pWbNmuzYsUPftgoVKmBiYpJlB5oJEyYwadIkihcv\nrl+WnJxM1apVCQsLA2Dfvn1UqFCBpKSkV7ZVMr5z584xYMAIevcewsGDB40dzhujatWqfPDBBwwb\nNgxbW9vX3/HyZWjUCG7c0N2LP3BAd2++CHqjnqMfMmQI/v7+fP755yiVSpYvX06fPn2wsrLKtG23\nbt24du1apuUKhYJjx45haWmZYbmjoyNbt27FxsaGtLQ0goKC2LVrF61atWLx4sXUqVOHLVu2sHjx\nYiZNmkSVKlVeGmtWyeFFYmNjOXXqFPfv36datWo0btyYypUrZ9jm0qVL9O7dO8v9W7Zsybx58zIt\nv337NqVLl9a/9vLy4p9//sm0XY0aNfj+++95+PAhDg4ObNy4kcjISP36hIQEatSogUKhoGfPnrz/\n/vuZyrh//z6bN29m+/btr9Xm7Byf//pvu5ydndFqtcTHx+Po6Khfvnr1alq1apXll4WsynnR8fmv\nHTt28OTJE7p06cLWrVv1X1qsra3ZuHEjLVu2xM3NjSFDhvDLL79gY2OT06ZK+eTs2bM0atSSpKQP\nAGu2bOnBzz+vJCgoyNihFXqJiYkMHPgeO3b8hp2dI4sWBdO9e7fcFfrnn9CiBdy/Dw0bwrZt4OCQ\nNwEXQG9UondycqJDhw6sXr2aIUOG8MMPP7Bv374st83qzPVl0tPTef/99zl27BhCCO7evcu5c+do\n1aoVVlZWbNy4kRo1atCmTRtGjBiRZRnbt2/no48+AiAuLg61Ws2vv/4KwOjRoxk8eHCW+7377rsA\nlChRgrZt23LgwIFMib5ChQqcPXs2W216XW+//TajRo2iZcuWWFlZ0axZM3bv3g2Au7s7UVFRODs7\nExsbS4cOHXByctLHDPDkyRM6dOjA+++/T9WqVbOs45NPPmHz5s2ALsEePnxY/+191apVr/zilBOh\noaFZfgHKjfj4eCZPnsyePbqewUKIDF9a3nrrLWbPnk39+vX5+uuvX3g8pILliy++JSnpQ0D3JVal\nKsGsWV/JRJ8HBg0axbZtaaSmXkSlus7Age9QurQXderUyVmBJ09CUBA8eqRL9r/8AkX8y/QblehB\nlzD79OmDi4sL/v7++kvH/9W1a1euX7+e5bpjx45lugrw5ZdfEh8fz8mTJ7GwsGD48OEZbglcvHgR\nBwcH7t69i0ajwdTUNFO5bdq0oU2bNoAueUVGRvLxxx+/sk3PJwohRJaXtSMiIujTp0+W+7do0YLP\nP/8803IvLy9u3bql74wWGRlJmTJlsixjzJgxjBkzBtBd0q74tMeqhYUFzs7OALi4uNCnTx+OHDmi\nT/QqlYp27doRFBTE+PHjX9jG6dOnM336dAAGDRrEoEGDaNy48Qu3f5nSpUtnuOLw4MEDTExMMpzN\nHz9+nEePHunfj6w8Oz7PLr9HRkbStGnTTNs9/35cuHCBu3fvUrt2bX3d27Zt49GjR0ybNg3Q3Vpw\ndXV9rasDUsGQkqIGnr9sbKfvkGoIT5484eHDh3h4eGBubm6wegqCnTt3kJp6DnAD3EhNHUh4+O6c\nJfrff4e2bXXPy3foABs2QBZXdIucPOgjkK/yIuS3335blCpVSmzdujUPItKZOHGiGD9+vBBCiDt3\n7ghXV1cxa9YsIYQQN27cEF5eXuLatWtiwIABYvLkya8s73U745UuXVoMHTpUCCHE/fv3hYeHR551\nzlu5cqVo1aqV0Gq14v79+y/sjCeEEDFPO7HExcWJ6tWriy1btuhjUqvVQgghkpKSRPPmzcWiRYuE\nEEIkJyeLpk2big8//DBbcQ0cOPC1OuMJIYRWqxUKhULfSU6IfzvjHT58WAghxCeffJKpM97QoUNf\nGdfMmTP1x/7KlSvC1dU1Qz1C6DoOvqyz3cCBAzN01tu8ebOoXr26iIuLExUrVhQ7dux4rXZKxhUe\nHi6UypICfhawQyiVviIkJNQgdS1a9K2wsLAVSqWnKFGitPjrr78MUk9B4e5eTsABoZtGTghr6y45\n68C6c6cQ1ta6Qnr1EuLp36XCIje5741M9GvWrBHe3t55EM2/IiMjRe3atUWlSpVEUFCQ6NOnj5g1\na5ZQq9Widu3aYt26dUIIXbLz9/cXO3fufGl5K1eu1H9ReBlvb28xdepUUaNGDeHr65tlD++c0mg0\nYuTIkcLHx0f4+PiI77//Xr9u2bJl4uOPP9a/rly5sqhYsaIoV66cWLx4sX755s2bRaVKlUTVqlWF\nv7+/+PDDD4VWqxVCCLFkyRJhamoqqlWrJgICAkRAQICYM2fOK+MaOHCgOHjw4Cu369y5s/D09BQm\nJibCw8NDBAUF6dcdPXpUVK5cWfj5+YmWLVuK+/fv69epVCrh4OAgLl++nKnMgIAA/ZeapKQk0a1b\nN+Hr6yveeustERYWpt9u7dq1wtPTU9jY2AgnJyfh6ekpLl26lGVbnr1nN2/eFKVKlRJXr14VQuh6\n7nt5eYmoqKhXtlUyvi1btogaNZqKqlUbix9+WGGQOs6cOfP0C8WNp4kvVHh6vmWQugqKX375RVhb\nlxBmZhNF0rhoAAAgAElEQVSFtXUn4etbJfu96zdvFsLcXJfkhwwRIj3dMMEaUG5y3xs5BO6QIUOo\nUKECEydOzKOoJEmSDC80NJTRo/eTlLT66RKBqakVCQmPUCqVeV7ftWvXOH/+PN7e3i8cTyI/nD59\nmt27d+Po6Ejfvn2z17t+zRoYOBA0Gt10swsXQjaeaiooCvQQuPHx8XTt2pUKFSrg7+/PiRMniIuL\no0WLFpQrV46WLVsSHx+v337u3Ln4+flRvnx5wsPD8zSW6Ohoypcvz/Xr1xk1alSeli1JkmRoZcuW\nBY4BCU+X/I6trZP+0da89NNP66hatT6DB/9I48ZdGDducp7X8bpq1KjB5MmTGTFiRPaS/PLl0L+/\nLslPm1Zok3yu5dFVhRfq37+/CAkJEUIIkZaWJuLj48UHH3wg5s2bJ4QQIjg4WH8v9OLFi6Jq1apC\nrVaLmzdvCh8fH6HRaDKUlw8hS5IkFUharVaMGDFOKJWewsGhubCxcRbh4eF5Xk9KSoqwsrIX8OfT\nWwRxQqksJU6fPp3ndRnMggVCf2P/6QBehVlucp9BL90/fvyYatWqcePGjQzLy5cvz8GDB3F1deXu\n3bs0adKEv//+m7lz52JiYqIfbCYoKIiZM2dSt25d/b5y9jpJkt50586dIyYmhqpVq+Lu7p7n5UdH\nR+PrW43k5Hv6Zfb27Vi1agidOnXK8/rylBDwyScwY4bu9ZIlUASu4BbYS/c3b97ExcWFQYMGUb16\ndYYOHUpSUhL37t3D1dUVAFdXV+7d032YoqOj8fT01O/v6elJVFSUIUOUJEkqdAICAmjdurVBkjzo\n/i7b2loB654uOUda2omCP66DEDBpki7Jm5hAaGiRSPK5ZdDn6NPT0zlz5gxLliyhVq1ajBs3juDg\n4AzbvGo406zWzZw5U/97kyZNaNKkSV6FLEmS9Ma7ceMGtrYOxMb2BYZhYSFYuXLlC8fRKBC0Wl1S\nX7YMzMxg7VrolssR9IzowIEDHDhwIE/KMmii9/T0xNPTk1q1agG6QWjmzp2Lm5sbd+/exc3NjZiY\nGEqUKAGAh4dHhkFC7ty5g4eHR6Zyn0/0kiRJUt7RaDQ0bdqOqKhRwHBgDxYWgwgMbGTs0F4sPR0G\nD4YffwRLS/j5Z93AOIXYf09iZ82aleOyDHrp3s3NjVKlSnHlyhUA9uzZQ8WKFWnfvj2rVq0CdCPA\nPbvn06FDB9avX49arebmzZtcvXpVP4KYJEmSZHhRUVHExSUixBjAEmiLqWkAZ86cMXZoWVOroWdP\nXZK3sYHt2wt9ks9rBh8Cd/HixfTp0we1Wo2Pjw+hoaFoNBq6d+9OSEgI3t7e+pnD/P396d69O/7+\n/piZmfHtt99maxY3SZIkKXecnJxIT08A7gCegIr09GsvnNzJqJKT4Z13YMcO3aQ0O3ZAvXrGjqrA\neSMHzJEkSSpo1Go1oaGh3LwZSb16dejYsaPRYgkOXsAnnyxCo2mHuflhOnSoxZo13+fqxCsxMZF3\n3x3Nrl27cHQsztKln9O6deucB/nkCbRvDwcPgrMzhIdDtWo5L6+Ay03uk4lekiTJyDQaDYGBbTh7\nVqBSNcLGZi1jxvRgzpyZRovp0KFDnD17ljJlytCuXbtcX13t0qUv27drSE2dB/yNUtmXY8f25Gzm\nyUePoHVrOHECSpaEPXvA3z9X8RV0MtFLkiQVYlOmTGHevE0IcRkwBe5hbl6Gx48fGmTUO2OwtnYg\nJeU6oJvN0tx8HHPmePL+++9nr6D796FlSzh/HkqXhr174QWzkBYlBfY5ekmSJOnlQkNXEhy8BCHK\noEvyAC4oFBaoVCpjhpanbGwcgFv61+bmN3FwcMheIVFREBioS/LlysGhQ29Eks8tmeglSZKMRKvV\nMm7cdGAl8BewGrgNjMXHx49ixYoZM7w89eWXc1AqO6JQTMfKqhvu7rfo1avX6xdw8yY0agR//w1V\nqujmli9VKttxpKSkkJycnO39CjOZ6CVJkoxk9Oj3SUhQAWWBHcBSoBqwik2bVhapp4769+/Lzp3r\nmTbNhODghpw5c/j1J6j5+29dkr95E2rXhv374enoqq9Lo9HQv/9wbG0dsbNzomvXfqjV6hy0pPCR\n9+glSZKM4NSpU9Sp0wCtdhz/JvkY4F2aN2/E7t3bjBtgQXHunO6efGwsNG4M27aBnV22i5k7dz6f\nfrodlSoMMMXauitjx9Zi7tycD0STn+Q9ekmSpFwKDw/HxyeA4sW96NNnqEHvjx87dozGjYPQagHe\nB7oB/YH3aNKkJjt3bjFY3YXK8ePw9tu6JB8UpHtOPptJPiEhga+++orly39CpXoPsAOUJCePZu/e\nowYJu6CRiV6SpDfeX3/9RadOfbhxYw5xcQfYvDmeAQNGGqy+GTO+IDl5LrohZrsC1VAo+lOsmAUb\nN67H1NT0FSVkX0JCAt26DaREibJUqdKAkydP5nkdeerAAWjeHOLjoXNn+PVXUCqzVURCQgIBAfWZ\nMuUYt25ZAb/r15maHsPbO/MQ60WRwUfGkyRJKuh27dqFRtMbaANASsq3/PZbOYPVp1KlAMWBhcAX\nwExcXBI4fvyQwUag69SpD0ePOpOauovY2D9o2rQtERGn8fLyMkh9ubJ9u27Eu5QU6NMHVq7UTVST\nTatXr+bu3QqkpGwA7gF1USjOYGvrgLX1JRYs+P1VRRQJ8oxekqQ3np2dHWZmt59bchulMvv3gV/X\n0KE9USonA4eBmiiVD1m8+DODzQ6nVqs5eHAXqanfAX5Ab6AF+/fvN0h9ufLzz9Cpky7JDxsGq1fn\nKMmD7oxerX52TF2BXVhaXmDFisFcvnyWUjnotV8YyUQvSdIbr3fv3ri6XsXSshcKxSyUyo588cWn\nBqtvwIB+fPnlB/j5vU+5clNYsmQm3bsbbkpVMzMzzMzM0Z3VAggUiqjX7/WeX1avhu7dIS0NJkzQ\nTTlrkvM01apVKywsVgH7gNtYWX1Ex47v0LVrVxwdHfMs7IJO9rqXJElCd/b3/fffExsbR1BQiwxT\nhBYFc+bM57PPvkelGoyV1Sl8fP7h1KmDWFlZGTs0naVL4b33dL/PmKH7yYPHC8PCwvjf/yaTkBBP\nmzZt+OGHRSizea+/IJBD4EqSJGWDEIL169ezf/9RvL09GDt2NDY2NsYOK0+Fh4czY8YCUlPVjBzZ\nlyFDBrN161b27z+Ep6cbI0aMKDhtnj8fJk369/fsDov7BpCJXpIkKRsmTZrGN9+EoVINxtLyGD4+\nNzl9+veCc3abA7/99htjx07jyZME6tatzu7dv5Oc/DXggFI5ni++mMDIkcOMHWZGQsDMmTB7tu71\nt9/CSMM97VCYyUQvSZL0mtRqNTY29qSn3wZKAAJb24b89NOHdOjQwdjh5cipU6cIDGyLSrUKKIOp\naVs0mlHA+Kdb7KFixRlcuHDEiFH+hxAwcSIsXKi7Dx8aCv37GzuqAis3uU8+XidJ0hslLS0NUABO\nT5coUChKFNrxzyMiIujRoz8q1SAgCACNpgHw/IA/Ksxy2HPdIDQa3f345cvB3BzWrdM9TpcNycnJ\nLF68hCtXImnYsCYDBgwoUkMG56UC9M5LkiQZno2NDQ0aNOX48aGkpk5EoTiGiclxAgOXGju0bLt0\n6RI1azYiObkREAnsBdKAeigU7yOEGeCIUjmbGTOWGDVWvfR0GDgQfvoJrKxg82bd3PLZkJaWRuPG\nrblwwYmUlCasW/cNJ06cZ+nShYaJuZCTl+4lSXrjJCQkMHz4eA4dOoanpwfff/8llStXNnZY2RIT\nE0OFClV5/DgQmI9uMhwPwBa4yOTJ/+POnYekpKgZMqQXrVq1yvMYhBCo1WosLS1fb4fUVOjZUzfK\nna0tbN0KOXi6Yf/+/XToMIHExNPonhKPx9zckwcPorG3t892eYWBHOtekiTpJdLT0zl+/DiHDh0i\nOTkZe3t71q0L4c6dCI4f313okjzA5MmzePKkJqAFQoB26Ka6PY6p6UQuXrzFjz8uZ9OmlTlO8klJ\nSXTu3AdLS1ucnNwJCQnVrwsJCUWpdESptKNmzSbcu3fvJSUBKhV06KBL8o6OsGdPjpK8rigVJibF\n+TeF2WFiYkFKSkqOyivq5KV7SZKKtKSkJBo1CuLq1UcoFFYUK5bM8eN7cXNzM3ZouXLrVjRabS9g\nBnAdGIeu7wFoNM24fj0813UMGTKGHTu0qNX/oFbfZsyYdpQt6421tTVjxkwjJeU4UI7z56fQpUt/\njhzZlXVBCQnQrh0cOgQuLrB7N1StmuO46tevj7n5CBSKrxHibSwsllK5chWDDR9c2MkzekmSirRP\nPgnm0qVSJCb+yZMnfxAd3Y4xYyYbO6wcu3v3LleuXKFp07oolaFAOGCPbprbJCAdS8vvqVevRq7r\nCg/fTWrqHHQdF6uSnDyE3bv3cvToUdLTuwIVAFPS06fzxx+Hsi4kLk43Oc2hQ+DhAb//nqskD+Dk\n5MTRo3tp0GAXnp696NBBRXj4L7Iz3gvIM3pJkoq0ixevk5LSmmfnNWlpbbh06SPjBpUDQgiGDx/L\n6tU/YmbmiIuLDUFBAWzZUhEhBJ6efty9WxKFwoxatWqzcOE3ua7Tyak4cXERQBlAYGkZgYtLXVxd\nXTE3/xW1WgOYAqdwcsriCsm9e9CiBfz1F5QpA3v36v7NA+XKlePQoe15UlZRJxO9JElFWt26Vdm7\ndy3Jyd0AcywtV1GrVu7OKPObEIIRI0YSEvI7Wu0tUlPtSUmZTalSJ0hKSgDA0tKSuLg40tLSKFGi\nRJ6c3S5bNp+OHXuh0fQATmFpGcn9+7707NmTatVWc+5cfYR4CyF2sGrVjxl3/ucf3Zn8lStQvrzu\nnrzHmzEtbEEje91LklSkpaWl0alTb/btO4BCYU7FiuXYuzesUPXOXrbse0aPnkJ6+lhg+tOlkTg5\nNSAu7o5B646IiODTTz/j55/3oVaPw9z8BsWK7ebcuaOcPHmShw8f0rBhQ/z8/P7d6fp1aNYMIiMh\nIAB27YISJQwaZ1EnB8yRJEl6AXNzc7Zt20hUVBTp6el4eXlhkosZ0fLb4cOH+fDDz0hPHwjsBiYB\nlkAYZcv6Grz+GzdusHlzOGr1NqAOaWkQH9+fdevWMX78+Mw7RETozuRjYqBuXd3c8k5OmbeT8o1M\n9JIkFXkKhQJPT09jh5FtBw8epHXrbiQnFwcaA7fRdYBzwtLyFmvWGHZI27Vr1zF06Iekpgp087nr\npKe7kZiYlHmHM2egVSt48ED36FxYGNjZGTRG6dXkpXtJkoqM9PR0fvjhBy5dukbNmlXp27dvoe6J\n3apVV8LD26DrVT8O3aN0F7GyWsnevdupX7++QesvX74Oly9/CmwFLgNfADdQKody9Ohuqj7fe/7o\nUWjTBh4/1v37f/8H1tYGje9NIi/dS5L0xtNqtbRp05UjR56gUrXExmYx+/cfZ8WK3Pc+N5a0tHTA\nHEgGWgHf4uqaxM6dBwgICDB4/enp6YASXYKfCrTGycmMjRvXZkzy+/bpBsNJSoKuXXXD21pYGDw+\n6fUUnhtVkiRJL3HmzBmOHr2ISrUT+JCkpD2sXbuWu3fvGju0HHvvvb6YmIwFlgN2QCRduwYZNMnH\nxsZy7tw5EhIS+N//BmJjMxzYDwSgVKrZuXMjzZs3/3eHbdt0Z/BJSTBggG6CGpnkCxSZ6CVJKhKS\nkpIwNXVBdwYMYIeZmT2JiYnGDCtXTE1NsbDwAQ4CXwFHWbFitcFuX3733Q94eZUjMLAfHh4+VKpU\ngXnz/ke1asE0aLCWbds2ULt27X932LgROnfWjWH/3nuwYgUUpFnyJEBeupckqYioXr06lpbRmJh8\njVbbBjOzlbi7F8Pb29vYoeVYXFwcpqb+/HtO5ktqqoq0tDQs8vis+dq1a4wfP5WUlD9ISfEFDtC5\nczcePLjDqFEjMu8QGgpDhoBWC5MmQXAwFOL+EEWZPKOXJKlIsLOz48iR3dSqtQ1n55YEBl7kwIHf\nCtY87K9p+/btdO8+iB079qHR/IZu+tl4zMwmUbNmozxP8gCXL1/GwqI68OyRvSZotVbExMRk3njJ\nEhg8WJfkZ8+WSb6Ak73uJUmSXiImJoaDBw+iVCpp1arV60/JmkO6R9omoVJ9hEJxHyurL7G1dSIh\n4QF16jRm06ZQShhg8JnLly9TrVpjkpP/ALyAY9jYtOPBgyisrKz+3TA4GKZM0f2+YAFMmJDnsUiZ\n5Sb3yUQvSZL0AufOnSMwMAgh6iPEPcqU0XL8+F6USqXB6ixXrhZXr84FdB3eFIqpTJig5Ysvgg1W\n5zMLFy5m6tSZWFj4kp5+nY0bV9G2bVvdSiFg+nT47DPd2fuyZTBsWLbKT0xMRKPR4ODgYIDoizY5\nH70kSZIBvPvuOBIS5vDkyWYSEw9z9aoHS5YY9nG9tDQ1YKt/LYQtKSlqg9b5zPjxo7ly5Rzbt3/J\nrVuXMib58eN1Sd7UFH78MVtJXqPR0L//MJycSuDi4kGrVp1RqVQGaoX0XzLRS5IkZeH+/fvcvn0b\nqPd0iYKUlLpERkYbtN533+2FldUgdNPPrkOp/Ir+/XsatM7nlSpVigYNGvw7t7tGA0OHwtdf6x6b\n27QJ+vTJVplffbWYn3++THr6PdLS4vj9dzMmTfrYANHn3JEjR+jYsQ9t2/Zk165dxg4nT8lEL0mS\n9B+DB4/A3b0scXGJwGdAOnAPpTKUJk0MNxrd+vUb+eyzYDSaWExNu1Kp0tds3bo+4yNt+SktDfr2\nhZAQ3Sh3YWG6x+myaf/+E6hUQ9GNBWBBSsp7/P77yTwPN6eOHDlCy5adCQtryPbtLenSZRDbtm0z\ndlh5RiZ6SZKk58ycOYvQ0M1oNNfQaq8CEYASMzNvxo3rTteuXQ1S782bNxk8eBQpKQdJS3uARhNK\nTEwUjRs3Nkh9r5SSohvlbv163Xj1O3fqxrHPAV/fUlhY/A7o7jGbmh6ibNlSeRhs7nz55XeoVDOA\nkcBgVKqFBAd/a+yw8kzhe+5EkiTJgBYu/AZoD7g9XfIHYE5CwmOs83Ds9vT0dL7+egknTpynYkUf\n/P3fwty8NsnJz4aWfQeVahT37t3DI7/ncU9Kgk6ddHPIOznpppmtVSvHxc2YMYXffnube/caAdZY\nW19j0aKDeRdvLmm1gn8HWgIwQ6PRGiucPCcTvSRJEnD+/Hl69RpGQkIC8DsQDzgC27C1dcnTJA/Q\nrdsAwsPvolL1JCwsjLJlfyE9/R7wECgO/AmkULx48dcqT6vVcvHiRdLS0qhUqVLOn7V//BjatoUj\nR3RzyO/eDVWq5Kysp5ycnPjzz2Ps37+f9PR0AgMDC1TP+9GjB7FrV2+Sk5WAJUrlRCZM+NLYYeUZ\n+XidJElvvEePHlG2bEXi4+cC+4BjwGOgNHCR0NBvGDhwYJ7VFxUVhY9PFVJTzwG9gb8AFf7+Vbh1\n6y5mZlVJSztJSMgSevXq8cryUlJSaNGiE2fPXsHExIqSJa04fHgXLi4upKen8+TJExwdHV89k9+D\nBxAUBKdPg6cn7N0L5crlRZMLvPDwcObMWUJ6uoZx4wbTtes7xg4pA/kcvSRJUg6lpKTQvXsftm27\nhRCngRTgfWAlJUq4sGhRMD16vDrZZseNGzeoXLkRKlV9wB1YCDzEyqoxn3zyLuXKlaNSpUqULVv2\ntcqbNesz5s07RXLyJsAUc/OJdO78CB8fDz7/fAEKhSleXj7s2fMrZcqUybqQmBho0QIuXgQfH91l\n+0I8fHBRIxO9JElSDnXrNoCwsFuo1beBvwFL4CEWFmWIjr752pfOX8fOnTuZOnUeycnJJCQ8Ijr6\nIXAC8Hm6xVwmTHjEggWfZ6vczp378euvzYCBT5ccpnjxXjx8mPi0fD/gc/z9N3Px4onMBURGQvPm\ncO0a+PvrLte7u+eskZJByAFzJEmSckCr1fLrrxtQq8OAOsDbwFQsLOozevToPE3y69ato3373pw9\n+z/+/juYR4/MsLIyRzcFLIAGa+tDlCnjle2yq1f3x9r6ZyANEJiZrScu7i7QBSgHKICJXLp0Co1G\nk3Hnq1ehUSNdkq9WDQ4elEm+iJFn9JIkvbGEEFhbO5Ca+hfgCazD3PwT3nuvNQsXLnz1Pe3XdObM\nGerUeZv09GnAB0+XHqFUqaEkJDxCiGpotTFUqlScAwd+y/Z4+qmpqbRu3ZUTJ85hYmKFp6c9V678\niVZbEd0ZvSVwCBubLiQmxv6744ULujP5e/egfn347TdwdMyTNhcEp06dYvv2HTg42DNgwAAcC3Hb\ncpP7ZK97SZLeWAqFgqlTpzBvXmtUqlGYm5/HzU3B7Nmz8yzJA0ye/Bnp6XWAhOeWPsbOzpHTpw9y\n9OhRbG1tCQwMzNFse5aWluzdG8aVK1dQq9VUqFCBgIAGXLyYBlRDd1a/h6+//vrfnU6fhpYtIS4O\nmjaFLVvA1vYFNRQ+W7dupWfPIaSkDMLcPIIFC5Zy/vwxnJycjB1a/hOFTCEMWZKkAm79+vWiX79h\nYvLkaeLhw4e5KissLEyUKuUvHBxKiu7dB4rNmzcLX98aApYLcBEwQ8AiYWJSXPz888951ILM7ty5\nI6pXbyxMTEyFnV1xsWLFin9XHjokhL29ECBEu3ZCJCfnef33798Xbdt2E2XLVhOdO/cV0dHReV7H\ny3h7VxYQLnQD9QthadlHzJ8/P19jyEu5yX3y0r0kSW+U06dP8+mnC0lMTGbIkB706NE9z8o+c+YM\nDRsGkZy8FiiJQtEcU1NXTE3TSE3VAPOBdZia7mPixEHMmzc3z+p+ESFExqsTe/ZAx46gUkH37rBm\nDZibv7iAHLh79y7e3pVJTW0LDAF+pXTp7fz995mMU94aUPHiXsTF7edZR0eFYgZTpmj57LNP8qX+\nvCY740mSJL2Gv/76i8DAIH79tTZ79rzD4MGTWbFiZZ6Vv2vXLtTq/uimmN2EEE1JTz9LauoFwAdz\n84G4up5k/vyp2UrySUlJDB06Bj+/mjRt2oHLly+/9r4ZknxYmG4wHJUKBg2CtWvzPMkDDBgwktRU\nE2AF0BCYz927ppw+fTrP63qR9u3bYm09EfgHOIyV1XLatAnKt/oLEnmPXpKkN8by5StJShoNjAFA\npSpJcPAkBg8emCflOzg4YGFxmuRk0CWYQHQ93gFm4OU1kmvXsp/s3nmnHwcPWpCS8g3Xrx+nXr2m\nXL587t8Z5v4jPj6egwcPYm5uzttvv60b1W/9et0ENRoNjB4NX30FJq93rqdSqYiOjsbd3R2lUvnK\n7S9fvg5oADVgBWjRaBIxN8CXihdZuvRLtNpxbNlSCxsbexYu/JoGDRrkW/0FiTyjlyTpjaHVasn4\nZ88kT28F9uvXDze3v7Gy6gncBb5EN8qeCkvLxTRqVCfbZapUKvbs2U5KymqgDkKMJS2tJvv3789y\n+8jISN56K4B+/b6hZ885VKlSD9XixdC7ty7JT5mim3L2NZP8zp07KVHCi4CAFri4eLJlS9gr9wkI\nqIxC4QZ0AlYC7+Dqakn16tVft9m5Zm1tzerV3/H48V2io6/k6S2aQidPegnko0IYsiRJBcTZs2eF\nUuksYJmAn4VS6SuWLv0uT+t4/PixWLBggahQobowMXEU4CbAVtSp87ZISEjIdnmpqanCzMxSwIOn\nHcu0wta2sfjll1+y3L51627C1HS2ftsJpnWFvkfaZ59lq+74+HhhY1NcwKGnRZwQSmVxcf/+/Zfu\nd/fuXeHjU0WYm7sJExMX4e1dQTx69ChbdUsZ5Sb3yUv3kiS9MQICAti7dyszZy4gKSmZIUM+ZsCA\nfnlah729PTY2NkRG2qDVRgNWmJlNw97+EnZ2dtkuz8LCgpEjRxMS0gqVaigWFscpWfIxrf4zZey1\na9do3bor165FAqMAmMJc5miO6zb4+msYMyZbdd+4cQNTU3d099kBamNu7sPVq1dfeNsAwNXVlYiI\nP4iIiMDCwoIKFSrk6eOKUjbl4ReOfFEIQ5Yk6SW++WaZKFmynHBxKSOmTZslNBqNsUPKtWHDRgv4\nUn8iDRdEyZLlclyeVqsV338fInr0GCymTJku4uPjM60vU6aSUCgWChgvoIuYwwdCgNCA2NWjV47q\nvX//vrCychRw+Wk7bggrq2Lizp07OW5Lbh08eFD4+VUXTk6eokuXvuLx48dGiyU/5Sb3FbqsKRO9\nJBUdGzZsFEqlj4CTAi4IpbKmmDv3C2OHlWuLFy8RSmUzASkChDA1/VS8/Xb7XJWp0WiESqXKtDwy\nMlK0a9ddKBSWAoRQ8EQsoowQINQgvm3cTKSnp+e43h9+CBXW1s7CwaGpsLZ2EYsXL815I3Lp6tWr\nwsbGWcAvAm4KS8sBomXLzkaLJz8V6ERfunRpUblyZREQECBq1aolhBDi4cOHonnz5sLPz0+0aNEi\nw72bOXPmCF9fX/HWW2+JXbt2ZQ5YJnpJKjI6deorIOS5M989okqVRsYOK9fS0tJEUFAXYWNTWtjb\nBwhPz3IiMjIyx+X98MMKYWVlJ0xNLUSVKvVFVFSUEEKIuLg44eJSWpiYzBBgI0w4L1YwUAgQKSjE\nqY8/zpP23Lx5U+zatUtcv349T8rLqWXLlglr60HPfV5UwtTUPFdfZAqL3OQ+g9+jVygUHDhwgGLF\niumXBQcH06JFCyZNmsS8efMIDg4mODiYiIgINmzYQEREBFFRUTRv3pwrV65g8pq9QyVJKlyKFbPH\nxOQ2Wu2zJZE4OtobM6Q8YWZmxvbt/8fFixdRqVRUrlxZ94hbDpw8eZIxYz4iJeUPwI+LF2fQuXM/\nTpzYy549e0hJqYhWOxNzyvAjtelBKkkoWNi4BR/NnJkn7fH29sa7AExZa2+v+7yAQPfY4j9YWNjI\nHPEK+XJ0xH8eXwkLC2PAgAEADBgwgF9//RWALVu2/D979xkfVfE1cPy3NduSUNIoodfQQeklgBTp\nHRA/SjQAACAASURBVEUQRaog2MEOSlP0ryKK8AARRDoISBEEDIQivQQQQq8hEAglfct5Xuwag4Ak\n2U1C8H5f6d07M2fWjzl7507h2WefRafTUaJECcqUKcOuXbtyIkSFQpEL3n33dby9v0erfQW1eiRm\n80g+/fR9t+o8efIkn376KV988QWXLl3yUKSZp1KpqFy5MrVr185ykgfYsWMHdnsXoDygxm5/h717\ntwKg0WiAVLxIZilL6EkKt4CDn07kvfBfH7sJcJ06daJYsVsYDF2BjzGZWvLpp+Meu356Wo480T/1\n1FNoNBoGDRrEgAEDiImJITAwEHDOzoyJiQHg8uXL1K1bN61s0aJFc/V/VIVCkb1Kly7NoUO7mD17\nDlarjZ49w6lUqVKW6rJarXTr9hwrV64C+qDRWBk79kn27t1KqVKlPBt4DipUqBBa7QJSUmw4/2Tv\nokCBQgC0aNGCwj6j+C6+LM3kItfR8k27jox+++1cjTm7GI1Gdu8OZ8aMGVy+HEPz5tNp2bJlbof1\nyMv2RL9t2zYKFSrEtWvXaNGiBRUqVLjrc5VK9a+/xu732eh0w1GhoaGEhoZ6KlyFQpHDihUrxgcf\nuPcUD/Dhh2NZtWonzv3kh2K3w61bH/DJJ5MIC5vqdv25pWvXrkybNpddu2oDFbHb1zFnzlwAvO12\nIgv5ort0gut6AyuGDuODSRNzN+BsZjabGTFiRG6Hke3Cw8MJDw/3SF3ZnugLFXL+8vT396dz587s\n2rWLwMBArly5QlBQENHR0QQEBABQpEgRLly4kFb24sWLFClS5J46R3vovZNCoXh8rFq1EYcjACib\ndk2kHNeuncxynadOnaJ37yGcPBlFpUqV+fHHqQQHB3sg2gc7ceIEx44do0yZMlSsWBGNRsP69T8T\nFhbGhx9+xpUrcfTuPZBl076k8bhx6Pbvh+BgCm7cSL+yZR/egCJP+OdD7JgxY7JcV7a+o09MTOTO\nnTuA81CG9evXU6VKFTp06MDs2bMBmD17Np06dQKgQ4cOLFiwgNTUVM6cOcOJEyeoXbt2doaoUCge\nE4GBfkAw8CFwCjiCVjuG7t3bZKm+hIQEGjRowa5drYmN3UhEhC/ly9ehR48X6Nv3JQICyhAcXIkZ\nM2Z5rA/Tps2gWrUG9O49lVq1mjJp0leAc2Tzk0++4MqVlxFJQX99EgHde8L+/VCmDGzdCkqSVzyI\n5yb/3+v06dNSrVo1qVatmlSqVEnGjx8vIs7ldc2bN7/v8rpx48ZJ6dKlpXz58vLrr7/eU2c2h6xQ\nKLLJnTt37rsO3FMiIyPFYvEXjaaGgK+oVBZ5990PxeFwZKm+7du3i49PLdcyrvkCRV1LAasLlBLY\nKbBF9PpgWbx4idvxx8bGujanOeFq84IYDAXl7NmzEh0dLQaDn4BIcc7ISUqJgNwKDhbJ4XPeFbnD\nndynnEevUCiyVUJCAp079+b339ch4qB//8F8993/smVJ1IULF1i1ahVarZYuXbpQsGDBLNcVGRlJ\n3brtSEyMApoCHwFlgDrAj8DTrjt/oHXr1axdu9it2CMjI2nQoCd37hxNu+brW49ffvmMJ554gnz5\n/CmRuoINvEAwF9mn9sK26mdqP/30v9SqeFwo59ErFIpH1uuvv0tEhBc2203s9iv8+OMfTJv2f9nS\nVnBwMEOGDGHAgAFuJXmAypUr06xZXUymlsBV4BjQCNAD0enuvIRO5/6f0pIlSwKxwAbXlR3YbCcp\nX748RqORWa+OIIKWBHOR7WoTkzt05cnWefd8davVypIlS/j+++85evTowwsoskx5olcoFNmqfPna\nREV9DdRzXZlB9+7bWLQoLDfDyhC73U5YWBhhYT+yffte4DvgFZzzmIcBycAU9u6N8MgRrOHh4XTs\n2JPUVCE11Ur+/PmpX78OP7zclwK9ekFcHBcqVODI2LG06tIlz64ft1qtNGnShsjIRByOisBK5s+f\nQYcOHXI7tEeWO7lPOb1OoVBki6SkJL799jsSE+NRqSIQqQcIev02SpUqmtvhZYhGo6F///4EBATQ\ns+fXJCc/D5iBF4H/odNBWNh0j52zHhoaSkTEb9Su3RSH4y2uX29P/JpP8FrdFhwO6NCB4IULCTYY\nPNJeblm0aBGHDqWSkBCBc2B5Ky+99BzXrimJPjsoiV6hUHhcamoqDRq05M8//UhO7gB8gl6/Hi+v\nFIKC4nnnna9yO8RMCQgIQKM5ByQBXYHK6HQ1iI6+8MBXBPHx8fTpM5CtW/8gKKgQ06ZNon79+v/a\nzvXr12ncuAUpKcWBd2nJOn62r8KEg/j27bEsWQI6nae7l+OuXr2K1VqVv98eV+fmzZjcDOmxpryj\nVygUHrdx40ZOnEghOXkpMBHYg822hbCwVzl4cDu+vr65HWKm1KlThzZtGmCx1MfL62VMppaMHz/+\ngUk+KSmJ4sWrsHx5IrGxazh8eDgtWnTk9OnTiAg2m+2+5X755RdSUioBCXRiCb/QHhNJzFLrufPd\nd49Fkgdo1KgRGs1i4CCQilb7IXXrNs3tsB5byhO9QqHwuMTERFSqQP5+liiDRqPnqaeecmvf99yi\nUqlYuPAHfvnlF86dO0fNms/RoEGDB97/4YdjuXHjInAY51B/BVJTV/HRR2NYtmwlycnx1K3blBUr\n5uHn55dWzuFwoFL50YvrzKYHWoSv8GN3zw70K5o3XndkxBNPPMG0aV/w8svNSUy8xRNPhLJ06U+5\nHdY9oqKiWLJkKVqthl69elE0j/43UCbjKRQKj7t69SrlylXj1q2PgYbo9V9Rs+YpduzY8NCyj4PG\njdsTEREO7Me5JE9QqWqg010hNXUjUBad7k0aNjzLpk0r08pdvXqVCSXL80XiTdTAOJUvv9avweYt\nGx/bE9rsdrvrcJ5Hy759+2jcuBXJyc+hVidjMq1g375tuXZugrK8TqFQPFICAgKIiFjPE0/MJyio\nI+3aJbFmjXvrzPOSKlXKotFUBVoBnwI90OlO43D0AioBeqzW0WzfHn5XuYCffuJLV5L/NrgsjjGj\nCN+84bFN8sAjmeQB3nrrYxISxmK3f4XV+j137gxk7NjPczusLFGG7hUKRbaoUqUKu3dvyu0wcsW4\ncR8SHt6SM2fspKRMQKXS4O3ty507ewAHzmes/RQo4DzFExEYOxY+/ND571OmMHTo0FyKPvdYrVaW\nLl3KlStXaNSoEbVq1cq1WOLibgF/P707HKW5du1ErsXjjsf3Z6JCoVBkwu3bt9mxYwcnTrj/xzxf\nvnzs37+VMWOGotNZsNvnc/36bGy2o3h51cNk6ofJ9AyzZn3jTPIjRzqTvFoNYWHwH0zyNpuNpk3b\n0b//t4wadZLGjdvx44+5996+e/e2mEwfAFHAIUym8fTs2S7X4nGLe7vv5rw8GLJCoXjE7du3T/Ln\nLyw+Pk+I0Rgogwe/muU98tPr1Km3wAzX3vUisFJKlqwk06ZNk2PHjonY7SJDhjg/1GpFFi3yQG/y\npiVLlojFUlfA5vquDorFUtAj/x2ywm63y8iRH0j+/EXFz6+4TJr0Za7E8Rd3cp8ydK9QKNyyf/9+\nNm/ejJ+fHz169ECv1+d2SA8VHR3N+PGfEx0dS/v2TzF69GfExU0CegG3+PHH+nTo8CtPu7mPvNls\nQKW6zt9zqG5RpEhxBg4cCDYbvPgizJkDXl6wdCm0betmz/Ku2NhYHI4Q4K939hVJTLyF3W5Hq835\nVKVWq5k48WMmTvw4x9v2NGXWvUKhyLLFi5fQt+9QHI7uaLVHqVDBzvbtvz3Syf7GjRuEhNTi+vVO\n2GyVMZm+JCnpOCK3AefSP73+FSZOLMVrr73mVluRkZHUq9eMhISXASMm0/9YvXoRofXrQ69ezuRu\nNsPKldCsmfudy8OOHj3Kk0+Gkpi4DKiJVvsRNWvuY+fOjbkd2iNBmXWvUChyxeDBr5KUtJKUlCkk\nJGzg2DENixYtyu2w/tWSJUu4c+dJbLYvgZdITFwJmID5rjuuo9Oto3Llym63VaVKFXbt2sywYfEM\nGhTN77+vIrROHejUyZnkfX3ht9/+80keICQkhAULZlKwYC+02gLUrn2IlSvn5XZYjwVl6F6hUGTZ\n7duxOJeLAaix2UK4fv16bob0UFarFYfDku6KNxqNlXz5xpCS8gWpqdEMHjyEFi1aeKS9kJAQvvnm\nC+e/3LkDbdpAeDj4+cH69VCjhkfayYz4+HgiIiJQqVQ0adLkkdnEqH379sTGts/tMB47yhO9QqHI\nsgYNnkKnGwXEAztRqxfTpEmTLNUlIpw/f56oqCjsdrtH40yvffv26HSrgalABEZjL/r0eYHz54+x\ndet8Tp2K5PPPx91TzuFwcODAAXbu3ElKSspdny1YsJDKlRtQsWJdpk+fcf+G4+KgRQsID0cKFeKd\n+k0o3LYX1as3Ztu2bZ7v6ANER0dToUJNevacSI8en1C5cu1H/seZwk2emQ+Yc/JgyArFYys2Nlaa\nNm0nWq1BChQoIosWLc5SPVarVTp2fFYMBn8xm4tLSMiTcu3aNQ9H+7cDBw5IaGh7CQmpJ2+99b6k\npqb+6/1JSUnSsGErMZtLibd3FSlZsrJER0eLiMiKFSvEZAoWWCOwUUymsjJr1g93VxATI1KtmgiI\no3hxaVa8okBtgR0Cc8VgKCCHDx++p90//vhDRo16T8aNGy8xMTEe6fszz/QTrXaka2a7Q3S6oTJo\n0AiP1K3IPu7kvjyXNZVEr1A8fr788msxmZoJJLmSzwjp1u35LNVltVrlzJkzcuvWLRERmTkzTAoX\nLi9+fsXl9dffEZvNluk6P/lkvBgMHQSsAg7RakdKp07PiYhI27bPCMxKt4RuhVSv3kjat39GKldu\nIO88P0Ds5cs7PyxXTtbPnClgETiVrsxwGTt23F1trlq1SozGAIEPRafrLwEBxeXKlStZ+k7Se+KJ\n5gK/pmt7kTRv3tnteh/k9u3bEh4eLnv37s21pXKPA3dynzJ0r1Aoct3u3ZEkJnYHDIAKq7U3e/ce\nynQ9x44do1ixClSq1Ah//yK89NJAXnnlIy5f/oHY2HV8/30EH31077D8wxw6FEVycnuc05pU2Gyd\nOHLkOOBcQgdx6e6+yJEjkaxZE0L84WEM+HEe6uPHkcqV+bxDV/p9NNHVz/RlYvHyunulwquvfkhS\n0g/AGKzW/+PGjdZMnTot07H/U+PGtTEYvgdSgESMxhk0bvyk2/Xez/HjxylVqjIdOoyiceNutGvX\nI1tfyyjuT0n0CoUi11WpUhajcQ3gPL5Vo1lJxYrlMl1P+/bPcOXKmyQmXiA19SizZy8jMfFNoC5Q\nnsTEz1i06JdM11urViWMxiU4k6Og18+jRg3nrPxRo4ZjNk8AxgKfode/g05XgzL27kTwJiUlgd0q\nNcOrPsFH323n4sUhrn52A74FXkWj+YU+ffrc1WZCQjwQnPbvNlsxbt+Oz3Ts/zRu3IeEhqrR6/3R\n6QJo0yaAd9550+16/+n06dN07vw816+/ye3bO0hI+JPw8KuEhYV5vC3FQ3hwZCFH5MGQFQrFQyQn\nJ7vegZcRH5+aEhxcQS5evJipOmw2m6hU6nQ7q4loNDVEpRog0EqgkEBlCQmpnen4UlNTpXXrLmI0\nBomXV4CYTEWkefOOsmXLFhEROXjwoAwc+Ir06/eyfPHFF1LfVF1i8BcBCaeB5NcYRK+3CMS4Yvuf\ngE5UqnxisfhLRETEPW0OH/62mEzNBY4JbBKTqZBs3rw5wzFbrVYZM2a8NGzYVnr3HnDP93njxg2J\ni4vL9HfxMA6HQ4YOfUMMBn8BH4Ez6V4TjJU33xzp8Tb/C9zJfXkuayqJXqF4PNntdtm7d69s375d\nEhMTs1SHv39xgcUCMwW+Er2+uKhU3gIfCZwXmCI+PkFp7+8zw+FwyOTJk8VgKCrwk8B0MZn8Zfv2\n7XfdlxQeLjfVGhGQtVSRgsb60rfvIDEafV0xOJOewdBFJk6c+MA5A6mpqTJs2Bvi719SihevLAsX\nLpJbt27JoUOH5MaNGw+Nt3fv/q55D8tFqx0lgYElsyWxpxcTEyOtW7cXjaaEQJxAW4EPBBwCN8Vs\nrik//fRTtsbwuFISvUKhUIjIzz//LCqVRaCNQE/Ras1iMAS7Eo0zwfr61svUk3F6tWo1E1iR7gn1\nS3n22Zf+vuH330XMZhGQg6XLSpe2PeV///tabDabjBz5gZjNNQV+Eo3mHfHzC5arV69muO21a9eK\n2VxQvL0risGQT+bOnffAe1NSUkSj0QvcTovVYnlaFi5cmKV+Z8SdO3ckOLi8qNWNBYa42r0gUEnA\nT7y88kn//sOUCXlZ5E7uUzbMUSgUj40tW3ag0fTFZpsCgM32GXb7x8BtwBdIwWaLxtvbO1P1bt68\nmd9+20hMTAygSvdJAlFRR5k8eTI9fXwIHDIEkpPhueeo+sMPLE23R/uECWMoXrwoK1euoHBhP8aM\n2Y6/v3+G2o+Pj6dbt94kJKwAGgBHGDCgCU2aNKJo0aIZ7EX2bh++YcMGbt4sisMxEhgG3ACKAq8R\nHDyJnTt/p1ChQtnWvuLBlESvUCgeG5cuXcNmq5fuSkN8fApgs4WSkNAZs/k3mjWrQ/Xq1TNcZ1jY\nbIYNe4/ExJfQar1RqV5C5GvgIjCBw4fbs/2NlQy2ufZkHzgQpk51HjmbjkqlYsiQgQwZMjDT/Tp/\n/jxqdUGcSR6gEnp9CCdOnLhvotfr9fTs2YflyzuTmDgcrXYnZvOftGrVKtNtZ5TzR4QGaAF0AcoB\nFgoUsLFq1Rolyeci5VAbhUKRI5KTk/nyy685fPgkdepUY+jQIWg0mocXzIQff/yJwYMnkJi4CvDF\naOzFoEHVqFu3BgcOHKJ8+bL06dMnU+0WKFCEuLhVQA2cM+6fpFQpDfHxt7l8uR3POaoQxotocLC4\nWGm6nz0BKtXDqs2U27dvExRUnKSk34HqwGmMxtr8+edeihcvft8yNpuNceM+47fftlGiRGE+/XQ0\nRYoU8Whc6d26dYsKFWpy7dqz2O0N8PKaRIMGBlauXIzZbM62dv8r3Ml9SqJXKBTZKiEhgXfeGU1Y\n2HySkqpht7fHZFpAmzbFWLx4jkfbEhHGjBnPZ59Nwmaz0qNHL2bN+tat0/QMBm9SUs4D+QHQ64cx\nblwJtm49QKEVGqbi7MNonmdZ5VMcitz6r/WdPHmSAwcOEBwcTJ06dTIcx8KFi+nXbwg6XTlSU6OY\nNGkcQ4cOynK/3HHgwAFmzvwRtVrFgAEvpB0AdOnSJV5//X3Onr1E06Z1+fjj9x/pkwzzEiXRKxSK\nR5LD4aBGjYYcOWLCbj8LHMc5vJuIwVCMkycPZstT5l9/I1QeeLLu1KkXv/4qpKRMBDagUr0OxDNK\n68V4axIAb/IBU00RvP56Mz755IMH1rVgwSL69RuKTtcQu/0Afft24dtvv8hwLNHR0Zw4cYKSJUsS\nHBz88ALZICIigtatu5CYOBywYzZ/S0TEemrkwuE8/yVu5b6szwHMHXkwZIXiP+vFFwcJFBD4XeDJ\ndLPV7WIyFZVTp07ldogPdefOHenZ80XJl6+waDT5RMX/5CM++KsjMlxnFqMxnwwcOFysVusD60lN\nTRWDwUfggKvoTTGbS8gff/yR6ZhsNpv83//9n7z66psSFhYmdrvdnS5miN1ul8GDX3WtjZ9218qD\nzp17Z3v7/3Xu5D5lZzyFQpHm2rVr7NmzxyOnme3du5f581fi3O61JnATGAPsRasdTqlSRShRooTb\n7TgcDs6ePcvVq1fdrut+LBYLCxbM4tixfWg1KiZxkdF8gh01gww1CF34I4mJcUyb9jVa7YPnN8fF\nxeFc6FTNdcUXjaY658+fz1Q8IkKXLr0ZMWIOX31VkGHDptG794AMlY2MjKRjx140atSOqVOnZ+oJ\nccqU75gzZwdQB0i/WiCA+PikTPVBkcM89nMjh+TBkBWKPOGHH34UozG/+PhUF5OpgCxb9rNb9S1d\nulS8vdsLtBDoKfB/AmVFp/OXLl16S2xsrNsxnzt3ToKCSotG4ydarbf07t0/255ukxMTZbpaKwKS\ngk66ME/M5rKydevWDJW32+0SGFhSYLbrSfigmEz+EhUVlak4Dh8+7DotL8lVT7wYDP5y5syZfy13\n4sQJsVj8RaX6UmCZmExVZOzYTx/a3r59+6Ro0fKug3jCBH4QKCewxbVjX0lZuHBRpvqgyDx3cl+e\ny5pKolcoPO/SpUtiNBYQOOJKHnvEZCqQpZ3Url69Kl269JFixUJEo/EV2CUwSqC2GAwF5fr16x6J\nOSUlRXx8gl2bszgE7ohO94RMn/5/HqlfxHkM78yZM2XmtGmS2K2bCEgiSCevVmKxVJEePV7I1AYw\nBw8elMDAkuLllV8MBh+ZPz/zG9j88ccf4uNTI93QuYjFUk4iIyP/tdyYMR+LRvNqunKHxN+/5L+W\niY+PlwIFigjME3hb4CXXd/29QEkxmQrLjBmzMt0HRea5k/uUdfQKhYJTp06h15cnKSnEdaUWGk0Q\n58+fJ1++fBmux2az0bjx05w61QirNQyVahwqVSMMhnyYzV6sW7eeAgUKuB2vzWajV6++3L6dAAzG\nuYmNBau1D9u27WHAgP5ut3HhwgVq1WqILeEJwlJ2YbRfxGE2c/6LL2glwoBixXj66aczNeGvatWq\nXL58ktjYWPLnz49Op8t0XFWqVMFsvk18/CQcjs5oNPMpWFBDuXL/fgiQM870Q/WOh8Z+4sQJrNZ8\nwLNAK6AxUA+TyQ+DIZWdOzdTpkyZTPdBkbOUd/QKhYJSpUqRmnocOOa6sg+bLZpixYplqp5jx45x\n8eJNrNb/AbURWY7ZXJolS2Zx5cppatas6ZF4R478kF9+OQhYgF9dV+3ASsqWzXjMEyZMxNs7EIPB\nl+7d+5KQkJD22fvvjyPpek/mJSbQ0X6ROAyMrNmAY0FBJCUlYTKZsjSrX61WExAQkKUkD2Aymdi6\ndT11627Ez+8pGjbcSUTEuocuY+vV61mMxnmoVJ8DSzCZnuO114b8a5mAgABSUy8DV4ECwFp0uj+Z\nMKElx48fUJJ8XuG5gYWckQdDVijyhFmzZovBkF98fGqKyVRAFi9emuk6oqKixGAIEkh0DQ+nitlc\nQg4ePOjRWAMDywhsFvATCBKoJ1BSvL0LS3JycobqeP31N10rAvYKXBOttpP06tU/7fP2TdpJOBVF\nQGLwl6p8IwUKlBCLpbro9a+IyVRSPv54okf7ld0OHz4snTv3ltDQDjJt2owMvXZ4//2PxWQqISbT\nS2I2l5Y33ng3ByJV/JM7uU9ZR69QKNLExMRw7tw5SpUqhZ+fX6bKXr16lUaNWhMVFYlzsLAzRmMC\ntWs72LTpF9Rqzw0glixZjbNnvwL8gFeAQ5QoEcSePREULFjwoeXj4uLw9y+C3f42MNp19TT58jUh\nLu4C3LjBlRo1CDp/nosU4imWcc4wFLs9Bqs1CjAB0ej15YiJuZCp1xt50datWzly5Ajly5cnNDQ0\nt8P5T3In9ylD9wqFIk1gYCC1a9fOdJK32WxUqFCHqKgngSTgOGr1Zp55JpB165Z5NMkDfPrp+xiN\nzwFr0GqrUrCgme3bN2YoyYNz4xmt1gxEpbt6DJPJDDExEBpK0PnzxPr40lwXx2ldM0JDi2A0lseZ\n5AEKodXm4+bNmx7t26OoYcOGDBo0SEnyeZQyGU+hULht+fLlxMXFAh/h/LNSAoejH8HBOry8vDze\nXo8e3QkI8GfJkpX4+uZj6NCdmTo0pUSJEuj1KlJSdgKdcZ6yFsbUdz+Fxo0hKgoqVMBvwwaOFS4M\nQGxsLKVLVwaWAy1Rqf6PAgVMnD59mrlz5xIYGEifPn0wGAwe769C4Q4l0SsUCrc5j2/1BXYBnQAH\nsIVChZ7LtjZDQ0Oz/IRpMplYu/Zn2rbtQmLiRlQqGzPfHUmHSZPg3DmoXh3WrYOAgLRDaf39/Vm3\nbjk9e/bj8uUeVKhQkx49nqd9+74kJz+HwbCV77//kR07Nij7u/+DiLBt2zYuXbpEzZo1KVu2bG6H\n9J+ivKNXKBRu279/P/XqNSclRQW0BI5jMkVz48bZbHmivx+bzcbq1auJi4ujUaNGlC5dOu2z3377\njZ9/Xk3+/D4MHz6UwMDAtDJXr17F/9o1dE8/DdHRULcurFkD+fP/a3sigtmcn6SkP4AKgGCxNGHW\nrFfo3r17Nvb0b8uXL2fgwFe5dSuWxo2fYtGiMPI/JO6cJiK8+OLLLFmyAY2mGlbrZubM+Z5u3brm\ndmh5irLXvUKhyHU//TRfjEZfUanUUqpUiJw7dy7H2k5NTZV69Z4Si6WOmM3PicnkJxs2bBARkZde\nGihQUGCSqFSDxN+/mMTExPxdeO9eET8/5y4yoaEit29nqE2r1SpqtVYgJW0TGpPpBZk+fXp2dPEu\nDodDFi9eLF5efgJbBeJErx8kzZt3yPa2M2vz5s1iNpcVuOP6nvaK0eibI/vzP07cyX15LmsqiV6h\neHQ5HA5JTU3N0Tbj4+OlevXaArUF7K5kslaKFq0gGzduFPAV2J6WjNXqPjJp0iRn4W3bRHx9nR88\n/bRYb9+Wd98dLRUq1JEGDVrLrl277mkvJSUlbVlao0atRacbInBFYK2YTH5y/PjxbO2vzWaTdu16\niE6XT2BAup3ubotWa8jWtrNi7ty5YrH0SBenQ3Q6s9y8eTO3Q8tT3Ml9yqx7hULhMSqVKssbwWTV\nwIGvEhmZDDTi74VETxIbe5nVq9cBOiAg7X6HI4iEhETYtAlatoRbt6BrV1i+nFffGc1XX/3OsWOf\ns21bD5o2bcOJEycAuH79Og0btsJotGA0+jBlylSWL/+JZs1iMJsrERz8OitWzH/oDnXumjlzJps2\nxWC1fgGc5u/d7o7h7Z2xVQc5qVatWtjtvwORAKhU0wkKKoqPj0/uBvZf4sEfHDkiD4asUOSq2UZO\nXwAAIABJREFUpKQk6ddvqPj7l5QyZWrKr7/+mtsh3eXOnTsyePCrUr16E3nmmX5y5cqVTJX38ysh\n8JNAUYEoAZuo1cMlNLSdjB8/QdTqqgLNBfYLfCfgI520RklWqZyPmM8/L+I6XtZi8Rc4l/b0qdMN\nk88++0xERFq16iI63csCqQInxGQqJps2bfL49/Eww4e/ITBRIFmgvqtvQ8RoDJQFCzK/d35OmDt3\nnhgMPqLX+0rRouXk6NGjuR1SnuNO7stzWVNJ9ApF5vTuPUAMhg4CxwVWidHoJwcOHMjtsETEOdTf\noEFL8fLqJbBBdLo3pXjxEElMTMxwHRUqPCmwzHXQikVAK8HBFSQmJkZu3LghRYuWE42mskBhAYv0\noLek4jyFboaXSeLSHbKTP38RgcNpid7Lq6989dVXIiJisfgJRKd9plK9I6NHj/H4d/IwYWFhYjLV\nFYgXSBSVqqOULh0ie/bsyfFYMsNqtUpsbGymDgFS/M2d3KcM3SsUj7nly5eTnPwdUA5oi9X6PGvX\nrs3tsAC4dOkSe/fuJyVlNtAcq/Uzbtwws3PnzgzX8f33kzCZBmIw7MNkakSpUhU4cmQXAQEB5M+f\nn8jInXz99WBef/0ZBukNzGMeOmx8xlu84VWNg5GRaXW9995bmEydgeloNG/h7b2JZ599FgA/vyBg\nj+tOB0bjPgoVCvLYd5FRzz//PJ06VcJgKIHFUpXixU8SHr6OWrVqpd1z9epVXnhhCA0btuW998aQ\nmpqa43H+k1arpWDBglk6H0DhHmUdvULxmDOZLMTHXwKKAKDVXsRiKZm7QbloNBpE7ICNv/8cpaLR\naO57v81mY926dWlL6IoXL06TJk3Yv38b69evx2KpR/fu3TGbzWll8uXLx9ChQ7k9fjw+qbEAfMDH\njOV1TLaKdy1He+ONEQQHF2bp0rUEBORn1KgdBAQ43+/PmjWZdu16oFI9jUp1ivLltfTt2zdD/YyO\njmbEiJFcvHiNli0b8t57b2d5LoNareann2Zw/vyHxMfHU7Zs2bvqSkhI4Mknm3D58tPYbIPYt28a\nhw/3ZcWK+VlqT/EY8ODIQo7IgyErFLnqhx/miMlUROAT0eufl6JFy2XpnPns4HA4pG3b7mI0Pi0w\nX7y8XpBKlWpLSkrKPfempKS4ltA9KRZLTzGb/WTz5s0Za2jChLTD20fqA0SjeVvM5lrSs+eLmRpK\nPnnypMycOVOWLl163xjv59ixY6LR/DVDfoloNE2lc+fnMtxmZq1Zs0a8vRulm+WeKDqd+ZH5b67I\nGndyn/JEr1A8hmJjYzl48CBBQUH07duH4sWDWb16HQULhjBo0Fe5eghLREQE3377A2q1ihEjBrBs\n2VwmTvycbduWEhJSijFjvr7vznJz587l4EEHiYk7AA2wkr59h3LmTOQ996YRgQ8+gHHjQKVCpk6l\nYZEi+Bw6RNmyI+nWrVumhpJLly5910Y8GdGlSy/s9jLANECF3d6GlSsLcvPmzfv+d1ixYgVjx36D\n3W5nxIh+9O3bJ1PtyT2bqihD5f95nvu9kTPyYMgKRY7asmWLWCz+4uvbWIzGwjJo0IhHZgLUxo0b\nxWQKEJgs8KWYTH6ybdu2DJX95JNPRK0ele5JNUZMpgIPLuBwiIwY4bxZoxGZO9dDvcgci6WgQMN0\ncSeLWm2SGzdu3HPv2rVrxWgs5JpcuEpMppIyZ07m4o6Pj5dixSqITveawHIxGttK+/Y9PdUdRS5x\nJ/fluaypJHqF4t/5+xcXWO1KKrfEbC4vv/32W6bquHnzphw9elTi4+M9GlvTph0FfkiX9L6Vjh17\nZais80dCcYEzAnbRal+Tpk3b3/9mm02kf39nI3q9yLJlHuxF5tSo0cg14/9tgTUCT0uVKnXue2+H\nDr0E/i/d97Nc6tRpmek2Y2Ji5IUXhkiDBm3k3XdHZ/g1g+LR5U7uU4buFYrHiM1mIzb2AtDadcUH\nkYacOnWKp556KkN1zJu3gP79h6DV+iMSx88/z89w2YexWm2AOd0VM6mptgfca2XBggXExMTQsGFD\nmjVrxtixbzBqVCXsdjvVq9dlwYJF9ysIffvC/PlgNMLPP0OrVh6JPysWLJhB/frNuXXrJ+z2MEqV\nKsSOHdvve69erwMS0l2JR6fL/J/pgIAAwsK+y1rAisePB39w5Ig8GLJCkaNKlKgkMMv1RHhRTKZg\n2b59e4bKXrhwQYzGggKHXOV/F4vFz2NP9gsXLnI9la8UWCYmUxFZtWrVPffdvHlTAgPLiEpVW1Sq\nYWIwBMnMmWEi4twCNiEh4f4NJCWJdOzofBz29hbJ6GS9bHbnzh3Ztm2bREZG/utrlF27donJ5Ccw\nSWCyGI0Bsn79+hyM9G63b98Wm82Wa+0r/uZO7stzWVNJ9ArFv4uMjBR//+JisZQSvd5bxo+flOGy\nGzZsEF/fJumGjkUsltLy559/eiy+efPmS61azeSJJ5rLsvsMqTscDqlS5QmBGvL33vVHxGDw/fe5\nBvHxIi1aOIPOn1/kPvvU5wW7d++W3r0HSM+e/SQ8PDxXYjh37pxUqFBLtFqjeHlZZMaMWbkSh+Jv\n7uQ+5ZhaheIxlJqaytmzZ/Hz86NAgQIZLnf69GkqV65DUtJeoBhwCKOxCVeunMuxvclv3LhBQEBh\n7PZngTDXVRtgICioFCkpifTs2Z3Jkz/7e/34rVvQrh1s3QoBAfDbb1C1ao7E+ziqXr0hhw+3xm5/\nD4jCZGrKli2/3LUpjyJnuZP7sn1nPLvdTo0aNWjfvj3g/J+4RYsWlCtXjpYtW3Lz5s20eydMmEDZ\nsmWpUKEC69evz+7QFIrHll6vp1y5chlO8mfOnCE8PByj0cj48R9hNNbC17cxRmMzZs2alqMHkGg0\nGlQqNbAK+B24BXRDpcrPlSuziYvbwuzZh3nrrQ+cBa5fh+bNnUm+aFGIiFCSvBscDgeRkX9gt4/E\nuTSvPA5He/7444/cDk2RRdme6L/++mtCQkLS1qpOnDiRFi1aEBUVRfPmzZk4cSIAR48eZeHChRw9\nepRff/2Vl19+GYfDkd3hKRT/eV98MZlKlWrTqdMHlClThWLFinDkyC6WLRvNiRMHeeaZHjkaj6+v\nL1279sTLqwjQGwhEowlH5G2gHlCKpKTPWbr0F7hyBUJDYe9eKF3ameSz+fS4nGS1Wvnhhx8YO3Ys\nGzduzJE21Wo1+fIFAX8l9lQ0mr0UKVIkR9pXZAMPvT64rwsXLkjz5s1l06ZN0q5dOxERKV++fNrp\nVNHR0VK+fHkRERk/frxMnDgxrWyrVq1kx44d99SZzSErFHmGw+GQS5cuydmzZ7O8Tj4qKkqMRn+B\n86534XvEaMz34MluOcRqtcqECZOkRo0GUqRIJSlWrLxoNIPTzR34WZqXrSlSpozzQkiIyKVLuRqz\np9lsNmnUqLWYzaGiVo8Uk6mETJr0ZY60vXr1ajGZ/MTbu6dYLFWkTZtuYrfbc6Rtxf25k/uy9Yn+\ntddeY9KkSajVfzcTExNDYGAgAIGBgcTExABw+fJlihYtmnZf0aJFuXTpUnaGp1DkWVarlY4dn6VU\nqSpUrFiXOnWacfv27UzXc/r0afT6qkCw60ot1GpfoqOjPRpvZmm1WkqXLsHx4+e5dOl9zp8fgt3+\nIzpdX9TqUVQx9OOXWxfh5EmoUQM2b4bChXMkth9+mEPBgsEYjb507dqHhISEhxfKgg0bNrB/fwwJ\nCRtwOCaSmLiZd999F6vVmi3tpdemTRsOHfqDqVPbs2zZF/zyy8K7/o4r8pZsW0e/atUqAgICqFGj\nBuHh4fe9R6VS/ev2kw/6bPTo0Wn/HBoaSmhoqBuRKhR5z6BBL7N69RUcjkuAjkOHBvDqq+8wa9a3\nmaqnTJkyJCfvAzYCzYDfUasTH4lh2kmTppGYOBno5LqSRMWKSxnc0Jv+izTorl6F+vVh9WpsFguv\nDnuDOXPmotPpef/9t3jtteEej2nLli28/PI7JCWtBEqwZs1Q+vcfzvz5Mz3eVlxcHCpVKZzb/QIU\nRURFUlJSlg/EyYysbPer8Jzw8PAH5s7MyrZEv337dlauXMmaNWtITk7m9u3b9OnTh8DAQK5cuUJQ\nUBDR0dFpJ0MVKVKECxcupJW/ePHiA//YpE/0CsV/zaZNm5g9+2ccjv8BBgBSUl5g5853MlVPbGws\nHTv2AkxAZzQaA0ajsHz5QgwGg8fjziznD/3083TMtA4IYsiC+XDjBjRrBitWgMXCR++NISxsL4mJ\nu4DbvP9+F4oUKUSPHt09GtO6db+RlNQfcM4+T06eyLp1DT3axl8aNGiAw/EKsBxogFb7OZUqVc/R\niZGK3PPPh9gxY8ZkvTIPvkJ4oPDw8LR39G+99Vbau/gJEybIyJEjRUTkyJEjUq1aNUlJSZHTp09L\nqVKl7vveMYdCVigeWZ069RZoJ9Ar3Trzt6RLlz6Zqqdr1z6i0w0XcAgkisEQKhMnfpZNUWfesmXL\nXKfuzRGYJs298onVbHa+k2/Xzrk5jkv58rUFItK9w58mPXv283hMX375pRgMPdK1s1ZKlKji8Xb+\nEhERISVKVBaTKb80btxGoqOjs60txaPNndyXY1vg/jUMP2rUKHr06MHMmTMpUaIEixY5t7AMCQmh\nR48ehISEoNVq+e677zJ1qpRC8V+h1WqAJjif9KoBWvT6C0yZ8i+nuN3Hvn2RWK3/h3MJlZHk5J4c\nPLgnU3XcunWLCRMmcfbsZZo1q8+AAS957P/bzp07s3ChjsmTf+DJ27F8fDAZTUIy9OgBc+dCuuHr\nggXzAycA59O1VnsCf3/3T+i7du0affu+zO7deyhWrDjfffcpRYrMIjq6I1ZrCbTaeUyd+qPb7TxI\nw4YN//10PoUiIzz4gyNH5MGQFQqP2r59uxiNfgJfC4wUvb6ALFmyJNP1tGnTXTSaD11PplYxGtvL\n+PGfZrj85cuXXSfRPSswXfT66jJs2BuZjuOhVqxwHkwDIi++6Dyw5h927twpZrOfaLWviJdXX/Hz\nC5aLFy+61axzh766rlPgTohKNU3y5y8sZ8+elenTp8vnn38uhw4dEhHnKoFt27bJxo0b5c6dOxlu\nY9euXbJgwQI5cuSIW7EqHn/u5L48lzWVRK9QOJN95869pX37ZzO0F/pfS/H+Wtoq4lz+GhxcXnx8\naorZXEYaNmwpycnJGY6hVq0GArVdQ/8icF00Gq9Mn5RmtVolLi7u/ksE5893HjELIsOGifzLEq/j\nx4/Lp59+Kl9++eVd/cyKixcvysyZM0Wvz5+ufyI+Pi3u2Zs/MTFRnnwyVCyWSuLjU18KFSot586d\ne2gbb7zxrphMxcTbu6uYTIEybdoMt2L+p507d0qtWqESHFxJBgx4RRITEz1avyJnKYleoVA8UHx8\nvDRp0kYMhoLi5ZVf2rbtnpaMExMTZdu2bbJnz55Mr5PW680CbdO9r04RtVqfqTX406fPFL3eLDqd\nRcqUqSZnzpz5+8MZM0RUKmflo0Y5z5fPAb///ruYzX7i7d1KwEvguqt/NrFYKsvmfxyU88kn48Vg\n6CJgExDRaD6RVq26PrD+mJgYadq0jahU+dPVHSVeXj5y+/Ztt+O32WyyYMECMRjyC8wW2C8GQyfp\n2jVzczgUjxYl0SsUigcaNuwNMRh6CqQKJInR2EY++mhslupyOBwyefK3UqlSfdFq8wkECPxP4A+B\nzlKx4hMZrmvPnj1iMhUSOC7gELV6olSq5Dqn/auv/j5VZ9y4LMWaVUFBpQTWupp/Q6CswHgxGltL\ngwYt7znN7dlnXxL4Pt0Pnt1SsmT1+9admpoq5crVELW6q0DoXYcHmc3F5NSpU27FnpqaKo0bPy1e\nXoUEnktX/03Rag1Z3lhJkfvcyX3KDggKxWNux479JCf3A3SAgaSkvmzbti9LdU2ZMpVRo77jyJGP\nsdleBuJRqb5HpepE/vx72bJlbYbr2rlzJyLtgHKACofjDY4e3Y1j7Fh49VXnTV99Be++m6VYs0JE\nuHr1PBDqujIJrbYkTZpsZNKkdmza9AsajeauMvXr18BkmofzHHkHev1Mateucd/6jx8/zuXLd3A4\nvgYOAztcnyzGYHDctWlYZkVFRfHWW2+xe7eVlJSPgfQbKF1Dp8v9JZOKXOK53xs5Iw+GrFDkql69\nXhKt9g3Xk51DvLxekldeeTNLdVWsWFdgU7onxbflyScbyJw5cyQp3XK3jFixYoVYLDUEkl11bZb/\nGSzOilUq59D9v3j//Y/Ez6+UBAaWkQkTJnnsabVq1fqiVk90vZs/KyZTsGzduvWB99tsNnnmmRfF\nyyufGI1BUqNGQ7lx48Z97z1x4oQYjYVcfV4tUEDAKPnzF5E9e/ZkOeZ33hktRmOA6PXFBcYK3Bao\nIPCiwFdiMpWViRM/z3L9itznTu7Lc1lTSfQKxcOlpqbKvn375ODBg3L58mUpXjxEvL3riLd3TalQ\noZbcvHkzS/VWq9ZYYHlaolepxsjAga9kqS673S4dOjwjFkuI+Fi6yndag7hecovMmycizlcFx44d\nk127dt317r9Nm44CRQV2CewTgyFEpkyZmqU4/unMmTNSsmRl8fIqIDqdSb744usMlbty5YqcO3fu\nX+c6OBwOadOmm5hMLQSmisHQWho1uvd1QGbs3r1bTKaiAlcFFgmECMQKXBeVqoEULlxOli5dmuX6\nFY8Gd3Kfch69QvGYuX79Og0btuLixQREUqlSpSSrVy/iwIEDaDQa6tati5eXV5bqXrlyJT169CMl\npSWgwWRay+7dWwgJCQEgNTWVsLAwzp49T/36ddOOp34QEeH3DRsoMXYspbZsAb0eFi2Cjh1xOBz0\n6TOQn39eg04XiMFwk4iIdVy9epUmTbricHwJ9HLV9At1637Ljh2/Zqlf94vr2rVr+Pj4eHyXQKvV\nyjfffMvevUeoXr0CI0a8gl6vz3Q9s2f/SFjYEu7cieX48QASEn4GBHgH+BKDwZfSpUuycePKtPNF\nFHmXW7nPIz81clAeDFmhyFHPPTdAdLqhrqFnmxgM3eTddz/ySN1z5swVLy9/0WieEa22vDRv3i5t\nyNxqtUq9ek+JydRSYLSYTOUePukvJUWkRw/nk7zJJJJuqeC8efPEbH5SIN41ejBZatZsLDNnzhSN\npqLAp+leIUyRp57q7JE+5gVTpkwVk6ms6wn+XQEfgVPy18l++fMXlgsXLiiT7x4j7uS+PJc1lUSv\nUPy7qlUb/eM9+lx5+ukebtdrs9nEYPAWOOyqN1nM5hDZsGGDiIisX7/e9c7d5vr8smi1hgeuzT93\n/LjsLRwsApJsMIhjy5a7Pv/ggw8FPkjXj0vi7R0gf/zxhxgMQQJ+rlnxb4tKZXLrHbenpKamyscf\nj5eWLbvJK6+8KXFxcdnSTokSVQW2pvtu2olGYxKLpbTky1dIdu7cmS3tKnKPO7lPmXWvUDxmqlcP\nQa9fiPNAGCtG41Jq1arkdr2JiYnYbDYgxHXFC5WqStqRtrdu3UKlCubv09YCUat1JCYm3lPXnvBw\nosqHUPPyBa5joYmtKKNWrb/rnkqVQjCbVwN3AFCr51O+fAh16tThww/fQK9PRqebjcHwPTNmfMPG\njRv54IOP2LMnc9v4elL37n2ZMGEz69d3Zfr0OOrVe4qUlBS36xURLl68mPZd37vNcA0GDerPnj2r\niY4+Te3atd1uU/EY8dzvjZyRB0NWKHLUjRs3pHLlOmI2lxKTKVgaNWqd6RnxD1KmTDVRqz8T52E6\nO8Vo9JOoqCgREYmOjhZv7wCBnwTOiU73mtSo0fDeSuLiZKfOuaXtZYKkEpECF0Svt9w11OxwOKRz\n516uYeliAmZ5442RaZ/HxMRIZGSknD17VgICSohe309UqvfEZAqQNWvWeKS/mXH16lXR630FEtNW\nOHh715KNGze6Ve+dO3ekXr2nxGDwFy+vAtKuXQ+ZPPnbdEP334jZ7CeHDx/2UE8UjyJ3cl+ey5pK\nolcoHs5ms8nhw4flzz//dOs9bVxcnPTq1V/KlKklbdp0l4iICKlQ4QlRq7Xi7e0nP//881337969\nWypWrC358hWWFi06y9WrV++u8No1cVSvLgJyDpOUIcqVFK+KRmO8J9ayZWsIfCJwQOCkmEzFJCIi\n4q57PvpojGi1g9INY6+ScuUyvnGPp0RHR4uXV35xbkz015a59TO0RfG/GThwuHh59RawinPDo1by\nyScTZPbsH6Vp047Svv2zj8RrC0X2cif3KbPuFQrFfTkcDmrXbkpkZAVSU/uh0awjIGAOUVEH0Ol0\n6PX6zJ1Ud/kytGgBR49ySq2hqcOHC7wPVAY+oHXrQqxdu/yu9rVaHSLJODf7AYNhMJMmVWbYsGGE\nh4fz3XezOXBgPydO9MQ52xzgMIULd+PSpWMe+ibuz2q18u2333Ho0HFq1Ahh8OBBtGjRiZ07vUlO\n7o9Wu4FChZbz5597MZvNWW6nWrXGHDo0BmjquvITTz+9kjVrFnqkH4q8wZ3cp7yjVygU93Xx4kWO\nHj1OaupUoA52+4ckJASwa9cuvLy8Mpfkz52Dxo3h6FGoVImLP80l1ihotVNQq/sQEuJg5crFAMyd\nOw9//+JYLAXQ6/MB61yVxKPRbKV06dKsX7+etm2fYfHiJzlxogEwCdgCnMRofI2uXTt49Lv4J4fD\nQevWXXj33dWEhVVk1KhldO3ah9WrF/HSS0WpUWMcXbteZefO391K8gDly5dCq/1r2aDg5bWOkJDS\n7ndC8d/hoVGFHJMHQ1Yo8qQrV66Il1e+tOVtYBeLpfI9Q+d/WbFihbRt+4x069ZX9u7d+/cHx4+L\nFC3qHMuuVUskNlZERM6fPy/Lli2Tbdu2pQ3Zb9261bX//U6Ba6LTPSVarbf4+jYVk6mY9O07WBwO\nhzRq1NY1F+Cv4fq+YjQGSsGCxWTIkNckNTU1276Xffv2ScGCRVyz/lNc7SeJ0RgkJ06c8Hh70dHR\nUrx4RfHxqS0WS1WpXLmORw6/UeQt7uQ+bW7/0FAoFI+mwMBAOnbsyKpVbUlMfA6DYT0BASqOHDmC\nv78/5cuXT7t3/vwF9O//NomJHwM3Wbu2Fdu2baCaWu0cro+JgYYNYdUq8PUFIDg4mODg4Lva/O23\nDSQlvQg4Z41brWFYLDVZvPgd/P39qV69uuu6DTCmK9mQFi2srFjxUzZ+IxAWNpt+/V7G+ZpgEfDX\nRjdeaDTeJCUlZbluq9WKTqe753pQUBBHj+5h165daRse3e8+heKBPPiDI0fkwZAVijzLZrPJV19N\nlm7d+krRomXFbK4tJtMLYjL5ydq1a0VEZNGixWI0FhZYk+4Je6yM7dRdJH9+54UWLUTi4x/a3uTJ\nk11Hvv5VzwYJDq54z30//TRPTKYSAisFFovJVEh+/fVXj/c/vf3794uXV0HX1rtJAhUFPhQ4IBrN\n21K6dNUsjSTs379fgoMriEqlloCAErJt27ZsiF6R17mT+/Jc1lQSvUKR8+bMmSNmcxPXsjoR2CRB\nQaVlyZKlYjIFC1QS2JCWoBsxWBJ1Oue/dOggksHlfXfu3JGyZauJydRedLoRYjT6y6pVq+57748/\n/iS1ajWT2rVbyIoVK2TPnj0ybtw4+fbbb+XOnTue7L6IiEydOlUMhucFvAVOClwU6CAqVT5p1Ki1\nXL58OdN1JiYmSsGCRQXmur7bFeLtHSDXr1/3ePyKvM2d3KcM3SsUeYSIMGtWGFu27KJs2WK89toI\ntyd6ZVRMTAypqTX4e/5uTW7cuMKUKbNJTPwM5xGtg4HPaUkEP/M9Rivw7LMwezZkcKjZYrGwf/82\n5s2bx82bN2nZ8jeqVat233t79+5F797Ove6XL19Oo0ZtSE19Hr1+L1988T0HDmzD29vbzZ7/rVCh\nQmi1R4BPgYZAI2Anw4cP4quvJmapzlOnTpGaagGec13pgFo9gSNHjtCoUSOPxK1Q5LnH4zwYskLh\nEYMHvyom0xMCU8Rg6CFVq9aTlJQUt+u1Wq1y+PBhiYqKeuCa+x07driOVz0iYBWt9jVp1OhpadGi\ni8As15P8bOlICUn+67G+f38RN05lywiHwyFjx34qKpWPwO9pIwpGY1f55ptv0u47ePCgPPVUJ6la\ntbF89NFYsVqtmW7LbrdL69ZdxGKpLkZjG9HpLDJx4kS34ndOePQViHbFfkOMxkA5fvy4W/UqHj/u\n5L48lzWVRK/4L4qPjxet1ijOY1nrC+QTtdpfpk+f7la9165dk4oVnxCLpbQYjYWlZctOD/zxMHNm\nmJhM+USt1kqdOs0lJiZGNm3aJEajv8A30os+Yv0r044YIeLGRj0HDhyQl14aKi++OER27Nhx33vs\ndrsMHz5C9PpyrhnwF9MSvVo9Sj7++BMRETl79qx4eweISjVFYKOYTI1lyJBXsxSX3W6XNWvWSFhY\nmBw7dizL/Utv9OjxYjIVF5Opn5jNZWT48Lc9Uq/i8aIkeoXiMXf9+nXR6SwCJQW+Ebgm8J34+ARJ\nfAYmuT1Ijx4viF7/ijhPuksRo/FpGTfu0wfe73A47plwtmXLFvm+Zj2x/5Vl338/Lck7HA5Zs2aN\nfP/997J79+4MxbRnzx4xmfwExgv8P3tnHhZl9b7xe/aZd4YBZFUBE0TEfV9zScP9p7lruaWpaS5l\nkdpimaW2mZq54JqaW6amiAuaqKm57xsiGIobIoIyMMDM/ftjRoKvoCCoYedzXV7F+57znOeckvs9\n2/N8R0ly486dO3OUeTC7Vii8CCwg0J9AdwLXCOyhTufBv/76iyQ5ffp0ajSDsh3wi6MkORdglApP\nVFQUa9duRoPBjdWqvfzQR8LevXs5Z86ch/opEDxACL1A8IJjtVpZrVp9Ar7ZBIt0cKie70xlBw4c\n4IIFC7g7W5a48uXrENiXzeZ8du7ct2DOTZ36j0PZlrKtVit79HiTen1l6nQDKUml+NPG0LK+AAAg\nAElEQVRPcx5rrmvXfgR+yObTYjZr9n85ymzZsoUGQ1UCIwgE2+/69yPgSLW6BJct+4WbN29maGgo\nv//+e+p0vbPZu0gHB7eC9bEQhITMp1xuJPANgWuUyX6km1uZQn2gCf57FEb7xGE8gaAYIJPJsHRp\nCKpXbwyrNQmAI4D7yMy8AWdn58fWnzLle0ycOA0yWXMAX2Hw4B6YOnUSKlUKQEzMWmRk1AdggU63\nETVq1MufUyTw5ZfA+PG2n2fOBN55J+v1/v37ERq6BykpJ2G78x6N996rigED+kGr1eZpNjXVbO/f\nA5yQlpaeo0x8fDyAQABjADQEcA2AAgaDGps2rcHAgSNw86YBMpkGWm00tNpMpKePhcUSCEn6DsHB\n7+Wvj4Vky5YtGDnyY1itngCCAQDkcJjNi3D69GnUq5fPsRYICkMRfnA8E4qhywJBkTF48Ejq9VUp\nl4+hXl+d/fq9/dg6u3btolJpyLaHbTvwdf78ed64cYN+flXp4FCZen1ZNm7cOs/88TmwWsng4Acb\n4uSiRQ8VWbt2LY3G/8uxAqHVuvDGjRuPNL1hwwZKkheBTQTCKUnluGjRzznKREVF2Zf3dxG4Qpms\nHT08vBkdHc3hw9+nWj3Evh1BKpUfs23bLhw8eAQ7dHidCxcuLlSin/xw8OBBVq/emDqdO4FP7WcI\nkuzjcJ+SVIrnzp17qj4IXiwKo32PrTl9+nTeuXPniRsoaoTQC/7LWK1Wrlu3jl9++SXXrFnzWMHa\nsmULtVpn2tK8/iO4jo6NGBERQZJMS0vjoUOHeOLECVoslsc7YbGQQ4fSrqLkqlU5/Nu7dy9/++03\n7tu3zy7GOwlkUiabRh+fCvkS2ZUrV7FKlZdZsWIDzpu3INcyYWFhdHHxolyuYPXqLzM2NpYk2bJl\nVwIrsvU3nNWrN318v4qIv//+mwaDG4GlBN6yby8MI1CdwMeUyyuzV68BT/1jQ/Bi8VSF/qOPPqKf\nnx+7devGzZs3P/f/OYXQC4oLVquV0dHRPHfuHDOf8jWzvPD1rUZgHW3R3JbbZ7mb6eDgztv2mPMF\nIiOD7NvXpqAaDblxY9Yrq9XKnj3fpF5fjkbj/1GSXDlp0iSWKFGaMpmc5cvXfCqx4P/3d9KkSd9Q\nklrY9+3N1Gq7cMSI4CJvNy8WLFhAvf4N+0fGVfvY9yXwGpVKHT/++OPn/ntUUPx4qkJP2k64bt68\nmT169KCfnx/HjRvHqKioJ260MAihFxQH0tPT2bZtV+p0HtTry7By5XpPJqyFxMXFh7YobkcJ+BNQ\nUKcrwV27dhXcmNlMduliE3m9nty+PcfrsLAw6vWVCZjsIhdBZ+dSJPlE99ZJW3jYLVu28Pr16/mu\nk5GRwe7d+1Gl0lOtdmDLlq/RZDI9UftPwooVK2gwvJq1dQAcpFyu4ieffMpjx449Mz8ELxaF0b58\npamVy+Xw9PSEh4cHFAoFEhMT0bVrVwQHBz+towMCQbFm8OCh2Lw5HqmpfyMlJQYXLtTBO+8U7O+L\nxWIptB9t27aGVjsGQGkAy6HTeWDz5rVo0qRJwQylpgKvvQb89pstKc22bUCLFjmKxMbGgqyHf5LN\nvIy7d28gIyMDSmXBzv2SxFtvjUCjRh3Qo8e3KFeuCiIiIvJVV6lUYtWqxYiPj8P165exdes66HS6\nx1V7ItLT07F3717s27cP6em2A4MdOnRAqVIJ0GheB/AdJKk3vvjiS0yc+EVWUh6B4JnyuC+BadOm\nsWbNmgwKCuKqVauy7tBaLBb6+vo+8RfGk5IPlwWC58qOHTuoULgQmJdtn3g//f1r56v+5s2bs5a7\nAwPr8NKlS0/sS0pKCrt3709JcqaLizcXLfqZGRkZDA0N5dKlS3n58uXHG0lOJps1s3XExYXMnoI2\nG9u3b6da7W5fQSBlsuksX77GE/kdHh5Ovb4CgWT7+G2li4vXE9l6Wty5c4cBATXp4FCNDg5VGRhY\nO+s8U3JyMidPnsJhw97lunXrnrOngheBwmjfY2uOHz8+z18GZ86ceeKGnxQh9IJ/O927v0mgA4HX\nCGTYl3A/YMeOrz+2bkxMjP0AWwSBDMrl37Js2cpFtqdrNpvZoMGrNBjq0GDoQb3e9dHL+HfukPXr\n20S+ZEkyj7/zly9fppubD9XqagQ0BAwsXdr/iffk586dS0kakO1DyUKZTEGz2cwJEyaxdOlAvvRS\nVf7889Insl8YrFYrz58/z44de2Q73W+lWj2YQ4aMeub+CP4bPFWh/7chhF7wb6dPn8EEviIQRKAc\ngUpUq13yld1s9erVdHDolE3grFSrjUW2v79gwQJKUnMCmXb7v/OllyrnXvjWLZorViQBXtPoOPO9\n4Dz32jt16k2FYoLdZhoVikEcNGj4E/t54MAB+xW7v+0257Fs2cr8+uvvKUk1CRwhEEFJ8s4zu93T\nIDExkX5+1SiXuxDwoC1N7oP/Vuv58svtnpkvgv8WhdG+fO3RCwSC/PPee29Dr/8BQAsAXaDRXMfK\nlfNQsmTJh8rGxcXh44/HY9SoD7B37164u7uDPAcgzV4iCoAFRqOxwH7Yfjfk5Nq1a0hLqwtAYX9S\nH7duXXu4clwcLI0aQX32LC6gBOqaf8SHcw9h8OCRubYVG3sNFkt9+08aWCwtcPny9QL7/IC6deti\n4sRgqNWVoNf7wMNjEjZuXIklS36DyfQ9gJoAmsJkGodly9Y+cTsFITMzE1Wr1sGlSzJYrbEA+gNY\nBCADQAa02mWoXz/3THsCwfNECL1AUMTUqFEDe/ZsQ+/el9C9+y2Ehf2KTp06PVTu6tWrqFq1Hr7+\nOgkzZiShadM2CAmZh6ZNK8NgqA+dbhAkqSlmzJgGVT7TvALArFlzYTC4QqXSok2brrh3717Wu4YN\nG0KrXQEgBoAVSuUU1KvXKKeBmBigcWMoLl7EabkRTXAWVzEQJtM6LF26MNdDgi1aNIJONw22dLVJ\nkKSZCApq9FC5gjB69EjEx8fh1KlduHLlAipVqgSDQQ/gnw8Imew6jMZnk6r39OnTuHEjEUAnABKA\n8QDuAnCDVuuFevVM+OKLT56JLwJBgSi6hYVnQzF0WSDIlXHjPqFCMdIe3KUkgS8I9Kanpy9/+eUX\nzp49+7GJYK5fv87w8PCsKGvbt2+nJPkQOEvgPjWaPuzaNWfs+qlTZ1CtlqhQaFi7dlPeunXrn5fn\nzpGlS5MA43196a1vk21pOpEKhTrXmABms5nduvWlQqGmQqHmgAHDnkrsgJ07d1KncyXwOeXy0TQa\n3XOcAzhy5Ahff/0tdu3aj9v/5/pfYTl+/Dg1Gg8CtQncs4/JVwwMrMXLly+Lu/GCp0phtE9mN1Bs\nkMlkuS5JCgTFjZEj38ePP7oCWAxgIQDbDFij6YtJk6pj9OjRj6y/detWdOnSG0plZaSnn8eIEYMg\nl1swZYoawGf2Upfh7NwYd+5cyVHXYrHAbDZDkqR/Hp44AQQFAfHxQJMmuPPzzwis1wwJCb1hsdSG\nJE1Dz56VsGDBT3n6ZDabQRK3b9+GwWCAk5NTQYflsRw5cgTLl6+GRqPGoEEDULZsWQDA0aNH0bhx\nK5hMYwDoodN9gV9/nY927doVSbuZmZmoXbspTp1KgtV6A4ADVKoknDt3CH5+fkXShkCQF4XSvqL5\n1nh2FEOXBYJcCQ0NpVzuTEAiEJM1c5bLx/Lzzyc8sm5mZiYNBhcCe+z1blOSfDh69GhqtZ2zBWv5\nneXK5eOK219/kU5ONgdatSJTUkiSsbGxfP31t/jyy+341VffPHaWfu3aNQYG1qZO506VSs/33hv7\n0Ew3IyODP/wwnb16DeSXX05mamrq4/3LB717DyLwbbYViF9Zp86rRWL7AUlJSRw+/H3WqtWMvXr1\ney5BkAT/TQqjfSJ7nUDwHLBarRg16mNYrV1gOxj3NoBpAGKg1S5E+/Zhj6yflJSE9PQMAC/bn7hA\noaiLKlWqoEyZCFy92hpWqw9ksvUICVn9aGciImBt3x7ylBSsgwzBZ2Kw9MQJNGjQAN7e3ggJmQaL\nJX8HAnv3fhsXL76KzMxJAO4gJKQZGjWqjS5dumSV6dHjTWzZEgeTqQd0ui0IDW2PP//cCoVCkbfh\nfGA2Z+CfYD0AICEzM7NQNv8Xo9GIH3/8rkhtCgRPnSL84HgmFEOXBYKHaNiwhf2+eQKBNAKjCLjT\nxaUsN23a9Nj6VquVbm4+BNbYZ6+XqNN58NSpUzSZTFy6dClnzZrFCxcuPNpQWBitWi0JcClqUoEk\nAmvp4ODOa9eusX//t6lUaqlUSmzZstNjQ8k6O5cmcDnbrPoLjhkzLuv9uXPnqNW6ZAuTm0mDIYAH\nDhzI17g9ij/++IM6nQeBVQRCKUl+XLhwcaHtCgT/BgqjfcVONYXQC4o74eHhdpF/ibbMbg/uyzfl\nolzSvebFoUOHWKJEaRoMZanRGDlr1tyCObJmDa0qFQlwDjSUwZIl0EZjczZt2pxKZV3a0quaqdV2\n5bBhox9psmrVRgTm2+2kU5KaMyQkhJcuXWK5ctWoUGgJOBM52qrD3bt3F8z3PAgLC2P9+i1Zq1Zz\nIfKCF4rCaJ84jCcQPGUyMzMxduxnWLVqPQwGA+rWrYAlS34DMBPAh7Bd1zoBb+8kXLx4HBqN5rE2\nSWLlypU4fPgoXFyc8fbbb6NEiRL5d2rpUqB/f8BqxVQ0wPs4CeAigJIAUqFQ+IDUwmr9CkBfe6Vd\nqFz5Y5w69WeeZk+ePImmTVuDrAiLJQ516pTD1q1rUbVqA0RG9oTV+h6AOgBqAxgEhSIMnp6/IDLy\neM6DgXmQkZGBhQsX4tKly6hTpya6du0KmUyW/34LBMWUwmifEHqB4Cnz7rtjMG/eQZhMPwC4ArX6\nDVgsLrBY3AC8DiAcMtkOXL4cCR8fn3zZ7NSpFzZvPgOzuTskKRzNmrkjNHT1Q6IXGxuLS5cuwd/f\nH15eXraHc+YAQ4cCAL7Tl0Bwyh4AGwCEAGgDhWIbyHhYrQMA3LM/l0Eun4i2bc9g48aVj/QtISEB\nBw8ehNFoRIMGDZCZmQmdTg+r1Qxb6I4EKBSN4eycjtq1ayAkZCq8vb0f22er1YpXX+2AAwfSYDI1\ng16/GoMGtcUPP0zJ15jlZk8uF6FEBMUDcepeIHgGWK1Wzp4dwrp1g9i8eUfu27cvX/Xc3X3t99of\n7Ft/Qm/vQKrVXlQofKlQOPHXX3/Ntx/jxo23n9S/mxVyVq/35ZH/STYzZ8486nQudHRsTJ3OxRYX\n/ttvHzjBSSVK0dMzgErlGPsp/U1UqcqwV69eVCq97OcHqhJ4mUAjKpWOjImJKciQkbSNm4ODK4ED\n9qZTaTBU4ebNmwtkZ8+ePTQYAmnLH2C7aaBS6ZmYmFggO7dv32bjxm0olytpMLhy8eIlBaovEDwP\nCqN9xU41hdALnhfffz+dklSRwEYC8ylJrvnKL16mTOVse/GkSjWEX3wxkdu3b+evv/7Kq1ev5tuH\nmzdvUq02EPDJdoWONBjqMyIiIqvc1atXqdOVIHDRXuYMJyo0WSI/TNaBwEGqVK9To3GlXv8SNZoS\nbNu2C5csWUKNxpXAJwROEhhAoASrVGn0RONGkuvXr6dO50qDoTs1mvL09CzP/v3fZnR09GPr/vzz\nUjo6elIuV1KhqJ/tg8lKnc69QONHki1adKBK9Y79EOQJSlJJ/vXXX0/aNYHgmSCEXiB4BpQpU4XA\n/mxC8znfffeDx9ZbsWIlJakUga+pVA6nq6s3r1+/nqPM/fv3+dFHn/G113rz66+/yzN5zKlTp2gw\nBBCoQuAz+/37GXR09GRSUlJWub1799LRsW6WIH6H0SRAi0zGwdqAbH3IpEZTgrt37+bnn0+kJHnS\nwaELlUonymSuBLwJvEyttiK//356ocYvMjKSPXu+QY3Gm8AiyuXj6eRU8pFCvXfvXkpSSQJH7af5\nHQnMJRBDpXIMAwNr02KxFMgPjcaBwJ1sH17v8euvvy5U3wSCp01htE/coxcI8ontnnd61s8yWTqU\nysff/e7Zswc8PNzx228b4ejojOHDD8DT0zPrfWZmJho3bo2zZ71gNrfCtm2/YN++I1i/fvlDtnx9\nfaFS3QPwCYBNAOZALk/Hli1hOe65lytXDhkZlyDDYczCfLyNuUgHcHLMGCyfuRmAFbb9chPIDHh4\neGDy5O9gNp8AUAbATSiV5VGihCNksusYOnQA3ntvxBON2wP8/f0RHr4HZnMYgMqwWgGT6QaWL1+O\n4ODgXOvs3LkTZnMfADXsT9ZDJusEJ6eJqFmzFpYt21jgfXZnZ3fcuHECQDMAVqjVJ+HuXvXJOyYQ\n/Nspwg+OZ0IxdFnwgjBv3gJKUlkCP1Mm+4Z6vWtWjPnCsHfvXhoMlbNdOTNRoymRZ1rbw4cPs2RJ\nP8rlKrq4eOV5NW3NytX8RaEmAZoA/vXZ50xPT2eNGi9Tq+1GYA4lqRH79BnEkydP0sGhQraZPuno\n2CDf197u3r3LJUuWcMGCBYyLi8vx7sSJE2zSpB0DAupSo8m+nUAqlSM5efLkPO3OmTOHktQu2zbF\ndpYuHZAvn/IiNDSUOp0rdbq3aDA0Zu3aTWk2mwtlUyB42hRG+4qdagqhFzxPVq/+lW3b9mCPHm/y\n5MmTD71PTU1ldHT0YwPLZCciIoJGY11mX07X6Tx5+fLlR9YzmUx5J1JJSyM7dSIBZkoSU7IF4UlJ\nSeGECV+yV6+BnDlzFi0WC1NSUujo6Ml/8qtHUK93ZXx8/GP9v3XrFkuX9qde356S1JOOjp48c+YM\nSVsIXQcHdwKzCPxJhaI8FYrqBLYRmE293pWRkZFZthYvXsJSpQLo4uLDkSODmZyczMqV61GvD6JG\nM5SS5FYk+efPnDnDWbNmceXKlULkBcUCIfQCwb+ArVu30mBwoV7vTb2+RL4FKSUlhd7eAVQqPyaw\nhxrNQNau3fTJs6GlpNji1QO2+PX5PGi2b98+OjuXolrtSAcHV4aHh+er3qhRwfbDbbYmZbLpbNGi\nI0ly9uzZ1On6ZfuIuU25XMvq1ZuxRYuOPHr0aJadrVu3UpK8COwlcIGS1JTBwZ8wNTWVS5Ys4fTp\n03nq1KmCj4dA8AIghF4geM7cvXuXBoMrgV12QdtHSXLJ14yYJOPi4vjaa28wMLA++/V7m3fv3s3x\nPj09PX+HzpKSyCZNbKrq5kYeP57jdUZGBkePHsfSpSvQ378WN2zYkOO9xWJhfHx8gVLMdu7cl8CC\nbGK+h4GB9UmSCxYsoCR1zvbub2q1xlw/YgYNGk7g+2xlD/Gll6rl2w+B4EWmMNonokUIBEXApUuX\nIJeXAtDE/qQBVCpfXLx48bF1SSI6Ohp9+nTG1q2rsXjxbDg6OgIAUlJS0LZtN+h0Bmi1BowfPzHv\noBl37gCvvgrs3g2UKmX7Z7VqOYp8+OGnmDNnH+LiVuHixYno0eMt7N+/P+u9XC6Hq6trgRLMtGnT\nFJL0I4DrAO5Bp5uMVq2aAgA6d+4MR8cTUCpHApgPSWqHDz8MzjWanbOzEQpFbLYnf8NodMi3HwKB\nIA+K7HPjGVEMXRb8B7h16xa1WqdsB81iqNWWeOwdb6vVyi5d+lCvL0+jsQP1eldu3749633//kOp\n1fYgkEogjpJUkStXruT69evZunU3duz4hi0hzI0bZJUqtqlw2bLkpUu5tufhUY7A6Wyz5gn84IMx\nheq71Wrlhx9+QpVKR4VCzR49+jMtLS3r/c2bNzlqVDC7devPxYuXZM3mjx07xt9//z0rCE9cXBxd\nXb2pUr1FmWwcJcktx1gIBP9lCqN94nqdQFAEuLm5YejQgZg5szrU6gqwWmMxZcpElC5d+pH1QkND\nsWXLSaSknACgBbAdPXsOQHz83wCAHTt2Iy3tF/u7UjCZhmD27AU4dOg8TKYvASTj7NbWOOnuAG1s\nLBAQAGzfDjwId/s/SJIetpl3JQCAUnkdDg6lCtV3mUwGk+keLBaCJM6cOY+EhASUKmWz6+7ujmnT\nvslR5733xiEkZBmUyqrIzDyIJUvmokuXzjh16iAWL/4ZJlMqOnfehurVqxfKN4FAgOI3PS6GLgv+\nA7z//kfU6/2o1Q6kRlOGgwYNz1e9mTNnUqsdkm2GnU65XJG1H1+3bgv+kw3OSrW6Dz08yhMIJUD6\nIooxcLZVrlaNvHkzh32r1crjx4/zjz/+4J07d7hmzRrqdJ4EvqJS+Q5dXb3zvMaXX954oz+BEgQi\n7dfgxrFu3eZ5lj906BAlyTtb0Joj1OkcmZ6eXig/BIIXmcJo31Pbo09LS0O9evVQvXp1VKxYEePG\njQMA3LlzB0FBQShfvjxatmyJu3fvZtWZPHky/P39UaFCBWzbtu1puSYQFJqzZ8+iceO28PWtjq5d\n38BPP4UgJeUA0tLmw2w+jKVLl+PKlSuPtVO7dm3I5aEAYgAQcvkMVKhQKysIzNy538HB4SPo9b1g\nMAShTJmTcHFxAaBEBZzDbjTBS0hElKs7sHMn4O6eZZsk3njjLTRs2AGvvTYeZctWxEsvvYQtW1Zh\n5Mg7GDfOFdu2/Y5Ro8ahevWmGDZsNFJSUgo0DgkJCVi5cgWAXgD8AcgAfIwjR/bmWefvv/+GUlkT\ngLP9SU1YrQokJiYWqG2BQJBPiu5742FSUlJI2k761qtXj3v27GFwcHBWuMkpU6ZwzBjb/uCZM2dY\nrVo1pqenMyYmhn5+frmeMn7KLgsEj+XmzZt0cipJmWwmgcNUqVpSocgeVpY0Gqvy8OHD+bI3Y8Ys\nqtV6ajQl+NJLlXjpf/bXr169ysWLF3PVqlVMSUnhokU/s4G2FG/BSAKMkKt4IJe97DVr1lCvr0Eg\nxe7Xcvr5/XOK/f79+/TyKk+lchyBHdRqe7Jp07YFutYXFRVFjcaFQH3+k2xmO52cSj9Ubv/+/UxK\nSmJkZCR1OrdsZwVW0s3Np8ChbAWC/xKF0b5nopopKSmsXbs2T58+zYCAAN64cYMkef36dQYE2KJc\nTZo0iVOmTMmq06pVK+7fv/9hh4XQC54zK1eupINDx2zCHk9AR2CVXexW0Nm5FO/du5dvm2lpabx5\n82b+RHbfPpoliQT4l4sHd2/dmmuxr7/+mkrl6Gx+3qVarc96v23bNhqNjXJsG2g0zll/P/NDRkYG\nvb0DCFSz/+lCQM81a9aQtG0dDB/+AXU6dxqNtejkVJJHjhzhkiXLqNUaqdN50tXV+6HMewKBICeF\n0b6ner3OarWievXq8PDwwCuvvIJKlSrh5s2b8PDwAAB4eHjg5s2bAIBr1679ky8bgJeXF+Li4p6m\newLBE6HVakHeAfDPNTeFIhOlS38CmUwDb+8J2L59IwwGQ456UVFRqF79ZWi1RpQvXxPHjh3LeqfR\naODu7p7rtbMc/PEHEBQEtckEdOmCetdi0bhly1yLVqtWDRrNRgDxAACZbBEqVPjnup1CoQBpztaP\nTJCWAl2tUyqV2LVrM2rUMEKlioSHx2GsX/8LunTpAgAIDw/HokUbkZp6AcnJh3H37lR07twHffq8\ngTt3buDChYO4fj0aNWvWzHebAoGgYDzVU/dyuRzHjx9HUlISWrVqhZ07d+Z4L5PJHvmLLa93n3/+\neda/N2vWDM2aNSsKdwWCfNGyZUuULv0FLl/uC7O5PvT6BRg0aDR++GEKLJbchTIjIwPNmrXFtWvD\nQG7ExYub0Lx5O8TEnIWTk1Ou7WzYsAEhISug12sxduxI1Lh2DejSBTCbgb59gQULAGXef4VbtWqF\nESNex9Sp5aBSlYCTkwq//RaW9b5Ro0YoXZqIjn4L6ektIEmL0br1/8HV1bVA41G2bFkcPbo713fn\nz59HZmYLAA/62AlXrvQGSeh0Onh7exeoLYHgv0JERAQiIiKKxljRLSw8mi+++ILffvstAwICslJ0\nXrt2LWvpfvLkyTmSW7Rq1SrXHNHP0GWBIE+SkpI4fvwE9ukzmIsWLX7skvv58+dpMPj+T9KYRty5\nc2eu5W2pbW3pXIGp7K1xoFWptFUcOpQswH52fHw8IyMjcz3VfvfuXb777ods3bobv/xySpGffN++\nfTv1+nIEbtv7/TN9fasUaRsCwX+BwmjfU1PN+Ph4JiYmkrQl32jcuDG3b9/O4ODgrL34yZMnP3QY\nz2w2Mzo6mr6+vrn+8hRCLyiO3Lx5kxqNo30/nwRSKEnePHHiRK7lK1VqSGAzAbIfFjETMpvIBweT\nBYyBb7FYuHbtWk6dOpV79uwpiu4UiA8++JhabQkajZXp4pJ3nwUCQd78K4X+5MmTrFGjBqtVq8Yq\nVarwm2++IUkmJCSwRYsW9Pf3Z1BQUNbHAEl+9dVX9PPzY0BAALds2ZK7w0LoBc+QpKQk9u07hH5+\nNRkU1OmhE/EF4YMPPqZeH0Cl8gPq9TXZq9eAPFcCAgPrE9jBYZiZtQSwtmbdAot8eno6X365JbXa\nalSrh1OSfPjttz88cR+elCtXrvDYsWNZN3EEAkHBKIz2yewGig0ymSzvWN8CQRFCEo0bt8bhwyVh\nNg+DXL4TLi6zEBl5Is999ccRFhaGkydPwt/fH507d87zHEpIyHxcGT4WEzMSAABjVXp02rMD9erV\ny3dbqampqFWrEc6duwUgCrboerFQqQJx9248JEl6oj4IBIJnT2G0T4TAFQjyICEhAYcOHUB6+m0A\nSlitdWE2h2Pv3r1o167dE9ls3bo12rRp8+jT9SQGX/kbyEiAFcAP5auiTciMAok8AEyf/iOiolQA\nqsEm8gDgDYVCQnJyshB6geA/gsheJxDkgVqtBpkBwGR/QpBJUKvVBbaVnJyMRo2CoFJpIUnO+P77\n6bkXJIHRo4EvvwQUCsiXLcP7F06gadOm+W4rLi4OISEh2LhxGzIyOgA4BGCTvR9T4OnpAfdsEfQE\nAsGLjVi6FwgewcCB72DlymMwmfpBo9kFf/9oHDmyO99in5iYiDfffAcbNmwGabfYDeoAACAASURB\nVATwGwBnaLVB+PXXGWjfvv0/hS0W4O23gfnzAbUaWLkS6NSpQP6eOXMGDRu2QGZmS2RmnkJ6uhXA\nFAAjAVyG0eiJ48d3o2zZsgWyKxAIni+F0T4xoxf8J7h8+TIaNWqFEiW8UK9eC0RFReWr3rx5P+Lb\nb/uiV69DGDOmAvbv355vkSeJVq06IzTUAHIvgDEAOgJwQlraEISHR/xTOCMD6NPHJvI6HbBhQ4FF\nHgBGjfoY9+59ApNpCdLTj0AmU0Au7wqtNgk1atTHokXTsXDhIsyaNQtpaWmwWq2YOnUGmjbtgF69\nBiImJqbAbQoEgn83YkYveOExm80oV64qrl0bAKu1J+TytXB3n4lLl0491X1qW6pWP6SnJwB4EESn\nDYC3ASzF5Ml1MHbsGCAtDejZE/j9d8DBAQgNBZo0KVBbW7duxebN27Fixe+4dWs+gAf1F6Ft2y0I\nCZmKwYPfQVjYPgCDIZcfQOXKKWjSpCEWLvwTJtOHUChOw2ici3PnjmZFrxQIBP8OxIxeIHgEFy5c\nQFKSHFbrGABlYLW+B5PJiNOnT+coZzabER8fX2QfklqtFlZrOoAk+xMrgFgA70Ol2gJHRyPSExOB\nDh1sIu/sDOzYUWCRnzVrLjp3HoLp011w+7YeMtl4AHcBXIVePx2dO7fG3r17ERa2BcA+AF/Cat2G\ns2ctmDPnJ5hMawF0hsUyHmlpzbB+/foi6b9AIPh3IIRe8MJjNBqRkZEA4L79SSoyMm7BaDRmlZk9\nOwRGowu8vQPg61sF0dHR+bKdnJyMN94YBB+fymjUqDXOnDmT9U6v12PYsOHQ61sAmArbbD4WQAKs\n1sH44v2VOOtTFggPt6WXjYgA6tQpcP/GjfsMJlMogLGwWg9ALr8GudwTGk0gRo58DQMG9EdY2A4A\nFgA+9loyWCw+sMW5z34DoGhXzKKiojBjxgzMmzcPSUlJj68gEAiKnkLc338uFEOXBc8Rq9VKq9XK\n3r0HUa+vQ+AL6vUN2KVLn6xgNcuXL6dC4UogigApl3/HwMA6+bLftGlbajR9CRynTDaLjo6evHnz\nZo72ly1bxiFDRrJ9+44E1ATOsARu8xBqkQBTXFzICxeeuI8ajYFAQlZoXY1mKKdOncqbN2+yWbP2\n1Omc6ODgTsCPwGACVwisJyCxXr0mlKQGBH6nXP4lnZxKZoWoPnv2LGfOnMlly5YxNTW1wH7t37+f\ner0rNZohlKTOLF3an7dv337ifgoE/2UKo33FTjWF0AvyQ0ZGBgcOfIdqtZ46nSPHjfuMS5cu5Ycf\njuPPP/+clfv8/PnzVKv1BPpni0OfQZlMzszMzEe2ce/ePSqV2mx52ElJasdPP/2USUlJOcpGRUVR\nq3UloKQH/uZJVCYBRskc+MtXXxWqr1279qVW25nAOQJrKEmu3LZtGyXJk8Bwe9jdVQT0BLwJONr/\nfEmt1pnjxn3KRo3asmvXvoyKiiJJbtmyhZLkSq12EPX6FqxcuR5NJlOB/KpZsymBZVljo1IN4scf\njy9UXwWC/ypC6AWC/+Gjjz6nJDW3i1wsJaka581b8FC5Dz8cR6CrPZd6ql2U/qCLi1dWmQMHDvCd\nd97j6NEfMjIykiT5yy/L2aHD65TJVNni11sJVKNOV5FubmWyRJMkw8LC6OgYRG+8zEg4kgBPowzL\napx5/vz5QvXVZDKxf/+h9PAox4oV6zE8PJwlS/oSUBHIzBJarbYzVSpnAnMJXLYn1qnLvXv3PmTT\n2zuQwNasful07Th79uwC+eXjU5nA0WwfUNM4cOA7heqrQPBfpTDaJ/boBS8koaE7YDJ9DMAVgDdM\nptHYuHHHQ+WsVgIIAFAVtghy/weZ7P+wfPkCAMAff/yBV15pj59+csUPPyhQq1YjBAePxaBBE7Bh\nQwuQdQE0APA+gOYAVEhNPYqEhBEYMGBkVjvlypWDd9ph7EEU/JGEo5DjFdzGtNWLERAQUKi+6nQ6\nLFo0CzduXMSZM3/Bw8MD9+4pAagBXH7QUwB/Qy7PBFAFQBkAR5GRcQnlypV7yGZiYry9HADIYDZX\nxa1b8QXyq127IOh04wEkADgPSfoR7du/+iRdFAgEhaEIPzieCcXQZcFzoGXLzpTJpmfNJpXKDzhk\nyMiHyp08eZKS5EpgNoFJVKu9ciwv16/fksDyLDsy2QSq1c4ETtufxdiXwV+yL4s3IHCPwCmWKlWe\nN2/etG0TnDrF+0YjCfAvhZ6lpBIMDd2Uwxer1cpdu3ZxxYoVvHjx4hP3PTY2llqtC4Hv7T59QKA+\nq1VryA0bNlCvd6GDgz8lyZm//bY2Vxvt2nWnWj2QQAqBk5Sk0ty9e3eB/EhNTWWvXgOo0Rjo4ODG\nqVOnP3GfBIL/OoXRvmKnmkLoBfnh9OnTNBo9qNP1oyR1o7t7GcbFxeVa9sCBAwwK6sz69Vtx9uyQ\nHBnlKld+mcD2bMvPs6lUGu0Cn0HAh8Db9mV7C4FuBMZSLg+iXK6lRlOCbT3KMNPJiQSY2qgR/9q+\nnfHx8Tl8sFqt7NnzTer1AXRw6EpJcuX69evz1Ver1cpvvpnKsmWr0d+/Nn/5ZTkHDRpBvb4agT5U\nqUqzbt2XaTabSdrOFpw9e5bJycl52kxMTOSrr3akQqGmg4MbFyxYlC9fBALB06Ew2icC5gheWK5e\nvYrQ0FAolUp06tQJLi4uBbYxdeoMfPrpAphMcwHchyS9iVdfbYDt26/DZOoFYAKAXwA8WJJeBZls\nKGxx8Q+gIeIRhlfhiDSgXTtgzRpAq83RBkn8+OOPGDNmFtLSjgHQATgIvb4NIiK24syZMyhfvjwa\nNGiQq4/Tp8/ERx+FwGQKyfJx9eo5SE1NxalTp1GhQgB69OgBubzgO3UkH52ARyAQPBMKpX1F8qnx\nDCmGLguKMVarlVOmfJdjtpyZmcnPP/+Kvr5VCXjYT+xbCKQTaM369RtTr+/HFgjnfUgkwNWQMS2X\nGbTFYmFQUEcqlS72Q4EPVg6slMlU1OlK0WB4g5JUhsHBn+TqY9WqjQlsy1Z3Drt16/+0h0YgEDxD\nCqN94jCeQPAIZDIZxox5H9HRxxEZeQgdO3ZA1659MWnSJNy+fRMuLhoAuwB4AygJne4oBg7sizaZ\nO7AJ7aCHCYvwCvooHdC991AsXrwk66ucJF55pRXCw08jMzMMwG4AZ+3tzgCpRWrqAdy/vwwm0xHM\nnBmCixcvPuSjXi8B+OegnEwWD4NB97SHRiAQFBOE0AsEBeCtt0Zi82Yr0tOvIDl5K0ymDDRvXhEe\nHnrI5WYolf7YNexdrEiPgwbpmKPywUD8hQzrYGzY8CqGD/8WEydOBgBs2LABf/11DkALAHUBfA+g\nPgAtSpb8CXq9CwAve8suUKvL4fr16w/5VK9eJQCDAUwCMBaSNB3BwSOe/mAIBIJigRB6gSCf3Lhx\nAxs3/g6z+VUAegDVkJY2BIGBfkhKug2r9Ri63huAnzNMUJKI6toVR/u1hEbbEVbrtwD6IyVlHb79\n9gcAQHR0NKzW+gDCAPwNoDeAT+HvH4iLF49DrU4HsAa2MLXhsFguomLFijl8Onz4MEJCVgD4GbZZ\n/UF4epZEYGBgkfX7wIEDCArqjAYNWmPOnHnijIxAUMxQPm8HBILnze7du3HgwAF4eXmhe/fuUCgU\nSEtLQ1paGpycnAAAx44dQ7NmbWAy1QQwG8BiAFuh0ZyFQuEJtdoXg9LCMAOjAABfaDzRdswYVN63\nD+SpbK3pYbFkAgBq1qwJtXoGMjOHAKgEQAOl0opNmw5CkiRs2/Y72rXrhjt3+sDBwRnr1v0KV1dX\nAEBqairOnTuHzZs3g2wPoIv9TyZiYrSwWCxQKBQoLKdOnULz5u1hMn0FwBOnTo2DyZSK0aNHPrau\nQCD4l1BUBwWeFcXQZcFz4sqVK+zUqTerVm3MYcNGMyUl5aEyU6fOoCT5UKV6j3p9Q7Zo0YFjx46n\nUqmlSqVnnTrNePv2bVat2ojAQvthNwuBNlSrK7JcuaqMiYnheJXuwUk4jsQo6vUuTEhI4OXLl2kw\nuBGYSeAPSlJTDh78z33+iROnUKXSU6FwpVZbgrNmzcrhn9Vq5b1793Jc+btw4QI9PMrSwaEy1WpH\nKpWBBNLszUewRInSRTaG778/hsD4bAf9/qKPT+Uisy8QCPJHYbSv2KmmEHpBfkhOTmbJkn5UKD4l\n8AeVynrU671YqVJDLl68hCSZnp5OlUqy34kngXRqtT7UagMI3CSQSaVyAB0dvQkYCERmE7wpbNGi\nNe8lJ5PjxpEALQCHadwoSSW4cWNoli8nTpxg8+Yd6OHhR1/fGhw0aHhW4pvLly/TwcGNMtkIAjMp\nST5cuHDxI/tWo0bjbMGA7lKhKEmt1p8ODp0pSa7cvHlzocbu+vXrPHfuHM1mMz/4YCxlsnHZ+r2H\nL71UtVD2BQJBwRFCLxD8D5s2baKDQzO7OP1KoAyBLQS2UpJe4ooVK5mYmEiVymAPdvMg8UoFApOy\nrrgB9QkMJdCLtsxvmQSuU6+vyDWrV5MjRtgqKhRMXbiQ58+f5/379x/yZ8CAYZSkxgRWUKUaRS+v\n8kxOTuYnn4ynQvFuNiHdzTJlHj1j1utdCFzPVucj9u3bjytXrmR0dPQTj5nVauXo0eOo0TjSYPBj\nqVLluHXrVur1rpTJviWwjJLkyzlzQp64DYFA8GQURvvEYTxBsSIxMRGtW3eBVmuEu3tZrF+/Ptdy\ntv3pNNgOsv0CYDKAVgBawmT6GnPnLoejoyP8/QOhUHwGIAlAGGSyK9Bq/wSQCaAngFMAPgLwE4Bo\nAAbI5WXw7oiu6BwWBvz4I6BW49bs2eixPhzdug3CuHETkJqamuVLeno6fv55PkymjQB6IiNjGpKS\nymDbtm1IT8+AxeKQzXMjMjIyHjkG/v6BkMnW2H+6D71+C9q1a4sePXrA29sbsbGxSElJKeDIAmFh\nYZg7dx3M5ku4fz8KN24Mw4cfTsT+/X+ga9czaN36d8yfPwlDhgwqsG2BQPAcKcIPjmdCMXRZUIQE\nBb1GtXoQbfnX91CS3Hns2LGHyqWmptLfvzrV6rcIvExgVrYZ8Fy2bt2VJHn16lXWq9eCarWeXl4B\n3Lp1K+vUaUat1pdAZQI17CsCtr15na45Z02fTvbo8SAvLe+tXUt39zJUKL4g8Ae12s5s06ZLDl8U\nCrU9brytmoNDO65atYpHjx61x9pfRmAnJak2x4+f+MgxOH/+PN3dX6LRWJU6nQf79h1Cq9XKEydO\n0N29DCWpFDUaB86ZM69AYztp0iQqFMHZximBGo1DgWwIBIKnQ2G0r9ipphD6/y7bt2+nLfXq3Swx\nUquHc+rUqSRtOegvXbrEW7dukbTFax81KpgNGrSgSuVEYAqBrylJrrmmZn1Aeno6hwwZQpVqKIF9\nBNwIdCFQgY3rNKWlXTtb40YjuWcP161bRweHltkEMo1KpS5HLPkuXfpQp2tLYCsVigl0c/PhnTt3\nSJIRERGsX78lK1VqyEmTvrUlwXkMKSkpPHz4cFbyG6vVylKlyhH42e7DRUqSJ0+cOJHv8V29ejX1\n+prZPkh+ZkBArXzXFwgETw8h9IIXnhMnTthnvu4EDmTtoev1QVy8eDFjY2NZtmxl6vXeVKuNHDky\nOMdJ9cOHD3PAgGEcMGAYDx06lGc7sbGxXLduHefOnUtJ8rIf1IulTNadlV+qQEvz5jY1L1GCV9av\nZ/36r1KvL0G5vHa2vf4kKpXaHKf8zWYzg4M/Ya1azdmpU29evny5SMcnKSmJSqWU7WODNBh6ccmS\nJbmWP3jwIEeOfJ8ffDCWUVFRJG0fC716DaAkedHRsQGdnUvx+PHjReqnQCB4MoTQC154Jk78kgrF\nBwRW0RZf/l0CjVm1agOmpqayQYMgKhQT7GKbQL2+Mn/77bcCtbFt2zbq9a40GttTry/HmjUbUaWS\nqFY7skbZykytVcumoJ6eTD10iCVL+lEu/47AOQJeBN4ksJSS1Jj9+g15SiORO1arlQ4OrgT+zDqN\nr9f7cs+ePQ+V3bFjByXJjcBEyuUf0sHBnRcuXMiyc/LkSUZERDAxMfGZ9kEgEOSNEHrBC8/UqVOp\n0fSxi9ghAsNpNLrRZDJx5MhgAjoCcdlmtOP5ySefFqiNEiW8COyw10+hwVCZv//+OxMuXKC1Rg2b\nYW9vMjKShw8fpoNDlRz72TKZKxs2bMXvv5/GzMzMpzQSeRMWFkZJcqWjY0tKkhffeef9XMvVrfsq\ngRVZvstkn3Hw4BHP2FuBQFAQCqN94tS9oFjQt29fODn9CaXybQA7IUnrMW3at1iyZBnmz98JoCps\noWQBwAy9fgfKlfPLl+3Lly8jMLAO7tyJA9DU/lSC2VwDYfPnw7FjR8iOHQPKlQP+/BPw94fRaERG\nRjwAk728BqQFer0ao0ePKpKodAWlTZs2iIw8juXLR2Hv3o2YOfO7rHe0fdQDAFJSTAA8sr3zQHKy\n6X/NCQSCFwSRj15QbIiPj8ePP/6EhIQkvPZaW2i1WrRu3QMm00QA9WC7PlcGMtlltGvXGOvXL89T\ncK1WK06ePImUlBT07DkQcXH9Qf4KoC+AUQCi4YM6+AMm+CEN1sBAyHfsAEqWBABs2bIFr73WG2az\nF4CuAEIBBEAuX4HU1PtQq9WP7IvFYsGKFSsQExODmjVrol27dkU1TA/1c+TIYISEzAYAvPnmIPj5\nlcGECUthMs0FcA+S1B9r1oSgTZs2T8UHgUBQeAqjfULoBcWSK1euIDCwJlJSmgFwBhAC4C6Aj1C3\n7jn89dcfkMlkudZNS0tDUNBrOHo0EqmpySCTAZgBRAHoAOAa/JGGHdDDG4k4Kjfi/LQv8foIW0a4\nEydOoGHDIJhM/QFsstepCKAllMoyuHXrOm7dugUfHx/odA+niyWJ//u/HoiIiIPJ1BSStBYjRvTA\n5MkTiniUgO++m4bPPlsNk+l3AHJIUieMG9cOCoUcc+cuhVqtxuefv4/XX+9V5G0LBIKio1DaV9h9\ng2dNMXRZ8BRYsWIFHRy62O/TVyTwKoEgOjmVzDpYlhcTJ06iTteRwNcEOhBwIHDKvmdtYmV48Doc\nSYC78TJdVQP4ww8/kCSPHDnCN954gwrFaAKJBDwJ6Ak4Uqn04auvtqNWa4ssZzR65HoYbv/+/dTr\n/QmY7W3eolptyPPw25kzZ/jDDz9wwYIFuUbdexTNmnUg8Fu2swQb2aBB6wLZEAgEz5/CaJ/YoxcU\nS5ydnUFeAmAEcBBAZygUEThz5jDKly//yLonT0YiNbU9bKlhW8CWja4FgH6oDX/sQjw8kYRtaIzW\neB/3Fb8jKCgIH374KRo37ojffjsBiyUawI8AygOIBHAEMpkOu3btRlraX7h/PwrJyYvQvn23hyLd\n3b17F0qlD4AHy/uuUCodkJyc/JCv27dvR506TTF27EWMGLEW1as3wv379/M9TqVLu0OhOJ71s1x+\nHKVLu+e7vkAgeAEowg+OZ0IxdFlQhFitVqalpTEzM5NNmrShXt+UCsWHlKQy/O67afmy8fXX31GS\nWhGYS6CuPQDPMTZGVSbZp77r4UUN3CiTGbl27VqePHmSklSKwG37TN6Xtvj5O7LNlhdTqfTNcZdd\nkkoyNjY2R/u3b9+mo6MngaUEblKh+IJ+flVzDZTj61uNwKasuAFabbesAEH54e+//6arqzclqSsl\nqQdLlChdqHj4AoHg+VAY7RP56AXFhvnzF2DEiPdhNqcgIKA6Nm5cgb179yIuLg716y9E8+bN82Xn\nvfdGIiJiP3buHI/MTAsyMz3QEgqsQyokAMuhQj/oYJHdwYYNq9G+fTts2rQJKlUVAC52K4cA+AI4\nC8DWrkJxFuQdADcAeAI4DDIV7u45Z9AuLi7YuTMMr78+GLGxo1C1ak2sXh0KufzhBbbExATY9v8B\nQIa0tIqIj0/I95j5+Pjg3Lmj2LBhAwCgffsZD/kjEAhebMRhPEGxYMWKFXj99cEA/gBQC8DXKF9+\nDS5cOPJE9kgiJiYG6enp+CmoA767GgMNMjEfPhiCVwD5GqxZsxSdOnUCAMTGxiIwsBZMpi329tfA\n0fEdWCxERsZrkMlMMBh2o1+/3pg1awHU6kBkZJzGhAnj4O7uBn9/fzRo0KDAfvbo8SY2bDAjLW0W\ngL8hSe0RGroEr7zyyhP1WyAQFE/EYTzBC4+ra2kC3bMti1spl6sfeTjt3r177Nq1Lw0GN5YqVZ7r\n1q17uNAvv9Ail5MAp6ElZehHlUrPZcuWPVR07dp11OmcqNW60sXFi4cOHWJMTAynT5/On376KSvG\nfmRkJMPDw/nRR59RkkrTYHidklSGY8d+VuB+37t3jx069KJaraeTU0nOn7+wwDYEAkHxpzDaJ2b0\ngmKBWi0hI8MXwBEAGgCnoFTWh9l8L9clbwDo2rUvQkMzYDaPADASQBTq1q2FtWuXoHTp0sC8ecCQ\nIQCJUx06YujtdGh1Ggwc2B1HjpyAyZSG3r27o2HDhlk2MzIykJCQADc3t0cGxbFdrysPs/k0AC8A\nt6HVVsTp0/vh55e/QD4CgUDwgMJon9ijFzx30tPTcePGDXh6euYZaKZmzYY4cOAOgLoAqgH4HcHB\n7+Yp8gCwefMmmM07ALwCYBiARTh48Bf4+FTEaHk6vs1MsxWcPBlVxo7FnwAuXbqEmjUb4f79/rBa\nS2LRotcwadI4+Pn5oXbt2nBxcUF6ejosFstjhV6tLmkPqAMArtBo/HD9+nUh9AKB4NlSRKsKz4xi\n6LLgEWzdupUGgyslqRQNBldu27Yt13JXrlxh+fI1qFTqqVCoOXLk6Mfa9vDwJfCK/YT8gyV/Cz+G\nU9ax+CV1G+WoM3z4aMpkH2VtDwBBlMtL0WhsQ63WmVqtAyWpFB0c3Lhjx448205JSaGTU0kCa+y2\nttHBwZ0JCQkFGyCBQCCgSGojKKbcuXOHer0rgd12MdxFvd41z8AxVquVt27dYmpqar7sr1q1moAT\ngZIE0ghYOQWjSYCZkLM/JtPVtUyOOv36vU3gh6zgMkAlAib7z1sJlLL/+w4aDG5MSkrKs/2DBw/S\n3f0lKpVaOjuXZERERL7HRiAQCLJTGO0TAXMEz42LFy9CofAB0Nj+pAkUCi9ERUXlWl4mk8HNzQ1a\nrTbHc7PZjNjYWJjN5hzPu3fvhm7d2gPQQoY2mIkmGIOpyADQC8uxGFXg5FQiR52+fbtBp/sGwGYA\nuwDUBvAgjO0rsF2dswJoDrncHdHR0Xn2r06dOrhxIxqJifFISIhD06ZN8ywrEAgETwsh9ILnhpeX\nF9LTY2CLUAcAl5Ge/je8vLweVS0H4eHhcHX1QrlytWEwuOLtt4ciMzMz631IyI9Q4CYWYjfewZ9I\nA9AJdfArdkGn64+ffpqSw17z5s2xbNlMVKgwASVL/g6Vaks2/34EUAW2vzaXkJ4eZzvU9whkMhkM\nBkOecfcFAoHgqVOEKwvPhGLosuARTJs2kzqdO43GNtTp3Dljxqx8101MTLQv/e+yL6fvJmBgmzZd\naLVaSZK3rl7lr7Bdn7sHic3xO4FR1GqNPHnyZJ62zWYzZ82axebNW1Gp1FGnc6ejYylqNC52X904\ne3ZIofsvEAgE+aEw2ieu1wmeOxcuXEBkZCTKly+PgICAh95fuXIFy5cvR2amBd27d4O/vz8AYO/e\nvWjS5E1YrZHZSteCWh2NixdPwMfNDezaFbKwMNyFHG1RHvtRA8AGLF78E/r165erP5mZmWjatC2O\nHZMhNfVlSNIyDBz4f5g27RtERkbi4sWLqFChQpYfRUlcXBwSEhLg7++fa+Y7gUDw30QEzBEUezIy\nMhgXF0ez2Zzj+cWLF+no6EmVaigVindpMLjx6NGjJMn33gu2Z46Lts/oYwg4U6crxYtHj5KvvGI7\neOfszA5e5QnIqdMZOW/evEf6Eh4eToOhOoFMu90bVKl0NJlMBeqTxWJhVFQUY2JislYYHsX7/9/e\nnQdEVb0NHP8OMwPMgOAOCCKGIiIIKq65YC6E5p7mXtpiWpbtZmbaT8W0zD1zqUxLLTX33dxywdwV\nLU1REUVxIZEBZmDO+8fQlK9LiwgyPJ+/nLuc+zy3iWfuveee88YQ5eJSQhUrVlWVLu2vjh49+q+O\nJ4RwXPdT++Q9elHg9uzZQ0xMRzIyLICZefO+oGNH29Cz//vfx6Sl9cdqHQbAzZtBvPXWCAYM6M3G\njTuATkAEUBM4ClQnokIagf37Q1wc+Pig3biRZSEhmM1m9Hr93z4vv3HjBk5OfsAf78mXQaPRYzKZ\n/vFV9o0bN2jevB3x8SdRKptHH63LypXf4eLicsft169fz/Tpi8jKOklWVinS0mbRsWPv/zzErxBC\n/EE644kCZTabefzxDly7NpmMjEtkZGykV68XOHfuHABXr/6O1VrxL3s8wu7d+3j66Y85fjwLuAws\nBSyAjvByyWzTmdHExUGFCrB9O4TYJoVxdnb+R53iHn30UWyT1swFzqDXv0lISBglS5b8mz3/9MYb\nQzl8OACT6SwZGefYsUMxevS4W7ZRSvHtt/Pp3PkZPvxwNBZLS/6cNKc7p04d/cfHE0KIu5FCL/LF\nwYMHWbVqFefPn79l+YULF8jKcgI65C6phV5fg/j4eAC6dGmN0TgaOAz8irPzu5jNBm7e/Ins7J+A\n60BX3N1TaFKpLHvdrOiOHoWgIFuR/w+j0Hl5ebF582pCQz+jRIlGPPbYWdav/+Ef/UhYsmQJPXo8\nz9Kla8nK6ontroAzGRnd2L370C3bjh07nuef/5BFixqya1cpzOaVwB9z0i/F3//2/gpCCPGv5d0T\nhPxRCEMu8l5++U1lNPopT89oZTSWVitXrrSvS09PV66uHgric5+Hpyij0cf+fNpqtapx4z5VpUsH\nqBIl/HJ7wb+au+1pBRuVVuuijq1apawVK9pGvAsLUyo5Od/zHDVqjDIa5fUbaAAAIABJREFUKymY\npjSaGgoG5I6ul6NcXHqoN98ccsv2Hh5eCn6xj8Kn1YYqvb6U8vSsrUqUKGfviyCEEPdT+6TXvXig\ndu7cScuWPUlPPwB4Artxc2vNjRsp9nHqv/56Hv37v45OV5fs7AO88spzxMYOv2N7u3fvpmnTDmRm\nhmCb4KYMIU4X2F/KDZeUFKhdG9auhX9xm/1esX/77SKMRlcGDHiBgICAO253/fp1YmKeJC4uDtgN\nhAIpaDRhODuXRK+HSpVKsn37Wtzd3e37ubmVwmQ6DNjexXd27s/rrxenbdu2VKtWDQ8Pj/vOQQjh\nGO6n9kmhFw/Ut99+S79+y7h5c6F9mV5fjKFD38JoNNKlSxf8/f357bffOHLkCBUrViQiIuKebTZs\nGMWOHaeBQ1TnHBtoRFnSuB4WRomffoI8KJCrV6/mySf7kJExCCenqxQr9g0HDuykYsWKt23bsWMv\nVq1yw2xeDOwHygOg0w2gXz8nevfuTc2aNdHpbu372r//a3z99UFMphHAr7i7v8ehQ7t55JFH7jt+\nIYRjkUIvHlrx8fHUqdMMk2k7UBn4Bo2mH1ptL5ycwNX1B37+eRtBQUG37XvlyhUOHDhAqVKlqFGj\nhv0ZucHgQWZmb+rQi7U8TglSWQv0MpYk8WrSbUPk/hfVqzfkyJG3gHYAODm9wyuvKD79dOxt2/r4\nBJGcvAz4HDgCjARO4Ob2Jvv377hjbmB7X/+DD0axdOk6SpcuyYQJ/6NGjRr3HbsQwvHcT+2Tznji\ngapWrRoTJozGxaUWRqMvzs4DUepFsrM/w2z+jLS0QQwdOvq2/fbs2UNgYCidO8fSuHEnunbta/+S\nKwVNWMpGmlOCVJZQk3aUx4SRixcv5knc6ekmwMv+2Wr1Ii3NdMdty5cvj0azDRgHNECjeRJ//4/Z\ntGnlXYs8gE6nY9SoD4iP38nWrSulyAshHggp9OKBe/75vly9epHjx3dRq1YdoLF9nVKVuHIl9bZ9\nunTpy40bk/n99x9JTz/GqlWHWLp0KQAfN3uMNVygGDeZhwdd+AUzA9FoTPj4+ORJzE8/3Rmj8RVg\nL7AOo/FjevTodMdtv/xyEp6eI/DwaI+7+xpq1Ajkl1/2ULdu3TyJRQgh7scDLfSJiYk0bdqUatWq\nERoayqRJkwC4du0aLVq0ICgoiJYtW5Ka+ucf+tjYWCpXrkxwcDDr169/kOGJfDRlynSqVo0gLm4r\nWu0QIB74CaPxf3Tu3Oq27S9cOA08nvvJgNnchFOnTsHixby0YTUGFF+7etAbKy5Gf4zGj1i48Os8\nuW0PMHToO7z1Vjv8/fsQFDSUr7+eTNOmTe+4bbVq1Thx4hBz5jzP4sWj2b17kwxfK4R4eNxfh/97\nu3jxojpw4IBSSqm0tDQVFBSkjh07pt566y310UcfKaWUGjNmjHrnnXeUUkrFx8er8PBwZTabVUJC\nggoMDFQ5OTm3tPmAQxYPwOLFi5XRWFnBSQXXlJNTeQUuCtyVwVBS7d69+7Z9wsLqK41mvH0IWje3\nQHXk7beVcrJNUKNef10pq1UlJiaqHTt2qJSUlALITAgh8sf91L4HekXv7e1t70Ht7u5O1apVSUpK\nYvny5fYJRZ5++mn7Ldlly5bRrVs39Ho9AQEBVKpUiT179jzIEEUeyszM5OjRoyQnJ9+yfOXKTZhM\nLwOVgJtYrWnAFiCNjIzZPP54h9vmkv/hh7n4+n6Om5s/zs6V+bZJCKFjx4LVCh98AB9/DBoNfn5+\nNGjQgNKlS9v3VUqxYsUKJk2axE8//fSg0xZCiIdavj2jP3PmDAcOHKBu3bpcunQJLy9bRycvLy8u\nXboE2EZJ++tc5H5+fiQlJeVXiOI+xMfH4+8fTIMGTxIQUJUhQ0bY1/n6lkGvPwJcAZpjK/j1cte2\nx2JxsQ95+4dHHnmEIUNe5bHHGrDk0Tq0Xb3CtmLcOBg+HO4ySp1Siu7dn6Nbt6G8/favREf34KOP\nxudxtrceLzZ2HKVK+VOypB/vvTcCq9X6wI4nhBD/Vr5ManPz5k06derExIkTKVas2C3rNBrNPYcW\nvdO64cOH2/8dFRVFVFRUXoUq/qN27XqQkvI+8CyQwqRJ9Tlx4hd++eUcZcuWpFSp46Sk1CMnpw6w\nGVvRLw2cIDv7mv2HH9iKZ82ajTh48DrDqEhrNgFgmTQJ/cCB94xj7969rFixmfT0o4AReJdhw6oy\nYMDzt3338sIXX3zFyJFzMJnWAjomTOhOyZLFeeONV/P8WEKIomPLli1s2bIlT9p64IXeYrHQqVMn\nevXqRfv27QHbVXxycjLe3t5cvHiRsmXLAuDr60tiYqJ93/Pnz+Pr63tbm38t9KLgKaVISDgK9Mxd\nUoaMjKYsX74Li2Uax4//jIfHXkqUcOPKlUFAFaAGUB2tdidTpky4ZRS42bO/4ODBOMbxIm8yhRyc\neEFbji5BQUT/TSwpKSlotZWwFXkAP3S6YqSmpnL58mXi4+MJCAigevXqeZL7woWrMJneA2wT55hM\nI/j++0lS6IUQ9+X/X8SOGDHi7hv/jQd6614pxbPPPktISAiDBg2yL2/bti1z5swBYM6cOfYfAG3b\ntmXBggWYzWYSEhI4efIkderUeZAhijyg0Wjw9a0MLMtdcgOrdT0Wy0igMVbrG1gsDShf3gedbjnw\nAbAYZ+fLDBzYl+ee63NLe5s2bGMa8CZTMKPnKRbypdX/tuf4d1KrVi2s1oPASiALjWYipUp5sHnz\nVsLC6tGr1+fUrx/D0KH/y5Pcy5QpjpPT6b+ci1OULOmZJ20LIUSeyJPugHexfft2pdFoVHh4uIqI\niFARERFqzZo16urVq6pZs2aqcuXKqkWLFur69ev2fUaNGqUCAwNVlSpV1Nq1a29r8wGHLP6jPXv2\nKE9Pb+XpWU8ZDN5KozEquJzba14pd/doNW3aNFWhQlVVrFiEcnMLVA0bRqvMzMxbG7JY1P6w6kqB\nMqFVMUxQME7pdB7q6tWr/yiW7du3Kx+fSsrJSadCQuqoQ4cOKVdXTwVHc+O5rAwGb/vEOffjxIkT\nysPDS+n1Lyqd7mXl7l5GHTp06L7bFUKIv7qf2idD4Io8k5qaytGjRylTpgxTp85i9uytmEwD0Ov3\n4u29kfj4n9Hr9Rw8eBAXFxfCw8PtE9sAkJUF3bvDkiWkazS003jxo9Lg5JTF0qVzeOKJJ245XnZ2\nNu+99yHff7+C4sU9+fTTETRp0sS+XimFRqMhISGBsLAmpKf/2eHP07Ml8+e/RkxMzH3nnZiYyIIF\nC7BarXTu3FnGqhdC5DkZ614UOKUU58+fx2w2U7FiRTQaDdOnz2Dduu1UqODD+++/c8srcLcxmaBT\nJ9vMc8WLk7FkCStSUsjMzKR58+aUK1futl1eeeUtZs/+GZNpLHAGo/Eldu3adNvzd7PZjLd3Ra5f\nn4Zt7PoDGI0tOX58H/7+/nl6HoQQ4kGQQi8KVHZ2Np069WL9+o04OblSubI/mzevpESJEv+sgbQ0\naNMGtm6FMmVg/Xr4mxnsAEqWLM/165uxva5nm3hm2DA3Pvhg2G3bxsXFERPTkcxMK5DBl1/OwN+/\nPGazmdq1a2M0Gm/bRwghHhb3U/vy5fU64dg+/XQSGzakkJmZCDhz/PjLDBjwJvPnz/77na9dg5gY\n2LMHypWDTZsgOBj489b73bi4uALX7J+12qsYDKXuuG3dunW5fPksycnJuLm5ER3dkePHL+Pk5I6H\nRyq7dm26ZQwHIYRwFDKpjbgvixYtZvDg/5GR0Q1wBZwwm3uzb9/hv9/50iVo2tRW5CtWhO3bOaXX\n07NnX4oXL49Wq8fLq+Jd3yX93//exWjsDExCq30NT8/19hEX70Sn0+Hn58ekSVM5cqQ0N28e5saN\nOC5e7Er//m/+l/SFEOKhJ1f04h/bv38/n3wyjawsC/369SQgIIDevV/Eau0OrAaeAbTodCuoWrXy\nvRs7fx6aNYMTJ6BKFdi4kdNmMzVqNCAtTQu8BbzE5cubadOmC7/+evC25/TPPdeXcuW8WbRoJaVK\nefLaa7tvGXjnbuLjT5GZGQ1oAcjJieHXX1f/+xMihBCFgBR68Y8cOHCARo2iMZkGA+6sWfM0L73U\nE52uCfAx8ARQDVB4e8Nnn22+a1s5J06gadECp3PnIDzc9ky+bFmmvz2Emzc7AkuA13K3jsbJKZJ9\n+/bdsUNeq1ataNXq9tnv7qVu3XBWrZqPydQDcMHZ+SsiI8P/VRtCCFFYyK178besVisDB76NyfQW\n8AbQD5NpCsuXb8JqPQxYgfXABzg7n+f48TsXZYDvPxxJcpVgnM6d46CrkcS5cyF3ZESTKROlvIF0\n4I9X4TLIyTlhHz3xTrGdPHmSs2fP/uOOKq+++jKPP+6Di4sfBoMf1arFM3XquH9+QoQQohCRQi/+\n1jPP9Gf37l/5c1hZAAOuru507NgUo7EGbm7dMBoH8eWXs3F3d79jO/HffEPUBx/gi2IzUTTJeoMn\ner5oX9+zZxeMxmlAV6AB0Adn55q0bt3ojiMkXr9+nVq1GhMR0Yzg4Dq0bt0Zi8Xyt/nodDoWL57H\n6dNHOHZsJ3v3bv3nbwgIIUQhI4Ve3NP58+f5/vvF5OTMAEYCC4FVuLq+xMCBz+Dq6oLFcgGLZRNl\nypSkadMmd2znzPz5lO/dmzJYWY0frZjPDfU+R4/G2Wd7q1evHkuWfE2NGr/h7+9BmzapfPfdGBYs\n+OKOve8HDnyHY8eqYTKdITPzHFu2pPPxxxP+cW7lypUjICDg1kF7hBDCwcgzenFP6enpaLUeQDTw\nFTAROECDBtVxcdEzb94GLJalQH2SkmLp2fNFNm1adksbv//wA6W798AdxSKa0R1fLDwNvEeJEj63\nFNro6Giio/9u6hqb/fuPYDaPw/Z71YWMjKfYvXsD48aNZ+/eo0REBPP666/i4uJi38dkMpGamoq3\nt7cUeCFEkSAD5oh7ys7OpkqVmpw925acnKexTVwzAReXkmi1lzCZtIA3kAbMolSp3ly5cta+/+/f\nfotrj564oJhDb55lNjkAeGAwGFi8eN5/Hoa2U6feLF/uQ3b2GMCKq2s3ypU7zsWL5cjIeBKDYTl1\n6uTw448rcXJyYvz4Sbz77hCcnIx4eZVm06YVBAYG3ucZEkKIB09GxhMP1IULF2jUKIbTpy9im152\nGvAKcBXYCrgAY4CFREaW4Oeff7Tt+P33ZD/1FDqlmEZZXuYCCi1wDSenchw+vI9q1arZj7N69Wr6\n9h3I9euXqFevCYsWfUWZMmXs681mM5mZmfYpbZOTk6lfvznXrjljtZp45JGSnDiRQGbmmdyYLLi5\nVWHHjh9IT0+nRYuumEzbgQpoNOMJCfmOo0d3P+jTJ4QQ9+1+ap/cuxT3ZLFYGDHiIxITfwM6AOuA\n48Bu4ElsBRWgAxpNAnPnTrN9/Oor6NoVnVKMpQ8v8QiK7sBkNJpGuLuXZuTI8aSmpgLwyy+/0Lnz\n01y6NAuzOYldu4Jo27a7PY7hw0fh5uZJqVI+1K4dxZUrV/D29ub48b2sWTOFzZvnMXfudLRaI+Cc\nu5cOJyd3zGYz+/btw2p9AqgAgFIvcfz4XvnRKIRweFLoxT0NGTKCefPisVh+BH4AXgKeBprnfjYB\nCphD48YNCQ4OhqlToU8fsFqZXq4ig6kNbASqA+NRSs+NGz+wZIkTLVq0RynFtm3bgDZAU8ATi2Us\ne/ZswWw28/jjbRgxYhrZ2afIzk7j0KHq9OzZDwAnJyfq169PZGQkISEhlC9fAr3+dWAPOt0QSpe2\nUr16dSpUqIBWuxPIyM1sM2XK+N9ziF0hhHAEUujFPS1duhaTaSRQF9gGfAs8CrgDQUAAEIhe/znf\nfPM5fPQRvPyybedPPqHR+hUULzGSYsXaA19g+2EQB9TGbJ7O0aPxXLx4kZIlS+Lk9Cu2d/IBTuDq\nWowpUz5j06ZDwPNAOcAJi+VNdu/exaOPRmMwuGM0ejJ16nR0Oh3btq2hbdurBAb2p1Wrs+zcuREX\nFxfatGlDTEw4bm7V8fBojbt7bxYs+CK/TqMQQhQYeUYv7ujKlSssXbqUUaMmc+bMm0AvIAnbVfkJ\noH7uv3XodCvZuGElTTZtgpEjURoN8S+/TNVPP0Wr1XLt2jWGDRvG55/vJDs7GziI7TfmTZydy3Hh\nQgIeHh40avQ4R49aMZsj0Onm0759c/bu/YWTJ6sDF4FVufstwGh8HYulIxbLBCABo7EZq1Z9TVRU\n1F1zUkqxe/duUlJSiIyMvOugPkII8bCRzngiTyUmJlKz5qOYTA3IyUklK2s7tiv649hmizsKlAHm\noNePYP63M+i0YwdMmEA20M+lLt/pzdSu7cuMGZ8ycOC77Nu3h6tXG2C1JgFeQDNgJr161eLrr2cA\nts52CxcuJCEhgalTv+TGjXpkZp7G1gHwJHADKItO9xM6HWRmnshtC5ycBtOqVTyNGzcmJiaG0NDQ\nfD1nQgjxIEmhF3lGKUXr1p1Yt64KVmts7tJ2aDRxKPU9ts54U4EmODsfonePVszUmmHWLLKArgxj\nKSOAbNzcGqPVniQ9fRA5OaFAb+Bd4CRa7Sbq1XuEbds23vY++5gxH/HBB8cwm+cAl4HaQHlcXbPR\n639j3boVdOv2PGfPjgVaAVY0mih0OhPQEL3+G5YvX0CzZs3y45QJIcQDJ73uRZ5QStG9+7OsW7cT\nq/Wvk7yYUCoWaIRtdLzReHruYd3KGczISoVZs8BgoKPWmaX8Md2rjqysWmRleZKT8x7QDtiORvMR\nYWEnGDr0ebZsWX/HQWuuXUvFbP7j/faywFKKFTvBl18OIiHhV+rXr8+XX07GaHwaN7deODvXRamz\nWCw7sFgmYDLN5qWXBj+4EyWEEIWIFHpht27dOlas2IPVOhj4BLgApKDVnsz99x9cqV09gqipU9F8\n+y24u8PatVyNbIRWOwZbL/zf0GoXodXqcz8DVESns7Bt2wqGD3+Po0ePMn/+fPbt23dLHE88EYPR\n+DmwCziPwfABnTt3oWvXrpQqVQqApk2bcvjwbiZPfozoaF/gOf581S+I69evPZiTJIQQhY0qZAph\nyIXG559/rozGvgqsCoYoKKZArzp16qbc3csojeZtBR+oUoZS6lqdOkqBUiVKKBUXp5RSKikpSVWv\nXl/pdK7K2dlNTZ48VYWG1lUuLj0UzFRGY0PVq9cLSimlxo79VBmNPqpYsc7KaPRTw4ePviWWefO+\nUV5egcrDw0v16vWCysjIuGvcGzduVEajn4K9Ci4qg6Gd6tv3pQd3ooQQIp/dT+2TZ/TCbt++fTRq\n1IaMjG1AJWAilSp9xa5dG+jb9yV2744joGRxNrgoPA8ftk0vu2EDVK9+Szvp6em4urqi1Wq5efMm\nY8Z8zIkTZ2nUKJKXXupPSkoKFSoEk5W1H5iObaKcVCZPHsXLL7/0n2KfPftL3nnnAzIy0mnfvgOz\nZk3GYDDc5xkRQoiHg3TGE3li4cLv6dnzmdxX4PR4eXmxadNyOnbsxZkzDXE3N2Wd5gUi1RWUnx+a\njRuhSpV/fZyDBw/SuHEP0tLCsD0SmAEk4+LSlbVrF9zzFTkhhCiKpDOeuG9nz56lT5/+ZGfvxPYa\n21QyM03cuHGDCxeyKGF+ly0MI1Jd4bRGx+mvvvpPRR7Ax8eH9PTz2EbLmwwEA1FkZb3GkiUr8iol\nIYQQSKEXueLj49HrawHh2Dq1PY3FYhvsxs9qYhtNCOMoxwimhUsprP7+/+k4V69e5Z13BuPk9BgQ\nCCTa1+l0iXh6uudBNkIIIf4g89ELACpUqEB29hEgBdtgOEewWm/SxNeXH7Mv4kMW+wmgnUsAJSp7\nYjab/1G7WVlZ6PV6nJyciI+Pp1Gjlty86UJ29kBsV/LPAP2A83h6bmDAgD0PKEMhhCia5IpeAFCt\nWjVef70/RmM4Hh4xGAyPsWjEe7jHxOBjzuJsOT9eqeZNcs5Ozp51p3bt5gwfPvqu7V27do2GDaNx\nc/PAYCjGJ59M5JlnBpKaOgyLZRTwJVAL28Q4S9FolgCQkZFx1zaFEEL8e9IZT9ziyJEjnDlzhppK\n4du3L1y9Sk5UFGtffJEOvfpisWwC6gGXMBgi2Lt3EyEhIbe107p1FzZuLI3ZPAk4j9H4GHq9md9/\n/xGoDAwDxuZuHQV8h5PT50RF7WDTpmX5k6wQQhQS0hlP5JmwsDDalCyJb69ecPUq5pYtCTt7haee\n/RSLpQq2KWovAl7o9WGcOXPmlv1TUlI4fvw4O3b8hNn8LranQwGYTL0oU6Y0ev00bAPoDEKrDQA6\nYxtW1xOrtQWnTiXkY7ZCCOH4pNALAC5cuMCkSZNYMmAA1hYt4MYN6NyZNwKqcCqpIenpu4D92Iay\nHQocxmLZT1BQkL2NESNiKV++EnXrtiMtLQP4OXeNFYNhLy+80IOQkJ9xcSmDXu9PkyaBGAyngTTA\nirPzDGrXrpnPmQshhGOTW/eCU6dOERnZiKY3Q5ifvRkXrPzeoQOe339P8+jObNrUDduVN8A6NJqe\naLUmnJy0ZGdnUKtWI4YOHUS3bq9gMu0GvIF30WgmYzS2RaM5S8WKOUREhJOQkESdOqG8997bWCwW\ngoJqcuPGNcAZd3c3TpzYh4+PT4GdCyGEeBjJrXtxX4YOHc3jvzdiYfZWXLAyhQY8k+MKWi2NG9fG\nYJgFmIAsDIYZtG7dBL3eE7P5J6zW0fz8cwo9e/bDam2IrcgD/A+lTEye3IIZM14mNTWVBQvc+Omn\nZ/nss4O88MKrDBz4DhkZT2F7xe4Q2dm1+OKLOQV1GoQQwiFJoRfUOLifb9T36MkmlsEMpBFLl6/H\n3b08ZcuWICamDHq9F87OZWnUyErDhrXJyekMfA6sAN4nLa0TWVnL+fO9+FX4+DxCnz59KFasGKmp\nPlgs44EOZGQsYcmS7/jxx5+wWDoDpYEAMjM7sm/fsYI5CUII4aDkPfoiJjk5mVGjxpGUlEKbNs14\n5kYqb/9yEIAhvEEs5YHhwFTS0zPo3/8VVq6cz6xZk7FarZQqVYpvvvkGnW4lZvMebPPFewJd0Oni\n0WiqYzCEYLX+xvTpM0lJScm93aT5SxQalNJy/Xo2Gs23KFUPyMZgWEKtWo/m7wkRQggHJ8/oi5Br\n164REhLJ1avtyM4OY5h+CCMslwBY2Tyap3buxWTKwfaOe/vcvabSuPFKtm5dY2/HYrHQpEkrdu3a\nAvwOGAFwd2/D8OFRBAcH8/77Yzh+/Fes1izatGnL7t17SE5uQ05OFLaJbDyAMUAobm4+KJVB3brV\nWbNmMS4uLgghhPiTPKMX/8iSJUtIS6tFdvZ4RvEbIyyXsAJq5kye2LCWs2d/QaPRANa/7GXF2dn5\nlnb0ej3btq2hQYMmODu3B9ah1X6IwXCYPn36MH/+Mo4dCyYz8yJm8wWWLfuNMmVKEBq6A632RSAS\n+Aooh4uLnqVLp7J37zo2blwuRV4IIfKYFHoHdPbsWb766iuWLFlCVlaWfbnFYgGrGxN5lSHEko2W\np7XO8OyzAJQuXZrWraOAF4Cvgc9xchrK8OFv33YMnU7H5s2ref31+kRGjqN9+9/4+edtlCxZkri4\n/WRlPQdoATeys/ty8KCOEyeS8PDQoNOZgR24uj5NnTp1aNasGVWrVsXJSb6OQgiR1+TWvYP57rvv\n6NHjeZRqjk6XRHCwll27NmIwGEg8c4YtlavSKzuTLPT0cg7BrXt9vvzyM/v+SimGDh3KggWrKVbM\njYkTR9GkSZN/FUNMTGc2bKhOTs772O4OdANCgccpVepJmjaN4sSJBOrXr8nHH4/E3V0mshFCiHuR\n+egFYBv0pnz5alits4BOgEKni+HTT5/g5X79oFcvWLiQDCctA/2qUPKpjowaNQy9Xp+ncZw7d456\n9R7j2rWSZGXdwDZJzjogmeLFG3H9elKeHk8IIRydPKMv4qxWKzNnzqRjx6ewWsH2DBxAQ3Z2PX45\neBg6dYKFC8HDA8PWLUw/dQiNRkPlyrUIDW3A+vXr8ywef39/fv31AJMnP4+LSzK22emOYjQ+S48e\nXfPsOEIIIf6eXNE7gF69XmDx4iNkZHgDx4EmwBQgCSN12eSWSb30G1CyJKxfD7Vq8dprg5kxYxcm\n03ggEaPxBbZuXU1kZOQ9j/Vvbdu2jUGDhpGa+judOrUmNnY4Op281SmEEP+G3LovwpKTkylfPojs\n7AvANWzPwgOAX/AAVuFKQ9LA2xs2bIDQUADKln2ElJRVQNXcloYxeLCV2NiRBZCFEEKIe5Fb90XY\nwYMHyc7WA26AP/A2cIVS1OFHytKQNM476ehbKZxt167Z9zMYjECK/bNOdxk3N0M+Ry+EEOJBk0Jf\niMXFxbFs2TI0GmfgFeAIoMObLLayk1okcRItDazj+fKnJ4mJeZKdO3cCEBv7HgZDd+ATtNpX8PRc\nRd++fVi+fDkTJ05k27ZtzJkzl9Kl/TEaS/DUU30wmUwFmK0QQoj/Qm7dF1LDh49m3LjpKBVKRsYu\noBoQjz9l2UQSlUjnpIuBxllTSaZP7l6T6Nr1EPPnz+bKlStERNTj8uV0IIcqVSoSHFyFNWsOk53d\nEFiE1QoWy0rAH1fXAXTuXIqvv/68oFIWQogiS57RFzHnz5+ncuVwMjOPAV7AEGAy1V29WJF5Gn8U\nlurVidF4sunQG9g6580GNtCsmY6NG1fSo8dzfP+9OxbLp4DC2TkGpeKxWE5gG9L2FaAEMCL3qKdw\nc3uUmzeT8z9hIYQo4uQZfRGzf/9+rNay2Io8wGjqGMqwyzkFfxQ8+ij6bdt4YchAXF37ARWBnUAk\n27btYeHC7/j558NYLG2xTTbjhNkcjlIV+GPcetvz/qN/OeoJ0tOzWLVqVT5lKYQQIi/IFX0hc/r0\naSIi6pGWZgbmAm2oxXjWa96kpFLQvDksXQpubmRkZFCqlC8ZGVGNMUnHAAARyUlEQVTAktwWduDm\n1onMTAs5OTGAH/ADcB2NxoRS84EWwKfAqNx/BwDfAB0pU2YDSUm/5PkgO0IIIe5OruiLkPHjp5Ce\n/jywBhhAQ5z5kTcoqRQp9euTk1vkATp37k1GRioQ+JcWKpCefoOcnG3YrvI3A4uAeSiVCbwGFAOW\nYpt+tjRQDtgIOHP9umLevHn5lK0QQoj7JYW+kElLM2G1egH1acEs1mGb8HWRrhxBh9N5rFVnzGYz\nb745hFWrlgDuwBxgA3Aa24Q1Ltg67+mBWUAY0DJ32x8AM7AbF5fywHzgCjAJWIrV2ooLFy7kZ8pC\nCCHugxT6QqZHj44YjWNpx4esoA1GLMyiKU9lnyM1fR87d6YxcOBAPvtsOeAMjARygD5ATeAAtufw\nCwAFXPxL6+FoNM2Akbi4dKN8+QwiIsLRaLYDQcAiXF1X8Oijj+ZnykIIIe6DPKMvhHYNHEjtKVPQ\nARPR8RoJKPxy13bH2XktZvO7wA1gBRCN7db7MWy3/H8BPsQ2YE4x4HXgQu62FwgOrk737h0ZNGgQ\nmZmZtGrVhQMHdqHVahk3biyvvPJS/iYshBBFnLxeV5TMnAn9+oFSxDq5McRqBHoD44CVQA+gA7bh\ncJcC84AvgTNABrY54gOAg0AMtiv6hthG1msFPIZe34OqVQ+zf/92tFotABkZGbi4uMic8UIIUQCk\nM15RMWECvPACKMUQJyNDrNOxzVS3DCgOdAWGAtOB34Ha2Ir8YeAZoCzwG7ZOeDGAN5CK7UdBKaAz\n8B4WyzR+++08p0+fth/aYDBIkRdCiEJI/nIXBkrByJHw2msAvOpkINZaEbgJTARM2Ap+CWy36w3A\nJqAD3t7nqF07HGfnj4HG/Pme/AhsPwJaYrttPxRoCwwGLFitWTg7O+dXhkIIIR6QB1ro+/bti5eX\nF2FhYfZl165do0WLFgQFBdGyZUtSU1Pt62JjY6lcuTLBwcF5Oj96oWexwIYNWDUaXtBVYJK1N9AM\neB9YDvQHdvLqq0/i7j4DjWYkMAuDYTqTJo1lz57NrFixBNu79JdyG90EVAE+o0cPX4KCKuDqegH4\nEoOhHU2bNsLf3z//cxVCCJGnHmih79OnD2vXrr1l2ZgxY2jRogUnTpygWbNmjBkzBoBjx46xcOFC\njh07xtq1axkwYABWq/VBhld4ODszvFYD2mpcmZndE2iH7fn7WGAfWu1sund/igkTJhAXt4U+fS7y\n1FN7+eGHL+jc+UkArly5hu0WfQBQAZgGdMDLqzzz5s3k4MHdvP12OO3b/8j77zdj2bL5aDSaAklX\nCCFEHlIPWEJCggoNDbV/rlKlikpOTlZKKXXx4kVVpUoVpZRSo0ePVmPGjLFvFx0drXbt2nVbe/kQ\n8kPnyJEjymDwUTBTQYSC3xV8ocBHabUe6qWXXldms/mu+1+6dEkZDCUVPKPAT4GbAj+l0birHTt2\n5GMmQggh/ov7qX26/P5hcenSJby8bGO0e3l5cemS7VbyhQsXqFevnn07Pz8/kpKS8ju8h9K5c+dw\ndg4jI+NZ4BDwCOBM8eJWPv10It26dbttSNrt27fz2Wdz0GqdaNasAc7Oj5CRMRvblfw6dLo4Fi/+\nhgYNGuR/QkIIIfJNvhf6v9JoNPe8PXy3dcOHD7f/OyoqiqioqDyO7OESGhqKxbIf2A9MBrzRaGLJ\nyanLK69M56OPphAX9yMeHh4AbNiwgXbtepKRMRTIYvHiN3Ifg/wKvAxEodc3loFvhBDiIbVlyxa2\nbNmSJ23le6H38vIiOTkZb29vLl68SNmyZQHw9fUlMTHRvt358+fx9fW9Yxt/LfRFgb+/P3PnzqBn\nz+YopScnx0pOzmDS0oYCioSEPowePY7Y2A+ZO3ceb701koyM8djeqYeMDD21ay/h6NGGODtXwmz+\njVmzplGqVKkCzUsIIcSd/f+L2BEjRtx947+R76/XtW3bljlz5gAwZ84c2rdvb1++YMECzGYzCQkJ\nnDx5kjp16uR3eA+tjh07kJR0mlGjBlOiREms1qa5azRkZTXmxImzvPPO+wwY8AmXLxuwjVv/B3d8\nfPw4deooq1d/yunT8XTv3rUAshBCCJHfHugVfbdu3di6dStXrlyhfPnyfPjhhwwePJguXbowe/Zs\nAgIC+O677wAICQmhS5cuhISEoNPpmDZtmvT6/oukpCRq147i+vXKmM3uwHigDpCJ0fgVjz7akcGD\nB5OdfQ7bBDavYZu0JgujcRj9+8/Gx8cHHx+fAsxCCCFEfpMhcAuBM2fOEBZWk5s3G2N7re4m0Bw4\njF6voWXLGIKDH2H8+AkolYZtdrq5ODkNpUKFkowf/4H9zokQQojCR4bAdXAvvvgmN2+GAzVyl7gD\n8ylevATLly9m8+atjB/vjFKB2IbB3YdGc5Nixczs3LlGirwQQhRhckVfCFSqVItTp54FYrHNMFcB\nJ6fn6dLFkzNnzrN7dy+gJ5AONKNYsSSqVw9l+vRxhIaGFmToQggh8oBc0Tu4Bg0icXHZCwzHNhmN\nD6GhF5g5cyJpaTfBPkWtG9CHmJgW/PTTGinyQgghpNAXBpMnj6VGjXO4uLyNTvc7tWpFMGDA0wB0\n794eo/Ft4AiwE6Mxlh495Fa9EEIIG7l1X0gopVi0aBFPPz2AnJyn0OkS8fY+zb592/nkk0nMnDkX\nZ2dnhg17g+ee61vQ4QohhMhD91P7pNAXIpUq1eDUqf8BTwDg4tKNUaMieeONNwo2MCGEEA+UPKMv\nIlJTrwFV7Z+zsqpy+fLVggtICCHEQ08KfSESHd0CV9ch2KabPYjROJPHH29R0GEJIYR4iEmhL0Rm\nzJhIq1bOuLgEULx4KyZN+pCmTZv+/Y5CCCGKLHlGL4QQQjzk5Bm9EEIIIe5ICr0QQgjhwKTQCyGE\nEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQ\nCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjh\nwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0Q\nQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5M\nCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGE\nEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA7soSv0a9euJTg4mMqVK/PRRx8VdDgPnS1b\nthR0CAWqKOdflHMHyV/y31LQIRRaD1Whz8nJ4eWXX2bt2rUcO3aM+fPnc/z48YIO66FS1L/sRTn/\nopw7SP6S/5aCDqHQeqgK/Z49e6hUqRIBAQHo9Xq6du3KsmXLCjosIYQQotB6qAp9UlIS5cuXt3/2\n8/MjKSmpACMSQgghCjeNUkoVdBB/WLx4MWvXrmXmzJkAzJs3j7i4OCZPnmzfplKlSpw6daqgQhRC\nCCHyXWBgIL/99tt/2leXx7HcF19fXxITE+2fExMT8fPzu2Wb/5qoEEIIURQ9VLfuIyMjOXnyJGfO\nnMFsNrNw4ULatm1b0GEJIYQQhdZDdUWv0+mYMmUK0dHR5OTk8Oyzz1K1atWCDksIIYQotB6qZ/RC\nCCGEyFsP1a37v/r++++pVq0aWq2W/fv337IuNjaWypUrExwczPr16+3L9+3bR1hYGJUrV+bVV1/N\n75AfqKIwkFDfvn3x8vIiLCzMvuzatWu0aNGCoKAgWrZsSWpqqn3d3b4HhVViYiJNmzalWrVqhIaG\nMmnSJKBonIPMzEzq1q1LREQEISEhvPvuu0DRyP2vcnJyqFGjBm3atAGKVv4BAQFUr16dGjVqUKdO\nHaBo5Z+amsqTTz5J1apVCQkJIS4uLu/yVw+p48ePq19//VVFRUWpffv22ZfHx8er8PBwZTabVUJC\nggoMDFRWq1UppVTt2rVVXFycUkqpmJgYtWbNmgKJPa9lZ2erwMBAlZCQoMxmswoPD1fHjh0r6LDy\n3LZt29T+/ftVaGiofdlbb72lPvroI6WUUmPGjFHvvPOOUurO34OcnJwCiTuvXLx4UR04cEAppVRa\nWpoKCgpSx44dKzLnID09XSmllMViUXXr1lXbt28vMrn/4ZNPPlHdu3dXbdq0UUoVre9/QECAunr1\n6i3LilL+vXv3VrNnz1ZK2f4fSE1NzbP8H9pC/4f/X+hHjx6txowZY/8cHR2tdu3apS5cuKCCg4Pt\ny+fPn6/69euXr7E+KDt37lTR0dH2z7GxsSo2NrYAI3pwEhISbin0VapUUcnJyUopWyGsUqWKUuru\n3wNH0q5dO7Vhw4Yidw7S09NVZGSkOnr0aJHKPTExUTVr1kz9+OOP6oknnlBKFa3vf0BAgLpy5cot\ny4pK/qmpqapixYq3Lc+r/B/aW/d3c+HChVteuftjUJ3/v9zX19dhBtspygMJXbp0CS8vLwC8vLy4\ndOkScPfvgaM4c+YMBw4coG7dukXmHFitViIiIvDy8rI/wigquQO89tprjBs3DienP/8sF6X8NRoN\nzZs3JzIy0j6WSlHJPyEhgTJlytCnTx9q1qzJ888/T3p6ep7lX6C97lu0aEFycvJty0ePHm1/RiVs\n/wMI23m417lwlPN08+ZNOnXqxMSJEylWrNgt6xz5HDg5OXHw4EF+//13oqOj2bx58y3rHTn3lStX\nUrZsWWrUqHHXMd0dOX+AHTt24OPjQ0pKCi1atCA4OPiW9Y6cf3Z2Nvv372fKlCnUrl2bQYMGMWbM\nmFu2uZ/8C7TQb9iw4V/v8/8H1Tl//jx+fn74+vpy/vz5W5b7+vrmSZwF7Z8MJOSovLy8SE5Oxtvb\nm4sXL1K2bFngzt8DR/jvbbFY6NSpE7169aJ9+/ZA0TsHnp6etG7dmn379hWZ3Hfu3Mny5ctZvXo1\nmZmZ3Lhxg169ehWZ/AF8fHwAKFOmDB06dGDPnj1FJn8/Pz/8/PyoXbs2AE8++SSxsbF4e3vnSf6F\n4ta9+ssbgG3btmXBggWYzWYSEhI4efIkderUwdvbGw8PD+Li4lBKMXfuXPsfysKuKA8k1LZtW+bM\nmQPAnDlz7P9N7/Y9KMyUUjz77LOEhIQwaNAg+/KicA6uXLli71GckZHBhg0bqFGjRpHIHWx3MRMT\nE0lISGDBggU89thjzJ07t8jkbzKZSEtLAyA9PZ3169cTFhZWZPL39vamfPnynDhxAoCNGzdSrVo1\n2rRpkzf552WHgry0ZMkS5efnp1xdXZWXl5d6/PHH7etGjRqlAgMDVZUqVdTatWvty/fu3atCQ0NV\nYGCgGjhwYEGE/cCsXr1aBQUFqcDAQDV69OiCDueB6Nq1q/Lx8VF6vV75+fmpL774Ql29elU1a9ZM\nVa5cWbVo0UJdv37dvv3dvgeF1fbt25VGo1Hh4eEqIiJCRUREqDVr1hSJc3D48GFVo0YNFR4ersLC\nwtTYsWOVUqpI5P7/bdmyxd7rvqjkf/r0aRUeHq7Cw8NVtWrV7H/jikr+Sil18OBBFRkZqapXr646\ndOigUlNT8yx/GTBHCCGEcGCF4ta9EEIIIf4bKfRCCCGEA5NCL4QQQjgwKfRCCCGEA5NCL4QQQjgw\nKfRCCCGEA5NCL4QQQjgwKfRCCCGEA5NCL4S4p59//pnw8HCysrJIT08nNDSUY8eOFXRYQoh/SEbG\nE0L8rffff5/MzEwyMjIoX74877zzTkGHJIT4h6TQCyH+lsViITIyEoPBwK5duwr1lKBCFDVy614I\n8beuXLlCeno6N2/eJCMjo6DDEUL8C3JFL4T4W23btqV79+6cPn2aixcvMnny5IIOSQjxD+kKOgAh\nxMPt66+/xsXFha5du2K1WmnQoAFbtmwhKiqqoEMTQvwDckUvhBBCODB5Ri+EEEI4MCn0QgghhAOT\nQi+EEEI4MCn0QgghhAOTQi+EEEI4MCn0QgghhAOTQi+EEEI4sP8Diwf1C+duoqkAAAAASUVORK5C\nYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x107806610>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 8
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"#### Comparing the results from the different implementations"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"As mentioned above, let us now confirm that the different implementations computed the same parameters (i.e., slope and y-axis intercept) as solution of the linear equation."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import prettytable\n",
|
|
"\n",
|
|
"params = [appr(x,y) for appr in [lin_lstsqr_mat, classic_lstsqr, numpy_lstsqr, scipy_lstsqr]]\n",
|
|
"\n",
|
|
"print(params)\n",
|
|
"\n",
|
|
"fit_table = prettytable.PrettyTable([\"\", \"slope\", \"y-intercept\"])\n",
|
|
"fit_table.add_row([\"matrix approach\", params[0][0], params[0][1]])\n",
|
|
"fit_table.add_row([\"classic approach\", params[1][0], params[1][1]])\n",
|
|
"fit_table.add_row([\"numpy function\", params[2][0], params[2][1]])\n",
|
|
"fit_table.add_row([\"scipy function\", params[3][0], params[3][1]])\n",
|
|
"\n",
|
|
"print(fit_table)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"[array([ 0.95181895, 107.01399744]), (0.95181895319126741, 107.01399744459181), array([ 0.95181895, 107.01399744]), (0.95181895319126764, 107.01399744459175)]\n",
|
|
"+------------------+----------------+---------------+\n",
|
|
"| | slope | y-intercept |\n",
|
|
"+------------------+----------------+---------------+\n",
|
|
"| matrix approach | 0.951818953191 | 107.013997445 |\n",
|
|
"| classic approach | 0.951818953191 | 107.013997445 |\n",
|
|
"| numpy function | 0.951818953191 | 107.013997445 |\n",
|
|
"| scipy function | 0.951818953191 | 107.013997445 |\n",
|
|
"+------------------+----------------+---------------+\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 9
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"#### Initial performance comparison"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"To get an initial impression of how the performances of the different least squares implementations compare against each other, let us do a quick benchmark using the `timeit` module via IPython's `%timeit` magic."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"for lab,appr in zip([\"matrix approach\",\"classic approach\",\n",
|
|
" \"numpy function\",\"scipy function\"],\n",
|
|
" [lin_lstsqr_mat, classic_lstsqr, \n",
|
|
" numpy_lstsqr, scipy_lstsqr]):\n",
|
|
" print(\"\\n{}: \".format(lab), end=\"\")\n",
|
|
" %timeit appr(x, y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"matrix approach: 10000 loops, best of 3: 158 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"classic approach: 1000 loops, best of 3: 1.6 ms per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"numpy function: 1000 loops, best of 3: 217 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"scipy function: 1000 loops, best of 3: 366 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 10
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"The timing above indicates that the \"classic\" approach (Python's standard library functions only) is significantly worse in performance than the other implemenations - roughly by a magnitude of 10. However, we should keep in mind that this experiment was done for a fixed sample size n=500."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"<a name=\"cython_nb\"></a>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Compiling the Python code via Cython in the IPython notebook"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Maybe we can speed things up a little bit via [Cython's C-extensions for Python](http://cython.org). Cython is basically a hybrid between C and Python and can be pictured as compiled Python code with type declarations. \n",
|
|
"Since we are working in an IPython notebook here, we can make use of the very convenient *IPython magic*: It will take care of the conversion to C code, the compilation, and eventually the loading of the function. \n",
|
|
"Let us also compile the functions for the other 3 least squares approaches - those already use numpy objects and therefore we don't expect any performance gain here, but it is good to be thorough.\n",
|
|
"\n",
|
|
"**Note** \n",
|
|
"Of course Cython has much more horsepower under its hood - more than I am showing in this section of this article (for example, I am not using Cython's type definitions via `cdef` here, but we will get to it [in a later section - Appendix II](#type_declarations)). \n",
|
|
"The focus of this section should be on how to speed up existing Python code by making only minimal changes to it. "
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%load_ext cythonmagic"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 11
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"import numpy as np\n",
|
|
"import scipy.stats\n",
|
|
"cimport numpy as np\n",
|
|
"\n",
|
|
"def cy_lin_lstsqr_mat(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)\n",
|
|
"\n",
|
|
"def cy_classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)\n",
|
|
"\n",
|
|
"def cy_numpy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return np.linalg.lstsq(X,y)[0]\n",
|
|
"\n",
|
|
"def cy_scipy_lstsqr(x,y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" return scipy.stats.linregress(x, y)[0:2]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 12
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### Comparing the compiled Cython code to the original Python code"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"for lab,appr in zip([\"matrix approach\",\"classic approach\",\n",
|
|
" \"numpy function\",\"scipy function\"],\n",
|
|
" [(lin_lstsqr_mat, cy_lin_lstsqr_mat), \n",
|
|
" (classic_lstsqr, cy_classic_lstsqr),\n",
|
|
" (numpy_lstsqr, cy_numpy_lstsqr),\n",
|
|
" (scipy_lstsqr, cy_scipy_lstsqr)]):\n",
|
|
" print(\"\\n\\n{}: \".format(lab))\n",
|
|
" %timeit appr[0](x, y)\n",
|
|
" %timeit appr[1](x, y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"matrix approach: \n",
|
|
"10000 loops, best of 3: 159 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"10000 loops, best of 3: 159 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"\n",
|
|
"classic approach: \n",
|
|
"1000 loops, best of 3: 1.62 ms per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"10000 loops, best of 3: 126 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"\n",
|
|
"numpy function: \n",
|
|
"1000 loops, best of 3: 218 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"1000 loops, best of 3: 220 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"\n",
|
|
"scipy function: \n",
|
|
"1000 loops, best of 3: 372 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"1000 loops, best of 3: 354 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 13
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"As we've seen before, our \"classic\" implementation of the least square method is pretty slow compared to the other approaches which use Numpy objects. This is not surprising, since Numpy is highly optimized and uses compiled C/C++ and Fortran code already. This explains why there is no significant difference if we used Cython to compile the numpy-objects-containing functions. \n",
|
|
"However, we were able to speed up the \"classic approach\" quite significantly via Cython, roughly by 1500%.\n",
|
|
"\n",
|
|
"The following 2 code blocks are just to visualize our results in a bar plot."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"funcs = ['classic_lstsqr', 'cy_classic_lstsqr', \n",
|
|
" 'lin_lstsqr_mat', 'numpy_lstsqr', 'scipy_lstsqr']\n",
|
|
"labels = ['classic approach','classic approach (cython)', \n",
|
|
" 'matrix approach', 'numpy function', 'scipy function']\n",
|
|
"\n",
|
|
"times = [timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000)\n",
|
|
" for f in funcs]\n",
|
|
"\n",
|
|
"times_rel = [times[0]/times[i+1] for i in range(len(times[1:]))]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 14
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"x_pos = np.arange(len(funcs))\n",
|
|
"plt.bar(x_pos, times, align='center', alpha=0.5)\n",
|
|
"plt.xticks(x_pos, labels, rotation=45)\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.title('Performance of different least square fit implementations')\n",
|
|
"plt.grid()\n",
|
|
"plt.show()\n",
|
|
"\n",
|
|
"x_pos = np.arange(len(funcs[1:]))\n",
|
|
"plt.bar(x_pos, times_rel, align='center', alpha=0.5, color=\"green\")\n",
|
|
"plt.xticks(x_pos, labels[1:], rotation=45)\n",
|
|
"plt.ylabel('relative performance gain')\n",
|
|
"plt.title('Performance gain compared to the classic least square implementation')\n",
|
|
"plt.grid()\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAFhCAYAAABwNN3iAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3X1cjff/B/DXSaWiG4XQrciEFHITo4yhKIahuStMGsbs\nhrERc5e53drMGG1GfJnbVAw7GbpxM7eRu50QNblLiur0/v3RzvXrdKOyTuec67yfj4eHrnNd57re\n7+u6zvU+1+dzXeeSEBGBMcaYztNTdwCMMcY0AxcExhhjALggMMYY+xcXBMYYYwC4IDDGGPsXFwTG\nGGMARF4QMjIy0KNHD5iZmeHTTz9Vdzhql5ubCz8/P1hYWGD48OEVTi+VSmFnZycMt2nTBseOHQMA\nEBGCgoJgaWmJLl26AADWrl0La2trmJmZ4fHjx6pJ4jWVzIVVXkpKCtzd3WFmZoZvv/0WISEhWLhw\nYaXfX9Xpq8LR0RFHjhxRybzVacuWLejbt2/NL5g0jIODAxkbG1PdunXJ2tqaAgMDKTs7+7XmtWDB\nAhoyZEg1R6i9fvnlF+rUqRPJ5fJKTf/HH3+Qra1tmeOOHTtGtra2lJOTQ0REeXl5ZGxsTBcvXqy2\neKvCwcGBjhw5Uu74V+VSXcaOHUtffPGFSpehDuPGjaMZM2aUOa4m1uurODo6vnK7q8OmTZvozTff\nrPT0f//9N0kkkkp/LlVJ484QJBIJoqKi8OzZM5w9exanT5+u8rcLIkJhYSFSU1Ph4uLyWnEUFBS8\n1vs0WWpqKlq0aAE9vf++2VNTU+Ho6AhjY2MAQHp6Ol68ePHa67uwsPA/xSORSEB8j2WFXme/Tk1N\nRatWrVQQDStOI/ZfNRekUkpW/E8++YQGDBhARETx8fHk6elJFhYW5ObmRlKpVJjOy8uL5syZQ926\ndSNjY2MaNWoUGRgYkKGhIdWtW5eOHDlCL1++pGnTplGTJk2oSZMmNH36dHr58iURFX3TsbGxobCw\nMGrUqBGNHj2aQkNDaejQoTRq1CgyNTUlV1dXunbtGi1evJgaNmxI9vb2dOjQISGGjRs3kouLC5ma\nmpKTkxOtW7dOGKeY/4oVK6hhw4bUuHFj2rRpkzA+JyeHZsyYQQ4ODmRubk5vvvkm5ebmVph3ScnJ\nyeTl5UUWFhbUunVr2rdvHxERzZ07lwwNDcnAwIDq1q1LGzduLPXenJwcGjt2LNWrV49atWpFy5Yt\nU/r25+DgQIcPH6YNGzaQkZER1apVi+rWrUsBAQFUp04dkkgkVLduXerVqxcREV25coV69+5NlpaW\n9MYbb9D//vc/YV5jx46lSZMmkY+PD9WpU4eOHDlCaWlpNHjwYGrQoAE1bdqUvvnmG2H6efPm0bvv\nvktjxowhU1NTat26NZ0+fZqIiEaNGkV6enrCmeXXX39dKreS32RftazExETq0qULWVhYUOPGjWnK\nlCmUl5cnjJ8+fTo1bNiQzMzMyNXVlS5dukTr1q1T2t/8/f3L3D5lvZeIKDMzk/z8/MjMzIw6depE\nX3zxhfAts6xvkF5eXrRhwwYiIrpx4wb17NmTrKysqH79+jRy5Eh68uSJ0nYLCwsjV1dXMjIyIrlc\nXul9qmfPnlSrVi0yMjIiU1NTunbtmnAm9Pz5czIyMiI9PT2qW7cumZqa0v3790vNo/iZk+JzsGzZ\nMmrQoAE1btyYdu/eTQcOHCBnZ2eytLSkJUuWKG33IUOG0PDhw8nU1JTat29P58+fF8YXP14UFhbS\nkiVLqFmzZmRlZUXDhg2jR48eKa3DTZs2kZ2dHVlaWtLatWspKSmJXF1dycLCgqZMmaIU908//UQu\nLi5Ur1496tu3L6WmpgrjJBIJ/fDDD+Ts7EwWFhY0efJkIir6/BX/bNSrV4+IiKKiosjd3Z3MzMzI\nzs6OQkNDhXnZ2dkJnx1TU1OKj48vdZZx4sQJ8vDwIHNzc+rYsSOdPHlSaV/48ssvqVu3bmRqakp9\n+vShzMxMIiLKzc2lkSNHkpWVFVlYWFDHjh0pIyOjzG1NRKSRBeHw4cNERHT79m1q3bo1zZ07l+7e\nvUtWVlYUExNDRES///47WVlZCYl7eXmRg4MDJScnk1wup/z8fAoMDKQvv/xSmPeXX35Jnp6e9ODB\nA3rw4AF17dpVGP/HH3+Qvr4+zZo1i/Ly8ig3N5fmzZtHRkZGdOjQISooKKAxY8aQg4MDLV68mAoK\nCmj9+vXUtGlTYf4HDhygW7duERFRXFwcmZiY0NmzZ5XmP2/ePCooKKDo6GgyMTERPrgffPAB9ezZ\nk+7duyd8YF++fFlu3g8ePCi17vLy8qhZs2a0ZMkSys/Pp6NHj5KpqSmlpKQQEVFoaCiNHj263HU/\nc+ZM6tGjBz1+/Jju3LlDrVu3Jjs7O6Vto/jwRUREKO2wMplM6aCVnZ1Ntra2FBERQXK5nP766y+q\nX78+JScnE1HRQcLc3FzYsXNycqh9+/b01VdfUX5+Pt26dYucnJzo4MGDRETCtoiJiaHCwkL6/PPP\nqUuXLmXGVpbiBUEul79yWWfOnKHExESSy+Ukk8nIxcWFVq9eTUREsbGx1KFDB3r69CkREV29elU4\nCJbc30p61XuHDx9Ow4cPp5ycHLp06RLZ2NhQ9+7diajsguDt7U0//fQTERUVhMOHD1NeXh49ePCA\nevToQdOnTxemdXBwoHbt2tHdu3fpxYsXVdqnSi6rZJ5SqbTCJqPi0ys+B1999ZXwGbKysqL33nuP\nsrOz6fLly2RsbEwymYyIira7gYEB/fbbb1RQUEDLly+npk2bUkFBAREpb/fVq1eTp6cnpaWlUV5e\nHgUHB1NAQIDSOgwJCaGXL1/SoUOHyNDQkAYNGkQPHjygtLQ0atiwIcXFxRER0Z49e6h58+Z09epV\nksvltHDhQuratauQk0QiIT8/P3r69Cndvn2bGjRoQLGxsURU+rOhWE+K4n/hwgWytramPXv2EFHp\nzw6RcrPTw4cPycLCgn799VeSy+UUGRlJ9erVE4qdl5cXNW/enK5fv065ubnk7e1Ns2bNIiKiH374\ngfz8/Cg3N5cKCwvp7NmzlJWVVe620riC4ODgQHXr1iULCwtycHCgyZMnU25uLi1durTUwaxv3770\n888/E1HRTjtv3jyl8YGBgUptus2aNRM+BEREBw8eJEdHRyIq2lENDQ2FMwaiop2xT58+wvC+ffuo\nbt26VFhYSEREWVlZJJFIhA94SYMGDaI1a9YI8zc2Nlba6A0bNhQOPMbGxnThwoVS86go7+KOHTtG\njRo1UnotICBA+DYyb948GjVqVJmxEpHSQZGI6Mcff1T6sBf/8JX8BlPyoLVt2zbhgKYwceJEmj9/\nPhEVFYSxY8cK4xISEsje3l5p+sWLF1NQUJAQ+9tvvy2MUxw4yoqtLMULQkXLKmnVqlX0zjvvEBHR\nkSNHqEWLFpSQkFCqzbfk/lbS0aNHy3xvQUEBGRgYCIWbiGj27NmvPEMoeZAubvfu3dSuXTth2NHR\nUelstCr7lGJZirORknlWpg+h5PTGxsalPkNJSUnC9B06dKC9e/cSUdF29/T0FMYVFhZS48aN6fjx\n40Juiu3u4uKitA/cu3ePDAwMSC6XC+vw3r17wngrKyuls9YhQ4YIn9d+/foprV+5XE4mJiZ0+/Zt\nIioqCCdOnBDGDxs2jJYuXUpEletDmDZtGn300UdEVPb2LT6PX375hTp37qz0fk9PT4qIiCCiou2z\naNEiYdz3339P/fr1I6KiVouuXbuWeWwpi766m6xKkkgk2Lt3L9566y2l11NTU7Fjxw7s379feK2g\noEBpuoquIrl37x4cHByEYXt7e9y7d08YbtCgAQwNDZXe07BhQ+FvY2Nj1K9fHxKJRBgGgOzsbJiZ\nmSEmJgbz58/H9evXUVhYiJycHLRt21Z4v5WVlVL7vYmJCbKzs5GZmYkXL16gWbNmpWKuTN7F8yu5\nDhwcHJCWlvbK9VLe++3t7Sv1vrKkpqYiMTER9erVE14rKCjAmDFjABRtZxsbG6Xp7927pzS9XC5H\njx49hGFra2vhbxMTE7x48QKFhYVV7hOpaFnXrl3DjBkzcObMGeTk5KCgoAAeHh4AgLfeegtTpkzB\n5MmTkZqaisGDB2P58uUwNTWtcLk9e/Ys873Pnz9HQUHBa6/7jIwMTJs2DcePH8ezZ89QWFgIS0tL\npWmKz7sq+5SCYp+vDlZWVqU+Q8W3rbGxMbKzs4VhW1tbpThsbW2VPrcKMpkM77zzjtL+oK+vj4yM\nDGG45HLKW25qaiqmTZuGjz/+WGkZaWlpwrps1KiR8LqJiQmeP39ebs6JiYmYNWsWLl++jLy8PLx8\n+RLDhg0rd/ri7t27V2p/cHBwUFoHxWMpnsfo0aNx584djBgxAk+ePMGoUaOwaNEi6OuXfejXuE7l\n8tjb22P06NF4/Pix8O/Zs2f47LPPhGkq2mmbNGkCmUwmDN++fRtNmjQp9/1V+RC8fPkSQ4YMwWef\nfYZ//vkHjx8/hq+vb6U6iurXrw8jIyPcuHGj1LjK5F08vzt37igtMzU1VekD9SqNGzfG7du3heHi\nf1eVvb09vLy8SsX93XffCdMUX7/29vZo2rSp0vRZWVmIiooqNW1ZqrKt7OzsXrmskJAQtGrVCjdu\n3MDTp0+xaNEipU7vqVOn4vTp00hOTsa1a9fw9ddfVzqGst7bsGFD6Ovrl7vu69SpAwDIyckRXktP\nTxf+nj17NmrVqoVLly7h6dOn2Lx5c6lO+pLrurL7VHkU86vsev8vBeXOnTvC34WFhbh7967S51bB\n3t4esbGxSnnl5OSgcePGVV6mvb09fvzxR6V5PX/+XLjE+lXKyvW9997DoEGDcPfuXTx58gSTJk0S\ntlFF68bGxgapqalKr6Wmpip9oSqPvr4+5s6di8uXL+PkyZOIiorCL7/8Uu70WlMQRo0ahf379+PQ\noUOQy+V48eIFpFKp0rffkgffksMBAQFYuHAhMjMzkZmZiQULFmD06NHlLrMyB3OFvLw85OXloX79\n+tDT00NMTAwOHTpUqffq6elh3LhxmDFjBu7fvw+5XI74+Hjk5eVVKm+FLl26wMTEBMuWLUN+fj6k\nUimioqIwYsSISsUxbNgwLFmyBE+ePMHdu3fx7bffVjr/kgYMGIBr167h119/RX5+PvLz83Hq1Clc\nvXoVQOl126lTJ5iammLZsmXIzc2FXC7HpUuXcPr06TKnL8na2ho3b96sVGwVLSs7OxumpqYwMTHB\n1atXsXbtWuFDe/r0aSQmJiI/Px8mJiYwMjJCrVq1hBhu3bpV7nLLe6+enh4GDx6M0NBQ5ObmIjk5\nGb/88ouwzAYNGsDGxgabN2+GXC7Hxo0blXLNzs5GnTp1YGZmhrS0NKFAlacq+5RC8fVPRU3NQs4P\nHz5EVlbWK99blc9SSWfOnMHu3btRUFCA1atXw8jIqMwD86RJkzB79myhmD548AD79u2r0rIUcU6a\nNAmLFy9GcnIyAODp06fYsWPHK99XfJ3cvXsX+fn5wvjs7GzUq1cPhoaGSEpKwtatW5W2r56eXrn7\nr4+PD65du4bIyEgUFBRg+/btuHr1KgYMGFAq7pL++OMPXLx4EXK5HKampjAwMBD217JoTUGwtbXF\n3r17sXjxYjRs2BD29vZYsWKF0ooo6xt+8de++OILeHh4oG3btmjbti08PDzwxRdfVPr95U0DAKam\npvjmm28wbNgwWFpaIjIyEgMHDnzle4tbvnw5XF1d0bFjR1hZWeHzzz9HYWFhuXmXdZmmgYEB9u/f\nj5iYGDRo0ABTpkzB5s2b0aJFi3LzKW7evHlwcHBA06ZN0a9fP4wZM6bc6StaN3Xr1sWhQ4ewbds2\n2NjYoHHjxvj888+Rl5dX5vv19PQQFRWFc+fOwcnJCQ0aNMDEiROFA01Fy/v888+xcOFC1KtXDytX\nriw3ZgCoVavWK5e1fPlybN26FWZmZpg4caJSQc3KysLEiRNhaWkJR0dH1K9fX7jpcfz48UhOTka9\nevUwePDgUst/1XvDw8ORnZ2NRo0aYdy4cQgKClLat9evX4+vv/4a9evXR3JyMrp16yaMmzdvHs6e\nPQtzc3P4+flhyJAhr9zOVdmnylrXxbdFy5YtERAQACcnJ1haWiqduZQ1fcl5lTVcctzAgQOxfft2\nWFpaYsuWLdi1a1eZB7Vp06bB398fffr0gZmZGTw9PZGUlFSp5ZScZtCgQZg5cyZGjBgBc3NzuLq6\n4uDBg6/MQfFar1690Lp1azRq1Ehocv7+++8xd+5cmJmZ4auvvlK6MdTExARz5sxBt27dYGlpicTE\nRKX5WVlZISoqCitWrED9+vWxfPlyREVFKTULlrd9MjIy8O6778Lc3BytWrWCt7f3K78ES+i/lO4K\njBs3DgcOHEDDhg1x8eLFUuMzMzMxatQopKeno6CgAJ988gkCAwNVFQ5jWiMiIgI//fQT/vzzT3WH\nolbz58/HjRs3sHnzZnWHohNUeoYQFBSE2NjYcseHh4ejXbt2OHfuHKRSKT7++GNR3hDGGHs9Kvy+\nysqg0oLQvXt3pSs5SmrcuLFwmp6VlQUrK6tye78Z0yUVNe/pCl4PNUulTUZA0aVgfn5+ZTYZFRYW\n4q233sK1a9fw7Nkz/O9//4OPj48qw2GMMVYOtXYqL168GO7u7rh37x7OnTuHyZMn49mzZ+oMiTHG\ndJZa22dOnjyJOXPmAACaNWuGpk2bIiUlRbgJSKF58+aVvqSQMcZYETc3N5w7d67S06v1DKFly5Y4\nfPgwgKLLo1JSUuDk5FRqups3bwrX+Yrx37x589QeA+fHuXF+4vt3/vz5Kh2TVXqGEBAQgLi4OGRm\nZsLOzg7z588XbtYIDg7G7NmzERQUBDc3NxQWFmLZsmWlbrnXBcXvnhYjMecn5twAzk/XqLQgREZG\nvnJ8/fr1lX5PhTHGmPpozZ3KYib2m/HEnJ+YcwM4P12j8stOq4MmPA1r1qwwpKfnqjWGqmrUyBhL\nl85UdxiMMTWp6rGT7wKrpPT0XDg6hqpk3jKZFI6O3iqYb2i1z/N1SKVSeHt7qzsMlRBzbgDnp2u4\nyYgxxhgALggaQRVnB5pEzN/AxJwbwPnpGi4IjDHGAHBB0AgymVTdIaiUVCpVdwgqI+bcAM5P13BB\nYIwxBoALgkbgPgTtJebcAM5P13BBYIwxBoALgkbgPgTtJebcAM5P13BBYIwxBoALgkbgPgTtJebc\nAM5P13BBYIwxBoALgkbgPgTtJebcAM5P13BBYIwxBkDFBWHcuHGwtraGq6trudNIpVK0a9cObdq0\n0dn2PO5D0F5izg3g/HSNSgtCUFAQYmNjyx3/5MkTTJ48Gfv378elS5ewc+dOVYbDGGPsFVRaELp3\n74569eqVO37r1q0YMmQIbG1tARQ9UlMXcR+C9hJzbgDnp2vU2odw/fp1PHr0CD179oSHhwc2b96s\nznAYY0ynqfWJafn5+Th79iyOHDmCnJwceHp6okuXLnB2di41bWBgIBwdHQEAFhYWcHd3F9r/FFVe\nlcPp6TL8u3jhG72i7f+/Diteq675lTzjqIn186phxWvqWr4qh729vTUqHs5Pt/OTSqWIiIgAAOF4\nWRUqf6ayTCaDn58fLl68WGpcWFgYcnNzERoaCgCYMGEC+vXrh6FDhyoHqQHPVA4MDFXZIzRVRSYL\nRUREqLrDYIypSVWPnWptMho4cCCOHz8OuVyOnJwcJCYmolWrVuoMSS24D0F7iTk3gPPTNSptMgoI\nCEBcXBwyMzNhZ2eH+fPnIz8/HwAQHByMli1bol+/fmjbti309PTw/vvv62RBYIwxTaDyJqPqwE1G\nr4ebjBjTbVrVZMQYY0xzcEHQANyHoL3EnBvA+ekaLgiMMcYAcEHQCPxbRtpLzLkBnJ+u4YLAGGMM\nABcEjcB9CNpLzLkBnJ+u4YLAGGMMABcEjcB9CNpLzLkBnJ+u4YLAGGMMABcEjcB9CNpLzLkBnJ+u\n4YLAGGMMABcEjcB9CNpLzLkBnJ+u4YLAGGMMABcEjcB9CNpLzLkBnJ+u4YLAGGMMABcEjcB9CNpL\nzLkBnJ+uUWlBGDduHKytreHq6vrK6U6dOgV9fX3s2rVLleEwxhh7BZUWhKCgIMTGxr5yGrlcjpkz\nZ6Jfv35qfyqaunAfgvYSc24A56drVFoQunfvjnr16r1ymm+//RZDhw5FgwYNVBkKY4yxCqi1DyEt\nLQ179+5FSEgIgKLnf+oi7kPQXmLODeD8dI2+Ohc+ffp0LF26VHgQ9KuajAIDA+Ho6AgAsLCwgLu7\nu7AxFad9qhxOT5fh38ULTTyKA7mmDivUxPrhYR7mYfUPS6VSREREAIBwvKwKCam44V4mk8HPzw8X\nL14sNc7JyUkoApmZmTAxMcH69evh7++vHOS/BUOdAgND4egYqpJ5y2RSlZwlyGShiIgIrfb5VpVU\nKhV2XrERc24A56ftqnrsVOsZwq1bt4S/g4KC4OfnV6oYMMYYqxkqLQgBAQGIi4tDZmYm7OzsMH/+\nfOTn5wMAgoODVblorcJ9CNpLzLkBnJ+uUWlBiIyMrPS0mzZtUmEkjDHGKsJ3KmsAvg9Be4k5N4Dz\n0zVcEBhjjAHggqARuA9Be4k5N4Dz0zVcEBhjjAHggqARuA9Be4k5N4Dz0zVcEBhjjAHggqARuA9B\ne4k5N4Dz0zVcEBhjjAHggqARuA9Be4k5N4Dz0zVcEBhjjAHggqARuA9Be4k5N4Dz0zVcEBhjjAHg\ngqARuA9Be4k5N4Dz0zVcEBhjjAHggqARuA9Be4k5N4Dz0zVcEBhjjAFQcUEYN24crK2t4erqWub4\nLVu2wM3NDW3btkW3bt1w4cIFVYajsbgPQXuJOTeA89M1Ki0IQUFBiI2NLXe8k5MTjh07hgsXLuDL\nL7/ExIkTVRkOY4yxV1BpQejevTvq1atX7nhPT0+Ym5sDADp37oy7d++qMhyNxX0I2kvMuQGcn67R\nmD6En376Cb6+vuoOgzHGdJa+ugMAgD/++AMbN27EiRMnyp0mMDAQjo6OAAALCwu4u7sL1V3RDqjK\n4fR0Gf5dvNDmr/hm/1+HExJWo1Ej92qbX8k+iZpYP68aXr16dY1vr5oaLt4GrQnxcH66nZ9UKkVE\nRAQACMfLqpAQEVX5XVUgk8ng5+eHixcvljn+woULGDx4MGJjY9G8efOyg5RIoOIwKxQYGApHx1CV\nzFsmk6qk2UgmC0VERGi1z7eqpFKpsPOKjZhzAzg/bVfVY6dam4xu376NwYMH49dffy23GOgC7kPQ\nXmLODeD8dI1Km4wCAgIQFxeHzMxM2NnZYf78+cjPzwcABAcHY8GCBXj8+DFCQkIAAAYGBkhKSlJl\nSIwxxsqh0oIQGRn5yvEbNmzAhg0bVBmCVlBVk5GmEPNpuZhzAzg/XaMxVxkxxhhTLy4IGkDMZweA\nuNtpxZwbwPnpGi4IjDHGAHBB0Aj8W0baS8y5AZyfruGCwBhjDAAXBI3AfQjaS8y5AZyfruGCwBhj\nDEAlCkJ2djbkcjkAICUlBfv27RNuLmPVg/sQtJeYcwM4P11TYUHo0aMHXr58ibS0NPTt2xebN29G\nYGBgDYTGGGOsJlVYEIgIJiYm2LVrFz744APs2LEDly5dqonYdAb3IWgvMecGcH66plJ9CPHx8diy\nZQv69+8PACgsLFRpUIwxxmpehQVh9erVWLJkCd555x20bt0aN2/eRM+ePWsiNp3BfQjaS8y5AZyf\nrqnwx+28vLzg5eUlDDdr1gzffPONSoNijDFW8yosCKdOncLixYshk8lQUFAAoOihCxcuXFB5cLqC\n+xC0l5hzAzg/XVNhQRg5ciSWL1+ONm3aQE+Pb1tgjDGxqvAI36BBA/j7+8PJyQmOjo7Cv8oYN24c\nrK2t4erqWu40H374IZydneHm5oa//vqr0oGLCfchaC8x5wZwfrqmwjOEefPmYfz48ejduzcMDQ0B\nFDUZDR48uMKZBwUFYerUqRgzZkyZ46Ojo3Hjxg1cv34diYmJCAkJQUJCQhVTYIwxVh0qLAg///wz\nUlJSUFBQoNRkVJmC0L17d8hksnLH79u3D2PHjgUAdO7cGU+ePEFGRgasra0rEbp4cB+C9hJzbgDn\np2sqLAinT5/G1atXIZFIqn3haWlpsLOzE4ZtbW1x9+5dnSsIjDGmCSrsQ+jatSuSk5NVFgARKQ2r\novBoOu5D0F5izg3g/HRNhWcI8fHxcHd3R9OmTVG7dm0A1XfZqY2NDe7cuSMM3717FzY2NmVOGxgY\nKHRmW1hYwN3dXTjdU2xUVQ6np8ug6EtXHMAVTT3/dTg9/Vy1zq9kgamJ9fOq4XPnzql1+TzMw7oy\nLJVKERERAQCVvvinOAmV/IpeQnl9AJVdmEwmg5+fHy5evFhqXHR0NMLDwxEdHY2EhARMnz69zE5l\niURS6kyipgUGhsLRMVStMVSVTBaKiIhQdYfBGFOTqh47KzxDeJ0qoxAQEIC4uDhkZmbCzs4O8+fP\nF346Ozg4GL6+voiOjkbz5s1Rp04dbNq06bWXxRhj7L+psCD8F5GRkRVOEx4ersoQtIJMJhX1lUZS\nqVQ4vRUbMecGcH66hm89ZowxBoALgkYQ89kBIO5rvcWcG8D56ZoKC8Jvv/0GZ2dnmJmZwdTUFKam\npjAzM6uJ2BhjjNWgCgvCZ599hn379iErKwvPnj3Ds2fPkJWVVROx6Qy+D0F7iTk3gPPTNRUWhEaN\nGsHFxaUmYmGMMaZGFV5l5OHhgeHDh2PQoEFV/nE7Vjnch6C9xJwbwPnpmgoLwtOnT2FsbIxDhw4p\nvc4FgTHGxKXCgqC4DZqpDt+HoL3EnBvA+emacgtCWFgYZs6cialTp5YaJ5FI+LnKjDEmMuUWhFat\nWgEAOnTooPQLpESkk79IqkpiPjsAxN1OK+bcAM5P15RbEPz8/AAU/cooY4wx8eM7lTUA34egvcSc\nG8D56RouCIwxxgBwQdAI3IegvcScG8D56ZoKC0JKSgp69eqF1q1bAwAuXLiAhQsXqjwwxhhjNavC\ngvD++++NtlMDAAAgAElEQVRj8eLFwl3Krq6ulXrOAas87kPQXmLODeD8dE2FBSEnJwedO3cWhiUS\nCQwMDCo189jYWLRs2RLOzs4ICwsrNT4zMxP9+vWDu7s72rRpwzfBMcaYGlVYEBo0aIAbN24Iwzt3\n7kTjxo0rnLFcLseUKVMQGxuL5ORkREZG4sqVK0rThIeHo127djh37hykUik+/vhjFBQUvEYa2o37\nELSXmHMDOD9dU+FPV4SHh2PixIm4evUqmjRpgqZNm2LLli0VzjgpKQnNmzcXnsk8YsQI7N27V+mX\nUxs3bowLFy4AALKysmBlZQV9fZU+1ZMxxlg5KjxDaNasGY4cOYLMzEykpKTgxIkTwkH+VdLS0mBn\nZycM29raIi0tTWma999/H5cvX0aTJk3g5uaGNWvWVD0DEeA+BO0l5twAzk/XVPh1/PHjx/jll18g\nk8mE5pzK/JZRZX7eYvHixXB3d4dUKsXNmzfx9ttv4/z58zA1Na1k+IwxxqpLhQXB19cXnp6eaNu2\nLfT09Cr9W0Y2Nja4c+eOMHznzh3Y2toqTXPy5EnMmTMHQNGZSNOmTZGSkgIPD49S8wsMDBTOTCws\nLODu7i60/ymqvCqH09NlUJwYKb7RK9r+/+uw4rXqml/JM46aWD+vGla8pq7lq3LY29tbo+Lh/HQ7\nP6lUKlycU5mWnJIkRESvmqB9+/Y4e/ZslWdcUFCAN954A0eOHEGTJk3QqVMnREZGKvUhzJgxA+bm\n5pg3bx4yMjLQoUMHXLhwAZaWlspBSiSoIEyVCwwMhaNjqFpjqCqZLBQREaHqDoMxpiZVPXZW2Ifw\n3nvv4ccff8T9+/fx6NEj4V9F9PX1ER4ejr59+6JVq1YYPnw4XFxcsG7dOqxbtw4AMHv2bJw+fRpu\nbm7o3bs3li1bVqoY6ALuQ9BeYs4N4Px0TYVNRkZGRvj000+xaNEi6OkV1Q+JRIJbt25VOHMfHx/4\n+PgovRYcHCz8Xb9+fezfv7+qMTPGGFOBCpuMmjZtilOnTqF+/fo1FVMp3GT0erjJiDHdVu1NRs7O\nzjA2Nv5PQTHGGNN8FRYEExMTuLu7Y+LEiZg6dSqmTp2KDz/8sCZi0xnch6C9xJwbwPnpmgr7EAYN\nGoRBgwYpvcaP0GSMMfGpsA9BE3AfwuvhPgTGdFtVj53lniG8++672LFjB1xdXctciOI3iBhjjIlD\nuQVB8btCUVFRpSoMNxlVr+J3KYtR8buUxUbMuQGcn64pt1O5SZMmAIDvv/8ejo6OSv++//77GguQ\nMcZYzajwKqNDhw6Vei06OlolwegqMZ8dAOL+zXkx5wZwfrqm3CajtWvX4vvvv8fNmzeV+hGePXuG\nbt261UhwjDHGak65Zwjvvfce9u/fD39/f0RFRWH//v3Yv38/zpw5U6kH5LDK4/sQtJeYcwM4P11T\n7hmCubk5zM3NsW3btpqMhzHGmJpU2IfAVI/7ELSXmHMDOD9dwwWBMcYYAC4IGoH7ELSXmHMDOD9d\nwwWBMcYYABUXhNjYWLRs2RLOzs4ICwsrcxqpVIp27dqhTZs2Otuex30I2kvMuQGcn66p8NdOX5dc\nLseUKVNw+PBh2NjYoGPHjvD391d6pvKTJ08wefJkHDx4ELa2tsjMzFRVOIwxxiqgsjOEpKQkNG/e\nHI6OjjAwMMCIESOwd+9epWm2bt2KIUOGwNbWFgDU+lQ2deI+BO0l5twAzk/XqKwgpKWlwc7OThi2\ntbVFWlqa0jTXr1/Ho0eP0LNnT3h4eGDz5s2qCocxxlgFVNZkVJlfRM3Pz8fZs2dx5MgR5OTkwNPT\nE126dIGzs3OpaQMDA+Ho6AgAsLCwgLu7u9D+p6jyqhxOT5fh38UL3+gVbf//dVjxWnXNr+QZR02s\nn1cNK15T1/JVOezt7a1R8XB+up2fVCpFREQEAAjHy6pQ2QNyEhISEBoaitjYWADAkiVLoKenh5kz\nZwrThIWFITc3F6GhoQCACRMmoF+/fhg6dKhykPyAnNfCD8hhTLdV9dipsiYjDw8PXL9+HTKZDHl5\nedi+fTv8/f2Vphk4cCCOHz8OuVyOnJwcJCYmolWrVqoKSWNxH4L2EnNuAOena1TWZKSvr4/w8HD0\n7dsXcrkc48ePh4uLC9atWwcACA4ORsuWLdGvXz+0bdsWenp6eP/993WyIDDGmCbgZypXEjcZMca0\njcY0GTHGGNMuXBA0APchaC8x5wZwfrqGCwJjjDEAXBA0Av+WkfYSc24A56druCAwxhgDwAVBI3Af\ngvYSc24A56druCAwxhgDwAVBI3AfgvYSc24A56druCAwxhgDwAVBI3AfgvYSc24A56druCAwxhgD\nwAVBI3AfgvYSc24A56druCAwxhgDwAVBI3AfgvYSc24A56druCAwxhgDwAVBI3AfgvYSc24A56dr\nVFoQYmNj0bJlSzg7OyMsLKzc6U6dOgV9fX3s2rVLleEwxhh7BZUVBLlcjilTpiA2NhbJycmIjIzE\nlStXypxu5syZ6Nevn9qfiqYu3IegvcScG8D56RqVFYSkpCQ0b94cjo6OMDAwwIgRI7B3795S0337\n7bcYOnQoGjRooKpQGGOMVYLKCkJaWhrs7OyEYVtbW6SlpZWaZu/evQgJCQFQ9PxPXcR9CNpLzLkB\nnJ+u0VfVjCtzcJ8+fTqWLl0qPAj6VU1GgYGBcHR0BABYWFjA3d1d2JiK0z5VDqeny/Dv4oUmHsWB\nXFOHFWpi/fAwD/Ow+oelUikiIiIAQDheVoWEVNRwn5CQgNDQUMTGxgIAlixZAj09PcycOVOYxsnJ\nSSgCmZmZMDExwfr16+Hv768c5L8FQ50CA0Ph6BiqknnLZFKVnCXIZKGIiAit9vlWlVQqFXZesRFz\nbgDnp+2qeuxU2RmCh4cHrl+/DplMhiZNmmD79u2IjIxUmubWrVvC30FBQfDz8ytVDBhjbNasMKSn\n51b7fNPTZYiIkFb7fBs1MsbSpTMrnlDDqKwg6OvrIzw8HH379oVcLsf48ePh4uKCdevWAQCCg4NV\ntWitw30I2kvMuQGak196eq5KztBfo1WlUmSyUNXMWMVUVhAAwMfHBz4+PkqvlVcINm3apMpQGGOM\nVYDvVNYAfB+C9hJzboD48xP7Z6+quCAwxhgDwAVBI3AfgvYSc26A+PMT+2evqrggMMYYA8AFQSOI\nvR1TzO3QYs4NEH9+Yv/sVRUXBMYYYwC4IGgEsbdjirkdWsy5AeLPT+yfvarigsAYYwwAFwSNIPZ2\nTDG3Q4s5N0D8+Yn9s1dVXBAYY4wB4IKgEcTejinmdmgx5waIPz+xf/aqigsCY4wxAFwQNILY2zHF\n3A4t5twA8ecn9s9eVXFBYIwxBoALgkYQezummNuhxZwbIP78xP7ZqyouCIwxxgDUQEGIjY1Fy5Yt\n4ezsjLCwsFLjt2zZAjc3N7Rt2xbdunXDhQsXVB2SxhF7O6aY26HFnBsg/vzE/tmrKpU+MU0ul2PK\nlCk4fPgwbGxs0LFjR/j7+8PFxUWYxsnJCceOHYO5uTliY2MxceJEJCQkqDIsxkSHnznMqoNKC0JS\nUhKaN28Ox38fXDpixAjs3btXqSB4enoKf3fu3Bl3795VZUgaSeztmGJuh9aU3PiZw69H7J+9qlJp\nk1FaWhrs7OyEYVtbW6SlpZU7/U8//QRfX19VhsQYY6wcKj1DkEgklZ72jz/+wMaNG3HixIkyxwcG\nBgpnGhYWFnB3dxe+nSnaOVU5nJ4uE74tKdodFd8u/utwQsJqNGrkXm3zK9kuWhPr51XDq1evrvHt\nVVPDxdvY1RmPqvbP4vtSde6f6ekyYb6cX/UNS6VSRERE/BuPI6pKQkRU5XdVUkJCAkJDQxEbGwsA\nWLJkCfT09DBzpnLb4YULFzB48GDExsaiefPmpYOUSKDCMCslMDBUJafkQNEOpIpTV5ksFBERodU+\n36qSSqUa07RS3TQlN1Xtn5qyb4o9P1Wp6rFTpU1GHh4euH79OmQyGfLy8rB9+3b4+/srTXP79m0M\nHjwYv/76a5nFQBeIvR1TEw6YqiLm3ADx75tiz6+qVNpkpK+vj/DwcPTt2xdyuRzjx4+Hi4sL1q1b\nBwAIDg7GggUL8PjxY4SEhAAADAwMkJSUpMqwGGOMlUGlBQEAfHx84OPjo/RacHCw8PeGDRuwYcMG\nVYeh0VR12qopNKFZRZWXZTZq5Fjt8wU049JMse+bYs+vqlReEBjTBKq6LBNQ3QFFUy7NZLqDf7pC\nA4j9G4q6zw5USezbjvPTLVwQGGOMAeAmI42gCe2YqmpjB1TXzs5t7KrH+ekWLggMgCrb2AFVtbNz\nGztj1YubjDSA2L+hiDk/MecGcH66hgsCY4wxAFwQNILYf5NdzPmJOTeA89M1XBAYY4wB4IKgEcTe\njinm/MScG8D56RouCIwxxgBwQdAIYm/HFHN+Ys4N4Px0DRcExhhjALggaASxt2OKOT8x5wZwfrqG\nCwJjjDEAKi4IsbGxaNmyJZydnREWFlbmNB9++CGcnZ3h5uaGv/76S5XhaCyxt2OKOT8x5wZwfrpG\nZQVBLpdjypQpiI2NRXJyMiIjI3HlyhWlaaKjo3Hjxg1cv34dP/74o/DUNF2Tnn5O3SGolJjzE3Nu\nAOena1RWEJKSktC8eXM4OjrCwMAAI0aMwN69e5Wm2bdvH8aOHQsA6Ny5M548eYKMjAxVhaSxXrx4\nou4QVErM+Yk5N4Dz0zUqKwhpaWmws7MThm1tbZGWllbhNHfv3lVVSIwxxl5BZQVBIpFUajoieq33\nicmTJzJ1h6BSYs5PzLkBnJ/OIRWJj4+nvn37CsOLFy+mpUuXKk0THBxMkZGRwvAbb7xB6enppebl\n5uZGAPgf/+N//I//VeGfm5tblY7bKntAjoeHB65fvw6ZTIYmTZpg+/btiIyMVJrG398f4eHhGDFi\nBBISEmBhYQFra+tS8zp3jjt+GGNM1VRWEPT19REeHo6+fftCLpdj/PjxcHFxwbp16wAAwcHB8PX1\nRXR0NJo3b446depg06ZNqgqHMcZYBSREJRrxGWOM6SS+U5kxxhgALghMh92/fx8zZ87EzZs38fDh\nQwBAYWGhmqP6fyVP3sVyMk9EoslFoayctDFHLggipzjAFRQUqDkSzdO4cWMAwJYtWzB58mScO3cO\nenp6GvFBJiLhEux79+7h8ePHorokWyKR4ODBg1i5ciW2bt2q7nCqhUQiwalTpxATE4O///4bEolE\no75gVAYXBJF69OgR0tLSoKenh9jYWMyePRurVq1Sd1gaQ/FBDQsLw6RJk+Dt7Q0fHx8cO3ZM7R/k\njIwM/PDDDwCA33//HQMHDsRbb72F3bt3IysrS21xVQdFoTt//jymTp2KjIwMxMTEIDg4WN2hvTZF\nTkeOHMHAgQPx22+/oWPHjvjrr7+gp6enVUVBZVcZMfV5/vw5VqxYgTp16sDV1RWzZs3C9OnTERYW\nhvT0dCxatAj6+rq56RXf/vX09JCXlwdDQ0M0bNgQkyZNQu3atREQEIDffvsNXbp0UfqWXpPxnTlz\nBidPnkRGRgYSExOxefNmXLhwARs3bsTz58/h7+8PMzOzGo2rukgkEsTFxeHXX3/FmjVr4OPjgxs3\nbmDx4sWYNGmSUAi1iUQiQXJyMnbu3Ilt27ahR48ecHNzQ69evXD06FG4u7ujsLAQenqa//27Vmho\naKi6g2DVy9DQEE+fPkVKSgr++usvDB06FBMnTsTw4cOxcuVKXL9+Hd7e3lqxg6qCorli06ZNSE5O\nRufOnQEA7dq1g4WFBT777DP069cPVlZWNRqXogDZ2NjA2NgYf/31FzIyMvDJJ5+gdevWMDY2xpYt\nW0BEcHJygpGRUY3G97pKFtbz589j0aJFcHBwgJeXF8zNzdG2bVtER0cjOjoaAwcOVGO0VSOXyyGX\ny7F06VKcPHkSb7zxBlxdXdGlSxfUqVMHgwcPxoABA9CkSRN1h1opXBBEhIiEbyIuLi4wNzfH8ePH\ncfPmTXTo0AF2dnbo378/5s+fjxs3bqBPnz6iapeuiOLAFB8fj8mTJ6Nfv35YsWIFMjIy0L17d9Sq\nVQvt27fHy5cvkZqaik6dOkEul9dI4VScuUgkEty7dw/t2rWDvr4+Tp06hYyMDHh6esLFxQW1atXC\nr7/+Cl9fX5iamqo8rv+qeF6pqakgIri7u+PNN9/El19+CScnJ7i4uMDCwgLt2rVDhw4dyrw5VZMU\nzyknJwfGxsbw9vbGP//8g9TUVFhaWsLGxgadO3eGmZkZ6tSpg2bNmqk56kqq0n3NTKMVFhYSEdH+\n/fspKCiIiIgOHz5M06ZNoxUrVtDff/9NRETp6el08uRJdYWpVlevXqWxY8fSunXriIgoLS2NunXr\nRrNnz6a8vDwiKlpn77//fo3Gpdh20dHR5OTkRCkpKZSTk0O7d++mDz74gFauXClMW9bPu2gquVxO\nREX7ZNeuXcnf35/Gjx9Ply9fpri4OGrevDnt3LlT6T2KdaGpFPHFxMRQ7969KTAwkL766isiIpo5\ncybNmDGDjh8/rpSHpuekwAVBZA4ePEitW7emAwcOCK8dOHCAZsyYQYsWLaJbt24Jr2vLTvpflMwx\nOjqaBgwYQAEBAcK6uHfvHrm5udEnn3wiTDd58mS6f/9+jcZ6+fJlat26NcXFxQmv5eTk0J49eygw\nMJCWLVtGRP9/kNXk7Zebmyv8nZqaSq1ataIzZ87QxYsX6ZdffiFfX19KT0+nXbt2ka2tLWVkZGh0\nPkRE+fn5wt9JSUnUqlUrioqKotOnT5O7uztNnTqVCgsL6YMPPqCPPvqIHj9+rMZoX49u9iyK2OnT\npxEaGgpfX1+8ePECRkZG8PX1hZ6eHvbt26d0SaXYm4uK53rr1i2YmJigV69esLGxwfr167Fnzx4M\nHjwYDg4OwqWCCuHh4TUeb0FBAd5880306NEDBQUFKCwshLGxMXr37g2JRAInJycAEJqwNHX7ZWRk\nIDIyEuPHjxeatezs7NC+fXsARZf7njlzBocOHcLo0aPRpUsXNGzYUJ0hV+iff/4RLk82NDRETk4O\nevfujf79+wMAzp49i06dOuHEiRNYsGABMjIyYGFhoeaoq043exVFgsq4Xv7+/fv47bffAEDodExM\nTIS3tzeWLFkiHFR0gUQigUQiQUxMDPr3748ZM2bAw8MD5ubmGD58OGQyGbZu3YrU1FQ0btwYXbt2\nrbGbpspajomJCWJjYxEVFQV9fX0YGhri4MGD+Pnnn+Hv7482bdqoPK7qULt2bfj4+CA7OxunT5+G\nvb09CgoKMGfOHACAlZUVLC0tce3aNQBAgwYNAGj2jVzp6enw8/PDw4cPcefOHZiZmeHIkSPCDY0S\niQQ9e/bE06dPYWVlhVatWqk54tfDBUFLFf/wyGQy4fGkH3/8MerVqyfcc5CUlITAwECcP38e5ubm\naolVnW7fvo158+Zh/fr12Lp1K4YPHw5/f3+0aNECgwcPRlpamtJ14ooiUhMUl2B+/fXXOHr0KJo1\na4ZVq1Zh5cqVCA8PR3R0NGbOnAkbG5saiee/ys/PR05ODiwsLGBnZ4clS5Zgw4YNuHz5MlasWAGZ\nTIZhw4Zh//792Lp1K3r16gUAwiXQmnjGk5+fDwBo27YtLC0tsXbtWixduhRt2rTByJEj0bFjR0il\nUkRFRSE6OlorzwqK4x+301L07xUz+/btQ2hoKGxsbGBjY4Np06bh77//xtq1a5GTk4PMzEwsXLgQ\nfn5+6g65RlCJSxyzs7MREhKCRYsWwd7eHgAwdepU1KpVC6tXr0ZGRobarmqJiYnBjBkzMH36dCxf\nvhwTJkxA//79kZmZiRUrVqBRo0YYOHAgBgwYoJZ7IqoiLy8PUqkU9evXx7Vr15CamopRo0Zh+fLl\nMDQ0xODBg+Hk5ISFCxfCwsICnTp1Qv/+/TU6r5cvX+LPP/+Era0tsrOzce3aNVhbW+P3338HEWHJ\nkiVYv369cCVYcHCwVmyrV6rxXgtWbf7880/q0KEDZWRk0Pr166lu3br00UcfkUwmo8LCQrp16xal\npqYSUVEHpKZ32lWHgoICIiJ69uwZ5efn08uXL2nQoEH07bffCtNs27aNZs6cqa4QqbCwkO7cuUOD\nBg2ia9eu0ZEjR6hZs2YUEBBAc+fOpWfPnpWaXhu23c6dO8nT05OaNm1Ke/bsISKiBw8e0NSpU+nT\nTz+lCxcuKE2v6XllZWXR/v37ydvbm5o0aUJXr14lIqITJ07Qp59+SrNmzaJHjx4RUVHnP5Hm51QR\nvg9Biz1//hy9e/fGrVu3sHLlSuzduxc//vgjDh8+jE6dOqF58+ZKzURa+62lEm7fvo28vDzUrVsX\ne/bswaRJk3Dx4kXUqlULgYGBmDVrFq5evYrTp09j7dq1GDduHFq0aFFj8VGxa9clEgnMzMzQrVs3\nPH/+HFOnTkViYiKsra3x8ccfw9DQEG5ubqhdu7bSezQR/dsXIpFIYG9vj5MnT6J27dro06cP6tat\ni/r166NLly44cOAALl26BE9PT6FvS1PzUmyr2rVrIycnB0uWLEHnzp3RtWtXNGnSBHZ2djAzM8P5\n8+chlUrh5eUFQ0ND6OnpaWxOlcUFQUsUP6A8fvwYcrkcNjY2sLW1xbp169C7d2/4+vri5cuXiI+P\nx9ChQ2FpaSm8X5t30spYuHAh5s6di44dO2Lt2rUICgqCnZ0dvvvuO9jb22P27Nl4+PAhsrKyMHHi\nRPTt27fGT+0lEgkuXLiA06dPo1atWmjSpAnS09Nx+PBhTJw4Ebm5ubh48SKmTJkCOzu7Govrv9LT\n08Pvv/+OzZs3Y9myZdDT08OePXtgZGQEFxcXFBQUwNXVFe3atdOavCQSCX7//XdYWloiMDAQDRo0\nwM6dO6Gvrw9nZ2cYGhrC0NAQPj4+sLa2Fs1d/3zZqRaRSCTYu3cvfvrpJzx9+hTvvfceevXqBQ8P\nD2zYsAH5+fnYvn07Vq5ciebNm6s73BqhuDP766+/RmFhIYYPH45Ro0ZhxIgRyM3NhZWVFZYtW4bM\nzExMmDBBeB/VcNeZRCLBnj17MHfuXDg5OcHY2BgtWrRAcHAwGjVqhN69e+POnTtYvXo12rRpozXt\n0IqruD7++GOsWrUKderUQVBQEHJzcxEVFYVTp05hw4YN+OOPP7TmKilFTtOmTcO3336Lvn37wszM\nDI8ePcLu3buRkJCAc+fOYc2aNWjatKm6w61e6mutYlV19epVat26NZ07d4527dpFc+bMoQULFlBS\nUhJ9//335OvrS/v37yci7W/LrIzs7Gy6dOkSERElJiZSVlYWzZo1i1xcXIS7eV++fEnR0dHk7e1N\nMplMuKmrJhTfBs+ePaMRI0bQ2bNniYgoLi6OZs2aRb/88gs9ePCAtm7dKtw9rk3bLi8vj6ZNm0Yx\nMTFERPTixQthXExMDK1atYpiY2PVFd5ryc7Opj59+tCRI0eI6P9vAPz777/pf//7Hw0YMEDoIxEb\nLggaTrEz3rt3j2JiYsjHx0cYl5iYSL169aLExEQi+v+7Q7XpgPJf3L59m8aNG0eTJ08mGxsbodNy\n0qRJ1LVrV8rIyCCioqLw4MGDGo2t+Po/ceIExcTEkKenJ23dupWIiu56Xb58OU2aNKnU+zR525UV\n2+jRo0t10p8/f17pbmVNzksRl+L/J0+ekLe3t9CJrOgwzszMJKKi/Ukxvabm9LrE0fAlUoWFhZBI\nJDh58iRGjhwJBwcHGBkZYceOHQCATp06oXXr1rh8+TIAwMDAQHivNjQ3/BeFhYWws7NDnz59sHHj\nRrz33ntwdXUFAKxduxZubm54++238c8//8DQ0BD169cHUPNNRSkpKfj000/Rtm1bfPLJJzh8+DDi\n4uKgr6+PDh064NGjR8jKyhLuhdCWTsnU1FQkJycDAMaNG4f8/Hzs3bsXAHDq1ClMmjQJ169fF6bX\nhrwyMjIAAObm5ujWrRtmzZqFR48ewdjYGMeOHcOAAQPwzz//KN03oek5VRV3KmswiUSCw4cPY8OG\nDQgJCYGnpycyMzNx+fJlHD16FLVq1cLXX3+NkJAQ2NraavxPGlQniUSCo0ePIiEhAXPmzMGuXbvw\n8uVLODo6wtjYGP3798fNmzfRsGFD4f4DxftqKr7z589j2LBhGDBgAPz9/VG7dm08f/4cCxYswLVr\n1xAWFoZZs2bB1dVVK7YZ/duvERUVhbFjx2LHjh24ffs2/Pz8cP/+fWzbtg3btm3DTz/9hPnz56NH\njx7qDrlCipyio6Px/vvv4+DBg6hXrx569uyJf/75BzNmzEBubi4WLVqE0NBQtG/fXiu21WtT8xkK\nK6HkKWhERARJJBL68ccfiYgoIyND+DXOCRMmKPUZ6Jrjx49Tnz59iKjoF0q9vLxoy5YttHXrVho6\ndKjw66U1tW7KakIYOXIktW/fXri3IC8vj86ePUu7d++mU6dO1Wh81eHKlSvk5+dHV69epcePH5On\npyctWLCAsrOz6eHDhxQfHy80tWhLk0piYiINHDiQ4uPjaenSpRQSEkJbtmyhnJwc2rFjB/322290\n7NgxItKenF4XFwQNo9jZ0tLShDbYyMhIql27Np04cUJpGrHcDFNZJXPMzMyksWPH0unTp4mo6Jde\nR48eTW+99RZt27ZNbfHFx8fT9u3b6fLly0RENG7cOOrXr5+wvUq+R9O3XfG29eDgYOrQoQPdvHmT\niIr6tnr06EEffvhhue/TNMX7DP755x/y9fWlgQMHCuN/+OEHCg4Ops2bNyvdJKgN2+q/4oKgQRQ7\nW1RUFHXq1In69OlDX331FT169Ih27NhBVlZWwjcVXVL8Q3jmzBkaMmQIXblyhQoKCmjDhg3k5eUl\nFM/Hjx8LnX81+eFVLOvYsWPUokULGjZsGA0fPpw+/fRTIiIKCgoib2/vMouCNjh37hw9e/aMzpw5\nQ6DbeIkAACAASURBVCNHjqSvv/6aZDIZERUVhc6dO9OVK1fUHGXVKC462LJlC7Vo0YI2bNggjPvm\nm29o3LhxlJaWpq7w1IILgoZJSEggHx8fOnv2LMXExFBYWBhNmjSJCgsL6YcffiATExN6/PhxjV4+\nqU7Fv5Vdu3aNnj9/TlOmTKFPPvmE/Pz86I8//qDhw4cLVxip86EkJ0+epL59+wpnLFevXqWQkBD6\n7rvviIjI399faCbSBor19/LlS5o+fTr179+fnj17RvHx8TRlyhRauXKl8EwJxZU32qCgoIAePHhA\nxsbGtH37diIi2rVrFw0YMIA2btwoTKf42RddwgVBgzx69IiGDRtG7du3F167ePEiBQQE0OHDh4mI\nhG9lukJxUDpw4AB17tyZUlJSiKjod2YiIiLonXfeIQsLC5owYYLaYlPYsmULSSQS4Ztmbm4uRUZG\nUnBw8Cvfp2mys7OVHgZDVNSE+cknn9C7775Lz549o4SEBBo/fjwtW7aMcnJyhN+Q0tTcFP1JRP//\ngKE9e/aQpaUl7d69m4iIdu/eTT179qT169erJUZNwAVBjcpqkzx8+DC1bduW5s+fL7w2ZcoUWrJk\nCRH9/1ObNPWDpwpXrlyhli1bCn0oxT158oQuX75M3t7ewk1fNaH4tnvw4IHQFLRp0yZycnISCnhM\nTAy9+eablJmZKRw0Ndnly5cpJCSEMjIy6NixY7RmzRph3P379+mjjz6iMWPG0PPnz+nEiRPCjYGa\n7PLly/TFF18QEVFycjIdOnRI2F7R0dFUu3Zt4UaznTt3UlJSktpiVTcuCGqkOKAcPnyYFi9eTOvX\nr6fMzEySSqU0ZMgQCgwMpLi4OGrdurVw16QuuHPnDm3evFkYPnbsGL377rvCcFlFccyYMTW6jhTL\n3rdvH3l5eVH37t3pxx9/pJSUFNq+fTuZmJjQhAkTaNCgQcI3UE2Xk5NDvXv3FppNjh49StbW1hQe\nHk5ERU0tR48epTZt2tDw4cO1otny6dOn5OXlRadOnaKsrCyaPn06jRs3jo4cOULPnz8nIqJVq1aR\nRCKh6Oho4X269IWrOL4xTU3o3+uf//zzT0yaNAl16tTB+vXr8c0338DAwABTp05FQkICPv/8c2zY\nsAFvvfUWCgoK1B12jSAibN68GefPnwcAODk54eHDhzh06BCAogeqHD16FGFhYSAi3Lx5Ezdv3qzR\nB8lIJBKcOXMGK1aswJo1azB16lSkpqZi27Zt6N+/P9asWYM///wTvr6+GDRoEORyuUY/EQwAjI2N\nMXLkSGzcuBE2Njbo2bMnDhw4gFWrVuG7775DrVq1ULt2bfTq1QszZ87Uih90k8vlyMnJQWRkJD78\n8EN89NFHsLe3x2+//Yb4+HgAQNeuXTF48GClfER9r8GrqLce6barV69SQECAcI9BWloaTZ8+nWbN\nmkVERFKplMaMGUNLly5VZ5g1StGssmbNGtqxYwcRFfUXLF++nD799FNaunQpSaVSat26NR06dEh4\n38OHD2s0zvv371NQUBB17dpVeO3EiRPUu3dvSkhIIKKiPgUbGxuKi4ur0dheR/G+GiMjI/Ly8qLs\n7GwiKnqgfNu2bWn8+PHUsGFD4XeLNP1btCK+8PBw0tfXF34mJC8vj+bOnUvjx4+n8ePHk7Ozs1be\nE6IKfKdyDaJ/zwoUP0lx7NgxxMXF4e7du+jatStsbGzg5uaGuXPnwt/fHy1btoS5uTmOHj2KN998\nEyYmJupOQeUU39Lu37+P1atXo2fPnrC2tkajRo1gYmKCAwcO4Pr16wgJCYGvry8KCgqgp6cHY2Nj\nlcZFxX5+XDFMRIiPj0dOTg46d+4MOzs7xMfHQy6Xo2PHjnB1dUWTJk3QsmVLpZ8i10SKvKysrODt\n7Q1LS0usWbMGHTp0gKurK/r164eWLVti9OjR6NGjh1b8Gqsivvv37+Ptt9/GqlWrULt2bXTr1g09\nevSAiYkJ6tSpg5EjR6J79+5K79FV/AjNGlL8gJKWliY0b5w4cQK//vornJ2dMWLECDx//hzvvvsu\nDhw4ABsbG+Tl5aGgoEAnikFJ8+bNw6ZNm5CUlIRGjRoJr7948QJGRkalDtKqUnw5x48fR25uLmrX\nro0ePXpg586dOHDgAExMTDB8+HBMmDAB69evh5eXl0pjqi7FD+xyuRy1atUCUPRbRRs3bkRKSgoW\nLlyo9HPqNbXeq9vp06fx9ttv46uvvsKUKVOUxmlrTtVOLeclOqj4KbmHhwd9/vnnNGfOHKGjbtCg\nQeTh4UG9e/emAwcOKL1HlxQWFip1Vn722Wf0xhtv0NmzZ5WahdSxbvbv30+tW7emdevWUZs2bYTO\n1127dpGbmxv17duXjh49SkRU6rJNTXb+/Hnh7+JXQt2+fZtmzZpF77zzDuXk5GjV/njnzh16+vSp\nELMir7Nnz1KtWrWUrp5i/4+bjGqI4tvl9OnTsXXrVpw7dw67du3CuXPnMHnyZDg5OSE9PR0eHh4Y\nM2aMzvxQnaL5TNH0o8hX8eCbt99+GwUFBdi7dy+uXr2KjIwMtGnTpsbXS2pq6v+1d+9xMef7H8Bf\nMxMxosRKyVHSEaHaSApJIpJ17bhvdhO5RLEuu07Ys87uKlFnd0MuueyidpFckppRq7aIPUqpHIot\nGqJMV1Mz798fme+Wdfa39qSZqc/zr6bm++j9/c7M9z2f2/uDNWvWICoqChKJBFevXoVIJAIRwcvL\nC927d0dlZSUEAgGGDh2qEQOu9LJ1MHv2bOTn58PFxaVJ3Lq6uvjrX//KddtpwnuRiCCRSBAQEAAH\nBwd07doVCoUCAoEAcrkcRkZGcHd3R6dOnWBmZqbqcNUOSwgtRC6XIycnB97e3iguLkZERAT27NmD\n8+fPQywWY8mSJdDS0kJKSgokEgmsra255ntr9OzZMzx79gy6urqIi4vDvn37uD13eTwe+Hw+5HI5\n+Hw+7O3tMWDAAHTr1g2HDx+Gq6vrWx8zeBWPx8P48eNRWlqKDRs2ICkpCb1798aKFSvQuXNnzJs3\nD2VlZcjOzoadnV2Lx/cmlIlAeYMfMmQIrl27huHDh6NDhw5Nbvy6urro1q2bqkJ9YzweDzo6OhCL\nxTh37hymTp3KfY6U76levXrBzMxMI8ZBWhpLCC2Ez+fjL3/5C7el40cffYSRI0ciNTUVhYWFsLOz\ng6OjI/h8PsaOHYsuXbqoOuS3pqqqCtu3b0dOTg7Ky8uxbt06uLu7Y+fOnSguLoazszP4fD74fD7X\ngujevTtMTU0xY8aMFh1PUd40OnToAH19fVy/fh26urpwc3NDQUEBunfvjlGjRsHc3BxmZmZwcnKC\nnp5ei8X3ZyinO9fW1oLP58PIyAjh4eHo06ePRn9r/uWXXyCRSNCtWzc4ODjg6tWrsLGxQefOnbn3\nEZta+vvUv12rgeiVcXrlY21tbRARpFIpsrKyIBaLkZmZibCwMAwcOBAA4OHh0WQAtTXq1KkTbG1t\n8fTpU5w6dQqrVq3C4sWLkZKSgp9++gmbNm3i1ly82vXSEl0xjV8/Ho/X5LFCoUBqair+8Y9/wNfX\nF56enhg7dizkcjl0dHTUNpHTy1lRSmKxGOvXr8fKlSuRlJSEOXPmYOfOnXj+/LkKo3wzjc9HKpXi\n448/xmeffYa1a9eirq4O+fn5OHv2LICWed+0BmyWUTOjRrMVbt26BX19fRgZGTV5zuXLlxESEoLq\n6mr4+PjA09OTO7Y1f2shIq4/FwDS0tIQGhoKuVyOL774An379sXjx4/h5uYGZ2dnBAcHq+x6ZGRk\n4NChQ/jXv/71m9flxIkTKCsrg4mJCdzc3DTidVPGmJmZiXbt2sHIyIib0vzZZ5/BzMwMsbGxuHLl\nCvr168eN4agz5Tk9evQIXbp0AY/HQ0VFBVatWoVBgwbh9OnTkMvliIqKgrm5uarD1QwtOIDdJjQu\naTBq1Chuv2Ml5QyayspKrtZ6W6izTvTrtYmNjaVFixYRUUPZjlWrVtGOHTuooKCAiIhKSkq4Dedb\nUuPZTVeuXPlNUbrX1SLShNdOGd/FixfJ0NCQFi5cSMbGxlypj5KSEsrJyaEpU6aQh4eHKkP9Qxpf\n85iYGLK2tqbBgwfTRx99xO3T8ODBA9q/fz85OztzCxjV/XVSBywhvAV37twhGxub15Y6ft0NpC29\nUS9evEiWlpbc1Fqihqm4AQEBtG3bNq6cMlHLXZfGexTcuXOH0tLS6NatWzR27Fh69uxZk+dq0nTS\nxm7evEnLli3jVk0fPnyYTE1Nf5N4582bR+Xl5aoI8Y1lZ2eTi4sL5eTk0C+//MKt8pdKpdxzvvvu\nO3J3d6fa2loVRqo51LtNqCEKCwuxcuVK7nFpaSm6d++OoUOHAgDXH15VVfXajbnVvbuhOWVkZGDL\nli2YNGkSamtrAQCTJk2Cq6srioqKftN//7aVl5djw4YNKCsrg1QqRVBQEHx8fBAcHAyxWIwvvvgC\nUVFRuHz5MhQKBbfBurpTXke5XA6ZTIYtW7YgMTERlZWVqK+vx4IFC7Bs2TKEhoZCoVAAAOLj45GW\nloa6ujpVhv5flZSUYNu2bVAoFCgtLUVISAgeP34MPT09GBsbY+3atRCLxTh27Bh3TOfOnVFRUcGd\nI/P72CyjZqCnpwcDAwPU1taia9eu0NfXR3x8PLp27QpjY2O0a9cOycnJOHr0KEaMGAGBQNAmkgC9\npm89KioK169fx8yZM7mba3p6Ouzt7TFmzBgYGhq2aIy1tbUYOnQoampq8PDhQyxevBi+vr4YPXo0\nbty4AXNzc/z4448QiUTo27cvevfu3aLx/S94PB6qqqogFAoxYcIEZGZmoqSkBJaWltDV1cXTp0+R\nn5+PadOmgcfjoaamBosXL/7NmJe6ePLkCSwsLCCTydCtWzfo6+vjzp07KC8vR58+fdCrVy+8ePEC\n5eXlcHR0hFwuR3FxMebMmdPi7yuNpeIWikZTKBRNuhAcHBxo1KhRRNRQnM3Pz482bNhAp0+fpn79\n+jUpxtbaNe4aKygooJycHO5nX19fCgkJIaKGDc4tLCy4gnAtGZ/SgwcP6MiRIzR69GgSi8VE1DBe\nMH/+fDp69Oh/PU7dxcbGkr29PW3evJmuXLlCFRUVNHPmTJowYQJt2rSJhg0bRidPnlR1mP+vxtdc\nJpPRhx9+SIsWLaK6ujpKSEggX19fmjlzJkVGRlK/fv0oLi5OhdFqNtZl9CfRyya5lpYWcnNzATTU\nJeLz+fD09ISfnx88PDxQW1uL+Ph4hIaGwtXVVe1LIDcnHo+HM2fOYPr06Vi3bh2WLl2KmpoaTJ48\nGSKRCC4uLli8eDG2b9+O4cOHqyTG+Ph4+Pr6wsbGBnPmzEFwcDCSkpIgEAgwbtw4FBUVqSSuP4Ma\nTS0tLi7G4cOHsWLFCnTp0gUHDx5ESkoKDh8+DAMDA9y4cQMhISGYNm0ad6w6ahxXdnY2+Hw+/P39\nIRQK4e/vDycnJ8ydOxdVVVWIj4/Hjh07MGHCBMjlchVGrcFUmY00WePaRGZmZtw+ukREjo6ONH36\ndO6xckBLE2akNKcff/yRbG1tSSKRUEREBOno6JC/vz8VFhaSQqGge/fucfvWtuS1Uf6fvLw8mjRp\nEjcTTCKRUHh4OE2ZMoWuXLlCGRkZXG0iTaA8r4yMDNq3bx+tX7+eiBpKdUdGRpK3tzfFxMRQdXU1\neXp60qpVq0gikaj1e1IZ24ULF8jU1JQyMzOpvr6ecnJyaOnSpbRq1SqSyWSUmJhI/v7+FBISQo8f\nP1Zx1JqLJYT/wfXr16l///70888/E1HDfsfKGSvDhw8nFxcXIiKN2FnqbcjJyaG0tDQ6f/482dnZ\nUWZmJjk6OtLEiRO5vZGVWuKmVFtbyyXnBw8eUGBgIA0cOJD279/PPefx48e0a9cuGj9+PLejljrf\nMJWUMYpEIurduzd5eXmRUCikrKwsImo4r71799LChQuppqaGHj16RPPmzaOSkhJVhv2H5OXl0aBB\ngyg5OZn7nUKhoJycHHr//ffJ19eXiIiOHDlC69evb/G9MVoTtjDtDRA1LZGbmZmJqKgo9O/fH8XF\nxThx4gTMzc2xceNG2NjYIDU1FQ4ODqoMucU0vjZlZWVo164ddHR0AABr166Fubk5lixZgvDwcERG\nRuLbb79tUlL5bauvr0dKSgoKCgqgo6OD7OxsTJs2DTExMSgvL4eHhwfGjBkDoGHwsrq6Gn369Gmx\n+JpDbm4u/P39sWnTJjg6OuLTTz9FdHQ0jh8/DktLSzx+/BgymQzGxsYAmpa7Vif0ymSE/Px8fP75\n5zh48CDkcjnkcjnat2+P+vp6FBQUoLq6GlZWVgCAiooKdO7cWVWhazw2y+gN8Xg8xMfH486dOzA1\nNUVycjLEYjHGjBmDFStWoLCwEDKZDO+++y569+7dpuqs83g8xMTEIDAwEAcOHIBMJuPq+hw9ehRS\nqRTHjx9HUFAQrK2tWzQ2Pp+PyspKBAUFITIyEsuWLcPIkSNhZGSEvLw85OXlgYhgZmaGTp06cXG/\nenNSN43jE4lEiI2NBRHB1dUVTk5OKCsrQ0BAAFxdXWFqasqV1iAitVyJ3Pjzcvv2bVRVVUFHRweB\ngYEwMDDAkCFDIBAIEB8fj6ioKEydOhU9e/bkCiFqa2ur+Aw0G0sIb0B5w9uwYQOcnZ0xdOhQODk5\nYfbs2bCyskJJSQl27NiBOXPmwMTEhDtGnW8ozYXH4yEvLw9LlizBV199hf79+yM3Nxe3b9+GnZ0d\n9PT0cP78eaxevRrjxo1TyeY2urq6OHnyJIyNjSEUCmFhYQFjY2OYmZnh2rVruHfvHmxsbJoUz1P3\n105ZVv3EiRPw8fGBoaEh/v3vf+PRo0cYOnQoRo8ejefPn6Nnz55NWjzqfF7KyQgrVqzA2LFj0b9/\nf5iZmSE8PBz379+HVCrFJ598Ak9PT1hYWABgtYqajSr6qTTVs2fPyNnZmXJzc0kul1NGRgYdOXKE\nqqurSSQSkYODA506dYqINKPfuTkoz/Phw4d04cIFmjhxIve39PR0cnFx4QZta2pquGNa4vo0/j8P\nHz7kfnfr1i1atmwZ/f3vfyeihj2bo6OjKT8//63H9DbcunWLevfuTTt27CAioqioKPLx8aFdu3Y1\neZ6mvCdv3LhBVlZW3DjTo0eP6Nq1a5SdnU2enp60cuVKOnv2LBFpzjlpCs1Ydqki9Ep3QX19PXg8\nHqKjo5GbmwuBQACRSITy8nIsXLgQ+/fvh4WFhdpO4WtuygJoqamp2LRpE77++mt06NAB0dHRmDVr\nFuzs7GBpacntEdCuXTvu2Jb6hsrj8XDu3Dls3boVDg4OaN++PbZv344FCxbgyJEjmD59Om7duoXo\n6GiNK4AmlUohFAphaWmJuLg4zJo1C0SENWvWoK6uDpcuXcL9+/e5loE6twoa69ChA6ysrCASiRAV\nFQWxWAwAWL9+PU6cOME9r618zloS6zL6L6hRV0NeXh74fD66d+8OExMTZGdnY+bMmQgICMDAgQMR\nFxeHGTNmwMDAgDteUz58/wsej4eEhATs27cPvr6+GDFiBEpLS5GdnQ2RSASBQICgoCD4+vrC2Ni4\nxXeB4/F4SEpKgr+/P7799lsUFRUhPDwc2dnZWLlyJaysrFBTU4OFCxfC0dGxRWJqDkSEu3fvwtvb\nG+bm5ujZsycMDAzg5OSEtWvXAgC8vb0xfPhwbgBZkwiFQkgkEhw9ehRTp06Fl5cXhEIh6urquMFj\noO10x7YoVTZP1JmysuWZM2fI1taWVq9eTX5+fk2Kr8XFxdHAgQObFGpr7V5tokdGRhKPx6O9e/cS\nUcNc/oSEBFq8eDF5e3tTbGzsa49rCXK5nC5dukRZWVkUFxdHdnZ2lJ2dTcOGDaMFCxY0ea66rxF5\nXXyBgYE0ZcoUunbtGr148YKIiHx9fcnQ0JAKCwtVEWazUk4Rvnr1Kg0aNIguXbqk4ohaP5YQXqEs\nSU3U0AduY2NDRUVF9Mknn9DgwYNp/vz5lJGRQZWVlTRx4kSV3vBUQXmexcXF3JjAsWPHSFtbm1JS\nUpo8R7kmoyVvtso1H7W1tU3imD9/PvdarV27tsn6EU2gPBexWExhYWFcKZAdO3aQh4cHxcfHU2xs\nLC1YsIBu376tylCbTX19PV27do2GDRtGp0+fJqK28zlTFdZl1EhZWRm2b98OiUSCwYMHo6ioCNOn\nT0dhYSHCw8MRFhaGGzduID4+HiNGjMAHH3yAQYMGtZmppfRyTOXcuXNYtmwZTp8+jfv372POnDmw\nsbHBvHnzMGLECK7PWjlm0JJNex6Ph1OnTmHdunVIT0+HUCiEubk54uPj0bFjRzx8+BBxcXE4fPgw\nLC0t1X5aKfDrdU9LS4OPjw+qq6tx9epVPH36FMuXL8fz58+RmJiIQ4cOwdfXF6NGjWpynKbi8/nQ\n09ODm5sbRowY0WY+Z6rEBpUbEQgEEAqFyMjIgI6ODqZMmQKgYTBr165dGD16NC5cuACJRMLNj1Zq\nC29SHo+H9PR0fP3119i9ezckEgkyMzPx8ccf45tvvsHTp0/h5uaG4uJidOnSpcWmAtIri+IOHjyI\nhQsXQiqVYvXq1di7dy+8vLywe/du5OfnIyAgQKMGkJXXfcuWLTh+/DiGDBmCY8eOITU1FREREfD2\n9oaWlhZXdl2ZCFrDe1IoFKJv377c49ZwTmpNdY0T9aFQKLgxg8rKSgoLCyM/Pz/64YcfiIho6dKl\n5OLiQomJiWRpacnVLWprzddnz56Rp6cnvfvuu9zvsrKyaM6cOZSQkEBEpJK+a+XrkJaWRl999RVt\n2bKF+1tkZCRZW1vTTz/9REREz58/547RpNfv4sWLJBAIKCgoiIgaNuo5fvw4eXt7086dO6m+vp7r\nLtOk82LUC+syeonP50MkEuHevXuYNm0a7t69i5s3b0JLSwt+fn5ISkpCeno6VqxYARcXF41vjv8R\n9EoTvWPHjtDX18eFCxfw5MkTODk5oUePHrh8+TIqKiowcuRI6OjogM/nt9j1Uf6flJQUvP/++3j6\n9Cl+/vlnmJubo1evXrC1tYWWlhbWr1+P2bNnQ1dXl4tLk14/MzMzWFlZITg4GPr6+rCyssKAAQNQ\nVVUFR0dHGBgYaOR5MWpGtflIfZw5c4asra3pwoULRERUXl5OISEhtHLlSjp//jwRtb2qpcpzTEhI\noH/+858UERFBpaWldPnyZZoxYwZ5eXlRUlISWVpacvvzqkJaWhqNGzeObt68SUREmzZtouXLl5NY\nLCaZTEZEREVFRSqLrzmdPXuWbGxsKDIyUtWhMK0QSwjUsFL1vffe47oVlDeR8vJy+vLLL2np0qUa\nURWyOSmTQXJyMvXr149CQ0PJzs6OAgMDKSUlhS5fvkwWFhbk4ODAXTdV7Td88eJF4vP53ErdFy9e\nUGBgIHl5eVFiYmKT5N0aEvnp06dpwIABVFxczHV1MkxzYAVA0NBdVFpaCqlUCuDXJrdMJkNAQAA2\nbNjQZNFZW6BckBceHo5169bBz88Pp06dglQqRWxsLJycnLB7927069cPSUlJAKCy/YbHjx+PkydP\nYt++ffjuu+/Qvn17bNq0CYaGhujRo0eTLpTW0J3y3nvvISkpCUZGRmpZrZTRXGwMAUD79u1RWVmJ\n/Px89OjRAwYGBkhJSYGfnx/Gjx+vkas9/wx62R+vUCjA4/GQnJyMpKQkFBUVwcHBAb169YKVlRUC\nAwMxZcoUWFhYQFdXFyKRCCNHjmxSFK6lWVhYwMTEBNu2bYO2tjZsbW0xduzYVpvIO3XqBEDzp5Yy\n6oXth/BScXEx9uzZA7FYDEdHR0RHRyMsLAzu7u6qDq1FUKMB5OLiYvTq1QtAw7agR48ehbm5OWbP\nno2qqirMmjUL586dQ69evSCTyVBfX6/SZNBYTEwMNm7ciISEBBgYGLBv0AzzBlhCaKS6uhrp6emQ\nSCQwMTGBvb19m1kMo/ymef78eWzevBmurq7g8/nYunUrkpOTERYWhqKiIujp6cHf3x+TJk1S22+n\nT548wTvvvKPqMBhG47CFaY0IhUI4Oztzj9tKMgB+rau/fv16REVF4dChQzh58iQePnyIPXv2oGPH\njjhw4ADMzMwwYcIEVYf7u5TJQF0TFsOoKzao/Dtay2rPP0Iul3M7mhUVFSEhIQEHDx5ESUkJfHx8\nYGtriylTpiA/Px/79u3jSoGrM3WPj2HUDWshMAAayna4uLiAx+Nh586d2LFjB0aMGAFTU1PcuXMH\nd+7cweTJk0FEGDZsmMpmFDEM8/awT3Ub9GpXivKxtrY2Xrx4AalUiqysLCgUCmRmZiIiIoLbqtDD\nw0NVYTMM85axQeU2pvG4yK1bt6Cvrw8jI6Mmz7l8+TJCQkJQXV0NHx8feHp6cseybhiGab1YQmhj\nlDf12NhYBAUFITg4GHZ2dtzfldtiVlVVgYigo6PTpgbXGaYtYwmhDfrPf/4DT09P7N27F0OHDm3y\nt9fd/FnLgGHaBjbLqA0oLCzEypUrucfKuvnKZFBfXw8AqKqqeu3MKpYMGKZtYAmhDTAxMYGXlxfu\n3bsHABgyZAj09fWRmJgImUwGLS0tJCcnY/v27aitrQVrNDJM28S6jFoxIoJcLuemiDo6OkIgEHAr\nj+/evQuhUAh7e3usXbsW33zzDVxdXVUcNcMwqsISQivVeCwgNzeXmzY6ZswY9OjRA1FRUUhISMC5\nc+cgk8ng7u6u1uUoGIZ5+1hCaKUa1yby8/PDiRMnYGtrCwAYOXIkDAwM8MMPPwAAXrx4AW1tbTab\niGHaOJYQWrEbN25g7ty5OH78OKytrXH//n306NEDHTt2hL29PXR0dJCQkMBNNWUYpm1jK5VbkVe/\n4WtpaWHmzJnIyspCXFwcTpw4AXNzc2zcuBFpaWlITU0FAJYMGIYBwGYZtTo8Hg/x8fGIi4tDTiLN\nSAAAA2VJREFU9+7dUVNTg2PHjsHU1BTHjx+Hqakpbty4AQBwcHAANWyjquKoGYZRBywhtCI8Hg8x\nMTFYs2YN6urqYGRkhG3btuHUqVP429/+hrq6Oly6dAlmZmZNjmFjBgzDACwhtCplZWUIDQ3F999/\nD3d3d1y/fh3ff/89FAoFxGIxlixZgsDAQIwZM4a1ChiG+Q02hqDBXp0iqtyjIDo6Grm5uRAIBBCJ\nRCgvL8fChQuxf/9+WFhYsGTAMMxrsRaChmp8U8/Ly8OzZ8/wzjvvIDAwEBUVFVi0aBEOHTqEiIgI\nXL16FR07duTWIgBsainDML/Fpp1qKLlcDoFAgNjYWGzduhWjRo2CQqHA6tWrYWpqCgC4ePEiAgIC\nEBQUhEmTJqk4YoZh1B1rIWiYyspKAA07nF29ehWbN29GTEwMOnXqBLFYjMDAQFy/fh1VVVUIDQ3F\nl19+ya1AZhiG+T2shaBBysrKEBwcDEtLS8ydOxfp6elo3749njx5gg0bNmDXrl2IiIiAVCpFcHAw\nDA0N2X4GDMP8YayFoEEEAgGEQiEyMjJw5swZDB8+HDY2NkhMTMSuXbswevRoGBsbo1u3bqiqqoKO\njg53LEsGDMP8f1hC0ADKqqVdunThxggSExNx8uRJAIBUKsWnn34KkUiE2NhYLF++HNbW1qxlwDDM\nG2FdRhpAOb1UJBLhxYsXcHJywp49e1BYWIjJkyfD1dUVH374IaqrqzFr1ixMnz6dVS1lGOaNsYSg\nIWJjYxEYGIjPP/8cbm5ueP78OQ4cOICCggJMnDgREydOZFVLGYb5n7AuIw1QUVGB/fv3Izw8HG5u\nbqirq4Ouri4++OADGBsb48yZM5BIJNDW1gbAylEwDPPnsJXKGoDP56O0tBRSqRTAr9/8ZTIZAgIC\nUFxcDAMDA1WGyDBMK8BaCBqgU6dO8PT0RGpqKnJycqClpYWUlBTMmzcPT548QZ8+fVQdIsMwrQAb\nQ9AQxcXF2LNnD8RiMRwdHREdHY2wsDC4u7urOjSGYVoJlhA0SHV1NdLT0yGRSGBiYgJ7e3s2gMww\nTLNhCUGDsWTAMExzYoPKGowlAoZhmhMbVGYYhmEAsITAMAzDvMQSAsMwDAOAJQSGYRjmJZYQGIZh\nGAAsITAMwzAvsYTAMAzDAAD+D41KT4VmEkzWAAAAAElFTkSuQmCC\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x1079680d0>"
|
|
]
|
|
},
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAbwAAAFhCAYAAAALEB8uAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdYFOfaBvB7qALSqyBFNEZQFKyIDWOJXYMaJZagJpZE\nj8YUOcYoJ8YWNZZoTEyixJ5jjI0gNkQ9KvZOBNtiBbtUhV2e7w+/nbCAqDjMLMvzuy6vZJadmXfu\n3Zln531ndgUiIjDGGGMGzkjpBjDGGGNy4ILHGGOsUuCCxxhjrFLggscYY6xS4ILHGGOsUuCCxxhj\nrFKQteClp6ejdevWsLGxweeffy7nqiukLl26YOXKlUo3Q2/5+Phg9+7dsq3PyMgIV65cKdd1RERE\n4Kuvviq35VtbW0OlUr3SPAkJCfD09CyfBhm4evXqYd++fZIvV6VSwcjICAUFBZIvW2mjRo3CN998\nUy7LNnnRE3x8fHDnzh0YGxvDysoKnTt3xqJFi2BlZfXKK1u6dClcXFyQkZFRpsZWNrGxsUo3Qa8J\nggBBEEr8W0REBDw9PTF16tQyLTs0NBSDBg3CsGHDXqeJr6y0bZJCZmZmuS37dbzu66Wvzp07p3QT\nZPWqr2N0dDR+/fVX7N+/X3xsyZIl5dW8F5/hCYKAmJgYZGZm4sSJEzh27NgrV18iQkFBAVJTU+Hn\n51emhqrV6jLNxyoGfXt9y7PovAh/F4R+0rf3KCsDegEfHx/avXu3OP3ZZ59Rt27diIjo0KFD1Lx5\nc7Kzs6MGDRpQQkKC+Lw2bdrQl19+SS1atCALCwsaOHAgmZqakpmZGVWtWpV2795NT58+pbFjx5K7\nuzu5u7vTuHHj6OnTp0REtGfPHvLw8KBZs2aRm5sbDRo0iKKioqhPnz40cOBAsra2poCAAEpJSaHp\n06eTi4sLeXl50Y4dO8Q2LFu2jPz8/Mja2pp8fX3pp59+Ev+mXf7cuXPJxcWFqlWrRsuXLxf/npOT\nQ+PHjydvb2+ytbWlli1bUm5u7gu3u6jjx49TYGAgWVtbU9++fendd9+lSZMmERHRgwcPqGvXruTs\n7Ez29vbUrVs3unHjhk6Gv/zyCxERLV++nFq0aEGfffYZ2dvbU40aNWjbtm3PXe+1a9fonXfeIWdn\nZ3J0dKTRo0cTEZFGo6GpU6eSt7c3ubi40ODBg+nx48dERHT16lUSBIGWL19Onp6e5ODgQEuWLKEj\nR45QQEAA2dnZicvRtikkJIRGjx5Ntra2VKdOHZ33ysvkr319Bw8eTAUFBTRjxgyqWbMmOTo60rvv\nvksPHjwQ51mxYgV5eXmRo6MjTZs2rdh7U+unn37Sea/16NGDiIiSkpKoTZs2ZGdnR3Xr1qUtW7aU\nmN3EiRPJ2NiYqlSpQlWrVqUxY8YQEZEgCPTjjz/SG2+8QXZ2dvTxxx/rzPfrr7+Sn58f2dvb09tv\nv02pqanPfX32798vvoc8PT3pt99+IyKiiIiIl35/LF++nHx9fcna2ppq1KhBq1evJiKiixcvUuvW\nrcnW1pacnJyoX79+4jyCINDly5eJqPT3eGF79uyh6tWri9M3b96ksLAwcnZ2pho1atDChQvFvx0+\nfJiCg4PJzs6OqlWrRqNHj6a8vDzx7+PGjSMXFxeysbGhgIAAOnfu3HNfr6JKmpeI6N69e9S9e3ey\nsbGhpk2b0qRJk6hly5ZE9M97WqPRiMspvF9dunSJ2rZtS46OjuTk5EQDBgygR48eic/19vamWbNm\nUUBAAFWpUoU0Gs0r7f/e3t7ie3TKlCmvdPxq06YNRUZGUtOmTcnGxoZ69uwp7g9Ft+vRo0c0dOhQ\nqlatGnl4eNCkSZPEv2n3008++YTs7OyoZs2adODAAVq2bBl5enqSi4uL+P4jInry5Al9+umn5OXl\nRa6urjRy5EjxfVHacfN5r6N2n7a2tiZ/f3/auHEjET3bH6tUqULGxsZUtWpVsre3JyKi999/X9wH\niIiWLl1KtWrVIgcHB+rRowfdunVL/NuL9smiXqrg7dq1i4ieHUTr1q1LkydPphs3bpCjo6N40N25\ncyc5OjrSvXv3xBfL29ubkpKSSKPRUH5+PkVERNBXX30lLvurr76i5s2b0927d+nu3bsUEhIi/n3P\nnj1kYmJCkZGRlJeXR7m5uTRlyhSqUqUK7dixg9RqNQ0ePJi8vb1p+vTppFar6eeff6YaNWqIy//r\nr7/oypUrRES0d+9esrS0pBMnTugsf8qUKaRWqyk2NpYsLS3FN/tHH31Ebdu2pVu3bolv8qdPnz53\nu+/evVssu6dPn5KXlxctXLiQ1Go1/fnnn2RmZiZu4/379+nPP/+k3NxcyszMpL59+1KvXr3E+UND\nQ+nXX38lomdvWlNTU/rll1+ooKCAlixZQu7u7iW+Zmq1murXr0/jx4+nnJwcevLkCR04cICInh2U\na9WqRVevXqWsrCwKCwujQYMGEdE/O9GoUaPo6dOntGPHDjIzM6NevXrR3bt36ebNm+Ti4kJ79+4V\n22RiYkLz588ntVpNv//+O9na2oo75cvkX/j1nT9/PjVv3pxu3rxJeXl5NGLECAoPDyciovPnz1PV\nqlVp//799PTpUxo/fjyZmJiUWPCIqNh7LS8vj2rWrEkzZsyg/Px8io+PJ2tra0pOTi5x/sLZawmC\nQN27d6fHjx/TtWvXyNnZmeLi4oiIaNOmTVSrVi26cOECaTQa+uabbygkJKTEZatUKrK2tqZ169aR\nWq2m+/fv06lTp8R2a3f20t4fWVlZZGNjQykpKURElJaWRufPnyciov79+9P06dOJ6Nl7UPvaa7dB\nW/Ce9x4vqnDB02g01LBhQ5o6dSrl5+fTlStXyNfXl7Zv305Ezz7gHT58mDQaDalUKvLz86P58+cT\nEVFcXBw1atRI/IB14cIFun37domvV1GlzduvXz/q168f5eTk0Llz58jDw4NatWpFRCUXvMKv7aVL\nl2jXrl2Ul5dHd+/epdatW9O4cePE53p7e1NQUBDduHGDnjx58kr7P5HuCcOrHr/atGlDHh4edP78\necrOzqbevXvTwIEDS9yuXr160ciRIyknJ4fu3LlDTZs2FT9gavfT6OhoKigooEmTJpGHh4f4YWTH\njh1kbW1N2dnZRPTsg0XPnj3p4cOHlJmZSd27d6d///vf4nuhtONmSa/j+vXrxdfq999/JysrK0pL\nSyMioujoaPHDiVbhZezevZucnJzo5MmT9PTpUxozZgy1bt1afG5p+2RJXljwvL29qWrVqmRnZ0fe\n3t708ccfU25uLs2cOVM8UGq9/fbb4ieF0NBQmjJlSrENKVy5a9asqXOWsn37dvLx8SGiZ8GamZnp\n7IBTpkyhjh07itNbtmyhqlWrUkFBARERZWRkkCAI4k5RVK9evWjBggXi8i0sLHR2BBcXF3FntbCw\noDNnzhRbxou2u7C9e/eSh4eHzmMtW7Z87o598uRJ8VMOUfGCV6tWLfFv2dnZJAgCpaenF1vOwYMH\nydnZWWfbtN566y1asmSJOJ2cnEympqak0WjEnajwJyhHR0f673//K0737t1bPIAtX768WNFt2rQp\nrVy5ssTtK5p/0dfXz89Pp4DdunWLTE1NSa1W03/+8x+x+Gm338zMrNSCV/i9tm/fPnJzc9N5Tnh4\nOEVFRZU4f2hoqHgWoCUIgk7xePfdd2nWrFlERNSpUyedAqnRaMjS0pKuXbtWbNnTp0+nsLCwl2p3\nYYXfH1lZWWRnZ0cbNmygnJwcnecNHjyYhg8frnM2WHgbLl++XOp7vKjCBS8xMZG8vLyKbc+QIUNK\nnHfevHn0zjvvENGzg1ft2rUpMTGx2HuztO0mIoqPjy9xXrVaTaampjofXCZOnFjqGV5JH2a0Nm7c\nSEFBQeK0j4+PTs/Pq+z/2vkLF7xXOX6FhoaKhYbo2RmRmZkZFRQU6GxXWloamZub65ydr1mzhtq2\nbUtEz/bTN954Q/zbmTNnSBAEunPnjviYo6MjnT59mgoKCsjKykr8UET07HiiLcSlHTeJXvw6EhEF\nBgbS5s2bxbaVVvCGDh1KEyZMEP+WlZVFpqamYu9JSfvkzJkzn7vulxrD27x5Mx4+fAiVSoVFixah\nSpUqSE1Nxfr162Fvby/+O3DgANLS0sR5X3Rl161bt+Dt7S1Oe3l54datW+K0s7MzzMzMdOZxcXER\n/9/CwgJOTk7ieIuFhQUAICsrCwCwbds2BAcHw9HREfb29oiNjcX9+/fF+R0dHWFk9E8ElpaWyMrK\nwr179/DkyRPUrFmzWJtfZrsLb5+Hh4fOY56enuIYTU5ODkaMGAEfHx/Y2tqiTZs2ePz48XPHcNzc\n3HTaWnhbC7t+/Tq8vb11tk3r9u3bxTJXq9VIT08XH3N1dRX/38LCoth0dna2OF10+7y9vXH79m0A\nL86/6OurUqnwzjvviLn6+/vDxMQE6enpuH37NqpXr66z/Y6OjiXFVKJbt24Vez96e3vj5s2bz52n\npHG8oq+BNv/U1FSMHTtWbLu2bSUt/8aNG/D19X1hm0t7f1hZWeH333/Hjz/+CHd3d3Tr1g3JyckA\ngG+//RZEhKZNm6JevXpYvnx5sWWX9h4vTWpqKm7duqXz/p8xYwbu3LkDAEhJSUG3bt1QrVo12Nra\n4ssvvxRf87feegujR4/Gxx9/DFdXV4wYMeKlL6Jp27ZtifPevXsXarVa57X18vJ66e1JT09H//79\nUb16ddja2mLQoEE671FA9zj2Kvt/SV7l+FV03V5eXsjPz8e9e/d0lpmamor8/HxUq1ZNbNPIkSNx\n9+5d8TlF92Hg2f5X+LGsrCzcvXsXOTk5aNSokbiszp0766zzecfN51mxYgWCgoLE5Z07d65Yxs9T\n9HhlZWUFR0dHnf3qeftkScp8W4KXlxcGDRqEhw8fiv8yMzPxxRdfiM950cC/u7u7ziXS165dg7u7\n+3Pnf5ULCZ4+fYrevXvjiy++wJ07d/Dw4UN06dLlpS4IcHJyQpUqVXDp0qVif3uZ7daqVq1asQPe\ntWvXxO2YO3cuUlJScOTIETx+/Bh79+4FPTvrfuntLImnpyeuXbsGjUZT7G8lZW5iYqKzQ7yKotuX\nmpoKd3f3l8q/6Ovp5eWFuLg4nWxzcnLg7u6OatWq4fr16+Jzc3JySt1pii7b3d0d169f11l/amqq\nThEtbf4X8fLywtKlS3Xanp2djeDg4GLP9fT0xOXLl1/Y9he9Pzp27IgdO3YgLS0NderUwYcffgjg\n2cFt6dKluHnzJn766Sd89NFHxW6nKO09XhpPT0/UqFFDZzszMjIQExMD4Nkl5f7+/rh06RIeP36M\nadOm6Vw6P2bMGBw7dgxJSUlISUnB7Nmzdba5NCXN6+LiAhMTE1y7dk18XuH/115NnpOTIz5WuDhN\nnDgRxsbGOHfuHB4/foyVK1cWu9S/cNteZf+XQtHtMjU1hZOTk85zPD09YW5ujvv374ttevz4Mc6e\nPfvK63NycoKFhQWSkpLEZT169Oilr6wv+jqmpqZi+PDhWLx4MR48eICHDx+iXr164nv4VWtEdnY2\n7t+/X+yD9ssqc8EbOHAgtm7dih07dkCj0eDJkydISEjQOQAWPXAXnQ4PD8c333yDe/fu4d69e/j6\n668xaNCg567zVQpBXl4e8vLy4OTkBCMjI2zbtg07dux4qXmNjIwwdOhQjB8/Hrdv34ZGo8GhQ4eQ\nl5f3UtutFRISAmNjYyxatAhqtRqbN2/G0aNHxb9nZWXBwsICtra2ePDgAf7zn/+89PaVplmzZqhW\nrRoiIyORk5ODJ0+e4ODBgwCeZT5v3jyoVCpkZWVh4sSJ6N+/f4lng89T+HW4c+cOFi5ciPz8fKxf\nvx4XLlxAly5dypT/yJEjMXHiRHEnv3v3LrZs2QIA6NOnD2JiYnDgwAHk5eVh8uTJpd6D5OrqqnOQ\nDw4OhqWlJb799lvk5+cjISEBMTEx6N+//3PnL60oaXPQZjFy5EhMnz4dSUlJAIDHjx9j/fr1Jc43\nYMAA7Nq1C+vXr4darcb9+/dx+vTpYsss7f1x584dbN68GdnZ2TA1NYWVlRWMjY0BAOvXr8eNGzcA\nAHZ2dhAEodjrW9p7vDRNmzaFtbU1vv32W+Tm5kKj0eDcuXM4duyY2GZra2tYWlriwoULWLJkiXhQ\nO3bsGA4fPoz8/HxYWlqiSpUqYpuLvl5FPW9eIyMjhIWFISoqCrm5uUhKSsKKFSvEdTo7O8PDwwMr\nV66ERqPBsmXLdF7XrKwsWFlZwcbGBjdv3hQL8PO8yv7/uogIq1atwt9//42cnBxMnjwZffv2LVYk\nqlWrho4dO2L8+PHIzMxEQUEBLl++XKb7/4yMjPDhhx9i3Lhx4hnizZs3X/rYWfR1zM7OhiAIcHJy\nQkFBAZYvX65zq4arqytu3LiB/Px8ne3W7gPh4eFYvnw5Tp8+jadPn2LixIkIDg5+7ln8i2pEmQte\n9erVsXnzZkyfPh0uLi7w8vLC3LlzS/0EX/Qeo0mTJqFx48aoX78+6tevj8aNG2PSpEkvPf/zngM8\nu8F24cKFePfdd+Hg4IC1a9eiZ8+epc5b2Jw5cxAQEIAmTZrA0dER//73v1FQUPDc7S7p4Gtqaoo/\n//wTv/76K+zt7bF69Wp069ZN7MYbN24ccnNz4eTkhJCQEHTu3Pm5bXqZbdcyMjLC1q1bcenSJXh5\necHT0xP//e9/AQBDhw7FoEGD0Lp1a/j6+sLS0hLff//9S2VS0nOaNWuGixcvwtnZGV999RU2bNgA\ne3v7MuU/duxY9OjRAx07doSNjQ2aN2+OI0eOAAD8/f2xePFivPfee3B3d4eDg0OpXebDhg1DUlIS\n7O3tERYWBlNTU2zduhXbtm2Ds7MzRo8ejZUrV6J27dolzj927Fj88ccfcHBwwLhx456bg3YbevXq\nhQkTJqB///6wtbVFQEAAtm/fXuJ8np6eiI2Nxdy5c+Ho6IigoCCcOXOm2DJLe38UFBRg3rx58PDw\ngKOjI/bv3y/ev3Ts2DEEBwfD2toaPXv2xMKFC+Hj41Ms8+e9x5+3rQBgbGyMmJgYnDp1Cr6+vnB2\ndsbw4cPFM4A5c+ZgzZo1sLGxwfDhw3U+UGRkZGD48OFwcHCAj48PnJycxC+gKPp6FVXavIsWLUJW\nVhbc3NwwdOhQDBkyROc49PPPP2P27NlwcnJCUlISWrRoIf5typQpOHHiBGxtbdG9e3f07t271H3g\nVfb/kjJ82eOX9v8HDRqEiIgIVKtWDXl5eVi4cGGJz12xYgXy8vLg7+8PBwcH9O3bVzyTfZVjBwDM\nmjULtWrVQnBwMGxtbdGhQwekpKS81LxFX0d/f398+umnaN68Odzc3HDu3Dm0bNlSfH67du1Qt25d\nuLm5id29hdvbrl07TJ06Fb1794a7uzuuXr2KdevWlZpfqcewUkcX9cCQIUPIxcWF6tWrV+xvc+bM\nIUEQ6P79+wq0rGyaNm1K0dHRSjdDEiUNODOmNEN5X5Z2cQ0rG73/Ls0hQ4YgLi6u2OPXr1/Hzp07\ndQY09dG+ffuQlpYGtVqN3377DefOnUOnTp2UbhZjrAIg/hICSel9wWvVqhXs7e2LPT5+/Hh8++23\nCrTo1SQnJyMwMBD29vaYN28e/vjjjzJfIKJvyvtrsBgrC0N6XxrKdugLgSrARwiVSoXu3buLVx1t\n3rwZCQkJmDdvHmrUqIHjx4/DwcFB4VYyxhjTZy/88mh9k5OTg+nTp2Pnzp3iYxWgZjPGGFNYhSt4\nly9fhkqlQoMGDQA8u4m3UaNGOHLkiM5NnQBQq1atF15azhhjTFeDBg1w6tQppZshOb0fwysqICAA\n6enpuHr1Kq5evYrq1avjxIkTxYod8Kw40v/f06HP/6ZMmaJ4GwzpH+fJWerrv4qSp/a+UEOj9wUv\nPDwcISEhSElJgaenZ7GvSTKEQd1X/UFOVjrOUzqcpbQ4T2XpfZfm2rVrS/17ef8CNWOMMcOg92d4\nlUFERITSTTAonKd0OEtpcZ7KqhC3JZSVIAgw4M1jjLFyYajHTj7D0wMJCQlKN8GgcJ7S4SylxXkq\niwseY4yxSoG7NBljjOkw1GMnn+ExxhirFLjg6QHu15cW5ykdzlJanKeyuOAxxhirFCr1GF5kVCTS\nHqXJ2CL95WbnhplRM5VuBmNMDxjqGJ7ef9NKeUp7lAafXj5KN0MvqDaplG4CY4yVK+7S1AOqUyql\nm2BQeJxEOpyltDhPZXHBY4wxVilwwdMDPoE+SjfBoISGhirdBIPBWUqL81QWFzzGGGOVAhc8PcBj\neNLicRLpcJbS4jyVxQWPMcZYpcAFTw/wGJ60eJxEOpyltDhPZXHBY4wxVilwwdMDPIYnLR4nkQ5n\nKS3OU1lc8BhjjFUKXPD0AI/hSYvHSaTDWUqL81QWFzzGGGOVAhc8PcBjeNLicRLpcJbS4jyVpfcF\nb+jQoXB1dUVAQID42Oeffw4/Pz80aNAAYWFhePz4sYItZIwxVhHofcEbMmQI4uLidB7r2LEjzp8/\nj9OnT6N27dqYMWOGQq2TBo/hSYvHSaTDWUqL81SW3he8Vq1awd7eXuexDh06wMjoWdObNWuGGzdu\nKNE0xhhjFYjeF7wXWbZsGbp06aJ0M14Lj+FJi8dJpMNZSovzVFaFLnjTpk2DmZkZ3nvvPaWbwhhj\nTM+ZKN2AsoqOjkZsbCx2795d6vMiIiLg4+MDALCzs0NgYKDYj552Iw049c8YmvZMq7JOaz99avPh\naZ4uTF/aU9GntfSlPaGhoUhISEB0dDQAiMdLQyQQESndiBdRqVTo3r07zp49CwCIi4vDp59+ir17\n98LJyem58wmCgNI2L2JcBHx6+Ujd3ApJtUmF6PnRSjeDMaYHXnTsrKj0vkszPDwcISEhSE5Ohqen\nJ5YtW4YxY8YgKysLHTp0QFBQED766COlm/laeAxPWkU/SbOy4yylxXkqS++7NNeuXVvssaFDhyrQ\nEsYYYxWZ3p/hVQZ8H560tGMU7PVxltLiPJXFBY8xxlilwAVPD/AYnrR4nEQ6nKW0OE9lccFjjDFW\nKXDB0wM8hictHieRDmcpLc5TWVzwGGOMVQpc8PQAj+FJi8dJpMNZSovzVBYXPMYYY5UCFzw9wGN4\n0uJxEulwltLiPJXFBY8xxlilwAVPD/AYnrR4nEQ6nKW0OE9lccFjjDFWKcj25dHJycmYM2cOVCoV\n1Go1gGc/QREfHy9XE/QWj+FJi8dJpMNZSovzVJZsBa9v374YNWoUPvjgAxgbGwN4VvAYY4wxOcjW\npWlqaopRo0ahWbNmaNy4MRo3boxGjRrJtXq9xmN40uJxEulwltLiPJUlW8Hr3r07Fi9ejNu3b+PB\ngwfiP8YYY0wOAsn0O+4+Pj4ldmFevXq13Nb5op+pjxgXAZ9ePuW2/opEtUmF6PnRSjeDMaYHXnTs\nrKhkG8NTqVRyrYoxxhgrptwL3u7du9GuXTts2LChxDO8sLCw8m6C3lOdUvGVmhJKSEjgq+EkwllK\ni/NUVrkXvH379qFdu3bYunUrFzzGGGOKkW0MTwk8hvfyeAyPMabFY3gSiImJQVJSEp48eSI+Nnny\nZDmbwMpRZFQk0h6lKd0MveBm54aZUTOVbgZjrBDZCt6IESOQm5uL+Ph4fPjhh1i/fj2aNWsm1+r1\nmqGM4aU9StOLM2Z9yFO1SaXo+qXCY07S4jyVJdt9eAcPHsSKFSvg4OCAKVOmIDExEcnJyS+cb+jQ\noXB1dUVAQID42IMHD9ChQwfUrl0bHTt2xKNHj8qz6YwxxgyAbAXPwsICAGBpaYmbN2/CxMQEaWkv\n7v4aMmQI4uLidB6bOXMmOnTogJSUFLRr1w4zZ1bsriOlz0YMDecpHT4bkRbnqSzZCl63bt3w8OFD\nfP7552jUqBF8fHwQHh7+wvlatWoFe3t7nce2bNmC999/HwDw/vvvY9OmTeXSZsYYY4ZDtoI3efJk\n2Nvbo3fv3lCpVLhw4QKmTp1apmWlp6fD1dUVAODq6or09HQpmyo7/i5NaXGe0uHvfpQW56ks2S5a\nKenGc1tbWwQEBMDFxaXMyxUEodRfXYiIiICPjw8AwM7ODoGBgWK3QtqNNODUP11g2gOl3NNaSq1f\nO63dGbX5vOo056k7/bp56sP0qVOn9Ko9FX1aX/NMSEhAdHQ0AIjHS0Mk2314Xbt2xaFDh9C2bVsA\nz8Ju2LAhrl69ismTJ2Pw4MHPnVelUqF79+44e/YsAKBOnTpISEiAm5sbbt++jbZt2+LChQvF5uP7\n8F6eFPfhcZ7/4PsaWUVmqPfhydalmZ+fj7///hsbNmzAhg0bkJSUBEEQcPjwYcyaNeuVltWjRw/8\n9ttvAIDffvsNvXr1Ko8mM8YYMyCyFbzr16+L424A4OLiguvXr8PR0RFmZmbPnS88PBwhISFITk6G\np6cnli9fjsjISOzcuRO1a9dGfHw8IiMj5diEcsNjTtLiPKXDY07S4jyVJdsYXtu2bdG1a1e8++67\nICJs2LABoaGhyM7Ohp2d3XPnW7t2bYmP79q1q7yayhhjzADJVvAWL16MDRs24MCBAwCe3U7Qu3dv\nCIKAPXv2yNUMvcT3jUmL85QO3zcmLc5TWbIVPEEQ0KdPH/Tp00euVTLGGGMi2cbw2PPxmJO0OE/p\n8JiTtDhPZXHBY4wxVinIWvBycnJe6gujKxsec5IW5ykdHnOSFuepLNkK3pYtWxAUFIS3334bAHDy\n5En06NFDrtUzxhir5GQreFFRUTh8+LD4RdBBQUG4cuWKXKvXazzmJC3OUzo85iQtzlNZshU8U1PT\nYvfbGRnxECJjjDF5yFZx6tati9WrV0OtVuPixYsYM2YMQkJC5Fq9XuMxJ2lxntLhMSdpcZ7Kkq3g\nff/99zh//jzMzc0RHh4OGxsbzJ8/X67VM8YYq+RkK3hWVlaYPn06jh07hmPHjmHatGmoUqWKXKvX\nazzmJC3OUzo85iQtzlNZshW89u3b49GjR+L0gwcPxCs2GWOMsfImW8G7d++ezkUrDg4OFf6XyqXC\nY07S4jzUAiASAAAgAElEQVSlw2NO0uI8lSVbwTM2NkZqaqo4rVKp+CpNxhhjspGt4kybNg2tWrXC\nwIEDMXDgQLRu3RrTp0+Xa/V6jcecpMV5SofHnKTFeSpLtl9L6NSpE44fP47ExEQIgoD58+fDyclJ\nrtUzxhir5GQreACQl5cHBwcHqNVqJCUlAQBat24tZxP0Eo85SYvzlA6POUmL81SWbAVvwoQJ+P33\n3+Hv7w9jY2PxcS54jDHG5CBbwdu4cSOSk5Nhbm4u1yorDNUpFZ+VSIjzlE5CQgKflUiI81SWbBet\n1KxZE3l5eXKtjjHGGNMh2xmehYUFAgMD0a5dO/EsTxAELFy4UK4m6C0+G5EW5ykdPhuRFuepLNkK\nXo8ePYr9/p0gCHKtnjHGWCUnW8GLiIiQa1UVDo85SYvzlA6POUmL81SWbGN4KSkp6NOnD/z9/VGj\nRg3UqFEDvr6+r7XMGTNmoG7duggICMB7772Hp0+fStRaxhhjhka2gjdkyBCMHDkSJiYmSEhIwPvv\nv48BAwaUeXkqlQo///wzTpw4gbNnz0Kj0WDdunUStlg+fDYiLc5TOnw2Ii3OU1myFbzc3Fy0b98e\nRARvb29ERUXhr7/+KvPybGxsYGpqipycHKjVauTk5MDDw0PCFjPGGDMkshW8KlWqQKPRoFatWli0\naBH+/PNPZGdnl3l5Dg4O+PTTT+Hl5QV3d3fY2dmhffv2ErZYPvzdj9LiPKXD3/0oLc5TWbJdtDJ/\n/nzk5ORg4cKF+Oqrr5CRkYHffvutzMu7fPky5s+fD5VKBVtbW/Tt2xerV68u1k0aEREBHx8fAICd\nnR0CAwPFboW0G2nAqX+6wLQHSrmntZRav3ZauzNq83nVac5Td/p189SH6VOnTulVeyr6tL7mmZCQ\ngOjoaAAQj5eGSCAiUroRZfH7779j586d+OWXXwAAK1euRGJiIhYvXiw+RxAElLZ5EeMi4NPLp7yb\nWiGoNqkQPT/6tZbBef5DijwZU8qLjp0VlWxdmkePHsU777yDoKAgBAQEICAgAPXr1y/z8urUqYPE\nxETk5uaCiLBr1y74+/tL2GLGGGOGRLYuzQEDBmDOnDmoV6+eJD/82qBBAwwePBiNGzeGkZERGjZs\niOHDh0vQUvnxfWPS4jylw/eNSYvzVJZsBc/Z2bnYN628ri+++AJffPGFpMtkjDFmmGQreFOmTMGw\nYcPQvn17mJmZAXjWTxwWFiZXE/QWn41Iy1DyjIyKRNqjNKWbgehN0Uo3AW52bpgZNVPpZrw2PrtT\nlmwF77fffkNycjLUarVOlyYXPMZKlvYojS8C+n+qTSqlm8AMgGwF79ixY7hw4QJ/YXQJeMxJWpyn\ndDhLafEYnrJku0ozJCQESUlJcq2OMcYY0yHbGd6hQ4cQGBiIGjVq6Pwe3pkzZ+Rqgt7iT9DS4jyl\nw1lKi8/ulCVLwSMiLF26FF5eXnKsjjHGGCtGti7Njz76CD4+PsX+Mf7uR6lxntLhLKXF36WpLFkK\nniAIaNSoEY4cOSLH6hhjjLFiZBvDS0xMxKpVq+Dt7Q0rKysAPIanxeMk0uI8pcNZSovH8JQlW8Hb\nvn07AIi3JRjiF5MyxhjTX7KN4fn4+ODRo0fYsmULtm7disePH/MY3v/jcRJpcZ7S4SylxWN4ypKt\n4C1YsAADBw7E3bt3kZ6ejoEDB2LhwoVyrZ4xxlglJ1uX5i+//ILDhw+L43eRkZEIDg7Gv/71L7ma\noLd4nERanKd0OEtp8RiesmQ7wwOg8x2aUvxEEGOMMfayZKs6Q4YMQbNmzRAVFYUpU6YgODgYQ4cO\nlWv1eo3HSaTFeUqHs5QWj+Epq9y7NK9cuQJfX1+MHz8ebdq0wf/+9z8IgoDo6GgEBQWV9+oZY4wx\nADIUvL59++L48eNo164ddu/ejUaNGpX3KiscHieRFucpHc5SWjyGp6xyL3gajQbTpk1DcnIyvvvu\nO5377wRBwPjx48u7CYwxxlj5j+GtW7cOxsbG0Gg0yMzMRFZWlvgvMzOzvFdfIfA4ibQ4T+lwltLi\nMTxllfsZXp06dfD555/D29sb4eHh5b06xhhjrESyXKVpbGyMOXPmyLGqConHSaTFeUqHs5QWj+Ep\nS7bbEjp06IA5c+bg+vXrePDggfiPMcYYk4Ns37Sybt06CIKAxYsX6zx+9epVuZqgt1SnVPxJWkKc\np3Q4S2klJCTwWZ6CZCt4KpVK8mU+evQIH3zwAc6fPw9BELBs2TIEBwdLvh7GGGMVn2xdmtnZ2Zg6\ndSo+/PBDAMDFixcRExPzWsscO3YsunTpgr///htnzpyBn5+fFE2VHX+ClhbnKR3OUlp8dqcsWb9a\nzMzMDAcPHgQAuLu748svvyzz8h4/foz9+/eLX09mYmICW1tbSdrKGGPM8MhW8C5fvowJEybAzMwM\nAMRfTSirq1evwtnZGUOGDEHDhg3x4YcfIicnR4qmyo7vdZIW5ykdzlJafB+esmQbwzM3N0dubq44\nffnyZZibm5d5eWq1GidOnMCiRYvQpEkTjBs3DjNnzsTXX3+t87yIiAjxh2bt7OwQGBgodiuk3UgD\nTv3TbaPdueWe1lJq/dpp7c6ozedVpzlP3WlDyDPtUprir6dUeerD9KlTp/SqPdrphIQEREdHA4BB\n/zC3QIW/66sc7dixA9OmTUNSUhI6dOiAAwcOIDo6Gm3bti3T8tLS0tC8eXPxKs///e9/mDlzps64\noCAIKG3zIsZFwKeXT5nWb2hUm1SInh/9WsvgPP/BeUpLijzZy3vRsbOiku0Mr2PHjmjYsCEOHz4M\nIsLChQvh5ORU5uW5ubnB09MTKSkpqF27Nnbt2oW6detK2GLGGGOGRLYxPCLC3r17sWvXLsTHx2P/\n/v2vvczvv/8eAwYMQIMGDXDmzBlMnDhRgpbKj8dJpMV5SoezlBaP4SlLtjO8jz76CJcvX0Z4eDiI\nCD/99BN27tyJH374oczLbNCgAY4ePSphKxljjBkq2Qrenj17kJSUBCOjZyeVERER8Pf3l2v1eo3v\ndZIW5ykdzlJafB+esmTr0qxVqxauXbsmTl+7dg21atWSa/WMMcYqOdkKXkZGBvz8/NCmTRuEhobC\n398fmZmZ6N69O3r06CFXM/QSj5NIi/OUDmcpLR7DU5ZsXZpF748D/rn0VRAEuZrBGGOskpKt4HHf\n9fPxOIm0OE/pcJbS4uOgsmTr0mSMMcaUxAVPD/A4ibQ4T+lwltLiMTxlyVrwcnJykJycLOcqGWOM\nMQAyFrwtW7YgKCgIb7/9NgDg5MmTlf7qTC0eJ5EW5ykdzlJaPIanLNkKXlRUFA4fPgx7e3sAQFBQ\nEK5cuSLX6hljjFVyshU8U1NT2NnZ6a7ciIcQAR4nkRrnKR3OUlo8hqcs2SpO3bp1sXr1aqjValy8\neBFjxoxBSEiIXKtnjDFWyclW8L7//nucP38e5ubmCA8Ph42NDebPny/X6vUaj5NIi/OUDmcpLR7D\nU5ZsN54nJydj+vTpmD59ulyrZIwxxkSyneGNHz8ederUwVdffYVz587JtdoKgcdJpMV5SoezlBaP\n4SlLtoKXkJCAPXv2wMnJCSNGjEBAQACmTp0q1+oZY4xVcrJeJlmtWjWMHTsWP/74Ixo0aFDiF0pX\nRjxOIi3OUzqcpbR4DE9ZshW8pKQkREVFoV69ehg9ejRCQkJw8+ZNuVbPGGOskpPtopWhQ4eif//+\n2L59Ozw8PORabYWgOqXiT9IS4jylY0hZRkZFIu1RmqJtSLuRBrfqboq2wc3ODTOjZiraBqXIVvAS\nExPlWhVjjBWT9igNPr18lG3EKeW7iVWbVIquX0nlXvD69u2L9evXIyAgoNjfBEHAmTNnyrsJek/p\nHcDQcJ7S4SylxXkqq9wL3oIFCwAAMTExICKdv/EvnTPGGJNLuV+04u7uDgD44Ycf4OPjo/Pvhx9+\nKO/VVwh8r5O0OE/pcJbS4jyVJdtVmjt27Cj2WGxs7GsvV6PRICgoCN27d3/tZTHGGDNc5d6luWTJ\nEvzwww+4fPmyzjheZmYmWrRo8drLX7BgAfz9/ZGZmfnay1IK9+tLi/OUDmcpLc5TWeVe8N577z10\n7twZkZGRmDVrljiOZ21tDUdHx9da9o0bNxAbG4svv/wS3333nRTNZYwxZqDKvUvT1tYWPj4+WLdu\nHby9vWFpaQkjIyNkZ2fj2rVrr7XsTz75BLNnz67wv6vH/frS4jylw1lKi/NUlmz34W3ZsgWffvop\nbt26BRcXF6SmpsLPzw/nz58v0/JiYmLg4uKCoKCgUr+QNSIiAj4+PgAAOzs7BAYGil/vk3YjTee+\nGO2bUe5pLaXWr53W5qjN51WnOU/daUPIM+1SmuKvJ+cp7bRW4XwSEhIQHR397Pn/f7w0RAIVvVeg\nnNSvXx/x8fHo0KEDTp48iT179mDlypVYtmxZmZY3ceJErFy5EiYmJnjy5AkyMjLQu3dvrFixQnyO\nIAjFboUoLGJchPI3ouoJ1SYVoudHv9YyOM9/cJ7S4jyl8zJZvujYWVHJ1hdoamoKJycnFBQUQKPR\noG3btjh27FiZlzd9+nRcv34dV69exbp16/DWW2/pFDvGGGOsMNkKnr29PTIzM9GqVSsMGDAA//rX\nv1C1alXJll+Rb2Lnfn1pcZ7S4SylxXkqS7aCt2nTJlhaWmLevHno1KkTatWqha1bt0qy7DZt2mDL\nli2SLIsxxphhku2iFe3ZnLGxMSIiIuRabYXA9+ZIi/OUDmcpLc5TWeVe8KpWrfrc7kZBEJCRkVHe\nTWCMMcbKv0szKysLmZmZJf7jYvcM9+tLi/OUDmcpLc5TWbLesb1//34sX74cAHD37l1cvXpVztUz\nxhirxGQreFFRUZg1axZmzJgBAMjLy8OAAQPkWr1e4359aXGe0uEspcV5Kku2grdx40Zs2bIFVlZW\nAAAPDw9kZWXJtXrGGGOVnGwFz9zcXOc7L7Ozs+Vatd7jfn1pcZ7S4SylxXkqS7aC17dvX4wYMQKP\nHj3C0qVL0a5dO3zwwQdyrZ4xxlglJ8t9eESEfv364cKFC7C2tkZKSgqmTp2KDh06yLF6vcf9+tLi\nPKXDWUqL81SWbDeed+nSBefOnUPHjh3lWiVjjDEmkqVLUxAENGrUCEeOHJFjdRUO9+tLi/OUDmcp\nLc5TWbKd4SUmJmLVqlXw9vYWr9QUBAFnzpyRqwmMMcYqMdkK3vbt2+VaVYXD/frS4jylw1lKi/NU\nlmwFz5B/RZcxxpj+k/WrxVjJuF9fWpyndDhLaXGeyuKCxxhjrFLggqcHuF9fWpyndDhLaXGeyuKC\nxxhjrFLggqcHuF9fWpyndDhLaXGeyuKCxxhjrFLggqcHuF9fWpyndDhLaXGeyuKCxxhjrFLggqcH\nuF9fWpyndDhLaXGeyqqwBe/69eto27Yt6tati3r16mHhwoVKN4kxxpgek+2rxaRmamqKefPmITAw\nEFlZWWjUqBE6dOgAPz8/pZv2yrhfX1qcp3Q4S2lxnsqqsGd4bm5uCAwMBABUrVoVfn5+uHXrlsKt\nYowxpq8qbMErTKVS4eTJk2jWrJnSTSkT7teXFucpHc5SWpynsipsl6ZWVlYW+vTpgwULFqBq1arF\n/h4RESH+UoOdnR0CAwMRGhoKAEi7kQac+qebQftmlHtaS6n1a6cTEhIAQMznVac5T91pQ8gz7VKa\n4q8n5ynttFbhfBISEhAdHf3s+Qb8yzYCEZHSjSir/Px8dOvWDZ07d8a4ceOK/V0QBJS2eRHjIuDT\ny6ccW1hxqDapED0/+rWWwXn+g/OUFucpnZfJ8kXHzoqqwnZpEhGGDRsGf3//EosdY4wxVliFLXgH\nDhzAqlWrsGfPHgQFBSEoKAhxcXFKN6tMuF9fWpyndDhLaXGeyqqwY3gtW7ZEQUGB0s1gjDFWQVTY\nMzxDwvfmSIvzlA5nKS3OU1lc8BhjjFUKXPD0APfrS4vzlA5nKS3OU1lc8BhjjFUKXPD0APfrS4vz\nlA5nKS3OU1lc8BhjjFUKXPD0APfrS4vzlA5nKS3OU1lc8BhjjFUKXPD0APfrS4vzlA5nKS3OU1lc\n8BhjjFUKXPD0APfrS4vzlA5nKS3OU1lc8BhjjFUKXPD0APfrS4vzlA5nKS3OU1lc8BhjjFUKXPD0\nAPfrS4vzlA5nKS3OU1lc8BhjjFUKXPD0APfrS4vzlA5nKS3OU1lc8BhjjFUKXPD0APfrS4vzlA5n\nKS3OU1lc8BhjjFUKXPD0APfrS4vzlA5nKS3OU1lc8BhjjFUKFbrgxcXFoU6dOnjjjTcwa9YspZtT\nZtyvLy3OUzqcpbQ4T2VV2IKn0WgwevRoxMXFISkpCWvXrsXff/+tdLPKJO1SmtJNMCicp3Q4S2lx\nnsqqsAXvyJEjqFWrFnx8fGBqaor+/ftj8+bNSjerTJ5kPVG6CQaF85QOZyktzlNZFbbg3bx5E56e\nnuJ09erVcfPmTQVbxBhjTJ9V2IInCILSTZDMo7RHSjfBoHCe0uEspcV5KksgIlK6EWWRmJiIqKgo\nxMXFAQBmzJgBIyMjTJgwQXxOYGAgTp8+rVQTGWOsQmrQoAFOnTqldDMkV2ELnlqtxptvvondu3fD\n3d0dTZs2xdq1a+Hn56d00xhjjOkhE6UbUFYmJiZYtGgR3n77bWg0GgwbNoyLHWOMseeqsGd4jDHG\n2KuosBetMMYYY6+CCx4r1e3btzFhwgRcvnwZ9+/fBwAUFBQo3CplFO0M4c6RsiEizu41lZQhZ/pi\nXPBYqapVqwYAWL16NT7++GOcOnUKRkZGlW7nIiLxVphbt27h4cOHBnVrjNwEQcD27dvx3XffYc2a\nNUo3p0ISBAFHjx7Ftm3bcPXqVQiCUGk/jL4sLnjsubQ7z6xZszBy5EiEhoaic+fO2LdvX6XaudLT\n0/Hjjz8CAHbu3ImePXvirbfewsaNG5GRkaFw6yoW7QeH06dPY8yYMUhPT8e2bdswYsQIpZtWYWgz\n3L17N3r27IkNGzagSZMmOHnyJIyMjCrNflkWFfYqTVZ+tGdvRkZGyMvLg5mZGVxcXDBy5EiYm5sj\nPDwcGzZsQHBwsM6ZjyEiIhw/fhwHDx5Eeno6Dh8+jJUrV+LMmTNYtmwZsrOz0aNHD9jY2Cjd1ApB\nEATs3bsXq1atwoIFC9C5c2dcunQJ06dPx8iRI8UPFuz5BEFAUlIS/vjjD6xbtw6tW7dGgwYN0K5d\nO8THxyMwMBAFBQUwMuLzmaKMo6KiopRuBNM/2i6n5cuXIykpCc2aNQMABAUFwc7ODl988QU6deoE\nR0dHhVtafrTF3MPDAxYWFjh58iTS09Px2WefoW7durCwsMDq1atBRPD19UWVKlWUbrJeKvqh6PTp\n05g2bRq8vb3Rpk0b2Nraon79+oiNjUVsbCx69uypYGv1m0ajgUajwcyZM3Hw4EG8+eabCAgIQHBw\nMKysrBAWFoZu3brB3d1d6abqJS54TIf24HTo0CF8/PHH6NSpE+bOnYv09HS0atUKxsbGaNiwIZ4+\nfYrU1FQ0bdoUGo3G4D5Nas9yBUHArVu3EBQUBBMTExw9ehTp6elo3rw5/Pz8YGxsjFWrVqFLly6w\ntrZWuNX6p3COqampICIEBgaiZcuW+Oqrr+Dr6ws/Pz/Y2dkhKCgIjRo1gqurq8Kt1i+FM8zJyYGF\nhQVCQ0Nx584dpKamwsHBAR4eHmjWrBlsbGxgZWWFmjVrKtxq/cT34bFikpOTMWPGDISEhGD48OG4\ndesW3n33XbRp0wZRUVEwNTXF7t278fvvv2Pp0qVKN7dcaAv/tm3bMHr0aGzbtg2enp7Yvn07du7c\niVq1auGTTz4B8GyMjw/SJdN2rcXExGDGjBlwcnKCs7Mzxo8fj3v37mHYsGGYOXMmevfuLc5j6N3k\nr0qbR1xcHObOnYvq1aujZs2amDRpEiIjI5Gfn4+wsDCEhISIuXGGz0Gs0isoKNCZjo2NpW7dulF4\neDhduXKFiIhu3bpFDRo0oM8++0x83scff0y3b9+Wta1yOn/+PNWtW5f27t0rPpaTk0ObNm2iiIgI\n+vbbb4mISKPREFHxHCuz3Nxc8f9TU1PJ39+fjh8/TmfPnqUVK1ZQly5dKC0tjf7880+qXr06paen\nc35F5Ofni/9/5MgR8vf3p5iYGDp27BgFBgbSmDFjqKCggD766CP65JNP6OHDhwq2tmLgi1YqOSp0\ngn/lyhVYWlqiXbt28PDwwM8//4xNmzYhLCwM3t7e4uXPWosWLVKiybJRq9Vo2bIlWrduDbVajYKC\nAlhYWKB9+/YQBAG+vr4AIHbn8ifqZ9LT07F27VoMGzZM7Ob19PREw4YNATy71eX48ePYsWMHBg0a\nhODgYLi4uCjZZL1z584d8VYgMzMz5OTkoH379ujatSsA4MSJE2jatCkOHDiAr7/+Gunp6bCzs1O4\n1frPsAZe2CsTBEHsuuvatSvGjx+Pxo0bw9bWFv369YNKpcKaNWuQmpqKatWqISQkxCBvHC5pmywt\nLREXF4eYmBiYmJjAzMwM27dvx2+//YYePXqgXr16CrVWv5mbm6Nz587IysrCsWPH4OXlBbVajS+/\n/BIA4OjoCAcHB6SkpAAAnJ2dAfCN04WlpaWhe/fuuH//Pq5fvw4bGxvs3r1b/PIHQRDQtm1bPH78\nGI6OjvD391e4xRUDFzyGa9euYcqUKfj555+xZs0a9OvXDz169EDt2rURFhaGmzdv6tzboy2ShkZ7\nyfzs2bMRHx+PmjVrYt68efjuu++waNEixMbGYsKECfDw8FC6qXopPz8fOTk5sLOzg6enJ2bMmIFf\nfvkF58+fx9y5c6FSqfDuu+9i69atWLNmDdq1awfg2RfBA3yGDDzLEADq168PBwcHLFmyBDNnzkS9\nevUwYMAANGnSBAkJCYiJiUFsbCyf1b0ivmilEqIiA9pZWVkYNWoUpk2bBi8vLwDAmDFjYGxsjPnz\n51eaizK2bduG8ePHY9y4cZgzZw4++OADdO3aFffu3cPcuXPh5uaGnj17olu3bnxRQBF5eXlISEiA\nk5MTUlJSkJqaioEDB2LOnDkwMzNDWFgYfH198c0338DOzg5NmzZF165dOcdCnj59iv3796N69erI\nyspCSkoKXF1dsXPnThARZsyYgZ9//lm8UnjEiBH8XnxFPIZXCRUUFMDY2BhZWVmoUqUKzMzMkJWV\nhS1btmD06NEAgJYtW+LkyZMAYPDFjohw8+ZNLF26FFu2bMH169dBRDh9+jRycnLw+eefY+vWrTrP\nZ7rMzMyQmZmJqKgopKWlYd68efDw8MCXX36Jr7/+Ghs2bMCgQYOwYMECcR7OUVdeXh6ePHmCUaNG\nISUlBfHx8XjzzTdhYWGBTZs24csvv8QXX3yBESNGIDc3FxYWFpzhK+L78CqRa9euIS8vD1WrVsWm\nTZswcuRInD17FsbGxoiIiEBkZCQuXLiAY8eOYcmSJRg6dChq166tdLPLBRW6t0kQBNjY2KBFixbI\nzs7GmDFjcPjwYbi6uuLTTz+FmZkZGjRoAHNzc5152D9jn4IgwMvLCwcPHoS5uTk6duyIqlWrwsnJ\nCcHBwfjrr79w7tw5NG/eXLxBn3N8RvteNDc3R05ODmbMmIFmzZohJCQE7u7u8PT0hI2NDU6fPo2E\nhAS0adMGZmZmMDIy4gxfERe8SuSbb77B5MmT0aRJEyxZsgRDhgyBp6cnFi9eDC8vL0ycOBH3799H\nRkYGhg8fjrffftugu0sEQcCZM2dw7NgxGBsbw93dHWlpadi1axeGDx+O3NxcnD17FqNHj4anp6fS\nzdVbRkZG2LlzJ1auXIlvv/0WRkZG2LRpE6pUqQI/Pz+o1WoEBAQgKCiIc3wOQRCwc+dOODg4ICIi\nAs7Ozvjjjz9gYmKCN954A2ZmZjAzM0Pnzp3h6upqcF/0IBfu0qwEtDf/zp49GwUFBejXrx8GDhyI\n/v37Izc3F46Ojvj2229x7949fPDBB+J8htxdIggCNm3ahMmTJ8PX1xcWFhaoXbs2RowYATc3N7Rv\n3x7Xr1/H/PnzUa9ePYMu/K9De4Xvp59+innz5sHKygpDhgxBbm4uYmJicPToUfzyyy/Ys2cPX9X6\nHNoMx44di++//x5vv/02bGxs8ODBA2zcuBGJiYk4deoUFixYgBo1aijd3IpNtjv+mCKysrLo3Llz\nRER0+PBhysjIoMjISPLz86O0tDQiInr69CnFxsZSaGgoqVQq8UZqQ1NQUCDe3JyZmUn9+/enEydO\nEBHR3r17KTIyklasWEF3796lNWvW0MGDB4vNx3Tl5eXR2LFjadu2bURE9OTJE/Fv27Zto3nz5lFc\nXJxSzasQsrKyqGPHjrR7924i+ucLDK5evUr//e9/qVu3brRp0yYlm2gw+AzPwD148ADfffedOPC9\nbds2zJgxA48ePUJYWBg2btwIFxcXtGvXDk2aNIGTk5PSTS4XVOgM7eDBg8jIyEBqaiouXLiAoKAg\nhISE4OjRozh48CAGDRqE8PBwcT6AL5nXoiJnuqampnjw4AESEhLQqVMncZzzzJkzCA0NRadOncT5\nAM4R+CdD7X/VajXy8vLE212ePHkCCwsLWFtbo2/fvujZsyfMzMw4QwlwR7ABKygogKenJzp27Ihl\ny5bhvffeQ0BAAABgyZIlaNCgATp06IA7d+7AzMxMLHZkwF2ZycnJ+Pzzz1G/fn189tln2LVrF/bu\n3QsTExM0atQIDx48QEZGhnjfIV8UULLU1FQkJSUBAIYOHYr8/Hxs3rwZAHD06FGMHDkSFy9eFJ/P\nORaXnp4OALC1tUWLFi0QGRmJBw8ewMLCAvv27UO3bt1w584dnfsUOcPXwwXPgBkZGSE+Ph5nzpzB\n1q1bcfr0afzyyy948OABAOCHH35Ahw4ddA5MgGF+gtT+6GhYWBjat28Pd3d3BAYGomHDhhg9ejTG\njcpl3zUAACAASURBVBuHIUOGYNCgQbCxseGLAkqgPSOJiYlBp06d0KdPH0yYMAF16tRBjRo18NNP\nP6F79+4YPHgwIiMjxQ9X7B/aDGNjY9GtWzf07t0bO3bsQEREBBo0aIAWLVpg9uzZGDVqFP7973/D\nxcWF34sS4hvPDZz2u/a2b9+O3bt3Y+rUqRg+fDgEQcCff/6JNWvWwNTU1CAvyiipC2jgwIH4+++/\nsXfvXlStWhX5+fk4d+4cUlNTUb16dTRu3Nggs5DKhQsX8MUXX2D27NlwdXVFly5d0LlzZ4wfPx5P\nnz5FSkoK7O3t8eabb3IX3HMcOXIE06dPR2RkJPbu3YvU1FS0bNkS77zzDv766y8YGRnB2dkZrVq1\n4gwlxmN4BqbowbpOnTril/W2a9cOGo0Gq1atws2bNzF8+HCYmpoCMNwdShAEJCYm4tq1a6hXrx5W\nrVqFYcOGoW/fvvjzzz9hYWGBoKAgBAUFATDs7tyy0r6nHj9+jPnz5+PWrVswNTWFnZ0dNmzYgP79\n++PevXtYsGABgoODdeY11PfVqyg8Znfv3j385z//gampKYKDgxEcHIyffvoJ+/btQ0FBAXr16oWq\nVauK8wGcoZT4PjwDod2pBEHAiRMnMGbMGNSvXx8eHh54+PAhZs+ejf79++PNN99E27Zt0adPHzRp\n0sRgz2a027V//34MHToUDx8+xL59+3DkyBEsWrQI8fHxWLx4Mfr16ycWfYDHSUqi7Q52dHSEj48P\nLl68iIcPH8LDwwPVq1cXfyS4ZcuWOhc9cY7PaHO4e/cuXFxcIAgC/vjjD1haWqJhw4Zo3Lgxrl69\nisTERLRo0UL8hQl+L0qPC54BKPxJ8OLFi/D19UViYiLOnj2LxYsXo2vXrrhw4QLq1q0LV1dXmJub\nw9LSUpzfEHcq7a+2T506FT/88AP+9a9/ISAgAPv370dqaiq++eYbbNy4EX5+fnB3d1e6uXpJ+6Eh\nLy8Pc+bMwdKlSzFixAj4+Phg//79SEtLg5ubGzw9PTF48GCD/wq6stJoNHjw4AG8vb3xxhtvoH//\n/qhevTrWrl2Lp0+fIigoCM2aNUNQUBCqV6+udHMNGhc8A6EdCB83bhzatWuHQYMGoXnz5hAEAStW\nrMCuXbuQmZmJHj166BQ4Qyp2Rc9W9+/fj9mzZ6Np06Zo2LAhqlatitzcXBw+fBjdunVDeHg43N3d\nDfYst6yys7NhZGQEY2NjAICxsTHq16+PS5cuYcWKFfjwww9RrVo1xMXF4c6dO2jYsCFMTU1hZGTE\nWf6//Px8MT8AsLKyQr169TB8+HC8+eabeOedd2BpaYmff/4Z+fn5aNiwIWxtbRVscSUhw71+TAZ/\n//031alThw4cOFDsb48ePaLz589TaGioeKO1oSl8c/jdu3cpJyeHiIiWL19Ovr6+tGvXLiJ6djN0\ny5Yt6d69e6RWqxVrr746f/48jRo1itLT02nfvn20YMEC8W+3b9+mTz75hAYPHkzZ2dl04MAB8UsN\n2D/Onz9PkyZNIiKipKQk2rFjh/h+jI2NJXNzc/FG8j/++IOOHDmiWFsrGy54FdT169dp5cqV4vS+\nffuob9++4nR+fj4Rkc43hAwePFj8NgdDo93OLVu2UJs2bahVq1a0dOlSSk5Opt9//50sLS3pgw8+\noF69etHGjRsVbq1+ysnJofbt29OyZcuIiCg+Pp5cXV1p0aJFRESkVqspPj6e6tWrR/369TPYb+R5\nHY8fP6Y2bdrQ0aNHKSMjg8aNG0dDhw6l3bt3U3Z2NhERzZs3jwRBoNjYWHE+/iYfefANHhUUEWHl\nypU4ffo0AMDX1xf379/Hjh07ADz7Uc34+HjMmjULRITLly/j8uXLBvvjpYIg4Pjx45g7dy4WLFiA\nMWPGIDU1FevWrUPXrl2xYMEC7N+/H126dEGvXr2g0Wj4iswiLCwsMGDAACxbtgweHh5o27Yt/vrr\nL8ybNw+LFy+GsbExzM3N0a5dO0yYMIHvDyuBRqNBTk4O1q5di3/961/45JNP4OXlhQ0bNuDQoUMA\ngJCQEISFhenkx93AMlG44LIy0HbFLViwgNavX09ERBkZGTRnzhz6/PPPaebMmZSQkEB169alHTt2\niPPdv39fkfbK4fbt2zRkyBAKCQkRHztw4AC1b9+eEhMTiYho9erV5OHhQXv37lWqmXpLe4bx119/\nUZUqVahNmzaUlZVFRERHjhyh+vXr07Bhw8jFxUX83kw+K9GlzWPRokVkYmJCI0eOJKJn3zc6efJk\nGjZsGA0bNozeeOMNOnr0qM48TB580UoFpP1kePv2bcyfPx9t27aFq6sr3NzcYGlpib/++gsXL17E\nqFGj0KVLF6jVahgZGcHCwkLhlkuHityjRP//u2yHDh1CTk4OmjVrBk9PTxw6dAgajQZNmjRBQEAA\n3N3dUadOHTg4OCjZfL2jzdHR0RGhoaFwcHDAggUL0KhRIwQEBKBTp06oU6cOBg0ahNatW/PFKSXQ\n5nH79m106NAB8+bNg7m5OVq0aIHWrVvD0tISVlZWGDBgAFq1aqUzD5MHf9NKBTdlyhQsX74cR44c\ngZubm/j4kydPUKVKFYO8ebXwNv3v/9q787Cqy/Tx4+/DQREEIVFIJJMBRr10MHJDMNdQlGwxMcYF\ntRwMc0XH5UolHU1zK2nSDLUoFxZDEVFUFjUxwaVGwV2RQVDckIOgcjh8fn/UOYHZd/KXduBwv/4S\nOZ/res5zfXjuZ72fgwe5d+8eFhYWdO/enS1btpCYmIiVlRVvvfUWY8aMISIigh49ehi51DVT1cCl\n0+kMOwtzc3NZv349Z8+eZcGCBbi5uVV7BkzrnXoajh49iq+vL//6178YP358td9JHRqHjPBqIf1o\nRqVS0atXL65du8asWbPw8fHBwsICS0tLzM3Nqx1GNyX677Rjxw4mT55Mq1atCAsLM6xBKT+vb/7w\nww8sXryYnj17Gka5ojr9Jbj6S0V1Oh1mZmbY2dnh5ubGhQsXiIqK4tVXX8Xc3NxQ96b2Tv1RV65c\nAaB+/fqoVCp0Oh3Ozs7069ePN998Ezs7O7p06WL4vNShcUjAqwUqKysN14iYmZkZ/lD0F7v6+vpS\nUVFBfHw8Z86cobCwkHbt2pn0H1Rubi5Tp04lJiaGwsJCMjMzSU1NRVEURo0aRZMmTbh79y5qtZqO\nHTtKsHsEfYcoMDCQc+fO0adPn2r1ZGtry1//+lfDlLkpv0//vxRFobCwkNDQULy9vXnmmWeorKxE\nrVaj0+lwcnLC39+fhg0b4urqauzi1nkS8Gqw27dvc/v2bWxtbUlKSmLt2rVkZWUZDpRX7ZF7eXnR\npk0b7O3t+frrr/H19TWpNbuHqVQq+vbty82bNw1JeJ977jnGjx+PjY0Nw4YNo6ioiOzsbDp37mzS\ndfG4Hh75e3h4cOTIEbp06UKDBg2qBTZbW1vs7e2NVdQaT6VSYW1tTVpaGomJibz++uuGaWH932fz\n5s1xdXWVdc8aQAJeDVVaWsqSJUs4deoUd+7cYfr06fj7+/Pxxx+Tn59Pr169MDMzw8zMzDACbNKk\nCS4uLrz55pvVUoeZEn2j0aBBAxo3bsyxY8ewtbXFz8+PnJwcmjRpwksvvYS7uzuurq706NEDOzs7\nYxe7RtHnGL1//z5mZmY4OTmxevVqnn/+eRmFPIa8vDwKCwuxt7fH29ubzMxMPD09sbGxMfxNytGD\nmkU2rdRgcXFxpKenU1RUhJeXF8HBwRQWFhIQEIC3tzcLFiwwXA5Zlan1JB/+PlV/3rp1K6tWraJ7\n9+6sWbOGLVu24OXlVW0Dhvj1Jon58+dz/PhxGjZsSFBQENevX2fz5s1s3rxZUlz9hqrvnUaj4b33\n3kOlUuHg4MD06dMJCgpi0KBBBAcHG7mk4rdIwKthFEUxrAEAHD58mJUrV6LT6Vi8eDF/+ctfuH79\nOn5+fvTq1Ytly5aZVHD7LUePHiUyMpJPP/30VwEwOjqaoqIiWrZsiZ+fn8kF/CdBXycnTpygXr16\nODk5YWtrS2pqKgsWLMDV1ZWEhAQOHjyIm5ubYX1Y/EJfh1evXqVRo0aoVCpKSkqYNGkS7dq1Y9u2\nbeh0OmJiYnB3dzd2ccUjyH14NZBarWbHjh3ExcWxfv16SktLSUhIYNu2bQwaNIiWLVuya9cuLl26\nZNINe9VG98GDB2i1WuCXUYp+FPfWW28ZnpH+26/pG2r9zdq+vr6kpqYSGRlJ7969adu2Lbdv3+b6\n9euEhoayfft2CXZVVB0db9++nbCwMHQ6HX5+frz77rtERUWRl5eHk5MTGzZs4PLly7i7u0vHqwaS\nt7qG0TdMM2fOZPDgwQD06dOHvn37kp+fz6ZNm8jJycHR0ZGuXbuaZAN/79494KdF/wsXLpCRkYGd\nnZ3hHjY9tVpNRUVFtWdlu/ev6Ud28fHxREVFERkZyYcffsiYMWP4/vvvcXR0pE2bNsTHx9OoUSOK\ni4uNXeQaRf9OnTp1ivDwcDZt2sTOnTvRarVERERQUlLCc889x9tvv80//vEPVq5cyYMHD+Q9rIEk\n4NVAR48e5YMPPmDAgAHcv38fgAEDBuDr68uVK1eqBTlT+6O6c+cOM2fOpKioCI1Gw9KlSwkODmbZ\nsmWkpaWxePFiYmJi2LdvH5WVlY9cwxS/jEp0Oh3l5eV88MEHpKSkcPfuXSoqKhgxYgTjxo1j5cqV\nVFZWArBnzx4OHz5sGEnXddeuXWPhwoVUVlZy8+ZNVqxYwfXr17Gzs8PZ2Zlp06aRlpbG5s2bDc/Y\n2NhQUlJiqFNRs0hrYWSPmva4evUqJ0+eZPDgwTRo0ACAjIwMevbsSdeuXU1+U8G0adMoLi6mqKiI\nNWvWAD8d0cjPz8fa2pqtW7dSXFxM/fr18fb2NnJpa7aysjJsbGxYv349EydOJDk5mXbt2tGiRQta\ntWrFyZMnDe+fk5MTKSkp1W4tr8vu3btHQEAA165dw8HBgaCgIIqKiti0aROBgYE0b96cESNGcOvW\nLSorK6msrMTS0pLPP/9cjsHUVE8pR6f4Hare4ZaTk6OcOnXK8O+QkBBlxYoViqIoSkZGhtK6dWtD\nEmRTVDWJ7n//+1/lm2++Ubp3766kpaUpivJTwuzhw4crGzZs+M3nRHUJCQmKl5eXEhYWphw8eFAp\nKSlRBg8erPTr10+ZPXu20qlTJyUuLs7Yxaxxqr5T5eXlyjvvvKOMHj1a0Wq1SnJyshISEqIMHjxY\n+eqrrxQ3NzclKSnJiKUVj0PO4RmZfiE8JCSEjIwMDhw4QIcOHXBwcCA2NpZ169YRHR3NokWL6N27\nt7GL+1Tp1y/nzp3LiBEjaNSoEV999RXNmzfHxcWFkpISCgoK6Nat26+eE9U3V+Tn57NkyRKCgoKo\nqKhg79692NjYMHnyZPbt28fFixdZsGAB/fr1Mzwr9Vi9DrOzs2natCnu7u785z//Yffu3YwdO5Zn\nnnmG1NRUCgoKCA0Nxd/f35AAQtRsEvCMSJ/8eNasWezatQuVSsXSpUsBGDhwIO+++y7du3dn2LBh\ndO7c2WQTzuob23PnzjFv3jzCwsLw9PSkRYsW6HQ6vvnmG1q0aIGTk5PhcL2eqdXFH6W/F/DgwYMo\nikJoaCguLi5otVqSkpIwNzdn0qRJ7Ny5k7y8PF588UWsrKykHqtQqVQkJSUxfPhwXn75Zdq0aYOr\nqyvff/89qampjB49GmdnZwoKCtDpdLi5uWFtbW3sYovfQbokRmZvb89nn33GsWPHiIiI4NChQ2Rm\nZhISEsL58+dxcXGhRYsWhs+bUsP04MEDw262vLw8Nm7cyOXLl8nKygLAwcGBN998k969ezN//nza\ntGlDr169THJn6h+l7zSkpaXxxhtvcPDgQT799FOysrJ49tlnGTBgAJ07d+bbb79FpVKxcuVKbt68\nKSO7h+g7Xv/85z+JjIzkb3/7G2q1mtatWzNx4kTu3LnDpEmT6N27Ny+++CKFhYWS4KAWkYPnf6Kq\nI7SioiLq1atn6BlOmzYNd3d3xo4dy+rVq/nqq6/YuHFjtWtZTElFRQXp6enk5ORgbW1NdnY2b7zx\nBvHx8dy5c4eBAwfSs2dPAG7cuEFZWRnPP/+8cQtdw505c4YpU6Ywe/ZsfHx8mD9/PrGxsURFRdG2\nbVuuX79OeXk5zs7OAJKN5mcPB/1z586xaNEivvzyS3Q6HTqdjvr161NRUUFOTg5lZWW0b98egJKS\nEmxsbIxVdPGYZJfmn0ylUhEfH8+6desoLi5m6NCh9OnTh44dO7J27Vq0Wi3R0dGsWLHCZIMdgLm5\nOfb29ixYsICTJ0+yfv16PDw8sLS0ZOPGjezevRutVouvry9NmzY1PCcjkuqq1seJEyfIy8tj+/bt\n+Pj4MHfuXNRqNQMGDCAxMZF27dpVe06CXfVEBadPn8bS0hJbW1sOHDhAVFQUgYGBqNVq9uzZw5Ej\nR3j//feBXzoLEuxqF1nD+xOpVCrOnj3L2LFj+fe//02rVq04c+YMp0+fpnPnztjZ2bFz504mT57M\nyy+/bJJrdlW/k62tLXFxcTg7O2NlZUXr1q1xdnbG1dWVI0eOcOnSJTw9PaslwjalungS9OvA0dHR\nBAcH06xZM3788UeuXr1Kx44d6d69O8XFxTz77LPVRshSj7/QbxwbP348vXv3plWrVri6urJ69Wpy\nc3PRaDS8//77DBkyhNatWwPIBpXa6k/eFVon6bc5FxQUKLt27VL69+9v+F1GRobSp08fJSMjQ1EU\nRbl3757hGVPbcl/1OxUUFBj+LysrSxk3bpwyZ84cRVEURaPRKLGxscq5c+eMVtbaJCsrS3nuueeU\n5cuXK4qiKDExMUpwcLDyySefVPucqb1PT8rx48eV9u3bK2fPnlUURVGuXr2qHDlyRMnOzlaGDBmi\nTJgwQdmxY4eiKFKHtZ1MaT5l+nyQhw4dYvbs2Xz22Wc0aNCA2NhYAgIC6Ny5M23btjXc21avXj3D\ns6bYC1epVCQmJjJv3jy8vb2pX78+S5YsYcSIEXzzzTcMGjSIrKwsYmNjJQHv/6DRaLCysqJt27Yk\nJSUREBCAoihMnToVrVbL3r17yc3NNYzsTPF9ehIaNGhA+/btSU1NJSYmhrS0NABmzJhBdHS04XOK\nbHeo9WRK8ylTqVQkJyezdu1aQkJC6Nq1Kzdv3iQ7O5vU1FTUajVLly4lJCQEZ2dnw1SJKTZOKpWK\n/fv3M2XKFDZu3MiVK1dYvXo12dnZTJgwgfbt23Pv3j2CgoLw8fExdnFrLEVRuHjxImPGjMHd3Z1n\nn30WR0dHevTowbRp0wAYM2YMXbp0MWxQEb/NysqKwsJCNmzYwOuvv86oUaOwsrJCq9UaNqeA5Gk1\nBTIR/RQ83BPMz89n48aN5OXlARAQEICfnx+3b99m06ZNhIeH06VLF5PvQVZWVqLVag3Z5bdt28b+\n/fs5ffo0QUFBODs7M3HiRPr27YuiKCZfH4+jan2oVCrc3Nzo2LEjixYt4scff6S8vJx27drRt29f\nFi9eTG5uLs2aNTNyqWuHhg0bMmHCBPbt28egQYMoKSlh1apVUn+myGiTqSZMP8+fn59vWJPbvHmz\nYmFhoaSnp1f7TFlZmeFnU1wf0Ol0iqIoyv3796t95+HDhysJCQmKoijKtGnTlFatWik//PCD0cpZ\n0+nrLi0tTQkPDzekoVu+fLkycOBAZc+ePUpCQoIyYsQI5fTp08Ysaq1VUVGhHDlyROnUqZOybds2\nRVFkzc7UyJTmE6b8vE08MTGRcePGsW3bNnJzc/n73/+Op6cnw4YNo2vXroZ1Ff2analOl6hUKrZu\n3cr06dPJyMjAysoKd3d39uzZg6WlJQUFBSQlJfH111/Ttm1bOXbwCPo6OXz4MMHBwZSVlZGZmcmt\nW7d47733KC4uJiUlhcjISEJCQnjppZeqPSd+HzMzM+zs7PDz86t29ZbUoemQg+dPQUZGBvPmzWPh\nwoUUFhZy4sQJcnJyWLVqFV988QWhoaHk5+fTqFEjk9zerDx0wH7kyJEMHToUjUZjqIPKyko+//xz\nzp07R2hoqOHuP2mkHy0jI4OwsDCWLFmCh4cHmzdv5tChQ3h4eDB69GjMzc25efMmTZo0kTp8QqQe\nTY/s0nzCioqKWLFiBYWFhXh6egLg7OzMhx9+SGpqKmPHjsXPzw87Ozsjl/TpUqlUZGRkcPToUTp0\n6EBgYCAAFhYW1bLJaDQaGjVqJL3p/6G4uJjk5GT27NmDh4cHAQEBmJmZkZycTGlpKRMmTKBx48bG\nLqZJkXfR9MiU5h/0cENtaWlJ48aN2bVrFzdu3KBHjx44ODiwb98+SkpK6NatG9bW1piZmZlkD1L/\nndLT0xk5ciS3bt3ihx9+wN3dnebNm9OhQwfMzc2ZMWMGgYGB2NraGurA1OriSXJ1daV9+/YsW7aM\nxo0b0759e9q0aUNpaSk+Pj44OjpKPQrxP8iU5h+kb+BTUlLIzMykadOmvPHGG2RlZfHpp59iY2PD\n6NGjGTduHOHh4SZ/xQ/8NP02e/Zsli9fjoeHB3PmzKGoqIjBgwfj4+NDvXr1yM/Pp3nz5sYuaq2T\nmJjInDlzmDRpEiNHjjR2cYSoVUxvAelPpA923333He+++y4NGzYkIiKC8PBw6tWrx4QJEzh8+DCz\nZs1i7dq19O7dm4qKCmMX+6krLi4mNTWV5ORkAObMmYO9vT2RkZF89913KIpiCHbS33o8/v7+hIWF\n8dFHHxmupxFC/D4S8P4AfW7M1atXM336dCZOnMjWrVvRaDQkJCTQo0cPPv/8c9zc3Ni/fz/wU9Jk\nU9e3b1/i4uJYu3YtmzZton79+syePZtmzZrh4OBQbcpNpt8e32uvvcb+/ftxcnKSBNBCPAbTb32f\nMP2oTp8yLDs7mxs3brB792769++Ps7Mz06dPp1+/fowfPx5vb2+0Wi0bNmww7KKrC1577TXMzc2Z\nM2cO5eXljBo1ioULF0qAe0L0N0iY4jqwEE+LrOE9hqobVKquQaWnp7Nhwwbc3d0JDAyktLSUgIAA\nEhMTad68OeXl5VRUVFTL+l9XxMfHM2vWLJKTk3F0dJQRiRDCaCTgPQZ9b3rnzp2EhYXh6+uLmZkZ\n8+bN48CBA4SHh3PlyhXs7OyYMmUKAwYMkB44P13gWvVOOyGEMAaZ0nwM+rvHZsyYQUxMDJGRkcTF\nxVFQUMCaNWuwtLRk/fr1uLq60q9fP2MXt8aQ6TchRE0gm1Yeg06nQ6PREBUVxZUrV0hOTubLL7/k\n2rVrBAcH06FDB1599VXOnTvH2rVrqaiokAa+CqkLIYQxyQjvMajVavr06YNKpeLjjz9m+fLldO3a\nFRcXF86fP8/58+d55ZVXUBSFTp061YkdmUIIUVtIi/wbHp5+0/9sYWHBgwcP0Gg0nDx5ksrKSk6c\nOEFERAStW7cGYODAgcYqthBCiN8gm1YeoepuzKysLBo3boyTk1O1z+zbt48VK1ZQVlZGcHAwQ4YM\nMTwrU3dCCFHzSMB7BH3QSkhIYOnSpSxbtozOnTsbfq8/g1daWoqiKFhbW0vyYyGEqOEk4P2GCxcu\nMGTIEL744gs6duxY7XePCm4yshNCiJpNdmn+7PLly0yYMMHwsz4rij7Y6XNglpaWPvKyVgl2QghR\ns0nA+1nLli0ZNWoUly5dAsDDw4PGjRuTkpJCeXk55ubmHDhwgCVLlnD//n1JeiyEELVMnZ/SVBQF\nnU5nOELg4+ODWq02ZE65ePEiVlZWeHl5MW3aNFatWoWvr6+RSy2EEOJx1emAV3Ut7syZM4ZjBT17\n9sTBwYGYmBiSk5NJTEykvLwcf39/SRcmhBC1VJ0PePrcmBMnTiQ6OpoOHToA0K1bNxwdHfn2228B\nePDgARYWFrIbUwghaqk6HfAAjh8/ztChQ4mKiuKFF14gNzcXBwcHLC0t8fLywtramuTkZMNRBCGE\nELVTncu08vAIzdzcnMGDB3Py5EmSkpKIjo7G3d2dWbNmcfjwYQ4dOgQgwU4IIWq5OtmKq1Qq9uzZ\nQ1JSEk2aNOHevXts3rwZFxcXoqKicHFx4fjx4wB4e3ujKIrsyhRCiFquzgU8lUpFfHw8U6dORavV\n4uTkxMKFC9m6dStvvfUWWq2WvXv34urqWu0ZWbMTQojarc4FvKKiIlauXMmWLVvw9/fn2LFjbNmy\nhcrKStLS0hg7dixz586lZ8+eMqoTQggTYvJreA8fIdDfURcbG8uZM2dQq9WkpqZy584dgoKCWLdu\nHa1bt5ZgJ4QQJsakR3hVg9bZs2e5ffs2TZs2Ze7cuZSUlDB69GgiIyOJiIggMzMTS0tLw1k8kKMH\nQghhSkz6WIJOp0OtVpOQkMC8efN46aWXqKysZPLkybi4uACwe/duQkNDWbp0KQMGDDByiYUQQjwt\nJjnCu3v3LvDTDeWZmZmEhYURHx9Pw4YNSUtLY+7cuRw7dozS0lJWrlzJRx99ZMigIoQQwjSZ3Aiv\nqKiIZcuW0bZtW4YOHUpGRgb169fnxo0bzJw5k08++YSIiAg0Gg3Lli2jWbNmcp+dEELUASY3wlOr\n1VhZWXH06FG2b99Oly5d8PT0JCUlhU8++YTu3bvj7OyMvb09paWlWFtbG56VYCeEEKbLZAKe/taD\nRo0aGdboUlJSiIuLA0Cj0TB//nxSU1NJSEjgvffe44UXXpCRnRBC1BEmM6WpP36QmprKgwcP6NGj\nB2vWrOHy5cu88sor+Pr68s4771BWVkZAQACDBg2SWw+EEKIOMZmAB5CQkMDcuXNZtGgRfn5+FBcX\ns379enJycujfvz/9+/eXWw+EEKKOMpkpzZKSEtatW8fq1avx8/NDq9Via2vL22+/jbOzM9u3b6ew\nsBALCwtA0oUJIURdYzKZVszMzLh58yYajQb4ZeRWXl5OaGgo+fn5ODo6GrOIQgghjMhkRngNtSO4\nUQAAALFJREFUGzZkyJAhHDp0iFOnTmFubk56ejrDhg3jxo0bPP/888YuohBCCCMyqTW8/Px81qxZ\nQ1paGj4+PsTGxhIeHo6/v7+xiyaEEMLITCrgAZSVlZGRkUFhYSEtW7bEy8tLNqgIIYQwvYD3MAl2\nQgghwIQ2rfwWCXRCCCHAhDatCCGEEP8XCXhCCCHqBAl4Qggh6gQJeEIIIeoECXhCCCHqBAl4Qggh\n6gQJeEIIIeqE/weOwIO8Og7UhQAAAABJRU5ErkJggg==\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x1078eeb10>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 16
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"sample_sizes\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Performance growth rates for different sample sizes"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In the previous section, we have seen how the different implemantations perform for a fixed sample size n=500. Now, let us take a look at the effect of different sample sizes on the relative performances for each approach. We will consider the sample sizes 10, 100, 1000, 10000, 100000, and 1000000."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"funcs = ['cy_classic_lstsqr', \n",
|
|
" 'lin_lstsqr_mat', 'numpy_lstsqr', 'scipy_lstsqr']\n",
|
|
"\n",
|
|
"orders_n = [10**n for n in range(1, 7)]\n",
|
|
"times_n = {f:[] for f in funcs}\n",
|
|
"\n",
|
|
"for n in orders_n:\n",
|
|
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
|
|
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
|
|
" for f in funcs:\n",
|
|
" times_n[f].append(timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 17
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"labels = [('cy_classic_lstsqr', 'Cython implementation'), \n",
|
|
" ('lin_lstsqr_mat', 'numpy matrix equation'),\n",
|
|
" ('numpy_lstsqr', 'numpy.linalg.lstsq()'), \n",
|
|
" ('scipy_lstsqr', 'scipy.stats.linregress()')] \n",
|
|
"\n",
|
|
"matplotlib.rcParams.update({'font.size': 12})\n",
|
|
"\n",
|
|
"fig = plt.figure(figsize=(10,8))\n",
|
|
"for lb in labels:\n",
|
|
" plt.plot(orders_n, times_n[lb[0]], alpha=0.5, label=lb[1], marker='o', lw=3)\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('performance gain relative to the slowest approach')\n",
|
|
"plt.xlim([1,max(orders_n) + max(orders_n) * 10])\n",
|
|
"plt.legend(loc=2)\n",
|
|
"plt.grid()\n",
|
|
"plt.xscale('log')\n",
|
|
"plt.yscale('log')\n",
|
|
"plt.title('Performance of least square fit implementations for different sample sizes')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAnMAAAIECAYAAAByl6h3AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXdYFcfXx7+79N7kAqLSBUHFih1BUGM0MVGjYAVrRM2r\nMVFjA3tJ1BjF+JNYKGrsaDSRKAIqmihYoogo1UazYUNAOO8fhA0LF7hcQBTn8zw8Dzs7c+bM2ZnZ\nc6ctR0QEBoPBYDAYDMZ7CV/fCjAYDAaDwWAw5Ic5cwwGg8FgMBjvMcyZYzAYDAaDwXiPYc4cg8Fg\nMBgMxnsMc+YYDAaDwWAw3mOYM8dgMBgMBoPxHsOcubfEmzdvMHbsWDRq1Ag8z+P06dP1rdJ7yb59\n+2BlZQVFRUWMHTtWahwvLy/07t37LWvGKPtsoqKiwPM8Hjx4UG1ZFhYWWL58eR1oWR5zc3MsW7bs\nreT1rsLzPHbt2lXfatRLPxkZGSmqp2WvAeDatWtwcnKCmpoaLC0tAQB3796Fm5sbNDU1oaCgUOd6\nfki8jfro4uKCiRMn1mkebxPmzJXCy8sLPM+D53koKSnB3NwckydPxuPHj2ss+8CBA9i9ezeOHj2K\njIwMdOnSpRY0/rAoLCzE2LFj4eHhgbt372L9+vVS43EcB47j3qpuISEh4PkPtzlJezZdu3ZFRkYG\nTExMAABnz54Fz/O4c+dOlfJiYmIwY8aMulYbQP3Ul5pw7949uR0dd3d3eHt7lwvPyMjA4MGDa0O9\nGvEu9JPdunUT1VsAmDVrFnR1dZGQkICLFy8CAJYvX46HDx/i6tWrSE9Pf+t6SmP8+PFwdXWtbzXe\nC0JDQ7F27dr6VqPWUKxvBd41nJ2dsXfvXrx58wYxMTGYMGEC7t69i6NHj8olLz8/H8rKyrh9+zZM\nTU3RuXPnGulXIu9D5MGDB3j58iX69esn6mjLQkRgZ2FXn6KiIgCQyymt6NlIJJJycWV5NgYGBtXW\n4UOjNuu4tOdUH7wL/aSSklI5eyQmJmLMmDFo1qyZSNeOHTvCysqqRroWFBRASUmpRjIY1UdXV7e+\nVahdiCEwZswYcnd3F4UtW7aMFBQU6PXr10REtHv3bnJ0dCRVVVUyNzenr7/+ml6+fCnE79mzJ40b\nN47mz59PJiYmZGxsTC4uLsRxnPBnYWFBRET5+fk0e/ZsMjU1JWVlZbK3t6ddu3aJ8uc4jn766Sfy\n9PQkHR0dGjZsGG3fvp0UFRUpIiKCWrZsSWpqauTq6krp6el06tQpcnR0JA0NDXJ3d6f79+8LspKT\nk+nzzz+nxo0bk7q6OrVq1YqCg4NF+fXs2ZPGjx9PixcvJmNjY9LX16fRo0fTixcvRPF+/fVXateu\nHamqqpKBgQH169ePnjx5Itz/6aefyNbWllRVVcnGxoaWLVtGb968qdT+58+fpx49epCamhrp6enR\n8OHDKSsri4iItm/fLrIhx3EUFRUl83Os6rn9+eef1LNnT9LX1ycdHR3q2bMnXbhwQSQjICCA7Ozs\nSFVVlfT19cnZ2Znu3btHERER5XTz9vausJzLli0jS0tLUlFRIUNDQ+rbty/l5uaKbGdqakrq6urU\nt29fCgwMJI7jhGdZ8vxLc/fu3XI2GT9+PFlZWZGamhpZWlrS3LlzKS8vT7jv6+tL1tbWtGfPHrK1\ntSVFRUW6efMmPX/+nL766itBh7Zt29LBgwcrLE9Fz6bELvfv36eUlJRycVxdXSuUaWZmRkuXLhVd\nL1iwgL788kvS0dEhIyMj2rRpE+Xm5pKPjw/p6emRqakpbdy4USSH4zhav349DRo0iDQ0NMjU1JTW\nr18vimNubk7Lli0TrvPz88nX15csLCxIVVWVHBwc6H//+185uRs2bKChQ4eShoYGmZmZ0cGDB+nx\n48fk4eFBWlpaZGlpSQcOHBCly8jIoDFjxpChoSFpaWlRt27d6PTp08L9EpudOHGCevToQerq6mRv\nb09//PGHKG9p/UlV7XvMmDEVtiGO42jnzp1C3AcPHtCwYcNIV1eX1NTUyMXFhWJiYqqlJ1HVdb00\nPXv2rLV+0sPDQ2oeRFW3r6rqrZ+fX4Xtvaq2UyJv586d1K9fP9LQ0KA5c+YQkWzvlsr6Zl9f33J6\nBQYGSrVBTk4OeXl5kbGxMamoqFDTpk3p66+/Fu7L0h/K0wZKyh8SEkK9evUS+qZff/21nOzS9bG6\nfRJRcZ84aNAgatSoEamqqpKlpSV9//335exZ+pmX/TM3Nxfi3759mwYNGkS6urqkp6dHffr0oWvX\nrsls07qGOXOlGDNmDPXu3VsUtmbNGuI4jl68eEHbt28nPT09CgkJoZSUFDp9+jS1bt2aRo0aJcTv\n2bMnaWlp0eTJkyk+Pp6uX79Ojx8/pm+++YYsLCwoMzOTHj58SERE33zzDRkYGND+/fvp9u3btHz5\ncuJ5nsLDwwV5HMeRgYEB+fv7U3JyMt2+fZu2b99OPM+Tq6srXbhwgS5dukQ2NjbUvXt3cnZ2pr//\n/puuXLlCdnZ2NGzYMEHWtWvXyN/fn/755x9KTk6mDRs2CE5haf11dXXp66+/poSEBPrzzz9JX1+f\nFixYIMTZtm0bKSkp0dKlS4Uybty4USiXr68vmZmZUWhoKKWmptLvv/9OzZo1E8koS3p6OmlpadGI\nESPo+vXrdPbsWWrdujU5OzsTEVFubi5dvHiROI6j3377jTIzMyk/P7/C51jamZPluR06dIj27dtH\nt27dohs3btD48eNJX1+fHj16REREMTExpKioSMHBwXTnzh26du0abd26le7du0f5+fnk7+9PHMdR\nZmYmZWZm0rNnz6TqduDAAdLW1qajR4/S3bt36cqVK7R+/XrhBRcaGkqKioq0bt06un37Nm3dupUk\nEgnxPF8tZ66oqIjmzZtHFy5coLS0NDpy5AiZmJiQr6+vkMbX15fU1dXJxcWFLly4QLdv36bnz5+T\ni4sLubq6UnR0NKWkpNCWLVtIWVlZVC9LU9GzKf1SLCwspCNHjhDHcRQTE0OZmZki578sZR0sMzMz\n0tXVpXXr1lFSUhItXbqUeJ6nvn37CmErVqwgnufpxo0bQjqO40hfX582btxIt2/fpvXr15OioiId\nPny4wrzGjBlDjo6OdOLECUpNTaU9e/aQrq4ubd26VSTX2NiYgoKCKCkpiXx8fEhDQ4P69OlDgYGB\nlJSURNOmTSMNDQ2hDr169YpatGhBQ4YModjYWEpKSqJly5aRiooKxcfHE9F/LxVHR0cKCwujxMRE\n8vb2Jm1tbcFely9fJo7j6NChQ6L+pKr2nZOTQ87OzuTh4SHU05I2VPrlWVRURE5OTtS2bVuKjo6m\na9eu0bBhw0hPT0/ISxY9q6rrZanNfjIxMVFqHrK0r7L1NiMjg5o2bUrfffcdZWZm0osXLygjI4O6\ndu1KI0eOFNp7UVFRlW2nxJlp0qQJ7dq1i1JTUyklJUXmd0tlffOLFy9oxIgR1K1bN+H5VmTradOm\nkaOjI124cIHu3r1L586do19++UW4X1V/KG8bKCl/48aNadeuXXTr1i2aP38+KSgo0OXLl0WyS9fH\n6vZJRESffPIJ9e7dm65evUppaWkUERFBu3fvFu67uLjQhAkTiKj4B0OJzTIzM+nGjRtkampKY8eO\nJaLiH2FGRkbk4+ND169fp1u3btG0adPIwMCAsrOzZbJpXcOcuVKUdQLi4uLI0tKSunTpQkTFL5Sy\nv9CjoqKI4zh6+vQpERU3OFtb23KyS0ZBSnj58iWpqKjQzz//LIr3+eefU69evYRrjuOEXw8llIyE\nXL16VQj7/vvvieM4unTpkhC2bt06atSoUaVlHjhwoFChS/Rv06aNKM7kyZMFGxARNW3alKZNmyZV\n3suXL0ldXZ3CwsJE4YGBgaSrq1uhHvPnz6emTZtSQUGBEHb16lXiOE4YuSjpCKKjoystU9nnKMtz\nK0thYSHp6ekJHcrBgwdJR0enQictODiYOI6rVC8iorVr11Lz5s1F5SxNt27daOTIkaKwb775Rq6R\nOWl529jYCNe+vr7E8zzdvXtXCIuIiCBVVVXKyckRpfX29qbPPvusQtnSnk3plyIR0ZkzZ4jjOEpL\nS6tQTgnSnLnPP/9cuC4qKiJtbW369NNPRWF6enqi0TmO42j06NEi2cOHD6cePXpIzSs5OZl4nqeE\nhARRmkWLFonaBcdxNGPGDOE6OzubOI6jr776Sgh78uQJcRxHx44dI6Li59akSZNyI9Surq40ffp0\nIvrPZocOHRLuZ2ZmEsdx9OeffxKRbM+6hLLt293dXeqocemX58mTJ4njOMHBJCLKy8sjExMTWrx4\nscx6VlXXpVGb/aQ0ZGlfZestUfn6SCR2BkrSVdV2StpJ6VFnItnfLVX1zePGjSMXF5cq7TBw4EDy\n8vKqMl4JZftDIvnaQEn5Fy5cKJLftWtXkeNauj7K2yc5OjqSn59fhffLPr8S8vPzycXFhZydnYUf\nO76+vtS5c2dRvKKiIrKysqIff/yRiKpv09rmw12xXQGRkZHQ0tKCuro6WrVqBWtra+zcuRPZ2dm4\nc+cOZsyYAS0tLeHv448/BsdxSExMFGS0b9++ynwSExORn58PZ2dnUbizszPi4uJEYU5OTuXScxyH\nVq1aCddGRkYAgNatW4vCHj16JKytefXqFebMmYOWLVvCwMAAWlpa+P3330UL0jmOg6OjoygvExMT\nZGZmAgCysrJw79499OnTR2q54uLikJubi0GDBons9OWXX+LZs2d49OhRhek6d+4MRcX/lnG2bt0a\nOjo6uHHjhtQ0siDrc0tJScGoUaNgY2MDHR0d6OjoICcnR7BNnz59YGlpCQsLC3h6eiIgIKDCslTG\nsGHDUFBQADMzM3h7eyMkJAQvXrwQ7sfHx6Nr166iNN26dZOr7AEBAejUqROMjY2hpaWFuXPnltt8\nYGRkhCZNmgjXFy9eRH5+PkxNTUX22rlzp6iOv23K1kuO42BoaCiq7xzHQSKRIDs7W5S27CL6rl27\nlmtjJcTExICI0L59e1H5V6xYUa78pfVp1KgRFBQURPro6upCWVkZWVlZAIptm5GRAV1dXZHss2fP\nlpPdpk0b4X+JRAIFBQWhDVaELO1bFuLi4mBgYAA7OzshTFlZGZ06dSpnt8r0rKquy0JN+8my1Gb7\nKkt12k5pXavzbqmsb64OPj4+2L9/P1q1aoXp06fj+PHjojWYVfWH0vSRpQ2UULZNduvWrcI2KW+f\nNH36dCxfvhydO3fGnDlzcObMmaoNA2Dy5Mm4f/8+QkNDhbWMFy9eRGxsrCh/bW1tpKWlCTpUZdO6\nhm2AKEPnzp0RGBgIRUVFNG7cWHAuShrMTz/9JHW3kKmpKYDiF4qGhkat6iRNHs/zoh14Jf+X3iJf\nEkZE4DgO3377LY4cOYJ169bB1tYW6urqmDlzJnJyckSyyy4c5jhOWBxfFSXx9u/fj+bNm5e7r6en\nJzUdx3F1UvFL9KnquQ0YMAASiQSbNm1C06ZNoaSkhO7duyM/Px9A8TOIiYlBdHQ0Tp48ic2bN2PW\nrFkIDw9Hu3btZNancePGuHnzJiIiInDq1CksWbIEs2fPxt9//y1yqipD2gaFgoIC0fW+ffswdepU\nrFq1Cj179oS2tjb27t2LefPmieKVrVtFRUXQ0dFBTExMuTzqe+NN2UXiHMdJDZO1rkqjJO358+eh\nrq5eTnZl+lSkY4nMoqIitGjRAqGhoeXSlc1Lmq2rKpes7VteSvoRWfWsjbpeHWq7360u1Wk7pXWV\ntY/iOK5GfXNp+vTpgzt37iAsLAyRkZEYOXIkWrVqhfDwcPA8X2V/WEJ120BFVNb3y9sneXl54aOP\nPsLx48cRERGBfv364fPPP0dwcHCFaVavXo3Q0FCcP39e9K4iIri7u2Pjxo3l0ujo6ACo2qZ1DXPm\nyqCqqiqcI1QaIyMjNG3aFDdv3sS4ceNqnI+1tTVUVFQQFRUFe3t7ITwqKko04labnDlzBiNHjsSQ\nIUMAFDeShISESneGlkUikaBJkyYICwvDgAEDyt13cHCAqqoqkpKS8NFHH8ks18HBAdu3bxft7Lp6\n9SpycnLQsmVLmeWURZbn9ujRI8THx2Pt2rXC+XT37t0r92uS53n06NEDPXr0wKJFi2Bvb4/du3ej\nXbt2Qqci7YVXFmVlZfTt2xd9+/bFkiVLYGRkhMOHD2PKlCmwt7dHdHQ0Jk+eLMSPjo4WpZdIJCgs\nLERWVpaw6+7SpUuiOKdPn0bbtm0xffp0ISwlJaVSvQCgY8eOePr0KXJzc+Hg4FBl/OpQYqPCwsJa\nlVsV58+fx5dffilcnzt3rsKylYyqp6WloX///rWqR8eOHREcHAwtLS0YGhrKLaciO8rSvpWVlfHm\nzZtK5Ts4OAhtokWLFgCAvLw8/P3335g6dWq1da2orstCbfeTsrQveZG37dTmu0VZWVnm9qWnpwcP\nDw94eHjA29sbXbp0QXx8PIyNjWXqD2vC+fPnRe+Hytpkhw4d5O6TjI2N4eXlBS8vL/Tr1w/Dhw/H\nzz//DE1NzXJxQ0ND4evri7CwMNjY2JTTYceOHTA1NYWKikqF+VVk09ruS6Xx3jlzmZmZGDRoEJSV\nlaGsrIxdu3a9tWMMli1bhnHjxkFPTw+ffvoplJSUEB8fj+PHj2Pz5s0AZD8WQ11dHV999RUWLFgg\nTBft378fR44cwcmTJ+tEf1tbW4SGhmLQoEHQ0NDA2rVrkZ6eDmNjYyGOLPr7+vpi8uTJMDIywuDB\ng1FUVISIiAh4enrCwMAAc+fOxdy5c8FxHNzc3PDmzRtcu3YNV65cwcqVK6XKnDp1KtavXw8vLy/M\nnTsXT548gY+PD5ydnWs8DVLVc9PT04OhoSG2bNkCS0tLPHz4ELNmzYKampog4/Dhw0hJSUGPHj1g\naGiI2NhY3L17V3jBWFhYCPG6desGdXV1qSMFW7duBRGhY8eO0NXVRXh4OJ4/fy7ImTlzJr744gs4\nOTmhX79+OHv2LEJCQkQOYqdOnaClpYU5c+bgu+++Q1JSEhYvXizKx87ODtu2bcORI0fg4OCAo0eP\n4tChQ1XaqlevXnB3d8egQYOwevVqtGrVCk+ePMG5c+egpqaG8ePHV/8B/IuZmRl4nsexY8cwdOhQ\nqKioCL9qy1K2Dkqrk7KGHTt2DP7+/ujTpw+OHz+OvXv3Yv/+/VLTWFtbY+zYsZgwYQJWr16Nzp07\n4+XLl4iNjRXqhbyMGDEC69atQ//+/bFs2TLY2NggMzMTp06dgr29PQYOHCiTnEaNGkFTUxNhYWFo\n0aIFVFRUoKenJ1P7trCwQEREBJKTk6GtrQ1dXV3R0gYAcHNzg5OTE4YPHw5/f39oa2tjyZIlyM/P\nFzlBVVFVXZeF2u4nK2pfVVFRXSsdXpO2U1vvFktLS+zfvx83btyARCKBtra21NGrefPmoUOHDrC3\ntwfP8wgJCYGWlhaaNWsGDQ2NKvvDmrJt2zbY2dmhffv2CAkJwV9//QV/f3+pcd3c3OSy69SpU9G/\nf380b94cr1+/xsGDB9GsWTPBkSttz7i4OIwcORJ+fn5o3rw5MjIyABTPdBkaGmLq1KnYunUrBg4c\niPnz56NJkya4d+8e/vjjDwwYMABdunSp1KZvhbezNK/2KCwsFP7fsWMHrVixotZke3l5ldvNWpbQ\n0FDq0qULqaurk7a2NrVp04aWLFki3K9oUaWfn59o8TkRUUFBAc2ZM0fYcu/g4CDabUNUfos2UfFC\naiUlJVFYcHAw8TwvCtu9ezfxPC/Y7O7du9S3b1/S0NAgExMT8vPzo3HjxomOiJCm/9KlS4VjAkrY\nuXMnOTo6koqKChkYGNCAAQNEmwl++eUXatOmDamqqpKenh517tyZNm/eXM4upfnrr7/I2dmZ1NTU\nSFdXl0aMGCHsFCIqXjzL83yVGyCkPceqnltUVJRwLICdnR0dOHCArK2tadGiRUREdPr0aerVqxcZ\nGhqSqqoqNW/enFatWiXKY/r06SSRSCo9muTgwYPUtWtX0tPTE46P2LZtmyjO+vXrydTUlNTU1Kh3\n797ljk4gIjp27Bi1aNGC1NTUqHv37hQWFkY8zwuL4gsKCmjSpEmkr69P2traNGLECNq4caOojkir\nk0TFu1PnzJlDFhYWpKysTMbGxtSvXz/RrueySHs2ERERol2CRESrV68mU1NTUlBQqPRokrILzqUt\nQC/9fEqws7MT7ZouOZrks88+I3V1dWrcuDGtW7eu0rwKCwtp9erVZGdnR8rKytSoUSNycXGh/fv3\ni+SWbZeKiorljoJQVVUV7YJ99OgRTZ48WWjzpqamNGjQILpy5UqFNpMmOygoiCwsLEhRUVFom7K0\n7+TkZHJ2diZNTc1KjyZJT08nDw8P0dEksbGxwn1Z9JSlrpelNvvJipDWvsruZi1bNlk2QBBV3XYq\n68PkebeU7ZsfP35MH3/8Meno6FR6NMmSJUuoZcuWpKmpSTo6OuTi4iLSqar+kEi+NlD6aBIXFxfh\nyJCqnqc8fdKUKVOoefPmpKamJryjSu90L21PaccrlT4eh4goLS2NRowYQYaGhqSiokJmZmY0atQo\nSk1NlcmmdQ1H9P6errphwwYoKytj0qRJ9a0Kg1FnREZGolevXrh37x4aN25c3+q8V5T8Qh4+fHh9\nq8JgfPCkpqbC0tISZ8+eLbcRhVEz3rtpVqB4LdXEiRPx9OlT4dMqDAaDwWAwGB8i9XY0ycaNG9Gh\nQweoqqqW+1bg48eP8fnnn0NTUxPm5ubYvXu36L6joyP+/vtvLF26FEuWLHmbajMY9UJVmyoYDAbj\nfYD1ZXVDvY3MmZqaYsGCBQgLC0Nubq7o3pQpU6CqqoqsrCxcvnwZ/fv3h6OjI+zt7UW7HbW1tZGX\nl1cf6jMYbw0XF5e3vgO0oVCTY0oYDEbtYm5uzvqyOqLe18wtWLAA9+7dw/bt2wEAL1++hL6+PuLi\n4mBtbQ0AGDNmDBo3bowVK1bgwoUL+Pbbb6GgoAAlJSVs3bpV6plFpqamePDgwVstC4PBYDAYDIY8\nODo64sqVK3KlrfcvQJT1JW/dugVFRUXBkQOKC1hyOrSTkxOioqJw6tQphIWFVXj45IMHD4Stx3Xx\n5+vr+07KlzVdZfHe1bK9D7Z7l8vHbPfuypclHbNdzdKxPq9ubPcul+99s93Vq1fl9qXq3ZkrO3/+\n4sULaGtri8K0tLTw/Pnzt6lWlbi4uLyT8mVNV1m81NRUufKWlYZsO+D9th+zXf3IlyUds13N0rE+\nT/50DbnuNRTb1bszRyQemdPU1MSzZ89EYTk5OdDS0nqbalVJQ2+cdQmzXc1oyB1bXfM+1z1mu5ql\nY32e/Okact1rKLard2eu7Mhc8+bN8ebNG9EHdK9evSrXJ538/PwQGRlZUxU/OLy8vOpbhfcaZj/5\nYbaTH2Y7+WG2qxnMfvLj5eWFyMhI+Pn51UhOvW2AKCwsREFBARYtWoT79+8jICAAioqKUFBQgKen\nJziOwy+//IJLly5hwIABOH/+vPCdQFmoqw+3MxgMBoPBYNQ2NfFb6m1kbsmSJVBXV8eqVasQEhIC\nNTU1LFu2DACwadMm5ObmQiKRYOTIkdi8eXO1HDlGzWCjmTWD2U9+mO3kh9lOfpjtagazn/zUlu3q\n7Zw5Pz+/CocV9fT0ZPooOIPBYDAYDMaHTr2fM1dXcBwHX19fuLi4lFuAqK+vjydPntSPYgzGB4ie\nnh4eP35c32owGAzGO0dkZCQiIyOxaNEiuadZG7QzV1HR2Ho6BuPtwtocg8FgVM57uWaOwWAwysLW\n3sgPs538MNvVDGY/+akt2zFnjsFgMBgMBuM9pkFPs1a0Zo5N+TAYbxfW5hgMBkM6bM1cJbA1cwzG\nuwNrcwwGg1E5bM0co9bw8vJC79696y1/CwsLLF++/K3kZW5uLpxt+KHC8zx27dpV32oIsLU38sNs\nJz/MdjWD2U9+2Jq5D5hHjx5h1qxZsLOzg5qaGoyMjNCzZ08EBwejsLBQJhlnz54Fz/O4c+eOKJzj\nuHKfWHubxMTEYMaMGW8lr/oua3W5d+8eeJ7H6dOnq53W3d0d3t7e5cIzMjIwePDg2lCPwWAwGPVE\nvR0a/C6TkJCGkyeTUFDAQ0mpCO7uVrC1NXsnZN69exfdu3eHsrIyFi9ejLZt20JJSQnR0dH44Ycf\n4OjoiNatW8ssr+yQbn1PhRkYGNRr/u8DtfmMJBJJrcmqDer7g97vM8x28sNsVzOY/eSntmzXoEfm\n/Pz8qj2EmZCQhh07EpGd3QtPn7ogO7sXduxIREJCmtx61KZMHx8fFBQU4NKlS/D09ISdnR2srKww\nevRoXLp0CdbW1tixYwf09PSQm5srSrt48WI0b94cqampcHZ2BlA8rcnzPHr16iXEIyJs2bIFZmZm\n0NHRwcCBA5GVlSWSFRgYCHt7e6ioqKBp06ZYsGCBaFTQxcUFEyZMwJIlS2BiYgIDAwOMGTMGL1++\nrLR8Zac+zc3NsXDhQkyePBm6urowNjbGzz//jNevX2PKlCnQ19dHkyZN4O/vL5LD8zx++uknDB48\nGJqammjSpAl++umnSvMuKCiAn58fLC0toaamhpYtW2LLli3l5G7cuBHDhg2DpqYmzM3NcejQITx5\n8gSenp7Q1taGlZUVDh48KEqXmZkJLy8vSCQSaGtro3v37jhz5oxwPzIyEjzP4+TJk3B2doaGhgYc\nHBxw/PhxIU6zZs0AAK6uruB5HpaWlgCAlJQUDBo0CKamptDQ0EDr1q0REhIipPPy8sKpU6cQGBgI\nnudFo3tlp1nT09Ph4eEBPT09qKurw9XVFbGxsdXSk8FgMBiyExkZWeEXsWSGGiiVFa2yexs3hpOv\nL1HPnuK/jz8uDpfnr1+/8HLyfH2J/P3Dq1WmR48ekYKCAi1btqzSeLm5uaSnp0eBgYFCWGFhIZmZ\nmdHq1aupsLCQjhw5QhzHUUxMDGVmZtKTJ0+IiGjMmDGko6NDw4cPp7i4ODp//jxZWFjQqFGjBFlH\njx4lBQXjqHA6AAAgAElEQVQFWrlyJd2+fZv27NlDenp6tGDBAiFOz549SVdXl77++mtKSEigP//8\nk/T19UVxpGFubi4qn5mZGenq6tK6desoKSmJli5dSjzPU9++fYWwFStWEM/zdOPGDSEdx3Gkr69P\nGzdupNu3b9P69etJUVGRDh8+XGFeY8aMIUdHRzpx4gSlpqbSnj17SFdXl7Zu3SqSa2xsTEFBQZSU\nlEQ+Pj6koaFBffr0ocDAQEpKSqJp06aRhoYGPXr0iIiIXr16RS1atKAhQ4ZQbGwsJSUl0bJly0hF\nRYXi4+OJiCgiIoI4jiNHR0cKCwujxMRE8vb2Jm1tbeHZXL58mTiOo0OHDlFmZiY9fPiQiIiuXbtG\n/v7+9M8//1BycjJt2LCBFBUVKSIigoiIcnJyyNnZmTw8PCgzM5MyMzMpPz9fKM/OnTuJiKioqIic\nnJyobdu2FB0dTdeuXaNhw4aRnp6ekJcsekpD1q6mRGdG9WG2kx9mu5rB7Cc/pW1XE5esQY/MyUNB\ngXSTFBbKb6qiIulp8/OrJzMxMRFFRUWwt7evNJ6qqipGjRqFgIAAIezEiRNIT0+Ht7c3eJ6Hnp4e\nAMDQ0BASiQS6urqi9Dt27IC9vT06d+6ML7/8EidPnhTur1y5EkOGDMHs2bNhbW2NoUOHws/PDz/8\n8APevHkjxDM3N8eaNWvQvHlz9O7dG8OGDRPJkRVXV1dMnz4dlpaWmDt3LjQ1NaGioiKEzZ49Gzo6\nOjh16pQo3YABAzBlyhRYW1vjq6++wtChQ/HDDz9IzSMlJQXBwcHYu3cv3N3dYWZmhqFDh2LGjBnY\nsGGDKK6npydGjRoFS0tLLFq0CK9evYKdnR1Gjx4NS0tLLF68GK9evcJff/0FANizZw+eP3+OX3/9\nFe3atRPK0bVrV/zvf/8Tyfbz80OfPn1gZWWFlStX4vnz57h48SIAoFGjRgCKP0cnkUiEKemWLVvC\nx8cHrVq1goWFBaZOnYr+/fsLI27a2tpQVlaGmpoaJBIJJBIJlJSUytng1KlTuHjxInbt2oWuXbui\nZcuWCAoKgqqqKjZt2iSzngwGg8F4u7A1c2VQUiqSGq6gID1cFnheelpl5erJpGqslZo0aRJatmyJ\nhIQE2NraIiAgAAMHDhQcgsqws7MTvexNTEyQmZkpXN+4cQOenp6iNM7Oznj9+jWSkpJga2sLAHB0\ndBTFMTExQVhYmMxlAIo3KZSWw3EcDA0NResCOY6DRCJBdna2KG2XLl1E1127dsXChQul5hMTEwMi\nQvv27UXhb968gaKiuJmU1qdRo0ZQUFAQ6aOrqwtlZWVhavrixYvIyMgQOcwAkJeXBw0NDVFYmzZt\nhP8lEgkUFBREtpfGq1evsHjxYhw9ehTp6enIz89HXl6eaOpcFuLi4mBgYAA7OzshTFlZGZ06dUJc\nXFyN9ZQFtvZGfpjt5IfZrmYw+8lPbdmOOXNlcHe3wo4d4XBxcRPC8vLC4eVljX99lGqTkFAsU0VF\nLNPNzbpacmxsbMDzPOLi4vDZZ59VGtfe3h7du3fHli1bMHv2bPz22284duyYTPmUHbWR5+wbjuOg\nrKxcLqyoqPpOsTR9pIXJI7uEkrTnz5+Hurp6OdmV6VORjiUyi4qK0KJFC4SGhpZLVzavsjYrrVtF\nfPvttzhy5AjWrVsHW1tbqKurY+bMmcjJyak0nawQUTkbyKMng8FgMOoGNs1aBltbM3h5WUMiOQVd\n3UhIJKf+deTk381aWzL19fXRr18/bNy4Ec+ePSt3v6CgAK9evRKuJ02ahKCgIGzZsgVNmjSBu7u7\ncK/kZSztKJOqjutwcHBAVFSUKCwqKgrq6uqwsrKqVpnqkvPnz4uuz507BwcHB6lxS0bk0tLSYGlp\nKfqzsLCokR4dO3ZEcnIytLS0ysk2NjaWWU5Fz+zMmTMYOXIkhgwZIky1JiQkiJ6jsrKyaApcGg4O\nDnj06BHi4+OFsLy8PPz9999o2bKlzHrWBHZelfww28kPs13NYPaTH3bOnAzIs5sVKHa+fHx6Yfp0\nF/j49KrxsSS1KXPTpk1QUlJC+/btsXv3bty4cQOJiYkICQlBx44dkZiYKMQdMmQIAGDp0qUYP368\nSI6ZmRl4nsexY8eQlZUlcg6rGoX77rvvcODAAaxatQq3bt3C3r17sWjRIsycOVOYkiQiuY7QKJtG\nmgxZw44dOwZ/f3/cvn0bGzZswN69ezFz5kypaaytrTF27FhMmDABISEhSExMxNWrV7Ft2zasXr26\n2uUozYgRI2BhYYH+/fvjxIkTSE1Nxd9//40VK1bg8OHDMstp1KgRNDU1ERYWhoyMDDx58gQAYGtr\ni9DQUFy8eBE3btzAxIkTkZ6eLiqfhYUFYmNjkZycjIcPH0p17Nzc3ODk5IThw4fj3LlzuH79OkaP\nHo38/HxMnjy5RjZgMBgMhnRqYzdrg3fmGtpcftOmTXHp0iV89tln8PPzQ/v27dGtWzcEBARg8uTJ\nopEnFRUVjBw5EkSEsWPHiuQYGRlhxYoVWLlyJRo3bixM21Z0kG7psH79+mHbtm0IDAxEq1at8PXX\nX2PKlCnw9fUVxS8rR5ZDeqWlqSpORWELFy7EyZMn0aZNG6xcuRLff/89Bg4cWGGaLVu2YMaMGVi2\nbBkcHBzg7u6O4ODgGo82qqioICoqCh06dIC3tzdsbW0xePBgxMTEwNzcvNIylIbnefj7+2Pv3r1o\n2rSpMJq4bt06mJmZwdXVFe7u7mjatCmGDBkikjdz5kw0atQIjo6OkEgkOHfunNQ8QkNDYWdnh/79\n+8PJyQlZWVk4ceIE9PX1ZdazJjS09vo2YbaTH2a7msHsJz8l34+vqTPHvs3awBk6dCgKCwtx4MCB\n+lblrcLzPEJCQjB8+PD6VoWBD6vNMRgMhjywb7MyyvHkyROEhYUhNDT0rX0ei8GoKWztjfww28kP\ns13NYPaTn9qyHdvN2kBp27YtHj9+jNmzZ6N79+71rQ6DwWAwGIw6gk2zMhiMOoe1OQaDwagcNs3K\nYDAYDAaD8YHSoJ05eY8mYTAY9QNrr/LDbCc/zHY1g9lPfiIjI2vlaJIGvWaupsZhMBgMBoPBqEtK\njidZtGiR3DLYmjkGg1HnsDbHYDAYlcPWzDEYDAaDwWB8oDBnjsFgvDOwtTfyw2wnP8x2NYPZT37Y\nt1kZjDogMjISPM/jwYMH9a1KnePn5wcbG5v6VoPBYDAYNYStmWM0eKytrTFq1CjRt2MroqCgAE+e\nPIGhoWGdfoP0bXL27Fk4OzsjNTUVzZo1E8JfvnyJvLw80XdX6wrW5hgMBqNyatJPNujdrAwGIPuH\n4d+8eQMlJSVIJJI61qh+KNtJaGhoQENDo560YTAYDEZtwaZZpZCQmAD/Pf748dcf4b/HHwmJCe+M\nTBcXF0yYMAFLliyBiYkJDAwMMGbMGLx8+VKI4+Xlhd69e4vShYSEgOf/e9wlU2z79u2DtbU1NDQ0\nMHjwYLx48QL79u2Dra0ttLW18cUXX+DZs2flZK9btw6mpqbQ0NDA0KFD8eTJEwDF05SKioq4d++e\nKP+goCDo6uoiNzdXarnk1efSpUvo168fjIyMoKWlBScnJ4SFhYnslZSUhEWLFoHneSgoKODOnTvC\ndOrvv/+O7t27Q01NDVu3bi03zbp69Wro6ekhLS1NkLl48WJIJBJkZGRU+JwyMzPh5eUFiUQCbW1t\ndO/eHWfOnBHFiYiIQOvWraGmpgZHR0dERESA53ns3LkTAJCamgqe53Hu3DlROmtra9EW9vXr16Nt\n27bQ0tKCiYkJPD09Bd1SU1Ph7OwMALCwsADP8+jVq5fI5qUJDAyEvb09VFRU0LRpUyxYsACFhYUi\ne1ZV/2oCW3sjP8x28sNsJx8JCWnw9T2FyZN/hL//KSQkpFWdiCGCrZmTAXkODU5ITMCOiB3INsrG\nU+OnyDbKxo6IHTVy6Gpb5v79+/H06VNERUXh119/xdGjR7Fq1SrhPsdxMo1GpaenIygoCKGhofjj\njz9w5swZDBo0CDt27MD+/fuFsOXLl4vSXbhwAVFRUfjzzz/x+++/48qVKxg3bhyA4pe9jY0Ntm3b\nJkoTEBCAESNGQE1NrVb1ef78OTw9PREZGYnLly+jb9+++PTTT3H79m0AwKFDh2Bubo5vvvkGGRkZ\nSE9PR5MmTYT0M2fOxHfffYebN29iwIAB5XSaNWsWOnXqBE9PTxQWFuL06dNYunQpAgMDYWxsLLUc\nubm5cHV1xcuXL3H8+HFcuXIFH3/8MXr37o2bN28CAB48eIABAwagY8eOuHz5MtasWYP/+7//A1D1\nSGLZ58txHNasWYPr16/j0KFDuHPnDjw8PAAAzZo1w+HDhwEAFy9eREZGBg4ePChV7rFjxzBu3DiM\nGTMGcXFxWLNmDfz9/cudfVRV/WMwGA2fhIQ0LF+eiKioXoiLa4PMzF7YsSOROXRywA4NrgJ5jHMy\n9iRUbFQQmRr5X6AS8M+v/6Bj945y6XHh7AW8avIKSP0vzMXGBeGXwmFrbVtteebm5lizZg0AoHnz\n5hg2bBhOnjyJxYsXAyieTpNl3j0vLw+BgYHCmqmhQ4di8+bNyMzMhIGBAQDAw8MD4eHhonREhODg\nYGhpaQEA/P390bdvXyQnJ8PS0hITJ07E+vXrsWDBAnAch5s3byI6OhobN26sdX169uwpkrFkyRL8\n9ttv2LdvH+bOnQs9PT0oKChAU1NT6vTp/Pnz0b9/f+G6xAksTVBQEBwdHTFt2jQcPXoU06ZNQ79+\n/Sosx549e/D8+XP8+uuvUFBQAADMnTsXJ0+exP/+9z+sW7cOmzZtgkQiQUBAAHieh52dHVasWIFP\nPvmkUhtJ46uvvhL+NzMzw8aNG9G+fXukp6fDxMQEenp6AABDQ8NKp5BXrlyJIUOGYPbs2QCKRwAz\nMjIwZ84cLFy4EIqKxd1FVfWvJri4uNRYxocKs538MNtVny1bkpCW5gYA4HkXpKUBFhZuCA8/BVtb\ns/pV7j2ipO7V9NDgBj0yJw8FVCA1vBCFUsNloQhFUsPzi/KrLYvjODg6OorCTExMkJmZWW1Zpqam\nosXvRkZGMDY2FhynkrCsrCxROnt7e8GRA4CuXbsCAG7cuAEAGD16NLKysoTpzl9++QUdOnQop3dt\n6JOdnQ0fHx+0aNECenp60NLSQlxcHO7cuSOTDZycnKqMI5FIsH37dmzevBmNGjWqchSqZARMV1cX\nWlpawt/Zs2eRmJgIoNhWTk5Ooqnvbt26yaRzWSIjI9G3b180a9YM2tra6NGjBwCIpoZl4caNG8KU\nbAnOzs54/fo1kpKShLDaqn8MBuP95OxZIC7uv75LWxto2rT4//x85lbUB8zqZVDilKSGK0BBbpl8\nBWZW5pXlkqesLE7HcRyKiv5zGHmeLzcyV1BQ3klVUhKXleM4qWGlZQPlF9KXxcDAAEOGDEFAQAAK\nCgoQFBSEiRMnVppGXn28vLwQHR2N77//HmfPnsWVK1fQpk0b5OfL5ijLugEgMjISCgoKyMzMxNOn\nTyuNW1RUhBYtWuDq1auiv5s3byIgIEAoR1V2LHH0KnuWd+7cwccffwxLS0vs2bMHsbGxOHLkCADI\nbIPqwHFclfWvJrC1S/LDbCc/zHayc/o0cPIkwPPFbV5HB9DRicS/A/dQVq6dvuBDobbqXoOeZpUH\n9/bu2BGxAy42LkJY3u08eHl4yTUlCgAJTYrXzKnYqIhkurm61VRdqRgZGeGvv/4ShV26dKnW5MfH\nx+P58+fC6FzJAn17e3shzqRJk+Dq6orNmzfj9evX8PT0rLX8S3PmzBl8//33wnq3ly9fIikpCa1a\ntRLiKCsrixbxV5eTJ09i7dq1OHbsGBYsWAAvLy8cPXq0wvgdO3YUpqENDQ2lxrG3t0dwcDCKiooE\npy06OloUpyTt/fv3hbCsrCzR9cWLF/H69Wv8+OOPUFFREcJKU+J8VWUDBwcHREVFwcfHRwiLioqC\nuro6rKysKk3LYDAaNkRAZCQQFVV8bWlphdTUcLRu7Ya7d4vD8vLC4eZmXW86fsiwkbky2FrbwsvV\nC5IsCXQzdCHJksDLVX5HrrZlyrIezt3dHTdv3sSmTZuQlJSEgIAA7Nu3T171y8FxHEaPHo24uDic\nPn0aU6ZMwcCBA2FpaSnE6datG2xtbfHtt9/C09Ozzo7AsLW1RUhICK5fv44rV67A09MTRUVFIhtZ\nWFjg7NmzuHv3Lh4+fFitc3yys7MxatQozJo1C3369MHu3btx5swZ/PjjjxWmGTFiBCwsLNC/f3+c\nOHECqamp+Pvvv7FixQphM8LkyZORnZ2NiRMnIj4+HuHh4Zg3b55IjpqaGrp164bVq1fjn3/+QWxs\nLEaPHi04bQBgY2MDjuPwww8/ICUlBaGhoViyZIlIjpmZGXiex7Fjx5CVlYWcnBypen/33Xc4cOAA\nVq1ahVu3bmHv3r1YtGgRZs6cKayXk3U9prywtUvyw2wnP8x2lUMEnDr1nyMHAJ06mWHlSmuYmJxC\nmzaARHIKXl7WbL1cNamtusdG5qRga21bI+etLmVK26laNszNzQ1Lly7F8uXLMXv2bHz66adYuHAh\npk2bVi05FYU5OTmhe/fu6N27N3JycvDxxx9jy5Yt5XQdP348ZsyYIdMUq7z6bN++HZMmTYKTkxOM\njY0xa9Ys5ObmiuIsWrQIEydOhK2tLfLy8pCSkiLIqkiXEry8vGBhYSEs7re0tMTmzZvh7e0NV1dX\nqesAVVRUEBUVhfnz58Pb2xvZ2dkwNDREp06d8PHHHwMAGjdujN9++w3Tp09H27Zt0bx5c6xfvx5u\nbuLR2m3btmHChAno2rUrTE1NsXLlStH6tdatW2PDhg1YuXIlli1bhg4dOuDHH38U8gGKR2pXrFiB\nlStXYvr06XB2dsapU6fK2bJfv37Ytm0bVq5ciYULF8LQ0BBTpkwRHbYs63NiMBgNAyLgxAmg9AlJ\n1taAhwegqGiGli2Z8/YuwL4AwagWXl5euH//Pk6cOFFl3FmzZiE8PByxsbFvQbOGAc/zCAkJwfDh\nw+tblVpF1jYXGRnJRknkhNlOfpjtpEMEhIUBpVft2NoCX3wBYY0cwOxXE0rbjn0BgvFOkZOTg1u3\nbiEgIAAbNmyob3UYDAaDUU2IgN9/B0ovwW3RAhgyBFCQfz8go45gzhyjWsgypTZw4EBcuHABnp6e\nGDly5FvSjNEQYL/u5YfZTn6Y7cQQAUePAqUnVRwcgEGDpDtyzH7yU1u2Y9OsDAajzmFtjsF4Pygq\nAo4cAa5c+S+sVSvg888Bnm2ZrFNq0k+yR8NgMN4Z2Hlf8sNsJz/MdsUUFQGhoWJHztGxYkeu5Jvj\nUxdOrbXvmH9osG+zMhgMBoPBqBWKioCDB4F//vkvrG1bYODAih25HRE7cFHlIh7rPK6V75gz5KdB\nT7P6+vrCxcWl3Jw0m/JhMN4urM0xGO8uhYXAgQPAv19kBAB06AD07w9UtER6w68bEJ75O/i/bkFF\nQRlGes2g2NEGlqr28BnqIz0RQyqRkZGIjIzEokWL5O4nG7Qzx9bMMRjvBqzNMRjvJm/eAPv3Azdv\n/hfm5AT061exI5dfmI8RcwfDMPYSxqa/Qqa+CvIbG+GKghb4Dj3g+/WKt6N8A4OtmWMwGA0CtnZJ\nfpjt5OdDtd2bN8DevWJHrkuXyh253IJcBF8NhsbFmxj34CUUCwnZd1+jyStFuCoroigu+e0o30Bg\n32ZlMBgMBoMhFwUFwJ49QGLif2HdugHu7hU7cs/yniHknxAUxt9Ah0f54F8SVDRVoaTMo0BVGW8e\nvYF9a0vpiRl1CptmZTAYdQ5rcwzGu0NBAbB7N5BcahDN2Rlwda3YkXv46iGCrwZDNS4BdtEJSLhx\nD4PylfC6kJBlZgJSVYOFiQX+sbNHLx+2Zk4e2DQr473Dz88PNjY2wvWOHTugpKRU6/nUllwvLy/0\n7t27FjSqOUSE9u3bY9++fQCAwsJCtGjRAn/88Uc9a8ZgMN518vOBnTvFjpyrK9CrV8WO3IPnD7Dt\n8jZoXY5Di7M3wRPQwb49fteR4GCn7jhrZo8LBk1xtAiwKvN9acbbgTlzjHqj9JckPDw88ODBg3rU\npnKq+zF5RUVFBAUF1Ykuu3btQl5eHr744gsAgIKCAubNm4fZs2fXSX5vkw917VJtwGwnPx+K7fLy\ngJAQIDX1vzA3N6Bnz4rTJD9Jxo7L2yG5EAfrC4ngOR6tjFpBy6Y1ogYPRsjAgdhjaIgLbm642KoV\nXtfBj/KGDFszV4ekJSQg6eRJ8AUFKFJSgpW7O8xsbd85me87pYeTVVVVoaqqWo/aVA4RVWv4uy6n\nFX/88UeMGzdOFDZ48GBMmTIFERERcHV1rZN8GQzG+8vr18WO3L17/4X17l28Tq4i4rLicPDGAVj+\nlQDTm/ehyCuitVFraNu0xCYtLdyzsYEmEZ6mp0PD0RGGSkoIv34dtpZs3dzbho3MlSEtIQGJO3ag\nV3Y2XJ4+Ra/sbCTu2IG0BPkPQqwtmS4uLpgwYQKWLFkCExMTGBgYYMyYMXj58iUA6VOBISEh4Eud\n+Fgyvblv3z5YW1tDQ0MDgwcPxosXL7Bv3z7Y2tpCW1sbX3zxBZ49eyakK5G9bt06mJqaQkNDA0OH\nDsWTJ08AFP+6UFRUxL3SPQWAoKAg6OrqIjc3t9KylZ0OLbk+d+4c2rVrBw0NDXTo0AExMTGidBMm\nTIC1tTXU1dVhZWWFefPmIT8/v9K8du/eDSsrK6ipqaFHjx44duwYeJ7HuXPnKk1Xmri4OPTt2xd6\nenrQ1NSEvb09QkJCAADm5uYoLCyEt7c3eJ6Hwr8fM3z27Bm8vb1hYmICVVVVNGvWDDNnzhRkvn79\nGpMnT4auri709fXh4+OD7777TjQdfevWLcTGxuLzzz8X6aOmpoaPPvpI0OF9hX3jUX6Y7eSnodsu\nNxcIChI7ch99VLkjd/H+RRy4thfNT8fB9OZ9qCiooK1xW2i3bI+UL77A+dxcFPz7g9WgY0co/Ttz\nUXnvyyhLbdU9NjJXhqSTJ+GmogKUGvp0A3Dqn39g1rGjfDIvXIDbq1eiMDcXF5wKD6/26Nz+/fsx\nduxYREVFIS0tDR4eHjAzM8PixYsBQKapwPT0dAQFBSE0NBSPHz/GkCFDMGjQICgpKWH//v149uwZ\nBg8ejOXLl2PlypVCugsXLkBDQwN//vknHj58iAkTJmDcuHE4ePAgXFxcYGNjg23btmHhwoVCmoCA\nAIwYMQJqamrVKicAFBUVYe7cudiwYQMaNWqEGTNmYOjQobh9+zYUFBRARDAyMsLu3bthZGSEq1ev\nYtKkSVBSUoKfn59UmbGxsRg5ciTmzZuHUaNG4caNG5g+fXq1plABwNPTE61bt8b58+ehqqqKmzdv\norCwEAAQExMDExMTrF27FsOGDRPSzJ8/H5cvX8aRI0dgYmKCu3fv4kapUzq/++47HDx4EMHBwbC1\ntUVAQAA2bdoEIyMjIU5kZCQaNWoEc3Pzcjp16tQJGzZsqFY5GAxGw+bVKyA4GEhP/y/s44+Lz5KT\nBhHhdNppRCWehEPkDRjcewR1JXW0NmoN1TYdcLNvX+x/9AhUVAQAUOI4tNLUhPa/P1qV67pADKkw\nZ64MfEGB9PB/X9Ryyfy30pcLr2IESRrm5uZYs2YNAKB58+YYNmwYTp48KThzskzt5eXlITAwEPr6\n+gCAoUOHYvPmzcjMzISBgQGA4jVs4eHhonREhODgYGhpaQEA/P390bdvXyQnJ8PS0hITJ07E+vXr\nsWDBAnAch5s3byI6OhobN26sdjlL8vvxxx/Rpk0bAMWjip07d0ZycjJsbGzAcRyWLl0qxG/WrBkS\nExPx888/V+jMrV27Ft27dxfsZWNjg4yMDEyePLlaut25cwczZ86EnZ0dAIicq0aNGgEAdHR0IJFI\nRGnatm2Ljv/+KGjSpAm6dOkCAHj58iU2b96MjRs34pNPPgEAfP/994iMjEROTo4g49atWzAzM5Oq\nk7m5OdLS0vDmzRsoKr6fTTsyMrLBj5LUFcx28tNQbffyZfGIXGbmf2GffAK0by89PhHhj8Q/cCnl\nHFqHX4NuZg60lLXQ2qg1lDp1wVVnZxx+9AhFRLC0tET85cto4+yM7IsXod25M/JiY+HWrt3bKVwD\nobbqHptmLUNRBYs3i/791SGXTGkftgNQpFy93zAcx8HR0VEUZmJigszSLVUGTE1NBUcOAIyMjGBs\nbCw4ciVhWVlZonT29vaCIwcAXbt2BQBhdGn06NHIyspCWFgYAOCXX35Bhw4dyuksK2XLa2JiAgCi\n8gYEBKBTp04wNjaGlpYW5s6dizt37lQoMz4+Hp07dxaFlb2WhW+++Qbjx4+Hq6srFi1ahMuXL1eZ\nxsfHB/v370erVq0wffp0HD9+XHC+k5KSkJeXJ9i0hG7duokc9JycHGhqakqVr62tDQB4+vRptcvD\nYDAaFi9eAIGB/zlyHFf8ndWKHLnCokIciD+Ay4ln4Xj8CnQzc6Cnqoc2xm2g5OqGv3v0wKF/HTkA\naG5piZXdusEiPh6aKSmQXL8Or3bt2Hq5euL9/Pleh1i5uyN8xw64lfKUw/PyYO3lBci5YcEqIaFY\npoqKWKYcW7iVyziAHMeh6N+RP57ny43MFUgZaSx7VAfHcVLDisqMKFY16mdgYIAhQ4YgICAAbm5u\nCAoKwvLlyysvUCXwPC+a/iz5v0Svffv2YerUqVi1ahV69uwJbW1t7N27F/PmzatUbnWnVKUxf/58\njBgxAsePH8epU6ewfPlyzJo1C0uWLKkwTZ8+fXDnzh2EhYUhMjISI0eORKtWrcqNgFaGrq4unj9/\nLvVeyQierq5u9QrzDtEQR0feFsx28tPQbPf8ebEj9/Bh8TXHAZ99BlT0uzq/MB97ru/BvbtxaPvn\nVcIAh3MAACAASURBVKg/y4VEQwK7Rnbg+n6EKHt7RDx+LMQ3UlbGKCMjaCoqoqOtbfFwH0Muaqvu\nsZG5MpjZ2sLaywunJBJE6urilEQCay+vGu08rQuZ0pBIJOWO97h06VKtyY+Pjxc5EiUbBuzt7YWw\nSZMm4bfffsPmzZvx+vVreHp61lr+ZTl9+jTatm2L6dOno23btrCyskJKSkqlaezt7cttdPjrr79k\nyq+sE2hhYYHJkydj3759WLRoEX7++WfhnrKysrCGrjR6enrw8PDA5s2bcezYMURFRSE+Ph5WVlZQ\nVlZGdHS0KH50dLQoXxsbG6SlpUnVLy0tDebm5u/tFCuDwag5z54BO3b858jxPDBoUMWO3KuCVwi8\nEoj01Gto9/tlqD/LhamWKVoY2oMb+BnCbG0R8e9GNwBoqqoKL2NjaLJ+5p2COXNSMLO1RS8fH7hM\nn45ePj614nTVhsyqjsdwd3fHzZs3sWnTJiQlJSEgIEA4WLY24DgOo0ePRlxcHE6fPo0pU6Zg4MCB\nsCw1rN6tWzfY2tri22+/haenJzQ0NAAAbm5umDt3bq3pAgB2dna4du0ajhw5gqSkJKxfvx6HDh2q\nNM3XX3+N6Oho+Pr64tatWzhy5AjWrl0rlK+0bH9/f1HaEtu/ePFCOAYkJSUFly9fxvHjx+Hg4CDE\ntbCwwKlTp/DgwQM8/LdXnTdvHg4dOoSEhATcvn0bISEh0NLSQrNmzaChoYEvv/wS8+fPx2+//YaE\nhATMmjULt27dEunQs2dPPHr0CKmlD4r6l7/++uu9H2H4UM77qguY7eSnodju6VNg+3bg0aPia54H\nhgwBWrWSHj/ndQ62Xd6GZyk30fb3y1B5lQdzXXNYG9qChg7F4aZN8VepUw2s1dQwysgIamWWHTUU\n+9UHtWU75sy9R0g7uLZ0mLu7O5YuXYrly5ejTZs2iIyMxMKFC8tNVVYmo7IwJycndO/eHb1790a/\nfv3g6OiIbdu2ldNz/PjxyM/Px8SJE4Ww5ORkZGRkVJlnZddlwyZNmoRRo0bB29sb7dq1w8WLF+Hn\n51epnHbt2mHnzp3YuXMnWrdujVWrVglTo6XPubt16xYelfSIZfRVUlLC06dPMW7cONjb2+Ojjz6C\niYkJdu3aJcRfs2YNYmNjYWFhIexGVVNTw8KFC9GhQwd07NgR169fxx9//CGsQ1y5ciU+++wzjBo1\nCp06dcKzZ88wZcoUkQNva2uLDh064ODBg6Iy5ubmIiwsDCNHjixnMwaD0fB58qR4RK5kEE1BARg6\nFCg1cSIi+2U2tl7eijfJiXAMuwKlvALY6NvAXNIchSNGYK+BAa68eCHEd9DQgKeREZQrWAPOqF/e\nu2+zXrhwAdOnT4eSkhJMTU0RFBQkdVqJfZu1dvHy8sL9+/dx4sSJKuPOmjUL4eHhiI2NfQua1Zyg\noCCMHTsWjx8/FjYRvCv4+flh586duH37thC2a9cuLFu2DHFxcUJYcHAwvv/+e/zzzz/1oWaVsDbH\nYNQdjx8Xr5Er2fiuoAAMGwY0by49/r1n97Dzn51QT74Lh6gbUCgktDBsAUkjM+QNH45flZSQUups\n0HZaWhhgYAC+FtYbMyrmg/o2a7NmzRAREYGoqCiYm5vj8OHD9a0S419ycnJw8eJFBAQEYMaMGfWt\nToX88MMPiI2NRUpKCvbu3Ys5c+Zg6NCh75wjVxHDhw+Hmpqa6Nusy5cvx+rVq+tZMwaD8bZ5+LB4\narXEkVNUBDw9K3bkEh8nIvBKILRvpqBlRByUiji0NmoNibEVXo0ZgyAFBZEj101HB58wR+6d571z\n5oyNjaHy765QJSUl4XR9Rt0iy7dJBw4ciJ49e2LQoEHv9HTftWvX8Mknn6BFixbC4cHSpovfBSqy\ne0xMjOjbrPHx8fjoo4/etnq1Dlt7Iz/MdvLzvtouO7t4arVkX5qSEjB8OGBtLT3+tcxr2HVtF4yu\np6DF2ZtQ5hTRxrgN9Eyt8Mzr/9m78/ioyrPx/5+Z7Jnsy8xkIQlZCJCVTUEUEFSQRbYiO0ZAbWuf\nWq1abB8EpLY/fVr7bautdSMkhF2oGyJrWFQ2yQIJBEJIICEBspB9z/n9MWSSsGiY7HC9X6+85D6Z\nOfd9Ls8kV869RbGqvp6c6mrj6x9xduZRF5ef/NnfU+PXHdzze7NmZWWxc+fOFrsNiI6zatWqn3xN\nT/lAr169uqub0GrLli1j2bJlXd0MIUQ3c+WKoWv1+m6OWFjA3Llwi81hADicfZivz27DLykLv8RM\nrM2tCdeFY+vdm8LZs4kpLeVaXR1g+CNygosLg3tIb4Xowidz7777LoMHD8ba2pqnn366xfcKCwuZ\nOnUqdnZ2+Pn5sW7duhbfLykpYcGCBaxevVqezAlxF+nps3G7ksTOdD0tdnl5hidyjYmcpSXMm3fr\nRE5RFPac38PXZ7cReCQdv8RMNBYaBugHYBvQl8tz5/JJSYkxkVOrVEx3c7ujRK6nxa876fS9Wb/5\n5hsSExMpaza7RaVSGbdFulNeXl4sXbqUb7755qZN2J9//nmsra25cuUKCQkJTJgwgYiICPr3709d\nXR2zZs1i2bJlLTYgF0IIIe52ly4Z9lpt/LVpZWVI5Hr1uvm1DUoDX535iuPZR+n3bRq6jMs4WDkQ\npg3DIrgfF6dMIa6ggKrrC7Gbq1TM1GoJsrXtxCsS7aFVT+Z+9atfMX/+fI4fP052djbZ2dlcvHiR\nixcvmlzx1KlTmTx5costpMCwR+WWLVtYuXIltra2DB8+nMmTJxMbGwvAunXrOHLkCCtXruThhx9m\n48aNJrdBCNG99JSu+u5IYme6nhK7nBzDXquNiZy1NSxYcOtErq6hjs2pm0m4eITQvSnoMi7jYuNC\nhC4Ci4gBnJsyhZhmiZyVWs18vd6kRK6nxK876tQxc3FxcSQnJ9PrVndMG904DffMmTOYm5sT2GwE\nZ0REhPGC58+fz/z581t17qioKOMG6E5OTkRGRsrjYCG6SPMNpRs/zzeWm7/2Vt+X8u3LiYmJ3ao9\nPamcmJjYrdpzq/KVK3Du3CiqqyEzMx5LS1ixYhQeHje/fsfuHew5vwc7H3PCd58gMymLMmtnRviG\noh5yH9FqNfu//BKf++8HIO/IER51dsbX1/eujV93LANER0cTHR1NW7Vqnbk+ffpw7NixDlm6YenS\npWRnZxsH2B84cIAnn3yS3Nxc42s+/PBD1q5dy969e1t9XllnTojuQz5zQpguKwvi4qCmxlC2tTU8\nkdPrb35teU05a5LXkH81i/CdydgXluHt4E2AcwCqESM4PmQIXxQWGj+PjubmLNDrcb1hf27R+dry\nc/K2T+YyMjKM//7tb3/LvHnzWLJkCfob7p7mWzmZ4saG29nZUdJs+xAwrF/WuEq+EEIIca84fx7W\nroXaWkNZo4GnngKt9ubXFlUWEZscS/nVSwzYkYRtSSX+zv70cuiFauxYvgsJYUeznW3cLCyYr9fj\nKPus9ni3HTMXGBho/PrFL37Bl19+yYMPPtjieHtMQLhx/Zo+ffpQV1dHenq68VhSUhKhoaF3fO7l\ny5e3eJx5L8vMzEStVt+0yfy9Ij4+HrVazaVLlwCJx40uXbqEq6srOTk5AJw/fx5XV1euXr3aqe2Q\nz6vpJHam666xy8homcjZ2UFU1K0Tuctll/kk4ROq8rIZuC0B25JKgl2D8XHyhcmT2d2vHzsKC42v\n97Cy4mkPj3ZJ5Lpr/HqC+Ph44uPjWb58eZvOc9tkrqGh4Se/6uvrTa64vr6eqqoq6urqqK+vp7q6\nmvr6ejQaDdOmTeP111+noqKCgwcP8sUXX7R6nFxzy5cvN/ZR3+t8fHzIy8vjvvvu65L6//jHP9K7\nd+87fl92djZqtZr9+/e3a3u6Oh7dzbJly5g5cyZeXl4A9O7dm6lTp5o8W10I0Tbp6S0TOQcHePpp\ncHe/+bUXii+wKnEVXLrEgG0J2FTWEqoNxcPJG2XGDLb5+nLg2jXj632trYnS69HI0l7dwqhRo9qc\nzLUqJc/JycHGxgYXFxfjscLCQqqqqvD09DSp4pUrV7b4RbFmzRqWL1/O66+/zr/+9S8WLlyIVqvF\nzc2N999/n379+plUjynSMjLYlZJCLWABPBISQnAbu5M74px3Qq1Wo73Vn3M9RHuPt2qveNTU1GBp\nadkOLbpZw/VZZmp1xy4HWVhYyJo1a256Srlw4ULGjh3Ln//8Z+zs7Dq0DY3kjy/TSexM191il5YG\nGzdC4/MSR0dD12qzX8FGZwrOsDFlI3aX8gndfQKrOgjThePkoKV+5kz+6+DAiWZDl/rY2jLD3R2L\ndvy50t3i15O0V+xa9X9z8uTJZGdntziWnZ3N1KlTTa54+fLlNz3pa9zNwdnZma1bt1JWVkZmZiaz\nZs0yuZ47lZaRQfTx41wNDeVaaChXQ0OJPn6ctGZjCLvynAcPHmT48OE4ODjg4OBAZGQkO3bsAODK\nlSs8/fTT6PV6bGxs6Nu3r3FiyY3dio3luLg4xowZg62tLQEBAWzYsMFY16hRo3juueda1K8oCgEB\nAbz55ps3te1Pf/oTAQEBWFtbo9VqGTduHFVVVURHR/P666+TlZWFWq1GrVYbE/m1a9dy//334+Tk\nhLu7OxMnTmyxqbyPjw8ADz/8MGq12jhGMzs7m+nTp+Pu7o6NjQ0BAQH85S9/aXUcbxePTZs2MXHi\nRDQaDQEBATftFqFWq/nnP//JnDlzcHJy4qmnngJg586dDB8+HFtbW7y9vVm4cCGFzbo0FEXh97//\nPe7u7jg4ODBv3jz+/ve/Y9Fs0PHy5csJCgpi48aN9O3bFysrK86ePUtZWRkvvPAC3t7eaDQaBg4c\nyNatW1sV+9bEatOmTeh0OgYMGNDinMOGDUOj0dxUlxCi45w61TKRc3IydK3eKpFLykti/cn1OGbm\nEb4zGdsGMwZ4DMDJ2YPa+fNZb2fHiWZrw4bb2TFTq23XRE50D616MnfmzBnCw8NbHAsLC+PUqVMd\n0qj20tjNeieZ766UFKwGDSK+2SNpAgJI3r+fISZuNHxk/34qIiKg2TlHDRrE7pMn7+jpXF1dHU88\n8QQLFy4kJiYGMOwzqtFoqKysZOTIkWg0GtauXUtAQADnzp0jPz//R8/56quv8pe//IX333+fmJgY\n5s6dS3BwMJGRkfz85z/n2Wef5Z133kGj0QCwZ88eLly4wKJFi1qcZ8uWLbz11lusXbuWiIgICgoK\n2LdvHwCzZs0iLS2NuLg4jh07BmA8X01NDa+//jr9+/enpKSE119/nQkTJpCSkoKFhQXHjx9n4MCB\nbNmyhQceeMC448cvf/lLqqqq2L17N05OTmRkZHD58uVWx/J2lixZwltvvcU//vEPPv74YxYvXswD\nDzzQYnzoihUreOONN3jzzTdpaGhgz549TJkyhbfffpuYmBiKiop49dVXmTZtmnEsyd/+9jf++c9/\n8v777zN06FA+//xz3njjjZvGjF66dIl///vfxMbG4uzsjF6vZ9KkSahUKjZu3Iinpyc7d+5k1qxZ\nfP3114wePfpHY3+7WOXl5Rm/v2/fPu6/vkRBcyqVivvvv589e/aYNMzBFPHNli8Rd0ZiZ7ruEruU\nFPj0U7j+UB4XF8MTOUfHm1/73cXv2HFuB7r0PPp+m4aNmRURughsXLRUzZ3LOkUhq6LC+Pr7HBx4\nvBX7rJqiu8SvJ2r8HdHWcYetSua0Wi1nz55t8Qvt3LlzuLm5tanyjmZKH3TtbY7Xt+ED0HCb99bc\n4XlKS0u5du0akyZNIiAgAMD4348//pjMzEzOnTtn7PpuXDPoxyxevJjZs2cDhq7vPXv28M477xAT\nE8PUqVP59a9/zfr1643J20cffcTEiRNvmtWclZWFXq9n7NixmJub4+3tTUREhPH7Go0GMzOzm7o2\no6KiWpRXrVqFm5sbx44dY9iwYcZ7zMXFpcV7L1y4wNSpU41/ZDQ+wWur//mf/+FnP/uZMR7//Oc/\n2bt3b4t7f+rUqfzyl780lhctWsQLL7zA888/bzwWHR2Nn58fycnJhIeH89e//pWXXnqJuXPnAvDi\niy9y5MgRNm/e3KL+qqoqYmNj8fb2Bgwf8EOHDnH58mXj0kDPPPMM33//Pf/85z8ZPXr0T8b+p2J1\n5swZHn744VvGw9fXlx9++OHOgiiEuGMnTsDWrU2JnKurIZG7cUUwRVHYlbGLby9+i1dqNkFH0tFY\naAjXhWOl9aB8zhxiq6vJq2n6DTPCyYmHnZw6JJETbdf40GnFihUmn6NVz1oXLlzI9OnT+eKLL0hN\nTeXzzz9n+vTpNz2duRvcbqUdszaM2VLf5r13OtLK2dmZxYsXM3bsWMaPH89bb73FmTNnAPjhhx8I\nCQm54zGMw4YNa1EePnw4KSkpAFhZWREVFcWHH34IQEFBAf/973955plnbjrPzJkzqa2txdfXl6ef\nfpo1a9a02PrtdhITE5k6dSr+/v44ODgYE9CsrKwffd9vfvMb/vSnPzF06FCWLFnCgQMHWnW9PyUy\nMtL478ZxdVeuXGnxmhsnTRw9epS//e1v2NvbG79CQkJQqVScPXuW4uJicnNzGTp0aIv33VgG0Ol0\nxkSu8dw1NTV4eXm1OH9cXJxxxvdPxf6nYlVSUnLbpX8cHBy41vwpdQeTv+5NJ7EzXVfHLikJtmxp\nSuTc3Axdqzcmcg1KA5+nfc63Fw7il5hJ0JF0HK0cGeAxACsvH4oXLOCTqqoWidxYFxdGOzt3aCLX\n1fHrydordq16MrdkyRIsLCx4+eWXyc7OplevXixevJiXXnqpXRrRnTwSEkL0Dz8watAg47HqH34g\nasQIgk2YjQmQpihEHz+O1Q3nHDNw4B2f64MPPuCFF15gx44d7Ny5k6VLl/Luu++226KsN57jueee\n469//SsnTpxg9+7daLVaHn/88Zve5+npyenTp9m7dy979uxh5cqV/O53v+Pw4cMtkpPmKioqeOyx\nxxgxYgTR0dHodDoURSEkJISamh9/bhkVFcW4cePYvn07e/fu5fHHH2fq1KnGbd9MdeNkBpVKZZyI\n0Kixi7iRoigsWbLkll2ROp2OuusbWLfmh+mN525oaMDR0dHYPX2rtv5U7H8qVk5OTpSWlt6yPcXF\nxTg7O/9ku4UQpklIgM8/h8YfvVqtYUHgG+cc1dbXsjl1M2n5pwk8ko73qRxcbVzp794fM18/8mfM\nILa4mOJmP2+ecHVlgKzRek9o1ZM5tVrNK6+8QlpaGuXl5Zw+fZqXX365w2fZtZUp68wF+/sTNXAg\n2pMncTp5Eu3Jk0QNHNimmaftfc6QkBBefPFFtm3bxqJFi/jggw8YNGgQqampxnXCWuv7779vUf7u\nu+8ICQkxlgMCAhg9ejQffvghH3/8MQsXLrxtUmJpacnYsWN56623OHHiBBUVFXz22WfG7924lM2p\nU6fIz8/nzTffZMSIEQQHB1PYbGXyxvcBt1wGR6/XExUVxerVq/noo4+Ii4tr1dPA9jZ48GBOnjyJ\nv7//TV8ajQZHR0c8PT1vmi166NChnzz3kCFDuHbtGpWVlTedu3mS/GOxhx+PVVBQEJmZmbesPysr\niz59+pgQFdPIelWmk9iZrqtid+wYfPZZUyKn0xm6Vm9M5KrqqliTvIYzV07R78BpvE/loLfTE6oN\nxaxPMLkzZ/LJtWvGRM5MpeJJd/dOS+Tk3jNde60z1+rVAmtqakhLSyM/P7/FL9vRo0e3qQEdydTg\nBPv7t/uyIe1xznPnzvHBBx/wxBNP4O3tzaVLl9i/fz+DBw9m9uzZvP322zzxxBO8/fbb+Pv7k5GR\nQUFBAU8++eRtz/nJJ5/Qt29fBg0axJo1azh06BDvvfdei9c899xzzJ07l4aGBhYvXgzA1q1bee21\n19i7dy8eHh58/PHHKIrCkCFDcHJyYvfu3ZSWltK/f3/AsG5ZXl4ehw4dIjAwEI1Gg6+vL1ZWVvzj\nH//gpZdeIjMzkyVLlrRIFt3c3LCzs+Obb76hX79+WFlZ4ezszK9+9SsmTJhAnz59qKqqYsuWLfj4\n+BiX0Hjttdc4evQou3btalPMW/O084033uCxxx7jt7/9LfPnz8fe3p6zZ8+yefNm3n33Xaytrfnt\nb3/LsmXL6Nu3L0OGDOGrr75i586dP/kH0ejRo3nkkUeYNm0ab7/9NmFhYRQVFfHdd99hY2PD4sWL\nfzL2PxWrkSNH3nJ2sqIoHDlyhLffftuEyAkhfsyRI7BtW1PZwwPmzzds1dVcaXUpa5LXcLX4EiH7\nUnG7WICPow+9nXqjCgsj6/HHWZufT/X1HgRLtZpZWi3+NjadeDWiLdpjzBxKKxw4cEDR6/WKs7Oz\nolarFWdnZ8XMzEzp3bt3a97eJX7s0lp52d1Obm6uMm3aNMXb21uxsrJSPD09lWeffVYpKSlRFEVR\n8vLylAULFihubm6KtbW10q9fP2X16tWKoijK+fPnFbVarXz77bfGskqlUtasWaOMGjVKsba2Vvz9\n/ZV169bdVG9tba2i1WqViRMnGo+tWrVKUavVSlZWlqIoirJlyxblgQceUJydnRVbW1slLCxM+eST\nT1qcY86cOYqLi4uiUqmUFStWKIqiKJs3b1aCgoIUa2trZeDAgcq+ffsUc3NzY7sVRVFiYmKU3r17\nK+bm5sZ77vnnn1f69Omj2NjYKK6ursrEiROV1NRU43uioqJa3J979+5V1Gq1kpOTc9t4NC83CgwM\nNLZVURRFpVIpcXFxN8XowIEDyiOPPKLY29srGo1G6devn/Liiy8qdXV1iqIoSkNDg/Laa68pbm5u\nip2dnTJ79mzlT3/6k2Jvb288x/Lly5WgoKCbzl1ZWaksWbJE6d27t2Jpaano9Xrl8ccfV/bu3duq\n2P9UrPLz8xVra2vlhx9+aFHvwYMHFY1Go5SWlt7UpjvVUz9zQnSE779XlGXLmr4++EBRKipufl1B\nRYHy/77/f8ob3/xB2fq7ycrep0YqF36z0PCmL75Q0kpLlZXnzyvLMjKUZRkZyv+XlaVcrKzs3IsR\n7aYtPydV10/wowYPHsycOXN46aWXcHZ2pqioiDfeeAMbGxteeeUV0zPJDvRjY8hk02/Dumr+/v4c\nPHiQBx544EdfW1BQQK9evdiwYQOTJk3qpBbe/RYuXMiJEyc4evRoVzeFZ599FjMzM/79738bjy1a\ntAgbGxvefffdNp9fPnNCGHz7Lezc2VTu1QvmzgVr65avyyvLY03yGqqLCwnfmYxDYTnBbsHo7fTw\n0EOcuO8+thYU0HD9c2VnZsZ8vR5dBy1iLjpeW35OtmrQ29mzZ/nNb34DNHU7LVmyhL/97W8mVSp6\nhrq6OvLy8vjDH/6At7e3JHJtkJuby3vvvUdqaippaWn85S9/ITY29pYzg7vCihUr2LhxY4u9WT/7\n7DOWLVvWqe2QsTemk9iZrrNit39/y0TOxwfmzbs5kcu8lsmqhFXUFuYzYHsijkUVhGpDDYncY49x\ndMgQtjRL5JwtLFjk4dFliZzce6Zrr9i1asyco6OjcVabp6cnKSkpuLm5UV5e3i6N6CimLBp8L/mp\n2ZUHDx5k9OjR+Pv7t3mW6L3OzMyMzZs38/rrr1NVVUVQUBDvv/9+t1nex8PDg4KCAmO5d+/eP7ng\ntBCidRQF9u2D5r+3/fxgzhy4Mf86nX+azambsSwqIXxHEnaV9YTpInC0cUKZOJEDAQHsafZZ1Vpa\nMl+nw9681UPgRTfTOAmiLVrVzfrCCy9w3333MXfuXP7yl7/wf//3f5ibmzNu3Dg+/vjjNjWgo0g3\nqxDdh3zmxL1KUWDvXsNTuUb+/jB7NljcsLDp8dzjfJH2BZqCEiJ2JKOpUxGuC8fOxhFl2jR2enjw\nXXGx8fXeVlbM1emwub4zjujZ2vJzslXJ3I0OHDhAaWkp48aN67bLk0gyJ0T3IZ85cS9SFNi1yzBO\nrlFgIMyc2TKRUxSFby9+y66MXTjlXSN09wnsFUsi9BFY2zrQMHMmXzg6ktBsPUh/GxtmabVYdtPf\nweLOdfiYuUYXLlzg+++/x9fXl/Hjx3fbRE4I0TPJ2BvTSexM1xGxUxT45puWiVyfPjBr1s2J3I5z\nO9iVsQvXC/mE70zGSWXDAI8BWNs7Uzd/Ppvs7Vskcv00GuZ0o0RO7j3TtVfsWnUn5ObmMnLkSAID\nA5k2bRqBgYGMGDGCS5cutUsjhBBCiLuFosDXX0PzdcH79jU8kWs+tK2+oZ7/nv4v32d/j+7cZUL3\npuBi4UCkPhJLJ1dqoqJYZ2HBqWbj0yPt7Jjh7o55N0nkRPfQqm7WyZMn4+vry5///Gc0Gg3l5eX8\n/ve/5/z583z++eed0c47Jt2sQnQf8pkT9wpFgS+/hB9+aDrWvz9Mnw7Nh7bV1teyMWUjZwvP4pWa\nTdCRdNxt3enn3g+1qxuVc+cSV11NdnW18T3DHB15rIP3WRVdp8PHzLm6upKbm9ti38rq6mo8PT1b\nzIDrTlQqFcuWLbvlbFYXFxeKioq6pmFC3IOcnZ0pLCzs6mYI0aEaGuCLLwz7rTYKC4OpU6H5g7TK\n2krWnljLxeIL+CVl4ZeYiae9J0EuQaj0ekpnzya2vJwrzfaoHu3szEOOjpLI3YUaZ7OuWLGiY5O5\noKAgNm3aRGRkpPFYUlIS06dPJz093aSKO5o8CTBdfHy8LOfSBhI/00nsTCexM117xK6hwbDPalJS\n07GICJg8uWUiV1JdwprkNVwpu0zgkXS8T+Xg6+iLn5MfKh8fip58kpjiYopqa43vGe/qyn0ODm1q\nX0eSe890zWPXlrylVQvTvPrqqzz66KMsWrQIX19fMjMzWbVqFStXrjSpUiGEEOJu0dAAW7fCiRNN\nxwYMgEmTWiZyBRUFxCTFUFJRRN/v0tCfu0ygSyDeDt4QGMiVKVOILSqitK4OALVKxRQ3N8KvqNP9\nOgAAIABJREFU76MsxO20emmSPXv2EBcXR25uLp6ensyePZsxY8Z0dPtMJk/mhBBCdLT6evj0U0hN\nbTo2aBBMnAjNe0QvlV5iTfIaqipL6b8vFfeLhfR164vOTgchIWRPmEBcfj6V9fUAmKtUzNBqCba1\n7eQrEl2lQ8fM1dXVERwcTGpqKlZWViZV0hUkmRNCCNGR6uth82Y4darp2H33weOPt0zkMooyWH9y\nPfWVFYTtOYnL5RJCtaG42LjAoEFkjB7N+vx8ahoaALBSq5mt1eJnY9PJVyS6UoeuM2dubo5araay\nstKkCkTPI2sGtY3Ez3QSO9NJ7ExnSuzq6mDDhpaJ3NChNydyKVdSiEuOQykrI3J7Im5XyojURxoS\nuYce4tTDDxN39aoxkbM1M+Mpvb5HJXJy75muU/dmffHFF5k5cyavvfYavXr1ajGbxt/fv10aIoQQ\nQvQEtbWGRK75/L/hw+GRR1omckdzjrLt7DYsyyqJ2JmMc1k94foBaCw18OijJIaH81l+vvFpjIO5\nOQt0Otxu3LBViJ/QqjFzt9vpQaVSUX+9f7+7+bGlSYQQQghT1NbCunWQkdF07KGHYPTopkROURT2\nZ+1nb+ZebIsrCN+RhEuNGeG6cKwtbGDSJA4FBLC92XI9rhYWzNfpcLpxw1Zx1+u0pUl6IhkzJ4QQ\noj3V1MDatZCZ2XRs1CgYObJlIvd1+tccyTmCXUEpETuScVGsCdeFY2FpjTJtGvGenuy7ds14Dr2l\nJfN0OuzMW9VZJu5SnbY3a05ODkePHiUnJ8ekykTPIOMf2kbiZzqJnekkdqZrTeyqq2HNmpaJ3OjR\nhmSuMZGrb6jn01OfciTnCE5514jcnohWZUekPhILGw3K7Nls1+tbJHI+1tZE6fU9OpGTe890nbo3\n64ULF3jooYfw9fVlwoQJ+Pr68tBDD5GVldUujRBCCCG6q6oqQyJ34ULTsUcfhREjmso19TWsPbGW\nk1dO4nohn/CdyXhauhKmC8NMY0f9/PlsdXTkcEmJ8T1BtrbM1+mwbr7PlxAmaFU366hRo4iMjOTN\nN99Eo9FQVlbG0qVLSUhI6LYZuXSzCiGEaKuqKoiNheYdUmPHwrBhTeWK2grikuPIKc1Bd+4yfQ+e\nxtvOk0CXQFQODtTOm8dmIK2iwvieUI2Gqe7umMn2XOK6Dt+b1cHBgfz8/BZ7s9bU1ODq6kppaalJ\nFXc0SeaEEEK0RWUlxMRAbm7TsfHjDWvJNSquKiY2OZb8iny8UrMJOpKOn5Mfvo6+qFxcqJ43j3U1\nNWRWVRnfM9jenvGurqglkRPNdPiYuaFDh3LkyJEWx44ePcqw5n+aiLtGd33a2lNI/EwnsTOdxM50\nt4pdeTmsXt0ykZs4sWUid7X8Kh8nfEx++VV8EzMJOpJOH9c+hn1W9XoqoqJYXV3dIpF70NGRCXdZ\nIif3nuk6dZ05f39/xo8fz8SJE/H29ubixYts27aNOXPmsHTpUsCQUb7xxhvt0ighhBCiqzQmcleu\nGMoqFTzxhGG/1UbZJdnEJcdRWVtB4JF0ep26RD/3/mg1WujVi5InnySmuJj82lrjex51cWG4o2Mn\nX424F7SqmzUqKqrpDc0eAzYuHqwoCiqVilWrVnVMK00g3axCCCHuVGmpoWv16lVDWaWCKVMgIqLp\nNemF6Ww4uYG62mqCv0vDKyOfUG0ozjbOEBBAwbRpxBQWUlxXd/0cKia6ujLI3r4Lrkj0FB0+Zq4n\nkmROCCHEnSgpMTyRKygwlFUqmDYNwsKaXnPi8gm2nt4KdXX0j0/BI6eEcF049lb2EBJC3sSJxF69\nSvn1BfXNVCqmubsTotF0wRWJnqRT1pk7c+YMf/zjH3n++ed58803OXPmjEkVdqbly5dLX74JJGZt\nI/EzncTOdBI708XHx1NcDNHRTYmcWg0/+1nLRO5w9mE+PfUpquoawncm451bzgCPAYZEbtAgLkyY\nQPSVK8ZEzkKtZrZWe9cncnLvma5x94fly5e36TytSubWrl3LwIEDOXHiBBqNhuTkZAYOHEhcXFyb\nKu9oy5cvl628hBBC3FJaWhbvvbeHuLhEFi3aw5kzhrVTzcxgxgwICTG8TlEU9p7fy9fpX2NRWUPk\nN0l4FdQyQD8AWwtbePBB0seMIfbqVaoaGgCwVquZr9MRaGvbVZcneohRo0a1OZlrVTdr7969Wb16\nNSOarZB44MAB5s+fT2bz5bC7EelmFUIIcTtpaVlER6fT0DCGxETDDg91dbsZODCQ55/3JTjY8LoG\npYFtZ7dx7NIxrMqqiNiZjL7KnDBtGBZmFvDoo5yMiGBrfj7113/n2JmZMU+nQ29l1YVXKHqatuQt\nrZrNWlZWdtMyJEOHDqW8vNykSoUQQoiutGvXOerrx5CUZEjkACwtx+DsvIfgYF8A6hrq2HJqC6lX\nU7EtriB8RxKeDRpCdCGYmZnDpEn8EBTEl/n5xl/CTubmzNfrcbWw6KpLE/egVnWzvvTSS7z22mtU\nVlYCUFFRwe9//3tefPHFDm2c6Boy/qFtJH6mk9iZTmJ3ZwoK1CQkGBK5a9fiUashNBScnQ2/Fqvr\nqolLjiP1aip2BaVEfp2AL06EakMxs7CEGTM46O/PF80SOXdLSxZ6eNxziZzce6br1HXm3nvvPS5f\nvszf//53nJ2dKSoqAkCv1/Pvf/8bMDwevNB84zohhBCiG8rOhmPHGmhcAk6tNkx0cHYGS8sGymvK\nWZO8htyyXBzzrhG2+wR+Nh4EOAegsrREmTmT3S4uHLz+uxDA08qKeTodtrLPqugCrRoz19rMsTtN\nNpAxc0IIIW6UmQlr18KlS1kkJqZjbT2G8HBwcIDq6t1Mm+POoYp9FFQW4HqxgJD4FAId/Ojl0AuV\nrS0Ns2fzla0tPzTbytLP2prZOh1W6lYvECHETWSduVuQZE4IIURzZ8/Chg1wfS1fysuzcHE5h42N\nGkvLBiKGO3CofB+lNaXozl2m78HT9HXpg4e9B9jbUz9vHltUKlKajRcPtrVlhrs75pLIiTbqlGQu\nISGBAwcOUFBQ0KKy7rqFlyRzpouPj+9WT1l7Gomf6SR2ppPY/bjUVPj0U7i+BBz29vDUU+DmZoid\n/wB/1p5YS1VdFV6ncgg+co7+7v1xs3UDZ2dq589nQ00N6dfHjgNE2Nkx2c3trtpn1RRy75mueew6\nfDbrBx98wIsvvshjjz3Gtm3bGD9+PDt27GDy5MkmVSqEEEJ0lqQk+O9/ofH3pLMzLFgAVwrS2LB7\nF98d+47ig8X49fZl0NVyApMuEqYLx8naCbRaqubOZW1FBReqqoznvN/BgXEuLsZtLYXoSq16MhcQ\nEMCqVasYMWKEcQLE119/zbp164iJiemMdt4xeTInhBDi2DH48sumspubIZHLvZJG9N5oijyKSMtP\nQ1EaGPxNPmPrnRgWNAw7Szvw9qZs1izWFBeTV1NjPMcoJydGOjlJIifaVYd3szo4OFBSUgKAq6sr\nV65cQa1W4+LiYpzZ2t1IMieEEPe2776DHTuayjqdIZHTaOC9De9xqCCe4u8SsaxrwDu3An9LcwbZ\n92V4+HAICODa9OnEFBZS2DjtFRjn4sJQR8cuuBpxt+vwvVm9vb05f/48AEFBQXz22WccOHAAK1nd\n+q4kawa1jcTPdBI700nsmigKxMe3TOS8vCAqypDIASSmHMJ822Gml9TwYEI+C69UY5urcLW8EkJC\nuPqzn/FJQYExkVOrVExxc5NE7hbk3jNdp64z98orr3Dq1Cl69+7NsmXLmD59OjU1NfzjH/9ol0Z0\nlMa9WWVgphBC3BsUxZDEff990zE/P5g9G6ysru+zmrmXouPHeUKlwj+7nDOVCvbO9jyiUvFZg4pL\nEyey5upVKq7PljBTqZjh7k7fxkxQiHYUHx/f5qTOpKVJqqurqampwd7evk2VdyTpZhVCiHuLosBX\nXxnGyTUKDISZM8HCwpDIbU/fzuGcwxT95xuePJaGo4UajYUGlUpFobUd306YQemCKGoaGgCwVKuZ\nrdXS28ami65K3Cs6fDbrjaysrKSLVQghRLfR0GCYsZqc3HSsXz+YPh3MzaFBaeCLtC9IyEvAqrya\ngNwSfKydUdWroBZKde7UDBtJQnA/fK4ncjZmZszT6fCS33eim5NVDsVNZPxD20j8TCexM929HLu6\nOti0qWUiFxEBM2YYErn6hnq2nNpCQl4CNiWVDPg6gf4evTjt6IG31pt0/77Ujp/G+/6BOPj7A2Bv\nbs7Ter0kcq1wL997bdWpY+aEEEKI7qi21rCrQ3p607HBg2HCBFCpoK6hjk0pm0grSENTWEbEzmR8\nzFwI7hPMXusL/NrCgqTycqoqKwkODsbJ1RUXCwvm63Q4W1h03YUJcQdkOy8hhBA9UnW1YZ/VrKym\nYw88AI8+akjkauprWH9yPRlFGThcKSZ81wl8rXQEugRyprKS6IAAckeMIPP6YsB1x44xJjSUl4cM\nwd5cnnWIztXhS5O4uLjc8rhWqzWpUiGEEKItKishJqZlIvfww02JXFVdFbFJsWQUZeCcU0jEjiT8\nbTwJdAlEZW3NjpAQzj/4oDGRA3AZOhTnq1clkRM9TquSudpmCyY2P1bfuMmduKvI+Ie2kfiZTmJn\nunspdmVlEB0NOTlNxx57DEaONCRy5TXlrE5czcWSi7hnXiVs9wkC7Xzxd/ZHZWdH5YIFfG9ubtzV\n4dqxYzibmxOh0RhOIO7IvXTvtbdOGTP30EMPAVBZWWn8d6Ps7GyGDRvWLo0QQgghWqOkBFavhoIC\nQ1mlMoyPGzz4+verS4hNiuVqxVX0Z3MJ/i6NPs5BeDl4gaMjhbNnE1dXx7VmDylczM0Js7NDDVh2\n/iUJ0WY/OmYuOjoagJ///Of85z//MfblqlQqdDodY8aMwaKbDhCVMXNCCHF3KSw0dK1eu2Yoq1Qw\nZYph5ipAUWURMUkxFFUV4Z1ykcCj5wh2DcbD3gNcXbkwaxbrKyupqK8n/+JFEtPS6PPgg/SytkYF\nVP/wA1EDBxJ8fUarEJ2pw/dmPX36NH379jWpgq4iyZwQQtw9rl41JHKlpYaymRn87GeGteQA8ivy\niUmKoaSqmN4JmfglX6Cfez+0Gi14eHBi2jT+W15O/fXfC+YqFQPKy8nKyKAGwxO5MSEhksiJLtPh\nEyCOHz9OamoqAGlpaYwYMYKHH36Y06dPm1Sp6N5k/EPbSPxMJ7Ez3d0cu9xcWLWqKZEzNzdsz9WY\nyOWV5bEqYRUlVcUEHU6n94mLhGpD0Wq0KD4+7Js6lU/LyoyJnMbMjCi9ngkhIfxy0iQi7e355aRJ\nksiZ6G6+9zpae8WuVcnc//7v/+Lq6grAb3/7W+677z5GjBjBL3/5y3ZphBBCCHErFy8axshVVBjK\nlpYwb55hmy6A7JJsohOjqagqpd+B0/ik5RGmDcPV1pW6oCC2jh/P3vJy4/ncLS15xsMDb2vrLrga\nITpGq7pZHRwcKCkpobKyEk9PT/Ly8rCwsMDV1ZWioqLOaOcdk25WIYTo2c6fh3Xr4PqkU6ytDYmc\nt7ehnHktk7Un1lJXU0X/+BT0OcWE68JxsHKgIjSUDcOGkdX4ZsDfxoYn3d2xNjPrgqsR4sd1+N6s\n7u7unD17lhMnTjBkyBCsrKwoLy+XZEkIIUSHOHMGNm40bNUFoNHA/Pmg1xvKZwvOsiFlA0pVFWF7\nTqK9Uk6EPhI7SzsKBg1ibWQkBc0SuUH29ox3dcVMlh4Rd6FWdbMuXbqUwYMHs2jRIl5++WUAdu3a\nRWRkZIc2TnQNGf/QNhI/00nsTHc3xS4lBdavb0rkHBzg6aebErnUq6msP7keVUUlkd8kob9ayQCP\nAdhZ2pH14IN8FB5OwfU3q1QqHnVxYeKPJHJ3U+y6gsTPdJ26N2tUVBQzZsxApVJha2sLwLBhw7j/\n/vvbpRF3oqSkhEceeYRTp05x+PBh+vfv3+ltEEII0TESE+Gzz6Cx48fZGRYsMPwXIDEvkc9Of4Zl\neRXhO5JwLW8gQh+JjYUNyWPG8FmvXtQ3NABgoVYzzc2NfhpNF12NEJ2j1XuzFhQU8NVXX5GXl8er\nr75KTk4OiqLg3Th4oZPU1dVx7do1XnnlFV5++WVCQkJu+ToZMyeEED3LkSOwbVtT2c3NkMg5OFz/\nfs4Rtp3dhk1JJRE7knCpVhOhi8DSwpr4sWPZp9MZ32tnZsZsnQ4vK6tOvgohTNPhS5Ps27eP4OBg\n1q5dy8qVKwE4e/Ysv/jFL0yqtC3Mzc1xc3Pr9HqFEEJ0nG+/bZnI6fWGrtXGRO7ghYNsO7sNTWEZ\nA75OwK3GnEh9JGaWNmyZOLFFIqe1tGSxh4ckcuKe0apk7oUXXmD9+vVs374d8+sbEA8dOpTDhw93\naONE15DxD20j8TOdxM50PTV2igJ798LOnU3HvL0hKsow6UFRFPac38OujF04XClmwPZE3BqsidRH\nUmdjR8wTT3DCxcX43gAbGxbq9Tjdwe5EPTV23YXEz3Sdus5cVlYWjzzySItjFhYW1NfXm1zxu+++\ny+DBg7G2tubpp59u8b3CwkKmTp2KnZ0dfn5+rFu37pbnUMmsJCGE6LEUBXbsgH37mo75+RlmrVpb\nGxK57enb2Z+1H+ecQiJ2JOGmtiNCF8E1e0c+mjiRC46OxvcOtrdnrk4nS4+Ie06rJkD069eP7du3\nM27cOOOx3bt3ExYWZnLFXl5eLF26lG+++YbKysoW33v++eextrbmypUrJCQkMGHCBCIiIm6a7CBj\n4jrGqFGjuroJPZrEz3QSO9P1tNg1NMBXX8EPPzQdCwqCJ58ECwtoUBr4Iu0LEvIScMu6Sv99qbhb\nuRCiDeGCiysbxoyh8vrEBpVKxWPOzgx1cDDpj/yeFrvuRuJnuvaKXauSuXfeeYeJEycyfvx4qqqq\nePbZZ/niiy/47LPPTK546tSpABw7dozs7Gzj8fLycrZs2UJKSgq2trYMHz6cyZMnExsby5///GcA\nxo8fT1JSEmlpaTz33HM89dRTt6wjKioKPz8/AJycnIiMjDQGrvHRppSlLGUpS7lzy7t3x3PwICiK\noZyZGY+vL8yaNQozM9i9ZzcHLxxE8VPQp+dRufkQWVaOjIoM4YSHJ3+3tqbhxAn8hg7FQq2mV2oq\n1TY2qLrJ9UlZyq0pN/47MzOTtmr1bNacnBzWrFlDVlYWPj4+zJs3r11msv7v//4vOTk5rFq1CoCE\nhAQefPBBypttv/LOO+8QHx/P559/3urzymxW08XHxxtvOnHnJH6mk9iZrqfErq4ONm+G5lt7R0bC\nE0+AWg11DXVsStlEWkEa3qnZBB5JR2+np49rMPG+vux/4AG4PrHBzsyMOTodnm2c6NBTYtddSfxM\n1zx2Hb4DxLVr1/Dy8uJ3v/udSZX8mBsfiZeVleHQOH3pOnt7e0obd1gWQgjRI9XWGhYDPneu6diQ\nITB+PKhUUFNfw/qT68koPIdfYiZ+SVl42Xvh5xrElqAgTg4ZYuiDBXSWlszR6XA0b9WvMSHuaq36\nFOj1evr168fIkSMZOXIkI0aMwNXVtV0acGMWamdnR0lJSYtjxcXF2Nvbt0t94qfJX1htI/EzncTO\ndN09dtXVsHYtZGU1HRs+HB55xJDIVdVVEZccx8XiCwQeScf7VA4+jj5oXQKI6d+fi5GRcD1xC7Sx\nYYZWi5Va3S5t6+6x6+4kfqZrr9i16pNQVFTEX//6VxwdHfnHP/6Bj48PYWFhPP/8821uwI1P5vr0\n6UNdXR3p6enGY0lJSYSGht7xuZcvX96ib1oIIUTnq6iA1atbJnKjRzclcuU15axOXE32tQv0PXga\n71M59HbqjYM2mI8jIrg4cKAxkRvi4MAcna7dEjkhulp8fDzLly9v0zlaPWYODJMTvv32W7Zv385H\nH32EjY0Nly9fNqni+vp6amtrWbFiBTk5OXz44YeYm5tjZmbG7NmzUalUfPTRRxw/fpyJEyfy/fff\n069fv9ZfmIyZM5mMf2gbiZ/pJHam666xKyuDmBi4cqXp2NixMGyY4d8l1SXEJsVSUHqZ/vEpuF0s\nIMgliBptABtCQ6nq3x9UKlQqFWOdnbnfxBmrP6a7xq6nkPiZrr3GzLXqT5tXX32VoUOH0rdvXz7+\n+GMCAwM5dOgQeXl5JlUKsHLlSmxtbXnrrbdYs2YNNjY2vPnmmwD861//orKyEq1Wy7x583j//ffv\nKJETQgjR9YqLYdWqpkROpYJJk5oSuaLKIlYlrKLwWi5hO5Nxu1hAsGswVzyDiR0wwJjIWajVzNJq\nGeroKOuLCnELrXoyp9Fo8PDwYNGiRYwcOZIhQ4ZgcQera3cFlUrFsmXLGDVqlPzFIIQQnayw0NC1\nWlxsKKvVMGUKhIcbyvkV+cQkxVBZXEDYrmQc88vo696Pk159OBAWBv7+ANibmzNHq8VDtuYSd6n4\n+Hji4+NZsWKFyU/mWpXM1dbWcvToUQ4cOMD+/ftJSEggJCSEESNGsHTpUpMq7mjSzSqEEF3j6lVD\n12rjIgRmZvCzn0FjB0teWR6xSbHUXSskfEcS9iVV9NGGcsAnmJTQUPDxAUB/fcaqg8xYFfeADu9m\ntbCw4IEHHuCZZ55h8eLFTJs2jcOHD7Ny5UqTKhXdm0waaRuJn+kkdqbrLrHLzTV0rTYmchYWMHt2\nUyKXXZJNdGI0DQX5RH6dgENJNf4ekXzpH0JKZKQxketja8vTHh6dksh1l9j1VBI/07VX7FqVzP36\n178mPDwcLy8v3nnnHZycnPj0008pLCxsl0YIIYTo+S5ehOhow+xVMKztO28eBAYaypnXMolJisHs\nSj4Dvk7AvqIOr15D2BwQQnZkJHh6AnC/gwOz2nHpESHudq3qZm0cezZ06FBsbGw6o11tJt2sQgjR\neTIyYN06w8LAADY2hkTOy8tQPltwlg0pG7C9XEjYrmRsa1U49B7GV738qQoNBVdXVCoV41xcuP+G\nheOFuBe0JW+5o6VJLly4QE5ODl5eXvhcfxTeXckECCGE6BxpabBpk2GrLgCNBhYsAJ3OUE69msqn\nqZ/ikJNP6J6T2ChmKEEj2O3lS0NYGDg6YqlW8zN3d/rY2nbdhQjRBdpjAkSrnmHn5uYycuRIAgMD\nmTZtGoGBgYwYMYJLly6ZVGlnWb58uSRyJpDxD20j8TOdxM50XRW7kydhw4amRM7BARYubErkEvMS\n2ZSyCefMPMMTOSwo7P8IO3v1piEyEhwdcTA3Z6Fe32WJnNx3bSPxM13jOnNtXTS4Vcncz3/+cyIi\nIigqKiI3N5eioiIGDBjAz3/+8zZVLoQQoudKSIBPP4WGBkPZxcWQyDXu9ngk5wj/Pf1fdOm5hMSn\nYG2uISN8HMc8e0FkJNjZ4WFlxWIPD/Sy9IgQJmtVN6urqyu5ublYWloaj1VXV+Pp6UlBQUGHNtBU\nMmZOCCE6zuHD8PXXTWV3d0PXauM22gcvHGRXxi68U7MJPJKO2taZlLBHuOziZlhsztqaYFtbpru7\nYykTHYTo+KVJXFxcSE1NbXHs9OnTODs7m1SpEEKInuvAgZaJnIcHPP20IZFTFIU95/ew69xO/BLO\nE3gknToHHUcjx3HZXWd4ImdtzVAHB2ZqtZLICdEOWr2d16OPPsqSJUv497//ze9+9zseffRRXnnl\nlY5uX5ssX75c+vJNIDFrG4mf6SR2puuM2CkK7N5t+GrUqxc89RTY2hoSue3p29mfuY/AI+n4JWVR\n6ubL4YhHKXXXQkQEKisrxru6Ms7VFXU32ZpL7ru2kfiZrnHyQ1vHzLVqNcZnnnmGgIAA4uLiSE5O\nxtPTk3Xr1jFmzJg2Vd7R2hocIYQQBooC27cbulcb9e5tWBDY0hIalAa+SPuCxEvH6fvtafTnLnPZ\nsy+ng+5DcXWDkBAszc2Z4e5OkMxYFcKocdWNFStWmHyOO1qapCeRMXNCCNE+Ghrgyy/h+PGmY336\nwJNPgrk51DfUs/X0VlJzk+m/LxXXC/mc7T2QHJ8wVFot9OuHg4UFc7RameggxG20JW+57ZO5pUuX\n3nRiVbNH4oqioFKpeOONN0yqWAghRPdXXw9btxqWIGkUEgLTphn2XK1rqGNTyibSc1MI23MS+8sl\nJPQdTrEuEJWnJwQF4WFtzRytFnvZY1WIDnHbMXMXL17k4sWLZGdnG78ajzX/EncfGf/QNhI/00ns\nTNcRsaurg40bWyZykZEwfbohkaupr2HtibVk5JwkYkcSVvkVfB/2sCGR8/GBPn3oq9HwtF7frRM5\nue/aRuJnuvaK3W0/XdHR0e1SgRBCiJ6npgbWrzds09Xovvvg8cdBpYKquirikuO4nJdO5I5kqqvg\nSPgYzOy1qPz9wceHYY6OPOrs3G0mOghxt2rVmLnU1FRcXFzQ6/WUlpbyf//3f5iZmfHKK69g200H\nssp2XkIIYZqqKli7Fi5caDr24IMwZowhkSuvKWdN8hquXcogfEcShSpbkvoOx1bjCkFBqL28eNzF\nhSGyx6oQP6k9tvNqVTIXHh7Opk2bCA4O5rnnnuPMmTNYW1vj5uZGbGysSRV3NJkAIYQQd66iAtas\ngea7NY4ZAw89ZPh3SXUJsUmxVORkErEjiQxbN9KD7sfOxgn69sVKr2eGuzuB3fQPfSG6qw5fNDgr\nK4vg4GAaGhrYsmULGzduZPPmzWzfvt2kSkX3JuMf2kbiZzqJnenaI3alpRAd3TKRGzeuKZErqixi\nVcIqqrPOEb49gUTnXpztMww7W2cICcHR05OFHh49LpGT+65tJH6m6/Axc81ZW1tTUlLCqVOn8PX1\nxd3dndraWqqqqtqlEUIIIbrWtWsQEwOFhYaySgWTJsHAgYZyfkU+MUkxmJ3Pon98Kt969aPSoy/2\nNg4QGoqnTsccrRa7bjzRQYi7Vau6WV988UUOHDhAaWkpv/rVr/if//kfDh8+zLPPPku0ec0XAAAg\nAElEQVRSUlJntPOOSTerEEK0TkGBIZErLjaU1WqYOhXCwgzlvLI8YpNisUnPxO/bdOJ7h6F288fW\n1hHCwuin1zPNzQ0L2ZpLCJO1JW9p9aLB33zzDZaWljz88MMAHDt2jJKSEkaPHm1SxR1NkjkhhPhp\nV64YErmyMkPZzAxmzIC+fQ3l7JJs1iSvwel0Ju4/ZLPXPxyNUy9s7JwgPJwHPDx41Nm5xTqkQog7\n1+Fj5gDGjh1rTOQABg8e3G0TOdE2Mv6hbSR+ppPYmc6U2F26BKtWNSVyFhYwZ05TIpd5LZOYpBjc\nktOxS7rCN0GDsHP2wcbBBfWAAUzy8eExF5cen8jJfdc2Ej/TdeqYuZ5q+fLlsjSJEELcwoULEBcH\n1dWGspWVIZHz9TWUzxacZcPJ9XgnnKMyu5bvAyLR2euxdHTBKiKCJ729CbCx6boLEOIu0bg0SVvI\n3qxCCHGPyciAdeugttZQtrGB+fPB09NQTr2ayqcpm/E9nEZuiQ1ntL7o7fRYOLviNGAAc7y80Fpa\ndt0FCHEX6pC9WYUQQtx90tIMW3TV1xvKdnawYAFotYZyYl4in6VuJeD7s5yucyVPp0Ov0WHhrsNr\nwABme3jIjFUhuplWj5mrqalh//79bNiwAYCysjLKGgdaiLuKjH9oG4mf6SR2pmtN7E6ehA0bmhI5\nR0d4+ummRO5IzhE+T9lC7wNnOK7y4LKz3vBETu9J//vuI8rL665M5OS+axuJn+naK3atSuZOnDhB\ncHAwzz77LIsWLQJg3759xn8LIYTo3o4fh08/hYYGQ9nFxZDIuboaygcvHOSblM/x3pfOIRs/yuxd\n0dvpMffqxYNDhzJDp5OlR4Toplo1Zm748OE899xzLFiwAGdnZ4qKiigvLycoKIhLzZcK70ZkzJwQ\nQhgcOgTNN+zRag1j5OztQVEU9mbu5bszu3H97iI/OPhiZmmLzk6HeS8fJt53HwNlj1UhOlyHrzPn\n7OxMYWEhKpXKmMwpioKLiwtFRUUmVdzRJJkTQgg4cAB2724qe3gYEjlbW0Mitz19Owln92N99Con\nHLywsrBBq9Fi6x/Ak0OG4N/DtuYSoqfq8HXmfH19OXbsWItjR48eJSgoyKRKRfcm4x/aRuJnOomd\n6W6MnaLArl0tEzkfH3jqKUMi16A08Hna5yScjqfueDHJjt5YW9iitdPhEtyXRcOG3TOJnNx3bSPx\nM12nrjP3xz/+kYkTJ/Lcc89RU1PDn/70J95//30+/PDDdmmEEEKI9qMo8PXXcORI0zF/f5g1Cywt\nob6hnq2nt3I27SjFaTVcttNia2GLu0ZLr5AQZg8ciMbMrOsuQAhxR1q9zlxCQgIffPABWVlZ+Pj4\n8MwzzzBo0KCObp/JVCoVy5Ytk0WDhRD3lIYG+PxzSExsOhYcbNiiy9wc6hrq2JSyifNpCVw+D8UW\ntthZ2uGqcSc0MpIpYWEy0UGITtS4aPCKFSs6fm/WnkbGzAkh7jX19bBlC6SkNB0LDYWpUw17rtbU\n17D+5HoyT53kUo4FVWYW2Fva42KvZcTgwYzu27fHb80lRE/V4WPmqqur+c9//sMvfvEL5s+fz4IF\nC4z/FXcfGf/QNhI/00nsTLd7dzwbNrRM5AYMgGnTDIlcVV0VsUmxnEk5RVauNVVmFjhaOeLmoGPK\n8OGM6dfvnk3k5L5rG4mf6Tp1zNxTTz1FcnIykyZNQqfTGY/fqx98IYToLtLSsti+/Ryff56MlVUD\n/v4BuLn5cv/9MG4cqFRQXlNObNIaMtIucCXfElQqnKyd0Nu7M3PUKHp7eXX1ZQgh2qBV3axOTk6c\nP38eZ2fnzmhTu5BuViHE3S4tLYuPPkonLW0MJSWGY3V1u1m8OJCnnvJFpYKS6hJWJ8ZyJu0KpYWG\nP8BdbFzwtXNl7tixuLm5deEVCCEadfjerL6+vlRXV5tUgRBCiI7x1VfnOHVqDM13VgwKGkNFxR5U\nKl+KKov4JCGGtLPF1BQZEjlXG1f627sya8IENI6OXdRyIUR7uu2Yud27d7Nnzx727NnDggULmDJl\nCmvXrjUea/wSdx8Z/9A2Ej/TSexar7gYDh5UGxO5a9fiCQwEX1+oqVGTX5HPv45Hc+JMGTVFhj28\n3G3dGebozlNTpkgi14zcd20j8TNdh4+ZW7RoUYsxcYqi8Ic//OGm150/f75dGiKEEKJ1CgogJgaq\nqhqMx3x8wNvb8O9K83z+37EYMs9VY15ciwoV7hp3xjm68fDkyaisrLqo5UKIjiBLkwghRA+Slwex\nsVBeDvn5WSQnpxMWNgZ3d8P3r1avp/K+01QWWmFVWo0KFR627jzppifyiScMi80JIbqdDl+aZPLk\nybc8Pm3aNJMqFUIIcecuXoToaEMiB+Dh4cvSpYGEhOzBySketetaCoekU1FgjVVpNWqVGj8bN571\n6EXklCmSyAlxl2pVMne7sXF79+5t18aI7kHGP7SNxM90ErvbO3eusWvVULa2hgULwKd3FYrrKY7k\nfMTXyndUZ9djXVaFWqWmn5ULz/cOwm/iRJBdHW5L7ru2kfiZrlPWmVu6dCkANTU1vP766y0e/2Vk\nZODn59cujRBCCHF7p07B5s2GHR4ANBqYPx+Ky9JY+f5KzuVdJqOkFrtroLIqQ+PTi/s1LjzVLwzb\nESMMi80JIe5aPzpmLioqCoC1a9cyd+7cpjepVOh0OhYtWkRgYGCHN9IUMmZOCHE3SEyEzz6Dxh9n\njo6GJ3KurvDC0l8TfzEL1UMPo24wR61A4fEERlVV8cEvfo35/fd3beOFEK3WYevMRUdHA/DAAw/w\n7LPPmlRBV1q+fDmjRo1i1KhRXd0UIYS4Y4cOwfbtTWVXV0Mi5+gI+dWVbLt0BcuHx2FVXW8cMxPZ\n24/8AwckkROih4iPj29zd2urBlH0xEQOmpI5cWdk/EPbSPxMJ7EzUBTYt69lIqfXw8KFYGvfwFdX\nsll07P9n787jo67u/Y+/ZrJvkISQQBYSIBA2ZUcgggGsWMUFFRBFRLnWttperb33/lprCd3sr/da\n7/3VKldUELe617WgAhHKIiD7YiQBsgKBrGRfZn5/fMlmWCbfycxkeT8fDx7JnG8y3zMfhvDJOZ9z\nzkfU+gbifz6RK//mW4aeKSDcXk19SIjH+t4V6X3nHMXPvLS0NFJSUkhNTXXqebS0SUSkE7Hb4bPP\nYNu25rYBA2DhQjvHbZX8LSODHTl7CT2WT1BdAzTY6VN1jugzpwns14vaei+ievf13AsQEbfTPnMi\nIp2EzQYffQR79jS3DR4MKXNrWX+ukH8WZJJ/4gB9ss/g1WCj4ng2JVlnGDFiBJUhQeDlxZn0Y/z0\nrruYOWuW516IiLSbM3mLkjkRkU6gvh7eew8OH25uSxzRQO+UEnZVlJJe8A21R4/Q6+w5/OrrmHQ6\nh9u8I9gTNYAPcnNpsFjwAm65/nolciJdkFuSuY0bN7JmzRry8vKIjY1l0aJFzJw509RN3UHJnHmN\nc/hijuJnXk+NXW0tvPUWZGQYj+3YCZlwjoYrSiipq+Sb7D0EHD2OX2UNw87mcXVRIeMHTsR/wd3G\nYaz03Nh1BMXOOYqfeS1j5/ITIF544QUWLFhA//79ue222+jXrx933XUXzz//vKmbioiIoboaXn21\nOZEr8aumKDmfcyMLOVVZxJGDaYQc/Jb4gtPcnL6LW0rLmTztDvwffqQpkRORns2hkbkhQ4bwzjvv\nMHr06Ka2/fv3c9ttt5HR+BOok9HInIh0dhUVxjmrp05BtVc9meFFBI2sID4eTpXkUrT/K6JOn2Vi\nXgbxpYUMjhhK7Lz7sUyapI2ARboZl0+z9unTh5MnT+Lr69vUVlNTQ3R0NIWFhaZu7GpK5kSkMyst\nNY7nKiiykdOrjOzepQwaYiM6xs6JnANYDuxjXE4mowpy8Ld4kTTsaiIWP2jsUSIi3Y7Lp1mTk5P5\n2c9+RsX5053Ly8v5+c9/ztSpU03dVDo37RnkHMXPvJ4Su8JCePElO99UVbAzJo8TYcUMHW4jsn8t\nGfs3MmjjOubv28Lo01n09glkzPVLiHjkF5dM5HpK7FxBsXOO4meeW85mbbRixQruvPNOevfuTXh4\nOEVFRUydOpU33nijQzohItJTnDoFz75Ry37/IkrCqrBYYOQI8PcvomzDP7h53076VZQCEBEaTdK9\nj+EzdryHey0inVm7tibJyckhPz+f6Oho4uLiXNkvp2maVUQ6m6NZDfz+HyWc8DsHFjtWK4waBb5V\nGQz89DWG52Vhxfi5FTtsEoMf+A8sffp4uNci4g4ur5kbO3Yse1ruYnnehAkT2LVrl6kbu5qSORHp\nLGx2Ox8cOceKHSXU0ACAtzdcOdJOQsbnDF33Nv719Ua71ZuBN95NzK2LwcvLk90WETdyec3chVas\n2u12jh07Zuqm0rmp/sE5ip953TF2J6qqWL47n/+3s7ApkfPxge8Pr2HWP57iyk/eaErkfENCGfnI\nH4i5/b52J3LdMXbuotg5R/Ezzy01c/fccw9grFxdvHhxq4zxxIkTjBw5skM6ISLS3ZTW1/NZURHr\nMyv4Jr25Pczbhx/2P07gS3+ioeJcU7v/kOGM/fFv8QuL8EBvRaQru+Q0a2pqKgBPPvkkv/zlL5uS\nOavVSlRUFPPmzSM8PNwtHW0vTbOKiCfU2WxsKS1lS1kZx3NsTZsBW21WrmwI5l+sb1P0z7ew2W0A\n2C0WQq+/lTF3PIxF06oiPZbLa+bWrl3L9ddfb+oGrvAf//EfbNu2jYSEBF566SW8vdsOMCqZExF3\nstvtHK6s5LOiIkrq68nOguMnjGuR5cFcU1PP9JI/Upizr+l76kKCGLj0MRLHdN6jEUXEPVxeM9eZ\nErl9+/aRn5/Ppk2bGDZsGO+8846nu9TtqP7BOYqfeV01dqdra3n51CneLiigpL6eY8eMRC64xo+x\n+f2YV5DJlMx/bZXIVSUmMGbZcx2WyHXV2HUGip1zFD/z3LrPXGeybds2Zs+eDRhJ5qpVq7jzzjs9\n3CsR6YkqGxrYWFLCrnPnsNvt2O3w7VE4m+vF0OIwYkp8uKrkDXpXvUVZQxUANi8rNbNSmDHv3/D3\nCfDwKxCR7qBd+8x1Bk8++SQjRozglltuISMjg2XLlvHaa6+1+TpNs4qIq9jsdr4+d44NJSVUNTSc\nb4P0IxZ8MkOILwklvPQ0407/FS/v7djOr2Kt6B1IyN33cfXE27FaHJoYEZEewuXTrK7wzDPPMGHC\nBPz9/bnvvvtaXSsqKmLu3LkEBweTkJDQ6qSJ0NBQysrKACgtLe20CzBEpHs6UVXF/+bn80lhYVMi\n12CDgr0BDNgbTWJhOAOztjMh6wksXluaErmCpFgS/u33TJ80T4mciHQoh36i2Gw2nn/+eWbOnMkV\nV1wBwKZNm3jrrbdM3zgmJoYnnniC+++/v821hx56CH9/fwoKCnjttdf40Y9+xOHDhwGYOnUqX3zx\nBQDr1q3j6quvNt0HuTDVPzhH8TOvM8eupK6OtwoKWH3qFKdra5vag/HBf2skUfujCK2oY+SBNSQU\nP40tKBMsUO/jRc73rmL6T/6LkbFjXda/zhy7zk6xc47iZ15Hxc6hZG7ZsmW8+OKLPPDAA2RnZwNG\nMvbHP/7R9I3nzp3LLbfcQp/vHFVTUVHBe++9x29/+1sCAwNJTk7mlltu4ZVXXgFg9OjRREVFMX36\ndI4cOcLtt99uug8iIpdTZ7ORVlzMM3l5HK6oaGr3sVqZGhBG4GfR1GUGEVZ8gtG7/kwIb+EVchaL\nBcoiQjiz6DZun7+MfsH9PPgqRKQ7c2gBxKpVq9izZw99+/blxz/+MQADBw7skBMgvjs//O233+Lt\n7U1iYmJT2+jRo1tlr3/6058ceu4lS5aQkJAAGNOzY8aMISUlBWjOhvW47eOUlJRO1Z+u9ljx6x6P\n7XY7kZMm8VlREfv++U8AEiZPBsCybx9DvUL4NmsWhWdsVG97iuqCrVgGl+IfUs/eUyWcHtiXax74\nITcOuZ7Nmza7pf+NOkP8utLjxrbO0p+u9rixrbP0p6s8bvx89erVOMuhBRDR0dFkZmYSEBBAWFgY\nxcXFnDt3jhEjRpCTk+NUB5544glyc3NZtWoVAJs3b2b+/PmcPHmy6WtWrlzJ66+/zsaNGx1+Xi2A\nEBGzTtfW8o/CQk5UV7dq7+/nx/fDwwmq8OeVV6D6VAnDD78DZdvwisgkOBhq/X04On0UyTPvZUy/\nMR56BSLS1bh8AcT3v/99fvazn1F9/gebzWbjiSee4KabbjJ105a+2/Hg4OCmBQ6NSktLCQkJcfpe\n4pjv/pYv7aP4mefp2FU2NPBJYSEr8vNbJXKBXl7cFBHBA/3741fqz6pV4H30CON2/ZW6c5/j3ddI\n5Ir7h5F+xwxunfNztydyno5dV6bYOUfxM6+jYufQNOuf//xnlixZQmhoKHV1dQQHB3PdddexZs0a\npztgsVhaPR46dCj19fVkZGQ0TbXu27ePUaNGtfu5U1NTSTk/7SUicjE2u51d586xscVWIwBWi4VJ\nISGkhIbi7+VFbi68/nIdMYc+Iyp/M2csBwmNLMc/0MKxsQnYk5O574o7CfYN9uCrEZGuJC0tzemk\nrl37zJ0+fZqsrCzi4uLo37+/UzduaGigrq6O5cuXk5eXx8qVK/H29sbLy4uFCxdisVh44YUX2L17\nN3PmzGHbtm0MHz7c4efXNKuIOOJ4VRVri4parVAFGBwQwPXh4fT19QXg2DH48MUzJO59B++KdM5a\nDxERWQcR/hyePpwho2dyw5Ab8LLqfFURaT+Xn836r//6r9x9991MmjTJ1E0uJDU1ld/85jdt2n79\n619TXFzM/fffz+eff05ERAR//OMf233Kg5I5EbmUkro6PisubrVCFSDMx4fZYWEkBQY2zRx8c8TO\n5v+3h0Hpn1Jhy6LUK4PISDtlQ/vybfIwZo+6hQnREzzxMkSkm3BLMvf2228TGBjI3XffzV133UVS\nUpKpG7qLkjnzWq5KkvZT/MxzR+zqbDb+WVrKltJS6lv8jPC1WpnWuzdTevXC29pcTrx/RzXpT31M\nxOn9FHKUKq+T9I2xkp2cSOnIRBZccScDeg9waZ8dofedeYqdcxQ/81rGzuULIP7nf/6HnJwcnnvu\nObKzs5k8eTLjx4/nqaeeMnVTd0lNTVVhpogAxmKrQxUVPJOXx5clJa0SuSuDg3k4JoZpoaGtErk9\nH+eR9+v/Jez015xiL9XeJwkZFsiBueNhwgR+MOHBTpHIiUjXlZaWRmpqqlPPYeps1ry8PJYsWcL6\n9eux2WxOdcBVNDInIo1O1dSwtqiozVYj0ee3Gonz92/VbrfZ2ffcVorfWU+tvYQCDmL1qaVhWn9O\nTE3kiphxzBk6Bx8vH3e+DBHpxpzJWxxazQpQXl7O+++/zxtvvNE0LNgRq1lFRFylsqGBjSUl7Dp3\nrtUPySAvL2aFhTEmOBjrd1bU28+Vc/B3f6fkqwzKOUkh32INsnL21hGUDu3HdYOv46qYq9qsxBcR\n8RSHplnnzZtHVFQUzz//PDfddBNZWVl8+umnLFq0yNX9Ew/Q1LRzFD/zOip2NrudHWVl/CUvj51l\nZU2JnNViYUrv3vwkJoZxISFtEjlbxjEO/3QFZ7/6lkKOUkg6Ff1CyHlgAtXD41l05SImx07ulImc\n3nfmKXbOUfzMc+s+cxMmTOC//uu/iI+P75Cbuov2mRPpeY5XVfGPoiIKLrPVSCsNDTR8sZFvXtzC\nqYIaznCYakrIGjUA2y0J9Avtz52j7iQsIMxNr0JEegq37zPXlahmTqRnudRWI9eHhzM0IODCI2ol\nJdS/+Q6H1+VysugcBRyk3MfGN9OHE3p1OKMiR3LLsFvw9bpAEigi0kFcUjM3bNgwvvnmGwDi4uIu\neuPs7GxTNxYR6Qjt3WqklcOHqXv3Qw7uqiav9DSFpJMb1pvMmcMZcIUf1w6aRXJccqecVhURaXTR\nZG7lypVNn7/yyisX/Br9gOuetGeQcxQ/89oTu8atRj4vLqa0vr7VtSuDg7k2LIxe3hf5EVdXB+vW\nUbt1F/v228kpP0aJJZfdAwdy7uo4hg0J4I4RtzOkzxAnX5H76H1nnmLnHMXPvI6K3UWTuWnTpjV9\nfubMGebNm9fma9555x2nOyAi0l6namr4R1ERWQ5uNdJKQQG88w41OQXs3ltHVtVhzvpX8eWIsfQa\n24uJSREsHLWQPoF9XPwqREQ6hkM1cyEhIZw7d65Ne1hYGMXFxS7pmLMsFgvLli3TAgiRbqSyoYEN\nxcV8XV5+wa1GxgYHX3zGwG6H3bth7VqqyurYsbeCnJqDHO0bzLakJAaO9CZlVBK3Db8NP28/N70i\nEenpGhdALF++3DXHeR07dgy73c7o0aPZv39/q2uZmZnce++95Ofnm7qxq2kBhEj3YbPb2XXuHBtL\nSqhqaGhqt1osXNWrF9f07o2/1yUOuK+uho8+gkOHKC+HrfvOkNvwLdsTB3I0uj/DR1iYN/EaUhJS\nVD4iIh7hsuO8EhMTGTJkCJWVlSQmJrb6s3jxYpYtW2bqptK5ac8g5yh+5l0odserqliRn8+nhYWt\nErnEgAB+FB3N7PDwSydyubmwYgUcOkRpqZ2Ne45zyPcEH44fQ0ZsNGPH+PGTGQuYMXBGl07k9L4z\nT7FzjuJnnlv2mWs8qmv69Ols2rSpQ24oIuKIi201Eu7jw+xLbTXSyG6HLVtgwwaw2ThTWE/aoSPs\n7ufHjsHjwNeLaRPCeGj6QiKDIl38akREXEf7zIlIp3KprUam9+7N5EttNdKovBzefx8yMwHIOVXJ\n+sxv2Dg0jqy+ffHxgZuvHsy/TL2DAJ8AV74cERGHuPxs1rq6Op599lm+/PJLCgsLm0bsLBaLRuxE\nxGnpx47x+cGD5NTWklFZSf+EBCJa7G95ZXAw3wsLI+RiW420lJkJ770H50f00rML+agwn7TxIyj3\n98fPDx64PpnbxszCanHoREMRkU7NoZ9kP/vZz/jf//1fpk+fzq5du7j99tspKChgxowZru6fU1JT\nUzWXb4Ji5hzFzzH1Nhunamr44OBBlm3ZwrqEBNYVF1N4xRXsTU/nbE4O0X5+LO3fn9v69r18ItfQ\nAJ9/Dq+8AhUV2O12dmVm87/1ZXw6eiTl/v4EBXjz63m3c8fY73W7RE7vO/MUO+cofuY1rmRNTU11\n6nkcGpl799132bZtG/Hx8SxbtoxHHnmE66+/nh/84AcsX77cqQ64krPBERHn2e12iuvrKaitpaCu\njtPnPxbW1WGz29mxaxeVo0cbydh5ARMnEpKRwQPTpjm2KKG4GN5911jsANTbGthw4gSrwsM5GWac\npxoR0ps/3n0nif36u+R1ioiY0biFmjP5lEM1c2FhYRQWFmK1Wunfvz8ZGRkEBgbSq1evC+4/1xmo\nZk7E/SoaGoxkrUXidqaujtrzpRkXsn3TJqqvvBIACxDj50eCvz8Rhw7xyE03Xf6mhw7Bhx9CTQ0A\nVXVVvF14mtfDo6n2Nc5THRiWwH8umUdE7yCnX6OIiCu4vGZu2LBh7Nq1i0mTJjF+/HiWL19OSEgI\nsbGxpm4qIl1brc3GmcZRthaJW0WL0bXLsVgshHl7E+3jQ4O/P0FeXvT28sLv/OKGyx5rX1cHa9fC\n1183NRVWl/IcNXwRFQ/nR/TG95vE75bMJsD/EtuXiIh0YQ4lc//zP/+D9/l6lT//+c/86Ec/ory8\nnOeff96lnRPP0Dl7zulO8bPZ7RTW1TVPj55P3Irr69v1G2SQlxdRvr5E+vgQ6etLlK8vfX188LVa\nSZ88mdW7d+M3fjwntm8nYfJkar7+mlnjxl38CU+fhnfegTNnAGMq9zhl/KmXF9/UGtuMWPDiuoQ5\n/NuisTiybqKr607vO3dT7Jyj+Jnn8rNZW5o0aVLT50OHDmX9+vVO31hEOg+73c65xinSFonbmbo6\nGtqRtPlYrUT6+LRJ3IIusalv0qBBLAHWHzzI2ePHiQwOZta4cSQNGnShjhojcWvXQn09AA22Br4K\nreb/EcSpMuNHmi8hzBu+gKXzYrncLiYiIl3dRWvm1q9f71Dh8cyZMzu8Ux1BNXMiF1bd0NBqIUJj\n4lZ9ibq277JaLPTx8WlO2M5/DPP2dt0pClVVxpFchw83NVVbGvggwc7rhV6Ulhn37UUsi8cv4PY5\nIXThAx1EpIdxSc3c0qVLHfqhfPz4cVM3dofU1NSmVSIiPU29zcbZllOk5z+WnR/RclQvb+/WI20+\nPkT4+Fx+496OlJNjrFYtKWlqKurlw8uD7GzItNC4Dqs/47h/2g1cO9NbiZyIdAmN25M4QydASBuq\nf3COu+N3ua0/HOVvtRJ5PmmL8vVt+jzgUueedrA2sbPZjCO5Nm40Pj/v6KBQ1kQU8/VBC5WVYMFK\nIt9nyfcmkJzcM7M4/bs1T7FzjuJnXsvYuXw1KxinQGzfvp38/HwWLFhAeXk5FouFoCAt9RdxFzNb\nf3yXl8VC3/OjbC0Tt15eXp3roPlz54wjuY4da2qy+fny5ehQ1loK2LfPQnU1+BDEKMt8Fs2JZ/x4\nD/ZXRMRDHBqZO3DgADfffDN+fn7k5uZSXl7OJ598wpo1a3jzzTfd0c9208icdGUdsfUHQJiPT1M9\nW2PiFu7jg1dnStouJCPDSOTOH8kFUN2vL28Pt7G/vJB9+6C2FoLpz5WWO7nr9t6MGuXB/oqIOMmZ\nvMWhZC45OZkHH3yQxYsXExYWRnFxMRUVFQwZMoT8/HxTN3Y1JXPSFXTk1h8tFyI01rf5dpGlnFnp\n6WR+8QXW6mpsx48zGIiPiDAuWiycGTecNWFZ5BVVsH+/sZA1iisZ4XUTd93pw5AhHu2+iIjTXJ7M\nhYWFUVRUZGzyeT6Zs9vthIeHU1xcbOrGrqZkzjzVPzjnQvHr6K0/Wk2R+vgQ3C7Jd18AACAASURB\nVIU3UstKTydj9Wpm2WykbdpEip8f6+vrSRwzhviBAzk8bRjvVe/hTGE9Bw9CQ4OFwXyPwb5TuPtu\nC/Hxnn4FnYP+3Zqn2DlH8TPPrTVz8fHx7Nq1i4kTJza17dy5kyH6dVikSfqxY3xx6BAH9u1jc1ER\nwxITCYyJMbX1h8VioU/jKtIWiZtLt/5wt4oKyM0l85lnmJWTA2VlxvYjfn7M8vbmi3PnSL92EFuL\nd3L2rLEjidUWwJXcQWzgYBYtguhoT78IERHPc2hk7uOPP2bp0qU8+OCDPPXUUzz++OOsWLGClStX\nMnv2bHf0s900MiffZbPbqbfbqWv8aLO1fnyR6458TU5WFluPHMEybhy159939bt2MSYpiYi4uEv2\nq5e3d5sVpH3dvfWHqzU0QEGBscVIbq7xp6gIgLTt20mprm7+WouF+oQB/LlPHZVzhnL6NHzzDQTa\nIxnFnUT1Cueee6BvXw+9FhERF3D5yNycOXNYu3Ytzz//PNdccw3Z2dm8//77jNfSsW6lcWSpDvAB\nrh058sK78HcAu91OgwNJkqPXHfma9kxnttfO9HTqxo41Tig4z3vCBI7v29eUzPlZrW1ORnD31h9u\nU15uJGyNyVt+vnGW6gXYWiatQUFUDIrjQNUJTtd7UZYHRzOgr30Ew7iVvuG+LF4MoaFueh0iIl3A\nZZO5+vp6kpKSOHz4MM8995w7+iQekH7sGKu+/hrruHGc2L6dmKuu4q87dnBbbS0D4uOdSrS++7Hx\nT3caObW1mPos2bWLmKuuItjLi6jAQO6KiiKqM2790VEaGuDUqdbJW4vNfS/Kywv692dwbCzvfL6O\ngdWlbCzIIrrqKHtDQshPnMLJoxYGMoMBTCMq0sI990BIiOtfUlekuiXzFDvnKH7mue1sVm9vb6xW\nK1VVVfj5+Tl9Q3fSCRCO++LQIRg3jq1lZZRUVpJ/7hwkJZG5fTsTu9jf+8VYLBa8z//xudhHq9Wh\n69+95turFyUhIVgtFvKDgxl0PuOIDAhgaGCgh195Bysra54qbRx1c+RUid69ITYW4uKMj/36gbc3\n1RnppOVv56PcbE6UFxPSP5ATdjvBp3yZEHonESQRGwt33w0BAa5/eSIi7uS2EyCeffZZPvjgA37x\ni18QFxfXanRhkIum4Zylmrn2+e+PPqJg5Ei2lpa2avffv5/J06e75J5eHZBEtScR87JYXDYyln7s\nGKt378avRelBzddfs+RiB8Z3FfX1cPJkc+LWuFDhcry9jdUJLZO3CwypVdVV8csXfsmh4EPUNtRi\ntxuldNXnAkk4nkLywH9n4EBYuBB8fV3w+kREOgmX18w9/PDDAHz++edtbtzQzk1MpXPyAbwAH4sF\nq8WCF8Zh6r29vBgYENDho1ne5+/TXSQNGsQSYP3Bg9QCvsCsrpbI2e1GotZykcLJk8Y06uWEhRkJ\nW2PyFhVlTKNeRGl1Kdtzt/P1ya85UniEEnsZRUVVlJdboCqEWL9BeFl8GTYM7rjDyA1FROTCHPoR\naWvHlgrSNV07ciSrd+8mefx4TmzfTsLkycbI0tSpJPXr5+nudQlJgwaRNGhQ16kfqaszkrWWyVvj\nifWX4uMDMTHNyVtsLAQHO3TL0+Wn2ZqzlQMFB7DZjZ8rleU1nKytorayH3Xp3oT0mUCB7TgDg84x\nb94lc0Jpocu87zohxc45ip95bquZk56h5cjS2ePHiQwO7nojS3JxdruxKKHlIoVTp1odXn9R4eHN\nU6WxscaoWzu2TbHb7WSVZrElewtHi462uR5gj8Py9SD8+8ZgqcvGgoXgohiGJcYpkRMRcYBDNXNd\nkWrmpEerrTUWJrRM3lqcc3pRvr7GqFvL5M3kAg6b3cY3Z79hS/YW8s7ltbmeEJrAlaHJ/O6xXHJO\nRlNiX4/dq5Y+vX2ZkDiLIQNP8sgjKabuLSLS1bi8Zk5EOrHGVQMtFykUFDg26hYR0XqRQt++7Rp1\nu5C6hjr2nd7H1pytFFUVtbpmwcLwvsOZGjcVn6pYXn0VqqtyCPJNIogkBg82ugLg69s2ARQRkbaU\nzEkbqn9wjsvjV1MDeXmttweprLz89/n5tV6kEBPToXt9VNVVsTN/J1/lfkVFXetRQG+rN2P6jWFK\n7BT6BPbhxAl45Q3jpQwaNJj9+9czatQsKivTgBRqatYza1Zih/WtJ9C/W/MUO+cofuZ5rGbuu4sh\nrN3pyCGRzsZuh8LC1osUCgpanTRxQRaLMcrWcpFC375GewcrqS5he+52dp/cTW1Dbatr/t7+TIqZ\nxKSYSQT7GoskDh2C995rXiQbExPPrbfCt99u4PDh/URG2pg1K5GkpPgO76uISHfkUM3c119/zcMP\nP8y+ffuobnGGYmfemkQ1c9IlVVcbo26NyVtennH4/OUEBLRO3GJiwN/fpV09VX6KrTlbOVhwsGll\naqPefr2ZEjeFcf3H4evVvEHcV1/B2rXNuWhIiLEZsBZMi0hP50ze4lAyN2rUKG6++WYWLVpE4HeK\noRMSEkzd2NWUzEmnZ7fDmTOtFymcPevYqFtkZOtFCn36uGTUrW2X7ZwoOcGWnC1kFGW0uR4VFEXy\ngGRG9h2Jl9WrxffBF1/Ali3NXxsRAYsW6ZxVERFwQzLXq1cvSktLu9S5kkrmzFP9g3MuGr+qqtaL\nFPLyjKKxywkMbL1IITraqH9zI5vdxpEzR9iSs4X8c/ltrg8MHUjygGQGhw1u83OioQE+/BD27Wtu\ni42Fu+5qu1BW7z3zFDvzFDvnKH7mtYydy1ezzp07l3Xr1nH99debuolIT5CVnk7mF1+w/8gRbAcO\nMHjsWOL9/ZuTt8LCyz+J1Wrs49YyeQsLc8uo24XUNdSx99RetuZspbi6uNU1CxZG9B3B1LipxPSK\nueD319TAW29BZmZzW1KScaqDj48rey4i0nM4NDI3f/58PvroI6ZNm0ZUVFTzN1ssrFmzxqUdNMti\nsbBs2TJSUlL0G4N0vIYGYwVpZSVUVJB18CAZ777LLJvNOEXh3DnW19SQOGYM8RERF3+e4ODWK0z7\n9+8Uh5BW1lWyM28nX+V9RWVd65Wy3lZvxvYby5S4KYQHhF/0OcrL4fXXje3uGo0fDzfe6PTuJyIi\n3UZaWhppaWksX77ctdOsqampF/7m8wlTZ6RpVmmXhgZjU93zyVnTx4u1tVgIBLBhxw5mXmB7kA1B\nQcycONF4YLUayVrL5K13b4+Nul1ISXUJ23K2sfvkbupsda2uBXgHNK1MDfINuuTzFBXBK69AcYvB\nvJQUuOaaTvVyRUQ6DZdPs14smZPuqVvUP9TXXz4ha9n2neSsvawttuxJKykhJTQUfH2xRkTAddcZ\nyVv//p12bvHkuZNszdnKoTOH2qxMDfUPZUrsFMb2H9tqZerF5OUZI3KNB05YLDBnjjEqdznd4r3n\nIYqdeYqdcxQ/81y+z9ymTZuYPn06ABs2bLjoE8ycOdPpTohcVl2d46NmlZWOLSxwhsVibAcSFASB\ngdiys42E0MfHGG0bPhz8/LBFRcHUqa7ti0l2u53jJcfZkr2FzOLMNtf7BfcjOS6ZkZEjsVocmxc9\netSokas7P6jn42PUxyUldWTPRUSkpYtOs44aNYqDBw8CxvYjF1vJevz4cdf1zgmaZu3k6uocHzWr\nqDDOGnUli8VYWnk+OWv18UJtAQGtCr+y0tPJWL2aWS1Wma6vqSFxyRLiO1kmY7PbOFRwiK05WzlZ\nfrLN9UFhg0iOS2ZQ2KB2rWDfu9dYtdo4SBkQYKxYbTyeS0RELs7lW5N0RUrm3Mhub07OHB09q6u7\n/PM6w2o1Eq9LJWTfTc6cLObKSk8nc/16rLW12Hx9GTxrVqdK5GobaptWppZUl7S6ZsHCyMiRJMcl\n0z+kf7ue126Hf/4T1q9vbgsNNfaQu9TaDxERaaZk7gKUzLVf09Yahw9z5ZAhDJ46lfjoaMeSNHck\nZ46OmgUFGacfeKjSvrPVj1TUVrAjbwc783e2WZnqY/VhbP+xTImdQlhAWLuf22aDf/wDdu5sbuvX\nzzjVISSk/X3tbLHrShQ78xQ75yh+5rl1n7nS0lJSU1P58ssvKSwsbDqf1WKxkJ2dberG0rlkpaeT\nsWIFsw4fxlpQQMqhQ6x/5x243NYaZnl5OT5qFhjo0eSsqyquKmZrzlb2nNpDva2+1bVAn8CmlamB\nPoEXeYZLq6+Hd9+FI0ea2wYOhAULXH6SmIiItODQyNyiRYvIycnh0Ucf5Z577uGVV17hP//zP7n9\n9tv52c9+5o5+tptG5tpnw1//ysy8PNi6tXV7y601LsXb2/FRs8BA4wQDJWcukX8uny3ZWzh85jB2\nWv8bCPUPZWrcVMb2G4uPl/mVtVVV8Le/QVZWc9uoUXDrrcZbQURE2sflI3Pr1q3jyJEjREREYLVa\nufXWW5k4cSI33XRTp03mpH2sdXWt/xe2WsHHB2tQECQmXj5J8/VVcuZBdrudzOJMtmRv4XhJ20VJ\n/YP7kzwgmRF9Rzi8MvViSkvhtdegoKC5bcoUYwcWvQVERNzPoWTObrfTu3dvAEJCQigpKaF///4c\nPXrUpZ0T97H5+BgJ3OTJpOXlkTJoEFgs2CIjjUp2cZg760cabA0cOnOILdlbOF1xus31wWGDSR6Q\nzMDQgR1ytnJBAbz6KpSVNbddd13H7b6i2hvzFDvzFDvnKH7muXyfuZauvPJKNm3axKxZs7j66qt5\n6KGHCAoKIqkTrdQT5wy+9lrWr17NLH9/o57NYjG21pg1y9Ndkwuobahl98ndbMvZRmlNaatrVouV\nkX1HMjVuartXpl5KVha88Ubz/speXsa06hVXdNgtRETEBIdq5jLPn5I9ePBgTp8+zS9/+UvKy8tZ\ntmwZI0aMcHknzVDNXPt19q01xFiZ+lXeV+zM20lVfVWraz5WH8b1H8eUuCmE+od26H0PH4b33jMW\nPYBR8rhgAQwa1KG3ERHpsbQ1yQUomZPupKiqiK05W9l7au8FV6ZeFXMVE2Mmml6Zeik7dhjbjzT+\ncwoONmbe+/Xr8FuJiPRYLl8A8eKLL16w3sbPz4/Y2FgmT56MX4ud76VrU/2DczoyfnlleWzJ2cKR\nM0farEwN8w9jatxUxvQb49TK1Iux22HDBti8ubmtTx8jkQtr/5Z0DtF7zzzFzjzFzjmKn3lurZlb\ns2YN27Zto1+/fsTGxpKbm8upU6eYMGECWef3Jvj73//OREe2sHBSWVkZ1157LUeOHOGrr77qtNO8\nImbZ7XYyijLYkrOFEyUn2lyPDokmOS6Z4X2HO70y9WIaGuCjj4wjuhrFxhrHcwV2/OCfiIg4waFp\n1oceeoikpCR++tOfAsZ/Nn/96185cuQIf/nLX/jDH/7AJ598wrZt21ze4fr6ekpKSvi3f/s3fv7z\nnzNy5MgLfp2mWaWrabA1cLDgIFtytlBQUdDmemJ4IslxySSEXvys5I5QWwtvvw0tF6sPHQp33GHs\nQCMiIh3P5TVzoaGhFBUVYW1xsHh9fT0RERGUlJRQU1ND3759KWu5X4GL3XfffUrmpFuoqa9h98nd\nbM/dfsGVqaMiRzE1bir9gl1fpFZRYewhl5/f3DZ2LNx0k7FzjYiIuIYzeYtDP56joqL48MMPW7V9\n8sknREVFAVBVVYWvfmXvNtLS0jzdhS7N0fiV15az/th6nt7+NOsy17VK5Hy9fJkcO5mfXvVTbht+\nm1sSuaIiePHF1oncNdfAzTe7L5HTe888xc48xc45ip95HRU7h2rm/vKXvzBv3jxGjRrVVDN34MAB\n3n77bQB27NjBT37yk8s+zzPPPMPq1as5ePAgCxcuZNWqVU3XioqKWLp0KZ9//jkRERE8+eSTLFy4\nEICnn36aDz/8kDlz5vDYY481fY8rp5pEXKWwspCtOVvZd3pfm5WpQT5BXBV7FROjJxLgE+C2PuXn\nGyNyFRXGY4sFbrwRJkxwWxdERMQkh7cmOXv2LJ9++in5+flER0dz44030qdPn3bd7P3338dqtbJu\n3TqqqqpaJXONiduLL77Inj17uPHGG9m6detFFzhomlW6mtyyXLZkb+Gbs9+0WZkaHhDO1LipjI4a\n7ZKVqZeSkQFvvWXUyoFxqtsdd8CwYW7thohIj9bl9pl74oknyM3NbUrmKioqCA8P59ChQyQmJgJw\n7733Eh0dzZNPPtnm+2+44Qb27dtHfHw8Dz74IPfee2+br1Ey137pGel88fUX1Nnr8LH4cO34a0lK\n1KbBzrDb7RwtOsqW7C1klWa1uR4TEkPygGSGRQxz2crUS9m3Dz74AGw243FAACxcCAMGuL0rIiI9\nmsv3meto3+3st99+i7e3d1MiBzB69OiLziV/+umnDt1nyZIlJCQkAMYijjFjxjTt59L43HpsPF7z\n2hrW7l5L7xm9yT+Qj9ViZe0/1/KTJT9hyKAhfLXlK6xYSZ6ejJfVi22bt2G1WJl+zXSsFitbNm3B\nYrEwY8YMrBYrm7/cjNViZcaMGZ3i9bnzcVpaGg22Bo6XHKcmtoYzlWc4sfcEAAljEgCoy6zjiqgr\nWHDNAiwWi9v7u3FjGgcPQmGh8fjEiTSCgiA1NYW+fT0Xv8a2zvT32VUe7927l0ceeaTT9KcrPf7v\n//5v/f/gxGPFz9xjgNWrV9MROsXI3ObNm5k/fz4nT55s+pqVK1fy+uuvs3HjRlP30Mhc+/z1zb+S\nH5HPlpwtlHxTQugw4ziooNwgJl5tfv9ACxasFitWixUvq1fz55bmzy91rWV7Z7zWsm4zPSOdf+z8\nB5t3bMYeaSc6PpqI6Iim61aLlSsir2Bq3FSigqPM/2U5yWaDdevgq6+a26Ki4O67oVcvj3ULMH7I\nNf7Ak/ZR7MxT7Jyj+JnXMnZdfmQuODi4zbYmpaWlhISEuLNbPVqdva6pjqsxkQNooMGp57Vjp8He\nQIO9gTpbnVPP1Rk1JqtFJ4vYc2QP1kFWbKONOcuCwwWMYQzRcdGM7z+eybGT6e3f26P9ra83zlg9\nfLi5LSEB7rwT/P091q0m+g/BPMXOPMXOOYqfeR0VO4eTudraWrZv387JkydZsGAB5eXlgJGItdd3\nV6EOHTqU+vp6MjIymqZa9+3bx6hRo9r93C2lpqaSkpKiN5oDfCw+WLAQGRSJ3W7HZrdhx05IYAgJ\noQnY7LamPw22hubP7Q2XvNbdNSar6RnpMBBsdlvTtcCkQHxKfXh03qNuXZl6MdXV8Le/wYkTzW0j\nR8LcucaiBxERcb+0tLRWU69mODTNeuDAAW6++Wb8/PzIzc2lvLycTz75hDVr1vDmm286fLOGhgbq\n6upYvnw5eXl5rFy5Em9vb7y8vFi4cCEWi4UXXniB3bt3M2fOHLZt28bw4cPNvTBNs7ZLekY6qzeu\nxm+IHyf2niBhTAI1R2tYMmOJ6UUQdrsdO3ZTSeCF2l1xzdF+XOxao+3/3E51bDUAlUcrGTN5DP2C\n+xF+OpxH7nykQ/6OnFFWBq++CgUtDpaYPBlmzza2IeksNF1jnmJnnmLnHMXPPLdOs/7whz9k+fLl\nLF68mLDzJ2ynpKTwwAMPtOtmv/3tb/nNb37T9PjVV18lNTWVX//61zz77LPcf//9REZGEhERwYoV\nK0wnctJ+SYlJLGEJ63ev52zRWSILIpk1Y5ZTq1ktFkvTNCQAXh3U2U6iZbL6zMlnOBN5BoDc4lyi\nQ6IB8LX6erKLAJw5YyRypS0Ol/je92Dq1M6VyImIiDkOjcyFhYVRVFSExWIhLCyM4uJi7HY74eHh\nFBcXu6Of7aaROXGnliObjZwd2ewI2dnwxhtQVWU8tlrh1lvhyis91iUREbkAl4/MxcfHs2vXLiZO\nbF7VuHPnToYMGWLqpu6imjlxl5Yjm7W2Wnytvk6PbDrryBF4911j0QOAry8sWACDB3usSyIi8h1u\nq5n7+OOPWbp0KQ8++CBPPfUUjz/+OCtWrGDlypXMnj3bqQ64ikbmzFP9g3M6Q/x27oRPP4XGfwJB\nQbBoEfTv79FuXVZniF1XpdiZp9g5R/Ezr6Nq5qyOfNGcOXNYu3YtZ86c4ZprriE7O5v333+/0yZy\nIj2V3Q4bNsAnnzQncuHh8C//0vkTORERMccjmwa7g0bmpKex2eCjj2DPnua2mBi46y5jZE5ERDov\nl4/MzZ07l82bN7dq27RpE3fccYepm4pIx6qtNfaQa5nIDRkC996rRE5EpLtzKJn78ssvmTJlSqu2\nKVOmsGHDBpd0qqOkpqY6XVTYEylmznF3/Coq4OWX4dtvm9vGjDFOdfD1/M4o7aL3nnmKnXmKnXMU\nP/MaFz+kpqY69TwOrWYNCAigoqKC3r2bjyKqqKjAt5P/T+FscEQ6u+JiYw+5wsLmtunTYcYM7SEn\nItIVNO66sXz5ctPP4VDN3H333Ud1dTUrVqygd+/elJaW8uMf/xgfHx9Wr15t+uaupJo56e5OnoTX\nXoPzJ+thscANN0CLHYRERKSLcHnN3FNPPUVZWRnh4eH07duX8PBwSktLefrpp03dVESck5kJq1Y1\nJ3Le3jB/vhI5EZGeyKFkLjw8nE8++YTc3Nymjx9//HHT0V7Svaj+wTmujt/+/caIXG2t8djfH+65\nB7rD6Xd675mn2Jmn2DlH8TOvo2LnUM1cIy8vLyIiIqiqquLYsWMADBo0qEM64go6AUK6E7sdtm2D\nzz5rbuvVy9gMODLSc/0SERHz3HYCxNq1a1m6dCknT55s/c0WCw0NDU51wFVUMyfdid0O69bB9u3N\nbZGRRiLXq5fn+iUiIh3DmbzFoWRu0KBB/Pu//zuLFy8mMDDQ1I3cTcmcdBf19fD3v8PBg81t8fGw\ncKExxSoiIl2fyxdAlJSU8OCDD3aZRE6co/oH53Rk/Kqrjfq4lonciBFGjVx3TOT03jNPsTNPsXOO\n4mdeR8XOoWRu6dKlvPTSSx1yQxFxzLlzxorV48eb2yZNgjvuMFavioiIgIPTrFdffTU7duwgPj6e\nfv36NX+zxcKmTZtc2kGzLBYLy5Yt0wII6ZLOnDE2Ay4tbW679lpITtZmwCIi3UnjAojly5e7tmbu\nYhsDWywW7r33XlM3djXVzElXlZMDr78OVVXGY6sVbrkFRo/2bL9ERMR1XL4AoitSMmdeWlqaRjOd\n4Ez80tPh7beNRQ9gnK06fz4kJnZc/zozvffMU+zMU+yco/iZ1zJ2zuQtDlfenD59mq+++orCwsJW\nN7v//vtN3VhEWvv6a/j4Y2MbEoCgILj7boiO9my/RESkc3NoZO7vf/87ixYtYsiQIRw8eJBRo0Zx\n8OBBrr76ajZu3OiOfrabRuakq7DbIS0NvvyyuS083NhDLjzcY90SERE3cvnWJI8//jgvvfQSe/bs\nITg4mD179vD8888zbtw4UzcVEYPNBh991DqRi46GpUuVyImIiGMcSuZycnKYP39+02O73c7ixYtZ\ns2aNyzomnqM9g5zjaPzq6uBvf4Pdu5vbEhNhyRJjirUn0nvPPMXOPMXOOYqfeW49mzUyMpJTp07R\nr18/EhIS2LZtGxEREdhstg7phEhPU1lprFjNzW1uGz0abr4ZvLw81y8REel6HKqZ++Mf/0hiYiJ3\n3HEHa9as4Qc/+AEWi4XHHnuM3/3ud+7oZ7tpnznprEpKjD3kzp5tbps2DWbO1B5yIiI9jdv2mfuu\nrKwsKioqGDFihKmbuoMWQEhndOqUkciVlxuPLRb4/veNkx1ERKTncvkCiO+Kj4/v1ImcOEf1D865\nWPyOHzeO52pM5Ly8YN48JXIt6b1nnmJnnmLnHMXPPLeezbp3715mzpxJWFgYPj4+TX98fX07pBMi\n3d3Bg8aIXE2N8djfH+65B/Q7kYiIOMuhadbhw4dzxx13MH/+fAICAlpdS+ykW9NrmlU6i23bYN26\n5se9ehmbAUdFea5PIiLSubj8OK+wsDCKioqwdKHqbCVz4ml2O3z2mZHMNerb19gMuHdvz/VLREQ6\nH5fXzC1evJjXXnvN1A2k61H9g3PS0tJoaID33mudyA0YAPffr0TuUvTeM0+xM0+xc47iZ55b95n7\nxS9+weTJk3nyySeJjIxsardYLGzYsKFDOiLSXdTWwmuvwbFjzW3Dh8Ntt4GPj+f6JSIi3ZND06zT\npk3D19eXuXPn4u/v3/zNFgtLly51aQfN0jSruFt6ehYff5zJ9u1WKipsDBo0mIiIeCZONLYfsZpa\nOy4iIj2BM3mLQyNze/fu5ezZs/j5+Zm6iaekpqZq02Bxi/T0LJ59NoP09FlUVxtte/eu54c/hBtu\niNdmwCIickGNmwY7w6GxgmnTpnH48GGnbuQJjcmctI/qH9rHboeVKzM5cMBI5EpK0rBYYOTIWZSV\nZSqRawe998xT7MxT7Jyj+JmXlpZGSkoKqampTj2PQyNzCQkJXHfdddx2221tauZ+85vfONUBka6s\ntBT+/nc4eNBK41HFFguMGgV9+kBtreZWRUTEtRyqmbvvvvuw2+2ttiZpfLxq1SqXdtAs1cyJK9nt\nsH8/fPqpsRHwjh0bqKycSXAwDBsGwcHG10VGbuDHP57p2c6KiEin59KauYaGBmJjY3n88cdbLX4Q\n6akqKuDjj+HIkea2wYMHU1i4nsTEWU0LHWpq1jNrVufcVFtERLqPy84BeXl58dxzz+norh5E9Q8X\nl54Ozz7bOpELD4d///d4li1LpF+/DZw9+99ERm5gyZJEkpLiPdfZLkjvPfMUO/MUO+cofua5dZ+5\nxYsX89xzz/HQQw91yE1FupqaGli7Fvbsad0+cSJ873tg/K4TT1JSPGlpVi28ERERt3GoZi45OZkd\nO3YQHR1NXFxcU+2cxWJh06ZNLu+kGaqZk45y4oSxyKGkpLktJARuuQU66dHEIiLSxbj8bNbVq1df\n9Mb33nuvqRu7mpI5cVZ9Paxf3/pILoArroAbboCAAM/0S0REuh+XJ3NdYCHXlQAAHWhJREFUkZI5\n8xr3venJ8vPh/ffhzJnmtoAAmDMHRo689PcqfuYpduYpduYpds5R/MxrGTuXnwBht9tZtWoVr7zy\nCnl5ecTGxrJo0SLuu+++VtuViHR1Nhts3gxffknTvnEAQ4bAzTcb06siIiKdiUMjc7///e9Zs2YN\njz32GAMGDCA7O5unn36au+++m1/96lfu6Ge7aWRO2uvsWWM0Li+vuc3XF2bPhnHj0EkOIiLiMi6f\nZk1ISODLL78kPr55m4WsrCymTZtGdna2qRu7mpI5cZTdDjt2wBdfQF1dc/uAAXDrrcbWIyIiIq7k\nTN7i0FlDlZWVREREtGrr06cP1Y0nindSqamp2v/GhJ4Us9JSeOUV+Mc/mhM5Ly+49lpYssRcIteT\n4tfRFDvzFDvzFDvnKH7mpaWlkZaW5vTZrA4lc9dffz2LFi3im2++oaqqiiNHjrB48WJmz57t1M1d\nLTU1VUWZckF2O+zbB889B8eONbdHRcEPfgBXX03TSQ4iIiKukpKS4nQy59A0a2lpKT/5yU948803\nqaurw8fHh/nz5/OXv/yF0NBQpzrgKppmlYu50HFcFouRwF1zDXg7tCxIRESk47ikZu6ZZ57h4Ycf\nBiAjI4PExEQaGho4e/YsEREReHl5me+xGyiZkwtJT4ePPoLy8ua28HCjNm7AAM/1S0REejaX1Mz9\n8pe/bPp83LhxgHFOa1RUVKdP5MQ53bH+oaYGPvwQ3nijdSI3YQL88Icdm8h1x/i5i2JnnmJnnmLn\nHMXPPJefzTpo0CAee+wxRowYQV1dHS+99BJ2u71pX7nGz++///4O6YiIq2RlGVuOfPc4rptvNvaP\nExER6couOs2anp7On/70J7KyskhLS2PatGkXfIKNGze6tINmaZpV6uthwwbjOK6Wb4VRo+DGG3Uc\nl4iIdB4u32du1qxZrF+/3tQNPEXJXM928iS8917b47huvNFI5kRERDoTl+4zV19fz5YtW6ipqTF1\nA+l6unL9g80GmzbBypWtE7nERPjRj9yTyHXl+HmaYmeeYmeeYuccxc88l9fMNX2BtzdJSUmcPXuW\nmJiYDrmpiCsUFhq1cbm5zW0+PsZxXOPH6zguERHpnhyaZv3Tn/7E3/72N376058SFxfXtAgCYObM\nmS7toFmaZu057HbYuRM+/7z1cVxxcTB3ro7jEhGRzs8tZ7M23ui7jh8/burGrqZkrmcoK4MPPoDM\nzOY2Ly+YMQOmTtUpDiIi0jW4/GzWEydOcOLECY4fP97mj3Q/XaH+wW6H/fvh2WdbJ3JRUfDAA549\njqsrxK+zUuzMU+zMU+yco/iZ57aauUZ1dXVs376d/Px8FixYQHl5ORaLhaCgoA7piIijKiuN47gO\nH25us1iMkbgZM3Qcl4iI9CwOTbMeOHCAm2++GT8/P3JzcykvL+eTTz5hzZo1vPnmm+7oZ7tpmrV7\n+vZb4ySHlqc4hIUZtXE6jktERLoql9fMJScn8+CDD7J48WLCwsIoLi6moqKCIUOGkJ+fb+rGrqZk\nrnupqYF162D37tbtEybAddeBr69n+iUiItIRXF4zd/jwYe65555WbYGBgVRVVZm6qTN27NjB1KlT\nueaaa7jrrruor693ex+6u85W/5CVBStWtE7kgoPh7rthzpzOl8h1tvh1JYqdeYqdeYqdcxQ/8zoq\ndg4lc/Hx8ezatatV286dOxnigYMtBwwYwMaNG/nyyy9JSEjggw8+cHsfxD3q643tRlavhuLi5vaR\nI+HHP9a5qiIiIuDgNOvHH3/M0qVLefDBB3nqqad4/PHHWbFiBStXrmT27Nnu6OcFLVu2jLFjx3Lr\nrbe2uaZp1q7t1CnjOK6CguY2f//m47i0AbCIiHQnLq+ZA9izZw/PP/88WVlZDBgwgAceeIDx48eb\numlHyMrKYuHChWzevBkvL68215XMdU02G2zZAmlp0NDQ3D54MNxyC/Tq5bGuiYiIuIzLa+YAxo4d\ny3PPPcenn37KihUrTCVyzzzzDBMmTMDf35/77ruv1bWioiLmzp1LcHAwCQkJvPHGG03Xnn76aWbM\nmMFTTz0FQFlZGYsXL+bll1++YCInzvFU/UNhIbz0Eqxf35zI+fgYo3GLFnWdRE71I+YpduYpduYp\nds5R/Mxz6z5zNTU1/O53v+ONN94gPz+fmJgYFixYwK9+9Sv8/f0dvllMTAxPPPEE69ata7N44qGH\nHsLf35+CggL27NnDjTfeyOjRoxkxYgSPPvoojz76KAD19fXceeedLFu2zCM1e9Lx7HbYtQs++6z1\ncVyxscaWI336eK5vIiIinZ1D06z3338/3377LY8//jgDBgwgOzub3//+9wwZMoRVq1a1+6ZPPPEE\nubm5Td9bUVFBeHg4hw4dIjExEYB7772X6OhonnzyyVbf+8orr/Doo49yxRVXAPCjH/2I+fPnt31h\nFgv33ntv01FkoaGhjBkzhpSUFKA5G9Zjzz4eNy6FDz6A9euNxwkJKXh5Qe/eaYwaBTNndq7+6rEe\n67Ee67Eed8Tjxs9PnDgBwMsvv+zamrnw8HAyMzMJCwtraisqKmLw4MEUt1xm6KBf/epX5OXlNSVz\ne/bs4eqrr6aioqLpa/785z+TlpbGhx9+2O7nB9XMdXZ2Oxw8CJ98AtXVze2RkXDbbdCvn+f6JiIi\n4m4ur5nr378/lZWVrdqqqqqIjo42dVPLd5YilpeX0+s7BVEhISGcO3fO1POLc1r+1uAKlZXwzjvw\n7rvNiZzFAsnJ8IMfdP1EztXx684UO/MUO/MUO+cofuZ1VOwcqpm75557+P73v8/DDz9MXFwc2dnZ\nPPvssyxevJgNGzY0fd3MmTMduul3M8/g4GDKyspatZWWlhISEuLQ80nXcfQofPBB2+O4br0V4uM9\n1y8REZGuyqFp1sa6s5Yjana7vc0I2/Hjxx26qSM1c/fccw9xcXH84Q9/cOg5v8tisbBs2TJSUlKa\n5qnFc2prjeO4vv66dfv48cZxXH5+numXiIiIJ6WlpZGWlsby5ctdv89cR2hoaKCuro7ly5eTl5fH\nypUr8fb2xsvLi4ULF2KxWHjhhRfYvXs3c+bMYdu2bQwfPtzUvVQz13lkZ8P777c+xSE4GG6+GYYO\n9Vy/REREOgu37DPXEX77298SGBjI//2//5dXX32VgIAAfv/73wPw7LPPUlVVRWRkJIsWLWLFihWm\nEzlxTkfN4Tcex7VqVetEbsQI4ziu7prIqX7EPMXOPMXOPMXOOYqfeW6tmesoqamppKamXvBaWFgY\n77//vju7Iy506pQxGnf6dHObjuMSERHpeG6dZnUn1cx5hs0GW7fCxo2tj+MaNMhY5NBVTnEQERFx\nhy5XM+dOqplzv6IiYzQuJ6e5zccHvvc9mDhRo3EiIiIX02Vq5qRraO8cfuNxXM891zqRi42FH/4Q\nJk3qWYmc6kfMU+zMU+zMU+yco/iZ1yVr5qT7KSuDDz+EjIzmNqsVUlLg6quNz0VERMR1uvU0q2rm\nXKvxOK6qqua2yEiYOxf69/dcv0RERLoK1cxdgmrmXKeqykjiDh5sbrNYYMoUmDkTvDXeKyIi0i6q\nmZMOdak5/IwMePbZ1olcaCgsWWKc5KBETvUjzlDszFPszFPsnKP4maeaOXGr2lr47DNjoUNL48bB\n7Nk6jktERMRTNM0ql5WTY2w5UlTU3BYUZBzHlZTkuX6JiIh0F87kLd16ZC41NVULIJxQXw9pabBl\ni7H9SKPhw2HOHCOhExEREfMaF0A4QyNz0iQ9PYsvvsjkyJH9xMRcSXX1YCyW+Kbr/v5www1wxRU9\na9+49kpLS9MvECYpduYpduYpds5R/MxrGTuNzInT0tOzWL06A1/fWWRmWjl0KIW6uvWMGQMREfEM\nGgS33AK9e3u6pyIiItKSRuYEgL/+dQPZ2TP55hsoLW1u79VrA7/61UwdxyUiIuJCGpkTp9XVWSkr\na53IhYTApElWJk3yXL9ERETk0rTPnADg42MjMhL69oWSkjQSEoxtR8LDbZ7uWpejPZfMU+zMU+zM\nU+yco/iZ11Gx69bJXGpqqt5kDrr22sHU1q5n6FAYOhQSEqC2dj2zZg32dNdERES6rbS0NFJTU516\nDtXMSZP09CzWr8+kttaKr6+NWbMGk5QUf/lvFBEREac4k7comRMRERHxMJ3NKh1KU9POUfzMU+zM\nU+zMU+yco/iZp5o5EREREdE0q4iIiIinaZpVREREpIfq1smctiYxRzFzjuJnnmJnnmJnnmLnHMXP\nvLS0tA7ZmqRbnwDhbHBEREREXCklJYWUlBSWL19u+jlUMyciIiLiYaqZExEREemhlMxJG6p/cI7i\nZ55iZ55iZ55i5xzFzzztMyciIiIiqpkTERER8TTVzImIiIj0UErmpA3VPzhH8TNPsTNPsTNPsXOO\n4meeauYcoE2DRUREpDPriE2DVTMnIiIi4mGqmRMRERHpoZTMSRuamnaO4meeYmeeYmeeYuccxc88\n1cyJiIiIiGrmRERERDxNNXMiIiIiPZSSOWlD9Q/OUfzMU+zMU+zMU+yco/iZp5o5EREREVHNnIiI\niIinqWZOREREpIdSMidtqP7BOYqfeYqdeYqdeYqdcxQ/81QzJyIiIiLdu2Zu2bJlpKSkkJKS4unu\niIiIiLSRlpZGWloay5cvN10z162TuW760kRERKSb0QII6VCqf3CO4meeYmeeYmeeYuccxc881cyJ\niIiIiKZZRURERDxN06wiIiIiPZSSOWlD9Q/OUfzMU+zMU+zMU+yco/iZp5o5EREREVHNnIiIiIin\nqWZOREREpIdSMidtqP7BOYqfeYqdeYqdeYqdcxQ/81QzJyIiIiKqmRMRERHxNNXMiYiIiPRQSuak\nDdU/OEfxM0+xM0+xM0+xc47iZ55q5kRERESk69XMnT59mttuuw1fX198fX15/fXX6dOnT5uvU82c\niIiIdBXO5C1dLpmz2WxYrcaA4ssvv8zJkyf5P//n/7T5OiVzIiIi0lX0qAUQjYkcQFlZGWFhYR7s\nTfek+gfnKH7mKXbmKXbmKXbOUfzM69E1c/v27eOqq67imWeeYeHChZ7uTrezd+9eT3ehS1P8zFPs\nzFPszFPsnKP4mddRsXNrMvfMM88wYcIE/P39ue+++1pdKyoqYu7cuQQHB5OQkMAbb7zRdO3pp59m\nxowZPPXU/2/v3mOauvswgD/lJtcqqONmEDdwjrBh5nBTAfE2JcpQMhUMeNuEADo1izqDggsQw6bE\nJd42k02ZUpTFZFMxMgd4C8JIkBjBcVlkbiywAYMWtJRy3j/20teCvoODO+2B55M04bS/c37fPmnh\nyzk9pwcBAAEBASgtLUV6ejrS0tKkfAqjwl9//WXqEmSN+YnH7MRjduIxu+FhfuI9r+wkbeY8PT2x\nd+9ebNy4ccBjSUlJsLW1RXNzM86cOYOEhARUVVUBALZv346ioiJ8+OGH0Ol0hnWUSiW0Wq1k9T/p\n396tLHb7g13PlLvFmd3w/JvzMzvTbH8w6zG74a3H33ni1xvJr72Rkp2kzdyKFSsQEREx4OzTzs5O\nnD9/HmlpabC3t8ecOXMQERGBr7/+esA27ty5g7lz52L+/PnIysrCzp07pSrfyEh+cz548EDU3IM1\nkrMD5J0fszPN9p9HM8fsxI9jdsMbJ+f8Rkp2Jjmbdc+ePfjtt9/w1VdfAQAqKioQFBSEzs5Ow5is\nrCwUFxfju+++EzWHj48P6uvrn0u9RERERP+mgIAA0Z+hs3rOtQyKQqEwWtZoNFAqlUb3OTk5Qa1W\ni56jrq5O9LpEREREcmGSs1n77wx0dHRER0eH0X3t7e1wcnKSsiwiIiIi2TFJM9d/z9zUqVPR09Nj\ntDetsrIS/v7+UpdGREREJCuSNnN6vR6PHz9GT08P9Ho9tFot9Ho9HBwcEBkZiZSUFHR1deHmzZu4\ncOECYmNjpSyPiIiISHYkbeb6zlbNzMzE6dOnYWdnh4yMDADA0aNH8ejRI7zwwguIiYnB8ePH8cor\nr0hZHhEREZHsyO67WYdr165dKCkpgbe3N7788ktYWZnkHBBZ6ujowMKFC1FdXY3S0lL4+fmZuiTZ\nKCsrw7Zt22BtbQ1PT09kZ2fztTdITU1NiIyMhI2NDWxsbJCTkzPg8kb0/6lUKmzduhXNzc2mLkU2\nHjx4gMDAQPj7+0OhUODcuXOYMGGCqcuSleLiYqSnp6O3txcffPABli9fbuqSZOH27dvYvXs3AKCx\nsRFLly5FVlbW/11Hll/nJVZlZSUaGxtx/fp1TJs2Dd98842pS5IVe3t75Ofn49133xX9ZcCjlZeX\nF4qKinDt2jV4e3vj22+/NXVJsjFx4kTcunULRUVFWLNmDU6cOGHqkmRFr9cjLy8PXl5epi5FdkJD\nQ1FUVITCwkI2ckP06NEjZGVl4fLlyygsLGQjNwRvvfUWioqKUFRUhNmzZ2PFihX/uM6oauZKSkqw\nePFiAMCSJUtw69YtE1ckL1ZWVvyFJpKbmxvGjBkDALC2toalpaWJK5IPC4v//Zrq6OiAs7OzCauR\nH5VKhVWrVg048Yz+2a1btxASEoLk5GRTlyI7JSUlsLOzQ3h4OCIjI9HU1GTqkmSnu7sbZWVlCA4O\n/sexo6qZa2trM1zuRKlUorW11cQV0WjT0NCA77//HuHh4aYuRVYqKyvx5ptv4vDhw4iOjjZ1ObLR\nt1du9erVpi5Fdjw8PFBfX4/r16+jubkZ58+fN3VJstLU1IS6ujpcvHgRmzZtwr59+0xdkuxcvXoV\nCxcuHNRYWTZzhw8fxhtvvAFbW1ts2LDB6LHW1lasWLECjo6O8Pb2hkqlMjw2btw4w/Xs2tvb4eLi\nImnd5kJsfk8arf/lDye7jo4OrF27FqdOnRqVe+aGk11AQABKS0uRnp6OtLQ0Kcs2C2KzO3369Kjf\nKyc2OxsbG9jZ2QEAIiMjUVlZKWnd5kJsfs7OzpgzZw6srKwwf/583Lt3T+rSTW64f2vz8vKwcuXK\nQc0ly2bO09MTe/fuxcaNGwc8lpSUBFtbWzQ3N+PMmTNISEhAVVUVAGD27Nm4evUqAODKlSsICgqS\ntG5zITa/J43Wz8yJza6npwdRUVFITU2Fr6+v1GWbBbHZ6XQ6wzilUgmtVitZzeZCbHbV1dXIzs5G\nWFgYamtrsW3bNqlLNzmx2Wk0GsO469ev8307xPwCAwNRXV0N4O/vVH/ppZckrdscDOdvrU6nQ3l5\n+eD7FEHG9uzZI6xfv96wrNFoBBsbG6G2ttZw39q1a4WPPvrIsLxjxw4hODhYiImJEXQ6naT1mhsx\n+YWFhQkeHh7CrFmzhJMnT0parzkZanbZ2dnC+PHjhdDQUCE0NFQ4e/as5DWbi6FmV1paKoSEhAjz\n5s0T3n77beHhw4eS12wuxLxn+wQGBkpSo7kaanb5+fnCjBkzhODgYGHdunWCXq+XvGZzIua1d+TI\nESEkJEQIDQ0Vfv75Z0nrNSdisrt8+bKwdevWQc8h62sjCP32DtXU1MDKygo+Pj6G+wICAlBcXGxY\n/uSTT6Qqz+yJyS8/P1+q8szaULOLjY3lRbD/a6jZzZw5E9euXZOyRLMl5j3bp6ys7N8uz6wNNbuw\nsDCEhYVJWaJZE/PaS0xMRGJiolQlmi0x2S1ZsgRLliwZ9ByyPMzap//nQDQaDZRKpdF9Tk5OUKvV\nUpYlG8xPPGYnHrMTj9mJx+yGh/mJJ0V2sm7m+ne7jo6OhhMc+rS3txvOYCVjzE88ZicesxOP2YnH\n7IaH+YknRXaybub6d7tTp05FT08P6urqDPdVVlbC399f6tJkgfmJx+zEY3biMTvxmN3wMD/xpMhO\nls2cXq/H48eP0dPTA71eD61WC71eDwcHB0RGRiIlJQVdXV24efMmLly4wM8q9cP8xGN24jE78Zid\neMxueJifeJJmJ+7cDNNKTU0VFAqF0e3jjz8WBEEQWltbheXLlwsODg7C5MmTBZVKZeJqzQ/zE4/Z\nicfsxGN24jG74WF+4kmZnUIQRukFw4iIiIhGAFkeZiUiIiKiv7GZIyIiIpIxNnNEREREMsZmjoiI\niEjG2MwRERERyRibOSIiIiIZYzNHREREJGNs5oiIiIhkjM0cEVE/69evx969e5/rNhMSEpCenv5c\nt0lEBABWpi6AiMjcKBSKAV+OPVzHjh17rtsjIurDPXNERE/BbzokIrlgM0dEZiUzMxOTJk2CUqnE\ntGnTUFhYCAAoKyvDrFmz4OzsDA8PD2zZsgU6nc6wnoWFBY4dOwZfX18olUqkpKSgvr4es2bNwrhx\n4xAVFWUYX1xcjEmTJmH//v2YOHEipkyZgpycnGfWdPHiRUyfPh3Ozs6YM2cO7t69+8yx27dvh6ur\nK8aOHYvXXnsNVVVVAIwP3YaHh8PJyclws7S0RHZ2NgDg/v37WLRoEcaPH49p06YhLy/vmXOFhoYi\nJSUFQUFBUCqVWLx4MVpaWgaZNBGNFGzmiMhs/PTTTzhy5AjKy8vR0dGBgoICeHt7AwCsrKzw2Wef\noaWlBSUlJfjhhx9w9OhRo/ULCgpQUVGB27dvIzMzE5s2bYJKpcIvv/yCu3fvQqVSGcY2NTWhpaUF\njY2NOHXqFOLi4lBbWzugpoqKCrz33ns4ceIEWltbER8fj3feeQfd3d0Dxl65cgU3btxAbW0t2tvb\nkZeXBxcXFwDGh24vXLgAtVoNtVqNc+fOwd3dHQsWLEBnZycWLVqEmJgY/PHHH8jNzUViYiKqq6uf\nmZlKpcLJkyfR3NyM7u5uHDhwYMi5E5G8sZkjIrNhaWkJrVaLe/fuQafTwcvLCy+++CIA4PXXX8fM\nmTNhYWGByZMnIy4uDteuXTNaf+fOnXB0dISfnx9effVVhIWFwdvbG0qlEmFhYaioqDAan5aWBmtr\na4SEhGDp0qU4e/as4bG+xuuLL75AfHw8AgMDoVAosHbtWowZMwa3b98eUL+NjQ3UajWqq6vR29uL\nl19+GW5ubobH+x+6rampwfr163Hu3Dl4enri4sWLmDJlCtatWwcLCwtMnz4dkZGRz9w7p1AosGHD\nBvj4+MDW1harVq3CnTt3hpA4EY0EbOaIyGz4+Pjg0KFD2LdvH1xdXREdHY3ff/8dwN+Nz7Jly+Du\n7o6xY8ciOTl5wCFFV1dXw892dnZGy7a2ttBoNIZlZ2dn2NnZGZYnT55smOtJDQ0NOHjwIJydnQ23\nX3/99alj582bh82bNyMpKQmurq6Ij4+HWq1+6nNtb29HREQEMjIyMHv2bMNcpaWlRnPl5OSgqanp\nmZk92Sza2dkZPUciGh3YzBGRWYmOjsaNGzfQ0NAAhUKBXbt2Afj70h5+fn6oq6tDe3s7MjIy0Nvb\nO+jt9j87ta2tDV1dXYblhoYGeHh4DFjPy8sLycnJaGtrM9w0Gg1Wr1791Hm2bNmC8vJyVFVVoaam\nBp9++umAMb29vVizZg0WLFiA999/32iuuXPnGs2lVqtx5MiRQT9PIhp92MwRkdmoqalBYWEhtFot\nxowZA1tbW1haWgIANBoNnJycYG9vj/v37w/qUh9PHtZ82tmpqamp0Ol0uHHjBi5duoSVK1caxvaN\n37RpE44fP46ysjIIgoDOzk5cunTpqXvAysvLUVpaCp1OB3t7e6P6n5w/OTkZXV1dOHTokNH6y5Yt\nQ01NDU6fPg2dTgedTocff/wR9+/fH9RzJKLRic0cEZkNrVaL3bt3Y+LEiXB3d8eff/6J/fv3AwAO\nHDiAnJwcKJVKxMXFISoqymhv29OuC9f/8SeX3dzcDGfGxsbG4vPPP8fUqVMHjJ0xYwZOnDiBzZs3\nw8XFBb6+voYzT/vr6OhAXFwcXFxc4O3tjQkTJmDHjh0Dtpmbm2s4nNp3RqtKpYKjoyMKCgqQm5sL\nT09PuLu7Y/fu3U892WIwz5GIRgeFwH/riGiUKS4uRmxsLB4+fGjqUoiIho175oiIiIhkjM0cEY1K\nPBxJRCMFD7MSERERyRj3zBERERHJGJs5IiIiIhljM0dEREQkY2zmiIiIiGSMzRwRERGRjP0HYdrQ\n0/EX3NkAAAAASUVORK5CYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10846f5d0>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 19
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"In this performance comparison using different sample sizes, we can see that our Cython approach is actually not so fast anymore. However, this is just the simplest approach to using Cython. \n",
|
|
"There are a lot of improvements that can be made. In a [later section](#showdown) we will come back to this comparison and see how the Cython version of our simple least squares implementation holds up against the other approaches, after we tweaked it a little bit.\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"cython_bonus\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Bonus: How to use Cython without the IPython magic"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"IPython's notebook is really great for explanatory analysis and documentation, but what if we want to compile our Python code via Cython without letting IPython's magic doing all the work? \n",
|
|
"These are the steps you would need."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 1. Creating a .pyx file containing the the desired code or function."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%file ccy_classic_lstsqr.pyx\n",
|
|
"\n",
|
|
"def ccy_classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"Writing ccy_classic_lstsqr.pyx\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 11
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 2. Creating a simple setup file"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%file setup.py\n",
|
|
"\n",
|
|
"from distutils.core import setup\n",
|
|
"from distutils.extension import Extension\n",
|
|
"from Cython.Distutils import build_ext\n",
|
|
"\n",
|
|
"setup(\n",
|
|
" cmdclass = {'build_ext': build_ext},\n",
|
|
" ext_modules = [Extension(\"ccy_classic_lstsqr\", [\"ccy_classic_lstsqr.pyx\"])]\n",
|
|
")"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"Writing setup.py\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 12
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"####3. Building and Compiling"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"!python3 setup.py build_ext --inplace"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"running build_ext\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"cythoning ccy_classic_lstsqr.pyx to ccy_classic_lstsqr.c\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"building 'ccy_classic_lstsqr' extension\r\n",
|
|
"creating build\r\n",
|
|
"creating build/temp.macosx-10.6-intel-3.4\r\n",
|
|
"/usr/bin/clang -fno-strict-aliasing -Werror=declaration-after-statement -fno-common -dynamic -DNDEBUG -g -fwrapv -O3 -Wall -Wstrict-prototypes -arch i386 -arch x86_64 -g -I/Library/Frameworks/Python.framework/Versions/3.4/include/python3.4m -c ccy_classic_lstsqr.c -o build/temp.macosx-10.6-intel-3.4/ccy_classic_lstsqr.o\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\u001b[1mccy_classic_lstsqr.c:2040:28: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_AsString'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE char* __Pyx_PyObject_AsString(PyObject* o) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2037:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function\r\n",
|
|
" '__Pyx_PyUnicode_FromString' [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyUnicode_FromString(char* c_str) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2104:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_IsTrue'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyObject_IsTrue(PyObject* x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2159:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyIndex_AsSsize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE Py_ssize_t __Pyx_PyIndex_AsSsize_t(PyObject* b) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2188:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_FromSize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject * __Pyx_PyInt_FromSize_t(size_t ival) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1584:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_From_long'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyInt_From_long(long value) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1631:27: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_long' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE long __Pyx_PyInt_As_long(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1731:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_int' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyInt_As_int(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"8 warnings generated.\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\u001b[1mccy_classic_lstsqr.c:2040:28: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_AsString'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE char* __Pyx_PyObject_AsString(PyObject* o) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2037:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function\r\n",
|
|
" '__Pyx_PyUnicode_FromString' [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyUnicode_FromString(char* c_str) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2104:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_IsTrue'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyObject_IsTrue(PyObject* x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2159:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyIndex_AsSsize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE Py_ssize_t __Pyx_PyIndex_AsSsize_t(PyObject* b) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2188:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_FromSize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject * __Pyx_PyInt_FromSize_t(size_t ival) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1584:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_From_long'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyInt_From_long(long value) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1631:27: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_long' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE long __Pyx_PyInt_As_long(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1731:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_int' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyInt_As_int(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"8"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
" warnings generated.\r\n",
|
|
"/usr/bin/clang -bundle -undefined dynamic_lookup -arch i386 -arch x86_64 -g build/temp.macosx-10.6-intel-3.4/ccy_classic_lstsqr.o -o /Users/sebastian/Github/python_reference/benchmarks/ccy_classic_lstsqr.so\r\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 13
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 4. Importing and running the code"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import ccy_classic_lstsqr\n",
|
|
"\n",
|
|
"%timeit classic_lstsqr(x, y)\n",
|
|
"%timeit cy_classic_lstsqr(x, y)\n",
|
|
"%timeit ccy_classic_lstsqr.ccy_classic_lstsqr(x, y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"100 loops, best of 3: 2.9 ms per loop\n",
|
|
"1000 loops, best of 3: 212 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"1000 loops, best of 3: 207 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 20
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"numba\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Appendix I: Cython vs. Numba"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Like we did with Cython before, we will use the minimalist approach to Numba and see how the two - Cython and Numba - compare against each other. \n",
|
|
"\n",
|
|
"Numba is using the [LLVM compiler infrastructure](http://llvm.org) for compiling Python code to machine code. Its strength is to work with NumPy arrays to speed-up the code. If you want to read more about Numba, please see refer to the original [website and documentation](http://numba.pydata.org/numba-doc/0.13/index.html)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"Here is our \"classic\" approach in Python, where I removed the list comprehensions, since they caused errors in the Numba compilation."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" for x_i in x:\n",
|
|
" var_x += (x_i - x_avg)**2\n",
|
|
" cov_xy = 0\n",
|
|
" for x_i, y_i in zip(x,y):\n",
|
|
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 22
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The Cython-compiled version of it:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%load_ext cythonmagic"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": []
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"\n",
|
|
"def cy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" for x_i in x:\n",
|
|
" var_x += (x_i - x_avg)**2\n",
|
|
" cov_xy = 0\n",
|
|
" for x_i, y_i in zip(x,y):\n",
|
|
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 26
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"And now the Numba-compiled version:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"from numba import jit\n",
|
|
"\n",
|
|
"@jit\n",
|
|
"def nmb_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" for x_i in x:\n",
|
|
" var_x += (x_i - x_avg)**2\n",
|
|
" cov_xy = 0\n",
|
|
" for x_i, y_i in zip(x,y):\n",
|
|
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
|
|
" \n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 27
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"Now, let us see how the different approaches compare against each other for different sample sizes."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"funcs = ['lstsqr', 'cy_lstsqr', 'nmb_lstsqr'] \n",
|
|
"orders_n = [10**n for n in range(1, 7)]\n",
|
|
"times_n = {f:[] for f in funcs}\n",
|
|
"\n",
|
|
"for n in orders_n:\n",
|
|
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
|
|
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
|
|
" for f in funcs:\n",
|
|
" times_n[f].append(timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 28
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%pylab inline"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": []
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"plt.figure(figsize=(10,8))\n",
|
|
"\n",
|
|
"for f in times_n.keys():\n",
|
|
" plt.plot(orders_n, times_n[f], alpha=0.5, label=f, marker='o', lw=2)\n",
|
|
"\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
|
|
"plt.legend(loc=2)\n",
|
|
"plt.grid()\n",
|
|
"\n",
|
|
"plt.title('Performance of a simple least square fit implementation')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAmEAAAH4CAYAAAACdDpdAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl4k2XW+PFv0n1vKV2A0gUKhULZBRSQQhFwYRlBliKL\nivO6jCvzc3RUFp0RxhnfcfB1m2GpClhABWRHliqiUtmkUKC00AJtKS2lQOmSNrl/fzxDpFCgSNts\n53Ndva4+SZ7kJCdPcnLfd050SimFEEIIIYRoVHpLByCEEEII4YikCBNCCCGEsAApwoQQQgghLECK\nMCGEEEIIC5AiTAghhBDCAqQIE0IIIYSwACnChM0pKCjg7rvvxtfXl//3//6fpcOxuPLycoYNG4a/\nvz9jx45tsNu57777+OyzzxrkuvV6PceOHbvl/ZKSkujXr18DRGT/duzYQZs2bfD19WXVqlXcd999\nfPrpp3Xe3xqfD9Zu9uzZPP7445YOQ1gRZ0sHIBxDZGQkZ86cwcnJCS8vL+69917+7//+Dy8vr1u+\nrn//+98EBwdz4cKFBojU9nzxxRecOXOG4uJi9PqG+1y1bt26BrtuaxYfH8/EiRN57LHHLB1KvZo+\nfTrPPvsszzzzDAAjRowwn5eUlMT8+fPZvn37dfd3tOfDzJkzycrKqnPhmZKSwsSJEzl58qT5tFde\neaWhwhM2SkbCRKPQ6XSsWbOGixcvsmfPHnbt2sVf/vKXW7oOpRQmk4mcnBzat2//m+Korq7+TftZ\ns5ycHNq2bdugBZgj0+l0lg7hpn7L8/rEiRPExsY2QDRCiDpTQjSCyMhItWXLFvP2H//4R/XAAw8o\npZT68ccf1Z133qn8/f1V586dVUpKivly/fv3V6+++qrq06eP8vDwUA8//LBycXFRrq6uytvbW23Z\nskVVVlaq5557TjVv3lw1b95cPf/886qyslIppdS2bdtUixYt1N/+9jcVGhqqJk6cqGbOnKlGjx6t\nHn74YeXj46Pi4uJURkaGeuutt1RwcLAKDw9XmzZtMsewYMEC1b59e+Xj46NatWqlPv74Y/N5l6//\nnXfeUcHBwapZs2Zq4cKF5vPLysrUiy++qCIiIpSfn5/q27evKi8vv+n9vlp6errq37+/8vf3Vx06\ndFBff/21Ukqp6dOnK1dXV+Xi4qK8vb3VggULrtl3586dqnfv3srf3181a9ZM/eEPf1AGg6HW2ykv\nL1cTJkxQgYGByt/fX91xxx3qzJkz5lzMmzdPKaXUwoUL1V133aVeeOEF5e/vr1q3bq127NihFixY\noFq2bKmCg4PVJ598Yr7eyZMnq//5n/9R99xzj/Lx8VH9+/dXOTk55vN1Op3KyspSSilVUVGhpk2b\npsLDw1VISIh64oknzI/Z1RYuXKj69u1r3j506JAaNGiQatKkiYqJiVHLli0zn7dmzRrVpUsX5evr\nq1q2bKlmzpx5w/tdUFCg/vznPysnJyfl7u6uvL291TPPPFOnx6ygoEAppdSxY8fU3XffrXx8fNQ9\n99yjnn76afXwww8rpbTnTlhYWI3rioiIMB8nN8ubTqdT77//voqOjlatWrVSSim1evVq1blzZ+Xv\n76/uuusutX///loft1atWim9Xq88PDyUj4+PqqysNOf30KFDys3NTTk5OSlvb28VEBBQ63VYw/Ph\n8vH39ttvq6CgINWsWTO1YsUKtXbtWtWmTRvVpEkTNXv2bPP1mkwmNXv2bNW6dWsVGBioxowZo4qL\ni5VSSh0/flzpdDr1ySefqPDwcNW0aVP117/+VSml1Pr162scZ126dFFKXf+1obS0VLm7uyu9Xq+8\nvb2Vj4+PysvLUzNmzDDnXymlVq1apWJjY5W/v7+Kj49Xhw4dqvFc+Mc//qE6deqk/Pz81NixY1VF\nRUWtuRC2S4ow0SgiIyPV5s2blVJKnThxQnXo0EFNnz5dnTp1SgUGBqr169crpZT65ptvVGBgoCoq\nKlJKaS/0ERERKj09XRmNRlVVVaWmTJmiXn/9dfN1v/766+rOO+9UhYWFqrCwUN11113m87dt26ac\nnZ3Vyy+/rAwGgyovL1czZsxQ7u7uatOmTaq6ulpNmjRJRUREqLfeektVV1er//znPyoqKsp8/WvX\nrlXHjh1TSin17bffKk9PT7Vnz54a1z9jxgxVXV2t1q1bpzw9PVVJSYlSSqmnnnpKDRgwQOXl5Smj\n0ah+/PFHVVlZed37XVhYeM1jZzAYVOvWrdXs2bNVVVWV2rp1q/Lx8VFHjhxRSik1c+ZMNXHixOs+\n9rt371Y7d+5URqNRZWdnq/bt26t333231st+9NFHatiwYaq8vFyZTCa1Z88edeHCBaWUUvHx8Wr+\n/PlKKe1N19nZWSUlJSmTyaRee+011aJFC3OhsGnTJuXj46MuXbqklNLedH18fNT27dvNRfOVxdOV\nb7rPP/+8GjFihDp37py6ePGiGjZsmHrllVdqjffKIqy0tFSFhYWppKQkZTQa1d69e1XTpk1Venq6\nUkqplJQUdeDAAaWUUvv371chISFq5cqVt3S/b/Ux6927t5o2bZoyGAzqu+++Uz4+PuZc1VaEXflh\n5WZ50+l0avDgwercuXOqoqJC7dmzRwUHB6vU1FRlMpnUJ598oiIjI80fSK529QejK+9nUlJSjfzU\nxhqeD5ePvzfffNN87AYGBqrExERVWlqqDh48qDw8PFR2drZSSql3331X3XnnnSo3N1cZDAb1P//z\nP2r8+PFKqV+LsN///veqoqJC/fLLL8rNzU0dPnxYKVX7cXaj14aUlJRr8jtz5kxzEXbkyBHl5eWl\nNm/erKqrq9Xbb7+toqOjVVVVlTk/vXr1Uvn5+aq4uFi1b99effTRRzfMibA9UoSJRhEREaG8vb2V\nv7+/ioiIUE8//bQqLy9Xc+bMueaFbciQIeZPzfHx8WrGjBk1zp8yZYp67bXXzNutW7c2FzNKKbVx\n40YVGRmplNJepF1dXWu8Ec2YMUMNHjzYvP31118rb29vZTKZlFJKXbhwQel0OnX+/Pla78vIkSPV\nv/71L/P1e3h4KKPRaD4/ODjY/Obp4eFR62jEze73lb777jsVGhpa47Tx48ebR3Ku/nR9M//85z/V\n7373u1rPW7BgwXVHUK5+023Tpo35vP379yudTmceNVNKqcDAQPXLL78opbQ33ctvdkppBZOTk5M6\ndeqUUurXN12TyaS8vLzMb8BKKfXDDz/UKIqvdGURlpycrPr161fj/N///vdq1qxZte773HPPqRde\neKFO9/vyiE9trrdvTk6OcnZ2VmVlZebTEhMT61yEXe3qvOl0OrVt2zbz9hNPPFHjw4lSSsXExKhv\nv/221uu7URF29Qhjbazh+XD5+Lv62E1NTTVfvnv37mrVqlVKKaXatWtX4z7n5eUpFxcXZTQazUVY\nbm6u+fyePXuqpUuXKqXqdpxd/dpwdX6vvI433nhDjR071nyeyWRSLVq0MOcrMjJSLV682Hz+Sy+9\npJ544okb3r6wPbIwXzQKnU7HqlWrGDhwYI3Tc3JyWL58OatXrzafVl1dXeNyLVu2vOF15+XlERER\nYd4ODw8nLy/PvB0UFISrq2uNfYKDg83/e3h40LRpU/PaHw8PDwBKS0vx9fVl/fr1zJo1i6NHj2Iy\nmSgrK6NTp07m/QMDA2usx/L09KS0tJSioiIqKipo3br1NTHX5X5fef+ufgwiIiLIzc294eNyWUZG\nBi+++CK7d++mrKyM6upqevToUetlLy8kHjduHCUlJTz88MP89a9/xdn52peKkJAQ8/+XH7OgoKAa\np5WWlgJa/sPCwszneXl50aRJE/Ly8mjRooX59MLCQsrKyujevbv5NPXftYA3k5OTw86dOwkICDCf\nVl1dzaRJkwDYuXMnL7/8MgcPHsRgMFBZWcmYMWPqdL9vtC7sevvm5eUREBBgfmxAy9uVC7VvpC55\nu/J5kZOTw6effsp7771nPq2qqor8/Pw63d7tstTzITAw8Jpj9+pYLt9uTk4Ov/vd72ocr87OzhQU\nFJi3Q0NDzf9fPpav52avDTeSl5dHeHi4eVun09GyZcsax/WVsXh4eNR4XRP2QVbyCosKDw9n4sSJ\nnDt3zvx38eJFXnrpJfNlbrYwunnz5mRnZ5u3T5w4QfPmza+7/60stK6srGTUqFG89NJLnDlzhnPn\nznHfffehlLrpvk2bNsXd3Z3MzMxrzqvL/b7y/p08ebLGbebk5NR4E7uRJ598ktjYWDIzMzl//jx/\n/etfr1vUODs7M336dA4ePMgPP/zAmjVrbqltwfUopWoUH6WlpRQXF9fIE2iPmYeHB+np6ebHpaSk\npE7fhA0PD6d///7XPKbvv/8+AImJiYwcOZJTp05RUlLCE088YX4cbnS/b/Z8ud6+zZs359y5c5SV\nlZkvm5OTY74+Ly+vGucZjUYKCwvN23XJ25WxhYeH8+qrr9a4/6Wlpb+pbUlDfxmhMZ4PtQkPD2fD\nhg01HqOysjKaNWt2032vfkxu9tpws8ewRYsW5OTkmLcvPyZXFqE3un1hH6QIExb18MMPs3r1ajZt\n2oTRaKSiooKUlJQanwavLniu3h4/fjx/+ctfKCoqoqioiDfeeIOJEyde9zbrUkBdZjAYMBgMNG3a\nFL1ez/r169m0aVOd9tXr9Tz66KO8+OKL5OfnYzQa+fHHHzEYDHW635f17t0bT09P3n77baqqqkhJ\nSWHNmjWMGzeuTnGUlpbi4+ODp6cnhw8f5sMPP7zuZVNSUkhLS8NoNOLj44OLiwtOTk51up2bWbdu\nHTt27MBgMPD6669z5513XvOGo9frefzxx3n++efNBUlubm6dHvP777+fjIwMFi1aRFVVFVVVVfz8\n888cPnwY0B6HgIAAXF1dSU1NZcmSJeY3thvd75CQELKysq57u9fbNzw8nB49ejBjxgyqqqr4/vvv\nWbNmjXm/tm3bUlFRwbp166iqquIvf/kLlZWV5vNvJW8Ajz/+OB999BGpqakopbh06RJr16694UjO\n9YSEhHDq1Cmqqqpued+6aujnQ22eeOIJ/vznP3PixAlAG2n7+uuv67RvaGgo2dnZ5tePm702hISE\ncPbs2esWjA899BBr165l69atVFVV8c477+Du7s5dd91V6+Vv5XVL2A4pwoRFhYWFsWrVKt566y2C\ng4MJDw/nnXfeqfGCU9tI1pWnvfbaa/To0YNOnTrRqVMnevTowWuvvVbn/a93GQAfHx/mzp3LmDFj\naNKkCZ9//nmNfkq17Xulf/zjH8TFxXHHHXcQGBjIK6+8gslkuu79rm2EysXFhdWrV7N+/XqCgoL4\nwx/+wGeffUbbtm2ve3+ujmHJkiX4+vry+9//nnHjxl338qdPn+ahhx7Cz8+P2NhYc4+sq9XlMbz6\nvMTERGbNmkVgYCB79+5l0aJFte77t7/9jejoaHr37o2fnx/33HMPGRkZ173eK3O1adMmkpOTadGi\nBc2aNeOVV17BYDAA8MEHHzB9+nR8fX158803a4wQ3eh+P/fcc3zxxRc0adKE559//pYesyVLlrBz\n506aNGnCG2+8waRJk8zPbT8/Pz744AOmTp1KWFgY3t7eNaYXb5a3qx/v7t2785///Ic//OEPNGnS\nhDZt2vzmUcyEhAQ6dOhAaGhojan767Hk8+FWbve5555j+PDhDB48GF9fX+68805SU1PrtO9DDz0E\naNOfPXr0uOlrQ7t27Rg/fjytWrWiSZMm5Ofn13icYmJiWLRoEc888wxBQUGsXbuW1atX1zr1fzk2\nGQ2zPzrVwOW10WikR48ehIWFsXr1aoqLixk7diw5OTlERkaybNky/P39Aa2b8IIFC3BycmLu3LkM\nHjy4IUMTQjSSRx55hLCwMN58801Lh2JRs2bNIjMzs8E6zdsKeT4IoWnwkbB//etfxMbGmiv4OXPm\nmD/JJCQkMGfOHADS09NZunQp6enpbNiwgaeeeqpOi3GFENZPplI08jho5HEQQtOgRdipU6dYt24d\nU6dONR90X3/9NZMnTwZg8uTJrFy5EoBVq1Yxfvx4XFxciIyMJDo6usYwsRDCdslUikYeB408DkJo\nGrRFxQsvvMDf//73GgsTCwoKzF8fDgkJMX81OC8vj969e5svFxYWVuev4AshrNvChQstHYJVmDFj\nhqVDsAryfBBC02BF2Jo1awgODqZr166kpKTUepmbfRqq7bwWLVpIrxQhhBBC2ITOnTuzb9++Ws9r\nsCLshx9+4Ouvv2bdunVUVFRw4cIFJk6cSEhICKdPnyY0NJT8/HzzN29atGhRo2/MqVOnau2XkpeX\nJ+sJrNDMmTOZOXOmpcMQV5CcWCfJi/WRnFgfe8rJjQabGmxN2FtvvcXJkyc5fvw4ycnJDBw4kM8+\n+4zhw4fzySefAPDJJ58wcuRIAIYPH05ycjIGg4Hjx49z9OhRevbs2VDhiXp2ZbNUYR0kJ9ZJ8mJ9\nJCfWx1Fy0mg/W3S5Enz55ZcZM2YM8+fPN7eoAIiNjWXMmDHExsbi7OzMBx98IAs3hRBCCGG3GrxP\nWH3T6XQyHWmFUlJSiI+Pt3QY4gqSE+skebE+khPrY085uVHdIkWYEEIIIazCkcwjbN69mSpVhYvO\nhUHdBxETHWPpsG7LjeoWu/nZoiZNmpi/bSl/tvHXpEkTSz9t7Nr1vpUsLEvyYn0kJ9bhSOYRkrYl\nURhSyO683RSGFJK0LYkjmUcsHVqDabQ1YQ3t3LlzMkJmY2TNnxBCiMs2796MWxs3CkoLSC9MJ8QQ\ngncbb7bs2WLzo2HXYzcjYUKImuxlPYW9kbxYH8mJdTCYDOSU5HCo6BA+MT4UlRWZT7dXdjMSJoQQ\nQgjbZDQZOVx4mOO+xwFoHdCaMN8wAFz1rpYMrUHJSJgQdkrWuVgnyYv1kZxYVkV1BYvTFuPS1AVT\nlokOQR0wHjei0+moPFpJQrcES4fYYGQkTAghhBAWUVJRwpK0JZy5dIaIiAge6vAQB48cJL04neAz\nwSQMSLDb9WBgRy0qHKV1RUpKChMnTqzxE0+2ylFyJoQQ4lp5F/NYkraEUkMpQZ5BJMYlEuARYOmw\n6p1DtKgQNc2cOZOJEydaOgwhhBDiGoeLDrNw70JKDaVE+UfxaNdH7bIAuxmHmI48ciSHzZuzqKrS\n4+JiYtCg1sTERDTa/vbkcjUv7SWsnz11nLYnkhfrIzlpXD+d+omNmRtRKLqEdmFY22E46Z1qXMZR\ncmL3I2FHjuSQlJRJYeFASkriKSwcSFJSJkeO5DTK/pedPHmSBx98kODgYJo2bcrTTz9NYGAgBw4c\nMF/mzJkzeHl5cfbs2Tpf79/+9jfCwsLw9fWlXbt2bN26lQ0bNjB79myWLl2Kj48PXbt2BSApKYnW\nrVvj6+tLq1atWLJkCQBGo5E//vGPBAUF0bp1a95//330ej0mkwnQvr792muv0adPH7y8vDh+/Pgt\n3XchhBDCpEysP7qeDZkbUCgGRA5gRMyIawowR2L3I2GbN2fh5pZAzS+/JLB//1buuOPmo1mpqVmU\nlf36zYz4eHBzS2DLlq11Hg0zGo088MADDBo0iMWLF+Pk5MTPP/8MwKJFi5gzZw4An3/+OYMGDSIw\nMLBO13vkyBHef/99du3aRWhoKCdOnKC6uppWrVrx5z//maysLD799FMALl26xHPPPceuXbto06YN\nBQUF5mLvP//5D2vXrmXfvn14enry4IMPXjPStWjRItavX09MTIy5OBPWzRE+RdoiyYv1kZw0PIPR\nwJfpX3Lk7BGcdE6MaDeCTiGdrnt5R8mJ3Y+EVVXVfheNxrrddZOp9ssZDHV/6FJTU8nPz+fvf/87\nHh4euLq60qdPHyZNmsTnn39uvtxnn312S+u4nJycqKys5ODBg1RVVREeHk6rVq0Abdrw6oWAer2e\ntLQ0ysvLCQkJITY2FoBly5bxwgsv0KJFCwICAvjzn/9cY1+dTseUKVNo3749er0eZ2e7r92FEELU\nk4uVF1m4dyFHzh7Bw9mDSZ0n3bAAcyR2/27q4nJ5Sq3m6cHBJp566ub7v/++icLCa093da37aNDJ\nkyeJiIhAr69ZuPXq1QsPDw9SUlIIDQ0lKyuL4cOH1/l6o6Ojeffdd5k5cyYHDx5kyJAh/O///i/N\nmjW75rJeXl4sXbqUf/zjHzz22GP06dOHd955h5iYGPLz82nZsqX5suHh4dfsf+X5wjY4ypoKWyN5\nsT6Sk4ZTUFrAkrQlnK88T4B7ABM6TaCpZ9Ob7ucoObH7kbBBg1pTWbmlxmmVlVtISGjdKPuDVsCc\nOHECo9F4zXmTJ09m0aJFfPbZZzz00EO4ut5aZ+Dx48ezfft2cnJy0Ol0/OlPfwJqXzg/ePBgNm3a\nxOnTp2nXrh2PP/44AM2aNePEiRPmy135/2WyEF8IIcStyCrOYsHeBZyvPE9L35ZM7Ta1TgWYI7H7\nIiwmJoIpU6IJDt6Kv38KwcFbmTIlus7ruW53f9BGvJo1a8bLL79MWVkZFRUV/PDDDwA8/PDDfPXV\nVyxevJhJkybd0n3LyMhg69atVFZW4ubmhru7O05O2gLH0NBQsrOzzdOKZ86cYdWqVVy6dAkXFxe8\nvLzMlx0zZgxz584lNzeXc+fOMWfOnGuKLunnZXsc4VOkLZK8WB/JSf3bk7+HxWmLqTRW0iGoA5M6\nT8LL1avO+ztKTux+OhK0Qup2Wkrc7v56vZ7Vq1fz7LPPEh4ejk6nY8KECdx11120bNmSbt26cezY\nMfr27Vun67tcIFVWVvLKK69w6NAhXFxc6NOnD//+978BeOihh1i0aBGBgYG0atWKNWvW8M9//pPJ\nkyej0+no2rUrH374IQCPP/44GRkZdO7cGT8/P6ZNm8a2bdtqvU0hhBDiepRSbD2+le0ntgPQN7wv\nCVEJ8h5yHdIx3wo89thjtGjRgjfeeMPSoQCQnZ1Nq1atqK6uvmYdW32y5ZzZAkdZU2FrJC/WR3JS\nP6pN1aw8vJIDZw6g1+m5v839dG/e/Tddlz3l5EbvdQ4xEmbNsrOz+eqrr9i3b5+lQxFCCCF+k7Kq\nMj5P+5yTF07i5uTGQx0eIrpJtKXDsnp2vybMmr3++uvExcXx0ksvERHx63TnW2+9hY+PzzV/999/\nf6PFJkPHts9ePkXaG8mL9ZGc3J6zZWeZt2ceJy+cxNfNl0e7PnrbBZij5ESmI4XFSM6EEMK25ZTk\nkHwgmfLqcpp5NyMxLhEfNx9Lh2VV5Ae8hXBAKTV/JkJYCcmL9ZGc/DZpBWl8+sunlFeX0zawLY90\nfaTeCjBHyYmsCRNCCCFEnSml2H5iO1uPbwWgZ4ueDI0eil4n4zq3SqYjhcVIzoQQwrYYTUbWZKxh\n7+m96NAxuPVgeof1lnXENyDfjhRCCCHEbamormDZwWUcO3cMF70LD7Z/kPZB7S0dlk2TsUMh7JSj\nrKmwNZIX6yM5ubmSihLm75nPsXPH8HLxYkqXKQ1agDlKTqQIawSRkZFs2bLl5hcUQgghrEzexTzm\n7ZlHYVkhQZ5BPN79cVr4trB0WHZB1oQ1gqioKObPn8/AgQNrPb+xOtRbG2vOmRBCCDhcdJgv07+k\nylRFlH8UYzuOxd3Z3dJh2RSHXxN2JPMIm3dvpkpV4aJzYVD3QcRExzTa/nXVEAWJ0Wg0/1C3EEII\nUVc/nfqJjZkbUSi6hHZhWNthOOnl/aQ+2f2wy5HMIyRtS6IwpJCS0BIKQwpJ2pbEkcwjjbL/lVJT\nU+nRowd+fn6Ehobyxz/+EYC7774bAH9/f3x8fNi5cyeZmZn0798ff39/goKCGDdunPl6vvnmG9q1\na4e/vz/PPPMM/fv3Z/78+QAkJSXRp08fXnzxRZo2bcqsWbNuOU5hHxxlTYWtkbxYH8lJTSZlYv3R\n9WzI3IBCMTBqICNiRjRqAeYoObH7kbDNuzfj1saNlOyUX090gf3J+7mj7x033T/1+1TKwsogW9uO\nj4zHrY0bW/ZsuaXRMKUUzz33HC+88AITJkygrKyMtLQ0ALZv305UVBTnz583T0eOHz+eoUOH8u23\n32IwGNi1axcARUVFjBo1iqSkJEaMGMF7773HRx99xOTJk3+NOTWVxMREzpw5g8FgqHOMQgghHJvB\naOCL9C/IOJuBk86JEe1G0Cmkk6XDslt2PxJWpapqPd2IsU77mzDVerrBdOvFjaurK0ePHqWoqAhP\nT0969eoF1D4N6erqSnZ2Nrm5ubi6unLXXXcBsG7dOjp27MiDDz6Ik5MTzz//PKGhoTX2bd68OU8/\n/TR6vR53d5m7d1SO8ttrtkbyYn0kJ5qLlRdZuHchGWcz8HD2YFLnSRYrwBwlJ3Y/EuaicwG0Eawr\nBXsG81T8Uzfd//2C9ykMKbzmdFe96y3FodPpmD9/PtOnT6d9+/ZERUUxY8aM6/4o99tvv83rr79O\nz549CQgIYNq0aTzyyCPk5eURFhZW47ItW7a84bYQQghxIwWlBSxJW8L5yvMEuAcwodMEmno2tXRY\nds/uR8IGdR9E5dHKGqdVHq0koVtCo+x/pejoaJYsWUJhYSF/+tOfGD16NOXl5bV2Gg4JCeHf//43\nubm5fPzxxzz11FNkZWXRvHlzTp48ab6cUqrGNiCdiwXgOGsqbI3kxfo4ek6yirNYsHcB5yvP09K3\nJVO7TbV4AeYoObH7IiwmOoYpA6YQfCYY/9P+BJ8JZsqAKXVez3W7+1+mlGLRokUUFmqjan5+fuh0\nOvR6PUFBQej1erKyssyXX758OadOnQK0Bfs6nQ4nJyfuu+8+Dh48yIoVK6iurmbu3LmcPn36lmIR\nQgghAPbk72Fx2mIqjZV0COrApM6T8HL1snRYDsPupyNBK6Rup6XE7e5/2caNG5k2bRplZWVERkaS\nnJyMm5sbAK+++ip9+vShurqa9evXs2vXLl544QXOnz9PSEgIc+fOJTIyEtAKtGeffZZHHnmEiRMn\n0qdPH/Nt6HQ6GQkTgOOsqbA1khfr44g5UUqx5fgWvj/xPQB9w/uSEJVgNe8fjpITadZqBwYMGMDE\niRN59NG+oDwJAAAgAElEQVRHLR3KLXHknAkhhKVUm6pZeXglB84cQK/Tc3+b++nevLulw7JbN3qv\ns/vpSEchxYy4mqOsqbA1khfr40g5Kasq45N9n3DgzAHcnNxIjEu0ygLMUXLiENORjsBahpCFEEJY\np7NlZ1mctpji8mJ83XyZEDeBEO8QS4fl0GQ6UliM5EwIIRpHTkkOyQeSKa8up5l3MxLjEvFx87F0\nWA7B4X87UgghhHBUaQVprDy8EqMy0jawLaNjR+PqdGu9LkXDkDVhQtgpR1lTYWskL9bHXnOilOK7\nnO/48tCXGJWRni16Mq7jOJsowOw1J1eTkTAhhBDCzhhNRtZkrGHv6b3o0DEkegi9WvSS9cNWRtaE\nCYuRnAkhRP2rqK5g6YGlHC85jovehVGxo2jXtJ2lw3JYsiZMCCGEcAAlFSUs3r+YwrJCvFy8SIxL\npIVvC0uHJa5D1oTZkJkzZzJx4sRb3i8yMpItW7Y0QETCmjnKmgpbI3mxPvaSk9wLuczbM4/CskKC\nPIN4vPvjNluA2UtObkaKMBvyW+fy6/JTRtnZ2ej1ekwm02+6DSGEEJZzuOgwSfuSKDWUEuUfxWPd\nHsPf3d/SYYmbaLDpyIqKCvr3709lZSUGg4ERI0Ywe/ZsZs6cybx58wgKCgLgrbfe4t577wVg9uzZ\nLFiwACcnJ+bOncvgwYPrJZacI0fI2rwZfVUVJhcXWg8aRERM3X8L8nb3ry+NsX6qIW7DaDTi5ORU\n79crbsxRfnvN1kherI8t50Qpxc7cnWzM3IhC0SW0C8PaDsNJb9uvuback1vRYCNh7u7ubNu2jX37\n9rF//362bdvG999/j06n48UXX2Tv3r3s3bvXXIClp6ezdOlS0tPT2bBhA0899VS9jMrkHDlCZlIS\nAwsLiS8pYWBhIZlJSeQcOdIo+4M2HfjOO+/QuXNn/P39GTduHJWVlaSkpBAWFsbf//53goODad68\nOStXrmTdunW0bduWwMBA5syZY74enU5HRUUF48aNw9fXl+7du7N///5bejxSU1Pp0aMHfn5+hIaG\n8sc//hGAu+++GwB/f398fHzYuXMnmZmZ9O/fH39/f4KCghg3bpz5er755hvatWuHv78/zzzzDP37\n92f+/PkAJCUl0adPH1588UWaNm3KrFmzbilGIYQQN2dSJtZnrmdD5gYUioFRAxkRM8LmCzBH0qAL\n8z09PQEwGAwYjUYCAgKA2kdbVq1axfjx43FxcSEyMpLo6GhSU1Pp3bv3bcWQtXkzCW5ucMX8cgKw\ndf9+Iu644+b7p6aSUFb26wnx8SS4ubF1y5Y6j4bpdDqWL1/Oxo0bcXNzo0+fPiQlJdGuXTsKCgqo\nrKwkPz+fhQsXMnXqVIYMGcLevXvJycmhR48ejB8/noiICJRSrFq1iuTkZBYvXsy7777LyJEjycjI\nwNm5bql87rnneOGFF5gwYQJlZWWkpaUBsH37dqKiojh//jx6vVabjx8/nqFDh/Ltt99iMBjYtWsX\nAEVFRYwaNYqkpCRGjBjBe++9x0cffcTkyZPNt5OamkpiYiJnzpzBYDDUKTZRv1JSUhzm06QtkbxY\nH1vMicFo4Iv0L8g4m4GTzomR7UYSFxJn6bDqjS3m5Ldo0DVhJpOJLl26EBISwoABA+jQoQMA7733\nHp07d+axxx6jpKQEgLy8PMLCwsz7hoWFkZube9sx6Kuqaj/daKzb/tcZjdPfYmHx7LPPEhoaSkBA\nAMOGDWPfvn0AuLi48Oqrr+Lk5MTYsWMpLi7m+eefx8vLi9jYWGJjY/nll1/M19OjRw8efPBBnJyc\nePHFF6moqOCnn36qcxyurq4cPXqUoqIiPD096dWrF1B7Yezq6kp2dja5ubm4urpy1113AbBu3To6\nduxojuP5558nNDS0xr7Nmzfn6aefRq/X4+7ufkuPlRBCiOu7WHmRhXsXknE2Aw9nDyZ1nmRXBZgj\nadCRML1ez759+zh//jxDhgwhJSWFJ598kunTpwPw+uuvM23aNPM01tWut5h8ypQpREZGAtr0WZcu\nXa4bg8nFRfvnqoraFBwMTz110/tgev99KCy89nTXW+s4fGWR4unpSV5eHgCBgYHm++nh4QFASMiv\nP6jq4eFBaWmpefvKQlWn0xEWFkZ+fn6d45g/fz7Tp0+nffv2REVFMWPGDO6///5aL/v222/z+uuv\n07NnTwICApg2bRqPPPLINQUzQMuWLW+4fT2XvwFz+ROPbNffdnx8vFXFI9vXfuPLWuKRbdvZLi4v\nJsc/h/OV5zmbfpZBrQYR4R9hNfHV13a8Db9+Xf4/Ozubm2m0Zq1vvvkmHh4e5jVIoH0jb9iwYaSl\npZnXPr388ssADB06lFmzZplHaswB32Kz1struhLc3MynbamsJHrKlDpNJ97u/gBRUVHMnz+fgQMH\nAjBr1iwyMzOZOnUqDz/8MCdPngSgurraPPoUHh4OQL9+/XjyySdJTExk5syZbNy4kR9//BHQRhrD\nwsJYvnw5ffr0qfPtX/bll1/y8MMPU1xczJkzZ4iKiqK6uto8HXmlHTt2MGjQIA4cOMCOHTv48MMP\nzXEopQgPD2fWrFk8+uijJCUlMX/+fLZv337Dx0WatQohRN1lFWex7OAyKo2VtPRtybiO4/By9bJ0\nWOImbvRe12DTkUVFReapxvLycr755hu6du3K6dOnzZdZsWIFcXHaEOrw4cNJTk7GYDBw/Phxjh49\nSs+ePW87joiYGKKnTGFrcDAp/v5sDQ6+pQLqdvevze0UHrt372bFihVUV1fz7rvv4u7ufkvr5hYt\nWkThf0f2/Pz80Ol06PV6goKC0Ov1ZGVlmS+7fPlyTp06BWgjjjqdDicnJ+677z4OHjxojmPu3Lk1\n8iqsw9WjLsI6SF6sjy3kZHfebhanLabSWEmHoA5M7jLZrgswW8hJfWiw6cj8/HwmT56MyWTCZDIx\nceJEEhISmDRpEvv27UOn0xEVFcXHH38MQGxsLGPGjCE2NhZnZ2c++OCDevuNq4iYmNsqmm53/6td\n2bfr6vt4o/us0+kYOXIkS5cuZfLkybRp04avvvrqlto/bNy4kWnTplFWVkZkZCTJycm4/XeU79VX\nX6VPnz5UV1ezfv16du3axQsvvMD58+cJCQlh7ty55mng5cuX8+yzz/LII48wceLEGiNxdelLJoQQ\n4uaUUmw5voXvT3wPQN/wviREJchrrJ2Q344U9WLAgAFMnDiRRx99tM77SM6EEOL6qk3VrDi0goOF\nB9Hr9Nzf5n66N+9u6bDELZLfjhSNQgoqIYSoH5cMl0g+kMzJCydxc3JjTIcxtG7S2tJhiXomP1tk\nB06cOIGPj881f76+vuY1XY1Bhseti6OsqbA1khfrY205OVt2lvl753Pywkn83Px4tOujDleAWVtO\nGoqMhNmB8PBwLl68aNEYtm3bZtHbF0IIe5BTkkPygWTKq8tp5t2MxLhEfNx8LB2WaCCyJkxYjORM\nCCF+lVaQxsrDKzEqI20D2zI6djSuTrfWk1JYH1kTJoQQQlgppRTbT2xn6/GtAPRs0ZOh0UPR62TF\nkL2TDAthpxxlTYWtkbxYH0vmxGgysurIKrYe34oOHUOjh3Jv9L0OX4A5ynFiNyNhAQEBsjDcxlz+\nQXchhHBEFdUVLD2wlOMlx3HRuzAqdhTtmrazdFiiEdnNmjAhhBDCVpRUlLB4/2IKywrxdvVmfMfx\ntPBtYemwRAOQNWFCCCGElci9kMvnBz6n1FBKkGcQEzpNwN/d39JhCQtw7ElnUW8cZf7elkhOrJPk\nxfo0Zk4OFx0maV8SpYZSWgW04rFuj0kBVgtHOU5kJEwIIYRoYEopdubuZGPmRhSKrqFdeaDtAzjp\n6/7bv8L+yJowIYQQogGZlIkNmRtIzU0FYGDUQPqF95MvkzkIWRMmhBBCWIDBaOCL9C/IOJuBk86J\nke1GEhcSZ+mwhJWQNWGiXjjK/L0tkZxYJ8mL9WmonFysvMjCvQvJOJuBh7MHkzpPkgKsjhzlOJGR\nMCGEEKKeFZQWsDhtMRcqL9DEowkT4iYQ6Blo6bCsXs6RI2Rt3sz+Q4cwHTxI60GDiIiJsXRYDUbW\nhAkhhBD1KLM4k+UHl1NprKSlb0vGdRyHl6uXpcOyejlHjpCZlESCmxsoBTodWyoriZ4yxaYLsRvV\nLTIdKYQQQtST3Xm7WZK2hEpjJR2COjC5y2QpwOooa/NmrQArLoaff4aKChLc3MjassXSoTUYKcJE\nvXCU+XtbIjmxTpIX61MfOVFKsfnYZlZnrMakTPQN78vo2NE462XVT13pKyogKwv27yclLw9OndJO\nNxgsHFnDkWeHEEIIcRuqjFWsPLySg4UH0ev03N/mfro3727psGxLcTGmXbsgPx90OggNhdatATC5\nulo4uIYja8KEEEKI3+iS4RLJB5I5eeEkbk5ujOkwhtZNWls6LNuyfz+sWUNOXh6Zhw+TEBcHfn4A\ndr8mTIowIYQQ4jcoKitiSdoSisuL8XPzIzEukRDvEEuHZTsqK2HdOvjlF227QwdyYmLI+v579AYD\nJldXWick2HQBBrIwXzQCWedifSQn1knyYn1+S05ySnKYv2c+xeXFNPNuxtRuU6UAuxV5efDxx1oB\n5uICw4fD6NFEdOrEwKeegi5dGPjUUzZfgN2MrAkTQgghbsH+gv2sOrwKozISExjDqNhRuDrZ77ql\neqUU/PADbNkCJpO29mv0aGja1NKRWYRMRwohhBB1oJRi+4ntbD2+FYBeLXoxJHoIep1MKtVJaSms\nWKF9AxKgd28YNAic7Xs8SH47UgghhLgNRpOR1Rmr2Xd6Hzp0DIkeQu+w3pYOy3ZkZmoF2KVL4OkJ\nI0dC27aWjsripHwX9ULWuVgfyYl1krxYn5vlpKK6gkX7F7Hv9D5c9C6M7ThWCrC6qq6GjRth0SKt\nAIuKgiefvGkB5ijHiYyECSGEENdRUlHC4v2LKSwrxNvVm/Edx9PCt4Wlw7INZ8/CF19ovb/0ehg4\nEO66S/tfALImTAghhKhV7oVclqQt4VLVJYI8g5jQaQL+7v6WDsv6KaV963HdOjAYICAARo2CsDBL\nR2YRsiZMCCGEuAWHiw7zZfqXVJmqaBXQijEdxuDu7G7psKxfZSWsWQNpadp2x47wwAPgLo9dbWRM\nUNQLR5m/tyWSE+skebE+V+ZEKcWPJ39k6YGlVJmq6BralQlxE6QAq4vcXPjoI60Ac3HRFt+PGvWb\nCjBHOU5kJEwIIYQATMrEhswNpOamAjAwaiD9wvuh0+ksHJmVUwp27ICtW7XeX82aacWXg/b+uhWy\nJkwIIYTDMxgNfJH+BRlnM3DSOTGy3UjiQuIsHZb1u3hRaz1x7Ji2feedkJBg972/boWsCRNCCCGu\n42LlRZakLSG/NB8PZw/GdRxHhH+EpcOyfkePagVYWRl4eWnTj23aWDoqmyJrwkS9cJT5e1siObFO\nkhfrUlBawJ/m/Yn80nyaeDRharepUoDdTHU1bNgAixdrBVirVvDEE/VagDnKcSIjYUIIIRxSZnEm\nyw8up6yqjJa+LRkfNx5PF09Lh2Xdioq03l+nT2v9vhIStN5fsm7uN5E1YUIIIRzO7rzdrD26FpMy\n0TG4IyPbjcRZL+MS16UU7Nun9f6qqtJ6f40eDS2kce3NyJowIYQQAq0FxeZjm9lxcgcA/cL7MTBq\noHwD8kYqKrTeXwcOaNtxcVrvLzc3y8ZlB2RNmKgXjjJ/b0skJ9ZJ8mI5VcYqvkj/gh0nd6DX6Rke\nM5yEVgl8++23lg7Nep06pfX+OnAAXF3hd7+DBx9s8ALMUY4TGQkTQghh9y4ZLpF8IJmTF07i5uTG\nmA5jaN2ktaXDsl4mk9b7a9u2X3t/jR4NgYGWjsyuyJowIYQQdq2orIjF+xdzruIcfm5+JMYlEuId\nYumwrNfFi/DVV3D8uLZ9113aAnwnJ8vGZaNkTZgQQgiHlFOSQ/KBZMqry2nm3YzEuER83HwsHZb1\nysiAlSt/7f31u99BdLSlo7JbsiZM1AtHmb+3JZIT6yR5aTz7C/bz6S+fUl5dTkxgDI90faTWAkxy\ngtb7a/16WLJEK8Bat4Ynn7RYAeYoOZGRMCGEEHZFKcV3Od+xLXsbAL1a9GJI9BD0Ohl3qFVhIXz5\npdb7y8lJm3q8807p/dUIZE2YEEIIu2E0GVmdsZp9p/ehQ8eQ6CH0Dutt6bCsk1Kwd682AlZVBU2a\naIvvmze3dGR2RdaECSGEsHsV1RUsPbCU4yXHcdG7MCp2FO2atrN0WNapogJWr4aDB7Xtzp3hvvuk\n91cjk7FZUS8cZf7elkhOrJPkpWGUVJQwf898jpccx9vVm0e6PlLnAszhcnLypNb76+BBrffXgw9q\nC/CtqABzlJzISJgQQgiblnshlyVpS7hUdYlgr2AS4xLxd/e3dFjWx2SC77+HlBTt/+bNtenHJk0s\nHZnDarA1YRUVFfTv35/KykoMBgMjRoxg9uzZFBcXM3bsWHJycoiMjGTZsmX4+2sHy+zZs1mwYAFO\nTk7MnTuXwYMHXxuwrAkTQgjxX4cKD/HVoa+oMlXRKqAVYzqMwd3Z3dJhWZ8LF7TeX9nZ2nafPjBw\noPT+agQ3qlsadGF+WVkZnp6eVFdX07dvX/7xj3/w9ddf07RpU1566SX+9re/ce7cOebMmUN6ejqJ\niYn8/PPP5ObmMmjQIDIyMtDra86YShEmhBBCKcVPp35iU9YmFIquoV15oO0DOOmlqLjG4cOwahWU\nl4O3tzb12Fp+LaCx3KhuadA1YZ6engAYDAaMRiMBAQF8/fXXTJ48GYDJkyezcuVKAFatWsX48eNx\ncXEhMjKS6OhoUlNTGzI8UY8cZf7elkhOrJPk5faZlIn1mevZmLURhSIhKoHhMcN/cwFmtzmproZ1\n6yA5WSvAoqO13l82UIDZbU6u0qBrwkwmE926dSMrK4snn3ySDh06UFBQQEiI9nMRISEhFBQUAJCX\nl0fv3r9+jTgsLIzc3NyGDE8IIYSNMRgNfJH+BRlnM3DSOTGy3UjiQuIsHZb1KSyEL76AggJtynHQ\nIOjdW3p/WZkGLcL0ej379u3j/PnzDBkyhG3bttU4X6fTobvBE+J6502ZMoXIyEgA/P396dKlC/Hx\n8cCv1bNsy7ajb8fHx1tVPLJ97ad7a4nHVrbXbVrH5uOb8Y3xxcPZg8iSSM4eOgv//RlIS8dnFdtK\nEe/rCxs2kHL0KPj6Ev/KK9CsmXXEV8fteBt+/br8f/bl9Xc30GjNWt988008PDyYN28eKSkphIaG\nkp+fz4ABAzh8+DBz5swB4OWXXwZg6NChzJo1i169etUMWNaECSGEwykoLWBx2mIuVF6giUcTJsRN\nINAz0NJhWZfycq33V3q6tt2li9b7y9XVsnE5OIusCSsqKqKkpASA8vJyvvnmG7p27crw4cP55JNP\nAPjkk08YOXIkAMOHDyc5ORmDwcDx48c5evQoPXv2bKjwRD27+hO+sDzJiXWSvNy6zOJMFuxdwIXK\nC4T7hTO129R6LcDsIicnTmi9v9LTtX5fo0bByJE2W4DZRU7qoMGmI/Pz85k8eTImkwmTycTEiRNJ\nSEiga9eujBkzhvnz55tbVADExsYyZswYYmNjcXZ25oMPPrjhVKUQQgj7tztvN2uPrsWkTHQM7sjI\ndiNx1kuLSzOTCbZvh/9ORdKihdb7KyDA0pGJOpDfjhRCCGF1lFJsPraZHSd3ANAvvB8DowbKh/Mr\nnT+v9f7KydEW3PfpAwMGSO8vKyO/HSmEEMJmVBmrWHl4JQcLD6LX6Xmg7QN0a9bN0mFZl0OH4Ouv\nf+399eCD0KqVpaMSt6jB1oQJx+Io8/e2RHJinSQvN3bJcIlPf/mUg4UHcXNyY0LchAYvwGwqJ1VV\nsHYtLF2qFWBt2mi9v+ysALOpnNwGGQkTQghhFYrKili8fzHnKs7h5+bHhE4TCPYKtnRY1uPMGa33\n15kz2pTjPfdAr17S+8uGyZowIYQQFpdTkkPygWTKq8tp5t2MxLhEfNx8LB2WdVAKdu+GDRu0LviB\ngdri+2bNLB2ZqANZEyaEEMJq7S/Yz6rDqzAqIzGBMYyKHYWrk222Vqh35eXa2q9Dh7Ttrl3h3ntt\ntvWEqEnWhIl64Sjz97ZEcmKdJC+/Ukrxbfa3fHXoK4zKSK8WvRjbcWyjF2BWm5OcHPjwQ60Ac3PT\nRr9GjHCIAsxqc1LPZCRMCCFEozOajKzOWM2+0/vQoWNo9FB6hfW6+Y6OwGSC776Db7/VpiLDwrTm\nq9L7y+7ImjAhhBCNqqK6gqUHlnK85DguehdGx44mpmmMpcOyDufPw5dfah3wdTro2xfi46X3lw2T\nNWFCCCGswrnycyxJW0JhWSHert4kxiXS3Ke5pcOyDunp2vqvigrw8dF6f0VFWToq0YBkTZioF44y\nf29LJCfWyZHzknshl3l75lFYVkiwVzBTu021igLM4jmpqtJ+eHvZMq0Aa9tW6/3lwAWYxXPSSGQk\nTAghRIM7VHiIrw59RZWpilYBrRjTYQzuzu6WDsvyCgq03l+FhdqU4+DB0LOn9P5yELImTAghRINR\nSvHTqZ/YlLUJhaJbs27c3+Z+nPQOvsZJKfj5Z9i0Sev91bSp9u3H0FBLRybqmawJE0II0ehMysT6\no+v5Oe9nABKiEugb3ld+hLusTFv7dfiwtt2tGwwd6hCtJ0RNsiZM1AtHmb+3JZIT6+QoeTEYDSQf\nSObnvJ9x0jkxqv0o+kX0s8oCrFFzkp0NH32kFWDu7vDQQzB8uBRgV3GU40RGwoQQQtSrC5UXWJK2\nhNOlp/Fw9mB83HjC/cItHZZlmUyQkgLbt2tTkS1bar2//P0tHZmwIFkTJoQQot6cLj3NkrQlXKi8\nQBOPJkyIm0CgZ6Clw7KskhKt99fJk9qC+379tN5fepmMcgSyJkwIIUSDyyzOZNnBZRiMBsL9whnX\ncRyeLp6WDsuyDh7U2k9UVICvr9b7KzLS0lEJKyFluKgXjjJ/b0skJ9bJXvOyK28XS9KWYDAa6Bjc\nkUmdJ9lMAdYgOTEYtMX3y5drBVi7dvDEE1KA1ZG9HidXk5EwIYQQv5lSis3HNrPj5A4A+oX3Y2DU\nQKtcgN9oTp/Wen8VFYGzs9b76447pPeXuIasCRNCCPGbVBmrWHF4BemF6eh1eh5o+wDdmnWzdFiW\noxSkpmq9v4xGCArSen+FhFg6MmFBsiZMCCFEvbpkuMTnBz7n1IVTuDm5MbbjWFoFtLJ0WJZTVgar\nVsGRI9p2jx4wZAi4uFg2LmHVZE2YqBeOMn9vSyQn1ske8lJUVsS8PfM4deEUfm5+PNbtMZsuwG47\nJ8ePw4cfagWYuzuMGQMPPCAF2G2wh+OkLmQkTAghRJ1ll2Sz9MBSyqvLae7TnPEdx+Pj5mPpsCzD\naNR6f33/vTYVGR6u9f7y87N0ZMJGyJowIYQQdbK/YD+rDq/CqIzEBMYwKnYUrk4O2un93Dmt99ep\nU9qC+/794e67pfeXuIasCRNCCPGbKaX4Luc7tmVvA6BXi14MiR6CXuegBceBA1rvr8pKrffXqFEQ\nEWHpqIQNctAjSNQ3R5m/tyWSE+tka3kxmoysOrKKbdnb0KHj3uh7ubfNvXZVgNU5JwaDtvj+iy+0\nAqx9e3jySSnAGoCtHSe/lYyECSGEqFV5VTnLDi7jeMlxXPQujI4dTUzTGEuHZRn5+dr04+XeX0OH\nQvfu0vtL3BZZEyaEEOIa58rPsThtMUVlRXi7epMYl0hzn+aWDqvxKQU7d8I332gL8YODtd5fwcGW\njkzYCFkTJoQQos5OXTjF52mfc6nqEsFewSTGJeLv7m/psBrfpUva9GNGhrZ9xx1a93tpPSHqif1M\n6guLcpT5e1siObFO1p6XQ4WHSNqXxKWqS7QKaMWjXR+1+wKs1pwcO6b1/srIAA8PGDsW7r9fCrBG\nYu3HSX2RkTAhhBAopfjx1I98k/UNCkW3Zt24v839OOmdLB1a4zIaYds22LFDm4qMiIAHH5TeX6JB\nyJowIYRwcCZlYv3R9fyc9zMACVEJ9A3v63g/wn3unPbNx9xcbcF9fDz06ye9v8RtkTVhQgghamUw\nGlh+cDlHi4/irHdmZLuRdAzuaOmwGl9aGqxZo7We8PPTen+Fh1s6KmHnpLwX9cJR5u9tieTEOllT\nXi5UXmDB3gUcLT6Kp4snkzpPcrwCzGAg5S9/0dpPVFZCbCw88YQUYBZmTcdJQ5KRMCGEcECnS0+z\nJG0JFyov0MSjCRPiJhDoGWjpsBpXfr42/ZiZCW3aaL2/unWT3l+i0ciaMCGEcDCZxZksO7gMg9FA\nuF844zqOw9PF09JhNR6l4KefYPNmbSF+SIjW+ysoyNKRCTska8KEEEIAsCtvF+uOrsOkTHQM7sjI\ndiNx1jvQW8GlS7ByJRw9qm337An33COtJ4RFyJowUS8cZf7elkhOrJOl8qKU4pusb1iTsQaTMtEv\nvB+j2o9yrAIsK0vr/XX0qNb7a9w4uO8+UnbssHRk4iqO8vrlQEefEEI4pipjFSsOryC9MB29Ts+w\ntsPo2qyrpcNqPEYjbN2q9f4CiIzUen/5+lo0LCFkTZgQQtixS4ZLfH7gc05dOIWbkxtjO46lVUAr\nS4fVeIqLtcX3eXlav6/4eOjbV3p/iUYja8KEEMIBFZUVsXj/Ys5VnMPPzY8JnSYQ7OVAPzy9f7/W\n+8tgAH9/rfdXy5aWjkoIM/koIOqFo8zf2xLJiXVqrLxkl2Qzf898zlWco7lPc6Z2m+o4BVhlJaxY\nAV99pRVgHTpovb+uU4DJsWJ9HCUnMhImhBB2Zn/BflYdXoVRGYkJjGFU7ChcnVwtHVbjyMvTph+L\ni7VvPN57L3TtKr2/hFWSNWFCCGEnlFJ8l/Md27K3AdA7rDeDWw9Gr3OASQ+l4McfYcsW6f0lrIqs\nCZJTubMAACAASURBVBNCCDtnNBlZnbGafaf3oUPH0Oih9ArrZemwGkdpqTb9mJWlbffqpfX+cpa3\nOGHdHODjkWgMjjJ/b0skJ9apIfJSXlXOov2L2Hd6Hy56F8Z1HOc4BVhmptb7KysLPD1h/HhtCvIW\nCjA5VqyPo+REPiYIIYQNO1d+jsVpiykqK8Lb1ZvEuESa+zS3dFgNz2jUph5/+EHbjoqC3/1Oen8J\nm9Kga8JOnjzJpEmTOHPmDDqdjt///vc8++yzzJw5k3nz5hH037n6t956i3vvvReA2bNns2DBApyc\nnJg7dy6DBw+uGbCsCRNCCABOXTjF52mfc6nqEsFewUyIm4Cfu5+lw2p4Z8/Cl1/+2vtrwADo00d6\nfwmrdKO6pUGLsNOnT3P69Gm6dOlCaWkp3bt3Z+XKlSxbtgwfHx9efPHFGpdPT08nMTGRn3/+mdzc\nXAYNGkRGRgb6Kw4sKcKEEAIOFR7iy0NfUm2qpnVAax7q8BDuzu6WDqthKaX1/lq79tfeX6NHQ1iY\npSMT4rpuVLc06MeG0NBQunTpAoC3tzft27cnNzcXoNaAVq1axfjx43FxcSEyMpLo6GhSU1MbMkRR\nTxxl/t6WSE6s0+3mRSnFDyd/YNnBZVSbqunWrBuJcYn2X4Bd7v21YoVWgHXsqPX+qocCTI4V6+Mo\nOWm0sdvs7Gz27t1L7969AXjvvffo3Lkzjz32GCUlJQDk5eURdsUBFRYWZi7ahBDC0ZmUiXVH17Ep\naxMKRUJUAsPaDsNJ72Tp0BpWbi589JE2CubiAiNGaN3v3e288BR2r1EW5peWljJ69Gj+9a9/4e3t\nzZNPPsn06dMBeP3115k2bRrz58+vdV9dLQ32pkyZQmRkJAD+/v506dKF+Ph44NfqWbZl29G34+Pj\nrSoe2b720/2t7F9ZXckbn7xB7sVcortFM7LdSIrSi/j2+LcWvz8Ntr1tGxw4QPy5c2AykXLhAvTv\nT3zXrtYRn2w32Ha8Db9+Xf4/Ozubm2nwZq1VVVU88MAD3HvvvTz//PPXnJ+dnc2wYcNIS0tjzpw5\nALz88ssADB06lFmzZtGr169ftZY1YUIIR3Oh8gJL0pZwuvQ0ni6ejOs4jnC/cEuH1bAuXtSmHo8d\n07Z794ZBg6T3l7A5FlsTppTiscceIzY2tkYBlp+fb/5/xYoVxMXFATB8+HCSk5MxGAwcP36co0eP\n0rNnz4YMUdSTqz/hC8uTnFinW83L6dLTzNszj9Olpwn0CGRqt6n2X4AdPapNPx47pvX+SkyEoUMb\nrACTY8X6OEpOGvQjxY4dO1i0aBGdOnWi63+Hj9966y0+//xz9u3bh06nIyoqio8//hiA2NhYxowZ\nQ2xsLM7OznzwwQe1TkcKIYQjOHr2KMvTl2MwGgj3C2dcx3F4unhaOqyGU12t9f768Udtu1UrrfeX\nj49l4xKigchvRwohhBXalbeLdUfXYVIm4oLjGNFuBM56O56KO3tW++Ht/Hyt39fAgVrvL/kgLmyc\n/HakEELYCKUUm49tZsfJHQDcHXE3AyIH2O+sgFLwyy+wbp3WeiIgQPvmo/T+Eg6gQdeECcfhKPP3\ntkRyYp1ulJcqYxXL05ez4+QO9Do9I2JGMDBqoP0WYBUV/5+9Ow+q6sz/PP5mBwFFAUHFiAqKKIj7\nlhiMS6KJRo1LxE60Ezud/v26O1M9VUlPZk3V1C9JzdRMp9OT/nVntbvRGI2JJtG0S8S4xV1BEcQF\nBARE2Xcu98wf3yjZFJF7Oefe+31VWe05Bu6DT1/4+jzf83lg82b49FMpwJKSHJb91Rn6XrEeT5kT\nXQlTSikLqG+pZ/2Z9RTVFBHgE8DyUcsZ0nuI2cNynqIiOXqoshL8/WHePBg9WrcflUfRnjCllDLZ\n9YbrpGemU9lUSa+AXqxMXknf4L5mD8s5DAP274c9e8Buh3795Oih8HCzR6aUU2hPmFJKWVR+VT4f\nnvmQJlsT/UP7k5aURoh/iNnDco4fZn9NmQIzZ2r2l/JY2hOmHMJT9u9dic6JNX13Xk6Xnubvp/9O\nk62JhIgEVqesdt8C7Px5+POfpQALDoaf/QweftgSBZi+V6zHU+bE/P/3K6WUhzEMg70Fe8nIzwBg\ncsxk5gydg7eXG/672GaDnTvh8GG5HjpUsr9C3LTYVKoTtCdMKaW6UZu9ja25WzlddhovvHgk7hEm\nxUzq+ANd0fXrkv1VWirZXzNnwtSp2nyvbis3t4Bduy7S2uqNn5+dWbOGMnz4ILOH1SV3qlu0CFNK\nqW7S2NrIhrMbyK/Kx8/bjyWJSxgeMdzsYTmeYcDJk7B9O7S2Qp8+kv01YIDZI1MWlptbwAcfXCAg\nYCa1tbJY2tKym9Wr41y6EDPt7EjlOTxl/96V6JxYS2VjJe+efJeMjAxC/EP4+Zifu2cB1tQk0RNb\nt0oBlpwMv/ylpQswfa9Yw65dF2lpmUlmJuzencGNGxAQMJPduy+aPTSn0Z4wpZRysqKaItZnrae+\ntZ6wwDB+MfYX9ArsZfawHK+wUAqwqirJ/nr0Ucn+UqoD5eVw5Ig3BQVy7e0t+b0ALS3uu16k25FK\nKeVE2eXZbD63GZvdxtDeQ1k6cimBvoFmD8ux7HbJ/srIkN/37y/ZX336mD0yZXGVlbB3r5xcdfjw\nVzQ1PUT//nDffVLHA/Tt+xX/8i8PmTvQLtCcMKWU6maGYXCo6BA7L+7EwGBsv7E8Gv8oPt4+Zg/N\nsWpq5Oih/Hy5njpVGvB93OzrVA5VUwNffw0nTkjd7u0NCxYMJS9vN6GhM2/9d83Nu5k5M87EkTqX\nroQph8jIyCA1NdXsYajv0Dkxj92wsz1vO0evHgVg1pBZTBs4DS8vL/eal9xcOfexsVG6qBcuhDjX\n+4HpVnNicfX1smh69Kikl3h5Sdtgaqqc3Z6bW8Du3RfJzs4kMTGZmTPd++lIXQlTSikHarY1syl7\nE3kVefh6+7IwYSGj+o4ye1iOZbPBjh1w5Ihcx8VJAabZX+o2mprg4EH45pv2Xq/ERJgxAyIj2/+7\n4cMHMXz4IDIyvD2iMNaVMKWUcpCa5hrWZa2jtK6UHn49eHLUk9zX6z6zh+VY5eWS/VVWJluOs2bB\n5Mma/aV+UkuL5PQePCgLpgDx8fDQQ3JsqCfQlTCllHKy0rpS1mWto6a5hvCgcFYmr6RPkBs1phuG\nNPB8+WV79teSJdKEr9QP2Gxw7Bjs2ydbkACxsVJ83edm/y7pCvd97lN1K83ZsR6dk+6TdyOP906+\nR01zDff1uo9nxz572wLMJeelsRE2boTPPpMCLCVFsr/cpABzyTmxqLY2OH4c3nxT6vX6eomIe/pp\nWLXq7gswT5kTXQlTSqkuOHb1GNvytmE37CT1TeLxhMfx9Xajb61Xrkj2V3U1BARI9ldystmjUhZj\nt8OZM5JSUlEh96KiZOVr2DDdrb4d7QlTSql7YBgGOy/t5GDhQQCmD5rOjNgZeLnLTxu7XfaSMjJk\nK3LAADl6SLO/1HcYBuTkwJ49cO2a3AsPl4b7kSO1+ALtCVNKKYdqbWvlk5xPyC7PxtvLm/nD5jOm\n3xizh+U4P8z+uv9++amq2V/qW4YBFy/CV1/B1atyr1cviZoYPVpyv1TH9K9JOYSn7N+7Ep0T56hv\nqWft6bVkl2cT4BPAz5J/1qkCzPLzkpMDf/6zFGAhIfDUU/IEpBsXYJafE4spKIAPPoB//EMKsJAQ\nmDcPfvMbGDPGMQWYp8yJroQppdRdut5wnfTMdCqbKukV0IuVySvpG9zX7GE5RmurZH8dlYBZ4uMl\n+ys42NxxKcu4elVWvi5ckOugIFkknTgR/PzMHZur0p4wpZS6C/lV+Xx45kOabE30D+1PWlIaIf5u\nEk567Zpkf127Jites2fDpEna0KMA+b/Fnj1w7pxcBwTAlCkSDxfoZsegOoP2hCmlVBecLj3N1tyt\ntBltJEQksHjEYvx9/M0eVtcZhuQJfPmlBDuFh0v2l6ekaKo7qqiQ5zKysuT/Kn5+suo1bRr06GH2\n6NyD9oQph/CU/XtXonPSdYZhkJGfwSc5n9BmtDE5ZjLLRi7rUgFmmXlpbISPPoLPP5cCbMwYyf7y\nwALMMnNiEdXVEgn3pz9BZqb0eE2cCL/9rSySdkcB5ilz0uFKWF1dHUFBQfj4+JCbm0tubi5z587F\nTzeAlVJurM3extbcrZwuO40XXsyNn8vEARPNHpZjFBTI0483s78eewySkswelTJZXZ0crn3sWPvh\n2mPGwIMPQliY2aNzTx32hI0dO5b9+/dTWVnJtGnTmDBhAv7+/qSnp3fXGL9He8KUUs7W2NrIhrMb\nyK/Kx8/bjyWJSxgeMdzsYXWd3Q5ffw1798r+UkyMZH/17m32yJSJGhvbD9dubZV7o0ZJ3EREhKlD\ncwtd6gkzDIMePXrw7rvv8i//8i+8+OKLjB492uGDVEopK6hsrCQ9K53rDdcJ9Q8lLSmNfqFusEVX\nXS2rXwUFssTxwAPyU9aNoyfUnTU3tx+u3dQk94YPl0i46Ghzx+Yp7qon7NChQ6Snp/Poo48CYLfb\nnToo5Xo8Zf/eleicdF5RTRHvnHiH6w3XiQqOYs3YNQ4vwEyZl+xsyf4qKIDQUMn+mjlTC7Bvedp7\npbUVDh2CN96QyImmJhgyBNasgRUrrFGAecqcdLgS9oc//IFXX32VRYsWMXLkSC5evMiMGTO6Y2xK\nKdVtssuz2XxuMza7jaG9h7Js5DICfAPMHlbXtLbCP/8pTT4gh/g9/rhmf3motjY4eVJ2pGtq5N7A\ngXK+4+DB5o7NU2lOmFLKoxmGwaGiQ+y8uBMDg3H9xjEvfh4+3i6+SvTD7K85c+QRN83+8jh2u8RM\nZGRAZaXci46W4is+Xv8v4Wxd6gk7evQo//Zv/0Z+fj42m+3WJ8zMzHTsKJVSqpvZDTvb8rZx7Kqs\nFM0aMotpA6e59iHchiErX//8pzziFhEh2V9W2GNS3cowJGB1zx4oL5d7ERHS85WYqMWXFXS4EjZs\n2DD+9//+34waNQrv7xwIFRsb6+yx/SRdCbOmjIwMUlNTzR6G+g6dkztrtjWzKXsTeRV5+Hr7sjBh\nIaP6jnL66zp1XhoaYOtWOf8RYOxYeOQR8HeDYFkncrf3imHI0UJffQUlJXIvLEyew0hOdo3Dtd1p\nTrq0EhYZGcmCBQscPiillDJLTXMN67LWUVpXSg+/Hjw56knu63Wf2cPqmvx8efqxpkbOkpk/H0aO\nNHtUqpvl50vxdeWKXIeGwvTpUo/rcxjW0+FK2I4dO9iwYQOzZs3C/9t/TXl5ebF48eJuGeAP6UqY\nUqorSutKSc9Mp7allvCgcFYmr6RPUB+zh3Xv7HbJ/fr66/bsryVLNF3TwxQXw+7dcOmSXPfoIYdr\nT5igh2ubrUsrYWvXriU3Nxebzfa97UizijCllLpXeTfy2Ji9kZa2Fgb1GsTyUcvp4efCh+BVVcHH\nH0NhoTT4TJ8u8ea65OExyspk5Ss3V64DAmDqVDlcO8DFH+71BB2uhA0fPpycnBzLNKrqSpg1udP+\nvbvQOfm+Y1ePsS1vG3bDTlLfJB5PeBxf7w7/HepwDpuXs2flgL+mJtlzWrxYcwbukSu+V27ckIb7\ns2fbD9eeNEkO1w4KMnt0XeeKc3I7XVoJmzp1KtnZ2YzU3gKllAsyDIOdl3ZysPAgANMHTWdG7AzL\n/MOy01pb4csv4fhxuR4+XLK/uuNUZWW6qirZfT59WnaifXxg/Hg5ACEkxOzRqc7qcCUsISGBixcv\nMnjwYAK+Xds0M6JCV8KUUnerta2VT3I+Ibs8G28vb+YPm8+YfmPMHta9Ky2V7cfycvD1leyvCRM0\na8AD1NVJ29/x4xK66u0NKSmy+9yrl9mjU3dyp7qlwyIsPz//J+9rRIVSysrqW+pZf2Y9RTVFBPoG\nsmzkMob0HmL2sO6NYcDRo7Bjh2R/RUZK831UlNkjU07W0AAHDsCRI7II6uXVfrh2eLjZo1N3o0tF\nmNVoEWZN7rR/7y48eU7K68tZl7WOyqZKwgLDWJm0ksjgSLOHBdzDvDQ0wJYt7Z3X48ZJ9pc+8uYw\nVnyvNDfL+Y6HDsnvARISJOW+b19zx9YdrDgn96pLPWFKKeVK8qvy+fDMhzTZmugf2p+0pDRC/F20\nWebyZcn+qq2V7K8FCyTqXLmt1lZZ9TpwQOpvgKFDpfgaMMDcsSnH05UwpZTbOF16mq25W2kz2kiI\nSGDxiMX4+7hgWnxbm3Rf79snW5H33SdPP2r2l9tqa5N+r337pOYGmfaZM2HQIHPHprpGV8KUUm7N\nMAz2FuwlIz8DgMkxk5kzdA7eXi5wPssP/TD768EH5ZcrnDWjOs1ulycd9+6VqQfo319WvoYO1Wcu\n3F2H7+qPP/6Y+Ph4evbsSWhoKKGhofTs2bM7xqZcSEZGhtlDUD/gKXNis9v4NOdTMvIz8MKLefHz\neCTuEcsWYHeclzNn4M9/lgKsZ09YtUpOW9YCzKnMeK8Yhkz3W29Jy19VlTxvsXw5/OIXEBfn2QWY\np3z/6nAl7MUXX+Tzzz9nxIgRnf7khYWFPP3001y7dg0vLy+ee+45fvvb31JRUcHy5cspKCggNjaW\njz76iLBvl9lfffVV3nvvPXx8fPjjH//InDlzOv9VKaU8QmNrIxvObiC/Kh8/bz+WjlzKsPBhZg+r\n81paJPvrxAm5TkiQ/i/N/nI7hgHnz0vQammp3OvdW2rtUaO03vY0HfaETZs2jQMHDtzTJy8tLaW0\ntJSUlBTq6uoYN24cn376Ke+//z4RERG8+OKLvP7661RWVvLaa6+RnZ1NWloaR48epbi4mFmzZnH+\n/PnvHZekPWFKKYDKxkrSs9K53nCdUP9Q0pLS6Bfaz+xhdV5pKWzaBNevS/bXww9L+qYnL4O4qUuX\n5IihoiK57tlTdppTUvSkKXfWpZ6w8ePHs3z5chYuXNjpA7yjo6OJjo4GICQkhBEjRlBcXMzWrVvZ\nu3cvAKtWrSI1NZXXXnuNLVu2sGLFCvz8/IiNjSUuLo4jR44wefLku/5ilVLur6imiPVZ66lvrScq\nOIq0pDR6BbpYYqVhyGNwO3ZIV3bfvvDEE5r95YYKC6X4unxZroODJeF+/Hipu5Xn6nD6q6urCQoK\nYseOHd+739kDvPPz8zl58iSTJk2irKyMqG+/0URFRVFWVgbA1atXv1dwxcTEUFxc3KnXUeZwp0wX\nd+Guc5Jdns3mc5ux2W0M7T2UZSOXEeDrOicVZ2RkkDphgjQCnT8vN8ePlxUwzf4yhbPeK6WlUnzd\nnObAQDnbcdIk8HfBh3a7k7t+//qhDouwDz74oMsvUldXxxNPPMEbb7xBaGjo9/7My8vrjme4uez5\nbkophzIMg0NFh9h5cScGBuP6jWNe/Dx8vF1sH+fqVfj3f2/P/nr8cbiHnltlXdevtx+uDVJwTZ4M\nU6fKlCt1022LsNdff52XXnqJ3/zmNz/6My8vL/74xz/e1Qu0trbyxBNP8NRTT7Fw4UJAVr9KS0uJ\njo6mpKSEvt/G/w4YMIDCwsJbH1tUVMSAn0inW7169a1jk8LCwkhJSblVMd98okKv9drTr1NTUy01\nnq5cT39wOtvytrFp2yYA1ixew7SB0261NZg9vru6bmsj4w9/gKwsiI2FQYPIiIyEsjJSvy3CLDVe\nve709WefZXD6NLS1pWIYUFiYwfDh8K//mkpwsPnjc6XrVBf+/nXz97c79vG7btuY/9lnnzF//nw+\n+OCD761GGYaBl5cXq1at6vCTG4bBqlWrCA8P5//+3/976/6LL75IeHg4L730Eq+99hpVVVXfa8w/\ncuTIrcb8CxcufO/1tTFfKc/SbGtmU/Ym8iry8PX2ZVHCIkb2HWn2sDqnslKyv4qK2rO/pk/XR+Hc\nRG2tHK594kT74dpjx8oUa6KTMu3syP379zN9+nSSk5NvFVKvvvoqEydOZNmyZVy5cuVHERX/9m//\nxnvvvYevry9vvPEGDz/88F1/Mco8GRkZt/41oKzBHeakprmGdVnrKK0rpYdfD1aMWsHAXgPNHlbn\nZGXB55/LAYC9epHRrx+pTz5p9qjUd9zre6WhAfbvl+crbDapr5OTITVVYifUvXOH7183mZaYf//9\n92O323/yz3bt2vWT919++WVefvllZw5LKeUCSutKSc9Mp7allvCgcFYmr6RPUB+zh3X3Wlpg2zY4\ndUquR4yQ7K/Dh80dl+qypqb2w7VbWuReYqJkfUVa45x45SL07EillOXk3chjY/ZGWtpaGNRrEMtH\nLaeHnwsFl5aUSPbXjRuSQfDIIzBunGZ/ubiWlvbDtRsb5V58vBwx1M8FI+pU99CzI5VSLuNo8VG2\n5W3DwCCpbxKPJzyOr7eLfKsyDPjmG9i1qz37a8kS+V/lsmy29sO16+rkXmysFF/33Wfq0JSL67Ar\nNDc3l5kzZzJypDTCZmZm8j//5/90+sCUa/nuUyHKGlxtTgzDYMfFHXyR9wUGBg8OepDFIxa7TgFW\nXw/r1sE//ykF2IQJcgjgDwowV5sXT3C7OWlrk2b7N9+E7dulABswAJ56So711ALMeTzlfdLhd7df\n/OIX/K//9b94/vnnAUhKSmLFihX8l//yX5w+OKWUZ2hta2Xzuc2cu34Oby9v5g+bz5h+Y8we1t27\neBE++UR+SgcFSfZXQoLZo1L36Obh2nv2QEWF3IuKkpWvYcN0V1k5Toc9YePHj+fYsWOMGTOGkydP\nApCSksKpm82m3Ux7wpRyL3UtdXx45kOKaooI9A1k2chlDOk9xOxh3Z22NolEv3m+bmwsLF6suQQu\nyjAgN1em9No1uRceLk87jhqlxZe6N13qCYuMjOTChQu3rjdt2kQ/7UBUSjlAeX056VnpVDVVERYY\nxsqklUQGu8jjZRUVkv1VXCw/nVNT5UBAzf5yOYbRfrj2zZPyevVqP1xbp1Q5S4crYRcvXuS5557j\n4MGD9O7dm8GDB5Oenn4rsb676UqYNblTpou7sPqcXK68zIazG2iyNTEgdAArklYQ4h9i9rDuTmYm\nfPHFrewvnnjirhuErD4vnubKFfh//y+DoKBUAEJCJGR17Fg9XNtM7vQ+6dJK2NChQ9m9ezf19fXY\n7fYfnf2olFKddbr0NFtzt9JmtJEQkcATI57Az8cFDq9ubpbsr9On5ToxEebPlz4w5VKuXpWVrwsX\noKxMYtzuvx8mTtRz1FX36XAlrLKykr/97W/k5+djs9nkgzpxdqSj6UqYUq7LMAz2FuwlIz8DgCkx\nU5g9dDbeXi6w33P1qmR/VVTIT+m5c2HMGG0UcjHXrknD/blzcu3vLwdrT56sh2sr5+jSSti8efOY\nMmUKycnJeHt73zo7UimlOsNmt/FZ7mecLjuNF17MjZ/LxAETzR5WxwxDotF375ZG/Kgoyf7SaHSX\nUlEBGRlyipRhyFbjxImy+tXDhXKAlXvpcCVs7NixnDhxorvG0yFdCbMmd9q/dxdWmpPG1kY2nN1A\nflU+/j7+LElcwrDwYWYPq2N1dfDpp7JnBfJTe86cLjULWWlePEFNDezdCydPgt0OPj5yeMEDD8DN\n7hqdE+txpznp0kpYWloaf/3rX5k/fz4BAQG37vfp40JnuCmlTFPZWEl6VjrXG64T6h9KWlIa/UJd\n4AnrCxck+6u+XpZKHn8chg83e1TqLtXXS8L9sWPth2uPGSNPPIaFmT06pUSHK2F/+tOf+M//+T8T\nFhaG97fP6Xp5eXHp0qVuGeAP6UqYUq6jqKaI9VnrqW+tJyo4irSkNHoF9jJ7WHfW1iZbjwcPyrVm\nf7mUxkaZusOH2w/XHjVKEkQiIkwdmvJQd6pbOizCBg8ezNGjR4mwyP97tQhTyjVkl2ez+dxmbHYb\ncX3iWJq4lADfgI4/0Ew3bkj219WrEg41YwZMm6ZBUS6gpUWO7Tx4EJqa5N6wYZJyHx1t7tiUZ7tT\n3dLhd5b4+HiC9PFr1QFPOefLlZg1J4ZhcODKAT46+xE2u41x/caxYtQK6xdgp0/DX/4iBVhYGPz8\n504JX9X3imPZbPLcxBtvSOREUxMMGQJr1kBa2t0VYDon1uMpc9JhT1iPHj1ISUlhxowZt3rCzIyo\nUEpZl92wsy1vG8euHgNg9pDZTB041dpPVDc3S/BqZqZcjxwp2V+aV2BpbW3SbP/119J8DzBwoKx8\nDR5s7tiUulsdbkd+8MEHP/4gLy9WrVrlrDHdkW5HKmVNzbZmNmZv5ELFBXy9fVmUsIiRfUeaPaw7\nKy6W7ceb2V/z5sk5NVYuGj2c3S4xExkZUFkp96KjpfiKj9epU9bTpZ4wq9EiTCnrqWmuIT0znbL6\nMnr49WDFqBUM7DXQ7GHdnmFI89Du3fJTPTpasr8s0vuqfswwJGB1zx4oL5d7ERHStpeYqMWXsq57\niqhYunQpGzduJCkp6Sc/YebNpXulcK9MF3fRXXNSWldKemY6tS21hAeFszJ5JX2CLBxhU1cn0RMX\nL8r15Mkwa1a3HRSo75XOMQxJC/nqKygpkXthYfK0Y3KyY1r2dE6sx1Pm5Lbfdd544w0APv/88x9V\ncJbu71BKdZu8G3lszN5IS1sLg3oN4slRTxLkZ+EHefLyJHz1ZvbXwoXyCJ2ypPx8Kb6uXJHr0ND2\nw7V9fEwdmlIO0eF25EsvvcTrr7/e4b3uotuRSlnD0eKjbMvbhoFBUt8kHk94HF/v7llN6jSbTbYe\nDx2S68GDJfvrZmS6spTiYim+bi5W9ughxwtNmKCHayvX06WesDFjxnDy5Mnv3UtKSiIrK8txI+wE\nLcKUMpdhGOy8tJODhRJm+uCgB0mNTbXuCvmNG3LwdkmJ7F099JCc2KzZX5ZTViY9Xzk5ch0Q0H64\ndoDFE06Uup17ygn785//TFJSErm5uSQlJd36FRsbS3JystMGq1yTp2S6uBJnzElrWysfnf2IjOEu\nyQAAIABJREFUg4UH8fbyZmHCQmYMnmHNAsww4NQpyf4qKYHeveGZZ2RJxcQCTN8rP3YzI/ff/10K\nMD8/mab/8B/kmCFnF2A6J9bjKXNy272DtLQ05s6dy+9//3tef/31W1VcaGgo4eHh3TZApZQ11LXU\nsT5rPcW1xQT6BrJ85HIG97ZoIFNzM3z+uWQZACQlwaOPavaXxVRXy+Hap061H649frxk5IaEmD06\npZxPIyqUUh0qry8nPSudqqYqwgLDWJm0ksjgSLOH9dOKimRZpbIS/P0l+2v0aM0wsJC6uvbDtdva\nZGEyJUVWvXpZ/GhRpTrrniIqlFIK4HLlZTac3UCTrYkBoQNYkbSCEH8LLlMYBhw4IB3ddjv06wdP\nPKHZXxbS0NB+uHZrq9TFSUkSN6EbLMoTaWeqcghP2b93JY6Yk1Olp/hH5j9osjUxImIEq1NWW7MA\nq62Fv/8ddu2SAmzKFHj2WUsWYJ74Xmlulm3HN96A/fulAEtIgOeflzrZ7ALME+fE6jxlTnQlTCn1\nI4ZhkJGfwd6CvQBMiZnC7KGz8fay4L/bzp+X7K+GBggOluyv+HizR6WQYuvoUSm8Ghrk3tCh8oDq\ngAHmjk0pK9CeMKXU99jsNrbmbiWzLBMvvJgbP5eJAyaaPawfs9lk5eubb+R6yBBYtEizvyygrQ1O\nnJDDtWtr5d5998HMmTBokLljU6q7aU+YUuquNLY28uGZDymoLsDfx58liUsYFm7BRPnr1yX7q7RU\nurpnzpRAKW2+N5XdDqdPy9ZjVZXc69dPpmfoUJ0epX7IgnsLyhV5yv69K+nsnFQ0VvDuyXcpqC4g\n1D+Un6f83HoFmGHAyZOS/VVaKtlfzz4L06a5zE94d3yvGAacPQtvvQVbtkgBFhkJy5bBc89BXJy1\np8cd58TVecqc6EqYUorC6kLWn1lPQ2sDUcFRpCWl0SvQYlkBTU2S/XXmjFwnJ0v2l0apm8Yw5DjO\nr76SmhikLp4xA0aN0kMJlOqI9oQp5eGyy7PZfG4zNruNuD5xLE1cSoCvxQqbwkLJ/qqqkuyvRx+V\n7C9lmsuX5TjOoiK57tlTcr5SUvRwbaW+S3vClFI/YhgGBwsPsvPSTgDG9RvHvPh5+Hhb6Ceo3S7Z\nX3v2yO/797dGpoEHKyyUla/Ll+U6OFgS7sePB1/9iaJUp+hisXIIT9m/dyV3mhO7YeeLvC9uFWCz\nh8zmsWGPWasAq6mR7K/du6UAmzpV+r9cvABz1fdKaSmsWwfvvisFWGCgNNy/8IIcsO3KBZirzok7\n85Q5ceG3jVLqXjTbmtmYvZELFRfw9fZlUcIiRvYdafawvi83Vzq8b2Z/LVok3d2q212/LguRZ8/K\ntb+/FF1TpkBQkLljU8rVaU+YUh6kprmG9Mx0yurL6OHXgxWjVjCw10Czh9XOZoOdO+VcG5DCa+FC\nPc3ZBFVVkJEhkROGIStdEybA/fdLXayUujvaE6aUoqS2hHVZ66htqSU8KJyVySvpE9TH7GG1Ky+X\n7K+yMunsnjlTllusnG3ghmprJWT1xIn2w7XHjYPp06X5XinlONoTphzCU/bvXcl35yTvRh7vn3qf\n2pZaBvUaxJqxa6xTgBmG/MT/61+lAOvTR3q/3DR81arvlYYG2LFDznc8elTa8EaPhl//Gh57zL0L\nMKvOiSfzlDnRlTCl3NzR4qNsy9uGgUFyVDILhi/A19sib/2mJvjss/aGo9GjYd48zf7qRk1NcOiQ\n/GppkXuJiZL1FRlp7tiUcnfaE6aUmzIMgx0Xd3Co6BAADw56kNTYVLyssrpUWCjbj9XV0u392GMS\nwKq6RUsLHDkiCSCNjXIvPl6Kr/79zR2bUu5Ee8KU8jCtba1sPreZc9fP4e3lzYLhC0iJTjF7WMJu\nh/37pevbbocBAyT7q49FtkfdnM0Gx4/Dvn1QVyf3YmPhoYfkkG2lVPfRnjDlEJ6yf+8K6lrq+ODU\nB2zftZ1A30CeSn7KOgVYTQ387W+S9mm3y5mPzzzjUQWYWe8Vu11a7958E7ZvlwJswAB46ilYtcqz\nCzD9/mU9njInuhKmlBspry8nPSudqqYqQvxDeHbMs0QGW6SxJydHsr8aGyVyYtEiGDrU7FG5PcOQ\n4zb37IGKCrnXt6+sfA0f7pbPPijlMrQnTCk3cbnyMhvObqDJ1sSA0AGsSFpBiL8F8rVaW+Wxu6NH\n5TouTgowDZtyKsOQzNuvvoJr1+ReeDikpsrh2lp8KdU9tCdMKTd3qvQUW3O3YjfsjIgYweIRi/Hz\n8TN7WPLTf9Mm+V8fH5g1S+LWtQJwGsOAS5ek+Coulnu9erUfru2tTShKWYa+HZVDeMr+vdUYhsGe\ny3v4NOdT7IadKTFTWDpyKX4+fubOiWFI9/fbb0sBFh4Oa9Zo+CrOfa9cuQIffCBHbhYXy67v3Lnw\nm9/A2LFagN2Ofv+yHk+ZE6e+JZ955hmioqJISkq6de9//I//QUxMDGPGjGHMmDFs37791p+9+uqr\nxMfHk5CQwI4dO5w5NKVcns1u45OcT9hbsBcvvHg0/lEejnsYby+Tf9I2NsJHH0n+V2urLL/88pfQ\nr5+543JjV6/CP/4B770HBQVypuOsWfDb38KkSa59uLZS7sypPWH79u0jJCSEp59+mqysLABeeeUV\nQkND+d3vfve9/zY7O5u0tDSOHj1KcXExs2bN4vz583j/4J9u2hOmFDS2NvLhmQ8pqC7A38efJYlL\nGBY+zOxhSQWwebNkfwUESPbXd/4RphyrvFy2Hc+dk2t/f1lsnDIFAgPNHZtSSpjWE/bAAw+Qn5//\no/s/NZgtW7awYsUK/Pz8iI2NJS4ujiNHjjB58mRnDlEpl1PRWMG6rHVcb7hOqH8oaUlp9As1eZXJ\nbpcDB/fula3IAQNgyRLo3dvccbmpigr5q87MbD9ce+JEOVy7Rw+zR6eUulum7Fu8+eabjB49mmef\nfZaqqioArl69SkxMzK3/JiYmhuKbXaXK8jxl/95shdWFvHPiHa43XCcqOIpfjPvFbQuwbpuT6mpY\nu1bCV0EqgWee0QLsNroyLzU1ssv7pz/B6dPS4zVhArzwAsyZowXYvdLvX9bjKXPS7Z0Cv/rVr/hv\n/+2/AfBf/+t/5T/+x//Iu++++5P/7e2OV1m9ejWxsbEAhIWFkZKSQmpqKtA+cXrdvdc3WWU87nh9\n9tpZ/s/6/0Ob0cash2axNHEph/YfMnd8a9fCgQOk9u8PISFk9O8Pvr6k+viY/vdl1etTp051+uMn\nTEhl3z7YuDGDtjYYPDiVlBTw9c0gOBhCQ63z9bni9U1WGY9eu/b1zd//1E7gDzk9Jyw/P5/58+ff\n6gm73Z+99tprAPz+978H4JFHHuGVV15h0qRJ3x+w9oQpD2MYBgcLD7Lz0k4Axvcfz7z4eeY24Le2\nwj//CceOyXV8PCxcqNlfDtbYCAcPwuHD7Ydrjxwp5ztGRJg7NqXU3bFUTlhJSQn9vn1K6pNPPrn1\n5OSCBQtIS0vjd7/7HcXFxeTl5TFx4sTuHp5SlmI37GzL28axq1LszB4ym6kDp5p7CPcPs79mz5ZH\n8Dw8esKRWlqk8DpwAJqa5N6wYZJyHx1t7tiUUo7j1CJsxYoV7N27l+vXrzNw4EBeeeWVW8vxXl5e\nDB48mL/85S8AJCYmsmzZMhITE/H19eWtt94y9weN6pSMjIxbS7LKMZptzWzM3siFigv4evuyKGER\nI/uOvOuPd/icGIasfP3zn3IKdESENN9rVdApd5oXm00OFti/H+rr5d7gwVJ8DRzYfWP0NPr9y3o8\nZU6cWoStX7/+R/eeeeaZ2/73L7/8Mi+//LIzh6SUS6huqmZd1jrK6svo4deDFaNWMLCXiT+FGxvl\n3MecHLkeM0ZSQP39zRuTG2lrg5Mn5QHTmhq5FxMDM2dKEaaUck96dqRSFlNSW8K6rHXUttQS0SOC\ntKQ0+gT1MW9A+fmS/VVTI9lf8+fL4YOqy+x2yMqCjAyorJR70dGy8hUfrzu8SrkDS/WEKaVu7/yN\n82zK3kRLWwuDeg3iyVFPEuQXZM5g7HYJo/r6a9mKjImBJ57Q6AkHMAwJWN2zRwJXQXZ3Z8yAxEQt\nvpTyFFqEKYfwlP17ZzpafJRtedswMEiOSmbB8AX4et/7W7RLc1JVJatfV65IRTB9upwA/W30hLo3\nhgHp6RnU16dSUiL3wsIgNRWSk/VsR7Po9y/r8ZQ50SJMKZPZDTs7L+7kUJFkfj046EFSY1PNezAl\nOxu2bpXH8kJDYfFibUxygPx8OWLo668hNlb+aqdPl4O1tbZVyjNpT5hSJmpta2Xzuc2cu34OHy8f\n5g+fT0p0ikmDaYUvv4Tjx+V6+HB4/HGNYe+i4mIpvi5elOsePeRQgQkTwM/P3LEppZxPe8KUsqC6\nljrWZ62nuLaYQN9Alo9czuDeJq04lZVJ9ld5uRxEOGeOVAnanHTPysqk5+vmA6UBATB1KkyeLL9X\nSintQFAO8cPjP9SdldeX886JdyiuLSYsMIxnxzzr8ALsrubEMODIEXj7bSnAIiJgzRo5DVoLsHty\n4wZ8/DH8+79LAebnJytfL7wgbXWHDmWYPUT1A/r9y3o8ZU50JUypbna58jIbzm6gydbEgNABrEha\nQYh/SPcPpKFBsr9yc+V63Dh4+GHN/rpH1dXyMOmpU/JgqY8PjB8PDzwAISZMr1LK+rQnTKludKr0\nFFtzt2I37IyIGMHiEYvx8zGhMei72V+BgZL9NfLu0/hVu7o62LdPDhNoa5MnHFNSZNWrVy+zR6eU\nMpv2hCllMsMwyMjPYG/BXgCmDpzKrCGzuv8QbrtdkkH37ZOtyIEDJfsrLKx7x+EGGhvlbMfDh+WZ\nBi8vSEqSuInwcLNHp5RyBdoTphzCU/bv74XNbuOTnE/YW7AXL7x4NP5R5gyd4/QC7EdzUlUF778v\nGQkgSzU//7kWYJ3U3Czbjn/4g5zx2NoKCQnw/PNSz3ZUgOl7xXp0TqzHU+ZEV8KUcqLG1kY+PPMh\nBdUF+Pv4syRxCcPCh3X/QM6ehc8+k+yvnj0l+ys2tvvH4cJaW9sP125okHtDh8oRQwMGmDs2pZRr\n0p4wpZykorGC9Mx0bjTeINQ/lLSkNPqF9uveQbS0SPbXiRNynZAACxZo9lcntLXJX9/XX0Ntrdy7\n7z4pvrSOVUp1RHvClOpmhdWFrD+znobWBqKCo1iZvJKeAT27dxClpZL9df26ZH89/LA8rqfRE3fF\nbofMTGmhq6qSe/36SfEVF6d/jUqprtOeMOUQnrJ/fzfOXjvL2tNraWhtIK5PHM+MeaZ7CzDDgMOH\nyXj5ZSnAIiPhF7/Q8NW7ZBiye/vWW/Dpp1KARUbCsmXw3HMQH9+1v0Z9r1iPzon1eMqc6EqYUg5i\nGAYHCw+y89JOAMb3H8+8+Hnd+wRkfb1kf50/L0s548fLCpiej9Mhw4C8PDliqLRU7vXuLU87JiXp\n4dpKKcfTnjClHMBu2Pni/BccL5FzF2cPmc3UgVO79xDuy5cl+6u2VrK/FiyAxMTue30XdvmyFF+F\nhXLds6ccrj1mjB6urZTqGu0JU8qJmm3NbMzeyIWKC/h6+7J4xGISI7ux+Glrk8al/ftlOee++yQr\nQZNCO1RUBLt3SxEGEBzcfri2r353VEo5mS6wK4fwlP37H6puqua9k+9xoeICwX7BrBq9qnsLsMpK\nyf7at0+uU1Nh9Wro1ctj5+RulJbCunXwzjtSgAUGSsP9Cy/AlCnOLcB0XqxH58R6PGVO9N96St2j\nktoS1mWto7allogeEaxMWknvoN7dN4AzZyT7q7lZ9s+eeAIGDeq+13dB16/Dnj3SeA9yTOakSTB1\nKgQFmTs2pZTn0Z4wpe7B+Rvn2ZS9iZa2FmLDYlk+cjlBft30U7ylBbZvh5Mn5XrECOn/0iritqqq\nZMf29GnZsfX1bT9cOzjY7NEppdyZ9oQp5UBHio+wPW87BgbJUcksGL4AX+9ueiuVlEj2140bUkk8\n8giMG6fRE7dRWyshqydOtB+uPXasnNjUs5tj25RS6oe0J0w5hCfs39sNO/+88E+25W3DwCA1NpVF\nCYu6pwAzDPjmG2liunED+vaV0Ko7hK96wpzcTkMD7NgBb7whRw3Z7ZCcDL/+Ncyfb24B5snzYlU6\nJ9bjKXOiK2FK3YXWtlY2n9vMuevn8PHyYf7w+aREp3TPi9fXS2poXp5cT5gAc+Zo9tdPaGqCQ4ek\nXm1ulnsjRsCMGVK3KqWUlWhPmFIdqGupY33Weopriwn0DWT5yOUM7j24e1780iXJ/qqrk56vBQuk\nqlDf09ICR47AgQPQ2Cj34uLkicf+/c0dm1LKs2lPmFL3qLy+nPSsdKqaqggLDGNl0koigyOd/8Jt\nbfIY34EDshU5aBAsXqzZXz9gs8Hx45LQUVcn9wYNgpkzJS5NKaWsTHvClEO44/795crLvHvyXaqa\nqhgQOoA1Y9d0TwFWUQHvvSfhqyB7aatWdboAc8c5uclul2b7N9+UB0Xr6mTF66mnJCbNygWYO8+L\nq9I5sR5PmRNdCVPqJ5wqPcXW3K3YDTsjIkaweMRi/Hy6oQcrKws+/1wamnr1kuwvK1cU3cwwJB4t\nI0OeTwDp9XroIRg+XB8SVUq5Fu0JU+o7DMMgIz+DvQV7AZg6cCqzh8x2/hmQzc2ypHPqlFwnJspj\nfJr9BUjxlZsrO7RlZXKvTx9ZJBw5Ug/XVkpZl/aEKXUXbHYbW3O3klmWiRdezIufx4QBE5z/wlev\nwscfy9KOn59kf40dq8s6SPF16ZIcrl1cLPd69ZKcr9Gj9XBtpZRr038/Kodw9f37xtZG/n7672SW\nZeLv409aUprzCzDDgIMH4d13pQCLipLsLweFr7r6nFy5AmvXwt//LgVYcDDMnQu/+Y3UqK5agLn6\nvLgjnRPr8ZQ50ZUw5fEqGitIz0znRuMNQv1DWZm8kuiQaOe+aF2dZH9duCDXEydK9pczT452ESUl\nsvJ1MxYtKAimTZO/In9/c8emlFKOpD1hyqMVVhey/sx6GlobiAqOYmXySnoGODlO/eJF+OST9uyv\nxx+HhATnvqYLKC+Xnq/sbLn294cpU+RXYKC5Y1NKqXulPWFK/YSz187ySc4n2Ow24vrEsTRxKQG+\nAc57wbY2WeI5cECuY2Ml+8vDDzGsrJSnHTMz2w/XnjhRVr/0cG2llDvTnjDlEK60f28YBvuv7Gdj\n9kZsdhvj+48nLSnNuQVYRYX0fh04II/yPfQQPP20Uwswq89JTY2kcbz5Jpw+LW1wEybACy/Izqy7\nFmBWnxdPpHNiPZ4yJ7oSpjxKm72NbXnbOF5yHIA5Q+cwJWaKcyMoTp+GL76Qs3XCwiT7a+BA572e\nxdXXSw7t0aOSeO/lBSkp8sRj795mj04ppbqP9oQpj9Fsa2Zj9kYuVFzA19uXxSMWkxiZ6MQXbJbi\nKzNTrkeOlOwvD21wamqSh0G/+UbqUZC/ktRUiOyGgwiUUsoM2hOmPF51UzXrstZRVl9GsF8wK5JW\nENMzxnkvePUqbNok25B+fpKtMGaMR2Z/tbTA4cOyE9vUJPeGDZOg1X79zB2bUkqZSXvClENYef++\npLaEd068Q1l9GRE9Ilgzdo3zCjDDkGrjnXekAIuOluwvE8JXzZ4Tm01Wvd54A3bvlgJs8GB49llI\nS/PcAszseVE/pnNiPZ4yJ7oSptza+Rvn2ZS9iZa2FmLDYlk+cjlBfk46CqiuTqInLl6U60mTYPZs\nj8v+amuT05f27pXme4CYGHkWYcgQc8emlFJWoj1hym0dKT7C9rztGBiMjhrN/OHz8fV2UkGUlyfh\nq/X10KOHZH8NH+6c17Iou739cO2KCrkXFSXF17BhHrkTq5RS2hOmPIvdsLPz4k4OFR0CIDU2lQcH\nPeicJyBtNtlrOySvxeDBkv0VGur417Iow4CcHIlAKy+Xe+Hh7Ydra/GllFI/TXvClENYZf++ta2V\nj85+xKGiQ/h4+bAoYRGpsanOKcBu3JDsr0OHJPtr5kx46inLFGDOnhPDkFOX3n4bNmyQAiwsTBYB\n//VfYdQoLcB+ilXeK6qdzon1eMqc6EqYcht1LXWsz1pPcW0xgb6BPDnqSWLDYh3/QoYh2V/btrVn\nfy1ZIo1PHqKgQBYAr1yR65AQmD5dnj/wsBY4pZS6Z9oTptxCeX056VnpVDVV0TuwN2lJaUQGOyF8\nqrlZYt6zsuR61Ch47DGPyf4qLpZtx5vPHgQFwf33yzFDfn7mjk0ppaxIe8KUW7tUeYmPzn5Ek62J\nmJ4xrBi1gmB/J5x5U1QEH38shx36+cG8eRL17gF7bteuSfGVkyPXAQHth2sHOPG0J6WUcmfaE6Yc\nwqz9+1Olp/hH5j9osjWRGJnIqtGrHF+AGYacs/Pee1KARUfDL39p+fBVR8xJRYXUnX/+sxRgfn5y\nsPYLL0jSvRZgnecpvS6uROfEejxlTpxahD3zzDNERUWRlJR0615FRQWzZ89m2LBhzJkzh6qqqlt/\n9uqrrxIfH09CQgI7duxw5tCUizMMg68uf8WnOZ9iN+xMHTiVpYlL8fNx8J5YbS38/e+wa5dkMEye\nDGvWQESEY1/HYqqrYetW+NOfZOfV21u2HH/7W4k+69HD7BEqpZTrc2pP2L59+wgJCeHpp58m69se\nmhdffJGIiAhefPFFXn/9dSorK3nttdfIzs4mLS2No0ePUlxczKxZszh//jze3t+vE7UnTNnsNrbk\nbCHrWhZeeDEvfh4TBkxw/Avl5Un4akODVB0LF0rglRurq4N9++DYMQld9faG0aPlcO2wMLNHp5RS\nrse0nrAHHniA/Pz8793bunUre/fuBWDVqlWkpqby2muvsWXLFlasWIGfnx+xsbHExcVx5MgRJk+e\n7MwhKhfT0NrAhjMbKKguwN/Hn6WJS4kPj3fsi9hssvL1zTdyPWQILFpkmegJZ2hslNOWDh+G1la5\nN2qUZH2Fh5s7NqWUclfd3hNWVlZGVFQUAFFRUZSVlQFw9epVYr7ziH9MTAzFxcXdPTx1j7pj/76i\nsYJ3T7xLQXUBof6hPDPmGccXYNevy7mP33wjy0CzZlkq+6sz7mZOmpvleKE//EHa3lpbJej/V7+S\n1A0twBzPU3pdXInOifV4ypyY+nSkl5fXHUM0b/dnq1evJjY2FoCwsDBSUlJITU0F2idOr7v3+iZn\nff6hY4ay/sx6so9m0yeoD79b/Tt6BvR03Os9+CCcOkXGn/4EbW2kjhkDS5aQkZcHe/ea/vfr6Otp\n01I5ehTWrs2guRliY1MZMgSCgjKIjISoKGuN152uT506Zanx6HU7q4xHr137+ubvf7gT+FOcnhOW\nn5/P/Pnzb/WEJSQkkJGRQXR0NCUlJcyYMYOcnBxee+01AH7/+98D8Mgjj/DKK68wadKk7w9Ye8I8\nztlrZ/kk5xNsdhtxfeJYmriUAF8HPpbX1CTZX2fOyHVSkmR/ueGjf21tcOIEfP21PHMAMHCghP1/\n++8apZRSDmSpnLAFCxawdu1aXnrpJdauXcvChQtv3U9LS+N3v/sdxcXF5OXlMXHixO4enrIQwzA4\nUHiAXZd2ATC+/3jmxc/D28vbcS9SVASbNkFVFfj7S/bX6NGWjp64F3Y7ZGZCRoZ8qQD9+snh2nFx\nbvflKqWUS3DgT7MfW7FiBVOnTiU3N5eBAwfy/vvv8/vf/56dO3cybNgwvvrqq1srX4mJiSxbtozE\nxETmzp3LW2+95Zzz/pRT/HBZv6va7G18fv7zWwXYnKFzeDT+UccVYHa7PAb43ntSlfTrJ9lfbhS+\nmpGRgWHA2bPw1lvw6afypUZGwrJl8NxzEB/vNl+uy3D0e0V1nc6J9XjKnDh1JWz9+vU/eX/Xrl0/\nef/ll1/m5ZdfduaQlAtotjXz0dmPuFh5EV9vXxaPWExiZKLjXqC2FjZvhsuX5XrqVFkScqNDDw0D\nCgvhL3+B0lK517s3pKbKbqu3U//5pZRS6m7o2ZHKUqqbqlmXtY6y+jKC/YJZkbSCmJ4OPBj7/HlZ\nEmpogOBgiZ6Ii3Pc57eAy5fliKHCQrkODZWcrzFjwMfH3LEppZSnsVRPmFK3U1JbwrqsddS21BLR\nI4KVSSvpHdTbMZ/cZoOdOyUIC2DoUCnAQkIc8/ktoKhIiq9Ll+S6Rw944AEYP14P11ZKKSvSTQnl\nEF3dvz9/4zzvn3qf2pZaYsNieXbMs44rwMrLJfvr8GHZh5szB372M7cpwEpLYf16+RIvXYLAQNld\nTUnJYMoULcCsxlN6XVyJzon1eMqc6EqYMt2R4iNsz9uOgcHoqNEsGL4AH28H7JsZBpw8Cdu3Swpp\nnz7wxBMwYEDXP7cFXL8uTzveTNbw94dJk6TFLShI/kwppZR1aU+YMo3dsLPj4g6+KZLjgVJjU3lw\n0IOOeSq2qQk++0weDQSJnZg3zy2yv6qqJOX+1CmpM318YMIEuP9+t1ncU0opt6E9YcpyWtpa2Hxu\nMznXc/Dx8mHB8AWMjh7tmE9eWAgff9ye/fXoo1KEubjaWknVOH68/XDtsWNh+nTo1cvs0SmllOos\n7QlTDtGZ/fu6ljo+OPUBOddzCPQN5KnRTzmmALPbJQr+/felAOvfH55/3uULsIYG2LED3ngDjhyR\nLzM5GX79a5g///YFmKf0VLganRfr0TmxHk+ZE10JU93qWv011mWto6qpit6BvUlLSiMyOLLrn7im\nRrK/bp7VNW2adKe7cCZDczMcOiS/mpvl3ogRMGMG9O1r7tiUUkp1nfaEqW5zqfISH539iCZbEzE9\nY1gxagXB/sFd/8Q5ObBlCzQ2SlPUokUSQeGiWltlxWv/fvmSQKLMHnpIFveUUkq5Du0JU6Y7WXKS\nz85/ht2wkxiZyKKERfj5dDE7obVVsr+OHJHruDhYuNBlu9NttvbDtevq5N6gQVJ8DRoRjk0JAAAg\nAElEQVRk7tiUUko5nvaEKYe43f69YRh8dfkrtuRuwW7YmTpwKksTl3a9ALuZ/XXkiGw5PvwwrFzp\nkgWY3S7F15tvwrZtUoD17y9RZqtX33sB5ik9Fa5G58V6dE6sx1PmRFfClNPY7Da25Gwh61oWXnjx\n6LBHGd9/fNc+qWFIxfLll+3ZX0uWuOQ+3c3DtffsgRs35F7fvrLyNXy4HqytlFLuTnvClFM0tDaw\n4cwGCqoL8PfxZ2niUuLD47v2SRsbJfsrO1uuU1Jg7lyXy/4yDDnC8quvoKxM7vXpIw33I0fq4dpK\nKeVOtCdMdauKxgrSM9O50XiDngE9SUtKIzokumuf9MoVyf6qrpai69FHJafBhRiGHK69ezcUF8u9\nnj0hNVVSNFz4QU6llFL3QP/NrRzi5v59YXUh75x4hxuNN4gOiWbN2DVdK8DsdomHf/99KcAGDIBf\n/tLlCrArV2DtWvjb36QACw6GRx6B3/5WAledUYB5Sk+Fq9F5sR6dE+vxlDnRlTDlMGevneWTnE+w\n2W3E94lnSeISAny7sFVYXS3ZXwUFcn3//bJn50JLRiUlsu2YlyfXQUESYTZxooT5K6WU8lzaE6a6\nzDAMDhQeYNelXQCM7z+eefHz8PbqwkLruXOwdavLZn+Vl0vD/c32NX9/mDJFfgUGmjs2pZRS3Ud7\nwpTTtNnb+CLvC06UnMALL2YPnc2UmCn3fgh3a6uc0XP0qFzHx0v2V7ADQl27QWUlZGRAZqb0gPn6\nyqrXtGku8yUopZTqJtoTpu5Zk62JdVnrOFFygsLThSwduZSpA6feewF27Rq8/bYUYD4+0jSVluYS\n1UtNDXz+uWR9nT4t8RLjx0vP15w55nwJntJT4Wp0XqxH58R6PGVOdCVM3ZPqpmrSs9K5Vn+NYL9g\nHol7hMTIxHv7ZIYBx49L9pfNBuHhkv3Vr59jB+0E9fVyvNDRozJ0Ly9JznjwQejd2+zRKaWUsjLt\nCVOddrX2Kuuz1lPbUktEjwhWJq2kd9A9VhyNjdL7de6cXI8ZI9lfFu9ab2qCgwfhm2+gpUXujRwp\ncRORDjiPXCmllHvQnjDlMLnXc9mUvYlWeyuxYbEsH7mcIL+ge/tkBQWS/VVTI9lfjz0GSUmOHbCD\ntbTA4cNw4IAUYgDDhslDmy6wcKeUUspCtCdM3bUjxUf48MyHtNpbGR01mqeSn7pVgHVq/95ul0cH\nP/hACrCYGHj+eUsXYDabrHq98YaErTY1QWwsPPustK1ZsQDzlJ4KV6PzYj06J9bjKXOiK2GqQ3bD\nzo6LO/im6BsAUmNTeXDQg/fWgF9dLatfV65IA9UDD8genkWzv9ra4NQpyYutqZF7MTFyvuPgwXq+\no1JKqXunPWHqjlraWth8bjM513Pw8fJhwfAFjI4efW+fLDtb+r+amiA0FBYvlkrGgux2OHNG4iYq\nKuReVJQUX8OGafGllFLq7mhPmLondS11rMtax9XaqwT6BvLkqCeJDYvt/CdqbZUnH48fl+thwyT7\nq0cPh47XEQwDcnJkt/TaNbkXHt5+uLYWX0oppRxFe8LUT7pWf413TrzD1dqr9A7szZqxa+5YgN12\n/76sDP76VynAfHzkyccVKyxXgBkGXLggMWUbNkgBFhYGjz8O//qvMGqU6xVgntJT4Wp0XqxH58R6\nPGVOdCVM/cilykt8dPYjmmxNxPSMYcWoFQT7dzJt1DAkPGvHDulqj4iQ7K/oLhzm7SQFBXK+480j\nKkNCYPp0OVjbV98hSimlnER7wtT3nCw5yWfnP8Nu2EmMTGRRwiL8fPw690kaGqT3KydHrseOlfR7\ni2V/FRdL8XXxolwHBckZ4RMngl8nv2SllFLqp2hPmOqQYRjsyd/D1wVfAzBt4DRmDZnV+Scg8/Nh\n82Z5lDAwEObPl2YqC7l2TYqvmzViQED74doBAeaOTSmllOfQIkxhs9vYkrOFrGtZeHt5My9+HuP7\nj+/U58j46itSAfbtk63IgQPhiSekscoiKiqk4f7MGRmin1/74doWa1FziIyMDFJTU80ehvoBnRfr\n0TmxHk+ZEy3CPFxDawMbzmygoLoAfx9/liYuJT48vnOfpKoKtm+XU6q9vKShKjUVvK3x3Ed1teR8\nnTol0RM+PjBunESUhYaaPTqllFKeSnvCPFhFYwXpmencaLxBz4CepCWlER3Sycb5s2fhs88smf1V\nVycLc8eOSejqdw/XttACnVJKKTemPWHqRwqrC1l/Zj0NrQ1Eh0STlpRGz4Ced/8JWlok++vECbke\nPlzyHCywr9fYKGc7Hj4sEWUgERMzZkjml1JKKWUF1tgvUt3qzLUzrD29lobWBuL7xPPzlJ93rgAr\nLZXsrxMnJMNh3jwyoqNNL8Cam2Xb8Y03YP9+KcCGD4df/UrSMTytAPOUnB1Xo/NiPTon1uMpc6Ir\nYR7EMAwOFB5g16VdAEzoP4G58XPx9rrLWtww4MgRyf5qa4PISKluoqLkfB+TtLZKJNn+/ZKOATBk\niBwxFBNj2rCUUkqpO9KeMA/RZm/ji7wvOFFyAi+8mD10NlNiptx9BEVDA2zZArm5cj1unGR/mRio\n1dYmi3Fffw21tXJv4ECYORNiY00bllJKKXWL9oR5uCZbExvPbuRi5UV8vX1ZPGIxiZGJd/8JLl+W\n7K/aWsn+WrAAEjvx8Q5mt0Nmpmw9VlbKvX79ZOUrLs71jhdSSinlmbQnzM1VN1Xz3sn3uFh5kWC/\nYFanrL77AqytDXbvhr/9TQqw++6D55//yQKsO/bvDUMexnzrLfj0UynAIiNh2TJ47jmIj9cC7Ls8\npafC1ei8WI/OifV4ypzoSpgbu1p7lXVZ66hrqSOiRwQrk1bSO6j33X1wZSV8/DEUFUll8+CD8suE\n7C/DgLw8CVotKZF7vXtLFFlSkmXiyJRSSqlO0Z4wN5V7PZdN2ZtotbcSGxbL8pHLCfILursPPnNG\nsr+am6FnT8n+MqnJ6vJlOWKosFCuQ0OlFhwzRkJXlVJKKSvTnjAPc7joMF9e+BIDg9FRo1kwfAE+\n3ndRsbS0SPL9yZNynZAg/V8mRE8UFUnxdemSXPfoIQn348fr4dpKKaXcg27kuBG7YefLC1+y/cJ2\nDAxmxM5gYcLCuyvASkok++vkScn+evRRWL78rgswR+3fl5XB+vXwzjtSgAUGSsP9Cy/IAdtagN09\nT+mpcDU6L9ajc2I9njInuhLmJlraWth8bjM513Pw8fLh8YTHSY5K7vgDDUOi5XfulEb8vn0l+6tv\nX+cP+juuX5eosTNn5NrPDyZPhqlTIegud1GVUkopV6I9YW6grqWOdVnruFp7lSDfIJaPWk5sWGzH\nH1hfL9lf58/L9fjx8PDD3brcVFXVfri2YUif14QJcP/9EBLSbcNQSimlnEJ7wtzYtfprpGemU91c\nTe/A3qxMXklEj4iOP/DSJcn+qquTpaYFC2DECOcP+Fu1tXK49vHjsgDn7Q1jx8L06dCrV7cNQyml\nlDKN9oS5sEuVl3j3xLtUN1cT0zOGNWPXdFyAtbXBrl3w979LATZokGR/dbEAu9v9+4YG2fn84x/l\nBCS7HZKT4de/hvnztQBzJE/pqXA1Oi/Wo3NiPZ4yJ6athMXGxtKzZ098fHzw8/PjyJEjVFRUsHz5\ncgoKCoiNjeWjjz4iLCzMrCFa2smSk3x2/jPshp3EyEQWJSzCz6eDbcTKSti0CYqLJfsrNVWWnroh\naKu5GQ4dkl/NzXJvxAiYMaPb28+UUkopSzCtJ2zw4MEcP36cPn363Lr34osvEhERwYsvvsjrr79O\nZWUlr7322vc+ztN7wgzDYE/+Hr4u+BqAaQOnMWvIrI7PgMzKgs8/lwqoVy944glJwHey1lZZ8dq/\nHxob5V5cnDzx2L+/019eKaWUMtWd6hZTi7Bjx44RHh5+615CQgJ79+4lKiqK0tJSUlNTycnJ+d7H\neXIRZrPb2JKzhaxrWXh7eTMvfh7j+4+/8we1tMC2bdL5DnLk0Pz5Tn/k0GZrP1y7rk7uDRokxdeg\nQU59aaWUUsoy7lS3mNYT5uXlxaxZsxg/fjxvv/02AGVlZURFRQEQFRVFWVmZWcOznIbWBv52+m9k\nXcvC38eftKS0jguwkhL4y1+kAPP1leJr6VKnFGA39+/tdokae/NNqf3q6mTF62c/g9WrtQDrTp7S\nU+FqdF6sR+fEejxlTkzrCTtw4AD9+vWjvLyc2bNnk5CQ8L0/9/Lyuu0W2+rVq4n99hidsLAwUlJS\nSE1NBdonzp2ua5prKAgr4EbjDa6dvcasIbOI6xN3+483DFIDA2HXLjIuXoSwMFJffhn69nXaeA1D\nMr7++tcMamogNjaVvn0hODiD++6DuDjr/H3qtV6beX3q1ClLjUev21llPHrt2tc3f5+fn09HLJET\n9sorrxASEsLbb79NRkYG0dHRlJSUMGPGDI/fjrxSfYUPz3xIQ2sD0SHRpCWl0TOg5+0/oK4OPv0U\nLlyQ64kTYfZsp2V/GYbEjH31laTdA/TpA6mpMGqUHq6tlFLKs1kuJ6yhoYG2tjZCQ0Opr69nx44d\n/Pf//t9ZsGABa9eu5aWXXmLt2rUsXLjQjOFZxplrZ/g051NsdhvxfeJZkriEAN+A23/AxYvwySft\n2V+PPy7nPzqBYbQfrl1UJPd69pTDtVNS9HBtpZRSqiOmrIRdvnyZRYsWAWCz2Vi5ciX/6T/9Jyoq\nKli2bBlXrly5bUSFJ6yEGYbB/iv72X15NwAT+k9gbvxcvL1us6zU1ibV0IEDch0bC4sXS1XkBIWF\nsHs33FxpDQ6WbcfnnkvFV+N/LSMjI+PWMrmyDp0X69E5sR53mhPLrYQNHjyYUzef1vuOPn36sGvX\nLhNGZB1t9ja+yPuCEyUn8MKLOUPnMDlm8u0jKCoqJPvr6lXZ+0tNlTN/nLAPWFIitV5enlwHBsK0\naTBpEhw8iBZgSimlVCdYoiesM9x5JazJ1sTGsxu5WHkRP28/Fo9YzIjIOyTZZ2ZK9ldLi1Ozv8rL\nYc8eyM6Wa3//9sO1AwMd/nJKKaWU27DcSpj6seqmatKz0rlWf41gv2DSktIY0HPAT//Hzc2S/3D6\ntFyPHAmPPebw6InKSsjIkFrPMGSl6+bh2sHBDn0ppZRS6v+3d6dRVZZrH8D/m2E7IiIoKqAyg4CA\nA6jnWBjHOJVa5jy+pafXrHztDNb5cFpnndYydZ1hnaxOrlX5UkvFBjulmbwqRI6gMhhKIfMQKDEL\nwmYP1/vhzq3kcEyB/cD+/z6xn/3sZ98P1wqv7vt6rtvu8Nk1Dai6UoV3st5BTWsNPAZ64DcTf3P7\nBKyqSvX+OndOPfE4dy6wYEGXJmDNzWqC7Y031NfodMDkycD//A+QkHDrBOynj3qT7TEm2sS4aA9j\noj32EhPOhNlAfmE+jmQegVGMqG+tR/PAZgwdNRS+Q32xKGwRBjjfIqESURsvpqSoQnxPT5V8DR/e\nZeNqbVXbC505ozre63RAZKQqM3Nz67KvISIiIrAmrMflF+Yj8atE9Avsh8rmShTWF8JUaMLiGYvx\n3Kzn4Ohwi94OLS2q9URRkXodG6t6f3VRJXx7uyqsT09X5WWA2t1o5swuzfGIiIjsDmvCNORI5hHo\nA/QorC9EZbNqsBUwOQAOjQ63TsAKC1UC1toKDByoen8FB3fJWDo6gIwMlYBd21w7MFDt7zhqVJd8\nBREREd0Ga8J6WLupHRd+uIDK5krooEOoRyjGDR0Hoxg7n2g2A4cOATt3qgTM1xd49tkuScBMJjXr\n9frranWzrU21Flu9Gli+/N4SMHtZv+9NGBNtYly0hzHRHnuJCWfCelBrRysyqzNR61ELJwcnhI8I\nx9D+qhmt3kF//cS6OmDv3uu9v2bOVA257rP3l9ms9vL++mtVfA8AXl5AfLzK8W7XioyIiIi6HmvC\nekjt1Vrs+mYXCooL8N3F7xA9PRqD9OoxQ0OBAU/NfArB/kGqH8SBA2qtcOhQ1fvLx+e+vttiUZtr\np6Wp3q6Aqut/6CEgKIjJFxERUXe5U97CJKwHlDeVIyk3CW2mNox2GY3JAycjPTcdHZYO6B30iJ8Y\nj2CfcSr5+uYb9aHwcNX76z66oYoA332nGq3W1Khj7u5qYi0sjMkXERFRd2MSZkMXai7g39/9GyaL\nCUHuQVgwfgH0jvrOJ33/vdp6qKFB9f569FG1C/Y9Zkki6kHK1FS1ogmohvpxcarlRDfsaNSn9vnq\nKxgTbWJctIcx0Z6+FBM+HWkDIoKTFSdxuPgwgM6bcJfl56PoyBE4dHTAUlEBf6MRY93dgZEjVe8v\nD497/t6yMpV8lZWp14MHAw88AEycyL0diYiItIQzYd3AIhYcLDiIM1VnAAAP+z+Mad7ToNPpUJaf\nj8LERMQDaq2woQEpJhMC/uu/MPbpp+85U6qqUslXYaF6PWCA2l4oJkZNrhEREVHP40xYD+owd+CT\nvE9wse4inBycMC9kHsJGhFnfLzpyBPEtLSoBMxoBZ2fER0Qg1WjE2HtIwGpqVM3Xt9+q1/36AdOm\nqQ22ubk2ERGRdrFPWBdq6WhBYk4iLtZdxACnAVgVuapTAgaTCQ7nzgG5uSoBc3NTmzK6u8PhWqv6\nu1RfD3z6KfD22yoBc3ZWXSw2bFC1Xz2dgNlLT5fehDHRJsZFexgT7bGXmHAmrIv80PoDduXuQmN7\nI9z6u2HFhBVwH+h+wwk/AJ98AktlpSq49/VVrSd+LL636PW3uXJnTU3A0aNAdrZqPeHoCEyaBMyY\nAbi4dMedERERUXdgTVgXKG0sxZ7ze9Buaof3EG8sDV9q7QEGESArC0hOBoxGlBmNKGxqQvwNxfcp\nBgMCnnoKY+/QDb+l5frm2mazyt2iooAHH1TtxIiIiEh72KKiG+VezsVn330Gs5gR4hGC+aHz4ez4\nYyV8Wxuwb9/1gq3ISODRR1FWWoqilBT1dKReD//4+NsmYG1t1zfXNv64s1F4uFpyvI+HKImIiKgH\nMAnrBiKC4+XHkVKSAgCI9YpFQkACHHQ/ltmVlqqireZmVS0/ezYQEXHX1zcYrm+u3d6ujgUHq0ar\nI0d28c10gb7U06WvYEy0iXHRHsZEe/pSTPh0ZBeziAUHLh5AZnUmdNAhISABU72nqjfNZrU547Fj\nainS21ttPeTmdlfXNhqBs2fVx69eVcf8/NQWQ97e3XRDRERE1OM4E/YzGUwGfJz3MQrrC+Hk4IT5\nofMROjxUvdnQoDbevlZ8P2OGKtpydPyP1zWbVbH9118DV66oYz4+Kvny9e3GGyIiIqJuw5mwLnLF\ncAW7cnfhUsslDHQeiKXhS+Hj+uPm2rm5wBdfqHXEIUOAJ58Exo275XXy88tw5EgRjEYHODpa4OPj\nj7KysWhoUO+PHKmSr8BA7u9IRETUV7FP2F2qaa3Bu1nv4lLLJbgPcMdvJv5GJWAGA/Dvf6sZMIMB\nCA0F1q27YwKWmFiImpqHUFAQh4MHH8Lf/laIgoIyeHgACxcCa9cCQUG9KwGzl54uvQljok2Mi/Yw\nJtpjLzHhTNhdKG4oxofnP4TBbIDPEB8sjViKgc4D1cbbe/eqzqnOzsCvf602abxD9nT4cBFaW+OR\nm6vaTgDA4MHxcHFJxXPPje2WzbWJiIhIe1gT9h+cu3QOn+d/DotYMH74eMwLmQdnByfgxAm1WaPF\nAnh6qo23hw+/47XKy4GXX05DdXUcAECvB8aOBUaNAoYNS8OLL8Z1/w0RERFRj2FN2D0QERwtO4qv\nSr8CAEz3mY5ZfrOga2lRy4/FxerEqVOBX/3qjhtvX7qk8rWLF4GmJgucnFTyNXr09Zp9vd7S3bdE\nREREGsLFr1swW8zYl78PX5V+BR10eDTwUTzs/zB0Fy+qzRqLi4FBg4Dly9US5G0SsPp6tVq5fbtK\nwPR6YPFif0RHp8DH53oCZjCkID7evwfvsOvZy/p9b8KYaBPjoj2MifbYS0w4E/YTBpMBH134CEUN\nRXB2cMaC8QsQ7OoHfPklcPq0OsnfH5g3Dxg8+JbXaG5WrSZu3N9xyhTVsWLQoLHIzwdSUlLR0eEA\nvd6C+PgABAeP7cG7JCIiIltjTdgNmg3N2PXNLlxuvYxBzoOwLGIZvNqdgU8+AWpqVDYVHw9Mm3bL\n4vurV9X+jqdPAyYT93ckIiKyd6wJuwuXWi5hd+5uNBua4THQA8vDl8HtQhHwf/+nMip3d9X5fvTo\nmz5rMKi9HU+eVD8DwPjxqtcX93ckIiKiW2FNGICi+iL8b/b/otnQjLGuY7EmeCnc9h0CDhxQCVh0\ntGre9ZMEzGRSyde2bcBXX6kEzN8f+O//BhYtsq8EzF7W73sTxkSbGBftYUy0x15iYvczYdnV2dh/\ncT8sYkH4iHA80S8STu8mqr2D+vcH5swBwsI6fcZiAc6dA9LSgKYmdczbWz0keZserURERESd2G1N\nmIggrTQNX5d9DQD4pdc0xJc6QHfypNp4e8wYtfXQDcVcIkBenpr1qq1Vxzw91bJjb+twT0RERN2P\nNWE/ca0FxbnL56CDDnOH/xLRacWqA75OB8TFAQ88gGvt60WAoiIgJQWorlbXcHMDZs4EwsPBLvdE\nRET0s9ld+tBuasfOb3bi3OVz0Dvq8ZQuGtGfZ6gEzNUVeOoplYT9mFlVVADvvw/s3KkSMBcXYPZs\n4IUXgAkTmIBdYy/r970JY6JNjIv2MCbaYy8xsauZsKb2JuzK3YWa1hq4oj+eKh8Ot4Is9WZYmMqu\nBgwAAFy+rLrc5+ertwcMAH75SyAmRm0TSURERHQ/7KYmrPpKNXbl7kJLRwvGXXHConwnDGxpVxnV\nI4+oJyB1OtTXq5qv8+fVMqRer3Ymmj5d1ekTERER3S27rwkrqCvAx3kfw2g0ILbUiF+VW+AMk9o5\ne/58wMMDV66oLvdZWde73E+erLrc36YxPhEREdE96/MVTZlVmUg6nwRd8xU8ll6HhDInOMNBTW2t\nWYO2QR44fFj1+jp7Vs1+RUUB69erCTImYHfHXtbvexPGRJsYF+1hTLTHXmLSZ2fCRAQpJSk4Xn4c\nHuW1+PUFA/z7j4bOxQV44gl0jAlA+kngxInrXe5DQ1W7ieHDbTt2IiIi6vv6ZE2YyWLCZ999hryq\ncwg8U4y42sEY5TIKCAyE6bHHkZk/GEePAq2t6nx/f5V8eXn1wA0QERGR3bhT3tLnkrA2Yxv2nN+D\n2pILmHDsIqbox2HY4OGwxM/CNwNikfa1Do2N6lxvb7Uft69vDw2eiIiI7Mqd8pY+VRPW0NaA97Le\nhenUCUxPvoBfDAiCm3cQ8h94Bv/KmorPPlcJ2IgRwJIlwJo1TMC6ir2s3/cmjIk2MS7aw5hoj73E\npFfXhOUX5uNI5hEYxYgWQwuu6n7ApIuVGHO5HRGeUWgYMx17TAmo/EoPQHW5j4sDIiLYZJWIiIhs\nq9cuR+YX5uPNpL9DX1sJQ1szmn+oRPAlIx70DUXImDgcc3kS54zjAagnHB98EJg4UbWeICIiIuoJ\nfbJP2Cf7d2JAdjZCmhrhVleL0U0dOOmgxynH/jg2Zj0MRlf073+9y71eb+sRExEREV3Xaxflak6c\nRdDlHzCmoh4jGwQWowu8MAxpLSZYXFwxYwawYYNKwpiAdT97Wb/vTRgTbWJctIcx0R57iYnmkrDk\n5GSEhIQgMDAQW7duveU5f4iJQG1qGsaW1GJAmxntFhdcGDIOVS4+0JuvYsMG9dTjj9tAUg/Iycmx\n9RDoJxgTbWJctIcx0R57iYmmkjCz2YwXXngBycnJyMvLQ1JSEr799tubzns89zymN7fDofYqfjAP\nwHm3cTAM7o/BZhN8vMaxy70NNF7r+0GawZhoE+OiPYyJ9thLTDSVhJ0+fRoBAQEYN24cnJ2dsWTJ\nEnz++ec3nRdhAXwFyIUDaq5a4CKDMNQwCBf7h2FkzEM2GDkRERHRz6Opwvzvv/8ePj4+1tfe3t7I\nyMi46TwBEDFAhwKLBQed3RDs9WsYHfXo8BqINctn9uCI6ZrS0lJbD4F+gjHRJsZFexgT7bGXmGiq\nRcXevXuRnJyMd955BwCwc+dOZGRk4I033rCeM1anQ7mtBkhERET0M0RGRt62xk1TM2FeXl6oqKiw\nvq6oqIC3t3enc8q0kzMSERER3TNN1YRNnjwZBQUFKC0tRUdHBz788EPMnTvX1sMiIiIi6nKamglz\ncnLCm2++iYSEBJjNZqxZswahoaG2HhYRERFRl9NUTRgRERGRvdDUcuR/cjeNXOnuVVRUYObMmQgL\nC0N4eDi2bdsGAKivr8esWbMQFBSEhx9+uFO/ls2bNyMwMBAhISE4dOiQ9XhmZiYiIiIQGBiIDRs2\nWI8bDAYsXrwYgYGBmDp1KsrKyqzvvf/++wgKCkJQUBA++OCDHrjj3sVsNiM6Ohpz5swBwLjYWmNj\nIxYsWIDQ0FCMHz8eGRkZjIkGbN68GWFhYYiIiMCyZctgMBgYlx62evVqeHp6IiIiwnrM1jEoKSlB\nbGwsAgMDsWTJEhiNxu66/fsjvYTJZBJ/f38pKSmRjo4OiYyMlLy8PFsPq1errq6W7OxsERG5cuWK\nBAUFSV5enmzcuFG2bt0qIiJbtmyRl19+WURELly4IJGRkdLR0SElJSXi7+8vFotFRESmTJkiGRkZ\nIiLyyCOPyMGDB0VE5K233pJ169aJiMiePXtk8eLFIiJSV1cnfn5+0tDQIA0NDdaf6bq///3vsmzZ\nMpkzZ46ICONiY6tWrZL33ntPRESMRqM0NjYyJjZWUlIivr6+0t7eLiIiixYtksTERMalhx09elSy\nsrIkPDzcesxWMWhsbBQRkYULF8qHH34oIiLPPvusvP322939a7gnvSYJO3nypCQkJFhfb968WTZv\n3mzDEfU9jz/+uBw+fFiCg4Pl0qVLIqISteDgYBERee2112TLli3W8xMSEuTUqbXZSFkAAAimSURB\nVFNSVVUlISEh1uNJSUmydu1a6znp6ekiov7h8vDwEBGR3bt3y7PPPmv9zNq1ayUpKal7b7AXqaio\nkPj4eElNTZXZs2eLiDAuNtTY2Ci+vr43HWdMbKuurk6CgoKkvr5ejEajzJ49Ww4dOsS42EBJSUmn\nJMyWMbBYLOLh4SFms1lERE6dOtUpf9CSXrMceatGrt9//70NR9S3lJaWIjs7G7Gxsbh8+TI8PT0B\nAJ6enrh8+TIAoKqqqlPLkGsx+OlxLy8va2xujJuTkxNcXV1RV1d322uR8tvf/hZ//etf4eBw/T9R\nxsV2SkpKMHz4cDz99NOYOHEinnnmGbS2tjImNjZs2DD8/ve/x5gxYzB69GgMHToUs2bNYlw0wJYx\nqK+vx9ChQ61/P2+8ltb0miRMp9PZegh9VktLC+bPn4/XX38dLi4und7T6XT83fewL774AiNGjEB0\ndDTkNs/NMC49y2QyISsrC8899xyysrIwaNAgbNmypdM5jEnPKyoqwj//+U+UlpaiqqoKLS0t2Llz\nZ6dzGBfb68kY9LZY95ok7G4audLPZzQaMX/+fKxcuRJPPPEEAPV/LZcuXQIAVFdXY8SIEQBujkFl\nZSW8vb3h5eWFysrKm45f+0x5udrjwGQyoampCe7u7oznHZw8eRL79u2Dr68vli5ditTUVKxcuZJx\nsSFvb294e3tjypQpAIAFCxYgKysLI0eOZExs6OzZs5g+fTrc3d3h5OSEJ598EqdOnWJcNMBWf6+8\nvLwwbNgwNDY2wmKxWK/l5eXVvTd8r2y9Hnq3jEaj+Pn5SUlJiRgMBhbmdwGLxSIrV66UF198sdPx\njRs3WtfsN2/efFNBpcFgkOLiYvHz87MWVMbExEh6erpYLJabCiqvrdknJSV1Kqj09fWVhoYGqa+v\nt/5MnaWlpVlrwhgX25oxY4bk5+eLiMif//xn2bhxI2NiYzk5ORIWFiZXr14Vi8Uiq1atkjfffJNx\nsYGf1oTZOgYLFy6UPXv2iIiqFWNhfhf48ssvJSgoSPz9/eW1116z9XB6vWPHjolOp5PIyEiJioqS\nqKgoOXjwoNTV1Ul8fLwEBgbKrFmzOv1h2bRpk/j7+0twcLAkJydbj589e1bCw8PF399f1q9fbz3e\n3t4uCxculICAAImNjZWSkhLrezt27JCAgAAJCAiQxMTEHrnn3iYtLc36dCTjYls5OTkyefJkmTBh\ngsybN08aGxsZEw3YunWrjB8/XsLDw2XVqlXS0dHBuPSwJUuWyKhRo8TZ2Vm8vb1lx44dNo9BcXGx\nxMTESEBAgCxatEg6Ojq695dwj9islYiIiMgGek1NGBEREVFfwiSMiIiIyAaYhBERERHZAJMwIiIi\nIhtgEkZERERkA0zCiIiIiGyASRgR2ZW4uDhkZmbe1zX279+PrVu3dtGIiMheOdl6AEREPakr9rGb\nM2cO5syZ00UjIiJ7xZkwIrKp1tZWPPbYY4iKikJERAQ+/vhjAMCrr76KmJgYREREYO3atdbz4+Li\n8Lvf/Q5TpkxBaGgozpw5g3nz5iEoKAivvPIKAKC0tBQhISFYsWIFxo8fj4ULF6Ktre2m7z506BCm\nT5+OSZMmYdGiRWhtbb3pnG3btiEsLAyRkZFYtmwZACAxMRHr168HAERFRSE6OhrR0dEYOHAgjh07\nhtbWVqxevRqxsbGYOHEi9u3bd9N109LSEBcXh4ULFyI0NBQrVqy4/18mEfUqTMKIyKaSk5Ph5eWF\nnJwc5ObmIiEhAQCwfv16nD59Grm5uWhra8MXX3wBQM1k9evXD2fOnMG6devw+OOPY/v27Th//jwS\nExPR0NAAALh48SKef/555OXlYciQIfjXv/7V6Xtra2uxadMmpKSkIDMzE5MmTcI//vGPm8a3detW\n5OTk4Ny5c9i+fbt1DNfk5OQgOzsbr776KqZMmYJp06Zh06ZNiI+PR0ZGBlJTU7Fx40ZcvXr1pmvn\n5OTg9ddfR15eHoqLi3HixImu+aUSUa/AJIyIbGrChAk4fPgw/vjHP+L48eMYMmQIACA1NRVTp07F\nhAkTkJqairy8POtn5s6dCwAIDw9HeHg4PD09odfr4efnh4qKCgCAj48Ppk2bBgBYsWIFjh8/bv28\niCA9PR15eXmYPn06oqOj8cEHH6C8vPyW41u2bBl27doFR0fHW95DQUEBXnrpJXz00UdwcnLCoUOH\nsGXLFkRHR2PmzJkwGAzWcd0oJiYGo0ePhk6nQ1RUFEpLS+/tl0hEvRJrwojIpgIDA5GdnY0DBw7g\nT3/6E+Lj4/HSSy/h+eefR2ZmJry8vPCXv/wF7e3t1s/069cPAODg4GD9+dprk8kEoPNslYjcsg5s\n1qxZ2L179x3Hd+DAARw9ehT79+/Hpk2bkJubixu33G1pacHixYvx7rvvwtPT03r8008/RWBg4B2v\nfePYHR0drWMnIvvAmTAisqnq6mr0798fy5cvxx/+8AdkZ2dbEy53d3e0tLRY68R+jvLycqSnpwMA\ndu/ejRkzZljf0+l0mDp1Kk6cOIGioiIAqjatoKCg0zVEBOXl5YiLi8OWLVvQ1NSElpaWTuesXr0a\nTz/9NH7xi19YjyUkJGDbtm3W19nZ2T97/ETU93EmjIhsKjc3Fxs3boSDgwOcnZ2xfft2uLq64pln\nnkF4eDhGjhyJ2NjYW372Tk86BgcH46233sLq1asRFhaGdevWdXrfw8MDiYmJWLp0KQwGAwBg06ZN\nnWavzGYzVq5ciaamJogINmzYAFdXV+v3lpeXY+/evSgoKMCOHTsAAO+99x5eeeUVvPjii5gwYQIs\nFgv8/PxuKs6/1djv96lNIupddHLjvDoRUR9QWlqKOXPmIDc319ZDISK6LS5HElGfxFklItI6zoQR\nERER2QBnwoiIiIhsgEkYERERkQ0wCSMiIiKyASZhRERERDbAJIyIiIjIBv4fz7qtiZ/BYakAAAAA\nSUVORK5CYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x1031a8710>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 32
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Without making any modifications to the original Python code - thereby we are not accounting for the particular strengths of Numba (Numpy) and Cython (static type declarations), we see that Cython performs significantly better than Numba."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"type_declarations\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Appendix II: Cython with and without type declarations"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In the sections above, we have been using the simplest approach to Cython without using static type declarations and thereby neglecting one of its major strengths. \n",
|
|
"Now, let us see how and if we can further improve the Cython implementation of our \"classic least squares approach\" by adding those type declarations."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Here is our \"classic\" approach in Python:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 21
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The Cython-compiled version of it:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%load_ext cythonmagic"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 23
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"def cy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 24
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"And now, the same code with static type declarations:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"def static_type_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" cdef double x_avg, y_avg, var_x, cov_xy, slope, y_interc, x_i, y_i\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 25
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"Now, let us see how the two functions (with and without static type declarations) compare against each other for different sample sizes."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"funcs = ['cy_lstsqr', 'static_type_lstsqr'] \n",
|
|
"labels = ['simple Cython', 'Cython w. type declarations']\n",
|
|
"orders_n = [10**n for n in range(1, 7)]\n",
|
|
"times_n = {f:[] for f in funcs}\n",
|
|
"\n",
|
|
"for n in orders_n:\n",
|
|
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
|
|
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
|
|
" for f in funcs:\n",
|
|
" times_n[f].append(timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 26
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%pylab inline"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": []
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"plt.figure(figsize=(10,8))\n",
|
|
"\n",
|
|
"for f in times_n.keys():\n",
|
|
" plt.plot(orders_n, times_n[f], alpha=0.5, label=f, marker='o', lw=2)\n",
|
|
"\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
|
|
"plt.legend(loc=2)\n",
|
|
"plt.grid()\n",
|
|
"\n",
|
|
"plt.title('Performance of a simple least square fit implementation')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAmcAAAH/CAYAAAASb3qiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdYFGf3N/DvotKLKIKooNgwImDvCkYsWKIYCyrqqmCL\nKUYTjfGx5JFcyeNPkxiNsaKJLdZoYktEERXfSDSigCAigopYiIKgSNn7/WPCxpUiILCz7PdzXVwy\nuzszZ+fsrId7zswohBACRERERCQLBtoOgIiIiIj+xeKMiIiISEZYnBERERHJCIszIiIiIhlhcUZE\nREQkIyzOiIiIiGSExRlVmNzcXEyaNAk2NjYwMDBAaGiotkPSSbt370aTJk1QvXp1TJo0qdLWq1Qq\n0adPH51al4GBAbZv314OEVFJvbyfnzp1qsz5DAkJgYGBAZKTkysgUu2tS642b96MGjVqaDsMKgSL\nMz2nVCphYGAAAwMD1KhRA40aNcL06dPx999/v/ay9+7dix07duDXX39FSkoKunTpUg4R65e8vDxM\nmjQJvr6+uHXrFr755ptKW/e3336LPXv2VMq6FAoFFApFpayrvHl5eWHixInaDkNrXt7Pu3btWuCz\n4+/vj169er1yWd26dUNKSgrs7e0rMmSdtXTpUjg5OZV6vtu3bxf6B7Kvr69eF6dyVl3bAZD29ezZ\nE7t27UJubi7+/PNPBAQE4NatW/j111/LtLzs7GwYGhoiLi4O9evXR+fOnV8rvvzl6aPk5GRkZmbC\n29u70v/DsrCwqLR1CSHA62Frz+vsY4Xt52UdjalRowZsbW3LNC+92sv7mLGxMYyNjbUUDRVLkF6b\nMGGC8PLy0ngsMDBQVKtWTWRlZQkhhNixY4dwd3cXxsbGolGjRuLDDz8UmZmZ6td7eHiIyZMniwUL\nFgh7e3tRt25d4enpKRQKhfrHyclJCCFEdna2mDt3rqhfv74wNDQULVu2FNu3b9dYv0KhECtXrhSj\nR48WVlZWYtSoUSIoKEhUr15dnDx5UrRq1UqYmJiIXr16ibt374oTJ04Id3d3YWZmJry8vMSdO3fU\ny7px44bw8fER9erVE6ampsLV1VX8+OOPGuvz8PAQ/v7+4rPPPhN169YVtWrVEuPHjxcZGRkar9u5\nc6do27atMDY2FrVr1xbe3t7i0aNH6udXrlwpnJ2dhbGxsWjWrJkIDAwUubm5xW7/c+fOiR49eggT\nExNhbW0txowZI+7fvy+EECIoKEhjGyoUCnHq1KlCl/Pbb78JDw8PUatWLWFlZSU8PDzE+fPni113\nWlqaUCqVom7dusLIyEg4ODiIDz/8UP38y5+N/OmVK1eK+vXrC3NzczF16lSRm5srvv32W+Ho6Cis\nra3FlClTRHZ2tsb2nTRpkpg7d66wsbERlpaWYsqUKerPV2HrEuLVn7vCKBQKsW3bNvX0kydPxHvv\nvSfq168vTE1NRZs2bcS+ffs05pk/f7544403hKmpqXBwcBDTpk0TaWlpJdpOEyZMKHGObt26JYYN\nGyZsbGyEsbGxaNy4sVi2bJn6+dTUVDFy5EhhZmYm7OzsxIIFC8T48eM1tkv+Z/VF//3vf0WjRo3U\n0xcuXBD9+/cXtra2wtzcXHTo0EEcPXpUY56GDRuKBQsWiOnTp4vatWuLzp07CyGE+PPPP0WfPn2E\nubm5qFOnjhg2bJhITEwscnt7eHgUup+/mM9FixYV2EZbtmwpdHknT54UCoVCvQ/nTx8+fFh07txZ\nmJiYiPbt24vo6GgREREhunbtKkxNTUXHjh1FdHS0ejn53xfHjx8XLVu2FMbGxqJTp07i0qVLRa5L\nCCHi4uLEsGHDRM2aNYW1tbXo27evuHLlSoHllvZ7SAhpH+3ataswMTER9evXFxMnThSpqanq5/O3\n2dq1a4Wjo6OwtLQUb731lrh375563S9vxyVLlgghhNi2bZvo2LGjsLKyEjY2NmLgwIHi2rVr6mW/\nPF9+nvLfz4sOHTok2rZtK4yMjIStra2YMWOGxn73qjipfLA403MTJkwQffr00Xhs+fLlQqFQiIyM\nDBEUFCSsra3F1q1bRUJCgggNDRVubm5i3Lhx6td7eHgICwsLMX36dHH16lURGRkp/v77bzFnzhzh\n5OQk7t27Jx4+fCiEEGLOnDmidu3aYs+ePSIuLk58/vnnwsDAQAQHB6uXp1AoRO3atcXq1avFjRs3\nRFxcnAgKChIGBgaiV69e4vz58+LixYuiWbNmonv37qJnz57ijz/+EJcuXRItWrQQo0aNUi/rypUr\nYvXq1eLy5cvixo0b4ttvv1V/ub4Yf82aNcWHH34oYmNjxW+//SZq1aol/vOf/6hfs2nTJlGjRg2x\ndOlS9XtctWqV+n0tWrRINGzYUPz888/i5s2b4vDhw8LR0VFjGS+7e/eusLCwEGPHjhWRkZHizJkz\nws3NTfTs2VMIIcSzZ89EeHi4UCgU4pdffhH37t3TKHpetH//frF7925x7do1ER0dLfz9/UWtWrU0\nvvxf9u677wp3d3dx/vx5cevWLREWFiY2bNigfl6pVGp8NiZMmCAsLS2FUqkUMTEx4pdffhHGxsai\nX79+YsKECSImJkYcOnRImJiYiDVr1mhs3/yCLH8+W1tbMWvWLI1lv1iElORzV5gXizOVSiU8PT1F\nr169xNmzZ0VCQoJYt26dMDQ01Pi8LV26VJw5c0YkJiaK4OBg0aJFCzFhwoQSbae0tDTRs2dP4evr\nK+7du1dsjgYPHiz69OkjIiIiRGJiojh58qTYsWOH+vmhQ4eKZs2aiZMnT4qoqCjh5+cnLC0tNXLg\n6ekpAgICNJb7cnEWEhIitmzZIqKjo0VcXJxYsGCBMDQ01PjPumHDhsLS0lIsWbJExMXFiatXr4qo\nqChhbm4uFi9eLGJjY0VkZKQYMWKEaN68uUYh/aKi9vMXv1cyMjLE2LFjRbdu3dTb6NmzZ4Uur6ji\nrG3btuLkyZMiOjpadOnSRbi5uYlu3bqJEydOiKtXr4ru3buLTp06qZeT/33Rrl07ERoaKi5fviwG\nDRok6tevr173y+tKSUkRdnZ2YsaMGSIyMlJcu3ZNvPvuu6J27driwYMHGsst7fdQcHCwMDU1FatW\nrRLXr18X4eHholevXsLDw0P9mgkTJggrKysxZswYERUVJc6dOyecnJzUn/lnz56JefPmCQcHB/V2\nzP8DMigoSPz666/ixo0b4tKlS+Ktt94SzZo1U38W//rrL6FQKMT+/fs18vRycRYRESGqVaum/i48\ncuSIcHR01NjvXhUnlQ8WZ3ru5f8Uo6KiROPGjUWXLl2EENKX+Nq1azXmOXXqlFAoFOLx48dCCOk/\nX2dn5wLLXrRokWjatKl6OjMzUxgZGWn8xy2EED4+PuLNN99UTysUigKjA/l/NUZERKgfW7ZsmVAo\nFOLixYvqx7766ithY2NT7HseMmSIxn9wHh4eonXr1hqvmT59unobCCGEg4ODePfddwtdXmZmpjA1\nNRXHjh3TeHzLli2iZs2aRcaxYMEC4eDgIHJyctSPRURECIVCIUJDQ4UQQiQkJAiFQiHOnj1b7Ht6\nWV5enrC2ttYYRXrZkCFDhFKpLPL5wkbO7OzsNOIdOHCgqFOnjkZBMmTIEDF8+HD1tIeHh3BychIq\nlUr92Lp164SxsbF4+vRpoesqyeeuMC8WZydPnhTGxsYao2BCCDFx4kQxdOjQIpexb98+YWRkpPF+\nittOXl5eYuLEiUU+n8/d3V0sXry40Ofi4uKEQqEQx48fVz+WnZ0t6tevX+rirKh1BwYGqqcbNmxY\nYKRywoQJwtfXV+OxrKwsYWpqKn7++ecil/3yfp6/rBeXP3nyZOHp6VlsjEIUXZwdOHBA/Zrdu3cL\nhUKhMQK6f/9+oVAo1CM8+d8XJ06cUL/m0aNHwtzcXGzcuLHQdS1atEg9gphPpVKJJk2aiK+//lpj\nuaX9HvLw8BCffPKJxrITExM1lpW/f724L3355ZfC3t5ePV2SXAshjcIqFAoRFhYmhJBGbQsb1X25\nOPPz89MocoUQ4sCBA8LAwEAkJSWVOE56fTwhgBASEgILCwuYmprC1dUVTZs2xbZt2/DgwQMkJSVh\n1qxZsLCwUP8MGDAACoUC169fVy+jXbt2r1zP9evXkZ2djZ49e2o83rNnT0RFRWk81rFjxwLzKxQK\nuLq6qqft7OwAAG5ubhqPpaamqnsrnj59innz5qFVq1aoXbs2LCwscPjwYSQlJWks193dXWNd9vb2\nuHfvHgDg/v37uH37Nvr27Vvo+4qKisKzZ88wbNgwje00bdo0pKenIzU1tcj5OnfujOrV/239dHNz\ng5WVFaKjowudpygJCQkYN24cmjVrBisrK1hZWSEtLU3jfb5sxowZ2LNnD1xdXfHBBx/g6NGjr+z7\neuONNzTitbOzg7Ozs0aPkZ2dHe7fv68xX8eOHTUa/rt27Yrnz58jPj6+wDpK87krTnh4OLKzs1G/\nfn2N5Wzbtk1jGfv27UPPnj3Vr/Pz80NOTg5SUlLKvJ0K88EHH+Dzzz9H586dMW/ePJw+fVr9XH6+\nu3btqn6sRo0a6NChQ6nX8+DBA8yYMQNvvPEGrK2tYWFhgaioqAKf+Zf3sfDwcOzfv19jW9nY2OD5\n8+cl3uYV5cX9s6j9HkCBz92LJyHVrFkTb7zxRpH7Vnh4OC5cuKDx/i0tLZGYmKjx/svyPRQeHo6v\nvvpKY9kuLi5QKBSIi4tTz9eiRQuNfenF76HiXLp0CT4+PmjcuDEsLS3RsGFDAEBiYuIr531RdHR0\nod/PQgiN7VbWOKnkeEIAoXPnztiyZQuqV6+OevXqqf/zzd/ZVq5cWeiZVvXr1wcgfVmZmZmVa0yF\nLc/AwEDjP/j836tVq1bgMSEEFAoFPvroIxw8eBBfffUVnJ2dYWpqitmzZyMtLU1j2S83QysUCqhU\nqhLFmv+6PXv2oHnz5gWet7a2LnQ+hUJRbk3wgwYNgq2tLb777js4ODigRo0a6N69O7Kzs4ucp2/f\nvkhKSsKxY8cQEhICPz8/uLq6Ijg4GAYGhf/d9mJhlv8eCnvs5W1XmveZP++rPnclWY6VlRX+/PPP\nAs/l5/uPP/7AyJEjMX/+fCxfvhzW1tY4d+4cJkyYoN52ZdlOhVEqlejfvz+OHj2KkydPwtvbGz4+\nPvjxxx+LnOfl7WZgYFDgsZycnALruX37NpYtWwYnJycYGxvD19e3wGfh5X1MCIHx48dj3rx5BeKo\nVatWid5jRXmxEMjfxwt77FX7bHGfQyEEvLy8sGrVqgLPWVlZqX8vy/eQEALz5s3DuHHjCiw7v7h7\n+T3lL+dV+87Tp0/Rt29f9OzZE5s3b4adnR2EEHBxcSl2/y9KSfbVssRJpcPijGBsbIzGjRsXeNzO\nzg4ODg6IiYnB5MmTX3s9TZs2hZGREU6dOoWWLVuqHz916pTGX6Ll6fTp0/Dz88Pw4cMBSF/esbGx\npTrz0dbWFg0aNMCxY8cwaNCgAs+7uLjA2NgY8fHx6N+/f4mX6+LigqCgIOTk5Ki/7CIiIpCWloZW\nrVqVeDmpqam4evUqVqxYob621O3btwuMIhTG2toavr6+8PX1xcSJE9GlSxdcvXoVLi4uhb6+rJe7\nCA8Ph0qlUhczYWFhMDIyQpMmTQq8trw+d+3bt8fjx4/x7NmzIt/PmTNnYGNjg88++0z92K5duwq8\nrrjtZGhoiNzc3BLFVLduXSiVSiiVSnh7e2PMmDFYs2aNen84e/YsvLy8AEhnUIaHh2vEbmtrizt3\n7mgs8+LFixp5OX36NJYtW6b+rGZmZiI+Pv6V+1j79u0RERFR6HfB6zI0NEReXl65L/dVzp07py7w\nHz9+jJiYGEyfPr3Q17Zv3x6bN29G/fr1YWRkVK5xtG/fHpGRka/ctq/avwrbjlevXsXDhw8RGBgI\nZ2dnANL+9WKxlP/HyKty4OLiUuByG6dOnYJCodD4HOrqZW90CQ9rUrECAwOxcuVKfP7554iMjERs\nbCx+/vlnTJs2Tf0aUcLLIJiamuK9997Df/7zH+zZswfXrl3D559/joMHD2L+/PkVEr+zszN+/vln\nhIeHIzo6GlOmTMHdu3c14i1J/IsWLcLatWuxdOlSXL16FVFRUVi1ahVSU1Nhbm6O+fPnY/78+fju\nu+8QGxuLqKgo7Ny5s9BRiHwzZ85Eeno6lEoloqKicObMGYwbNw49e/ZEt27dSvwera2tUadOHaxb\ntw5xcXE4d+4cRo8eDRMTk2Ln+/TTT7F//37ExsYiLi4OW7duhYWFBRwdHYucp6x/HaempuKdd95B\nTEwMDh06hIULF2LatGlFxliSz92r9O7dG15eXhg2bBgOHDiAGzdu4MKFC/j222+xYcMGANLhmQcP\nHmDTpk24ceMGfvjhB6xZs0ZjOa/aTk5OTrhw4QJu3LiBhw8fFlmozZw5E0eOHEF8fDyioqKwb98+\nODo6wtzcHE2bNsVbb72Fd955ByEhIYiOjoa/vz8yMjI0luHl5YXjx49jz549uH79Or744gucOXNG\nIy/Ozs7YunUrIiMjcenSJYwePRoqlarAZ/5l8+fPx9WrV+Hn54fw8HAkJCTg5MmT+OCDD5CQkFDi\n7V6Yxo0bIyYmBtHR0Xj48GGZRnRKS6FQYO7cuTh9+jSuXLmC8ePHw9LSEmPGjCn09TNnzkReXh6G\nDBmCM2fO4ObNmzhz5gw+/fRTnDt37rVi+eyzz3DgwAHMnj0bly5dQnx8PI4ePQp/f388f/5c/bpX\n7V+NGzdGSkoK/t//+394+PAhnj17hoYNG8LIyAgrV65EfHw8goOD8f7772sUUDY2NjA3N8exY8eQ\nkpKCR48eFbr8jz76CBcvXsSHH36ImJgYHD16FO+++y78/PzQoEGDEsdJr4/FmZ571cU//fz8sGvX\nLvz666/o1KkTOnbsiCVLlmjsqEUto7DHAwMDERAQgA8++ACurq7Yvn07tm3bVqILVBa1juIe++qr\nr9CwYUP06tULXl5ecHBwwPDhwwsclnh5OS8/NnnyZGzevBl79uxBmzZt4OHhgWPHjqkP6S1YsAAr\nVqzA+vXr0bp1a/To0QPffPNNsReMtLW1xW+//Ybbt2+jQ4cOGDx4MNzc3Apc+PVVf6UaGBhg9+7d\niI+Ph5ubGyZNmoRZs2a9cnTQxMQECxcuRPv27dGhQwdERkbiyJEj6uubvbwNSrKdippvxIgRsLCw\nQPfu3TF69GgMHjwYX3zxRZHzlORzVxIHDx7EsGHDMGvWLLzxxhsYNGgQjhw5gqZNmwIABg4ciE8/\n/RTz58+Hm5sbdu3ahWXLlmnE8qrtNHv2bNjY2MDd3R12dnYICwsrMp78z72HhweePXuGI0eOqJ/b\ntGkTWrdujUGDBsHT0xMODg7w8fHR+I9wwoQJeOedd/DOO++gQ4cOuHPnDt577z2NeIOCgqBSqdCx\nY0cMGzYMAwYMQIcOHQo9FPeiFi1aICwsDBkZGejXrx9cXFwwZcoUZGVloWbNmkW+p5LuPx06dEDX\nrl1ha2uLnTt3Fru84qZL+piBgQE+//xzTJ06FR06dMD9+/dx6NAhjet6vTiPra0tzp07BxsbGwwb\nNgwtWrSAn58fbt26hXr16r1WPJ6enjhx4gQuX76Mnj17wt3dHR9++CEsLS3V3yHFfY/mGzp0KEaM\nGIGBAwfC1tYWy5Ytg42NDbZu3Yrff/8drVq1wscff4zly5drHHI3MDDA6tWrsWvXLjg4OGj0CL+4\nfFdXVxw8eBChoaFo3bo1xo8fj8GDB+P777/XeH1JtwGVnUJUUgns5+eH4OBgZGZmwsbGBpMnT8an\nn34KAAgODsY777yDW7duoVOnTti8ebPGX+9z587Fxo0bAUhXmn7xS52I5K1Xr15o1qwZ1q1bp+1Q\ndI5SqURycjJ+++03bYeiUzZv3oyAgIAC/XhEuqLSRs4++eQTJCQkID09HUeOHMG3336LY8eO4eHD\nhxg2bBgCAwPx6NEjtG/fHqNGjVLPt3btWhw4cACXL1/G5cuX8csvv2Dt2rWVFTYRvaaSHvamwnHb\nEemfSivO8pum89WoUQN16tTBvn374OrqirfffhuGhoZYvHgxIiIicO3aNQDAli1bMGfOHNSrVw/1\n6tXDnDlzsHnz5soKm4he06sOnVPRuO3KjtuNdFml9pzNmDEDZmZmcHFxwaeffoq2bdsiKipK4xo2\npqamaNq0qfq6V9HR0RrPu7m5FbgmFhHJ18mTJ3lIs4yCgoJ4SLMMlEplpZx0QFRRKvVSGt999x1W\nr16NU6dOYfjw4Wjbti0yMzNRp04djddZWlriyZMnAICMjAyNa8xYWloWOIMJkK59lJycXLFvgIiI\niKgcuLu749KlS4U+V+lnayoUCnh6emLEiBHYsWMHzM3NkZ6ervGatLQ09ZlQLz+flpYGc3PzAstN\nTk5W97bwRz4/ixYt0noM/GFOdOGHeZHfD3Miz5+qkpeIiIgiayWtXUojJydHfYjzxQDzL5iYf8E7\nFxcXjcoyIiKiVBfoJO26efOmtkOglzAn8sS8yA9zIk/6kJdKKc4ePHiAnTt3IjMzE3l5eTh27Bh2\n796NIUOGwMfHB5GRkdi3bx+ysrKwZMkStG7dWn0bnPHjx2PFihVITk7GnTt3sGLFCiiVysoIm4iI\niKjSVUrPmUKhwPfff4/p06dDCIHmzZvjxx9/VN/Ud+/evZg5cyb8/PzQuXNnjQsUTp06FTdu3FDf\neiQgIABTpkypjLCpHLCQlh/mRJ6YF/lhTuRJH/JSaRehrWi88SoRERHpiuLqFt6+iSpUSEiItkOg\nlzAn8sS8yA9zIk/6kBcWZ0REREQyojeHNWvVqoVHjx5VYkRE5cva2hp///23tsMgIqJyUFzdojfF\nGXvSSNfxM0xEVHWw54yI1PShX0MXMS/yw5zIkz7khcUZERERkYzwsCaRjuBnmIio6uBhTSIiIiId\nweKMSM/oQ7+GLmJe5Ic5kSd9yAuLMz1nYGCA7du3azsMIiIi+gd7zv4RG5uI48fjkZNjgBo1VPDy\nagJn54Zljqe8l1dRDAwMsHXrVowZM+aVr926dSvGjx8PlUpVCZHRy9hzRkRUdRT3nV4pNz6Xu9jY\nRGzefB1GRr3Vj23eHAylEmUqqMp7efooOzsbhoaG2g6DiIhkQlcGPcoDizMAx4/Hw8ioNzQPY/fG\n5csn0KFD6RN//nw8nj79tzDz9ASMjHojOPhEmT9Iq1evxurVq3Hjxg1YWVmhR48ecHV1xY4dOxAT\nE6Px2kmTJiEpKQnHjx8v9Xo2bNiA5cuX4+bNmzA1NUWrVq2wfft2xMXFYfz48QCk0TYAUCqV2LRp\nE86cOYO5c+fiypUrAIDGjRvjf//7H/r27QsAiIiIwPTp03Hx4kU4Ojpi6dKl+PjjjxEQEIBPP/1U\nvcxvvvkG586dw+HDh+Ht7Y0dO3aUaVtR8UJCQuDp6antMOglzIv8MCfykT/ooVD0RnJyCBo1erNK\nD3qwOAOQk1N4611eXtla8lSqwufLzi7b8hYtWoQVK1bgyy+/RN++fZGZmYkjR45g3LhxWLp0KUJD\nQ9GzZ08AwJMnT7B7925s2rSp1Ou5cOECpk+fjqCgIHh4eCAtLQ3nz58HAHTr1g2rVq3CzJkzkZKS\nAgAwMTFBbm4u3nrrLUyaNAk//PADACAyMhKmpqYAgGfPnmHAgAFo06YNwsPDkZmZiffeew8PHjyA\nQqHQWP+SJUvw2WefITAwkIdOiYhI7fhxadAjKgowMgIaNXr9QQ85Y3EGoEYNqRB4+Q8kW1sVZswo\n/fJWr1bhwYOCjxsalr7gyMzMxP/+9z8EBgZixgvBuLu7AwAGDBiA9evXq4uz7du3w9TUFD4+PqVe\nV1JSEszMzDBkyBBYWFjAwcEBrVq1Uj9vaWkJALC1tVU/9ujRIzx+/BiDBw9GkyZNAED9LwBs27YN\n6enp2LZtG6ysrAAAQUFBcHV1LbB+Hx8fjfdIFYMjAfLEvMgPcyIf8fEGuHwZEAKwtvaEEIBCUfZB\nD7mrmu+qlLy8muD582CNx54/D0bv3k2KmKPylhcVFYXnz5+rDxG+bOrUqdi7dy/S0tIAAOvXr8eE\nCRNQvXrp6+6+ffuicePGcHJywujRo7F+/XqkpqYWO4+1tTX8/f3Rr18/DBgwAF9++SWuXbumfj46\nOhotW7ZUF2YA4OLiojGdr2PHjqWOmYiIqi6VCjh2DIiJUUEIwNERaNlSKsyAsg166AIWZ5COVyuV\nTWFrewI1a4bA1vYElMqmZR4qLe/lFad///6wtbXFDz/8gEuXLuHixYsICAgo07LMzMzw559/Yv/+\n/WjevDm+//57NG3aFBcvXix2vnXr1uHChQvo06cPTp06hVatWmHdunXq50t6hqGZmVmZ4qbS0Ydr\nBOki5kV+mBPtev4c2LkTOHcOaNq0CZo0CUbjxkBiYsg/z5d9EEXueFjzH87ODcu1eCqv5bVs2RLG\nxsY4duyYxiHGfAYGBggICMD69esRExMDDw8PNGvWrMzrMzAwQI8ePdCjRw8sWbIELVu2xI4dO9C2\nbVv12ZNCiAL9Yi4uLnBxccGsWbMwffp0rFu3DlOmTEHLli2xfv16pKWlqUfLoqKi1CN9REREL0tL\nA7ZvB+7dA0xMgNmzGyIrCwgOPoGHDy/D1laF3r0rZtBDDlicyZy5uTlmz56NxYsXw8TEBF5eXnj2\n7BmOHDmCefPmAQAmT56MJUuW4Nq1awgKCirzug4cOICEhAT06NEDderUwYULF3Dr1i20bNkSAODk\n5KR+Xbdu3WBqaoqUlBSsW7cOb731Fho0aIDk5GScPn0a7dq1AwCMHTsWCxcuhJ+fHwIDA/H06VO8\n//77MDExec0tQ2XFPhp5Yl7khznRjtu3pRGzjAzAxgYYMwaoVQsA8gc93tRyhBWPhzV1wH//+18E\nBgZi5cqVcHV1Rb9+/fDXX3+pn69bty4GDhwICwsLDB8+vMzrqVWrFn755Rd4e3vD2dkZ8+bNw3/+\n8x9MnDh++DUsAAAgAElEQVQRANChQwe8//77mDp1Kuzs7PDuu+/CzMwM169fh6+vL5ydnTF8+HD1\nmZ2AdEbn4cOHkZqaio4dO2LcuHH48MMPNU4qICIiAoDISGDzZqkwa9wYmDw5vzDTL7xDQBXRsWNH\n9OjRA8uXL9d2KCXi5OSEgIAAzJ8/X9uh6Izy+gzz2k3yxLzID3NSeYQAQkOBkyel6fbtAW9voFq1\ngq+tKnnhHQKqsIcPH+LXX3/FX3/9hV27dmk7nBKryoUyERGVXG4ucOAAcOWKdBZmv35Ap07/npGp\nj1ic6ThbW1vUqlUL3377LRo1aqTxnLe3N86cOVPofD179sShQ4cqIcLCvXxCAVWeqvAXZ1XEvMgP\nc1LxMjKAn34Cbt0CDA2B4cOB5s2Ln0cf8sLDmlVYcnIysrKyCn3OxMQE9vb2lRwRvQ59/AwTUdV1\n/750Rubjx4CVldT4b2en7agqT3Hf6SzOiHQEe86qNuZFfpiTihMXB+zZI13LrEEDwNcXMDcv2bxV\nJS/sOSMiIiKtEwI4fx44elT6vVUrYMgQoEYNbUcmLxw5I9IR/AwTkS7Ly5OKsvBwadrTE/Dw0N/G\nf46cERERkdZkZQG7dwPx8UD16tJomaurtqOSL16ElkjP8H6B8sS8yA9zUj7+/hvYsEEqzMzMgAkT\nXq8w04e8cOSMiIiIKkRionSpjKdPAVtb6YzMmjW1HZX8seeMSEfwM0xEuiQiAjh4UOo1a9ZMuoaZ\nkZG2o5KP4r7TeViTNBgYGGD79u3aDqPCLV68GM2aNdN2GEREVY4QQHAwsH+/VJh17gyMHs3CrDRY\nnP0j9nosVv+0Gl/v/Bqrf1qN2OuxslpeYW7fvg0DAwOEhoaWel4vLy/1Dc1flJKSgrfffrs8wkPT\npk2xZMmScllWRSjNXQrk/l5KQx/6NXQR8yI/zEnp5eQAu3YBp08DBgbAwIFA//7S7+VFH/LCnjNI\nhdTmk5th1Ozfsn7zyc1QQgnnps5aX96rlOehLltb23Jbltxv0VSa7VZZ70WlUgGQRjCJiHTJkyfA\njh1AcjJgbAyMGAE0aaLtqHQTe84ArP5pNR7YPUDIzRCNx81um6FD9w6ljuX8mfN42uCpetqzkScA\nwPa+LWaMnFHq5Z05cwZz587FlStXAACNGzfG//73P/Tv31/jdY0aNcKNGzeQkJCA2bNn448//sDj\nx4/RpEkTfPzxx/Dz8wMAKJVK/PDDDxrzhoSEoGfPnjAwMMDWrVsxZswYAEBGRgYWLFiAffv24f79\n+7C3t8eUKVPwySefFBuzp6enxoieQqFAfHw83nzzTQQEBGjMn5mZCXt7e6xZswZjx46Fp6cnmjRp\ngjp16mDjxo3Izs6Gr68vVq5cCaMXxsW//fZbrF69GomJiXBwcIBSqcTcuXNRrVq1V27TxYsXY9u2\nbYiLiwMgjUK+//77CA0NRUZGBurVq4fp06djzpw5Bd4LANy8eRP29vaYO3cudu/ejQcPHqBWrVrw\n8PDAjh07AEjF38KFC7F27Vo8e/YMAwcORKdOnfDxxx8jJydHI47AwEAsXLgQ8fHxiIyMhLNzwSKe\nPWdEJFd370qFWXo6YG0tNf7XqaPtqOSN1zl7hRyRU+jjecgr0/JUUBX6eLYqu9TLys3NxVtvvYVJ\nkyapC6rIyEiYmpri4sWLaNu2Lfbt24euXbuqi5LMzEx4eXlhyZIlMDc3x6FDhzBx4kQ0aNAAnp6e\nWLlyJRISElCvXj188803AABra+sC6xZCYNCgQbh9+zZWrVoFNzc33LlzB7Gxrz5Eu3//frRr1w7D\nhw/HnDlzAAA2NjaYMmUKNmzYoFGc7dy5E4aGhhgxYoT6sT179sDX1xdnzpxBXFwcJk+eDDMzM6xY\nsQKAVNRs3rwZ33zzDVq3bo3o6GhMmzYNWVlZ+Oyzz0q9nWfMmIGsrCwEBwejZs2auHHjBlJSUop9\nL19//TV2796Nbdu2oXHjxkhJSUFYWJh6mStXrsRXX32FNWvWoEuXLti/fz+WLFlSYBQuOTkZa9as\nwY8//ghra2vUrVu31PETEWlLTAywd690SLNhQ2DUKMDUVNtR6TYWZwBqKKT7RuSPcOWzNbXFDM/S\nj3StvieNxL3M0MCw1Mt68uQJHj9+jMGDB6PJP+PD+f/evn0bAFCrVi2Nw5GtWrVCq1at1NMzZ87E\n8ePHsX37dnh6esLS0hKGhoYwMTEp9jDmiRMnEBoaij///BNt27YFII3OdevW7ZVxW1tbo1q1ajA3\nN9dYx6RJk7Bo0SIEBwejd+/eAIANGzZg3LhxMDT8d/vUrl0b33//PRQKBZydnbF06VK89957CAwM\nhBACy5Ytw/79+9G3b18AQMOGDfHf//4X77//fpmKs6SkJPj4+MDNzQ0A4Ojo+Mr3kpSUhObNm6Nn\nz54AgAYNGqB9+/bq55ctW4ZZs2Zh3LhxAICPPvoI58+fx4EDBzTWnZWVhR9//BENGjQoddxlUVXu\nS1fVMC/yw5wUTwggLAw4flz6vXVrYNAg6SKzFUkf8sLGFgBe7bzwPO65xmPP456jd9veWl+etbU1\n/P390a9fPwwYMABffvklrl27Vuw8T58+xbx589CqVSvUrl0bFhYWOHz4MJKSkkq17gsXLsDa2lpd\nmJUHW1tbDBkyBOvXrwcgjQL+8ccfCAgI0Hhdx44dNUaYunbtiufPnyM+Ph5RUVF49uwZhg0bBgsL\nC/XPtGnTkJ6ejtTU1FLH9cEHH+Dzzz9H586dMW/ePJw+ffqV80ycOBFXrlxB06ZNMX36dOzbt099\nuDI9PR3Jycno2rWrxjzdunUrMIxtZ2dXaYUZEVF5yMuTLpPx++9SYeblJV31v6ILM33B4gyAc1Nn\nKHspYXvfFjVTasL2vi2UvcrevF/ey1u3bh0uXLiAPn364NSpU2jVqhXWrVtX5Os/+ugjbNu2DYsX\nL0ZISAguXbqEAQMG4Pnz50XOU5mmTZuGn3/+GampqdiwYQO6du2Kli1barymuN6q/Kb5PXv2ICIi\nQv0TGRmJuLi4Qg/RvopSqURiYiKmTZuGu3fvwtvbWz3iVRR3d3ckJCTg//7v/2BoaIj3338frVu3\nxpMnT0q1bjMzs1LH+zqq+l+cuop5kR/mpHBPnwI//gj89Zd0w/JRo4Du3SvvHpn6kBfWuP9wbupc\nrmdSlvfyXFxc4OLiglmzZmH69OlYt24dfHx8AAB5eZq9cadPn4afnx+GDx8OQCpmYmNjYW9vr36N\noaEhcnNzi11nu3bt8OjRI1y4cAHt2rUrdcyGhoYFYgOAXr16wdHREd9//z22bt2K5cuXF3hNeHg4\nVCqV+qzFsLAwGBkZoUmTJsjLy4OxsTHi4+MLnBTxOurWrQulUgmlUglvb2+MGTMGa9asgbm5eZHv\nxczMDEOHDsXQoUMxf/582NvbIzQ0FAMHDkT9+vVx9uxZeHt7q19/9uxZ2Z/FSkRUlIcPge3bpVsy\nWVhI1y+rV0/bUVU9HDmTufj4eMydOxdnz55FYmIizp07h9DQULi4uMDGxgbm5uY4duwYUlJS8OjR\nIwCAs7Mzfv75Z4SHhyM6OhpTpkzB3bt3NUajnJyccOHCBdy4cQMPHz4stFDr3bs3evTogVGjRuHg\nwYNISEjA2bNnsXHjxhLF7uTkhDNnzuDWrVt4+PChev0KhQJTpkzBZ599BpVKhVGjRhWYNzU1Fe+8\n8w5iYmJw6NAhLFy4ENOmTYOJiQnMzc0xf/58zJ8/H9999x1iY2MRFRWFnTt3Yt68eWXZzJg5cyaO\nHDmiPmy6b98+ODo6wtzcvMj3smzZMmzfvh1RUVFISEjAxo0bUb16dTRv3hwAMHv2bHzzzTfYunUr\n4uLisHz5cgQHB5cpvvKkD9cI0kXMi/wwJ5pu3JDukfn334C9PRAQoJ3CTB/ywuJM5szMzHD9+nX4\n+vrC2dkZw4cPR/fu3bFq1SooFAqsXr0au3btgoODg3p066uvvkLDhg3Rq1cveHl5wcHBAcOHD9cY\nsZk9ezZsbGzg7u4OW1tbjbMMX3To0CEMGDAA06ZNQ4sWLTBu3LgS93QtWbIEjx8/hrOzM+zs7HDr\n1i31c/kXwB07diyMjY015lMoFBgxYgQsLCzQvXt3jB49GoMHD8YXX3yhfs2CBQuwYsUKrF+/Hq1b\nt0aPHj3wzTffwMnJqUSxKRSKAiNYH3zwAVxdXeHh4YFnz57hyJEjRb6XpKQkWFlZYcWKFejatSvc\n3Nxw4MAB7N27V33ngffffx/vvfceZs2ahTZt2uCPP/7AwoULNYrkwuIgIpKbCxeArVuBrCygRQtg\n4kTA0lLbUVVdvM4ZaUVUVBRcXV0REREBV1dXjed69eqFZs2aFdtXp6s2b96MgIAA9YkDpcHPMBFV\nNpVKavo/d06a7t4d6N278vrLqjJe54xkIzs7Gw8ePMAnn3yCN998s0BhBkgnA7AIISLSrufPpeuX\nXbsGVKsmXSajTRttR6UfeFiTyuTzzz/XuIzFiz+WxYx1b9++HY6OjkhMTMSaNWsKfc3rHuo7ffp0\nkbFZWFjg7NmzZV52edD2YUx96NfQRcyL/OhzTtLSgE2bpMLMxAQYN04+hZk+5IWHNalMHj16pD4B\noTCNGzeuxGg0ZWVlITk5ucjn69WrV6DPTReU12dYHy7gqIuYF/nR15zcvg3s3AlkZAA2NtKtmGrV\n0nZU/6oqeSnuO53FGZGO4GeYiCpaZCTw889Abi7QuLF083ITE21HVTWx54yIiIiKJAQQGgqcPClN\nt2sHDBgg9ZpR5WPPGZGe0Yd+DV3EvMiPvuQkNxfYt08qzBQKoH9/qflfroWZPuRFb0bOrK2ttd6I\nTfQ6ynJbKiKi4mRmSv1lt24BhobA8OHAP9fRJi3Sm54zIiIi+tf9+9KtmB4/BqyspMZ/OzttR6U/\n2HNGREREanFxwJ490rXMGjQAfH2Bf+5WRzLAnjOqUPrQG6BrmBN5Yl7kpyrmRAjgjz+kEbPnz4FW\nrYAJE3SrMKuKeXkZR86IiIj0gEoFHDkChIdL056egIcHb8UkR+w5IyIiquKysoDdu4H4eKB6dWDI\nEKCQu+dRJWLPGRERkZ569Eg6jPngAWBmJvWXOThoOyoqDnvOqELpQ2+ArmFO5Il5kZ+qkJPERGD9\neqkws7UFAgJ0vzCrCnl5FY6cERERVUEREcDBg0BeHtCsmXQNMyMjbUdFJcGeMyIioipECODECeD0\naWm6c2egb1/AgMfKZIU9Z0RERHogJwfYvx+IjpaKMW9voEMHbUdFpcU6miqUPvQG6BrmRJ6YF/nR\ntZw8eQIEBUmFmbExMHZs1SzMdC0vZcGRMyIiIh139y6wYweQng5YW0u3YqpTR9tRUVmx54yIiEiH\nxcQAe/dKhzQbNgRGjQJMTbUdFb0Ke86IiIiqGCGAsDDg+HHp99atgUGDpIvMkm6rlJ6z7OxsTJ48\nGY0aNYKlpSXatGmDo0ePAgBu3rwJAwMDWFhYqH8CAwM15p87dy5sbGxgY2ODefPmVUbIVE70oTdA\n1zAn8sS8yI+cc5KXJ10m4/ffpcLMy0u66r8+FGZyzkt5qZQ05ubmwtHREaGhoXB0dMShQ4cwcuRI\nREZGql+Tnp4ORSE3+Fq7di0OHDiAy5cvAwD69OkDJycnTJ06tTJCJyIikpWnT4Fdu4CbN4EaNQAf\nH6BlS21HReVJaz1n7u7uWLx4Mdq0aYPGjRsjJycH1apVK/C6rl27YtKkSfD39wcABAUFYd26dTh3\n7pzG69hzRkREVd3Dh9KtmP7+G7CwAEaPBurV03ZUVBbF1S1auZTGvXv3cO3aNbi4uKgfa9iwIRwc\nHDBp0iSkpqaqH4+Ojoa7u7t62s3NDVFRUZUaLxERkbbduAFs2CAVZvb20q2YWJhVTZVenOXk5GDs\n2LFQKpVo3rw56tSpgz///BNJSUm4cOECnjx5grFjx6pfn5GRASsrK/W0paUlMjIyKjtsKiN96A3Q\nNcyJPDEv8iOnnFy4AGzdCmRlAS1aABMnApaW2o5KO+SUl4pSqa2DKpUK48aNg7GxMVatWgUAMDMz\nQ9u2bQEAtra2WLVqFezt7ZGZmQkzMzOYm5sjPT1dvYy0tDSYm5sXunylUolGjRoBAGrWrInWrVvD\n09MTwL/J5HTlTueTSzyc5rRcpy9duiSreDj9L23Go1IB//d/IYiOBho18kS3bkD16iEIC9P+9tHW\n9KVLl2QVT2k+TyEhIbh58yZepdJ6zoQQmDRpEpKSknD48GEYFXH31Xv37sHe3h5paWmwsLBAt27d\nMHHiRHXP2caNG7Fx40aEhYVpzMeeMyIiqkqeP5euX3btGlCtmnSZjDZttB0VlRdZ9JxNnz4dMTEx\nOHjwoEZhdv78ecTGxkKlUiE1NRXvvfceevXqBQsLCwDA+PHjsWLFCiQnJ+POnTtYsWIFlEplZYVN\nRERU6dLSgE2bpMLMxAQYN46FmT6plOIsMTER69atQ0REBOrWrau+ntn27dtx48YNeHt7w9LSEq6u\nrjAxMcGOHTvU806dOhWDBw+Gq6sr3NzcMHjwYEyZMqUywqZy8PLhAdI+5kSemBf50VZObt8G1q8H\n7t0DatcG/P2Bfzp2CPqxr1RKz1nDhg2hUqmKfN7X17fY+b/88kt8+eWX5R0WERGRrERFAfv3A7m5\ngJMTMHKkNHJG+oX31iQiItIyIYDQUODkSWm6XTtgwACp14yqJt5bk4iISKZyc4EDB4ArVwCFAujb\nF+jcWfqd9FOlnRBA+kkfegN0DXMiT8yL/FRGTjIzgS1bpMLM0FC64n+XLizMiqMP+wpHzoiIiLTg\n/n3pVkyPHwNWVsCYMYCdnbajIjlgzxkREVEli4sD9uyRrmVWv740YlbE9dWpimLPGRERkQwIAZw/\nDxw9Kv3eqhUwZAhQo4a2IyM5Yc8ZVSh96A3QNcyJPDEv8lPeOVGpgMOHgSNHpMLMwwN4+20WZqWl\nD/sKR86IiIgqWFYWsHs3EB8PVK8ujZa5umo7KpIr9pwRERFVoEePpMb/Bw8AMzPA1xdwcNB2VKRt\n7DkjIiLSgqQkYOdO4OlTwNZWOiOzZk1tR0Vyx54zqlD60Buga5gTeWJe5Od1cxIRIV3D7OlToFkz\nYPJkFmblQR/2FY6cERERlSMhgBMngNOnpelOnYB+/QADDodQCbHnjIiIqJzk5Eg3Lo+Olooxb2+g\nQwdtR0VyxJ4zIiKiCvbkCbBjB5CcDBgZASNHAk2aaDsq0kUcZKUKpQ+9AbqGOZEn5kV+SpOTu3eB\n9eulwszaGvD3Z2FWUfRhX+HIGRER0WuIiQH27pUOaTo6SpfKMDXVdlSky9hzRkREVAZCAGFhwPHj\n0u/u7sDgwdJFZolehT1nRERE5SgvD/j1V+Cvv6Tp3r2B7t0BhUK7cVHVwJ4zqlD60Buga5gTeWJe\n5KeonDx9Cvz4o1SY1aghNf736MHCrLLow77CkTMiIqISevhQuhXT338DFhbA6NFAvXrajoqqGvac\nERERlUBCAvDTT9JNzO3tpcLM0lLbUZGuYs8ZERHRa7hwATh0CFCpgBYtgGHDAENDbUdFVRV7zqhC\n6UNvgK5hTuSJeZGfkJAQqFTAsWPAL79IhVm3bsCoUSzMtEkf9hWOnBERERUiOxvYuRO4dk26FdPg\nwUCbNtqOivQBe86IiIhekpYmNf7fuweYmEijZY0aaTsqqkrYc0ZERFRCd+5I98jMyABq1wbGjJH+\nJaos7DmjCqUPvQG6hjmRJ+ZFHqKigKAgqTDLygqBvz8LM7nRh32FI2dERKT3hABCQ4GTJ6Xpdu2k\n+2OamGg3LtJP7DkjIiK9lpsLHDwIXL4sXeW/b1+gc2de8Z8qFnvOiIiICpGZKZ2ReeuWdHmMt98G\nnJ21HRXpO/acUYXSh94AXcOcyBPzUvnu3wfWr5cKMysrYNIkzcKMOZEnfcgLR86IiEjvXL8O7N4N\nPH8O1K8v3YrJ3FzbURFJ2HNGRER65Y8/gKNHpZMAXFyAoUOBGjW0HRXpG/acERGR3lOpgCNHgPBw\nadrDA/D0ZOM/yQ97zqhC6UNvgK5hTuSJealYWVnAtm1SYVatmnTj8l69ii/MmBN50oe8cOSMiIiq\ntEePpFsxPXgAmJkBvr6Ag4O2oyIqGnvOiIioykpKki6V8fQpYGsr3YqpZk1tR0XEnjMiItJDERHS\nxWXz8oBmzYDhwwEjI21HRfRq7DmjCqUPvQG6hjmRJ+al/AgBnDgB7N8vFWadOkmXyihtYcacyJM+\n5IUjZ0REVGXk5EhFWXQ0YGAAeHsDHTpoOyqi0mHPGRERVQlPngA7dgDJydIo2ciRQJMm2o6KqHDs\nOSMioirt7l2pMEtPB6ytpcb/OnW0HRVR2bDnjCqUPvQG6BrmRJ6Yl7KLiQE2bZIKM0dHwN+/fAoz\n5kSe9CEvHDkjIiKdJARw7hzw++/S7+7uwODBQHX+z0Y6jj1nRESkc/LygEOHgIsXpenevYHu3Xkr\nJtId7DkjIqIq49kz4KefgJs3pRuW+/gALVtqOyqi8sOeM6pQ+tAboGuYE3liXkomNRXYsEEqzCws\ngIkTK64wY07kSR/ywpEzIiLSCQkJ0ohZVhZQt650RqalpbajIip/7DkjIiLZu3gR+PVXQKUCWrQA\nhg0DDA21HRVR2bHnjIiIdJJKBRw/DoSFSdPdugFeXmz8p6qNPWdUofShN0DXMCfyxLwUlJ0tHcYM\nC5NuxTRkCNCnT+UVZsyJPOlDXjhyRkREspOWJl3xPyUFMDEBRo0CGjXSdlRElYM9Z0REJCt37kiF\nWUYGULu21Phfu7a2oyIqX+w5IyIinRAVBezfD+TmAk5O0s3LTUy0HRVR5WLPGVUofegN0DXMiTzp\ne16EAEJDgd27pcKsXTvAz0+7hZm+50Su9CEvHDkjIiKtys0FDh4ELl+Wmv379gU6d+YZmaS/2HNG\nRERak5kJ7NwJ3LolXbfs7bcBZ2dtR0VU8dhzRkREsnP/PrB9O/D4MWBlBYweLV35n0jfseeMKpQ+\n9AboGuZEnvQtL9evAxs3SoVZ/fpAQID8CjN9y4mu0Ie8cOSMiIgq1fnzwJEj0kkALi7A0KFAjRra\njopIPthzRkRElUKlAo4elYozAPDwADw92fhP+ok9Z0REpFVZWdJlMuLjgWrVpFsxublpOyoieWLP\nGVUofegN0DXMiTxV5bw8eiT1l8XHA2ZmgFKpG4VZVc6JLtOHvHDkjIiIKkxSknSpjKdPAVtb6VZM\nNWtqOyoieauUkbPs7GxMnjwZjRo1gqWlJdq0aYOjR4+qnw8ODkaLFi1gZmaGN998E0lJSRrzz507\nFzY2NrCxscG8efMqI2QqJ56entoOgV7CnMhTVcxLRASwZYtUmDVtCkyerFuFWVXMSVWgD3mplOIs\nNzcXjo6OCA0NRXp6OpYuXYqRI0ciKSkJDx8+xLBhwxAYGIhHjx6hffv2GDVqlHretWvX4sCBA7h8\n+TIuX76MX375BWvXrq2MsImIqAyEAE6ckO6RmZcHdOokjZgZGWk7MiLdUCnFmampKRYtWgRHR0cA\nwMCBA+Hk5IQ///wT+/btg6urK95++20YGhpi8eLFiIiIwLVr1wAAW7ZswZw5c1CvXj3Uq1cPc+bM\nwebNmysjbCoH+tAboGuYE3mqKnnJyZEa/0NDAQMDYOBAwNtb+l3XVJWcVDX6kBet7C737t3DtWvX\n0KpVK0RFRcHd3V39nKmpKZo2bYqoqCgAQHR0tMbzbm5u6ueIiEg+njwBgoKA6GhplGzMGKBDB21H\nRaR7Kv2EgJycHIwdOxZKpRLNmzdHZmYm6tSpo/EaS0tLPHnyBACQkZEBKysrjecyMjIqNWYqO33o\nDdA1zIk86XpeUlKkWzGlpwPW1lJh9tJXu87R9ZxUVfqQl0otzlQqFcaNGwdjY2OsWrUKAGBubo70\n9HSN16WlpcHCwqLQ59PS0mBubl7o8pVKJRo1agQAqFmzJlq3bq1OYv4wKKc5zWlOc7p8p3/4IQSh\noUCDBp5wdATs7UMQFSWf+DjNaTlM5/9+8+ZNvEql3SFACIFJkyYhKSkJhw8fhtE/naHr16/Hli1b\ncObMGQBQj6RdunQJzZs3R7du3TBx4kT4+/sDADZu3IiNGzciLCxM843wDgGyFBISov6AkjwwJ/Kk\ni3kRAjh3Dvj9d+l3d3dg8GCgehW5SJMu5kQfVJW8FFe3GFRWENOnT0dMTAwOHjyoLswAwMfHB5GR\nkdi3bx+ysrKwZMkStG7dGs2bNwcAjB8/HitWrEBycjLu3LmDFStWQKlUVlbYRERUiLw84JdfgN9+\nkwqz3r2le2RWlcKMSJsqZeQsMTERTk5OMDY2RrVq1dSPr1u3DqNHj0ZwcDBmzpyJxMREdO7cGZs3\nb1af2QlI1znbsGEDACAgIABffPFFwTfCkTMiokrx7Bnw00/AzZvSDct9fICWLbUdFZFuKa5u4Y3P\niYioxFJTpcb/1FTAwgIYPRqoV0/bURHpHlkc1iT99GIjJMkDcyJPupCXhARgwwapMKtbFwgIqNqF\nmS7kRB/pQ17YHUBERK908SLw66+ASgU4OwNvvw0YGmo7KqKqiYc1iYioSCoVcPw4kH+CfLduUvO/\nAY+7EL2W4uoWjpwREVGhsrOBvXuB2FipGBs0CGjbVttREVV9/NuHKpQ+9AboGuZEnuSWl7Q0YNMm\nqTAzMQHGj9e/wkxuOSGJPuSFI2dERKThzh1gxw4gIwOoXVu6FVPt2tqOikh/sOeMiIjUoqKA/fuB\n3FzAyQkYOVIaOSOi8sWeMyIiKpYQwOnTwIkT0nS7dsCAAcAL1w0nokrCnjOqUPrQG6BrmBN50mZe\ncnOl0bITJwCFAujXT2r+1/fCjPuKPOlDXjhyRkSkxzIzgZ07gVu3pOuWvf22dB0zItIe9pwREemp\n+3Tl9LwAACAASURBVPelWzE9fgxYWUm3YqpbV9tREekH9pwREZGG69eB3buB58+B+vUBX1/pXplE\npH3sOaMKpQ+9AbqGOZGnyszL+fPAtm1SYebiAiiVLMwKw31FnvQhLxw5IyLSEyoVcPSoVJwBgIcH\n4OkpnQRARPLBnjMiIj2QlSUdxoyPl87CHDIEcHPTdlRE+os9Z0REeuzRI6nx/8EDwMxM6i9zcNB2\nVERUFPacUYXSh94AXcOcyFNF5SUpCVi/XirM6tQB/P1ZmJUU9xV50oe8cOSMiKiKiogADh4E8vKA\npk2B4cMBY2NtR0VEr8KeMyKiKkYI4ORJIDRUmu7USbrqvwGPlRDJBnvOiIj0RE6OdCum6GipGOvf\nH+jYUdtREVFp8O8oqlD60Buga5gTeSqPvDx5AgQFSYWZkREwZgwLs9fBfUWe9CEvHDkjIqoCUlKk\nMzLT0wFra6kwq1NH21ERUVmw54yISMfFxgJ79wLZ2YCjIzBqlHTJDCKSL/acERFVQUIA584Bv/8u\n/e7uDgweDFTnNzuRTmPPGVUofegN0DXMiTyVNi95ecAvvwC//SYVZr17A0OHsjArT9xX5Ekf8sLd\nmIhIxzx7Bvz0E3DzJlCjBuDjA7Rsqe2oiKi8sOeMiEiHpKZKjf+pqYC5OTB6NFC/vrajIqLSYs8Z\nEVEVkJAA7NoljZzVrSsVZlZW2o6KiMobe86oQulDb4CuYU7k6VV5uXgR+PFHqTBzdgYmTWJhVtG4\nr8iTPuSFI2dERDKmUgHHjwNhYdJ0t25S8z9vxURUdbHnjIhIprKzpeuXxcZKxdigQUDbttqOiojK\nA3vOiIh0TFoasGOHdOV/ExPpwrKNGmk7KiKqDBwYpwqlD70BuoY5kacX83LnDrB+vVSY1a4N+Puz\nMNMG7ivypA954cgZEZGMREUB+/cDubmAkxMwcqQ0ckZE+oM9Z0REMiAEcPo0cOKENN22LTBwIFCt\nmnbjIqKKwZ4zIiIZy80FDh4ELl8GFAqgb1+gc2fpdyLSP+w5owqlD70BuoY5kZfMTGDLFuDgwRAY\nGgK+vkCXLizM5ID7ijzpQ144ckZEpCX370u3Ynr8GDA1lS4sW7eutqMiIm1jzxkRkRZcvw7s3g08\nfy7dG9PXF7Cw0HZURFRZXrvn7P79+zAxMYGFhQVyc3Pxww8/oFq1ahg3bhwMeJlqIqJSOX8eOHJE\nOgnAxQUYOhSoUUPbURGRXJSosho0aBCuX78OAPj000+xfPlyfPXVV/jwww8rNDjSffrQG6BrmBPt\nUamAw4elHyEADw9g+HCpMGNe5Ic5kSd9yEuJRs7i4uLQunVrAMDWrVsRFhYGCwsLtGzZEl9//XWF\nBkhEVBVkZQF79kiHM6tVA4YMAdzctB0VEclRiXrObGxscPv2bcTFxcHX1xdRUVHIy8uDlZUVMjIy\nKiPOV2LPGRHJ1aNHUuP/gweAmZl0KyZHR21HRUTa9No9Z/3798fIkSORmpqKUaNGAQCio6PRoEGD\n8ouSiKgKSkoCdu4Enj4F6tQBxowBrK21HRURyVmJes42bNiAgQMHwt/fH/PnzwcAPHz4EIsXL67I\n2KgK0IfeAF3DnFSey5ela5g9fQo0bQpMnlx0Yca8yA9zIk/6kJcSjZwZGxtj6tSpGo/16tWrQgIi\nItJ1QgAnTwKhodJ0p05Av34AT24nopIoUc/Z48ePsXLlSvz1118aPWYKhQK//fZbhQZYUuw5IyI5\nyMmRblweHS0VY/37Ax07ajsqIpKb1+45GzFiBFQqFXx8fGBsbKyxYCIikjx5AuzYASQnA0ZGwIgR\n0uFMIqLSKNHImZWVFe7fvw8jI6PKiKlMOHImTyEhIfD09NR2GPQC5qRipKRIZ2Smp0t9ZWPGSCcA\nlBTzIj/MiTxVlbwUV7eUqAOia9euiImJKdegiIiqithYYNMmqTBzdAT8/UtXmBERvahEI2f37t2D\nt7c3unTpAjs7O3Wlp1AosHDhwgoPsiQ4ckZElU0I4Nw54Pffpd/d3YHBg4HqJWoYISJ99to9Z/Pn\nz8edO3dw7949pKenl2twRET/n717j66qPvf9/05CLuQOua8IBIgBEiCErFjRagWl1WK1bKpCW/tD\ntHV0t/Z09OjWfcZuj213xz5nnO62p3Xvobtq7XFv8QZqtd4KNhaq0qwECAQIEgiXrNwJuV/Xmr8/\nvrIkCMglyZxrrc9rDIfMuZLFA49Lvsz5zM83GPl88Mc/QlWVOb7+evjsZ0GjuCJyqc7ryllSUhK1\ntbW4XK6JqOmi6MqZM4XKbEAoUU8uXX8/PPcc1Nebq2R/93dQWHhp76m+OI964kyh0pdLvnI2c+ZM\noqOjx7QoEZFg1N5uBv/b2yExEdasgdxcu6sSkVByXlfOfv7zn7Nx40buu+8+srKyRr22bNmycSvu\nQujKmYiMt0OH4PnnzZWz7GyzMEtJsbsqEQlG51q3nNfiLC8v76yZZocOHbq06saIFmciMp6qquC1\n18DvhzlzYNUqiImxuyoRCVaXHKVRX1/PoUOHzviPyLmEwx5owUY9uTB+P7z9NvzhD+bHV10Fd9wx\n9gsz9cV51BNnCoe+6IFvEZGzGBqCDRtMjllkJNx8MyxebHdVIhLqzuu2ZjDQbU0RGUudnWYrpqYm\nmDwZbr8dZs60uyoRCRWX/LSmiEg4aWgwC7OeHkhLM1sxpaXZXZWIhIvzmjkTuVjhMBsQbNSTc6up\ngd/9zizMZs40WzFNxMJMfXEe9cSZwqEvF3TlrKWlhZ6enlHnZs2aNaYFiYjYwbJgyxZ45x1zvHgx\nrFgBUVH21iUi4ee8Zs7efPNN7r77bhobG0d/c0QEPp9v3Iq7EJo5E5GLNTJinsasrjbbLy1fDkuW\naCsmERk/l5xzNmvWLP7hH/6Bb3zjG8THx495gWNBizMRuRi9vWYrpiNHTDzGqlUmx0xEZDxdcs7Z\niRMnuPfeex27MBPnCofZgGCjnnyspQUef9wszJKTYd06+xZm6ovzqCfOFA59Oa/F2d13382TTz55\nST/RI488gtvtJi4ujrvuuitwvr6+nsjISJKSkgL//OxnPxv1vQ8++CDp6emkp6fz0EMPXVIdIiIA\nBw7AE09AR4fZG/Ob3zRbMomI2O28bmt+9rOf5W9/+xszZswg+5T/e0VERPCXv/zlvH6il156icjI\nSN566y36+/v53e9+B5jF2axZs/D5fGfcIuqxxx7jl7/8Je98NKW7fPlyvve973HvvfeO/oXotqaI\nnKe//Q3eeMM8BFBUBF/+MkRH212ViISTS845u+eee7jnnnvO+Mbna+XKlQB4PB6OHTv2idf9fj9R\nZ3gs6ve//z33338/LpcLgPvvv5//+I//+MTiTETk0/j98OabZnEGcO21sHSpBv9FxFnOa3G2du3a\nMfsJz7ZKnDFjBhERESxfvpz/83/+D2kfBQvt2bOH4uLiwNctXLiQmpqaMatHxld5eTnXXXed3WXI\nKcK1JwMD8OKL5nZmVBTceissXGh3VR8L1744mXriTOHQl7Muzp5++mnuvPNOAJ544omzXiVbt27d\nBf2Ep79PRkYGHo+HRYsW0dbWxne+8x2+9rWv8eabbwLQ09NDSkpK4OuTk5M/kbUmInIuHR3wzDPQ\n2goJCWbj8unT7a5KROTMzro4W79+fWBx9vTTT4/Z4uz0K2cJCQks/mgn4czMTB555BFycnLo7e0l\nISGBxMREurq6Al/f2dlJYmLiGd977dq15OXlAZCamsqiRYsCq+uTT3foWMfhfnzdddc5qp7xPj5y\nBH72s3IGB6Gs7Dq++lXYubOcgwedUd+pxyc5pR4d69iJxyfPOaWeC/l8l5eXU19fz6eZ8I3Pf/jD\nH3Ls2LHAAwGna25uJicnh87OTpKSkrj66qu56667AjNvTzzxBE888QTvvffeqO/TAwEicrrqanjl\nFfD5ID8fvvIViIuzuyoRkTHIORsLPp+PgYEBRkZG8Pl8DA4OMjIywt/+9jdqa2vx+/20t7fzve99\nj6VLl5KUlATAN77xDX7xi1/g9XppaGjgF7/4xZjOwMn4Ov2KgNgvHHpiWWYbpo0bzcLsiivM5uVO\nXpiFQ1+CjXriTOHQlwvaW/NS/PSnP+UnP/lJ4Pg///M/efjhhykoKOB//I//QUtLC8nJyXz+859n\n/fr1ga+79957OXjwIAsWLADgm9/8Jt/61rcmqmwRCTLDw/Dyy2YD88hIuPFGszgTEQkWE35bc7zo\ntqaIdHfDs89CQwPExsJtt5nbmSIiTnPJOWciIk7X1GSeyOzqgtRUcxszM9PuqkRELtx5z5zt3buX\nn/zkJ3znO98BYN++fVRXV49bYRIawmE2INiEYk9qa+HJJ83CbPp0sxVTsC3MQrEvwU49caZw6Mt5\nLc5eeOEFrr32WhoaGvh//+//AdDd3c0PfvCDcS1ORORcLAvee8/cyhwaMqGy3/iGyTITEQlW5zVz\nNnfuXJ599lkWLVrElClT6OjoYHh4mJycHNra2iaizk+lmTOR8OLzwR//CFVV5njZMrjmGm3FJCLB\n4ZJnzlpbW1l4hn1OIiMnLIlDRCSgvx+efx4OHYJJk2DlSrOBuYhIKDiv1dXixYt5+umnR5177rnn\nuELPp8unCIfZgGAT7D1pb4fHHzcLs8REuOuu0FiYBXtfQpF64kzh0JfzunL2m9/8huXLl/PEE0/Q\n19fH5z//efbv38/bb7893vWJiAQcOmSumPX3Q3Y2rFkDp2y9KyISEs4756y3t5fXXnuNw4cPM336\ndFasWBFI8XcCzZyJhLaqKnjtNfD7Yc4cWLUKYmLsrkpE5OKca92iEFoRcTS/HzZtMk9lAlx1Fdxw\ng0n/FxEJVpe8t+bhw4dZt24dJSUlXH755YF/CgoKxrRQCT3hMBsQbIKpJ0ND8NxzZmEWGQm33AKf\n/3xoLsyCqS/hQj1xpnDoy3nNnN12223MmzePn/70p8Q5eedgEQkZnZ2wfr1J/p88GW6/HWbOtLsq\nEZHxd163NVNSUjh+/DhRUVETUdNF0W1NkdDR0GAWZj09kJZmtmJKS7O7KhGxU+2BWjZVbmLYGiY6\nIpobSm9gTv4cu8u6aJd8W/Pmm2/m3XffHdOiRETOpKYGfvc7szCbORPuuUcLM5FwV3uglqf+/BQN\n6Q20ZrTSmtXKU39+itoDtXaXNi7O68pZW1sbS5YsoaCggMxTNqyLiIjgySefHNcCz5eunDlTeXk5\n1113nd1lyCmc2hPLgi1b4J13zPHixbBiBTj4gv2Ycmpfwpl64gyWZfHT3/+U3Qm7ae1tJeZoDEuu\nWQJAZksmf3/739tc4cW55B0C1q1bR0xMDPPmzSMuLi7whhHaJ0VExsDICPzhD1BdbbZfWr4clizR\nVkwi4WxwZJCdzTvxeD28d+w9Bi4bAGDYPxz4miH/kF3ljavzunKWlJREQ0MDycnJE1HTRdGVM5Hg\n1Ntrnsg8csTklq1aZXLMRCQ8NfU0UdFQwa6WXQz5zOJr5/s7SZqbhCvJRdykjx9MDOsrZwsXLqS9\nvd3RizMRCT6trfDMM9DRAcnJZvA/O9vuqkRkog37hqlprcHj9XCs61jgfF5qHmWuMm533c7T7z5N\n7JTYwGuDHw5y/dLr7Sh33J3X4mzZsmV84Qtf4K677iIrKwsgcFtz3bp141qgBDfNbDiPU3py4AC8\n8AIMDkJuLqxeDQ7adGTCOaUv8jH1ZPy197Xj8XrY0bSD/pF+AOImxVGcVYzb5SYjIcN8YSasjVzL\n5qrN7Nm9h8L5hVy/9PqgflrzXM5rcbZlyxZcLtcZ99LU4kxELtTf/gZvvGEeAigshJUrITra7qpE\nZCL4/D5q22vxeD0c7DgYOO9KcuF2uZmfOZ+YqE/uzTYnfw5z8udQnhn6i2Zt3yQiE8bvhzffNIsz\ngGuvhaVLNfgvEg66Bruo9FZS1VhF91A3ANGR0czPnE9ZbhmuJJfNFU6si5o5O/VpTL/ff9Y3jwzF\nfVREZMwNDMCLL5rbmVFRcOutsHCh3VWJyHiyLIu6jjo8Xg/72/fjt8x6Ij0+HbfLTXFWMZOjJ9tc\npfOcdXGWnJxMd7dZ2U6adOYvi4iIwOfzjU9lEhI0s+E8dvSko8MM/re2Qny8mS+bPn1CS3A8fVac\nRz25eH3DfWxv3E5lYyXH+48DEBkRSVFGEWW5ZcxImXHRcVzh0JezLs5qamoCPz548ODZvkxE5JyO\nHoVnnzWRGRkZ5onMKVPsrkpExpplWRztOorH66GmpQafZS7epMSmUOoqZXHOYhJjEm2uMjic18zZ\nz3/+c+6///5PnP/FL37BD37wg3Ep7EJp5kzEeaqr4ZVXwOeD/Hz4ylcgLu7Tv09EgsfgyCDVzdV4\nvB6ae5sBiCCC/Kn5lOWWkT81n8gIjUCd7lzrlvMOoT15i/NUU6ZMoaOj49IrHANanIk4h2XBn/8M\nf/mLOb7iCrjxRtCIqkjoaOppwuP1UN1cHQiLTYhOoCSnhNKcUqZM1iXyc7noENp33nkHy7Lw+Xy8\nc3LDu4/U1dUplFY+VTjMBgSb8e7J8DC8/LLZwDwiAm66ySzO5Nz0WXEe9eSTRvwj1LSYsNijXUcD\n52ekzKAst4y56XOZFHleKV0XLRz6cs7fwXXr1hEREcHg4CB333134HxERARZWVn85je/GfcCRSR4\ndHeb+bKGBoiNhdtuM7czRSS4He8/HgiL7RvuAyA2KpbibBMWm5mQaXOFoeW8bmveeeedPP300xNR\nz0XTbU0RezU1wfr10NkJqalm8D9T/78WCVp+y09tmwmLreuoC5zPScyhLLfsrGGxcn4ueeYsGGhx\nJmKf2lrYsAGGhmDaNBOVkZBgd1UicjG6BruoaqyiqrGKrsEuACZFTjJhsS4TFnuxMRjysUve+Fzk\nYoXDbECwGcueWBa8/z786U/mxwsXwi23wFmiEeUc9FlxnnDqiWVZHOw4iMfroba9NhAWmzY5DbfL\nzaLsRY4Jiw2Hvuh/oSJyUXw++OMfoarKHC9bBtdco62YRIJJ33AfO5p24PF6RoXFFmYUUuYqIy81\nT1fJbKDbmiJywfr74fnn4dAhc5Vs5UooKrK7KhE5H5ZlcazrmAmLba1hxD8CfBwWW5JdQlJsks1V\nhj7d1hSRMdPebrZiam+HxERYswZyc+2uSkQ+zZBvKBAW29TTBJwSFusq4/K0yxUW6xBanMm4CofZ\ngGBzKT2pr4fnnjNXzrKzzcIsJWVMywtb+qw4T6j0pLmnORAWO+gbBCA+Op6S7BLcLnfQhcWGSl/O\nRYszETkvVVXw2mvg98OcObBqFcToKXoRRxrxj7CndQ8er4cjnUcC56enTKfMVca8jHnjHhYrF08z\nZyJyTn4/bNoE771njq+6Cm64QVsxiThRR38HHq+H7U3bR4XFLsxaiNvlJisxy+YK5STNnInIRRka\nMvlltbVmMXbzzbB4sd1Vicip/Jaf/e378Xg9HDh+IHA+OzGbMlcZC7IWKCw2yGhxJuMqHGYDgs35\n9qSrywz+NzXB5Mlw++0wc+b41xeu9FlxHqf3pHuwm6rGKiobK0eFxRZlFFGWW0ZuUm5IxmA4vS9j\nQYszEfmEhgazR2Z3N6Slma2Y0tLsrkpELMvi0IlDeLwe9rXt+0RYbHF2MfHR8TZXKZdKM2ciMsqe\nPbBxI4yMmCtlt99urpyJiH36h/sDYbHt/e2ACYudkzaHstwyZqbODMmrZKFMM2ci8qksC7ZsgXfe\nMceLF8OKFRAVZW9dIuHKsiwauhvweD3sbtkdCItNjk2mNKeUkpwSkmOTba5SxoMWZzKuwmE2INic\nqScjI/CHP0B1tdl+aflyWLJEWzFNJH1WnMeungz5htjVvAuP10NjT2Pg/OwpsynLLaMgrSCsw2LD\n4bOixZlImOvtNcGyR46Y3LJVq0yOmYhMrJbeFjxeDzubdn4iLLbUVcrUyVNtrlAmimbORMJYa6t5\nIrOjA5KTzeB/drbdVYmEjxH/CHtb9+LxejjceThwflryNMpyyyjMKFRYbIjSzJmIfMKBA/DCCzA4\nCC6X2YopSXsdi0yIjv4OKhsr2d64nd7hXgBiomJYmLWQMleZwmLDnBZnMq7CYTYg2JSXl5OQcB1v\nvGHS/wsLYeVKiI62u7Lwps+K84x1T/yWnw/bPwyExVqYqyZZCVmU5ZaxIHMBsZNix+znC1Xh8FnR\n4kwkjPj9sG2b2bgc4NprYelSDf6LjKeeoR4TFuutpHOwEzBhsYUZhZS5yrgs+TLFYMgomjkTCRMD\nA/Dii+Z2ZlQU3HILFBfbXZVIaLIsi/oT9Xi8Hva27Q2ExU6dPBW3y82i7EUKiw1zmjkTCXMdHbB+\nPbS0QHw8rF4N06fbXZVI6Okf7mdn8048Xg9tfW0ARBDB3PS5lLnKmDVllq6SyafS4kzGVTjMBjjd\n0aNmK6beXsjIgOnTy5k+/Tq7y5LT6LPiPBfSk4auj8Nih/3DACTFJLE4ZzGlrlKFxY6hcPisaHEm\nEsKqq+GVV8Dng9mz4bbb4IMP7K5KJDQM+YbY3bIbj9eDt9sbOD9ryizKXCYsNipSW2zIhdPMmUgI\nsiwoL4d33zXHV1wBN94IkeEbKi4yZlp7W01YbPNOBkYGAJg8aTIlOSWU5pSSFp9mc4USDDRzJhJG\nhofh5ZehpsY8hXnTTWZxJiIXz+f3sbfNhMXWn6gPnL8s+TLKXCYsNjpKeTQyNrQ4k3EVDrMBTtLd\nbebLGhogNtbcxszPH/016okzqS/OU15ezqIrF1HpraSqsWpUWOyCzAWU5ZaRnagtNSZaOHxWtDgT\nCRFNTeaJzM5OSE01WzFlZtpdlUjw8Vt+Dhw/wKaDm3iXdwNhsZkJmZS5yliYtVBhsTKuNHMmEgJq\na2HDBhgagmnTTFRGQoLdVYkEl56hHrY3bqeysZITAycAiIqIMmGxuWVMS56mGAwZM5o5EwlRlmWe\nvnz7bfPjhQtNuOwkfbJFzotlWRzuPGzCYlv34rN8AEyJmxIIi02I0d90ZGLp2S0ZV+Xl5XaXELJ8\nPnjtNXjrLbMwW7bM7JH5aQsz9cSZ1JeJNTAywLZj2/j3in/nqR1PsbtlN37Lz5y0OXx94df53me+\nx/DBYS3MHCgcPiv6+7VIEOrvh+efh0OHzGJs5UooKrK7KhHn83Z78Xg97GreFQiLTYxJpDSnlMU5\ni0mJS7G5QhHNnIkEnfZ2eOYZ8+/ERFizBnJz7a5KxLmGfcOBsNiG7obA+ZmpMynLLWNO2hyFxcqE\n08yZSIior4fnnjNXzrKzzcIsRX/RFzmjtr42PF4PO5p2jAqLXZS9iFJXKenx6TZXKHJmWpzJuAqH\nPJqJUlVlZsz8fpgzB1atgpiYC38f9cSZ1Jex4fP72Ne2D4/Xw6EThwLnc5NyKcstoyij6LzDYtUT\nZwqHvmhxJuJwfj9s3gx//as5vuoquOEGbcUkcqrOgU4qG01YbM9QDwDRkdEszFqI2+UmJynH5gpF\nzp9mzkQcbGgINm6EffvMYmzFCigttbsqEWewLIsDxw/g8XrY374/EBabEZ9BWa4Ji42bFGdzlSJn\ndq51y4T93fuRRx7B7XYTFxfHXXfdNeq1zZs3M3fuXBISEli2bBlHjhwZ9fqDDz5Ieno66enpPPTQ\nQxNVsoiturrgySfNwiwuDu68UwszEYDeoV62HtnKr7f9mv/a9V/UttcSGRHJ/Mz53LXoLv6+7O+5\nIvcKLcwkaE3Y4iw3N5cf/vCHrFu3btT5trY2Vq1axc9+9jM6Ojpwu93ccccdgdcfe+wxXnnlFaqr\nq6murubVV1/lsccem6iy5RKFQx7NePB64be/NVsypaXBN78JM2eOzXurJ86kvpybZVkcPnGYDXs2\n8Iv3f8Gmg5voGOggNS6VG2bdwA+W/ICvFH6FGakzxizFXz1xpnDoy4TNnK1cuRIAj8fDsWPHAuc3\nbtzI/PnzWbVqFQAPP/ww6enp7N+/n4KCAn7/+99z//3343K5ALj//vv5j//4D+69996JKl1kQu3Z\nAy+9BMPDkJcHd9wBkyfbXZWIPQZGBqhursbj9dDS2wJABBEUpBVQ5ipj9tTZREZoAFNCy4Q/EHD6\n/dWamhqKi4sDx/Hx8eTn51NTU0NBQQF79uwZ9frChQupqamZsHrl0oT6EzVjybJg61Yz/A9QUgI3\n3wxRYxy/pJ44k/oyWmN3owmLbdnFkG8IMGGxi3MWszhnMalxqeNeg3riTOHQlwlfnJ1+ubm3t5eM\njIxR55KTk+nu7gagp6eHlFOCnJKTk+np6Rn/QkUm0MgIvPoq7NwJERGwfDksWWJ+LBIuhn3D1LTW\n4PF6ONb18R2WvNQ8ylxlzE2fq7BYCQu2XzlLTEykq6tr1LnOzk6SkpLO+HpnZyeJiYlnfO+1a9eS\nl5cHQGpqKosWLQqssE/eo9bxxB6fPOeUepx43NsLP/5xOS0tcPnl17FqFTQ1lfPuu+Pz853eG7t/\n/To2xzt27OD73/++Y+qZyONX3nyF2vZarBkW/SP91O+oJyYqhpU3rsTtclNTUUPriVaKriua0PpO\nnrP790fHo49/9atfBeWf7yd/XF9fz6eZ8CiNH/7whxw7dozf/e53APz2t7/l97//PVu3bgU+vpK2\nY8cOCgoKuPrqq7nrrru45557AHjiiSd44okneO+990b/QhSl4Ujl5eWB/0Dlk1pbzVZMHR2QnGwS\n/3PGOY5JPXGmcOuLz++jtr0Wj9fDwY6DgfOuJBdlrjLmZ84/77DY8RJuPQkWodKXc61bJmxx5vP5\nGB4e5sc//jENDQ389re/ZdKkSXR0dJCfn8+TTz7JF7/4RX70ox+xdevWwOLrscce4//+3//Lpk2b\nsCyLz3/+8/y3//bf+Na3vjX6F6LFmQSZAwfghRdgcBBcLrMw++iCsUjI6hrsotJrwmK7h8z4jyBk\neAAAIABJREFUSnRkNAuyFuB2uXEluWyuUGRiOGJx9vDDD/OTn/zkE+d+9KMfsXnzZr773e9y+PBh\nrrzySp566immT58e+LoHH3yQxx9/HIBvfvOb/K//9b8+8f5anEkwqaiAN94w6f+FhbByJUTbe5FA\nZNxYlkVdRx0er4fattpAWGx6fDplrjKKs4uVSSZhxxGLs/GmxZkzhcrl57Hi98Nbb8G2beb42mth\n6dKJHfxXT5wpFPvSN9zH9sbteLweOgY6AIiMiGRe+jzKcsuYkTJ2mWTjIRR7EgpCpS/nWrdob02R\nCTIwAC++aG5nRkXBLbfAKSkxIiHBsiyOdh3F4/VQ01KDz/IBkBKbgtvlpiSnhMSYMz/UJSKGrpyJ\nTICODli/HlpaID4eVq+GU+7ciwS9wZHBQFhsc28zYMJi86fmU5ZbRv7UfIXFipxCV85EbHT0KDz7\nLPT2QkYGfPWrMGWK3VWJjI2mniY8Xg/VzdWBsNiE6AQW5yym1FU6IWGxIqFGizMZV6EyG3Cxqqvh\nlVfA54PZs+G228wm5nYK9544VTD1ZcQ/Qk2LCYs92nU0cH5GygzKcsuYlz4vJMJig6kn4SQc+qLF\nmcg4sCwoL4d33zXHV1wBN94IkbqrI0HseP9xPF4P2xu30z/SD0BsVCyLshdR6iolMyHT5gpFQoNm\nzkTG2PAwvPwy1NSYpzBvuskszkSCkd/yU9tmwmLrOuoC53MScyjLNWGxMVExNlYoEpw0cyYyQXp6\nzOB/QwPExprbmPn5dlclcuG6Bruoaqyi0lsZCIudFDmJBZkfh8U6OQZDJJhpcSbjKhxmA05qajIL\ns85OSE01g/+ZDrzLE049CSZO6ItlWRzsOGjCYttr8Vt+wITFul1uirOKmRw92dYaJ5ITeiKfFA59\n0eJMZAzU1sKGDTA0BNOmmaiMhAS7qxI5P33Dfexo2oHH6+F4/3HAhMUWZRThdrnJS83TVTKRCaSZ\nM5FLYFnwwQfw9tvmxwsXmnDZSfprjzicZVkc6zpmwmJbaxjxjwAmLLbUVUpJdglJsdrsVWS8aOZM\nZBz4fPD661BZaY6XLYNrrpnYrZhELtTgyCC7Wnbh8Xpo6mkCTgmLdZVxedrlCosVsZkWZzKuQnU2\noL8fnn8eDh0yV8lWroSiIrurOj+h2pNgN959ae5pDoTFDvoGAYiPjjdhsTmlTJmsZOTT6bPiTOHQ\nFy3ORC5Qezs884z5d2IirFkDubl2VyXySSP+Efa07sHj9XCk80jg/PSU6ZS5ypiXMY9JkfpjQMRp\nNHMmcgHq6+G558yVs6ws80RmSordVYmMdrz/OJXeSrY3badvuA8wYbHF2cW4XW6FxYo4gGbORMbA\n9u3w6qvg98OcOfB3f2eyzEScwG/52d++H4/Xw4HjBwLnsxOzKXOVsSBrgcJiRYKEFmcyrkJhNsDv\nh82b4a9/NcdXXQU33BC8WzGFQk9C0cX2pXuw24TFNlbSNdgFmLDY+Znzcbvc5CblKgbjIumz4kzh\n0BctzkTOYWgINm6EffvMYmzFCigttbsqCXeWZXHoxCE8Xg/72vYFwmLTJqfhdrlZlL0orMJiRUKN\nZs5EzqKrywz+NzVBXBzccQfMnGl3VRLO+of7A2Gx7f3tgAmLnZs+F7fLzczUmbpKJhIkNHMmcoG8\nXrMVU3c3TJ0KX/sapKXZXZWEI8uyaOhuwOP1sLtldyAsNjk2mdKcUhbnLFZYrEiI0eJMxlUwzgbs\n2QMvvQTDw5CXB7ffDvHxdlc1doKxJ+Hg9L4M+YbY1WzCYht7GgPnZ0+ZTVluGQVpBQqLHWf6rDhT\nOPRFizORj1gWbN1qhv8BSkrg5pshKsreuiS8tPS24PF62Nm0c1RYbEl2CaWuUqZOnmpzhSIy3jRz\nJgKMjJiYjJ07zfZLy5fDkiXaikkmxoh/hL2te/F4PRzuPBw4Py15GmW5ZRRmFCosViTEaOZM5Bz6\n+uDZZ+HIEYiOhlWrYO5cu6uScNDR30FlYyXbG7fTO9wLQExUDMVZJiw2KzHL5gpFxA5anMm4cvps\nQGureSKzowOSk81WTDk5dlc1vpzek1Dnt/x82P5hICzWwvzNuXNfJ1+75WssyFxA7CSlGzuBPivO\nFA590eJMwlZdndm8fHAQXC6zMEvSQ28yTnqGekxYrLeSzsFOwITFFmUU4Xa5OWAdwO1y21yliDiB\nZs4kLFVUwBtvmPT/wkJYudLc0hQZS5ZlUX+iHo/Xw962vYGw2KmTpwbCYuOjQ+hRYBE5b5o5E/mI\n3w9vvQXbtpnja6+FpUs1+C9jq3+4n53NO/F4PbT1tQEmLHZe+jzcLjezpsxSWKyInJUWZzKunDQb\nMDgIL74IH35o4jFuuQWKi+2uauI5qSehpqHr47DYYf8wAEkxSZS6TFhscmzyWb9XfXEe9cSZwqEv\nWpxJWOjoMIn/LS0mUHb1apg+3e6qJBQM+YbY3bIbj9eDt9sbOD97ymzcLjcFaQVERSosT0TOn2bO\nJOQdPWqiMnp7ISMDvvpVmDLF7qok2LX2tpqw2OadDIwMADB50mRKckoozSklLV77fYnI2WnmTMJW\ndTW88gr4fDB7Ntx2m9nEXORi+Pw+9raZsNj6E/WB85clX0aZy4TFRkfpyRIRuTRanMm4sms2wLKg\nvBzefdccl5XBTTdBpLYiDIt5jbF2YuAEld5KqhqrRoXFLsxaiNvlJjsx+5J/DvXFedQTZwqHvmhx\nJiFneBhefhlqasxTmDfdBFdcYXdVEmz8lp8Dxw/g8Xr4sP3DQFhsZkImZa4yFmYtVFisiIwLzZxJ\nSOnpMYP/DQ0QG2tuY+bn212VBJOeoR62N26nsrGSEwMnAIiKiKIo04TFTkuephgMEblkmjmTsNDU\nZBZmnZ2QmmoG/zMz7a5KgoFlWRzuPGzCYlv34rN8AEyJmxIIi02ISbC5ShEJF1qcybiaqNmA2lrY\nsAGGhmDaNBOVkaA/S88oHOY1ztfAyAA7m0xYbGtfKwARRDA3fS5ul5vZU2ZP2FUy9cV51BNnCoe+\naHEmQc2y4IMP4O23zY8XLjThspP0X7acg7fbi8frYVfzrlFhsYtzFrM4ZzEpcSk2Vygi4UwzZxK0\nfD54/XWorDTHy5bBNddoKyY5s2HfcCAstqG7IXB+1pRZuF1u5qTNUVisiEwYzZxJyOnvh+efh0OH\nzFWylSuhqMjuqsSJ2vra8Hg97GjaMSosdlH2IkpdpaTHp9tcoYjIaFqcybgaj9mA9nZ45hnz78RE\nWLMGcnPH9KcIaeEwr+Hz+9jXto8Kb8WosNjcpFzKcssoyihyXFhsOPQl2KgnzhQOfdHiTIJKfT08\n95y5cpaVZZ7ITNF4kHykc6CTykYTFtsz1ANAdGR0ICw2JynH5gpFRD6dZs4kaGzfDq+9ZmbNCgpg\n1SqTZSbhzW/5qTteh8frYX/7/kBYbEZ8BmW5Jiw2bpL27BIRZ9HMmQQ1y4JNm+CvfzXHV10FN9yg\nrZjCXe9QL9ubtuPxekaFxRZmFOJ2uZmeMl1hsSISlLQ4k3F1qbMBQ0OwcSPs22cWYytWQGnp2NUX\njoJ5XsOyLI50HsHj9bCndU8gLDY1LhW3y01JdknQhsUGc19ClXriTOHQFy3OxLG6uszgf1MTxMXB\nHXfAzJl2VyV2GBgZoLq5Go/XQ0tvC2DCYuekzTFhsVNnExmhS6kiEho0cyaO5PWarZi6u2HqVDP4\nn67Eg7DT2N1owmJbdjHkGwIgMSaRxTmLKc0pVVisiAQtzZxJUNmzB156CYaHIS8Pbr8d4uPtrkom\nyrBvmJrWGjxeD8e6jgXOz0ydidvlZm76XIXFikhI0+JMxtWFzAZYFmzdCps3m+OSErj5ZojSn8Nj\nyqnzGu197YGw2P6RfgDiJsWxKHsRbpc75MNindqXcKaeOFM49EWLM3GEkRF49VXYudNsv3TDDeap\nTD1sF9p8fh+17bVUNFRw6MShwPncpFzcLjfzM+c7LixWRGS8aeZMbNfXB88+C0eOQHS0yS+bO9fu\nqmQ8dQ50UtVYRVVjFd1D3YAJi12QtQC3y40ryWVzhSIi40szZ+JYra3micyODkhONlsx5SjEPSRZ\nlkVdhwmLrW2rHRUW63a5Kc4uVlisiAhanMk4O9dsQF0dvPACDAyAy2UWZklJE1tfOJroeY3eoV52\nNO3A4/XQMdABmLDYeRnzcLvczEiZobBYwmOOJtioJ84UDn3R4kxsUVEBb7wBfj8UFsLKleaWpoQG\ny7I42nUUj9dDTUvNqLDY0pxSSnJKSIxJtLlKERFn0syZTCi/H956C7ZtM8fXXAPLlmnwP1QMjgwG\nwmKbe5sBExZ7edrluF1u8qfmKyxWRATNnIlDDA7Ciy/Chx+aeIxbboHiYrurkrHQ1NOEx+uhurk6\nEBabEJ1gwmJdpaTGpdpcoYhI8NDiTMbVydmAEyfM4H9LiwmUXb0apk+3u7rwNFbzGiP+EWpaaqjw\nVowKi81LzcPtcjMvfZ7CYi9AOMzRBBv1xJnCoS9anMm4O3rURGX09kJGhtmKacoUu6uSi9Xe105l\nYyXbG7cHwmJjo2IDYbEZCRk2VygiEtw0cybjatcueOUVEzI7ezbcdpvZxFyCi9/yU9tWi8froa6j\nLnDeleQKhMXGRMXYWKGISHDRzJlMOMuC8nJ4911zXFYGN90EkZoFDypdg11UNVZR6a0MhMVOipzE\ngkwTFpubnGtzhSIioUeLMxlzw8Pmatnu3VBfX863v30dn/mM3VXJSZ82r2FZFgc7DlLhrWB/+378\nlh+A9Ph0ExabVczk6MkTVG34CIc5mmCjnjhTOPRFizMZUz09sH49NDRAbKzZI1MLs+DQN9wXCIs9\n3n8cgMiISIoyinC73OSl5iksVkRkAmjmTMZMc7N5IrOzE1JTzeB/ZqbdVcm5WJbFsa5jJiy2tYYR\n/wgAKbEplLpKKckuISlW2zaIiIw1zZzJuNu/32SYDQ3BtGkmKiMhwe6q5GwGRwbZ1bILj9dDU08T\n8FFY7FQTFnt52uUKixURsYkWZ3JJLAs++ADeftv8eMECuPVWmPTRf1nhMBsQTJp7mnnypSex8qxA\nWGx8dLwJi80pZcpkZZzYRZ8V51FPnCkc+qLFmVw0nw9efx0qK83x0qVw7bXaislpRvwj7GndQ0VD\nBUe7jlLfXk/etDxmpMwwYbEZ85gUqf8ViIg4hWNmzq677jq2bdvGpI8uuVx22WXs3bsXgM2bN/Od\n73yHo0eP8pnPfIannnqK6afFy2vmbGL198Pzz8OhQ+Yq2cqVUFRkd1VyquP9x6n0VrK9aTt9w32A\nCYstzi7G7XKTmaCBQBERu5xr3eKYxdnSpUu58847Wbdu3ajzbW1t5Ofn88QTT/ClL32Jf/qnf2LL\nli28//77o75Oi7OJ095uBv/b2yExEdasgVzFXTmC3/Kzv30/Hq+HA8cPBM5nJ2ZT5ipjQdYChcWK\niDhA0DwQcKYiN27cyPz581m1ahUADz/8MOnp6ezfv5+CgoKJLjHs1dfDc8+ZK2dZWeaJzJSUs399\nOMwGOEH3YLcJi22spGuwCzBhsfMz55uw2KTcQAyGeuJM6ovzqCfOFA59cdTi7B//8R956KGHmDNn\nDj/72c/43Oc+R01NDcXFxYGviY+PJz8/n927d2txNsG2b4fXXjOzZgUFsGqVyTITe1iWxaETh6ho\nqKC2vTYQFps2OQ23y82i7EUKixURCUKOWZz97//9vykqKiImJob169fzpS99iR07dtDb20tGxuiN\nlJOTk+np6fnEe6xdu5a8vDwAUlNTWbRoUWB1XV5eDqDjizi2LPjXfy1n927Iy7uOJUsgOrqc9993\nRn3hdtw/3M+TLz1JbVstUwunAnB4x2Gmp0zn//vy/8fM1Jm8++67bKvbdsbvv+666xz169Hxx8cn\nOaUeHevYiccnzzmlngv5fJeXl1NfX8+ncczM2eluuukmVqxYwYEDBxgeHubf/u3fAq8tWLCAn/zk\nJ6xcuTJwTjNn42NoCDZuhH37zL6YK1ZAaandVYUfy7Jo6G7A4/Wwu2V3ICw2OTaZ0pxSFucsVlis\niEgQOde6JXKCa7lgRUVF7Ny5M3Dc29tLXV0dRXo0cNx1dcHvfmcWZnFx8PWvX/jC7PQrAnJhhnxD\nVHoreazyMR6vepwdTTsY8Y+QPzWf1fNX8/0rv8/n8j53QQsz9cSZ1BfnUU+cKRz64ojbmp2dnXzw\nwQd87nOfY9KkSTz33HNs2bKF3/zmN6SmpvLAAw+wceNGvvjFL/LjH/+YRYsWad5snHm9Zo/M7m6Y\nOtUM/qen211V+GjpbcHj9bCzaSeDvkHAhMWWZJdQ6ipl6uSpNlcoIiLjxRG3Ndva2vjiF7/Ivn37\niIqKYt68efz0pz/l+uuvB0zO2Xe/+10OHz7MlVdeqZyzcbZnD7z0EgwPQ14e3H47xMfbXVXoG/GP\nsLd1LxXeCo50Hgmcn54yHbfLTWFGocJiRURCRFDknF0qLc4unWXB1q2webM5LimBm2+GqCh76wp1\nHf0dVDZWsr1xO73DvQDERMVQnGXCYrMSs2yuUERExlrQ5JyJfUZG4NVXYedOs/3SDTfAVVdd+lZM\npz5RIx/zW34+bP+QCm8FdcfrsDAf0OzEbNwuNwsyFxA7aXxyStQTZ1JfnEc9caZw6IsWZ0JfHzz7\nLBw5AtHRJr9s7ly7qwpNPUM9JizWW0nnYCdgwmKLMopwu9xclnxZICxWRETCk25rhrnWVrMVU0cH\nJCebrZhycuyuKrRYlkX9iXoqvBXsa9sXCIudOnlqICw2PlpDfSIi4US3NeWM6urghRdgYABcLrMw\nS1JU1pjpH+5nZ/NOPF4PbX1tAERGRDIvfR5ul5tZU2bpKpmIiHyCFmdhqqIC3ngD/H4oLISVK80t\nzbEWDrMBp7IsC2+3lwpvxaiw2KSYJEpdJiw2OTbZ1hrDrSfBQn1xHvXEmcKhL1qchRm/H956C7Zt\nM8fXXAPLll364H+4G/INsbtlNxUNFTT2NAbOz54yG7fLzZz0OURGOD7zWUREHEAzZ2FkcBBefBE+\n/NDEY9xyC5yyp7xchNbeVhMW27yTgZEBACZPmkxJTgmlOaWkxafZXKGIiDiRZs6EEyfM4H9LiwmU\nveMOmDHD7qqCk8/vY2/bXioaKjjceThwflryNNwuN0WZRQqLFRGRi6Y/QcLA0aMmKqO3FzIyzOD/\n1Ana/SeUZgNODJyg0ltJVWPVqLDYhVkLcbvcZCdm21zh+QmlnoQS9cV51BNnCoe+aHEW4nbtglde\nMSGzs2fDbbeZTczl/PgtPweOH6CioYIDxw8EwmKzErJwu9wszFo4bmGxIiISnjRzFqIsC8rL4d13\nzXFZGdx0E0RqJv289Az1sL1xO5WNlZwYOAFAVEQURZkmLHZa8jTFYIiIyEXTzFmYGR42V8t27zZP\nYd54I1xxhZ7I/DSWZXG48zAVDSYs1mf5AJgSNyUQFpsQk2BzlSIiEuq0OAsxPT1mvuzYMYiNha98\nBS6/3L56gmE2YGBkgJ1NJiy2ta8VgAgimJs+F7fLzewps0PqKlkw9CQcqS/Oo544Uzj0RYuzENLc\nbJ7I7OyE1FT46lchM9PuqpzL2+2losGExQ77hwETFrs4ZzGLcxaTEpdic4UiIhKONHMWIvbvNxlm\nQ0MwbRqsXg0JugP3CcO+YRMW663A2+0NnJ81ZZYJi02bQ1RklI0ViohIONDMWQizLPjgA3j7bfPj\nBQvg1lthkjo7SmtvK5WNlexo2jEqLHZR9iLcLrfCYkVExDH0R3gQ8/ng9dehstIcL10K117rrMF/\nO2cDfH4f+9r2UeGtoP5EfeD8ZcmXmbDYjCKio8ZhQ1GHC4d5jWCkvjiPeuJM4dAXLc6CVH8/vPAC\nHDxorpJ9+cswf77dVTnDiYETVDVWUdVYRc9QDwDRkdGBsNicpBybKxQRETk7zZwFoePH4b/+C9rb\nITHRzJdddpndVdnLb/mpO15HhbeCD9s/DITFZiZkBsJi4yYpfVdERJxBM2chpL4ennvOXDnLyjJP\nZKaE8UOFvUO9bG/ajsfrGRUWW5hRiNvlZnrK9JCKwRARkdCnxVkQ2b4dXnvNzJoVFMCqVSbLzMnG\nYzbAsiyOdB6hwlvB3ta9o8JiS12llGSXKCz2HMJhXiMYqS/Oo544Uzj0RYuzIGBZsGkT/PWv5njJ\nEli+PPy2YhoYGaC6uRqP10NLbwtgwmLnpM3B7XKTPzVfV8lERCToaebM4YaGYONG2LfPLMZWrIDS\nUrurmliN3Y1UeCvY1bwrEBabGJPI4pzFlOaUKixWRESCjmbOglRXF6xfD42NEBcHt98Os2bZXdXE\nGPYNU9NaQ0VDBQ3dDYHzM1Nn4na5mZs+V2GxIiISkrQ4c5Da2sNs2lTH8HAkvb1+urpmM3nyDKZO\nNYP/6el2V3jhLnQ2oK2vDY/XMyosNm5SXCAsNj0+CH8THCYc5jWCkfriPOqJM4VDX7Q4c4ja2sM8\n9dQBYmOvp7UV9u6FoaHNrFgB99wzg/h4uyscPz6/j9r2WioaKjh04lDgfG5SLm6Xm/mZ88MyLFZE\nRMKTZs4c4t/+7R1aWpZx5Agc+mh9kp0NV1/9Dvfdt8ze4sZJ50BnICy2e6gbMGGxC7IW4Ha5cSW5\nbK5QRERkfGjmLAgMDESydy+0mIcQmTXLbGDu84XWI5mWZVHXUUdFQwX72/cHwmIz4jNwu9wUZxcr\nLFZERMJaaP3JH6S6u8Hj8dPSAlFRZhum6dPNHpkxMX67y7sk5eXlgAmL/euRv/Lrbb/mP6v/k9r2\nWiIjIpmfOZ+1i9by92V/z2cu+4wWZhPgZE/EWdQX51FPnCkc+qIrZzZraIBnn4W0tNm0tm5m0aLr\nSUw0rw0Obub66/PtLfASWJZFc08zG/ZsYE/rnkBYbGpcKqU5pZTklJAYk2hzlSIiIs6imTMb7doF\nr7wCIyMwYwYsWnSY99+vY2gokpgYP9dfP5s5c2bYXeYFGxwZpLq5mgpvxaiw2MvTLg+ExUZG6KKt\niIiEr3OtW7Q4s4FlwTvvwJYt5ri0FL74RXNLM5g19TRR0VDBrpZdDPmGAEiITjBhsa5SUuNSba5Q\nRETEGc61btHliwk2OGg2Lt+yxST+33QT3Hxz8C7Mhn3D7GzayeNVj/Oo51EqGysZ8g2Rl5rHVwq/\nwuLBxVw/63otzBwkHOY1gpH64jzqiTOFQ180czaBTpwwif/NzSbx/7bbYPZsu6u6OO197YGw2P6R\nfsCExRZnFeN2uclIyACgLbLNzjJFRESCjm5rTpDDh80Vs74+k/S/Zg2kpdld1YXxW35q22qp8FZw\nsONg4LwryRUIi42JirGxQhERkeCgnDObVVXBH/8IPh/k58NXvmKunAWLrsEuqhqrqPRWjgqLnZ85\nH7fLTW5yrs0VioiIhA4tzsaR3w9vvQXbtpnjJUtg+XIza+Z0lmVxsOMgFV4TFuu3TN5aeny6CYvN\nKmZy9ORPfZ9w2AMt2KgnzqS+OI964kzh0BctzsZJfz+8+CLU1Zlh/5tvhpISu6v6dH3Dfexo2oHH\n6+F4/3EAIiMiKcoowu1yk5eaR0REhM1VioiIhC7NnI2DtjYz+N/eDgkJcMcdJvHfqSzL4ljXMSq8\nFexp3cOIfwSAlNgUSl2lLM5ZrLBYERGRMaSZswl04IC5YjYwYDYuX70aUh2aIjE4Msiull1UNFTQ\n3NsMfBQWO9WExV6edrnCYkVERCaYFmdjxLLggw/g7bfNj+fNg5UrIcaBDy829zRT4a2gurl6VFhs\nSU4JpTmlTJk8Zcx+rnCYDQg26okzqS/Oo544Uzj0RYuzMTAyYp7G3L7dHH/uc3DddWbjcqcY8Y+w\np3UPFQ0VHO06Gjg/I2UGbpebeRnzmBSp/xxERETsppmzS9Tba/LLjhyB6Gj48pehqGjCyzir4/3H\nA2GxfcN9AMRGxVKcbcJiMxMyba5QREQk/GjmbJw0NZnB/85OSE4282Uul91VmbDY/e37qWiooK6j\nLnA+JzEHt8vNgqwFCosVERFxKC3OLtLevbBxIwwPw2WXmScyk5Lsral7sJvKxkqqGqvoGuwCYFLk\npI/DYpNyJzwGIxxmA4KNeuJM6ovzqCfOFA590eLsAlkW/OUv8Oc/m+PiYvjSl2CSTb+TlmVx6MQh\nKhoqqG2vDYTFpk1Ow+1ysyh70XmFxYqIiIgzaObsAgwPw8svQ02NGfa/4Qa46ip7Bv/7hvvY2bQT\nj9dDe387YMJi56bPxe1yMzN1psJiRUREHEozZ2Ogq8vMlzU2QmwsrFoFBQUTW4NlWTR0N1DRUEFN\na00gLDY5NpnSHBMWmxRr871VERERuSRanJ2HY8fg2WehpwemTIE1ayBzAh9yHPINUd1cjcfroamn\nCTBhsflT83G73BSkFTg2LDYcZgOCjXriTOqL86gnzhQOfdHi7FPs3AmvvmqyzPLy4PbbIT5+fH6u\n2gO1bKrcxLA1THRENIvmLeJE3Amqm6sZ9A0CEB8dT0l2CW6Xe0zDYkVERMQZNHN2Fn4/bN4Mf/2r\nOS4rgxtvNJuYj4faA7U89eeniM6PprW3FW+3l/aadhYVLiLdlc70lOm4XW4KMwoVFisiIhLkNHN2\ngQYHYcMG2L8fIiPhppvM4my8+Pw+nvnLMxyacoi2o22BWbLYy2Pxtfv49i3fJisxa/wKEBEREcdw\n5qCSjY4fh8cfNwuzyZPhzjvHZ2Hm8/uoO17HH2r/wM/f+znbvNto6mlixD9CYkwiBWkFLJm2hDkZ\nc4J6YVZeXm53CXIa9cSZ1BfnUU+cKRz6oitnpzh0CJ5/Hvr7ISPDDP5PnTp27++3/NSfqKempYa9\nbXsD2ykBpMSkkJ2aTWZCJvHRHw+1xUQqyV9ERCScaObsIxUV8MYbZtasoMBEZcTGXnor9btAAAAS\n70lEQVRdfsvPkc4j7G7Zzd7WvfQO9wZeS49PZ37mfAozCulo7OCpPz9F7OUf/6SDHw6ydula5uTP\nufRCRERExDHOtW4J+8WZzwdvvmkWZwBXXw3XX29mzS6WZVkc6TxCTWsNe1r30DPUE3gtbXIaRZlF\nFGUUkZmQOSootvZALZurNjPkHyImMobrF1+vhZmIiEgI0uLsLPr64IUXzO3MqCi45RazHdPFsCyL\nY13H2N2ymz2te+ge6g68NiVuCvMz51OUWURWQlZYJfeHQx5NsFFPnEl9cR71xJlCpS96WvMMWltN\n4v/x45CYaDYunzbtwt7jZGJ/TUsNNa01gc3GAVLjUinKKKIos4icxJywWpCJiIjIxQvLK2f795uo\njMFByMmB1ashJeX8fh7LsvB2e6lpraGmpYbOwc7AaymxKYFblq4klxZkIiIicka6cvYRy4L33oNN\nm8yPi4rg1lsh5lMeiLQsi6aepsCCrGOgI/BacmwyhRmFzM+cT25SrhZkIiIicknCZnE2MmK2Ydq5\n0xwvXQrXXgtnW0tZlkVzb3PgluXx/uOB15JikijMKKQos4hpydO0IDuHUJkNCCXqiTOpL86jnjhT\nOPQlLBZnPT1m4/JjxyA6GlauhMLCM39tS29LYEHW1tcWOJ8Yk2gWZBlFTEuZ5tiNxkVERCS4heTM\nWW3tYTZtqmN4OJK+Pj9dXbOJi5tBSooJls3OHv29rb2tgVuWrX2tgfPx0fGBBdmM1BlakImIiMiY\nCKuZs9rawzz11AFiY6+npQX27YOhoc3ceCN885szSEw0X9fe1x5YkDX3Nge+f/KkyYFblnmpeVqQ\niYiIyIQKisXZ8ePHufvuu/nTn/5Eeno6//Iv/8KaNWvO+LWbNtXR2XsZnup/43jnMBH+aPLTbyAl\npY6hqCS2HDa3LJt6mgLfEzcpjnnp8yjKLGJm6kyiIqMm6pcW8sJhNiDYqCfOpL44j3riTOHQl6BY\nnH3nO98hLi6OlpYWtm/fzooVKyguLqbwtMGxX/2qnD/8cSt1Ix1EzEiBDEie2s+x1n/m9WNRtG/7\nS+Br4ybFMTd9LkUZRcyaMksLsnGyY8eOkP8QBRv1xJnUF+dRT5wpHPri+MVZb28vGzdupKamhvj4\neK6++mpuvfVWnn76af7lX/5l1Nf+w1PfgsEooguLSIhpJjGjm67obkiGow39XBs1hznpcyjKKGL2\n1NlMinT8Lz/onThxwu4S5DTqiTOpL86jnjhTOPTF8auT/fv3M2nSJPLz8wPniouLKS8v/8TXDn/h\nBOw9wXBiA1ExM4mPnkIEUcT6R7jq8sU8cPUDWpCJiIiIozl+pdLT00NycvKoc0lJSXR3d3/yiyOH\nICkKUoeI7O/gsphZJE1KZPasNAr9BVqY2aC+vt7uEuQ06okzqS/Oo544Uzj0xfFRGtu3b+ezn/0s\nvb29gXM///nP+ctf/sIf/vCHwLmI1EnQ6bOjRBEREZELUlxczI4dO874muMvJRUUFDAyMsKBAwcC\ntzZ37tzJ/PnzR32ddWLEjvJERERExpTjr5wBrFmzhoiICB5//HGqqqq4+eabef/995k3b57dpYmI\niIiMqaBIWP33f/93+vv7yczM5Otf/zqPPvqoFmYiIiISkoLiypmIiIhIuAiKK2ciIiIi4SLoF2fH\njx9n5cqVJCYmkpeXx/r16+0uKSgNDQ1x9913k5eXR3JyMiUlJbz55puB1zdv3szcuXNJSEhg2bJl\nHDlyZNT3P/jgg6Snp5Oens5DDz006rX6+nqWLl1KQkIC8+bNY/PmzaNef+aZZ5gxYwaJiYmsXLmS\njo6OwGuDg4OsW7eOlJQUcnJy+OUvfzkOv3rn+/DDD4mLi+POO+8MnFNP7PXss88yb948EhMTyc/P\nZ+vWrYD6Ypdjx47xpS99ibS0NHJycrjvvvvw+cwT/OrJxHjkkUdwu93ExcVx1113jXrNqT3YsWMH\npaWlJCQk4Ha72blz51j8Vlw6K8itXr3aWr16tdXb22tt3brVSklJsWpqauwuK+j09vZaDz/8sHX4\n8GHLsizrtddes5KSkqzDhw9bra2tVnJysvXiiy9ag4OD1gMPPGBdeeWVge999NFHrTlz5lgNDQ1W\nQ0ODVVhYaD366KOB16+88krrv//3/24NDAxYGzZssFJTU63W1lbLsixr9+7dVlJSkrVlyxarp6fH\n+upXv2qtXr068L0PPfSQde2111onTpyw9u7da2VnZ1tvvvnmBP2uOMfy5cuta665xrrzzjsty7Ks\n1tZWKyUlRT2xydtvv23NmDHD2rZtm2VZluX1eq2GhgZ9Vmy0cuVKa+3atdbg4KDV1NRkLViwwPr1\nr3+tnkygjRs3Wi+//LL17W9/21q7dm3gvFP/fzU4OGhNnz7d+tWvfmUNDQ1Zv/71r60ZM2ZYQ0ND\n4/1b9amCenHW09NjxcTEWB9++GHg3De+8Q3roYcesrGq0LFw4UJrw4YN1mOPPWZdffXVgfO9vb3W\n5MmTrdraWsuyLGvJkiXWb3/728DrTz75ZOCDV1tba8XGxlo9PT2B16+99trAB+8f//Efra997WuB\n1+rq6qyYmJjA17tcLutPf/pT4PUf/ehHoz544WD9+vXW7bffbj388MPW17/+dcuyLPXEZkuWLLGe\nfPLJT5xXX+xTUFBgvfHGG4HjBx54wLr33nvVExv80z/906jFmVN78NZbb1m5ubmjap8+fbojFtBB\nfVvzbFs71dTU2FhVaGhubmb//v3Mnz+fmpoaiouLA6/Fx8eTn58f+H3es2fPqNcXLlwYeK2mpoZZ\ns2aRkJAQeP3UHp3+3rNmzSI2Npb9+/fT0dFBY2PjWd87HHR1dfE//+f/5Je//CXWKc/uqCf28fl8\nVFZW0tLSwuWXX860adO47777GBgYUF9s9IUvfIFnnnmG/v5+GhoaeOONN7jppps+8Xuunow/67Tn\nDJ36uaipqWHhwoWjanXKGiKoF2cXtLWTnLfh4WG+9rWvsXbtWgoKCujt7f3E73NycnLg97mnp4eU\nlJRRr/X09JzxNTA9Ovl6b2/vJ14/+d4nv+b09w6n/v7whz/knnvuweVyERERQUREBIB6YqPm5maG\nh4fZsGEDW7duZceOHWzfvp1//ud/Vl9s9PDDD7N7926Sk5OZNm0aZWVl3HrrrWf8c0I9GV8n/z91\nklM/F2d6b6f0KKgXZ4mJiXR1dY0619nZSVJSkk0VBT+/38+dd95JXFwcjzzyCPDpv8+nv97Z2Uli\nYuJ5f29nZ+cZXz/5Hqe/d7j0d8eOHWzevJnvf//7gPnb6Mm/kaon9pk8eTIA9913H1lZWaSlpfGD\nH/yA119/XX2xiWVZfOELX+C2226jr6+PtrY2jh8/zoMPPqie2OD0K2dO7cHZ3vv0haQdgnpxdurW\nTiedaWsnOT+WZXH33XfT2trKhg0biIqKAqCoqGjUEyy9vb3U1dVRVFQUeP3U/cFO7UFRUREHDx4M\n/A3m5Ounfu+p711XV8fQ0BAFBQVMmTKFnJycs753qHv33Xepr69n+vTp5OTk8K//+q9s2LCB0tJS\n9cRGU6ZM4bLLLjvja+qLPdra2qisrOS73/0u0dHRTJ06lbVr1/L666+rJzY4/cqZU3tQVFREdXX1\nqFqrq6sD720rG+fdxsTq1autNWvWWL29vdaWLVuslJQUa8+ePXaXFZTuvfde68orrxw1eGlZHz9p\ns2HDBqu/v9964IEHrCVLlgRef/TRR6158+ZZDQ0N1rFjx6zCwkLrscceC7x+5ZVXWvfff7/V3///\nt3dvIVF1bRzA/6P16ngYdTLGEx7CSoJCkoJKUhEJyUqi0qnsrJIpEVQqkholIhnphdnhpiJmTC/T\nCyXF8CIzQSEys4KsqDR1sDFrGvH5Ll7aNKl8vt/X24z2/8EGF3ud9lo3j2vN2vuLctJmaGhIRESe\nPHkiGo1GOWmj1+tFr9crZfPy8iQmJkZMJpP09PSIn5+fNDY2/ssj4RjGx8dlYGBABgYG5MOHD3Ly\n5EnZsWOHDA0NcU7srLCwUNasWSODg4MyMjIi0dHRUlhYyHmxk8nJSQkICJCysjKZmJgQk8kkycnJ\nsmfPHs7JbzQxMSFfvnyRvLw8SUtLk69fv8rExITDzoHFYpGQkBCprKyUr1+/SmVlpYSGhorVav1N\nIzazOR+cjYyMSHJysri7u0tISIgYjUZ7d2lOevXqlahUKlGr1eLh4aFcBoNBRETu3bsnERERolar\nJS4uTnnlxnenT58WrVYrWq1WcnNzp9QdGxsrarVaIiIipLm52ea+wWCQ4OBgcXd3l+TkZDGZTMo9\ni8Uihw4dEo1GIzqdTi5duvQvjYDjKy4uVl6lIcI5sSer1SpZWVni7e0tfn5+cvz4cbFYLCLCebGX\n9vZ2iY6OFm9vb/H19ZWUlBQZHBwUEc7J71JUVCQqlcrmOnv2rIg47hx0dXVJVFSUqNVqiYqKku7u\n7l85JP8zfr6JiIiIyIHM6d+cEREREc03DM6IiIiIHAiDMyIiIiIHwuCMiIiIyIEwOCMiIiJyIAzO\niIiIiBwIgzMiIiIiB8LgjIj+eAcOHMCZM2d+aZ1Hjx7F+fPnf2mdRPRnWGDvDhAR2ZtKpZryPcD/\nV3V19S+tj4j+HFw5IyICwI+lEJGjYHBGRHZVVlaGoKAgaDQaREREoKWlBQDQ0dGBdevWwcfHBwEB\nAcjJyYHValXKOTk5obq6GkuXLoVGo0FhYSFevnyJdevWwdvbG6mpqUr+1tZWBAUFobS0FIsXL0ZY\nWBgMBsOMfaqvr0dkZCR8fHywYcMGPH78eMa8J06cgE6ng5eXF1atWoWenh4AtlulW7Zsgaenp3I5\nOzvj1q1bAIDe3l4kJCRg0aJFiIiIQF1d3YxtxcbGorCwENHR0dBoNNi0aROGh4dnOdJENFcwOCMi\nu3n27BmqqqrQ2dmJT58+oampCaGhoQCABQsWoLKyEsPDw3jw4AGam5tx+fJlm/JNTU3o6upCe3s7\nysrKkJ6eDqPRiNevX+Px48cwGo1K3oGBAQwPD+Pdu3e4efMmMjIy8Pz58yl96urqwuHDh3H9+nWM\njIwgMzMTW7duxbdv36bkbWxsRFtbG54/f47R0VHU1dVBq9UCsN0qvXv3LsxmM8xmM2pra+Hv74/4\n+Hh8/vwZCQkJ2Lt3Lz5+/IiamhpkZWXh6dOnM46Z0WjEjRs3MDg4iG/fvqG8vPwfjzsROTYGZ0Rk\nN87OzrBYLHjy5AmsViuCg4OxZMkSAMDq1auxdu1aODk5ISQkBBkZGbh//75N+dOnT8PDwwMrVqzA\nypUrkZiYiNDQUGg0GiQmJqKrq8sm/7lz57Bw4UJs3LgRmzdvxp07d5R73wOpa9euITMzE2vWrIFK\npcK+ffvg4uKC9vb2Kf3/66+/YDab8fTpU0xOTmL58uXw8/NT7v+8VdrX14cDBw6gtrYWgYGBqK+v\nR1hYGPbv3w8nJydERkZi+/btM66eqVQqHDx4EOHh4XB1dcWuXbvQ3d39D0aciOYCBmdEZDfh4eGo\nqKhAcXExdDod9Ho93r9/D+DvQCYpKQn+/v7w8vJCQUHBlC08nU6n/K1Wq23Srq6uGBsbU9I+Pj5Q\nq9VKOiQkRGnrR/39/bh48SJ8fHyU6+3bt9PmjYuLQ3Z2No4dOwadTofMzEyYzeZpn3V0dBTbtm1D\nSUkJ1q9fr7T18OFDm7YMBgMGBgZmHLMfgz+1Wm3zjEQ0PzA4IyK70uv1aGtrQ39/P1QqFXJzcwH8\n/SqKFStW4MWLFxgdHUVJSQkmJydnXe/Ppy9NJhPGx8eVdH9/PwICAqaUCw4ORkFBAUwmk3KNjY0h\nJSVl2nZycnLQ2dmJnp4e9PX14cKFC1PyTE5OYvfu3YiPj8eRI0ds2oqJibFpy2w2o6qqatbPSUTz\nD4MzIrKbvr4+tLS0wGKxwMXFBa6urnB2dgYAjI2NwdPTE25ubujt7Z3Vqyl+3Eac7vRlUVERrFYr\n2tra0NDQgJ07dyp5v+dPT0/HlStX0NHRARHB58+f0dDQMO0KVWdnJx4+fAir1Qo3Nzeb/v/YfkFB\nAcbHx1FRUWFTPikpCX19fbh9+zasViusVisePXqE3t7eWT0jEc1PDM6IyG4sFgvy8/OxePFi+Pv7\nY2hoCKWlpQCA8vJyGAwGaDQaZGRkIDU11WY1bLr3kv18/8e0n5+fcvIzLS0NV69exbJly6bkjYqK\nwvXr15GdnQ2tVoulS5cqJyt/9unTJ2RkZECr1SI0NBS+vr44derUlDpramqU7cvvJzaNRiM8PDzQ\n1NSEmpoaBAYGwt/fH/n5+dMePpjNMxLR/KAS/htGRPNca2sr0tLS8ObNG3t3hYjov+LKGREREZED\nYXBGRH8Ebv8R0VzBbU0iIiIiB8KVMyIiIiIHwuCMiIiIyIEwOCMiIiJyIAzOiIiIiBwIgzMiIiIi\nB/IfaLkgtnNsZy4AAAAASUVORK5CYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10ed0dd90>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 27
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"The improvement is pretty significant when static type declarations are used. \n",
|
|
"One more experiment to see by how much we could improve our \"classic least squares\" code via Cython compared to the initial Python implementation:\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"x = [x_i*random.randrange(8,12)/10 for x_i in range(500)]\n",
|
|
"y = [y_i*random.randrange(8,12)/10 for y_i in range(100,600)]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 30
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"funcs = ['classic_lstsqr', 'cy_lstsqr', 'static_type_lstsqr', \n",
|
|
" 'lin_lstsqr_mat', 'numpy_lstsqr', 'scipy_lstsqr']\n",
|
|
"labels = ['classic approach','classic approach (cython)', \n",
|
|
" 'classic approach (cython + type decl.)',\n",
|
|
" 'matrix approach', 'numpy function', 'scipy function']\n",
|
|
"\n",
|
|
"times = [timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000)\n",
|
|
" for f in funcs]\n",
|
|
"\n",
|
|
"times_rel = [times[0]/times[i+1] for i in range(len(times[1:]))]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 31
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%pylab inline"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": []
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"x_pos = np.arange(len(funcs[1:]))\n",
|
|
"plt.bar(x_pos, times_rel, align='center', alpha=0.5, color=\"green\")\n",
|
|
"plt.xticks(x_pos, labels[1:], rotation=90)\n",
|
|
"plt.ylabel('rel. performance gain')\n",
|
|
"plt.title('Performance gain compared to the classic least square'\\\n",
|
|
" '(n={})'.format(len(x)))\n",
|
|
"plt.grid()\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAdUAAAHnCAYAAADuC8dRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdUFPcWB/DvIEhHepGuIGAJaNBn1NhiLyHYY8WWRJNn\nNM0WItanSSwxaiwxYkQxsUejGGM3MZYoJCoqlgUsoKCiokjxvj88zDICiro4uz/u5xzOYX87O3vv\nlrk7c6dIRERgjDHG2AszUjsAxhhjTBRcVBljjDEd4aLKGGOM6QgXVcYYY0xHuKgyxhhjOsJFlTHG\nGNMRVYtqfn4+Bg0aBEdHRxgZGWHfvn1qhiOsPXv2wMjICFeuXFE7FKFERESgdevWqsYQFRUFf39/\nVZ7bx8cHU6dOfWnP17x5c7zzzjvP/XiNRgMjIyP8+eefOoyKPY6I8Oqrr2LNmjVqh6IzMTExaNiw\nYZmmfWpRjYiIgJGREYyMjGBiYgIfHx8MGzYMN27ceOFA161bh9jYWGzZsgVpaWl47bXXXnierLjG\njRsjLS0Nbm5uaociHEmSSr3v0qVLOvuxqMt56YokSU/MX9c2btyIWbNmvbTn0xU/Pz9MnDhR7TBe\nmlWrVuHBgwfo3r17uT5P0dpU+FepUiU8fPhQMd3WrVsREhICMzMz+Pr6Yvbs2cXmdejQITRq1Ajm\n5uaoWrUqxo0bp5hP7969cfPmTaxbt+6pcZVpTbVp06ZIS0tDcnIy5s6di/Xr16N///5leWiJcnNz\nAQBJSUlwd3dHw4YN4ezsDBMTkxeaHyuZiYkJnJ2dX+oC0FDk5+e/0OPLcu4UXZ5fpSKfq8XW1hZW\nVlZqh/HMRPjePcsyds6cORg8eHA5RvOIJElybSr8u3r1KoyMtGXt6NGjCAsLQ8eOHZGQkICoqCiM\nGzcOixYtkqdJTU1F69atERQUhGPHjuG7777DokWLMH78eHkaIyMjDBgwAHPnzn16YPQUAwYMoFat\nWinGpk6dSpUqVaKcnBwiIoqNjaXg4GAyMzMjHx8f+uijjyg7O1uevlmzZjR48GD6/PPPyc3NjVxd\nXal58+YkSZL85+vrS0REubm5NHr0aHJ3d6fKlStTzZo1adWqVYrnlySJ5s6dS2+//TZVqVKFevbs\nScuWLSNjY2PavXs31a5dm8zNzalFixZ09epV2rVrFwUHB5OlpSW1atWKLl++LM/rwoULFB4eTlWr\nViULCwuqU6cOrVixQvF8zZo1oyFDhtCkSZPI1dWV7O3tqX///nT37l3FdKtXr6Z69eqRmZkZOTg4\nUPv27enmzZvy/XPnzqWAgAAyMzMjf39/mjp1KuXn5z/x9f/999+pdu3aZGZmRiEhIbRv3z6SJIli\nYmLkacaNG0dBQUFkYWFBnp6e9N5771FWVpZ8/+7du0mSJDnvwts7duyg119/nSwsLKhmzZq0bdu2\nJ8ZCRLRjxw5q0qQJWVhYUJUqVahZs2Z0/vx5+f6vvvqKfH19qXLlylS9enWaM2eO4vHe3t4UGRlJ\n7733HlWpUoVcXFxowYIFdP/+fRo+fDjZ2dmRu7s7zZs3T/E4SZLom2++oS5dupClpSW5u7vTN998\no5hmzpw5FBISQlZWVuTq6kq9evWiq1evFnsdfv31V2rcuDGZmZnRwoULy/TeZGZmUo8ePcjS0pJc\nXFzo888/p/79+xf7bjwec0mfcSKi6OhoCgoKosqVK5OHhwd9/vnnT/wslDavCRMmkJ+fH23atIkC\nAgLI0tKSmjdvTklJSYrHHz16lFq3bk1WVlbk5OREXbp0oeTk5FKfj4goLy+PoqKiqFq1amRqakru\n7u703//+V77fx8eHpk6dKt9euXIlNWjQgKpUqUKOjo7UsWNHOnv2rGKeU6dOlefn5OREbdu2pfv3\n7xMRUWpqKnXp0oUcHR3JzMyMqlWrRl999ZX82MLvYVHz5s2joKAgMjU1JWdnZ+ratWup+Vy8eJEk\nSaI//vhDHktLS6MBAwaQk5MTWVtbU+PGjWnfvn2Kxw0ZMoSqV69O5ubmVK1aNRo3bhw9ePBAvv9J\ncTdr1qzYe1fa637ixAlq06YN2drakqWlJQUFBSmWRRqNhtq2bUvm5ubk6elJc+fOLfaaeHt705Qp\nUxTzHTx4MDVv3ly+/dtvv1GzZs3I3t5e/g4fPnxY8ZjHl7G9evWSH9uoUSMyNzcnd3d3GjhwIGVm\nZsqPO3PmDEmSRBcvXiw2vwULFlDfvn3J2tqaPDw86H//+1+Jr0NZlVSbHvf2229T48aNFWOffvop\n+fj4yLfHjh1Lnp6eimnmz59PlpaWdO/ePXns5MmTJEkSpaSkPPE5y1RUW7durRibOXMmSZJEd+/e\npWXLlpGdnR3FxMTQxYsXad++ffTKK69Qv3795OmbNWtG1tbWNGzYMEpMTKQTJ07QjRs36JNPPiFf\nX19KT0+njIwMIiL65JNPyMHBgdauXUtJSUk0bdo0MjIyop07d8rzkySJHBwcaP78+XThwgVKSkqi\nZcuWkZGREbVo0YIOHz5Mx44dI39/f2rSpAk1bdqUDh06RPHx8RQYGEg9e/aU5/Xvv//S/Pnz6Z9/\n/qELFy7Qt99+KxfnovHb2trSRx99RGfOnKHffvuN7O3tKTIyUp7mhx9+IBMTE5oyZYqc47x58+S8\nJkyYQN7e3rRx40bSaDS0detW8vLyUszjcZcuXSJzc3MaOnQoJSYm0s6dO6levXokSRKtXLlSnm7K\nlCl04MABSk5Opp07d1JgYCANGDBAvr+0ohocHEzbt2+nc+fO0cCBA8nGxkbxI+BxO3bsoEqVKtGo\nUaPon3/+oTNnzlB0dDSdOXOGiB4t4MzNzWnJkiV07tw5WrhwIZmZmdHSpUvleXh7e5OtrS3Nnj2b\nzp8/T1OmTCEjIyNq27atPPa///2PjIyM6NSpU4r33N7enubNm0dJSUn0zTffkLGxMW3atEme5ptv\nvqGdO3eSRqOhgwcPUqNGjahZs2bFXofAwEDasmULaTQaunTpUpnem7feeov8/f1p9+7ddPLkSerb\nty/Z2NgU+24Udfz4cZIkiTZs2KD4jG/ZsoUqVapE06dPp6SkJPrpp5/Izs7uiZ+F0uY1YcIEsrS0\npPbt29OxY8coISGBXn31VXr99dflx548eZKsrKwoKiqKzpw5QydOnKDu3btTjRo15B/GJenfvz85\nOztTTEwMXbhwgY4cOaL4IfN4UV22bBlt2bKFLly4QPHx8fTmm2+Sv78/5ebmEhHRunXryMbGhrZs\n2UKpqakUHx9P33zzjVxUO3fuTK1bt6aEhARKTk6m3bt3U2xsrDz/5s2b09ChQ+XbX3zxBVlZWdH8\n+fMpKSmJ4uPjn7igfryo3rt3j4KCgqhbt270999/0/nz52nq1KlkampKiYmJRET08OFDGj9+PB0+\nfJiSk5Ppl19+ITc3N5owYYI83yfFfePGDfL19aVPP/2U0tPTKT09nQoKCkqMr06dOtSnTx9KTEyk\nixcv0rZt22jLli1yHHXr1qUGDRrQ4cOHKT4+nlq3bk02NjaK1+Tx94ToUVFt0aKFfHvDhg20Zs0a\nOnv2LJ06dYqGDBlC9vb2iuL4+DL23LlztHPnTrKwsKB58+bRuXPn6MiRI9SiRQvFd2zRokXk5ORU\nLDdJksjFxYW+//57unDhAs2fP58kSVIs1999912ysrJ64l/RFayIiAiysbEhV1dX8vX1pa5du9LJ\nkycVz+vl5UWTJ09WjP3++++K5WHTpk1p8ODBimnOnTtX7AfYw4cPydbWlqKjo4vlV9Qzr6mePHmS\nqlWrRq+99hoRPVpILlq0SPGYvXv3kiRJdOvWLSJ6VJQCAgKKzbvwV3ah7OxsMjU1pe+++04xXXh4\nOLVs2VK+LUlSsV+sy5YtI0mSKCEhQR776quvSJIkOnbsmDw2e/ZscnR0fGLOYWFhig9qs2bNKCQk\nRDHNsGHD5NeAiMjT01PxK76o7OxssrCwoO3btyvGly9fTra2tqXGMW7cOPL19aWHDx/KY3FxccWK\n6uPWr19Ppqam8u3SiuqGDRvkadLT00mSJPrtt99KnW+TJk2oc+fOpd7v4eFBo0ePVoyNGjWKqlWr\nJt/29vam8PBw+fbDhw/JxsaG3nzzTcWYnZ2dYm1VkiTq37+/Yt69e/dWFI/HHTt2jCRJoitXrhCR\nNu+ia/lleW+SkpJIkiT6/fff5ftzc3PJ3d39iUU1NTWVJEmivXv3KsabNGmi+GFH9OgHgbm5OeXl\n5T3TvCZMmEDGxsZykSUi+umnn8jIyEhemxowYIC8plEoJyeHLCwsaOPGjSU+X2HO69atKzW/khbg\nRWVmZpIkSfTnn38SEdGsWbOoRo0apeYYHBxMUVFRpc6vaFG9e/cumZmZ0cyZM0ud/nGPF9Vly5aR\nh4dHsS0ELVu2pJEjR5Y6n1mzZpG/v3+Z4/bz86OJEyc+Nb4qVaqUusDesWMHSZKk2AJx/fp1+Ud3\nodKKatE11ccVFBSQnZ2dYplS0jK2WbNmNHbsWMVYcnKyYrn78ccfU2hoaLHnkCSJPvzwQ8VYUFCQ\nYn7Xrl2j8+fPP/Hvzp078vSxsbG0ceNGOnHiBP3+++/Url07srCwoBMnTsjTVK5cmZYsWaJ43hMn\nTpAkSXT06FEiIqpRowaNHz9eMc3du3dJkiRau3atYvyVV14pNu3jytRT3bNnD6ytrWFhYYE6derA\nz88PK1euxPXr15GSkoJRo0bB2tpa/uvQoQMkScK5c+fkebz66qtPfZ5z584hNzcXTZs2VYw3bdoU\nJ0+eVIw1aNCg2OMlSUKdOnXk2y4uLgCAV155RTGWmZkp96bu3buHMWPGoHbt2nBwcIC1tTW2bt2K\nlJQUxXyDg4MVz+Xm5ob09HQAwLVr13Dp0iW0adOmxLxOnjyJ+/fvo0uXLorX6b333sPt27eRmZlZ\n4uNOnTqF+vXrK3oyJe2Btn79ejRt2hTu7u6wtrZG3759kZeXh7S0tBLnWygkJET+39nZGZUqVZJz\nKsmxY8dKzfH27du4fPlyie+dRqNBTk4OgOKvpSRJcHJyUrxHkiTB2dkZ169fV8zr8R3ZGjVqpPhc\n7NmzB23btoWXlxdsbGzw+uuvAwCSk5MVjyv62SnLe3Pq1Cn5+QqZmJigfv36pbxST3bq1KkSX6ec\nnBycP3/+medXtWpVODg4yLfd3NxARLh27RoA4MiRI9iwYYMiP0dHRzx48EDxHS3q2LFjAFDq+12S\n+Ph4hIeHo1q1arCxsYG3tzcA7evfs2dP5OXlwdvbGwMHDkRMTAzu3r0rP37kyJGYNm0aGjZsiDFj\nxmD//v2lPtfJkyfx4MGDZ4rvcUeOHEFaWhpsbW0Vr83+/fsVr8uSJUvwn//8B66urrC2tsa4ceMU\ny4dniftJPvnkEwwZMgQtWrTAxIkTcfz4cfm+U6dOwdHREX5+fvKYo6MjAgICnvl5Ll68iH79+sHf\n3x9VqlRBlSpVkJWVpcgJKL6MPXLkCGbPnq14rWrVqgVJkpCUlAQAyMrKKrXvXXR5Azz63BZ+RgHA\nyckJ1apVe+Jf0Xn36tULYWFhqFWrFt544w388ssv8PDwKFvf8znZ2Njg1q1bT5zGuCwzatiwIZYv\nXw5jY2NUrVoVxsaPHla4AJ47dy5atGhR7HHu7u4AHi0kLS0tnyn4pylpfkZGRooCVPh/pUqVio0R\nESRJwqeffopffvkFs2fPRkBAACwsLPDxxx8jKytLMe/KlSsrbkuSVGwvs9IUTrd27VrUqFGj2P12\ndnYlPq4sOzgcOnQIPXr0wLhx4zBz5kzY2dnh4MGDGDBgwFN3Lng8p6KxlqfHd0iTJKnEsWeJJSUl\nBR06dMCAAQMQFRUFR0dHpKamolWrVsVeh6Kfned9bwD92WmopM8moM2NiNC/f3+MGTOm2GPt7e11\nEsO9e/fQpk0bNG3aFNHR0XBxcQERoVatWvLrX7VqVZw+fRq7d+/Grl27MHnyZIwePRqHDh2Ch4cH\nIiIi0K5dO8TFxWH37t1o3749wsPDsWLFCp3E+LiHDx8iKCgIGzduLHafhYUFAGDNmjX44IMPMGPG\nDDRr1gw2Njb4+eefFTux6Cruzz//HH369EFcXBx27dqFadOm4bPPPsPkyZNLfczjn0EjI6NiY3l5\neYrbnTp1grOzMxYsWABPT0+YmJigSZMmT/yeFD7XmDFj0K9fv2JxFK7A2Nra4s6dOyXG+rRl6Hvv\nvYeVK1eW+NhCixcvxttvv13ifSYmJqhbty40Go085ubmhqtXryqmK6xbhUdDlGWaQllZWbC1tX1i\njGVaUzUzM0O1atXg5eUlF1Tg0Qvp6emJ06dPl/irwtTUtCyzl/n5+cHU1BR79+5VjO/du1exBqpL\n+/fvR9++fdGtWzfUqVMHvr6+OHPmzDPtsefs7AwPDw9s3769xPtr1aoFMzMznD9/vsTXqejeakXV\nrFkTR44cUXzw/vrrL8U0Bw4cgKOjIyZNmoT69evDz88PqampZY79Wbz66qul5mhjYwMPD48S37tq\n1arBzMzshZ//4MGDitt//vknatWqBeDRr+icnBzMmTMHr732Gvz9/Z+6pg6U7b2pWbMmAOCPP/6Q\nH5ebm4sjR448cd6FC5GCgoJiz1nS62RhYYHq1as/07zKIjQ0FAkJCSXmV9oCol69egBQ6vv9uMTE\nRGRkZGDq1Klo2rQpAgICcOPGjWIL+MqVK6Nt27aYMWMG/v33X9y7dw+bNm2S73d1dUVERASWL1+O\n77//HitXrlSszRaqWbMmzMzMyhxfSerXr48LFy7A2tq62Ovi6uoKANi3bx/q1q2LkSNHom7duqhe\nvTouXrxYbPnwpLgrV65c5vfN19cXw4YNw5o1azBx4kR89913cr4ZGRmKNeiMjAycOXNG8XhnZ2dc\nvnxZMXb8+HE53szMTCQmJmLMmDFo3bo1AgMDYWpqqlhjLE1oaChOnDhR4ueosAD7+/sX2zJUVpMn\nT0ZCQsIT/zp37lzq4wsKCvDPP//Ay8tLHmvcuHGxz0hcXBx8fHxQtWpVeZodO3YoPqtxcXGwtLRE\n3bp15TEiQmpqaok/vosq05rqk0ydOhWDBw+GnZ0d3nzzTZiYmCAxMRFxcXFYuHChHExZftVbWFhg\nxIgRiIyMlDcJrl27Fr/88gt+//33Fw21RAEBAdi4cSO6dOkCS0tLzJo1C1evXpW/VGWNf8KECRg2\nbBhcXFzQtWtXPHz4ELt378bbb78NBwcHjBs3DuPGjYMkSXjjjTeQn5+Pf//9F/Hx8Zg+fXqJ8xw+\nfDhmz56NYcOGYeTIkUhLS5N/IRd+SQIDA3H9+nX88MMPaN68OQ4cOCB/EXUtMjIS7du3x6hRozBw\n4ECYmpri4MGDaNSoEWrUqIGxY8fi448/hr+/P5o1a4Zdu3Zh4cKFWLBggTyPkl7Hso79+uuvmD9/\nPtq0aYO4uDj8/PPPWLt2LYBHX2ZJkvD111+jd+/eSEhIeOIv/EJWVlZPfW/8/Pzw5ptv4v3338ei\nRYvg7OyM6dOnl7iwL8rR0RFWVlbYvn07goKCYGpqCjs7O4wdOxadO3fGjBkzEB4ejvj4eEycOBEf\nf/yx4kdrWeZVFuPGjUODBg3Qt29ffPjhh3B0dIRGo8GmTZvw4YcfwtfXt9hj/Pz80KdPHwwfPhw5\nOTlo2LAhbty4gYMHD2LEiBEAlO+Rt7c3TE1NMXfuXHz00UfQaDQYM2aMovgsXboURIT69evD1tYW\nO3fuxJ07d+QfLR988AE6duyIGjVqICcnB+vXr4eXl5e8ya/o99DKygoff/wxoqKiYG5ujlatWuH+\n/fvYtm1biWvkJenTpw9mz56Njh07YurUqfD390d6ejp27dqFmjVrIiwsDIGBgfjhhx/wyy+/oFat\nWtiyZQs2bNigyP1pcfv6+uLAgQNITU2Fubk5HBwcihXl7OxsfPbZZ+jWrRt8fHxw69YtxMXFyT8a\nW7VqheDgYPTt2xfffvstTExMMHr06GJrf61atcKCBQsQHh4OLy8vLFy4ECkpKXJ7wM7ODk5OTli8\neDGqVauGjIwMfPbZZzA3N3/q6zVp0iS0adMGH3/8Mfr16wdra2skJSVh7dq1mDdvHszMzNCsWTNk\nZmZCo9HAx8fnifN7fLnq5OQEJyenp8ZR+HpFRkaiW7du8mbkr776ChqNBqtWrZKnGzVqFBo1aoTP\nP/8cffv2xaFDhzBv3jzMmTNHnmbYsGGYN28ehg4dilGjRuH8+fP44osv8N///lfxuiQmJiIrKwvN\nmzd/cnBP7LjSoz2snrQzBhHRxo0b6bXXXiMLCwuysbGhkJAQxR5Xj++1VygqKkrR8Cd6tBv/mDFj\n5ENqatWqpdgDkIhK3FFn2bJlZGJiohhbsWIFGRkZKcZiY2PJyMhI3gMvNTWV2rZtS5aWluTm5kZR\nUVHF9pYrKf4pU6YoDpEgenRIQXBwMJmampKDgwN16tRJ3lmLiOj777+nkJAQMjMzIzs7O2rYsKF8\nSEdpCg+pMTU1peDgYNq2bRtJkkTr16+Xp4mMjCQXFxeytLSkjh07yjkW7rq/e/duMjIyUuyoVPR2\nIWNjY1q+fPkT49m+fTu99tprZG5uTlWqVKGWLVsqdp8vPKTGxMSEqlevXuywl5J2pChpR47AwEDF\n3rCFh9S89dZbZGFhQVWrVqXZs2crHjN//nzy9PQkc3Nzev311ykuLo6MjIzknXtKy5vo6e9N0UNq\nnJycaNy4cSXuGf+4H3/8kXx9fcnY2FjxeVm+fLl8SI27uzt9/vnnpe4V+qR5lfQd2r9/v+L9J3q0\nl3tYWBjZ2dmRubk5+fn50bvvvks3btwo9fny8vIoMjKSfHx85EN/Ro0aJd//+Hu5du1a8vf3JzMz\nM6pXrx7t3btX8Zlav349NWrUiOzs7OTD13744Qf58e+//z7VqFGDzM3N5e9P0T3AS/oefvPNNxQQ\nEECVK1cmFxcX6tGjR6n5XLx4kYyMjBR7dGZmZtKwYcPk5Y27uzt16dKF4uPj5dfg3XffJXt7e7Kx\nsaE+ffrQvHnzFMuVp8V99OhRqlevHpmbmxd7Xwrl5ORQ7969ydfXl8zMzMjZ2Zl69epFly5dkqfR\naDTUpk0bMjMzkw+pefw1uXPnDvXr14/s7OzI2dmZJk6cSEOGDFEsz/bu3SsfAhkYGEjr1q0r9h0s\nbWfI/fv3U6tWrcja2lo+7GfUqFGKnb3q169fbAeykubXqlUrGjhwYAnv1NPdv3+f2rVrR66urvL7\nFhYWRsePHy827a+//iovl318fIotN4iI/vrrL2rUqBGZmZmRq6srjRs3TrGDKNGjZf6Tdows9NSi\nakj69OlDrq6uZG1tTb6+vorjtX7//XcKCAggCwsLatGixVOP0dNXhXtWF93DrSJ42h7PjFVEpa2w\nqGnlypVUs2ZNtcPQqYKCAvL396c1a9Y8dVqhTqg/duxYXLx4Ebdv38a2bdvw7bffYvv27cjIyECX\nLl0wdepU3Lx5E6GhoejZs6fa4ZbJd999hz///BMajQZbt27F0KFD0bBhQ3mzEGOs4qIyttZept69\ne8Pc3Fyoc/+uWrUKDg4O6Nat21OnfeGeqj55vNCYmJjAyckJ69evR506ddC1a1cAkPcOPXv27FOb\nzmpLSUnB9OnTkZ6eDldXV7Rp0wYzZsxQOyzGmB542edfLqujR4+qHYJO9e3bF3379i3TtBLp28+c\nFzR8+HAsX74cDx48wLx58/Dee+/hww8/RH5+PubPny9P98orryAqKgpdunRRMVrGGGMiEWpNFQAW\nLFiA+fPnY+/evejWrRvq1auH7OzsYnuV2djYFNt708/P77kOvmeMsYosODgY8fHxaoehF4TqqRaS\nJAnNmzdH9+7dERsbCysrK9y+fVsxTVZWFqytrRVj58+fl3sUIv5NmDBB9Rg4P86vouVWEfJLSEh4\nmYt4vSZkUS2Ul5cHS0tL1KpVS/GmZ2dn4/z58xVuZ5+iZxoREednuETODRA/P6YlTFG9fv06Vq9e\njezsbBQUFGD79u1Ys2YNwsLCEB4ejhMnTmD9+vXIycnBxIkTERISovc7KTHGGDMswhRVSZKwcOFC\neHh4wMHBAZGRkVixYgXq168PR0dHrFu3DuPHj4e9vT2OHj2K1atXqx3ySxcREaF2COWK8zNcIucG\niJ8f0xJu798XIUkS+OVgjLFnw8tOLWHWVNnT7dmzR+0QyhXnZ7hEzg0QPz+mxUWVMcYY0xHe/FsE\nb8JgjLFnx8tOLV5TZYwxxnREuDMqsdLt2bPn6dcCLGdjosYg7dbTLx7+PNIupcHVw/XpEz4jV1tX\nTI8q+Zq3L5M+vH/lReTcAPHzY1pcVNlLlXYrDT5v+ZTPzOMBnxDdz1uzUaPzeTLGxMSbfysQ0X8p\nl0dB1Sciv38i5waInx/T4qLKGGOM6QgX1QpE9GPlNPEatUMoVyK/fyLnBoifH9PiosoYY4zpCBfV\nCkT0vg73VA2XyLkB4ufHtLioMsYYYzrCRbUCEb2vwz1VwyVyboD4+TEtLqqMMcaYjnBRrUBE7+tw\nT9VwiZwbIH5+TIuLKmOMMaYjXFQrENH7OtxTNVwi5waInx/T4qLKGGOM6QgX1QpE9L4O91QNl8i5\nAeLnx7S4qDLGGGM6wkW1AhG9r8M9VcMlcm6A+PkxLS6qjDHGmI5wUa1ARO/rcE/VcImcGyB+fkyL\niypjjDGmI1xUKxDR+zrcUzVcIucGiJ8f0+KiyhhjjOkIF9UKRPS+DvdUDZfIuQHi58e0hCmqubm5\nGDx4MHx8fGBjY4O6desiLi4OAKDRaGBkZARra2v5b+rUqSpHzBhjTDTCFNX8/Hx4eXlh3759uH37\nNqZMmYIePXogJSVFnub27du4c+cO7ty5g/Hjx6sYrTpE7+twT9VwiZwbIH5+TEuYomphYYEJEybA\ny8sLANCxY0f4+vri77//lqd5+PChWuExxhirAIQpqo9LT0/H2bNnUatWLXnM29sbnp6eGDRoEDIz\nM1WMTh13NaWwAAAgAElEQVSi93W4p2q4RM4NED8/pmWsdgDlIS8vD3369EFERARq1KiB7OxsHD16\nFCEhIcjIyMD777+PPn36yD3XoiIiIuDj4wMAsLW1RUhIiPyFKNyEw7ef/3bapTT4wAeAdnNtYTHU\n19uF9OH149t8Wx9u79mzB9HR0QAgLy/ZIxIRkdpB6NLDhw/Ru3dv3L17F5s2bUKlSpWKTZOeng43\nNzfcuXMHlpaW8rgkSRDs5VDYs2eP/AVRS8TICPi85VMu89bEa8plbVWzUYPoOdE6n++z0of3r7yI\nnBsgfn6iLzufhVBrqkSEwYMH4/r169i6dWuJBbUo7rEyxhjTJaGK6rBhw3D69Gn8/vvvMDU1lccP\nHz6MKlWqwN/fHzdv3sSIESPQokULWFtbqxjtyyfyL2WAe6qGTOTcAPHzY1rC7KiUnJyMxYsXIyEh\nAa6urvLxqKtWrcKFCxfQvn172NjYoE6dOjA3N0dsbKzaITPGGBOMMGuq3t7eT9yc26tXr5cYjX4S\nva9TXj1VfSHy+ydyboD4+TEtYdZUGWOMMbVxUa1ARP+lLPJaKiD2+ydyboD4+TEtLqqMMcaYjnBR\nrUAKD94WFZ/713CJnBsgfn5Mi4sqY4wxpiN6t/fvtWvXcPfuXcVYtWrVVIpGLKL3dbinarhEzg0Q\nPz+mpTdFNS4uDoMHD8bVq1cV45IkoaCgQKWoGGOMsbLTm82/w4cPR2RkJO7evYuHDx/Kf1xQdUf0\nvg73VA2XyLkB4ufHtPRmTfXWrVt49913IUmS2qEwxhhjz0Vv1lQHDx6MH374Qe0whCZ6X4d7qoZL\n5NwA8fNjWnqzpnrw4EF88803mD59OlxdXeVxSZKwb98+FSNjjDHGykZviuqQIUMwZMiQYuO8OVh3\nRD//KJ/713CJnBsgfn5MS2+KakREhNohMMYYYy9E1aK6YsUK9OvXDwCwdOnSUtdKBw0a9DLDEpbo\nv5RFXksFxH7/RM4NED8/pqVqUY2NjZWL6ooVK7ioMsYYM2iqFtWtW7fK//NxXOVP9L4O91QNl8i5\nAeLnx7T0pqdaFBGBiOTbRkZ6c+QPY4wxViq9qVaXL19GeHg47O3tYWxsLP+ZmJioHZowRP+lLPJa\nKiD2+ydyboD4+TEtvSmq7733HkxMTLBr1y5YWVnh2LFjCAsLw3fffad2aIwxxliZ6E1R/eOPP/DD\nDz8gJCQEABASEoKlS5di1qxZKkcmDtH71nzuX8Mlcm6A+PkxLb0pqoWbewHAzs4O165dg6WlJS5f\nvqxyZIwxxljZ6E1RbdCgAbZt2wYAaNu2LXr27Inw8HCEhoaqHJk4RO/rcE/VcImcGyB+fkxLb/b+\nXbFihbzH7+zZszFz5kzcvXsXI0eOVDkyxhhjrGz0Zk3Vzs4O9vb2AAALCwtERkZixowZcHNzUzky\ncYje1+GequESOTdA/PyYlt6sqUZGRspnVCIi+f/KlSvD09MT7dq1g4uLi5ohMsYYY08kUdGzLKio\nZ8+e2LhxIxo0aABPT0+kpKTgyJEj6NSpEy5duoQTJ05g7dq1aN++fbnFIEkS9OTlEFbEyAj4vOWj\ndhjPRLNRg+g50WqHwZje4mWnlt5s/iUirF69Gvv378eqVatw4MAB/Pzzz6hUqRIOHTqEBQsWYOzY\nsWqHyRhjjJVKb4pqXFwc3nzzTcVYx44d5T2C+/Tpg/Pnz5f6+NzcXAwePBg+Pj6wsbFB3bp1ERcX\nJ9+/c+dOBAYGwtLSEi1btkRKSkr5JKLHRO/rcE/VcImcGyB+fkxLb4pq9erVsWDBAsXYwoUL4efn\nBwDIyMiApaVlqY/Pz8+Hl5cX9u3bh9u3b2PKlCno0aMHUlJSkJGRgS5dumDq1Km4efMmQkND0bNn\nz3LNhzHGWMWjNz3VY8eOITw8HAUFBXB3d8fly5dRqVIlrF+/Hq+++ir27duHM2fOYOjQoWWeZ3Bw\nMCZMmICMjAz8+OOPOHDgAADg3r17cHR0RHx8PGrUqCFPz32B8sc9VcbEw8tOLb3Z+7devXpISkrC\nX3/9hStXrsDNzQ2NGjWST6jftGlTNG3atMzzS09Px9mzZ1G7dm3Mnz8fwcHB8n0WFhbw8/PDiRMn\nFEWVMcYYexF6s/kXeHT4TNOmTdGrVy80a9bsua9Qk5eXhz59+iAiIgI1atRAdnY2bGxsFNPY2Njg\n7t27ugjbYIje1+GequESOTdA/PyYlt6sqerKw4cP0a9fP5iZmWHevHkAACsrK9y+fVsxXVZWFqyt\nrYs9PiIiAj4+PgAAW1tbhISEyKcYK/xiGOrt+Ph41eNJu5QGH/gA0BbBwtMLvujttHNpOp3f40Wa\n3z++zbcf3d6zZw+io6MBQF5eskf0pqeqC0SEQYMGISUlBVu3boWpqSkAYMmSJVi+fLncU83OzoaT\nkxP3VFXAPVXGxMPLTi292vz7ooYNG4bTp0/jl19+kQsqAISHh+PEiRNYv349cnJyMHHiRISEhHA/\nlTHGmE7pVVEt3Ev3yy+/BABcvnwZqampZXpscnIyFi9ejISEBLi6usLa2hrW1taIjY2Fo6Mj1q1b\nh/Hjx8Pe3h5Hjx7F6tWryzMVvVS4+UZU3FM1XCLnBoifH9PSm57q3r170bVrV4SGhuKPP/7AZ599\nhqSkJMycORObN29+6uO9vb3x8OHDUu9/4403kJiYqMuQGWOMMQW96amGhITg66+/RqtWrWBnZ4eb\nN28iJycHXl5euHbt2kuJgfsC5Y97qoyJh5edWnqz+Tc5ORmtWrVSjJmYmKCgoECliBhjjLFnozdF\nNSgoSHGuXuDR+Xrr1KmjUkTiEb2vwz1VwyVyboD4+TEtvempzpo1C506dUKHDh2Qk5ODd955B5s3\nb8amTZvUDo0xxhgrE73pqQKP9vaNiYlBcnIyvLy80LdvX3h4eLy05+e+QPnjnipj4uFlp5berKnm\n5OTAyckJo0ePlsdyc3ORk5MDMzMzFSNjjDHGykZveqqtW7fGsWPHFGN///032rVrp1JE4hG9r8M9\nVcMlcm6A+PkxLb0pqv/++y8aNGigGGvQoIF8vlPGGGNM3+lNUbW1tUV6erpi7Nq1a7CyslIpIvEU\nnhhbVIUnwheVyO+fyLkB4ufHtPSmqHbt2hV9+vTBv//+i3v37uGff/5Bv3790L17d7VDY4wxxspE\nb4rqlClTEBQUhP/85z+wsrJCw4YNERgYiP/9739qhyYM0fs63FM1XCLnBoifH9PSm71/zc3NMX/+\nfHz77bfIyMiAo6MjjIz0puYzxhhjT6U3RRV4dOHwM2fO4O7du4rxli1bqhSRWETv63BP1XCJnBsg\nfn5MS2+KanR0NN5//31YWVnBwsJCcd/FixdViooxxhgrO73Zvjpu3DisXbsW6enpuHjxouKP6Ybo\nfR3uqRoukXMDxM+PaelNUS0oKECbNm3UDoMxxhh7bnpTVEePHo3Jkyc/8ULj7MWI3tfhnqrhEjk3\nQPz8mJbe9FRnzZqF9PR0fPnll3BwcJDHJUlCSkqKipExxhhjZaM3RTUmJkbtEIS3Z88eoX8xa+I1\nQq+tivz+iZwbIH5+TEtviip/4BhjjBk6vSmqAHD8+HHs378fmZmZimvzTZo0ScWoxCH6DxeR11IB\nsd8/kXMDxM+PaenNjkqLFy9GkyZNsHv3bkyfPh3//vsvZs6ciXPnzqkdGmOMMVYmelNUZ8yYgW3b\ntmHDhg2wsLDAhg0bsHbtWhgb69XKtEET/Vg5Pk7VcImcGyB+fkxLb4rq9evX0bRpUwCAkZERCgoK\n0K5dO2zevFnlyBhjjLGy0ZvVQA8PD1y8eBG+vr7w9/fHpk2b4OjoCFNTU7VDE4bofR3uqRoukXMD\nxM+PaelNUf3000+RmJgIX19fTJgwAV27dkVubi7mzp2rdmiMMcZYmejN5t+BAweiQ4cOAID27dvj\n5s2buHnzJoYPH65yZOIQva/DPVXDJXJugPj5MS29KaqFbt++jStXriAzMxN37tzBlStXyvS4efPm\nITQ0FGZmZhg4cKA8rtFoYGRkBGtra/lv6tSp5RU+Y4yxCkxvNv/u2LED7777LjQajWJckiQUFBQ8\n9fHu7u6IjIzE9u3bcf/+/WL33759G5Ik6SpcgyR6X4d7qoZL5NwA8fNjWnqzpjpkyBCMGzcOWVlZ\nyM3Nlf8ePHhQpseHh4cjLCxMcd7govhE/Ywxxsqb3hTVnJwcDBw4ENbW1jA2Nlb8PYuiZ2Iqytvb\nG56enhg0aBAyMzN1EbLBEb2vwz1VwyVyboD4+TEtvSmqI0eOxJdffllqUSyrxzfxOjk54ejRo0hJ\nScHff/+NO3fuoE+fPi/0HIwxxlhJ9Kan2q1bN7Ru3RrTpk2Do6OjPC5JEi5cuFDm+TxelC0tLVGv\nXj0AgLOzM+bNmwc3NzdkZ2fD0tKy2OMjIiLg4+MDALC1tUVISIjcDyn8tWmotwvH1Iwn7VIafOAD\nQLtmWdgLfdHbhWO6mt/ja778/pXf7ebNm+tVPJzfk2/v2bMH0dHRACAvL9kjEr3oqqGOvPLKK6hb\nty66desGc3NzxX2tWrUq83wiIyNx6dIlLFu2rMT709PT4ebmhqysLFhbWyvukyTphdeU2ZNFjIyA\nz1s+aofxTDQbNYieE612GIzpLV52aunNmqpGo8Hx48dRqVKl53p8QUEB8vLykJ+fj4KCAjx48ACV\nKlXCsWPHUKVKFfj7++PmzZsYMWIEWrRoUaygVgRF13JExNdTNVwi5waInx/T0puealhYGHbt2vXc\nj588eTIsLCwwY8YMxMTEwNzcHNOmTcOFCxfQvn172NjYoE6dOjA3N0dsbKwOI2eMMcYe0ZvNv927\nd8eWLVvQtGlTODs7y+OSJOHHH398KTHwJozyx5t/GRMPLzu19Gbzb+3atVGrVi35duGbVNFP2MAY\nY8xw6EVRzc/Px/nz57F48WKYmZmpHY6wRO/rcE/VcImcGyB+fkxLL3qqxsbG2LFjx3PvpMQYY4zp\nA70oqgAwatQofPHFF8jNzVU7FGGJ/ktZ5LVUQOz3T+TcAPHzY1p6sfkXAObOnYv09HTMmjULTk5O\nci9VkiSkpKSoHB1jjDH2dHpTVGNiYtQOQXii93W4p2q4RM4NED8/pqU3RZU/cIwxxgyd3vRUc3Nz\n8cUXX8DX1xempqbw9fXlHquOif7DReS1VEDs90/k3ADx82NaerOmOnr0aBw+fBiLFi2Cl5cXUlJS\nMGnSJNy+fRtz5sxROzzGGGPsqfRmTfXnn3/Gpk2b0KZNGwQGBqJNmzbYuHEjfv75Z7VDE0bhVSZE\nxddTNVwi5waInx/T0puiyhhjjBk6vSmq3bt3x5tvvom4uDgkJiZi27ZtCAsLQ/fu3dUOTRii93W4\np2q4RM4NED8/pqU3PdUvv/wSU6ZMwQcffIArV66gatWqePvtt/H555+rHRpjjDFWJqquqX766afy\n/wcOHMCkSZNw7tw53Lt3D+fOncPkyZNhamqqYoRiEb2vwz1VwyVyboD4+TEtVYvqokWL5P/DwsJU\njIQxxhh7capu/g0JCUG3bt0QFBQkH6f6+DX5JEnCpEmTVIpQLKL3dbinarhEzg0QPz+mpWpRXbNm\nDRYvXozk5GQQEVJTUxX3V9TrqY6JGoO0W2lqh1FmrraumB41Xe0wGGNMdaoWVRcXF0RGRuLhw4d4\n8OABlixZAmNjvdl3SjVpt9Lg85aPzudbXufG1WzU6Hyez4PP/Wu4RM4NED8/pqUXh9RIkoR169bB\nyEgvwmGMMcaei15UMUmSUK9ePZw5c0btUIQm8locIH5+Iq/piJwbIH5+TEtvtrU2b94c7du3R0RE\nBDw9PSFJktxTHTRokNrhMcYYY0+lN0X1wIED8PHxwd69e4vdx0VVN0TvOYqen8h9OZFzA8TPj2np\nTVHlg6MZY4wZOr3oqRbKzMzEjz/+iC+//BIAcPnyZVy6dEnlqMQh8locIH5+Iq/piJwbIH5+TEtv\niurevXsREBCAVatWYfLkyQCApKQkDBs2TOXIGGOMsbLRm6L64YcfYvXq1YiLi5OPVW3YsCEOHTqk\ncmTiEP3cuKLnJ3KLROTcAPHzY1p6U1STk5PRqlUrxZiJiQkKCgpUiogxxhh7NnpTVIOCghAXF6cY\n27lzJ+rUqVOmx8+bNw+hoaEwMzPDwIEDi80nMDAQlpaWaNmyJVJSUnQWtyERvecoen4i9+VEzg0Q\nPz+mpTdFddasWejbty/69++PnJwcvPPOOxgwYIC809LTuLu7IzIystjhNxkZGejatSumTp2Kmzdv\nIjQ0FD179iyPFBhjjFVwelNUGzZsiISEBNSqVQsDBw5EtWrVcOTIETRo0KBMjw8PD0dYWBgcHBwU\n4+vXr0ft2rXRtWtXVK5cGVFRUUhISMDZs2fLIw29JnrPUfT8RO7LiZwbIH5+TEtvjlMFHq1tfvrp\np8jIyICTk9NzXaHm8UvHnTx5EsHBwfJtCwsL+Pn54cSJE6hRo8YLx8xYUeV5haG0S2mI3hit8/ny\nVYYY0x29Kao3b97EiBEj8PPPPyMvLw8mJibo3r075s6dC3t7+zLP5/FCnJ2dDScnJ8WYjY0N7t69\nq5O4DYnoPUd9yK+8rjAEAD4on/nqw1WGRO85ip4f09Kbojpw4EAYGxsjPj4eXl5eSElJwRdffIGB\nAwdi06ZNZZ7P42uqVlZWuH37tmIsKysL1tbWJT4+IiICPj4+AABbW1uEhITIX4jCTTjlfbtQ4ebM\nwmKhr7cLlSW/tEtpcnHQl/g5v7Lnx7f5dvPmzbFnzx5ER0cDgLy8ZI9I9HgVUkmVKlVw9epVWFhY\nyGP37t2Dm5sbsrKyyjyfyMhIXLp0CcuWLQMALFmyBMuXL8eBAwcAaNdc4+Pji23+LTyJv9oiRkYY\n3PVUo+dEl2na8soN4Pyee77PkF95Ef3cuKLnpy/LTn2gNzsqBQYGQqPRKMaSk5MRGBhYpscXFBQg\nJycH+fn5KCgowIMHD1BQUIDw8HCcOHEC69evR05ODiZOnIiQkBDupzLGGNM5vdn827JlS7Rp0wb9\n+/eHp6cnUlJSEBMTg379+uGHH3546mXgJk+ejEmTJsm3Y2JiEBUVhS+++ALr1q3DBx98gL59+6Jh\nw4ZYvXr1y0pLr+hDz7E8cX6GS+S1OED8/JiW3hTVgwcPws/PDwcPHsTBgwcBANWrV1fcBkq/DFxU\nVBSioqJKvO+NN95AYmKizmNmjDHGitKbosrHcZU/0a83yvkZLtF7jqLnx7T0pqfKGGOMGTouqhWI\nqGs5hTg/wyX6Wpzo+TEtLqqMMcaYjnBRrUBEPzcu52e4RN+nQvT8mBYXVcYYY0xH9L6olnY6Qfbs\nRO7JAZyfIRO95yh6fkxL74vq1q1b1Q6BMcYYKxO9L6qvv/662iEIQ+SeHMD5GTLRe46i58e0VD35\nw9KlS594zdSnnZqQMcYY0yeqFtUVK1aU6ULkXFR1Q+SeHMD5GTLRe46i58e0VC2qvEmEMcaYSPSq\np5qZmYkff/wRX375JQDg8uXLuHTpkspRiUPknhzA+Rky0X9gi54f09Kborp3714EBARg1apVmDx5\nMgAgKSkJw4YNUzkyxhhjrGz0pqh++OGHWL16NeLi4mBs/GirdMOGDXHo0CGVIxOHyD05gPMzZKL3\nHEXPj2npzaXfkpOT0apVK8WYiYkJCgoKVIqIMfa4MVFjkHYrTe0wnomrrSumR01XOwxWQehNUQ0K\nCkJcXBzatWsnj+3cuRN16tRRMSqxiHw9ToDzexnSbqXB5y3dx1CeuWk2asplvs+Cr6dacehNUZ01\naxY6deqEDh06ICcnB++88w42b96MTZs2qR0aY4wxViZ6U1QbNGiAhIQExMTEwMrKCl5eXjhy5Ag8\nPDzUDk0Yaq/llDfOz3CJnBvAPdWKRC+Kan5+PqytrXHr1i2MHj1a7XAYY4yx56IXe/8aGxvD398f\nGRkZaociNJGPcwQ4P0Mmcm4AH6dakejFmioA9O3bF507d8aIESPg6empOH1hy5YtVYyMMcYYKxu9\nKaoLFiwAAEycOLHYfRcvXnzZ4QhJ9L4V52e4RM4N4J5qRaI3RVWj0agdAmOMMfZC9KKnyl4O0ftW\nnJ/hEjk3gHuqFQkXVcYYY0xHuKhWIKL3rTg/wyVybgD3VCsSLqqMMcaYjlSYotq8eXOYm5vD2toa\n1tbWCAoKUjukl070vhXnZ7hEzg3gnmpFUmGKqiRJmD9/Pu7cuYM7d+4gMTFR7ZAYY4wJpsIUVQAg\nIrVDUJXofSvOz3CJnBvAPdWKpEIV1bFjx8LJyQlNmjTB3r171Q6HMcaYYPTm5A/lbcaMGahVqxYq\nV66M2NhYdO7cGfHx8ahWrZpiuoiICPj4+AAAbG1tERISIv/KLOyLlPftQoV9psJf8S96+6+1f8HV\nz1Vn83u8D1aW/NIupcEHun1+zs/w8ysai5r5ldftot9tNZ6/PPKJjo4GAHl5yR6RqIJuE23fvj06\nduyIDz74QB6TJEkvNhFHjIwwqAtBazZqED0nukzTllduAOf33PPVg/zK+yLlZc2vvIh+kXJ9WXbq\ngwq1+beiE71vxfkZLpFzA7inWpFUiKKalZWF7du3IycnB/n5+Vi5ciX279+Pdu3aqR0aY4wxgVSI\nnmpeXh4iIyNx+vRpVKpUCUFBQdi0aRP8/PzUDu2lKs9NbPqA8zNc+pLbmKgxSLuVpvP5pl1Kg6uH\nq87n62rriulR03U+X/b8KkRRdXR0xOHDh9UOgzGm59JupZVPTzy+fDZxazZqdD5P9mIqxOZf9og+\nrAmUJ87PcImcGyB+fkyLiypjjDGmI1xUKxDRz6/K+RkukXMDxM+PaXFRZYwxxnSEi2oFInpfh/Mz\nXCLnBoifH9PiosoYY4zpCBfVCkT0vg7nZ7hEzg0QPz+mxUWVMcYY0xEuqhWI6H0dzs9wiZwbIH5+\nTIuLKmOMMaYjXFQrENH7Opyf4RI5N0D8/JgWF1XGGGNMR7ioViCi93U4P8Mlcm6A+PkxLS6qjDHG\nmI5wUa1ARO/rcH6GS+TcAPHzY1pcVBljjDEd4aJagYje1+H8DJfIuQHi58e0uKgyxhhjOsJFtQIR\nva/D+RkukXMDxM+PaXFRZYwxxnSEi2oFInpfh/MzXCLnBoifH9PiosoYY4zpCBfVCkT0vg7nZ7hE\nzg0QPz+mxUWVMcYY0xEuqhWI6H0dzs9wiZwbIH5+TIuLKmOMMaYjXFQrENH7Opyf4RI5N0D8/JhW\nhSmqN27cQHh4OKysrODj44PY2Fi1Q3rp0s6lqR1CueL8DJfIuQHi58e0jNUO4GV5//33YWZmhmvX\nruH48ePo2LEjgoODUbNmTbVDe2ly7uaoHUK54vwMl8i5AeLnx7QqxJpqdnY21q9fj8mTJ8PCwgKN\nGzdGWFgYVqxYoXZojDHGBFIhiurZs2dhbGwMPz8/eSw4OBgnT55UMaqX71baLbVDKFecn+ESOTdA\n/PyYlkREpHYQ5W3//v3o0aMHrl69Ko8tWbIEq1atwu7du+WxkJAQJCQkqBEiY4wZrODgYMTHx6sd\nhl6oED1VKysr3L59WzGWlZUFa2trxRh/KBhjjL2ICrH5t0aNGsjPz8e5c+fksYSEBNSuXVvFqBhj\njImmQmz+BYC3334bkiTh+++/x7Fjx9CpUyccPHgQQUFBaofGGGNMEBViTRUAFixYgPv378PZ2Rl9\n+/bFwoULuaAyxhjTqQqzpsoYY4yVtwqxo1JFlJeXhzNnzuDWrVuwtbVFQEAATExM1A5LZ1JTUxEf\nH4+srCzY2toiODgYnp6eaoelM5mZmfj6668RHx+Pu3fvyuOSJGHfvn0qRqYbDx48QHR0dIn5/fjj\njypGphsXLlzA+PHjS8wvJSVFxchYeeOiKpgtW7Zg0aJF2LlzJ0xMTGBtbY07d+4gNzcXb7zxBt57\n7z106tRJ7TCfS25uLhYvXoxFixbhwoUL8PPzk/M7d+4cfHx8MGzYMLzzzjuoXLmy2uG+kN69eyM3\nNxc9evSAubm5PC5JkopR6c6AAQPwzz//oHPnznBxcYEkSSAiYfLr3bs3/Pz8MGvWLMX7x8THm38F\n0rhxY9ja2qJPnz5o1qwZ3N3d5fsuX76MvXv3YuXKlbh16xb++OMPFSN9PjVr1kSLFi3Qp08fNGjQ\nAMbG2t+E+fn5OHz4MFauXIndu3fj1KlTKkb64mxsbHDt2jWYmZmpHUq5sLW1xcWLF2FnZ6d2KOXC\nxsYGN2/eRKVKldQOhb1kXFQF8s8//+CVV17R2XT6Jj09HS4uLk+d7tq1a3B2dn4JEZWfJk2aIDo6\nWnEWMJEEBwdj+/btcHV1VTuUctGpUydERUUhNDRU7VDYS8ZFlTE9sXTpUnnzp0ajwapVqzBo0CC5\n8BRuHh00aJCaYerEzJkzsWbNGowYMaJYYW3ZsqVKUenO+++/j59++gldunRR/BCUJAmTJk1SMTJW\n3rioCkr0HUFKM336dIwZM0btMJ5L8+bNFT3F0nqMRU+taah8fHxK7Z9evHjxJUejexEREfL/hXkW\nvp/Lli1TKSr2MnBRFVSvXr3kHUHMzc0VO4JMmDBB7fDKTYcOHbB161a1w2CMVVBcVAUl+o4govvt\nt9/g7e2NgIAAeezMmTNISUlB69atVYxMd/Lz8/Hnn3/i8uXLcHd3R6NGjRQ7nxm6s2fPIjY2Fleu\nXIG7uzt69eqFGjVqqB0WK2cV5oxKFY23tzcePHigdhjsOQ0fPrzYBR+srKwwfPhwlSLSrdOnTyMo\nKAi9e/fG3Llz0bt3bwQGBiIxMVHt0HRi8+bNCA0NxZkzZ2Bvb4/Tp08jNDQUmzZtUjs0Vs54TVVQ\nIu4IUpaTO4hycH2VKlWQlZWlGHv48CFsbW2LXXHJELVo0QIdOnTAJ598IrcmZs6ciV9//VWInnHt\n2jqvgUsAACAASURBVLXx7bffokWLFvLYnj178MEHH+DEiRMqRsbKGxdVQYm4I8iePXvKNF3z5s3L\nNY6XISQkBDNnzsQbb7whj+3atQujRo0S4pq/dnZ2yMjIUBzHmZeXBycnJ9y6ZfgX9Lazs8P169cV\nm7NFyo+VTpwGBlPQaDRqh6BzIhTLspo4cSK6du2KwYMHo3r16jh37hyWLVsmzJ6jVatWxZ49exQ/\nGvbv3684YYkhCw4Oxtdffy3viU5EmDVrFkJCQlSOjJU3XlMVmMg7goSHh+Ojjz7C66+/Lo/t27cP\nc+fOxdq1a1WMTHcOHz6MpUuX4tKlS/D09MTgwYNRv359tcPSiV9++QW9e/dGp06d4OXlheTkZPz6\n66+IiYnBW2+9pXZ4LywxMRGdO3dGdnY2PD09kZqaCgsLC2zevBk1a9ZUOzxWjrioCur06dPo3Lkz\n7t+/L3+pzczMsHnzZiEueWdvb49r164V27zm4uKCGzduqBgZK6uzZ8/ip59+kveO7d69u2JvZ0OX\nl5eHv/76C1euXEHVqlXxn//8x+DPSc2ejouqoETfEcTd3R2nTp1ClSpV5LFbt24hMDAQaWlpKkam\nO8ePH8f+/fuRmZmJol9TPiMPY/qLi6qgRN8RZODAgcjJycHChQvlPWWHDx8OExMTREdHqx3eC1u8\neDFGjRqFNm3aYOvWrejQoQN+++03hIWFYdWqVWqH91yGDh2KJUuWAAD69etX4jSGfMavwMBAnD59\nGkDpe6qLsnc6K50YDTZWjOg7gsycORP9+vWDvb097O3tcePGDbRv3x4rVqxQOzSdmDFjBrZt24am\nTZvCzs4OGzZswLZt2xAbG6t2aM+tWrVq8v/Vq1eXt6AUZciXfiv8wQCg1M+hIefHyobXVAUl+o4g\nha5evYrU1FR4enrCzc1N7XB0xsbGRj4e1cHBAdeuXYORkRHs7e1x8+ZNlaN7cVevXi3x/Spt3NCs\nWbMG3bt3Lza+du1adOvWTYWI2MvCZ1QS1Jtvvoljx46hVq1auHPnDurUqYO///5bqIKamZmJHTt2\nYM+ePXBzc8Ply5eRmpqqdlg64eHhIR9P7O/vj02bNmH//v0wNTVVOTLdKG2HpFq1ar3kSMpHaVcS\nGjp06EuOhL1svPlXYDVq1EBkZKTaYZSLvXv3omvXrggNDcUff/yBzz77DElJSZg5cyY2b96sdngv\n7NNPP0ViYiJ8fX0xYcIEdO3aFbm5uZg7d67aoelESRvIbt++DSMjw/6df+HCBRARiAgXLlxQ3Hf+\n/HmYm5urFBl7WXjzr6AyMzPx9ddfl3jpt3379qkYmW6EhITg66+/RqtWrWBnZ4ebN28iJycHXl5e\nuHbtmtrh6dyDBw+Qm5tb7HzAhqZwB57Cw0yKyszMxNtvv42lS5eqEZpOPOlHgYuLC6KiovDuu+++\nxIjYy8ZrqoLq3bs3cnNz0aNHD8WvY1F2lEhOTkarVq0UYyYmJigoKFApIt27ceMGNm/eLB/H2alT\nJ7VDemGFO/C0b98eMTEx8hqrJElwcXFBYGCgmuG9sIcPHwIAmjZtKsSPV/bseE1VUDY2Nrh27RrM\nzMzUDqVcNGrUCF988QXatWsnr6n+9ttvmDZtWpnPEazPDh48iI4dOyIwMBDe3t5ITk7G6dOnsWXL\nFjRq1Ejt8F7YvXv3YGFhoXYY5ebSpUuwsLCAvb29PHbjxg3k5OQUW0NngiEmpMaNG1NSUpLaYZSb\ngwcPkoODA/Xr14/MzMxo6NCh5OrqSocOHVI7NJ2oX78+xcbGKsZWr15NoaGhKkWkW+Hh4bRv3z7F\n2N69e6lr164qRaRboaGhlJCQoBhLSEigBg0aqBQRe1l4TVUgS5culTfvajQarFq1CoMGDZIv/UZE\nkCSp1D0TDc3ly5cRExOD5ORkeHl5oW/fvvDw8FA7LJ2wtbXFjRs3FD26/Px8ODo6CnHyDtFPM1n0\nkKhCRIQqVaoIcek+VjruqQpkxYoVip6ph4cHduzYUWw6UYqqu7s7Ro8erXYY5cLf3x+xsbHo06eP\nPLZmzRr4+fmpGJXumJubIzs7W3GayezsbGHOjevs7IykpCT4+/vLY+fPn4ejo6OKUbGXgddUmcF4\n/NR2hT8gCtfACxnqae6K+vPPP9GxY0cEBATIJ+84e/YstmzZgsaNG6sd3gsT/TST06ZNw+rVqzF1\n6lT50n2RkZHo0aMHxo8fr3Z4rBwZ9kFhrFR169YtcTw0NPQlR6I71atXh5+fH/z8/GBra4uNGzei\noKAAnp6eKCgowKZNm2Bra6t2mC+MiODq6orTp0/j/fffx6uvvor//ve/OH/+vBAFFXh0msnbt2/D\n3t4eTk5OsLe3R1ZWFmbPnq12aDoxZswY9OvXD5988gnq16+Pzz77DP369cPYsWPVDo2VM15TFZS1\ntTXu3LmjGCMiODg4CNGzatOmDSIjIxXXUz1w4AAmTZqE3377TcXIXhwRwdLSEnfv3jX4kyE8jain\nmWQVFxdVwRRuIv3pp5/Qq1cvxZlrNBoNgEcn1jd0NjY2yMzMhImJiTyWl5cHe3v7Yj8mDFHjxo3x\n/fffC3Ht2ye5du2a4uQkgPLE+4bszJkzSEhIKJafKPs0sJLxjkqCqV69OoBH/cbq1avLRdXIyAhN\nmjQp8STfhqhu3boYO3YsJk+eDHNzc9y7dw8TJkwodbO3oWnRogXat2+PiIgIeHp6yld0EWXv7bi4\nOAwePBhXr15VjEuSJMQJPKZNm4ZJkyYhODi42PG4Irx/rHS8piqo7du3o23btmqHUW4uXryI3r17\n4+jRo/LJH0JDQ7Fq1Sr4+vqqHd4La968OYCSz4AlwkXmq1Wrhs8++wz9+/cX8iQQTk5O2LlzJ155\n5RW1Q2EvGRdVQYWEhGDAgAHo3bs3XFxc1A6n3KSkpODKlStwc3ODt7e32uGwMrK3t0dmZqYwp818\nnLe3N86ePSvMVYVY2VWKioqKUjsIpnvOzs7YvHkzRowYgQMHDsDIyAj+/v6Kg+1FUKVKFXh4eAix\n1+/jbt26hbVr12L79u3QaDTw9PQU5ionGRkZSE1NRb169dQOpVw4ODhg8eLFePXVV2FpaSlfuebx\nw7+YeHhNVXA3btzAzz//jJiYGJw4cQLh4eHo168fWrZsqXZo7Al27dqFLl26ICAgQHHu33Xr1hW7\nkIAhatKkCQ4fPgxvb2/5jF+AOFdRKm2vbVF6xqx0XFQrgHv37mH9+vX4f3v3HlRltb8B/NkgChps\n2KLIZSOJlqh5z9Q0OZaKZCocURMBD5QTpgV2oV8iqUdPZWqOnuw4ZV62t8JjeQm1Kc1rZygjLQxR\nUTdXBTd3hM3t94fDe9ypeSY2rN61n8+MM7HYfzyMyfdd613ru959910YjUZ07twZGo0GH3zwAcaM\nGSM6Ht1FQEAAFi9ejKlTpypjycnJWLhwITIyMgQms457NXjQaDSIiopq3TAtoGmn/d34+fm1Wg5q\nfSyqkmpsbMShQ4ewdetW7Nu3D0OHDkVkZCRCQ0Ph5OSE3bt3Y86cOSgoKBAdle7C1dUVN27cgL29\nvTJWW1uLTp06SdH7l0hWLKqS6tKlCzp27IjIyEiEh4fftdF8YGCgqq9J+/XXX5GcnIxr167hgw8+\nQEZGBsxmsxQ7LufNm4fu3bvj5ZdfVsbWrFmDCxcuYO3atQKTWcftlz/8lgxHTn7bUhP4705uGdpo\n0r2xqErq+++/x6OPPio6RotJTk7GnDlzEBoaiu3bt6O8vBzff/89/u///g9ff/216HjN9vjjjyM1\nNRWdO3eGt7c3cnNzcf36dTz22GPKL2c1v38MDAy0KKoFBQVKG0YZjgwtWrRIOVsM3Pr5/v3vfyM8\nPByrV68WnI5aEouqpDZv3owBAwZYzNrOnDmDs2fP3vUpWm169uyJnTt3on///so51draWnh6eqKo\nqEh0vGb7X5rKy/L+scknn3yCc+fOYcWKFaKjtIgffvgBixYtwv79+0VHoRbEoiopX19f/PTTT9Dp\ndMrYjRs3MGDAABiNRoHJrKNjx44oLCyEnZ2dRVH19vbG9evXRcejP6C+vh7u7u4oLi4WHaVF1NXV\nwc3NTYo2mnRvch1aJEV5ebnFXZUAlCu2ZDBw4EAYDAaLmdqnn36KIUOGCExlPY2Njfjkk0+wY8cO\n5OXlwdvbG9OmTUNMTIwU5xwbGhosvq6qqoLBYICbm5ugRNb1zTffWPw9VVZWYufOnejdu7fAVNQa\nWFQlFRAQgF27dmHatGnK2Oeffy5Ng/a1a9dizJgx2LBhA6qqqjB27FhkZmaq/oaaJgkJCdizZw/i\n4uLg6+sLo9GIlStX4vz583jvvfdEx2u2uzUh8fb2xkcffSQgjfX99uGnQ4cO6N+/P3bs2CEwFbUG\nLv9K6sSJEwgODsaYMWPQrVs3XLp0CV9//TVSUlIwYsQI0fGsorKyEvv378fVq1fh6+uLp59+Gs7O\nzqJjWUWnTp3w448/Qq/XK2PZ2dkYMGCAat8ZFxcXKzPRq1evWtyg1KFDB3Tq1ElUNKvYu3cvJk6c\nCAAwm81o27at4EQkAouqxK5evYrt27cjJycHer0e4eHhFr+kZZCTk6Msj3p7e4uOYzX+/v44ffq0\nRfvFkpISDBo0CJcuXRKY7I9zcXFBWVkZAOCpp56SYpf27W6/w/j2n5VsC4sqqZLRaER4eDi+++47\n6HQ6mEwmDBs2DFu3bpWisf7atWvxxRdfICEhAXq9HkajEStWrMCkSZMQHBysfE5Nd496eHjgm2++\nQUBAAFxdXe/5fl+tF7P36NEDL730Enr16oVnnnnmnrt82SJUbiyqEomPj8frr78OT0/Pe34mPz8f\ny5cvx/vvv9+KyawvMDAQ/fv3x7Jly9ChQwdUVFRg4cKFSEtLU3VDiyb/S2FRWx/ZDz/8EK+88gqq\nq6vv+Rm1/Uy3O3nyJJKSkmA0GpGVlQVfX9+7fu7y5cutnIxaE4uqRNavX49ly5YhICAAo0aNwsMP\nPwxnZ2eUlZUhMzMTR48eRUZGBhITE/H888+LjtssLi4uKCoqsnhvZTab0bFjRx5Z+BOrra1FQUEB\nAgICkJ6ejrv9+pGhN66/v79ql+mpeVhUJWM2m7Fnzx4cOHAAv/zyC0pKSuDm5oa+ffsiODgYEyZM\ngIODg+iYzTZ27FgkJSVZbLo6efIkFi9eLM0OYJllZmbioYceEh2DyOpYVEmVXnjhBWzfvh0TJkyA\nj48PsrOzkZKSghkzZsDd3R3AraXEJUuWCE76x9TW1mLdunU4evQobty4oZzrVHNrQiJboM4dAWTz\nqqurERoairZt26KwsBDt2rVDSEgIqqurkZOTg+zsbGRnZ4uO+YfNnz8f69evxxNPPIEffvgBf/3r\nX3H9+nX85S9/ER2NiH4HZ6pEf0JeXl747rvv0LVrV6UTVkZGBmbPns2ZKtGfGGeqpEqTJ0/G559/\njtraWtFRWsTNmzeVM8Xt27dHZWUlHn74YaSlpQlOZh1nzpwRHaFFrV69GoWFhaJjkAAsqqRKTzzx\nBJYsWQIPDw/Exsbi1KlToiNZVc+ePfHDDz8AAAYNGoTFixdj6dKld70XV42efPJJ9OvXDytWrEB+\nfr7oOFZ3+PBh+Pn5YcKECfj0009RU1MjOhK1Ei7/Sqy0tBTnz59HRUWFxbhMh8/T09NhMBiwY8cO\ntG3bFjNnzsTMmTPh7+8vOlqzpKamok2bNhg4cCAyMzMRGxuLiooKrFixAiNHjhQdr9lqa2uRkpIC\ng8GAgwcPYvjw4YiMjERoaCjat28vOp5VFBUVYefOndi6dSsyMjIwZcoUREREYNSoUaKjUQtiUZXU\npk2b8OKLL+KBBx6445eUjIfPjx07hrlz5yI9PR0dOnTAkCFDsHLlSvTr1090NLqPkpISJCcnY82a\nNbhy5QpCQkIwe/ZsaXpUA7eWuyMjI/Hzzz9Dr9fj+eefR1xcHB544AHR0cjKuPwrqTfffBO7du3C\ntWvXcPnyZYs/smhqZNGtWzfMnj0b06ZNw+XLl3Ht2jUEBwdj8uTJoiPSfVRUVOCLL77Ap59+itzc\nXEybNg09evRAREQE5syZIzpeszQ2NuLrr7/GrFmzEBgYiM6dO2PLli3YunUr0tLSEBQUJDoitQDO\nVCXl4eGBvLw82Nvbi47SIgYPHozLly9j6tSpiIqKwtChQ+/4jJ+fH65cudL64ei+9u/fj61bt+LL\nL7/E448/jqioKISEhMDR0REAYDKZ4Ovre8erC7V49dVXsWPHDmi1WkRGRmLmzJkW78Nra2vh5uam\n2p+P7o1FVVKrVq1CWVkZkpKSVNug/Pfs2rULEydO5PVaKtWnTx9ERUUhPDwcXl5ed/3MRx99pNp2\nmi+++CJmzZqFRx999J6f+fXXX6W535j+i0VVIr+91q2goAAODg7o2LGjMqbRaGA0Gls7mtUNGDDg\nrsdLBg8erOyaJRItNzcXeXl58PLykupqQrq3NqIDkPUYDAbREVrNxYsX7xhrbGxEVlaWgDTWFxMT\ngzVr1qBDhw7KWF5eHqKjo3Hw4EGByayjpqYGS5cuxY4dO5SiM336dCQmJipLwGom+9WEdG8sqhIJ\nDAwUHaHFRUREALj1SzkyMtLilpMrV66gd+/eoqJZVWVlJfr164ctW7Zg+PDh2LlzJ+bNm4eYmBjR\n0awiNjYWmZmZWLt2LXx9fWE0GrFs2TLk5uZi48aNouM1W2RkJAYNGoSDBw9aXE0YFRUlxdWEdG9c\n/pVUSEgI5s+fb3Gm8dixY1izZg127dolMFnzLFq0CADw9ttv480331SKqp2dHTw8PBAWFgadTicw\nofVs27YNcXFx6NmzJ/Lz87Fp0yZpjpnodDpcunQJbm5uypjJZIK/vz+Ki4sFJrMOXk1ouzhTldTR\no0eRnJxsMTZs2DDVHzNpKqpDhw6V/kiCl5cXHB0dcenSJfTq1Uv1DS1u5+npiaqqKouievPmzXtu\nWlKboUOHIjU11eIh6Pvvv8ewYcMEpqLWwKIqKScnJ1RWVkKr1SpjlZWV0uyWlb2gvvrqqzAYDPjw\nww8xYcIELFiwAH379sUHH3yAqVOnio7XbBERERg/fjzmzp0LvV4Po9GIdevWITIyEocPH1Y+p9bu\nX926dVPuL/7t1YQLFy4EoO6rCeneuPwrqb/97W+orq7Gv/71L+WWkzlz5sDBwQGbNm0SHY/uIzg4\nGBs3boSHh4cyduzYMURFRUnRwMPPzw/ArcLSpLGx0eJrQL3dv2bNmqX8t0ajUV5TNP18TT+rDO+P\nyRKLqqRMJhMiIiJw8OBBZffh+PHjYTAYLJbcSF3Kysrg4uIiOgYR3QOLquTy8/ORnZ0NvV4PT09P\n0XHodxw7dgxPPPEEAFgsgf6WWpdEZXflyhVlBv57R7u6devWSolIBBZVG9DY2Ghx9ES2DkunTp3C\n8OHDRcdotj59+uCXX34BcGt59LdLoU3UuiR6u59++gnz589HWlqaRas+jUYDs9ksMNkf5+zsrOzs\nvde/MY1Gg/r6+taMRa2MRVVSubm5mDt3Lo4ePYrS0lKLdzqy/aN2c3OT4hjG7err66Xt2wwAAQEB\nmDJlCqZOnQonJyeL73Xv3l1QKqLm4+5fSb3wwgtwcnLC4cOHMWrUKBw9ehSLFy/G+PHjRUej+6ir\nq4OzszNKSkrQrl070XFaREFBAZYsWXLP2bja5ebmwsnJyeLMtMlkQnV1tTTHhuju5FoHJMXJkyfx\nySefoH///gCA/v37Y8OGDVi1apXgZHQ/bdq0QY8ePVBUVCQ6SouJjIzEtm3bRMdoMZMmTUJOTo7F\nWE5ODkJCQgQlotbC5V9Jde7cGUajEY6OjvDz80Nqaiq0Wi3c3d1V39Hl994Jy7K8vXz5cuzcuRMv\nvfQS9Hq9xYxOho1KBQUFGDp0KDp06IDOnTsr4xqN5nc3aamFi4sLysrKLMYaGxuh1WrvGCe5cPlX\nUkOGDMGBAwcQEhKCcePGYdq0aXBycsLgwYNFR2u2hoYG5b8bGxuh0+mke6e6bt06AMDixYvv+J4M\nG5XCwsLg7+9vcYcqAGmWgzt37owLFy6gR48eytilS5fg7u4uMBW1Bs5UJVVSUoKGhgbodDpUVVVh\n5cqVqKioQFxcnHRHa2TcqCQ7Z2dnFBUVSfvO+B//+Ad27tyJZcuWwd/fHxcvXsTChQsxdepULFiw\nQHQ8akEsqqR6MhbVSZMmYc+ePXeMh4aGYvfu3QISWVdwcDCWLVuGAQMGiI7SIurr67Fq1Sps2LBB\nOSf+3HPPYf78+dIdaSNLLKqSMpvNWLp0KQwGA/Ly8uDt7Y2ZM2ciMTFRmv6/TU6cOCHN7S1Nbj/z\neDtZHiDmzJmD5ORkhIaG3vFOlf1wSc34TlVSCQkJSE1Nxfr165X7KpcsWYKysjKsXr1adDyrkqmg\nNjVbN5vNSEpKsmjakZWVpXTsUbuqqio8/fTTMJvNyi7Zu/X+VavDhw/Dz88P3bp1Q35+PhISEmBv\nb4+3334bXbp0ER2PWhBnqpLy9vbGmTNnLDZGFBUVoW/fvsjLyxOYjH5PUyP27du3Izw8XBnXaDTw\n8PBATEwMmyOoQM+ePfHVV1/B19cXzz77LDQaDRwdHVFUVIS9e/eKjkctiDNVoj+RphuEhg8fjtmz\nZ4sN04Jk742bl5cHX19f1NbW4tChQ7h69SratWsn3SZBuhOLqqTCwsIwceJEJCUloWvXrrhy5QqW\nLl2KsLAw0dHof9BUUMvLy1FUVGSxDCxD0bnXbFuWc8YuLi4oKChAeno6evfuDWdnZ9TU1KC2tlZ0\nNGphLKqSWr58OZYuXYq5c+ciLy8PXl5eePbZZ5GYmCg6Gv0Pzp07h/DwcJw5c8ZiXJaic/tZY+BW\nM4hFixZh5MiRghJZ17x58zBkyBDU1NQoexhOnjyJgIAAwcmopfGdqoTq6uoQExOD9evXWxysl0lN\nTQ02bdqEn3766Y5bTrZs2SIwmXWMGjUKAwcOxFtvvYUHH3wQly9fxptvvolhw4YhIiJCdLwWUV1d\njYcffhhXr14VHcUqzp8/D3t7e2VWnpmZiZqaGjzyyCOCk1FLYlGVlKenJ4xGIxwcHERHaRHTp0/H\n2bNn8cwzz8DJyQkajUbZPfrWW2+Jjtdsrq6uKCwshIODA7RaLUpLS1FZWYk+ffpI0VHpbs6cOYOn\nnnoKhYWFoqMQ/WFc/pVUfHw8kpKSsHjxYunOpQLAwYMHcfnyZbi5uYmO0iKcnJxgNpvh4OCATp06\n4erVq9DpdLhx44boaFbx22XeqqoqpKenIykpSVAiIutgUZXUmjVrcO3aNaxatQqdOnVSzv9pNBoY\njUbB6Zqva9euqKmpER2jxYwYMQLJycmYNWsWpkyZgvHjx6Ndu3ZSNNMHgJiYGIuvO3TogH79+uGh\nhx4SlIjIOrj8K6lvv/32nt8LDAxstRwtZeXKlUhOTsZLL710x2F6WQpPk/r6emzfvh0VFRWIjIxE\nhw4dREciontgUSVV8vPzu2f3HVnfOcpE9o1mZLu4/CupmpoaLF26FDt27FCO1EyfPh2JiYlS7Ai+\ncuWK6AgtqqSkBGvWrEFaWtodReerr74SmMw6oqKilI1mHh4eyrgsbQrJdrGoSio2NhaZmZlYu3at\n0vt32bJlyM3NxcaNG0XHs4q6ujqcOnUKubm58Pb2xvDhw9GmjRz/S4eFhaGhoUHa+0Zl32hGtovL\nv5LS6XS4dOmSxS8tk8kEf39/KW45ycjIwDPPPIObN29Cr9cjOzsbjo6O2LdvnxQH7LVaLa5fvy7t\nfaP9+vXDoUOH2FyepCPHYz3dwdPTE1VVVRZF9ebNm/Dy8hKYynpiY2Mxe/ZsvPrqq8oZ1ZUrV2LO\nnDk4cuSI6HjNNnz4cGRkZKBfv36io7SIyMhITJ482SY2mpFt4UxVUu+88w62b9+OuXPnQq/Xw2g0\nYt26dZgxYwYeffRR5XNq/QXm5uaGoqIi2NvbK2O1tbXo1KkTSkpKBCazjmvXrmH8+PEYNmwYPDw8\nlN6/Go1GirOc3GhGsmJRlVTTvZu3/+K6232Vav0F1rt3b6xZswZPPvmkMnb48GHMmzcP6enpApNZ\nR0xMDPbv34+RI0fCycnJ4nsGg0FQKiK6HxZVUqW9e/dixowZmDBhAnx9fXH16lV8+eWX2Lp1KyZP\nniw6XrM5Ozvj/Pnz0izXE9kKO9EBqOXU19fj5MmTSE5OxsmTJ6W43aTJxIkT8eOPP6J3794oLy/H\nI488gtOnT0tRUAHgwQcflLZvM5HMOFOV1NmzZzF58mRUV1fDx8cHOTk5cHR0xO7du9G/f3/R8eg+\nVqxYgd27d2PevHkW5zgB9b4HJ7IFLKqSGjRoEGbMmIH58+dDo9GgoaEBq1evxrZt23D69GnR8Zrt\nxo0bWLFixV078hw7dkxgMuvgRh4idWJRlZSLiwuKi4stdsfW1dVBp9OhrKxMYDLrGDduHMxmM6ZO\nnWqxkUej0SAqKkpgMiKyZTynKqng4GDs2bMHoaGhyti+ffsQHBwsMJX1fPfdd7h+/boULReJSB4s\nqpKqq6vD9OnTMXjwYPj4+CA7OxunT5/GpEmTEBERAUDdzcv79u2LnJwcdO/eXXQUIiIFi6qk+vTp\ngz59+ihf9+rVC+PGjVPe093tzOqf3YYNG5TMo0ePRlBQEKKjo5WOPE0/U3R0tMiYRGTD+E6VVCMw\nMPC+zSwASNGmkIjUiUVVYmazGefPn0dRURFu/2vmkQwiopbB5V9JnThxAmFhYaipqUFpaSm0Wi3K\nysrg6+uLrKws0fGabcCAAUhLS7tjfPDgwfjhhx8EJCIiYkclacXFxeG1116DyWSCi4sLTCYTkpKS\nEBsbKzqaVVy8ePGOscbGRikeGIhIvbj8KymtVovi4mLY2dnB1dUVJSUlMJvN8PPzQ15enuh4zSIG\nfQAAEA1JREFUf1jTzuVPP/0U06dPt1jWvnLlCgDg+PHjIqIREXH5V1ZarRalpaVwc3ODl5cX0tPT\n4e7ujsrKStHRmsXf3x/AreNA/v7+SlG1s7PDiBEjEBYWJjIeEdk4FlVJhYSEICUlBeHh4YiOjsbo\n0aPRpk0bTJkyRXS0Zlm0aBEAYNiwYRg3bpzYMEREv8HlXxtx/PhxlJeXIygoCHZ26n+V3r9/f0RF\nRWHGjBl3NJwnIhKFRZVUaffu3TAYDPjqq6/wxBNPICIiAqGhoWxbSERCsaiSqplMJnz22WfYunUr\nfvnlF4SEhCAiIoJncYlICBZVUr2qqirs3r0b7777LoxGIzp37gyNRoMPPvgAY8aMER2PiGyI+l+u\nkU1qbGzEwYMHMXPmTHh6esJgMOCNN95AQUEBLly4gHfeeUc5fkNE1Fo4U5VUWloaOnbsCF9fX2XM\naDSiuLgY/fr1E5jMOrp06YKOHTsiMjIS4eHh8PHxueMzgYGB+Pbbb1s/HBHZLBZVSfXu3Rv79u1D\nt27dlLGLFy8iNDQUZ8+eFZjMOr7//ns8+uijomMQEVng8q+ksrOzLQoqcKtxwuXLlwUlsq5z587d\n8XBw5swZGAwGQYmIiFhUpeXj44PTp09bjKWlpcHb21tQIutauHDhHUu+Pj4+WLBggaBERETsqCSt\n+Ph4TJo0CQkJCfD398fFixexYsUKaYpOeXk5tFqtxVhTa0YiIlFYVCX1/PPPw9XVFR9//DFycnKg\n1+uxatUq1bcpbBIQEIBdu3Zh2rRpytjnn3+OgIAAgamIyNZxoxKp0okTJxAcHIwxY8agW7duuHTp\nEr7++mukpKRgxIgRouMRkY1iUZWIwWBQzmZu2LABGo3mrp+Ljo5uzVgt5urVq9i+fbsyEw8PD4de\nrxcdi4hsGIuqRIKDg5GSkgLg1hnNexXVI0eOtGYsIiKbwaJKqhEfH4/XX38dnp6e9/xMfn4+li9f\njvfff78VkxER3cKNSpIqLCyEo6MjnJ2dUVdXhy1btsDe3h4RERGqvfqtZ8+eeOyxxxAQEIBRo0bh\n4YcfhrOzM8rKypCZmYmjR48iIyMDiYmJoqMSkY3iTFVSQ4YMwfr16zFgwAAkJCRg//79cHBwQGBg\nIFavXi063h9mNpuxZ88eHDhwAL/88gtKSkrg5uaGvn37Ijg4GBMmTICDg4PomERko1hUJeXm5gaT\nyQSNRgNvb2+cOnUKzs7O6NWrFwoKCkTHIyKSEpd/JWVvb4+amhpcuHABrq6u6Nq1K+rr61FRUSE6\nGhGRtFhUJRUUFISpU6fixo0bSoOEc+fO3fU2FyIisg4u/0qquroamzdvRtu2bREREYE2bdrgyJEj\nuHbtGqZPny46HhGRlFhUbcTNmzdhZ2eHdu3aiY5CRCQtdZ6toPt65ZVXkJqaCgD48ssvodPp4Obm\nhr179wpOZj2lpaVITU3F4cOHLf4QEYnCmaqkunTpgqysLLRv3x5DhgxBQkICtFot4uPj8fPPP4uO\n12ybNm3Ciy++iAceeADt27e3+J4sd8YSkfqwqEqq6Rq0oqIiBAQEoLCwEADg7OyM8vJywemaz8vL\nCxs2bMD48eNFRyEiUnD3r6R69OiBbdu24cKFCxgzZgyAW12WfjurU6v6+nqMHTtWdAwiIgt8pyqp\ndevW4Z///CeOHDmCJUuWAAAOHTokTSFKSEjA3//+dzQ0NIiOQkSk4PIvqcZvr3UrKCiAg4MDOnbs\nqIxpNBoYjcbWjkZEBIDLv1Izm804f/48ioqKcPuz0+jRowWm+uMMBoPoCEREv4szVUmdOHECYWFh\nqKmpQWlpKbRaLcrKyuDr64usrCzR8YiIpMR3qpKKi4vDa6+9BpPJBBcXF5hMJiQlJSE2NlZ0NKsI\nCQnB8ePHLcaOHTuGKVOmCEpERMSZqrS0Wi2Ki4thZ2cHV1dXlJSUwGw2w8/PD3l5eaLjNZtOp8P1\n69fRps1/32DU1tbCw8MDJpNJYDIismWcqUqq6ZwqcOtMZ3p6OoqLi1FZWSk4mXU4OTnd8bNUVlai\nbdu2ghIREbGoSiskJAQpKSkAgOjoaIwePRoDBw6UZnl07NixeOGFF5QHh9LSUrz44osICgoSnIyI\nbBmXf23E8ePHUV5ejqCgINjZqf9ZymQyISIiAgcPHoROp4PJZML48eNhMBjg5uYmOh4R2SgWVVK1\n/Px8ZGdnQ6/Xw9PTU3QcIrJxLKoSGTly5H0/o9FocOzYsVZI03oaGxstzuHKMBMnInVi8weJxMTE\n3PczGo2mFZK0vNzcXMydOxdHjx5FaWmpUlQ1Gg3q6+sFpyMiW8WiKpFZs2aJjtBqXnjhBTg5OeHw\n4cMYNWoUjh49isWLF/PWGiISisu/kpo3bx6effZZDB8+XBk7deoUPvvsM6xevVpgMuvQ6XQwGo14\n4IEHlONDJpMJw4cPR0ZGhuh4RGSjWFQl5e7ujtzcXLRr104Zq66uhl6vV+5WVbPOnTvDaDTC0dER\nfn5+SE1NhVarhbu7uxT3xRKROnFHh6Ts7OzuuBatoaEBsjxDDRkyBAcOHAAAjBs3DtOmTUNISAgG\nDx4sOBkR2TLOVCUVGhqKBx98EO+99x7s7OxQX1+PN954AxcvXsTnn38uOl6zlZSUoKGhATqdDlVV\nVVi5ciUqKioQFxfHozVEJAyLqqSys7MxYcIE5Ofno2vXrjAajfD09MS+ffvuuJeUiIisg0VVYvX1\n9UhNTVWaIzz22GPSnOE0m81YunQpDAYD8vLy4O3tjZkzZyIxMZH9f4lIGBZVUqX4+Hikpqbirbfe\ngq+vL4xGI5YsWYLBgwdLsbuZiNSJRZVUydvbG2fOnIG7u7syVlRUhL59+0pxtR0RqZMca4FERER/\nAiyqpEphYWGYOHEiDh48iF9//RUHDhzApEmTEBYWJjoaEdkwLv+SKjVtVNq+fTvy8vLg5eWFZ599\nFomJiRYNL4iIWhOLKqlOXV0dYmJisH79ejg6OoqOQ0SkYFElVfL09ITRaISDg4PoKERECr5TJVWK\nj49HUlISzGaz6ChERArOVEmVfHx8cO3aNdjZ2aFTp07KPbEajQZGo1FwOiKyVbxPlVRp69atoiMQ\nEd2BM1UiIiIr4TtVUqWamhosXLgQ3bt3R/v27dG9e3ckJiaiurpadDQismFc/iVVio2NRWZmJtau\nXav0/l22bBlyc3OxceNG0fGIyEZx+ZdUSafT4dKlS3Bzc1PGTCYT/P39UVxcLDAZEdkyLv+SKnl6\neqKqqspi7ObNm/Dy8hKUiIiIy7+kUhERERg/fjzmzp0LvV4Po9GIdevWITIyEocPH1Y+N3r0aIEp\nicjWcPmXVMnPzw8AlPOpANDY2GjxNQBcvny5NWMRkY1jUSUiIrISLv+SatXX1+M///mPckvN0KFD\nYW9vLzoWEdkwFlVSpbNnz2Ly5Mmorq6Gj48PcnJy4OjoiN27d6N///6i4xGRjeLyL6nSoEGDMGPG\nDMyfPx8ajQYNDQ1YvXo1tm3bhtOnT4uOR0Q2ikWVVMnFxQXFxcUWy711dXXQ6XQoKysTmIyIbBnP\nqZIqBQcHY8+ePRZj+/btQ3BwsKBEREScqZJKTZkyBXv37sXgwYPh4+OD7OxsnD59GpMmTYKjoyOA\nW8dttmzZIjgpEdkSblQiVerTpw/69OmjfN2rVy+MGzdOOad6tzOrREQtjTNVIiIiK+FMlVTLbDbj\n/PnzKCoqwu3PhmxNSESisKiSKp04cQJhYWGoqalBaWkptFotysrK4Ovri6ysLNHxiMhGcfcvqVJc\nXBxee+01mEwmuLi4wGQyISkpCbGxsaKjEZEN4ztVUiWtVovi4mLY2dnB1dUVJSUlMJvN8PPzQ15e\nnuh4RGSjOFMlVdJqtSgtLQUAeHl5IT09HcXFxaisrBScjIhsGYsqqVJISAhSUlIAANHR0Rg9ejQG\nDhyIKVOmCE5GRLaMy78khePHj6O8vBxBQUGws+OzIhGJwaJKRERkJXykJyIishIWVSIiIithUSUi\nIrISFlVSpbS0NBiNRosxo9GIM2fOCEpERMSiSio1c+ZM1NXVWYyZzWZEREQISkRExN2/pFIuLi4o\nKyuzGGtsbISLiwvKy8sFpSIiW8eZKqmSj48PTp8+bTGWlpYGb29vQYmIiHhLDalUfHw8Jk2ahISE\nBPj7++PixYtYsWIFFixYIDoaEdkwLv+SaiUnJ+Pjjz9GTk4O9Ho9nnvuObYpJCKhWFSJiIishMu/\npBoGg0HZ3bthwwZoNJq7fi46Oro1YxERKThTJdUIDg5WbqYJDAy8Z1E9cuRIa8YiIlKwqBIREVkJ\nj9SQKhUWFirnUevq6vDJJ59g8+bNaGhoEJyMiGwZiyqp0tNPP42LFy8CABYsWICVK1fi/fffx/z5\n8wUnIyJbxuVfUiU3NzeYTCZoNBp4e3vj1KlTcHZ2Rq9evVBQUCA6HhHZKO7+JVWyt7dHTU0NLly4\nAFdXV3Tt2hX19fWoqKgQHY2IbBiLKqlSUFAQpk6dihs3bmDatGkAgHPnzsHHx0dwMiKyZVz+JVWq\nrq7G5s2b0bZtW0RERKBNmzY4cuQIrl27hunTp4uOR0Q2ikWVpHDz5k3Y2dmhXbt2oqMQkQ3j7l9S\npVdeeQWpqakAgC+//BI6nQ5ubm7Yu3ev4GREZMs4UyVV6tKlC7KystC+fXsMGTIECQkJ0Gq1iI+P\nx88//yw6HhHZKBZVUiWtVovS0lIUFRUhICAAhYWFAABnZ2deUk5EwnD3L6lSjx49sG3bNly4cAFj\nxowBcKvLUvv27QUnIyJbxqJKqrRu3Tq8/PLLaNu2LTZs2AAAOHToEMaOHSs4GRHZMi7/EhERWQln\nqqRaZrMZ58+fR1FREW5/Nhw9erTAVERky1hUSZVOnDiBsLAw1NTUoLS0FFqtFmVlZfD19UVWVpbo\neERko3hOlVQpLi4Or732GkwmE1xcXGAymZCUlITY2FjR0YjIhvGdKqmSVqtFcXEx7Ozs4OrqipKS\nEpjNZvj5+SEvL090PCKyUZypkio1nVMFAC8vL6Snp6O4uBiVlZWCkxGRLWNRJVUKCQlBSkoKACA6\nOhqjR4/GwIEDMWXKFMHJiMiWcfmXpHD8+HGUl5cjKCgIdnZ8ViQiMVhUiYiIrIRHakg1Ro4ced/P\naDQaHDt2rBXSEBHdiUWVVCMmJua+n9FoNK2QhIjo7rj8S0REZCXc0UGqNG/ePJw6dcpi7NSpU4iL\nixOUiIiIM1VSKXd3d+Tm5qJdu3bKWHV1NfR6vXK3KhFRa+NMlVTJzs4ODQ0NFmMNDQ3gMyIRicSi\nSqo0YsQIJCYmKoW1vr4eb7311v+0Q5iIqKVw+ZdUKTs7GxMmTEB+fj66du0Ko9EIT09P7Nu3D3q9\nXnQ8IrJRLKqkWvX19UhNTUV2djb0ej0ee+wxdlMiIqFYVImIiKyEj/VERERWwqJKRERkJSyqRERE\nVsKiSkREZCX/D2lbGZgZrg2GAAAAAElFTkSuQmCC\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10ed1da90>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 35
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"This is a pretty significant performance gain. The \"Cython + type declarations\" approach sped up our initial Python code 25 times."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"explicit_loops\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"# Appendix III: Cython performance after replacing list comprehensions by explicit for loops"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In Python, we have those wonderful list, set, and dictionary comprehensions, which do not only look prettier and are easier to read (at least most of the time) than nested loop structures, but they also additionally come with some small performance benefits. \n",
|
|
"Does this also apply in Cython? Let's check it out."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"This is the code for our \"classic\" least squares approach that we have been using in the previous sections:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def lstsqr_comprehensions(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 46
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"And here is a version where I replaced the list comprehensions by for-loops:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def lstsqr_loops(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" for x_i in x:\n",
|
|
" var_x += (x_i - x_avg)**2\n",
|
|
" cov_xy = 0\n",
|
|
" for x_i, y_i in zip(x,y):\n",
|
|
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 48
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"Finally, the Cython versions of the two functions (with and without using list comprehensions) that we have defined above:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%load_ext cythonmagic"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": []
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"\n",
|
|
"def cy_lstsqr_comprehensions(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" cdef double x_avg, y_avg, var_x, cov_xy, slope, y_interc, x_i, y_i\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 49
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"\n",
|
|
"def cy_lstsqr_loops(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" cdef double x_avg, y_avg, var_x, cov_xy, slope, y_interc, x_i, y_i\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" for x_i in x:\n",
|
|
" var_x += (x_i - x_avg)**2\n",
|
|
" cov_xy = 0\n",
|
|
" for x_i, y_i in zip(x,y):\n",
|
|
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 50
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"We will generate some sample data for different sample sizes and take a look at the results for the regular Python functions, and the Cython code separately."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"funcs = ['lstsqr_comprehensions', 'lstsqr_loops',\n",
|
|
" 'cy_lstsqr_comprehensions', 'cy_lstsqr_loops'] \n",
|
|
"\n",
|
|
"orders_n = [10**n for n in range(1, 6)]\n",
|
|
"times_n = {f:[] for f in funcs}\n",
|
|
"\n",
|
|
"for n in orders_n:\n",
|
|
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
|
|
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
|
|
" for f in funcs:\n",
|
|
" times_n[f].append(timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 52
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"plt.figure(figsize=(8,6))\n",
|
|
"plt.plot(orders_n, times_n['lstsqr_comprehensions'], alpha=0.5, \n",
|
|
" label='list comprehensions', marker='o', lw=2)\n",
|
|
"plt.plot(orders_n, times_n['lstsqr_loops'], alpha=0.5, \n",
|
|
" label='for-loops', marker='o', lw=2)\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.legend(loc=2)\n",
|
|
"plt.grid()\n",
|
|
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
|
|
"plt.title('Performance comparison list comprehensions and for-loops')\n",
|
|
"plt.show()\n",
|
|
"\n",
|
|
"plt.figure(figsize=(8,6))\n",
|
|
"plt.plot(orders_n, times_n['cy_lstsqr_comprehensions'], alpha=0.5, \n",
|
|
" label='list comprehensions (Cython', marker='o', lw=2)\n",
|
|
"plt.plot(orders_n, times_n['cy_lstsqr_loops'], alpha=0.5, \n",
|
|
" label='for-loops (Cython)', marker='o', lw=2)\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.legend(loc=2)\n",
|
|
"plt.grid()\n",
|
|
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
|
|
"plt.title('Performance comparison list comprehensions and for-loops in Cython')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAfEAAAGJCAYAAACaQwrRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd4VFX++PH3pBHSG0kIaZDQEkoQBKSGLh1pCwiC4FdZ\nle+6+lt1UcEO+oW1rS7qIqjoioB0WJASpIgBaUpIIJCENEJCgCSkTDJzfn/cZTaBVFIn+byeJ8+T\nOzPnzLmfuclnzj3nnqtTSimEEEIIYXYs6rsBQgghhLg3ksSFEEIIMyVJXAghhDBTksSFEEIIMyVJ\nXAghhDBTksSFEEIIMyVJ3AylpaUxYMAAnJyc+Mtf/lLfzRFlOHjwIB06dKjT9wwPD2flypUAfPPN\nN4wYMaJO378hKR6LujJq1Ci+/vrrOn3PmhQYGMjevXtLfS4vL4+xY8fi4uLCH/7wh2q/16uvvsqs\nWbOqXU9TZ1XfDWgqAgMDuXr1KpaWltjb2zNy5Ej+/ve/Y29vX+W6PvvsMzw9PcnKyqqFloqa0r9/\nf6Kjo+v0PXU6HTqdDoCHH36Yhx9+uMIyc+bMwc/PjzfeeKO2m1eniseiruzYsaNO36+mlRez9evX\nc/XqVTIzM7GwqH7/r64/m8ZKeuJ1RKfTsW3bNrKzszlx4gTHjx/nzTffrFIdSimMRiMJCQl07Njx\nntpRVFR0T+VE1Uica5fEt+4lJCTQrl27e0rgpX1ess5YzZAkXg98fHx48MEH+f333wE4evQoffr0\nwdXVlbCwMA4cOGB6bXh4OC+//DL9+vXD3t6e2bNn89VXX/Huu+/i6OjIvn370Ov1PPPMM7Rq1YpW\nrVrx5z//Gb1eD0BERAS+vr68++67tGzZkrlz5/Laa68xZcoUZs2ahZOTE126dOHChQssWbIELy8v\nAgIC+PHHH01tWLVqFSEhITg5OREUFMRnn31meu52/X/729/w8vLCx8eH1atXm57Py8vjueeeIzAw\nEBcXF/r3709+fn6F+32nxMREJk6ciKenJx4eHixYsAAAo9HIm2++SWBgIF5eXsyePdt0hiI+Ph4L\nCwtWr16Nv78/7u7urFixgmPHjtGlSxdcXV1N9QCsXr2avn37smDBAlxcXOjYsSP79u2rUhxux3ne\nvHlERETg5+dnes0777yDr68vTk5OdOjQwVR3QUFBhZ9fWfEtz+rVq+nfvz+g/cP885//jJeXF87O\nznTp0oWzZ8/y2Wef8e2335qOp/Hjx5da19mzZxk2bBju7u54e3uzZMmSSrf9//7v//D09MTHx4dN\nmzaxY8cO2rVrh7u7O0uXLjW9x6uvvsrkyZOZNm0aTk5OdO/enTNnzpieDwwM5N1336VLly44Ojpi\nNBorPIbi4+Pp168fTk5OjBgxgmvXrpmeq+jvbtGiRaWWzc/PZ+bMmXh4eODq6krPnj1JT083lbt9\nCl8pVeGx+dVXXxEQEECLFi14++23Te8fGRlJjx49cHZ2xtvbm+eee67Uz+XGjRuMGTMGT09P3Nzc\nGDt2LMnJyZXaD4Cvv/6agIAAPDw8Srz/nRYvXswbb7zB2rVrcXR0ZNWqVZXavy+++IKAgACGDh1a\nZt23bdmyhdDQUFxdXRk0aFCJs1jnzp0jPDwcV1dXOnXqxNatW03PzZkzh/nz5zN8+HCcnJwIDw/n\n8uXLpudLO+4bFSXqRGBgoNqzZ49SSqnLly+r0NBQtWjRIpWUlKTc3d3Vzp07lVJK/fjjj8rd3V1l\nZGQopZQaOHCgCggIUFFRUcpgMKjCwkI1Z84c9corr5jqfuWVV9QDDzyg0tPTVXp6uurTp4/p+f37\n9ysrKyv14osvKr1er/Ly8tTixYuVra2t2r17tyoqKlKPPPKICggIUG+//bYqKipSn3/+uWrdurWp\n/u3bt6tLly4ppZQ6cOCAsrOzUydOnChR/+LFi1VRUZHasWOHsrOzUzdu3FBKKfXkk0+qQYMGqZSU\nFGUwGNTPP/+sCgoKytzv9PT0u2JXVFSkunTpop599lmVm5ur8vPz1eHDh5VSSq1cuVIFBweruLg4\nlZOToyZOnKhmzZqllFIqLi5O6XQ69cc//lEVFBSo3bt3KxsbGzVhwgSVnp6ukpOTlaenpzpw4IBS\nSqlVq1YpKysr9f7776uioiK1du1a5ezsrDIzMysdh+Jx3r9/v/L19VVKKRUdHa38/PxUamqqUkqp\nhIQEdfHixUp/fmXF907h4eFq5cqVpv3p16+fUkqpf//736p79+7q5s2bpvbcbsudx9OdsrKylLe3\nt/rb3/6mCgoKVHZ2tvrll18q3fY33njDdFy5u7urGTNmqJycHHX27FnVvHlzFR8fr5RSavHixcra\n2lpt2LBBFRUVqWXLlqnWrVuroqIipZRSAQEBqlu3biopKUnl5+dX6m8nKChIXbhwQeXl5anw8HD1\n4osvKqVUpcoGBweXWnbFihVq7NixKi8vTxmNRnXixAmVlZV1V/wrc2w+/vjjKj8/X50+fVo1a9ZM\nRUdHK6WU6t27t1qzZo1SSqlbt26po0ePlvrZXLt2Tf3www8qLy9PZWdnqylTpqgJEyaYni9vP86e\nPascHBzUwYMHVUFBgXr22WeVlZWV2rt3b6nv9eqrr5raX9n9mz17tulv9k6LFy9WM2fOVEopFRMT\no+zt7dWePXtUUVGRevfdd1VwcLAqLCxUer1eBQUFqSVLlqjCwkK1b98+5ejoqGJiYpRSSs2ePVs5\nOjqa9uNPf/pTpY77xkKSeB0JCAhQDg4OysXFRQUEBKinnnpK5eXlqaVLl5b4w1BKqREjRqgvv/xS\nKaX9U1i8eHGJ5+fMmaNefvll03ZQUJDpn5FSSu3atUsFBgYqpbR/pDY2NqqgoMD0/OLFi9Xw4cNN\n21u2bFEODg7KaDQqpbR/2jqdznTg32nChAnqgw8+MNXfvHlzZTAYTM97enqqX375RRkMBtW8eXN1\n5syZu+qoaL+LO3LkiGrRokWJ97ht8ODB6h//+IdpOyYmRllbWyuDwWD6R5KSkmJ63t3dXX3//fem\n7UmTJqn3339fKaUlPR8fnxL19+zZU3399deVisOdcS6exC9cuKA8PT3Vnj17lF6vL1FPRZ9fWfEt\nTVlJfO/evapdu3bq6NGjd8XxzuPpTt9++6267777Sn2uMm2/87iKjIw0vb579+5q8+bNSintuHzg\ngQdMzxmNRtWyZUt16NAhpZT2RXjVqlWm5yvzt/PWW2+Znvvkk0/Ugw8+WO2yX3zxherTp0+px3Xx\n+Ffm2ExOTjY937NnT7V27VqllFIDBgxQixcvLvVLbXlOnjypXF1dS7SnrP147bXX1PTp003P3bp1\nS9nY2JSZxIsn3cruX1xcXJltLV7f66+/rv7whz+YnjMajapVq1YqIiJC/fTTT8rb27tE2enTp6tX\nX31VKaUl8eL7kZOToywtLVVSUpLat29fmcd9YyGn0+uITqdj8+bNXL9+nfj4eP7+979ja2tLQkIC\n69atw9XV1fRz+PBhrly5Yipb/JRsaVJSUggICDBt+/v7k5KSYtpu0aIFNjY2Jcp4enqafm/evDke\nHh6miSbNmzcHICcnB4CdO3fSu3dv3N3dcXV1ZceOHSVOybm7u5cYJ7OzsyMnJ4eMjAzy8/MJCgq6\nq82V2e/bEhMTCQgIKHUsLjU19a59LyoqIi0tzfSYl5dXiX29c/vWrVum7VatWpWoPyAggNTU1ErF\nobQ43xYcHMz777/Pq6++ipeXF9OnTzfVW9HnV1Z8q2Lw4ME8/fTTPPXUU3h5efHEE0+QnZ1dqbKJ\niYm0adOm1Ocq0/Y7j6s74198X3x9fU2/63Q6fH19S9RX/G+hMseQt7d3qe9VnbKzZs1ixIgRTJs2\njVatWvHCCy+UOuZbmWOz+HsU/1xXrlzJ+fPn6dixIz179mT79u131Q+Qm5vLE088QWBgIM7Ozgwc\nOJCbN2+WGG8uaz9SUlJKxNvOzg53d/dS36c0ldm/25/XN998g6OjI46OjowePfquulJSUvD39zdt\n63Q6/Pz8SE5OJjU19a7/gQEBAabj4vZxcpu9vT1ubm6kpKQwaNCgez7uzYUk8Xrm7+/PrFmzuH79\nuuknOzub559/3vSaimZx+vj4EB8fb9q+fPkyPj4+ZZavyqzQgoICJk2axPPPP8/Vq1e5fv06o0aN\nqtSkFA8PD2xtbYmNjb3rucrs921+fn5cvnwZg8Fw13Ol7buVlVWJRFEVxccTQftn7+PjU6k4VBTX\n6dOnc/DgQRISEtDpdLzwwgtl7kPxz6+mLFiwgOPHjxMVFcX58+f5v//7v0q129/fn0uXLpX6XE23\nPTEx0fS70WgkKSmpzGO5KsfQnapT1srKikWLFnH27FmOHDnCtm3b+Oqrr+56XXWOzeDgYL799lvS\n09N54YUXmDx5Mnl5eXe9bvny5Zw/f57IyEhu3rzJgQMHUNoZ1grfw8fHp0S8c3NzS3wpvdOdx0ll\n9q/4lRLZ2dlkZ2eX+oWkVatWJCQkmLaVUiQmJuLr62tqZ/F9SkhIMH3hvv3a23JycsjMzDQdN2Ud\n942FJPF6NnPmTLZu3cru3bsxGAzk5+cTERFRIpnc+Qd55/b06dN58803ycjIICMjg9dff73c6y8r\n8wd+m16vR6/X4+HhgYWFBTt37mT37t2VKmthYcHcuXN59tlnSU1NxWAw8PPPP6PX6yu137f16tWL\nli1b8uKLL5Kbm0t+fj5Hjhwx7ft7771HfHw8OTk5LFy4kGnTplVpBm3xeFy9epUPP/yQwsJC1q1b\nR3R0NKNGjapWHADOnz/Pvn37KCgooFmzZtja2mJpaWnah6p8fvfi+PHj/PLLLxQWFmJnZ1fi/b28\nvMpM0gBjxowhNTWVDz74gIKCArKzs4mMjKyVtv/6669s3LiRoqIi3n//fWxtbendu3epr72Xv52a\nKLt//35+++03DAYDjo6OWFtbm2JZXHWOzTVr1pgmyzk7O6PT6Uotl5OTQ/PmzXF2diYzM5PXXnvt\nrteUtR+TJk1i27ZtHD58GL1ez6JFizAajWW2qbT/O9X927ttypQpbN++nX379lFYWMjy5cuxtbWl\nT58+9OzZEzs7O959910KCwuJiIhg27ZtTJs2zVR+x44dpv145ZVXeOCBB2jVqlW5x31jIUm8nvn6\n+rJ582befvttPD098ff3Z/ny5eX28O68lvPll1+mR48edOnShS5dutCjRw9efvnlSpcv6zUAjo6O\nfPjhh0ydOhU3Nzf+9a9/3TWDubye3LJly+jcuTP3338/7u7u/PWvf8VoNJa536X9E7GwsGDr1q3E\nxsbi7++Pn58f33//PQBz585l1qxZDBgwgDZt2mBnZ8dHH31UqbaV9ppevXpx4cIFWrRowSuvvMKG\nDRtwdXW95zjcfqygoIC//vWvtGjRgpYtW5KRkWGa4V3Vz6+yin/OWVlZPP7447i5uREYGIiHh4dp\noaB58+YRFRWFq6srEydOvKseBwcHfvzxR7Zu3UrLli1p164dERER99T28vZFp9Mxfvx41q5di5ub\nG9988w0//PBDmf90q/q3Uzwe1SmblpbGlClTcHZ2JiQkhPDw8FK/uFTn2Ny1axedOnXC0dGRP//5\nz3z33Xc0a9bsrtc988wz5OXl4eHhQZ8+fRg5cmS5MS++H6GhoXz88cfMmDEDHx8f3Nzcyh26u/P/\nRnX/9orX1759e9asWcOCBQto0aIF27dvZ+vWrVhZWWFjY8PWrVvZuXMnLVq04Omnn+brr7+mXbt2\npnpmzJjBa6+9hru7OydPnmTNmjVA+cd9Y6FTVemWVUF+fj4DBw6koKAAvV7P+PHjWbJkCa+++ir/\n/Oc/adGiBQBvv/02I0eOBGDJkiV88cUXWFpa8uGHHzJ8+PDaaJoQpVq9ejUrV67k4MGD9d2UJum1\n114jNjbWrFc8E3Xv0UcfxdfXt9EtVlRZtbZim62tLfv378fOzo6ioiL69evHoUOH0Ol0PPvsszz7\n7LMlXh8VFcXatWuJiooiOTmZoUOHcv78+RpZGUgI0fDVUn9CNHJN/bip1QxpZ2cHaOOqBoMBV1dX\noPSgb968menTp2NtbU1gYCDBwcGmcTch6kJ9LNMp/kviL+5FUz9uajWJG41GwsLC8PLyYtCgQYSG\nhgLw0Ucf0bVrV+bNm8eNGzeAuy938PX1LXWSkxC1Zfbs2fz000/13Ywma/HixaXO8haiPKtWreL1\n11+v72bUm1pN4hYWFpw6dYqkpCR++uknIiIi+OMf/0hcXBynTp2iZcuWZS4nCLJAvhBCCFGeOrmL\nmbOzM6NHj+b48eOEh4ebHn/ssccYO3YsoF0nWPxav6SkpLsW3rj9uuKLPwghhBCNWdeuXTl16lSp\nz9VaTzwjI8N0qjwvL48ff/yRbt26lVgRaePGjXTu3BmAcePG8d1336HX64mLi+PChQv07NnzrnpT\nUlJMixnIz739LF68uN7bYO4/EkOJYUP4kRg2jTiePn26zFxbaz3x1NRUZs+ejdFoxGg0MmvWLIYM\nGcIjjzzCqVOn0Ol0tG7dmk8//RSAkJAQpk6dSkhICFZWVnzyySdyOr2WFF9lSdwbiWH1SQyrT2JY\nM8w5jrWWxDt37syJEyfuery8iSsLFy5k4cKFtdUkIYQQolGRi7CboDlz5tR3E8yexLD6JIbVJzGs\nGeYcx1pbsa226HQ6zKzJQgghxD0rL+81mp64m5ub6aJ/+ZGf+vxxc3Or7z8Hs3B7/XVx7ySGNcOc\n41gnl5jVhevXr0sPXTQIOp1MyBRC1I1Gczq9rMeFqGtyLAohalJ5/1Mazel0IYQQoqmRJC6EqBfm\nPA7ZUEgMa4Y5x1GSeB0IDAxk3759gHb/9P/5n/+p5xbVn8DAQPbu3Vun79mpUye5sYkQolFqNBPb\nGrLiE50qu5hNeHg4s2bNYt68ebXVrHpxewZ3Xfr999/r9P1E5RS/j4K4NxLDmmHOcZSeeANljjOc\ni4qK6rsJQgjRpDT6JB4Tk8DHH+/j/fcj+PjjfcTEJNRLHbe9+uqrzJo1C4D8/HxmzpyJh4cHrq6u\n9OzZk6tXr/LSSy9x8OBBnn76aRwdHfnf//3fUus6dOgQffr0wdXVFX9/f7788ksAbt68ySOPPIKn\npyeBgYG89dZbppmNq1evpm/fvjz77LO4uroSHBzMkSNHWLVqFf7+/nh5eZVYGnfOnDnMnz+f4cOH\n4+TkRHh4OJcvXzY9b2FhwSeffELbtm1p3749ANu2bSMsLAxXV1f69u3Lb7/9VqLdJ0+epGvXrri4\nuDBt2jQKCgpMz5VXNjAwkOXLl5daNiMjgzFjxuDq6oq7uzsDBgwoUe72KfyCggKeeeYZWrVqRatW\nrfjzn/+MXq8HtHExX19f/va3v+Hl5YWPjw+rV6821bNjxw5CQ0NxcnLC19eX5cuXV+YjF2Uw53HI\nhkJiWDPMOY6NOonHxCSwenUs6emDuXEjnPT0waxeHVulJFwTdRRX/HTyl19+SVZWFklJSWRmZvLp\np5/SvHlz3nrrLfr378/HH39MdnY2H3744V31JCQkMGrUKP70pz+RkZHBqVOnCAsLA2DBggVkZ2cT\nFxfHgQMH+Oqrr1i1apWpbGRkJF27diUzM5Pp06czdepUTpw4wcWLF1mzZg1PP/00ubm5ptd/++23\nLFq0iIyMDMLCwnj44YdLtGXz5s0cO3aMqKgoTp48ybx58/j888/JzMzkiSeeYNy4cRQWFgKglGLd\nunXs2rWLuLg4zpw5Y0qUFZXV6XRlll2+fDl+fn5kZGRw9epVlixZUmrM33rrLSIjIzl9+jSnT58m\nMjKSN9980/TatLQ0srKySElJYeXKlTz11FPcvHkTgHnz5vHZZ5+RlZXF2bNnGTx4cNUPACGEqEGN\nekx8z56LNGs2hJJfsoZw5sw+7r8/oFJ1REZeJDd3iGk7PByaNRvC3r37aN++cnUUd/vWcgA2NjZc\nu3aNCxcu0LlzZ7p163bXa8vy7bffMmzYMP7whz8A2op1bm5uGAwG1q5dy+nTp7G3t8fe3p7nnnuO\nr7/+mrlz5wLQunVrZs+eDcDUqVN56623WLRoEdbW1gwbNgwbGxtiY2Pp0qULAGPGjKFfv36AlgSd\nnZ1JTk423e/9r3/9Ky4uLgB89tlnPPHEE9x///0APPLII7z99tscPXqU/v37o9Pp+N///V+8vb0B\nGDt2rOk+uRWVBcosa2NjQ2pqKvHx8QQFBdG3b98y4/b3v/8dDw8PABYvXswTTzzB66+/DoC1tTWL\nFi3CwsKCkSNH4uDgQExMDD179sTGxoazZ8/SuXNnnJ2d7/q8RNWY8zhkQyExrBnmHMdG3RMvLCx9\n9wyGyu+20Vj6a/X66odu1qxZjBgxgmnTptGqVSteeOGFEuPK5Y2LJyUl0aZNm7sez8jIoLCwkICA\n/37B8Pf3Jzk52bTt5eVl+r158+YAtGjRosRjOTk5pjb4+vqanrO3t8fNzY2UlBTTY35+fqbfExIS\nWL58Oa6urqafpKSkEq+/nYTvfK/qlP3LX/5CcHAww4cPJygoiHfeeafUuKWkpNwVm+L1u7u7Y2Hx\n38/Wzs7O9B4bNmxgx44dBAYGEh4eztGjR0t9DyGEqCuNuidubW0EtN5zcZ6eRp58snJ1fPyxkfT0\nux+3sTFWr3GAlZUVixYtYtGiRabT4+3bt2fu3LkVTmzz8/MjMjLyrsc9PDywtrYmPj6ejh07AnD5\n8uUSibgqlFIkJiaatnNycsjMzMTHx8f0WPG2+vv789JLL1XplrK3y1e1bPH3dXBwYNmyZSxbtsx0\nqrtnz54MGjSoRBkfH5+7YlN8X8rTo0cPNm3ahMFg4KOPPmLq1Kkl5geIqomIiDDrHlBDIDGsGeYc\nx0bdEx86NIiCgpLXJBcU7GXIkKA6raMsERER/PbbbxgMBhwdHbG2tsbS0hLQessXL14ss+zDDz/M\nnj17WLduHUVFRVy7do3Tp09jaWnJ1KlTeemll8jJySEhIYH33nuPmTNn3nM7d+zYweHDh9Hr9bzy\nyis88MADplPpd/qf//kfVqxYQWRkJEopbt26xfbt20292dLcHjaoatniww3btm0jNjYWpRROTk5Y\nWlqW6FHfNn36dN58800yMjLIyMjg9ddfN000LE9hYSHffPMNN2/exNLSEkdHR9NnJYQQ9aVRJ/H2\n7QOYMycYT899uLhE4Om5jzlzgqs0ll0TdRRXfJLVlStXmDJlCs7OzoSEhJiuDQf405/+xPr163Fz\nc+OZZ565qx4/Pz927NjB8uXLcXd3p1u3bpw5cwaAjz76CHt7e9q0aUP//v15+OGHefTRR+96/+Jt\nKq+9M2bM4LXXXsPd3Z2TJ0+yZs2aMst2796dzz//nKeffho3Nzfatm3LV199VeZ7FG9PdcrGxsYy\nbNgwHB0d6dOnD0899RQDBw68q8zLL79Mjx496NKlC126dKFHjx68/PLLlYrFmjVraN26Nc7Oznz2\n2Wd88803Zb5WVMxcez4NicSwZphzHOUGKKJcjz76KL6+vrzxxhv13RSzIceiEKImyQ1QxD2TZCRq\nizlfm9tQSAxrhjnHUZK4KFd9LJMqhBCicuR0uhA1TI5FIURNktPpQgghRCMkSVwIUS/MeRyyoZAY\n1gxzjqMkcSGEEMJMyZi4EDVMjkUhRE2SMXEhhBCiEZIkXgdiYmIICwvDycmJv//979WqKzw8nJUr\nV9ZQy4SoP+Y8DtlQSAxrhjnHsVHfAKWhePfddxkyZIjptpnVIddtCyFEzYiJjWHPr3s4d/YcZ9PO\nMrT7UNoHt6/vZlWJ9MTrQEJCAiEhIVUuZzAYaqE1QjQM5rxedUMhMbx3MbExrN6/mrMOZ3Ee6Ey6\nVzqr968mJjamvptWJY0+icfExvDx2o95/7v3+Xjtx/f0AVWnjsGDBxMREcHTTz+Nk5MTZ86c4ZFH\nHsHT05PAwEDeeust04SF1atX07dvX5599lk8PDx47bXXyq1bKcWbb75JYGAgXl5ezJ49m6ysLNPz\nW7ZsITQ0FFdXVwYNGkR0dLTpucDAQJYuXUpoaChubm7MnTuXgoICQLsn+ZgxY3B1dcXd3Z0BAwbI\nRC0hRKPy72P/Js41jqj0KKIzolFK0axtM/ae2Ftx4QakUSfx29+00r3SueF9456+aVW3jn379tG/\nf38+/vhjsrKyWLZsGdnZ2cTFxXHgwAG++uorVq1aZXp9ZGQkQUFBXL16tcL7aq9atYovv/ySiIgI\nLl26RE5ODk8//TQA58+fZ8aMGXz44YdkZGQwatQoxo4dS1FRkan8t99+y+7du7l48SLnz5/nzTff\nBGD58uX4+fmRkZHB1atXWbJkiZzCFzXOnMchGwqJ4b25knOFny7/xJWcK1joLNBf1Jue0xv15ZRs\neBr1mPieX/fQrG0zIuIj/vugNZz57gz397u/UnVEHook1zcX4rXt8MBw07e1qo6dGAwG1q5dy+nT\np7G3t8fe3p7nnnuOr7/+mrlz5wLg4+PDU089BYCtrW259X3zzTc899xzBAYGArBkyRI6derEqlWr\nWLt2LWPGjGHIkCEA/L//9//44IMPOHLkCAMGDECn0/H000+b7gv+0ksvsWDBAt544w1sbGxITU0l\nPj6eoKAg+vbtW6X9FEKIhkgpxbGUY+y+uJu8wjzsre0JaRFC+vV0U0fFxsKmnltZNY26J16oCkt9\n3EDlx5qNGEt9/F6+rWVkZFBYWEhAwH/vRe7v709ycrJp28/Pz/T7/PnzcXR0xNHRkaVLl95VX2pq\n6l11FRUVkZaWRmpqKv7+/qbndDodfn5+Zb6Xv78/KSkpAPzlL38hODiY4cOHExQUxDvvvFPlfRWi\nIjKeW30Sw8rLK8zj+7Pfs+PCDoqMRYztNZZOOZ2wt7EnMCwQgIILBQy5b0j9NrSKGnVP3FpnDWi9\n5+I87Tx5MvzJStXxcdrHpHul3/X4vXxb8/DwwNramvj4eDp27AjA5cuX8fX1Nb2m+GnrFStWsGLF\nijLr8/EYfVaPAAAgAElEQVTxIT4+3rR9+fJlrKys8Pb2xsfHh99++830nFKKxMREU8/79uuL/+7j\n4wOAg4MDy5YtY9myZZw9e5bBgwdz//33M3jw4CrvsxBC1LfEm4msj1rPzYKbNLNsxrj24wj1DCUm\nNoa9J/aiN+qxsbBhyKAhMju9IRnafSgFFwpKPFbVb1o1UcdtlpaWTJ06lZdeeomcnBwSEhJ47733\nmDlzZpXrApg+fTrvvfce8fHx5OTksHDhQqZNm4aFhQVTpkxh+/bt7Nu3j8LCQpYvX46trS19+vQB\ntKT+ySefkJycTGZmJm+99RbTpk0DYNu2bcTGxqKUwsnJCUtLSywtLe+pjUKURcZzq09iWD6lFAcT\nDrLq1CpuFtyklWMr5veYT6hnKADtg9vz5NQnCfMO48mpT5pdAodG3hNvH9yeOcyp1jetmqijuI8+\n+ogFCxbQpk0bbG1tefzxx3n00UeBql8DPnfuXFJSUhgwYAD5+fk8+OCDfPTRR1q727dnzZo1LFiw\ngOTkZLp168bWrVuxsrIyvdeMGTMYPnw4KSkpTJgwgZdffhmA2NhYFixYQHp6Oq6urjz11FMMHDjw\nnvZXCCHqQ44+hx/O/cCl65cA6OPXhyGth2Bp0bg6JLJ2ehPVunVrVq5cKafIa4Eci0LUr4uZF/nh\n3A/cKryFnbUdD3V4iLbubeu7WfesvP8pjbonLoQQoukwGA3sj9/PocuHAGjt0pqJHSfi2MyxnltW\nexr1mLgQouGS8dzqkxj+1438G6w+tZpDlw+hQ8fg1oOZ1XVWpRK4Ocex1pJ4fn4+vXr1IiwsjJCQ\nEP76178CkJmZybBhw2jXrh3Dhw/nxo0bpjJLliyhbdu2dOjQgd27d9dW0wQQFxcnp9KFEI3CufRz\nrDi+gsSsRJyaOTEnbA4DAgZgoWv8/dRaHRPPzc3Fzs6OoqIi+vXrx7Jly9iyZQseHh48//zzvPPO\nO1y/fp2lS5cSFRXFjBkzOHbsGMnJyQwdOpTz589jYVHyQ5AxcdHQybEoRN0oMhaxK3YXx1KOAdDe\nvT3jO4zHztquUuVjYhLYs+cihYUWWFsbGTo0iPbtAyouWMfq7X7idnZaIPV6PQaDAVdXV7Zs2cLs\n2bMBmD17Nps2bQJg8+bNTJ8+HWtrawIDAwkODiYyMrI2myeEEMJMZeRm8Pmvn3Ms5RiWOktGBo9k\nWqdpVUrgq1fHkp4+mBs3wklPH8zq1bHExCTUcstrVq0mcaPRSFhYGF5eXgwaNIjQ0FDS0tLw8vIC\nwMvLi7S0NABSUlJKLHri6+tbYnUxIUTjYs7jkA1FU4yhUopTV07x6fFPSbuVhltzNx677zF6+faq\n0iW6e/ZcxMJiCGfPwu+/RwDQrNkQ9u69WEstrx21OjvdwsKCU6dOcfPmTUaMGMH+/ftLPF/RddFy\n0w0hhBC3FRQVsP3Cds6knQGgi1cXRrcdTTOrZlWuKzXVgmPHQK+H/HwIDQWdDvR68xpHr5NLzJyd\nnRk9ejS//vorXl5eXLlyBW9vb1JTU/H09ASgVatWJCYmmsokJSWVWCK0uDlz5phu+uHi4kJYWBiu\nrq6S9EWD4OTkZPr9dk/p9hrXsv3f7fDw8AbVHnPcvv1YQ2lPbW6nZqfy9tdvk63Ppu19bRndbjTX\nz13n57Sfq1SfwQBFReGcOGHk6tUI7O1h4MBwdDqIj4/AxeUEUL/7e/v34stql6XWJrZlZGRgZWWF\ni4sLeXl5jBgxgsWLF7Nr1y7c3d154YUXWLp0KTdu3CgxsS0yMtI0sS02NvauxCyThoQQoulQShGZ\nHMnui7sxKANe9l5MCZ2Ch51Hleu6ehU2bIC0NLh2LYHr12MJChrC7TRTULCXOXOCG9zktnpZ7CU1\nNZXZs2djNBoxGo3MmjWLIUOG0K1bN6ZOncrKlSsJDAzk+++/ByAkJISpU6cSEhKClZUVn3zyifSs\na0nxb+7i3kgMq09iWH2NPYa5hblsjt5MzLUYAO73uZ/hQcOxtrSuUj1KQWQk/PgjFBWBmxs89lgA\nt27B3r37iIo6Q0hIF4YMaXgJvCK1lsQ7d+7MiRMn7nrczc2NPXv2lFpm4cKFLFy4sLaaJIQQwkwk\n3Ehgw7kNZBVkYWtly/j24+nYomOV68nOhs2bITZW277vPnjwQbCxAQigffsAIiIszPbLUKNZO10I\nIYT5MyojBxMOEhEfgULh5+THpJBJuNi6VLmu6GjYsgVyc6F5cxg3DjpW/XtAvZO104UQQjR42QXZ\n/HDuB+JuxKFDR3///oQHhlf5zmN6PezaBb/+qm0HBcGECeDYCJdQN6+59KJGFJ8BKe6NxLD6JIbV\n15hieOHaBVYcX0HcjTjsre2Z2WUmQ9pU/dahKSnw6adaAre01E6dz5xZfgI35zhKT1wIIUS9MRgN\n7I3by5HEIwC0cW3DxI4TcbBxqFI9RiMcPgz792u/e3rCpEnwn7XFGi0ZExdCCFEvruddZ33UepKz\nk7HQWTC49WD6+vWt8pVJN27Axo2Q8J8VU3v3hqFDwaqRdFNlTFwIIUSDcvbqWbbEbKHAUIBzM2cm\nh0zGz9mvyvX89hts2wYFBeDgoI19BwfXQoMbKBkTb4LMefynoZAYVp/EsPrMMYaFhkK2xmxlXdQ6\nCgwFdPToyPwe86ucwPPztYVbNmzQEniHDvDkk/eWwM0xjrdJT1wIIUSduHrrKuuj1nP11lWsLKwY\nETSCHj49qnz6PCEBfvgBbt4Ea2tt8tp990FTXB9MxsSFEELUKqUUJ6+cZOeFnRQaC/Gw82ByyGS8\nHbyrVI/BABERcOiQtgqbj482ec3dvXba3VDImLgQQoh6kV+Uz7bz2/j96u8AhHmHMartKGwsbapU\nz7Vr2qnzlBStxz1gAAwcqF1G1pTJmHgTZM7jPw2FxLD6JIbV19BjmJyVzKfHP+X3q79jY2nDxI4T\nmdBhQpUSuFLaNd8rVmgJ3MUF5syBwYNrLoE39DiWR3riQgghapRSip+TfmbPpT0YlZGWDi2ZHDIZ\nd7uqnfe+dQu2btWWTwXo0gVGjQJb21potJmSMXEhhBA15pb+FpuiN3Eh8wIAvVr1YljQMKwsqtZn\njI2FTZsgJ0dL2qNHQ+fOtdHihk/GxIUQQtS6+BvxbIjaQLY+m+ZWzZnQYQLtPdpXqY7CQtizB375\nRdsOCICHHtJOo4u7yZh4E2TO4z8NhcSw+iSG1ddQYmhURvbH7efLU1+Src/G39mf+T3mVzmBp6XB\n559rCdzCQlt1bfbs2k/gDSWO90J64kIIIe5ZVkEWG6I2kHAzAR06BgQMIDwwHAtd5fuISsHRo1oP\n3GDQLhmbNEm7hEyUT8bEhRBC3JOYjBg2RW8irygPBxsHJnWcRGvX1lWqIytLG/u+dEnb7tEDhg8H\nm6pdgdaoyZi4EEKIGlNkLGLPpT0cTToKQLBbMA91eAh7G/sq1XPuHGzZAnl5YGcH48dD+6qdgW/y\nZEy8CTLn8Z+GQmJYfRLD6quPGGbmZbLyxEqOJh3FQmfB8KDhPNz54SolcL0eNm+GtWu1BB4crK17\nXl8J3JyPRemJCyGEqJTf0n5j6/mt6A16XGxdmBwyGV8n3yrVkZSkrXuemandKnTYMOjZs2mue14T\nZExcCCFEufQGPTsv7OTklZMAhLYIZWz7sdhaVX7VFaMRDh6EAwe03728tMlrnp611erGQ8bEhRBC\n3JO0nDTWRa0jIzcDKwsrRgaP5L6W91XpzmPXr2u978REbbtPH23ZVCvJQNUmY+JNkDmP/zQUEsPq\nkxhWX23GUCnF8ZTjfH7iczJyM2hh14LHuz9Od5/ulU7gSsHp09q654mJ4OgIjzyizT5vSAncnI/F\nBhRGIYQQDUF+UT5bYrYQlR4FwH0t72Nk8EisLa0rXUdeHmzbBmfPatshITBmjDYLXdQcGRMXQghh\nkpSVxPqo9dzIv0Ezy2aMbT+WTp6dqlRHXBxs3KhdA25jAyNHQliYTF67VzImLoQQolxKKY4kHmFv\n3F6MyoiPow+TQybj1tyt0nUYDLBvHxw5op1K9/WFiRPBrfJViCqSMfEmyJzHfxoKiWH1SQyrr6Zi\nmKPPYc2ZNfx46UeMysgDvg8wr9u8KiXw9HT45z/h8GFte+BAePRR80jg5nwsSk9cCCGasEvXL/HD\nuR/I0edgZ23HhA4TaOfertLllYLjx2HXLigqAldXrfft51eLjRYmMiYuhBBN0O07jx26fAiFItAl\nkIkdJ+LUzKnSdeTkaMumnj+vbYeFaePfzZrVUqObKBkTF0IIYXIz/ybro9aTmJWIDh2DAgfRP6B/\nle48dv68tnTqrVtgawtjx0JoaC02WpRKxsSbIHMe/2koJIbVJzGsvnuJYXRGNCuOryAxKxFHG0dm\nh81mYODASifwwkLYvh2+/VZL4K1bwx//aN4J3JyPRemJCyFEE1BkLGL3xd1EJkcC0M69HRM6TMDO\nuvIXbqemaiuvpaeDpaW26lqfPnLpWH2SMXEhhGjkMnIzWB+1nis5V7DUWTIsaBi9WvWq0sprR45o\nl48ZDNCihTZ5rWXLWm64AGRMXAghmqzTV06z/cJ29AY9bs3dmBwyGR9Hn0qXv3lTW7glPl7b7tlT\nu/OYdeUXbxO1SMbEmyBzHv9pKCSG1ScxrL7yYqg36Nl4biMbozeiN+jp7NmZJ7o/UaUEfvYs/OMf\nWgK3t4cZM2DUqMaXwM35WJSeuBBCNDJXcq6w7uw6ruVdw9rCmlFtRxHmHVbp0+cFBbBjh3bzEoB2\n7WD8eC2Ri4ZFxsSFEKKRUEpxLOUYu2J3YVAGPO09mRIyhRb2LSpdR2KiNnnt+nWtxz18OPToIZPX\n6pOMiQshRCOXV5jH5pjNRGdEA9DDpwcjgkZU+s5jBgP89JP2o5Q2aW3iRG0Sm2i4ZEy8CTLn8Z+G\nQmJYfRLD6rsdw8s3L7Pi+AqiM6KxtbJlSsgUxrQbU+kEnpkJq1bBgQPadr9+8NhjTSeBm/OxWGtJ\nPDExkUGDBhEaGkqnTp348MMPAXj11Vfx9fWlW7dudOvWjZ07d5rKLFmyhLZt29KhQwd2795dW00T\nQohGwaiM/JTwE6tPreZmwU18nXx5ovsThHpWbuUVpeDkSVixApKSwMkJZs+GoUO168BFw1drY+JX\nrlzhypUrhIWFkZOTQ/fu3dm0aRPff/89jo6OPPvssyVeHxUVxYwZMzh27BjJyckMHTqU8+fPY2FR\n8nuGjIkLIQRkF2SzMXojl65fAqCffz8GBQ7C0qJy2Tc3F7ZuhXPntO1OnWD0aGjevLZaLO5VvYyJ\ne3t74+3tDYCDgwMdO3YkOTkZoNTGbN68menTp2NtbU1gYCDBwcFERkbSu3fv2mqiEEKYpdjMWDae\n28itwlvYW9vzUMeHCHYLrnT5S5e0a7+zs7WblYwaBV26yOQ1c1QnY+Lx8fGcPHnSlJA/+ugjunbt\nyrx587hx4wYAKSkp+Pr6msr4+vqakr6oWeY8/tNQSAyrT2JYdQajgR8v/siaM2u4VXiL/Nh85veY\nX+kEXlSk3TL0q6+0BO7vD/PnQ9euTTuBm/OxWOtJPCcnh8mTJ/PBBx/g4ODAH//4R+Li4jh16hQt\nW7bkueeeK7NsZa9pFEKIxu563nVWnVrF4cTDWOgsGNx6MMODhuPYzLFS5a9ehc8/h59/BgsLbd3z\nOXO0+38L81Wrl5gVFhYyadIkZs6cyYQJEwDw9PQ0Pf/YY48xduxYAFq1akViYqLpuaSkJFq1alVq\nvXPmzCEwMBAAFxcXwsLCCA8PB/77jUq2y9++raG0R7ab3nZ4eHiDak9D3vYM9WRLzBaij0djb23P\nCzNfwN/Zn4i4CCIiIsotrxTY2YXz448QGxuBoyO88EI4vr4NZ/9ku+T27d/jb691W45am9imlGL2\n7Nm4u7vz3nvvmR5PTU2l5X9WzX/vvfc4duwY3377rWliW2RkpGliW2xs7F29cZnYJoRoKgoNhey6\nuIvjKccB6ODRgfHtx9PcunKzz3JyYNMmiI3Vtu+7Dx58EGxsaqvFojbUy8S2w4cPs2bNGrp06UK3\nbt0AePvtt/nXv/7FqVOn0Ol0tG7dmk8//RSAkJAQpk6dSkhICFZWVnzyySdyOr2WFP/mLu6NxLD6\nJIblS7+Vzvqo9aTdSsNSZ8mI4BHc73N/if+L5cUwJgY2b9ZmoTdvDuPGQceOddR4M2POx2KtJfF+\n/fphNBrvenzkyJFlllm4cCELFy6srSYJIUSDp5Ti1JVT7Liwg0JjIe7N3ZkcMpmWjpW776der01e\n+/VXbbtNG3joIXCs3NC5MDOydroQQjQQBUUFbDu/jd+u/gZAV6+ujGo7imZWzSpVPiUFNmyAa9e0\nxVqGDoXevZv2zPPGQNZOF0KIBi4lO4X1UevJzMvExtKG0W1H09W7a6XKGo1w+DDs36/97ukJkyaB\nl1ctN1rUO1k7vQkqPgNS3BuJYfVJDDVKKY4mHWXliZVk5mXi7eDN490fr1QCj4iI4MYN+PJL2LtX\nS+C9e8Pjj0sCrwpzPhalJy6EEPUktzCXTdGbOH/tPAA9W/VkeNBwrCwq96/50iU4ehTy88HBASZM\ngODKL9wmGgEZExdCiHqQcCOBDec2kFWQha2VLePbj6dji8pNH8/Ph+3b4Tdt6JwOHWDsWLC3r8UG\ni3ojY+JCCNFAGJWRgwkHiYiPQKHwc/JjUsgkXGxdKlU+IUFb9/zGDbC21q77vu8+mbzWVMmYeBNk\nzuM/DYXEsPqaYgyzCrL46vRX7I/fD0B///482u3RSiVwg0Eb9169WkvgPj7QqVME3btLAq8ucz4W\npScuhBB14Py182yK3kRuYS4ONg5M7DiRNq5tKlX22jXt0rGUFC1hDxgAAwfCwYO13GjR4MmYuBBC\n1CKD0cCeS3v4OelnAIJcg3io40M42DhUWFYpOHEC/v1vKCwEFxdt4ZaAgNputWhIZExcCCHqQWZe\nJuuj1pOSnWK681hfv76VWlI6Nxe2bIHoaG27Sxftvt+2trXcaGFWZEy8CTLn8Z+GQmJYfY09hr9f\n/Z1Pj39KSnYKLrYuPBr2KP38+1UqgcfGwiefaAnc1lZbuGXixLsTeGOPYV0x5zhKT1wIIWpQoaGQ\nnbE7OZF6AoCQFiGMaz8OW6uKu9CFhbBnD/zyi7YdEKCdPnep3MR10QTJmLgQQtSQq7eusu7sOtJz\n07GysOLB4Afp3rJ7pXrfaWna5LWrV8HCAgYNgr59td9F0yZj4kIIUYuUUpxIPcHO2J0UGYvwsPNg\nSsgUvBwqXvtUKW3VtT17tMvI3N210+c+PnXQcGH25DteE2TO4z8NhcSw+hpLDPOL8lkftZ6t57dS\nZCyim3c3Hu/+eKUSeHY2fP21dutQgwF69IAnnqh8Am8sMaxv5hxH6YkLIcQ9Ss5KZn3Ueq7nX8fG\n0oax7cbS2atzpcqeO6fNPs/LAzs7GDdOWz5ViKqQMXEhhKgipRQ/J/3Mnkt7MCojLR1aMjlkMu52\n7hWW1eth5044eVLbDg7WblziUPFl46KJkjFxIYSoIbf0t9gYvZHYzFgAevv2ZmiboZW681hSEvzw\nA2RmgpUVDBsGPXvKsqni3smYeBNkzuM/DYXEsPrMMYZx1+NYcXwFsZmxNLdqzvRO03kw+MEKE7jR\nCAcOwBdfaAncy0u753evXtVL4OYYw4bInOMoPXEhhKiAURmJiI/gYMJBFIoA5wAmhUzCqZlThWWv\nX9d634mJ2vYDD8CQIVpPXIjqkjFxIYQox838m/xw7gcSbiagQ8eAgAEMDByIha78E5lKwZkzsGMH\nFBSAo6O2cEubyt3zRAgTGRMXQoh7EJMRw6boTeQV5eFo48jEjhNp7dq6wnJ5ebBtG5w9q22HhMCY\nMdosdCFqkoyJN0HmPP7TUEgMq68hx7DIWMTOCzv51+//Iq8oj7ZubZnfY36lEnhcHPzjH1oCt7GB\n8eNhypTaSeANOYbmxJzjKD1xIYQo5lruNdZHrSc1JxVLnSVD2wylt2/vCpdONRhg3z44ckQ7le7r\nq920xM2tjhoumiQZExdCiP84k3aGbee3oTfocbV1ZXLIZFo5taqwXHq6NnktNVWbbT5ggPZjaVkH\njRaNnoyJCyFEOfQGPTsu7ODUlVMAdPLsxJh2Yyq885hScPw47N6t3YHM1VXrffv51UWrhZAx8SbJ\nnMd/GgqJYfU1lBheybnCZ79+xqkrp7C2sGZc+3FM6jipwgR+6xb861+wfbuWwMPCYP78uk3gDSWG\n5s6c4yg9cSFEk6SU4njKcXZd3EWRsQhPe08mh0zG096zwrIXLsCmTVoit7WFsWMhNLQOGi3EHWRM\nXAjR5OQV5rElZgvnMs4B0L1ldx4MfhBrS+tyyxUWaqfOjx3Ttlu31tY9d3au7RaLpkzGxIUQ4j8S\nbyayPmo9Nwtu0syyGWPbj6WTZ6cKy6WmapPX0tO1CWuDB0OfPrLuuahfMibeBJnz+E9DITGsvrqO\noVKKQ5cPserUKm4W3KSVYyvm95hfYQJXCg4fhn/+U0vgLVrAY49B3771n8DlOKwZ5hxH6YkLIRq9\nHH0OG89t5OL1iwD08evDkNZDsLQo/xqwmze1se+4OG27Z0/tzmPW5Z91F6LOyJi4EKJRu5h5kY3R\nG8nR52BnbcdDHR6irXvbCsudPQtbt0J+PtjbayuvtWtXBw0W4g4yJi6EaHIMRgP74/dz+PJhFIrW\nLq2Z2HEijs0cyy1XUKDdtOT0aW27XTstgdvb10GjhagiGRNvgsx5/KehkBhWX23G8Eb+DVafWs2h\ny4cAGBQ4iFldZ1WYwBMTYcUKLYFbW8Po0TB9esNN4HIc1gxzjqP0xIUQjcq59HNsjtlMflE+Ts2c\nmNRxEgEuAeWWMRrhwAH46SdtIlvLltrKay1a1FGjhbhHMiYuhGgUioxF7IrdxbEU7SLu9u7tGd9h\nPHbW5d8+LDNTu3QsKUmbbd63LwwaJOuei4ZDxsSFEI1aRm4G686uI+1WGpY6S4YFDaNXq17l3nlM\nKTh1CnbuBL0enJy03ndgYN21W4jqkjHxJsicx38aColh9dVEDJVSnLpyik+Pf0rarTTcmrsx7755\nFd46NDcX1q2DzZu1BN6pE/zxj+aXwOU4rBnmHMdaS+KJiYkMGjSI0NBQOnXqxIcffghAZmYmw4YN\no127dgwfPpwbN26YyixZsoS2bdvSoUMHdu/eXVtNE0I0AgVFBWyM3sim6E0UGgvp4tWFJ7o/gY+j\nT7nlLl2Cf/wDoqKgWTN46CGYNAmaN6+jhgtRg2ptTPzKlStcuXKFsLAwcnJy6N69O5s2bWLVqlV4\neHjw/PPP884773D9+nWWLl1KVFQUM2bM4NixYyQnJzN06FDOnz+PhUXJ7xkyJi6ESM1OZV3UOjLz\nMrG2sGZ0u9F09epabu+7qAj27oWff9a2/f21BO7qWkeNFuIe1cuYuLe3N97e3gA4ODjQsWNHkpOT\n2bJlCwcOHABg9uzZhIeHs3TpUjZv3sz06dOxtrYmMDCQ4OBgIiMj6d27d201UQhhZpRSRCZHsvvi\nbgzKgJe9F1NCp+Bh51FuuatXYcMGSEsDCwsYOBD699d+F8KcVXgI5+TkYDAYAIiJiWHLli0UFhZW\n6U3i4+M5efIkvXr1Ii0tDS8vLwC8vLxIS0sDICUlBV9fX1MZX19fkpOTq/Q+onLMefynoZAYVl9V\nY5hbmMt3v3/HztidGJSB+33u57H7His3gSsFv/wCn32mJXA3N5g7V0vijSGBy3FYM8w5jhX2xAcM\nGMChQ4e4fv06I0aM4P7772ft2rV88803lXqDnJwcJk2axAcffICjY8mFFnQ6Xbmnv8p6bs6cOQT+\nZwaKi4sLYWFhhIeHA//9MGS77O1Tp041qPaY4/ZtDaU9jX27dVhrNpzbwJlfzmBjacMz054hpEVI\nueVzcmDJkgiSkyEwMJz77oPmzSOIjQVf34a1f/e6ferUqQbVHnPdvq0htSciIoL4+HgqUuGYeLdu\n3Th58iQfffQReXl5PP/883Tt2pXTt9ckLEdhYSFjxoxh5MiRPPPMMwB06NCBiIgIvL29SU1NZdCg\nQURHR7N06VIAXnzxRQAefPBBXnvtNXr16lWywTImLkSTYVRGDl0+xP64/SgUvk6+TA6ZjIutS7nl\nYmK0mee5udqEtXHjoGPHOmq0EDWsvLxXqRNKP//8M9988w2jR48GwGg0VlhGKcW8efMICQkxJXCA\ncePG8eWXXwLw5ZdfMmHCBNPj3333HXq9nri4OC5cuEDPnj0r0zwhRCOUXZDN16e/Zl/cPhSKfv79\neDTs0XITuF4P27bBv/6lJfA2bbRLxySBi8aqwiT+/vvvs2TJEh566CFCQ0O5ePEigwYNqrDiw4cP\ns2bNGvbv30+3bt3o1q0b//73v3nxxRf58ccfadeuHfv27TP1vENCQpg6dSohISGMHDmSTz75pNxT\n7eLe3XkKSVSdxLD6yovhhWsXWHF8BXE34rC3tmdWl1kMbTO03FuHpqTAp5/C8ePaamsjRsCsWdoi\nLo2VHIc1w5zjWOGY+MCBAxk4cKBpOygoyHTNd3n69etXZo99z549pT6+cOFCFi5cWGHdQojGyWA0\nsDduL0cSjwDQxrUNEztOxMHGocwyRiMcPgz792u/e3pq133/Z/6sEI1ahWPix44d4+233yY+Pp6i\noiKtkE7HmTNn6qSBd5IxcSEap+t511kftZ7k7GQsdBYMChxEP/9+5Z6Ru3EDNm6EhARtu3dvGDoU\nrGRBadGIlJf3Kkzi7dq1Y9myZXTq1KnEwiuB9bQ+oSRxIRqfs1fPsiVmCwWGApybOTM5ZDJ+zn7l\nlvntN9i+HfLzwcEBJkyA4OA6arAQdahaE9tatGjBuHHjaNOmDYGBgaYfYb7MefynoZAYVl9ERASF\nhsM/ACwAACAASURBVEK2xmxlXdQ6CgwFdPToyPwe88tN4Pn52l3HNmzQfu/QQZu81hQTuByHNcOc\n41jhSafFixczb948hg4dio2NDaB9K5g4cWKtN04I0Xhdz7vO5yc+5+qtq1hZWDEiaAQ9fHqUe/o8\nIUE7fX7jBlhbw4MPwn33abcQFaIpqvB0+sMPP0xMTAyhoaElTqevWrWq1htXGjmdLoR5U0px8spJ\ndl7YSaGxEA87DyaHTMbbwbvMMgYDRETAoUPaKmw+PtrkNXf3umu3EPWlWmPi7du3Jzo6usFc7iVJ\nXAjzVVBUwNbzW/n96u8AhHmHMartKGwsbcosc+2advo8OVnrcffrB+Hh2mVkQjQF1RoT79OnD1FR\nUTXeKFF/zHn8p6GQGFZdSnYKK46v4Perv2NjaYNvpi8TOkwoM4ErBb/+CitWaAncxQXmzIEhQySB\n3ybHYc0w5zhWOCb+888/ExYWRuvWrWnWrBlQv5eYCSHMi1KKo0lH2XNpDwZlwNvBmykhU/gt8rcy\ny+TmwpYtEB2tbXfpAqNGga1tHTVaCDNR4en0shZgl0vMhBAVuaW/xaboTVzIvABAr1a9GBY0DCuL\nsvsPsbGwaRPk5ECzZjBmDHTuXFctFqLhqdaYeEMjSVwI8xB/I54NURvI1mfT3Ko54zuMp4NHhzJf\nX1QEP/6o3ToUICAAHnpIO40uRFNW7RugiMbFnMd/GgqJYdmMysj+uP18eepLsvXZ+Dv7M7/H/LsS\nePEYpqVp9/z+5RftPt9DhsDs2ZLAKyLHYc0w5zjK4oRCiBqTVZDFhqgNJNxMQIeOAQEDCA8Mx0JX\nen9BKTh6FPbs0S4jc3fXLh3z8anjhgthpuR0uhCiRpy/dp5N0ZvILczFwcaBiR0n0sa1TZmvz87W\nxr4vXtS2u3fX7jxmU/bVZkI0SeXlvQp74hs2bODFF18kLS3NVIlOpyMrK6tmWymEMEtFxiL2XNrD\n0aSjAAS7BfNQh4ewt7Evs8y5c9rs87w8sLODceO05VOFEFVT4Zj4888/z5YtW8jKyiI7O5vs7GxJ\n4GbOnMd/GgqJoSYzL5MvTn7B0aSjWOgsGNZmGA93frjMBK7Xw+bNsHYtnDsXQXAwPPmkJPB7Jcdh\nzTDnOFbYE/f29qZjx4510RYhhBn5Le03tp7fit6gx8XWhckhk/F18i3z9cnJ2k1LMjO1W4X27AkP\nPyzrngtRHRWOif/pT3/iypUrTJgwoUHcAEXGxIWoX3qDnp0XdnLyykkAQluEMrb9WGytSl+JxWjk\n/7d351FRn/fix98z7AqCoGyCguwoirvGmOCCO65oqm0WTYyxtz3tbW9r2tPc2+ScRHLu7fnd5t6k\nJo25Jm1iEnHfccO4xCgqiRFRRBBkcWGTfYB5fn9847QEjMsAM8N8XufkHL7Dw/DhE/Tj8/083+fh\n6FE4ckT72M9PW7zm69uVUQthu8zqiVdVVeHm5kZaWlqr1+UUMyHsz42aG6RmpXKr7haOekemh09n\nRMCIe56tUFGhnTpWUKBdjxunPT7mKM/FCNEhZHW6HUpPTychIcHSYdg0e8uhUoozJWfYe2UvzcZm\n+vboS3JsMn7ufvcYD998A7t3Q2MjeHhoG7cM/KfF6vaWw84gOewY1p7HR5qJv/nmm6xevZqf//zn\n7b7hW2+91XERCiGsVkNzA9svbSfrlnYQ0vCA4UwPn37Pg0vq62HXLvhWO6iM2Fht69QePboqYiHs\nxz1n4jt27CApKYn169e3ulWmlEKn0/Hss892WZD/TGbiQnSd63euk5qVSmVDJS4OLsyOnE2c3703\nMs/P126fV1Vpz3vPmAHx8bJ4TQhzyN7pQoiHopTiROEJDuYdxKiMBHoEkhybjLebd7vjW1rg0CE4\ncUK7lR4UBAsWgHf7w4UQD0H2Thet2PIzkdaiO+ew1lDLx+c/Zv/V/RiVkXFB43h+2PP3LOC3b8P7\n78Px49r1k0/CsmX3L+DdOYddRXLYMWw5j7JGVAhhcrXiKpsvbqbGUEMPpx7Mi55HpE9ku2OVgowM\nSEuDpibo3VubfQcHd3HQQtgxuZ0uhMCojKTnp3P02lEUihCvEBbELKCXS692x9fWajuvXb6sXQ8d\nCjNnaud/CyE6llnPiV+6dImf/vSnlJaWcuHCBb755hu2b9/OH/7whw4PVAjR9aoaqth0cRMFVQXo\n0JEQksATA56458ljOTnawSW1teDqCklJMGhQFwcthAAeoCe+YsUK3njjDdNubXFxcWzYsKHTAxOd\nx5b7P9aiu+Qw+3Y2azPWUlBVgIezB8/GP3vPo0ObmrTnvj/+WCvgISGwatWjF/DukkNLkhx2DFvO\n431n4nV1dYwZM8Z0rdPpcHJy6tSghBCdq9nYTFpuGqeKTgEQ6RPJvOh59HBq/2Hu0lJt3/Nbt8DB\nASZNgscek0fHhLC0+xbxvn37cuXKFdN1amoqAQEBnRqU6FzWvDORrbDlHJbVlbExayOlNaU46ByY\nMnAKY4PGtrt1qlLaY2OHDmmPkfXtqy1e64i/Amw5h9ZCctgxbDmP913Ylpuby4svvsiJEyfo3bs3\noaGhfPzxx4SEhHRRiK3JwjYhHt3XpV+zK2cXhhYD3m7eJMcmE+gR2O7Yqiqt952Xp12PHg2JiSA3\n4oToWh2y2UttbS1GoxEPD48ODe5hSRE3n7XvE2wLbC2HhhYDuy7v4usbXwMw2HcwSZFJuDi2v5z8\nwgXYsQMaGqBnT5g7FyLbf9LskdlaDq2R5LBjWHsezVqdXlFRwUcffUR+fj7Nzc2mN5S904WwDaU1\npWy8sJGy+jKc9E7MjJhJvH98u7fPGxthzx7IzNSuIyNhzhxwd+/ioIUQD+S+M/Fx48Yxbtw44uLi\n0Ov1sne6EDZCKcXp4tPsu7KPFtWCb09fFsUuom/Pvu2OLyyEzZu140OdnGDqVBg5UhavCWFpZt1O\nHz58OGfPnu2UwB6FFHEh7q++qZ5tl7aRfTsbgJGBI5kWNg0nh7YNbaMRvvgCjhzRFrIFBGiL1/q2\nX+uFEF3MrL3Tly5dynvvvUdJSQnl5eWm/4TtsuVnIq2FNeewoKqAtRlryb6djYuDC4tiFzE7cna7\nBby8HD74AO7+OOPHwwsvdE0Bt+Yc2grJYcew5Tzetyfu6urKb37zG15//XX0eq3m63Q6rl692unB\nCSEenFEZOV5wnMP5hzEqI/08+pEcm0xvt95txiql9b337AGDAXr1gvnzITTUAoELIR7ZfW+nh4aG\ncvr0afr06dNVMf0guZ0uRFs1hho2X9zM1QrtH9fjg8czKXQSDnqHNmPr6mDnTsjK0q4HD4ZZs8DN\nrSsjFkI8KLNWp0dEROAmf7qFsFpXyq+w5eIWaptq6enUk/kx8wn3Dm937NWrsGULVFdrh5XMnAlD\nhsjiNSFs1X2LeI8ePYiPj2fixIm4fHdEkTxiZtus/ZlIW2ANOWwxtnAo7xDHC7WDvEO9QlkQswAP\nl7Z7OTQ3a7uunTihXQcHa4vXere9095lrCGHtk5y2DFsOY/3LeLz5s1j3rx5rV5r7/nS9ixfvpxd\nu3bh6+vL+fPnAfjjH//I+++/T9/vVs688cYbzJgxA4A1a9bwwQcf4ODgwFtvvcXUqVMf6ocRwl5U\nNlSSmpXK9TvX0aFjYuhEHu//eLsHl9y8qT06VloKej08+SRMmKB9LISwbZ16nvjRo0dxd3fnmWee\nMRXxV199FQ8PD371q1+1GpuVlcXSpUs5ffo0RUVFTJkyhcuXL5sW05kClp64sHNZt7LYfmk7Dc0N\n9HLpRXJsMv09+7cZpxScOgX792szcW9vbfYdFGSBoIUQj+yReuKLFi1i48aNxMXFtfuG33zzzX2/\n8YQJE8jPz2/zenvBbNu2jSVLluDk5ERISAjh4eGcOnWKsWPH3vf7CGEPmlqa2Je7j4ziDACi+0Qz\nN2oubk5t16zU1Gj7nt89u2j4cJg+Hb47UVgI0U3cs4j/+c9/BmDnzp1tiu6D3k6/l//5n//ho48+\nYuTIkfzpT3/Cy8uL4uLiVgU7KCiIoqIis76PaJ8t93+sRVfn8FbtLVKzUrlRewMHnQNTw6Yyut/o\ndv8sXroE27Zpq9Dd3LRtU2NiuizUBya/h+aTHHYMW87jPYt4YKB2stE777zDm2++2epzq1evbvPa\ng1q1ahX//u//DsArr7zCr3/9a9atW9fu2Hv9Y+G5554znaLm5eVFfHy86X/A3Yf25fre15mZmVYV\njy1e39XZ3+/w4cNcKb/Czb43aTI2UZ5VzpMhTzImaEyb8QYD/OlP6Vy6BCEhCQwcCD4+6dy4ATEx\nls2XXHfOdeZ3m9xbSzy2en2XNcWTnp7e7p3s77tvT3zYsGGcO3eu1WtxcXGmHvf95Ofnk5SU1O74\nf/5cSkoKAC+//DIA06dP59VXX2XMmDGtA5aeuLATjc2N7Ly8k/M3tT87Q/2GMjNiZrsnjxUXw6ZN\nUFYGDg4wZQqMHSuPjgnRHTxST/wvf/kL77zzDrm5ua364tXV1YwfP/6RgykpKSEgIACALVu2mN57\nzpw5LF26lF/96lcUFRWRk5PD6NGjH/n7CGHLiquLSc1Kpby+HCe9E7MiZxHvH99mnNGoPTZ26JD2\nsa8vLFwIfn4WCFoI0eXuWcSXLl3KjBkzePnll3nzzTdN/wrw8PDAx8fngd58yZIlHDlyhNu3bxMc\nHMyrr75K+ne3c3U6HaGhobz77rsAxMbGsnjxYmJjY3F0dOSdd94xu/cu2pduw/0fa9FZOVRK8VXR\nV+zP3U+LasHf3Z/k2GT69Gi7Y2JVlfbo2LVr2vWYMdoM3KntFulWSX4PzSc57Bi2nMd7FnFPT088\nPT359NNPH/nNN2zY0Oa15cuX33P873//e37/+98/8vcTwpbVNdWxNXsrl8suAzC632imhk3FUd/2\nj+n587BrFzQ0aGd9z5sH4e1v0iaE6MY69TnxziA9cdEdXau8xqaLm7jTeAdXR1fmRs0lpm/bJeUN\nDbB7N9x9wjM6GpKSoGfPLg5YCNFlzNo7XQjReYzKyNFrR0nPT0ehCO4VzMLYhXi5erUZe+2atu95\nZaV2y3z6dO35b+k6CWG/ZONFO/T9xyrEw+uIHFY3VvPR1x9xOP8wABP6T+C5+OfaFPCWFjh4ENav\n1wp4YCC89BKMGGHbBVx+D80nOewYtpxHmYkLYQE5ZTlsyd5CXVMd7s7uzI+eT5h3WJtxZWXa4rWi\nIq1gT5gACQnaY2RCCCE9cSG6UIuxhYN5BzlReAKAsN5hzI+Zj7uze6txSsHZs7B3LzQ1gaentu/5\ngAGWiFoIYUnSExfCCpTXl5OalUpxdTF6nZ5JoZMYHzy+zaOUdXWwfTtkZ2vXcXEwaxa4ulogaCGE\nVZOeuB2y5f6PtXjYHH5781vezXiX4upivFy9WBa/jMf7P96mgF+5Au+8oxVwFxdt45aFC7tnAZff\nQ/NJDjuGLedRZuJCdKKmlib2XtnLmZIzAMT0iWFO1Jw2J481N8OBA3DypHY9YADMnw9ebRepCyGE\nifTEhegkN2tvsvHCRm7V3cJR78i0sGmMDBzZZvZ944a27/nNm6DXw8SJMH689rEQQkhPXIgupJTi\nbMlZ9lzZQ7OxmT49+rAodhF+7n7fG6fNvA8c0B4j8/HRbp1/d4CgEELcl/xb3w7Zcv/HWtwrhw3N\nDaRmpbLj8g6ajc0M8x/GiyNebFPAq6vh73+Hffu0Aj5iBKxcaV8FXH4PzSc57Bi2nEeZiQvRQYru\nFJGalUpFQwXODs7MjpzNEL8hbcZdvKitPq+vhx49YM4cbftUIYR4WNITF8JMSim+vP4lB64ewKiM\nBLgHkBybjE+P1qf9GQzac99nz2rX4eHawSXu7u28qRBCfEd64kJ0klpDLVuzt5JTngPA2KCxTBk4\npc3JY0VF2uK18nJwdITERBg92ra3TRVCWJ70xO2QLfd/rEV6ejp5FXmszVhLTnkObo5uLBm8hOnh\n01sVcKMRjhyBdeu0Au7nBy++qJ39be8FXH4PzSc57Bi2nEeZiQvxkIzKyLmScxzhCArFAM8BLIxd\nSC+XXq3GVVRop44VFGjX48bB5MnaTFwIITqC9MSFeAhVDVVsvriZa1XX0KHjiQFP8GTIk+h1/7ip\npZR23vfu3dDYCB4e2sYtAwdaMHAhhM2SnrgQHeDS7Utszd5KfXM9Hs4eLIhZQGjv0FZj6uth1y74\n9lvtOiYGkpK0VehCCNHRpCduh2y5/2MJzcZm9l7Zy4ZvN1DfXE+EdwSxtbFtCnh+PqxdqxVwZ2eY\nOxcWL5YCfi/ye2g+yWHHsOU8ykxciB9QVldGalYqJTUl6HV6pgycwrigcRwpP2Ia09IChw/D8ePa\nrfSgIO3YUG9vCwYuhLAL0hMX4h6+ufENOy/vxNBioLdrb5Jjk+nXq1+rMbdva4+OlZRoq82feEL7\nz8HBQkELIbod6YkL8RAMLQZ25+wmszQTgEF9B5EUlYSr4z/OA1UKMjIgLQ2amqB3b232HRxsqaiF\nEPZIeuJ2yJb7P52ttKaU9868R2ZpJk56J+ZEzSE5NrlVAa+thVdeSWfXLq2ADx0KL70kBfxhye+h\n+SSHHcOW8ygzcSHQtk7NKM5gX+4+mo3N9O3Rl0WDFuHb07fVuJwc2LoVrl/X9jtPSoJBgywUtBDC\n7klPXNi9+qZ6dlzeQdatLABGBIxgevh0nBycTGOammD/fjh1SrsOCdGe/fb0tEDAQgi7Ij1xIe6h\nsKqQTRc3UdlQiYuDC0lRSQz2HdxqTGmptnjt1i1twdqkSfDYY7JtqhDC8qQnbodsuf/TUZRSHCs4\nxv9l/h+VDZX08+jHSyNfalXAlYITJ+Cvf9UKeN++8MILMH48HDmSbrnguwn5PTSf5LBj2HIeZSYu\n7E6NoYYtF7eQW5ELwGPBjzE5dDIO+n88F3bnjrbveV6edj1qFEydCk5O7b2jEEJYhvTEhV3JLc9l\nS/YWagw19HDqwfzo+UT4RLQac+EC7NypbaHas6e281pkpIUCFkLYPemJC7vXYmwhPT+dYwXHUChC\nvEJYGLMQDxcP05jGRtizBzK1x8OJjIQ5c8Dd3UJBCyHEfUhP3A7Zcv/nUVQ2VLI+cz1HC44CMDFk\nIs8MfaZVAS8s1PY9z8zUbpnPmgVLlty7gNtbDjuD5NB8ksOOYct5lJm46NYu3rrItkvbaGhuoJdL\nLxbGLGSA1wDT541G+OIL7T+jEQICtJ3X+va1YNBCCPGApCcuuqVmYzP7ruzjdPFpAKJ8opgbPZce\nTv84Uqy8HDZv1jZu0em0x8YmTZJ9z4UQ1kV64sKu3K67zcYLG7lRewMHnQOJYYmM6TcG3XcPdisF\nX38Nu3eDwQC9emkbt4SG3ueNhRDCykhP3A7Zcv/nfjJLM3k3411u1N7A282b54c/z9igsaYCXl8P\nGzdqW6caDNqWqatWPXwB78457CqSQ/NJDjuGLedRZuKiW2hsbmR3zm6+vvE1AHG+ccyOnI2Lo4tp\nzNWrWvG+cwdcXGDmTBgyRHZeE0LYLumJC5tXUl1CalYqZfVlOOmdmBkxk3j/eNPsu7kZDh3Sdl8D\n7bSxBQu040OFEMLaSU9cdEtKKU4VnSItN40W1YJfTz+SY5Pp2/MfS8tv3tQWr5WWgl4PTz4JEyZo\nHwshhK3r1L/Kli9fjp+fH3FxcabXysvLSUxMJDIykqlTp1JZWWn63Jo1a4iIiCA6Opq0tLTODM2u\n2XL/5666pjo+/fZT9lzZQ4tqYVTgKF4Y/oKpgCulnTj23ntaAff2huXLtSLeEQW8O+TQ0iSH5pMc\ndgxbzmOnFvFly5axd+/eVq+lpKSQmJjI5cuXmTx5MikpKQBkZWXx2WefkZWVxd69e/npT3+K0Wjs\nzPCEjSqoKmBtxloulV3C1dGVxYMWMytyluno0Joa+OQTbfV5czMMGwYrV0JQkIUDF0KIDtbpPfH8\n/HySkpI4f/48ANHR0Rw5cgQ/Pz9KS0tJSEggOzubNWvWoNfrWb16NQDTp0/nj3/8I2PHjm0dsPTE\n7ZZRGTlWcIzDeYdRKIJ6BZEcm4yXq5dpzKVLsG0b1NWBm5u2bWpMjAWDFkIIM1lVT/zGjRv4+fkB\n4Ofnx40bNwAoLi5uVbCDgoIoKirq6vCElapurGbzxc3kVWrHij3e/3Emhkw0nTxmMEBaGmRkaOMH\nDoR587RnwIUQoruy6PIenU5nWkF8r8+Ljmdr/Z8r5VdYm7GWvMo8ejr15OkhTzNl4BRTAS8u1nrf\nGRnabmvTpsHTT3duAbe1HFojyaH5JIcdw5bz2OUz8bu30f39/SkpKcHX1xeAfv36UVhYaBp3/fp1\n+vXr1+57PPfcc4SEhADg5eVFfHw8CQkJwD/+Z8j1va8zMzOtKp57XbcYW/h/G/4f3976lpD4EAb2\nHkjfm30p/KaQsIQwjEZ4++10zp6FAQMS8PUFf/90GhtBp+vc+O6ypnzJtf1dZ3535J61xGOr13dZ\nUzzp6enk5+dzP13eE//tb3+Lj48Pq1evJiUlhcrKSlJSUsjKymLp0qWcOnWKoqIipkyZwpUrV9rM\nxqUnbh8q6itIzUqlqLoIvU7PxJCJPN7/cdPvQ1WV9ujYtWva+DFjYMoU7QQyIYToTizWE1+yZAlH\njhzh9u3bBAcH89prr/Hyyy+zePFi1q1bR0hICJ9//jkAsbGxLF68mNjYWBwdHXnnnXfkdrqdunDz\nAtsvbaexpRFPF08Wxi6kv2d/0+fPn4ddu6ChQTsqdN48CA+3YMBCCGEhsmObHUpPTzfdvrEmTS1N\n7MvdR0axtjotuk80c6Pm4ubkBmhFe/du+OYbbXx0NCQlQc+eXR+rtebQlkgOzSc57BjWnkerWp0u\nRHtu1d5iY9ZGbtbexEHnwLTwaYwKHGW6G3PtGmzZApWV2i3z6dNh+HDZ91wIYd9kJi4sSinFudJz\n7MnZQ5OxCR83HxYNWoS/uz8ALS1w5AgcPartwhYYCAsXgo+PhQMXQoguIjNxYZUamxvZcXkH3978\nFoB4/3hmRszE2cEZgLIybfFaUZE2454wARIStMfIhBBCyHnidun7j1VYQnF1MWsz1vLtzW9xdnBm\nfvR85kXPw9nBGaXgzBlYu1Yr4J6e8NxzMHmy9RRwa8ihrZMcmk9y2DFsOY8yExddSinFyesnOXD1\nAC2qBX93fxbFLsKnh3Z/vK4Otm+H7GxtfFwczJoFrq4WDFoIIayU9MRFl6lrqmNr9lYul10GYEy/\nMSSGJeKo1/4tmZsLW7dCdTW4uMDs2VoRF0IIeyY9cWFx+ZX5bMraRLWhGjdHN+ZGzyW6TzSgnTR2\n4ACcPKmNHTAA5s8HL68feEMhhBDSE7dHXdn/MSoj6fnpfJj5IdWGavp79uelkS+ZCviNG9q+5ydP\naud8T54Mzz5r/QXclnto1kJyaD7JYcew5TzKTFx0mjuNd9iUtYlrVdfQoeOJAU+QEJKAXqdHKfjq\nK9i/X3uMzMdHe3QsMNDSUQshhO2QnrjoFJfLLrM1eyt1TXW4O7uzIGYBA3sPBLSe99atWg8cYMQI\n7eQxZ2cLBiyEEFZKeuKiy7QYWzhw9QBfXv8SgHDvcOZFz8Pd2R2Aixdhxw5tFXqPHjBnjrZ9qhBC\niIcnPXE71Fn9n/L6ctadW8eX179Er9OTODCRH8f9GHdndwwG7dGxzz7TCnh4OKxaZbsF3JZ7aNZC\ncmg+yWHHsOU8ykxcdIjzN86z8/JOGlsa8XL1Ijk2maBeQYC2YcumTVBeDo6OkJgIo0fLvudCCGEu\n6YkLsxhaDOzJ2cO50nMAxPaNZU7UHFwdXTEa4dgxSE8HoxH8/LTFa76+lo1ZCCFsifTERae4UXOD\n1KxUbtXdwlHvyPTw6YwIGIFOp6OiQjt1rKBAGztunPb4mKP8xgkhRIeRnrgdMrf/o5QioziDv579\nK7fqbtG3R19WDF/ByMCRgI5vvtH2PS8oAA8PeOYZbfV5dyrgttxDsxaSQ/NJDjuGLeexG/21KrpC\nQ3MDOy7t4MKtCwAMDxjO9PDpODs409AAO3fCt9qhZMTEQFKStgpdCCFEx5OeuHhg1+9cJzUrlcqG\nSlwcXJgdOZs4P21z8/x87fZ5VZX2vPeMGRAfL4vXhBDCXNITF2ZRSnGi8AQH8w5iVEYCPQJJjk3G\n282blhY4fBiOHwelICgIFiwAb29LRy2EEN2f9MTt0MP0f2oNtXx8/mP2X92PURkZFzSO54c9j7eb\nN7dvw/vvayvQAZ58EpYts48Cbss9NGshOTSf5LBj2HIeZSYu7ulqxVU2X9xMjaGGHk49mBc9j0if\nSJSCjAzYtw+amqB3b232HRxs6YiFEMK+SE9ctHH35LGj146iUAzwHMDC2IX0culFba2289qlS9rY\noUNh5kzt/G8hhBAdT3ri4oFVNVSx6eImCqoK0KEjISSBJwY8gV6nJydHO7ikthZcXbWV54MGWTpi\nIYSwX9ITt0P36v9k385mbcZaCqoK8HD24Nn4Z0kISaClWc/u3fDxx1oBDwnR9j235wJuyz00ayE5\nNJ/ksGPYch5lJi5oNjazP3c/XxV9BUCkTyTzoufRw6kHpaXavue3boGDA0yaBI89Jo+OCSGENZCe\nuJ0rqytjY9ZGSmtKcdA5MGXgFMYGjQV0fPklHDwILS3Qp4+273lAgKUjFkII+yI9cdGur0u/ZlfO\nLgwtBnq79mbRoEUEegRy5462cUtenjZu1CiYOhWcnCwbrxBCiNakJ26H9h/cz9bsrWzJ3oKhxcBg\n38G8NPIlAj0CycqCv/xFK+A9e8LSpTBrlhTw77PlHpq1kByaT3LYMWw5jzITtzOlNaXsuLQDbwdv\nnPROzIiYwTD/YRgMOrbuhMxMbVxkJMyZA+7ulo1XCCHEvUlP3E4opThdfJq03DSajc349vRl/5mk\n8AAAGD9JREFUUewi+vbsS2EhbN4MFRXaSWPTpsHIkbJ4TQghrIH0xO1cfVM92y5tI/t2NgAjA0cy\nLWwaDjon0tPhiy/AaNQWrS1YAH37WjZeIYQQD0Z64t1cYVUhazPWkn07GxcHFxbFLsK92J3qKic+\n+ADS07WDS8aPhxdekAL+oGy5h2YtJIfmkxx2DFvOo8zEuymlFMcKjnE4/zBGZaSfRz+SY5Pxcu3N\nuivpnDgBBgP06gXz50NoqKUjFkII8bCkJ94N1Rhq2HxxM1crrgIwPng8k0InYWh0YMcOyMrSxg0a\nBLNng5ubBYMVQgjxg6Qnbkdyy3PZfHEztU219HTqyfyY+YR7h5OXpz37feeOdljJzJkwZIgsXhNC\nCFsmPfFuosXYwoGrB/jbN3+jtqmWUK9QXhr5EiG9wklLgw8/1Ap4cDAMHpzO0KFSwM1hyz00ayE5\nNJ/ksGPYch5lJt4NVDZUkpqVyvU719GhY2LoRB7v/zi3b+n5eDOUloJeD08+CRMmaKvRhRBC2D7p\nidu4rFtZbL+0nYbmBnq59CI5NpngXv05fRrS0qC5Gby9tUfHgoIsHa0QQoiH9UN1T4q4jWpqaSIt\nN43TxacBiPKJYm70XIyNPdi2DXJytHHDhsH06VofXAghhO35obpnsZ54SEgIQ4YMYdiwYYwePRqA\n8vJyEhMTiYyMZOrUqVRWVloqPKt2q/YW7599n9PFp3HQOTAjfAY/GvwjCq/24C9/0Qq4mxs89RTM\nndu2gNty/8daSA7NJzk0n+SwY9hyHi1WxHU6Henp6Zw7d45Tp04BkJKSQmJiIpcvX2by5MmkpKRY\nKjyrpJTiXMk53jvzHjdqb+Dj5sMLw19gmO8Ydu3SsWED1NbCwIGwahXExFg6YiGEEJ3JYrfTQ0ND\nycjIwMfHx/RadHQ0R44cwc/Pj9LSUhISEsjOzm71dfZ6O72xuZGdl3dy/uZ5AIb4DWFWxCzKbrqw\neTPcvg0ODjBlCowdKyvPhRCiu7DKnvjAgQPx9PTEwcGBlStXsmLFCnr37k1FRQWgzTq9vb1N16aA\n7bCIF1cXk5qVSnl9OU56J2ZFzmKIbzwnTsChQ9q+576+2uI1f39LRyuEEKIjWWVP/Pjx45w7d449\ne/bw9ttvc/To0Vaf1+l06Ox8OqmU4uT1k6w7u47y+nL8evqxcuRKQt3i+egjOHBAK+BjxsCKFQ9e\nwG25/2MtJIfmkxyaT3LYMWw5jxZ7TjwgIACAvn37Mn/+fE6dOmW6je7v709JSQm+vr7tfu1zzz1H\nSEgIAF5eXsTHx5OQkAD843+GrV+PHj+abdnb2HdwHwCLZy1mathUPlp/jJMnITAwAXd3CAhIx80N\nnJwe/P0zMzMt/vPZ+vVd1hKPXNvndWZmplXFY6vXd1lTPOnp6eTn53M/FrmdXldXR0tLCx4eHtTW\n1jJ16lT+4z/+gwMHDuDj48Pq1atJSUmhsrKyzeI2e7idfq3yGpsubuJO4x1cHV2ZGzWXUI8Ydu+G\nb77RxkRFwZw50LOnZWMVQgjRuayuJ56Xl8f8+fMBaG5u5sc//jG/+93vKC8vZ/HixRQUFBASEsLn\nn3+Ol5dX64C7cRE3KiNHrx0lPT8dhSK4VzALYxdy56YXmzdDZSU4OWnPfQ8fLovXhBDCHlhdETdH\ndy3i1Y3VbLq4ifzKfHToeLz/40wITuDYUQeOHtXO/A4MhIUL4Z8W9D+S9PR00+0b8Wgkh+aTHJpP\nctgxrD2PcoqZlcspy2FL9hbqmupwd3ZnfvR8vFQYH66HoiJtxj1hAiQkaI+RCSGEECAzcYtqMbZw\nMO8gJwpPABDWO4x50fPJueDO3r1gMICnp/bo2IABFg5WCCGERchM3ApV1FeQmpVKUXURep2eSaGT\nGOYznh1bdNzd3yYuDmbNAldXy8YqhBDCOsl54hbw7c1vWZuxlqLqIrxcvVgWv4yApsdZu1Yr4C4u\nWu974cLOKeDff6xCPDzJofkkh+aTHHYMW86jzMS7UFNLE3uv7OVMyRkAYvrEMDNsDsePuHHypDZm\nwACYPx++tyhfCCGEaEN64l3kZu1NUrNSuVl7E0e9I9PCphHsMJItW3TcuAF6PUycCOPHax8LIYQQ\nII+YWZRSirMlZ9l7ZS9Nxib69OjDwphkrl3w58ABaG7WHhlbuFB7hEwIIYT4Z1a5d7o9aGhuYNPF\nTey4vIMmYxPx/vEsiXyRA1v92btXK+AjRsDKlV1bwG25/2MtJIfmkxyaT3LYMWw5j9IT7yRFd4pI\nzUqloqECZwdnZkfOxql8COveg7o66NFD2zY1OtrSkQohhLBVcju9g1y6cokDZw5gMBq4XnUdg6cB\nnwAfAtwDmBOezOkvfDh7VhsbHg5z54KHh2VjFkIIYf3kOfFOdunKJdYfXo9+oJ6Lty9S7lpO84Vm\nnvV9lql+y9j4kSPl5eDoCImJMHq07HsuhBDCfNIT7wAHzhzA0N9ARnEG5fXlOOodGTounqyTTXz4\nf1oB9/ODF1/Uzv62dAG35f6PtZAcmk9yaD7JYcew5TzKTLwD5Fflc7z8S8rKa3GhJ30J4GK+I85X\nDYwNgXHjYPJkbSYuhBBCdBTpiZuhxdjCvtx9pKz7T/Jdyumli8WlNoLyMj0tzVeJaorg3ddfYeBA\nS0cqhBDCVklPvBPUGGrYeGEj16quodd50Ts3hGbPAZTVap/vcbsfI0cESwEXQgjRaaQn/giu37nO\nuxnvcq3qGh7OHsQ7LcX9+ssYzvrilOtFUKUvkyOew88nxNKhtsuW+z/WQnJoPsmh+SSHHcOW8ygz\n8Yd0pvgMu3N206JaCPLoT0D5Yg6dOYUTUUT3iSI2FtzctLHOzkWWDVYIIUS3Jj3xB9RsbGZPzh7T\n4SXRHqOpOjONkmIHysquUVZ2hfDwyaZ9zxsbD/Lcc+FERclB4EIIIR6d7J1upjuNd/j8wudcv3Md\nB50jEWo2V0/EYzCApycsWAANDdc4eDAXg0GPs7ORyZPDpIALIYQwmxRxMxRUFfD5hc+pMdTQQ+9J\nr8KnKM3RNjofPBhmz+6cM787U3p6OgkJCZYOw6ZJDs0nOTSf5LBjWHseZXX6I1BKcbr4NHuv7MWo\njLg3h9L0dTKl1T1xcYFZsyAuzvIbtwghhLBfMhNvR1NLE7tydpFZmonRCG5lj9GQNQWd0hMcrN0+\n7927U0MQQgghAJmJP5Sqhio+u/AZxdXFGBqccLwyh8bbcTjo4ckEmDAB0+I1IYQQwpKkHP2TvIo8\n3j3zLkV3iqm+1RtjxvPob8fRuzcsWwZPPtk9CrgtPxNpLSSH5pMcmk9y2DFsOY8yE0frf5+8fpL9\nV/fT0GikMi+M3iXJOOFGfDzMmAEuLpaOUgghhGjN7nviTS1NbL+0nfM3z1NeDo05E/Cvn4ibq57Z\ns7UV6EIIIYSlSE/8HirqK7T+951SCvKc6Vk4jwBiGTBAW7zm6WnpCIUQQoh76wYd3keTW57Le2fe\nI/dGKdnnfOhb+AJ++limTIFnn+3eBdyW+z/WQnJoPsmh+SSHHcOW82h3M3GlFMcLj3Pg6kGuX1dU\nXY0kyrgAPx9XFi6EwEBLRyiEEEI8GLvqiRtaDGzN3kpmURbZ2eBR/iQhJDBiuI7p08HZuYODFUII\nIcwkPXGgrK6Mzy58xsWCm1y55EKYYQHBblHMmQMxMZaOTgghhHh4dtETv1x2mbWn/8rxzJvknu9D\nnGEFowdGsWqVfRZwW+7/WAvJofkkh+aTHHYMW85jt56JK6X44toX7Pw2nQtZih51MYzSz2PaFBfG\njZN9z4UQQti2btsTb2huYPPFLRzMvEReno4BxkkM93mc5GQdAQFdEKgQQgjRAeyuJ36r9hYfnvmM\n4+duU13hyiAWMn1UBFOngpOTpaMTQgghOka364lfvHWRN/b9lX1Hb2Oo8ONxtxf52ZIIZs2SAn6X\nLfd/rIXk0HySQ/NJDjuGLeex28zEjcrI/px01h/+gpIS8GUwM8PmkDzfGXd3S0cnhBBCdLxu0ROv\nb6pn3Zeb2fVlDvX1OiIdElmeOI4xY3SyeE0IIYRN65Y98T37D7F+61aqmqrJrc7F1TMEf//BTPJJ\nZuXigfj5WTpCIYQQonNZXU987969REdHExERwZtvvtnumD37D/Ha/73PZe9mMnpd45afnusF2Yxy\niuL3q6SA348t93+sheTQfJJD80kOO4Yt59GqinhLSws/+9nP2Lt3L1lZWWzYsIGLFy+2GbfitX/j\nmnc5+TVZNDcbcW32IzxuGrnFh3C02XsLXSczM9PSIdg8yaH5JIfmkxx2DFvOo1UV8VOnThEeHk5I\nSAhOTk786Ec/Ytu2bW3GFXtepbT2DIb6aryM4YT3jqanmwMGY4sForY9lZWVlg7B5kkOzSc5NJ/k\nsGPYch6tqogXFRURHBxsug4KCqKoqKjNONWzBeVpQFU1McA7CEcHbfWas96hy2IVQgghLM2qirju\nAZeS69290Bc406yqufsVjZcv89y8uZ0XXDeSn59v6RBsnuTQfJJD80kOO4Yt59GqHjE7efIkf/zj\nH9m7dy8Aa9asQa/Xs3r1atMYvacb6k6DpUIUQgghutTQoUPv2be3qiLe3NxMVFQUBw8eJDAwkNGj\nR7NhwwZi7PGoMSGEEOI+rGott6OjI//7v//LtGnTaGlp4fnnn5cCLoQQQtyDVc3EhRBCCPHgrGph\n2w95kE1g7ElhYSETJ05k0KBBDB48mLfeeguA8vJyEhMTiYyMZOrUqa0enVizZg0RERFER0eTlpZm\nev3MmTPExcURERHBL37xC9PrjY2NPPXUU0RERDB27FiuXbvWdT9gF2ppaWHYsGEkJSUBksOHVVlZ\nSXJyMjExMcTGxvLVV19JDh/SmjVrGDRoEHFxcSxdupTGxkbJ4X0sX74cPz8/4uLiTK91Vc4+/PBD\nIiMjiYyM5KOPPurkn/Q+lA1obm5WYWFhKi8vTxkMBjV06FCVlZVl6bAsqqSkRJ07d04ppVR1dbWK\njIxUWVlZ6je/+Y168803lVJKpaSkqNWrVyullLpw4YIaOnSoMhgMKi8vT4WFhSmj0aiUUmrUqFHq\nq6++UkopNWPGDLVnzx6llFJvv/22WrVqlVJKqU8//VQ99dRTXfozdpU//elPaunSpSopKUkppSSH\nD+mZZ55R69atU0op1dTUpCorKyWHDyEvL0+FhoaqhoYGpZRSixcvVuvXr5cc3scXX3yhzp49qwYP\nHmx6rStyVlZWpgYOHKgqKipURUWF6WNLsYkifuLECTVt2jTT9Zo1a9SaNWssGJH1mTt3rtq/f7+K\niopSpaWlSimt0EdFRSmllHrjjTdUSkqKafy0adPUl19+qYqLi1V0dLTp9Q0bNqiVK1eaxpw8eVIp\npf3l3KdPn676cbpMYWGhmjx5sjp06JCaPXu2UkpJDh9CZWWlCg0NbfO65PDBlZWVqcjISFVeXq6a\nmprU7NmzVVpamuTwAeTl5bUq4l2Rs08++US99NJLpq9ZuXKl2rBhQyf9hPdnE7fTH3QTGHuVn5/P\nuXPnGDNmDDdu3MDvu83j/fz8uHHjBgDFxcUEBQWZvuZuDr//er9+/Uy5/ee8Ozo64unpSXl5eVf9\nWF3iX//1X/nP//xP9Pp//FGQHD64vLw8+vbty7Jlyxg+fDgrVqygtrZWcvgQvL29+fWvf03//v0J\nDAzEy8uLxMREyeEj6OyclZWV3fO9LMUmiviDbgJjj2pqali4cCF//vOf8fDwaPU5nU4nufsBO3fu\nxNfXl2HDht3zmD/J4Q9rbm7m7Nmz/PSnP+Xs2bP07NmTlJSUVmMkhz8sNzeX//7v/yY/P5/i4mJq\namr4+9//3mqM5PDh2UvObKKI9+vXj8LCQtN1YWFhq38J2aumpiYWLlzI008/zbx58wDtX5+lpaUA\nlJSU4OvrC7TN4fXr1wkKCqJfv35cv369zet3v6agoADQ/rKuqqrC29u7S362rnDixAm2b99OaGgo\nS5Ys4dChQzz99NOSw4cQFBREUFAQo0aNAiA5OZmzZ8/i7+8vOXxAGRkZPPbYY/j4+ODo6MiCBQv4\n8ssvJYePoLP/7Pr4+FhdPbKJIj5y5EhycnLIz8/HYDDw2WefMWfOHEuHZVFKKZ5//nliY2P55S9/\naXp9zpw5fPjhh4C2gvJucZ8zZw6ffvopBoOBvLw8cnJyGD16NP7+/vTq1YuvvvoKpRR/+9vfmDt3\nbpv3Sk1NZfLkyV38U3auN954g8LCQvLy8vj000+ZNGkSf/vb3ySHD8Hf35/g4GAuX74MwIEDBxg0\naBBJSUmSwwcUHR3NyZMnqa+vRynFgQMHiI2NlRw+gq74szt16lTS0tKorKykoqKC/fv3M23aNAv8\ntN+xWDf+Ie3evVtFRkaqsLAw9cYbb1g6HIs7evSo0ul0aujQoSo+Pl7Fx8erPXv2qLKyMjV58mQV\nERGhEhMTW62afP3111VYWJiKiopSe/fuNb2ekZGhBg8erMLCwtTPf/5z0+sNDQ1q0aJFKjw8XI0Z\nM0bl5eV15Y/YpdLT002r0yWHDyczM1ONHDlSDRkyRM2fP19VVlZKDh/Sm2++qWJjY9XgwYPVM888\nowwGg+TwPn70ox+pgIAA5eTkpIKCgtQHH3zQZTn74IMPVHh4uAoPD1fr16/vkp/3XmSzFyGEEMJG\n2cTtdCGEEEK0JUVcCCGEsFFSxIUQQggbJUVcCCGEsFFSxIUQQggbJUVcCCGEsFFSxIUQrSQkJHDm\nzBmz3mPHjh1yZLAQXcDR0gEIIaxLR+w5nZSUZDqfXQjReWQmLoSVq62tZdasWcTHxxMXF8fGjRsB\neO211xg9ejRxcXGsXLnSND4hIYFf/epXjBo1ipiYGE6fPs38+fOJjIzklVdeAbST76Kjo/nJT35C\nbGwsixYtor6+vs33TktL47HHHmPEiBEsXryY2traNmPeeustBg0axNChQ1m6dCkA69ev5+c//zkA\n8fHxDBs2jGHDhtGjRw+OHj1KbW0ty5cvZ8yYMQwfPpzt27e3ed/09HQSEhJYtGgRMTEx/OQnPzE/\nmUJ0NxbdL04IcV+pqalqxYoVpuuqqiqllFLl5eWm155++mm1Y8cOpZRSCQkJ6uWXX1ZKKfXnP/9Z\nBQQEqNLSUtXY2KiCgoJUeXm5ysvLUzqdTp04cUIppdTy5cvVf/3Xf5m+/syZM+rWrVvqiSeeUHV1\ndUoppVJSUtRrr73WJr7AwEBlMBhaxbZ+/Xr1s5/9rNW47du3qyeeeEI1NTWp3/3ud+rvf/+7Ukqp\niooKFRkZqWpra1uNP3z4sPL09FRFRUXKaDSqcePGqWPHjj1KCoXotmQmLoSVGzJkCPv37+fll1/m\n2LFj9OrVC4BDhw4xduxYhgwZwqFDh8jKyjJ9zd0DggYPHszgwYPx8/PD2dmZgQMHmk5gCg4OZty4\ncQD85Cc/4dixY6avV0px8uRJsrKyeOyxxxg2bBgfffSR6VSn78e3dOlSPv74YxwcHNr9GXJycvjt\nb3/L559/jqOjI2lpaaSkpDBs2DAmTpxIY2Njq5Oh7ho9ejSBgYHodDri4+PJz89/tCQK0U1JT1wI\nKxcREcG5c+fYtWsXf/jDH5g8eTK//e1v+Zd/+RfOnDlDv379ePXVV2loaDB9jYuLCwB6vd708d3r\n5uZmgFZ9b6VUu33wxMREPvnkkx+Mb9euXXzxxRfs2LGD119/nfPnz7c6n72mpoannnqK999/Hz8/\nP9PrmzdvJiIi4gff+59jd3BwMMUuhNDITFwIK1dSUoKrqys//vGP+bd/+zfOnTtnKtg+Pj7U1NSY\n+uQPo6CggJMnTwLwySefMGHCBNPndDodY8eO5fjx4+Tm5gJabz4nJ6fVeyilKCgoICEhgZSUFKqq\nqqipqWk1Zvny5Sxbtozx48ebXps2bRpvvfWW6frcuXMPHb8QQmbiQli98+fP85vf/Aa9Xo+TkxNr\n167F09OTFStWMHjwYPz9/RkzZky7X/tDK82joqJ4++23Wb58OYMGDWLVqlWtPt+nTx/Wr1/PkiVL\naGxsBOD1119vNXtuaWnh6aefpqqqCqUUv/jFL/D09DR934KCAjZt2kROTg4ffPABAOvWreOVV17h\nl7/8JUOGDMFoNDJw4MA2i9vai93cVfNCdDdyFKkQdig/P5+kpCTOnz9v6VCEEGaQ2+lC2CmZ1Qph\n+2QmLoQQQtgomYkLIYQQNkqKuBBCCGGjpIgLIYQQNkqKuBBCCGGjpIgLIYQQNkqKuBBCCGGj/j8b\nURKDPTGQxwAAAABJRU5ErkJggg==\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10e8f8610>"
|
|
]
|
|
},
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAeoAAAGJCAYAAABFDXDOAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl8TXf++PFXQoJE9kgiO0ntgtZSFLG2lNYoKtagqr/B\nTKtT7bSKKqodVBedfnVUSmyli30pGqNUaRGqxJpYEksESSSyfn5/nMltQja5N7n3JO/n4+Eh5957\nznmf9z03n5zz/tzPx0oppRBCCCGERbI2dwBCCCGEKJo01EIIIYQFk4ZaCCGEsGDSUAshhBAWTBpq\nIYQQwoJJQy2EEEJYMGmoi3Ht2jU6d+6Mo6Mjr732mrnDEUXYu3cvjRo1qtB9hoaGsmTJEgBWrFjB\nk08+WaH7tyT5c1FR+vTpw/Llyyt0n6YUGBjIrl27Cn0uPT2dfv364ezszPPPP2/0vmbMmMGIESOM\n3o6pWNJ7Fx4ezttvv23uMEpU6RrqwMBA7OzscHBwwMvLi9GjR3P37t0ybWvx4sV4eHiQnJzMv/71\nLxNHKkylU6dOnDp1qkL3aWVlhZWVFQDDhg1j+/btJa6jl18KDyt/LirKli1bLKrxeVjF5WzdunVc\nv36dpKQk1qxZY5J9WRJj37uVK1fSunVrHBwc8Pb2pk+fPuzbt6/E9SIiIujUqVOBx8xx7pZFpWuo\nrays2LRpEykpKRw+fJhff/2VWbNmPdQ2lFLk5uYSFxdH48aNyxRHdnZ2mdYTD0fyXL4kvxUvLi6O\nBg0aYG398L+eC3u/KtOYVgsWLOCVV15h6tSpXL9+nUuXLjFhwgQ2bNhg7tDKVaVrqPPz9vbmqaee\n4vfffwfgwIEDdOjQARcXF1q2bMmePXsMrw0NDWXq1Kk88cQT2NvbM2rUKJYtW8YHH3yAg4MDu3fv\nJjMzk5dffhkfHx98fHx45ZVXyMzMBCAqKgpfX18++OAD6taty5gxY3jnnXcYNGgQI0aMwNHRkZCQ\nEM6cOcN7772Hp6cnAQEB/PDDD4YYli5dSpMmTXB0dCQoKIjFixcbnsvb/oIFC/D09MTb25uIiAjD\n8+np6bz66qsEBgbi7OxMp06duHfvXonHfb9Lly4xYMAAPDw8cHd3Z9KkSQDk5uYya9YsAgMD8fT0\nZNSoUSQnJwMQGxuLtbU1ERER+Pv74+bmxueff86hQ4cICQnBxcXFsB3Q/rLt2LEjkyZNwtnZmcaN\nG7N79+6HykNenseOHUtUVBR+fn6G17z//vv4+vri6OhIo0aNDNvOyMgo8f0rKr/Fyf+XulKKV155\nBU9PT5ycnAgJCeHEiRMsXryYlStXGs6nZ599ttBtnThxgp49e+Lm5oaXlxfvvfdeqWP/17/+hYeH\nB97e3nz//fds2bKFBg0a4Obmxty5cw37mDFjBgMHDmTIkCE4Ojry2GOPcezYMcPzgYGBfPDBB4SE\nhODg4EBubm6J51BsbCxPPPEEjo6OPPnkk9y8edPwXEmfu2nTphW67r179xg+fDju7u64uLjQtm1b\nbty4YVgv73a7UqrEc3PZsmUEBARQp04d5syZY9j/wYMHad26NU5OTnh5efHqq68W+r7cvn2bvn37\n4uHhgaurK/369ePKlSulOg6A5cuXExAQgLu7e4H932/69Om8++67rFmzBgcHB5YuXVqq4/vyyy8J\nCAigR48eRW47z4YNG2jatCkuLi507dq1wN2okydPEhoaiouLC82aNWPjxo2G58LDw3nppZfo1asX\njo6OhIaGcvHiRcPzhZ33hcn/3kVERPDEE0/w2muv4erqSv369dm2bVuh6925c4fp06fz2Wef0b9/\nf2rVqkW1atV4+umnef/997l69Sr29vYkJSUZ1jl8+DAeHh78/vvvvPTSS/z88884ODjg6upqeE1S\nUhJ9+/bF0dGRxx9/nPPnzxue279/P23atMHZ2Zm2bdvy888/FziO4t5zk1KVTGBgoNq5c6dSSqmL\nFy+qpk2bqmnTpqnLly8rNzc3tXXrVqWUUj/88INyc3NTiYmJSimlunTpogICAtQff/yhcnJyVFZW\nlgoPD1dvv/22Ydtvv/22at++vbpx44a6ceOG6tChg+H5H3/8UVWvXl298cYbKjMzU6Wnp6vp06er\nmjVrqh07dqjs7Gw1cuRIFRAQoObMmaOys7PVF198oerVq2fY/ubNm9X58+eVUkrt2bNH2dnZqcOH\nDxfY/vTp01V2drbasmWLsrOzU7dv31ZKKfXXv/5Vde3aVcXHx6ucnBz1888/q4yMjCKP+8aNGw/k\nLjs7W4WEhKjJkyertLQ0de/ePbVv3z6llFJLlixRwcHB6sKFCyo1NVUNGDBAjRgxQiml1IULF5SV\nlZX6f//v/6mMjAy1Y8cOZWtrq/r3769u3Lihrly5ojw8PNSePXuUUkotXbpUVa9eXS1cuFBlZ2er\nNWvWKCcnJ5WUlFTqPOTP848//qh8fX2VUkqdOnVK+fn5qYSEBKWUUnFxcercuXOlfv+Kyu/9QkND\n1ZIlSwzH88QTTyillNq2bZt67LHH1J07dwzx5MVy//l0v+TkZOXl5aUWLFigMjIyVEpKivrll19K\nHfu7775rOK/c3NzU0KFDVWpqqjpx4oSqVauWio2NVUopNX36dGVjY6O++eYblZ2drebNm6fq1aun\nsrOzlVJKBQQEqFatWqnLly+re/fuleqzExQUpM6cOaPS09NVaGioeuONN5RSqlTrBgcHF7ru559/\nrvr166fS09NVbm6uOnz4sEpOTn4g/6U5N1988UV17949FR0drWrUqKFOnTqllFLq8ccfV5GRkUop\npe7evasOHDhQ6Htz8+ZN9e2336r09HSVkpKiBg0apPr37294vrjjOHHihKpdu7bau3evysjIUJMn\nT1bVq1dXu3btKnRfM2bMMMRf2uMbNWqU4TN7v+nTp6vhw4crpZSKiYlR9vb2aufOnSo7O1t98MEH\nKjg4WGVlZanMzEwVFBSk3nvvPZWVlaV2796tHBwcVExMjFJKqVGjRikHBwfDcfz9738v1Xl/v/s/\nOzY2Nuo///mPys3NVf/+97+Vt7d3oett3bpVVa9eXeXk5BT6vFJK9enTR/373/82LL/88svqb3/7\nm1JKqYiICEO8eUaNGqXc3NzUoUOHVHZ2tho2bJgaMmSIUkp7z52dnVVkZKTKyclRq1atUi4uLobf\nU8W956ZW6RrqgIAAVbt2beXs7KwCAgLUhAkTVHp6upo7d26Bk18ppZ588kn11VdfKaW0k2f69OkF\nng8PD1dTp041LAcFBRl+4Sil1Pbt21VgYKBSSvtlaWtrqzIyMgzPT58+XfXq1cuwvGHDBlW7dm2V\nm5urlNJ+MVtZWRlO7vv1799fffTRR4bt16pVq8BJ6uHhoX755ReVk5OjatWqpY4dO/bANko67vz2\n79+v6tSpU+gHoVu3bgU+ADExMcrGxkbl5OQYflnEx8cbnndzc1Nff/21Yfm5555TCxcuVEppH877\nP4xt27ZVy5cvL1Ue7s9z/ob6zJkzysPDQ+3cuVNlZmYW2E5J719R+S1MUQ31rl27VIMGDdSBAwce\nyOP959P9Vq5cqR599NFCnytN7PefVwcPHjS8/rHHHlPr169XSmnnZfv27Q3P5ebmqrp166qffvpJ\nKaX9sbt06VLD86X57MyePdvw3Geffaaeeuopo9f98ssvVYcOHQo9r/PnvzTn5pUrVwzPt23bVq1Z\ns0YppVTnzp3V9OnTC/3DtThHjhxRLi4uBeIp6jjeeecdFRYWZnju7t27ytbWtsiGOn/DWtrju3Dh\nQpGx5t/ezJkz1fPPP294Ljc3V/n4+KioqCj13//+V3l5eRVYNywsTM2YMUMppTVq+Y8jNTVVVatW\nTV2+fFnt3r27yPP+fvd/doKDgwvkxsrKSl27du2B9SIjIx+I736rV69WHTt2VEppFx5eXl7q0KFD\nhn3d31CHh4ercePGGZa3bNmiGjVqpJRSatmyZapdu3YFXt++fXsVERFhOI6i3nNTq3S3vq2srFi/\nfj23bt0iNjaWTz/9lJo1axIXF8fatWtxcXEx/Nu3bx9Xr141rJv/9mlh4uPjCQgIMCz7+/sTHx9v\nWK5Tpw62trYF1vHw8DD8XKtWLdzd3Q2dF2rVqgVAamoqAFu3buXxxx/Hzc0NFxcXtmzZUuBWipub\nW4G6lZ2dHampqSQmJnLv3j2CgoIeiLk0x53n0qVLBAQEFFobS0hIeODYs7OzuXbtmuExT0/PAsd6\n/3L+Tn0+Pj4Fth8QEEBCQkKp8lBYnvMEBwezcOFCZsyYgaenJ2FhYYbtlvT+FZXfh9GtWzcmTpzI\nhAkT8PT0ZPz48aSkpJRq3UuXLlG/fv1CnytN7PefV/fnP/+x+Pr6Gn62srLC19e3wPbyfxZKcw55\neXkVui9j1h0xYgRPPvkkQ4YMwcfHh9dff73QGmxpzs38+8j/vi5ZsoTTp0/TuHFj2rZty+bNmx/Y\nPkBaWhrjx48nMDAQJycnunTpwp07dwrUf4s6jvj4+AL5trOzw83NrdD9FKY0x5f3fq1YsQIHBwcc\nHBx4+umnH9hWfHw8/v7+hmUrKyv8/Py4cuUKCQkJD/wODAgIMJwXeedJHnt7e1xdXYmPj6dr165l\nPu/vf2+AQj93bm5uJCYmkpubW+S2nn32Wf744w9iY2P54YcfcHJyonXr1sXuv6jPyf25goL5uD/2\n+z9jplTpGuqi+Pv7M2LECG7dumX4l5KSwpQpUwyvKan3n7e3N7GxsYblixcv4u3tXeT6D9ObMCMj\ng+eee44pU6Zw/fp1bt26RZ8+fUrVEcTd3Z2aNWty9uzZB54rzXHn8fPz4+LFi+Tk5DzwXGHHXr16\n9QIn+cPIX98D7Re6t7d3qfJQUl7DwsLYu3cvcXFxWFlZ8frrrxd5DPnfP1OZNGkSv/76K3/88Qen\nT582fGOgpLj9/f0L1MfyM3Xsly5dMvycm5vL5cuXizyXH+Ycup8x61avXp1p06Zx4sQJ9u/fz6ZN\nm1i2bNkDrzPm3AwODmblypXcuHGD119/nYEDB5Kenv7A6+bPn8/p06c5ePAgd+7cYc+ePSjtjmSJ\n+/D29i6Q77S0tGJrmfefJ6U5vvzfQEhJSSElJaXQPzp8fHyIi4szLCuluHTpEr6+voY48x9TXFyc\n4Y/qvNfmSU1NJSkpyXDeFHXem0r79u2pUaMG3333XZGvqVmzJoMGDSIyMpLIyEhGjhxpeO5he3ff\nnysomI+KVGUa6uHDh7Nx40Z27NhBTk4O9+7dIyoqqkCDcf+H7v7lsLAwZs2aRWJiIomJicycObPY\nrxmU5kOcJzMzk8zMTNzd3bG2tmbr1q3s2LGjVOtaW1szZswYJk+eTEJCAjk5Ofz8889kZmaW6rjz\ntGvXjrp16/LGG2+QlpbGvXv32L9/v+HYP/zwQ2JjY0lNTeXNN99kyJAhD9UzNX8+rl+/zscff0xW\nVhZr167l1KlT9OnTx6g8AJw+fZrdu3eTkZFBjRo1qFmzJtWqVTMcw8O8f2Xx66+/8ssvv5CVlYWd\nnV2B/Xt6ehbZEAP07duXhIQEPvroIzIyMkhJSeHgwYPlEvtvv/3Gd999R3Z2NgsXLqRmzZo8/vjj\nhb62LJ8dU6z7448/cvz4cXJycnBwcMDGxsaQy/yMOTcjIyMNHdScnJywsrIqdL3U1FRq1aqFk5MT\nSUlJvPPOOw+8pqjjeO6559i0aRP79u0jMzOTadOmFXtVWNjvHWM/e3kGDRrE5s2b2b17N1lZWcyf\nP5+aNWvSoUMH2rZti52dHR988AFZWVlERUWxadMmhgwZYlh/y5YthuN4++23ad++PT4+PsWe96bi\n5OTEzJkzmTBhAuvXryctLY2srCy2bt1q+GMcYOTIkSxdupQNGzYU+Ix4eXlx+fJlsrKyDI8V9zu6\nd+/enD59mlWrVpGdnc2aNWs4deoUffv2LdX6plRlGmpfX1/Wr1/PnDlz8PDwwN/fn/nz5xd7pXb/\nd+ymTp1K69atCQkJISQkhNatWzN16tRSr1/UawAcHBz4+OOPGTx4MK6urqxateqBnsHF/UU4b948\nmjdvTps2bXBzc+Of//wnubm5RR53Yb8orK2t2bhxI2fPnsXf3x8/Pz++/vprAMaMGcOIESPo3Lkz\n9evXx87Ojk8++aRUsRX2mnbt2nHmzBnq1KnD22+/zTfffIOLi0uZ85D3WEZGBv/85z+pU6cOdevW\nJTEx0dBz+mHfv9LK/z4nJyfz4osv4urqSmBgIO7u7obBcsaOHcsff/yBi4sLAwYMeGA7tWvX5ocf\nfmDjxo3UrVuXBg0aEBUVVabYizsWKysrnn32WdasWYOrqysrVqzg22+/LfIX68N+dvLnw5h1r127\nxqBBg3BycqJJkyaEhoYW+seJMefm9u3badasGQ4ODrzyyiusXr2aGjVqPPC6l19+mfT0dNzd3enQ\noQO9e/cuNuf5j6Np06YsWrSIoUOH4u3tjaura7Fltvt/bxj72cu/vYYNGxIZGcmkSZOoU6cOmzdv\nZuPGjVSvXh1bW1s2btzI1q1bqVOnDhMnTmT58uU0aNDAsJ2hQ4fyzjvv4ObmxpEjR4iMjASKP+9L\nG1tpjmfy5MksWLCAWbNmGc6nzz77jL/85S+G13Ts2BFra2see+yxAnnu1q0bTZs2xcvLy1CSLG7/\nbm5ubNq0ifnz5+Pu7s68efPYtGlTgR7jRb3npmalyulPgjFjxrB582Y8PDw4fvw4AK+99hqbNm3C\n1taWoKAgli5dipOTU3nsXliwiIgIlixZwt69e80dSpX0zjvvcPbsWYsZHUrow+jRo/H19eXdd981\ndygl6tGjB0OHDmXMmDHmDsUkyu2KevTo0Q98H65Xr16cOHGC6OhoGjRoYLjSEUJUnIq6XScqF72c\nN4cOHeLw4cMmGX7VUpRbQ92pUydcXFwKPNazZ09DXaVdu3Zcvny5vHYvLJhehu2rrCT/oiz0cN6M\nGjWKnj17snDhQuzt7c0djsmU261v0EbN6devn+HWd379+vUjLCyMoUOHltfuhRBCCN0zS2ey2bNn\nY2trK420EEIIUYLqFb3DiIgItmzZUuQUb6B9fy3/l8qFEEKIyqxFixYcPXq00Ocq9Ip627Zt/Otf\n/2L9+vXUrFmzyNfFx8cbBhOQf2X7N336dLPHoPd/kkPJo6X8kxxW/hxGR0cX2SaWW0MdFhZGhw4d\niImJwc/Pjy+//JJJkyaRmppKz549adWqFX/961/La/dVXv6RjETZSA5NQ/JoPMmh8fScw3K79b1q\n1aoHHqss32kTQgihDzExcezceY4//rjKokW76dEjiIYNA0pe0YJUmZHJqprw8HBzh6B7kkPTkDwa\nT3JYNjExcUREnCUhoRsNG77BjRvdiIg4S0xMXMkrW5By/XpWWVlZWWGBYQkhhNCRRYt2c/FiN37/\nHWrVgqZNwcoKPDx289e/djN3eAUU1+5VeK9vY7i6unLr1i1zhyFEpeLi4kJSUlK5bT8qKorQ0NBy\n235VIDksm2vXrDl8GLKyIDExigYNQrG1hcxMfd1M1lVDfevWLbnSFsLELH20KSHK4rff4LffcsnK\nAldXsLeHvGnsbW2Lnr3MEunq1rfcEhfC9ORzJSqT3FzYvh1++QUSE+NITDxLw4bdyft7NCNjF+Hh\nwRbXoay4z6E01EJUcfK5EpVFejqsWwfnzkG1atC3L9jZxbFr1zkyM62xtc2le3fL7PUtDbUQokjl\n/bmS+qrxJIclS0yEVavg5k3tNvfzz4O//5/PW3oOi/sc6quibsECAwPZvXs3AHPmzGHcuHFmjsh8\nAgMDix0itjw0a9aM//73vxW6zxs3btC4cWMyMjLKZfszZsxgxIgR5bJtISqTs2fhP//RGmkvLxg3\nrmAjrXfSUJtI/g45b775Jl988UWJ64SGhrJkyZLyDMsszDEd3u+//07nzp0rdJ9z585l9OjR1KhR\nw/DY9u3b6dy5M46Ojnh4eBAaGsrGjRtL3FZUVBR+fn4FHqssnbws+SpGLySHhVMKDhyAFSvg3j1o\n3BjGjAFn5wdfq+ccSkNtRnr8RZydnW3uECxCRkYGy5YtY/jw4YbH1q1bx+DBgwkPD+fKlStcv36d\nmTNnlqqhLoyUeYQoWnY2bNgA27ZpDXaXLjB48J89uyuTStFQx8TEsWjRbhYujGLRot1lGnXGFNvI\nk/+W5b179xg+fDju7u64uLjQtm1brl+/zltvvcXevXuZOHEiDg4O/O1vfyt0Wz/99BMdOnTAxcUF\nf39/vvrqKwDu3LnDyJEj8fDwIDAwkNmzZxt+sUdERNCxY0cmT56Mi4sLwcHB7N+/n6VLl+Lv74+n\npyfLli0z7CM8PJyXXnqJXr164ejoSGhoKBcvXjQ8b21tzWeffcYjjzxCw4YNAdi0aRMtW7bExcWF\njh07PjDn+JEjR2jRogXOzs4MGTKkwO3h4tYNDAxk/vz5ha6bmJhI3759cXFxwc3NrcAVdP7b7RkZ\nGbz88sv4+Pjg4+PDK6+8QmZmJqBdufr6+rJgwQI8PT3x9vYmIiLCsJ0tW7bQtGlTHB0d8fX1Zf78\n+YW+L7/88gvOzs54e3sDWqM6efJkpk2bxpgxY3BwcACgc+fOLF68mMzMTNzc3Pj9998N27h+/Tr2\n9vZcvHiR3r17Ex8fj4ODA46OjiQkJGBlZUVmZiajRo3C0dGRZs2a8dtvvxnWP3nyJKGhobi4uNCs\nWbMCfxCEh4czYcIE+vbti6OjI48//jjnz58v9FjKW1RUlFn2W5lIDgu6exeWLYMjR8DGBgYNgq5d\nobhrHz3nUPcNdd4QcTdudOP27dAyDRFnim3kl//W71dffUVycjKXL18mKSmJ//u//6NWrVrMnj2b\nTp06sWjRIlJSUvj4448f2E5cXBx9+vTh73//O4mJiRw9epSWLVsCMGnSJFJSUrhw4QJ79uxh2bJl\nLF261LDuwYMHadGiBUlJSYSFhTF48GAOHz7MuXPniIyMZOLEiaSlpRlev3LlSqZNm0ZiYiItW7Zk\n2LBhBWJZv349hw4d4o8//uDIkSOMHTuWL774gqSkJMaPH88zzzxDVlYWoDVaa9euZfv27Vy4cIFj\nx44ZGsOS1rWysipy3fnz5+Pn50diYiLXr1/nvffeKzTns2fP5uDBg0RHRxMdHc3BgweZNWuW4bXX\nrl0jOTmZ+Ph4lixZwoQJE7hz5w4AY8eOZfHixSQnJ3PixAm6dSt89KLjx48b/mgBiImJ4fLlywwc\nOLDQ19va2jJkyBAiIyMNj61atYoePXrg7+/Ptm3b8Pb2JiUlheTkZOrWrYtSig0bNhAWFsadO3d4\n5plnmDhxIgBZWVn069ePp556ihs3bvDJJ58wbNgwTp8+bdj+mjVrmDFjBrdu3SI4OJi33nqr0NiE\n0JOrV2HxYrh4ERwdYfRobcSxykxXA54UZufOc9So0Z2Cfyx159ix3bRpU7ou+AcPniMtrbthOTQU\natTozq5du8vUjT9v2jLQfkHfvHmTM2fO0Lx5c1q1avXAa4uycuVKevbsyfPPPw9oI7O5urqSk5PD\nmjVriI6Oxt7eHnt7e1599VWWL19umPikXr16jBo1CoDBgwcze/Zspk2bho2NDT179sTW1pazZ88S\nEhICQN++fXniiScAraFzcnLiypUr+Pj4APDPf/4T5/8VfhYvXsz48eNp06YNACNHjmTOnDkcOHCA\nTp06YWVlxd/+9je8vLwA6Nevn2Ge1ZLWBYpc19bWloSEBGJjYwkKCqJjx45F5u3TTz/F3d0dgOnT\npzN+/HhmzpwJgI2NDdOmTcPa2prevXtTu3ZtYmJiaNu2Lba2tpw4cYLmzZvj5OT0wPuV5/bt24ar\nZoCbN28CULdu3SLfz5EjRzJ48GDmzp0LwPLly3njjTeAos+DTp068dRTTwEwfPhwFi5cCMCBAwe4\ne/euYf2uXbvSt29fVq1axfTp0wEYMGAArVu3BmDYsGFMnjy5yNjKk55rg5ZCcqg5eRK++w4yM8HX\nV+vZne9jWCw951D3V9RZWYUfQk5O6Q8tN7fw15pimLkRI0bw5JNPMmTIEHx8fHj99dcL1HmLq1Nf\nvnyZ+vXrP/B4YmIiWVlZBAT8+UeEv78/V65cMSx7enoafq5VqxYAderUKfBYamqqIQZfX1/Dc/b2\n9ri6uhIfH294LH9Hp7i4OObPn4+Li4vh3+XLlwu8Pq+hvX9fxqz72muvERwcTK9evQgKCuL9998v\nNG/x8fEP5Cb/9t3c3LC2/vO9tbOzM+zjm2++YcuWLQQGBhIaGsqBAwcK3YerqyspKSkFtgmQkJBQ\n6OsB2rVrR61atYiKiuLUqVOcO3eOZ555psjXQ8H30c7Ojnv37pGbm0t8fPwDnc8CAgIMx2llZfXA\nOZB3jELojVLw3//CmjVaI92iBYSHl76R1jvdX1Hb2GhDwd3/x5KHRy6lne560aJcbtx48HFTDDNX\nvXp1pk2bxrRp0wy3shs2bMiYMWNK7Ezm5+fHwYMHH3jc3d0dGxsbYmNjady4MQAXL14s0Ng+DKUU\nly5dMiynpqaSlJRkqL9CwT8o/P39eeutt3jzzTdLvY+89R923fz7rV27NvPmzWPevHmG29Jt27al\na9euBdbx9vZ+IDf5j6U4rVu35vvvvycnJ4dPPvmEwYMHF6jX5wkJCeHDDz80LDds2BA/Pz/WrVvH\nq6++WuT2R40aRWRkJJ6engwaNAjb//V8KexcKO788Pb25tKlSyilDK+Li4ujUaNGpTrOimTp31/V\ng6qcw6wsWL8efv9dq0H36AEdOhRfjy6MnnOo+yvqHj2CyMgo+J3djIxddO8eVKHbKEpUVBTHjx8n\nJycHBwcHbGxsqFatGqBdLZ07d67IdYcNG8bOnTtZu3Yt2dnZ3Lx5k+joaKpVq8bgwYN56623SE1N\nJS4ujg8//LBAD+SHtWXLFvbt20dmZiZvv/027du3N9z2vt+4ceP4/PPPOXjwIEop7t69y+bNm4u9\nYsu7tfubivxFAAAgAElEQVSw6+a/Jbxp0ybOnj2LUgpHR0eqVatW4Mo4T1hYGLNmzSIxMZHExERm\nzpxZqu8jZ2VlsWLFCu7cuUO1atVwcHAwvFf3a9OmDbdv3y5wBbtgwQLeffddIiIiSE5OJjc3l59+\n+onx48cb1hs+fDjffvstK1asYOTIkYbHPT09uXnzJsnJyYUe+/3atWuHnZ0dH3zwAVlZWURFRbFp\n0yaGDBlS4rpC6EVyMixdqjXStrYQFgYdOz58I613um+oGzYMIDw8GA+P3Tg7R+Hhsfuhx3E1xTby\ny9+x6erVqwwaNAgnJyeaNGlCaGioodH4+9//zrp163B1deXll19+YDt+fn5s2bKF+fPn4+bmRqtW\nrTh27BgAn3zyCfb29tSvX59OnToxbNgwRo8e/cD+88dUXLxDhw7lnXfewc3NjSNHjhTo9HT/uo89\n9hhffPEFEydOxNXVlUceeYRly5YVuY/88Riz7tmzZ+nZsycODg506NCBCRMm0KVLlwfWmTp1Kq1b\ntyYkJISQkBBat27N1KlTS5WLyMhI6tWrh5OTE4sXL2bFihWFvs7W1pbw8PACeXruuedYs2YNX375\nJT4+Pnh5eTFt2jT69+9veI2fnx+PPvoo1tbWhj4BAI0aNSIsLIz69evj6upq6PVd1Ptoa2vLxo0b\n2bp1K3Xq1GHixIksX76cBg0aPJC30hx3edLrVYwlqYo5vHxZ6zQWHw8uLvDCC/C/07tM9JxDGUJU\nMHr0aHx9fXn33XfNHYquJCYm0qlTJ44ePVpg0JOSjB07Fh8fH0PnNnOTz5WwNMeOad+Rzs6GwEDt\n+9F2duaOqnzJEKKiWPJLumzc3d05efLkQzXSsbGxfPvtt4wdO7YcI7Msev7+qqWoKjlUCnbuhG+/\n1Rrp1q1hxAjTNNJ6zqE01MIsQ35WRW+//TbNmzdnypQpBXqlCyEgIwNWr4affgJra3j6aW32qyK6\niVQpcutbiCpOPlfC3G7d0ma+un4datXSRhor5JuplVpxn0Pdfz1LCCGEfsXGwtdfQ1oauLvD0KHg\n6mruqCyL3PoWQpQrPdcGLUVlzeFvv2ljdqelwSOPaD27y6uR1nMO5YpaCCFEhcrJge3bIW88pw4d\ntIFMChkWQSA1aiGqPPlciYqUng5r18L581pHsX794H9zDVVpUqMWQghhdjduaJ3GkpLA3h6GDIH7\nhqwXhZAbDSYSExNDy5YtcXR05NNPPzV6e6GhoSxZssQEkZlOWFgY69evL5dtx8bGYm1tTW6u8eOr\n3+8f//gHn3/+ucm3K0pHz7VBS1EZcnjmDPznP1oj7eUFL75YsY20nnMoDbWJfPDBB3Tv3p3k5GTD\nnMHGsLTvNh87doxjx47x7LPPGh5LSEhg7NixeHt74+joSOPGjZkxY0aBea6LEhgYyO7du8szZIN/\n/OMfzJkzxzDntRCi4igF+/fDypXad6WbNIExY8DJydyR6Yc01CYSFxdHkyZNyrRuTk6OiaMxvf/7\nv/8rMOlHUlIS7du3JyMjgwMHDpCcnMwPP/zAnTt3ip1oJE9F1kW9vLxo1KgRGzZsqJD9iYL0PMay\npdBrDrOztZmvduzQGuzQUO070v+bNK5C6TWHUEka6pizMSxas4iFqxeyaM0iYs7GVOg2unXrRlRU\nFBMnTsTR0ZGzZ89y584dRo4ciYeHB4GBgcyePdvQMEVERNCxY0cmT56Mu7s777zzTrHbV0oxa9Ys\nAgMD8fT0ZNSoUQVmWdqwYQNNmzbFxcWFrl27curUKcNzgYGBzJ07l6ZNm+Lq6sqYMWPIyMgAtLGq\n+/bti4uLC25ubnTu3LnIxnPbtm0FJsBYsGABTk5OREZG4u/vD4Cvry8ffvghzZs3Z8KECfzjH/8o\nsI1nnnmGhQsXMnLkSC5evEi/fv1wcHBg3rx5htdERkYSEBBAnTp1mDNnjuHxjIwMXn75ZXx8fPDx\n8eGVV14hMzMT0G5p+fr6smDBAjw9PfH29iYiIqLAvkNDQ9m8eXOxeRZCmE5qKnz1FRw9CjY2WgMd\nGlr1Zr4yBd031DFnY4j4MYIbnje47XWbG543iPgx4qEaWmO3sXv3bjp16sSiRYtITk4mODiYSZMm\nkZKSwoULF9izZw/Lli1j6dKlhnUOHjxIUFAQ169fL3Fu5qVLl/LVV18RFRXF+fPnSU1NNdxeP336\nNEOHDuXjjz8mMTGRPn360K9fP7Kzsw3rr1y5kh07dnDu3DlOnz7NrFmzAJg/fz5+fn4kJiZy/fp1\n3nvvvUJvt9+9e5cLFy7QsGFDw2M7d+5kwIABRcYcHh7OqlWrDA1/YmIiu3btYtiwYSxbtgx/f382\nbdpESkpKgQZ93759nD59ml27djFz5kxiYrT3YPbs2Rw8eJDo6Giio6M5ePCg4TgArl27RnJyMvHx\n8SxZsoQJEyZw584dw/ONGjUiOjq62DyL8qHn2qCl0FsOExLgiy/g0iVwdNRudTdtat6Y9JbD/HTf\n63vnbzup8UgNomKj/nzQBo6tPkabJ9qUahsHfzpImm8axGrLoYGh1HikBrsO76JhcMNi180vr1HK\nyclhzZo1REdHY29vj729Pa+++irLly9nzJgxAHh7ezNhwgQAatasWex2V6xYwauvvkpgYCAA7733\nHs2aNWPp0qWsWbOGvn370r17d0Crx3700Ufs37+fzp07Y2VlxcSJEw1zS7/11ltMmjSJd999F1tb\nWxISEoiNjSUoKIiOHTsWuv/bt28D4ODgYHgsKSmJunXrFhlzmzZtcHJyYteuXfTo0YPVq1fTtWtX\n6tSpU+yxTp8+nRo1ahASEkKLFi2Ijo6mYcOGrFy5kk8//RR3d3fD68aPH2+YgcrGxoZp06ZhbW1N\n7969qV27NjExMbRt29YQe95xCCHKzx9/wHffQVYW+PpqPbtr1zZ3VPqm+yvqLFV4B6EcSl/3zaXw\nnsaZuZkPFUve1WhiYiJZWVkFJl7w9/fnypUrhmW/fN0dX3rpJRwcHHBwcGDu3LkPbDchIeGBbWVn\nZ3Pt2jUSEhIMt57zYvDz8ytyX/7+/sTHxwPw2muvERwcTK9evQgKCuL9998v9LicnZ0BSElJMTzm\n5uZm2E5RRo4caZivOTIy0jAPd3G8vLwMP9vZ2ZGamgpAfHz8AznIv383Nzes842WkH/dvNjzjkNU\nLD3XBi2FHnKoFOzZow0HmpUFLVpAeLjlNNJ6yGFRdH9FbWNlA2hXwfl52Hnw19C/lmobi64t4obn\njQcet7UuW48Hd3d3bGxsiI2NpXHjxgBcvHgRX19fw2vy32L+/PPPi/36kLe3N7GxsYblixcvUr16\ndby8vPD29ub48eOG55RSXLp0yXAFnff6/D97e3sDULt2bebNm8e8efM4ceIE3bp1o02bNnTr1q3A\n/u3t7QkKCiImJoYOHToA0KNHD7777jumT59eZO/04cOH07x5c6Kjozl16hT9+/cv9PhLIy8H+fOZ\ndxylcfLkSVrKqApClIusLPj+ezhxQqtB9+wJ7dtLPdpUdH9F3eOxHmScySjwWMaZDLo/2r1CtwF/\n3vquVq0agwcP5q233iI1NZW4uDg+/PDDAr2mH0ZYWBgffvghsbGxpKam8uabbzJkyBCsra0ZNGgQ\nmzdvZvfu3WRlZTF//nxq1qxpaFCVUnz22WdcuXKFpKQkZs+ezZAhQwDYtGkTZ8+eRSmFo6Mj1apV\no1oRc8r16dOHPXv2GJYnT55McnIyo0aNMvwhcOXKFV599VXDHw6+vr60bt2akSNHMnDgwALzNnt6\nepaqd3j+HMyaNYvExEQSExOZOXNmqa7Q8+zZs4fevXuX+vXCdPRcG7QUlpzDO3fgyy+1RrpGDW1S\njQ4dLK+RtuQclkT3DXXD4IaEdw3H47oHzled8bjuQXjX8IeqLZtiG1DwKvGTTz7B3t6e+vXr06lT\nJ4YNG8bo0aMNr3uYK8oxY8YwYsQIOnfuTP369bGzs+OTTz7RYm/YkMjISCZNmkSdOnXYvHkzGzdu\npHr16oZ9DR061HB7+5FHHmHq1KkAnD17lp49e+Lg4ECHDh2YMGFCgZ7d+b344ousWLHCsOzi4sL+\n/fuxsbGhXbt2ODo60qNHD5ydnQkODja8btSoURw/fvyBRvWf//wns2bNwsXFhQULFjyQv/tNnTqV\n1q1bExISQkhICK1btzYcR0nrJiQkcPLkyQJX9EII412+rHUaS0jQJtN44QVtcg1hWjLWdyVXr149\nlixZ8sDt7LIYNmwYgwcPLjDoSUn27t3L8OHDiYuLM3r/ZfWPf/yD4OBgXnrpJbPFYMnkcyXKIjoa\nNmzQJtioV0/7+pWdnbmj0i8Z61uYRP4r6tLIyspi4cKFjBs3rpwiKp3839MWQhgnNxd27YJ9+7Tl\ntm3hySe1CTZE+dD9rW9hmU6ePImLiwvXrl3j5ZdfNnc4woz0XBu0FJaSw4wMWL1aa6StraFvX+jT\nRx+NtKXksCzkirqSu3Dhgln227hx4wJfjxJC6FtSkjbz1Y0bUKsWDB6s3fIW5U9q1EJUcfK5EiW5\ncEH7fnR6OtSpA2FhWucxYTpSoxZCCFEmhw7B1q1abbpBA3juOe1rWKLiSI1aCFGu9FwbtBTmyGFO\nDmzerP3LzYWOHbXhQPXaSOv5PJQraiGEEAWkpcHatdot72rV4JlntCFBhXnoqkbt6urKrVu3zBCR\nEJWXi4sLSUlJ5g5DWIgbN7ROY0lJ2jjdQ4Zok2uI8lVcjVpXDbUQQojyc+YMrFunfQ2rbl2tkXZy\nMndUVUNx7Z7UqCspPddjLIXk0DQkj8Yr7xwqBfv3w8qVWiPdtKk2h3RlaqT1fB6WW0M9ZswYPD09\nad68ueGxpKQkevbsSYMGDejVq5fMDyyEEGaWna3NfLVjh9Zgd+0KAweCjY25IxN5yu3W9969e6ld\nuzYjR440zKY0ZcoU3N3dmTJlCu+//z63bt0qdP5lufUthBDlLzVVG2ns8mWtYf7LX6BJE3NHVTWZ\nrUYdGxtLv379DA11o0aN2LNnD56enly9epXQ0FBOnTr1UAELIYQwXkKC1mksOVm7xR0WBl5e5o6q\n6rKYGvW1a9fw9PQEtPmIr127VpG7r1L0XI+xFJJD05A8Gs/UOTxxQptDOjkZ/Pxg3LjK30jr+Tw0\n2/eoH3ZOZiGEEMZRCvbsgbw2q1UrePppqC4jali0Cn178m55e3l5kZCQgIeHR5GvDQ8PJzAwEABn\nZ2datmxJaGgo8OdfRrJc/HIeS4lHlqvmct5jlhKPXpfzlHX9Dh1C+f572LJFWx4/PpTHH4c9eyzj\n+Kract7PsbGxlKRCa9RTpkzBzc2N119/nblz53L79m3pTCaEEOXszh2tHn31qjYE6MCB8Mgj5o5K\n5GeWGnVYWBgdOnQgJiYGPz8/li5dyhtvvMEPP/xAgwYN2L17N2+88UZ57b7Ku/+vcPHwJIemIXk0\nnjE5vHQJFi/WGmlXV3jhharZSOv5PCy3W9+rVq0q9PGdO3eW1y6FEELkc/QobNyoTbBRvz4MGqTN\nJS30RYYQFUKISiY3F3bu1EYbA2jbFp58UptgQ1gmmY9aCCGqiHv34JtvtHG7ra2hTx9o3drcUQlj\nyFjflZSe6zGWQnJoGpJH45U2hzdvwn/+ozXSdnYwcqQ00nn0fB7KFbUQQlQC589rc0inp4OHhzbS\nmIuLuaMSpiA1aiGE0DGl4NAh2LZNq003bAgDBmhfwxL6ITVqIYSohHJyYOtW+PVXbfmJJ6BbN602\nLSoPeTsrKT3XYyyF5NA0JI/GKyyHaWmwfLnWSFevrl1F9+ghjXRR9HweyhW1EELozPXr2khjt26B\ngwM8/zz4+po7KlFepEYthBA6EhOjff0qMxO8vWHIEHB0NHdUwlhSoxZCCJ1TCvbtg127tJ+bNYNn\nnwUbG3NHJsqbVDMqKT3XYyyF5NA0JI/G27Uriu++00YbU0rrMPbcc9JIPww9n4dyRS2EEBYsJUX7\n6pW9Pdjawl/+Ao0bmzsqUZGkRi2EEBYqPh5Wr4bkZHB21gYx8fQ0d1SiPEiNWgghdOb332H9esjK\nAn9/rWe3vb25oxLmIDXqSkrP9RhLITk0Dcnjw1EKfvwR1q3TGulHH4WAgChppI2k5/NQGmohhLAQ\nmZnw9dewZw9YWcFTT0G/fjI9ZVUnNWohhLAAt29rg5hcuwY1a8LAgRAcbO6oREWRGrUQQliwixdh\nzRq4exfc3LROY+7u5o5KWAq59V1J6bkeYykkh6YheSzekSPw1VdaIx0UBC+88GAjLTk0np5zKFfU\nQghhBrm58MMP8PPP2vLjj0OvXjKphniQ1KiFEKKC3bun9eo+e1brKPb001rvblF1SY1aCCEsxM2b\nWqexxESws9O+Hx0QYO6ohCWTmyyVlJ7rMZZCcmgaksc/nTsHX3yhNdKenvDii6VrpCWHxtNzDuWK\nWgghyplScPAgbN+u1aYbNdLG7K5Rw9yRCT2QGrUQQpSjnBzYsgV++01b7tRJm/3Kysq8cQnLIjVq\nIYQwg7Q07fvRcXFQvbo2f3Tz5uaOSuiN1KgrKT3XYyyF5NA0qmoer12DxYu1RtrBAUaPLnsjXVVz\naEp6zqFcUQshhImdOgXffquN3e3jA0OGaI21EGUhNWohhDARpeCnn2D3bu3n5s3hmWfAxsbckQlL\nJzVqIYQoZ1lZsGEDHD+uLXfvDk88IZ3GhPGkRl1J6bkeYykkh6ZRFfKYkgIREVojbWur3eru1Ml0\njXRVyGF503MO5YpaCCGMcOUKrF6tNdbOztrMV56e5o5KVCZSoxZCiDI6fhzWr4fsbG2EscGDwd7e\n3FEJPZIatRBCmJBSWoexvXu15Ucf1SbWqFbNvHGJyklq1JWUnusxlkJyaBqVLY8ZGdogJnv3ajXo\n3r2hX7/ybaQrWw7NQc85lCtqIYQopdu3tZmvrl2DmjVh0CAICjJ3VKKykxq1EEKUQlycdiWdlgZu\nbjB0qPa/EKYgNWohhDDC4cOwebM2wUZwMAwcqF1RC1ERpEZdSem5HmMpJIemoec85ubCtm3aQCY5\nOdC+vXYlXdGNtJ5zaCn0nEO5ohZCiEKkp8O6dXDunNZRrG9faNXK3FGJqkhq1EIIcZ/ERK3T2M2b\n2vein38e/P3NHZWozKRGLYQQpXTuHKxdC/fugZeXNhyos7O5oxJVmdSoKyk912MsheTQNPSSR6Xg\nwAGIjNQa6caNYcwYy2ik9ZJDS6bnHMoVtRCiysvJ0Xp1Hz6sLXfpAqGhMvOVsAxSoxZCVGl372rf\nj754EapXh/79oVkzc0clqhqpUQshRCGuXdM6jd2+DY6OWj3a29vcUQlRkNSoKyk912MsheTQNCw1\nj6dOwZIlWiPt4wPjxlluI22pOdQTPefQLA31e++9R9OmTWnevDlDhw4lIyPDHGEIIaogpeC//9Xm\nkM7MhJAQGD0aHBzMHZkQhavwGnVsbCzdunXj5MmT1KhRg+eff54+ffowatSoP4OSGrUQohxkZWnz\nR//+u9ZRrHt36NhROo0J87OoGrWjoyM2NjakpaVRrVo10tLS8PHxqegwhBBVTHKydhUdHw+2tvDc\nc9CwobmjEqJkFX7r29XVlVdffRV/f3+8vb1xdnamR48eFR1GpafneoylkByahiXk8coV+OILrZF2\ncYEXXtBXI20JOdQ7Peewwhvqc+fOsXDhQmJjY4mPjyc1NZUVK1ZUdBhCiCri+HFYuhRSUiAwUOs0\n5uFh7qiEKL0Kv/X966+/0qFDB9z+N5HrgAED2L9/P8OGDSvwuvDwcAIDAwFwdnamZcuWhIaGAn/+\nZSTLxS/nsZR4ZLlqLuc9VtH779IllF27IDJSWx44MJTevWHvXvPmQz7PspwnKiqK2NhYSlLhncmi\no6MZNmwYhw4dombNmoSHh9O2bVsmTJjwZ1DSmUwIYYSMDPj2W4iJAWtreOopaNNGOo0Jy1Vcu1fh\nt75btGjByJEjad26NSEhIQC8+OKLFR1GpXf/X+Hi4UkOTaOi83jrlvb96JgYqFULhg+Htm313UjL\nuWg8PefQLCOTTZkyhSlTpphj10KISiw2Fr7+GtLSwN0dwsLgf1U2IXRLxvoWQlQKv/2mTayRmwvB\nwTBwINSsae6ohCgdi/oetRBCmFJuLmzbBgcPassdOkCPHlptWojKQE7lSkrP9RhLITk0jfLMY3q6\nNn/0wYNQrZo281WvXpWvkZZz0Xh6zqFcUQshdCkxEVauhKQksLfXZr7y8zN3VEKYntSohRC6c+YM\nrFunfQ3Ly0vrNObkZO6ohCg7qVELISoFpeDAAdixQ/u5SRPtdretrbkjE6L8VLJKjsij53qMpZAc\nmoap8pidrc18tX271kh36QKDBlWNRlrORePpOYdyRS2EsHipqbBmDVy6BDY22lV006bmjkqIiiE1\naiGERbt6FVatgjt3wNFRq0fXrWvuqIQwLalRCyF06eRJbczurCzw9dV6dteube6ohKhYUqOupPRc\nj7EUkkPTKEselYI9e7Tb3VlZ0KIFhIdX3UZazkXj6TmHckUthLAoWVnw/fdw4oQ2kUaPHtpoY3qe\nVEMIY0iNWghhMZKTtXp0QgLUqAHPPQcNGpg7KiHKn9SohRAW7/JlWL1a6+Ht6qp1GqtTx9xRCWF+\nUqOupPRcj7EUkkPTKE0eo6MhIkJrpOvVgxdekEY6PzkXjafnHMoVtRDCbHJzYdcu2LdPW27TBp56\nSptgQwihkRq1EMIsMjLgm2/g9GlttqvevbWGWoiqSGrUQgiLcuuWNvPVjRtQqxYMHqzd8hZCPEhq\n1JWUnusxlkJyaBr35/HCBVi8WGuk69SBceOkkS6JnIvG03MO5YpaCFFhfv0VtmzRatMNGmhfv6pR\nw9xRCWHZpEYthCh3OTmwbRscOqQtd+wI3btrtWkhhNSohRBmlJ4OX3+t3fKuVg2eeUYbElQIUTry\n92wlped6jKWQHBrvxg2YMiWKCxe0cbrDw6WRLgs5F42n5xzKFbUQolycOQPr1kFKCjRrps185eRk\n7qiE0B+pUQshTEop+Pln+OEH7eemTeHZZ8HW1tyRCWG5pEYthKgQ2dmwaRMcPaotd+0KnTvLzFdC\nGKPEGnVqaio5OTkAxMTEsGHDBrKysso9MGEcPddjLIXk8OGkpsJXX2mNtI2NNohJly6wZ0+UuUPT\nPTkXjafnHJbYUHfu3JmMjAyuXLnCk08+yfLlywkPD6+A0IQQepGQAF98AZcuaXXosWOhSRNzRyVE\n5VBijbpVq1YcOXKETz75hPT0dKZMmUKLFi2Ijo4uv6CkRi2EbvzxB3z3HWRlgZ8fPP+81sNbCFF6\nRteof/75Z1asWMGSJUsAyM3NNV10QghdUgr27IG8O4otW0LfvlBder4IYVIl3vpeuHAh7733Hn/5\ny19o2rQp586do2vXrhURmzCCnusxlkJyWLTMTFi7VmukraygVy+tZ3dhjbTk0XiSQ+PpOYcl/u3b\npUsXunTpYlgOCgri448/LteghBCW684dWL1aq0vXqAEDB8Ijj5g7KiEqrxJr1IcOHWLOnDnExsaS\nnZ2trWRlxbFjx8ovKKlRC2GRLl3SGum7d8HVFcLCtBmwhBDGKa7dK7GhbtCgAfPmzaNZs2ZY5xtB\nPzAw0KRBFghKGmohLM7Ro7BxozbBRv36MGiQNpe0EMJ4xbV7Jdao69SpwzPPPEP9+vUJDAw0/BOW\nTc/1GEshOdTk5sKOHfD991oj3bYtDBtW+kZa8mg8yaHx9JzDEmvU06dPZ+zYsfTo0QPb/40BaGVl\nxYABA8o9OCGEed27B998o43bbW0NffpA69bmjkqIqqXEW9/Dhg0jJiaGpk2bFrj1vXTp0vILSm59\nC2F2SUmwapU2A1atWtr3o+VmmhDlw6gadcOGDTl16hRWFThYrzTUQpjXhQvaHNLp6eDhoXUac3Ex\nd1RCVF5G1ag7dOjAH3/8YfKgRPnScz3GUlTVHB46BMuXa410gwbacKDGNNJVNY+mJDk0np5zWGKN\n+ueff6Zly5bUq1ePGjVqAOX/9SwhRMXLyYGtW+HXX7XlJ56Abt202rQQwnxKvPUdGxtb6OPy9Swh\nKo+0NO1Wd2ysNrrYM89ASIi5oxKi6jCqRm0O0lALUXGuX9c6jd26pU2mMWQI+PqaOyohqhajatRC\nn/Rcj7EUVSGHp0/DkiVaI+3tDS++aPpGuirksbxJDo2n5xzKPDdCVEFKwf79sHOn9nOzZtqkGjY2\n5o5MCHE/ufUtRBWTna0NBZo3pXy3btCpkzYLlhDCPIy69f3NN9/wyCOP4OjoiIODAw4ODjg6Opo8\nSCFE+UtJgYgIrZG2tdUGMencWRppISxZiQ31lClT2LBhA8nJyaSkpJCSkkJycnJFxCaMoOd6jKWo\nbDmMj4cvvoDLl8HJCcaMgcaNy3+/lS2P5iA5NJ6ec1hiQ+3l5UVjE3+ab9++zcCBA2ncuDFNmjTh\nwIEDJt2+EKKgEydg6VJITgZ/f63TmJeXuaMSQpRGiTXqv//971y9epX+/fubbFKOUaNG0aVLF8aM\nGUN2djZ3797Fycnpz6CkRi2ESSgFUVGwZ4+23KoVPP209l1pIYTlMOp71OHh4YaN5FfWSTnu3LlD\nq1atOH/+fJGvkYZaCONlZsJ338HJk1oN+sknoV07qUcLYYksasCTo0ePMn78eJo0aUJ0dDSPPfYY\nH330EXZ2dn8GJQ210aKioggNDTV3GLqm5xzevg2rV8PVq1CzJgwcCMHB5olFz3m0FJJD41l6Dotr\n94q8Afb+++/z+uuvM2nSpEI3+PHHH5cpmOzsbA4fPsynn35KmzZtePnll5k7dy4zZ84s8Lrw8HDD\nMKXOzs60bNnSkOS8TgGyXPTy0aNHLSoePS7nsZR4Sru8Zk0UP/4IXl6huLmBv38Uly9DcLB54jl6\n9KHJ3WgAACAASURBVKhZ81EZluXzXPk+z3k/FzVMd35FXlFv3LiRfv36ERERUeC2t1IKKysrRo0a\nVeLGC3P16lXat2/PhQsXAPjpp5+YO3cumzZt+jMouaIWokyOHIFNm7QJNurXh0GDtLmkhRCWrUxX\n1P369QP+rFGbipeXF35+fpw+fZoGDRqwc+dOmjZtatJ9CFHV5ObCDz/Azz9ry+3aaTVpaxkkWAjd\nM8vH+JNPPmHYsGG0aNGCY8eO8eabb5ojjErt/ts94uHpJYf37sHKlVojbW0N/fpB796W00jrJY+W\nTHJoPD3n0Cxf0mjRogWHDh0yx66FqFRu3tRmvkpMBDs7baSxgABzRyWEMCUZ61sInTp/HtauhfR0\n8PCAsDBwcTF3VEKIsjBqrO+YmBi6d+9uqCMfO3aMWbNmmTZCIUSpKQUHD0JkpNZIN2wIY8dKIy1E\nZVViQz1u3DjmzJljGJWsefPmrFq1qtwDE8bRcz3GUlhiDnNytF7dW7ZoHcg6dYIhQ6BGDXNHVjRL\nzKPeSA6Np+ccllijTktLo127doZlKysrbGTSWiEqXFoafP01xMZqQ4A++yw0b27uqIQQ5a3EhrpO\nnTqcPXvWsLxu3Trq1q1brkEJ4+V9uV6UnSXl8Pp1rdPYrVvg4KBdRfv4mDuq0rGkPOqV5NB4es5h\niZ3Jzp07x4svvsj+/ftxcXGhXr16rFixwjBqWLkEJZ3JhDCIiYFvvtHG7vb21hppmRJeiMrFqM5k\nQUFB7Nq1i8TERGJiYti3b1+5NtLCNPRcj7EU5s6hUrB3rzZmd2YmNGsGo0frr5E2dx4rA8mh8fSc\nwxJvfd+6dYtly5YRGxtLdnY2YNxY30KIkmVlwYYNcPy4tty9OzzxhMx8JURVVOKt7/bt29O+fXua\nN2+OtbW10WN9lyooufUtqrCUFO0q+soVsLWFAQOgUSNzRyWEKE9GTXP56KOPcvjw4XIJrCjSUIuq\nKj5e6zSWkgLOztogJp6e5o5KCFHejKpRDx06lMWLF5OQkEBSUpLhn7Bseq7HWIqKzuHvv8OXX2qN\ndEAAjBtXORppOReNJzk0np5zWGKNumbNmrz22mvMnj0b6/+N8m9lZcX58+fLPTghqgKl4Mcf4b//\n1ZYffRSefhqqVTNvXEIIy1Dire969epx6NAh3N3dKyomufUtqozMTPj2Wzh1Suso9tRT0LatdBoT\noqop03zUeR555BFqyczzQpjc7dtaPfraNahZEwYNgqAgc0clhLA0Jdao7ezsaNmyJS+++CKTJk1i\n0qRJ/O1vf6uI2IQR9FyPsRTlmcO4OFi8WGuk3dy0enRlbaTlXDSe5NB4es5hiVfU/fv3p3///gUe\ns5L7ckKU2eHDsHmzNsFGcDAMHKhdUQshRGFkPmohKkhuLuzYAQcOaMuPPw69eoF1ife1hBCVXZlq\n1IMGDWLt2rU0L2R6HisrK44dO2a6CIWo5O7dg7Vr4dw5rTd3377QqpW5oxJC6EGRV9Tx8fF4e3sT\nFxf3QCtvZWVFQEBA+QUlV9RGi4qK0vVsMZbAVDm8eRNWrtT+t7eH558Hf3/j49MLOReNJzk0nqXn\nsEwDnnh7ewPw2WefERgYWODfZ599Vj6RClHJnDsHX3yhNdKenlqnsarUSAshjFdijbpVq1YcOXKk\nwGPNmzfneN5sAeURlFxRC51TCn75BbZv135u1Egbs9vW1tyRCSEsUZlq1P/+97/57LPPOHfuXIE6\ndUpKCh07djR9lEJUEjk5Wq/uvCHyO3eGrl1lEBMhRNkUeUV9584dbt26xRtvvMH7779vaOkdHBxw\nc3Mr36Dkitpoll6P0YOy5PDuXfj6a+170tWrQ//+2jzSVZmci8aTHBrP0nNYpitqJycnnJycWL16\ndbkFJkRlcu2aNtLY7dvg4KDNfPW/rh5CCFFm8j1qIUzg1CltzO7MTPDxgSFDtMZaCCFKw6ixvoUQ\nRVMKfvoJdu3SlkNCoF8/sLExb1xCiMpDxkSqpPQ8rq2lKCmHWVnaVfSuXVpHsR494C9/kUb6fnIu\nGk9yaDw951CuqIUog+RkWL0a4uO1r1w99xw0bGjuqIQQlZHUqIV4SFeuaI10Sgo4O8PQoeDhYe6o\nhBB6JjVqIUzk+HFYvx6ysyEwEAYPBjs7c0clhKjMpEZdSem5HmMp8udQKa0W/c03WiP92GMwYoQ0\n0qUh56LxJIfG03MO5YpaiBJkZMB332lfwbK2hqeegjZtZKQxIUTFkBq1EMW4dUsbxOT6dahZU7vV\nXb++uaMSQlQ2UqMWogzi4mDNGkhLA3d3baSxch49VwghHiA16kpKz/UYS/DbbzBjRhRpaRAcDC+8\nII10Wcm5aDzJofH0nEO5ohYin9xcbWrKX37ROpC1bw89e2q1aSGEMAepUQvxP+npsHYtnD8P1apB\n377QqpW5oxJCVAVSoxaiBImJWqexmzfB3h6efx78/c0dlRBCSI260tJzPaainT0L//mP1kh7ecG4\ncVojLTk0Dcmj8SSHxtNzDuWKWlRZSsGBA7Bjh/Zz48bapBq2tuaOTAgh/iQ1alElZWfD5s3/v707\nj26ruvYH/pUseR5kyfEQybFsWXYGJ7HJSPgBDm4IFBICSchQoCF9PEpb2rR9Hd5qu1Zf14KE1RFW\nWavrteW5tIUQhkLCkIYMJpiQAEn8mhJe4siSLc+OZFmWrPme3x+3OUFkwI5s3Stpf/7y1ZGsox3H\n2+fufe8BTp4Uj2++GWhspJuYEEKkQTVqQj7F6xWvj+7qErekXLMGmDNH6lkRQqbCmXNnsP/4foRY\nCGqFGl9Y8AXUVifWVndUo05SiVyPmUr9/cB//7eYpPPzgQcfvHKSphhODopj7CiG1+bMuTNoPtSM\nvml9eN/+PoZKhtB8qBlnzp2RemoTQitqkjI++QR45RUgFAIMBrGzOy9P6lkRQqaC0+fE7/f/HhaN\nBa4uF3wuH2ZhFjLMGThw4kBCraqpRk2SHmPA4cPAoUPi8fz5wKpVgIr+TCUkaUSECLpGutDubMdZ\nx1mcHzuPo61H4Tf4AQAFGQWYVzIPaco0aPo12LZxm8QzjkY1apKyQiFx/+h//lNsFPvCF4Bly6hp\njJBk4A16cc55DmcdZ3HOeQ6BSICPZaoyYcg1QF2khjZLC3Wamo+lKxPr0g7JEnUkEsHChQthMBiw\nZ88eqaaRtFpaWtDY2Cj1NCTldgM7dwK9vUBGBrB2LVBTM/7XUwwnB8UxdhRDEWMMA94BnHWcxVnH\nWfS4e8BwcRU6LXsaanQ1qNHVoLygHO2l7Wg+1Ay1WQ1bmw3GeiMC7QE0LW+S8FNMnGSJ+sknn8Ts\n2bMxOjoq1RRIEuvuFpO0xwMUFoo7XxUXSz0rQshEBSNBWIetOOs4i3ZnO9wBNx9LU6ShsrASZq0Z\nNboaFGYVRr22troWW7AFB04cwHnneRQPFqNpeVNC1acBiWrU3d3d2LJlC370ox/hV7/61SUraqpR\nk1j84x/A7t3itdJGo7iHdHa21LMihIyXy+8SE7OjHVaXFWEhzMfy0vNg1omJuaqwCulpiXUa+0pk\nV6P+9re/jZ///Odwu92f/2RCxkkQgIMHgdZW8XjRIuC228QNNggh8iUwAfYRO28EG/QO8jEFFNDn\n6fkp7dLcUihSrMkk7on69ddfR3FxMRoaGujawCmUajWtQAB4+WXg7FlxS8rbbxcTdSxSLYZTheIY\nu2SMoS/ki2oE84V9fCwjLQMmrQk1uhpUa6uRm54b8/slcgzjnqiPHDmC3bt3480334Tf74fb7cYD\nDzyAZ599Nup5W7ZsgdFoBABoNBrU19fzIF9I8HR85eO2tjZZzWcqj/fsacGBA4BG04isLGDGjBZ4\nvQAQ2/e/QOrPl+jHbW1tsppPIh4nw//nm2++GUNjQ3jh9Rdgd9uRY84BA4OtzQYAWHD9AtToauD4\nxIGSnBI0zWma1Pe/QC7xuPC1zWbD55H0Oup33nkHv/jFL6hGTa6ZzQbs2gWMjQHTpolNY1qt1LMi\nhABAWAhHNYK5/C4+plQoYdQYeSOYLlsn4UylJ7sa9aelWq2BTJ6PPgLefFOsTZvN4uVXmZlSz4qQ\n1OYOuNHuEGvNHcMdCAkhPpajzolqBMtU0X/Y8aA7kyWplgSux3yeSAT4+9+BDz4Qj5ctE29kopzk\nO9cncwzjieIYOznHUGACekd7+bXN/Z7+qPGy3DLeCDY9b7pkizM5xxCQ+YqakInw+YAXXwQ6OsRu\n7lWrgPp6qWdFSGrxh/2wOC38lPZYaIyPpaelo6qwCjW6Gpi1ZuRl0A31Y0UrapIwhoaA558HnE4g\nN1fcVKO8XOpZEZL8GGNw+Bx81dw10gWBCXy8MLNQTMw6M4waI1RKWgNOFK2oScJrbwdeekm8DKus\nDNi4ESgokHpWhCSvsBBGp6uTX9vs9Dn5mFKhREVBBT+lXZRdRP1GU4gSdZKSez1mvBgD3n8fePtt\n8evZs4E1a4D0ONyMKFliKDWKY+ziFUNP0MMbwSzDFgQjQT6WpcrijWCmQhOy1FlTPp/JlMg/h5So\niWyFw8DrrwP/ugwXjY3AzTfTzleETBbGGPo8ffyUdu9ob9R4SU4JXzXr8/VQKia5Y5OMC9WoiSx5\nPMALLwB2O6BWA3ffLa6mCSGxCYQD6Bju4I1gnqCHj6mUKlQVVvFrmwsyqb4UL1SjJgmlr0/c+Wpk\nRKxDb9wo1qUJIdfG6XPyTS5sLhsiLMLHCjIK+CntSk1l1L7NRB4oUSepRK3HnD4N/O1vQCgkdnRv\n2CB2eEshUWMoNxTH2E00hhEhArvbzk9pnx87z8cUUKA8v5yf0i7OKU6JRrBE/jmkRE1kgTHg8GHg\n0CHxuL4euPNOQEU/oYSMizfo5ZtcWIYt8If9fCxTlYlqbTXf5CJbTfu+JhKqURPJhULAq68CH38s\nNoqtWAFcfz01jRFyNYwxDHgH+Kq5x90Dhou/N6dlT+PXNpfnlyNNSfu9yhnVqIlsjYyI9ei+PiAj\nA1i3TrxvNyHkUqFIKKoRzB1w87E0RRoqCyt5I1hhVqGEMyWTiRJ1kkqEeozdLnZ2ezzijlebNok7\nYMlFIsQwEVAcY+Pyu7Bzz07k1ebB6rIiLIT5WF56XtQmF+lpcbjBQIJK5J9DStREEm1twJ494gYb\nlZXA+vVANpXNCIHABHS7u/kp7UHvIGw9NhinGQEA+jw9bwQrzS1NiUawVEc1ahJXggDs3w8cOSIe\nL14MrFwpbrBBSKryhXy8Eeyc8xx8YR8fy0jLgElr4o1guekSXQZBphTVqIksBALi/brb28UtKb/4\nRWDhQqlnRUj8McYwNDbEV832EXtUI5guS8cbwSoKKqgRLMVRok5ScqvHOJ3izldDQ0BWFnDvveIp\nbzmTWwwTFcVRFBbCsA5b+SYXLr+LjykVShgLjPyUti5bF/VaimHsEjmGlKjJlLNagV27xL2kp00T\nm8a0WqlnRcjUcwfcfJOLjuEOhIQQH8tR50Q1gmWqMiWcKZEzqlGTKfXhh8Bbb4m16ZoaYO1a8TIs\nQpKRwAT0jvbyU9r9nv6o8bLcMr5qnp43nRrBCEc1ahJ3kQiwd6+YqAHghhuApiaxNk1IMvGH/bA4\nLfza5rHQGB9TK9UwaU0wa80w68zIz8iXcKYkUVGiTlJS1mPGxoAXXxRPeatUwOrVwLx5kkwlJolc\n05KTZIsjYwwOn4NvctE50gmBCXxck6nhq2ajxgiVMvZfs8kWQykkcgwpUZNJNTQEPPccMDwsbqax\ncSNgMEg9K0JiExbC6HR18kYwp8/Jx5QKJSoKKnhyLsouolPaZFJRjZpMmrNngZdfFi/DKisTm8by\n6UwfSVCeoIc3glmGLQhGgnwsS5XFG8FMhSZkqbMknClJBlSjJlOKMfEGJvv3i1/PmQOsWQOoaVtb\nkkAYY+jz9PFGsN7R3qjxkpwSvmrW5+uhVFDDBYkPStRJKl71mHBYvBXo//6veHzLLcCNNybHzleJ\nXNOSEznHMRAORG1y4Ql6+JhKqUJVYRXf5KIgs0Cyeco5hokikWNIiZpcM49H3Pmqu1tcPd9zDzBr\nltSzIuTqnD4nbwSzuWyIsAgfK8go4Ke0KzWVUKfRaSEiPapRk2vS1yfeacztBgoKxHp0aanUsyLk\nUhEhArvbzk9pnx87z8cUUMCQb+CntItziqkRjEiCatRkUn38MfDqq0AoBMyYAWzYAOTkSD0rQi7y\nBr18kwvLsAX+sJ+PZaoyUa2t5ptcZKtp2zYib5Sok9RU1GMYA1pagHfeEY8bGoA77hCvlU5GiVzT\nkpN4xJExhgHvAF8197h7oja5mJY9jW9yUZ5fnnCbXNDPYuwSOYZJ+iuWTLZgUFxFnz4tNordeiuw\ndGlyNI2RxBSKhNAx3MGvbXYH3HwsTZEGo+biJheFWYUSzpSQ2FCNmnyukRGxHt3fL96ne/16oLpa\n6lmRVOTyu/i1zVaXFWEhzMfy0vOiNrlIT0uXcKaETAzVqMk1s9vFzm6vV9zxavNmoKhI6lmRVCEw\nAd3ubn5Ke9A7GDWuz9PzVXNpbik1gpGkRIk6SU1GPaatTbxGOhIBqqrElXRWCt2AKZFrWnIy0Tj6\nQj7eCHbOeQ6+sI+PZaRlwKQ18Uaw3PTcKZix/NDPYuwSOYaUqMklBEG8y9iRI+LxkiXAypW08xWZ\nGowxDI0N8Wubu0a6ohrBtFlavmquKKhIuEYwQmJFNWoSxe8X79fd3i4m5jvuABYskHpWJNmEhTCs\nw1beCObyu/jYZze50GXrJJwpIfFBNWoyLg6H2DR2/jyQnQ3cey9gNEo9K5Is3AE3bwTrGO5ASAjx\nsRx1TlQjWKYqU8KZEiIvlKiT1ETrMR0d4h7SPh9QXCzeaawwxa9oSeSalhwITEDvaC92vbEL2eZs\n9Hv6o8bLcsv4tc36PD01gl0F/SzGLpFjSIk6xTEGfPghsHevWJuurRXv2Z2RIfXMSCLyh/2wOC28\nEcwb8sI2YIOxzAi1Ug2T1gSz1gyzzoz8DNoDlZDxoBp1CotEgLfeAj76SDy+8UZx9yta2JDxYozB\n4XPwRrDOkU4ITODjmkwNrzUbNUaolLQ2IORyqEZNLjE2BuzaBdhs4i1AV68G5s2TelYkEUSECDpH\nOvm1zU6fk499thGsKLuITmkTEiNK1EnqavWYwUGxaWx4GMjLAzZuBPT6+M4vESRyTWuyeYIe3ghm\nGbYgGAnysSxVFm8EMxWakKWOvtie4hg7imHsEjmGlKhTzJkz4uVXwSAwfbqYpPOpVEg+gzGGPk8f\nXzX3jvZGjZfklPBGMEO+AUoFXWRPyFShGnWKYAx47z3gwAHx67o64K67ALVa6pkRuQiEA1GbXHiC\nHj6mUqpQqankp7QLMgsknCkhyYdq1CkuHAZ27wb+8Q/x+JZbxMYxKh0Sp8/JT2nbXDZEWISP5Wfk\n88RcqamEOo3+qiNECpSok9SFeszoqLipRk8PkJ4O3H03MGuW1LNLDIlc07qSiBCB3W3np7TPj53n\nYwooUJ5fzpNzcU7xpDSCJWMc441iGLtEjiEl6iTW2ysmabcb0GjEm5iUlEg9KxJv3qCXb3JhGbbA\nH/bzsUxVJqq11XyTi2x1toQzJYRcDtWok9Q//wm8+qp42nvGDGDDBiAnR+pZkXhgjGHAO8BXzT3u\nnqhNLqZlT+Nd2uX55bTJBSEyQDXqFMIYcOgQcPiweHzddeLGGmn0uziphSKhqEYwd8DNx9IUaTBq\njPyUdmFWit8blpAEE/dEbbfb8cADD2BwcBAKhQL//u//jm9+85vxnkZSCgaBv/0N+OQTwGZrwVe/\n2oglS6hp7FrJvabl8rt4I5jVZUVYCPOxvPS8qE0u0tPSJZun3OOYCCiGsUvkGMY9UavVavz6179G\nfX09PB4PFixYgBUrVmAWdTjFxOUSb2IyMABkZgIrVgBLl0o9KzKZBCag293NT2kPegejxvV5er5q\nLs0tpTuCEZIkJK9Rr1mzBo8++iiampr4Y1SjnpiuLuCFFwCvF9DpxKaxoiKpZ0Umgy/k441g55zn\n4Av7+Fh6WjqqtdV8k4vc9FwJZ0oIiYVsa9Q2mw0nT57EkiVLpJxGQjtxAnjjDXGDDZMJWLcOyMr6\n/NcReWKMYWhsiG9y0TXSFdUIps3S8lVzRUEFNYIRkgIkS9Qejwfr1q3Dk08+idxcWglMlCAA+/YB\nR4+Kx0uXArfeCij/dSfHRK7HyEW8YhgWwrC5bPyUtsvv4mNKhRLGgouNYLps3ZTPZ7LRz2LsKIax\nS+QYSpKoQ6EQ1q5di/vuuw9r1qy57HO2bNkCo9EIANBoNKivr+dBbmlpAYCUPd63rwXvvAOo1Y1I\nSwNKSlqQmQkolRef39bWJpv5JurxBVPx/b1BL0rrSnHWcRb7D+5HhEVgrDcCAPpP9cNQYMA9t9+D\nqsIqHG09ioArAF25TlbxGe9xW1ubrOaTiMf0/1ne/5+vdT4tLS2w2Wz4PHGvUTPG8OUvfxk6nQ6/\n/vWvLz8pqlFfkcMhNo2dPw9kZ4vXR1dUSD0r8nkEJqB3tJevmvs9/VHjZbllfJMLfZ6eGsEISTFX\ny3txT9Stra246aabMG/ePP7LaPv27bjtttsuTooS9WVZLMCLLwJ+v3iHsU2bxDuOEXnyh/2wOC28\nEcwb8vIxtVKNqsIqnpzzM2gLM0JSmawS9XhQoo7GGPDBB8Df/y7WpmfOBO65R7x395W0JHA9Ri4m\nGkPGGBw+B7+2uXOkEwIT+LgmU8NrzUaNESplatxviH4WY0cxjJ3cYyjbrm/y+SIR4M03gePHxeOb\nbgKWL6ebmMhFRIigc6STn9J2+px8TKlQoqKggifnouwiOqVNCJkwWlHLmNcL7NoFdHYCKpW4f/Tc\nuVLPiniCHr5qtgxbEIwE+ViWKgtmnRlmrRnV2mpkqelaOULI56MVdQIaGBCbxlwuIC8P2LgR0Oul\nnlVqYoyhz9PHr23uGe2JGi/JKeG36zTkG6BUKCWaKSEkGVGilqH/+z/glVfEe3fr9WKSzsub2PeQ\nez1G7gLhAHa+vhOFswpx1nEWnqCHj6mUKlRqKnkjmCaTOvquhn4WY0cxjF0ix5AStYwwBrS2AgcP\nil/PnQusXg2o1VLPLDU4fU5+StvmssFis8CoMQIA8jPyea25UlMJdRr9oxBC4oNq1DIRCgG7dwOn\nTomNYk1NwA03UNPYVIoIEdjddt4Idn7sPB9TQAFDvoEn5+KcYmoEI4RMGapRy9zoKLBzJ9DTI15y\ntXYtUFsr9ayS01hoLKoRzB/287FMVSbf5KJaW42c9BwJZ0oIISJK1BLr6RGT9OioePOSTZvEm5nE\nKpHrMZOJMYYB7wBvBOt2d0dtcjEtexpvBCvPL4/a5IJiODkojrGjGMYukWNIiVpCp04Br70GhMPi\nbUDvvRfIoUVczEKREDqGO9DuFFfO7oCbj6Up0mDUXNzkojCrUMKZEkLI56MatQQYExvG3n1XPF6w\nAPjiF4E02rHwmrn8Ln5K2+qyIiyE+Vhuei5PzFWFVUhPu8ot3QghRAJUo5aRQAD429/ES7CUSmDl\nSmDxYmoamyiBCeh2d/NGsEHvYNS4Pk/PL58qyy2jRjBCSMKiRB1HLpd4E5OBASAzE1i/HjCZpua9\nErkecyW+kA/nnOf4Jhe+sI+Ppael80Yws86M3PTY9zhPxhhKgeIYO4ph7BI5hpSo46SzE3jhBWBs\nDCgqEpvGdDqpZyVvjDEMjQ3xRrCuka6oRjBtlpaf0q4oqIhqBCOEkGRBNeo4OHECeOMNcYON6mpg\n3TpxRU0uFRbCsLls/JS2y+/iY5/d5EKXTX/pEEKSA9WoJSII4taUx46Jx9dfD6xYIdamyUXugJs3\ngnUMdyAkhPhYjjqHXz5VVViFTBX9hUMISS2UqKeIzwe89BJgsYjd3HfeCTQ0xO/95VyPEZiA3tFe\nvmru9/RHjZfllvHkrM/TS9YIJucYJhKKY+wohrFL5BhSop4C58+LTWMOh3hd9IYNwIwZUs9KWv6w\nHxanBe3OdrQ72uENefmYWqlGVWEV79LOz8iXcKaEECIvVKOeZOfOiStpvx8oLRV3vtKk4OZKjDE4\nfA5+SrtzpBMCE/i4JlPDa81GjREqJf3NSAhJXVSjjgPGxFr03/8ufj1rFnD33eK9u1NFRIigc6ST\nn9J2+px87NONYGadGdOyp9G1zYQQMg6UqCdBOCx2dZ88KR7ffDPQ2CjtTUziVY/xBD1RjWCBSICP\nZamyYNaZ+SYXWeqsKZ/PZErkmpacUBxjRzGMXSLHkBJ1jLxe8frori5ApQLWrAHq6qSe1dRhjKHP\n08evbe4Z7YkaL8kp4Y1ghnwDlApqcSeEkFhQjToG/f1i09jICJCfL9ajp0+XelaTLxAORG1y4Ql6\n+JhKqUKlppKf0tZkpmBBnhBCYkQ16kl05kwn9u+3wG5X4vRpATNmmFBfX4ENG4C8PKlnN3mcPic/\npW1z2RBhET6Wn5HPG8EqNZVQp6klnCkhhCQ3StQTcOZMJ5qbz6G/vwlWq/hYb+8BPPIIkJdXIe3k\nPmOi9ZiIEIHdbeeNYOfHzvMxBRQozy/nq+aSnJKUaARL5JqWnFAcY0cxjF0ix5AS9QS89poFn3zS\nBNe/7mpZVQWUlzfhnXcOYs4ceSXq8RgLjfFVs2XYAn/Yz8cyVZl8k4tqbTVy0mmjbEIIkQLVqMeB\nMeDDD4Gf/rQFY2ONUKuBmTMvbqqh0bRg27ZGSec4HowxDHgHeCNYt7s7apOLouwifkq7PL+cNrkg\nhJA4oRp1DJxO4LXXxN2vAAHFxeLGGp++Pjo9XbjSyyUXioRgdVn5KW13wM3H0hRpMGqM/JS2Nksr\n4UwJIYRcDiXqK7hwA5MDB4BQSLwV6Ne/bkJr6wGkpzfx5wUCB9DUVC3hTC/l8ruwc89O5NXmkFMO\nXwAAEZhJREFUweqyIiyE+Vhuei5fNVcVViE9LYXuyDJBiVzTkhOKY+wohrFL5BhSor4Mh0NcRXd1\nicdz5wK33w5kZ1eguho4cOAggkEl0tMFNDVVo7ZW2vq0wAR0u7v5qnnQOwhbjw3GaUYAgD5Pz69t\nLsstS4lGMEIISRZUo/4UQbi4ig6HgdxccdermTPjPpXP5Qv5cM55jm9y4Qv7+Fh6WjpMhSZ+Sjs3\nPVfCmRJCCPk8VKMeh/PnxVW03S4ez58P3HYbkCWTu14yxjA0NsS7tO1ue9QmF9osLT+lPaNgBm1y\nQQghSSLlf5sLAvD++8ChQ+IqOi8PWLUKqKmRemZAWAjD5rLxU9ouv4uPKRVKfkewGl0NdNm6qNcm\ncj1GLiiGk4PiGDuKYewSOYYpnaiHhoBXXwV6/nW76vp6YOVKaVfR7oA7apOLkBDiYznqHL7JhUlr\nQqYqU7qJEkIIiYuUrFELAnDkiLiKjkTE+3SvWgWYzVP2llfEGEPPaA+/trnP0xc1XpZbxhvB9Hl6\nagQjhJAkRDXqTxkcFFfRvb3i8XXXAbfeCmTGcXHqD/thcVp4I5g35OVjaqUaVYVVvBEsPyM/fhMj\nhBAiOymTqCMR4L33gHfeEb8uKBBX0dVxugTaMebgtebOkc6oRjBNpobXmo0a46Q0giVyPUYuKIaT\ng+IYO4ph7BI5himRqAcGxFV037/OKi9cCKxYAWRkTN17RoQIOkc6eXJ2+px8TKlQoqKggq+ap2VP\no1PahBBCLiupa9SRCNDaChw+LH6t0QCrV4ubaUwFT9AT1QgWiAT4WJYqizeCVWurkaWWyXVfhBBC\nJJeSNer+fnEV3d8vHi9aBHzhC7Gvos+cO4P9x/cjxEJQQYV5s+ZBKBDQ7mhHz2hP1HOLc4r5KW1D\nvgFKhTK2NyeEEJJykm5FHYmIK+h33xW7uwsLxVV0ZWXs8zpz7gz+cOAPGDOMwelzwuFzYOzMGOpn\n16NoehFUShW/ttmsM0OTqYn9Ta9RItdj5IJiODkojrGjGMZO7jFMmRV1X5+4ih4YEI+XLAGamqJ3\nupqoiBBBz2gPOoY78PtXf4/eol6woYvBzKnNQcQRweaVm1GpqYQ6TR3jpyCEEEIuSooVdTgsrqJb\nW8VVtFYrrqKNxom/N2MMDp8DHcMdsDgtsLlsvNZ8tPUoAoYA8jPyoc3SQpetQ446B4UDhdi2cdvE\n34wQQghBkq+oe3vFVfTgIKBQAEuXArfcMrFV9FhoDB3DHTw5jwRGosaLsotQVVgFoUyAMEO45PKp\ndCVtFUkIIWRqJGyiDoeBlhbxDmOCAOh0wF13ATNmjOO1QhhdI108Mfd7+sFw8S+ZbHU2qgqrUFVY\nBVOhCQWZBQAAk8KE5kPNUJkvhi3QHkDT8qZL3kNqcq/HJAKK4eSgOMaOYhi7RI5hQibq7m5xp6uh\nIXEVvWwZsHw5oL5CeZgxhkHvICzDFnQMd6DT1Rl1D+00RRoqNBU8MZfmll72uuba6lpswRYcOHEA\nQSGIdGU6mpY3oba6dqo+KiGEkBSXUDXqUOjiKpoxoKhIXEWXl1/6PUYDozwxdwx3wBP0RI2X5JTA\npDWhqrAKFQUV1ARGCCFEMglboz5zphP791sQCinh8Qjw+01QqSqgUAA33AA0Nl5cRQcjQXS6Only\nHvQORn2vvPQ8npirCquQm54b/w9ECCGETJAkiXrv3r3Ytm0bIpEI/u3f/g0/+MEPLnnOmTOdaG4+\nB5WqCVareLo7HD6A5cuBhx+uwHS9gL7RPlh6xcRsH7EjwiL89WqlGkaNkSfnVLtNZyLXY+SCYjg5\nKI6xoxjGLpFjGPdEHYlE8I1vfAP79++HXq/HokWLsHr1asyaNSvqeZs2/Q90JY3oHXsagUgICkGN\nav0i+LVv4ciIFlabFb6wjz9fAQX0eXqxzqw1oTy/HGnKtHh/PNloa2tL2B9KuaAYTg6KY+wohrFL\n5BjGPVF/8MEHqK6uhvFfFzlv3LgRr7322iWJ+p+eNxDxtUKz0IAMTRDpBcP4uOt5jPYVIWeoHoC4\n65Sp0AST1oRKTSXdP/tTXC6X1FNIeBTDyUFxjB3FMHaJHMO4J+qenh6Uf6r7y2Aw4NixY5c8LzTP\nAuSFMcJs0OsMAABVVSaEPj/uMN8Bk9aEwszClDqdTQghJPXEPVGPO7GqI0BZBLC7UIj/hyxokRYZ\nwo2zK7FIv2hqJ5kEbDab1FNIeBTDyUFxjB3FMHaJHMO4X5519OhR/PSnP8XevXsBANu3b4dSqYxq\nKFMWZIG5/fGcFiGEECKZ+fPno62t7bJjcU/U4XAYtbW1OHDgAKZPn47Fixfj+eefv6RGTQghhBAJ\nTn2rVCr89re/xcqVKxGJRPCVr3yFkjQhhBByBbK8MxkhhBBCREqpJ/BZe/fuxcyZM2E2m/HEE09I\nPR1J2e12LF++HHPmzEFdXR2eeuopAIDT6cSKFStQU1ODW2+9Neqyg+3bt8NsNmPmzJnYt28ff/z4\n8eOYO3cuzGYzvvWtb/HHA4EANmzYALPZjKVLl6KzszN+HzCOIpEIGhoasGrVKgAUw4lyuVxYt24d\nZs2ahdmzZ+PYsWMUwwnavn075syZg7lz52Lz5s0IBAIUw3HYunUrSkpKMHfuXP5YvOL2pz/9CTU1\nNaipqcGzzz47xZ/0KpiMhMNhZjKZmNVqZcFgkM2fP5+dPn1a6mlJpq+vj508eZIxxtjo6Cirqalh\np0+fZt/73vfYE088wRhjbMeOHewHP/gBY4yxjz/+mM2fP58Fg0FmtVqZyWRigiAwxhhbtGgRO3bs\nGGOMsdtvv5299dZbjDHGnn76afbII48wxhjbuXMn27BhQ1w/Y7z88pe/ZJs3b2arVq1ijDGK4QQ9\n8MAD7I9//CNjjLFQKMRcLhfFcAKsViurrKxkfr+fMcbYvffey5qbmymG43D48GF24sQJVldXxx+L\nR9wcDgerqqpiw8PDbHh4mH8tBVkl6iNHjrCVK1fy4+3bt7Pt27dLOCN5ueuuu9jbb7/NamtrWX9/\nP2NMTOa1tbWMMcYef/xxtmPHDv78lStXsvfff5/19vaymTNn8seff/559vDDD/PnHD16lDEm/gIu\nKiqK18eJG7vdzpqamtjBgwfZnXfeyRhjFMMJcLlcrLKy8pLHKYbj53A4WE1NDXM6nSwUCrE777yT\n7du3j2I4TlarNSpRxyNuzz33HPvqV7/KX/Pwww+z559/foo+4dXJ6tT35W6G0tPTI+GM5MNms+Hk\nyZNYsmQJBgYGUFJSAgAoKSnBwMAAAKC3txcGg4G/5kL8Pvu4Xq/ncf10zFUqFQoKCuB0OuP1seLi\n29/+Nn7+859Dqbz4404xHD+r1Ypp06bhwQcfxHXXXYeHHnoIXq+XYjgBWq0W3/3udzFjxgxMnz4d\nGo0GK1asoBheo6mOm8PhuOL3koKsEjXdZezyPB4P1q5diyeffBJ5eXlRYwqFguJ2Fa+//jqKi4vR\n0NBwxS3kKIZXFw6HceLECXzta1/DiRMnkJOTgx07dkQ9h2J4dRaLBb/5zW9gs9nQ29sLj8eDv/zl\nL1HPoRhem1SIm6wStV6vh91u58d2uz3qL5pUFAqFsHbtWtx///1Ys2YNAPEvyP7+fgBAX18fiouL\nAVwav+7ubhgMBuj1enR3d1/y+IXXdHV1ARB/IY+MjECr1cbls8XDkSNHsHv3blRWVmLTpk04ePAg\n7r//forhBBgMBhgMBixaJN4RcN26dThx4gRKS0sphuP00UcfYdmyZdDpdFCpVLjnnnvw/vvvUwyv\n0VT//9XpdLLKR7JK1AsXLkR7eztsNhuCwSBeeOEFrF69WuppSYYxhq985SuYPXs2tm3bxh9fvXo1\n/vSnPwEQuxIvJPDVq1dj586dCAaDsFqtaG9vx+LFi1FaWor8/HwcO3YMjDH8+c9/xl133XXJ93rp\npZfQ1NQU5085tR5//HHY7XZYrVbs3LkTt9xyC/785z9TDCegtLQU5eXlOHv2LABg//79mDNnDlat\nWkUxHKeZM2fi6NGj8Pl8YIxh//79mD17NsXwGsXj/++tt96Kffv2weVyYXh4GG+//TZWrlwpwaeF\nvLq+GWPszTffZDU1NcxkMrHHH39c6ulI6t1332UKhYLNnz+f1dfXs/r6evbWW28xh8PBmpqamNls\nZitWrIjqRHzssceYyWRitbW1bO/evfzxjz76iNXV1TGTycQeffRR/rjf72fr169n1dXVbMmSJcxq\ntcbzI8ZVS0sL7/qmGE5MW1sbW7hwIZs3bx67++67mcvlohhO0BNPPMFmz57N6urq2AMPPMCCwSDF\ncBw2btzIysrKmFqtZgaDgT3zzDNxi9szzzzDqqurWXV1NWtubo7L570cuuEJIYQQImOyOvVNCCGE\nkGiUqAkhhBAZo0RNCCGEyBglakIIIUTGKFETQgghMkaJmhBCCJExStSEpKjGxkYcP348pu+xZ8+e\nlN+OlpCpppJ6AoQQaUzGPZJXrVrF9/gmhEwNWlETIhNerxd33HEH6uvrMXfuXLz44osAgJ/97GdY\nvHgx5s6di4cffpg/v7GxEd/5znewaNEizJo1Cx9++CHuvvtu1NTU4Cc/+QkAcde1mTNn4r777sPs\n2bOxfv16+Hy+S9573759WLZsGRYsWIB7770XXq/3kuc89dRTmDNnDubPn4/NmzcDAJqbm/Hoo48C\nAOrr69HQ0ICGhgZkZ2fj3XffhdfrxdatW7FkyRJcd9112L179yXft6WlBY2NjVi/fj1mzZqF++67\nL/ZgEpJMJLsnGiEkyksvvcQeeughfjwyMsIYY8zpdPLH7r//frZnzx7GGGONjY3shz/8IWOMsSef\nfJKVlZWx/v5+FggEmMFgYE6nk1mtVqZQKNiRI0cYY4xt3bqV/eIXv+CvP378OBsaGmI33XQTGxsb\nY4wxtmPHDvazn/3skvlNnz6dBYPBqLk1Nzezb3zjG1HP2717N7vppptYKBRi//mf/8n+8pe/MMYY\nGx4eZjU1Nczr9UY9/9ChQ6ygoID19PQwQRDY9ddfz1pbW68lhIQkJVpREyIT8+bNw9tvv40f/vCH\naG1tRX5+PgDg4MGDWLp0KebNm4eDBw/i9OnT/DUXNq2pq6tDXV0dSkpKkJ6ejqqqKr7zT3l5Oa6/\n/noAwH333YfW1lb+esYYjh49itOnT2PZsmVoaGjAs88+y3cT+uz8Nm/ejL/+9a9IS0u77Gdob2/H\n97//fezatQsqlQr79u3Djh070NDQgOXLlyMQCETtSHTB4sWLMX36dCgUCtTX18Nms11bEAlJQlSj\nJkQmzGYzTp48iTfeeAM//vGP0dTUhO9///v4+te/juPHj0Ov1+O//uu/4Pf7+WsyMjIAAEqlkn99\n4TgcDgOI3uedMXbZuvSKFSvw3HPPXXV+b7zxBg4fPow9e/bgsccew6lTp6L2+PZ4PNiwYQP+8Ic/\noKSkhD/+yiuvwGw2X/V7f3ruaWlpfO6EEKpREyIbfX19yMzMxJe+9CX8x3/8B06ePMmTsk6ng8fj\n4XXriejq6sLRo0cBAM899xxuvPFGPqZQKLB06VK89957sFgsAMRaeXt7e9T3YIyhq6sLjY2N2LFj\nB0ZGRuDxeKKes3XrVjz44IO44YYb+GMrV67EU089xY9Pnjw54fkTkupoRU2ITJw6dQrf+973oFQq\noVar8bvf/Q4FBQV46KGHUFdXh9LSUixZsuSyr71aB3dtbS2efvppbN26FXPmzMEjjzwSNV5UVITm\n5mZs2rQJgUAAAPDYY49FrYIjkQjuv/9+jIyMgDGGb33rWygoKODv29XVhZdffhnt7e145plnAAB/\n/OMf8ZOf/ATbtm3DvHnzIAgCqqqqLmkou9zcY+1GJySZ0DaXhCQxm82GVatW4dSpU1JPhRByjejU\nNyFJjlanhCQ2WlETQgghMkYrakIIIUTGKFETQgghMkaJmhBCCJExStSEEEKIjFGiJoQQQmSMEjUh\nhBAiY/8fzj2UNX7XML4AAAAASUVORK5CYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10565c6d0>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 71
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"As we can see in the first plot, the list comprehensions lead to a slightly increased performance in regular Python code. \n",
|
|
"But the second plot is quite interesting: List comprehensions in Cython are significantly slower than the regular for-loop structures. \n",
|
|
"Apparently, Cython has no difficulties turning the explicit for-loop into for-loop in C with basic float arithmetic. However, the list comprehension version is constantly writing to memory while it is iterating and appending new values.\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"Let us do a quick comparison by how much we were able to improve the performance of the simple least square implementation using Cython so far:\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"x = [x_i*random.randrange(8,12)/10 for x_i in range(500)]\n",
|
|
"y = [y_i*random.randrange(8,12)/10 for y_i in range(100,600)]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 72
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"funcs = ['lstsqr_comprehensions', 'cy_lstsqr_comprehensions', \n",
|
|
" 'cy_lstsqr_loops'] \n",
|
|
"labels = ['list comprehensions', 'list comprehensions (Cython)', \n",
|
|
" 'for-loops (Cython)']\n",
|
|
"\n",
|
|
"times = [timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000)\n",
|
|
" for f in funcs]\n",
|
|
"\n",
|
|
"times_rel = [times[0]/times[i+1] for i in range(len(times[1:]))]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 73
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"#%pylab inline\n",
|
|
"#import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"plt.figure(figsize=(8,6))\n",
|
|
"x_pos = np.arange(len(funcs[1:]))\n",
|
|
"plt.bar(x_pos, times_rel, align='center', alpha=0.5, color=\"green\")\n",
|
|
"plt.xticks(x_pos, labels[1:], rotation=90)\n",
|
|
"plt.ylabel('relative performance gain')\n",
|
|
"plt.title('Performance gain compared to the classic least square implementation')\n",
|
|
"ftext = 'For-loops in Cython are {:.2f}x faster then list comprehensions'\\\n",
|
|
" .format(times[1]/times[2],1)\n",
|
|
"plt.figtext(.15,.8, ftext, fontsize=11, ha='left')\n",
|
|
"plt.xlim([-1,len(funcs[1:])])\n",
|
|
"plt.ylim([0,max(times_rel)*1.2])\n",
|
|
"plt.grid()\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAesAAAIBCAYAAABpxJfYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl4DXf7P/D3SSSWJJLIIoLkWC9LgqCoIomdqiq11Rba\n0qqiSqlS6VdrKS1NaUurYntqeRShqmpXtVQpJZLYYk+sQRKRnJP790d+mScn2wnmTA7n/bou12Uy\nZ2bumfnM3Ocz98wcnYgIiIiIyGrZFXcAREREVDgmayIiIivHZE1ERGTlmKyJiIisHJM1ERGRlWOy\nJiIisnJM1v9fYmIiWrVqhbJly2LcuHHFHY7V69y5M5YtW1bcYVgtvV6P7du3a7Y8Ozs7nDt3zqLL\nCAsLw+TJky02fxcXF8THxz/SNLt27ULlypUtE9AzLiAgAHv27FF9vvHx8bCzs0NmZqbq8y5ub7/9\nNj799NNiWXaJYlmqSvR6Pa5fvw57e3s4OTmhU6dOmDdvHpycnB55XgsXLoS3tzfu3btngUifPZs3\nby7uEKyaTqeDTqfLd1xYWBgqV66MqVOnPta8Q0JCMGDAALz++utPEuIjK2yd1HD//n2LzftJPOn+\nslYnTpwo7hA09aj7MTIyEosWLcLevXuVv3377beWCs+sp7pnrdPpsGnTJty/fx9HjhzB4cOHH/lb\nj4ggMzMTFy5cQO3atR8rDoPB8FjT0dPB2vavJROmOXyHknWytjZKFiBPMb1eL9u3b1eGx44dK126\ndBERkf3798vzzz8vbm5uUr9+fdm1a5fyueDgYPnoo4/khRdekNKlS0v//v3FwcFBHB0dxdnZWbZv\n3y4PHz6UUaNGia+vr/j6+sro0aPl4cOHIiKyc+dOqVixosycOVN8fHxkwIABEh4eLq+++qr0799f\nXFxcJDAwUOLi4mTatGni7e0tfn5+snXrViWGH3/8UWrXri0uLi5StWpVWbBggTIue/5ffPGFeHt7\nS4UKFWTx4sXK+NTUVBkzZoz4+/uLq6urtGjRQh48eGB2vXP7+++/pUGDBuLi4iI9e/aUXr16yaRJ\nk0RE5Pbt2/Liiy+Kl5eXuLu7S5cuXeTy5csm2/CHH34QEZHFixfLCy+8IGPHjhV3d3epUqWK/Prr\nrwUu9+LFi/LKK6+Il5eXeHh4yIgRI0RExGg0ytSpU8Xf31+8vb1l4MCBcvfuXREROX/+vOh0Olm8\neLFUrlxZypUrJ99++60cOnRIAgMDxc3NTZlPdkzNmzeXESNGiKurq9SqVcukrRRl+2fv34EDB0pm\nZqZMnz5dqlWrJh4eHtKrVy+5ffu2Ms3SpUvFz89PPDw85LPPPsvTNrMtWLDApK117dpVRESio6Ml\nODhY3NzcpG7duhIVFZXvtps4caLY29tLqVKlxNnZWd59910REdHpdPLdd99JjRo1xM3NTd555x2T\n6RYtWiS1a9cWd3d36dChg1y4cKHA/bN3716lDVWuXFmWLFkiIiJhYWFFbh+LFy+WqlWriouLi1Sp\nUkVWrFghIiKnT5+WVq1aiaurq3h6ekrv3r2VaXQ6nZw9e1ZECm/jOe3cuVMqVaqkDF+5ckW6d+8u\nXl5eUqVKFYmIiFDGHTx4UJo1ayZubm5SoUIFGTFihKSnpyvjR48eLd7e3lK2bFkJDAyUEydOFLi/\ncstvWhGRmzdvyksvvSRly5aVJk2ayKRJk6RFixYi8r82bTQalfnkPK7OnDkjoaGh4uHhIZ6entKv\nXz9JSkpSPuvv7y8zZ86UwMBAKVWqlBiNxkc6/v39/ZU2OmXKlEc6fwUHB8uECROkSZMmUrZsWXn5\n5ZeV4yH3eiUlJcmQIUOkQoUKUrFiRZk0aZIyLvs4fe+998TNzU2qVasm+/btkx9//FEqV64s3t7e\nSvsTEUlLS5P3339f/Pz8pHz58vLWW28p7aKw82ZB+zH7mHZxcZE6derIunXrRCTreCxVqpTY29uL\ns7OzuLu7i4jIoEGDlGNARGThwoVSvXp1KVeunHTt2lWuXr2qjDN3TD6qpz5Zb9u2TUSyEkDdunXl\n448/lsuXL4uHh4eSMH7//Xfx8PCQmzdvikhWQ/P395fo6GgxGo2SkZEhYWFhMnnyZGXekydPluef\nf15u3LghN27ckObNmyvjd+7cKSVKlJAJEyZIenq6PHjwQKZMmSKlSpWSrVu3isFgkIEDB4q/v79M\nmzZNDAaDfP/991KlShVl/r/88oucO3dORER2794tZcqUkSNHjpjMf8qUKWIwGGTz5s1SpkwZ5UAd\nPny4hIaGytWrV5UD9OHDhwWu940bN/Jsu4cPH4qfn59ERESIwWCQn3/+WRwdHZV1vHXrlvz888/y\n4MEDuX//vvTs2VO6deumTB8SEiKLFi0SkawDzsHBQX744QfJzMyUb7/9Vnx9ffPdZwaDQerVqydj\nxoyR1NRUSUtLk3379olIVkKpXr26nD9/XpKTk6V79+4yYMAAEfnfCeDtt9+Whw8fytatW8XR0VG6\ndesmN27ckCtXroi3t7fs3r1bialEiRIyd+5cMRgMsmrVKnF1dVVOKEXZ/jn379y5c+X555+XK1eu\nSHp6ugwbNkz69u0rIiInT54UZ2dn2bt3rzx8+FDGjBkjJUqUyDdZi0ietpaeni7VqlWT6dOnS0ZG\nhuzYsUNcXFwkNjY23+lzbvtsOp1OXnrpJbl7965cvHhRvLy8ZMuWLSIisn79eqlevbrExMSI0WiU\nTz/9VJo3b57vvOPj48XFxUVWrlwpBoNBbt26Jf/8848Sd/aJqrD2kZycLGXLlpW4uDgREUlISJCT\nJ0+KiEifPn1k2rRpIpLVBrP3ffY6ZCfrgtp4bjmTtdFolIYNG8rUqVMlIyNDzp07J1WrVpXffvtN\nRLK+nB48eFCMRqPEx8dL7dq1Ze7cuSIismXLFmnUqJHy5TAmJkauXbuW7/7KrbBpe/fuLb1795bU\n1FQ5ceKEVKxYUVq2bCki+SfrnPv2zJkzsm3bNklPT5cbN25Iq1atZPTo0cpn/f39JSgoSC5fvixp\naWmPdPyLmHZ2HvX8FRwcLBUrVpSTJ09KSkqK9OjRQ/r375/venXr1k3eeustSU1NlevXr0uTJk2U\nL8fZx2lkZKRkZmbKpEmTpGLFisoXqa1bt4qLi4ukpKSISNaXopdfflnu3Lkj9+/fl5deekk+/PBD\npS0Udt7Mbz+uWbNG2VerVq0SJycnSUhIEBGRyMhI5YtVtpzz2L59u3h6esrRo0fl4cOH8u6770qr\nVq2UzxZ2TD6OpzpZ+/v7i7Ozs7i5uYm/v7+888478uDBA5kxY4Zyks/WoUMH5RtaSEiITJkyxWR8\nzhORiEi1atVMeoe//fab6PV6EclqFI6OjiYnjylTpkj79u2V4aioKHF2dpbMzEwREbl3757odDrl\ngM6tW7du8tVXXynzL126tMlB7O3trZxoSpcuLcePH88zD3PrndPu3bulYsWKJn9r0aJFgSelo0eP\nKt8uRfIm6+rVqyvjUlJSRKfTSWJiYp75/Pnnn+Ll5WWybtlat24t3377rTIcGxsrDg4OYjQalRNA\nzm+uHh4esnr1amW4R48eysl38eLFeb4wNGnSRJYtW5bv+uXe/rn3b+3atU2S79WrV8XBwUEMBoN8\n8sknSuLOXn9HR8dCk3XOtrZnzx7x8fEx+Uzfvn0lPDw83+lDQkKU3lc2nU5nkvh69eolM2fOFBGR\njh07miR3o9EoZcqUkYsXL+aZ97Rp06R79+5FijunnO0jOTlZ3NzcZO3atZKammryuYEDB8rQoUNN\neuE51+Hs2bOFtvHccibrAwcOiJ+fX571GTx4cL7TzpkzR1555RURyTrx1qxZUw4cOJCnbRa23iIi\nO3bsyHdag8EgDg4OJl+6Jk6cWGjPOr8vYtnWrVsnQUFByrBerze54vYox3/29DmT9aOcv0JCQpQk\nKZLVE3V0dJTMzEyT9UpISJCSJUuaXBX5z3/+I6GhoSKSdZzWqFFDGXf8+HHR6XRy/fp15W8eHh5y\n7NgxyczMFCcnJ+ULnUjW+ST7S0Rh500R8/tRRKRBgwayYcMGJbbCkvWQIUNk/Pjxyrjk5GRxcHBQ\nrlrld0zOmDGj0OUX5qmvWW/YsAF37txBfHw85s2bh1KlSuHChQtYs2YN3N3dlX/79u1DQkKCMq25\nO0ivXr0Kf39/ZdjPzw9Xr15Vhr28vODo6Ggyjbe3t/L/0qVLw9PTU6kvli5dGgCQnJwMAPj111/R\nrFkzeHh4wN3dHZs3b8atW7eU6T08PGBn97/dU6ZMGSQnJ+PmzZtIS0tDtWrV8sRclPXOuX4VK1Y0\n+VvlypWVmmRqaiqGDRsGvV4PV1dXBAcH4+7duwXWLH18fExizbmuOV26dAn+/v4m65bt2rVreba5\nwWBAYmKi8rfy5csr/y9dunSe4ZSUFGU49/r5+/vj2rVrAMxv/9z7Nz4+Hq+88oqyXevUqYMSJUog\nMTER165dQ6VKlUzW38PDI7/NlK+rV6/maY/+/v64cuVKgdPkV7fOvQ+yt/+FCxcwatQoJfbs2PKb\n/+XLl1G1alWzMRfWPpycnLBq1Sp899138PX1RZcuXRAbGwsA+PzzzyEiaNKkCQICArB48eI88y6s\njRfmwoULuHr1qkn7nz59Oq5fvw4AiIuLQ5cuXVChQgW4urrio48+UvZ569atMWLECLzzzjsoX748\nhg0bVuQb3kJDQ/Od9saNGzAYDCb71s/Pr8jrk5iYiD59+qBSpUpwdXXFgAEDTNooYHoee5TjPz+P\ncv7KvWw/Pz9kZGTg5s2bJvO8cOECMjIyUKFCBSWmt956Czdu3FA+k/sYBrKOv5x/S05Oxo0bN5Ca\nmopGjRop8+rUqZPJMgs6bxZk6dKlCAoKUuZ34sSJPNu4ILnPV05OTvDw8DA5rgo6Jh/HU52sC+Ln\n54cBAwbgzp07yr/79+/jgw8+UD5j7iYdX19fk8dILl68CF9f3wKnf5Sbfh4+fIgePXrggw8+wPXr\n13Hnzh107ty5SDfveHp6olSpUjhz5kyecUVZ72wVKlTIc7K+ePGish5ffPEF4uLicOjQIdy9exe7\nd++GZF2JKfJ65qdy5cq4ePEijEZjnnH5bfMSJUqYHMyPIvf6XbhwAb6+vkXa/rn3p5+fH7Zs2WKy\nbVNTU+Hr64sKFSrg0qVLymdTU1MLPeBzz9vX1xeXLl0yWf6FCxdMvgAUNr05fn5+WLhwoUnsKSkp\naNasWZ7PVq5cGWfPnjUbu7n20b59e2zduhUJCQmoVasW3nzzTQBZJ+aFCxfiypUrWLBgAYYPH57n\nkbPC2nhhKleujCpVqpis571797Bp0yYAWY/d1KlTB2fOnMHdu3fx2WefmTxe9O677+Lw4cOIjo5G\nXFwcZs2aZbLOhclvWm9vb5QoUQIXL15UPpfz/9lPraSmpip/y5lYJ06cCHt7e5w4cQJ3797FsmXL\n8jwOlTO2Rzn+1ZB7vRwcHODp6WnymcqVK6NkyZK4deuWEtPdu3fx77//PvLyPD09Ubp0aURHRyvz\nSkpKKvITPLn344ULFzB06FDMnz8ft2/fxp07dxAQEKC04UfNESkpKbh161aeToJanslk3b9/f2zc\nuBFbt26F0WhEWloadu3aZXLyzp10cg/37dsXn376KW7evImbN2/i//7v/zBgwIACl/koSSw9PR3p\n6enw9PSEnZ0dfv31V2zdurVI09rZ2WHIkCEYM2YMrl27BqPRiP379yM9Pb1I652tefPmsLe3x7x5\n82AwGLBhwwb89ddfyvjk5GSULl0arq6uuH37Nj755JMir19hmjZtigoVKmDChAlITU1FWloa/vzz\nTwBZ23zOnDmIj49HcnIyJk6ciD59+uTbCy9Izv1w/fp1REREICMjA2vWrEFMTAw6d+78WNv/rbfe\nwsSJE5UT1I0bNxAVFQUAePXVV7Fp0ybs27cP6enp+Pjjjwt9xrR8+fImCapZs2YoU6YMPv/8c2Rk\nZGDXrl3YtGkT+vTpU+D0hSXU7O2QvS3eeustTJs2DdHR0QCAu3fvYs2aNflO169fP2zbtg1r1qyB\nwWDArVu3cOzYsTzzLKx9XL9+HRs2bEBKSgocHBzg5OQEe3t7AMCaNWtw+fJlAICbmxt0Ol2e/VtY\nGy9MkyZN4OLigs8//xwPHjyA0WjEiRMncPjwYSVmFxcXlClTBjExMfj222+VE/Lhw4dx8OBBZGRk\noEyZMihVqpQSc+79lVtB09rZ2aF79+4IDw/HgwcPEB0djaVLlyrL9PLyQsWKFbFs2TIYjUb8+OOP\nJvs1OTkZTk5OKFu2LK5cuaJ8eSjIoxz/T0pEsHz5cpw6dQqpqan4+OOP0bNnzzwJrkKFCmjfvj3G\njBmD+/fvIzMzE2fPnn2s57vt7Ozw5ptvYvTo0UrP/MqVK0U+d+bejykpKdDpdPD09ERmZiYWL15s\n8jhb+fLlcfnyZWRkZJisd/Yx0LdvXyxevBjHjh3Dw4cPMXHiRDRr1qzAqydP2tF5JpN1pUqVsGHD\nBkybNg3e3t7w8/PDF198UWjPKfczpJMmTULjxo1Rr1491KtXD40bN8akSZOKPH1BnwGyXv4QERGB\nXr16oVy5cvjpp5/w8ssvFzptTrNnz0ZgYCCee+45eHh44MMPP0RmZmaB651f4nBwcMDPP/+MRYsW\nwd3dHStWrECXLl2US7+jR4/GgwcP4OnpiebNm6NTp04FxlSUdc9mZ2eHjRs34syZM/Dz80PlypWx\nevVqAMCQIUMwYMAAtGrVClWrVkWZMmXw9ddfF2mb5PeZpk2b4vTp0/Dy8sLkyZOxdu1auLu7P9b2\nHzVqFLp27Yr27dujbNmyeP7553Ho0CEAQJ06dTB//ny89tpr8PX1Rbly5Qots7z++uuIjo6Gu7s7\nunfvDgcHB2zcuBG//vorvLy8MGLECCxbtgw1a9bMd/pRo0bhv//9L8qVK4fRo0cXuB2y16Fbt24Y\nP348+vTpA1dXVwQGBuK3337Ld7rKlStj8+bN+OKLL+Dh4YGgoCAcP348zzwLax+ZmZmYM2cOKlas\nCA8PD+zdu1d5PvXw4cNo1qwZXFxc8PLLLyMiIgJ6vT7PNi+ojRe0rgBgb2+PTZs24Z9//kHVqlXh\n5eWFoUOHKj2v2bNn4z//+Q/Kli2LoUOHmnwZunfvHoYOHYpy5cpBr9fD09NTeTlS7v2VW2HTzps3\nD8nJyfDx8cGQIUMwePBgk/PQ999/j1mzZsHT0xPR0dF44YUXlHFTpkzBkSNH4Orqipdeegk9evQo\n9Bh4lOM/v21Y1PNX9v8HDBiAsLAwVKhQAenp6YiIiMj3s0uXLkV6ejrq1KmDcuXKoWfPnsoVhEc5\ndwDAzJkzUb16dTRr1gyurq5o164d4uLiijRt7v1Yp04dvP/++3j++efh4+ODEydOoEWLFsrn27Rp\ng7p168LHx0cpEeSMt02bNpg6dSp69OgBX19fnD9/HitXrix0+z3JY5c6edJ0T8+Mpk2bYvjw4Rg0\naFBxh/LE8nuhAVFxe1baZWhoKAYMGIAhQ4YUdyg245nsWVPR7NmzBwkJCTAYDFiyZAlOnDiBjh07\nFndYRPQUYD9PW0/160bpycTGxqJXr15ISUlBtWrV8N///vexb+ayNpZ+NSbR43iW2uWzsh5PC14G\nJyIisnK8DE5ERGTlrPYyeEhICHbv3l3cYRAREWkiODgYu3btynec1V4G1+l0vIGBVBUWFobIyMji\nDoOeEWxPpLbC8h4vgxMREVk5JmuyGdkv3yBSA9sTaYnJmmxGSEhIcYdAzxC2J9ISkzUREZGVY7Im\nIiKycrwbnIiIyArwbnAiIqKnGJM12YyCXjZA9DjYnkhLTNZERERWjjVrIiIiK8CaNRER0VOMyZps\nBmuMpCa2J9ISkzUREZGVY82aiIjICrBmTURE9BRjsiabwRojqYntibTEZE1ERGTlWLMmIiKyAqxZ\nExERPcWYrMlmsMZIamJ7Ii0xWRMREVk51qyJiIisAGvWRERETzEma7IZrDGSmtieSEtM1kRERFaO\nNWsiIiIrwJo1ERHRU4zJmmwGa4ykJrYn0hKTNRERkZVjzZqIiMgKsGZNRET0FGOyJpvBGiOpie2J\ntMRkTUREZOWeyWSt1+tRu3ZtBAUFISgoCO+///4TzS8yMhI9e/ZUKbrHs2DBAsydO/expv3qq68Q\nEBCAgIAANGzYEEOHDsXdu3cLnSYyMhKnT582GS7ubfA4pk6dioCAANSvXx9jx47F1q1bC/28iKBt\n27bw8vIy+fv06dMRGBiI2rVrIywsDOnp6Y8cy6RJk1C7dm0EBwc/8rRA3n3yJI4dO4Y1a9aY/M3O\nzg6pqamqzD8/YWFhmD9/PoCitecNGzbgr7/+slg8TyokJKRIn9Pr9YiOjrZsMAD+/vtv9O/f3+LL\noeJRorgDsASdToe1a9eiTp06jzV9ZmYm7Oz+9z1Gp9OpFdpjGzZs2GNNN2nSJOzduxc7d+5UEtC6\ndetw+/ZtuLq6FjhdZGQkvLy8UKNGDQDWsQ2y5d4/hWnatCnGjRuHUqVK4fjx4wgODkZCQgJKliyZ\n7+fnzZsHvV6P48ePK3/bunUrVq5ciUOHDqF06dIYOnQo5syZg/Hjxz9S3F9++SUuXboEDw+PR5ou\nW+59UlT5ba+jR4/il19+yfMFzJI3dep0OqUdFaU9r1u3Ds899xyee+45i8WkBqPRCHt7+wLHa3Wz\nbKNGjbB8+XKLL4eKxzPZswbyP+ls2bIFDRs2RP369dG2bVucPXsWQFbtqV69ehgyZAiCgoKwZcuW\nQuc1c+ZMBAYGIjAwEEOGDEFKSgoAIDk5GYMHD1bGzZo1S5kmJCQE7733Hpo2bYoaNWrgo48+UsZ9\n8sknypWAhg0b5tvrDQ8Px7hx4wBknbTbt2+PPn36ICAgAC1atEBiYmKeaZKTk/Hll1/ihx9+MOkp\nvvLKK6hSpQq6dOmC//73v8rff/75Z3To0AGRkZH4+++/MXLkSAQFBWH79u0AgHv37uW7TKPRiLFj\nxyrrPW7cOGRmZgLI6k29/fbbaNOmDWrWrIlBgwbliTN7Hh07dsRzzz2HgIAADBkyBBkZGcr6tm3b\nFt27d0dgYCD+/fdfHDx4EK1bt0bjxo3RuHFjbN68Od/5tm/fHqVKlQIA3Lp1CyKCW7du5fvZ06dP\nY9WqVZgwYYLJPj9+/DhatmyJ0qVLAwA6duyIFStWAACWL1+OZs2awWAwIDMzE23btsXChQvzzLtl\ny5ZIS0tD69at8cEHHyAxMVGJPyAgwCTxb9iwAfXq1UNQUBACAwOxe/duLF682GSf7NixA0BWW2za\ntCkaNWqErl27KvskPDwcPXv2RIcOHVC3bl2TNnXr1i1MmTIF27ZtQ1BQEEaPHq2Mi4iIQJMmTVCt\nWjX8/PPPyt8L2t7x8fHw9PTEpEmT0LBhQ9SqVQv79u3Ld/vmlLM9//nnn2jUqBGCgoIQEBCAlStX\nYuvWrdi4cSNmzJiBoKCgfJPQlStX0KNHD9SvXx/169fHjBkzAACJiYl45ZVXUL9+fdSrVw/Lli1T\nptHr9Zg8eTKaN28OPz8/rFixAl988QWaNGmCGjVqYO/evSbrNXbsWGU+f/zxh8m4Pn36oFGjRli0\naBGuXbuGnj17omnTpqhXrx6mT59uEuvq1avRvHlzVKlSRbm6AACxsbHo3LkzmjRpggYNGiAyMlIZ\nZ2dnh+nTp+fZH6mpqejZsyfq1q2LBg0aoHfv3gCyzmM5v9gsXboU9erVQ/369dG9e3fcuHEDQOHn\nj/z2BVkJsVJPEpq/v7/UqlVLGjRoIA0aNJCtW7dKYmKieHl5yalTp0REZNGiRdK0aVMREdm5c6fY\n29vLgQMH8p3f4sWL5dVXXxURkc2bN0tAQIDcv39fREQGDhwo48ePFxGRDz74QMLCwkRE5N69e1K3\nbl359ddfRUQkODhYOnToIEajUZKTkyUwMFA2bdokt27dEjc3N0lLSxMRkeTkZDEYDHliCA8Pl7Fj\nxyrxuLu7y+XLl0VE5M0335SPPvoozzQHDx4UNze3ArfTli1bJDQ0VBlu3bq1REVFiYhISEiI/PLL\nLybboKBlfvPNN9K2bVvJyMiQ9PR0adOmjXz77bciIjJo0CBp2bKlPHz4UNLT06Vu3bry+++/5xvP\nrVu3REQkMzNTBg4cKN99952ybGdnZzl37pyIiNy5c0eCgoLk2rVrIiJy9epVqVSpkiQlJRW4riIi\n48ePl0aNGuU7zmg0SnBwsBw7dkzOnz8vnp6eyrgdO3ZIzZo15ebNm5KRkSG9e/eWsmXLKuNff/11\nef/99+WTTz6R3r17F7h8nU4nKSkpIiKSlpYmycnJIiKSnp4urVu3li1btoiISP369ZW2mJmZKffu\n3RORvPtk2bJlMnToUMnMzBSRrP3Qr18/ERGZMmWK+Pn5Kds0t8jISKVN54xv/vz5IiKyb98+qVix\noogUvL3v3r0r58+fF51Op8S1YsUKeeGFF/JdZlhYmDL/8PBwGTdunIiIdO3aVX766Sflc9n7Mefn\n8xMSEiKzZ89Whm/evCkiIr169ZKPP/5YRESuXbsmvr6+cvLkSRER0ev18sEHH4iIyF9//SWlS5eW\nb775RkREVq9eLS1atBARUdZr2bJlIiKya9cuqVSpkqSnpyvjpkyZoiy7bdu2smfPHhERefjwobRo\n0UJp53q9XlnX+Ph4cXZ2lpSUFMnIyJCGDRtKTEyMiGSdM2rWrCmxsbGF7o+ff/5ZOnTokGd77dy5\nUxo3biwiIv/++6/4+vpKQkKCiIhMnjxZaZuFHcsvv/xyvvuCtFFY3rOZy+AbN25E/fr1UatWLQBZ\nPb7hw4crveIaNWqgadOmZue9bds29O3bF87OzgCAoUOHYtSoUQCA7du3IyIiAgDg4uKCvn37Ytu2\nbejYsSN0Oh0GDRoEOzs7ODk5oU+fPtixYwc6deqE6tWrY8CAAWjfvj26dOkCJycns3G88MILqFix\nIgCgWbMyheJmAAAgAElEQVRm+P333x9hC2Vp3749Ro8ejZiYGIgIzp07hy5duijjJdcVhYKWuX37\ndgwePBglSmQ1p8GDB2PdunV46623oNPp0K1bNzg6OgIAGjZsiLNnz6Jt27Ym887MzMSsWbOwZcsW\nGI1G3Llzx2Q7tGjRAlWqVAGQ9e3//Pnz6NSpkzLezs4OZ8+eRcOGDfNd1927d+Onn37Ctm3b8h0/\ne/ZsBAcHo169eoiPjzcZFxoainfeeUfppbdp08Zke8+bNw8NGzaEwWDAkSNH8p1/bgaDAWPHjsX+\n/fshIkhISMCxY8fQoUMHtG7dGqNHj0aPHj3QqVMn1K1bV5ku5z6JiorC33//rayzwWCAm5ubMv7F\nF19EuXLl8l1+7n2brU+fPgCyygdXr15Fenp6gdv7zJkzKFeuHJydndG5c2dluqLeI5IdQ+vWrfHp\np5/i7NmzaNeuHZo0aWI2zuTkZOzfv1+56gNAKS9s374dc+bMAQD4+Pigc+fO2LFjh3I+yO6JBgUF\nIS0tTRlu2LAhzpw5o8zP0dFRqQEHBwejdOnSiI2NhbOzM0qVKoXw8HAAQEpKCnbt2oWbN2+axBcT\nE6O08+zt6u/vD3d3d1y+fBkGgwExMTHKOADIyMjAqVOnULNmTZPpcu6PBg0a4NSpUxgxYgRCQkLw\n4osv5tk+O3fuxIsvvojy5csDyCo71K9fXxlf0LEcGhpa4L6g4vVMJuv8mKu5ZidfAOjevTvOnz8P\nnU6HPXv25JlPzhNI7pNJ7nE5l5vfODs7Oxw4cAD79u3Djh070KhRI2zZsgWBgYGFxpt9aRfIOnEa\nDIY8n6lTpw7S0tJw+vTpfOucOp0OI0aMwPz586HT6ZTkmnN8UZdZ2HrnrA/b29vnG+uKFSuwb98+\n/PHHH3BycsL06dMRFxenjM+5fwCgXr162L17d5755Gf//v0YMGAAoqKiCqz37t27F8ePH8fSpUth\nMBhw584dVK1aFcePH4ezszNGjhyJkSNHAsi6pJkzgV67dg0pKSmws7PD3bt388Sany+//BJJSUk4\ndOgQHB0dMWzYMDx48EAZd/LkSWzfvh09e/bEmDFj8MYbbwDIu08mT56MsLCwPPPX6XRF+tKXW/Y+\nzq7BGgwGiEiB2zs+Pr5I+7cwo0aNQteuXfH777/j3XffRfv27TF16lRlPQpTUDIvrD3mXsecw7lj\nzz1ttpzbNvuegMOHDxdYu8557GQvR0Tg6emJo0ePFrh++e2PKlWqIDo6Gtu2bcOvv/6KiRMn4t9/\n/zWZztx5qqBjubB9QcXrma1Z59a0aVMcO3YMsbGxAIAlS5agYcOG+Z7Qfv75Zxw9ehRHjhzJc+Jt\n27YtVq1aheTkZIgIfvjhB7Rv314Zt2jRIgDA/fv3sWrVKrRr1w5A1sGyfPlyGI1GpKSkYM2aNWjd\nujWSk5Nx/fp1tGrVCuHh4QgICMDJkyfzxFTQSakwzs7OeO+99zB06FClXiUiWL9+Pc6fPw8AGDRo\nENavX4/Vq1crCQEAypYti6SkpCItp23btliyZAkMBgMyMjKwZMkSZb2L6u7du/D09ISTkxPu3r2L\nFStWFHiibt68OU6fPm3ynGtBdw3/9ddf6N27N9auXVvo+mzcuBEXLlzA+fPn8ccff8Dd3R3nzp1T\n9n9CQgIA4M6dO5g5cybGjh0LAEhPT0fv3r0xa9YsTJkyBX369IHRaCzS+laoUAGOjo64cuUKNmzY\noKxvbGws6tati5EjR6J///44fPgwgLz7pGvXrpg/f77yt4cPHyo3xplrL66urmafCMj2KNvbnOy4\ncsYXFxeHKlWqYOjQoRg5cqQy78LaoLOzM5o3b670oAEo9yK0bdsW33//PYCs/fbrr7+idevWjxxr\neno6/vOf/wDI+jKXlpamXJkD/vectYuLC1q2bGlSp7506VK+95HkVKtWLZQpU8akHh8TE4P79+8X\nOt2VK1eg0+nw8ssv48svv8SNGzdw584dk8+EhIRg8+bNSgzff/+9cp4qTEH7goqfzfSsvby8sGzZ\nMrz22mswGAzw9vZWDpKcd6nmJ+f4jh074vjx43j++ecBAM899xwmTZoEIKuXM2LECKVXPHDgQOUA\n0el0qFWrFpo3b47bt2+jd+/e6Ny5My5fvoxXX30VDx48QGZmJho1aoTu3bsXGkPueAuLf9q0aZgz\nZ47ymImIoFWrVggNDQWQddLr1KkT0tLSTO5SHjp0KN5//33MmjULs2fPLnSZQ4cOxZkzZxAUFKRs\nozfffNPks7nXJbeBAwdiw4YNqF27Nry9vREcHKz0NHMv283NDVFRURg3bhxGjx6N9PR0VKtWDVFR\nUXnm/c477+Dhw4cYOnQokpOT4ezsjOXLl6Nu3bpYsGABrl69ik8++cRkmvx6U+3bt0dmZiYyMjLw\n7rvvomvXrgCA8ePHo2HDhujVqxcAYMeOHZg8eTKmTZuWZx1zznPkyJHo2bMnAgMDUalSJZOywIcf\nfojTp0+jRIkScHd3V74A5twnX3zxBfr374+bN28qj4JlZmbinXfeQb169cy26TZt2mD27Nlo0KAB\nQkJCMHfu3AL3k7u7e77be+PGjXnWK7/h/MbljO/rr7/Gzp074ejoiFKlSuHrr78GAAwYMABhYWFY\ns2YN3n///TyPJS1fvhzvvPMOlixZAnt7e/Tr1w/jxo1DRESEctlXRDBz5kzUrl270HjyG/bw8MA/\n//yDzz//HADw008/KaWe3NOtWLEC7733HurVqwcgK4EvXrxYuQydH3t7e2zcuBGjR4/GrFmzYDQa\n4ePjg9WrVxca2/Hjx/Hhhx8CyLoxc+LEifDx8UFMTIzymYCAAMyYMQPt2rWDTqdDtWrVsGDBgjzb\nPvdwQfuCih/fDa6R0NBQjBs3TqntWQuDwYD69etj6dKlaNSoUXGHQ2QV4uPj8dxzzylXpIi0wHeD\nU76ioqJQvXp1dOjQgYmaKBdrercAEXvWZDN27dpV5LdOEZnD9kRqY8+aiIjoKWbRnvX06dOxfPly\n2NnZITAwEIsXL0ZKSgp69+6NCxcuQK/XY/Xq1SbPhiqBsWdNREQ2pFh61vHx8fj+++9x5MgR/Pvv\nvzAajVi5cqVyh2JcXBzatGmjvCKQiIiI8mexZF22bFk4ODggNTUVBoMBqamp8PX1RVRUlPJ+6Oxn\nfIm0wN8fJjWxPZGWLJasy5Urh/fffx9+fn7w9fWFm5sb2rVrh8TEROXZw/Lly5t9cQAREZGts9hL\nUc6ePYu5c+ciPj4erq6u6NmzZ55fzjH34oawsDDo9XoAWS/CyH6BA/C/b7Uc5vCjDGezlng4/HQP\nZ7OWeDj8dA1n/z/37xHkx2I3mK1atQq///47fvjhBwDAsmXLcODAAezYsQM7d+6Ej48Prl27htDQ\nUMTExOQNjDeYERGRDSmWG8xq1aqFAwcO4MGDBxARbNu2DXXq1MFLL72EJUuWAMh6P3e3bt0sFQKR\nidy9IaInwfZEWrLYZfD69etj4MCBaNy4Mezs7NCwYUMMHToU9+/fR69evbBo0SLl0S0iIiIqGN9g\nRkSqmRA+AQlJCcUdBlmAj5sPZoTzUVtLKizv2cyvbhGR5SUkJUDfTV/cYZAFxK+PL+4QbBpfN0o2\ngzVGUlP8P/HFHQLZECZrIiIiK8dkTTYj+xlHIjXoG+iLOwSyIUzWREREVo7JmmwGa9akJtasSUtM\n1kRERFaOyZpsBmvWpCbWrElLTNZERERWjsmabAZr1qQm1qxJS0zWREREVo7JmmwGa9akJtasSUtM\n1kRERFaOyZpsBmvWpCbWrElLTNZERERWjsmabAZr1qQm1qxJS0zWREREVo7JmmwGa9akJtasSUtM\n1kRERFaOyZpsBmvWpCbWrElLTNZERERWjsmabAZr1qQm1qxJS0zWREREVo7JmmwGa9akJtasSUtM\n1kRERFaOyZpsBmvWpCbWrElLTNZERERWjsmabAZr1qQm1qxJS0zWREREVo7JmmwGa9akJtasSUtM\n1kRERFaOyZpsBmvWpCbWrElLTNZERERWjsmabAZr1qQm1qxJS0zWREREVo7JmmwGa9akJtasSUtM\n1kRERFaOyZpsBmvWpCbWrElLTNZERERWjsmabAZr1qQm1qxJS0zWREREVo7JmmwGa9akJtasSUtM\n1kRERFaOyZpsBmvWpCbWrElLTNZERERWjsmabAZr1qQm1qxJS0zWREREVo7JmmwGa9akJtasSUsl\nzH0gNjYWs2fPRnx8PAwGAwBAp9Nhx44dFg+OiIiIipCse/bsibfffhtvvPEG7O3tAWQla6Knza5d\nu9i7JtXE/xPP3jVpxmyydnBwwNtvv61FLERERJQPszXrl156CfPnz8e1a9dw+/Zt5R/R04a9alIT\ne9WkJbM968jISOh0OsyePdvk7+fPn7dYUERERPQ/ZpN1fHy8BmEQWR5r1qQm1qxJSwUm6+3bt6NN\nmzZYu3ZtvjeUde/e3aKBERERUZYCk/WePXvQpk0bbNy4kcmangnsVZOa2KsmLRWYrD/55BMAWTVr\nIiIiKj5ma9YAsGnTJkRHRyMtLU3528cff2yxoIgsgTVrUhNr1qQls49uDRs2DKtXr0ZERAREBKtX\nr8aFCxe0iI2IiIhQhGT9559/YunSpShXrhymTJmCAwcOIDY2VovYiFTFXjWpib1q0pLZZF26dGkA\nQJkyZXDlyhWUKFECCQkJFg+MiIiIsphN1l26dMGdO3cwbtw4NGrUCHq9Hn379i3yApKSkvDqq6+i\ndu3aqFOnDg4ePIjbt2+jXbt2qFmzJtq3b4+kpKQnWgmiouDvWZOa+HvWpCWzyfrjjz+Gu7s7evTo\ngfj4eMTExGDq1KlFXsCoUaPQuXNnnDp1CsePH0etWrUwY8YMtGvXDnFxcWjTpg1mzJjxRCtBRET0\nLNOJiBT2gfxeiuLq6orAwEB4e3sXOvO7d+8iKCgI586dM/l7rVq1sHv3bpQvXx4JCQkICQlBTEyM\naWA6HcyERkRWJmx0GPTd9MUdBllA/Pp4RM6NLO4wnmmF5T2zj279+OOP2L9/P0JDQwFkXUps2LAh\nzp8/j48//hgDBw4scNrz58/Dy8sLgwcPxrFjx9CoUSPMnTsXiYmJKF++PACgfPnySExMfJz1IiIi\nsglmL4NnZGTg1KlTWLt2LdauXYvo6GjodDocPHgQM2fOLHRag8GAI0eOYPjw4Thy5AicnJzyXPLW\n6XT8fWzSBGvWpCbWrElLZnvWly5dUnrBAODt7Y1Lly7Bw8MDjo6OhU5bqVIlVKpUCc899xwA4NVX\nX8X06dPh4+ODhIQE+Pj44Nq1awVeTg8LC4NerwcAuLm5oUGDBsrjN9knXg5zuKjD//zzj1XF8ywO\nZ8tOZNmPNz2LwwlnEqwqHouv7+X/PQVkLe3taR/O/n9RfjDLbM16+PDhuHDhAnr16gURwdq1a1Gp\nUiXMnj0bXbp0wc6dOwtdQKtWrfDDDz+gZs2aCA8PR2pqKgDAw8MD48ePx4wZM5CUlJRvj5s1a6Kn\nC2vWzy7WrC2vsLxnNllnJ+h9+/YBAF544QX06NGjyJeujx07hjfeeAPp6emoVq0aFi9eDKPRiF69\neuHixYvQ6/VYvXo13Nzcihw0EVknJutnF5O15T1Rsi4uTNaktl18N7jF2VKytrV3gzNZW15hec/s\nDWZERERUvJisyWawV01qsqVeNRW/IiXr1NRU/ngHERFRMTGbrKOiohAUFIQOHToAAI4ePYquXbta\nPDAiteV+vIjoSfA5a9KS2WQdHh6OgwcPwt3dHQDyfX0oERERWY7ZZO3g4JDnsSo7O5a66enDmjWp\niTVr0pLZrFu3bl2sWLECBoMBp0+fxrvvvovmzZtrERsRERGhCMn666+/xsmTJ1GyZEn07dsXZcuW\nxdy5c7WIjUhVrFmTmlizJi2ZfTe4k5MTpk2bhmnTpmkRDxEREeVitmfdtm1bJCUlKcO3b99W7gwn\nepqwZk1qYs2atGQ2Wd+8edPkBrNy5crx96eJiIg0ZDZZ29vb48KFC8pwfHw87wanpxJr1qQm1qxJ\nS2Zr1p999hlatmyJVq1aAQD27NmDhQsXWjwwIiIiymI2WXfs2BF///03Dhw4AJ1Oh7lz58LT01OL\n2IhUxZo1qYk1a9KS2WQNAOnp6ShXrhwMBgOio6MBQOlpExERkWWZTdbjx4/HqlWrUKdOHdjb2yt/\nZ7Kmpw1/z5rUZGu/Z03Fy2yyXrduHWJjY1GyZEkt4iEiIqJczN7WXa1aNaSnp2sRC5FFsVdNamKv\nmrRktmddunRpNGjQAG3atFF61zqdDhERERYPjoiIiIqQrLt27Zrn96t1Op3FAiKyFNasSU2sWZOW\nzCbrsLAwDcIgIiKigphN1nFxcZg4cSKio6Px4MEDAFk963Pnzlk8OCI1sVdNamKvmrRk9gazwYMH\n46233kKJEiWwa9cuDBo0CP369dMiNiIiIkIRkvWDBw/Qtm1biAj8/f0RHh6OX375RYvYiFTFd4OT\nmvhucNKS2cvgpUqVgtFoRPXq1TFv3jz4+voiJSVFi9iIiIgIRUjWc+fORWpqKiIiIjB58mTcu3cP\nS5Ys0SI2IlWxZk1qYs2atGQ2WTdp0gQA4OLigsjISEvHQ0RERLmYrVn/9ddfeOWVVxAUFITAwEAE\nBgaiXr16WsRGpCrWrElNrFmTlsz2rPv164fZs2cjICAAdnZmczsRERGpzGyy9vLyyvMGM6KnEWvW\npCbWrElLZpP1lClT8Prrr6Nt27ZwdHQEkPVSlO7du1s8OCIiIipCsl6yZAliY2NhMBhMLoMzWdPT\nhu8GJzXx3eCkJbPJ+vDhw4iJieGPdxARERUTs3eMNW/eHNHR0VrEQmRR7FWTmtirJi2Z7Vnv378f\nDRo0QJUqVUx+z/r48eMWD46IiIjMJGsRwcKFC+Hn56dVPEQWw5o1qYk1a9KS2Z718OHDceLECS1i\nISIionwUWrPW6XRo1KgRDh06pFU8RBbDXjWpib1q0pLZnvWBAwewfPly+Pv7w8nJCQBr1kRERFoy\nm6x/++03AFAe3RIRy0ZEZCGsWZOaWLMmLZl9dEuv1yMpKQlRUVHYuHEj7t69C71er0FoREREBBQh\nWX/11Vfo378/bty4gcTERPTv3x8RERFaxEakKvaqSU3sVZOWzF4G/+GHH3Dw4EGlXj1hwgQ0a9YM\nI0eOtHhwREREVISeNQCTd4LzZzLpacXfsyY18fesSUtme9aDBw9G06ZN0b17d4gI1q9fjyFDhmgR\nGxEREaGQZH3u3DlUrVoVY8aMQXBwMP744w/odDpERkYiKChIyxiJVMGaNamJNWvSUoHJumfPnvj7\n77/Rpk0bbN++HY0aNdIyLiIiIvr/CkzWRqMRn332GWJjY/Hll1+aPF+t0+kwZswYTQIkUgufsyY1\n8Tlr0lKBd4utXLkS9vb2MBqNuH//PpKTk5V/9+/f1zJGIiIim1Zgz7pWrVoYN24c/P390bdvXy1j\nIrII9qpJTexVk5YKfQ7L3t4es2fP1ioWIiIiyofZh6bbtWuH2bNn49KlS7h9+7byj+hpw+esSU18\nzpq0ZPY565UrV0Kn02H+/Pkmfz9//rzFgiIiIqL/MZus4+PjNQiDyPJYsyY1sWZNWjJ7GTwlJQVT\np07Fm2++CQA4ffo0Nm3aZPHAiIiIKIvZZD148GA4Ojrizz//BAD4+vrio48+snhgRGpjzZrUxJo1\naclssj579izGjx8PR0dHAFB+fYuIiIi0YTZZlyxZEg8ePFCGz549i5IlS1o0KCJLYM2a1MSaNWnJ\n7A1m4eHh6NixIy5fvozXXnsN+/btQ2RkpAahEREREVCEZN2+fXs0bNgQBw8ehIggIiICnp6eWsRG\npCq+G5zUxHeDk5bMJmsRwe7du5WfyMzIyMArr7yiRWxERESEItSshw8fjgULFqBevXoICAjAggUL\nMHz4cC1iI1IVe9WkJvaqSUtme9Y7d+5EdHQ07Oyy8npYWBjq1KlT5AUYjUY0btwYlSpVwsaNG3H7\n9m307t0bFy5cgF6vx+rVq+Hm5vb4a0BERPSMM9uzrl69Oi5evKgMX7x4EdWrVy/yAr766ivUqVMH\nOp0OADBjxgy0a9cOcXFxaNOmDWbMmPEYYRM9Oj5nTWric9akJbPJ+t69e6hduzaCg4MREhKCOnXq\n4P79+3jppZfQtWvXQqe9fPkyNm/ejDfeeAMiAgCIiorCoEGDAACDBg3C+vXrVVgNIiKiZ5fZy+D/\n93//l+dvOp0OIqL0lgvy3nvvYdasWbh3757yt8TERJQvXx4AUL58eSQmJj5qzESPhTVrUhNr1qQl\ns8n6cU9wmzZtgre3N4KCggq8/KjT6cwmfCIiIltnNlk/rj///BNRUVHYvHkz0tLScO/ePQwYMADl\ny5dHQkICfHx8cO3aNXh7exc4j7CwMOj1egCAm5sbGjRooHx5yP4CwGEOF3X4n3/+wejRo60mnmdx\nOFt2PTe79/ksDiecSUCzV5tZTTwWX9/LCchmLe3taR/O/n9Rft1SJ9nFZAvavXs3Zs+ejY0bN+KD\nDz6Ah4cHxo8fjxkzZiApKSnfm8yyL7UTqWUXX4picWGjw6Dvpi/uMDRhay9FiV8fj8i5kcUdxjOt\nsLxn9gYzAEhNTUVsbOwTBwEAEyZMwO+//46aNWtix44dmDBhwhPNl6iomKhJTbaUqKn4mU3WUVFR\nCAoKQocOHQAAR48eNXsXeG7BwcGIiooCAJQrVw7btm1DXFwctm7dymesiYiIzDCbrMPDw3Hw4EG4\nu7sDAIKCgnDu3DmLB0akttx1VaInweesSUtmk7WDg0Oe3m/228yIiIjI8sxm3bp162LFihUwGAw4\nffo03n33XTRv3lyL2IhUxZo1qYk1a9KS2WT99ddf4+TJkyhZsiT69u2LsmXLYu7cuVrERkRERCjC\nc9axsbGYNm0apk2bpkU8RBbDR7dITbb26BYVL7M96zFjxqBWrVqYPHkyTpw4oUVMRERElIPZZL1r\n1y7s3LkTnp6eGDZsGAIDAzF16lQtYiNSFXvVpCb2qklLRbqtu0KFChg1ahS+++471K9fP98f9yAi\nIiLLMJuso6OjER4ejoCAAIwYMQLNmzfHlStXtIiNSFV8zprUxOesSUtmbzAbMmQI+vTpg99++w0V\nK1bUIiYiIiLKwWyyPnDggBZxEFkca9akJtasSUsFJuuePXtizZo1CAwMzDNOp9Ph+PHjFg2MiIiI\nshSYrL/66isAwKZNm/L8ZFf2L2gRPU34nDWpic9Zk5YKvMHM19cXAPDNN99Ar9eb/Pvmm280C5CI\niMjWmb0bfOvWrXn+tnnzZosEQ2RJ7FWTmtirJi0VeBn822+/xTfffIOzZ8+a1K3v37+PF154QZPg\niIiIqJBk/dprr6FTp06YMGECZs6cqdStXVxc4OHhoVmARGphzZrUxJo1aanAZO3q6gpXV1esXLkS\nAHD9+nWkpaUhJSUFKSkp8PPz0yxIIiIiW2a2Zh0VFYUaNWqgSpUqCA4Ohl6vR6dOnbSIjUhV7FWT\nmtirJi2ZTdaTJk3C/v37UbNmTZw/fx7bt29H06ZNtYiNiIiIUIRk7eDgAE9PT2RmZsJoNCI0NBSH\nDx/WIjYiVfHd4KQmvhuctGT2daPu7u64f/8+WrZsiX79+sHb2xvOzs5axEZEREQoQs96/fr1KFOm\nDObMmYOOHTuievXq2LhxoxaxEamKNWtSE2vWpCWzPevsXrS9vT3CwsIsHQ8RERHlUmDP2tnZGS4u\nLvn+K1u2rJYxEqmCNWtSE2vWpKUCe9bJyclaxkHFYEL4BCQkJRR3GJpJuJyAyPWRxR2GJnzcfDAj\nfEZxh0FEKjF7GRwA9u7dizNnzmDw4MG4ceMGkpOTUaVKFUvHRhaWkJQAfTd9cYehGT30xR2CZuLX\nxxd3CM881qxJS2ZvMAsPD8fMmTMxffp0AEB6ejr69etn8cCIiIgoi9lkvW7dOkRFRcHJyQkAULFi\nRV4ip6cSa4ykJrYn0pLZZF2yZEnY2f3vYykpKRYNiIiIiEyZTdY9e/bEsGHDkJSUhIULF6JNmzZ4\n4403tIiNSFWsMZKa2J5IS4XeYCYi6N27N2JiYuDi4oK4uDhMnToV7dq10yo+IiIim2f2bvDOnTvj\nxIkTaN++vRbxEFkMf3+Y1MT2RFoq9DK4TqdDo0aNcOjQIa3iISIiolzM9qwPHDiA5cuXw9/fX7kj\nXKfT4fjx4xYPjkhN7AWRmtieSEtmk/Vvv/2mRRxERERUALPJWq/XaxAGkeWxxkhqYnsiLZl9dIuI\niIiKF5M12Qz2gkhNbE+kJSZrIiIiK8dkTTaD73ImNbE9kZaYrImIiKwckzXZDNYYSU1sT6QlJmsi\nIiIrx2RNNoM1RlIT2xNpicmaiIjIyjFZk81gjZHUxPZEWmKyJiIisnJM1mQzWGMkNbE9kZaYrImI\niKwckzXZDNYYSU1sT6QlJmsiIiIrx2RNNoM1RlIT2xNpicmaiIjIyjFZk81gjZHUxPZEWmKyJiIi\nsnJM1mQzWGMkNbE9kZaYrImIiKwckzXZDNYYSU1sT6QlJmsiIiIrx2RNNoM1RlIT2xNpicmaiIjI\nylk0WV+6dAmhoaGoW7cuAgICEBERAQC4ffs22rVrh5o1a6J9+/ZISkqyZBhEAFhjJHWxPZGWLJqs\nHRwcMGfOHJw8eRIHDhzA/PnzcerUKcyYMQPt2rVDXFwc2rRpgxkzZlgyDCIioqeaRZO1j48PGjRo\nAABwdnZG7dq1ceXKFURFRWHQoEEAgEGDBmH9+vWWDIMIAGuMpC62J9KSZjXr+Ph4HD16FE2bNkVi\nYiLKly8PAChfvjwSExO1CoOIiOipU0KLhSQnJ6NHjx746quv4OLiYjJOp9NBp9PlO11YWBj0ej0A\nwM6JhrcAABkuSURBVM3NDQ0aNEBISAgAYNeuXQDA4ScYTricAD30AP7XS8iuwz2rw9msJR5LDSdc\nTsCuXbs0b1/Zinv92Z7UH064nKCsrzWcv56F4ez/x8fHwxydiIjZTz2BjIwMdOnSBZ06dcLo0aMB\nALVq1cKuXbvg4+ODa9euITQ0FDExMaaB6XSwcGg2L2x0GPTd9MUdBllA/Pp4RM6N1Hy5bFPPruJq\nU7aksLxn0cvgIoLXX38dderUURI1AHTt2hVLliwBACxZsgTdunWzZBhEAFhjJHWxPZGWLHoZfN++\nfVi+fDnq1auHoKAgAMD06dMxYcIE9OrVC4sWLYJer8fq1astGQYREdFTzaLJukWLFsjMzMx33LZt\n2yy5aKI8+FwsqYntibTEN5gRERFZOSZrshmsMZKa2J5IS0zWREREVo7JmmwGa4ykJrYn0hKTNRER\nkZVjsiabwRojqYntibTEZE1ERGTlmKzJZrDGSGpieyItMVkTERFZOSZrshmsMZKa2J5IS0zWRERE\nVo7JmmwGa4ykJrYn0hKTNRERkZVjsiabwRojqYntibTEZE1ERGTlmKzJZrDGSGpieyItMVkTERFZ\nOSZrshmsMZKa2J5IS0zWREREVo7JmmwGa4ykJrYn0hKTNRERkZVjsiabwRojqYntibTEZE1ERGTl\nmKzJZrDGSGpieyItMVkTERFZOSZrshmsMZKa2J5IS0zWREREVo7JmmwGa4ykJrYn0hKTNRERkZVj\nsiabwRojqYntibTEZE1ERGTlmKzJZrDGSGpieyItMVkTERFZOSZrshmsMZKa2J5IS0zWREREVo7J\nmmwGa4ykJrYn0hKTNRERkZVjsiabwRojqYntibTEZE1ERGTlmKzJZrDGSGpieyItMVkTERFZOSZr\nshmsMZKa2J5IS0zWREREVo7JmmwGa4ykJrYn0hKTNRERkZVjsiabwRojqYntibTEZE1ERGTlmKzJ\nZrDGSGpieyItMVkTERFZOSZrshmsMZKa2J5IS0zWREREVo7JmmwGa4ykJrYn0hKTNRERkZVjsiab\nwRojqYntibTEZE1ERGTlmKzJZrDGSGpieyItMVkTERFZOSZrshmsMZKa2J5IS0zWREREVo7JmmwG\na4ykJrYn0hKTNRERkZVjsiabwRojqYntibRUbMl6y5YtqFWrFmrUqIGZM2cWVxhkQxLOJBR3CPQM\nYXsiLRVLsjYajRgxYgS2bNmC6Oho/PTTTzh16lRxhEI2JC05rbhDoGcI2xNpqViS9aFDh1C9enXo\n9Xo4ODigT58+2LBhQ3GEQkREZPWKJVlfuXIFlStXVoYrVaqEK1euFEcoZEOSEpKKOwR6hrA9kZZK\nFMdCdTqd2c/Ur1+/SJ+jJ/RVcQegrWO/HSvuEDSz5KslxbNgG2pTttSegGJsUzaifv36BY4rlmRd\nsWJFXLp0SRm+dOkSKlWqZPKZf/75R+uwiIiIrFKxXAZv3LgxTp8+jfj4eKSnp2PVqlXo2rVrcYRC\nRERk9YqlZ12iRAnMmzcPHTp0gNFoxOuvv47atWsXRyhERERWTyciUtxBEBERUcGKpWdNpIWkpCTs\n378f8fHx0Ol00Ov1eP755+Hq6lrcoRERPRL2rOmZs3fvXsyaNQvx8fEICgqCr68vRATXrl3D0aNH\nodfr8cEHH6BFixbFHSo9RU6ePIk9e/aYfPlr2bIl6tatW9yhkQ1gz5qeOevWrcMXX3yBGjVq5Ds+\nLi4O3333HZM1FcmyZcvw9ddfw8PDA02aNEHVqlWVL39jx47FzZs3MWrUKPTv37+4Q6VnGHvWRESF\niIiIwODBg+Hi4pLv+Hv37iEyMhIjR47UODKyJUzW9MxKS0vD2rVrEf//2rvT4Bqvxw/g3yeJJCUJ\nWWiYlsgdRUK2G0sUjaVqplmaCFGSEAxVzVQtpdUhaf20xthipowlU0KsY6tSSyUlipCShdFK4toS\nQSJyJUqW+3uRcf/Nn5bEzz15zv1+Xsm5XnxfZPK95zznnEenQ3V1NYC6C3nmzp0rOBkRUcNwGZyk\nFRoailatWkGr1cLW1lZ0HFK527dvY82aNU99+UtKShKcjMwBy5qkdfPmTRw8eFB0DJJEaGgo+vfv\nj3fffRcWFnX3SfFKZDIVljVJq0+fPsjOzoaXl5foKCSBhw8fYuHChaJjkJniM2uSVteuXZGXl4eO\nHTvCxsYGQN1MKDs7W3AyUqOvvvoKAQEBeP/990VHITPEsiZp6XQ6AP+3VPnkV93NzU1QIlIzOzs7\nVFZWwtraGs2aNQNQ97tVXl4uOBmZA5Y1Se38+fM4fvw4FEVBv379/vUVdERETZWQt24RmcLy5csR\nFRWFO3fuoLi4GFFRUUhMTBQdi1Rsz549mD59OmbMmIEff/xRdBwyI5xZk7S6d++OU6dOoUWLFgCA\niooK9O7dGzk5OYKTkRrNnj0bZ86cwejRo2EwGLBlyxb4+/vj22+/FR2NzAB3g5PUnhyx+f//Jmqo\nn376CefPn4elpSUAYOzYsfDx8WFZk0mwrElasbGx6NWrF8LDw2EwGLB7926MGzdOdCxSKUVRUFZW\nBmdnZwB1b3XjOWsyFS6Dk9QyMzORnp5u3GDm6+srOhKp1ObNmzF79mwEBgYCAH799Vd89913GDly\npNhgZBZY1iS1mpoa3Lp1C9XV1cZZUPv27QWnIrUqLCzEmTNnoCgKevbsCVdXV9GRyEywrElaK1as\nQEJCAtq0aWN8zgiAG8yo0W7evGm8G/zJl7/+/fsLTkXmgGVN0tJoNMjIyDA+YyR6GbNmzcLWrVvh\n4eFR78sfj3CRKXCDGUmrffv2cHBwEB2DJLFr1y788ccfxqtriUyJZU3SWbx4MQDA3d0dgYGBCAoK\ngrW1NYC6Hb3Tpk0TGY9USqPR4PHjxyxrEoJlTdLR6/VQFAXt27fHm2++icePH+Px48eiY5FKxcXF\nAQCaN28OHx8fDBo0qN6LYXgrHpkCy5qkEx8fDwDYtm0bRowYUe+zbdu2CUhEaqbVao2byYKDg+u9\nGIbnrMlUuMGMpOXr64tz5849d4zoRSxbtgxTp0597hjRq8CyJukcOHAA+/fvx9atWzFy5EjjqzH1\nej0uXryIjIwMwQlJjZ71Rc/Hxwfnz58XlIjMCZfBSTrt2rWDVqvF3r17odVqjcuV9vb2WLp0qeh4\npDKbN29GSkoKrly5guDgYOO4Xq/nsUAyGZY1Scfb2xve3t5wcnJCUFAQX+BBL6VPnz5o27Yt7t69\nixkzZhhXahwcHODl5SU4HZkLLoOTtEaPHo2TJ08iIiIC48aNQ5cuXURHIhVLTExEdHQ0HB0dRUch\nM8QpB0lr06ZNOHfuHNzd3TF27FgEBARg9erV0Ov1oqORChUXF6NHjx4YMWIEfv75Z3CeQ6ZkGf/k\nnAuRhGxtbeHm5oaamhocPnwYJSUlWLBgAQCgV69egtORmgwaNAiffPIJHBwc8MMPP+CLL77ArVu3\n4ObmBicnJ9HxSHKcWZO09uzZg7CwMAQGBqKqqgpnzpzBgQMHkJ2djSVLloiORypkYWEBV1dXvP76\n67C0tMS9e/cQERGBmTNnio5GkuMza5LWmDFjMH78+Ge+FenIkSMYPHiwgFSkVsuXL8eGDRvg7OyM\nCRMmICwsDM2aNUNtbS06deqE/Px80RFJYtwNTtK5fPkyiouLsX79+nrj6enpaNu2LTQaDYuaGqy0\ntBQ7d+5Ehw4d6o1bWFjwzVv0ynEZnKQzderUZ75ty8HBgbdNUYNlZGRg//79SEhIqFfU+/fvR2Zm\nJgDAw8NDVDwyEyxrkk5xcfEzz796eXnhypUrAhKRms2aNeuZZezh4YEZM2YISETmiGVN0ikrK/vH\nz/766y8TJiEZ6PV6uLm5PTXu5uaGu3fvmj4QmSWWNUnH398fq1evfmp8zZo10Gq1AhKRmv3bl7+H\nDx+aMAmZM+4GJ+ncunULYWFhsLa2NpZzZmYmHj16hF27dqFt27aCE5KaTJo0CS4uLpg/f77xlZi1\ntbWYN28eiouLn/nFkOh/jWVNUjIYDEhNTUVubi4URYGnpycGDhwoOhap0IMHDzBhwgRkZGTAx8cH\nAJCVlQV/f3+sXbsW9vb2ghOSOWBZk3T0ev1z/4C+yP8h+rv8/HxcuHABiqLAw8MDGo1GdCQyIyxr\nks7gwYPRuXNnhIaGwt/f33gVZElJCc6ePYvdu3fj8uXLOHLkiOCkpAb5+fnPLeYX+T9EL4NlTVI6\nevQoUlJScOLECRQWFgKoe8913759MXr0aAQGBooNSKoRGRmJiooKhISEwN/fH23btoXBYEBRURHO\nnj2LvXv3wt7eHlu2bBEdlSTGsiYieo68vDxs2bIFJ06cwNWrVwEAHTp0QN++ffHhhx/C3d1dcEKS\nHcuaiIioieM5ayIioiaOZU1ERNTEsaxJWnl5ecbrRVNTU5GYmPivt1ERETVVLGuS1rBhw2BlZYW8\nvDxMmjQJ169fx6hRo0THIpVKT0/HgwcPAADJycmYNm2acbMZ0avGsiZpWVhYwMrKCjt37kRcXBwW\nLVqEoqIi0bFIpSZPnowWLVogKysLS5YsgUajQUxMjOhYZCZY1iQta2trpKSkYMOGDQgKCgIAVFVV\nCU5FamVlZQVFUbB7925MmTIFU6ZMgV6vFx2LzATLmqSVlJSEkydPYs6cOejYsSMKCgoQFRUlOhap\nlL29PRYsWICNGzciKCgINTU1/PJHJsNz1kREL6CoqAgpKSno2bMn+vXrh2vXriEtLY1L4WQSLGuS\nVnp6OhISEqDT6VBdXQ0AUBQFBQUFgpORWhUVFSEjIwMWFhbo0aMHXF1dRUciM8GyJml17twZy5Yt\ng5+fHywtLY3jLi4uAlORWq1duxZff/01BgwYAABIS0vD3LlzMX78eMHJyBywrElavXr1wunTp0XH\nIEm89dZbOHnyJJydnQHUvcUtICAAf/75p+BkZA6sRAcgelUGDBiAmTNnIjw8HDY2NsZxPz8/galI\nrVxcXGBnZ2f82c7Ojqs0ZDKcWZO0AgMDoSjKU+OpqakC0pDaRUdHIzc3F6GhoQCAPXv2wMvLC15e\nXlAUBdOmTROckGTGmTVJKy0tTXQEkohGo4FGozF+AQwNDYWiKMZbzYheJc6sSVplZWVISEjAsWPH\nANTNtOfOnYuWLVsKTkZq9uQiFHt7e8FJyJzwUhSS1rhx4+Dg4IDt27dj27ZtsLe3R2xsrOhYpFI5\nOTnw9fWFp6cnPD09odVqkZubKzoWmQnOrEla3t7eyMrKeu4Y0YsICAjAggUL6h3d+vLLL/Hbb78J\nTkbmgDNrktZrr72G48ePG39OT09H8+bNBSYiNausrDQWNVD3WKWiokJgIjIn3GBG0lq1ahViYmJw\n//59AICjoyPWr18vOBWpVceOHfHNN98gOjoaBoMBmzZtgru7u+hYZCa4DE7SKy8vBwA4ODgITkJq\nVlpainnz5uHEiRMAgH79+iE+Ph6Ojo6Ck5E5YFmTdJKTkxEdHY3FixfXO2dtMBh4HpZeGneDkwhc\nBifpVFZWAqj7o/qssiZqjJycHMTExKCkpAQA0Lp1a6xfvx7dunUTnIzMAWfWREQvgLvBSSTuBidp\nff755ygvL0dVVRUGDRoEFxcXJCcni45FKsXd4CQSy5qkdfDgQTg4OGDfvn1wc3NDfn4+Fi1aJDoW\nqdST3eA6nQ5XrlzB/PnzuRucTIZlTdKqrq4GAOzbtw8RERFo2bIln1lToyUlJeH27dsIDw/HsGHD\ncOfOHSQlJYmORWaCG8xIWsHBwejSpQtsbW2xcuVK3L59G7a2tqJjkUo5OTlhxYoVomOQmeIGM5Ja\nSUkJWrVqBUtLS1RUVECv18PV1VV0LFKR4ODgf/xMURTs3bvXhGnIXHFmTVK7dOkSrl69iqqqKgB1\nf1xjYmIEpyI1mT59+j9+xscqZCqcWZO0oqKiUFBQAB8fH1haWhrHuZRJLyszMxNarVZ0DDIjLGuS\nVteuXXHx4kXOfuh/ztfXF+fOnRMdg8wId4OTtLp164aioiLRMYiIXhqfWZO07ty5Aw8PD/Ts2RM2\nNjYAuCGIGqe6uhpjxozBpk2bAABz584VnIjMDcuapBUfHw+grqCfPO3hkjg1hpWVFa5evYpHjx7B\nxsYGYWFhoiORmeEza5KaTqdDXl4eBg8ejMrKSlRXV/NVmdQo0dHRuHTpEkJCQtC8eXMA4FvcyGQ4\nsyZprV69GmvWrEFpaSny8/Nx48YNTJ48Gb/88ovoaKRCGo0GGo0GtbW1ePDgAd/iRibFmTVJy9vb\nGxkZGejdu7dx52737t2Rk5MjOBmpGd9nTSJwNzhJy8bGxrixDKjbJMSZEDVWTk4OfH194enpCU9P\nT2i1WuTm5oqORWaCZU3Seuedd/Cf//wHlZWVOHz4MIYPH/6vV0cS/ZuJEydiyZIluHbtGq5du4bF\nixdj4sSJomORmeAyOEmrpqYG69atw6FDhwAA7733HiZMmMDZNTWKt7c3srKynjtG9CqwrImIXsAH\nH3wArVaL6OhoGAwGbNq0CZmZmdi1a5foaGQGWNYkrfT0dCQkJECn0xnfba0oCgoKCgQnIzUqLS3F\nvHnzcOLECQBAv379EB8fD0dHR8HJyBywrElanTt3xrJly+Dn51fvRR4uLi4CU5HaREdHIzk5GcuW\nLcPUqVNFxyEzxbImafXq1QunT58WHYNUzsPDA0eOHMHQoUORlpb21OdOTk6mD0Vmh2VN0snMzAQA\nbN++HTU1NQgPD693hMvPz09UNFKhxMRErFy5EgUFBWjXrl29z/hYhUyFZU3SCQwMNO74ftYtU6mp\nqSJikcp99NFHWLVqlegYZKZY1kRERE0cL0Uhad26dQvjx4/H0KFDAQAXL17EunXrBKciImo4ljVJ\na+zYsRgyZAgKCwsBAJ06dcLSpUsFpyIiajiWNUnr7t27iIyMNB7batasGays+KI5IlIfljVJy87O\nDiUlJcafT506hZYtWwpMRETUOJxmkLQWL16M4OBgFBQUoE+fPrhz5w527NghOhYRUYOxrElKNTU1\nOHbsGI4dO4ZLly7BYDCgc+fOsLa2Fh2NiKjBeHSLpNWjRw+cOXNGdAwiopfGsiZpffbZZ6iqqkJk\nZCRatGhhvCCFN5gRkdqwrElaf7/J7O94gxkRqQ3LmoiIqInj0S2S1t27dxEXFwdfX1/4+fnh008/\nrXeUi4hILVjWJK2RI0eiTZs22LlzJ3bs2IHWrVsjMjJSdCwiogbjMjhJq1u3bsjNza031r17d+Tk\n5AhKRETUOJxZk7SGDBmCzZs3o7a2FrW1tdi6dSuGDBkiOhYRUYNxZk3SsrOzQ2VlJSws6r6T1tbW\nokWLFgAARVFQXl4uMh4R0QtjWRMRETVxvG6UpJadnQ2dTofq6mrjWHh4uMBEREQNx7ImacXGxiIn\nJweenp7GpXCAZU1E6sNlcJKWh4cHLly48MxbzIiI1IS7wUlaPXr0wMWLF0XHICJ6aZxZk7TS0tIQ\nEhICV1dX2NjYAKjbBZ6dnS04GRFRw7CsSVoajQZLly5Ft27d6j2zdnNzExeKiKgRuMGMpNWmTRuE\nhISIjkFE9NI4syZpffzxxygrK0NwcDCsra0B1C2Dczc4EakNZ9YkrcrKSlhbW+PQoUP1xlnWRKQ2\nnFkTERE1cTy6RdK6fv06wsLC0Lp1a7Ru3RrDhg3DjRs3RMciImowljVJKzY2FiEhISgsLERhYSGC\ng4MRGxsrOhYRUYNxGZyk5e3tjaysrOeOERE1dZxZk7ScnZ2RnJyMmpoaVFdXY+PGjXBxcREdi4io\nwTizJmnpdDrExcXh1KlTAIA+ffpgxYoVaN++veBkREQNw7ImIiJq4rgMTtKKiYlBWVmZ8ed79+5h\n3LhxAhMRETUOy5qklZ2djVatWhl/dnR0xO+//y4wERFR47CsSVoGgwGlpaXGn0tLS1FTUyMwERFR\n4/C6UZLW9OnTERAQgBEjRsBgMGD79u2YM2eO6FhERA3GDWYktQsXLuDo0aNQFAUDBw6Eh4eH6EhE\nRA3GsiYiImri+MyaiIioiWNZExERNXEsa5LWrFmzXmiMiKipY1mTtA4dOvTU2P79+wUkISJ6OTy6\nRdJZuXIlvv/+e+Tn56N79+7Gcb1ej7fffltgMiKixuFucJLO/fv3ce/ePcyePRsLFy7Ek19xBwcH\nODk5CU5HRNRwLGuSVl5eHt544w3Y2toiNTUVOTk5iImJqXcFKRGRGvCZNUkrIiICVlZWyMvLw6RJ\nk3D9+nWMGjVKdCwiogZjWZO0FEWBlZUVdu7cibi4OCxatAhFRUWiYxERNRjLmqRlbW2NlJQUbNiw\nAUFBQQCAqqoqwamIiBqOZU3SSkpKwsmTJzFnzhx07NgRBQUFiIqKEh2LiKjBuMGMiIioieM5a5LO\n8OHDsX379npnrJ9QFAXZ2dkCUhERNR5n1iSdwsJCtGvXDjqd7pmfu7m5mTQPEdHLYlkTERE1cVwG\nJ+nY2dlBUZRnfqYoCsrLy02ciIjo5XBmTURE1MTx6BYREVETx7ImIiJq4ljWRERETRzLmoiIqIlj\nWRMRETVxLGsiIqIm7r+eoHMw3W5vGAAAAABJRU5ErkJggg==\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10e919d10>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 88
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"showdown\"></a>\n",
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Final Comparison: Cython vs. NumPy vs. SciPy for least squares fitting"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"To wrap it up, let us compare the Cython code of our simple least squares fit implementation to the Numpy and Scipy functions - after we made some improvements by adding static type declarations and explicit for loops."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%load_ext cythonmagic"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 1
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"\n",
|
|
"def cy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" cdef double x_avg, y_avg, temp, var_x, cov_xy, slope, y_interc, x_i, y_i\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" cov_xy = 0\n",
|
|
" for x_i, y_i in zip(x,y):\n",
|
|
" temp = (x_i - x_avg)\n",
|
|
" var_x += temp**2\n",
|
|
" cov_xy += temp*(y_i - y_avg)\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 2
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import numpy as np\n",
|
|
"import scipy.stats"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 3
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def lin_lstsqr_mat(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 4
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def numpy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return np.linalg.lstsq(X,y)[0]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 5
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def scipy_lstsqr(x,y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" return scipy.stats.linregress(x, y)[0:2]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 6
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"funcs = ['cy_lstsqr', 'lin_lstsqr_mat',\n",
|
|
" 'numpy_lstsqr', 'scipy_lstsqr'] \n",
|
|
"\n",
|
|
"orders_n = [10**n for n in range(1, 6)]\n",
|
|
"times_n = {f:[] for f in funcs}\n",
|
|
"\n",
|
|
"for n in orders_n:\n",
|
|
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
|
|
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
|
|
" for f in funcs:\n",
|
|
" times_n[f].append(min(timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f)\n",
|
|
" .repeat(repeat=3, number=1000)))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 7
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%pylab inline"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 9
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"labels = [('cy_lstsqr', 'Cython implementation'), \n",
|
|
" ('lin_lstsqr_mat', 'numpy matrix equation'),\n",
|
|
" ('numpy_lstsqr', 'numpy.linalg.lstsq()'), \n",
|
|
" ('scipy_lstsqr', 'scipy.stats.linregress()')] \n",
|
|
"\n",
|
|
"matplotlib.rcParams.update({'font.size': 12})\n",
|
|
"\n",
|
|
"fig = plt.figure(figsize=(10,8))\n",
|
|
"for lb in labels:\n",
|
|
" plt.plot(orders_n, times_n[lb[0]], alpha=0.5, label=lb[1], marker='o', lw=3)\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('time per computation in milliseconds [ms]')\n",
|
|
"plt.xlim([1,max(orders_n) + max(orders_n) * 10])\n",
|
|
"plt.legend(loc=2)\n",
|
|
"plt.grid()\n",
|
|
"plt.xscale('log')\n",
|
|
"plt.yscale('log')\n",
|
|
"plt.title('Performance of least square fit implementations for different sample sizes')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAnIAAAIECAYAAACdVcNJAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXdYVMfXx7/30lnpsICodEFQsXcRFDVYYixRsGKLEWNe\njYldAbsmaoxiTIiFYjdKjCZiA+wFLFFEFBTEQlGxIVLP+wdyf1xYYEFYLPN5nn2e3bkz5545d2bu\n2akcEREYDAaDwWAwGB8cfG0rwGAwGAwGg8GoGsyRYzAYDAaDwfhAYY4cg8FgMBgMxgcKc+QYDAaD\nwWAwPlCYI8dgMBgMBoPxgcIcOQaDwWAwGIwPFObIKYi8vDyMGTMGhoaG4HkeJ06cqG2VPkh2794N\na2trKCsrY8yYMTLjeHl5oXv37grWjFHy2URGRoLneTx8+LDSsiwtLbFkyZIa0LI0FhYWWLx4sULu\n9b7C8zy2bdtW22rUSjsZEREhKqclfwPAtWvX0KZNG2hoaMDKygoAkJycjG7duqFOnTpQUlKqcT0/\nJRRRHl1cXPDVV1/V6D0UBXPkiuHl5QWe58HzPFRUVGBhYYGJEyfi6dOn7yz7zz//xPbt23HgwAGk\npKSgffv21aDxp0V+fj7GjBkDDw8PJCcnY82aNTLjcRwHjuMUqltISAh4/tOtTrKeTYcOHZCSkgJT\nU1MAwKlTp8DzPO7du1ehvKioKEydOrWm1QZQO+XlXbh//36VnRw3NzeMHj26VHhKSgoGDhxYHeq9\nE+9DO9mxY0dRuQWA6dOnQ1dXF3Fxcbh48SIAYMmSJXj8+DGuXr2KR48eKVxPWYwbNw6urq61rcYH\nQWhoKFatWlXbalQLyrWtwPuGs7Mzdu3ahby8PERFRWH8+PFITk7GgQMHqiQvJycHqqqquH37NszM\nzNCuXbt30q9I3qfIw4cPkZmZCXd3d1EjWxIiAtvnuvIUFBQAQJUc0rKejVQqLRVXnmdjYGBQaR0+\nNaqzjMt6TrXB+9BOqqiolLJHfHw8Ro0ahQYNGoh0bd26Naytrd9J19zcXKioqLyTDEbl0dXVrW0V\nqg9iCIwaNYrc3NxEYYsXLyYlJSV68+YNERFt376dnJycSF1dnSwsLOi7776jzMxMIX6XLl1o7Nix\nNHfuXDI1NSUTExNycXEhjuOEj6WlJRER5eTk0IwZM8jMzIxUVVXJwcGBtm3bJro/x3H0yy+/kKen\nJ+no6NCQIUNo8+bNpKysTOHh4dS4cWPS0NAgV1dXevToER0/fpycnJxIIpGQm5sbPXjwQJB1584d\n6t+/P9WtW5c0NTWpSZMmFBwcLLpfly5daNy4cbRgwQIyMTEhfX19GjlyJL169UoUb8eOHdSiRQtS\nV1cnAwMDcnd3p4yMDOH6L7/8QnZ2dqSurk62tra0ePFiysvLK9f+Z8+epc6dO5OGhgbp6enR0KFD\nKS0tjYiINm/eLLIhx3EUGRkp93Os6LkdPnyYunTpQvr6+qSjo0NdunShCxcuiGQEBASQvb09qaur\nk76+Pjk7O9P9+/cpPDy8lG6jR48uM5+LFy8mKysrUlNTIyMjI+rZsydlZWWJbGdmZkaamprUs2dP\nCgwMJI7jhGdZ9PyLk5ycXMom48aNI2tra9LQ0CArKyuaPXs2ZWdnC9d9fHzIxsaGdu7cSXZ2dqSs\nrEw3b96kly9f0rfffivo0Lx5c9q7d2+Z+Snr2RTZ5cGDB3T37t1ScVxdXcuUaW5uTosWLRL9njdv\nHn399deko6NDxsbGtH79esrKyiJvb2/S09MjMzMzWrdunUgOx3G0Zs0aGjBgAEkkEjIzM6M1a9aI\n4lhYWNDixYuF3zk5OeTj40OWlpakrq5Ojo6O9Ntvv5WSu3btWho8eDBJJBIyNzenvXv30tOnT8nD\nw4O0tLTIysqK/vzzT1G6lJQUGjVqFBkZGZGWlhZ17NiRTpw4IVwvstmRI0eoc+fOpKmpSQ4ODvTv\nv/+K7i2rPamofo8aNarMOsRxHG3dulWI+/DhQxoyZAjp6uqShoYGubi4UFRUVKX0JKq4rBenS5cu\n1dZOenh4yLwHUcX1q6Jy6+vrW2Z9r6juFMnbunUrubu7k0QioZkzZxKRfO+W8tpmHx+fUnoFBgbK\ntMHz58/Jy8uLTExMSE1NjerXr0/fffedcF2e9rAqdaAo/yEhIdS1a1ehbdqxY0cp2cXLY2XbJKLC\nNnHAgAFkaGhI6urqZGVlRT/++GMpexZ/5iU/FhYWQvzbt2/TgAEDSFdXl/T09KhHjx507do1uW1a\nkzBHrhijRo2i7t27i8JWrlxJHMfRq1evaPPmzaSnp0chISF09+5dOnHiBDVt2pRGjBghxO/SpQtp\naWnRxIkTKTY2lq5fv05Pnz6l77//niwtLSk1NZUeP35MRETff/89GRgY0J49e+j27du0ZMkS4nme\njh07JsjjOI4MDAzI39+f7ty5Q7dv36bNmzcTz/Pk6upKFy5coEuXLpGtrS116tSJnJ2d6fz583Tl\nyhWyt7enIUOGCLKuXbtG/v7+9N9//9GdO3do7dq1gkNYXH9dXV367rvvKC4ujg4fPkz6+vo0b948\nIc6mTZtIRUWFFi1aJORx3bp1Qr58fHzI3NycQkNDKTExkf755x9q0KCBSEZJHj16RFpaWjRs2DC6\nfv06nTp1ipo2bUrOzs5ERJSVlUUXL14kjuPo77//ptTUVMrJySnzORZ35OR5bvv27aPdu3fTrVu3\n6MaNGzRu3DjS19enJ0+eEBFRVFQUKSsrU3BwMN27d4+uXbtGGzdupPv371NOTg75+/sTx3GUmppK\nqamp9OLFC5m6/fnnn6StrU0HDhyg5ORkunLlCq1Zs0Z4uYWGhpKysjKtXr2abt++TRs3biSpVEo8\nz1fKkSsoKKA5c+bQhQsXKCkpifbv30+mpqbk4+MjpPHx8SFNTU1ycXGhCxcu0O3bt+nly5fk4uJC\nrq6udPr0abp79y79/vvvpKqqKiqXxSnr2RR/Iebn59P+/fuJ4ziKioqi1NRUkeNfkpLOlbm5Oenq\n6tLq1aspISGBFi1aRDzPU8+ePYWwpUuXEs/zdOPGDSEdx3Gkr69P69ato9u3b9OaNWtIWVmZ/vrr\nrzLvNWrUKHJycqIjR45QYmIi7dy5k3R1dWnjxo0iuSYmJhQUFEQJCQnk7e1NEomEevToQYGBgZSQ\nkECTJ08miUQilKHXr19To0aNaNCgQRQdHU0JCQm0ePFiUlNTo9jYWCL63wvFycmJwsLCKD4+nkaP\nHk3a2tqCvS5fvkwcx9G+fftE7UlF9fv58+fk7OxMHh4eQjktqkPFX5wFBQXUpk0bat68OZ0+fZqu\nXbtGQ4YMIT09PeFe8uhZUVkvSXW2k/Hx8TLvIU/9KlluU1JSqH79+jRr1ixKTU2lV69eUUpKCnXo\n0IGGDx8u1PeCgoIK606RI1OvXj3atm0bJSYm0t27d+V+t5TXNr969YqGDRtGHTt2FJ5vWbaePHky\nOTk50YULFyg5OZnOnDlDf/zxh3C9ovawqnWgKP9169albdu20a1bt2ju3LmkpKREly9fFskuXh4r\n2yYREfXt25e6d+9OV69epaSkJAoPD6ft27cL111cXGj8+PFEVPhnochmqampdOPGDTIzM6MxY8YQ\nUeEfMGNjY/L29qbr16/TrVu3aPLkyWRgYEDp6ely2bQmYY5cMUo6ADExMWRlZUXt27cnosKXScl/\n5pGRkcRxHD179oyICiubnZ1dKdlFvR9FZGZmkpqaGv3666+ieP3796euXbsKvzmOE/41FFHUA3L1\n6lUh7McffySO4+jSpUtC2OrVq8nQ0LDcPPfr108ozEX6N2vWTBRn4sSJgg2IiOrXr0+TJ0+WKS8z\nM5M0NTUpLCxMFB4YGEi6urpl6jF37lyqX78+5ebmCmFXr14ljuOEHouiRuD06dPl5qnkc5TnuZUk\nPz+f9PT0hMZk7969pKOjU6aDFhwcTBzHlasXEdGqVauoYcOGonwWp2PHjjR8+HBR2Pfff1+lHjlZ\n97a1tRV++/j4EM/zlJycLISFh4eTuro6PX/+XJR29OjR9MUXX5QpW9azKf5CJCI6efIkcRxHSUlJ\nZcopQpYj179/f+F3QUEBaWtr0+effy4K09PTE/XKcRxHI0eOFMkeOnQode7cWea97ty5QzzPU1xc\nnCiNn5+fqF5wHEdTp04VfqenpxPHcfTtt98KYRkZGcRxHB08eJCICp9bvXr1SvVMu7q60pQpU4jo\nfzbbt2+fcD01NZU4jqPDhw8TkXzPuoiS9dvNzU1mb3HxF+fRo0eJ4zjBuSQiys7OJlNTU1qwYIHc\nelZU1mVRne2kLOSpXyXLLVHp8kgkdgSK0lVUd4rqSfHeZiL53y0Vtc1jx44lFxeXCu3Qr18/8vLy\nqjBeESXbQ6Kq1YGi/M+fP18kv0OHDiKntXh5rGqb5OTkRL6+vmVeL/n8isjJySEXFxdydnYW/uj4\n+PhQu3btRPEKCgrI2tqafv75ZyKqvE2rk093dnYZREREQEtLC5qammjSpAlsbGywdetWpKen4969\ne5g6dSq0tLSET69evcBxHOLj4wUZLVu2rPA+8fHxyMnJgbOzsyjc2dkZMTExorA2bdqUSs9xHJo0\naSL8NjY2BgA0bdpUFPbkyRNhLs3r168xc+ZMNG7cGAYGBtDS0sI///wjmnzOcRycnJxE9zI1NUVq\naioAIC0tDffv30ePHj1k5ismJgZZWVkYMGCAyE5ff/01Xrx4gSdPnpSZrl27dlBW/t+0zaZNm0JH\nRwc3btyQmUYe5H1ud+/exYgRI2BrawsdHR3o6Ojg+fPngm169OgBKysrWFpawtPTEwEBAWXmpTyG\nDBmC3NxcmJubY/To0QgJCcGrV6+E67GxsejQoYMoTceOHauU94CAALRt2xYmJibQ0tLC7NmzSy00\nMDY2Rr169YTfFy9eRE5ODszMzET22rp1q6iMK5qS5ZLjOBgZGYnKO8dxkEqlSE9PF6UtOWG+Q4cO\npepYEVFRUSAitGzZUpT/pUuXlsp/cX0MDQ2hpKQk0kdXVxeqqqpIS0sDUGjblJQU6OrqimSfOnWq\nlOxmzZoJ36VSKZSUlIQ6WBby1G95iImJgYGBAezt7YUwVVVVtG3btpTdytOzorIuD+/aTpakOutX\nSSpTd4rrWpl3S3ltc2Xw9vbGnj170KRJE0yZMgWHDh0SzbmsqD2UpY88daCIknWyY8eOZdbJqrZJ\nU6ZMwZIlS9CuXTvMnDkTJ0+erNgwACZOnIgHDx4gNDRUmLt48eJFREdHi+6vra2NpKQkQYeKbFqT\nsMUOJWjXrh0CAwOhrKyMunXrCo5FUWX55ZdfZK4KMjMzA1D4MpFIJNWqkyx5PM+LVtoVfS++DL4o\njIjAcRx++OEH7N+/H6tXr4adnR00NTUxbdo0PH/+XCS75CRhjuOEifAVURRvz549aNiwYanrenp6\nMtNxHFcjhb5In4qeW58+fSCVSrF+/XrUr18fKioq6NSpE3JycgAUPoOoqCicPn0aR48exYYNGzB9\n+nQcO3YMLVq0kFufunXr4ubNmwgPD8fx48excOFCzJgxA+fPnxc5VOUhazFCbm6u6Pfu3bvxzTff\nYPny5ejSpQu0tbWxa9cuzJkzRxSvZNkqKCiAjo4OoqKiSt2jthfZlJwQznGczDB5y6ositKePXsW\nmpqapWSXp09ZOhbJLCgoQKNGjRAaGloqXcl7ybJ1RfmSt35XlaJ2RF49q6OsV4bqbncrS2XqTnFd\n5W2jOI57p7a5OD169MC9e/cQFhaGiIgIDB8+HE2aNMGxY8fA83yF7WERla0DZVFe21/VNsnLywuf\nffYZDh06hPDwcLi7u6N///4IDg4uM82KFSsQGhqKs2fPit5VRAQ3NzesW7euVBodHR0AFdu0JmGO\nXAnU1dWFfYKKY2xsjPr16+PmzZsYO3bsO9/HxsYGampqiIyMhIODgxAeGRkp6mmrTk6ePInhw4dj\n0KBBAAorSFxcXLkrQEsilUpRr149hIWFoU+fPqWuOzo6Ql1dHQkJCfjss8/kluvo6IjNmzeLVnBd\nvXoVz58/R+PGjeWWUxJ5ntuTJ08QGxuLVatWCfvP3b9/v9S/SJ7n0blzZ3Tu3Bl+fn5wcHDA9u3b\n0aJFC6FBkfWyK4mqqip69uyJnj17YuHChTA2NsZff/2FSZMmwcHBAadPn8bEiROF+KdPnxall0ql\nyM/PR1pamrC67tKlS6I4J06cQPPmzTFlyhQh7O7du+XqBQCtW7fGs2fPkJWVBUdHxwrjV4YiG+Xn\n51er3Io4e/Ysvv76a+H3mTNnysxbUW96UlISevfuXa16tG7dGsHBwdDS0oKRkVGV5ZRlR3nqt6qq\nKvLy8sqV7+joKNSJRo0aAQCys7Nx/vx5fPPNN5XWtayyLg/V3U7KU7+qSlXrTnW+W1RVVeWuX3p6\nevDw8ICHhwdGjx6N9u3bIzY2FiYmJnK1h+/C2bNnRe+H8upkq1atqtwmmZiYwMvLC15eXnB3d8fQ\noUPx66+/ok6dOqXihoaGwsfHB2FhYbC1tS2lw5YtW2BmZgY1NbUy71eWTau7LS3JB+fIXbhwAVOm\nTIGKigrMzMwQFBQkGo6rSRYvXoyxY8dCT08Pn3/+OVRUVBAbG4tDhw5hw4YNAOTf+kJTUxPffvst\n5s2bJwwR7dmzB/v378fRo0drRH87OzuEhoZiwIABkEgkWLVqFR49egQTExMhjjz6+/j4YOLEiTA2\nNsbAgQNRUFCA8PBweHp6wsDAALNnz8bs2bPBcRy6deuGvLw8XLt2DVeuXMGyZctkyvzmm2+wZs0a\neHl5Yfbs2cjIyIC3tzecnZ3feeijouemp6cHIyMj/P7777CyssLjx48xffp0aGhoCDL++usv3L17\nF507d4aRkRGio6ORnJwsvFwsLS2FeB07doSmpqbMHoKNGzeCiNC6dWvo6uri2LFjePnypSBn2rRp\n+PLLL9GmTRu4u7vj1KlTCAkJETmHbdu2hZaWFmbOnIlZs2YhISEBCxYsEN3H3t4emzZtwv79++Ho\n6IgDBw5g3759Fdqqa9eucHNzw4ABA7BixQo0adIEGRkZOHPmDDQ0NDBu3LjKP4C3mJubg+d5HDx4\nEIMHD4aamprwb7YkJcugrDIpb9jBgwfh7++PHj164NChQ9i1axf27NkjM42NjQ3GjBmD8ePHY8WK\nFWjXrh0yMzMRHR0tlIuqMmzYMKxevRq9e/fG4sWLYWtri9TUVBw/fhwODg7o16+fXHIMDQ1Rp04d\nhIWFoVGjRlBTU4Oenp5c9dvS0hLh4eG4c+cOtLW1oaurW6r97NatG9q0aYOhQ4fC398f2traWLhw\nIXJyckQOUEVUVNblobrbybLqV0WUVdaKh79L3amud4uVlRX27NmDGzduQCqVQltbW2av1Zw5c9Cq\nVSs4ODiA53mEhIRAS0sLDRo0gEQiqbA9fFc2bdoEe3t7tGzZEiEhITh37hz8/f1lxu3WrVuV7PrN\nN9+gd+/eaNiwId68eYO9e/eiQYMGghNX3J4xMTEYPnw4fH190bBhQ6SkpAAoHOEyMjLCN998g40b\nN6Jfv36YO3cu6tWrh/v37+Pff/9Fnz590L59+3JtWuMoZipe9fHo0SNhK5BZs2bRnj17qk22l5dX\nqVWrJQkNDaX27duTpqYmaWtrU7NmzWjhwoXC9bImUPr6+oommhMR5ebm0syZM4Vl9Y6OjqJVNUSl\nl2ETFU6aVlFREYUFBwcTz/OisO3btxPP85Sfn09EhZOke/bsSRKJhExNTcnX15fGjh0r2gZClv6L\nFi0StgIoYuvWreTk5ERqampkYGBAffr0ES0c+OOPP6hZs2akrq5Oenp61K5dO9qwYUMpuxTn3Llz\n5OzsTBoaGqSrq0vDhg0TVgQRFU6U5Xm+wsUOsp5jRc8tMjJSWPpvb29Pf/75J9nY2JCfnx8REZ04\ncYK6du1KRkZGpK6uTg0bNqTly5eL7jFlyhSSSqXlbj+yd+9e6tChA+np6QlbRGzatEkUZ82aNWRm\nZkYaGhrUvXv3UtsjEBEdPHiQGjVqRBoaGtSpUycKCwsjnueFCfC5ubk0YcIE0tfXJ21tbRo2bBit\nW7dOVEZklUmiwlWoM2fOJEtLS1JVVSUTExNyd3cXrW4uiaxnEx4eLloNSES0YsUKMjMzIyUlpXK3\nHyk5uVzWZPPiz6cIe3t70eroou1HvvjiC9LU1KS6devS6tWry71Xfn4+rVixguzt7UlVVZUMDQ3J\nxcVF1NbIqpfKysqltntQV1cXrXZ98uQJTZw4UajzZmZmNGDAALpy5UqZNpMlOygoiCwtLUlZWVmo\nm/LU7zt37pCzszPVqVOn3O1HHj16RB4eHqLtR6Kjo4Xr8ugpT1kvSXW2k2Uhq36VXLVaMm/yLHYg\nqrjulNeGVeXdUrJtfvr0KfXq1Yt0dHTK3X5k4cKF1LhxY6pTpw7p6OiQi4uLSKeK2kOiqtWB4tuP\nuLi4CNuCVPQ8q9ImTZo0iRo2bEgaGhrCO6r4ivbi9pS1hVLxLXCIiJKSkmjYsGFkZGREampqZG5u\nTiNGjKDExES5bFqTcEQf7s6pPj4+aN68Ob744ovaVoXBqDEiIiLQtWtX3L9/H3Xr1q1tdT4oiv4Z\nDx06tLZVYTA+eRITE2FlZYVTp06VWnTCqDof7KrVpKQkHDlyBH379q1tVRgMBoPBYDBqhVpz5Nat\nW4dWrVpBXV291Nl/T58+Rf/+/VGnTh1YWFhg+/btousvXrzAyJEjERgYyA4rZnwSVLSAgsFgMD4E\nWFtW/dTa0Oq+ffvA8zzCwsKQlZWFzZs3C9c8PT0BFE6WvXz5Mnr37o0zZ87AwcEBeXl5+Pzzz/H9\n99+ja9eutaE6g8FgMBgMxvuBQmbilcPcuXNFuyG/evWKVFVV6fbt20LYyJEjhfPogoKCyMDAgFxc\nXMjFxYV27twpU27dunUJAPuwD/uwD/uwD/uwz3v/cXJyqpIfVetz5KhEh+CtW7egrKwMGxsbIczJ\nyUnY9XnEiBF4/PgxwsPDER4ejsGDB8uU+/DhQ2F5sSI+Pj4+Ck0vT/zy4pR1Td5wWfHe1QaKtHdl\nZdSUvStjS3mewfts8+ou41W9zuxd9fisTak+GaxN+bjLeFXsffXq1Sr5UbXuyJUcL3/16hW0tbVF\nYVpaWnj58qUi1ao0Li4uCk0vT/zy4pR1Td5wWfESExMr1Km6eFd7V1ZGTdm7rGvyhCnS3rLuX9Pp\nK4pf1evM3lWPz9qU6pPB2pSPu4wr0t61vv3I3Llz8eDBA2GO3OXLl9GpUydkZmYKcX766SecOHEC\n+/fvl1tuTR35xCgbLy8vbNmypbbV+GRg9lYszN6Kh9lcsTB7K5aS9q6q3/Le9cg1bNgQeXl5osNw\nr169WqVjmnx9fREREfGuKjLkxMvLq7ZV+KRg9lYszN6Kh9lcsTB7K5Yie0dERMDX17fKcmqtRy4/\nPx+5ubnw8/PDgwcPEBAQAGVlZSgpKcHT0xMcx+GPP/7ApUuX0KdPH5w9e1Y4908eWI8cg8FgMBiM\nD4UPrkdu4cKF0NTUxPLlyxESEgINDQ0sXrwYALB+/XpkZWVBKpVi+PDh2LBhQ6WcOEbtwHo/FQuz\nt2Jh9lY8zOaKhdlbsVSXvRVz2rwMfH19y+xK1NPTk+uAbwaDwWAwGIxPmVpf7FBTlNdFqa+vj4yM\nDAVrxGB8uujp6eHp06e1rQaDwWC8t1R1aLXWeuQUga+vL1xcXEot+c3IyGDz5xgMBcKO5WEwGAzZ\nREREvNMw6yfZI8cWQjAYiuVjqHMRERHVstcYQ36YzRULs7diKWnvD26xA4PBYDAYDAbj3WA9cgwG\no8ZhdY7BYDDKh/XIMRgMBoPBYHxifNSOHDvZofJ4eXmhe/futXZ/S0tLLFmyRCH3srCwEPYu/FTh\neR7btm2rbTU+CFhboniYzRULs7diKbL3u57s8NE7ch/jxM0nT55g+vTpsLe3h4aGBoyNjdGlSxcE\nBwcjPz9fLhmnTp0Cz/O4d++eKJzjuFpdYRgVFYWpU6cq5F61ndfKcv/+ffA8jxMnTlQ6rZubG0aP\nHl0qPCUlBQMHDqwO9RgMBoNRBVxcXN7Jkfuotx+pKnFxSTh6NAG5uTxUVArg5mYNOzvz90JmcnIy\nOnXqBFVVVSxYsADNmzeHiooKTp8+jZ9++glOTk5o2rSp3PJKjsfX9jwmAwODWr3/h0B1PiOpVFpt\nsj52PsY/he87zOaKhdlbsVSXvT/qHrmqEBeXhC1b4pGe3hXPnrkgPb0rtmyJR1xc0nsh09vbG7m5\nubh06RI8PT1hb28Pa2trjBw5EpcuXYKNjQ22bNkCPT09ZGVlidIuWLAADRs2RGJiIpydnQEUDmXy\nPI+uXbsK8YgIv//+O8zNzaGjo4N+/fohLS1NJCswMBAODg5QU1ND/fr1MW/ePFFvoIuLC8aPH4+F\nCxfC1NQUBgYGGDVqFDIzM8vNX8nhTgsLC8yfPx8TJ06Erq4uTExM8Ouvv+LNmzeYNGkS9PX1Ua9e\nPfj7+4vk8DyPX375BQMHDkSdOnVQr149/PLLL+XeOzc3F76+vrCysoKGhgYaN26M33//vZTcdevW\nYciQIahTpw4sLCywb98+ZGRkwNPTE9ra2rC2tsbevXtF6VJTU+Hl5QWpVAptbW106tQJJ0+eFK5H\nRESA53kcPXoUzs7OkEgkcHR0xKFDh4Q4DRo0AAC4urqC53lYWVkBAO7evYsBAwbAzMwMEokETZs2\nRUhIiJDOy8sLx48fR2BgIHieF/XqlRxaffToETw8PKCnpwdNTU24uroiOjq6UnoyGAwGQ4HQR0p5\nWSvv2rp1x8jHh6hLF/GnV6/C8Kp83N2PlZLn40Pk73+sUnl68uQJKSkp0eLFi8uNl5WVRXp6ehQY\nGCiE5efnk7m5Oa1YsYLy8/Np//79xHEcRUVFUWpqKmVkZBAR0ahRo0hHR4eGDh1KMTExdPbsWbK0\ntKQRI0Z+6IEfAAAgAElEQVQIsg4cOEBKSkq0bNkyun37Nu3cuZP09PRo3rx5QpwuXbqQrq4ufffd\ndxQXF0eHDx8mfX19URxZWFhYiPJnbm5Ourq6tHr1akpISKBFixYRz/PUs2dPIWzp0qXE8zzduHFD\nSMdxHOnr69O6devo9u3btGbNGlJWVqa//vqrzHuNGjWKnJyc6MiRI5SYmEg7d+4kXV1d2rhxo0iu\niYkJBQUFUUJCAnl7e5NEIqEePXpQYGAgJSQk0OTJk0kikdCTJ0+IiOj169fUqFEjGjRoEEVHR1NC\nQgItXryY1NTUKDY2loiIwsPDieM4cnJyorCwMIqPj6fRo0eTtra28GwuX75MHMfRvn37KDU1lR4/\nfkxERNeuXSN/f3/677//6M6dO7R27VpSVlam8PBwIiJ6/vw5OTs7k4eHB6WmplJqairl5OQI+dm6\ndSsRERUUFFCbNm2oefPmdPr0abp27RoNGTKE9PT0hHvJo6csPoampsieDMXBbK5YmL0VS0l7V7Wd\nZD1yJcjNlW2S/Pyqm6qgQHbanJzKyYyPj0dBQQEcHBzKjaeuro4RI0YgICBACDty5AgePXqE0aNH\ng+d56OnpAQCMjIwglUqhq6srSr9lyxY4ODigXbt2+Prrr3H06FHh+rJlyzBo0CDMmDEDNjY2GDx4\nMHx9ffHTTz8hLy9PiGdhYYGVK1eiYcOG6N69O4YMGSKSIy+urq6YMmUKrKysMHv2bNSpUwdqampC\n2IwZM6Cjo4Pjx4+L0vXp0weTJk2CjY0Nvv32WwwePBg//fSTzHvcvXsXwcHB2LVrF9zc3GBubo7B\ngwdj6tSpWLt2rSiup6cnRowYASsrK/j5+eH169ewt7fHyJEjYWVlhQULFuD169c4d+4cAGDnzp14\n+fIlduzYgRYtWgj56NChA3777TeRbF9fX/To0QPW1tZYtmwZXr58iYsXLwIADA0NARQeMSeVSoVh\n6MaNG8Pb2xtNmjSBpaUlvvnmG/Tu3VvoadPW1oaqqio0NDQglUohlUqhoqJSygbHjx/HxYsXsW3b\nNnTo0AGNGzdGUFAQ1NXVsX79ern1ZDAYDIbi+KjnyJV1RFd5qKgUyAxXUpIdLg88LzutqmrlZFIl\n5kZNmDABjRs3RlxcHOzs7BAQEIB+/foJzkB52Nvbi170pqamSE1NFX7fuHEDnp6eojTOzs548+YN\nEhISYGdnBwBwcnISxTE1NUVYWJjceQAKFyQUl8NxHIyMjETzADmOg1QqRXp6uiht+/btRb87dOiA\n+fPny7xPVFQUiAgtW7YUhefl5UFZWVxNiutjaGgIJSUlkT66urpQVVUVhqMvXryIlJQUkbMMANnZ\n2ZBIJKKwZs2aCd+lUimUlJREtpfF69evsWDBAhw4cACPHj1CTk4OsrOzRcPl8hATEwMDAwPY29sL\nYaqqqmjbti1iYmLeWc8PHTZ/SPEwmysWZm/FUmTvdz2i66N35CqLm5s1tmw5BheXbkJYdvYxeHnZ\n4K1/Umni4gplqqmJZXbrZlMpOba2tuB5HjExMfjiiy/Kjevg4IBOnTrh999/x4wZM/D333/j4MGD\nct2nZG9NVTYp5DgOqqqqpcIKCirvEMvSR1ZYVWQXUZT27Nmz0NTULCW7PH3K0rFIZkFBARo1aoTQ\n0NBS6Ureq6TNiutWFj/88AP279+P1atXw87ODpqampg2bRqeP39ebjp5IaJSNqiKngwGg8EoTVGH\nk5+fX5XSs6HVEtjZmcPLywZS6XHo6kZAKj3+1omr+qrV6pKpr68Pd3d3rFu3Di9evCh1PTc3F69f\nvxZ+T5gwAUFBQfj9999Rr149uLm5CdeKXsSytiupaEsOR0dHREZGisIiIyOhqakJa2vrSuWpJjl7\n9qzo95kzZ+Do6CgzblFPXFJSEqysrEQfS0vLd9KjdevWuHPnDrS0tErJNjExkVtOWc/s5MmTGD58\nOAYNGiQMr8bFxYmeo6qqqmjYWxaOjo548uQJYmNjhbDs7GycP38ejRs3llvPjxW2x5biYTZXLMze\niqW67M0cORnY2ZnD27srpkxxgbd313feeqQ6Za5fvx4qKipo2bIltm/fjhs3biA+Ph4hISFo3bo1\n4uPjhbiDBg0CACxatAjjxo0TyTE3NwfP8zh48CDS0tJEjmFFvW+zZs3Cn3/+ieXLl+PWrVvYtWsX\n/Pz8MG3aNGEYkoiqtE1GyTSyZMgbdvDgQfj7++P27dtYu3Ytdu3ahWnTpslMY2NjgzFjxmD8+PEI\nCQlBfHw8rl69ik2bNmHFihWVzkdxhg0bBktLS/Tu3RtHjhxBYmIizp8/j6VLl+Kvv/6SW46hoSHq\n1KmDsLAwpKSkICMjAwBgZ2eH0NBQXLx4ETdu3MBXX32FR48eifJnaWmJ6Oho3LlzB48fP5bp1HXr\n1g1t2rTB0KFDcebMGVy/fh0jR45ETk4OJk6c+E42YDAYDEbNwBy5D4z69evj0qVL+OKLL+Dr64uW\nLVuiY8eOCAgIwMSJE0U9Tmpqahg+fDiICGPGjBHJMTY2xtKlS7Fs2TLUrVtXGKota5Pc4mHu7u7Y\ntGkTAgMD0aRJE3z33XeYNGkSfHx8RPFLypFnA15ZaSqKU1bY/PnzcfToUTRr1gzLli3Djz/+iH79\n+pWZ5vfff8fUqVOxePFiODo6ws3NDcHBwe/cy6impobIyEi0atUKo0ePhp2dHQYOHIioqChYWFiU\nm4fi8DwPf39/7Nq1C/Xr1xd6EVevXg1zc3O4urrCzc0N9evXx6BBg0Typk2bBkNDQzg5OUEqleLM\nmTMy7xEaGgp7e3v07t0bbdq0QVpaGo4cOQJ9fX259fxYYfOHFA+zuWJh9lYs1WVvjqrSbfIBUN68\nrk/pAO/BgwcjPz8ff/75Z22rolB4nkdISAiGDh1a26ow8GnVOQaDwagKVW0nWY/cR0pGRgbCwsIQ\nGhqqsCOvGIyPGTZ/SPEwmysWZm/FUl32/uhXrVZ2+5GPhebNm+Pp06eYMWMGOnXqVNvqMBgMBoPB\nkMG7bj/ChlYZDEaNw+ocg8FglA8bWmUwGAwGg8H4xGCOHIPBYMgBmz+keJjNFQuzt2Jh+8gxGAwG\ng8FgfOKwOXIMBqPGYXWOwWAwyofNkWMwGAwGg8H4xGCOHIPBYMgBmz+keJjNFQuzt2Jhc+QYjBog\nIiICPM/j4cOHta1KjePr6wtbW9vaVoPBYDAY78BHPUfOx8dH5obAbL7Op4WNjQ1GjBghOgu2LHJz\nc5GRkQEjI6OP5kzRU6dOwdnZGYmJiWjQoIEQnpmZiezsbNE5qjUFq3MMBoMhm6INgf38/KrUTn70\nJzswGPI6ZHl5eVBRUYFUKq1hjWqHkg2ERCKBRCKpJW0YDAaDAUDocPLz86tSeja0KoO4+Dj47/TH\nzzt+hv9Of8TFx703Ml1cXDB+/HgsXLgQpqamMDAwwKhRo5CZmSnE8fLyQvfu3UXpQkJCwPP/e9xF\nw2q7d++GjY0NJBIJBg4ciFevXmH37t2ws7ODtrY2vvzyS7x48aKU7NWrV8PMzAwSiQSDBw9GRkYG\ngMJ/FsrKyrh//77o/kFBQdDV1UVWVpbMfFVVn0uXLsHd3R3GxsbQ0tJCmzZtEBYWJrJXQkIC/Pz8\nwPM8lJSUcO/ePWEI9Z9//kGnTp2goaGBjRs3lhpaXbFiBfT09JCUlCTIXLBgAaRSKVJSUsp8Tqmp\nqfDy8oJUKoW2tjY6deqEkydPiuKEh4ejadOm0NDQgJOTE8LDw8HzPLZu3QoASExMBM/zOHPmjCid\njY2NqMKvWbMGzZs3h5aWFkxNTeHp6SnolpiYCGdnZwCApaUleJ5H165dRTYvTmBgIBwcHKCmpob6\n9etj3rx5yM/PF9mzovL3scLmDykeZnPFwuytWNgcuRoiLj4OW8K3IN04Hc9MniHdOB1bwre8kzNX\n3TL37NmDZ8+eITIyEjt27MCBAwewfPly4TrHcXL1Qj169AhBQUEIDQ3Fv//+i5MnT2LAgAHYsmUL\n9uzZI4QtWbJElO7ChQuIjIzE4cOH8c8//+DKlSsYO3YsgMIXva2tLTZt2iRKExAQgGHDhkFDQ6Na\n9Xn58iU8PT0RERGBy5cvo2fPnvj8889x+/ZtAMC+fftgYWGB77//HikpKXj06BHq1asnpJ82bRpm\nzZqFmzdvok+fPqV0mj59Otq2bQtPT0/k5+fjxIkTWLRoEQIDA2FiYiIzH1lZWXB1dUVmZiYOHTqE\nK1euoFevXujevTtu3rwJAHj48CH69OmD1q1b4/Lly1i5ciX+7//+D0DFPYglny/HcVi5ciWuX7+O\nffv24d69e/Dw8AAANGjQAH/99RcA4OLFi0hJScHevXtlyj148CDGjh2LUaNGISYmBitXroS/v3+p\nf4kVlT8Gg8FgKI6Pemi1KhyNPgo1WzVEJEb8L1AF+G/Hf2jdqXWVZF44dQGv670GEv8X5mLrgmOX\njsHOxq7S8iwsLLBy5UoAQMOGDTFkyBAcPXoUCxYsAFA4hCbPOHt2djYCAwOFOVKDBw/Ghg0bkJqa\nCgMDAwCAh4cHjh07JkpHRAgODoaWlhYAwN/fHz179sSdO3dgZWWFr776CmvWrMG8efPAcRxu3ryJ\n06dPY926ddWuT5cuXUQyFi5ciL///hu7d+/G7NmzoaenByUlJdSpU0fmkOncuXPRu3dv4XeRA1ic\noKAgODk5YfLkyThw4AAmT54Md3f3MvOxc+dOvHz5Ejt27ICSkhIAYPbs2Th69Ch+++03rF69GuvX\nr4dUKkVAQAB4noe9vT2WLl2Kvn37lmsjWXz77bfCd3Nzc6xbtw4tW7bEo0ePYGpqCj09PQCAkZFR\nucPGy5Ytw6BBgzBjxgwAhT1/KSkpmDlzJubPnw9l5cLmoqLy97FScq4to+ZhNlcszN6KpbrszXrk\nSpBLuTLD85EvM1weClAgMzynIKfSsjiOg5OTkyjM1NQUqamplZZlZmYmmuhubGwMExMTwWkqCktL\nSxOlc3BwEJw4AOjQoQMA4MaNGwCAkSNHIi0tTRji/OOPP9CqVatSeleHPunp6fD29kajRo2gp6cH\nLS0txMTE4N69e3LZoE2bNhXGkUql2Lx5MzZs2ABDQ8MKe5+Ker50dXWhpaUlfE6dOoX4+HgAhbZq\n06aNaLi7Y8eOculckoiICPTs2RMNGjSAtrY2OnfuDACi4WB5uHHjhjAMW4SzszPevHmDhIQEIay6\nyh+DwWAw3h3WI1cCFU5FZrgSlKosky/DX1blVaskT1VVnI7jOBQU/M9Z5Hm+VI9cbm5pB1VFRZxX\njuNkhhWXDZSeNF8SAwMDDBo0CAEBAejWrRuCgoJKDc/Koir6eHl54f79+/jxxx9haWkJdXV1eHh4\nICdHPidZ3sn+ERERUFJSQmpqKp49ewZDQ8My4xYUFKBRo0YIDQ0tdU1TU1PIR0V2LHLyynuW9+7d\nQ69evTBq1Cj4+vrC0NAQycnJcHNzk9sGlYHjuArL38dKREQE67FQMMzmiiEuPg5/n/sbsTGxaNGs\nBdxaulVptIhROaqrfDNHrgRuLd2wJXwLXGxdhLDs29nw8vCqcsGOq1c4R07NVk0ks5trt3dVVybG\nxsY4d+6cKOzSpUvVJj82NhYvX74UeuWKJuM7ODgIcSZMmABXV1ds2LABb968gaenZ7XdvzgnT57E\njz/+KMxvy8zMREJCApo0aSLEUVVVFU3YryxHjx7FqlWrcPDgQcybNw9eXl44cOBAmfFbt24tDD0b\nGRnJjOPg4IDg4GAUFBQIDtvp06dFcYrSPnjwQAhLS0sT/b548SLevHmDn3/+GWpqakJYcYocr4ps\n4OjoiMjISHh7ewthkZGR0NTUhLW1dblpGQzGh0lcfBw2HN6AG1o3kMFnwMjACFvCt8ALVX/nMRQL\nG1otgZ2NHbxcvSBNk0I3RRfSNCm8XN+tQFenTHnmv7m5ueHmzZtYv349EhISEBAQgN27d1dV/VJw\nHIeRI0ciJiYGJ06cwKRJk9CvXz9YWVkJcTp27Ag7Ozv88MMP8PT0rLFtLuzs7BASEoLr16/jypUr\n8PT0REFBgchGlpaWOHXqFJKTk/H48eNK7dOTnp6OESNGYPr06ejRowe2b9+OkydP4ueffy4zzbBh\nw2BpaYnevXvjyJEjSExMxPnz57F06VJh4cHEiRORnp6Or776CrGxsTh27BjmzJkjkqOhoYGOHTti\nxYoV+O+//xAdHY2RI0cKDhsA2NraguM4/PTTT7h79y5CQ0OxcOFCkRxzc3PwPI+DBw8iLS0Nz58/\nl6n3rFmz8Oeff2L58uW4desWdu3aBT8/P0ybNk2YHyfv/MuPEdYzpHiYzWuefWf3IUYrBtn52dC0\n1cS11GtQtVHFsUvHKk7MeCfYHLkaxM7GDt6DvTHFYwq8B3tXy7+S6pIpa0VqybBu3bph0aJFWLJk\nCZo1a4aIiAjMnz+/1ErHiuSUFdamTRt06tQJ3bt3h7u7O5ycnEqtUgWAcePGIScnB1999VW15EtW\n2ObNm1FQUIA2bdpgwIAB6NWrF1q3bi2K4+fnh2fPnsHOzg7GxsZITk4WZJWlSxFeXl6wtLQUJvJb\nWVlhw4YNmDlzJq5evSozvZqaGiIjI9GqVSuMHj0adnZ2GDhwIKKiomBhYQEAqFu3Lv7++29cuHAB\nzZs3x9SpU7F69epSsjZt2oQ6deqgQ4cOGDp0KCZMmABTU1PhetOmTbF27Vr89ttvcHR0xKpVq/Dz\nzz+L8mBsbIylS5di2bJlqFu3Lvr37y/Tlu7u7ti0aRMCAwPRpEkTfPfdd5g0aZJoI2V5nxODwXj/\nSXmVgjPJZ5B1PwPaRx/A8PB91D+diczkJ1Waw82oHT7qkx3KyhrbZb7qeHl54cGDBzhy5EiFcadP\nn45jx44hOjpaAZp9HPA8j5CQEAwdOrS2ValWPoY6x+ZrKR5m85rjwYsHCP4vGMd3/wOzhEQMfpGL\nu69V4dDYEuE5eVBr0xWzp3zcK9Frm5Llu6rt5Ec9R87X11fmEV2MmuX58+e4desWAgICsHbt2tpW\nh8FgMBjFSHqWhG3XtiE7PxuWz4D+yTmwIWU8f50N7bTn6KwkQfoz1suuKIqO6KoqrEeOUSlGjx6N\nBw8e4PDhw2XGcXFxwYULF+Dp6YmNGzcqULsPH9Yjx2AwapI7GXew/dp25BbkAkTQ/iUMY5LfIPN1\nJgiEHIkE2u064bq1LVymTKltdT8pqtpOMkeOwWDUOKzOMRi1z60nt7ArZhfyCvIAIjS59ACaYYlw\nz8krjKCvDzg6AkpKOC6VomuxFeyMmqeq7SRb7MBgMBhywM6hVDzM5tVHTFoMdlzfgbyCPHAFhOYX\n78P9qT4cGtpjy5s3WKuri4kFBfBPT8eWx49h3a1mtsdi/I/qKt8f9Rw5BoPBYDA+da6mXEXozVAQ\nCFwBoeWFZLi9kkJdRR1vVPNwrksXxHTogGfXruGVnR20nz5FexXZm+Mz3j/Y0CqDwahxWJ1jMGqH\n6IfROHDrQKETl1+Atufvw/W1MdSUC/ejXK2sjPDPP8eLtxuGG6qowFEigfH16/CuwtnPjKrDVq0y\nGAwGg8EQOHf/HA7FHwIA8PkF6HDmPpxzTKCqXHjay8tWrXD62TPBiQMAiVLhcZRsF7kPBzZHjsFg\nMOSAzddSPMzmVedE0on/OXF5+eh8+j665JhCVanQiXvarh02OTnhdV6ekEZy7Ros1dXBAajaSeCM\nylBd5Zs5cgwGg8FgfCQQEY7dOYbjd48DAJRy8uB66gE659WFilLhvLfUzp2xycEBGXl5sLKyQkF0\nNOw1NWH0dl5cdnQ0ujk61loeGJWDzZFjMBg1DqtzDEbNQ0QISwjDufvnAADKOXnoevoh2pIZlPjC\nIdN7rq7YZmGBNwUFhXE4Di1fv8bdhATkoLAnrpujI+yKnZ3NUAxs+xHGB4Wvry9sbW2F31u2bIFK\nDaySqi65Xl5e6N69ezVo9O4QEVq2bIndu3cDAPLz89GoUSP8+++/tawZg8GoLYgIB28fFJw4lTe5\n6HHqEdqhnuDE3e7eHcHFnDg1nscIExO4OzjAu29fTOnbF959+zIn7gODOXKMWqP4QeseHh54+PBh\nLWpTPpU9GF5ZWRlBQUE1osu2bduQnZ2NL7/8EgCgpKSEOXPmYMaMGTVyP0YhbL6W4mE2l48CKkDo\nzVBEPYwCAKhm5eCz0yloxZmB5wpf89c++wzbzcyQ+9aJkygpwcvEBObq6oIcZm/FwvaRq0GS4uKQ\ncPQo+NxcFKiowNrNDeZ2du+dzA+d4l3I6urqUC/WoLxvEFGlurxrcijx559/xtixY0VhAwcOxKRJ\nkxAeHg5XV9cauS+DwXj/yC/Ix97YvYhJjwEAqGVmo9eZdDRVrlf455PjcKFXL/xrZCS0SbrKyhhh\nYgIDtlfcRwHrkStBUlwc4rdsQdf0dLg8e4au6emI37IFSXFxtS7TxcUF48ePx8KFC2FqagoDAwOM\nGjUKmZmZAGQP/4WEhIDn//eYi4Y0d+/eDRsbG0gkEgwcOBCvXr3C7t27YWdnB21tbXz55Zd48eKF\nkK5I9urVq2FmZgaJRILBgwcjIyMDQOE/C2VlZdy/f190/6CgIOjq6iIrK6vcvJUcAi36febMGbRo\n0QISiQStWrVCVFSUKN348eNhY2MDTU1NWFtbY86cOcjJKX/h/Pbt22FtbQ0NDQ107twZBw8eBM/z\nOHPmTLnpihMTE4OePXtCT08PderUgYODA0JCQgAAFhYWyM/Px+jRo8HzPJTeLud/8eIFRo8eDVNT\nU6irq6NBgwaYNm2aIPPNmzeYOHEidHV1oa+vD29vb8yaNUs0BH3r1i1ER0ejf//+In00NDTw2Wef\nCTowqh8XF5faVuGTg9m8fPIK8rAzZqfgxKm/zELfM4/RVNms8M8kzyOib1/8Y2goOHFSVVWMMTWV\n6cQxeyuW6rI365ErQcLRo+impgYU6/LsBuD4f//BvHXrqsm8cAHdXr8WhXVzccHxY8cq3Su3Z88e\njBkzBpGRkUhKSoKHhwfMzc2xYMECAJBr+O/Ro0cICgpCaGgonj59ikGDBmHAgAFQUVHBnj178OLF\nCwwcOBBLlizBsmXLhHQXLlyARCLB4cOH8fjxY4wfPx5jx47F3r174eLiAltbW2zatAnz588X0gQE\nBGDYsGHQ0NCoVD4BoKCgALNnz8batWthaGiIqVOnYvDgwbh9+zaUlJRARDA2Nsb27dthbGyMq1ev\nYsKECVBRUYGvr69MmdHR0Rg+fDjmzJmDESNG4MaNG5gyZUqlhk0BwNPTE02bNsXZs2ehrq6Omzdv\nIv/tXkxRUVEwNTXFqlWrMGTIECHN3LlzcfnyZezfvx+mpqZITk7GjRs3hOuzZs3C3r17ERwcDDs7\nOwQEBGD9+vUwNjYW4kRERMDQ0BAWFhaldGrbti3Wrl1bqXwwGIwPk5z8HOy4vgN3Mu4AADSev0a/\n889gp1K30IlTUsK/ffvigo6OkKaemhqGGRtD4+2fS8bHAXPkSsDn5soOL7ZhYqVlvp2TUCq8gp4j\nWVhYWGDlypUAgIYNG2LIkCE4evSo4MjJM5yXnZ2NwMBA6OvrAwAGDx6MDRs2IDU1FQYGBgAK56wd\nO3ZMlI6IEBwcDC0tLQCAv78/evbsiTt37sDKygpfffUV1qxZg3nz5oHjONy8eROnT5/GunXrKp3P\novv9/PPPaNasGYDC3sR27drhzp07sLW1BcdxWLRokRC/QYMGiI+Px6+//lqmI7dq1Sp06tRJsJet\nrS1SUlIwceLESul27949TJs2Dfb29gAgcqwMDQ0BADo6OpBKpaI0zZs3R+u3fwjq1auH9u3bAwAy\nMzOxYcMGrFu3Dn3f7qb+448/IiIiAs+fPxdk3Lp1C+bm5jJ1srCwQFJSEvLy8qCszKp2dRMREcF6\nLBQMs7lssvOyse3aNiQ9TwIASDIy8cWFF7BRNQXHcchXVkbo55/j2tu2GgCsNTQwRCqFKl/2QByz\nt2KpLnt/1EOrvr6+lZ5MWFDGnIGCd/gHU1BGxSlQrdyWixzHwcnJSRRmamqK1NTUSskxMzMTnDgA\nMDY2homJieDEFYWlpaWJ0jk4OAhOHAB06NABAIRepZEjRyItLQ1hYWEAgD/++AOtWrUqpbO8lMyv\nqakpAIjyGxAQgLZt28LExARaWlqYPXs27t27V6bM2NhYtGvXThRW8rc8fP/99xg3bhxcXV3h5+eH\ny5cvV5jG29sbe/bsQZMmTTBlyhQcOnRIcLwTEhKQnZ0t2LSIjh07ipzz58+fo06dOjLla2trAwCe\nPXtW6fwwGIwPg6zcLARdDRKcuDpPXmLghZewVSt04nJVVbGjXz+RE+cokcCzAieOUXtERESU2fkg\nDx/13/aqGMbazQ3HtmxBt2Je8rHsbNh4eQFVXJxgHRdXKFNNTSyzW7dKy1It4fxxHIeCtz1+PM+X\n6pHLldHDWHI7Do7jZIYVlOhJrKi3z8DAAIMGDUJAQAC6deuGoKAgLFmypPwMlQPP86Ihz6LvRXrt\n3r0b33zzDZYvX44uXbpAW1sbu3btwpw5c8qVW9lhVFnMnTsXw4YNw6FDh3D8+HEsWbIE06dPx8KF\nC8tM06NHD9y7dw9hYWGIiIjA8OHD0aRJk1I9n+Whq6uLly9fyrxW1HOnq6tbucww5IL1VCgeZnMx\nmTmZCP4vGCmvUgAA2ukvMDA6C+bqJgCAN+rq2NanD+5JJEKaVlpa6GVgAF6Odo/ZW7EU2dvFxQUu\nLi7w8/OrkhzmnpfA3M4ONl5eOC6VIkJXF8elUth4eb3TCtOakCkLqVRaaguPS5cuVZv82NhYkRNR\ntDjAwcFBCJswYQL+/vtvbNiwAW/evIGnp2e13b8kJ06cQPPmzTFlyhQ0b94c1tbWuHv3brlpHBwc\nShC5cD8AACAASURBVC1qOHfunFz3K+kAWlpaYuLEidi9ezf8/Pzw66+/CtdUVVWFOXPF0dPTg4eH\nBzZs2ICDBw8iMjISsbGxsLa2hqqqKk6fPi2Kf/r0adF9bW1tkZSUJFO/pKQkWFhYsGFVBuMj5GX2\nS2y5skVw4nRSnmFwdDbM1Qvn0L7S1MTmvn1FTpyzri56y+nEMT5cWIsvA3M7u2p3sqpDZkVbYLi5\nuWHFihVYv349evbsiePHjwubxlYHHMdh5MiRWLRoEZ48eYJJkyahX79+sCq2eWTHjh1hZ2eHH374\nAaNGjYLkbaPSrVs3tG3b9p166Epib2+PTZs2Yf/+/XB0dMSBAwewb9++ctN89913aN26NXx8fDBs\n2DDcvHkTq1atEvJXXPbkyZMxadIkIazI9q9evcKMGTMwaNAgWFhY4NmzZzh06BAcix1pY2lpiePH\nj6Nnz55QVVWFoaEh5syZg1atWsHBwQE8zyMkJARaWlpo0KABJBIJvv76a8ydOxfGxsZo2LAhNm7c\niFu3bokWO3Tp0gVPnjxBYmJiqQUP586dY/+oaxA2f0jxMJsX8uzNMwRdDcLTrKcAAL2HGRj8Xz5M\n1Y0AABlaWghyd0dGsUVlPfX10b7YQgd5YPZWLGyO3CeIrE1pi4e5ublh0aJFWLJkCZo1a4aIiAjM\nnz+/1PBkeTLKC2vTpg06deqE7t27w93dHU5OTti0aVMpPceNG4ecnBx89dVXQtidO3eQkpJS4T3L\n+10ybMKECRgxYgRGjx6NFi1a4OLFi/D19S1XTosWLbB161Zs3boVTZs2xfLly4Xh0OL72N26dQtP\nnjyRqa+KigqePXuGsWPHwsHBAZ999hlMTU2xbds2If7KlSsRHR0NS0tLwRHT0NDA/Pnz0apVK7Ru\n3RrXr1/Hv//+K8w7XLZsGb744guMGDECbdu2xYsXLzBp0iSR825nZ4dWrVph7969ojxmZWUhLCwM\nw4cPL2UzBoPx4fI06yk2X94sOHGG95/C4z+CqXrhoqpUXV1s7NVLcOJ4jsMXhoaVduIYHy7srFWG\nXHh5eeHBgwc4cuRIhXGnT5+OY8eOITo6WgGavTtBQUEYM2YMnj59KiwYeF/w9fXF1q1bcfv2bSFs\n27ZtWLx4MWJiYoSw4OBg/Pjjj/jvv/9qQ80KYXWOwag86ZnpCLoahJc5hVNajJOe4MubPAzV9AAA\nyYaG2NqtG968/ROqzHH4UiqFnaZmrenMqDrsrFVGrfP8+XNcvHgRAQEBmDp1am2rUyY//fQToqOj\ncffuXezatQszZ87E4MGD3zsnriyGDh0KDQ0N0VmrS5YswYoVK2pZMwaDUV2kvErB5iubBSfO7O4T\nDLmpJDhx8cbGCHJzE5w4NZ7HcGNj5sR9gjBHjiEX8pw12q9fP3Tp0gUDBgx4r4f4rl27hr59+6JR\no0bCxsCyhojfB8qye1RUlOis1djYWHz22WeKVu+Tgp1DqXg+VZvff3EfW65swevcwo3k68en48tb\nytBXK1yRft3MDNu6dkXu250Qis5NtajCxuvF+VTtXVuws1YZCmXz5s0VxvlQGoHAwMDaVkFufHx8\n4OPjU9tqMBgMBZH0LAlbr21FTn7hhvGWt9LR/64atNUKRwwumpvjn44dQW+3jNJRVsZIdm7qJw2b\nI8dgMGocVucYjIpJeJqAHdd3ILegcP9P29g09EvWRB3VOiAAJ6ysEN6uHfDWaTNSVcUIY2Nosy2H\nPgqq2k6yp89gMBgMRi0T9zgOu2J2IZ/yASI0upGOPg8kkKhKQAAONWyI861bA2+dNrO356ZqsnNT\nP3nYHDkGg8GQgw9l6sDHxKdi85i0GOyM2Sk4cU2upeHzh1qQqEqQD2CfgwPOt2kjOHHWGhoYZWJS\n7U7cp2Lv9wU2R47BYDAYjA+cKylX8NfNv0AggAjNr6Si5xNdqKuoI5fjsLtxY9xq1gx4e06qo0SC\n/oaGUGbnpjLewubIMRiMGofVOQajNFEPo3Dg1oHCH0RofSkVbhl6UFNWwxuex/amTZHUpIngxLXU\n0mJHbn3EsDlyDMb/s3ff4VFWaePHvzOT3ie9kYQkkEACofcSQAWlKEVAiiKwuq8ur65eP3V1keKq\nq++q767uu64VaQKyoIIgAiH0DgkkQCAJSUiBkN7LzDy/Px4yKRBInUkm53NdXvCcZJ7nzG0Ybs65\nzzmCIAidxPEbx9mTtAcAhU5i6NlbjC9yxsLMghKVivX9+nEzLAzuJG2jnZwY7+T0wG2ghK5HjM12\nESkpKSiVyrsOjO8qoqOjUSqVZGZmAiIeDWVmZuLi4kJGRgYA169fx8XFhdu3bxu5Zx2HqB8yPFON\n+aHUQ7VJnFbHyNM3mVDkgoXKgnwzM74ZOLBeEveIszMT1Op2T+JMNd4dVVvFWyRyXYSfnx83b95k\nyJAhRnn+X/7yF7p3797s16Wnp6NUKjl06FCb9sfY8ehoVqxYwZw5c/Dx8QGge/fuTJ8+ndWrVxu5\nZ4JgOiRJYn/yfqKuRwGg1OoYe+oWkaVumKvMyTY355tBg8jr1QsUCv25qSPEuanCfYip1XtISE5m\nX3w81YA58FBYGCGBgR3uns2hVCpxd3c32PPaWlvXV7VVPKqqqrCwsGiDHt1Np9MBcl/bU15eHuvX\nr79rdHLx4sVMnDiR999/Hzs7u3btQ2cQGRlp7C50OaYUc0mS2JO0hxPpJwBQarSMP3mb4ZXuqJQq\nblhasnHQIMqDgwH53NRZbm6E2toarI+mFO/OoK3iLUbkGkhITmbNuXPcDg+nIDyc2+HhrDl3joTk\n5A5xzyNHjjBy5EgcHBxwcHCgX79+/PbbbwBkZ2fz7LPP4unpibW1NaGhofoTGRpOJdZcb9iwgQkT\nJmBjY0NQUBCbN2/WPysyMpLnn3++3vMlSSIoKIh33333rr699957BAUFYWVlhbu7O5MmTaKiooI1\na9bw9ttvk5qailKpRKlU6kd6Nm7cyNChQ3FycsLNzY0pU6bUOyDez88PgHHjxqFUKgm8k/ymp6cz\nc+ZM3NzcsLa2JigoiL/97W9NjmNj8fjhhx+YMmUKtra2BAUF3XUKhFKp5NNPP2XevHk4OTnxzDPP\nALB3715GjhyJjY0Nvr6+LF68mLy8vHpxe/PNN3Fzc8PBwYEFCxbw97//HfM6u7GvXLmSHj16sGXL\nFkJDQ7G0tOTatWuUlJTw0ksv4evri62tLQMGDGD79u1Nin1TYvXDDz/g4eFB//79691z+PDh2Nra\n3vUsQRCaR5Ikdl7dqU/iVFUaHj6RzYgqOYlLtLZm7ZAh+iSu5txUQyZxQuclRuQa2Bcfj+XAgUQX\nFNQ2BgVx4dAhBrewPuHUoUOURURAnXtGDhzI/ri4Zo3KaTQapk2bxuLFi1m7di0gnxtqa2tLeXk5\nY8eOxdbWlo0bNxIUFERSUhI5OTn3vedrr73G3/72Nz7//HPWrl3L/PnzCQkJoV+/fvz+97/nueee\n4+OPP8b2zgdKVFQUaWlpLFmypN59tm3bxgcffMDGjRuJiIggNzeXgwcPAjB37lwSEhLYsGEDZ86c\nAdDfr6qqirfffpvevXtTVFTE22+/zeTJk4mPj8fc3Jxz584xYMAAtm3bxogRI1Dd2TfphRdeoKKi\ngv379+Pk5ERycjK3bt1qciwb88Ybb/DBBx/wj3/8g6+//pqlS5cyYsQIevToof+eVatWsXr1at59\n9110Oh1RUVE88cQTfPjhh6xdu5b8/Hxee+01ZsyYoa+B+OSTT/j000/5/PPPGTZsGD///DOrV6++\nq+YlMzOTf/3rX6xbtw61Wo2npydTp05FoVCwZcsWvL292bt3L3PnzmX37t2MHz/+vrFvLFY3b97U\nf/3gwYMMHTr0rlgoFAqGDh1KVFQUCxcubHVsO7vo6GgxYmFgphBznaTjxys/cuHWBQDMqjRMPJHL\nQK0HSoWSOFtbtg8ejNbfHwAblYoFHh543zlH1ZBMId6dSVvFu9MlckVFRTz00ENcvnyZkydP0rt3\n7za9f3Uj7dpWFJnqGnltVTPvU1xcTEFBAVOnTiUoKAhA/+vXX39NSkoKSUlJeHt7A+B/54PhfpYu\nXcpTTz0FwDvvvENUVBQff/wxa9euZfr06fz3f/83mzZt0iduX331FVOmTMHT07PefVJTU/H09GTi\nxImYmZnh6+tLRESE/uu2traoVKq7pjMXLVpU7/rbb7/F1dWVM2fOMHz4cFxdXQFwdnau99q0tDSm\nT59O3759gdqRu9ZatmwZs2bN0sfj008/5cCBA/USuenTp/PCCy/or5csWcJLL73Eiy++qG9bs2YN\nAQEBXLhwgb59+/LRRx/xyiuvMH/+fAD++Mc/curUKbZu3Vrv+RUVFaxbtw5fX19A/oN+4sQJbt26\nhYODfNbi7373O44fP86nn37K+PHjHxj7B8Xq6tWrjBs37p7x8Pf35+zZs80LoiAIAGh1Wv5z+T9c\nun0JAPOKah47kUs/yQOFQsFpe3t2DR6M1K0bIJ+butDDA9d2KtcQTFOnm1q1sbFh165dzJo1q132\npWrs2GFVK56lbOS1zf2jqlarWbp0KRMnTuSxxx7jgw8+4OrVqwCcPXuWsLAwfRLXVMOHD693PXLk\nSOLj4wGwtLRk0aJFfPnllwDk5uby448/8rvf/e6u+8yZM4fq6mr8/f159tlnWb9+PSUlJQ98fkxM\nDNOnTycwMBAHBwd98pmamnrf17388su89957DBs2jDfeeIPDhw836f0+SL9+/fS/r6mjy87Orvc9\nDRdInD59mk8++QR7e3v9f2FhYSgUCq5du0ZhYSFZWVkMGzas3usaXgN4eHjok7iae1dVVeHj41Pv\n/hs2bCAxMRF4cOwfFKuioiLs7e3vGQ8HBwcK6o5Od2FipMLwOnPMNToNm+M365M4i/Iqph3Po5/k\nAQoFhxwd+WXoUH0S52ZhwWIvL6MmcZ053p1RW8W7043ImZmZ6Udp2sNDYWGsOXuWyIED9W2VZ8+y\naMwYQlqw6hIgQZJYc+4clg3uOWHAgGbf64svvuCll17it99+Y+/evSxfvpzPPvuszTZcbXiP559/\nno8++oiLFy+yf/9+3N3defTRR+96nbe3N1euXOHAgQNERUXxzjvv8Prrr3Py5Ml6iUldZWVlPPLI\nI4wZM4Y1a9bg4eGBJEmEhYVRVXX/8cpFixYxadIkfv31Vw4cOMCjjz7K9OnTWbduXcvfPNy1cEGh\nUOgXHdSwbVC3IkkSb7zxxj2nHz08PNBoNPp7PUjDe+t0OhwdHfVT0vfq64Ni/6BYOTk5UVxcfM/+\nFBYWolarH9hvQRBqVWmr2BS3ieR8uQ7asrSSx08W0EvhDgoFe5ydOTFoEHh5AeLcVKF1Ot2IXHsL\nCQxk0YABuMfF4RQXh3tcHIsGDGjVCtO2vmdYWBh//OMf2bVrF0uWLOGLL75g4MCBXLp0Sb8PWFMd\nP3683vWxY8cICwvTXwcFBTF+/Hi+/PJLvv76axYvXtxoQmJhYcHEiRP54IMPuHjxImVlZfz000/6\nr2m12nrff/nyZXJycnj33XcZM2YMISEh5OXl1Usma5KVhq8F8PT0ZNGiRXz33Xd89dVXbNiwoUmj\ngG1t0KBBxMXFERgYeNd/tra2ODo64u3tfdeq0BMnTjzw3oMHD6agoIDy8vK77l03Qb5f7OH+serR\nowcpKSn3fH5qaio9e/ZsQVRMj9hjy/A6Y8wrNZWsv7Ben8RZlVQw82QRvRTu6BQKfnRz48SQIfok\nLtDamqfb4dzUluiM8e7MOv1Zq5999hlr1qwhLi6Op556Sr+6EuTtEJYsWcLevXtxdXXl/fff19dx\n1dVemyOGBAa2+dYgbXHPpKQkvvjiC6ZNm4avry+ZmZkcOnSIQYMG8dRTT/Hhhx8ybdo0PvzwQwID\nA0lOTiY3N5fZs2c3es9vvvmG0NBQBg4cyPr16zlx4gT//Oc/633P888/z/z589HpdCxduhSA7du3\n86c//YkDBw7g5eXF119/jSRJDB48GCcnJ/bv309xcbG+hrF79+7cvHmTEydOEBwcjK2tLf7+/lha\nWvKPf/yDV155hZSUFN544416/19dXV2xs7Njz5499OrVC0tLS9RqNX/4wx+YPHkyPXv2pKKigm3b\ntuHn56ffJuNPf/oTp0+fZt++fa2KeVNGOVevXs0jjzzCq6++ysKFC7G3t+fatWts3bqVzz77DCsr\nK1599VVWrFhBaGgogwcP5pdffmHv3r0P3Fpk/PjxPPTQQ8yYMYMPP/yQPn36kJ+fz7Fjx7C2tmbp\n0qUPjP2DYjV27Nh7rkKWJIlTp07x4YcftiBygtD1lFeXs/7CejKK5X9QWxeWMetMOUEqN6oVCra6\nu5MwcCC4uQHQ29aWGeLcVKGVjPbT4+Pjw/Lly1m8ePFdX3vxxRexsrIiOzubDRs28F//9V9cunTp\nru/ramc32trakpiYyNy5cwkJCWHWrFmMGjWKzz77DGtraw4ePEh4eDhz586ld+/eLFu2TL8FBdw7\n8f3rX//KF198QUREBBs2bGDDhg316sQAnnjiCZycnJg0aZJ+w9jCwkKuXbtGdbW8PMTZ2Zlvv/2W\ncePG0bt3b/73f/+XL7/8Ul9EP336dJ588kkmT56Mu7s7//M//4Orqyvr169n7969hIeH89prr/HR\nRx/VS26USiX//Oc/2bJlC926dWNgnenpl19+mT59+jB27FjKy8vZvXu3/ms3b94kucH2Lg3f/4Ou\nG2trKDIykqioKC5cuMCYMWOIiIjglVdewcHBQb+9yMsvv8wf/vAHXnrpJQYMGMCpU6d49dVXsayz\nMk2hUNzzeT///DMzZszgj3/8I7169WLKlCns3r2b4DtbFTwo9g+K1cyZM8nOzubcuXP1nnvs2DFK\nSkqYMWPGA2PQFYj6IcPrTDEvrSplTcwafRJnU1DK3NPlBKlcqFAqWe/lRcLgwfokboC9PbPc3DpU\nEteZ4m0K2ireCsnI2dDy5ctJT0/Xj8iVlpbi7OxMfHy8/i+qZ555Bm9vb95//30AHnvsMWJjY/H3\n9+f555/X7+VV1/1qxsQB3vK+aYGBgRw5coQRI0bc93tzc3Pp1q0bmzdvZurUqQbqoelbvHgxFy9e\n5PTp08buCs899xwqlYp//etf+rYlS5ZgbW3NZ5991ur7iz9zgikrqixibexacsrk7Z7s8kqYe64K\nXzNn+dxUb29u9u8Pd+pNRzk6GuTILaFzaennpNEXOzTs9NWrVzEzM9MncQARERH15pJ37drVpHsv\nWrSIgIAAQC7o7tevn/gXRzNoNBpycnJYuXIlvr6+IolrhaysLLZt28a4ceNQqVTs2LGDdevW3TWN\nbSyrVq0iPDycP//5z/j4+HD9+nV++uknLl++3GbPqLtnUs2f5850HRMTw8svv9xh+tMVrmvaOkp/\n7nVdUFHAn7/5MyVVJQT0C8DhdjH+P6WQaGaPXbA7a729OafTQUICAcOG8YizM1Xnz3Owg/S/7nVN\nW0fpj6lfx8TEUFBQ0GiNclN1uBG5w4cPM3v2bLKysvTf8+WXX7Jx40YOHDjQ5PuKEbn7S0lJISgo\niMOHDzc6IhcdHc348eMJDAxk3bp1d21VIjRddnY2c+bM4cKFC1RUVNCjRw+WLVt218bKpsoU/sxF\ni81SDa6jxzy3LJe1sWsprCwEwCm7iKdidXiYO5Ftbs46X1+K+/UDBwcUCgXTXFzo38hWPx1BR4+3\nqWkYb5MZkbOzs6OoqKheW2FhYaP7XAktExAQcM+VoHVFRkbetfWG0DLu7u7N+oeI0PGIv+AMryPH\nPLs0m7Wxaympkld/u2QVMvciuFk4kW5pyQZfX8r79QM7O1R3zk3t1cGP3OrI8TZFbRVvo1dZNqwR\n6NmzJxqNRr/ZKUBsbCzh4eGG7pogCIIg3CWrOIs1MWv0SZx7ZiHzLipws3AkycqKtd26Ud6/P9jZ\nYaGUz03t6Emc0HkZLZHTarVUVFSg0WjQarVUVlai1WqxtbVlxowZvP3225SVlXHkyBF27NjRorMe\nV65cWW/uXxAEoaXEZ4nhdcSYpxel813sd5RVlwHgfaOQefFKXCwciLexYaOfH1UDBoCtLTYqFYs8\nPelubW3kXjdNR4y3KauJd3R0NCtXrmzxfYyWyL3zzjvY2NjwwQcfsH79eqytrfV7Wf3f//0f5eXl\nuLu7s2DBAj7//HN69erV7GesXLlSDBULgiAIbSKlIIW1sWup0MjbOnVLLWDuFRVO5vacsbdnq58f\n2v79wdoaRzMzFnt64l1niyFBuJfIyMhWJXJGX+zQXsRiB0HoOMSfOaGzS8xLZHPcZqp18t6ZAdfz\nmZlogZ25LUccHdnv7Q0REWBpiau5OQs9PXE0M3oZutCJdNrFDsagFvv3CIJBifNahc4sISeBLfFb\n0EryArEeifk8kWyBjYUtv6nVHPf2hr59wcICb0tLFohzUwUDajSRa2pNmqWlJV999VWbdagt1Uyt\nNpxezcvLM06HTJxYum5YIt6GJeJteB0h5nHZcWy7vA2dJK/gD72ax+Op1lhaWPOTqysxnp5yEmdu\nTndra+a6u2OpNPo6whbpCPHuSmriHR0d3ar6xEYTuS1btvDmm28+cHryo48+6tCJnCAIgiC0RMzN\nGH668hMSEkgSfa7kMznDBpWFNZvd3Ejw9IQ+fcDMjF62tswU56YKLVAz4LRq1aoWvb7RGrmgoCCS\nkpIeeIOQkBASEhJa9PD2JGpyBEEQhJY6nXGaX679Il9IEv0v5TMpyxbJwppN7u6keHjISZxKxQB7\ne6a4uKAUJTtCK7Q0b+mSix0EQRAEoTHHbxxnT9Ie+UKSGHwxj4dv21NtbsV6Dw+yPD0hPByUSkY6\nOvKQqLsW2kBL85YWjQEnJye3+mwwwfSIPYgMS8TbsES8Dc/QMZckiUOph+olccNj83jktgNlljZ8\n4+VFlre3Pol72NmZh52dTSaJEz/jhtVW8W5SIjd37lyOHTsGwLfffktYWBi9e/fusLVxgiAIgtAc\nkiSx//p+oq5HAaDQSYw+l8uEPEcKrGz4xtOTXG9vCAtDoVIxzdWVkY6ORu61IDRxatXNzY2MjAws\nLCwIDw/n3//+N05OTjz++OP1jtLqSBQKBStWrLjnqlVBEARBqCFJEr8m/srJjJMAKLQ6Is/lM6rY\niSxrGza4u1Pu7Q0hIaiUyk5xbqrQedSsWl21alX71cg5OTlRUFBARkYGQ4YMISMjAwB7e3uKi4ub\n32sDEDVygiAIwoPoJB07r+7kXNY5AJRaHRPO5jO8VM11axs2u7tT5eMDPXtioVQy192dwE5y5FZT\nJSSksm9fEtXVSszNdTz0UBAhIf7G7laX0641chEREbz//vusXr2ayZMnA5Ceno6jGFYW6hD1FYYl\n4m1YIt6G194x10k6frzyY20Sp9Ey8bScxF2xtWOjhwdV3bpBz57YqFQ84+lpkkncmjWJXLkynkOH\n4Pbt8axZk0hCQqqxu2byDFoj9/XXX3PhwgUqKip45513ADh+/Djz589vk04IgiAIgiFpdVq2XtrK\nhVsXAFBVa5l8qoAh5c6ct3fgBzc3tH5+EByMw51zU31M8NzUffuSKC6eQFwcXL8OeXlgaTmB/fsf\nvP2Y0DGI7UcEQRCELkWj07A5bjPX8q4BYFalYerpIvpUqTnm5MQ+tRoCAsDf3+TPTX3jjWhOnoyk\n5q9LGxsYPBjU6mhefjnSqH3ratr9rNXDhw9z/vx5iouL9Q9TKBS8+eabzX6ooTR2RJcgCILQNVVp\nq9gUt4nk/GQAzCuqeeJMCb2q1exzduaYoyMEBkK3bnhbWjLfwwNbEz03NT4eLl7U6ZM4a2v5tDGF\nAiwsdMbtXBfS2iO6mjQit2zZMrZs2cLo0aOxblAfsG7duhY/vD2JETnDE+f0GZaIt2GJeBteW8e8\nQlPBxosbSStMA8C8vIpZZ8oI1jiyw82NGDs7CA4GH59Of27qg8TFwbZtkJ2dSkxMIvb2E1Cro+nZ\nM5LKyv0sWhQsFjy0s4Y/3+06Ird+/Xri4+Px9vZu9gMEQRAEwdjKq8tZd2EdmcWZAFiWVvLk2XIC\nJDU/eLhxxcYGevYELy9CbWyY5eZmsuemXrgA27eDJIGrqz+RkaBWR3H9+gXc3XVMmCCSuM6kSSNy\nffv2JSoqCldXV0P0qU2IETlBEAQBoLSqlLWxa7lVegsAq5IK5p6txAsnvvfwIMXKCkJDwcOD/vb2\nTDXhc1NjYuCnn9BPp7q5wTPPgJ2dcfsltPNZq6dPn+a9995j3rx5eHh41PvamDFjmv1QQxCJnCAI\nglBUWcTa2LXklOUAYF1Uzrxz1Tgrndjg4UGmlRX06gVuboxwdORhEz439dw52LGjNolzd5eTOLG3\nccfQrlOrZ8+eZdeuXRw+fPiuGrkbN240+6GCaRI1RIYl4m1YIt6G19qYF1QU8F3Md+RX5ANgW1DG\n/Bgttiq1fOSWhQWEhYGLCw+p1Yxycmqjnnc8Z87Azp21156e8PTT8irVGuJn3LDaKt5NSuTeeust\ndu7cycMPP9zqBwqCIAhCe8sty+W72O8oqiwCwD6vlAWxEkoLZ7728KDIwgLCw1E4OzPFxYWB9vZG\n7nH7OXUKdu2qvfbykpM4E9vbuMtq0tSqn58fiYmJWFhYGKJPbUJMrQqCIHRN2aXZrI1dS0lVCQDq\n3DLmXdBRZenMBg8Pyu4kcSq1mplubvQ24bnFEyfg119rr318YMECkcR1RO16RNfq1at5+eWXycrK\nQqfT1fuvI1u5cqU4VkcQBKELySrOYk3MGn0S53K7lIWxEsXWrnzn6UmZpSX07YuFszPzPTxMOok7\ndqx+EufrCwsXiiSuo4mOjmblypUtfn2TRuSUjSzBVigUaLXaFj+8PYkROcMT9RWGJeJtWCLeG3SW\nqAAAIABJREFUhtfcmN8ovMGGixuo0FQA4H6rlHlxkGXvxlY3N7QWFtC3LzaOjsz38DDJI7dqHDkC\n+/bVXvv5wfz5cL+3LH7GDcug+8glJyc3+8aCIAiCYCgpBSlsvLiRKm0VAN5Zpcy9pCDR0Z0dLi5I\nd0biHBwdWejhgVsnKhVqrkOHICqq9trfX07iTPgtd2nirFVBEAShU0vMS2RT3CY0Og0A3TJKmH1F\nyQW1J3udneVhqL59cbmTxDmZmxu5x+1DkuDgQahbUdS9Ozz1lEjiOoM2r5Fbvnx5k26wYsWKZj9U\nEARBENrClZwrfH/xe30SF5BewpzLKk64+shJnJUV9OuHl1rNYi8vk07iDhyon8QFBsK8eSKJM3WN\njsjZ2dlx4cKF+75YkiQGDhxIQUFBu3SuNcSInOGJ+grDEvE2LBFvw3tQzOOy49h2eRs6SV54F5xS\nzBOJ5uz38OG8vb1c1R8RQYCjI095eJjsuamSJNfDHT1a2xYcDHPmQHPyVvEzbljtXiNXVlZGcHDw\nA29gacLFooIgCELHFHMzhp+u/ISE/Bdf6PVipiRb8IuXL5dtbeXjCvr2JdTJyaTPTZUk+O03OH68\ntq1nT5g9G8yaVAUvdHaiRk4QBEHoVE5nnOaXa7/or8OTinkkxZLt3t24bm0tHxzaty/91Gqmubqa\n7LmpkiRvL3LyZG1bSAg8+aRI4jqjdl212lmtXLmSyMhIMVQsCIJgIo7dOMZvSb/pr/tfLWZMhg2b\nfH3JtLQEe3vo25fhLi48YsLnpkqSfFrD6dO1bb16waxZoFIZr19C80VHR7dqz1sxIie0GVFfYVgi\n3oYl4m14dWMuSRKHUg9xIOUAdxoYklDCkJt2bPLxJcfcHBwdoU8fJri6MsrR0aSTuJ074ezZ2raw\nMJgxo3VJnPgZNyyD7iMnCIIgCMYiSRL7r+/nSNqRmgaGXyohIs+Btb4+FJmZgVqNIjycKe7uJn1u\nqk4HO3bA+fO1bX36wPTpYKJlgMIDiBE5QRAEocOSJIlfE3/lZMbJmgbGxBXTo1DN917elKlU4OKC\nKiyMmSZ+5JZOBz/9BLGxtW0REfD44yKJMwXtOiKXnZ2NtbU19vb2aDQa1q5di0qlYuHChY0e3yUI\ngiAIraGTdOy8upNzWecAUOgkxl0sxqfMlXXenlQpleDmhkXv3szx9CTIhA8R1elg+3a4eLG2rV8/\nmDZNJHFdXZP+90+ZMoXExEQA3nrrLT766CM++eQTXnnllXbtnNC5tKZYU2g+EW/DEvE2nITEBD7d\n9CmPLXuMz3/4nJzMHBRaHQ/HluBS4c5GTy85iXN3xzo8nKe9vEw6idNq4T//qZ/EDRjQ9iNx4mfc\nsNoq3k36Ebh27Rr9+vUDYP369ezatYuoqCg2bdrUJp0QBEEQBJCTuG+jvuWg8iA37W5S5lvGxbjz\nDNt/AyuNJ1vdPdAqFODlhX14OM96eeFrZWXsbrebmiQuPr62bdAgmDoVTHQth9BMTaqRc3V1JT09\nnWvXrjF37lzi4+PRarU4OjpSUlJiiH42m6iREwRB6Hw+2fgJB5UHKaiQTwxSaXTMuFiNhTacjEEj\n5W/y8cGlVy+TPjcV5CTuhx/gypXatiFD4NFHRRJnitq1Rm7SpEnMnj2b3Nxc5syZA8ClS5fw9fVt\n9gMFQRAE4V5ultzkUNohCjzlJM5Mo2NWrIZiu1DOq/3xBejWDa/QUBZ4emJrwhumaTSwZQtcvVrb\nNmwYTJwokjihviZNrX711VdMnjyZpUuX8uabbwKQm5vLypUr27NvQicj6isMS8TbsES821dcdhxf\nn/uaSk0l2qxS1HtuEPD3a8QWe3HK0QsFCvD3x793b57pAknc5s31k7iRI9s/iRM/44bVVvFu0oic\nlZUVzz//fL02sWmgIAiC0Fo6Scf+5P0cvSGf+O5lpcZm80WCbdw45u6LyswORfJNHMY9REjv3sxy\nc8PchJdpVlfDpk2QlFTbNno0jB8vRuKEe2u0Rm7hwoX1v/HOT5AkSfV2y167dm07dq/lFAoFK1as\nEEd0CYIgdFDl1eVsvbSVpPzarCX/66NIRdZcHTeOQhsbufHqNQb5+vL3l14y2XNTAaqq4Pvv4fr1\n2raxYyEyUiRxpqzmiK5Vq1a1qEau0X/WBAUFERwcTHBwME5OTvz4449otVq6deuGVqvlp59+wsnJ\nqVWdb281Z60KgiAIHcutklt8cfYLfRKn0EmMvK4lp9yehKnTqHBSY2lhiaWjE0GDBqFMSzP5JG7j\nxvpJ3Lhx8n8m/LYF5BnO1pSqNTq1WvemjzzyCL/88gujR4/Wtx05coTVq1e3+MGC6RHn9BmWiLdh\niXi3nUu3L/HjlR+p0lYBYFVSwcgEFYk2vlz1LsTWzAwUCgqSk+kfGopfZSW3LSyM3Ov2U1kJGzZA\nWlpt24QJ8pSqIYmfccNqq3g3qUbuxIkTDBs2rF7b0KFDOX78eKs7IAiCIHQNOknHgesHOJx2WN/m\nmlaEOtedKGcPJIUCOysr8pRK3G1s8NNo8K+sJFmjoUdwsBF73n4qKuQk7saN2raHH5YXNwhCUzRp\nH7mxY8cyePBg3nnnHaytrSkrK2PFihWcPHmSQ4cOGaKfzSb2kRMEQeg4KjQV/OfSf7iWdw0ARZUG\nu6vVlFkEoLW4cyqDQkGupSXXc3NxdHfHXKtFUqmwy8vjvx9+mJDAQCO+g7ZXUQHr1kFGRm3bxIkw\nfLjx+iQYT0vzliYlctevX2fevHmcOXMGtVpNfn4+gwYNYuPGjXTv3r1FHW5vIpETBEHoGG6X3mZT\n3CZyy3MBqM7VoLlpg4W1ByrlnW1ErKwI6tuXScHB5KWnsz8+nirAApgQFmZySVx5uZzEZWbWtj36\nKAwdarw+CcbVrolcjbS0NDIzM/Hy8sLf37/ZDzMkkcgZnqivMCwRb8MS8W6ZKzlX2H55O5XaSip0\nKgpv6DAvd0Bt6aTfAUHt7s7EESMIcXSstyuCqca8rAzWroWbN2vbJk+GwYON1ycw3Xh3VA3j3a4n\nO9SwsrLC3d0drVZLcnIyAIEm9q8kQRAEofUkSeJg6kGiU6LRoiCr3IaKG1q8cMDWyhYAC6WSMeHh\nDOvXDzMT3huurtJSOYm7dUu+VihgyhQYONC4/RI6ryaNyP36668sWbKErKys+i9WKNBqte3WudYQ\nI3KCIAjGUampZNvlbVzJTSAbW27lmuN0swxPK1csVPLq0wgrKx56+GHsXVyM3FvDKSmRk7jsbPla\noYBp06B/f+P2S+gY2nVqNTAwkNdee42nn34am5oNGjs4kcgJgiAYXm5ZLt/Hfc/1siKSNU4oM8tw\nK9LgZuOGSqnCu6qKR3v2pNuYMdBFRuEAiovhu+8gJ0e+VijgiScgIsK4/RI6jpbmLU36U1RQUMDz\nzz/faZI4wTjEOX2GJeJtWCLeD3Y19yqfnfmKo2UScaXO2FzNw6dUiYetB44SPF5Zye8mTaJbZGST\nkjhTiXlREaxZUz+JmzGj4yVxphLvzqKt4t2kRG7JkiV88803bfJAQRAEwbRIksSBlIN8ePEXDmtc\nKbulwyvxFl5mTrhZqRlVVMQytZr+zzyDws/P2N01qMJCOYnLlRfsolTCrFnQp49RuyWYkCZNrY4a\nNYpTp07h7++Pp6dn7YsVCrGPnCAIQhdWpa3i8/gd/JqXR2WVAre0HGxLq3G3dadPlZaJpaW4TJwI\nffsau6sGV1AgT6fm58vXNUlc797G7ZfQMbVrjdyaNWsafegzzzzT7IcagkjkBEEQ2ldScTbvxv1G\ncqUGm4JSXG7kYquwIMTckSkFRfRwcYGZM0GtNnZXDS4/X07iCgrka5UKnnwSQkON2y+h4zLIPnKd\niUjkDE/sQWRYIt6GJeJdq1Kn4/sbl9iQeh5NdTXOGXnY55XgYmbD9Eolw0tKUY0ZA2PHtmpBQ2eN\neV6enMQVFsrXKhXMmQM9exq3Xw/SWePdWRl0HzlJkvj2229Zt24dGRkZ+Pr6smDBAp599tl6mzcK\ngiAIpkuSJGJKSvjq+nni85KxKKvEO/U2lpUaxlSrmFVciZ2dHTz7LHSxWrgaublyEldUJF+bmcHc\nuWCiR8UKHUCTRuTeffdd1q5dy6uvvoqfnx9paWl88sknzJ8/nz//+c+G6GezKRQKVqxYQWRkpPgX\nhiAIQitlVFayIyebqIyLZJfewiG7CPXNfHzKSnmm0owQLCE8XN7d1srK2N01ipwcOYkrLpavzczg\nqacgKMi4/RI6tujoaKKjo1m1alX7Ta0GBARw8ODBesdypaamMnr0aNLS0pr9UEMQU6uCIAitV6zR\nsD8/n+MFOcRlx1FRWohrWg4u+YWMzcnmCQsPLK3t5DOm+vaV99bogrKz5c1+S0rka3NzmDcPOuhx\n5EIH1K77yJWVleHq6lqvzcXFhYqKimY/UDBdYg8iwxLxNqyuFm+NTsfRwkI+zcjgQM4NzmaeRcq5\nje+VdIYkJfDCjRs8aeWDpV93+P3v5U3R2jiJ6ywxv3VLHomrSeIsLGDBgs6XxHWWeJuKtop3k2rk\nJk2axIIFC3j//ffx9/cnJSWFt956i4kTJ7ZJJwRBEISOQZIkrpWX82teHrnV1aQXpZOccw3nzDzC\nklMYnJHEIHs/vFwCYPRoeUGDSmXsbhvNzZvySFxZmXxdk8R10RJBwQiaNLVaWFjIsmXL2Lx5M9XV\n1ZibmzN79mw+/fRTnJycDNHPZhNTq4IgCM2TU1XFr3l5JJaXo5V0XM29Sv7tNIKvpjEy6RLdy0oJ\ncwvD0b2bfDRBQICxu2xUWVlyEldeLl9bWspJXLduxu2X0DkZZPsRrVZLTk4Orq6uqDr4v8BEIicI\ngtA0FVotBwsLOVlUhE6SqNBUEpcdh+WNNMadO0ev2xmoLewJcwvDMmKAvKDB2trY3TaqjAxYtw5q\nKoysrGDhQvDxMW6/hM6rXWvkvvvuO2JjY1GpVHh4eKBSqYiNjWXdunXNfqBgukR9hWGJeBuWKcZb\nkiTOFRfzaUYGxwsL0UkSBRUFxKSdpO/JYyzdt5vw7HR8bT2J8BuC5czZ8tEEBkriOmrM09Plkbia\nJM7aGp5+uvMncR013qbKoDVyy5cvJyYmpl6br68vU6dOZeHChW3SEUEQBMFwblRUsDsvj8zKSgAk\nILM4g/LEkzx78DAehQUoUNDDpSdePQeimDULXFyM2+kOIC0NNmyAO2HDxkZO4uqcXikIBtWkqVW1\nWk1OTk696VSNRoOLiwuFNVtXdzBialUQBOFuRRoN+/LzuVCzxBLQSToyci7T49huhsbEowDMleaE\neYTjNGEyjBvXpRc01EhNlZO4qir52tZWTuI8PIzbL8E0tOvJDr169WLr1q3MmTNH37Z9+3Z69erV\n7AcKgiAIhqfR6ThWVMThwkKqdTp9u1ZXhTY5mmm/7MCxQE7u7C3sCQsejtWTT3W+PTTayfXrsHEj\nVFfL13Z2chLn7m7cfglCk0bkjhw5wmOPPcbDDz9MYGAgSUlJ7Nu3j127djFq1ChD9LPZxIic4Ylz\n+gxLxNuwOmu8JUniSlkZv+Xnk1+ThdzhThlm+78m+Nh5lDr589LTzpMeI6ehevwJed7QiDpKzJOS\n4PvvQaORr+3t4ZlnoMH2qp1eR4l3V2HQs1ZHjRrFxYsX2bhxI+np6QwZMoS///3vdBNrrAVBEDqs\n7DvbiSTX7I9xh4eFBb5FiWjW/wN1Ri4AChQEuofgO+d3KAYM6LInNDSUmAibNtUmcQ4OchInygWF\njqLZ24/cunULb2/v9uxTmxAjcoIgdFXlWi3RBQWcLi5GV+dz0FqlYoyjPaXHN6P78T9YVMgjdOZK\nc0L6jMN14XOmN8zUClevwubNoNXK146OchLn7GzcfgmmqV1H5PLz83nxxRfZunUrZmZmlJWV8fPP\nP3Pq1Cn+8pe/NPuhgiAIQtvT3dlOJKqggLKa7AP5L4jB9vYMMpc4v2Ylludi9V+zs7Aj9PEl2E2a\nJhY01JGQAFu21CZxTk5yEqdWG7dfgtBQk/aR+/3vf4+DgwOpqalYWloCMHz4cDZt2tSunRM6F7EH\nkWGJeBtWR493akUFX2RmsjM3t14S193amt97e9Ov4AYXVj9XL4lzdg8g4v99hN3k6R0yiTNWzC9f\nrj8Sp1bDokWmn8R19J9xU2PQfeT2799PVlYW5ubm+jY3Nzeys7PbpBOCIAhCyxRqNPyWl0d8aWm9\ndiczMx5xdqaXtTUJu9eRtW0tZnUSPO/B4+mx6FUUtraG7nKHFh8P//kP1CzsdXaWR+IcHY3bL0Fo\nTJNq5IKDgzl06BDe3t6o1Wry8/NJS0vjkUce4cqVK4boZ7OJGjlBEExZtU7H0cJCjhYV1dtOxFyp\nZLSjI8MdHFCWlnDh36spjDuj/7rSwpLAuf+F77jHxYKGBi5ehO3ba5M4Fxc5iXNwMG6/hK6hXWvk\nli5dyqxZs/jLX/6CTqfj+PHjvPnmmzz//PPNfqAgCILQcpIkcamsjN/y8iisWUp5Rx87Ox5Sq3E0\nM6P0UiyXvnyP0vxb+q8rPL3o+8JqnPx6GLrbHV5sLPz4I9T8PerqKidx9vbG7ZcgPEiTauRef/11\n5syZwx/+8Aeqq6t59tlnefzxx3n55Zfbu39CJyLqKwxLxNuwOkK8b1VV8d3Nm/yQnV0vifOytGSx\nlxcz3dxwBHK2refCR6/VS+KUI0YyfNXXnSqJM1TMY2LqJ3Hu7nJNXFdL4jrCz3hXYtAaOYVCwUsv\nvcRLL73UJg8VBEEQmq5Mq+VAQQFniovrTb3YqFRMUKvpb2eHUqGA7GzSv/07yVeOo5Pk+cEqawuc\n5y1h4KjZKMRU6l3OnYMdO2qTOA8P+cQGUToodBZNqpGLiooiICCAwMBAsrKyeP3111GpVLz//vt4\nGuGk4Ndff53jx48TEBDAN998g5nZ3fmoqJETBKGz00kSp4uLiS4ooLzOQgWlQsEQe3sinZywUqlA\nktCeOknSpn+RmZ+q/74if0/Clr5JULe+xuh+h3fmDOzcWXvt6SkncUY+0ELoolqatzRpavWFF17Q\nJ0uvvPIKGo0GhULBc8891+wHtlZsbCyZmZkcOnSI0NBQtm7davA+CIIgtLfk8nI+z8xkd25uvSQu\nyNqa//L2ZpKLi5zElZZSsX4NF7/9qz6J06mU5IwbyqjX/ymSuEacOlU/ifP2lmviRBIndDZNSuQy\nMzPx8/OjurqaPXv28O9//5vPP/+co0ePtnf/7nL8+HEmTpwIwKRJk4zSB+HeRH2FYYl4G5ah4p1f\nXc3m7GzW3rxJdlWVvt3Z3JynPDxY4OGBm4WF3JiURNH/fsD56E0UVBQAUKK2pejpuUydvxpnm859\njlR7xfz4cdi1q/bax0ceibO2bpfHdRriM8WwDFoj5+DgwM2bN4mPjycsLAx7e3sqKyupbnAAsyHk\n5+fj5eWl71deXp7B+yAIgtDWqnQ6jhQWcqywEE2d6RULpZIxjo4Mc3DATHnn394aDezfz629P5KQ\nm6Cvh0vv7YvfzMWMDhwn6uEacfQo7N1be92tG8yfD1ZWxuuTILRGk0bkli1bxpAhQ5g3bx4vvPAC\nAEePHqVXr14tfvBnn33GoEGDsLKy4tlnn633tby8PKZPn46dnR0BAQF8//33+q85OTlRVFQEQGFh\nIc7i0LsOIzIy0thd6FJEvA2rveItSRIXS0r4LCODQwUF9ZK4CDs7lvn4MMrJqTaJu30b3ZdfkPTL\nei7nXEYn6aiyMufKxEEMWfI2Y4LGm0wS19YxP3y4fhLn5wcLFogkrob4TDGstop3k0bkXn/9dZ54\n4glUKhXBwcEA+Pr68tVXX7X4wT4+Pixfvpw9e/ZQXl5e72svvvgiVlZWZGdnc/78eSZPnkxERAS9\ne/dmxIgRfPzxxyxcuJA9e/YwatSoFvdBEATBmDIrK/k1L4+0iop67T6Wljzq7Ixv3QxDkuDsWap2\n7eRyZiz5FfkA5Po4k/PwSGYNeQZXG3HgfWMOHoQDB2qvAwJg3jyomaUWhM6qSSNyACEhIfokDqBn\nz5706dOnxQ+ePn06jz/+OC4u9Ws4SktL2bZtG++88w42NjaMHDmSxx9/nHXr1gEQERGBh4cHY8aM\n4fLly8ycObPFfRDalqivMCwRb8Nqy3iXarX8nJPDl1lZ9ZI4O5WKJ1xdWerlVT+JKyuDzZsp2baJ\nc2knyK/IR6dScm1IMFVzZvHMqBdNMolri5hLkpzA1U3iuncXSdy9iM8Uw2r3GrnQ0FD98VvdunW7\n5/coFArS0tJa1YGGS22vXr2KmZlZvaQxIiKi3hv+8MMPm3TvRYsWERAQAMhTsv369dMPZdbcT1y3\n3XVMTEyH6o+pX4t4d754jx47llNFRXyzezfVkkTAsGEApJ08SW8bG5ZNmYKlUln/9cnJRP/P/5Cf\nl4mLTTE6ScfxkgpS+/oz97EFjPUfy8GDB40en/a4rtHS148dG0lUFKxbJ18HBEQSFAReXtEcO2b8\n99fRrmt0lP6Y+nVMTAzR0dGkpKTQGo3uI3f48GFGjx5d76H3UtOxllq+fDnp6el8++23+ufOnj2b\nrKws/fd8+eWXbNy4kQN1/0n1AGIfOUEQOpLEsjJ+zcsjp8EisZ42Nkx0dsbF3Lz+C7RaiIpCd/Qo\nKfnJpBWmAZAR6sONoaE80edJQl1DDdX9TkeSYN8+eXFDjeBgmDsX7rH1qCAYXZuftVqTxEH7FkA2\n7LSdnZ1+MUONwsJC7LvaWSmCIJiE3Opq9uTlcbWsrF67i7k5k5yd6XGvjctycmDbNqpvpHI55zJ5\n5XlUWZmTMDIUqWcPloQ/hZutm4HeQecjSfDbb/I2IzV69oTZs0USJ5ieRn+kly9f3mh2WNOuUChY\nvXp1qzrQcHVVz5490Wg0JCYm6qdXY2NjCQ8Pb9VzhPYXHR3drkm/UJ+It2E1N96VOh2HCgo4UVSE\nts7nqKVSyVgnJ4Y6OKBquLpUkuD8edi9m9LSAuKy4yjXlJPn48yVUaH4+4Qxs/dMrMy6xjLLlvyM\nSxL8+iucPFnbFhoKTz4JKlXb9s/UiM8Uw2qreDeayN24ceO+S9hrErmW0mq1VFdXo9Fo0Gq1VFZW\nYmZmhq2tLTNmzODtt9/mq6++4ty5c+zYsYPjdf9p1UQrV64kMjJS/GAKgmAwkiQRW1LCvvx8Suqc\nyKBQKOhvZ8d4Jyfs7jUsVF4OP/8Mly9zu/Q2V3KuUK3QkTwkmPRePoz2H8O47uNQKpQGfDediyTJ\nG/2ePl3b1rs3zJwpkjih44qOjr5vCduDNOms1fawcuXKu0bzVq5cydtvv01+fj6LFy9m7969uLq6\n8te//pW5c+c26/6iRk4QBENLr6hgd14eGZWV9dq7WVnxqLMz3paW937h9euwfTtSYSEpBSmkFqZS\n6mjD5bG9qXRV80ToE4S5hxngHXRekgQ7dsC5c7VtYWEwY4ZI4oTOoaV5S6OJXHJycpNuEBgY2OyH\nGoJI5ARBMJRijYb9+fnElJTUa7c3M+NhtZo+trb3nsHQauV9MY4eRaOt5vLty+SW55IR4k3S4CAc\n7VyZGz4XDzsPA72TzkmnkwczY2Jq2/r0genTQSkGMIVOos0TOWUTfvoVCgXaOlMHHYlI5AxP1FcY\nloi3Yd0r3hqdjpPFxRwsKKBKp9O3qxQKRjg6MtrREYvGPktzc+E//4HMTMqqy4jLjqNQWc2VkSHk\n+rkSpA5iVu9ZWJt33QNAm/IzrtPBTz9BbGxtW0QEPP64SOKaS3ymGFbDeLf5qlVdnQ8lQRAEoZYk\nSVwtL2dPXh55DbYTCb2znYi64XYitS+Wh45274aqKnLKcrh8+zK3vRy4MiqCKhtLRnQbwUOBD4l6\nuAfQ6WD7drh4sbatf3+YOlUkcULXYbQaufamUChYsWKFWOwgCEKbyqmq4te8PBIbHC3oZmHBo87O\nBFrfZwStvBx27oT4eCRJIrUwleSiVJIHBpLe2xdzlQXTQqbRx6Plp+Z0FVotbNsG8fG1bQMHwpQp\nYCJHzQpdRM1ih1WrVrXt1OrEiRPZs2cPUH9PuXovVig4dOhQsx9qCGJqVRCEtpCQnMy++HjKdDpS\nKipQenvj4uur/7qVUsk4tZpB9vZ3bydSV2qqnHkUFqLRabiSc4U08zIujelFiYs9TlZOzAmbg5e9\nlwHeVeem1cLWrXD5cm3b4MHw2GMiiRM6rzafWn366af1v1+yZEmjDxWEGqK+wrBEvNuXRqfj5LVr\nrDl7lqr+/Yk7ehT7gQPRnDlDP0nCzc+PgXZ2jFOrsb3fskitVj6x/fBhkCTKq8u5mH2RxEAnEgf3\nQmemortTd54MexIb83tsDtyF3bMuUQM//AAJCbVtQ4fCpEkiiWst8ZliWO2+j9z8+fP1v1+0aFGr\nHyQIgtARVep05FRXc7uqSv61upqc6mryNRpOHD9OWUQEVFToN/U1GzSIgvh4/jx0KJ6NbSdSIy9P\nHoVLT5cvy/OILbpG/OggcvzkQ+6H+Q7jkaBHRD1cE2g0sGULXL1a2zZ8ODzyiEjihK6ryTVyhw4d\n4vz585SWlgK1GwK/+eab7drBlhJTq4Ig1JAkiVKttl6iVvNrkUbT6OtOHDpERd+++mtLpZIgKyt6\nXL3KH6dOvd8D5WWUu3ZBVRWSJHGj6AbnLPO5PDqUSltLzJRmTO05lQjPiLZ8qyaruho2b4bExNq2\nkSPhoYdEEieYhjafWq1r2bJlbNmyhdGjR2N9v0LeDkac7CAIXYskSRRoNPdM2MqbuVWSQqHATqHA\nxtwcG6USO5UKN3NzVAoF9x2Hq6iQFzTExQGg1Wm5nH+Vkz1tuRHeFxQKHCwdmBs+F29775a/2S6k\nuho2bYKkpNq2MWNg3DiRxAmdn0FOdlCr1cTHx+Pt3Xk+dMSInOGJ+grD6srx1koSuQ3Sp/j9AAAg\nAElEQVQStdtVVeRqNFQ3c+sklUKBs7k5bubmuNb51dXcnOSUFNacO4flwIGknDhBwLBhVJ49y6IB\nAwi512boaWnyVGpBAQDl1eWcqbzOqWHdKHa1B8Df0Z8nw57EzsKu1XEwddHR0YwYEcn338uHX9SI\njISxY0US19a68meKMbT7PnJ1devWDQsLi2bfXBAEoTVq6tca1rDlazTomvmBZ6FU1kvUan5V3xll\nu5eQwEAWAfvj4si5fh13Ozsm3CuJ0+nkBQ2HDsnTqkB+eT5R6gIuRYagNZcXQwzxGcLEoImolOLM\nqKaoroYNG+QFvzXGj5dH4wRBkDVpRO706dO89957zJs3Dw+P+kfFjOmgf6LEiJwgdA6SJFGm0921\n2OD2A+rXGmOrUtVP2CwscDU3x0Glap+V9vn58ijcjRuA/H7Sqm6zM0TB7QA3AFQKFZN7TmaA14C2\nf74JSkhIZffuJE6cUFJUpCMwMAhXV38eeghGjTJ27wShfbTriNzZs2fZtWsXhw8fvqtG7sadDy9B\nEIT7kSSJQo3mrtq12y2oXwNwMjOrl6jVJG42hjwh/cIF+OUXqKwE5Hq485b57B3sQKWdFQD2FvbM\nCZ+Dr4Pv/e4k3JGQkMpXXyWSkDCBoiK5LSZmPy++CKNG+Ru3c4LQATUpkXvrrbfYuXMnDz/8cHv3\nR+jERH2FYXXUeGslibx7LDbIqa5udv2aUqHApcFUqJu5OS7m5o2fYdpO6sW7okJekXrhgv7r5boq\nfvOrJibQBUkpj/x1c+jG7LDZ2FvaG7SvndmuXUlcuTKB4mIoKIjGySmS0NAJ5OdHASKRa08d9TPF\nVLX7PnJ12draMnbs2FY/zNDEqlVBaD9VNfuvNahhy2uD+rWa39+vfs1obtyQD7u/s6ABINdKYnOo\ngmwnW33bQK+BPNrjUcyUTfqYFYCyMjh2TElxcW1bjx7g4wNVVWKfPcE0GWTV6po1azh16hTLly+/\nq0ZO2UFPJhY1coLQNvT7rzWoYStsQf2azZ0tPGoStXavX2sDqQkJJO3bh7KyEl1aGkFaLf4uLoA8\nXXzNz44t/sVozOTPQpVCxaM9HmWQ9yBjdrvTKS2Fdevg55+jKCsbD0DPnlCzWYK7exQvvDDeiD0U\nhPbV0rylSYlcY8maQqFA24LaFkMQiZwgNF1N/dq99l8ra4P6tZrEzaD1a20gNSGBxDVrmKDTwZUr\nUFjIfo2G4H798PXxJjrcjsP2efrvt7OwY3bYbPwc/YzY686ntBS++w6ysyEnJ5XY2ER6956A151j\nZysr97NoUTAhIWJqVTBd7ZrIpaSkNPq1gICAZj/UEEQiZ3iivsKwWhLvmvq1eyVsnbl+rc1JEmRl\nEfXBB4xPTobiYqILCoh0cgLgVy8Psn4/glQpX/8SH3sf5oTPwcHSwVi97pSKi2HtWrh9W75WKKBv\n31SyspK4dOkCvXv3ZcKEIJHEGYD4DDcsg+4j11GTNUEQ7q2q7v5rdWrYWlO/1jBh65D1a61RVQXJ\nyfJBnteuQXExyoQEeWFDDYWCEi9XjrmUoqyTxPX37M/knpNFPVwzFRXJI3G5ufK1QgEzZkCfPv6A\nP9HRSpFYCMIDNPms1c5GjMgJpiohOZl98fFUAzqdjn4hITj6+NSrYWuL+rWaqdGOXL/WaoWFcuJ2\n9ap8dECDuEWdOsX4sjJQKJCcnLjlak1CdRY/O9lg/8RglAolk4InMdh7sOnGqJ0UFspJXN6dmWml\nEmbOhLAw4/ZLEIylXadWOyORyAmGIEkSWklCC2hqfi9J+t9r7nytblvd9nu9pm57w6+np6Vx+NIl\nlAMGUKHTUS1JaM6coV9ICK7dujWpz45mZndtltsZ69daRJIgI0NO3BIS4Natxr/XxoZUa2tOHzmE\nX1UhWeW3KakqIdbeAd3M4XgEyUdtBTgFGKz7pqKgQE7i8u8MaiqVMGsW9O5t3H4JgjG169RqZyW2\nHzGMmhGiyxcv0qtPHx4KC7v3OZStUDdhuitRMmAida97GdKpS5coi4gArZaCM2dwGjQIs0GDuB4b\nWy+RUyoUOJuZ3bVZrqsp1K81V2WlPGWakCBPmZaWNv697u7yUsmQEPDxoTzpKjtuHqE0M5PbRfk4\n+NiQaysx0cGN5wY+h6OVo+Heh4nIz5eTuJrdW1QqePJJCA29+3tFzZZhiXgbVk28W7v9iMknckL7\nupKUxN9OnsRs4EDS8/Op7NGDk8eOMbG4GB8/vzZNpATQNZi+UyoU2CiVuFlZMV6t1idszqZWv9Zc\n+fm1U6YpKdDYyluVCrp3l5O3Hj1ArdZ/Ka0wjb/8/BfSe9yCHq4UXjFDEepEN1sPnMudRRLXAnl5\nsGYN+hMbVCqYM0cOvyB0VTUDTqtWrWrR65uUyCUnJ/PWW28RExNDSUmJvl2hUJCWltaiBwumYf+l\nSyT16oVUVgZ9+nCtvBzCwth4/jyDHbrG6j2VQoFKocCs7q932mva6rbf1Xaf9ob3Utjbk29nh1Kh\nwGL8eCyVShSAu60tY+6sqOySdDpIT6+dMq1ZAnkvtrZy5tCzJwQGgqVlvS9nFmcSdT2KxLxEcspz\n9O3qUDVBzkH42PugvdUxt13qyHJy5JG4ms1+zcxg7lwIDm78NWJ0yLBEvA2rreLdpERu3rx5BAcH\n8/HHH9911qrQtVVz73l9bTuMBt0v+blXwnRXQtTERKo591IpFAYtcp/brx9rzp3DcuBAfVvl2bNM\nGNAFD2OvqICkJDlxS0yUjwVojKdn7ZSpt7e8PLKB7NJsDlw/wOWcy/o2JUoUKPCy98LP0Q8rM/n8\nVAulRZu/HVN2+7acxNWMA5ibw1NPyXm0IAit06RE7tKlSxw9ehRVVyiGFprFHHA3N0cCbp86hefQ\noSgBtZUVY52cmpxIPWgUy9AJU0cVEhjIImB/XByXLl6kd58+TBgwoM1rEjus3NzaKdPUVHkk7l7M\nzOQp05AQecrUsfFp0NyyXKJToonLjkOi9h8kChQ8OvhRkpOScQxwJCUmhYB+AVReq2TCuAlt/c5M\nVna2nMTVlCaam8P8+dCUXa1EzZZhiXgblkHPWh0zZgznz59n0CBx5IxQ30NhYaTfGSGytrIiwNqa\nyrNnWTR4MCF16o2EthMSGEhIYCDR9vam/6Gr1cpnm9Ykbzk5jX+vvX3tlGn37mBx/1GzgooCDqYc\nJPZWLDqpfkIY5hZGZEAkbrZuJCQmsP/cfnLycnDPdmfCuAmEBIe0xbszeTdvypv91gyWWljISZy/\n2NtXENpMk7YfefHFF9m8eTMzZsyod9aqQqFg9erV7drBlhLbjxhOQnIy++PjqQIsgAntsGpV6ELK\ny+Wp0pop07ob8jbk7V2bvHl53XPKtKHiymIOpx3mbOZZtFL9WreeLj0Z3308nnaerX0XXV5WlpzE\nlZfL15aWsGABNHGXHEHoctp1+5HS0lKmTJlCdXU16enpgLwdhJjqEqB2hEgQWkSS5JG2mlG3Gzca\nnzI1N5cLq2qmTO3tm/yY/9/enYdFWe7/A3/PsO+LAgKyqARqpJSlaYoImllaaWVa4kKn+qb1q07L\nOS0qHu3q6nvazmnzHMtySTRbvqUtWsAorrQgleICCijuIjuyzDy/Px5hGBYdhpn7meX9ui6ufO5n\nmOfDp4k+Pvfnue+6pjrsKN2B3LJcNOsMF/7tH9Af46LHIcKPVYY5lJUBa9boa3B3dyA1FQgPVzYu\nIntkVCH3ySefWDgMy+A6cmKxv0Ism863Viv3uLUUb+XlXb/Wz09/1y06Wi7muuFS8yXsOr4Le07s\nQaO20eBchG8Ekvslo19Av6u+j03nW6Djx4G1a+Xl+wDAw0Mu4sLCuv9ezLlYzLdYFl9Hrri4uHWP\n1aNHj3b5Bv2t+E4M15EjsiK1tfop06Ii/f/p21Op5Fs3LcVbSIhRU6btNWobsffEXuw8vhOXmg2n\nZ0O9Q5HcLxkxgTGcWTCj0lK5iGu8XC97egKzZ8sPDRNR53q6jlyXPXI+Pj6ovrzgj7qLleBVKhW0\nXS20qTD2yBEpTJLkRxZb7rqdOCGPdcbVFRgwQJ4yjYkBvL1Nvmyzrhm/nPwFOSU5qG0y3MUhyDMI\nyf2SMbD3QBZwZlZcDKxbpy/ivLzkIq5NWzURXQH3Wm2HhRyRApqb5f+jtxRvLfswdcbfXy7cYmPl\nxxide7bRjFanRd7pPGwv2Y6qhiqDc4EegUiKTkJ8cDzUKgfbokyAY8fkIq6pST729gbmzAGCgpSN\ni8iWcK9VUhz7K8SymnzX1Mh7mB46JO9p2tjY+etUKvmRxZYp06Agk6ZM29NJOvx+5ndsK96Gi5cu\nGpzzc/PD2OixGBoyFE7qnq2DaTX5tjJFRUBGhlzDA/LzJ3PmAL179/y9mXOxmG+xhK4jR0TUSpLk\nBcJa7rqVlXX9Wjc3eaq0ZcrU09OMYUg4cO4Asouzcb7OcH05b1dvJEYl4obQG+Cs5q85SzlyBNiw\nQV/E+frKRVyvXsrGReRIOLVKRFfX1CTPn7UUb1VVXb82MFA/ZRoZKe+MbkaSJOHwhcPILs7G6ZrT\nBuc8nD0wOnI0hocPh4tT955upe45dAj47DP5AWRAfrh47lyA64ATmYZTq0RkXlVV+inTY8f0DVDt\nqdVywdYyZdqrl1mmTNuTJAnHKo4h61gWTlSdMDjn5uSGURGjcHPfm+Hm7Gb2a5OhggJg40b9cn/+\n/nIR5++vaFhEDqnbhZyu3UKdXT3RSo6H/RVimT3fkiQvx3/okHzX7dSprl/r4SFPlcbGyv/08DBf\nHJ0orSxF1rEsFFcUG4y7qF0wou8I3BJxCzxcLBsDP9+y/fuBL77QF3GBgfJ06hW2szUZcy4W8y2W\n0B65X3/9FY8//jjy8/Nxqc12Oda8/AgRGaGxUX5AoWXKtKam69f27q2fMo2IkO/EWdjJ6pPIOpaF\nwvJCg3EnlRNuCr8JoyNHw9vV9KVKqHv++AP46it9Ederl1zE+foqGxeRIzOqRy4+Ph533nknZs2a\nBc92zcotiwZbG/bIEXWhslJfuB07pu9Ub0+tlndSaJkyDQwUFuLZ2rPIPpaNgvMFhiGp1Li+z/VI\njEqEn7sFbgFRl/Lzgf/7P/1SgL17y0VcN3ZJI6IrsOg6cr6+vqisrLSpBTRZyBFdptMBJ0/qp0zP\nnOn6tZ6e8h6msbHyAr3u7uLiBHCh7gI0xRr8efZPSND/96uCCkNChmBs9FgEeogrKEmWlwd8842+\niAsOlhf77cG6zUTUjkUfdpg6dSq2bNmC2267rdsXUBL3WhWL/RViXTHfDQ3yAl+HD8sPLNTWdv46\nQP6/cmysPG0aHi5kyrS9iksV2F6yHftO74NOMuzDvTboWiRFJyHIS9nVZR318/3rr8CmTfrjkBC5\niPPysvy1HTXnSmG+xbL4Xqtt1dfXY+rUqRgzZgxC2uy3olKpsHr1apMvbmnca5UcysWL+inT4mL9\nuhDtOTkB/frpp0wVfNSwuqEaOaU5+PXkr9BKhvHG9orFuOhxCPUJVSg6+vln4Ntv9cehoUBqqlmX\nAyRyeBbba7WtrgoilUqFxYsXm3RhS+PUKtmrkkOHUPTTT1A3NEBXW4sB4eGIqq8Hzp3r+pu8vPSF\nW//+8kK9CqprqsOO0h3ILctFs86wR69/QH+Mix6HCL8IhaIjANi7F/j+e/1xWJhcxFn4AWUih8W9\nVtthIUdWT6uVnxptapL/2fbP7f95+c8lR4+icOtWpKhU8kMLzc3IbG5GTEICotrvidSnj37KNCzM\nImu7ddel5kvYfXw3dp/YjUat4VZeEb4RSO6XjH4B/RSKjlrs2gVs3ao/7tsXmDVLeMskkUOx+ILA\n2dnZWL16NcrKytC3b1/MmjULycnJ3b4g2S+77K9oX2x1UWAZfa7tn9utyWiMotxcpNTVAQA0FRVI\n8vdHirMzso4dQ1SfPvLdtthY+YEFSyzsZaJGbSP2ntiLXcd3ob653uBcqHcokvslIyYwxqofqLLL\nz3cnduwAfvpJfxwZCTz4oDI3cR0l59aC+RZL6DpyH374IV588UX85S9/wYgRI1BaWooHHngA//jH\nP/DII4/0OAiiHtFqe15gdXXOytZJVLcv/lxdgV69oI6OBp5/Xj62Is26Zvxy8hfklOSgtsnwgYsg\nzyAk90vGwN4DrbqAcyTbtgHZ2frjqCi5iLOyjxURtWHU1Oo111yDzz//HEOHDm0d+/333zFt2jQU\nFhZe4TuVw6lVcVp7tpqaoHNxwYDx4xEVF2f4Ip3OvAVW239aWbFlNLUacHGR/y/Z/p+djbm4IOvr\nr5FcXS1/r4eHvP6DSoWs4GAkz5+v9E/USqvTIu90HraXbEdVg+G+rIEegUiKTkJ8cDzUKu4MYw0k\nCdBo5EKuRb9+wMyZLOKIRLHo1Gp5eTkGDRpkMBYXF4eLFy92+4JkX0oKClD48stIUavlgkqrRebm\nzcCwYYgKDLT9YkulumJh1aNzTk7d7lsbEBSEzE8+QUqbea7MhgbEpKSY+yc3iU7S4Y8zf0BTrMHF\nS4a/H/zc/DA2eiyGhgyFk9pJoQipPUkCsrKAnBz92IABwIwZ8keViKybUXfk7rzzTkRGRuK1116D\nl5cXampq8MILL6C4uBib2i4wZEV4R06MrHffRfIXXwCS1NqzBQBZXl5IvukmMUG0FFs9LazMVGxZ\nWsmhQyjKzMTvBw5gyODBGJCS0vEOqGCSJOHAuQPILs7G+brzBue8Xb0xJnIMhoUNg7O629s7Ww17\n7B+SJODHH+WHG1rExMhFnLMV/Kuyx5xbM+ZbrPb5tugdueXLl2PGjBnw8/NDYGAgysvLMWrUKGRk\nZHT7gmRf1M3N8jRfuztu6vZ34NoXW+Ysuqyw2LKkqLg4RMXFQW0Fv3QlScLhC4eRXZyN0zWnDc55\nOHtgdORoDA8fDhcn3tqxNpIEbNkC7NmjH4uNBaZPt44ijoiM063lR44fP46TJ08iLCwMERHWvcYT\n78iJkfXee0jev18+cHKSv9RqZIWEIPnRR/VFl4MVW/ZOkiQcqziGrGNZOFF1wuCcm5MbRkWMws19\nb4abs7Lr1VHnJEleIy43Vz82cCBw333yf6pEJJ7Z15GTJKn1STLdFZZJUCuwnY8xWMiJUXLoEAo7\n69maO1fx6T6yjNLKUmQdy0JxRbHBuIvaBSP6jsCoiFHwdOHS/9ZKkoDNm+Wtt1oMHgzccw+LOCIl\nmVq3dFmF+fr6tv7Z2dm50y8XdsI6vKi4OMTMnYus4GC8ff48soKDWcQJ0pO9+Uxxsvok1v6+Fivz\nVhoUcU4qJ9zc92Y8efOTGN9/vN0WcaLzbQmSBHzzjWERFx8P3HuvdRZx9pBzW8J8i2WufHfZCbG/\nZboMwNGjR81yMbJP1tSzReZ3tvYsso9lo+B8gcG4WqXG9X2uR2JUIvzcrWfxYeqcTgd8/TWQn68f\nGzIEuPtuuc2ViGyTUT1yr7/+Op599tkO42+++Sb++te/WiSwnuLUKlHPXKi7AE2xBn+e/RMS9P8t\nqaDCkJAhGBs9FoEegQpGSMbS6YCvvgL++EM/lpAA3Hknizgia2HRvVZ9fHxQXV3dYTwgIMBq15JT\nqVRYvHgxkpKSeJeIqBsqL1ViW8k27Du9DzrJsD/22qBrkRSdhCCvIIWio+7SaoEvvwTaTLJg2DBg\n8mQ+f0RkDTQaDTQaDZYsWWL+Qi4rKwuSJGHKlCnYvHmzwbmioiIsW7YMJSUl3Y9aAN6RE49rEIll\n7nxXN1QjpzQHv578FVrJcPmY2F6xGBc9DqE+oWa7nq2xxc+3Vgt8/jlQ0GZW/KabgNtvt40izhZz\nbsuYb7GErCOXlpYGlUqFhoYGPPTQQwYXCwkJwTvvvNPtCxKRdalrqsPO0p3ILctFk67J4Fz/gP4Y\nFz0OEX7WvdwQddTcDGzcCBw6pB8bMQK47TbbKOKIyDhGTa2mpqZizZo1IuIxG96RI7qyS82XsPv4\nbuw5sQcN2gaDcxG+EUjul4x+Af0Uio56orkZ2LABOHJEPzZyJHDrrSziiKyVRXvkbBELOaLONWob\nsffEXuw6vgv1zfUG50K9Q5HcLxkxgTGt60iSbWlqAtavB4qK9GOjRwMpKSziiKyZ2deRa6uyshJP\nP/00brjhBkRFRSEiIgIRERGIjIzs9gXJfnENIrG6m+9mXTP2nNiDf+35FzKPZRoUcUGeQbj/2vvx\nyLBHcE2va1jEdcIWPt9NTUBGhmERl5hou0WcLeTcnjDfYll8Hbm2FixYgOPHj2PRokWt06z//Oc/\ncc8995glCCKyHK1Oi7zTedhesh1VDVUG5wI9ApEUnYT44HioVVyHwpY1NgLr1gHFxfqxceOAsWMV\nC4mIBDBqajUoKAgFBQXo3bs3/Pz8UFlZibKyMkyZMgW//fabiDi7jVOr5Oh0kg5/nPkDmmINLl4y\nXCbIz80PY6PHYmjIUDiprXBJf+qWhgbg00+B0lL9WEoKMGaMcjERUfdY5KnVFpIkwc9PXrndx8cH\nFRUVCA0NxZG2nbREZBUkScKBcweQXZyN83XnDc55u3pjTOQYDAsbBme1Uf/5k5W7dEku4o4f149N\nmADccotyMRGROEbNpQwZMgTbt28HAIwePRoLFizA//zP/yCO+2lSG+yvEKt9viVJwuELh/GfX/+D\njQc2GhRxHs4emNB/Ap4c8SRG9B3BIs4E1vj5vnQJWLPGsIibONF+ijhrzLk9Y77FEtojt2LFitY/\n/+tf/8KLL76IyspKrF692ixBEJHpJEnCsYpjyDqWhRNVJwzOuTm5YVTEKNzc92a4ObspFCFZQn09\nsHo1cOqUfuz224Hhw5WLiYjEM6pHbu/evRgxYkSH8dzcXAy30t8a7JEje3Wo8BB++vUnNElNqL5U\nDefezmjwNlwHzkXtghF9R2BUxCh4ungqFClZSl2dXMSdPq0fmzwZuPFG5WIiop5RZK/VwMBAlJeX\nd/uiIrCQI3t08MhBfJj5IZqjm1FaWYry+nI0FzYjYXACeof1hpPKCTeG3YgxUWPg7eqtdLhkAbW1\nchF35ox8rFIBU6YAN9ygbFxE1DMWedhBp9O1vqlOZ7h5dlFREZyd2WdDetynz3RanRY1jTWoaaxB\ndWO1/s8N1QZjmZmZqO1bC5wGKg5WwH+gP5xjnHHs6DFMHDYRiVGJ8HP3U/rHsUvW8PmuqQFWrQLO\nnZOPVSrgrruAhARFw7IYa8i5I2G+xTJXvq9YibUt1NoXbWq1Gi+99FKPAyCyZw3NDR0KtJbirO1Y\nXVOdUe+nhbbDWIhXCIZEDsGUuCnmDp+sSHW1XMSdv/wMi0oFTJ0KDBmibFxEpKwrTq0WX15ZMjEx\nETk5Oa1351QqFYKCguDpab29N5xaJUuRJAl1TXVd3j1rO96obTTrtXN35KIxshGuTq7wcfVBpF8k\nvFy9EHw2GPOnzzfrtch6VFbKRVxLJ4taDUybBsTHKxsXEZmPRaZWo6OjAQClbVeZJLJTxk5v1jTW\nQCfprv6G3aCCCl6uXvBx9YG3qze8Xb3h4yb/ue1YWWgZPt3+Kdyu0T+B2nCkASnjUswaD1mPigq5\niLt4eU1ntRq4915g8GBl4yIi62DUww6pqakdv/Hyxn3WugQJ78iJZ639Feae3uwOZ7WzQTHWUpy1\nH/N08TR6i6xDhYeQ+VsmDvx5AIPjByPlhhTExXBNR0tT4vN98aJcxFVUyMdOTsB99wEDBwoNQzHW\n+jvFXjHfYrXPt0V3dhgwYIDBBU6fPo0vvvgCDz74YLcvSGQOSk5vAoC7s7tRBZqbk5vZN6CPi4lD\nXEwcNMH8pWvPysuBTz4Bqi5vj+vkBNx/PxAbq2hYRGRljLoj15lffvkF6enp2Lx5s7ljMgvekbNN\ntjC96e3qDRcnF7Nem6itCxfkIq5l1SdnZ2DGDCAmRtGwiMiCLLqOXGeam5sREBDQ6fpy1oCFnDht\nF6h1Ublg/LDxHab6rGl6s6sCzcvVy+jpTSJLOXdOnk6tqZGPXVyAmTOB/v2VjYuILMuiU6uZmZkG\n00O1tbVYv349rr322m5fsKeqqqowfvx4FBQUYO/evRjMjl9FFRwpwAdbPwD6A8X7itF7cG9s/2I7\nRg0dBd8QX8WnN71dveHu7G726U1rwH4WsUTk++xZuYirrZWPXVyABx8ELj935nD4GReL+RZLyDpy\nLR566CGD/xF6eXkhISEBGRkZPQ6guzw9PfHdd9/hueee4x03K7D1l6343et34AxQUVmBqotVQIg8\nftPom7r9fi3Tm8YUaJzeJHty+rS8Y0Pd5ZvSrq5yERcVpWxcRGTdjCrkWtaTswbOzs7o3bu30mHQ\nZZJKgpPKCVpJC/+B/q3j7ReuvdL0ZttxTm8aj39zFsuS+T51Si7i6uvlYzc3YNYsICLCYpe0CfyM\ni8V8i2WufBu9x1ZFRQW+/fZbnDx5EmFhYbj99tsREBBgliDIdrmoXODn7gedpIOrkytcnVzh5uSG\nkKYQzBk6x+6nN4l6qqwMWLMGuHRJPnZ3l4u4vn2VjYuIbINRtz6ysrIQHR2Nf//73/j555/x73//\nG9HR0fjpp5+6dbF3330XN954I9zd3TFv3jyDc+Xl5Zg6dSq8vb0RHR1tMG371ltvYdy4cXjjjTcM\nvoeFgfLGDxuPuKo4JPRJgGeZJ2ICYxB8Nhhzxs1Bv4B+CPIKgoeLB/9dWYBGo1E6BIdiiXyfOCHf\niWsp4jw8gNmzWcS14GdcLOZbLHPl26g7cgsWLMB///tfTJ8+vXVs48aNePzxx3Hw4EGjLxYeHo6F\nCxdiy5YtqG+ZQ2hzDXd3d5w9exZ5eXm44447MHToUAwePBhPP/00nn766Q7vxx455cXFxGEu5iLz\nt0ycLz+P4LPBSBnHBWqJrqa0FPj0U6ChQT729ARSU4HQUGXjIiLbYtTyI/7+/isKHnQAACAASURB\nVLhw4QKcnJxax5qamhAUFISKliXHu2HhwoU4ceIEPv74YwDyU7CBgYHYv38/Yi4vlDRnzhyEhYXh\n1Vdf7fD9t99+O/Lz8xEVFYVHH30Uc+bM6fiDqVSYM2dO6zZj/v7+SEhIaJ2TbqmEecxjHvNY9PH6\n9Rr89BPQt698fOqUBhMnAtOmWUd8POYxjy1/3PLnlucQVq1aZbl15J544gnExMTgySefbB3797//\njSNHjuCdd97p9kVffvlllJWVtRZyeXl5GD16NGpbnrkH8Oabb0Kj0eCbb77p9vsDXEeOiKzTsWPA\nunVAU5N87O0tT6cGBysbFxEpy9S6RW3Mi3777Tc8++yzCA8Px/DhwxEeHo5nnnkGeXl5GDNmDMaM\nGYPExMRuBdtWTU0NfH19DcZ8fHysdrFh6lzbv2WQ5THfYpkj30VF8nRqSxHn4wPMncsiriv8jIvF\nfItlrnwb1SP38MMP4+GHH77ia7rTzN6+4vT29kZVy4aCl1VWVsLHx8fo9yQismZHjgAbNgDNzfKx\nry8wZw7Qq5eycRGRbTOqkJs7d65ZL9q+6IuNjUVzczMKCwtbe+Ty8/MRHx/fo+ukp6cjKSmpdV6a\nLIt5Fov5Fqsn+T50CPjsM0B7eXlFPz+5iAsMNE9s9oqfcbGYb7Ha9sz15O6c0Xutbt++HXl5ea19\nbJIkQaVS4cUXXzT6YlqtFk1NTViyZAnKysqwYsUKODs7w8nJCTNnzoRKpcKHH36I3377DZMnT8bu\n3bsxaNAg034w9sgRkRUoKAA+/1xfxPn7y9Op/v5X/DYicjAW7ZF74okncN999yEnJwcFBQUoKCjA\nwYMHUVBQ0K2LLV26FJ6ennjttdewdu1aeHh44JVXXgEAvP/++6ivr0dwcDBmzZqF5cuXm1zEkTLY\nXyEW8y2WKfk+cADYuFFfxAUGAvPmsYgzFj/jYjHfYgntkVu7di3279+PsLCwHl0sPT0d6enpnZ4L\nCAjAV1991aP3JyKyFn/+CXz5JaDTyce9esnTqe2e6yIi6hGjplaHDBmCrKwsm9rjlFOrRKSU338H\nvvoKaPkV1Lu3XMTx+S0i6oqpdYtRd+Q++ugjPPzww3jggQcQEhJicK47y46IxocdiEi0vDzgm2/0\nRVxQkFzEeXsrGxcRWSchDzssX74cTz75JHx8fODh4WFw7vjx4yZf3JJ4R048jUbDolkg5lssY/L9\n66/Apk3645AQebFfLy/Lxmav+BkXi/kWq32+LXpH7qWXXsLmzZsxYcKEbl+AiMgR/Pwz8O23+uM+\nfeQiztNTuZiIyP4ZdUcuMjIShYWFcHV1FRGTWfCOHBGJsncv8P33+uOwMCA1FWg3gUFE1CWLLj/y\nj3/8A0899RROnToFnU5n8EVE5Mh27TIs4vr2le/EsYgjIhGMKuTS0tKwfPlyhIeHw9nZufXLxcXF\n0vH1SHp6OtfFEYi5Fov5FquzfO/YAWzdqj+OiJDvxLm7i4vLnvEzLhbzLVZLvjUaTZdLsxnDqB65\no0ePmnwBJfUkMUREV7J9O5CVpT+OigIeeABwc1MuJiKyPS2rayxZssSk7zd6iy4A0Ol0OHPmDEJC\nQqBWG3UzTzHskSMiS5AkYNs2oO3Ni379gJkzARtqIyYiK2PRHrmqqirMnj0b7u7uCA8Ph7u7O2bP\nno3KyspuX5CIyFZJknwXrm0RN2CAfCeORRwRKcHovVZra2vx559/oq6urvWfTzzxhKXjIxvC/gqx\nmG+xsrM1+OknICdHPxYTA8yYAVh5u7DN4mdcLOZbLKF7rf7www84evQovC6vahkbG4tPPvkE/fv3\nN0sQRETW6tChEvz4YxG2bPkdWq0O/fsPQO/eUYiNBaZPB5yN+i1KRGQZRvXIRUdHQ6PRIDo6unWs\nuLgYiYmJKC0ttWR8JlOpVFi8eDG36CIikx06VIJPPilEaWkKysrksebmTEybFoMnn4yCk5Oy8RGR\n7WvZomvJkiUm9cgZVcgtW7YMq1atwjPPPIOoqCgUFxfjrbfeQmpqKhYuXGhS4JbGhx2IqKfeeScL\nO3Yk48wZ/VhQEJCYmIUnnkhWLjAisjsWfdjhxRdfxAsvvICNGzfimWeewRdffIG//e1vePnll7t9\nQbJf7K8Qi/m2rKYmIDdX3VrEVVRoEBwMDBoEaLXW/dS+veBnXCzmWyyhPXJqtRppaWlIS0szy0WJ\niKxZfT2wbh1w4YJ+95rAQLmIU6kAV1fuakNE1sGoqdUnnngCM2fOxKhRo1rHdu3ahc8++wxvv/22\nRQM0FadWicgU1dXAmjXA2bPA+fMl2LevEAMGpCA6Wi7iGhoyMXduDOLiopQOlYjsiKl1i1GFXO/e\nvVFWVga3NkuWX7p0CRERETh37ly3LyoCCzki6q7ycmD1aqCiQj82cGAJysuL0NiohqurDikpA1jE\nEZHZWbRHTq1WQ6cznErQ6XQslMgA+yvEYr7N69Qp4KOP9EWcWg1MmwbMmBGF+fOTkZAAzJ+fzCJO\nIH7GxWK+xTJXvo0q5EaPHo2XX365tZjTarVYvHgxxowZY5YgLCU9PZ0fTCK6quJi4JNPgNpa+djF\nRV7od8gQJaMiIkeg0Wh6tDe8UVOrx48fx+TJk3Hq1ClERUWhtLQUoaGh2LRpEyIiIky+uCVxapWI\njHHwIPD550Bzs3zs7i5vuRUZqWxcRORYLNojB8h34XJzc3H8+HFERERgxIgRUKut9xF8FnJEdDV5\necA338h7qAKAjw8waxYQEqJsXETkeCzaIwcATk5OGDlyJKZPn46RI0dadRFHyuA0tljMd8/s3Al8\n/bW+iAsMBNLSui7imG/xmHOxmG+xhK4jR0RkLyQJ+PFHYNcu/VifPvKdOG9v5eIiIjKF0VOrtoZT\nq0TUnk4HbNokT6m2iI6WH2xwd1csLCIiy02tSpKEo0ePormlE5iIyAY1NQGffWZYxA0cKN+JYxFH\nRLbKqEa3+Ph49sTRVbG/Qizm23iXLgFr18pPqLa4/npg+nTA2cgGE+ZbPOZcLOZbLGHryKlUKlx/\n/fU4dOiQWS5IRCRSTY28RlxJiX7slluAO++UF/0lIrJlRvXIvfzyy1i7di3mzp2LiIiI1nlclUqF\ntLQ0EXF2m0qlwuLFi5GUlISkpCSlwyEiBVy8KO+bWl6uH5swQS7kiIisgUajgUajwZIlSyy3jlxL\nIaRSqTqcy87O7vZFReDDDkSO7cwZeTq1ulo+VquBKVPkKVUiImtj8QWBbQ0LOfE0Gg3vfgrEfHet\ntBRYt07ujQPkPrh775UfbjAV8y0ecy4W8y1W+3ybWrcYvY7chQsX8O233+L06dN4/vnnUVZWBkmS\n0Ldv325flIjIUg4flp9ObXnQ3s0NmDlTXmaEiMjeGHVHbtu2bbjnnntw4403YufOnaiuroZGo8Eb\nb7yBTZs2iYiz23hHjsjx5OfLuzXodPKxl5e8vEhoqLJxERFdjUWnVhMSEvD6669j/PjxCAgIwMWL\nF3Hp0iVERkbi7NmzJgVsaSzkiBzLnj3ADz/ojwMCgNRUeestIiJrZ9G9VktKSjB+/HiDMRcXF2i1\n2m5fkOwX1yASi/mWSRKQmWlYxIWEyPummrOIY77FY87FYr7FEraOHAAMGjQIP7T9LQkgMzMT1113\nnVmCICIyhU4HbN4M5OToxyIjgblzAR8fxcIiIhLGqKnVPXv2YPLkybj99tuxceNGpKamYtOmTfj6\n668xfPhwEXF2G6dWiexbczPw5ZfAgQP6sdhY4L77ABcX5eIiIjKFxZcfKSsrw9q1a1FSUoLIyEjM\nmjXLqp9YZSFHZL8aGoD164Fjx/RjQ4fKuzU4OSkXFxGRqYSsI6fT6XD+/HkEBQV1ujiwNWEhJx7X\nIBLLUfNdWwt8+ilw8qR+7OabgYkTAUv+WnLUfCuJOReL+RbLXOvIGdUjd/HiRaSmpsLDwwN9+vSB\nu7s7Zs2ahfK2+95YofT0dDZvEtmRigpg5UrDIi4lxfJFHBGRpWg0GqSnp5v8/Ubdkbv77rvh7OyM\npUuXIjIyEqWlpVi0aBEaGxvx9ddfm3xxS+IdOSL7cvasvOVWVZV8rFIBkycDw4YpGxcRkTlYdGrV\nz88Pp06dgqenZ+tYXV0dQkNDUVlZ2e2LisBCjsh+nDghT6fW18vHTk7APfcAgwcrGxcRkblYdGp1\n4MCBKC4uNhgrKSnBwJ5sXEh2h9PYYjlKvgsLgVWr9EWcq6u8W4PoIs5R8m1NmHOxmG+xzJVvo/Za\nTU5Oxq233orZs2cjIiICpaWlWLt2LVJTU7Fy5UpIkgSVSoW0tDSzBEVEBAB//gl89RXQsva4p6dc\nxIWFKRsXEZG1MGpqteWpirZPqrYUb21lZ2ebN7oe4NQqkW3LzQW+/17euQEA/PzkLbd691Y2LiIi\nSxCy/IgtYSFHZJskCdi2DWg76xAUJBdxvr6KhUVEZFEW7ZEjMgb7K8Syx3xLknwXru2P1rcvMG+e\n8kWcPebb2jHnYjHfYgntkSMisjStVu6H+/NP/diAAcD998sPOBARUUecWiUixTU2Ahs2AEVF+rH4\neGDqVG65RUSOwdS6hXfkiEhRdXXAunXyWnEthg8HJk3ibg1ERFdjdI9cQUEB/vGPf2DBggUAgIMH\nD+L333+3WGBke9hfIZY95LuqCvj4Y8MiLinJOos4e8i3rWHOxWK+xTJXvo0q5DZu3IjExESUlZVh\n9erVAIDq6mr89a9/NUsQROR4zp8HPvoIOHdOPlapgNtvlws5ayviiIislVE9cgMHDsT69euRkJCA\ngIAAXLx4EU1NTQgNDcX58+dFxNlt7JEjsl4nT8r7ptbVycdOTnI/XHy8snERESnFoj1y586dw5Ah\nQzqMq9VcvYSIuufoUWD9evkBBwBwcQFmzJCfUCUiou4xqhK74YYbsGbNGoOxDRs2YPjw4RYJimwT\n+yvEssV8HzgAfPqpvojz8ADmzLGNIs4W823rmHOxmG+xhK4j984772DChAn46KOPUFdXh1tvvRWH\nDx/G1q1bzRKEpaSnpyMpKal1izEiUs6vvwKbN+u33PL1lXdrCApSNi4iIiVpNJoeFXVGryNXW1uL\nzZs3o6SkBJGRkbjjjjvg4+Nj8oUtjT1yRNZBkoCcHCArSz/Wq5dcxPn7KxcXEZE14V6r7bCQI1Ke\nJAFbtgB79ujHwsKABx8EvLyUi4uIyNpYdK/VkpISpKWl4frrr8c111zT+hUbG9vtC5L9Yn+FWNae\n75Ytt9oWcf36yT1xtljEWXu+7RFzLhbzLZbQHrn77rsPgwYNwtKlS+Hu7m6WCxOR/WpqAjZuBA4f\n1o8NHgxMmwY4cz8ZIiKzMWpq1c/PD+Xl5XCyoU0PObVKpIz6ennLrePH9WPDhgF33AFwxSIios5Z\ndGp18uTJ2LZtW7ffnIgcS3W1vOVW2yIuMRGYPJlFHBGRJRh1R+78+fMYOXIkYmNjERwcrP9mlQor\nV660aICm4h058TQaDZd6Ecja8l1eDqxeDVRU6Mduuw24+WblYjIna8u3I2DOxWK+xWqfb4vu7JCW\nlgZXV1cMGjQI7u7urRdTcUNEIgJw6pS85VZtrXysVgN33QUMHapsXERE9s6oO3I+Pj4oKyuDr6+v\niJjMgnfkiMQoLgYyMoCGBvnYxQW47z6AD7UTERnPonfkhgwZggsXLthUIUdElnfwIPD550Bzs3zs\n7g488AAQGalsXEREjsKo9uPk5GRMnDgRr776KlauXImVK1fio48+str+OFIG1yASS+l85+UBGzbo\nizgfH2DePPst4pTOtyNizsVivsUSuo5cTk4OwsLCOt1bNS0tzSyBEJHt2LkT+PFH/XFgoLzlVkCA\ncjERETkibtFFREaTJLmA27VLP9anDzBrFuDtrVxcRES2zuw9cm2fStXpdF2+gZqLQxE5BJ0O2LRJ\nnlJtER0NzJgh98YREZF4XVZhbR9scHZ27vTLxcVFSJBkG9hfIZbIfDc1AZ99ZljEDRwo34lzlCKO\nn2/xmHOxmG+xLN4jt3///tY/Hz161CwXIyLbc+mSvLxISYl+7PrrgSlTuFsDEZHSjOqRe/311/Hs\ns892GH/zzTfx17/+1SKB9RR75Ih6rqZGXuj39Gn92C23AOPHA1wPnIjIfEytW4xeELi6urrDeEBA\nAC5evNjti4rAQo6oZy5eBNaskbfeajFhglzIERGReZlat1xxYiQrKwuZmZnQarXIysoy+FqxYgUX\nCCYD7K8Qy5L5PnMGWLlSX8SpVPKWW45cxPHzLR5zLhbzLZaQdeTS0tKgUqnQ0NCAhx56qHVcpVIh\nJCQE77zzjlmC6I7c3Fw89dRTcHFxQXh4OFavXg1nZ6OWwyMiI5SWAuvWyb1xAODsDNx7r/xwAxER\nWRejplZTU1OxZs0aEfFc1enTpxEQEAA3Nze8+OKLGDZsGO65554Or+PUKlH3HT4sP53asluDmxsw\nc6a8zAgREVmORfdatZYiDgD69OnT+mcXFxc4OTkpGA2R/cjPB77+Wl4vDgC8vOTlRUJDlY2LiIi6\nZrOLB5SUlODHH3/ElClTlA6FLmN/hVjmzPeePcBXX+mLOH9/4KGHWMS1xc+3eMy5WMy3WObKt9BC\n7t1338WNN94Id3d3zJs3z+BceXk5pk6dCm9vb0RHRyMjI6P13FtvvYVx48bhjTfeAABUVVVh9uzZ\nWLVqFe/IEfWAJAGZmcAPP+jHgoPlIi4wULm4iIjIOEL3Wv3qq6+gVquxZcsW1NfX4+OPP249N3Pm\nTADARx99hLy8PNxxxx3YtWsXBg8ebPAezc3NuPPOO/Hss88iOTm5y2uxR47oynQ64NtvgV9/1Y9F\nRso9cR4eysVFROSILLqOnLktXLgQJ06caC3kamtrERgYiP379yMmJgYAMGfOHISFheHVV181+N41\na9bg6aefxnXXXQcAeOyxxzB9+vQO12AhR9S15mbgyy+BAwf0Y7GxwH33Adx5j4hIPIs+7GBu7QM9\nfPgwnJ2dW4s4ABg6dGin88epqalITU016jpz585F9OXH7fz9/ZGQkICkpCQA+rlpHpvveN++fXjq\nqaesJh57PzY13w0NwOLFGpw+DURHy+fVag1CQgAXF+v5+aztmJ9v8cctY9YSj70ft4xZSzz2frxv\n3z5UVFSguLgYPWEVd+RycnIwffp0nDp1qvU1K1aswLp165CdnW3SNXhHTjyNRtP6QSXLMyXftbXA\np58CJ0/qx26+GZg4kVtuXQ0/3+Ix52Ix32K1z7dN35Hz9vZGVVWVwVhlZSV8fHxEhkU9xF8AYnU3\n3xUV8pZbFy7ox1JSgNGjWcQZg59v8ZhzsZhvscyVb7VZ3qWbVO3+rxEbG4vm5mYUFha2juXn5yM+\nPl50aER26dw5ecutliJOpQKmTAHGjGERR0Rky4QWclqtFpcuXUJzczO0Wi0aGhqg1Wrh5eWFadOm\nYdGiRairq8OOHTuwadMmo3vhupKenm4w90+WxVyLZWy+T5yQi7iWm95OTvJDDcOGWS42e8TPt3jM\nuVjMt1gt+dZoNEhPTzf5fYQWckuXLoWnpydee+01rF27Fh4eHnjllVcAAO+//z7q6+sRHByMWbNm\nYfny5Rg0aFCPrpeens5bxeTQCguBVauA+nr52NUVePBBoN2qPkREpJCkpKQeFXKKPOwgAh92IEf3\n55/ybg1arXzs6SlvuRUWpmxcRETUkU097EBElpWbC3z/vbxzAwD4+QGpqUDv3srGRURE5qXIww6i\nsEdOLOZarM7yLUmARgN8952+iAsKkrfcYhHXM/x8i8eci8V8i2WuHjm7viPXk8QQ2RpJku/C5ebq\nx/r2BR54QJ5WJSIi65OUlISkpCQsWbLEpO9njxyRHdBq5X64P//Ujw0YANx/v/yAAxERWTf2yBE5\nqMZGYMMGoKhIPxYfD0ydKi81QkRE9suue+RILPZXiKXRaFBXB6xebVjEDR8O3HMPizhz4+dbPOZc\nLOZbLHPl267vyLWsI8e15Mge1dYCH38s79rQIikJGDuWuzUQEdkKjUbTo6KOPXJENubQoRL83/8V\nYfduNRobdejffwCCgqIwaZJ8N46IiGwPe+SIHMDBgyV4881CHDuWgqYmeez33zPx3HPA8OFRygZH\nRETCsUeOzIb9FZZ16hSwbFkRDh+Wi7iKCg3UaiAhIQXHjxdd/Q2oR/j5Fo85F4v5Fos9ckQOoroa\nyMoC9u0Dzp/X/93LyQlISAB8fYHGRv6djIjIEbFHjshKNTUBe/YAOTnyEiMAkJubhfr6ZISHA1FR\ngIuLPB4cnIX585OVC5aIiHqEPXKd4FOrZIskCThwAPjxR6CiwvBccvIAnDiRCX//lNaxhoZMpKTE\nCI6SiIjMgU+tdoF35MTTaDQsmnvo5Enghx+A0lLD8eBgYOJEebeGQ4dKkJlZhAMHfsfgwUOQkjIA\ncXF80MHS+PkWjzkXi/kWq32+eUeOyIZVVwOZmXIfXFuenkByMnDDDYD6chtcXFwU4uKioNGo+UuX\niMjB8Y4ckYKamoDdu+U+uJblRAD5QYYRI4DERMDdXbn4iIhIDN6RI7IhkgTs3y/3wVVWGp4bOBCY\nMAHo1UuZ2IiIyHZwzQIyG65BZJyyMmDlSuDzzw2LuJAQYPZsYMYM44o45lss5ls85lws5lssriNH\nZGOqquQ+uPx8w3EvL7kP7vrr9X1wRERExrDrHrnFixdz+RFSXFMTsHOn/NW+D+7mm4ExY9gHR0Tk\nqFqWH1myZIlJPXJ2XcjZ6Y9GNkKSgD//lPvgqqoMzw0aJPfBBQYqExsREVkXU+sWTuSQ2bC/Qu/E\nCeCjj4AvvjAs4vr0AebMAe6/v+dFHPMtFvMtHnMuFvMtFnvkiKxQZaXcB/f774bjXl5ASoq8Nyr7\n4IiIyFw4tUpkBo2NwK5dnffBjRwp98G5uSkXHxERWTeuI0ekAEkC/vgD+Omnjn1wgwfLfXABAcrE\nRkRE9o+TPGQ2jtZfcfw48OGHwJdfduyDmzsXmD7dskWco+Vbacy3eMy5WMy3WOyRI1JIZaV8B+6P\nPwzHvb3lPrihQ9kHR0REYrBHjshIjY3Ajh1yL1xzs37c2Vnugxs9mn1wRERkGvbIdSI9PZ0LAlOP\nSZK8G0NmJlBdbXju2muB8ePZB0dERKZpWRDYVLwjR2aj0WjsrmguLQV++AE4edJwPDQUuO02ICpK\nmbgA+8y3NWO+xWPOxWK+xWqfb96RIzKjigp5R4b9+w3Hvb3lO3BDhwIqlTKxERERteAdOaI2Ghrk\nPrjduzv2wY0aJffBuboqFx8REdkn3pEj6gFJAvbtk/vgamoMz8XHy3fh/P2ViY2IiKgrXCSBzMZW\n1yAqKQH++1/g668Ni7iwMCAtDbj3Xuss4mw137aK+RaPOReL+RaL68gR9dDFi3If3IEDhuM+PvId\nuCFD2AdHRETWjT1y5HAaGoCcHLkPTqvVjzs7A7fcIn+xD46IiERijxzRVeh0ch9cVlbHPrjrrpPv\nwvn5KRMbERGRKdgjR2Zjzf0VxcVyH9w33xgWceHhwEMPAffcY3tFnDXn2x4x3+Ix52Ix32KxR47I\nCOXlch9cQYHhuK+vfAfuuuvYB0dERLbLrnvkFi9ezC26HFRDA7B9O7Bnj2EfnIuL3AM3ahT74IiI\nSHktW3QtWbLEpB45uy7k7PRHoyvQ6YC8PLkPrrbW8NyQIfJdOF9fZWIjIiLqiql1C3vkyGyU7q84\ndgz4z3+ATZsMi7i+fYG//AWYNs2+ijil8+1omG/xmHOxmG+x2CNHdNmFC3If3MGDhuN+fvIduPh4\n9sEREZF94tQq2axLl+Q+uL17O/bBjR4t98G5uCgXHxERkbG4jhw5DJ0O+O03uQ+urs7w3NChQEqK\nfU2hEhERdYU9cmQ2Ivorjh4Fli8HNm82LOIiIoCHHwamTnWcIo79LGIx3+Ix52Ix32KxR44cyoUL\nwNatwKFDhuN+fsCECcC117IPjoiIHA975Miq1dfr++B0Ov24q6vcBzdyJPvgiIjI9rFHjuyKTgf8\n+iuQnd2xDy4hQe6D8/FRJjYiIiJrwR45MhtzzfcXFQEffAB8+61hERcZCTzyCHD33SziAPaziMZ8\ni8eci8V8i8UeObI758/LfXCHDxuO+/sDt94KDBrEPjgiIqK22CNHiquvB7ZtA3JzO/bBJSYCN98M\nOPOvHEREZMfYI0c2R6vV98HV1+vHVSrg+uuB5GTA21u5+IiIiKwde+TIbLoz319YKK8H9913hkVc\nVJTcB3fnnSzirob9LGIx3+Ix52Ix32KxR45s0rlzch/ckSOG4wEBch/cwIHsgyMiIjKWXffILV68\nGElJSUhKSlI6HIdXVyf3wf38s2EfnJub3Ac3YgT74IiIyPFoNBpoNBosWbLEpB45uy7k7PRHsyla\nLfDLL4BG07EP7oYbgHHjOIVKRERkat3CHjkym7bz/ZIkT59+8AHw/feGRVx0NPDoo8CUKSzieoL9\nLGIx3+Ix52Ix32KxR46s1tmzch9cYaHheGCg3AcXF8c+OCIiInPg1Cr12KFDJfjppyLU1qpx7JgO\nzs4D0KtXVOt5Nzdg7Fhg+HD2wREREXWG68iRIg4dKsHHHxfi/PkUFBcDzc1Ac3MmEhKAoKAoDBsm\n98F5eSkdKRERkf1hjxz1yOefFyE/PwWFhcD58xoAgLNzCqqqivA//wNMnswizlLYzyIW8y0ecy4W\n8y0We+TIKqjVajQ06I89PIABA4ABA9QICVEuLiIiIkfAHjnqkffey8LPPyfjxAl5V4bwcECtBoKD\nszB/frLS4REREdkE9siRIsaPH4DS0kyEhaXA1VUea2jIREpKjLKBEREROQD2yFGPxMVFIS0tBn37\nZuH8+bcRHJyFuXNjEBcXdfVvph5hP4tYzLd4zLlYzLdY7JEjqxEXF4W4ik2AbAAADuVJREFUuCho\nNGpuh0ZERCQQe+SIiIiIFMYtuoiIiIgcDAs5Mhv2V4jFfIvFfIvHnIvFfItlrnyzkCMiIiKyUeyR\nIyIiIlIYe+SIiIiIHAwLOTIb9leIxXyLxXyLx5yLxXyLxR45IiIiIgdncz1yZ86cwbRp0+Dq6gpX\nV1esW7cOvXr16vA69sgRERGRrTC1brG5Qk6n00Gtlm8krlq1CqdOncLf//73Dq9jIUdERES2wmEe\ndmgp4gCgqqoKAQEBCkZDbbG/QizmWyzmWzzmXCzmWyyH7pHLz8/HiBEj8O6772LmzJlKh0OX7du3\nT+kQHArzLRbzLR5zLhbzLZa58i20kHv33Xdx4403wt3dHfPmzTM4V15ejqlTp8Lb2xvR0dHIyMho\nPffWW29h3LhxeOONNwAAQ4cOxd69e7Fs2TIsXbpU5I9AV1BRUaF0CA6F+RaL+RaPOReL+RbLXPkW\nWsiFh4dj4cKFSEtL63BuwYIFcHd3x9mzZ/Hpp5/isccew4EDBwAATz/9NLKzs/HMM8+gqamp9Xt8\nfX3R0NAgLP4r6ekt0u5+vzGvv9Jrujpn7LjSt+DNcf3uvIel8t3VOWPHRLK2z7ip55lv01/P3ynm\new/+TrHvz7jIfAst5KZOnYq77rqrw1OmtbW1+PLLL7F06VJ4enrilltuwV133YU1a9Z0eI99+/Zh\n7NixSE5Oxptvvonnn39eVPhXZM8fyM7GO3tdcXHxVWMyF/7SFZvvzq5v6e+3tkLO0fN9tdfwdwp/\np3SXPX/GReZbkadWX375ZZSVleHjjz8GAOTl5WH06NGora1tfc2bb74JjUaDb775xqRrxMTEoKio\nyCzxEhEREVnS0KFDTeqbc7ZALFelUqkMjmtqauDr62sw5uPjg+rqapOvUVhYaPL3EhEREdkCRZ5a\nbX8T0NvbG1VVVQZjlZWV8PHxERkWERERkU1RpJBrf0cuNjYWzc3NBnfR8vPzER8fLzo0IiIiIpsh\ntJDTarW4dOkSmpubodVq0dDQAK1WCy8vL0ybNg2LFi1CXV0dduzYgU2bNiE1NVVkeEREREQ2RWgh\n1/JU6muvvYa1a9fCw8MDr7zyCgDg/fffR319PYKDgzFr1iwsX74cgwYNEhkeERERkU2xub1We+pv\nf/sbdu/ejejoaKxcuRLOzoo87+EwqqqqMH78eBQUFGDv3r0YPHiw0iHZtdzcXDz11FNwcXFBeHg4\nVq9ezc+4BZ05cwbTpk2Dq6srXF1dsW7dug7LK5FlZGRk4Mknn8TZs2eVDsWuFRcX46abbkJ8fDxU\nKhU+++wz9O7dW+mw7JpGo8GyZcug0+nw//7f/8Pdd999xdfb5BZdpsrPz8fJkyexfft2DBw4EJ9/\n/rnSIdk9T09PfPfdd7j33ntN2gyYuicyMhLZ2dnYtm0boqOj8fXXXysdkl0LCgrCzp07kZ2djQce\neAArVqxQOiSHoNVqsXHjRkRGRiodikNISkpCdnY2srKyWMRZWH19Pd588018//33yMrKumoRBzhY\nIbd7925MnDgRAHDbbbdh586dCkdk/5ydnfkfvkB9+vSBm5sbAMDFxQVOTk4KR2Tf1Gr9r9CqqioE\nBAQoGI3jyMjIwPTp0zs8OEeWsXPnTiQmJuKll15SOhS7t3v3bnh4eGDKlCmYNm0azpw5c9XvcahC\n7uLFi61Lmvj6+qK8vFzhiIgso6SkBD/++COmTJmidCh2Lz8/HyNGjMC7776LmTNnKh2O3Wu5G3f/\n/fcrHYpDCAsLQ1FREbZv346zZ8/iyy+/VDoku3bmzBkUFhZi8+bNePjhh5Genn7V77HJQu7dd9/F\njTfeCHd3d8ybN8/gXHl5OaZOnQpvb29ER0cjIyOj9Zy/v3/renWVlZUIDAwUGrctMzXnbfFvz8br\nSb6rqqowe/ZsrFq1infkjNSTfA8dOhR79+7FsmXLsHTpUpFh2zRTc7527VrejTOBqfl2dXWFh4cH\nAGDatGnIz88XGretMjXfAQEBuOWWW+Ds7Izk5GTs37//qteyyUIuPDwcCxcuRFpaWodzCxYsgLu7\nO86ePYtPP/0Ujz32GA4cOAAAGDVqFH766ScAwJYtWzB69GihcdsyU3PeFnvkjGdqvpubmzFjxgws\nXrwY11xzjeiwbZap+W5qamp9na+vLxoaGoTFbOtMzXlBQQFWr16NSZMm4ciRI3jqqadEh26TTM13\nTU1N6+u2b9/O3ytGMjXfN910EwoKCgDIe8sPGDDg6heTbNjLL78szZ07t/W4pqZGcnV1lY4cOdI6\nNnv2bOnvf/976/Fzzz0njRkzRpo1a5bU1NQkNF57YErOJ02aJIWFhUkjR46UPvnkE6Hx2rru5nv1\n6tVSr169pKSkJCkpKUnasGGD8JhtWXfzvXfvXikxMVEaN26cdOutt0rHjx8XHrOtM+V3SoubbrpJ\nSIz2pLv5/u6776Rhw4ZJY8aMkebMmSNptVrhMdsyUz7f7733npSYmCglJSVJR48eveo1bHpdAqnd\nHZ7Dhw/D2dkZMTExrWNDhw6FRqNpPf7f//1fUeHZJVNy/t1334kKz+50N9+pqalcSLsHupvv4cOH\nY9u2bSJDtDum/E5pkZuba+nw7E538z1p0iRMmjRJZIh2xZTP9/z58zF//nyjr2GTU6st2vdI1NTU\nwNfX12DMx8cH1dXVIsOya8y5WMy3WMy3eMy5WMy3WCLybdOFXPtK19vbu/VhhhaVlZWtT6pSzzHn\nYjHfYjHf4jHnYjHfYonIt00Xcu0r3djYWDQ3N6OwsLB1LD8/H/Hx8aJDs1vMuVjMt1jMt3jMuVjM\nt1gi8m2ThZxWq8WlS5fQ3NwMrVaLhoYGaLVaeHl5Ydq0aVi0aBHq6uqwY8cObNq0iT1DZsCci8V8\ni8V8i8eci8V8iyU03z19IkMJixcvllQqlcHXkiVLJEmSpPLycunuu++WvLy8pKioKCkjI0PhaO0D\ncy4W8y0W8y0ecy4W8y2WyHyrJImLexERERHZIpucWiUiIiIiFnJERERENouFHBEREZGNYiFHRERE\nZKNYyBERERHZKBZyRERERDaKhRwRERGRjWIhR0RERGSjWMgREbUzd+5cLFy40Kzv+dhjj2HZsmVm\nfU8iImelAyAisjYqlarDZtc99cEHH5j1/YiIAN6RIyLqFHcvJCJbwEKOiKzKa6+9hr59+8LX1xcD\nBw5EVlYWACA3NxcjR45EQEAAwsLC8MQTT6Cpqan1+9RqNT744ANcc8018PX1xaJFi1BUVISRI0fC\n398fM2bMaH29RqNB37598eqrryIoKAj9+vXDunXruoxp8+bNSEhIQEBAAG655Rb88ccfXb726aef\nRkhICPz8/DBkyBAcOHAAgOF07ZQpU+Dj49P65eTkhNWrVwMADh48iAkTJqBXr14YOHAgNm7c2OW1\nkpKSsGjRIowePRq+vr6YOHEiLly4YGSmicgesJAjIqtx6NAhvPfee/jll19QVVWFrVu3Ijo6GgDg\n7OyMf/3rX7hw4QJ2796NzMxMvP/++wbfv3XrVuTl5WHPnj147bXX8PDDDyMjIwOlpaX4448/kJGR\n0fraM2fO4MKFCzh58iRWrVqFRx55BEeOHOkQU15eHh566CGsWLEC5eXlePTRR3HnnXeisbGxw2u3\nbNmCnJwcHDlyBJWVldi4cSMCAwMBGE7Xbtq0CdXV1aiursZnn32G0NBQpKSkoLa2FhMmTMCsWbNw\n7tw5rF+/HvPnz0dBQUGXOcvIyMAnn3yCs2fPorGxEa+//nq3805EtouFHBFZDScnJzQ0NGD//v1o\nampCZGQk+vfvDwC44YYbMHz4cKjVakRFReGRRx7Btm3bDL7/+eefh7e3NwYPHozrrrsOkyZNQnR0\nNHx9fTFp0iTk5eUZvH7p0qVwcXFBYmIi7rjjDmzYsKH1XEvR9d///hePPvoobrrpJqhUKsyePRtu\nbm7Ys2dPh/hdXV1RXV2NgoIC6HQ6xMXFoU+fPq3n20/XHj58GHPnzsVnn32G8PBwbN68Gf369cOc\nOXOgVquRkJCAadOmdXlXTqVSYd68eYiJiYG7uzumT5+Offv2dSPjRGTrWMgRkdWIiYnB22+/jfT0\ndISEhGDmzJk4deoUALnomTx5MkJDQ+Hn54eXXnqpwzRiSEhI6589PDwMjt3d3VFTU9N6HBAQAA8P\nj9bjqKio1mu1VVJSgjfeeAMBAQGtXydOnOj0tePGjcPjjz+OBQsWICQkBI8++iiqq6s7/VkrKytx\n11134ZVXXsGoUaNar7V3716Da61btw5nzpzpMmdtC0UPDw+Dn5GI7B8LOSKyKjNnzkROTg5KSkqg\nUqnwt7/9DYC8fMfgwYNRWFiIyspKvPLKK9DpdEa/b/unUC9evIi6urrW45KSEoSFhXX4vsjISLz0\n0ku4ePFi61dNTQ3uv//+Tq/zxBNP4JdffsGBAwdw+PBh/POf/+zwGp1OhwceeAApKSn4y1/+YnCt\nsWPHGlyruroa7733ntE/JxE5FhZyRGQ1Dh8+jKysLDQ0NMDNzQ3u7u5wcnICANTU1MDHxweenp44\nePCgUct5tJ3K7Owp1MWLF6OpqQk5OTn49ttvcd9997W+tuX1Dz/8MJYvX47c3FxIkoTa2lp8++23\nnd75+uWXX7B37140NTXB09PTIP6213/ppZdQV1eHt99+2+D7J0+ejMOHD2Pt2rVoampCU1MTfv75\nZxw8eNCon5GIHA8LOSKyGg0NDXjhhRcQFBSE0NBQnD9/Hq+++ioA4PXXX8e6devg6+uLRx55BDNm\nzDC4y9bZum/tz7c97tOnT+sTsKmpqfjPf/6D2NjYDq8dNmwYVqxYgccffxyBgYG45pprWp8wba+q\nqgqPPPIIAgMDER0djd69e+O5557r8J7r169vnUJteXI1IyMD3t7e2Lp1K9avX4/w8HCEhobihRde\n6PTBCmN+RiKyfyqJf50jIgej0WiQmpqK48ePKx0KEVGP8I4cERERkY1iIUdEDolTkERkDzi1SkRE\nRGSjeEeOiIiIyEaxkCMiIiKyUSzkiIiIiGwUCzkiIiIiG8VCjoiIiMhG/X9xqo7C5o2nRAAAAABJ\nRU5ErkJggg==\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10762ab00>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 10
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"So, using a few tweaks, such as static type declarations and explicit for-loops instead of list comprehensions, we managed to increase the performance of our least squares fit implementation quite significantly - it outperforms the alternative functions in Numpy and Scipy now."
|
|
]
|
|
}
|
|
],
|
|
"metadata": {}
|
|
}
|
|
]
|
|
} |