mirror of
https://github.com/rasbt/python_reference.git
synced 2024-11-27 22:11:13 +00:00
2399 lines
600 KiB
Plaintext
2399 lines
600 KiB
Plaintext
{
|
|
"metadata": {
|
|
"name": "",
|
|
"signature": "sha256:b8a2adab4cfa8ac1064656d4b3e3121a2acc1060e034c98ce29986312939c9ac"
|
|
},
|
|
"nbformat": 3,
|
|
"nbformat_minor": 0,
|
|
"worksheets": [
|
|
{
|
|
"cells": [
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[Sebastian Raschka](http://www.sebastianraschka.com) \n",
|
|
"last updated: 05/06/2014\n",
|
|
"\n",
|
|
"- [Link to this IPython Notebook on GitHub](https://github.com/rasbt/python_reference/blob/master/benchmarks/cython_least_squares.ipynb) \n",
|
|
"- [Link to the GitHub repository](https://github.com/rasbt/python_reference)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### The code in this notebook was executed in Python 3.4.0"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<hr>\n",
|
|
"I am really looking forward to your comments and suggestions to improve and \n",
|
|
"extend this little collection! Just send me a quick note \n",
|
|
"via Twitter: [@rasbt](https://twitter.com/rasbt) \n",
|
|
"or Email: [bluewoodtree@gmail.com](mailto:bluewoodtree@gmail.com)\n",
|
|
"<hr>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"# Implementing the least squares fit method for linear regression and speeding it up via Cython"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"sections\"></a>\n",
|
|
"<br>\n",
|
|
"<br>\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#Sections"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"- [Introduction](#introduction)\n",
|
|
"- [Least squares fit implementations](#implementations)\n",
|
|
"- [Generating sample data and benchmarking](#sample_data)\n",
|
|
"- [Compiling the Python code via Cython in the IPython notebook](#cython_nb)\n",
|
|
"- [Performance growth rates for different sample sizes](#sample_sizes)\n",
|
|
"- [Bonus: How to use Cython without the IPython magic](#cython_bonus)\n",
|
|
"- [Appendix I: Cython vs. Numba](#numba)\n",
|
|
"- [Appendix II: Cython with and without type declarations](#type_declarations)\n",
|
|
"- [Appendix III: Cython performance after replacing list comprehensions by explicit for loops](#explicit_loops)\n",
|
|
"- [Final Comparison: Cython vs. NumPy vs. SciPy for least squares fitting](#showdown)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"introduction\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
" \n",
|
|
"(Note that this chart just reflects my rather objective thoughts after experimenting with Cython, and it is not based on real numbers or benchmarks.)\n",
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Introduction"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
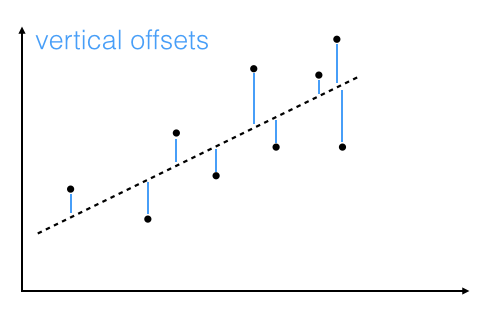
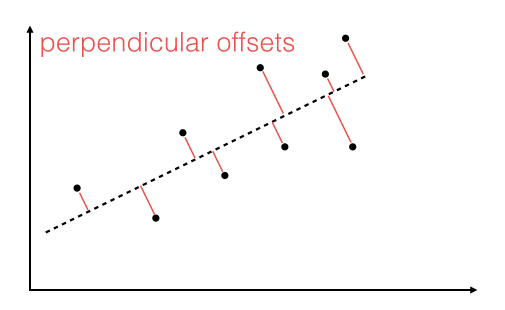
"Linear regression via the least squares method is the simplest approach to performing a regression analysis of a dependent and a explanatory variable. The objective is to find the best-fitting straight line through a set of points that minimizes the sum of the squared offsets from the line. \n",
|
|
"The offsets come in 2 different flavors: perpendicular and vertical - with respect to the line. \n",
|
|
" \n",
|
|
" \n",
|
|
"\n",
|
|
"As Michael Burger summarizes it nicely in his article \"[Problems of Linear Least Square Regression - And Approaches to Handle Them](http://www.arsa-conf.com/archive/?vid=1&aid=2&kid=60101-220)\": \"the perpendicular offset method delivers a more precise result but is are more complicated to handle. Therefore normally the vertical offsets are used.\" \n",
|
|
"Here, we will also use the method of computing the vertical offsets.\n",
|
|
"\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In more mathematical terms, our goal is to compute the best fit to *n* points $(x_i, y_i)$ with $i=1,2,...n,$ via linear equation of the form \n",
|
|
"$f(x) = a\\cdot x + b$. \n",
|
|
"Here, we assume that the y-component is functionally dependent on the x-component. \n",
|
|
"In a cartesian coordinate system, $b$ is the intercept of the straight line with the y-axis, and $a$ is the slope of this line."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In order to obtain the parameters for the linear regression line for a set of multiple points, we can re-write the problem as matrix equation \n",
|
|
"$\\pmb X \\; \\pmb a = \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\Rightarrow\\Bigg[ \\begin{array}{cc}\n",
|
|
"x_1 & 1 \\\\\n",
|
|
"... & 1 \\\\\n",
|
|
"x_n & 1 \\end{array} \\Bigg]$\n",
|
|
"$\\bigg[ \\begin{array}{c}\n",
|
|
"a \\\\\n",
|
|
"b \\end{array} \\bigg]$\n",
|
|
"$=\\Bigg[ \\begin{array}{c}\n",
|
|
"y_1 \\\\\n",
|
|
"... \\\\\n",
|
|
"y_n \\end{array} \\Bigg]$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"With a little bit of calculus, we can rearrange the term in order to obtain the parameter vector $\\pmb a = [a\\;b]^T$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\Rightarrow \\pmb a = (\\pmb X^T \\; \\pmb X)^{-1} \\pmb X^T \\; \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"The more classic approach to obtain the slope parameter $a$ and y-axis intercept $b$ would be:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$a = \\frac{S_{x,y}}{\\sigma_{x}^{2}}\\quad$ (slope)\n",
|
|
"\n",
|
|
"\n",
|
|
"$b = \\bar{y} - a\\bar{x}\\quad$ (y-axis intercept)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"where \n",
|
|
"\n",
|
|
"\n",
|
|
"$S_{xy} = \\sum_{i=1}^{n} (x_i - \\bar{x})(y_i - \\bar{y})\\quad$ (covariance)\n",
|
|
"\n",
|
|
"\n",
|
|
"$\\sigma{_x}^{2} = \\sum_{i=1}^{n} (x_i - \\bar{x})^2\\quad$ (variance)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"implementations\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"## Least squares fit implementations"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 1. The matrix approach"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"First, let us implement the equation:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\pmb a = (\\pmb X^T \\; \\pmb X)^{-1} \\pmb X^T \\; \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"which I will refer to as the \"matrix approach\"."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import numpy as np\n",
|
|
"\n",
|
|
"def lin_lstsqr_mat(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 36
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 2. The classic approach"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Next, we will calculate the parameters separately, using only standard library functions in Python, which I will call the \"classic approach\"."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$a = \\frac{S_{x,y}}{\\sigma_{x}^{2}}\\quad$ (slope)\n",
|
|
"\n",
|
|
"\n",
|
|
"$b = \\bar{y} - a\\bar{x}\\quad$ (y-axis intercept)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 37
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 3. Using the lstsq numpy function"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"For our convenience, `numpy` has a function that can also compute the leat squares solution of a linear matrix equation. For more information, please refer to the [documentation](http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.lstsq.html)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def numpy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return np.linalg.lstsq(X,y)[0]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 38
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 4. Using the linregress scipy function"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The last approach is using `scipy.stats.linregress()`, which returns a tuple of 5 different attributes, where the 1st value in the tuple is the slope, and the second value is the y-axis intercept, respectively. The documentation for this function can be found [here](http://docs.scipy.org/doc/scipy-0.13.0/reference/generated/scipy.stats.linregress.html)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import scipy.stats\n",
|
|
"\n",
|
|
"def scipy_lstsqr(x,y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" return scipy.stats.linregress(x, y)[0:2]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 39
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name='sample_data'></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Generating sample data and benchmarking"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In order to test our different least squares fit implementation, we will generate some sample data: \n",
|
|
"- 500 sample points for the x-component within the range [0,500) \n",
|
|
"- 500 sample points for the y-component within the range [100,600) \n",
|
|
"\n",
|
|
"where each sample point is multiplied by a random value within\n",
|
|
"the range [0.8, 12)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"x = [x_i*random.randrange(8,12)/10 for x_i in range(500)]\n",
|
|
"y = [y_i*random.randrange(8,12)/10 for y_i in range(100,600)]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 40
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"#### Visualization"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"To check how our dataset is distributed, and how the straight line, which we obtain via the least square fit method, we will plot it in a scatter plot. \n",
|
|
"Note that we are using our \"matrix approach\" here for simplicity, but after plotting the data, we will check whether all of the four different implementations yield the same parameters."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%pylab inline\n",
|
|
"from matplotlib import pyplot as plt\n",
|
|
"\n",
|
|
"slope, intercept = lin_lstsqr_mat(x, y)\n",
|
|
"\n",
|
|
"line_x = [round(min(x)) - 1, round(max(x)) + 1]\n",
|
|
"line_y = [slope*x_i + intercept for x_i in line_x]\n",
|
|
"\n",
|
|
"plt.figure(figsize=(8,8))\n",
|
|
"plt.scatter(x,y)\n",
|
|
"plt.plot(line_x, line_y, color='red', lw='2')\n",
|
|
"\n",
|
|
"plt.ylabel('y')\n",
|
|
"plt.xlabel('x')\n",
|
|
"plt.title('Linear regression via least squares fit')\n",
|
|
"\n",
|
|
"ftext = 'y = ax + b = {:.3f} + {:.3f}x'\\\n",
|
|
" .format(slope, intercept)\n",
|
|
"plt.figtext(.15,.8, ftext, fontsize=11, ha='left')\n",
|
|
"\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAfoAAAH4CAYAAACi3S9CAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdUVMfbwPHv0lm6giAgooBRbNi7GCv2EnvXWOPPnhg1\nGksSxRhjoiYaE0SNsb4xEY0Fe+zGmijGLkZARRERFljYnfeP1Y0ELJRlAedzDkf2lpln7q48e++d\nO6MQQggkSZIkSSqSTIwdgCRJkiRJhiMTvSRJkiQVYTLRS5IkSVIRJhO9JEmSJBVhMtFLkiRJUhEm\nE70kSZIkFWEy0UtGd+jQIcqXL2/sMAqtSpUq8fvvv+drnSNHjuTTTz/N0b7e3t7s3bs3jyN6s/3y\nyy+UKlUKe3t7zp07Z5TPhFRwKeRz9FJ+8fb2JiQkhGbNmhk7FMmIypQpQ0hICE2bNjVI+QcOHKBf\nv378888/Bim/IPLx8eGrr76iffv2mdbNnDmT69ev8+OPPxohMqkgkGf0Ur5RKBQoFApjh6Gn0Wjy\nZJvXJYRAfq+Wnsmrz5YQgtu3b+Pv758n5UlFj0z0ktEdOHCAUqVK6V97e3uzYMECqlatiqOjIz17\n9iQ1NVW/ftu2bQQEBODk5ESDBg3466+/9OuCg4Px9fXF3t6eihUr8uuvv+rXrVy5kgYNGjBhwgSc\nnZ2ZNWtWplhmzpxJ165d6devHw4ODqxatYrHjx/z7rvv4u7ujqenJ9OnT0er1QKg1WqZOHEiLi4u\nlC1bliVLlmBiYqJf36RJE6ZNm0aDBg2wsbHh5s2b/P3337Ro0YLixYtTvnx5Nm3apK9/+/btVKxY\nEXt7ezw9PVmwYAEADx48oF27djg5OVG8eHEaN26c4Xg9uxSemprKuHHj8PDwwMPDg/Hjx6NWq/XH\n2dPTky+//BJXV1fc3d1ZuXJllu/Jhg0bqFWrVoZlCxcupGPHjgAMHDiQ6dOnA/Do0SPatWtHiRIl\nKFasGO3btycqKirLcv9LCKF/z5ydnenRowePHj3Sr+/WrRslS5bE0dGRwMBAIiIiXnisvvzyS1Qq\nFa1btyY6Oho7Ozvs7e25e/dupnpfdJwB5s+fr3+vV6xYgYmJCTdu3AB072dISIh+25UrV9KoUSP9\n67Fjx+Ll5YWDgwM1a9bk8OHD+nXZ/Wxdu3aNwMBAHB0dcXFxoWfPnpnakZqaip2dHRqNhqpVq+Ln\n5wf8+5nYuXMnc+fOZcOGDdjZ2VGtWrXXel+kIkZIUj7x9vYWe/fuzbR8//79wtPTM8N2derUETEx\nMSIuLk5UqFBBLFu2TAghxJkzZ0SJEiXEyZMnhVarFatWrRLe3t5CrVYLIYTYtGmTiImJEUIIsWHD\nBmFjYyPu3r0rhBAiNDRUmJmZiSVLlgiNRiOSk5MzxTJjxgxhbm4utmzZIoQQIjk5WXTq1EmMGDFC\nqFQqcf/+fVG7dm3x3XffCSGEWLp0qfD39xdRUVHi0aNHolmzZsLExERoNBohhBCBgYGidOnSIiIi\nQmg0GhEfHy88PT3FypUrhUajEWfPnhXOzs7i0qVLQggh3NzcxOHDh4UQQsTHx4szZ84IIYSYPHmy\nGDFihEhPTxfp6en6bf57XKdPny7q1asnYmNjRWxsrKhfv76YPn26/jibmZmJGTNmiPT0dLF9+3ah\nVCpFfHx8puOgUqmEnZ2duHr1qn5ZzZo1xYYNG4QQQgwcOFBf7sOHD8XmzZtFcnKyePLkiejWrZvo\n1KlT1h+C/8T71VdfiXr16omoqCihVqvF8OHDRa9evfTbhoaGisTERKFWq8W4ceNEQECAft2LjtWB\nAwcyfJ6y8qJ9d+zYIVxdXcXFixdFUlKS6NWrl1AoFOL69etCCCGaNGkiQkJCMsTXsGFD/es1a9aI\nuLg4odFoxIIFC4Sbm5tITU0VQmT/s9WzZ08xZ84cIYQQqamp4siRIy9sz/Mx/vcYz5w5U/Tr1++l\nx0Mq2uQZvVQgjRkzBjc3N5ycnGjfvj3nzp0DYPny5QwfPpxatWqhUCjo378/lpaWHDt2DICuXbvi\n5uYGQPfu3fHz8+PEiRP6ct3d3Rk1ahQmJiZYWVllWXf9+vXp0KEDAI8fP2bHjh0sXLgQa2trXFxc\nGDduHOvXrwdg48aNjBs3Dnd3dxwdHZkyZUqGy/MKhYKBAwdSoUIFTExM2LlzJ2XKlGHAgAGYmJgQ\nEBBAly5d2LhxIwAWFhZcvHiRhIQEHBwc9GdgFhYWxMTEcOvWLUxNTWnQoEGWsa9du5aPP/4YZ2dn\nnJ2dmTFjRoZ7s+bm5nz88ceYmprSunVrbG1tuXz5cqZyrK2t6dixI+vWrQPg6tWrXL58WX9cAH07\nixUrRufOnbGyssLW1papU6dy8ODBrN/Y//juu+/49NNPcXd3x9zcnBkzZvB///d/+rPagQMHYmNj\no193/vx5njx58tJjJV7j9siL9t24cSODBw/G398fpVKZ5VWfl+nTpw9OTk6YmJgwYcIEUlNTMxzf\n7Hy2LCwsuHXrFlFRUVhYWFC/fv1sxfKMkLeM3ngy0UsF0rNkDbqkk5iYCEBkZCQLFizAyclJ/3Pn\nzh1iYmIAWL16NdWqVdOvu3DhAg8fPtSX9fwtghfx9PTU/x4ZGUlaWholS5bUlzlixAhiY2MBiImJ\nyVDm8/tmVWdkZCQnTpzIEP/atWu5d+8eAD///DPbt2/H29ubJk2acPz4cQA++OADfH19admyJT4+\nPsybNy/L2KOjoyldurT+tZeXF9HR0frXxYsXx8Tk3//2SqVSf2z/q3fv3vpEv3btWn0y/y+VSsXw\n4cPx9vbGwcGBwMBAHj9+/FrJ5datW3Tu3Fl/LPz9/TEzM+PevXtoNBomT56Mr68vDg4OlClTBoVC\nwYMHD156rF7Hi/b97/vp5eX12mUCfPHFF/j7++Po6IiTkxOPHz/WxwvZ+2x9/vnnCCGoXbs2lSpV\nIjQ0NFuxSNIzZsYOQJJex7NOfF5eXnz00UdMnTo10zaRkZEMGzaMffv2Ua9ePRQKBdWqVct0hv2q\nep7fplSpUlhaWvLw4cMMCfKZkiVLZujdnVVP7+fL8/LyIjAwkPDw8Czrr1mzJr/++isajYbFixfT\nvXt3bt++ja2tLV988QVffPEFFy9epGnTptSuXZu33347w/7u7u7cunWLChUqAHD79m3c3d1f2uYX\nad68ObGxsZw/f57169fz1VdfZdmuBQsWcOXKFU6ePEmJEiU4d+4c1atXRwjxyuPt5eVFaGgo9erV\ny7Tuxx9/JCwsjL1791K6dGni4+MpVqyY/v180bF6nQ6fL9q3ZMmS3L59W7/d878D2NjYkJSUpH/9\n/P3/Q4cOMX/+fPbt20fFihUBMsT7/DGDV3+2XF1dWb58OQBHjhyhefPmBAYGUrZs2Ve273kFqQOs\nZBzyjF7KV2q1mpSUFP3P6/Y8fvbHcujQoSxbtoyTJ08ihCApKYnffvuNxMREkpKSUCgUODs7o9Vq\nCQ0N5cKFC9mK779noSVLlqRly5ZMmDCBJ0+eoNVquX79uv4Z5e7du/P1118THR1NfHw88+bNy/SH\n9fky27Vrx5UrV1izZg1paWmkpaXxxx9/8Pfff5OWlsZPP/3E48ePMTU1xc7ODlNTU0DXAfHatWsI\nIbC3t8fU1DTL5NCrVy8+/fRTHjx4wIMHD5g9ezb9+vXL1jF4xtzcnG7duvH+++/z6NEjWrRokaFN\nz9qVmJiItbU1Dg4OxMXFZety94gRI5g6dao+ocbGxhIWFqYv19LSkmLFipGUlJThy93LjpWrqysP\nHz4kISEhyzpftm/37t1ZuXIlly5dQqVSZWpLQEAAmzdvJjk5mWvXrhESEqJ/v588eYKZmRnOzs6o\n1Wpmz579whjg1Z+tTZs2cefOHQAcHR1RKBRZvuev4ubmxq1bt+Tl+zeYTPRSvmrTpg1KpVL/M2vW\nrFc+dvf8+ho1avD999/zv//9j2LFiuHn58fq1asB8Pf3Z+LEidSrVw83NzcuXLhAw4YNsyzndep6\nZvXq1ajVavz9/SlWrBjdunXTn8kNHTqUli1bUqVKFWrUqEHbtm0zJeHny7O1tSU8PJz169fj4eFB\nyZIlmTJlir5n/Jo1ayhTpgwODg4sX76cn376CdD1wG7RogV2dnbUr1+fUaNGERgYmCn+adOmUbNm\nTapUqUKVKlWoWbMm06ZNyzKW19G7d2/27t1Lt27dMrXpWVnjxo0jOTkZZ2dn6tevT+vWrV+7nrFj\nx9KhQwdatmyJvb099erV4+TJkwD079+f0qVL4+HhQaVKlfRXaZ550bEqX748vXr1omzZshQrVizL\nXvcv2jcoKIhx48bRtGlTypUrl2nMh/Hjx2NhYYGrqyuDBg2ib9+++nVBQUEEBQVRrlw5vL29sba2\nznDpP7ufrVOnTlG3bl3s7Ozo2LEjixYtwtvbO8vj+LLj3a1bN0B326ZmzZov3E4qugw6YM7ly5cz\nPBJy48YNPvnkE/r27UuPHj2IjIzE29ubjRs34ujoCMDcuXNZsWIFpqamLFq0iJYtWxoqPEnKczt2\n7GDkyJHcunXL2KFIecTExIRr165l+5K5JBUUBj2jf+uttzh79ixnz57l9OnTKJVKOnfuTHBwMC1a\ntODKlSs0a9aM4OBgACIiItiwYQMRERHs3LmT9957T9/7VpIKopSUFLZv3056ejpRUVHMmjWLLl26\nGDssSZIkvXy7dL9nzx58fX0pVaoUYWFhDBgwAIABAwboBzXZsmULvXr1wtzcHG9vb3x9ffWX8SSp\nIBJCMHPmTIoVK0b16tWpWLEis2fPNnZYUh6Sndmkwi7fet2vX7+eXr16AXDv3j1cXV0BXceZZ48W\nRUdHU7duXf0+np6erz3CliQZg7W1tfwyWsTl5TDIkmQM+ZLo1Wo1W7duzfLZ39fpiPU8X19frl+/\nnucxSpIkSVJB5ePjw7Vr13K0b75cut+xYwc1atTAxcUF0J3FP+tZGhMTQ4kSJQDw8PDI8BzynTt3\n8PDwyFDW9evX9Y/2vIk/M2bMMHoMsv2y7bL9sv2y/fn7k5sT3HxJ9OvWrdNftgfo0KEDq1atAmDV\nqlV06tRJv3z9+vWo1Wpu3rzJ1atXqV27dn6EKEmSJElFksEv3SclJbFnzx6+//57/bLJkyfTvXt3\nQkJC9I/Xge456O7du+uHwfz2229lRxhJkiRJygWDJ3obG5sMYz2DbljIPXv2ZLn91KlTsxzeVNJp\n0qSJsUMwqje5/W9y20G2X7a/ibFDKLQMOmCOISgUCgpZyJIkSZKUK7nJfXIIXEmSJEkqwmSilyRJ\nkqQiTCZ6SZIkSSrCZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIkwmekmSJEkqwmSilyRJkqQiTCZ6\nSZIkSSrCZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIkwmekmSJEkqwmSilyRJkqQiTCZ6SZIkSSrC\nZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIszM2AFIkiRJWYuNjWXHjh2YmJjQtm1bnJycjB2SVAgp\nhBDC2EFkh0KhoJCFLEmSlG03btygdu1AUlLqAOnY2p7nzJkjuLu750v9f/75JzNnzichIYn+/bvQ\nv3/ffKlXylpucp88o5ckSSqAJk78mEePRqDVfgRAauqHTJv2KStWfGvwuv/880/q1GlCSso0wINj\nxz7m8eMERo9+z+B1S3lP3qOXJEkqgKKi7qHV1tC/Tk+vwe3bdw1e78OHDwkMbEVKyhBgAtADlWo1\n8+d/Y/C6AU6cOMHIkWMZO/Z9/v7773yps6iTiV6SJKkAatWqMUrlF8Bj4CFK5Ve0bh1o8HqnTp1N\nQoInYPrcUpN8uWW6f/9+mjZtz7JlJVm8WEmtWo25ePGiwest6mSilyRJKoA+/ngy77zjg6lpCczM\nPBgwoA7jx482eL2XLt1Aq+0P/AB8A/yCiUkPxo4dZvC6P/poHirVV8BkhJhNUtJ4Pv98scHrLepk\nopckSSqAzM3NWb36O1JTVaSkJPHttwsxMTH8n+yGDWtgbb0bCAMOYGLyPs2a+TNx4liD152cnAIU\n178WwpnExGSD1qlSqRg+fCzly9chKKgr169fN2h9xiA740mSJBVgpqamr94olx49esSOHTtQKBSM\nHTuSs2ffY//+NoCCRo0aERa2AYVCYfA4hgzpyaRJE1GpbAAVSuVsBg9eZtA6O3fuw++/W5CSspCr\nVw9Tp04Trlw5T7FixQxab36SiV6SJOkN9s8//1CzZiNUqiqAwMZmKqdOHcLc3BwhBK6urvmS5AHe\ne284arWab78dh5mZGR9/PJ+2bdsapK7k5GQ++mgWu3dvR4gngAVabX3U6gMcOHCALl26GKReY5DP\n0UuSJBnZX3/9RUxMDJUrV6ZkyZL5WnfPnoP5v//zRKOZDYCZ2VR69XrI6tXf5Wsc+UkIQZMmbTlx\nwoLU1J3APcABENjZNWbt2g9p166dkaPMKDe5T96jlyRJMqIxYyZRt24Q3bvPw8+vCrt3787X+v/5\n5y4aTS396/T0WkRGRudrDPnt+vXr/PHHeVJTNwHDgCBgBebmg3Fze0KzZs2MHGHekolekiTJSA4f\nPsyKFT+jUl3k8eO9JCX9TNeuffLlquW6devx9q7C+fOnMDObDyQAj1Eqv6Zly0YGr9+YhBAoFKbo\nUuBXQD9MTafRo4eCP/44iLW1tZEjzFsy0UuSJBnJjRs3UCjqAo5PlzRCpUokMTHRoPXu3buXd9+d\nSGTkIpKSdiNEJAqFM6amJejevQKTJ080aP3G5uPjg79/WSwt3wV2Y2FxET8/d0JCluHg4GDs8PKc\nTPSSJElGUqVKFTSafcDNp0vW4eLijq2trUHr3bhxC8nJE4AmQFU0mp/x8ipPcnIioaFL86WnvzGZ\nmJiwb99WBg1yombN+fTuLThyJBwLCwtjh2YQste9JEmSkQQEBDBv3sd88EFVzMycsLaG7du3GLyX\nu4ODLaamd9Boni25g52dHebm5gattyCxs7Nj6dKFxg4jX8he95IkSUaWkJBAbGwspUqVypezyjt3\n7lC1al0SEjqQnl4Ca+tv+eWXH2nVqpXB65ZyJje5TyZ6SZKkN1B0dDQ//BBCUlIyXbt2platWq/e\nSTIameglSZIkqQiTz9FLkiRJkpQlmeglSZIk6UWEgEWLIC7O2JHkmEz0kiRJkpQVrRZGj4axY6FD\nB93rQkg+XidJkiRJ/5WeDkOHwsqVYGEBkyZBPkwTbAgy0UuSJEnS89Rq6NsXNm0CpRK2bIHmzY0d\nVY4Vzq8nkiRJ0hsvKSmJLl36olQ64uzsxY8//pT7QlNS4J13dEne3h7Cwwt1kgf5eJ0kSZJUSPXo\nMYgtW1JITV0M3MTauiPh4Rtp2LBhzgpMTISOHWHfPiheHHbtgho18jTmnJKP10mSJElvnF27dpGa\nOg9wBmqRkjKY3bv35Kyw+Hho2VKX5N3c4ODBApPkc0smekmSJKlQcnAoBlzWv7a0vEzx4sWyX1Bs\nLDRtCseOgZcXHDoEFSvmXaBGJhN9Ieft7U1ERIRBytZoNIwaNQpfX1/8/PwICQl54bZz586lcuXK\nVKhQgYEDB6JWqwG4desWZmZmVKtWTf/z6NEjAI4ePUqDBg2oWLEiFStWZNKkSXkaf58+ffDw8MDE\nxASVSpVh3fHjx6latSpvvfUWrVq1IjY2Vh/T87F6eHhQ4wXf6lUqFT169MDPz48KFSrw22+/6det\nWbOGKlWqYG5uzjfffJPl/gcOHMDU1PSF6yVJermlSz9HqeyDufk4lMqOeHpeYdCgQdkrJDoaAgPh\n7Fnw89MleV9fwwRsLKKQKYQh50hoaKiYOXPmK7fz9vYWFy5cMEgMq1atEq1atRJCCBEbGys8PT3F\nrVu3Mm23a9cuUaVKFaFSqYQQQgwdOlQEBwcLIYS4efOmcHZ2zrL8CxcuiGvXrgkhhEhNTRUNGzYU\nP/744yvjGjBggDhw4MArt9u/f7+4f/++UCgUIikpSb9co9EIHx8fceTIESGEEJ9++qkYPHhwlmV0\n6tRJLFiwIMt1s2bNEsOGDRNCCHH16lXh5uYmEhMT9W2LiIgQ/fv3F998802mfRMSEkSdOnVE+/bt\nxZIlS17ZFkmSsnbu3Dnx+eefi++++048efIkezvfvClE2bJCgBCVKgkRE2OQGPNCbnLfG3VGP3/+\nfP73v//pX9+7dw83NzdSUlJyXfa9e/do2rQpNWvWpFKlSnz44Yf6dUOHDmXChAn67cqWLcuff/75\n0vKyM03lmjVrqFmzJn5+fnl6drhx40aGDRsGgLOzM506dWLTpk2Ztvvzzz9p1KgR1tbWAAQFBfHT\nT6/u/VqxYkV8fHwAsLCwICAggNu3b79yP4VC8VrHp0mTJri4uGRafvr0aaytralfvz4Aw4cPZ+PG\njZm2u3//PuHh4fTr1y/L8jdu3Mjw4cMB8PX1pWbNmuzYsUPftgoVKmBiYpJlB5oJEyYwadIkihcv\nrl+WnJxM1apVCQsLA2Dfvn1UqFCBpKSkV7ZVMr5z584xYMAIevcewsGDB40dzhujatWqfPDBBwwb\nNgxbW9vX3/HyZWjUCG7c0N2LP3BAd2++CHqjnqMfMmQI/v7+fP755yiVSpYvX06fPn2wsrLKtG23\nbt24du1apuUKhYJjx45haWmZYbmjoyNbt27FxsaGtLQ0goKC2LVrF61atWLx4sXUqVOHLVu2sHjx\nYiZNmkSVKlVeGmtWyeFFYmNjOXXqFPfv36datWo0btyYypUrZ9jm0qVL9O7dO8v9W7Zsybx58zIt\nv337NqVLl9a/9vLy4p9//sm0XY0aNfj+++95+PAhDg4ObNy4kcjISP36hIQEatSogUKhoGfPnrz/\n/vuZyrh//z6bN29m+/btr9Xm7Byf//pvu5ydndFqtcTHx+Po6Khfvnr1alq1apXll4WsynnR8fmv\nHTt28OTJE7p06cLWrVv1X1qsra3ZuHEjLVu2xM3NjSFDhvDLL79gY2OT06ZK+eTs2bM0atSSpKQP\nAGu2bOnBzz+vJCgoyNihFXqJiYkMHPgeO3b8hp2dI4sWBdO9e7fcFfrnn9CiBdy/Dw0bwrZt4OCQ\nNwEXQG9UondycqJDhw6sXr2aIUOG8MMPP7Bv374st83qzPVl0tPTef/99zl27BhCCO7evcu5c+do\n1aoVVlZWbNy4kRo1atCmTRtGjBiRZRnbt2/no48+AiAuLg61Ws2vv/4KwOjRoxk8eHCW+7377rsA\nlChRgrZt23LgwIFMib5ChQqcPXs2W216XW+//TajRo2iZcuWWFlZ0axZM3bv3g2Au7s7UVFRODs7\nExsbS4cOHXByctLHDPDkyRM6dOjA+++/T9WqVbOs45NPPmHz5s2ALsEePnxY/+191apVr/zilBOh\noaFZfgHKjfj4eCZPnsyePbqewUKIDF9a3nrrLWbPnk39+vX5+uuvX3g8pILliy++JSnpQ0D3JVal\nKsGsWV/JRJ8HBg0axbZtaaSmXkSlus7Age9QurQXderUyVmBJ09CUBA8eqRL9r/8AkX8y/QblehB\nlzD79OmDi4sL/v7++kvH/9W1a1euX7+e5bpjx45lugrw5ZdfEh8fz8mTJ7GwsGD48OEZbglcvHgR\nBwcH7t69i0ajwdTUNFO5bdq0oU2bNoAueUVGRvLxxx+/sk3PJwohRJaXtSMiIujTp0+W+7do0YLP\nP/8803IvLy9u3bql74wWGRlJmTJlsixjzJgxjBkzBtBd0q74tMeqhYUFzs7OALi4uNCnTx+OHDmi\nT/QqlYp27doRFBTE+PHjX9jG6dOnM336dAAGDRrEoEGDaNy48Qu3f5nSpUtnuOLw4MEDTExMMpzN\nHz9+nEePHunfj6w8Oz7PLr9HRkbStGnTTNs9/35cuHCBu3fvUrt2bX3d27Zt49GjR0ybNg3Q3Vpw\ndXV9rasDUsGQkqIGnr9sbKfvkGoIT5484eHDh3h4eGBubm6wegqCnTt3kJp6DnAD3EhNHUh4+O6c\nJfrff4e2bXXPy3foABs2QBZXdIucPOgjkK/yIuS3335blCpVSmzdujUPItKZOHGiGD9+vBBCiDt3\n7ghXV1cxa9YsIYQQN27cEF5eXuLatWtiwIABYvLkya8s73U745UuXVoMHTpUCCHE/fv3hYeHR551\nzlu5cqVo1aqV0Gq14v79+y/sjCeEEDFPO7HExcWJ6tWriy1btuhjUqvVQgghkpKSRPPmzcWiRYuE\nEEIkJyeLpk2big8//DBbcQ0cOPC1OuMJIYRWqxUKhULfSU6IfzvjHT58WAghxCeffJKpM97QoUNf\nGdfMmTP1x/7KlSvC1dU1Qz1C6DoOvqyz3cCBAzN01tu8ebOoXr26iIuLExUrVhQ7dux4rXZKxhUe\nHi6UypICfhawQyiVviIkJNQgdS1a9K2wsLAVSqWnKFGitPjrr78MUk9B4e5eTsABoZtGTghr6y45\n68C6c6cQ1ta6Qnr1EuLp36XCIje5741M9GvWrBHe3t55EM2/IiMjRe3atUWlSpVEUFCQ6NOnj5g1\na5ZQq9Widu3aYt26dUIIXbLz9/cXO3fufGl5K1eu1H9ReBlvb28xdepUUaNGDeHr65tlD++c0mg0\nYuTIkcLHx0f4+PiI77//Xr9u2bJl4uOPP9a/rly5sqhYsaIoV66cWLx4sX755s2bRaVKlUTVqlWF\nv7+/+PDDD4VWqxVCCLFkyRJhamoqqlWrJgICAkRAQICYM2fOK+MaOHCgOHjw4Cu369y5s/D09BQm\nJibCw8NDBAUF6dcdPXpUVK5cWfj5+YmWLVuK+/fv69epVCrh4OAgLl++nKnMgIAA/ZeapKQk0a1b\nN+Hr6yveeustERYWpt9u7dq1wtPTU9jY2AgnJyfh6ekpLl26lGVbnr1nN2/eFKVKlRJXr14VQuh6\n7nt5eYmoqKhXtlUyvi1btogaNZqKqlUbix9+WGGQOs6cOfP0C8WNp4kvVHh6vmWQugqKX375RVhb\nlxBmZhNF0rhoAAAgAElEQVSFtXUn4etbJfu96zdvFsLcXJfkhwwRIj3dMMEaUG5y3xs5BO6QIUOo\nUKECEydOzKOoJEmSDC80NJTRo/eTlLT66RKBqakVCQmPUCqVeV7ftWvXOH/+PN7e3i8cTyI/nD59\nmt27d+Po6Ejfvn2z17t+zRoYOBA0Gt10swsXQjaeaiooCvQQuPHx8XTt2pUKFSrg7+/PiRMniIuL\no0WLFpQrV46WLVsSHx+v337u3Ln4+flRvnx5wsPD8zSW6Ohoypcvz/Xr1xk1alSeli1JkmRoZcuW\nBY4BCU+X/I6trZP+0da89NNP66hatT6DB/9I48ZdGDducp7X8bpq1KjB5MmTGTFiRPaS/PLl0L+/\nLslPm1Zok3yu5dFVhRfq37+/CAkJEUIIkZaWJuLj48UHH3wg5s2bJ4QQIjg4WH8v9OLFi6Jq1apC\nrVaLmzdvCh8fH6HRaDKUlw8hS5IkFUharVaMGDFOKJWewsGhubCxcRbh4eF5Xk9KSoqwsrIX8OfT\nWwRxQqksJU6fPp3ndRnMggVCf2P/6QBehVlucp9BL90/fvyYatWqcePGjQzLy5cvz8GDB3F1deXu\n3bs0adKEv//+m7lz52JiYqIfbCYoKIiZM2dSt25d/b5y9jpJkt50586dIyYmhqpVq+Lu7p7n5UdH\nR+PrW43k5Hv6Zfb27Vi1agidOnXK8/rylBDwyScwY4bu9ZIlUASu4BbYS/c3b97ExcWFQYMGUb16\ndYYOHUpSUhL37t3D1dUVAFdXV+7d032YoqOj8fT01O/v6elJVFSUIUOUJEkqdAICAmjdurVBkjzo\n/i7b2loB654uOUda2omCP66DEDBpki7Jm5hAaGiRSPK5ZdDn6NPT0zlz5gxLliyhVq1ajBs3juDg\n4AzbvGo406zWzZw5U/97kyZNaNKkSV6FLEmS9Ma7ceMGtrYOxMb2BYZhYSFYuXLlC8fRKBC0Wl1S\nX7YMzMxg7VrolssR9IzowIEDHDhwIE/KMmii9/T0xNPTk1q1agG6QWjmzp2Lm5sbd+/exc3NjZiY\nGEqUKAGAh4dHhkFC7ty5g4eHR6Zyn0/0kiRJUt7RaDQ0bdqOqKhRwHBgDxYWgwgMbGTs0F4sPR0G\nD4YffwRLS/j5Z93AOIXYf09iZ82aleOyDHrp3s3NjVKlSnHlyhUA9uzZQ8WKFWnfvj2rVq0CdCPA\nPbvn06FDB9avX49arebmzZtcvXpVP4KYJEmSZHhRUVHExSUixBjAEmiLqWkAZ86cMXZoWVOroWdP\nXZK3sYHt2wt9ks9rBh8Cd/HixfTp0we1Wo2Pjw+hoaFoNBq6d+9OSEgI3t7e+pnD/P396d69O/7+\n/piZmfHtt99maxY3SZIkKXecnJxIT08A7gCegIr09GsvnNzJqJKT4Z13YMcO3aQ0O3ZAvXrGjqrA\neSMHzJEkSSpo1Go1oaGh3LwZSb16dejYsaPRYgkOXsAnnyxCo2mHuflhOnSoxZo13+fqxCsxMZF3\n3x3Nrl27cHQsztKln9O6deucB/nkCbRvDwcPgrMzhIdDtWo5L6+Ay03uk4lekiTJyDQaDYGBbTh7\nVqBSNcLGZi1jxvRgzpyZRovp0KFDnD17ljJlytCuXbtcX13t0qUv27drSE2dB/yNUtmXY8f25Gzm\nyUePoHVrOHECSpaEPXvA3z9X8RV0MtFLkiQVYlOmTGHevE0IcRkwBe5hbl6Gx48fGmTUO2OwtnYg\nJeU6oJvN0tx8HHPmePL+++9nr6D796FlSzh/HkqXhr174QWzkBYlBfY5ekmSJOnlQkNXEhy8BCHK\noEvyAC4oFBaoVCpjhpanbGwcgFv61+bmN3FwcMheIVFREBioS/LlysGhQ29Eks8tmeglSZKMRKvV\nMm7cdGAl8BewGrgNjMXHx49ixYoZM7w89eWXc1AqO6JQTMfKqhvu7rfo1avX6xdw8yY0agR//w1V\nqujmli9VKttxpKSkkJycnO39CjOZ6CVJkoxk9Oj3SUhQAWWBHcBSoBqwik2bVhapp4769+/Lzp3r\nmTbNhODghpw5c/j1J6j5+29dkr95E2rXhv374enoqq9Lo9HQv/9wbG0dsbNzomvXfqjV6hy0pPCR\n9+glSZKM4NSpU9Sp0wCtdhz/JvkY4F2aN2/E7t3bjBtgQXHunO6efGwsNG4M27aBnV22i5k7dz6f\nfrodlSoMMMXauitjx9Zi7tycD0STn+Q9ekmSpFwKDw/HxyeA4sW96NNnqEHvjx87dozGjYPQagHe\nB7oB/YH3aNKkJjt3bjFY3YXK8ePw9tu6JB8UpHtOPptJPiEhga+++orly39CpXoPsAOUJCePZu/e\nowYJu6CRiV6SpDfeX3/9RadOfbhxYw5xcQfYvDmeAQNGGqy+GTO+IDl5LrohZrsC1VAo+lOsmAUb\nN67H1NT0FSVkX0JCAt26DaREibJUqdKAkydP5nkdeerAAWjeHOLjoXNn+PVXUCqzVURCQgIBAfWZ\nMuUYt25ZAb/r15maHsPbO/MQ60WRwUfGkyRJKuh27dqFRtMbaANASsq3/PZbOYPVp1KlAMWBhcAX\nwExcXBI4fvyQwUag69SpD0ePOpOauovY2D9o2rQtERGn8fLyMkh9ubJ9u27Eu5QU6NMHVq7UTVST\nTatXr+bu3QqkpGwA7gF1USjOYGvrgLX1JRYs+P1VRRQJ8oxekqQ3np2dHWZmt59bchulMvv3gV/X\n0KE9USonA4eBmiiVD1m8+DODzQ6nVqs5eHAXqanfAX5Ab6AF+/fvN0h9ufLzz9Cpky7JDxsGq1fn\nKMmD7oxerX52TF2BXVhaXmDFisFcvnyWUjnotV8YyUQvSdIbr3fv3ri6XsXSshcKxSyUyo588cWn\nBqtvwIB+fPnlB/j5vU+5clNYsmQm3bsbbkpVMzMzzMzM0Z3VAggUiqjX7/WeX1avhu7dIS0NJkzQ\nTTlrkvM01apVKywsVgH7gNtYWX1Ex47v0LVrVxwdHfMs7IJO9rqXJElCd/b3/fffExsbR1BQiwxT\nhBYFc+bM57PPvkelGoyV1Sl8fP7h1KmDWFlZGTs0naVL4b33dL/PmKH7yYPHC8PCwvjf/yaTkBBP\nmzZt+OGHRSizea+/IJBD4EqSJGWDEIL169ezf/9RvL09GDt2NDY2NsYOK0+Fh4czY8YCUlPVjBzZ\nlyFDBrN161b27z+Ep6cbI0aMKDhtnj8fJk369/fsDov7BpCJXpIkKRsmTZrGN9+EoVINxtLyGD4+\nNzl9+veCc3abA7/99htjx07jyZME6tatzu7dv5Oc/DXggFI5ni++mMDIkcOMHWZGQsDMmTB7tu71\nt9/CSMM97VCYyUQvSZL0mtRqNTY29qSn3wZKAAJb24b89NOHdOjQwdjh5cipU6cIDGyLSrUKKIOp\naVs0mlHA+Kdb7KFixRlcuHDEiFH+hxAwcSIsXKi7Dx8aCv37GzuqAis3uU8+XidJ0hslLS0NUABO\nT5coUChKFNrxzyMiIujRoz8q1SAgCACNpgHw/IA/Ksxy2HPdIDQa3f345cvB3BzWrdM9TpcNycnJ\nLF68hCtXImnYsCYDBgwoUkMG56UC9M5LkiQZno2NDQ0aNOX48aGkpk5EoTiGiclxAgOXGju0bLt0\n6RI1azYiObkREAnsBdKAeigU7yOEGeCIUjmbGTOWGDVWvfR0GDgQfvoJrKxg82bd3PLZkJaWRuPG\nrblwwYmUlCasW/cNJ06cZ+nShYaJuZCTl+4lSXrjJCQkMHz4eA4dOoanpwfff/8llStXNnZY2RIT\nE0OFClV5/DgQmI9uMhwPwBa4yOTJ/+POnYekpKgZMqQXrVq1yvMYhBCo1WosLS1fb4fUVOjZUzfK\nna0tbN0KOXi6Yf/+/XToMIHExNPonhKPx9zckwcPorG3t892eYWBHOtekiTpJdLT0zl+/DiHDh0i\nOTkZe3t71q0L4c6dCI4f313okjzA5MmzePKkJqAFQoB26Ka6PY6p6UQuXrzFjz8uZ9OmlTlO8klJ\nSXTu3AdLS1ucnNwJCQnVrwsJCUWpdESptKNmzSbcu3fvJSUBKhV06KBL8o6OsGdPjpK8rigVJibF\n+TeF2WFiYkFKSkqOyivq5KV7SZKKtKSkJBo1CuLq1UcoFFYUK5bM8eN7cXNzM3ZouXLrVjRabS9g\nBnAdGIeu7wFoNM24fj0813UMGTKGHTu0qNX/oFbfZsyYdpQt6421tTVjxkwjJeU4UI7z56fQpUt/\njhzZlXVBCQnQrh0cOgQuLrB7N1StmuO46tevj7n5CBSKrxHibSwsllK5chWDDR9c2MkzekmSirRP\nPgnm0qVSJCb+yZMnfxAd3Y4xYyYbO6wcu3v3LleuXKFp07oolaFAOGCPbprbJCAdS8vvqVevRq7r\nCg/fTWrqHHQdF6uSnDyE3bv3cvToUdLTuwIVAFPS06fzxx+Hsi4kLk43Oc2hQ+DhAb//nqskD+Dk\n5MTRo3tp0GAXnp696NBBRXj4L7Iz3gvIM3pJkoq0ixevk5LSmmfnNWlpbbh06SPjBpUDQgiGDx/L\n6tU/YmbmiIuLDUFBAWzZUhEhBJ6efty9WxKFwoxatWqzcOE3ua7Tyak4cXERQBlAYGkZgYtLXVxd\nXTE3/xW1WgOYAqdwcsriCsm9e9CiBfz1F5QpA3v36v7NA+XKlePQoe15UlZRJxO9JElFWt26Vdm7\ndy3Jyd0AcywtV1GrVu7OKPObEIIRI0YSEvI7Wu0tUlPtSUmZTalSJ0hKSgDA0tKSuLg40tLSKFGi\nRJ6c3S5bNp+OHXuh0fQATmFpGcn9+7707NmTatVWc+5cfYR4CyF2sGrVjxl3/ucf3Zn8lStQvrzu\nnrzHmzEtbEEje91LklSkpaWl0alTb/btO4BCYU7FiuXYuzesUPXOXrbse0aPnkJ6+lhg+tOlkTg5\nNSAu7o5B646IiODTTz/j55/3oVaPw9z8BsWK7ebcuaOcPHmShw8f0rBhQ/z8/P7d6fp1aNYMIiMh\nIAB27YISJQwaZ1EnB8yRJEl6AXNzc7Zt20hUVBTp6el4eXlhkosZ0fLb4cOH+fDDz0hPHwjsBiYB\nlkAYZcv6Grz+GzdusHlzOGr1NqAOaWkQH9+fdevWMX78+Mw7RETozuRjYqBuXd3c8k5OmbeT8o1M\n9JIkFXkKhQJPT09jh5FtBw8epHXrbiQnFwcaA7fRdYBzwtLyFmvWGHZI27Vr1zF06Iekpgp087nr\npKe7kZiYlHmHM2egVSt48ED36FxYGNjZGTRG6dXkpXtJkoqM9PR0fvjhBy5dukbNmlXp27dvoe6J\n3apVV8LD26DrVT8O3aN0F7GyWsnevdupX7++QesvX74Oly9/CmwFLgNfADdQKody9Ohuqj7fe/7o\nUWjTBh4/1v37f/8H1tYGje9NIi/dS5L0xtNqtbRp05UjR56gUrXExmYx+/cfZ8WK3Pc+N5a0tHTA\nHEgGWgHf4uqaxM6dBwgICDB4/enp6YASXYKfCrTGycmMjRvXZkzy+/bpBsNJSoKuXXXD21pYGDw+\n6fUUnhtVkiRJL3HmzBmOHr2ISrUT+JCkpD2sXbuWu3fvGju0HHvvvb6YmIwFlgN2QCRduwYZNMnH\nxsZy7tw5EhIS+N//BmJjMxzYDwSgVKrZuXMjzZs3/3eHbdt0Z/BJSTBggG6CGpnkCxSZ6CVJKhKS\nkpIwNXVBdwYMYIeZmT2JiYnGDCtXTE1NsbDwAQ4CXwFHWbFitcFuX3733Q94eZUjMLAfHh4+VKpU\ngXnz/ke1asE0aLCWbds2ULt27X932LgROnfWjWH/3nuwYgUUpFnyJEBeupckqYioXr06lpbRmJh8\njVbbBjOzlbi7F8Pb29vYoeVYXFwcpqb+/HtO5ktqqoq0tDQs8vis+dq1a4wfP5WUlD9ISfEFDtC5\nczcePLjDqFEjMu8QGgpDhoBWC5MmQXAwFOL+EEWZPKOXJKlIsLOz48iR3dSqtQ1n55YEBl7kwIHf\nCtY87K9p+/btdO8+iB079qHR/IZu+tl4zMwmUbNmozxP8gCXL1/GwqI68OyRvSZotVbExMRk3njJ\nEhg8WJfkZ8+WSb6Ak73uJUmSXiImJoaDBw+iVCpp1arV60/JmkO6R9omoVJ9hEJxHyurL7G1dSIh\n4QF16jRm06ZQShhg8JnLly9TrVpjkpP/ALyAY9jYtOPBgyisrKz+3TA4GKZM0f2+YAFMmJDnsUiZ\n5Sb3yUQvSZL0AufOnSMwMAgh6iPEPcqU0XL8+F6USqXB6ixXrhZXr84FdB3eFIqpTJig5Ysvgg1W\n5zMLFy5m6tSZWFj4kp5+nY0bV9G2bVvdSiFg+nT47DPd2fuyZTBsWLbKT0xMRKPR4ODgYIDoizY5\nH70kSZIBvPvuOBIS5vDkyWYSEw9z9aoHS5YY9nG9tDQ1YKt/LYQtKSlqg9b5zPjxo7ly5Rzbt3/J\nrVuXMib58eN1Sd7UFH78MVtJXqPR0L//MJycSuDi4kGrVp1RqVQGaoX0XzLRS5IkZeH+/fvcvn0b\nqPd0iYKUlLpERkYbtN533+2FldUgdNPPrkOp/Ir+/XsatM7nlSpVigYNGvw7t7tGA0OHwtdf6x6b\n27QJ+vTJVplffbWYn3++THr6PdLS4vj9dzMmTfrYANHn3JEjR+jYsQ9t2/Zk165dxg4nT8lEL0mS\n9B+DB4/A3b0scXGJwGdAOnAPpTKUJk0MNxrd+vUb+eyzYDSaWExNu1Kp0tds3bo+4yNt+SktDfr2\nhZAQ3Sh3YWG6x+myaf/+E6hUQ9GNBWBBSsp7/P77yTwPN6eOHDlCy5adCQtryPbtLenSZRDbtm0z\ndlh5RiZ6SZKk58ycOYvQ0M1oNNfQaq8CEYASMzNvxo3rTteuXQ1S782bNxk8eBQpKQdJS3uARhNK\nTEwUjRs3Nkh9r5SSohvlbv163Xj1O3fqxrHPAV/fUlhY/A7o7jGbmh6ibNlSeRhs7nz55XeoVDOA\nkcBgVKqFBAd/a+yw8kzhe+5EkiTJgBYu/AZoD7g9XfIHYE5CwmOs83Ds9vT0dL7+egknTpynYkUf\n/P3fwty8NsnJz4aWfQeVahT37t3DI7/ncU9Kgk6ddHPIOznpppmtVSvHxc2YMYXffnube/caAdZY\nW19j0aKDeRdvLmm1gn8HWgIwQ6PRGiucPCcTvSRJEnD+/Hl69RpGQkIC8DsQDzgC27C1dcnTJA/Q\nrdsAwsPvolL1JCwsjLJlfyE9/R7wECgO/AmkULx48dcqT6vVcvHiRdLS0qhUqVLOn7V//BjatoUj\nR3RzyO/eDVWq5Kysp5ycnPjzz2Ps37+f9PR0AgMDC1TP+9GjB7FrV2+Sk5WAJUrlRCZM+NLYYeUZ\n+XidJElvvEePHlG2bEXi4+cC+4BjwGOgNHCR0NBvGDhwYJ7VFxUVhY9PFVJTzwG9gb8AFf7+Vbh1\n6y5mZlVJSztJSMgSevXq8cryUlJSaNGiE2fPXsHExIqSJa04fHgXLi4upKen8+TJExwdHV89k9+D\nBxAUBKdPg6cn7N0L5crlRZMLvPDwcObMWUJ6uoZx4wbTtes7xg4pA/kcvSRJUg6lpKTQvXsftm27\nhRCngRTgfWAlJUq4sGhRMD16vDrZZseNGzeoXLkRKlV9wB1YCDzEyqoxn3zyLuXKlaNSpUqULVv2\ntcqbNesz5s07RXLyJsAUc/OJdO78CB8fDz7/fAEKhSleXj7s2fMrZcqUybqQmBho0QIuXgQfH91l\n+0I8fHBRIxO9JElSDnXrNoCwsFuo1beBvwFL4CEWFmWIjr752pfOX8fOnTuZOnUeycnJJCQ8Ijr6\nIXAC8Hm6xVwmTHjEggWfZ6vczp378euvzYCBT5ccpnjxXjx8mPi0fD/gc/z9N3Px4onMBURGQvPm\ncO0a+PvrLte7u+eskZJByAFzJEmSckCr1fLrrxtQq8OAOsDbwFQsLOozevToPE3y69ato3373pw9\n+z/+/juYR4/MsLIyRzcFLIAGa+tDlCnjle2yq1f3x9r6ZyANEJiZrScu7i7QBSgHKICJXLp0Co1G\nk3Hnq1ehUSNdkq9WDQ4elEm+iJFn9JIkvbGEEFhbO5Ca+hfgCazD3PwT3nuvNQsXLnz1Pe3XdObM\nGerUeZv09GnAB0+XHqFUqaEkJDxCiGpotTFUqlScAwd+y/Z4+qmpqbRu3ZUTJ85hYmKFp6c9V678\niVZbEd0ZvSVwCBubLiQmxv6744ULujP5e/egfn347TdwdMyTNhcEp06dYvv2HTg42DNgwAAcC3Hb\ncpP7ZK97SZLeWAqFgqlTpzBvXmtUqlGYm5/HzU3B7Nmz8yzJA0ye/Bnp6XWAhOeWPsbOzpHTpw9y\n9OhRbG1tCQwMzNFse5aWluzdG8aVK1dQq9VUqFCBgIAGXLyYBlRDd1a/h6+//vrfnU6fhpYtIS4O\nmjaFLVvA1vYFNRQ+W7dupWfPIaSkDMLcPIIFC5Zy/vwxnJycjB1a/hOFTCEMWZKkAm79+vWiX79h\nYvLkaeLhw4e5KissLEyUKuUvHBxKiu7dB4rNmzcLX98aApYLcBEwQ8AiYWJSXPz888951ILM7ty5\nI6pXbyxMTEyFnV1xsWLFin9XHjokhL29ECBEu3ZCJCfnef33798Xbdt2E2XLVhOdO/cV0dHReV7H\ny3h7VxYQLnQD9QthadlHzJ8/P19jyEu5yX3y0r0kSW+U06dP8+mnC0lMTGbIkB706NE9z8o+c+YM\nDRsGkZy8FiiJQtEcU1NXTE3TSE3VAPOBdZia7mPixEHMmzc3z+p+ESFExqsTe/ZAx46gUkH37rBm\nDZibv7iAHLh79y7e3pVJTW0LDAF+pXTp7fz995mMU94aUPHiXsTF7edZR0eFYgZTpmj57LNP8qX+\nvCY740mSJL2Gv/76i8DAIH79tTZ79rzD4MGTWbFiZZ6Vv2vXLtTq/uimmN2EEE1JTz9LauoFwAdz\n84G4up5k/vyp2UrySUlJDB06Bj+/mjRt2oHLly+/9r4ZknxYmG4wHJUKBg2CtWvzPMkDDBgwktRU\nE2AF0BCYz927ppw+fTrP63qR9u3bYm09EfgHOIyV1XLatAnKt/oLEnmPXpKkN8by5StJShoNjAFA\npSpJcPAkBg8emCflOzg4YGFxmuRk0CWYQHQ93gFm4OU1kmvXsp/s3nmnHwcPWpCS8g3Xrx+nXr2m\nXL587t8Z5v4jPj6egwcPYm5uzttvv60b1W/9et0ENRoNjB4NX30FJq93rqdSqYiOjsbd3R2lUvnK\n7S9fvg5oADVgBWjRaBIxN8CXihdZuvRLtNpxbNlSCxsbexYu/JoGDRrkW/0FiTyjlyTpjaHVasn4\nZ88kT28F9uvXDze3v7Gy6gncBb5EN8qeCkvLxTRqVCfbZapUKvbs2U5KymqgDkKMJS2tJvv3789y\n+8jISN56K4B+/b6hZ885VKlSD9XixdC7ty7JT5mim3L2NZP8zp07KVHCi4CAFri4eLJlS9gr9wkI\nqIxC4QZ0AlYC7+Dqakn16tVft9m5Zm1tzerV3/H48V2io6/k6S2aQidPegnko0IYsiRJBcTZs2eF\nUuksYJmAn4VS6SuWLv0uT+t4/PixWLBggahQobowMXEU4CbAVtSp87ZISEjIdnmpqanCzMxSwIOn\nHcu0wta2sfjll1+y3L51627C1HS2ftsJpnWFvkfaZ59lq+74+HhhY1NcwKGnRZwQSmVxcf/+/Zfu\nd/fuXeHjU0WYm7sJExMX4e1dQTx69ChbdUsZ5Sb3yUv3kiS9MQICAti7dyszZy4gKSmZIUM+ZsCA\nfnlah729PTY2NkRG2qDVRgNWmJlNw97+EnZ2dtkuz8LCgpEjRxMS0gqVaigWFscpWfIxrf4zZey1\na9do3bor165FAqMAmMJc5miO6zb4+msYMyZbdd+4cQNTU3d099kBamNu7sPVq1dfeNsAwNXVlYiI\nP4iIiMDCwoIKFSrk6eOKUjbl4ReOfFEIQ5Yk6SW++WaZKFmynHBxKSOmTZslNBqNsUPKtWHDRgv4\nUn8iDRdEyZLlclyeVqsV338fInr0GCymTJku4uPjM60vU6aSUCgWChgvoIuYwwdCgNCA2NWjV47q\nvX//vrCychRw+Wk7bggrq2Lizp07OW5Lbh08eFD4+VUXTk6eokuXvuLx48dGiyU/5Sb3FbqsKRO9\nJBUdGzZsFEqlj4CTAi4IpbKmmDv3C2OHlWuLFy8RSmUzASkChDA1/VS8/Xb7XJWp0WiESqXKtDwy\nMlK0a9ddKBSWAoRQ8EQsoowQINQgvm3cTKSnp+e43h9+CBXW1s7CwaGpsLZ2EYsXL815I3Lp6tWr\nwsbGWcAvAm4KS8sBomXLzkaLJz8V6ERfunRpUblyZREQECBq1aolhBDi4cOHonnz5sLPz0+0aNEi\nw72bOXPmCF9fX/HWW2+JXbt2ZQ5YJnpJKjI6deorIOS5M989okqVRsYOK9fS0tJEUFAXYWNTWtjb\nBwhPz3IiMjIyx+X98MMKYWVlJ0xNLUSVKvVFVFSUEEKIuLg44eJSWpiYzBBgI0w4L1YwUAgQKSjE\nqY8/zpP23Lx5U+zatUtcv349T8rLqWXLlglr60HPfV5UwtTUPFdfZAqL3OQ+g9+jVygUHDhwgGLF\niumXBQcH06JFCyZNmsS8efMIDg4mODiYiIgINmzYQEREBFFRUTRv3pwrV65g8pq9QyVJKlyKFbPH\nxOQ2Wu2zJZE4OtobM6Q8YWZmxvbt/8fFixdRqVRUrlxZ94hbDpw8eZIxYz4iJeUPwI+LF2fQuXM/\nTpzYy549e0hJqYhWOxNzyvAjtelBKkkoWNi4BR/NnJkn7fH29sa7AExZa2+v+7yAQPfY4j9YWNjI\nHPEK+XJ0xH8eXwkLC2PAgAEADBgwgF9//RWALVu2/D979xkfVfE1cPy3NduSUNIoodfQQeklgBTp\nHRA/SjQAACAASURBVEUQRaog2MEOSlP0ryKK8AARRDoISBEEDIQivQQQQq8hEAglfct5Xuwag4Ak\n2U1C8H5f6d07M2fWjzl7507h2WefRafTUaJECcqUKcOuXbtyIkSFQpEL3n33dby9v0erfQW1eiRm\n80g+/fR9t+o8efIkn376KV988QWXLl3yUKSZp1KpqFy5MrVr185ykgfYsWMHdnsXoDygxm5/h717\ntwKg0WiAVLxIZilL6EkKt4CDn07kvfBfH7sJcJ06daJYsVsYDF2BjzGZWvLpp+Meu356Wo480T/1\n1FNoNBoGDRrEgAEDiImJITAwEHDOzoyJiQHg8uXL1K1bN61s0aJFc/V/VIVCkb1Kly7NoUO7mD17\nDlarjZ49w6lUqVKW6rJarXTr9hwrV64C+qDRWBk79kn27t1KqVKlPBt4DipUqBBa7QJSUmw4/2Tv\nokCBQgC0aNGCwj6j+C6+LM3kItfR8k27jox+++1cjTm7GI1Gdu8OZ8aMGVy+HEPz5tNp2bJlbof1\nyMv2RL9t2zYKFSrEtWvXaNGiBRUqVLjrc5VK9a+/xu732eh0w1GhoaGEhoZ6KlyFQpHDihUrxgcf\nuPcUD/Dhh2NZtWonzv3kh2K3w61bH/DJJ5MIC5vqdv25pWvXrkybNpddu2oDFbHb1zFnzlwAvO12\nIgv5ort0gut6AyuGDuODSRNzN+BsZjabGTFiRG6Hke3Cw8MJDw/3SF3ZnugLFXL+8vT396dz587s\n2rWLwMBArly5QlBQENHR0QQEBABQpEgRLly4kFb24sWLFClS5J46R3vovZNCoXh8rFq1EYcjACib\ndk2kHNeuncxynadOnaJ37yGcPBlFpUqV+fHHqQQHB3sg2gc7ceIEx44do0yZMlSsWBGNRsP69T8T\nFhbGhx9+xpUrcfTuPZBl076k8bhx6Pbvh+BgCm7cSL+yZR/egCJP+OdD7JgxY7JcV7a+o09MTOTO\nnTuA81CG9evXU6VKFTp06MDs2bMBmD17Np06dQKgQ4cOLFiwgNTUVM6cOcOJEyeoXbt2doaoUCge\nE4GBfkAw8CFwCjiCVjuG7t3bZKm+hIQEGjRowa5drYmN3UhEhC/ly9ehR48X6Nv3JQICyhAcXIkZ\nM2Z5rA/Tps2gWrUG9O49lVq1mjJp0leAc2Tzk0++4MqVlxFJQX99EgHde8L+/VCmDGzdCkqSVzyI\n5yb/3+v06dNSrVo1qVatmlSqVEnGjx8vIs7ldc2bN7/v8rpx48ZJ6dKlpXz58vLrr7/eU2c2h6xQ\nKLLJnTt37rsO3FMiIyPFYvEXjaaGgK+oVBZ5990PxeFwZKm+7du3i49PLdcyrvkCRV1LAasLlBLY\nKbBF9PpgWbx4idvxx8bGujanOeFq84IYDAXl7NmzEh0dLQaDn4BIcc7ISUqJgNwKDhbJ4XPeFbnD\nndynnEevUCiyVUJCAp079+b339ch4qB//8F8993/smVJ1IULF1i1ahVarZYuXbpQsGDBLNcVGRlJ\n3brtSEyMApoCHwFlgDrAj8DTrjt/oHXr1axdu9it2CMjI2nQoCd37hxNu+brW49ffvmMJ554gnz5\n/CmRuoINvEAwF9mn9sK26mdqP/30v9SqeFwo59ErFIpH1uuvv0tEhBc2203s9iv8+OMfTJv2f9nS\nVnBwMEOGDGHAgAFuJXmAypUr06xZXUymlsBV4BjQCNAD0enuvIRO5/6f0pIlSwKxwAbXlR3YbCcp\nX748RqORWa+OIIKWBHOR7WoTkzt05cnWefd8davVypIlS/j+++85evTowwsoskx5olcoFNmqfPna\nREV9DdRzXZlB9+7bWLQoLDfDyhC73U5YWBhhYT+yffte4DvgFZzzmIcBycAU9u6N8MgRrOHh4XTs\n2JPUVCE11Ur+/PmpX78OP7zclwK9ekFcHBcqVODI2LG06tIlz64ft1qtNGnShsjIRByOisBK5s+f\nQYcOHXI7tEeWO7lPOb1OoVBki6SkJL799jsSE+NRqSIQqQcIev02SpUqmtvhZYhGo6F///4EBATQ\ns+fXJCc/D5iBF4H/odNBWNh0j52zHhoaSkTEb9Su3RSH4y2uX29P/JpP8FrdFhwO6NCB4IULCTYY\nPNJeblm0aBGHDqWSkBCBc2B5Ky+99BzXrimJPjsoiV6hUHhcamoqDRq05M8//UhO7gB8gl6/Hi+v\nFIKC4nnnna9yO8RMCQgIQKM5ByQBXYHK6HQ1iI6+8MBXBPHx8fTpM5CtW/8gKKgQ06ZNon79+v/a\nzvXr12ncuAUpKcWBd2nJOn62r8KEg/j27bEsWQI6nae7l+OuXr2K1VqVv98eV+fmzZjcDOmxpryj\nVygUHrdx40ZOnEghOXkpMBHYg822hbCwVzl4cDu+vr65HWKm1KlThzZtGmCx1MfL62VMppaMHz/+\ngUk+KSmJ4sWrsHx5IrGxazh8eDgtWnTk9OnTiAg2m+2+5X755RdSUioBCXRiCb/QHhNJzFLrufPd\nd49Fkgdo1KgRGs1i4CCQilb7IXXrNs3tsB5byhO9QqHwuMTERFSqQP5+liiDRqPnqaeecmvf99yi\nUqlYuPAHfvnlF86dO0fNms/RoEGDB97/4YdjuXHjInAY51B/BVJTV/HRR2NYtmwlycnx1K3blBUr\n5uHn55dWzuFwoFL50YvrzKYHWoSv8GN3zw70K5o3XndkxBNPPMG0aV/w8svNSUy8xRNPhLJ06U+5\nHdY9oqKiWLJkKVqthl69elE0j/43UCbjKRQKj7t69SrlylXj1q2PgYbo9V9Rs+YpduzY8NCyj4PG\njdsTEREO7Me5JE9QqWqg010hNXUjUBad7k0aNjzLpk0r08pdvXqVCSXL80XiTdTAOJUvv9avweYt\nGx/bE9rsdrvrcJ5Hy759+2jcuBXJyc+hVidjMq1g375tuXZugrK8TqFQPFICAgKIiFjPE0/MJyio\nI+3aJbFmjXvrzPOSKlXKotFUBVoBnwI90OlO43D0AioBeqzW0WzfHn5XuYCffuJLV5L/NrgsjjGj\nCN+84bFN8sAjmeQB3nrrYxISxmK3f4XV+j137gxk7NjPczusLFGG7hUKRbaoUqUKu3dvyu0wcsW4\ncR8SHt6SM2fspKRMQKXS4O3ty507ewAHzmes/RQo4DzFExEYOxY+/ND571OmMHTo0FyKPvdYrVaW\nLl3KlStXaNSoEbVq1cq1WOLibgF/P707HKW5du1ErsXjjsf3Z6JCoVBkwu3bt9mxYwcnTrj/xzxf\nvnzs37+VMWOGotNZsNvnc/36bGy2o3h51cNk6ofJ9AyzZn3jTPIjRzqTvFoNYWHwH0zyNpuNpk3b\n0b//t4wadZLGjdvx44+5996+e/e2mEwfAFHAIUym8fTs2S7X4nGLe7vv5rw8GLJCoXjE7du3T/Ln\nLyw+Pk+I0Rgogwe/muU98tPr1Km3wAzX3vUisFJKlqwk06ZNk2PHjonY7SJDhjg/1GpFFi3yQG/y\npiVLlojFUlfA5vquDorFUtAj/x2ywm63y8iRH0j+/EXFz6+4TJr0Za7E8Rd3cp8ydK9QKNyyf/9+\nNm/ejJ+fHz169ECv1+d2SA8VHR3N+PGfEx0dS/v2TzF69GfExU0CegG3+PHH+nTo8CtPu7mPvNls\nQKW6zt9zqG5RpEhxBg4cCDYbvPgizJkDXl6wdCm0betmz/Ku2NhYHI4Q4K939hVJTLyF3W5Hq835\nVKVWq5k48WMmTvw4x9v2NGXWvUKhyLLFi5fQt+9QHI7uaLVHqVDBzvbtvz3Syf7GjRuEhNTi+vVO\n2GyVMZm+JCnpOCK3AefSP73+FSZOLMVrr73mVluRkZHUq9eMhISXASMm0/9YvXoRofXrQ69ezuRu\nNsPKldCsmfudy8OOHj3Kk0+Gkpi4DKiJVvsRNWvuY+fOjbkd2iNBmXWvUChyxeDBr5KUtJKUlCkk\nJGzg2DENixYtyu2w/tWSJUu4c+dJbLYvgZdITFwJmID5rjuuo9Oto3Llym63VaVKFXbt2sywYfEM\nGhTN77+vIrROHejUyZnkfX3ht9/+80keICQkhAULZlKwYC+02gLUrn2IlSvn5XZYjwVl6F6hUGTZ\n7duxOJeLAaix2UK4fv16bob0UFarFYfDku6KNxqNlXz5xpCS8gWpqdEMHjyEFi1aeKS9kJAQvvnm\nC+e/3LkDbdpAeDj4+cH69VCjhkfayYz4+HgiIiJQqVQ0adLkkdnEqH379sTGts/tMB47yhO9QqHI\nsgYNnkKnGwXEAztRqxfTpEmTLNUlIpw/f56oqCjsdrtH40yvffv26HSrgalABEZjL/r0eYHz54+x\ndet8Tp2K5PPPx91TzuFwcODAAXbu3ElKSspdny1YsJDKlRtQsWJdpk+fcf+G4+KgRQsID0cKFeKd\n+k0o3LYX1as3Ztu2bZ7v6ANER0dToUJNevacSI8en1C5cu1H/seZwk2emQ+Yc/JgyArFYys2Nlaa\nNm0nWq1BChQoIosWLc5SPVarVTp2fFYMBn8xm4tLSMiTcu3aNQ9H+7cDBw5IaGh7CQmpJ2+99b6k\npqb+6/1JSUnSsGErMZtLibd3FSlZsrJER0eLiMiKFSvEZAoWWCOwUUymsjJr1g93VxATI1KtmgiI\no3hxaVa8okBtgR0Cc8VgKCCHDx++p90//vhDRo16T8aNGy8xMTEe6fszz/QTrXaka2a7Q3S6oTJo\n0AiP1K3IPu7kvjyXNZVEr1A8fr788msxmZoJJLmSzwjp1u35LNVltVrlzJkzcuvWLRERmTkzTAoX\nLi9+fsXl9dffEZvNluk6P/lkvBgMHQSsAg7RakdKp07PiYhI27bPCMxKt4RuhVSv3kjat39GKldu\nIO88P0Ds5cs7PyxXTtbPnClgETiVrsxwGTt23F1trlq1SozGAIEPRafrLwEBxeXKlStZ+k7Se+KJ\n5gK/pmt7kTRv3tnteh/k9u3bEh4eLnv37s21pXKPA3dynzJ0r1Aoct3u3ZEkJnYHDIAKq7U3e/ce\nynQ9x44do1ixClSq1Ah//yK89NJAXnnlIy5f/oHY2HV8/30EH31077D8wxw6FEVycnuc05pU2Gyd\nOHLkOOBcQgdx6e6+yJEjkaxZE0L84WEM+HEe6uPHkcqV+bxDV/p9NNHVz/RlYvHyunulwquvfkhS\n0g/AGKzW/+PGjdZMnTot07H/U+PGtTEYvgdSgESMxhk0bvyk2/Xez/HjxylVqjIdOoyiceNutGvX\nI1tfyyjuT0n0CoUi11WpUhajcQ3gPL5Vo1lJxYrlMl1P+/bPcOXKmyQmXiA19SizZy8jMfFNoC5Q\nnsTEz1i06JdM11urViWMxiU4k6Og18+jRg3nrPxRo4ZjNk8AxgKfode/g05XgzL27kTwJiUlgd0q\nNcOrPsFH323n4sUhrn52A74FXkWj+YU+ffrc1WZCQjwQnPbvNlsxbt+Oz3Ts/zRu3IeEhqrR6/3R\n6QJo0yaAd9550+16/+n06dN07vw816+/ye3bO0hI+JPw8KuEhYV5vC3FQ3hwZCFH5MGQFQrFQyQn\nJ7vegZcRH5+aEhxcQS5evJipOmw2m6hU6nQ7q4loNDVEpRog0EqgkEBlCQmpnen4UlNTpXXrLmI0\nBomXV4CYTEWkefOOsmXLFhEROXjwoAwc+Ir06/eyfPHFF1LfVF1i8BcBCaeB5NcYRK+3CMS4Yvuf\ngE5UqnxisfhLRETEPW0OH/62mEzNBY4JbBKTqZBs3rw5wzFbrVYZM2a8NGzYVnr3HnDP93njxg2J\ni4vL9HfxMA6HQ4YOfUMMBn8BH4Ez6V4TjJU33xzp8Tb/C9zJfXkuayqJXqF4PNntdtm7d69s375d\nEhMTs1SHv39xgcUCMwW+Er2+uKhU3gIfCZwXmCI+PkFp7+8zw+FwyOTJk8VgKCrwk8B0MZn8Zfv2\n7XfdlxQeLjfVGhGQtVSRgsb60rfvIDEafV0xOJOewdBFJk6c+MA5A6mpqTJs2Bvi719SihevLAsX\nLpJbt27JoUOH5MaNGw+Nt3fv/q55D8tFqx0lgYElsyWxpxcTEyOtW7cXjaaEQJxAW4EPBBwCN8Vs\nrik//fRTtsbwuFISvUKhUIjIzz//LCqVRaCNQE/Ras1iMAS7Eo0zwfr61svUk3F6tWo1E1iR7gn1\nS3n22Zf+vuH330XMZhGQg6XLSpe2PeV///tabDabjBz5gZjNNQV+Eo3mHfHzC5arV69muO21a9eK\n2VxQvL0risGQT+bOnffAe1NSUkSj0QvcTovVYnlaFi5cmKV+Z8SdO3ckOLi8qNWNBYa42r0gUEnA\nT7y88kn//sOUCXlZ5E7uUzbMUSgUj40tW3ag0fTFZpsCgM32GXb7x8BtwBdIwWaLxtvbO1P1bt68\nmd9+20hMTAygSvdJAlFRR5k8eTI9fXwIHDIEkpPhueeo+sMPLE23R/uECWMoXrwoK1euoHBhP8aM\n2Y6/v3+G2o+Pj6dbt94kJKwAGgBHGDCgCU2aNKJo0aIZ7EX2bh++YcMGbt4sisMxEhgG3ACKAq8R\nHDyJnTt/p1ChQtnWvuLBlESvUCgeG5cuXcNmq5fuSkN8fApgs4WSkNAZs/k3mjWrQ/Xq1TNcZ1jY\nbIYNe4/ExJfQar1RqV5C5GvgIjCBw4fbs/2NlQy2ufZkHzgQpk51HjmbjkqlYsiQgQwZMjDT/Tp/\n/jxqdUGcSR6gEnp9CCdOnLhvotfr9fTs2YflyzuTmDgcrXYnZvOftGrVKtNtZ5TzR4QGaAF0AcoB\nFgoUsLFq1Rolyeci5VAbhUKRI5KTk/nyy685fPgkdepUY+jQIWg0mocXzIQff/yJwYMnkJi4CvDF\naOzFoEHVqFu3BgcOHKJ8+bL06dMnU+0WKFCEuLhVQA2cM+6fpFQpDfHxt7l8uR3POaoQxotocLC4\nWGm6nz0BKtXDqs2U27dvExRUnKSk34HqwGmMxtr8+edeihcvft8yNpuNceM+47fftlGiRGE+/XQ0\nRYoU8Whc6d26dYsKFWpy7dqz2O0N8PKaRIMGBlauXIzZbM62dv8r3Ml9SqJXKBTZKiEhgXfeGU1Y\n2HySkqpht7fHZFpAmzbFWLx4jkfbEhHGjBnPZ59Nwmaz0qNHL2bN+tat0/QMBm9SUs4D+QHQ64cx\nblwJtm49QKEVGqbi7MNonmdZ5VMcitz6r/WdPHmSAwcOEBwcTJ06dTIcx8KFi+nXbwg6XTlSU6OY\nNGkcQ4cOynK/3HHgwAFmzvwRtVrFgAEvpB0AdOnSJV5//X3Onr1E06Z1+fjj9x/pkwzzEiXRKxSK\nR5LD4aBGjYYcOWLCbj8LHMc5vJuIwVCMkycPZstT5l9/I1QeeLLu1KkXv/4qpKRMBDagUr0OxDNK\n68V4axIAb/IBU00RvP56Mz755IMH1rVgwSL69RuKTtcQu/0Afft24dtvv8hwLNHR0Zw4cYKSJUsS\nHBz88ALZICIigtatu5CYOBywYzZ/S0TEemrkwuE8/yVu5b6szwHMHXkwZIXiP+vFFwcJFBD4XeDJ\ndLPV7WIyFZVTp07ldogPdefOHenZ80XJl6+waDT5RMX/5CM++KsjMlxnFqMxnwwcOFysVusD60lN\nTRWDwUfggKvoTTGbS8gff/yR6ZhsNpv83//9n7z66psSFhYmdrvdnS5miN1ul8GDX3WtjZ9218qD\nzp17Z3v7/3Xu5D5lZzyFQpHm2rVr7NmzxyOnme3du5f581fi3O61JnATGAPsRasdTqlSRShRooTb\n7TgcDs6ePcvVq1fdrut+LBYLCxbM4tixfWg1KiZxkdF8gh01gww1CF34I4mJcUyb9jVa7YPnN8fF\nxeFc6FTNdcUXjaY658+fz1Q8IkKXLr0ZMWIOX31VkGHDptG794AMlY2MjKRjx140atSOqVOnZ+oJ\nccqU75gzZwdQB0i/WiCA+PikTPVBkcM89nMjh+TBkBWKPOGHH34UozG/+PhUF5OpgCxb9rNb9S1d\nulS8vdsLtBDoKfB/AmVFp/OXLl16S2xsrNsxnzt3ToKCSotG4ydarbf07t0/255ukxMTZbpaKwKS\ngk66ME/M5rKydevWDJW32+0SGFhSYLbrSfigmEz+EhUVlak4Dh8+7DotL8lVT7wYDP5y5syZfy13\n4sQJsVj8RaX6UmCZmExVZOzYTx/a3r59+6Ro0fKug3jCBH4QKCewxbVjX0lZuHBRpvqgyDx3cl+e\ny5pKolcoPO/SpUtiNBYQOOJKHnvEZCqQpZ3Url69Kl269JFixUJEo/EV2CUwSqC2GAwF5fr16x6J\nOSUlRXx8gl2bszgE7ohO94RMn/5/HqlfxHkM78yZM2XmtGmS2K2bCEgiSCevVmKxVJEePV7I1AYw\nBw8elMDAkuLllV8MBh+ZPz/zG9j88ccf4uNTI93QuYjFUk4iIyP/tdyYMR+LRvNqunKHxN+/5L+W\niY+PlwIFigjME3hb4CXXd/29QEkxmQrLjBmzMt0HRea5k/uUdfQKhYJTp06h15cnKSnEdaUWGk0Q\n58+fJ1++fBmux2az0bjx05w61QirNQyVahwqVSMMhnyYzV6sW7eeAgUKuB2vzWajV6++3L6dAAzG\nuYmNBau1D9u27WHAgP5ut3HhwgVq1WqILeEJwlJ2YbRfxGE2c/6LL2glwoBixXj66aczNeGvatWq\nXL58ktjYWPLnz49Op8t0XFWqVMFsvk18/CQcjs5oNPMpWFBDuXL/fgiQM870Q/WOh8Z+4sQJrNZ8\nwLNAK6AxUA+TyQ+DIZWdOzdTpkyZTPdBkbOUd/QKhYJSpUqRmnocOOa6sg+bLZpixYplqp5jx45x\n8eJNrNb/AbURWY7ZXJolS2Zx5cppatas6ZF4R478kF9+OQhYgF9dV+3ASsqWzXjMEyZMxNs7EIPB\nl+7d+5KQkJD22fvvjyPpek/mJSbQ0X6ROAyMrNmAY0FBJCUlYTKZsjSrX61WExAQkKUkD2Aymdi6\ndT11627Ez+8pGjbcSUTEuocuY+vV61mMxnmoVJ8DSzCZnuO114b8a5mAgABSUy8DV4ECwFp0uj+Z\nMKElx48fUJJ8XuG5gYWckQdDVijyhFmzZovBkF98fGqKyVRAFi9emuk6oqKixGAIEkh0DQ+nitlc\nQg4ePOjRWAMDywhsFvATCBKoJ1BSvL0LS3JycobqeP31N10rAvYKXBOttpP06tU/7fP2TdpJOBVF\nQGLwl6p8IwUKlBCLpbro9a+IyVRSPv54okf7ld0OHz4snTv3ltDQDjJt2owMvXZ4//2PxWQqISbT\nS2I2l5Y33ng3ByJV/JM7uU9ZR69QKNLExMRw7tw5SpUqhZ+fX6bKXr16lUaNWhMVFYlzsLAzRmMC\ntWs72LTpF9Rqzw0glixZjbNnvwL8gFeAQ5QoEcSePREULFjwoeXj4uLw9y+C3f42MNp19TT58jUh\nLu4C3LjBlRo1CDp/nosU4imWcc4wFLs9Bqs1CjAB0ej15YiJuZCp1xt50datWzly5Ajly5cnNDQ0\nt8P5T3In9ylD9wqFIk1gYCC1a9fOdJK32WxUqFCHqKgngSTgOGr1Zp55JpB165Z5NMkDfPrp+xiN\nzwFr0GqrUrCgme3bN2YoyYNz4xmt1gxEpbt6DJPJDDExEBpK0PnzxPr40lwXx2ldM0JDi2A0lseZ\n5AEKodXm4+bNmx7t26OoYcOGDBo0SEnyeZQyGU+hULht+fLlxMXFAh/h/LNSAoejH8HBOry8vDze\nXo8e3QkI8GfJkpX4+uZj6NCdmTo0pUSJEuj1KlJSdgKdcZ6yFsbUdz+Fxo0hKgoqVMBvwwaOFS4M\nQGxsLKVLVwaWAy1Rqf6PAgVMnD59mrlz5xIYGEifPn0wGAwe769C4Q4l0SsUCrc5j2/1BXYBnQAH\nsIVChZ7LtjZDQ0Oz/IRpMplYu/Zn2rbtQmLiRlQqGzPfHUmHSZPg3DmoXh3WrYOAgLRDaf39/Vm3\nbjk9e/bj8uUeVKhQkx49nqd9+74kJz+HwbCV77//kR07Nij7u/+DiLBt2zYuXbpEzZo1KVu2bG6H\n9J+ivKNXKBRu279/P/XqNSclRQW0BI5jMkVz48bZbHmivx+bzcbq1auJi4ujUaNGlC5dOu2z3377\njZ9/Xk3+/D4MHz6UwMDAtDJXr17F/9o1dE8/DdHRULcurFkD+fP/a3sigtmcn6SkP4AKgGCxNGHW\nrFfo3r17Nvb0b8uXL2fgwFe5dSuWxo2fYtGiMPI/JO6cJiK8+OLLLFmyAY2mGlbrZubM+Z5u3brm\ndmh5irLXvUKhyHU//TRfjEZfUanUUqpUiJw7dy7H2k5NTZV69Z4Si6WOmM3PicnkJxs2bBARkZde\nGihQUGCSqFSDxN+/mMTExPxdeO9eET8/5y4yoaEit29nqE2r1SpqtVYgJW0TGpPpBZk+fXp2dPEu\nDodDFi9eLF5efgJbBeJErx8kzZt3yPa2M2vz5s1iNpcVuOP6nvaK0eibI/vzP07cyX15LmsqiV6h\neHQ5HA5JTU3N0Tbj4+OlevXaArUF7K5kslaKFq0gGzduFPAV2J6WjNXqPjJp0iRn4W3bRHx9nR88\n/bRYb9+Wd98dLRUq1JEGDVrLrl277mkvJSUlbVlao0atRacbInBFYK2YTH5y/PjxbO2vzWaTdu16\niE6XT2BAup3ubotWa8jWtrNi7ty5YrH0SBenQ3Q6s9y8eTO3Q8tT3Ml9yqx7hULhMSqVKssbwWTV\nwIGvEhmZDDTi74VETxIbe5nVq9cBOiAg7X6HI4iEhETYtAlatoRbt6BrV1i+nFffGc1XX/3OsWOf\ns21bD5o2bcOJEycAuH79Og0btsJotGA0+jBlylSWL/+JZs1iMJsrERz8OitWzH/oDnXumjlzJps2\nxWC1fgGc5u/d7o7h7Z2xVQc5qVatWtjtvwORAKhU0wkKKoqPj0/uBvZf4sEfHDkiD4asUOSq2UZO\nXwAAIABJREFUpKQk6ddvqPj7l5QyZWrKr7/+mtsh3eXOnTsyePCrUr16E3nmmX5y5cqVTJX38ysh\n8JNAUYEoAZuo1cMlNLSdjB8/QdTqqgLNBfYLfCfgI520RklWqZyPmM8/L+I6XtZi8Rc4l/b0qdMN\nk88++0xERFq16iI63csCqQInxGQqJps2bfL49/Eww4e/ITBRIFmgvqtvQ8RoDJQFCzK/d35OmDt3\nnhgMPqLX+0rRouXk6NGjuR1SnuNO7stzWVNJ9ApF5vTuPUAMhg4CxwVWidHoJwcOHMjtsETEOdTf\noEFL8fLqJbBBdLo3pXjxEElMTMxwHRUqPCmwzHXQikVAK8HBFSQmJkZu3LghRYuWE42mskBhAYv0\noLek4jyFboaXSeLSHbKTP38RgcNpid7Lq6989dVXIiJisfgJRKd9plK9I6NHj/H4d/IwYWFhYjLV\nFYgXSBSVqqOULh0ie/bsyfFYMsNqtUpsbGymDgFS/M2d3KcM3SsUj7nly5eTnPwdUA5oi9X6PGvX\nrs3tsAC4dOkSe/fuJyVlNtAcq/Uzbtwws3PnzgzX8f33kzCZBmIw7MNkakSpUhU4cmQXAQEB5M+f\nn8jInXz99WBef/0ZBukNzGMeOmx8xlu84VWNg5GRaXW9995bmEydgeloNG/h7b2JZ599FgA/vyBg\nj+tOB0bjPgoVCvLYd5FRzz//PJ06VcJgKIHFUpXixU8SHr6OWrVqpd1z9epVXnhhCA0btuW998aQ\nmpqa43H+k1arpWDBglk6H0DhHmUdvULxmDOZLMTHXwKKAKDVXsRiKZm7QbloNBpE7ICNv/8cpaLR\naO57v81mY926dWlL6IoXL06TJk3Yv38b69evx2KpR/fu3TGbzWll8uXLx9ChQ7k9fjw+qbEAfMDH\njOV1TLaKdy1He+ONEQQHF2bp0rUEBORn1KgdBAQ43+/PmjWZdu16oFI9jUp1ivLltfTt2zdD/YyO\njmbEiJFcvHiNli0b8t57b2d5LoNareann2Zw/vyHxMfHU7Zs2bvqSkhI4Mknm3D58tPYbIPYt28a\nhw/3ZcWK+VlqT/EY8ODIQo7IgyErFLnqhx/miMlUROAT0eufl6JFy2XpnPns4HA4pG3b7mI0Pi0w\nX7y8XpBKlWpLSkrKPfempKS4ltA9KRZLTzGb/WTz5s0Za2jChLTD20fqA0SjeVvM5lrSs+eLmRpK\nPnnypMycOVOWLl163xjv59ixY6LR/DVDfoloNE2lc+fnMtxmZq1Zs0a8vRulm+WeKDqd+ZH5b67I\nGndyn/JEr1A8hmJjYzl48CBBQUH07duH4sWDWb16HQULhjBo0Fe5eghLREQE3377A2q1ihEjBrBs\n2VwmTvycbduWEhJSijFjvr7vznJz587l4EEHiYk7AA2wkr59h3LmTOQ996YRgQ8+gHHjQKVCpk6l\nYZEi+Bw6RNmyI+nWrVumhpJLly5910Y8GdGlSy/s9jLANECF3d6GlSsLcvPmzfv+d1ixYgVjx36D\n3W5nxIh+9O3bJ1PtyT2bqihD5f95nvu9kTPyYMgKRY7asmWLWCz+4uvbWIzGwjJo0IhHZgLUxo0b\nxWQKEJgs8KWYTH6ybdu2DJX95JNPRK0ele5JNUZMpgIPLuBwiIwY4bxZoxGZO9dDvcgci6WgQMN0\ncSeLWm2SGzdu3HPv2rVrxWgs5JpcuEpMppIyZ07m4o6Pj5dixSqITveawHIxGttK+/Y9PdUdRS5x\nJ/fluaypJHqF4t/5+xcXWO1KKrfEbC4vv/32W6bquHnzphw9elTi4+M9GlvTph0FfkiX9L6Vjh17\nZais80dCcYEzAnbRal+Tpk3b3/9mm02kf39nI3q9yLJlHuxF5tSo0cg14/9tgTUCT0uVKnXue2+H\nDr0E/i/d97Nc6tRpmek2Y2Ji5IUXhkiDBm3k3XdHZ/g1g+LR5U7uU4buFYrHiM1mIzb2AtDadcUH\nkYacOnWKp556KkN1zJu3gP79h6DV+iMSx88/z89w2YexWm2AOd0VM6mptgfca2XBggXExMTQsGFD\nmjVrxtixbzBqVCXsdjvVq9dlwYJF9ysIffvC/PlgNMLPP0OrVh6JPysWLJhB/frNuXXrJ+z2MEqV\nKsSOHdvve69erwMS0l2JR6fL/J/pgIAAwsK+y1rAisePB39w5Ig8GLJCkaNKlKgkMMv1RHhRTKZg\n2b59e4bKXrhwQYzGggKHXOV/F4vFz2NP9gsXLnI9la8UWCYmUxFZtWrVPffdvHlTAgPLiEpVW1Sq\nYWIwBMnMmWEi4twCNiEh4f4NJCWJdOzofBz29hbJ6GS9bHbnzh3Ztm2bREZG/utrlF27donJ5Ccw\nSWCyGI0Bsn79+hyM9G63b98Wm82Wa+0r/uZO7stzWVNJ9ArFv4uMjBR//+JisZQSvd5bxo+flOGy\nGzZsEF/fJumGjkUsltLy559/eiy+efPmS61azeSJJ5rLsvsMqTscDqlS5QmBGvL33vVHxGDw/fe5\nBvHxIi1aOIPOn1/kPvvU5wW7d++W3r0HSM+e/SQ8PDxXYjh37pxUqFBLtFqjeHlZZMaMWbkSh+Jv\n7uQ+5ZhaheIxlJqaytmzZ/Hz86NAgQIZLnf69GkqV65DUtJeoBhwCKOxCVeunMuxvclv3LhBQEBh\n7PZngTDXVRtgICioFCkpifTs2Z3Jkz/7e/34rVvQrh1s3QoBAfDbb1C1ao7E+ziqXr0hhw+3xm5/\nD4jCZGrKli2/3LUpjyJnuZP7sn1nPLvdTo0aNWjfvj3g/J+4RYsWlCtXjpYtW3Lz5s20eydMmEDZ\nsmWpUKEC69evz+7QFIrHll6vp1y5chlO8mfOnCE8PByj0cj48R9hNNbC17cxRmMzZs2alqMHkGg0\nGlQqNbAK+B24BXRDpcrPlSuziYvbwuzZh3nrrQ+cBa5fh+bNnUm+aFGIiFCSvBscDgeRkX9gt4/E\nuTSvPA5He/7444/cDk2RRdme6L/++mtCQkLS1qpOnDiRFi1aEBUVRfPmzZk4cSIAR48eZeHChRw9\nepRff/2Vl19+GYfDkd3hKRT/eV98MZlKlWrTqdMHlClThWLFinDkyC6WLRvNiRMHeeaZHjkaj6+v\nL1279sTLqwjQGwhEowlH5G2gHlCKpKTPWbr0F7hyBUJDYe9eKF3ameSz+fS4nGS1Wvnhhx8YO3Ys\nGzduzJE21Wo1+fIFAX8l9lQ0mr0UKVIkR9pXZAMPvT64rwsXLkjz5s1l06ZN0q5dOxERKV++fNrp\nVNHR0VK+fHkRERk/frxMnDgxrWyrVq1kx44d99SZzSErFHmGw+GQS5cuydmzZ7O8Tj4qKkqMRn+B\n86534XvEaMz34MluOcRqtcqECZOkRo0GUqRIJSlWrLxoNIPTzR34WZqXrSlSpozzQkiIyKVLuRqz\np9lsNmnUqLWYzaGiVo8Uk6mETJr0ZY60vXr1ajGZ/MTbu6dYLFWkTZtuYrfbc6Rtxf25k/uy9Yn+\ntddeY9KkSajVfzcTExNDYGAgAIGBgcTExABw+fJlihYtmnZf0aJFuXTpUnaGp1DkWVarlY4dn6VU\nqSpUrFiXOnWacfv27UzXc/r0afT6qkCw60ot1GpfoqOjPRpvZmm1WkqXLsHx4+e5dOl9zp8fgt3+\nIzpdX9TqUVQx9OOXWxfh5EmoUQM2b4bChXMkth9+mEPBgsEYjb507dqHhISEhxfKgg0bNrB/fwwJ\nCRtwOCaSmLiZd999F6vVmi3tpdemTRsOHfqDqVPbs2zZF/zyy8K7/o4r8pZsW0e/atUqAgICqFGj\nBuHh4fe9R6VS/ev2kw/6bPTo0Wn/HBoaSmhoqBuRKhR5z6BBL7N69RUcjkuAjkOHBvDqq+8wa9a3\nmaqnTJkyJCfvAzYCzYDfUasTH4lh2kmTppGYOBno5LqSRMWKSxnc0Jv+izTorl6F+vVh9WpsFguv\nDnuDOXPmotPpef/9t3jtteEej2nLli28/PI7JCWtBEqwZs1Q+vcfzvz5Mz3eVlxcHCpVKZzb/QIU\nRURFUlJSlg/EyYysbPer8Jzw8PAH5s7MyrZEv337dlauXMmaNWtITk7m9u3b9OnTh8DAQK5cuUJQ\nUBDR0dFpJ0MVKVKECxcupJW/ePHiA//YpE/0CsV/zaZNm5g9+2ccjv8BBgBSUl5g5853MlVPbGws\nHTv2AkxAZzQaA0ajsHz5QgwGg8fjziznD/3083TMtA4IYsiC+XDjBjRrBitWgMXCR++NISxsL4mJ\nu4DbvP9+F4oUKUSPHt09GtO6db+RlNQfcM4+T06eyLp1DT3axl8aNGiAw/EKsBxogFb7OZUqVc/R\niZGK3PPPh9gxY8ZkvTIPvkJ4oPDw8LR39G+99Vbau/gJEybIyJEjRUTkyJEjUq1aNUlJSZHTp09L\nqVKl7vveMYdCVigeWZ069RZoJ9Ar3Trzt6RLlz6Zqqdr1z6i0w0XcAgkisEQKhMnfpZNUWfesmXL\nXKfuzRGYJs298onVbHa+k2/Xzrk5jkv58rUFItK9w58mPXv283hMX375pRgMPdK1s1ZKlKji8Xb+\nEhERISVKVBaTKb80btxGoqOjs60txaPNndyXY1vg/jUMP2rUKHr06MHMmTMpUaIEixY5t7AMCQmh\nR48ehISEoNVq+e677zJ1qpRC8V+h1WqAJjif9KoBWvT6C0yZ8i+nuN3Hvn2RWK3/h3MJlZHk5J4c\nPLgnU3XcunWLCRMmcfbsZZo1q8+AAS957P/bzp07s3ChjsmTf+DJ27F8fDAZTUIy9OgBc+dCuuHr\nggXzAycA59O1VnsCf3/3T+i7du0affu+zO7deyhWrDjfffcpRYrMIjq6I1ZrCbTaeUyd+qPb7TxI\nw4YN//10PoUiIzz4gyNH5MGQFQqP2r59uxiNfgJfC4wUvb6ALFmyJNP1tGnTXTSaD11PplYxGtvL\n+PGfZrj85cuXXSfRPSswXfT66jJs2BuZjuOhVqxwHkwDIi++6Dyw5h927twpZrOfaLWviJdXX/Hz\nC5aLFy+61axzh766rlPgTohKNU3y5y8sZ8+elenTp8vnn38uhw4dEhHnKoFt27bJxo0b5c6dOxlu\nY9euXbJgwQI5cuSIW7EqHn/u5L48lzWVRK9QOJN95869pX37ZzO0F/pfS/H+Wtoq4lz+GhxcXnx8\naorZXEYaNmwpycnJGY6hVq0GArVdQ/8icF00Gq9Mn5RmtVolLi7u/ksE5893HjELIsOGifzLEq/j\nx4/Lp59+Kl9++eVd/cyKixcvysyZM0Wvz5+ufyI+Pi3u2Zs/MTFRnnwyVCyWSuLjU18KFSot586d\ne2gbb7zxrphMxcTbu6uYTIEybdoMt2L+p507d0qtWqESHFxJBgx4RRITEz1avyJnKYleoVA8UHx8\nvDRp0kYMhoLi5ZVf2rbtnpaMExMTZdu2bbJnz55Mr5PW680CbdO9r04RtVqfqTX406fPFL3eLDqd\nRcqUqSZnzpz5+8MZM0RUKmflo0Y5z5fPAb///ruYzX7i7d1KwEvguqt/NrFYKsvmfxyU88kn48Vg\n6CJgExDRaD6RVq26PrD+mJgYadq0jahU+dPVHSVeXj5y+/Ztt+O32WyyYMECMRjyC8wW2C8GQyfp\n2jVzczgUjxYl0SsUigcaNuwNMRh6CqQKJInR2EY++mhslupyOBwyefK3UqlSfdFq8wkECPxP4A+B\nzlKx4hMZrmvPnj1iMhUSOC7gELV6olSq5Dqn/auv/j5VZ9y4LMWaVUFBpQTWupp/Q6CswHgxGltL\ngwYt7znN7dlnXxL4Pt0Pnt1SsmT1+9admpoq5crVELW6q0DoXYcHmc3F5NSpU27FnpqaKo0bPy1e\nXoUEnktX/03Rag1Z3lhJkfvcyX3KDggKxWNux479JCf3A3SAgaSkvmzbti9LdU2ZMpVRo77jyJGP\nsdleBuJRqb5HpepE/vx72bJlbYbr2rlzJyLtgHKACofjDY4e3Y1j7Fh49VXnTV99Be++m6VYs0JE\nuHr1PBDqujIJrbYkTZpsZNKkdmza9AsajeauMvXr18BkmofzHHkHev1Mateucd/6jx8/zuXLd3A4\nvgYOAztcnyzGYHDctWlYZkVFRfHWW2+xe7eVlJSPgfQbKF1Dp8v9JZOKXOK53xs5Iw+GrFDkql69\nXhKt9g3Xk51DvLxekldeeTNLdVWsWFdgU7onxbflyScbyJw5cyQp3XK3jFixYoVYLDUEkl11bZb/\nGSzOilUq59D9v3j//Y/Ez6+UBAaWkQkTJnnsabVq1fqiVk90vZs/KyZTsGzduvWB99tsNnnmmRfF\nyyufGI1BUqNGQ7lx48Z97z1x4oQYjYVcfV4tUEDAKPnzF5E9e/ZkOeZ33hktRmOA6PXFBcYK3Bao\nIPCiwFdiMpWViRM/z3L9itznTu7Lc1lTSfQKxcOlpqbKvn375ODBg3L58mUpXjxEvL3riLd3TalQ\noZbcvHkzS/VWq9ZYYHlaolepxsjAga9kqS673S4dOjwjFkuI+Fi6yndag7hecovMmycizlcFx44d\nk127dt317r9Nm44CRQV2CewTgyFEpkyZmqU4/unMmTNSsmRl8fIqIDqdSb744usMlbty5YqcO3fu\nX+c6OBwOadOmm5hMLQSmisHQWho1uvd1QGbs3r1bTKaiAlcFFgmECMQKXBeVqoEULlxOli5dmuX6\nFY8Gd3Kfch69QvGYuX79Og0btuLixQREUqlSpSSrVy/iwIEDaDQa6tati5eXV5bqXrlyJT169CMl\npSWgwWRay+7dWwgJCQEgNTWVsLAwzp49T/36ddOOp34QEeH3DRsoMXYspbZsAb0eFi2Cjh1xOBz0\n6TOQn39eg04XiMFwk4iIdVy9epUmTbricHwJ9HLV9At1637Ljh2/Zqlf94vr2rVr+Pj4eHyXQKvV\nyjfffMvevUeoXr0CI0a8gl6vz3Q9s2f/SFjYEu7cieX48QASEn4GBHgH+BKDwZfSpUuycePKtPNF\nFHmXW7nPIz81clAeDFmhyFHPPTdAdLqhrqFnmxgM3eTddz/ySN1z5swVLy9/0WieEa22vDRv3i5t\nyNxqtUq9ek+JydRSYLSYTOUePukvJUWkRw/nk7zJJJJuqeC8efPEbH5SIN41ejBZatZsLDNnzhSN\npqLAp+leIUyRp57q7JE+5gVTpkwVk6ms6wn+XQEfgVPy18l++fMXlgsXLiiT7x4j7uS+PJc1lUSv\nUPy7qlUb/eM9+lx5+ukebtdrs9nEYPAWOOyqN1nM5hDZsGGDiIisX7/e9c7d5vr8smi1hgeuzT93\n/LjsLRwsApJsMIhjy5a7Pv/ggw8FPkjXj0vi7R0gf/zxhxgMQQJ+rlnxb4tKZXLrHbenpKamyscf\nj5eWLbvJK6+8KXFxcdnSTokSVQW2pvtu2olGYxKLpbTky1dIdu7cmS3tKnKPO7lPmXWvUDxmqlcP\nQa9fiPNAGCtG41Jq1arkdr2JiYnYbDYgxHXFC5WqStqRtrdu3UKlCubv09YCUat1JCYm3lPXnvBw\nosqHUPPyBa5joYmtKKNWrb/rnkqVQjCbVwN3AFCr51O+fAh16tThww/fQK9PRqebjcHwPTNmfMPG\njRv54IOP2LMnc9v4elL37n2ZMGEz69d3Zfr0OOrVe4qUlBS36xURLl68mPZd37vNcA0GDerPnj2r\niY4+Te3atd1uU/EY8dzvjZyRB0NWKHLUjRs3pHLlOmI2lxKTKVgaNWqd6RnxD1KmTDVRqz8T52E6\nO8Vo9JOoqCgREYmOjhZv7wCBnwTOiU73mtSo0fDeSuLiZKfOuaXtZYKkEpECF0Svt9w11OxwOKRz\n516uYeliAmZ5442RaZ/HxMRIZGSknD17VgICSohe309UqvfEZAqQNWvWeKS/mXH16lXR630FEtNW\nOHh715KNGze6Ve+dO3ekXr2nxGDwFy+vAtKuXQ+ZPPnbdEP334jZ7CeHDx/2UE8UjyJ3cl+ey5pK\nolcoHs5ms8nhw4flzz//dOs9bVxcnPTq1V/KlKklbdp0l4iICKlQ4QlRq7Xi7e0nP//881337969\nWypWrC358hWWFi06y9WrV++u8No1cVSvLgJyDpOUIcqVFK+KRmO8J9ayZWsIfCJwQOCkmEzFJCIi\n4q57PvpojGi1g9INY6+ScuUyvnGPp0RHR4uXV35xbkz015a59TO0RfG/GThwuHh59RawinPDo1by\nyScTZPbsH6Vp047Svv2zj8RrC0X2cif3KbPuFQrFfTkcDmrXbkpkZAVSU/uh0awjIGAOUVEH0Ol0\n6PX6zJ1Ud/kytGgBR49ySq2hqcOHC7wPVAY+oHXrQqxdu/yu9rVaHSLJODf7AYNhMJMmVWbYsGGE\nh4fz3XezOXBgPydO9MQ52xzgMIULd+PSpWMe+ibuz2q18u2333Ho0HFq1Ahh8OBBtGjRiZ07vUlO\n7o9Wu4FChZbz5597MZvNWW6nWrXGHDo0BmjquvITTz+9kjVrFnqkH4q8wZ3cp7yjVygU93Xx4kWO\nHj1OaupUoA52+4ckJASwa9cuvLy8Mpfkz52Dxo3h6FGoVImLP80l1ihotVNQq/sQEuJg5crFAMyd\nOw9//+JYLAXQ6/MB61yVxKPRbKV06dKsX7+etm2fYfHiJzlxogEwCdgCnMRofI2uXTt49Lv4J4fD\nQevWXXj33dWEhVVk1KhldO3ah9WrF/HSS0WpUWMcXbteZefO391K8gDly5dCq/1r2aDg5bWOkJDS\n7ndC8d/hoVGFHJMHQ1Yo8qQrV66Il1e+tOVtYBeLpfI9Q+d/WbFihbRt+4x069ZX9u7d+/cHx4+L\nFC3qHMuuVUskNlZERM6fPy/Lli2Tbdu2pQ3Zb9261bX//U6Ba6LTPSVarbf4+jYVk6mY9O07WBwO\nhzRq1NY1F+Cv4fq+YjQGSsGCxWTIkNckNTU1276Xffv2ScGCRVyz/lNc7SeJ0RgkJ06c8Hh70dHR\nUrx4RfHxqS0WS1WpXLmORw6/UeQt7uQ+bW7/0FAoFI+mwMBAOnbsyKpVbUlMfA6DYT0BASqOHDmC\nv78/5cuXT7t3/vwF9O//NomJHwM3Wbu2Fdu2baCaWu0cro+JgYYNYdUq8PUFIDg4mODg4Lva/O23\nDSQlvQg4Z41brWFYLDVZvPgd/P39qV69uuu6DTCmK9mQFi2srFjxUzZ+IxAWNpt+/V7G+ZpgEfDX\nRjdeaDTeJCUlZbluq9WKTqe753pQUBBHj+5h165daRse3e8+heKBPPiDI0fkwZAVijzLZrPJV19N\nlm7d+krRomXFbK4tJtMLYjL5ydq1a0VEZNGixWI0FhZYk+4Je6yM7dRdJH9+54UWLUTi4x/a3uTJ\nk11Hvv5VzwYJDq54z30//TRPTKYSAisFFovJVEh+/fVXj/c/vf3794uXV0HX1rtJAhUFPhQ4IBrN\n21K6dNUsjSTs379fgoMriEqlloCAErJt27ZsiF6R17mT+/Jc1lQSvUKR8+bMmSNmcxPXsjoR2CRB\nQaVlyZKlYjIFC1QS2JCWoBsxWBJ1Oue/dOggksHlfXfu3JGyZauJydRedLoRYjT6y6pVq+57748/\n/iS1ajWT2rVbyIoVK2TPnj0ybtw4+fbbb+XOnTue7L6IiEydOlUMhucFvAVOClwU6CAqVT5p1Ki1\nXL58OdN1JiYmSsGCRQXmur7bFeLtHSDXr1/3ePyKvM2d3KcM3SsUeYSIMGtWGFu27KJs2WK89toI\ntyd6ZVRMTAypqTX4e/5uTW7cuMKUKbNJTPwM5xGtg4HPaUkEP/M9Rivw7LMwezZkcKjZYrGwf/82\n5s2bx82bN2nZ8jeqVat233t79+5F797Ove6XL19Oo0ZtSE19Hr1+L1988T0HDmzD29vbzZ7/rVCh\nQmi1R4BPgYZAI2Anw4cP4quvJmapzlOnTpGaagGec13pgFo9gSNHjtCoUSOPxK1Q5LnH4zwYskLh\nEYMHvyom0xMCU8Rg6CFVq9aTlJQUt+u1Wq1y+PBhiYqKeuCa+x07driOVz0iYBWt9jVp1OhpadGi\ni8As15P8bOlICUn+67G+f38RN05lywiHwyFjx34qKpWPwO9pIwpGY1f55ptv0u47ePCgPPVUJ6la\ntbF89NFYsVqtmW7LbrdL69ZdxGKpLkZjG9HpLDJx4kS34ndOePQViHbFfkOMxkA5fvy4W/UqHj/u\n5L48lzWVRK/4L4qPjxet1ijOY1nrC+QTtdpfpk+f7la9165dk4oVnxCLpbQYjYWlZctOD/zxMHNm\nmJhM+USt1kqdOs0lJiZGNm3aJEajv8A30os+Yv0r044YIeLGRj0HDhyQl14aKi++OER27Nhx33vs\ndrsMHz5C9PpyrhnwF9MSvVo9Sj7++BMRETl79qx4eweISjVFYKOYTI1lyJBXsxSX3W6XNWvWSFhY\nmBw7dizL/Utv9OjxYjIVF5Opn5jNZWT48Lc9Uq/i8aIkeoXiMXf9+nXR6SwCJQW+Ebgm8J34+ARJ\nfAYmuT1Ijx4viF7/ijhPuksRo/FpGTfu0wfe73A47plwtmXLFvm+Zj2x/5Vl338/Lck7HA5Zs2aN\nfP/997J79+4MxbRnzx4xmfwExgv8P3tnHhZl9b7xe/aZd4YBZFUBE0TEfV9zScP9p7lruaWpaS5l\nkdpimaW2mZq54JqaW6amiAuaqKm57xsiGIobIoIyMMDM/ftjRoKvoCCoYedzXV7F+57znOeckvs9\n2/N8R0ly486dO3OUeTC7Vii8CCwg0J9AdwLXCOyhTufBv/76iyQ5ffp0ajSDsh3wi6MkORdglApP\nVFQUa9duRoPBjdWqvfzQR8LevXs5Z86ch/opEDxACL1A8IJjtVpZrVp9Ar7ZBIt0cKie70xlBw4c\n4IIFC7g7W5a48uXrENiXzeZ8du7ct2DOTZ36j0PZlrKtVit79HiTen1l6nQDKUml+NPG0LK+AAAg\nAElEQVRPcx5rrmvXfgR+yObTYjZr9n85ymzZsoUGQ1UCIwgE2+/69yPgSLW6BJct+4WbN29maGgo\nv//+e+p0vbPZu0gHB7eC9bEQhITMp1xuJPANgWuUyX6km1uZQn2gCf57FEb7xGE8gaAYIJPJsHRp\nCKpXbwyrNQmAI4D7yMy8AWdn58fWnzLle0ycOA0yWXMAX2Hw4B6YOnUSKlUKQEzMWmRk1AdggU63\nETVq1MufUyTw5ZfA+PG2n2fOBN55J+v1/v37ERq6BykpJ2G78x6N996rigED+kGr1eZpNjXVbO/f\nA5yQlpaeo0x8fDyAQABjADQEcA2AAgaDGps2rcHAgSNw86YBMpkGWm00tNpMpKePhcUSCEn6DsHB\n7+Wvj4Vky5YtGDnyY1itngCCAQDkcJjNi3D69GnUq5fPsRYICkMRfnA8E4qhywJBkTF48Ejq9VUp\nl4+hXl+d/fq9/dg6u3btolJpyLaHbTvwdf78ed64cYN+flXp4FCZen1ZNm7cOs/88TmwWsng4Acb\n4uSiRQ8VWbt2LY3G/8uxAqHVuvDGjRuPNL1hwwZKkheBTQTCKUnluGjRzznKREVF2Zf3dxG4Qpms\nHT08vBkdHc3hw9+nWj3Evh1BKpUfs23bLhw8eAQ7dHidCxcuLlSin/xw8OBBVq/emDqdO4FP7WcI\nkuzjcJ+SVIrnzp17qj4IXiwKo32PrTl9+nTeuXPniRsoaoTQC/7LWK1Wrlu3jl9++SXXrFnzWMHa\nsmULtVpn2tK8/iO4jo6NGBERQZJMS0vjoUOHeOLECVoslsc7YbGQQ4fSrqLkqlU5/Nu7dy9/++03\n7tu3zy7GOwlkUiabRh+fCvkS2ZUrV7FKlZdZsWIDzpu3INcyYWFhdHHxolyuYPXqLzM2NpYk2bJl\nVwIrsvU3nNWrN318v4qIv//+mwaDG4GlBN6yby8MI1CdwMeUyyuzV68BT/1jQ/Bi8VSF/qOPPqKf\nnx+7devGzZs3P/f/OYXQC4oLVquV0dHRPHfuHDOf8jWzvPD1rUZgHW3R3JbbZ7mb6eDgztv2mPMF\nIiOD7NvXpqAaDblxY9Yrq9XKnj3fpF5fjkbj/1GSXDlp0iSWKFGaMpmc5cvXfCqx4P/3d9KkSd9Q\nklrY9+3N1Gq7cMSI4CJvNy8WLFhAvf4N+0fGVfvY9yXwGpVKHT/++OPn/ntUUPx4qkJP2k64bt68\nmT169KCfnx/HjRvHqKioJ260MAihFxQH0tPT2bZtV+p0HtTry7By5XpPJqyFxMXFh7YobkcJ+BNQ\nUKcrwV27dhXcmNlMduliE3m9nty+PcfrsLAw6vWVCZjsIhdBZ+dSJPlE99ZJW3jYLVu28Pr16/mu\nk5GRwe7d+1Gl0lOtdmDLlq/RZDI9UftPwooVK2gwvJq1dQAcpFyu4ieffMpjx449Mz8ELxaF0b58\npamVy+Xw9PSEh4cHFAoFEhMT0bVrVwQHBz+towMCQbFm8OCh2Lw5HqmpfyMlJQYXLtTBO+8U7O+L\nxWIptB9t27aGVjsGQGkAy6HTeWDz5rVo0qRJwQylpgKvvQb89pstKc22bUCLFjmKxMbGgqyHf5LN\nvIy7d28gIyMDSmXBzv2SxFtvjUCjRh3Qo8e3KFeuCiIiIvJVV6lUYtWqxYiPj8P165exdes66HS6\nx1V7ItLT07F3717s27cP6em2A4MdOnRAqVIJ0GheB/AdJKk3vvjiS0yc+EVWUh6B4JnyuC+BadOm\nsWbNmgwKCuKqVauy7tBaLBb6+vo+8RfGk5IPlwWC58qOHTuoULgQmJdtn3g//f1r56v+5s2bs5a7\nAwPr8NKlS0/sS0pKCrt3709JcqaLizcXLfqZGRkZDA0N5dKlS3n58uXHG0lOJps1s3XExYXMnoI2\nG9u3b6da7W5fQSBlsuksX77GE/kdHh5Ovb4CgWT7+G2li4vXE9l6Wty5c4cBATXp4FCNDg5VGRhY\nO+s8U3JyMidPnsJhw97lunXrnrOngheBwmjfY2uOHz8+z18GZ86ceeKGnxQh9IJ/O927v0mgA4HX\nCGTYl3A/YMeOrz+2bkxMjP0AWwSBDMrl37Js2cpFtqdrNpvZoMGrNBjq0GDoQb3e9dHL+HfukPXr\n20S+ZEkyj7/zly9fppubD9XqagQ0BAwsXdr/iffk586dS0kakO1DyUKZTEGz2cwJEyaxdOlAvvRS\nVf7889Insl8YrFYrz58/z44de2Q73W+lWj2YQ4aMeub+CP4bPFWh/7chhF7wb6dPn8EEviIQRKAc\ngUpUq13yld1s9erVdHDolE3grFSrjUW2v79gwQJKUnMCmXb7v/OllyrnXvjWLZorViQBXtPoOPO9\n4Dz32jt16k2FYoLdZhoVikEcNGj4E/t54MAB+xW7v+0257Fs2cr8+uvvKUk1CRwhEEFJ8s4zu93T\nIDExkX5+1SiXuxDwoC1N7oP/Vuv58svtnpkvgv8WhdG+fO3RCwSC/PPee29Dr/8BQAsAXaDRXMfK\nlfNQsmTJh8rGxcXh44/HY9SoD7B37164u7uDPAcgzV4iCoAFRqOxwH7Yfjfk5Nq1a0hLqwtAYX9S\nH7duXXu4clwcLI0aQX32LC6gBOqaf8SHcw9h8OCRubYVG3sNFkt9+08aWCwtcPny9QL7/IC6deti\n4sRgqNWVoNf7wMNjEjZuXIklS36DyfQ9gJoAmsJkGodly9Y+cTsFITMzE1Wr1sGlSzJYrbEA+gNY\nBCADQAa02mWoXz/3THsCwfNECL1AUMTUqFEDe/ZsQ+/el9C9+y2Ehf2KTp06PVTu6tWrqFq1Hr7+\nOgkzZiShadM2CAmZh6ZNK8NgqA+dbhAkqSlmzJgGVT7TvALArFlzYTC4QqXSok2brrh3717Wu4YN\nG0KrXQEgBoAVSuUU1KvXKKeBmBigcWMoLl7EabkRTXAWVzEQJtM6LF26MNdDgi1aNIJONw22dLVJ\nkKSZCApq9FC5gjB69EjEx8fh1KlduHLlAipVqgSDQQ/gnw8Imew6jMZnk6r39OnTuHEjEUAnABKA\n8QDuAnCDVuuFevVM+OKLT56JLwJBgSi6hYVnQzF0WSDIlXHjPqFCMdIe3KUkgS8I9Kanpy9/+eUX\nzp49+7GJYK5fv87w8PCsKGvbt2+nJPkQOEvgPjWaPuzaNWfs+qlTZ1CtlqhQaFi7dlPeunXrn5fn\nzpGlS5MA43196a1vk21pOpEKhTrXmABms5nduvWlQqGmQqHmgAHDnkrsgJ07d1KncyXwOeXy0TQa\n3XOcAzhy5Ahff/0tdu3aj9v/5/pfYTl+/Dg1Gg8CtQncs4/JVwwMrMXLly+Lu/GCp0phtE9mN1Bs\nkMlkuS5JCgTFjZEj38ePP7oCWAxgIQDbDFij6YtJk6pj9OjRj6y/detWdOnSG0plZaSnn8eIEYMg\nl1swZYoawGf2Upfh7NwYd+5cyVHXYrHAbDZDkqR/Hp44AQQFAfHxQJMmuPPzzwis1wwJCb1hsdSG\nJE1Dz56VsGDBT3n6ZDabQRK3b9+GwWCAk5NTQYflsRw5cgTLl6+GRqPGoEEDULZsWQDA0aNH0bhx\nK5hMYwDoodN9gV9/nY927doVSbuZmZmoXbspTp1KgtV6A4ADVKoknDt3CH5+fkXShkCQF4XSvqL5\n1nh2FEOXBYJcCQ0NpVzuTEAiEJM1c5bLx/Lzzyc8sm5mZiYNBhcCe+z1blOSfDh69GhqtZ2zBWv5\nneXK5eOK219/kU5ONgdatSJTUkiSsbGxfP31t/jyy+341VffPHaWfu3aNQYG1qZO506VSs/33hv7\n0Ew3IyODP/wwnb16DeSXX05mamrq4/3LB717DyLwbbYViF9Zp86rRWL7AUlJSRw+/H3WqtWMvXr1\ney5BkAT/TQqjfSJ7nUDwHLBarRg16mNYrV1gOxj3NoBpAGKg1S5E+/Zhj6yflJSE9PQMAC/bn7hA\noaiLKlWqoEyZCFy92hpWqw9ksvUICVn9aGciImBt3x7ylBSsgwzBZ2Kw9MQJNGjQAN7e3ggJmQaL\nJX8HAnv3fhsXL76KzMxJAO4gJKQZGjWqjS5dumSV6dHjTWzZEgeTqQd0ui0IDW2PP//cCoVCkbfh\nfGA2Z+CfYD0AICEzM7NQNv8Xo9GIH3/8rkhtCgRPnSL84HgmFEOXBYKHaNiwhf2+eQKBNAKjCLjT\nxaUsN23a9Nj6VquVbm4+BNbYZ6+XqNN58NSpUzSZTFy6dClnzZrFCxcuPNpQWBitWi0JcClqUoEk\nAmvp4ODOa9eusX//t6lUaqlUSmzZstNjQ8k6O5cmcDnbrPoLjhkzLuv9uXPnqNW6ZAuTm0mDIYAH\nDhzI17g9ij/++IM6nQeBVQRCKUl+XLhwcaHtCgT/BgqjfcVONYXQC4o74eHhdpF/ibbMbg/uyzfl\nolzSvebFoUOHWKJEaRoMZanRGDlr1tyCObJmDa0qFQlwDjSUwZIl0EZjczZt2pxKZV3a0quaqdV2\n5bBhox9psmrVRgTm2+2kU5KaMyQkhJcuXWK5ctWoUGgJOBM52qrD3bt3F8z3PAgLC2P9+i1Zq1Zz\nIfKCF4rCaJ84jCcQPGUyMzMxduxnWLVqPQwGA+rWrYAlS34DMBPAh7Bd1zoBb+8kXLx4HBqN5rE2\nSWLlypU4fPgoXFyc8fbbb6NEiRL5d2rpUqB/f8BqxVQ0wPs4CeAigJIAUqFQ+IDUwmr9CkBfe6Vd\nqFz5Y5w69WeeZk+ePImmTVuDrAiLJQ516pTD1q1rUbVqA0RG9oTV+h6AOgBqAxgEhSIMnp6/IDLy\neM6DgXmQkZGBhQsX4tKly6hTpya6du0KmUyW/34LBMWUwmifEHqB4Cnz7rtjMG/eQZhMPwC4ArX6\nDVgsLrBY3AC8DiAcMtkOXL4cCR8fn3zZ7NSpFzZvPgOzuTskKRzNmrkjNHT1Q6IXGxuLS5cuwd/f\nH15eXraHc+YAQ4cCAL7Tl0Bwyh4AGwCEAGgDhWIbyHhYrQMA3LM/l0Eun4i2bc9g48aVj/QtISEB\nBw8ehNFoRIMGDZCZmQmdTg+r1Qxb6I4EKBSN4eycjtq1ayAkZCq8vb0f22er1YpXX+2AAwfSYDI1\ng16/GoMGtcUPP0zJ15jlZk8uF6FEBMUDcepeIHgGWK1Wzp4dwrp1g9i8eUfu27cvX/Xc3X3t99of\n7Ft/Qm/vQKrVXlQofKlQOPHXX3/Ntx/jxo23n9S/mxVyVq/35ZH/STYzZ8486nQudHRsTJ3OxRYX\n/ttvHzjBSSVK0dMzgErlGPsp/U1UqcqwV69eVCq97OcHqhJ4mUAjKpWOjImJKciQkbSNm4ODK4ED\n9qZTaTBU4ebNmwtkZ8+ePTQYAmnLH2C7aaBS6ZmYmFggO7dv32bjxm0olytpMLhy8eIlBaovEDwP\nCqN9xU41hdALnhfffz+dklSRwEYC8ylJrvnKL16mTOVse/GkSjWEX3wxkdu3b+evv/7Kq1ev5tuH\nmzdvUq02EPDJdoWONBjqMyIiIqvc1atXqdOVIHDRXuYMJyo0WSI/TNaBwEGqVK9To3GlXv8SNZoS\nbNu2C5csWUKNxpXAJwROEhhAoASrVGn0RONGkuvXr6dO50qDoTs1mvL09CzP/v3fZnR09GPr/vzz\nUjo6elIuV1KhqJ/tg8lKnc69QONHki1adKBK9Y79EOQJSlJJ/vXXX0/aNYHgmSCEXiB4BpQpU4XA\n/mxC8znfffeDx9ZbsWIlJakUga+pVA6nq6s3r1+/nqPM/fv3+dFHn/G113rz66+/yzN5zKlTp2gw\nBBCoQuAz+/37GXR09GRSUlJWub1799LRsW6WIH6H0SRAi0zGwdqAbH3IpEZTgrt37+bnn0+kJHnS\nwaELlUonymSuBLwJvEyttiK//356ocYvMjKSPXu+QY3Gm8AiyuXj6eRU8pFCvXfvXkpSSQJH7af5\nHQnMJRBDpXIMAwNr02KxFMgPjcaBwJ1sH17v8euvvy5U3wSCp01htE/coxcI8ontnnd61s8yWTqU\nysff/e7Zswc8PNzx228b4ejojOHDD8DT0zPrfWZmJho3bo2zZ71gNrfCtm2/YN++I1i/fvlDtnx9\nfaFS3QPwCYBNAOZALk/Hli1hOe65lytXDhkZlyDDYczCfLyNuUgHcHLMGCyfuRmAFbb9chPIDHh4\neGDy5O9gNp8AUAbATSiV5VGihCNksusYOnQA3ntvxBON2wP8/f0RHr4HZnMYgMqwWgGT6QaWL1+O\n4ODgXOvs3LkTZnMfADXsT9ZDJusEJ6eJqFmzFpYt21jgfXZnZ3fcuHECQDMAVqjVJ+HuXvXJOyYQ\n/Nspwg+OZ0IxdFnwgjBv3gJKUlkCP1Mm+4Z6vWtWjPnCsHfvXhoMlbNdOTNRoymRZ1rbw4cPs2RJ\nP8rlKrq4eOV5NW3NytX8RaEmAZoA/vXZ50xPT2eNGi9Tq+1GYA4lqRH79BnEkydP0sGhQraZPuno\n2CDf197u3r3LJUuWcMGCBYyLi8vx7sSJE2zSpB0DAupSo8m+nUAqlSM5efLkPO3OmTOHktQu2zbF\ndpYuHZAvn/IiNDSUOp0rdbq3aDA0Zu3aTWk2mwtlUyB42hRG+4qdagqhFzxPVq/+lW3b9mCPHm/y\n5MmTD71PTU1ldHT0YwPLZCciIoJGY11mX07X6Tx5+fLlR9YzmUx5J1JJSyM7dSIBZkoSU7IF4UlJ\nSeGECV+yV6+BnDlzFi0WC1NSUujo6Ml/8qtHUK93ZXx8/GP9v3XrFkuX9qde356S1JOOjp48c+YM\nSVsIXQcHdwKzCPxJhaI8FYrqBLYRmE293pWRkZFZthYvXsJSpQLo4uLDkSODmZyczMqV61GvD6JG\nM5SS5FYk+efPnDnDWbNmceXKlULkBcUCIfQCwb+ArVu30mBwoV7vTb2+RL4FKSUlhd7eAVQqPyaw\nhxrNQNau3fTJs6GlpNji1QO2+PX5PGi2b98+OjuXolrtSAcHV4aHh+er3qhRwfbDbbYmZbLpbNGi\nI0ly9uzZ1On6ZfuIuU25XMvq1ZuxRYuOPHr0aJadrVu3UpK8COwlcIGS1JTBwZ8wNTWVS5Ys4fTp\n03nq1KmCj4dA8AIghF4geM7cvXuXBoMrgV12QdtHSXLJ14yYJOPi4vjaa28wMLA++/V7m3fv3s3x\nPj09PX+HzpKSyCZNbKrq5kYeP57jdUZGBkePHsfSpSvQ378WN2zYkOO9xWJhfHx8gVLMdu7cl8CC\nbGK+h4GB9UmSCxYsoCR1zvbub2q1xlw/YgYNGk7g+2xlD/Gll6rl2w+B4EWmMNonokUIBEXApUuX\nIJeXAtDE/qQBVCpfXLx48bF1SSI6Ohp9+nTG1q2rsXjxbDg6OgIAUlJS0LZtN+h0Bmi1BowfPzHv\noBl37gCvvgrs3g2UKmX7Z7VqOYp8+OGnmDNnH+LiVuHixYno0eMt7N+/P+u9XC6Hq6trgRLMtGnT\nFJL0I4DrAO5Bp5uMVq2aAgA6d+4MR8cTUCpHApgPSWqHDz8MzjWanbOzEQpFbLYnf8NodMi3HwKB\nIA+K7HPjGVEMXRb8B7h16xa1WqdsB81iqNWWeOwdb6vVyi5d+lCvL0+jsQP1eldu3749633//kOp\n1fYgkEogjpJUkStXruT69evZunU3duz4hi0hzI0bZJUqtqlw2bLkpUu5tufhUY7A6Wyz5gn84IMx\nheq71Wrlhx9+QpVKR4VCzR49+jMtLS3r/c2bNzlqVDC7devPxYuXZM3mjx07xt9//z0rCE9cXBxd\nXb2pUr1FmWwcJcktx1gIBP9lCqN94nqdQFAEuLm5YejQgZg5szrU6gqwWmMxZcpElC5d+pH1QkND\nsWXLSaSknACgBbAdPXsOQHz83wCAHTt2Iy3tF/u7UjCZhmD27AU4dOg8TKYvASTj7NbWOOnuAG1s\nLBAQAGzfDjwId/s/SJIetpl3JQCAUnkdDg6lCtV3mUwGk+keLBaCJM6cOY+EhASUKmWz6+7ujmnT\nvslR5733xiEkZBmUyqrIzDyIJUvmokuXzjh16iAWL/4ZJlMqOnfehurVqxfKN4FAgOI3PS6GLgv+\nA7z//kfU6/2o1Q6kRlOGgwYNz1e9mTNnUqsdkm2GnU65XJG1H1+3bgv+kw3OSrW6Dz08yhMIJUD6\nIooxcLZVrlaNvHkzh32r1crjx4/zjz/+4J07d7hmzRrqdJ4EvqJS+Q5dXb3zvMaXX954oz+BEgQi\n7dfgxrFu3eZ5lj906BAlyTtb0Joj1OkcmZ6eXig/BIIXmcJo31Pbo09LS0O9evVQvXp1VKxYEePG\njQMA3LlzB0FBQShfvjxatmyJu3fvZtWZPHky/P39UaFCBWzbtu1puSYQFJqzZ8+iceO28PWtjq5d\n38BPP4UgJeUA0tLmw2w+jKVLl+PKlSuPtVO7dm3I5aEAYgAQcvkMVKhQKysIzNy538HB4SPo9b1g\nMAShTJmTcHFxAaBEBZzDbjTBS0hElKs7sHMn4O6eZZsk3njjLTRs2AGvvTYeZctWxEsvvYQtW1Zh\n5Mg7GDfOFdu2/Y5Ro8ahevWmGDZsNFJSUgo0DgkJCVi5cgWAXgD8AcgAfIwjR/bmWefvv/+GUlkT\ngLP9SU1YrQokJiYWqG2BQJBPiu5742FSUlJI2k761qtXj3v27GFwcHBWuMkpU6ZwzBjb/uCZM2dY\nrVo1pqenMyYmhn5+frmeMn7KLgsEj+XmzZt0cipJmWwmgcNUqVpSocgeVpY0Gqvy8OHD+bI3Y8Ys\nqtV6ajQl+NJLlXjpf/bXr169ysWLF3PVqlVMSUnhokU/s4G2FG/BSAKMkKt4IJe97DVr1lCvr0Eg\nxe7Xcvr5/XOK/f79+/TyKk+lchyBHdRqe7Jp07YFutYXFRVFjcaFQH3+k2xmO52cSj9Ubv/+/UxK\nSmJkZCR1OrdsZwVW0s3Np8ChbAWC/xKF0b5nopopKSmsXbs2T58+zYCAAN64cYMkef36dQYE2KJc\nTZo0iVOmTMmq06pVK+7fv/9hh4XQC54zK1eupINDx2zCHk9AR2CVXexW0Nm5FO/du5dvm2lpabx5\n82b+RHbfPpoliQT4l4sHd2/dmmuxr7/+mkrl6Gx+3qVarc96v23bNhqNjXJsG2g0zll/P/NDRkYG\nvb0DCFSz/+lCQM81a9aQtG0dDB/+AXU6dxqNtejkVJJHjhzhkiXLqNUaqdN50tXV+6HMewKBICeF\n0b6ner3OarWievXq8PDwwCuvvIJKlSrh5s2b8PDwAAB4eHjg5s2bAIBr1679ky8bgJeXF+Li4p6m\newLBE6HVakHeAfDPNTeFIhOlS38CmUwDb+8J2L59IwwGQ456UVFRqF79ZWi1RpQvXxPHjh3LeqfR\naODu7p7rtbMc/PEHEBQEtckEdOmCetdi0bhly1yLVqtWDRrNRgDxAACZbBEqVPjnup1CoQBpztaP\nTJCWAl2tUyqV2LVrM2rUMEKlioSHx2GsX/8LunTpAgAIDw/HokUbkZp6AcnJh3H37lR07twHffq8\ngTt3buDChYO4fj0aNWvWzHebAoGgYDzVU/dyuRzHjx9HUlISWrVqhZ07d+Z4L5PJHvmLLa93n3/+\neda/N2vWDM2aNSsKdwWCfNGyZUuULv0FLl/uC7O5PvT6BRg0aDR++GEKLJbchTIjIwPNmrXFtWvD\nQG7ExYub0Lx5O8TEnIWTk1Ou7WzYsAEhISug12sxduxI1Lh2DejSBTCbgb59gQULAGXef4VbtWqF\nESNex9Sp5aBSlYCTkwq//RaW9b5Ro0YoXZqIjn4L6ektIEmL0br1/8HV1bVA41G2bFkcPbo713fn\nz59HZmYLAA/62AlXrvQGSeh0Onh7exeoLYHgv0JERAQiIiKKxljRLSw8mi+++ILffvstAwICslJ0\nXrt2LWvpfvLkyTmSW7Rq1SrXHNHP0GWBIE+SkpI4fvwE9ukzmIsWLX7skvv58+dpMPj+T9KYRty5\nc2eu5W2pbW3pXIGp7K1xoFWptFUcOpQswH52fHw8IyMjcz3VfvfuXb777ods3bobv/xySpGffN++\nfTv1+nIEbtv7/TN9fasUaRsCwX+BwmjfU1PN+Ph4JiYmkrQl32jcuDG3b9/O4ODgrL34yZMnP3QY\nz2w2Mzo6mr6+vrn+8hRCLyiO3Lx5kxqNo30/nwRSKEnePHHiRK7lK1VqSGAzAbIfFjETMpvIBweT\nBYyBb7FYuHbtWk6dOpV79uwpiu4UiA8++JhabQkajZXp4pJ3nwUCQd78K4X+5MmTrFGjBqtVq8Yq\nVarwm2++IUkmJCSwRYsW9Pf3Z1BQUNbHAEl+9dVX9PPzY0BAALds2ZK7w0LoBc+QpKQk9u07hH5+\nNRkU1OmhE/EF4YMPPqZeH0Cl8gPq9TXZq9eAPFcCAgPrE9jBYZiZtQSwtmbdAot8eno6X365JbXa\nalSrh1OSfPjttz88cR+elCtXrvDYsWNZN3EEAkHBKIz2yewGig0ymSzvWN8CQRFCEo0bt8bhwyVh\nNg+DXL4TLi6zEBl5Is999ccRFhaGkydPwt/fH507d87zHEpIyHxcGT4WEzMSAABjVXp02rMD9erV\ny3dbqampqFWrEc6duwUgCrboerFQqQJx9248JEl6oj4IBIJnT2G0T4TAFQjyICEhAYcOHUB6+m0A\nSlitdWE2h2Pv3r1o167dE9ls3bo12rRp8+jT9SQGX/kbyEiAFcAP5auiTciMAok8AEyf/iOiolQA\nqsEm8gDgDYVCQnJyshB6geA/gsheJxDkgVqtBpkBwGR/QpBJUKvVBbaVnJyMRo2CoFJpIUnO+P77\n6bkXJIHRo4EvvwQUCsiXLcP7F06gadOm+W4rLi4OISEh2LhxGzIyOgA4BGCTvR9T4OnpAfdsEfQE\nAsGLjVi6FwgewcCB72DlymMwmfpBo9kFf/9oHDmyO99in5iYiDfffAcbNmwGabfYDeoAACAASURB\nVATwGwBnaLVB+PXXGWjfvv0/hS0W4O23gfnzAbUaWLkS6NSpQP6eOXMGDRu2QGZmS2RmnkJ6uhXA\nFAAjAVyG0eiJ48d3o2zZsgWyKxAIni+F0T4xoxf8J7h8+TIaNWqFEiW8UK9eC0RFReWr3rx5P+Lb\nb/uiV69DGDOmAvbv355vkSeJVq06IzTUAHIvgDEAOgJwQlraEISHR/xTOCMD6NPHJvI6HbBhQ4FF\nHgBGjfoY9+59ApNpCdLTj0AmU0Au7wqtNgk1atTHokXTsXDhIsyaNQtpaWmwWq2YOnUGmjbtgF69\nBiImJqbAbQoEgn83YkYveOExm80oV64qrl0bAKu1J+TytXB3n4lLl0491X1qW6pWP6SnJwB4EESn\nDYC3ASzF5Ml1MHbsGCAtDejZE/j9d8DBAQgNBZo0KVBbW7duxebN27Fixe+4dWs+gAf1F6Ft2y0I\nCZmKwYPfQVjYPgCDIZcfQOXKKWjSpCEWLvwTJtOHUChOw2ici3PnjmZFrxQIBP8OxIxeIHgEFy5c\nQFKSHFbrGABlYLW+B5PJiNOnT+coZzabER8fX2QfklqtFlZrOoAk+xMrgFgA70Ol2gJHRyPSExOB\nDh1sIu/sDOzYUWCRnzVrLjp3HoLp011w+7YeMtl4AHcBXIVePx2dO7fG3r17ERa2BcA+AF/Cat2G\ns2ctmDPnJ5hMawF0hsUyHmlpzbB+/foi6b9AIPh3IIRe8MJjNBqRkZEA4L79SSoyMm7BaDRmlZk9\nOwRGowu8vQPg61sF0dHR+bKdnJyMN94YBB+fymjUqDXOnDmT9U6v12PYsOHQ61sAmArbbD4WQAKs\n1sH44v2VOOtTFggPt6WXjYgA6tQpcP/GjfsMJlMogLGwWg9ALr8GudwTGk0gRo58DQMG9EdY2A4A\nFgA+9loyWCw+sMW5z34DoGhXzKKiojBjxgzMmzcPSUlJj68gEAiKnkLc338uFEOXBc8Rq9VKq9XK\n3r0HUa+vQ+AL6vUN2KVLn6xgNcuXL6dC4UogigApl3/HwMA6+bLftGlbajR9CRynTDaLjo6evHnz\nZo72ly1bxiFDRrJ9+44E1ATOsARu8xBqkQBTXFzICxeeuI8ajYFAQlZoXY1mKKdOncqbN2+yWbP2\n1Omc6ODgTsCPwGACVwisJyCxXr0mlKQGBH6nXP4lnZxKZoWoPnv2LGfOnMlly5YxNTW1wH7t37+f\ner0rNZohlKTOLF3an7dv337ifgoE/2UKo33FTjWF0AvyQ0ZGBgcOfIdqtZ46nSPHjfuMS5cu5Ycf\njuPPP/+clfv8/PnzVKv1BPpni0OfQZlMzszMzEe2ce/ePSqV2mx52ElJasdPP/2USUlJOcpGRUVR\nq3UloKQH/uZJVCYBRskc+MtXXxWqr1279qVW25nAOQJrKEmu3LZtGyXJk8Bwe9jdVQT0BLwJONr/\nfEmt1pnjxn3KRo3asmvXvoyKiiJJbtmyhZLkSq12EPX6FqxcuR5NJlOB/KpZsymBZVljo1IN4scf\njy9UXwWC/ypC6AWC/+Gjjz6nJDW3i1wsJaka581b8FC5Dz8cR6CrPZd6ql2U/qCLi1dWmQMHDvCd\nd97j6NEfMjIykiT5yy/L2aHD65TJVNni11sJVKNOV5FubmWyRJMkw8LC6OgYRG+8zEg4kgBPowzL\napx5/vz5QvXVZDKxf/+h9PAox4oV6zE8PJwlS/oSUBHIzBJarbYzVSpnAnMJXLYn1qnLvXv3PmTT\n2zuQwNasful07Th79uwC+eXjU5nA0WwfUNM4cOA7heqrQPBfpTDaJ/boBS8koaE7YDJ9DMAVgDdM\nptHYuHHHQ+WsVgIIAFAVtghy/weZ7P+wfPkCAMAff/yBV15pj59+csUPPyhQq1YjBAePxaBBE7Bh\nQwuQdQE0APA+gOYAVEhNPYqEhBEYMGBkVjvlypWDd9ph7EEU/JGEo5DjFdzGtNWLERAQUKi+6nQ6\nLFo0CzduXMSZM3/Bw8MD9+4pAagBXH7QUwB/Qy7PBFAFQBkAR5GRcQnlypV7yGZiYry9HADIYDZX\nxa1b8QXyq127IOh04wEkADgPSfoR7du/+iRdFAgEhaEIPzieCcXQZcFzoGXLzpTJpmfNJpXKDzhk\nyMiHyp08eZKS5EpgNoFJVKu9ciwv16/fksDyLDsy2QSq1c4ETtufxdiXwV+yL4s3IHCPwCmWKlWe\nN2/etG0TnDrF+0YjCfAvhZ6lpBIMDd2Uwxer1cpdu3ZxxYoVvHjx4hP3PTY2llqtC4Hv7T59QKA+\nq1VryA0bNlCvd6GDgz8lyZm//bY2Vxvt2nWnWj2QQAqBk5Sk0ty9e3eB/EhNTWWvXgOo0Rjo4ODG\nqVOnP3GfBIL/OoXRvmKnmkLoBfnh9OnTNBo9qNP1oyR1o7t7GcbFxeVa9sCBAwwK6sz69Vtx9uyQ\nHBnlKld+mcD2bMvPs6lUGu0Cn0HAh8Db9mV7C4FuBMZSLg+iXK6lRlOCbT3KMNPJiQSY2qgR/9q+\nnfHx8Tl8sFqt7NnzTer1AXRw6EpJcuX69evz1Ver1cpvvpnKsmWr0d+/Nn/5ZTkHDRpBvb4agT5U\nqUqzbt2XaTabSdrOFpw9e5bJycl52kxMTOSrr3akQqGmg4MbFyxYlC9fBALB06Ew2icC5gheWK5e\nvYrQ0FAolUp06tQJLi4uBbYxdeoMfPrpAphMcwHchyS9iVdfbYDt26/DZOoFYAKAXwA8WJJeBZls\nKGxx8Q+gIeIRhlfhiDSgXTtgzRpAq83RBkn8+OOPGDNmFtLSjgHQATgIvb4NIiK24syZMyhfvjwa\nNGiQq4/Tp8/ERx+FwGQKyfJx9eo5SE1NxalTp1GhQgB69OgBubzgO3UkH52ARyAQPBMKpX1F8qnx\nDCmGLguKMVarlVOmfJdjtpyZmcnPP/+Kvr5VCXjYT+xbCKQTaM369RtTr+/HFgjnfUgkwNWQMS2X\nGbTFYmFQUEcqlS72Q4EPVg6slMlU1OlK0WB4g5JUhsHBn+TqY9WqjQlsy1Z3Drt16/+0h0YgEDxD\nCqN94jCeQPAIZDIZxox5H9HRxxEZeQgdO3ZA1659MWnSJNy+fRMuLhoAuwB4AygJne4oBg7sizaZ\nO7AJ7aCHCYvwCvooHdC991AsXrwk66ucJF55pRXCw08jMzMMwG4AZ+3tzgCpRWrqAdy/vwwm0xHM\nnBmCixcvPuSjXi8B+OegnEwWD4NB97SHRiAQFBOE0AsEBeCtt0Zi82Yr0tOvIDl5K0ymDDRvXhEe\nHnrI5WYolf7YNexdrEiPgwbpmKPywUD8hQzrYGzY8CqGD/8WEydOBgBs2LABf/11DkALAHUBfA+g\nPgAtSpb8CXq9CwAve8suUKvL4fr16w/5VK9eJQCDAUwCMBaSNB3BwSOe/mAIBIJigRB6gSCf3Lhx\nAxs3/g6z+VUAegDVkJY2BIGBfkhKug2r9Ri63huAnzNMUJKI6toVR/u1hEbbEVbrtwD6IyVlHb79\n9gcAQHR0NKzW+gDCAPwNoDeAT+HvH4iLF49DrU4HsAa2MLXhsFguomLFijl8Onz4MEJCVgD4GbZZ\n/UF4epZEYGBgkfX7wIEDCArqjAYNWmPOnHnijIxAUMxQPm8HBILnze7du3HgwAF4eXmhe/fuUCgU\nSEtLQ1paGpycnAAAx44dQ7NmbWAy1QQwG8BiAFuh0ZyFQuEJtdoXg9LCMAOjAABfaDzRdswYVN63\nD+SpbK3pYbFkAgBq1qwJtXoGMjOHAKgEQAOl0opNmw5CkiRs2/Y72rXrhjt3+sDBwRnr1v0KV1dX\nAEBqairOnTuHzZs3g2wPoIv9TyZiYrSwWCxQKBQoLKdOnULz5u1hMn0FwBOnTo2DyZSK0aNHPrau\nQCD4l1BUBwWeFcXQZcFz4sqVK+zUqTerVm3MYcNGMyUl5aEyU6fOoCT5UKV6j3p9Q7Zo0YFjx46n\nUqmlSqVnnTrNePv2bVat2ojAQvthNwuBNlSrK7JcuaqMiYnheJXuwUk4jsQo6vUuTEhI4OXLl2kw\nuBGYSeAPSlJTDh78z33+iROnUKXSU6FwpVZbgrNmzcrhn9Vq5b1793Jc+btw4QI9PMrSwaEy1WpH\nKpWBBNLszUewRInSRTaG778/hsD4bAf9/qKPT+Uisy8QCPJHYbSv2KmmEHpBfkhOTmbJkn5UKD4l\n8AeVynrU671YqVJDLl68hCSZnp5OlUqy34kngXRqtT7UagMI3CSQSaVyAB0dvQkYCERmE7wpbNGi\nNe8lJ5PjxpEALQCHadwoSSW4cWNoli8nTpxg8+Yd6OHhR1/fGhw0aHhW4pvLly/TwcGNMtkIAjMp\nST5cuHDxI/tWo0bjbMGA7lKhKEmt1p8ODp0pSa7cvHlzocbu+vXrPHfuHM1mMz/4YCxlsnHZ+r2H\nL71UtVD2BQJBwRFCLxD8D5s2baKDQzO7OP1KoAyBLQS2UpJe4ooVK5mYmEiVymAPdvMg8UoFApOy\nrrgB9QkMJdCLtsxvmQSuU6+vyDWrV5MjRtgqKhRMXbiQ58+f5/379x/yZ8CAYZSkxgRWUKUaRS+v\n8kxOTuYnn4ynQvFuNiHdzTJlHj1j1utdCFzPVucj9u3bjytXrmR0dPQTj5nVauXo0eOo0TjSYPBj\nqVLluHXrVur1rpTJviWwjJLkyzlzQp64DYFA8GQURvvEYTxBsSIxMRGtW3eBVmuEu3tZrF+/Ptdy\ntv3pNNgOsv0CYDKAVgBawmT6GnPnLoejoyP8/QOhUHwGIAlAGGSyK9Bq/wSQCaAngFMAPgLwE4Bo\nAAbI5WXw7oiu6BwWBvz4I6BW49bs2eixPhzdug3CuHETkJqamuVLeno6fv55PkymjQB6IiNjGpKS\nymDbtm1IT8+AxeKQzXMjMjIyHjkG/v6BkMnW2H+6D71+C9q1a4sePXrA29sbsbGxSElJKeDIAmFh\nYZg7dx3M5ku4fz8KN24Mw4cfTsT+/X+ga9czaN36d8yfPwlDhgwqsG2BQPAcKcIPjmdCMXRZUIQE\nBb1GtXoQbfnX91CS3Hns2LGHyqWmptLfvzrV6rcIvExgVrYZ8Fy2bt2VJHn16lXWq9eCarWeXl4B\n3Lp1K+vUaUat1pdAZQI17CsCtr15na45Z02fTvbo8SAvLe+tXUt39zJUKL4g8Ae12s5s06ZLDl8U\nCrU9brytmoNDO65atYpHjx61x9pfRmAnJak2x4+f+MgxOH/+PN3dX6LRWJU6nQf79h1Cq9XKEydO\n0N29DCWpFDUaB86ZM69AYztp0iQqFMHZximBGo1DgWwIBIKnQ2G0r9ipphD6/y7bt2+nLfXq3Swx\nUquHc+rUqSRtOegvXbrEW7dukbTFax81KpgNGrSgSuVEYAqBrylJrrmmZn1Aeno6hwwZQpVqKIF9\nBNwIdCFQgY3rNKWlXTtb40YjuWcP161bRweHltkEMo1KpS5HLPkuXfpQp2tLYCsVigl0c/PhnTt3\nSJIRERGsX78lK1VqyEmTvrUlwXkMKSkpPHz4cFbyG6vVylKlyhH42e7DRUqSJ0+cOJHv8V29ejX1\n+prZPkh+ZkBArXzXFwgETw8h9IIXnhMnTthnvu4EDmTtoev1QVy8eDFjY2NZtmxl6vXeVKuNHDky\nOMdJ9cOHD3PAgGEcMGAYDx06lGc7sbGxXLduHefOnUtJ8rIf1IulTNadlV+qQEvz5jY1L1GCV9av\nZ/36r1KvL0G5vHa2vf4kKpXaHKf8zWYzg4M/Ya1azdmpU29evny5SMcnKSmJSqWU7WODNBh6ccmS\nJbmWP3jwIEeOfJ8ffDCWUVFRJG0fC716DaAkedHRsQGdnUvx+PHjReqnQCB4MoTQC154Jk78kgrF\nBwRW0RZf/l0CjVm1agOmpqayQYMgKhQT7GKbQL2+Mn/77bcCtbFt2zbq9a40GttTry/HmjUbUaWS\nqFY7skbZykytVcumoJ6eTD10iCVL+lEu/47AOQJeBN4ksJSS1Jj9+g15SiORO1arlQ4OrgT+zDqN\nr9f7cs+ePQ+V3bFjByXJjcBEyuUf0sHBnRcuXMiyc/LkSUZERDAxMfGZ9kEgEOSNEHrBC8/UqVOp\n0fSxi9ghAsNpNLrRZDJx5MhgAjoCcdlmtOP5ySefFqiNEiW8COyw10+hwVCZv//+OxMuXKC1Rg2b\nYW9vMjKShw8fpoNDlRz72TKZKxs2bMXvv5/GzMzMpzQSeRMWFkZJcqWjY0tKkhffeef9XMvVrfsq\ngRVZvstkn3Hw4BHP2FuBQFAQCqN94tS9oFjQt29fODn9CaXybQA7IUnrMW3at1iyZBnmz98JoCps\noWQBwAy9fgfKlfPLl+3Lly8jMLAO7tyJA9DU/lSC2VwDYfPnw7FjR8iOHQPKlQP+/BPw94fRaERG\nRjwAk728BqQFer0ao0ePKpKodAWlTZs2iIw8juXLR2Hv3o2YOfO7rHe0fdQDAFJSTAA8sr3zQHKy\n6X/NCQSCFwSRj15QbIiPj8ePP/6EhIQkvPZaW2i1WrRu3QMm00QA9WC7PlcGMtlltGvXGOvXL89T\ncK1WK06ePImUlBT07DkQcXH9Qf4KoC+AUQCi4YM6+AMm+CEN1sBAyHfsAEqWBABs2bIFr73WG2az\nF4CuAEIBBEAuX4HU1PtQq9WP7IvFYsGKFSsQExODmjVrol27dkU1TA/1c+TIYISEzAYAvPnmIPj5\nlcGECUthMs0FcA+S1B9r1oSgTZs2T8UHgUBQeAqjfULoBcWSK1euIDCwJlJSmgFwBhAC4C6Aj1C3\n7jn89dcfkMlkudZNS0tDUNBrOHo0EqmpySCTAZgBRAHoAOAa/JGGHdDDG4k4Kjfi/LQv8foIW0a4\nEydOoGHDIJhM/QFsstepCKAllMoyuHXrOm7dugUfHx/odA+niyWJ//u/HoiIiIPJ1BSStBYjRvTA\n5MkTiniUgO++m4bPPlsNk+l3AHJIUieMG9cOCoUcc+cuhVqtxuefv4/XX+9V5G0LBIKio1DaV9h9\ng2dNMXRZ8BRYsWIFHRy62O/TVyTwKoEgOjmVzDpYlhcTJ06iTteRwNcEOhBwIHDKvmdtYmV48Doc\nSYC78TJdVQP4ww8/kCSPHDnCN954gwrFaAKJBDwJ6Ak4Uqn04auvtqNWa4ssZzR65HoYbv/+/dTr\n/QmY7W3eolptyPPw25kzZ/jDDz9wwYIFuUbdexTNmnUg8Fu2swQb2aBB6wLZEAgEz5/CaJ/YoxcU\nS5ydnUFeAmAEcBBAZygUEThz5jDKly//yLonT0YiNbU9bKlhW8CWja4FgH6oDX/sQjw8kYRtaIzW\neB/3Fb8jKCgIH374KRo37ojffjsBiyUawI8AygOIBHAEMpkOu3btRlraX7h/PwrJyYvQvn23hyLd\n3b17F0qlD4AHy/uuUCodkJyc/JCv27dvR506TTF27EWMGLEW1as3wv379/M9TqVLu0OhOJ71s1x+\nHKVLu+e7vkAgeAEowg+OZ0IxdFlQhFitVqalpTEzM5NNmrShXt+UCsWHlKQy/O67afmy8fXX31GS\nWhGYS6CuPQDPMTZGVSbZp77r4UUN3CiTGbl27VqePHmSklSKwG37TN6Xtvj5O7LNlhdTqfTNcZdd\nkkoyNjY2R/u3b9+mo6MngaUEblKh+IJ+flVzDZTj61uNwKasuAFabbesAEH54e+//6arqzclqSsl\nqQdLlChdqHj4AoHg+VAY7RP56AXFhvnzF2DEiPdhNqcgIKA6Nm5cgb179yIuLg716y9E8+bN82Xn\nvfdGIiJiP3buHI/MTAsyMz3QEgqsQyokAMuhQj/oYJHdwYYNq9G+fTts2rQJKlUVAC52K4cA+AI4\nC8DWrkJxFuQdADcAeAI4DDIV7u45Z9AuLi7YuTMMr78+GLGxo1C1ak2sXh0KufzhBbbExATY9v8B\nQIa0tIqIj0/I95j5+Pjg3Lmj2LBhAwCgffsZD/kjEAhebMRhPEGxYMWKFXj99cEA/gBQC8DXKF9+\nDS5cOPJE9kgiJiYG6enp+CmoA767GgMNMjEfPhiCVwD5GqxZsxSdOnUCAMTGxiIwsBZMpi329tfA\n0fEdWCxERsZrkMlMMBh2o1+/3pg1awHU6kBkZJzGhAnj4O7uBn9/fzRo0KDAfvbo8SY2bDAjLW0W\ngL8hSe0RGroEr7zyyhP1WyAQFE/EYTzBC4+ra2kC3bMti1spl6sfeTjt3r177Nq1Lw0GN5YqVZ7r\n1q17uNAvv9Ail5MAp6ElZehHlUrPZcuWPVR07dp11OmcqNW60sXFi4cOHWJMTAynT5/On376KSvG\nfmRkJMPDw/nRR59RkkrTYHidklSGY8d+VuB+37t3jx069KJaraeTU0nOn7+wwDYEAkHxpzDaJ2b0\ngmKBWi0hI8MXwBEAGgCnoFTWh9l8L9clbwDo2rUvQkMzYDaPADASQBTq1q2FtWuXoHTp0sC8ecCQ\nIQCJUx06YujtdGh1Ggwc2B1HjpyAyZSG3r27o2HDhlk2MzIykJCQADc3t0cGxbFdrysPs/k0AC8A\nt6HVVsTp0/vh55e/QD4CgUDwgMJon9ijFzx30tPTcePGDXh6euYZaKZmzYY4cOAOgLoAqgH4HcHB\n7+Yp8gCwefMmmM07ALwCYBiARTh48Bf4+FTEaHk6vs1MsxWcPBlVxo7FnwAuXbqEmjUb4f79/rBa\nS2LRotcwadI4+Pn5oXbt2nBxcUF6ejosFstjhV6tLmkPqAMArtBo/HD9+nUh9AKB4NlSRKsKz4xi\n6LLgEWzdupUGgyslqRQNBldu27Yt13JXrlxh+fI1qFTqqVCoOXLk6Mfa9vDwJfCK/YT8gyV/Cz+G\nU9ax+CV1G+WoM3z4aMpkH2VtDwBBlMtL0WhsQ63WmVqtAyWpFB0c3Lhjx448205JSaGTU0kCa+y2\nttHBwZ0JCQkFGyCBQCCgSGojKKbcuXOHer0rgd12MdxFvd41z8AxVquVt27dYmpqar7sr1q1moAT\ngZIE0ghYOQWjSYCZkLM/JtPVtUyOOv36vU3gh6zgMkAlAib7z1sJlLL/+w4aDG5MSkrKs/2DBw/S\n3f0lKpVaOjuXZERERL7HRiAQCLJTGO0TAXMEz42LFy9CofAB0Nj+pAkUCi9ERUXlWl4mk8HNzQ1a\nrTbHc7PZjNjYWJjN5hzPu3fvhm7d2gPQQoY2mIkmGIOpyADQC8uxGFXg5FQiR52+fbtBp/sGwGYA\nuwDUBvAgjO0rsF2dswJoDrncHdHR0Xn2r06dOrhxIxqJifFISIhD06ZN8ywrEAgETwsh9ILnhpeX\nF9LTY2CLUAcAl5Ge/je8vLweVS0H4eHhcHX1QrlytWEwuOLtt4ciMzMz631IyI9Q4CYWYjfewZ9I\nA9AJdfArdkGn64+ffpqSw17z5s2xbNlMVKgwASVL/g6Vaks2/34EUAW2vzaXkJ4eZzvU9whkMhkM\nBkOecfcFAoHgqVOEKwvPhGLosuARTJs2kzqdO43GNtTp3Dljxqx8101MTLQv/e+yL6fvJmBgmzZd\naLVaSZK3rl7lr7Bdn7sHic3xO4FR1GqNPHnyZJ62zWYzZ82axebNW1Gp1FGnc6ejYylqNC52X904\ne3ZIofsvEAgE+aEw2ieu1wmeOxcuXEBkZCTKly+PgICAh95fuXIFy5cvR2amBd27d4O/vz8AYO/e\nvWjS5E1YrZHZSteCWh2NixdPwMfNDezaFbKwMNyFHG1RHvtRA8AGLF78E/r165erP5mZmWjatC2O\nHZMhNfVlSNIyDBz4f5g27RtERkbi4sWLqFChQpYfRUlcXBwSEhLg7++fa+Y7gUDw30QEzBEUezIy\nMhgXF0ez2Zzj+cWLF+no6EmVaigVindpMLjx6NGjJMn33gu2Z46Lts/oYwg4U6crxYtHj5KvvGI7\neOfszA5e5QnIqdMZOW/evEf6Eh4eToOhOoFMu90bVKl0NJlMBeqTxWJhVFQUY2JislYYHsX7/9/e\nnQdEVb0NHP8OMwPMgOAOCCKGIiIIKq65YC6E5p7mXtpiWpbtZmbaT8W0zD1zqUxLLTX33dxywdwV\nLU1REUVxIZEBZmDO+8fQlK9LiwgyPJ+/nLuc+zy3iWfuveee88YQ5eJSQhUrVlWVLu2vjh49+q+O\nJ4RwXPdT++Q9elHg9uzZQ0xMRzIyLICZefO+oGNH29Cz//vfx6Sl9cdqHQbAzZtBvPXWCAYM6M3G\njTuATkAEUBM4ClQnokIagf37Q1wc+Pig3biRZSEhmM1m9Hr93z4vv3HjBk5OfsAf78mXQaPRYzKZ\n/vFV9o0bN2jevB3x8SdRKptHH63LypXf4eLicsft169fz/Tpi8jKOklWVinS0mbRsWPv/zzErxBC\n/EE644kCZTabefzxDly7NpmMjEtkZGykV68XOHfuHABXr/6O1VrxL3s8wu7d+3j66Y85fjwLuAws\nBSyAjvByyWzTmdHExUGFCrB9O4TYJoVxdnb+R53iHn30UWyT1swFzqDXv0lISBglS5b8mz3/9MYb\nQzl8OACT6SwZGefYsUMxevS4W7ZRSvHtt/Pp3PkZPvxwNBZLS/6cNKc7p04d/cfHE0KIu5FCL/LF\nwYMHWbVqFefPn79l+YULF8jKcgI65C6phV5fg/j4eAC6dGmN0TgaOAz8irPzu5jNBm7e/Ins7J+A\n60BX3N1TaFKpLHvdrOiOHoWgIFuR/w+j0Hl5ebF582pCQz+jRIlGPPbYWdav/+Ef/UhYsmQJPXo8\nz9Kla8nK6ontroAzGRnd2L370C3bjh07nuef/5BFixqya1cpzOaVwB9z0i/F3//2/gpCCPGv5d0T\nhPxRCEMu8l5++U1lNPopT89oZTSWVitXrrSvS09PV66uHgric5+Hpyij0cf+fNpqtapx4z5VpUsH\nqBIl/HJ7wb+au+1pBRuVVuuijq1apawVK9pGvAsLUyo5Od/zHDVqjDIa5fUbaAAAIABJREFUKymY\npjSaGgoG5I6ul6NcXHqoN98ccsv2Hh5eCn6xj8Kn1YYqvb6U8vSsrUqUKGfviyCEEPdT+6TXvXig\ndu7cScuWPUlPPwB4Artxc2vNjRsp9nHqv/56Hv37v45OV5fs7AO88spzxMYOv2N7u3fvpmnTDmRm\nhmCb4KYMIU4X2F/KDZeUFKhdG9auhX9xm/1esX/77SKMRlcGDHiBgICAO253/fp1YmKeJC4uDtgN\nhAIpaDRhODuXRK+HSpVKsn37Wtzd3e37ubmVwmQ6DNjexXd27s/rrxenbdu2VKtWDQ8Pj/vOQQjh\nGO6n9kmhFw/Ut99+S79+y7h5c6F9mV5fjKFD38JoNNKlSxf8/f357bffOHLkCBUrViQiIuKebTZs\nGMWOHaeBQ1TnHBtoRFnSuB4WRomffoI8KJCrV6/mySf7kJExCCenqxQr9g0HDuykYsWKt23bsWMv\nVq1yw2xeDOwHygOg0w2gXz8nevfuTc2aNdHpbu372r//a3z99UFMphHAr7i7v8ehQ7t55JFH7jt+\nIYRjkUIvHlrx8fHUqdMMk2k7UBn4Bo2mH1ptL5ycwNX1B37+eRtBQUG37XvlyhUOHDhAqVKlqFGj\nhv0ZucHgQWZmb+rQi7U8TglSWQv0MpYk8WrSbUPk/hfVqzfkyJG3gHYAODm9wyuvKD79dOxt2/r4\nBJGcvAz4HDgCjARO4Ob2Jvv377hjbmB7X/+DD0axdOk6SpcuyYQJ/6NGjRr3HbsQwvHcT+2Tznji\ngapWrRoTJozGxaUWRqMvzs4DUepFsrM/w2z+jLS0QQwdOvq2/fbs2UNgYCidO8fSuHEnunbta/+S\nKwVNWMpGmlOCVJZQk3aUx4SRixcv5knc6ekmwMv+2Wr1Ii3NdMdty5cvj0azDRgHNECjeRJ//4/Z\ntGnlXYs8gE6nY9SoD4iP38nWrSulyAshHggp9OKBe/75vly9epHjx3dRq1YdoLF9nVKVuHIl9bZ9\nunTpy40bk/n99x9JTz/GqlWHWLp0KQAfN3uMNVygGDeZhwdd+AUzA9FoTPj4+ORJzE8/3Rmj8RVg\nL7AOo/FjevTodMdtv/xyEp6eI/DwaI+7+xpq1Ajkl1/2ULdu3TyJRQgh7scDLfSJiYk0bdqUatWq\nERoayqRJkwC4du0aLVq0ICgoiJYtW5Ka+ucf+tjYWCpXrkxwcDDr169/kOGJfDRlynSqVo0gLm4r\nWu0QIB74CaPxf3Tu3Oq27S9cOA08nvvJgNnchFOnTsHixby0YTUGFF+7etAbKy5Gf4zGj1i48Os8\nuW0PMHToO7z1Vjv8/fsQFDSUr7+eTNOmTe+4bbVq1Thx4hBz5jzP4sWj2b17kwxfK4R4eNxfh/97\nu3jxojpw4IBSSqm0tDQVFBSkjh07pt566y310UcfKaWUGjNmjHrnnXeUUkrFx8er8PBwZTabVUJC\nggoMDFQ5OTm3tPmAQxYPwOLFi5XRWFnBSQXXlJNTeQUuCtyVwVBS7d69+7Z9wsLqK41mvH0IWje3\nQHXk7beVcrJNUKNef10pq1UlJiaqHTt2qJSUlALITAgh8sf91L4HekXv7e1t70Ht7u5O1apVSUpK\nYvny5fYJRZ5++mn7Ldlly5bRrVs39Ho9AQEBVKpUiT179jzIEEUeyszM5OjRoyQnJ9+yfOXKTZhM\nLwOVgJtYrWnAFiCNjIzZPP54h9vmkv/hh7n4+n6Om5s/zs6V+bZJCKFjx4LVCh98AB9/DBoNfn5+\nNGjQgNKlS9v3VUqxYsUKJk2axE8//fSg0xZCiIdavj2jP3PmDAcOHKBu3bpcunQJLy9bRycvLy8u\nXboE2EZJ++tc5H5+fiQlJeVXiOI+xMfH4+8fTIMGTxIQUJUhQ0bY1/n6lkGvPwJcAZpjK/j1cte2\nx2JxsQ95+4dHHnmEIUNe5bHHGrDk0Tq0Xb3CtmLcOBg+HO4ySp1Siu7dn6Nbt6G8/favREf34KOP\nxudxtrceLzZ2HKVK+VOypB/vvTcCq9X6wI4nhBD/Vr5ManPz5k06derExIkTKVas2C3rNBrNPYcW\nvdO64cOH2/8dFRVFVFRUXoUq/qN27XqQkvI+8CyQwqRJ9Tlx4hd++eUcZcuWpFSp46Sk1CMnpw6w\nGVvRLw2cIDv7mv2HH9iKZ82ajTh48DrDqEhrNgFgmTQJ/cCB94xj7969rFixmfT0o4AReJdhw6oy\nYMDzt3338sIXX3zFyJFzMJnWAjomTOhOyZLFeeONV/P8WEKIomPLli1s2bIlT9p64IXeYrHQqVMn\nevXqRfv27QHbVXxycjLe3t5cvHiRsmXLAuDr60tiYqJ93/Pnz+Pr63tbm38t9KLgKaVISDgK9Mxd\nUoaMjKYsX74Li2Uax4//jIfHXkqUcOPKlUFAFaAGUB2tdidTpky4ZRS42bO/4ODBOMbxIm8yhRyc\neEFbji5BQUT/TSwpKSlotZWwFXkAP3S6YqSmpnL58mXi4+MJCAigevXqeZL7woWrMJneA2wT55hM\nI/j++0lS6IUQ9+X/X8SOGDHi7hv/jQd6614pxbPPPktISAiDBg2yL2/bti1z5swBYM6cOfYfAG3b\ntmXBggWYzWYSEhI4efIkderUeZAhijyg0Wjw9a0MLMtdcgOrdT0Wy0igMVbrG1gsDShf3gedbjnw\nAbAYZ+fLDBzYl+ee63NLe5s2bGMa8CZTMKPnKRbypdX/tuf4d1KrVi2s1oPASiALjWYipUp5sHnz\nVsLC6tGr1+fUrx/D0KH/y5Pcy5QpjpPT6b+ci1OULOmZJ20LIUSeyJPugHexfft2pdFoVHh4uIqI\niFARERFqzZo16urVq6pZs2aqcuXKqkWLFur69ev2fUaNGqUCAwNVlSpV1Nq1a29r8wGHLP6jPXv2\nKE9Pb+XpWU8ZDN5KozEquJzba14pd/doNW3aNFWhQlVVrFiEcnMLVA0bRqvMzMxbG7JY1P6w6kqB\nMqFVMUxQME7pdB7q6tWr/yiW7du3Kx+fSsrJSadCQuqoQ4cOKVdXTwVHc+O5rAwGb/vEOffjxIkT\nysPDS+n1Lyqd7mXl7l5GHTp06L7bFUKIv7qf2idD4Io8k5qaytGjRylTpgxTp85i9uytmEwD0Ov3\n4u29kfj4n9Hr9Rw8eBAXFxfCw8PtE9sAkJUF3bvDkiWkazS003jxo9Lg5JTF0qVzeOKJJ245XnZ2\nNu+99yHff7+C4sU9+fTTETRp0sS+XimFRqMhISGBsLAmpKf/2eHP07Ml8+e/RkxMzH3nnZiYyIIF\nC7BarXTu3FnGqhdC5DkZ614UOKUU58+fx2w2U7FiRTQaDdOnz2Dduu1UqODD+++/c8srcLcxmaBT\nJ9vMc8WLk7FkCStSUsjMzKR58+aUK1futl1eeeUtZs/+GZNpLHAGo/Eldu3adNvzd7PZjLd3Ra5f\nn4Zt7PoDGI0tOX58H/7+/nl6HoQQ4kGQQi8KVHZ2Np069WL9+o04OblSubI/mzevpESJEv+sgbQ0\naNMGtm6FMmVg/Xr4mxnsAEqWLM/165uxva5nm3hm2DA3Pvhg2G3bxsXFERPTkcxMK5DBl1/OwN+/\nPGazmdq1a2M0Gm/bRwghHhb3U/vy5fU64dg+/XQSGzakkJmZCDhz/PjLDBjwJvPnz/77na9dg5gY\n2LMHypWDTZsgOBj489b73bi4uALX7J+12qsYDKXuuG3dunW5fPksycnJuLm5ER3dkePHL+Pk5I6H\nRyq7dm26ZQwHIYRwFDKpjbgvixYtZvDg/5GR0Q1wBZwwm3uzb9/hv9/50iVo2tRW5CtWhO3bOaXX\n07NnX4oXL49Wq8fLq+Jd3yX93//exWjsDExCq30NT8/19hEX70Sn0+Hn58ekSVM5cqQ0N28e5saN\nOC5e7Er//m/+l/SFEOKhJ1f04h/bv38/n3wyjawsC/369SQgIIDevV/Eau0OrAaeAbTodCuoWrXy\nvRs7fx6aNYMTJ6BKFdi4kdNmMzVqNCAtTQu8BbzE5cubadOmC7/+evC25/TPPdeXcuW8WbRoJaVK\nefLaa7tvGXjnbuLjT5GZGQ1oAcjJieHXX1f/+xMihBCFgBR68Y8cOHCARo2iMZkGA+6sWfM0L73U\nE52uCfAx8ARQDVB4e8Nnn22+a1s5J06gadECp3PnIDzc9ky+bFmmvz2Emzc7AkuA13K3jsbJKZJ9\n+/bdsUNeq1ataNXq9tnv7qVu3XBWrZqPydQDcMHZ+SsiI8P/VRtCCFFYyK178besVisDB76NyfQW\n8AbQD5NpCsuXb8JqPQxYgfXABzg7n+f48TsXZYDvPxxJcpVgnM6d46CrkcS5cyF3ZESTKROlvIF0\n4I9X4TLIyTlhHz3xTrGdPHmSs2fP/uOOKq+++jKPP+6Di4sfBoMf1arFM3XquH9+QoQQohCRQi/+\n1jPP9Gf37l/5c1hZAAOuru507NgUo7EGbm7dMBoH8eWXs3F3d79jO/HffEPUBx/gi2IzUTTJeoMn\ner5oX9+zZxeMxmlAV6AB0Adn55q0bt3ojiMkXr9+nVq1GhMR0Yzg4Dq0bt0Zi8Xyt/nodDoWL57H\n6dNHOHZsJ3v3bv3nbwgIIUQhI4Ve3NP58+f5/vvF5OTMAEYCC4FVuLq+xMCBz+Dq6oLFcgGLZRNl\nypSkadMmd2znzPz5lO/dmzJYWY0frZjPDfU+R4/G2Wd7q1evHkuWfE2NGr/h7+9BmzapfPfdGBYs\n+OKOve8HDnyHY8eqYTKdITPzHFu2pPPxxxP+cW7lypUjICDg1kF7hBDCwcgzenFP6enpaLUeQDTw\nFTAROECDBtVxcdEzb94GLJalQH2SkmLp2fNFNm1adksbv//wA6W798AdxSKa0R1fLDwNvEeJEj63\nFNro6Giio/9u6hqb/fuPYDaPw/Z71YWMjKfYvXsD48aNZ+/eo0REBPP666/i4uJi38dkMpGamoq3\nt7cUeCFEkSAD5oh7ys7OpkqVmpw925acnKexTVwzAReXkmi1lzCZtIA3kAbMolSp3ly5cta+/+/f\nfotrj564oJhDb55lNjkAeGAwGFi8eN5/Hoa2U6feLF/uQ3b2GMCKq2s3ypU7zsWL5cjIeBKDYTl1\n6uTw448rcXJyYvz4Sbz77hCcnIx4eZVm06YVBAYG3ucZEkKIB09GxhMP1IULF2jUKIbTpy9im152\nGvAKcBXYCrgAY4CFREaW4Oeff7Tt+P33ZD/1FDqlmEZZXuYCCi1wDSenchw+vI9q1arZj7N69Wr6\n9h3I9euXqFevCYsWfUWZMmXs681mM5mZmfYpbZOTk6lfvznXrjljtZp45JGSnDiRQGbmmdyYLLi5\nVWHHjh9IT0+nRYuumEzbgQpoNOMJCfmOo0d3P+jTJ4QQ9+1+ap/cuxT3ZLFYGDHiIxITfwM6AOuA\n48Bu4ElsBRWgAxpNAnPnTrN9/Oor6NoVnVKMpQ8v8QiK7sBkNJpGuLuXZuTI8aSmpgLwyy+/0Lnz\n01y6NAuzOYldu4Jo27a7PY7hw0fh5uZJqVI+1K4dxZUrV/D29ub48b2sWTOFzZvnMXfudLRaI+Cc\nu5cOJyd3zGYz+/btw2p9AqgAgFIvcfz4XvnRKIRweFLoxT0NGTKCefPisVh+BH4AXgKeBprnfjYB\nCphD48YNCQ4OhqlToU8fsFqZXq4ig6kNbASqA+NRSs+NGz+wZIkTLVq0RynFtm3bgDZAU8ATi2Us\ne/ZswWw28/jjbRgxYhrZ2afIzk7j0KHq9OzZDwAnJyfq169PZGQkISEhlC9fAr3+dWAPOt0QSpe2\nUr16dSpUqIBWuxPIyM1sM2XK+N9ziF0hhHAEUujFPS1duhaTaSRQF9gGfAs8CrgDQUAAEIhe/znf\nfPM5fPQRvPyybedPPqHR+hUULzGSYsXaA19g+2EQB9TGbJ7O0aPxXLx4kZIlS+Lk9Cu2d/IBTuDq\nWowpUz5j06ZDwPNAOcAJi+VNdu/exaOPRmMwuGM0ejJ16nR0Oh3btq2hbdurBAb2p1Wrs+zcuREX\nFxfatGlDTEw4bm7V8fBojbt7bxYs+CK/TqMQQhQYeUYv7ujKlSssXbqUUaMmc+bMm0AvIAnbVfkJ\noH7uv3XodCvZuGElTTZtgpEjURoN8S+/TNVPP0Wr1XLt2jWGDRvG55/vJDs7GziI7TfmTZydy3Hh\nQgIeHh40avQ4R49aMZsj0Onm0759c/bu/YWTJ6sDF4FVufstwGh8HYulIxbLBCABo7EZq1Z9TVRU\n1F1zUkqxe/duUlJSiIyMvOugPkII8bCRzngiTyUmJlKz5qOYTA3IyUklK2s7tiv649hmizsKlAHm\noNePYP63M+i0YwdMmEA20M+lLt/pzdSu7cuMGZ8ycOC77Nu3h6tXG2C1JgFeQDNgJr161eLrr2cA\nts52CxcuJCEhgalTv+TGjXpkZp7G1gHwJHADKItO9xM6HWRmnshtC5ycBtOqVTyNGzcmJiaG0NDQ\nfD1nQgjxIEmhF3lGKUXr1p1Yt64KVmts7tJ2aDRxKPU9ts54U4EmODsfonePVszUmmHWLLKArgxj\nKSOAbNzcGqPVniQ9fRA5OaFAb+Bd4CRa7Sbq1XuEbds23vY++5gxH/HBB8cwm+cAl4HaQHlcXbPR\n639j3boVdOv2PGfPjgVaAVY0mih0OhPQEL3+G5YvX0CzZs3y45QJIcQDJ73uRZ5QStG9+7OsW7cT\nq/Wvk7yYUCoWaIRtdLzReHruYd3KGczISoVZs8BgoKPWmaX8Md2rjqysWmRleZKT8x7QDtiORvMR\nYWEnGDr0ebZsWX/HQWuuXUvFbP7j/faywFKKFTvBl18OIiHhV+rXr8+XX07GaHwaN7deODvXRamz\nWCw7sFgmYDLN5qWXBj+4EyWEEIWIFHpht27dOlas2IPVOhj4BLgApKDVnsz99x9cqV09gqipU9F8\n+y24u8PatVyNbIRWOwZbL/zf0GoXodXqcz8DVESns7Bt2wqGD3+Po0ePMn/+fPbt23dLHE88EYPR\n+DmwCziPwfABnTt3oWvXrpQqVQqApk2bcvjwbiZPfozoaF/gOf581S+I69evPZiTJIQQhY0qZAph\nyIXG559/rozGvgqsCoYoKKZArzp16qbc3csojeZtBR+oUoZS6lqdOkqBUiVKKBUXp5RSKikpSVWv\nXl/pdK7K2dlNTZ48VYWG1lUuLj0UzFRGY0PVq9cLSimlxo79VBmNPqpYsc7KaPRTw4ePviWWefO+\nUV5egcrDw0v16vWCysjIuGvcGzduVEajn4K9Ci4qg6Gd6tv3pQd3ooQQIp/dT+2TZ/TCbt++fTRq\n1IaMjG1AJWAilSp9xa5dG+jb9yV2744joGRxNrgoPA8ftk0vu2EDVK9+Szvp6em4urqi1Wq5efMm\nY8Z8zIkTZ2nUKJKXXupPSkoKFSoEk5W1H5iObaKcVCZPHsXLL7/0n2KfPftL3nnnAzIy0mnfvgOz\nZk3GYDDc5xkRQoiHg3TGE3li4cLv6dnzmdxX4PR4eXmxadNyOnbsxZkzDXE3N2Wd5gUi1RWUnx+a\njRuhSpV/fZyDBw/SuHEP0tLCsD0SmAEk4+LSlbVrF9zzFTkhhCiKpDOeuG9nz56lT5/+ZGfvxPYa\n21QyM03cuHGDCxeyKGF+ly0MI1Jd4bRGx+mvvvpPRR7Ax8eH9PTz2EbLmwwEA1FkZb3GkiUr8iol\nIYQQSKEXueLj49HrawHh2Dq1PY3FYhvsxs9qYhtNCOMoxwimhUsprP7+/+k4V69e5Z13BuPk9BgQ\nCCTa1+l0iXh6uudBNkIIIf4g89ELACpUqEB29hEgBdtgOEewWm/SxNeXH7Mv4kMW+wmgnUsAJSp7\nYjab/1G7WVlZ6PV6nJyciI+Pp1Gjlty86UJ29kBsV/LPAP2A83h6bmDAgD0PKEMhhCia5IpeAFCt\nWjVef70/RmM4Hh4xGAyPsWjEe7jHxOBjzuJsOT9eqeZNcs5Ozp51p3bt5gwfPvqu7V27do2GDaNx\nc/PAYCjGJ59M5JlnBpKaOgyLZRTwJVAL28Q4S9FolgCQkZFx1zaFEEL8e9IZT9ziyJEjnDlzhppK\n4du3L1y9Sk5UFGtffJEOvfpisWwC6gGXMBgi2Lt3EyEhIbe107p1FzZuLI3ZPAk4j9H4GHq9md9/\n/xGoDAwDxuZuHQV8h5PT50RF7WDTpmX5k6wQQhQS0hlP5JmwsDDalCyJb69ecPUq5pYtCTt7haee\n/RSLpQq2KWovAl7o9WGcOXPmlv1TUlI4fvw4O3b8hNn8LranQwGYTL0oU6Y0ev00bAPoDEKrDQA6\nYxtW1xOrtQWnTiXkY7ZCCOH4pNALAC5cuMCkSZNYMmAA1hYt4MYN6NyZNwKqcCqpIenpu4D92Iay\nHQocxmLZT1BQkL2NESNiKV++EnXrtiMtLQP4OXeNFYNhLy+80IOQkJ9xcSmDXu9PkyaBGAyngTTA\nirPzDGrXrpnPmQshhGOTW/eCU6dOERnZiKY3Q5ifvRkXrPzeoQOe339P8+jObNrUDduVN8A6NJqe\naLUmnJy0ZGdnUKtWI4YOHUS3bq9gMu0GvIF30WgmYzS2RaM5S8WKOUREhJOQkESdOqG8997bWCwW\ngoJqcuPGNcAZd3c3TpzYh4+PT4GdCyGEeBjJrXtxX4YOHc3jvzdiYfZWXLAyhQY8k+MKWi2NG9fG\nYJgFmIAsDIYZtG7dBL3eE7P5J6zW0fz8cwo9e/bDam2IrcgD/A+lTEye3IIZM14mNTWVBQvc+Omn\nZ/nss4O88MKrDBz4DhkZT2F7xe4Q2dm1+OKLOQV1GoQQwiFJoRfUOLifb9T36MkmlsEMpBFLl6/H\n3b08ZcuWICamDHq9F87OZWnUyErDhrXJyekMfA6sAN4nLa0TWVnL+fO9+FX4+DxCnz59KFasGKmp\nPlgs44EOZGQsYcmS7/jxx5+wWDoDpYEAMjM7sm/fsYI5CUII4aDkPfoiJjk5mVGjxpGUlEKbNs14\n5kYqb/9yEIAhvEEs5YHhwFTS0zPo3/8VVq6cz6xZk7FarZQqVYpvvvkGnW4lZvMebPPFewJd0Oni\n0WiqYzCEYLX+xvTpM0lJScm93aT5SxQalNJy/Xo2Gs23KFUPyMZgWEKtWo/m7wkRQggHJ8/oi5Br\n164REhLJ1avtyM4OY5h+CCMslwBY2Tyap3buxWTKwfaOe/vcvabSuPFKtm5dY2/HYrHQpEkrdu3a\nAvwOGAFwd2/D8OFRBAcH8/77Yzh+/Fes1izatGnL7t17SE5uQ05OFLaJbDyAMUAobm4+KJVB3brV\nWbNmMS4uLgghhPiTPKMX/8iSJUtIS6tFdvZ4RvEbIyyXsAJq5kye2LCWs2d/QaPRANa/7GXF2dn5\nlnb0ej3btq2hQYMmODu3B9ah1X6IwXCYPn36MH/+Mo4dCyYz8yJm8wWWLfuNMmVKEBq6A632RSAS\n+Aooh4uLnqVLp7J37zo2blwuRV4IIfKYFHoHdPbsWb766iuWLFlCVlaWfbnFYgGrGxN5lSHEko2W\np7XO8OyzAJQuXZrWraOAF4Cvgc9xchrK8OFv33YMnU7H5s2ref31+kRGjqN9+9/4+edtlCxZkri4\n/WRlPQdoATeys/ty8KCOEyeS8PDQoNOZgR24uj5NnTp1aNasGVWrVsXJSb6OQgiR1+TWvYP57rvv\n6NHjeZRqjk6XRHCwll27NmIwGEg8c4YtlavSKzuTLPT0cg7BrXt9vvzyM/v+SimGDh3KggWrKVbM\njYkTR9GkSZN/FUNMTGc2bKhOTs772O4OdANCgccpVepJmjaN4sSJBOrXr8nHH4/E3V0mshFCiHuR\n+egFYBv0pnz5alits4BOgEKni+HTT5/g5X79oFcvWLiQDCctA/2qUPKpjowaNQy9Xp+ncZw7d456\n9R7j2rWSZGXdwDZJzjogmeLFG3H9elKeHk8IIRydPKMv4qxWKzNnzqRjx6ewWsH2DBxAQ3Z2PX45\neBg6dYKFC8HDA8PWLUw/dQiNRkPlyrUIDW3A+vXr8ywef39/fv31AJMnP4+LSzK22emOYjQ+S48e\nXfPsOEIIIf6eXNE7gF69XmDx4iNkZHgDx4EmwBQgCSN12eSWSb30G1CyJKxfD7Vq8dprg5kxYxcm\n03ggEaPxBbZuXU1kZOQ9j/Vvbdu2jUGDhpGa+judOrUmNnY4Op281SmEEP+G3LovwpKTkylfPojs\n7AvANWzPwgOAX/AAVuFKQ9LA2xs2bIDQUADKln2ElJRVQNXcloYxeLCV2NiRBZCFEEKIe5Fb90XY\nwYMHyc7WA26AP/A2cIVS1OFHytKQNM476ehbKZxt167Z9zMYjECK/bNOdxk3N0M+Ry+EEOJBk0Jf\niMXFxbFs2TI0GmfgFeAIoMObLLayk1okcRItDazj+fKnJ4mJeZKdO3cCEBv7HgZDd+ATtNpX8PRc\nRd++fVi+fDkTJ05k27ZtzJkzl9Kl/TEaS/DUU30wmUwFmK0QQoj/Qm7dF1LDh49m3LjpKBVKRsYu\noBoQjz9l2UQSlUjnpIuBxllTSaZP7l6T6Nr1EPPnz+bKlStERNTj8uV0IIcqVSoSHFyFNWsOk53d\nEFiE1QoWy0rAH1fXAXTuXIqvv/68oFIWQogiS57RFzHnz5+ncuVwMjOPAV7AEGAy1V29WJF5Gn8U\nlurVidF4sunQG9g6580GNtCsmY6NG1fSo8dzfP+9OxbLp4DC2TkGpeKxWE5gG9L2FaAEMCL3qKdw\nc3uUmzeT8z9hIYQo4uQZfRGzf/9+rNay2Io8wGjqGMqwyzkFfxQ8+ij6bdt4YchAXF37ARWBnUAk\n27btYeHC7/j558NYLG2xTTbjhNkcjlIV+GPcetvz/qN/OeoJ0tOzWLVqVT5lKYQQIi/IFX0hc/r0\naSIi6pGWZgbmAm2oxXjWa96kpFLQvDksXQpubmRkZFCqlC8ZGVGNMUnHAAARyUlEQVTAktwWduDm\n1onMTAs5OTGAH/ADcB2NxoRS84EWwKfAqNx/BwDfAB0pU2YDSUm/5PkgO0IIIe5OruiLkPHjp5Ce\n/jywBhhAQ5z5kTcoqRQp9euTk1vkATp37k1GRioQ+JcWKpCefoOcnG3YrvI3A4uAeSiVCbwGFAOW\nYpt+tjRQDtgIOHP9umLevHn5lK0QQoj7JYW+kElLM2G1egH1acEs1mGb8HWRrhxBh9N5rFVnzGYz\nb745hFWrlgDuwBxgA3Aa24Q1Ltg67+mBWUAY0DJ32x8AM7AbF5fywHzgCjAJWIrV2ooLFy7kZ8pC\nCCHugxT6QqZHj44YjWNpx4esoA1GLMyiKU9lnyM1fR87d6YxcOBAPvtsOeAMjARygD5ATeAAtufw\nCwAFXPxL6+FoNM2Akbi4dKN8+QwiIsLRaLYDQcAiXF1X8Oijj+ZnykIIIe6DPKMvhHYNHEjtKVPQ\nARPR8RoJKPxy13bH2XktZvO7wA1gBRCN7db7MWy3/H8BPsQ2YE4x4HXgQu62FwgOrk737h0ZNGgQ\nmZmZtGrVhQMHdqHVahk3biyvvPJS/iYshBBFnLxeV5TMnAn9+oFSxDq5McRqBHoD44CVQA+gA7bh\ncJcC84AvgTNABrY54gOAg0AMtiv6hthG1msFPIZe34OqVQ+zf/92tFotABkZGbi4uMic8UIIUQCk\nM15RMWECvPACKMUQJyNDrNOxzVS3DCgOdAWGAtOB34Ha2Ir8YeAZoCzwG7ZOeDGAN5CK7UdBKaAz\n8B4WyzR+++08p0+fth/aYDBIkRdCiEJI/nIXBkrByJHw2msAvOpkINZaEbgJTARM2Ap+CWy36w3A\nJqAD3t7nqF07HGfnj4HG/Pme/AhsPwJaYrttPxRoCwwGLFitWTg7O+dXhkIIIR6QB1ro+/bti5eX\nF2FhYfZl165do0WLFgQFBdGyZUtSU1Pt62JjY6lcuTLBwcF5Oj96oWexwIYNWDUaXtBVYJK1N9AM\neB9YDvQHdvLqq0/i7j4DjWYkMAuDYTqTJo1lz57NrFixBNu79JdyG90EVAE+o0cPX4KCKuDqegH4\nEoOhHU2bNsLf3z//cxVCCJGnHmih79OnD2vXrr1l2ZgxY2jRogUnTpygWbNmjBkzBoBjx46xcOFC\njh07xtq1axkwYABWq/VBhld4ODszvFYD2mpcmZndE2iH7fn7WGAfWu1sund/igkTJhAXt4U+fS7y\n1FN7+eGHL+jc+UkArly5hu0WfQBQAZgGdMDLqzzz5s3k4MHdvP12OO3b/8j77zdj2bL5aDSaAklX\nCCFEHlIPWEJCggoNDbV/rlKlikpOTlZKKXXx4kVVpUoVpZRSo0ePVmPGjLFvFx0drXbt2nVbe/kQ\n8kPnyJEjymDwUTBTQYSC3xV8ocBHabUe6qWXXldms/mu+1+6dEkZDCUVPKPAT4GbAj+l0birHTt2\n5GMmQggh/ov7qX26/P5hcenSJby8bGO0e3l5cemS7VbyhQsXqFevnn07Pz8/kpKS8ju8h9K5c+dw\ndg4jI+NZ4BDwCOBM8eJWPv10It26dbttSNrt27fz2Wdz0GqdaNasAc7Oj5CRMRvblfw6dLo4Fi/+\nhgYNGuR/QkIIIfJNvhf6v9JoNPe8PXy3dcOHD7f/OyoqiqioqDyO7OESGhqKxbIf2A9MBrzRaGLJ\nyanLK69M56OPphAX9yMeHh4AbNiwgXbtepKRMRTIYvHiN3Ifg/wKvAxEodc3loFvhBDiIbVlyxa2\nbNmSJ23le6H38vIiOTkZb29vLl68SNmyZQHw9fUlMTHRvt358+fx9fW9Yxt/LfRFgb+/P3PnzqBn\nz+YopScnx0pOzmDS0oYCioSEPowePY7Y2A+ZO3ceb701koyM8djeqYeMDD21ay/h6NGGODtXwmz+\njVmzplGqVKkCzUsIIcSd/f+L2BEjRtx947+R76/XtW3bljlz5gAwZ84c2rdvb1++YMECzGYzCQkJ\nnDx5kjp16uR3eA+tjh07kJR0mlGjBlOiREms1qa5azRkZTXmxImzvPPO+wwY8AmXLxuwjVv/B3d8\nfPw4deooq1d/yunT8XTv3rUAshBCCJHfHugVfbdu3di6dStXrlyhfPnyfPjhhwwePJguXbowe/Zs\nAgIC+O677wAICQmhS5cuhISEoNPpmDZtmvT6/oukpCRq147i+vXKmM3uwHigDpCJ0fgVjz7akcGD\nB5OdfQ7bBDavYZu0JgujcRj9+8/Gx8cHHx+fAsxCCCFEfpMhcAuBM2fOEBZWk5s3G2N7re4m0Bw4\njF6voWXLGIKDH2H8+AkolYZtdrq5ODkNpUKFkowf/4H9zokQQojCR4bAdXAvvvgmN2+GAzVyl7gD\n8ylevATLly9m8+atjB/vjFKB2IbB3YdGc5Nixczs3LlGirwQQhRhckVfCFSqVItTp54FYrHNMFcB\nJ6fn6dLFkzNnzrN7dy+gJ5AONKNYsSSqVw9l+vRxhIaGFmToQggh8oBc0Tu4Bg0icXHZCwzHNhmN\nD6GhF5g5cyJpaTfBPkWtG9CHmJgW/PTTGinyQgghpNAXBpMnj6VGjXO4uLyNTvc7tWpFMGDA0wB0\n794eo/Ft4AiwE6Mxlh495Fa9EEIIG7l1X0gopVi0aBFPPz2AnJyn0OkS8fY+zb592/nkk0nMnDkX\nZ2dnhg17g+ee61vQ4QohhMhD91P7pNAXIpUq1eDUqf8BTwDg4tKNUaMieeONNwo2MCGEEA+UPKMv\nIlJTrwFV7Z+zsqpy+fLVggtICCHEQ08KfSESHd0CV9ch2KabPYjROJPHH29R0GEJIYR4iEmhL0Rm\nzJhIq1bOuLgEULx4KyZN+pCmTZv+/Y5CCCGKLHlGL4QQQjzk5Bm9EEIIIe5ICr0QQgjhwKTQCyGE\nEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQ\nCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjh\nwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0Q\nQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5M\nCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGE\nEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA7soSv0a9euJTg4mMqVK/PRRx8VdDgPnS1b\nthR0CAWqKOdflHMHyV/y31LQIRRaD1Whz8nJ4eWXX2bt2rUcO3aM+fPnc/z48YIO66FS1L/sRTn/\nopw7SP6S/5aCDqHQeqgK/Z49e6hUqRIBAQHo9Xq6du3KsmXLCjosIYQQotB6qAp9UlIS5cuXt3/2\n8/MjKSmpACMSQgghCjeNUkoVdBB/WLx4MWvXrmXmzJkAzJs3j7i4OCZPnmzfplKlSpw6daqgQhRC\nCCHyXWBgIL/99tt/2leXx7HcF19fXxITE+2fExMT8fPzu2Wb/5qoEEIIURQ9VLfuIyMjOXnyJGfO\nnMFsNrNw4ULatm1b0GEJIYQQhdZDdUWv0+mYMmUK0dHR5OTk8Oyzz1K1atWCDksIIYQotB6qZ/RC\nCCGEyFsP1a37v/r++++pVq0aWq2W/fv337IuNjaWypUrExwczPr16+3L9+3bR1hYGJUrV+bVV1/N\n75AfqKIwkFDfvn3x8vIiLCzMvuzatWu0aNGCoKAgWrZsSWpqqn3d3b4HhVViYiJNmzalWrVqhIaG\nMmnSJKBonIPMzEzq1q1LREQEISEhvPvuu0DRyP2vcnJyqFGjBm3atAGKVv4BAQFUr16dGjVqUKdO\nHaBo5Z+amsqTTz5J1apVCQkJIS4uLu/yVw+p48ePq19//VVFRUWpffv22ZfHx8er8PBwZTabVUJC\nggoMDFRWq1UppVTt2rVVXFycUkqpmJgYtWbNmgKJPa9lZ2erwMBAlZCQoMxmswoPD1fHjh0r6LDy\n3LZt29T+/ftVaGiofdlbb72lPvroI6WUUmPGjFHvvPOOUurO34OcnJwCiTuvXLx4UR04cEAppVRa\nWpoKCgpSx44dKzLnID09XSmllMViUXXr1lXbt28vMrn/4ZNPPlHdu3dXbdq0UUoVre9/QECAunr1\n6i3LilL+vXv3VrNnz1ZK2f4fSE1NzbP8H9pC/4f/X+hHjx6txowZY/8cHR2tdu3apS5cuKCCg4Pt\ny+fPn6/69euXr7E+KDt37lTR0dH2z7GxsSo2NrYAI3pwEhISbin0VapUUcnJyUopWyGsUqWKUuru\n3wNH0q5dO7Vhw4Yidw7S09NVZGSkOnr0aJHKPTExUTVr1kz9+OOP6oknnlBKFa3vf0BAgLpy5cot\ny4pK/qmpqapixYq3Lc+r/B/aW/d3c+HChVteuftjUJ3/v9zX19dhBtspygMJXbp0CS8vLwC8vLy4\ndOkScPfvgaM4c+YMBw4coG7dukXmHFitViIiIvDy8rI/wigquQO89tprjBs3DienP/8sF6X8NRoN\nzZs3JzIy0j6WSlHJPyEhgTJlytCnTx9q1qzJ888/T3p6ep7lX6C97lu0aEFycvJty0ePHm1/RiVs\n/wMI23m417lwlPN08+ZNOnXqxMSJEylWrNgt6xz5HDg5OXHw4EF+//13oqOj2bx58y3rHTn3lStX\nUrZsWWrUqHHXMd0dOX+AHTt24OPjQ0pKCi1atCA4OPiW9Y6cf3Z2Nvv372fKlCnUrl2bQYMGMWbM\nmFu2uZ/8C7TQb9iw4V/v8/8H1Tl//jx+fn74+vpy/vz5W5b7+vrmSZwF7Z8MJOSovLy8SE5Oxtvb\nm4sXL1K2bFngzt8DR/jvbbFY6NSpE7169aJ9+/ZA0TsHnp6etG7dmn379hWZ3Hfu3Mny5ctZvXo1\nmZmZ3Lhxg169ehWZ/AF8fHwAKFOmDB06dGDPnj1FJn8/Pz/8/PyoXbs2AE8++SSxsbF4e3vnSf6F\n4ta9+ssbgG3btmXBggWYzWYSEhI4efIkderUwdvbGw8PD+Li4lBKMXfuXPsfysKuKA8k1LZtW+bM\nmQPAnDlz7P9N7/Y9KMyUUjz77LOEhIQwaNAg+/KicA6uXLli71GckZHBhg0bqFGjRpHIHWx3MRMT\nE0lISGDBggU89thjzJ07t8jkbzKZSEtLAyA9PZ3169cTFhZWZPL39vamfPnynDhxAoCNGzdSrVo1\n2rRpkzf552WHgry0ZMkS5efnp1xdXZWXl5d6/PHH7etGjRqlAgMDVZUqVdTatWvty/fu3atCQ0NV\nYGCgGjhwYEGE/cCsXr1aBQUFqcDAQDV69OiCDueB6Nq1q/Lx8VF6vV75+fmpL774Ql29elU1a9ZM\nVa5cWbVo0UJdv37dvv3dvgeF1fbt25VGo1Hh4eEqIiJCRUREqDVr1hSJc3D48GFVo0YNFR4ersLC\nwtTYsWOVUqpI5P7/bdmyxd7rvqjkf/r0aRUeHq7Cw8NVtWrV7H/jikr+Sil18OBBFRkZqapXr646\ndOigUlNT8yx/GTBHCCGEcGCF4ta9EEIIIf4bKfRCCCGEA5NCL4QQQjgwKfRCCCGEA5NCL4QQQjgw\nKfRCCCGEA5NCL4QQQjgwKfRCCCGEA5NCL4S4p59//pnw8HCysrJIT08nNDSUY8eOFXRYQoh/SEbG\nE0L8rffff5/MzEwyMjIoX74877zzTkGHJIT4h6TQCyH+lsViITIyEoPBwK5duwr1lKBCFDVy614I\n8beuXLlCeno6N2/eJCMjo6DDEUL8C3JFL4T4W23btqV79+6cPn2aixcvMnny5IIOSQjxD+kKOgAh\nxMPt66+/xsXFha5du2K1WmnQoAFbtmwhKiqqoEMTQvwDckUvhBBCODB5Ri+EEEI4MCn0QgghhAOT\nQi+EEEI4MCn0QgghhAOTQi+EEEI4MCn0QgghhAOTQi+EEEI4sP8Diwf1C+duoqkAAAAASUVORK5C\nYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10f9e8a50>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 42
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"#### Comparing the results from the different implementations"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"As mentioned above, let us confirm that the different implementation computed the same parameters (i.e., slope and y-axis intercept) as solution for the linear equation."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import prettytable\n",
|
|
"\n",
|
|
"params = [appr(x,y) for appr in [lin_lstsqr_mat, classic_lstsqr, numpy_lstsqr, scipy_lstsqr]]\n",
|
|
"\n",
|
|
"print(params)\n",
|
|
"\n",
|
|
"fit_table = prettytable.PrettyTable([\"\", \"slope\", \"y-intercept\"])\n",
|
|
"fit_table.add_row([\"matrix approach\", params[0][0], params[0][1]])\n",
|
|
"fit_table.add_row([\"classic approach\", params[1][0], params[1][1]])\n",
|
|
"fit_table.add_row([\"numpy function\", params[2][0], params[2][1]])\n",
|
|
"fit_table.add_row([\"scipy function\", params[3][0], params[3][1]])\n",
|
|
"\n",
|
|
"print(fit_table)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"[array([ 0.95181895, 107.01399744]), (0.95181895319126741, 107.01399744459181), array([ 0.95181895, 107.01399744]), (0.95181895319126764, 107.01399744459175)]\n",
|
|
"+------------------+----------------+---------------+\n",
|
|
"| | slope | y-intercept |\n",
|
|
"+------------------+----------------+---------------+\n",
|
|
"| matrix approach | 0.951818953191 | 107.013997445 |\n",
|
|
"| classic approach | 0.951818953191 | 107.013997445 |\n",
|
|
"| numpy function | 0.951818953191 | 107.013997445 |\n",
|
|
"| scipy function | 0.951818953191 | 107.013997445 |\n",
|
|
"+------------------+----------------+---------------+\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 43
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"#### Initial performance comparison"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"For a first impression how the performances of the different least squares implementations compare against each other, let us do a quick benchmark using the `timeit` module via IPython's `%timeit` magic."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"for lab,appr in zip([\"matrix approach\",\"classic approach\",\n",
|
|
" \"numpy function\",\"scipy function\"],\n",
|
|
" [lin_lstsqr_mat, classic_lstsqr, \n",
|
|
" numpy_lstsqr, scipy_lstsqr]):\n",
|
|
" print(\"\\n{}: \".format(lab), end=\"\")\n",
|
|
" %timeit appr(x, y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"matrix approach: 10000 loops, best of 3: 163 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"classic approach: 1000 loops, best of 3: 1.55 ms per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"numpy function: 1000 loops, best of 3: 221 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"scipy function: 1000 loops, best of 3: 362 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 44
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"The timing above indicates, that the \"classic\" approach (Python's standard library functions only) is significantly worse in performance than the other implemenations - roughly by a magnitude of 10."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"<a name=\"cython_nb\"></a>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Compiling the Python code via Cython in the IPython notebook"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Maybe we can speed things up a little bit via [Cython's C-extensions for Python](http://cython.org). Cython is basically a hybrid between C and Python and can be pictured as compiled Python code with type declarations. \n",
|
|
"Since we are working in an IPython notebook here, we can make use of the IPython magic: It will automatically convert it to C code, compile it, and load the function. \n",
|
|
"Just to be thorough, let us also compile the other functions, which already use numpy objects.\n",
|
|
"\n",
|
|
"**Note** \n",
|
|
"Of course Cython has much more horsepower under its hood - more than I am showing in this article (for example, I am not using Cython's type definitions via `cdef` here). Here, I want to focus on how to speed up existing Python code by making only minimal changes to it. \n",
|
|
"[In a later section - Appendix II](#type_declarations) We will see how static type declarations can further improve the performance via Cython."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%load_ext cythonmagic"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"The cythonmagic extension is already loaded. To reload it, use:\n",
|
|
" %reload_ext cythonmagic\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 45
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"import numpy as np\n",
|
|
"import scipy.stats\n",
|
|
"cimport numpy as np\n",
|
|
"\n",
|
|
"def cy_lin_lstsqr_mat(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)\n",
|
|
"\n",
|
|
"def cy_classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)\n",
|
|
"\n",
|
|
"def cy_numpy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return np.linalg.lstsq(X,y)[0]\n",
|
|
"\n",
|
|
"def cy_scipy_lstsqr(x,y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" return scipy.stats.linregress(x, y)[0:2]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 46
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### Comparing the compiled Cython code to the original Python code"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"for lab,appr in zip([\"matrix approach\",\"classic approach\",\n",
|
|
" \"numpy function\",\"scipy function\"],\n",
|
|
" [(lin_lstsqr_mat, cy_lin_lstsqr_mat), \n",
|
|
" (classic_lstsqr, cy_classic_lstsqr),\n",
|
|
" (numpy_lstsqr, cy_numpy_lstsqr),\n",
|
|
" (scipy_lstsqr, cy_scipy_lstsqr)]):\n",
|
|
" print(\"\\n\\n{}: \".format(lab))\n",
|
|
" %timeit appr[0](x, y)\n",
|
|
" %timeit appr[1](x, y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"matrix approach: \n",
|
|
"10000 loops, best of 3: 165 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"10000 loops, best of 3: 166 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"\n",
|
|
"classic approach: \n",
|
|
"1000 loops, best of 3: 1.59 ms per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"10000 loops, best of 3: 127 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"\n",
|
|
"numpy function: \n",
|
|
"1000 loops, best of 3: 220 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"1000 loops, best of 3: 221 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"\n",
|
|
"scipy function: \n",
|
|
"1000 loops, best of 3: 361 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"1000 loops, best of 3: 367 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 47
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"As we've seen before, our \"classic\" implementation of the least square method is pretty slow compared to using numpy's functions. This is not surprising, since numpy is highly optmized and uses compiled C/C++ and Fortran code already. This explains why there is no significant difference if we used Cython to compile the numpy-objects-containing functions. \n",
|
|
"However, we were able to speed up the \"classic approach\" quite significantly, roughly by 1500%.\n",
|
|
"\n",
|
|
"The following 2 code blocks are just to visualize our results in a bar plot."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"funcs = ['classic_lstsqr', 'cy_classic_lstsqr', \n",
|
|
" 'lin_lstsqr_mat', 'numpy_lstsqr', 'scipy_lstsqr']\n",
|
|
"labels = ['classic approach','classic approach (cython)', \n",
|
|
" 'matrix approach', 'numpy function', 'scipy function']\n",
|
|
"\n",
|
|
"times = [timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000)\n",
|
|
" for f in funcs]\n",
|
|
"\n",
|
|
"times_rel = [times[0]/times[i+1] for i in range(len(times[1:]))]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 50
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"#%pylab inline\n",
|
|
"#import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"x_pos = np.arange(len(funcs))\n",
|
|
"plt.bar(x_pos, times, align='center', alpha=0.5)\n",
|
|
"plt.xticks(x_pos, labels, rotation=45)\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.title('Performance of different least square fit implementations')\n",
|
|
"plt.grid()\n",
|
|
"plt.show()\n",
|
|
"\n",
|
|
"x_pos = np.arange(len(funcs[1:]))\n",
|
|
"plt.bar(x_pos, times_rel, align='center', alpha=0.5, color=\"green\")\n",
|
|
"plt.xticks(x_pos, labels[1:], rotation=45)\n",
|
|
"plt.ylabel('relative performance gain')\n",
|
|
"plt.title('Performance gain compared to the classic least square implementation')\n",
|
|
"plt.grid()\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAFhCAYAAABwNN3iAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XlcFPX/B/DXIiCgHAJeHIIIJiKCigeagmkqKGhqKnnh\nkWhqmh2alqJ5YZ5FmWnKN1M0yxMBTW0xD8Ajj0TwalFRSLwQQWGX9+8P2vmxHALmsruz7+fj4UNm\nZ3bm/Z6ZnffO5zMzKyEiAmOMMb1noOkAGGOMaQcuCIwxxgBwQWCMMfYvLgiMMcYAcEFgjDH2Ly4I\njDHGAIi8IGRlZaFbt26wsLDAxx9/rOlwNC4/Px9BQUGwsrLC0KFDK51eKpXC0dFRGG7VqhWOHj0K\nACAijBkzBtbW1ujUqRMAYO3atWjYsCEsLCzw8OFD9STxkkrnwqouLS0N3t7esLCwwNdff41JkyZh\n4cKFVX5/daevDmdnZxw+fFgt89akLVu2oHfv3jW/YNIyTk5OZGpqSnXr1qWGDRtSaGgo5ebmvtS8\nFixYQIMGDXrFEequH3/8kTp06EAKhaJK0//+++/k4OBQ7rijR4+Sg4MD5eXlERFRQUEBmZqa0sWL\nF19ZvNXh5OREhw8frnD8i3J5VUaPHk2fffaZWpehCWPHjqUZM2aUO64m1uuLODs7v3C7a8KmTZvo\n9ddfr/L0f//9N0kkkip/LtVJ684QJBIJYmJi8OTJE5w9exanT5+u9rcLIkJRURHS09Ph7u7+UnHI\n5fKXep82S09PR/PmzWFg8N83e3p6OpydnWFqagoAyMzMxLNnz156fRcVFf2neCQSCYjvsazUy+zX\n6enpaNmypRqiYSVpxf6r4YJURumK/9FHH1G/fv2IiOjkyZPk6+tLVlZW5OXlRVKpVJjOz8+P5syZ\nQ126dCFTU1MaMWIEGRkZkbGxMdWtW5cOHz5Mz58/p2nTppGdnR3Z2dnR9OnT6fnz50RU/E3H3t6e\nIiIiqFGjRjRy5EgKDw+nwYMH04gRI8jc3Jw8PT3pypUrtHjxYmrQoAE1adKEDh48KMSwceNGcnd3\nJ3Nzc3JxcaF169YJ45TzX7FiBTVo0IAaN25MmzZtEsbn5eXRjBkzyMnJiSwtLen111+n/Pz8SvMu\nLSUlhfz8/MjKyoo8PDxo7969REQ0d+5cMjY2JiMjI6pbty5t3LixzHvz8vJo9OjRVK9ePWrZsiUt\nW7ZM5dufk5MTHTp0iDZs2EAmJiZUq1Ytqlu3LoWEhFCdOnVIIpFQ3bp1qUePHkREdPnyZerZsydZ\nW1vTa6+9Rj///LMwr9GjR9PEiRMpICCA6tSpQ4cPH6aMjAwaOHAg1a9fn5o2bUpfffWVMP28efPo\n7bffplGjRpG5uTl5eHjQ6dOniYhoxIgRZGBgIJxZfvnll2VyK/1N9kXLSkpKok6dOpGVlRU1btyY\npkyZQgUFBcL46dOnU4MGDcjCwoI8PT3pr7/+onXr1qnsb8HBweVun/LeS0SUnZ1NQUFBZGFhQR06\ndKDPPvtM+JZZ3jdIPz8/2rBhAxERXbt2jbp37042NjZka2tLw4cPp0ePHqlst4iICPL09CQTExNS\nKBRV3qe6d+9OtWrVIhMTEzI3N6crV64IZ0JPnz4lExMTMjAwoLp165K5uTndvXu3zDxKnjkpPwfL\nli2j+vXrU+PGjWnXrl20f/9+cnNzI2tra1qyZInKdh80aBANHTqUzM3NqW3btnT+/HlhfMnjRVFR\nES1ZsoSaNWtGNjY2NGTIEHrw4IHKOty0aRM5OjqStbU1rV27lpKTk8nT05OsrKxoypQpKnH/8MMP\n5O7uTvXq1aPevXtTenq6ME4ikdB3331Hbm5uZGVlRZMnTyai4s9fyc9GvXr1iIgoJiaGvL29ycLC\nghwdHSk8PFyYl6Ojo/DZMTc3p5MnT5Y5yzh+/Dj5+PiQpaUltW/fnk6cOKGyL3z++efUpUsXMjc3\np169elF2djYREeXn59Pw4cPJxsaGrKysqH379pSVlVXutiYi0sqCcOjQISIiunnzJnl4eNDcuXPp\n9u3bZGNjQ3FxcURE9Ntvv5GNjY2QuJ+fHzk5OVFKSgopFAoqLCyk0NBQ+vzzz4V5f/755+Tr60v3\n7t2je/fuUefOnYXxv//+OxkaGtKsWbOooKCA8vPzad68eWRiYkIHDx4kuVxOo0aNIicnJ1q8eDHJ\n5XJav349NW3aVJj//v376caNG0RElJCQQGZmZnT27FmV+c+bN4/kcjnFxsaSmZmZ8MF97733qHv3\n7nTnzh3hA/v8+fMK8753716ZdVdQUEDNmjWjJUuWUGFhIR05coTMzc0pLS2NiIjCw8Np5MiRFa77\nmTNnUrdu3ejhw4d069Yt8vDwIEdHR5Vto/zwRUVFqeywMplM5aCVm5tLDg4OFBUVRQqFgv7880+y\ntbWllJQUIio+SFhaWgo7dl5eHrVt25a++OILKiwspBs3bpCLiwsdOHCAiEjYFnFxcVRUVESffvop\nderUqdzYylOyICgUihcu68yZM5SUlEQKhYJkMhm5u7vT6tWriYgoPj6e2rVrR48fPyYiotTUVOEg\nWHp/K+1F7x06dCgNHTqU8vLy6K+//iJ7e3vq2rUrEZVfEPz9/emHH34gouKCcOjQISooKKB79+5R\nt27daPr06cK0Tk5O1KZNG7p9+zY9e/asWvtU6WWVzlMqlVbaZFRyeuXn4IsvvhA+QzY2NvTOO+9Q\nbm4uXbp0iUxNTUkmkxFR8XY3MjKiX3/9leRyOS1fvpyaNm1KcrmciFS3++rVq8nX15cyMjKooKCA\nwsLCKCQkRGUdTpo0iZ4/f04HDx4kY2NjGjBgAN27d48yMjKoQYMGlJCQQEREu3fvJldXV0pNTSWF\nQkELFy6kzp07CzlJJBIKCgqix48f082bN6l+/foUHx9PRGU/G8r1pCz+Fy5coIYNG9Lu3buJqOxn\nh0i12en+/ftkZWVFP/30EykUCoqOjqZ69eoJxc7Pz49cXV3p6tWrlJ+fT/7+/jRr1iwiIvruu+8o\nKCiI8vPzqaioiM6ePUs5OTkVbiutKwhOTk5Ut25dsrKyIicnJ5o8eTLl5+fT0qVLyxzMevfuTf/7\n3/+IqHinnTdvnsr40NBQlTbdZs2aCR8CIqIDBw6Qs7MzERXvqMbGxsIZA1HxztirVy9heO/evVS3\nbl0qKioiIqKcnBySSCTCB7y0AQMG0Jo1a4T5m5qaqmz0Bg0aCAceU1NTunDhQpl5VJZ3SUePHqVG\njRqpvBYSEiJ8G5k3bx6NGDGi3FiJSOWgSET0/fffq3zYS374Sn+DKX3Q2rZtm3BAU5owYQLNnz+f\niIoLwujRo4VxiYmJ1KRJE5XpFy9eTGPGjBFif/PNN4VxygNHebGVp2RBqGxZpa1atYreeustIiI6\nfPgwNW/enBITE8u0+Zbe30o7cuRIue+Vy+VkZGQkFG4iotmzZ7/wDKH0QbqkXbt2UZs2bYRhZ2dn\nlbPR6uxTymUpz0ZK51mVPoTS05uampb5DCUnJwvTt2vXjvbs2UNExdvd19dXGFdUVESNGzemY8eO\nCbkpt7u7u7vKPnDnzh0yMjIihUIhrMM7d+4I421sbFTOWgcNGiR8Xvv06aOyfhUKBZmZmdHNmzeJ\nqLggHD9+XBg/ZMgQWrp0KRFVrQ9h2rRp9MEHHxBR+du35Dx+/PFH6tixo8r7fX19KSoqioiKt8+i\nRYuEcd9++y316dOHiIpbLTp37lzusaU8hppusipNIpFgz549eOONN1ReT09Px44dO7Bv3z7hNblc\nrjJdZVeR3LlzB05OTsJwkyZNcOfOHWG4fv36MDY2VnlPgwYNhL9NTU1ha2sLiUQiDANAbm4uLCws\nEBcXh/nz5+Pq1asoKipCXl4eWrduLbzfxsZGpf3ezMwMubm5yM7OxrNnz9CsWbMyMVcl75L5lV4H\nTk5OyMjIeOF6qej9TZo0qdL7ypOeno6kpCTUq1dPeE0ul2PUqFEAirezvb29yvR37txRmV6hUKBb\nt27CcMOGDYW/zczM8OzZMxQVFVW7T6SyZV25cgUzZszAmTNnkJeXB7lcDh8fHwDAG2+8gSlTpmDy\n5MlIT0/HwIEDsXz5cpibm1e63O7du5f73qdPn0Iul7/0us/KysK0adNw7NgxPHnyBEVFRbC2tlaZ\npuS8q7NPKSn3+VfBxsamzGeo5LY1NTVFbm6uMOzg4KASh4ODg8rnVkkmk+Gtt95S2R8MDQ2RlZUl\nDJdeTkXLTU9Px7Rp0/Dhhx+qLCMjI0NYl40aNRJeNzMzw9OnTyvMOSkpCbNmzcKlS5dQUFCA58+f\nY8iQIRVOX9KdO3fK7A9OTk4q66BkLCXzGDlyJG7duoVhw4bh0aNHGDFiBBYtWgRDw/IP/VrXqVyR\nJk2aYOTIkXj48KHw78mTJ/jkk0+EaSrbae3s7CCTyYThmzdvws7OrsL3V+dD8Pz5cwwaNAiffPIJ\n/vnnHzx8+BCBgYFV6iiytbWFiYkJrl27VmZcVfIumd+tW7dUlpmenq7ygXqRxo0b4+bNm8Jwyb+r\nq0mTJvDz8ysT9zfffCNMU3L9NmnSBE2bNlWZPicnBzExMWWmLU91tpWjo+MLlzVp0iS0bNkS165d\nw+PHj7Fo0SKVTu+pU6fi9OnTSElJwZUrV/Dll19WOYby3tugQQMYGhpWuO7r1KkDAMjLyxNey8zM\nFP6ePXs2atWqhb/++guPHz/G5s2by3TSl17XVd2nKqKcX1XX+38pKLdu3RL+Lioqwu3bt1U+t0pN\nmjRBfHy8Sl55eXlo3LhxtZfZpEkTfP/99yrzevr0qXCJ9YuUl+s777yDAQMG4Pbt23j06BEmTpwo\nbKPK1o29vT3S09NVXktPT1f5QlURQ0NDzJ07F5cuXcKJEycQExODH3/8scLpdaYgjBgxAvv27cPB\ngwehUCjw7NkzSKVSlW+/pQ++pYdDQkKwcOFCZGdnIzs7GwsWLMDIkSMrXGZVDuZKBQUFKCgogK2t\nLQwMDBAXF4eDBw9W6b0GBgYYO3YsZsyYgbt370KhUODkyZMoKCioUt5KnTp1gpmZGZYtW4bCwkJI\npVLExMRg2LBhVYpjyJAhWLJkCR49eoTbt2/j66+/rnL+pfXr1w9XrlzBTz/9hMLCQhQWFuLUqVNI\nTU0FUHbddujQAebm5li2bBny8/OhUCjw119/4fTp0+VOX1rDhg1x/fr1KsVW2bJyc3Nhbm4OMzMz\npKamYu3atcKH9vTp00hKSkJhYSHMzMxgYmKCWrVqCTHcuHGjwuVW9F4DAwMMHDgQ4eHhyM/PR0pK\nCn788UdhmfXr14e9vT02b94MhUKBjRs3quSam5uLOnXqwMLCAhkZGUKBqkh19imlkuufipuahZzv\n37+PnJycF763Op+l0s6cOYNdu3ZBLpdj9erVMDExKffAPHHiRMyePVsopvfu3cPevXurtSxlnBMn\nTsTixYuRkpICAHj8+DF27NjxwveVXCe3b99GYWGhMD43Nxf16tWDsbExkpOTsXXrVpXta2BgUOH+\nGxAQgCtXriA6OhpyuRzbt29Hamoq+vXrVybu0n7//XdcvHgRCoUC5ubmMDIyEvbX8uhMQXBwcMCe\nPXuwePFiNGjQAE2aNMGKFStUVkR53/BLvvbZZ5/Bx8cHrVu3RuvWreHj44PPPvusyu+vaBoAMDc3\nx1dffYUhQ4bA2toa0dHR6N+//wvfW9Ly5cvh6emJ9u3bw8bGBp9++imKiooqzLu8yzSNjIywb98+\nxMXFoX79+pgyZQo2b96M5s2bV5hPSfPmzYOTkxOaNm2KPn36YNSoURVOX9m6qVu3Lg4ePIht27bB\n3t4ejRs3xqeffoqCgoJy329gYICYmBicO3cOLi4uqF+/PiZMmCAcaCpb3qeffoqFCxeiXr16WLly\nZYUxA0CtWrVeuKzly5dj69atsLCwwIQJE1QKak5ODiZMmABra2s4OzvD1tZWuOlx3LhxSElJQb16\n9TBw4MAyy3/ReyMjI5Gbm4tGjRph7NixGDNmjMq+vX79enz55ZewtbVFSkoKunTpIoybN28ezp49\nC0tLSwQFBWHQoEEv3M7V2afKW9clt0WLFi0QEhICFxcXWFtbq5y5lDd96XmVN1x6XP/+/bF9+3ZY\nW1tjy5Yt2LlzZ7kHtWnTpiE4OBi9evWChYUFfH19kZycXKXllJ5mwIABmDlzJoYNGwZLS0t4enri\nwIEDL8xB+VqPHj3g4eGBRo0aCU3O3377LebOnQsLCwt88cUXKjeGmpmZYc6cOejSpQusra2RlJSk\nMj8bGxvExMRgxYoVsLW1xfLlyxETE6PSLFjR9snKysLbb78NS0tLtGzZEv7+/i/8Eiyh/1K6KzF2\n7Fjs378fDRo0wMWLF8uMz87OxogRI5CZmQm5XI6PPvoIoaGh6gqHMZ0RFRWFH374AX/88YemQ9Go\n+fPn49q1a9i8ebOmQ9ELaj1DGDNmDOLj4yscHxkZiTZt2uDcuXOQSqX48MMPRXlDGGPs5ajx+yor\nh1oLQteuXVWu5CitcePGwml6Tk4ObGxsKuz9ZkyfVNa8py94PdQstTYZAcWXggUFBZXbZFRUVIQ3\n3ngDV65cwZMnT/Dzzz8jICBAneEwxhirgEY7lRcvXgxvb2/cuXMH586dw+TJk/HkyRNNhsQYY3pL\no+0zJ06cwJw5cwAAzZo1Q9OmTZGWlibcBKTk6upa5UsKGWOMFfPy8sK5c+eqPL1GzxBatGiBQ4cO\nASi+PCotLQ0uLi5lprt+/bpwna8Y/82bN0/jMXB+nBvnJ75/58+fr9YxWa1nCCEhIUhISEB2djYc\nHR0xf/584WaNsLAwzJ49G2PGjIGXlxeKioqwbNmyMrfc64OSd0+LkZjzE3NuAOenb9RaEKKjo184\n3tbWVuV5KowxxjRHZ+5UFjOx34wn5vzEnBvA+ekbtV92+irwr2Exxlj1VffYyWcIWkAqlWo6BLUS\nc35izg3g/PQNFwTGGGMAuMmIMcZEi5uMGGOMvRQuCFpA7O2YYs5PzLkBnJ++4YLAGGMMAPchMMaY\naHEfAmOMsZfCBUELiL0dU8z5iTk3gPPTN1wQGGOMAeA+BMYYEy3uQ2CMMfZSuCBoAbG3Y4o5PzHn\nBnB++oYLAmOMMQBq7kMYO3Ys9u/fjwYNGuDixYvlTiOVSvHBBx+gsLAQtra25VZs7kNgjLHqq+6x\nU60F4Y8//kDdunUxatSocgvCo0eP0KVLFxw4cAAODg7Izs6Gra1t2SC1oCDMmhWBzMx8jcZQXY0a\nmWLp0pmaDoMxpiHVPXaq9Sc0u3bt+sLfLN26dSsGDRoEBwcHACi3GGiLzMx8ODuHq2XeMpkUzs7+\naphv+Cuf58uQSqXw9/fXdBhqIebcAM5P32i0D+Hq1at48OABunfvDh8fH2zevFmT4TDGmF5T6xlC\nZQoLC3H27FkcPnwYeXl58PX1RadOneDm5lZm2tDQUDg7OwMArKys4O3tLVR2Zb+DOoczM2X4d/GQ\nyYrHK7/V/9dh5Wuvan7KYaWaWD8vGla+pqnlq3PY399fq+Lh/PQ7P6lUiqioKAAQjpfVofYb02Qy\nGYKCgsrtQ4iIiEB+fj7Cw8MBAOPHj0efPn0wePBg1SC1oA8hNDRcbU1G6iKThSMqKlzTYTDGNESn\nbkzr378/jh07BoVCgby8PCQlJaFly5aaDEkjSn+jFxvlNxgxEnNuAOenb9TaZBQSEoKEhARkZ2fD\n0dER8+fPR2FhIQAgLCwMLVq0QJ8+fdC6dWsYGBjg3Xff1cuCwBhj2oCfZVRF3GTEGNM1OtVkxBhj\nTHtwQdAC3Iegu8ScG8D56RsuCIwxxgBwQdAK6rhLWZuUvB9BbMScG8D56RsuCIwxxgBwQdAK3Ieg\nu8ScG8D56RsuCIwxxgBwQdAK3Iegu8ScG8D56RsuCIwxxgBwQdAK3Iegu8ScG8D56RsuCIwxxgBw\nQdAK3Iegu8ScG8D56RsuCIwxxgBwQdAK3Iegu8ScG8D56RsuCIwxxgBwQdAK3Iegu8ScG8D56Ru1\nFoSxY8eiYcOG8PT0fOF0p06dgqGhIXbu3KnOcBhjjL2AWgvCmDFjEB8f/8JpFAoFZs6ciT59+mj8\nV9E0hfsQdJeYcwM4P32j1oLQtWtX1KtX74XTfP311xg8eDDq16+vzlAYY4xVQqN9CBkZGdizZw8m\nTZoEoPj3P/UR9yHoLjHnBnB++sZQkwufPn06li5dKvwQ9IuajEJDQ+Hs7AwAsLKygre3t7Axlad9\n6hzOzJTh38ULTTzKA7m2DivVxPrhYR7mYc0PS6VSREVFAYBwvKwOCam54V4mkyEoKAgXL14sM87F\nxUUoAtnZ2TAzM8P69esRHBysGuS/BUOTQkPD4ewcrpZ5y2RStZwlyGThiIoKf+XzrS6pVCrsvGIj\n5twAzk/XVffYqdEzhBs3bgh/jxkzBkFBQWWKAWOMsZqh1oIQEhKChIQEZGdnw9HREfPnz0dhYSEA\nICwsTJ2L1inch6C7xJwbwPnpG7UWhOjo6CpPu2nTJjVGwhhjrDJ8p7IW4PsQdJeYcwM4P33DBYEx\nxhgALghagfsQdJeYcwM4P33DBYExxhgALghagfsQdJeYcwM4P33DBYExxhgALghagfsQdJeYcwM4\nP33DBYExxhgALghagfsQdJeYcwM4P33DBYExxhgALghagfsQdJeYcwM4P33DBYExxhgALghagfsQ\ndJeYcwM4P33DBYExxhgALghagfsQdJeYcwM4P33DBYExxhgANReEsWPHomHDhvD09Cx3/JYtW+Dl\n5YXWrVujS5cuuHDhgjrD0Vrch6C7xJwbwPnpG7UWhDFjxiA+Pr7C8S4uLjh69CguXLiAzz//HBMm\nTFBnOIwxxl5ArQWha9euqFevXoXjfX19YWlpCQDo2LEjbt++rc5wtBb3IeguMecGcH76Rmv6EH74\n4QcEBgZqOgzGGNNbhpoOAAB+//13bNy4EcePH69wmtDQUDg7OwMArKys4O3tLVR3ZTugOoczM2X4\nd/FCm7/ym/1/HU5MXI1Gjbxf2fxK90nUxPp50fDq1atrfHvV1HDJNmhtiIfz0+/8pFIpoqKiAEA4\nXlaHhIio2u+qBplMhqCgIFy8eLHc8RcuXMDAgQMRHx8PV1fX8oOUSKDmMCsVGhoOZ+dwtcxbJpOq\npdlIJgtHVFT4K59vdUmlUmHnFRsx5wZwfrquusdOjTYZ3bx5EwMHDsRPP/1UYTHQB9yHoLvEnBvA\n+ekbtTYZhYSEICEhAdnZ2XB0dMT8+fNRWFgIAAgLC8OCBQvw8OFDTJo0CQBgZGSE5ORkdYbEGGOs\nAmotCNHR0S8cv2HDBmzYsEGdIegEdTUZaQsxn5aLOTeA89M3WnOVEWOMMc3igqAFxHx2AIi7nVbM\nuQGcn77hgsAYYwwAFwStwM8y0l1izg3g/PQNFwTGGGMAuCBoBe5D0F1izg3g/PQNFwTGGGMAqlAQ\ncnNzoVAoAABpaWnYu3evcHMZezW4D0F3iTk3gPPTN5UWhG7duuH58+fIyMhA7969sXnzZoSGhtZA\naIwxxmpSpQWBiGBmZoadO3fivffew44dO/DXX3/VRGx6g/sQdJeYcwM4P31TpT6EkydPYsuWLejb\nty8AoKioSK1BMcYYq3mVFoTVq1djyZIleOutt+Dh4YHr16+je/fuNRGb3uA+BN0l5twAzk/fVPpw\nOz8/P/j5+QnDzZo1w1dffaXWoBhjjNW8SgvCqVOnsHjxYshkMsjlcgDFP7pw4cIFtQenL7gPQXeJ\nOTeA89M3lRaE4cOHY/ny5WjVqhUMDPi2BcYYE6tKj/D169dHcHAwXFxc4OzsLPyrirFjx6Jhw4bw\n9PSscJr3338fbm5u8PLywp9//lnlwMWE+xB0l5hzAzg/fVPpGcK8efMwbtw49OzZE8bGxgCKm4wG\nDhxY6czHjBmDqVOnYtSoUeWOj42NxbVr13D16lUkJSVh0qRJSExMrGYKjDHGXoVKC8L//vc/pKWl\nQS6XqzQZVaUgdO3aFTKZrMLxe/fuxejRowEAHTt2xKNHj5CVlYWGDRtWIXTx4D4E3SXm3ADOT99U\nWhBOnz6N1NRUSCSSV77wjIwMODo6CsMODg64ffu23hUExhjTBpX2IXTu3BkpKSlqC4CIVIbVUXi0\nHfch6C4x5wZwfvqm0jOEkydPwtvbG02bNkXt2rUBvLrLTu3t7XHr1i1h+Pbt27C3ty932tDQUKEz\n28rKCt7e3sLpnnKjqnM4M1MGZV+68gCubOr5r8OZmede6fxKF5iaWD8vGj537pxGl8/DPKwvw1Kp\nFFFRUQBQ5Yt/SpJQ6a/opVTUB1DVhclkMgQFBeHixYtlxsXGxiIyMhKxsbFITEzE9OnTy+1Ulkgk\nZc4kalpoaDicncM1GkN1yWThiIoK13QYjDENqe6xs9IzhJepMkohISFISEhAdnY2HB0dMX/+fOHR\n2WFhYQgMDERsbCxcXV1Rp04dbNq06aWXxRhj7L+ptCD8F9HR0ZVOExkZqc4QdIJMJhX1lUZSqVQ4\nvRUbMecGcH76hm89ZowxBoALglYQ89kBIO5rvcWcG8D56ZtKC8Kvv/4KNzc3WFhYwNzcHObm5rCw\nsKiJ2BhjjNWgSgvCJ598gr179yInJwdPnjzBkydPkJOTUxOx6Q2+D0F3iTk3gPPTN5UWhEaNGsHd\n3b0mYmGMMaZBlV5l5OPjg6FDh2LAgAHVfrgdqxruQ9BdYs4N4Pz0TaUF4fHjxzA1NcXBgwdVXueC\nwBhj4lJpQVDeBs3Uh+9D0F1izg3g/PRNhQUhIiICM2fOxNSpU8uMk0gk/LvKjDEmMhUWhJYtWwIA\n2rVrp/IEUiLSyyeSqpOYzw4AcbfTijk3gPPTNxUWhKCgIADFTxlljDEmfnynshbg+xB0l5hzAzg/\nfcMFgTHGGAAuCFqB+xB0l5hzAzg/fVNpQUhLS0OPHj3g4eEBALhw4QIWLlyo9sAYY4zVrEoLwrvv\nvovFixdHMEfbAAAgAElEQVQLdyl7enpW6XcOWNVxH4LuEnNuAOenbyotCHl5eejYsaMwLJFIYGRk\nVKWZx8fHo0WLFnBzc0NERESZ8dnZ2ejTpw+8vb3RqlUrvgmOMcY0qNKCUL9+fVy7dk0Y/uWXX9C4\nceNKZ6xQKDBlyhTEx8cjJSUF0dHRuHz5sso0kZGRaNOmDc6dOwepVIoPP/wQcrn8JdLQbdyHoLvE\nnBvA+embSh9dERkZiQkTJiA1NRV2dnZo2rQptmzZUumMk5OT4erqKvwm87Bhw7Bnzx6VJ6c2btwY\nFy5cAADk5OTAxsYGhoZq/VVPxhhjFaj0DKFZs2Y4fPgwsrOzkZaWhuPHjwsH+RfJyMiAo6OjMOzg\n4ICMjAyVad59911cunQJdnZ28PLywpo1a6qfgQhwH4LuEnNuAOenbyr9Ov7w4UP8+OOPkMlkQnNO\nVZ5lVJXHWyxevBje3t6QSqW4fv063nzzTZw/fx7m5uZVDJ8xxtirUmlBCAwMhK+vL1q3bg0DA4Mq\nP8vI3t4et27dEoZv3boFBwcHlWlOnDiBOXPmACg+E2natCnS0tLg4+NTZn6hoaHCmYmVlRW8vb2F\n9j9llVfncGamDMoTI+U3emXb/38dVr72quZX+oyjJtbPi4aVr2lq+eoc9vf316p4OD/9zk8qlQoX\n51SlJac0CRHRiyZo27Ytzp49W+0Zy+VyvPbaazh8+DDs7OzQoUMHREdHq/QhzJgxA5aWlpg3bx6y\nsrLQrl07XLhwAdbW1qpBSiSoJEy1Cw0Nh7NzuEZjqC6ZLBxRUeGaDoMxpiHVPXZW2ofwzjvv4Pvv\nv8fdu3fx4MED4V9lDA0NERkZid69e6Nly5YYOnQo3N3dsW7dOqxbtw4AMHv2bJw+fRpeXl7o2bMn\nli1bVqYY6APuQ9BdYs4N4Pz0TaVNRiYmJvj444+xaNEiGBgU1w+JRIIbN25UOvOAgAAEBASovBYW\nFib8bWtri3379lU3ZsYYY2pQaZNR06ZNcerUKdja2tZUTGVwk9HL4SYjxvTbK28ycnNzg6mp6X8K\nijHGmPartCCYmZnB29sbEyZMwNSpUzF16lS8//77NRGb3uA+BN0l5twAzk/fVNqHMGDAAAwYMEDl\nNf4JTcYYE59K+xC0AfchvBzuQ2BMv1X32FnhGcLbb7+NHTt2wNPTs9yFKJ9BxBhjTBwqLAjK5wrF\nxMSUqTDcZPRqlbxLWYxK3qUsNmLODeD89E2Fncp2dnYAgG+//RbOzs4q/7799tsaC5AxxljNqPQq\no4MHD5Z5LTY2Vi3B6Csxnx0A4n7mvJhzAzg/fVNhk9HatWvx7bff4vr16yr9CE+ePEGXLl1qJDjG\nGGM1p8IzhHfeeQf79u1DcHAwYmJisG/fPuzbtw9nzpyp0g/ksKrj+xB0l5hzAzg/fVPhGYKlpSUs\nLS2xbdu2moyHMcaYhlTah8DUj/sQdJeYcwM4P33DBYExxhgALghagfsQdJeYcwM4P33DBYExxhgA\nNReE+Ph4tGjRAm5uboiIiCh3GqlUijZt2qBVq1Z6257HfQi6S8y5AZyfvqn0aacvS6FQYMqUKTh0\n6BDs7e3Rvn17BAcHq/ym8qNHjzB58mQcOHAADg4OyM7OVlc4jDHGKqG2M4Tk5GS4urrC2dkZRkZG\nGDZsGPbs2aMyzdatWzFo0CA4ODgAgEZ/lU2TuA9Bd4k5N4Dz0zdqKwgZGRlwdHQUhh0cHJCRkaEy\nzdWrV/HgwQN0794dPj4+2Lx5s7rCYYwxVgm1NRlV5YmohYWFOHv2LA4fPoy8vDz4+vqiU6dOcHNz\nKzNtaGgonJ2dAQBWVlbw9vYW2v+UVV6dw5mZMvy7eOEbvbLt/78OK197VfMrfcZRE+vnRcPK1zS1\nfHUO+/v7a1U8nJ9+5yeVShEVFQUAwvGyOtT2AzmJiYkIDw9HfHw8AGDJkiUwMDDAzJkzhWkiIiKQ\nn5+P8PBwAMD48ePRp08fDB48WDVI/oGcl8I/kMOYfqvusVNtTUY+Pj64evUqZDIZCgoKsH37dgQH\nB6tM079/fxw7dgwKhQJ5eXlISkpCy5Yt1RWS1uI+BN0l5twAzk/fqK3JyNDQEJGRkejduzcUCgXG\njRsHd3d3rFu3DgAQFhaGFi1aoE+fPmjdujUMDAzw7rvv6mVBYIwxbcC/qVxF3GTEGNM1WtNkxBhj\nTLdwQdAC3Iegu8ScG8D56RsuCIwxxgBwQdAK/Cwj3SXm3ADOT99wQWCMMQaAC4JW4D4E3SXm3ADO\nT99wQWCMMQaAC4JW4D4E3SXm3ADOT99wQWCMMQaAC4JW4D4E3SXm3ADOT99wQWCMMQaAC4JW4D4E\n3SXm3ADOT99wQWCMMQaAC4JW4D4E3SXm3ADOT99wQWCMMQaAC4JW4D4E3SXm3ADOT9+otSDEx8ej\nRYsWcHNzQ0RERIXTnTp1CoaGhti5c6c6w2GMMfYCaisICoUCU6ZMQXx8PFJSUhAdHY3Lly+XO93M\nmTPRp08fjf8qmqZwH4LuEnNuAOenb9RWEJKTk+Hq6gpnZ2cYGRlh2LBh2LNnT5npvv76awwePBj1\n69dXVyiMMcaqQG0FISMjA46OjsKwg4MDMjIyykyzZ88eTJo0CUDx73/qI+5D0F1izg3g/PSNobpm\nXJWD+/Tp07F06VLhh6Bf1GQUGhoKZ2dnAICVlRW8vb2Fjak87VPncGamDP8uXmjiUR7ItXVYqSbW\nDw/zMA9rflgqlSIqKgoAhONldUhITQ33iYmJCA8PR3x8PABgyZIlMDAwwMyZM4VpXFxchCKQnZ0N\nMzMzrF+/HsHBwapB/lswNCk0NBzOzuFqmbdMJlXLWYJMFo6oqPBXPt/qkkqlws4rNmLODeD8dF11\nj51qO0Pw8fHB1atXIZPJYGdnh+3btyM6Olplmhs3bgh/jxkzBkFBQWWKAWOMsZqhtoJgaGiIyMhI\n9O7dGwqFAuPGjYO7uzvWrVsHAAgLC1PXonUO9yHoLjHnBnB++kZtBQEAAgICEBAQoPJaRYVg06ZN\n6gyFMabDZs2KQGZmvqbDqLJGjUyxdOnMyifUMmotCKxq1NWHoC3E3E4r5twA7ckvMzNfLX146uy/\n00X86ArGGGMAuCBoBTGfHQDibqcVc26A+PMT+2evurggMMYYA8AFQSvws4x0l5hzA8Sfn9g/e9XF\nBYExxhgALghaQeztmGJuhxZzboD48xP7Z6+6uCAwxhgDwAVBK4i9HVPM7dBizg0Qf35i/+xVFxcE\nxhhjALggaAWxt2OKuR1azLkB4s9P7J+96uKCwBhjDAAXBK0g9nZMMbdDizk3QPz5if2zV11cEBhj\njAHggqAVxN6OKeZ2aDHnBog/P7F/9qqLCwJjjDEANVAQ4uPj0aJFC7i5uSEiIqLM+C1btsDLywut\nW7dGly5dcOHCBXWHpHXE3o4p5nZoMecGiD8/sX/2qkutP5CjUCgwZcoUHDp0CPb29mjfvj2Cg4Ph\n7u4uTOPi4oKjR4/C0tIS8fHxmDBhAhITE9UZFmOio65fFMvMlCEqSvrK56urvygmdmotCMnJyXB1\ndYWzszMAYNiwYdizZ49KQfD19RX+7tixI27fvq3OkLSS2NsxxdwOrS25qesXxf796L5y2vKLYmL/\n7FWXWpuMMjIy4OjoKAw7ODggIyOjwul/+OEHBAYGqjMkxhhjFVDrGYJEIqnytL///js2btyI48eP\nlzs+NDRUONOwsrKCt7e38O1M2c6pzuHMTJnwbUnZ7qj8dvFfhxMTV6NRI+9XNr/S7aI1sX5eNLx6\n9eoa3141NVyyjV2T8ahr/yy5L73K/TMzUybMl/N7dcNSqRRRUVH/xuOM6pIQEVX7XVWUmJiI8PBw\nxMfHAwCWLFkCAwMDzJyp2nZ44cIFDBw4EPHx8XB1dS0bpEQCNYZZJaGh4Wo5JQfU+0PfUVHhr3y+\n1aUtP9SuDtqSm7r2T23ZN8Wen7pU99ip1iYjHx8fXL16FTKZDAUFBdi+fTuCg4NVprl58yYGDhyI\nn376qdxioA/E3o6pDQdMdRFzboD4902x51ddam0yMjQ0RGRkJHr37g2FQoFx48bB3d0d69atAwCE\nhYVhwYIFePjwISZNmgQAMDIyQnJysjrDYowxVg61FgQACAgIQEBAgMprYWFhwt8bNmzAhg0b1B2G\nVlPXaau20JZmFXUQc26A+PdNsedXXWovCIxpA127Th/ga/VZzeOCoAXE/g1FG75B69p1+oB2XKsv\n9n1T7PlVFz/LiDHGGAAuCFpB7M9TEfPzcMS+7Tg//cIFgTHGGADuQ9AK2tCOqa5OVyWxPiBNG7ad\nOnF++oULAgOgvk5XddKGTlfGxISbjLSA2NsxxZyfmHMDOD99wwWBMcYYAC4IWkHs7Zhizk/MuQGc\nn77hgsAYYwwAFwStIPZ2TDHnJ+bcAM5P33BBYIwxBoALglYQezummPMTc24A56dvuCAwxhgDoOaC\nEB8fjxYtWsDNzQ0RERHlTvP+++/Dzc0NXl5e+PPPP9UZjtYSezummPMTc24A56dv1FYQFAoFpkyZ\ngvj4eKSkpCA6OhqXL19WmSY2NhbXrl3D1atX8f333wu/mqZvMjPPaToEtRJzfmLODeD89I3aCkJy\ncjJcXV3h7OwMIyMjDBs2DHv27FGZZu/evRg9ejQAoGPHjnj06BGysrLUFZLWevbskaZDUCsx5yfm\n3ADOT9+orSBkZGTA0dFRGHZwcEBGRkal09y+fVtdITHGGHsBtRUEiURSpemI6KXeJyaPHsk0HYJa\niTk/MecGcH56h9Tk5MmT1Lt3b2F48eLFtHTpUpVpwsLCKDo6Whh+7bXXKDMzs8y8vLy8CAD/43/8\nj//xv2r88/LyqtZxW22Pv/bx8cHVq1chk8lgZ2eH7du3Izo6WmWa4OBgREZGYtiwYUhMTISVlRUa\nNmxYZl7nznHHD2OMqZvaCoKhoSEiIyPRu3dvKBQKjBs3Du7u7li3bh0AICwsDIGBgYiNjYWrqyvq\n1KmDTZs2qSscxhhjlZAQlWrEZ4wxppf4TmXGGGMAuCAwPXb37l3MnDkT169fx/379wEARUVFGo7q\n/5U+eRfLyTwRiSYXpfJy0sUcuSCInPIAJ5fLNRyJ9mncuDEAYMuWLZg8eTLOnTsHAwMDrfggE5Fw\nCfadO3fw8OFDUV2SLZFIcODAAaxcuRJbt27VdDivhEQiwalTpxAXF4e///4bEolEq75gVAUXBJF6\n8OABMjIyYGBggPj4eMyePRurVq3SdFhaQ/lBjYiIwMSJE+Hv74+AgAAcPXpU4x/krKwsfPfddwCA\n3377Df3798cbb7yBXbt2IScnR2NxvQrKQnf+/HlMnToVWVlZiIuLQ1hYmKZDe2nKnA4fPoz+/fvj\n119/Rfv27fHnn3/CwMBAp4qC2q4yYprz9OlTrFixAnXq1IGnpydmzZqF6dOnIyIiApmZmVi0aBEM\nDfVz0yu//RsYGKCgoADGxsZo0KABJk6ciNq1ayMkJAS//vorOnXqpPItvSbjO3PmDE6cOIGsrCwk\nJSVh8+bNuHDhAjZu3IinT58iODgYFhYWNRrXqyKRSJCQkICffvoJa9asQUBAAK5du4bFixdj4sSJ\nQiHUJRKJBCkpKfjll1+wbds2dOvWDV5eXujRoweOHDkCb29vFBUVwcBA+79/1woPDw/XdBDs1TI2\nNsbjx4+RlpaGP//8E4MHD8aECRMwdOhQrFy5ElevXoW/v79O7KDqoGyu2LRpE1JSUtCxY0cAQJs2\nbWBlZYVPPvkEffr0gY2NTY3GpSxA9vb2MDU1xZ9//omsrCx89NFH8PDwgKmpKbZs2QIigouLC0xM\nTGo0vpdVurCeP38eixYtgpOTE/z8/GBpaYnWrVsjNjYWsbGx6N+/vwajrR6FQgGFQoGlS5fixIkT\neO211+Dp6YlOnTqhTp06GDhwIPr16wc7OztNh1olXBBEhIiEbyLu7u6wtLTEsWPHcP36dbRr1w6O\njo7o27cv5s+fj2vXrqFXr16iapeujPLAdPLkSUyePBl9+vTBihUrkJWVha5du6JWrVpo27Ytnj9/\njvT0dHTo0AEKhaJGCqfyzEUikeDOnTto06YNDA0NcerUKWRlZcHX1xfu7u6oVasWfvrpJwQGBsLc\n3Fztcf1XJfNKT08HEcHb2xuvv/46Pv/8c7i4uMDd3R1WVlZo06YN2rVrV+7NqdqkZE55eXkwNTWF\nv78//vnnH6Snp8Pa2hr29vbo2LEjLCwsUKdOHTRr1kzDUVdRte5rZlqtqKiIiIj27dtHY8aMISKi\nQ4cO0bRp02jFihX0999/ExFRZmYmnThxQlNhalRqaiqNHj2a1q1bR0REGRkZ1KVLF5o9ezYVFBQQ\nUfE6e/fdd2s0LuW2i42NJRcXF0pLS6O8vDzatWsXvffee7Ry5Uph2vIe76KtFAoFERXvk507d6bg\n4GAaN24cXbp0iRISEsjV1ZV++eUXlfco14W2UsYXFxdHPXv2pNDQUPriiy+IiGjmzJk0Y8YMOnbs\nmEoe2p6TEhcEkTlw4AB5eHjQ/v37hdf2799PM2bMoEWLFtGNGzeE13VlJ/0vSucYGxtL/fr1o5CQ\nEGFd3Llzh7y8vOijjz4Spps8eTLdvXu3RmO9dOkSeXh4UEJCgvBaXl4e7d69m0JDQ2nZsmVE9P8H\nWW3efvn5+cLf6enp1LJlSzpz5gxdvHiRfvzxRwoMDKTMzEzauXMnOTg4UFZWllbnQ0RUWFgo/J2c\nnEwtW7akmJgYOn36NHl7e9PUqVOpqKiI3nvvPfrggw/o4cOHGoz25ehnz6KInT59GuHh4QgMDMSz\nZ89gYmKCwMBAGBgYYO/evSqXVIq9uahkrjdu3ICZmRl69OgBe3t7rF+/Hrt378bAgQPh5OQkXCqo\nFBkZWePxyuVyvP766+jWrRvkcjmKiopgamqKnj17QiKRwMXFBQCEJixt3X5ZWVmIjo7GuHHjhGYt\nR0dHtG3bFkDx5b5nzpzBwYMHMXLkSHTq1AkNGjTQZMiV+ueff4TLk42NjZGXl4eePXuib9++AICz\nZ8+iQ4cOOH78OBYsWICsrCxYWVlpOOrq089eRZGgcq6Xv3v3Ln799VcAEDodk5KS4O/vjyVLlggH\nFX0gkUggkUgQFxeHvn37YsaMGfDx8YGlpSWGDh0KmUyGrVu3Ij09HY0bN0bnzp1r7Kap8pZjZmaG\n+Ph4xMTEwNDQEMbGxjhw4AD+97//ITg4GK1atVJ7XK9C7dq1ERAQgNzcXJw+fRpNmjSBXC7HnDlz\nAAA2NjawtrbGlStXAAD169cHoN03cmVmZiIoKAj379/HrVu3YGFhgcOHDws3NEokEnTv3h2PHz+G\njY0NWrZsqeGIXw4XBB1V8sMjk8mEnyf98MMPUa9ePeGeg+TkZISGhuL8+fOwtLTUSKyadPPmTcyb\nNw/r16/H1q1bMXToUAQHB6N58+YYOHAgMjIyVK4TVxaRmqC8BPPLL7/EkSNH0KxZM6xatQorV65E\nZGQkYmNjMXPmTNjb29dIPP9VYWEh8vLyYGVlBUdHRyxZsgQbNmzApUuXsGLFCshkMgwZMgT79u3D\n1q1b0aNHDwAQLoHWxjOewsJCAEDr1q1hbW2NtWvXYunSpWjVqhWGDx+O9u3bQyqVIiYmBrGxsTp5\nVlASP9xOR9G/V8zs3bsX4eHhsLe3h729PaZNm4a///4ba9euRV5eHrKzs7Fw4UIEBQVpOuQaQaUu\ncczNzcWkSZOwaNEiNGnSBAAwdepU1KpVC6tXr0ZWVpbGrmqJi4vDjBkzMH36dCxfvhzjx49H3759\nkZ2djRUrVqBRo0bo378/+vXrp5F7IqqjoKAAUqkUtra2uHLlCtLT0zFixAgsX74cxsbGGDhwIFxc\nXLBw4UJYWVmhQ4cO6Nu3r1bn9fz5c/zxxx9wcHBAbm4urly5goYNG+K3334DEWHJkiVYv369cCVY\nWFiYTmyrF6rxXgv2yvzxxx/Url07ysrKovXr11PdunXpgw8+IJlMRkVFRXTjxg1KT08nouIOSG3v\ntHsV5HI5ERE9efKECgsL6fnz5zRgwAD6+uuvhWm2bdtGM2fO1FSIVFRURLdu3aIBAwbQlStX6PDh\nw9SsWTMKCQmhuXPn0pMnT8pMrwvb7pdffiFfX19q2rQp7d69m4iI7t27R1OnTqWPP/6YLly4oDK9\ntueVk5ND+/btI39/f7Kzs6PU1FQiIjp+/Dh9/PHHNGvWLHrw4AERFXf+E2l/TpXh+xB02NOnT9Gz\nZ0/cuHEDK1euxJ49e/D999/j0KFD6NChA1xdXVWaiXT2W0sV3Lx5EwUFBahbty52796NiRMn4uLF\ni6hVqxZCQ0Mxa9YspKam4vTp01i7di3Gjh2L5s2b11h8VOLadYlEAgsLC3Tp0gVPnz7F1KlTkZSU\nhIYNG+LDDz+EsbExvLy8ULt2bZX3aCP6ty9EIpGgSZMmOHHiBGrXro1evXqhbt26sLW1RadOnbB/\n/3789ddf8PX1Ffq2tDUv5baqXbs28vLysGTJEnTs2BGdO3eGnZ0dHB0dYWFhgfPnz0MqlcLPzw/G\nxsYwMDDQ2pyqiguCjih5QHn48CEUCgXs7e3h4OCAdevWoWfPnggMDMTz589x8uRJDB48GNbW1sL7\ndXknrYqFCxdi7ty5aN++PdauXYsxY8bA0dER33zzDZo0aYLZs2fj/v37yMnJwYQJE9C7d+8aP7WX\nSCS4cOECTp8+jVq1asHOzg6ZmZk4dOgQJkyYgPz8fFy8eBFTpkyBo6NjjcX1XxkYGOC3337D5s2b\nsWzZMhgYGGD37t0wMTGBu7s75HI5PD090aZNG53JSyKR4LfffoO1tTVCQ0NRv359/PLLLzA0NISb\nmxuMjY1hbGyMgIAANGzYUDR3/fNlpzpEIpFgz549+OGHH/D48WO888476NGjB3x8fLBhwwYUFhZi\n+/btWLlyJVxdXTUdbo1Q3pn95ZdfoqioCEOHDsWIESMwbNgw5Ofnw8bGBsuWLUN2djbGjx8vvI9q\nuOtMIpFg9+7dmDt3LlxcXGBqaormzZsjLCwMjRo1Qs+ePXHr1i2sXr0arVq10pl2aOVVXB9++CFW\nrVqFOnXqYMyYMcjPz0dMTAxOnTqFDRs24Pfff9eZq6SUOU2bNg1ff/01evfuDQsLCzx48AC7du1C\nYmIizp07hzVr1qBp06aaDvfV0lxrFauu1NRU8vDwoHPnztHOnTtpzpw5tGDBAkpOTqZvv/2WAgMD\nad++fUSk+22ZVZGbm0t//fUXERElJSVRTk4OzZo1i9zd3YW7eZ8/f06xsbHk7+9PMplMuKmrJpTc\nBk+ePKFhw4bR2bNniYgoISGBZs2aRT/++CPdu3ePtm7dKtw9rkvbrqCggKZNm0ZxcXFERPTs2TNh\nXFxcHK1atYri4+M1Fd5Lyc3NpV69etHhw4eJ6P9vAPz777/p559/pn79+gl9JGLDBUHLKXfGO3fu\nUFxcHAUEBAjjkpKSqEePHpSUlERE/393qC4dUP6Lmzdv0tixY2ny5Mlkb28vdFpOnDiROnfuTFlZ\nWURUXBTu3btXo7GVXP/Hjx+nuLg48vX1pa1btxJR8V2vy5cvp4kTJ5Z5nzZvu/JiGzlyZJlO+vPn\nz6vcrazNeSnjUv7/6NEj8vf3FzqRlR3G2dnZRFS8Pymn19acXpY4Gr5EqqioCBKJBCdOnMDw4cPh\n5OQEExMT7NixAwDQoUMHeHh44NKlSwAAIyMj4b260NzwXxQVFcHR0RG9evXCxo0b8c4778DT0xMA\nsHbtWnh5eeHNN9/EP//8A2NjY9ja2gKo+aaitLQ0fPzxx2jdujU++ugjHDp0CAkJCTA0NES7du3w\n4MED5OTkCPdC6EqnZHp6OlJSUgAAY8eORWFhIfbs2QMAOHXqFCZOnIirV68K0+tCXllZWQAAS0tL\ndOnSBbNmzcKDBw9gamqKo0ePol+/fvjnn39U7pvQ9pyqizuVtZhEIsGhQ4ewYcMGTJo0Cb6+vsjO\nzsalS5dw5MgR1KpVC19++SUmTZoEBwcHrX+kwaskkUhw5MgRJCYmYs6cOdi5cyeeP38OZ2dnmJqa\nom/fvrh+/ToaNGgg3H+gfF9NxXf+/HkMGTIE/fr1Q3BwMGrXro2nT59iwYIFuHLlCiIiIjBr1ix4\nenrqxDajf/s1YmJiMHr0aOzYsQM3b95EUFAQ7t69i23btmHbtm344YcfMH/+fHTr1k3TIVdKmVNs\nbCzeffddHDhwAPXq1UP37t3xzz//YMaMGcjPz8eiRYsQHh6Otm3b6sS2emkaPkNhpZQ+BY2KiiKJ\nRELff/89ERFlZWUJT+McP368Sp+Bvjl27Bj16tWLiIqfUOrn50dbtmyhrVu30uDBg4Wnl9bUuimv\nCWH48OHUtm1b4d6CgoICOnv2LO3atYtOnTpVo/G9CpcvX6agoCBKTU2lhw8fkq+vLy1YsIByc3Pp\n/v37dPLkSaGpRVeaVJKSkqh///508uRJWrp0KU2aNIm2bNlCeXl5tGPHDvr111/p6NGjRKQ7Ob0s\nLghaRrmzZWRkCG2w0dHRVLt2bTp+/LjKNGK5GaaqSueYnZ1No0ePptOnTxNR8ZNeR44cSW+88QZt\n27ZNY/GdPHmStm/fTpcuXSIiorFjx1KfPn2E7VX6Pdq+7Uq2rYeFhVG7du3o+vXrRFTct9WtWzd6\n//33K3yftinZZ/DPP/9QYGAg9e/fXxj/3XffUVhYGG3evFnlJkFd2Fb/FRcELaLc2WJiYqhDhw7U\nq1cv+uKLL+jBgwe0Y8cOsrGxEb6p6JOSH8IzZ87QoEGD6PLlyySXy2nDhg3k5+cnFM+HDx8KnX81\n+eFVLuvo0aPUvHlzGjJkCA0dOpQ+/vhjIiIaM2YM+fv7l1sUdMG5c+foyZMndObMGRo+fDh9+eWX\nJO9I+x8AACAASURBVJPJiKi4KHTs2JEuX76s4SirR3nRwZYtW6h58+a0YcMGYdxXX31FY8eOpYyM\nDE2FpxFcELRMYmIiBQQE0NmzZykuLo4iIiJo4sSJVFRURN999x2ZmZnRw4cPa/TySU0q+a3sypUr\n9PTpU5oyZQp99NFHFBQURL///jsNHTpUuMJIkz9KcuLECerdu7dwxpKamkqTJk2ib775hoiIgoOD\nhWYiXaBcf8+fP6fp06dT37596cmTJ3Ty5EmaMmUKrVy5UvhNCeWVN7pALpfTvXv3yNTUlLZv305E\nRDt37qR+/frRxo0bhemUj33RJ1wQtMiDBw9oyJAh1LZtW+G1ixcvUkhICB06dIiISPhWpi+UB6X9\n+/dTx44dKS0tjYiKnzMTFRVFb731FllZWdH48eM1FpvSli1bSCKRCN808/PzKTo6msLCwl74Pm2T\nm5ur8mMwRMVNmB999BG9/fbb9OTJE0pMTKRx48bRsmXLKC8vT3iGlLbmpuxPIvr/HxjavXs3WVtb\n065du4iIaNeuXdS9e3dav369RmLUBlwQNKi8NslDhw5R69ataf78+cJrU6ZMoSVLlhDR//9qk7Z+\n8NTh8uXL1KJFC6EPpaRHjx7RpUuXyN/fX7jpqyaU3Hb37t0TmoI2bdpELi4uQgGPi4uj119/nbKz\ns4WDpja7dOkSTZo0ibKysujo0aO0Zs0aYdzdu3fpgw8+oFGjRtHTp0/p+PHjwo2B2uzSpUv02Wef\nERFRSkoKHTx4UNhesbGxVLt2beFGs19++YWSk5M1FqumcUHQIOUB5dChQ7R48WJav349ZWdnk1Qq\npUGDBlFoaCglJCSQh4eHcNekPrh16xZt3rxZGD569Ci9/fbbwnB5RXHUqFE1uo6Uy967dy/5+flR\n165d6fvvv6e0tDTavn07mZmZ0fjx42nAgAHCN1Btl5eXRz179hSaTY4cOUINGzakyMhIIipuajly\n5Ai1atWKhg4dqhPNlo8fPyY/Pz86deoU5eTk0PTp02ns2LF0+PBhevr0KRERrVq1iiQSCcXGxgrv\n06cvXCXxjWkaQv9e//zHH39g4sSJqFOnDtavX4+vvvoKRkZGmDp1KhITE/Hpp59iw4YNeOONNyCX\nyzUddo0gImzevBnnz58HALi4uOD+/fs4ePAggOIfVDly5AgiIiJARLh+/TquX79eoz8kI5FIcObM\nGaxYsQJr1qzB1KlTkZ6ejm3btqFv375Ys2YN/vjjDwQGBmLAgAFQKBRa/YtgAGBqaorhw4dj48aN\nsLe3R/fu3bF//36sWrUK33zzDWrVqoXatWujR48emDlzpk480E2hUCAvLw/R0dF4//338cEHH6BJ\nkyb49ddfcfLkSQBA586dMXDgQJV8RH2vwYtoth7pt9TUVAoJCRHuMcjIyKDp06fTrFmziIhIKpXS\nqFGjaOnSpZoMs0Ypm1XWrFlDO3bsIKLi/oLly5fTxx9/TEuXLiWpVEoeHh508OBB4X3379+v0Tjv\n3r1LY8aMoc6dOwuvHT9+nHr27EmJiYlEVNynYG9vTwkJCTUa28so2VdjYmJCfn5+lJubS0TFPyjf\nunVrGjduHDVo0EB4bpG2f4tWxhcZGUmGhobCY0IKCgpo7ty5NG7cOBo3bhy5ubnp5D0h6sB3Ktcg\n+vesQPlIiqNHjyIhIQG3b99G586dYW9vDy8vL8ydOxfBwcFo0aIFLC0tceTIEbz++uswMzPTdApq\np/yWdvfuXaxevRrdu3dHw4YN0ahRI5iZmWH//v24evUqJk2ahMDAQMjlchgYGMDU1FStcVGJx48r\nh4kIJ0+eRF5eHjp27AhHR0ecPHkSCoUC7du3h6enJ+zs7NCiRQuVR5FrI2VeNjY28Pf3h7W1Ndas\nWYN27drB09MTffr0QYsWLTBy5Eh069ZNJ57Gqozv7t27ePPNN7Fq1SrUrl0bXbp0Qbdu3WBmZoY6\ndepg+PDh6Nq1q8p79BX/hGYNKXlAycjIEJo3jh8/jp9++glubm4YNmwYnj59irfffhv79++Hvb09\nCgoKIJfL9aIYlDZv3jxs2rQJycnJaNSokfD6s2fPYGJiUuYgrS4ll3Ps2DHk5+ejdu3a6NatG375\n5Rfs378fZmZmGDp0KMaPH4/169fDz89PrTG9KiUP7AqFArVq1QJQ/KyijRs3Ii0tDQsXLlR5nHpN\nrfdX7fTp03jzzTfxxRdfYMqUKSrjdDWnV04j5yV6qOQpuY+PD3366ac0Z84coaNuwIAB5OPjQz17\n9qT9+/ervEefFBUVqXRWfvLJJ/Taa6/R2bNnVZqFNLFu9u3bRx4eHrRu3Tpq1aqV0Pm6c+dO8vLy\not69e9ORI0eIiMpctqnNzp8/L/xd8kqomzdv0qxZs+itt96ivLw8ndofb926RY8fPxZiVuZ19uxZ\nqlWrlsrVU+z/cZNRDVF+u5w+fTq2bt2Kc+fOYefOnTh37hwmT54MFxcXZGZmwsfHB6NGjdKbB9Up\nm8+UTT/KfJU/fPPmm29CLpdjz549SE1NRVZWFlq1alXj6yU9PR0ffvghfv75Z2Rl/V979x4Xc77/\nAfw1MxFTRFopOUo6IlQbSSEkIqxrR26b3UQuUWuxu07Ys87uKqGzuyGXXHapdpFckppRq7aS9ohS\nORRbNESZrqZm3r8/Mt8t6+xv7UkzU5/nX03N99H7+52Z73s+t/dHgoyMDIhEIhARvLy8YGBggKqq\nKggEAgwbNkwjBlzpRetg3rx5KCgogIuLS7O49fT08Ne//pXrttOE9yIRQSKRICAgAI6OjujevTsU\nCgUEAgHkcjmMjY3h7u4OHR0dmJubqzpctcMSQiuRy+XIzc2Ft7c3SkpKEB4ejr179+L8+fMQi8VY\ntmwZtLS0kJKSAolEAhsbG6753hY9ffoUT58+hZ6eHuLi4rB//35uz10ejwc+nw+5XA4+nw8HBwcM\nHDgQPXr0wJEjR+Dq6vrGxwxexuPxMHHiRJSVlWHjxo1ISkpCnz59sGrVKnTp0gULFixAeXk5cnJy\nYG9v3+rxvQ5lIlDe4IcOHYqrV69ixIgR6NSpU7Mbv56eHnr06KGqUF8bj8eDrq4uxGIxzp07hxkz\nZnCfI+V7qnfv3jA3N9eIcZDWxhJCK+Hz+fjLX/7Cben44YcfYtSoUUhNTUVRURHs7e3h5OQEPp+P\n8ePHo2vXrqoO+Y2prq7G9u3bkZubi4qKCqxfvx7u7u7YuXMnSkpKMG7cOPD5fPD5fK4FYWBgADMz\nM8yePbtVx1OUN41OnTpBX18f165dg56eHtzc3FBYWAgDAwOMHj0aFhYWMDc3h7OzM7p169Zq8f0Z\nyunOdXV14PP5MDY2RlhYGPr27avR35p/+eUXSCQS9OjRA46OjsjIyICtrS26dOnCvY/Y1NLfp/7t\nWg1EL43TKx9ra2uDiCCVSnHjxg2IxWJkZ2cjNDQUgwYNAgBMmzat2QBqW6SjowM7Ozs8efIEp06d\nwpo1a7B06VKkpKTgp59+wqZNm7g1Fy93vbRGV0zT14/H4zV7rFAokJqain/84x/w9fWFh4cHxo8f\nD7lcDl1dXbVN5PRiVpSSWCzGhg0bsHr1aiQlJcHT0xM7d+7Es2fPVBjl62l6PlKpFB9//DE+++wz\nrFu3DvX19SgoKMDZs2cBtM77pi1gs4xaGDWZrXDz5k3o6+vD2Ni42XMuX76MkJAQ1NTUwMfHBx4e\nHtyxbflbCxFx/bkAkJaWht27d0Mul+OLL75Av3798OjRI7i5uWHcuHEIDg5W2fXIzMzE4cOH8a9/\n/es3r0tkZCTKy8thamoKNzc3jXjdlDFmZ2ejQ4cOMDY25qY0f/bZZzA3N0dsbCyuXLmC/v37c2M4\n6kx5Tg8fPkTXrl3B4/FQWVmJNWvWYPDgwTh9+jTkcjmioqJgYWGh6nA1QysOYLcLTUsajB49mtvv\nWEk5g6aqqoqrtd4e6qwT/XptYmNjacmSJUTUWLZjzZo1tGPHDiosLCQiotLSUm7D+dbUdHbTlStX\nflOU7lW1iDThtVPGd/HiRTIyMqLFixeTiYkJV+qjtLSUcnNzafr06TRt2jRVhvqHNL3mMTExZGNj\nQ0OGDKEPP/yQ26fh/v37dODAARo3bhy3gFHdXyd1wBLCG3D79m2ytbV9ZanjV91A2tMb9eLFi2Rl\nZcVNrSVqnIobEBBA27Zt48opE7XedWm6R8Ht27cpLS2Nbt68SePHj6enT582e64mTSdt6vr167Ri\nxQpu1fSRI0fIzMzsN4l3wYIFVFFRoYoQX1tOTg65uLhQbm4u/fLLL9wqf6lUyj3nu+++I3d3d6qr\nq1NhpJpDvduEGqKoqAirV6/mHpeVlcHAwADDhg0DAK4/vLq6+pUbc6t7d0NLyszMxJYtWzBlyhTU\n1dUBAKZMmQJXV1cUFxf/pv/+TauoqMDGjRtRXl4OqVSKoKAg+Pj4IDg4GGKxGF988QWioqJw+fJl\nKBQKboN1dae8jnK5HDKZDFu2bEFiYiKqqqrQ0NCARYsWYcWKFdi9ezcUCgUAID4+Hmlpaaivr1dl\n6P9VaWkptm3bBoVCgbKyMoSEhODRo0fo1q0bTExMsG7dOojFYhw/fpw7pkuXLqisrOTOkfl9bJZR\nC+jWrRsMDQ1RV1eH7t27Q19fH/Hx8ejevTtMTEzQoUMHJCcn49ixYxg5ciQEAkG7SAL0ir71qKgo\nXLt2DXPmzOFurunp6XBwcMDYsWNhZGTUqjHW1dVh2LBhqK2txYMHD7B06VL4+vpizJgxyMrKgoWF\nBX788UeIRCL069cPffr0adX4/hc8Hg/V1dUQCoWYNGkSsrOzUVpaCisrK+jp6eHJkycoKCjAzJkz\nwePxUFtbi6VLl/5mzEtdPH78GJaWlpDJZOjRowf09fVx+/ZtVFRUoG/fvujduzeeP3+OiooKODk5\nQS6Xo6SkBJ6enq3+vtJYKm6haDSFQtGsC8HR0ZFGjx5NRI3F2fz8/Gjjxo10+vRp6t+/f7NibG1d\n066xwsJCys3N5X729fWlkJAQImrc4NzS0pIrCNea8Sndv3+fjh49SmPGjCGxWExEjeMFCxcupGPH\njv3X49RdbGwsOTg40ObNm+nKlStUWVlJc+bMoUmTJtGmTZto+PDhdPLkSVWH+f9qes1lMhm9//77\ntGTJEqqvr6eEhATy9fWlOXPmUEREBPXv35/i4uJUGK1mY11GfxK9aJJraWkhLy8PQGNdIj6fDw8P\nD/j5+WHatGmoq6tDfHw8du/eDVdXV7UvgdySeDwezpw5g1mzZmH9+vVYvnw5amtrMXXqVIhEIri4\nuGDp0qXYvn07RowYoZIY4+Pj4evrC1tbW3h6eiI4OBhJSUkQCASYMGECiouLVRLXn0FNppaWlJTg\nyJEjWLVqFbp27YpDhw4hJSUFR44cgaGhIbKyshASEoKZM2dyx6qjpnHl5OSAz+fD398fQqEQ/v7+\ncHZ2xvz581FdXY34+Hjs2LEDkyZNglwuV2HUGkyV2UiTNa1NZG5uzu2jS0Tk5OREs2bN4h4rB7Q0\nYUZKS/rxxx/Jzs6OJBIJhYeHk66uLvn7+1NRUREpFAq6e/cut29ta14b5f/Jz8+nKVOmcDPBJBIJ\nhYWF0fTp0+nKlSuUmZnJ1SbSBMrzyszMpP3799OGDRuIqLFUd0REBHl7e1NMTAzV1NSQh4cHrVmz\nhiQSiVq/J5WxXbhwgczMzCg7O5saGhooNzeXli9fTmvWrCGZTEaJiYnk7+9PISEh9OjRIxVHrblY\nQvgfXLt2jQYMGEA///wzETXud6ycsTJixAhycXEhItKInaXehNzcXEpLS6Pz58+Tvb09ZWdnk5OT\nE02ePJnbG1mpNW5KdXV1XHK+f/8+BQYG0qBBg+jAgQPccx49ekS7du2iiRMncjtqqfMNU0kZo0gk\noj59+pCXlxcJhUK6ceMGETWe1759+2jx4sVUW1tLDx8+pAULFlBpaakqw/5D8vPzafDgwZScnMz9\nTqFQUG5uLr377rvk6+tLRERHjx6lDRs2tPreGG0JW5j2Goial8jNzs5GVFQUBgwYgJKSEkRGRsLC\nwgIfffQRbG1tkZqaCkdHR1WG3GqaXpvy8nJ06NABurq6AIB169bBwsICy5YtQ1hYGCIiIvDtt982\nK6n8pjU0NCAlJQWFhYXQ1dVFTk4OZs6ciZiYGFRUVGDatGkYO3YsgMbBy5qaGvTt27fV4msJeXl5\n8Pf3x6ZNm+Dk5IRPP/0U0dHROHHiBKysrPDo0SPIZDKYmJgAaF7uWp3QS5MRCgoK8Pnnn+PQoUOQ\ny+WQy+Xo2LEjGhoaUFhYiJqaGlhbWwMAKisr0aVLF1WFrvHYLKPXxOPxEB8fj9u3b8PMzAzJyckQ\ni8UYO3YsVq1ahaKiIshkMrz99tvo06dPu6qzzuPxEBMTg8DAQBw8eBAymYyr63Ps2DFIpVKcOHEC\nQUFBsLGxadXY+Hw+qqqqEBQUhIiICKxYsQKjRo2CsbEx8vPzkZ+fDyKCubk5dHR0uLhfvjmpm6bx\niUQixMbGgojg6uoKZ2dnlJeXIyAgAK6urjAzM+NKaxCRWq5Ebvp5uXXrFqqrq6Grq4vAwEAYGhpi\n6NChEAgEiI+PR1RUFGbMmIFevXpxhRC1tbVVfAaajSWE16C84W3cuBHjxo3DsGHD4OzsjHnz5sHa\n2hqlpaXYsWMHPD09YWpqyh2jzjeUlsLj8ZCfn49ly5bhq6++woABA5CXl4dbt27B3t4e3bp1w/nz\n57F27VpMmDBBJZvb6Onp4eTJkzAxMYFQKISlpSVMTExgbm6Oq1ev4u7du7C1tW1WPE/dXztlWfXI\nyEj4+PjAyMgI//73v/Hw4UMMGzYMY8aMwbNnz9CrV69mLR51Pi/lZIRVq1Zh/PjxGDBgAMzNzREW\nFoZ79+5BKpXik08+gYeHBywtLQGwWkUtRhX9VJrq6dOnNG7cOMrLyyO5XE6ZmZl09OhRqqmpIZFI\nRI6OjnTq1Cki0ox+55agPM8HDx7QhQsXaPLkydzf0tPTycXFhRu0ra2t5Y5pjevT9P88ePCA+93N\nmzdpxYoV9Pe//52IGvdsjo6OpoKCgjce05tw8+ZN6tOnD+3YsYOIiKKiosjHx4d27drV7Hma8p7M\nysoia2trbpzp4cOHdPXqVcrJySEPDw9avXo1nT17log055w0hWYsu1QReqm7oKGhATweD9HR0cjL\ny4NAIIBIJEJFRQUWL16MAwcOwNLSUm2n8LU0ZQG01NRUbNq0CV9//TU6deqE6OhozJ07F/b29rCy\nsuL2COjQoQN3bGt9Q+XxeDh37hy2bt0KR0dHdOzYEdu3b8eiRYtw9OhRzJo1Czdv3kR0dLTGFUCT\nSqUQCoWwsrJCXFwc5s6dCyLCBx98gPr6ely6dAn37t3jWgbq3CpoqlOnTrC2toZIJEJUVBTEYjEA\nYMOGDYiMjOSe114+Z62JdRn9F9SkqyE/Px98Ph8GBgYwNTVFTk4O5syZg4CAAAwaNAhxcXGYPXs2\nDA0NueM15cP3v+DxeEhISMD+/fvh6+uLkSNHoqysDDk5ORCJRBAIBAgKCoKvry9MTExafRc4Ho+H\npKQk+Pv749tvv0VxcTHCwsKQk5OD1atXw9raGrW1tVi8eDGcnJxaJaaWQES4c+cOvL29YWFhgV69\nesHQ0BDOzs5Yt24dAMDb2xsjRozgBpA1iVAohEQiwbFjxzBjxgx4eXlBKBSivr6eGzwG2k93bKtS\nZfNEnSkrW545c4bs7Oxo7dq15Ofn16z4WlxcHA0aNKhZoba27uUmekREBPF4PNq3bx8RNc7lT0hI\noKVLl5K3tzfFxsa+8rjWIJfL6dKlS3Tjxg2Ki4sje3t7ysnJoeHDh9OiRYuaPVfd14i8Kr7AwECa\nPn06Xb16lZ4/f05ERL6+vmRkZERFRUWqCLNFKacIZ2Rk0ODBg+nSpUsqjqjtYwnhJcqS1ESNfeC2\ntrZUXFxMn3zyCQ0ZMoQWLlxImZmZVFVVRZMnT1bpDU8VlOdZUlLCjQkcP36ctLW1KSUlpdlzlGsy\nWvNmq1zzUVdX1yyOhQsXcq/VunXrmq0f0QTKcxGLxRQaGsqVAtmxYwdNmzaN4uPjKTY2lhYtWkS3\nbt1SZagtpqGhga5evUrDhw+n06dPE1H7+ZypCusyaqK8vBzbt2+HRCLBkCFDUFxcjFmzZqGoqAhh\nYWEIDQ1FVlYW4uPjMXLkSLz33nsYPHhwu5laSi/GVM6dO4cVK1bg9OnTuHfvHjw9PWFra4sFCxZg\n5MiRXJ+1csygNZv2PB4Pp06dwvr165Geng6hUAgLCwvEx8ejc+fOePDgAeLi4nDkyBFYWVmp/bRS\n4NfrnpaWBh8fH9TU1CAjIwNPnjzBypUr8ezZMyQmJuLw4cPw9fXF6NGjmx2nqfh8Prp16wY3NzeM\nHDmy3XzOVIkNKjchEAggFAqRmZkJXV1dTJ8+HUDjYNauXbswZswYXLhwARKJhJsfrdQe3qQ8Hg/p\n6en4+uuvsWfPHkgkEmRnZ+Pjjz/GN998gydPnsDNzQ0lJSXo2rVrq00FpJcWxR06dAiLFy+GVCrF\n2rVrsW/fPnh5eWHPnj0oKChAQECARg0gK6/7li1bcOLECQwdOhTHjx9HamoqwsPD4e3tDS0tLa7s\nujIRtIX3pFAoRL9+/bjHbeGc1JrqGifqQ6FQcGMGVVVVFBoaSn5+fvTDDz8QEdHy5cvJxcWFEhMT\nycrKiqtb1N6ar0+fPiUPDw96++23ud/duHGDPD09KSEhgYhIJX3XytchLS2NvvrqK9qyZQv3t4iI\nCLKxsaGffvqJiIiePXvGHaNJr9/FixdJIBBQUFAQETVu1HPixAny9vamnTt3UkNDA9ddpknnxagX\n1mX0Ap/Ph0gkwt27dzFz5kzcuXMH169fh5aWFvz8/JCUlIT09HSsWrUKLi4uGt8c/yPopSZ6586d\noa+vjwsXLuDx48dwdnZGz549cfnyZVRWVmLUqFHQ1dUFn89vteuj/D8pKSl499138eTJE/z888+w\nsLBA7969YWdnBy0tLWzYsAHz5s2Dnp4eF5cmvX7m5uawtrZGcHAw9PX1YW1tjYEDB6K6uhpOTk4w\nNDTUyPNi1Ixq85H6OHPmDNnY2NCFCxeIiKiiooJCQkJo9erVdP78eSJqf1VLleeYkJBA//znPyk8\nPJzKysro8uXLNHv2bPLy8qKkpCSysrLi9udVhbS0NJowYQJdv36diIg2bdpEK1euJLFYTDKZjIiI\niouLVRZfSzp79izZ2tpSRESEqkNh2iCWEKhxpeo777zDdSsobyIVFRX05Zdf0vLlyzWiKmRLUiaD\n5ORk6t+/P+3evZvs7e0pMDCQUlJS6PLly2RpaUmOjo7cdVPVfsMXL14kPp/PrdR9/vw5BQYGkpeX\nFyUmJjZL3m0hkZ8+fZoGDhxIJSUlXFcnw7QEVgAEjd1FZWVlkEqlAH5tcstkMgQEBGDjxo3NFp21\nB8oFeWFhYVi/fj38/Pxw6tQpSKVSxMbGwtnZGXv27EH//v2RlJQEACrbb3jixIk4efIk9u/fj+++\n+w4dO3bEpk2bYGRkhJ49ezbrQmkL3SnvvPMOkpKSYGxsrJbVShnNxcYQAHTs2BFVVVUoKChAz549\nYWhoiJSUFPj5+WHixIkaudrzz6AX/fEKhQI8Hg/JyclISkpCcXExHB0d0bt3b1hbWyMwMBDTp0+H\npaUl9PT0IBKJMGrUqGZF4VqbpaUlTE1NsW3bNmhra8POzg7jx49vs4lcR0cHgOZPLWXUC9sP4YWS\nkhLs3bsXYrEYTk5OiI6ORmhoKNzd3VUdWqugJgPIJSUl6N27N4DGbUGPHTsGCwsLzJs3D9XV1Zg7\ndy7OnTuH3r17QyaToaGhQaXJoKmYmBh89NFHSEhIgKGhIfsGzTCvgSWEJmpqapCeng6JRAJTU1M4\nODi0m8Uwym+a58+fx+bNm+Hq6go+n4+tW7ciOTkZoaGhKC4uRrdu3eDv748pU6ao7bfTx48f4623\n3lJ1GAyjcdjCtCaEQiHGjRvHPW4vyQD4ta7+hg0bEBUVhcOHD+PkyZN48OAB9u7di86dO+PgwYMw\nNzfHpEmTVB3u71ImA3VNWAyjrtig8u9oK6s9/wi5XM7taFZcXIyEhAQcOnQIpaWl8PHxgZ2dHaZP\nn46CggLs37+fKwWuztQ9PoZRN6yFwABoLNvh4uICHo+HnTt3YseOHRg5ciTMzMxw+/Zt3L59G1On\nTgURYfjw4SqbUcQwzJvDPtXt0MtdKcrH2traeP78OaRSKW7cuAGFQoHs7GyEh4dzWxVOmzZNVWEz\nDPOGsUHldqbpuMjNmzehr68PY2PjZs+5fPkyQkJCUFNTAx8fH3h4eHDHsm4Yhmm7WEJoZ5Q39djY\nWAQFBSE4OBj29vbc35XbYlZXV4OIoKur264G1xmmPWMJoR36z3/+Aw8PD+zbtw/Dhg1r9rdX3fxZ\ny4Bh2gc2y6gdKCoqwurVq7nHyrr5ymTQ0NAAAKiurn7lzCqWDBimfWAJoR0wNTWFl5cX7t69CwAY\nOnQo9PX1kZiYCJlMBi0tLSQnJ2P79u2oq6sDazQyTPvEuozaMCKCXC7npog6OTlBIBBwK4/v3LkD\noVAIBwcHrFu3Dt988w1cXV1VHDXDMKrCEkIb1XQsIC8vj5s2OnbsWPTs2RNRUVFISEjAuXPnIJPJ\n4O7urtblKBiGefNYQmijmtYm8vPzQ2RkJOzs7AAAo0aNgqGhIX744QcAwPPnz6Gtrc1mEzFMO8cS\nQhuWlZWF+fPn48SJE7CxscG9e/fQs2dPdO7cGQ4ODtDV1UVCQgI31ZRhmPaNrVRuQ17+hq+lpYU5\nc+bgxo0biIuLQ2RkJCwsLPDRRx8hLS0NqampAMCSAcMwANgsozaHx+MhPj4ecXFxMDAwQG1tW/uv\nOwAAA19JREFULY4fPw4zMzOcOHECZmZmyMrKAgA4OjqCGrdRVXHUDMOoA5YQ2hAej4eYmBh88MEH\nqK+vh7GxMbZt24ZTp07hb3/7G+rr63Hp0iWYm5s3O4aNGTAMA7CE0KaUl5dj9+7d+P777+Hu7o5r\n167h+++/h0KhgFgsxrJlyxAYGIixY8eyVgHDML/BxhA02MtTRJV7FERHRyMvLw8CgQAikQgVFRVY\nvHgxDhw4AEtLS5YMGIZ5JdZC0FBNb+r5+fl4+vQp3nrrLQQGBqKyshJLlizB4cOHER4ejoyMDHTu\n3JlbiwCwqaUMw/wWm3aqoeRyOQQCAWJjY7F161aMHj0aCoUCa9euhZmZGQDg4sWLCAgIQFBQEKZM\nmaLiiBmGUXeshaBhqqqqADTucJaRkYHNmzcjJiYGOjo6EIvFCAwMxLVr11BdXY3du3fjyy+/5FYg\nMwzD/B7WQtAg5eXlCA4OhpWVFebPn4/09HR07NgRjx8/xsaNG7Fr1y6Eh4dDKpUiODgYRkZGbD8D\nhmH+MNZC0CACgQBCoRCZmZk4c+YMRowYAVtbWyQmJmLXrl0YM2YMTExM0KNHD1RXV0NXV5c7liUD\nhmH+PywhaABl1dKuXbtyYwSJiYk4efIkAEAqleLTTz+FSCRCbGwsVq5cCRsbG9YyYBjmtbAuIw2g\nnF4qEonw/PlzODs7Y+/evSgqKsLUqVPh6uqK999/HzU1NZg7dy5mzZrFqpYyDPPaWELQELGxsQgM\nDMTnn38ONzc3PHv2DAcPHkRhYSEmT56MyZMns6qlDMP8T1iXkQaorKzEgQMHEBYWBjc3N9TX10NP\nTw/vvfceTExMcObMGUgkEmhrawNg5SgYhvlz2EplDcDn81FWVgapVArg12/+MpkMAQEBKCkpgaGh\noSpDZBimDWAtBA2go6MDDw8PpKamIjc3F1paWkhJScGCBQvw+PFj9O3bV9UhMgzTBrAxBA1RUlKC\nvXv3QiwWw8nJCdHR0QgNDYW7u7uqQ2MYpo1gCUGD1NTUID09HRKJBKampnBwcGADyAzDtBiWEDQY\nSwYMw7QkNqiswVgiYBimJbFBZYZhGAYASwgMwzDMCywhMAzDMABYQmAYhmFeYAmBYRiGAcASAsMw\nDPMCSwgMwzAMAOD/ANLifp9XPWcHAAAAAElFTkSuQmCC\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10eeafd50>"
|
|
]
|
|
},
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAbwAAAFhCAYAAAALEB8uAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdYFGfXBvB7qNJ7EaSIxgiKghWxYVBj16BGiSWoiSXR\naEyR1xjljbFrLNGYmESJPTHGGuyK+tl7I4JtsYIFlSqwy/n+8N2JC4iKw8yynN91eSWz7Mw8c+/O\nnJ3nmdkViIjAGGOMGTgjpRvAGGOMyYELHmOMsQqBCx5jjLEKgQseY4yxCoELHmOMsQqBCx5jjLEK\nQdaCl5qaihYtWsDW1hZffPGFnKsulzp06IBly5Yp3Qy95evri127dsm2PiMjI1y9erVM1xEVFYWv\nv/66zJZvY2MDlUr1SvPEx8fDy8urbBpk4GrXro19+/ZJvlyVSgUjIyMUFBRIvmylDRs2DN9++22Z\nLNvkRU/w9fXF3bt3YWxsDCsrK7Rv3x7z58+HlZXVK69s0aJFcHV1RXp6eqkaW9HExcUp3QS9JggC\nBEEo9m9RUVHw8vLCxIkTS7XssLAw9OvXD4MGDXqdJr6ykrZJChkZGWW27Nfxuq+Xvjp//rzSTZDV\nq76OsbGx+PXXX7F//37xsYULF5ZV8158hicIAjZv3oyMjAycPHkSx48ff+XqS0QoKChAcnIy/P39\nS9VQtVpdqvlY+aBvr29ZFp0X4e+C0E/69h5lpUAv4OvrS7t27RKnP//8c+rUqRMRER06dIiaNGlC\n9vb2VLduXYqPjxef17JlS/rqq6+oadOmZGFhQX379iVTU1MyMzMja2tr2rVrF+Xm5tLIkSPJw8OD\nPDw8aNSoUZSbm0tERHv27CFPT0+aNm0aubu7U79+/SgmJoZ69OhBffv2JRsbGwoMDKSkpCSaPHky\nubq6kre3N23fvl1sw+LFi8nf359sbGzIz8+PfvrpJ/Fv2uXPmjWLXF1dqXLlyrRkyRLx79nZ2TR6\n9Gjy8fEhOzs7atasGeXk5Lxwuws7ceIEBQUFkY2NDfXs2ZPeffddGjduHBERpaWlUceOHcnFxYUc\nHByoU6dOdPPmTZ0Mf/nlFyIiWrJkCTVt2pQ+//xzcnBwoKpVq9KWLVueu97r16/TO++8Qy4uLuTk\n5ETDhw8nIiKNRkMTJ04kHx8fcnV1pf79+9Pjx4+JiOjatWskCAItWbKEvLy8yNHRkRYuXEhHjx6l\nwMBAsre3F5ejbVNoaCgNHz6c7OzsqGbNmjrvlZfJX/v69u/fnwoKCmjKlClUrVo1cnJyonfffZfS\n0tLEeZYuXUre3t7k5OREkyZNKvLe1Prpp5903mtdunQhIqKEhARq2bIl2dvbU61atWjjxo3FZjd2\n7FgyNjamSpUqkbW1NY0YMYKIiARBoB9//JHeeOMNsre3p48//lhnvl9//ZX8/f3JwcGB3n77bUpO\nTn7u67N//37xPeTl5UW//fYbERFFRUW99PtjyZIl5OfnRzY2NlS1alVasWIFERFdunSJWrRoQXZ2\nduTs7Ey9evUS5xEEga5cuUJEJb/Hn7Vnzx6qUqWKOH3r1i2KiIggFxcXqlq1Ks2bN0/825EjRygk\nJITs7e2pcuXKNHz4cMrLyxP/PmrUKHJ1dSVbW1sKDAyk8+fPP/f1Kqy4eYmI7t+/T507dyZbW1tq\n1KgRjRs3jpo1a0ZE/76nNRqNuJxn96vLly9Tq1atyMnJiZydnalPnz706NEj8bk+Pj40bdo0CgwM\npEqVKpFGo3ml/d/Hx0d8j06YMOGVjl8tW7ak6OhoatSoEdna2lLXrl3F/aHwdj169IgGDhxIlStX\nJk9PTxo3bpz4N+1++umnn5K9vT1Vq1aNDhw4QIsXLyYvLy9ydXUV339ERE+ePKHPPvuMvL29yc3N\njYYOHSq+L0o6bj7vddTu0zY2NhQQEEDr1q0joqf7Y6VKlcjY2Jisra3JwcGBiIjef/99cR8gIlq0\naBFVr16dHB0dqUuXLnT79m3xby/aJwt7qYK3c+dOInp6EK1VqxaNHz+ebt68SU5OTuJBd8eOHeTk\n5ET3798XXywfHx9KSEggjUZD+fn5FBUVRV9//bW47K+//pqaNGlC9+7do3v37lFoaKj49z179pCJ\niQlFR0dTXl4e5eTk0IQJE6hSpUq0fft2UqvV1L9/f/Lx8aHJkyeTWq2mn3/+mapWrSou/++//6ar\nV68SEdHevXvJ0tKSTp48qbP8CRMmkFqtpri4OLK0tBTf7B999BG1atWKbt++Lb7Jc3Nzn7vd9+7d\nK5Jdbm4ueXt707x580itVtNff/1FZmZm4jY+ePCA/vrrL8rJyaGMjAzq2bMndevWTZw/LCyMfv31\nVyJ6+qY1NTWlX375hQoKCmjhwoXk4eFR7GumVqupTp06NHr0aMrOzqYnT57QgQMHiOjpQbl69ep0\n7do1yszMpIiICOrXrx8R/bsTDRs2jHJzc2n79u1kZmZG3bp1o3v37tGtW7fI1dWV9u7dK7bJxMSE\n5syZQ2q1mn7//Xeys7MTd8qXyf/Z13fOnDnUpEkTunXrFuXl5dGQIUMoMjKSiIguXLhA1tbWtH//\nfsrNzaXRo0eTiYlJsQWPiIq81/Ly8qhatWo0ZcoUys/Pp927d5ONjQ0lJiYWO/+z2WsJgkCdO3em\nx48f0/Xr18nFxYW2bt1KRETr16+n6tWr08WLF0mj0dC3335LoaGhxS5bpVKRjY0NrV69mtRqNT14\n8IBOnz4ttlu7s5f0/sjMzCRbW1tKSkoiIqKUlBS6cOECERH17t2bJk+eTERP34Pa1167DdqC97z3\neGHPFjyNRkP16tWjiRMnUn5+Pl29epX8/Pxo27ZtRPT0A96RI0dIo9GQSqUif39/mjNnDhERbd26\nlerXry9+wLp48SLduXOn2NersJLm7dWrF/Xq1Yuys7Pp/Pnz5OnpSc2bNyei4gves6/t5cuXaefO\nnZSXl0f37t2jFi1a0KhRo8Tn+vj4UHBwMN28eZOePHnySvs/ke4Jw6sev1q2bEmenp504cIFysrK\nou7du1Pfvn2L3a5u3brR0KFDKTs7m+7evUuNGjUSP2Bq99PY2FgqKCigcePGkaenp/hhZPv27WRj\nY0NZWVlE9PSDRdeuXenhw4eUkZFBnTt3pv/85z/ie6Gk42Zxr+OaNWvE1+r3338nKysrSklJISKi\n2NhY8cOJ1rPL2LVrFzk7O9OpU6coNzeXRowYQS1atBCfW9I+WZwXFjwfHx+ytrYme3t78vHxoY8/\n/phycnJo6tSp4oFS6+233xY/KYSFhdGECROKbMizlbtatWo6Zynbtm0jX19fInoarJmZmc4OOGHC\nBGrbtq04vXHjRrK2tqaCggIiIkpPTydBEMSdorBu3brR3LlzxeVbWFjo7Aiurq7izmphYUFnz54t\nsowXbfez9u7dS56enjqPNWvW7Lk79qlTp8RPOURFC1716tXFv2VlZZEgCJSamlpkOQcPHiQXFxed\nbdN66623aOHCheJ0YmIimZqakkajEXeiZz9BOTk50R9//CFOd+/eXTyALVmypEjRbdSoES1btqzY\n7Sucf+HX19/fX6eA3b59m0xNTUmtVtN///tfsfhpt9/MzKzEgvfse23fvn3k7u6u85zIyEiKiYkp\ndv6wsDDxLEBLEASd4vHuu+/StGnTiIioXbt2OgVSo9GQpaUlXb9+vciyJ0+eTBERES/V7mc9+/7I\nzMwke3t7Wrt2LWVnZ+s8r3///jR48GCds8Fnt+HKlSslvscLe7bgHT58mLy9vYtsz4ABA4qdd/bs\n2fTOO+8Q0dODV40aNejw4cNF3pslbTcR0e7du4udV61Wk6mpqc4Hl7Fjx5Z4hlfchxmtdevWUXBw\nsDjt6+ur0/PzKvu/dv5nC96rHL/CwsLEQkP09IzIzMyMCgoKdLYrJSWFzM3Ndc7OV65cSa1atSKi\np/vpG2+8If7t7NmzJAgC3b17V3zMycmJzpw5QwUFBWRlZSV+KCJ6ejzRFuKSjptEL34diYiCgoJo\nw4YNYttKKngDBw6kMWPGiH/LzMwkU1NTsfekuH1y6tSpz133S43hbdiwAQ8fPoRKpcL8+fNRqVIl\nJCcnY82aNXBwcBD/HThwACkpKeK8L7qy6/bt2/Dx8RGnvb29cfv2bXHaxcUFZmZmOvO4urqK/29h\nYQFnZ2dxvMXCwgIAkJmZCQDYsmULQkJC4OTkBAcHB8TFxeHBgwfi/E5OTjAy+jcCS0tLZGZm4v79\n+3jy5AmqVatWpM0vs93Pbp+np6fOY15eXuIYTXZ2NoYMGQJfX1/Y2dmhZcuWePz48XPHcNzd3XXa\n+uy2PuvGjRvw8fHR2TatO3fuFMlcrVYjNTVVfMzNzU38fwsLiyLTWVlZ4nTh7fPx8cGdO3cAvDj/\nwq+vSqXCO++8I+YaEBAAExMTpKam4s6dO6hSpYrO9js5ORUXU7Fu375d5P3o4+ODW7duPXee4sbx\nCr8G2vyTk5MxcuRIse3athW3/Js3b8LPz++FbS7p/WFlZYXff/8dP/74Izw8PNCpUyckJiYCAKZP\nnw4iQqNGjVC7dm0sWbKkyLJLeo+XJDk5Gbdv39Z5/0+ZMgV3794FACQlJaFTp06oXLky7Ozs8NVX\nX4mv+VtvvYXhw4fj448/hpubG4YMGfLSF9G0atWq2Hnv3bsHtVqt89p6e3u/9Pakpqaid+/eqFKl\nCuzs7NCvXz+d9yigexx7lf2/OK9y/Cq8bm9vb+Tn5+P+/fs6y0xOTkZ+fj4qV64stmno0KG4d++e\n+JzC+zDwdP979rHMzEzcu3cP2dnZqF+/vris9u3b66zzecfN51m6dCmCg4PF5Z0/f75Ixs9T+Hhl\nZWUFJycnnf3qeftkcUp9W4K3tzf69euHhw8fiv8yMjLw5Zdfis950cC/h4eHziXS169fh4eHx3Pn\nf5ULCXJzc9G9e3d8+eWXuHv3Lh4+fIgOHTq81AUBzs7OqFSpEi5fvlzkby+z3VqVK1cucsC7fv26\nuB2zZs1CUlISjh49isePH2Pv3r2gp2fdL72dxfHy8sL169eh0WiK/K24zE1MTHR2iFdRePuSk5Ph\n4eHxUvkXfj29vb2xdetWnWyzs7Ph4eGBypUr48aNG+Jzs7OzS9xpCi/bw8MDN27c0Fl/cnKyThEt\naf4X8fb2xqJFi3TanpWVhZCQkCLP9fLywpUrV17Y9he9P9q2bYvt27cjJSUFNWvWxIcffgjg6cFt\n0aJFuHXrFn766Sd89NFHRW6nKOk9XhIvLy9UrVpVZzvT09OxefNmAE8vKQ8ICMDly5fx+PFjTJo0\nSefS+REjRuD48eNISEhAUlISZsyYobPNJSluXldXV5iYmOD69evi8579f+3V5NnZ2eJjzxansWPH\nwtjYGOfPn8fjx4+xbNmyIpf6P9u2V9n/pVB4u0xNTeHs7KzzHC8vL5ibm+PBgwdimx4/foxz5869\n8vqcnZ1hYWGBhIQEcVmPHj166SvrC7+OycnJGDx4MBYsWIC0tDQ8fPgQtWvXFt/Dr1ojsrKy8ODB\ngyIftF9WqQte3759sWnTJmzfvh0ajQZPnjxBfHy8zgGw8IG78HRkZCS+/fZb3L9/H/fv38c333yD\nfv36PXedr1II8vLykJeXB2dnZxgZGWHLli3Yvn37S81rZGSEgQMHYvTo0bhz5w40Gg0OHTqEvLy8\nl9purdDQUBgbG2P+/PlQq9XYsGEDjh07Jv49MzMTFhYWsLOzQ1paGv773/++9PaVpHHjxqhcuTKi\no6ORnZ2NJ0+e4ODBgwCeZj579myoVCpkZmZi7Nix6N27d7Fng8/z7Otw9+5dzJs3D/n5+VizZg0u\nXryIDh06lCr/oUOHYuzYseJOfu/ePWzcuBEA0KNHD2zevBkHDhxAXl4exo8fX+I9SG5ubjoH+ZCQ\nEFhaWmL69OnIz89HfHw8Nm/ejN69ez93/pKKkjYHbRZDhw7F5MmTkZCQAAB4/Pgx1qxZU+x8ffr0\nwc6dO7FmzRqo1Wo8ePAAZ86cKbLMkt4fd+/exYYNG5CVlQVTU1NYWVnB2NgYALBmzRrcvHkTAGBv\nbw9BEIq8viW9x0vSqFEj2NjYYPr06cjJyYFGo8H58+dx/Phxsc02NjawtLTExYsXsXDhQvGgdvz4\ncRw5cgT5+fmwtLREpUqVxDYXfr0Ke968RkZGiIiIQExMDHJycpCQkIClS5eK63RxcYGnpyeWLVsG\njUaDxYsX67yumZmZsLKygq2tLW7duiUW4Od5lf3/dRERli9fjn/++QfZ2dkYP348evbsWaRIVK5c\nGW3btsXo0aORkZGBgoICXLlypVT3/xkZGeHDDz/EqFGjxDPEW7duvfSxs/DrmJWVBUEQ4OzsjIKC\nAixZskTnVg03NzfcvHkT+fn5Otut3QciIyOxZMkSnDlzBrm5uRg7dixCQkKeexb/ohpR6oJXpUoV\nbNiwAZMnT4arqyu8vb0xa9asEj/BF77HaNy4cWjQoAHq1KmDOnXqoEGDBhg3btxLz/+85wBPb7Cd\nN28e3n33XTg6OmLVqlXo2rVrifM+a+bMmQgMDETDhg3h5OSE//znPygoKHjudhd38DU1NcVff/2F\nX3/9FQ4ODlixYgU6deokduONGjUKOTk5cHZ2RmhoKNq3b//cNr3MtmsZGRlh06ZNuHz5Mry9veHl\n5YU//vgDADBw4ED069cPLVq0gJ+fHywtLfH999+/VCbFPadx48a4dOkSXFxc8PXXX2Pt2rVwcHAo\nVf4jR45Ely5d0LZtW9ja2qJJkyY4evQoACAgIAALFizAe++9Bw8PDzg6OpbYZT5o0CAkJCTAwcEB\nERERMDU1xaZNm7Blyxa4uLhg+PDhWLZsGWrUqFHs/CNHjsSff/4JR0dHjBo16rk5aLehW7duGDNm\nDHr37g07OzsEBgZi27Ztxc7n5eWFuLg4zJo1C05OTggODsbZs2eLLLOk90dBQQFmz54NT09PODk5\nYf/+/eL9S8ePH0dISAhsbGzQtWtXzJs3D76+vkUyf957/HnbCgDGxsbYvHkzTp8+DT8/P7i4uGDw\n4MHiGcDMmTOxcuVK2NraYvDgwTofKNLT0zF48GA4OjrC19cXzs7O4hdQFH69Citp3vnz5yMzMxPu\n7u4YOHAgBgwYoHMc+vnnnzFjxgw4OzsjISEBTZs2Ff82YcIEnDx5EnZ2dujcuTO6d+9e4j7wKvt/\ncRm+7PFL+//9+vVDVFQUKleujLy8PMybN6/Y5y5duhR5eXkICAiAo6MjevbsKZ7JvsqxAwCmTZuG\n6tWrIyQkBHZ2dmjTpg2SkpJeat7Cr2NAQAA+++wzNGnSBO7u7jh//jyaNWsmPj88PBy1atWCu7u7\n2N37bHvDw8MxceJEdO/eHR4eHrh27RpWr15dYn4lHsNKHF3UAwMGDCBXV1eqXbt2kb/NnDmTBEGg\nBw8eKNCy0mnUqBHFxsYq3QxJFDfgzJjSDOV9WdLFNax09P67NAcMGICtW7cWefzGjRvYsWOHzoCm\nPtq3bx9SUlKgVqvx22+/4fz582jXrp3SzWKMlQPEX0IgKb0veM2bN4eDg0ORx0ePHo3p06cr0KJX\nk5iYiKCgIDg4OGD27Nn4888/S32BiL4p66/BYqw0DOl9aSjboS8EKgcfIVQqFTp37ixedbRhwwbE\nx8dj9uzZqFq1Kk6cOAFHR0eFW8kYY0yfvfDLo/VNdnY2Jk+ejB07doiPlYOazRhjTGHlruBduXIF\nKpUKdevWBfD0Jt769evj6NGjOjd1AkD16tVfeGk5Y4wxXXXr1sXp06eVbobk9H4Mr7DAwECkpqbi\n2rVruHbtGqpUqYKTJ08WKXbA0+JI/7unQ5//TZgwQfE2GNI/zpOz1Nd/5SVP7X2hhkbvC15kZCRC\nQ0ORlJQELy+vIl+TZAiDuq/6g5ysZJyndDhLaXGeytL7Ls1Vq1aV+Pey/gVqxhhjhkHvz/Aqgqio\nKKWbYFA4T+lwltLiPJVVLm5LKC1BEGDAm8cYY2XCUI+dfIanB+Lj45VugkHhPKXDWUqL81QWFzzG\nGGMVAndpMsYY02Gox04+w2OMMVYhcMHTA9yvLy3OUzqcpbQ4T2VxwWOMMVYhVOgxvOiYaKQ8SpGx\nRfrL3d4dU2OmKt0MxpgeMNQxPL3/ppWylPIoBb7dfJVuhl5QrVcp3QTGGCtT3KWpB1SnVUo3waDw\nOIl0OEtpcZ7K4oLHGGOsQuCCpwd8g3yVboJBCQsLU7oJBoOzlBbnqSwueIwxxioELnh6gMfwpMXj\nJNLhLKXFeSqLCx5jjLEKgQueHuAxPGnxOIl0OEtpcZ7K4oLHGGOsQuCCpwd4DE9aPE4iHc5SWpyn\nsrjgMcYYqxC44OkBHsOTFo+TSIezlBbnqSwueIwxxioELnh6gMfwpMXjJNLhLKXFeSpL7wvewIED\n4ebmhsDAQPGxL774Av7+/qhbty4iIiLw+PFjBVvIGGOsPND7gjdgwABs3bpV57G2bdviwoULOHPm\nDGrUqIEpU6Yo1Dpp8BietHicRDqcpbQ4T2XpfcFr3rw5HBwcdB5r06YNjIyeNr1x48a4efOmEk1j\njDFWjuh9wXuRxYsXo0OHDko347XwGJ60eJxEOpyltDhPZZXrgjdp0iSYmZnhvffeU7opjDHG9JyJ\n0g0ordjYWMTFxWHXrl0lPi8qKgq+vr4AAHt7ewQFBYn96Ck3U4DT/46hac+0Kuq09tOnNh+e5uln\n6Ut7yvu0lr60JywsDPHx8YiNjQUA8XhpiAQiIqUb8SIqlQqdO3fGuXPnAABbt27FZ599hr1798LZ\n2fm58wmCgJI2L2pUFHy7+Urd3HJJtV6F2DmxSjeDMaYHXnTsLK/0vkszMjISoaGhSExMhJeXFxYv\nXowRI0YgMzMTbdq0QXBwMD766COlm/laeAxPWoU/SbPS4yylxXkqS++7NFetWlXksYEDByrQEsYY\nY+WZ3p/hVQR8H560tGMU7PVxltLiPJXFBY8xxliFwAVPD/AYnrR4nEQ6nKW0OE9lccFjjDFWIXDB\n0wM8hictHieRDmcpLc5TWVzwGGOMVQhc8PQAj+FJi8dJpMNZSovzVBYXPMYYYxUCFzw9wGN40uJx\nEulwltLiPJXFBY8xxliFwAVPD/AYnrR4nEQ6nKW0OE9lccFjjDFWIcj25dGJiYmYOXMmVCoV1Go1\ngKc/QbF79265mqC3eAxPWjxOIh3OUlqcp7JkK3g9e/bEsGHD8MEHH8DY2BjA04LHGGOMyUG2Lk1T\nU1MMGzYMjRs3RoMGDdCgQQPUr19frtXrNR7DkxaPk0iHs5QW56ks2Qpe586dsWDBAty5cwdpaWni\nP8YYY0wOAsn0O+6+vr7FdmFeu3atzNb5op+pjxoVBd9uvmW2/vJEtV6F2DmxSjeDMaYHXnTsLK9k\nG8NTqVRyrYoxxhgroswL3q5duxAeHo61a9cWe4YXERFR1k3Qe6rTKr5SU0Lx8fF8NZxEOEtpcZ7K\nKvOCt2/fPoSHh2PTpk1c8BhjjClGtjE8JfAY3svjMTzGmBaP4Ulg8+bNSEhIwJMnT8THxo8fL2cT\nGGOMVVCy3ZYwZMgQ/PHHH5g3bx6ICH/88QeSk5PlWr1e4/vwpMX3OkmHs5QW56ks2QrewYMHsXTp\nUjg6OmLChAk4fPgwEhMTXzjfwIED4ebmhsDAQPGxtLQ0tGnTBjVq1EDbtm3x6NGjsmw6Y4wxAyBb\nwbOwsAAAWFpa4tatWzAxMUFKSsoL5xswYAC2bt2q89jUqVPRpk0bJCUlITw8HFOnTi2TNsuFr9CU\nFl8FJx3OUlqcp7JkK3idOnXCw4cP8cUXX6B+/frw9fVFZGTkC+dr3rw5HBwcdB7buHEj3n//fQDA\n+++/j/Xr15dJmxljjBkO2Qre+PHj4eDggO7du0OlUuHixYuYOHFiqZaVmpoKNzc3AICbmxtSU1Ol\nbKrseAxPWjxOIh3OUlqcp7Jku0qzuBvP7ezsEBgYCFdX11IvVxCEEn91ISoqCr6+vgAAe3t7BAUF\nid0KKTdTgNP/dilqC4/c01pKrV87rd0ZtfmU12ktfWlPeZ4+ffq0XrWnvE/ra57x8fGIjY0FAPF4\naYhkuw+vY8eOOHToEFq1agXgadj16tXDtWvXMH78ePTv3/+586pUKnTu3Bnnzp0DANSsWRPx8fFw\nd3fHnTt30KpVK1y8eLHIfHwf3suT4j686JhopDx68bhsReBu746pMeV7bJlVXHwf3mvKz8/HP//8\nI3ZFpqamol+/fjhy5AhatGhRYsErrEuXLvjtt98wZswY/Pbbb+jWrVtZNZu9gpRHKfwB4n9U61VK\nN4ExVohsY3g3btwQix0AuLq64saNG3BycoKZmdlz54uMjERoaCgSExPh5eWFJUuWIDo6Gjt27ECN\nGjWwe/duREdHy7EJZYbH8KTFeUqncDcxez2cp7JkO8Nr1aoVOnbsiHfffRdEhLVr1yIsLAxZWVmw\nt7d/7nyrVq0q9vGdO3eWVVMZY4wZINkK3oIFC7B27VocOHAAwNPbCbp37w5BELBnzx65mqGX+D48\naXGe0tFe4MCkwXkqS7aCJwgCevTogR49esi1SsYYY0wk2xgeez4ec5IW5ykdHnOSFuepLC54jDHG\nKgRZC152dvZLfWF0RcNjTtLiPKXDY07S4jyVJVvB27hxI4KDg/H2228DAE6dOoUuXbrItXrGGGMV\nnGwFLyYmBkeOHBG/CDo4OBhXr16Va/V6jcecpMV5SofHnKTFeSpLtoJnampa5H47IyMeQmSMMSYP\n2SpOrVq1sGLFCqjValy6dAkjRoxAaGioXKvXazzmJC3OUzo85iQtzlNZshW877//HhcuXIC5uTki\nIyNha2uLOXPmyLV6xhhjFZxsBc/KygqTJ0/G8ePHcfz4cUyaNAmVKlWSa/V6jcecpMV5SofHnKTF\neSpLtoLXunVrPHr0SJxOS0sTr9hkjDHGyppsBe/+/fs6F604OjqW+18qlwqPOUmL85QOjzlJi/NU\nlmwFz9hOClWnAAAgAElEQVTYGMnJyeK0SqXiqzQZY4zJRraKM2nSJDRv3hx9+/ZF37590aJFC0ye\nPFmu1es1HnOSFucpHR5zkhbnqSzZfi2hXbt2OHHiBA4fPgxBEDBnzhw4OzvLtXrGGGMVnGwFDwDy\n8vLg6OgItVqNhIQEAECLFi3kbIJe4jEnaXGe0uExJ2lxnsqSreCNGTMGv//+OwICAmBsbCw+zgWP\nMcaYHGQreOvWrUNiYiLMzc3lWmW5oTqt4rMSCXGe0omPj+ezEglxnsqS7aKVatWqIS8vT67VMcYY\nYzpkO8OzsLBAUFAQwsPDxbM8QRAwb948uZqgt/hsRFqcp3T4bERanKeyZCt4Xbp0KfL7d4IgyLV6\nxhhjFZxsBS8qKkquVZU7POYkLc5TOjzmJC3OU1myjeElJSWhR48eCAgIQNWqVVG1alX4+fm91jKn\nTJmCWrVqITAwEO+99x5yc3Mlai1jjDFDI1vBGzBgAIYOHQoTExPEx8fj/fffR58+fUq9PJVKhZ9/\n/hknT57EuXPnoNFosHr1aglbLB8+G5EW5ykdPhuRFuepLNkKXk5ODlq3bg0igo+PD2JiYvD333+X\nenm2trYwNTVFdnY21Go1srOz4enpKWGLGWOMGRLZCl6lSpWg0WhQvXp1zJ8/H3/99ReysrJKvTxH\nR0d89tln8Pb2hoeHB+zt7dG6dWsJWywf/u5HaXGe0uHvfpQW56ks2S5amTNnDrKzszFv3jx8/fXX\nSE9Px2+//Vbq5V25cgVz5syBSqWCnZ0devbsiRUrVhTpJo2KioKvry8AwN7eHkFBQWK3QsrNFOD0\nv11g2gOl3NNaSq1fO63dGbX5vOo056k7/bp56sP06dOn9ao95X1aX/OMj49HbGwsAIjHS0MkEBEp\n3YjS+P3337Fjxw788ssvAIBly5bh8OHDWLBggfgcQRBQ0uZFjYqCbzffsm5quaBar0LsnNjXWgbn\n+S8p8mRMKS86dpZXsnVpHjt2DO+88w6Cg4MRGBiIwMBA1KlTp9TLq1mzJg4fPoycnBwQEXbu3ImA\ngAAJW8wYY8yQyNal2adPH8ycORO1a9eW5Idf69ati/79+6NBgwYwMjJCvXr1MHjwYAlaKj++b0xa\nnKd0+L4xaXGeypKt4Lm4uBT5ppXX9eWXX+LLL7+UdJmMMcYMk2wFb8KECRg0aBBat24NMzMzAE/7\niSMiIuRqgt7isxFpcZ7S4bMRaXGeypKt4P32229ITEyEWq3W6dLkgscYY0wOshW848eP4+LFi/yF\n0cXgMSdpcZ7S4TEnaXGeypLtKs3Q0FAkJCTItTrGGGNMh2xneIcOHUJQUBCqVq2q83t4Z8+elasJ\neovPRqTFeUqHz0akxXkqS5aCR0RYtGgRvL295VgdY4wxVoRsZ3gfffQRzp8/L9fqyhUec5KWoeQZ\nHRONlEcpirYh5WYK3Ku4K9oGAHC3d8fUmKlKN+O18RiesmQpeIIgoH79+jh69CgaNWokxyoZK/dS\nHqUo/1Vtp/Wji1i1XqV0E5gBkO0M7/Dhw1i+fDl8fHxgZWUFgMfwtPThgGJIOE/pcJbS4rM7ZclW\n8LZt2wYA4m0JhvjFpIwxxvSXbLcl+Pr64tGjR9i4cSM2bdqEx48fG/TPULwK/v02aXGe0uEspcW/\nh6cs2Qre3Llz0bdvX9y7dw+pqano27cv5s2bJ9fqGWOMVXCydWn+8ssvOHLkiDh+Fx0djZCQEHzy\nySdyNUFv8TiJtDhP6XCW0uIxPGXJdoYHQOc7NKX4iSDGGGPsZclWdQYMGIDGjRsjJiYGEyZMQEhI\nCAYOHCjX6vUaj5NIi/OUDmcpLR7DU1aZd2levXoVfn5+GD16NFq2bIn/+7//gyAIiI2NRXBwcFmv\nnjHGGAMgQ8Hr2bMnTpw4gfDwcOzatQv169cv61WWOzxOIi3OUzqcpbR4DE9ZZV7wNBoNJk2ahMTE\nRHz33Xc6998JgoDRo0eXdRMYY4yxsh/DW716NYyNjaHRaJCRkYHMzEzxX0ZGRlmvvlzgcRJpcZ7S\n4SylxWN4yirzM7yaNWviiy++gI+PDyIjI8t6dYwxxlixZLlK09jYGDNnzpRjVeUSj5NIi/OUDmcp\nLR7DU5ZstyW0adMGM2fOxI0bN5CWlib+Y4wxxuQg2zetrF69GoIgYMGCBTqPX7t2Ta4m6C1D+f02\nfcF5SoezlBb/Hp6yZCt4KpVK8mU+evQIH3zwAS5cuABBELB48WKEhIRIvh7GGGPln2xdmllZWZg4\ncSI+/PBDAMClS5ewefPm11rmyJEj0aFDB/zzzz84e/Ys/P39pWiq7PgTtLQ4T+lwltLisztlyfrV\nYmZmZjh48CAAwMPDA1999VWpl/f48WPs379f/HoyExMT2NnZSdJWxhhjhke2gnflyhWMGTMGZmZm\nACD+akJpXbt2DS4uLhgwYADq1auHDz/8ENnZ2VI0VXZ8r5O0OE/pcJbS4vvwlCXbGJ65uTlycnLE\n6StXrsDc3LzUy1Or1Th58iTmz5+Phg0bYtSoUZg6dSq++eYbnedFRUWJPzRrb2+PoKAgsVsh5WYK\ncPrfbhvtzi33tJZS69dOa3dGbT6vOs156k4bQp4pl1MUfz2lylMfpk+fPq1X7dFOx8fHIzY2FgAM\n+oe5BXr2u77K0Pbt2zFp0iQkJCSgTZs2OHDgAGJjY9GqVatSLS8lJQVNmjQRr/L8v//7P0ydOlVn\nXFAQBJS0eVGjouDbzbdU6zc0qvUqxM6Jfa1lcJ7/4jylJUWe7OW96NhZXsl2hte2bVvUq1cPR44c\nARFh3rx5cHZ2LvXy3N3d4eXlhaSkJNSoUQM7d+5ErVq1JGwxY4wxQyLbGB4RYe/evdi5cyd2796N\n/fv3v/Yyv//+e/Tp0wd169bF2bNnMXbsWAlaKj8eJ5EW5ykdzlJaPIanLNnO8D766CNcuXIFkZGR\nICL89NNP2LFjB3744YdSL7Nu3bo4duyYhK1kjDFmqGQreHv27EFCQgKMjJ6eVEZFRSEgIECu1es1\nvtdJWpyndDhLafF9eMqSrUuzevXquH79ujh9/fp1VK9eXa7VM8YYq+BkK3jp6enw9/dHy5YtERYW\nhoCAAGRkZKBz587o0qWLXM3QSzxOIi3OUzqcpbR4DE9ZsnVpFr4/Dvj30ldBEORqBmOMsQpKtoLH\nfdfPx+Mk0uI8pcNZSouPg8qSrUuTMcYYUxIXPD3A4yTS4jylw1lKi8fwlCVrwcvOzkZiYqKcq2SM\nMcYAyFjwNm7ciODgYLz99tsAgFOnTlX4qzO1eJxEWpyndDhLafEYnrJkK3gxMTE4cuQIHBwcAADB\nwcG4evWqXKtnjDFWwclW8ExNTWFvb6+7ciMeQgR4nERqnKd0OEtp8RiesmSrOLVq1cKKFSugVqtx\n6dIljBgxAqGhoXKtnjHGWAUnW8H7/vvvceHCBZibmyMyMhK2traYM2eOXKvXazxOIi3OUzqcpbR4\nDE9Zst14npiYiMmTJ2Py5MlyrZIxxhgTyXaGN3r0aNSsWRNff/01zp8/L9dqywUeJ5EW5ykdzlJa\nPIanLNkKXnx8PPbs2QNnZ2cMGTIEgYGBmDhxolyrZ4wxVsHJeplk5cqVMXLkSPz444+oW7dusV8o\nXRHxOIm0OE/pcJbS4jE8ZclW8BISEhATE4PatWtj+PDhCA0Nxa1bt+RaPWOMsQpOtoI3cOBA2Nvb\nY9u2bdi7dy8++ugjuLq6yrV6vcbjJNLiPKXDWUqLx/CUJdtVmocPH5ZrVYwxxlgRZV7wevbsiTVr\n1iAwMLDI3wRBwNmzZ8u6CXqPx0mkxXlKx5CyjI6JRsqjFKWbgdj1sYqu393eHVNjpiraBqWUecGb\nO3cuAGDz5s0gIp2/8S+dM8bkkvIoBb7dfJVuhuJU61VKN0ExZT6G5+HhAQD44Ycf4Ovrq/Pvhx9+\nKOvVlws8TiItzlM6nKW0OE9lyXbRyvbt24s8FhcX99rL1Wg0CA4ORufOnV97WYwxxgxXmXdpLly4\nED/88AOuXLmiM46XkZGBpk2bvvby586di4CAAGRkZLz2spRiSOMk+oDzlA5nKS3OU1llXvDee+89\ntG/fHtHR0Zg2bZo4jmdjYwMnJ6fXWvbNmzcRFxeHr776Ct99950UzWWMMWagyrxL087ODr6+vli9\nejV8fHxgaWkJIyMjZGVl4fr166+17E8//RQzZswo97+rx/360uI8pcNZSovzVJZs9+Ft3LgRn332\nGW7fvg1XV1ckJyfD398fFy5cKNXyNm/eDFdXVwQHB5d4M2dUVBR8fX0BAPb29ggKChK/3iflZgpw\n+t9uBu2bUe5pLaXWr53W5qjN51WnOU/daUPIM+VyiuKvJ+cp7bTWs/nEx8cjNjb26fP/d7w0RAIV\nvlegjNSpUwe7d+9GmzZtcOrUKezZswfLli3D4sWLS7W8sWPHYtmyZTAxMcGTJ0+Qnp6O7t27Y+nS\npeJzBEEocivEs6JGRfFlyv+jWq9C7JzY11oG5/kvzlNanKd0XibLFx07yyvZ+gJNTU3h7OyMgoIC\naDQatGrVCsePHy/18iZPnowbN27g2rVrWL16Nd566y2dYscYY4w9S7aC5+DggIyMDDRv3hx9+vTB\nJ598Amtra8mWX55vYud+fWlxntLhLKXFeSpLtoK3fv16WFpaYvbs2WjXrh2qV6+OTZs2SbLsli1b\nYuPGjZIsizHGmGGS7aIV7dmcsbExoqKi5FptucD35kiL85QOZyktzlNZZV7wrK2tn9vdKAgC0tPT\ny7oJjDHGWNl3aWZmZiIjI6PYf1zsnuJ+fWlxntLhLKXFeSpL1ju29+/fjyVLlgAA7t27h2vXrsm5\nesYYYxWYbAUvJiYG06ZNw5QpUwAAeXl56NOnj1yr12vcry8tzlM6nKW0OE9lyVbw1q1bh40bN8LK\nygoA4OnpiczMTLlWzxhjrIKTreCZm5vrfOdlVlaWXKvWe9yvLy3OUzqcpbQ4T2XJVvB69uyJIUOG\n4NGjR1i0aBHCw8PxwQcfyLV6xhhjFZws9+EREXr16oWLFy/CxsYGSUlJmDhxItq0aSPH6vUe9+tL\ni/OUDmcpLc5TWbLdeN6hQwecP38ebdu2lWuVjDHGmEiWLk1BEFC/fn0cPXpUjtWVO9yvLy3OUzqc\npbQ4T2XJdoZ3+PBhLF++HD4+PuKVmoIg4OzZs3I1gTHGWAUmW8Hbtm2bXKsqd7hfX1qcp3Q4S2lx\nnsqSreAZ8q/oMsYY03+yfrUYKx7360uL85QOZyktzlNZXPAYY4xVCFzw9AD360uL85QOZyktzlNZ\nXPAYY4xVCFzw9AD360uL85QOZyktzlNZXPAYY4xVCFzw9AD360uL85QOZyktzlNZXPAYY4xVCFzw\n9AD360uL85QOZyktzlNZ5bbg3bhxA61atUKtWrVQu3ZtzJs3T+kmMcYY02OyfbWY1ExNTTF79mwE\nBQUhMzMT9evXR5s2beDv7690014Z9+tLi/OUDmcpLc5TWeX2DM/d3R1BQUEAAGtra/j7++P27dsK\nt4oxxpi+KrcF71kqlQqnTp1C48aNlW5KqXC/vrQ4T+lwltLiPJVVbrs0tTIzM9GjRw/MnTsX1tbW\nRf4eFRUl/lKDvb09goKCEBYWBgBIuZkCnP63m0H7ZpR7Wkup9Wun4+PjAUDM51WnOU/daUPIM+Vy\niuKvJ+cp7bTWs/nEx8cjNjb26fMN+JdtBCIipRtRWvn5+ejUqRPat2+PUaNGFfm7IAgoafOiRkXB\nt5tvGbaw/FCtVyF2TuxrLYPz/BfnKS3OUzovk+WLjp3lVbnt0iQiDBo0CAEBAcUWO8YYY+xZ5bbg\nHThwAMuXL8eePXsQHByM4OBgbN26VelmlQr360uL85QOZyktzlNZ5XYMr1mzZigoKFC6GYwxxsqJ\ncnuGZ0j43hxpcZ7S4SylxXkqiwseY4yxCoELnh7gfn1pcZ7S4SylxXkqiwseY4yxCoELnh7gfn1p\ncZ7S4SylxXkqiwseY4yxCoELnh7gfn1pcZ7S4SylxXkqiwseY4yxCoELnh7gfn1pcZ7S4SylxXkq\niwseY4yxCoELnh7gfn1pcZ7S4SylxXkqiwseY4yxCoELnh7gfn1pcZ7S4SylxXkqiwseY4yxCoEL\nnh7gfn1pcZ7S4SylxXkqiwseY4yxCoELnh7gfn1pcZ7S4SylxXkqiwseY4yxCoELnh7gfn1pcZ7S\n4SylxXkqiwseY4yxCoELnh7gfn1pcZ7S4SylxXkqiwseY4yxCqFcF7ytW7eiZs2aeOONNzBt2jSl\nm1Nq3K8vLc5TOpyltDhPZZXbgqfRaDB8+HBs3boVCQkJWLVqFf755x+lm1UqKZdTlG6CQeE8pcNZ\nSovzVFa5LXhHjx5F9erV4evrC1NTU/Tu3RsbNmxQulml8iTzidJNMCicp3Q4S2lxnsoqtwXv1q1b\n8PLyEqerVKmCW7duKdgixhhj+qzcFjxBEJRugmQepTxSugkGhfOUDmcpLc5TWQIRkdKNKI3Dhw8j\nJiYGW7duBQBMmTIFRkZGGDNmjPicoKAgnDlzRqkmMsZYuVS3bl2cPn1a6WZIrtwWPLVajTfffBO7\ndu2Ch4cHGjVqhFWrVsHf31/ppjHGGNNDJko3oLRMTEwwf/58vP3229BoNBg0aBAXO8YYY89Vbs/w\nGGOMsVdRbi9aYYwxxl4FFzxWojt37mDMmDG4cuUKHjx4AAAoKChQuFXKKNwZwp0jpUNEnN1rKi5D\nzvTFuOCxElWuXBkAsGLFCnz88cc4ffo0jIyMKtzORUTirTC3b9/Gw4cPDerWGLkJgoBt27bhu+++\nw8qVK5VuTrkkCAKOHTuGLVu24Nq1axAEocJ+GH1ZXPDYc2l3nmnTpmHo0KEICwtD+/btsW/fvgq1\nc6WmpuLHH38EAOzYsQNdu3bFW2+9hXXr1iE9PV3h1pUv2g8OZ86cwYgRI5CamootW7ZgyJAhSjet\n3NBmuGvXLnTt2hVr165Fw4YNcerUKRgZGVWY/bI0yu1VmqzsaM/ejIyMkJeXBzMzM7i6umLo0KEw\nNzdHZGQk1q5di5CQEJ0zH0NERDhx4gQOHjyI1NRUHDlyBMuWLcPZs2exePFiZGVloUuXLrC1tVW6\nqeWCIAjYu3cvli9fjrlz56J9+/a4fPkyJk+ejKFDh4ofLNjzCYKAhIQE/Pnnn1i9ejVatGiBunXr\nIjw8HLt370ZQUBAKCgpgZMTnM4UZx8TExCjdCKZ/tF1OS5YsQUJCAho3bgwACA4Ohr29Pb788ku0\na9cOTk5OCre07GiLuaenJywsLHDq1Cmkpqbi888/R61atWBhYYEVK1aAiODn54dKlSop3WS9VPhD\n0ZkzZzBp0iT4+PigZcuWsLOzQ506dRAXF4e4uDh07dpVwdbqN41GA41Gg6lTp+LgwYN48803ERgY\niJCQEFhZWSEiIgKdOnWCh4eH0k3VS1zwmA7twenQoUP4+OOP0a5dO8yaNQupqalo3rw5jI2NUa9e\nPeTm5iI5ORmNGjWCRqMxuE+T2rNcQRBw+/ZtBAcHw8TEBMeOHUNqaiqaNGkCf39/GBsbY/ny5ejQ\noQNsbGwUbrX+eTbH5ORkEBGCgoLQrFkzfP311/Dz84O/vz/s7e0RHByM+vXrw83NTeFW65dnM8zO\nzoaFhQXCwsJw9+5dJCcnw9HREZ6enmjcuDFsbW1hZWWFatWqKdxq/cT34bEiEhMTMWXKFISGhmLw\n4MG4ffs23n33XbRs2RIxMTEwNTXFrl278Pvvv2PRokVKN7dMaAv/li1bMHz4cGzZsgVeXl7Ytm0b\nduzYgerVq+PTTz8F8HSMjw/SxdN2rW3evBlTpkyBs7MzXFxcMHr0aNy/fx+DBg3C1KlT0b17d3Ee\nQ+8mf1XaPLZu3YpZs2ahSpUqqFatGsaNG4fo6Gjk5+cjIiICoaGhYm6c4XMQq/AKCgp0puPi4qhT\np04UGRlJV69eJSKi27dvU926denzzz8Xn/fxxx/TnTt3ZG2rnC5cuEC1atWivXv3io9lZ2fT+vXr\nKSoqiqZPn05ERBqNhoiK5liR5eTkiP+fnJxMAQEBdOLECTp37hwtXbqUOnToQCkpKfTXX39RlSpV\nKDU1lfMrJD8/X/z/o0ePUkBAAG3evJmOHz9OQUFBNGLECCooKKCPPvqIPv30U3r48KGCrS0f+KKV\nCo6eOcG/evUqLC0tER4eDk9PT/z8889Yv349IiIi4OPjI17+rDV//nwlmiwbtVqNZs2aoUWLFlCr\n1SgoKICFhQVat24NQRDg5+cHAGJ3Ln+ifio1NRWrVq3CoEGDxG5eLy8v1KtXD8DTW11OnDiB7du3\no1+/fggJCYGrq6uSTdY7d+/eFW8FMjMzQ3Z2Nlq3bo2OHTsCAE6ePIlGjRrhwIED+Oabb5Camgp7\ne3uFW63/DGvghb0yQRDErruOHTti9OjRaNCgAezs7NCrVy+oVCqsXLkSycnJqFy5MkJDQw3yxuHi\ntsnS0hJbt27F5s2bYWJiAjMzM2zbtg2//fYbunTpgtq1ayvUWv1mbm6O9u3bIzMzE8ePH4e3tzfU\najW++uorAICTkxMcHR2RlJQEAHBxcQHAN04/KyUlBZ07d8aDBw9w48YN2NraYteuXeKXPwiCgFat\nWuHx48dwcnJCQECAwi0uH7jgMVy/fh0TJkzAzz//jJUrV6JXr17o0qULatSogYiICNy6dUvn3h5t\nkTQ02kvmZ8yYgd27d6NatWqYPXs2vvvuO8yfPx9xcXEYM2YMPD09lW6qXsrPz0d2djbs7e3h5eWF\nKVOm4JdffsGFCxcwa9YsqFQqvPvuu9i0aRNWrlyJ8PBwAE+/CB7gM2TgaYYAUKdOHTg6OmLhwoWY\nOnUqateujT59+qBhw4aIj4/H5s2bERcXx2d1r4gvWqmAqNCAdmZmJoYNG4ZJkybB29sbADBixAgY\nGxtjzpw5FeaijC1btmD06NEYNWoUZs6ciQ8++AAdO3bE/fv3MWvWLLi7u6Nr167o1KkTXxRQSF5e\nHuLj4+Hs7IykpCQkJyejb9++mDlzJszMzBAREQE/Pz98++23sLe3R6NGjdCxY0fO8Rm5ubnYv38/\nqlSpgszMTCQlJcHNzQ07duwAEWHKlCn4+eefxSuFhwwZwu/FV8RjeBVQQUEBjI2NkZmZiUqVKsHM\nzAyZmZnYuHEjhg8fDgBo1qwZTp06BQAGX+yICLdu3cKiRYuwceNG3LhxA0SEM2fOIDs7G1988QU2\nbdqk83ymy8zMDBkZGYiJiUFKSgpmz54NT09PfPXVV/jmm2+wdu1a9OvXD3PnzhXn4Rx15eXl4cmT\nJxg2bBiSkpKwe/duvPnmm7CwsMD69evx1Vdf4csvv8SQIUOQk5MDCwsLzvAV8X14Fcj169eRl5cH\na2trrF+/HkOHDsW5c+dgbGyMqKgoREdH4+LFizh+/DgWLlyIgQMHokaNGko3u0zQM/c2CYIAW1tb\nNG3aFFlZWRgxYgSOHDkCNzc3fPbZZzAzM0PdunVhbm6uMw/7d+xTEAR4e3vj4MGDMDc3R9u2bWFt\nbQ1nZ2eEhITg77//xvnz59GkSRPxBn3O8Snte9Hc3BzZ2dmYMmUKGjdujNDQUHh4eMDLywu2trY4\nc+YM4uPj0bJlS5iZmcHIyIgzfEVc8CqQb7/9FuPHj0fDhg2xcOFCDBgwAF5eXliwYAG8vb0xduxY\nPHjwAOnp6Rg8eDDefvttg+4uEQQBZ8+exfHjx2FsbAwPDw+kpKRg586dGDx4MHJycnDu3DkMHz4c\nXl5eSjdXbxkZGWHHjh1YtmwZpk+fDiMjI6xfvx6VKlWCv78/1Go1AgMDERwczDk+hyAI2LFjBxwd\nHREVFQUXFxf8+eefMDExwRtvvAEzMzOYmZmhffv2cHNzM7gvepALd2lWANqbf2fMmIGCggL06tUL\nffv2Re/evZGTkwMnJydMnz4d9+/fxwcffCDOZ8jdJYIgYP369Rg/fjz8/PxgYWGBGjVqYMiQIXB3\nd0fr1q1x48YNzJkzB7Vr1zbowv86tFf4fvbZZ5g9ezasrKwwYMAA5OTkYPPmzTh27Bh++eUX7Nmz\nh69qfQ5thiNHjsT333+Pt99+G7a2tkhLS8O6detw+PBhnD59GnPnzkXVqlWVbm75Jtsdf0wRmZmZ\ndP78eSIiOnLkCKWnp1N0dDT5+/tTSkoKERHl5uZSXFwchYWFkUqlEm+kNjQFBQXizc0ZGRnUu3dv\nOnnyJBER7d27l6Kjo2np0qV07949WrlyJR08eLDIfExXXl4ejRw5krZs2UJERE+ePBH/tmXLFpo9\nezZt3bpVqeaVC5mZmdS2bVvatWsXEf37BQbXrl2jP/74gzp16kTr169XsokGg8/wDFxaWhq+++47\nceB7y5YtmDJlCh49eoSIiAisW7cOrq6uCA8PR8OGDeHs7Kx0k8sEPXOGdvDgQaSnpyM5ORkXL15E\ncHAwQkNDcezYMRw8eBD9+vVDZGSkOB/Al8xrUaEzXVNTU6SlpSE+Ph7t2rUTxznPnj2LsLAwtGvX\nTpwP4ByBfzPU/letViMvL0+83eXJkyewsLCAjY0Nevbsia5du8LMzIwzlAB3BBuwgoICeHl5oW3b\ntli8eDHee+89BAYGAgAWLlyIunXrok2bNrh79y7MzMzEYkcG3JWZmJiIL774AnXq1MHnn3+OnTt3\nYu/evTAxMUH9+vWRlpaG9PR08b5DviigeMnJyUhISAAADBw4EPn5+diwYQMA4NixYxg6dCguXbok\nPp9zLCo1NRUAYGdnh6ZNmyI6OhppaWmwsLDAvn370KlTJ9y9e1fnPkXO8PVwwTNgRkZG2L17N86e\nPYtNmzbhzJkz+OWXX5CWlgYA+OGHH9CmTRudAxNgmJ8gtT86GhERgdatW8PDwwNBQUGoV68ehg8f\njowINqMAACAASURBVFGjRmHAgAHo168fbG1t+aKAYmjPSDZv3ox27dqhR48eGDNmDGrWrImqVavi\np59+QufOndG/f39ER0eLH67Yv7QZxsXFoVOnTujevTu2b9+OqKgo1K1bF02bNsWMGTMwbNgw/Oc/\n/4Grqyu/FyXEN54bOO137W3btg27du3CxIkTMXjwYAiCgL/++gsrV66EqampQV6UUVwXUN++ffHP\nP/9g7969sLa2Rn5+Ps6fP4/k5GRUqVIFDRo0MMgspHLx4kV8+eWXmDFjBtzc3NChQwe0b98eo0eP\nRm5uLpKSkuDg4IA333yTu+Ce4+jRo5g8eTKio6Oxd+9eJCcno1mzZnjnnXfw999/w8jICC4uLmje\nvDlnKDEewzMwhQ/WNWvWFL+sNzw8HBqNBsuXL8etW7cwePBgmJqaAjDcHUoQBBw+fBjXr19H7dq1\nsXz5cgwaNAg9e/bEX3/9BQsLCwQHByM4OBiAYXfnlpb2PfX48WPMmTMHt2/fhqmpKezt7bF27Vr0\n7t0b9+/fx9y5cxESEqIzr6G+r17Fs2N29+/fx3//+1+YmpoiJCQEISEh+Omnn7Bv3z4UFBSgW7du\nsLa2FucDOEMp8X14BkK7UwmCgJMnT2LEiBGoU6cOPD098fDhQ8yYMQO9e/fGm2++iVatWqFHjx5o\n2LChwZ7NaLdr//79GDhwIB4+fIh9+/bh6NGjmD9/Pnbv3o0FCxagV69eYtEHeJykONruYCcnJ/j6\n+uLSpUt4+PAhPD09UaVKFfFHgps1a6Zz0RPn+JQ2h3v37sHV1RWCIODPP/+EpaUl6tWrhwYNGuDa\ntWs4fPgwmjZtKv7CBL8XpccFzwA8+0nw0qVL8PPzw+HDh3Hu3DksWLAAHTt2xMWLF1GrVi24ubnB\n3NwclpaW4vyGuFNpf7V94sSJ+OGHH/DJJ58gMDAQ+/fvR3JyMr799lusW7cO/v7+8PDwULq5ekn7\noSEvLw8zZ87EokWLMGTIEPj6+mL//v1ISUmBu7s7vLy80L9/f4P/CrrS0mg0SEtLg4+PD9544w30\n7t0bVapUwapVq5Cbm4vg4GA0btwYwcHBqFKlitLNNWhc8AyEdiB81KhRCA8PR79+/dCkSRMIgoCl\nS5di586dyMjIQJcuXXQKnCEVu8Jnq/v378eMGTPQqFEj1KtXD9bW1sjJycGRI0fQqVMnREZGwsPD\nw2DPcksrKysLRkZGMDY2BgAYGxujTp06uHz5MpYuXYoPP/wQlStXxtatW3H37l3Uq1cPpqamMDIy\n4iz/Jz8/X8wPAKysrFC7dm0MHjwYb775Jt555x1YWlri559/Rn5+PurVqwc7OzsFW1xByHCvH5PB\nP//8QzVr1qQDBw4U+dujR4/owoULFBYWJt5obWievTn83r17lJ2dTURES5YsIT8/P9q5cycRPb0Z\nulmzZnT//n1Sq9WKtVdfXbhwgYYNG0apqam0b98+mjt3rvi3O3fu0Keffkr9+/enrKwsOnDggPil\nBuxfFy5coHHjxhERUUJCAm3fvl18P8bFxZG5ubl4I/mff/5JR48eVaytFQ0XvHLqxo0btGzZMnF6\n37591LNnT3E6Pz+fiEjnG0L69+8vfpuDodFu58aNG6lly5bUvHlzWrRoESUmJtLvv/9OlpaW9MEH\nH1C3bt1o3bp1CrdWP2VnZ1Pr1q1p8eLFRES0e/ducnNzo/nz5xMRkVqtpt27d1Pt2rWpV69eBvuN\nPK/j8ePH1LJlSzp27Bilp6fTqFGjaODAgbRr1y7KysoiIqLZs2eTIAgUFxcnzsff5CMPvsGjnCIi\nLFu2DGfOnAEA+Pn54cGDB9i+fTuApz+quXv3bkybNg1EhCtXruDKlSsG++OlgiDgxIkTmDVrFubO\nnYsRI0YgOTkZq1evRseOHTF37lzs378fHTp0QLdu3aDRaPiKzEIsLCzQp08fLF68GJ6enmjVqhX+\n/vtvzJ49GwsWLICxsTHMzc0RHh6OMWPG8P1hxdBoNMjOzsaqVavwySef4NNPP4W3tzfWrl2LQ4cO\nAQBCQ0MRERGhkx93A8tE4YLLSkHbFTd37lxas2YNERGlp6fTzJkz6YsvvqCpU6dSfHw81apVi7Zv\n3y7O9+DBA0XaK4c7d+7QgAEDKDQ0VHzswIED1Lp1azp8+DAREa1YsYI8PT1p7969SjVTb2nPMP7+\n+2+qVKkStWzZkjIzM4mI6OjRo1SnTh0aNGgQubq6it+byWclurR5zJ8/n0xMTGjo0KFE9PT7RseP\nH0+DBg2iQYMG0RtvvEHHjh3TmYfJgy9aKYe0nwzv3LmDOXPmoFWrVnBzc4O7uzssLS3x999/49Kl\nSxg2bBg6dOgAtVoNIyMjWFhYKNxy6VChe5Tof7/LdujQIWRnZ6Nx48bw8vLCoUOHoNFo0LBhQwQG\nBsLDwwM1a9aEo6Ojks3XO9ocnZycEBYWBkdHR8ydOxf169dHYGAg2rVrh5o1a6Jfv35o0aIFX5xS\nDG0ed+7cQZs2bTB79myYm5ujadOmaNGiBSwtLWFlZYU+ffqgefPmOvMwefA3rZRzEyZMwJIlS3D0\n6FG4u7uLjz958gSVKlUyyJtX/7+9e4/r+e4fP/749ImUUhNFGrqqCzeuzJxS5riIZptDuJjG5soy\nx7gcbkPjYsxp5JrDwjSnDhZpEeuAYcppF+VMuihySp8U+vTp/ftj+3xWxvea39inPj3vf0mf9+32\n+rxu717P1/H5KvudDh48yMOHD7GwsKBTp05s27aN+Ph4rKysGDRoECNHjiQsLIzOnTsbudQVU9nA\npdPpDDsLs7KyWL9+PefPn2fu3Lm4ubmVewZM6516GY4dO4aPjw//+te/GDNmTLnfSR0ah4zwKiH9\naEalUtG1a1du3rzJ9OnT8fb2xsLCAktLS8zNzcsdRjcl+u/03XffMWHCBJo0aUJISIhhDUr5ZX3z\n5MmTLFiwgC5duhhGuaI8/SW4+ktFdTodZmZm2NnZ4ebmxqVLl4iIiODtt9/G3NzcUPem9k79Udev\nXwegevXqqFQqdDodzs7O9OzZk/79+2NnZ0f79u0Nn5c6NA4JeJVAaWmp4RoRMzMzwx+K/mJXHx8f\nSkpKiI2N5dy5c+Tm5tKiRQuT/oPKyspi0qRJREVFkZubS1paGsnJySiKwvDhw6lTpw4PHjxArVbT\npk0bCXZPoe8QDR48mAsXLtC9e/dy9WRra8tf//pXw5S5Kb9P/78URSE3N5fg4GC8vLx45ZVXKC0t\nRa1Wo9PpcHJyws/Pj5o1a+Lq6mrs4lZ5EvAqsHv37nHv3j1sbW1JSEhg7dq1pKenGw6Ul+2Re3p6\n0qxZM+zt7fnmm2/w8fExqTW7J6lUKnr06MGdO3cMSXhfffVVxowZg42NDUOHDiUvL4+MjAzatWtn\n0nXxvJ4c+Xt4eHD06FHat29PjRo1ygU2W1tb7O3tjVXUCk+lUmFtbU1KSgrx8fG8++67hmlh/d9n\ngwYNcHV1lXXPCkACXgVVWFjIwoULOXPmDPfv32fKlCn4+fnxxRdfkJ2dTdeuXTEzM8PMzMwwAqxT\npw4uLi7079+/XOowU6JvNGrUqEHt2rU5fvw4tra2+Pr6kpmZSZ06dXjjjTdwd3fH1dWVzp07Y2dn\nZ+xiVyj6HKOPHj3CzMwMJycnVq1aRaNGjWQU8hyuXbtGbm4u9vb2eHl5kZaWRqtWrbCxsTH8TcrR\ng4pFNq1UYDExMRw6dIi8vDw8PT0JDAwkNzcXf39/vLy8mDt3ruFyyLJMrSf55Pcp+/P27dtZuXIl\nnTp1Ys2aNWzbtg1PT89yGzDEbzdJzJkzhxMnTlCzZk0CAgK4desWW7duZevWrZLi6hnKvncajYaP\nP/4YlUqFg4MDU6ZMISAggH79+hEYGGjkkopnkYBXwSiKYlgDADhy5AjLly9Hp9OxYMEC/vKXv3Dr\n1i18fX3p2rUrixcvNqng9izHjh0jPDycFStW/CYARkZGkpeXR+PGjfH19TW5gP8i6Ovk1KlTVKtW\nDScnJ2xtbUlOTmbu3Lm4uroSFxfHwYMHcXNzM6wPi1/p6/DGjRvUqlULlUpFQUEB48ePp0WLFuzY\nsQOdTkdUVBTu7u7GLq54CrkPrwJSq9V89913xMTEsH79egoLC4mLi2PHjh3069ePxo0bs3v3bq5c\nuWLSDXvZRvfx48dotVrg11GKfhQ3aNAgwzPSf/stfUOtv1nbx8eH5ORkwsPD6datG82bN+fevXvc\nunWL4OBgdu7cKcGujLKj4507dxISEoJOp8PX15ePPvqIiIgIrl27hpOTE5s2beLq1au4u7tLx6sC\nkre6gtE3TNOmTWPAgAEAdO/enR49epCdnc2WLVvIzMzE0dGRDh06mGQD//DhQ+DnRf9Lly6RmpqK\nnZ2d4R42PbVaTUlJSblnZbv3b+lHdrGxsURERBAeHs5nn33GyJEj+fHHH3F0dKRZs2bExsZSq1Yt\n8vPzjV3kCkX/Tp05c4bQ0FC2bNnCrl270Gq1hIWFUVBQwKuvvsoHH3zAP/7xD5YvX87jx4/lPayA\nJOBVQMeOHePTTz+ld+/ePHr0CIDevXvj4+PD9evXywU5U/ujun//PtOmTSMvLw+NRsOiRYsIDAxk\n8eLFpKSksGDBAqKioti3bx+lpaVPXcMUv45KdDodxcXFfPrppyQlJfHgwQNKSkoYNmwYo0ePZvny\n5ZSWlgKwd+9ejhw5YhhJV3U3b95k3rx5lJaWcufOHZYuXcqtW7ews7PD2dmZyZMnk5KSwtatWw3P\n2NjYUFBQYKhTUbFIa2FkT5v2uHHjBqdPn2bAgAHUqFEDgNTUVLp06UKHDh1MflPB5MmTyc/PJy8v\njzVr1gA/H9HIzs7G2tqa7du3k5+fT/Xq1fHy8jJyaSu2oqIibGxsWL9+PePGjSMxMZEWLVrQsGFD\nmjRpwunTpw3vn5OTE0lJSeVuLa/KHj58iL+/Pzdv3sTBwYGAgADy8vLYsmULgwcPpkGDBgwbNoy7\nd+9SWlpKaWkplpaWrF69Wo7BVFQvKUen+B3K3uGWmZmpnDlzxvDvoKAgZenSpYqiKEpqaqrStGlT\nQxJkU1Q2ie5///tfZePGjUqnTp2UlJQURVF+Tpj93nvvKZs2bXrmc6K8uLg4xdPTUwkJCVEOHjyo\nFBQUKAMGDFB69uypzJgxQ2nbtq0SExNj7GJWOGXfqeLiYuXDDz9URowYoWi1WiUxMVEJCgpSBgwY\noGzYsEFxc3NTEhISjFha8TzkHJ6R6RfCg4KCSE1N5cCBA7Ru3RoHBweio6NZt24dkZGRzJ8/n27d\nuhm7uC+Vfv1y1qxZDBs2jFq1arFhwwYaNGiAi4sLBQUF5OTk0LFjx988J8pvrsjOzmbhwoUEBARQ\nUlLC999/j42NDRMmTGDfvn1cvnyZuXPn0rNnT8OzUo/l6zAjI4O6devi7u7Of/7zH/bs2cOoUaN4\n5ZVXSE5OJicnh+DgYPz8/AwJIETFJgHPiPTJj6dPn87u3btRqVQsWrQIgD59+vDRRx/RqVMnhg4d\nSrt27Uw24ay+sb1w4QKzZ88mJCSEVq1a0bBhQ3Q6HRs3bqRhw4Y4OTkZDtfrmVpd/FH6ewEPHjyI\noigEBwfj4uKCVqslISEBc3Nzxo8fz65du7h27Rqvv/46VlZWUo9lqFQqEhISeO+993jzzTdp1qwZ\nrq6u/PjjjyQnJzNixAicnZ3JyclBp9Ph5uaGtbW1sYstfgfpkhiZvb09X375JcePHycsLIzDhw+T\nlpZGUFAQFy9exMXFhYYNGxo+b0oN0+PHjw272a5du8bmzZu5evUq6enpADg4ONC/f3+6devGnDlz\naNasGV27djXJnal/lL7TkJKSQt++fTl48CArVqwgPT2devXq0bt3b9q1a8e3336LSqVi+fLl3Llz\nR0Z2T9B3vP75z38SHh7O3/72N9RqNU2bNmXcuHHcv3+f8ePH061bN15//XVyc3MlwUElIgfP/0Rl\nR2h5eXlUq1bN0DOcPHky7u7ujBo1ilWrVrFhwwY2b95c7loWU1JSUsKhQ4fIzMzE2tqajIwM+vbt\nS2xsLPfv36dPnz506dIFgNu3b1NUVESjRo2MW+gK7ty5c0ycOJEZM2bg7e3NnDlziI6OJiIigubN\nm3Pr1i2Ki4txdnYGkGw0v3gy6F+4cIH58+fz9ddfo9Pp0Ol0VK9enZKSEjIzMykqKqJly5YAFBQU\nYGNjY6yii+ckuzT/ZCqVitjYWNatW0d+fj5Dhgyhe/futGnThrVr16LVaomMjGTp0qUmG+wAzM3N\nsbe3Z+7cuZw+fZr169fj4eGBpaUlmzdvZs+ePWi1Wnx8fKhbt67hORmRlFe2Pk6dOsW1a9fYuXMn\n3t7ezJo1C7VaTe/evYmPj6dFixblnpNgVz5RwdmzZ7G0tMTW1pYDBw4QERHB4MGDUavV7N27l6NH\nj/LJJ58Av3YWJNhVLrKG9ydSqVScP3+eUaNG8e9//5smTZpw7tw5zp49S7t27bCzs2PXrl1MmDCB\nN9980yTX7Mp+J1tbW2JiYnB2dsbKyoqmTZvi7OyMq6srR48e5cqVK7Rq1apcImxTqosXQb8OHBkZ\nSWBgIPXr1+enn37ixo0btGnThk6dOpGfn0+9evXKjZClHn+l3zg2ZswYunXrRpMmTXB1dWXVqlVk\nZWWh0Wj45JNPGDhwIE2bNgWQDSqV1Z+8K7RK0m9zzsnJUXbv3q306tXL8LvU1FSle/fuSmpqqqIo\nivLw4UPDM6a25b7sd8rJyTH8X3p6ujJ69Ghl5syZiqIoikajUaKjo5ULFy4YrayVSXp6uvLqq68q\nS5YsURRFUaKiopTAwEBl2bJl5T5nau/Ti3LixAmlZcuWyvnz5xVFUZQbN24oR48eVTIyMpSBAwcq\nY8eOVb777jtFUaQOKzuZ0nzJ9PkgDx8+zIwZM/jyyy+pUaMG0dHR+Pv7065dO5o3b264t61atWqG\nZ02xF65SqYiPj2f27Nl4eXlRvXp1Fi5cyLBhw9i4cSP9+vUjPT2d6OhoScD7P2g0GqysrGjevDkJ\nCQn4+/ujKAqTJk1Cq9Xy/fffk5WVZRjZmeL79CLUqFGDli1bkpycTFRUFCkpKQBMnTqVyMhIw+cU\n2e5Q6cmU5kumUqlITExk7dq1BAUF0aFDB+7cuUNGRgbJycmo1WoWLVpEUFAQzs7OhqkSU2ycVCoV\n+/fvZ+LEiWzevJnr16+zatUqMjIyGDt2LC1btuThw4cEBATg7e1t7OJWWIqicPnyZUaOHIm7uzv1\n6tXD0dGRzp07M3nyZABGjhxJ+/btDRtUxLNZWVmRm5vLpk2bePfddxk+fDhWVlZotVrD5hSQPK2m\nQCaiX4Ine4LZ2dls3ryZa9euAeDv74+vry/37t1jy5YthIaG0r59e5PvQZaWlqLVag3Z5Xfs2MH+\n/fs5e/YsAQEBODs7M27cOHr06IGiKCZfH8+jbH2oVCrc3Nxo06YN8+fP56effqK4uJgWLVrQo0cP\nFixYQFZWFvXr1zdyqSuHmjVrMnbsWPbt20e/fv0oKChg5cqVUn+myGiTqSZMP8+fnZ1tWJPbunWr\nYmFhoRw6dKjcZ4qKigw/m+L6gE6nUxRFUR49elTuO7/33ntKXFycoiiKMnnyZKVJkybKyZMnjVbO\nik5fdykpKUpoaKghDd2SJUuUPn36KHv37lXi4uKUYcOGKWfPnjVmUSutkpIS5ejRo0rbtm2VHTt2\nKIoia3amRqY0XzDll23i8fHxjB49mh07dpCVlcXf//53WrVqxdChQ+nQoYNhXUW/Zmeq0yUqlYrt\n27czZcoUUlNTsbKywt3dnb1792JpaUlOTg4JCQl88803NG/eXI4dPIW+To4cOUJgYCBFRUWkpaVx\n9+5dPv74Y/Lz80lKSiI8PJygoCDeeOONcs+J38fMzAw7Ozt8fX3LXb0ldWg65OD5S5Camsrs2bOZ\nN28eubm5nDp1iszMTFauXMlXX31FcHAw2dnZ1KpVyyS3NytPHLB///33GTJkCBqNxlAHpaWlrF69\nmgsXLhAcHGy4+08a6adLTU0lJCSEhQsX4uHhwdatWzl8+DAeHh6MGDECc3Nz7ty5Q506daQOXxCp\nR9MjuzRfsLy8PJYuXUpubi6tWrUCwNnZmc8++4zk5GRGjRqFr68vdnZ2Ri7py6VSqUhNTeXYsWO0\nbt2awYMHA2BhYVEum4xGo6FWrVrSm/4f8vPzSUxMZO/evXh4eODv74+ZmRmJiYkUFhYyduxYateu\nbeximhR5F02PTGn+QU821JaWltSuXZvdu3dz+/ZtOnfujIODA/v27aOgoICOHTtibW2NmZmZSfYg\n9d/p0KFDvP/++9y9e5eTJ0/i7u5OgwYNaN26Nebm5kydOpXBgwdja2trqANTq4sXydXVlZYtW7J4\n8WJq165Ny5YtadasGYWFhXh7e+Po6Cj1KMT/IFOaf5C+gU9KSiItLY26devSt29f0tPTWbFiBTY2\nNowYMYLRo0cTGhpq8lf8wM/TbzNmzGDJkiV4eHgwc+ZM8vLyGDBgAN7e3lSrVo3s7GwaNGhg7KJW\nOvHx8cycOZPx48fz/vvvG7s4QlQqpreA9CfSB7sffviBjz76iJo1axIWFkZoaCjVqlVj7NixHDly\nhOnTp7N27Vq6detGSUmJsYv90uXn55OcnExiYiIAM2fOxN7envDwcH744QcURTEEO+lvPR8/Pz9C\nQkL4/PPPDdfTCCF+Hwl4f4A+N+aqVauYMmUK48aNY/v27Wg0GuLi4ujcuTOrV6/Gzc2N/fv3Az8n\nTTZ1PXr0ICYmhrVr17JlyxaqV6/OjBkzqF+/Pg4ODuWm3GT67fm988477N+/HycnJ0kALcRzMP3W\n9wXTj+r0KcMyMjK4ffs2e/bsoVevXjg7OzNlyhR69uzJmDFj8PLyQqvVsmnTJsMuuqrgnXfewdzc\nnJkzZ1JcXMzw4cOZN2+eBLgXRH+DhCmuAwvxssga3nMou0Gl7BrUoUOH2LRpE+7u7gwePJjCwkL8\n/f2Jj4+nQYMGFBcXU1JSUi7rf1URGxvL9OnTSUxMxNHRUUYkQgijkYD3HPS96V27dhESEoKPjw9m\nZmbMnj2bAwcOEBoayvXr17Gzs2PixIn07t1beuD8fIFr2TvthBDCGGRK8zno7x6bOnUqUVFRhIeH\nExMTQ05ODmvWrMHS0pL169fj6upKz549jV3cCkOm34QQFYFsWnkOOp0OjUZDREQE169fJzExka+/\n/pqbN28SGBhI69atefvtt7lw4QJr166lpKREGvgypC6EEMYkI7znoFar6d69OyqVii+++IIlS5bQ\noUMHXFxcuHjxIhcvXuStt95CURTatm1bJXZkCiFEZSEt8jM8Of2m/9nCwoLHjx+j0Wg4ffo0paWl\nnDp1irCwMJo2bQpAnz59jFVsIYQQzyCbVp6i7G7M9PR0ateujZOTU7nP7Nu3j6VLl1JUVERgYCAD\nBw40PCtTd0IIUfFIwHsKfdCKi4tj0aJFLF68mHbt2hl+rz+DV1hYiKIoWFtbS/JjIYSo4CTgPcOl\nS5cYOHAgX331FW3atCn3u6cFNxnZCSFExSa7NH9x9epVxo4da/hZnxVFH+z0OTALCwufelmrBDsh\nhKjYJOD9onHjxgwfPpwrV64A4OHhQe3atUlKSqK4uBhzc3MOHDjAwoULefTokSQ9FkKISqbKT2kq\nioJOpzMcIfD29katVhsyp1y+fBkrKys8PT2ZPHkyK1euxMfHx8ilFkII8byqdMAruxZ37tw5w7GC\nLl264ODgQFRUFImJicTHx1NcXIyfn5+kCxNCiEqqygc8fW7McePGERkZSevWrQHo2LEjjo6OfPvt\ntwA8fvwYCwsL2Y0phBCVVJUOeAAnTpxgyJAhRERE8Nprr5GVlYWDgwOWlpZ4enpibW1NYmKi4SiC\nEEKIyqnKZVp5coRmbm7OgAEDOH36NAkJCURGRuLu7s706dM5cuQIhw8fBpBgJ4QQlVyVbMVVKhV7\n9+4lISGBOnXq8PDhQ7Zu3YqLiwsRERG4uLhw4sQJALy8vFAURXZlCiFEJVflAp5KpSI2NpZJkyah\n1WpxcnJi3rx5bN++nUGDBqHVavn+++9xdXUt94ys2QkhROVW5QJeXl4ey5cvZ9u2bfj5+XH8+HG2\nbdtGaWkpKSkpjBo1ilmzZtGlSxcZ1QkhhAkx+TW8J48Q6O+oi46O5ty5c6jVapKTk7l//z4BAQGs\nW7eOpk2bSrATQggTY9IjvLJB6/z589y7d4+6desya9YsCgoKGDFiBOHh4YSFhZGWloalpaXhLB7I\n0QMhhDAlJn0sQafToVariYuLY/bs2bzxxhuUlpYyYcIEXFxcANizZw/BwcEsWrSI3r17G7nEQggh\nXhaTHOE9ePAA+PmG8rS0NEJCQoiNjaVmzZqkpKQwa9Ysjh8/TmFhIcuXL+fzzz83ZFARQghhmkxu\nhJeXl8fixYtp3rw5Q4YMITU1lerVq3P79m2mTZvGsmXLCAsLQ6PRsHjxYurXry/32QkhRBVgciM8\ntVqNlZUVx44dY+fOnbRv355WrVqRlJTEsmXL6NSpE87Oztjb21NYWIi1tbXhWQl2Qghhukwm4Olv\nPahVq5ZhjS4pKYmYmBgANBoNc+bMITk5mbi4OD7++GNee+01GdkJIUQVYTJTmvrjB8nJyTx+/JjO\nnTuzZs0arl69yltvvYWPjw8ffvghRUVF+Pv7069fP7n1QAghqhCTCXgAcXFxzJo1i/nz5+Pr60t+\nfj7r168nMzOTXr160atXL7n1QAghqiiTmdIsKChg3bp1rFq1Cl9fX7RaLba2tnzwwQc4Ozuzc+dO\ncnNzsbCwACRdmBBCVDUmk2nFzMyMO3fuoNFogF9HbsXFxQQHB5OdnY2jo6MxiyiEEMKITGaEj5ET\naQAAALJJREFUV7NmTQYOHMjhw4c5c+YM5ubmHDp0iKFDh3L79m0aNWpk7CIKIYQwIpNaw8vOzmbN\nmjWkpKTg7e1NdHQ0oaGh+Pn5GbtoQgghjMykAh5AUVERqamp5Obm0rhxYzw9PWWDihBCCNMLeE+S\nYCeEEAJMaNPKs0igE0IIASa0aUUIIYT4v0jAE0IIUSVIwBNCCFElSMATQghRJUjAE0IIUSVIwBNC\nCFElSMATQghRJfw/5a9/wr1GWjoAAAAASUVORK5CYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10eeac310>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 51
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"sample_sizes\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Performance growth rates for different sample sizes"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In the plot above, we've seen how the different implemantations perform for a fixed sample size n=500. Now, let us take a look at the effect of the sample size on the relative performances for each approach. We will consider the sample sizes 10, 100, 1000, 10000, 100000, and 1000000."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"funcs = ['cy_classic_lstsqr', \n",
|
|
" 'lin_lstsqr_mat', 'numpy_lstsqr', 'scipy_lstsqr']\n",
|
|
"\n",
|
|
"orders_n = [10**n for n in range(1, 7)]\n",
|
|
"times_n = {f:[] for f in funcs}\n",
|
|
"\n",
|
|
"for n in orders_n:\n",
|
|
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
|
|
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
|
|
" for f in funcs:\n",
|
|
" times_n[f].append(timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 22
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"#%pylab inline\n",
|
|
"#import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"plt.figure(figsize=(10,8))\n",
|
|
"\n",
|
|
"for f in times_n.keys():\n",
|
|
" plt.plot(orders_n, times_n[f], alpha=0.5, label=f, marker='o', lw=2)\n",
|
|
"\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
|
|
"plt.legend(loc=2)\n",
|
|
"plt.grid()\n",
|
|
"\n",
|
|
"plt.title('Performance of least square fit implementations for different sample sizes')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAmEAAAH4CAYAAAACdDpdAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XlcVOX+B/DPDLIz7JvsCl4VV9IQxQWFXCqXXFBLBDW9\nppZbtyxTKXOrvLef3bxXCyXF3VLLJU2QUivJzA0MFQUUUFAUZZEZZr6/P+YyMayDMMyZme/79fIl\nZ+ac5zznfM+c+c5znvMcERERGGOMMcZYixLrugKMMcYYY8aIkzDGGGOMMR3gJIwxxhhjTAc4CWOM\nMcYY0wFOwhhjjDHGdICTMMYYY4wxHeAkzIDdvXsX/fv3h62tLf7xj3/oujo6V1ZWhuHDh8Pe3h7j\nx4+v8X5sbCyioqJ0UDP9t2/fPnh7e8PW1hbnz59H586d8dNPP2m8fGPn11RmZibEYjEUCkWzl61r\nr732Gj788MMWXWdlnCUSCS5cuNDs5Vf9DGZnZ0MikaByFKXazmdTpkyBo6MjQkJCmr0uhiA5ORne\n3t7NWubJkyfRoUOHZi3TmLXSdQWYOj8/P+Tn58PExATW1tYYNmwY/v3vf8Pa2rrRZW3cuBGurq54\n9OiRFmqqf/bu3Yv8/HwUFhZCLK75+0MkEmm9Dn5+fti0aRMGDRqk9XW1pDfffBPr16/H8OHDAQCX\nL19WvRcbG4uMjAxs3bq1zuWrzm8MYmJi4O3tjeXLl2s0f3x8POLi4nDy5EnVa//5z3+0Vb06VY9z\nc6v6GfTx8cHjx49V09XPZydPnsTx48eRm5sLCwsLrdSnLpmZmWjbti0qKipqPZcYsn79+uHPP//U\ndTUMhnEdPXpAJBLh4MGDePz4Mc6dO4ezZ882+tcuEUGhUCArKwsdO3Z8qnpUVFQ81XJClpWVhb/9\n7W91njRbYtxikUjUIutpisbGnoiQnZ2NwMBALdWICUFT49zU1sjq57OsrCz4+fk9VQLWXOc3oX+W\nmR4gJih+fn6UmJiomn7zzTfpxRdfJCKiX375hXr37k329vbUrVs3Sk5OVs03YMAAWrx4MYWGhpKl\npSVNmjSJTE1NyczMjGxsbCgxMZHKy8tp7ty55OHhQR4eHjRv3jwqLy8nIqITJ06Qp6cnrVmzhtzd\n3SkqKopiY2Np7NixNGnSJJJIJNSlSxe6evUqrVy5klxdXcnHx4eOHTumqsOmTZuoY8eOJJFIqG3b\ntrRhwwbVe5Xlr127llxdXal169a0efNm1fulpaW0YMEC8vX1JTs7O+rbty+VlZU1uN3VpaWl0YAB\nA8je3p46depE3377LRERLV26lMzMzMjU1JRsbGxo06ZNNZZdtmwZTZo0STVd33rr29aCggJ64YUX\nyN7enhwdHalfv36kUCho0qRJJBaLydLSkmxsbOjjjz+uUYe6liUiOnfuHAUFBZFEIqHx48fT+PHj\n6b333iMios2bN1Pfvn3VyhKJRJSRkUFERAcPHqTu3buTra0teXt7U2xsrGq+mzdvkkgkori4OPLx\n8aEBAwYQEVFcXBx17NiRHBwcaMiQIZSVlVWjvk+ePCFra2sSiURkbW1NAQEBRETk6+tLx48fpyNH\njqjt9+7du9caN19fX9Vxv2zZskYddwMGDKBFixZRcHAw2dra0siRI6mwsFBt2+RyORERPXz4kKZO\nnUqtW7cmT09Peu+991Tvbd68mfr06UPz588ne3t78vf3p9OnT9OmTZvI29ubXF1d6auvvlLb9oUL\nF5KPjw+5ubnRzJkzVcdsfcf7hg0b1D6bI0aMICKiVatWkb+/P0kkEgoMDKR9+/YRkfKYtrCwIBMT\nE7KxsSEHBwciIoqOjlbFn4ho48aNFBAQQI6OjjRixAjKzc1VOxb++9//Urt27cje3p5mz56teu/a\ntWvUv39/srOzI2dnZxo/frzGca7r81ZZv5kzZ9KwYcPI2tpa7bxW6caNG9S/f3+SSCT03HPP0Zw5\nc1SfwcrYVVRUUHR0tNo+27Bhg9o+qTyev/vuO+rWrRvZ29tTnz596OLFi2rH2Jo1a6hLly5kYWFB\ncrm8wXPqkiVLKDQ0lCQSCQ0ePJju3btHRETe3t4kEonIxsaGbGxs6Ndff62xbWfOnKEePXqQra0t\nubm50YIFC1TvjR07ltzd3cnOzo769+9Pqampavvttddeo2HDhpGNjQ317duX8vLy6I033iB7e3vq\n0KED/fHHH2rbtWrVKgoMDCQHBweaMmUKPXnyhIiUx6GXl5dq3pycHBo9ejS5uLhQmzZtaN26dTXq\nXenQoUMUGBhIEomEPD096ZNPPqlR5s6dO1X7wMbGhszMzCgsLEx1zNT1+ajvPGdsOAkTGD8/Pzp+\n/DgREWVnZ1OnTp1o6dKldPv2bXJycqIjR44QEdEPP/xATk5OqpPCgAEDyNfXl9LS0kgul5NMJqOY\nmBhasmSJquwlS5ZQ7969qaCggAoKCqhPnz6q90+cOEGtWrWiRYsWkVQqpbKyMlq2bBlZWFjQsWPH\nqKKigiZPnky+vr60cuVKqqiooC+++ILatGmjKv/QoUN048YNIiL68ccfycrKis6dO6dW/rJly6ii\nooIOHz5MVlZW9PDhQyIimjVrFg0cOJByc3NVJ8fy8vI6t7ugoKDGvpNKpeTv70+rVq0imUxGSUlJ\nJJFIKD09nYiIYmNjKSoqqs59XzUJa2h/17atlSfGRYsW0cyZM6miooIqKiro1KlTavGt7cuoUl3L\nlpeXk4+PD3366adUUVFBe/fuJVNTU1X8GkrCkpOT6fLly0REdPHiRXJzc6P9+/cT0V9fdtHR0VRa\nWkplZWW0f/9+CggIoD///JPkcjl9+OGH1KdPnzrrXXVd1bezof1eff7GHncDBgwgT09PSk1NpZKS\nEhozZkyNL/LKRGvUqFE0c+ZMKi0tpfz8fAoODlYl0Js3b6ZWrVpRfHw8KRQKeu+998jT05PmzJlD\nUqmUjh07RhKJhEpKSoiIaN68eTRy5Eh68OABPX78mIYPH07vvPMOETV8vFf/bBIR7dmzh/Ly8oiI\naNeuXWRtbU137twhIqL4+Pga8a1aRmJiIjk7O9Mff/xB5eXl9Prrr1P//v3V4jN8+HAqKiqi7Oxs\ncnFxoaNHjxIR0YQJE2jlypVEpDzOTp8+XWecqsa5oc9bdHQ02dnZ0c8//0xEpEoMqgoJCaGFCxeS\nVCqln376iSQSiepYqR676vus+j45d+4cubq6UkpKCikUCvrqq6/Iz8+PpFIpESmTlaCgILp9+zY9\nefJEo3NqQEAAXbt2jcrKyigsLIwWLVpERESZmZlqdatNSEgIJSQkEBFRSUmJWqK2efNmKi4uJqlU\nSvPmzVP7cRIdHU3Ozs507tw5evLkCQ0aNIh8fX1p69atquNy4MCBqvl9fX2pS5cudPv2bSosLKTQ\n0FBVcl41YZLL5fTMM8/Q8uXLSSaT0Y0bN6ht27aq46A6d3d31fnn4cOHaufyqoldpUePHlHHjh1p\n48aNRFT/56O+c6Sx4SRMYHx9fcnGxobs7e3J19eXZs+eTWVlZbR69eoaX2RDhgxR/TIPCwujZcuW\nqb0fExOj9kvZ399fdcIhIjp69Cj5+fkRkfKDZWZmpmoZI1J+GQ4ePFg1/e2335KNjY3qF8ujR49I\nJBJRUVFRrdsyatQo+r//+z9V+ZaWlmonLVdXVzpz5gzJ5XKytLRU+9VaqaHtruqnn34id3d3tdcm\nTpyo+pVcvaWruqrvN2a91bd16dKlNHLkSLp+/XqN+RpKwupa9scffyQPDw+116om0Q0lYdXNnTuX\n5s+fT0R/fdndvHlT9f7QoUMpLi5ONS2Xy8nKyoqys7NrLa++JKyh/V7b/I057sLCwlQndyJl64yZ\nmRkpFAq1L/I7d+6Qubm56tc4EdH27dtVX2ibN2+mdu3aqd67ePEiiUQiys/PV73m5OREFy5cIIVC\nQdbW1mrb/PPPP6uSw/qOd6Kan83adO/enQ4cOKCqW31J2NSpU+ntt99WvVdcXEympqaq1kuRSKSW\nXEVGRtKaNWuIiGjy5Mk0Y8YMun37dr31qSyncpsb+rxFR0dTdHR0nWVlZWVRq1atqLS0VPXayy+/\nXGcCXX2fVd8nM2fOrJHYtm/fnn766SciUh5jVVvfNTmnrlixQvXe+vXraejQobXWrTb9+/enZcuW\n1fqDsaoHDx6QSCSiR48eqbZzxowZqvc/++wzCgwMVE1fvHiR7O3tVdN+fn5qLfGHDx8mf39/IlJP\nmH799Vfy8fFRW/fKlStpypQptdbLx8eHNmzYUOP8XlsSJpfL6YUXXqBZs2YRETX4+ajvHGlsuE+Y\nwIhEIhw4cAAPHjxAZmYm/v3vf8PCwgJZWVnYs2cPHBwcVP9Onz6NO3fuqJZt6C6Y3Nxc+Pr6qqZ9\nfHyQm5urmnZxcYGZmZnaMq6urqq/LS0t4ezsrOo8a2lpCQAoLi4GABw5cgQhISFwcnKCg4MDDh8+\njPv376uWd3JyUuuPZWVlheLiYty7dw9PnjyBv79/jTprst1Vt6/6PvD19UVOTk69+6U2Da23vm39\nxz/+gYCAAAwePBj+/v5Ys2aNxuuta9nc3Fx4enrW2DZNnTlzBgMHDoSrqyvs7e2xYcMGtdgA6sdP\nVlYW5s6dq9p2JycnAHiqffk0GnPcAep19/HxgUwmw71799TKzMrKgkwmQ+vWrVXbNXPmTBQUFKjm\ncXNzU1svoPxcVH2tuLgYBQUFKC0tRY8ePVRlDRs2TG2ddR3vddmyZQuCgoJU5V2+fLlGjOqSl5en\ndjxYW1vDyclJLV7u7u5qdans9P7RRx+BiBAcHIzOnTtj8+bNGq2zrs9b5TlFJBLVe07Kzc2Fg4OD\naj9XLv+0srKysHbtWrXP7O3bt9XOcdWP8YbOLVX3WWXsNRUXF4erV6+iY8eOCA4OxqFDhwAAcrkc\nixYtQkBAAOzs7NCmTRsAUDt2qh7/FhYWNT4P1etR/fivus1Vt7dyn1f+W7VqFfLz82ut/9dff43D\nhw/Dz88PYWFh+PXXX+vc1sWLF6OkpATr1q0DgAY/H005RxoavjtST/j4+CAqKgobN26sc56G7u7z\n8PBAZmamqnNrdnY2PDw86ly+MXcLlpeXY8yYMUhISMDIkSNhYmKCl156SaOOq87OzrCwsMD169fR\ntWtXtfc02e5KHh4euHXrFohIVfesrKynup26vvU2tK02Njb45JNP8MknnyA1NRWDBg1CcHAwBg4c\n2OA+rW3ZZ599Fh4eHjUSoKysLAQEBABQfumWlpaq3quepL788st44403cPToUZiZmWH+/Pk1kpTq\nd6YtWbIEEydO1GBv1a8l7jrNzs5W+9vU1BTOzs4oKSlRve7t7Q1zc3Pcv3+/yXe0OTs7w9LSEmlp\naWjdunWjl6++T7KysjBjxgwkJSWhd+/eEIlECAoKUh1Tmn62K5WUlOD+/fs1EvfauLm5qY7z06dP\nIyIiAgMGDEDbtm0bXGdTPm+tW7fGgwcPUFpaCisrK9XyJiYmGi1fnY+PDxYvXox33323znmqH+Oa\nnlvqK6cuAQEB2L59OwBlQjN27FgUFhZi7969+Pbbb5GYmAhfX188fPgQjo6OTerkX/34r3per+Tt\n7Y02bdrg6tWrGpXZs2dP7N+/H3K5HJ999hkiIyPV1lNp586d2LVrF3777TdV7Br6fNR1njO0u8Y1\nwS1hemLSpEn47rvvcOzYMcjlcjx58gTJyclqX8zVP8TVpydOnIgPP/wQ9+7dw7179/DBBx/UOy5W\nY04KUqkUUqkUzs7OEIvFOHLkCI4dO6bRsmKxGFOnTsWCBQuQl5cHuVyOX375BVKpVKPtrhQSEgIr\nKyt89NFHkMlkSE5OxsGDBzFhwgSNt6NSfettaFsPHjyI69evg4hga2sLExMT1Ze+m5sbMjIy6lzv\noUOHaixrYmKC3r17o1WrVli3bh1kMhm++eYb/Pbbb6rlunXrhtTUVFy4cAFPnjxBbGysWrnFxcVw\ncHCAmZkZUlJSsH379nq/SGbOnImVK1ciLS0NAFBUVIQ9e/Y0ej8CytaEzMxMrd1JRkRISEjAlStX\nUFpaiqVLl2LcuHE1tq9169YYPHgwFixYgMePH0OhUCAjI+OpxicTi8WYPn065s2bp2pJy8nJ0fiY\nd3Nzw40bN1TTJSUlEIlEcHZ2hkKhwObNm9WG7XBzc8Pt27chk8nUtrtyn06cOBGbN2/GhQsXUF5e\njnfffRchISHw8fGpdf1VY7Fnzx7cvn0bAGBvbw+RSKRRktrQ562hePv6+qJnz55YtmwZZDIZTp06\nhYMHD9Y5f0PlTZ8+Hf/973+RkpICIkJJSQkOHTpUZ+vV05xTK7m4uEAsFtf7WU5ISFAdG3Z2dqr9\nWlxcDHNzczg6OqKkpKRG0tjYzwkRYf369cjJyUFhYSFWrFhR6zkvODgYEokEH330EcrKyiCXy3H5\n8mWcPXu2xrwymQzbtm1DUVERTExMIJFIak2O//jjD7z++uvYt2+fqrUcaPjzUdd5zhhxEqYnvLy8\ncODAAaxcuRKurq7w8fHB2rVr1T6wtbVkVX3tvffeQ8+ePdG1a1d07doVPXv2xHvvvafx8nXNAwAS\niQTr1q1DZGQkHB0dsWPHDowcObLeZav65JNP0KVLFzz77LNwcnLCO++8A4VCUed213a7u6mpKb77\n7jscOXIELi4umDNnDrZu3Yq//e1vdW5PXdtb3/5uaFuvX7+O5557DhKJBH369MHs2bMxYMAAAMA7\n77yDDz/8EA4ODvjnP/9Zow7Xrl2rdVlTU1N88803iI+Ph5OTE3bv3o3Ro0er4v+3v/0NS5cuRURE\nBNq3b49+/fqpbev69euxdOlS2NraYvny5TUGq62+X0aNGoW3334bEyZMgJ2dHbp06YKjR4/Wu+/q\nMm7cOADKy3M9e/asc76qZWl63FX+HRUVhZiYGLRu3RpSqVR1WaT6vFu2bIFUKkVgYCAcHR0xbtw4\nVauhJuutas2aNQgICEBISAjs7Ozw3HPPqbUy1LfstGnTkJaWBgcHB4wePRqBgYFYuHAhevfuDXd3\nd1y+fBl9+/ZVzR8eHo5OnTrB3d1ddWmqan3Dw8OxfPlyjBkzBh4eHrh58yZ27txZ7/6rfO3s2bMI\nCQmBRCLByJEjsW7dOvj5+dVa76rlNPXzBgDbt2/HmTNn4OjoiA8++ADR0dF1rq96edWne/TogS++\n+AJz5syBo6Mj2rVrhy1bttRZh8aeU6uuz8rKCosXL0ZoaCgcHByQkpJSo/yjR4+ic+fOkEgkmD9/\nPnbu3Alzc3NMnjwZvr6+8PT0ROfOnVUtn5puZ231evnll1WX9tq1a1fred3ExAQHDx7E+fPn0bZt\nW7i4uGDGjBl1jiOZkJCANm3awM7ODhs3bsS2bdtqlHngwAE8fPgQffv2hUQigUQiwQsvvACg/s9H\nXec5YyQiLf08ffLkCQYMGIDy8nJIpVKMHDkSq1atQmxsLL788ktVP4uVK1di2LBhAIBVq1Zh06ZN\nMDExwbp16zB48GBtVI0xgzBlyhR4eXlpPOCnoRo4cCCioqIwdepUXVeFsRbXpk0bxMXFGeWlPEOg\ntT5hFhYWOHHiBKysrFBRUYG+ffvi1KlTEIlEWLBgARYsWKA2f1paGnbt2oW0tDTk5OQgIiICV69e\nNbrRiBnTlLYu7+kj3heMMX2k1QynsrOlVCqFXC6Hg4MDgNpPmAcOHMDEiRNhamoKPz8/BAQE1NrE\nyxhT0uRyj7Hg/cAY00davTtSoVDgmWeeQUZGBl577TV06tQJe/fuxWeffYYtW7agZ8+eWLt2Lezt\n7ZGbm6v2EFYvL68Wux2eMX2k6VAChu7EiRO6rgJjOnPz5k1dV4E1gVaTMLFYjPPnz6OoqAhDhgxB\ncnIyXnvtNSxduhQAsGTJEixcuBBxcXG1Ll/br1tPT89ax0BhjDHGGBOabt264fz587W+1yIdruzs\n7PDCCy/g7NmzcHV1VV1GefXVV1WXHD09PXHr1i3VMrdv3651jJvc3FzVrdn8Txj/li1bpvM68D+O\niz7845gI8x/HRXj/DCkmFy5cqDM/0loSdu/ePTx8+BAAUFZWhh9++AFBQUFqg0ju27cPXbp0AQCM\nGDECO3fuhFQqxc2bN3Ht2jUEBwdrq3qsGVUdJJIJB8dFeDgmwsRxER5jiYnWLkfm5eUhOjoaCoUC\nCoUCUVFRCA8Px+TJk3H+/HmIRCK0adMGGzZsAAAEBgYiMjISgYGBaNWqFdavX8+dbRljjDFmsLQ2\nTpi2iEQi6FmVDV5ycjLCwsJ0XQ1WDcdFeDgmwsRxER5Dikl9eQsnYYwxxhhjWlJf3mIwI6E6Ojqq\nOvzzP/6n6T9HR0ddH7pak5ycrOsqsGo4JsLEcREeY4mJVoeoaEkPHjzgFjLWaCIR9ztkjDGmGwZz\nObKu1xmrDx83jDHGtKm+7xmDuRzJGGOMMaZPOAljzEAZS58KfcIxESaOi/AYS0w4CWOMMcYY0wHu\nE2YgwsLCEBUVhWnTpjV72dnZ2ejUqRMePXr0VB3Zk5OTERUVpfZYKqEw9uOGMcaYdnGfMCNQOeSC\nNvj4+ODx48dav5MwNjYWUVFRWl0HY4wxJhQGM0RFXdLTs3D8eAZkMjFMTRWIiPBH+/a+LV4G053K\nXyDGNhyFIY04bSg4JsLEcREeY4mJQbeEpadnIT7+OgoKBuHhwzAUFAxCfPx1pKdntWgZt27dwujR\no+Hq6gpnZ2fMnj0bTk5OuHz5smqe/Px8WFtb4/79+/WWdeDAAXTv3h12dnYICAjAsWPHasyTkZGB\nQYMGwdnZGS4uLpg0aRKKiopU769ZswZeXl6wtbVFhw4dkJSUBABISUlBz549YWdnB3d3dyxcuBCA\n8kGqYrEYCoUCAFBYWIgpU6bA09MTjo6OeOmllzTeF3Wt//vvv8eqVauwa9cuSCQSBAUFAQDi4+Ph\n7+8PW1tbtG3bFtu3bwcAyOVyvPnmm3BxcYG/vz8+//xztTqGhYXhvffeQ2hoKKytrXHz5s1G1ZEx\nxhjTNoNuCTt+PAPm5uFQv8kiHBcvJuHZZzVryUpJyUBpabhqOiwMMDcPR2JikkatYXK5HC+++CIi\nIiKwbds2mJiY4LfffgMAJCQkYPXq1QCAHTt2ICIiAk5OTvXUJQXR0dH4+uuvER4ejtzcXDx+/LjW\neRcvXoz+/fujqKgIY8aMQWxsLP71r38hPT0dn3/+Oc6ePQt3d3dkZ2ejoqICADB37lzMnz8fr7zy\nCkpLS3Hp0qVay46KioKtrS3S0tJgbW2NX375pcH9UKmu9bdt2xbvvvsuMjIysGXLFgBASUkJ5s6d\ni7Nnz6Jdu3a4e/euKkn94osvcOjQIZw/fx5WVlYYPXp0jZauhIQEHDlyBO3bt1clZ8bEGH5F6huO\niTBxXITHWGJi0EmYTFZ7Q59crnkDoEJR+7xSqWZlpKSkIC8vDx9//DHEYuUyoaGhaNWqFSIjI1VJ\n2NatW7Fo0aJ6y4qLi8O0adMQHq5MCj08PGqdz9/fH/7+/gAAZ2dnzJ8/Hx988AEAwMTEBOXl5UhN\nTYWTkxN8fHxUy5mZmeHatWu4d+8enJ2d0atXrxpl5+Xl4fvvv0dhYSHs7OwAAP369dNoXzS0fiKq\n0XlRLBbj0qVL8PLygpubG9zc3AAAu3fvxvz58+Hp6QkAePfdd/Hjjz+qlhOJRIiJiUHHjh1V5TDG\nGGNCYtBJmKlp5aUp9dddXRWYNUuzMj7/XIGCgpqvm5lp1rJy69Yt+Pr61kgCevXqBUtLSyQnJ8Pd\n3R0ZGRkYMWJEvWXdvn0bL7zwQoPrvHv3LubOnYtTp07h8ePHUCgUqmckBgQE4NNPP0VsbCxSU1Mx\nZMgQ/POf/0Tr1q0RFxeHpUuXomPHjmjTpg2WLVtWY323bt2Co6OjKgFrrPrWX521tTV27dqFTz75\nBNOmTUNoaCjWrl2L9u3bIy8vD97e3qp5qyZzlaq+b4yMpU+FPuGYCBPHRXiMJSYG3TwQEeGP8vJE\ntdfKyxMRHu7fYmV4e3sjOzsbcrm8xnvR0dFISEjA1q1bMW7cOJiZmTVY1vXr1xtc57vvvgsTExNc\nvnwZRUVF2Lp1q9rluIkTJ+LkyZPIysqCSCTC22+/DUCZIG3fvh0FBQV4++23MXbsWJSVldWoQ2Fh\noVofs8aqa/21dZwfPHgwjh07hjt37qBDhw6YPn06AKB169bIzs5WzVf170rG1hGfMcaYfjHoJKx9\ne1/ExATA1TUJ9vbJcHVNQkxMQKPubGxqGb169ULr1q2xaNEilJaW4smTJ/j5558BAJMmTcI333yD\nbdu2YfLkyQ2WNW3aNGzevBlJSUlQKBTIyclBenp6jfmKi4thbW0NW1tb5OTk4OOPP1a9d/XqVSQl\nJaG8vBzm5uawsLCAiYkJAGUfqoL/NfvZ2dlBJBLVaMFr3bo1hg0bhlmzZuHhw4eQyWT46aefNNoX\nDa3f3d0dmZmZqkuS+fn5OHDgAEpKSmBqagpra2vVvJGRkVi3bh1ycnLw4MEDrF69ukbSZezjfxnD\nr0h9wzERJo6L8BhNTEjP1FVlIW9KdnY2jRo1ipycnMjZ2Znmzp2rei88PJzatGmjcVn79u2jrl27\nkkQioYCAADp27BgREYWFhVFcXBwREaWmplKPHj3IxsaGgoKCaO3ateTt7U1ERBcvXqTg4GCSSCTk\n6OhIw4cPp7y8PCIimjRpErm6upKNjQ117tyZDhw4QEREN2/eJLFYTHK5nIiICgsLKTo6mtzc3MjB\nwYHGjBlTb51PnDih0frv379Pffv2JQcHB+rRowfl5eXRgAEDyM7Ojuzt7WngwIF05coVIiKqqKig\n+fPnk5OTE7Vt25Y+//xzEolEqjpW3R/1EfJxwxhjTP/V9z3DI+br2LRp0+Dp6anqOM+eTmZmJtq2\nbYuKiopGdcLX1+NGE8bSp0KfcEyEieMiPIYUk/q+Zwy6Y77QZWZm4ptvvsH58+d1XRXGGGOMtTCD\n7hMmZEvHNwwaAAAgAElEQVSWLEGXLl3w1ltvwdf3r/5lK1euhEQiqfFPk7sidUkI9eaO+OoM5Vek\nIeGYCBPHRXiMJSZ8OZIZNT5uGGOMaRM/wJsxI5Ss/qgIJgAcE2HiuAiPscSEkzDGGGOMMR3gy5HM\nqPFxwxhjTJv4ciRjjDHGmMBwEsaYgTKWPhX6hGMiTBwX4TGWmHASxmqVmZkJsVis9sxJxhhjjDUf\n7hPGaqXpCPTx8fGIi4vDyZMnW7B2zYePG8YYY9pk1CPmp19Px/Hfj0NGMpiKTBHRIwLtA9q3eBms\n8RQKRaMeQcQYY4zpE4P+hku/no74E/EocCvAQ/eHKHArQPyJeKRfT2+xMvz8/LB27Vp069YN9vb2\nmDBhAsrLyxEfH49+/fqpzSsWi3Hjxg0AQExMDGbNmoXnn38eEokE/fr1w507dzB37lw4ODigY8eO\nao878vPzw+rVq9GpUyc4Ojpi6tSpKC8vBwB07twZBw8eVM0rk8ng7OyMCxcuaLwf4uPj4e/vD1tb\nW7Rt2xbbt2/Hn3/+iZkzZ+KXX36BRCKBo6MjAODw4cPo1KkTbG1t4eXlhbVr16rK+fjjj+Hh4QEv\nLy9s2rSpxja/9tpreP7552FjY2M0fQK0hfef8HBMhInjIjzGEhODbgk7/vtxmLczR3Jm8l8vmgIX\nd17Es32f1aiMlFMpKPUqBTKV02F+YTBvZ47Ec4katYaJRCLs2bMHR48ehbm5OUJDQxEfHw8LC4sG\nl92zZw+OHTuGwMBAPP/88wgJCcGHH36ITz/9FEuXLsWCBQuQlJSkmn/79u04duwYrKysMHz4cHz4\n4YdYvnw5oqOjkZCQgBdffBGAMkny9PREt27dNNoHJSUlmDt3Ls6ePYt27drh7t27uH//Pjp06IAN\nGzbgyy+/VLscOW3aNOzduxehoaEoKipSJVnff/891q5di6SkJPj5+eHVV1+tsa4dO3bgyJEj6N27\ntyqJZIwxxgyRQbeEyUhW6+tyyDUuQ4HaO6ZLFVKNy3jjjTfg7u4OBwcHDB8+XKMHdotEIowePRpB\nQUEwNzfHSy+9BGtra0yaNAkikQiRkZH4448/1OafM2cOPD094eDggMWLF2PHjh0AgFdeeQWHDh1C\ncXExAGDr1q2IiorSuP6AspXu0qVLKCsrg5ubGwIDAwGg1uvcZmZmSE1NxaNHj2BnZ4egoCAAwO7d\nuzF16lQEBgbCysoK77//fo1lR40ahd69ewMAzM3NG1VHps5Ynr2mTzgmwsRxER5jiYlBt4SZikwB\nKFuvqnK1csWssFkalfH53c9R4FZQ43UzsZnG9XB3d1f9bWVlhdzcXI2Wc3V1Vf1tYWGhNm1paalK\nqip5e3ur/vbx8VGtx8PDA6Ghodi7dy9GjRqF77//Hp999pnG9be2tsauXbvwySefYNq0aQgNDcXa\ntWvRvn3tLYFff/01PvzwQyxatAhdu3bF6tWrERISgry8PDz77F8tkD4+PmrLiUQieHl5aVwvxhhj\nTJ8ZdEtYRI8IlF9Tv6RVfq0c4c+Et2gZtbG2tkZpaalq+s6dO00qDwCys7PV/vbw8FBNV16S3LNn\nD/r06YPWrVs3quzBgwfj2LFjuHPnDjp06IDp06cDUCZO1fXs2RP79+9HQUEBRo0ahcjISABA69at\na9SRaY+x9KnQJxwTYeK4CI+xxMSgk7D2Ae0RMzAGrvmusL9jD9d8V8QMjGnUnY3NUUZVlZfvunXr\nhtTUVFy4cAFPnjxBbGxsrfM1ptz169cjJycHhYWFWLFiBSZMmKB6/6WXXsK5c+ewbt06TJ48uVFl\n5+fn48CBAygpKYGpqSmsra1hYmICAHBzc8Pt27chkykv/cpkMmzbtg1FRUUwMTGBRCJRzRsZGYn4\n+HhcuXIFpaWlNS5H8lARjDHGjIlBX44ElElUU4eTaI4yKolEIohEIrRr1w5Lly5FREQErKyssHLl\nSnzxxRc15qtruvK1qn+//PLLGDx4MHJzczFq1Ci89957qvctLCwwevRo7Nq1C6NHj9a4roByqIh/\n/etfiI6OhkgkQlBQEP7zn/8AAMLDw9GpUye4u7vDxMQEOTk5SEhIwOuvvw65XI4OHTpg27ZtAICh\nQ4di3rx5GDRoEExMTLB8+XJs37693m1kT89Y+lToE46JMHFchMdYYsKDtRqINm3aIC4uDoMGDapz\nnuXLl+PatWvYsmVLC9asfmKxGNevX0fbtm11sn5jP24YY4xpFz/Am6GwsBCbNm3CjBkzdF0V1kKM\npU+FPuGYCBPHRXiMJSachBmBL774Aj4+Phg2bBj69u2ren3btm2QSCQ1/nXp0qXF6saXHxljjBkr\nvhzJjBofN4wxxrSJL0cyxhhjjAkMJ2GMGShj6VOhTzgmwsRxER5jiQknYYwxxhhjOsB9wphR4+OG\nMcaYNnGfMMYYY4wxgeEkTMv8/PyQmJiIVatWqZ63+LRiY2MRFRXVTDVjhs5Y+lToE46JMHFchMdY\nYsJJmJZVPornnXfeUXss0dOWpYmwsDDExcU1aV26ZgjbwBhjjNXH4J8dmZWejozjxyGWyaAwNYV/\nRAR82zfuOZDNUUZz0LTvkrYGQK2oqECrVi1zyPAgrk1nLM9e0yccE2HiuAiPscTEoFvCstLTcT0+\nHoMKChD28CEGFRTgenw8stLTW7QMIlK7lJiZmQmxWIwtW7bA19cXLi4uWLlyZaO27cmTJ5g0aRKc\nnZ3h4OCA4OBg5OfnY/HixTh58iTmzJkDiUSCN954AwAwf/58uLm5wc7ODl27dkVqaioA4P79+xgx\nYgTs7OzQq1cvLFmyBP369VOtRywWY/369WjXrh3aN5B4isVi/Oc//0G7du1ga2uLpUuXIiMjA717\n94a9vT0mTJgAmUwGAHj48CFefPFFuLq6wtHREcOHD0dOTg4A1LkNjDHGmCEx6JawjOPHEW5uDlS5\nthwOIOniRfg++6xmZaSkILy09K8XwsIQbm6OpMTERrWG1dayc/r0aVy9ehXp6ekIDg7G6NGj0aFD\nB43K++qrr/Do0SPcvn0b5ubmOH/+PCwtLbFixQr8/PPPiIqKwtSpUwEAR48excmTJ3Ht2jXY2toi\nPT0ddnZ2AIDZs2fDysoKd+7cwY0bNzBkyJAaD9M+cOAAfvvtN1haWjZYr2PHjuGPP/5AdnY2goKC\ncOrUKezYsQOOjo7o3bs3duzYgcmTJ0OhUGDatGnYu3cvKioqMHXqVMyZMwf79u2rdRtY4yUnJxvN\nr0l9wTERJo6LcKSnZ+H48QxcuXIRHTt2RUSEP9q399V1tbTGoFvCxP9rdanxulyueRkKRe2vS6VP\nVaeqli1bBnNzc3Tt2hXdunXDhQsXNF7WzMwM9+/fx7Vr1yASiRAUFASJRKJ6v+qlSzMzMzx+/BhX\nrlyBQqFA+/bt4e7uDrlcjm+++QYffPABLC0t0alTJ0RHR9e47PnOO+/A3t4e5ubmDdbrrbfego2N\nDQIDA9GlSxcMGzYMfn5+sLW1xbBhw/DHH38AABwdHfHSSy/BwsICNjY2ePfdd/Hjjz+qlcVDRzDG\nmPFIT89CfPx15OcPQmFhdxQUDEJ8/HWkp2fpumpaY9AtYQpTU+Uf1X7hKFxdgVmzNCvj88+BgoKa\nr5uZNbV6cHd3V/1tZWWFkpISjZeNiorCrVu3MGHCBDx8+BCTJk3CihUrVH22qra8DRw4EHPmzMHs\n2bORlZWF0aNH45NPPkFJSQkqKirg7e2tmtfHx6fGuqq+3xA3NzfV35aWljWm79y5AwAoLS3F/Pnz\ncfToUTx48AAAUFxcDCJS1Z37hTUN/7IXHo6JMHFchOH48QyIxeG4dAkoLQ2DTAaYm4cjMTHJYFvD\nDLolzD8iAonl5WqvJZaXwz88vEXLaC5Vk5JWrVph6dKlSE1Nxc8//4yDBw9iy5YtNear9Prrr+Ps\n2bNIS0vD1atX8fHHH8PV1RWtWrVCdna2ar6qf9e23uaydu1aXL16FSkpKSgqKsKPP/4IIlK1fnEC\nxhhjxuXePTF+/x0oLATkcqCsTPm6VGq4qYrhbhkA3/btERATgyRXVyTb2yPJ1RUBMTGN6svVHGUA\nml1aa2iequ8nJyfj0qVLkMvlkEgkMDU1hYmJCQBla1RGRoZq3rNnz+LMmTOQyWSwsrKChYUFTExM\nIBaLMXr0aMTGxqKsrAxpaWnYsmVLsyZAVetc9e/i4mJYWlrCzs4OhYWFeP/999WWq74NrPGMZZwd\nfcIxESaOi24RAb//DqSkKPDkCSCRAC4uybC1Vb5vZlZ7tyBDYNBJGKBMogbNmoWwefMwaNaspxpa\noqllVI4VVjW5qS3RaSj5qVrGnTt3MG7cONjZ2SEwMBBhYWGquy/nzp2LvXv3wtHREfPmzcOjR48w\nY8YMODo6ws/PD87OzvjHP/4BAPj3v/+N4uJiuLu7Y+rUqZgyZYpastSYhKyhbapa/3nz5qGsrAzO\nzs7o06cPhg0bpjZv9W1gjDFmeGQy4Ntvge++A9q08YeLSyKCgoDKHj/l5YkID/fXbSW1SGvPjnzy\n5AkGDBiA8vJySKVSjBw5EqtWrUJhYSHGjx+PrKws+Pn5Yffu3bC3twcArFq1Cps2bYKJiQnWrVuH\nwYMH16wwPztSq+Lj4xEXF4eTJ0/quiotgo8bxhjTjQcPgN27gbw8wNQUePFFwMIiC4mJGZBKxTAz\nUyA8XP/vjqzve0ZrHfMtLCxw4sQJWFlZoaKiAn379sWpU6fw7bff4rnnnsNbb72FNWvWYPXq1Vi9\nejXS0tKwa9cupKWlIScnBxEREbh69SrEYoNvrGOMMcaMytWrwDffAE+eAI6OwPjxgPI+Ll+9T7oa\nQ6sZjpWVFQBAKpVCLpfDwcEB3377LaKjowEA0dHR2L9/PwDlWFQTJ06Eqakp/Pz8EBAQgJSUFG1W\nT5CGDRsGiURS49/q1atbZP3VL5tWdfLkyVrrZlt54Z4JCvdzER6OiTBxXFqOQgGcOAFs365MwNq3\nB2bMqEzA/mIsMdHqEBUKhQLPPPMMMjIy8Nprr6FTp064e/euatgCNzc33L17FwCQm5uLkJAQ1bJe\nXl6qEdSNyZEjR3S6/ujoaFWSXF2/fv3w+PHjFq4RY4wxQ1BaCnz9NZCRAYhEwKBBQN++yr+NlVaT\nMLFYjPPnz6OoqAhDhgzBiRMn1N6vr9Wl8v3axMTEwM/PDwBgb2+P7t27N1udmfGpOlp25a8vQ5gO\nCwsTVH14GqrXhFIfnubplprOzQVWrEhGSQkQGBiGsWOB7Oxk/Pij4Z2/Kv/OzMxEQ7TWMb+65cuX\nw9LSEl9++SWSk5Ph7u6OvLw8DBw4EH/++afqctuiRYsAAEOHDsX777+PXr16qVeYO+azZsTHDWOM\naQ8RcO4ccPiwcuwvLy9g3Djgf0/OMwr1fc9orU/YvXv38PDhQwBAWVkZfvjhBwQFBWHEiBH46quv\nACiffzhq1CgAwIgRI7Bz505IpVLcvHkT165dQ3BwsLaqx5jBq/qrjAkDx0SYOC7aIZMBBw4oh5+Q\ny4FnnwViYjRLwIwlJlq7HJmXl4fo6GgoFAooFApERUUhPDwcQUFBiIyMRFxcnGqICgAIDAxEZGQk\nAgMD0apVK6xfv55HTWeMMcb00IMHwK5dwJ07fw0/0a2brmslPC12ObK58OVI1pz4uGGMseZV9/AT\nxkknlyPZ05NIJBp16Htafn5+SExM1Fr5jDHGjI9CASQl/TX8RIcOtQ8/wf7CSZgAPX78WHX3pzY0\ndFcqAGRmZkIsFkOhMNxndhk6Y+lToU84JsLEcWm60lJg2zbgp5+UQ06EhytbwCwsnq48Y4mJVoeo\nEIL0GzdwPDUVMgCmACI6dUL7tm1bvAx9pY1LdXK5XPWwccYYY/otJ0f5+KGiIsDaGhgzBjCSr8gm\nM+iWsPQbNxB/7hwKOnfGw86dUdC5M+LPnUP6jRstWsaaNWvg5eUFW1tbdOjQAUlJSVAoFFi5ciUC\nAgJga2uLnj17qganFYvFuPG/8mNiYjBz5kwMHjwYtra2CAsLQ3Z2NgBg9uzZePPNN9XWNWLECHz6\n6aca1y0lJQU9e/aEnZ0d3N3dVeX1798fgHIcNolEgjNnzuD69esYMGAA7O3t4eLiggkTJqjK+eGH\nH9ChQwfY29vj9ddfx4ABAxAXFwdA+TzK0NBQLFiwAM7Oznj//fc1rh97epVj1zDh4JgIE8fl6RAB\nv/8ObNqkTMC8vIC//715EjBjiYlBt4QdT02FeY8eSP7fUBkAAH9/XPzpJzyr4Z2XKT/9hNJu3YD/\nlRFmbw/zHj2QePmyRq1h6enp+Pzzz3H27Fm4u7sjOzsbFRUVWLt2LXbu3IkjR46gXbt2uHjxIiwt\nLWstY/v27Th8+DCCg4Px1ltv4ZVXXsHJkycRExODUaNG4eOPP4ZIJMK9e/eQmJioSn40MXfuXMyf\nPx+vvPIKSktLcenSJQDKRxS1adMGRUVFqud3Tpw4EUOHDsWPP/4IqVSKs2fPAlAORzJmzBjEx8dj\n5MiR+Oyzz/Df//5XbeT9lJQUvPzyy8jPz4dUKtW4fowxxoRHJgMOHQLOn1dOP/ssMGQI0Mqgs4rm\nZ9AtYbI6Xpc3YugLRR3zappGmJiYoLy8HKmpqZDJZPDx8UHbtm0RFxeHFStWoF27dgCArl27wtHR\nsdYyXnzxRfTt2xdmZmZYsWIFfvnlF+Tk5ODZZ5+FnZ2dqpP9zp07MXDgQLi4uGi8fWZmZrh27Rru\n3bsHKysr1eC4tV2GNDMzQ2ZmJnJycmBmZoY+ffoAAA4fPozOnTtj9OjRMDExwbx58+Du7q62rIeH\nB2bPng2xWAyLp+0kwBrFWPpU6BOOiTBxXBrnwQMgLk6ZgJmaAqNHAy+80LwJmLHExKBzVtP//R9m\nb6/2uqujI2a1aaNRGZ9fvoyCassDgJmGdQgICMCnn36K2NhYpKamYsiQIVi7di1u3boFf3//BpcX\niUTw8vJSTVtbW8PR0RG5ubnw9PTE5MmTkZCQgIiICCQkJGD+/Pka1kwpLi4OS5cuRceOHdGmTRss\nW7YML7zwQq3zfvTRR1iyZAmCg4Ph4OCAhQsXYsqUKcjNzVWrIwB4e3vXO80YY0z/8PATzcugW8Ii\nOnVC+e+/q71W/vvvCO/UqUXLmDhxIk6ePImsrCyIRCK8/fbb8Pb2xvXr1xtclohw69Yt1XRxcTEK\nCwvh4eEBAJg0aRIOHDiACxcu4M8//1Q9gUBTAQEB2L59OwoKCvD2229j7NixKCsrq/XuSTc3N2zc\nuBE5OTnYsGEDZs2ahYyMDHh4eKjVsXqdgbqfA8q0x1j6VOgTjokwcVwa1tLDTxhLTAw6CWvfti1i\nnnkGrpcvw/7yZbhevoyYZ55p1J2NTS3j6tWrSEpKQnl5OczNzWFhYYFWrVrh1VdfxZIlS3D9+nUQ\nES5evIjCwsJayzh8+DBOnz4NqVSKJUuWoHfv3vD09AQAeHl5oWfPnpg8eTLGjh0Lc3NzjbcNABIS\nElBQUAAAsLOzg0gkglgshouLC8RiMTIyMlTz7tmzB7dv3wag7LAvEolgYmKC559/Hqmpqdi3bx8q\nKiqwbt063Llzp1H1YIwxJkzVh5+IiGja8BPsLwZ9ORJQJlFNHU6iKWWUl5fjnXfewZUrV2BqaorQ\n0FBs3LgRrq6uKC8vx+DBg3Hv3j107NgR+/btA6DeaiQSifDyyy/j/fffxy+//IIePXogISFBbR3R\n0dGYPHky1q1b1+j6HT16FAsXLkRpaSn8/Pywc+dOVSK3ePFihIaGoqKiAkeOHMHZs2cxf/58FBUV\nwc3NDevWrVONZ7Znzx688cYbmDJlCqKiohAaGqq2DdwS1vKSk5ON5tekvuCYCBPHpW66Gn7CWGLC\njy0SuClTpsDLywvLly+vc56TJ09i0qRJyMrKasGa1W/gwIGIiorC1KlTdV2VehnqcQMYz0lMn3BM\nhInjUlPl8BNHjigfvu3lBURGAra2LbN+Q4pJfd8zBt8Spu8aShBkMhk+/fRTTJ8+vYVqpDlDTW70\nhaGcwAwJx0SYOC7qqg8/ERysHH6iJcfYNpaYGHSfMENQ36W8K1euwMHBAXfv3sW8efNUr2dnZ0Mi\nkdT4Z2trq+rT1RL4EiRjjOmXwsKaw088/3zLJmDGhC9HMqNmyMeNITXnGwqOiTBxXJSENPyEIcWE\nL0cyxhhjrFYKBZCcrLz7EVAOPzFqFN/92BK4JYwZNT5uGGPGrLQU+PprICNDOfxEeDgQGqr8mzUP\nbgljjDHGmJrqw0+MHQto+DAZ1kwMpmO+g4ODqhM7/+N/mv5zcHDQ9aGrNcby7DV9wjERJmOLCxFw\n9iywaZMyAfPyAv7+d0BICZixxMRgWsLqGm2eaZ8hdaBkjDFDJpMBBw8CFy4op3Ux/AT7i8H0CWOM\nMcZY3QoLgV27gLt3lcNPDB8OdO2q61oZvvryFoNpCWOMMcZY7dLTgX37hDH8BPuLwfQJY7pjLNfu\n9Q3HRXg4JsJkyHFRKICkJGDHDmUC1qEDMGOG8BMwQ45JVdwSxhhjjBmgkhLl8BM3biiHnIiIAPr0\n4eEnhIT7hDHGGGMGhoefEA7uE8YYY4wZASLg99+BI0cAuVw5/ERkJGBrq+uasdpwnzDWZMZy7V7f\ncFyEh2MiTIYSF5kM2L9fOQSFXA706gVMmaKfCZihxKQh3BLGGGOM6bnqw0+MGAF06aLrWrGGcJ8w\nxhhjTI9VHX7CyUk5/ISrq65rxSpxnzDGGGPMwCgUwIkTwMmTyumOHYGRIwELC93Wi2mO+4SxJjOW\na/f6huMiPBwTYdLHuJSUAAkJygRMJAKee07ZAd9QEjB9jMnT4JYwxhhjTI/cvg3s2cPDTxgC7hPG\nGGOM6QEi4OxZ4PvvlXc/ensD48bp592PxoT7hDHGGGN6TCZTDj1x4YJyulcvYPBgwMREt/ViTcN9\nwliTGcu1e33DcREejokwCT0uhYXAl18qEzBTU2DMGGDYMMNOwIQek+bCLWGMMcaYQPHwE4aN+4Qx\nxhhjAlPb8BOjRgHm5rqtF2s87hPGGGOM6YmSEuDrr4EbN5TDT0REAH36KP9mhoX7hLEmM5Zr9/qG\n4yI8HBNhElJcbt8GNmxQJmDW1kB0NBAaanwJmJBiok3cEsYYY4zpGA8/YZy4TxhjjDGmQzIZ8N13\nwMWLymkefsKwcJ8wxhhjTIAKC4Fdu4C7d5XDT4wYAXTpoutasZbCfcJYkxnLtXt9w3ERHo6JMOkq\nLn/+qez/dfeucviJ6dM5AatkLJ8VbgljjDHGWpBCASQlAadOKad5+AnjxX3CGGOMsRZSUgLs3Qvc\nvMnDTxgL7hPGGGOM6djt28Du3cCjR8rhJ8aNA/z8dF0rpkvcJ4w1mbFcu9c3HBfh4ZgIk7bjQgT8\n9huwebMyAfP2BmbO5ASsPsbyWeGWMMYYY0xLpFLg4EEefoLVjvuEMcYYY1pw/77y8iMPP2HcuE8Y\nY4wx1oL+/BPYtw8oL1cOPzF+PODqqutaMaHhPmGsyYzl2r2+4bgID8dEmJozLgoFcPw4sHOnMgHr\n2BGYMYMTsMYyls8Kt4QxxhhjzaDq8BNisXL4id69efgJVjfuE8YYY4w1EQ8/werCfcIYY4wxLagc\nfuLoUUAuB3x8lAmYRKLrmjF9wH3CWJMZy7V7fcNxER6OiTA9bVykUmXn+8OHlQlYSAgQHc0JWHMw\nls8Kt4QxxhhjjXT/PrBrF5CfD5iZKYef6NxZ17Vi+kZrfcJu3bqFyZMnIz8/HyKRCDNmzMAbb7yB\n2NhYfPnll3BxcQEArFy5EsOGDQMArFq1Cps2bYKJiQnWrVuHwYMH16ww9wljjDGmQ1WHn3B2BiIj\n+e5HVrf68hatJWF37tzBnTt30L17dxQXF6NHjx7Yv38/du/eDYlEggULFqjNn5aWhpdffhm//fYb\ncnJyEBERgatXr0IsVr9iykkYY4wxXVAogKQk4NQp5XRgIDByJGBurtt6MWGrL2/RWp8wd3d3dO/e\nHQBgY2ODjh07IicnBwBqrcyBAwcwceJEmJqaws/PDwEBAUhJSdFW9VgzMpZr9/qG4yI8HBNh0iQu\nJSXA1q3KBEwsVj56aNw4TsC0xVg+Ky3SMT8zMxN//PEHQkJCAACfffYZunXrhmnTpuHhw4cAgNzc\nXHh5eamW8fLyUiVtjDHGmK7cugVs2KAc/8vGBpg8GejTh8f/Yk2n9Y75xcXFGDt2LP7v//4PNjY2\neO2117B06VIAwJIlS7Bw4ULExcXVuqyojiM8JiYGfv8bgMXe3h7du3dHWFgYgL+yZ55u2elKQqkP\nT4chLCxMUPXhaaheE0p9eLr+6RMnkvHnn8C9e2GQy4HS0mQEBwN+fsKonyFPh+nx+avy78zMTDRE\nq4O1ymQyvPjiixg2bBjmzZtX4/3MzEwMHz4cly5dwurVqwEAixYtAgAMHToU77//Pnr16qVeYe4T\nxhhjTMukUuDgQeDiReV0SAjw3HOAiYlu68X0j076hBERpk2bhsDAQLUELC8vT/X3vn370OV/j5Qf\nMWIEdu7cCalUips3b+LatWsIDg7WVvVYM6qa/TPh4LgID8dEmKrH5f594MsvlQmYmRkwdiwwdCgn\nYC3JWD4rWrscefr0aSQkJKBr164ICgoCoByOYseOHTh//jxEIhHatGmDDRs2AAACAwMRGRmJwMBA\ntGrVCuvXr6/zciRjjDGmDVeuAPv3/zX8xPjxwP9GVGKs2fGzIxljjBk9Hn6CaQs/O5IxxhirQ3Ex\n8PXXyrsfxWJl36+QEL77kWmf1vqEMeNhLNfu9Q3HRXg4JsJz6xbwj38kq4afiI4GevfmBEzXjOWz\nwi1hjDHGjA4R8NtvwNGjQFkZ4OOjHHyVH77NWhL3CWOMMWZUpFLgu++AS5eU0zz8BNMm7hPGGGOM\nQaOxlSQAACAASURBVDn8xK5dQH6+cviJkSOBTp10XStmrLhPGGsyY7l2r284LsLDMdGtK1eAjRuV\nCZizMzB9ujIB47gIj7HEhFvCGGOMGTSFAkhMBE6fVk7z8BNMKLhPGGOMMYPFw08wXeM+YYwxxozO\nrVvA7t3A48fK4SfGjQN8fXVdK8b+wn3CWJMZy7V7fcNxER6OScsgAs6cATZvViZgPj7A3/9edwLG\ncREeY4kJt4QxxhgzGNWHn+jdG4iI4OEnmDBxnzDGGGMGgYefYELEfcIYY4wZtCtXgP37gfJy5fAT\n48cDLi66rhVj9eM+YazJjOXavb7huAgPx6T5KRTADz8oW8DKy5UtX9OnNy4B47gIj7HEhFvCGGOM\n6aXiYmDvXiAzk4efYPqJ+4QxxhjTOzz8BNMX3CeMMcaYQSACUlKAo0eVlyJ9fYGxYwGJRNc1Y6zx\nuE8YazJjuXavbzguwsMxaRqpFPjmG+DIEWUC1rs3MHly0xMwjovwGEtMuCWMMcaY4PHwE8wQcZ8w\nxhhjglZ1+AkXFyAykoefYPqD+4QxxhjTOwoFcPw48PPPyulOnYARIwBzc93Wi7Hmwn3CWJMZy7V7\nfcNxER6OieaKi4EtW5QJmFgMDBmi7ICvjQSM4yI8xhITbgljjDEmKDz8BDMW3CeMMcaYIPDwE8wQ\ncZ8wxhhjgiaVAt9+C1y+rJzu3RuIiABMTHRbL8a0ifuEsSYzlmv3+objIjwck9rduwd88YUyATMz\nU15+HDKk5RIwjovwGEtMuCWMMcaYzqSlAQcO8PATzDhxnzDGGGMtrrbhJ0aOVLaEMWZIuE8YY4wx\nwSguBvbuBTIzlcNPDB4M9OoFiES6rhnTtaz0dGQcPw6xTAaFqSn8IyLg2769rqulNdwnjDWZsVy7\n1zccF+HhmADZ2cCGDcoEzMYGiIkBQkJ0m4BxXIQhKz0d1+PjMSg/H0hJwaCCAlyPj0dWerquq6Y1\nnIQxxhjTOiLg11+B+Hjl+F++vsDMmYCPj65rxoQi4/hxhJeXA+fPA+npQEUFws3NkZGYqOuqaQ33\nCWOMMaZV1Yef6NMHCA/n4SdYFQ8fInnePIRlZiqnTU2BLl0AW1sk29sjbN48nVavKbhPGGOMMZ24\ndw/YtQsoKFB2uh81CggM1HWtmGA8eQKcPAn8+isU+fnKToJeXsom0lbKFEVhwHdr8OVI1mTcn0KY\nOC7CY2wxSUsDNm5UJmAuLsCMGcJMwIwtLoIglysfj7BuHXD6NCCXw3/oUCR27w60bYvk27cBAInl\n5fAPD9dxZbWHW8IYY4w1q+rDT3TuDIwYwcNPMCg7B169Cvzwg7KZFFB2EBw8GL6enkB6OpISE3Hx\n3j0oXF0REB5u0HdHcp8wxhhjzaa4GNizB8jK4uEnWDW5ucCxY8pbYwHAyQl47jmgfXuDPkC4Txhj\njDGty85WJmCPHysfuj1uHN/9yAAUFQFJScCFC8ppKytgwACgZ0+jvzuD+4SxJuP+FMLEcREeQ41J\nbcNP/P3v+pOAGWpcdK68HEhMBD77TJmAmZgob4194w1l82g9CZixxIRbwhhjjD01Hn6C1aBQAOfO\nASdOACUlytc6d1YeGA4Ouq2bwHCfMMYYY0+Fh59gaoiA69eV/b4KCpSveXsDQ4Yoh50wUtwnjDHG\nWLNKSwP271e2hLm4AOPHA87Ouq4V05k7d5TJ140bymkHByAiQpmVG3Cn+6biPmGsyYzl2r2+4bgI\njyHERKFQftfu3q1MwDp3BqZP1+8EzBDiojOPHwMHDigfCHrjBmBhoWz5mj0b6NTpqRMwY4kJt4Qx\nxhjTSPXhJ4YMAYKDuaHDKEmlyoHgTp8GZDLlAdGrF9C/v/LuR6YR7hPGGGOsQdnZytav4mIefsKo\nKRTKOx2TkpStYADQsaPy0qOTk27rJlDcJ4wxxthTIQLOnFFeglQoAD8/YOxYwMZG1zVjLS4jQ3kg\n3L2rnPb0VI7G6+ur23rpMe4TxprMWK7d6xuOi/DoW0ykUuDrr4Hvv1cmYH36AJMnG14Cpm9xaXH5\n+cC2bcDWrcoEzM4OGDMGePVVrSVgxhITbgljjDFWQ9XhJ8zNgZEjefgJo1NcrBzr69w5ZZOouTnQ\nrx8QEgK04vShOXCfMMYYY2p4+AkjJ5MBv/wCnDqlPAjE/8/enQe3fd93/n/i4AXgC1ESRYoUL12W\nRF0UKZKSKB625SuNvUnd2j97d2NPuslus9NuJzvjeLLHrPdo7Gk702Qz7iSts3Emma6dpHHceFvb\nsk2Qog5S92Xd4iGSIkXxwBcgCeL4/v74QLQs6yZAfAG8HzOZ6AvbxIf8CMCbn8/7+/pYoboampvB\n6Uz06JKO9IQJIYS4o3AYdu5Un7+g4ieeekoFsYo0YBhw9Kg6asjrVY+tWqWa7hctSuzYUpT0hIlZ\nS5e9+2Qj82I+Zp4Tnw9+9jNVgFmt8MQTqu0nHQowM8/LnOnqgh//GH7zG1WAFRbCCy/Ac88lpABL\nlzmRlTAhhEhz3d0q/0viJ9LQ8DB8+CGcPq2u3W51xuOGDRIANwekJ0wIIdKUYcDeveozWOIn0ozf\nDx4P7N+vJj8zE7Zvh61bISMj0aNLKdITJoQQ4nMCAXj3XThxQl3X16sFEKs0qaS2UEgFv7W2qr8E\nFotqun/wQam+E0BebmLW0mXvPtnIvJiPWebkyhX4u79TBVhWlrr78ZFH0rcAM8u8xJVhwPHj8MMf\nqqXPQABWrIA//mN48knTFWBpMSfISpgQQqSVEyfUecvT05CfD888I/ETKa+nB95/H/r61HVBgUq6\nX748seMS8esJ6+3t5Wtf+xpDQ0NYLBa++c1v8qd/+qeMjIzw7LPP0t3dTXl5OW+//Ta5ubkAfO97\n3+MnP/kJNpuNH/zgBzz66KNfHLD0hAkhxD27MX5i/Xq1AJIOdz+mrZERter16afq2uWChx6Cysr0\nXfZMgNvVLXErwi5fvszly5eprKzE5/NRXV3NO++8w//5P/+HvLw8XnrpJV577TVGR0d59dVXOXny\nJM8//zydnZ309fWxY8cOzpw5g/WGvyhShAkhxL3RdfjVr9RdkFYrPPYY1NbKzW8pa3JSNd13dqrq\nOyNDnTlVXy9VdwLcrm6JWym8ePFiKisrAXC5XKxZs4a+vj7effddXnjhBQBeeOEF3nnnHQB++9vf\n8txzz5GRkUF5eTkrVqygo6MjXsMTMZQue/fJRubFfBIxJ93d8KMfqf/XNHjxRairkwLseinzWgmF\n1FLn97+vbnuNRGDTJviTP1GN90lUgKXMnNzBnPSEdXV1cejQIerq6hgcHKSgoACAgoICBqOnsff3\n97Nly5aZ/6a4uJi+a/vXQggh7onET6QRw1Bbjh9+CKOj6rFly1Tf1+LFiR2buK24F2E+n4+nn36a\n73//+2ia9rl/ZrFYsNzm17Fb/bMXX3yR8vJyAHJzc6msrKS5uRn4rHqW67m9vsYs45HrZpqbm001\nHrlm5rF4P9/Wrc28+y689566/pf/spmHH4bWVnP9POQ6BtdXrtCs69DTQ0tXF8ybR/O///ewciUt\nHg+cOmWu8d7ldXMSv39d+3NXVxd3Etew1mAwyJe//GWeeOIJ/uzP/gyA1atX09LSwuLFixkYGODB\nBx/k1KlTvPrqqwC8/PLLADz++OO88sor1NXVfX7A0hMmhBC3dOUKvPWWCkLPyoKvfAXWrEn0qETM\njY6qMx6PH1fXTqfacqyqSuqm+9PnTrPzwE6CRpAMSwY7qnewasWqRA9rVhLSE2YYBn/0R39ERUXF\nTAEG8NRTT/Hmm28C8Oabb/KVr3xl5vH/+3//L9PT01y8eJGzZ89SW1sbr+GJGLq++hfmIfNiPvGe\nkxMn4G//VhVg+fnwjW9IAXY3kuq1MjWlth1/+ENVgNnt0NAAf/qnsHlz0hdgP/3kp5ybd45/PvfP\nXCm4wk8/+Smnz51O9NDiJm7bke3t7fz85z9nw4YNbNq0CVARFC+//DLPPPMMb7zxxkxEBUBFRQXP\nPPMMFRUV2O12Xn/99dtuVQohhFDCYfW5vHevupb4iRQUDqsjhjwemJhQj23YoI45mDcvsWOLkbd2\nvcWn2qeMXR5jzDeGHtDRVmp8dPCjpF8NuxU5O1IIIZKYrqvDt3t6JH4iJRmGOlz7ww/h6lX1WFmZ\nmuiiosSOLQYMw+Di2EU8XR7eeu8tpoqnsFvtLNGWUOwuJsOWQe7lXP7s//uzO38xk5KzI4UQIgV1\nd6sCzOdT8RPPPAMlJYkelYiZ/n744AO41uC9cKE6X2rVqqSvsg3D4PzoeTxdHnq9vQBkWbNYnLuY\nYncxdutn5UmmNXWXdJN381iYRlL1U6QRmRfzidWcGIaKg3rzTVWAlZfDv/23UoDdL9O9VsbH4R/+\nAX78Y1WAORzwxBPwrW/B6tVJXYAZhsHZq2d549Ab/Pzoz+n19pJjz+HhpQ/zP57+HxReKcRutdN1\nuAuAwNkAD1c9nNhBx9EdV8J8Ph85OTnYbDZOnz7N6dOneeKJJ8jIyJiL8QkhhLhOIKDOfjx5Ul3X\n16u2oCTuxxbXBAKwa5eqsEMhsNlgyxbVeJ+dnejRzYphGJy5egZPt4d+vR8AR4aDbSXbqCmqIcue\nBUCWLYuPDn7E8Mgw+UP5PPzgwynbDwZ30RNWVVXFrl27GB0dpb6+npqaGjIzM/nFL34xV2P8HOkJ\nE0KkK4mfSFGRCBw8CJ98An6/emzdOlVdz5+f2LHNkmEYnBo+hafbw2XfZQCcGU7qS+vZXLSZTFvq\nbjVeM6ueMMMwcDgcvPHGG3zrW9/ipZdeYuPGjTEfpBBCiFs7cUKtgE1Pq/iJZ59VLUIiiRkGnD2r\nmu6vXFGPlZSopvvi4sSObZYMw+DT4U/xdHkY9KuTcVyZLraXbqe6sJoMm+ymwV025u/Zs4df/OIX\nvPHGGwBEIpG4Dkokl5brEsCFeci8mM/9zInET8RfQl4rly+rpvsLF9T1/Pmq6X7NmqTu+YoYEU5e\nOUlrdytD/iEA3FlutpduZ9PiTXddfKXL+9cdi7C//uu/5nvf+x5f/epXWbt2LefPn+fBBx+ci7EJ\nIURauzF+4vHHoaYmqT+jha7Dxx/D4cNqJSw7G5qa1MTakzewIGJEOD50nNbuVoYnhgGYlzVPFV+F\nmz53t6P4jOSECSGECUn8RIqZnob2dti9G4JB1XRfU6MKsJycRI/uvkWMCMcGj9Ha3crVSZVjlpud\nS0NpA5WLK7FZbQkeYeLNqiess7OTP//zP6erq4tQKDTzBY8ePRrbUQohhJiJn9i5U/VrL10Kf/AH\n6mhAkYQiEbXq9cknahUM1JbjI4/AggWJHdsshCNhjg4epbW7ldGpUQDmZ8+nsayRDQUbpPi6S3dc\nCXvggQf4y7/8S9atW4f1unugy8vL4z22m5KVMPNJl737ZCPzYj53mpMb4ye2b4eHHpL4iXiL22vl\n/HnV9zWoGtNZsgQefVQl3iepcCTM4cuHaetpY2xqDICFOQtpLGtkfcF6rJbY/GVNpfevWa2ELVq0\niKeeeirmgxJCCPGZG+MnvvpVlcspktDQkCq+zp1T17m5Km5i3bqkbegLRUIcGjjErp5djAfGAchz\n5NFY1si6/HUxK77SzR1Xwj744APeeustduzYQWb0dhyLxcLv//7vz8kAbyQrYUKIVHP8OLz7rsRP\nJD2fT207Hjyo9pWzsqCxEerqkrbpPhQJcXDgILt6duENeAHId+bTWNZIxaIKKb7uwqxWwt58801O\nnz5NKBT63HZkooowIYRIFRI/kSKCQdXIt2uXqqSt1s+a7pO0mS8YDnJg4ADtPe3o06qXrcBZQFN5\nE2vy1mBJ0hU9s7njStiqVas4deqUaX7gshJmPqm0d59KZF7M5/o5uT5+wmZT+ZwSP5EY9/1aMQw4\nehQ++gi8apWIVatU031eXkzHOFemw9Ps79/P7t7d+KZ9ACx2LaaprInVeavnrBZIpfevWa2Ebdu2\njZMnT7J27dqYD0wIIdJRVxf86ldq98rthj/8Q4mfSDpdXfD++zAwoK4LC1XT/dKlCR3W/ZoOT9PR\n18Hu3t1MBCcAKNKKaCpr4oGFD5hmISbV3HElbPXq1Zw/f56lS5eSlaUO2ExkRIWshAkhkpXET6SA\n4WG1h3z6tLp2u1XT/YYNSbmMGQgF6OjrYM+lPTPF1xJtCc3lzaxYsEKKrxi4Xd1yxyKsq6vrpo9L\nRIUQQtw9iZ9Icn4/eDywf7+qoDMz1SRu3QoZyXcO4lRoin2X9rH30l4mQ5MAlLhLaCpvYvn85VJ8\nxdCsijCzkSLMfFJp7z6VyLyYx9AQvP027N/fwqpVzRI/YTK3fa2EQurOibY2VUlbLFBVBQ8+CC7X\nnI4zFiaDk+y9tJd9ffuYCk0BUDavjKbyJpbmLjVN8ZVK71+z6gkTQghx/66Pn8jNhW9+U+InkoJh\nqMnbuRPGVS4WK1eqpvv8/MSO7T5MBCdU8XVpH4FwAICluUtpKm+iPLc8sYNLY7ISJoQQcXBj/MSG\nDfDlL0v8RFLo6VFN93196rqgQDXdL1+e2HHdB/+0nz2X9tDR18F0eBqAZfOX0VTWRFlu8ib3JxNZ\nCRNCiDkk8RNJamREVc6ffqquXS7VuFdZmXTNe75pH7t7d9PZ10kwEgRgxYIVNJU1UTJPbsU1izsW\nYb/+9a95+eWXGRwcnKnkLBYL3muZKCLtpdLefSqReUmMG+MnnnkGiovVP5M5MaeW99+n2TCgs1Mt\nYWZkQH09bNuWdEuXekCnvbedA/0HZoqvBxY+QFNZE0vcSxI8uruXLq+VOxZhL730Er/73e9Ys2bN\nXIxHCCGSksRPJKFQSBVev/41FBWppcpNm1TTvdud6NHdE2/AS3tPOwcGDhCKhABYnbeaxrJGirSi\nBI9O3Mode8Lq6+tpb2+fq/HckfSECSHMRuInkoxhqMnauRNGR9Vjy5apvq/FixM7tns0PjXOrp5d\nHBw4SNgIA7Ambw1N5U0sdiXX95KqZtUTtnnzZp599lm+8pWvmOIAbyGEMJNr8RPDw+q8ZomfMLlL\nl1TTfW+vul60SBVfK1YkVdPe2NQYbd1tHL58mLARxoKFtYvW0ljWSIGrINHDE3fpjkXY+Pg4OTk5\nfPDBB597XIowcU267N0nG5mX+Dt+XK2ABYPqBrpnnrl9/ITMSQKNjqozHo8fV9dOp9p2rKqipbWV\n5pUrEzu+uzQ6OUpbjyq+IkYECxbW56+noayBfGfyRWfcSrq8Vu5YhP30pz+dg2EIIUTyCIfhgw9g\n3z51LfETJjY1Ba2tarLCYbDbVcr99u1q6TJJXJ24SltPG0cHj84UXxsLNtJQ1kCeIzkPCxe36Ql7\n7bXX+M53vsOf/MmffPE/slj4wQ9+EPfB3Yz0hAkhEknX1fZjb6+Kn3j8cdi8Oal2stJDOKyOGPJ4\nYEKdicjGjapZb968xI7tHgxPDNPa3cqxwWMYGFgtVjYUbKChtIGFDkn9TQb31RNWUVEBQHV19eeO\nMTAMwzTHGgghxFzq6lL5X37/F+MnhEkYhjpc+8MP4epV9Vh5uer7KkqeuwSv+K/Q2t3K8aHjM8XX\npsWbaChtYH7O/EQPT8SIJOaLWUuXvftkI/MSO4YBu3erlqLZxE/InMRZf7/aJ+7qUtcLF6pjhlat\nuu1SpZnmZdA3SGt3KyevnMTAwGaxsalwE9tLt5ObnZvo4c0ZM83JbElivhBC3KdAAN5557MQdYmf\nMKHxcVUhHz2qrh0OaG6G6mq1Z5wELvsu4+ny8Omw+otms9ioKqxie+l25mUnz/apuDeyEiaEELcw\nNARvvaV2tSR+woQCAdi1S6XkhkKq4NqyBRoaIDs70aO7K/16P54uD6evngbAbrVTXVhNfWk97qzk\nCowVNycrYUIIcY+OHYN33/0sfuLZZ2HBgkSPSgBqT/jAAWhpUQ16AOvWwY4dkJscW3Z93j483R7O\nXD0DQIY1g81Fm9lWsg0tS0vw6BLn9IUL7DxxgiCQAexYu5ZVy5Ylelhxc8cF9dOnT/Pwww+zdu1a\nAI4ePcr//J//M+4DE8mjpaUl0UMQNyHzcn/CYfinf1In2QSDKn7i3/yb2BRgMiezZBhw5gz8zd/A\ne++pAqykRE3QH/zBfRdgczkvveO9/Pzoz/nbg3/LmatnyLBmUF9Sz3/Y8h94bMVjaV+A/fTgQYbW\nrWOv18uVdev46cGDnL5wIdFDi5s7roR94xvf4C/+4i/4d//u3wGwfv16nnvuOf7zf/7PcR+cEELM\nJa9X3f0o8RMmdPmyarq/9oE8f75qul+zJikmqHusG0+3hwujavyZtkxql9SytXgrzkw5YBTgn44f\n58q6dfR7vVyenGSFYZBVXc1Hx4+n7GrYHYuwiYkJ6urqZq4tFgsZGRlxHZRILqlyB0uqkXm5Nxcv\nwq9+Fd/4CZmT++D1wscfw5EjaiUsJwcaG6GmRgWvxkC85sUwDLrHu2npaqFrrAuALFsWdcV1bCne\ngiPDEZfnTTZXpqfp0HU+HBvDPzkJwKKaGiYjETSbjekEjy+e7vg3eNGiRZw7d27m+le/+hWFhYVx\nHZQQQsyVa/ETO3eqPy9bBk8/fe/xEyLGpqehvV1NTjColiZra1UBlpOT6NHdlmEYXBy7iKfLQ/d4\nNwDZ9my2FG+hbkkdORnmHv9ciBgGZyYm2KfrXIwWXkYkQq7dzpKsLPIyMri2vpnKB1Hc8e7I8+fP\n881vfpPdu3czf/58li5dyi9+8QvKy8vnaIifJ3dHmk8q5bmkEpmXO7sxfqKhQR0nGK/4CZmTuxCJ\nwOHDavXL51OPVVSopvs43RkRq3kxDIPzo+fxdHno9aoDwnPsOar4Kq4j254cd2zG00Q4zEFdp1PX\nGQ+FAMi0WtnocpE7PMzvjh0jq7qarr17Kd+yhcCBA7xYVZXU25Gzujty+fLlfPTRR/j9fiKRCJqW\nvk2DQojUIfETJnT+vOr7GhxU18XFKum+tDSx47oDwzA4O3IWT5eHPr0PAEeGg63FW6ldUkuWPXnO\nqIyX/kCADq+X434/oWhBsjAjgxpNo9LlIttmg4ULycvI4KPjxxm+eJF8l4uHk7wAu5M7roSNjo7y\ns5/9jK6uLkLRqlXOjhRCJDOJnzCZoSFVfF1rfcnNVStfa9eauuneMAzOXD2Dp9tDv94PgDPDybaS\nbWwu2pz2xVcoEuHkxAQdXi+XAgFAfYavzMmhVtNYnpOTFscgzmol7Etf+hJbt25lw4YNWK1WOTtS\nCJG0wmH1Wb9vn7reuBG+/GWQe40SxOeDTz6BgwdVQ15Wlur5qquLWdN9PBiGwanhU3i6PVz2XQbA\nlemaKb4ybancxXRn3lCI/brOAV3HHw4DkGOzscnlokbTmC8vuBl3XAmrqqri4MGDczWeO5KVMPOR\nPhdzknn5PDPET8icRAWDKuV+1y7VgG+1qsloblZHDs2xu50XwzA4eeUkrd2tDPrVlqmWqVFfWk91\nYTUZtvQtLgzDoHtqig5d59TEBJHo5/TizExq3W7WO51k3EOzZSq9Vma1Evb888/z4x//mCeffJKs\nrM+WVhfI2r0QIknMRfyEuAuGoaImPv5YVcWgDtd+5BHIy0vs2G4jYkQ4eeUkni4PVyauAODOcrO9\ndDtVhVXYreZdtYu36UiEoz4fHbrO0LQKk7BaLKxzOql1uynJypLds9u440rYD3/4Q/7Tf/pP5Obm\nYo1WsRaLhQsJSrCVlTAhxN2S+AkTuXgR3n9fha4CFBbCY49Bgu60vxsRI8LxoeO0drcyPDEMwLys\neTSUNVC5uDKti6+rwSCdXi+HfT6mIhEAXDYbmzWNak1DM/F28ly7Xd1yxyJs6dKldHZ2kmeS31Kk\nCBNC3I2pKfjtb+cufkLcwvCwasQ7o85IxO2Ghx9W50GZdIUkYkQ4OniUtu42rk5eBSA3O5eGUlV8\n2ay2BI8wMQzD4NzkJPu8Xs5Fs70ASrOzqdU01jid2Ew6p4k0q+3IlStXkmPyYDyRWKm0d59K0nle\nro+fyM5W8ROrViV6VGk2J36/OmD7wAGV/ZWZCdu3w9atprsT4tq8hCNhjgweoa27jdGpUQAW5Cyg\nobSBDQUb0rb4mgyHORzdchwNBgGwWyxsiDbaF2bF/i7QdHmt3LEIczgcVFZW8uCDD870hCUyokII\nIW5H4icSLBSCvXuhrU2l4VosnzXdu1yJHt1NhSNhDvQfoK2njbGpMQAW5iyksayR9QXrsVrSc/n0\nciBAp65z1O8nGN1yzLXbqXG72eRy4bClZ1EaS3fcjvzpT3/6xf/IYuGFF16I15huS7YjhRA3Ew6r\nlqOODnUt8RNzzDDg+HHVgDc+rh5buVI13efnJ3ZstxCKhDg0cIhdPbsYD6gx5znyaCprYm3+2rQs\nvsKGwalotlf31NTM48tzcqh1u1mZk4NVthzvyax6wsxGijAhxI1ujJ944gmorjZty1Hq6e5WfV99\nKi2eggKVdL98eWLHdQuhSIgD/Qdo723HG1B3aeY782ksa6RiUUVaFl++UIgDPh/7dR09GsyeZbVS\nGd1yzMtM7+yz2bivnrA//MM/5Je//CXr16+/6Rc8evRo7EYoklq67N0nm3SZl2SKn0i5Obl6Va18\nXbv7QdPgoYfUMqQJ74AIhoMcGDhAe087+rQOQIGzgJy+HF5oeiHtohQMw+BSIECHrnPS7yccLRQW\nZWZSq2lscLnIStA8ptxr5RZuWYR9//vfB+B3v/vdFyq4dPuLKoQwH4mfSKCJCWhtVXu/kYja862v\nh23bVAO+yUyHp9nfv5/2nnb8QT8Aha5CmsqbWLVwFR6/J60+14KRCMf9fjp0nYHrjhNa43RSq2mU\nZ2en1c8jke64Hfmd73yH11577Y6PzRXZjhRCTE3BO+/AqVPqurFR9X2bcPEltYRCqvBqbVWTc7EH\nDwAAIABJREFUYLFAZaVa/dK0RI/uCwKhAJ39nezu3c1EcAKAIq2IprImHlj4QNoVGmPBIJ26zkGf\nj8nocUIOm41qTWOzpjFPsr3iYlY9YZs2beLQoUOfe2z9+vUcO3YsdiO8B1KECZHeBgfh7bfNFz+R\n0gwDTp5Uy46jKrqB5ctV31dBQWLHdhOBUICOvg529+5mMqTyrIrdxTSVNbFiwYq0Kr4Mw+DC1BQd\nXi9nJidnPj+LsrKoc7tZ63Bgl99e4uq+esL+5m/+htdff53z589/ri9M13Xq6+tjP0qRtNJl7z7Z\npOK8HD0K//iPyRs/kZRz0turmu57e9X1okWq+FqxwnR3PkyFpth3aR97Lu1hKqTu7Ctxl9Bc3syy\n+ctuWXwl5bzcQSAS4YjPR4fXy3A028tmsbDO5aLW7WZJHLK9YikV5+RmblmEPf/88zzxxBO8/PLL\nvPbaazNVnKZpLFy48K6++Ne//nXee+898vPzZ1bO/tt/+2/83d/9HYsWLQLgz//8z3niiScA+N73\nvsdPfvITbDYbP/jBD3j00Udn9c0JIVKDxE8kwOioWvk6cUJdO53qyIGqKtPt+04GJ9l7aS/7+vbN\nFF9l88poLm+mPLc8rVa+rkxP06nrHPb5mI5me7nt9pnjhJyS7WUqcY2oaGtrw+Vy8bWvfW2mCHvl\nlVfQNI1vf/vbn/t3T548yfPPP09nZyd9fX3s2LGDM2fOzJxXOTNg2Y4UIq14vWr78dIliZ+YE5OT\nKmh13z5V/drtquG+vh5MtnoyEZxgT+8eOvo6CIRVg/nS3KU0lTdRnlue2MHNoYhhcGZigg5d58J1\nxwmVZ2dT63az2uGQbK8EmtWxRbPR0NBAV1fXFx6/2WB++9vf8txzz5GRkUF5eTkrVqygo6ODLVu2\nxHOIQggTuz5+Yt48FT+xZEmiR5WiwmHYv18dNXTtg3zjRtV0P29eQod2I/+0nz2XVPE1HZ4GYPn8\n5TSVN1E6rzTBo5s7E+EwB3WdTl1nPJrtlWG1stHppNbtJt+Ed6qKz0vIrRD/+3//b372s5+xefNm\n/uqv/orc3Fz6+/s/V3AVFxfTdy34T5hauuzdJ5tknhfDgPZ2+Oijz+In/uAPwOFI9Mhmx5RzYhjq\nNtOdO9XdDgDl5fDYY1BYmNCh3cg37WN37246+zoJRlSf04oFK2gqa6JkXsl9f11Tzstt9AcCdHi9\nHPf7CUUXNRZmZFCjaVS6XGSnwJZjss3J/ZrzIuyP//iP+a//9b8C8F/+y3/hP/7H/8gbb7xx03/3\nVvv4L774IuXl5QDk5uZSWVk5M1ktLS0Acj2H14cPHzbVeOQ6ua+np2FkpJlTp6Crq4UNG+Bf/atm\nrFZzjG8214cPHzbVeFp+9Svo7KQ5J0ddj4zA5s00/+t/DRZL4scXva7eWk17bzu/fO+XhI0w5ZXl\nPLDwATJ6MljEIko2lMzq619jlu/3ZtehSIQ333+fU34/zupqALr27aM4M5MXH3+c5Tk5eDwe9ppk\nvOl8fe3PN9sJvFHcjy3q6uriySefvGmkxfX/7NVXXwXg5ZdfBuDxxx/nlVdeoa6u7vMDlp4wIVLW\n4CC89RaMjEj8RFyNj6tlxmsnnzgc0Nysmu1MtIriDXjZ1bOLgwMHCUXUdtvqvNU0ljVSpBUleHRz\nwxsKsV/XOaDr+KPZXtlWK1XRbK8FcneK6SWsJ+xmBgYGKIwucf/mN7+Zib946qmneP755/n2t79N\nX18fZ8+epba2dq6HJ4RIkOvjJxYvVv1fyRQ/kRQCAdV0v3evCl612WDLFmhoUFWvSYxPjc8UX2FD\nFR4ViypoLGtksWtxgkcXf4Zh0D01RYeuc2pigkj0A3xxZia1bjfrnU4yrNYEj1LEQlyLsOeeew6P\nx8Pw8DAlJSW88sortES3rywWC0uXLuVHP/oRABUVFTzzzDNUVFRgt9t5/fXX0+q24mTW0pIee/fJ\nJlnm5cb4icpK+L3fS834iYTNSSQCBw5AS4u6ywFg3TrYsQNyc+d+PLcwNjVGW3cbhy8fJmyEsWBh\n7aK1NJY1UuCKXyisWV4r05EIx/x+OrxeBqfVDQdWi4V10Ub7kqystPlcNMucxFtci7C///u//8Jj\nX//612/573/3u9/lu9/9bjyHJIQwEYmfiDPDgLNnVdjq8LB6rLRUha2a6JTzkckR2rrbODJ4hIgR\nwYKF9fnraSxrZJFzUaKHF3cj0eOEDuk6U9FsL5fNNpPtpclxQikr7j1hsSY9YUKkBomfiLPLl9US\n48WL6nrBAnjkEVi92jRV7tWJq7T1tHF08OhM8bWhYAMNZQ3kOfISPby4MgyDc5OTdOg6ZycmZh4v\nyc6mVtOocDqxmWSexOyYqidMCJHeboyfWL4cnn46+eMnTMPrhY8/hiNH1A84JweamqCmxjRN91f8\nV2jraePY4DEMDKwWK5sWb6KhrIEFOandCDgZDnPY56NT1xmJHidkt1hY73JRq2kUmiwQV8SXFGFi\n1tJl7z7ZmHFepqbgnXdULBVAY6O6KS9deozjOifT06q63b1b3d1gs0FtrfohRyMoEm3IP0Rrdysn\nhk58vvgqbWB+zvyEjWsuXiuD09N0eL0c9fsJRrccc+12atxuNrlcOExSIJuFGd+/4kGKMCHEnLgx\nfuL3fx8eeCDRo0oBkQgcPqxWv3w+9VhFhWq6N8ntpYO+QTzdHk5eOQmAzWJjU+EmtpduJzfbPDcG\nxFrYMDg1MUGH10v31NTM48tzcqh1u1mZkyPHCaU56QkTQsTdjfETzz4L8xO38JE6zp1TTfdDQ+q6\nuFg13Zea4+ieAX2A1u5WPh3+FFDFV3VRNfUl9czLNtdRSLHkC4U44POxX9fRo8cJZVmtVLpc1Gga\neZmZCR6hmEvSEyaESIhwGP75n6GzU12ncvzEnBochA8/VEUYqJiJHTtg7VpTNN336/14ujycvnoa\nALvVTnVhNfWl9biz3AkeXXwYhsGlQIAOXeek3084+qG7KDOTWk1jg8tFVrrsu4u7JkWYmLV02btP\nNomeF4mf+KJZz4nPp7YdDx1STffZ2Spota4OTBBjcMl7CU+Xh7MjZwHIsGawuWgz20q2oWVpCR7d\nrc1mXoKRCCf8fvbpOgOBAKBWPtY4ndRqGuXZ2WmT7RVLiX7/miuJf9UKIVLOhQsqfmJiQuInYiIY\nVA337e2qAd9qVXc7Njeb4rbS3vFePN0ezo2olbkMawa1S2rZVrINZ6YzwaOLj7FgkP26zkGfj4no\ncUIOm43q6HFC80xQFAvzk54wIUTMGAbs2qUWayR+IgYMQ0VNfPQR6Lp6bPVqtfWYl/gcre6xbjzd\nHi6MXgAg05ZJ3ZI6thRvScniyzAMLk5N0eH1cnpycuazqCgri1pNY53TiV22HMUNpCdMCBF3U1Pw\nm9/AadUGlHbxEzF38aIKW718WV0XFsJjj0F5eUKHZRgGXWNdeLo9dI11AZBly6KuWBVfjozUq7gD\nkQhHfD46vF6Go9leNouFtdFsryVpdJyQiC0pwsSspcvefbKZy3mR+Im7c1dzcuWKaro/c0Zdu91q\n5Wv9+oQ21BmGwcWxi3i6PHSPdwOQbc9mS/EW6pbUkZNhjiyy+3GreRmenqZD1zns8zEdzfZy2+1s\n1jSqXC5csuUYN+nyuSJ/g4QQsyLxEzHi96sDtg8cUNlfmZmq6X7LloTeTmoYBudHz+Pp8tDr7QUg\nx57D1pKt1C6pJduenbCxxUPEMDgzMUGHrnNhcnLm8fLsbGrdblY7HJLtJWJGesKEEPclFFK7ZRI/\nMUvBIOzbB21tEAio1a7qarWX63IlbFiGYXB25CyeLg99eh8AjgwH20q2UVNUQ5Y9tY7XmQiHOajr\ndOo649FsrwyrlY1OJzVuNwWS7SXuk/SECSFianwcfvnLz+InvvQlqKpK7/iJe2YYcOyYarofH1eP\nrVypwlYXLUrgsAxOXz2Np8vDgG8AAGeGUxVfS2rItKVWMdIfCNDh9XLc7ycU/aBckJFBraZR6XKR\nLccJiTiSIkzMWrrs3SebeM2LxE/cv5k56e5WSfd9aoWJxYtV8bVsWcLGZhgGp4ZP4en2cNmnbgZw\nZbqoL6mnuqg6pYqvsGFwwu+nw+vlUiBA1969LN26lQccDmo1jeU5OdJon2Dp8rkiRZgQ4q5I/EQM\njI+rOxg+Vcf4oGnw0EOwcWPCbiM1DIOTV07S2t3KoH9QDStTY3vpdqoKq8iwpc7+sjcU4oCuc0DX\n8UWzvbKtVtY6nfzRkiUskL10McekJ0wIcUc3xk80Nan/SfzEXZqYAI9HNdBFIqpxbvt22LpVNeAn\nQMSIcGLoBK3drVyZuAKAO8s9U3zZranxO7phGPREtxw/nZggEv38KMjMpNbtZoPTSYb8RRZxJD1h\nQoj7JvETsxAKQUcHtLaqStZiUc1zDz6oVsESIGJEOD50nNbuVoYnhgGYlzWPhrIGKhdXpkzxNR2J\ncCy65Tg4PQ2A1WJhrdNJrdtNqWR7CRNIjVebSKh02btPNrGYlyNH4He/k/iJe2YYcPIk7NwJo6Pq\nseXLaXE6aX7qqYQMKRwJc2zoGK3drYxMjgCQm51LY1kjGws2YrOmRgP6SDBIp65zSNeZimZ7uaLH\nCVVrGu6bZHvJe5j5pMucSBEmhPiCG+MnNm1Sd0BKy8xd6O1VP7xLl9R1fr5qul++XG1JzrFwJMyR\nwSO0dbcxOqUKwgU5C2gobWBDwYaUKL4Mw+Dc5CQdus65644TKsnOplbTqHA6scmqlzAh6QkTQnzO\n+Di8/ba6cU/iJ+7B6Kha+TpxQl07narpftOmhDTPhSIhDl8+zK6eXYxNjQGwMGchjWWNrC9Yj9WS\n/H1Qk+Ewh30+OnWdkehxQnaLhfXR44QKs1Iry0wkJ+kJE0LclRvjJ559FoqKEj0qk5ucVEGr+/ZB\nOAx2O2zbBvX1kIAiIBQJcWjgELt6djEeUPljeY48msqaWJu/NiWKr8HpaTq8Xo76/QSjW465djs1\nbjebXC4cku0lkoQUYWLW0mXvPtncy7zcGD+xYoVqwJf4idsIh9V+rcejCjFQURMPP6zOe7yJeL5W\nguEgBwcOsqtnF/q0DkC+M5+msibWLFqT9MVX2DA4NTFBh9dL99TUzOPLc3KodbtZmZNz38cJyXuY\n+aTLnEgRJkSak/iJe2QYcOqUOmR7RDW4U14Ojz0GhYVzPpxgOMj+/v2097bjm/YBUOAsoKm8iTV5\na5L+DkBfKMRBn4/9uo43epxQltVKpctFjaaRJ8cJiSQmPWFCpLHLl1X/17X4iaefVifniFvo61NJ\n993d6jovDx55RGV2zHGxMx2eprOvk929u/EH/QAUugppKm9i1cJVSV18GYZBXyBAh65zwu8nHH3P\nX5SZSa2mscHlIkt+SxBJQnrChBBfIPET92BsTJ3xeOyYunY41AHb1dXq7oU5FAgF6OxXxddEcAKA\nIq2I5vJmVi5YmdTFVzASUccJ6Tr9gQCgPsBWOxzUut0szc5O6u9PiBtJESZmLV327pPNreYlFIJ/\n/mfYv19dS/zEbUxNqWa5vXvVD85uhy1bVNp9dvY9f7nZvFamQlN09HWwp3cPkyHVg1bsLqaprIkV\nC1YkdXEyFgyyX9c56PMxET1OyGGzUeVysVnTyI3zX055DzOfdJkTKcKESCPXx0/Y7Z/FT4gbRCJw\n4AC0tIBfbfWxfr1qus/NndOhTIWm2HdpH3su7WEqpBrSS+eV0lTWxLL5y5K2+DIMg4tTU3R4vZy+\nLturKCuLWk1jndOJXbYcRYqTnjAh0sT18RO5ufDMMxI/8QWGAWfPqr6vYXWkD6Wlqul+yZI5Hcpk\ncJK9l/ay99JeAmG1NVeeW05TWRPlueVJW3wFIhGO+Hx0eL0MR7O9bNeOE9I0lshxQiLFSE+YEGlM\n4ifu0sCAKr4uXlTXCxaopvvVq+e06X4iOMGe3j109HXMFF9Lc5fSVK6Kr2Q1PD1Nh65zxOcjEM32\nctvtbNY0qlwuXDc5TkiIVCd/68WspcvefbJpaWlhy5ZmiZ+4E69XVahHjqgqNSdH/ZBqamLedH+7\n14p/2s/u3t109ncyHVYHTi+fv5ym8iZK55XGdBxzJWIYnJmYoEPXuXAtSw0oz86m1u1mlcNhiuOE\n5D3MfNJlTqQIEyJFjYzAj36kTtPJyVGrXxI/cZ1AANrbYc8edYuozQa1tdDYqH5gc8Q37VPFV18n\nwYjanlu5YCVN5U0Uu4vnbByxNBEOc8jno9PrZSya7ZVhtbLR6aTG7aZAsr2EAKQnTIiUdOQI/OM/\nqhv6CgtV/5fET0RFInDoEHzyCfhUuCkVFbBjh9qCnCN6QKe9t539/fsJRVShsmrhKhrLGlnintv+\ns1gZiGZ7HfP5CEXfpxdkZFCraVS6XGTLcUIiDUlPmBBpQuIn7uDcOdX3NTSkrouLVdN9ScmcDcEb\n8LKrZxcHBw7OFF+r81bTVNZEoTb3ifuzFTYMTkazvXqjxwlZLBZWOhzUahorcnKk0V6IW5AiTMxa\nuuzdm92N8RP5+S38i3/RnOhhmcPgoCq+zp9X17m5auVr7do5a7ofnxrn9V++Tqg0RNhQWVgViypo\nLGtksWvxnIwhlryhEAd0nQO6ji+a7ZVttbJJ06jRNBYkUeUv72Hmky5zIkWYECng/Hn49a8/Hz9x\n5kyiR2UCuq62HQ8dUk332dmq56u2VlWqc2B0cpRdPbs4fPkw56+eZ2nJUtblr6OxrJF8Z/6cjCFW\nDMOgJxCgw+vl04kJItEtloLMTGrdbtY7nWTKXR9C3DXpCRMiiRkGtLWpOkPiJ64zPa0a7tvb1Z+t\nVnW3Y1PTnP1wRiZHaOtu48jgESJGBAsW1hesp6G0gUXORXMyhliZjkQ45vfT4fUyOK3u3LRaLKyJ\nHidUKtleQtyS9IQJkYImJ+Gdd1T8hMWijjJsbEzz+IlIBI4eVec86rp6bPVqlfe1cOGcDOHqxFVa\nu1s5NnRspvjaWLCRhrIG8hx5czKGWBkJBunUdQ7pOlPRbC+nzcZmTaNa03BLtpcQsyKvIDFr6bJ3\nbyaXL8Nbb90+fiLt5uXCBdX3dfmyui4qgkcfhfLyOXn6K/4rtPW0cWzwGAYGVouVTYs30VDWwIIc\ndddlMsyJYRicm5ykQ9c5d91xQiXZ2dRqGmscjpQ7TigZ5iXdpMucSBEmRJI5fBh+9zuJn5hx5Qp8\n+OFnTXDz5qkzHtevn5Om+yH/EK3drZwYOvH54qu0gfk5yTMxU9eyvXSdkehxQnaLhfXRRvuirKwE\nj1CI1CM9YUIkiRvjJ6qqVPxE2u4I+f3qgO0DB9Q2ZFYWbN8OW7bMSSbHoG8QT7eHk1dOAmCz2NhU\nuIntpdvJzZ7bQ75nY3B6mk6vlyN+P8HolmOu3U6N280mlwuHZHsJMSvSEyZEkrsxfuJLX1JFWFoK\nBmHvXnUgZiDwWdN9czM4nXF/+gF9AE+3h1PDpwBVfFUXVVNfUs+87Hlxf/5YCBsGpycm6PB66Ypm\newEsy8mhVtN4wOHAKo32QsSdFGFi1tJl7z5RbhY/UVR05/8u5ebFMODYMdV0Pz6uHnvgAdV0vyj+\ndxv2efto7W7l9FV1EKfdamdz0Wa2lWzDneW+q6+R6DnxhUIc9PnYr+t4o8cJZVqtVLpc1Ggai9L0\nOKFEz4v4onSZEynChDCpm8VPPP30nB5raB7d3fD++9Dfr64XL1ZN98uWxf2pL3kv4enycHbkLAAZ\n1gw2F22mvrQeV6Yr7s8/W4Zh0Bc9TuiE3084ui2Sl5FBrdvNRpeLrBRrtBciWUhPmBAmNDkJv/mN\n6jW3WFS8VVPTnIW7m8fVq6rp/pTa+kPTVNP9hg1xz+LoGe/B0+Xh/KhK2c+0ZVJTVMO2km04M+O/\n7TlboUiE49HjhPoDAUC9f67KyaHW7WZpdrZkewkxB6QnTIgkcjfxEylvYgI8HujsVE33mZlQXw9b\nt6o/x1H3WDctXS1cHLsIqOKrbkkdW0u24sgwfwruWDDIfl3noM/HRPQ4IYfNRpXLxWZNIzeJjhMS\nItVJESZmLV327ufCjfETzz6r+sDuR1LOSygEHR3Q2gpTU2rpr6oKHnxQrYLFiWEYdI114en20DXW\nBUCWLYstxVvYUryFnIzY7AHHa04Mw+Di1BQdXi+nr8v2KszKok7TWOt0kiFbjreUlK+VFJcucyJF\nmBAmEArBP/2TSluANIyfMAw4cQJ27oSxMfXY8uWq76ugII5Pa3Bh9AKebg894z0AZNuz2VK8hbol\ndTErvuIlEIlwJJrtdSV6nJDNYmGty0WtprFEjhMSwtSkJ0yIBEv7+IneXtV0f+mSus7PV8XXihVx\ne0rDMDg/eh5Pl4deby8AOfYctpZspXZJLdn27Lg9dywMT0/Tqesc9vkIRLO9NLudGk2jyuXClTbV\nuxDmJz1hQpjU/cZPpISRERU3ceKEuna51Lbjpk1xa7o3DIOzI2fxdHno0/sAcGQ42FayjZqiGrLs\n5k2FjxgGZycn6fB6OT85OfN4WXY2dW43qxwObLLqJURSkSJMzFq67N3HkmGotqeWFvXnlStVA34s\n4ydMOy+Tk+qb7+iAcFil22/dqhrv43Q0jmEYnL56Gk+XhwHfAADODKcqvpbUkGmbm3ys+5mTiWvH\nCXm9jEWzvTKsVjY4ndS63RSkabZXLJn2tZLG0mVOpAgTYo7dGD/R3Jwm8RPhsLrb0eNRPwSLBSor\n4aGHwH13Yaf3yjAMPh3+lNbuVi771MHerkwX9SX1bC7aTIbNvHcKDkSzvY75fISiWxkLMjKo0TQq\nXS5y5DghIZKe9IQJMYdujJ94+um4tj6Zg2GonK8PP1RbkABLl6q+r8LCuDxlxIjw6ZVP8XR7GPIP\nAaBlamwv3U5VYZVpi6+wYXAymu3Ve91xQisdDmo1jRU5OdJoL0SSkZ4wIUzg+viJoiLV/3W/8RNJ\no68PPvhAJd4D5OWp4mvlyrgs/UWMCCeGTtDa3cqViSsAuLPcNJQ2sKlwE3arOd/y9FCI/brOAV3H\nF832yrZa2aRp1GgaCyTbS4iUZM53JJFU0mXv/n4lKn4iofMyNqaa7o8dU9cOh2q6r6qCOGyjRYwI\nxwaP0drdytXJqwDMy5pHQ1kDlYsrTVN8XT8nhmHQEwjQ4fXy6cQEkehvygWZmdS63ax3OsmUbK85\nIe9h5pMucxLXd6avf/3rvPfee+Tn53Ms+mY8MjLCs88+S3d3N+Xl5bz99tvkRpcDvve97/GTn/wE\nm83GD37wAx599NF4Dk+IuBsbU/ET/f2q6Pq931M3/6WsqSnYtQv27lXVp90OW7bA9u2QHfvYh3Ak\nzLEhVXyNTKqtzvnZ82koa2BjwUZsVvP1TU1HIhzz++nwehmMZntZLRbWRhvtSyXbS4i0EdeesLa2\nNlwuF1/72tdmirCXXnqJvLw8XnrpJV577TVGR0d59dVXOXnyJM8//zydnZ309fWxY8cOzpw5g/WG\n3wSlJ0wki3PnVPzE5KTadnz22bi1QCVeOKyW+lpaVN4GwPr16pzHOOy5hiNhjgweoa27jdGpUQAW\n5CygsayR9fnrTVl8jQSDdOo6h3SdqWi2l9NmY7OmUa1puCXbS4iUlLCesIaGBrq6uj732LvvvovH\n4wHghRdeoLm5mVdffZXf/va3PPfcc2RkZFBeXs6KFSvo6Ohgy5Yt8RyiEDE3F/ETpmEY6jbPDz+E\n4WH1WGkpPPYYLFkS86cLRUIcvnyYXT27GJtSyfp5jjwayxpZl78Oq8Vc23eGYXB+cpJ9us65644T\nKs7Kos7tZo3DgV22HIVIW3P+q9fg4CAF0WNICgoKGBwcBKC/v/9zBVdxcTF9fX1zPTxxH9Jl7/5u\n3Bg/8eCD0NiYmPiJuM/LwIBqur+oDrpmwQJ45BFYvTrm33AoEuLgwEF29ezCG/ACsMixiMayRtbm\nrzVd8TUVDnPY56ND1xkJBgGwWyxw5Ahff+IJiuKUhybuj7yHmU+6zElC178tFsttex9u9c9efPFF\nysvLAcjNzaWysnJmslpaWgDkeg6vDx8+bKrxJOp6YAD+1/9qweeDNWuaefppuHSpBY/HHOOL2bXf\nT/P0NBw9SsvFi5CZSfPXvw41NbS0tcHgYMyeb+dHOzkzcobJJZPo0zpdh7vIzc7lG7//DdYsWkOr\np5XWT1tN8/P5hw8/5PTEBJHKSoKRCF179+K02Xju0Uep0jR+/M47nNmzhyKTjFeu1fU1ZhmPXCf3\n9bU/37gTeDNxzwnr6uriySefnOkJW716NS0tLSxevJiBgQEefPBBTp06xauvvgrAyy+/DMDjjz/O\nK6+8Ql1d3ecHLD1hwoQOHYL33kvx+IlAANrbYc8eCAbVXY51ddDQEPO91mA4yP7+/bT3tuOb9gFQ\n4CygqbyJNXlrTNW4HjYMTk9M0OH10nVdtteynBxqNY0HHA6sJhqvEGJumSon7KmnnuLNN9/kO9/5\nDm+++SZf+cpXZh5//vnn+fa3v01fXx9nz56ltrZ2rocnxD25MX6iuhqeeCL+8RNzKhJRVeYnn4BP\nFUSsXQs7dsD8+TF9qunwNJ19nezu3Y0/6Aeg0FVIU3kTqxauMlXx5Q+HOaDr7Nd1vNHjhDKtVipd\nLmo0jUWZmQkeoRDC7OL6UfHcc8/h8XgYHh6mpKSE//7f/zsvv/wyzzzzDG+88cZMRAVARUUFzzzz\nDBUVFdjtdl5//XVTveGKW2tpSY+9+xuZPX4iJvNy7pzq+xpSqfMUF6um+5KSWY/veoFQgM5+VXxN\nBNXdlUu0JTSVN7FywUrTvBcYhkFf9DihE34/4ehvt3kZGdS63Wx0uciyWm/536fra8XsZF7MJ13m\nJK5F2N///d/f9PGdO3fe9PHvfve7fPe7343nkISIiZSPnxgcVMXX+fPqev58tfJVURHRw9evAAAg\nAElEQVTTpvup0BQdfR3s6d3DZGgSgGJ3Mc3lzSyfv9w0xVcoEuF49Dih/kAAUFsMqx0Oat1ulmZn\nm2asQojkIWdHCnEPUj5+QtfVtuOhQ+obzM5Wt3fW1sZ0j3UyOMm+vn3svbSXqZDqoyqdV0pTWRPL\n5i8zTUEzFgyyX9c56PMxET1OKMdmo9rlYrOmkSvHCQkh7sBUPWFCJKvJSfiHf4CzZxMfPxFz09Oq\n4b69Xf3ZalWFV1OTOnIoRiaCE+y9tJd9l/YRCKsVpfLccprKmijPLTdF8WUYBl1TU+zzejl9XbZX\nYVYWdZrGWqeTjNtsOQohxN2SIkzMWjrs3Q8MwFtvqT6wnBx4+mlYsSLRo7q9u5qXSASOHIGPP1ar\nYABr1qitx4ULYzaWieAEe3r3sK9vH9NhdVTPsvnLaCxrpDy3PGbPMxuBSISj0WyvK9HjhGwWCxUu\nF7WaRnEMjhNKh9dKMpJ5MZ90mRMpwoS4g5SNn7hwQfV9Xb6srouKVNN9WVnMnsI/7Wd37246+ztn\niq/l85fTVN5E6bzSmD3PbAxPT9Op6xz2+QhEjxPS7HZ1nJDLhSulbnUVQpiJ9IQJcQspGz9x5Yo6\nZujMGXU9b54643H9+pjtrfqmfbT3tLO/fz/BiEqMX7lgJU3lTRS7i2PyHLMRMQzOTk7S4fVyfnJy\n5vGy7Gxq3W5WOxzYTLA1KoRIftITJsQ9Mnv8xH3x+dQdBQcPqm3IrCwVtFpXBzFqMNcDOu29qvgK\nRVR21qqFq2gqb6JIK4rJc8zGRDjMIZ+PTq+XsWi2V4bVygank1q3mwLJ9hJCzCEpwsSspdre/fXx\nE/Pnq+3HZIyfmJmXYBD27oVdu1TqvdUKNTXQ3AxOZ0yeyxvwsqtnFwcHDs4UX2vy1tBY1kihlvgf\n3kA02+uYz0co+hvp/IwMajWNSpeLHJttTsaRaq+VVCHzYj7pMidShAkRlXLxE4YBR4/CRx/B+Lh6\n7IEH1CHbixbF5CnGpsbY1bOLQwOHCBsqwqFiUQWNZY0sdi2OyXPcr7BhcDKa7dV73XFCKx0OajWN\nFTk5prgbUwiRvqQnTAi+GD/R3Jzk8RNdXarpvr9fXS9eDI8+CsuWxeTLj06O0tbTxuHLh4kYESxY\nWJu/lsayRvKd+TF5jvulh0Ls13UO6Dq+aLZXttXKJk1js6axULK9hBBzSHrChLiNZIyfuKWrV1XT\n/alT6lrTVNP9hg1qG3KWRiZHaOtu48jgkZnia0PBBhpKG1jkjM3q2v0wDIPeQIAOr5eTExNEom94\n+ZmZ1LndrHc6yZRsLyGEyUgRJmYtmffuUyZ+YmICPB7o7FRN95mZtDgcNH/rWxCDZvOrE1dp7W7l\n2NAxIkYEq8VK5eJKGkobWOiIXZ7YvQpGIhzz++nwerkczfayWixUOJ3UahplJjtOKJlfK6lM5sV8\n0mVOpAgTaSkUgv/3/9SNgpDE8ROhEOzbB21tMDWl9k+rqlSc/4EDsy7Arviv0NrdyvGh4xgYWC1W\nNi3eRENZAwtyFsTom7h3o8EgnbrOQV1nKprt5bTZqI5uObqTbiKFEOlIesJE2hkbU9uPAwOq6Pry\nl6GyMtGjukeGASdOwM6d6hsCtYf6yCNQUDDrLz/kH6K1u5UTQycwMLBZbFQurmR76Xbm58yf9de/\nH4ZhcH5ykg5d5+x1xwkVZ2VR63ZT4XBgly1HIYTJSE+YEFE3xk88+6zqWU8qvb3w/vtw6ZK6zs9X\nTfcxaGS77LtMa3crJ6+cBMBmsVFVWEV9aT252YnZp50Khzns89Gp61wNquBXu8XCOpeLWreboqys\nhIxLCCFmS4owMWvJsHdvGKplyuNRf37gAfjqV5MsfmJkRK18nVQFEi4XPPSQWsa7yQrQvczLgD6A\np9vDqWHV0G+32qkqrGJ76XbcWe5YfQf3ZGh6mg6vl6N+P9PRLcd5djs1mkaVpuGYo2yvWEqG10o6\nknkxn3SZEynCRMq7MX7ioYdUULyJ+rVvb3JSBZh1dEA4rNLtt22D+vpZ93z1efvwdHs4c1UdYWS3\n2tlctJn6knq0LC0Wo78nEcPg1MQEHV4vXddley3LyaFW03jA4cCaNBMnhBC3Jz1hIqVdHz/hcKj4\nieXLEz2quxQOq7sdPR5ViFkssHGjqiLds1uduuS9hKfLw9mRswBkWDOoWVLDtpJtuDJdsRj9PfGH\nwxzQdfbrOt7ocUKZViuVLhc1msYiOU5ICJGkpCdMpKWDB9UdkEkXP2EY8OmnautxZEQ9tnSp6vua\n5flJPeM9eLo8nB89D0CmLZOaIlV8OTNjc4TRveiLZnsd9/sJR9+k8jIyqHW72ehykSWN9kKIFCZF\nmJg1s+3d3xg/sXkzPP54ksRP9PWppvueHnWdl6eKr5Ur73n/9Pp56RrrwtPl4eLYRQCybFnULqll\na8lWHBmOWH4HdxSKRDgR3XLsCwQA9ZviKoeDOrebpSbL9ools71WhCLzYj7pMifJ8LEkxF0bHYW3\n307C+ImxMbXydfy4unY61dlJVVVwnw3ohmFwcfQiLV0tdI93A6r42lK8hS3FW8jJmNu7EsavO05o\nInqcUI7NRlV0yzFXjhMSQqQZ6QkTKePsWdWAn1TxE1NTKmh13z61hGe3w5YtsH07ZGff15c0DIML\noxfwdHvoGVcratn2bLYWb6WuuI5s+/193fsdS9fUFB26zqmJiZnXbmFWFrWaxjqnkwzZchRCpDDp\nCRMpLSnjJ8JhlWjf0qKOHAJ1vuNDD91345phGJwbOYen28Mlr8oQy7HnsLVkK7VLaue0+ApEIhz1\n+ejQda5EjxOyWSxUuFzUahrFWVkpu+UohBB3S4owMWuJ3LufnFThq+fOJUn8hGHAmTPqkO3hYfVY\nWZnq+1qy5D6/pMGZq2fwdHvo1/sBcGQ4yLmUwzef/iZZ9rkLMx2enqZT1zns8xGIZntpdjubNY1q\nlwtXUjTmxU+69LkkG5kX80mXOUnvd0SR1Pr7Vf9X0sRPDAyopvuuLnW9YIE6Zmj16vuqGg3D4PTV\n03i6PAz4BgBwZjipL61nc9FmdrftnpMCLGIYnJ2cpMPr5fzk5MzjZdnZ1LrdrHY4sJm2KhZCiMSR\nnjCRlK6Pn1iyRMVPzJuX6FHdwvg4fPwxHDmirnNyVNP95s331XRvGAafDn+Kp8vDoH8QAFemi/oS\nVXxl2OamwX0iHOaQz0en18tYNNsrw2plg9NJjaaxWI4TEkII6QkTqSMYVMXXoUPq2tTxE4EAtLfD\n7t2qWrTZoK5O7ZfeR8NaxIhw8spJWrtbGfIPAaBlamwv3U5VYdWcFV8DgQAdus4xn49Q9I1lfkYG\ntZpGpctFThIeJySEEIlgxo8ukWTmau8+aeInIhFVJX7yCfh86rG1a2HHDnXb5r1+OSPCiaETtHa3\ncmXiCgDuLDcNpQ1sKtyE3Xrzl3Es5yVsGHzq97NP1+m97jihlQ4HtZrGipwcabS/C+nS55JsZF7M\nJ13mRIowkRSSIn7CMNQdAh9+CENqpYqSEtV0X1Jyz18uYkQ4NniM1u5Wrk5eBSA3O5eG0gY2Lt54\ny+IrlvRQaOY4IV802yv72nFCbjcLJdtLCCHum/SECVOLRFT0RGuryeMnBgfhgw/gvDoOiPnz1cpX\nRcU9N92HI2GODh6lraeNkUl1bNH87Pk0lDWwsWAjNmt8t/sMw6A3epzQyYkJItHXW35mJrWaxgaX\ni0zJ9hJCiLsiPWEiKU1MqNUvU8dP6Lradjx0SFWJ2dnQ2Ai1tffcqBaOhDkyeIS27jZGp0YBWJCz\ngMayRtbnr4978RWMRDjm99Ph9XI5mu1ltViocDqp1TTKUvg4ISGESAQpwsSsxWPv3vTxE9PTquG+\nvV3dLWC1qqb7xkY14HsQioQ4fPkwbd1tjAfGAchz5NFY1si6/HVYLfe36nS38zIaDNKp6xzy+ZiM\nbjk6bTaqNY3NmobblHc9JKd06XNJNjIv5pMucyLvrsJ0Dh6E995TofKmi5+IRFTUxMcfq1UwgDVr\n1NbjwoX39KVCkRAHBw6yq2cX3oAXgEWORTSVN1GxqOK+i6+7YRgG5ycn6dB1zk5OziyVF2dlUet2\nU+FwYJctRyGEiCvpCROmYfr4iQsXVNjqoMrmoqgIHntMJd7fg2A4yIGBA7T3tKNPq0Iu35lPU5kq\nvuK55TcVDnPY56NT17kaDAJgt1hY53RS43azRLK9hBAipqQnTJjejfETTz4JGzcmelRRQ0Pqjsez\nZ9X1vHlq5WvduntqUJsOT3Og/wDtve34plV0xWLXYprKmlidtzquxdfQ9DQdXi9H/X6mo8cJzbPb\nqdE0NmkaTsn2Ev9/e3ceHPV1JXr8291qrd2tFUlIAu0SiwAJUItdODJmMmO8xMZ2HNuVOM/PcTKu\nZBY7MzWTSiX1HEOlMm/iSWZcWTw4ydhx8pyZeIkxtrEQi4RAILOIXRsSQoDW7pbUUnff98dtd8Bs\nAiS6JZ1Plav4/fTrX9/WkdHh3vM7Vwhx20kSJm7Zra7dh2z7CadTb7BdV6eL7iMi9JMBZWVwA60Z\nhr3D7Gnfw67Tu3CNuABIs6ZRnllOQWLBuCVfWz/+mFS7ndr+fpov6u2VExWF3WqlIDoaoxTa31ZT\npc5lopG4hJ6pEhNJwkTQfNp+Yts2fVxYqNtPREYGd1yMjEBNDWzfrgvwjUa9Nrp6NcTEjPo2bo+b\n2vZaqtuqGRgZACDdmk55Vjn5Cfnjlny5vF72ORz8v/PnSfb3Kws3GllgsWC3WpkWHj4u7yuEEOLG\nSE2YCIortZ9YsSLI7SeUggMH4KOPoF8XylNQoDfZnjZt1LcZ8gzp5Ot0NYMevaH1DNsMyrPKyY3P\nHbfkq93f2+uQy4XX//9IotmM3WZjQUwMkbLkKIQQt53UhImQ8tn2Ew8+CDk5QR5Uc7NutnrmjD6e\nPl13us/OHvUtBkcG2d2+m5q2GoY8evlvZuxMVmetJjsue1ySL4/Px+GBAWr7+2l3uwH9P3xhdDR2\nm40c6e0lhBAhS5IwcctGu3avlG4/8ac/hVD7iQsXdNH9sWP62GbT03ILFox6Wm5gZICathp2t+3G\n7dWJUFZcFuWZ5WTFZY1LEtTn8bDX4aDO4WDA39srymRiocXCYquVeLOZyspKcqdATcVEMlXqXCYa\niUvomSoxkSRM3BafbT9RWqq7OwSt/cTAgC6637tXF6eFh+v10KVLR1107xp2Ud1WTW17LcNe3WE+\nJz6H8sxyMuNurG3FaCilaB4aotbh4OjAQGB6OzU8nDKbjaKYGMzS20sIISYMqQkT4+7i9hNmM9x9\ndxDbT3g8sHu3LrofGtKzXQsXwh13gMUyqls4h51Un65mz5k9geQrLyGPVZmrmBk7c8yHPOzz8YnT\nSa3DwfmLthOa699OKCMiQpYchRAiRElNmAiaEyfgzTd1vpOQoJcfg9J+Qik4fBg+/FAXowHk5em6\nr+TkUd3C4Xaw6/Qu9p7Zy4hPNzrNT8inPKucDFvGmA/5wvAwexwO6p1O3P7eXtawMBZbrSy0WLCG\nTBdbIYQQN0P+Fhe37Epr9yHVfqK1VRfdt7Xp45QUnXyNcjPKfnc/O1t3UtdRh8fnAaAwsZDyrHLS\nrGljOlSfUpwYHKS2v59Tg4OB85mRkdhtNmZFR2Ma5azXVKmpmEgkJqFJ4hJ6pkpMJAkTY25gQM9+\nnToV5PYT3d165quhQR9bLHowxcW699d19A31saN1B/s69uFVuvh9dtJsVmWuYrp1+pgOddDrZb9/\nO6Ee/3ZCZqORef4lx1TZTkgIISYdqQkTY+rMGXjjDejrC2L7icFBPQW3Z49+DNNshmXLYPlyXYB/\nHb1Dvexo3cH+jv14lRcDBuZMm8OqzFWkWFLGdKhn3W5qHQ4OOJ14/D/X8Waz3k7IYiFKensJIcSE\nJjVhYtyFRPsJrxdqa6GqSidiBoOe9frc53TrievoGexhe+t26s/W41M+DBgoSi5iVeYqkmNGVzc2\nqmEqxRGXi1qHg9aLthPKi4rCbrORFxUl2wkJIcQUIEmYuGUffliJy7U6eO0nlIIjR/TSY3e3Pped\nrQcxiqcAuge7qWqp4kDngUDyNT9lPqsyV5EUnTRmw3R4PNQ5HOx1OHD6e3tFGI2UWCyU2mwk3sB+\nlKMxVWoqJhKJSWiSuISeqRITScLELenp0bNfNluQ2k+0temi+9ZWfTxtmt5mKD//ukVoFwYusL1l\nOwc6D6BQGA1GilOLWTlzJYnRiWMyPKUUp/3bCTUMDODzT0knh4djt1qZb7EQLr29hBBiSpKaMHHT\njh/X+z9+2n7i4Yf1g4e3RW+vnvk6dEgfx8ToDbYXLbpu0f1513mqWqo4dO7QJcnXipkrSIhKGJPh\njfh8HHS5qO3v5+xFvb1mRUdjt1rJlO2EhBBiSpCaMDGmgtp+YmhIN1qtqdE1YGFhusv9ihVwnScI\nO52dVLVU0XC+AYXCZDAFkq/4qPgxGV7PyAh7HA72O50M+pccY0wmFlmtLLJaiZXeXkIIIfzkN4K4\nIVdqP+HxVBIZuXp839jrhbo6vdXQwIA+N38+VFRct/r/rPNsIPkCMBlMLJy+kBUzVxAbeetPDiil\nODU4SK3DwYnBwcC/eDIiIrDbbMyJjiYsCEuOU6WmYiKRmIQmiUvomSoxkSRMjFp7u95+6LPtJyor\nx/FNldLrnh98oDfbBsjM1EX3addulNrh6GBbyzaOXjgKQJgxjEXTF7F85nJsEdd/WvJ6hrxePvEv\nOXb5e3uZDAaKLBbsNhvp0ttLCCHENUhNmLiuz7afyMiA9etvQ/uJM2d00X1zsz5OTNRF94WF1yy6\nb+9vZ1vLNo53HQd08rU4bTHLZyzHGmG95WGd828n9InTybB/O6HYT7cTslqJkd5eQggh/KQmTNy0\nkRF4912or9fHt6X9RF8fbN0Kn3yij6OjobwcFi+GayQ4p/tOs61lGye7TwJgNpopTS9l2YxlWMJH\ntzn31fiU4tjAALUOB00XbSeUHRWF3WqlMDpaensJIYS4IZKEiavq6dHd78+evXb7iTFbu3e7YccO\nqK4Gj0cnXGVlsGrVNav+W/ta2da8jVM9pwAIN4VjT7ezNGMpMeExtzQkl9fLPoeDPQ4H/R69b2S4\n0cgCi4VSq5XkUXTgD5apUlMxkUhMQpPEJfRMlZgELQnLysrCZrNhMpkwm83U1tbS3d3Nww8/TEtL\nC1lZWfzud78jLi4uWEOc0m5r+wmfT693fvwxuFz6XFGRLrqPv/pTi829zWxr3kZTbxMAEaYIyjLK\nWJKxhGhz9C0Nqd3f2+uQy4XXP42caDZjt9lYEBNDpCw5CiGEuEVBqwnLzs6mrq6OhIQ/92V6/vnn\nSUpK4vnnn2fjxo309PSwYcOGS14nNWHjy+fThfZVVfp41iy4775xaj+hFJw8qeu+zp/X52bM0Oud\nGRlXeYmiqbeJbc3baOlrASAyLJKydJ18RZmjbno4Hp+PwwMD1Pb30+52A/rnrcC/nVCO9PYSQghx\ng66VtwQ1Cdu7dy+JiX/uTD5r1iy2bdtGSkoKZ8+eZfXq1Rw9evSS10kSNn6u1H5ixYrrNp6/OWfP\n6uSrsVEfx8fDnXfCnDlXfEOlFI09jWxr2UZrn+6OHxUWxZKMJZRllBEZdvNZYp/Hw16Hg30OBy5/\nb68ok4mFFguLrVbix3g7ISGEEFNHSCZhOTk5xMbGYjKZePrpp3nqqaeIj4+np6cH0L90ExISAseB\nAUsSNi4ubj8REwMPPKDbT4zGDa3dOxy66L6+Xs+ERUbqovvS0itW+yulONl9km0t22jrbwN08rVs\nxjLs6XYiwm6uDYRSiuahIWodDo4ODAR+plLDwymz2SiKicE8wbcTmio1FROJxCQ0SVxCz2SKSUg+\nHblz506mT5/O+fPnWbNmDbNmzbrk6waD4apLP1/+8pfJysoCIC4ujuLi4kCwKv1Nq+R4dMcff1zJ\n8eNw7txqvF5wuSopLYWcnNHfr76+/vrvt2wZ7NpF5a9/DV4vq3NyoKyMSgC3m9X+BOzT68vLyzne\ndZyfvfkzuga7yCrOItocTVRbFIVJhazMXHlTn/eDrVtpHBzEW1zMueFhmmtqMBgM3F1Rgd1q5WR1\nNX0GA+YQiY8cT67jev9jxqEyHjnWx58KlfHI8cQ+/vTPzZ+2V7qGkOgT9r3vfQ+LxcLPf/5zKisr\nSU1NpaOjgzvuuEOWI8fRbWk/4fPpVhNbt+pZMIDZs/XSY+Llm2QrpTh64ShVLVV0ODsAiDHHsHzm\nchanLSbcFH5Tw+gaGWFPfz/7nU7c/t5eFpOJxf7thKyynZAQQohxEHIzYQMDA3i9XqxWKy6Xiy1b\ntvDd736Xe+65h1dffZVvf/vbvPrqq9x3333BGN6U0N2tlx8/bT+xbp3eBWhMnTql6746O/Vxejrc\ndZfueP8ZSimOXDjCtuZtdLr09ZZwCytmrmDR9EWYTTdel+VTipODg9T293Pyot5eMyMjsVutzI6J\nwSSF9kIIIYIkKDNhTU1N3H///QB4PB6+9KUv8Y//+I90d3fz0EMP0draetUWFTITduvGuv1EZeVn\n1u7PndPbDJ04oY9jY/XMV1HRZUX3PuWj4XwDVS1VnHOdA8AabmXFzBUsnL7wppKvQa+X/U4nexwO\nevzbCZmNRubFxGC3WkmdItsJXRYXEXQSk9AkcQk9kykmITcTlp2dHaiNuFhCQgIffvhhEEY0NYx7\n+wmnU/f62rdPF91HRMDKlbBkyWVrnD7l49C5Q1S1VHFhQO8JGRsRy4qZKyiZXkKY8cZ/NM+63dQ6\nHBxwOvH4f+DjzWZKrVZKLBaipLeXEEKIEBISNWE3QmbCbs5n209UVMDy5WPUfmJkRHe537EDhofB\naNRbDJWX60ctL+JTPg52HqSqpYquwS4A4iLjWDlzJcWpxZiMN5YoeZXiiMtFrcNB69BQ4Hyev7dX\nXlSUbCckhBAiaEJuJkzcXrfSfuKalIIDB+Cjj6C/X58rLNSbbCclXXKp1+flQOcBqlqq6BnSbUfi\nI+NZlbmK+Snzbzj5cng81Dkc1DmdOPzbCUUYjZRYLJTabCRKby8hhBAhTpKwSUwpqKuD994Dr1c3\noX/oIbDZxuDmzc3w/vvQ0UFlczOrly7VRffZ2Zdc5vV5qT9bz/bW7fQO9QKQEJXAqsxVzEued0PJ\nl1KK0/7thBoGBvD5/2WRHB6O3WplvsVCuNE4Bh9ucphMNRWThcQkNElcQs9UiYkkYZPUZ9tP2O26\n/cQtl0VduKCL7o8d08c2m26r/9WvXrK26fF52N+xnx2tO+hz9wGQFJ3EqsxVFCUXYTSMPlka8fk4\n6HJR29/P2eFhAIwGA3P8hfaZsp2QEEKICUhqwiahcWk/4XLBtm2wd6+u8A8P18nX0qX6Tfw8Pg/7\nOvaxo3UH/W69RDktehrlWeXMmTbnhpKvnpERvZ2Q08mgfzuhaJOJRVYri61WYqW3lxBCiBAnNWFT\nyLFj8N//PXbtJ/B4oKYGtm8Ht1vPdi1aBHfcARZL4LIR7wh1HXXsbN2JY1g3ZU2JSaE8q5zZSbNH\nPVOllKJxaIja/n6ODw4GfnDTIyKw22zMjY4mTJYchRBCTAKShE0SY95+Qik4dEgX3ffqWi7y8nTd\nV3Jy4LJh7zA/e/NnDGUM4Rx2ApBqSaU8s5xZSbNGnXwNeb184l9y7PL39jIZDBRZLNhtNtKnSG+v\nsTRVaiomEolJaJK4hJ6pEhNJwiaBMW8/0dqqi+7b2/VxSopOvnJzA5cMe4fZ076HXad3cfjMYbKS\ns0izplGeWU5BYsGok69zw8PscTj4xOlk2L+dUGxYGIutVhZarcRIby8hhBCTlNSETXCfbT/x4IOX\nPaA4et3duuj+yBF9bLHA5z4HxcW69xfg9ripba+luq2agZEBANKt6azOWk1eQt6oki+fUhwbGKDW\n4aDpou2EsqOisFutFEZHS28vIYQQk4LUhE1CY9p+YnBQF93v2aNvZjbDsmV6Oi1cb5g95Blid9tu\natpqGPToxGmGbQblWeXkxueOKvlyeb3sczjY63DQ5+/tFW40ssBiodRqJTn85jbnFkIIISYiScIm\noJEReOcd+OQTfXzT7Sc8Hp14bdumK/kNBigp0UX3/mxucGSQ3e06+Rry6I70mbGZlGeVkx2XjcFg\nuO7afbu/t9chlwuv/18DiWYzdpuNBTExRMqS47iYKjUVE4nEJDRJXELPVImJJGETTHc3vPEGdHbe\nQvsJpfSS4wcfQI/uXk9Ojq77Sk0FYGBkgJq2Gna37cbtdQOQHZdNeVY5WXFZ130Lj8/H4YEBavv7\naXfr1xsMBgqjo7HbbORIby8hhBBTnNSETSBj0n6irQ22bNHF9wDTpunkKy8PDAZcwy6q26qpba9l\n2Ksbo+bE51CeWU5mXOZ1b9/36XZCDgcuf2+vKJNJbydktRIv2wkJIYSYQqQmbILz+eDjj3WrLrjJ\n9hM9PbrdxKFD+jgmRi87LlwIRiPOYSe7Tu9iT/seRny6RUReQh7lmeXMiJ1xzVsrpWgZGqLW4eDo\nRdsJpYaHY7fZmBcTg1l6ewkhhBCXkCQsxLlcuv1EY6Mu2brzTl0zP+qVvKEhnb3V1Oii+7Aw3eV+\nxQqIiMDhdrDr9C72ntkbSL4KEgsozywn3ZZ+zVsP+3wccDr5zfvvE7d4MaC3EyqKicFuszEjIkKW\nHINoqtRUTCQSk9AkcQk9UyUmkoSFsFtqP+H16i2Gtm3TjcRAF49VVEBsLP3ufnae2EpdRx0en35S\ncVbSLFZlriLNmnbNW3eNjLCnv5/9Tidun49ej4cMk4nFViuLrFassp2QEEIIcV1SExaClNL50+bN\nN9F+QildPPbBB9DVpc9lZurHJ9PS6BvqY0frDvZ17MOrdM3W7KTZlGeVk2pJvfCfGkwAABnASURB\nVOptfUpxcnCQ2v5+Tl7U22tmZCR2q5XZMTGYZNZLCCGEuMS18hZJwkLMZ9tPlJXpuvlRdXE4c0YX\n3Tc36+PERFizBgoL6XX3sb1lO/Vn6/EqLwYMzJk2h1WZq0ixXL26f9DrZb/TyR6Hgx7/dkJhBgPz\n/YX202U7ISGEEOKqJAmbID7bfuKee2DevFG8sK9PF90fOKCPo6OhvBwWL6ZnuJ/trTr58ikfBgwU\nJRexMnMlyTHJV73lWbebWoeDgy4XI/7thOLCwrDbbJRYLERdlBVOlbX7iUbiEnokJqFJ4hJ6JlNM\n5OnICeDi9hOJibr9RPLVcyTN7YYdO6C6WjdeNZlgyRJYuZIun4vtJ97mQOeBQPI1P2U+qzJXkRSd\ndMXbeZXiiMtFrcNB69BQ4HxeVBR2m428qCjZTkgIIYQYIzITFmSfbT8xezbce+912k/4fLBvn36h\ny6XPFRVBRQUXIrxUtVRxsPMgCoXRYGR+ynxWzlxJYnTiFW/n9HioczrZ63Dg8G8nFGE06t5eNhuJ\n0ttLCCGEuCkyExZijh1r4cMPT+F0Gjl82IfNlsu0aZnXbz+hFJw4oYvuz5/X52bMgLVrOR8fQVXL\nVg6dOxRIvkpSS1gxcwUJUQlXuJWizb/k2HDRdkLTwsOxW63Mt1iIkN5eQgghxLiRJOw2O3ashU2b\nTuJ2V3D4sF5RNBg+4p/+CZYvv0ZH+rNnddF9Y6M+jo+HNWvonJFAVet2Gk42oFCYDCaKU4tZmbmS\nuMi4y24z4vNxyL/k2HHRdkKzY2KwW61k3cR2QpNp7X4ykbiEHolJaJK4hJ6pEhNJwm6zLVtOce5c\nBY2NemLLZoO5cys4fnwrd955hSTM4YCtW6G+Xr8gMhLKyzk7ewbb2nZypO4IACaDiYXTF7Ji5gpi\nI2Mvu03PyAh7HQ72OZ0M+rcTijaZWGS1sthqJVZ6ewkhhBC3ldSE3UY9PfD1r1fS0bEagPR0yM0F\noxHi4ir51rdW//ni4WHYuRN27dJ9K0wmKC3lzMJ8tnXWcqzrGABhxjAWTV/E8pnLsUVc2khMKUXj\n0BC1/f0cHxwMfN/SIyKw22zMjY4mTJYchRBCiHEjNWFBppSeyHrvPejr8xEeDoWF+inIT4WH6zYQ\n+Hz64o8/1rNgAHPmcMY+h0rHAY43/BoAs9HM4rTFLJuxDGuE9ZL3c/t81Dud7Onv54K/t5fJYKDI\nYsFus5Euvb2EEEKIoJOZsHHmcsHbb8PRo/o4Lq6FtraTWCwVgWvc7o/48pfzKAzz6Lqvzk79hfR0\nziydx1bfSU52nwR08lWaXsqyGcuwhFsuea/zw8PUOhx84nQy7O/tZQsLo9RqZaHVSsyoOr7euKmy\ndj/RSFxCj8QkNElcQs9kionMhAXJ0aM6AXO5dCnXX/4lzJuXyfHj8NFHWxkeNhIe7uOu4jjy9myH\nkzrRIi6ODvscPojuoPHCZgDCTeHY0+0szVhKTHhM4D18SnFsYIBah4Omi7YTyo6Kwm61UhgdLb29\nhBBCiBAkM2HjwO3WS4/19fo4Oxvuuw9i/fXyLceOcerDDzE6nfiamsg1m8lMTISICDpK8vkgqZ9G\nZysAEaYIyjLKWJKxhGhzdOA9XF4v+xwO9joc9Pl7e4UbjSzwbyeUHB5+Wz+zEEIIIS4n2xbdRs3N\n8D//A729EBYGd96p93/8dDKq5dgxTr7yChXnzkFrK3i9fOj1EvvAWo7akzg1fBaAyLBIlmQsoSy9\njChzVOD+Z9xuavv7OeRy4fF/HxLNZkqtVootFiLHaclRCCGEEDdOliNvA49Hb99YU6ML8dPS4P77\nYdq0iy7y+Ti1aRNLdu2kvasTn/LRHx1OdGYiv22uxlpcSlRYlE6+MsqIDNNt8z0+Hw0DA9T299N2\nUW+vguho7FYruVFRN9zbayxNprX7yUTiEnokJqFJ4hJ6pkpMJAkbAx0det/Hc+d0u4lVq/R/l0xK\nNTbCli0M7NhOZ2crA3FGGhOMdEcO4rvQis+aS0V2BfZ0OxFh+unFfo+HvQ4HdQ4HLn9vryiTSW8n\nZLUSL9sJCSGEEBOWLEfeAp9Pt/KqrASvV7ec+MIXdP+vgHPn9DZDJ06glOKn7/6O3LhBOmMUGAwY\nDUZiI2LZE5XL//nP/4dSipahIWodDo4ODODzf9bU8HDsNhvzYmIwS28vIYQQYkKQ5chx0N2tZ79O\nn9bHdjusWQOBySmHQ2dn+/aBUvSqQXZlmXh7aTxpTS7uMIYRGxGLNcLKthEfhvkF7O3vp9bh4Nzw\nMABGg4GimBjsNhszIiKCuuQohBBCiLElSdgNUgrq6uD993Uje5sN7r1Xd74HdKf76mo9RTY8jGPE\nxd402JVjZiQqnIiOJDqTY/nPkwqjIYxho5EoewHRmQswdXUBYDGZWGy1sshqxToBthOaKmv3E43E\nJfRITEKTxCX0TJWYhP5v+BDicMAf//jndl7z5uneX1FRXNbp3jXs4kD8MNsLIhiIjSbcFE55xlJK\nvGVs+PgdvF9ZioMIBjHj2bGX8plRzIyMxG61MjsmBpPMegkhhBCTmtSEjdLhw/DOOzA4qJOuu++G\nuXP9Xzx5Utd9dXYyODLIkYh+qgoi6U2NJcwYhj3dzvIZyzGZIvmnN9+kdkYGZx09KBRGDOTHJrLi\nTAf/eP/9t/1zCSGEEGL8SE3YLRgchD/9CQ4e1Md5eXr50WpFby+0ZQucOsWQZ4iTvgvsyI/gbFYy\nJmMYpdMXsipzFUOGCCodDj5xXuDw4CCmyChyo2NIi4hgeng4ZoOBqHPng/o5hRBCCHF7SRJ2DadO\n6eXH/n5dcL92LSxaBAanA/64FerrGfa4aRrsYFd2GKdnpaFMJkpSi1mZuYrzKoL/7umncfBC4J7J\nYWHYYmJINJu5eMFxIve3nypr9xONxCX0SExCk8Ql9EyVmEgSdgUjI3p1sbZWH2dk6MaridZhqNwJ\nu3YxMjRAq7ON2jRoXJ7BSKSZouQiymau4rQ3gl93OegZ6QXAbDSywP+UY8/SpWzatw/DokWB93PX\n1VGxcGEwPqoQQgghgkRqwj6jvR3+8Afo6tKNV++4A5Yv9WH8ZD98/DGe/l7a+tvYH+/mePEMBmOj\nmZU0i6L0lTR5IzjgcjHi8wEQbzZj928nFHVR59ZjjY18dPgww+gZsIq5cynMyRm3zySEEEKI4JC9\nI0fB64WqKti+XT/oOG0afOF+xXTXSdiyBW/nWdod7TRE9HOkZAZ9KbFkx+WSOX0FLSqKpsHBwL1y\no6Ios9nIi4rCKE85CiGEEFOWJGHXcf68brx65ozeaHvJEqiYe5awrVvwnTpJh6ODY75zHFmQzvms\naaTEZpGcvIzTKppejweAcKORBRYLdquVaeETucLrxk2VtfuJRuISeiQmoUniEnomU0zk6cirUAp2\n74YPP9QbcMfFwf0V/WSe2orvF/V0ODo4NdDO0aIUzsxaQJQtk+lJds4ZrHSOKMBDwkVLjpGXbBYp\nhBBCCHF1U3YmrK9PP/nY2KiPF8518xfWnZj37ORc3xmaHK2cyI2naUEmI3HZRCUsxB0WH3iiMe+i\nJUfZTkgIIYQQVyLLkRdRCg4cgPfeg6EhiI708VBuHZlNH9N1oZWmniaa0qM5tjCPrqQ8wuPmERWV\nhAEDEUYjxRYLpVYrSVNsyVEIIYQQN06SML+BAd31vqEBUIrFtuPcqbYwcP4ETT1NtMUa2F82h9Op\nBUTEzWZaTAoGDCSazdhtNootFiKMxrH9QJPAZFq7n0wkLqFHYhKaJC6hZzLFRGrCgOPH4a23wOmE\nhKEz3Bu1hdhz9RzpbaI9fISa8gUcn1lAbGw+6ZbpGA1G8qOjKbNayZUlRyGEEEKMsUk/EzY8DO+/\nD3V1EDHUR5nzI4rMO+gYbKLFOMR2ewlHsgpIjssh3ZZOtCmMEosFu81Ggtk8jp9ECCGEEJPdlF2O\nbG3VrScc54fIatvBYuOHjESc5IjRzY6SBRzNziMtIYsMWwapEZGU2WzMlyVHIYQQQoyRKZeEeTxQ\nWQm7tnuZfqaOggvvEp14lIMWxe7Zs2nKziQ1KYuZsTOYa7Fht9nIiYyUJcebNJnW7icTiUvokZiE\nJolL6JlMMZlSNWGdnfCHNxXehmMUN76FOe4A+/PD+CR7Dh2Z00lMyWZ5fBZL4hKxW63Ey5KjEEII\nIYJg0syE+XxQXQ17/qedjONv4TTVcWqWmeaMNLrSE4lNy2XRtFxWJyQz32IhXJYchRBCCDHOJu1y\n5MYf/ojfv/cnfBgZ6fewwjeD/Pw4TuSacUyPpS81jpjMXO5Mm01F4nSyZMlRCCGEELfRtZKwCTsd\ntPGHP+LXH24hbelyshaVknHPat6fD39IdXO2KAMWL+CJ5Xfzcsld/K+MHLKlzcS4qaysDPYQxBVI\nXEKPxCQ0SVxCz1SJScglYZs3b2bWrFnk5+ezcePGK14Tf9dd/N83XifTvhSHNYqm7OmcnZZI9LIy\nGnv7efpz9/KfZetYn5ZDnNR8jbv6+vpgD0FcgcQl9EhMQpPEJfRMlZiEVBLm9Xr567/+azZv3kxD\nQwOvv/46R44cuew69fT/5nxuLvXRZnpjrXhNBkyeIVK7e5jefoG/SM3BLDVft01vb2+whyCuQOIS\neiQmoUniEnqmSkxCKlOpra0lLy+PrKwszGYzjzzyCH/84x8vu05FRGIsLqbbBzED/aSdO096lwPL\nkAeDzxeEkQshhBBC3JiQSsLa29uZMWNG4DgjI4P29vbLrjP6vMTEx6Hq6khyDBPpNWDAwMnqatZ/\n/i9v55AF0NzcHOwhiCuQuIQeiUlokriEnqkSk5B6OvLNN99k8+bN/PznPwfgN7/5Dbt37+bf/u3f\nAteYUlLwnTsXrCEKIYQQQozaggULrlrjFlLNWtPT0zl9+nTg+PTp02RkZFxyjbez83YPSwghhBBi\nzIXUcuTixYs5ceIEzc3NDA8P88Ybb3DPPfcEe1hCCCGEEGMupGbCwsLC+MlPfsLatWvxer189atf\nZfbs2cEelhBCCCHEmAupmjAhhBBCiKkipJYjr2U0TVzFjTl9+jR33HEHc+fOpaioiJdeegmA7u5u\n1qxZQ0FBAXfdddcl/VpefPFF8vPzmTVrFlu2bAmcr6urY968eeTn5/PNb34zcN7tdvPwww+Tn5/P\nkiVLaGlpCXzt1VdfpaCggIKCAn71q1/dhk88cXi9XkpKSli3bh0gMQkFvb29PPjgg8yePZs5c+aw\ne/duiUuQvfjii8ydO5d58+bx6KOP4na7JSZB8OSTT5KSksK8efMC54Idh6amJsrKysjPz+eRRx5h\nZGRkvD7+rVETgMfjUbm5uaqpqUkNDw+rBQsWqIaGhmAPa8Lr6OhQ+/fvV0op5XA4VEFBgWpoaFDP\nPfec2rhxo1JKqQ0bNqhvf/vbSimlDh8+rBYsWKCGh4dVU1OTys3NVT6fTymlVGlpqdq9e7dSSqnP\nf/7z6r333lNKKfXTn/5UPfPMM0oppX7729+qhx9+WCmlVFdXl8rJyVE9PT2qp6cn8Geh/ehHP1KP\nPvqoWrdunVJKSUxCwBNPPKF++ctfKqWUGhkZUb29vRKXIGpqalLZ2dlqaGhIKaXUQw89pDZt2iQx\nCYKqqiq1b98+VVRUFDgXrDj09vYqpZRav369euONN5RSSn3ta19T//Ef/zHe34abMiGSsF27dqm1\na9cGjl988UX14osvBnFEk9O9996rPvjgA1VYWKjOnj2rlNKJWmFhoVJKqR/84Adqw4YNgevXrl2r\nqqur1ZkzZ9SsWbMC519//XX19NNPB66pqalRSulfXElJSUoppV577TX1ta99LfCap59+Wr3++uvj\n+wEniNOnT6uKigq1detWdffddyullMQkyHp7e1V2dvZl5yUuwdPV1aUKCgpUd3e3GhkZUXfffbfa\nsmWLxCRImpqaLknCghkHn8+nkpKSlNfrVUopVV1dfUkOEUomxHLkaJu4ipvX3NzM/v37KSsro7Oz\nk5SUFABSUlLo9LcFOXPmzCUtQz6Nw2fPp6enB+JzcezCwsKIjY2lq6vrqvcS8Dd/8zf88Ic/xHjR\n1lsSk+Bqampi2rRpfOUrX2HhwoU89dRTuFwuiUsQJSQk8Hd/93fMnDmTtLQ04uLiWLNmjcQkRAQz\nDt3d3cTFxQX+Dr34XqFmQiRhBoMh2EOY1JxOJw888AA//vGPsVqtl3zNYDDI9/82euedd0hOTqak\npAR1lWdmJCa3n8fjYd++fXz9619n3759xMTEsGHDhkuukbjcXqdOneJf//VfaW5u5syZMzidTn7z\nm99cco3EJDTczjhMtHhPiCRsNE1cxc0ZGRnhgQce4PHHH+e+++4D9L9azp49C0BHRwfJycnA5XFo\na2sjIyOD9PR02traLjv/6WtaW1sB/Yusr6+PxMREielV7Nq1i7feeovs7Gy++MUvsnXrVh5//HGJ\nSZBlZGSQkZFBaWkpAA8++CD79u0jNTVV4hIke/fuZdmyZSQmJhIWFsYXvvAFqqurJSYhIlh/Z6Wn\np5OQkEBvby8+/17SbW1tpKenj+8HvlnBXg8djZGREZWTk6OampqU2+2Wwvwx4vP51OOPP66+9a1v\nXXL+ueeeC6zZv/jii5cVVLrdbtXY2KhycnICBZV2u13V1NQon893WUHlp2v2r7/++iUFldnZ2aqn\np0d1d3cH/iz+rLKyMlATJjEJvpUrV6pjx44ppZT67ne/q5577jmJSxDV19eruXPnqoGBAeXz+dQT\nTzyhfvKTn0hMguSzNWHBjsP69evVb3/7W6WUrhWTwvxb9Kc//UkVFBSo3Nxc9YMf/CDYw5kUtm/f\nrgwGg1qwYIEqLi5WxcXF6r333lNdXV2qoqJC5efnqzVr1lzyl8sLL7ygcnNzVWFhodq8eXPg/N69\ne1VRUZHKzc1Vzz77bOD80NCQWr9+vcrLy1NlZWWqqakp8LVXXnlF5eXlqby8PLVp06bb8pknksrK\nysDTkRKT4Kuvr1eLFy9W8+fPV/fff7/q7e2VuATZxo0b1Zw5c1RRUZF64okn1PDwsMQkCB555BE1\nffp0ZTabVUZGhnrllVeCHofGxkZlt9tVXl6eeuihh9Tw8PD4fhNukjRrFUIIIYQIgglREyaEEEII\nMdlIEiaEEEIIEQSShAkhhBBCBIEkYUIIIYQQQSBJmBBCCCFEEEgSJoQQQggRBJKECSGmlNWrV1NX\nV3dL93j77bfZuHHjGI1ICDFVhQV7AEIIcTuNxT5269atY926dWM0IiHEVCUzYUKIoHK5XPzVX/0V\nxcXFzJs3j9///vcAfP/738dutzNv3jyefvrpwPWrV6/mb//2byktLWX27Nns2bOH+++/n4KCAr7z\nne8A0NzczKxZs3jssceYM2cO69evZ3Bw8LL33rJlC8uWLWPRokU89NBDuFyuy6556aWXmDt3LgsW\nLODRRx8FYNOmTTz77LMAFBcXU1JSQklJCdHR0Wzfvh2Xy8WTTz5JWVkZCxcu5K233rrsvpWVlaxe\nvZr169cze/ZsHnvssVv/ZgohJhRJwoQQQbV582bS09Opr6/n4MGDrF27FoBnn32W2tpaDh48yODg\nIO+88w6gZ7IiIiLYs2cPzzzzDPfeey8vv/wyhw4dYtOmTfT09ABw/PhxvvGNb9DQ0IDNZuPf//3f\nL3nfCxcu8MILL/DRRx9RV1fHokWL+Jd/+ZfLxrdx40bq6+v55JNPePnllwNj+FR9fT379+/n+9//\nPqWlpSxdupQXXniBiooKdu/ezdatW3nuuecYGBi47N719fX8+Mc/pqGhgcbGRnbu3Dk231QhxIQg\nSZgQIqjmz5/PBx98wD/8wz+wY8cObDYbAFu3bmXJkiXMnz+frVu30tDQEHjNPffcA0BRURFFRUWk\npKQQHh5OTk4Op0+fBmDGjBksXboUgMcee4wdO3YEXq+UoqamhoaGBpYtW0ZJSQm/+tWvaG1tveL4\nHn30Uf7rv/4Lk8l0xc9w4sQJnn/+eX73u98RFhbGli1b2LBhAyUlJdxxxx243e7AuC5mt9tJS0vD\nYDBQXFxMc3PzzX0ThRATktSECSGCKj8/n/379/Puu+/yz//8z1RUVPD888/zjW98g7q6OtLT0/ne\n977H0NBQ4DUREREAGI3GwJ8/PfZ4PMCls1VKqSvWga1Zs4bXXnvtmuN79913qaqq4u233+aFF17g\n4MGDXLzlrtPp5OGHH+YXv/gFKSkpgfN/+MMfyM/Pv+a9Lx67yWQKjF0IMTXITJgQIqg6OjqIjIzk\nS1/6En//93/P/v37AwlXYmIiTqczUCd2I1pbW6mpqQHgtddeY+XKlYGvGQwGlixZws6dOzl16hSg\na9NOnDhxyT2UUrS2trJ69Wo2bNhAX18fTqfzkmuefPJJvvKVr7B8+fLAubVr1/LSSy8Fjvfv33/D\n4xdCTH4yEyaECKqDBw/y3HPPYTQaMZvNvPzyy8TGxvLUU09RVFREamoqZWVlV3zttZ50LCws5Kc/\n/SlPPvkkc+fO5Zlnnrnk60lJSWzatIkvfvGLuN1uAF544YVLZq+8Xi+PP/44fX19KKX45je/SWxs\nbOB9W1tbefPNNzlx4gSvvPIKAL/85S/5zne+w7e+9S3mz5+Pz+cjJyfnsuL8K439Vp/aFEJMLAZ1\n8by6EEJMAs3Nzaxbt46DBw8GeyhCCHFVshwphJiUZFZJCBHqZCZMCCGEECIIZCZMCCGEECIIJAkT\nQgghhAgCScKEEEIIIYJAkjAhhBBCiCCQJEwIIYQQIgj+P2WGO4pdoAcIAAAAAElFTkSuQmCC\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10f9e1050>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 34
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"In this performance comparison for different sample sizes, we see that our Cython approach is actually not so fast anymore. However, this is just the simplest approach to using Cython. There are a lot of tweaks that can be made. In a [later section](#showdown) we will come back to this comparison and see how the Cython version of our simple least squares implementation holds up against the other approaches\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"cython_bonus\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Bonus: How to use Cython without the IPython magic"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"IPython's notebook is really great for explanatory analysis and documentation, but what if we want to compile our Python code via Cython without letting IPython's magic doing all the work? \n",
|
|
"These are the steps you would need."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 1. Creating a .pyx file containing the the desired code or function."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%file ccy_classic_lstsqr.pyx\n",
|
|
"\n",
|
|
"def ccy_classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"Writing ccy_classic_lstsqr.pyx\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 11
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 2. Creating a simple setup file"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%file setup.py\n",
|
|
"\n",
|
|
"from distutils.core import setup\n",
|
|
"from distutils.extension import Extension\n",
|
|
"from Cython.Distutils import build_ext\n",
|
|
"\n",
|
|
"setup(\n",
|
|
" cmdclass = {'build_ext': build_ext},\n",
|
|
" ext_modules = [Extension(\"ccy_classic_lstsqr\", [\"ccy_classic_lstsqr.pyx\"])]\n",
|
|
")"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"Writing setup.py\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 12
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"####3. Building and Compiling"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"!python3 setup.py build_ext --inplace"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"running build_ext\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"cythoning ccy_classic_lstsqr.pyx to ccy_classic_lstsqr.c\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"building 'ccy_classic_lstsqr' extension\r\n",
|
|
"creating build\r\n",
|
|
"creating build/temp.macosx-10.6-intel-3.4\r\n",
|
|
"/usr/bin/clang -fno-strict-aliasing -Werror=declaration-after-statement -fno-common -dynamic -DNDEBUG -g -fwrapv -O3 -Wall -Wstrict-prototypes -arch i386 -arch x86_64 -g -I/Library/Frameworks/Python.framework/Versions/3.4/include/python3.4m -c ccy_classic_lstsqr.c -o build/temp.macosx-10.6-intel-3.4/ccy_classic_lstsqr.o\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\u001b[1mccy_classic_lstsqr.c:2040:28: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_AsString'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE char* __Pyx_PyObject_AsString(PyObject* o) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2037:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function\r\n",
|
|
" '__Pyx_PyUnicode_FromString' [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyUnicode_FromString(char* c_str) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2104:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_IsTrue'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyObject_IsTrue(PyObject* x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2159:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyIndex_AsSsize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE Py_ssize_t __Pyx_PyIndex_AsSsize_t(PyObject* b) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2188:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_FromSize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject * __Pyx_PyInt_FromSize_t(size_t ival) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1584:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_From_long'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyInt_From_long(long value) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1631:27: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_long' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE long __Pyx_PyInt_As_long(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1731:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_int' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyInt_As_int(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"8 warnings generated.\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\u001b[1mccy_classic_lstsqr.c:2040:28: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_AsString'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE char* __Pyx_PyObject_AsString(PyObject* o) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2037:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function\r\n",
|
|
" '__Pyx_PyUnicode_FromString' [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyUnicode_FromString(char* c_str) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2104:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_IsTrue'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyObject_IsTrue(PyObject* x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2159:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyIndex_AsSsize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE Py_ssize_t __Pyx_PyIndex_AsSsize_t(PyObject* b) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2188:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_FromSize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject * __Pyx_PyInt_FromSize_t(size_t ival) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1584:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_From_long'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyInt_From_long(long value) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1631:27: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_long' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE long __Pyx_PyInt_As_long(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1731:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_int' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyInt_As_int(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"8"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
" warnings generated.\r\n",
|
|
"/usr/bin/clang -bundle -undefined dynamic_lookup -arch i386 -arch x86_64 -g build/temp.macosx-10.6-intel-3.4/ccy_classic_lstsqr.o -o /Users/sebastian/Github/python_reference/benchmarks/ccy_classic_lstsqr.so\r\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 13
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 4. Importing and running the code"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import ccy_classic_lstsqr\n",
|
|
"\n",
|
|
"%timeit classic_lstsqr(x, y)\n",
|
|
"%timeit cy_classic_lstsqr(x, y)\n",
|
|
"%timeit ccy_classic_lstsqr.ccy_classic_lstsqr(x, y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"100 loops, best of 3: 2.9 ms per loop\n",
|
|
"1000 loops, best of 3: 212 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"1000 loops, best of 3: 207 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 20
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"numba\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Appendix I: Cython vs. Numba"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Like we did with Cython before, we will use the minimalist approach to Numba and see how they compare against each other. \n",
|
|
"\n",
|
|
"Numba is using the [LLVM compiler infrastructure](http://llvm.org) for compiling Python code to machine code. Its strength is to work with NumPy arrays to speed-up code. If you want to read more about Numba, see the original [website and documentation](http://numba.pydata.org/numba-doc/0.13/index.html)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Here is our \"classic\" approach in Python, where I removed the list comprehensions, since they caused errors in the Numba compilation."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" for x_i in x:\n",
|
|
" var_x += (x_i - x_avg)**2\n",
|
|
" cov_xy = 0\n",
|
|
" for x_i, y_i in zip(x,y):\n",
|
|
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 22
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The Cython-compiled version of it:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%load_ext cythonmagic"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": []
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"\n",
|
|
"def cy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" for x_i in x:\n",
|
|
" var_x += (x_i - x_avg)**2\n",
|
|
" cov_xy = 0\n",
|
|
" for x_i, y_i in zip(x,y):\n",
|
|
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 26
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"And now the Numba-compiled version:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"from numba import jit\n",
|
|
"\n",
|
|
"@jit\n",
|
|
"def nmb_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" for x_i in x:\n",
|
|
" var_x += (x_i - x_avg)**2\n",
|
|
" cov_xy = 0\n",
|
|
" for x_i, y_i in zip(x,y):\n",
|
|
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
|
|
" \n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 27
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"Now, let us see how the different approaches compare against each other for different sample sizes."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"funcs = ['lstsqr', 'cy_lstsqr', 'nmb_lstsqr'] \n",
|
|
"orders_n = [10**n for n in range(1, 7)]\n",
|
|
"times_n = {f:[] for f in funcs}\n",
|
|
"\n",
|
|
"for n in orders_n:\n",
|
|
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
|
|
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
|
|
" for f in funcs:\n",
|
|
" times_n[f].append(timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 28
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"#%pylab inline\n",
|
|
"#import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"plt.figure(figsize=(10,8))\n",
|
|
"\n",
|
|
"for f in times_n.keys():\n",
|
|
" plt.plot(orders_n, times_n[f], alpha=0.5, label=f, marker='o', lw=2)\n",
|
|
"\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
|
|
"plt.legend(loc=2)\n",
|
|
"plt.grid()\n",
|
|
"\n",
|
|
"plt.title('Performance of a simple least square fit implementation')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAmEAAAH4CAYAAAACdDpdAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl4k2XW+PFv0n1vKV2A0gUKhULZBRSQQhFwYRlBliKL\nivO6jCvzc3RUFp0RxhnfcfB1m2GpClhABWRHliqiUtmkUKC00AJtKS2lQOmSNrl/fzxDpFCgSNts\n53Ndva4+SZ7kJCdPcnLfd050SimFEEIIIYRoVHpLByCEEEII4YikCBNCCCGEsAApwoQQQgghLECK\nMCGEEEIIC5AiTAghhBDCAqQIE0IIIYSwACnChM0pKCjg7rvvxtfXl//3//6fpcOxuPLycoYNG4a/\nvz9jx45tsNu57777+OyzzxrkuvV6PceOHbvl/ZKSkujXr18DRGT/duzYQZs2bfD19WXVqlXcd999\nfPrpp3Xe3xqfD9Zu9uzZPP7445YOQ1gRZ0sHIBxDZGQkZ86cwcnJCS8vL+69917+7//+Dy8vr1u+\nrn//+98EBwdz4cKFBojU9nzxxRecOXOG4uJi9PqG+1y1bt26BrtuaxYfH8/EiRN57LHHLB1KvZo+\nfTrPPvsszzzzDAAjRowwn5eUlMT8+fPZvn37dfd3tOfDzJkzycrKqnPhmZKSwsSJEzl58qT5tFde\neaWhwhM2SkbCRKPQ6XSsWbOGixcvsmfPHnbt2sVf/vKXW7oOpRQmk4mcnBzat2//m+Korq7+TftZ\ns5ycHNq2bdugBZgj0+l0lg7hpn7L8/rEiRPExsY2QDRCiDpTQjSCyMhItWXLFvP2H//4R/XAAw8o\npZT68ccf1Z133qn8/f1V586dVUpKivly/fv3V6+++qrq06eP8vDwUA8//LBycXFRrq6uytvbW23Z\nskVVVlaq5557TjVv3lw1b95cPf/886qyslIppdS2bdtUixYt1N/+9jcVGhqqJk6cqGbOnKlGjx6t\nHn74YeXj46Pi4uJURkaGeuutt1RwcLAKDw9XmzZtMsewYMEC1b59e+Xj46NatWqlPv74Y/N5l6//\nnXfeUcHBwapZs2Zq4cKF5vPLysrUiy++qCIiIpSfn5/q27evKi8vv+n9vlp6errq37+/8vf3Vx06\ndFBff/21Ukqp6dOnK1dXV+Xi4qK8vb3VggULrtl3586dqnfv3srf3181a9ZM/eEPf1AGg6HW2ykv\nL1cTJkxQgYGByt/fX91xxx3qzJkz5lzMmzdPKaXUwoUL1V133aVeeOEF5e/vr1q3bq127NihFixY\noFq2bKmCg4PVJ598Yr7eyZMnq//5n/9R99xzj/Lx8VH9+/dXOTk55vN1Op3KyspSSilVUVGhpk2b\npsLDw1VISIh64oknzI/Z1RYuXKj69u1r3j506JAaNGiQatKkiYqJiVHLli0zn7dmzRrVpUsX5evr\nq1q2bKlmzpx5w/tdUFCg/vznPysnJyfl7u6uvL291TPPPFOnx6ygoEAppdSxY8fU3XffrXx8fNQ9\n99yjnn76afXwww8rpbTnTlhYWI3rioiIMB8nN8ubTqdT77//voqOjlatWrVSSim1evVq1blzZ+Xv\n76/uuusutX///loft1atWim9Xq88PDyUj4+PqqysNOf30KFDys3NTTk5OSlvb28VEBBQ63VYw/Ph\n8vH39ttvq6CgINWsWTO1YsUKtXbtWtWmTRvVpEkTNXv2bPP1mkwmNXv2bNW6dWsVGBioxowZo4qL\ni5VSSh0/flzpdDr1ySefqPDwcNW0aVP117/+VSml1Pr162scZ126dFFKXf+1obS0VLm7uyu9Xq+8\nvb2Vj4+PysvLUzNmzDDnXymlVq1apWJjY5W/v7+Kj49Xhw4dqvFc+Mc//qE6deqk/Pz81NixY1VF\nRUWtuRC2S4ow0SgiIyPV5s2blVJKnThxQnXo0EFNnz5dnTp1SgUGBqr169crpZT65ptvVGBgoCoq\nKlJKaS/0ERERKj09XRmNRlVVVaWmTJmiXn/9dfN1v/766+rOO+9UhYWFqrCwUN11113m87dt26ac\nnZ3Vyy+/rAwGgyovL1czZsxQ7u7uatOmTaq6ulpNmjRJRUREqLfeektVV1er//znPyoqKsp8/WvX\nrlXHjh1TSin17bffKk9PT7Vnz54a1z9jxgxVXV2t1q1bpzw9PVVJSYlSSqmnnnpKDRgwQOXl5Smj\n0ah+/PFHVVlZed37XVhYeM1jZzAYVOvWrdXs2bNVVVWV2rp1q/Lx8VFHjhxRSik1c+ZMNXHixOs+\n9rt371Y7d+5URqNRZWdnq/bt26t333231st+9NFHatiwYaq8vFyZTCa1Z88edeHCBaWUUvHx8Wr+\n/PlKKe1N19nZWSUlJSmTyaRee+011aJFC3OhsGnTJuXj46MuXbqklNLedH18fNT27dvNRfOVxdOV\nb7rPP/+8GjFihDp37py6ePGiGjZsmHrllVdqjffKIqy0tFSFhYWppKQkZTQa1d69e1XTpk1Venq6\nUkqplJQUdeDAAaWUUvv371chISFq5cqVt3S/b/Ux6927t5o2bZoyGAzqu+++Uz4+PuZc1VaEXflh\n5WZ50+l0avDgwercuXOqoqJC7dmzRwUHB6vU1FRlMpnUJ598oiIjI80fSK529QejK+9nUlJSjfzU\nxhqeD5ePvzfffNN87AYGBqrExERVWlqqDh48qDw8PFR2drZSSql3331X3XnnnSo3N1cZDAb1P//z\nP2r8+PFKqV+LsN///veqoqJC/fLLL8rNzU0dPnxYKVX7cXaj14aUlJRr8jtz5kxzEXbkyBHl5eWl\nNm/erKqrq9Xbb7+toqOjVVVVlTk/vXr1Uvn5+aq4uFi1b99effTRRzfMibA9UoSJRhEREaG8vb2V\nv7+/ioiIUE8//bQqLy9Xc+bMueaFbciQIeZPzfHx8WrGjBk1zp8yZYp67bXXzNutW7c2FzNKKbVx\n40YVGRmplNJepF1dXWu8Ec2YMUMNHjzYvP31118rb29vZTKZlFJKXbhwQel0OnX+/Pla78vIkSPV\nv/71L/P1e3h4KKPRaD4/ODjY/Obp4eFR62jEze73lb777jsVGhpa47Tx48ebR3Ku/nR9M//85z/V\n7373u1rPW7BgwXVHUK5+023Tpo35vP379yudTmceNVNKqcDAQPXLL78opbQ33ctvdkppBZOTk5M6\ndeqUUurXN12TyaS8vLzMb8BKKfXDDz/UKIqvdGURlpycrPr161fj/N///vdq1qxZte773HPPqRde\neKFO9/vyiE9trrdvTk6OcnZ2VmVlZebTEhMT61yEXe3qvOl0OrVt2zbz9hNPPFHjw4lSSsXExKhv\nv/221uu7URF29Qhjbazh+XD5+Lv62E1NTTVfvnv37mrVqlVKKaXatWtX4z7n5eUpFxcXZTQazUVY\nbm6u+fyePXuqpUuXKqXqdpxd/dpwdX6vvI433nhDjR071nyeyWRSLVq0MOcrMjJSLV682Hz+Sy+9\npJ544okb3r6wPbIwXzQKnU7HqlWrGDhwYI3Tc3JyWL58OatXrzafVl1dXeNyLVu2vOF15+XlERER\nYd4ODw8nLy/PvB0UFISrq2uNfYKDg83/e3h40LRpU/PaHw8PDwBKS0vx9fVl/fr1zJo1i6NHj2Iy\nmSgrK6NTp07m/QMDA2usx/L09KS0tJSioiIqKipo3br1NTHX5X5fef+ufgwiIiLIzc294eNyWUZG\nBi+++CK7d++mrKyM6upqevToUetlLy8kHjduHCUlJTz88MP89a9/xdn52peKkJAQ8/+XH7OgoKAa\np5WWlgJa/sPCwszneXl50aRJE/Ly8mjRooX59MLCQsrKyujevbv5NPXftYA3k5OTw86dOwkICDCf\nVl1dzaRJkwDYuXMnL7/8MgcPHsRgMFBZWcmYMWPqdL9vtC7sevvm5eUREBBgfmxAy9uVC7VvpC55\nu/J5kZOTw6effsp7771nPq2qqor8/Pw63d7tstTzITAw8Jpj9+pYLt9uTk4Ov/vd72ocr87OzhQU\nFJi3Q0NDzf9fPpav52avDTeSl5dHeHi4eVun09GyZcsax/WVsXh4eNR4XRP2QVbyCosKDw9n4sSJ\nnDt3zvx38eJFXnrpJfNlbrYwunnz5mRnZ5u3T5w4QfPmza+7/60stK6srGTUqFG89NJLnDlzhnPn\nznHfffehlLrpvk2bNsXd3Z3MzMxrzqvL/b7y/p08ebLGbebk5NR4E7uRJ598ktjYWDIzMzl//jx/\n/etfr1vUODs7M336dA4ePMgPP/zAmjVrbqltwfUopWoUH6WlpRQXF9fIE2iPmYeHB+np6ebHpaSk\npE7fhA0PD6d///7XPKbvv/8+AImJiYwcOZJTp05RUlLCE088YX4cbnS/b/Z8ud6+zZs359y5c5SV\nlZkvm5OTY74+Ly+vGucZjUYKCwvN23XJ25WxhYeH8+qrr9a4/6Wlpb+pbUlDfxmhMZ4PtQkPD2fD\nhg01HqOysjKaNWt2032vfkxu9tpws8ewRYsW5OTkmLcvPyZXFqE3un1hH6QIExb18MMPs3r1ajZt\n2oTRaKSiooKUlJQanwavLniu3h4/fjx/+ctfKCoqoqioiDfeeIOJEyde9zbrUkBdZjAYMBgMNG3a\nFL1ez/r169m0aVOd9tXr9Tz66KO8+OKL5OfnYzQa+fHHHzEYDHW635f17t0bT09P3n77baqqqkhJ\nSWHNmjWMGzeuTnGUlpbi4+ODp6cnhw8f5sMPP7zuZVNSUkhLS8NoNOLj44OLiwtOTk51up2bWbdu\nHTt27MBgMPD6669z5513XvOGo9frefzxx3n++efNBUlubm6dHvP777+fjIwMFi1aRFVVFVVVVfz8\n888cPnwY0B6HgIAAXF1dSU1NZcmSJeY3thvd75CQELKysq57u9fbNzw8nB49ejBjxgyqqqr4/vvv\nWbNmjXm/tm3bUlFRwbp166iqquIvf/kLlZWV5vNvJW8Ajz/+OB999BGpqakopbh06RJr16694UjO\n9YSEhHDq1Cmqqqpued+6aujnQ22eeOIJ/vznP3PixAlAG2n7+uuv67RvaGgo2dnZ5tePm702hISE\ncPbs2esWjA899BBr165l69atVFVV8c477+Du7s5dd91V6+Vv5XVL2A4pwoRFhYWFsWrVKt566y2C\ng4MJDw/nnXfeqfGCU9tI1pWnvfbaa/To0YNOnTrRqVMnevTowWuvvVbn/a93GQAfHx/mzp3LmDFj\naNKkCZ9//nmNfkq17Xulf/zjH8TFxXHHHXcQGBjIK6+8gslkuu79rm2EysXFhdWrV7N+/XqCgoL4\nwx/+wGeffUbbtm2ve3+ujmHJkiX4+vry+9//nnHjxl338qdPn+ahhx7Cz8+P2NhYc4+sq9XlMbz6\nvMTERGbNmkVgYCB79+5l0aJFte77t7/9jejoaHr37o2fnx/33HMPGRkZ173eK3O1adMmkpOTadGi\nBc2aNeOVV17BYDAA8MEHHzB9+nR8fX158803a4wQ3eh+P/fcc3zxxRc0adKE559//pYesyVLlrBz\n506aNGnCG2+8waRJk8zPbT8/Pz744AOmTp1KWFgY3t7eNaYXb5a3qx/v7t2785///Ic//OEPNGnS\nhDZt2vzmUcyEhAQ6dOhAaGhojan767Hk8+FWbve5555j+PDhDB48GF9fX+68805SU1PrtO9DDz0E\naNOfPXr0uOlrQ7t27Rg/fjytWrWiSZMm5Ofn13icYmJiWLRoEc888wxBQUGsXbuW1atX1zr1fzk2\nGQ2zPzrVwOW10WikR48ehIWFsXr1aoqLixk7diw5OTlERkaybNky/P39Aa2b8IIFC3BycmLu3LkM\nHjy4IUMTQjSSRx55hLCwMN58801Lh2JRs2bNIjMzs8E6zdsKeT4IoWnwkbB//etfxMbGmiv4OXPm\nmD/JJCQkMGfOHADS09NZunQp6enpbNiwgaeeeqpOi3GFENZPplI08jho5HEQQtOgRdipU6dYt24d\nU6dONR90X3/9NZMnTwZg8uTJrFy5EoBVq1Yxfvx4XFxciIyMJDo6usYwsRDCdslUikYeB408DkJo\nGrRFxQsvvMDf//73GgsTCwoKzF8fDgkJMX81OC8vj969e5svFxYWVuev4AshrNvChQstHYJVmDFj\nhqVDsAryfBBC02BF2Jo1awgODqZr166kpKTUepmbfRqq7bwWLVpIrxQhhBBC2ITOnTuzb9++Ws9r\nsCLshx9+4Ouvv2bdunVUVFRw4cIFJk6cSEhICKdPnyY0NJT8/HzzN29atGhRo2/MqVOnau2XkpeX\nJ+sJrNDMmTOZOXOmpcMQV5CcWCfJi/WRnFgfe8rJjQabGmxN2FtvvcXJkyc5fvw4ycnJDBw4kM8+\n+4zhw4fzySefAPDJJ58wcuRIAIYPH05ycjIGg4Hjx49z9OhRevbs2VDhiXp2ZbNUYR0kJ9ZJ8mJ9\nJCfWx1Fy0mg/W3S5Enz55ZcZM2YM8+fPN7eoAIiNjWXMmDHExsbi7OzMBx98IAs3hRBCCGG3GrxP\nWH3T6XQyHWmFUlJSiI+Pt3QY4gqSE+skebE+khPrY085uVHdIkWYEEIIIazCkcwjbN69mSpVhYvO\nhUHdBxETHWPpsG7LjeoWu/nZoiZNmpi/bSl/tvHXpEkTSz9t7Nr1vpUsLEvyYn0kJ9bhSOYRkrYl\nURhSyO683RSGFJK0LYkjmUcsHVqDabQ1YQ3t3LlzMkJmY2TNnxBCiMs2796MWxs3CkoLSC9MJ8QQ\ngncbb7bs2WLzo2HXYzcjYUKImuxlPYW9kbxYH8mJdTCYDOSU5HCo6BA+MT4UlRWZT7dXdjMSJoQQ\nQgjbZDQZOVx4mOO+xwFoHdCaMN8wAFz1rpYMrUHJSJgQdkrWuVgnyYv1kZxYVkV1BYvTFuPS1AVT\nlokOQR0wHjei0+moPFpJQrcES4fYYGQkTAghhBAWUVJRwpK0JZy5dIaIiAge6vAQB48cJL04neAz\nwSQMSLDb9WBgRy0qHKV1RUpKChMnTqzxE0+2ylFyJoQQ4lp5F/NYkraEUkMpQZ5BJMYlEuARYOmw\n6p1DtKgQNc2cOZOJEydaOgwhhBDiGoeLDrNw70JKDaVE+UfxaNdH7bIAuxmHmI48ciSHzZuzqKrS\n4+JiYtCg1sTERDTa/vbkcjUv7SWsnz11nLYnkhfrIzlpXD+d+omNmRtRKLqEdmFY22E46Z1qXMZR\ncmL3I2FHjuSQlJRJYeFASkriKSwcSFJSJkeO5DTK/pedPHmSBx98kODgYJo2bcrTTz9NYGAgBw4c\nMF/mzJkzeHl5cfbs2Tpf79/+9jfCwsLw9fWlXbt2bN26lQ0bNjB79myWLl2Kj48PXbt2BSApKYnW\nrVvj6+tLq1atWLJkCQBGo5E//vGPBAUF0bp1a95//330ej0mkwnQvr792muv0adPH7y8vDh+/Pgt\n3XchhBDCpEysP7qeDZkbUCgGRA5gRMyIawowR2L3I2GbN2fh5pZAzS+/JLB//1buuOPmo1mpqVmU\nlf36zYz4eHBzS2DLlq11Hg0zGo088MADDBo0iMWLF+Pk5MTPP/8MwKJFi5gzZw4An3/+OYMGDSIw\nMLBO13vkyBHef/99du3aRWhoKCdOnKC6uppWrVrx5z//maysLD799FMALl26xHPPPceuXbto06YN\nBQUF5mLvP//5D2vXrmXfvn14enry4IMPXjPStWjRItavX09MTIy5OBPWzRE+RdoiyYv1kZw0PIPR\nwJfpX3Lk7BGcdE6MaDeCTiGdrnt5R8mJ3Y+EVVXVfheNxrrddZOp9ssZDHV/6FJTU8nPz+fvf/87\nHh4euLq60qdPHyZNmsTnn39uvtxnn312S+u4nJycqKys5ODBg1RVVREeHk6rVq0Abdrw6oWAer2e\ntLQ0ysvLCQkJITY2FoBly5bxwgsv0KJFCwICAvjzn/9cY1+dTseUKVNo3749er0eZ2e7r92FEELU\nk4uVF1m4dyFHzh7Bw9mDSZ0n3bAAcyR2/27q4nJ5Sq3m6cHBJp566ub7v/++icLCa093da37aNDJ\nkyeJiIhAr69ZuPXq1QsPDw9SUlIIDQ0lKyuL4cOH1/l6o6Ojeffdd5k5cyYHDx5kyJAh/O///i/N\nmjW75rJeXl4sXbqUf/zjHzz22GP06dOHd955h5iYGPLz82nZsqX5suHh4dfsf+X5wjY4ypoKWyN5\nsT6Sk4ZTUFrAkrQlnK88T4B7ABM6TaCpZ9Ob7ucoObH7kbBBg1pTWbmlxmmVlVtISGjdKPuDVsCc\nOHECo9F4zXmTJ09m0aJFfPbZZzz00EO4ut5aZ+Dx48ezfft2cnJy0Ol0/OlPfwJqXzg/ePBgNm3a\nxOnTp2nXrh2PP/44AM2aNePEiRPmy135/2WyEF8IIcStyCrOYsHeBZyvPE9L35ZM7Ta1TgWYI7H7\nIiwmJoIpU6IJDt6Kv38KwcFbmTIlus7ruW53f9BGvJo1a8bLL79MWVkZFRUV/PDDDwA8/PDDfPXV\nVyxevJhJkybd0n3LyMhg69atVFZW4ubmhru7O05O2gLH0NBQsrOzzdOKZ86cYdWqVVy6dAkXFxe8\nvLzMlx0zZgxz584lNzeXc+fOMWfOnGuKLunnZXsc4VOkLZK8WB/JSf3bk7+HxWmLqTRW0iGoA5M6\nT8LL1avO+ztKTux+OhK0Qup2Wkrc7v56vZ7Vq1fz7LPPEh4ejk6nY8KECdx11120bNmSbt26cezY\nMfr27Vun67tcIFVWVvLKK69w6NAhXFxc6NOnD//+978BeOihh1i0aBGBgYG0atWKNWvW8M9//pPJ\nkyej0+no2rUrH374IQCPP/44GRkZdO7cGT8/P6ZNm8a2bdtqvU0hhBDiepRSbD2+le0ntgPQN7wv\nCVEJ8h5yHdIx3wo89thjtGjRgjfeeMPSoQCQnZ1Nq1atqK6uvmYdW32y5ZzZAkdZU2FrJC/WR3JS\nP6pN1aw8vJIDZw6g1+m5v839dG/e/Tddlz3l5EbvdQ4xEmbNsrOz+eqrr9i3b5+lQxFCCCF+k7Kq\nMj5P+5yTF07i5uTGQx0eIrpJtKXDsnp2vybMmr3++uvExcXx0ksvERHx63TnW2+9hY+PzzV/999/\nf6PFJkPHts9ePkXaG8mL9ZGc3J6zZWeZt2ceJy+cxNfNl0e7PnrbBZij5ESmI4XFSM6EEMK25ZTk\nkHwgmfLqcpp5NyMxLhEfNx9Lh2VV5Ae8hXBAKTV/JkJYCcmL9ZGc/DZpBWl8+sunlFeX0zawLY90\nfaTeCjBHyYmsCRNCCCFEnSml2H5iO1uPbwWgZ4ueDI0eil4n4zq3SqYjhcVIzoQQwrYYTUbWZKxh\n7+m96NAxuPVgeof1lnXENyDfjhRCCCHEbamormDZwWUcO3cMF70LD7Z/kPZB7S0dlk2TsUMh7JSj\nrKmwNZIX6yM5ubmSihLm75nPsXPH8HLxYkqXKQ1agDlKTqQIawSRkZFs2bLl5hcUQgghrEzexTzm\n7ZlHYVkhQZ5BPN79cVr4trB0WHZB1oQ1gqioKObPn8/AgQNrPb+xOtRbG2vOmRBCCDhcdJgv07+k\nylRFlH8UYzuOxd3Z3dJh2RSHXxN2JPMIm3dvpkpV4aJzYVD3QcRExzTa/nXVEAWJ0Wg0/1C3EEII\nUVc/nfqJjZkbUSi6hHZhWNthOOnl/aQ+2f2wy5HMIyRtS6IwpJCS0BIKQwpJ2pbEkcwjjbL/lVJT\nU+nRowd+fn6Ehobyxz/+EYC7774bAH9/f3x8fNi5cyeZmZn0798ff39/goKCGDdunPl6vvnmG9q1\na4e/vz/PPPMM/fv3Z/78+QAkJSXRp08fXnzxRZo2bcqsWbNuOU5hHxxlTYWtkbxYH8lJTSZlYv3R\n9WzI3IBCMTBqICNiRjRqAeYoObH7kbDNuzfj1saNlOyUX090gf3J+7mj7x033T/1+1TKwsogW9uO\nj4zHrY0bW/ZsuaXRMKUUzz33HC+88AITJkygrKyMtLQ0ALZv305UVBTnz583T0eOHz+eoUOH8u23\n32IwGNi1axcARUVFjBo1iqSkJEaMGMF7773HRx99xOTJk3+NOTWVxMREzpw5g8FgqHOMQgghHJvB\naOCL9C/IOJuBk86JEe1G0Cmkk6XDslt2PxJWpapqPd2IsU77mzDVerrBdOvFjaurK0ePHqWoqAhP\nT0969eoF1D4N6erqSnZ2Nrm5ubi6unLXXXcBsG7dOjp27MiDDz6Ik5MTzz//PKGhoTX2bd68OU8/\n/TR6vR53d5m7d1SO8ttrtkbyYn0kJ5qLlRdZuHchGWcz8HD2YFLnSRYrwBwlJ3Y/EuaicwG0Eawr\nBXsG81T8Uzfd//2C9ykMKbzmdFe96y3FodPpmD9/PtOnT6d9+/ZERUUxY8aM6/4o99tvv83rr79O\nz549CQgIYNq0aTzyyCPk5eURFhZW47ItW7a84bYQQghxIwWlBSxJW8L5yvMEuAcwodMEmno2tXRY\nds/uR8IGdR9E5dHKGqdVHq0koVtCo+x/pejoaJYsWUJhYSF/+tOfGD16NOXl5bV2Gg4JCeHf//43\nubm5fPzxxzz11FNkZWXRvHlzTp48ab6cUqrGNiCdiwXgOGsqbI3kxfo4ek6yirNYsHcB5yvP09K3\nJVO7TbV4AeYoObH7IiwmOoYpA6YQfCYY/9P+BJ8JZsqAKXVez3W7+1+mlGLRokUUFmqjan5+fuh0\nOvR6PUFBQej1erKyssyXX758OadOnQK0Bfs6nQ4nJyfuu+8+Dh48yIoVK6iurmbu3LmcPn36lmIR\nQgghAPbk72Fx2mIqjZV0COrApM6T8HL1snRYDsPupyNBK6Rup6XE7e5/2caNG5k2bRplZWVERkaS\nnJyMm5sbAK+++ip9+vShurqa9evXs2vXLl544QXOnz9PSEgIc+fOJTIyEtAKtGeffZZHHnmEiRMn\n0qdPH/Nt6HQ6GQkTgOOsqbA1khfr44g5UUqx5fgWvj/xPQB9w/uSEJVgNe8fjpITadZqBwYMGMDE\niRN59NG+oDwJAAAgAElEQVRHLR3KLXHknAkhhKVUm6pZeXglB84cQK/Tc3+b++nevLulw7JbN3qv\ns/vpSEchxYy4mqOsqbA1khfr40g5Kasq45N9n3DgzAHcnNxIjEu0ygLMUXLiENORjsBahpCFEEJY\np7NlZ1mctpji8mJ83XyZEDeBEO8QS4fl0GQ6UliM5EwIIRpHTkkOyQeSKa8up5l3MxLjEvFx87F0\nWA7B4X87UgghhHBUaQVprDy8EqMy0jawLaNjR+PqdGu9LkXDkDVhQtgpR1lTYWskL9bHXnOilOK7\nnO/48tCXGJWRni16Mq7jOJsowOw1J1eTkTAhhBDCzhhNRtZkrGHv6b3o0DEkegi9WvSS9cNWRtaE\nCYuRnAkhRP2rqK5g6YGlHC85jovehVGxo2jXtJ2lw3JYsiZMCCGEcAAlFSUs3r+YwrJCvFy8SIxL\npIVvC0uHJa5D1oTZkJkzZzJx4sRb3i8yMpItW7Y0QETCmjnKmgpbI3mxPvaSk9wLuczbM4/CskKC\nPIN4vPvjNluA2UtObkaKMBvyW+fy6/JTRtnZ2ej1ekwm02+6DSGEEJZzuOgwSfuSKDWUEuUfxWPd\nHsPf3d/SYYmbaLDpyIqKCvr3709lZSUGg4ERI0Ywe/ZsZs6cybx58wgKCgLgrbfe4t577wVg9uzZ\nLFiwACcnJ+bOncvgwYPrJZacI0fI2rwZfVUVJhcXWg8aRERM3X8L8nb3ry+NsX6qIW7DaDTi5ORU\n79crbsxRfnvN1kherI8t50Qpxc7cnWzM3IhC0SW0C8PaDsNJb9uvuback1vRYCNh7u7ubNu2jX37\n9rF//362bdvG999/j06n48UXX2Tv3r3s3bvXXIClp6ezdOlS0tPT2bBhA0899VS9jMrkHDlCZlIS\nAwsLiS8pYWBhIZlJSeQcOdIo+4M2HfjOO+/QuXNn/P39GTduHJWVlaSkpBAWFsbf//53goODad68\nOStXrmTdunW0bduWwMBA5syZY74enU5HRUUF48aNw9fXl+7du7N///5bejxSU1Pp0aMHfn5+hIaG\n8sc//hGAu+++GwB/f398fHzYuXMnmZmZ9O/fH39/f4KCghg3bpz5er755hvatWuHv78/zzzzDP37\n92f+/PkAJCUl0adPH1588UWaNm3KrFmzbilGIYQQN2dSJtZnrmdD5gYUioFRAxkRM8LmCzBH0qAL\n8z09PQEwGAwYjUYCAgKA2kdbVq1axfjx43FxcSEyMpLo6GhSU1Pp3bv3bcWQtXkzCW5ucMX8cgKw\ndf9+Iu644+b7p6aSUFb26wnx8SS4ubF1y5Y6j4bpdDqWL1/Oxo0bcXNzo0+fPiQlJdGuXTsKCgqo\nrKwkPz+fhQsXMnXqVIYMGcLevXvJycmhR48ejB8/noiICJRSrFq1iuTkZBYvXsy7777LyJEjycjI\nwNm5bql87rnneOGFF5gwYQJlZWWkpaUBsH37dqKiojh//jx6vVabjx8/nqFDh/Ltt99iMBjYtWsX\nAEVFRYwaNYqkpCRGjBjBe++9x0cffcTkyZPNt5OamkpiYiJnzpzBYDDUKTZRv1JSUhzm06QtkbxY\nH1vMicFo4Iv0L8g4m4GTzomR7UYSFxJn6bDqjS3m5Ldo0DVhJpOJLl26EBISwoABA+jQoQMA7733\nHp07d+axxx6jpKQEgLy8PMLCwsz7hoWFkZube9sx6Kuqaj/daKzb/tcZjdPfYmHx7LPPEhoaSkBA\nAMOGDWPfvn0AuLi48Oqrr+Lk5MTYsWMpLi7m+eefx8vLi9jYWGJjY/nll1/M19OjRw8efPBBnJyc\nePHFF6moqOCnn36qcxyurq4cPXqUoqIiPD096dWrF1B7Yezq6kp2dja5ubm4urpy1113AbBu3To6\nduxojuP5558nNDS0xr7Nmzfn6aefRq/X4+7ufkuPlRBCiOu7WHmRhXsXknE2Aw9nDyZ1nmRXBZgj\nadCRML1ez759+zh//jxDhgwhJSWFJ598kunTpwPw+uuvM23aNPM01tWut5h8ypQpREZGAtr0WZcu\nXa4bg8nFRfvnqoraFBwMTz110/tgev99KCy89nTXW+s4fGWR4unpSV5eHgCBgYHm++nh4QFASMiv\nP6jq4eFBaWmpefvKQlWn0xEWFkZ+fn6d45g/fz7Tp0+nffv2REVFMWPGDO6///5aL/v222/z+uuv\n07NnTwICApg2bRqPPPLINQUzQMuWLW+4fT2XvwFz+ROPbNffdnx8vFXFI9vXfuPLWuKRbdvZLi4v\nJsc/h/OV5zmbfpZBrQYR4R9hNfHV13a8Db9+Xf4/Ozubm2m0Zq1vvvkmHh4e5jVIoH0jb9iwYaSl\npZnXPr388ssADB06lFmzZplHaswB32Kz1struhLc3MynbamsJHrKlDpNJ97u/gBRUVHMnz+fgQMH\nAjBr1iwyMzOZOnUqDz/8MCdPngSgurraPPoUHh4OQL9+/XjyySdJTExk5syZbNy4kR9//BHQRhrD\nwsJYvnw5ffr0qfPtX/bll1/y8MMPU1xczJkzZ4iKiqK6uto8HXmlHTt2MGjQIA4cOMCOHTv48MMP\nzXEopQgPD2fWrFk8+uijJCUlMX/+fLZv337Dx0WatQohRN1lFWex7OAyKo2VtPRtybiO4/By9bJ0\nWOImbvRe12DTkUVFReapxvLycr755hu6du3K6dOnzZdZsWIFcXHaEOrw4cNJTk7GYDBw/Phxjh49\nSs+ePW87joiYGKKnTGFrcDAp/v5sDQ6+pQLqdvevze0UHrt372bFihVUV1fz7rvv4u7ufkvr5hYt\nWkThf0f2/Pz80Ol06PV6goKC0Ov1ZGVlmS+7fPlyTp06BWgjjjqdDicnJ+677z4OHjxojmPu3Lk1\n8iqsw9WjLsI6SF6sjy3kZHfebhanLabSWEmHoA5M7jLZrgswW8hJfWiw6cj8/HwmT56MyWTCZDIx\nceJEEhISmDRpEvv27UOn0xEVFcXHH38MQGxsLGPGjCE2NhZnZ2c++OCDevuNq4iYmNsqmm53/6td\n2bfr6vt4o/us0+kYOXIkS5cuZfLkybRp04avvvrqlto/bNy4kWnTplFWVkZkZCTJycm4/XeU79VX\nX6VPnz5UV1ezfv16du3axQsvvMD58+cJCQlh7ty55mng5cuX8+yzz/LII48wceLEGiNxdelLJoQQ\n4uaUUmw5voXvT3wPQN/wviREJchrrJ2Q344U9WLAgAFMnDiRRx99tM77SM6EEOL6qk3VrDi0goOF\nB9Hr9Nzf5n66N+9u6bDELZLfjhSNQgoqIYSoH5cMl0g+kMzJCydxc3JjTIcxtG7S2tJhiXomP1tk\nB06cOIGPj881f76+vuY1XY1Bhseti6OsqbA1khfrY205OVt2lvl753Pywkn83Px4tOujDleAWVtO\nGoqMhNmB8PBwLl68aNEYtm3bZtHbF0IIe5BTkkPygWTKq8tp5t2MxLhEfNx8LB2WaCCyJkxYjORM\nCCF+lVaQxsrDKzEqI20D2zI6djSuTrfWk1JYH1kTJoQQQlgppRTbT2xn6/GtAPRs0ZOh0UPR62TF\nkL2TDAthpxxlTYWtkbxYH0vmxGgysurIKrYe34oOHUOjh3Jv9L0OX4A5ynFiNyNhAQEBsjDcxlz+\nQXchhHBEFdUVLD2wlOMlx3HRuzAqdhTtmrazdFiiEdnNmjAhhBDCVpRUlLB4/2IKywrxdvVmfMfx\ntPBtYemwRAOQNWFCCCGElci9kMvnBz6n1FBKkGcQEzpNwN/d39JhCQtw7ElnUW8cZf7elkhOrJPk\nxfo0Zk4OFx0maV8SpYZSWgW04rFuj0kBVgtHOU5kJEwIIYRoYEopdubuZGPmRhSKrqFdeaDtAzjp\n6/7bv8L+yJowIYQQogGZlIkNmRtIzU0FYGDUQPqF95MvkzkIWRMmhBBCWIDBaOCL9C/IOJuBk86J\nke1GEhcSZ+mwhJWQNWGiXjjK/L0tkZxYJ8mL9WmonFysvMjCvQvJOJuBh7MHkzpPkgKsjhzlOJGR\nMCGEEKKeFZQWsDhtMRcqL9DEowkT4iYQ6Blo6bCsXs6RI2Rt3sz+Q4cwHTxI60GDiIiJsXRYDUbW\nhAkhhBD1KLM4k+UHl1NprKSlb0vGdRyHl6uXpcOyejlHjpCZlESCmxsoBTodWyoriZ4yxaYLsRvV\nLTIdKYQQQtST3Xm7WZK2hEpjJR2COjC5y2QpwOooa/NmrQArLoaff4aKChLc3MjassXSoTUYKcJE\nvXCU+XtbIjmxTpIX61MfOVFKsfnYZlZnrMakTPQN78vo2NE462XVT13pKyogKwv27yclLw9OndJO\nNxgsHFnDkWeHEEIIcRuqjFWsPLySg4UH0ev03N/mfro3727psGxLcTGmXbsgPx90OggNhdatATC5\nulo4uIYja8KEEEKI3+iS4RLJB5I5eeEkbk5ujOkwhtZNWls6LNuyfz+sWUNOXh6Zhw+TEBcHfn4A\ndr8mTIowIYQQ4jcoKitiSdoSisuL8XPzIzEukRDvEEuHZTsqK2HdOvjlF227QwdyYmLI+v579AYD\nJldXWick2HQBBrIwXzQCWedifSQn1knyYn1+S05ySnKYv2c+xeXFNPNuxtRuU6UAuxV5efDxx1oB\n5uICw4fD6NFEdOrEwKeegi5dGPjUUzZfgN2MrAkTQgghbsH+gv2sOrwKozISExjDqNhRuDrZ77ql\neqUU/PADbNkCJpO29mv0aGja1NKRWYRMRwohhBB1oJRi+4ntbD2+FYBeLXoxJHoIep1MKtVJaSms\nWKF9AxKgd28YNAic7Xs8SH47UgghhLgNRpOR1Rmr2Xd6Hzp0DIkeQu+w3pYOy3ZkZmoF2KVL4OkJ\nI0dC27aWjsripHwX9ULWuVgfyYl1krxYn5vlpKK6gkX7F7Hv9D5c9C6M7ThWCrC6qq6GjRth0SKt\nAIuKgiefvGkB5ijHiYyECSGEENdRUlHC4v2LKSwrxNvVm/Edx9PCt4Wlw7INZ8/CF19ovb/0ehg4\nEO66S/tfALImTAghhKhV7oVclqQt4VLVJYI8g5jQaQL+7v6WDsv6KaV963HdOjAYICAARo2CsDBL\nR2YRsiZMCCGEuAWHiw7zZfqXVJmqaBXQijEdxuDu7G7psKxfZSWsWQNpadp2x47wwAPgLo9dbWRM\nUNQLR5m/tyWSE+skebE+V+ZEKcWPJ39k6YGlVJmq6BralQlxE6QAq4vcXPjoI60Ac3HRFt+PGvWb\nCjBHOU5kJEwIIYQATMrEhswNpOamAjAwaiD9wvuh0+ksHJmVUwp27ICtW7XeX82aacWXg/b+uhWy\nJkwIIYTDMxgNfJH+BRlnM3DSOTGy3UjiQuIsHZb1u3hRaz1x7Ji2feedkJBg972/boWsCRNCCCGu\n42LlRZakLSG/NB8PZw/GdRxHhH+EpcOyfkePagVYWRl4eWnTj23aWDoqmyJrwkS9cJT5e1siObFO\nkhfrUlBawJ/m/Yn80nyaeDRharepUoDdTHU1bNgAixdrBVirVvDEE/VagDnKcSIjYUIIIRxSZnEm\nyw8up6yqjJa+LRkfNx5PF09Lh2Xdioq03l+nT2v9vhIStN5fsm7uN5E1YUIIIRzO7rzdrD26FpMy\n0TG4IyPbjcRZL+MS16UU7Nun9f6qqtJ6f40eDS2kce3NyJowIYQQAq0FxeZjm9lxcgcA/cL7MTBq\noHwD8kYqKrTeXwcOaNtxcVrvLzc3y8ZlB2RNmKgXjjJ/b0skJ9ZJ8mI5VcYqvkj/gh0nd6DX6Rke\nM5yEVgl8++23lg7Nep06pfX+OnAAXF3hd7+DBx9s8ALMUY4TGQkTQghh9y4ZLpF8IJmTF07i5uTG\nmA5jaN2ktaXDsl4mk9b7a9u2X3t/jR4NgYGWjsyuyJowIYQQdq2orIjF+xdzruIcfm5+JMYlEuId\nYumwrNfFi/DVV3D8uLZ9113aAnwnJ8vGZaNkTZgQQgiHlFOSQ/KBZMqry2nm3YzEuER83HwsHZb1\nysiAlSt/7f31u99BdLSlo7JbsiZM1AtHmb+3JZIT6yR5aTz7C/bz6S+fUl5dTkxgDI90faTWAkxy\ngtb7a/16WLJEK8Bat4Ynn7RYAeYoOZGRMCGEEHZFKcV3Od+xLXsbAL1a9GJI9BD0Ohl3qFVhIXz5\npdb7y8lJm3q8807p/dUIZE2YEEIIu2E0GVmdsZp9p/ehQ8eQ6CH0Dutt6bCsk1Kwd682AlZVBU2a\naIvvmze3dGR2RdaECSGEsHsV1RUsPbCU4yXHcdG7MCp2FO2atrN0WNapogJWr4aDB7Xtzp3hvvuk\n91cjk7FZUS8cZf7elkhOrJPkpWGUVJQwf898jpccx9vVm0e6PlLnAszhcnLypNb76+BBrffXgw9q\nC/CtqABzlJzISJgQQgiblnshlyVpS7hUdYlgr2AS4xLxd/e3dFjWx2SC77+HlBTt/+bNtenHJk0s\nHZnDarA1YRUVFfTv35/KykoMBgMjRoxg9uzZFBcXM3bsWHJycoiMjGTZsmX4+2sHy+zZs1mwYAFO\nTk7MnTuXwYMHXxuwrAkTQgjxX4cKD/HVoa+oMlXRKqAVYzqMwd3Z3dJhWZ8LF7TeX9nZ2nafPjBw\noPT+agQ3qlsadGF+WVkZnp6eVFdX07dvX/7xj3/w9ddf07RpU1566SX+9re/ce7cOebMmUN6ejqJ\niYn8/PPP5ObmMmjQIDIyMtDra86YShEmhBBCKcVPp35iU9YmFIquoV15oO0DOOmlqLjG4cOwahWU\nl4O3tzb12Fp+LaCx3KhuadA1YZ6engAYDAaMRiMBAQF8/fXXTJ48GYDJkyezcuVKAFatWsX48eNx\ncXEhMjKS6OhoUlNTGzI8UY8cZf7elkhOrJPk5faZlIn1mevZmLURhSIhKoHhMcN/cwFmtzmproZ1\n6yA5WSvAoqO13l82UIDZbU6u0qBrwkwmE926dSMrK4snn3ySDh06UFBQQEiI9nMRISEhFBQUAJCX\nl0fv3r9+jTgsLIzc3NyGDE8IIYSNMRgNfJH+BRlnM3DSOTGy3UjiQuIsHZb1KSyEL76AggJtynHQ\nIOjdW3p/WZkGLcL0ej379u3j/PnzDBkyhG3bttU4X6fTobvBE+J6502ZMoXIyEgA/P396dKlC/Hx\n8cCv1bNsy7ajb8fHx1tVPLJ97ad7a4nHVrbXbVrH5uOb8Y3xxcPZg8iSSM4eOgv//RlIS8dnFdtK\nEe/rCxs2kHL0KPj6Ev/KK9CsmXXEV8fteBt+/br8f/bl9Xc30GjNWt988008PDyYN28eKSkphIaG\nkp+fz4ABAzh8+DBz5swB4OWXXwZg6NChzJo1i169etUMWNaECSGEwykoLWBx2mIuVF6giUcTJsRN\nINAz0NJhWZfycq33V3q6tt2li9b7y9XVsnE5OIusCSsqKqKkpASA8vJyvvnmG7p27crw4cP55JNP\nAPjkk08YOXIkAMOHDyc5ORmDwcDx48c5evQoPXv2bKjwRD27+hO+sDzJiXWSvNy6zOJMFuxdwIXK\nC4T7hTO129R6LcDsIicnTmi9v9LTtX5fo0bByJE2W4DZRU7qoMGmI/Pz85k8eTImkwmTycTEiRNJ\nSEiga9eujBkzhvnz55tbVADExsYyZswYYmNjcXZ25oMPPrjhVKUQQgj7tztvN2uPrsWkTHQM7sjI\ndiNx1kuLSzOTCbZvh/9ORdKihdb7KyDA0pGJOpDfjhRCCGF1lFJsPraZHSd3ANAvvB8DowbKh/Mr\nnT+v9f7KydEW3PfpAwMGSO8vKyO/HSmEEMJmVBmrWHl4JQcLD6LX6Xmg7QN0a9bN0mFZl0OH4Ouv\nf+399eCD0KqVpaMSt6jB1oQJx+Io8/e2RHJinSQvN3bJcIlPf/mUg4UHcXNyY0LchAYvwGwqJ1VV\nsHYtLF2qFWBt2mi9v+ysALOpnNwGGQkTQghhFYrKili8fzHnKs7h5+bHhE4TCPYKtnRY1uPMGa33\n15kz2pTjPfdAr17S+8uGyZowIYQQFpdTkkPygWTKq8tp5t2MxLhEfNx8LB2WdVAKdu+GDRu0LviB\ngdri+2bNLB2ZqANZEyaEEMJq7S/Yz6rDqzAqIzGBMYyKHYWrk222Vqh35eXa2q9Dh7Ttrl3h3ntt\ntvWEqEnWhIl64Sjz97ZEcmKdJC+/Ukrxbfa3fHXoK4zKSK8WvRjbcWyjF2BWm5OcHPjwQ60Ac3PT\nRr9GjHCIAsxqc1LPZCRMCCFEozOajKzOWM2+0/vQoWNo9FB6hfW6+Y6OwGSC776Db7/VpiLDwrTm\nq9L7y+7ImjAhhBCNqqK6gqUHlnK85DguehdGx44mpmmMpcOyDufPw5dfah3wdTro2xfi46X3lw2T\nNWFCCCGswrnycyxJW0JhWSHert4kxiXS3Ke5pcOyDunp2vqvigrw8dF6f0VFWToq0YBkTZioF44y\nf29LJCfWyZHzknshl3l75lFYVkiwVzBTu021igLM4jmpqtJ+eHvZMq0Aa9tW6/3lwAWYxXPSSGQk\nTAghRIM7VHiIrw59RZWpilYBrRjTYQzuzu6WDsvyCgq03l+FhdqU4+DB0LOn9P5yELImTAghRINR\nSvHTqZ/YlLUJhaJbs27c3+Z+nPQOvsZJKfj5Z9i0Sev91bSp9u3H0FBLRybqmawJE0II0ehMysT6\no+v5Oe9nABKiEugb3ld+hLusTFv7dfiwtt2tGwwd6hCtJ0RNsiZM1AtHmb+3JZIT6+QoeTEYDSQf\nSObnvJ9x0jkxqv0o+kX0s8oCrFFzkp0NH32kFWDu7vDQQzB8uBRgV3GU40RGwoQQQtSrC5UXWJK2\nhNOlp/Fw9mB83HjC/cItHZZlmUyQkgLbt2tTkS1bar2//P0tHZmwIFkTJoQQot6cLj3NkrQlXKi8\nQBOPJkyIm0CgZ6Clw7KskhKt99fJk9qC+379tN5fepmMcgSyJkwIIUSDyyzOZNnBZRiMBsL9whnX\ncRyeLp6WDsuyDh7U2k9UVICvr9b7KzLS0lEJKyFluKgXjjJ/b0skJ9bJXvOyK28XS9KWYDAa6Bjc\nkUmdJ9lMAdYgOTEYtMX3y5drBVi7dvDEE1KA1ZG9HidXk5EwIYQQv5lSis3HNrPj5A4A+oX3Y2DU\nQKtcgN9oTp/Wen8VFYGzs9b76447pPeXuIasCRNCCPGbVBmrWHF4BemF6eh1eh5o+wDdmnWzdFiW\noxSkpmq9v4xGCArSen+FhFg6MmFBsiZMCCFEvbpkuMTnBz7n1IVTuDm5MbbjWFoFtLJ0WJZTVgar\nVsGRI9p2jx4wZAi4uFg2LmHVZE2YqBeOMn9vSyQn1ske8lJUVsS8PfM4deEUfm5+PNbtMZsuwG47\nJ8ePw4cfagWYuzuMGQMPPCAF2G2wh+OkLmQkTAghRJ1ll2Sz9MBSyqvLae7TnPEdx+Pj5mPpsCzD\naNR6f33/vTYVGR6u9f7y87N0ZMJGyJowIYQQdbK/YD+rDq/CqIzEBMYwKnYUrk4O2un93Dmt99ep\nU9qC+/794e67pfeXuIasCRNCCPGbKaX4Luc7tmVvA6BXi14MiR6CXuegBceBA1rvr8pKrffXqFEQ\nEWHpqIQNctAjSNQ3R5m/tyWSE+tka3kxmoysOrKKbdnb0KHj3uh7ubfNvXZVgNU5JwaDtvj+iy+0\nAqx9e3jySSnAGoCtHSe/lYyECSGEqFV5VTnLDi7jeMlxXPQujI4dTUzTGEuHZRn5+dr04+XeX0OH\nQvfu0vtL3BZZEyaEEOIa58rPsThtMUVlRXi7epMYl0hzn+aWDqvxKQU7d8I332gL8YODtd5fwcGW\njkzYCFkTJoQQos5OXTjF52mfc6nqEsFewSTGJeLv7m/psBrfpUva9GNGhrZ9xx1a93tpPSHqif1M\n6guLcpT5e1siObFO1p6XQ4WHSNqXxKWqS7QKaMWjXR+1+wKs1pwcO6b1/srIAA8PGDsW7r9fCrBG\nYu3HSX2RkTAhhBAopfjx1I98k/UNCkW3Zt24v839OOmdLB1a4zIaYds22LFDm4qMiIAHH5TeX6JB\nyJowIYRwcCZlYv3R9fyc9zMACVEJ9A3v63g/wn3unPbNx9xcbcF9fDz06ye9v8RtkTVhQgghamUw\nGlh+cDlHi4/irHdmZLuRdAzuaOmwGl9aGqxZo7We8PPTen+Fh1s6KmHnpLwX9cJR5u9tieTEOllT\nXi5UXmDB3gUcLT6Kp4snkzpPcrwCzGAg5S9/0dpPVFZCbCw88YQUYBZmTcdJQ5KRMCGEcECnS0+z\nJG0JFyov0MSjCRPiJhDoGWjpsBpXfr42/ZiZCW3aaL2/unWT3l+i0ciaMCGEcDCZxZksO7gMg9FA\nuF844zqOw9PF09JhNR6l4KefYPNmbSF+SIjW+ysoyNKRCTska8KEEEIAsCtvF+uOrsOkTHQM7sjI\ndiNx1jvQW8GlS7ByJRw9qm337An33COtJ4RFyJowUS8cZf7elkhOrJOl8qKU4pusb1iTsQaTMtEv\nvB+j2o9yrAIsK0vr/XX0qNb7a9w4uO8+UnbssHRk4iqO8vrlQEefEEI4pipjFSsOryC9MB29Ts+w\ntsPo2qyrpcNqPEYjbN2q9f4CiIzUen/5+lo0LCFkTZgQQtixS4ZLfH7gc05dOIWbkxtjO46lVUAr\nS4fVeIqLtcX3eXlav6/4eOjbV3p/iUYja8KEEMIBFZUVsXj/Ys5VnMPPzY8JnSYQ7OVAPzy9f7/W\n+8tgAH9/rfdXy5aWjkoIM/koIOqFo8zf2xLJiXVqrLxkl2Qzf898zlWco7lPc6Z2m+o4BVhlJaxY\nAV99pRVgHTpovb+uU4DJsWJ9HCUnMhImhBB2Zn/BflYdXoVRGYkJjGFU7ChcnVwtHVbjyMvTph+L\ni7VvPN57L3TtKr2/hFWSNWFCCGEnlFJ8l/Md27K3AdA7rDeDWw9Gr3OASQ+l4McfYcsW6f0lrIqs\nCZJTubMAACAASURBVBNCCDtnNBlZnbGafaf3oUPH0Oih9ArrZemwGkdpqTb9mJWlbffqpfX+cpa3\nOGHdHODjkWgMjjJ/b0skJ9apIfJSXlXOov2L2Hd6Hy56F8Z1HOc4BVhmptb7KysLPD1h/HhtCvIW\nCjA5VqyPo+REPiYIIYQNO1d+jsVpiykqK8Lb1ZvEuESa+zS3dFgNz2jUph5/+EHbjoqC3/1Oen8J\nm9Kga8JOnjzJpEmTOHPmDDqdjt///vc8++yzzJw5k3nz5hH037n6t956i3vvvReA2bNns2DBApyc\nnJg7dy6DBw+uGbCsCRNCCABOXTjF52mfc6nqEsFewUyIm4Cfu5+lw2p4Z8/Cl1/+2vtrwADo00d6\nfwmrdKO6pUGLsNOnT3P69Gm6dOlCaWkp3bt3Z+XKlSxbtgwfHx9efPHFGpdPT08nMTGRn3/+mdzc\nXAYNGkRGRgb6Kw4sKcKEEAIOFR7iy0NfUm2qpnVAax7q8BDuzu6WDqthKaX1/lq79tfeX6NHQ1iY\npSMT4rpuVLc06MeG0NBQunTpAoC3tzft27cnNzcXoNaAVq1axfjx43FxcSEyMpLo6GhSU1MbMkRR\nTxxl/t6WSE6s0+3mRSnFDyd/YNnBZVSbqunWrBuJcYn2X4Bd7v21YoVWgHXsqPX+qocCTI4V6+Mo\nOWm0sdvs7Gz27t1L7969AXjvvffo3Lkzjz32GCUlJQDk5eURdsUBFRYWZi7ahBDC0ZmUiXVH17Ep\naxMKRUJUAsPaDsNJ72Tp0BpWbi589JE2CubiAiNGaN3v3e288BR2r1EW5peWljJ69Gj+9a9/4e3t\nzZNPPsn06dMBeP3115k2bRrz58+vdV9dLQ32pkyZQmRkJAD+/v506dKF+Ph44NfqWbZl29G34+Pj\nrSoe2b720/2t7F9ZXckbn7xB7sVcortFM7LdSIrSi/j2+LcWvz8Ntr1tGxw4QPy5c2AykXLhAvTv\nT3zXrtYRn2w32Ha8Db9+Xf4/Ozubm2nwZq1VVVU88MAD3HvvvTz//PPXnJ+dnc2wYcNIS0tjzpw5\nALz88ssADB06lFmzZtGr169ftZY1YUIIR3Oh8gJL0pZwuvQ0ni6ejOs4jnC/cEuH1bAuXtSmHo8d\n07Z794ZBg6T3l7A5FlsTppTiscceIzY2tkYBlp+fb/5/xYoVxMXFATB8+HCSk5MxGAwcP36co0eP\n0rNnz4YMUdSTqz/hC8uTnFinW83L6dLTzNszj9Olpwn0CGRqt6n2X4AdPapNPx47pvX+SkyEoUMb\nrACTY8X6OEpOGvQjxY4dO1i0aBGdOnWi63+Hj9966y0+//xz9u3bh06nIyoqio8//hiA2NhYxowZ\nQ2xsLM7OznzwwQe1TkcKIYQjOHr2KMvTl2MwGgj3C2dcx3F4unhaOqyGU12t9f768Udtu1UrrfeX\nj49l4xKigchvRwohhBXalbeLdUfXYVIm4oLjGNFuBM56O56KO3tW++Ht/Hyt39fAgVrvL/kgLmyc\n/HakEELYCKUUm49tZsfJHQDcHXE3AyIH2O+sgFLwyy+wbp3WeiIgQPvmo/T+Eg6gQdeECcfhKPP3\ntkRyYp1ulJcqYxXL05ez4+QO9Do9I2JGMDBqoP0WYBUV/5+9Ow+q6sz/PP5mBwFFAUHFiAqKKIj7\nlhiMS6KJRo1LxE60Ezud/v26O1M9VUlPZk3V1C9JzdRMp9OT/nVntbvRGI2JJtG0S8S4xV1BEcQF\nBARE2Xcu98wf3yjZFJF7Oefe+31VWe05Bu6DT1/4+jzf83lg82b49FMpwJKSHJb91Rn6XrEeT5kT\nXQlTSikLqG+pZ/2Z9RTVFBHgE8DyUcsZ0nuI2cNynqIiOXqoshL8/WHePBg9WrcflUfRnjCllDLZ\n9YbrpGemU9lUSa+AXqxMXknf4L5mD8s5DAP274c9e8Buh3795Oih8HCzR6aUU2hPmFJKWVR+VT4f\nnvmQJlsT/UP7k5aURoh/iNnDco4fZn9NmQIzZ2r2l/JY2hOmHMJT9u9dic6JNX13Xk6Xnubvp/9O\nk62JhIgEVqesdt8C7Px5+POfpQALDoaf/QweftgSBZi+V6zHU+bE/P/3K6WUhzEMg70Fe8nIzwBg\ncsxk5gydg7eXG/672GaDnTvh8GG5HjpUsr9C3LTYVKoTtCdMKaW6UZu9ja25WzlddhovvHgk7hEm\nxUzq+ANd0fXrkv1VWirZXzNnwtSp2nyvbis3t4Bduy7S2uqNn5+dWbOGMnz4ILOH1SV3qlu0CFNK\nqW7S2NrIhrMbyK/Kx8/bjyWJSxgeMdzsYTmeYcDJk7B9O7S2Qp8+kv01YIDZI1MWlptbwAcfXCAg\nYCa1tbJY2tKym9Wr41y6EDPt7EjlOTxl/96V6JxYS2VjJe+efJeMjAxC/EP4+Zifu2cB1tQk0RNb\nt0oBlpwMv/ylpQswfa9Yw65dF2lpmUlmJuzencGNGxAQMJPduy+aPTSn0Z4wpZRysqKaItZnrae+\ntZ6wwDB+MfYX9ArsZfawHK+wUAqwqirJ/nr0Ucn+UqoD5eVw5Ig3BQVy7e0t+b0ALS3uu16k25FK\nKeVE2eXZbD63GZvdxtDeQ1k6cimBvoFmD8ux7HbJ/srIkN/37y/ZX336mD0yZXGVlbB3r5xcdfjw\nVzQ1PUT//nDffVLHA/Tt+xX/8i8PmTvQLtCcMKWU6maGYXCo6BA7L+7EwGBsv7E8Gv8oPt4+Zg/N\nsWpq5Oih/Hy5njpVGvB93OzrVA5VUwNffw0nTkjd7u0NCxYMJS9vN6GhM2/9d83Nu5k5M87EkTqX\nroQph8jIyCA1NdXsYajv0Dkxj92wsz1vO0evHgVg1pBZTBs4DS8vL/eal9xcOfexsVG6qBcuhDjX\n+4HpVnNicfX1smh69Kikl3h5Sdtgaqqc3Z6bW8Du3RfJzs4kMTGZmTPd++lIXQlTSikHarY1syl7\nE3kVefh6+7IwYSGj+o4ye1iOZbPBjh1w5Ihcx8VJAabZX+o2mprg4EH45pv2Xq/ERJgxAyIj2/+7\n4cMHMXz4IDIyvD2iMNaVMKWUcpCa5hrWZa2jtK6UHn49eHLUk9zX6z6zh+VY5eWS/VVWJluOs2bB\n5Mma/aV+UkuL5PQePCgLpgDx8fDQQ3JsqCfQlTCllHKy0rpS1mWto6a5hvCgcFYmr6RPkBs1phuG\nNPB8+WV79teSJdKEr9QP2Gxw7Bjs2ydbkACxsVJ83edm/y7pCvd97lN1K83ZsR6dk+6TdyOP906+\nR01zDff1uo9nxz572wLMJeelsRE2boTPPpMCLCVFsr/cpABzyTmxqLY2OH4c3nxT6vX6eomIe/pp\nWLXq7gswT5kTXQlTSqkuOHb1GNvytmE37CT1TeLxhMfx9Xajb61Xrkj2V3U1BARI9ldystmjUhZj\nt8OZM5JSUlEh96KiZOVr2DDdrb4d7QlTSql7YBgGOy/t5GDhQQCmD5rOjNgZeLnLTxu7XfaSMjJk\nK3LAADl6SLO/1HcYBuTkwJ49cO2a3AsPl4b7kSO1+ALtCVNKKYdqbWvlk5xPyC7PxtvLm/nD5jOm\n3xizh+U4P8z+uv9++amq2V/qW4YBFy/CV1/B1atyr1cviZoYPVpyv1TH9K9JOYSn7N+7Ep0T56hv\nqWft6bVkl2cT4BPAz5J/1qkCzPLzkpMDf/6zFGAhIfDUU/IEpBsXYJafE4spKIAPPoB//EMKsJAQ\nmDcPfvMbGDPGMQWYp8yJroQppdRdut5wnfTMdCqbKukV0IuVySvpG9zX7GE5RmurZH8dlYBZ4uMl\n+ys42NxxKcu4elVWvi5ckOugIFkknTgR/PzMHZur0p4wpZS6C/lV+Xx45kOabE30D+1PWlIaIf5u\nEk567Zpkf127Jites2fDpEna0KMA+b/Fnj1w7pxcBwTAlCkSDxfoZsegOoP2hCmlVBecLj3N1tyt\ntBltJEQksHjEYvx9/M0eVtcZhuQJfPmlBDuFh0v2l6ekaKo7qqiQ5zKysuT/Kn5+suo1bRr06GH2\n6NyD9oQph/CU/XtXonPSdYZhkJGfwSc5n9BmtDE5ZjLLRi7rUgFmmXlpbISPPoLPP5cCbMwYyf7y\nwALMMnNiEdXVEgn3pz9BZqb0eE2cCL/9rSySdkcB5ilz0uFKWF1dHUFBQfj4+JCbm0tubi5z587F\nTzeAlVJurM3extbcrZwuO40XXsyNn8vEARPNHpZjFBTI0483s78eewySkswelTJZXZ0crn3sWPvh\n2mPGwIMPQliY2aNzTx32hI0dO5b9+/dTWVnJtGnTmDBhAv7+/qSnp3fXGL9He8KUUs7W2NrIhrMb\nyK/Kx8/bjyWJSxgeMdzsYXWd3Q5ffw1798r+UkyMZH/17m32yJSJGhvbD9dubZV7o0ZJ3EREhKlD\ncwtd6gkzDIMePXrw7rvv8i//8i+8+OKLjB492uGDVEopK6hsrCQ9K53rDdcJ9Q8lLSmNfqFusEVX\nXS2rXwUFssTxwAPyU9aNoyfUnTU3tx+u3dQk94YPl0i46Ghzx+Yp7qon7NChQ6Snp/Poo48CYLfb\nnToo5Xo8Zf/eleicdF5RTRHvnHiH6w3XiQqOYs3YNQ4vwEyZl+xsyf4qKIDQUMn+mjlTC7Bvedp7\npbUVDh2CN96QyImmJhgyBNasgRUrrFGAecqcdLgS9oc//IFXX32VRYsWMXLkSC5evMiMGTO6Y2xK\nKdVtssuz2XxuMza7jaG9h7Js5DICfAPMHlbXtLbCP/8pTT4gh/g9/rhmf3motjY4eVJ2pGtq5N7A\ngXK+4+DB5o7NU2lOmFLKoxmGwaGiQ+y8uBMDg3H9xjEvfh4+3i6+SvTD7K85c+QRN83+8jh2u8RM\nZGRAZaXci46W4is+Xv8v4Wxd6gk7evQo//Zv/0Z+fj42m+3WJ8zMzHTsKJVSqpvZDTvb8rZx7Kqs\nFM0aMotpA6e59iHchiErX//8pzziFhEh2V9W2GNS3cowJGB1zx4oL5d7ERHS85WYqMWXFXS4EjZs\n2DD+9//+34waNQrv7xwIFRsb6+yx/SRdCbOmjIwMUlNTzR6G+g6dkztrtjWzKXsTeRV5+Hr7sjBh\nIaP6jnL66zp1XhoaYOtWOf8RYOxYeOQR8HeDYFkncrf3imHI0UJffQUlJXIvLEyew0hOdo3Dtd1p\nTrq0EhYZGcmCBQscPiillDJLTXMN67LWUVpXSg+/Hjw56knu63Wf2cPqmvx8efqxpkbOkpk/H0aO\nNHtUqpvl50vxdeWKXIeGwvTpUo/rcxjW0+FK2I4dO9iwYQOzZs3C/9t/TXl5ebF48eJuGeAP6UqY\nUqorSutKSc9Mp7allvCgcFYmr6RPUB+zh3Xv7HbJ/fr66/bsryVLNF3TwxQXw+7dcOmSXPfoIYdr\nT5igh2ubrUsrYWvXriU3Nxebzfa97UizijCllLpXeTfy2Ji9kZa2Fgb1GsTyUcvp4efCh+BVVcHH\nH0NhoTT4TJ8u8ea65OExyspk5Ss3V64DAmDqVDlcO8DFH+71BB2uhA0fPpycnBzLNKrqSpg1udP+\nvbvQOfm+Y1ePsS1vG3bDTlLfJB5PeBxf7w7/HepwDpuXs2flgL+mJtlzWrxYcwbukSu+V27ckIb7\ns2fbD9eeNEkO1w4KMnt0XeeKc3I7XVoJmzp1KtnZ2YzU3gKllAsyDIOdl3ZysPAgANMHTWdG7AzL\n/MOy01pb4csv4fhxuR4+XLK/uuNUZWW6qirZfT59WnaifXxg/Hg5ACEkxOzRqc7qcCUsISGBixcv\nMnjwYAK+Xds0M6JCV8KUUnerta2VT3I+Ibs8G28vb+YPm8+YfmPMHta9Ky2V7cfycvD1leyvCRM0\na8AD1NVJ29/x4xK66u0NKSmy+9yrl9mjU3dyp7qlwyIsPz//J+9rRIVSysrqW+pZf2Y9RTVFBPoG\nsmzkMob0HmL2sO6NYcDRo7Bjh2R/RUZK831UlNkjU07W0AAHDsCRI7II6uXVfrh2eLjZo1N3o0tF\nmNVoEWZN7rR/7y48eU7K68tZl7WOyqZKwgLDWJm0ksjgSLOHBdzDvDQ0wJYt7Z3X48ZJ9pc+8uYw\nVnyvNDfL+Y6HDsnvARISJOW+b19zx9YdrDgn96pLPWFKKeVK8qvy+fDMhzTZmugf2p+0pDRC/F20\nWebyZcn+qq2V7K8FCyTqXLmt1lZZ9TpwQOpvgKFDpfgaMMDcsSnH05UwpZTbOF16mq25W2kz2kiI\nSGDxiMX4+7hgWnxbm3Rf79snW5H33SdPP2r2l9tqa5N+r337pOYGmfaZM2HQIHPHprpGV8KUUm7N\nMAz2FuwlIz8DgMkxk5kzdA7eXi5wPssP/TD768EH5ZcrnDWjOs1ulycd9+6VqQfo319WvoYO1Wcu\n3F2H7+qPP/6Y+Ph4evbsSWhoKKGhofTs2bM7xqZcSEZGhtlDUD/gKXNis9v4NOdTMvIz8MKLefHz\neCTuEcsWYHeclzNn4M9/lgKsZ09YtUpOW9YCzKnMeK8Yhkz3W29Jy19VlTxvsXw5/OIXEBfn2QWY\np3z/6nAl7MUXX+Tzzz9nxIgRnf7khYWFPP3001y7dg0vLy+ee+45fvvb31JRUcHy5cspKCggNjaW\njz76iLBvl9lfffVV3nvvPXx8fPjjH//InDlzOv9VKaU8QmNrIxvObiC/Kh8/bz+WjlzKsPBhZg+r\n81paJPvrxAm5TkiQ/i/N/nI7hgHnz0vQammp3OvdW2rtUaO03vY0HfaETZs2jQMHDtzTJy8tLaW0\ntJSUlBTq6uoYN24cn376Ke+//z4RERG8+OKLvP7661RWVvLaa6+RnZ1NWloaR48epbi4mFmzZnH+\n/PnvHZekPWFKKYDKxkrSs9K53nCdUP9Q0pLS6Bfaz+xhdV5pKWzaBNevS/bXww9L+qYnL4O4qUuX\n5IihoiK57tlTdppTUvSkKXfWpZ6w8ePHs3z5chYuXNjpA7yjo6OJjo4GICQkhBEjRlBcXMzWrVvZ\nu3cvAKtWrSI1NZXXXnuNLVu2sGLFCvz8/IiNjSUuLo4jR44wefLku/5ilVLur6imiPVZ66lvrScq\nOIq0pDR6BbpYYqVhyGNwO3ZIV3bfvvDEE5r95YYKC6X4unxZroODJeF+/Hipu5Xn6nD6q6urCQoK\nYseOHd+739kDvPPz8zl58iSTJk2irKyMqG+/0URFRVFWVgbA1atXv1dwxcTEUFxc3KnXUeZwp0wX\nd+Guc5Jdns3mc5ux2W0M7T2UZSOXEeDrOicVZ2RkkDphgjQCnT8vN8ePlxUwzf4yhbPeK6WlUnzd\nnObAQDnbcdIk8HfBh3a7k7t+//qhDouwDz74oMsvUldXxxNPPMEbb7xBaGjo9/7My8vrjme4uez5\nbkophzIMg0NFh9h5cScGBuP6jWNe/Dx8vF1sH+fqVfj3f2/P/nr8cbiHnltlXdevtx+uDVJwTZ4M\nU6fKlCt1022LsNdff52XXnqJ3/zmNz/6My8vL/74xz/e1Qu0trbyxBNP8NRTT7Fw4UJAVr9KS0uJ\njo6mpKSEvt/G/w4YMIDCwsJbH1tUVMSAn0inW7169a1jk8LCwkhJSblVMd98okKv9drTr1NTUy01\nnq5cT39wOtvytrFp2yYA1ixew7SB0261NZg9vru6bmsj4w9/gKwsiI2FQYPIiIyEsjJSvy3CLDVe\nve709WefZXD6NLS1pWIYUFiYwfDh8K//mkpwsPnjc6XrVBf+/nXz97c79vG7btuY/9lnnzF//nw+\n+OCD761GGYaBl5cXq1at6vCTG4bBqlWrCA8P5//+3/976/6LL75IeHg4L730Eq+99hpVVVXfa8w/\ncuTIrcb8CxcufO/1tTFfKc/SbGtmU/Ym8iry8PX2ZVHCIkb2HWn2sDqnslKyv4qK2rO/pk/XR+Hc\nRG2tHK594kT74dpjx8oUa6KTMu3syP379zN9+nSSk5NvFVKvvvoqEydOZNmyZVy5cuVHERX/9m//\nxnvvvYevry9vvPEGDz/88F1/Mco8GRkZt/41oKzBHeakprmGdVnrKK0rpYdfD1aMWsHAXgPNHlbn\nZGXB55/LAYC9epHRrx+pTz5p9qjUd9zre6WhAfbvl+crbDapr5OTITVVYifUvXOH7183mZaYf//9\n92O323/yz3bt2vWT919++WVefvllZw5LKeUCSutKSc9Mp7allvCgcFYmr6RPUB+zh3X3Wlpg2zY4\ndUquR4yQ7K/Dh80dl+qypqb2w7VbWuReYqJkfUVa45x45SL07EillOXk3chjY/ZGWtpaGNRrEMtH\nLaeHnwsFl5aUSPbXjRuSQfDIIzBunGZ/ubiWlvbDtRsb5V58vBwx1M8FI+pU99CzI5VSLuNo8VG2\n5W3DwCCpbxKPJzyOr7eLfKsyDPjmG9i1qz37a8kS+V/lsmy29sO16+rkXmysFF/33Wfq0JSL67Ar\nNDc3l5kzZzJypDTCZmZm8j//5/90+sCUa/nuUyHKGlxtTgzDYMfFHXyR9wUGBg8OepDFIxa7TgFW\nXw/r1sE//ykF2IQJcgjgDwowV5sXT3C7OWlrk2b7N9+E7dulABswAJ56So711ALMeTzlfdLhd7df\n/OIX/K//9b94/vnnAUhKSmLFihX8l//yX5w+OKWUZ2hta2Xzuc2cu34Oby9v5g+bz5h+Y8we1t27\neBE++UR+SgcFSfZXQoLZo1L36Obh2nv2QEWF3IuKkpWvYcN0V1k5Toc9YePHj+fYsWOMGTOGkydP\nApCSksKpm82m3Ux7wpRyL3UtdXx45kOKaooI9A1k2chlDOk9xOxh3Z22NolEv3m+bmwsLF6suQQu\nyjAgN1em9No1uRceLk87jhqlxZe6N13qCYuMjOTChQu3rjdt2kQ/7UBUSjlAeX056VnpVDVVERYY\nxsqklUQGu8jjZRUVkv1VXCw/nVNT5UBAzf5yOYbRfrj2zZPyevVqP1xbp1Q5S4crYRcvXuS5557j\n4MGD9O7dm8GDB5Oenn4rsb676UqYNblTpou7sPqcXK68zIazG2iyNTEgdAArklYQ4h9i9rDuTmYm\nfPHFrewvnnjirhuErD4vnubKFfh//y+DoKBUAEJCJGR17Fg9XNtM7vQ+6dJK2NChQ9m9ezf19fXY\n7fYfnf2olFKddbr0NFtzt9JmtJEQkcATI57Az8cFDq9ubpbsr9On5ToxEebPlz4w5VKuXpWVrwsX\noKxMYtzuvx8mTtRz1FX36XAlrLKykr/97W/k5+djs9nkgzpxdqSj6UqYUq7LMAz2FuwlIz8DgCkx\nU5g9dDbeXi6w33P1qmR/VVTIT+m5c2HMGG0UcjHXrknD/blzcu3vLwdrT56sh2sr5+jSSti8efOY\nMmUKycnJeHt73zo7UimlOsNmt/FZ7mecLjuNF17MjZ/LxAETzR5WxwxDotF375ZG/Kgoyf7SaHSX\nUlEBGRlyipRhyFbjxImy+tXDhXKAlXvpcCVs7NixnDhxorvG0yFdCbMmd9q/dxdWmpPG1kY2nN1A\nflU+/j7+LElcwrDwYWYPq2N1dfDpp7JnBfJTe86cLjULWWlePEFNDezdCydPgt0OPj5yeMEDD8DN\n7hqdE+txpznp0kpYWloaf/3rX5k/fz4BAQG37vfp40JnuCmlTFPZWEl6VjrXG64T6h9KWlIa/UJd\n4AnrCxck+6u+XpZKHn8chg83e1TqLtXXS8L9sWPth2uPGSNPPIaFmT06pUSHK2F/+tOf+M//+T8T\nFhaG97fP6Xp5eXHp0qVuGeAP6UqYUq6jqKaI9VnrqW+tJyo4irSkNHoF9jJ7WHfW1iZbjwcPyrVm\nf7mUxkaZusOH2w/XHjVKEkQiIkwdmvJQd6pbOizCBg8ezNGjR4mwyP97tQhTyjVkl2ez+dxmbHYb\ncX3iWJq4lADfgI4/0Ew3bkj219WrEg41YwZMm6ZBUS6gpUWO7Tx4EJqa5N6wYZJyHx1t7tiUZ7tT\n3dLhd5b4+HiC9PFr1QFPOefLlZg1J4ZhcODKAT46+xE2u41x/caxYtQK6xdgp0/DX/4iBVhYGPz8\n504JX9X3imPZbPLcxBtvSOREUxMMGQJr1kBa2t0VYDon1uMpc9JhT1iPHj1ISUlhxowZt3rCzIyo\nUEpZl92wsy1vG8euHgNg9pDZTB041dpPVDc3S/BqZqZcjxwp2V+aV2BpbW3SbP/119J8DzBwoKx8\nDR5s7tiUulsdbkd+8MEHP/4gLy9WrVrlrDHdkW5HKmVNzbZmNmZv5ELFBXy9fVmUsIiRfUeaPaw7\nKy6W7ceb2V/z5sk5NVYuGj2c3S4xExkZUFkp96KjpfiKj9epU9bTpZ4wq9EiTCnrqWmuIT0znbL6\nMnr49WDFqBUM7DXQ7GHdnmFI89Du3fJTPTpasr8s0vuqfswwJGB1zx4oL5d7ERHStpeYqMWXsq57\niqhYunQpGzduJCkp6Sc/YebNpXulcK9MF3fRXXNSWldKemY6tS21hAeFszJ5JX2CLBxhU1cn0RMX\nL8r15Mkwa1a3HRSo75XOMQxJC/nqKygpkXthYfK0Y3KyY1r2dE6sx1Pm5Lbfdd544w0APv/88x9V\ncJbu71BKdZu8G3lszN5IS1sLg3oN4slRTxLkZ+EHefLyJHz1ZvbXwoXyCJ2ypPx8Kb6uXJHr0ND2\nw7V9fEwdmlIO0eF25EsvvcTrr7/e4b3uotuRSlnD0eKjbMvbhoFBUt8kHk94HF/v7llN6jSbTbYe\nDx2S68GDJfvrZmS6spTiYim+bi5W9ughxwtNmKCHayvX06WesDFjxnDy5Mnv3UtKSiIrK8txI+wE\nLcKUMpdhGOy8tJODhRJm+uCgB0mNTbXuCvmNG3LwdkmJ7F099JCc2KzZX5ZTViY9Xzk5ch0Q0H64\ndoDFE06Uup17ygn785//TFJSErm5uSQlJd36FRsbS3JystMGq1yTp2S6uBJnzElrWysfnf2IjOEu\nyQAAIABJREFUg4UH8fbyZmHCQmYMnmHNAsww4NQpyf4qKYHeveGZZ2RJxcQCTN8rP3YzI/ff/10K\nMD8/mab/8B/kmCFnF2A6J9bjKXNy272DtLQ05s6dy+9//3tef/31W1VcaGgo4eHh3TZApZQ11LXU\nsT5rPcW1xQT6BrJ85HIG97ZoIFNzM3z+uWQZACQlwaOPavaXxVRXy+Hap061H649frxk5IaEmD06\npZxPIyqUUh0qry8nPSudqqYqwgLDWJm0ksjgSLOH9dOKimRZpbIS/P0l+2v0aM0wsJC6uvbDtdva\nZGEyJUVWvXpZ/GhRpTrrniIqlFIK4HLlZTac3UCTrYkBoQNYkbSCEH8LLlMYBhw4IB3ddjv06wdP\nPKHZXxbS0NB+uHZrq9TFSUkSN6EbLMoTaWeqcghP2b93JY6Yk1Olp/hH5j9osjUxImIEq1NWW7MA\nq62Fv/8ddu2SAmzKFHj2WUsWYJ74Xmlulm3HN96A/fulAEtIgOeflzrZ7ALME+fE6jxlTnQlTCn1\nI4ZhkJGfwd6CvQBMiZnC7KGz8fay4L/bzp+X7K+GBggOluyv+HizR6WQYuvoUSm8Ghrk3tCh8oDq\ngAHmjk0pK9CeMKXU99jsNrbmbiWzLBMvvJgbP5eJAyaaPawfs9lk5eubb+R6yBBYtEizvyygrQ1O\nnJDDtWtr5d5998HMmTBokLljU6q7aU+YUuquNLY28uGZDymoLsDfx58liUsYFm7BRPnr1yX7q7RU\nurpnzpRAKW2+N5XdDqdPy9ZjVZXc69dPpmfoUJ0epX7IgnsLyhV5yv69K+nsnFQ0VvDuyXcpqC4g\n1D+Un6f83HoFmGHAyZOS/VVaKtlfzz4L06a5zE94d3yvGAacPQtvvQVbtkgBFhkJy5bBc89BXJy1\np8cd58TVecqc6EqYUorC6kLWn1lPQ2sDUcFRpCWl0SvQYlkBTU2S/XXmjFwnJ0v2l0apm8Yw5DjO\nr76SmhikLp4xA0aN0kMJlOqI9oQp5eGyy7PZfG4zNruNuD5xLE1cSoCvxQqbwkLJ/qqqkuyvRx+V\n7C9lmsuX5TjOoiK57tlTcr5SUvRwbaW+S3vClFI/YhgGBwsPsvPSTgDG9RvHvPh5+Hhb6Ceo3S7Z\nX3v2yO/797dGpoEHKyyUla/Ll+U6OFgS7sePB1/9iaJUp+hisXIIT9m/dyV3mhO7YeeLvC9uFWCz\nh8zmsWGPWasAq6mR7K/du6UAmzpV+r9cvABz1fdKaSmsWwfvvisFWGCgNNy/8IIcsO3KBZirzok7\n85Q5ceG3jVLqXjTbmtmYvZELFRfw9fZlUcIiRvYdafawvi83Vzq8b2Z/LVok3d2q212/LguRZ8/K\ntb+/FF1TpkBQkLljU8rVaU+YUh6kprmG9Mx0yurL6OHXgxWjVjCw10Czh9XOZoOdO+VcG5DCa+FC\nPc3ZBFVVkJEhkROGIStdEybA/fdLXayUujvaE6aUoqS2hHVZ66htqSU8KJyVySvpE9TH7GG1Ky+X\n7K+yMunsnjlTllusnG3ghmprJWT1xIn2w7XHjYPp06X5XinlONoTphzCU/bvXcl35yTvRh7vn3qf\n2pZaBvUaxJqxa6xTgBmG/MT/61+lAOvTR3q/3DR81arvlYYG2LFDznc8elTa8EaPhl//Gh57zL0L\nMKvOiSfzlDnRlTCl3NzR4qNsy9uGgUFyVDILhi/A19sib/2mJvjss/aGo9GjYd48zf7qRk1NcOiQ\n/GppkXuJiZL1FRlp7tiUcnfaE6aUmzIMgx0Xd3Co6BAADw56kNTYVLyssrpUWCjbj9XV0u392GMS\nwKq6RUsLHDkiCSCNjXIvPl6Kr/79zR2bUu5Ee8KU8jCtba1sPreZc9fP4e3lzYLhC0iJTjF7WMJu\nh/37pevbbocBAyT7q49FtkfdnM0Gx4/Dvn1QVyf3YmPhoYfkkG2lVPfRnjDlEJ6yf+8K6lrq+ODU\nB2zftZ1A30CeSn7KOgVYTQ387W+S9mm3y5mPzzzjUQWYWe8Vu11a7958E7ZvlwJswAB46ilYtcqz\nCzD9/mU9njInuhKmlBspry8nPSudqqYqQvxDeHbMs0QGW6SxJydHsr8aGyVyYtEiGDrU7FG5PcOQ\n4zb37IGKCrnXt6+sfA0f7pbPPijlMrQnTCk3cbnyMhvObqDJ1sSA0AGsSFpBiL8F8rVaW+Wxu6NH\n5TouTgowDZtyKsOQzNuvvoJr1+ReeDikpsrh2lp8KdU9tCdMKTd3qvQUW3O3YjfsjIgYweIRi/Hz\n8TN7WPLTf9Mm+V8fH5g1S+LWtQJwGsOAS5ek+Coulnu9erUfru2tTShKWYa+HZVDeMr+vdUYhsGe\ny3v4NOdT7IadKTFTWDpyKX4+fubOiWFI9/fbb0sBFh4Oa9Zo+CrOfa9cuQIffCBHbhYXy67v3Lnw\nm9/A2LFagN2Ofv+yHk+ZE6e+JZ955hmioqJISkq6de9//I//QUxMDGPGjGHMmDFs37791p+9+uqr\nxMfHk5CQwI4dO5w5NKVcns1u45OcT9hbsBcvvHg0/lEejnsYby+Tf9I2NsJHH0n+V2urLL/88pfQ\nr5+543JjV6/CP/4B770HBQVypuOsWfDb38KkSa59uLZS7sypPWH79u0jJCSEp59+mqysLABeeeUV\nQkND+d3vfve9/zY7O5u0tDSOHj1KcXExs2bN4vz583j/4J9u2hOmFDS2NvLhmQ8pqC7A38efJYlL\nGBY+zOxhSQWwebNkfwUESPbXd/4RphyrvFy2Hc+dk2t/f1lsnDIFAgPNHZtSSpjWE/bAAw+Qn5//\no/s/NZgtW7awYsUK/Pz8iI2NJS4ujiNHjjB58mRnDlEpl1PRWMG6rHVcb7hOqH8oaUlp9As1eZXJ\nbpcDB/fula3IAQNgyRLo3dvccbmpigr5q87MbD9ce+JEOVy7Rw+zR6eUulum7Fu8+eabjB49mmef\nfZaqqioArl69SkxMzK3/JiYmhuKbXaXK8jxl/95shdWFvHPiHa43XCcqOIpfjPvFbQuwbpuT6mpY\nu1bCV0EqgWee0QLsNroyLzU1ssv7pz/B6dPS4zVhArzwAsyZowXYvdLvX9bjKXPS7Z0Cv/rVr/hv\n/+2/AfBf/+t/5T/+x//Iu++++5P/7e2OV1m9ejWxsbEAhIWFkZKSQmpqKtA+cXrdvdc3WWU87nh9\n9tpZ/s/6/0Ob0cash2axNHEph/YfMnd8a9fCgQOk9u8PISFk9O8Pvr6k+viY/vdl1etTp051+uMn\nTEhl3z7YuDGDtjYYPDiVlBTw9c0gOBhCQ63z9bni9U1WGY9eu/b1zd//1E7gDzk9Jyw/P5/58+ff\n6gm73Z+99tprAPz+978H4JFHHuGVV15h0qRJ3x+w9oQpD2MYBgcLD7Lz0k4Axvcfz7z4eeY24Le2\nwj//CceOyXV8PCxcqNlfDtbYCAcPwuHD7Ydrjxwp5ztGRJg7NqXU3bFUTlhJSQn9vn1K6pNPPrn1\n5OSCBQtIS0vjd7/7HcXFxeTl5TFx4sTuHp5SlmI37GzL28axq1LszB4ym6kDp5p7CPcPs79mz5ZH\n8Dw8esKRWlqk8DpwAJqa5N6wYZJyHx1t7tiUUo7j1CJsxYoV7N27l+vXrzNw4EBeeeWVW8vxXl5e\nDB48mL/85S8AJCYmsmzZMhITE/H19eWtt94y9weN6pSMjIxbS7LKMZptzWzM3siFigv4evuyKGER\nI/uOvOuPd/icGIasfP3zn3IKdESENN9rVdApd5oXm00OFti/H+rr5d7gwVJ8DRzYfWP0NPr9y3o8\nZU6cWoStX7/+R/eeeeaZ2/73L7/8Mi+//LIzh6SUS6huqmZd1jrK6svo4deDFaNWMLCXiT+FGxvl\n3MecHLkeM0ZSQP39zRuTG2lrg5Mn5QHTmhq5FxMDM2dKEaaUck96dqRSFlNSW8K6rHXUttQS0SOC\ntKQ0+gT1MW9A+fmS/VVTI9lf8+fL4YOqy+x2yMqCjAyorJR70dGy8hUfrzu8SrkDS/WEKaVu7/yN\n82zK3kRLWwuDeg3iyVFPEuQXZM5g7HYJo/r6a9mKjImBJ57Q6AkHMAwJWN2zRwJXQXZ3Z8yAxEQt\nvpTyFFqEKYfwlP17ZzpafJRtedswMEiOSmbB8AX4et/7W7RLc1JVJatfV65IRTB9upwA/W30hLo3\nhgHp6RnU16dSUiL3wsIgNRWSk/VsR7Po9y/r8ZQ50SJMKZPZDTs7L+7kUJFkfj046EFSY1PNezAl\nOxu2bpXH8kJDYfFibUxygPx8OWLo668hNlb+aqdPl4O1tbZVyjNpT5hSJmpta2Xzuc2cu34OHy8f\n5g+fT0p0ikmDaYUvv4Tjx+V6+HB4/HGNYe+i4mIpvi5elOsePeRQgQkTwM/P3LEppZxPe8KUsqC6\nljrWZ62nuLaYQN9Alo9czuDeJq04lZVJ9ld5uRxEOGeOVAnanHTPysqk5+vmA6UBATB1KkyeLL9X\nSintQFAO8cPjP9SdldeX886JdyiuLSYsMIxnxzzr8ALsrubEMODIEXj7bSnAIiJgzRo5DVoLsHty\n4wZ8/DH8+79LAebnJytfL7wgbXWHDmWYPUT1A/r9y3o8ZU50JUypbna58jIbzm6gydbEgNABrEha\nQYh/SPcPpKFBsr9yc+V63Dh4+GHN/rpH1dXyMOmpU/JgqY8PjB8PDzwAISZMr1LK+rQnTKludKr0\nFFtzt2I37IyIGMHiEYvx8zGhMei72V+BgZL9NfLu0/hVu7o62LdPDhNoa5MnHFNSZNWrVy+zR6eU\nMpv2hCllMsMwyMjPYG/BXgCmDpzKrCGzuv8QbrtdkkH37ZOtyIEDJfsrLKx7x+EGGhvlbMfDh+WZ\nBi8vSEqSuInwcLNHp5RyBdoTphzCU/bv74XNbuOTnE/YW7AXL7x4NP5R5gyd4/QC7EdzUlUF778v\nGQkgSzU//7kWYJ3U3Czbjn/4g5zx2NoKCQnw/PNSz3ZUgOl7xXp0TqzHU+ZEV8KUcqLG1kY+PPMh\nBdUF+Pv4syRxCcPCh3X/QM6ehc8+k+yvnj0l+ys2tvvH4cJaW9sP125okHtDh8oRQwMGmDs2pZRr\n0p4wpZykorGC9Mx0bjTeINQ/lLSkNPqF9uveQbS0SPbXiRNynZAACxZo9lcntLXJX9/XX0Ntrdy7\n7z4pvrSOVUp1RHvClOpmhdWFrD+znobWBqKCo1iZvJKeAT27dxClpZL9df26ZH89/LA8rqfRE3fF\nbofMTGmhq6qSe/36SfEVF6d/jUqprtOeMOUQnrJ/fzfOXjvL2tNraWhtIK5PHM+MeaZ7CzDDgMOH\nyXj5ZSnAIiPhF7/Q8NW7ZBiye/vWW/Dpp1KARUbCsmXw3HMQH9+1v0Z9r1iPzon1eMqc6EqYUg5i\nGAYHCw+y89JOAMb3H8+8+Hnd+wRkfb1kf50/L0s548fLCpiej9Mhw4C8PDliqLRU7vXuLU87JiXp\n4dpKKcfTnjClHMBu2Pni/BccL5FzF2cPmc3UgVO79xDuy5cl+6u2VrK/FiyAxMTue30XdvmyFF+F\nhXLds6ccrj1mjB6urZTqGu0JU8qJmm3NbMzeyIWKC/h6+7J4xGISI7ux+Glrk8al/ftlOee++yQr\nQZNCO1RUBLt3SxEGEBzcfri2r353VEo5mS6wK4fwlP37H6puqua9k+9xoeICwX7BrBq9qnsLsMpK\nyf7at0+uU1Nh9Wro1ctj5+RulJbCunXwzjtSgAUGSsP9Cy/AlCnOLcB0XqxH58R6PGVO9N96St2j\nktoS1mWto7allogeEaxMWknvoN7dN4AzZyT7q7lZ9s+eeAIGDeq+13dB16/Dnj3SeA9yTOakSTB1\nKgQFmTs2pZTn0Z4wpe7B+Rvn2ZS9iZa2FmLDYlk+cjlBft30U7ylBbZvh5Mn5XrECOn/0iritqqq\nZMf29GnZsfX1bT9cOzjY7NEppdyZ9oQp5UBHio+wPW87BgbJUcksGL4AX+9ueiuVlEj2140bUkk8\n8giMG6fRE7dRWyshqydOtB+uPXasnNjUs5tj25RS6oe0J0w5hCfs39sNO/+88E+25W3DwCA1NpVF\nCYu6pwAzDPjmG2liunED+vaV0Ko7hK96wpzcTkMD7NgBb7whRw3Z7ZCcDL/+Ncyfb24B5snzYlU6\nJ9bjKXOiK2FK3YXWtlY2n9vMuevn8PHyYf7w+aREp3TPi9fXS2poXp5cT5gAc+Zo9tdPaGqCQ4ek\nXm1ulnsjRsCMGVK3KqWUlWhPmFIdqGupY33Weopriwn0DWT5yOUM7j24e1780iXJ/qqrk56vBQuk\nqlDf09ICR47AgQPQ2Cj34uLkicf+/c0dm1LKs2lPmFL3qLy+nPSsdKqaqggLDGNl0koigyOd/8Jt\nbfIY34EDshU5aBAsXqzZXz9gs8Hx45LQUVcn9wYNgpkzJS5NKaWsTHvClEO44/795crLvHvyXaqa\nqhgQOoA1Y9d0TwFWUQHvvSfhqyB7aatWdboAc8c5uclul2b7N9+UB0Xr6mTF66mnJCbNygWYO8+L\nq9I5sR5PmRNdCVPqJ5wqPcXW3K3YDTsjIkaweMRi/Hy6oQcrKws+/1wamnr1kuwvK1cU3cwwJB4t\nI0OeTwDp9XroIRg+XB8SVUq5Fu0JU+o7DMMgIz+DvQV7AZg6cCqzh8x2/hmQzc2ypHPqlFwnJspj\nfJr9BUjxlZsrO7RlZXKvTx9ZJBw5Ug/XVkpZl/aEKXUXbHYbW3O3klmWiRdezIufx4QBE5z/wlev\nwscfy9KOn59kf40dq8s6SPF16ZIcrl1cLPd69ZKcr9Gj9XBtpZRr038/Kodw9f37xtZG/n7672SW\nZeLv409aUprzCzDDgIMH4d13pQCLipLsLweFr7r6nFy5AmvXwt//LgVYcDDMnQu/+Y3UqK5agLn6\nvLgjnRPr8ZQ50ZUw5fEqGitIz0znRuMNQv1DWZm8kuiQaOe+aF2dZH9duCDXEydK9pczT452ESUl\nsvJ1MxYtKAimTZO/In9/c8emlFKOpD1hyqMVVhey/sx6GlobiAqOYmXySnoGODlO/eJF+OST9uyv\nxx+HhATnvqYLKC+Xnq/sbLn294cpU+RXYKC5Y1NKqXulPWFK/YSz187ySc4n2Ow24vrEsTRxKQG+\nAc57wbY2WeI5cECuY2Ml+8vDDzGsrJSnHTMz2w/XnjhRVr/0cG2llDvTnjDlEK60f28YBvuv7Gdj\n9kZsdhvj+48nLSnNuQVYRYX0fh04II/yPfQQPP20Uwswq89JTY2kcbz5Jpw+LW1wEybACy/Izqy7\nFmBWnxdPpHNiPZ4yJ7oSpjxKm72NbXnbOF5yHIA5Q+cwJWaKcyMoTp+GL76Qs3XCwiT7a+BA572e\nxdXXSw7t0aOSeO/lBSkp8sRj795mj04ppbqP9oQpj9Fsa2Zj9kYuVFzA19uXxSMWkxiZ6MQXbJbi\nKzNTrkeOlOwvD21wamqSh0G/+UbqUZC/ktRUiOyGgwiUUsoM2hOmPF51UzXrstZRVl9GsF8wK5JW\nENMzxnkvePUqbNok25B+fpKtMGaMR2Z/tbTA4cOyE9vUJPeGDZOg1X79zB2bUkqZSXvClENYef++\npLaEd068Q1l9GRE9Ilgzdo3zCjDDkGrjnXekAIuOluwvE8JXzZ4Tm01Wvd54A3bvlgJs8GB49llI\nS/PcAszseVE/pnNiPZ4yJ7oSptza+Rvn2ZS9iZa2FmLDYlk+cjlBfk46CqiuTqInLl6U60mTYPZs\nj8v+amuT05f27pXme4CYGHkWYcgQc8emlFJWoj1hym0dKT7C9rztGBiMjhrN/OHz8fV2UkGUlyfh\nq/X10KOHZH8NH+6c17Iou739cO2KCrkXFSXF17BhHrkTq5RS2hOmPIvdsLPz4k4OFR0CIDU2lQcH\nPeicJyBtNtlrOySvxeDBkv0VGur417Iow4CcHIlAKy+Xe+Hh7Ydra/GllFI/TXvClENYZf++ta2V\nj85+xKGiQ/h4+bAoYRGpsanOKcBu3JDsr0OHJPtr5kx46inLFGDOnhPDkFOX3n4bNmyQAiwsTBYB\n//VfYdQoLcB+ilXeK6qdzon1eMqc6EqYcht1LXWsz1pPcW0xgb6BPDnqSWLDYh3/QoYh2V/btrVn\nfy1ZIo1PHqKgQBYAr1yR65AQmD5dnj/wsBY4pZS6Z9oTptxCeX056VnpVDVV0TuwN2lJaUQGOyF8\nqrlZYt6zsuR61Ch47DGPyf4qLpZtx5vPHgQFwf33yzFDfn7mjk0ppaxIe8KUW7tUeYmPzn5Ek62J\nmJ4xrBi1gmB/J5x5U1QEH38shx36+cG8eRL17gF7bteuSfGVkyPXAQHth2sHOPG0J6WUcmfaE6Yc\nwqz9+1Olp/hH5j9osjWRGJnIqtGrHF+AGYacs/Pee1KARUfDL39p+fBVR8xJRYXUnX/+sxRgfn5y\nsPYLL0jSvRZgnecpvS6uROfEejxlTpxahD3zzDNERUWRlJR0615FRQWzZ89m2LBhzJkzh6qqqlt/\n9uqrrxIfH09CQgI7duxw5tCUizMMg68uf8WnOZ9iN+xMHTiVpYlL8fNx8J5YbS38/e+wa5dkMEye\nDGvWQESEY1/HYqqrYetW+NOfZOfV21u2HH/7W4k+69HD7BEqpZTrc2pP2L59+wgJCeHpp58m69se\nmhdffJGIiAhefPFFXn/9dSorK3nttdfIzs4mLS2No0ePUlxczKxZszh//jze3t+vE7UnTNnsNrbk\nbCHrWhZeeDEvfh4TBkxw/Avl5Un4akODVB0LF0rglRurq4N9++DYMQld9faG0aPlcO2wMLNHp5RS\nrse0nrAHHniA/Pz8793bunUre/fuBWDVqlWkpqby2muvsWXLFlasWIGfnx+xsbHExcVx5MgRJk+e\n7MwhKhfT0NrAhjMbKKguwN/Hn6WJS4kPj3fsi9hssvL1zTdyPWQILFpkmegJZ2hslNOWDh+G1la5\nN2qUZH2Fh5s7NqWUclfd3hNWVlZGVFQUAFFRUZSVlQFw9epVYr7ziH9MTAzFxcXdPTx1j7pj/76i\nsYJ3T7xLQXUBof6hPDPmGccXYNevy7mP33wjy0CzZlkq+6sz7mZOmpvleKE//EHa3lpbJej/V7+S\n1A0twBzPU3pdXInOifV4ypyY+nSkl5fXHUM0b/dnq1evJjY2FoCwsDBSUlJITU0F2idOr7v3+iZn\nff6hY4ay/sx6so9m0yeoD79b/Tt6BvR03Os9+CCcOkXGn/4EbW2kjhkDS5aQkZcHe/ea/vfr6Otp\n01I5ehTWrs2guRliY1MZMgSCgjKIjISoKGuN152uT506Zanx6HU7q4xHr137+ubvf7gT+FOcnhOW\nn5/P/Pnzb/WEJSQkkJGRQXR0NCUlJcyYMYOcnBxee+01AH7/+98D8Mgjj/DKK68wadKk7w9Ye8I8\nztlrZ/kk5xNsdhtxfeJYmriUAF8HPpbX1CTZX2fOyHVSkmR/ueGjf21tcOIEfP21PHMAMHCghP1/\n++8apZRSDmSpnLAFCxawdu1aXnrpJdauXcvChQtv3U9LS+N3v/sdxcXF5OXlMXHixO4enrIQwzA4\nUHiAXZd2ATC+/3jmxc/D28vbcS9SVASbNkFVFfj7S/bX6NGWjp64F3Y7ZGZCRoZ8qQD9+snh2nFx\nbvflKqWUS3DgT7MfW7FiBVOnTiU3N5eBAwfy/vvv8/vf/56dO3cybNgwvvrqq1srX4mJiSxbtozE\nxETmzp3LW2+95Zzz/pRT/HBZv6va7G18fv7zWwXYnKFzeDT+UccVYHa7PAb43ntSlfTrJ9lfbhS+\nmpGRgWHA2bPw1lvw6afypUZGwrJl8NxzEB/vNl+uy3D0e0V1nc6J9XjKnDh1JWz9+vU/eX/Xrl0/\nef/ll1/m5ZdfduaQlAtotjXz0dmPuFh5EV9vXxaPWExiZKLjXqC2FjZvhsuX5XrqVFkScqNDDw0D\nCgvhL3+B0lK517s3pKbKbqu3U//5pZRS6m7o2ZHKUqqbqlmXtY6y+jKC/YJZkbSCmJ4OPBj7/HlZ\nEmpogOBgiZ6Ii3Pc57eAy5fliKHCQrkODZWcrzFjwMfH3LEppZSnsVRPmFK3U1JbwrqsddS21BLR\nI4KVSSvpHdTbMZ/cZoOdOyUIC2DoUCnAQkIc8/ktoKhIiq9Ll+S6Rw944AEYP14P11ZKKSvSTQnl\nEF3dvz9/4zzvn3qf2pZaYsNieXbMs44rwMrLJfvr8GHZh5szB372M7cpwEpLYf16+RIvXYLAQNld\nTUnJYMoULcCsxlN6XVyJzon1eMqc6EqYMt2R4iNsz9uOgcHoqNEsGL4AH28H7JsZBpw8Cdu3Swpp\nnz7wxBMwYEDXP7cFXL8uTzveTNbw94dJk6TFLShI/kwppZR1aU+YMo3dsLPj4g6+KZLjgVJjU3lw\n0IOOeSq2qQk++0weDQSJnZg3zy2yv6qqJOX+1CmpM318YMIEuP9+t1ncU0opt6E9YcpyWtpa2Hxu\nMznXc/Dx8mHB8AWMjh7tmE9eWAgff9ye/fXoo1KEubjaWknVOH68/XDtsWNh+nTo1cvs0SmllOos\n7QlTDtGZ/fu6ljo+OPUBOddzCPQN5KnRTzmmALPbJQr+/felAOvfH55/3uULsIYG2LED3ngDjhyR\nLzM5GX79a5g///YFmKf0VLganRfr0TmxHk+ZE10JU93qWv011mWto6qpit6BvUlLSiMyOLLrn7im\nRrK/bp7VNW2adKe7cCZDczMcOiS/mpvl3ogRMGMG9O1r7tiUUkp1nfaEqW5zqfISH539iCZbEzE9\nY1gxagXB/sFd/8Q5ObBlCzQ2SlPUokUSQeGiWltlxWv/fvmSQKLMHnpIFveUUkq5Du0JU6Y7WXKS\nz85/ht2wkxiZyKKERfj5dDE7obVVsr+OHJHruDhYuNBlu9NttvbDtevq5N6gQVJ8DRoRjk0JAAAg\nAElEQVRk7tiUUko5nvaEKYe43f69YRh8dfkrtuRuwW7YmTpwKksTl3a9ALuZ/XXkiGw5PvwwrFzp\nkgWY3S7F15tvwrZtUoD17y9RZqtX33sB5ik9Fa5G58V6dE6sx1PmRFfClNPY7Da25Gwh61oWXnjx\n6LBHGd9/fNc+qWFIxfLll+3ZX0uWuOQ+3c3DtffsgRs35F7fvrLyNXy4HqytlFLuTnvClFM0tDaw\n4cwGCqoL8PfxZ2niUuLD47v2SRsbJfsrO1uuU1Jg7lyXy/4yDDnC8quvoKxM7vXpIw33I0fq4dpK\nKeVOtCdMdauKxgrSM9O50XiDngE9SUtKIzokumuf9MoVyf6qrpai69FHJafBhRiGHK69ezcUF8u9\nnj0hNVVSNFz4QU6llFL3QP/NrRzi5v59YXUh75x4hxuNN4gOiWbN2DVdK8DsdomHf/99KcAGDIBf\n/tLlCrArV2DtWvjb36QACw6GRx6B3/5WAledUYB5Sk+Fq9F5sR6dE+vxlDnRlTDlMGevneWTnE+w\n2W3E94lnSeISAny7sFVYXS3ZXwUFcn3//bJn50JLRiUlsu2YlyfXQUESYTZxooT5K6WU8lzaE6a6\nzDAMDhQeYNelXQCM7z+eefHz8PbqwkLruXOwdavLZn+Vl0vD/c32NX9/mDJFfgUGmjs2pZRS3Ud7\nwpTTtNnb+CLvC06UnMALL2YPnc2UmCn3fgh3a6uc0XP0qFzHx0v2V7ADQl27QWUlZGRAZqb0gPn6\nyqrXtGku8yUopZTqJtoTpu5Zk62JdVnrOFFygsLThSwduZSpA6feewF27Rq8/bYUYD4+0jSVluYS\n1UtNDXz+uWR9nT4t8RLjx0vP15w55nwJntJT4Wp0XqxH58R6PGVOdCVM3ZPqpmrSs9K5Vn+NYL9g\nHol7hMTIxHv7ZIYBx49L9pfNBuHhkv3Vr59jB+0E9fVyvNDRozJ0Ly9JznjwQejd2+zRKaWUsjLt\nCVOddrX2Kuuz1lPbUktEjwhWJq2kd9A9VhyNjdL7de6cXI8ZI9lfFu9ab2qCgwfhm2+gpUXujRwp\ncRORDjiPXCmllHvQnjDlMLnXc9mUvYlWeyuxYbEsH7mcIL+ge/tkBQWS/VVTI9lfjz0GSUmOHbCD\ntbTA4cNw4IAUYgDDhslDmy6wcKeUUspCtCdM3bUjxUf48MyHtNpbGR01mqeSn7pVgHVq/95ul0cH\nP/hACrCYGHj+eUsXYDabrHq98YaErTY1QWwsPPustK1ZsQDzlJ4KV6PzYj06J9bjKXOiK2GqQ3bD\nzo6LO/im6BsAUmNTeXDQg/fWgF9dLatfV65IA9UDD8genkWzv9ra4NQpyYutqZF7MTFyvuPgwXq+\no1JKqXunPWHqjlraWth8bjM513Pw8fJhwfAFjI4efW+fLDtb+r+amiA0FBYvlkrGgux2OHNG4iYq\nKuReVJQUX8OGafGllFLq7mhPmLondS11rMtax9XaqwT6BvLkqCeJDYvt/CdqbZUnH48fl+thwyT7\nq0cPh47XEQwDcnJkt/TaNbkXHt5+uLYWX0oppRxFe8LUT7pWf413TrzD1dqr9A7szZqxa+5YgN12\n/76sDP76VynAfHzkyccVKyxXgBkGXLggMWUbNkgBFhYGjz8O//qvMGqU6xVgntJT4Wp0XqxH58R6\nPGVOdCVM/cilykt8dPYjmmxNxPSMYcWoFQT7dzJt1DAkPGvHDulqj4iQ7K/oLhzm7SQFBXK+480j\nKkNCYPp0OVjbV98hSimlnER7wtT3nCw5yWfnP8Nu2EmMTGRRwiL8fPw690kaGqT3KydHrseOlfR7\ni2V/FRdL8XXxolwHBckZ4RMngl8nv2SllFLqp2hPmOqQYRjsyd/D1wVfAzBt4DRmDZnV+Scg8/Nh\n82Z5lDAwEObPl2YqC7l2TYqvmzViQED74doBAeaOTSmllOfQIkxhs9vYkrOFrGtZeHt5My9+HuP7\nj+/U58j46itSAfbtk63IgQPhiSekscoiKiqk4f7MGRmin1/74doWa1FziIyMDFJTU80ehvoBnRfr\n0TmxHk+ZEy3CPFxDawMbzmygoLoAfx9/liYuJT48vnOfpKoKtm+XU6q9vKShKjUVvK3x3Ed1teR8\nnTol0RM+PjBunESUhYaaPTqllFKeSnvCPFhFYwXpmencaLxBz4CepCWlER3Sycb5s2fhs88smf1V\nVycLc8eOSejqdw/XttACnVJKKTemPWHqRwqrC1l/Zj0NrQ1Eh0STlpRGz4Ced/8JWlok++vECbke\nPlzyHCywr9fYKGc7Hj4sEWUgERMzZkjml1JKKWUF1tgvUt3qzLUzrD29lobWBuL7xPPzlJ93rgAr\nLZXsrxMnJMNh3jwyoqNNL8Cam2Xb8Y03YP9+KcCGD4df/UrSMTytAPOUnB1Xo/NiPTon1uMpc6Ir\nYR7EMAwOFB5g16VdAEzoP4G58XPx9rrLWtww4MgRyf5qa4PISKluoqLkfB+TtLZKJNn+/ZKOATBk\niBwxFBNj2rCUUkqpO9KeMA/RZm/ji7wvOFFyAi+8mD10NlNiptx9BEVDA2zZArm5cj1unGR/mRio\n1dYmi3Fffw21tXJv4ECYORNiY00bllJKKXWL9oR5uCZbExvPbuRi5UV8vX1ZPGIxiZGJd/8JLl+W\n7K/aWsn+WrAAEjvx8Q5mt0Nmpmw9VlbKvX79ZOUrLs71jhdSSinlmbQnzM1VN1Xz3sn3uFh5kWC/\nYFanrL77AqytDXbvhr/9TQqw++6D55//yQKsO/bvDUMexnzrLfj0UynAIiNh2TJ47jmIj9cC7Ls8\npafC1ei8WI/OifV4ypzoSpgbu1p7lXVZ66hrqSOiRwQrk1bSO6j33X1wZSV8/DEUFUll8+CD8suE\n7C/DgLw8CVotKZF7vXtLFFlSkmXiyJRSSqlO0Z4wN5V7PZdN2ZtotbcSGxbL8pHLCfILursPPnNG\nsr+am6FnT8n+MqnJ6vJlOWKosFCuQ0OlFhwzRkJXlVJKKSvTnjAPc7joMF9e+BIDg9FRo1kwfAE+\n3ndRsbS0SPL9yZNynZAg/V8mRE8UFUnxdemSXPfoIQn348fr4dpKKaXcg27kuBG7YefLC1+y/cJ2\nDAxmxM5gYcLCuyvASkok++vkScn+evRRWL78rgswR+3fl5XB+vXwzjtSgAUGSsP9Cy/IAdtagN09\nT+mpcDU6L9ajc2I9njInuhLmJlraWth8bjM513Pw8fLh8YTHSY5K7vgDDUOi5XfulEb8vn0l+6tv\nX+cP+juuX5eosTNn5NrPDyZPhqlTIegud1GVUkopV6I9YW6grqWOdVnruFp7lSDfIJaPWk5sWGzH\nH1hfL9lf58/L9fjx8PDD3brcVFXVfri2YUif14QJcP/9EBLSbcNQSimlnEJ7wtzYtfprpGemU91c\nTe/A3qxMXklEj4iOP/DSJcn+qquTpaYFC2DECOcP+Fu1tXK49vHjsgDn7Q1jx8L06dCrV7cNQyml\nlDKN9oS5sEuVl3j3xLtUN1cT0zOGNWPXdFyAtbXBrl3w979LATZokGR/dbEAu9v9+4YG2fn84x/l\nBCS7HZKT4de/hvnztQBzJE/pqXA1Oi/Wo3NiPZ4yJ6athMXGxtKzZ098fHzw8/PjyJEjVFRUsHz5\ncgoKCoiNjeWjjz4iLCzMrCFa2smSk3x2/jPshp3EyEQWJSzCz6eDbcTKSti0CYqLJfsrNVWWnroh\naKu5GQ4dkl/NzXJvxAiYMaPb28+UUkopSzCtJ2zw4MEcP36cPn363Lr34osvEhERwYsvvsjrr79O\nZWUlr7322vc+ztN7wgzDYE/+Hr4u+BqAaQOnMWvIrI7PgMzKgs8/lwqoVy944glJwHey1lZZ8dq/\nHxob5V5cnDzx2L+/019eKaWUMtWd6hZTi7Bjx44RHh5+615CQgJ79+4lKiqK0tJSUlNTycnJ+d7H\neXIRZrPb2JKzhaxrWXh7eTMvfh7j+4+/8we1tMC2bdL5DnLk0Pz5Tn/k0GZrP1y7rk7uDRokxdeg\nQU59aaWUUsoy7lS3mNYT5uXlxaxZsxg/fjxvv/02AGVlZURFRQEQFRVFWVmZWcOznIbWBv52+m9k\nXcvC38eftKS0jguwkhL4y1+kAPP1leJr6VKnFGA39+/tdokae/NNqf3q6mTF62c/g9WrtQDrTp7S\nU+FqdF6sR+fEejxlTkzrCTtw4AD9+vWjvLyc2bNnk5CQ8L0/9/Lyuu0W2+rVq4n99hidsLAwUlJS\nSE1NBdonzp2ua5prKAgr4EbjDa6dvcasIbOI6xN3+483DFIDA2HXLjIuXoSwMFJffhn69nXaeA1D\nMr7++tcMamogNjaVvn0hODiD++6DuDjr/H3qtV6beX3q1ClLjUev21llPHrt2tc3f5+fn09HLJET\n9sorrxASEsLbb79NRkYG0dHRlJSUMGPGDI/fjrxSfYUPz3xIQ2sD0SHRpCWl0TOg5+0/oK4OPv0U\nLlyQ64kTYfZsp2V/GYbEjH31laTdA/TpA6mpMGqUHq6tlFLKs1kuJ6yhoYG2tjZCQ0Opr69nx44d\n/Pf//t9ZsGABa9eu5aWXXmLt2rUsXLjQjOFZxplrZ/g051NsdhvxfeJZkriEAN+A23/AxYvwySft\n2V+PPy7nPzqBYbQfrl1UJPd69pTDtVNS9HBtpZRSqiOmrIRdvnyZRYsWAWCz2Vi5ciX/6T/9Jyoq\nKli2bBlXrly5bUSFJ6yEGYbB/iv72X15NwAT+k9gbvxcvL1us6zU1ibV0IEDch0bC4sXS1XkBIWF\nsHs33FxpDQ6WbcfnnkvFV+N/LSMjI+PWMrmyDp0X69E5sR53mhPLrYQNHjyYUzef1vuOPn36sGvX\nLhNGZB1t9ja+yPuCEyUn8MKLOUPnMDlm8u0jKCoqJPvr6lXZ+0tNlTN/nLAPWFIitV5enlwHBsK0\naTBpEhw8iBZgSimlVCdYoiesM9x5JazJ1sTGsxu5WHkRP28/Fo9YzIjIOyTZZ2ZK9ldLi1Ozv8rL\nYc8eyM6Wa3//9sO1AwMd/nJKKaWU27DcSpj6seqmatKz0rlWf41gv2DSktIY0HPAT//Hzc2S/3D6\ntFyPHAmPPebw6InKSsjIkFrPMGSl6+bh2sHBDn0ppZRS6v+3d6dRVZZrH8D/m2E7IiIoKqAyg4CA\nA6jnWBjHOJVa5jy+pafXrHztDNb5cFpnndYydZ1hnaxOrlX5UkvFBjulmbwqRI6gMhhKIfMQKDEL\nwmYP1/vhzq3kcEyB/cD+/z6xn/3sZ98P1wqv7vt6rtvu8Nk1Dai6UoV3st5BTWsNPAZ64DcTf3P7\nBKyqSvX+OndOPfE4dy6wYEGXJmDNzWqC7Y031NfodMDkycD//A+QkHDrBOynj3qT7TEm2sS4aA9j\noj32EhPOhNlAfmE+jmQegVGMqG+tR/PAZgwdNRS+Q32xKGwRBjjfIqESURsvpqSoQnxPT5V8DR/e\nZeNqbVXbC505ozre63RAZKQqM3Nz67KvISIiIrAmrMflF+Yj8atE9Avsh8rmShTWF8JUaMLiGYvx\n3Kzn4Ohwi94OLS2q9URRkXodG6t6f3VRJXx7uyqsT09X5WWA2t1o5swuzfGIiIjsDmvCNORI5hHo\nA/QorC9EZbNqsBUwOQAOjQ63TsAKC1UC1toKDByoen8FB3fJWDo6gIwMlYBd21w7MFDt7zhqVJd8\nBREREd0Ga8J6WLupHRd+uIDK5krooEOoRyjGDR0Hoxg7n2g2A4cOATt3qgTM1xd49tkuScBMJjXr\n9frranWzrU21Flu9Gli+/N4SMHtZv+9NGBNtYly0hzHRHnuJCWfCelBrRysyqzNR61ELJwcnhI8I\nx9D+qhmt3kF//cS6OmDv3uu9v2bOVA257rP3l9ms9vL++mtVfA8AXl5AfLzK8W7XioyIiIi6HmvC\nekjt1Vrs+mYXCooL8N3F7xA9PRqD9OoxQ0OBAU/NfArB/kGqH8SBA2qtcOhQ1fvLx+e+vttiUZtr\np6Wp3q6Aqut/6CEgKIjJFxERUXe5U97CJKwHlDeVIyk3CW2mNox2GY3JAycjPTcdHZYO6B30iJ8Y\nj2CfcSr5+uYb9aHwcNX76z66oYoA332nGq3W1Khj7u5qYi0sjMkXERFRd2MSZkMXai7g39/9GyaL\nCUHuQVgwfgH0jvrOJ33/vdp6qKFB9f569FG1C/Y9Zkki6kHK1FS1ogmohvpxcarlRDfsaNSn9vnq\nKxgTbWJctIcx0Z6+FBM+HWkDIoKTFSdxuPgwgM6bcJfl56PoyBE4dHTAUlEBf6MRY93dgZEjVe8v\nD497/t6yMpV8lZWp14MHAw88AEycyL0diYiItIQzYd3AIhYcLDiIM1VnAAAP+z+Mad7ToNPpUJaf\nj8LERMQDaq2woQEpJhMC/uu/MPbpp+85U6qqUslXYaF6PWCA2l4oJkZNrhEREVHP40xYD+owd+CT\nvE9wse4inBycMC9kHsJGhFnfLzpyBPEtLSoBMxoBZ2fER0Qg1WjE2HtIwGpqVM3Xt9+q1/36AdOm\nqQ22ubk2ERGRdrFPWBdq6WhBYk4iLtZdxACnAVgVuapTAgaTCQ7nzgG5uSoBc3NTmzK6u8PhWqv6\nu1RfD3z6KfD22yoBc3ZWXSw2bFC1Xz2dgNlLT5fehDHRJsZFexgT7bGXmHAmrIv80PoDduXuQmN7\nI9z6u2HFhBVwH+h+wwk/AJ98AktlpSq49/VVrSd+LL636PW3uXJnTU3A0aNAdrZqPeHoCEyaBMyY\nAbi4dMedERERUXdgTVgXKG0sxZ7ze9Buaof3EG8sDV9q7QEGESArC0hOBoxGlBmNKGxqQvwNxfcp\nBgMCnnoKY+/QDb+l5frm2mazyt2iooAHH1TtxIiIiEh72KKiG+VezsVn330Gs5gR4hGC+aHz4ez4\nYyV8Wxuwb9/1gq3ISODRR1FWWoqilBT1dKReD//4+NsmYG1t1zfXNv64s1F4uFpyvI+HKImIiKgH\nMAnrBiKC4+XHkVKSAgCI9YpFQkACHHQ/ltmVlqqireZmVS0/ezYQEXHX1zcYrm+u3d6ujgUHq0ar\nI0d28c10gb7U06WvYEy0iXHRHsZEe/pSTPh0ZBeziAUHLh5AZnUmdNAhISABU72nqjfNZrU547Fj\nainS21ttPeTmdlfXNhqBs2fVx69eVcf8/NQWQ97e3XRDRERE1OM4E/YzGUwGfJz3MQrrC+Hk4IT5\nofMROjxUvdnQoDbevlZ8P2OGKtpydPyP1zWbVbH9118DV66oYz4+Kvny9e3GGyIiIqJuw5mwLnLF\ncAW7cnfhUsslDHQeiKXhS+Hj+uPm2rm5wBdfqHXEIUOAJ58Exo275XXy88tw5EgRjEYHODpa4OPj\nj7KysWhoUO+PHKmSr8BA7u9IRETUV7FP2F2qaa3Bu1nv4lLLJbgPcMdvJv5GJWAGA/Dvf6sZMIMB\nCA0F1q27YwKWmFiImpqHUFAQh4MHH8Lf/laIgoIyeHgACxcCa9cCQUG9KwGzl54uvQljok2Mi/Yw\nJtpjLzHhTNhdKG4oxofnP4TBbIDPEB8sjViKgc4D1cbbe/eqzqnOzsCvf602abxD9nT4cBFaW+OR\nm6vaTgDA4MHxcHFJxXPPje2WzbWJiIhIe1gT9h+cu3QOn+d/DotYMH74eMwLmQdnByfgxAm1WaPF\nAnh6qo23hw+/47XKy4GXX05DdXUcAECvB8aOBUaNAoYNS8OLL8Z1/w0RERFRj2FN2D0QERwtO4qv\nSr8CAEz3mY5ZfrOga2lRy4/FxerEqVOBX/3qjhtvX7qk8rWLF4GmJgucnFTyNXr09Zp9vd7S3bdE\nREREGsLFr1swW8zYl78PX5V+BR10eDTwUTzs/zB0Fy+qzRqLi4FBg4Dly9US5G0SsPp6tVq5fbtK\nwPR6YPFif0RHp8DH53oCZjCkID7evwfvsOvZy/p9b8KYaBPjoj2MifbYS0w4E/YTBpMBH134CEUN\nRXB2cMaC8QsQ7OoHfPklcPq0OsnfH5g3Dxg8+JbXaG5WrSZu3N9xyhTVsWLQoLHIzwdSUlLR0eEA\nvd6C+PgABAeP7cG7JCIiIltjTdgNmg3N2PXNLlxuvYxBzoOwLGIZvNqdgU8+AWpqVDYVHw9Mm3bL\n4vurV9X+jqdPAyYT93ckIiKyd6wJuwuXWi5hd+5uNBua4THQA8vDl8HtQhHwf/+nMip3d9X5fvTo\nmz5rMKi9HU+eVD8DwPjxqtcX93ckIiKiW2FNGICi+iL8b/b/otnQjLGuY7EmeCnc9h0CDhxQCVh0\ntGre9ZMEzGRSyde2bcBXX6kEzN8f+O//BhYtsq8EzF7W73sTxkSbGBftYUy0x15iYvczYdnV2dh/\ncT8sYkH4iHA80S8STu8mqr2D+vcH5swBwsI6fcZiAc6dA9LSgKYmdczbWz0keZserURERESd2G1N\nmIggrTQNX5d9DQD4pdc0xJc6QHfypNp4e8wYtfXQDcVcIkBenpr1qq1Vxzw91bJjb+twT0RERN2P\nNWE/ca0FxbnL56CDDnOH/xLRacWqA75OB8TFAQ88gGvt60WAoiIgJQWorlbXcHMDZs4EwsPBLvdE\nRET0s9ld+tBuasfOb3bi3OVz0Dvq8ZQuGtGfZ6gEzNUVeOoplYT9mFlVVADvvw/s3KkSMBcXYPZs\n4IUXgAkTmIBdYy/r970JY6JNjIv2MCbaYy8xsauZsKb2JuzK3YWa1hq4oj+eKh8Ot4Is9WZYmMqu\nBgwAAFy+rLrc5+ertwcMAH75SyAmRm0TSURERHQ/7KYmrPpKNXbl7kJLRwvGXXHConwnDGxpVxnV\nI4+oJyB1OtTXq5qv8+fVMqRer3Ymmj5d1ekTERER3S27rwkrqCvAx3kfw2g0ILbUiF+VW+AMk9o5\ne/58wMMDV66oLvdZWde73E+erLrc36YxPhEREdE96/MVTZlVmUg6nwRd8xU8ll6HhDInOMNBTW2t\nWYO2QR44fFj1+jp7Vs1+RUUB69erCTImYHfHXtbvexPGRJsYF+1hTLTHXmLSZ2fCRAQpJSk4Xn4c\nHuW1+PUFA/z7j4bOxQV44gl0jAlA+kngxInrXe5DQ1W7ieHDbTt2IiIi6vv6ZE2YyWLCZ999hryq\ncwg8U4y42sEY5TIKCAyE6bHHkZk/GEePAq2t6nx/f5V8eXn1wA0QERGR3bhT3tLnkrA2Yxv2nN+D\n2pILmHDsIqbox2HY4OGwxM/CNwNikfa1Do2N6lxvb7Uft69vDw2eiIiI7Mqd8pY+VRPW0NaA97Le\nhenUCUxPvoBfDAiCm3cQ8h94Bv/KmorPPlcJ2IgRwJIlwJo1TMC6ir2s3/cmjIk2MS7aw5hoj73E\npFfXhOUX5uNI5hEYxYgWQwuu6n7ApIuVGHO5HRGeUWgYMx17TAmo/EoPQHW5j4sDIiLYZJWIiIhs\nq9cuR+YX5uPNpL9DX1sJQ1szmn+oRPAlIx70DUXImDgcc3kS54zjAagnHB98EJg4UbWeICIiIuoJ\nfbJP2Cf7d2JAdjZCmhrhVleL0U0dOOmgxynH/jg2Zj0MRlf073+9y71eb+sRExEREV3Xaxflak6c\nRdDlHzCmoh4jGwQWowu8MAxpLSZYXFwxYwawYYNKwpiAdT97Wb/vTRgTbWJctIcx0R57iYnmkrDk\n5GSEhIQgMDAQW7duveU5f4iJQG1qGsaW1GJAmxntFhdcGDIOVS4+0JuvYsMG9dTjj9tAUg/Iycmx\n9RDoJxgTbWJctIcx0R57iYmmkjCz2YwXXngBycnJyMvLQ1JSEr799tubzns89zymN7fDofYqfjAP\nwHm3cTAM7o/BZhN8vMaxy70NNF7r+0GawZhoE+OiPYyJ9thLTDSVhJ0+fRoBAQEYN24cnJ2dsWTJ\nEnz++ec3nRdhAXwFyIUDaq5a4CKDMNQwCBf7h2FkzEM2GDkRERHRz6Opwvzvv/8ePj4+1tfe3t7I\nyMi46TwBEDFAhwKLBQed3RDs9WsYHfXo8BqINctn9uCI6ZrS0lJbD4F+gjHRJsZFexgT7bGXmGiq\nRcXevXuRnJyMd955BwCwc+dOZGRk4I033rCeM1anQ7mtBkhERET0M0RGRt62xk1TM2FeXl6oqKiw\nvq6oqIC3t3enc8q0kzMSERER3TNN1YRNnjwZBQUFKC0tRUdHBz788EPMnTvX1sMiIiIi6nKamglz\ncnLCm2++iYSEBJjNZqxZswahoaG2HhYRERFRl9NUTRgRERGRvdDUcuR/cjeNXOnuVVRUYObMmQgL\nC0N4eDi2bdsGAKivr8esWbMQFBSEhx9+uFO/ls2bNyMwMBAhISE4dOiQ9XhmZiYiIiIQGBiIDRs2\nWI8bDAYsXrwYgYGBmDp1KsrKyqzvvf/++wgKCkJQUBA++OCDHrjj3sVsNiM6Ohpz5swBwLjYWmNj\nIxYsWIDQ0FCMHz8eGRkZjIkGbN68GWFhYYiIiMCyZctgMBgYlx62evVqeHp6IiIiwnrM1jEoKSlB\nbGwsAgMDsWTJEhiNxu66/fsjvYTJZBJ/f38pKSmRjo4OiYyMlLy8PFsPq1errq6W7OxsERG5cuWK\nBAUFSV5enmzcuFG2bt0qIiJbtmyRl19+WURELly4IJGRkdLR0SElJSXi7+8vFotFRESmTJkiGRkZ\nIiLyyCOPyMGDB0VE5K233pJ169aJiMiePXtk8eLFIiJSV1cnfn5+0tDQIA0NDdaf6bq///3vsmzZ\nMpkzZ46ICONiY6tWrZL33ntPRESMRqM0NjYyJjZWUlIivr6+0t7eLiIiixYtksTERMalhx09elSy\nsrIkPDzcesxWMWhsbBQRkYULF8qHH34oIiLPPvusvP322939a7gnvSYJO3nypCQkJFhfb968WTZv\n3mzDEfU9jz/+uBw+fFiCg4Pl0qVLIqISteDgYBERee2112TLli3W8xMSEuTUqbXZSFkAAAimSURB\nVFNSVVUlISEh1uNJSUmydu1a6znp6ekiov7h8vDwEBGR3bt3y7PPPmv9zNq1ayUpKal7b7AXqaio\nkPj4eElNTZXZs2eLiDAuNtTY2Ci+vr43HWdMbKuurk6CgoKkvr5ejEajzJ49Ww4dOsS42EBJSUmn\nJMyWMbBYLOLh4SFms1lERE6dOtUpf9CSXrMceatGrt9//70NR9S3lJaWIjs7G7Gxsbh8+TI8PT0B\nAJ6enrh8+TIAoKqqqlPLkGsx+OlxLy8va2xujJuTkxNcXV1RV1d322uR8tvf/hZ//etf4eBw/T9R\nxsV2SkpKMHz4cDz99NOYOHEinnnmGbS2tjImNjZs2DD8/ve/x5gxYzB69GgMHToUs2bNYlw0wJYx\nqK+vx9ChQ61/P2+8ltb0miRMp9PZegh9VktLC+bPn4/XX38dLi4und7T6XT83fewL774AiNGjEB0\ndDTkNs/NMC49y2QyISsrC8899xyysrIwaNAgbNmypdM5jEnPKyoqwj//+U+UlpaiqqoKLS0t2Llz\nZ6dzGBfb68kY9LZY95ok7G4audLPZzQaMX/+fKxcuRJPPPEEAPV/LZcuXQIAVFdXY8SIEQBujkFl\nZSW8vb3h5eWFysrKm45f+0x5udrjwGQyoampCe7u7oznHZw8eRL79u2Dr68vli5ditTUVKxcuZJx\nsSFvb294e3tjypQpAIAFCxYgKysLI0eOZExs6OzZs5g+fTrc3d3h5OSEJ598EqdOnWJcNMBWf6+8\nvLwwbNgwNDY2wmKxWK/l5eXVvTd8r2y9Hnq3jEaj+Pn5SUlJiRgMBhbmdwGLxSIrV66UF198sdPx\njRs3WtfsN2/efFNBpcFgkOLiYvHz87MWVMbExEh6erpYLJabCiqvrdknJSV1Kqj09fWVhoYGqa+v\nt/5MnaWlpVlrwhgX25oxY4bk5+eLiMif//xn2bhxI2NiYzk5ORIWFiZXr14Vi8Uiq1atkjfffJNx\nsYGf1oTZOgYLFy6UPXv2iIiqFWNhfhf48ssvJSgoSPz9/eW1116z9XB6vWPHjolOp5PIyEiJioqS\nqKgoOXjwoNTV1Ul8fLwEBgbKrFmzOv1h2bRpk/j7+0twcLAkJydbj589e1bCw8PF399f1q9fbz3e\n3t4uCxculICAAImNjZWSkhLrezt27JCAgAAJCAiQxMTEHrnn3iYtLc36dCTjYls5OTkyefJkmTBh\ngsybN08aGxsZEw3YunWrjB8/XsLDw2XVqlXS0dHBuPSwJUuWyKhRo8TZ2Vm8vb1lx44dNo9BcXGx\nxMTESEBAgCxatEg6Ojq695dwj9islYiIiMgGek1NGBEREVFfwiSMiIiIyAaYhBERERHZAJMwIiIi\nIhtgEkZERERkA0zCiIiIiGyASRgR2ZW4uDhkZmbe1zX279+PrVu3dtGIiMheOdl6AEREPakr9rGb\nM2cO5syZ00UjIiJ7xZkwIrKp1tZWPPbYY4iKikJERAQ+/vhjAMCrr76KmJgYREREYO3atdbz4+Li\n8Lvf/Q5TpkxBaGgozpw5g3nz5iEoKAivvPIKAKC0tBQhISFYsWIFxo8fj4ULF6Ktre2m7z506BCm\nT5+OSZMmYdGiRWhtbb3pnG3btiEsLAyRkZFYtmwZACAxMRHr168HAERFRSE6OhrR0dEYOHAgjh07\nhtbWVqxevRqxsbGYOHEi9u3bd9N109LSEBcXh4ULFyI0NBQrVqy4/18mEfUqTMKIyKaSk5Ph5eWF\nnJwc5ObmIiEhAQCwfv16nD59Grm5uWhra8MXX3wBQM1k9evXD2fOnMG6devw+OOPY/v27Th//jwS\nExPR0NAAALh48SKef/555OXlYciQIfjXv/7V6Xtra2uxadMmpKSkIDMzE5MmTcI//vGPm8a3detW\n5OTk4Ny5c9i+fbt1DNfk5OQgOzsbr776KqZMmYJp06Zh06ZNiI+PR0ZGBlJTU7Fx40ZcvXr1pmvn\n5OTg9ddfR15eHoqLi3HixImu+aUSUa/AJIyIbGrChAk4fPgw/vjHP+L48eMYMmQIACA1NRVTp07F\nhAkTkJqairy8POtn5s6dCwAIDw9HeHg4PD09odfr4efnh4qKCgCAj48Ppk2bBgBYsWIFjh8/bv28\niCA9PR15eXmYPn06oqOj8cEHH6C8vPyW41u2bBl27doFR0fHW95DQUEBXnrpJXz00UdwcnLCoUOH\nsGXLFkRHR2PmzJkwGAzWcd0oJiYGo0ePhk6nQ1RUFEpLS+/tl0hEvRJrwojIpgIDA5GdnY0DBw7g\nT3/6E+Lj4/HSSy/h+eefR2ZmJry8vPCXv/wF7e3t1s/069cPAODg4GD9+dprk8kEoPNslYjcsg5s\n1qxZ2L179x3Hd+DAARw9ehT79+/Hpk2bkJubixu33G1pacHixYvx7rvvwtPT03r8008/RWBg4B2v\nfePYHR0drWMnIvvAmTAisqnq6mr0798fy5cvxx/+8AdkZ2dbEy53d3e0tLRY68R+jvLycqSnpwMA\ndu/ejRkzZljf0+l0mDp1Kk6cOIGioiIAqjatoKCg0zVEBOXl5YiLi8OWLVvQ1NSElpaWTuesXr0a\nTz/9NH7xi19YjyUkJGDbtm3W19nZ2T97/ETU93EmjIhsKjc3Fxs3boSDgwOcnZ2xfft2uLq64pln\nnkF4eDhGjhyJ2NjYW372Tk86BgcH46233sLq1asRFhaGdevWdXrfw8MDiYmJWLp0KQwGAwBg06ZN\nnWavzGYzVq5ciaamJogINmzYAFdXV+v3lpeXY+/evSgoKMCOHTsAAO+99x5eeeUVvPjii5gwYQIs\nFgv8/PxuKs6/1djv96lNIupddHLjvDoRUR9QWlqKOXPmIDc319ZDISK6LS5HElGfxFklItI6zoQR\nERER2QBnwoiIiIhsgEkYERERkQ0wCSMiIiKyASZhRERERDbAJIyIiIjIBv4fz7qtiZ/BYakAAAAA\nSUVORK5CYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x1031a8710>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 32
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Without making any modifications to the original code in order to account for the strengths of Numba (Numpy) and Cython (static type declarations), we see that Cython performs significantly better than Numba."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"type_declarations\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Appendix II: Cython with and without type declarations"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In the sections above, we have been using the simplest approach to Cython without using static type declarations and thereby neglecting one of its major strengths. \n",
|
|
"Let us now see how we can further improve the Cython implementation of our \"classic least squares approach\" by adding those type declarations."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Here is our \"classic\" approach in Python:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 44
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The Cython-compiled version of it:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%load_ext cythonmagic"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": []
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"def cy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 45
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"And now, the same code with static type declarations:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"def static_type_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" cdef double x_avg, y_avg, var_x, cov_xy, slope, y_interc, x_i, y_i\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 55
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"Now, let us see how the two functions (with and without static type declarations) compare against each other for different sample sizes."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"funcs = ['cy_lstsqr', 'static_type_lstsqr'] \n",
|
|
"labels = ['simple Cython', 'Cython w. type declarations']\n",
|
|
"orders_n = [10**n for n in range(1, 7)]\n",
|
|
"times_n = {f:[] for f in funcs}\n",
|
|
"\n",
|
|
"for n in orders_n:\n",
|
|
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
|
|
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
|
|
" for f in funcs:\n",
|
|
" times_n[f].append(timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 58
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"#%pylab inline\n",
|
|
"#import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"plt.figure(figsize=(10,8))\n",
|
|
"\n",
|
|
"for f in times_n.keys():\n",
|
|
" plt.plot(orders_n, times_n[f], alpha=0.5, label=f, marker='o', lw=2)\n",
|
|
"\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
|
|
"plt.legend(loc=2)\n",
|
|
"plt.grid()\n",
|
|
"\n",
|
|
"plt.title('Performance of a simple least square fit implementation')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAmEAAAH4CAYAAAACdDpdAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdYVGf6N/Dv0KQN0osComhUXBVs2BJRsUaxYzCiJkZT\nNm3NrtFsVEyylrzJpq1J1KhYY4sNW4gFW1xL1JiIgqKAAqIoFqQMwzzvH+fnLChNYZgzc76f6+K6\n5szMOdwz9wxz8zz3PEclhBAgIiIiojplYewAiIiIiJSIRRgRERGREbAIIyIiIjICFmFERERERsAi\njIiIiMgIWIQRERERGQGLMDI52dnZeO655+Dk5IR//OMfxg7H6AoKCjB48GA4Oztj9OjRBvs9AwcO\nxMqVKw1ybAsLC1y+fPmJ94uNjcWzzz5rgIjM35EjR9CsWTM4OTlh69atGDhwIFasWFHt/eX4epC7\nuXPnYtKkScYOg2TEytgBkDIEBATgxo0bsLS0hIODAwYMGID//Oc/cHBweOJjLVq0CJ6enrh3754B\nIjU9GzduxI0bN3D79m1YWBju/6qdO3ca7NhyFhYWhujoaEycONHYodSqmTNn4u2338Zbb70FABgy\nZIj+ttjYWCxZsgSHDh2qcH+lvR5iYmKQkpJS7cIzISEB0dHRuHr1qv666dOnGyo8MlEcCaM6oVKp\nsH37dty/fx+nTp3CyZMn8cknnzzRMYQQ0Ol0SEtLQ8uWLZ8qDq1W+1T7yVlaWhqeeeYZgxZgSqZS\nqYwdQpWe5nWdnp6OoKAgA0RDRNUmiOpAQECA2Lt3r37773//uxg0aJAQQoijR4+KLl26CGdnZ9G2\nbVuRkJCgv1+PHj3EP//5T9GtWzdhZ2cnxo4dK6ytrYWNjY1wdHQUe/fuFUVFReKdd94RDRo0EA0a\nNBDvvvuuKCoqEkIIsX//ftGwYUMxf/584e3tLaKjo0VMTIwYOXKkGDt2rFCr1aJ169YiOTlZzJkz\nR3h6egp/f38RHx+vj2Hp0qWiZcuWQq1WiyZNmoiFCxfqb3t4/M8//1x4enoKHx8fsWzZMv3t+fn5\nYsqUKaJRo0aifv36onv37qKgoKDKx/2oxMRE0aNHD+Hs7CxatWoltm3bJoQQYubMmcLGxkZYW1sL\nR0dHsXTp0sf2PXbsmOjcubNwdnYWPj4+4s033xQajabc31NQUCBefPFF4ebmJpydnUXHjh3FjRs3\n9Ln44YcfhBBCLFu2THTt2lX87W9/E87OziIwMFAcOXJELF26VPj5+QlPT0+xfPly/XHHjx8vXn31\nVdGnTx+hVqtFjx49RFpamv52lUolUlJShBBCFBYWivfee0/4+/sLLy8v8dprr+mfs0ctW7ZMdO/e\nXb99/vx5ER4eLlxdXUXz5s3F+vXr9bdt375dBAcHCycnJ+Hn5ydiYmIqfdzZ2dnigw8+EJaWlsLW\n1lY4OjqKt956q1rPWXZ2thBCiMuXL4vnnntOqNVq0adPH/HXv/5VjB07VgghvXZ8fX3LHKtRo0b6\n90lVeVOpVGLBggWiadOmokmTJkIIIeLi4kTbtm2Fs7Oz6Nq1qzh79my5z1uTJk2EhYWFsLOzE2q1\nWhQVFenze/78eVGvXj1haWkpHB0dhYuLS7nHkMPr4eH779NPPxUeHh7Cx8dHbN68WezYsUM0a9ZM\nuLq6irlz5+qPq9PpxNy5c0VgYKBwc3MTkZGR4vbt20IIIa5cuSJUKpVYvny58Pf3F+7u7uJf//qX\nEEKIXbt2lXmfBQcHCyEq/tuQl5cnbG1thYWFhXB0dBRqtVpkZmaKWbNm6fMvhBBbt24VQUFBwtnZ\nWYSFhYnz58+XeS189tlnok2bNqJ+/fpi9OjRorCwsNxckOliEUZ1IiAgQOzZs0cIIUR6erpo1aqV\nmDlzprh27Zpwc3MTu3btEkII8csvvwg3NzeRk5MjhJD+0Ddq1EgkJiaKkpISUVxcLCZMmCBmzJih\nP/aMGTNEly5dxM2bN8XNmzdF165d9bfv379fWFlZiWnTpgmNRiMKCgrErFmzhK2trYiPjxdarVaM\nGzdONGrUSMyZM0dotVqxePFi0bhxY/3xd+zYIS5fviyEEOLAgQPC3t5enDp1qszxZ82aJbRardi5\nc6ewt7cXd+7cEUII8cYbb4iePXuKzMxMUVJSIo4ePSqKiooqfNw3b9587LnTaDQiMDBQzJ07VxQX\nF4t9+/YJtVotkpKShBBCxMTEiOjo6Aqf+99++00cO3ZMlJSUiNTUVNGyZUvx5Zdflnvf77//Xgwe\nPFgUFBQInU4nTp06Je7duyeEECIsLEwsWbJECCF96FpZWYnY2Fih0+nEhx9+KBo2bKgvFOLj44Va\nrRYPHjwQQkgfumq1Whw6dEhfNJcunkp/6L777rtiyJAhIjc3V9y/f18MHjxYTJ8+vdx4SxdheXl5\nwtfXV8TGxoqSkhJx+vRp4e7uLhITE4UQQiQkJIg///xTCCHE2bNnhZeXl9iyZcsTPe4nfc46d+4s\n3nvvPaHRaMTBgweFWq3W56q8Iqz0PytV5U2lUom+ffuK3NxcUVhYKE6dOiU8PT3F8ePHhU6nE8uX\nLxcBAQH6f0ge9eg/RqUfZ2xsbJn8lEcOr4eH77+PP/5Y/951c3MTY8aMEXl5eeLcuXPCzs5OpKam\nCiGE+PLLL0WXLl1ERkaG0Gg04tVXXxVRUVFCiP8VYZMnTxaFhYXi999/F/Xq1RMXLlwQQpT/Pqvs\nb0NCQsJj+Y2JidEXYUlJScLBwUHs2bNHaLVa8emnn4qmTZuK4uJifX5CQ0NFVlaWuH37tmjZsqX4\n/vvvK80JmR4WYVQnGjVqJBwdHYWzs7No1KiR+Otf/yoKCgrEvHnzHvvD1q9fP/1/zWFhYWLWrFll\nbp8wYYL48MMP9duBgYH6YkYIIX7++WcREBAghJD+SNvY2JT5IJo1a5bo27evfnvbtm3C0dFR6HQ6\nIYQQ9+7dEyqVSty9e7fcxzJ06FDx1Vdf6Y9vZ2cnSkpK9Ld7enrqPzzt7OzKHY2o6nGXdvDgQeHt\n7V3muqioKP1IzqP/XVfliy++EMOGDSv3tqVLl1Y4gvLoh26zZs30t509e1aoVCr9qJkQQri5uYnf\nf/9dCCF96D78sBNCKpgsLS3FtWvXhBD/+9DV6XTCwcFB/wEshBC//vprmaK4tNJF2Nq1a8Wzzz5b\n5vbJkyeL2bNnl7vvO++8I/72t79V63E/HPEpT0X7pqWlCSsrK5Gfn6+/bsyYMdUuwh71aN5UKpXY\nv3+/fvu1114r88+JEEI0b95cHDhwoNzjVVaEPTrCWB45vB4evv8efe8eP35cf//27duLrVu3CiGE\naNGiRZnHnJmZKaytrUVJSYm+CMvIyNDf3qlTJ7Fu3TohRPXeZ4/+bXg0v6WP8dFHH4nRo0frb9Pp\ndKJhw4b6fAUEBIjVq1frb586dap47bXXKv39ZHrYmE91QqVSYevWrejVq1eZ69PS0rBhwwbExcXp\nr9NqtWXu5+fnV+mxMzMz0ahRI/22v78/MjMz9dseHh6wsbEps4+np6f+sp2dHdzd3fW9P3Z2dgCA\nvLw8ODk5YdeuXZg9ezYuXrwInU6H/Px8tGnTRr+/m5tbmX4se3t75OXlIScnB4WFhQgMDHws5uo8\n7tKP79HnoFGjRsjIyKj0eXkoOTkZU6ZMwW+//Yb8/HxotVp06NCh3Ps+bCR+4YUXcOfOHYwdOxb/\n+te/YGX1+J8KLy8v/eWHz5mHh0eZ6/Ly8gBI+ff19dXf5uDgAFdXV2RmZqJhw4b662/evIn8/Hy0\nb99ef534v17AqqSlpeHYsWNwcXHRX6fVajFu3DgAwLFjxzBt2jScO3cOGo0GRUVFiIyMrNbjrqwv\nrKJ9MzMz4eLion9uAClvpRu1K1OdvJV+XaSlpWHFihX45ptv9NcVFxcjKyurWr+vpoz1enBzc3vs\nvftoLA9/b1paGoYNG1bm/WplZYXs7Gz9tre3t/7yw/dyRar621CZzMxM+Pv767dVKhX8/PzKvK9L\nx2JnZ1fm7xqZB3byklH5+/sjOjoaubm5+p/79+9j6tSp+vtU1RjdoEEDpKam6rfT09PRoEGDCvd/\nkkbroqIijBgxAlOnTsWNGzeQm5uLgQMHQghR5b7u7u6wtbXFpUuXHrutOo+79OO7evVqmd+ZlpZW\n5kOsMq+//jqCgoJw6dIl3L17F//6178qLGqsrKwwc+ZMnDt3Dr/++iu2b9/+RMsWVEQIUab4yMvL\nw+3bt8vkCZCeMzs7OyQmJuqflzt37lTrm7D+/v7o0aPHY8/pggULAABjxozB0KFDce3aNdy5cwev\nvfaa/nmo7HFX9XqpaN8GDRogNzcX+fn5+vumpaXpj+fg4FDmtpKSEty8eVO/XZ28lY7N398f//zn\nP8s8/ry8vKdatsTQX0aoi9dDefz9/bF79+4yz1F+fj58fHyq3PfR56Sqvw1VPYcNGzZEWlqafvvh\nc1K6CK3s95N5YBFGRjV27FjExcUhPj4eJSUlKCwsREJCQpn/Bh8teB7djoqKwieffIKcnBzk5OTg\no48+QnR0dIW/szoF1EMajQYajQbu7u6wsLDArl27EB8fX619LSws8PLLL2PKlCnIyspCSUkJjh49\nCo1GU63H/VDnzp1hb2+PTz/9FMXFxUhISMD27dvxwgsvVCuOvLw8qNVq2Nvb48KFC/juu+8qvG9C\nQgL++OMPlJSUQK1Ww9raGpaWltX6PVXZuXMnjhw5Ao1GgxkzZqBLly6PfeBYWFhg0qRJePfdd/UF\nSUZGRrWe8+effx7JyclYtWoViouLUVxcjBMnTuDChQsApOfBxcUFNjY2OH78ONasWaP/YKvscXt5\neSElJaXC31vRvv7+/ujQoQNmzZqF4uJiHD58GNu3b9fv98wzz6CwsBA7d+5EcXExPvnkExQVFelv\nf5K8AcCkSZPw/fff4/jx4xBC4MGDB9ixY0elIzkV8fLywrVr11BcXPzE+1aXoV8P5XnttdfwwQcf\nID09HYA00rZt27Zq7evt7Y3U1FT934+q/jZ4eXnh1q1bFRaMo0aNwo4dO7Bv3z4UFxfj888/h62t\nLbp27Vru/Z/k7xaZDhZhZFS+vr7YunUr5syZA09PT/j7++Pzzz8v8wenvJGs0td9+OGH6NChA9q0\naYM2bdqgQ4cO+PDDD6u9f0X3AQC1Wo2vv/4akZGRcHV1xY8//lhmPaXy9i3ts88+Q+vWrdGxY0e4\nublh+vTp0Ol0FT7u8kaorK2tERcXh127dsHDwwNvvvkmVq5ciWeeeabCx/NoDGvWrIGTkxMmT56M\nF154ocL7X79+HaNGjUL9+vURFBSkXyPrUdV5Dh+9bcyYMZg9ezbc3Nxw+vRprFq1qtx958+fj6ZN\nm6Jz586oX78++vTpg+Tk5AqPWzpX8fHxWLt2LRo2bAgfHx9Mnz4dGo0GAPDtt99i5syZcHJywscf\nf1xmhKiyx/3OO+9g48aNcHV1xbvvvvtEz9maNWtw7NgxuLq64qOPPsK4ceP0r+369evj22+/xSuv\nvAJfX184OjqWmV6sKm+PPt/t27fH4sWL8eabb8LV1RXNmjV76lHM3r17o1WrVvD29i4zdV8RY74e\nnuT3vvPOO4iIiEDfvn3h5OSELl264Pjx49Xad9SoUQCk6c8OHTpU+behRYsWiIqKQpMmTeDq6oqs\nrKwyz1Pz5s2xatUqvPXWW/Dw8MCOHTsQFxdX7tT/w9g4GmZ+VMJA5XVhYSF69OiBoqIiaDQaDBky\nBHPnzkVMTAx++OEHfa/AnDlzMGDAAADSasJLly6FpaUlvv76a/Tt29cQoRFRHXvppZfg6+uLjz/+\n2NihGNXs2bNx6dIlg600byr4eiCSGKwx39bWFvv374e9vT20Wi26d++Ow4cPQ6VSYcqUKZgyZUqZ\n+ycmJmLdunVITExERkYGwsPDkZyczAUoicwAp1IkfB4kfB6IJAatcOzt7QFIc+clJSX6by2V9wbc\nunUroqKiYG1tjYCAADRt2rTMMDERmS5OpUj4PEj4PBBJDLpEhU6nQ7t27ZCSkoLXX38drVq1wsaN\nG/HNN99gxYoV6NChAz7//HM4OzsjMzMTnTt31u/r6+tb7a/gE5G8LVu2zNghyMKsWbOMHYIs8PVA\nJDFoEWZhYYEzZ87g7t276NevHxISEvD6669j5syZAIAZM2bgvffew5IlS8rdv7z/lBo2bMi1UoiI\niMgktG3bFmfOnCn3tjppuKpfvz6ef/55nDx5Ep6envqh6FdeeUU/5diwYcMy68Zcu3at3PVSMjMz\nIaSV/vkjk59Zs2YZPQb+MC+m8MOcyPOHeZHfjznl5Pfff6+wPjJYEZaTk4M7d+4AAAoKCvDLL78g\nJCQE169f199n8+bNaN26NQAgIiICa9euhUajwZUrV3Dx4kV06tTJUOFRLSq9UCrJB/MiP8yJPDEv\n8qOUnBhsOjIrKwvjx4+HTqeDTqdDdHQ0evfujXHjxuHMmTNQqVRo3LgxFi5cCAAICgpCZGQkgoKC\nYGVlhW+//ZaNm0RERGS2DLZOmKGoVCqYWMhmLyEhAWFhYcYOgx7BvMgPcyJPzIv8mFNOKqtbWIQR\nERERGUhldYvZrITq6uqqb/jnD39q+uPq6mrsl3SNJSQkGDsEegRzIk/Mi/woJScGXaKiLuXm5nKE\njGqNSsV+RCIiMiyzmY6s6Hqip8HXExER1YbKPk/MZjqSiIiIyJSwCCMyU0rpqTAlzIk8MS/yo5Sc\nsAgjIiIiMgL2hJmQhIQEREdHlzm9ExmGEl5PRERkeOwJU5iYmBhER0cbOwwiIiKqhNksUVGRpKQ0\n7NmTguJiC1hb6xAeHojmzRvV+THMwcNKnss3mAZzWnHaXDAn8sS8yI9ScmLWI2FJSWmIjb2Emzd7\n4c6dMNy82QuxsZeQlJRWp8e4evUqhg8fDk9PT7i7u+Ovf/0r3Nzc8Oeff+rvc+PGDTg4OODWrVvV\nPu78+fPh6+sLJycntGjRAvv27cPu3bsxd+5crFu3Dmq1GiEhIQCA2NhYBAYGwsnJCU2aNMGaNWsA\nACUlJfj73/8ODw8PBAYGYsGCBbCwsIBOpwMAhIWF4cMPP0S3bt3g4OCAK1euVDs+IiIiqphZj4Tt\n2ZOCevV6o+yXLHrj7Nl96NixeiNZx4+nID+/t347LAyoV6839u7dV63RsJKSEgwaNAjh4eFYvXo1\nLC0tceLECQDAqlWrMG/ePADAjz/+iPDwcLi5uVUrrqSkJCxYsAAnT56Et7c30tPTodVq0aRJE3zw\nwQdISUnBihUrAAAPHjzAO++8g5MnT6JZs2bIzs7WF3uLFy/Gjh07cObMGdjb22P48OGPjXStWrUK\nu3btQvPmzfXFGcmfEv6LNDXMiTwxL/KjlJyY9UhYcXH5D6+kpPoPW6cr/74aTfWOcfz4cWRlZeH/\n/b//Bzs7O9jY2KBbt24YN24cfvzxR/39Vq5c+UR9XJaWligqKsK5c+dQXFwMf39/NGnSBIA0bfho\nE6CFhQX++OMPFBQUwMvLC0FBQQCA9evX429/+xsaNmwIFxcXfPDBB2X2ValUmDBhAlq2bAkLCwtY\nWZl13U5ERFRnzPoT1dr64ZRa2es9PXV4443qHWPBAh1u3nz8ehub6o0IXb16FY0aNYKFRdmiLTQ0\nFHZ2dkhISIC3tzdSUlIQERFRvaAANG3aFF9++SViYmJw7tw59OvXD//+97/h4+Pz2H0dHBywbt06\nfPbZZ5g4cSK6deuGzz//HM2bN0dWVhb8/Pz09/X3939s/9K3k+lQSk+FKWFO5Il5kR+l5MSsR8LC\nwwNRVLS3zHVFRXvRu3dgnR3Dz88P6enpKCkpeey28ePHY9WqVVi5ciVGjRoFGxubascFAFFRUTh0\n6BDS0tKgUqnw/vvvAyi/cb5v376Ij4/H9evX0aJFC0yaNAkA4OPjg/T0dP39Sl9+iI34REREtc+s\ni7DmzRthwoSm8PTcB2fnBHh67sOECU2f6JuNNT1GaGgofHx8MG3aNOTn56OwsBC//vorAGDs2LHY\ntGkTVq9ejXHjxj3RY0tOTsa+fftQVFSEevXqwdbWFpaWlgAAb29vpKam6qcVb9y4ga1bt+LBgwew\ntraGg4OD/r6RkZH4+uuvkZGRgdzcXMybN++xoovrZZkmJfwXaWqYE3liXuRHKTkx6+lIQCqiarqc\nRE2OYWFhgbi4OLz99tvw9/eHSqXCiy++iK5du8LPzw/t2rXD5cuX0b1792od72GBVFRUhOnTp+P8\n+fOwtrZGt27dsGjRIgDAqFGjsGrVKri5uaFJkybYvn07vvjiC4wfPx4qlQohISH47rvvAACTJk1C\ncnIy2rZti/r16+O9997D/v37y/2dREREVHu4Yr6RTZw4EQ0bNsRHH31k7FAAAKmpqWjSpAm0Wu1j\nfWxKYqqvp9KU0lNhSpgTeWJe5MecclLZ54nZj4TJWWpqKjZt2oQzZ84YOxQiIiKqY8od6jCyGTNm\noHXr1pg6dSoaNfrfVOecOXOgVqsf+3n++efrLDZOP5oHc/kv0pwwJ/LEvMiPUnLC6UiicvD1RERE\ntYEn8CZSoISyp4ogGWBO5Il5kR+l5IRFGBEREZERcDqSqBx8PRERUW3gdCQRERGRzLAIIzJTSump\nMCXMiTwxL/KjlJywCDNhc+fO1Z8D0lSFhYVhyZIlxg6DiIiozrEnzEhiYmKQkpKClStXVuv+CQkJ\niI6OxtWrV2sthgkTJsDPzw8ff/xxrR3zSfXs2RPR0dF4+eWXK72fhYUFLl26hCZNmtRJXKb2eiIi\nInlS9Ir5SZeSsOe3PSgWxbBWWSO8fTiaN21e58egmjNEUaTVamFlZfZvAyIikiGzno5MupSE2P2x\nuOl1E3e87+Cm103E7o9F0qWkOj3G/Pnz4evrCycnJ7Ro0QI7d+7E3LlzsW7dOqjVaoSEhAAAli1b\nhqCgIDg5OSEwMFB/Qu4HDx5gwIAByMzMhFqthpOTE7KyshATE4Po6Gj97zl8+DC6du0KFxcX+Pv7\nY/ny5RXGtGjRIqxZswaffvop1Go1IiIi8Nlnn2HkyJFl7vf222/j3XffBSBNHU6fPh2hoaGoX78+\nhg4ditzcXP19//vf/+p/f3BwMA4cOFDt5wgALl26hB49esDZ2RkeHh6IiooCADz33HMAgLZt20Kt\nVmPDhg3IycnBoEGD4OLiAjc3Nzz33HP6Iu306dNo164dnJyc8MILL+CFF17AjBkzAEgjir6+vvj0\n00/h4+ODiRMnPlGMpkQpPRWmhDmRJ+ZFfpSSE7MeAtjz2x7Ua1YPCakJ/7vSGji79iw6du9YrWMc\nP3wc+b75QKq0HRYQhnrN6mHvqb3VGg1LSkrCggULcPLkSXh7eyM9PR1arRYffPABUlJSsGLFCv19\nvby8sGPHDjRu3BgHDx7EgAED0LFjR4SEhGD37t0YO3ZsmenI0qcXSktLw8CBA7F48WKMHDkSd+/e\nrXTqcvLkyTh69Cj8/Pz0Jw+/fv06YmJicPfuXdSvXx9arRbr1q3D7t279futXLkS8fHxCAgIwLhx\n4/D2229j5cqVyMjIwKBBg7Bq1Sr0798fe/bswYgRI3DhwgW4u7tX67meMWMG+vfvjwMHDkCj0eDk\nyZMAgIMHD8LCwgJnz57VT0dOnz4dfn5+yMnJASAVgCqVChqNBkOHDsWUKVPw5ptvYsuWLYiKisK0\nadP0vyc7Oxu5ublIT09HSUlJtWIjIiKqbWY9ElYsisu9vgTV/+DVQVfu9Rqdplr7W1paoqioCOfO\nnUNxcTH8/f3RpEkTCCEem14bOHAgGjduDEAa/enbty8OHToEoPypuNLXrVmzBn369MHo0aNhaWkJ\nV1dXtG3btsr4Sh/D29sbzz77LDZs2AAA2L17N9zd3fUjdSqVCuPGjUNQUBDs7e3x8ccfY/369dDp\ndFi1ahUGDhyI/v37AwDCw8PRoUMH7Ny5s1rPEwDY2NggNTUVGRkZsLGxQdeuXSu9b1ZWFlJTU2Fp\naYlu3boBkIoxrVaLd955B5aWlhgxYgQ6dixbcFtYWGD27NmwtraGra1tteMzNUo595opYU7kiXmR\nH6XkxKxHwqxV1gCk0avSPO098UbYG9U6xoLsBbjpdfOx620sbKq1f9OmTfHll18iJiYG586dQ79+\n/fDvf/+73Pvu2rULs2fPxsWLF6HT6ZCfn482bdpU6/dcvXq1VprWx48fj++//x6vvPIKVq1ahXHj\nxpW53c/PT3/Z398fxcXFyMnJQVpaGjZs2IC4uDj97VqtFr169ar27/70008xY8YMdOrUCS4uLnjv\nvffw0ksvlXvff/zjH4iJiUHfvn0BSCN777//PjIzM9GwYcMy9y19gnQA8PDwgI1N9fJHRERkKGY9\nEhbePhxFF4vKXFd0sQi92/Wu02NERUXh0KFDSEtLg0qlwvvvvw8Li7JPfVFREUaMGIGpU6fixo0b\nyM3NxcCBA/UjVaWnHsvj7++PlJSUasdU0TGHDBmCs2fP4s8//8SOHTvw4osvlrk9PT29zGVra2t4\neHjA398f0dHRyM3N1f/cv38fU6dOrXY8Xl5eWLRoETIyMrBw4UK88cYbuHz5crn3dXR0xGeffYaU\nlBRs27YN//73v7Fv3z40aNAAGRkZZe6blpZW5eM2R0rpqTAlzIk8MS/yo5ScmHUR1rxpc0zoOQGe\nNzzhfN0Znjc8MaHnhCf6ZmNNj5GcnIx9+/ahqKgI9erVg62tLSwtLeHl5YXU1FR9kaXRaKDRaODu\n7g4LCwvs2rUL8fHx+uN4eXnh1q1buHfvXrm/Z8yYMdizZw82bNgArVaLW7du4ffff680Ni8vr8eK\nHDs7O4wYMQJjxoxBaGgofH199bcJIbBq1SqcP38e+fn5mDlzJkaNGgWVSoWxY8ciLi4O8fHxKCkp\nQWFhIRISEh4riCqzYcMGXLt2DQDg7OwMlUqlL1a9vLzKFJk7duzApUuXIISAk5MTLC0tYWlpiS5d\nusDKygogt9nSAAAgAElEQVRff/01iouLsWnTJpw4caLaMRAREdUZYWIqClmuD+Xs2bOiU6dOQq1W\nC1dXVzF48GCRlZUlbt26Jbp37y5cXFxE+/bthRBCLFiwQHh5eQlnZ2cRHR0toqKixIwZM/THevnl\nl4Wbm5twcXERmZmZIiYmRkRHR+tvP3TokAgNDRVOTk7Cz89PrFixotLYLl68KIKDg4Wzs7MYNmxY\nmeOoVCoRGxtb5v5hYWFi+vTpolOnTsLJyUlERESIW7du6W8/duyY6NGjh3B1dRUeHh5i0KBBIj09\nvdIYwsLCxJIlS4QQQkydOlU0bNhQODo6isDAQLF48WL9/b7//nvh4+MjnJ2dxfr168UXX3whAgIC\nhIODg/D19RWffPKJ/r4nT54UISEhQq1Wi9GjR4vRo0eLDz/8UAghxP79+4Wfn1+lMQkh39cTERGZ\nlso+T7hYKz3m6tWraNGiBbKzs+Ho6Ki/vroLq8rNSy+9BF9f3ydalJavJyIiqg08gTdVm06nw+ef\nf46oqKgyBdhDpliYmGLMtUEpPRWmhDmRJ+ZFfpSSE7P+diQBrVq1KtNM/9CiRYv0i6E+9ODBA3h5\neaFx48Zl1gYr7Wma2h0dHcvdb/fu3fqlJQxJpVIpphmfiIhMB6cjicrB1xMREdUGTkcSERERyQyL\nMCIzpZSeClPCnMgT8yI/SskJizAiIiIiIzCbnjBXV1fk5uYaISIyRy4uLrh9+7axwyAiIhNXWU+Y\n2RRhRERERHLDxnwyKKXM3Zsa5kV+mBN5Yl7kRyk5YRFGREREZAScjiQiIiIyEE5HEhEREckMizCq\nMaXM3Zsa5kV+mBN5Yl7kRyk5YRFGREREZATsCSMiIiIyEPaEEREREckMizCqMaXM3Zsa5kV+mBN5\nYl7kIykpDQsW7MObb36JBQv2ISkpzdghGRSLMCIiIjK6pKQ0xMZeQkZGL2RkBOPmzV6Ijb1k1oWY\nwYqwwsJChIaGIjg4GEFBQZg+fToA4Pbt2+jTpw+eeeYZ9O3bF3fu3NHvM3fuXDRr1gwtWrRAfHy8\noUKjWhYWFmbsEKgczIv8MCfyxLzIw549KSgo6I2TJ4G7d8OQlwfUq9cbe/emGDs0gzFYEWZra4v9\n+/fjzJkzOHv2LPbv34/Dhw9j3rx56NOnD5KTk9G7d2/MmzcPAJCYmIh169YhMTERu3fvxhtvvAGd\nTmeo8IiIiEgmhACSky3w+++ARgM4OQE2NtJtGo35TtoZ9JHZ29sDADQaDUpKSuDi4oJt27Zh/Pjx\nAIDx48djy5YtAICtW7ciKioK1tbWCAgIQNOmTXH8+HFDhke1hP0U8sS8yA9zIk/Mi3EVFgLr1wMX\nL+ogBODvD9Svn6AvwmxszHdAxqBFmE6nQ3BwMLy8vNCzZ0+0atUK2dnZ8PLyAgB4eXkhOzsbAJCZ\nmQlfX1/9vr6+vsjIyDBkeERERGRE2dnA4sXA+fNAixaBeOaZvWjSBFCppNuLivaid+9A4wZpQFaG\nPLiFhQXOnDmDu3fvol+/fti/f3+Z21UqFVQPn+lyVHTbhAkTEBAQAABwdnZGcHCwfk7/4X803K7b\n7YfkEg+3wxAWFiareLgN/XVyiYfb3Dbm9g8/JODoUcDPLwxeXkC7dldw585N5OXtg7OzBVJT/412\n7RqgefPesoi3utsPL6empqIqdbZY68cffww7Ozv88MMPSEhIgLe3N7KystCzZ09cuHBB3xs2bdo0\nAED//v0xe/ZshIaGlg2Yi7USERGZLK0W2L0bOHlS2g4OBp5/HrC2Nm5chmKUxVpzcnL033wsKCjA\nL7/8gpCQEERERGD58uUAgOXLl2Po0KEAgIiICKxduxYajQZXrlzBxYsX0alTJ0OFR7WodPVP8sG8\nyA9zIk/MS925cwdYtkwqwCwtgcGDgSFDHi/AlJITg01HZmVlYfz48dDpdNDpdIiOjkbv3r0REhKC\nyMhILFmyBAEBAVi/fj0AICgoCJGRkQgKCoKVlRW+/fbbSqcqiYiIyHRcugT89BNQUAA4OwORkUCD\nBsaOyrh47kgiIiIyGJ0OOHgQOHBAWoqiWTNg+HDAzs7YkdWNyuoWgzbmExERkXLl50ujXykp0jce\ne/UCnn32f99+VDqD9YSRcihl7t7UMC/yw5zIE/NiGBkZwMKFUgFmbw+MHQs891z1CjCl5IQjYURE\nRFRrhJAa73fvBkpKAF9fYNQooH59Y0cmP+wJIyIiolqh0QDbtwNnz0rboaFA377SNyGVij1hRERE\nZFA5OdLph27ckJaciIgAWrc2dlTyxp4wqjGlzN2bGuZFfpgTeWJeai4xUTr90I0bgLs7MHlyzQow\npeSEI2FERET0VEpKgD17gKNHpe1WraQRsHr1jBuXqWBPGBERET2x+/eBDRuA9HTAwkLq/QoN5fIT\nj2JPGBEREdWa1FSpAHvwAFCrpdXv/fyMHZXpYU8Y1ZhS5u5NDfMiP8yJPDEv1ScEcPgwsHy5VIA1\nbgy89lrtF2BKyQlHwoiIiKhKhYXAli3AhQvS9rPPAj17SlOR9HTYE0ZERESVun5dWn7i9m3A1hYY\nNgxo3tzYUZkG9oQRERHRUzlzRlqAVasFfHyk/i8XF2NHZR44iEg1ppS5e1PDvMgPcyJPzEv5tFog\nLk6agtRqgXbtgJdfrpsCTCk54UgYERERlZGbK00/ZmUBVlbA888DISHGjsr8sCeMiIiI9JKTgU2b\npEZ8Fxdp+tHHx9hRmS72hBEREVGldDogIQE4eFDabt4cGDoUsLMzalhmjT1hVGNKmbs3NcyL/DAn\n8sS8SGt+rVolFWAqFRAeDrzwgvEKMKXkhCNhRERECnb1qrT6/b17gIMDMHKktAgrGR57woiIiBRI\nCOD4ceDnn6WpSD8/YNQowMnJ2JGZF/aEERERkZ5GA2zbBvz5p7TduTPQpw9gaWncuJSGPWFUY0qZ\nuzc1zIv8MCfypLS83LwJLF4sFWA2NtLoV//+8irAlJITjoQREREpxJ9/SiNgGg3g4QGMHg24uxs7\nKuViTxgREZGZKykB4uOBY8ek7datgcGDpZEwMiz2hBERESnUvXvStx+vXpWmHPv1Azp2lJaiIONi\nTxjVmFLm7k0N8yI/zIk8mXNeLl8GFi6UCjAnJ+Cll4BOneRfgJlzTkrjSBgREZGZEQI4fBjYt0+6\nHBgIDB8urQNG8sGeMCIiIjNSUABs3iydAxIAevSQfiw492UU7AkjIiJSgKwsYP16IDdXOuXQ8OFA\ns2bGjooqwrqYakwpc/emhnmRH+ZEnswlL6dOAUuWSAVYgwbAq6+abgFmLjmpCkfCiIiITFhxMbBz\nJ3D6tLTdoYO0+KoVP+Fljz1hREREJur2bWn68fp1qegaNAgIDjZ2VFQae8KIiIjMzIULwJYtQGEh\n4OoqrX7v5WXsqOhJsCeMakwpc/emhnmRH+ZEnkwtLzodsGcPsHatVIC1aAFMnmxeBZip5eRpcSSM\niIjIROTlAT/9BFy5Ii05ER4OdOki/8VXqXzsCSMiIjIB6enS6Yfu3wccHYGRI4GAAGNHRVVhTxgR\nEZGJEgL473+BX36RpiIbNZIKMLXa2JFRTbEnjGpMKXP3poZ5kR/mRJ7knJeiImn06+efpQKsa1dg\n3DjzL8DknJPaxJEwIiIiGbpxQ1p+IicHqFcPGDoUaNnS2FFRbWJPGBERkcycPQvExUkLsXp6SstP\nuLkZOyp6GuwJIyIiMgFaLRAfDxw/Lm23aSMtwGpjY9y4yDDYE0Y1ppS5e1PDvMgPcyJPcsnL3bvA\nsmVSAWZpKRVfw4YpswCTS04MjSNhRERERpaSIq3/lZ8P1K8PREYCDRsaOyoyNPaEERERGYkQwMGD\nQEKCdLlpU2D4cMDe3tiRUW1hTxgREZHM5OcDmzcDFy9KK9737Ak89xxXv1cS9oRRjSll7t7UMC/y\nw5zIkzHykpkJLFokFWB2dsCLLwI9erAAe0gp7xWOhBEREdURIYDffgN27QJKSqS+r8hIqQ+MlIc9\nYURERHWguBjYvh34/Xdpu2NHoF8/wIrDIWaNPWFERERGdOuWtPp9djZgbQ0MHiytAUbKxp4wqjGl\nzN2bGuZFfpgTeTJ0Xs6fl/q/srOlVe8nTWIBVhWlvFc4EkZERGQAOh2wZw/w66/SdlAQMGSIdB5I\nIoA9YURERLXu/n1g40YgLQ2wsAD69AE6d+a3H5WIPWFERER1JC0N2LAByMsD1Gpg1CjA39/YUZEc\nsSeMakwpc/emhnmRH+ZEnmorL0JIU4/Ll0sFWEAA8OqrLMCehlLeKxwJIyIiqqHCQmDrVqkJHwC6\ndwd69ZKmIokqYrCesKtXr2LcuHG4ceMGVCoVJk+ejLfffhsxMTH44Ycf4OHhAQCYM2cOBgwYAACY\nO3culi5dCktLS3z99dfo27fv4wGzJ4yIiGQkOxtYtw64fRuwtQWGDgVatDB2VCQXldUtBivCrl+/\njuvXryM4OBh5eXlo3749tmzZgvXr10OtVmPKlCll7p+YmIgxY8bgxIkTyMjIQHh4OJKTk2HxyL8R\nLMKIiEgufv9dWoC1uBjw8gJGjwZcXY0dFclJZXWLwQZKvb29ERwcDABwdHREy5YtkZGRAQDlBrN1\n61ZERUXB2toaAQEBaNq0KY4fP26o8KgWKWXu3tQwL/LDnMjT0+RFq5WKr82bpQIsOBh45RUWYLVF\nKe+VOpmtTk1NxenTp9G5c2cAwDfffIO2bdti4sSJuHPnDgAgMzMTvr6++n18fX31RRsREZFc3LkD\nLF0KnDwpnXIoIkJa/8va2tiRkakxeGN+Xl4eRo4cia+++gqOjo54/fXXMXPmTADAjBkz8N5772HJ\nkiXl7quqYEGVCRMmICAgAADg7OyM4OBghIWFAfhf9cztut1+SC7xcDsMYWFhsoqH29BfJ5d4uP3k\n29euARkZYSgoAHJyEtCzJ9CunXziM5ftMBP++/XwcmpqKqpi0MVai4uLMWjQIAwYMADvvvvuY7en\npqZi8ODB+OOPPzBv3jwAwLRp0wAA/fv3x+zZsxEaGlo2YPaEERFRHdPpgAMHgIMHpaUonnkGGDYM\nsLMzdmQkd0bpCRNCYOLEiQgKCipTgGVlZekvb968Ga1btwYAREREYO3atdBoNLhy5QouXryITp06\nGSo8qkWlq3+SD+ZFfpgTeaoqL/n5wOrVUhEGAL17A1FRLMAMSSnvFYNNRx45cgSrVq1CmzZtEBIS\nAkBajuLHH3/EmTNnoFKp0LhxYyxcuBAAEBQUhMjISAQFBcHKygrffvtthdORREREdeHaNWn1+7t3\nAXt7YORIoEkTY0dF5oLnjiQiInqEEFLj/e7dQEkJ4OsLREYCTk7GjoxMDc8dSUREVE0aDRAXB/zx\nh7QdGgr07QtYWho3LjI/BusJI+VQyty9qWFe5Ic5kafSecnJAX74QSrAbGyk6ccBA1iA1TWlvFc4\nEkZERAQgMRHYskUaCXN3l1a//78z7BEZBHvCiIhI0UpKgD17gKNHpe2//AUYPBioV8+4cZF5YE8Y\nERFROe7dAzZuBNLTAQsLoF8/oFMngF/Op7rAnjCqMaXM3Zsa5kV+mBN5uXIFWLgQOHgwAU5OwEsv\nSU34LMCMTynvFY6EERGRoggBHDkC7N0rXfb2Bl59FXBwMHZkpDTsCSMiIsUoLAQ2bwaSkqTt554D\nwsKkqUgiQ2BPGBERKd7168C6dUBuLmBrCwwfLp0DkshYWPtTjSll7t7UMC/yw5wYz+nT0vpfubmA\nj480/fiwAGNe5EcpOeFIGBERmS2tFti5Ezh1Stpu1w4YOBCw4qcfyQB7woiIyCzl5gLr1wNZWVLR\n9fzzQEiIsaMipWFPGBERKUpyMrBpk9SI7+IirX7v7W3sqIjKYk8Y1ZhS5u5NDfMiP8yJ4el00tIT\na9ZIBVjz5lL/V2UFGPMiP0rJCUfCiIjILDx4APz0E3D5srTgau/eQLduXHyV5Is9YUREZPKuXgU2\nbJBOQ+TgAIwcCTRubOyoiNgTRkREZkoI4Phx4OefpalIf3+pAHNyMnZkRFVjTxjVmFLm7k0N8yI/\nzEnt0mik6cddu6QCrEsXYPz4Jy/AmBf5UUpOOBJGREQm5+ZNafX7nBzAxgYYMgRo1crYURE9GfaE\nERGRSfnzT2DbNmkkzNMTiIwE3N2NHRVR+dgTRkREJq+kBIiPB44dk7ZbtwYGD5ZGwohMEXvCqMaU\nMndvapgX+WFOnt69e8CyZVIBZmkprX4/fHjtFGDMi/woJSccCSMiIlm7fBnYuBHIzwfq1wdGjQJ8\nfY0dFVHNsSeMiIhkSQjg0CFg/37pcmAgMGIEYG9v7MiIqo89YUREZFIKCoDNm6VzQAJAjx7SjwWb\naMiM8OVMNaaUuXtTw7zID3NSPZmZwMKFUgFmZwe8+CLQs6fhCjDmRX6UkhOOhBERkSwIAZw+Dezc\nCWi1QIMG0vITzs7GjozIMNgTRkRERldcDOzYAZw5I2136AD07w9YcaiATBx7woiISLZu3wbWrweu\nXwesrYFBg4C2bY0dFZHhsSeMakwpc/emhnmRH+bkcRcuSP1f168Drq7AK6/UfQHGvMiPUnLCkTAi\nIqpzOh2wdy9w5Ii03bKldP5HW1vjxkVUl9gTRkREdSovT1p8NTVV+sZjeDjQpQugUhk7MqLax54w\nIiKShfR0YMMG4P59wNFRWv2+USNjR0VkHOwJoxpTyty9qWFe5EfJORECOHoUiI2VCrBGjYBXX5VH\nAabkvMiVUnLCkTAiIjKooiJg61YgMVHa7toV6N1bOhE3kZKxJ4yIiAzmxg1g3Trg1i2gXj1g6FCp\nCZ9IKdgTRkREde7sWSAuTlqI1ctLWv3ezc3YURHJB3vCqMaUMndvapgX+VFKTrRaafX7TZukAqxt\nW2n9L7kWYErJiylRSk44EkZERLXm7l1p9fuMDKnna+BAoF07Lj9BVB72hBERUa24dEka/crPl066\nHRkpnYSbSMnYE0ZERAYjBHDggPQjBNC0KTB8OGBvb+zIiOSNPWFUY0qZuzc1zIv8mGNO8vOB1auB\nhw+tZ0/gxRdNqwAzx7yYOqXkhCNhRET0VDIypP6vu3elomvECCAw0NhREZkO9oQREdETEQL47Tdg\n1y6gpARo2FDq/6pf39iREckPe8KIiKhWaDTA9u3SGmAA0KkT0LcvYMVPE6Inxp4wqjGlzN2bGuZF\nfkw9J7duAT/8IBVg1tbS9OPAgaZfgJl6XsyRUnJi4m8dIiKqC+fPA1u2SOeBdHeXph89PY0dFZFp\nY08YERFVqKQE2LsX+PVXaTsoCBgyRDoPJBFVjT1hRET0xO7fBzZuBNLSAAsLqfcrNJSr3xPVFvaE\nUY0pZe7e1DAv8mNKOUlNBRYulAowtRqYMAHo3Nk8CzBTyotSKCUnHAkjIiI9IaSpx717AZ0OaNxY\nasB3dDR2ZETmhz1hREQEACgslJrvL1yQtrt3B3r1kqYiiejpsCeMiIgqlZ0NrFsH3L4N2NoCw4YB\nzZsbOyoi88b/b6jGlDJ3b2qYF/mRa07OnJHW/7p9G/D2BiZPVlYBJte8KJlScsKRMCIihdJqpVMP\n/fabtB0SIi2+am1t3LiIlMJgPWFXr17FuHHjcOPGDahUKkyePBlvv/02bt++jdGjRyMtLQ0BAQFY\nv349nJ2dAQBz587F0qVLYWlpia+//hp9+/Z9PGD2hBER1didO9LJtzMzpRXvBw4E2rUzdlRE5qey\nusVgRdj169dx/fp1BAcHIy8vD+3bt8eWLVuwbNkyuLu7Y+rUqZg/fz5yc3Mxb948JCYmYsyYMThx\n4gQyMjIQHh6O5ORkWDzSEcoijIioZi5eBDZtAgoKABcXafV7Hx9jR0VkniqrWwzWE+bt7Y3g4GAA\ngKOjI1q2bImMjAxs27YN48ePBwCMHz8eW7ZsAQBs3boVUVFRsLa2RkBAAJo2bYrjx48bKjyqRUqZ\nuzc1zIv8GDsnOh2wfz+werVUgD3zjNT/pfQCzNh5occpJSd10hOWmpqK06dPIzQ0FNnZ2fDy8gIA\neHl5ITs7GwCQmZmJzp076/fx9fVFRkZGXYRHRGT2HjyQRr9SUqQFV3v1kpagMMfFV4lMhcGLsLy8\nPIwYMQJfffUV1Gp1mdtUKhVUlfwFqOi2CRMmICAgAADg7OyM4OBghIWFAfhf9cztut1+SC7xcDsM\nYWFhsoqH29BfV9e/v2nTMKxfD5w9mwBbW2Dq1DA0aWL854Pb3K5oO8yE/349vJyamoqqGHSx1uLi\nYgwaNAgDBgzAu+++CwBo0aIFEhIS4O3tjaysLPTs2RMXLlzAvHnzAADTpk0DAPTv3x+zZ89GaGho\n2YDZE0ZEVC1CACdOAD//LJ2I288PGDUKcHIydmREymGUnjAhBCZOnIigoCB9AQYAERERWL58OQBg\n+fLlGDp0qP76tWvXQqPR4MqVK7h48SI6depkqPCoFpWu/kk+mBf5qcucaDTS9OPOnVIB1rmzdP5H\nFmCP43tFfpSSE4NNRx45cgSrVq1CmzZtEBISAkBagmLatGmIjIzEkiVL9EtUAEBQUBAiIyMRFBQE\nKysrfPvtt5VOVRIRUflycqTV72/eBGxsgIgI4C9/MXZURPQonjuSiMiMnDsHbN0qjYR5eEjLT3h4\nGDsqIuXiuSOJiMxcSQnwyy/Af/8rbf/lL9IImI2NceMioooZrCeMlEMpc/emhnmRH0Pl5N49IDZW\nKsAsLIABA4ARI1iAVRffK/KjlJxUORKWl5cHOzs7WFpaIikpCUlJSRgwYACseXIxIiKju3IF2LhR\nWgfMyUn69qOfn7GjIqLqqLInrF27djh8+DByc3PRrVs3dOzYETY2Nli9enVdxVgGe8KIiKTlJw4f\nBvbtky43aSKNfjk4GDsyIiqtRktUCCFgb2+PTZs24Y033sCGDRvw559/1nqQRERUPQUFwNq1wN69\nUgH23HPA2LEswIhMTbV6wo4ePYrVq1fj+eefBwDodDqDBkWmRSlz96aGeZGf2shJVhawaBGQlATY\n2QFjxkinILJgh+9T43tFfpSSkyp7wr788kvMnTsXw4YNQ6tWrZCSkoKePXvWRWxERFTK6dPAjh2A\nViuddDsyEnBxMXZURPS0uE4YEZHMFRdLK9+fPi1tt28vfQPSiosMEclejdYJO3HiBObMmYPU1FRo\ntVr9Ac+ePVu7URIR0WNyc6XV769fl4quQYOA4GBjR0VEtaHKLoIXX3wRL730En766SfExcUhLi4O\n27Ztq4vYyEQoZe7e1DAv8vOkOUlKAhYulAowV1fglVdYgBkC3yvyo5ScVDkS5uHhgYiIiLqIhYiI\nAOh0wP79wKFD0nbz5sCwYYCtrXHjIqLaVWVPWHx8PNatW4fw8HDY/N/yyyqVCsOHD6+TAB/FnjAi\nMmcPHkiLr165AqhUQO/eQLdu0mUiMj016glbvnw5kpKSoNVqYVHqO9DGKsKIiMxVejqwYQNw/z7g\n6AiMHAkEBBg7KiIylCpHwpo3b44LFy5AJZN/wzgSJj8JCQkICwszdhj0COZFfirKiRDAsWNAfLw0\nFenvL51+SK2u+xiViO8V+TGnnNRoJKxr165ITExEq1ataj0wIiKlKyoCtm0Dzp2Ttrt0AcLDAUtL\n48ZFRIZX5UhYixYtkJKSgsaNG6NevXrSTkZcooIjYURkLm7elJafyMkB6tUDhgwBgoKMHRUR1abK\n6pYqi7DU1NRyrw8wUqMCizAiMgd//AHExQEaDeDpKa1+7+5u7KiIqLbV6ATeAQEB5f4QPaSU9VxM\nDfMiPwkJCSgpkVa//+knqQBr00Za/4sFmPHwvSI/SskJT3pBRFRH8vKAZcuAa9eknq/+/YEOHbj8\nBJFS8dyRRER1ICVFGv3Kzwfq15emHxs2NHZURGRoNfp2JBERPT0hpJXv9++XLgcGAiNGAPb2xo6M\niIytyp6wn376Cc2aNYOTkxPUajXUajWcnJzqIjYyEUqZuzc1zIvxFRQAa9YA+/ZJ287OCXjxRRZg\ncsP3ivwoJSdVjoRNnToV27dvR8uWLesiHiIis5CZCaxfD9y5A9jZSaNf164BFlX+60tESlFlT1i3\nbt1w5MiRuoqnSuwJIyI5EwI4dUr6BmRJCdCggdT/5exs7MiIyBhq1BPWoUMHjB49GkOHDpXFCbyJ\niOSquBjYsQM4c0ba7tgR6NcPsGL3LRGVo8qB8bt378LOzg7x8fHYvn07tm/fjri4uLqIjUyEUubu\nTQ3zUrdu3QJ++EEqwKytgWHDgOefL1uAMSfyxLzIj1JyUuX/Z7GxsXUQBhGR6bpwAdi8WToPpJub\nNP3o5WXsqIhI7irsCZs/fz7ef/99vPXWW4/vpFLh66+/Nnhw5WFPGBHJhU4H7N0LPGybbdlSOv+j\nra1x4yIi+XiqnrCg/zuLbPv27aEqtZyzEKLMNhGREuXlARs3Aqmp0jcew8OBLl24+j0RVR9XzKca\nS0hIQFhYmLHDoEcwL4aTlgZs2CAVYo6OwKhRQKNGVe/HnMgT8yI/5pQTrphPRFQLhACOHgX27JGm\nIhs1kgowR0djR0ZEpogjYURE1VBUBGzZApw/L2136wb07s3FV4mochwJIyKqgexsafX7W7eAevWA\noUOlJnwiopqo8n+4pKQk9O7dG61atQIAnD17Fp988onBAyPToZT1XEwN81I7fv9dWv/r1i1p2YnJ\nk5++AGNO5Il5kR+l5KTKImzSpEmYM2eOfrX81q1b48cffzR4YERExqTVAtu3S+t/FRcDbdsCr7wi\nrQNGRFQbquwJ69ChA06ePImQkBCcPn0aABAcHIwzD8/LUcfYE0ZEhnbnjvTtx4wMwNISGDgQaNeO\ny08Q0ZOrUU+Yh4cHLl26pN/euHEjfHx8ai86IiIZuXQJ+OknoKBAOul2ZKR0Em4iotpW5XTkf/7z\nHzFBi0sAACAASURBVLz66qu4cOECGjRogC+++ALfffddXcRGJkIpc/emhnl5MjodkJAArF4tFWDN\nmgGvvlq7BRhzIk/Mi/woJSdVjoQFBgZi7969ePDgAXQ6HdRqdV3ERURUZ/LzgU2bpFEwlQro1Qt4\n9llOPxKRYVXZE5abm4sVK1YgNTUVWq1W2onnjiQiM5GRIS0/cfcuYG8PjBgBBAYaOyoiMhc16gkb\nOHAgunTpgjZt2sDCwoLnjiQisyAEcPIksHs3UFIC+PpKq9/Xr2/syIhIKaocCWvXrh1OnTpVV/FU\niSNh8mNO5/gyJ8xLxTQaafmJs2el7U6dgH79pG9CGhJzIk/Mi/yYU05qNBI2ZswYLFq0CIMHD0a9\nevX017u6utZehEREdSQnR5p+vHEDsLYGIiKA1q2NHRURKVGVI2H/+c9/8M9//hPOzs6w+L+TpKlU\nKly+fLlOAnwUR8KI6GklJgJbt0rngXR3l5af8PQ0dlREZM4qq1uqLMIaN26MEydOwN3d3SDBPSkW\nYUT0pEpKgD17gKNHpe1WraQRsFKD+0REBlFZ3VLlOmHNmjWDnZ1drQdF5kMp67mYGuZFcv8+sHy5\nVIBZWAD9+wMjRxqnAGNO5Il5kR+l5KTKnjB7e3sEBwejZ8+e+p4wYy5RQURUXampwMaNQF4eoFZL\n33709zd2VEREkiqnI2NjYx/fSaXC+PHjDRVTpTgdSURVEQI4cgTYu1e63LixNPrl4GDsyIhIaWrU\nEyY3LMKIqDKFhcCWLcCFC9L2s88CPXtKU5FERHXtqXrCRo0aBQBo3br1Yz9t2rQxTKRkkpQyd29q\nlJiX69eBRYukAszWFoiKAnr3lk8BpsScmALmRX6UkpMKe8K++uorAMD27dsfq+C4Yj4Ryc2ZM9IC\nrFot4O0tLT/B5QyJSM6qnI58//33MX/+/CqvqyucjiSi0rRaYNcu4LffpO2QEGDgQGkhViIiY6tR\nT1hISAhOnz5d5rrWrVvjjz/+qL0InwCLMCJ6KDdXWv0+KwuwspKKr3btjB0VEdH/PFVP2HfffYfW\nrVsjKSmpTD9YQEAAe8KoDKXM3Zsac89LcrLU/5WVBbi4ABMnyr8AM/ecmCrmRX6UkpMKi7AxY8Yg\nLi4OERER2L59O+Li4hAXF4fffvsNq1evrtbBX375ZXh5eaF1qROzxcTEwNfXFyEhIQgJCcGuXbv0\nt82dOxfNmjVDixYtEB8fX4OHRUTmSqcD9u0D1qwBCgqA5s2ByZMBHx9jR0ZE9GQMukTFoUOH4Ojo\niHHjxumnL2fPng21Wo0pU6aUuW9iYiLGjBmDEydOICMjA+Hh4UhOTtafr1IfMKcjiRTrwQPgp5+A\ny5cBlQro1Qvo3l26TEQkRzU6bVFNPPvss3BxcXns+vKC2bp1K6KiomBtbY2AgAA0bdoUx48fN2R4\nRGRCrl4FFi6UCjAHB2DcOGkNMBZgRGSqjLJ6zjfffIO2bdti4sSJuHPnDgAgMzMTvr6++vv4+voi\nIyPDGOHRE1LK3L2pMZe8CAEcOwYsWwbcuwf4+QGvviqtgm9qzCUn5oZ5kR+l5KTKc0fWttdffx0z\nZ84EAMyYMQPvvfcelixZUu59K1qPbMKECQgICAAAODs7Izg4GGFhYQD+lzhu1932mTNnZBUPt81n\n+5dfEvDrr4AQ0ra9fQICAgAnJ3nE96TbZ86ckVU83Ja2H5JLPNw27e2Hl1NTU1EVg5+2KDU1FYMH\nDy53SYvSt82bNw8AMG3aNABA//79MXv2bISGhpYNmD1hRIpw86a0/MTNm4CNDTBkCNCqlbGjIiJ6\nMkbrCStPVlaW/vLmzZv135yMiIjA2rVrodFocOXKFVy8eBGdOnWq6/CISAb+/BNYvFgqwDw8gEmT\nWIARkfkxaBEWFRWFrl27IikpCX5+fli6dCnef/99tGnTBm3btsWBAwfwxRdfAACCgoIQGRmJoKAg\nDBgwAN9+++3/b+/eg6K87/2Bv7mLiiCXBQWVOwi73hKviQaDl6aJd8FokzS1zS9NezJN26PJyZxO\nJ5mx4vScM6c5TU/O5MQxmZ7YRE28xMQYMKgx3pV0FxS5LSgiK1e577L7/f3xLRsRxQssz7P7vF8z\nnfHZBfzip5iP3+/neT98PJKbuHVLn9TBHetitwMHDgA7dwJWK2AwyAYsIkLplQ0Od6yJFrAu6qOV\nmrh0Jmz79u19Xlu/fv0dP/7111/H66+/7solEZFK3bgB7Ngh74L08QEWLwamT+fdj0TkuVw+EzbY\nOBNG5HnKy2X+V1sbMGqUfPj2TTdLExG5rf76liG/O5KIqIcQwDffyAR8IYD4eGDVKpkDRkTk6YZ8\nMJ88j1bO7t2N2uvS0QFs3w7k5ckG7LHHgGee8ewGTO010SrWRX20UhPuhBHRkKupkfETjY1AYCCw\nYgWQnKz0qoiIhhZnwohoSJ07B3z+OdDdDYwdK+e/QkKUXhURkWtwJoyIFGezyebr/Hl5/dBDwBNP\nAL78W4iINIozYTRgWjm7dzdqqktDA/Dee7IB8/UFli8HlizRXgOmpprQ91gX9dFKTTT2VyARDbWL\nF4Hdu4HOTiA0VB4/RkUpvSoiIuVxJoyIXMLhkNET33wjr1NT5Q7YsGHKrouIaChxJoyIhlRrqwxf\nraiQifcLFgBz5jD9nojoZpwJowHTytm9u1GqLlVVwP/8j2zARo4Efvxj4JFH2IAB/FlRK9ZFfbRS\nE+6EEdGgEAI4cQL46it5FDl+PJCVBQQFKb0yInIXxaXFyD2biwuFF1BYW4gFDy1ASmKK0styGc6E\nEdGAdXUBe/YARUXyes4cIDNTPoibiOheFJcWY2veVtyIvoEbXTeQFJaErpIuPD//ebduxDgTRkQu\nY7HI9Pu6OiAgAFi2DEhLU3pVROQu7A47ShtK8cfP/ojy0eVw1DkAAGODxmJE0gjknctz6yasP5wJ\nowHTytm9uxmKuhiNwLvvygZMpwP+3/9jA9Yf/qyoE+sy9BzCgYrGCuwt3ot/+/bfsN20HVdar8Ah\nHBgVMAojqkfA38cfAGB1WBVeretwJ4yI7lt3N3DwIHDqlLyeNAl46inA31/ZdRGRegkhUN1SDZPF\nhEJLIVqsLc73IkdEYmLYRPhH+yPQLxDmWjP8fPwAAP7envsXC2fCiOi+NDfL48fqajnz9cQT8hFE\nvPuRiG7H0maBsdYIk8WExs5G5+ujh42GIdIAvU4P3QgdikuLse3rbQhICnB+jKfPhLEJI6J7VlYm\n87/a24HgYJl+Hx2t9KqISG0aOxphsphgtBhhabM4Xw/yD0K6Lh0GnQFjg8bC65Z/vRWXFiPvXB6s\nDiv8vf2ROS3TrRswgE0YuVh+fj4yMjKUXgbdYjDrIgRw5AiQny9/nZgIrFwJDB8+KF9eM/izok6s\ny+Bo6WpB4fVCmCwmXLlxxfl6oG8g0iLSoNfpMSFkAry97j6O7kk14d2RRPTA2tuBTz8FSkrkkWNG\nBjBvHuDN23qINK/D1oELdRdgrDXC3GSGgGw2/H38kRKWAkOkAQmjE+Djzbya2+FOGBHd0dWrcv6r\nqQkIDARWrZK7YESkXVa7FcV1xTBZTChtKIVd2AEAPl4+SApLgl6nR3JYsvPuRq3jThgR3RchgLNn\ngS++AOx2OfeVlQWEhCi9MiJSQk+Wl9FiRHFdMWwOGwDAC16IHx0Pg86A1PBUBPoFKrxS98ImjAbM\nk87uPcmD1sVmAz77DPjuO3k9fTqweDHgy78tBow/K+rEutyeQzhgbjLDZDGh6HoROrs7ne/FjIqB\nQWdAui4dI/1HDvrvrZWa8K9VInKqr5fHj7W1gJ8fsGSJzAAjIm3oyfIy1hpReL0QrdZW53uRIyJh\niDQgPSIdowNHK7hKz8GZMCICAFy4AOzeLZ8DGRYGrFkjU/CJyPPdLcvLoDMgYkSEgit0X5wJI6I7\ncjiA3Fzg22/ldVqafP5jQED/n0dE7q2xoxFGi2y87ifLiwYPmzAaMK2c3bube6lLSwuwcydQWSkj\nJxYuBGbNYvq9q/BnRZ20VJeeLC9jrRHVLdXO1x8ky8uVtFITNmFEGlVZCezYAbS2AkFBwOrVwIQJ\nSq+KiAYbs7zUizNhRBojBHD8uDyCdDiA2FjZgI0c/BuciEghzPJSD86EEREAoLMT2LNHDuEDwKOP\nAo8/zvR7Ik/Q7ehGWUNZv1leEyMmYpjvMIVXSj3YhNGAaeXs3t3cWpfaWuCjj4CGBjl0v2IFkJqq\n3Pq0iD8r6uTOdekvy2vcqHHQ6/Quy/JyJXeuyf1gE0akAd99JwNYbTYgMlLGT4SGKr0qInoQ95Ll\npdfpETKMj7hQO86EEXmw7m7gwAHgzBl5PWUK8OSTMoiViNxLbWstTBZTnyyv0MBQ6HV6ZnmpFGfC\niDSoqUmm31+9Kh859MQTwLRpjJ8gcif9ZXnpdXrodXpmebkxNmE0YFo5u3cnJSXAH/+Yj7FjMxAS\nAmRnA2PHKr0q4s+KOqmtLnfL8jJEGjA+eLziWV6upLaauAqbMCIP4nAAhw8DR44AViuQlASsXAkE\nBiq9MiLqT4etA0XXi2CymJjlpSGcCSPyEO3twK5dQFmZPHKcPx+YO5fHj0Rq1ZPlZbQYUdZQdtss\nr5SwFPj5cIjTnXEmjMjDXbki0++bm4Hhw4FVq4CEBKVXRUS36nZ0o7ShFCaLiVlexCaMBk4rZ/dq\nJIS88/HAAcBuB2JigKwsIDiYdVEj1kSdXF0XT83yciWt/KywCSNyU1YrsG8fYDTK65kzgUWLAB+O\njBApjlledC84E0bkhurqZPyExQL4+wNLlwJ6vdKrIiJmedGtOBNG5EGKioDdu+VOWHi4TL+P4N/p\nRIphlhc9KDZhNGBaObtXmt0O5OYCx4/L6/R0uQMWEHD7j2dd1Ic1UacHqQuzvFxLKz8rbMKI3MCN\nG8DOnUBVFeDtDSxeDMyYwfgJoqHUX5ZXangq9Do9s7zovnAmjEjlKipkA9bWBgQFyfT7ceOUXhWR\nNtwty8ugMyA5LJlZXnRHnAkjckNCAMeOAXl58tdxccDq1cCIEUqvjMiz9ZfllTA6AXqdnlleNCjY\nhNGAaeXsfih1dgKffgoUF8vruXNlAr73fYyXsC7qw5qoU35+PuY9Ng/mJjOMtUZcqLvALC+FaeVn\nhU0YkcpcuwZ89BHQ2AgMGwasWAGkpCi9KiLPI4TAlRtXcPLKSZw5fqZXllfUyCjnnY3M8iJX4UwY\nkYqcPw/s3w90dwNjxsj5r9GjlV4VkWepba11Rko0dTY5Xw8NDIVBJ0NUmeVFg4UzYUQq190NfP45\ncO6cvJ42DXjiCcCPs75Eg6Kho8EZososL1ILNmE0YFo5u3eVxkaZfl9TA/j6Ak8+CUydOvCvy7qo\nD2sytO41y+vI4SOIToxWcKV0K638rLAJI1LQpUvAJ5/IQfzRo+Xx45gxSq+KyH31ZHkZLUZUNlUy\ny4tUjTNhRApwOICvvwaOHpXXKSlyAH8Y73gnum/M8iI140wYkYq0tQG7dgHl5TLxPjMTeOQRpt8T\n3Q9meZEnYBNGA6aVs/vBcPkysGOHfAzRiBEyfDUuzjW/F+uiPqzJwDiEo98sL0OkAWkRafed5cW6\nqI9WauLSJmz9+vXYv38/dDodjEYjAKChoQFr1qxBZWUlYmNj8fHHHyMkRGawbN68GVu3boWPjw/e\neustLFq0yJXLIxoyQgCnTgFffimPIseNA7KygFGjlF4Zkbr1ZHmZLCYUXi9klhd5FJfOhB09ehQj\nR47Ec88952zCNm7ciPDwcGzcuBFbtmxBY2MjcnJyUFRUhHXr1uH06dOorq7GggULcOnSJXjfEhHO\nmTByN1YrsHcvYDLJ69mzgQULAB/OBRPdlhACljYLs7zIIyg2EzZ37lyYzeZer+3duxeHDx8GAPz4\nxz9GRkYGcnJysGfPHqxduxZ+fn6IjY1FYmIiTp06hVmzZrlyiUQudf26TL+vqwP8/YFly4D0dKVX\nRaROPVlexlojrrdfd74+KmAU0iPSYYg0YMzIMczyIo8x5DNhtbW1iIyMBABERkaitrYWAHD16tVe\nDVdMTAyqq6tv+zVIXbRydn+/TCa5A2a1AhERwJo1QHj40P3+rIv6sCZ9tXS1OENUb83yStelQ6/T\nY0LwBJc2XqyL+milJooO5nt5efX7g3Wn955//nnExsYCAEJCQjBlyhRnsfLz8wGA10N4XVBQoKr1\nKH1ttwNWawZOngTM5nzExQEvvJABf391rI/Xyl0XFBSoaj1KXc94ZAYuXL+AHZ/vwLXWa4idEgsA\nuPL3KxgfPB5rn1qL+NHxOHrkKMxXzYjNiHXpenqo5c+H1+593fPrW08Cb8flOWFmsxlLlixxzoSl\npqYiPz8fUVFRqKmpwfz583Hx4kXk5OQAAF577TUAwA9+8AO88cYbmDlzZu8FcyaMVOzGDZl+f+WK\nnPlavBiYPp3xE0RWuxUX6y7CZDGhtKEUDuEAwCwv8nyqyglbunQp3n//fbz66qt4//33sXz5cufr\n69atw29+8xtUV1ejpKQEM2bMGOrlET2w8nJg506gvV3e9ZidDcTEKL0qIuX0ZHkZa424VH+JWV5E\nt3BpE7Z27VocPnwYdXV1GDduHN5880289tpryM7OxnvvveeMqACAtLQ0ZGdnIy0tDb6+vvjLX/7C\n4Us3kZ+f79yO1SIhZPL911/LXyckACtXyhwwJWm9LmqkhZq4KsvLlbRQF3ejlZq4tAnbvn37bV/P\nzc297euvv/46Xn/9dVcuiWhQdXQAn34qnwEJAI89Jv/n7a3suoiGErO8iB4Mnx1J9ICuXpXzX01N\nQGCg3P1KSlJ6VURDg1leRPdGVTNhRO5OCOD8eeDzz4HubmDsWDn/FcJ/5JMGMMuLaPCwCaMB08rZ\nPQDYbMD+/cA/kgbw8MPAD34A+KrwJ0lLdXEX7lqTO2V5DfcbjrSItCHJ8nIld62LJ9NKTVT4nw4i\ndWpokMeP164Bfn7AU08BkycrvSoi12i3tePC9QswWoyobKqEgDxO8ffxR2p4Kgw6A+JHx8PHm8/f\nInpQnAkjugcXLwK7dwOdnUBoqEy//8eDH4g8Rn9ZXslhydDr9MzyIrpPnAkjekAOB5CXBxw7Jq9T\nU4Hly4FhjDUiD3G3LC9DpAGp4anM8iJyATZhNGCeenbf2irDV81mGTmxYAEwe7b7pN97al3cmVpq\n4hAOVDRWwGQx3THLKz0iHSP8FQ67GyJqqQt9Tys1YRNGdBtVVcCOHUBLCzByJLB6NfCPx5USuaWe\nLC+jxYhCSyHabG3O95jlRaQMzoQR3UQI4MQJ4Kuv5FHkhAmyAQsKUnplRPdPCIHatlrnnY3M8iIa\nepwJI7oHXV3Anj1AUZG8njMHyMyUD+ImcifM8iJyD2zCaMA84ezeYgE++giorwcCAuTw/cSJSq9q\nYDyhLp7GlTXx9CwvV+LPivpopSZswkjz/v53YN8+GcSq08n4ibAwpVdFdHfM8iJyb5wJI83q7ga+\n/BI4fVpeT54MPPkk4O+v7LqI+nOnLC9fb18khSYxy4tIZTgTRnSL5maZfl9dLWe+nngCeOgh94mf\nIG25U5aXt5c3s7yI3BibMBowdzu7Ly0FPvkEaG8HgoPlw7ejo5Ve1eBzt7powf3UpL8sr/HB46HX\n6TWV5eVK/FlRH63UhE0YaYYQwOHD8n9CAImJwMqVwPDhSq+MSLpblpdBZ0C6Lp1ZXkQegjNhpAnt\n7XL3q7RUHjlmZADz5vH4kZTXX5ZXWGCYM0SVWV5E7okzYaRp1dVy/qu5We56rVwpd8GIlNTQ0QBj\nrREmi6lPlldP48UsLyLPxiaMBkytZ/dCAGfPAl98Adjtcu4rO1vOgWmBWuuiZfsP7kfoxFAYLUZc\nbbnqfL0ny8ugM2B88Hg2XkOMPyvqo5WasAkjj2SzAZ99Bnz3nbyePh1YvBjw5f/jaYi129pRdL0I\nJosJ+UX5iPWPBSCzvCaGT4Rep2eWF5FGcSaMPE59vUy/t1gAPz9gyRJg0iSlV0Va0tXdheL6Yhhr\njShrLGOWF5GGcSaMNOPCBWD3bvkcyLAwmX6v0ym9KtKCbkc3SupLYLKYmOVFRPeETRgNmBrO7u12\nIC8P+PZbeZ2WBixbJp8DqVVqqIun68nyMlqMuFh38a5ZXqyJOrEu6qOVmrAJI7fX0gLs3AlUVgLe\n3sDChcCsWYyfINdglhcRDRbOhJFbM5tlA9baCgQFAVlZwPjxSq+KPM29ZHkZIg0IHx6u4CqJSI04\nE0YeRwh59JiXBzgcQGwssHo1MHKk0isjT8IsLyJyJTZhNGBDfXbf2SmH7y9elNePPgo8/rg8iqTv\naWWmYrDd6LqBQkuhS7K8WBN1Yl3URys1YRNGbqW2VsZPNDQAw4YBy5cDqalKr4rc3c1ZXpVNlRCQ\nRwfM8iIiV+JMGLmNggJg/34ZxBoVJdPvQ0OVXhW5q7tleRkiDUgKTWKWFxENCGfCyK11d8tHD509\nK6+nTAGefFIGsRLdj/6yvBJDE6HX6ZnlRURDhk0YDZgrz+6bmuTDt69elY8c+uEPgalTGT9xL7Qy\nU3E3N2d5Xbh+AV32Lud744PHw6AzIC0izZnl5UqsiTqxLuqjlZqwCSPVKikBPvkE6OgAQkJk+v2Y\nMUqvityBEAKXb1yGyWK6Y5aXXqdH8DCNPM2diFSJM2GkOg4HcPiw/B8AJCcDK1YAgYHKrovUrSfL\nqydSormr2fleWGAYDJGy8WKWFxENJc6Ekdtobwd27QLKyuSR4+OPywgKHj/SnfRkeRktRtS11zlf\n78nyMugMiBoZxSwvIlIdNmE0YIN1dn/lipz/unEDGD5chq/Gxw98fVrlyTMVrszyciVProk7Y13U\nRys1YRNGihMCOH0a+PJL+SDucePk44dGjVJ6ZaQmzPIiIk/DmTBSlNUK7NsHGI3yeuZMYNEiwIf/\nHSUwy4uI3B9nwkiV6upk+v3164C/P7B0KaDXK70qUhqzvIhIK9iE0YA9yNl9YSGwZ4/cCQsPl/ET\nERGuWZ9WudNMhZqyvFzJnWqiJayL+milJmzCaEjZ7cBXXwEnTshrvR5YsgQICFB2XTT0+svyGjNy\nDPQ6PbO8iMijcSaMhsyNG8COHcDly4C3N7B4MTBjBuMntIRZXkSkNZwJI8VVVAA7dwJtbfKux6ws\neRckaUN9ez1MFhOzvIiIbsImjAasv7N7IYBjx4C8PPnr+Hhg1SpghHuP9rgFpWcqbnTdgMligsli\n6pPllR6RDr1Or8osL1dSuiZ0e6yL+milJmzCyGU6OoDdu4HiYnk9bx6QkSGPIskz9WR5GWuNqGqu\ncmZ5BfgEIDU8FYZIA+JC4pjlRUQEzoSRi9TUyPT7xkZg2DBg5Ur5DEjyPMzyIiK6M86E0ZA6fx7Y\nvx/o7gbGjAGys4HRo5VeFQ2mm7O8iuuL0e3oBsAsLyKi+8EmjAas5+zeZgM+/1w2YQAwbRrwwx8C\nvvx/mSIGe6bCIRwobyyHyWLy6CwvV9LKnIu7YV3URys14X8eaVA0Nsr0+2vXZNP15JPA1KlKr4oG\nilleRESuw5kwGrDiYuDTT4HOTnnsuGYNEBWl9KroQTHLi4ho8HAmjFzC4QC+/ho4elRep6QAK1bI\nQXxyP8zyIiIaWmzC6IG0tcnw1YoKwGzOx89+loFHHmH6vZrcy0wFs7yGllbmXNwN66I+WqkJmzC6\nb1VV8vFDLS0ydHXxYuDRR5VeFd0rZnkREakDZ8LongkBnDwJHDwojyLHj5ePHwoKUnpldDdd3V24\nWHcRJoupT5ZXclgy9Do9s7yIiFyAM2E0YF1dwN69QGGhvJ49G1iwAPDhZolq9WR5GS1GXKq/1CfL\ny6AzIDU8FQG+AQqvlIhIm9iE0V1dvy7jJ+rqAH9/YPlyIC3t+/e1cnbvDm7O8tp/cD+iJ0U735sQ\nPAF6nZ5ZXgriz4o6sS7qo5WaKNaExcbGYtSoUfDx8YGfnx9OnTqFhoYGrFmzBpWVlYiNjcXHH3+M\nkJAQpZZIAIxGYN8+wGoFdDqZfh/OZAJV6cnyMtYaUXS9yJnlZXPYmOVFRKRiis2ExcXF4ezZswgN\nDXW+tnHjRoSHh2Pjxo3YsmULGhsbkZOT0+vzOBM2NOx24MsvgVOn5LXBACxZInfCSHlCCFxrvea8\ns5FZXkRE6tRf36JoE3bmzBmEhYU5X0tNTcXhw4cRGRmJa9euISMjAxcvXuz1eWzCXK+5Wd79eOWK\nnPn6wQ+Ahx9m/IQa1LfXw2iRIarM8iIiUj9VNmHx8fEIDg6Gj48PXnzxRbzwwgsYPXo0GhsbAch/\n6YeGhjqvnQtmE+ZSZWXArl1AezsQHCzvfoyJ6f9ztHJ2r5QHzfJiXdSHNVEn1kV9PKkmqrw78tix\nYxgzZgyuX7+OhQsXIjU1tdf7Xl5ed/zX/PPPP4/Y2FgAQEhICKZMmeIsVn5+PgDw+j6vH3ssA0eP\nAlu3yuvMzAysWgWcOpWP0tL+P7+goEDx9Xva9YxHZqDoehF27N+B2rZaxE6JBQBU/70a44PHY+2S\ntYgLicPRI0dRcbUCEzImqGr9vL79dUFBgarWw2t53UMt6+G1e1/3/NpsNuNuVJET9sYbb2DkyJF4\n9913kZ+fj6ioKNTU1GD+/Pk8jhwCHR3AJ58AJSXyyHHePOCxxwBvb6VXpi3M8iIi8jyqO45sb2+H\n3W5HUFAQ2trasGjRIvz+979Hbm4uwsLC8OqrryInJwdNTU0czHexq1eBjz8GmpqAwEBg5UogKUnp\nVWlHf1le8aPjmeVFROTmVNeEVVRUYMWKFQCA7u5u/OhHP8K//Mu/oKGhAdnZ2aiqqrpjRAWbsMEh\nBHDuHPD55/JOyLFjZfzEgySC5OfnO7dj6e5uzvK6cP0CuuxdzvcGM8uLdVEf1kSdWBf18aSaElba\nYwAAGBNJREFUqG4mLC4uzjkbcbPQ0FDk5uYqsCJtsdmA/fuBnhI8/LC8A9KX0b0uc6csLwAYM3IM\nDJEGpEekM8uLiEhDVDETdj+4EzYwDQ0y/b62FvDzA556Cpg8WelVeab+srzCh4c7Q1SZ5UVE5LlU\ntxNGyrh4Efj0U/kcyNBQYM0aIDJS6VV5njtleQUHBDsbL2Z5ERERmzANcDiAvDzg2DF5PXEisGwZ\nMGzY4Hx9Tzq7f1DNnc0ovF4IY60RNa01ztdH+I1AWkQaDJEGjBs1bkgbL9ZFfVgTdWJd1EcrNWET\n5uFaW4GdOwGzWUZOLFgAzJ7N9PvB0G5rR6GlECaLCZXNlc7XA3wCMDFiIvQ6PeJHx8Pbi1kfRETU\nF2fCPFhlpXz8UGsrMHKkTL+fMEHpVbm3niwvo8WI8sbyPlleBp0BSWFJ8PXmv2+IiIgzYZojBHD8\nOJCbK48iJ0wAVq8GgoKUXpl76i/LKzE0kVleRET0QNiEeZiuLmD3buDCBXn9yCNAZqZr0+898ex+\nqLK8XMkT6+LuWBN1Yl3URys1YRPmQWprZfp9fT0QEAAsXy6H8One3JzlVXi9EO22dud7zPIiIqLB\nxpkwD/H3vwP79skg1shImX4fFqb0qtTvXrK8DDoDwobzD5OIiO4fZ8I8WHc38OWXwOnT8nryZBnA\n6sdnPPeLWV5ERKQ0NmFurKlJ3v1YXQ34+AA//CEwbdrQx0+4y9m9GrO8XMld6qIlrIk6sS7qo5Wa\nsAlzU6WlwK5dQEeHfOh2drZ8CDf11mZtQ9H1ImZ5ERGR6nAmzM04HMCRI8DhwzKKIikJWLECGD5c\n6ZWpB7O8iIhILTgT5iHa24FPPpG7YF5ewPz5wLx5TL8HZJbXpfpLMFlMfbK8kkKToNfpmeVFRESq\nwibMTVRXy/iJ5ma567VqFZCQoPSqJKXO7nuyvIy1Rlysu9gny8sQaUBaRBqG+2lzm1ArMxXuhDVR\nJ9ZFfbRSEzZhKicEcOYMcOAAYLcD0dFy/itYo1FVQghUNVfBZDHdMctLr9NjVMAoBVdJRER0d5wJ\nUzGrFfjsM5kBBgAzZgCLFgG+Gmude7K8jBYjCi2FzPIiIiK3wZkwN1RXJ48fLRaZ+bV0KWAwKL2q\noVXXXucMUWWWFxEReRo2YSpUVATs2SOfAxkeLo8fdTqlV3Vng3l2r7UsL1fSykyFO2FN1Il1UR+t\n1IRNmIrY7UBuLnD8uLxOT5c7YAEefkMfs7yIiEiLOBOmEi0tMv2+qgrw9pazXzNnem78BLO8iIhI\nCzgTpnJmM7BzJ9DaCgQFAVlZwPjxSq9q8NnsNpQ0lDDLi4iICGzCFFFcXInc3DJYrd64fNkBmy0B\nYWETEBcn879GjlR6hfenv7N7u8OOiqYKZnkpQCszFe6ENVEn1kV9tFITNmFDrLi4Etu2lcLHJxMX\nL8q7ILu78/DTnwLPPjsB3h4w9tRfltfYoLHOOxuZ5UVERFrGmbAh9vbbh1BW9jguXJAP3/b1BVJT\ngbS0Q/jFLx5XenkP7G5ZXgadDFFllhcREWkJZ8JUorsbMJm8ceGCvB45Ut4BGRgIWK3uuQXWk+Vl\nrDWivqPe+XpPlpch0oDIEZGMlCAiIroFm7AhcuUKsHs3UFkp7wIcNw6IjQV8fOT7/v4O5RZ3n5o7\nm50hqjWtNTAXmBE7JRYj/EYgXZcOvU7PLC8V0MpMhTthTdSJdVEfrdSETZiL2WzA11/L7C8hgGnT\nEtDYmIeIiEznx3R15SEzM1HBVd5dT5aX0WJEVXOV8/UAnwAkhiZi7aS1iBsdxywvIiKie8SZMBe6\nfFkm39fVybyvOXOAjAygvLwSeXny7kh/fwcyMxOQkjJB6eX20dXdhQt1F2CymPpkeaWEpUCv0zPL\ni4iIqB/99S1swlzAZgMOHQJOnJC7XxERwLJlQEyM0iu7u/6yvBJGJzDLi4iI6D5wMH8IVVXJ3a/6\nern79eijcvfLV8V/0nfK8vKC1z1leWnl7N7dsC7qw5qoE+uiPlqpiYpbA/diswF5ecDJk9/vfi1f\nDkRHK72y22OWFxERkbJ4HDkIKivl7ldDg3zu4yOPAI89pr7dr5uzvEwWE2503XC+xywvIiKiwcfj\nSBexWuXsV8/ul04nd7/GjlV6Zb0xy4uIiEh92IQ9oFt3v+bOBebNU8/u161ZXj1ckeWllbN7d8O6\nqA9rok6si/popSYqaRnch9X6/ewXAERGyjsf1bD71V+W18SIiTDoDMzyIiIiUgnOhN0Hs1nufjU2\n9t796km9VwKzvIiIiNSLM2EDZLUCubnAqVPyOipK7n6NGaPMenqyvIy1RpQ0lPTK8koKTYIh0oCU\nsBRmeREREakYm7C7qKiQu19NTXL3a948uQM21Ltfdocd5Y3lMFlMfbK8YkNiodfp+83yciWtnN27\nG9ZFfVgTdWJd1EcrNWETdgddXXL36/RpeR0VJe98jIoaujX0ZHkZLUYUXS/qk+Vl0BmQrktnlhcR\nEZEb4kzYbZSXA3v3yt0vHx+5+/Xoo0Oz+yWEQE1rjfPORmZ5ERERuS/OhN2jri7gq6+AM2fk9Zgx\ncvcrMnJwf5/i0mLkns2FTdjg5+WHBQ8tQNjYMBhrZYgqs7yIiIg8H3fC/qGsTO5+NTfLHa/HHpPJ\n94O9+1VcWoxtX29DQFIAOrs7YWmz4Op3V5GYmIjwseEAXJPl5UpaObt3N6yL+rAm6sS6qI8n1YQ7\nYf3o6gIOHgTOnpXXY8fKOx8He/cLkEeNnx7/FLW6WtTX1KO5q1m+MR6oMldhwbQFzPIiIiLSCE3v\nhJWWAvv2fb/7lZEhd7+8B7H/sdltMDeZUdJQgkv1l3Ag9wA6YzoByEiJsMAw6EboEN8cj9+u++3g\n/cZERESkOO6E3aKzU+5+nTsnr6Oj5e6XTjc4X7+5sxmX6i+hpKEEFY0VsDlszveG+QxD8IhghA0P\nQ2hgqDNENbAtcHB+cyIiInILmmvCSkrk7teNG3L3a/58YM6cge1+OYQDl5svO3e7LG2WXu+PGTkG\nyWHJSApLQkt0Cz7I/wABEd8HqXaVdCFzfuaDL0BhnnR270lYF/VhTdSJdVEfrdREM01YZyfw5ZfA\n+fPyOjpa3vkYEfFgX6/d1o7ShlJcqr+EsoYydHR3ON/z9/FHwugEJIUlISk0CUEBQd9/4ijgea/n\nkXcuD1aHFf7e/sicn4mUxJQBfHdERETkbjQxE3bpktz9amkBfH3l7tfs2fe3+yWEwLXWayhpKEFJ\nfQmu3LgCge/XERYY5tztGh88ns9qJCIiIu3OhHV0yN2vggJ5HRMjd7/Cw+/t8612K8oby+V8V30J\nWqwtzvd8vHwQGxKLpLAkJIclIzQw1AXfAREREXkqj23Cbt39evxxYNasu+9+NXQ0OJsuc5MZdmF3\nvhfkH+RsuuJHx8Pfx9/F34V70MrZvbthXdSHNVEn1kV9tFITj2vCOjqAAweA776T1+PGyTsf77T7\nZXfYUdlc6Wy8bk6r94IXxo0a55ztihoZpfrgVCIiInIPHjUTVlwsd79aW+XuV2YmMHNm392vlq4W\n52xXWWMZrHar871hvsOQGJqI5LBkJIYmYrjfcFd+O0REROTBPHYmrLi4Erm5ZWhr80ZJiQMBAQkI\nD5+A8ePl7lfYP55xLYRAdUs1SuplhERNa02vrxM5ItK52zUueBzT6omIiMjl3LYJKy6uxLZtpbhx\nIxMlJYDVCjgcefjFL4Ds7AmwOjpRaCnDpfpLKG0oRZutzfm5ft5+iBsdJ+9mDE1C8LBgBb8T96eV\ns3t3w7qoD2uiTqyL+milJqprwg4cOIBXXnkFdrsdP/vZz/Dqq6/2+Zi33z6Eysp6fGeahPKmtyG8\nbQj098Wk1Kk4XbsHHd8F4fKNy3AIh/NzQoaFOJuu2JBY+Pn4DeW35dEKCgo08cPiblgX9WFN1Il1\nUR+t1ERVTZjdbsc//dM/ITc3F9HR0Zg+fTqWLl2KiRMn9vq4X7/zEnxrx2FU8kT46gUCQhrQPrwB\nR8v/hvHV4QhqngJvL2/EhsQ6G6/w4eEcqneRpqYmpZdAt8G6qA9rok6si/popSaqasJOnTqFxMRE\nxMbGAgCefvpp7Nmzp08TZvthI2yHy2GNu4SxY+Jh/0dv5RsfCFyzISstCwmhCRjmO2yIvwMiIiKi\ne6OqJqy6uhrjxo1zXsfExODkyZN9P9DHCiR6w26/hkCvqRiGEAxHGHzsdZg7MRbpuvQhXDWZzWal\nl0C3wbqoD2uiTqyL+milJqqKqNi1axcOHDiAd999FwDw17/+FSdPnsR//dd/OT/GK8QXaLbf6UsQ\nERERqcbkyZNR0PPonluoaicsOjoaly9fdl5fvnwZMTExvT5GNHUP9bKIiIiIBp2qArEefvhhlJSU\nwGw2w2q14qOPPsLSpUuVXhYRERHRoFPVTpivry/+/Oc/Y/HixbDb7fjpT3/aZyifiIiIyBOoaiaM\niIiISCtUdRzZnwMHDiA1NRVJSUnYsmWL0svxCJcvX8b8+fORnp4OvV6Pt956CwDQ0NCAhQsXIjk5\nGYsWLeqV17J582YkJSUhNTUVBw8edL5+9uxZGAwGJCUl4Ve/+pXz9a6uLqxZswZJSUmYNWsWKisr\nne+9//77SE5ORnJyMj744IMh+I7dh91ux9SpU7FkyRIArIkaNDU1YfXq1Zg4cSLS0tJw8uRJ1kVh\nmzdvRnp6OgwGA9atW4euri7WRAHr169HZGQkDAaD8zWl61BRUYGZM2ciKSkJTz/9NGw2m6u+/YER\nbqC7u1skJCSIiooKYbVaxeTJk0VRUZHSy3J7NTU14vz580IIIVpaWkRycrIoKioSGzZsEFu2bBFC\nCJGTkyNeffVVIYQQhYWFYvLkycJqtYqKigqRkJAgHA6HEEKI6dOni5MnTwohhHjiiSfEF198IYQQ\n4u233xYvvfSSEEKIv/3tb2LNmjVCCCHq6+tFfHy8aGxsFI2Njc5fk/Tv//7vYt26dWLJkiVCCMGa\nqMBzzz0n3nvvPSGEEDabTTQ1NbEuCqqoqBBxcXGis7NTCCFEdna22LZtG2uigCNHjohz584JvV7v\nfE2pOjQ1NQkhhMjKyhIfffSREEKIn//85+K///u/Xf3H8EDcogn79ttvxeLFi53XmzdvFps3b1Zw\nRZ5p2bJl4quvvhIpKSni2rVrQgjZqKWkpAghhPjDH/4gcnJynB+/ePFicfz4cXH16lWRmprqfH37\n9u3ixRdfdH7MiRMnhBDyP1zh4eFCCCE+/PBD8fOf/9z5OS+++KLYvn27a79BN3H58mWRmZkpDh06\nJJ566ikhhGBNFNbU1CTi4uL6vM66KKe+vl4kJyeLhoYGYbPZxFNPPSUOHjzImiikoqKiVxOmZB0c\nDocIDw8XdrtdCCHE8ePHe/UQauIWx5G3C3Gtrq5WcEWex2w24/z585g5cyZqa2sRGRkJAIiMjERt\nbS0A4OrVq70iQ3rqcOvr0dHRzvrcXDtfX18EBwejvr7+jl+LgF//+tf44x//CG/v7388WRNlVVRU\nICIiAj/5yU8wbdo0vPDCC2hra2NdFBQaGorf/va3GD9+PMaOHYuQkBAsXLiQNVEJJevQ0NCAkJAQ\n59+hN38ttXGLJozPfHSt1tZWrFq1Cn/6058QFBTU6z0vLy/++Q+hzz77DDqdDlOnToW4wz0zrMnQ\n6+7uxrlz5/CLX/wC586dw4gRI5CTk9PrY1iXoVVWVob//M//hNlsxtWrV9Ha2oq//vWvvT6GNVGH\noayDu9XbLZqwewlxpQdjs9mwatUqPPvss1i+fDkA+a+Wa9euAQBqamqg0+kA9K3DlStXEBMTg+jo\naFy5cqXP6z2fU1VVBUD+h6y5uRlhYWGs6R18++232Lt3L+Li4rB27VocOnQIzz77LGuisJiYGMTE\nxGD69OkAgNWrV+PcuXOIiopiXRRy5swZzJkzB2FhYfD19cXKlStx/Phx1kQllPo7Kzo6GqGhoWhq\naoLD4XB+rejoaNd+ww9K6fPQe2Gz2UR8fLyoqKgQXV1dHMwfJA6HQzz77LPilVde6fX6hg0bnGf2\nmzdv7jNQ2dXVJcrLy0V8fLxzoHLGjBnixIkTwuFw9Bmo7Dmz3759e6+Byri4ONHY2CgaGhqcv6bv\n5efnO2fCWBPlzZ07VxQXFwshhPj9738vNmzYwLooqKCgQKSnp4v29nbhcDjEc889J/785z+zJgq5\ndSZM6TpkZWWJv/3tb0IIOSvGwfwB+vzzz0VycrJISEgQf/jDH5Rejkc4evSo8PLyEpMnTxZTpkwR\nU6ZMEV988YWor68XmZmZIikpSSxcuLDXXy6bNm0SCQkJIiUlRRw4cMD5+pkzZ4RerxcJCQni5Zdf\ndr7e2dkpsrKyRGJiopg5c6aoqKhwvrd161aRmJgoEhMTxbZt24bke3Yn+fn5zrsjWRPlFRQUiIcf\nflhMmjRJrFixQjQ1NbEuCtuyZYtIS0sTer1ePPfcc8JqtbImCnj66afFmDFjhJ+fn4iJiRFbt25V\nvA7l5eVixowZIjExUWRnZwur1eraP4QHxLBWIiIiIgW4xUwYERERkadhE0ZERESkADZhRERERApg\nE0ZERESkADZhRERERApgE0ZERESkADZhRKQpGRkZOHv27IC+xr59+7Bly5ZBWhERaZWv0gsgIhpK\ng/EcuyVLlmDJkiWDtCIi0iruhBGRotra2vDkk09iypQpMBgM2LFjBwDgzTffxIwZM2AwGPDiiy86\nPz4jIwO/+c1vMH36dEycOBGnT5/GihUrkJycjN/97ncAALPZjNTUVDzzzDNIS0tDVlYWOjo6+vze\nBw8exJw5c/DQQw8hOzsbbW1tfT7mrbfeQnp6OiZPnox169YBALZt24aXX34ZADBlyhRMnToVU6dO\nxfDhw3H06FG0tbVh/fr1mDlzJqZNm4a9e/f2+br5+fnIyMhAVlYWJk6ciGeeeWbgf5hE5FbYhBGR\nog4cOIDo6GgUFBTAaDRi8eLFAICXX34Zp06dgtFoREdHBz777DMAcicrICAAp0+fxksvvYRly5bh\nnXfegclkwrZt29DY2AgAuHTpEn75y1+iqKgIo0aNwl/+8pdev29dXR02bdqEvLw8nD17Fg899BD+\n4z/+o8/6tmzZgoKCAnz33Xd45513nGvoUVBQgPPnz+PNN9/E9OnTMXv2bGzatAmZmZk4efIkDh06\nhA0bNqC9vb3P1y4oKMCf/vQnFBUVoby8HMeOHRucP1QicgtswohIUZMmTcJXX32F1157Dd988w1G\njRoFADh06BBmzZqFSZMm4dChQygqKnJ+ztKlSwEAer0eer0ekZGR8Pf3R3x8PC5fvgwAGDduHGbP\nng0AeOaZZ/DNN984P18IgRMnTqCoqAhz5szB1KlT8cEHH6Cqquq261u3bh3+7//+Dz4+Prf9HkpK\nSrBx40Z8/PHH8PX1xcGDB5GTk4OpU6di/vz56Orqcq7rZjNmzMDYsWPh5eWFKVOmwGw2P9gfIhG5\nJc6EEZGikpKScP78eezfvx//+q//iszMTGzcuBG//OUvcfbsWURHR+ONN95AZ2en83MCAgIAAN7e\n3s5f91x3d3cD6L1bJYS47RzYwoUL8eGHH/a7vv379+PIkSPYt28fNm3aBKPRiJsfudva2oo1a9bg\nf//3fxEZGel8/ZNPPkFSUlK/X/vmtfv4+DjXTkTawJ0wIlJUTU0Nhg0bhh/96Ef453/+Z5w/f97Z\ncIWFhaG1tdU5J3Y/qqqqcOLECQDAhx9+iLlz5zrf8/LywqxZs3Ds2DGUlZUBkLNpJSUlvb6GEAJV\nVVXIyMhATk4Ompub0dra2utj1q9fj5/85Cd45JFHnK8tXrwYb731lvP6/Pnz971+IvJ83AkjIkUZ\njUZs2LAB3t7e8PPzwzvvvIPg4GC88MIL0Ov1iIqKwsyZM2/7uf3d6ZiSkoK3334b69evR3p6Ol56\n6aVe74eHh2Pbtm1Yu3Yturq6AACbNm3qtXtlt9vx7LPPorm5GUII/OpXv0JwcLDz962qqsKuXbtQ\nUlKCrVu3AgDee+89/O53v8Mrr7yCSZMmweFwID4+vs9w/u3WPtC7NonIvXiJm/fViYg8gNlsxpIl\nS2A0GpVeChHRHfE4kog8EneViEjtuBNGREREpADuhBEREREpgE0YERERkQLYhBEREREpgE0YERER\nkQLYhBEREREp4P8DGaETtWbn1E4AAAAASUVORK5CYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10eea0790>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 59
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"The improvement is pretty significant when static type declarations are used. One more experiment to see by how much we could improve our \"classic least squares\" code via Cython compared to the initial Python implementation.\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"x = [x_i*random.randrange(8,12)/10 for x_i in range(500)]\n",
|
|
"y = [y_i*random.randrange(8,12)/10 for y_i in range(100,600)]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 60
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"funcs = ['classic_lstsqr', 'cy_lstsqr', 'static_type_lstsqr', \n",
|
|
" 'lin_lstsqr_mat', 'numpy_lstsqr', 'scipy_lstsqr']\n",
|
|
"labels = ['classic approach','classic approach (cython)', \n",
|
|
" 'classic approach (cython + type decl.)',\n",
|
|
" 'matrix approach', 'numpy function', 'scipy function']\n",
|
|
"\n",
|
|
"times = [timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000)\n",
|
|
" for f in funcs]\n",
|
|
"\n",
|
|
"times_rel = [times[0]/times[i+1] for i in range(len(times[1:]))]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 61
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"#%pylab inline\n",
|
|
"#import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"x_pos = np.arange(len(funcs[1:]))\n",
|
|
"plt.bar(x_pos, times_rel, align='center', alpha=0.5, color=\"green\")\n",
|
|
"plt.xticks(x_pos, labels[1:], rotation=90)\n",
|
|
"plt.ylabel('relative performance gain')\n",
|
|
"plt.title('Performance gain compared to the classic least square implementation')\n",
|
|
"plt.grid()\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAbwAAAG/CAYAAAAjJGJxAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl8Dff3P/DXJGLLLhFJSHIRSgiJKLEmqb3WWoLakqBo\naX3ThSoV9aH0Ux+EVmk1UdUWpYSiisYeEhVbKrFdSyQRImSP3Lx/f+SXaa5ESNw7c+d9z/PxyOOR\nu82cc+/cOXfmzLxHYIwxEEIIIZwzkTsAQgghRApU8AghhBgFKniEEEKMAhU8QgghRoEKHiGEEKNA\nBY8QQohRkLTgpaWloXv37rCyssKHH34o5awV6fXXX8fGjRvlDsNgqVQqHDx4ULL5mZiY4Pr163qd\nR1BQEObNm6e36VtaWkKtVlfpNdHR0XBxcdFPQJxr3bo1jhw5ovPpqtVqmJiYoLi4WOfTltu0adPw\nn//8Ry/TrvG8J6hUKty7dw+mpqYwNzdHv379sHr1apibm1d5ZuvWrYODgwMeP35crWCNzZ49e+QO\nwaAJggBBECp8LCgoCC4uLli4cGG1pu3v749x48Zh4sSJLxNilVWWky5kZWXpbdov42U/L0N18eJF\nuUOQVFU/x8jISKxfvx5Hjx4V71uzZo2+wnv+Fp4gCNi9ezeysrLw999/Iy4ursrVlzGG4uJi3Lx5\nEy1btqxWoEVFRdV6HVEGQ/t89Vl0nofGgjBMhraMkmpgz6FSqdjBgwfF2x988AEbMGAAY4yxkydP\nsk6dOjEbGxvWtm1bFh0dLT7Pz8+PffLJJ6xLly6sTp06bOzYsczMzIzVrFmTWVhYsIMHD7KCggL2\n3nvvMWdnZ+bs7MxmzpzJCgoKGGOM/fXXX6xhw4Zs6dKlzNHRkY0bN46FhYWx4cOHs7FjxzJLS0vm\n6enJkpKS2OLFi5mDgwNzdXVl+/fvF2P4/vvvWcuWLZmlpSVr0qQJW7t2rfhY6fSXLVvGHBwcmJOT\nE4uIiBAfz83NZaGhoczNzY1ZW1uzrl27sry8vOfm/bQzZ84wLy8vZmlpyUaMGMECAwPZ3LlzGWOM\nZWRksP79+7P69eszW1tbNmDAAHbnzh2t9/C7775jjDEWERHBunTpwj744ANma2vLGjduzPbu3fvM\n+d66dYu98cYbrH79+szOzo5Nnz6dMcaYRqNhCxcuZG5ubszBwYGNHz+ePXr0iDHG2I0bN5ggCCwi\nIoK5uLiwevXqsTVr1rDTp08zT09PZmNjI06nNKbOnTuz6dOnM2tra9aiRQutZeVF3v/Sz3f8+PGs\nuLiYff7556xp06bMzs6OBQYGsoyMDPE1P/zwA3N1dWV2dnZs0aJF5ZbNUmvXrtVa1gYNGsQYYywh\nIYH5+fkxGxsb1qpVKxYVFVXhezdnzhxmamrKateuzSwsLNiMGTMYY4wJgsC++eYb1qxZM2ZjY8Pe\neecdrdetX7+etWzZktna2rI+ffqwmzdvPvPzOXr0qLgMubi4sA0bNjDGGAsKCnrh5SMiIoI1adKE\nWVpassaNG7NNmzYxxhi7cuUK6969O7O2tmb29vZs5MiR4msEQWDXrl1jjFW+jJf1119/sUaNGom3\nk5OT2dChQ1n9+vVZ48aNWXh4uPjYqVOnmK+vL7OxsWFOTk5s+vTprLCwUHx85syZzMHBgVlZWTFP\nT0928eLFZ35eT6votYwxdv/+fTZw4EBmZWXFOnTowObOncu6du3KGPt3mdZoNOJ0yn6vrl69ygIC\nApidnR2zt7dnY8aMYZmZmeJz3dzc2NKlS5mnpyerXbs202g0Vfr+u7m5icvo/Pnzq7T+8vPzY7Nn\nz2YdOnRgVlZWbPDgweL34em8MjMzWUhICHNycmINGzZkc+fOFR8r/Z7+3//9H7OxsWFNmzZlx48f\nZ99//z1zcXFhDg4O4vLHGGP5+fns/fffZ66urqxBgwZs6tSp4nJR2XrzWZ9j6Xfa0tKSeXh4sN9+\n+40xVvJ9rF27NjM1NWUWFhbM1taWMcbYhAkTxO8AY4ytW7eOubu7s3r16rFBgwaxu3fvio897zv5\ntBcqeAcOHGCMlaxEW7VqxT799FN2584dZmdnJ650//zzT2ZnZ8fu378vflhubm4sISGBaTQa9uTJ\nExYUFMTmzZsnTnvevHmsU6dOLD09naWnp7POnTuLj//111+sRo0abPbs2aywsJDl5eWx+fPns9q1\na7P9+/ezoqIiNn78eObm5sYWL17MioqK2LfffssaN24sTv/3339n169fZ4wxdvjwYVa3bl32999/\na01//vz5rKioiO3Zs4fVrVtXXNjffvttFhAQwO7evSsu5AUFBc/MOz09vdx7V1BQwFxdXVl4eDgr\nKipi27dvZzVr1hRzfPDgAdu+fTvLy8tjWVlZbMSIEWzIkCHi6/39/dn69esZYyULrZmZGfvuu+9Y\ncXExW7NmDXN2dq7wMysqKmJt2rRhoaGhLDc3l+Xn57Pjx48zxkpWyu7u7uzGjRssOzubDR06lI0b\nN44x9u+XaNq0aaygoIDt37+f1axZkw0ZMoSlp6ez5ORk5uDgwA4fPizGVKNGDbZixQpWVFTENm/e\nzKytrcUv5Yu8/2U/3xUrVrBOnTqx5ORkVlhYyKZMmcJGjx7NGGPs0qVLzMLCgh09epQVFBSw0NBQ\nVqNGjQoLHmOs3LJWWFjImjZtyj7//HP25MkTdujQIWZpackSExMrfH3Z976UIAhs4MCB7NGjR+zW\nrVusfv36bN++fYwxxnbs2MHc3d3Z5cuXmUajYf/5z39Y586dK5y2Wq1mlpaW7JdffmFFRUXswYMH\nLD4+Xoy79Mte2fKRnZ3NrKysWFJSEmOMsdTUVHbp0iXGGGOjRo1iixcvZoyVLIOln31pDqUF71nL\n+NPKFjyNRsPatWvHFi5cyJ48ecKuX7/OmjRpwv744w/GWMkPvFOnTjGNRsPUajVr2bIlW7FiBWOM\nsX379jEfHx/xB9bly5dZSkpKhZ/X0yp77ciRI9nIkSNZbm4uu3jxImvYsCHr1q0bY6ziglf2s716\n9So7cOAAKywsZOnp6ax79+5s5syZ4nPd3NyYt7c3u3PnDsvPz6/S958x7Q2Gqq6//Pz8WMOGDdml\nS5dYTk4OGzZsGBs7dmyFeQ0ZMoRNnTqV5ebmsnv37rEOHTqIPzBLv6eRkZGsuLiYzZ07lzVs2FD8\nMbJ//35maWnJcnJyGGMlPywGDx7MHj58yLKystjAgQPZxx9/LC4Lla03K/oct27dKn5WmzdvZubm\n5iw1NZUxxlhkZKT446RU2WkcPHiQ2dvbs7Nnz7KCggI2Y8YM1r17d/G5lX0nK/Lcgufm5sYsLCyY\njY0Nc3NzY++88w7Ly8tjS5YsEVeUpfr06SP+UvD392fz588vl0jZyt20aVOtrZQ//viDqVQqxljJ\nG1uzZk2tL+D8+fNZ7969xdtRUVHMwsKCFRcXM8YYe/z4MRMEQfxSPG3IkCFs5cqV4vTr1Kmj9UVw\ncHAQv6x16tRh58+fLzeN5+Vd1uHDh1nDhg217uvateszv9hnz54Vf+UwVr7gubu7i4/l5OQwQRBY\nWlpauemcOHGC1a9fXyu3Uq+99hpbs2aNeDsxMZGZmZkxjUYjfonK/oKys7NjW7ZsEW8PGzZMXIFF\nRESUK7odOnRgGzdurDC/p9//pz/fli1bahWwu3fvMjMzM1ZUVMQWLFggFr/S/GvWrFlpwSu7rB05\ncoQ5OjpqPWf06NEsLCyswtf7+/uLWwGlBEHQKh6BgYFs6dKljDHG+vbtq1UgNRoNq1u3Lrt161a5\naS9evJgNHTr0heIuq+zykZ2dzWxsbNi2bdtYbm6u1vPGjx/P3nrrLa2twbI5XLt2rdJl/GllC15M\nTAxzdXUtl09wcHCFr12+fDl74403GGMlK6/mzZuzmJiYcstmZXkzxtihQ4cqfG1RUREzMzPT+uEy\nZ86cSrfwKvoxU+q3335j3t7e4m2VSqW156cq3//S15cteFVZf/n7+4uFhrGSLaKaNWuy4uJirbxS\nU1NZrVq1tLbOf/rpJxYQEMAYK/meNmvWTHzs/PnzTBAEdu/ePfE+Ozs7du7cOVZcXMzMzc3FH0WM\nlaxPSgtxZetNxp7/OTLGmJeXF9u5c6cYW2UFLyQkhM2aNUt8LDs7m5mZmYl7Tyr6Ti5ZsuSZ836h\nHt7OnTvx8OFDqNVqrF69GrVr18bNmzexdetW2Nrain/Hjx9Hamqq+NrnHdl19+5duLm5ibddXV1x\n9+5d8Xb9+vVRs2ZNrdc4ODiI/9epUwf29vZiv6VOnToAgOzsbADA3r174evrCzs7O9ja2mLPnj14\n8OCB+Ho7OzuYmPz7FtStWxfZ2dm4f/8+8vPz0bRp03Ixv0jeZfNr2LCh1n0uLi5ijyY3NxdTpkyB\nSqWCtbU1/Pz88OjRo2f2cBwdHbViLZtrWbdv34abm5tWbqVSUlLKvedFRUVIS0sT72vQoIH4f506\ndcrdzsnJEW8/nZ+bmxtSUlIAPP/9f/rzVavVeOONN8T31cPDAzVq1EBaWhpSUlLQqFEjrfzt7Owq\nepsqdPfu3XLLo5ubG5KTk5/5mor6eE9/BqXv/82bN/Hee++JsZfGVtH079y5gyZNmjw35sqWD3Nz\nc2zevBnffPMNnJ2dMWDAACQmJgIAvvjiCzDG0KFDB7Ru3RoRERHlpl3ZMl6Zmzdv4u7du1rL/+ef\nf4579+4BAJKSkjBgwAA4OTnB2toan3zyifiZv/baa5g+fTreeecdNGjQAFOmTHnhg2gCAgIqfG16\nejqKioq0PltXV9cXzictLQ2jRo1Co0aNYG1tjXHjxmkto4D2eqwq3/+KVGX99fS8XV1d8eTJE9y/\nf19rmjdv3sSTJ0/g5OQkxjR16lSkp6eLz3n6OwyUfP/K3pednY309HTk5ubCx8dHnFa/fv205vms\n9eaz/PDDD/D29hand/HixXLv8bM8vb4yNzeHnZ2d1vfqWd/JilT7tARXV1eMGzcODx8+FP+ysrLw\n0Ucfic95XuPf2dlZ6xDpW7duwdnZ+Zmvr8qBBAUFBRg2bBg++ugj3Lt3Dw8fPsTrr7/+QgcE2Nvb\no3bt2rh69Wq5x14k71JOTk7lVni3bt0S81i2bBmSkpJw+vRpPHr0CIcPHwYr2ep+4Twr4uLiglu3\nbkGj0ZR7rKL3vEaNGlpfiKp4Or+bN2/C2dn5hd7/pz9PV1dX7Nu3T+u9zc3NhbOzM5ycnHD79m3x\nubm5uZV+aZ6etrOzM27fvq01/5s3b2oV0cpe/zyurq5Yt26dVuw5OTnw9fUt91wXFxdcu3btubE/\nb/no3bs39u/fj9TUVLRo0QKTJ08GULJyW7duHZKTk7F27Vq8/fbb5U6nqGwZr4yLiwsaN26slefj\nx4+xe/duACWHlHt4eODq1at49OgRFi1apHXo/IwZMxAXF4eEhAQkJSXhv//9r1bOlanotQ4ODqhR\nowZu3bolPq/s/6VHk+fm5or3lS1Oc+bMgampKS5evIhHjx5h48aN5Q71LxtbVb7/uvB0XmZmZrC3\nt9d6jouLC2rVqoUHDx6IMT169AgXLlyo8vzs7e1Rp04dJCQkiNPKzMx84SPrn/4cb968ibfeegtf\nffUVMjIy8PDhQ7Ru3VpchqtaI3JycvDgwYNyP7RfVLUL3tixY7Fr1y7s378fGo0G+fn5iI6O1loB\nPr3ifvr26NGj8Z///Af379/H/fv38dlnn2HcuHHPnGdVCkFhYSEKCwthb28PExMT7N27F/v373+h\n15qYmCAkJAShoaFISUmBRqPByZMnUVhY+EJ5l+rcuTNMTU2xevVqFBUVYefOnYiNjRUfz87ORp06\ndWBtbY2MjAwsWLDghfOrTMeOHeHk5ITZs2cjNzcX+fn5OHHiBICS93z58uVQq9XIzs7GnDlzMGrU\nqAq3Bp+l7Odw7949hIeH48mTJ9i6dSsuX76M119/vVrv/9SpUzFnzhzxS56eno6oqCgAwPDhw7F7\n924cP34chYWF+PTTTys9B6lBgwZaK3lfX1/UrVsXX3zxBZ48eYLo6Gjs3r0bo0aNeubrKytKpe9D\n6XsxdepULF68GAkJCQCAR48eYevWrRW+bsyYMThw4AC2bt2KoqIiPHjwAOfOnSs3zcqWj3v37mHn\nzp3IycmBmZkZzM3NYWpqCgDYunUr7ty5AwCwsbGBIAjlPt/KlvHKdOjQAZaWlvjiiy+Ql5cHjUaD\nixcvIi4uTozZ0tISdevWxeXLl7FmzRpxpRYXF4dTp07hyZMnqFu3LmrXri3G/PTn9bRnvdbExARD\nhw5FWFgY8vLykJCQgB9++EGcZ/369dGwYUNs3LgRGo0G33//vdbnmp2dDXNzc1hZWSE5OVkswM9S\nle//y2KM4ccff8Q///yD3NxcfPrppxgxYkS5IuHk5ITevXsjNDQUWVlZKC4uxrVr16p1/p+JiQkm\nT56MmTNniluIycnJL7zufPpzzMnJgSAIsLe3R3FxMSIiIrRO1WjQoAHu3LmDJ0+eaOVd+h0YPXo0\nIiIicO7cORQUFGDOnDnw9fV95lb882pEtQteo0aNsHPnTixevBgODg5wdXXFsmXLKv0F//Q5RnPn\nzkX79u3Rpk0btGnTBu3bt8fcuXNf+PXPeg5QcoJteHg4AgMDUa9ePfz8888YPHhwpa8t68svv4Sn\npydeffVV2NnZ4eOPP0ZxcfEz865o5WtmZobt27dj/fr1sLW1xaZNmzBgwABxN97MmTORl5cHe3t7\ndO7cGf369XtmTC+SeykTExPs2rULV69ehaurK1xcXLBlyxYAQEhICMaNG4fu3bujSZMmqFu3Llat\nWvVC70lFz+nYsSOuXLmC+vXrY968edi2bRtsbW2r9f6/9957GDRoEHr37g0rKyt06tQJp0+fBgB4\neHjgq6++wptvvglnZ2fUq1ev0l3mEydOREJCAmxtbTF06FCYmZlh165d2Lt3L+rXr4/p06dj48aN\naN68eYWvf++99/Drr7+iXr16mDlz5jPfh9IchgwZglmzZmHUqFGwtraGp6cn/vjjjwpf5+Ligj17\n9mDZsmWws7ODt7c3zp8/X26alS0fxcXFWL58ORo2bAg7OzscPXpUPH8pLi4Ovr6+sLS0xODBgxEe\nHg6VSlXuPX/WMv6sXAHA1NQUu3fvRnx8PJo0aYL69evjrbfeErcAvvzyS/z000+wsrLCW2+9pfWD\n4vHjx3jrrbdQr149qFQq2NvbiwNQPP15Pa2y165evRrZ2dlwdHRESEgIgoODtdZD3377Lf773//C\n3t4eCQkJ6NKli/jY/Pnz8ffff8Pa2hoDBw7EsGHDKv0OVOX7X9F7+KLrr9L/x40bh6CgIDg5OaGw\nsBDh4eEVPveHH35AYWEhPDw8UK9ePYwYMULckq3KugMAli5dCnd3d/j6+sLa2hq9evVCUlLSC732\n6c/Rw8MD77//Pjp16gRHR0dcvHgRXbt2FZ/fo0cPtGrVCo6OjuLu3rLx9ujRAwsXLsSwYcPg7OyM\nGzdu4Jdffqn0/at0HVZpd9EA3Lp1i/n7+zMPDw/WqlUr8aCH+fPns4YNGzIvLy/m5eVV6SH6hqRD\nhw4sMjJS7jB0oqKGMyFy42W5rOzgGlI9zx1pRW5mZmZYvnw5vLy8kJ2dDR8fH/Tq1QuCICA0NBSh\noaFyh1ipI0eOoHnz5rC3t8emTZtw8eJF9O3bV+6wCCEKwGgQAp0y+ILn6OgoHoVjYWGBli1bivvL\nlbAwJCYmIjAwEDk5OWjatCl+/fXXah8gYmj0PQwWIdXB03LJSx6GQmBKqBr/n1qthp+fHy5duoRl\ny5YhIiIC1tbWaN++PZYtWwYbGxu5QySEEGKgFHN5oOzsbAwfPhwrV66EhYUFpk2bhhs3biA+Ph5O\nTk54//335Q6REEKIAVPEFt6TJ08wYMAA9OvXr8Ij5tRqNQYOHFjuvBN3d/fnHlpOCCFEW9u2bREf\nHy93GDpn8D08xhgmTpwIDw8PrWKXkpICJycnAMBvv/0GT0/Pcq+9du2aIvp81RUWFoawsDBZY5gd\nNhupmS82ykRVxcfEw8vXS+fTdbRxxJKwJTqfblUYwmenT5SfsvHaOzT4gnf8+HH8+OOPaNOmDby9\nvQEAixcvxs8//4z4+HgIgoDGjRtj7dq1MkcqvapeyFMfUjNToRqi0su04y/H62Xa6h1qnU+zyjEY\nwGenT5QfMUQGX/C6du1a4Umd/fr1kyEaQgghSqWYg1ZIeUFBQXKHoFdefXW/O9NQ8P7ZUX7EEFHB\nUzB/f3+5Q9ArlZdK7hD0hvfPjvIjhogKnoJFR0fLHYJeqePVcoegN7x/dpQfMURU8AghhBgFKngK\nxvtuFdqlqVyUHzFEVPAIIYQYBSp4CsZ7H4F6eMpF+RFDRAWPEEKIUaCCp2C89xGoh6dclB8xRFTw\nCCGEGAUqeArGex+BenjKRfkRQ0QFjxBCiFGggqdgvPcRqIenXJQfMURU8AghhBgFKngKxnsfgXp4\nykX5EUNEBY8QQohRoIKnYLz3EaiHp1yUHzFEVPAIIYQYBSp4CsZ7H4F6eMpF+RFDRAWPEEKIUaCC\np2C89xGoh6dclB8xRFTwCCGEGAUqeArGex+BenjKRfkRQ0QFjxBCiFGggqdgvPcRqIenXJQfMURU\n8AghhBgFKngKxnsfgXp4ykX5EUNEBY8QQohRoIKnYLz3EaiHp1yUHzFEVPAIIYQYBSp4CsZ7H4F6\neMpF+RFDRAWPEEKIUaCCp2C89xGoh6dclB8xRFTwCCGEGAUqeArGex+BenjKRfkRQ0QFjxBCiFEw\n+IJ3+/ZtBAQEoFWrVmjdujXCw8MBABkZGejVqxeaN2+O3r17IzMzU+ZIpcd7H4F6eMpF+RFDZPAF\nz8zMDMuXL8elS5cQExODr776Cv/88w+WLFmCXr16ISkpCT169MCSJUvkDpUQQogBM/iC5+joCC8v\nLwCAhYUFWrZsieTkZERFRWHChAkAgAkTJmDHjh1yhikL3vsI1MNTLsqPGCKDL3hlqdVqnD17Fh07\ndkRaWhoaNGgAAGjQoAHS0tJkjo4QQoghqyF3AC8qOzsbw4YNw8qVK2Fpaan1mCAIEAShwtcFBQVB\npVIBAGxsbODl5SXufy/9labU26X3yRlP6p1UqKAC8O8WWWnv7WVvl96nq+k9vcUo5+fn7+8v+/JD\n+VF+pbejo6MRGRkJAOL6kkcCY4zJHcTzPHnyBAMGDEC/fv0wc+ZMAECLFi0QHR0NR0dHpKSkICAg\nAJcvX9Z6nSAIUEB6ihY0MwiqISq5w6gS9Q41IldEyh0GIQaL13Wnwe/SZIxh4sSJ8PDwEIsdAAwa\nNAgbNmwAAGzYsAFDhgyRK0TZlP5C4xX18JSL8iOGyOB3aR4/fhw//vgj2rRpA29vbwDA559/jtmz\nZyMwMBDr16+HSqXCli1bZI6UEEKIIZNsl2ZiYiK+/PJLqNVqFBUVlcxcEHDo0CG9zZPXzXJDQrs0\nCeEPr+tOybbwRowYgWnTpmHSpEkwNTUFgGceaEIIIYTommQ9PDMzM0ybNg0dO3ZE+/bt0b59e/j4\n+Eg1ey7x3kegHp5yUX7EEElW8AYOHIivvvoKKSkpyMjIEP8IIYQQKUjWw1OpVBXuwrxx44be5snr\nfmhDQj08QvjD67pTsh6eWq2WalaEEEJIOXrfpXnw4EEAwLZt27B9+/Zyf6T6eO8jUA9PuSg/Yoj0\nvoV35MgR9OjRA7t27apwl+bQoUP1HQIhhBCijKHFqovX/dCGhHp4hPCH13WnpCOt7N69GwkJCcjP\nzxfv+/TTT6UMgRBCiJGS7LSEKVOmYMuWLQgPDwdjDFu2bMHNmzelmj2XeO8jUA9PuSg/YogkK3gn\nTpzADz/8gHr16mH+/PmIiYlBYmKiVLMnhBBi5CQreHXq1AEA1K1bF8nJyahRowZSU1Olmj2Xyl4X\nj0dlr4vHG94/O8qPGCLJengDBgzAw4cP8eGHH4pDik2ePFmq2RNCCDFykm3hffrpp7C1tcWwYcOg\nVqtx+fJlLFy4UKrZc4n3PgL18JSL8iOGSLItvG3btpU7D8/a2hqenp5wcHCQKgxCCCFGSrLz8Pr3\n74+TJ08iICAAQMkvpHbt2uHGjRv49NNPMX78eJ3Pk9dzSQwJnYdHCH94XXdKtoX35MkT/PPPP2jQ\noAEAIC0tDePGjcOpU6fQvXt3vRQ8QgghpJRkPbzbt2+LxQ4AHBwccPv2bdjZ2aFmzZpShcEV3vsI\n1MNTLsqPGCLJtvACAgLQv39/BAYGgjGGbdu2wd/fHzk5ObCxsZEqDEIIIUZKsh5eaZE7fvw4AKBL\nly4YNmxYhQNK6wqv+6ENCfXwCOEPr+tOybbwBEHA8OHDMXz4cKlmSQghhIgk6+ER3eO9j0A9POWi\n/IghooJHCCHEKEha8HJzc2nAaB3ifTw/GktTuSg/YogkK3hRUVHw9vZGnz59AABnz57FoEGDpJo9\nIYQQIydZwQsLC8OpU6dga2sLAPD29sb169elmj2XeO8jUA9PuSg/YogkK3hmZmblzrczMaEWIiGE\nEGlIVnFatWqFTZs2oaioCFeuXMGMGTPQuXNnqWbPJd77CNTDUy7KjxgiyQreqlWrcOnSJdSqVQuj\nR4+GlZUVVqxYIdXsCSGEGDnJCp65uTkWL16MuLg4xMXFYdGiRahdu7ZUs+cS730E6uEpF+VHDJFk\nBa9nz57IzMwUb2dkZIhHbBJCCCH6JlnBu3//vtZBK/Xq1UNaWppUs+cS730E6uEpF+VHDJFkBc/U\n1BQ3b94Ub6vVajpKkxBCiGQkqziLFi1Ct27dMHbsWIwdOxbdu3fH4sWLpZo9l3jvI1APT7koP2KI\nJLtaQt++fXHmzBnExMRAEASsWLEC9vb2Us2eEEKIkZN0n2JhYSHq1asHS0tLJCQk4MiRI899TUhI\nCBo0aABPT0/xvrCwMDRq1Aje3t7w9vbGvn379Bm2weK9j0A9POWi/IghkmwLb9asWdi8eTM8PDxg\namoq3t+TNxc5AAAgAElEQVS9e/dKXxccHIwZM2Zg/Pjx4n2CICA0NBShoaF6i5cQQghfJNvC++23\n35CYmIg9e/Zg165d4t/zdOvWTRx/sywer8ZbVbz3EaiHp1yUHzFEkhW8pk2borCwUGfTW7VqFdq2\nbYuJEydqnd9HCCGEVERgEm0qDR06FOfOnUOPHj1Qq1atkpkLAsLDw5/7WrVajYEDB+LChQsAgHv3\n7qF+/foAgHnz5iElJQXr168v9zpBEGhLUM+CZgZBNUQldxhVot6hRuSKSLnDIMRg8brulKyHN2jQ\noHLXvxMEoVrTcnBwEP+fNGkSBg4c+MznBgUFQaVSAQBsbGzg5eUlNpxLd0vQ7erfTr2TChVUAP7d\nBVl6sImh3i5lCO8f3abbhnA7OjoakZGRACCuL3kk2Rbey3h6Cy8lJQVOTk4AgOXLlyM2NhY//fRT\nudfx+iulVHR0tLjwykWfW3jqeLVejtQ0hC08Q/js9InyUzZe152SbeElJSVhzpw5SEhIQF5eHoCS\nN/V5F4EdPXo0Dh8+jPv378PFxQULFixAdHQ04uPjIQgCGjdujLVr10qRAiGEEAWTbAuvS5cuWLBg\nAUJDQ7Fr1y5ERERAo9Fg4cKFepsnr79SDAn18AjhD6/rTsmO0szLy0PPnj3BGIObmxvCwsLw+++/\nSzV7QgghRk6ygle7dm1oNBq4u7tj9erV2L59O3JycqSaPZdKm868ovPwlIvyI4ZIsh7eihUrkJub\ni/DwcMybNw+PHz/Ghg0bpJo9IYQQI6eIozSri9f90IaEeniE8IfXdadkW3ixsbFYvHgx1Go1ioqK\nAJS8qefPn5cqBEIIIUZMsh7emDFjEBwcjG3btonjaEZFRUk1ey7x3kegHp5yUX7EEEm2hVe/fv1y\nI60QQgghUpGsh7d//35s3rwZPXv2RM2aNUtmLggYOnSo3ubJ635oQ0I9PEL4w+u6U7ItvA0bNiAx\nMRFFRUUwMfl3T6o+Cx4hhBBSSrKCFxcXh8uXL1d7wGhSHu/j+elrLE1DwPtnR/kRQyTZQSudO3dG\nQkKCVLMjhBBCtEjWw2vRogWuXbuGxo0ba10PT5+nJfC6H9qQUA+PEP7wuu6UZJcmYwzr1q2Dq6ur\nFLMjhBBCypFsl+bbb78NlUpV7o9UH+/nAtF5eMpF+RFDJEnBEwQBPj4+OH36tBSzI4QQQsqRrIf3\nyiuv4OrVq3Bzc4O5uXnJzKmHp3jUwyOEP7yuOyU7LeGPP/4AAPG0BB7fTEIIIYZLsh6eSqVCZmYm\noqKisGvXLjx69Ih6eC+J9z4C9fCUi/Ijhkiygrdy5UqMHTsW6enpSEtLw9ixYxEeHi7V7AkhhBg5\nyXp4np6eiImJEft3OTk58PX1xYULF/Q2T0PZDz07bDZSM1PlDuOFOdo4YknYkhd6LvXwCOGPoaw7\ndU2yHh4ArTE0y/7Pu9TMVEUVBfUOtdwhEEKIzklWdYKDg9GxY0eEhYVh/vz58PX1RUhIiFSz5xLP\nPS6A7/x47wFRfsQQ6X0L7/r162jSpAlCQ0Ph5+eHY8eOQRAEREZGwtvbW9+zJ4QQQgBIUPBGjBiB\nM2fOoEePHjh48CB8fHz0PUujweuVBErxnB/vI+1TfsQQ6b3gaTQaLFq0CImJifjf//6n1QgVBAGh\noaH6DoEQQgjRfw/vl19+gampKTQaDbKyspCdnS3+ZWVl6Xv2XOO5xwXwnR/vPSDKjxgivW/htWjR\nAh9++CHc3NwwevRofc+OEEIIqZAkR2mampriyy+/lGJWRoXnHhfAd36894AoP2KIJDstoVevXvjy\nyy9x+/ZtZGRkiH+EEEKIFCQreL/88gu++uordO/eHT4+PuIfqT6ee1wA3/nx3gOi/IghkmykFbVa\nLdWsCCGEkHIk28LLycnBwoULMXnyZADAlStXsHv3bqlmzyWee1wA3/nx3gOi/IghknRosZo1a+LE\niRMAAGdnZ3zyySdSzZ4QQoiRk6zgXbt2DbNmzULNmjUBQLxqAqk+nntcAN/58d4DovyIIZKs4NWq\nVQt5eXni7WvXrqFWrVpSzZ4QQoiRk+yglbCwMPTt2xd37tzBm2++iePHjyMyMlKq2XOJ5x4XwHd+\nvPeAKD9iiCQreL1790a7du1w6tQpMMYQHh4Oe3v7574uJCQEv//+OxwcHMSLxWZkZGDkyJG4efMm\nVCoVtmzZAhsbG32nQAghRMEk26XJGMPhw4dx4MABHDp0CEePHn2h1wUHB2Pfvn1a9y1ZsgS9evVC\nUlISevTogSVLXuzq3LzhuccF8J0f7z0gyo8YIskK3ttvv421a9eiTZs2aN26NdauXYu33377ua/r\n1q0bbG1tte6LiorChAkTAAATJkzAjh079BIzIYQQfki2S/Ovv/5CQkICTExKamxQUBA8PDyqNa20\ntDQ0aNAAANCgQQOkpaXpLE4l4bnHBfCdH+89IMqPGCLJCp67uztu3boFlUoFALh16xbc3d1ferqC\nIEAQhGc+HhQUJM7TxsYGXl5e4sJaultC37dLle6iK12RG+rtUi+SX+qdVKhgWPHrMj+6TbeN4XZ0\ndLR4EGHp+pJHAit7RVY96t69O2JjY9GhQwcIgoDTp0/j1VdfhZWVFQRBQFRU1DNfq1arMXDgQPGg\nlRYtWiA6OhqOjo5ISUlBQEAALl++XO51giBAovQqFTQzCKohKp1PVx2v1stWkHqHGpErIl/oufrK\nDTCM/PQlOjqa660Eyk/ZDGXdqWuSbeF99tln5e4rfVMr20KryKBBg7BhwwbMmjULGzZswJAhQ3QV\nJiGEEE5JVvCq+2to9OjROHz4MO7fvw8XFxd89tlnmD17NgIDA7F+/XrxtARjxHOPC+A7P563DgDK\njxgmyQpedf38888V3n/gwAGJIyGEEKJkkp2WQHSP5/PUAL7ze/qAJt5QfsQQSVrwcnNzkZiYKOUs\nCSGEEAAS7tKMiorChx9+iIKCAqjVapw9exbz58+v9OhMUjmee1yAYeQ3O2w2UjNT9TLtyB2Repmu\no40jloTJO/oQ7z0u3vPjlaSDR586dQoBAQEAAG9vb1y/fl2q2RNSLamZqXo77UJf1DvUcodAiEGS\nbJemmZlZuQGeS0ddIdXDc48L4Ds/nnMD+O9x8Z4frySrOK1atcKmTZtQVFSEK1euYMaMGejcubNU\nsyeEEGLkJCt4q1atwqVLl1CrVi2MHj0aVlZWWLFihVSz55Ih9Lj0ief8eM4N4L/HxXt+vJKsh5eY\nmIjFixdj8eLFUs2SEEIIEUm2hRcaGooWLVpg3rx5uHjxolSz5RrvfSCe8+M5N4D/Hhfv+fFKsoIX\nHR2Nv/76C/b29pgyZQo8PT2xcOFCqWZPCCHEyEl6mKSTkxPee+89fPPNN2jbtm2FA0qTF8d7H4jn\n/HjODeC/x8V7frySrOAlJCQgLCwMrVu3xvTp09G5c2ckJydLNXtCCCFGTrKCFxISAhsbG/zxxx84\nfPgw3n77bTg4OEg1ey7x3gfiOT+ecwP473Hxnh+vJDtKMyYmRqpZEUIIIeXoveCNGDECW7duhaen\nZ7nHBEHA+fPn9R0Ct3jvA/GcH8+5Afz3uHjPj1d6L3grV64EAOzevbvcJeOreqVzQgghpLr03sNz\ndnYGAHz99ddQqVRaf19//bW+Z8813vtAPOfHc24A/z0u3vPjlWQHrezfv7/cfXv27JFq9oQQQoyc\n3ndprlmzBl9//TWuXbum1cfLyspCly5d9D17rvHeB+I5P55zA/jvcfGeH6/0XvDefPNN9OvXD7Nn\nz8bSpUvFPp6lpSXs7Oz0PXtCCCEEgAS7NK2traFSqfDLL7/Azc0NdevWhYmJCXJycnDr1i19z55r\nvPeBeM6P59wA/ntcvOfHK8l6eFFRUWjWrBkaN24MPz8/qFQq9OvXT6rZE0IIMXKSFby5c+fi5MmT\naN68OW7cuIGDBw+iY8eOUs2eS7z3gXjOj+fcAP57XLznxyvJCp6ZmRns7e1RXFwMjUaDgIAAxMXF\nSTV7QgghRk6ygmdra4usrCx069YNY8aMwbvvvgsLCwupZs8l3vtAPOfHc24A/z0u3vPjlWQFb8eO\nHahbty6WL1+Ovn37wt3dHbt27ZJq9oQQQoycZINHl27NmZqaIigoSKrZco33PhDP+fGcG8B/j4v3\n/Hil94JnYWHxzDEzBUHA48eP9R0CIYQQov9dmtnZ2cjKyqrwj4rdy+G9D8RzfjznBvDf4+I9P15J\n1sMDgKNHjyIiIgIAkJ6ejhs3bkg5e0IIIUZMsh5eWFgY4uLikJSUhODgYBQWFmLMmDE4ceKEVCFw\nh/c+EM/5GUpus8NmIzUzVS/TjtwRqZfpOto4YknYEr1M+0VRD0+ZJCt4v/32G86ePQsfHx8AQMOG\nDZGdnS3V7AkhFUjNTIVqiEruMKpEvUMtdwhEoSTbpVmrVi2YmPw7u5ycHKlmzS3e+0A858dzbgD/\n+VEPT5kkK3gjRozAlClTkJmZiXXr1qFHjx6YNGmSVLMnhBBi5CTZpckYw8iRI3H58mVYWloiKSkJ\nCxcuRK9evaSYPbcMpQ+kLzznx3NuAP/5UQ9PmSTr4b3++uu4ePEievfuLdUsCSGEEJEkuzQFQYCP\njw9Onz6t0+mqVCq0adMG3t7e6NChg06nrQS890l4zo/n3AD+86MenjJJtoUXExODH3/8EW5ubjA3\nNwdQUgjPnz9f7WkKgoDo6GjUq1dPV2ESQgjhlGQF748//tDLdBljepmuEvDeJ+E5P55zA/jPj3p4\nyiRZwVOpVDqfpiAI6NmzJ0xNTTFlyhRMnjxZ5/MghBDCB8kKnj4cP34cTk5OSE9PR69evdCiRQt0\n69ZN6zlBQUFisbWxsYGXl5f466x0P7y+b5cq7WuU/vp92dsxv8bA0d1RZ9N7uu/yIvml3kmFCrqd\nvzHkVzYWyk9/+enrdtnvthzz10c+kZGRAPSzcWIoBMbJPsEFCxbAwsIC77//vnifIAgGscszaGaQ\nXkazUMer9bLrSL1DjcgVkS/0XH3lBvCdn75yAyg/KURHR3O9W9NQ1p26Jung0bqUm5uLrKwsACWj\ntuzfvx+enp4yRyUt3vskPOfHc24A//nxXOx4pthdmmlpaXjjjTcAAEVFRRgzZgyd40cIIeSZFLuF\n17hxY8THxyM+Ph4XL17Exx9/LHdIkuP9XCee8+M5N4D//Og8PGVSbMEjhBBCqoIKnoLx3ifhOT+e\ncwP4z496eMpEBY8QQohRoIKnYLz3SXjOj+fcAP7zox6eMlHBI4QQYhSo4CkY730SnvPjOTeA//yo\nh6dMij0PjxBCnmd22GykZqbKHcYLc7RxxJKwJXKHwS0qeAqmz+GbDAHP+fGcG2A4+aVmpipq6DT1\nDrXOp0n+Rbs0CSGEGAUqeApmCL+g9Ynn/HjODaD8iGGigkcIIcQoUMFTMN7PdeI5P55zAyg/Ypio\n4BFCCDEKVPAUjPc+As/58ZwbQPkRw0QFjxBCiFGggqdgvPcReM6P59wAyo8YJip4hBBCjAIVPAXj\nvY/Ac3485wZQfsQwUcEjhBBiFKjgKRjvfQSe8+M5N4DyI4aJCh4hhBCjQAVPwXjvI/CcH8+5AZQf\nMUxU8AghhBgFKngKxnsfgef8eM4NoPyIYaKCRwghxChQwVMw3vsIPOfHc24A5UcMExU8QgghRoEK\nnoLx3kfgOT+ecwMoP2KYqOARQggxClTwFIz3PgLP+fGcG0D5EcNEBY8QQohRoIKnYLz3EXjOj+fc\nAMqPGCYqeIQQQowCFTwF472PwHN+POcGUH7EMFHBI4QQYhQUXfD27duHFi1aoFmzZli6dKnc4UiO\n9z4Cz/nxnBtA+RHDpNiCp9FoMH36dOzbtw8JCQn4+eef8c8//8gdlqRSr6bKHYJe8Zwfz7kBlB8x\nTIoteKdPn4a7uztUKhXMzMwwatQo7Ny5U+6wJJWfnS93CHrFc3485wZQfsQwKbbgJScnw8XFRbzd\nqFEjJCcnyxgRIYQQQ6bYgicIgtwhyC4zNVPuEPSK5/x4zg2g/IhhEhhjTO4gqiMmJgZhYWHYt28f\nAODzzz+HiYkJZs2aJT7Hy8sL586dkytEQghRpLZt2yI+Pl7uMHROsQWvqKgIr7zyCg4ePAhnZ2d0\n6NABP//8M1q2bCl3aIQQQgxQDbkDqK4aNWpg9erV6NOnDzQaDSZOnEjFjhBCyDMpdguPEEIIqQrF\nHrRizPLz81FQUCB3GHrDe36EEHkodpemMSkuLsaOHTvw888/48SJEyguLgZjDKampujUqRPGjBmD\nIUOGKPbIVd7zK5WcnAy1Wg2NRgPGGARBQPfu3eUOSycSExPx5ZdfQq1Wo6ioCEDJkdSHDh2SOTLd\n2LZtG2bPno20tDSU7hQTBAGPHz+WOTJSFbRLUwG6d++Obt26YdCgQfDy8kKtWrUAAAUFBTh79iyi\noqJw7NgxHDlyROZIq4f3/ABg1qxZ2Lx5Mzw8PGBqairev2vXLhmj0p02bdpg2rRpaNeunZifIAjw\n8fGROTLdaNq0KXbv3k3HCSgcFTwFKCgoEIvAyzzHUPGeHwA0b94cFy5cUHQOlfHx8cGZM2fkDkNv\nunTpguPHj8sdBnlJtEtTAcquJDUaDdLS0sTdRgDg6uqq6BXpi8Su5PyAki2EwsJCxefxLAMHDsRX\nX32FoUOHauVYr149GaPSnfbt22PkyJEYMmQIatasCaBkC3bo0KEyR0aqgrbwFGTVqlVYsGABHBwc\ntHaLXbhwQcao9Kt///74/fff5Q6j2mbMmAEAuHv3LuLj49GjRw+xIAiCgPDwcDnD0xmVSlWuxyoI\nAq5fvy5TRLoVFBQEoPwITxERETJEQ6qLCp6CNG3aFKdPn4adnZ3coUjm7t27cHZ2ljuMaouMjBRX\nkqUHqpT9f8KECXKGR4hRoYKnIAEBAdi/fz/MzMzkDoVUUXZ2NurUqSNumWs0GuTn58Pc3FzmyHSj\nsLAQa9aswZEjRyAIAvz8/DB16lRultXbt2/j3XffxbFjxwCUHGi1cuVKNGrUSObISFVQwVOQkJAQ\nJCUloX///lp9hNDQUJkjezmenp7PfEwQBJw/f17CaPTD19cXBw4cgIWFBQAgKysLffr0wYkTJ2SO\nTDcmTpyIoqIiTJgwAYwxbNy4ETVq1MB3330nd2g60bNnT4wZMwZjx44FAGzatAmbNm3Cn3/+KXNk\npCrooBUFcXV1haurKwoLC1FYWKi1i0zJeDk0vzL5+flisQMAS0tL5ObmyhiRbsXGxmr9MOnRowfa\ntGkjY0S6lZ6ejuDgYPF2UFAQli9fLmNEpDqo4ClIWFgYgJKtA6BkpckDlUoFALhx4wYcHR1Rp04d\nAEBeXh7S0tJkjEx3zM3NcebMGfG8tLi4ODFPHtSoUQNXr16Fu7s7AODatWuoUYOf1YudnR02btyI\nN998E4wx/PLLL7C3t5c7LFJFtEtTQS5cuIDx48fjwYMHAID69etjw4YNaN26tcyR6YaPjw9Onjwp\n7q4tKChAly5dEBcXJ3NkLy82NhajRo2Ck5MTACAlJQWbN29G+/btZY5MNw4ePIjg4GA0btwYAKBW\nqxEREYHXXntN5sh0Q61WY8aMGYiJiQEAdO7cGatWrYKrq6vMkZGqoIKnIJ06dcLixYsREBAAAIiO\njsacOXO46QN5eXmVuwZX27ZtubmmYWFhIRITEyEIAl555RVuDugolZ+fr5Ufr+ccEuXiZ5+DEcjN\nzRWLHQD4+/sjJydHxoh0y97eHjt37sTgwYMBADt37uRqt1FiYiISEhKQn5+Pv//+GwAwfvx4maN6\nOQcPHkSPHj2wbds2CIIgjjN59epVAFD8idlLly7FrFmzxPMpy+LpPEpjQQVPQRo3boyFCxdi3Lhx\nYIxh06ZNaNKkidxh6cw333yDMWPGYPr06QCARo0aYePGjTJHpRthYWE4fPgwLl26hP79+2Pv3r3o\n2rWr4gvekSNH0KNHD+zatavCA6iUXvA8PDwAlOxuL5sfLweMGRvapakgGRkZmD9/vjimX7du3RAW\nFgZbW1uZI9Ot7OxsMMa4OSgHAFq3bo1z586hXbt2OHfuHNLS0jBmzBgcOHBA7tB04vr16+V+fFV0\nn1Jt2bIFgYGBz72PGDYqeMRgpKam4pNPPkFycjL27duHhIQEnDx5EhMnTpQ7tJf26quvIjY2Fj4+\nPjh06BCsrKzQokULJCYmyh2aTrRr107cTVuKpwGlvb29cfbs2efeRwwb7dJUEN6vORYUFITg4GAs\nWrQIANCsWTMEBgZyU/AePnyIyZMno3379jA3N0fnzp3lDuul/fPPP0hISEBmZia2b98u7up7/Pgx\n8vPz5Q7vpe3duxd79uxBcnIy3n33XbFHmZWVxd1BR8aACp6CjBgxAtOmTcOkSZO0rjnGi/v372Pk\nyJFYsmQJAMDMzIybc7m+/vprAMDUqVPRt29fPH78mIsTs5OSkrBr1y48evRIawABS0tLfPvttzJG\nphvOzs7w8fHBzp074ePjIxZ0S0tLOvFcgfhYmxgJMzMzTJs2Te4w9MbCwkI8xxAAYmJiYG1tLWNE\nurVz506tsSZ5KHiDBw/G4MGDcfLkSXTq1EnucHSubdu2aNu2LYYOHQpzc3OtsVALCgpkjo5UlYnc\nAZDny8jIwIMHD8RrjqWkpCAjI0P848WyZcswcOBAXL9+HZ07d8a4ceO4Oex79uzZCA8PR6tWrdCy\nZUuEh4fj448/ljssnVmzZg0yMzPF2w8fPkRISIiMEelW7969kZeXJ97Ozc1Fz549ZYyIVAcdtKIA\nFV1rrKwbN25IGI1+PXnyRDyQg6eTsz09PREfH6+1heDl5cXNtQwrGjSgovuUivf8jAXt0lQAtVoN\noGQki9q1a2s9xsOBAWVPWi5b2JOSkgAo/1wuoKTXmpmZKV7LMDMzk6v+K2MMGRkZ4hXOMzIyoNFo\nZI5Kd3gfC9VYUMFTkM6dO5c79Lui+5Sm9KTle/fu4cSJE+L4i3/99Rc6d+7MRcH7+OOP0a5dOwQE\nBIAxhsOHD4sH5/Dg/fffR6dOnRAYGAjGGLZu3YpPPvlE7rB0ZsWKFQgMDCw3FipRFip4CpCSkoK7\nd+8iNzcXf//9t9ah3zxcYiYyMhIA0KtXLyQkJGitVHi4InhxcTFMTExw8uRJxMbGQhAELFmyRMyT\nB+PHjxfPMRQEAb/99ps4SgkPXn31Vfzzzz9cj4VqDKiHpwAbNmxAZGQk4uLitEbXt7S0RFBQEBdb\nQADQokUL/PPPP+KuvuLiYnh4eODy5csyR/byeDoJ+1k0Gg1SU1NRVFQkfoY8XU3gxIkTuHHjhlZ+\nSh8azthQwVOQX3/9FcOHD5c7DL2ZPn06kpKSxGuObd68Gc2aNcOqVavkDu2lzZ49G/b29hg5ciTM\nzc3F+0t7Xkq3atUqLFiwAA4ODuKBOQC4OShn7NixuH79Ory8vLTy42HZNCZU8BSkSZMmGDZsGIKD\ng7naXVTW9u3bcfToUQBA9+7d8cYbb8gckW5UdKStIAi4fv26TBHpVtOmTXH69GnxoBzetGzZEgkJ\nCVwdaGSMqOApyOPHj/HLL78gMjISGo0GISEhGD16NKysrOQOjRi5gIAA7N+/n9u+1ogRI7By5Uo4\nOzvLHQp5CVTwFCo6OhpjxozBw4cPMWLECMybNw/u7u5yh0WeIS8vD19//TWOHTsGQRDQrVs3TJs2\nrdxpJkoVEhKCpKQk9O/fX7xivSAICA0NlTky3fD390d8fDw6dOggXthWEARERUXJHBmpCjpKU0GK\niorw+++/IyIiAmq1Gu+//z7efPNNHDt2DK+//rp43hoxPOPHj4eVlZU4APFPP/2EcePGYevWrXKH\nphOurq5wdXVFYWEhCgsLubteXFhYmNwhEB2gLTwFadKkCfz9/TFp0qRyI+3PmDGDiwZ6bm4ubt++\njVdeeUXuUHTKw8MDCQkJz72PEKI/tIWnIOfPn4eFhUWFj/FQ7KKiovDhhx+ioKAAarUaZ8+exfz5\n87nYbdSuXTutAZZjYmLEUTt4EBAQUO4+ni5dZWFhIW6xFhYW4smTJ7CwsMDjx49ljoxUBRU8BXnn\nnXewcuVK2NjYACgZvumDDz7A999/L3NkuhEWFoZTp06JK09vb29ujmKMi4tDly5d4OLiAkEQcOvW\nLbzyyivw9PSEIAg4f/683CG+lP/+97/i//n5+di2bRs3l3YCgOzsbPH/4uJiREVFISYmRsaISHXw\ns0QagXPnzonFDig5h0vpw4qVZWZmppUfAJiY8HFBj3379gH49/qFvHUSyg6IAABdu3bFq6++KlM0\n+mViYoIhQ4YgLCyMq+HhjAEVPAXhfYDeVq1aYdOmTSgqKsKVK1cQHh7OxVXBgZLz8M6cOYNjx47B\nxMQEXbp0Qbt27eQOS2fKXqaquLgYcXFxXO3u27Ztm/h/cXExzpw5Q4NHKxAVPAXhfYDeVatWYdGi\nRahVqxZGjx6NPn36YN68eXKHpROfffYZtm7diqFDh4IxhuDgYAwfPpyb/Nq1ayduvdaoUQMqlQrr\n16+XOSrd2b17t/h/aX47d+6UMSJSHXSUpsJcunRJHKD3tdde43LElUePHkEQBK5OqG/evDnOnz8v\nnneXl5eHtm3bKv5Ukq1bt2LEiBG4fv06mjRpInc4Ojdr1iwsXboUW7ZsQWBgoNzhkJfER4OEc1lZ\nWeL/rVq1wowZMzB9+nStYlf2OUoVGxsLT09PtGnTBp6enmjbti3i4uLkDksnGjZsqHXF7Pz8fDRq\n1EjGiHRj8eLFAMDtGK+///47GGP4/PPP5Q6F6ADt0lSAN954A6+88goGDx6M9u3ba/XwYmNjsWPH\nDly5cgUHDhyQOdKXExISgq+//hrdunUDABw7dgwhISGKP4IRAKysrNCqVSv07t0bAPDnn3+iQ4cO\nmKWd018AABrKSURBVDFjBgRBQHh4uMwRVo+dnR169eqF69evY+DAgVqP8TASSb9+/WBra4vs7GxY\nWlpqPVZ6iS6iHLRLUyEOHTqEn376CcePH8fdu3cBAM7OzujatSvGjBkDf39/eQPUAW9vb5w9e1br\nvnbt2nFxJGrpNf8qIgiCYq/7V1hYiL///hvjxo3Dd999p3X0qSAI8PPzkzE63Rk0aJDiizehgkcM\nyMyZM5GXl4fRo0cDADZv3ozatWtj3LhxAMDVUY28uXfvHhwcHOQOg5BKUcEjBsPf37/S8Rf/+usv\nCaPRraSkJMyZMwcJCQliL4+nywMRogTUwyMG48CBA1yNzlFWcHAwFixYgNDQUERHRyMiIoKrcygJ\nUQI6SpMYjObNm+PDDz/kckDlvLw89OzZE4wxuLm5ISwsDL///rvcYenMgwcP5A5Br6KiolBcXCx3\nGOQlUcFTGI1Gg7t37+LWrVviHy/i4+PRrFkzTJo0CR07dsTatWu5OQqudu3a0Gg0cHd3x+rVq7F9\n+3bk5OTIHZbO+Pr6YsSIEdizZw93w6YBJf1kd3d3fPTRR7h8+bLc4ZBqoh6egqxatQoLFiyAg4MD\nTE1NxfsvXLggY1T6wdsFbk+fPo2WLVsiMzMT8+bNw+PHj/HRRx/B19dX7tB0ori4GAcOHMD333+P\n2NhYBAYGIjg4GM2bN5c7NJ159OgRfv75Z0RGRkIQBAQHB2P06NHlTlcghosKnoI0bdoUp0+fhp2d\nndyh6MXTF7gdP368eIHbOXPmKH5UEmNx6NAhjB07Fjk5OfDy8sLnn3/OzZio9+/fx8aNG7FixQp4\neHjgypUrePfdd/Huu+/KHRp5AXweIcApV1dXrobbelrz5s3h7++Pjz76SGsFOXz4cBw+fFjGyMjz\n3L9/H5s2bcIPP/yABg0aYPXq1Rg4cCDOnTuH4cOHQ61Wyx3iS9m5cyciIyNx5coVjB8/HrGxsXBw\ncEBubi48PDyo4CkEbeEpwLJlywAACQkJuHz5MgYMGICaNWsCKDm0PTQ0VM7wdObYsWPo2rXrc+8j\nhqd58+YYO3YsQkJCyg2ZtmTJEsyePVumyHRjwoQJmDhxIrp3717usQMHDqBnz54yREWqigqeAoSF\nhWldR+3pc9Xmz58vR1g6V9GoKhWNvsKLwsJC8YeL0hUXF8PExASPHz+GIAhc9rVSUlJw+vRpmJiY\n4NVXX4Wjo6PcIZEqol2aChAWFiZ3CHp18uRJnDhxAvfu3cP//vc/8Si/rKwsbg4F9/PzQ2RkJBo3\nbgyg5CCWSZMmcTFOKACcOXMGISEh4lG1NjY2WL9+fbkLwyrVd999h88++wwBAQFgjGH69On49NNP\nMXHiRLlDI1VABU9BevXqha1bt4pXBc/IyMDo0aPxxx9/yBzZyyksLERWVhY0Go3WVR+srKzw66+/\nyhiZ7syZMwf9+vXDjBkzkJycjL1791Y6vqbS8DzwNwB88cUXOHv2rHjA2IMHD9CpUycqeApDBU9B\n0tPTxWIHAPXq1UNaWpqMEemGn58f/Pz8EBQUBJVKJXc4etGnTx+sWbMGvXr1Qv369XH27FmudonV\nqFFDLHYA0LVrV65GzbG3t4eFhYV428LCAvb29jJGRKqDnyXSCJiamuLmzZtwc3MDAKjVapiY8DN2\nAK/FDgAWLlyIzZs34+jRozh//jz8/PywbNkyDBgwQO7QdMLPzw9TpkzRGvjbz89P7MkqfeDvpk2b\nwtfXF4MHDwZQctRmmzZtsGzZMq4OHOMdFTwFWbRoEbp16yYeKXbkyBGsW7dO5qjIi3jw4AFiY2NR\np04ddOrUCX379sWkSZO4KXjx8fEQBAELFiwA8O/BVfHx8QCUPfA3UFLwmjZtKh4wNnjwYAiCgOzs\nbJkjI1VBR2kqTHp6OmJiYiAIAnx9fWm3CiGEvCAqeArz8OFDJCUlIT8/X/y1WdG5QUq2YcMGxV4Q\n9WnvvfceVq5cWe5q4AAfVwQv9fDhQ/zwww9Qq9UoKioCAEVfyb2UsXx+xoJ2aSrIt99+i/DwcNy5\ncwdeXl6IiYlBp06dcOjQIblD06kVK1ZwU/DGjx8PAPjggw/KDapc2bX/lOb1119Hp06d0KZNG5iY\nmFR4vqgSlX5+77//frnHeMjP2NAWnoK0bt0asbGx6NSpE+Lj43H58mV8/PHH+O233+QOTad4O9m8\nqKgI48ePx08//SR3KHpT0aABPMnOzkadOnXEQds1Gg3y8/Nhbm4uc2SkKmgLT0Fq166NOnXqAADy\n8/PRokULJCYmyhyVbgQEBIj/X716VbwtCILit2Br1KiBW7duoaCgALVq1ZI7HL148803sW7dOgwc\nOFArx3r16skYle706NEDBw8eFE9NyM3NRZ8+fXDixAmZIyNVQQVPQVxcXPDw4UMMGTIEvXr1gq2t\nLTeH8kdEREAQBDDG0L9/f0RGRnJ1XbXGjRuja9euGDRoEOrWrQuAr3FQa9eujQ8//BCLFi0ST5UR\nBAHXr1+XOTLdKCgo0DoPz9LSErm5uTJGRKqDCp6ClO66DAsLg7+/Px4/foy+ffvKHJVulC3cNWvW\nFM815EXpYe3FxcVcHsq+bNkyXLt2jdujhs3NzXHmzBn4+PgAAOLi4sS9LUQ5qOApTHx8PI4ePQqg\n5OhMXgYfLqt0vEmeeHh4IDAwUOu+LVu2yBSN7jVr1ozrArBixQoEBgbCyckJQMlA0ps3b5Y5KlJV\ndNCKgqxcuRLffvsthg4dCsYYduzYgcmTJ9O1uBSgogNxeDo4Z8iQIbh06RICAgLEHh4PpyWUVVhY\niMTERAiCgFdeeQVmZmZyh0SqiAqegnh6eiImJkY8MiwnJwe+vr64cOGCzJGRZ9m7dy/27NmDzZs3\nY9SoUVpXgkhISMDp06dljlA3KhoIWxAEbk4v2bJlC/r27QsrKyssXLgQZ8+exdy5cxU/ZJqxoV2a\nClN27EyextHklbOzM3x8fLBz5074+PiIBc/KygrLly+XOTrdCQoKkjsEvVq4cCECAwNx7NgxHDx4\nEB988AGmTp3KzQ8WY0EFT0GCg4PRsWNHrV2aISEhcodFKtG2bVu0bdsWb775Jpf91lIV9V15Okqz\n9Py73bt3Y/LkyRgwYADmzZsnc1SkqqjgKURxcTE6duwIPz8/HDt2DIIgIDIyEt7e3nKHplMajQZp\naWni8FQA4OrqKmNEuqFWqzFnzhwkJCQgLy8PAF8FITY2Vvw/Pz8fv/76Kx48eCBjRLrVsGFDvPXW\nW/jzzz8xe/Zs5Ofnc3NxYmNCPTwF8fLyEkef59GqVauwYMECODg4iL+oAXDRo+zSpQsWLFiA0NBQ\n7Nq1CxEREdBoNFi4cKHcoekNT6Ov5OTkYN++fWjTpg2aNWuGlJQUXLhwAb1795Y7NFIFVPAU5IMP\nPoCvry+GDRvG5Th+TZs2xenTp8WrSvOkdOXv6ekpFnCeCsKZM2f+X3v3FhPV1b4B/NlACKYjAqIh\nJFJwkALVEYuAKIrxEIwnhKqJJWCkaEMMTYuNjUERjxfWQ6WtPahYSTXxUFLUqjUGTasRUZGDEDBi\nKVKJEvfggEKQYf8viPMvsV/7pUy/tffi+SVe7B0vnkTiy7v2u9Zy/Ez29vbi5s2b+PLLL1FZWSk4\nGdH/45KmgXz11VfYvXs3XF1d4eHhAaBvWcxmswlO5hwBAQHw9PQUHeNf4eHhAbvdjuDgYHz++efw\n9/fHs2fPRMdymjVr1jgKnpubGwIDA6XaZ0hyYIdHupGeno67d+9i3rx5jgEPWY7fKisrQ1hYGNra\n2rBhwwbYbDasXbsWkyZNEh2NaNBgh2cgmqahqKgIV65cgYuLC+Li4pCUlCQ6ltMEBAQgICAA3d3d\n6O7uluaKGQCIjo4G0HcG45/tWTO6rq4ufP/992hsbITdbnf82+Xm5oqORuTADs9AMjMz0dDQgGXL\nlkHTNBw7dgxmsxn79u0THc2p2tvbAfQVB1ncuHED27dvf+WC1KqqKsHJnCMhIQFeXl6IjIzsN3D0\nZ/fIEYnCgmcgoaGhqK2tdWw47+3tRXh4OOrq6gQnc47q6mqkpaU5xtlHjBiBw4cPY+zYsYKTDVxI\nSAh27tyJsWPH9jswQJbbLsaOHYs7d+6IjkH0l7ikaSDBwcFoampy/CfZ1NSE4OBgsaGcaNWqVdi9\ne7fjLrzLly9j1apVUtw5NmLECCxcuFB0jH/N5MmTUVVVBYvFIjoK0X/EDs9Apk2bhhs3biA6OhqK\noqCsrAxRUVHw9PSEoig4deqU6IgDMn78+FfG2P/snRFduHABx44dw6xZs/oN5CQnJwtO5hxhYWG4\nd+8egoKC+h0eLcuSLcmBHZ6BbN68GQAcgxx//F1FhuGOoKAgbNmyBampqdA0DUeOHMHo0aNFx3KK\nw4cPo76+Hj09Pf2WNGUpeOfOnRMdgehvscMzmJaWFpSVlcHFxQVRUVHw8/MTHclpVFXFxo0bcfXq\nVQDA1KlTkZeXB29vb8HJBu6NN95AXV2dFL+YEBkVC56BHDhwAJs3b+73jSs3Nxfvvvuu4GT0d1as\nWIGPPvoIb775pugoRIMWC56BhISE4Nq1a46jt548eYLY2FjcvXtXcDLnqK+vx86dO18Z3S8pKRGc\nbOBCQ0PR0NDAb1xEAvEbnoH4+vrCZDI5nk0mE3x9fQUmcq4lS5YgMzMTGRkZjr1csiwBnj9/XnQE\nokGPHZ6BpKam4s6dO0hMTAQAFBcXw2KxwGKxSHEEV2RkJG7duiU6BhFJih2egZjNZpjNZkfXk5iY\nCEVR0NHRITjZwKiqCk3TsGDBAnzxxRdITk52LPsBgI+Pj8B0RCQLdngkXGBg4F8uXf7666//wzRE\nJCsWPAN5/PgxduzY8cqt2TIMdQB9BxC/vPbor94REf0TLn//V0gvUlJSEBoaivv37yMvLw+BgYGY\nOHGi6FhOM3ny5P/qHRHRP8FveAby5MkTZGRkID8/H/Hx8YiPj5ei4LW0tODhw4d4/vw5ysvLHVfL\n2Gw2PH/+XHQ8IpIEC56BvDyD0c/PD2fOnIG/vz+sVqvgVAN34cIFfPvtt/j999/7XSczdOhQbN++\nXWAyIpIJv+EZyOnTpzF16lQ8ePAAWVlZsNlsyMvLk+YU/pMnT2Lx4sWiYxCRpFjwSDdGjx6Nt99+\nGytWrEB4eLjoOEQkGQ6tkG5UVFRgzJgxyMjIQExMDL7++mvYbDbRsYhIEuzwSJcuX76MlJQUWK1W\nLFmyBBs2bJDqslsi+t9jh0e60dPTg+LiYixatAgffPAB1qxZg/v372PBggWYO3eu6HhEZHAseAay\nbt26flOZVqsV69evF5jIuUJCQlBcXIy1a9eioqIC2dnZ8PPzw+LFi5GQkCA6HhEZHJc0DSQiIgIV\nFRX93k2YMAG3b98WlMi5Ojo6+t0GQUTkTOzwDKS3txddXV2O587OTnR3dwtM5FyrV69GW1ub41lV\nVaSnpwtMREQy4cZzA0lJScHMmTORnp4OTdNw6NAhpKWliY7lNJWVlfDy8nI8+/j4oLy8XGAiIpIJ\nC56BfPzxx7BYLLh48SIURUFubq5U37Y0TYOqqo7rgFRVhd1uF5yKiGTBb3ikG4WFhdi2bRuWLl0K\nTdNw4sQJ5OTkSNXFEpE4LHgGMGXKFFy9ehUmk+mVe+NeHrIsi5qaGpSUlEBRFMyYMYMnrhCR07Dg\nkXDt7e0YOnTogP8OEdFf4ZSmgTQ0NDimNC9duoT8/Px+U41GlZSUhNWrV+PChQtQVdXxXlVV/PTT\nT8jMzERSUpLAhEQkA3Z4BjJ+/HjcunULjY2NmDt3LhITE1FTU4OzZ8+KjjZgJSUlOHr0KK5evYqH\nDx8CAPz9/REXF4eUlBRMnz5dbEAiMjwWPAN5ucl8x44dGDJkCLKysqTaeE5E9G/ikqaBuLu74+jR\noygsLMT8+fOhaRpevHghOhYRkSGw4BlIQUEBSktLkZOTg6CgIDQ2NiI1NVV0LCIiQ+CSpkGpqorm\n5mZYLBbRUYiIDIEnrRhIfHw8Tp8+jZ6eHkRGRmLEiBGYMmUK9uzZIzqa09jtdjx69Ag9PT2OdwEB\nAQITEZEsWPAM5OnTp/D09MSBAweQlpaGTZs2Ydy4caJjOc1nn32GTZs2YeTIkXB1dXW8r66uFpiK\niGTBgmcgdrsdLS0tOH78OLZu3QoAr5y8YmSffvop6uvrMXz4cNFRiEhCHFoxkJeHRZvNZkRHR6Oh\noQFjxowRHctpAgIC4OnpKToGEUmKQysk3K5duwAAtbW1qKurw/z58+Hu7g6gr4PNzs4WGY+IJMEl\nTQPp7OzEwYMHUVtbi87OTgB9BaGgoEBwsoFpb2+HoigICAjAqFGj0N3dLdXFtkSkD+zwDGTx4sUI\nCwvDkSNHsHHjRnz33XcICwtDfn6+6GhERLrHb3gGcu/ePWzZsgUmkwnLly/H2bNncf36ddGxnGb2\n7Nn9DsNWVVWqC26JSCwWPAN5+V1r2LBhqK6uRltbG1pbWwWncp7W1lZ4eXk5nn18fPDo0SOBiYhI\nJix4BrJy5UqoqoqtW7di4cKFCA8Px9q1a0XHchpXV1f89ttvjufGxka4uPBHlIicg9/wSDfOnz+P\nVatWYdq0aQCAn3/+Gd988w3mzJkjOBkRyYAFzwBeju3/kaIo0DRNurH91tZWlJaWQlEUTJo0Cb6+\nvqIjEZEkuC3BAF6O7Q8Gbm5uGDlyJLq6ulBbWwsAjo6PiGgg2OGRbuzfvx/5+flobm5GREQESktL\nERsbi5KSEtHRiEgCnAgwkOXLl/cb27darUhPTxeYyLn27t2LsrIyvP7667h06RJu376NYcOGiY5F\nRJJgwTOQysrKfmP73t7eKC8vF5jIuTw8PDBkyBAAQFdXF0JDQ1FfXy84FRHJgt/wDETTNKiqCh8f\nHwB9G7PtdrvgVM4zatQoWK1WLFq0CLNnz4a3tzcCAwNFxyIiSfAbnoEUFhZi27ZtWLp0KTRNw4kT\nJ5CTk4O0tDTR0Zzu8uXLsNlsmDNnjmPDPRHRQLDgGUxNTQ1KSkqgKApmzJiB8PBw0ZGcqqKiAr/8\n8guAvunM8ePHC05ERLJgwSPd2Lt3L/bv34/k5GRomoYffvgBK1euxPvvvy86GhFJgAWPdGPcuHEo\nLS3Fa6+9BgB49uwZJk2ahOrqasHJiEgGnNIkXfnj2Zk8R5OInIlTmqQbK1asQExMTL8lTZn2GRKR\nWFzSJF3o7e3FtWvX4OHhgStXrkBRFEydOhUTJkwQHY2IJMGCR7oRERGBiooK0TGISFL8SEK6MWvW\nLJw8eRL8HYyI/g3s8Eg3TCYTnj9/DldXV3h4eADouwbJZrMJTkZEMmDBIyKiQYFTmqQbmqahqKgI\nV65cgYuLC+Li4pCUlCQ6FhFJgh0e6UZmZiYaGhqwbNkyaJqGY8eOwWw2Y9++faKjEZEEWPBIN0JD\nQ1FbW+vYcN7b24vw8HDU1dUJTkZEMuCUJulGcHAwmpqaHM9NTU0IDg4WmIiIZMIOj3Rj2rRpuHHj\nBqKjo6EoCsrKyhAVFQVPT08oioJTp06JjkhEBsahFdKNzZs3A+jbigCg3368l++IiP4pdnikKy0t\nLSgrK4OLiwuioqLg5+cnOhIRSYLf8Eg3Dhw4gJiYGBQVFeHkyZOIiYnBwYMHRcciIkmwwyPdCAkJ\nwbVr1zB8+HAAwJMnTxAbG4u7d+8KTkZEMmCHR7rh6+sLk8nkeDaZTPD19RWYiIhkwg6PdCM1NRV3\n7txBYmIiAKC4uBgWiwUWiwWKoiA7O1twQiIyMk5pkm6YzWaYzWbHRGZiYiIURUFHR4fgZEQkA3Z4\nREQ0KLDDI914/PgxduzYgdraWnR2dgLo239XUlIiOBkRyYBDK6QbKSkpCA0Nxf3795GXl4fAwEBM\nnDhRdCwikgSXNEk33nrrLZSXl8NisaCqqgoAMHHiRNy8eVNwMiKSAZc0STfc3d0BAH5+fjhz5gz8\n/f1htVoFpyIiWbDgkW7k5OSgra0Nu3btQlZWFmw2G/bs2SM6FhFJgkuaREQ0KHBohYiIBgUWPCIi\nGhRY8IiIaFBgwSPdWLduXb+pTKvVivXr1wtMREQyYcEj3Th37hy8vb0dz97e3vjxxx8FJiIimbDg\nkW709vaiq6vL8dzZ2Ynu7m6BiYhIJtyHR7qRkpKCmTNnIj09HZqm4dChQ0hLSxMdi4gkwX14pCvn\nzp3DxYsXoSgKZs+ejYSEBNGRiEgSLHhERDQo8BseCTdlyhQAgMlkwtChQ/v98fT0FJyOiGTBDo+I\niAYFdnikGw0NDY4pzUuXLiE/Px9tbW2CUxGRLFjwSDeSk5Ph5uaGe/fu4b333sODBw/wzjvviI5F\nRJJgwSPdcHFxgZubG4qKipCVlYVPPvkELS0tomMRkSRY8Eg33N3dcfToURQWFmL+/PnQNA0vXrwQ\nHYuIJMGCR7pRUFCA0tJS5OTkICgoCI2NjUhNTRUdi4gkwSlN0iVVVdHc3AyLxSI6ChFJgh0e6UZ8\nfDxsNhtUVUVkZCQyMjLw4Ycfio5FRJJgwSPdePr0KTw9PVFUVIS0tDSUlZXh4sWLomMRkSRY8Eg3\n7HY7WlpacPz4ccybNw8AoCiK4FREJAsWPNKN3NxcJCQkwGw2Izo6Gg0NDRgzZozoWEQkCQ6tEBHR\noMD78Eg3Ojs7cfDgQdTW1qKzsxNA35JmQUGB4GREJAMuaZJupKam4tGjRzh//jymT5+O5uZmmEwm\n0bGISBJc0iTdiIiIQEVFBSwWC6qqqvDixQvExcXh+vXroqMRkQTY4ZFuuLu7AwCGDRuG6upqtLW1\nobW1VXAqIpIFv+GRbqxcuRKqqmLr1q1YuHAhOjo6sGXLFtGxiEgSXNIkIqJBgR0eCbdr165X3imK\nAk3ToCgKsrOzBaQiItmw4JFw7e3tPFGFiP51XNIkIqJBgVOapBvLly9HW1ub49lqtSI9PV1gIiKS\nCQse6UZlZSW8vLwcz97e3igvLxeYiIhkwoJHuqFpGlRVdTyrqgq73S4wERHJhEMrpBtr1qxBbGws\nli5dCk3TcOLECeTk5IiORUSS4NAK6UpNTQ1KSkqgKApmzJiB8PBw0ZGISBIseERENCjwGx4REQ0K\nLHhERDQosOAREdGgwIJHRESDAgseERENCv8HW+pAuTxU0ZIAAAAASUVORK5CYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x106418090>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 63
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"This is a pretty significant performance gain. The \"Cython + type declarations\" approach sped up our initial Python code 25 times."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"explicit_loops\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"# Appendix III: Cython performance after replacing list comprehensions by explicit for loops"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"List, set and dictionary comprehensions in Python do not only look prettier and are easier to read (at least most of the time) than nested loop structures, but they also come with some small performance benefits. \n",
|
|
"Does this also apply in Cython? Let's check it out."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"This is the code for our \"classic\" least squares approach that we have been using in the previous sections:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def lstsqr_comprehensions(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 46
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"And here is a version where I replaced the list comprehensions by for-loops:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def lstsqr_loops(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" for x_i in x:\n",
|
|
" var_x += (x_i - x_avg)**2\n",
|
|
" cov_xy = 0\n",
|
|
" for x_i, y_i in zip(x,y):\n",
|
|
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 48
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"Finally, the Cython versions of the two functions (with and without using list comprehensions) that we have defined above:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%load_ext cythonmagic"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": []
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"\n",
|
|
"def cy_lstsqr_comprehensions(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" cdef double x_avg, y_avg, var_x, cov_xy, slope, y_interc, x_i, y_i\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 49
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"\n",
|
|
"def cy_lstsqr_loops(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" cdef double x_avg, y_avg, var_x, cov_xy, slope, y_interc, x_i, y_i\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" for x_i in x:\n",
|
|
" var_x += (x_i - x_avg)**2\n",
|
|
" cov_xy = 0\n",
|
|
" for x_i, y_i in zip(x,y):\n",
|
|
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 50
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"We will generate some sample data for different sample sizes and take a look at the results for the regular Python functions, and the Cython code separately."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"funcs = ['lstsqr_comprehensions', 'lstsqr_loops',\n",
|
|
" 'cy_lstsqr_comprehensions', 'cy_lstsqr_loops'] \n",
|
|
"\n",
|
|
"orders_n = [10**n for n in range(1, 6)]\n",
|
|
"times_n = {f:[] for f in funcs}\n",
|
|
"\n",
|
|
"for n in orders_n:\n",
|
|
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
|
|
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
|
|
" for f in funcs:\n",
|
|
" times_n[f].append(timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 52
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"plt.figure(figsize=(8,6))\n",
|
|
"plt.plot(orders_n, times_n['lstsqr_comprehensions'], alpha=0.5, \n",
|
|
" label='list comprehensions', marker='o', lw=2)\n",
|
|
"plt.plot(orders_n, times_n['lstsqr_loops'], alpha=0.5, \n",
|
|
" label='for-loops', marker='o', lw=2)\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.legend(loc=2)\n",
|
|
"plt.grid()\n",
|
|
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
|
|
"plt.title('Performance comparison list comprehensions and for-loops')\n",
|
|
"plt.show()\n",
|
|
"\n",
|
|
"plt.figure(figsize=(8,6))\n",
|
|
"plt.plot(orders_n, times_n['cy_lstsqr_comprehensions'], alpha=0.5, \n",
|
|
" label='list comprehensions (Cython', marker='o', lw=2)\n",
|
|
"plt.plot(orders_n, times_n['cy_lstsqr_loops'], alpha=0.5, \n",
|
|
" label='for-loops (Cython)', marker='o', lw=2)\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.legend(loc=2)\n",
|
|
"plt.grid()\n",
|
|
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
|
|
"plt.title('Performance comparison list comprehensions and for-loops in Cython')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAfEAAAGJCAYAAACaQwrRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd4VFX++PH3pBHSG0kIaZDQEkoQBKSGLh1pCwiC4FdZ\nle+6+lt1UcEO+oW1rS7qIqjoioB0WJASpIgBaUpIIJCENEJCgCSkTDJzfn/cZTaBVFIn+byeJ8+T\nOzPnzLmfuclnzj3nnqtTSimEEEIIYXYs6rsBQgghhLg3ksSFEEIIMyVJXAghhDBTksSFEEIIMyVJ\nXAghhDBTksSFEEIIMyVJ3AylpaUxYMAAnJyc+Mtf/lLfzRFlOHjwIB06dKjT9wwPD2flypUAfPPN\nN4wYMaJO378hKR6LujJq1Ci+/vrrOn3PmhQYGMjevXtLfS4vL4+xY8fi4uLCH/7wh2q/16uvvsqs\nWbOqXU9TZ1XfDWgqAgMDuXr1KpaWltjb2zNy5Ej+/ve/Y29vX+W6PvvsMzw9PcnKyqqFloqa0r9/\nf6Kjo+v0PXU6HTqdDoCHH36Yhx9+uMIyc+bMwc/PjzfeeKO2m1eniseiruzYsaNO36+mlRez9evX\nc/XqVTIzM7GwqH7/r64/m8ZKeuJ1RKfTsW3bNrKzszlx4gTHjx/nzTffrFIdSimMRiMJCQl07Njx\nntpRVFR0T+VE1Uica5fEt+4lJCTQrl27e0rgpX1ess5YzZAkXg98fHx48MEH+f333wE4evQoffr0\nwdXVlbCwMA4cOGB6bXh4OC+//DL9+vXD3t6e2bNn89VXX/Huu+/i6OjIvn370Ov1PPPMM7Rq1YpW\nrVrx5z//Gb1eD0BERAS+vr68++67tGzZkrlz5/Laa68xZcoUZs2ahZOTE126dOHChQssWbIELy8v\nAgIC+PHHH01tWLVqFSEhITg5OREUFMRnn31meu52/X/729/w8vLCx8eH1atXm57Py8vjueeeIzAw\nEBcXF/r3709+fn6F+32nxMREJk6ciKenJx4eHixYsAAAo9HIm2++SWBgIF5eXsyePdt0hiI+Ph4L\nCwtWr16Nv78/7u7urFixgmPHjtGlSxdcXV1N9QCsXr2avn37smDBAlxcXOjYsSP79u2rUhxux3ne\nvHlERETg5+dnes0777yDr68vTk5OdOjQwVR3QUFBhZ9fWfEtz+rVq+nfvz+g/cP885//jJeXF87O\nznTp0oWzZ8/y2Wef8e2335qOp/Hjx5da19mzZxk2bBju7u54e3uzZMmSSrf9//7v//D09MTHx4dN\nmzaxY8cO2rVrh7u7O0uXLjW9x6uvvsrkyZOZNm0aTk5OdO/enTNnzpieDwwM5N1336VLly44Ojpi\nNBorPIbi4+Pp168fTk5OjBgxgmvXrpmeq+jvbtGiRaWWzc/PZ+bMmXh4eODq6krPnj1JT083lbt9\nCl8pVeGx+dVXXxEQEECLFi14++23Te8fGRlJjx49cHZ2xtvbm+eee67Uz+XGjRuMGTMGT09P3Nzc\nGDt2LMnJyZXaD4Cvv/6agIAAPDw8Srz/nRYvXswbb7zB2rVrcXR0ZNWqVZXavy+++IKAgACGDh1a\nZt23bdmyhdDQUFxdXRk0aFCJs1jnzp0jPDwcV1dXOnXqxNatW03PzZkzh/nz5zN8+HCcnJwIDw/n\n8uXLpudLO+4bFSXqRGBgoNqzZ49SSqnLly+r0NBQtWjRIpWUlKTc3d3Vzp07lVJK/fjjj8rd3V1l\nZGQopZQaOHCgCggIUFFRUcpgMKjCwkI1Z84c9corr5jqfuWVV9QDDzyg0tPTVXp6uurTp4/p+f37\n9ysrKyv14osvKr1er/Ly8tTixYuVra2t2r17tyoqKlKPPPKICggIUG+//bYqKipSn3/+uWrdurWp\n/u3bt6tLly4ppZQ6cOCAsrOzUydOnChR/+LFi1VRUZHasWOHsrOzUzdu3FBKKfXkk0+qQYMGqZSU\nFGUwGNTPP/+sCgoKytzv9PT0u2JXVFSkunTpop599lmVm5ur8vPz1eHDh5VSSq1cuVIFBweruLg4\nlZOToyZOnKhmzZqllFIqLi5O6XQ69cc//lEVFBSo3bt3KxsbGzVhwgSVnp6ukpOTlaenpzpw4IBS\nSqlVq1YpKysr9f7776uioiK1du1a5ezsrDIzMysdh+Jx3r9/v/L19VVKKRUdHa38/PxUamqqUkqp\nhIQEdfHixUp/fmXF907h4eFq5cqVpv3p16+fUkqpf//736p79+7q5s2bpvbcbsudx9OdsrKylLe3\nt/rb3/6mCgoKVHZ2tvrll18q3fY33njDdFy5u7urGTNmqJycHHX27FnVvHlzFR8fr5RSavHixcra\n2lpt2LBBFRUVqWXLlqnWrVuroqIipZRSAQEBqlu3biopKUnl5+dX6m8nKChIXbhwQeXl5anw8HD1\n4osvKqVUpcoGBweXWnbFihVq7NixKi8vTxmNRnXixAmVlZV1V/wrc2w+/vjjKj8/X50+fVo1a9ZM\nRUdHK6WU6t27t1qzZo1SSqlbt26po0ePlvrZXLt2Tf3www8qLy9PZWdnqylTpqgJEyaYni9vP86e\nPascHBzUwYMHVUFBgXr22WeVlZWV2rt3b6nv9eqrr5raX9n9mz17tulv9k6LFy9WM2fOVEopFRMT\no+zt7dWePXtUUVGRevfdd1VwcLAqLCxUer1eBQUFqSVLlqjCwkK1b98+5ejoqGJiYpRSSs2ePVs5\nOjqa9uNPf/pTpY77xkKSeB0JCAhQDg4OysXFRQUEBKinnnpK5eXlqaVLl5b4w1BKqREjRqgvv/xS\nKaX9U1i8eHGJ5+fMmaNefvll03ZQUJDpn5FSSu3atUsFBgYqpbR/pDY2NqqgoMD0/OLFi9Xw4cNN\n21u2bFEODg7KaDQqpbR/2jqdznTg32nChAnqgw8+MNXfvHlzZTAYTM97enqqX375RRkMBtW8eXN1\n5syZu+qoaL+LO3LkiGrRokWJ97ht8ODB6h//+IdpOyYmRllbWyuDwWD6R5KSkmJ63t3dXX3//fem\n7UmTJqn3339fKaUlPR8fnxL19+zZU3399deVisOdcS6exC9cuKA8PT3Vnj17lF6vL1FPRZ9fWfEt\nTVlJfO/evapdu3bq6NGjd8XxzuPpTt9++6267777Sn2uMm2/87iKjIw0vb579+5q8+bNSintuHzg\ngQdMzxmNRtWyZUt16NAhpZT2RXjVqlWm5yvzt/PWW2+Znvvkk0/Ugw8+WO2yX3zxherTp0+px3Xx\n+Ffm2ExOTjY937NnT7V27VqllFIDBgxQixcvLvVLbXlOnjypXF1dS7SnrP147bXX1PTp003P3bp1\nS9nY2JSZxIsn3cruX1xcXJltLV7f66+/rv7whz+YnjMajapVq1YqIiJC/fTTT8rb27tE2enTp6tX\nX31VKaUl8eL7kZOToywtLVVSUpLat29fmcd9YyGn0+uITqdj8+bNXL9+nfj4eP7+979ja2tLQkIC\n69atw9XV1fRz+PBhrly5Yipb/JRsaVJSUggICDBt+/v7k5KSYtpu0aIFNjY2Jcp4enqafm/evDke\nHh6miSbNmzcHICcnB4CdO3fSu3dv3N3dcXV1ZceOHSVOybm7u5cYJ7OzsyMnJ4eMjAzy8/MJCgq6\nq82V2e/bEhMTCQgIKHUsLjU19a59LyoqIi0tzfSYl5dXiX29c/vWrVum7VatWpWoPyAggNTU1ErF\nobQ43xYcHMz777/Pq6++ipeXF9OnTzfVW9HnV1Z8q2Lw4ME8/fTTPPXUU3h5efHEE0+QnZ1dqbKJ\niYm0adOm1Ocq0/Y7j6s74198X3x9fU2/63Q6fH19S9RX/G+hMseQt7d3qe9VnbKzZs1ixIgRTJs2\njVatWvHCCy+UOuZbmWOz+HsU/1xXrlzJ+fPn6dixIz179mT79u131Q+Qm5vLE088QWBgIM7Ozgwc\nOJCbN2+WGG8uaz9SUlJKxNvOzg53d/dS36c0ldm/25/XN998g6OjI46OjowePfquulJSUvD39zdt\n63Q6/Pz8SE5OJjU19a7/gQEBAabj4vZxcpu9vT1ubm6kpKQwaNCgez7uzYUk8Xrm7+/PrFmzuH79\nuuknOzub559/3vSaimZx+vj4EB8fb9q+fPkyPj4+ZZavyqzQgoICJk2axPPPP8/Vq1e5fv06o0aN\nqtSkFA8PD2xtbYmNjb3rucrs921+fn5cvnwZg8Fw13Ol7buVlVWJRFEVxccTQftn7+PjU6k4VBTX\n6dOnc/DgQRISEtDpdLzwwgtl7kPxz6+mLFiwgOPHjxMVFcX58+f5v//7v0q129/fn0uXLpX6XE23\nPTEx0fS70WgkKSmpzGO5KsfQnapT1srKikWLFnH27FmOHDnCtm3b+Oqrr+56XXWOzeDgYL799lvS\n09N54YUXmDx5Mnl5eXe9bvny5Zw/f57IyEhu3rzJgQMHUNoZ1grfw8fHp0S8c3NzS3wpvdOdx0ll\n9q/4lRLZ2dlkZ2eX+oWkVatWJCQkmLaVUiQmJuLr62tqZ/F9SkhIMH3hvv3a23JycsjMzDQdN2Ud\n942FJPF6NnPmTLZu3cru3bsxGAzk5+cTERFRIpnc+Qd55/b06dN58803ycjIICMjg9dff73c6y8r\n8wd+m16vR6/X4+HhgYWFBTt37mT37t2VKmthYcHcuXN59tlnSU1NxWAw8PPPP6PX6yu137f16tWL\nli1b8uKLL5Kbm0t+fj5Hjhwx7ft7771HfHw8OTk5LFy4kGnTplVpBm3xeFy9epUPP/yQwsJC1q1b\nR3R0NKNGjapWHADOnz/Pvn37KCgooFmzZtja2mJpaWnah6p8fvfi+PHj/PLLLxQWFmJnZ1fi/b28\nvMpM0gBjxowhNTWVDz74gIKCArKzs4mMjKyVtv/6669s3LiRoqIi3n//fWxtbendu3epr72Xv52a\nKLt//35+++03DAYDjo6OWFtbm2JZXHWOzTVr1pgmyzk7O6PT6Uotl5OTQ/PmzXF2diYzM5PXXnvt\nrteUtR+TJk1i27ZtHD58GL1ez6JFizAajWW2qbT/O9X927ttypQpbN++nX379lFYWMjy5cuxtbWl\nT58+9OzZEzs7O959910KCwuJiIhg27ZtTJs2zVR+x44dpv145ZVXeOCBB2jVqlW5x31jIUm8nvn6\n+rJ582befvttPD098ff3Z/ny5eX28O68lvPll1+mR48edOnShS5dutCjRw9efvnlSpcv6zUAjo6O\nfPjhh0ydOhU3Nzf+9a9/3TWDubye3LJly+jcuTP3338/7u7u/PWvf8VoNJa536X9E7GwsGDr1q3E\nxsbi7++Pn58f33//PQBz585l1qxZDBgwgDZt2mBnZ8dHH31UqbaV9ppevXpx4cIFWrRowSuvvMKG\nDRtwdXW95zjcfqygoIC//vWvtGjRgpYtW5KRkWGa4V3Vz6+yin/OWVlZPP7447i5uREYGIiHh4dp\noaB58+YRFRWFq6srEydOvKseBwcHfvzxR7Zu3UrLli1p164dERER99T28vZFp9Mxfvx41q5di5ub\nG9988w0//PBDmf90q/q3Uzwe1SmblpbGlClTcHZ2JiQkhPDw8FK/uFTn2Ny1axedOnXC0dGRP//5\nz3z33Xc0a9bsrtc988wz5OXl4eHhQZ8+fRg5cmS5MS++H6GhoXz88cfMmDEDHx8f3Nzcyh26u/P/\nRnX/9orX1759e9asWcOCBQto0aIF27dvZ+vWrVhZWWFjY8PWrVvZuXMnLVq04Omnn+brr7+mXbt2\npnpmzJjBa6+9hru7OydPnmTNmjVA+cd9Y6FTVemWVUF+fj4DBw6koKAAvV7P+PHjWbJkCa+++ir/\n/Oc/adGiBQBvv/02I0eOBGDJkiV88cUXWFpa8uGHHzJ8+PDaaJoQpVq9ejUrV67k4MGD9d2UJum1\n114jNjbWrFc8E3Xv0UcfxdfXt9EtVlRZtbZim62tLfv378fOzo6ioiL69evHoUOH0Ol0PPvsszz7\n7LMlXh8VFcXatWuJiooiOTmZoUOHcv78+RpZGUgI0fDVUn9CNHJN/bip1QxpZ2cHaOOqBoMBV1dX\noPSgb968menTp2NtbU1gYCDBwcGmcTch6kJ9LNMp/kviL+5FUz9uajWJG41GwsLC8PLyYtCgQYSG\nhgLw0Ucf0bVrV+bNm8eNGzeAuy938PX1LXWSkxC1Zfbs2fz000/13Ywma/HixaXO8haiPKtWreL1\n11+v72bUm1pN4hYWFpw6dYqkpCR++uknIiIi+OMf/0hcXBynTp2iZcuWZS4nCLJAvhBCCFGeOrmL\nmbOzM6NHj+b48eOEh4ebHn/ssccYO3YsoF0nWPxav6SkpLsW3rj9uuKLPwghhBCNWdeuXTl16lSp\nz9VaTzwjI8N0qjwvL48ff/yRbt26lVgRaePGjXTu3BmAcePG8d1336HX64mLi+PChQv07NnzrnpT\nUlJMixnIz739LF68uN7bYO4/EkOJYUP4kRg2jTiePn26zFxbaz3x1NRUZs+ejdFoxGg0MmvWLIYM\nGcIjjzzCqVOn0Ol0tG7dmk8//RSAkJAQpk6dSkhICFZWVnzyySdyOr2WFF9lSdwbiWH1SQyrT2JY\nM8w5jrWWxDt37syJEyfuery8iSsLFy5k4cKFtdUkIYQQolGRi7CboDlz5tR3E8yexLD6JIbVJzGs\nGeYcx1pbsa226HQ6zKzJQgghxD0rL+81mp64m5ub6aJ/+ZGf+vxxc3Or7z8Hs3B7/XVx7ySGNcOc\n41gnl5jVhevXr0sPXTQIOp1MyBRC1I1Gczq9rMeFqGtyLAohalJ5/1Mazel0IYQQoqmRJC6EqBfm\nPA7ZUEgMa4Y5x1GSeB0IDAxk3759gHb/9P/5n/+p5xbVn8DAQPbu3Vun79mpUye5sYkQolFqNBPb\nGrLiE50qu5hNeHg4s2bNYt68ebXVrHpxewZ3Xfr999/r9P1E5RS/j4K4NxLDmmHOcZSeeANljjOc\ni4qK6rsJQgjRpDT6JB4Tk8DHH+/j/fcj+PjjfcTEJNRLHbe9+uqrzJo1C4D8/HxmzpyJh4cHrq6u\n9OzZk6tXr/LSSy9x8OBBnn76aRwdHfnf//3fUus6dOgQffr0wdXVFX9/f7788ksAbt68ySOPPIKn\npyeBgYG89dZbppmNq1evpm/fvjz77LO4uroSHBzMkSNHWLVqFf7+/nh5eZVYGnfOnDnMnz+f4cOH\n4+TkRHh4OJcvXzY9b2FhwSeffELbtm1p3749ANu2bSMsLAxXV1f69u3Lb7/9VqLdJ0+epGvXrri4\nuDBt2jQKCgpMz5VXNjAwkOXLl5daNiMjgzFjxuDq6oq7uzsDBgwoUe72KfyCggKeeeYZWrVqRatW\nrfjzn/+MXq8HtHExX19f/va3v+Hl5YWPjw+rV6821bNjxw5CQ0NxcnLC19eX5cuXV+YjF2Uw53HI\nhkJiWDPMOY6NOonHxCSwenUs6emDuXEjnPT0waxeHVulJFwTdRRX/HTyl19+SVZWFklJSWRmZvLp\np5/SvHlz3nrrLfr378/HH39MdnY2H3744V31JCQkMGrUKP70pz+RkZHBqVOnCAsLA2DBggVkZ2cT\nFxfHgQMH+Oqrr1i1apWpbGRkJF27diUzM5Pp06czdepUTpw4wcWLF1mzZg1PP/00ubm5ptd/++23\nLFq0iIyMDMLCwnj44YdLtGXz5s0cO3aMqKgoTp48ybx58/j888/JzMzkiSeeYNy4cRQWFgKglGLd\nunXs2rWLuLg4zpw5Y0qUFZXV6XRlll2+fDl+fn5kZGRw9epVlixZUmrM33rrLSIjIzl9+jSnT58m\nMjKSN9980/TatLQ0srKySElJYeXKlTz11FPcvHkTgHnz5vHZZ5+RlZXF2bNnGTx4cNUPACGEqEGN\nekx8z56LNGs2hJJfsoZw5sw+7r8/oFJ1REZeJDd3iGk7PByaNRvC3r37aN++cnUUd/vWcgA2NjZc\nu3aNCxcu0LlzZ7p163bXa8vy7bffMmzYMP7whz8A2op1bm5uGAwG1q5dy+nTp7G3t8fe3p7nnnuO\nr7/+mrlz5wLQunVrZs+eDcDUqVN56623WLRoEdbW1gwbNgwbGxtiY2Pp0qULAGPGjKFfv36AlgSd\nnZ1JTk423e/9r3/9Ky4uLgB89tlnPPHEE9x///0APPLII7z99tscPXqU/v37o9Pp+N///V+8vb0B\nGDt2rOk+uRWVBcosa2NjQ2pqKvHx8QQFBdG3b98y4/b3v/8dDw8PABYvXswTTzzB66+/DoC1tTWL\nFi3CwsKCkSNH4uDgQExMDD179sTGxoazZ8/SuXNnnJ2d7/q8RNWY8zhkQyExrBnmHMdG3RMvLCx9\n9wyGyu+20Vj6a/X66odu1qxZjBgxgmnTptGqVSteeOGFEuPK5Y2LJyUl0aZNm7sez8jIoLCwkICA\n/37B8Pf3Jzk52bTt5eVl+r158+YAtGjRosRjOTk5pjb4+vqanrO3t8fNzY2UlBTTY35+fqbfExIS\nWL58Oa6urqafpKSkEq+/nYTvfK/qlP3LX/5CcHAww4cPJygoiHfeeafUuKWkpNwVm+L1u7u7Y2Hx\n38/Wzs7O9B4bNmxgx44dBAYGEh4eztGjR0t9DyGEqCuNuidubW0EtN5zcZ6eRp58snJ1fPyxkfT0\nux+3sTFWr3GAlZUVixYtYtGiRabT4+3bt2fu3LkVTmzz8/MjMjLyrsc9PDywtrYmPj6ejh07AnD5\n8uUSibgqlFIkJiaatnNycsjMzMTHx8f0WPG2+vv789JLL1XplrK3y1e1bPH3dXBwYNmyZSxbtsx0\nqrtnz54MGjSoRBkfH5+7YlN8X8rTo0cPNm3ahMFg4KOPPmLq1Kkl5geIqomIiDDrHlBDIDGsGeYc\nx0bdEx86NIiCgpLXJBcU7GXIkKA6raMsERER/PbbbxgMBhwdHbG2tsbS0hLQessXL14ss+zDDz/M\nnj17WLduHUVFRVy7do3Tp09jaWnJ1KlTeemll8jJySEhIYH33nuPmTNn3nM7d+zYweHDh9Hr9bzy\nyis88MADplPpd/qf//kfVqxYQWRkJEopbt26xfbt20292dLcHjaoatniww3btm0jNjYWpRROTk5Y\nWlqW6FHfNn36dN58800yMjLIyMjg9ddfN000LE9hYSHffPMNN2/exNLSEkdHR9NnJYQQ9aVRJ/H2\n7QOYMycYT899uLhE4Om5jzlzgqs0ll0TdRRXfJLVlStXmDJlCs7OzoSEhJiuDQf405/+xPr163Fz\nc+OZZ565qx4/Pz927NjB8uXLcXd3p1u3bpw5cwaAjz76CHt7e9q0aUP//v15+OGHefTRR+96/+Jt\nKq+9M2bM4LXXXsPd3Z2TJ0+yZs2aMst2796dzz//nKeffho3Nzfatm3LV199VeZ7FG9PdcrGxsYy\nbNgwHB0d6dOnD0899RQDBw68q8zLL79Mjx496NKlC126dKFHjx68/PLLlYrFmjVraN26Nc7Oznz2\n2Wd88803Zb5WVMxcez4NicSwZphzHOUGKKJcjz76KL6+vrzxxhv13RSzIceiEKImyQ1QxD2TZCRq\nizlfm9tQSAxrhjnHUZK4KFd9LJMqhBCicuR0uhA1TI5FIURNktPpQgghRCMkSVwIUS/MeRyyoZAY\n1gxzjqMkcSGEEMJMyZi4EDVMjkUhRE2SMXEhhBCiEZIkXgdiYmIICwvDycmJv//979WqKzw8nJUr\nV9ZQy4SoP+Y8DtlQSAxrhjnHsVHfAKWhePfddxkyZIjptpnVIddtCyFEzYiJjWHPr3s4d/YcZ9PO\nMrT7UNoHt6/vZlWJ9MTrQEJCAiEhIVUuZzAYaqE1QjQM5rxedUMhMbx3MbExrN6/mrMOZ3Ee6Ey6\nVzqr968mJjamvptWJY0+icfExvDx2o95/7v3+Xjtx/f0AVWnjsGDBxMREcHTTz+Nk5MTZ86c4ZFH\nHsHT05PAwEDeeust04SF1atX07dvX5599lk8PDx47bXXyq1bKcWbb75JYGAgXl5ezJ49m6ysLNPz\nW7ZsITQ0FFdXVwYNGkR0dLTpucDAQJYuXUpoaChubm7MnTuXgoICQLsn+ZgxY3B1dcXd3Z0BAwbI\nRC0hRKPy72P/Js41jqj0KKIzolFK0axtM/ae2Ftx4QakUSfx29+00r3SueF9456+aVW3jn379tG/\nf38+/vhjsrKyWLZsGdnZ2cTFxXHgwAG++uorVq1aZXp9ZGQkQUFBXL16tcL7aq9atYovv/ySiIgI\nLl26RE5ODk8//TQA58+fZ8aMGXz44YdkZGQwatQoxo4dS1FRkan8t99+y+7du7l48SLnz5/nzTff\nBGD58uX4+fmRkZHB1atXWbJkiZzCFzXOnMchGwqJ4b25knOFny7/xJWcK1joLNBf1Jue0xv15ZRs\neBr1mPieX/fQrG0zIuIj/vugNZz57gz397u/UnVEHook1zcX4rXt8MBw07e1qo6dGAwG1q5dy+nT\np7G3t8fe3p7nnnuOr7/+mrlz5wLg4+PDU089BYCtrW259X3zzTc899xzBAYGArBkyRI6derEqlWr\nWLt2LWPGjGHIkCEA/L//9//44IMPOHLkCAMGDECn0/H000+b7gv+0ksvsWDBAt544w1sbGxITU0l\nPj6eoKAg+vbtW6X9FEKIhkgpxbGUY+y+uJu8wjzsre0JaRFC+vV0U0fFxsKmnltZNY26J16oCkt9\n3EDlx5qNGEt9/F6+rWVkZFBYWEhAwH/vRe7v709ycrJp28/Pz/T7/PnzcXR0xNHRkaVLl95VX2pq\n6l11FRUVkZaWRmpqKv7+/qbndDodfn5+Zb6Xv78/KSkpAPzlL38hODiY4cOHExQUxDvvvFPlfRWi\nIjKeW30Sw8rLK8zj+7Pfs+PCDoqMRYztNZZOOZ2wt7EnMCwQgIILBQy5b0j9NrSKGnVP3FpnDWi9\n5+I87Tx5MvzJStXxcdrHpHul3/X4vXxb8/DwwNramvj4eDp27AjA5cuX8fX1Nb2m+GnrFStWsGLF\nijLr8/EYfVaPAAAgAElEQVTxIT4+3rR9+fJlrKys8Pb2xsfHh99++830nFKKxMREU8/79uuL/+7j\n4wOAg4MDy5YtY9myZZw9e5bBgwdz//33M3jw4CrvsxBC1LfEm4msj1rPzYKbNLNsxrj24wj1DCUm\nNoa9J/aiN+qxsbBhyKAhMju9IRnafSgFFwpKPFbVb1o1UcdtlpaWTJ06lZdeeomcnBwSEhJ47733\nmDlzZpXrApg+fTrvvfce8fHx5OTksHDhQqZNm4aFhQVTpkxh+/bt7Nu3j8LCQpYvX46trS19+vQB\ntKT+ySefkJycTGZmJm+99RbTpk0DYNu2bcTGxqKUwsnJCUtLSywtLe+pjUKURcZzq09iWD6lFAcT\nDrLq1CpuFtyklWMr5veYT6hnKADtg9vz5NQnCfMO48mpT5pdAodG3hNvH9yeOcyp1jetmqijuI8+\n+ogFCxbQpk0bbG1tefzxx3n00UeBql8DPnfuXFJSUhgwYAD5+fk8+OCDfPTRR1q727dnzZo1LFiw\ngOTkZLp168bWrVuxsrIyvdeMGTMYPnw4KSkpTJgwgZdffhmA2NhYFixYQHp6Oq6urjz11FMMHDjw\nnvZXCCHqQ44+hx/O/cCl65cA6OPXhyGth2Bp0bg6JLJ2ehPVunVrVq5cKafIa4Eci0LUr4uZF/nh\n3A/cKryFnbUdD3V4iLbubeu7WfesvP8pjbonLoQQoukwGA3sj9/PocuHAGjt0pqJHSfi2MyxnltW\nexr1mLgQouGS8dzqkxj+1438G6w+tZpDlw+hQ8fg1oOZ1XVWpRK4Ocex1pJ4fn4+vXr1IiwsjJCQ\nEP76178CkJmZybBhw2jXrh3Dhw/nxo0bpjJLliyhbdu2dOjQgd27d9dW0wQQFxcnp9KFEI3CufRz\nrDi+gsSsRJyaOTEnbA4DAgZgoWv8/dRaHRPPzc3Fzs6OoqIi+vXrx7Jly9iyZQseHh48//zzvPPO\nO1y/fp2lS5cSFRXFjBkzOHbsGMnJyQwdOpTz589jYVHyQ5AxcdHQybEoRN0oMhaxK3YXx1KOAdDe\nvT3jO4zHztquUuVjYhLYs+cihYUWWFsbGTo0iPbtAyouWMfq7X7idnZaIPV6PQaDAVdXV7Zs2cLs\n2bMBmD17Nps2bQJg8+bNTJ8+HWtrawIDAwkODiYyMrI2myeEEMJMZeRm8Pmvn3Ms5RiWOktGBo9k\nWqdpVUrgq1fHkp4+mBs3wklPH8zq1bHExCTUcstrVq0mcaPRSFhYGF5eXgwaNIjQ0FDS0tLw8vIC\nwMvLi7S0NABSUlJKLHri6+tbYnUxIUTjYs7jkA1FU4yhUopTV07x6fFPSbuVhltzNx677zF6+faq\n0iW6e/ZcxMJiCGfPwu+/RwDQrNkQ9u69WEstrx21OjvdwsKCU6dOcfPmTUaMGMH+/ftLPF/RddFy\n0w0hhBC3FRQVsP3Cds6knQGgi1cXRrcdTTOrZlWuKzXVgmPHQK+H/HwIDQWdDvR68xpHr5NLzJyd\nnRk9ejS//vorXl5eXLlyBW9vb1JTU/H09ASgVatWJCYmmsokJSWVWCK0uDlz5phu+uHi4kJYWBiu\nrq6S9EWD4OTkZPr9dk/p9hrXsv3f7fDw8AbVHnPcvv1YQ2lPbW6nZqfy9tdvk63Ppu19bRndbjTX\nz13n57Sfq1SfwQBFReGcOGHk6tUI7O1h4MBwdDqIj4/AxeUEUL/7e/v34stql6XWJrZlZGRgZWWF\ni4sLeXl5jBgxgsWLF7Nr1y7c3d154YUXWLp0KTdu3CgxsS0yMtI0sS02NvauxCyThoQQoulQShGZ\nHMnui7sxKANe9l5MCZ2Ch51Hleu6ehU2bIC0NLh2LYHr12MJChrC7TRTULCXOXOCG9zktnpZ7CU1\nNZXZs2djNBoxGo3MmjWLIUOG0K1bN6ZOncrKlSsJDAzk+++/ByAkJISpU6cSEhKClZUVn3zyifSs\na0nxb+7i3kgMq09iWH2NPYa5hblsjt5MzLUYAO73uZ/hQcOxtrSuUj1KQWQk/PgjFBWBmxs89lgA\nt27B3r37iIo6Q0hIF4YMaXgJvCK1lsQ7d+7MiRMn7nrczc2NPXv2lFpm4cKFLFy4sLaaJIQQwkwk\n3Ehgw7kNZBVkYWtly/j24+nYomOV68nOhs2bITZW277vPnjwQbCxAQigffsAIiIszPbLUKNZO10I\nIYT5MyojBxMOEhEfgULh5+THpJBJuNi6VLmu6GjYsgVyc6F5cxg3DjpW/XtAvZO104UQQjR42QXZ\n/HDuB+JuxKFDR3///oQHhlf5zmN6PezaBb/+qm0HBcGECeDYCJdQN6+59KJGFJ8BKe6NxLD6JIbV\n15hieOHaBVYcX0HcjTjsre2Z2WUmQ9pU/dahKSnw6adaAre01E6dz5xZfgI35zhKT1wIIUS9MRgN\n7I3by5HEIwC0cW3DxI4TcbBxqFI9RiMcPgz792u/e3rCpEnwn7XFGi0ZExdCCFEvruddZ33UepKz\nk7HQWTC49WD6+vWt8pVJN27Axo2Q8J8VU3v3hqFDwaqRdFNlTFwIIUSDcvbqWbbEbKHAUIBzM2cm\nh0zGz9mvyvX89hts2wYFBeDgoI19BwfXQoMbKBkTb4LMefynoZAYVp/EsPrMMYaFhkK2xmxlXdQ6\nCgwFdPToyPwe86ucwPPztYVbNmzQEniHDvDkk/eWwM0xjrdJT1wIIUSduHrrKuuj1nP11lWsLKwY\nETSCHj49qnz6PCEBfvgBbt4Ea2tt8tp990FTXB9MxsSFEELUKqUUJ6+cZOeFnRQaC/Gw82ByyGS8\nHbyrVI/BABERcOiQtgqbj482ec3dvXba3VDImLgQQoh6kV+Uz7bz2/j96u8AhHmHMartKGwsbapU\nz7Vr2qnzlBStxz1gAAwcqF1G1pTJmHgTZM7jPw2FxLD6JIbV19BjmJyVzKfHP+X3q79jY2nDxI4T\nmdBhQpUSuFLaNd8rVmgJ3MUF5syBwYNrLoE39DiWR3riQgghapRSip+TfmbPpT0YlZGWDi2ZHDIZ\nd7uqnfe+dQu2btWWTwXo0gVGjQJb21potJmSMXEhhBA15pb+FpuiN3Eh8wIAvVr1YljQMKwsqtZn\njI2FTZsgJ0dL2qNHQ+fOtdHihk/GxIUQQtS6+BvxbIjaQLY+m+ZWzZnQYQLtPdpXqY7CQtizB375\nRdsOCICHHtJOo4u7yZh4E2TO4z8NhcSw+iSG1ddQYmhURvbH7efLU1+Src/G39mf+T3mVzmBp6XB\n559rCdzCQlt1bfbs2k/gDSWO90J64kIIIe5ZVkEWG6I2kHAzAR06BgQMIDwwHAtd5fuISsHRo1oP\n3GDQLhmbNEm7hEyUT8bEhRBC3JOYjBg2RW8irygPBxsHJnWcRGvX1lWqIytLG/u+dEnb7tEDhg8H\nm6pdgdaoyZi4EEKIGlNkLGLPpT0cTToKQLBbMA91eAh7G/sq1XPuHGzZAnl5YGcH48dD+6qdgW/y\nZEy8CTLn8Z+GQmJYfRLD6quPGGbmZbLyxEqOJh3FQmfB8KDhPNz54SolcL0eNm+GtWu1BB4crK17\nXl8J3JyPRemJCyGEqJTf0n5j6/mt6A16XGxdmBwyGV8n3yrVkZSkrXuemandKnTYMOjZs2mue14T\nZExcCCFEufQGPTsv7OTklZMAhLYIZWz7sdhaVX7VFaMRDh6EAwe03728tMlrnp611erGQ8bEhRBC\n3JO0nDTWRa0jIzcDKwsrRgaP5L6W91XpzmPXr2u978REbbtPH23ZVCvJQNUmY+JNkDmP/zQUEsPq\nkxhWX23GUCnF8ZTjfH7iczJyM2hh14LHuz9Od5/ulU7gSsHp09q654mJ4OgIjzyizT5vSAncnI/F\nBhRGIYQQDUF+UT5bYrYQlR4FwH0t72Nk8EisLa0rXUdeHmzbBmfPatshITBmjDYLXdQcGRMXQghh\nkpSVxPqo9dzIv0Ezy2aMbT+WTp6dqlRHXBxs3KhdA25jAyNHQliYTF67VzImLoQQolxKKY4kHmFv\n3F6MyoiPow+TQybj1tyt0nUYDLBvHxw5op1K9/WFiRPBrfJViCqSMfEmyJzHfxoKiWH1SQyrr6Zi\nmKPPYc2ZNfx46UeMysgDvg8wr9u8KiXw9HT45z/h8GFte+BAePRR80jg5nwsSk9cCCGasEvXL/HD\nuR/I0edgZ23HhA4TaOfertLllYLjx2HXLigqAldXrfft51eLjRYmMiYuhBBN0O07jx26fAiFItAl\nkIkdJ+LUzKnSdeTkaMumnj+vbYeFaePfzZrVUqObKBkTF0IIYXIz/ybro9aTmJWIDh2DAgfRP6B/\nle48dv68tnTqrVtgawtjx0JoaC02WpRKxsSbIHMe/2koJIbVJzGsvnuJYXRGNCuOryAxKxFHG0dm\nh81mYODASifwwkLYvh2+/VZL4K1bwx//aN4J3JyPRemJCyFEE1BkLGL3xd1EJkcC0M69HRM6TMDO\nuvIXbqemaiuvpaeDpaW26lqfPnLpWH2SMXEhhGjkMnIzWB+1nis5V7DUWTIsaBi9WvWq0sprR45o\nl48ZDNCihTZ5rWXLWm64AGRMXAghmqzTV06z/cJ29AY9bs3dmBwyGR9Hn0qXv3lTW7glPl7b7tlT\nu/OYdeUXbxO1SMbEmyBzHv9pKCSG1ScxrL7yYqg36Nl4biMbozeiN+jp7NmZJ7o/UaUEfvYs/OMf\nWgK3t4cZM2DUqMaXwM35WJSeuBBCNDJXcq6w7uw6ruVdw9rCmlFtRxHmHVbp0+cFBbBjh3bzEoB2\n7WD8eC2Ri4ZFxsSFEKKRUEpxLOUYu2J3YVAGPO09mRIyhRb2LSpdR2KiNnnt+nWtxz18OPToIZPX\n6pOMiQshRCOXV5jH5pjNRGdEA9DDpwcjgkZU+s5jBgP89JP2o5Q2aW3iRG0Sm2i4ZEy8CTLn8Z+G\nQmJYfRLD6rsdw8s3L7Pi+AqiM6KxtbJlSsgUxrQbU+kEnpkJq1bBgQPadr9+8NhjTSeBm/OxWGtJ\nPDExkUGDBhEaGkqnTp348MMPAXj11Vfx9fWlW7dudOvWjZ07d5rKLFmyhLZt29KhQwd2795dW00T\nQohGwaiM/JTwE6tPreZmwU18nXx5ovsThHpWbuUVpeDkSVixApKSwMkJZs+GoUO168BFw1drY+JX\nrlzhypUrhIWFkZOTQ/fu3dm0aRPff/89jo6OPPvssyVeHxUVxYwZMzh27BjJyckMHTqU8+fPY2FR\n8nuGjIkLIQRkF2SzMXojl65fAqCffz8GBQ7C0qJy2Tc3F7ZuhXPntO1OnWD0aGjevLZaLO5VvYyJ\ne3t74+3tDYCDgwMdO3YkOTkZoNTGbN68menTp2NtbU1gYCDBwcFERkbSu3fv2mqiEEKYpdjMWDae\n28itwlvYW9vzUMeHCHYLrnT5S5e0a7+zs7WblYwaBV26yOQ1c1QnY+Lx8fGcPHnSlJA/+ugjunbt\nyrx587hx4wYAKSkp+Pr6msr4+vqakr6oWeY8/tNQSAyrT2JYdQajgR8v/siaM2u4VXiL/Nh85veY\nX+kEXlSk3TL0q6+0BO7vD/PnQ9euTTuBm/OxWOtJPCcnh8mTJ/PBBx/g4ODAH//4R+Li4jh16hQt\nW7bkueeeK7NsZa9pFEKIxu563nVWnVrF4cTDWOgsGNx6MMODhuPYzLFS5a9ehc8/h59/BgsLbd3z\nOXO0+38L81Wrl5gVFhYyadIkZs6cyYQJEwDw9PQ0Pf/YY48xduxYAFq1akViYqLpuaSkJFq1alVq\nvXPmzCEwMBAAFxcXwsLCCA8PB/77jUq2y9++raG0R7ab3nZ4eHiDak9D3vYM9WRLzBaij0djb23P\nCzNfwN/Zn4i4CCIiIsotrxTY2YXz448QGxuBoyO88EI4vr4NZ/9ku+T27d/jb691W45am9imlGL2\n7Nm4u7vz3nvvmR5PTU2l5X9WzX/vvfc4duwY3377rWliW2RkpGliW2xs7F29cZnYJoRoKgoNhey6\nuIvjKccB6ODRgfHtx9PcunKzz3JyYNMmiI3Vtu+7Dx58EGxsaqvFojbUy8S2w4cPs2bNGrp06UK3\nbt0AePvtt/nXv/7FqVOn0Ol0tG7dmk8//RSAkJAQpk6dSkhICFZWVnzyySdyOr2WFP/mLu6NxLD6\nJIblS7+Vzvqo9aTdSsNSZ8mI4BHc73N/if+L5cUwJgY2b9ZmoTdvDuPGQceOddR4M2POx2KtJfF+\n/fphNBrvenzkyJFlllm4cCELFy6srSYJIUSDp5Ti1JVT7Liwg0JjIe7N3ZkcMpmWjpW776der01e\n+/VXbbtNG3joIXCs3NC5MDOydroQQjQQBUUFbDu/jd+u/gZAV6+ujGo7imZWzSpVPiUFNmyAa9e0\nxVqGDoXevZv2zPPGQNZOF0KIBi4lO4X1UevJzMvExtKG0W1H09W7a6XKGo1w+DDs36/97ukJkyaB\nl1ctN1rUO1k7vQkqPgNS3BuJYfVJDDVKKY4mHWXliZVk5mXi7eDN490fr1QCj4iI4MYN+PJL2LtX\nS+C9e8Pjj0sCrwpzPhalJy6EEPUktzCXTdGbOH/tPAA9W/VkeNBwrCwq96/50iU4ehTy88HBASZM\ngODKL9wmGgEZExdCiHqQcCOBDec2kFWQha2VLePbj6dji8pNH8/Ph+3b4Tdt6JwOHWDsWLC3r8UG\ni3ojY+JCCNFAGJWRgwkHiYiPQKHwc/JjUsgkXGxdKlU+IUFb9/zGDbC21q77vu8+mbzWVMmYeBNk\nzuM/DYXEsPqaYgyzCrL46vRX7I/fD0B///482u3RSiVwg0Eb9169WkvgPj7QqVME3btLAq8ucz4W\npScuhBB14Py182yK3kRuYS4ONg5M7DiRNq5tKlX22jXt0rGUFC1hDxgAAwfCwYO13GjR4MmYuBBC\n1CKD0cCeS3v4OelnAIJcg3io40M42DhUWFYpOHEC/v1vKCwEFxdt4ZaAgNputWhIZExcCCHqQWZe\nJuuj1pOSnWK681hfv76VWlI6Nxe2bIHoaG27Sxftvt+2trXcaGFWZEy8CTLn8Z+GQmJYfY09hr9f\n/Z1Pj39KSnYKLrYuPBr2KP38+1UqgcfGwiefaAnc1lZbuGXixLsTeGOPYV0x5zhKT1wIIWpQoaGQ\nnbE7OZF6AoCQFiGMaz8OW6uKu9CFhbBnD/zyi7YdEKCdPnep3MR10QTJmLgQQtSQq7eusu7sOtJz\n07GysOLB4Afp3rJ7pXrfaWna5LWrV8HCAgYNgr59td9F0yZj4kIIUYuUUpxIPcHO2J0UGYvwsPNg\nSsgUvBwqXvtUKW3VtT17tMvI3N210+c+PnXQcGH25DteE2TO4z8NhcSw+hpLDPOL8lkftZ6t57dS\nZCyim3c3Hu/+eKUSeHY2fP21dutQgwF69IAnnqh8Am8sMaxv5hxH6YkLIcQ9Ss5KZn3Ueq7nX8fG\n0oax7cbS2atzpcqeO6fNPs/LAzs7GDdOWz5ViKqQMXEhhKgipRQ/J/3Mnkt7MCojLR1aMjlkMu52\n7hWW1eth5044eVLbDg7WblziUPFl46KJkjFxIYSoIbf0t9gYvZHYzFgAevv2ZmiboZW681hSEvzw\nA2RmgpUVDBsGPXvKsqni3smYeBNkzuM/DYXEsPrMMYZx1+NYcXwFsZmxNLdqzvRO03kw+MEKE7jR\nCAcOwBdfaAncy0u753evXtVL4OYYw4bInOMoPXEhhKiAURmJiI/gYMJBFIoA5wAmhUzCqZlThWWv\nX9d634mJ2vYDD8CQIVpPXIjqkjFxIYQox838m/xw7gcSbiagQ8eAgAEMDByIha78E5lKwZkzsGMH\nFBSAo6O2cEubyt3zRAgTGRMXQoh7EJMRw6boTeQV5eFo48jEjhNp7dq6wnJ5ebBtG5w9q22HhMCY\nMdosdCFqkoyJN0HmPP7TUEgMq68hx7DIWMTOCzv51+//Iq8oj7ZubZnfY36lEnhcHPzjH1oCt7GB\n8eNhypTaSeANOYbmxJzjKD1xIYQo5lruNdZHrSc1JxVLnSVD2wylt2/vCpdONRhg3z44ckQ7le7r\nq920xM2tjhoumiQZExdCiP84k3aGbee3oTfocbV1ZXLIZFo5taqwXHq6NnktNVWbbT5ggPZjaVkH\njRaNnoyJCyFEOfQGPTsu7ODUlVMAdPLsxJh2Yyq885hScPw47N6t3YHM1VXrffv51UWrhZAx8SbJ\nnMd/GgqJYfU1lBheybnCZ79+xqkrp7C2sGZc+3FM6jipwgR+6xb861+wfbuWwMPCYP78uk3gDSWG\n5s6c4yg9cSFEk6SU4njKcXZd3EWRsQhPe08mh0zG096zwrIXLsCmTVoit7WFsWMhNLQOGi3EHWRM\nXAjR5OQV5rElZgvnMs4B0L1ldx4MfhBrS+tyyxUWaqfOjx3Ttlu31tY9d3au7RaLpkzGxIUQ4j8S\nbyayPmo9Nwtu0syyGWPbj6WTZ6cKy6WmapPX0tO1CWuDB0OfPrLuuahfMibeBJnz+E9DITGsvrqO\noVKKQ5cPserUKm4W3KSVYyvm95hfYQJXCg4fhn/+U0vgLVrAY49B3771n8DlOKwZ5hxH6YkLIRq9\nHH0OG89t5OL1iwD08evDkNZDsLQo/xqwmze1se+4OG27Z0/tzmPW5Z91F6LOyJi4EKJRu5h5kY3R\nG8nR52BnbcdDHR6irXvbCsudPQtbt0J+PtjbayuvtWtXBw0W4g4yJi6EaHIMRgP74/dz+PJhFIrW\nLq2Z2HEijs0cyy1XUKDdtOT0aW27XTstgdvb10GjhagiGRNvgsx5/KehkBhWX23G8Eb+DVafWs2h\ny4cAGBQ4iFldZ1WYwBMTYcUKLYFbW8Po0TB9esNN4HIc1gxzjqP0xIUQjcq59HNsjtlMflE+Ts2c\nmNRxEgEuAeWWMRrhwAH46SdtIlvLltrKay1a1FGjhbhHMiYuhGgUioxF7IrdxbEU7SLu9u7tGd9h\nPHbW5d8+LDNTu3QsKUmbbd63LwwaJOuei4ZDxsSFEI1aRm4G686uI+1WGpY6S4YFDaNXq17l3nlM\nKTh1CnbuBL0enJy03ndgYN21W4jqkjHxJsicx38aColh9dVEDJVSnLpyik+Pf0rarTTcmrsx7755\nFd46NDcX1q2DzZu1BN6pE/zxj+aXwOU4rBnmHMdaS+KJiYkMGjSI0NBQOnXqxIcffghAZmYmw4YN\no127dgwfPpwbN26YyixZsoS2bdvSoUMHdu/eXVtNE0I0AgVFBWyM3sim6E0UGgvp4tWFJ7o/gY+j\nT7nlLl2Cf/wDoqKgWTN46CGYNAmaN6+jhgtRg2ptTPzKlStcuXKFsLAwcnJy6N69O5s2bWLVqlV4\neHjw/PPP884773D9+nWWLl1KVFQUM2bM4NixYyQnJzN06FDOnz+PhUXJ7xkyJi6ESM1OZV3UOjLz\nMrG2sGZ0u9F09epabu+7qAj27oWff9a2/f21BO7qWkeNFuIe1cuYuLe3N97e3gA4ODjQsWNHkpOT\n2bJlCwcOHABg9uzZhIeHs3TpUjZv3sz06dOxtrYmMDCQ4OBgIiMj6d27d201UQhhZpRSRCZHsvvi\nbgzKgJe9F1NCp+Bh51FuuatXYcMGSEsDCwsYOBD699d+F8KcVXgI5+TkYDAYAIiJiWHLli0UFhZW\n6U3i4+M5efIkvXr1Ii0tDS8vLwC8vLxIS0sDICUlBV9fX1MZX19fkpOTq/Q+onLMefynoZAYVl9V\nY5hbmMt3v3/HztidGJSB+33u57H7His3gSsFv/wCn32mJXA3N5g7V0vijSGBy3FYM8w5jhX2xAcM\nGMChQ4e4fv06I0aM4P7772ft2rV88803lXqDnJwcJk2axAcffICjY8mFFnQ6Xbmnv8p6bs6cOQT+\nZwaKi4sLYWFhhIeHA//9MGS77O1Tp041qPaY4/ZtDaU9jX27dVhrNpzbwJlfzmBjacMz054hpEVI\nueVzcmDJkgiSkyEwMJz77oPmzSOIjQVf34a1f/e6ferUqQbVHnPdvq0htSciIoL4+HgqUuGYeLdu\n3Th58iQfffQReXl5PP/883Tt2pXTt9ckLEdhYSFjxoxh5MiRPPPMMwB06NCBiIgIvL29SU1NZdCg\nQURHR7N06VIAXnzxRQAefPBBXnvtNXr16lWywTImLkSTYVRGDl0+xP64/SgUvk6+TA6ZjIutS7nl\nYmK0mee5udqEtXHjoGPHOmq0EDWsvLxXqRNKP//8M9988w2jR48GwGg0VlhGKcW8efMICQkxJXCA\ncePG8eWXXwLw5ZdfMmHCBNPj3333HXq9nri4OC5cuEDPnj0r0zwhRCOUXZDN16e/Zl/cPhSKfv79\neDTs0XITuF4P27bBv/6lJfA2bbRLxySBi8aqwiT+/vvvs2TJEh566CFCQ0O5ePEigwYNqrDiw4cP\ns2bNGvbv30+3bt3o1q0b//73v3nxxRf58ccfadeuHfv27TP1vENCQpg6dSohISGMHDmSTz75pNxT\n7eLe3XkKSVSdxLD6yovhhWsXWHF8BXE34rC3tmdWl1kMbTO03FuHpqTAp5/C8ePaamsjRsCsWdoi\nLo2VHIc1w5zjWOGY+MCBAxk4cKBpOygoyHTNd3n69etXZo99z549pT6+cOFCFi5cWGHdQojGyWA0\nsDduL0cSjwDQxrUNEztOxMHGocwyRiMcPgz792u/e3pq133/Z/6sEI1ahWPix44d4+233yY+Pp6i\noiKtkE7HmTNn6qSBd5IxcSEap+t511kftZ7k7GQsdBYMChxEP/9+5Z6Ru3EDNm6EhARtu3dvGDoU\nrGRBadGIlJf3Kkzi7dq1Y9myZXTq1KnEwiuB9bQ+oSRxIRqfs1fPsiVmCwWGApybOTM5ZDJ+zn7l\nlvntN9i+HfLzwcEBJkyA4OA6arAQdahaE9tatGjBuHHjaNOmDYGBgaYfYb7MefynoZAYVl9ERASF\nhsM/ACwAACAASURBVEK2xmxlXdQ6CgwFdPToyPwe88tN4Pn52l3HNmzQfu/QQZu81hQTuByHNcOc\n41jhSafFixczb948hg4dio2NDaB9K5g4cWKtN04I0Xhdz7vO5yc+5+qtq1hZWDEiaAQ9fHqUe/o8\nIUE7fX7jBlhbw4MPwn33abcQFaIpqvB0+sMPP0xMTAyhoaElTqevWrWq1htXGjmdLoR5U0px8spJ\ndl7YSaGxEA87DyaHTMbbwbvMMgYDRETAoUPaKmw+PtrkNXf3umu3EPWlWmPi7du3Jzo6usFc7iVJ\nXAjzVVBUwNbzW/n96u8AhHmHMartKGwsbcosc+2advo8OVnrcffrB+Hh2mVkQjQF1RoT79OnD1FR\nUTXeKFF/zHn8p6GQGFZdSnYKK46v4Perv2NjaYNvpi8TOkwoM4ErBb/+CitWaAncxQXmzIEhQySB\n3ybHYc0w5zhWOCb+888/ExYWRuvWrWnWrBlQv5eYCSHMi1KKo0lH2XNpDwZlwNvBmykhU/gt8rcy\ny+TmwpYtEB2tbXfpAqNGga1tHTVaCDNR4en0shZgl0vMhBAVuaW/xaboTVzIvABAr1a9GBY0DCuL\nsvsPsbGwaRPk5ECzZjBmDHTuXFctFqLhqdaYeEMjSVwI8xB/I54NURvI1mfT3Ko54zuMp4NHhzJf\nX1QEP/6o3ToUICAAHnpIO40uRFNW7RugiMbFnMd/GgqJYdmMysj+uP18eepLsvXZ+Dv7M7/H/LsS\nePEYpqVp9/z+5RftPt9DhsDs2ZLAKyLHYc0w5zjK4oRCiBqTVZDFhqgNJNxMQIeOAQEDCA8Mx0JX\nen9BKTh6FPbs0S4jc3fXLh3z8anjhgthpuR0uhCiRpy/dp5N0ZvILczFwcaBiR0n0sa1TZmvz87W\nxr4vXtS2u3fX7jxmU/bVZkI0SeXlvQp74hs2bODFF18kLS3NVIlOpyMrK6tmWymEMEtFxiL2XNrD\n0aSjAAS7BfNQh4ewt7Evs8y5c9rs87w8sLODceO05VOFEFVT4Zj4888/z5YtW8jKyiI7O5vs7GxJ\n4GbOnMd/GgqJoSYzL5MvTn7B0aSjWOgsGNZmGA93frjMBK7Xw+bNsHYtnDsXQXAwPPmkJPB7Jcdh\nzTDnOFbYE/f29qZjx4510RYhhBn5Le03tp7fit6gx8XWhckhk/F18i3z9cnJ2k1LMjO1W4X27AkP\nPyzrngtRHRWOif/pT3/iypUrTJgwoUHcAEXGxIWoX3qDnp0XdnLyykkAQluEMrb9WGytSl+JxWjk\n/7d351FRn/fix98z7AqCoGyCguwoirvGmOCCO65oqm0WTYyxtz3tbW9r2tPc2+ScRHLu7fnd5t6k\nJo25Jm1iEnHfccO4xCgqiRFRRBBkcWGTfYB5fn9847QEjMsAM8N8XufkHL7Dw/DhE/Tj8/083+fh\n6FE4ckT72M9PW7zm69uVUQthu8zqiVdVVeHm5kZaWlqr1+UUMyHsz42aG6RmpXKr7haOekemh09n\nRMCIe56tUFGhnTpWUKBdjxunPT7mKM/FCNEhZHW6HUpPTychIcHSYdg0e8uhUoozJWfYe2UvzcZm\n+vboS3JsMn7ufvcYD998A7t3Q2MjeHhoG7cM/KfF6vaWw84gOewY1p7HR5qJv/nmm6xevZqf//zn\n7b7hW2+91XERCiGsVkNzA9svbSfrlnYQ0vCA4UwPn37Pg0vq62HXLvhWO6iM2Fht69QePboqYiHs\nxz1n4jt27CApKYn169e3ulWmlEKn0/Hss892WZD/TGbiQnSd63euk5qVSmVDJS4OLsyOnE2c3703\nMs/P126fV1Vpz3vPmAHx8bJ4TQhzyN7pQoiHopTiROEJDuYdxKiMBHoEkhybjLebd7vjW1rg0CE4\ncUK7lR4UBAsWgHf7w4UQD0H2Thet2PIzkdaiO+ew1lDLx+c/Zv/V/RiVkXFB43h+2PP3LOC3b8P7\n78Px49r1k0/CsmX3L+DdOYddRXLYMWw5j7JGVAhhcrXiKpsvbqbGUEMPpx7Mi55HpE9ku2OVgowM\nSEuDpibo3VubfQcHd3HQQtgxuZ0uhMCojKTnp3P02lEUihCvEBbELKCXS692x9fWajuvXb6sXQ8d\nCjNnaud/CyE6llnPiV+6dImf/vSnlJaWcuHCBb755hu2b9/OH/7whw4PVAjR9aoaqth0cRMFVQXo\n0JEQksATA56458ljOTnawSW1teDqCklJMGhQFwcthAAeoCe+YsUK3njjDdNubXFxcWzYsKHTAxOd\nx5b7P9aiu+Qw+3Y2azPWUlBVgIezB8/GP3vPo0ObmrTnvj/+WCvgISGwatWjF/DukkNLkhx2DFvO\n431n4nV1dYwZM8Z0rdPpcHJy6tSghBCdq9nYTFpuGqeKTgEQ6RPJvOh59HBq/2Hu0lJt3/Nbt8DB\nASZNgscek0fHhLC0+xbxvn37cuXKFdN1amoqAQEBnRqU6FzWvDORrbDlHJbVlbExayOlNaU46ByY\nMnAKY4PGtrt1qlLaY2OHDmmPkfXtqy1e64i/Amw5h9ZCctgxbDmP913Ylpuby4svvsiJEyfo3bs3\noaGhfPzxx4SEhHRRiK3JwjYhHt3XpV+zK2cXhhYD3m7eJMcmE+gR2O7Yqiqt952Xp12PHg2JiSA3\n4oToWh2y2UttbS1GoxEPD48ODe5hSRE3n7XvE2wLbC2HhhYDuy7v4usbXwMw2HcwSZFJuDi2v5z8\nwgXYsQMaGqBnT5g7FyLbf9LskdlaDq2R5LBjWHsezVqdXlFRwUcffUR+fj7Nzc2mN5S904WwDaU1\npWy8sJGy+jKc9E7MjJhJvH98u7fPGxthzx7IzNSuIyNhzhxwd+/ioIUQD+S+M/Fx48Yxbtw44uLi\n0Ov1sne6EDZCKcXp4tPsu7KPFtWCb09fFsUuom/Pvu2OLyyEzZu140OdnGDqVBg5UhavCWFpZt1O\nHz58OGfPnu2UwB6FFHEh7q++qZ5tl7aRfTsbgJGBI5kWNg0nh7YNbaMRvvgCjhzRFrIFBGiL1/q2\nX+uFEF3MrL3Tly5dynvvvUdJSQnl5eWm/4TtsuVnIq2FNeewoKqAtRlryb6djYuDC4tiFzE7cna7\nBby8HD74AO7+OOPHwwsvdE0Bt+Yc2grJYcew5Tzetyfu6urKb37zG15//XX0eq3m63Q6rl692unB\nCSEenFEZOV5wnMP5hzEqI/08+pEcm0xvt95txiql9b337AGDAXr1gvnzITTUAoELIR7ZfW+nh4aG\ncvr0afr06dNVMf0guZ0uRFs1hho2X9zM1QrtH9fjg8czKXQSDnqHNmPr6mDnTsjK0q4HD4ZZs8DN\nrSsjFkI8KLNWp0dEROAmf7qFsFpXyq+w5eIWaptq6enUk/kx8wn3Dm937NWrsGULVFdrh5XMnAlD\nhsjiNSFs1X2LeI8ePYiPj2fixIm4fHdEkTxiZtus/ZlIW2ANOWwxtnAo7xDHC7WDvEO9QlkQswAP\nl7Z7OTQ3a7uunTihXQcHa4vXere9095lrCGHtk5y2DFsOY/3LeLz5s1j3rx5rV5r7/nS9ixfvpxd\nu3bh6+vL+fPnAfjjH//I+++/T9/vVs688cYbzJgxA4A1a9bwwQcf4ODgwFtvvcXUqVMf6ocRwl5U\nNlSSmpXK9TvX0aFjYuhEHu//eLsHl9y8qT06VloKej08+SRMmKB9LISwbZ16nvjRo0dxd3fnmWee\nMRXxV199FQ8PD371q1+1GpuVlcXSpUs5ffo0RUVFTJkyhcuXL5sW05kClp64sHNZt7LYfmk7Dc0N\n9HLpRXJsMv09+7cZpxScOgX792szcW9vbfYdFGSBoIUQj+yReuKLFi1i48aNxMXFtfuG33zzzX2/\n8YQJE8jPz2/zenvBbNu2jSVLluDk5ERISAjh4eGcOnWKsWPH3vf7CGEPmlqa2Je7j4ziDACi+0Qz\nN2oubk5t16zU1Gj7nt89u2j4cJg+Hb47UVgI0U3cs4j/+c9/BmDnzp1tiu6D3k6/l//5n//ho48+\nYuTIkfzpT3/Cy8uL4uLiVgU7KCiIoqIis76PaJ8t93+sRVfn8FbtLVKzUrlRewMHnQNTw6Yyut/o\ndv8sXroE27Zpq9Dd3LRtU2NiuizUBya/h+aTHHYMW87jPYt4YKB2stE777zDm2++2epzq1evbvPa\ng1q1ahX//u//DsArr7zCr3/9a9atW9fu2Hv9Y+G5554znaLm5eVFfHy86X/A3Yf25fre15mZmVYV\njy1e39XZ3+/w4cNcKb/Czb43aTI2UZ5VzpMhTzImaEyb8QYD/OlP6Vy6BCEhCQwcCD4+6dy4ATEx\nls2XXHfOdeZ3m9xbSzy2en2XNcWTnp7e7p3s77tvT3zYsGGcO3eu1WtxcXGmHvf95Ofnk5SU1O74\nf/5cSkoKAC+//DIA06dP59VXX2XMmDGtA5aeuLATjc2N7Ly8k/M3tT87Q/2GMjNiZrsnjxUXw6ZN\nUFYGDg4wZQqMHSuPjgnRHTxST/wvf/kL77zzDrm5ua364tXV1YwfP/6RgykpKSEgIACALVu2mN57\nzpw5LF26lF/96lcUFRWRk5PD6NGjH/n7CGHLiquLSc1Kpby+HCe9E7MiZxHvH99mnNGoPTZ26JD2\nsa8vLFwIfn4WCFoI0eXuWcSXLl3KjBkzePnll3nzzTdN/wrw8PDAx8fngd58yZIlHDlyhNu3bxMc\nHMyrr75K+ne3c3U6HaGhobz77rsAxMbGsnjxYmJjY3F0dOSdd94xu/cu2pduw/0fa9FZOVRK8VXR\nV+zP3U+LasHf3Z/k2GT69Gi7Y2JVlfbo2LVr2vWYMdoM3KntFulWSX4PzSc57Bi2nMd7FnFPT088\nPT359NNPH/nNN2zY0Oa15cuX33P873//e37/+98/8vcTwpbVNdWxNXsrl8suAzC632imhk3FUd/2\nj+n587BrFzQ0aGd9z5sH4e1v0iaE6MY69TnxziA9cdEdXau8xqaLm7jTeAdXR1fmRs0lpm/bJeUN\nDbB7N9x9wjM6GpKSoGfPLg5YCNFlzNo7XQjReYzKyNFrR0nPT0ehCO4VzMLYhXi5erUZe+2atu95\nZaV2y3z6dO35b+k6CWG/ZONFO/T9xyrEw+uIHFY3VvPR1x9xOP8wABP6T+C5+OfaFPCWFjh4ENav\n1wp4YCC89BKMGGHbBVx+D80nOewYtpxHmYkLYQE5ZTlsyd5CXVMd7s7uzI+eT5h3WJtxZWXa4rWi\nIq1gT5gACQnaY2RCCCE9cSG6UIuxhYN5BzlReAKAsN5hzI+Zj7uze6txSsHZs7B3LzQ1gaentu/5\ngAGWiFoIYUnSExfCCpTXl5OalUpxdTF6nZ5JoZMYHzy+zaOUdXWwfTtkZ2vXcXEwaxa4ulogaCGE\nVZOeuB2y5f6PtXjYHH5781vezXiX4upivFy9WBa/jMf7P96mgF+5Au+8oxVwFxdt45aFC7tnAZff\nQ/NJDjuGLedRZuJCdKKmlib2XtnLmZIzAMT0iWFO1Jw2J481N8OBA3DypHY9YADMnw9ebRepCyGE\nifTEhegkN2tvsvHCRm7V3cJR78i0sGmMDBzZZvZ944a27/nNm6DXw8SJMH689rEQQkhPXIgupJTi\nbMlZ9lzZQ7OxmT49+rAodhF+7n7fG6fNvA8c0B4j8/HRbp1/d4CgEELcl/xb3w7Zcv/HWtwrhw3N\nDaRmpbLj8g6ajc0M8x/GiyNebFPAq6vh73+Hffu0Aj5iBKxcaV8FXH4PzSc57Bi2nEeZiQvRQYru\nFJGalUpFQwXODs7MjpzNEL8hbcZdvKitPq+vhx49YM4cbftUIYR4WNITF8JMSim+vP4lB64ewKiM\nBLgHkBybjE+P1qf9GQzac99nz2rX4eHawSXu7u28qRBCfEd64kJ0klpDLVuzt5JTngPA2KCxTBk4\npc3JY0VF2uK18nJwdITERBg92ra3TRVCWJ70xO2QLfd/rEV6ejp5FXmszVhLTnkObo5uLBm8hOnh\n01sVcKMRjhyBdeu0Au7nBy++qJ39be8FXH4PzSc57Bi2nEeZiQvxkIzKyLmScxzhCArFAM8BLIxd\nSC+XXq3GVVRop44VFGjX48bB5MnaTFwIITqC9MSFeAhVDVVsvriZa1XX0KHjiQFP8GTIk+h1/7ip\npZR23vfu3dDYCB4e2sYtAwdaMHAhhM2SnrgQHeDS7Utszd5KfXM9Hs4eLIhZQGjv0FZj6uth1y74\n9lvtOiYGkpK0VehCCNHRpCduh2y5/2MJzcZm9l7Zy4ZvN1DfXE+EdwSxtbFtCnh+PqxdqxVwZ2eY\nOxcWL5YCfi/ye2g+yWHHsOU8ykxciB9QVldGalYqJTUl6HV6pgycwrigcRwpP2Ia09IChw/D8ePa\nrfSgIO3YUG9vCwYuhLAL0hMX4h6+ufENOy/vxNBioLdrb5Jjk+nXq1+rMbdva4+OlZRoq82feEL7\nz8HBQkELIbod6YkL8RAMLQZ25+wmszQTgEF9B5EUlYSr4z/OA1UKMjIgLQ2amqB3b232HRxsqaiF\nEPZIeuJ2yJb7P52ttKaU9868R2ZpJk56J+ZEzSE5NrlVAa+thVdeSWfXLq2ADx0KL70kBfxhye+h\n+SSHHcOW8ygzcSHQtk7NKM5gX+4+mo3N9O3Rl0WDFuHb07fVuJwc2LoVrl/X9jtPSoJBgywUtBDC\n7klPXNi9+qZ6dlzeQdatLABGBIxgevh0nBycTGOammD/fjh1SrsOCdGe/fb0tEDAQgi7Ij1xIe6h\nsKqQTRc3UdlQiYuDC0lRSQz2HdxqTGmptnjt1i1twdqkSfDYY7JtqhDC8qQnbodsuf/TUZRSHCs4\nxv9l/h+VDZX08+jHSyNfalXAlYITJ+Cvf9UKeN++8MILMH48HDmSbrnguwn5PTSf5LBj2HIeZSYu\n7E6NoYYtF7eQW5ELwGPBjzE5dDIO+n88F3bnjrbveV6edj1qFEydCk5O7b2jEEJYhvTEhV3JLc9l\nS/YWagw19HDqwfzo+UT4RLQac+EC7NypbaHas6e281pkpIUCFkLYPemJC7vXYmwhPT+dYwXHUChC\nvEJYGLMQDxcP05jGRtizBzK1x8OJjIQ5c8Dd3UJBCyHEfUhP3A7Zcv/nUVQ2VLI+cz1HC44CMDFk\nIs8MfaZVAS8s1PY9z8zUbpnPmgVLlty7gNtbDjuD5NB8ksOOYct5lJm46NYu3rrItkvbaGhuoJdL\nLxbGLGSA1wDT541G+OIL7T+jEQICtJ3X+va1YNBCCPGApCcuuqVmYzP7ruzjdPFpAKJ8opgbPZce\nTv84Uqy8HDZv1jZu0em0x8YmTZJ9z4UQ1kV64sKu3K67zcYLG7lRewMHnQOJYYmM6TcG3XcPdisF\nX38Nu3eDwQC9emkbt4SG3ueNhRDCykhP3A7Zcv/nfjJLM3k3411u1N7A282b54c/z9igsaYCXl8P\nGzdqW6caDNqWqatWPXwB78457CqSQ/NJDjuGLedRZuKiW2hsbmR3zm6+vvE1AHG+ccyOnI2Lo4tp\nzNWrWvG+cwdcXGDmTBgyRHZeE0LYLumJC5tXUl1CalYqZfVlOOmdmBkxk3j/eNPsu7kZDh3Sdl8D\n7bSxBQu040OFEMLaSU9cdEtKKU4VnSItN40W1YJfTz+SY5Pp2/MfS8tv3tQWr5WWgl4PTz4JEyZo\nHwshhK3r1L/Kli9fjp+fH3FxcabXysvLSUxMJDIykqlTp1JZWWn63Jo1a4iIiCA6Opq0tLTODM2u\n2XL/5666pjo+/fZT9lzZQ4tqYVTgKF4Y/oKpgCulnTj23ntaAff2huXLtSLeEQW8O+TQ0iSH5pMc\ndgxbzmOnFvFly5axd+/eVq+lpKSQmJjI5cuXmTx5MikpKQBkZWXx2WefkZWVxd69e/npT3+K0Wjs\nzPCEjSqoKmBtxloulV3C1dGVxYMWMytyluno0Joa+OQTbfV5czMMGwYrV0JQkIUDF0KIDtbpPfH8\n/HySkpI4f/48ANHR0Rw5cgQ/Pz9KS0tJSEggOzubNWvWoNfrWb16NQDTp0/nj3/8I2PHjm0dsPTE\n7ZZRGTlWcIzDeYdRKIJ6BZEcm4yXq5dpzKVLsG0b1NWBm5u2bWpMjAWDFkIIM1lVT/zGjRv4+fkB\n4Ofnx40bNwAoLi5uVbCDgoIoKirq6vCElapurGbzxc3kVWrHij3e/3Emhkw0nTxmMEBaGmRkaOMH\nDoR587RnwIUQoruy6PIenU5nWkF8r8+Ljmdr/Z8r5VdYm7GWvMo8ejr15OkhTzNl4BRTAS8u1nrf\nGRnabmvTpsHTT3duAbe1HFojyaH5JIcdw5bz2OUz8bu30f39/SkpKcHX1xeAfv36UVhYaBp3/fp1\n+vXr1+57PPfcc4SEhADg5eVFfHw8CQkJwD/+Z8j1va8zMzOtKp57XbcYW/h/G/4f3976lpD4EAb2\nHkjfm30p/KaQsIQwjEZ4++10zp6FAQMS8PUFf/90GhtBp+vc+O6ypnzJtf1dZ3535J61xGOr13dZ\nUzzp6enk5+dzP13eE//tb3+Lj48Pq1evJiUlhcrKSlJSUsjKymLp0qWcOnWKoqIipkyZwpUrV9rM\nxqUnbh8q6itIzUqlqLoIvU7PxJCJPN7/cdPvQ1WV9ujYtWva+DFjYMoU7QQyIYToTizWE1+yZAlH\njhzh9u3bBAcH89prr/Hyyy+zePFi1q1bR0hICJ9//jkAsbGxLF68mNjYWBwdHXnnnXfkdrqdunDz\nAtsvbaexpRFPF08Wxi6kv2d/0+fPn4ddu6ChQTsqdN48CA+3YMBCCGEhsmObHUpPTzfdvrEmTS1N\n7MvdR0axtjotuk80c6Pm4ubkBmhFe/du+OYbbXx0NCQlQc+eXR+rtebQlkgOzSc57BjWnkerWp0u\nRHtu1d5iY9ZGbtbexEHnwLTwaYwKHGW6G3PtGmzZApWV2i3z6dNh+HDZ91wIYd9kJi4sSinFudJz\n7MnZQ5OxCR83HxYNWoS/uz8ALS1w5AgcPartwhYYCAsXgo+PhQMXQoguIjNxYZUamxvZcXkH3978\nFoB4/3hmRszE2cEZgLIybfFaUZE2454wARIStMfIhBBCyHnidun7j1VYQnF1MWsz1vLtzW9xdnBm\nfvR85kXPw9nBGaXgzBlYu1Yr4J6e8NxzMHmy9RRwa8ihrZMcmk9y2DFsOY8yExddSinFyesnOXD1\nAC2qBX93fxbFLsKnh3Z/vK4Otm+H7GxtfFwczJoFrq4WDFoIIayU9MRFl6lrqmNr9lYul10GYEy/\nMSSGJeKo1/4tmZsLW7dCdTW4uMDs2VoRF0IIeyY9cWFx+ZX5bMraRLWhGjdHN+ZGzyW6TzSgnTR2\n4ACcPKmNHTAA5s8HL68feEMhhBDSE7dHXdn/MSoj6fnpfJj5IdWGavp79uelkS+ZCviNG9q+5ydP\naud8T54Mzz5r/QXclnto1kJyaD7JYcew5TzKTFx0mjuNd9iUtYlrVdfQoeOJAU+QEJKAXqdHKfjq\nK9i/X3uMzMdHe3QsMNDSUQshhO2QnrjoFJfLLrM1eyt1TXW4O7uzIGYBA3sPBLSe99atWg8cYMQI\n7eQxZ2cLBiyEEFZKeuKiy7QYWzhw9QBfXv8SgHDvcOZFz8Pd2R2Aixdhxw5tFXqPHjBnjrZ9qhBC\niIcnPXE71Fn9n/L6ctadW8eX179Er9OTODCRH8f9GHdndwwG7dGxzz7TCnh4OKxaZbsF3JZ7aNZC\ncmg+yWHHsOU8ykxcdIjzN86z8/JOGlsa8XL1Ijk2maBeQYC2YcumTVBeDo6OkJgIo0fLvudCCGEu\n6YkLsxhaDOzJ2cO50nMAxPaNZU7UHFwdXTEa4dgxSE8HoxH8/LTFa76+lo1ZCCFsifTERae4UXOD\n1KxUbtXdwlHvyPTw6YwIGIFOp6OiQjt1rKBAGztunPb4mKP8xgkhRIeRnrgdMrf/o5QioziDv579\nK7fqbtG3R19WDF/ByMCRgI5vvtH2PS8oAA8PeOYZbfV5dyrgttxDsxaSQ/NJDjuGLeexG/21KrpC\nQ3MDOy7t4MKtCwAMDxjO9PDpODs409AAO3fCt9qhZMTEQFKStgpdCCFEx5OeuHhg1+9cJzUrlcqG\nSlwcXJgdOZs4P21z8/x87fZ5VZX2vPeMGRAfL4vXhBDCXNITF2ZRSnGi8AQH8w5iVEYCPQJJjk3G\n282blhY4fBiOHwelICgIFiwAb29LRy2EEN2f9MTt0MP0f2oNtXx8/mP2X92PURkZFzSO54c9j7eb\nN7dvw/vvayvQAZ58EpYts48Cbss9NGshOTSf5LBj2HIeZSYu7ulqxVU2X9xMjaGGHk49mBc9j0if\nSJSCjAzYtw+amqB3b232HRxs6YiFEMK+SE9ctHH35LGj146iUAzwHMDC2IX0culFba2289qlS9rY\noUNh5kzt/G8hhBAdT3ri4oFVNVSx6eImCqoK0KEjISSBJwY8gV6nJydHO7ikthZcXbWV54MGWTpi\nIYSwX9ITt0P36v9k385mbcZaCqoK8HD24Nn4Z0kISaClWc/u3fDxx1oBDwnR9j235wJuyz00ayE5\nNJ/ksGPYch5lJi5oNjazP3c/XxV9BUCkTyTzoufRw6kHpaXavue3boGDA0yaBI89Jo+OCSGENZCe\nuJ0rqytjY9ZGSmtKcdA5MGXgFMYGjQV0fPklHDwILS3Qp4+273lAgKUjFkII+yI9cdGur0u/ZlfO\nLgwtBnq79mbRoEUEegRy5462cUtenjZu1CiYOhWcnCwbrxBCiNakJ26H9h/cz9bsrWzJ3oKhxcBg\n38G8NPIlAj0CycqCv/xFK+A9e8LSpTBrlhTw77PlHpq1kByaT3LYMWw5jzITtzOlNaXsuLQDbwdv\nnPROzIiYwTD/YRgMOrbuhMxMbVxkJMyZA+7ulo1XCCHEvUlP3E4opThdfJq03DSajc349vRl/5mk\n8AAAGD9JREFUUewi+vbsS2EhbN4MFRXaSWPTpsHIkbJ4TQghrIH0xO1cfVM92y5tI/t2NgAjA0cy\nLWwaDjon0tPhiy/AaNQWrS1YAH37WjZeIYQQD0Z64t1cYVUhazPWkn07GxcHFxbFLsK92J3qKic+\n+ADS07WDS8aPhxdekAL+oGy5h2YtJIfmkxx2DFvOo8zEuymlFMcKjnE4/zBGZaSfRz+SY5Pxcu3N\nuivpnDgBBgP06gXz50NoqKUjFkII8bCkJ94N1Rhq2HxxM1crrgIwPng8k0InYWh0YMcOyMrSxg0a\nBLNng5ubBYMVQgjxg6Qnbkdyy3PZfHEztU219HTqyfyY+YR7h5OXpz37feeOdljJzJkwZIgsXhNC\nCFsmPfFuosXYwoGrB/jbN3+jtqmWUK9QXhr5EiG9wklLgw8/1Ap4cDAMHpzO0KFSwM1hyz00ayE5\nNJ/ksGPYch5lJt4NVDZUkpqVyvU719GhY2LoRB7v/zi3b+n5eDOUloJeD08+CRMmaKvRhRBC2D7p\nidu4rFtZbL+0nYbmBnq59CI5NpngXv05fRrS0qC5Gby9tUfHgoIsHa0QQoiH9UN1T4q4jWpqaSIt\nN43TxacBiPKJYm70XIyNPdi2DXJytHHDhsH06VofXAghhO35obpnsZ54SEgIQ4YMYdiwYYwePRqA\n8vJyEhMTiYyMZOrUqVRWVloqPKt2q/YW7599n9PFp3HQOTAjfAY/GvwjCq/24C9/0Qq4mxs89RTM\nndu2gNty/8daSA7NJzk0n+SwY9hyHi1WxHU6Henp6Zw7d45Tp04BkJKSQmJiIpcvX2by5MmkpKRY\nKjyrpJTiXMk53jvzHjdqb+Dj5sMLw19gmO8Ydu3SsWED1NbCwIGwahXExFg6YiGEEJ3JYrfTQ0ND\nycjIwMfHx/RadHQ0R44cwc/Pj9LSUhISEsjOzm71dfZ6O72xuZGdl3dy/uZ5AIb4DWFWxCzKbrqw\neTPcvg0ODjBlCowdKyvPhRCiu7DKnvjAgQPx9PTEwcGBlStXsmLFCnr37k1FRQWgzTq9vb1N16aA\n7bCIF1cXk5qVSnl9OU56J2ZFzmKIbzwnTsChQ9q+576+2uI1f39LRyuEEKIjWWVP/Pjx45w7d449\ne/bw9ttvc/To0Vaf1+l06Ox8OqmU4uT1k6w7u47y+nL8evqxcuRKQt3i+egjOHBAK+BjxsCKFQ9e\nwG25/2MtJIfmkxyaT3LYMWw5jxZ7TjwgIACAvn37Mn/+fE6dOmW6je7v709JSQm+vr7tfu1zzz1H\nSEgIAF5eXsTHx5OQkAD843+GrV+PHj+abdnb2HdwHwCLZy1mathUPlp/jJMnITAwAXd3CAhIx80N\nnJwe/P0zMzMt/vPZ+vVd1hKPXNvndWZmplXFY6vXd1lTPOnp6eTn53M/FrmdXldXR0tLCx4eHtTW\n1jJ16lT+4z/+gwMHDuDj48Pq1atJSUmhsrKyzeI2e7idfq3yGpsubuJO4x1cHV2ZGzWXUI8Ydu+G\nb77RxkRFwZw50LOnZWMVQgjRuayuJ56Xl8f8+fMBaG5u5sc//jG/+93vKC8vZ/HixRQUFBASEsLn\nn3+Ol5dX64C7cRE3KiNHrx0lPT8dhSK4VzALYxdy56YXmzdDZSU4OWnPfQ8fLovXhBDCHlhdETdH\ndy3i1Y3VbLq4ifzKfHToeLz/40wITuDYUQeOHtXO/A4MhIUL4Z8W9D+S9PR00+0b8Wgkh+aTHJpP\nctgxrD2PcoqZlcspy2FL9hbqmupwd3ZnfvR8vFQYH66HoiJtxj1hAiQkaI+RCSGEECAzcYtqMbZw\nMO8gJwpPABDWO4x50fPJueDO3r1gMICnp/bo2IABFg5WCCGERchM3ApV1FeQmpVKUXURep2eSaGT\nGOYznh1bdNzd3yYuDmbNAldXy8YqhBDCOsl54hbw7c1vWZuxlqLqIrxcvVgWv4yApsdZu1Yr4C4u\nWu974cLOKeDff6xCPDzJofkkh+aTHHYMW86jzMS7UFNLE3uv7OVMyRkAYvrEMDNsDsePuHHypDZm\nwACYPx++tyhfCCGEaEN64l3kZu1NUrNSuVl7E0e9I9PCphHsMJItW3TcuAF6PUycCOPHax8LIYQQ\nII+YWZRSirMlZ9l7ZS9Nxib69OjDwphkrl3w58ABaG7WHhlbuFB7hEwIIYT4Z1a5d7o9aGhuYNPF\nTey4vIMmYxPx/vEsiXyRA1v92btXK+AjRsDKlV1bwG25/2MtJIfmkxyaT3LYMWw5j9IT7yRFd4pI\nzUqloqECZwdnZkfOxql8COveg7o66NFD2zY1OtrSkQohhLBVcju9g1y6cokDZw5gMBq4XnUdg6cB\nnwAfAtwDmBOezOkvfDh7VhsbHg5z54KHh2VjFkIIYf3kOfFOdunKJdYfXo9+oJ6Lty9S7lpO84Vm\nnvV9lql+y9j4kSPl5eDoCImJMHq07HsuhBDCfNIT7wAHzhzA0N9ARnEG5fXlOOodGTounqyTTXz4\nf1oB9/ODF1/Uzv62dAG35f6PtZAcmk9yaD7JYcew5TzKTLwD5Fflc7z8S8rKa3GhJ30J4GK+I85X\nDYwNgXHjYPJkbSYuhBBCdBTpiZuhxdjCvtx9pKz7T/Jdyumli8WlNoLyMj0tzVeJaorg3ddfYeBA\nS0cqhBDCVklPvBPUGGrYeGEj16quodd50Ts3hGbPAZTVap/vcbsfI0cESwEXQgjRaaQn/giu37nO\nuxnvcq3qGh7OHsQ7LcX9+ssYzvrilOtFUKUvkyOew88nxNKhtsuW+z/WQnJoPsmh+SSHHcOW8ygz\n8Yd0pvgMu3N206JaCPLoT0D5Yg6dOYUTUUT3iSI2FtzctLHOzkWWDVYIIUS3Jj3xB9RsbGZPzh7T\n4SXRHqOpOjONkmIHysquUVZ2hfDwyaZ9zxsbD/Lcc+FERclB4EIIIR6d7J1upjuNd/j8wudcv3Md\nB50jEWo2V0/EYzCApycsWAANDdc4eDAXg0GPs7ORyZPDpIALIYQwmxRxMxRUFfD5hc+pMdTQQ+9J\nr8KnKM3RNjofPBhmz+6cM787U3p6OgkJCZYOw6ZJDs0nOTSf5LBjWHseZXX6I1BKcbr4NHuv7MWo\njLg3h9L0dTKl1T1xcYFZsyAuzvIbtwghhLBfMhNvR1NLE7tydpFZmonRCG5lj9GQNQWd0hMcrN0+\n7927U0MQQgghAJmJP5Sqhio+u/AZxdXFGBqccLwyh8bbcTjo4ckEmDAB0+I1IYQQwpKkHP2TvIo8\n3j3zLkV3iqm+1RtjxvPob8fRuzcsWwZPPtk9CrgtPxNpLSSH5pMcmk9y2DFsOY8yE0frf5+8fpL9\nV/fT0GikMi+M3iXJOOFGfDzMmAEuLpaOUgghhGjN7nviTS1NbL+0nfM3z1NeDo05E/Cvn4ibq57Z\ns7UV6EIIIYSlSE/8HirqK7T+951SCvKc6Vk4jwBiGTBAW7zm6WnpCIUQQoh76wYd3keTW57Le2fe\nI/dGKdnnfOhb+AJ++limTIFnn+3eBdyW+z/WQnJoPsmh+SSHHcOW82h3M3GlFMcLj3Pg6kGuX1dU\nXY0kyrgAPx9XFi6EwEBLRyiEEEI8GLvqiRtaDGzN3kpmURbZ2eBR/iQhJDBiuI7p08HZuYODFUII\nIcwkPXGgrK6Mzy58xsWCm1y55EKYYQHBblHMmQMxMZaOTgghhHh4dtETv1x2mbWn/8rxzJvknu9D\nnGEFowdGsWqVfRZwW+7/WAvJofkkh+aTHHYMW85jt56JK6X44toX7Pw2nQtZih51MYzSz2PaFBfG\njZN9z4UQQti2btsTb2huYPPFLRzMvEReno4BxkkM93mc5GQdAQFdEKgQQgjRAeyuJ36r9hYfnvmM\n4+duU13hyiAWMn1UBFOngpOTpaMTQgghOka364lfvHWRN/b9lX1Hb2Oo8ONxtxf52ZIIZs2SAn6X\nLfd/rIXk0HySQ/NJDjuGLeex28zEjcrI/px01h/+gpIS8GUwM8PmkDzfGXd3S0cnhBBCdLxu0ROv\nb6pn3Zeb2fVlDvX1OiIdElmeOI4xY3SyeE0IIYRN65Y98T37D7F+61aqmqrJrc7F1TMEf//BTPJJ\nZuXigfj5WTpCIYQQonNZXU987969REdHExERwZtvvtnumD37D/Ha/73PZe9mMnpd45afnusF2Yxy\niuL3q6SA348t93+sheTQfJJD80kOO4Yt59GqinhLSws/+9nP2Lt3L1lZWWzYsIGLFy+2GbfitX/j\nmnc5+TVZNDcbcW32IzxuGrnFh3C02XsLXSczM9PSIdg8yaH5JIfmkxx2DFvOo1UV8VOnThEeHk5I\nSAhOTk786Ec/Ytu2bW3GFXtepbT2DIb6aryM4YT3jqanmwMGY4sForY9lZWVlg7B5kkOzSc5NJ/k\nsGPYch6tqogXFRURHBxsug4KCqKoqKjNONWzBeVpQFU1McA7CEcHbfWas96hy2IVQgghLM2qirju\nAZeS69290Bc406yqufsVjZcv89y8uZ0XXDeSn59v6RBsnuTQfJJD80kOO4Yt59GqHjE7efIkf/zj\nH9m7dy8Aa9asQa/Xs3r1atMYvacb6k6DpUIUQgghutTQoUPv2be3qiLe3NxMVFQUBw8eJDAwkNGj\nR7NhwwZi7PGoMSGEEOI+rGott6OjI//7v//LtGnTaGlp4fnnn5cCLoQQQtyDVc3EhRBCCPHgrGph\n2w95kE1g7ElhYSETJ05k0KBBDB48mLfeeguA8vJyEhMTiYyMZOrUqa0enVizZg0RERFER0eTlpZm\nev3MmTPExcURERHBL37xC9PrjY2NPPXUU0RERDB27FiuXbvWdT9gF2ppaWHYsGEkJSUBksOHVVlZ\nSXJyMjExMcTGxvLVV19JDh/SmjVrGDRoEHFxcSxdupTGxkbJ4X0sX74cPz8/4uLiTK91Vc4+/PBD\nIiMjiYyM5KOPPurkn/Q+lA1obm5WYWFhKi8vTxkMBjV06FCVlZVl6bAsqqSkRJ07d04ppVR1dbWK\njIxUWVlZ6je/+Y168803lVJKpaSkqNWrVyullLpw4YIaOnSoMhgMKi8vT4WFhSmj0aiUUmrUqFHq\nq6++UkopNWPGDLVnzx6llFJvv/22WrVqlVJKqU8//VQ99dRTXfozdpU//elPaunSpSopKUkppSSH\nD+mZZ55R69atU0op1dTUpCorKyWHDyEvL0+FhoaqhoYGpZRSixcvVuvXr5cc3scXX3yhzp49qwYP\nHmx6rStyVlZWpgYOHKgqKipURUWF6WNLsYkifuLECTVt2jTT9Zo1a9SaNWssGJH1mTt3rtq/f7+K\niopSpaWlSimt0EdFRSmllHrjjTdUSkqKafy0adPUl19+qYqLi1V0dLTp9Q0bNqiVK1eaxpw8eVIp\npf3l3KdPn676cbpMYWGhmjx5sjp06JCaPXu2UkpJDh9CZWWlCg0NbfO65PDBlZWVqcjISFVeXq6a\nmprU7NmzVVpamuTwAeTl5bUq4l2Rs08++US99NJLpq9ZuXKl2rBhQyf9hPdnE7fTH3QTGHuVn5/P\nuXPnGDNmDDdu3MDvu83j/fz8uHHjBgDFxcUEBQWZvuZuDr//er9+/Uy5/ee8Ozo64unpSXl5eVf9\nWF3iX//1X/nP//xP9Pp//FGQHD64vLw8+vbty7Jlyxg+fDgrVqygtrZWcvgQvL29+fWvf03//v0J\nDAzEy8uLxMREyeEj6OyclZWV3fO9LMUmiviDbgJjj2pqali4cCF//vOf8fDwaPU5nU4nufsBO3fu\nxNfXl2HDht3zmD/J4Q9rbm7m7Nmz/PSnP+Xs2bP07NmTlJSUVmMkhz8sNzeX//7v/yY/P5/i4mJq\namr4+9//3mqM5PDh2UvObKKI9+vXj8LCQtN1YWFhq38J2aumpiYWLlzI008/zbx58wDtX5+lpaUA\nlJSU4OvrC7TN4fXr1wkKCqJfv35cv369zet3v6agoADQ/rKuqqrC29u7S362rnDixAm2b99OaGgo\nS5Ys4dChQzz99NOSw4cQFBREUFAQo0aNAiA5OZmzZ8/i7+8vOXxAGRkZPPbYY/j4+ODo6MiCBQv4\n8ssvJYePoLP/7Pr4+FhdPbKJIj5y5EhycnLIz8/HYDDw2WefMWfOHEuHZVFKKZ5//nliY2P55S9/\naXp9zpw5fPjhh4C2gvJucZ8zZw6ffvopBoOBvLw8cnJyGD16NP7+/vTq1YuvvvoKpRR/+9vfmDt3\nbpv3Sk1NZfLkyV38U3auN954g8LCQvLy8vj000+ZNGkSf/vb3ySHD8Hf35/g4GAuX74MwIEDBxg0\naBBJSUmSwwcUHR3NyZMnqa+vRynFgQMHiI2NlRw+gq74szt16lTS0tKorKykoqKC/fv3M23aNAv8\ntN+xWDf+Ie3evVtFRkaqsLAw9cYbb1g6HIs7evSo0ul0aujQoSo+Pl7Fx8erPXv2qLKyMjV58mQV\nERGhEhMTW62afP3111VYWJiKiopSe/fuNb2ekZGhBg8erMLCwtTPf/5z0+sNDQ1q0aJFKjw8XI0Z\nM0bl5eV15Y/YpdLT002r0yWHDyczM1ONHDlSDRkyRM2fP19VVlZKDh/Sm2++qWJjY9XgwYPVM888\nowwGg+TwPn70ox+pgIAA5eTkpIKCgtQHH3zQZTn74IMPVHh4uAoPD1fr16/vkp/3XmSzFyGEEMJG\n2cTtdCGEEEK0JUVcCCGEsFFSxIUQQggbJUVcCCGEsFFSxIUQQggbJUVcCCGEsFFSxIUQrSQkJHDm\nzBmz3mPHjh1yZLAQXcDR0gEIIaxLR+w5nZSUZDqfXQjReWQmLoSVq62tZdasWcTHxxMXF8fGjRsB\neO211xg9ejRxcXGsXLnSND4hIYFf/epXjBo1ipiYGE6fPs38+fOJjIzklVdeAbST76Kjo/nJT35C\nbGwsixYtor6+vs33TktL47HHHmPEiBEsXryY2traNmPeeustBg0axNChQ1m6dCkA69ev5+c//zkA\n8fHxDBs2jGHDhtGjRw+OHj1KbW0ty5cvZ8yYMQwfPpzt27e3ed/09HQSEhJYtGgRMTEx/OQnPzE/\nmUJ0NxbdL04IcV+pqalqxYoVpuuqqiqllFLl5eWm155++mm1Y8cOpZRSCQkJ6uWXX1ZKKfXnP/9Z\nBQQEqNLSUtXY2KiCgoJUeXm5ysvLUzqdTp04cUIppdTy5cvVf/3Xf5m+/syZM+rWrVvqiSeeUHV1\ndUoppVJSUtRrr73WJr7AwEBlMBhaxbZ+/Xr1s5/9rNW47du3qyeeeEI1NTWp3/3ud+rvf/+7Ukqp\niooKFRkZqWpra1uNP3z4sPL09FRFRUXKaDSqcePGqWPHjj1KCoXotmQmLoSVGzJkCPv37+fll1/m\n2LFj9OrVC4BDhw4xduxYhgwZwqFDh8jKyjJ9zd0DggYPHszgwYPx8/PD2dmZgQMHmk5gCg4OZty4\ncQD85Cc/4dixY6avV0px8uRJsrKyeOyxxxg2bBgfffSR6VSn78e3dOlSPv74YxwcHNr9GXJycvjt\nb3/L559/jqOjI2lpaaSkpDBs2DAmTpxIY2Njq5Oh7ho9ejSBgYHodDri4+PJz89/tCQK0U1JT1wI\nKxcREcG5c+fYtWsXf/jDH5g8eTK//e1v+Zd/+RfOnDlDv379ePXVV2loaDB9jYuLCwB6vd708d3r\n5uZmgFZ9b6VUu33wxMREPvnkkx+Mb9euXXzxxRfs2LGD119/nfPnz7c6n72mpoannnqK999/Hz8/\nP9PrmzdvJiIi4gff+59jd3BwMMUuhNDITFwIK1dSUoKrqys//vGP+bd/+zfOnTtnKtg+Pj7U1NSY\n+uQPo6CggJMnTwLwySefMGHCBNPndDodY8eO5fjx4+Tm5gJabz4nJ6fVeyilKCgoICEhgZSUFKqq\nqqipqWk1Zvny5Sxbtozx48ebXps2bRpvvfWW6frcuXMPHb8QQmbiQli98+fP85vf/Aa9Xo+TkxNr\n167F09OTFStWMHjwYPz9/RkzZky7X/tDK82joqJ4++23Wb58OYMGDWLVqlWtPt+nTx/Wr1/PkiVL\naGxsBOD1119vNXtuaWnh6aefpqqqCqUUv/jFL/D09DR934KCAjZt2kROTg4ffPABAOvWreOVV17h\nl7/8JUOGDMFoNDJw4MA2i9vai93cVfNCdDdyFKkQdig/P5+kpCTOnz9v6VCEEGaQ2+lC2CmZ1Qph\n+2QmLoQQQtgomYkLIYQQNkqKuBBCCGGjpIgLIYQQNkqKuBBCCGGjpIgLIYQQNkqKuBBCCGGj/j8b\nURKDPTGQxwAAAABJRU5ErkJggg==\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10e8f8610>"
|
|
]
|
|
},
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAeoAAAGJCAYAAABFDXDOAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl8TXf++PFXQoJE9kgiO0ntgtZSFLG2lNYoKtagqr/B\nTKtT7bSKKqodVBedfnVUSmyli30pGqNUaRGqxJpYEksESSSyfn5/nMltQja5N7n3JO/n4+Eh5957\nznmf9z03n5zz/tzPx0oppRBCCCGERbI2dwBCCCGEKJo01EIIIYQFk4ZaCCGEsGDSUAshhBAWTBpq\nIYQQwoJJQy2EEEJYMGmoi3Ht2jU6d+6Mo6Mjr732mrnDEUXYu3cvjRo1qtB9hoaGsmTJEgBWrFjB\nk08+WaH7tyT5c1FR+vTpw/Llyyt0n6YUGBjIrl27Cn0uPT2dfv364ezszPPPP2/0vmbMmMGIESOM\n3o6pWNJ7Fx4ezttvv23uMEpU6RrqwMBA7OzscHBwwMvLi9GjR3P37t0ybWvx4sV4eHiQnJzMv/71\nLxNHKkylU6dOnDp1qkL3aWVlhZWVFQDDhg1j+/btJa6jl18KDyt/LirKli1bLKrxeVjF5WzdunVc\nv36dpKQk1qxZY5J9WRJj37uVK1fSunVrHBwc8Pb2pk+fPuzbt6/E9SIiIujUqVOBx8xx7pZFpWuo\nrays2LRpEykpKRw+fJhff/2VWbNmPdQ2lFLk5uYSFxdH48aNyxRHdnZ2mdYTD0fyXL4kvxUvLi6O\nBg0aYG398L+eC3u/KtOYVgsWLOCVV15h6tSpXL9+nUuXLjFhwgQ2bNhg7tDKVaVrqPPz9vbmqaee\n4vfffwfgwIEDdOjQARcXF1q2bMmePXsMrw0NDWXq1Kk88cQT2NvbM2rUKJYtW8YHH3yAg4MDu3fv\nJjMzk5dffhkfHx98fHx45ZVXyMzMBCAqKgpfX18++OAD6taty5gxY3jnnXcYNGgQI0aMwNHRkZCQ\nEM6cOcN7772Hp6cnAQEB/PDDD4YYli5dSpMmTXB0dCQoKIjFixcbnsvb/oIFC/D09MTb25uIiAjD\n8+np6bz66qsEBgbi7OxMp06duHfvXonHfb9Lly4xYMAAPDw8cHd3Z9KkSQDk5uYya9YsAgMD8fT0\nZNSoUSQnJwMQGxuLtbU1ERER+Pv74+bmxueff86hQ4cICQnBxcXFsB3Q/rLt2LEjkyZNwtnZmcaN\nG7N79+6HykNenseOHUtUVBR+fn6G17z//vv4+vri6OhIo0aNDNvOyMgo8f0rKr/Fyf+XulKKV155\nBU9PT5ycnAgJCeHEiRMsXryYlStXGs6nZ599ttBtnThxgp49e+Lm5oaXlxfvvfdeqWP/17/+hYeH\nB97e3nz//fds2bKFBg0a4Obmxty5cw37mDFjBgMHDmTIkCE4Ojry2GOPcezYMcPzgYGBfPDBB4SE\nhODg4EBubm6J51BsbCxPPPEEjo6OPPnkk9y8edPwXEmfu2nTphW67r179xg+fDju7u64uLjQtm1b\nbty4YVgv73a7UqrEc3PZsmUEBARQp04d5syZY9j/wYMHad26NU5OTnh5efHqq68W+r7cvn2bvn37\n4uHhgaurK/369ePKlSulOg6A5cuXExAQgLu7e4H932/69Om8++67rFmzBgcHB5YuXVqq4/vyyy8J\nCAigR48eRW47z4YNG2jatCkuLi507dq1wN2okydPEhoaiouLC82aNWPjxo2G58LDw3nppZfo1asX\njo6OhIaGcvHiRcPzhZ33hcn/3kVERPDEE0/w2muv4erqSv369dm2bVuh6925c4fp06fz2Wef0b9/\nf2rVqkW1atV4+umnef/997l69Sr29vYkJSUZ1jl8+DAeHh78/vvvvPTSS/z88884ODjg6upqeE1S\nUhJ9+/bF0dGRxx9/nPPnzxue279/P23atMHZ2Zm2bdvy888/FziO4t5zk1KVTGBgoNq5c6dSSqmL\nFy+qpk2bqmnTpqnLly8rNzc3tXXrVqWUUj/88INyc3NTiYmJSimlunTpogICAtQff/yhcnJyVFZW\nlgoPD1dvv/22Ydtvv/22at++vbpx44a6ceOG6tChg+H5H3/8UVWvXl298cYbKjMzU6Wnp6vp06er\nmjVrqh07dqjs7Gw1cuRIFRAQoObMmaOys7PVF198oerVq2fY/ubNm9X58+eVUkrt2bNH2dnZqcOH\nDxfY/vTp01V2drbasmWLsrOzU7dv31ZKKfXXv/5Vde3aVcXHx6ucnBz1888/q4yMjCKP+8aNGw/k\nLjs7W4WEhKjJkyertLQ0de/ePbVv3z6llFJLlixRwcHB6sKFCyo1NVUNGDBAjRgxQiml1IULF5SV\nlZX6f//v/6mMjAy1Y8cOZWtrq/r3769u3Lihrly5ojw8PNSePXuUUkotXbpUVa9eXS1cuFBlZ2er\nNWvWKCcnJ5WUlFTqPOTP848//qh8fX2VUkqdOnVK+fn5qYSEBKWUUnFxcercuXOlfv+Kyu/9QkND\n1ZIlSwzH88QTTyillNq2bZt67LHH1J07dwzx5MVy//l0v+TkZOXl5aUWLFigMjIyVEpKivrll19K\nHfu7775rOK/c3NzU0KFDVWpqqjpx4oSqVauWio2NVUopNX36dGVjY6O++eYblZ2drebNm6fq1aun\nsrOzlVJKBQQEqFatWqnLly+re/fuleqzExQUpM6cOaPS09NVaGioeuONN5RSqlTrBgcHF7ru559/\nrvr166fS09NVbm6uOnz4sEpOTn4g/6U5N1988UV17949FR0drWrUqKFOnTqllFLq8ccfV5GRkUop\npe7evasOHDhQ6Htz8+ZN9e2336r09HSVkpKiBg0apPr37294vrjjOHHihKpdu7bau3evysjIUJMn\nT1bVq1dXu3btKnRfM2bMMMRf2uMbNWqU4TN7v+nTp6vhw4crpZSKiYlR9vb2aufOnSo7O1t98MEH\nKjg4WGVlZanMzEwVFBSk3nvvPZWVlaV2796tHBwcVExMjFJKqVGjRikHBwfDcfz9738v1Xl/v/s/\nOzY2Nuo///mPys3NVf/+97+Vt7d3oett3bpVVa9eXeXk5BT6vFJK9enTR/373/82LL/88svqb3/7\nm1JKqYiICEO8eUaNGqXc3NzUoUOHVHZ2tho2bJgaMmSIUkp7z52dnVVkZKTKyclRq1atUi4uLobf\nU8W956ZW6RrqgIAAVbt2beXs7KwCAgLUhAkTVHp6upo7d26Bk18ppZ588kn11VdfKaW0k2f69OkF\nng8PD1dTp041LAcFBRl+4Sil1Pbt21VgYKBSSvtlaWtrqzIyMgzPT58+XfXq1cuwvGHDBlW7dm2V\nm5urlNJ+MVtZWRlO7vv1799fffTRR4bt16pVq8BJ6uHhoX755ReVk5OjatWqpY4dO/bANko67vz2\n79+v6tSpU+gHoVu3bgU+ADExMcrGxkbl5OQYflnEx8cbnndzc1Nff/21Yfm5555TCxcuVEppH877\nP4xt27ZVy5cvL1Ue7s9z/ob6zJkzysPDQ+3cuVNlZmYW2E5J719R+S1MUQ31rl27VIMGDdSBAwce\nyOP959P9Vq5cqR599NFCnytN7PefVwcPHjS8/rHHHlPr169XSmnnZfv27Q3P5ebmqrp166qffvpJ\nKaX9sbt06VLD86X57MyePdvw3Geffaaeeuopo9f98ssvVYcOHQo9r/PnvzTn5pUrVwzPt23bVq1Z\ns0YppVTnzp3V9OnTC/3DtThHjhxRLi4uBeIp6jjeeecdFRYWZnju7t27ytbWtsiGOn/DWtrju3Dh\nQpGx5t/ezJkz1fPPP294Ljc3V/n4+KioqCj13//+V3l5eRVYNywsTM2YMUMppTVq+Y8jNTVVVatW\nTV2+fFnt3r27yPP+fvd/doKDgwvkxsrKSl27du2B9SIjIx+I736rV69WHTt2VEppFx5eXl7q0KFD\nhn3d31CHh4ercePGGZa3bNmiGjVqpJRSatmyZapdu3YFXt++fXsVERFhOI6i3nNTq3S3vq2srFi/\nfj23bt0iNjaWTz/9lJo1axIXF8fatWtxcXEx/Nu3bx9Xr141rJv/9mlh4uPjCQgIMCz7+/sTHx9v\nWK5Tpw62trYF1vHw8DD8XKtWLdzd3Q2dF2rVqgVAamoqAFu3buXxxx/Hzc0NFxcXtmzZUuBWipub\nW4G6lZ2dHampqSQmJnLv3j2CgoIeiLk0x53n0qVLBAQEFFobS0hIeODYs7OzuXbtmuExT0/PAsd6\n/3L+Tn0+Pj4Fth8QEEBCQkKp8lBYnvMEBwezcOFCZsyYgaenJ2FhYYbtlvT+FZXfh9GtWzcmTpzI\nhAkT8PT0ZPz48aSkpJRq3UuXLlG/fv1CnytN7PefV/fnP/+x+Pr6Gn62srLC19e3wPbyfxZKcw55\neXkVui9j1h0xYgRPPvkkQ4YMwcfHh9dff73QGmxpzs38+8j/vi5ZsoTTp0/TuHFj2rZty+bNmx/Y\nPkBaWhrjx48nMDAQJycnunTpwp07dwrUf4s6jvj4+AL5trOzw83NrdD9FKY0x5f3fq1YsQIHBwcc\nHBx4+umnH9hWfHw8/v7+hmUrKyv8/Py4cuUKCQkJD/wODAgIMJwXeedJHnt7e1xdXYmPj6dr165l\nPu/vf2+AQj93bm5uJCYmkpubW+S2nn32Wf744w9iY2P54YcfcHJyonXr1sXuv6jPyf25goL5uD/2\n+z9jplTpGuqi+Pv7M2LECG7dumX4l5KSwpQpUwyvKan3n7e3N7GxsYblixcv4u3tXeT6D9ObMCMj\ng+eee44pU6Zw/fp1bt26RZ8+fUrVEcTd3Z2aNWty9uzZB54rzXHn8fPz4+LFi+Tk5DzwXGHHXr16\n9QIn+cPIX98D7Re6t7d3qfJQUl7DwsLYu3cvcXFxWFlZ8frrrxd5DPnfP1OZNGkSv/76K3/88Qen\nT582fGOgpLj9/f0L1MfyM3Xsly5dMvycm5vL5cuXizyXH+Ycup8x61avXp1p06Zx4sQJ9u/fz6ZN\nm1i2bNkDrzPm3AwODmblypXcuHGD119/nYEDB5Kenv7A6+bPn8/p06c5ePAgd+7cYc+ePSjtjmSJ\n+/D29i6Q77S0tGJrmfefJ6U5vvzfQEhJSSElJaXQPzp8fHyIi4szLCuluHTpEr6+voY48x9TXFyc\n4Y/qvNfmSU1NJSkpyXDeFHXem0r79u2pUaMG3333XZGvqVmzJoMGDSIyMpLIyEhGjhxpeO5he3ff\nnysomI+KVGUa6uHDh7Nx40Z27NhBTk4O9+7dIyoqqkCDcf+H7v7lsLAwZs2aRWJiIomJicycObPY\nrxmU5kOcJzMzk8zMTNzd3bG2tmbr1q3s2LGjVOtaW1szZswYJk+eTEJCAjk5Ofz8889kZmaW6rjz\ntGvXjrp16/LGG2+QlpbGvXv32L9/v+HYP/zwQ2JjY0lNTeXNN99kyJAhD9UzNX8+rl+/zscff0xW\nVhZr167l1KlT9OnTx6g8AJw+fZrdu3eTkZFBjRo1qFmzJtWqVTMcw8O8f2Xx66+/8ssvv5CVlYWd\nnV2B/Xt6ehbZEAP07duXhIQEPvroIzIyMkhJSeHgwYPlEvtvv/3Gd999R3Z2NgsXLqRmzZo8/vjj\nhb62LJ8dU6z7448/cvz4cXJycnBwcMDGxsaQy/yMOTcjIyMNHdScnJywsrIqdL3U1FRq1aqFk5MT\nSUlJvPPOOw+8pqjjeO6559i0aRP79u0jMzOTadOmFXtVWNjvHWM/e3kGDRrE5s2b2b17N1lZWcyf\nP5+aNWvSoUMH2rZti52dHR988AFZWVlERUWxadMmhgwZYlh/y5YthuN4++23ad++PT4+PsWe96bi\n5OTEzJkzmTBhAuvXryctLY2srCy2bt1q+GMcYOTIkSxdupQNGzYU+Ix4eXlx+fJlsrKyDI8V9zu6\nd+/enD59mlWrVpGdnc2aNWs4deoUffv2LdX6plRlGmpfX1/Wr1/PnDlz8PDwwN/fn/nz5xd7pXb/\nd+ymTp1K69atCQkJISQkhNatWzN16tRSr1/UawAcHBz4+OOPGTx4MK6urqxateqBnsHF/UU4b948\nmjdvTps2bXBzc+Of//wnubm5RR53Yb8orK2t2bhxI2fPnsXf3x8/Pz++/vprAMaMGcOIESPo3Lkz\n9evXx87Ojk8++aRUsRX2mnbt2nHmzBnq1KnD22+/zTfffIOLi0uZ85D3WEZGBv/85z+pU6cOdevW\nJTEx0dBz+mHfv9LK/z4nJyfz4osv4urqSmBgIO7u7obBcsaOHcsff/yBi4sLAwYMeGA7tWvX5ocf\nfmDjxo3UrVuXBg0aEBUVVabYizsWKysrnn32WdasWYOrqysrVqzg22+/LfIX68N+dvLnw5h1r127\nxqBBg3BycqJJkyaEhoYW+seJMefm9u3badasGQ4ODrzyyiusXr2aGjVqPPC6l19+mfT0dNzd3enQ\noQO9e/cuNuf5j6Np06YsWrSIoUOH4u3tjaura7Fltvt/bxj72cu/vYYNGxIZGcmkSZOoU6cOmzdv\nZuPGjVSvXh1bW1s2btzI1q1bqVOnDhMnTmT58uU0aNDAsJ2hQ4fyzjvv4ObmxpEjR4iMjASKP+9L\nG1tpjmfy5MksWLCAWbNmGc6nzz77jL/85S+G13Ts2BFra2see+yxAnnu1q0bTZs2xcvLy1CSLG7/\nbm5ubNq0ifnz5+Pu7s68efPYtGlTgR7jRb3npmalyulPgjFjxrB582Y8PDw4fvw4AK+99hqbNm3C\n1taWoKAgli5dipOTU3nsXliwiIgIlixZwt69e80dSpX0zjvvcPbsWYsZHUrow+jRo/H19eXdd981\ndygl6tGjB0OHDmXMmDHmDsUkyu2KevTo0Q98H65Xr16cOHGC6OhoGjRoYLjSEUJUnIq6XScqF72c\nN4cOHeLw4cMmGX7VUpRbQ92pUydcXFwKPNazZ09DXaVdu3Zcvny5vHYvLJhehu2rrCT/oiz0cN6M\nGjWKnj17snDhQuzt7c0djsmU261v0EbN6devn+HWd379+vUjLCyMoUOHltfuhRBCCN0zS2ey2bNn\nY2trK420EEIIUYLqFb3DiIgItmzZUuQUb6B9fy3/l8qFEEKIyqxFixYcPXq00Ocq9Ip627Zt/Otf\n/2L9+vXUrFmzyNfFx8cbBhOQf2X7N336dLPHoPd/kkPJo6X8kxxW/hxGR0cX2SaWW0MdFhZGhw4d\niImJwc/Pjy+//JJJkyaRmppKz549adWqFX/961/La/dVXv6RjETZSA5NQ/JoPMmh8fScw3K79b1q\n1aoHHqss32kTQgihDzExcezceY4//rjKokW76dEjiIYNA0pe0YJUmZHJqprw8HBzh6B7kkPTkDwa\nT3JYNjExcUREnCUhoRsNG77BjRvdiIg4S0xMXMkrW5By/XpWWVlZWWGBYQkhhNCRRYt2c/FiN37/\nHWrVgqZNwcoKPDx289e/djN3eAUU1+5VeK9vY7i6unLr1i1zhyFEpeLi4kJSUlK5bT8qKorQ0NBy\n235VIDksm2vXrDl8GLKyIDExigYNQrG1hcxMfd1M1lVDfevWLbnSFsLELH20KSHK4rff4LffcsnK\nAldXsLeHvGnsbW2Lnr3MEunq1rfcEhfC9ORzJSqT3FzYvh1++QUSE+NITDxLw4bdyft7NCNjF+Hh\nwRbXoay4z6E01EJUcfK5EpVFejqsWwfnzkG1atC3L9jZxbFr1zkyM62xtc2le3fL7PUtDbUQokjl\n/bmS+qrxJIclS0yEVavg5k3tNvfzz4O//5/PW3oOi/sc6quibsECAwPZvXs3AHPmzGHcuHFmjsh8\nAgMDix0itjw0a9aM//73vxW6zxs3btC4cWMyMjLKZfszZsxgxIgR5bJtISqTs2fhP//RGmkvLxg3\nrmAjrXfSUJtI/g45b775Jl988UWJ64SGhrJkyZLyDMsszDEd3u+//07nzp0rdJ9z585l9OjR1KhR\nw/DY9u3b6dy5M46Ojnh4eBAaGsrGjRtL3FZUVBR+fn4FHqssnbws+SpGLySHhVMKDhyAFSvg3j1o\n3BjGjAFn5wdfq+ccSkNtRnr8RZydnW3uECxCRkYGy5YtY/jw4YbH1q1bx+DBgwkPD+fKlStcv36d\nmTNnlqqhLoyUeYQoWnY2bNgA27ZpDXaXLjB48J89uyuTStFQx8TEsWjRbhYujGLRot1lGnXGFNvI\nk/+W5b179xg+fDju7u64uLjQtm1brl+/zltvvcXevXuZOHEiDg4O/O1vfyt0Wz/99BMdOnTAxcUF\nf39/vvrqKwDu3LnDyJEj8fDwIDAwkNmzZxt+sUdERNCxY0cmT56Mi4sLwcHB7N+/n6VLl+Lv74+n\npyfLli0z7CM8PJyXXnqJXr164ejoSGhoKBcvXjQ8b21tzWeffcYjjzxCw4YNAdi0aRMtW7bExcWF\njh07PjDn+JEjR2jRogXOzs4MGTKkwO3h4tYNDAxk/vz5ha6bmJhI3759cXFxwc3NrcAVdP7b7RkZ\nGbz88sv4+Pjg4+PDK6+8QmZmJqBdufr6+rJgwQI8PT3x9vYmIiLCsJ0tW7bQtGlTHB0d8fX1Zf78\n+YW+L7/88gvOzs54e3sDWqM6efJkpk2bxpgxY3BwcACgc+fOLF68mMzMTNzc3Pj9998N27h+/Tr2\n9vZcvHiR3r17Ex8fj4ODA46OjiQkJGBlZUVmZiajRo3C0dGRZs2a8dtvvxnWP3nyJKGhobi4uNCs\nWbMCfxCEh4czYcIE+vbti6OjI48//jjnz58v9FjKW1RUlFn2W5lIDgu6exeWLYMjR8DGBgYNgq5d\nobhrHz3nUPcNdd4QcTdudOP27dAyDRFnim3kl//W71dffUVycjKXL18mKSmJ//u//6NWrVrMnj2b\nTp06sWjRIlJSUvj4448f2E5cXBx9+vTh73//O4mJiRw9epSWLVsCMGnSJFJSUrhw4QJ79uxh2bJl\nLF261LDuwYMHadGiBUlJSYSFhTF48GAOHz7MuXPniIyMZOLEiaSlpRlev3LlSqZNm0ZiYiItW7Zk\n2LBhBWJZv349hw4d4o8//uDIkSOMHTuWL774gqSkJMaPH88zzzxDVlYWoDVaa9euZfv27Vy4cIFj\nx44ZGsOS1rWysipy3fnz5+Pn50diYiLXr1/nvffeKzTns2fP5uDBg0RHRxMdHc3BgweZNWuW4bXX\nrl0jOTmZ+Ph4lixZwoQJE7hz5w4AY8eOZfHixSQnJ3PixAm6dSt89KLjx48b/mgBiImJ4fLlywwc\nOLDQ19va2jJkyBAiIyMNj61atYoePXrg7+/Ptm3b8Pb2JiUlheTkZOrWrYtSig0bNhAWFsadO3d4\n5plnmDhxIgBZWVn069ePp556ihs3bvDJJ58wbNgwTp8+bdj+mjVrmDFjBrdu3SI4OJi33nqr0NiE\n0JOrV2HxYrh4ERwdYfRobcSxykxXA54UZufOc9So0Z2Cfyx159ix3bRpU7ou+AcPniMtrbthOTQU\natTozq5du8vUjT9v2jLQfkHfvHmTM2fO0Lx5c1q1avXAa4uycuVKevbsyfPPPw9oI7O5urqSk5PD\nmjVriI6Oxt7eHnt7e1599VWWL19umPikXr16jBo1CoDBgwcze/Zspk2bho2NDT179sTW1pazZ88S\nEhICQN++fXniiScAraFzcnLiypUr+Pj4APDPf/4T5/8VfhYvXsz48eNp06YNACNHjmTOnDkcOHCA\nTp06YWVlxd/+9je8vLwA6Nevn2Ge1ZLWBYpc19bWloSEBGJjYwkKCqJjx45F5u3TTz/F3d0dgOnT\npzN+/HhmzpwJgI2NDdOmTcPa2prevXtTu3ZtYmJiaNu2Lba2tpw4cYLmzZvj5OT0wPuV5/bt24ar\nZoCbN28CULdu3SLfz5EjRzJ48GDmzp0LwPLly3njjTeAos+DTp068dRTTwEwfPhwFi5cCMCBAwe4\ne/euYf2uXbvSt29fVq1axfTp0wEYMGAArVu3BmDYsGFMnjy5yNjKk55rg5ZCcqg5eRK++w4yM8HX\nV+vZne9jWCw951D3V9RZWYUfQk5O6Q8tN7fw15pimLkRI0bw5JNPMmTIEHx8fHj99dcL1HmLq1Nf\nvnyZ+vXrP/B4YmIiWVlZBAT8+UeEv78/V65cMSx7enoafq5VqxYAderUKfBYamqqIQZfX1/Dc/b2\n9ri6uhIfH294LH9Hp7i4OObPn4+Li4vh3+XLlwu8Pq+hvX9fxqz72muvERwcTK9evQgKCuL9998v\nNG/x8fEP5Cb/9t3c3LC2/vO9tbOzM+zjm2++YcuWLQQGBhIaGsqBAwcK3YerqyspKSkFtgmQkJBQ\n6OsB2rVrR61atYiKiuLUqVOcO3eOZ555psjXQ8H30c7Ojnv37pGbm0t8fPwDnc8CAgIMx2llZfXA\nOZB3jELojVLw3//CmjVaI92iBYSHl76R1jvdX1Hb2GhDwd3/x5KHRy6lne560aJcbtx48HFTDDNX\nvXp1pk2bxrRp0wy3shs2bMiYMWNK7Ezm5+fHwYMHH3jc3d0dGxsbYmNjady4MQAXL14s0Ng+DKUU\nly5dMiynpqaSlJRkqL9CwT8o/P39eeutt3jzzTdLvY+89R923fz7rV27NvPmzWPevHmG29Jt27al\na9euBdbx9vZ+IDf5j6U4rVu35vvvvycnJ4dPPvmEwYMHF6jX5wkJCeHDDz80LDds2BA/Pz/WrVvH\nq6++WuT2R40aRWRkJJ6engwaNAjb//V8KexcKO788Pb25tKlSyilDK+Li4ujUaNGpTrOimTp31/V\ng6qcw6wsWL8efv9dq0H36AEdOhRfjy6MnnOo+yvqHj2CyMgo+J3djIxddO8eVKHbKEpUVBTHjx8n\nJycHBwcHbGxsqFatGqBdLZ07d67IdYcNG8bOnTtZu3Yt2dnZ3Lx5k+joaKpVq8bgwYN56623SE1N\nJS4ujg8//LBAD+SHtWXLFvbt20dmZiZvv/027du3N9z2vt+4ceP4/PPPOXjwIEop7t69y+bNm4u9\nYsu7tfubivxFAAAgAElEQVSw6+a/Jbxp0ybOnj2LUgpHR0eqVatW4Mo4T1hYGLNmzSIxMZHExERm\nzpxZqu8jZ2VlsWLFCu7cuUO1atVwcHAwvFf3a9OmDbdv3y5wBbtgwQLeffddIiIiSE5OJjc3l59+\n+onx48cb1hs+fDjffvstK1asYOTIkYbHPT09uXnzJsnJyYUe+/3atWuHnZ0dH3zwAVlZWURFRbFp\n0yaGDBlS4rpC6EVyMixdqjXStrYQFgYdOz58I613um+oGzYMIDw8GA+P3Tg7R+Hhsfuhx3E1xTby\ny9+x6erVqwwaNAgnJyeaNGlCaGioodH4+9//zrp163B1deXll19+YDt+fn5s2bKF+fPn4+bmRqtW\nrTh27BgAn3zyCfb29tSvX59OnToxbNgwRo8e/cD+88dUXLxDhw7lnXfewc3NjSNHjhTo9HT/uo89\n9hhffPEFEydOxNXVlUceeYRly5YVuY/88Riz7tmzZ+nZsycODg506NCBCRMm0KVLlwfWmTp1Kq1b\ntyYkJISQkBBat27N1KlTS5WLyMhI6tWrh5OTE4sXL2bFihWFvs7W1pbw8PACeXruuedYs2YNX375\nJT4+Pnh5eTFt2jT69+9veI2fnx+PPvoo1tbWhj4BAI0aNSIsLIz69evj6upq6PVd1Ptoa2vLxo0b\n2bp1K3Xq1GHixIksX76cBg0aPJC30hx3edLrVYwlqYo5vHxZ6zQWHw8uLvDCC/C/07tM9JxDGUJU\nMHr0aHx9fXn33XfNHYquJCYm0qlTJ44ePVpg0JOSjB07Fh8fH0PnNnOTz5WwNMeOad+Rzs6GwEDt\n+9F2duaOqnzJEKKiWPJLumzc3d05efLkQzXSsbGxfPvtt4wdO7YcI7Msev7+qqWoKjlUCnbuhG+/\n1Rrp1q1hxAjTNNJ6zqE01MIsQ35WRW+//TbNmzdnypQpBXqlCyEgIwNWr4affgJra3j6aW32qyK6\niVQpcutbiCpOPlfC3G7d0ma+un4datXSRhor5JuplVpxn0Pdfz1LCCGEfsXGwtdfQ1oauLvD0KHg\n6mruqCyL3PoWQpQrPdcGLUVlzeFvv2ljdqelwSOPaD27y6uR1nMO5YpaCCFEhcrJge3bIW88pw4d\ntIFMChkWQSA1aiGqPPlciYqUng5r18L581pHsX794H9zDVVpUqMWQghhdjduaJ3GkpLA3h6GDIH7\nhqwXhZAbDSYSExNDy5YtcXR05NNPPzV6e6GhoSxZssQEkZlOWFgY69evL5dtx8bGYm1tTW6u8eOr\n3+8f//gHn3/+ucm3K0pHz7VBS1EZcnjmDPznP1oj7eUFL75YsY20nnMoDbWJfPDBB3Tv3p3k5GTD\nnMHGsLTvNh87doxjx47x7LPPGh5LSEhg7NixeHt74+joSOPGjZkxY0aBea6LEhgYyO7du8szZIN/\n/OMfzJkzxzDntRCi4igF+/fDypXad6WbNIExY8DJydyR6Yc01CYSFxdHkyZNyrRuTk6OiaMxvf/7\nv/8rMOlHUlIS7du3JyMjgwMHDpCcnMwPP/zAnTt3ip1oJE9F1kW9vLxo1KgRGzZsqJD9iYL0PMay\npdBrDrOztZmvduzQGuzQUO070v+bNK5C6TWHUEka6pizMSxas4iFqxeyaM0iYs7GVOg2unXrRlRU\nFBMnTsTR0ZGzZ89y584dRo4ciYeHB4GBgcyePdvQMEVERNCxY0cmT56Mu7s777zzTrHbV0oxa9Ys\nAgMD8fT0ZNSoUQVmWdqwYQNNmzbFxcWFrl27curUKcNzgYGBzJ07l6ZNm+Lq6sqYMWPIyMgAtLGq\n+/bti4uLC25ubnTu3LnIxnPbtm0FJsBYsGABTk5OREZG4u/vD4Cvry8ffvghzZs3Z8KECfzjH/8o\nsI1nnnmGhQsXMnLkSC5evEi/fv1wcHBg3rx5htdERkYSEBBAnTp1mDNnjuHxjIwMXn75ZXx8fPDx\n8eGVV14hMzMT0G5p+fr6smDBAjw9PfH29iYiIqLAvkNDQ9m8eXOxeRZCmE5qKnz1FRw9CjY2WgMd\nGlr1Zr4yBd031DFnY4j4MYIbnje47XWbG543iPgx4qEaWmO3sXv3bjp16sSiRYtITk4mODiYSZMm\nkZKSwoULF9izZw/Lli1j6dKlhnUOHjxIUFAQ169fL3Fu5qVLl/LVV18RFRXF+fPnSU1NNdxeP336\nNEOHDuXjjz8mMTGRPn360K9fP7Kzsw3rr1y5kh07dnDu3DlOnz7NrFmzAJg/fz5+fn4kJiZy/fp1\n3nvvvUJvt9+9e5cLFy7QsGFDw2M7d+5kwIABRcYcHh7OqlWrDA1/YmIiu3btYtiwYSxbtgx/f382\nbdpESkpKgQZ93759nD59ml27djFz5kxiYrT3YPbs2Rw8eJDo6Giio6M5ePCg4TgArl27RnJyMvHx\n8SxZsoQJEyZw584dw/ONGjUiOjq62DyL8qHn2qCl0FsOExLgiy/g0iVwdNRudTdtat6Y9JbD/HTf\n63vnbzup8UgNomKj/nzQBo6tPkabJ9qUahsHfzpImm8axGrLoYGh1HikBrsO76JhcMNi180vr1HK\nyclhzZo1REdHY29vj729Pa+++irLly9nzJgxAHh7ezNhwgQAatasWex2V6xYwauvvkpgYCAA7733\nHs2aNWPp0qWsWbOGvn370r17d0Crx3700Ufs37+fzp07Y2VlxcSJEw1zS7/11ltMmjSJd999F1tb\nWxISEoiNjSUoKIiOHTsWuv/bt28D4ODgYHgsKSmJunXrFhlzmzZtcHJyYteuXfTo0YPVq1fTtWtX\n6tSpU+yxTp8+nRo1ahASEkKLFi2Ijo6mYcOGrFy5kk8//RR3d3fD68aPH2+YgcrGxoZp06ZhbW1N\n7969qV27NjExMbRt29YQe95xCCHKzx9/wHffQVYW+PpqPbtr1zZ3VPqm+yvqLFV4B6EcSl/3zaXw\nnsaZuZkPFUve1WhiYiJZWVkFJl7w9/fnypUrhmW/fN0dX3rpJRwcHHBwcGDu3LkPbDchIeGBbWVn\nZ3Pt2jUSEhIMt57zYvDz8ytyX/7+/sTHxwPw2muvERwcTK9evQgKCuL9998v9LicnZ0BSElJMTzm\n5uZm2E5RRo4caZivOTIy0jAPd3G8vLwMP9vZ2ZGamgpAfHz8AznIv383Nzes842WkH/dvNjzjkNU\nLD3XBi2FHnKoFOzZow0HmpUFLVpAeLjlNNJ6yGFRdH9FbWNlA2hXwfl52Hnw19C/lmobi64t4obn\njQcet7UuW48Hd3d3bGxsiI2NpXHjxgBcvHgRX19fw2vy32L+/PPPi/36kLe3N7GxsYblixcvUr16\ndby8vPD29ub48eOG55RSXLp0yXAFnff6/D97e3sDULt2bebNm8e8efM4ceIE3bp1o02bNnTr1q3A\n/u3t7QkKCiImJoYOHToA0KNHD7777jumT59eZO/04cOH07x5c6Kjozl16hT9+/cv9PhLIy8H+fOZ\ndxylcfLkSVrKqApClIusLPj+ezhxQqtB9+wJ7dtLPdpUdH9F3eOxHmScySjwWMaZDLo/2r1CtwF/\n3vquVq0agwcP5q233iI1NZW4uDg+/PDDAr2mH0ZYWBgffvghsbGxpKam8uabbzJkyBCsra0ZNGgQ\nmzdvZvfu3WRlZTF//nxq1qxpaFCVUnz22WdcuXKFpKQkZs+ezZAhQwDYtGkTZ8+eRSmFo6Mj1apV\no1oRc8r16dOHPXv2GJYnT55McnIyo0aNMvwhcOXKFV599VXDHw6+vr60bt2akSNHMnDgwALzNnt6\nepaqd3j+HMyaNYvExEQSExOZOXNmqa7Q8+zZs4fevXuX+vXCdPRcG7QUlpzDO3fgyy+1RrpGDW1S\njQ4dLK+RtuQclkT3DXXD4IaEdw3H47oHzled8bjuQXjX8IeqLZtiG1DwKvGTTz7B3t6e+vXr06lT\nJ4YNG8bo0aMNr3uYK8oxY8YwYsQIOnfuTP369bGzs+OTTz7RYm/YkMjISCZNmkSdOnXYvHkzGzdu\npHr16oZ9DR061HB7+5FHHmHq1KkAnD17lp49e+Lg4ECHDh2YMGFCgZ7d+b344ousWLHCsOzi4sL+\n/fuxsbGhXbt2ODo60qNHD5ydnQkODja8btSoURw/fvyBRvWf//wns2bNwsXFhQULFjyQv/tNnTqV\n1q1bExISQkhICK1btzYcR0nrJiQkcPLkyQJX9EII412+rHUaS0jQJtN44QVtcg1hWjLWdyVXr149\nlixZ8sDt7LIYNmwYgwcPLjDoSUn27t3L8OHDiYuLM3r/ZfWPf/yD4OBgXnrpJbPFYMnkcyXKIjoa\nNmzQJtioV0/7+pWdnbmj0i8Z61uYRP4r6tLIyspi4cKFjBs3rpwiKp3839MWQhgnNxd27YJ9+7Tl\ntm3hySe1CTZE+dD9rW9hmU6ePImLiwvXrl3j5ZdfNnc4woz0XBu0FJaSw4wMWL1aa6StraFvX+jT\nRx+NtKXksCzkirqSu3Dhgln227hx4wJfjxJC6FtSkjbz1Y0bUKsWDB6s3fIW5U9q1EJUcfK5EiW5\ncEH7fnR6OtSpA2FhWucxYTpSoxZCCFEmhw7B1q1abbpBA3juOe1rWKLiSI1aCFGu9FwbtBTmyGFO\nDmzerP3LzYWOHbXhQPXaSOv5PJQraiGEEAWkpcHatdot72rV4JlntCFBhXnoqkbt6urKrVu3zBCR\nEJWXi4sLSUlJ5g5DWIgbN7ROY0lJ2jjdQ4Zok2uI8lVcjVpXDbUQQojyc+YMrFunfQ2rbl2tkXZy\nMndUVUNx7Z7UqCspPddjLIXk0DQkj8Yr7xwqBfv3w8qVWiPdtKk2h3RlaqT1fB6WW0M9ZswYPD09\nad68ueGxpKQkevbsSYMGDejVq5fMDyyEEGaWna3NfLVjh9Zgd+0KAweCjY25IxN5yu3W9969e6ld\nuzYjR440zKY0ZcoU3N3dmTJlCu+//z63bt0qdP5lufUthBDlLzVVG2ns8mWtYf7LX6BJE3NHVTWZ\nrUYdGxtLv379DA11o0aN2LNnD56enly9epXQ0FBOnTr1UAELIYQwXkKC1mksOVm7xR0WBl5e5o6q\n6rKYGvW1a9fw9PQEtPmIr127VpG7r1L0XI+xFJJD05A8Gs/UOTxxQptDOjkZ/Pxg3LjK30jr+Tw0\n2/eoH3ZOZiGEEMZRCvbsgbw2q1UrePppqC4jali0Cn178m55e3l5kZCQgIeHR5GvDQ8PJzAwEABn\nZ2datmxJaGgo8OdfRrJc/HIeS4lHlqvmct5jlhKPXpfzlHX9Dh1C+f572LJFWx4/PpTHH4c9eyzj\n+Kract7PsbGxlKRCa9RTpkzBzc2N119/nblz53L79m3pTCaEEOXszh2tHn31qjYE6MCB8Mgj5o5K\n5GeWGnVYWBgdOnQgJiYGPz8/li5dyhtvvMEPP/xAgwYN2L17N2+88UZ57b7Ku/+vcPHwJIemIXk0\nnjE5vHQJFi/WGmlXV3jhharZSOv5PCy3W9+rVq0q9PGdO3eW1y6FEELkc/QobNyoTbBRvz4MGqTN\nJS30RYYQFUKISiY3F3bu1EYbA2jbFp58UptgQ1gmmY9aCCGqiHv34JtvtHG7ra2hTx9o3drcUQlj\nyFjflZSe6zGWQnJoGpJH45U2hzdvwn/+ozXSdnYwcqQ00nn0fB7KFbUQQlQC589rc0inp4OHhzbS\nmIuLuaMSpiA1aiGE0DGl4NAh2LZNq003bAgDBmhfwxL6ITVqIYSohHJyYOtW+PVXbfmJJ6BbN602\nLSoPeTsrKT3XYyyF5NA0JI/GKyyHaWmwfLnWSFevrl1F9+ghjXRR9HweyhW1EELozPXr2khjt26B\ngwM8/zz4+po7KlFepEYthBA6EhOjff0qMxO8vWHIEHB0NHdUwlhSoxZCCJ1TCvbtg127tJ+bNYNn\nnwUbG3NHJsqbVDMqKT3XYyyF5NA0JI/G27Uriu++00YbU0rrMPbcc9JIPww9n4dyRS2EEBYsJUX7\n6pW9Pdjawl/+Ao0bmzsqUZGkRi2EEBYqPh5Wr4bkZHB21gYx8fQ0d1SiPEiNWgghdOb332H9esjK\nAn9/rWe3vb25oxLmIDXqSkrP9RhLITk0Dcnjw1EKfvwR1q3TGulHH4WAgChppI2k5/NQGmohhLAQ\nmZnw9dewZw9YWcFTT0G/fjI9ZVUnNWohhLAAt29rg5hcuwY1a8LAgRAcbO6oREWRGrUQQliwixdh\nzRq4exfc3LROY+7u5o5KWAq59V1J6bkeYykkh6YheSzekSPw1VdaIx0UBC+88GAjLTk0np5zKFfU\nQghhBrm58MMP8PPP2vLjj0OvXjKphniQ1KiFEKKC3bun9eo+e1brKPb001rvblF1SY1aCCEsxM2b\nWqexxESws9O+Hx0QYO6ohCWTmyyVlJ7rMZZCcmgaksc/nTsHX3yhNdKenvDii6VrpCWHxtNzDuWK\nWgghyplScPAgbN+u1aYbNdLG7K5Rw9yRCT2QGrUQQpSjnBzYsgV++01b7tRJm/3Kysq8cQnLIjVq\nIYQwg7Q07fvRcXFQvbo2f3Tz5uaOSuiN1KgrKT3XYyyF5NA0qmoer12DxYu1RtrBAUaPLnsjXVVz\naEp6zqFcUQshhImdOgXffquN3e3jA0OGaI21EGUhNWohhDARpeCnn2D3bu3n5s3hmWfAxsbckQlL\nJzVqIYQoZ1lZsGEDHD+uLXfvDk88IZ3GhPGkRl1J6bkeYykkh6ZRFfKYkgIREVojbWur3eru1Ml0\njXRVyGF503MO5YpaCCGMcOUKrF6tNdbOztrMV56e5o5KVCZSoxZCiDI6fhzWr4fsbG2EscGDwd7e\n3FEJPZIatRBCmJBSWoexvXu15Ucf1SbWqFbNvHGJyklq1JWUnusxlkJyaBqVLY8ZGdogJnv3ajXo\n3r2hX7/ybaQrWw7NQc85lCtqIYQopdu3tZmvrl2DmjVh0CAICjJ3VKKykxq1EEKUQlycdiWdlgZu\nbjB0qPa/EKYgNWohhDDC4cOwebM2wUZwMAwcqF1RC1ERpEZdSem5HmMpJIemoec85ubCtm3aQCY5\nOdC+vXYlXdGNtJ5zaCn0nEO5ohZCiEKkp8O6dXDunNZRrG9faNXK3FGJqkhq1EIIcZ/ERK3T2M2b\n2vein38e/P3NHZWozKRGLYQQpXTuHKxdC/fugZeXNhyos7O5oxJVmdSoKyk912MsheTQNPSSR6Xg\nwAGIjNQa6caNYcwYy2ik9ZJDS6bnHMoVtRCiysvJ0Xp1Hz6sLXfpAqGhMvOVsAxSoxZCVGl372rf\nj754EapXh/79oVkzc0clqhqpUQshRCGuXdM6jd2+DY6OWj3a29vcUQlRkNSoKyk912MsheTQNCw1\nj6dOwZIlWiPt4wPjxlluI22pOdQTPefQLA31e++9R9OmTWnevDlDhw4lIyPDHGEIIaogpeC//9Xm\nkM7MhJAQGD0aHBzMHZkQhavwGnVsbCzdunXj5MmT1KhRg+eff54+ffowatSoP4OSGrUQohxkZWnz\nR//+u9ZRrHt36NhROo0J87OoGrWjoyM2NjakpaVRrVo10tLS8PHxqegwhBBVTHKydhUdHw+2tvDc\nc9CwobmjEqJkFX7r29XVlVdffRV/f3+8vb1xdnamR48eFR1GpafneoylkByahiXk8coV+OILrZF2\ncYEXXtBXI20JOdQ7Peewwhvqc+fOsXDhQmJjY4mPjyc1NZUVK1ZUdBhCiCri+HFYuhRSUiAwUOs0\n5uFh7qiEKL0Kv/X966+/0qFDB9z+N5HrgAED2L9/P8OGDSvwuvDwcAIDAwFwdnamZcuWhIaGAn/+\nZSTLxS/nsZR4ZLlqLuc9VtH779IllF27IDJSWx44MJTevWHvXvPmQz7PspwnKiqK2NhYSlLhncmi\no6MZNmwYhw4dombNmoSHh9O2bVsmTJjwZ1DSmUwIYYSMDPj2W4iJAWtreOopaNNGOo0Jy1Vcu1fh\nt75btGjByJEjad26NSEhIQC8+OKLFR1GpXf/X+Hi4UkOTaOi83jrlvb96JgYqFULhg+Htm313UjL\nuWg8PefQLCOTTZkyhSlTpphj10KISiw2Fr7+GtLSwN0dwsLgf1U2IXRLxvoWQlQKv/2mTayRmwvB\nwTBwINSsae6ohCgdi/oetRBCmFJuLmzbBgcPassdOkCPHlptWojKQE7lSkrP9RhLITk0jfLMY3q6\nNn/0wYNQrZo281WvXpWvkZZz0Xh6zqFcUQshdCkxEVauhKQksLfXZr7y8zN3VEKYntSohRC6c+YM\nrFunfQ3Ly0vrNObkZO6ohCg7qVELISoFpeDAAdixQ/u5SRPtdretrbkjE6L8VLJKjsij53qMpZAc\nmoap8pidrc18tX271kh36QKDBlWNRlrORePpOYdyRS2EsHipqbBmDVy6BDY22lV006bmjkqIiiE1\naiGERbt6FVatgjt3wNFRq0fXrWvuqIQwLalRCyF06eRJbczurCzw9dV6dteube6ohKhYUqOupPRc\nj7EUkkPTKEselYI9e7Tb3VlZ0KIFhIdX3UZazkXj6TmHckUthLAoWVnw/fdw4oQ2kUaPHtpoY3qe\nVEMIY0iNWghhMZKTtXp0QgLUqAHPPQcNGpg7KiHKn9SohRAW7/JlWL1a6+Ht6qp1GqtTx9xRCWF+\nUqOupPRcj7EUkkPTKE0eo6MhIkJrpOvVgxdekEY6PzkXjafnHMoVtRDCbHJzYdcu2LdPW27TBp56\nSptgQwihkRq1EMIsMjLgm2/g9GlttqvevbWGWoiqSGrUQgiLcuuWNvPVjRtQqxYMHqzd8hZCPEhq\n1JWUnusxlkJyaBr35/HCBVi8WGuk69SBceOkkS6JnIvG03MO5YpaCFFhfv0VtmzRatMNGmhfv6pR\nw9xRCWHZpEYthCh3OTmwbRscOqQtd+wI3btrtWkhhNSohRBmlJ4OX3+t3fKuVg2eeUYbElQIUTry\n92wlped6jKWQHBrvxg2YMiWKCxe0cbrDw6WRLgs5F42n5xzKFbUQolycOQPr1kFKCjRrps185eRk\n7qiE0B+pUQshTEop+Pln+OEH7eemTeHZZ8HW1tyRCWG5pEYthKgQ2dmwaRMcPaotd+0KnTvLzFdC\nGKPEGnVqaio5OTkAxMTEsGHDBrKysso9MGEcPddjLIXk8OGkpsJXX2mNtI2NNohJly6wZ0+UuUPT\nPTkXjafnHJbYUHfu3JmMjAyuXLnCk08+yfLlywkPD6+A0IQQepGQAF98AZcuaXXosWOhSRNzRyVE\n5VBijbpVq1YcOXKETz75hPT0dKZMmUKLFi2Ijo4uv6CkRi2EbvzxB3z3HWRlgZ8fPP+81sNbCFF6\nRteof/75Z1asWMGSJUsAyM3NNV10QghdUgr27IG8O4otW0LfvlBder4IYVIl3vpeuHAh7733Hn/5\ny19o2rQp586do2vXrhURmzCCnusxlkJyWLTMTFi7VmukraygVy+tZ3dhjbTk0XiSQ+PpOYcl/u3b\npUsXunTpYlgOCgri448/LteghBCW684dWL1aq0vXqAEDB8Ijj5g7KiEqrxJr1IcOHWLOnDnExsaS\nnZ2trWRlxbFjx8ovKKlRC2GRLl3SGum7d8HVFcLCtBmwhBDGKa7dK7GhbtCgAfPmzaNZs2ZY5xtB\nPzAw0KRBFghKGmohLM7Ro7BxozbBRv36MGiQNpe0EMJ4xbV7Jdao69SpwzPPPEP9+vUJDAw0/BOW\nTc/1GEshOdTk5sKOHfD991oj3bYtDBtW+kZa8mg8yaHx9JzDEmvU06dPZ+zYsfTo0QPb/40BaGVl\nxYABA8o9OCGEed27B998o43bbW0NffpA69bmjkqIqqXEW9/Dhg0jJiaGpk2bFrj1vXTp0vILSm59\nC2F2SUmwapU2A1atWtr3o+VmmhDlw6gadcOGDTl16hRWFThYrzTUQpjXhQvaHNLp6eDhoXUac3Ex\nd1RCVF5G1ag7dOjAH3/8YfKgRPnScz3GUlTVHB46BMuXa410gwbacKDGNNJVNY+mJDk0np5zWGKN\n+ueff6Zly5bUq1ePGjVqAOX/9SwhRMXLyYGtW+HXX7XlJ56Abt202rQQwnxKvPUdGxtb6OPy9Swh\nKo+0NO1Wd2ysNrrYM89ASIi5oxKi6jCqRm0O0lALUXGuX9c6jd26pU2mMWQI+PqaOyohqhajatRC\nn/Rcj7EUVSGHp0/DkiVaI+3tDS++aPpGuirksbxJDo2n5xzKPDdCVEFKwf79sHOn9nOzZtqkGjY2\n5o5MCHE/ufUtRBWTna0NBZo3pXy3btCpkzYLlhDCPIy69f3NN9/wyCOP4OjoiIODAw4ODjg6Opo8\nSCFE+UtJgYgIrZG2tdUGMencWRppISxZiQ31lClT2LBhA8nJyaSkpJCSkkJycnJFxCaMoOd6jKWo\nbDmMj4cvvoDLl8HJCcaMgcaNy3+/lS2P5iA5NJ6ec1hiQ+3l5UVjE3+ab9++zcCBA2ncuDFNmjTh\nwIEDJt2+EKKgEydg6VJITgZ/f63TmJeXuaMSQpRGiTXqv//971y9epX+/fubbFKOUaNG0aVLF8aM\nGUN2djZ3797Fycnpz6CkRi2ESSgFUVGwZ4+23KoVPP209l1pIYTlMOp71OHh4YaN5FfWSTnu3LlD\nq1atOH/+fJGvkYZaCONlZsJ338HJk1oN+sknoV07qUcLYYksasCTo0ePMn78eJo0aUJ0dDSPPfYY\nH330EXZ2dn8GJQ210aKioggNDTV3GLqm5xzevg2rV8PVq1CzJgwcCMHB5olFz3m0FJJD41l6Dotr\n94q8Afb+++/z+uuvM2nSpEI3+PHHH5cpmOzsbA4fPsynn35KmzZtePnll5k7dy4zZ84s8Lrw8HDD\nMKXOzs60bNnSkOS8TgGyXPTy0aNHLSoePS7nsZR4Sru8Zk0UP/4IXl6huLmBv38Uly9DcLB54jl6\n9KHJ3WgAACAASURBVKhZ81EZluXzXPk+z3k/FzVMd35FXlFv3LiRfv36ERERUeC2t1IKKysrRo0a\nVeLGC3P16lXat2/PhQsXAPjpp5+YO3cumzZt+jMouaIWokyOHIFNm7QJNurXh0GDtLmkhRCWrUxX\n1P369QP+rFGbipeXF35+fpw+fZoGDRqwc+dOmjZtatJ9CFHV5ObCDz/Azz9ry+3aaTVpaxkkWAjd\nM8vH+JNPPmHYsGG0aNGCY8eO8eabb5ojjErt/ts94uHpJYf37sHKlVojbW0N/fpB796W00jrJY+W\nTHJoPD3n0Cxf0mjRogWHDh0yx66FqFRu3tRmvkpMBDs7baSxgABzRyWEMCUZ61sInTp/HtauhfR0\n8PCAsDBwcTF3VEKIsjBqrO+YmBi6d+9uqCMfO3aMWbNmmTZCIUSpKQUHD0JkpNZIN2wIY8dKIy1E\nZVViQz1u3DjmzJljGJWsefPmrFq1qtwDE8bRcz3GUlhiDnNytF7dW7ZoHcg6dYIhQ6BGDXNHVjRL\nzKPeSA6Np+ccllijTktLo127doZlKysrbGTSWiEqXFoafP01xMZqQ4A++yw0b27uqIQQ5a3EhrpO\nnTqcPXvWsLxu3Trq1q1brkEJ4+V9uV6UnSXl8Pp1rdPYrVvg4KBdRfv4mDuq0rGkPOqV5NB4es5h\niZ3Jzp07x4svvsj+/ftxcXGhXr16rFixwjBqWLkEJZ3JhDCIiYFvvtHG7vb21hppmRJeiMrFqM5k\nQUFB7Nq1i8TERGJiYti3b1+5NtLCNPRcj7EU5s6hUrB3rzZmd2YmNGsGo0frr5E2dx4rA8mh8fSc\nwxJvfd+6dYtly5YRGxtLdnY2YNxY30KIkmVlwYYNcPy4tty9OzzxhMx8JURVVOKt7/bt29O+fXua\nN2+OtbW10WN9lyooufUtqrCUFO0q+soVsLWFAQOgUSNzRyWEKE9GTXP56KOPcvjw4XIJrCjSUIuq\nKj5e6zSWkgLOztogJp6e5o5KCFHejKpRDx06lMWLF5OQkEBSUpLhn7Bseq7HWIqKzuHvv8OXX2qN\ndEAAjBtXORppOReNJzk0np5zWGKNumbNmrz22mvMnj0b6/+N8m9lZcX58+fLPTghqgKl4Mcf4b//\n1ZYffRSefhqqVTNvXEIIy1Dire969epx6NAh3N3dKyomufUtqozMTPj2Wzh1Suso9tRT0LatdBoT\noqop03zUeR555BFqyczzQpjc7dtaPfraNahZEwYNgqAgc0clhLA0Jdao7ezsaNmyJS+++CKTJk1i\n0qRJ/O1vf6uI2IQR9FyPsRTlmcO4OFi8WGuk3dy0enRlbaTlXDSe5NB4es5hiVfU/fv3p3///gUe\ns5L7ckKU2eHDsHmzNsFGcDAMHKhdUQshRGFkPmohKkhuLuzYAQcOaMuPPw69eoF1ife1hBCVXZlq\n1IMGDWLt2rU0L2R6HisrK44dO2a6CIWo5O7dg7Vr4dw5rTd3377QqpW5oxJC6EGRV9Tx8fF4e3sT\nFxf3QCtvZWVFQEBA+QUlV9RGi4qK0vVsMZbAVDm8eRNWrtT+t7eH558Hf3/j49MLOReNJzk0nqXn\nsEwDnnh7ewPw2WefERgYWODfZ599Vj6RClHJnDsHX3yhNdKenlqnsarUSAshjFdijbpVq1YcOXKk\nwGPNmzfneN5sAeURlFxRC51TCn75BbZv135u1Egbs9vW1tyRCSEsUZlq1P/+97/57LPPOHfuXIE6\ndUpKCh07djR9lEJUEjk5Wq/uvCHyO3eGrl1lEBMhRNkUeUV9584dbt26xRtvvMH7779vaOkdHBxw\nc3Mr36Dkitpoll6P0YOy5PDuXfj6a+170tWrQ//+2jzSVZmci8aTHBrP0nNYpitqJycnnJycWL16\ndbkFJkRlcu2aNtLY7dvg4KDNfPW/rh5CCFFm8j1qIUzg1CltzO7MTPDxgSFDtMZaCCFKw6ixvoUQ\nRVMKfvoJdu3SlkNCoF8/sLExb1xCiMpDxkSqpPQ8rq2lKCmHWVnaVfSuXVpHsR494C9/kUb6fnIu\nGk9yaDw951CuqIUog+RkWL0a4uO1r1w99xw0bGjuqIQQlZHUqIV4SFeuaI10Sgo4O8PQoeDhYe6o\nhBB6JjVqIUzk+HFYvx6ysyEwEAYPBjs7c0clhKjMpEZdSem5HmMp8udQKa0W/c03WiP92GMwYoQ0\n0qUh56LxJIfG03MO5YpaiBJkZMB332lfwbK2hqeegjZtZKQxIUTFkBq1EMW4dUsbxOT6dahZU7vV\nXb++uaMSQlQ2UqMWogzi4mDNGkhLA3d3baSxch49VwghHiA16kpKz/UYS/DbbzBjRhRpaRAcDC+8\nII10Wcm5aDzJofH0nEO5ohYin9xcbWrKX37ROpC1bw89e2q1aSGEMAepUQvxP+npsHYtnD8P1apB\n377QqpW5oxJCVAVSoxaiBImJWqexmzfB3h6efx78/c0dlRBCSI260tJzPaainT0L//mP1kh7ecG4\ncVojLTk0Dcmj8SSHxtNzDuWKWlRZSsGBA7Bjh/Zz48bapBq2tuaOTAgh/iQ1alElZWfD5s3/v707\nj26ruvYH/pUseR5kyfEQybFsWXYGJ7HJSPgBDm4IFBICSchQoCF9PEpb2rR9Hd5qu1Zf14KE1RFW\nWavrteW5tIUQhkLCkIYMJpiQAEn8mhJe4siSLc+OZFmWrPme3x+3OUFkwI5s3Stpf/7y1ZGsox3H\n2+fufe8BTp4Uj2++GWhspJuYEEKkQTVqQj7F6xWvj+7qErekXLMGmDNH6lkRQqbCmXNnsP/4foRY\nCGqFGl9Y8AXUVifWVndUo05SiVyPmUr9/cB//7eYpPPzgQcfvHKSphhODopj7CiG1+bMuTNoPtSM\nvml9eN/+PoZKhtB8qBlnzp2RemoTQitqkjI++QR45RUgFAIMBrGzOy9P6lkRQqaC0+fE7/f/HhaN\nBa4uF3wuH2ZhFjLMGThw4kBCraqpRk2SHmPA4cPAoUPi8fz5wKpVgIr+TCUkaUSECLpGutDubMdZ\nx1mcHzuPo61H4Tf4AQAFGQWYVzIPaco0aPo12LZxm8QzjkY1apKyQiFx/+h//lNsFPvCF4Bly6hp\njJBk4A16cc55DmcdZ3HOeQ6BSICPZaoyYcg1QF2khjZLC3Wamo+lKxPr0g7JEnUkEsHChQthMBiw\nZ88eqaaRtFpaWtDY2Cj1NCTldgM7dwK9vUBGBrB2LVBTM/7XUwwnB8UxdhRDEWMMA94BnHWcxVnH\nWfS4e8BwcRU6LXsaanQ1qNHVoLygHO2l7Wg+1Ay1WQ1bmw3GeiMC7QE0LW+S8FNMnGSJ+sknn8Ts\n2bMxOjoq1RRIEuvuFpO0xwMUFoo7XxUXSz0rQshEBSNBWIetOOs4i3ZnO9wBNx9LU6ShsrASZq0Z\nNboaFGYVRr22troWW7AFB04cwHnneRQPFqNpeVNC1acBiWrU3d3d2LJlC370ox/hV7/61SUraqpR\nk1j84x/A7t3itdJGo7iHdHa21LMihIyXy+8SE7OjHVaXFWEhzMfy0vNg1omJuaqwCulpiXUa+0pk\nV6P+9re/jZ///Odwu92f/2RCxkkQgIMHgdZW8XjRIuC228QNNggh8iUwAfYRO28EG/QO8jEFFNDn\n6fkp7dLcUihSrMkk7on69ddfR3FxMRoaGujawCmUajWtQAB4+WXg7FlxS8rbbxcTdSxSLYZTheIY\nu2SMoS/ki2oE84V9fCwjLQMmrQk1uhpUa6uRm54b8/slcgzjnqiPHDmC3bt3480334Tf74fb7cYD\nDzyAZ599Nup5W7ZsgdFoBABoNBrU19fzIF9I8HR85eO2tjZZzWcqj/fsacGBA4BG04isLGDGjBZ4\nvQAQ2/e/QOrPl+jHbW1tsppPIh4nw//nm2++GUNjQ3jh9Rdgd9uRY84BA4OtzQYAWHD9AtToauD4\nxIGSnBI0zWma1Pe/QC7xuPC1zWbD55H0Oup33nkHv/jFL6hGTa6ZzQbs2gWMjQHTpolNY1qt1LMi\nhABAWAhHNYK5/C4+plQoYdQYeSOYLlsn4UylJ7sa9aelWq2BTJ6PPgLefFOsTZvN4uVXmZlSz4qQ\n1OYOuNHuEGvNHcMdCAkhPpajzolqBMtU0X/Y8aA7kyWplgSux3yeSAT4+9+BDz4Qj5ctE29kopzk\nO9cncwzjieIYOznHUGACekd7+bXN/Z7+qPGy3DLeCDY9b7pkizM5xxCQ+YqakInw+YAXXwQ6OsRu\n7lWrgPp6qWdFSGrxh/2wOC38lPZYaIyPpaelo6qwCjW6Gpi1ZuRl0A31Y0UrapIwhoaA558HnE4g\nN1fcVKO8XOpZEZL8GGNw+Bx81dw10gWBCXy8MLNQTMw6M4waI1RKWgNOFK2oScJrbwdeekm8DKus\nDNi4ESgokHpWhCSvsBBGp6uTX9vs9Dn5mFKhREVBBT+lXZRdRP1GU4gSdZKSez1mvBgD3n8fePtt\n8evZs4E1a4D0ONyMKFliKDWKY+ziFUNP0MMbwSzDFgQjQT6WpcrijWCmQhOy1FlTPp/JlMg/h5So\niWyFw8DrrwP/ugwXjY3AzTfTzleETBbGGPo8ffyUdu9ob9R4SU4JXzXr8/VQKia5Y5OMC9WoiSx5\nPMALLwB2O6BWA3ffLa6mCSGxCYQD6Bju4I1gnqCHj6mUKlQVVvFrmwsyqb4UL1SjJgmlr0/c+Wpk\nRKxDb9wo1qUJIdfG6XPyTS5sLhsiLMLHCjIK+CntSk1l1L7NRB4oUSepRK3HnD4N/O1vQCgkdnRv\n2CB2eEshUWMoNxTH2E00hhEhArvbzk9pnx87z8cUUKA8v5yf0i7OKU6JRrBE/jmkRE1kgTHg8GHg\n0CHxuL4euPNOQEU/oYSMizfo5ZtcWIYt8If9fCxTlYlqbTXf5CJbTfu+JhKqURPJhULAq68CH38s\nNoqtWAFcfz01jRFyNYwxDHgH+Kq5x90Dhou/N6dlT+PXNpfnlyNNSfu9yhnVqIlsjYyI9ei+PiAj\nA1i3TrxvNyHkUqFIKKoRzB1w87E0RRoqCyt5I1hhVqGEMyWTiRJ1kkqEeozdLnZ2ezzijlebNok7\nYMlFIsQwEVAcY+Pyu7Bzz07k1ebB6rIiLIT5WF56XtQmF+lpcbjBQIJK5J9DStREEm1twJ494gYb\nlZXA+vVANpXNCIHABHS7u/kp7UHvIGw9NhinGQEA+jw9bwQrzS1NiUawVEc1ahJXggDs3w8cOSIe\nL14MrFwpbrBBSKryhXy8Eeyc8xx8YR8fy0jLgElr4o1guekSXQZBphTVqIksBALi/brb28UtKb/4\nRWDhQqlnRUj8McYwNDbEV832EXtUI5guS8cbwSoKKqgRLMVRok5ScqvHOJ3izldDQ0BWFnDvveIp\nbzmTWwwTFcVRFBbCsA5b+SYXLr+LjykVShgLjPyUti5bF/VaimHsEjmGlKjJlLNagV27xL2kp00T\nm8a0WqlnRcjUcwfcfJOLjuEOhIQQH8tR50Q1gmWqMiWcKZEzqlGTKfXhh8Bbb4m16ZoaYO1a8TIs\nQpKRwAT0jvbyU9r9nv6o8bLcMr5qnp43nRrBCEc1ahJ3kQiwd6+YqAHghhuApiaxNk1IMvGH/bA4\nLfza5rHQGB9TK9UwaU0wa80w68zIz8iXcKYkUVGiTlJS1mPGxoAXXxRPeatUwOrVwLx5kkwlJolc\n05KTZIsjYwwOn4NvctE50gmBCXxck6nhq2ajxgiVMvZfs8kWQykkcgwpUZNJNTQEPPccMDwsbqax\ncSNgMEg9K0JiExbC6HR18kYwp8/Jx5QKJSoKKnhyLsouolPaZFJRjZpMmrNngZdfFi/DKisTm8by\n6UwfSVCeoIc3glmGLQhGgnwsS5XFG8FMhSZkqbMknClJBlSjJlOKMfEGJvv3i1/PmQOsWQOoaVtb\nkkAYY+jz9PFGsN7R3qjxkpwSvmrW5+uhVFDDBYkPStRJKl71mHBYvBXo//6veHzLLcCNNybHzleJ\nXNOSEznHMRAORG1y4Ql6+JhKqUJVYRXf5KIgs0Cyeco5hokikWNIiZpcM49H3Pmqu1tcPd9zDzBr\nltSzIuTqnD4nbwSzuWyIsAgfK8go4Ke0KzWVUKfRaSEiPapRk2vS1yfeacztBgoKxHp0aanUsyLk\nUhEhArvbzk9pnx87z8cUUMCQb+CntItziqkRjEiCatRkUn38MfDqq0AoBMyYAWzYAOTkSD0rQi7y\nBr18kwvLsAX+sJ+PZaoyUa2t5ptcZKtp2zYib5Sok9RU1GMYA1pagHfeEY8bGoA77hCvlU5GiVzT\nkpN4xJExhgHvAF8197h7oja5mJY9jW9yUZ5fnnCbXNDPYuwSOYZJ+iuWTLZgUFxFnz4tNordeiuw\ndGlyNI2RxBSKhNAx3MGvbXYH3HwsTZEGo+biJheFWYUSzpSQ2FCNmnyukRGxHt3fL96ne/16oLpa\n6lmRVOTyu/i1zVaXFWEhzMfy0vOiNrlIT0uXcKaETAzVqMk1s9vFzm6vV9zxavNmoKhI6lmRVCEw\nAd3ubn5Ke9A7GDWuz9PzVXNpbik1gpGkRIk6SU1GPaatTbxGOhIBqqrElXRWCt2AKZFrWnIy0Tj6\nQj7eCHbOeQ6+sI+PZaRlwKQ18Uaw3PTcKZix/NDPYuwSOYaUqMklBEG8y9iRI+LxkiXAypW08xWZ\nGowxDI0N8Wubu0a6ohrBtFlavmquKKhIuEYwQmJFNWoSxe8X79fd3i4m5jvuABYskHpWJNmEhTCs\nw1beCObyu/jYZze50GXrJJwpIfFBNWoyLg6H2DR2/jyQnQ3cey9gNEo9K5Is3AE3bwTrGO5ASAjx\nsRx1TlQjWKYqU8KZEiIvlKiT1ETrMR0d4h7SPh9QXCzeaawwxa9oSeSalhwITEDvaC92vbEL2eZs\n9Hv6o8bLcsv4tc36PD01gl0F/SzGLpFjSIk6xTEGfPghsHevWJuurRXv2Z2RIfXMSCLyh/2wOC28\nEcwb8sI2YIOxzAi1Ug2T1gSz1gyzzoz8DNoDlZDxoBp1CotEgLfeAj76SDy+8UZx9yta2JDxYozB\n4XPwRrDOkU4ITODjmkwNrzUbNUaolLQ2IORyqEZNLjE2BuzaBdhs4i1AV68G5s2TelYkEUSECDpH\nOvm1zU6fk499thGsKLuITmkTEiNK1EnqavWYwUGxaWx4GMjLAzZuBPT6+M4vESRyTWuyeYIe3ghm\nGbYgGAnysSxVFm8EMxWakKWOvtie4hg7imHsEjmGlKhTzJkz4uVXwSAwfbqYpPOpVEg+gzGGPk8f\nXzX3jvZGjZfklPBGMEO+AUoFXWRPyFShGnWKYAx47z3gwAHx67o64K67ALVa6pkRuQiEA1GbXHiC\nHj6mUqpQqankp7QLMgsknCkhyYdq1CkuHAZ27wb+8Q/x+JZbxMYxKh0Sp8/JT2nbXDZEWISP5Wfk\n88RcqamEOo3+qiNECpSok9SFeszoqLipRk8PkJ4O3H03MGuW1LNLDIlc07qSiBCB3W3np7TPj53n\nYwooUJ5fzpNzcU7xpDSCJWMc441iGLtEjiEl6iTW2ysmabcb0GjEm5iUlEg9KxJv3qCXb3JhGbbA\nH/bzsUxVJqq11XyTi2x1toQzJYRcDtWok9Q//wm8+qp42nvGDGDDBiAnR+pZkXhgjGHAO8BXzT3u\nnqhNLqZlT+Nd2uX55bTJBSEyQDXqFMIYcOgQcPiweHzddeLGGmn0uziphSKhqEYwd8DNx9IUaTBq\njPyUdmFWit8blpAEE/dEbbfb8cADD2BwcBAKhQL//u//jm9+85vxnkZSCgaBv/0N+OQTwGZrwVe/\n2oglS6hp7FrJvabl8rt4I5jVZUVYCPOxvPS8qE0u0tPSJZun3OOYCCiGsUvkGMY9UavVavz6179G\nfX09PB4PFixYgBUrVmAWdTjFxOUSb2IyMABkZgIrVgBLl0o9KzKZBCag293NT2kPegejxvV5er5q\nLs0tpTuCEZIkJK9Rr1mzBo8++iiampr4Y1SjnpiuLuCFFwCvF9DpxKaxoiKpZ0Umgy/k441g55zn\n4Av7+Fh6WjqqtdV8k4vc9FwJZ0oIiYVsa9Q2mw0nT57EkiVLpJxGQjtxAnjjDXGDDZMJWLcOyMr6\n/NcReWKMYWhsiG9y0TXSFdUIps3S8lVzRUEFNYIRkgIkS9Qejwfr1q3Dk08+idxcWglMlCAA+/YB\nR4+Kx0uXArfeCij/dSfHRK7HyEW8YhgWwrC5bPyUtsvv4mNKhRLGgouNYLps3ZTPZ7LRz2LsKIax\nS+QYSpKoQ6EQ1q5di/vuuw9r1qy57HO2bNkCo9EIANBoNKivr+dBbmlpAYCUPd63rwXvvAOo1Y1I\nSwNKSlqQmQkolRef39bWJpv5JurxBVPx/b1BL0rrSnHWcRb7D+5HhEVgrDcCAPpP9cNQYMA9t9+D\nqsIqHG09ioArAF25TlbxGe9xW1ubrOaTiMf0/1ne/5+vdT4tLS2w2Wz4PHGvUTPG8OUvfxk6nQ6/\n/vWvLz8pqlFfkcMhNo2dPw9kZ4vXR1dUSD0r8nkEJqB3tJevmvs9/VHjZbllfJMLfZ6eGsEISTFX\ny3txT9Stra246aabMG/ePP7LaPv27bjtttsuTooS9WVZLMCLLwJ+v3iHsU2bxDuOEXnyh/2wOC28\nEcwb8vIxtVKNqsIqnpzzM2gLM0JSmawS9XhQoo7GGPDBB8Df/y7WpmfOBO65R7x395W0JHA9Ri4m\nGkPGGBw+B7+2uXOkEwIT+LgmU8NrzUaNESplatxviH4WY0cxjJ3cYyjbrm/y+SIR4M03gePHxeOb\nbgKWL6ebmMhFRIigc6STn9J2+px8TKlQoqKggifnouwiOqVNCJkwWlHLmNcL7NoFdHYCKpW4f/Tc\nuVLPiniCHr5qtgxbEIwE+ViWKgtmnRlmrRnV2mpkqelaOULI56MVdQIaGBCbxlwuIC8P2LgR0Oul\nnlVqYoyhz9PHr23uGe2JGi/JKeG36zTkG6BUKCWaKSEkGVGilqH/+z/glVfEe3fr9WKSzsub2PeQ\nez1G7gLhAHa+vhOFswpx1nEWnqCHj6mUKlRqKnkjmCaTOvquhn4WY0cxjF0ix5AStYwwBrS2AgcP\nil/PnQusXg2o1VLPLDU4fU5+StvmssFis8CoMQIA8jPyea25UlMJdRr9oxBC4oNq1DIRCgG7dwOn\nTomNYk1NwA03UNPYVIoIEdjddt4Idn7sPB9TQAFDvoEn5+KcYmoEI4RMGapRy9zoKLBzJ9DTI15y\ntXYtUFsr9ayS01hoLKoRzB/287FMVSbf5KJaW42c9BwJZ0oIISJK1BLr6RGT9OioePOSTZvEm5nE\nKpHrMZOJMYYB7wBvBOt2d0dtcjEtexpvBCvPL4/a5IJiODkojrGjGMYukWNIiVpCp04Br70GhMPi\nbUDvvRfIoUVczEKREDqGO9DuFFfO7oCbj6Up0mDUXNzkojCrUMKZEkLI56MatQQYExvG3n1XPF6w\nAPjiF4E02rHwmrn8Ln5K2+qyIiyE+Vhuei5PzFWFVUhPu8ot3QghRAJUo5aRQAD429/ES7CUSmDl\nSmDxYmoamyiBCeh2d/NGsEHvYNS4Pk/PL58qyy2jRjBCSMKiRB1HLpd4E5OBASAzE1i/HjCZpua9\nErkecyW+kA/nnOf4Jhe+sI+Ppael80Yws86M3PTY9zhPxhhKgeIYO4ph7BI5hpSo46SzE3jhBWBs\nDCgqEpvGdDqpZyVvjDEMjQ3xRrCuka6oRjBtlpaf0q4oqIhqBCOEkGRBNeo4OHECeOMNcYON6mpg\n3TpxRU0uFRbCsLls/JS2y+/iY5/d5EKXTX/pEEKSA9WoJSII4taUx46Jx9dfD6xYIdamyUXugJs3\ngnUMdyAkhPhYjjqHXz5VVViFTBX9hUMISS2UqKeIzwe89BJgsYjd3HfeCTQ0xO/95VyPEZiA3tFe\nvmru9/RHjZfllvHkrM/TS9YIJucYJhKKY+wohrFL5BhSop4C58+LTWMOh3hd9IYNwIwZUs9KWv6w\nHxanBe3OdrQ72uENefmYWqlGVWEV79LOz8iXcKaEECIvVKOeZOfOiStpvx8oLRV3vtKk4OZKjDE4\nfA5+SrtzpBMCE/i4JlPDa81GjREqJf3NSAhJXVSjjgPGxFr03/8ufj1rFnD33eK9u1NFRIigc6ST\nn9J2+px87NONYGadGdOyp9G1zYQQMg6UqCdBOCx2dZ88KR7ffDPQ2CjtTUziVY/xBD1RjWCBSICP\nZamyYNaZ+SYXWeqsKZ/PZErkmpacUBxjRzGMXSLHkBJ1jLxe8frori5ApQLWrAHq6qSe1dRhjKHP\n08evbe4Z7YkaL8kp4Y1ghnwDlApqcSeEkFhQjToG/f1i09jICJCfL9ajp0+XelaTLxAORG1y4Ql6\n+JhKqUKlppKf0tZkpmBBnhBCYkQ16kl05kwn9u+3wG5X4vRpATNmmFBfX4ENG4C8PKlnN3mcPic/\npW1z2RBhET6Wn5HPG8EqNZVQp6klnCkhhCQ3StQTcOZMJ5qbz6G/vwlWq/hYb+8BPPIIkJdXIe3k\nPmOi9ZiIEIHdbeeNYOfHzvMxBRQozy/nq+aSnJKUaARL5JqWnFAcY0cxjF0ix5AS9QS89poFn3zS\nBNe/7mpZVQWUlzfhnXcOYs4ceSXq8RgLjfFVs2XYAn/Yz8cyVZl8k4tqbTVy0mmjbEIIkQLVqMeB\nMeDDD4Gf/rQFY2ONUKuBmTMvbqqh0bRg27ZGSec4HowxDHgHeCNYt7s7apOLouwifkq7PL+cNrkg\nhJA4oRp1DJxO4LXXxN2vAAHFxeLGGp++Pjo9XbjSyyUXioRgdVn5KW13wM3H0hRpMGqM/JS2Nksr\n4UwJIYRcDiXqK7hwA5MDB4BQSLwV6Ne/bkJr6wGkpzfx5wUCB9DUVC3hTC/l8ruwc89O5NXmkFMO\nXwAAEZhJREFUweqyIiyE+Vhuei5fNVcVViE9LYXuyDJBiVzTkhOKY+wohrFL5BhSor4Mh0NcRXd1\nicdz5wK33w5kZ1eguho4cOAggkEl0tMFNDVVo7ZW2vq0wAR0u7v5qnnQOwhbjw3GaUYAgD5Pz69t\nLsstS4lGMEIISRZUo/4UQbi4ig6HgdxccdermTPjPpXP5Qv5cM55jm9y4Qv7+Fh6WjpMhSZ+Sjs3\nPVfCmRJCCPk8VKMeh/PnxVW03S4ez58P3HYbkCWTu14yxjA0NsS7tO1ue9QmF9osLT+lPaNgBm1y\nQQghSSLlf5sLAvD++8ChQ+IqOi8PWLUKqKmRemZAWAjD5rLxU9ouv4uPKRVKfkewGl0NdNm6qNcm\ncj1GLiiGk4PiGDuKYewSOYYpnaiHhoBXXwV6/nW76vp6YOVKaVfR7oA7apOLkBDiYznqHL7JhUlr\nQqYqU7qJEkIIiYuUrFELAnDkiLiKjkTE+3SvWgWYzVP2llfEGEPPaA+/trnP0xc1XpZbxhvB9Hl6\nagQjhJAkRDXqTxkcFFfRvb3i8XXXAbfeCmTGcXHqD/thcVp4I5g35OVjaqUaVYVVvBEsPyM/fhMj\nhBAiOymTqCMR4L33gHfeEb8uKBBX0dVxugTaMebgtebOkc6oRjBNpobXmo0a46Q0giVyPUYuKIaT\ng+IYO4ph7BI5himRqAcGxFV037/OKi9cCKxYAWRkTN17RoQIOkc6eXJ2+px8TKlQoqKggq+ap2VP\no1PahBBCLiupa9SRCNDaChw+LH6t0QCrV4ubaUwFT9AT1QgWiAT4WJYqizeCVWurkaWWyXVfhBBC\nJJeSNer+fnEV3d8vHi9aBHzhC7Gvos+cO4P9x/cjxEJQQYV5s+ZBKBDQ7mhHz2hP1HOLc4r5KW1D\nvgFKhTK2NyeEEJJykm5FHYmIK+h33xW7uwsLxVV0ZWXs8zpz7gz+cOAPGDOMwelzwuFzYOzMGOpn\n16NoehFUShW/ttmsM0OTqYn9Ta9RItdj5IJiODkojrGjGMZO7jFMmRV1X5+4ih4YEI+XLAGamqJ3\nupqoiBBBz2gPOoY78PtXf4/eol6woYvBzKnNQcQRweaVm1GpqYQ6TR3jpyCEEEIuSooVdTgsrqJb\nW8VVtFYrrqKNxom/N2MMDp8DHcMdsDgtsLlsvNZ8tPUoAoYA8jPyoc3SQpetQ446B4UDhdi2cdvE\n34wQQghBkq+oe3vFVfTgIKBQAEuXArfcMrFV9FhoDB3DHTw5jwRGosaLsotQVVgFoUyAMEO45PKp\ndCVtFUkIIWRqJGyiDoeBlhbxDmOCAOh0wF13ATNmjOO1QhhdI108Mfd7+sFw8S+ZbHU2qgqrUFVY\nBVOhCQWZBQAAk8KE5kPNUJkvhi3QHkDT8qZL3kNqcq/HJAKK4eSgOMaOYhi7RI5hQibq7m5xp6uh\nIXEVvWwZsHw5oL5CeZgxhkHvICzDFnQMd6DT1Rl1D+00RRoqNBU8MZfmll72uuba6lpswRYcOHEA\nQSGIdGU6mpY3oba6dqo+KiGEkBSXUDXqUOjiKpoxoKhIXEWXl1/6PUYDozwxdwx3wBP0RI2X5JTA\npDWhqrAKFQUV1ARGCCFEMglboz5zphP791sQCinh8Qjw+01QqSqgUAA33AA0Nl5cRQcjQXS6Only\nHvQORn2vvPQ8npirCquQm54b/w9ECCGETJAkiXrv3r3Ytm0bIpEI/u3f/g0/+MEPLnnOmTOdaG4+\nB5WqCVareLo7HD6A5cuBhx+uwHS9gL7RPlh6xcRsH7EjwiL89WqlGkaNkSfnVLtNZyLXY+SCYjg5\nKI6xoxjGLpFjGPdEHYlE8I1vfAP79++HXq/HokWLsHr1asyaNSvqeZs2/Q90JY3oHXsagUgICkGN\nav0i+LVv4ciIFlabFb6wjz9fAQX0eXqxzqw1oTy/HGnKtHh/PNloa2tL2B9KuaAYTg6KY+wohrFL\n5BjGPVF/8MEHqK6uhvFfFzlv3LgRr7322iWJ+p+eNxDxtUKz0IAMTRDpBcP4uOt5jPYVIWeoHoC4\n65Sp0AST1oRKTSXdP/tTXC6X1FNIeBTDyUFxjB3FMHaJHMO4J+qenh6Uf6r7y2Aw4NixY5c8LzTP\nAuSFMcJs0OsMAABVVSaEPj/uMN8Bk9aEwszClDqdTQghJPXEPVGPO7GqI0BZBLC7UIj/hyxokRYZ\nwo2zK7FIv2hqJ5kEbDab1FNIeBTDyUFxjB3FMHaJHMO4X5519OhR/PSnP8XevXsBANu3b4dSqYxq\nKFMWZIG5/fGcFiGEECKZ+fPno62t7bJjcU/U4XAYtbW1OHDgAKZPn47Fixfj+eefv6RGTQghhBAJ\nTn2rVCr89re/xcqVKxGJRPCVr3yFkjQhhBByBbK8MxkhhBBCREqpJ/BZe/fuxcyZM2E2m/HEE09I\nPR1J2e12LF++HHPmzEFdXR2eeuopAIDT6cSKFStQU1ODW2+9Neqyg+3bt8NsNmPmzJnYt28ff/z4\n8eOYO3cuzGYzvvWtb/HHA4EANmzYALPZjKVLl6KzszN+HzCOIpEIGhoasGrVKgAUw4lyuVxYt24d\nZs2ahdmzZ+PYsWMUwwnavn075syZg7lz52Lz5s0IBAIUw3HYunUrSkpKMHfuXP5YvOL2pz/9CTU1\nNaipqcGzzz47xZ/0KpiMhMNhZjKZmNVqZcFgkM2fP5+dPn1a6mlJpq+vj508eZIxxtjo6Cirqalh\np0+fZt/73vfYE088wRhjbMeOHewHP/gBY4yxjz/+mM2fP58Fg0FmtVqZyWRigiAwxhhbtGgRO3bs\nGGOMsdtvv5299dZbjDHGnn76afbII48wxhjbuXMn27BhQ1w/Y7z88pe/ZJs3b2arVq1ijDGK4QQ9\n8MAD7I9//CNjjLFQKMRcLhfFcAKsViurrKxkfr+fMcbYvffey5qbmymG43D48GF24sQJVldXxx+L\nR9wcDgerqqpiw8PDbHh4mH8tBVkl6iNHjrCVK1fy4+3bt7Pt27dLOCN5ueuuu9jbb7/NamtrWX9/\nP2NMTOa1tbWMMcYef/xxtmPHDv78lStXsvfff5/19vaymTNn8seff/559vDDD/PnHD16lDEm/gIu\nKiqK18eJG7vdzpqamtjBgwfZnXfeyRhjFMMJcLlcrLKy8pLHKYbj53A4WE1NDXM6nSwUCrE777yT\n7du3j2I4TlarNSpRxyNuzz33HPvqV7/KX/Pwww+z559/foo+4dXJ6tT35W6G0tPTI+GM5MNms+Hk\nyZNYsmQJBgYGUFJSAgAoKSnBwMAAAKC3txcGg4G/5kL8Pvu4Xq/ncf10zFUqFQoKCuB0OuP1seLi\n29/+Nn7+859Dqbz4404xHD+r1Ypp06bhwQcfxHXXXYeHHnoIXq+XYjgBWq0W3/3udzFjxgxMnz4d\nGo0GK1asoBheo6mOm8PhuOL3koKsEjXdZezyPB4P1q5diyeffBJ5eXlRYwqFguJ2Fa+//jqKi4vR\n0NBwxS3kKIZXFw6HceLECXzta1/DiRMnkJOTgx07dkQ9h2J4dRaLBb/5zW9gs9nQ29sLj8eDv/zl\nL1HPoRhem1SIm6wStV6vh91u58d2uz3qL5pUFAqFsHbtWtx///1Ys2YNAPEvyP7+fgBAX18fiouL\nAVwav+7ubhgMBuj1enR3d1/y+IXXdHV1ARB/IY+MjECr1cbls8XDkSNHsHv3blRWVmLTpk04ePAg\n7r//forhBBgMBhgMBixaJN4RcN26dThx4gRKS0sphuP00UcfYdmyZdDpdFCpVLjnnnvw/vvvUwyv\n0VT//9XpdLLKR7JK1AsXLkR7eztsNhuCwSBeeOEFrF69WuppSYYxhq985SuYPXs2tm3bxh9fvXo1\n/vSnPwEQuxIvJPDVq1dj586dCAaDsFqtaG9vx+LFi1FaWor8/HwcO3YMjDH8+c9/xl133XXJ93rp\npZfQ1NQU5085tR5//HHY7XZYrVbs3LkTt9xyC/785z9TDCegtLQU5eXlOHv2LABg//79mDNnDlat\nWkUxHKeZM2fi6NGj8Pl8YIxh//79mD17NsXwGsXj/++tt96Kffv2weVyYXh4GG+//TZWrlwpwaeF\nvLq+GWPszTffZDU1NcxkMrHHH39c6ulI6t1332UKhYLNnz+f1dfXs/r6evbWW28xh8PBmpqamNls\nZitWrIjqRHzssceYyWRitbW1bO/evfzxjz76iNXV1TGTycQeffRR/rjf72fr169n1dXVbMmSJcxq\ntcbzI8ZVS0sL7/qmGE5MW1sbW7hwIZs3bx67++67mcvlohhO0BNPPMFmz57N6urq2AMPPMCCwSDF\ncBw2btzIysrKmFqtZgaDgT3zzDNxi9szzzzDqqurWXV1NWtubo7L570cuuEJIYQQImOyOvVNCCGE\nkGiUqAkhhBAZo0RNCCGEyBglakIIIUTGKFETQgghMkaJmhBCCJExStSEpKjGxkYcP348pu+xZ8+e\nlN+OlpCpppJ6AoQQaUzGPZJXrVrF9/gmhEwNWlETIhNerxd33HEH6uvrMXfuXLz44osAgJ/97GdY\nvHgx5s6di4cffpg/v7GxEd/5znewaNEizJo1Cx9++CHuvvtu1NTU4Cc/+QkAcde1mTNn4r777sPs\n2bOxfv16+Hy+S9573759WLZsGRYsWIB7770XXq/3kuc89dRTmDNnDubPn4/NmzcDAJqbm/Hoo48C\nAOrr69HQ0ICGhgZkZ2fj3XffhdfrxdatW7FkyRJcd9112L179yXft6WlBY2NjVi/fj1mzZqF++67\nL/ZgEpJMJLsnGiEkyksvvcQeeughfjwyMsIYY8zpdPLH7r//frZnzx7GGGONjY3shz/8IWOMsSef\nfJKVlZWx/v5+FggEmMFgYE6nk1mtVqZQKNiRI0cYY4xt3bqV/eIXv+CvP378OBsaGmI33XQTGxsb\nY4wxtmPHDvazn/3skvlNnz6dBYPBqLk1Nzezb3zjG1HP2717N7vppptYKBRi//mf/8n+8pe/MMYY\nGx4eZjU1Nczr9UY9/9ChQ6ygoID19PQwQRDY9ddfz1pbW68lhIQkJVpREyIT8+bNw9tvv40f/vCH\naG1tRX5+PgDg4MGDWLp0KebNm4eDBw/i9OnT/DUXNq2pq6tDXV0dSkpKkJ6ejqqqKr7zT3l5Oa6/\n/noAwH333YfW1lb+esYYjh49itOnT2PZsmVoaGjAs88+y3cT+uz8Nm/ejL/+9a9IS0u77Gdob2/H\n97//fezatQsqlQr79u3Djh070NDQgOXLlyMQCETtSHTB4sWLMX36dCgUCtTX18Nms11bEAlJQlSj\nJkQmzGYzTp48iTfeeAM//vGP0dTUhO9///v4+te/juPHj0Ov1+O//uu/4Pf7+WsyMjIAAEqlkn99\n4TgcDgOI3uedMXbZuvSKFSvw3HPPXXV+b7zxBg4fPow9e/bgsccew6lTp6L2+PZ4PNiwYQP+8Ic/\noKSkhD/+yiuvwGw2X/V7f3ruaWlpfO6EEKpREyIbfX19yMzMxJe+9CX8x3/8B06ePMmTsk6ng8fj\n4XXriejq6sLRo0cBAM899xxuvPFGPqZQKLB06VK89957sFgsAMRaeXt7e9T3YIyhq6sLjY2N2LFj\nB0ZGRuDxeKKes3XrVjz44IO44YYb+GMrV67EU089xY9Pnjw54fkTkupoRU2ITJw6dQrf+973oFQq\noVar8bvf/Q4FBQV46KGHUFdXh9LSUixZsuSyr71aB3dtbS2efvppbN26FXPmzMEjjzwSNV5UVITm\n5mZs2rQJgUAAAPDYY49FrYIjkQjuv/9+jIyMgDGGb33rWygoKODv29XVhZdffhnt7e145plnAAB/\n/OMf8ZOf/ATbtm3DvHnzIAgCqqqqLmkou9zcY+1GJySZ0DaXhCQxm82GVatW4dSpU1JPhRByjejU\nNyFJjlanhCQ2WlETQgghMkYrakIIIUTGKFETQgghMkaJmhBCCJExStSEEEKIjFGiJoQQQmSMEjUh\nhBAiY/8fzj2UNX7XML4AAAAASUVORK5CYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10565c6d0>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 71
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"As we can see in the first plot, the list comprehensions lead to a slightly increased performance in regular Python code. \n",
|
|
"But the second plot is quite interesting: List comprehensions in Cython are significantly slower than the regular for-loop structures.\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"Let us do a quick comparison by how much we were able to improve the performance of the simple least square implementation using Cython so far:\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"x = [x_i*random.randrange(8,12)/10 for x_i in range(500)]\n",
|
|
"y = [y_i*random.randrange(8,12)/10 for y_i in range(100,600)]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 72
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"funcs = ['lstsqr_comprehensions', 'cy_lstsqr_comprehensions', \n",
|
|
" 'cy_lstsqr_loops'] \n",
|
|
"labels = ['list comprehensions', 'list comprehensions (Cython)', \n",
|
|
" 'for-loops (Cython)']\n",
|
|
"\n",
|
|
"times = [timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000)\n",
|
|
" for f in funcs]\n",
|
|
"\n",
|
|
"times_rel = [times[0]/times[i+1] for i in range(len(times[1:]))]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 73
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"#%pylab inline\n",
|
|
"#import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"plt.figure(figsize=(8,6))\n",
|
|
"x_pos = np.arange(len(funcs[1:]))\n",
|
|
"plt.bar(x_pos, times_rel, align='center', alpha=0.5, color=\"green\")\n",
|
|
"plt.xticks(x_pos, labels[1:], rotation=90)\n",
|
|
"plt.ylabel('relative performance gain')\n",
|
|
"plt.title('Performance gain compared to the classic least square implementation')\n",
|
|
"ftext = 'For-loops in Cython are {:.2f}x faster then list comprehensions'\\\n",
|
|
" .format(times[1]/times[2],1)\n",
|
|
"plt.figtext(.15,.8, ftext, fontsize=11, ha='left')\n",
|
|
"plt.xlim([-1,len(funcs[1:])])\n",
|
|
"plt.ylim([0,max(times_rel)*1.2])\n",
|
|
"plt.grid()\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAesAAAIBCAYAAABpxJfYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl4DXf7P/D3SSSWJJLIIoLkWC9LgqCoIomdqiq11Rba\n0qqiSqlS6VdrKS1NaUurYntqeRShqmpXtVQpJZLYYk+sQRKRnJP790d+mScn2wnmTA7n/bou12Uy\nZ2bumfnM3Ocz98wcnYgIiIiIyGrZFXcAREREVDgmayIiIivHZE1ERGTlmKyJiIisHJM1ERGRlWOy\nJiIisnJM1v9fYmIiWrVqhbJly2LcuHHFHY7V69y5M5YtW1bcYVgtvV6P7du3a7Y8Ozs7nDt3zqLL\nCAsLw+TJky02fxcXF8THxz/SNLt27ULlypUtE9AzLiAgAHv27FF9vvHx8bCzs0NmZqbq8y5ub7/9\nNj799NNiWXaJYlmqSvR6Pa5fvw57e3s4OTmhU6dOmDdvHpycnB55XgsXLoS3tzfu3btngUifPZs3\nby7uEKyaTqeDTqfLd1xYWBgqV66MqVOnPta8Q0JCMGDAALz++utPEuIjK2yd1HD//n2LzftJPOn+\nslYnTpwo7hA09aj7MTIyEosWLcLevXuVv3377beWCs+sp7pnrdPpsGnTJty/fx9HjhzB4cOHH/lb\nj4ggMzMTFy5cQO3atR8rDoPB8FjT0dPB2vavJROmOXyHknWytjZKFiBPMb1eL9u3b1eGx44dK126\ndBERkf3798vzzz8vbm5uUr9+fdm1a5fyueDgYPnoo4/khRdekNKlS0v//v3FwcFBHB0dxdnZWbZv\n3y4PHz6UUaNGia+vr/j6+sro0aPl4cOHIiKyc+dOqVixosycOVN8fHxkwIABEh4eLq+++qr0799f\nXFxcJDAwUOLi4mTatGni7e0tfn5+snXrViWGH3/8UWrXri0uLi5StWpVWbBggTIue/5ffPGFeHt7\nS4UKFWTx4sXK+NTUVBkzZoz4+/uLq6urtGjRQh48eGB2vXP7+++/pUGDBuLi4iI9e/aUXr16yaRJ\nk0RE5Pbt2/Liiy+Kl5eXuLu7S5cuXeTy5csm2/CHH34QEZHFixfLCy+8IGPHjhV3d3epUqWK/Prr\nrwUu9+LFi/LKK6+Il5eXeHh4yIgRI0RExGg0ytSpU8Xf31+8vb1l4MCBcvfuXREROX/+vOh0Olm8\neLFUrlxZypUrJ99++60cOnRIAgMDxc3NTZlPdkzNmzeXESNGiKurq9SqVcukrRRl+2fv34EDB0pm\nZqZMnz5dqlWrJh4eHtKrVy+5ffu2Ms3SpUvFz89PPDw85LPPPsvTNrMtWLDApK117dpVRESio6Ml\nODhY3NzcpG7duhIVFZXvtps4caLY29tLqVKlxNnZWd59910REdHpdPLdd99JjRo1xM3NTd555x2T\n6RYtWiS1a9cWd3d36dChg1y4cKHA/bN3716lDVWuXFmWLFkiIiJhYWFFbh+LFy+WqlWriouLi1Sp\nUkVWrFghIiKnT5+WVq1aiaurq3h6ekrv3r2VaXQ6nZw9e1ZECm/jOe3cuVMqVaqkDF+5ckW6d+8u\nXl5eUqVKFYmIiFDGHTx4UJo1ayZubm5SoUIFGTFihKSnpyvjR48eLd7e3lK2bFkJDAyUEydOFLi/\ncstvWhGRmzdvyksvvSRly5aVJk2ayKRJk6RFixYi8r82bTQalfnkPK7OnDkjoaGh4uHhIZ6entKv\nXz9JSkpSPuvv7y8zZ86UwMBAKVWqlBiNxkc6/v39/ZU2OmXKlEc6fwUHB8uECROkSZMmUrZsWXn5\n5ZeV4yH3eiUlJcmQIUOkQoUKUrFiRZk0aZIyLvs4fe+998TNzU2qVasm+/btkx9//FEqV64s3t7e\nSvsTEUlLS5P3339f/Pz8pHz58vLWW28p7aKw82ZB+zH7mHZxcZE6derIunXrRCTreCxVqpTY29uL\ns7OzuLu7i4jIoEGDlGNARGThwoVSvXp1KVeunHTt2lWuXr2qjDN3TD6qpz5Zb9u2TUSyEkDdunXl\n448/lsuXL4uHh4eSMH7//Xfx8PCQmzdvikhWQ/P395fo6GgxGo2SkZEhYWFhMnnyZGXekydPluef\nf15u3LghN27ckObNmyvjd+7cKSVKlJAJEyZIenq6PHjwQKZMmSKlSpWSrVu3isFgkIEDB4q/v79M\nmzZNDAaDfP/991KlShVl/r/88oucO3dORER2794tZcqUkSNHjpjMf8qUKWIwGGTz5s1SpkwZ5UAd\nPny4hIaGytWrV5UD9OHDhwWu940bN/Jsu4cPH4qfn59ERESIwWCQn3/+WRwdHZV1vHXrlvz888/y\n4MEDuX//vvTs2VO6deumTB8SEiKLFi0SkawDzsHBQX744QfJzMyUb7/9Vnx9ffPdZwaDQerVqydj\nxoyR1NRUSUtLk3379olIVkKpXr26nD9/XpKTk6V79+4yYMAAEfnfCeDtt9+Whw8fytatW8XR0VG6\ndesmN27ckCtXroi3t7fs3r1bialEiRIyd+5cMRgMsmrVKnF1dVVOKEXZ/jn379y5c+X555+XK1eu\nSHp6ugwbNkz69u0rIiInT54UZ2dn2bt3rzx8+FDGjBkjJUqUyDdZi0ietpaeni7VqlWT6dOnS0ZG\nhuzYsUNcXFwkNjY23+lzbvtsOp1OXnrpJbl7965cvHhRvLy8ZMuWLSIisn79eqlevbrExMSI0WiU\nTz/9VJo3b57vvOPj48XFxUVWrlwpBoNBbt26Jf/8848Sd/aJqrD2kZycLGXLlpW4uDgREUlISJCT\nJ0+KiEifPn1k2rRpIpLVBrP3ffY6ZCfrgtp4bjmTtdFolIYNG8rUqVMlIyNDzp07J1WrVpXffvtN\nRLK+nB48eFCMRqPEx8dL7dq1Ze7cuSIismXLFmnUqJHy5TAmJkauXbuW7/7KrbBpe/fuLb1795bU\n1FQ5ceKEVKxYUVq2bCki+SfrnPv2zJkzsm3bNklPT5cbN25Iq1atZPTo0cpn/f39JSgoSC5fvixp\naWmPdPyLmHZ2HvX8FRwcLBUrVpSTJ09KSkqK9OjRQ/r375/venXr1k3eeustSU1NlevXr0uTJk2U\nL8fZx2lkZKRkZmbKpEmTpGLFisoXqa1bt4qLi4ukpKSISNaXopdfflnu3Lkj9+/fl5deekk+/PBD\npS0Udt7Mbz+uWbNG2VerVq0SJycnSUhIEBGRyMhI5YtVtpzz2L59u3h6esrRo0fl4cOH8u6770qr\nVq2UzxZ2TD6OpzpZ+/v7i7Ozs7i5uYm/v7+888478uDBA5kxY4Zyks/WoUMH5RtaSEiITJkyxWR8\nzhORiEi1atVMeoe//fab6PV6EclqFI6OjiYnjylTpkj79u2V4aioKHF2dpbMzEwREbl3757odDrl\ngM6tW7du8tVXXynzL126tMlB7O3trZxoSpcuLcePH88zD3PrndPu3bulYsWKJn9r0aJFgSelo0eP\nKt8uRfIm6+rVqyvjUlJSRKfTSWJiYp75/Pnnn+Ll5WWybtlat24t3377rTIcGxsrDg4OYjQalRNA\nzm+uHh4esnr1amW4R48eysl38eLFeb4wNGnSRJYtW5bv+uXe/rn3b+3atU2S79WrV8XBwUEMBoN8\n8sknSuLOXn9HR8dCk3XOtrZnzx7x8fEx+Uzfvn0lPDw83+lDQkKU3lc2nU5nkvh69eolM2fOFBGR\njh07miR3o9EoZcqUkYsXL+aZ97Rp06R79+5FijunnO0jOTlZ3NzcZO3atZKammryuYEDB8rQoUNN\neuE51+Hs2bOFtvHccibrAwcOiJ+fX571GTx4cL7TzpkzR1555RURyTrx1qxZUw4cOJCnbRa23iIi\nO3bsyHdag8EgDg4OJl+6Jk6cWGjPOr8vYtnWrVsnQUFByrBerze54vYox3/29DmT9aOcv0JCQpQk\nKZLVE3V0dJTMzEyT9UpISJCSJUuaXBX5z3/+I6GhoSKSdZzWqFFDGXf8+HHR6XRy/fp15W8eHh5y\n7NgxyczMFCcnJ+ULnUjW+ST7S0Rh500R8/tRRKRBgwayYcMGJbbCkvWQIUNk/Pjxyrjk5GRxcHBQ\nrlrld0zOmDGj0OUX5qmvWW/YsAF37txBfHw85s2bh1KlSuHChQtYs2YN3N3dlX/79u1DQkKCMq25\nO0ivXr0Kf39/ZdjPzw9Xr15Vhr28vODo6Ggyjbe3t/L/0qVLw9PTU6kvli5dGgCQnJwMAPj111/R\nrFkzeHh4wN3dHZs3b8atW7eU6T08PGBn97/dU6ZMGSQnJ+PmzZtIS0tDtWrV8sRclPXOuX4VK1Y0\n+VvlypWVmmRqaiqGDRsGvV4PV1dXBAcH4+7duwXWLH18fExizbmuOV26dAn+/v4m65bt2rVreba5\nwWBAYmKi8rfy5csr/y9dunSe4ZSUFGU49/r5+/vj2rVrAMxv/9z7Nz4+Hq+88oqyXevUqYMSJUog\nMTER165dQ6VKlUzW38PDI7/NlK+rV6/maY/+/v64cuVKgdPkV7fOvQ+yt/+FCxcwatQoJfbs2PKb\n/+XLl1G1alWzMRfWPpycnLBq1Sp899138PX1RZcuXRAbGwsA+PzzzyEiaNKkCQICArB48eI88y6s\njRfmwoULuHr1qkn7nz59Oq5fvw4AiIuLQ5cuXVChQgW4urrio48+UvZ569atMWLECLzzzjsoX748\nhg0bVuQb3kJDQ/Od9saNGzAYDCb71s/Pr8jrk5iYiD59+qBSpUpwdXXFgAEDTNooYHoee5TjPz+P\ncv7KvWw/Pz9kZGTg5s2bJvO8cOECMjIyUKFCBSWmt956Czdu3FA+k/sYBrKOv5x/S05Oxo0bN5Ca\nmopGjRop8+rUqZPJMgs6bxZk6dKlCAoKUuZ34sSJPNu4ILnPV05OTvDw8DA5rgo6Jh/HU52sC+Ln\n54cBAwbgzp07yr/79+/jgw8+UD5j7iYdX19fk8dILl68CF9f3wKnf5Sbfh4+fIgePXrggw8+wPXr\n13Hnzh107ty5SDfveHp6olSpUjhz5kyecUVZ72wVKlTIc7K+ePGish5ffPEF4uLicOjQIdy9exe7\nd++GZF2JKfJ65qdy5cq4ePEijEZjnnH5bfMSJUqYHMyPIvf6XbhwAb6+vkXa/rn3p5+fH7Zs2WKy\nbVNTU+Hr64sKFSrg0qVLymdTU1MLPeBzz9vX1xeXLl0yWf6FCxdMvgAUNr05fn5+WLhwoUnsKSkp\naNasWZ7PVq5cGWfPnjUbu7n20b59e2zduhUJCQmoVasW3nzzTQBZJ+aFCxfiypUrWLBgAYYPH57n\nkbPC2nhhKleujCpVqpis571797Bp0yYAWY/d1KlTB2fOnMHdu3fx2WefmTxe9O677+Lw4cOIjo5G\nXFwcZs2aZbLOhclvWm9vb5QoUQIXL15UPpfz/9lPraSmpip/y5lYJ06cCHt7e5w4cQJ3797FsmXL\n8jwOlTO2Rzn+1ZB7vRwcHODp6WnymcqVK6NkyZK4deuWEtPdu3fx77//PvLyPD09Ubp0aURHRyvz\nSkpKKvITPLn344ULFzB06FDMnz8ft2/fxp07dxAQEKC04UfNESkpKbh161aeToJanslk3b9/f2zc\nuBFbt26F0WhEWloadu3aZXLyzp10cg/37dsXn376KW7evImbN2/i//7v/zBgwIACl/koSSw9PR3p\n6enw9PSEnZ0dfv31V2zdurVI09rZ2WHIkCEYM2YMrl27BqPRiP379yM9Pb1I652tefPmsLe3x7x5\n82AwGLBhwwb89ddfyvjk5GSULl0arq6uuH37Nj755JMir19hmjZtigoVKmDChAlITU1FWloa/vzz\nTwBZ23zOnDmIj49HcnIyJk6ciD59+uTbCy9Izv1w/fp1REREICMjA2vWrEFMTAw6d+78WNv/rbfe\nwsSJE5UT1I0bNxAVFQUAePXVV7Fp0ybs27cP6enp+Pjjjwt9xrR8+fImCapZs2YoU6YMPv/8c2Rk\nZGDXrl3YtGkT+vTpU+D0hSXU7O2QvS3eeustTJs2DdHR0QCAu3fvYs2aNflO169fP2zbtg1r1qyB\nwWDArVu3cOzYsTzzLKx9XL9+HRs2bEBKSgocHBzg5OQEe3t7AMCaNWtw+fJlAICbmxt0Ol2e/VtY\nGy9MkyZN4OLigs8//xwPHjyA0WjEiRMncPjwYSVmFxcXlClTBjExMfj222+VE/Lhw4dx8OBBZGRk\noEyZMihVqpQSc+79lVtB09rZ2aF79+4IDw/HgwcPEB0djaVLlyrL9PLyQsWKFbFs2TIYjUb8+OOP\nJvs1OTkZTk5OKFu2LK5cuaJ8eSjIoxz/T0pEsHz5cpw6dQqpqan4+OOP0bNnzzwJrkKFCmjfvj3G\njBmD+/fvIzMzE2fPnn2s57vt7Ozw5ptvYvTo0UrP/MqVK0U+d+bejykpKdDpdPD09ERmZiYWL15s\n8jhb+fLlcfnyZWRkZJisd/Yx0LdvXyxevBjHjh3Dw4cPMXHiRDRr1qzAqydP2tF5JpN1pUqVsGHD\nBkybNg3e3t7w8/PDF198UWjPKfczpJMmTULjxo1Rr1491KtXD40bN8akSZOKPH1BnwGyXv4QERGB\nXr16oVy5cvjpp5/w8ssvFzptTrNnz0ZgYCCee+45eHh44MMPP0RmZmaB651f4nBwcMDPP/+MRYsW\nwd3dHStWrECXLl2US7+jR4/GgwcP4OnpiebNm6NTp04FxlSUdc9mZ2eHjRs34syZM/Dz80PlypWx\nevVqAMCQIUMwYMAAtGrVClWrVkWZMmXw9ddfF2mb5PeZpk2b4vTp0/Dy8sLkyZOxdu1auLu7P9b2\nHzVqFLp27Yr27dujbNmyeP7553Ho0CEAQJ06dTB//ny89tpr8PX1Rbly5Qots7z++uuIjo6Gu7s7\nunfvDgcHB2zcuBG//vorvLy8MGLECCxbtgw1a9bMd/pRo0bhv//9L8qVK4fRo0cXuB2y16Fbt24Y\nP348+vTpA1dXVwQGBuK3337Ld7rKlStj8+bN+OKLL+Dh4YGgoCAcP348zzwLax+ZmZmYM2cOKlas\nCA8PD+zdu1d5PvXw4cNo1qwZXFxc8PLLLyMiIgJ6vT7PNi+ojRe0rgBgb2+PTZs24Z9//kHVqlXh\n5eWFoUOHKj2v2bNn4z//+Q/Kli2LoUOHmnwZunfvHoYOHYpy5cpBr9fD09NTeTlS7v2VW2HTzps3\nD8nJyfDx8cGQIUMwePBgk/PQ999/j1mzZsHT0xPR0dF44YUXlHFTpkzBkSNH4Orqipdeegk9evQo\n9Bh4lOM/v21Y1PNX9v8HDBiAsLAwVKhQAenp6YiIiMj3s0uXLkV6ejrq1KmDcuXKoWfPnsoVhEc5\ndwDAzJkzUb16dTRr1gyurq5o164d4uLiijRt7v1Yp04dvP/++3j++efh4+ODEydOoEWLFsrn27Rp\ng7p168LHx0cpEeSMt02bNpg6dSp69OgBX19fnD9/HitXrix0+z3JY5c6edJ0T8+Mpk2bYvjw4Rg0\naFBxh/LE8nuhAVFxe1baZWhoKAYMGIAhQ4YUdyg245nsWVPR7NmzBwkJCTAYDFiyZAlOnDiBjh07\nFndYRPQUYD9PW0/160bpycTGxqJXr15ISUlBtWrV8N///vexb+ayNpZ+NSbR43iW2uWzsh5PC14G\nJyIisnK8DE5ERGTlrPYyeEhICHbv3l3cYRAREWkiODgYu3btynec1V4G1+l0vIGBVBUWFobIyMji\nDoOeEWxPpLbC8h4vgxMREVk5JmuyGdkv3yBSA9sTaYnJmmxGSEhIcYdAzxC2J9ISkzUREZGVY7Im\nIiKycrwbnIiIyArwbnAiIqKnGJM12YyCXjZA9DjYnkhLTNZERERWjjVrIiIiK8CaNRER0VOMyZps\nBmuMpCa2J9ISkzUREZGVY82aiIjICrBmTURE9BRjsiabwRojqYntibTEZE1ERGTlWLMmIiKyAqxZ\nExERPcWYrMlmsMZIamJ7Ii0xWRMREVk51qyJiIisAGvWRERETzEma7IZrDGSmtieSEtM1kRERFaO\nNWsiIiIrwJo1ERHRU4zJmmwGa4ykJrYn0hKTNRERkZVjzZqIiMgKsGZNRET0FGOyJpvBGiOpie2J\ntMRkTUREZOWeyWSt1+tRu3ZtBAUFISgoCO+///4TzS8yMhI9e/ZUKbrHs2DBAsydO/expv3qq68Q\nEBCAgIAANGzYEEOHDsXdu3cLnSYyMhKnT582GS7ubfA4pk6dioCAANSvXx9jx47F1q1bC/28iKBt\n27bw8vIy+fv06dMRGBiI2rVrIywsDOnp6Y8cy6RJk1C7dm0EBwc/8rRA3n3yJI4dO4Y1a9aY/M3O\nzg6pqamqzD8/YWFhmD9/PoCitecNGzbgr7/+slg8TyokJKRIn9Pr9YiOjrZsMAD+/vtv9O/f3+LL\noeJRorgDsASdToe1a9eiTp06jzV9ZmYm7Oz+9z1Gp9OpFdpjGzZs2GNNN2nSJOzduxc7d+5UEtC6\ndetw+/ZtuLq6FjhdZGQkvLy8UKNGDQDWsQ2y5d4/hWnatCnGjRuHUqVK4fjx4wgODkZCQgJKliyZ\n7+fnzZsHvV6P48ePK3/bunUrVq5ciUOHDqF06dIYOnQo5syZg/Hjxz9S3F9++SUuXboEDw+PR5ou\nW+59UlT5ba+jR4/il19+yfMFzJI3dep0OqUdFaU9r1u3Ds899xyee+45i8WkBqPRCHt7+wLHa3Wz\nbKNGjbB8+XKLL4eKxzPZswbyP+ls2bIFDRs2RP369dG2bVucPXsWQFbtqV69ehgyZAiCgoKwZcuW\nQuc1c+ZMBAYGIjAwEEOGDEFKSgoAIDk5GYMHD1bGzZo1S5kmJCQE7733Hpo2bYoaNWrgo48+UsZ9\n8sknypWAhg0b5tvrDQ8Px7hx4wBknbTbt2+PPn36ICAgAC1atEBiYmKeaZKTk/Hll1/ihx9+MOkp\nvvLKK6hSpQq6dOmC//73v8rff/75Z3To0AGRkZH4+++/MXLkSAQFBWH79u0AgHv37uW7TKPRiLFj\nxyrrPW7cOGRmZgLI6k29/fbbaNOmDWrWrIlBgwbliTN7Hh07dsRzzz2HgIAADBkyBBkZGcr6tm3b\nFt27d0dgYCD+/fdfHDx4EK1bt0bjxo3RuHFjbN68Od/5tm/fHqVKlQIA3Lp1CyKCW7du5fvZ06dP\nY9WqVZgwYYLJPj9+/DhatmyJ0qVLAwA6duyIFStWAACWL1+OZs2awWAwIDMzE23btsXChQvzzLtl\ny5ZIS0tD69at8cEHHyAxMVGJPyAgwCTxb9iwAfXq1UNQUBACAwOxe/duLF682GSf7NixA0BWW2za\ntCkaNWqErl27KvskPDwcPXv2RIcOHVC3bl2TNnXr1i1MmTIF27ZtQ1BQEEaPHq2Mi4iIQJMmTVCt\nWjX8/PPPyt8L2t7x8fHw9PTEpEmT0LBhQ9SqVQv79u3Ld/vmlLM9//nnn2jUqBGCgoIQEBCAlStX\nYuvWrdi4cSNmzJiBoKCgfJPQlStX0KNHD9SvXx/169fHjBkzAACJiYl45ZVXUL9+fdSrVw/Lli1T\nptHr9Zg8eTKaN28OPz8/rFixAl988QWaNGmCGjVqYO/evSbrNXbsWGU+f/zxh8m4Pn36oFGjRli0\naBGuXbuGnj17omnTpqhXrx6mT59uEuvq1avRvHlzVKlSRbm6AACxsbHo3LkzmjRpggYNGiAyMlIZ\nZ2dnh+nTp+fZH6mpqejZsyfq1q2LBg0aoHfv3gCyzmM5v9gsXboU9erVQ/369dG9e3fcuHEDQOHn\nj/z2BVkJsVJPEpq/v7/UqlVLGjRoIA0aNJCtW7dKYmKieHl5yalTp0REZNGiRdK0aVMREdm5c6fY\n29vLgQMH8p3f4sWL5dVXXxURkc2bN0tAQIDcv39fREQGDhwo48ePFxGRDz74QMLCwkRE5N69e1K3\nbl359ddfRUQkODhYOnToIEajUZKTkyUwMFA2bdokt27dEjc3N0lLSxMRkeTkZDEYDHliCA8Pl7Fj\nxyrxuLu7y+XLl0VE5M0335SPPvoozzQHDx4UNze3ArfTli1bJDQ0VBlu3bq1REVFiYhISEiI/PLL\nLybboKBlfvPNN9K2bVvJyMiQ9PR0adOmjXz77bciIjJo0CBp2bKlPHz4UNLT06Vu3bry+++/5xvP\nrVu3REQkMzNTBg4cKN99952ybGdnZzl37pyIiNy5c0eCgoLk2rVrIiJy9epVqVSpkiQlJRW4riIi\n48ePl0aNGuU7zmg0SnBwsBw7dkzOnz8vnp6eyrgdO3ZIzZo15ebNm5KRkSG9e/eWsmXLKuNff/11\nef/99+WTTz6R3r17F7h8nU4nKSkpIiKSlpYmycnJIiKSnp4urVu3li1btoiISP369ZW2mJmZKffu\n3RORvPtk2bJlMnToUMnMzBSRrP3Qr18/ERGZMmWK+Pn5Kds0t8jISKVN54xv/vz5IiKyb98+qVix\noogUvL3v3r0r58+fF51Op8S1YsUKeeGFF/JdZlhYmDL/8PBwGTdunIiIdO3aVX766Sflc9n7Mefn\n8xMSEiKzZ89Whm/evCkiIr169ZKPP/5YRESuXbsmvr6+cvLkSRER0ev18sEHH4iIyF9//SWlS5eW\nb775RkREVq9eLS1atBARUdZr2bJlIiKya9cuqVSpkqSnpyvjpkyZoiy7bdu2smfPHhERefjwobRo\n0UJp53q9XlnX+Ph4cXZ2lpSUFMnIyJCGDRtKTEyMiGSdM2rWrCmxsbGF7o+ff/5ZOnTokGd77dy5\nUxo3biwiIv/++6/4+vpKQkKCiIhMnjxZaZuFHcsvv/xyvvuCtFFY3rOZy+AbN25E/fr1UatWLQBZ\nPb7hw4crveIaNWqgadOmZue9bds29O3bF87OzgCAoUOHYtSoUQCA7du3IyIiAgDg4uKCvn37Ytu2\nbejYsSN0Oh0GDRoEOzs7ODk5oU+fPtixYwc6deqE6tWrY8CAAWjfvj26dOkCJycns3G88MILqFix\nIgCgWbMyheJmAAAgAElEQVRm+P333x9hC2Vp3749Ro8ejZiYGIgIzp07hy5duijjJdcVhYKWuX37\ndgwePBglSmQ1p8GDB2PdunV46623oNPp0K1bNzg6OgIAGjZsiLNnz6Jt27Ym887MzMSsWbOwZcsW\nGI1G3Llzx2Q7tGjRAlWqVAGQ9e3//Pnz6NSpkzLezs4OZ8+eRcOGDfNd1927d+Onn37Ctm3b8h0/\ne/ZsBAcHo169eoiPjzcZFxoainfeeUfppbdp08Zke8+bNw8NGzaEwWDAkSNH8p1/bgaDAWPHjsX+\n/fshIkhISMCxY8fQoUMHtG7dGqNHj0aPHj3QqVMn1K1bV5ku5z6JiorC33//rayzwWCAm5ubMv7F\nF19EuXLl8l1+7n2brU+fPgCyygdXr15Fenp6gdv7zJkzKFeuHJydndG5c2dluqLeI5IdQ+vWrfHp\np5/i7NmzaNeuHZo0aWI2zuTkZOzfv1+56gNAKS9s374dc+bMAQD4+Pigc+fO2LFjh3I+yO6JBgUF\nIS0tTRlu2LAhzpw5o8zP0dFRqQEHBwejdOnSiI2NhbOzM0qVKoXw8HAAQEpKCnbt2oWbN2+axBcT\nE6O08+zt6u/vD3d3d1y+fBkGgwExMTHKOADIyMjAqVOnULNmTZPpcu6PBg0a4NSpUxgxYgRCQkLw\n4osv5tk+O3fuxIsvvojy5csDyCo71K9fXxlf0LEcGhpa4L6g4vVMJuv8mKu5ZidfAOjevTvOnz8P\nnU6HPXv25JlPzhNI7pNJ7nE5l5vfODs7Oxw4cAD79u3Djh070KhRI2zZsgWBgYGFxpt9aRfIOnEa\nDIY8n6lTpw7S0tJw+vTpfOucOp0OI0aMwPz586HT6ZTkmnN8UZdZ2HrnrA/b29vnG+uKFSuwb98+\n/PHHH3BycsL06dMRFxenjM+5fwCgXr162L17d5755Gf//v0YMGAAoqKiCqz37t27F8ePH8fSpUth\nMBhw584dVK1aFcePH4ezszNGjhyJkSNHAsi6pJkzgV67dg0pKSmws7PD3bt388Sany+//BJJSUk4\ndOgQHB0dMWzYMDx48EAZd/LkSWzfvh09e/bEmDFj8MYbbwDIu08mT56MsLCwPPPX6XRF+tKXW/Y+\nzq7BGgwGiEiB2zs+Pr5I+7cwo0aNQteuXfH777/j3XffRfv27TF16lRlPQpTUDIvrD3mXsecw7lj\nzz1ttpzbNvuegMOHDxdYu8557GQvR0Tg6emJo0ePFrh++e2PKlWqIDo6Gtu2bcOvv/6KiRMn4t9/\n/zWZztx5qqBjubB9QcXrma1Z59a0aVMcO3YMsbGxAIAlS5agYcOG+Z7Qfv75Zxw9ehRHjhzJc+Jt\n27YtVq1aheTkZIgIfvjhB7Rv314Zt2jRIgDA/fv3sWrVKrRr1w5A1sGyfPlyGI1GpKSkYM2aNWjd\nujWSk5Nx/fp1tGrVCuHh4QgICMDJkyfzxFTQSakwzs7OeO+99zB06FClXiUiWL9+Pc6fPw8AGDRo\nENavX4/Vq1crCQEAypYti6SkpCItp23btliyZAkMBgMyMjKwZMkSZb2L6u7du/D09ISTkxPu3r2L\nFStWFHiibt68OU6fPm3ynGtBdw3/9ddf6N27N9auXVvo+mzcuBEXLlzA+fPn8ccff8Dd3R3nzp1T\n9n9CQgIA4M6dO5g5cybGjh0LAEhPT0fv3r0xa9YsTJkyBX369IHRaCzS+laoUAGOjo64cuUKNmzY\noKxvbGws6tati5EjR6J///44fPgwgLz7pGvXrpg/f77yt4cPHyo3xplrL66urmafCMj2KNvbnOy4\ncsYXFxeHKlWqYOjQoRg5cqQy78LaoLOzM5o3b670oAEo9yK0bdsW33//PYCs/fbrr7+idevWjxxr\neno6/vOf/wDI+jKXlpamXJkD/vectYuLC1q2bGlSp7506VK+95HkVKtWLZQpU8akHh8TE4P79+8X\nOt2VK1eg0+nw8ssv48svv8SNGzdw584dk8+EhIRg8+bNSgzff/+9cp4qTEH7goqfzfSsvby8sGzZ\nMrz22mswGAzw9vZWDpKcd6nmJ+f4jh074vjx43j++ecBAM899xwmTZoEIKuXM2LECKVXPHDgQOUA\n0el0qFWrFpo3b47bt2+jd+/e6Ny5My5fvoxXX30VDx48QGZmJho1aoTu3bsXGkPueAuLf9q0aZgz\nZ47ymImIoFWrVggNDQWQddLr1KkT0tLSTO5SHjp0KN5//33MmjULs2fPLnSZQ4cOxZkzZxAUFKRs\nozfffNPks7nXJbeBAwdiw4YNqF27Nry9vREcHKz0NHMv283NDVFRURg3bhxGjx6N9PR0VKtWDVFR\nUXnm/c477+Dhw4cYOnQokpOT4ezsjOXLl6Nu3bpYsGABrl69ik8++cRkmvx6U+3bt0dmZiYyMjLw\n7rvvomvXrgCA8ePHo2HDhujVqxcAYMeOHZg8eTKmTZuWZx1zznPkyJHo2bMnAgMDUalSJZOywIcf\nfojTp0+jRIkScHd3V74A5twnX3zxBfr374+bN28qj4JlZmbinXfeQb169cy26TZt2mD27Nlo0KAB\nQkJCMHfu3AL3k7u7e77be+PGjXnWK7/h/MbljO/rr7/Gzp074ejoiFKlSuHrr78GAAwYMABhYWFY\ns2YN3n///TyPJS1fvhzvvPMOlixZAnt7e/Tr1w/jxo1DRESEctlXRDBz5kzUrl270HjyG/bw8MA/\n//yDzz//HADw008/KaWe3NOtWLEC7733HurVqwcgK4EvXrxYuQydH3t7e2zcuBGjR4/GrFmzYDQa\n4ePjg9WrVxca2/Hjx/Hhhx8CyLoxc+LEifDx8UFMTIzymYCAAMyYMQPt2rWDTqdDtWrVsGDBgjzb\nPvdwQfuCih/fDa6R0NBQjBs3TqntWQuDwYD69etj6dKlaNSoUXGHQ2QV4uPj8dxzzylXpIi0wHeD\nU76ioqJQvXp1dOjQgYmaKBdrercAEXvWZDN27dpV5LdOEZnD9kRqY8+aiIjoKWbRnvX06dOxfPly\n2NnZITAwEIsXL0ZKSgp69+6NCxcuQK/XY/Xq1SbPhiqBsWdNREQ2pFh61vHx8fj+++9x5MgR/Pvv\nvzAajVi5cqVyh2JcXBzatGmjvCKQiIiI8mexZF22bFk4ODggNTUVBoMBqamp8PX1RVRUlPJ+6Oxn\nfIm0wN8fJjWxPZGWLJasy5Urh/fffx9+fn7w9fWFm5sb2rVrh8TEROXZw/Lly5t9cQAREZGts9hL\nUc6ePYu5c+ciPj4erq6u6NmzZ55fzjH34oawsDDo9XoAWS/CyH6BA/C/b7Uc5vCjDGezlng4/HQP\nZ7OWeDj8dA1n/z/37xHkx2I3mK1atQq///47fvjhBwDAsmXLcODAAezYsQM7d+6Ej48Prl27htDQ\nUMTExOQNjDeYERGRDSmWG8xq1aqFAwcO4MGDBxARbNu2DXXq1MFLL72EJUuWAMh6P3e3bt0sFQKR\nidy9IaInwfZEWrLYZfD69etj4MCBaNy4Mezs7NCwYUMMHToU9+/fR69evbBo0SLl0S0iIiIqGN9g\nRkSqmRA+AQlJCcUdBlmAj5sPZoTzUVtLKizv2cyvbhGR5SUkJUDfTV/cYZAFxK+PL+4QbBpfN0o2\ngzVGUlP8P/HFHQLZECZrIiIiK8dkTTYj+xlHIjXoG+iLOwSyIUzWREREVo7JmmwGa9akJtasSUtM\n1kRERFaOyZpsBmvWpCbWrElLTNZERERWjsmabAZr1qQm1qxJS0zWREREVo7JmmwGa9akJtasSUtM\n1kRERFaOyZpsBmvWpCbWrElLTNZERERWjsmabAZr1qQm1qxJS0zWREREVo7JmmwGa9akJtasSUtM\n1kRERFaOyZpsBmvWpCbWrElLTNZERERWjsmabAZr1qQm1qxJS0zWREREVo7JmmwGa9akJtasSUtM\n1kRERFaOyZpsBmvWpCbWrElLTNZERERWjsmabAZr1qQm1qxJS0zWREREVo7JmmwGa9akJtasSUtM\n1kRERFaOyZpsBmvWpCbWrElLTNZERERWjsmabAZr1qQm1qxJS0zWREREVo7JmmwGa9akJtasSUtM\n1kRERFaOyZpsBmvWpCbWrElLTNZERERWjsmabAZr1qQm1qxJS0zWREREVo7JmmwGa9akJtasSUtM\n1kRERFaOyZpsBmvWpCbWrElLTNZERERWjsmabAZr1qQm1qxJS0zWREREVo7JmmwGa9akJtasSUsl\nzH0gNjYWs2fPRnx8PAwGAwBAp9Nhx44dFg+OiIiIipCse/bsibfffhtvvPEG7O3tAWQla6Knza5d\nu9i7JtXE/xPP3jVpxmyydnBwwNtvv61FLERERJQPszXrl156CfPnz8e1a9dw+/Zt5R/R04a9alIT\ne9WkJbM968jISOh0OsyePdvk7+fPn7dYUERERPQ/ZpN1fHy8BmEQWR5r1qQm1qxJSwUm6+3bt6NN\nmzZYu3ZtvjeUde/e3aKBERERUZYCk/WePXvQpk0bbNy4kcmangnsVZOa2KsmLRWYrD/55BMAWTVr\nIiIiKj5ma9YAsGnTJkRHRyMtLU3528cff2yxoIgsgTVrUhNr1qQls49uDRs2DKtXr0ZERAREBKtX\nr8aFCxe0iI2IiIhQhGT9559/YunSpShXrhymTJmCAwcOIDY2VovYiFTFXjWpib1q0pLZZF26dGkA\nQJkyZXDlyhWUKFECCQkJFg+MiIiIsphN1l26dMGdO3cwbtw4NGrUCHq9Hn379i3yApKSkvDqq6+i\ndu3aqFOnDg4ePIjbt2+jXbt2qFmzJtq3b4+kpKQnWgmiouDvWZOa+HvWpCWzyfrjjz+Gu7s7evTo\ngfj4eMTExGDq1KlFXsCoUaPQuXNnnDp1CsePH0etWrUwY8YMtGvXDnFxcWjTpg1mzJjxRCtBRET0\nLNOJiBT2gfxeiuLq6orAwEB4e3sXOvO7d+8iKCgI586dM/l7rVq1sHv3bpQvXx4JCQkICQlBTEyM\naWA6HcyERkRWJmx0GPTd9MUdBllA/Pp4RM6NLO4wnmmF5T2zj279+OOP2L9/P0JDQwFkXUps2LAh\nzp8/j48//hgDBw4scNrz58/Dy8sLgwcPxrFjx9CoUSPMnTsXiYmJKF++PACgfPnySExMfJz1IiIi\nsglmL4NnZGTg1KlTWLt2LdauXYvo6GjodDocPHgQM2fOLHRag8GAI0eOYPjw4Thy5AicnJzyXPLW\n6XT8fWzSBGvWpCbWrElLZnvWly5dUnrBAODt7Y1Lly7Bw8MDjo6OhU5bqVIlVKpUCc899xwA4NVX\nX8X06dPh4+ODhIQE+Pj44Nq1awVeTg8LC4NerwcAuLm5oUGDBsrjN9knXg5zuKjD//zzj1XF8ywO\nZ8tOZNmPNz2LwwlnEqwqHouv7+X/PQVkLe3taR/O/n9RfjDLbM16+PDhuHDhAnr16gURwdq1a1Gp\nUiXMnj0bXbp0wc6dOwtdQKtWrfDDDz+gZs2aCA8PR2pqKgDAw8MD48ePx4wZM5CUlJRvj5s1a6Kn\nC2vWzy7WrC2vsLxnNllnJ+h9+/YBAF544QX06NGjyJeujx07hjfeeAPp6emoVq0aFi9eDKPRiF69\neuHixYvQ6/VYvXo13Nzcihw0EVknJutnF5O15T1Rsi4uTNaktl18N7jF2VKytrV3gzNZW15hec/s\nDWZERERUvJisyWawV01qsqVeNRW/IiXr1NRU/ngHERFRMTGbrKOiohAUFIQOHToAAI4ePYquXbta\nPDAiteV+vIjoSfA5a9KS2WQdHh6OgwcPwt3dHQDyfX0oERERWY7ZZO3g4JDnsSo7O5a66enDmjWp\niTVr0pLZrFu3bl2sWLECBoMBp0+fxrvvvovmzZtrERsRERGhCMn666+/xsmTJ1GyZEn07dsXZcuW\nxdy5c7WIjUhVrFmTmlizJi2ZfTe4k5MTpk2bhmnTpmkRDxEREeVitmfdtm1bJCUlKcO3b99W7gwn\nepqwZk1qYs2atGQ2Wd+8edPkBrNy5crx96eJiIg0ZDZZ29vb48KFC8pwfHw87wanpxJr1qQm1qxJ\nS2Zr1p999hlatmyJVq1aAQD27NmDhQsXWjwwIiIiymI2WXfs2BF///03Dhw4AJ1Oh7lz58LT01OL\n2IhUxZo1qYk1a9KS2WQNAOnp6ShXrhwMBgOio6MBQOlpExERkWWZTdbjx4/HqlWrUKdOHdjb2yt/\nZ7Kmpw1/z5rUZGu/Z03Fy2yyXrduHWJjY1GyZEkt4iEiIqJczN7WXa1aNaSnp2sRC5FFsVdNamKv\nmrRktmddunRpNGjQAG3atFF61zqdDhERERYPjoiIiIqQrLt27Zrn96t1Op3FAiKyFNasSU2sWZOW\nzCbrsLAwDcIgIiKigphN1nFxcZg4cSKio6Px4MEDAFk963Pnzlk8OCI1sVdNamKvmrRk9gazwYMH\n46233kKJEiWwa9cuDBo0CP369dMiNiIiIkIRkvWDBw/Qtm1biAj8/f0RHh6OX375RYvYiFTFd4OT\nmvhucNKS2cvgpUqVgtFoRPXq1TFv3jz4+voiJSVFi9iIiIgIRUjWc+fORWpqKiIiIjB58mTcu3cP\nS5Ys0SI2IlWxZk1qYs2atGQ2WTdp0gQA4OLigsjISEvHQ0RERLmYrVn/9ddfeOWVVxAUFITAwEAE\nBgaiXr16WsRGpCrWrElNrFmTlsz2rPv164fZs2cjICAAdnZmczsRERGpzGyy9vLyyvMGM6KnEWvW\npCbWrElLZpP1lClT8Prrr6Nt27ZwdHQEkPVSlO7du1s8OCIiIipCsl6yZAliY2NhMBhMLoMzWdPT\nhu8GJzXx3eCkJbPJ+vDhw4iJieGPdxARERUTs3eMNW/eHNHR0VrEQmRR7FWTmtirJi2Z7Vnv378f\nDRo0QJUqVUx+z/r48eMWD46IiIjMJGsRwcKFC+Hn56dVPEQWw5o1qYk1a9KS2Z718OHDceLECS1i\nISIionwUWrPW6XRo1KgRDh06pFU8RBbDXjWpib1q0pLZnvWBAwewfPly+Pv7w8nJCQBr1kRERFoy\nm6x/++03AFAe3RIRy0ZEZCGsWZOaWLMmLZl9dEuv1yMpKQlRUVHYuHEj7t69C71er0FoREREBBQh\nWX/11Vfo378/bty4gcTERPTv3x8RERFaxEakKvaqSU3sVZOWzF4G/+GHH3Dw4EGlXj1hwgQ0a9YM\nI0eOtHhwREREVISeNQCTd4LzZzLpacXfsyY18fesSUtme9aDBw9G06ZN0b17d4gI1q9fjyFDhmgR\nGxEREaGQZH3u3DlUrVoVY8aMQXBwMP744w/odDpERkYiKChIyxiJVMGaNamJNWvSUoHJumfPnvj7\n77/Rpk0bbN++HY0aNdIyLiIiIvr/CkzWRqMRn332GWJjY/Hll1+aPF+t0+kwZswYTQIkUgufsyY1\n8Tlr0lKBd4utXLkS9vb2MBqNuH//PpKTk5V/9+/f1zJGIiIim1Zgz7pWrVoYN24c/P390bdvXy1j\nIrII9qpJTexVk5YKfQ7L3t4es2fP1ioWIiIiyofZh6bbtWuH2bNn49KlS7h9+7byj+hpw+esSU18\nzpq0ZPY565UrV0Kn02H+/Pkmfz9//rzFgiIiIqL/MZus4+PjNQiDyPJYsyY1sWZNWjJ7GTwlJQVT\np07Fm2++CQA4ffo0Nm3aZPHAiIiIKIvZZD148GA4Ojrizz//BAD4+vrio48+snhgRGpjzZrUxJo1\naclssj579izGjx8PR0dHAFB+fYuIiIi0YTZZlyxZEg8ePFCGz549i5IlS1o0KCJLYM2a1MSaNWnJ\n7A1m4eHh6NixIy5fvozXXnsN+/btQ2RkpAahEREREVCEZN2+fXs0bNgQBw8ehIggIiICnp6eWsRG\npCq+G5zUxHeDk5bMJmsRwe7du5WfyMzIyMArr7yiRWxERESEItSshw8fjgULFqBevXoICAjAggUL\nMHz4cC1iI1IVe9WkJvaqSUtme9Y7d+5EdHQ07Oyy8npYWBjq1KlT5AUYjUY0btwYlSpVwsaNG3H7\n9m307t0bFy5cgF6vx+rVq+Hm5vb4a0BERPSMM9uzrl69Oi5evKgMX7x4EdWrVy/yAr766ivUqVMH\nOp0OADBjxgy0a9cOcXFxaNOmDWbMmPEYYRM9Oj5nTWric9akJbPJ+t69e6hduzaCg4MREhKCOnXq\n4P79+3jppZfQtWvXQqe9fPkyNm/ejDfeeAMiAgCIiorCoEGDAACDBg3C+vXrVVgNIiKiZ5fZy+D/\n93//l+dvOp0OIqL0lgvy3nvvYdasWbh3757yt8TERJQvXx4AUL58eSQmJj5qzESPhTVrUhNr1qQl\ns8n6cU9wmzZtgre3N4KCggq8/KjT6cwmfCIiIltnNlk/rj///BNRUVHYvHkz0tLScO/ePQwYMADl\ny5dHQkICfHx8cO3aNXh7exc4j7CwMOj1egCAm5sbGjRooHx5yP4CwGEOF3X4n3/+wejRo60mnmdx\nOFt2PTe79/ksDiecSUCzV5tZTTwWX9/LCchmLe3taR/O/n9Rft1SJ9nFZAvavXs3Zs+ejY0bN+KD\nDz6Ah4cHxo8fjxkzZiApKSnfm8yyL7UTqWUXX4picWGjw6Dvpi/uMDRhay9FiV8fj8i5kcUdxjOt\nsLxn9gYzAEhNTUVsbOwTBwEAEyZMwO+//46aNWtix44dmDBhwhPNl6iomKhJTbaUqKn4mU3WUVFR\nCAoKQocOHQAAR48eNXsXeG7BwcGIiooCAJQrVw7btm1DXFwctm7dymesiYiIzDCbrMPDw3Hw4EG4\nu7sDAIKCgnDu3DmLB0akttx1VaInweesSUtmk7WDg0Oe3m/228yIiIjI8sxm3bp162LFihUwGAw4\nffo03n33XTRv3lyL2IhUxZo1qYk1a9KS2WT99ddf4+TJkyhZsiT69u2LsmXLYu7cuVrERkRERCjC\nc9axsbGYNm0apk2bpkU8RBbDR7dITbb26BYVL7M96zFjxqBWrVqYPHkyTpw4oUVMRERElIPZZL1r\n1y7s3LkTnp6eGDZsGAIDAzF16lQtYiNSFXvVpCb2qklLRbqtu0KFChg1ahS+++471K9fP98f9yAi\nIiLLMJuso6OjER4ejoCAAIwYMQLNmzfHlStXtIiNSFV8zprUxOesSUtmbzAbMmQI+vTpg99++w0V\nK1bUIiYiIiLKwWyyPnDggBZxEFkca9akJtasSUsFJuuePXtizZo1CAwMzDNOp9Ph+PHjFg2MiIiI\nshSYrL/66isAwKZNm/L8ZFf2L2gRPU34nDWpic9Zk5YKvMHM19cXAPDNN99Ar9eb/Pvmm280C5CI\niMjWmb0bfOvWrXn+tnnzZosEQ2RJ7FWTmtirJi0VeBn822+/xTfffIOzZ8+a1K3v37+PF154QZPg\niIiIqJBk/dprr6FTp06YMGECZs6cqdStXVxc4OHhoVmARGphzZrUxJo1aanAZO3q6gpXV1esXLkS\nAHD9+nWkpaUhJSUFKSkp8PPz0yxIIiIiW2a2Zh0VFYUaNWqgSpUqCA4Ohl6vR6dOnbSIjUhV7FWT\nmtirJi2ZTdaTJk3C/v37UbNmTZw/fx7bt29H06ZNtYiNiIiIUIRk7eDgAE9PT2RmZsJoNCI0NBSH\nDx/WIjYiVfHd4KQmvhuctGT2daPu7u64f/8+WrZsiX79+sHb2xvOzs5axEZEREQoQs96/fr1KFOm\nDObMmYOOHTuievXq2LhxoxaxEamKNWtSE2vWpCWzPevsXrS9vT3CwsIsHQ8RERHlUmDP2tnZGS4u\nLvn+K1u2rJYxEqmCNWtSE2vWpKUCe9bJyclaxkHFYEL4BCQkJRR3GJpJuJyAyPWRxR2GJnzcfDAj\nfEZxh0FEKjF7GRwA9u7dizNnzmDw4MG4ceMGkpOTUaVKFUvHRhaWkJQAfTd9cYehGT30xR2CZuLX\nxxd3CM881qxJS2ZvMAsPD8fMmTMxffp0AEB6ejr69etn8cCIiIgoi9lkvW7dOkRFRcHJyQkAULFi\nRV4ip6cSa4ykJrYn0pLZZF2yZEnY2f3vYykpKRYNiIiIiEyZTdY9e/bEsGHDkJSUhIULF6JNmzZ4\n4403tIiNSFWsMZKa2J5IS4XeYCYi6N27N2JiYuDi4oK4uDhMnToV7dq10yo+IiIim2f2bvDOnTvj\nxIkTaN++vRbxEFkMf3+Y1MT2RFoq9DK4TqdDo0aNcOjQIa3iISIiolzM9qwPHDiA5cuXw9/fX7kj\nXKfT4fjx4xYPjkhN7AWRmtieSEtmk/Vvv/2mRRxERERUALPJWq/XaxAGkeWxxkhqYnsiLZl9dIuI\niIiKF5M12Qz2gkhNbE+kJSZrIiIiK8dkTTaD73ImNbE9kZaYrImIiKwckzXZDNYYSU1sT6QlJmsi\nIiIrx2RNNoM1RlIT2xNpicmaiIjIyjFZk81gjZHUxPZEWmKyJiIisnJM1mQzWGMkNbE9kZaYrImI\niKwckzXZDNYYSU1sT6QlJmsiIiIrx2RNNoM1RlIT2xNpicmaiIjIyjFZk81gjZHUxPZEWmKyJiIi\nsnJM1mQzWGMkNbE9kZaYrImIiKwckzXZDNYYSU1sT6QlJmsiIiIrx2RNNoM1RlIT2xNpicmaiIjI\nylk0WV+6dAmhoaGoW7cuAgICEBERAQC4ffs22rVrh5o1a6J9+/ZISkqyZBhEAFhjJHWxPZGWLJqs\nHRwcMGfOHJw8eRIHDhzA/PnzcerUKcyYMQPt2rVDXFwc2rRpgxkzZlgyDCIioqeaRZO1j48PGjRo\nAABwdnZG7dq1ceXKFURFRWHQoEEAgEGDBmH9+vWWDIMIAGuMpC62J9KSZjXr+Ph4HD16FE2bNkVi\nYiLKly8PAChfvjwSExO1CoOIiOipU0KLhSQnJ6NHjx746quv4OLiYjJOp9NBp9PlO11YWBj0ej0A\nwM6JhrcAABkuSURBVM3NDQ0aNEBISAgAYNeuXQDA4ScYTricAD30AP7XS8iuwz2rw9msJR5LDSdc\nTsCuXbs0b1/Zinv92Z7UH064nKCsrzWcv56F4ez/x8fHwxydiIjZTz2BjIwMdOnSBZ06dcLo0aMB\nALVq1cKuXbvg4+ODa9euITQ0FDExMaaB6XSwcGg2L2x0GPTd9MUdBllA/Pp4RM6N1Hy5bFPPruJq\nU7aksLxn0cvgIoLXX38dderUURI1AHTt2hVLliwBACxZsgTdunWzZBhEAFhjJHWxPZGWLHoZfN++\nfVi+fDnq1auHoKAgAMD06dMxYcIE9OrVC4sWLYJer8fq1astGQYREdFTzaLJukWLFsjMzMx33LZt\n2yy5aKI8+FwsqYntibTEN5gRERFZOSZrshmsMZKa2J5IS0zWREREVo7JmmwGa4ykJrYn0hKTNRER\nkZVjsiabwRojqYntibTEZE1ERGTlmKzJZrDGSGpieyItMVkTERFZOSZrshmsMZKa2J5IS0zWRERE\nVo7JmmwGa4ykJrYn0hKTNRERkZVjsiabwRojqYntibTEZE1ERGTlmKzJZrDGSGpieyItMVkTERFZ\nOSZrshmsMZKa2J5IS0zWREREVo7JmmwGa4ykJrYn0hKTNRERkZVjsiabwRojqYntibTEZE1ERGTl\nmKzJZrDGSGpieyItMVkTERFZOSZrshmsMZKa2J5IS0zWREREVo7JmmwGa4ykJrYn0hKTNRERkZVj\nsiabwRojqYntibTEZE1ERGTlmKzJZrDGSGpieyItMVkTERFZOSZrshmsMZKa2J5IS0zWREREVo7J\nmmwGa4ykJrYn0hKTNRERkZVjsiabwRojqYntibTEZE1ERGTlmKzJZrDGSGpieyItMVkTERFZOSZr\nshmsMZKa2J5IS0zWREREVo7JmmwGa4ykJrYn0hKTNRERkZVjsiabwRojqYntibTEZE1ERGTlmKzJ\nZrDGSGpieyItMVkTERFZOSZrshmsMZKa2J5IS0zWREREVo7JmmwGa4ykJrYn0hKTNRERkZVjsiab\nwRojqYntibTEZE1ERGTlmKzJZrDGSGpieyItMVkTERFZOSZrshmsMZKa2J5IS0zWREREVo7JmmwG\na4ykJrYn0hKTNRERkZVjsiabwRojqYntibRUbMl6y5YtqFWrFmrUqIGZM2cWVxhkQxLOJBR3CPQM\nYXsiLRVLsjYajRgxYgS2bNmC6Oho/PTTTzh16lRxhEI2JC05rbhDoGcI2xNpqViS9aFDh1C9enXo\n9Xo4ODigT58+2LBhQ3GEQkREZPWKJVlfuXIFlStXVoYrVaqEK1euFEcoZEOSEpKKOwR6hrA9kZZK\nFMdCdTqd2c/Ur1+/SJ+jJ/RVcQegrWO/HSvuEDSz5KslxbNgG2pTttSegGJsUzaifv36BY4rlmRd\nsWJFXLp0SRm+dOkSKlWqZPKZf/75R+uwiIiIrFKxXAZv3LgxTp8+jfj4eKSnp2PVqlXo2rVrcYRC\nRERk9YqlZ12iRAnMmzcPHTp0gNFoxOuvv47atWsXRyhERERWTyciUtxBEBERUcGKpWdNpIWkpCTs\n378f8fHx0Ol00Ov1eP755+Hq6lrcoRERPRL2rOmZs3fvXsyaNQvx8fEICgqCr68vRATXrl3D0aNH\nodfr8cEHH6BFixbFHSo9RU6ePIk9e/aYfPlr2bIl6tatW9yhkQ1gz5qeOevWrcMXX3yBGjVq5Ds+\nLi4O3333HZM1FcmyZcvw9ddfw8PDA02aNEHVqlWVL39jx47FzZs3MWrUKPTv37+4Q6VnGHvWRESF\niIiIwODBg+Hi4pLv+Hv37iEyMhIjR47UODKyJUzW9MxKS0vD2rVrEf//2rvT4Bqvxw/g3yeJJCUJ\nWWiYlsgdRUK2G0sUjaVqplmaCFGSEAxVzVQtpdUhaf20xthipowlU0KsY6tSSyUlipCShdFK4toS\nQSJyJUqW+3uRcf/Nn5bEzz15zv1+Xsm5XnxfZPK95zznnEenQ3V1NYC6C3nmzp0rOBkRUcNwGZyk\nFRoailatWkGr1cLW1lZ0HFK527dvY82aNU99+UtKShKcjMwBy5qkdfPmTRw8eFB0DJJEaGgo+vfv\nj3fffRcWFnX3SfFKZDIVljVJq0+fPsjOzoaXl5foKCSBhw8fYuHChaJjkJniM2uSVteuXZGXl4eO\nHTvCxsYGQN1MKDs7W3AyUqOvvvoKAQEBeP/990VHITPEsiZp6XQ6AP+3VPnkV93NzU1QIlIzOzs7\nVFZWwtraGs2aNQNQ97tVXl4uOBmZA5Y1Se38+fM4fvw4FEVBv379/vUVdERETZWQt24RmcLy5csR\nFRWFO3fuoLi4GFFRUUhMTBQdi1Rsz549mD59OmbMmIEff/xRdBwyI5xZk7S6d++OU6dOoUWLFgCA\niooK9O7dGzk5OYKTkRrNnj0bZ86cwejRo2EwGLBlyxb4+/vj22+/FR2NzAB3g5PUnhyx+f//Jmqo\nn376CefPn4elpSUAYOzYsfDx8WFZk0mwrElasbGx6NWrF8LDw2EwGLB7926MGzdOdCxSKUVRUFZW\nBmdnZwB1b3XjOWsyFS6Dk9QyMzORnp5u3GDm6+srOhKp1ObNmzF79mwEBgYCAH799Vd89913GDly\npNhgZBZY1iS1mpoa3Lp1C9XV1cZZUPv27QWnIrUqLCzEmTNnoCgKevbsCVdXV9GRyEywrElaK1as\nQEJCAtq0aWN8zgiAG8yo0W7evGm8G/zJl7/+/fsLTkXmgGVN0tJoNMjIyDA+YyR6GbNmzcLWrVvh\n4eFR78sfj3CRKXCDGUmrffv2cHBwEB2DJLFr1y788ccfxqtriUyJZU3SWbx4MQDA3d0dgYGBCAoK\ngrW1NYC6Hb3Tpk0TGY9USqPR4PHjxyxrEoJlTdLR6/VQFAXt27fHm2++icePH+Px48eiY5FKxcXF\nAQCaN28OHx8fDBo0qN6LYXgrHpkCy5qkEx8fDwDYtm0bRowYUe+zbdu2CUhEaqbVao2byYKDg+u9\nGIbnrMlUuMGMpOXr64tz5849d4zoRSxbtgxTp0597hjRq8CyJukcOHAA+/fvx9atWzFy5EjjqzH1\nej0uXryIjIwMwQlJjZ71Rc/Hxwfnz58XlIjMCZfBSTrt2rWDVqvF3r17odVqjcuV9vb2WLp0qeh4\npDKbN29GSkoKrly5guDgYOO4Xq/nsUAyGZY1Scfb2xve3t5wcnJCUFAQX+BBL6VPnz5o27Yt7t69\nixkzZhhXahwcHODl5SU4HZkLLoOTtEaPHo2TJ08iIiIC48aNQ5cuXURHIhVLTExEdHQ0HB0dRUch\nM8QpB0lr06ZNOHfuHNzd3TF27FgEBARg9erV0Ov1oqORChUXF6NHjx4YMWIEfv75Z3CeQ6ZkGf/k\nnAuRhGxtbeHm5oaamhocPnwYJSUlWLBgAQCgV69egtORmgwaNAiffPIJHBwc8MMPP+CLL77ArVu3\n4ObmBicnJ9HxSHKcWZO09uzZg7CwMAQGBqKqqgpnzpzBgQMHkJ2djSVLloiORypkYWEBV1dXvP76\n67C0tMS9e/cQERGBmTNnio5GkuMza5LWmDFjMH78+Ge+FenIkSMYPHiwgFSkVsuXL8eGDRvg7OyM\nCRMmICwsDM2aNUNtbS06deqE/Px80RFJYtwNTtK5fPkyiouLsX79+nrj6enpaNu2LTQaDYuaGqy0\ntBQ7d+5Ehw4d6o1bWFjwzVv0ynEZnKQzderUZ75ty8HBgbdNUYNlZGRg//79SEhIqFfU+/fvR2Zm\nJgDAw8NDVDwyEyxrkk5xcfEzz796eXnhypUrAhKRms2aNeuZZezh4YEZM2YISETmiGVN0ikrK/vH\nz/766y8TJiEZ6PV6uLm5PTXu5uaGu3fvmj4QmSWWNUnH398fq1evfmp8zZo10Gq1AhKRmv3bl7+H\nDx+aMAmZM+4GJ+ncunULYWFhsLa2NpZzZmYmHj16hF27dqFt27aCE5KaTJo0CS4uLpg/f77xlZi1\ntbWYN28eiouLn/nFkOh/jWVNUjIYDEhNTUVubi4URYGnpycGDhwoOhap0IMHDzBhwgRkZGTAx8cH\nAJCVlQV/f3+sXbsW9vb2ghOSOWBZk3T0ev1z/4C+yP8h+rv8/HxcuHABiqLAw8MDGo1GdCQyIyxr\nks7gwYPRuXNnhIaGwt/f33gVZElJCc6ePYvdu3fj8uXLOHLkiOCkpAb5+fnPLeYX+T9EL4NlTVI6\nevQoUlJScOLECRQWFgKoe8913759MXr0aAQGBooNSKoRGRmJiooKhISEwN/fH23btoXBYEBRURHO\nnj2LvXv3wt7eHlu2bBEdlSTGsiYieo68vDxs2bIFJ06cwNWrVwEAHTp0QN++ffHhhx/C3d1dcEKS\nHcuaiIioieM5ayIioiaOZU1ERNTEsaxJWnl5ecbrRVNTU5GYmPivt1ERETVVLGuS1rBhw2BlZYW8\nvDxMmjQJ169fx6hRo0THIpVKT0/HgwcPAADJycmYNm2acbMZ0avGsiZpWVhYwMrKCjt37kRcXBwW\nLVqEoqIi0bFIpSZPnowWLVogKysLS5YsgUajQUxMjOhYZCZY1iQta2trpKSkYMOGDQgKCgIAVFVV\nCU5FamVlZQVFUbB7925MmTIFU6ZMgV6vFx2LzATLmqSVlJSEkydPYs6cOejYsSMKCgoQFRUlOhap\nlL29PRYsWICNGzciKCgINTU1/PJHJsNz1kREL6CoqAgpKSno2bMn+vXrh2vXriEtLY1L4WQSLGuS\nVnp6OhISEqDT6VBdXQ0AUBQFBQUFgpORWhUVFSEjIwMWFhbo0aMHXF1dRUciM8GyJml17twZy5Yt\ng5+fHywtLY3jLi4uAlORWq1duxZff/01BgwYAABIS0vD3LlzMX78eMHJyBywrElavXr1wunTp0XH\nIEm89dZbOHnyJJydnQHUvcUtICAAf/75p+BkZA6sRAcgelUGDBiAmTNnIjw8HDY2NsZxPz8/galI\nrVxcXGBnZ2f82c7Ojqs0ZDKcWZO0AgMDoSjKU+OpqakC0pDaRUdHIzc3F6GhoQCAPXv2wMvLC15e\nXlAUBdOmTROckGTGmTVJKy0tTXQEkohGo4FGozF+AQwNDYWiKMZbzYheJc6sSVplZWVISEjAsWPH\nANTNtOfOnYuWLVsKTkZq9uQiFHt7e8FJyJzwUhSS1rhx4+Dg4IDt27dj27ZtsLe3R2xsrOhYpFI5\nOTnw9fWFp6cnPD09odVqkZubKzoWmQnOrEla3t7eyMrKeu4Y0YsICAjAggUL6h3d+vLLL/Hbb78J\nTkbmgDNrktZrr72G48ePG39OT09H8+bNBSYiNausrDQWNVD3WKWiokJgIjIn3GBG0lq1ahViYmJw\n//59AICjoyPWr18vOBWpVceOHfHNN98gOjoaBoMBmzZtgru7u+hYZCa4DE7SKy8vBwA4ODgITkJq\nVlpainnz5uHEiRMAgH79+iE+Ph6Ojo6Ck5E5YFmTdJKTkxEdHY3FixfXO2dtMBh4HpZeGneDkwhc\nBifpVFZWAqj7o/qssiZqjJycHMTExKCkpAQA0Lp1a6xfvx7dunUTnIzMAWfWREQvgLvBSSTuBidp\nff755ygvL0dVVRUGDRoEFxcXJCcni45FKsXd4CQSy5qkdfDgQTg4OGDfvn1wc3NDfn4+Fi1aJDoW\nqdST3eA6nQ5XrlzB/PnzuRucTIZlTdKqrq4GAOzbtw8RERFo2bIln1lToyUlJeH27dsIDw/HsGHD\ncOfOHSQlJYmORWaCG8xIWsHBwejSpQtsbW2xcuVK3L59G7a2tqJjkUo5OTlhxYoVomOQmeIGM5Ja\nSUkJWrVqBUtLS1RUVECv18PV1VV0LFKR4ODgf/xMURTs3bvXhGnIXHFmTVK7dOkSrl69iqqqKgB1\nf1xjYmIEpyI1mT59+j9+xscqZCqcWZO0oqKiUFBQAB8fH1haWhrHuZRJLyszMxNarVZ0DDIjLGuS\nVteuXXHx4kXOfuh/ztfXF+fOnRMdg8wId4OTtLp164aioiLRMYiIXhqfWZO07ty5Aw8PD/Ts2RM2\nNjYAuCGIGqe6uhpjxozBpk2bAABz584VnIjMDcuapBUfHw+grqCfPO3hkjg1hpWVFa5evYpHjx7B\nxsYGYWFhoiORmeEza5KaTqdDXl4eBg8ejMrKSlRXV/NVmdQo0dHRuHTpEkJCQtC8eXMA4FvcyGQ4\nsyZprV69GmvWrEFpaSny8/Nx48YNTJ48Gb/88ovoaKRCGo0GGo0GtbW1ePDgAd/iRibFmTVJy9vb\nGxkZGejdu7dx52737t2Rk5MjOBmpGd9nTSJwNzhJy8bGxrixDKjbJMSZEDVWTk4OfH194enpCU9P\nT2i1WuTm5oqORWaCZU3Seuedd/Cf//wHlZWVOHz4MIYPH/6vV0cS/ZuJEydiyZIluHbtGq5du4bF\nixdj4sSJomORmeAyOEmrpqYG69atw6FDhwAA7733HiZMmMDZNTWKt7c3srKynjtG9CqwrImIXsAH\nH3wArVaL6OhoGAwGbNq0CZmZmdi1a5foaGQGWNYkrfT0dCQkJECn0xnfba0oCgoKCgQnIzUqLS3F\nvHnzcOLECQBAv379EB8fD0dHR8HJyBywrElanTt3xrJly+Dn51fvRR4uLi4CU5HaREdHIzk5GcuW\nLcPUqVNFxyEzxbImafXq1QunT58WHYNUzsPDA0eOHMHQoUORlpb21OdOTk6mD0Vmh2VN0snMzAQA\nbN++HTU1NQgPD693hMvPz09UNFKhxMRErFy5EgUFBWjXrl29z/hYhUyFZU3SCQwMNO74ftYtU6mp\nqSJikcp99NFHWLVqlegYZKZY1kRERE0cL0Uhad26dQvjx4/H0KFDAQAXL17EunXrBKciImo4ljVJ\na+zYsRgyZAgKCwsBAJ06dcLSpUsFpyIiajiWNUnr7t27iIyMNB7batasGays+KI5IlIfljVJy87O\nDiUlJcafT506hZYtWwpMRETUOJxmkLQWL16M4OBgFBQUoE+fPrhz5w527NghOhYRUYOxrElKNTU1\nOHbsGI4dO4ZLly7BYDCgc+fOsLa2Fh2NiKjBeHSLpNWjRw+cOXNGdAwiopfGsiZpffbZZ6iqqkJk\nZCRatGhhvCCFN5gRkdqwrElaf7/J7O94gxkRqQ3LmoiIqInj0S2S1t27dxEXFwdfX1/4+fnh008/\nrXeUi4hILVjWJK2RI0eiTZs22LlzJ3bs2IHWrVsjMjJSdCwiogbjMjhJq1u3bsjNza031r17d+Tk\n5AhKRETUOJxZk7SGDBmCzZs3o7a2FrW1tdi6dSuGDBkiOhYRUYNxZk3SsrOzQ2VlJSws6r6T1tbW\nokWLFgAARVFQXl4uMh4R0QtjWRMRETVxvG6UpJadnQ2dTofq6mrjWHh4uMBEREQNx7ImacXGxiIn\nJweenp7GpXCAZU1E6sNlcJKWh4cHLly48MxbzIiI1IS7wUlaPXr0wMWLF0XHICJ6aZxZk7TS0tIQ\nEhICV1dX2NjYAKjbBZ6dnS04GRFRw7CsSVoajQZLly5Ft27d6j2zdnNzExeKiKgRuMGMpNWmTRuE\nhISIjkFE9NI4syZpffzxxygrK0NwcDCsra0B1C2Dczc4EakNZ9YkrcrKSlhbW+PQoUP1xlnWRKQ2\nnFkTERE1cTy6RdK6fv06wsLC0Lp1a7Ru3RrDhg3DjRs3RMciImowljVJKzY2FiEhISgsLERhYSGC\ng4MRGxsrOhYRUYNxGZyk5e3tjaysrOeOERE1dZxZk7ScnZ2RnJyMmpoaVFdXY+PGjXBxcREdi4io\nwTizJmnpdDrExcXh1KlTAIA+ffpgxYoVaN++veBkREQNw7ImIiJq4rgMTtKKiYlBWVmZ8ed79+5h\n3LhxAhMRETUOy5qklZ2djVatWhl/dnR0xO+//y4wERFR47CsSVoGgwGlpaXGn0tLS1FTUyMwERFR\n4/C6UZLW9OnTERAQgBEjRsBgMGD79u2YM2eO6FhERA3GDWYktQsXLuDo0aNQFAUDBw6Eh4eH6EhE\nRA3GsiYiImri+MyaiIioiWNZExERNXEsa5LWrFmzXmiMiKipY1mTtA4dOvTU2P79+wUkISJ6OTy6\nRdJZuXIlvv/+e+Tn56N79+7Gcb1ej7fffltgMiKixuFucJLO/fv3ce/ePcyePRsLFy7Ek19xBwcH\nODk5CU5HRNRwLGuSVl5eHt544w3Y2toiNTUVOTk5iImJqXcFKRGRGvCZNUkrIiICVlZWyMvLw6RJ\nk3D9+nWMGjVKdCwiogZjWZO0FEWBlZUVdu7cibi4OCxatAhFRUWiYxERNRjLmqRlbW2NlJQUbNiw\nAUFBQQCAqqoqwamIiBqOZU3SSkpKwsmTJzFnzhx07NgRBQUFiIqKEh2LiKjBuMGMiIioieM5a5LO\n8OHDsX379npnrJ9QFAXZ2dkCUhERNR5n1iSdwsJCtGvXDjqd7pmfu7m5mTQPEdHLYlkTERE1cVwG\nJ+nY2dlBUZRnfqYoCsrLy02ciIjo5XBmTURE1MTx6BYREVETx7ImIiJq4ljWRERETRzLmoiIqIlj\nWRMRETVxLGsiIqIm7r+eoHMw3W5vGAAAAABJRU5ErkJggg==\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10e919d10>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 88
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"showdown\"></a>\n",
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Final Comparison: Cython vs. NumPy vs. SciPy for least squares fitting"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"To wrap it up, let us compare the Cython code of our simple least squares fit implementation to the Numpy and Scipy functions - after we made some improvements by adding static type declarations and explicit for loops."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%load_ext cythonmagic"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 1
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"\n",
|
|
"def cy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" cdef double x_avg, y_avg, temp, var_x, cov_xy, slope, y_interc, x_i, y_i\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" for x_i, y_i in zip(x,y):\n",
|
|
" temp = (x_i - x_avg)\n",
|
|
" var_x += temp**2\n",
|
|
" cov_xy += temp*(y_i - y_avg)\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 2
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import numpy as np\n",
|
|
"import scipy.stats"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 3
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def lin_lstsqr_mat(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 4
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def numpy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return np.linalg.lstsq(X,y)[0]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 5
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def scipy_lstsqr(x,y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" return scipy.stats.linregress(x, y)[0:2]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 6
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"funcs = ['cy_lstsqr', 'lin_lstsqr_mat',\n",
|
|
" 'numpy_lstsqr', 'scipy_lstsqr'] \n",
|
|
"\n",
|
|
"orders_n = [10**n for n in range(1, 6)]\n",
|
|
"times_n = {f:[] for f in funcs}\n",
|
|
"\n",
|
|
"for n in orders_n:\n",
|
|
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
|
|
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
|
|
" for f in funcs:\n",
|
|
" times_n[f].append(min(timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f)\n",
|
|
" .repeat(repeat=3, number=1000)))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 26
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"#%pylab inline\n",
|
|
"#import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"labels = [('cy_lstsqr', 'Cython implementation'), \n",
|
|
" ('lin_lstsqr_mat', 'numpy matrix equation'),\n",
|
|
" ('numpy_lstsqr', 'numpy.linalg.lstsq()'), \n",
|
|
" ('scipy_lstsqr', 'scipy.stats.linregress()')] \n",
|
|
"\n",
|
|
"matplotlib.rcParams.update({'font.size': 12})\n",
|
|
"\n",
|
|
"fig = plt.figure(figsize=(10,8))\n",
|
|
"for lb in labels:\n",
|
|
" plt.plot(orders_n, times_n[lb[0]], alpha=0.5, label=lb[1], marker='o', lw=3)\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('performance gain relative to the slowest approach')\n",
|
|
"plt.xlim([1,max(orders_n) + max(orders_n) * 10])\n",
|
|
"plt.legend(loc=2)\n",
|
|
"plt.grid()\n",
|
|
"plt.xscale('log')\n",
|
|
"plt.yscale('log')\n",
|
|
"plt.title('Performance of least square fit implementations for different sample sizes')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAnIAAAIECAYAAACdVcNJAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXdYVMfXx7/30vsuZQFR6YKgYtdYEBQ1RBNjiYIVLDG2\nvBrzsytg10SNUYyRqDQ1ligxmkgsgDVRsCuioCAqxYqKCAjn/QO54cICC8Jimc/z7PPszp05c+bc\nO3PPTuWIiMBgMBgMBoPBeOfg61oBBoPBYDAYDEb1YI4cg8FgMBgMxjsKc+QYDAaDwWAw3lGYI8dg\nMBgMBoPxjsIcOQaDwWAwGIx3FObIMRgMBoPBYLyjMEdOSbx69QojR46EsbExeJ7H0aNH61qld5Kd\nO3fC1tYWqqqqGDlypNw4Pj4+6N69u5I1Y5S+NzExMeB5Hvfu3auyLGtrayxevLgWtCyLlZUVFi1a\npJS83lZ4nsfWrVvrWo06aSejo6NFz2np3wBw6dIltG3bFlpaWrCxsQEApKamolu3btDV1YWKikqt\n6/khoYzn0c3NDV9++WWt5qEsmCNXAh8fH/A8D57noaamBisrK4wbNw6PHj16Y9m//fYbtm3bhn37\n9iE9PR0fffRRDWj8YVFQUICRI0fCy8sLqampWL16tdx4HMeB4zil6hYeHg6e/3Crk7x706FDB6Sn\np8Pc3BwAcPz4cfA8j9u3b1cqLzY2FlOmTKlttQHUzfPyJty5c6faTo6Hhwd8fX3LhKenp6N///41\nod4b8Ta0kx07dhQ9twAwbdo0SCQSJCQk4MyZMwCAxYsX48GDB7hw4QLS0tKUrqc8Ro8eDXd397pW\n450gIiICK1eurGs1agTVulbgbcPV1RU7duzAq1evEBsbizFjxiA1NRX79u2rlry8vDyoq6vjxo0b\nsLCwQPv27d9Iv2J5HyL37t1DdnY2PD09RY1saYgIbJ/rqlNYWAgA1XJIy7s3MpmsTFxF7o2RkVGV\ndfjQqMlnXN59qgvehnZSTU2tjD0SExMxYsQINGzYUKRrmzZtYGtr+0a65ufnQ01N7Y1kMKqORCKp\naxVqDmIIjBgxgjw8PERhixYtIhUVFXr58iUREW3bto1cXFxIU1OTrKys6JtvvqHs7GwhfpcuXWjU\nqFE0Z84cMjc3JzMzM3JzcyOO44SPtbU1ERHl5eXR9OnTycLCgtTV1cnJyYm2bt0qyp/jOPrxxx/J\n29ubDAwMaNCgQbR582ZSVVWlqKgoatKkCWlpaZG7uzulpaXRkSNHyMXFhXR0dMjDw4Pu3r0ryLp5\n8yb17duX6tWrR9ra2tS0aVMKCwsT5delSxcaPXo0zZ8/n8zMzMjQ0JCGDx9Oz58/F8X79ddfqWXL\nlqSpqUlGRkbk6elJjx8/Fq7/+OOP5ODgQJqammRvb0+LFi2iV69eVWj/U6dOUefOnUlLS4ukUikN\nHjyYMjMziYho8+bNIhtyHEcxMTEK38fK7tvff/9NXbp0IUNDQzIwMKAuXbrQ6dOnRTKCgoLI0dGR\nNDU1ydDQkFxdXenOnTsUFRVVRjdfX99yy7lo0SKysbEhDQ0NMjExoZ49e1JOTo7IdhYWFqStrU09\ne/akkJAQ4jhOuJfF978kqampZWwyevRosrW1JS0tLbKxsaFZs2ZRbm6ucN3Pz4/s7Oxo+/bt5ODg\nQKqqqnTt2jV69uwZff3114IOLVq0oN27d5dbnvLuTbFd7t69S7du3SoTx93dvVyZlpaWtHDhQtHv\nuXPn0ldffUUGBgZkampK69ato5ycHBo/fjxJpVKysLCgtWvXiuRwHEerV6+mfv36kY6ODllYWNDq\n1atFcaysrGjRokXC77y8PPLz8yNra2vS1NQkZ2dn+vnnn8vIXbNmDQ0cOJB0dHTI0tKSdu/eTY8e\nPSIvLy/S09MjGxsb+u2330Tp0tPTacSIEWRiYkJ6enrUsWNHOnr0qHC92GYHDx6kzp07k7a2Njk5\nOdFff/0lyltee1JZ/R4xYkS5dYjjONqyZYsQ9969ezRo0CCSSCSkpaVFbm5uFBsbWyU9iSp/1kvS\npUuXGmsnvby85OZBVHn9quy59ff3L7e+V1Z3iuVt2bKFPD09SUdHh2bMmEFEir1bKmqb/fz8yugV\nEhIi1wZZWVnk4+NDZmZmpKGhQQ0aNKBvvvlGuK5Ie1idOlBc/vDwcOratavQNv36669lZJd8Hqva\nJhEVtYn9+vUjY2Nj0tTUJBsbG/ruu+/K2LPkPS/9sbKyEuLfuHGD+vXrRxKJhKRSKfXo0YMuXbqk\nsE1rE+bIlWDEiBHUvXt3UdiKFSuI4zh6/vw5bd68maRSKYWHh9OtW7fo6NGj1KxZMxo2bJgQv0uX\nLqSnp0fjxo2j+Ph4unz5Mj169Ii+/fZbsra2poyMDHrw4AEREX377bdkZGREu3btohs3btDixYuJ\n53k6fPiwII/jODIyMqLAwEC6efMm3bhxgzZv3kw8z5O7uzudPn2azp49S/b29tSpUydydXWlf//9\nl86fP0+Ojo40aNAgQdalS5coMDCQLl68SDdv3qQ1a9YIDmFJ/SUSCX3zzTeUkJBAf//9NxkaGtLc\nuXOFOJs2bSI1NTVauHChUMa1a9cK5fLz8yNLS0uKiIig5ORk+vPPP6lhw4YiGaVJS0sjPT09GjJk\nCF2+fJmOHz9OzZo1I1dXVyIiysnJoTNnzhDHcfTHH39QRkYG5eXllXsfSzpyity3PXv20M6dO+n6\n9et09epVGj16NBkaGtLDhw+JiCg2NpZUVVUpLCyMbt++TZcuXaKNGzfSnTt3KC8vjwIDA4njOMrI\nyKCMjAx6+vSpXN1+++030tfXp3379lFqaiqdP3+eVq9eLbzcIiIiSFVVlVatWkU3btygjRs3kkwm\nI57nq+TIFRYW0uzZs+n06dOUkpJCe/fuJXNzc/Lz8xPS+Pn5kba2Nrm5udHp06fpxo0b9OzZM3Jz\ncyN3d3c6ceIE3bp1izZs2EDq6uqi57Ik5d2bki/EgoIC2rt3L3EcR7GxsZSRkSFy/EtT2rmytLQk\niURCq1atoqSkJFq4cCHxPE89e/YUwpYsWUI8z9PVq1eFdBzHkaGhIa1du5Zu3LhBq1evJlVVVfr9\n99/LzWvEiBHk4uJCBw8epOTkZNq+fTtJJBLauHGjSK6ZmRmFhoZSUlISjR8/nnR0dKhHjx4UEhJC\nSUlJNGnSJNLR0RGeoRcvXlDjxo1pwIABFBcXR0lJSbRo0SLS0NCg+Ph4IvrvheLi4kKRkZGUmJhI\nvr6+pK+vL9jr3LlzxHEc7dmzR9SeVFa/s7KyyNXVlby8vITntLgOlXxxFhYWUtu2balFixZ04sQJ\nunTpEg0aNIikUqmQlyJ6Vvasl6Ym28nExES5eShSv0o/t+np6dSgQQOaOXMmZWRk0PPnzyk9PZ06\ndOhAQ4cOFep7YWFhpXWn2JGpX78+bd26lZKTk+nWrVsKv1sqapufP39OQ4YMoY4dOwr3tzxbT5o0\niVxcXOj06dOUmppKJ0+epF9++UW4Xll7WN06UFz+evXq0datW+n69es0Z84cUlFRoXPnzolkl3we\nq9omERF9+umn1L17d7pw4QKlpKRQVFQUbdu2Tbju5uZGY8aMIaKiPwvFNsvIyKCrV6+ShYUFjRw5\nkoiK/oCZmprS+PHj6fLly3T9+nWaNGkSGRkZ0f379xWyaW3CHLkSlHYArly5QjY2NvTRRx8RUdHL\npPQ/85iYGOI4jp48eUJERZXNwcGhjOzi3o9isrOzSUNDg3766SdRvL59+1LXrl2F3xzHCf8aiinu\nAblw4YIQ9t133xHHcXT27FkhbNWqVWRsbFxhmfv06SM8zMX6N2/eXBRn3Lhxgg2IiBo0aECTJk2S\nKy87O5u0tbUpMjJSFB4SEkISiaRcPebMmUMNGjSg/Px8IezChQvEcZzQY1HcCJw4caLCMpW+j4rc\nt9IUFBSQVCoVGpPdu3eTgYFBuQ5aWFgYcRxXoV5ERCtXrqRGjRqJylmSjh070tChQ0Vh3377bbV6\n5OTlbW9vL/z28/MjnucpNTVVCIuKiiJNTU3KysoSpfX19aXPP/+8XNny7k3JFyIR0bFjx4jjOEpJ\nSSlXTjHyHLm+ffsKvwsLC0lfX58+++wzUZhUKhX1ynEcR8OHDxfJHjx4MHXu3FluXjdv3iSe5ykh\nIUGUJiAgQFQvOI6jKVOmCL/v379PHMfR119/LYQ9fvyYOI6j/fv3E1HRfatfv36Znml3d3eaPHky\nEf1nsz179gjXMzIyiOM4+vvvv4lIsXtdTOn67eHhIbe3uOSL89ChQ8RxnOBcEhHl5uaSubk5zZ8/\nX2E9K3vW5VGT7aQ8FKlfpZ9borLPI5HYEShOV1ndKa4nJXubiRR/t1TWNo8aNYrc3NwqtUOfPn3I\nx8en0njFlG4PiapXB4rLP2/ePJH8Dh06iJzWks9jddskFxcX8vf3L/d66ftXTF5eHrm5uZGrq6vw\nR8fPz4/at28vildYWEi2trb0ww8/EFHVbVqTfLizs8shOjoaenp60NbWRtOmTWFnZ4ctW7bg/v37\nuH37NqZMmQI9PT3h88knn4DjOCQmJgoyWrVqVWk+iYmJyMvLg6urqyjc1dUVV65cEYW1bdu2THqO\n49C0aVPht6mpKQCgWbNmorCHDx8Kc2levHiBGTNmoEmTJjAyMoKenh7+/PNP0eRzjuPg4uIiysvc\n3BwZGRkAgMzMTNy5cwc9evSQW64rV64gJycH/fr1E9npq6++wtOnT/Hw4cNy07Vv3x6qqv9N22zW\nrBkMDAxw9epVuWkUQdH7duvWLQwbNgz29vYwMDCAgYEBsrKyBNv06NEDNjY2sLa2hre3N4KCgsot\nS0UMGjQI+fn5sLS0hK+vL8LDw/H8+XPhenx8PDp06CBK07Fjx2qVPSgoCO3atYOZmRn09PQwa9as\nMgsNTE1NUb9+feH3mTNnkJeXBwsLC5G9tmzZInrGlU3p55LjOJiYmIied47jIJPJcP/+fVHa0hPm\nO3ToUKaOFRMbGwsiQqtWrUTlX7JkSZnyl9TH2NgYKioqIn0kEgnU1dWRmZkJoMi26enpkEgkItnH\njx8vI7t58+bCd5lMBhUVFaEOloci9VsRrly5AiMjIzg6Ogph6urqaNeuXRm7VaRnZc+6IrxpO1ma\nmqxfpalK3Smpa1XeLRW1zVVh/Pjx2LVrF5o2bYrJkyfjwIEDojmXlbWH8vRRpA4UU7pOduzYsdw6\nWd02afLkyVi8eDHat2+PGTNm4NixY5UbBsC4ceNw9+5dRERECHMXz5w5g7i4OFH++vr6SElJEXSo\nzKa1CVvsUIr27dsjJCQEqqqqqFevnuBYFFeWH3/8Ue6qIAsLCwBFLxMdHZ0a1UmePJ7nRSvtir+X\nXAZfHEZE4DgO//vf/7B3716sWrUKDg4O0NbWxtSpU5GVlSWSXXqSMMdxwkT4yiiOt2vXLjRq1KjM\ndalUKjcdx3G18tAX61PZfevduzdkMhnWrVuHBg0aQE1NDZ06dUJeXh6AonsQGxuLEydO4NChQ1i/\nfj2mTZuGw4cPo2XLlgrrU69ePVy7dg1RUVE4cuQIFixYgOnTp+Pff/8VOVQVIW8xQn5+vuj3zp07\nMXHiRCxbtgxdunSBvr4+duzYgdmzZ4vilX62CgsLYWBggNjY2DJ51PUim9ITwjmOkxum6LMqj+K0\np06dgra2dhnZFelTno7FMgsLC9G4cWNERESUSVc6L3m2rqxcitbv6lLcjiiqZ00861WhptvdqlKV\nulNSV0XbKI7j3qhtLkmPHj1w+/ZtREZGIjo6GkOHDkXTpk1x+PBh8DxfaXtYTFXrQHlU1PZXt03y\n8fHBxx9/jAMHDiAqKgqenp7o27cvwsLCyk2zfPlyRERE4NSpU6J3FRHBw8MDa9euLZPGwMAAQOU2\nrU2YI1cKTU1NYZ+gkpiamqJBgwa4du0aRo0a9cb52NnZQUNDAzExMXBychLCY2JiRD1tNcmxY8cw\ndOhQDBgwAEBRBUlISKhwBWhpZDIZ6tevj8jISPTu3bvMdWdnZ2hqaiIpKQkff/yxwnKdnZ2xefNm\n0QquCxcuICsrC02aNFFYTmkUuW8PHz5EfHw8Vq5cKew/d+fOnTL/InmeR+fOndG5c2cEBATAyckJ\n27ZtQ8uWLYUGRd7LrjTq6uro2bMnevbsiQULFsDU1BS///47JkyYACcnJ5w4cQLjxo0T4p84cUKU\nXiaToaCgAJmZmcLqurNnz4riHD16FC1atMDkyZOFsFu3blWoFwC0adMGT548QU5ODpydnSuNXxWK\nbVRQUFCjcivj1KlT+Oqrr4TfJ0+eLLdsxb3pKSkp6NWrV43q0aZNG4SFhUFPTw8mJibVllOeHRWp\n3+rq6nj16lWF8p2dnYU60bhxYwBAbm4u/v33X0ycOLHKupb3rCtCTbeTitSv6lLdulOT7xZ1dXWF\n65dUKoWXlxe8vLzg6+uLjz76CPHx8TAzM1OoPXwTTp06JXo/VFQnW7duXe02yczMDD4+PvDx8YGn\npycGDx6Mn376Cbq6umXiRkREwM/PD5GRkbC3ty+jQ3BwMCwsLKChoVFufuXZtKbb0tK8c47c6dOn\nMXnyZKipqcHCwgKhoaGi4bjaZNGiRRg1ahSkUik+++wzqKmpIT4+HgcOHMD69esBKL71hba2Nr7+\n+mvMnTtXGCLatWsX9u7di0OHDtWK/g4ODoiIiEC/fv2go6ODlStXIi0tDWZmZkIcRfT38/PDuHHj\nYGpqiv79+6OwsBBRUVHw9vaGkZERZs2ahVmzZoHjOHTr1g2vXr3CpUuXcP78eSxdulSuzIkTJ2L1\n6tXw8fHBrFmz8PjxY4wfPx6urq5vPPRR2X2TSqUwMTHBhg0bYGNjgwcPHmDatGnQ0tISZPz++++4\ndesWOnfuDBMTE8TFxSE1NVV4uVhbWwvxOnbsCG1tbbk9BBs3bgQRoU2bNpBIJDh8+DCePXsmyJk6\ndSq++OILtG3bFp6enjh+/DjCw8NFzmG7du2gp6eHGTNmYObMmUhKSsL8+fNF+Tg6OmLTpk3Yu3cv\nnJ2dsW/fPuzZs6dSW3Xt2hUeHh7o168fli9fjqZNm+Lx48c4efIktLS0MHr06KrfgNdYWlqC53ns\n378fAwcOhIaGhvBvtjSln0F5z6SiYfv370dgYCB69OiBAwcOYMeOHdi1a5fcNHZ2dhg5ciTGjBmD\n5cuXo3379sjOzkZcXJzwXFSXIUOGYNWqVejVqxcWLVoEe3t7ZGRk4MiRI3ByckKfPn0UkmNsbAxd\nXV1ERkaicePG0NDQgFQqVah+W1tbIyoqCjdv3oS+vj4kEkmZ9rNbt25o27YtBg8ejMDAQOjr62PB\nggXIy8sTOUCVUdmzrgg13U6WV78qo7xnrWT4m9Sdmnq32NjYYNeuXbh69SpkMhn09fXl9lrNnj0b\nrVu3hpOTE3ieR3h4OPT09NCwYUPo6OhU2h6+KZs2bYKjoyNatWqF8PBw/PPPPwgMDJQbt1u3btWy\n68SJE9GrVy80atQIL1++xO7du9GwYUPBiStpzytXrmDo0KHw9/dHo0aNkJ6eDqBohMvExAQTJ07E\nxo0b0adPH8yZMwf169fHnTt38Ndff6F379746KOPKrRpraOcqXg1R1pamrAVyMyZM2nXrl01JtvH\nx6fMqtXSRERE0EcffUTa2tqkr69PzZs3pwULFgjXy5tA6e/vL5poTkSUn59PM2bMEJbVOzs7i1bV\nEJVdhk1UNGlaTU1NFBYWFkY8z4vCtm3bRjzPU0FBAREVTZLu2bMn6ejokLm5Ofn7+9OoUaNE20DI\n03/hwoXCVgDFbNmyhVxcXEhDQ4OMjIyod+/eooUDv/zyCzVv3pw0NTVJKpVS+/btaf369WXsUpJ/\n/vmHXF1dSUtLiyQSCQ0ZMkRYEURUNFGW5/lKFzvIu4+V3beYmBhh6b+joyP99ttvZGdnRwEBAURE\ndPToUeratSuZmJiQpqYmNWrUiJYtWybKY/LkySSTySrcfmT37t3UoUMHkkqlwhYRmzZtEsVZvXo1\nWVhYkJaWFnXv3r3M9ghERPv376fGjRuTlpYWderUiSIjI4nneWECfH5+Po0dO5YMDQ1JX1+fhgwZ\nQmvXrhU9I/KeSaKiVagzZswga2trUldXJzMzM/L09BStbi6NvHsTFRUlWg1IRLR8+XKysLAgFRWV\nCrcfKT25XN5k85L3pxhHR0fR6uji7Uc+//xz0tbWpnr16tGqVasqzKugoICWL19Ojo6OpK6uTsbG\nxuTm5iZqa+TVS1VV1TLbPWhqaopWuz58+JDGjRsn1HkLCwvq168fnT9/vlybyZMdGhpK1tbWpKqq\nKtRNRer3zZs3ydXVlXR1dSvcfiQtLY28vLxE24/ExcUJ1xXRU5FnvTQ12U6Wh7z6VXrVaumyKbLY\ngajyulNRG1add0vptvnRo0f0ySefkIGBQYXbjyxYsICaNGlCurq6ZGBgQG5ubiKdKmsPiapXB0pu\nP+Lm5iZsC1LZ/axOmzRhwgRq1KgRaWlpCe+okivaS9pT3hZKJbfAISJKSUmhIUOGkImJCWloaJCl\npSUNGzaMkpOTFbJpbcIRvbs7p/r5+aFFixb4/PPP61oVBqPWiI6ORteuXXHnzh3Uq1evrtV5pyj+\nZzx48OC6VoXB+OBJTk6GjY0Njh8/XmbRCaP6vLOrVlNSUnDw4EF8+umnda0Kg8FgMBgMRp1QZ47c\n2rVr0bp1a2hqapY5++/Ro0fo27cvdHV1YWVlhW3btomuP336FMOHD0dISAg7rJjxQVDZAgoGg8F4\nF2BtWc1TZ0Ore/bsAc/ziIyMRE5ODjZv3ixc8/b2BlA0WfbcuXPo1asXTp48CScnJ7x69QqfffYZ\nvv32W3Tt2rUuVGcwGAwGg8F4O1DKTLwKmDNnjmg35OfPn5O6ujrduHFDCBs+fLhwHl1oaCgZGRmR\nm5sbubm50fbt2+XKrVevHgFgH/ZhH/ZhH/ZhH/Z56z8uLi7V8qPqfI4cleoQvH79OlRVVWFnZyeE\nubi4CLs+Dxs2DA8ePEBUVBSioqIwcOBAuXLv3bsnLC9WxsfPz0+p6RWJX1Gc8q4pGi4v3pvaQJn2\nrqqM2rJ3VWypyD14m21e0894da8ze1c/PmtTak4Ga1Pe72e8Ova+cOFCtfyoOnfkSo+XP3/+HPr6\n+qIwPT09PHv2TJlqVRk3NzelplckfkVxyrumaLi8eMnJyZXqVFO8qb2rKqO27F3eNUXClGlvefnX\ndvrK4lf3OrN39eOzNqXmZLA25f1+xpVp7zrffmTOnDm4e/euMEfu3Llz6NSpE7Kzs4U433//PY4e\nPYq9e/cqLLe2jnxilI+Pjw+Cg4PrWo0PBmZv5cLsrXyYzZULs7dyKW3v6votb12PXKNGjfDq1SvR\nYbgXLlyo1jFN/v7+iI6OflMVGQri4+NT1yp8UDB7Kxdmb+XDbK5cmL2VS7G9o6Oj4e/vX205ddYj\nV1BQgPz8fAQEBODu3bsICgqCqqoqVFRU4O3tDY7j8Msvv+Ds2bPo3bs3Tp06JZz7pwisR47BYDAY\nDMa7wjvXI7dgwQJoa2tj2bJlCA8Ph5aWFhYtWgQAWLduHXJyciCTyTB06FCsX7++Sk4co25gvZ/K\nhdlbuTB7Kx9mc+XC7K1casreyjltXg7+/v7ldiVKpVKFDvhmMBgMBoPB+JCp88UOtUVFXZSGhoZ4\n/PixkjViMD5cpFIpHj16VNdqMBgMxltLdYdW66xHThn4+/vDzc2tzJLfx48fs/lzDIYSYcfyMBgM\nhnyio6PfaJj1g+yRYwshGAzl8j7Uuejo6BrZa4yhOMzmyoXZW7mUtvc7t9iBwWAwGAwGg/FmsB45\nBoNR67A6x2AwGBXDeuQYDAaDwWAwPjDea0eOnexQdXx8fNC9e/c6y9/a2hqLFy9WSl5WVlbC3oUf\nKjzPY+vWrXWtxjsBa0uUD7O5cmH2Vi7F9n7Tkx3ee0fufZy4+fDhQ0ybNg2Ojo7Q0tKCqakpunTp\ngrCwMBQUFCgk4/jx4+B5Hrdv3xaFcxxXpysMY2NjMWXKFKXkVddlrSp37twBz/M4evRoldN6eHjA\n19e3THh6ejr69+9fE+oxGAwGoxq4ubm9kSP3Xm8/Ul0SElJw6FAS8vN5qKkVwsPDFg4Olm+FzNTU\nVHTq1Anq6uqYP38+WrRoATU1NZw4cQLff/89XFxc0KxZM4XllR6Pr+t5TEZGRnWa/7tATd4jmUxW\nY7Led97HP4VvO8zmyoXZW7nUlL3f6x656pCQkILg4ETcv98VT5644f79rggOTkRCQspbIXP8+PHI\nz8/H2bNn4e3tDUdHR9ja2mL48OE4e/Ys7OzsEBwcDKlUipycHFHa+fPno1GjRkhOToarqyuAoqFM\nnufRtWtXIR4RYcOGDbC0tISBgQH69OmDzMxMkayQkBA4OTlBQ0MDDRo0wNy5c0W9gW5ubhgzZgwW\nLFgAc3NzGBkZYcSIEcjOzq6wfKWHO62srDBv3jyMGzcOEokEZmZm+Omnn/Dy5UtMmDABhoaGqF+/\nPgIDA0VyeJ7Hjz/+iP79+0NXVxf169fHjz/+WGHe+fn58Pf3h42NDbS0tNCkSRNs2LChjNy1a9di\n0KBB0NXVhZWVFfbs2YPHjx/D29sb+vr6sLW1xe7du0XpMjIy4OPjA5lMBn19fXTq1AnHjh0TrkdH\nR4PneRw6dAiurq7Q0dGBs7MzDhw4IMRp2LAhAMDd3R08z8PGxgYAcOvWLfTr1w8WFhbQ0dFBs2bN\nEB4eLqTz8fHBkSNHEBISAp7nRb16pYdW09LS4OXlBalUCm1tbbi7uyMuLq5KejIYDAZDidB7SkVF\nq+ja2rWHyc+PqEsX8eeTT4rCq/Px9DxcRp6fH1Fg4OEqlenhw4ekoqJCixYtqjBeTk4OSaVSCgkJ\nEcIKCgrI0tKSli9fTgUFBbR3717iOI5iY2MpIyODHj9+TEREI0aMIAMDAxo8eDBduXKFTp06RdbW\n1jRs2DDAEwgXAAAgAElEQVRB1r59+0hFRYWWLl1KN27coO3bt5NUKqW5c+cKcbp06UISiYS++eYb\nSkhIoL///psMDQ1FceRhZWUlKp+lpSVJJBJatWoVJSUl0cKFC4nneerZs6cQtmTJEuJ5nq5evSqk\n4ziODA0Nae3atXTjxg1avXo1qaqq0u+//15uXiNGjCAXFxc6ePAgJScn0/bt20kikdDGjRtFcs3M\nzCg0NJSSkpJo/PjxpKOjQz169KCQkBBKSkqiSZMmkY6ODj18+JCIiF68eEGNGzemAQMGUFxcHCUl\nJdGiRYtIQ0OD4uPjiYgoKiqKOI4jFxcXioyMpMTERPL19SV9fX3h3pw7d444jqM9e/ZQRkYGPXjw\ngIiILl26RIGBgXTx4kW6efMmrVmzhlRVVSkqKoqIiLKyssjV1ZW8vLwoIyODMjIyKC8vTyjPli1b\niIiosLCQ2rZtSy1atKATJ07QpUuXaNCgQSSVSoW8FNFTHu9DU1NsT4byYDZXLszeyqW0vavbTrIe\nuVLk58s3SUFB9U1VWCg/bV5e1WQmJiaisLAQTk5OFcbT1NTEsGHDEBQUJIQdPHgQaWlp8PX1Bc/z\nkEqlAAATExPIZDJIJBJR+uDgYDg5OaF9+/b46quvcOjQIeH60qVLMWDAAEyfPh12dnYYOHAg/P39\n8f333+PVq1dCPCsrK6xYsQKNGjVC9+7dMWjQIJEcRXF3d8fkyZNhY2ODWbNmQVdXFxoaGkLY9OnT\nYWBggCNHjojS9e7dGxMmTICdnR2+/vprDBw4EN9//73cPG7duoWwsDDs2LEDHh4esLS0xMCBAzFl\nyhSsWbNGFNfb2xvDhg2DjY0NAgIC8OLFCzg6OmL48OGwsbHB/Pnz8eLFC/zzzz8AgO3bt+PZs2f4\n9ddf0bJlS6EcHTp0wM8//yyS7e/vjx49esDW1hZLly7Fs2fPcObMGQCAsbExgKIj5mQymTAM3aRJ\nE4wfPx5NmzaFtbU1Jk6ciF69egk9bfr6+lBXV4eWlhZkMhlkMhnU1NTK2ODIkSM4c+YMtm7dig4d\nOqBJkyYIDQ2FpqYm1q1bp7CeDAaDwVAe7/UcufKO6KoINbVCueEqKvLDFYHn5adVV6+aTKrC3Kix\nY8eiSZMmSEhIgIODA4KCgtCnTx/BGagIR0dH0Yve3NwcGRkZwu+rV6/C29tblMbV1RUvX75EUlIS\nHBwcAAAuLi6iOObm5oiMjFS4DEDRgoSScjiOg4mJiWgeIMdxkMlkuH//vijtRx99JPrdoUMHzJs3\nT24+sbGxICK0atVKFP7q1SuoqoqrSUl9jI2NoaKiItJHIpFAXV1dGI4+c+YM0tPTRc4yAOTm5kJH\nR0cU1rx5c+G7TCaDioqKyPbyePHiBebPn499+/YhLS0NeXl5yM3NFQ2XK8KVK1dgZGQER0dHIUxd\nXR3t2rXDlStX3ljPdx02f0j5MJsrF2Zv5VJs7zc9ouu9d+SqioeHLYKDD8PNrZsQlpt7GD4+dnjt\nn1SZhIQimRoaYpndutlVSY69vT14nseVK1fw+eefVxjXyckJnTp1woYNGzB9+nT88ccf2L9/v0L5\nlO6tqc4mhRzHQV1dvUxYYWHVHWJ5+sgLq47sYorTnjp1Ctra2mVkV6RPeToWyywsLETjxo0RERFR\nJl3pvErbrKRu5fG///0Pe/fuxapVq+Dg4ABtbW1MnToVWVlZFaZTFCIqY4Pq6MlgMBiMshR3OAUE\nBFQrPRtaLYWDgyV8fOwgkx2BRBINmezIayeu+qtWa0qmoaEhPD09sXbtWjx9+rTM9fz8fLx48UL4\nPXbsWISGhmLDhg2oX78+PDw8hGvFL2J525VUtiWHs7MzYmJiRGExMTHQ1taGra1tlcpUm5w6dUr0\n++TJk3B2dpYbt7gnLiUlBTY2NqKPtbX1G+nRpk0b3Lx5E3p6emVkm5mZKSynvHt27NgxDB06FAMG\nDBCGVxMSEkT3UV1dXTTsLQ9nZ2c8fPgQ8fHxQlhubi7+/fdfNGnSRGE931fYHlvKh9lcuTB7K5ea\nsjdz5OTg4GCJ8eO7YvJkN4wf3/WNtx6pSZnr1q2DmpoaWrVqhW3btuHq1atITExEeHg42rRpg8TE\nRCHugAEDAAALFy7E6NGjRXIsLS3B8zz279+PzMxMkWNYWe/bzJkz8dtvv2HZsmW4fv06duzYgYCA\nAEydOlUYhiSiam2TUTqNPBmKhu3fvx+BgYG4ceMG1qxZgx07dmDq1Kly09jZ2WHkyJEYM2YMwsPD\nkZiYiAsXLmDTpk1Yvnx5lctRkiFDhsDa2hq9evXCwYMHkZycjH///RdLlizB77//rrAcY2Nj6Orq\nIjIyEunp6Xj8+DEAwMHBAREREThz5gyuXr2KL7/8EmlpaaLyWVtbIy4uDjdv3sSDBw/kOnXdunVD\n27ZtMXjwYJw8eRKXL1/G8OHDkZeXh3Hjxr2RDRgMBoNROzBH7h2jQYMGOHv2LD7//HP4+/ujVatW\n6NixI4KCgjBu3DhRj5OGhgaGDh0KIsLIkSNFckxNTbFkyRIsXboU9erVE4Zqy9skt2SYp6cnNm3a\nhJCQEDRt2hTffPMNJkyYAD8/P1H80nIU2YBXXprK4pQXNm/ePBw6dAjNmzfH0qVL8d1336FPnz7l\nptmwYQOmTJmCRYsWwdnZGR4eHggLC3vjXkYNDQ3ExMSgdevW8PX1hYODA/r374/Y2FhYWVlVWIaS\n8DyPwMBA7NixAw0aNBB6EVetWgVLS0u4u7vDw8MDDRo0wIABA0Typk6dCmNjY7i4uEAmk+HkyZNy\n84iIiICjoyN69eqFtm3bIjMzEwcPHoShoaHCer6vsPlDyofZXLkweyuXmrI3R9XpNnkHqGhe14d0\ngPfAgQNRUFCA3377ra5VUSo8zyM8PByDBw+ua1UY+LDqHIPBYFSH6raTrEfuPeXx48eIjIxERESE\n0o68YjDeZ9j8IeXDbK5cmL2VS03Z+71ftVrV7UfeF1q0aIFHjx5h+vTp6NSpU12rw2AwGAwGQw5v\nuv0IG1plMBi1DqtzDAaDUTFsaJXBYDAYDAbjA4M5cgwGg6EAbP6Q8mE2Vy7M3sqF7SPHYDAYDAaD\n8YHD5sgxGIxah9U5BoPBqBg2R47BYDAYDAbjA4M5cgwGg6EAbP6Q8mE2Vy7M3sqFzZFjMGqB6Oho\n8DyPe/fu1bUqtY6/vz/s7e3rWg0Gg8FgvAHv9Rw5Pz8/uRsCs/k6HxZ2dnYYNmyY6CzY8sjPz8fj\nx49hYmLy3pwpevz4cbi6uiI5ORkNGzYUwrOzs5Gbmys6R7W2YHWOwWAw5FO8IXBAQEC12sn3/mQH\nBkNRh+zVq1dQU1ODTCarZY3qhtINhI6ODnR0dOpIGwaDwWAAEDqcAgICqpWeDa3KISExAYHbA/HD\nrz8gcHsgEhIT3hqZbm5uGDNmDBYsWABzc3MYGRlhxIgRyM7OFuL4+Pige/fuonTh4eHg+f9ud/Gw\n2s6dO2FnZwcdHR30798fz58/x86dO+Hg4AB9fX188cUXePr0aRnZq1atgoWFBXR0dDBw4EA8fvwY\nQNE/C1VVVdy5c0eUf2hoKCQSCXJycuSWq7r6nD17Fp6enjA1NYWenh7atm2LyMhIkb2SkpIQEBAA\nnuehoqKC27dvC0Oof/75Jzp16gQtLS1s3LixzNDq8uXLIZVKkZKSIsicP38+ZDIZ0tPTy71PGRkZ\n8PHxgUwmg76+Pjp16oRjx46J4kRFRaFZs2bQ0tKCi4sLoqKiwPM8tmzZAgBITk4Gz/M4efKkKJ2d\nnZ2owq9evRotWrSAnp4ezM3N4e3tLeiWnJwMV1dXAIC1tTV4nkfXrl1FNi9JSEgInJycoKGhgQYN\nGmDu3LkoKCgQ2bOy5+99hc0fUj7M5sqF2Vu5sDlytURCYgKCo4Jx3/Q+npg9wX3T+wiOCn4jZ66m\nZe7atQtPnjxBTEwMfv31V+zbtw/Lli0TrnMcp1AvVFpaGkJDQxEREYG//voLx44dQ79+/RAcHIxd\nu3YJYYsXLxalO336NGJiYvD333/jzz//xPnz5zFq1CgARS96e3t7bNq0SZQmKCgIQ4YMgZaWVo3q\n8+zZM3h7eyM6Ohrnzp1Dz5498dlnn+HGjRsAgD179sDKygrffvst0tPTkZaWhvr16wvpp06dipkz\nZ+LatWvo3bt3GZ2mTZuGdu3awdvbGwUFBTh69CgWLlyIkJAQmJmZyS1HTk4O3N3dkZ2djQMHDuD8\n+fP45JNP0L17d1y7dg0AcO/ePfTu3Rtt2rTBuXPnsGLFCvzf//0fgMp7EEvfX47jsGLFCly+fBl7\n9uzB7du34eXlBQBo2LAhfv/9dwDAmTNnkJ6ejt27d8uVu3//fowaNQojRozAlStXsGLFCgQGBpb5\nl1jZ88dgMBgM5fFeD61Wh0Nxh6Bhr4Ho5Oj/AtWAi79eRJtObaol8/Tx03hR/wWQ/F+Ym70bDp89\nDAc7hyrLs7KywooVKwAAjRo1wqBBg3Do0CHMnz8fQNEQmiLj7Lm5uQgJCRHmSA0cOBDr169HRkYG\njIyMAABeXl44fPiwKB0RISwsDHp6egCAwMBA9OzZEzdv3oSNjQ2+/PJLrF69GnPnzgXHcbh27RpO\nnDiBtWvX1rg+Xbp0EclYsGAB/vjjD+zcuROzZs2CVCqFiooKdHV15Q6ZzpkzB7169RJ+FzuAJQkN\nDYWLiwsmTZqEffv2YdKkSfD09Cy3HNu3b8ezZ8/w66+/QkVFBQAwa9YsHDp0CD///DNWrVqFdevW\nQSaTISgoCDzPw9HREUuWLMGnn35aoY3k8fXXXwvfLS0tsXbtWrRq1QppaWkwNzeHVCoFAJiYmFQ4\nbLx06VIMGDAA06dPB1DU85eeno4ZM2Zg3rx5UFUtai4qe/7eV0rPtWXUPszmyoXZW7nUlL1Zj1wp\n8ilfbngBCuSGK0IhCuWG5xXmVVkWx3FwcXERhZmbmyMjI6PKsiwsLEQT3U1NTWFmZiY4TcVhmZmZ\nonROTk6CEwcAHTp0AABcvXoVADB8+HBkZmYKQ5y//PILWrduXUbvmtDn/v37GD9+PBo3bgypVAo9\nPT1cuXIFt2/fVsgGbdu2rTSOTCbD5s2bsX79ehgbG1fa+1Tc8yWRSKCnpyd8jh8/jsTERABFtmrb\ntq1ouLtjx44K6Vya6Oho9OzZEw0bNoS+vj46d+4MAKLhYEW4evWqMAxbjKurK16+fImkpCQhrKae\nPwaD8XaQkJiAFVtWYFn4shqbTsRQHsyRK4UapyY3XAUq1ZbJl2NmdV69WvLU1cXpOI5DYeF/ziLP\n82V65PLzyzqoamrisnIcJzespGyg7KT50hgZGWHAgAEICgpCfn4+QkND8eWXX1aYprr6+Pj44MSJ\nE/juu+9w/PhxnD9/Hs2bN0denmJOsqKT/aOjo6GiooKMjAw8efKkwriFhYVo3LgxLly4IPpcu3YN\nQUFBQjkqs2Oxk1fRvbx9+zY++eQT2NjYYPv27YiLi8PevXsBQGEbVAWO4yp9/t5X2Pwh5cNsXvsk\nJCZgw6ENOESHsCd+D+4a333j6UQMxaip55sNrZbCo5UHgqOC4WbvJoTl3siFj5dPtYZBASChftEc\nOQ17DZHMbu7d3lRduZiamuKff/4RhZ09e7bG5MfHx+PZs2dCr1zxZHwnJychztixY+Hu7o7169fj\n5cuX8Pb2rrH8S3Ls2DF89913wvy27OxsJCUloWnTpkIcdXV10YT9qnLo0CGsXLkS+/fvx9y5c+Hj\n44N9+/aVG79NmzbC0LOJiYncOE5OTggLC0NhYaHgsJ04cUIUpzjt3bt3hbDMzEzR7zNnzuDly5f4\n4YcfoKGhIYSVpNjxqswGzs7OiImJwfjx44WwmJgYaGtrw9bWtsK0DAbj3WTfv/twVfcqcl7l4GXB\nS1zMuIhWdq2qPfWHoXxYj1wpHOwc4OPuA1mmDJJ0CWSZMvi4V9+Jq2mZisx/8/DwwLVr17Bu3Tok\nJSUhKCgIO3furK76ZeA4DsOHD8eVK1dw9OhRTJgwAX369IGNjY0Qp2PHjnBwcMD//vc/eHt719o2\nFw4ODggPD8fly5dx/vx5eHt7o7CwUGQja2trHD9+HKmpqXjw4EGV9um5f/8+hg0bhmnTpqFHjx7Y\ntm0bjh07hh9++KHcNEOGDIG1tTV69eqFgwcPIjk5Gf/++y+WLFkiLDwYN24c7t+/jy+//BLx8fE4\nfPgwZs+eLZKjpaWFjh07Yvny5bh48SLi4uIwfPhwwWEDAHt7e3Ach++//x63bt1CREQEFixYIJJj\naWkJnuexf/9+ZGZmIisrS67eM2fOxG+//YZly5bh+vXr2LFjBwICAjB16lRhfpyi8y/fR9j8IeXD\nbF67PM19ihOpJ5Dzqmg3AamjFJYGluA4rlpTfxhVg82Rq0Uc7BwwfuB4TPaajPEDx9fIv5Kakilv\nRWrpsG7dumHhwoVYvHgxmjdvjujoaMybN6/MSsfK5JQX1rZtW3Tq1Andu3eHp6cnXFxcyqxSBYDR\no0cjLy9PoWHV6uqzefNmFBYWom3btujXrx8++eQTtGnTRhQnICAAT548gYODA0xNTZGamirIKk+X\nYnx8fGBtbS1M5LexscH69esxY8YMXLhwQW56DQ0NxMTEoHXr1vD19YWDgwP69++P2NhYWFlZAQDq\n1auHP/74A6dPn0aLFi0wZcoUrFq1qoysTZs2QVdXFx06dMDgwYMxduxYmJubC9ebNWuGNWvW4Oef\nf4azszNWrlyJH374QVQGU1NTLFmyBEuXLkW9evXQt29fubb09PTEpk2bEBISgqZNm+Kbb77BhAkT\nRBspK3qfGAzG283T3KcIPh+Ml69eoiAtG8Z/pcIlKgeaf9/C89sPqj31h6F83uuTHcorGttlvvr4\n+Pjg7t27OHjwYKVxp02bhsOHDyMuLk4Jmr0f8DyP8PBwDB48uK5VqVHehzoXHR3NeoiUDLN57ZD1\nMgshF0LwKOcRUmNvQGVnNCa/UsHZ7AJYtrRG5JMCdJs8D+49yl+dz3hzSj/f1W0n3+seOX9/fzZZ\ntg7IysrCmTNnEBQUhClTptS1OgwGg8F4TdbLLASfD8ajnEcAAFnifSziTGGQowGNHKBB/BNMtm0J\nSrxVx5p+OERHR7/RSVSsR45RJXx9fXH37l38/fff5cZxc3PD6dOn4e3tjY0bNypRu3cf1iPHYDBq\niycvnyDkfAgevyw6iUfnWS4cfzqNT1+8XgjF80CTJoChIaIlErhNnlyH2n54VLedZI4cg8GodVid\nYzDqlicvnyD4fDCevCzaPkn3aS6GXyBcPnURFllZOKStjfz69aGmoQEPbW3ctbND1xIr2Bm1Dxta\nZTAYjFqETdNQPszmNUMZJy7rJUacJ8gKNAGZDAHGxrg+aBBi6tXD/fbtEZCbCziwrUdqG7aPHIPB\nYDAYjAp5nPMYweeDkZVbtO1QkRMHmJAmACBeRweqw4cjJicHzzMzwenpoaGvL66lpaFrXSrOUBg2\ntMpgMGodVucYDOVT2onTf5qL4ecJxoVFThzU1PCtmRliW7YU0mjzPNro60N6+TImV+PsZ0b1YUOr\nDAaDwWAwAACPch6Jnbislxh+rvA/J05dHacGDMBVlf+On9TieTTT1QUHgO0i9+7AHDkGg8FQADZf\nS/kwm1eP0k6cwZOXGHGOYExaAABSV8eR/v0Rqa4OGxsbvIqNha6KCgwvX4YmzyM3Lg7dnJ3rsggf\nBGyOHIPBYDAYDBEPXzxEyIUQPM19CgAweJyD4RcAI7x24jQ08Gffvjjz+gxm4wYN4KmhAZ3kZCSm\npECmr49uLVvCocSRi4y3GzZHjsFg1DqszjEYtc/DFw8RfD4Yz/KeAQCkj19i6AUSnLgCDQ1E9O2L\nSyXPa9bWxkATE6jxbICurmFz5BjvFP7+/rC3txd+BwcHQ01NrcbzqSm5Pj4+6N69ew1o9OYQEVq1\naoWdO3cCAAoKCtC4cWP89ddfdawZg8GoKx68eCB24h7lYNj5QsGJy9fSwvbPPxc5cU10dOAlkzEn\n7h2H3T1GnVHyoHUvLy/cu3evDrWpmKoeDK+qqorQ0NBa0WXr1q3Izc3FF198AQBQUVHB7NmzMX36\n9FrJj1EEm6+lfJjNFePBiwcIOR8iOHGGD3Mw7ALBkNMGALzU0kL4Z5/huqamkKa1nh76mZhApUS7\nxuytXNgcuVokJSEBSYcOgc/PR6GaGmw9PGD5hpsj1obMd52SXciamprQLNHIvG0QUZW6vGtzKPGH\nH37AqFGjRGH9+/fHhAkTEBUVBXd391rJl8FgvH0U98Q9z3sOADB88ALDLgJSvsiJy9bRQXjv3kgr\n0b52lkjQVSKp0p9TxtsL65ErRUpCAhKDg9H1/n24PXmCrvfvIzE4GCkJCXUu083NDWPGjMGCBQtg\nbm4OIyMjjBgxAtnZ2QDkD/+Fh4eDL9FtXjykuXPnTtjZ2UFHRwf9+/fH8+fPsXPnTjg4OEBfXx9f\nfPEFnj59KqQrlr1q1SpYWFhAR0cHAwcOxOPHRWf2RUdHQ1VVFXfu3BHlHxoaColEgpycnArLVnoI\ntPj3yZMn0bJlS+jo6KB169aIjY0VpRszZgzs7Oygra0NW1tbzJ49G3l5eRXmtW3bNtja2kJLSwud\nO3fG/v37wfM8Tp48WWG6kly5cgU9e/aEVCqFrq4unJycEB4eDgCwsrJCQUEBfH19wfM8VF4v73/6\n9Cl8fX1hbm4OTU1NNGzYEFOnThVkvnz5EuPGjYNEIoGhoSHGjx+PmTNnioagr1+/jri4OPTt21ek\nj5aWFj7++GNBB0bN4+bmVtcqfHAwm1fM/ez7IifOqJQTl6Wnh029eomcuB6Ghugmlcp14pi9lUtN\n2Zv1yJUi6dAhdNPQAEp0eXYDcOTiRVi2aVM9madPo9uLF6Kwbm5uOHL4cJV75Xbt2oWRI0ciJiYG\nKSkp8PLygqWlJebPnw8ACv3DSktLQ2hoKCIiIvDo0SMMGDAA/fr1g5qaGnbt2oWnT5+if//+WLx4\nMZYuXSqkO336NHR0dPD333/jwYMHGDNmDEaNGoXdu3fDzc0N9vb22LRpE+bNmyekCQoKwpAhQ6Cl\npVWlcgJAYWEhZs2ahTVr1sDY2BhTpkzBwIEDcePGDaioqICIYGpqim3btsHU1BQXLlzA2LFjoaam\nBn9/f7ky4+LiMHToUMyePRvDhg3D1atXMXny5Cr/M/X29kazZs1w6tQpaGpq4tq1aygoKDp4OjY2\nFubm5li5ciUGDRokpJkzZw7OnTuHvXv3wtzcHKmpqbh69apwfebMmdi9ezfCwsLg4OCAoKAgrFu3\nDqampkKc6OhoGBsbw8rKqoxO7dq1w5o1a6pUDgaD8W5S7MRl5xf9kTd+8AJDLgBSlSIn7oG+PkI/\n/hhPX7e9HMfhUyMjtNTTqzOdGbUDc+RKwefnyw9//ZKulszCQvnhlfQcycPKygorVqwAADRq1AiD\nBg3CoUOHBEdOkeG83NxchISEwNDQEAAwcOBArF+/HhkZGTAyMgJQNGft8OHDonREhLCwMOi9bggC\nAwPRs2dP3Lx5EzY2Nvjyyy+xevVqzJ07FxzH4dq1azhx4gTWrl1b5XIW5/fDDz+gefPmAIp6E9u3\nb4+bN2/C3t4eHMdh4cKFQvyGDRsiMTERP/30U7mO3MqVK9GpUyfBXvb29khPT8e4ceOqpNvt27cx\ndepUODo6AoDIsTI2NgYAGBgYQCaTidK0aNECbV7/Iahfvz4++ugjAEB2djbWr1+PtWvX4tPXu6l/\n9913iI6ORlZWliDj+vXrsLS0lKuTlZUVUlJS8OrVK6iqsqpd00RHR7MeCyXDbC6fzOxMhJwP+c+J\nu5+NoZc4SF47cfckEoT36IEXr504FY5DfxMTOOnoVCiX2Vu51JS93+uhVX9//ypPJiwsZ4VjYYnd\nr6tKYTkrggrVq7Z3NsdxcHFxEYWZm5sjIyOjSnIsLCwEJw4ATE1NYWZmJjhxxWGZmZmidE5OToIT\nBwAdOnQAAKFXafjw4cjMzERkZCQA4JdffkHr1q3L6Kwopctrbm4OAKLyBgUFoV27djAzM4Oenh5m\nzZqF27dvlyszPj4e7du3F4WV/q0I3377LUaPHg13d3cEBATg3LlzlaYZP348du3ahaZNm2Ly5Mk4\ncOCA4HgnJSUhNzdXsGkxHTt2FDnnWVlZ0NXVlStfX18fAPDkyZMql4fBYLwblHbiTDJfO3Gvh1OT\nDQ0RUsKJU+d5DDY1rdSJY9Qd0dHR5XY+KMJ7/be9Ooax9fDA4eBgdCvhJR/OzYWdjw9QzcUJtgkJ\nRTJLLPs+nJsLu27dqixLvZTzx3EcCl/3+PE8X6ZHLl9OD2Pp7Tg4jpMbVliqJ7Gy3j4jIyMMGDAA\nQUFB6NatG0JDQ7F48eKKC1QBPM+LhjyLvxfrtXPnTkycOBHLli1Dly5doK+vjx07dmD27NkVyq2J\nCb5z5szBkCFDcODAARw5cgSLFy/GtGnTsGDBgnLT9OjRA7dv30ZkZCSio6MxdOhQNG3atEzPZ0VI\nJBI8e/ZM7rXinjuJRFK1wjAUgvVUKB9mczEZzzMQciEEL/KLpurIMrIx+PJ/PXHXjYywo1s3vHrt\nxGmpqGCITIb6Ci4kY/ZWLsX2dnNzg5ubGwICAqol573ukasOlg4OsPPxwRGZDNESCY7IZLDz8Xmj\nFaa1IVMeMpmszBYeZ8+erTH58fHxIieieHGAk5OTEDZ27Fj88ccfWL9+PV6+fAlvb+8ay780R48e\nRYsWLTB58mS0aNECtra2uHXrVoVpnJycyixq+OeffxTKr7QDaG1tjXHjxmHnzp0ICAjATz/9JFxT\nV1cX5syVRCqVwsvLC+vXr8f+/fsRExOD+Ph42NraQl1dHSdOnBDFP3HihChfe3t7pKSkyNUvJSUF\nVr/46b0AACAASURBVFZWbFiVwXgPSX+eLnLiTEs5cRdlMvxawonTVVGBj5mZwk4c492FtfhysHRw\nqHEnqyZkVrYFhoeHB5YvX45169ahZ8+eOHLkiLBpbE3AcRyGDx+OhQsX4uHDh5gwYQL69OkDmxJH\nuXTs2BEODg743//+hxEjRkDndXd+t27d0K5duzfqoSuNo6MjNm3ahL1798LZ2Rn79u3Dnj17Kkzz\nzTffoE2bNvDz88OQIUNw7do1rFy5UihfSdmTJk3ChAkThLBi2z9//hzTp0/HgAEDYGVlhSdPnuDA\ngQNwLnE2obW1NY4cOYKePXtCXV0dxsbGmD17Nlq3bg0nJyfwPI/w8HDo6emhYcOG0NHRwVdffYU5\nc+bA1NQUjRo1wsaNG3H9+nXRYocuXbrg4cOHSE5OLrPg4Z9//mH/qGsRNn9I+TCbF5H+PB2hF0L/\nc+LSn2PwFQ4Gr52402Zm+NPVFXjtxEnV1DDc1BTSKm6GzuytXNgcuQ8QeZvSlgzz8PDAwoULsXjx\nYjRv3hzR0dGYN29emeHJimRUFNa2bVt06tQJ3bt3h6enJ1xcXLBp06Yyeo4ePRp5eXn48ssvhbCb\nN28iPT290jwr+l06bOzYsRg2bBh8fX3RsmVLnDlzBv7+/hXKadmyJbZs2YItW7agWbNmWLZsmTAc\nWnIfu+vXr+Phw4dy9VVTU8OTJ08watQoODk54eOPP4a5uTm2bt0qxF+xYgXi4uJgbW0tOGJaWlqY\nN28eWrdujTZt2uDy5cv466+/hHmHS5cuxeeff45hw4ahXbt2ePr0KSZMmCBy3h0cHNC6dWvs3r1b\nVMacnBxERkZi6NChZWzGYDDeXdKepSHk/H89cWbpzzHkCg8DFR0QgJh69UROnExdHSPNzKrsxDHe\nXdhZqwyF8PHxwd27d3Hw4MFK406bNg2HDx9GXFycEjR7c0JDQzFy5Eg8evRIWDDwtuDv748tW7bg\nxo0bQtjWrVuxaNEiXLlyRQgLCwvDd999h4sXL9aFmpXC6hyDUXXSnqUh9EIocl4V7cNpnvYc3lc4\n6KsWOXGR9evjn44dgdd/QutraGCIqSm03mBxHqPuYGetMuqcrKwsnDlzBkFBQZgyZUpdq1Mu33//\nPeLi4nDr1i3s2LEDM2bMwMCBA986J648Bg8eDC0tLdFZq4sXL8by5cvrWDMGg1FT3Ht2T+TE1bv3\nTHDiCgH8bmkpcuJstbQw3MyMOXEfIMyRYyiEImeN9unTB126dEG/fv3e6iG+S5cu4dNPP0Xjxo2F\njYHlDRG/DZRn99jYWNFZq/Hx8fj444+Vrd4HBTuHUvl8qDYv7cRZ3H0Gr6s89FV18IrjsMPaGufb\ntxecOCcdHXjLZFAvZ6srRflQ7V1XsLNWGUpl8+bNlcZ5VxqBkJCQulZBYfz8/ODn51fXajAYDCVx\n9+ldhF0Mw8tXLwEA9e88w6B4HnpqOsjlOPxqbY1bbdsCr7ezaqGnh0+NjMCzc1M/WNgcOQaDUeuw\nOsdgVE4ZJy71KQZdU4Gemg5e8Dy22NjgbuvWghPXwcAA3cs5N5Xx7lHddlLhHrnIyEicP38ez58/\nF2VafNQRg8FgMBiM6nHn6R2EXQhDbkEuAKDB7SwMvK4GPTVtPFVRQZiNDe63aiU4cd2kUnQyMGBO\nHEOxOXITJ07EsGHDcPbsWdy5cwd37txBamoqUlNTa1s/BoPBeCt4V6YOvE98KDZPzUoVOXENb2dh\nYIIq9FS18UhVFZvs7HD/dU8cx3HoZWSEzhJJjTtxH4q93xaUOkduy5YtuHjxIho0aFAjmTIYDAaD\nwShy4sIvhgtOnGVKFr64rgpdNR2kq6sj3MYGz1u0ANTVwXMc+hkbo0k55y0zPkwUmiPXqFEjxMbG\nvjPbMwBsjhyD8TbB6hyDUZbbWbcRfjEceQV5AACr5CwMuKEGXTVtpGpoYIuNDV42bw6oq0OV4zBI\nJoO9tnYda82oLarbTpbryN28eVP4fvDgQezfvx8zZsyAmZmZKF7J45neJpgjx2C8PbA6x2CIKe3E\nWd96gv6J6tBV00ailha2W1sjv3lzQE0NGjyPwaamsGTnpr7X1PiGwHZ2dsJn3Lhx2LdvHzp16iQK\nt7e3fyOlGcojOTkZPM+XOTD+QyE6Oho8z+Pevf9n777DoyrTxo9/ZzLpddIbpEISQg1BmoaqgIIs\noNJEIthe3V3Xjr5Lta2+q/5cdXWtkaqCILIqSklognRIgUBIIxXSe5s5vz+GTDKhTcqUhOdzXbnk\nnJmc88ztZHLnKfeTB4h4tJWXl4ebmxu5ubkAZGRk4ObmxuXLl03cMvMh5g8ZX0+NeVZZlm4Sl16q\nTeKS7ezYEBysTeLsLSyI9fY2ShLXU+Ntrroq3tdN5NRq9U2/VCpVlzRCMLzevXtTUFDAbbfdZpL7\nv/baawQFBbX7+3JycpDL5ezdu7dL22PqeJib5cuXM3v2bPz8/AAICgpixowZYlW6IHSxrLIs1iWu\n0yZxIell3HcliTvm4MCm4GBUgwaBpSXOCgWLfHzwubJSVRCuRa/FDrm5udja2uLq6qo9V1JSQl1d\nHb6+vgZrnKmkpqezMzmZRsASmBgZSVgnh5ANcc32kMvleHp6Gu1+Xa2rh+W6Kh4NDQ1YWVl1QYuu\nplarAU1bDamkpIS1a9de1Tu5aNEiJk2axJtvvomDmFzN2LFjTd2EW05Pi3lmWSbrTq+jUd0IQOiF\nUmamW2NnZcd+Z2d29u4NAweCQoG7pSULvL1xVhivbn9Pi7e566p46/UbYvr06eTk5Oicy8nJYcaM\nGV3SCHOSmp5O3PHjXO7fn7L+/bncvz9xx4+T2mrOoCmvuX//fkaPHo2TkxNOTk4MHjyY3377DYBL\nly7x8MMP4+3tja2tLeHh4dodGdoOJTYfr1u3jgkTJmBnZ0dISAjffvut9l5jx47l8ccf17m/JEmE\nhITw+uuvX9W2N954g5CQEGxsbPD09GTy5MnU1dURFxfHsmXLyMrKQi6XI5fLtT0969evZ/jw4bi4\nuODh4cHUqVN1Nojv3bs3AOPGjUMul2vnZObk5DBr1iw8PDywtbUlJCSEf/7zn3rH8Xrx2LhxI1On\nTsXe3p6QkJCrdoGQy+V88MEHzJs3DxcXFxYuXAho5pGOHj0aOzs7/P39WbRoESUlJTpxe+WVV/Dw\n8MDJyYkHH3yQ999/H0tLS+1zVqxYQZ8+ffjuu+8IDw/H2tqa8+fPU1VVxdNPP42/vz/29vZERUWx\nZcsWvWKvT6w2btyIl5cXQ4YM0bnmyJEjsbe3v+pegiC0X0Zphm4Sl1bCzHRrbC3t2KFU6iRxvtbW\nLPLxMWoSJ3Rfer1Lzp07x8CBA3XODRgwgDNnzhikUaa0MzkZ66FDSSgrazkZEsLpvXsZ1sGaPYf3\n7qVm0CBodc2xQ4eyKympXb1yTU1N3HvvvSxatIjVq1cDmn1D7e3tqa2tZcyYMdjb27N+/XpCQkK4\ncOECRUVFN7zmiy++yD//+U8++eQTVq9ezfz58wkLC2Pw4ME88cQTPPbYY7z77rvY29sDsHv3brKz\ns1m8eLHOdTZv3sxbb73F+vXrGTRoEMXFxezZsweAOXPmkJqayrp16zh69CiA9noNDQ0sW7aMfv36\nUVFRwbJly7jnnntITk7G0tKS48ePExUVxebNmxk1ahQWVzaEfvLJJ6mrq2PXrl24uLiQnp5OYWGh\n3rG8niVLlvDWW2/xr3/9iy+++IJHHnmEUaNG6cwHXblyJatWreL1119HrVaze/du/vSnP/H222+z\nevVqSktLefHFF5k5c6Z2DsR7773HBx98wCeffMKIESP48ccfWbVq1VV1oPLy8vj4449Zs2YNSqUS\nb29vpk2bhkwm47vvvsPX15cdO3YwZ84cfvnlF8aPH3/D2F8vVgUFBdrH9+zZw/Dhw6+KhUwmY/jw\n4ezevZsFCxZ0OrbdXUJCguixMLKeEvOM0gzWJ67XJnF9zpcwI9MGG0s7/uvmxjE/PxgwABQKAm1s\nmOvlhbWBe+KvpafEu7voqnjrlch5enpy/vx5nV9mFy5cwN3dvdMNaK+KigomTpzImTNn+OOPP+jX\nr1+XXr/xOudVnSi8qL7O9za08zqVlZWUlZUxbdo0QkJCALT//eKLL8jMzOTChQva4e6AgICbXvOR\nRx5h7ty5ALz66qvs3r2bd999l9WrVzNjxgz++te/8s0332gTt88//5ypU6detXo5KysLb29vJk2a\nhEKhwN/fn0GDBmkft7e3x8LC4qrhzNjYWJ3jr776Cnd3d44ePcrIkSO17zFXV1ed783OzmbGjBna\nPzCae+466y9/+Qv33XefNh4ffPAB8fHxOu/9GTNm8OSTT2qPFy9ezNNPP81TTz2lPRcXF0dgYCCn\nT59m4MCBvPPOOzz77LPMnz8fgGeeeYbDhw+zadMmnfvX1dWxZs0a/P39Ac0P+qFDhygsLNSW/3n0\n0Uc5ePAgH3zwAePHj79p7G8Wq3PnzjFu3LhrxiMgIIBjx461L4iCIGill6azIXGDNonre66YP2XZ\nYm1px/ceHiT7+GiTuDA7O+7z8MDSBEmc0H3p9W5ZtGgRs2bNYtu2baSkpPDjjz8ya9asq3pljMHO\nzo6ff/6Z++67zyDlDCyvc96iE/eSX+d72zuzSqlU8sgjjzBp0iTuvvtu3nrrLc6dOwfAsWPHiIyM\nbPecxZEjR+ocjx49muTkZACsra2JjY3ls88+A6C4uJgffviBRx999KrrzJ49m8bGRgICAnj44YdZ\nu3atznZu13Py5ElmzJhBcHAwTk5O2uQzKyvrht/3t7/9jTfeeIMRI0awZMkS9u3bp9frvZnBgwdr\n/908j+7SpUs6z2m7QOLIkSO89957ODo6ar8iIyORyWScP3+e8vJy8vPzGTFihM73tT0G8PLy0iZx\nzdduaGjAz89P5/rr1q0jLS0NuHnsbxariooKHB0drxkPJycnylr3Tt/CRE+F8XX3mKeXpuv0xIWn\napI4hZU9G7y8NEncleHUgQ4OPODpadIkrrvHu7vpqnjr1SO3ZMkSLC0tef7558nJyaFXr1488sgj\nPPvss13SiPZQKBQG7QmcGBlJ3LFjjB06VHuu/tgxYmNiCOvAqkuAVEki7vhxrNtcc0JUVLuv9emn\nn/L000/z22+/sWPHDpYuXcqHH37YZXW62l7j8ccf55133iExMZFdu3bh6enJlClTrvo+X19fzp49\nS3x8PLt37+bVV1/lpZde4o8//tBJTFqrqanhrrvuIiYmhri4OLy8vJAkicjISBoabtxfGRsby+TJ\nk9m+fTvx8fFMmTKFGTNmsGbNmo6/eLhq4YJMJtMuOmjWPCzcTJIklixZcs3hRy8vL5qamrTXupm2\n11ar1Tg7O2uHpK/V1pvF/maxcnFxobKy8prtKS8vR6lU3rTdgiDoulBygQ1JG2hSa37+w88WMf2i\nPVjbs8bTk4teXpqeOAsLhjs5MdnVVeybKnSIXqm/XC7nhRdeIDU1lerqas6ePcvzzz9v8NV0phAW\nHExsVBSeSUm4JCXhmZREbFRUp1aYdvU1IyMjeeaZZ/j5559ZvHgxn376KUOHDiUlJUVbB0xfBw8e\n1Dn+/fffiYyM1B6HhIQwfvx4PvvsM7744gsWLVp03Q8bKysrJk2axFtvvUViYiI1NTVs3bpV+1jb\ncjVnzpyhqKiI119/nZiYGMLCwigpKdFJJpuTlWuVuvH29iY2Npavv/6azz//nHXr1unVC9jVoqOj\nSUpKIjg4+Kove3t7nJ2d8fX1vWpV6KFDh2567WHDhlFWVkZtbe1V126dIN8o9nDjWPXp04fMzMxr\n3j8rK4u+fft2ICo9j6ixZXzdNeZpJWk6SVy/FE0Sp7JxIM7bWyeJG+viYjZJXHeNd3dl1L1WQTMp\nPTU1laKiIp1ftOPHj+/QjT/88EPi4uJISkpi7ty52tWVoCmHsHjxYnbs2IG7uztvvvmmdh5Xa4Z6\n44cFB3d5aZCuuOaFCxf49NNPuffee/H39ycvL4+9e/cSHR3N3Llzefvtt7n33nt5++23CQ4OJj09\nneLiYh544IHrXvPLL78kPDycoUOHsnbtWg4dOsRHH32k85zHH3+c+fPno1areeSRRwDYsmULL7/8\nMvHx8fj4+PDFF18gSRLDhg3DxcWFXbt2UVlZqZ3DGBQUREFBAYcOHSI0NBR7e3sCAgKwtrbmX//6\nF88++yyZmZksWbJE5/+ru7s7Dg4O/Prrr0RERGBtbY1SqeTPf/4z99xzD3379qWuro7NmzfTu3dv\nbZmMl19+mSNHjrBz585OxVyfXs5Vq1Zx11138dxzz7FgwQIcHR05f/48mzZt4sMPP8TGxobnnnuO\n5cuXEx4ezrBhw/jpp5/YsWPHTf8YGj9+PBMnTmTmzJm8/fbbDBgwgNLSUn7//XdsbW155JFHbhr7\nm8VqzJgx11yFLEkShw8f5u233+5A5ATh1pRWksY3Sd+0SuIuMy3XgTpbR9Z4eVHi4QH9+4OFBZNd\nXRnh7GziFgvdnqSHffv2Sd7e3pJSqZTkcrmkVColCwsLKSgoSJ9vv6bNmzdLP/zwg/Q///M/Umxs\nrM5jc+bMkebMmSNVV1dL+/fvl5ydnaXk5GSd58TGxkpJSUnXvf6NXpqeL9vs5OfnSzNnzpT8/f0l\na2trydfXV3rsscekiooKSZIkqaCgQHrooYckd3d3ycbGRoqIiJC+/vprSZIkKSMjQ5LL5dKBAwe0\nxzKZTFq7dq00duxYycbGRgoODpY2bNhw1X0bGxslT09PaerUqdpzX331lSSXy6WsrCxJkjT/P0eN\nGiUplUrJzs5OGjBggPTll1/qXGPevHmSq6urJJPJpJUrV0qSJEmbNm2S+vTpI9nY2EhRUVHSnj17\nJIVCoW23JEnS6tWrpaCgIEmhUGjfc0899ZTUt29fydbWVnJzc5OmTp0qpaSkaL8nNjZW5/0ZHx8v\nyeVyKTc397rxaH3cLDQ0VNtWSZIkmUwmrVu37qoY7du3T5o4caLk6Ogo2dvbSxEREdIzzzwjNTU1\nSZIkSWq1Wnr55Zcld3d3ycHBQZo7d670xhtvSI6OjtprrFixQurTp89V166trZWWLFkiBQUFSVZW\nVpK3t7c0ZcoUKT4+Xq/Y3yxWRUVFko2NjXTs2DGd++7fv1+yt7eXKisrr2pTe3XXnzlBaI9zReek\nVQmrpOXxy6Xlu5dJGz96Sqp55UWp8LXXpH9+9pm0/IcfpOVpadLKjAzpZBf8XAk9S0c/J6+712pr\n0dHRzJs3j2effRalUklpaSmrVq3C1taWF154oVOJ5NKlS8nJydH2yFVXV+Pq6kpycjKhoaEALFy4\nEF9fX958800A7r77bk6dOkVAQACPP/64tpZXa2Kv1RvLzMwkODiY/fv3M2rUqBs+t7i4mF69evHt\nt98ybdo0I7Ww51u0aBGJiYkcOXLE1E3hsccew8LCgo8//lh7bvHixdja2vLhhx92+vriZ07o6c4V\nn+PbpG9RSSqQJPonFzG1wJFiOyfWenlR6+4O/fujsLDgPg8PwtvMhxWEjn5O6jW0ev78ef72t78B\nLUNNS5YsITAwsNOJXNtGnzt3DoVCoU3iAAYNGqQzlvzzzz/rde3Y2FgCAwMBzYTuwYMHi1U57dDU\n1ERRURErVqzA399fJHGdkJ+fz+bNmxk3bhwWFhZs27aNNWvWXDWMbSorV66kf//+/P3vf8fPz4+M\njAy2bt3apbUiW9dMav557k7HJ0+e1H4OmkN7boXj5nPm0p7rHa/Zuob4jHh6D+4NkoRsy0mcSu3J\nj+zFBk9PzuXng40NfRUK5np6kvXHHxSYUfu7W7x7yvHJkycpKyu77hxlfenVI9e7d29OnTqFUqmk\nX79+bNy4EXd3d/r27Ut5eXmnGtC2R27fvn088MAD5Ofna5/z2WefsX79euLj4/W+ruiRu7HMzExC\nQkLYt2/fdXvkEhISGD9+PMHBwaxZs+aqUiWC/i5dusTs2bM5ffo0dXV19OnTh7/85S8mKeFjCj3h\nZy5BFEs1uu4Q89SiVL5L/k7bEzco8TJTLjmR6eTKRg8PVG5uEBmJnaUl87288DPjfVO7Q7x7krbx\nNmiP3IwZM/j555+ZP38+ixYtYvz48SgUCm3h1M5o22gHBwcqKip0zpWXl1+3zpXQMYGBgddcCdra\n2LFjryq9IXSMp6dnu/4QEcyP+AVnfOYe87NFZ9mYvLEliTt9iSmXnTnr4s5WNzckd3fo1w8nKysW\neHnhYWWYfZm7irnHu6fpqnjrlci9//772n8///zzDB8+nMrKSiZPntzpBrRdedq3b1+amppIS0vT\nDq+eOnWK/v37d/pegiAIgtAVzhad5bvk71BLapAkhpy6xKQiZ066erLd1RWuJHGuVlY85OWFi+X1\nys0LQue0qxBcdnY2Bw8eJCAggLvvvrtTdeRUKhV1dXU0NTWhUqmor69HpVJhb2/PzJkzWbZsGTU1\nNezfv59t27Z1aK/HFStW6Iz9C4IgdJT4LDE+c435mctndJO4k4VMKnLhoLu3ThLnbW3NIm/vbpPE\nmWu8e6rmeCckJLBixYoOX0evTCw/P58xY8YQGhrKzJkzCQ0NJSYmhry8vA7f+NVXX8XOzo633nqL\ntWvXYmtrq61l9e9//5va2lo8PT158MEH+eSTT4iIiGj3PVasWCG6igVBEIQuk3I5hY0pG7VJXNTJ\nQiYVK9nt6cMeFxfw8IB+/ehta0ustzcOCr3LtQq3qLFjx3YqkdNrscP06dMJCAjgzTffxN7enurq\nal555RUyMjL48ccfO3xzQxKLHQTBfIifOaEnSL6UzPdnvtcmcUOPFzCh1JXt3n6cdnDQJHEREYTa\n2THbxPumCt1PRz8n9Urk3NzcyM/P19mHsr6+Hl9fX4qLi9t9U2O4UUBcXV0pLS01cosE4dalVCop\nKSkxdTMEocOuSuKO5TOu3J0fffw5Z2cHnp4QHk5/BwdmeHhgYQZbbgndS0cTOb3+XHB1dSUlJUXn\n3NmzZ81+M+3rzZFr3s9TfHXtV3x8vMnbcCt9dad494QkTswfMj5ziXnSpSSdJG7Y0XxiKjzY6Ndb\nk8R5eUF4ONFOTszsxkmcucT7VtFVc+T0Grx/8cUXufPOO1m8eDEBAQFkZmby1Vdf8eqrr3b4xsbQ\nmcAIgiAIQmJhIpvPbEZCQqaWiD6Wx6gqb77x8yff2lqTxIWFcYdSyXgXF4PtAS70XGPHjmXs2LGs\nXLmyQ9+v19AqwO7du1m3bh35+fn4+voyd+5cJkyY0KGbGoOYkyMIgiB0RtskbtjRfIbVePOtXy+K\nLC3B2xv69uVONzdGOzuburlCN2ewOXJNTU2EhYWRkpKCtRlXpG5LJHKCIAhCR50uPM2WM1u0Sdxt\nh3MZ1ODHt769KFcowMcHWd++THN3J0oUrBe6gMHmyCkUCuRyObW1tR1qmHDrEPMrjEvE27hEvI3P\nVDE/VXBKJ4kbfjiXfo3+rPPrrU3iLMLCuN/Ts0clceI9blxdFW+95sg988wzzJ49m5dffplevXrp\nzAEIDg7ukoYIgiAIgqmdLDjJ1rNbNUmcSs2Iw/kEq3uz3s+ferkcfH2x7NuXOV5ehNjamrq5gqDf\nHLnr7eAgk8luul+nqchkMpYvX66dRCgIgiAIN9I2iRv5Rx6+BPKDjx9NMhn4+WHTty/zvbzoZWNj\n6uZ2mdTULHbuvEBjoxxLSzUTJ4YQFhZg6mbdMhISEkhISGDlypWGmSPXXYk5coIgCIK+TuSf4MfU\nH7VJ3KhDubhZhPJfL2/UV5I4h7AwFnh749Wqpmp3l5qaRVxcGjU1E5DLwdkZ6ut3ERsbKpI5IzNo\nHblmubm5HDlyhNzc3HbfSOj5xPwK4xLxNi4Rb+MzVsyP5x/XJnFylZrRh3JxsOzLtuYkzt8fZXg4\ni3x8elQSB7Bz5wVqaiaQmAh79iRQVgbW1hPYteuCqZvW43XV+1uvRC47O5s77riDgIAA7rnnHgIC\nArjjjjvIysrqkkYIgiAIgikcyzumk8SNOpiL3CacXz29kGQy6NULzytJnKulpamb2+UKC+UkJoJa\nrfk6dw4kCRoaxPZi3YVe/6ceeughhg4dSnl5OZcuXaKsrIzo6GgWLlxo6PYJ3YiYi2hcIt7GJeJt\nfIaO+bG8Y2w7tw1Ak8T9nkO9fSR73Tw0T+jdG7+ICGJ9fHBU6LU2sFvJzoaTJ9Wo1ZpjT8+x9O8P\nMhlYWalN27hbQFe9v/WaI+fk5ERRUZHOXqsNDQ24ublRWVnZJQ3pamKxgyAIgnA9R/OO8t9z/wVA\n3qRi1MFcyp0GkujsonlCQADB4eHM8fLC6joL/rqzixdhzRrIy8vi5Mk07OwmMHgw2NmJOXLG1tnF\nDnq9O0eMGMHhw4d1zh05coSRI0e2+4bGtGLFCpHEGZGYQ2RcIt7GJeJtfIaK+ZHcI7pJ3O95FLoM\n1kniIvr1Y14PTeJyc2HtWmhoAHf3AEaODGXChN3U1Pw/PD13iyTOSJrf32PHjjX8XqvBwcHcfffd\nTJ06FX9/fy5evMjPP//MvHnzWLp0KaDpAVu1alWHGyIIgiAIhnY49zA/n/8Z0CRxI37P46J7FFl2\n9ponBAYypH9/prm5Ie+B+6bm5Wl64urrNcd2dvDkkwF4egaQkCAXnR/dkF5Dq7GxsS3f0Gp5bHNh\nYEmSkMlkfPXVV4ZpZQeI8iOCIAhCa62TOItGFcMO5pPpGUWBjZ3mCYGBjBw4kLuUSp3C9z1Ffj6s\nXg3NGzXZ2cHCheDlZdp2CRoG22u1uxKJnCAIgtDsj5w/+CXtF0CTxEUfKiDNcyjF1lcK+wYFMX7Q\nIO5wdu6RSVxBAXz9dUsSZ2urSeK8vU3bLqGFwevInTt3jtdee42nnnqK119/nXPnzrX7ZkLPmrOD\nTwAAIABJREFUJuYQGZeIt3GJeBtfV8X8UM6hliSuoYkhhy6R4hWtTeJkwcHcM2QIMS4uPTKJu3RJ\ntyfOxgYeeujqJE68x43LqHXk1q9fT1RUFImJidjb23P69GmioqJYt25dlzRCEARBEAzh4MWDbE/b\nDmiSuIF/FJHiPZRKK2sA5CEhzIyKYpiTkymbaTCXL2t64mpqNMfNSZyPj2nbJXQdvYZWg4KC+Prr\nr4mJidGe27dvHwsWLCAzM9OQ7eswMbQqCIJwa/v94u/8duE3ABQNTUQcKSHVewgNFprCvoqQEB4Y\nOpS+dnambKbBFBVBXBxUVWmOra1hwQLw9zdps4Tr6Gjeoteq1aqqqqtKjYwYMYLq6up239CYmsuP\niFU4giAIt5a2SVzo0TJSvKNQWWh+7VmHhjIvOpoAGxtTNtNgios1PXHNSZyVFTz4oEjizFFzHbmO\n0mto9dlnn+Xll1+m9soAe01NDa+88grPPPNMh29sDKKOnHGJ+RXGJeJtXCLextfRmB/IPtCSxNU3\nEnCsklTvIdokzr5PH2KHDeuxSVxJiSaJa67X35zE9ep14+8T73HjMmoduY8++ojCwkLef/99lEol\npaWlAHh7e/Pxxx8Dmi7B7OzsDjdEEARBEDprf/Z+dqbvBDRJnN/JWtK8BiG7UtjXuW9fHho2DLce\nuG8qQGmpJomrqNAcW1rCvHnQu7dp2yUYjl5z5PTN0s2p90vMkRMEQbi17Mvax66MXQBY1jXifrqB\nXI8I5DJNEuceFsaCYcNw7oH7pgKUlWnmxJWVaY4VCpg/H4KCTNosQU+ijlwbIpETBEG4dezN2svu\njN0AKGobcEpWU+TWV5vE+YSH8+CwYdhbWJiymQZTXq5J4q4MmKFQwNy5EBJi0mYJ7WDQxQ4AJ06c\nYN++fRQXF+vcSGzLJTRLSEgwq17Znk7E27hEvI1P35jvydxDfGY8ABa1DdickekkcQEREcwbNgzr\nHrhvKmiGUb/+uiWJs7CAOXPan8SJ97hxdVW89XpXf/rpp9x+++3Ex8fzj3/8g8TERN555x3S0tI6\n3QBBEARB6KiEzARtEqeobcAiVUGFMkSbxPWNjOTBHpzEVVZqkriSEs2xhQXMng2hoaZtl2A8eg2t\nhoSE8NVXXxETE6Nd7PDLL7+wYcMGVq9ebYx2tpsYWhUEQejZEjITSMhMAMCithHVeSvUjr20SdzA\n/v2ZPnQoFj1wtwbQlBaJi9PUiwOQyzVJXFiYSZsldJBB58g5OTlRcWUJjJubG5cuXUIul+Pq6qpd\nwWpuZDIZy5cvF3XkBEEQehhJkkjITGBP1h4AZDWNNKbbILf30yRxMhm3DRjAlCFDeuSWWwDV1Zok\n7vJlzbFcDvffDxERJm2W0AHNdeRWrlxpuL1W/f39ycjIAKBPnz5s3bqVffv2YW1t3e4bGpOoI2dc\nogaRcYl4G5eIt/FdK+aSJBGfGa9N4qhuojbDDgt7f20SN2bgwB6fxH39tW4SN2tW55M48R43LqPW\nkXvhhRc4c+YMQUFBLF++nFmzZtHQ0MC//vWvDt9YEARBENpDkiR2Z+xmX/Y+ANRVTdRkO2Bv56VJ\n2mQyJg8ezIhBg0zcUsOpqYHVq+HSJc2xTAYzZ0JkpGnbJZhOh8qP1NfX09DQgKOjoyHa1CXEHDlB\nEISeQ5IkdmXsYn/2fgAaq1TUXHTAycYTmUyGDJgeFcXggQNN21ADqq3V9MQVFGiOZTKYMQN68Eu+\npYg6cm2IRE4QBKFnaJvE1VdLVF10wNXaHZlMhgVw/7BhhPfgbqm6Ok1PXF6e5lgmg+nTYfBg07ZL\n6DodzVt65npswSTE/ArjEvE2LhFv40tISECSJHam79QmcTVVUJnjqE3irID5t93W45O4NWtakjiA\ne+/t+iROvMeNq6vi3TP3KREEQRC6PUmS2JG+g98v/g5AZZWc2lx7PKxckclk2EoSD44ciV94uIlb\najj19bB2LeTmtpybNg2GDDFdmwTzIoZWBUEQBLOSmpbKjqM7SLycyMXyiwQHB2Ph5E1Dri2eV5I4\nR0nioVGj8OjBRdMaGjRJXHZ2y7l77oFhw0zXJsFwDDq06urqes3znp6e7b6hIAiCIFxPaloqcfFx\nHLI6RKpjKjX+NRy7UEh5uoU2iXNVqVh8++09Polbt043iZsyRSRxwtX0SuQaGxuveU6lUnV5g4Tu\nS8yvMC4Rb+MS8TaO347+RpZrFjkVOZSeLaNR7Y+XfTCKOhUymQwvlYpFY8bg0qePqZtqMI2NsGED\nZGW1nJs0CYYPN+x9xXvcuIwyR+6OO+4AoLa2VvvvZjk5OYwcObJLGiEIgiAIdU11/JH7B+fJorTE\nhspcN7zqrPFwagAH6NXYyLzx47Ft727w3UhzEnelBj8Ad90F4tetcD03nCMXFxcHwBNPPMF//vMf\n7ditTCbDy8uLCRMmYGlpaZSGtpfYoksQBKH7KKsrY33ier75bjPpKhtkETFYyhxQyCyQJ59molri\n3adfwCooyNRNNZimJvjmG0hLazk3cSLcfrvp2iQYXme36NJrscPZs2cJ72argsRiB0EQhO4hpyKH\nDYkbqG6sZtu2VIqCo/G0skWODJlMRmNZOXeUV/D/Xn3d1E01mKYm+PZbOH++5dz48RATY7o2CcZl\n0MUOx48fJyUlBYDU1FRiYmIYN24cZ8+ebfcNhZ5LzK8wLhFv4xLxNoykS0nEnYyjpLGOs5Ib5ZIS\nP2snFJIFlWfP41VWwQSFFQ2NPXdOtkoFGzfqJnFjxxo/iRPvcePqqnjrlcj9/e9/x83NDYDnnnuO\n2267jZiYGJ588skuaYQgCIJwa5Ekib1Ze/ku5XvS1XYcbfKG7AZcatVYKSyxsbSid30Dgx2dsXNR\nYtXQYOomG0RzEpea2nIuJgbGjDFdm4TuRa+hVScnJyoqKqitrcXX15eCggIsLS1xc3OjtLTUGO1s\nNzG0KgiCYJ6a1E38eHYb8ZfOkYYr6moVvhfL8bV0JTn1PFJpKeGhodgqlWBlRf3x44R5ehL797+b\nuuldSqWC77+HKwNegGY+3IQJmi24hFtLR/MWvXZ28PDw4Pz58yQmJjJs2DCsra2prq4WiZIgCILQ\nLjWNNXx+eiMJlTWUSJ44F5bjXVSPp5073k0qJslkpBcUUCOX02BpiVVTE3YKBePuv9/UTe9SajVs\n2aKbxI0aJZI4of30GlpdunQp0dHRLF68mOeffx6AnTt3Mljs1iu0IuZXGJeIt3GJeHdeTtUlnjvy\nDVsq1ZQ3WOJ1oZBeJU0E2rpzT1k5T5SUEBMby7h//pPwQYMACB84kHF/+QsBPaj4b3MSl5TUcm7E\nCLjzTtMmceI9blxG3Ws1NjaW+++/H5lMhp2dHQAjR45kuKGrEwqCIAjdniRJ/JR/jn+n/UGNWo5t\neQ3u2UV4WDoxtknOhKJc7P39YdYscHYmAAgIC0OekNDjykep1bB1KyQmtpy77TZNwV/REyd0hN57\nrRYXF/PTTz9RUFDAiy++SG5uLpIk4e/vb+g2doiYIycIgmB6F+vq+E/GKQ4UngW1GmV+Kc6XKxks\ns+OB6kZ8GhtbZvfL9Rok6rYkCX78EU6caDk3bBjcfbdI4oSO5y16JXJ79uxh1qxZREdHc+DAASor\nK0lISOCdd95h27ZtHWqwoYlEThAEwXQqmprYUVLC1pwksiuyUdQ14pF1GY/KGubXK7itEWROTjBz\nJgQGmrq5BidJsG0bHD/ecm7oUJg6VSRxgoZB68g9/fTTfPPNN2zfvh2FQjMaO2LECP74449231Do\nucT8CuMS8TYuEW/9NKnV7Csr4/2L2XyTeYTs8iwcSqrodTaHmIvZvFauYngjyMLC4IknbpjE9ZSY\nSxL89JNuEjdkiPklcT0l3t2FUefIZWVlMXHiRJ1zlpaWqFQ9t0CjIAiCoD9JkkitqeHX0lIK6qpJ\nupREVW057heLiczM5K6SEoa7hKCwtNZsHnrbbeaVxRiIJMEvv8DRoy3nBg2CadNuiZcvGIFeQ6uj\nRo1i2bJlTJ48GaVSSWlpKb/99htvvPGG2WbwYmhVEATBOC43NLC9pIQLtbVUNVSTeCkRqaKCPuey\nuP1CCsPkDoQoQ5B5eMB994G3t6mbbBSSBL/+CocOtZwbMABmzOjx0wGFDjBoHbl3332XqVOncvfd\nd1NXV8djjz3Gtm3b2Lp1a7tvKAiCIPQMtSoVCWVlHKmsRC1JFNeWkHIpGWVBEeOPHSP8ch5hrqH4\nOflpxhKnTAErK1M32ygkCXbs0E3i+vcXSZzQ9fR6O40YMYJTp04RGRnJww8/THBwMEeOHOG2224z\ndPuEbsRce2d7KhFv4xLxbqGWJI5WVPBBbi5/VFSgliRyKnJJyT3BiBMneWTHLwwoKmCw1wD8PII1\nvXDTp7c7ieuuMZck2LULfv+95Vy/fpp1HeacxHXXeHdXRp0jV1ZWhp+fHy+99FKX3FQQBEHonrLq\n6viluJiCK3ufSkiklVxAyj7FY3sO4FVWirWFNQN9BmMf1FeTxCmVJm618UgSxMfD/v0t5yIiNCXy\nzDmJE7ovvebI2djYEBERwZgxYxgzZgwxMTG4ubkZo30dJpPJWL58OWPHju1xBSUFQRCMrfxKOZGk\n6mrtuSa1iqzLifQ7upsRRxORAY5WjgzwGoDVmPEwbhxYWJiu0SaQkKD5ahYWBg88cMuFQWiHhIQE\nEhISWLlypeHqyNXW1nLw4EH27NnD3r17OXz4MMHBwcTExPDRRx91qOGGJhY7CIIgdF6jWs3vFRXs\nLy+nUa3WnlepG6jPTGDE9p9xvVwOgIedB+GB0VjMug9CQkzVZJPZuxd272457tMHZs8GhV5jX8Kt\nzqAFgZtVV1dz4MABtm/fzueff46trS2FhYXtvqkxiETO+BJ64HY65kzE27hutXhLksSZmhp+Kymh\nrKlJ5zEfeT2q/XH0TTiColFThirAOYDA6InIZswAB4cuaUN3ivn+/bBzZ8txaCjMmdO9krjuFO+e\noG28Dbpq9cUXX2Tv3r3k5uYyatQoxowZw6FDh4iIiGj3DQVBEATzVnilnEhGba3OeW8rK0IbCylZ\n9w6e53IBkCGjr2c4Pn9aACNH3pLF0Q4c0E3igoNFT5xgPHr1yNnb2+Pj48PixYsZM2YMw4YNw9LS\n0hjt6zDRIycIgtA+tSoV8VfKibT+/LSzsGCciwuNZ3dTtu5T7MprAFDIFUSEjcbtwcfAz89UzTap\ngwc1teKaBQXBvHlg5r8iBTNk0KHVxsZGjhw5wr59+9i7dy8nTpwgMjKSmJgYli5d2qEGG5pI5ARB\nEPSjliSOVVayu6yM2lY79shlMoY5OnKHowPHtryP6tdfkKs1n6u2Clv6TZiD48w5YG1tqqab1B9/\naHZtaBYYqEnibpFSeUIXM8ocuZKSEvbs2cOuXbtYvXo1dXV1NFxZgm5uRCJnfGJ+hXGJeBtXT413\nZm0tv5SUUNjmszzY1pbJrq441lZy+N//i5R6VvuYo6M7kQ89j030cIMOpZpzzI8c0eyf2qx3b3jw\nwe6dxJlzvHsio86R++tf/0pCQgLnz58nOjqaMWPG8P333zNy5Mh231AQBEEwvbLGRn4rLSWlVTkR\nAKWlJZOUSsLs7Cg7e5Kjn6xCKi/VPu4SFMGAJ1di4eFp7CabjWPHdJO4Xr1g/vzuncQJ3ZdePXLN\n9dhGjBiBra2tMdrVaaJHThAE4WqNajX7y8s5UF5OU6vPSEu5nBhnZ0Y6OaEACn76lrQfvqRJ1ah9\njvv4aUTO/SuyW3gC2IkT0Hp3Sn9/WLDglh1dFrqQUYZWs7Ozyc3Nxc/Pj969e7f7ZsYkEjlBEIQW\nkiSRXF3NjtJSytuUExno4MBEpRInhQLKy8n+8j0yTu1BQvMZqrKxJiD2aUJH3G2KppuNkyc1SVzz\nrxZfX3joIbCxMW27hJ6ho3mLXhuG5OfnM2bMGEJDQ5k5cyahoaHExMSQl5fX7hsKPZfYp8+4RLyN\nqzvHu6C+nriCAjZdvqyTxPlYW7PIx4eZHh44KRRIKSmkvfE86acStElcrb83EUv/ZZIkzpxifvq0\nbhLn46PpietJSZw5xftW0FXx1iuRe+KJJxg0aBClpaXk5+dTWlrKkCFDeOKJJ7qkEYIgCELXq1Gp\n+G9REf/Jzyerrk573t7Cgnvd3XnUx4feNjbQ2EjTj1tJ+XA5OYXnAZBkMspGRjHylX/j6xdmqpdg\nFpKSYMuWliTO21uTxHWTmUZCD6fX0Kqbmxv5+flYtZrJWV9fj6+vL8XFxQZtYEeJoVVBEG5VKkni\naGUl8aWl1LXaVksukzHcyYkxzs7YNG/+eekSdd+sIyU5nor6CgDq7K2pnX4Pd49/HGvFrT35KzkZ\nvv8emsPo5QULF4KdnWnbJfQ8Bl216urqSkpKCoMHD9aeO3v2LEqlst03FARBEAwn/Uo5kcttyomE\nXikn4t78B7kkwfHjVP24iaTcE9Q1aXrsLgd44HjfPKb3n45cptegTY915oxuEufhoZkTJ5I4wZzo\n9VP64osvcuedd7JkyRI+/vhjXnrpJe68805eeOEFQ7dP6EbE/ArjEvE2LnOPd2ljI98UFrK6oEAn\niXO1tGSulxfzvbxakri6Oti0iZLvvuZE9mHqmupQW8g5NzKM3o88x+QBM8wiiTNlzM+ehY0bW5I4\nd3dNT5y9vcmaZHDm/h7vaboq3nr1yD366KOEhISwbt06Tp8+ja+vLxs2bGDChAld0ghBEAShYxrU\navaVl3OwTTkRqyvlREY4OaGQt0rKLl6E778nNzuZ8yWa+XDVLvacHz+Ie0Y/TB+3PsZ+CWbn3Dnd\nJM7NTZPEOTiYtl2CcC3tKj/SnYg5coIg9GSSJJF4pZxIZZtyIoOulBNxbL1ru1oNBw6g3r2b9OLz\n5FTkAJAX5svl26OYM2QBXg5exnwJZiktDTZsgOadylxdITYWnJxM2izhFtDlc+SWLl161UVlrbZi\nkSQJmUzGqlWr2n1TQRAEoePy6uv5paSEi61WogL4WVszxdUV/7Y1MSorYfNmmi6c58zlMxTXFtNk\npSB1VBhWAwazqP8cHK0djfgKzNOFC/DNNy1JnFKp6YkTSZxgzq6byF28eFEncWurOZEThGZinz7j\nEvE2LnOId7VKxa7SUk5UVen8ke1gYcFEpZJBDg5Xfy6fOwc//EBdRQmJhYlUN1ZT7ulMSkwEIUFR\nzAifgaWFee7UYMyYZ2RoeuKaOzddXDRJnLOzUW5vFszhPX4r6ap4XzeRi4uL6/TFBUEQhM5TSRKH\nKypIKCujvlU5EQuZjBFOTsS4uGAtb7M4oakJdu6EQ4eorK8k8VIi9eoGsgYFkDUokNGBdzAhaIL4\ngxzIzIT161uSOGdnTRLn4mLSZgmCXvSaI5eSkoKrqyve3t5UVlbyf//3f1hYWPDCCy9gZ4J12C+9\n9BIHDx4kMDCQL7/8EoXi6nxUzJETBKEnSKupYXtJCUWNjTrn+9rZMcnVFbdr7XtaXAybNkF+Pper\nL3Om6Ay1tgrOxPSjwseVaX2nMcRniJFegXnLyoJ166B5oa+Tk2ZOnKurSZsl3IIMukXXnDlzKC8v\nB+D5559n3759HDp0iMcff7zdN+ysU6dOkZeXx969ewkPD2fTpk1Gb4MgCIKhlTQ2sr6wkLWFhTpJ\nnJulJfO9vJjn5XXtJO7UKfjPf5Dy8sguzyb5cjKX/JUcvXcY9f4+LBi4QCRxV1y8qJvEOTpqeuJE\nEid0J3olcllZWYSFhaFWq9m8eTPfffcdmzZtYvv27YZu31UOHjzIpEmTAJg8eTIHDhwwehuEaxM1\niIxLxNu4jBXverWaHSUlfJSby7maGu15a7mcu1xdedLPjz7XGgmpr4fNm2HLFtT1dZwrPkdaeQbn\nbwslaXx/HJVeLI5aTJAyyCivoysYMuY5ObB2bUsS5+CgSeLc3Ax2S7MnPlOMy6h15GxsbKioqODM\nmTMEBATg4eFBY2MjdW1WTBlDaWkpPj4+ADg5OVFSUmL0NgiCIHQ1SZI4VVXFztJSqpqXTaIZbhns\n4MAEFxccrjGNBIC8PM1QakkJjapGki8nk2fdQMrUoVS5OhDgHMDs/rOxsxRbEgDk5sKaNZrcFzRF\nfhcu1BT9FYTuRq8euXnz5jF+/HgeeughFi5cCMDx48cJDg7u8I0//PBDoqOjsbGx4eGHH9Z5rKSk\nhBkzZuDg4EBgYCAbNmzQPubi4kJFhWY/wPLyclxFH7jZEKudjEvE27gMGe/c+nq+yM/nh6IinSSu\nl40Nj/r4MN3d/dpJnCTB77/DF19ASQm1jbWcKDjBGX8bjl1J4gZ5DWLBoAXdMokzRMzz83WTODs7\nTRLn4dHlt+p2xGeKcXVVvPXqkXvvvff49ddfsbKyYty4cQBYWFjw3nvvdfjGfn5+LF26lF9//ZXa\n2lqdx5566ilsbGy4dOkSJ06c4J577mHQoEH069ePUaNG8e6777JgwQJ+/fVXbr/99g63QRAEwZSq\nmprYWVrKyaoqnfOOCgV3KpUMsLe//qrS6mrYskVTwRYoqyvjVFkqySMDuRSsKew7Pmg8d/S+Q6xM\nvaKgAFav1uxQBi1JnKenadslCJ1h8p0dli5dSk5ODl999RUA1dXVuLq6kpycTGhoKAALFy7E19eX\nN998E9Ds/Xro0CECAgL46quvxKpVMyFqEBmXiLdxdWW8VZLEoYoK9l6jnMgoZ2fucHbGqm05kdbS\n0zXz4a4kgIVVhRyR5ZF8Rzi1TrYo5ApmhM8g0jOyS9prKl0Z88JC+PpraJ52aGurSeK8vbvk8j2C\n+Ewxrrbx7vKdHYylbaPPnTuHQqHQJnEAgwYN0pkU+Pbbb+t17djYWAIDAwHNkOzgwYO1QWu+njju\nuuOTJ0+aVXt6+rGId/eM97maGj786ScqmpoIHDECgMxDh+htbc1fp03D1dLy+t9/xx0QH0/C2rUA\njAkIILMsk08b8sgP9SHQyRZ7S3sCywK5nHIZrvQ0mUP8OnLcrLPX27IlgV9/BW9vzXFeXgKTJrUc\nm8vrNfVxM3NpT08/PnnyJAkJCWRmZtIZZtcjt2/fPh544AHy8/O1z/nss89Yv3498fHxel9X9MgJ\ngmBOihoa+LW0lPOtVqICeFhZMdnVlRBb2xtfoLQUvv9es9wSUEtqkqoziB+ipNRPM1fY096TeQPm\n4WIjKtk2u3wZ4uI0I9EA1tbw0EPg52fSZgnCVXpMj5yDg4N2MUOz8vJyHB3FPoCCIHQ/dSoVe8vL\nOVRRgbrV552NXM5YFxeGOTlhcbM5bElJsG2bdoZ+g6qBg1aXODChFw22VgCEuoZyX7/7sFHY3OhK\nt5SiIs1wauskbsECkcQJPYtc3yc2NDSwd+9evv32WwCqqqqoajNBtyPaTsLt27cvTU1NpF2ZwAua\nIsD9+/fv9L0Ew2rbPS8Yloi3cbU33pIkcaKykg9yc/m9vFybxMlkMoY6OvIXf39GODvfOIlraIAf\nf9SUFrmSxFU11bLFv4r42/20Sdww32HMGzCvxyVxnXmPFxdrkrjmX1NWVvDgg+Dv3zVt64nEZ4px\ndVW89eqRS0xM5N5778Xa2pqcnBxmz57Nnj17WL16tTaxay+VSkVjYyNNTU2oVCrq6+tRKBTY29sz\nc+ZMli1bxueff87x48fZtm0bBw8ebPc9VqxYwdixY7Xj0oIgCMZwsa6OX0pKyGuucXFFbxsbpri6\n4mNtffOLFBRoEriiIu2pImsVGwbKKL5SdkmGjMmhk7nN7zaxMrWVkhJNEldZqTm2tIT586FXL9O2\nSxCuJSEhoVNJnV5z5EaPHs3jjz/OQw89hFKppLS0lOrqavr06UNeXl6HbrxixQpWrVp11blly5ZR\nWlrKokWL2LFjB+7u7vzjH/9gzpw57bq+mCMnCIKxVTY1saO0lNNtRiucFAruUiqJvFE5kWaSBEeO\nwG+/teziDqT52fFtYBWNlpqBFCsLK+7rdx993fp2+evozkpLNXPiruwqqU3irqx7EwSz1dG8Ra9E\nTqlUUlJSgkwm0yZykiTh6upKaWlphxpsaCKREwTBWJrUag5WVLCvvJyGVuVEFDIZo52dGX2zciLN\namo0Q6lnz2pPqRUKDg105TfHQriSBDpZOzFvwDy8HUTtjNbKyjRJXFmZ5lihgHnzoBO16wXBaDqa\nt+g1Ry4gIICjR4/qnDty5Ah9+vRp9w2FnkvMrzAuEW/jula8JUnibHU1H+Xlsau0VCeJ62dvz5/9\n/BinVOqXxGVlwSef6CRxTZ7ubInx4DenS9okztfRl0ejHr0lkrj2vMfLyzXDqa2TuLlzRRLXHuIz\nxbiMOkfutddeY+rUqTz++OM0NDTwxhtv8Mknn/DZZ591SSMEQRC6m8sNDWwvKeFCm51pPK2smOLq\nStDNyok0U6th717Ys0czrHpF9dCBrPXIJ7+upRRThHsEMyJmYGVh1SWvoaeoqNAkcc0DRBYWMHs2\nhISYtl2CYAx615E7ceIEn376KVlZWfTu3ZtHH32UoUOHGrp9HSaTyVi+fLlY7CAIQpeqU6lIKCvj\ncGWlTjkRWwsLxrm4EO3oiFzfhQfl5ZodGrKyWs7Z2VE4cSRr6w5T2VCpPT2612gmBk8UixraqKzU\nDKcWF2uOm5O4vmLqoNBNNC92WLlypeHmyHVHYo6cIAhdITU9nZ3JydQDhfX1qLy9cWhViEwmkxHt\n6Mg4FxfsLCz0v/CZM5r5cK179AIDOTemPxsv/kqjuhEAuUzO1L5TifKJ6qJX1HNUVWmSuOaFvXI5\nPPAAhIebtFmC0CEGLQhcX19PXFwcJ0+epKqqSnszmUzG6tWr231ToWdKSEgQvZ9GJOJteElpaXx6\n7BiNgwdzcv9+rKOiaDp6lMFqNe69ehFoY8MUNze8rNox1NnYqFmReuRIyzm5HGnMGA6+4KiHAAAg\nAElEQVQGWrAj4yckNB/mNgobZkfOJkgZ1MWvrHu40Xu8uloznNo6ibv/fpHEdYb4TDGuroq3Xonc\nwoULOX36NNOmTcPLy0t7XnTxC4LQ3UmSRI1aTVFj41Vfvx04QPXAgVBTQ61ajTWgiI4mPzGRJ4cO\nJcLOrn2fg5cva2rDFRa2nHN2RjXjT/xUn8jxjOPa0662rswbMA93O/eue7E9RE0NrF6tCSdokrhZ\nsyAiwrTtEgRT0Gto1cXFhYyMDJRKpTHa1CXE0KogCK2pJYmypiaKGhu53CZhq1Wprvk9h/bupW7g\nQO2xXCajt7U1A86f57l779X/5pIEx4/D9u2aHrlm/fpRO3kiGzP+S3ppuvZ0b+fezOk/BztLu3a/\nzp6utlbTE1dQoDmWyWDmTBgwwLTtEoTOMujQakBAAPVtKpR3B2JnB0G49TRcp3etuLERVTs/JC0A\nW7kcOwsLHCws8LGywkYux7Y9vXB1dZp9UpOTW84pFDB5MiX9gliftJ6impbdGwZ6DeTesHtRyE2+\nFbbZqa3V9MS1TuJmzBBJnNC9GWxnh127dmmHDE6cOMHGjRv561//ire3bu2i8ePHd/jmhiR65IxP\nzK8wrls53pIkUaVSXbN3raLVbgj6spLLcbe0vOrrcnY2a0+exHroUDIPHSJwxAjqjx0jNiqKMH0K\nlF28CN9/31LcDMDTE+67j2zrOr5J+oaaxhrtQ+MCxxETECOmrVzR+j1eV6dJ4po3E5LJYPp0GDzY\ndO3raW7lzxRTaBvvLu+RW7x4sc6HiSRJ/O///u9Vz8vIyGj3TQVBEPShkiRKrtG7VtTYSH2r4rv6\nclQo8LhGwuZoYXHN5MkzNJRYuZxdSUkUZWTg6eDABH2SOEmC/fshPl5TJ65ZdDRMmsTpkjNsPbkV\nlaQZ0lXIFfwp/E/09+zf7td0K6ivh7VrW5I4gGnTRBInCCDKjwiCYAZqVSqKr9G7VtrUpFOrTR8W\nMhmu10jW3C0tsdZnh4XOqqyELVsgvWXOGzY2cO+9SBER7MnaQ0JmgvYhe0t75vSfQy9nsaP7tTQn\ncRcvtpybNg3MuIypIHSIQefITZ8+na1bt151fubMmWzevLndNxUE4dYjSRLlVxYbtP2qus5igxux\nkcvxsLK6KllzUSiwMNXQ5PnzmiSupmW4lF69YNYsmpwc2HpmM4mXErUPedh5MG/APJS23WchmTE1\nNMC6dbpJ3D33iCROEFrTq0fO0dGRysrKq84rlUpKm/dEMTOiR874xPwK4zLXeDeq1ZQ0NXG5oUF3\nsUFTE40dGA51USiu2btmf53hUEO5YbybmmDXLjh4sOWcTAZ33AFjx1LdVMs3Sd9wsaIlIwlRhnB/\n5P3YKGwM2/BuKDU1i+3bL/Djj6exth5IcHAI7u4BTJkCw4ebunU9l7l+pvRUBp8jB7B06VIAGhoa\nWLZsmc4N0tPTCQwMbPcNjUmsWhUEw7hR7bWypqZ2fxgpZDLcLC2vmr/mZmmJpTGGQzujuFhTGy6/\nZU9UHB01NTGCgrhcfZn1iesprWv5ozfaN5opoVOwkLdjJ4hbRGpqFl9+mUZq6gSKi+W4uIzl5Mld\n/PnPMHx4gKmbJwhdzmCrVgFiY2MBWL9+PfPnz2/5JpkMLy8vFi9eTGhoaIdvbkiiR04QOq8jtddu\nxN7C4pq9a84Khf77k5qTU6fgp580Y4DN+vaFP/0J7OxIL03nu+TvqGuqA0CGjLtC7mKE/wixMvU6\n3n9/NwkJ42k92BMSAkOH7ubJJ82zSoIgdAWD9MjFxcUBMGrUKB577LEONUwQBPPXlbXXZDIZymus\nDnWztGzfXqTmrL5ek8CdPt1yzsIC7roLbrsNZDKO5R3jp/M/oZY0w8lWFlbMiphFmHuYiRpt/urr\n4eBBuU4SFxysmWbY0GDmPbOCYCJ6LXYQSZygDzG/wrjaG29j1V5zVShQmPtwaAdo452XpxlKLSlp\nedDNDe67D3x8UEtqdl7Ywe8Xf9c+7GTtxNz+c/Fx9DF+w7uJ2lrN6tSKipZ5lDY2CfTuPRYAK6v2\nz68U2kd8hhuXUfdaFQSh+zB17bWeJis1lQs7d3I6JQX1tm2ENDYS4Ora8oTBg+Huu8HKigZVA5vP\nbOZs0Vntwz4OPswdMBcnaycTtL57qK6GNWs0OzYEB4dw8uQuwsIm0Dx6X1+/iwkTzHMajyCYmqgj\nJwjdTGp6OjuTk6lRq6lXqYjs0wcHP7/uXXvNTGWlppIWF8cEmQzOnoWSEnY1NRE6eDABfn4wdap2\nf6iK+go2JG4gv6pl0UO4ezgzI2ZiZWFlqpdg9iorNTs2XL7ccq5//ywuXbpAQ4McKys1EyaEEBYm\nFjoIPVtH8xaRyAlCK5IkoZIk1Gh6tlSShKr1v2/ymArNAgFDPZafnc3hs2eRDx2qnbvWdPQog8PC\ncO9184KyZll7zRypVJCTw+5332V8ZiZUVGh2a7hit48P4z/6CK70zOVX5rM+cT2VDS1lmkb1GsXE\n4InIZbduInwz5eXw9dcto9Ri2y3hVmbQgsAA8fHxrF69mtzcXPz9/XnwwQfNdp/VZqL8iHE09xCd\nSUwkYsAAJkZGEhYcjNQ26elEgmSsx9rbk2VsiefPI0VFoZIkyo4exSU6GkV0NBmnTukkcuZSe63b\nkCS4dEmzG0N6OmRlQUMD8tRUzSafQEJZGWNdXKBXL+SDB2uTuNSiVDalbKJR3QiAXCbnnj73MNRX\nVK29kdJSTRLXvA2tXK6p2NK/1S5lYs6WcYl4G1dzvDtbfkSvRO7zzz/nlVde4ZFHHmH48OFkZ2cz\nb948Vq1aZdYLIVasWGHqJvR4qenp/DkhAfnQoRQVFnK2Vy++i49nUG4urv7+pm5ej6NulYTJ0JTz\nsJfL8bSz4z4Pj+5Te80clJe3JG4ZGVBVddVT1K3jaGsLAweCqytqW1skSeJQziF+u/AbEpo/AGwU\nNjwQ+QDBypvsxXqLKyrSJHHNdeYtLOD++yE83LTtEgRTaO5wWrlyZYe+X6+h1T59+rBp0yYGDRqk\nPXf69GlmzpxJWlpah25saGJo1Tg+2raN7/39aTuF3v7UKYaNGWOSNnWWhUzW8gXIW/3b1I998fPP\nFA8YgPzKY81pnWdSEk9Om2b0WHUrdXWahK05eSsuvvHzXVzIsrYm7fhxJnh4gJVmntuu+nqCHlpA\nikU6R/OOap+utFEyb8A8POw9DPkqur3CQs2cuOpqzbFCAXPmgJmWJBUEozHo0GpJSQkRERE658LC\nwsx2ey7BeBrRvPlo8+ZTXek5ulZSIufqBKX1sc7jRn5M3vx6zNTUAQOIO34cRavNJuuPHWNCVJQJ\nW2Wmmpo0m3Q2J255eVe9T3XY2mqKljV/KZUEAKSmsnvXLuQNDaitrPAfczsHGo5xofSC9lt7OfVi\nTv852FvZG/xldWd5eZrVqbW1mmMrK5g7F4KCTNsuQejO9ErkRo8ezbPPPstbb72Fvb09VVVVvPzy\ny4waNcrQ7RPMnCUQ7eiIDLh46BCBI0ciBzyVSv4cGGjWSVF3FBYcTCywKymJlMRE+g0YwISoKMKC\nxVAekqSpX9GcuGVnQ2Pj9Z+vUEBAQEvi5u2tmW3fRkBYGAFhYSQkJDBk+CDWJ67nck3LEssBngOY\nHj4dhVxUc7qRixc1deLq6zXH1tYwfz707n397xFztoxLxNu4jFpH7pNPPmHOnDk4Ozvj6upKSUkJ\no0aNYsOGDZ1ugNC9TYyMJO74cayHDsVSLsdSJqP+2DHuiooSSZyBhAUHExYcTIKjo/jQLS3VnedW\nU3P958pk4Ovbkrj16qVJ5m4iNS2Vncd2cvj4YSoOVuAX4Ie7rzsAYwPHMiZgjHiv30RmJqxf37KT\nma0tLFig+d8hCELntKv8yMWLF8nLy8PX15deepQ6MCUxR854UtPT2ZWcTANgBUy4smpVELpcTY3u\nPLebTe9wc2tJ3AIDNRlEO6SmpfJV/Ff/v707j4+qvvoH/pnJvi9kI7uQEIggYSesgaiAsggIAkIA\neYSK2GJtbRWV8CDlsa3Y/kSl0goEJCDuAiqaEII2EFBA1kBYAmEJS/aFZJKZ3x/XmcmQBGYmM9/Z\nPu/XK69y7yz35HQ6Pbn33PNFWVgZzpSegVKlRGNhI3rf3xv/M/J/8EDoA8b/Lg6isBDYskW60g0A\nXl5AWhoQGmrZuIisjVnnyPXq1QuHDh1qsb9v3744ePBgK6+wPBZyRHZAoZAukaoLt2vX7t7n5uWl\nLdzuuw/w9zf60PWN9Vjy7yU45n1Ms+g9ALjIXTBcNRyvzH7F6Pd2FAUFwEcfQbNCg48PMHs2EBRk\n2biIrJFZb3Zo7c5UlUqFc+fOGXxAkThHTiz2V4hll/lWKoGrV7WF26VL2lM5rXFxkc60qYu3kJBW\n+9wMUXG7AvmX8/HT1Z9w7OYx3HaXirjyU+UI7xGOHiE94H3Lu13HcATHjwOffCL9VwoAfn5SEdd8\ndbN7scvPuBVjvsUSMkdu1qxZAID6+nqkpaXpVIoXLlzA/fffb/SBReAcOSIrp1JJY/2b97ndvt32\n8+VyICJCW7hFRkpDyEzgStUV5F3Kw/Ebx6FUSdWHHNIcOWe5M0K8QtC7Y284y53hKueSW3dz5Ajw\n+efak6eBgVIR5+dn2biIrJFZ58ipC6GVK1fi5Zdf1hRycrkcoaGhmDJlCgIN+fNKIF5aJbJS1dW6\nfW4VFXd/fnCwtnCLiQHc3U0WilKlxOlbp5F3KQ9FFUUtHleUKnD5wmVEJUXBSS4VjPVn6jFnxBwk\nxCWYLA57cvAgsH27djs4WOqJ8/GxXExEtsCsPXLffPMNRo8ebVRglsJCjshKNDRIS16pC7eSkrs/\n38dHt8/N19f0ITU14PC1w9hXvA+ldaUtHo/1j0VyZDK6dOiC02dPI+vnLDQoG+Aqd0Vq71QWcW3Y\ntw/45hvtdmioVMR5cbwe0T2ZtZCzRSzkxGN/hVhWm2+lErh8WVu4FRdru91b4+am2+cWFNTuPre2\nVNZXIv9yPg5eOahzAwMgrZHaI6QHBkYOREefji1ea7X5thJ79wJZWdrt8HBpxIiBNwrrYM7FYr7F\nujPfZr3ZgYioTSqVtHimunC7cEE79bU1Tk5Sb5u6cAsPN1mfW1ta639T83D2QN/wvugX0Q++bqY/\n+2fvVCogJwfYs0e7LzoamDHDpFfBiagNPCNHRIarqtIWbufOaVc/b0toqG6fm6v5bxa4V/9boEcg\nkiOT0TOsJ1ydePOCMVQq4LvvgP/+V7vvvvukZbcE/FdMZFd4Ro6IzKe+XjrTpi7cbty4+/P9/HT7\n3LzFjevQt/8tvkM85DK5sLjsjUoF7NwJHDig3RcfD0ydKk2FISIx9CrklEol/v3vf2PLli24ceMG\njh49itzcXFy7dg1Tp041d4xkI9hfIZZZ893UJPW2qQu3y5e1A8Fa4+4uFWzq4i0w0Gx9bm1R97/9\ndOUn1DXW6Twml8nRPaQ7BkYORLiPcetC8fOtpVQCX30FNJ8T360bMHmyXque6Y05F4v5FkvoWqtL\nly7Frl27sHjxYvzmN78BAERERGDx4sUs5IjsgUoFXL+uLdyKirQLY7bGyUlqhFIXbh07SjPeLOBq\n1VXkFefh2PVjLfrf3J3d0Te8L/pH9Gf/m4k0NUkz4o4e1e7r0QN47DGztzoSUSv06pGLjIzEoUOH\nEBwcjICAAJSVlUGpVCIwMBDl5eUi4jQYe+SI7qGiQrfPraam7efKZEBYmLZwi4626PUzlUol9b8V\n5+FC+YUWjwd6BGJg5EAkhSWx/82EmpqAjz8GTp7U7uvVCxg3zmJ1PJHdMGuPnFKphPcdPS41NTXw\n4YRHIttRV6fb53br1t2fHxCg2+fm6SkkzLtpaGrAkWtHsK94H27VtYw/xi8GyVHS/Df2v5mWQiGt\nm3rmjHZfv37AI48Iv4pORM3oVciNGTMGv//97/HWW28BkAq7V199FePGjTNrcO3FtVbFYn+FWPfM\nd2OjtFapunC7cuXuC857eur2uQUEmDxmY1XVV2nmv7XW/3Z/8P0YGDkQEb4RZovBkT/fDQ1AZqa0\nIIdacjLw8MPmLeIcOeeWwHyLJWStVbVVq1Zhzpw58Pf3h0KhgLe3Nx5++GFkZGQYfWARuNYqORSV\nCrh2TbfP7W4Lzjs7S6NA1IVbWJjVnVq5Vn0NeZek/rcmle5QYXdnd/Tp2Af9I/rDz52LeJpLfT3w\n4YfAxYvafcOGASNGWN3HhcgmmXWt1TuVlJSgqKgIUVFR6Nix5eRza8IeObJXRQUFOPv995ArFFA2\nNKBz586IUSql0yW1tW2/UCaThu+qC7eoKNPeYmgiKpUKZ0rPIO9SHs6Xn2/xeIB7gKb/zc3ZzQIR\nOo66OmDTJummZbXUVGDoUMvFRGSvzLpE1+9+9zs8+eST6N+/v1HBWQILObJqKpXUdHS3n4aGFvuK\nzp1D4a5dSJXJgMpK4PZtZDU2Ii4pCTFBQS2P06GDtnCLjW3feklmpmhS4EiJ1P92s/Zmi8ej/aKR\nHJmMhKAE9r8JUFMDbNwoneRVGz0aGDjQcjER2TOzDwR+7LHH4OnpiSeffBIzZsxAQgIXjSZddtNf\noVRKlyTbKKYMKbzafN7dLnnexdn8fKT+etYtp7wcKf7+SHV2Rvb581Ih5+WlLdw6dZIG81q56oZq\nTf9brUL3jKJcJkdicCIGRg5EpG+khSKU2M3nWw9VVUBGhu7c57Fjgb59xcbhSDm3Bsy3WELnyP3z\nn//EqlWrkJ2djc2bN2PgwIHo1KkTZsyYgRdeeKHdQRDpTak0XTHV1mNGFlkiyO8cyuvkBPj5QR4V\nBTzzDBASYjONSyXVJcgrzsPRkqMt+t/cnNzQJ1zqf/N397dQhI6pogLYsAEo/XVRDJkMmDABSEqy\nbFxE1Dqj1lq9fPky5syZg6ysLCjvNu3dgnhpVRxNz1Z9PZRyOToPHYqY++4z7Rks9b+bmu4dkK1w\ncbn3j6urznb2F19gZFWVNLTLwwPw8QHkcmSHhGDkwoWW/o3uSaVSobC0EHnFeThXdq7F4/7u/hgY\nORC9wnqx/80CSkulM3Hq8aByOTBpEtC9u2XjInIEZr+0Wl1djc8++wyZmZma04HWftcqmV/RqVMo\n/M1vpJ6tXz+AWR9/DLTVs2UrWimiDCm47vlcZ2ejzpx1Dg1F1vr1SHXTFjlZ9fWIS0015W9vcoom\nBX4p+QV5xXmt9r9F+UYhOSoZXYO6sv/NQm7elM7EVVVJ205OwJQpQNeulo2LiO5Or0JuypQp2Llz\nJ3r37o0ZM2Zgw4YNCA4ONndsZAPOZmUhVS4HlMrWe7ZMTSYzTSF1t8eNLLJEiElIAObMQXZWFn45\ncQIPJCYiLjVV2m+FqhuqceDyARy4cqBF/5sMMk3/W5RflIUi1J899w+VlEhn4tSLezg7A9OmAXFx\nlo3LnnNujZhvsYT2yPXt2xd///vfERMT0+4Dkn2RKxTS9Rf1JXYnJ8DJCXJXV6lfy9QFl5OT1RZZ\nosQkJCAmIQFyK/7SLakuwb7iffil5JdW+996d+yNAZED2P9mBa5cke5Orft1zrKrKzB9ujQbmois\nn1E9craAPXJiZL/zDkZevSoVczKZpsiylZ4tMh2VSoWzZWeRdykPZ8vOtnjc390fAyIGoHfH3ux/\nsxKXLklz4urrpW03N2DmTGnEIBGJZfIeua5du+LUqVMAgKg2/lctk8lwsfm4b3I4nR98UOrZajZY\n1hZ6tsh0GpWNUv/bpTzcqL3R4vFI30gkRyajW3A39r9ZkQsXgM2bpXuJAOnemVmzpJnRRGQ72jwj\nt3fvXgz9dXx3W2uAyWQyDB8+3GzBtQfPyIlTVFCAs816tjpbcc+WPbF0P0tNQw0OXDmAA5cPoEZR\no/OYDDJ0C+6G5Mhkm+h/04el821KhYXAli3aSTteXkBaGhAaatm47mRPObcFzLdYd+bb5GfkhjZb\ng+XGjRuYMmVKi+d8/PHHBh+Q7I8t9GyR6Vyvua7pf2tU6s7cc3VylfrfIgYgwCPAQhHS3Zw6BWzb\npp3k4+MDzJ4N2PJN5kSOTK8eOR8fH1Sp70lvJiAgAGVlZWYJrL14Ro7IdFQqFc6VnUNecR4KSwtb\nPO7n5ocBkVL/m7uzuwUiJH0cOwZ8+qn23iQ/P6mICwy0bFxEZKY5cufOnYNKpZK+xM/pDu88e/Ys\nPKx43UYASE9PR0pKCs8SERmpUdmIoyVHkVech+s111s8HuETgeSoZHQL6gYnuZMFIiR9HT4MfPGF\nZtwjAgOlIs4GVnEjsms5OTlttrDp465n5OTythuTQ0NDkZ6ejgULFhh9cHPiGTnx2F8hljnzXdNQ\ng4NXDiL/cn6r/W9dg7oiOSoZUb5RkDnIOBhb/nwfPAhs367dDg6WeuJ8fCwXkz5sOee2iPkWy+w9\ncgA0y28NGzYMubm5Br85EdmWGzU3sK94H46UHGm1/61XWC8MiByAQA9ei7MV+/YB33yj3Q4Lk+5O\n9fKyXExEZDqcI0fk4NT9b/uK9+FM6ZkWj/u6+WJAxAD0Ce/D/jcbs3cvkJWl3Y6IkObEWXlXDJFD\nMutaqwqFAu+++y727NmDW7duac7UyWQynqkjslHq/rd9xftQUlPS4vFwn3AkRyYjMTiR/W82RqUC\ndu8Gmn89R0cDTz4pDf0lIvuh13TO3//+9/jXv/6FYcOG4eDBg5g8eTKuX7+OESNGmDs+siHtadYk\nwxmb75qGGuy5sAf/2PcPfFHwhU4Rp+5/m5s0F0/3fho9QnuwiPuVrXy+VSrgu+90i7j77pPOxNla\nEWcrObcXzLdYpsq3XmfkPvnkE+Tl5SEmJgZLly7F4sWLMXr0aMyfPx/Lli0zSSBEZF53639zkbug\nV8deGBg5kP1vNkylAnbuBA4c0O6LjwemTpWWKiYi+6NXj1xAQABu3boFuVyOjh07orCwEJ6envD1\n9W11vpw1YI8ckdT/dr78PPIu5bXa/+bj6oMBkQPQp2MfeLiwccqWKZXAV18Bhw5p93XrBkyeDDjr\n9Sc7EVmSWXvkunbtioMHD6J///7o06cPli1bBh8fH0RGRhp8QCIyv0ZlI45dP4a8S3mt9r919O6I\n5Khk3B98Py+d2oGmJuCzz6SBv2o9egCPPQY48b9eIrumV4/cP//5Tzj/+ifdqlWr8NNPP2H79u14\n//33zRoc2Rb2V4jVWr5rFbXILcrFP/b9A5+f+rxF/1tChwTMSZqD+X3m44HQB1jEGcBaP9+NjcDH\nH+sWcb16ARMn2n4RZ605t1fMt1hCe+T69++v+XeXLl2Q1fx+diKyuJu1N6X+t2tHoFAqdB5zkbsg\nKSwJAyMHooNnBwtFSOagUAAffQScaXbVvF8/4JFHAAeZ00zk8NrskcvKytJrYvvIkSNNHpQpsEeO\n7FVBYQG+/+l7NCgbUHW7Cp6hnqj2rG7xPB9XH/SP6I++4X3Z/2aHGhqAzEzg/HntvkGDgIceYhFH\nZIuMrVvaLORiY2P1KuTON/8WsSIs5MheqFQq1DfVo1ZRi19O/4LMPZlQxipxtfoqqhuq0VjYiKTE\nJASFBwEAwrzDkByZjO4h3Xnp1E7V1wMffghcvKjdN3w4kJLCIo7IVpm8kLN1LOTE4zp9+lE0KVCr\nqG3zp0ZR02KfUiUN4c7/IR+1kbUAgPJT5fDv6g8A8Cr2wswJMzEwciBi/fX7I4wMYy2f77o6YNMm\n4PJl7b7UVGDoUMvFZC7WknNHwXyLJWSt1eYUCgX27duHK1eu4IknnkB1dTVkMhm8uGAfObAmZdNd\ni7LWfu7sYTOEEkqdbblMjjDvMCRGJ2J6j+nt/XXIytXUABkZQEmzG5FHjwYGDrRcTERkWXqdkTt6\n9CjGjx8PNzc3FBcXo7q6Gjt27EBGRga2bt0qIk6D8YwcGUqpUuJ2423prFhDy7Nirf3UN9ULic3V\nyRWeLp7Yv3c/6qPr4SJ3gZerFzp6d4SLkwtCrodg4dSFQmIhy6iqkoq4Gze0+8aOBfr2tVxMRGQ6\nZr20OnjwYCxYsABpaWkICAhAWVkZampqEB8fjytXrhgVsLmxkHNszfvK9P2pU9RBBfN/ZpxkTvB0\n8Wz1x8vVq8U+D2cPuDhJY/kLCguwfvd6uMVr11qqP1OPOSPmICEuweyxk2WUl0tFXGmptC2TARMm\nAElJlo2LiEzHrIVcQEAASktLIZPJNIWcSqVCYGAgysrKjArY3FjIiWeu/gqVSgWF8u59Za39qPvK\nzEkGWZtFWVs/rk6u7ephKygsQNbPWThx7AQSuycitXcqizgBLNU/VFoKbNgAVFRI23K5tFrD/fcL\nD0U49myJxXyLJbRHLiYmBgcPHkS/fv00+w4cOID4+HiDD0j2Rz0O4+TxkzhechwP9nnwroVFo7IR\ndYo6gxr+71wb1Fw8nD0MKsrcnd2F31iQEJeAhLgE5ITwS9fe3bwpFXHqlRCdnIApU4CuXS0bFxFZ\nD73OyG3fvh3z5s3DggUL8Oabb2LJkiVYs2YN1q5di1GjRomI02A8IyfGqTOn8O+sf0PWSQaFUiHd\nkXm6Fg/2eRBB4UFW0Vem74+HswfHdZDVKCmRLqfW1Ejbzs7AtGlAXJxl4yIi8zD7+JFDhw7h/fff\nR1FREaKjo/H000+jT58+Bh9QFBZyYvy/zP+HT+s/bbHfq9gL/Yb0a+UVxnGSObXaP3a3H2c5Vwon\n23TlCrBxozRqBABcXYEZM4DYWIuGRURmZLZLq42NjUhISMCJEyfw3nvvGRWcKVVWVuLBBx/EyZMn\nsX//fiQmJlo6JIemlCkhl8mhVCl15po1oanN18hl8jYvYbZVrLnIXTgb7Q7sZxFLVL4vXZLmxNX/\neuLazQ2YOROIijL7oa0OP+NiMd9imSrf9yzknJ2dIZfLUVdXBzc3t3s93ew8PbUBJHkAACAASURB\nVD2xc+dO/PGPf+QZNyvgInOBh7MHlColGlwa0MGjA1ycXBAcEIyHOj1kNX1lRLbg/Hlp2a2GBmnb\nwwOYNQsID7dsXERkvfS6tPruu+/iiy++wEsvvYSoqCid/xPu1KmTWQNsy9y5c/GHP/wB97dx6xYv\nrYrBcRhEplFYCGzZAjT+el+PlxeQlgaEhlo2LiISw6x3rS5atAgA8N1337U4aFNT25fQyP4lxCVg\nDuYg6+csNCgb4Cp3ReoIjsMgMsSpU8C2bYD669THB5g9GwgKsmxcRGT95Po8SalUtvpjaBG3evVq\n9O3bF+7u7pg7d67OY6WlpZg4cSK8vb0RGxuLzMxMzWNvvfUWRowYgTfffFPnNbw8Zx0S4hKwcOpC\nJIUlYeHUhSziBMnJybF0CA7FXPk+dgz46CNtEefvD8ydyyIO4GdcNOZbLFPlW+htfREREXj11Vfx\n7bffok59O9avnn32Wbi7u+P69es4dOgQHn30UfTs2ROJiYl4/vnn8fzzz7d4P146JSJbdvgw8MUX\ngPqrLDBQOhPn52fZuIjIdggt5CZOnAgAOHjwIIqLizX7a2pq8Omnn+L48ePw9PTE4MGDMWHCBGzc\nuBErV65s8T6PPPIIjhw5goKCAixYsACzZ89u9Xhz5sxB7K/36/v7+yMpKUlzh4i6Eua2abfVrCUe\ne99Ws5Z47H1bzRTvV1AAXL0qbV+4kAM/P+CFF1Lg42M9vy+3uc1t836fpKen48KFC2gPvefImdIr\nr7yCy5cvY926dQCkGXVDhgxBjXryJYBVq1YhJycHX375pVHH4M0ORGSt9u0DvvlGux0WJt2d6uVl\nuZiIyLKMrVvkZojlnu7sbauuroavr6/OPh8fH1Sp16Uhm9D8rwwyP+ZbLFPle+9e3SIuIkK6nMoi\nriV+xsVivsUyVb4NvrSqVOouRC6XG14L3llxent7o7KyUmdfRUUFfHx8DH5vIiJrpFIBu3cDubna\nfdHRwJNPSkN/iYiMoVcV9tNPPyE5ORmenp5wdnbW/Li4uBh10DvPyHXp0gWNjY0oLCzU7Dty5Ai6\nd+9u1Purpaen8y8MgdTX/0kM5lus9uRbpQJ27dIt4u67T1qxgUVc2/gZF4v5Fqt5z1x6errR76NX\nj1z37t0xfvx4zJw5E56enjqPxRqw+F9TUxMUCgWWLVuGy5cvY+3atXB2doaTkxOmT58OmUyGf//7\n3/j5558xduxY5OXloVu3bgb/UgB75IjIOqhUwM6dwIED2n3x8cDUqYCRfwsTkR0ya4/cxYsXsWLF\nCiQmJiI2NlbnxxDLly+Hp6cn3njjDWzatAkeHh5YsWIFAGn1iLq6OoSEhGDmzJlYs2aN0UUcWQbP\nforFfItlTL6VSmm8SPMirls3YNo0FnH64GdcLOZbLKE9chMnTsS3336L0aNHt+tg6enpbZ4+DAgI\nwGeffdau9ycishZNTcBnn0kDf9V69AAmTgSMaC0mImqVXpdWp06diq+++gpDhw5FaLOF/2QyGTIy\nMswaoLF4aZWILKWxEfjkE+DkSe2+Xr2AceNYxBFR68y61mpiYiISExNbPag1S09PR0pKChs4iUgY\nhUJacuvMGe2+/v2BMWMAK//KJCILyMnJaddlVosMBBaBZ+TEy8nJYdEsEPMtlj75bmgAMjOB8+e1\n+wYNAh56iEWcMfgZF4v5FuvOfJv8jFxubi6GDRsGAMjOzm7zDUaOHGnwQYmI7M3t28DmzcDFi9p9\nw4cDKSks4ojIfNo8I9e9e3cc+7VLNzY2ts3LqOeb/+lpRXhGjohEqasDNm4ErlzR7ktNBYYOtVxM\nRGRbjK1beGmViKgdamqAjAygpES7b/RoYOBAy8VERLbHptZaFYUrO4jFXIvFfIvVWr6rqoB167RF\nnEwm3ZnKIs40+BkXi/kWS53v9q7soNddqxUVFUhPT8eePXtw69YtzXqrMpkMF5s3hFiZ9iSGiOhu\nysulM3GlpdK2TAY89hjQs6dl4yIi26KerrFs2TKjXq/XpdWZM2fi0qVLeP755zFr1ixs3LgRf/vb\n3zB58mT8/ve/N+rA5sZLq0RkLqWlwIYNQEWFtC2XA5MnA/ffb9m4iMh2mbVHLjg4GCdPnkRQUBD8\n/PxQUVGBy5cvY9y4cfj555+NCtjcWMgRkTncuCGdiauqkradnKR1UxMSLBsXEdk2s/bIqVQq+Pn5\nAQB8fHxQXl6Ojh074kzziZfk8NhfIRbzLVZOTg6uXQPWr9cWcc7OwPTpLOLMhZ9xsZhvsYSutfrA\nAw8gNzcXqampGDJkCJ599ll4eXkhgd9eRGTnCgqK8P33Z3HgwC8oK1MiKqozgoJi4OoKzJgBxMZa\nOkIicmR6XVo9e/YsAKBz584oKSnByy+/jOrqaixdurTVpbusgUwmw9KlS7lEFxEZraCgCOvXF+L2\n7VT88gvQ1AQ0Nmahf/84PP98DKKiLB0hEdk69RJdy5Yt4xy55tgjR0Tt9c472SgoGIljx4Bfb9aH\nszMwcmQ2Xn6Zq9oQkemYfImu5v7zn/+0urKDm5sbIiMjMXDgQLi5uRl8cLIvXKdPLObb/IqK5Dh6\nFFCpgPLyHAQHp6BnT8DT065HcFoNfsbFYr7FMlW+9SrkMjIykJeXh7CwMERGRqK4uBjXrl1D3759\nUVRUBAD4/PPP0a9fv3YHRERkDfbvB44dU0L9B7KLC9CrF+DpCbi6Ki0bHBHRr/S6tPrss88iISEB\nv/3tbwFId7G+8847OHnyJN5++2385S9/wY4dO5CXl2f2gPXFS6tEZAyVCti9G8jNBW7eLMLhw4Xw\n9U1Fz56AmxtQX5+FOXPikJAQY+lQiciOmHWOnL+/P0pLSyGXay8nNDY2IigoCOXl5aivr0dwcDAq\nKysNDsBcWMgRkaGUSmDHDuCnn7T7nJ2L4O19FoAcrq5KpKZ2ZhFHRCZn1jlyoaGh+PLLL3X27dix\nA6GhoQCAuro6uLq6Gnxwsi+cQSQW821ajY3Atm26RVx8PPDiizFYvHgkkpKAhQtHsogTiJ9xsZhv\nsYTOkXv77bcxZcoUdO/eXdMjd/ToUWzbtg0AkJ+fj+eee84kAZlSeno6x48Q0T3V1wNbtgDnz2v3\nPfAAMGGCtHIDEZG5qMePGEvv8SM3b97Ezp07ceXKFYSHh+PRRx9Fhw4djD6wufHSKhHpo7oa+PBD\n4OpV7b6BA4FRo4BWbtYnIjILs/bI2SIWckR0L2VlwMaNQGmpdt+DDwKDB7OIIyKxzNojR6QP9leI\nxXy3T0kJ8J//aIs4mQwYPx4YMqT1Io75Fo85F4v5FktojxwRkT0pKgIyM4Hbt6VtZ2fg8ceBrl0t\nGxcRkaF4aZWIHEpBgXR3amOjtO3mBkyfDsTGWjQsInJwZr+02tDQgNzcXGzduhUAUF1djerqaoMP\nSERkKYcPA1u3aos4b29g7lwWcURku/Qq5I4ePYqEhATMnz8f8+bNAwDs2bNH828igP0VojHfhvnx\nR+Dzz6WhvwAQEAA89RQQFqbf65lv8ZhzsZhvsUyVb70Kud/85jdYtmwZTp06BRcXFwBASkoK9u7d\na5IgiIjMRaUCdu0CvvtOuy8sDJg3DwgMtFxcRESmoFePXEBAAEpLSyGTyRAQEICysjKoVCoEBgai\nrKxMRJwGk8lkWLp0KQcCEzkwpRL48kvpkqpaTIzUE+fubrm4iIjU1AOBly1bZr45cklJSVi7di36\n9eunKeTy8/OxaNEi5OfnGxW4ufFmByLHplBINzWcPq3d17WrdHeqM+/XJyIrY9abHV5//XWMHTsW\nr732GhoaGvCXv/wFjz/+OJYvX27wAcl+sb9CLOa7bXV10qDf5kVc797A1KnGF3HMt3jMuVjMt1hC\ne+TGjh2Lb775Bjdu3MDw4cNx8eJFfPbZZxg1apRJgiAiMpWqKmDdOuDiRe2+oUOBceMAOUegE5Gd\n4Rw5IrIbt25JZ+LKy7X7Ro0CkpMtFxMRkT7Meml14sSJLe5Qzc3NxeOPP27wAYmIzOHKFeCDD7RF\nnFwOTJrEIo6I7JtehdyePXuQfMe3YXJyMrKzs80SFNkm9leIxXxrnT8PrF8P1NRI2y4u0p2pDzxg\numMw3+Ix52Ix32IJXWvVw8MDNTU18PPz0+yrqamBq6urSYIgIjLWiRPAJ58ATU3StocHMGMGEBVl\n2biIiETQq0du7ty5uH37NtasWQM/Pz9UVFRg4cKFcHFxwfr16wWEaTj2yBHZv4MHgR07pKG/AODr\nC8ycCYSEWDYuIiJDmbVH7s0330RlZSUCAwMRHByMwMBAVFRU4K233jL4gERE7aVSAXv2ANu3a4u4\nDh2kJbdYxBGRI9GrkAsMDMSOHTtQXFys+c/t27cjICDA3PGRDWF/hViOmm+VCvj6a2D3bu2+8HCp\niPP3N99xHTXflsSci8V8iyW0R07NyckJQUFBqKurw7lz5wAAnTp1Mkkg5pCens4luojsSFMT8Nln\nwLFj2n2dOgFPPAG4uVkuLiIiY6mX6DKWXj1y33zzDebNm4erV6/qvlgmQ5O6w9jKsEeOyL40NABb\ntwJnz2r33X8/MHEil9wiIttnbN2iVyHXqVMnvPjii0hLS4Onp6dRAYrGQo7IftTWAh9+CFy+rN3X\nrx8wZgxXayAi+2DWmx3Ky8uxYMECmyniyDLYXyGWo+S7okIa9Nu8iEtJAR55RGwR5yj5tibMuVjM\nt1hC11qdN28ePvjgA5MckIhIXzduAP/5D3DzprQtkwGPPioVcjKZRUMjIrIKel1aHTJkCPLz8xET\nE4OwsDDti2Uy5ObmmjVAY/HSKpFtKy6WLqfW1UnbTk7Sklv332/ZuIiIzMGsPXJtDf2VyWSYPXu2\nwQcVgYUcke0qLJRubFAopG1XV2DaNOkOVSIie2TWQs4WsZATLycnh6NeBLLXfB89Ko0YUSqlbU9P\nabWG8HDLxmWv+bZmzLlYzLdYd+bb2LpF75v2S0pKsH//fty6dUvnQE899ZTBByUias3+/dKwXzV/\nf2DWLGnVBiIiakmvM3Kff/45Zs6cifj4eBw7dgzdu3fHsWPHMGTIEOxuPl7divCMHJHtUKmklRqa\nt9yGhEhn4nx9LRcXEZEoZh0/smTJEnzwwQc4dOgQvL29cejQIbz//vvo3bu3wQckImpOqZTWTG1e\nxEVFAXPnsogjIroXvQq5S5cuYerUqZptlUqFtLQ0ZGRkmC0wsj2cQSSWPeS7sRHYtg346Sftvi5d\ngLQ0wMPDcnG1xh7ybWuYc7GYb7GErrUaEhKCa9euISwsDLGxscjLy0NQUBCU6m5kIiID3b4NbNkC\nXLig3dezJzB+vDRqhIiI7k2vHrn/+7//Q1xcHB5//HFkZGRg/vz5kMlkeOGFF/D666+LiNNg7JEj\nsl7V1cCmTcC1a9p9ycnAww9z0C8ROSah40eKiopQU1ODxMREgw8oCgs5IutUVgZs3AiUlmr3PfQQ\nMGgQizgiclxmvdnhTjExMVZdxJFlsL9CLFvM97Vr0pJb6iJOJgMmTAAGD7b+Is4W823rmHOxmG+x\nhK61evjwYYwcORIBAQFwcXHR/Li6upokCHNJT0/nB5PIShQVAevWSZdVAcDZGXjiCaBXL8vGRURk\nSTk5OUhPTzf69XpdWu3WrRsef/xxTJ06FR533EoWFxdn9MHNiZdWiazHqVPAxx9Ld6kCgJsbMGMG\nEBNj2biIiKyFWXvkAgICUFpaCpm1X/tohoUckXU4dAj48ktp6C8AeHtLg37DwiwbFxGRNTFrj1xa\nWho+/PBDg9+cHAsvY4tl7flWqYAffwS++EJbxAUGAvPm2WYRZ+35tkfMuVjMt1hC58i99NJLGDhw\nIFauXImQkBDNfplMhuzsbJMEQkT2Q6UCvvsO+O9/tfvCwqQzcd7elouLiMje6HVpdejQoXB1dcXE\niRPh7u6ufbFMhnnz5pk1QGPx0iqRZTQ1SZdSjxzR7ouNBaZNA5p9fRARUTNm7ZHz8fHBzZs34ebm\nZlRwlsBCjkg8hUJacuv0ae2+bt2AyZOlu1SJiKh1Zu2RGzp0KE6cOGHwm5NjYX+FWNaW77o6ICND\nt4jr0weYMsU+ijhry7cjYM7FYr7FEtojFxsbi4cffhiTJk1q0SP3v//7vyYJhIhsV2WltOTW9eva\nfcOGASNGWP+gXyIiW6bXpdW5c+dCpVLpjB9Rb69bt86sARqLl1aJxLh1S1pyq7xcu2/0aGDgQMvF\nRERka4ytW+55Rq6pqQmRkZFYsmSJzo0ORERXrkhn4mprpW25HHjsMeCBBywbFxGRo7hnj5yTkxPe\ne+89q1+OiyyP/RViWTrf584B69drizgXF2m1Bnst4iydb0fEnIvFfIsldK3VtLQ0vPfeeyY5IBHZ\nvuPHgQ8/BBoapG0PD2D2bMBKV+wjIrJbevXIDR48GPn5+QgPD0dUVJSmV04mkyE3N9fsQRqDPXJE\n5nHgALBzp3a1Bl9fYNYsIDjYsnEREdkys86RW79+fZsHnT17tsEHFYGFHJFpqVRAbi6we7d2X1CQ\nVMT5+VkuLiIie2DWQs4WsZATLycnBykpKZYOw2GIzLdKBXz9NZCfr90XEQE8+STg6SkkBIvj51s8\n5lws5lusO/Nt1oHAKpUKH3zwAUaMGIEuXbpg5MiR+OCDD1goETmApibgk090i7jOnaWeOEcp4oiI\nrJVeZ+RWrFiBjIwMvPDCC4iOjsbFixfx1ltv4cknn8Qrr7wiIk6D8YwcUfvV1wMffQScPavd1707\nMHEi4ORkubiIiOyNWS+txsbGYs+ePYiJidHsKyoqwtChQ3Hx4kWDDyoCCzmi9qmpATZvBi5f1u7r\n3x8YM4arNRARmZpZL63W1tYiKChIZ1+HDh1w+/Ztgw9I9osziMQyZ77Ly4F163SLuBEjHLuI4+db\nPOZcLOZbLKFz5EaPHo2ZM2fi1KlTqKurw8mTJ5GWloZRo0aZJAhD5OfnY9CgQRg+fDhmzJiBxsZG\n4TEQ2bPr14EPPgBu3pS2ZTJg7Fhg+HDHLeKIiKyVXpdWKyoq8Nxzz2Hr1q1QKBRwcXHB1KlT8fbb\nb8Pf319EnBrXrl1DQEAA3Nzc8PLLL6NPnz6YPHlyi+fx0iqR4S5dki6n1tVJ205OwOTJQGKiZeMi\nIrJ3Jr+0unr1as2/b9y4gYyMDNTW1uLq1auora3Fxo0bhRdxABAWFgY3NzcAgIuLC5zYcU1kEmfO\nABkZ2iLO1VUaL8IijojIerVZyL388suaf/fu3RuAtO5qaGioVRRPRUVF+O677zBu3DhLh0K/Yn+F\nWKbM9y+/AJmZgEIhbXt5AXPmAJ06mewQNo+fb/GYc7GYb7FMlW/nth7o1KkTXnjhBSQmJkKhUGjm\nxqmX51L/+6mnntL7YKtXr8b69etx7NgxTJ8+HevWrdM8Vlpainnz5uG7775DUFAQVq5cienTpwMA\n3nrrLXz55ZcYO3YsXnjhBVRWViItLQ0bNmywiqKSyJbt2wd88412299fWq2hQwfLxURERPpps0eu\noKAAf/3rX1FUVIScnBwMHTq01TfY3Xy9nnv47LPPIJfL8e2336Kurk6nkFMXbf/5z39w6NAhPPro\no/jvf/+LxDuu6zQ2NmL8+PH4wx/+gJEjR7b9i7FHjuiuVCogOxvYu1e7LyREKuJ8fCwXFxGRIzLr\nHLnU1FRkZWUZFVhrXn31VRQXF2sKuZqaGgQGBuL48eOIi4sDAMyePRvh4eFYuXKlzms3btyI559/\nHj169AAAPPPMM5g6dWqLY7CQI2qbUgls3w78/LN2X3Q0MH064OFhubiIiByVsXVLm5dW1RobG/Hj\njz+ivr5ec5NBe90Z6OnTp+Hs7Kwp4gCgZ8+erV4/njVrFmbNmqXXcebMmYPY2FgAgL+/P5KSkjTr\nmqnfm9um2z58+DAWL15sNfHY+7ax+W5sBP73f3Nw8SIQGys93tiYg+howMPDen4/a9vm51v8tnqf\ntcRj79vqfdYSj71vHz58GOXl5bhw4QLaQ68zcj179sTOnTsRERHRroOp3XlGbu/evZg6dSquXr2q\nec7atWuxefNmgy7dNsczcuLl5ORoPqhkfsbk+/ZtYMsWoPn3RlISMG4cl9y6F36+xWPOxWK+xboz\n32Y7IwcATz75JMaNG4ff/va3iIqK0tzwAOCufWptuTNQb29vVFZW6uyrqKiADxt1bAq/AMQyNN/V\n1cCmTcC1a9p9gwYBDz3EQb/64OdbPOZcLOZbLFPlW69C7t133wUALFu2rMVj58+fN/igsjv+X6NL\nly5obGxEYWGh5vLqkSNH0L17d4Pfm4haKi0FNm4Eysq0+x56CBg82HIxERFR+8n1edKFCxdw4cIF\nnD9/vsWPIZqamnD79m00NjaiqakJ9fX1aGpqgpeXFyZNmoTXXnsNtbW1+OGHH/DVV1/p3QvXlvT0\ndJ1r/2RezLVY+ub72jVpyS11ESeXAxMmsIgzFD/f4jHnYjHfYqnznZOTg/T0dKPfR69CDgAUCgX2\n7t2LrVu3AgCqq6tRU1Nj0MGWL18OT09PvPHGG9i0aRM8PDywYsUKANJZv7q6OoSEhGDmzJlYs2YN\nunXrZtD73yk9PZ2nismhXbgArFsnXVYFAGdn4IkngF69LBoWERH9KiUlpV2FnF43Oxw9ehTjx4+H\nm5sbiouLUV1djR07diAjI0NT2Fkb3uxAju7UKeDjj4HGRmnb3V0aLxITY9m4iIioJbPOkRs8eDAW\nLFiAtLQ0BAQEoKysDDU1NYiPj8eVK1eMCtjcWMiRIzt0CPjyS2noLwB4e0uDfkNDLRsXERG1zti6\nRa9LqydOnGjRr+bp6Yk69eraVoo9cmIx12K1lm+VCvjhB+CLL7RFXGAgMG8ei7j24udbPOZcLOZb\nLKE9cjExMTh48KDOvgMHDiA+Pt7oA4vAHjlyJCoVsGsX8P332n0dOwJPPQUEBFguLiIiapuQHrnt\n27dj3rx5WLBgAd58800sWbIEa9aswdq1azFq1CijD25OvLRKjqSpSbqUeuSIdt999wHTpgEmWpCF\niIjMyKw9cgBw6NAhvP/++ygqKkJ0dDSefvpp9OnTx+ADisJCjhxFQwOwbRtw5ox2X7duwOTJ0l2q\nRERk/cxeyNkaFnLicXkXsXJycjBgQAo2bwYuXdLu79MHePRRaV4cmQ4/3+Ix52Ix32KZaokuvb7q\n6+vr8eqrryIuLg6enp6Ij4/HK6+8gtu3bxt8QJF4swPZs5oaadBv8yJu2DBg7FgWcUREtqK9Nzvo\ndUbuqaeewunTp7FkyRJER0fj4sWLWLFiBeLj4zUL31sbnpEje1VQUITPPz+LvDw5GhqU6NSpM4KC\nYjBmDDBggKWjIyIiY5j10mpgYCDOnj2LgGa3vpWWlqJz584oa754oxVhIUf26NSpIvztb4W4eDEV\nCoW0T6nMwh/+EIfx4znpl4jIVpn10mrHjh1RW1urs6+urg7h4eEGH5DsFy9jm49KJd3MsHTpWZw9\nKxVx5eU5kMuBpKRUFBeftXSIdo+fb/GYc7GYb7FMlW+97mmbNWsWxowZg0WLFiEqKgoXL17Eu+++\ni7S0NGRnZ2ueN3LkSJMERURaly5Js+GKioCKCu3fXk5OQFIS4OsLNDSwKY6IyBHpdWk1NjZWerJM\nptmnUql0tgHg/Pnzpo2uHXhplWzd9etAVhZQUKDdl5+fjdu3RyIqCoiK0o4XCQnJxsKF/EOKiMhW\nGVu36HVG7sKFCwa/sTVQr+zA26nJlpSXAzk50nDf5v+blsuBCRM648yZLHh7p2r219dnITU1Tnyg\nRETUbjk5Oe26zMo5cmQynEHUPjU1wN69wIED0koNzfXoAYwYIa2bWlBQhKysszhx4hckJj6A1NTO\nSEjgjQ7mxs+3eMy5WMy3WKaaI8e570QWVl8P7NsH/Pe/0r+bi48HUlOBsDDtvoSEGCQkxCAnR84v\nXSIiB8czckQW0tQEHDwI5OZKZ+Oai4wEHnwQ+LU9lYiI7BzPyBHZCJUKOHoUyM6W+uGaCw6WzsAl\nJAB33EtERETUAmcWkMlwBtHdqVTA6dPAmjXAp5/qFnF+fsBjjwHPPAN07apfEcd8i8V8i8eci8V8\niyV0jhwRtc/Fi9IsuIsXdfd7egJDhwL9+mlHiRAREenLrnvkli5dyvEjZFGtzYIDAFdXIDlZ+nF3\nt0xsRERkeerxI8uWLTPfWqu2iDc7kCWVlwO7dwO//KI7C87JCejTBxg2DPD2tlx8RERkXcy61iqR\nPthfId19+s03wNtv6w70lcmABx4AFi0CHnnENEUc8y0W8y0ecy4W8y0We+SIrEh9PZCXJ82Ca2jQ\nfay1WXBERESmwEurRO3Q2Aj89FPrs+CioqRZcDFcdIGIiO6Bc+SIBFIqpVlwu3e3nAUXEiKdgevS\nhbPgiIjIvNgjRybjCP0V6llw//oX8Nlnrc+C+81vxAz0dYR8WxPmWzzmXCzmWyz2yBEJdrdZcMOG\nAX37chYcERGJxR45onsoKZFmwZ0+rbtfPQtu0CDAzc0ysRERkX1gj1wr0tPTORCYjHa3WXB9+0or\nMnAWHBERtYd6ILCxeEaOTCYnJ8cuiuaaGuku1IMHgaYm7X6ZDOjRAxgxAggIsFx8avaSb1vBfIvH\nnIvFfIt1Z755Ro6one42C65LF+lO1NBQy8RGRETUGp6RI4fX2CidfcvNBWprdR/jLDgiIhKBZ+SI\nDMRZcEREZOs4R45MxlZmEKlUQEEBsGZNy1lw/v7AxIniZsG1h63k214w3+Ix52Ix32JxjhyRETgL\njoiI7Al75Mgh3G0W3KBB0jw4zoIjIiJLYY8cUSvKyqQeuKNHW58FN2wY4OVlufiIiIjagz1yZDLW\n1F9RXQ18/TWwerXuQF+ZDOjZE1i0CBgzxraLOGvKtyNgvsVjzsVivsVifYHyAQAAEfxJREFUjxxR\nK+rrpTlweXmcBUdERPbPrnvkli5dyiW6HMTdZsFFR0uz4KKjLRMbERFRW9RLdC1btsyoHjm7LuTs\n9FejZpRK6dLp7t1ARYXuY5wFR0REtsLYuoU9cmQyIvsrms+C+/xz3SLOlmbBtQf7WcRivsVjzsVi\nvsVijxw5rKIiaRbcpUu6+728pLtQ+/ThLDgiInIMvLRKNqOkRCrgzpzR3c9ZcEREZOs4R47s1t1m\nwfXrBwwdattjRIiIiIzFHjkyGVP3V1RXAzt3tj0L7rnngNGjHbeIYz+LWMy3eMy5WMy3WOyRI7t1\nt1lwCQnSnaghIZaJjYiIyJqwR46sRmMjcOAAsHcvZ8EREZFjYY8c2ax7zYJ78EEgPt5+x4gQEREZ\niz1yZDKGXu9XqYBTp4D33mt9FtykSdIsOA70bR37WcRivsVjzsVivsVijxzZNM6CIyIiaj/2yJFQ\n164BWVmtz4IbPBgYOJCz4IiIyPGwR46sWlkZkJ0tzYJrjrPgiIiIjMceOTKZ1q73q2fBvf22bhEn\nkwFJSZwF1x7sZxGL+RaPOReL+RaLPXJk1W7flmbB7dvHWXBERETmYtc9ckuXLkVKSgpSUlIsHY7D\nuNssuJgYaZRIVJRlYiMiIrI2OTk5yMnJwbJly4zqkbPrQs5OfzWrU1BQhF27zqKoSI7z55Xo2LEz\ngoJiNI+HhkoFXFwcx4gQERG1xti6hT1y1C6nThXhzTcL8fXXI/H998CtWyNx+HAhbt4sQkCAdhYc\nB/qaHvtZxGK+xWPOxWK+xWKPHFmFzMyzOH06VWefh0cqPD2zsWhRDJycLBQYERGRA+ClVWqXt97K\nQVZWCqqrpVEiUVHST4cOOVi8OMXS4REREdkEzpEji3B1VaJTJ6C0VFrQ3tVVu5+IiIjMiz1y1C4P\nPtgZXl5ZiIsDrlzJAQDU12chNbWzReNyBOxnEYv5Fo85F4v5Fos9cmQVEhJiMGcOkJWVjZs3f0FI\niBKpqXFISIi552uJiIiofdgjR0RERGRhHD9CRERE5GBYyJHJsL9CLOZbLOZbPOZcLOZbLFPlm4Uc\nERERkY1ijxwRERGRhbFHjoiIiMjBsJAjk2F/hVjMt1jMt3jMuVjMt1jskSMiIiJycOyRIyIiIrIw\n9sgRERERORgWcmQy7K8Qi/kWi/kWjzkXi/kWiz1yRERERA7O5nrkSkpKMGnSJLi6usLV1RWbN29G\nhw4dWjyPPXJERERkK4ytW2yukFMqlZDLpROJGzZswNWrV/HnP/+5xfNYyBEREZGtcJibHdRFHABU\nVlYiICDAgtFQc+yvEIv5Fov5Fo85F4v5Fsuhe+SOHDmCAQMGYPXq1Zg+fbqlw6FfHT582NIhOBTm\nWyzmWzzmXCzmWyxT5VtoIbd69Wr07dsX7u7umDt3rs5jpaWlmDhxIry9vREbG4vMzEzNY2+99RZG\njBiBN998EwDQs2dP7N+/H6+//jqWL18u8leguygvL7d0CA6F+RaL+RaPOReL+RbLVPkWWshFRETg\n1VdfxVNPPdXisWeffRbu7u64fv06PvzwQzzzzDM4ceIEAOD555/H7t278cILL0ChUGhe4+vri/r6\nemHx3017T5Ea+np9nn+357T1mL77LX0K3hTHN+Q9zJXvth7Td59I1vYZN/Zx5tv45/M7xXTvwe8U\n+/6Mi8y30EJu4sSJmDBhQou7TGtqavDpp59i+fLl8PT0xODBgzFhwgRs3LixxXscPnwYw4cPx8iR\nI7Fq1Sq8+OKLosK/K3v+QLa2v7XnXbhw4Z4xmQq/dMXmu7Xjm/v11lbIOXq+7/UcfqfwO8VQ9vwZ\nF5lvi9y1+sorr+Dy5ctYt24dAODQoUMYMmQIampqNM9ZtWoVcnJy8OWXXxp1jLi4OJw9e9Yk8RIR\nERGZU8+ePY3qm3M2Qyz3JJPJdLarq6vh6+urs8/HxwdVVVVGH6OwsNDo1xIRERHZAovctXrnSUBv\nb29UVlbq7KuoqICPj4/IsIiIiIhsikUKuTvPyHXp0gWNjY06Z9GOHDmC7t27iw6NiIiIyGYILeSa\nmppw+/ZtNDY2oqmpCfX19WhqaoKXlxcmTZqE1157DbW1tfjhhx/w1VdfYdasWSLDIyIiIrIpQgs5\n9V2pb7zxBjZt2gQPDw+sWLECAPDuu++irq4OISEhmDlzJtasWYNu3bqJDI+IiIjIptjcWqvt9ac/\n/Ql5eXmIjY3FBx98AGdni9zv4TAqKyvx4IMP4uTJk9i/fz8SExMtHZJdy8/Px+LFi+Hi4oKIiAhk\nZGTwM25GJSUlmDRpElxdXeHq6orNmze3GK9E5pGZmYnf/e53uH79uqVDsWsXLlxAv3790L17d8hk\nMnz00UcICgqydFh2LScnB6+//jqUSiV++9vf4rHHHrvr821yiS5jHTlyBFeuXEFubi66du2Kjz/+\n2NIh2T1PT0/s3LkTjz/+uFGLAZNhoqOjsXv3buzZswexsbH44osvLB2SXQsODsaPP/6I3bt3Y8aM\nGVi7dq2lQ3IITU1N2LZtG6Kjoy0dikNISUnB7t27kZ2dzSLOzOrq6rBq1Sp8/fXXyM7OvmcRBzhY\nIZeXl4dRo0YBAEaPHo0ff/zRwhHZP2dnZ/4PX6CwsDC4ubkBAFxcXODk5GThiOybXK79Cq2srERA\nQIAFo3EcmZmZmDp1aosb58g8fvzxRwwbNgxLliyxdCh2Ly8vDx4eHhg3bhwmTZqEkpKSe77GoQq5\nsrIyzUgTX19flJaWWjgiIvMoKirCd999h3Hjxlk6FLt35MgRDBgwAKtXr8b06dMtHY7dU5+Ne+KJ\nJywdikMIDw/H2bNnkZubi+vXr+PTTz+1dEh2raSkBIWFhdi+fTuefvpppKen3/M1NlnIrV69Gn37\n9oW7uzvmzp2r81hpaSkmTpwIb29vxMbGIjMzU/OYv7+/Zl5dRUUFAgMDhcZty4zNeXP861l/7cl3\nZWUl0tLSsGHDBp6R01N78t2zZ0/s378fr7/+OpYvXy4ybJtmbM43bdrEs3FGMDbfrq6u8PDwAABM\nmjQJR44cERq3rTI23wEBARg8eDCcnZ0xcuRIHD9+/J7HsslCLiIiAq+++iqeeuqpFo89++yzcHd3\nx/Xr1/Hhhx/imWeewYkTJwAAgwYNwvfffw8A+PbbbzFkyBChcdsyY3PeHHvk9GdsvhsbGzFt2jQs\nXboU8fHxosO2WcbmW6FQaJ7n6+uL+vp6YTHbOmNzfvLkSWRkZGDMmDE4c+YMFi9eLDp0m2Rsvqur\nqzXPy83N5feKnozNd79+/XDy5EkA0trynTt3vvfBVDbslVdeUc2ZM0ezXV1drXJ1dVWdOXNGsy8t\nLU315z//WbP9xz/+UTV06FDVzJkzVQqFQmi89sCYnI8ZM0YVHh6uSk5OVq1fv15ovLbO0HxnZGSo\nOnTooEpJSVGlpKSotm7dKjxmW2Zovvfv368aNmyYasSIEaqHH35YdenSJeEx2zpjvlPU+vXrJyRG\ne2Jovnfu3Knq06ePaujQoarZs2ermpqahMdsy4z5fL/zzjuqYcOGqVJSUlTnzp275zFsei6B6o4z\nPKdPn4azszPi4uI0+3r27ImcnBzN9l//+ldR4dklY3K+c+dOUeHZHUPzPWvWLA7SbgdD892/f3/s\n2bNHZIh2x5jvFLX8/Hxzh2d3DM33mDFjMGbMGJEh2hVjPt8LFy7EwoUL9T6GTV5aVbuzR6K6uhq+\nvr46+3x8fFBVVSUyLLvGnIvFfIvFfIvHnIvFfIslIt82XcjdWel6e3trbmZQq6io0NypSu3HnIvF\nfIvFfIvHnIvFfIslIt82XcjdWel26dIFjY2NKCws1Ow7cuQIunfvLjo0u8Wci8V8i8V8i8eci8V8\niyUi3zZZyDU1NeH27dtobGxEU1MT6uvr0dTUBC8vL0yaNAmvvfYaamtr8cMPP+Crr75iz5AJMOdi\nMd9iMd/iMediMd9iCc13e+/IsISlS5eqZDKZzs+yZctUKpVKVVpaqnrsscdUXl5eqpiYGFVmZqaF\no7UPzLlYzLdYzLd4zLlYzLdYIvMtU6k43IuIiIjIFtnkpVUiIiIiYiFHREREZLNYyBERERHZKBZy\nRERERDaKhRwRERGRjWIhR0RERGSjWMgRERER2SgWckREREQ2ioUcEdEd5syZg1dffdWk7/nMM8/g\n9ddfN+l7EhE5WzoAIiJrI5PJWix23V7vvfeeSd+PiAjgGTkiolZx9UIisgUs5IjIqrzxxhuIjIyE\nr68vunbtiuzsbABAfn4+kpOTERAQgPDwcDz33HNQKBSa18nlcrz33nuIj4+Hr68vXnvtNZw9exbJ\nycnw9/fHtGnTNM/PyclBZGQkVq5cieDgYNx3333YvHlzmzFt374dSUlJCAgIwODBg3H06NE2n/v8\n888jNDQUfn5+eOCBB3DixAkAupdrx40bBx8fH82Pk5MTMjIyAACnTp3CQw89hA4dOqBr167Ytm1b\nm8dKSUnBa6+9hiFDhsDX1xejRo3CrVu39Mw0EdkDFnJEZDUKCgrwzjvv4ODBg6isrMSuXbsQGxsL\nAHB2dsY///lP3Lp1C3l5ecjKysK7776r8/pdu3bh0KFD2LdvH9544w08/fTTyMzMxMWLF3H06FFk\nZmZqnltSUoJbt27hypUr2LBhA+bPn48zZ860iOnQoUOYN28e1q5di9LSUixYsADjx49HQ0NDi+d+\n++232Lt3L86cOYOKigps27YNgYGBAHQv13711VeoqqpCVVUVPvroI3Ts2BGpqamoqanBQw89hJkz\nZ+LGjRvYsmULFi5ciJMnT7aZs8zMTKxfvx7Xr19HQ0MD/v73vxucdyKyXSzkiMhqODk5ob6+HseP\nH4dCoUB0dDQ6deoEAOjduzf69+8PuVyOmJgYzJ8/H3v27NF5/Ysvvghvb28kJiaiR48eGDNmDGJj\nY+Hr64sxY8bg0KFDOs9fvnw5XFxcMGzYMDz66KPYunWr5jF10fX+++9jwYIF6NevH2QyGdLS0uDm\n5oZ9+/a1iN/V1RVVVVU4efIklEolEhISEBYWpnn8zsu1p0+fxpw5c/DRRx8hIiIC27dvx3333YfZ\ns2dDLpcjKSkJkyZNavOsnEwmw9y5cxEXFwd3d3dMnToVhw8fNiDjRGTrWMgRkdWIi4vDP/7xD6Sn\npyM0NBTTp0/H1atXAUhFz9ixY9GxY0f4+flhyZIlLS4jhoaGav7t4eGhs+3u7o7q6mrNdkBAADw8\nPDTbMTExmmM1V1RUhDfffBMBAQGan+Li4lafO2LECCxatAjPPvssQkNDsWDBAlRVVbX6u1ZUVGDC\nhAlYsWIFBg0apDnW/v37dY61efNmlJSUtJmz5oWih4eHzu9IRPaPhRwRWZXp06dj7969KCoqgkwm\nw5/+9CcA0viOxMREFBYWoqKiAitWrIBSqdT7fe+8C7WsrAy1tbWa7aKiIoSHh7d4XXR0NJYsWYKy\nsjLNT3V1NZ544olWj/Pcc8/h4MGDOHHiBE6fPo2//e1vLZ6jVCoxY8YMpKam4n/+5390jjV8+HCd\nY1VVVeGdd97R+/ckIsfCQo6IrMbp06eRnZ2N+vp6uLm5wd3dHU5OTgCA6upq+Pj4wNPTE6dOndJr\nnEfzS5mt3YW6dOlSKBQK7N27Fzt27MCUKVM0z1U//+mnn8aaNWuQn58PlUqFmpoa7Nixo9UzXwcP\nHsT+/fuhUCjg6empE3/z4y9ZsgS1tbX4xz/+ofP6sWPH4vTp09i0aRMUCgUUCgUOHDiAU6dO6fU7\nEpHjYSFHRFajvr4eL730EoKDg9GxY0fcvHkTK1euBAD8/e9/x+bNm+Hr64v58+dj2rRpOmfZWpv7\ndufjzbfDwsI0d8DOmjUL//rXv9ClS5cWz+3Tpw/Wrl2LRYsWITAwEPHx8Zo7TO9UWVmJ+fPnIzAw\nELGxsQgKCsIf//jHFu+5ZcsWzSVU9Z2rmZmZ8Pb2xq5du7BlyxZERESgY8eOeOmll1q9sUKf35GI\n7J9MxT/niMjB5OTkYNasWbh06ZKlQyEiaheekSMiIiKyUSzkiMgh8RIkEdkDXlolIiIislE8I0dE\nRERko1jIEREREdkoFnJERERENoqFHBEREZGNYiFHREREZKP+P8n938hzEeMBAAAAAElFTkSuQmCC\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x111098fd0>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 70
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"So, using a few tweaks, such as static type declarations and explicit for-loops instead of list comprehensions, we managed to increase the performance of our least squares fit implementation quite significantly - it outperforms the alternative functions in Numpy and Scipy now."
|
|
]
|
|
}
|
|
],
|
|
"metadata": {}
|
|
}
|
|
]
|
|
} |