mirror of
https://github.com/rasbt/python_reference.git
synced 2024-11-30 15:31:12 +00:00
1274 lines
280 KiB
Plaintext
1274 lines
280 KiB
Plaintext
{
|
|
"metadata": {
|
|
"name": "",
|
|
"signature": "sha256:5d04280c23460c2481423dabf313f3ad28f40fb4ad915967d83e3a08231c8b3d"
|
|
},
|
|
"nbformat": 3,
|
|
"nbformat_minor": 0,
|
|
"worksheets": [
|
|
{
|
|
"cells": [
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[Sebastian Raschka](http://www.sebastianraschka.com) \n",
|
|
"last updated: 05/09/2014\n",
|
|
"\n",
|
|
"- [Link to this IPython Notebook on GitHub](https://github.com/rasbt/python_reference/blob/master/benchmarks/cython_least_squares.ipynb) \n",
|
|
"- [Link to the GitHub repository](https://github.com/rasbt/python_reference)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### The code in this notebook was executed in Python 3.4.0"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<hr>\n",
|
|
"I am really looking forward to your comments and suggestions to improve and \n",
|
|
"extend this little collection! Just send me a quick note \n",
|
|
"via Twitter: [@rasbt](https://twitter.com/rasbt) \n",
|
|
"or Email: [bluewoodtree@gmail.com](mailto:bluewoodtree@gmail.com)\n",
|
|
"<hr>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"# Implementing the least squares fit method for linear regression and speeding it up via Cython"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"sections\"></a>\n",
|
|
"<br>\n",
|
|
"<br>\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#Sections"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"- [Introduction](#introduction)\n",
|
|
"- [Least squares fit implementations](#implementations)\n",
|
|
" - [1. The matrix approach in (C)Python and NumPy](#matrix_approach)\n",
|
|
" - [2. The classic approach in (C)Python, Cython, and Numba](#classic_approach)\n",
|
|
" - [3. Using the `numpy.linalg.lstsq` function](#numpy_func)\n",
|
|
" - [4. Using the `scipy.stats.linregress` function](#scipy_func)\n",
|
|
"- [Generating sample data and benchmarking](#sample_data)\n",
|
|
" - [Performance growth rates: (C)Python vs. Cython vs. Numba](#performance1)\n",
|
|
" - [Performance growth rates: NumPy and SciPy library functions](#performance2)\n",
|
|
"- [Bonus: How to use Cython without the IPython magic](#cython_bonus)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"introduction\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
" \n",
|
|
"(Note that this chart just reflects my rather objective thoughts after experimenting with Cython, and it is not based on real numbers or benchmarks.)\n",
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"# Introduction"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
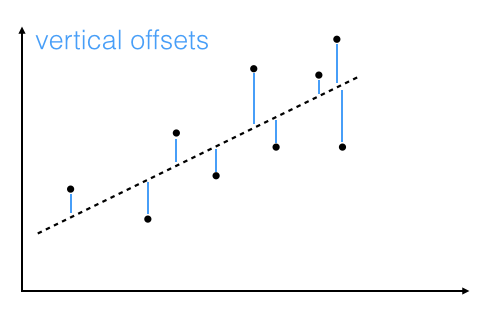
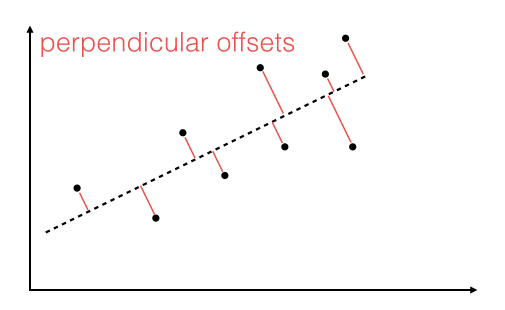
"Linear regression via the least squares method is the simplest approach to performing a regression analysis of a dependent and a explanatory variable. The objective is to find the best-fitting straight line through a set of points that minimizes the sum of the squared offsets from the line. \n",
|
|
"The offsets come in 2 different flavors: perpendicular and vertical - with respect to the line. \n",
|
|
" \n",
|
|
" \n",
|
|
"\n",
|
|
"As Michael Burger summarizes it nicely in his article \"[Problems of Linear Least Square Regression - And Approaches to Handle Them](http://www.arsa-conf.com/archive/?vid=1&aid=2&kid=60101-220)\": \"the perpendicular offset method delivers a more precise result but is are more complicated to handle. Therefore normally the vertical offsets are used.\" \n",
|
|
"Here, we will also use the method of computing the vertical offsets.\n",
|
|
"\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In more mathematical terms, our goal is to compute the best fit to *n* points $(x_i, y_i)$ with $i=1,2,...n,$ via linear equation of the form \n",
|
|
"$f(x) = a\\cdot x + b$. \n",
|
|
"We further have to assume that the y-component is functionally dependent on the x-component. \n",
|
|
"In a cartesian coordinate system, $b$ is the intercept of the straight line with the y-axis, and $a$ is the slope of this line."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In order to obtain the parameters for the linear regression line for a set of multiple points, we can re-write the problem as matrix equation \n",
|
|
"$\\pmb X \\; \\pmb a = \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\Rightarrow\\Bigg[ \\begin{array}{cc}\n",
|
|
"x_1 & 1 \\\\\n",
|
|
"... & 1 \\\\\n",
|
|
"x_n & 1 \\end{array} \\Bigg]$\n",
|
|
"$\\bigg[ \\begin{array}{c}\n",
|
|
"a \\\\\n",
|
|
"b \\end{array} \\bigg]$\n",
|
|
"$=\\Bigg[ \\begin{array}{c}\n",
|
|
"y_1 \\\\\n",
|
|
"... \\\\\n",
|
|
"y_n \\end{array} \\Bigg]$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"With a little bit of calculus, we can rearrange the term in order to obtain the parameter vector $\\pmb a = [a\\;b]^T$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\Rightarrow \\pmb a = (\\pmb X^T \\; \\pmb X)^{-1} \\pmb X^T \\; \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"The more classic approach to obtain the slope parameter $a$ and y-axis intercept $b$ would be:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$a = \\frac{S_{x,y}}{\\sigma_{x}^{2}}\\quad$ (slope)\n",
|
|
"\n",
|
|
"\n",
|
|
"$b = \\bar{y} - a\\bar{x}\\quad$ (y-axis intercept)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"where \n",
|
|
"\n",
|
|
"\n",
|
|
"$S_{xy} = \\sum_{i=1}^{n} (x_i - \\bar{x})(y_i - \\bar{y})\\quad$ (covariance)\n",
|
|
"\n",
|
|
"\n",
|
|
"$\\sigma{_x}^{2} = \\sum_{i=1}^{n} (x_i - \\bar{x})^2\\quad$ (variance)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"implementations\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"# Least squares fit implementations"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name='matrix_approach'></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 1. The matrix approach in (C)Python and NumPy"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"First, let us implement the equation:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\pmb a = (\\pmb X^T \\; \\pmb X)^{-1} \\pmb X^T \\; \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"which I will refer to as the \"matrix approach\"."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### Matrix approach implemented in NumPy and (C)Python"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import numpy as np\n",
|
|
"\n",
|
|
"def py_matrix_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 9
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name='classic_approach'></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 2. The classic approach in (C)Python, Cython, and Numba"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Next, we will calculate the parameters separately, using standard library functions in Python only, which I will call the \"classic approach\"."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$a = \\frac{S_{x,y}}{\\sigma_{x}^{2}}\\quad$ (slope)\n",
|
|
"\n",
|
|
"\n",
|
|
"$b = \\bar{y} - a\\bar{x}\\quad$ (y-axis intercept)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Note: I refrained from using list comprehensions and convenience functions such as `zip()` in\n",
|
|
"order to maximize the performance for the Cython compilation into C code in the later sections.\n",
|
|
" "
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### Implemented in (C)Python"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def py_classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" len_x = len(x)\n",
|
|
" x_avg = sum(x)/len_x\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" cov_xy = 0\n",
|
|
" for i in range(len_x):\n",
|
|
" temp = (x[i] - x_avg)\n",
|
|
" var_x += temp**2\n",
|
|
" cov_xy += temp*(y[i] - y_avg)\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc) "
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 1
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### Implemented in Cython"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Maybe we can speed things up a little bit via [Cython's C-extensions for Python](http://cython.org). Cython is basically a hybrid between C and Python and can be pictured as compiled Python code with type declarations. \n",
|
|
"Since we are working in an IPython notebook here, we can make use of the very convenient *IPython magic*: It will take care of the conversion to C code, the compilation, and eventually the loading of the function. "
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%load_ext cythonmagic"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 2
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"def cy_classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" cdef double x_avg, y_avg, var_x, cov_xy,\\\n",
|
|
" slope, y_interc, x_i, y_i\n",
|
|
" cdef int len_x\n",
|
|
" len_x = len(x)\n",
|
|
" x_avg = sum(x)/len_x\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" cov_xy = 0\n",
|
|
" for i in range(len_x):\n",
|
|
" temp = (x[i] - x_avg)\n",
|
|
" var_x += temp**2\n",
|
|
" cov_xy += temp*(y[i] - y_avg)\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 3
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### Implemented in Numba"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Like we did with Cython before, we will use the minimalist approach to Numba and see how the two - Cython and Numba - compare against each other. \n",
|
|
"\n",
|
|
"Numba is using the [LLVM compiler infrastructure](http://llvm.org) for compiling Python code to machine code. Its strength is to work with NumPy arrays to speed-up the code. If you want to read more about Numba, please see refer to the original [website and documentation](http://numba.pydata.org/numba-doc/0.13/index.html)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"from numba import jit\n",
|
|
"\n",
|
|
"@jit\n",
|
|
"def numba_classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" len_x = len(x)\n",
|
|
" x_avg = sum(x)/len_x\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = 0\n",
|
|
" cov_xy = 0\n",
|
|
" for i in range(len_x):\n",
|
|
" temp = (x[i] - x_avg)\n",
|
|
" var_x += temp**2\n",
|
|
" cov_xy += temp*(y[i] - y_avg)\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 4
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name='numpy_func'></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 3. Using the `numpy.linalg.lstsq` function"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"For our convenience, `numpy` has a function that can computes the least squares solution of a linear matrix equation. For more information, please refer to the [documentation](http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.lstsq.html)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def numpy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return np.linalg.lstsq(X,y)[0]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 5
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name='scipy_func'></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 4. Using the `scipy.stats.linregress` function"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Also scipy has a least squares function, `scipy.stats.linregress()`, which returns a tuple of 5 different attributes, where the 1st value in the tuple is the slope, and the second value is the y-axis intercept, respectively. \n",
|
|
"The documentation for this function can be found [here](http://docs.scipy.org/doc/scipy-0.13.0/reference/generated/scipy.stats.linregress.html)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import scipy.stats\n",
|
|
"\n",
|
|
"def scipy_lstsqr(x,y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" return scipy.stats.linregress(x, y)[0:2]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 6
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name='sample_data'></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"# Generating sample data and benchmarking"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"#### Visualization"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"To check how our dataset is distributed, and how the least squares regression line looks like, we will plot the results in a scatter plot. \n",
|
|
"Note that we are only using our \"matrix approach\" to visualize the results - for simplicity. We expect all 4 approaches to produce similar results, which we will confirm after visualizing the data."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%matplotlib inline"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 7
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"from matplotlib import pyplot as plt\n",
|
|
"import random\n",
|
|
"\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"x = [x_i*random.randrange(8,12)/10 for x_i in range(500)]\n",
|
|
"y = [y_i*random.randrange(8,12)/10 for y_i in range(100,600)]\n",
|
|
"\n",
|
|
"slope, intercept = py_matrix_lstsqr(x, y)\n",
|
|
"\n",
|
|
"line_x = [round(min(x)) - 1, round(max(x)) + 1]\n",
|
|
"line_y = [slope*x_i + intercept for x_i in line_x]\n",
|
|
"\n",
|
|
"plt.figure(figsize=(8,8))\n",
|
|
"plt.scatter(x,y)\n",
|
|
"plt.plot(line_x, line_y, color='red', lw='2')\n",
|
|
"\n",
|
|
"plt.ylabel('y')\n",
|
|
"plt.xlabel('x')\n",
|
|
"plt.title('Linear regression via least squares fit')\n",
|
|
"\n",
|
|
"ftext = 'y = ax + b = {:.3f} + {:.3f}x'\\\n",
|
|
" .format(slope, intercept)\n",
|
|
"plt.figtext(.15,.8, ftext, fontsize=11, ha='left')\n",
|
|
"\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAfoAAAH4CAYAAACi3S9CAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdUVMfbwPHv0lm6giAgooBRbNi7GCv2EnvXWOPPnhg1\nGksSxRhjoiYaE0SNsb4xEY0Fe+zGmijGLkZARRERFljYnfeP1Y0ELJRlAedzDkf2lpln7q48e++d\nO6MQQggkSZIkSSqSTIwdgCRJkiRJhiMTvSRJkiQVYTLRS5IkSVIRJhO9JEmSJBVhMtFLkiRJUhEm\nE70kSZIkFWEy0UtGd+jQIcqXL2/sMAqtSpUq8fvvv+drnSNHjuTTTz/N0b7e3t7s3bs3jyN6s/3y\nyy+UKlUKe3t7zp07Z5TPhFRwKeRz9FJ+8fb2JiQkhGbNmhk7FMmIypQpQ0hICE2bNjVI+QcOHKBf\nv378888/Bim/IPLx8eGrr76iffv2mdbNnDmT69ev8+OPPxohMqkgkGf0Ur5RKBQoFApjh6Gn0Wjy\nZJvXJYRAfq+Wnsmrz5YQgtu3b+Pv758n5UlFj0z0ktEdOHCAUqVK6V97e3uzYMECqlatiqOjIz17\n9iQ1NVW/ftu2bQQEBODk5ESDBg3466+/9OuCg4Px9fXF3t6eihUr8uuvv+rXrVy5kgYNGjBhwgSc\nnZ2ZNWtWplhmzpxJ165d6devHw4ODqxatYrHjx/z7rvv4u7ujqenJ9OnT0er1QKg1WqZOHEiLi4u\nlC1bliVLlmBiYqJf36RJE6ZNm0aDBg2wsbHh5s2b/P3337Ro0YLixYtTvnx5Nm3apK9/+/btVKxY\nEXt7ezw9PVmwYAEADx48oF27djg5OVG8eHEaN26c4Xg9uxSemprKuHHj8PDwwMPDg/Hjx6NWq/XH\n2dPTky+//BJXV1fc3d1ZuXJllu/Jhg0bqFWrVoZlCxcupGPHjgAMHDiQ6dOnA/Do0SPatWtHiRIl\nKFasGO3btycqKirLcv9LCKF/z5ydnenRowePHj3Sr+/WrRslS5bE0dGRwMBAIiIiXnisvvzyS1Qq\nFa1btyY6Oho7Ozvs7e25e/dupnpfdJwB5s+fr3+vV6xYgYmJCTdu3AB072dISIh+25UrV9KoUSP9\n67Fjx+Ll5YWDgwM1a9bk8OHD+nXZ/Wxdu3aNwMBAHB0dcXFxoWfPnpnakZqaip2dHRqNhqpVq+Ln\n5wf8+5nYuXMnc+fOZcOGDdjZ2VGtWrXXel+kIkZIUj7x9vYWe/fuzbR8//79wtPTM8N2derUETEx\nMSIuLk5UqFBBLFu2TAghxJkzZ0SJEiXEyZMnhVarFatWrRLe3t5CrVYLIYTYtGmTiImJEUIIsWHD\nBmFjYyPu3r0rhBAiNDRUmJmZiSVLlgiNRiOSk5MzxTJjxgxhbm4utmzZIoQQIjk5WXTq1EmMGDFC\nqFQqcf/+fVG7dm3x3XffCSGEWLp0qfD39xdRUVHi0aNHolmzZsLExERoNBohhBCBgYGidOnSIiIi\nQmg0GhEfHy88PT3FypUrhUajEWfPnhXOzs7i0qVLQggh3NzcxOHDh4UQQsTHx4szZ84IIYSYPHmy\nGDFihEhPTxfp6en6bf57XKdPny7q1asnYmNjRWxsrKhfv76YPn26/jibmZmJGTNmiPT0dLF9+3ah\nVCpFfHx8puOgUqmEnZ2duHr1qn5ZzZo1xYYNG4QQQgwcOFBf7sOHD8XmzZtFcnKyePLkiejWrZvo\n1KlT1h+C/8T71VdfiXr16omoqCihVqvF8OHDRa9evfTbhoaGisTERKFWq8W4ceNEQECAft2LjtWB\nAwcyfJ6y8qJ9d+zYIVxdXcXFixdFUlKS6NWrl1AoFOL69etCCCGaNGkiQkJCMsTXsGFD/es1a9aI\nuLg4odFoxIIFC4Sbm5tITU0VQmT/s9WzZ08xZ84cIYQQqamp4siRIy9sz/Mx/vcYz5w5U/Tr1++l\nx0Mq2uQZvVQgjRkzBjc3N5ycnGjfvj3nzp0DYPny5QwfPpxatWqhUCjo378/lpaWHDt2DICuXbvi\n5uYGQPfu3fHz8+PEiRP6ct3d3Rk1ahQmJiZYWVllWXf9+vXp0KEDAI8fP2bHjh0sXLgQa2trXFxc\nGDduHOvXrwdg48aNjBs3Dnd3dxwdHZkyZUqGy/MKhYKBAwdSoUIFTExM2LlzJ2XKlGHAgAGYmJgQ\nEBBAly5d2LhxIwAWFhZcvHiRhIQEHBwc9GdgFhYWxMTEcOvWLUxNTWnQoEGWsa9du5aPP/4YZ2dn\nnJ2dmTFjRoZ7s+bm5nz88ceYmprSunVrbG1tuXz5cqZyrK2t6dixI+vWrQPg6tWrXL58WX9cAH07\nixUrRufOnbGyssLW1papU6dy8ODBrN/Y//juu+/49NNPcXd3x9zcnBkzZvB///d/+rPagQMHYmNj\no193/vx5njx58tJjJV7j9siL9t24cSODBw/G398fpVKZ5VWfl+nTpw9OTk6YmJgwYcIEUlNTMxzf\n7Hy2LCwsuHXrFlFRUVhYWFC/fv1sxfKMkLeM3ngy0UsF0rNkDbqkk5iYCEBkZCQLFizAyclJ/3Pn\nzh1iYmIAWL16NdWqVdOvu3DhAg8fPtSX9fwtghfx9PTU/x4ZGUlaWholS5bUlzlixAhiY2MBiImJ\nyVDm8/tmVWdkZCQnTpzIEP/atWu5d+8eAD///DPbt2/H29ubJk2acPz4cQA++OADfH19admyJT4+\nPsybNy/L2KOjoyldurT+tZeXF9HR0frXxYsXx8Tk3//2SqVSf2z/q3fv3vpEv3btWn0y/y+VSsXw\n4cPx9vbGwcGBwMBAHj9+/FrJ5datW3Tu3Fl/LPz9/TEzM+PevXtoNBomT56Mr68vDg4OlClTBoVC\nwYMHD156rF7Hi/b97/vp5eX12mUCfPHFF/j7++Po6IiTkxOPHz/WxwvZ+2x9/vnnCCGoXbs2lSpV\nIjQ0NFuxSNIzZsYOQJJex7NOfF5eXnz00UdMnTo10zaRkZEMGzaMffv2Ua9ePRQKBdWqVct0hv2q\nep7fplSpUlhaWvLw4cMMCfKZkiVLZujdnVVP7+fL8/LyIjAwkPDw8Czrr1mzJr/++isajYbFixfT\nvXt3bt++ja2tLV988QVffPEFFy9epGnTptSuXZu33347w/7u7u7cunWLChUqAHD79m3c3d1f2uYX\nad68ObGxsZw/f57169fz1VdfZdmuBQsWcOXKFU6ePEmJEiU4d+4c1atXRwjxyuPt5eVFaGgo9erV\ny7Tuxx9/JCwsjL1791K6dGni4+MpVqyY/v180bF6nQ6fL9q3ZMmS3L59W7/d878D2NjYkJSUpH/9\n/P3/Q4cOMX/+fPbt20fFihUBMsT7/DGDV3+2XF1dWb58OQBHjhyhefPmBAYGUrZs2Ve273kFqQOs\nZBzyjF7KV2q1mpSUFP3P6/Y8fvbHcujQoSxbtoyTJ08ihCApKYnffvuNxMREkpKSUCgUODs7o9Vq\nCQ0N5cKFC9mK779noSVLlqRly5ZMmDCBJ0+eoNVquX79uv4Z5e7du/P1118THR1NfHw88+bNy/SH\n9fky27Vrx5UrV1izZg1paWmkpaXxxx9/8Pfff5OWlsZPP/3E48ePMTU1xc7ODlNTU0DXAfHatWsI\nIbC3t8fU1DTL5NCrVy8+/fRTHjx4wIMHD5g9ezb9+vXL1jF4xtzcnG7duvH+++/z6NEjWrRokaFN\nz9qVmJiItbU1Dg4OxMXFZety94gRI5g6dao+ocbGxhIWFqYv19LSkmLFipGUlJThy93LjpWrqysP\nHz4kISEhyzpftm/37t1ZuXIlly5dQqVSZWpLQEAAmzdvJjk5mWvXrhESEqJ/v588eYKZmRnOzs6o\n1Wpmz579whjg1Z+tTZs2cefOHQAcHR1RKBRZvuev4ubmxq1bt+Tl+zeYTPRSvmrTpg1KpVL/M2vW\nrFc+dvf8+ho1avD999/zv//9j2LFiuHn58fq1asB8Pf3Z+LEidSrVw83NzcuXLhAw4YNsyzndep6\nZvXq1ajVavz9/SlWrBjdunXTn8kNHTqUli1bUqVKFWrUqEHbtm0zJeHny7O1tSU8PJz169fj4eFB\nyZIlmTJlir5n/Jo1ayhTpgwODg4sX76cn376CdD1wG7RogV2dnbUr1+fUaNGERgYmCn+adOmUbNm\nTapUqUKVKlWoWbMm06ZNyzKW19G7d2/27t1Lt27dMrXpWVnjxo0jOTkZZ2dn6tevT+vWrV+7nrFj\nx9KhQwdatmyJvb099erV4+TJkwD079+f0qVL4+HhQaVKlfRXaZ550bEqX748vXr1omzZshQrVizL\nXvcv2jcoKIhx48bRtGlTypUrl2nMh/Hjx2NhYYGrqyuDBg2ib9+++nVBQUEEBQVRrlw5vL29sba2\nznDpP7ufrVOnTlG3bl3s7Ozo2LEjixYtwtvbO8vj+LLj3a1bN0B326ZmzZov3E4qugw6YM7ly5cz\nPBJy48YNPvnkE/r27UuPHj2IjIzE29ubjRs34ujoCMDcuXNZsWIFpqamLFq0iJYtWxoqPEnKczt2\n7GDkyJHcunXL2KFIecTExIRr165l+5K5JBUUBj2jf+uttzh79ixnz57l9OnTKJVKOnfuTHBwMC1a\ntODKlSs0a9aM4OBgACIiItiwYQMRERHs3LmT9957T9/7VpIKopSUFLZv3056ejpRUVHMmjWLLl26\nGDssSZIkvXy7dL9nzx58fX0pVaoUYWFhDBgwAIABAwboBzXZsmULvXr1wtzcHG9vb3x9ffWX8SSp\nIBJCMHPmTIoVK0b16tWpWLEis2fPNnZYUh6Sndmkwi7fet2vX7+eXr16AXDv3j1cXV0BXceZZ48W\nRUdHU7duXf0+np6erz3CliQZg7W1tfwyWsTl5TDIkmQM+ZLo1Wo1W7duzfLZ39fpiPU8X19frl+/\nnucxSpIkSVJB5ePjw7Vr13K0b75cut+xYwc1atTAxcUF0J3FP+tZGhMTQ4kSJQDw8PDI8BzynTt3\n8PDwyFDW9evX9Y/2vIk/M2bMMHoMsv2y7bL9sv2y/fn7k5sT3HxJ9OvWrdNftgfo0KEDq1atAmDV\nqlV06tRJv3z9+vWo1Wpu3rzJ1atXqV27dn6EKEmSJElFksEv3SclJbFnzx6+//57/bLJkyfTvXt3\nQkJC9I/Xge456O7du+uHwfz2229lRxhJkiRJygWDJ3obG5sMYz2DbljIPXv2ZLn91KlTsxzeVNJp\n0qSJsUMwqje5/W9y20G2X7a/ibFDKLQMOmCOISgUCgpZyJIkSZKUK7nJfXIIXEmSJEkqwmSilyRJ\nkqQiTCZ6SZIkSSrCZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIkwmekmSJEkqwmSilyRJkqQiTCZ6\nSZIkSSrCZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIkwmekmSJEkqwmSilyRJkqQiTCZ6SZIkSSrC\nZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIszM2AFIkiRJWYuNjWXHjh2YmJjQtm1bnJycjB2SVAgp\nhBDC2EFkh0KhoJCFLEmSlG03btygdu1AUlLqAOnY2p7nzJkjuLu750v9f/75JzNnzichIYn+/bvQ\nv3/ffKlXylpucp88o5ckSSqAJk78mEePRqDVfgRAauqHTJv2KStWfGvwuv/880/q1GlCSso0wINj\nxz7m8eMERo9+z+B1S3lP3qOXJEkqgKKi7qHV1tC/Tk+vwe3bdw1e78OHDwkMbEVKyhBgAtADlWo1\n8+d/Y/C6AU6cOMHIkWMZO/Z9/v7773yps6iTiV6SJKkAatWqMUrlF8Bj4CFK5Ve0bh1o8HqnTp1N\nQoInYPrcUpN8uWW6f/9+mjZtz7JlJVm8WEmtWo25ePGiwest6mSilyRJKoA+/ngy77zjg6lpCczM\nPBgwoA7jx482eL2XLt1Aq+0P/AB8A/yCiUkPxo4dZvC6P/poHirVV8BkhJhNUtJ4Pv98scHrLepk\nopckSSqAzM3NWb36O1JTVaSkJPHttwsxMTH8n+yGDWtgbb0bCAMOYGLyPs2a+TNx4liD152cnAIU\n178WwpnExGSD1qlSqRg+fCzly9chKKgr169fN2h9xiA740mSJBVgpqamr94olx49esSOHTtQKBSM\nHTuSs2ffY//+NoCCRo0aERa2AYVCYfA4hgzpyaRJE1GpbAAVSuVsBg9eZtA6O3fuw++/W5CSspCr\nVw9Tp04Trlw5T7FixQxab36SiV6SJOkN9s8//1CzZiNUqiqAwMZmKqdOHcLc3BwhBK6urvmS5AHe\ne284arWab78dh5mZGR9/PJ+2bdsapK7k5GQ++mgWu3dvR4gngAVabX3U6gMcOHCALl26GKReY5DP\n0UuSJBnZX3/9RUxMDJUrV6ZkyZL5WnfPnoP5v//zRKOZDYCZ2VR69XrI6tXf5Wsc+UkIQZMmbTlx\nwoLU1J3APcABENjZNWbt2g9p166dkaPMKDe5T96jlyRJMqIxYyZRt24Q3bvPw8+vCrt3787X+v/5\n5y4aTS396/T0WkRGRudrDPnt+vXr/PHHeVJTNwHDgCBgBebmg3Fze0KzZs2MHGHekolekiTJSA4f\nPsyKFT+jUl3k8eO9JCX9TNeuffLlquW6devx9q7C+fOnMDObDyQAj1Eqv6Zly0YGr9+YhBAoFKbo\nUuBXQD9MTafRo4eCP/44iLW1tZEjzFsy0UuSJBnJjRs3UCjqAo5PlzRCpUokMTHRoPXu3buXd9+d\nSGTkIpKSdiNEJAqFM6amJejevQKTJ080aP3G5uPjg79/WSwt3wV2Y2FxET8/d0JCluHg4GDs8PKc\nTPSSJElGUqVKFTSafcDNp0vW4eLijq2trUHr3bhxC8nJE4AmQFU0mp/x8ipPcnIioaFL86WnvzGZ\nmJiwb99WBg1yombN+fTuLThyJBwLCwtjh2YQste9JEmSkQQEBDBv3sd88EFVzMycsLaG7du3GLyX\nu4ODLaamd9Boni25g52dHebm5gattyCxs7Nj6dKFxg4jX8he95IkSUaWkJBAbGwspUqVypezyjt3\n7lC1al0SEjqQnl4Ca+tv+eWXH2nVqpXB65ZyJje5TyZ6SZKkN1B0dDQ//BBCUlIyXbt2platWq/e\nSTIameglSZIkqQiTz9FLkiRJkpQlmeglSZIk6UWEgEWLIC7O2JHkmEz0kiRJkpQVrRZGj4axY6FD\nB93rQkg+XidJkiRJ/5WeDkOHwsqVYGEBkyZBPkwTbAgy0UuSJEnS89Rq6NsXNm0CpRK2bIHmzY0d\nVY4Vzq8nkiRJ0hsvKSmJLl36olQ64uzsxY8//pT7QlNS4J13dEne3h7Cwwt1kgf5eJ0kSZJUSPXo\nMYgtW1JITV0M3MTauiPh4Rtp2LBhzgpMTISOHWHfPiheHHbtgho18jTmnJKP10mSJElvnF27dpGa\nOg9wBmqRkjKY3bv35Kyw+Hho2VKX5N3c4ODBApPkc0smekmSJKlQcnAoBlzWv7a0vEzx4sWyX1Bs\nLDRtCseOgZcXHDoEFSvmXaBGJhN9Ieft7U1ERIRBytZoNIwaNQpfX1/8/PwICQl54bZz586lcuXK\nVKhQgYEDB6JWqwG4desWZmZmVKtWTf/z6NEjAI4ePUqDBg2oWLEiFStWZNKkSXkaf58+ffDw8MDE\nxASVSpVh3fHjx6latSpvvfUWrVq1IjY2Vh/T87F6eHhQ4wXf6lUqFT169MDPz48KFSrw22+/6det\nWbOGKlWqYG5uzjfffJPl/gcOHMDU1PSF6yVJermlSz9HqeyDufk4lMqOeHpeYdCgQdkrJDoaAgPh\n7Fnw89MleV9fwwRsLKKQKYQh50hoaKiYOXPmK7fz9vYWFy5cMEgMq1atEq1atRJCCBEbGys8PT3F\nrVu3Mm23a9cuUaVKFaFSqYQQQgwdOlQEBwcLIYS4efOmcHZ2zrL8CxcuiGvXrgkhhEhNTRUNGzYU\nP/744yvjGjBggDhw4MArt9u/f7+4f/++UCgUIikpSb9co9EIHx8fceTIESGEEJ9++qkYPHhwlmV0\n6tRJLFiwIMt1s2bNEsOGDRNCCHH16lXh5uYmEhMT9W2LiIgQ/fv3F998802mfRMSEkSdOnVE+/bt\nxZIlS17ZFkmSsnbu3Dnx+eefi++++048efIkezvfvClE2bJCgBCVKgkRE2OQGPNCbnLfG3VGP3/+\nfP73v//pX9+7dw83NzdSUlJyXfa9e/do2rQpNWvWpFKlSnz44Yf6dUOHDmXChAn67cqWLcuff/75\n0vKyM03lmjVrqFmzJn5+fnl6drhx40aGDRsGgLOzM506dWLTpk2Ztvvzzz9p1KgR1tbWAAQFBfHT\nT6/u/VqxYkV8fHwAsLCwICAggNu3b79yP4VC8VrHp0mTJri4uGRafvr0aaytralfvz4Aw4cPZ+PG\njZm2u3//PuHh4fTr1y/L8jdu3Mjw4cMB8PX1pWbNmuzYsUPftgoVKmBiYpJlB5oJEyYwadIkihcv\nrl+WnJxM1apVCQsLA2Dfvn1UqFCBpKSkV7ZVMr5z584xYMAIevcewsGDB40dzhujatWqfPDBBwwb\nNgxbW9vX3/HyZWjUCG7c0N2LP3BAd2++CHqjnqMfMmQI/v7+fP755yiVSpYvX06fPn2wsrLKtG23\nbt24du1apuUKhYJjx45haWmZYbmjoyNbt27FxsaGtLQ0goKC2LVrF61atWLx4sXUqVOHLVu2sHjx\nYiZNmkSVKlVeGmtWyeFFYmNjOXXqFPfv36datWo0btyYypUrZ9jm0qVL9O7dO8v9W7Zsybx58zIt\nv337NqVLl9a/9vLy4p9//sm0XY0aNfj+++95+PAhDg4ObNy4kcjISP36hIQEatSogUKhoGfPnrz/\n/vuZyrh//z6bN29m+/btr9Xm7Byf//pvu5ydndFqtcTHx+Po6Khfvnr1alq1apXll4WsynnR8fmv\nHTt28OTJE7p06cLWrVv1X1qsra3ZuHEjLVu2xM3NjSFDhvDLL79gY2OT06ZK+eTs2bM0atSSpKQP\nAGu2bOnBzz+vJCgoyNihFXqJiYkMHPgeO3b8hp2dI4sWBdO9e7fcFfrnn9CiBdy/Dw0bwrZt4OCQ\nNwEXQG9UondycqJDhw6sXr2aIUOG8MMPP7Bv374st83qzPVl0tPTef/99zl27BhCCO7evcu5c+do\n1aoVVlZWbNy4kRo1atCmTRtGjBiRZRnbt2/no48+AiAuLg61Ws2vv/4KwOjRoxk8eHCW+7377rsA\nlChRgrZt23LgwIFMib5ChQqcPXs2W216XW+//TajRo2iZcuWWFlZ0axZM3bv3g2Au7s7UVFRODs7\nExsbS4cOHXByctLHDPDkyRM6dOjA+++/T9WqVbOs45NPPmHz5s2ALsEePnxY/+191apVr/zilBOh\noaFZfgHKjfj4eCZPnsyePbqewUKIDF9a3nrrLWbPnk39+vX5+uuvX3g8pILliy++JSnpQ0D3JVal\nKsGsWV/JRJ8HBg0axbZtaaSmXkSlus7Age9QurQXderUyVmBJ09CUBA8eqRL9r/8AkX8y/QblehB\nlzD79OmDi4sL/v7++kvH/9W1a1euX7+e5bpjx45lugrw5ZdfEh8fz8mTJ7GwsGD48OEZbglcvHgR\nBwcH7t69i0ajwdTUNFO5bdq0oU2bNoAueUVGRvLxxx+/sk3PJwohRJaXtSMiIujTp0+W+7do0YLP\nP/8803IvLy9u3bql74wWGRlJmTJlsixjzJgxjBkzBtBd0q74tMeqhYUFzs7OALi4uNCnTx+OHDmi\nT/QqlYp27doRFBTE+PHjX9jG6dOnM336dAAGDRrEoEGDaNy48Qu3f5nSpUtnuOLw4MEDTExMMpzN\nHz9+nEePHunfj6w8Oz7PLr9HRkbStGnTTNs9/35cuHCBu3fvUrt2bX3d27Zt49GjR0ybNg3Q3Vpw\ndXV9rasDUsGQkqIGnr9sbKfvkGoIT5484eHDh3h4eGBubm6wegqCnTt3kJp6DnAD3EhNHUh4+O6c\nJfrff4e2bXXPy3foABs2QBZXdIucPOgjkK/yIuS3335blCpVSmzdujUPItKZOHGiGD9+vBBCiDt3\n7ghXV1cxa9YsIYQQN27cEF5eXuLatWtiwIABYvLkya8s73U745UuXVoMHTpUCCHE/fv3hYeHR551\nzlu5cqVo1aqV0Gq14v79+y/sjCeEEDFPO7HExcWJ6tWriy1btuhjUqvVQgghkpKSRPPmzcWiRYuE\nEEIkJyeLpk2big8//DBbcQ0cOPC1OuMJIYRWqxUKhULfSU6IfzvjHT58WAghxCeffJKpM97QoUNf\nGdfMmTP1x/7KlSvC1dU1Qz1C6DoOvqyz3cCBAzN01tu8ebOoXr26iIuLExUrVhQ7dux4rXZKxhUe\nHi6UypICfhawQyiVviIkJNQgdS1a9K2wsLAVSqWnKFGitPjrr78MUk9B4e5eTsABoZtGTghr6y45\n68C6c6cQ1ta6Qnr1EuLp36XCIje5741M9GvWrBHe3t55EM2/IiMjRe3atUWlSpVEUFCQ6NOnj5g1\na5ZQq9Widu3aYt26dUIIXbLz9/cXO3fufGl5K1eu1H9ReBlvb28xdepUUaNGDeHr65tlD++c0mg0\nYuTIkcLHx0f4+PiI77//Xr9u2bJl4uOPP9a/rly5sqhYsaIoV66cWLx4sX755s2bRaVKlUTVqlWF\nv7+/+PDDD4VWqxVCCLFkyRJhamoqqlWrJgICAkRAQICYM2fOK+MaOHCgOHjw4Cu369y5s/D09BQm\nJibCw8NDBAUF6dcdPXpUVK5cWfj5+YmWLVuK+/fv69epVCrh4OAgLl++nKnMgIAA/ZeapKQk0a1b\nN+Hr6yveeustERYWpt9u7dq1wtPTU9jY2AgnJyfh6ekpLl26lGVbnr1nN2/eFKVKlRJXr14VQuh6\n7nt5eYmoqKhXtlUyvi1btogaNZqKqlUbix9+WGGQOs6cOfP0C8WNp4kvVHh6vmWQugqKX375RVhb\nlxBmZhNF0rhoAAAgAElEQVSFtXUn4etbJfu96zdvFsLcXJfkhwwRIj3dMMEaUG5y3xs5BO6QIUOo\nUKECEydOzKOoJEmSDC80NJTRo/eTlLT66RKBqakVCQmPUCqVeV7ftWvXOH/+PN7e3i8cTyI/nD59\nmt27d+Po6Ejfvn2z17t+zRoYOBA0Gt10swsXQjaeaiooCvQQuPHx8XTt2pUKFSrg7+/PiRMniIuL\no0WLFpQrV46WLVsSHx+v337u3Ln4+flRvnx5wsPD8zSW6Ohoypcvz/Xr1xk1alSeli1JkmRoZcuW\nBY4BCU+X/I6trZP+0da89NNP66hatT6DB/9I48ZdGDducp7X8bpq1KjB5MmTGTFiRPaS/PLl0L+/\nLslPm1Zok3yu5dFVhRfq37+/CAkJEUIIkZaWJuLj48UHH3wg5s2bJ4QQIjg4WH8v9OLFi6Jq1apC\nrVaLmzdvCh8fH6HRaDKUlw8hS5IkFUharVaMGDFOKJWewsGhubCxcRbh4eF5Xk9KSoqwsrIX8OfT\nWwRxQqksJU6fPp3ndRnMggVCf2P/6QBehVlucp9BL90/fvyYatWqcePGjQzLy5cvz8GDB3F1deXu\n3bs0adKEv//+m7lz52JiYqIfbCYoKIiZM2dSt25d/b5y9jpJkt50586dIyYmhqpVq+Lu7p7n5UdH\nR+PrW43k5Hv6Zfb27Vi1agidOnXK8/rylBDwyScwY4bu9ZIlUASu4BbYS/c3b97ExcWFQYMGUb16\ndYYOHUpSUhL37t3D1dUVAFdXV+7d032YoqOj8fT01O/v6elJVFSUIUOUJEkqdAICAmjdurVBkjzo\n/i7b2loB654uOUda2omCP66DEDBpki7Jm5hAaGiRSPK5ZdDn6NPT0zlz5gxLliyhVq1ajBs3juDg\n4AzbvGo406zWzZw5U/97kyZNaNKkSV6FLEmS9Ma7ceMGtrYOxMb2BYZhYSFYuXLlC8fRKBC0Wl1S\nX7YMzMxg7VrolssR9IzowIEDHDhwIE/KMmii9/T0xNPTk1q1agG6QWjmzp2Lm5sbd+/exc3NjZiY\nGEqUKAGAh4dHhkFC7ty5g4eHR6Zyn0/0kiRJUt7RaDQ0bdqOqKhRwHBgDxYWgwgMbGTs0F4sPR0G\nD4YffwRLS/j5Z93AOIXYf09iZ82aleOyDHrp3s3NjVKlSnHlyhUA9uzZQ8WKFWnfvj2rVq0CdCPA\nPbvn06FDB9avX49arebmzZtcvXpVP4KYJEmSZHhRUVHExSUixBjAEmiLqWkAZ86cMXZoWVOroWdP\nXZK3sYHt2wt9ks9rBh8Cd/HixfTp0we1Wo2Pjw+hoaFoNBq6d+9OSEgI3t7e+pnD/P396d69O/7+\n/piZmfHtt99maxY3SZIkKXecnJxIT08A7gCegIr09GsvnNzJqJKT4Z13YMcO3aQ0O3ZAvXrGjqrA\neSMHzJEkSSpo1Go1oaGh3LwZSb16dejYsaPRYgkOXsAnnyxCo2mHuflhOnSoxZo13+fqxCsxMZF3\n3x3Nrl27cHQsztKln9O6deucB/nkCbRvDwcPgrMzhIdDtWo5L6+Ay03uk4lekiTJyDQaDYGBbTh7\nVqBSNcLGZi1jxvRgzpyZRovp0KFDnD17ljJlytCuXbtcX13t0qUv27drSE2dB/yNUtmXY8f25Gzm\nyUePoHVrOHECSpaEPXvA3z9X8RV0MtFLkiQVYlOmTGHevE0IcRkwBe5hbl6Gx48fGmTUO2OwtnYg\nJeU6oJvN0tx8HHPmePL+++9nr6D796FlSzh/HkqXhr174QWzkBYlBfY5ekmSJOnlQkNXEhy8BCHK\noEvyAC4oFBaoVCpjhpanbGwcgFv61+bmN3FwcMheIVFREBioS/LlysGhQ29Eks8tmeglSZKMRKvV\nMm7cdGAl8BewGrgNjMXHx49ixYoZM7w89eWXc1AqO6JQTMfKqhvu7rfo1avX6xdw8yY0agR//w1V\nqujmli9VKttxpKSkkJycnO39CjOZ6CVJkoxk9Oj3SUhQAWWBHcBSoBqwik2bVhapp4769+/Lzp3r\nmTbNhODghpw5c/j1J6j5+29dkr95E2rXhv374enoqq9Lo9HQv/9wbG0dsbNzomvXfqjV6hy0pPCR\n9+glSZKM4NSpU9Sp0wCtdhz/JvkY4F2aN2/E7t3bjBtgQXHunO6efGwsNG4M27aBnV22i5k7dz6f\nfrodlSoMMMXauitjx9Zi7tycD0STn+Q9ekmSpFwKDw/HxyeA4sW96NNnqEHvjx87dozGjYPQagHe\nB7oB/YH3aNKkJjt3bjFY3YXK8ePw9tu6JB8UpHtOPptJPiEhga+++orly39CpXoPsAOUJCePZu/e\nowYJu6CRiV6SpDfeX3/9RadOfbhxYw5xcQfYvDmeAQNGGqy+GTO+IDl5LrohZrsC1VAo+lOsmAUb\nN67H1NT0FSVkX0JCAt26DaREibJUqdKAkydP5nkdeerAAWjeHOLjoXNn+PVXUCqzVURCQgIBAfWZ\nMuUYt25ZAb/r15maHsPbO/MQ60WRwUfGkyRJKuh27dqFRtMbaANASsq3/PZbOYPVp1KlAMWBhcAX\nwExcXBI4fvyQwUag69SpD0ePOpOauovY2D9o2rQtERGn8fLyMkh9ubJ9u27Eu5QU6NMHVq7UTVST\nTatXr+bu3QqkpGwA7gF1USjOYGvrgLX1JRYs+P1VRRQJ8oxekqQ3np2dHWZmt59bchulMvv3gV/X\n0KE9USonA4eBmiiVD1m8+DODzQ6nVqs5eHAXqanfAX5Ab6AF+/fvN0h9ufLzz9Cpky7JDxsGq1fn\nKMmD7oxerX52TF2BXVhaXmDFisFcvnyWUjnotV8YyUQvSdIbr3fv3ri6XsXSshcKxSyUyo588cWn\nBqtvwIB+fPnlB/j5vU+5clNYsmQm3bsbbkpVMzMzzMzM0Z3VAggUiqjX7/WeX1avhu7dIS0NJkzQ\nTTlrkvM01apVKywsVgH7gNtYWX1Ex47v0LVrVxwdHfMs7IJO9rqXJElCd/b3/fffExsbR1BQiwxT\nhBYFc+bM57PPvkelGoyV1Sl8fP7h1KmDWFlZGTs0naVL4b33dL/PmKH7yYPHC8PCwvjf/yaTkBBP\nmzZt+OGHRSizea+/IJBD4EqSJGWDEIL169ezf/9RvL09GDt2NDY2NsYOK0+Fh4czY8YCUlPVjBzZ\nlyFDBrN161b27z+Ep6cbI0aMKDhtnj8fJk369/fsDov7BpCJXpIkKRsmTZrGN9+EoVINxtLyGD4+\nNzl9+veCc3abA7/99htjx07jyZME6tatzu7dv5Oc/DXggFI5ni++mMDIkcOMHWZGQsDMmTB7tu71\nt9/CSMM97VCYyUQvSZL0mtRqNTY29qSn3wZKAAJb24b89NOHdOjQwdjh5cipU6cIDGyLSrUKKIOp\naVs0mlHA+Kdb7KFixRlcuHDEiFH+hxAwcSIsXKi7Dx8aCv37GzuqAis3uU8+XidJ0hslLS0NUABO\nT5coUChKFNrxzyMiIujRoz8q1SAgCACNpgHw/IA/Ksxy2HPdIDQa3f345cvB3BzWrdM9TpcNycnJ\nLF68hCtXImnYsCYDBgwoUkMG56UC9M5LkiQZno2NDQ0aNOX48aGkpk5EoTiGiclxAgOXGju0bLt0\n6RI1azYiObkREAnsBdKAeigU7yOEGeCIUjmbGTOWGDVWvfR0GDgQfvoJrKxg82bd3PLZkJaWRuPG\nrblwwYmUlCasW/cNJ06cZ+nShYaJuZCTl+4lSXrjJCQkMHz4eA4dOoanpwfff/8llStXNnZY2RIT\nE0OFClV5/DgQmI9uMhwPwBa4yOTJ/+POnYekpKgZMqQXrVq1yvMYhBCo1WosLS1fb4fUVOjZUzfK\nna0tbN0KOXi6Yf/+/XToMIHExNPonhKPx9zckwcPorG3t892eYWBHOtekiTpJdLT0zl+/DiHDh0i\nOTkZe3t71q0L4c6dCI4f313okjzA5MmzePKkJqAFQoB26Ka6PY6p6UQuXrzFjz8uZ9OmlTlO8klJ\nSXTu3AdLS1ucnNwJCQnVrwsJCUWpdESptKNmzSbcu3fvJSUBKhV06KBL8o6OsGdPjpK8rigVJibF\n+TeF2WFiYkFKSkqOyivq5KV7SZKKtKSkJBo1CuLq1UcoFFYUK5bM8eN7cXNzM3ZouXLrVjRabS9g\nBnAdGIeu7wFoNM24fj0813UMGTKGHTu0qNX/oFbfZsyYdpQt6421tTVjxkwjJeU4UI7z56fQpUt/\njhzZlXVBCQnQrh0cOgQuLrB7N1StmuO46tevj7n5CBSKrxHibSwsllK5chWDDR9c2MkzekmSirRP\nPgnm0qVSJCb+yZMnfxAd3Y4xYyYbO6wcu3v3LleuXKFp07oolaFAOGCPbprbJCAdS8vvqVevRq7r\nCg/fTWrqHHQdF6uSnDyE3bv3cvToUdLTuwIVAFPS06fzxx+Hsi4kLk43Oc2hQ+DhAb//nqskD+Dk\n5MTRo3tp0GAXnp696NBBRXj4L7Iz3gvIM3pJkoq0ixevk5LSmmfnNWlpbbh06SPjBpUDQgiGDx/L\n6tU/YmbmiIuLDUFBAWzZUhEhBJ6efty9WxKFwoxatWqzcOE3ua7Tyak4cXERQBlAYGkZgYtLXVxd\nXTE3/xW1WgOYAqdwcsriCsm9e9CiBfz1F5QpA3v36v7NA+XKlePQoe15UlZRJxO9JElFWt26Vdm7\ndy3Jyd0AcywtV1GrVu7OKPObEIIRI0YSEvI7Wu0tUlPtSUmZTalSJ0hKSgDA0tKSuLg40tLSKFGi\nRJ6c3S5bNp+OHXuh0fQATmFpGcn9+7707NmTatVWc+5cfYR4CyF2sGrVjxl3/ucf3Zn8lStQvrzu\nnrzHmzEtbEEje91LklSkpaWl0alTb/btO4BCYU7FiuXYuzesUPXOXrbse0aPnkJ6+lhg+tOlkTg5\nNSAu7o5B646IiODTTz/j55/3oVaPw9z8BsWK7ebcuaOcPHmShw8f0rBhQ/z8/P7d6fp1aNYMIiMh\nIAB27YISJQwaZ1EnB8yRJEl6AXNzc7Zt20hUVBTp6el4eXlhkosZ0fLb4cOH+fDDz0hPHwjsBiYB\nlkAYZcv6Grz+GzdusHlzOGr1NqAOaWkQH9+fdevWMX78+Mw7RETozuRjYqBuXd3c8k5OmbeT8o1M\n9JIkFXkKhQJPT09jh5FtBw8epHXrbiQnFwcaA7fRdYBzwtLyFmvWGHZI27Vr1zF06Iekpgp087nr\npKe7kZiYlHmHM2egVSt48ED36FxYGNjZGTRG6dXkpXtJkoqM9PR0fvjhBy5dukbNmlXp27dvoe6J\n3apVV8LD26DrVT8O3aN0F7GyWsnevdupX7++QesvX74Oly9/CmwFLgNfADdQKody9Ohuqj7fe/7o\nUWjTBh4/1v37f/8H1tYGje9NIi/dS5L0xtNqtbRp05UjR56gUrXExmYx+/cfZ8WK3Pc+N5a0tHTA\nHEgGWgHf4uqaxM6dBwgICDB4/enp6YASXYKfCrTGycmMjRvXZkzy+/bpBsNJSoKuXXXD21pYGDw+\n6fUUnhtVkiRJL3HmzBmOHr2ISrUT+JCkpD2sXbuWu3fvGju0HHvvvb6YmIwFlgN2QCRduwYZNMnH\nxsZy7tw5EhIS+N//BmJjMxzYDwSgVKrZuXMjzZs3/3eHbdt0Z/BJSTBggG6CGpnkCxSZ6CVJKhKS\nkpIwNXVBdwYMYIeZmT2JiYnGDCtXTE1NsbDwAQ4CXwFHWbFitcFuX3733Q94eZUjMLAfHh4+VKpU\ngXnz/ke1asE0aLCWbds2ULt27X932LgROnfWjWH/3nuwYgUUpFnyJEBeupckqYioXr06lpbRmJh8\njVbbBjOzlbi7F8Pb29vYoeVYXFwcpqb+/HtO5ktqqoq0tDQs8vis+dq1a4wfP5WUlD9ISfEFDtC5\nczcePLjDqFEjMu8QGgpDhoBWC5MmQXAwFOL+EEWZPKOXJKlIsLOz48iR3dSqtQ1n55YEBl7kwIHf\nCtY87K9p+/btdO8+iB079qHR/IZu+tl4zMwmUbNmozxP8gCXL1/GwqI68OyRvSZotVbExMRk3njJ\nEhg8WJfkZ8+WSb6Ak73uJUmSXiImJoaDBw+iVCpp1arV60/JmkO6R9omoVJ9hEJxHyurL7G1dSIh\n4QF16jRm06ZQShhg8JnLly9TrVpjkpP/ALyAY9jYtOPBgyisrKz+3TA4GKZM0f2+YAFMmJDnsUiZ\n5Sb3yUQvSZL0AufOnSMwMAgh6iPEPcqU0XL8+F6USqXB6ixXrhZXr84FdB3eFIqpTJig5Ysvgg1W\n5zMLFy5m6tSZWFj4kp5+nY0bV9G2bVvdSiFg+nT47DPd2fuyZTBsWLbKT0xMRKPR4ODgYIDoizY5\nH70kSZIBvPvuOBIS5vDkyWYSEw9z9aoHS5YY9nG9tDQ1YKt/LYQtKSlqg9b5zPjxo7ly5Rzbt3/J\nrVuXMib58eN1Sd7UFH78MVtJXqPR0L//MJycSuDi4kGrVp1RqVQGaoX0XzLRS5IkZeH+/fvcvn0b\nqPd0iYKUlLpERkYbtN533+2FldUgdNPPrkOp/Ir+/XsatM7nlSpVigYNGvw7t7tGA0OHwtdf6x6b\n27QJ+vTJVplffbWYn3++THr6PdLS4vj9dzMmTfrYANHn3JEjR+jYsQ9t2/Zk165dxg4nT8lEL0mS\n9B+DB4/A3b0scXGJwGdAOnAPpTKUJk0MNxrd+vUb+eyzYDSaWExNu1Kp0tds3bo+4yNt+SktDfr2\nhZAQ3Sh3YWG6x+myaf/+E6hUQ9GNBWBBSsp7/P77yTwPN6eOHDlCy5adCQtryPbtLenSZRDbtm0z\ndlh5RiZ6SZKk58ycOYvQ0M1oNNfQaq8CEYASMzNvxo3rTteuXQ1S782bNxk8eBQpKQdJS3uARhNK\nTEwUjRs3Nkh9r5SSohvlbv163Xj1O3fqxrHPAV/fUlhY/A7o7jGbmh6ibNlSeRhs7nz55XeoVDOA\nkcBgVKqFBAd/a+yw8kzhe+5EkiTJgBYu/AZoD7g9XfIHYE5CwmOs83Ds9vT0dL7+egknTpynYkUf\n/P3fwty8NsnJz4aWfQeVahT37t3DI7/ncU9Kgk6ddHPIOznpppmtVSvHxc2YMYXffnube/caAdZY\nW19j0aKDeRdvLmm1gn8HWgIwQ6PRGiucPCcTvSRJEnD+/Hl69RpGQkIC8DsQDzgC27C1dcnTJA/Q\nrdsAwsPvolL1JCwsjLJlfyE9/R7wECgO/AmkULx48dcqT6vVcvHiRdLS0qhUqVLOn7V//BjatoUj\nR3RzyO/eDVWq5Kysp5ycnPjzz2Ps37+f9PR0AgMDC1TP+9GjB7FrV2+Sk5WAJUrlRCZM+NLYYeUZ\n+XidJElvvEePHlG2bEXi4+cC+4BjwGOgNHCR0NBvGDhwYJ7VFxUVhY9PFVJTzwG9gb8AFf7+Vbh1\n6y5mZlVJSztJSMgSevXq8cryUlJSaNGiE2fPXsHExIqSJa04fHgXLi4upKen8+TJExwdHV89k9+D\nBxAUBKdPg6cn7N0L5crlRZMLvPDwcObMWUJ6uoZx4wbTtes7xg4pA/kcvSRJUg6lpKTQvXsftm27\nhRCngRTgfWAlJUq4sGhRMD16vDrZZseNGzeoXLkRKlV9wB1YCDzEyqoxn3zyLuXKlaNSpUqULVv2\ntcqbNesz5s07RXLyJsAUc/OJdO78CB8fDz7/fAEKhSleXj7s2fMrZcqUybqQmBho0QIuXgQfH91l\n+0I8fHBRIxO9JElSDnXrNoCwsFuo1beBvwFL4CEWFmWIjr752pfOX8fOnTuZOnUeycnJJCQ8Ijr6\nIXAC8Hm6xVwmTHjEggWfZ6vczp378euvzYCBT5ccpnjxXjx8mPi0fD/gc/z9N3Px4onMBURGQvPm\ncO0a+PvrLte7u+eskZJByAFzJEmSckCr1fLrrxtQq8OAOsDbwFQsLOozevToPE3y69ato3373pw9\n+z/+/juYR4/MsLIyRzcFLIAGa+tDlCnjle2yq1f3x9r6ZyANEJiZrScu7i7QBSgHKICJXLp0Co1G\nk3Hnq1ehUSNdkq9WDQ4elEm+iJFn9JIkvbGEEFhbO5Ca+hfgCazD3PwT3nuvNQsXLnz1Pe3XdObM\nGerUeZv09GnAB0+XHqFUqaEkJDxCiGpotTFUqlScAwd+y/Z4+qmpqbRu3ZUTJ85hYmKFp6c9V678\niVZbEd0ZvSVwCBubLiQmxv6744ULujP5e/egfn347TdwdMyTNhcEp06dYvv2HTg42DNgwAAcC3Hb\ncpP7ZK97SZLeWAqFgqlTpzBvXmtUqlGYm5/HzU3B7Nmz8yzJA0ye/Bnp6XWAhOeWPsbOzpHTpw9y\n9OhRbG1tCQwMzNFse5aWluzdG8aVK1dQq9VUqFCBgIAGXLyYBlRDd1a/h6+//vrfnU6fhpYtIS4O\nmjaFLVvA1vYFNRQ+W7dupWfPIaSkDMLcPIIFC5Zy/vwxnJycjB1a/hOFTCEMWZKkAm79+vWiX79h\nYvLkaeLhw4e5KissLEyUKuUvHBxKiu7dB4rNmzcLX98aApYLcBEwQ8AiYWJSXPz888951ILM7ty5\nI6pXbyxMTEyFnV1xsWLFin9XHjokhL29ECBEu3ZCJCfnef33798Xbdt2E2XLVhOdO/cV0dHReV7H\ny3h7VxYQLnQD9QthadlHzJ8/P19jyEu5yX3y0r0kSW+U06dP8+mnC0lMTGbIkB706NE9z8o+c+YM\nDRsGkZy8FiiJQtEcU1NXTE3TSE3VAPOBdZia7mPixEHMmzc3z+p+ESFExqsTe/ZAx46gUkH37rBm\nDZibv7iAHLh79y7e3pVJTW0LDAF+pXTp7fz995mMU94aUPHiXsTF7edZR0eFYgZTpmj57LNP8qX+\nvCY740mSJL2Gv/76i8DAIH79tTZ79rzD4MGTWbFiZZ6Vv2vXLtTq/uimmN2EEE1JTz9LauoFwAdz\n84G4up5k/vyp2UrySUlJDB06Bj+/mjRt2oHLly+/9r4ZknxYmG4wHJUKBg2CtWvzPMkDDBgwktRU\nE2AF0BCYz927ppw+fTrP63qR9u3bYm09EfgHOIyV1XLatAnKt/oLEnmPXpKkN8by5StJShoNjAFA\npSpJcPAkBg8emCflOzg4YGFxmuRk0CWYQHQ93gFm4OU1kmvXsp/s3nmnHwcPWpCS8g3Xrx+nXr2m\nXL587t8Z5v4jPj6egwcPYm5uzttvv60b1W/9et0ENRoNjB4NX30FJq93rqdSqYiOjsbd3R2lUvnK\n7S9fvg5oADVgBWjRaBIxN8CXihdZuvRLtNpxbNlSCxsbexYu/JoGDRrkW/0FiTyjlyTpjaHVasn4\nZ88kT28F9uvXDze3v7Gy6gncBb5EN8qeCkvLxTRqVCfbZapUKvbs2U5KymqgDkKMJS2tJvv3789y\n+8jISN56K4B+/b6hZ885VKlSD9XixdC7ty7JT5mim3L2NZP8zp07KVHCi4CAFri4eLJlS9gr9wkI\nqIxC4QZ0AlYC7+Dqakn16tVft9m5Zm1tzerV3/H48V2io6/k6S2aQidPegnko0IYsiRJBcTZs2eF\nUuksYJmAn4VS6SuWLv0uT+t4/PixWLBggahQobowMXEU4CbAVtSp87ZISEjIdnmpqanCzMxSwIOn\nHcu0wta2sfjll1+y3L51627C1HS2ftsJpnWFvkfaZ59lq+74+HhhY1NcwKGnRZwQSmVxcf/+/Zfu\nd/fuXeHjU0WYm7sJExMX4e1dQTx69ChbdUsZ5Sb3yUv3kiS9MQICAti7dyszZy4gKSmZIUM+ZsCA\nfnlah729PTY2NkRG2qDVRgNWmJlNw97+EnZ2dtkuz8LCgpEjRxMS0gqVaigWFscpWfIxrf4zZey1\na9do3bor165FAqMAmMJc5miO6zb4+msYMyZbdd+4cQNTU3d099kBamNu7sPVq1dfeNsAwNXVlYiI\nP4iIiMDCwoIKFSrk6eOKUjbl4ReOfFEIQ5Yk6SW++WaZKFmynHBxKSOmTZslNBqNsUPKtWHDRgv4\nUn8iDRdEyZLlclyeVqsV338fInr0GCymTJku4uPjM60vU6aSUCgWChgvoIuYwwdCgNCA2NWjV47q\nvX//vrCychRw+Wk7bggrq2Lizp07OW5Lbh08eFD4+VUXTk6eokuXvuLx48dGiyU/5Sb3FbqsKRO9\nJBUdGzZsFEqlj4CTAi4IpbKmmDv3C2OHlWuLFy8RSmUzASkChDA1/VS8/Xb7XJWp0WiESqXKtDwy\nMlK0a9ddKBSWAoRQ8EQsoowQINQgvm3cTKSnp+e43h9+CBXW1s7CwaGpsLZ2EYsXL815I3Lp6tWr\nwsbGWcAvAm4KS8sBomXLzkaLJz8V6ERfunRpUblyZREQECBq1aolhBDi4cOHonnz5sLPz0+0aNEi\nw72bOXPmCF9fX/HWW2+JXbt2ZQ5YJnpJKjI6deorIOS5M989okqVRsYOK9fS0tJEUFAXYWNTWtjb\nBwhPz3IiMjIyx+X98MMKYWVlJ0xNLUSVKvVFVFSUEEKIuLg44eJSWpiYzBBgI0w4L1YwUAgQKSjE\nqY8/zpP23Lx5U+zatUtcv349T8rLqWXLlglr60HPfV5UwtTUPFdfZAqL3OQ+g9+jVygUHDhwgGLF\niumXBQcH06JFCyZNmsS8efMIDg4mODiYiIgINmzYQEREBFFRUTRv3pwrV65g8pq9QyVJKlyKFbPH\nxOQ2Wu2zJZE4OtobM6Q8YWZmxvbt/8fFixdRqVRUrlxZ94hbDpw8eZIxYz4iJeUPwI+LF2fQuXM/\nTpzYy549e0hJqYhWOxNzyvAjtelBKkkoWNi4BR/NnJkn7fH29sa7AExZa2+v+7yAQPfY4j9YWNjI\nHPEK+XJ0xH8eXwkLC2PAgAEADBgwgF9//RWALVu2/D979xkfVfE1cPy3NduSUNIoodfQQeklgBTp\nHRA/SjQAACAASURBVEUQRaog2MEOSlP0ryKK8AARRDoISBEEDIQivQQQQq8hEAglfct5Xuwag4Ak\n2U1C8H5f6d07M2fWjzl7507h2WefRafTUaJECcqUKcOuXbtyIkSFQpEL3n33dby9v0erfQW1eiRm\n80g+/fR9t+o8efIkn376KV988QWXLl3yUKSZp1KpqFy5MrVr185ykgfYsWMHdnsXoDygxm5/h717\ntwKg0WiAVLxIZilL6EkKt4CDn07kvfBfH7sJcJ06daJYsVsYDF2BjzGZWvLpp+Meu356Wo480T/1\n1FNoNBoGDRrEgAEDiImJITAwEHDOzoyJiQHg8uXL1K1bN61s0aJFc/V/VIVCkb1Kly7NoUO7mD17\nDlarjZ49w6lUqVKW6rJarXTr9hwrV64C+qDRWBk79kn27t1KqVKlPBt4DipUqBBa7QJSUmw4/2Tv\nokCBQgC0aNGCwj6j+C6+LM3kItfR8k27jox+++1cjTm7GI1Gdu8OZ8aMGVy+HEPz5tNp2bJlbof1\nyMv2RL9t2zYKFSrEtWvXaNGiBRUqVLjrc5VK9a+/xu732eh0w1GhoaGEhoZ6KlyFQpHDihUrxgcf\nuPcUD/Dhh2NZtWonzv3kh2K3w61bH/DJJ5MIC5vqdv25pWvXrkybNpddu2oDFbHb1zFnzlwAvO12\nIgv5ort0gut6AyuGDuODSRNzN+BsZjabGTFiRG6Hke3Cw8MJDw/3SF3ZnugLFXL+8vT396dz587s\n2rWLwMBArly5QlBQENHR0QQEBABQpEgRLly4kFb24sWLFClS5J46R3vovZNCoXh8rFq1EYcjACib\ndk2kHNeuncxynadOnaJ37yGcPBlFpUqV+fHHqQQHB3sg2gc7ceIEx44do0yZMlSsWBGNRsP69T8T\nFhbGhx9+xpUrcfTuPZBl076k8bhx6Pbvh+BgCm7cSL+yZR/egCJP+OdD7JgxY7JcV7a+o09MTOTO\nnTuA81CG9evXU6VKFTp06MDs2bMBmD17Np06dQKgQ4cOLFiwgNTUVM6cOcOJEyeoXbt2doaoUCge\nE4GBfkAw8CFwCjiCVjuG7t3bZKm+hIQEGjRowa5drYmN3UhEhC/ly9ehR48X6Nv3JQICyhAcXIkZ\nM2Z5rA/Tps2gWrUG9O49lVq1mjJp0leAc2Tzk0++4MqVlxFJQX99EgHde8L+/VCmDGzdCkqSVzyI\n5yb/3+v06dNSrVo1qVatmlSqVEnGjx8vIs7ldc2bN7/v8rpx48ZJ6dKlpXz58vLrr7/eU2c2h6xQ\nKLLJnTt37rsO3FMiIyPFYvEXjaaGgK+oVBZ5990PxeFwZKm+7du3i49PLdcyrvkCRV1LAasLlBLY\nKbBF9PpgWbx4idvxx8bGujanOeFq84IYDAXl7NmzEh0dLQaDn4BIcc7ISUqJgNwKDhbJ4XPeFbnD\nndynnEevUCiyVUJCAp079+b339ch4qB//8F8993/smVJ1IULF1i1ahVarZYuXbpQsGDBLNcVGRlJ\n3brtSEyMApoCHwFlgDrAj8DTrjt/oHXr1axdu9it2CMjI2nQoCd37hxNu+brW49ffvmMJ554gnz5\n/CmRuoINvEAwF9mn9sK26mdqP/30v9SqeFwo59ErFIpH1uuvv0tEhBc2203s9iv8+OMfTJv2f9nS\nVnBwMEOGDGHAgAFuJXmAypUr06xZXUymlsBV4BjQCNAD0enuvIRO5/6f0pIlSwKxwAbXlR3YbCcp\nX748RqORWa+OIIKWBHOR7WoTkzt05cnWefd8davVypIlS/j+++85evTowwsoskx5olcoFNmqfPna\nREV9DdRzXZlB9+7bWLQoLDfDyhC73U5YWBhhYT+yffte4DvgFZzzmIcBycAU9u6N8MgRrOHh4XTs\n2JPUVCE11Ur+/PmpX78OP7zclwK9ekFcHBcqVODI2LG06tIlz64ft1qtNGnShsjIRByOisBK5s+f\nQYcOHXI7tEeWO7lPOb1OoVBki6SkJL799jsSE+NRqSIQqQcIev02SpUqmtvhZYhGo6F///4EBATQ\ns+fXJCc/D5iBF4H/odNBWNh0j52zHhoaSkTEb9Su3RSH4y2uX29P/JpP8FrdFhwO6NCB4IULCTYY\nPNJeblm0aBGHDqWSkBCBc2B5Ky+99BzXrimJPjsoiV6hUHhcamoqDRq05M8//UhO7gB8gl6/Hi+v\nFIKC4nnnna9yO8RMCQgIQKM5ByQBXYHK6HQ1iI6+8MBXBPHx8fTpM5CtW/8gKKgQ06ZNon79+v/a\nzvXr12ncuAUpKcWBd2nJOn62r8KEg/j27bEsWQI6nae7l+OuXr2K1VqVv98eV+fmzZjcDOmxpryj\nVygUHrdx40ZOnEghOXkpMBHYg822hbCwVzl4cDu+vr65HWKm1KlThzZtGmCx1MfL62VMppaMHz/+\ngUk+KSmJ4sWrsHx5IrGxazh8eDgtWnTk9OnTiAg2m+2+5X755RdSUioBCXRiCb/QHhNJzFLrufPd\nd49Fkgdo1KgRGs1i4CCQilb7IXXrNs3tsB5byhO9QqHwuMTERFSqQP5+liiDRqPnqaeecmvf99yi\nUqlYuPAHfvnlF86dO0fNms/RoEGDB97/4YdjuXHjInAY51B/BVJTV/HRR2NYtmwlycnx1K3blBUr\n5uHn55dWzuFwoFL50YvrzKYHWoSv8GN3zw70K5o3XndkxBNPPMG0aV/w8svNSUy8xRNPhLJ06U+5\nHdY9oqKiWLJkKVqthl69elE0j/43UCbjKRQKj7t69SrlylXj1q2PgYbo9V9Rs+YpduzY8NCyj4PG\njdsTEREO7Me5JE9QqWqg010hNXUjUBad7k0aNjzLpk0r08pdvXqVCSXL80XiTdTAOJUvv9avweYt\nGx/bE9rsdrvrcJ5Hy759+2jcuBXJyc+hVidjMq1g375tuXZugrK8TqFQPFICAgKIiFjPE0/MJyio\nI+3aJbFmjXvrzPOSKlXKotFUBVoBnwI90OlO43D0AioBeqzW0WzfHn5XuYCffuJLV5L/NrgsjjGj\nCN+84bFN8sAjmeQB3nrrYxISxmK3f4XV+j137gxk7NjPczusLFGG7hUKRbaoUqUKu3dvyu0wcsW4\ncR8SHt6SM2fspKRMQKXS4O3ty507ewAHzmes/RQo4DzFExEYOxY+/ND571OmMHTo0FyKPvdYrVaW\nLl3KlStXaNSoEbVq1cq1WOLibgF/P707HKW5du1ErsXjjsf3Z6JCoVBkwu3bt9mxYwcnTrj/xzxf\nvnzs37+VMWOGotNZsNvnc/36bGy2o3h51cNk6ofJ9AyzZn3jTPIjRzqTvFoNYWHwH0zyNpuNpk3b\n0b//t4wadZLGjdvx44+5996+e/e2mEwfAFHAIUym8fTs2S7X4nGLe7vv5rw8GLJCoXjE7du3T/Ln\nLyw+Pk+I0Rgogwe/muU98tPr1Km3wAzX3vUisFJKlqwk06ZNk2PHjonY7SJDhjg/1GpFFi3yQG/y\npiVLlojFUlfA5vquDorFUtAj/x2ywm63y8iRH0j+/EXFz6+4TJr0Za7E8Rd3cp8ydK9QKNyyf/9+\nNm/ejJ+fHz169ECv1+d2SA8VHR3N+PGfEx0dS/v2TzF69GfExU0CegG3+PHH+nTo8CtPu7mPvNls\nQKW6zt9zqG5RpEhxBg4cCDYbvPgizJkDXl6wdCm0betmz/Ku2NhYHI4Q4K939hVJTLyF3W5Hq835\nVKVWq5k48WMmTvw4x9v2NGXWvUKhyLLFi5fQt+9QHI7uaLVHqVDBzvbtvz3Syf7GjRuEhNTi+vVO\n2GyVMZm+JCnpOCK3AefSP73+FSZOLMVrr73mVluRkZHUq9eMhISXASMm0/9YvXoRofXrQ69ezuRu\nNsPKldCsmfudy8OOHj3Kk0+Gkpi4DKiJVvsRNWvuY+fOjbkd2iNBmXWvUChyxeDBr5KUtJKUlCkk\nJGzg2DENixYtyu2w/tWSJUu4c+dJbLYvgZdITFwJmID5rjuuo9Oto3Llym63VaVKFXbt2sywYfEM\nGhTN77+vIrROHejUyZnkfX3ht9/+80keICQkhAULZlKwYC+02gLUrn2IlSvn5XZYjwVl6F6hUGTZ\n7duxOJeLAaix2UK4fv16bob0UFarFYfDku6KNxqNlXz5xpCS8gWpqdEMHjyEFi1aeKS9kJAQvvnm\nC+e/3LkDbdpAeDj4+cH69VCjhkfayYz4+HgiIiJQqVQ0adLkkdnEqH379sTGts/tMB47yhO9QqHI\nsgYNnkKnGwXEAztRqxfTpEmTLNUlIpw/f56oqCjsdrtH40yvffv26HSrgalABEZjL/r0eYHz54+x\ndet8Tp2K5PPPx91TzuFwcODAAXbu3ElKSspdny1YsJDKlRtQsWJdpk+fcf+G4+KgRQsID0cKFeKd\n+k0o3LYX1as3Ztu2bZ7v6ANER0dToUJNevacSI8en1C5cu1H/seZwk2emQ+Yc/JgyArFYys2Nlaa\nNm0nWq1BChQoIosWLc5SPVarVTp2fFYMBn8xm4tLSMiTcu3aNQ9H+7cDBw5IaGh7CQmpJ2+99b6k\npqb+6/1JSUnSsGErMZtLibd3FSlZsrJER0eLiMiKFSvEZAoWWCOwUUymsjJr1g93VxATI1KtmgiI\no3hxaVa8okBtgR0Cc8VgKCCHDx++p90//vhDRo16T8aNGy8xMTEe6fszz/QTrXaka2a7Q3S6oTJo\n0AiP1K3IPu7kvjyXNZVEr1A8fr788msxmZoJJLmSzwjp1u35LNVltVrlzJkzcuvWLRERmTkzTAoX\nLi9+fsXl9dffEZvNluk6P/lkvBgMHQSsAg7RakdKp07PiYhI27bPCMxKt4RuhVSv3kjat39GKldu\nIO88P0Ds5cs7PyxXTtbPnClgETiVrsxwGTt23F1trlq1SozGAIEPRafrLwEBxeXKlStZ+k7Se+KJ\n5gK/pmt7kTRv3tnteh/k9u3bEh4eLnv37s21pXKPA3dynzJ0r1Aoct3u3ZEkJnYHDIAKq7U3e/ce\nynQ9x44do1ixClSq1Ah//yK89NJAXnnlIy5f/oHY2HV8/30EH31077D8wxw6FEVycnuc05pU2Gyd\nOHLkOOBcQgdx6e6+yJEjkaxZE0L84WEM+HEe6uPHkcqV+bxDV/p9NNHVz/RlYvHyunulwquvfkhS\n0g/AGKzW/+PGjdZMnTot07H/U+PGtTEYvgdSgESMxhk0bvyk2/Xez/HjxylVqjIdOoyiceNutGvX\nI1tfyyjuT0n0CoUi11WpUhajcQ3gPL5Vo1lJxYrlMl1P+/bPcOXKmyQmXiA19SizZy8jMfFNoC5Q\nnsTEz1i06JdM11urViWMxiU4k6Og18+jRg3nrPxRo4ZjNk8AxgKfode/g05XgzL27kTwJiUlgd0q\nNcOrPsFH323n4sUhrn52A74FXkWj+YU+ffrc1WZCQjwQnPbvNlsxbt+Oz3Ts/zRu3IeEhqrR6/3R\n6QJo0yaAd9550+16/+n06dN07vw816+/ye3bO0hI+JPw8KuEhYV5vC3FQ3hwZCFH5MGQFQrFQyQn\nJ7vegZcRH5+aEhxcQS5evJipOmw2m6hU6nQ7q4loNDVEpRog0EqgkEBlCQmpnen4UlNTpXXrLmI0\nBomXV4CYTEWkefOOsmXLFhEROXjwoAwc+Ir06/eyfPHFF1LfVF1i8BcBCaeB5NcYRK+3CMS4Yvuf\ngE5UqnxisfhLRETEPW0OH/62mEzNBY4JbBKTqZBs3rw5wzFbrVYZM2a8NGzYVnr3HnDP93njxg2J\ni4vL9HfxMA6HQ4YOfUMMBn8BH4Ez6V4TjJU33xzp8Tb/C9zJfXkuayqJXqF4PNntdtm7d69s375d\nEhMTs1SHv39xgcUCMwW+Er2+uKhU3gIfCZwXmCI+PkFp7+8zw+FwyOTJk8VgKCrwk8B0MZn8Zfv2\n7XfdlxQeLjfVGhGQtVSRgsb60rfvIDEafV0xOJOewdBFJk6c+MA5A6mpqTJs2Bvi719SihevLAsX\nLpJbt27JoUOH5MaNGw+Nt3fv/q55D8tFqx0lgYElsyWxpxcTEyOtW7cXjaaEQJxAW4EPBBwCN8Vs\nrik//fRTtsbwuFISvUKhUIjIzz//LCqVRaCNQE/Ras1iMAS7Eo0zwfr61svUk3F6tWo1E1iR7gn1\nS3n22Zf+vuH330XMZhGQg6XLSpe2PeV///tabDabjBz5gZjNNQV+Eo3mHfHzC5arV69muO21a9eK\n2VxQvL0risGQT+bOnffAe1NSUkSj0QvcTovVYnlaFi5cmKV+Z8SdO3ckOLi8qNWNBYa42r0gUEnA\nT7y88kn//sOUCXlZ5E7uUzbMUSgUj40tW3ag0fTFZpsCgM32GXb7x8BtwBdIwWaLxtvbO1P1bt68\nmd9+20hMTAygSvdJAlFRR5k8eTI9fXwIHDIEkpPhueeo+sMPLE23R/uECWMoXrwoK1euoHBhP8aM\n2Y6/v3+G2o+Pj6dbt94kJKwAGgBHGDCgCU2aNKJo0aIZ7EX2bh++YcMGbt4sisMxEhgG3ACKAq8R\nHDyJnTt/p1ChQtnWvuLBlESvUCgeG5cuXcNmq5fuSkN8fApgs4WSkNAZs/k3mjWrQ/Xq1TNcZ1jY\nbIYNe4/ExJfQar1RqV5C5GvgIjCBw4fbs/2NlQy2ufZkHzgQpk51HjmbjkqlYsiQgQwZMjDT/Tp/\n/jxqdUGcSR6gEnp9CCdOnLhvotfr9fTs2YflyzuTmDgcrXYnZvOftGrVKtNtZ5TzR4QGaAF0AcoB\nFgoUsLFq1Rolyeci5VAbhUKRI5KTk/nyy685fPgkdepUY+jQIWg0mocXzIQff/yJwYMnkJi4CvDF\naOzFoEHVqFu3BgcOHKJ8+bL06dMnU+0WKFCEuLhVQA2cM+6fpFQpDfHxt7l8uR3POaoQxotocLC4\nWGm6nz0BKtXDqs2U27dvExRUnKSk34HqwGmMxtr8+edeihcvft8yNpuNceM+47fftlGiRGE+/XQ0\nRYoU8Whc6d26dYsKFWpy7dqz2O0N8PKaRIMGBlauXIzZbM62dv8r3Ml9SqJXKBTZKiEhgXfeGU1Y\n2HySkqpht7fHZFpAmzbFWLx4jkfbEhHGjBnPZ59Nwmaz0qNHL2bN+tat0/QMBm9SUs4D+QHQ64cx\nblwJtm49QKEVGqbi7MNonmdZ5VMcitz6r/WdPHmSAwcOEBwcTJ06dTIcx8KFi+nXbwg6XTlSU6OY\nNGkcQ4cOynK/3HHgwAFmzvwRtVrFgAEvpB0AdOnSJV5//X3Onr1E06Z1+fjj9x/pkwzzEiXRKxSK\nR5LD4aBGjYYcOWLCbj8LHMc5vJuIwVCMkycPZstT5l9/I1QeeLLu1KkXv/4qpKRMBDagUr0OxDNK\n68V4axIAb/IBU00RvP56Mz755IMH1rVgwSL69RuKTtcQu/0Afft24dtvv8hwLNHR0Zw4cYKSJUsS\nHBz88ALZICIigtatu5CYOBywYzZ/S0TEemrkwuE8/yVu5b6szwHMHXkwZIXiP+vFFwcJFBD4XeDJ\ndLPV7WIyFZVTp07ldogPdefOHenZ80XJl6+waDT5RMX/5CM++KsjMlxnFqMxnwwcOFysVusD60lN\nTRWDwUfggKvoTTGbS8gff/yR6ZhsNpv83//9n7z66psSFhYmdrvdnS5miN1ul8GDX3WtjZ9218qD\nzp17Z3v7/3Xu5D5lZzyFQpHm2rVr7NmzxyOnme3du5f581fi3O61JnATGAPsRasdTqlSRShRooTb\n7TgcDs6ePcvVq1fdrut+LBYLCxbM4tixfWg1KiZxkdF8gh01gww1CF34I4mJcUyb9jVa7YPnN8fF\nxeFc6FTNdcUXjaY658+fz1Q8IkKXLr0ZMWIOX31VkGHDptG794AMlY2MjKRjx140atSOqVOnZ+oJ\nccqU75gzZwdQB0i/WiCA+PikTPVBkcM89nMjh+TBkBWKPOGHH34UozG/+PhUF5OpgCxb9rNb9S1d\nulS8vdsLtBDoKfB/AmVFp/OXLl16S2xsrNsxnzt3ToKCSotG4ydarbf07t0/255ukxMTZbpaKwKS\ngk66ME/M5rKydevWDJW32+0SGFhSYLbrSfigmEz+EhUVlak4Dh8+7DotL8lVT7wYDP5y5syZfy13\n4sQJsVj8RaX6UmCZmExVZOzYTx/a3r59+6Ro0fKug3jCBH4QKCewxbVjX0lZuHBRpvqgyDx3cl+e\ny5pKolcoPO/SpUtiNBYQOOJKHnvEZCqQpZ3Url69Kl269JFixUJEo/EV2CUwSqC2GAwF5fr16x6J\nOSUlRXx8gl2bszgE7ohO94RMn/5/HqlfxHkM78yZM2XmtGmS2K2bCEgiSCevVmKxVJEePV7I1AYw\nBw8elMDAkuLllV8MBh+ZPz/zG9j88ccf4uNTI93QuYjFUk4iIyP/tdyYMR+LRvNqunKHxN+/5L+W\niY+PlwIFigjME3hb4CXXd/29QEkxmQrLjBmzMt0HRea5k/uUdfQKhYJTp06h15cnKSnEdaUWGk0Q\n58+fJ1++fBmux2az0bjx05w61QirNQyVahwqVSMMhnyYzV6sW7eeAgUKuB2vzWajV6++3L6dAAzG\nuYmNBau1D9u27WHAgP5ut3HhwgVq1WqILeEJwlJ2YbRfxGE2c/6LL2glwoBixXj66aczNeGvatWq\nXL58ktjYWPLnz49Op8t0XFWqVMFsvk18/CQcjs5oNPMpWFBDuXL/fgiQM870Q/WOh8Z+4sQJrNZ8\nwLNAK6AxUA+TyQ+DIZWdOzdTpkyZTPdBkbOUd/QKhYJSpUqRmnocOOa6sg+bLZpixYplqp5jx45x\n8eJNrNb/AbURWY7ZXJolS2Zx5cppatas6ZF4R478kF9+OQhYgF9dV+3ASsqWzXjMEyZMxNs7EIPB\nl+7d+5KQkJD22fvvjyPpek/mJSbQ0X6ROAyMrNmAY0FBJCUlYTKZsjSrX61WExAQkKUkD2Aymdi6\ndT11627Ez+8pGjbcSUTEuocuY+vV61mMxnmoVJ8DSzCZnuO114b8a5mAgABSUy8DV4ECwFp0uj+Z\nMKElx48fUJJ8XuG5gYWckQdDVijyhFmzZovBkF98fGqKyVRAFi9emuk6oqKixGAIEkh0DQ+nitlc\nQg4ePOjRWAMDywhsFvATCBKoJ1BSvL0LS3JycobqeP31N10rAvYKXBOttpP06tU/7fP2TdpJOBVF\nQGLwl6p8IwUKlBCLpbro9a+IyVRSPv54okf7ld0OHz4snTv3ltDQDjJt2owMvXZ4//2PxWQqISbT\nS2I2l5Y33ng3ByJV/JM7uU9ZR69QKNLExMRw7tw5SpUqhZ+fX6bKXr16lUaNWhMVFYlzsLAzRmMC\ntWs72LTpF9Rqzw0glixZjbNnvwL8gFeAQ5QoEcSePREULFjwoeXj4uLw9y+C3f42MNp19TT58jUh\nLu4C3LjBlRo1CDp/nosU4imWcc4wFLs9Bqs1CjAB0ej15YiJuZCp1xt50datWzly5Ajly5cnNDQ0\nt8P5T3In9ylD9wqFIk1gYCC1a9fOdJK32WxUqFCHqKgngSTgOGr1Zp55JpB165Z5NMkDfPrp+xiN\nzwFr0GqrUrCgme3bN2YoyYNz4xmt1gxEpbt6DJPJDDExEBpK0PnzxPr40lwXx2ldM0JDi2A0lseZ\n5AEKodXm4+bNmx7t26OoYcOGDBo0SEnyeZQyGU+hULht+fLlxMXFAh/h/LNSAoejH8HBOry8vDze\nXo8e3QkI8GfJkpX4+uZj6NCdmTo0pUSJEuj1KlJSdgKdcZ6yFsbUdz+Fxo0hKgoqVMBvwwaOFS4M\nQGxsLKVLVwaWAy1Rqf6PAgVMnD59mrlz5xIYGEifPn0wGAwe769C4Q4l0SsUCrc5j2/1BXYBnQAH\nsIVChZ7LtjZDQ0Oz/IRpMplYu/Zn2rbtQmLiRlQqGzPfHUmHSZPg3DmoXh3WrYOAgLRDaf39/Vm3\nbjk9e/bj8uUeVKhQkx49nqd9+74kJz+HwbCV77//kR07Nij7u/+DiLBt2zYuXbpEzZo1KVu2bG6H\n9J+ivKNXKBRu279/P/XqNSclRQW0BI5jMkVz48bZbHmivx+bzcbq1auJi4ujUaNGlC5dOu2z3377\njZ9/Xk3+/D4MHz6UwMDAtDJXr17F/9o1dE8/DdHRULcurFkD+fP/a3sigtmcn6SkP4AKgGCxNGHW\nrFfo3r17Nvb0b8uXL2fgwFe5dSuWxo2fYtGiMPI/JO6cJiK8+OLLLFmyAY2mGlbrZubM+Z5u3brm\ndmh5irLXvUKhyHU//TRfjEZfUanUUqpUiJw7dy7H2k5NTZV69Z4Si6WOmM3PicnkJxs2bBARkZde\nGihQUGCSqFSDxN+/mMTExPxdeO9eET8/5y4yoaEit29nqE2r1SpqtVYgJW0TGpPpBZk+fXp2dPEu\nDodDFi9eLF5efgJbBeJErx8kzZt3yPa2M2vz5s1iNpcVuOP6nvaK0eibI/vzP07cyX15LmsqiV6h\neHQ5HA5JTU3N0Tbj4+OlevXaArUF7K5kslaKFq0gGzduFPAV2J6WjNXqPjJp0iRn4W3bRHx9nR88\n/bRYb9+Wd98dLRUq1JEGDVrLrl277mkvJSUlbVlao0atRacbInBFYK2YTH5y/PjxbO2vzWaTdu16\niE6XT2BAup3ubotWa8jWtrNi7ty5YrH0SBenQ3Q6s9y8eTO3Q8tT3Ml9yqx7hULhMSqVKssbwWTV\nwIGvEhmZDDTi74VETxIbe5nVq9cBOiAg7X6HI4iEhETYtAlatoRbt6BrV1i+nFffGc1XX/3OsWOf\ns21bD5o2bcOJEycAuH79Og0btsJotGA0+jBlylSWL/+JZs1iMJsrERz8OitWzH/oDnXumjlzJps2\nxWC1fgGc5u/d7o7h7Z2xVQc5qVatWtjtvwORAKhU0wkKKoqPj0/uBvZf4sEfHDkiD4asUOSq2UZO\nXwAAIABJREFUpKQk6ddvqPj7l5QyZWrKr7/+mtsh3eXOnTsyePCrUr16E3nmmX5y5cqVTJX38ysh\n8JNAUYEoAZuo1cMlNLSdjB8/QdTqqgLNBfYLfCfgI520RklWqZyPmM8/L+I6XtZi8Rc4l/b0qdMN\nk88++0xERFq16iI63csCqQInxGQqJps2bfL49/Eww4e/ITBRIFmgvqtvQ8RoDJQFCzK/d35OmDt3\nnhgMPqLX+0rRouXk6NGjuR1SnuNO7stzWVNJ9ApF5vTuPUAMhg4CxwVWidHoJwcOHMjtsETEOdTf\noEFL8fLqJbBBdLo3pXjxEElMTMxwHRUqPCmwzHXQikVAK8HBFSQmJkZu3LghRYuWE42mskBhAYv0\noLek4jyFboaXSeLSHbKTP38RgcNpid7Lq6989dVXIiJisfgJRKd9plK9I6NHj/H4d/IwYWFhYjLV\nFYgXSBSVqqOULh0ie/bsyfFYMsNqtUpsbGymDgFS/M2d3KcM3SsUj7nly5eTnPwdUA5oi9X6PGvX\nrs3tsAC4dOkSe/fuJyVlNtAcq/Uzbtwws3PnzgzX8f33kzCZBmIw7MNkakSpUhU4cmQXAQEB5M+f\nn8jInXz99WBef/0ZBukNzGMeOmx8xlu84VWNg5GRaXW9995bmEydgeloNG/h7b2JZ599FgA/vyBg\nj+tOB0bjPgoVCvLYd5FRzz//PJ06VcJgKIHFUpXixU8SHr6OWrVqpd1z9epVXnhhCA0btuW998aQ\nmpqa43H+k1arpWDBglk6H0DhHmUdvULxmDOZLMTHXwKKAKDVXsRiKZm7QbloNBpE7ICNv/8cpaLR\naO57v81mY926dWlL6IoXL06TJk3Yv38b69evx2KpR/fu3TGbzWll8uXLx9ChQ7k9fjw+qbEAfMDH\njOV1TLaKdy1He+ONEQQHF2bp0rUEBORn1KgdBAQ43+/PmjWZdu16oFI9jUp1ivLltfTt2zdD/YyO\njmbEiJFcvHiNli0b8t57b2d5LoNareann2Zw/vyHxMfHU7Zs2bvqSkhI4Mknm3D58tPYbIPYt28a\nhw/3ZcWK+VlqT/EY8ODIQo7IgyErFLnqhx/miMlUROAT0eufl6JFy2XpnPns4HA4pG3b7mI0Pi0w\nX7y8XpBKlWpLSkrKPfempKS4ltA9KRZLTzGb/WTz5s0Za2jChLTD20fqA0SjeVvM5lrSs+eLmRpK\nPnnypMycOVOWLl163xjv59ixY6LR/DVDfoloNE2lc+fnMtxmZq1Zs0a8vRulm+WeKDqd+ZH5b67I\nGndyn/JEr1A8hmJjYzl48CBBQUH07duH4sWDWb16HQULhjBo0Fe5eghLREQE3377A2q1ihEjBrBs\n2VwmTvycbduWEhJSijFjvr7vznJz587l4EEHiYk7AA2wkr59h3LmTOQ996YRgQ8+gHHjQKVCpk6l\nYZEi+Bw6RNmyI+nWrVumhpJLly5910Y8GdGlSy/s9jLANECF3d6GlSsLcvPmzfv+d1ixYgVjx36D\n3W5nxIh+9O3bJ1PtyT2bqihD5f95nvu9kTPyYMgKRY7asmWLWCz+4uvbWIzGwjJo0IhHZgLUxo0b\nxWQKEJgs8KWYTH6ybdu2DJX95JNPRK0ele5JNUZMpgIPLuBwiIwY4bxZoxGZO9dDvcgci6WgQMN0\ncSeLWm2SGzdu3HPv2rVrxWgs5JpcuEpMppIyZ07m4o6Pj5dixSqITveawHIxGttK+/Y9PdUdRS5x\nJ/fluaypJHqF4t/5+xcXWO1KKrfEbC4vv/32W6bquHnzphw9elTi4+M9GlvTph0FfkiX9L6Vjh17\nZais80dCcYEzAnbRal+Tpk3b3/9mm02kf39nI3q9yLJlHuxF5tSo0cg14/9tgTUCT0uVKnXue2+H\nDr0E/i/d97Nc6tRpmek2Y2Ji5IUXhkiDBm3k3XdHZ/g1g+LR5U7uU4buFYrHiM1mIzb2AtDadcUH\nkYacOnWKp556KkN1zJu3gP79h6DV+iMSx88/z89w2YexWm2AOd0VM6mptgfca2XBggXExMTQsGFD\nmjVrxtixbzBqVCXsdjvVq9dlwYJF9ysIffvC/PlgNMLPP0OrVh6JPysWLJhB/frNuXXrJ+z2MEqV\nKsSOHdvve69erwMS0l2JR6fL/J/pgIAAwsK+y1rAisePB39w5Ig8GLJCkaNKlKgkMMv1RHhRTKZg\n2b59e4bKXrhwQYzGggKHXOV/F4vFz2NP9gsXLnI9la8UWCYmUxFZtWrVPffdvHlTAgPLiEpVW1Sq\nYWIwBMnMmWEi4twCNiEh4f4NJCWJdOzofBz29hbJ6GS9bHbnzh3Ztm2bREZG/utrlF27donJ5Ccw\nSWCyGI0Bsn79+hyM9G63b98Wm82Wa+0r/uZO7stzWVNJ9ArFv4uMjBR//+JisZQSvd5bxo+flOGy\nGzZsEF/fJumGjkUsltLy559/eiy+efPmS61azeSJJ5rLsvsMqTscDqlS5QmBGvL33vVHxGDw/fe5\nBvHxIi1aOIPOn1/kPvvU5wW7d++W3r0HSM+e/SQ8PDxXYjh37pxUqFBLtFqjeHlZZMaMWbkSh+Jv\n7uQ+5ZhaheIxlJqaytmzZ/Hz86NAgQIZLnf69GkqV65DUtJeoBhwCKOxCVeunMuxvclv3LhBQEBh\n7PZngTDXVRtgICioFCkpifTs2Z3Jkz/7e/34rVvQrh1s3QoBAfDbb1C1ao7E+ziqXr0hhw+3xm5/\nD4jCZGrKli2/3LUpjyJnuZP7sn1nPLvdTo0aNWjfvj3g/J+4RYsWlCtXjpYtW3Lz5s20eydMmEDZ\nsmWpUKEC69evz+7QFIrHll6vp1y5chlO8mfOnCE8PByj0cj48R9hNNbC17cxRmMzZs2alqMHkGg0\nGlQqNbAK+B24BXRDpcrPlSuziYvbwuzZh3nrrQ+cBa5fh+bNnUm+aFGIiFCSvBscDgeRkX9gt4/E\nuTSvPA5He/7444/cDk2RRdme6L/++mtCQkLS1qpOnDiRFi1aEBUVRfPmzZk4cSIAR48eZeHChRw9\nepRff/2Vl19+GYfDkd3hKRT/eV98MZlKlWrTqdMHlClThWLFinDkyC6WLRvNiRMHeeaZHjkaj6+v\nL1279sTLqwjQGwhEowlH5G2gHlCKpKTPWbr0F7hyBUJDYe9eKF3ameSz+fS4nGS1Wvnhhx8YO3Ys\nGzduzJE21Wo1+fIFAX8l9lQ0mr0UKVIkR9pXZAMPvT64rwsXLkjz5s1l06ZN0q5dOxERKV++fNrp\nVNHR0VK+fHkRERk/frxMnDgxrWyrVq1kx44d99SZzSErFHmGw+GQS5cuydmzZ7O8Tj4qKkqMRn+B\n86534XvEaMz34MluOcRqtcqECZOkRo0GUqRIJSlWrLxoNIPTzR34WZqXrSlSpozzQkiIyKVLuRqz\np9lsNmnUqLWYzaGiVo8Uk6mETJr0ZY60vXr1ajGZ/MTbu6dYLFWkTZtuYrfbc6Rtxf25k/uy9Yn+\ntddeY9KkSajVfzcTExNDYGAgAIGBgcTExABw+fJlihYtmnZf0aJFuXTpUnaGp1DkWVarlY4dn6VU\nqSpUrFiXOnWacfv27UzXc/r0afT6qkCw60ot1GpfoqOjPRpvZmm1WkqXLsHx4+e5dOl9zp8fgt3+\nIzpdX9TqUVQx9OOXWxfh5EmoUQM2b4bChXMkth9+mEPBgsEYjb507dqHhISEhxfKgg0bNrB/fwwJ\nCRtwOCaSmLiZd999F6vVmi3tpdemTRsOHfqDqVPbs2zZF/zyy8K7/o4r8pZsW0e/atUqAgICqFGj\nBuHh4fe9R6VS/ev2kw/6bPTo0Wn/HBoaSmhoqBuRKhR5z6BBL7N69RUcjkuAjkOHBvDqq+8wa9a3\nmaqnTJkyJCfvAzYCzYDfUasTH4lh2kmTppGYOBno5LqSRMWKSxnc0Jv+izTorl6F+vVh9WpsFguv\nDnuDOXPmotPpef/9t3jtteEej2nLli28/PI7JCWtBEqwZs1Q+vcfzvz5Mz3eVlxcHCpVKZzb/QIU\nRURFUlJSlg/EyYysbPer8Jzw8PAH5s7MyrZEv337dlauXMmaNWtITk7m9u3b9OnTh8DAQK5cuUJQ\nUBDR0dFpJ0MVKVKECxcupJW/ePHiA//YpE/0CsV/zaZNm5g9+2ccjv8BBgBSUl5g5853MlVPbGws\nHTv2AkxAZzQaA0ajsHz5QgwGg8fjziznD/3083TMtA4IYsiC+XDjBjRrBitWgMXCR++NISxsL4mJ\nu4DbvP9+F4oUKUSPHt09GtO6db+RlNQfcM4+T06eyLp1DT3axl8aNGiAw/EKsBxogFb7OZUqVc/R\niZGK3PPPh9gxY8ZkvTIPvkJ4oPDw8LR39G+99Vbau/gJEybIyJEjRUTkyJEjUq1aNUlJSZHTp09L\nqVKl7vveMYdCVigeWZ069RZoJ9Ar3Trzt6RLlz6Zqqdr1z6i0w0XcAgkisEQKhMnfpZNUWfesmXL\nXKfuzRGYJs298onVbHa+k2/Xzrk5jkv58rUFItK9w58mPXv283hMX375pRgMPdK1s1ZKlKji8Xb+\nEhERISVKVBaTKb80btxGoqOjs60txaPNndyXY1vg/jUMP2rUKHr06MHMmTMpUaIEixY5t7AMCQmh\nR48ehISEoNVq+e677zJ1qpRC8V+h1WqAJjif9KoBWvT6C0yZ8i+nuN3Hvn2RWK3/h3MJlZHk5J4c\nPLgnU3XcunWLCRMmcfbsZZo1q8+AAS957P/bzp07s3ChjsmTf+DJ27F8fDAZTUIy9OgBc+dCuuHr\nggXzAycA59O1VnsCf3/3T+i7du0affu+zO7deyhWrDjfffcpRYrMIjq6I1ZrCbTaeUyd+qPb7TxI\nw4YN//10PoUiIzz4gyNH5MGQFQqP2r59uxiNfgJfC4wUvb6ALFmyJNP1tGnTXTSaD11PplYxGtvL\n+PGfZrj85cuXXSfRPSswXfT66jJs2BuZjuOhVqxwHkwDIi++6Dyw5h927twpZrOfaLWviJdXX/Hz\nC5aLFy+61axzh766rlPgTohKNU3y5y8sZ8+elenTp8vnn38uhw4dEhHnKoFt27bJxo0b5c6dOxlu\nY9euXbJgwQI5cuSIW7EqHn/u5L48lzWVRK9QOJN95869pX37ZzO0F/pfS/H+Wtoq4lz+GhxcXnx8\naorZXEYaNmwpycnJGY6hVq0GArVdQ/8icF00Gq9Mn5RmtVolLi7u/ksE5893HjELIsOGifzLEq/j\nx4/Lp59+Kl9++eVd/cyKixcvysyZM0Wvz5+ufyI+Pi3u2Zs/MTFRnnwyVCyWSuLjU18KFSot586d\ne2gbb7zxrphMxcTbu6uYTIEybdoMt2L+p507d0qtWqESHFxJBgx4RRITEz1avyJnKYleoVA8UHx8\nvDRp0kYMhoLi5ZVf2rbtnpaMExMTZdu2bbJnz55Mr5PW680CbdO9r04RtVqfqTX406fPFL3eLDqd\nRcqUqSZnzpz5+8MZM0RUKmflo0Y5z5fPAb///ruYzX7i7d1KwEvguqt/NrFYKsvmfxyU88kn48Vg\n6CJgExDRaD6RVq26PrD+mJgYadq0jahU+dPVHSVeXj5y+/Ztt+O32WyyYMECMRjyC8wW2C8GQyfp\n2jVzczgUjxYl0SsUigcaNuwNMRh6CqQKJInR2EY++mhslupyOBwyefK3UqlSfdFq8wkECPxP4A+B\nzlKx4hMZrmvPnj1iMhUSOC7gELV6olSq5Dqn/auv/j5VZ9y4LMWaVUFBpQTWupp/Q6CswHgxGltL\ngwYt7znN7dlnXxL4Pt0Pnt1SsmT1+9admpoq5crVELW6q0DoXYcHmc3F5NSpU27FnpqaKo0bPy1e\nXoUEnktX/03Rag1Z3lhJkfvcyX3KDggKxWNux479JCf3A3SAgaSkvmzbti9LdU2ZMpVRo77jyJGP\nsdleBuJRqb5HpepE/vx72bJlbYbr2rlzJyLtgHKACofjDY4e3Y1j7Fh49VXnTV99Be++m6VYs0JE\nuHr1PBDqujIJrbYkTZpsZNKkdmza9AsajeauMvXr18BkmofzHHkHev1Mateucd/6jx8/zuXLd3A4\nvgYOAztcnyzGYHDctWlYZkVFRfHWW2+xe7eVlJSPgfQbKF1Dp8v9JZOKXOK53xs5Iw+GrFDkql69\nXhKt9g3Xk51DvLxekldeeTNLdVWsWFdgU7onxbflyScbyJw5cyQp3XK3jFixYoVYLDUEkl11bZb/\nGSzOilUq59D9v3j//Y/Ez6+UBAaWkQkTJnnsabVq1fqiVk90vZs/KyZTsGzduvWB99tsNnnmmRfF\nyyufGI1BUqNGQ7lx48Z97z1x4oQYjYVcfV4tUEDAKPnzF5E9e/ZkOeZ33hktRmOA6PXFBcYK3Bao\nIPCiwFdiMpWViRM/z3L9itznTu7Lc1lTSfQKxcOlpqbKvn375ODBg3L58mUpXjxEvL3riLd3TalQ\noZbcvHkzS/VWq9ZYYHlaolepxsjAga9kqS673S4dOjwjFkuI+Fi6yndag7hecovMmycizlcFx44d\nk127dt317r9Nm44CRQV2CewTgyFEpkyZmqU4/unMmTNSsmRl8fIqIDqdSb744usMlbty5YqcO3fu\nX+c6OBwOadOmm5hMLQSmisHQWho1uvd1QGbs3r1bTKaiAlcFFgmECMQKXBeVqoEULlxOli5dmuX6\nFY8Gd3Kfch69QvGYuX79Og0btuLixQREUqlSpSSrVy/iwIEDaDQa6tati5eXV5bqXrlyJT169CMl\npSWgwWRay+7dWwgJCQEgNTWVsLAwzp49T/36ddOOp34QEeH3DRsoMXYspbZsAb0eFi2Cjh1xOBz0\n6TOQn39eg04XiMFwk4iIdVy9epUmTbricHwJ9HLV9At1637Ljh2/Zqlf94vr2rVr+Pj4eHyXQKvV\nyjfffMvevUeoXr0CI0a8gl6vz3Q9s2f/SFjYEu7cieX48QASEn4GBHgH+BKDwZfSpUuycePKtPNF\nFHmXW7nPIz81clAeDFmhyFHPPTdAdLqhrqFnmxgM3eTddz/ySN1z5swVLy9/0WieEa22vDRv3i5t\nyNxqtUq9ek+JydRSYLSYTOUePukvJUWkRw/nk7zJJJJuqeC8efPEbH5SIN41ejBZatZsLDNnzhSN\npqLAp+leIUyRp57q7JE+5gVTpkwVk6ms6wn+XQEfgVPy18l++fMXlgsXLiiT7x4j7uS+PJc1lUSv\nUPy7qlUb/eM9+lx5+ukebtdrs9nEYPAWOOyqN1nM5hDZsGGDiIisX7/e9c7d5vr8smi1hgeuzT93\n/LjsLRwsApJsMIhjy5a7Pv/ggw8FPkjXj0vi7R0gf/zxhxgMQQJ+rlnxb4tKZXLrHbenpKamyscf\nj5eWLbvJK6+8KXFxcdnSTokSVQW2pvtu2olGYxKLpbTky1dIdu7cmS3tKnKPO7lPmXWvUDxmqlcP\nQa9fiPNAGCtG41Jq1arkdr2JiYnYbDYgxHXFC5WqStqRtrdu3UKlCubv09YCUat1JCYm3lPXnvBw\nosqHUPPyBa5joYmtKKNWrb/rnkqVQjCbVwN3AFCr51O+fAh16tThww/fQK9PRqebjcHwPTNmfMPG\njRv54IOP2LMnc9v4elL37n2ZMGEz69d3Zfr0OOrVe4qUlBS36xURLl68mPZd37vNcA0GDerPnj2r\niY4+Te3atd1uU/EY8dzvjZyRB0NWKHLUjRs3pHLlOmI2lxKTKVgaNWqd6RnxD1KmTDVRqz8T52E6\nO8Vo9JOoqCgREYmOjhZv7wCBnwTOiU73mtSo0fDeSuLiZKfOuaXtZYKkEpECF0Svt9w11OxwOKRz\n516uYeliAmZ5442RaZ/HxMRIZGSknD17VgICSohe309UqvfEZAqQNWvWeKS/mXH16lXR630FEtNW\nOHh715KNGze6Ve+dO3ekXr2nxGDwFy+vAtKuXQ+ZPPnbdEP334jZ7CeHDx/2UE8UjyJ3cl+ey5pK\nolcoHs5ms8nhw4flzz//dOs9bVxcnPTq1V/KlKklbdp0l4iICKlQ4QlRq7Xi7e0nP//881337969\nWypWrC358hWWFi06y9WrV++u8No1cVSvLgJyDpOUIcqVFK+KRmO8J9ayZWsIfCJwQOCkmEzFJCIi\n4q57PvpojGi1g9INY6+ScuUyvnGPp0RHR4uXV35xbkz015a59TO0RfG/GThwuHh59RawinPDo1by\nyScTZPbsH6Vp047Svv2zj8RrC0X2cif3KbPuFQrFfTkcDmrXbkpkZAVSU/uh0awjIGAOUVEH0Ol0\n6PX6zJ1Ud/kytGgBR49ySq2hqcOHC7wPVAY+oHXrQqxdu/yu9rVaHSLJODf7AYNhMJMmVWbYsGGE\nh4fz3XezOXBgPydO9MQ52xzgMIULd+PSpWMe+ibuz2q18u2333Ho0HFq1Ahh8OBBtGjRiZ07vUlO\n7o9Wu4FChZbz5597MZvNWW6nWrXGHDo0BmjquvITTz+9kjVrFnqkH4q8wZ3cp7yjVygU93Xx4kWO\nHj1OaupUoA52+4ckJASwa9cuvLy8Mpfkz52Dxo3h6FGoVImLP80l1ihotVNQq/sQEuJg5crFAMyd\nOw9//+JYLAXQ6/MB61yVxKPRbKV06dKsX7+etm2fYfHiJzlxogEwCdgCnMRofI2uXTt49Lv4J4fD\nQevWXXj33dWEhVVk1KhldO3ah9WrF/HSS0WpUWMcXbteZefO391K8gDly5dCq/1r2aDg5bWOkJDS\n7ndC8d/hoVGFHJMHQ1Yo8qQrV66Il1e+tOVtYBeLpfI9Q+d/WbFihbRt+4x069ZX9u7d+/cHx4+L\nFC3qHMuuVUskNlZERM6fPy/Lli2Tbdu2pQ3Zb9261bX//U6Ba6LTPSVarbf4+jYVk6mY9O07WBwO\nhzRq1NY1F+Cv4fq+YjQGSsGCxWTIkNckNTU1276Xffv2ScGCRVyz/lNc7SeJ0RgkJ06c8Hh70dHR\nUrx4RfHxqS0WS1WpXLmORw6/UeQt7uQ+bW7/0FAoFI+mwMBAOnbsyKpVbUlMfA6DYT0BASqOHDmC\nv78/5cuXT7t3/vwF9O//NomJHwM3Wbu2Fdu2baCaWu0cro+JgYYNYdUq8PUFIDg4mODg4Lva/O23\nDSQlvQg4Z41brWFYLDVZvPgd/P39qV69uuu6DTCmK9mQFi2srFjxUzZ+IxAWNpt+/V7G+ZpgEfDX\nRjdeaDTeJCUlZbluq9WKTqe753pQUBBHj+5h165daRse3e8+heKBPPiDI0fkwZAVijzLZrPJV19N\nlm7d+krRomXFbK4tJtMLYjL5ydq1a0VEZNGixWI0FhZYk+4Je6yM7dRdJH9+54UWLUTi4x/a3uTJ\nk11Hvv5VzwYJDq54z30//TRPTKYSAisFFovJVEh+/fVXj/c/vf3794uXV0HX1rtJAhUFPhQ4IBrN\n21K6dNUsjSTs379fgoMriEqlloCAErJt27ZsiF6R17mT+/Jc1lQSvUKR8+bMmSNmcxPXsjoR2CRB\nQaVlyZKlYjIFC1QS2JCWoBsxWBJ1Oue/dOggksHlfXfu3JGyZauJydRedLoRYjT6y6pVq+57748/\n/iS1ajWT2rVbyIoVK2TPnj0ybtw4+fbbb+XOnTue7L6IiEydOlUMhucFvAVOClwU6CAqVT5p1Ki1\nXL58OdN1JiYmSsGCRQXmur7bFeLtHSDXr1/3ePyKvM2d3KcM3SsUeYSIMGtWGFu27KJs2WK89toI\ntyd6ZVRMTAypqTX4e/5uTW7cuMKUKbNJTPwM5xGtg4HPaUkEP/M9Rivw7LMwezZkcKjZYrGwf/82\n5s2bx82bN2nZ8jeqVat233t79+5F797Ove6XL19Oo0ZtSE19Hr1+L1988T0HDmzD29vbzZ7/rVCh\nQmi1R4BPgYZAI2Anw4cP4quvJmapzlOnTpGaagGec13pgFo9gSNHjtCoUSOPxK1Q5LnH4zwYskLh\nEYMHvyom0xMCU8Rg6CFVq9aTlJQUt+u1Wq1y+PBhiYqKeuCa+x07driOVz0iYBWt9jVp1OhpadGi\ni8As15P8bOlICUn+67G+f38RN05lywiHwyFjx34qKpWPwO9pIwpGY1f55ptv0u47ePCgPPVUJ6la\ntbF89NFYsVqtmW7LbrdL69ZdxGKpLkZjG9HpLDJx4kS34ndOePQViHbFfkOMxkA5fvy4W/UqHj/u\n5L48lzWVRK/4L4qPjxet1ijOY1nrC+QTtdpfpk+f7la9165dk4oVnxCLpbQYjYWlZctOD/zxMHNm\nmJhM+USt1kqdOs0lJiZGNm3aJEajv8A30os+Yv0r044YIeLGRj0HDhyQl14aKi++OER27Nhx33vs\ndrsMHz5C9PpyrhnwF9MSvVo9Sj7++BMRETl79qx4eweISjVFYKOYTI1lyJBXsxSX3W6XNWvWSFhY\nmBw7dizL/Utv9OjxYjIVF5Opn5jNZWT48Lc9Uq/i8aIkeoXiMXf9+nXR6SwCJQW+Ebgm8J34+ARJ\nfAYmuT1Ijx4viF7/ijhPuksRo/FpGTfu0wfe73A47plwtmXLFvm+Zj2x/5Vl338/Lck7HA5Zs2aN\nfP/997J79+4MxbRnzx4xmfwExgv8P3tnHhZl9b7xe/aZd4YBZFUBE0TEfV9zScP9p7lruaWpaS5l\nkdpimaW2mZq54JqaW6amiAuaqKm57xsiGIobIoIyMMDM/ftjRoKvoCCoYedzXV7F+57znOeckvs9\n2/N8R0ly486dO3OUeTC7Vii8CCwg0J9AdwLXCOyhTufBv/76iyQ5ffp0ajSDsh3wi6MkORdglApP\nVFQUa9duRoPBjdWqvfzQR8LevXs5Z86ch/opEDxACL1A8IJjtVpZrVp9Ar7ZBIt0cKie70xlBw4c\n4IIFC7g7W5a48uXrENiXzeZ8du7ct2DOTZ36j0PZlrKtVit79HiTen1l6nQDKUml+NPG0LK+AAAg\nAElEQVRPcx5rrmvXfgR+yObTYjZr9n85ymzZsoUGQ1UCIwgE2+/69yPgSLW6BJct+4WbN29maGgo\nv//+e+p0vbPZu0gHB7eC9bEQhITMp1xuJPANgWuUyX6km1uZQn2gCf57FEb7xGE8gaAYIJPJsHRp\nCKpXbwyrNQmAI4D7yMy8AWdn58fWnzLle0ycOA0yWXMAX2Hw4B6YOnUSKlUKQEzMWmRk1AdggU63\nETVq1MufUyTw5ZfA+PG2n2fOBN55J+v1/v37ERq6BykpJ2G78x6N996rigED+kGr1eZpNjXVbO/f\nA5yQlpaeo0x8fDyAQABjADQEcA2AAgaDGps2rcHAgSNw86YBMpkGWm00tNpMpKePhcUSCEn6DsHB\n7+Wvj4Vky5YtGDnyY1itngCCAQDkcJjNi3D69GnUq5fPsRYICkMRfnA8E4qhywJBkTF48Ejq9VUp\nl4+hXl+d/fq9/dg6u3btolJpyLaHbTvwdf78ed64cYN+flXp4FCZen1ZNm7cOs/88TmwWsng4Acb\n4uSiRQ8VWbt2LY3G/8uxAqHVuvDGjRuPNL1hwwZKkheBTQTCKUnluGjRzznKREVF2Zf3dxG4Qpms\nHT08vBkdHc3hw9+nWj3Evh1BKpUfs23bLhw8eAQ7dHidCxcuLlSin/xw8OBBVq/emDqdO4FP7WcI\nkuzjcJ+SVIrnzp17qj4IXiwKo32PrTl9+nTeuXPniRsoaoTQC/7LWK1Wrlu3jl9++SXXrFnzWMHa\nsmULtVpn2tK8/iO4jo6NGBERQZJMS0vjoUOHeOLECVoslsc7YbGQQ4fSrqLkqlU5/Nu7dy9/++03\n7tu3zy7GOwlkUiabRh+fCvkS2ZUrV7FKlZdZsWIDzpu3INcyYWFhdHHxolyuYPXqLzM2NpYk2bJl\nVwIrsvU3nNWrN318v4qIv//+mwaDG4GlBN6yby8MI1CdwMeUyyuzV68BT/1jQ/Bi8VSF/qOPPqKf\nnx+7devGzZs3P/f/OYXQC4oLVquV0dHRPHfuHDOf8jWzvPD1rUZgHW3R3JbbZ7mb6eDgztv2mPMF\nIiOD7NvXpqAaDblxY9Yrq9XKnj3fpF5fjkbj/1GSXDlp0iSWKFGaMpmc5cvXfCqx4P/3d9KkSd9Q\nklrY9+3N1Gq7cMSI4CJvNy8WLFhAvf4N+0fGVfvY9yXwGpVKHT/++OPn/ntUUPx4qkJP2k64bt68\nmT169KCfnx/HjRvHqKioJ260MAihFxQH0tPT2bZtV+p0HtTry7By5XpPJqyFxMXFh7YobkcJ+BNQ\nUKcrwV27dhXcmNlMduliE3m9nty+PcfrsLAw6vWVCZjsIhdBZ+dSJPlE99ZJW3jYLVu28Pr16/mu\nk5GRwe7d+1Gl0lOtdmDLlq/RZDI9UftPwooVK2gwvJq1dQAcpFyu4ieffMpjx449Mz8ELxaF0b58\npamVy+Xw9PSEh4cHFAoFEhMT0bVrVwQHBz+towMCQbFm8OCh2Lw5HqmpfyMlJQYXLtTBO+8U7O+L\nxWIptB9t27aGVjsGQGkAy6HTeWDz5rVo0qRJwQylpgKvvQb89pstKc22bUCLFjmKxMbGgqyHf5LN\nvIy7d28gIyMDSmXBzv2SxFtvjUCjRh3Qo8e3KFeuCiIiIvJVV6lUYtWqxYiPj8P165exdes66HS6\nx1V7ItLT07F3717s27cP6em2A4MdOnRAqVIJ0GheB/AdJKk3vvjiS0yc+EVWUh6B4JnyuC+BadOm\nsWbNmgwKCuKqVauy7tBaLBb6+vo+8RfGk5IPlwWC58qOHTuoULgQmJdtn3g//f1r56v+5s2bs5a7\nAwPr8NKlS0/sS0pKCrt3709JcqaLizcXLfqZGRkZDA0N5dKlS3n58uXHG0lOJps1s3XExYXMnoI2\nG9u3b6da7W5fQSBlsuksX77GE/kdHh5Ovb4CgWT7+G2li4vXE9l6Wty5c4cBATXp4FCNDg5VGRhY\nO+s8U3JyMidPnsJhw97lunXrnrOngheBwmjfY2uOHz8+z18GZ86ceeKGnxQh9IJ/O927v0mgA4HX\nCGTYl3A/YMeOrz+2bkxMjP0AWwSBDMrl37Js2cpFtqdrNpvZoMGrNBjq0GDoQb3e9dHL+HfukPXr\n20S+ZEkyj7/zly9fppubD9XqagQ0BAwsXdr/iffk586dS0kakO1DyUKZTEGz2cwJEyaxdOlAvvRS\nVf7889Insl8YrFYrz58/z44de2Q73W+lWj2YQ4aMeub+CP4bPFWh/7chhF7wb6dPn8EEviIQRKAc\ngUpUq13yld1s9erVdHDolE3grFSrjUW2v79gwQJKUnMCmXb7v/OllyrnXvjWLZorViQBXtPoOPO9\n4Dz32jt16k2FYoLdZhoVikEcNGj4E/t54MAB+xW7v+0257Fs2cr8+uvvKUk1CRwhEEFJ8s4zu93T\nIDExkX5+1SiXuxDwoC1N7oP/Vuv58svtnpkvgv8WhdG+fO3RCwSC/PPee29Dr/8BQAsAXaDRXMfK\nlfNQsmTJh8rGxcXh44/HY9SoD7B37164u7uDPAcgzV4iCoAFRqOxwH7Yfjfk5Nq1a0hLqwtAYX9S\nH7duXXu4clwcLI0aQX32LC6gBOqaf8SHcw9h8OCRubYVG3sNFkt9+08aWCwtcPny9QL7/IC6deti\n4sRgqNWVoNf7wMNjEjZuXIklS36DyfQ9gJoAmsJkGodly9Y+cTsFITMzE1Wr1sGlSzJYrbEA+gNY\nBCADQAa02mWoXz/3THsCwfNECL1AUMTUqFEDe/ZsQ+/el9C9+y2Ehf2KTp06PVTu6tWrqFq1Hr7+\nOgkzZiShadM2CAmZh6ZNK8NgqA+dbhAkqSlmzJgGVT7TvALArFlzYTC4QqXSok2brrh3717Wu4YN\nG0KrXQEgBoAVSuUU1KvXKKeBmBigcWMoLl7EabkRTXAWVzEQJtM6LF26MNdDgi1aNIJONw22dLVJ\nkKSZCApq9FC5gjB69EjEx8fh1KlduHLlAipVqgSDQQ/gnw8Imew6jMZnk6r39OnTuHEjEUAnABKA\n8QDuAnCDVuuFevVM+OKLT56JLwJBgSi6hYVnQzF0WSDIlXHjPqFCMdIe3KUkgS8I9Kanpy9/+eUX\nzp49+7GJYK5fv87w8PCsKGvbt2+nJPkQOEvgPjWaPuzaNWfs+qlTZ1CtlqhQaFi7dlPeunXrn5fn\nzpGlS5MA43196a1vk21pOpEKhTrXmABms5nduvWlQqGmQqHmgAHDnkrsgJ07d1KncyXwOeXy0TQa\n3XOcAzhy5Ahff/0tdu3aj9v/5/pfYTl+/Dg1Gg8CtQncs4/JVwwMrMXLly+Lu/GCp0phtE9mN1Bs\nkMlkuS5JCgTFjZEj38ePP7oCWAxgIQDbDFij6YtJk6pj9OjRj6y/detWdOnSG0plZaSnn8eIEYMg\nl1swZYoawGf2Upfh7NwYd+5cyVHXYrHAbDZDkqR/Hp44AQQFAfHxQJMmuPPzzwis1wwJCb1hsdSG\nJE1Dz56VsGDBT3n6ZDabQRK3b9+GwWCAk5NTQYflsRw5cgTLl6+GRqPGoEEDULZsWQDA0aNH0bhx\nK5hMYwDoodN9gV9/nY927doVSbuZmZmoXbspTp1KgtV6A4ADVKoknDt3CH5+fkXShkCQF4XSvqL5\n1nh2FEOXBYJcCQ0NpVzuTEAiEJM1c5bLx/Lzzyc8sm5mZiYNBhcCe+z1blOSfDh69GhqtZ2zBWv5\nneXK5eOK219/kU5ONgdatSJTUkiSsbGxfP31t/jyy+341VffPHaWfu3aNQYG1qZO506VSs/33hv7\n0Ew3IyODP/wwnb16DeSXX05mamrq4/3LB717DyLwbbYViF9Zp86rRWL7AUlJSRw+/H3WqtWMvXr1\ney5BkAT/TQqjfSJ7nUDwHLBarRg16mNYrV1gOxj3NoBpAGKg1S5E+/Zhj6yflJSE9PQMAC/bn7hA\noaiLKlWqoEyZCFy92hpWqw9ksvUICVn9aGciImBt3x7ylBSsgwzBZ2Kw9MQJNGjQAN7e3ggJmQaL\nJX8HAnv3fhsXL76KzMxJAO4gJKQZGjWqjS5dumSV6dHjTWzZEgeTqQd0ui0IDW2PP//cCoVCkbfh\nfGA2Z+CfYD0AICEzM7NQNv8Xo9GIH3/8rkhtCgRPnSL84HgmFEOXBYKHaNiwhf2+eQKBNAKjCLjT\nxaUsN23a9Nj6VquVbm4+BNbYZ6+XqNN58NSpUzSZTFy6dClnzZrFCxcuPNpQWBitWi0JcClqUoEk\nAmvp4ODOa9eusX//t6lUaqlUSmzZstNjQ8k6O5cmcDnbrPoLjhkzLuv9uXPnqNW6ZAuTm0mDIYAH\nDhzI17g9ij/++IM6nQeBVQRCKUl+XLhwcaHtCgT/BgqjfcVONYXQC4o74eHhdpF/ibbMbg/uyzfl\nolzSvebFoUOHWKJEaRoMZanRGDlr1tyCObJmDa0qFQlwDjSUwZIl0EZjczZt2pxKZV3a0quaqdV2\n5bBhox9psmrVRgTm2+2kU5KaMyQkhJcuXWK5ctWoUGgJOBM52qrD3bt3F8z3PAgLC2P9+i1Zq1Zz\nIfKCF4rCaJ84jCcQPGUyMzMxduxnWLVqPQwGA+rWrYAlS34DMBPAh7Bd1zoBb+8kXLx4HBqN5rE2\nSWLlypU4fPgoXFyc8fbbb6NEiRL5d2rpUqB/f8BqxVQ0wPs4CeAigJIAUqFQ+IDUwmr9CkBfe6Vd\nqFz5Y5w69WeeZk+ePImmTVuDrAiLJQ516pTD1q1rUbVqA0RG9oTV+h6AOgBqAxgEhSIMnp6/IDLy\neM6DgXmQkZGBhQsX4tKly6hTpya6du0KmUyW/34LBMWUwmifEHqB4Cnz7rtjMG/eQZhMPwC4ArX6\nDVgsLrBY3AC8DiAcMtkOXL4cCR8fn3zZ7NSpFzZvPgOzuTskKRzNmrkjNHT1Q6IXGxuLS5cuwd/f\nH15eXraHc+YAQ4cCAL7Tl0Bwyh4AGwCEAGgDhWIbyHhYrQMA3LM/l0Eun4i2bc9g48aVj/QtISEB\nBw8ehNFoRIMGDZCZmQmdTg+r1Qxb6I4EKBSN4eycjtq1ayAkZCq8vb0f22er1YpXX+2AAwfSYDI1\ng16/GoMGtcUPP0zJ15jlZk8uF6FEBMUDcepeIHgGWK1Wzp4dwrp1g9i8eUfu27cvX/Xc3X3t99of\n7Ft/Qm/vQKrVXlQofKlQOPHXX3/Ntx/jxo23n9S/mxVyVq/35ZH/STYzZ8486nQudHRsTJ3OxRYX\n/ttvHzjBSSVK0dMzgErlGPsp/U1UqcqwV69eVCq97OcHqhJ4mUAjKpWOjImJKciQkbSNm4ODK4ED\n9qZTaTBU4ebNmwtkZ8+ePTQYAmnLH2C7aaBS6ZmYmFggO7dv32bjxm0olytpMLhy8eIlBaovEDwP\nCqN9xU41hdALnhfffz+dklSRwEYC8ylJrvnKL16mTOVse/GkSjWEX3wxkdu3b+evv/7Kq1ev5tuH\nmzdvUq02EPDJdoWONBjqMyIiIqvc1atXqdOVIHDRXuYMJyo0WSI/TNaBwEGqVK9To3GlXv8SNZoS\nbNu2C5csWUKNxpXAJwROEhhAoASrVGn0RONGkuvXr6dO50qDoTs1mvL09CzP/v3fZnR09GPr/vzz\nUjo6elIuV1KhqJ/tg8lKnc69QONHki1adKBK9Y79EOQJSlJJ/vXXX0/aNYHgmSCEXiB4BpQpU4XA\n/mxC8znfffeDx9ZbsWIlJakUga+pVA6nq6s3r1+/nqPM/fv3+dFHn/G113rz66+/yzN5zKlTp2gw\nBBCoQuAz+/37GXR09GRSUlJWub1799LRsW6WIH6H0SRAi0zGwdqAbH3IpEZTgrt37+bnn0+kJHnS\nwaELlUonymSuBLwJvEyttiK//356ocYvMjKSPXu+QY3Gm8AiyuXj6eRU8pFCvXfvXkpSSQJH7af5\nHQnMJRBDpXIMAwNr02KxFMgPjcaBwJ1sH17v8euvvy5U3wSCp01htE/coxcI8ontnnd61s8yWTqU\nysff/e7Zswc8PNzx228b4ejojOHDD8DT0zPrfWZmJho3bo2zZ71gNrfCtm2/YN++I1i/fvlDtnx9\nfaFS3QPwCYBNAOZALk/Hli1hOe65lytXDhkZlyDDYczCfLyNuUgHcHLMGCyfuRmAFbb9chPIDHh4\neGDy5O9gNp8AUAbATSiV5VGihCNksusYOnQA3ntvxBON2wP8/f0RHr4HZnMYgMqwWgGT6QaWL1+O\n4ODgXOvs3LkTZnMfADXsT9ZDJusEJ6eJqFmzFpYt21jgfXZnZ3fcuHECQDMAVqjVJ+HuXvXJOyYQ\n/Nspwg+OZ0IxdFnwgjBv3gJKUlkCP1Mm+4Z6vWtWjPnCsHfvXhoMlbNdOTNRoymRZ1rbw4cPs2RJ\nP8rlKrq4eOV5NW3NytX8RaEmAZoA/vXZ50xPT2eNGi9Tq+1GYA4lqRH79BnEkydP0sGhQraZPuno\n2CDf197u3r3LJUuWcMGCBYyLi8vx7sSJE2zSpB0DAupSo8m+nUAqlSM5efLkPO3OmTOHktQu2zbF\ndpYuHZAvn/IiNDSUOp0rdbq3aDA0Zu3aTWk2mwtlUyB42hRG+4qdagqhFzxPVq/+lW3b9mCPHm/y\n5MmTD71PTU1ldHT0YwPLZCciIoJGY11mX07X6Tx5+fLlR9YzmUx5J1JJSyM7dSIBZkoSU7IF4UlJ\nSeGECV+yV6+BnDlzFi0WC1NSUujo6Ml/8qtHUK93ZXx8/GP9v3XrFkuX9qde356S1JOOjp48c+YM\nSVsIXQcHdwKzCPxJhaI8FYrqBLYRmE293pWRkZFZthYvXsJSpQLo4uLDkSODmZyczMqV61GvD6JG\nM5SS5FYk+efPnDnDWbNmceXKlULkBcUCIfQCwb+ArVu30mBwoV7vTb2+RL4FKSUlhd7eAVQqPyaw\nhxrNQNau3fTJs6GlpNji1QO2+PX5PGi2b98+OjuXolrtSAcHV4aHh+er3qhRwfbDbbYmZbLpbNGi\nI0ly9uzZ1On6ZfuIuU25XMvq1ZuxRYuOPHr0aJadrVu3UpK8COwlcIGS1JTBwZ8wNTWVS5Ys4fTp\n03nq1KmCj4dA8AIghF4geM7cvXuXBoMrgV12QdtHSXLJ14yYJOPi4vjaa28wMLA++/V7m3fv3s3x\nPj09PX+HzpKSyCZNbKrq5kYeP57jdUZGBkePHsfSpSvQ378WN2zYkOO9xWJhfHx8gVLMdu7cl8CC\nbGK+h4GB9UmSCxYsoCR1zvbub2q1xlw/YgYNGk7g+2xlD/Gll6rl2w+B4EWmMNonokUIBEXApUuX\nIJeXAtDE/qQBVCpfXLx48bF1SSI6Ohp9+nTG1q2rsXjxbDg6OgIAUlJS0LZtN+h0Bmi1BowfPzHv\noBl37gCvvgrs3g2UKmX7Z7VqOYp8+OGnmDNnH+LiVuHixYno0eMt7N+/P+u9XC6Hq6trgRLMtGnT\nFJL0I4DrAO5Bp5uMVq2aAgA6d+4MR8cTUCpHApgPSWqHDz8MzjWanbOzEQpFbLYnf8NodMi3HwKB\nIA+K7HPjGVEMXRb8B7h16xa1WqdsB81iqNWWeOwdb6vVyi5d+lCvL0+jsQP1eldu3749633//kOp\n1fYgkEogjpJUkStXruT69evZunU3duz4hi0hzI0bZJUqtqlw2bLkpUu5tufhUY7A6Wyz5gn84IMx\nheq71Wrlhx9+QpVKR4VCzR49+jMtLS3r/c2bNzlqVDC7devPxYuXZM3mjx07xt9//z0rCE9cXBxd\nXb2pUr1FmWwcJcktx1gIBP9lCqN94nqdQFAEuLm5YejQgZg5szrU6gqwWmMxZcpElC5d+pH1QkND\nsWXLSaSknACgBbAdPXsOQHz83wCAHTt2Iy3tF/u7UjCZhmD27AU4dOg8TKYvASTj7NbWOOnuAG1s\nLBAQAGzfDjwId/s/SJIetpl3JQCAUnkdDg6lCtV3mUwGk+keLBaCJM6cOY+EhASUKmWz6+7ujmnT\nvslR5733xiEkZBmUyqrIzDyIJUvmokuXzjh16iAWL/4ZJlMqOnfehurVqxfKN4FAgOI3PS6GLgv+\nA7z//kfU6/2o1Q6kRlOGgwYNz1e9mTNnUqsdkm2GnU65XJG1H1+3bgv+kw3OSrW6Dz08yhMIJUD6\nIooxcLZVrlaNvHkzh32r1crjx4/zjz/+4J07d7hmzRrqdJ4EvqJS+Q5dXb3zvMaXX954oz+BEgQi\n7dfgxrFu3eZ5lj906BAlyTtb0Joj1OkcmZ6eXig/BIIXmcJo31Pbo09LS0O9evVQvXp1VKxYEePG\njQMA3LlzB0FBQShfvjxatmyJu3fvZtWZPHky/P39UaFCBWzbtu1puSYQFJqzZ8+iceO28PWtjq5d\n38BPP4UgJeUA0tLmw2w+jKVLl+PKlSuPtVO7dm3I5aEAYgAQcvkMVKhQKysIzNy538HB4SPo9b1g\nMAShTJmTcHFxAaBEBZzDbjTBS0hElKs7sHMn4O6eZZsk3njjLTRs2AGvvTYeZctWxEsvvYQtW1Zh\n5Mg7GDfOFdu2/Y5Ro8ahevWmGDZsNFJSUgo0DgkJCVi5cgWAXgD8AcgAfIwjR/bmWefvv/+GUlkT\ngLP9SU1YrQokJiYWqG2BQJBPiu5742FSUlJI2k761qtXj3v27GFwcHBWuMkpU6ZwzBjb/uCZM2dY\nrVo1pqenMyYmhn5+frmeMn7KLgsEj+XmzZt0cipJmWwmgcNUqVpSocgeVpY0Gqvy8OHD+bI3Y8Ys\nqtV6ajQl+NJLlXjpf/bXr169ysWLF3PVqlVMSUnhokU/s4G2FG/BSAKMkKt4IJe97DVr1lCvr0Eg\nxe7Xcvr5/XOK/f79+/TyKk+lchyBHdRqe7Jp07YFutYXFRVFjcaFQH3+k2xmO52cSj9Ubv/+/UxK\nSmJkZCR1OrdsZwVW0s3Np8ChbAWC/xKF0b5nopopKSmsXbs2T58+zYCAAN64cYMkef36dQYE2KJc\nTZo0iVOmTMmq06pVK+7fv/9hh4XQC54zK1eupINDx2zCHk9AR2CVXexW0Nm5FO/du5dvm2lpabx5\n82b+RHbfPpoliQT4l4sHd2/dmmuxr7/+mkrl6Gx+3qVarc96v23bNhqNjXJsG2g0zll/P/NDRkYG\nvb0DCFSz/+lCQM81a9aQtG0dDB/+AXU6dxqNtejkVJJHjhzhkiXLqNUaqdN50tXV+6HMewKBICeF\n0b6ner3OarWievXq8PDwwCuvvIJKlSrh5s2b8PDwAAB4eHjg5s2bAIBr1679ky8bgJeXF+Li4p6m\newLBE6HVakHeAfDPNTeFIhOlS38CmUwDb+8J2L59IwwGQ456UVFRqF79ZWi1RpQvXxPHjh3LeqfR\naODu7p7rtbMc/PEHEBQEtckEdOmCetdi0bhly1yLVqtWDRrNRgDxAACZbBEqVPjnup1CoQBpztaP\nTJCWAl2tUyqV2LVrM2rUMEKlioSHx2GsX/8LunTpAgAIDw/HokUbkZp6AcnJh3H37lR07twHffq8\ngTt3buDChYO4fj0aNWvWzHebAoGgYDzVU/dyuRzHjx9HUlISWrVqhZ07d+Z4L5PJHvmLLa93n3/+\neda/N2vWDM2aNSsKdwWCfNGyZUuULv0FLl/uC7O5PvT6BRg0aDR++GEKLJbchTIjIwPNmrXFtWvD\nQG7ExYub0Lx5O8TEnIWTk1Ou7WzYsAEhISug12sxduxI1Lh2DejSBTCbgb59gQULAGXef4VbtWqF\nESNex9Sp5aBSlYCTkwq//RaW9b5Ro0YoXZqIjn4L6ektIEmL0br1/8HV1bVA41G2bFkcPbo713fn\nz59HZmYLAA/62AlXrvQGSeh0Onh7exeoLYHgv0JERAQiIiKKxljRLSw8mi+++ILffvstAwICslJ0\nXrt2LWvpfvLkyTmSW7Rq1SrXHNHP0GWBIE+SkpI4fvwE9ukzmIsWLX7skvv58+dpMPj+T9KYRty5\nc2eu5W2pbW3pXIGp7K1xoFWptFUcOpQswH52fHw8IyMjcz3VfvfuXb777ods3bobv/xySpGffN++\nfTv1+nIEbtv7/TN9fasUaRsCwX+BwmjfU1PN+Ph4JiYmkrQl32jcuDG3b9/O4ODgrL34yZMnP3QY\nz2w2Mzo6mr6+vrn+8hRCLyiO3Lx5kxqNo30/nwRSKEnePHHiRK7lK1VqSGAzAbIfFjETMpvIBweT\nBYyBb7FYuHbtWk6dOpV79uwpiu4UiA8++JhabQkajZXp4pJ3nwUCQd78K4X+5MmTrFGjBqtVq8Yq\nVarwm2++IUkmJCSwRYsW9Pf3Z1BQUNbHAEl+9dVX9PPzY0BAALds2ZK7w0LoBc+QpKQk9u07hH5+\nNRkU1OmhE/EF4YMPPqZeH0Cl8gPq9TXZq9eAPFcCAgPrE9jBYZiZtQSwtmbdAot8eno6X365JbXa\nalSrh1OSfPjttz88cR+elCtXrvDYsWNZN3EEAkHBKIz2yewGig0ymSzvWN8CQRFCEo0bt8bhwyVh\nNg+DXL4TLi6zEBl5Is999ccRFhaGkydPwt/fH507d87zHEpIyHxcGT4WEzMSAABjVXp02rMD9erV\ny3dbqampqFWrEc6duwUgCrboerFQqQJx9248JEl6oj4IBIJnT2G0T4TAFQjyICEhAYcOHUB6+m0A\nSlitdWE2h2Pv3r1o167dE9ls3bo12rRp8+jT9SQGX/kbyEiAFcAP5auiTciMAok8AEyf/iOiolQA\nqsEm8gDgDYVCQnJyshB6geA/gsheJxDkgVqtBpkBwGR/QpBJUKvVBbaVnJyMRo2CoFJpIUnO+P77\n6bkXJIHRo4EvvwQUCsiXLcP7F06gadOm+W4rLi4OISEh2LhxGzIyOgA4BGCTvR9T4OnpAfdsEfQE\nAsGLjVi6FwgewcCB72DlymMwmfpBo9kFf/9oHDmyO99in5iYiDfffAcbNmwGabfYDeoAACAASURB\nVATwGwBnaLVB+PXXGWjfvv0/hS0W4O23gfnzAbUaWLkS6NSpQP6eOXMGDRu2QGZmS2RmnkJ6uhXA\nFAAjAVyG0eiJ48d3o2zZsgWyKxAIni+F0T4xoxf8J7h8+TIaNWqFEiW8UK9eC0RFReWr3rx5P+Lb\nb/uiV69DGDOmAvbv355vkSeJVq06IzTUAHIvgDEAOgJwQlraEISHR/xTOCMD6NPHJvI6HbBhQ4FF\nHgBGjfoY9+59ApNpCdLTj0AmU0Au7wqtNgk1atTHokXTsXDhIsyaNQtpaWmwWq2YOnUGmjbtgF69\nBiImJqbAbQoEgn83YkYveOExm80oV64qrl0bAKu1J+TytXB3n4lLl0491X1qW6pWP6SnJwB4EESn\nDYC3ASzF5Ml1MHbsGCAtDejZE/j9d8DBAQgNBZo0KVBbW7duxebN27Fixe+4dWs+gAf1F6Ft2y0I\nCZmKwYPfQVjYPgCDIZcfQOXKKWjSpCEWLvwTJtOHUChOw2ici3PnjmZFrxQIBP8OxIxeIHgEFy5c\nQFKSHFbrGABlYLW+B5PJiNOnT+coZzabER8fX2QfklqtFlZrOoAk+xMrgFgA70Ol2gJHRyPSExOB\nDh1sIu/sDOzYUWCRnzVrLjp3HoLp011w+7YeMtl4AHcBXIVePx2dO7fG3r17ERa2BcA+AF/Cat2G\ns2ctmDPnJ5hMawF0hsUyHmlpzbB+/foi6b9AIPh3IIRe8MJjNBqRkZEA4L79SSoyMm7BaDRmlZk9\nOwRGowu8vQPg61sF0dHR+bKdnJyMN94YBB+fymjUqDXOnDmT9U6v12PYsOHQ61sAmArbbD4WQAKs\n1sH44v2VOOtTFggPt6WXjYgA6tQpcP/GjfsMJlMogLGwWg9ALr8GudwTGk0gRo58DQMG9EdY2A4A\nFgA+9loyWCw+sMW5z34DoGhXzKKiojBjxgzMmzcPSUlJj68gEAiKnkLc338uFEOXBc8Rq9VKq9XK\n3r0HUa+vQ+AL6vUN2KVLn6xgNcuXL6dC4UogigApl3/HwMA6+bLftGlbajR9CRynTDaLjo6evHnz\nZo72ly1bxiFDRrJ9+44E1ATOsARu8xBqkQBTXFzICxeeuI8ajYFAQlZoXY1mKKdOncqbN2+yWbP2\n1Omc6ODgTsCPwGACVwisJyCxXr0mlKQGBH6nXP4lnZxKZoWoPnv2LGfOnMlly5YxNTW1wH7t37+f\ner0rNZohlKTOLF3an7dv337ifgoE/2UKo33FTjWF0AvyQ0ZGBgcOfIdqtZ46nSPHjfuMS5cu5Ycf\njuPPP/+clfv8/PnzVKv1BPpni0OfQZlMzszMzEe2ce/ePSqV2mx52ElJasdPP/2USUlJOcpGRUVR\nq3UloKQH/uZJVCYBRskc+MtXXxWqr1279qVW25nAOQJrKEmu3LZtGyXJk8Bwe9jdVQT0BLwJONr/\nfEmt1pnjxn3KRo3asmvXvoyKiiJJbtmyhZLkSq12EPX6FqxcuR5NJlOB/KpZsymBZVljo1IN4scf\njy9UXwWC/ypC6AWC/+Gjjz6nJDW3i1wsJaka581b8FC5Dz8cR6CrPZd6ql2U/qCLi1dWmQMHDvCd\nd97j6NEfMjIykiT5yy/L2aHD65TJVNni11sJVKNOV5FubmWyRJMkw8LC6OgYRG+8zEg4kgBPowzL\napx5/vz5QvXVZDKxf/+h9PAox4oV6zE8PJwlS/oSUBHIzBJarbYzVSpnAnMJXLYn1qnLvXv3PmTT\n2zuQwNasful07Th79uwC+eXjU5nA0WwfUNM4cOA7heqrQPBfpTDaJ/boBS8koaE7YDJ9DMAVgDdM\nptHYuHHHQ+WsVgIIAFAVtghy/weZ7P+wfPkCAMAff/yBV15pj59+csUPPyhQq1YjBAePxaBBE7Bh\nQwuQdQE0APA+gOYAVEhNPYqEhBEYMGBkVjvlypWDd9ph7EEU/JGEo5DjFdzGtNWLERAQUKi+6nQ6\nLFo0CzduXMSZM3/Bw8MD9+4pAagBXH7QUwB/Qy7PBFAFQBkAR5GRcQnlypV7yGZiYry9HADIYDZX\nxa1b8QXyq127IOh04wEkADgPSfoR7du/+iRdFAgEhaEIPzieCcXQZcFzoGXLzpTJpmfNJpXKDzhk\nyMiHyp08eZKS5EpgNoFJVKu9ciwv16/fksDyLDsy2QSq1c4ETtufxdiXwV+yL4s3IHCPwCmWKlWe\nN2/etG0TnDrF+0YjCfAvhZ6lpBIMDd2Uwxer1cpdu3ZxxYoVvHjx4hP3PTY2llqtC4Hv7T59QKA+\nq1VryA0bNlCvd6GDgz8lyZm//bY2Vxvt2nWnWj2QQAqBk5Sk0ty9e3eB/EhNTWWvXgOo0Rjo4ODG\nqVOnP3GfBIL/OoXRvmKnmkLoBfnh9OnTNBo9qNP1oyR1o7t7GcbFxeVa9sCBAwwK6sz69Vtx9uyQ\nHBnlKld+mcD2bMvPs6lUGu0Cn0HAh8Db9mV7C4FuBMZSLg+iXK6lRlOCbT3KMNPJiQSY2qgR/9q+\nnfHx8Tl8sFqt7NnzTer1AXRw6EpJcuX69evz1Ver1cpvvpnKsmWr0d+/Nn/5ZTkHDRpBvb4agT5U\nqUqzbt2XaTabSdrOFpw9e5bJycl52kxMTOSrr3akQqGmg4MbFyxYlC9fBALB06Ew2icC5gheWK5e\nvYrQ0FAolUp06tQJLi4uBbYxdeoMfPrpAphMcwHchyS9iVdfbYDt26/DZOoFYAKAXwA8WJJeBZls\nKGxx8Q+gIeIRhlfhiDSgXTtgzRpAq83RBkn8+OOPGDNmFtLSjgHQATgIvb4NIiK24syZMyhfvjwa\nNGiQq4/Tp8/ERx+FwGQKyfJx9eo5SE1NxalTp1GhQgB69OgBubzgO3UkH52ARyAQPBMKpX1F8qnx\nDCmGLguKMVarlVOmfJdjtpyZmcnPP/+Kvr5VCXjYT+xbCKQTaM369RtTr+/HFgjnfUgkwNWQMS2X\nGbTFYmFQUEcqlS72Q4EPVg6slMlU1OlK0WB4g5JUhsHBn+TqY9WqjQlsy1Z3Drt16/+0h0YgEDxD\nCqN94jCeQPAIZDIZxox5H9HRxxEZeQgdO3ZA1659MWnSJNy+fRMuLhoAuwB4AygJne4oBg7sizaZ\nO7AJ7aCHCYvwCvooHdC991AsXrwk66ucJF55pRXCw08jMzMMwG4AZ+3tzgCpRWrqAdy/vwwm0xHM\nnBmCixcvPuSjXi8B+OegnEwWD4NB97SHRiAQFBOE0AsEBeCtt0Zi82Yr0tOvIDl5K0ymDDRvXhEe\nHnrI5WYolf7YNexdrEiPgwbpmKPywUD8hQzrYGzY8CqGD/8WEydOBgBs2LABf/11DkALAHUBfA+g\nPgAtSpb8CXq9CwAve8suUKvL4fr16w/5VK9eJQCDAUwCMBaSNB3BwSOe/mAIBIJigRB6gSCf3Lhx\nAxs3/g6z+VUAegDVkJY2BIGBfkhKug2r9Ri63huAnzNMUJKI6toVR/u1hEbbEVbrtwD6IyVlHb79\n9gcAQHR0NKzW+gDCAPwNoDeAT+HvH4iLF49DrU4HsAa2MLXhsFguomLFijl8Onz4MEJCVgD4GbZZ\n/UF4epZEYGBgkfX7wIEDCArqjAYNWmPOnHnijIxAUMxQPm8HBILnze7du3HgwAF4eXmhe/fuUCgU\nSEtLQ1paGpycnAAAx44dQ7NmbWAy1QQwG8BiAFuh0ZyFQuEJtdoXg9LCMAOjAABfaDzRdswYVN63\nD+SpbK3pYbFkAgBq1qwJtXoGMjOHAKgEQAOl0opNmw5CkiRs2/Y72rXrhjt3+sDBwRnr1v0KV1dX\nAEBqairOnTuHzZs3g2wPoIv9TyZiYrSwWCxQKBQoLKdOnULz5u1hMn0FwBOnTo2DyZSK0aNHPrau\nQCD4l1BUBwWeFcXQZcFz4sqVK+zUqTerVm3MYcNGMyUl5aEyU6fOoCT5UKV6j3p9Q7Zo0YFjx46n\nUqmlSqVnnTrNePv2bVat2ojAQvthNwuBNlSrK7JcuaqMiYnheJXuwUk4jsQo6vUuTEhI4OXLl2kw\nuBGYSeAPSlJTDh78z33+iROnUKXSU6FwpVZbgrNmzcrhn9Vq5b1793Jc+btw4QI9PMrSwaEy1WpH\nKpWBBNLszUewRInSRTaG778/hsD4bAf9/qKPT+Uisy8QCPJHYbSv2KmmEHpBfkhOTmbJkn5UKD4l\n8AeVynrU671YqVJDLl68hCSZnp5OlUqy34kngXRqtT7UagMI3CSQSaVyAB0dvQkYCERmE7wpbNGi\nNe8lJ5PjxpEALQCHadwoSSW4cWNoli8nTpxg8+Yd6OHhR1/fGhw0aHhW4pvLly/TwcGNMtkIAjMp\nST5cuHDxI/tWo0bjbMGA7lKhKEmt1p8ODp0pSa7cvHlzocbu+vXrPHfuHM1mMz/4YCxlsnHZ+r2H\nL71UtVD2BQJBwRFCLxD8D5s2baKDQzO7OP1KoAyBLQS2UpJe4ooVK5mYmEiVymAPdvMg8UoFApOy\nrrgB9QkMJdCLtsxvmQSuU6+vyDWrV5MjRtgqKhRMXbiQ58+f5/379x/yZ8CAYZSkxgRWUKUaRS+v\n8kxOTuYnn4ynQvFuNiHdzTJlHj1j1utdCFzPVucj9u3bjytXrmR0dPQTj5nVauXo0eOo0TjSYPBj\nqVLluHXrVur1rpTJviWwjJLkyzlzQp64DYFA8GQURvvEYTxBsSIxMRGtW3eBVmuEu3tZrF+/Ptdy\ntv3pNNgOsv0CYDKAVgBawmT6GnPnLoejoyP8/QOhUHwGIAlAGGSyK9Bq/wSQCaAngFMAPgLwE4Bo\nAAbI5WXw7oiu6BwWBvz4I6BW49bs2eixPhzdug3CuHETkJqamuVLeno6fv55PkymjQB6IiNjGpKS\nymDbtm1IT8+AxeKQzXMjMjIyHjkG/v6BkMnW2H+6D71+C9q1a4sePXrA29sbsbGxSElJKeDIAmFh\nYZg7dx3M5ku4fz8KN24Mw4cfTsT+/X+ga9czaN36d8yfPwlDhgwqsG2BQPAcKcIPjmdCMXRZUIQE\nBb1GtXoQbfnX91CS3Hns2LGHyqWmptLfvzrV6rcIvExgVrYZ8Fy2bt2VJHn16lXWq9eCarWeXl4B\n3Lp1K+vUaUat1pdAZQI17CsCtr15na45Z02fTvbo8SAvLe+tXUt39zJUKL4g8Ae12s5s06ZLDl8U\nCrU9brytmoNDO65atYpHjx61x9pfRmAnJak2x4+f+MgxOH/+PN3dX6LRWJU6nQf79h1Cq9XKEydO\n0N29DCWpFDUaB86ZM69AYztp0iQqFMHZximBGo1DgWwIBIKnQ2G0r9ipphD6/y7bt2+nLfXq3Swx\nUquHc+rUqSRtOegvXbrEW7dukbTFax81KpgNGrSgSuVEYAqBrylJrrmmZn1Aeno6hwwZQpVqKIF9\nBNwIdCFQgY3rNKWlXTtb40YjuWcP161bRweHltkEMo1KpS5HLPkuXfpQp2tLYCsVigl0c/PhnTt3\nSJIRERGsX78lK1VqyEmTvrUlwXkMKSkpPHz4cFbyG6vVylKlyhH42e7DRUqSJ0+cOJHv8V29ejX1\n+prZPkh+ZkBArXzXFwgETw8h9IIXnhMnTthnvu4EDmTtoev1QVy8eDFjY2NZtmxl6vXeVKuNHDky\nOMdJ9cOHD3PAgGEcMGAYDx06lGc7sbGxXLduHefOnUtJ8rIf1IulTNadlV+qQEvz5jY1L1GCV9av\nZ/36r1KvL0G5vHa2vf4kKpXaHKf8zWYzg4M/Ya1azdmpU29evny5SMcnKSmJSqWU7WODNBh6ccmS\nJbmWP3jwIEeOfJ8ffDCWUVFRJG0fC716DaAkedHRsQGdnUvx+PHjReqnQCB4MoTQC154Jk78kgrF\nBwRW0RZf/l0CjVm1agOmpqayQYMgKhQT7GKbQL2+Mn/77bcCtbFt2zbq9a40GttTry/HmjUbUaWS\nqFY7skbZykytVcumoJ6eTD10iCVL+lEu/47AOQJeBN4ksJSS1Jj9+g15SiORO1arlQ4OrgT+zDqN\nr9f7cs+ePQ+V3bFjByXJjcBEyuUf0sHBnRcuXMiyc/LkSUZERDAxMfGZ9kEgEOSNEHrBC8/UqVOp\n0fSxi9ghAsNpNLrRZDJx5MhgAjoCcdlmtOP5ySefFqiNEiW8COyw10+hwVCZv//+OxMuXKC1Rg2b\nYW9vMjKShw8fpoNDlRz72TKZKxs2bMXvv5/GzMzMpzQSeRMWFkZJcqWjY0tKkhffeef9XMvVrfsq\ngRVZvstkn3Hw4BHP2FuBQFAQCqN94tS9oFjQt29fODn9CaXybQA7IUnrMW3at1iyZBnmz98JoCps\noWQBwAy9fgfKlfPLl+3Lly8jMLAO7tyJA9DU/lSC2VwDYfPnw7FjR8iOHQPKlQP+/BPw94fRaERG\nRjwAk728BqQFer0ao0ePKpKodAWlTZs2iIw8juXLR2Hv3o2YOfO7rHe0fdQDAFJSTAA8sr3zQHKy\n6X/NCQSCFwSRj15QbIiPj8ePP/6EhIQkvPZaW2i1WrRu3QMm00QA9WC7PlcGMtlltGvXGOvXL89T\ncK1WK06ePImUlBT07DkQcXH9Qf4KoC+AUQCi4YM6+AMm+CEN1sBAyHfsAEqWBABs2bIFr73WG2az\nF4CuAEIBBEAuX4HU1PtQq9WP7IvFYsGKFSsQExODmjVrol27dkU1TA/1c+TIYISEzAYAvPnmIPj5\nlcGECUthMs0FcA+S1B9r1oSgTZs2T8UHgUBQeAqjfULoBcWSK1euIDCwJlJSmgFwBhAC4C6Aj1C3\n7jn89dcfkMlkudZNS0tDUNBrOHo0EqmpySCTAZgBRAHoAOAa/JGGHdDDG4k4Kjfi/LQv8foIW0a4\nEydOoGHDIJhM/QFsstepCKAllMoyuHXrOm7dugUfHx/odA+niyWJ//u/HoiIiIPJ1BSStBYjRvTA\n5MkTiniUgO++m4bPPlsNk+l3AHJIUieMG9cOCoUcc+cuhVqtxuefv4/XX+9V5G0LBIKio1DaV9h9\ng2dNMXRZ8BRYsWIFHRy62O/TVyTwKoEgOjmVzDpYlhcTJ06iTteRwNcEOhBwIHDKvmdtYmV48Doc\nSYC78TJdVQP4ww8/kCSPHDnCN954gwrFaAKJBDwJ6Ak4Uqn04auvtqNWa4ssZzR65HoYbv/+/dTr\n/QmY7W3eolptyPPw25kzZ/jDDz9wwYIFuUbdexTNmnUg8Fu2swQb2aBB6wLZEAgEz5/CaJ/YoxcU\nS5ydnUFeAmAEcBBAZygUEThz5jDKly//yLonT0YiNbU9bKlhW8CWja4FgH6oDX/sQjw8kYRtaIzW\neB/3Fb8jKCgIH374KRo37ojffjsBiyUawI8AygOIBHAEMpkOu3btRlraX7h/PwrJyYvQvn23hyLd\n3b17F0qlD4AHy/uuUCodkJyc/JCv27dvR506TTF27EWMGLEW1as3wv379/M9TqVLu0OhOJ71s1x+\nHKVLu+e7vkAgeAEowg+OZ0IxdFlQhFitVqalpTEzM5NNmrShXt+UCsWHlKQy/O67afmy8fXX31GS\nWhGYS6CuPQDPMTZGVSbZp77r4UUN3CiTGbl27VqePHmSklSKwG37TN6Xtvj5O7LNlhdTqfTNcZdd\nkkoyNjY2R/u3b9+mo6MngaUEblKh+IJ+flVzDZTj61uNwKasuAFabbesAEH54e+//6arqzclqSsl\nqQdLlChdqHj4AoHg+VAY7RP56AXFhvnzF2DEiPdhNqcgIKA6Nm5cgb179yIuLg716y9E8+bN82Xn\nvfdGIiJiP3buHI/MTAsyMz3QEgqsQyokAMuhQj/oYJHdwYYNq9G+fTts2rQJKlUVAC52K4cA+AI4\nC8DWrkJxFuQdADcAeAI4DDIV7u45Z9AuLi7YuTMMr78+GLGxo1C1ak2sXh0KufzhBbbExATY9v8B\nQIa0tIqIj0/I95j5+Pjg3Lmj2LBhAwCgffsZD/kjEAhebMRhPEGxYMWKFXj99cEA/gBQC8DXKF9+\nDS5cOPJE9kgiJiYG6enp+CmoA767GgMNMjEfPhiCVwD5GqxZsxSdOnUCAMTGxiIwsBZMpi329tfA\n0fEdWCxERsZrkMlMMBh2o1+/3pg1awHU6kBkZJzGhAnj4O7uBn9/fzRo0KDAfvbo8SY2bDAjLW0W\ngL8hSe0RGroEr7zyyhP1WyAQFE/EYTzBC4+ra2kC3bMti1spl6sfeTjt3r177Nq1Lw0GN5YqVZ7r\n1q17uNAvv9Ail5MAp6ElZehHlUrPZcuWPVR07dp11OmcqNW60sXFi4cOHWJMTAynT5/On376KSvG\nfmRkJMPDw/nRR59RkkrTYHidklSGY8d+VuB+37t3jx069KJaraeTU0nOn7+wwDYEAkHxpzDaJ2b0\ngmKBWi0hI8MXwBEAGgCnoFTWh9l8L9clbwDo2rUvQkMzYDaPADASQBTq1q2FtWuXoHTp0sC8ecCQ\nIQCJUx06YujtdGh1Ggwc2B1HjpyAyZSG3r27o2HDhlk2MzIykJCQADc3t0cGxbFdrysPs/k0AC8A\nt6HVVsTp0/vh55e/QD4CgUDwgMJon9ijFzx30tPTcePGDXh6euYZaKZmzYY4cOAOgLoAqgH4HcHB\n7+Yp8gCwefMmmM07ALwCYBiARTh48Bf4+FTEaHk6vs1MsxWcPBlVxo7FnwAuXbqEmjUb4f79/rBa\nS2LRotcwadI4+Pn5oXbt2nBxcUF6ejosFstjhV6tLmkPqAMArtBo/HD9+nUh9AKB4NlSRKsKz4xi\n6LLgEWzdupUGgyslqRQNBldu27Yt13JXrlxh+fI1qFTqqVCoOXLk6Mfa9vDwJfCK/YT8gyV/Cz+G\nU9ax+CV1G+WoM3z4aMpkH2VtDwBBlMtL0WhsQ63WmVqtAyWpFB0c3Lhjx448205JSaGTU0kCa+y2\nttHBwZ0JCQkFGyCBQCCgSGojKKbcuXOHer0rgd12MdxFvd41z8AxVquVt27dYmpqar7sr1q1moAT\ngZIE0ghYOQWjSYCZkLM/JtPVtUyOOv36vU3gh6zgMkAlAib7z1sJlLL/+w4aDG5MSkrKs/2DBw/S\n3f0lKpVaOjuXZERERL7HRiAQCLJTGO0TAXMEz42LFy9CofAB0Nj+pAkUCi9ERUXlWl4mk8HNzQ1a\nrTbHc7PZjNjYWJjN5hzPu3fvhm7d2gPQQoY2mIkmGIOpyADQC8uxGFXg5FQiR52+fbtBp/sGwGYA\nuwDUBvAgjO0rsF2dswJoDrncHdHR0Xn2r06dOrhxIxqJifFISIhD06ZN8ywrEAgETwsh9ILnhpeX\nF9LTY2CLUAcAl5Ge/je8vLweVS0H4eHhcHX1QrlytWEwuOLtt4ciMzMz631IyI9Q4CYWYjfewZ9I\nA9AJdfArdkGn64+ffpqSw17z5s2xbNlMVKgwASVL/g6Vaks2/34EUAW2vzaXkJ4eZzvU9whkMhkM\nBkOecfcFAoHgqVOEKwvPhGLosuARTJs2kzqdO43GNtTp3Dljxqx8101MTLQv/e+yL6fvJmBgmzZd\naLVaSZK3rl7lr7Bdn7sHic3xO4FR1GqNPHnyZJ62zWYzZ82axebNW1Gp1FGnc6ejYylqNC52X904\ne3ZIofsvEAgE+aEw2ieu1wmeOxcuXEBkZCTKly+PgICAh95fuXIFy5cvR2amBd27d4O/vz8AYO/e\nvWjS5E1YrZHZSteCWh2NixdPwMfNDezaFbKwMNyFHG1RHvtRA8AGLF78E/r165erP5mZmWjatC2O\nHZMhNfVlSNIyDBz4f5g27RtERkbi4sWLqFChQpYfRUlcXBwSEhLg7++fa+Y7gUDw30QEzBEUezIy\nMhgXF0ez2Zzj+cWLF+no6EmVaigVindpMLjx6NGjJMn33gu2Z46Lts/oYwg4U6crxYtHj5KvvGI7\neOfszA5e5QnIqdMZOW/evEf6Eh4eToOhOoFMu90bVKl0NJlMBeqTxWJhVFQUY2JislYYHsX7/9/e\nnQdEVb0NHP8OMwPMgOAOCCKGIiIIKq65YC6E5p7mXtpiWpbtZmbaT8W0zD1zqUxLLTX33dxywdwV\nLU1REUVxIZEBZmDO+8fQlK9LiwgyPJ+/nLuc+zy3iWfuveee88YQ5eJSQhUrVlWVLu2vjh49+q+O\nJ4RwXPdT++Q9elHg9uzZQ0xMRzIyLICZefO+oGNH29Cz//vfx6Sl9cdqHQbAzZtBvPXWCAYM6M3G\njTuATkAEUBM4ClQnokIagf37Q1wc+Pig3biRZSEhmM1m9Hr93z4vv3HjBk5OfsAf78mXQaPRYzKZ\n/vFV9o0bN2jevB3x8SdRKptHH63LypXf4eLicsft169fz/Tpi8jKOklWVinS0mbRsWPv/zzErxBC\n/EE644kCZTabefzxDly7NpmMjEtkZGykV68XOHfuHABXr/6O1VrxL3s8wu7d+3j66Y85fjwLuAws\nBSyAjvByyWzTmdHExUGFCrB9O4TYJoVxdnb+R53iHn30UWyT1swFzqDXv0lISBglS5b8mz3/9MYb\nQzl8OACT6SwZGefYsUMxevS4W7ZRSvHtt/Pp3PkZPvxwNBZLS/6cNKc7p04d/cfHE0KIu5FCL/LF\nwYMHWbVqFefPn79l+YULF8jKcgI65C6phV5fg/j4eAC6dGmN0TgaOAz8irPzu5jNBm7e/Ins7J+A\n60BX3N1TaFKpLHvdrOiOHoWgIFuR/w+j0Hl5ebF582pCQz+jRIlGPPbYWdav/+Ef/UhYsmQJPXo8\nz9Kla8nK6ontroAzGRnd2L370C3bjh07nuef/5BFixqya1cpzOaVwB9z0i/F3//2/gpCCPGv5d0T\nhPxRCEMu8l5++U1lNPopT89oZTSWVitXrrSvS09PV66uHgric5+Hpyij0cf+fNpqtapx4z5VpUsH\nqBIl/HJ7wb+au+1pBRuVVuuijq1apawVK9pGvAsLUyo5Od/zHDVqjDIa5fUbaAAAIABJREFUKymY\npjSaGgoG5I6ul6NcXHqoN98ccsv2Hh5eCn6xj8Kn1YYqvb6U8vSsrUqUKGfviyCEEPdT+6TXvXig\ndu7cScuWPUlPPwB4Artxc2vNjRsp9nHqv/56Hv37v45OV5fs7AO88spzxMYOv2N7u3fvpmnTDmRm\nhmCb4KYMIU4X2F/KDZeUFKhdG9auhX9xm/1esX/77SKMRlcGDHiBgICAO253/fp1YmKeJC4uDtgN\nhAIpaDRhODuXRK+HSpVKsn37Wtzd3e37ubmVwmQ6DNjexXd27s/rrxenbdu2VKtWDQ8Pj/vOQQjh\nGO6n9kmhFw/Ut99+S79+y7h5c6F9mV5fjKFD38JoNNKlSxf8/f357bffOHLkCBUrViQiIuKebTZs\nGMWOHaeBQ1TnHBtoRFnSuB4WRomffoI8KJCrV6/mySf7kJExCCenqxQr9g0HDuykYsWKt23bsWMv\nVq1yw2xeDOwHygOg0w2gXz8nevfuTc2aNdHpbu372r//a3z99UFMphHAr7i7v8ehQ7t55JFH7jt+\nIYRjkUIvHlrx8fHUqdMMk2k7UBn4Bo2mH1ptL5ycwNX1B37+eRtBQUG37XvlyhUOHDhAqVKlqFGj\nhv0ZucHgQWZmb+rQi7U8TglSWQv0MpYk8WrSbUPk/hfVqzfkyJG3gHYAODm9wyuvKD79dOxt2/r4\nBJGcvAz4HDgCjARO4Ob2Jvv377hjbmB7X/+DD0axdOk6SpcuyYQJ/6NGjRr3HbsQwvHcT+2Tznji\ngapWrRoTJozGxaUWRqMvzs4DUepFsrM/w2z+jLS0QQwdOvq2/fbs2UNgYCidO8fSuHEnunbta/+S\nKwVNWMpGmlOCVJZQk3aUx4SRixcv5knc6ekmwMv+2Wr1Ii3NdMdty5cvj0azDRgHNECjeRJ//4/Z\ntGnlXYs8gE6nY9SoD4iP38nWrSulyAshHggp9OKBe/75vly9epHjx3dRq1YdoLF9nVKVuHIl9bZ9\nunTpy40bk/n99x9JTz/GqlWHWLp0KQAfN3uMNVygGDeZhwdd+AUzA9FoTPj4+ORJzE8/3Rmj8RVg\nL7AOo/FjevTodMdtv/xyEp6eI/DwaI+7+xpq1Ajkl1/2ULdu3TyJRQgh7scDLfSJiYk0bdqUatWq\nERoayqRJkwC4du0aLVq0ICgoiJYtW5Ka+ucf+tjYWCpXrkxwcDDr169/kOGJfDRlynSqVo0gLm4r\nWu0QIB74CaPxf3Tu3Oq27S9cOA08nvvJgNnchFOnTsHixby0YTUGFF+7etAbKy5Gf4zGj1i48Os8\nuW0PMHToO7z1Vjv8/fsQFDSUr7+eTNOmTe+4bbVq1Thx4hBz5jzP4sWj2b17kwxfK4R4eNxfh/97\nu3jxojpw4IBSSqm0tDQVFBSkjh07pt566y310UcfKaWUGjNmjHrnnXeUUkrFx8er8PBwZTabVUJC\nggoMDFQ5OTm3tPmAQxYPwOLFi5XRWFnBSQXXlJNTeQUuCtyVwVBS7d69+7Z9wsLqK41mvH0IWje3\nQHXk7beVcrJNUKNef10pq1UlJiaqHTt2qJSUlALITAgh8sf91L4HekXv7e1t70Ht7u5O1apVSUpK\nYvny5fYJRZ5++mn7Ldlly5bRrVs39Ho9AQEBVKpUiT179jzIEEUeyszM5OjRoyQnJ9+yfOXKTZhM\nLwOVgJtYrWnAFiCNjIzZPP54h9vmkv/hh7n4+n6Om5s/zs6V+bZJCKFjx4LVCh98AB9/DBoNfn5+\nNGjQgNKlS9v3VUqxYsUKJk2axE8//fSg0xZCiIdavj2jP3PmDAcOHKBu3bpcunQJLy9bRycvLy8u\nXboE2EZJ++tc5H5+fiQlJeVXiOI+xMfH4+8fTIMGTxIQUJUhQ0bY1/n6lkGvPwJcAZpjK/j1cte2\nx2JxsQ95+4dHHnmEIUNe5bHHGrDk0Tq0Xb3CtmLcOBg+HO4ySp1Siu7dn6Nbt6G8/favREf34KOP\nxudxtrceLzZ2HKVK+VOypB/vvTcCq9X6wI4nhBD/Vr5ManPz5k06derExIkTKVas2C3rNBrNPYcW\nvdO64cOH2/8dFRVFVFRUXoUq/qN27XqQkvI+8CyQwqRJ9Tlx4hd++eUcZcuWpFSp46Sk1CMnpw6w\nGVvRLw2cIDv7mv2HH9iKZ82ajTh48DrDqEhrNgFgmTQJ/cCB94xj7969rFixmfT0o4AReJdhw6oy\nYMDzt3338sIXX3zFyJFzMJnWAjomTOhOyZLFeeONV/P8WEKIomPLli1s2bIlT9p64IXeYrHQqVMn\nevXqRfv27QHbVXxycjLe3t5cvHiRsmXLAuDr60tiYqJ93/Pnz+Pr63tbm38t9KLgKaVISDgK9Mxd\nUoaMjKYsX74Li2Uax4//jIfHXkqUcOPKlUFAFaAGUB2tdidTpky4ZRS42bO/4ODBOMbxIm8yhRyc\neEFbji5BQUT/TSwpKSlotZWwFXkAP3S6YqSmpnL58mXi4+MJCAigevXqeZL7woWrMJneA2wT55hM\nI/j++0lS6IUQ9+X/X8SOGDHi7hv/jQd6614pxbPPPktISAiDBg2yL2/bti1z5swBYM6cOfYfAG3b\ntmXBggWYzWYSEhI4efIkderUeZAhijyg0Wjw9a0MLMtdcgOrdT0Wy0igMVbrG1gsDShf3gedbjnw\nAbAYZ+fLDBzYl+ee63NLe5s2bGMa8CZTMKPnKRbypdX/tuf4d1KrVi2s1oPASiALjWYipUp5sHnz\nVsLC6tGr1+fUrx/D0KH/y5Pcy5QpjpPT6b+ci1OULOmZJ20LIUSeyJPugHexfft2pdFoVHh4uIqI\niFARERFqzZo16urVq6pZs2aqcuXKqkWLFur69ev2fUaNGqUCAwNVlSpV1Nq1a29r8wGHLP6jPXv2\nKE9Pb+XpWU8ZDN5KozEquJzba14pd/doNW3aNFWhQlVVrFiEcnMLVA0bRqvMzMxbG7JY1P6w6kqB\nMqFVMUxQME7pdB7q6tWr/yiW7du3Kx+fSsrJSadCQuqoQ4cOKVdXTwVHc+O5rAwGb/vEOffjxIkT\nysPDS+n1Lyqd7mXl7l5GHTp06L7bFUKIv7qf2idD4Io8k5qaytGjRylTpgxTp85i9uytmEwD0Ov3\n4u29kfj4n9Hr9Rw8eBAXFxfCw8PtE9sAkJUF3bvDkiWkazS003jxo9Lg5JTF0qVzeOKJJ245XnZ2\nNu+99yHff7+C4sU9+fTTETRp0sS+XimFRqMhISGBsLAmpKf/2eHP07Ml8+e/RkxMzH3nnZiYyIIF\nC7BarXTu3FnGqhdC5DkZ614UOKUU58+fx2w2U7FiRTQaDdOnz2Dduu1UqODD+++/c8srcLcxmaBT\nJ9vMc8WLk7FkCStSUsjMzKR58+aUK1futl1eeeUtZs/+GZNpLHAGo/Eldu3adNvzd7PZjLd3Ra5f\nn4Zt7PoDGI0tOX58H/7+/nl6HoQQ4kGQQi8KVHZ2Np069WL9+o04OblSubI/mzevpESJEv+sgbQ0\naNMGtm6FMmVg/Xr4mxnsAEqWLM/165uxva5nm3hm2DA3Pvhg2G3bxsXFERPTkcxMK5DBl1/OwN+/\nPGazmdq1a2M0Gm/bRwghHhb3U/vy5fU64dg+/XQSGzakkJmZCDhz/PjLDBjwJvPnz/77na9dg5gY\n2LMHypWDTZsgOBj489b73bi4uALX7J+12qsYDKXuuG3dunW5fPksycnJuLm5ER3dkePHL+Pk5I6H\nRyq7dm26ZQwHIYRwFDKpjbgvixYtZvDg/5GR0Q1wBZwwm3uzb9/hv9/50iVo2tRW5CtWhO3bOaXX\n07NnX4oXL49Wq8fLq+Jd3yX93//exWjsDExCq30NT8/19hEX70Sn0+Hn58ekSVM5cqQ0N28e5saN\nOC5e7Er//m/+l/SFEOKhJ1f04h/bv38/n3wyjawsC/369SQgIIDevV/Eau0OrAaeAbTodCuoWrXy\nvRs7fx6aNYMTJ6BKFdi4kdNmMzVqNCAtTQu8BbzE5cubadOmC7/+evC25/TPPdeXcuW8WbRoJaVK\nefLaa7tvGXjnbuLjT5GZGQ1oAcjJieHXX1f/+xMihBCFgBR68Y8cOHCARo2iMZkGA+6sWfM0L73U\nE52uCfAx8ARQDVB4e8Nnn22+a1s5J06gadECp3PnIDzc9ky+bFmmvz2Emzc7AkuA13K3jsbJKZJ9\n+/bdsUNeq1ataNXq9tnv7qVu3XBWrZqPydQDcMHZ+SsiI8P/VRtCCFFYyK178besVisDB76NyfQW\n8AbQD5NpCsuXb8JqPQxYgfXABzg7n+f48TsXZYDvPxxJcpVgnM6d46CrkcS5cyF3ZESTKROlvIF0\n4I9X4TLIyTlhHz3xTrGdPHmSs2fP/uOOKq+++jKPP+6Di4sfBoMf1arFM3XquH9+QoQQohCRQi/+\n1jPP9Gf37l/5c1hZAAOuru507NgUo7EGbm7dMBoH8eWXs3F3d79jO/HffEPUBx/gi2IzUTTJeoMn\ner5oX9+zZxeMxmlAV6AB0Adn55q0bt3ojiMkXr9+nVq1GhMR0Yzg4Dq0bt0Zi8Xyt/nodDoWL57H\n6dNHOHZsJ3v3bv3nbwgIIUQhI4Ve3NP58+f5/vvF5OTMAEYCC4FVuLq+xMCBz+Dq6oLFcgGLZRNl\nypSkadMmd2znzPz5lO/dmzJYWY0frZjPDfU+R4/G2Wd7q1evHkuWfE2NGr/h7+9BmzapfPfdGBYs\n+OKOve8HDnyHY8eqYTKdITPzHFu2pPPxxxP+cW7lypUjICDg1kF7hBDCwcgzenFP6enpaLUeQDTw\nFTAROECDBtVxcdEzb94GLJalQH2SkmLp2fNFNm1adksbv//wA6W798AdxSKa0R1fLDwNvEeJEj63\nFNro6Giio/9u6hqb/fuPYDaPw/Z71YWMjKfYvXsD48aNZ+/eo0REBPP666/i4uJi38dkMpGamoq3\nt7cUeCFEkSAD5oh7ys7OpkqVmpw925acnKexTVwzAReXkmi1lzCZtIA3kAbMolSp3ly5cta+/+/f\nfotrj564oJhDb55lNjkAeGAwGFi8eN5/Hoa2U6feLF/uQ3b2GMCKq2s3ypU7zsWL5cjIeBKDYTl1\n6uTw448rcXJyYvz4Sbz77hCcnIx4eZVm06YVBAYG3ucZEkKIB09GxhMP1IULF2jUKIbTpy9im152\nGvAKcBXYCrgAY4CFREaW4Oeff7Tt+P33ZD/1FDqlmEZZXuYCCi1wDSenchw+vI9q1arZj7N69Wr6\n9h3I9euXqFevCYsWfUWZMmXs681mM5mZmfYpbZOTk6lfvznXrjljtZp45JGSnDiRQGbmmdyYLLi5\nVWHHjh9IT0+nRYuumEzbgQpoNOMJCfmOo0d3P+jTJ4QQ9+1+ap/cuxT3ZLFYGDHiIxITfwM6AOuA\n48Bu4ElsBRWgAxpNAnPnTrN9/Oor6NoVnVKMpQ8v8QiK7sBkNJpGuLuXZuTI8aSmpgLwyy+/0Lnz\n01y6NAuzOYldu4Jo27a7PY7hw0fh5uZJqVI+1K4dxZUrV/D29ub48b2sWTOFzZvnMXfudLRaI+Cc\nu5cOJyd3zGYz+/btw2p9AqgAgFIvcfz4XvnRKIRweFLoxT0NGTKCefPisVh+BH4AXgKeBprnfjYB\nCphD48YNCQ4OhqlToU8fsFqZXq4ig6kNbASqA+NRSs+NGz+wZIkTLVq0RynFtm3bgDZAU8ATi2Us\ne/ZswWw28/jjbRgxYhrZ2afIzk7j0KHq9OzZDwAnJyfq169PZGQkISEhlC9fAr3+dWAPOt0QSpe2\nUr16dSpUqIBWuxPIyM1sM2XK+N9ziF0hhHAEUujFPS1duhaTaSRQF9gGfAs8CrgDQUAAEIhe/znf\nfPM5fPQRvPyybedPPqHR+hUULzGSYsXaA19g+2EQB9TGbJ7O0aPxXLx4kZIlS+Lk9Cu2d/IBTuDq\nWowpUz5j06ZDwPNAOcAJi+VNdu/exaOPRmMwuGM0ejJ16nR0Oh3btq2hbdurBAb2p1Wrs+zcuREX\nFxfatGlDTEw4bm7V8fBojbt7bxYs+CK/TqMQQhQYeUYv7ujKlSssXbqUUaMmc+bMm0AvIAnbVfkJ\noH7uv3XodCvZuGElTTZtgpEjURoN8S+/TNVPP0Wr1XLt2jWGDRvG55/vJDs7GziI7TfmTZydy3Hh\nQgIeHh40avQ4R49aMZsj0Onm0759c/bu/YWTJ6sDF4FVufstwGh8HYulIxbLBCABo7EZq1Z9TVRU\n1F1zUkqxe/duUlJSiIyMvOugPkII8bCRzngiTyUmJlKz5qOYTA3IyUklK2s7tiv649hmizsKlAHm\noNePYP63M+i0YwdMmEA20M+lLt/pzdSu7cuMGZ8ycOC77Nu3h6tXG2C1JgFeQDNgJr161eLrr2cA\nts52CxcuJCEhgalTv+TGjXpkZp7G1gHwJHADKItO9xM6HWRmnshtC5ycBtOqVTyNGzcmJiaG0NDQ\nfD1nQgjxIEmhF3lGKUXr1p1Yt64KVmts7tJ2aDRxKPU9ts54U4EmODsfonePVszUmmHWLLKArgxj\nKSOAbNzcGqPVniQ9fRA5OaFAb+Bd4CRa7Sbq1XuEbds23vY++5gxH/HBB8cwm+cAl4HaQHlcXbPR\n639j3boVdOv2PGfPjgVaAVY0mih0OhPQEL3+G5YvX0CzZs3y45QJIcQDJ73uRZ5QStG9+7OsW7cT\nq/Wvk7yYUCoWaIRtdLzReHruYd3KGczISoVZs8BgoKPWmaX8Md2rjqysWmRleZKT8x7QDtiORvMR\nYWEnGDr0ebZsWX/HQWuuXUvFbP7j/faywFKKFTvBl18OIiHhV+rXr8+XX07GaHwaN7deODvXRamz\nWCw7sFgmYDLN5qWXBj+4EyWEEIWIFHpht27dOlas2IPVOhj4BLgApKDVnsz99x9cqV09gqipU9F8\n+y24u8PatVyNbIRWOwZbL/zf0GoXodXqcz8DVESns7Bt2wqGD3+Po0ePMn/+fPbt23dLHE88EYPR\n+DmwCziPwfABnTt3oWvXrpQqVQqApk2bcvjwbiZPfozoaF/gOf581S+I69evPZiTJIQQhY0qZAph\nyIXG559/rozGvgqsCoYoKKZArzp16qbc3csojeZtBR+oUoZS6lqdOkqBUiVKKBUXp5RSKikpSVWv\nXl/pdK7K2dlNTZ48VYWG1lUuLj0UzFRGY0PVq9cLSimlxo79VBmNPqpYsc7KaPRTw4ePviWWefO+\nUV5egcrDw0v16vWCysjIuGvcGzduVEajn4K9Ci4qg6Gd6tv3pQd3ooQQIp/dT+2TZ/TCbt++fTRq\n1IaMjG1AJWAilSp9xa5dG+jb9yV2744joGRxNrgoPA8ftk0vu2EDVK9+Szvp6em4urqi1Wq5efMm\nY8Z8zIkTZ2nUKJKXXupPSkoKFSoEk5W1H5iObaKcVCZPHsXLL7/0n2KfPftL3nnnAzIy0mnfvgOz\nZk3GYDDc5xkRQoiHg3TGE3li4cLv6dnzmdxX4PR4eXmxadNyOnbsxZkzDXE3N2Wd5gUi1RWUnx+a\njRuhSpV/fZyDBw/SuHEP0tLCsD0SmAEk4+LSlbVrF9zzFTkhhCiKpDOeuG9nz56lT5/+ZGfvxPYa\n21QyM03cuHGDCxeyKGF+ly0MI1Jd4bRGx+mvvvpPRR7Ax8eH9PTz2EbLmwwEA1FkZb3GkiUr8iol\nIYQQSKEXueLj49HrawHh2Dq1PY3FYhvsxs9qYhtNCOMoxwimhUsprP7+/+k4V69e5Z13BuPk9BgQ\nCCTa1+l0iXh6uudBNkIIIf4g89ELACpUqEB29hEgBdtgOEewWm/SxNeXH7Mv4kMW+wmgnUsAJSp7\nYjab/1G7WVlZ6PV6nJyciI+Pp1Gjlty86UJ29kBsV/LPAP2A83h6bmDAgD0PKEMhhCia5IpeAFCt\nWjVef70/RmM4Hh4xGAyPsWjEe7jHxOBjzuJsOT9eqeZNcs5Ozp51p3bt5gwfPvqu7V27do2GDaNx\nc/PAYCjGJ59M5JlnBpKaOgyLZRTwJVAL28Q4S9FolgCQkZFx1zaFEEL8e9IZT9ziyJEjnDlzhppK\n4du3L1y9Sk5UFGtffJEOvfpisWwC6gGXMBgi2Lt3EyEhIbe107p1FzZuLI3ZPAk4j9H4GHq9md9/\n/xGoDAwDxuZuHQV8h5PT50RF7WDTpmX5k6wQQhQS0hlP5JmwsDDalCyJb69ecPUq5pYtCTt7haee\n/RSLpQq2KWovAl7o9WGcOXPmlv1TUlI4fvw4O3b8hNn8LranQwGYTL0oU6Y0ev00bAPoDEKrDQA6\nYxtW1xOrtQWnTiXkY7ZCCOH4pNALAC5cuMCkSZNYMmAA1hYt4MYN6NyZNwKqcCqpIenpu4D92Iay\nHQocxmLZT1BQkL2NESNiKV++EnXrtiMtLQP4OXeNFYNhLy+80IOQkJ9xcSmDXu9PkyaBGAyngTTA\nirPzDGrXrpnPmQshhGOTW/eCU6dOERnZiKY3Q5ifvRkXrPzeoQOe339P8+jObNrUDduVN8A6NJqe\naLUmnJy0ZGdnUKtWI4YOHUS3bq9gMu0GvIF30WgmYzS2RaM5S8WKOUREhJOQkESdOqG8997bWCwW\ngoJqcuPGNcAZd3c3TpzYh4+PT4GdCyGEeBjJrXtxX4YOHc3jvzdiYfZWXLAyhQY8k+MKWi2NG9fG\nYJgFmIAsDIYZtG7dBL3eE7P5J6zW0fz8cwo9e/bDam2IrcgD/A+lTEye3IIZM14mNTWVBQvc+Omn\nZ/nss4O88MKrDBz4DhkZT2F7xe4Q2dm1+OKLOQV1GoQQwiFJoRfUOLifb9T36MkmlsEMpBFLl6/H\n3b08ZcuWICamDHq9F87OZWnUyErDhrXJyekMfA6sAN4nLa0TWVnL+fO9+FX4+DxCnz59KFasGKmp\nPlgs44EOZGQsYcmS7/jxx5+wWDoDpYEAMjM7sm/fsYI5CUII4aDkPfoiJjk5mVGjxpGUlEKbNs14\n5kYqb/9yEIAhvEEs5YHhwFTS0zPo3/8VVq6cz6xZk7FarZQqVYpvvvkGnW4lZvMebPPFewJd0Oni\n0WiqYzCEYLX+xvTpM0lJScm93aT5SxQalNJy/Xo2Gs23KFUPyMZgWEKtWo/m7wkRQggHJ8/oi5Br\n164REhLJ1avtyM4OY5h+CCMslwBY2Tyap3buxWTKwfaOe/vcvabSuPFKtm5dY2/HYrHQpEkrdu3a\nAvwOGAFwd2/D8OFRBAcH8/77Yzh+/Fes1izatGnL7t17SE5uQ05OFLaJbDyAMUAobm4+KJVB3brV\nWbNmMS4uLgghhPiTPKMX/8iSJUtIS6tFdvZ4RvEbIyyXsAJq5kye2LCWs2d/QaPRANa/7GXF2dn5\nlnb0ej3btq2hQYMmODu3B9ah1X6IwXCYPn36MH/+Mo4dCyYz8yJm8wWWLfuNMmVKEBq6A632RSAS\n+Aooh4uLnqVLp7J37zo2blwuRV4IIfKYFHoHdPbsWb766iuWLFlCVlaWfbnFYgGrGxN5lSHEko2W\np7XO8OyzAJQuXZrWraOAF4Cvgc9xchrK8OFv33YMnU7H5s2ref31+kRGjqN9+9/4+edtlCxZkri4\n/WRlPQdoATeys/ty8KCOEyeS8PDQoNOZgR24uj5NnTp1aNasGVWrVsXJSb6OQgiR1+TWvYP57rvv\n6NHjeZRqjk6XRHCwll27NmIwGEg8c4YtlavSKzuTLPT0cg7BrXt9vvzyM/v+SimGDh3KggWrKVbM\njYkTR9GkSZN/FUNMTGc2bKhOTs772O4OdANCgccpVepJmjaN4sSJBOrXr8nHH4/E3V0mshFCiHuR\n+egFYBv0pnz5alits4BOgEKni+HTT5/g5X79oFcvWLiQDCctA/2qUPKpjowaNQy9Xp+ncZw7d456\n9R7j2rWSZGXdwDZJzjogmeLFG3H9elKeHk8IIRydPKMv4qxWKzNnzqRjx6ewWsH2DBxAQ3Z2PX45\neBg6dYKFC8HDA8PWLUw/dQiNRkPlyrUIDW3A+vXr8ywef39/fv31AJMnP4+LSzK22emOYjQ+S48e\nXfPsOEIIIf6eXNE7gF69XmDx4iNkZHgDx4EmwBQgCSN12eSWSb30G1CyJKxfD7Vq8dprg5kxYxcm\n03ggEaPxBbZuXU1kZOQ9j/Vvbdu2jUGDhpGa+judOrUmNnY4Op281SmEEP+G3LovwpKTkylfPojs\n7AvANWzPwgOAX/AAVuFKQ9LA2xs2bIDQUADKln2ElJRVQNXcloYxeLCV2NiRBZCFEEKIe5Fb90XY\nwYMHyc7WA26AP/A2cIVS1OFHytKQNM476ehbKZxt167Z9zMYjECK/bNOdxk3N0M+Ry+EEOJBk0Jf\niMXFxbFs2TI0GmfgFeAIoMObLLayk1okcRItDazj+fKnJ4mJeZKdO3cCEBv7HgZDd+ATtNpX8PRc\nRd++fVi+fDkTJ05k27ZtzJkzl9Kl/TEaS/DUU30wmUwFmK0QQoj/Qm7dF1LDh49m3LjpKBVKRsYu\noBoQjz9l2UQSlUjnpIuBxllTSaZP7l6T6Nr1EPPnz+bKlStERNTj8uV0IIcqVSoSHFyFNWsOk53d\nEFiE1QoWy0rAH1fXAXTuXIqvv/68oFIWQogiS57RFzHnz5+ncuVwMjOPAV7AEGAy1V29WJF5Gn8U\nlurVidF4sunQG9g6580GNtCsmY6NG1fSo8dzfP+9OxbLp4DC2TkGpeKxWE5gG9L2FaAEMCL3qKdw\nc3uUmzeT8z9hIYQo4uQZfRGzf/9+rNay2Io8wGjqGMqwyzkFfxQ8+ij6bdt4YchAXF37ARWBnUAk\n27btYeHC7/j558NYLG2xTTbjhNkcjlIV+GPcetvz/qN/OeoJ0tOzWLVqVT5lKYQQIi/IFX0hc/r0\naSIi6pGWZgbmAm2oxXjWa96kpFLQvDksXQpubmRkZFCqlC8ZGVGNMUnHAAARyUlEQVTAktwWduDm\n1onMTAs5OTGAH/ADcB2NxoRS84EWwKfAqNx/BwDfAB0pU2YDSUm/5PkgO0IIIe5OruiLkPHjp5Ce\n/jywBhhAQ5z5kTcoqRQp9euTk1vkATp37k1GRioQ+JcWKpCefoOcnG3YrvI3A4uAeSiVCbwGFAOW\nYpt+tjRQDtgIOHP9umLevHn5lK0QQoj7JYW+kElLM2G1egH1acEs1mGb8HWRrhxBh9N5rFVnzGYz\nb745hFWrlgDuwBxgA3Aa24Q1Ltg67+mBWUAY0DJ32x8AM7AbF5fywHzgCjAJWIrV2ooLFy7kZ8pC\nCCHugxT6QqZHj44YjWNpx4esoA1GLMyiKU9lnyM1fR87d6YxcOBAPvtsOeAMjARygD5ATeAAtufw\nCwAFXPxL6+FoNM2Akbi4dKN8+QwiIsLRaLYDQcAiXF1X8Oijj+ZnykIIIe6DPKMvhHYNHEjtKVPQ\nARPR8RoJKPxy13bH2XktZvO7wA1gBRCN7db7MWy3/H8BPsQ2YE4x4HXgQu62FwgOrk737h0ZNGgQ\nmZmZtGrVhQMHdqHVahk3biyvvPJS/iYshBBFnLxeV5TMnAn9+oFSxDq5McRqBHoD44CVQA+gA7bh\ncJcC84AvgTNABrY54gOAg0AMtiv6hthG1msFPIZe34OqVQ+zf/92tFotABkZGbi4uMic8UIIUQCk\nM15RMWECvPACKMUQJyNDrNOxzVS3DCgOdAWGAtOB34Ha2Ir8YeAZoCzwG7ZOeDGAN5CK7UdBKaAz\n8B4WyzR+++08p0+fth/aYDBIkRdCiEJI/nIXBkrByJHw2msAvOpkINZaEbgJTARM2Ap+CWy36w3A\nJqAD3t7nqF07HGfnj4HG/Pme/AhsPwJaYrttPxRoCwwGLFitWTg7O+dXhkIIIR6QB1ro+/bti5eX\nF2FhYfZl165do0WLFgQFBdGyZUtSU1Pt62JjY6lcuTLBwcF5Oj96oWexwIYNWDUaXtBVYJK1N9AM\neB9YDvQHdvLqq0/i7j4DjWYkMAuDYTqTJo1lz57NrFixBNu79JdyG90EVAE+o0cPX4KCKuDqegH4\nEoOhHU2bNsLf3z//cxVCCJGnHmih79OnD2vXrr1l2ZgxY2jRogUnTpygWbNmjBkzBoBjx46xcOFC\njh07xtq1axkwYABWq/VBhld4ODszvFYD2mpcmZndE2iH7fn7WGAfWu1sund/igkTJhAXt4U+fS7y\n1FN7+eGHL+jc+UkArly5hu0WfQBQAZgGdMDLqzzz5s3k4MHdvP12OO3b/8j77zdj2bL5aDSaAklX\nCCFEHlIPWEJCggoNDbV/rlKlikpOTlZKKXXx4kVVpUoVpZRSo0ePVmPGjLFvFx0drXbt2nVbe/kQ\n8kPnyJEjymDwUTBTQYSC3xV8ocBHabUe6qWXXldms/mu+1+6dEkZDCUVPKPAT4GbAj+l0birHTt2\n5GMmQggh/ov7qX26/P5hcenSJby8bGO0e3l5cemS7VbyhQsXqFevnn07Pz8/kpKS8ju8h9K5c+dw\ndg4jI+NZ4BDwCOBM8eJWPv10It26dbttSNrt27fz2Wdz0GqdaNasAc7Oj5CRMRvblfw6dLo4Fi/+\nhgYNGuR/QkIIIfJNvhf6v9JoNPe8PXy3dcOHD7f/OyoqiqioqDyO7OESGhqKxbIf2A9MBrzRaGLJ\nyanLK69M56OPphAX9yMeHh4AbNiwgXbtepKRMRTIYvHiN3Ifg/wKvAxEodc3loFvhBDiIbVlyxa2\nbNmSJ23le6H38vIiOTkZb29vLl68SNmyZQHw9fUlMTHRvt358+fx9fW9Yxt/LfRFgb+/P3PnzqBn\nz+YopScnx0pOzmDS0oYCioSEPowePY7Y2A+ZO3ceb701koyM8djeqYeMDD21ay/h6NGGODtXwmz+\njVmzplGqVKkCzUsIIcSd/f+L2BEjRtx947+R76/XtW3bljlz5gAwZ84c2rdvb1++YMECzGYzCQkJ\nnDx5kjp16uR3eA+tjh07kJR0mlGjBlOiREms1qa5azRkZTXmxImzvPPO+wwY8AmXLxuwjVv/B3d8\nfPw4deooq1d/yunT8XTv3rUAshBCCJHfHugVfbdu3di6dStXrlyhfPnyfPjhhwwePJguXbowe/Zs\nAgIC+O677wAICQmhS5cuhISEoNPpmDZtmvT6/oukpCRq147i+vXKmM3uwHigDpCJ0fgVjz7akcGD\nB5OdfQ7bBDavYZu0JgujcRj9+8/Gx8cHHx+fAsxCCCFEfpMhcAuBM2fOEBZWk5s3G2N7re4m0Bw4\njF6voWXLGIKDH2H8+AkolYZtdrq5ODkNpUKFkowf/4H9zokQQojCR4bAdXAvvvgmN2+GAzVyl7gD\n8ylevATLly9m8+atjB/vjFKB2IbB3YdGc5Nixczs3LlGirwQQhRhckVfCFSqVItTp54FYrHNMFcB\nJ6fn6dLFkzNnzrN7dy+gJ5AONKNYsSSqVw9l+vRxhIaGFmToQggh8oBc0Tu4Bg0icXHZCwzHNhmN\nD6GhF5g5cyJpaTfBPkWtG9CHmJgW/PTTGinyQgghpNAXBpMnj6VGjXO4uLyNTvc7tWpFMGDA0wB0\n794eo/Ft4AiwE6Mxlh495Fa9EEIIG7l1X0gopVi0aBFPPz2AnJyn0OkS8fY+zb592/nkk0nMnDkX\nZ2dnhg17g+ee61vQ4QohhMhD91P7pNAXIpUq1eDUqf8BTwDg4tKNUaMieeONNwo2MCGEEA+UPKMv\nIlJTrwFV7Z+zsqpy+fLVggtICCHEQ08KfSESHd0CV9ch2KabPYjROJPHH29R0GEJIYR4iEmhL0Rm\nzJhIq1bOuLgEULx4KyZN+pCmTZv+/Y5CCCGKLHlGL4QQQjzk5Bm9EEIIIe5ICr0QQgjhwKTQCyGE\nEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQ\nCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjh\nwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0Q\nQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5M\nCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGE\nEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA7soSv0a9euJTg4mMqVK/PRRx8VdDgPnS1b\nthR0CAWqKOdflHMHyV/y31LQIRRaD1Whz8nJ4eWXX2bt2rUcO3aM+fPnc/z48YIO66FS1L/sRTn/\nopw7SP6S/5aCDqHQeqgK/Z49e6hUqRIBAQHo9Xq6du3KsmXLCjosIYQQotB6qAp9UlIS5cuXt3/2\n8/MjKSmpACMSQgghCjeNUkoVdBB/WLx4MWvXrmXmzJkAzJs3j7i4OCZPnmzfplKlSpw6daqgQhRC\nCCHyXWBgIL/99tt/2leXx7HcF19fXxITE+2fExMT8fPzu2Wb/5qoEEIIURQ9VLfuIyMjOXnyJGfO\nnMFsNrNw4ULatm1b0GEJIYQQhdZDdUWv0+mYMmUK0dHR5OTk8Oyzz1K1atWCDksIIYQotB6qZ/RC\nCCGEyFsP1a37v/r++++pVq0aWq2W/fv337IuNjaWypUrExwczPr16+3L9+3bR1hYGJUrV+bVV1/N\n75AfqKIwkFDfvn3x8vIiLCzMvuzatWu0aNGCoKAgWrZsSWpqqn3d3b4HhVViYiJNmzalWrVqhIaG\nMmnSJKBonIPMzEzq1q1LREQEISEhvPvuu0DRyP2vcnJyqFGjBm3atAGKVv4BAQFUr16dGjVqUKdO\nHaBo5Z+amsqTTz5J1apVCQkJIS4uLu/yVw+p48ePq19//VVFRUWpffv22ZfHx8er8PBwZTabVUJC\nggoMDFRWq1UppVTt2rVVXFycUkqpmJgYtWbNmgKJPa9lZ2erwMBAlZCQoMxmswoPD1fHjh0r6LDy\n3LZt29T+/ftVaGiofdlbb72lPvroI6WUUmPGjFHvvPOOUurO34OcnJwCiTuvXLx4UR04cEAppVRa\nWpoKCgpSx44dKzLnID09XSmllMViUXXr1lXbt28vMrn/4ZNPPlHdu3dXbdq0UUoVre9/QECAunr1\n6i3LilL+vXv3VrNnz1ZK2f4fSE1NzbP8H9pC/4f/X+hHjx6txowZY/8cHR2tdu3apS5cuKCCg4Pt\ny+fPn6/69euXr7E+KDt37lTR0dH2z7GxsSo2NrYAI3pwEhISbin0VapUUcnJyUopWyGsUqWKUuru\n3wNH0q5dO7Vhw4Yidw7S09NVZGSkOnr0aJHKPTExUTVr1kz9+OOP6oknnlBKFa3vf0BAgLpy5cot\ny4pK/qmpqapixYq3Lc+r/B/aW/d3c+HChVteuftjUJ3/v9zX19dhBtspygMJXbp0CS8vLwC8vLy4\ndOkScPfvgaM4c+YMBw4coG7dukXmHFitViIiIvDy8rI/wigquQO89tprjBs3DienP/8sF6X8NRoN\nzZs3JzIy0j6WSlHJPyEhgTJlytCnTx9q1qzJ888/T3p6ep7lX6C97lu0aEFycvJty0ePHm1/RiVs\n/wMI23m417lwlPN08+ZNOnXqxMSJEylWrNgt6xz5HDg5OXHw4EF+//13oqOj2bx58y3rHTn3lStX\nUrZsWWrUqHHXMd0dOX+AHTt24OPjQ0pKCi1atCA4OPiW9Y6cf3Z2Nvv372fKlCnUrl2bQYMGMWbM\nmFu2uZ/8C7TQb9iw4V/v8/8H1Tl//jx+fn74+vpy/vz5W5b7+vrmSZwF7Z8MJOSovLy8SE5Oxtvb\nm4sXL1K2bFngzt8DR/jvbbFY6NSpE7169aJ9+/ZA0TsHnp6etG7dmn379hWZ3Hfu3Mny5ctZvXo1\nmZmZ3Lhxg169ehWZ/AF8fHwAKFOmDB06dGDPnj1FJn8/Pz/8/PyoXbs2AE8++SSxsbF4e3vnSf6F\n4ta9+ssbgG3btmXBggWYzWYSEhI4efIkderUwdvbGw8PD+Li4lBKMXfuXPsfysKuKA8k1LZtW+bM\nmQPAnDlz7P9N7/Y9KMyUUjz77LOEhIQwaNAg+/KicA6uXLli71GckZHBhg0bqFGjRpHIHWx3MRMT\nE0lISGDBggU89thjzJ07t8jkbzKZSEtLAyA9PZ3169cTFhZWZPL39vamfPnynDhxAoCNGzdSrVo1\n2rRpkzf552WHgry0ZMkS5efnp1xdXZWXl5d6/PHH7etGjRqlAgMDVZUqVdTatWvty/fu3atCQ0NV\nYGCgGjhwYEGE/cCsXr1aBQUFqcDAQDV69OiCDueB6Nq1q/Lx8VF6vV75+fmpL774Ql29elU1a9ZM\nVa5cWbVo0UJdv37dvv3dvgeF1fbt25VGo1Hh4eEqIiJCRUREqDVr1hSJc3D48GFVo0YNFR4ersLC\nwtTYsWOVUqpI5P7/bdmyxd7rvqjkf/r0aRUeHq7Cw8NVtWrV7H/jikr+Sil18OBBFRkZqapXr646\ndOigUlNT8yx/GTBHCCGEcGCF4ta9EEIIIf4bKfRCCCGEA5NCL4QQQjgwKfRCCCGEA5NCL4QQQjgw\nKfRCCCGEA5NCL4QQQjgwKfRCCCGEA5NCL4S4p59//pnw8HCysrJIT08nNDSUY8eOFXRYQoh/SEbG\nE0L8rffff5/MzEwyMjIoX74877zzTkGHJIT4h6TQCyH+lsViITIyEoPBwK5duwr1lKBCFDVy614I\n8beuXLlCeno6N2/eJCMjo6DDEUL8C3JFL4T4W23btqV79+6cPn2aixcvMnny5IIOSQjxD+kKOgAh\nxMPt66+/xsXFha5du2K1WmnQoAFbtmwhKiqqoEMTQvwDckUvhBBCODB5Ri+EEEI4MCn0QgghhAOT\nQi+EEEI4MCn0QgghhAOTQi+EEEI4MCn0QgghhAOTQi+EEEI4sP8Diwf1C+duoqkAAAAASUVORK5C\nYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10a57ca10>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 10
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"#### Comparing the results from the different implementations"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"As mentioned above, let us now confirm that the different implementations computed the same parameters (i.e., slope and y-axis intercept) as solution of the linear equation."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import prettytable\n",
|
|
"\n",
|
|
"params = [appr(x,y) for appr in [py_matrix_lstsqr, py_classic_lstsqr, numpy_lstsqr, scipy_lstsqr]]\n",
|
|
"\n",
|
|
"print(params)\n",
|
|
"\n",
|
|
"fit_table = prettytable.PrettyTable([\"\", \"slope\", \"y-intercept\"])\n",
|
|
"fit_table.add_row([\"matrix approach\", params[0][0], params[0][1]])\n",
|
|
"fit_table.add_row([\"classic approach\", params[1][0], params[1][1]])\n",
|
|
"fit_table.add_row([\"numpy function\", params[2][0], params[2][1]])\n",
|
|
"fit_table.add_row([\"scipy function\", params[3][0], params[3][1]])\n",
|
|
"\n",
|
|
"print(fit_table)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"[array([ 0.95181895, 107.01399744]), (0.9518189531912674, 107.01399744459181), array([ 0.95181895, 107.01399744]), (0.95181895319126764, 107.01399744459175)]\n",
|
|
"+------------------+--------------------+--------------------+\n",
|
|
"| | slope | y-intercept |\n",
|
|
"+------------------+--------------------+--------------------+\n",
|
|
"| matrix approach | 0.951818953191 | 107.013997445 |\n",
|
|
"| classic approach | 0.9518189531912674 | 107.01399744459181 |\n",
|
|
"| numpy function | 0.951818953191 | 107.013997445 |\n",
|
|
"| scipy function | 0.951818953191 | 107.013997445 |\n",
|
|
"+------------------+--------------------+--------------------+\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 12
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name='performance1'></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"# Performance growth rates: (C)Python vs. Cython vs. Numba"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Now, finally let us take a look at the effect of different sample sizes on the relative performances for each approach."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"funcs = ['py_classic_lstsqr', 'cy_classic_lstsqr', 'numba_classic_lstsqr']\n",
|
|
"\n",
|
|
"orders_n = [10**n for n in range(1, 7)]\n",
|
|
"perf1 = {f:[] for f in funcs}\n",
|
|
"\n",
|
|
"for n in orders_n:\n",
|
|
" x_list = ([x_i*np.random.randint(8,12)/10 for x_i in range(n)])\n",
|
|
" y_list = ([y_i*np.random.randint(10,14)/10 for y_i in range(n)])\n",
|
|
" for f in funcs:\n",
|
|
" perf1[f].append(timeit.Timer('%s(x_list,y_list)' %f, \n",
|
|
" 'from __main__ import %s, x_list, y_list' %f).timeit(1000))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 14
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"from matplotlib import pyplot as plt\n",
|
|
"\n",
|
|
"labels = [ ('py_classic_lstsqr', '\"classic\" least squares in reg. (C)Python'),\n",
|
|
" ('cy_classic_lstsqr', '\"classic\" least squares in Cython'),\n",
|
|
" ('numba_classic_lstsqr','\"classic\" least squares in Numba')\n",
|
|
" ]\n",
|
|
"\n",
|
|
"plt.rcParams.update({'font.size': 12})\n",
|
|
"\n",
|
|
"fig = plt.figure(figsize=(10,8))\n",
|
|
"for lb in labels:\n",
|
|
" plt.plot(orders_n, perf1[lb[0]], alpha=0.5, label=lb[1], marker='o', lw=3)\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('time per computation in milliseconds [ms]')\n",
|
|
"#plt.xlim([1,max(orders_n) + max(orders_n) * 10])\n",
|
|
"plt.legend(loc=4)\n",
|
|
"plt.grid()\n",
|
|
"plt.xscale('log')\n",
|
|
"plt.yscale('log')\n",
|
|
"max_perf = max( py/cy for py,cy in zip(perf1['py_classic_lstsqr'],\n",
|
|
" perf1['cy_classic_lstsqr']) )\n",
|
|
"min_perf = min( py/cy for py,cy in zip(perf1['py_classic_lstsqr'],\n",
|
|
" perf1['cy_classic_lstsqr']) )\n",
|
|
"ftext = 'Using Cython is {:.2f}x to '\\\n",
|
|
" '{:.2f}x faster than regular (C)Python'\\\n",
|
|
" .format(min_perf, max_perf)\n",
|
|
"plt.figtext(.14,.75, ftext, fontsize=11, ha='left')\n",
|
|
"plt.title('Performance of least square fit implementations')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAnYAAAIECAYAAACUvmMzAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdcFMf/P/DXHnA06UUFRKoISBWwI1VjL2lqNGqiH6OJ\n+eg3McnHfBSMMcbkl6omGjVqJPqJmogoKjbOgsbeC1JVUEBRUIrAwfz+2NzCUg89ysH7+Xj4eHhz\nu7MzN7vc3HtnZjnGGAMhhBBCCFF7kpYuACGEEEIIUQ3q2BFCCCGEtBHUsSOEEEIIaSOoY0cIIYQQ\n0kZQx44QQgghpI2gjh0hhBBCSBtBHTvSZsnlcrz11lswNzeHRCLB0aNHW7pIamnbtm1wdHSEpqYm\n3nrrrVq3mTJlCsLDw5u5ZKR62xw5cgQSiQT37t1rdF729vb44osvmqCUNdnZ2WHJkiXNcqzWSiKR\nYPPmzS1dDNIGUceOtKgpU6ZAIpFAIpFAS0sLdnZ2mDlzJh49evTCef/555/YsmULdu/ejaysLPTp\n00cFJW5fysvL8dZbb2HcuHG4e/cufvjhh1q34zgOHMc1a9mioqIgkbTfP2G1tU3fvn2RlZWFzp07\nAwCOHz8OiUSCO3fuNJjf2bNnMXfu3KYuNoCWOV9eREZGxnP/OAwLC8PUqVNrpGdlZeHll19WRfEI\nEdFs6QIQEhgYiK1bt0Iul+Ps2bOYPn067t69i927dz9XfqWlpZBKpUhKSoK1tTV69+79QuVT5Nce\n3bt3D4WFhRgyZIjQWagNYwy01nnjVVRUAMBzdVDrahtLS8sa2yrTNmZmZo0uQ3ujynO8tnYiRBXa\n789d0mpoaWnB0tISVlZWGDlyJP79739j3759KCkpAQD873//g7e3N3R1dWFvb48PPvgARUVFwv5B\nQUGYNm0aFixYACsrK3Tt2hXBwcFYuHAhUlNTIZFI4ODgAAAoKyvDJ598AhsbG2hra8Pd3R1btmwR\nlUcikWD58uWYMGECjI2N8eabb2LDhg3Q0tKCTCaDh4cH9PT0EBISgqysLMTHx8Pb2xsdOnRAeHi4\n6DZYWloaxo4dC2tra+jr68PT0xNRUVGi4wUFBWH69OlYvHgxOnfuDDMzM0yePBmFhYWi7f744w/0\n7NkTurq6MDc3x9ChQ5GXlye8v3z5cnTv3h26urro1q0bvvjiC5SXl9f72f/9998IDAyEnp4eTE1N\n8cYbb+DBgwcAgA0bNqBr164A+M53YyMWDbXbgQMHEBQUBDMzMxgbGyMoKAhnzpwR5bF27Vq4urpC\nV1cXZmZmGDhwIDIzMyGTyfDmm28CgBDxres2MQB88cUXcHR0hI6ODiwtLfHSSy/h2bNnos/OxsYG\n+vr6eOmll/Dbb7+Jbmkq2r+q2qI406dPh5OTE/T09ODo6IhPP/0UpaWlwvuRkZFwdnbG1q1b0b17\nd2hrayMpKQkFBQX497//LZTB19cXO3bsqLM+dbWNTCYTyp2eno7AwEAA/G1WiUSCkJCQOvOsfnvU\nzs4OCxcuxMyZM2FsbIxOnTrh559/xrNnz/Duu+/C1NQUNjY2WLlypSgfiUSCH3/8ES+//DI6dOgA\nGxsb/Pjjj3UeF+Cvy8jISDg4OEBXVxc9evTAL7/8UiPfFStW4PXXX0eHDh1gZ2eHHTt24PHjxxg/\nfjwMDQ3h6OiIv/76S7RfdnY2pkyZAktLSxgaGqJ///44duyY8L7iMzt48CACAwOhr68Pd3d37Nu3\nT9jG1tYWABAcHCz6e9LQ9T1lyhQcPnwYGzduFM5TxflS/Vbs/fv3MW7cOJiYmEBPTw/BwcE4d+5c\no8oJNHyuk3aAEdKCJk+ezMLDw0Vp33zzDeM4jhUUFLD169czExMTFhUVxdLS0tjRo0eZp6cnmzRp\nkrD9wIEDmYGBAZs5cya7ceMGu3r1Knv06BH78MMPmb29PcvOzmYPHz5kjDH24YcfMjMzM7Z9+3aW\nlJTEvvjiCyaRSNihQ4eE/DiOY2ZmZmzlypUsNTWVJSUlsfXr1zOJRMKCg4PZ6dOn2fnz55mzszPr\n378/CwwMZKdOnWIXL15k3bt3Z6+//rqQ15UrV9jKlSvZ5cuXWWpqKlu+fDnT1NRk8fHxovIbGxuz\n//u//2OJiYls//79zNTUlC1YsEDY5tdff2VaWlrs888/F+q4YsUKoV4RERGsa9euLDo6mqWnp7M9\ne/YwW1tbUR7V3b9/nxkYGLA33niDXb16lR0/fpx5enqywMBAxhhjxcXF7MyZM4zjOLZr1y6WnZ3N\nSktL62zHsLAw4bUy7bZjxw62bds2duvWLXb9+nU2bdo0ZmpqynJzcxljjJ09e5ZpamqyTZs2sTt3\n7rArV66wdevWsYyMDFZaWspWrlzJOI5j2dnZLDs7mz158qTWsv3555/M0NCQ7d69m929e5ddvHiR\n/fDDD6y4uJgxxlh0dDTT1NRk3333HUtKSmLr1q1jlpaWTCKRsMzMTKE+mpqaonzv3r3LOI5jR44c\nYYwxVlFRwT799FN2+vRpdvv2bRYTE8M6d+7MIiIihH0iIiKYnp4eCwoKYqdPn2ZJSUns6dOnLCgo\niAUHB7OEhASWlpbGfvnlFyaVSkXnZVV1tU18fDzjOI5lZmay8vJyFhMTwziOY2fPnmXZ2dns8ePH\ndZ4PdnZ2bMmSJcLrrl27MmNjY/bdd9+xlJQU9vnnnzOJRMIGDx4spC1dupRJJBJ2/fp1YT+O45ip\nqSlbsWIFS0pKYj/88APT1NRkO3furPNYkydPZl5eXuzAgQMsPT2d/fHHH8zY2JitW7dOlG+nTp3Y\nb7/9xlJSUtisWbOYvr4+GzRoENu4cSNLSUlhs2fPZvr6+sI5VFRUxFxdXdkrr7zCzp07x1JSUtiS\nJUuYtrY2u3HjBmOMCZ+Zl5cXi4uLY8nJyWzq1KnM0NBQ+LwuXLjAOI5jO3bsEP09aej6zs/PZ4GB\ngWzcuHHCeaq4hjiOY7///rtw7gQEBDAfHx+WkJDArly5wl5//XVmYmIiHEuZcjZ0rpP2gTp2pEVV\n7xBcu3aNOTg4sD59+jDG+C+X1atXi/Y5cuQI4ziO5eXlMcb4jpGLi0uNvCMiIpiTk5PwurCwkGlr\na7Off/5ZtN2YMWNYSEiI8JrjODZt2jTRNuvXr2ccx7FLly4JaV9//TXjOI6dP39eSPvuu++Yubl5\nvXUeNWoUmz59uvB64MCBzNvbW7TNzJkzhc+AMca6dOnCZs+eXWt+hYWFTE9Pj8XFxYnSN27cyIyN\njessx3//+1/WpUsXVlZWJqRdunSJcRzHjh49yhhjLC0tjXEcxxISEuqtU/V2VKbdqisvL2cmJibC\nl91ff/3FjIyM6uywbdq0iXEcV2+5GGPs22+/Zd26dRPVs6p+/fqxiRMnitI+/PBDoYPEmHIdu7qO\n7ezsLLyOiIhgEomE3b17V0iLj49nOjo6LD8/X7Tv1KlT2ejRo+vMu7a2qdqxY4yxY8eOMY7j2O3b\nt+vMR6G2jt2YMWOE1xUVFczQ0JCNHDlSlGZiYsJWrFghpHEcx958801R3hMmTGADBgyo9VipqalM\nIpGwxMRE0T6LFi0SXRccx7G5c+cKrx88eMA4jmPvv/++kPb48WPGcRyLjY1ljPHtZmNjw+RyuSjv\n4OBgNmfOHMZY5We2Y8cO4f3s7GzGcRzbv38/Y0y5tlaofn2HhYWxqVOn1tiuasfu4MGDjOM4obPJ\nGGMlJSWsc+fO7LPPPlO6nA2d66R9oFuxpMXJZDIYGBhAT08PHh4ecHJywu+//44HDx7gzp07mDt3\nLgwMDIR/Q4cOBcdxSE5OFvLo2bNng8dJTk5GaWmpcHtKITAwENeuXROlBQQE1Nif4zh4eHgIrzt2\n7AgA8PT0FKXl5uYKY3GKiorwySefoEePHjAzM4OBgQH27NkjGszOcRy8vLxEx+rcuTOys7MBADk5\nOcjIyMCgQYNqrde1a9dQXFyMsWPHij6nd955B0+ePEFubm6d+/Xu3RuampVDbT09PWFkZITr16/X\nuo8ylG23tLQ0TJo0Cc7OzjAyMoKRkRHy8/OFz2bQoEFwcHCAvb09xo8fjzVr1tRZl/q8/vrrKCsr\nQ9euXTF16lRERUWhoKBAeP/GjRvo27evaJ9+/fo9V93XrFmDXr16oVOnTjAwMMD8+fNrTFzo2LEj\nbGxshNdnzpxBaWkprK2tRZ/X77//LjrHm1v185LjOFhYWIjOd47jYGlpKdy+V6g+Ualv3741rjGF\ns2fPgjGGnj17iuq/dOnSGvWvWh5zc3NoaGiIymNsbAypVIqcnBwA/GeblZUFY2NjUd7Hjx+vkbe3\nt7fwf0tLS2hoaAjXYF2Uub6Vce3aNZiZmaF79+5CmlQqRa9evWp8bvWVs6FznbQPNHmCtLjevXtj\n48aN0NTUhJWVldDRUPyx+vHHHxEcHFxjP2trawD8l4u+vr5Ky1RbfhKJRDSTT/F/DQ2NGmmMMXAc\nh3nz5iEmJgbfffcdXFxcoKenhw8++AD5+fmivKtPzuA4ThhY3xDFdtu3b0e3bt1qvG9iYlLrfhzH\nNcmEB0V5Gmq34cOHw9LSEj/99BO6dOkCLS0t9O/fXxiTpq+vj7NnzyIhIQEHDx7EqlWr8NFHH+HQ\noUPw9fVVujxWVla4efMm4uPjcfjwYSxevBgff/wxTp06Jepg1ae2yQ1lZWWi19u2bcN7772HZcuW\nYeDAgTA0NMTWrVvx6aefirarfm5VVFTAyMgIZ8+erXGMlp60U31cIcdxtaYpe67WRrHvyZMnoaen\nVyPv+spTVxkVeVZUVMDV1RXR0dE19qt+rNo+64bqpez1/bwUf0eULacqznWi/ihiR1qcjo4OHBwc\nYGtrK4oedezYEV26dMHNmzfh4OBQ45+2tnajjuPk5ARtbW0cOXJElH7kyBFRJE6Vjh07hokTJ+KV\nV16Bh4cH7O3tkZiY2KilHiwtLWFjY4O4uLha33d3d4eOjg5SUlJq/ZzqmnHp7u6Ov//+W9RBuXTp\nEvLz89GjR4/GVbQKZdotNzcXN27cwCeffILw8HBhIoEi0qIgkUgwYMAALFq0COfOnUPnzp2FyS6K\nLzhlOqdSqRSDBw/GsmXLcOXKFRQVFWHnzp0AADc3NyQkJIi2r/7a0tIS5eXlovKdP39etM3Ro0fh\n4+ODOXPmwMfHB46OjkhLS2uwbP7+/sjLy0NxcXGNz+pFv4wVn1FDk2hU7eTJk6LXJ06cgLu7e63b\nKqLtt2/frlF/e3v7FyqHv78/UlNTYWBgUCPvTp06KZ1PXZ+jMte3VCqFXC6vN393d3fhmlAoKSnB\nqVOnGn0t1neuk/ZB7SJ22dnZGDt2LKRSKaRSKTZv3kzT9NuwJUuW4O2334aJiQlGjhwJLS0t3Lhx\nA/v27cOqVasAKL/Uhp6eHt5//30sWLBAuKW0fft2xMTE4ODBg01SfhcXF0RHR2Ps2LHQ19fHt99+\ni/v374u+VJQpf0REBGbOnImOHTvi5ZdfRkVFBeLj4zF+/HiYmZlh/vz5mD9/PjiOQ2hoKORyOa5c\nuYKLFy/iyy+/rDXP9957Dz/88AOmTJmC+fPn4/Hjx5g1axYCAwOf+1akQkPtZmJiAgsLC/zyyy9w\ncHDAw4cP8dFHH0FXV1fIY+fOnUhLS8OAAQNgYWGBc+fO4e7du3BzcwMA4Ut/586d6NevH/T09GqN\ntK5btw6MMfj7+8PY2BiHDh3C06dPhXw++OADvPrqqwgICMCQIUNw/PhxREVFib6ce/XqBQMDA3zy\nySf4z3/+g5SUFHz22Wei43Tv3h2//vorYmJi4O7ujt27d9c7s1UhJCQEYWFhGDt2LL766it4eHjg\n8ePHOHHiBHR1dTFt2rTGN8A/unbtColEgtjYWLz22mvQ1taGkZFRrdtWPwdrOyeVTYuNjcXKlSsx\naNAg7Nu3D1u3bsX27dtr3cfJyQlvvfUWpk+fjq+++gq9e/dGYWEhzp07J5wXz+uNN97Ad999h2HD\nhmHJkiVwdnZGdnY2Dh8+DDc3N4waNUqpfMzNzdGhQwfExcXB1dUV2traMDExUer6tre3R3x8PFJT\nU2FoaAhjY2PRD1gACA0NRUBAACZMmICVK1fC0NAQixcvRmlpKWbOnKl0fRs610n7oHYROwsLCyQk\nJCA+Ph4TJkzAmjVrWrpI5AU0tFDpxIkTsXXrVuzevRu9evVCQEAAFi1aJIpk1JVHbelLlizB9OnT\nMWfOHHh4eGDz5s34/fffa71lWFt+jU377rvvhOVXwsLC0KVLF7zyyis1bulWz6d62ttvv40NGzZg\n+/bt8PHxwcCBAxEXFyd8Qfz3v//Ft99+izVr1sDb2xsDBgzADz/8UG/Ew9LSEvv370dGRgb8/f0x\nYsQIobPbUB1rq3PV7RpqN4lEgm3btiElJQWenp546623MHfuXNF6bKampti1axeGDBkCFxcXfPLJ\nJ1iwYIGw2Ku/vz/+/e9/Y8aMGejYsSNmz55da9lMTU2xfv16BAcHw83NDd9//z3WrFkjtPno0aPx\nzTff4KuvvoKXlxe2bNmCZcuWiTofJiYm2LJlC/7++294eXlhyZIl+Prrr0V1njFjBiZNmoSpU6fC\n19cXZ86cQWRkZINtDQAxMTEYO3Ys5s6dC1dXVwwfPhx79+6Fk5NTg597fWkdO3bE0qVL8eWXX8LK\nygpjxoxROq/nOd8VFi5ciIMHD8Lb2xtffvklvv76a1Enqvo+v/zyC+bOnYslS5bA3d0dYWFh2LRp\nExwdHessrzIUEXo/Pz9MnToVLi4uePnll3H27FnY2dnVW4eqJBIJVq5cia1bt6JLly5ClFGZ6/uD\nDz6Aubk5vLy8YGlpiRMnTtR6jOjoaHTv3h3Dhg1DQEAAcnJycODAAZiamipdzobOddI+cKwpBtk0\nk+XLl0MqlWLGjBktXRRCSBsik8kQEhKCjIwMWFlZtXRx1IpEIkFUVBQmTJjQ0kUhpF1Su1uxAD8O\n6F//+hfy8vJqLGhKCCGEENJetdit2BUrVsDPzw86Ojo1nqP36NEjjBkzRlhdvPqTAby8vHDq1Cl8\n/vnnWLx4cXMWmxDSTqjTs0wJIUShxSJ21tbWWLBgAeLi4lBcXCx6791334WOjg5ycnJw4cIFDBs2\nDF5eXnBzc0NZWZkwvd3Q0FB47BQhhKhKUFBQs88kbSteZOkTQsiLa/ExdgsWLEBGRgbWr18PACgs\nLISpqSmuXbsmDByePHkyrKyssHTpUpw+fRrz5s2DhoYGtLS0sG7dulqXBLC2thY9s5MQQgghpLVy\ndHRUyaLkLT4rtnq/8tatW9DU1BTNBvPy8hJW3w4ICMCRI0dw+PBhxMXF1bnO071794RlJFryX0RE\nRIvn1Zj9lNm2vm2e573a0lX5ubWGtmur7dda204d2+9F266+99Xt2lN1OdrLtdda2k/drj1ltm2O\nay8lJUUl/aoW79hVH8dSUFAAQ0NDUZqBgQGePn3anMVSmaCgoBbPqzH7KbNtfds8z3u1paenpzdY\njqamyrZ7kfxac/u11rYD1K/9XrTt6ntf3a49gP52NvReXdu3hvZTt2tPmW2b49pTlRa/Ffvf//4X\nmZmZwq3YCxcuoH///igsLBS2+X//7//h6NGjiImJUTrfpnpcEmkeU6ZMwYYNG1q6GOQ5UNupN2o/\n9Ubtp75U1W9pdRG7bt26QS6Xi+4zX7p06bkecRQZGQmZTPaiRSQtYMqUKS1dBPKcqO3UG7WfeqP2\nUz8ymQyRkZEqy6/FInbl5eUoKyvDokWLkJmZiTVr1kBTUxMaGhoYP348OI7D2rVrcf78eQwfPhwn\nT56Eq6ur0vlTxI4QQggh6kLtI3aLFy+Gnp4eli1bhqioKOjq6mLJkiUAgJ9++gnFxcWwtLTExIkT\nsWrVqkZ16oj6o0ir+qK2U2/UfuqN2o+02Dp2kZGRdYYeTUxMlHp4NiGEEEIIqdTikyeaCsdxiIiI\nQFBQUJPOPiGEEEIIeV4ymQwymQyLFi1Sya3YNt2xa6NVI4QQQkgbo/Zj7AipD40TUV/UduqN2k+9\nUfuRFhtjRwghhBDS3iUm3sb+/ap56gTQxm/F0hg7QgghhLRWiYm38Z//bMfVq0+RlERj7OpFY+wI\nIYQQ0lpVVAAffHAYFy+GgDHgyBEaY0faMBonor6o7dQbtZ96o/ZTD7m5wK+/AjduSKDqGBSNsSOE\nEEIIaQaMAadPAwcPAmVlgERSAQAwMFDdMehWLCGEEEJIE8vLA3buBNLSKtMePbqNR4+S4egYis8+\no1uxDYqMjKSwNCGEEEJaDGPA+fPATz+JO3UdOwLz53fFoEEPcPbsZJUdjyJ2pFWSyWQ0m1lNUdup\nN2o/9Ubt17o8fQrExABJSZVpHAf07w8MHAhoalZNV02/hcbYEUIIIYSoEGPA1avAnj1AcXFlurk5\nMHo0YGPTdMemiB0hhBBCiIoUFgKxscD16+L03r2B0FBAS6v2/ShiRwghhBDSity8CezaxXfuFIyN\n+SidnV3zlKFNT54g6osmvagvajv1Ru2n3qj9WkZxMbBjB/C//4k7dX5+wMyZ9Xfqbicm4vDKlSor\nS5uO2EVGRtIjxQghhBDSZJKT+QkST55UphkaAiNHAk5O9e97OzER2xctwtPMTJWVh8bYEUIIIYQ0\nUkkJsH8/cO6cON3LC3jpJUBXt+E8Dq9ciZCUFODmTXB799IYO0IIIYSQ5paeDkRH84sOK+jrA8OH\nA66uSmYil0Ny9Spw44ZKy0Zj7EirRONE1Be1nXqj9lNv1H5Nq6wM2LcP2LBB3KlzdQVmzWpEpy4j\nA1i9GhW3b6u8jBSxI4QQQghpQEYGH6V7+LAyTUcHGDYM6NGDX3i4QXI5EB8PnDgBMAZHBwccungR\noebmKisnjbEjhBBCCKmDXA4cOQIcP84vPKzg7MxPkDAwUDKjjAz+YbEPHlSmSaW47eyMlJwchL73\nHo2xI4QQQghpKllZ/DIm2dmVaVIpPznCx+f5onQCe3tg1Cg8e5iNG+cOqqzMbXqMXWRkJI03UFPU\nbuqL2k69UfupN2o/1aioAI4eBdasEXfq7O35sXS+vkp26v4ZS4eEhMpOnVTK3799800kPszGolWL\nsDFmo8rK3qYjdpGRkS1dBEIIIYSokQcP+LF0VZeW09ICwsKAgADVROlgbAwA2HN6Dyp6V0CvQA/Y\nrJry0xg7QgghhLR7FRXAqVPAoUN8v0zBxgYYMwYwM1MyozrG0iE8nH8UxT89w8SHiZi3Zh6edOZX\nNj4y9QiNsSOEEEIIeVGPH/NRuqqrj2hoAMHBQN++gESZgWtKRumKyoqwL3kfLmdfhrxcXkdmz69N\nj7Ej6ovGiagvajv1Ru2n3qj9Gocx4OxZ4OefxZ26zp2Bf/0L6N9fyU5dA2PpFJ26mw9v4qczP+Fy\n9mUAgIODAyRpEvSw7KGyOlHEjhBCCCHtTn4+/4zXlJTKNIkEGDAACAzkI3YNakSUbm/SXlzJuSLa\nPcQnBNN9pyPhcoIKasSjMXaEEEIIaTcYAy5fBvbuBZ49q0y3sODH0llZKZmRkmPprj+4jthbsSgs\nKxQ2M5AaYHi34XAxdxHSVNVvoYgdIYQQQtqFggJg927g5s3KNI7jx9EFBwOayvSKlIzSFZYWYk/S\nHlx7cE20u3cnbwx2HAxdLV0V1Kgm6tiRVkkmkyEoKKili0GeA7WdeqP2U2/UfnW7dg2IjQWKiirT\nTE2B0aMBW1slM1EiSscY46N0SbEoKqs8mKG2IUZ0GwFnM2fVVKgObbpjFxkZiaCgIDrJCSGEkHaq\nqAjYswe4elWcHhDAr00nlSqRiZJRuoLSAuxJ2oPrD66Ldvfp5IPBToOho6lTI2uZTKbSSS80xo4Q\nQgghbdKtW/wEiYKCyjQjI74v5uCgZCZKRumu5lzF3uS9NaJ0I11GwsnUqcHD0Bg7QgghhJBalJQA\n+/YBFy6I0318gMGDAZ2agbOalIzSPS15itikWNx8eFO0e8/OPTHIcRC0NbVfsDaNQx070irROBH1\nRW2n3qj91Bu1H5CaygfY8vMr0zp0AEaOBLp1UzITJaN0V3KuYG/SXhTLi4XNjLSNMNJlJBxNHVVT\noUaijh0hhBBC1F5pKXDwIHD6tDi9Rw9g6FBAT0+JTBoRpdt9azcScxNFu/tZ+SHcIbzZo3RV0Rg7\nQgghhKi1u3eBHTuAR48q0/T0+Ac/uLsrmYmSUbpL2ZewL3kfnskrF8Ez1jHGKJdRsDexf+460Bg7\nQgghhLRrdQXYXFyAESP4W7DPnUm1KN2TkifYlbgLSY+SRLsHWAcgzCEMUg1lptc2PerYkVaJxomo\nL2o79Ubtp97aU/vdu8dH6aoG2LS1gSFDAC8v4cEP9VMySncx6yL2Je9DSXmJsJmJjglGdR8FO2M7\nldVJFahjRwghhBC1UV4OHDsGHD0KVFRUpjs48AE2IyMlMlEySpf/LB+7bu1C8qNk0e69rHsh1CG0\n1UTpqqIxdoQQQghRCzk5fJTu/v3KNC0tYNAg0eNZ66dklO78/fPYn7JfFKUz1TXFKJdR6GrcVXWV\n+geNsSOEEEJIu1BRAZw8CRw+zEfsFGxt+UeCmZoqkYmSUbq8Z3mISYxB6uNUYRMOHHrb9EaIfQi0\nNLRUVKumQR070iq1p3EibQ21nXqj9lNvbbH9cnOB6Gh+5quCpiYQGgr06gVIJEpkomSU7tz9c9if\nsh+l5aXCZma6ZhjdfTS6GHVRXaWaEHXsCCGEENLqMMavSXfwIFBWVpluZQWMGQNYWCiRiZJRusfF\njxGTGIO0vDRhEw4c+nTpg2C74FYfpauqTY+xi4iIQFBQUJv79UIIIYS0ZXl5fIAtrbKfBYkECAoC\n+vdXbZTuzL0zOJh6UBSlM9czx+juo2FjaKOyOtVFJpNBJpNh0aJFKhlj16Y7dm20aoQQQkibxBj/\nfNe4OP55rwodO/Jj6Tp3ViITJaN0j4ofISYxBul56cImHDj0s+2HILsgaEqa96YmTZ4gbVpbHCfS\nXlDbqTd/k3VSAAAgAElEQVRqP/Wmzu339CkQEwMkVVn/l+P4CN3Agfy4ugYpGaU7nXkaB1MPoqyi\n8h6vhZ4FRncfDWtDa9VVqgVQx44QQgghLYYx4OpVYM8eoLi4Mt3MjB9LZ6PM3VAlo3S5RbnYmbgT\nd/LvCJtIOAn6demHgXYDmz1K1xToViwhhBBCWkRhIRAbC1y/Lk7v3Zuf9aqlzJwFJaJ0FawCpzJO\n4VDaIcgr5MJmlvqWGN19NKwMrFRToRdAt2IJIYQQorZu3gR27eI7dwrGxvxYOjs7JTJQMkr3sOgh\ndt7cibtPKtdLkXASDLAdgMCugdCQaKimQq0EdexIq6TO40TaO2o79Ubtp97Uof2ePQP27gUuXRKn\n9+zJP0FCW1uJTJSM0v2d8TcOpx0WRek6deiEUS6j0NlAmZkY6oc6doQQQghpFsnJ/ASJJ08q0wwM\n+ACbk5MSGSgZpXtQ+AA7E3ci40mGsImEkyCwayAG2A5oc1G6qmiMHSGEEEKaVGkpsH8/cPasON3T\nExgyBNDVVSITJaN0J+6egCxdJorSde7QGaO6j0KnDp1UU6EmQGPsCCGEENLq3b7NPxLs8ePKNH19\nYPhwwNVViQyUjNLlFOZg582dyHyaKWyiwWlgoN1A9OvSr01H6aqijh1pldRhnAipHbWdeqP2U2+t\nqf3KyoDDh4G//xb3x1xd+U6dvr4SmSgZpUu4kwBZugzlrFzYzMrACqNcRqFjh46qq5QaoI4dIYQQ\nQlQqMxPYsQN4+LAyTUcHGDoU8PDgFx6ul5JRuuyCbETfjMb9gvvCJhqcBoLsgtDPth8knDLPHmtb\naIwdIYQQQlSivBw4cgQ4dkzcH3N2BkaMAAwNlchEiShdeUU5jt85jqO3j4qidNYG1hjVfRQs9S1V\nV6lmQmPsCCGEENJqZGXxUbrs7Mo0qRR46SXAx0d1UbqsgixE34xGVkGWsImmRBPBdsHo06VPu4zS\nVUUdO9IqtaZxIqRxqO3UG7WfemuJ9quoAI4f5yN15ZXBM9jZ8YsN/9Mfq5+SUbpjd47h6O2jqGAV\nwmY2hjYY3X00zPXMVVYndUYdO0IIIYQ8l4cP+ShdZuVEVGhq8v2xgADVRenuP72P6JvRyC6sDAdq\nSjQRYh+C3ja9232Uriq1G2N3+vRpzJkzB1paWrC2tsZvv/0GTc2a/VMaY0cIIYQ0Dcb42a6HDvF9\nMwUbGz5KZ65M8EyJKJ28Qo6jt4/i+J3joiidrZEtRrmMgpmemeoq1cJU1W9Ru45dVlYWTExMoK2t\njfnz56Nnz554+eWXa2xHHTtCCCFE9R4/5telu327Mk1DAwgOBvr2BSQNBc+UjNLde3oP0TejkVOY\nI2yiJdFCqEMoAqwD2lyUrt1OnujUqXLVaC0tLWhotI8FB9sbGuejvqjt1Bu1n3pryvZjDDh3jn+C\nRGlpZXqnTsCYMUBHZZaLUzJKdyT9CBLuJoiidF2NumJU91Ew1TVVXaXaILXr2Cncvn0bBw4cwMKF\nC1u6KIQQQkib9uQJ3x9LSalMk0iAAQOAwEA+YlcvJaN0mU8yEX0zGg+KKjt+WhIthDmEIcA6AFyD\ng/ZIi92KXbFiBTZs2ICrV69i/PjxWL9+vfDeo0eP8Pbbb+PAgQMwNzfH0qVLMX78eOH9J0+eYMSI\nEVi7di2cnZ1rzZ9uxRJCCCEvhjHg8mVg717g2bPKdAsLPkpnZaVEJkpG6eLT4nHi7gkwVH532xnb\nYaTLyHYRpVP7W7HW1tZYsGAB4uLiUFxcLHrv3XffhY6ODnJycnDhwgUMGzYMXl5ecHNzg1wux7hx\n4xAREVFnp44QQgghL6agANi9G7h5szKN44A+fYCQEH72a72UjNLdzb+LnYk78bCo8jEVUg0pwh3C\n4WflR1G6RmrxyRMLFixARkaGELErLCyEqakprl27BicnJwDA5MmTYWVlhaVLl2LTpk2YO3cuPDw8\nAAAzZ87Ea6+9ViNfitipNxrno76o7dQbtZ96U1X7Xb/Od+qKiirTTEz4KJ2trRIZKBGlKysvQ3x6\nPE7ePSmK0tkb22Oky0iY6Jq8cD3UidpH7BSqV+LWrVvQ1NQUOnUA4OXlBZlMBgCYNGkSJk2apFTe\nU6ZMgZ2dHQDA2NgY3t7ewgmvyI9et87XFy9ebFXlodf0ml7T6/bwurgY+OorGdLSADs7/v30dBlc\nXICZM4MglTaQn1wO2fffA1evIuif719ZejrQqROC5swBjI0hk8mQXZCNHIsc5BbnIv1iOgCgW89u\nGOQ4CE8Tn+LSqUut4vNoyteK/6enp0OVWl3E7tixY3jttddw/37lA33XrFmDzZs3Iz4+Xul8KWJH\nCCGEKO/WLWDXLuDp08o0Q0P+rqmjoxIZKBmlO5R2CKcyTomidI4mjhjhMgLGOso8pqJtarMRuw4d\nOuDJkyeitPz8fBgYGDRnsQghhJB2oaQEiIsDzp8Xp/v4AIMHAzo6DWSg5Fi623m3sTNxJx4VPxI2\n0dbQxmCnwfDp5ENj6VRE0tIFqN6Q3bp1g1wuR3JyspB26dIl9OjRo9F5R0ZGikKeRH1Qu6kvajv1\nRu2n3hrbfmlpwE8/iTt1HToA48fzfbIGO3UZGcDq1UBCQmWnTioFhg0D3nwTMDZGaXkp9ibtxfqL\n60WdOidTJ8zynwXfzr7tulMnk8kQGRmpsvxaLGJXXl6OsrIyyOVylJeXo6SkBJqamtDX18fYsWOx\ncOFCrF27FufPn8euXbtw8uTJRh9DlR8UIYQQ0laUlQEHDwKnTonT3d35PpmeXgMZKBmlS3uchpjE\nGDx+9ljYREdTB4MdB8O7k3e77tApBAUFISgoCIsWLVJJfi0WsVu8eDH09PSwbNkyREVFQVdXF0uW\nLAEA/PTTTyguLoalpSUmTpyIVatWwdXVtUnLI5FIUFR1+g8Ac3Nz3Llzp8597t27h5CQEJWX5cyZ\nMwgPD4eTkxMCAgIQGhqKY8eO1bvPpUuXsG3bNlFabXVSpenTpyMhIUHp7e/du4fg4GAYGxvD39+/\n3m2nTJkCV1dX+Pj4wMfHBwcOHBDee/bsGWbOnIlu3brB09MTM2bMaHTZIyMjUVZW1uj9du7cCT8/\nP3h4eKBHjx749ttv69z2ww8/hIODAyQSCa5fvy5679atW+jTpw9cXFzQt29fUYRaWdHR0XBzc0PP\nnj1x69atRu9/5MgR0ef6IvLz8/HVV18BqBwgHBQUhNjYWJXk31I2bNiAV199VSV5ZWdno0+fPsLr\nsrIyLFy4EC4uLvDy8oKvry8+/PBDyOVy7N69G++++65of4lEAi8vL3h7e8PX1xeHDx9u8JjVz/Mp\nU6Zg5cqV9e6jaD+inpRpv7t3gVWrxJ06XV3glVeAV19VolOnZJQu9lYsNl7aKOrUdTPrhln+s+DT\nmW69NpUWi9hFRkbWGVEzMTHBjh07mrdAtWjopLOyslLqj2tjXLlyBcOHD0dUVBTCw8MBAKmpqcIs\n0bpcuHABsbGxNb6EmnICyZo1axq1fYcOHfD5558jPz8fERER9W7LcRz+/PNPuLm51Xjvo48+gp6e\nntCZycnJqbFNQz777DPMmzcPWlpajdqvc+fO2L17Nzp16oQnT56gZ8+eCAgIQP/+/WtsO2bMGMyZ\nMwcDBgyo8d4777yD2bNnY8KECfj9998xY8YMHDp0qFFlWb16NRYvXlzrs5KVER8fj8LCQuE8a4yK\nigpIJJW/Cx8/foyvv/4aH330kZDWnH+0q5dHVZ6nDnWVZdmyZXjnnXeE11OnTkVJSQnOnz8PfX19\nlJeX49dff0VJSQmGDx+OTz/9FBkZGbCxsRH2OXnyJPT09BATE4PXX38dD6oOUq9F9fOcvkjbN7kc\nkMnE/TEA6NYNGDmSvwXbYAZKROlSH6ciJjEGec/yhE10NHUwxGkIPDt60nnYxFp8jF1TUtUYO8YY\nZs2aBVdXV3h7ewtf4unp6TA3Nxe2k0gkWLp0KQICAuDo6Ii//vpLeO/PP/+Eq6srfH198cUXX9QZ\nTVu2bBmmTZsm+rJ1cHDA2LFjsW3bNgwfPlxILykpgZWVFe7cuYOFCxfi4MGD8PHxwZw5c4Rtfvzx\nx1rLs2/fPvj6+sLLywthYWFI+ec5MTKZDN7e3njnnXeE6MDNqqtTVlE1IvPLL7/Azc0NPj4+8PLy\nQmJiYo3tDQ0N0a9fP+g1+HOQj8rV1iktKCjApk2bsHjxYiHN0tISAHDz5k3Y2toKUdZFixaJnlii\noIiE9O3bFz4+Pnjy5Amys7MxZswYeHl5wdPTE5s2baq1XAEBAcLzig0NDeHq6lpnVLdfv36iL2UF\nxcLbirKNGzcO58+fR25urtJ1mDt3Lo4fP46PPvoIoaGhAIA33ngD/v7+8PT0xNixY5GXx/9RTUxM\nRJ8+feDt7Q0PDw988803uHr1KlavXo3ffvsNPj4+QrRtz5496N+/P/z8/NC3b1+c+ucnvUwmg6en\nJ9566y34+Phg3759NT7TvLw8+Pj4CGtMAnxUcMCAAXB0dMR//vMfIf2bb75BQEAAfH190bdvX1y6\ndEl4r77rqKrIyEi8+uqrGDx4MNzd3ZGXl1dn+QHg008/hbOzM3r37o2PP/5YiBpXj8pVfV31HMzK\nykJISAj8/PzQo0cPfPzxx3WWJT8/X1RWuVyOzZs345VXXgEAJCUlITo6GmvXroW+vj4AQENDA9On\nTxdejx07Fr/99lutdQ8LC0Nubi4yMjJgZWWFrKws4b33338fS5cuxXvvvQeAP899fX2FMl29ehWh\noaHo1q0bJk+eLOynuAYcHR1rXAN2dnaIiIhA3759YW9v32DUj7Scur7z7t8HfvkFOH68sk+mrQ2M\nHs2Pp2uwU6dElK5EXoLdt3bjt0u/iTp1LmYueNf/XXh18qJOXS1UPcYOrI1qbNU4jmOFhYWiNHNz\nc3b79m12/vx55urqKqTn5eUxxhhLS0tj5ubmojxWrlzJGGMsISGBWVtbM8YYy8rKYmZmZiw5OZkx\nxth3331X6/EYY8zNzY3t3Lmz1jLK5XLWtWtXlpaWxhhj7LfffmNjx45ljDG2YcMG9sorr9SoU23l\nyc7OZhYWFuzGjRuMMcbWrVvHevXqxRhjLD4+nmlpabGLFy8yxhhbsmQJe+ONN2otT1BQEIuNjWWM\nMWZkZMSysrIYY4yVlpayoqKiWvdRHMPPz6/O9xljrFOnTszDw4N5eHiwWbNmCZ/5xYsXmaOjI5s3\nbx7z8/NjQUFB7Pjx48J+mzZtYr1792ZxcXHMxcWFPX36tNb8q3/+r732Glu4cCFjjLH79+8zKysr\ndvXq1XrLeOPGDWZhYcHu379f73Z2dnbs2rVrwuuzZ88yd3d30TZubm7swoULjapD1c+fMcYePnwo\n/P/TTz9ln3zyCWOMsffff58tXbpUeE/xWUZGRrJ58+YJ6cnJyaxPnz7syZMnjDHGrl69ymxtbRlj\nfJtpaGiwv//+u9aypKenC9dCfHw8Y4yxgQMHsnHjxjHGGMvPz2fm5ubCNfDgwQNh3wMHDrDevXsL\nr+s6b6uLiIhgtra2LDc3t8Hyx8TEMC8vL1ZUVMQqKirY2LFjmb+/P2OMsfXr14uunaqvq/7/2bNn\nrKCggDHGn+MhISFs3759tZalutOnTzMfHx/h9R9//MG8vb1r3VZh//79LCQkRPS5KI6/fv16oW6f\nfPIJW7RoEWOMsadPnzJLS0vh861+nk+ePJkNGDCAlZSUsNLSUubu7s4OHDjAGKu8BuLj44VrQHHe\n2tnZCedKeno669ChQ61/v0jLU1x/CnI5Y/HxjC1axFhEROW/jRsZ++dPQf3Kyhjbv5+xyEhxBhs2\nMPb4sbBZcm4y+/bEtywiPkL49+WxL9mlrEusoqJCRbVr21TVJWvTETtV4DgOjo6OKCsrw1tvvYWo\nqKh6b2+OGzcOANCrVy/cu3cPpaWlOHXqFHx9feH4z0JAU6dOfa6yaGhoYMaMGVi1ahUAYOXKlUL0\nqa4y1VUeLy8vdO/eHQA/7ubixYsoLCwEAGHMj2K/lKpPfa5DSEgI3nzzTaxYsQIZGRnQ1dV9rjoq\nnD17FpcvX8bZs2fBGBOiD+Xl5UhNTYWvry/OnDmDZcuWYezYsXj6z8JLEydOhIuLC8aMGYMtW7ag\nQ4M/Q3mHDh0Sxup16tQJQ4cOrXfdxPv372P06NH4+eefhQieqjSmDlXbfePGjfDz84Onpye2bNki\nRMEGDhyItWvXYuHChYiPj4eRkVGt+8fFxSElJQWBgYHw8fHBxIkTUV5eLtzuc3Z2Rq9evRosh2KM\nD8dxQuRLEd1UnEtnz55FYGAgPDw88MEHH9QYalDbeVsdx3EYNmwYTE1N6y1/Tk4O4uPj8frrr0NX\nVxccx2Hy5MmNHqYgl8vx4YcfwtvbG35+frh69aoo0li1LNWlpaXB2tq6UceztrZGamqqKE0RZf7j\njz8QHR0NgI+Wrl+/HuXl5YiKisLgwYNFdxKq4jgOo0ePhlQqhZaWFnx9fYVjKK6BoKAg4RqoOtRE\n0SZdu3aFiYkJMjIyGlUf0jyqjrHLyQHWruVvv1ZU8GlaWnyQbdIkoMqfgtopEaV7Jn+GmMQYbLq8\nCfkllZHq7ubd8W7Au3TrtQW0+Dp2rYWFhQUePnwI23+elSKXy5Gfnw8LCwvo6Ojg2rVrkMlkOHjw\nID7++GNcuHCh1nx0/pkbrqGhIeTTGL6+vjh16hRGjhxZ6/v/+te/4OPjgxEjRiA/P7/ByRvPUx6d\nKvPbNTQ0lNrnr7/+wpkzZ3D48GEEBwdj1apVeOmll2rdVpmLXPElKJVKMXPmTIwaNQoAYGtrC01N\nTeFLJiAgAObm5khKSoKvry9KS0tx7do1mJiYiG5PKaPqFz1jrM5y5uTkIDw8HB9//PFzjW/r0qUL\nMjMzhWOUl5fj3r176NKlCwA0qg6KMh47dgyrVq3CyZMnYWZmhs2bNwtjIMeOHYu+ffsiLi4OX375\nJX799Vds2rSp1o7NSy+9hI0bN9Z6LGU7yVXVdi6VlpbilVdewfHjx+Ht7Y179+7VuGVd23krlUpr\n5K+4bdlQ+asv/Fn1/5qamqhQfOuBHwZQm2+//RZ5eXk4ffo0pFIpZsyYIWzLcVyNslQ/flU+Pj5I\nSkpCXl4ejI1rX5C1tsVKFWPsqrKxsYGfnx+io6Px008/NTj2VVtbW/h/9eu7vmvgef4ukJZRUQGc\nPAkcPgyUl1em29ryt17r+P1RScmxdMmPkhGTGIMnJZVrz+pp6WGo81C4W7hTh66FtOmIXWPG2IWH\nh2P16tXC619++QV9+vSBjo4OHj58iMLCQgwaNAhLly6FkZFRjV/S9enVqxfOnz8v7FPXFycAzJs3\nD2vWrBENpE9LSxPGGZmZmSEsLAzjx48XzZozMjKqMa6nLr1798alS5eEcXAbN26Er69vvV9M9Skv\nL0dKSgr8/f3x8ccfY9CgQfVO9mgoUlJUVITdu3cL2/7vf/+Dj48PAH6mcnBwsDCb89atW8jJyREe\nQTdv3jz4+/tj//79eOedd5CZmVnrMQwMDIQxaAA/ZknxhZiVlYW9e/fW2mnOzc1FeHg4Zs+e3ajI\na9U6W1pawtvbG5s3bwYAbNmyBb6+vjAzM2tUHarKy8uDkZERTE1NUVJSgl9//VV4Lzk5GZaWlpg8\neTIWLlyIM2fOAKh5zgwaNAj79u0TzeBVbNsQQ0NDFBUVoby8XHTN1dbWz549Q3l5udCZ++mnn5Q6\nRnXV866v/EFBQdi+fTuKi4tRUVGBTZs2CV86Tk5OuHz5MkpLS1FaWort27fXerz8/Hx07twZUqkU\nmZmZ2LlzZ731rMrOzk7Ujs7Ozhg5ciRmzJiBgoICAPx1tG7dOiFynpGRAXt7e6U+i9mzZ2POnDmQ\nSqWiqGr187w+imtAJpPVew2Q1ikx8TZWrjyMt9/+HpMmHcaWLbeFTp2mJjBoEDBlihKdOiWjdDtv\n7kTU5ShRp87Nwg2z/Gehh2UP6tQ1gqrH2LX5jp2yU/e///57pKenw8vLCz4+PoiLixMGD9+9exfh\n4eHw9vaGl5cXhg4dit69ewMQ/xKvfiIrXnfs2BGrVq3C0KFD0bNnTzx8+BBaWlq1TiLw9PTErl27\nsHTpUjg5OcHT0xPTpk0T3e57++238fjxY9HA59DQUBQWFsLb21uYPFFXeSwsLLBp0yZMmDABXl5e\n2Lx5M6KiooRtqtepoQu0vLwcU6dOhaenJ7y9vZGVlVXrEiSKL/PXXnsNly9fRpcuXfDZZ58B4G/N\nDRs2DADfsfq///s/eHl5wcPDA8nJyaIv/1WrVuGLL76Ap6cnxo8fj6ioKBgaGiI6OhpHjx7F999/\nDzc3N0RERGD8+PGiaIzCBx98gJCQEPj6+uLJkyf48ccfcenSJXh5eWHQoEFYtmxZrUvsfPnll0hO\nTsaqVauEpVgUHfWqdQD4QeyK6FxYWJhoUsGqVauwfPlyuLi4YOXKlcLt9cbUoaohQ4bA0dER3bp1\nQ1BQEHr27Cm027Zt2+Dp6QlfX1+8//77+OGHHwDws3bPnDkjTJ5wcnJCVFQU3n77bXh7e8PNzU0U\n/anvPDA1NcUbb7wBDw8PzJ49u959DA0N8dlnn8Hf3x9+fn7o0KGDUtdRddXPzfrKP2LECAwePBie\nnp7o06cPrK2tYWhoCID/oRMWFgZ3d3eEh4fDzc1NyLfqMd5//30kJCTAw8MD06ZNQ1hYWJ1lqc7b\n2xuZmZmiCVMbN26Es7MzevbsCQ8PD3h6eiIxMVGIqJ04caLGMeoSGBgIXV1dzJo1S5Re9TxXdOLr\nykdxDbz99tv1XgOk9UlMvI0NG5Jx8WIIzp/3RmZmCC5eTMbDh7dhZQXMmAH07QvUO3FcLgcOHADW\nrRM/EszeHpg1C/D3BzgOt3JvYeXplbiQVXnXSk9LD6+6vYrX3F9DB2njI/vtXVBQkEo7di3+rNim\n0tqeFVtQUCDcylq/fj3Wr1+Po0ePPlden3/+ObKzs7F8+XJVFpGQNk1xDVZUVGDatGmwsbERflg0\nhzlz5sDHx0f0g6w+3t7e2L17d60zq6tLS0tD//79kZKSIrplStqHr746jBMnQlA1OMtxgJfXYXzz\nTQj+GdFQNyWe8VpcVox9yftwKfuSaFd3C3cMdR4Kfenz3fEhldrMs2Lbix9//BHbtm2DXC6HmZlZ\no9eAU3B3d4dUKkVcXJyKS0hI2/bmm28iPT0dxcXF8PPzE6251xz+85//YPTo0Up17GJjY+tcLqe6\nhQsXYv369fj222+pU9fOMAacPg3IZBJUXT1LXx/o3h3o0kVSf6dOybF0iQ8TsevWLhSUFlQeQ0sf\nw7oNg5tFzbVGScuiiB1plWQyGa2Ar6ao7dQbtZ96ePgQiIkB7twBTp8+jKIifjykVCpD795BkEgA\nS8vDmDWrjnGSSkTpisqKsC95Hy5nXxbt6mHpgSHOQ6Cn1fCapER5FLFTgmKMHf2RIoQQ0hYoZrzG\nx/MBNwBwcHBEUtIh9OgRitxcfixdSckhhIY61cxAySjdjQc3EJsUK4rSdZB2wPBuw9HdvHtTVrHd\nkclkKnmYggJF7AghhBA1kJPDB9mqTpSXSIABA4COHW9DJktBaakEUmkFQkMd4eLSVZyBklG6PUl7\ncDXnqmhXz46eGOI0BLpaL7ZGKambqvot1LEjhBBCWrHycn71kSNHxOvSde7MB9kaXCNdySjd9QfX\nEXsrFoVlhcImBlIDDO82HC7mLiqsEakN3YolbRqN81Ff1Hbqjdqvdbl/nw+yVV2rXEMDCArilzCp\nPjmiRvspEaUrLC3EnqQ9uPbgmigv707eGOw4mKJ0aoY6doQQQkgrI5cDR48Cx49XPg4MAGxs+CCb\nhYUSGTQQpWOM4VrOVexJ2oOisspptYbahhjRbQSczZxVWynSLOhWLCGEENKKZGYC0dHiIJumJhAa\nCvTq1cBCw4BSUbqC0gLE3orFjYc3RLv6dPLBYKfB0NGkpXOaG92KVQLNiiWEEKIuysoAmaxmkK1r\nV2DkSOCfpw7W6nZiIlLi4iC5cQMVd+7A0d4eXc3N+TerRemuZl/BnqQ9KJYXC/sbahtipMtIOJnW\nMpOWNKlmmxU7adIkpTLQ1tbG2rVrVVYgVaGInXqjcT7qi9pOvVH7tYw7d/ggW25uZZpUCoSFCU/z\nqtPtxEQkL1+O0NRUyO7dQ5CxMQ7J5XDy90fXCROEKN3TkqeITYrFzYc3Rfv37NwTgxwHQVtTu4lq\nR5TR5BG7rVu3Yv78+XUeRFGAb775plV27AghhJDWrrQUOHSIf4JE1a9bBwc+SvfPhNW6yeVIWb4c\noVfFy5OEmpvjsLU1uvr7gzGGy1mXsC95nyhKZ6RthJEuI+Fo6qjCGpGWVmfEztHRESkpKQ1m4OLi\ngsTERJUX7EVRxI4QQkhrlpbGPz3i8ePKNG1tYPBgwMen/igdAGEwnmzXLgQ9e8anaWjwvUIrK8hM\nTNBz5tvYdWsXbuXeEu3qZ+WHcIdwitK1IrSOXQOoY0cIIaQ1KikB9u8Hzp0Tpzs7AyNGAIaGDWQg\nl/OD8RISAMZw+PRphBQV8eE9FxdAVxeMMfymU4r7A4zwTP5M2NVYxxijXEbB3sRe5fUiL0ZV/ZaG\n5tbUKjU1Fenp6S98cELqosqBpKR5UdupN2q/ppWUBKxcKe7U6eoCY8YAEyYo0anLzARWr+bXQfmn\nE+Do4oJDdnaAlxdk2dkokZfgx4wLuGL9VNSpC7AOwCz/WdSpa+OU6tiNGzcOJ06cAACsX78e7u7u\ncHNzo7F1hBBCiBKKi/klTH7/HXjypDLd1RV4913Ay6uBW69yOXDwILB2rXgZEzs7dF24EJIJr2Ph\n3RtYkXYREy/vxmVXA3Sw5WfFmuiYYIr3FAx1HgqphrRpKkhaDaVuxVpYWCAzMxNSqRQ9evTA6tWr\nYeN/7AEAACAASURBVGxsjFGjRiE5Obk5ytloHMchIiKCljshhBDSom7eBHbvBgoKKtP09IBhwwA3\nN+XH0tVYl+6fKbOJKbew+sBqpJmk4fEzfsCePFkObzdvDPMfhlCHUOrQtWKK5U4WLVrUfGPsjI2N\nkZeXh8zMTAQEBCDznycQGxgY4OnTpy9ciKZAY+wIIYS0pMJCYO9eoNqEVfToAQwZAujrN5CBXM4/\nIDYhQfz4CTs7fl06ExMwxvDxLx/jnM45lLPKB8nqauqir7wvFkxZoLL6kKbVrAsUe3l5YenSpUhP\nT8ewYcMAABkZGTAyMnrhAhBSG1pLS31R26k3ar8Xxxhw/TqwZw/fuVPo0AEYPhzo3l2JTO7d46N0\nOTmVaVpa/NMj/lnY7mHRQ8QkxuDyg8sot+E7dXk389AjoAfsje1hkGOg2ooRtaBUx27dunVYsGAB\npFIpvvrqKwDAyZMn8cYbbzRp4QghhBB1UlAAxMYCN8RP6oK3N7+Mia5uAxnUFaXr2pWP0pmaoryi\nHCfvnoQsXQZ5hRySf4bL62npwdzUXHh6hFRCt1/bI1ruhBBCCHlBjAGXLwP79vETJRQMDfklTJyd\nlcikrihdWBgQEABwHO4/vY+YxBjcL7gvbJJ7Pxe5Gblw8nOChOM7eSVJJZgSPAUuTi4qqiFpas2+\njt2xY8dw4cIFPH36VDg4x3GYP3/+CxeiKVDHjhBCSHN48gTYtYtfyqQqPz/+zql2Q2sAl5fzUbrj\nx+uM0skr5DiSfgQJdxNQwSq36dyhM0Z1H4X8rHwcOn8IpRWlkEqkCPUNpU6dmmnWMXazZ8/G1q1b\nMWDAAOg2GEcm5MXROB/1RW2n3qj9lMcYcOECEBfHLzqsYGzMPw7MwUGJTO7f56N02dmVadWidHfy\n72DnzZ3ILa58kKymRBPBdsHo06UPJJwEnZw6wcXJhdqPKNexi4qKwrVr12BlZdXU5SGEEEJavbw8\n/nFgqamVaRzH98VCQ/nVSOqlRJSuRF6CQ2mHcDrztGjXrkZdMdJlJMz0zFRXIdJmKHUr1tPTE4cP\nH4a5uXlzlEkl6FYsIYQQVWMMOHOGXyu4tLQy3cyM74/Z2iqRSV1RutBQoFcvgOOQlJuE3bd2I78k\nX9hEW0Mb4Y7h6Nm5J7gGF78j6qZZx9idOXMGX3zxBSZMmICOHTuK3gsMDHzhQjQF6tgRQghRpdxc\nPkp3+3ZlGscBffoAwcF836xe5eXA0aPAsWPiKJ2tLTB6NGBqiqKyIsQlx+FS9iXRrt3MumGY8zAY\n6dAyY21Vs46xO3fuHPbs2YNjx47VGGN39+7dFy5EU4mMjKQnT6gpGieivqjt1Bu1X00VFcDffwOH\nD/OrkShYWPBROhsbJTLJyuKjdFlZlWlVonQMwPWca9iTtAeFZZWL3+lp6WGI0xD0sOyhVJSO2k/9\nKJ48oSpKdew+/fRT7N69G+Hh4So7cHOIjIxs6SIQQghRYw8eADt3AhkZlWkSCdC/PxAYCGg29C1a\nX5Ru1CjAzAxPS54iNikWNx/eFO3qYemBl5xegr60oUdUEHWmCEAtWrRIJfkpdSvW1tYWycnJkDY4\nGrT1oFuxhBBCnld5OXDiBCCT8f9X6NSJ74917qxEJvVF6QICwDgOF7IuYH/KfjyTPxM2MdQ2xDDn\nYXAxp+VK2pNmHWO3YcMGnD59GgsWLKgxxk4ikbxwIZoCdewIIYQ8j6wsPkp3v3INYGhoAAMHAv36\n8f+vV3k5H6E7erTOKN2j4kfYlbgLaXlpol39rPwQ5hAGHU0d1VWIqIVm7djV1XnjOA7lVX/KtCLU\nsVNvNE5EfVHbqbf23H513TW1tub7Y5aWSmRSW5ROU1MYS1fBAacyTuFw2mGUVZQJm5jqmmKky0jY\nGdu9UB3ac/upu2adPJFadaEeQgghpI2p7Wlempr8bNc+ffhxdfWqK0rXpQvfKzQ3R05hDnbe3InM\np5nC2xw49O3SF0F2QdDSaGhaLSENo2fFEkIIabfkcn4cXUICv0adgq0t//QIpZZvzc7me4VV791W\nidLJUYHjd47j2O1jKGeVd7k66nfEqO6jYGVAi/+TZojYLViwAIsXL24wg4iICJXN5CCEEEKay927\n/Fi6hw8r0xRP8/L3VzJKd/w4H6WrOiypSpQu40kGYhJjkFNYGQrU4DQw0G4g+nXpBw1JQwP2CGmc\nOiN2HTp0wOXLl+vdmTGGnj17Ii8vr0kK9yIoYqfeaJyI+qK2U2/tof3KyoBDh4BTp8RROnt7Pkpn\nYqJEJnVF6UJCgN69UcrkiE+Lx98Zf4Oh8iBdDLtgpMtIWOhbqK5CVbSH9murmjxiV1RUBCcnpwYz\n0NbWfuFCEEIIIc0hPZ1/esSjR5Vp2tpAeDjQsyf/JIl61RWls7Hhnx5hbo7Ux6nYlbgLj589Ft7W\nkmghzCEM/tb+kHCtczUJ0jbQGDtCCCFtXkkJ/3zXM2fE6U5OwIgRgJEyT+pqIEr3rKIU+1P24/z9\n86LdHE0cMcJlBIx1jF+8IqTNatZZsYQQQoi6Sknho3T5+ZVpOjrASy8BXv+fvfuOjvI6Ez/+naLe\nOxISEqo0U2x6Fb2YYhwHG8fENnZibxwf/36bdn6OicHeTc5uNol343WctRPjEve1Te8gquggQIBA\nEqoIBOoSKtN+f7xoRkMdaQp60fM5xyfMHc373jfXY66ee+/zDHEgSmc2K1G6nTtvG6U7e/Us686t\no6GtwXYPvS+zUmcxJGaIQ+XAhHAFidiJbkn2iaiXjJ263U/j19ICmzbBsWP27RkZMHcuBAU5cJHK\nSiVKd/Gira1DHpRG4zU2nN9A7pVcu48NiBrAnLQ5BHoHOv8gnXA/jV9PIxE7Byxfvtxag00IIUTP\nce4crFkDDbYAGv7+MHs2DBrkRJSud2945BEskZGcuHyCjfkbaTY2W98O9A5kTtocBkQNcO0DiftW\nVlYWWVlZLrueROyEEELcN65dg40b4cakDgMHwpw5EBDgwEXuEqWrbatn7bm15Ffn231sWK9hzEiZ\ngZ+Xn/MPInocj0bsKisr8fPzIygoCKPRyEcffYROp2PJkiXdtlasEEKInuX0aVi3DpqabG2BgcqE\nboAjATSzWclUnJV12yjdoYuH2Fq4lTZTm/XtUN9Q5qXPIyU8xWXPIkRXORSxGzlyJH/9618ZNmwY\nv/rVr1i7di1eXl5kZmby1ltveaKfnSYRO3WTfSLqJWOnbmocv8ZGWL9emdh1NGQIzJypLMHe1ZUr\nSpSu3FbuC51OidKNHcvVlmpW562mpK7E+rYGDaPiRzGl7xS8dd6ueRgnqXH8hMKjEbvz588zdOhQ\nAD755BP27dtHUFAQAwYM6LYTOyGEEPc3iwVOnoQNG6DZts2NoCAlhUl6ugMXMZth3z7YsePmKN2C\nBZgiI9hXupesoiy7cmBR/lHMz5hPQkiC6x5ICBdwKGIXGRlJWVkZ58+f54knniA3NxeTyURISAiN\njY2e6GenScROCCHuX/X1yrJrXp59+4MPwowZSjqTu7pLlK6i6TKr8lZxqfGS9W2tRsuEPhOYkDgB\nvfa+Pn8oPMyjEbtZs2axaNEiqqqqePzxxwE4ffo08fHxTndACCGEcJTFAsePK2lMWlps7aGhSpQu\nxZFtbreL0sXFwSOPYIgIY2fRdvaV7sNsMdveDopjQcYCYgJjXPdAQriYQxG7lpYWPvzwQ7y9vVmy\nZAl6vZ6srCwuXbrEE0884Yl+dppE7NRN9omol4ydunXn8autVVKYFBTYt48cCVOnKqXB7up2UbrM\nTBg3juL6Ulbnraaqucr6tl6rZ0rfKYyOH93ty4F15/ETd+bRiJ2vry8vvPCCXZv8iyOEEMITLBY4\nfBi2bIE222FUwsNh/nxISnLgImYzZGcrUTqj0dZ+PUrXGh7C1vwNHLpoX3MsKTSJ+RnzCfcLd8mz\nCOFut43YLVmyxP4Hr2dztFgsdqVRPvroIzd2r+skYieEEOpXXa2UAysqsrVpNDB6tFKi1cvLgYtc\nvapE6crKbG0donTnawpYc24N9a311rd9dD7MSJnBg7EPSjkw4RFuj9ilpKRY/2W+evUqH374IfPm\nzSMxMZHi4mLWrl3L008/7XQHhBBCiBuZzXDwIGzbBgaDrT0yEhYsgARHDqPeJUp3LSyQjXnfceKy\nfTbj9Ih05qbPJdgn2DUPI4QHObTHbsaMGSxbtowJEyZY2/bs2cMbb7zB5s2b3drBrpKInbrJPhH1\nkrFTt+4wflevwqpVUFpqa9NqYdw4mDRJKQLh0EVuFaWbNAnL2LHkVp9lw/kNNBls2Yz9vfyZkzaH\ngVEDVRul6w7jJ7rGo3vs9u/fz+jRo+3aRo0aRXZ2ttMdEEIIIcB2WDUryz7AFhOjROni4hy8yP79\nsH27/UViY+GRR6gP9WPdma/Iq7LPkzI4ZjCzUmfh7+VINmMhui+HInaTJk1ixIgRvPnmm/j5+XHt\n2jVef/11Dhw4wK5duzzRz06TiJ0QQqjH5ctKlK5jeVatFiZOhAkTlGDbXd0q1NchSne0MofNBZtp\nNbVa3w72CWZu+lzSIxzJZiyE+3g0Yrdy5UqefPJJgoODCQsLo6amhuHDh/Ppp5863QEhhBA9l8kE\ne/bArl03p5RbsECJ1t3VXaJ01cFerD71CUW1RXYfGxE3gmnJ0/DRO5InRQh1cChi166kpISLFy8S\nGxtLYmKiO/vlNInYqZvsE1EvGTt18+T4VVQo2+AuX7a16fXKYdWxY5WI3V1VVSkXuTFKN3Ei5nFj\n2V9xiO0XtmM02yZ8EX4RzM+YT2Jo9/57rCvk+6deHo3YtfP19SU6OhqTyURhYSEAycnJTneiM+rr\n65k2bRpnzpzhwIEDDBgwwKP3F0II4RyjEXbuhL17lWBbu/h4JUoXFeXARcxmOHBAOTbbMUrXqxcs\nXMjlAFids5LyBlsiYq1Gy9iEsUxKnISXzpE8KUKoj0MRu40bN/Lcc89RUVFh/2GNBlPH2LkHGI1G\namtr+cUvfsHPf/5zBg4ceMufk4idEEJ0P2Vlyja4K1dsbV5eSk66UaOciNJptTBpEsaxo9ldto/d\nJbvtyoH1CuzF/Iz5xAU5cgJDCM/zaMTuJz/5CcuWLeOHP/wh/v739sSQXq8nMjLynvZBCCFE5xgM\nSjq57GylkkS7pCSlekS4I4Ud7hSle+QRSv0MrD72Pleu2WaNOo2OzKRMxiaMRad15ASGEOrm0MSu\ntraWF154QbV5fYT6yD4R9ZKxUzd3jF9xsRKlq662tXl7w/TpMHy4UknirqqqlIuUlNjarh+bbRs7\niu0lOzlw9gAWbLPGhOAEFvRbQKR/zwkGyPdPOFTN+LnnnuPvf/+7S2/89ttvM3z4cHx9fXn22Wft\n3quurmbhwoUEBgaSlJTEZ599dstryERTCCG6r7Y2WL8ePvjAflKXkgI/+QmMGOHApM5iUU68vvuu\n/aSuVy/48Y8pHNKHd47+lf1l+62TOm+dN3PS5rB02NIeNakTAhzcYzd+/HgOHjxIYmIivXr1sn1Y\no+lyHrtvv/0WrVbLpk2baG5u5oMPPrC+t3jxYgD+9re/cezYMR5++GH27dtnd1Di2WeflT12QgjR\nTRUWKjVea2ttbT4+MHMmDBvmYJSuulrZS3eLKF3z6OFsLtrGsUvH7D6SGp7K3PS5hPqGuuZBhPAQ\nV81bHJrYrVy58radcLZe7LJlyygrK7NO7JqamggPDyc3N5fU1FQAnn76aeLi4vjd734HwJw5c8jJ\nySExMZEXXnjhln1o71tSUhIAoaGhDB061BqizsrKApDX8lpey2t57cLXLS3wxz9mce4cJCUp7xcV\nZREfD7/8ZSbBwQ5cb8cOOHOGzJoaMBjIKipS3h81Ch55hA8PbGZ/2X5iBilJ7oqOF+Gt8+al77/E\n4JjB7Ny5s9v8/yGv5fXtXrf/uej6v98ffvih5yZ27vTaa69RXl5undgdO3aM8ePH09Rkq9/3xz/+\nkaysLFavXu3wdSVip25ZWVnWL4FQFxk7dXNm/M6fhzVroL7e1ubnB7NnwwMPdCJKt2qVsjGvnVYL\nEybQOPpB1hdu4vSV03YfGRg1kNlpswn0DuxSv+8n8v1TL4+eirVYLHzwwQd8/PHHlJeXEx8fz1NP\nPcWzzz7r9D63Gz/f2NhIcHCwXVtQUBANDQ1O3UcIIYR7NDfDxo2Qk2Pf3r8/PPwwBDoy37JY4OBB\n2LpVOULbLiYGy4IF5Ggr2XTkXZqNzda3Ar0DeTjtYfpH9XfNgwhxH3BoYvfb3/6Wjz76iJ/97Gf0\n6dOHkpISfv/733Px4kVee+01pzpw4+w0MDCQ+o6/7gF1dXUEBQU5dR+hLvIbp3rJ2KlbZ8fvzBlY\ntw4aG21tAQEwZw7cZgv0ze4QpasdOZg1+espqCmw+8iDsQ8yPXk6fl5+nerv/U6+f8Khid17773H\nzp077cqIzZw5kwkTJjg9sbsxYpeeno7RaCQ/P9+6xy4nJ4dBgwZ1+trLly8nMzNT/kUXQggXa2pS\nTrzm5tq3P/CAsvTqUMrTO0TpzAvmc8hcxrajf6XN1GZ9K8w3jHkZ80gOS3bNgwhxj2VlZdntu3OW\nQ3vsoqOjuXDhAgEBAda2xsZGkpOTqays7NKNTSYTBoOBFStWUF5eznvvvYder0en07F48WI0Gg3v\nv/8+R48eZe7cuWRnZ9O/v+Phdtljp26yT0S9ZOzU7W7jZ7Eok7n16+HaNVt7UBDMnQsZGQ7eqKZG\nidJd3zgOKFG68eO5MnwAq/PXUVpvqyyhQcPo+NFM7jsZb513p56pJ5Hvn3q5at6ideSHZs2axVNP\nPcXZs2dpbm7mzJkz/PCHP2TmzJldvvGbb76Jv78///Zv/8Ynn3yCn58f//qv/wrAO++8Q3NzM9HR\n0Tz11FO8++67nZrUCSGEcL2GBvjiC/j6a/tJ3bBhSl46hyZ17VG6d96xn9RFR2Na+iy7UvS8e+w9\nu0ldlH8Uzz34HDNTZ8qkToi7cChiV1dXx8svv8wXX3yBwWDAy8uLRYsW8ec//5nQ0O6ZK0ij0fD6\n66/LUqwQQjjJYlEORmzcCC0ttvaQEJg3D67vmrm7O0TpLg5LZVX+Oi43Xba9pdEyMXEi4/uMR691\naOeQEKrTvhS7YsUKz6c7MZlMXL16lcjISHS67l1zT5ZihRDCeXV1SgqT/Hz79uHDlZJgPj4OXMRi\ngUOHlL10bbb9ckRHY5j3MFlt59hXus+uHFjvoN7Mz5hPTGCMax5EiG7Oo0uxH374ITk5Oeh0OmJi\nYtDpdOTk5PDxxx873QEhbsWVG0mFZ8nYqVv7+FkscOSIsmLacVIXFgZPP63sp3NoUldTAx9+qGzK\na5/UXT/xWrRoBn+5uIq9pXutkzovrRczU2by3IPPyaSuC+T7JxyKbS9btozjx4/btcXHxzNv3jyW\nLFnilo4JIYS4N2pqlHJgFy7Y2jQaGDUKpkwBb0e2uVkscPgwbNliH6WLiqJ13hy2tORy+NQndh/p\nG9qXeRnzCPcLd82DCNEDObQUGxYWxtWrV+2WX41GIxEREdTV1bm1g10lS7FCCOG4vLxitmwpID9f\nS0GBmcTEFCIjlRRXERGwYAH06ePgxW43Mxw/nnODYllbuJH6Vlu+Uh+dDzNTZzKs1zCnk94LoVYe\nrTzRv39/vv76ax5//HFr27ffftvtT6pKHjshhLi7vLxi/vu/8ykunkr77+rHj29j2DCYPz+RzEzw\n8nLgQneI0l2bM4MNzSc4eWa33UcyIjJ4OP1hgn2CEaInuid57Pbs2cOcOXOYPn06ycnJFBQUsHXr\nVtavX8/48eNd1hlXkoidukkuJvWSsVOX5mb42c+2c+bMFCwWqK3NIjQ0k4AAGDt2O7/+9RTHLlRb\nq5x4vSFKZxk7llMDItlQtIVrBluOlACvAOakzWFA1ACJ0rmQfP/Uy6MRu/Hjx3Py5Ek+/fRTysrK\nGDlyJP/5n/9JQkKC0x0QQgjheWYzHDsG27ZBYaGWjn+fJCYq/wQEOHC+rv2UxebNN0XpGmZPZU3T\nUc6d32v3kSExQ5iZOhN/L0fKUwghOqPT6U4uX75MXFycO/vkEhKxE0KIWysthQ0b4OJF5fXBg9u5\ndm0KYWFKTrr2IkPR0dv5yU/uELGrrVX20hUW2tquR+mOZASxpXgHraZW61shPiHMTZ9LWkSaG55K\nCHXzaMSupqaGl156ia+//hq9Xs+1a9dYvXo1Bw8e5F/+5V+c7oQQQgj3a2hQUsnl5Ni3Dx6cQnX1\nNmJjp9K+Ktrauo2pU2+Tefh2UbrISGpmTmJV0xGKCovsPjKy90im9p2Kj96RHClCiK5yKI/diy++\nSHBwMMXFxfhcT1w0ZswYPv/8c7d2zlnLly+XnD4qJeOmXjJ23Y/JBPv2wdtv20/q9HrIzIQ330zk\nZz9LJSZmO1evvkV09HaeeSaVjIzEmy9WWwsffwxr19omdRoN5rFj2DvnAf67YhVFtUXWH4/wi+DZ\noc8yJ22OTOo8QL5/6pOVlcXy5ctddj2HlmIjIyOpqKjAy8uLsLAwampqAAgODqa+vv4un743ZClW\n3WQDsHrJ2HUv+flKKbCrV+3b+/eHmTPhxqqQtx0/iwWOHlWidK225VUiI6mcPpbvGg9zseGitVmr\n0TIuYRyTkiZJOTAPku+ferlq3uLQxC41NZVdu3YRFxdnndiVlJQwY8YMzp4963Qn3EEmdkKInqym\nBjZtghv/Ex0VBbNnQ3JyJy5WV6fspSsosLVpNJhGj2JXXy27K/Zjtpitb/UK7MWCjAXEBsU69xBC\n9CAe3WP3/PPP89hjj/Ev//IvmM1msrOzefXVV3nhhRec7oAQQgjXMRhg925l6dVotLX7+CjLriNH\ngsOlvu8Qpbs4eQTfNh3mysUr1ma9Vk9mUiZj4seg03bveuJC3K8cithZLBb+67/+i7/+9a8UFRXR\np08fXnzxRV555ZVum39IInbqJssJ6iVjd29YLHD6tDIHu7Eg0LBhMHUqBAbe/TrW8btNlM4wcjjb\nEs0cqDxqre8K0CekD/Mz5hPpH+maBxJdIt8/9fJoxE6j0fDKK6/wyiuvOH1DIYQQrnX5spK+pKjI\nvr13b2XZNT7+7tcozsujYOtWTpw+jXnDBlIMBhKDO1SDiIigKHMo3zUdobay1trsrfNmevJ0hscN\n77a/6AvRkzgUsdu+fTtJSUkkJydTUVHBr371K3Q6Hb/73e/o1auXJ/rZaRqNhtdff11Kigkh7lvN\nzZCVBYcOKQmH2wUEwLRpMHQoODLXKs7LI3/lSqZaLHDuHFRXs81oJHXoUBKjomgd8SAbE1o5VnXK\n7nOp4anMS59HiG+Iax9MiB6kvaTYihUrPHd4ol+/fmzevJk+ffqwePFiNBoNvr6+XL16ldWrVzvd\nCXeQpVghxP2qY9WIa7YqXWi1yh66zEzw9XX8etvffpspOTlKomGTydYeHU38qy+w+toxGtsare1+\nej9mp83mgegHJEonhIt4dCn24sWL9OnTB4PBwKZNm6z57GJj5cSTcA/ZJ6JeMnbudWPViHbJycqy\na1RUJy9YWYl2925lPRfIqq0lMzQUQ1wMOXFe7Krdbffjg6IHMTt1NgHeAU48hXAX+f4JhyZ2wcHB\nXLp0idzcXAYOHEhQUBCtra0YDAZ3908IIQTQ2AhbttxcNSIkRMlH17+/Y8uuVgYD7NoFe/dibmjg\nWvM1ahpqqGhrZXekF9faSigzhhN0/ceDvIN4OP1h+kX2c9UjCSHcwKGJ3csvv8zIkSNpbW3lrbfe\nAmDv3r3079/frZ0TPZf8xqleMnauZTLBgQOwc6d9xhG9HsaPh3HjwMurkxctLFQqR1RXAxAWEcY/\nzp9kWFII2iAtBeYr7Kgwoh+dTBDwUOxDTE+Zjq++E+u74p6Q759waI8dQF5eHjqdjtRUpXbguXPn\naG1t5YEHHnBrB7tK9tgJIdSus1Uj7qqpSclafOKEXfOWinN82beWy6fz8TaaadVpqB0QSowmkd+/\n8Hv6hvV17kGEEHfl0T12ABkZGXav09PTnb65ELcj+0TUS8bOeXeqGjFrFqSkdPKCFgscP64kuWtu\ntjX7+HBhZBrvHDxOTa9r0CuO2rO1hPYLJSk4gaHNQ2VSpzLy/RO3ndj169fPWi4sISHhlj+j0Wgo\nKSlxT89cYPny5ZLuRAihGi6tGtHu6lVl2fWGJHc1afGs62skv+0UraY2a7uvzpcHYx8k2CcYv0q/\nLj+LEMIx7elOXOW2S7G7d+9mwoQJ1pveTnedNMlSrBBCLVxVNcKO0Qh79yoHJDqkMGkN8mfPAyHs\n8b5krRxx9eJVcvNySRueRmxgLBqNhtbzrTwz+RkyUjNudwchhAu5at7i8B47tZGJnRBCDSorlfQl\nFy7Yt3emasRNiothzRq7zXlmDZxNDWNt70auYctooNVoGdl7JLHGWPae2EubuQ1vrTdTH5wqkzoh\nPMjtE7tly5bd9ibt7RqNhjfeeMPpTriDTOzUTfaJqJeMnWNcVTXipotu2QJHj9o1Xw7RszZDQ6m/\nfYqq1PBUZqXOsqvvKuOnbjJ+6uX2wxOlpaV3zCjePrETQgjhOLNZOcewdatrqkYAylruqVPKEdqm\nJmtzo8bI7lQvDsYasGht/72O8ItgVuos0iLSnHsYIUS3I0uxQgjhIberGtG3r7LsGh3dhYvW1MC6\ndUpulOsMJgO5kWY2pmlo8fe2tvvqfZmUOImRvUei03b2FIYQwp3cHrErLCx06ALJyclOd0IIIe5n\nLq8aAcqBiOxsJXPx9SpAFouFMurZ1F9HWZzttIUGDQ/FPcTkpMlSCkyI+9xtI3ZarfbuH9ZoMHU4\nbdWdSMRO3WSfiHrJ2Nm4pWoEQFmZcjjien1XgJqWWvbFGjnaPxSTt+139qTQJGalzqJXYC+HlCzL\n+AAAIABJREFULi3jp24yfurl9oidueNuXiGEEJ1SUKAsu7qsagQos8Nt25QTF9f/Amg2NJOrq2Ln\nQ8E0RNkOQYT6hjIjZQb9I/vLfmghepD7eo/d66+/LgmKhRAe5fKqEe3OnIH166GhAQCj2Uhx00V2\np+gp7hdrPRzhpfViQuIExsSPwUvXlXCgEMKT2hMUr1ixwr3pTmbOnMmmTZsArImKb/qwRsOuXbuc\n7oQ7yFKsEMKTDAbYs0fJCeyyqhGgZCzesME6U7RYLFxuusyRgAZOjkigJdB2hHZIzBCmJk8l2CfY\nuYcRQnic25dif/jDH1r//Nxzz922E0K4g+wTUa+eNnZ3qhoxdKiSk67TVSNAyYty6JCy9NqmlPyq\nb63ndHMpR4dEUZmUaj1x0TuoN7PTZhMf3JVsxvZ62vjdb2T8xG0ndj/4wQ+sf37mmWc80RchhFAV\nt1SNALh0STkcUV4OQKuxlcKaQo711lKYmY7RR1liDfIOYlryNAbHDJZftIUQQCf22O3atYtjx47R\ndD35ZXuC4ldffdWtHewqWYoVQriLW6pGgBKZy8qC/fvBbMZkNlFWX8YZzVXOjE6lLiYEAL1Wz5j4\nMUxInIC3zvvO1xRCqILbl2I7evnll/nyyy+ZMGECfn5+Tt9UCCHUyC1VI9qdP68kGq6txWKxcOXa\nFfLri8jrH03pA8Mw65QUVAOiBjA9eTphfmFOP48Q4v7jUMQuLCyM3Nxc4uLiPNEnl5CInbrJPhH1\nul/HrqxMOZTq0qoRoGQv3rhRKQkGNLY1cr7qPEVhGs6NSac5xB+AmIAYZqfNJik0qesP4YD7dfx6\nChk/9fJoxC4hIQFvbwn3CyF6nsZGJUJ3/Lh9u1NVI0A5dXH0qFKSoqWFNlMbF2ouUGq4Sv6IFC6l\nxIBGg7+XP1P6TuHB2AfRau6eOF4I0bM5FLE7dOgQv/3tb3nyySeJiYmxe2/ixIlu65wzJGInhHDG\nnapGjBunVI7oUtUIgCtXlMMRJSWYLWbK68spqi2iPDmSguEpGPy80Wq0jOo9iklJk/DVd3V9Vwih\nFh6N2B05coT169eze/fum/bYlZaWOt0JIYToTu5UNWLGDAjr6vY2oxF27YK9e7EYjVQ3V5NfnU+1\nH5ybPoiaOOXCaeFpzEydSaR/5F0uKIQQ9hyK2EVERPD5558zffp0T/TJJSRip26yT0S91Dx2bqsa\nAUpOlLVroaqKprYmCmoKqGqpoWRQAsVDEjHrdUT6RzIzZSZpEWlOPYcz1Dx+QsZPzTwasQsICGDS\npElO30wIIbojt1WNAOX47ObNcPw4BpOB4rpiyuvLqY0K4tyM4TSFBeCr92VS4iRG9h6JTtvVGwkh\nhIMRu5UrV3Lw4EGWLVt20x47rbZ7buaViJ0Q4m7cVjWi/eInTsCmTViamqhorOBCzQWa9RYKH0rm\nYnosGo2Wh+IeYnLSZAK8A5x+HiGEerlq3uLQxO52kzeNRoPJZHK6E+6g0Wh4/fXXyczMlLC0EOIm\nbqsaAVBVpeSkKyykprmG/Op8mgxNVCZFkT8ylTZ/H5JCk5iVOotegb2ceg4hhLplZWWRlZXFihUr\nPDexKyoquu17SUlJTnfCHSRip26yT0S9uvvY3alqxNSpMGxYF9OXgHKUdu9e2LWL5uYGCmoKuHrt\nKi0BPpwfnU5VQgShvqHMSJlB/8j+3bIMWHcfP3FnMn7q5dE9dt118iaEEI5ya9UIgJISWLsW46WL\nlNSVUFpXilljoWxAPEXD+qLz9WNKn/GMiR+Dl66reVKEEOLOHK4VqzYSsRNCtHNb1QiAlhbYuhXL\noUNcbrpMYU0hbaY2GiKCyBubTmNEEENihjA1eSrBPsFOPYcQ4v7l0T12aiQTOyGE26pGgO3kxYYN\n1F0tJ786n4a2Bkx6HRce7Et5v97EhcQzO2028cHObNgTQvQEHl2KFcLTZJ+IenWHsXNr1QiA2lpY\nt47WM6corCnkctNlAK4mRHB+VBre4VE8kjyNwTGDu+U+ujvpDuMnuk7GT8jETghxX3Fb1QhQNurt\n349p21ZKqwopqVNKgrX6e5M/Mo2avr0Y22cc4/uMx1sn9bWFEJ7n0FJsYWEhv/71rzl+/DiNjY22\nD2s0lJSUuLWDXSVLsUL0LLerGhEZqeyjc6pqBMDFi1hWr+ZKwQkKawppMbZg0cDF9DguPJRMeu/B\nTE+eTpifMzNHIURP5dGl2CeffJLU1FT++Mc/3lQrVggh7iW3Vo0AZS13xw4adm0lv+o8da1KJuOm\n0ADyxqbj1zedp9JmkxSa5MxjCCGESzgUsQsODqampgadU/919CyJ2Kmb7BNRL0+NnVurRrTLy6N1\n9XcUFR+norECALNOS9HQJKqGpDMldTrDYoeh1XTPCjxdId89dZPxUy+PRuwmTpzIsWPHGD58uNM3\nFEIIZ7m1agRAfT3mdesoP7iVotoiTBalwk51XBj5YzIY0n8yTyZNwlfvTOI7IYRwPYcidi+99BJf\nfPEFjz76qF2tWI1GwxtvvOHWDnaVROyEuP+0tMCOHW6qGgFgNmM5dIira7+ksOI0zcZmANp8vSgY\nkUrw8HHMTJtFpH+kcw8ihBA38GjErqmpiblz52IwGCgrKwPAYrGo7hi/EEKdLBY4dsyNVSMALl+m\n4etPuXBqN9XN1dbmitRe1E0cybSB80iLSHPyJkII4V6SoFh0S7JPRL1cPXZurRoBYDDQum0zJRs+\n52JdGRaU/25cC/GnePwDDBuzkBFxI9Bp1bPH2Bny3VM3GT/1cnvErqioyFojtrCw8LYXSE5OdroT\nQghxI7dWjbjOnH+esn+8S2nxCQxmg9Km1VAyOJGoGQv5Yeo0ArwDnLuJEEJ40G0jdkFBQTQ0NACg\n1d76xJdGo8FkMrmvd06QiJ0Q6uT2qhEATU1c/vpDSvaso8nQZG2ujQmhedY0Jo/4Pr0Cezl5EyGE\ncFyPrhX7q1/9iuzsbJKSkvj73/+OXn9z4FEmdkKoj1urRgBYLNTv38WFL/9KTY1tbdfgo6dy7BCG\nzV5K/6gBsn9YCOFxrpq3qC75Uk5ODhcvXmTXrl3069ePr7/++l53SbhBVlbWve6C6KKujF1NDXz+\nOXz8sf2kLjISliyBxx93flLXeqmc3N//kmN/XW43qatKicP/lV/w+JJ/Y0D0wB4/qZPvnrrJ+AnV\n1YrNzs5m5syZAMyaNYsPPviAJ5544h73SgjRFW6vGgFYDAYK1nzIpQ1fYTTY1nabA33RzZ3PjMlL\nCPIJcu4mQgjRTahuYldTU0NsbCygVMSorq6+yyeEGsmpLvVyZOw8UjUCuHgymwsf/xeGygrbvTUa\nmkcOY/Cil4mP6Ov8Te4z8t1TNxk/cc+WYt9++22GDx+Or68vzz77rN171dXVLFy4kMDAQJKSkvjs\ns8+s74WGhlJfXw9AXV0d4eHhHu23EMI5lZXw0Ufw1Vf2k7q4OHj+eXjkEecndfW1l8n+7//HuT/8\nP7tJXVuvKKL/72vMfvEPMqkTQtyXOj2xM5vNdv90Ve/evVm2bBlLly696b2XXnoJX19fKisr+cc/\n/sE//dM/cfr0aQDGjh3L1q1bAdi0aRPjx4/vch9E9yX7RNTrdmPX0qIcjHj3XftSYAEBMH8+/OhH\nzpcCMxjbOLzxAw79v6dpPZRtbTd7exHwyCIy3/yYgYOn9vh9dHci3z11k/ETDi3FHjlyhJ/+9Kfk\n5OTQ0tJibXcm3cnChQsBOHz4sLWaBShVLr755htyc3Px9/dn3LhxLFiwgI8//pjf/e53DBkyhJiY\nGCZOnEhiYiK//OUvu3R/IYRneKJqhMVi4ez5bIo/+W98S8rpuC3PZ9BQ+i35v4TFJDp3EyGEUAGH\nJnZPP/008+fP529/+xv+/v4u7cCNR3vPnTuHXq8nNTXV2jZkyBC730L+/d//3aFrP/PMM9Yky6Gh\noQwdOtS6/6D9evK6e75ub+su/ZHXjr/OzMy0vk5NzWT9eti3T3mdlKT8fEtLFqNGwaxZzt+voraM\nlb/9Jd65Z3goKgSA45dq0QeGsPCXv6H3yKnKz5+50C3+/+nurzuOX3foj7yW8btfX7f/uaioCFdy\nKI9dcHAwdXV1blm+WLZsGWVlZXzwwQcA7N69m0WLFlFRYdsX89577/Hpp5+yY8cOh68reeyE8Ky8\nvGK2bi3AYNBiMpnx8Unh6lX7KJkrq0Y0tTWxN/sLDN99Q0BNo7Vdr/MiZvI8Uh77EVpfP+duIoQQ\nHuL2kmIdLVy4kE2bNjFr1iynb3ijGx8iMDDQejiiXV1dHUFBko6gJ8nqEK0T3V9eXjErV+bj5TWV\nw4ezaG2dQmvrNoYOhcjIRJdWjTCZTRws3E3pNyuJOlOE9/X/hGjQEJn8AClPv4JvYorzD9VDyXdP\n3WT8hEMTu+bmZhYuXMiECROIiYmxtms0Gj766COnOnBjFDA9PR2j0Uh+fr51OTYnJ4dBgwZ1+trL\nly+3hqaFEO6jROqmcuIEXLwIoaGg10/lwoXtjB+fyMyZzicYtlgsnK86x8GtHxG16xDR19qs74UG\nRZO08BlCM2cpm/eEEEIlsrKy7JZnneXQUuzy5ctv/WGNhtdff71LNzaZTBgMBlasWEF5eTnvvfce\ner0enU7H4sWL0Wg0vP/++xw9epS5c+eSnZ1N//79Hb6+LMUK4RlmM7zyShanTmXS8Svn7w/DhmXx\nr/+a6fQ9rjRdYduxb9Bv2kxkaZXtHl7+9HloKr2eeE6ZTQohhEp5dCn2dhM7Z7z55pu88cYb1tef\nfPIJy5cv5ze/+Q3vvPMOS5cuJTo6msjISN59991OTeqEEJ5RXQ3ffgsFBWbrpE6rhb59oXdv6NWr\n6ymRAJoNzWQVbufitu9IOlqIzqicwtdr9STE9Sd+0fPoHhjs/IY9IYS4TzgUsQPYsWMHH330EeXl\n5cTHx/PUU08xZcoUd/evyyRip26yT6R7s1jgyBHYtEkpC3b1ajHHj+cTHj4Vf/8s+vXLpLV1G888\nk0pGRufTjJgtZo5cPMLBw6vosyuHoKoG63txQXH0mbwQ39lzwU8OR7iafPfUTcZPvTwasXv//fd5\n9dVXef755xk1ahQlJSU8+eSTvPHGG/z4xz92uhPuInvshHC9hgZYvRrOn7e1RUcn8uKLUFu7nbNn\nTxAdbWbq1K5N6gprCtl8Zi0Bew8x4HQZmuv/oQv1DSU5fRTBj/0A+vRx1eMIIcQ9dU/22KWlpfH1\n118zZMgQa9uJEyd49NFHyc/Pd1lnXEkidkK4Xm4urF0Lzc22tqgoePRRuF7Cucuqm6vZXLCZyuN7\nSd9/Ht9GJRm6r96X5KgMomY9imb8eNDp7nIlIYRQH1fNWxya2EVERFBRUYG3t7e1rbW1lbi4OKqq\nqu7wyXtHJnZCuE5zM6xfDydP2to0Ghg9GqZOBb1Dsf9bazW2srtkN4fzskg+kEd00RUAdBodfUL6\nED9kArr5CyAiwsmnEEKI7stV8xaH8gKMGzeOf/7nf6apqQmAxsZGfv7znzN27FinOyDErbgyLC2c\nU1AAf/mL/aQuJASeflpJNnzjpM7RsbNYLBy/dJw/H/gvCrd8yfBv91sndTEBMYxMyyTxmVfQPfOs\nTOo8SL576ibjJxz6Pfvdd9/liSeeICQkhPDwcKqrqxk7diyfffaZu/vnFNljJ0TXGQywZQscPGjf\nPnQozJrlXH3X0rpSNuRvoK7kPOnZ5wiprAMg2CeY1PBUgkdOUGaNLi5hKIQQ3c092WPXrrS0lIsX\nLxIXF0dCQoLLOuEOshQrRNeVlSlpTDrutAgIgHnzoF+/rl+3vrWeLQVbyK3IITGnmIRTJWjNFrx1\n3qSEpRCd0A/NvHmQnOz8QwghhIq4fY+dxWKxVoUwm2+fi0rbTbO8y8ROiM4zmWDnTti9G7tkwxkZ\nMH++MrnrCoPJwL7Sfewp2UNAeSUZ+87h19CMVqMlITiBhLAk9BMnwYQJztccE0IIFXJ7upPg4GAa\nGpTcUfrb7IzWaDSYTCanOyHEjSQXk+dduQLffAMVFbY2Hx9l2XXoUMdzAHccO4vFQu6VXLYUbOFa\n3VVSDuXTq+AyAFH+UaSEp+DbN00JBUZHu/iJRFfId0/dZPzEbSd2ubm51j8XFhZ6pDNCCM+zWGD/\nfti2DYxGW3tSEjzySNcrdVU0VLAhfwMltcX0KrjMoEMFeLUaCPQOJDU8ldDQXjBtGjz0kFSOEEII\nF3Foj91//Md/8POf//ym9j/+8Y/88z//s1s65qz2OrZyeEKI26urg+++gwsXbG16vZLCZPTozs23\n8vLz2HpkK42GRgprCvGO8CY+wI/07HOEXarFS+tF37C+xAbGohk0SAkFBgW5/qGEEEJF2g9PrFix\nwnN57IKCgqzLsh2FhYVRU1PjdCfcQfbYCXF7Fgvk5MCGDdDaamvv1UtJNtzZVdG8/DxW7ljJlZgr\nXKi5gMVkpH9WNbOaAwgO8KN3cG+SQpPQh0fCww9DWpprH0gIIVTOIyXFtm/fjsViwWQysX37drv3\nCgoKCA4OdroDQtyK7BNxn6YmpXrEmTO2No1GObcwaVLXCjtsOLSBM03HMH9ZgFdhPcONZiKCvDDp\ndYxIn4i/dwCMGQOZmdAh0bnofuS7p24yfuKOE7ulS5ei0WhobW3lueees7ZrNBpiYmL485//7PYO\nCiFcJy9PqfN6Pdc4AOHhsHAhdDWDUWVTJduPrKfXydM8XtvGhYprjAzwJrvJC+ID8U9MVQ5HOFtz\nTAghxF05tBS7ZMkSPv74Y0/0x2VkKVYIm9ZW2LgRjh2zbx8xAqZP73oQ7eTlk6w99Q0XX/uAZ+pq\n0ZnBW+eNn94Pi07Lt71T+NmqzdBN0yIJIUR34ZGl2HZqm9QJIWyKi5Vkw7W1tragIFiwAFJTu3ZN\nk9nEpvMbKN25hgePXyCkyYy2yYJ/cADeOm+uBftR6R9C/OARMqkTQggPcmhiV1dXx/Lly9m5cydV\nVVXWhMUajYaSkhK3dtAZUlJMvWSfiPOMRti+HbKz7ZMNDxqknF/w8+vadetb69m48W38s/aSUaOs\n6foEBpLsHUGN2cAWvZahMQkMiu2LuXf3rlAjbibfPXWT8VMfV5cUc2hi99JLL1FaWspvfvMb67Ls\n73//e773ve+5rCPusHz58nvdBSHuiUuXlGTDlZW2Nl9fmDtXmdh1VXHeQU598keiSy9Z2yL9I0kY\nN5zDVdVMTUggrbiYEUlJbGttJXXqVCeeQggh7n/tAagVK1a45HoO7bGLiorizJkzREZGEhISQl1d\nHeXl5cybN4+jR4+6pCOuJnvsRE9kNsPevZCVpZQHa5eSoiy9dvUgu6W+ntNfvM2VfVus4T8NGpJi\n0ukzezGasWMpvnCBgm3b0La1Yfb2JmXqVBIzMpx/KCGE6AHcXiu2o8jISCoqKvDy8iI+Pp5Tp04R\nHBxMSEjILfPbdQcysRM9TXW1speutNTW5uUFM2bA8OFdLO7Q1kbbrh2cWfV3ahou266r9yZ16iJi\n5j0BgYHOd14IIXo4V81bHNrVPHjwYHbt2gXA+PHjeemll3jxxRfJkN/GhZu4cr/B/c5igcOH4S9/\nsZ/UxcfDiy8qJ187Pakzm+HIEep//68c+/wtu0kdaekMef1dYhY/f8tJnYydusn4qZuMn3Boj917\n771n/fN//ud/8uqrr1JXV8dHH33kto4JIe6uoQFWrYL8fFubVqvkAR4/vgsHUi0W5WJbtnCp8ATn\nqs5htiiHpRrDAwme+xjjMpeg03Yhi7EQQgi3c2gp9sCBA4waNeqm9oMHDzJy5Ei3dMxZshQr7ne5\nuUoFieZmW1tUlFISrEu5gC9dgs2bMRfkc77qPBWNFQC0+vtQOjyNsQ+/yIAYJ05eCCGEuC2P5rGb\nNm3aLffSzZo1i+rqaqc74S6S7kTcj5qbYf16OHnS1qbRwOjRMHUq6B36VndQX6/kRcnJocXQTG5l\nLg1tDZj0Okoe6EPLiGF8f+iTRPpHuvQ5hBBCuD7dyR0jdmazGYvFQmhoKHV1dXbvFRQUMG7cOCo7\n5lPoRiRip26Si+nWCgqUpdf6eltbaCg88ggkJXXyYq2tyhHa7GwwGKhurub0ldMYLCYq0mMpGppE\neuKDzM+Yj7fO8dIUMnbqJuOnbjJ+6uWRiJ2+w6/++hvCAFqtll//+tdOd0AIcXdtbbB1Kxw8aN8+\ndCjMng0+Pp24mNkMR4/Cjh3Q1ITFYqG4rpii2iKq4iMoGJ5MS1gQM1NmMrL3SDRdOk4rhBDiXrhj\nxK6oqAiAiRMnsnv3butMUqPREBUVhb+/v0c62RUSsRP3i7IyJY1JVZWtLSAA5s2Dfv06cSGLBc6f\nh82b4epVAAwmA2eunqHYr42CESnUxoYR7BPM9wd8n4QQqRohhBCe4tE8dmokEzuhdiYT7NwJu3fb\nlwTr10+Z1AUEdOJiFRXKhO7CBWtTQ2sDR68VcHpwLJeTo0GjoW9oXx4b8BgB3p25uBBCCGd5dGK3\nZMmSW3YA6LYpT2Rip249fZ/IlStKSbCKClubj4+y7DpkSCfy0tXVWQ9GtLNYLFxsq2JLXAsl/WMx\n65XUJRP6TGBy38loNZ3NkWKvp4+d2sn4qZuMn3p59FRsSkqK3Q0vXbrE//7v//KDH/zA6Q4IIWws\nFti/H7ZtA6PR1p6UpByQCA118EItLbBnj3KxDhcyYeFgnJntfYIx+CmnXH31vjzS7xH6RXZmXVcI\nIUR31OWl2MOHD7N8+XLWrl3r6j65hETshNrU1sJ338H1ra2Akrpk6lQllYlDUTqTCY4cUYrFXrtm\n91Zjcjxfx9VSpG+0tsUExPD4oMcJ9wt3yTMIIYTomnu+x85oNBIWFia1YoVwksWirJRu2KBkIGnX\nq5eSbDg62sGL5OXBli32pywA4uIoGJ7CV9cO0WJssTYPiRnC3PS5eOm8XPMgQgghusyjS7Hbtm2z\nS3nQ1NTE559/zsCBA53ugBC30lP2iTQ1KdUjzpyxtWk0MGECTJoEOkcqd5WXKwcjiovt20NCME+d\nwo6AK+wu3W1t1ml0zEmbw4OxD7ollUlPGbv7lYyfusn4CYcmds8995zdXwABAQEMHTqUzz77zG0d\ncwWpPCG6s7w8WL1amdy1Cw9XonTx8Q5coLZW2YzXsQQFgK8vTJhA07BBfH3uOy6U2k7ChviEsGjg\nInoH93bNQwghhHCKRytPqJksxYruqrUVNm6EY8fs20eMgOnTwftuRR5aWpQcKAcO2J+w0GqVi0ya\nRKmhiq9Of0V9q61ERWp4Ko/2fxR/r+6bf1IIIXoqjy7FAtTW1rJu3TouXrxIXFwcc+bMISwszOkO\nCNGTFBcryYZra21tQUGwYAGkpt7lwyYTHD6sJLe74WAE/fvDtGlYwsM5WH6QTQWbMFvMAGjQMClp\nEhMTJzqdykQIIUT35lDEbvv27Tz66KNkZGSQmJhIcXExZ8+e5X//93+ZNm2aJ/rZaRKxU7f7bZ+I\n0aikk8vOtk82PGgQPPww+Pnd4cMWC5w9q9QUu/FgRO/eMHMm9OlDm6mNNXlrOFlpW5r10/vxaP9H\nSYtIc+0D3cH9NnY9jYyfusn4qZdHI3YvvfQS//M//8OiRYusbV999RU//elPOXv2rNOdEOJ+dumS\nkmy4stLW5uenTOgGDbrLh8vKlIMRJSX27aGhMG0aDBwIGg1Xr13ly9wvqWyy3SQuKI5FAxcR6uto\n8jshhBBq51DELjQ0lKqqKnQdjugZDAaioqKo7bim1I1IxE7ca2Yz7N2rpJQzmWztqakwfz4EB9/h\nwzU1ysGIU6fs2319YeJEGDlSSXIHnL5ymu/Ofkebqc36Yw/FPsTstNnotQ7vthBCCHEPeTRit2TJ\nEt5++21eeeUVa9tf/vKXW5YaE0JAdbWyl6601Nbm5QUzZsDw4XdINtzcbDsY0XE2qNMpByMmTgR/\n5fCDyWxi24Vt7CvdZ/0xvVbP3PS5DO011A1PJYQQortzKGI3btw4Dh48SHR0NL1796a8vJzKykpG\njRplTYOi0WjYtWuX2zvsKInYqZta94lYLErhh02bwGCwtcfHw8KFEBFxmw+aTHDokHIwornZ/r0B\nA5Rl13BbdYiG1ga+Pv01xXW23HVhvmE8PuhxegX2cuETdZ5ax04oZPzUTcZPvTwasfvRj37Ej370\no7t2SIierKEBVq2C/Hxbm1YLmZkwfrzy55tYLEp24q1blTBfR/HxysGIhAS75uLaYr46/RWNbbbS\nYBkRGSzsvxBfva/rHkgIIYTqSB47IVzg1ClYt84+2BYVpSQbjo29zYdKS5WDER3XawHCwpQI3YAB\ndmu2FouF7LJsthZutUtlMqXvFMb3GS+/XAkhhIp5PI/drl27OHbsGE3X0+RbLBY0Gg2vvvqq050Q\nQq2am2H9evviDxoNjB4NU6dazzfYq65WInSnT9u3+/kpe+hGjLjpg63GVlblreL0Fdtn/L38eWzA\nYySHJbvwiYQQQqiZQxO7l19+mS+//JIJEybgd8eEW0K4hhr2iRQUwHffKUuw7UJD4ZFHICnpFh9o\nboZdu+DgwZsPRowapRSIvcX3q7Kpki9OfUFVsy2HXXxwPIsGLiLY505Ha+8NNYyduD0ZP3WT8RMO\nTew++eQTcnNziYuLc3d/hOj22tqUgNvBg/btQ4fC7Nng43PDB4xG5Yd37VLKgXU0aJAS2rtNFZeT\nl0+yOm81BrPtJMbI3iOZmTITnVZ3y88IIYTouRzaYzd48GC2b99OZGSkJ/rkEhqNhtdff53MzEz5\n7UW4TFmZksakYwGIgACYNw/69bvhhy0WyM1V8tHV1Ni/16ePkvskPv6W9zGZTWwq2MTBctvs0Uvr\nxfyM+TwQ84CLnkYIIcS9lpWVRVZWFitWrHDJHjuHJnaHDh3it7/9LU8++SQxMTF2702cfxizAAAg\nAElEQVScONHpTriDHJ4QrmQyKZlIdu+2LwnWr58yqQsIuOEDJSXKwYiyMvv28HCYPl354G0OO9S3\n1vNl7peU1ds+G+EXweODHic6INpFTySEEKI78ejhiSNHjrB+/Xp279590x670htP9AnhAt1pn8iV\nK0pJsIoKW5uPj7LsOmTIDfOzqiplnfbMGfuL+PkpeU+GD1f21N1GYU0hX5/+mmuGa9a2AVEDWJCx\nAB/9jWu83VN3GjvReTJ+6ibjJxya2P36179m7dq1TJ8+3d39EaLbsFhg/35lJdVotLUnJSkHJEI7\nlmC9dk0J6R06pNQSa6fTKUdkJ0xQyoHd9l4W9pTsYfuF7VhQfmPTarRMS57GmPgxkspECCGEQxxa\niu3Tpw/5+fl4e3t7ok8uIUuxwhm1tcqJ16IiW5ter5xzGD26Q5TOaFTKf+3effPBiAceUD5gNwO8\nWYuxhW/PfEteVZ61LdA7kO8P+D6JoYmueSAhhBDdmqvmLQ5N7FauXMnBgwdZtmzZTXvstLdMp3/v\nycROdIXFAjk5sGEDtLba2mNjlZJg0dEdfvDUKSWcV1trf5HEROVgRO/ed73fpcZLfHHqC2pabIcr\nEkMSeWzAYwT5BLngiYQQQqiBRyd2t5u8aTQaTB3zcXUjMrFTt3uxT6SpCdasgbNnbW0ajbKKOmlS\nh61xxcVKMdiLF+0vEBGhHIzIyLjtwYiOjl86ztpzazGabeu8YxPGMrXvVFWnMpE9Puom46duMn7q\n5dHDE4WFhU7fSIjuLC8PVq9WJnftwsOVkmDWjCRXryoHIzrO/AD8/ZWDEQ89dMeDEe2MZiMbzm/g\nSMURa5u3zptH+j3CgKgBzj+MEEKIHqtTtWLNZjOXL18mJiam2y7BtpOInXBEayts3AjHjtm3jxih\nBN+8vVFmezt3wuHD9gcj9Hplw9348Xc8GNFRbUstX+Z+ycUGW7Qvyj+Kxwc9TqS/evJECiGEcC2P\nRuzq6+v56U9/yueff47RaESv1/PEE0/w5z//mZCQEKc7IcS9UFysJBvuuEUuKAgWLIDUVMBggD3X\nD0Z03HAHMHgwTJly14MRHZ2vOs83Z76h2dhsbXsg+gHmZczDW6eeg0lCCCG6L4fCbi+//DJNTU2c\nOnWKa9euWf/35Zdfdnf/RA+VlZXltmsbjUru4JUr7Sd1gwbBT34CqSkWOHEC3n5bWXrtOKlLSoIf\n/1hZo3VwUmexWMgqyuLTk59aJ3VajZY5aXN4tP+j992kzp1jJ9xPxk/dZPyEQxG7jRs3UlhYSMD1\n9Prp6emsXLmS5ORkt3ZOCFerqFCidJWVtjY/P3j4YWVix4ULyqyvYzZigMhIZW02Pd2hgxHtrhmu\n8c2Zb8ivzre2BfsE8/0B3ychJMHJpxFCCCHsObTHLikpiaysLJKSkqxtRUVFTJw4kZKSEnf2r8tk\nj53oyGyGvXshK0spD9YuNRXmz4fg1itKdC4vz/6DAQG2gxGd3FdaXl/Ol7lfUtdaZ23rG9qXxwY8\nRoD3jTXIhBBC9GQe3WP3/PPPM336dH72s5+RmJhIUVERf/rTn/jRj37kdAeEcLfqaiVK17H6nZeX\nkmpueL9GNDuz4OjRmw9GjBmjHIzw6VwpL4vFwtGKo6w/vx6TxTaLnNBnApP7Tkar6d4Hj4QQQqiX\nQxE7s9nMypUr+cc//kFFRQVxcXEsXryYpUuXdttSRxKxUzdX5GKyWODIESXlnMFga4+Ph4VzDUSc\ny4Y9e6CtzfamRqMUgJ08GbpwMMhgMrDu/DqOXzpubfPV+7Kw30IyIjOceRzVkDxa6ibjp24yfurl\n0YidVqtl6dKlLF261OkbOqu+vp5p06Zx5swZDhw4wIABkvdL3KyhAVatgnzb1ja0WsicZGF8UA7a\nT7dDfb39h/r2VcJ4sbFdumd1czVfnPqCy02XrW29AnuxaOAiwv3Cu3RNIYQQojMciti9/PLLLF68\nmLFjx1rb9u3bx5dffslbb73l1g7eyGg0Ultbyy9+8Qt+/vOfM3DgwFv+nETseq5Tp2DdOmi2ZRUh\nKgq+/1Ah0cc3w6VL9h+IilImdKmpnToY0VHe1Ty+PfstLUZbvdihvYbycNrDeOm8unRNIYQQPYdH\nS4pFRkZSXl6OT4e9Ri0tLSQkJHDlyhWnO9EVzz77rEzshJ3mZli/Hk6etLVpNDCxXyUTW7egKzxv\n/4HAQGXJddiwTh+MaGe2mNlxYQe7S3Zb23QaHXPS5vBg7IPddquCEEKI7sVV8xaH/jbTarWYO24s\nR9l3JxMn4S6dzcVUUADvvGM/qYvya+TF3muYfPYv9pM6Ly+l+OvLL3fptGu7prYmPs752G5SF+ob\nynMPPsdDcQ/12Emd5NFSNxk/dZPxEw79jTZ+/Hhee+016+TOZDLx+uuvM2HChE7d7O2332b48OH4\n+vry7LPP2r1XXV3NwoULCQwMJCkpic8++8z63p/+9CcmT57MH/7wB7vP9NS/OIVNW5uy7Prxx8q+\nOgCdqY1pXjt5ofW/iCk7opyiACV8N2yYMqGbPLnTp107Kq0r5a9H/sqF2gvWttTwVH780I+JC4pz\n5pGEEEKILnNoKba0tJS5c+dSUVFBYmIiJSUlxMbGsmbNGhISHE+y+u2336LVatm0aRPNzc188MEH\n1vcWL14MwN/+9jeOHTvGww8/zL59+257OEKWYkVZmZLGpKpKea2xmEmqy2G2z3ai/Rrsfzg5WdlH\n16uXU/e0WCwcLD/IpoJNmC3KLzoaNExKmsTExImSykQIIUSXeHSPHShRuoMHD1JaWkpCQgKjRo1C\n28UlrGXLllFWVmad2DU1NREeHk5ubi6pqakAPP3008TFxfG73/3ups/PmTOHnJwcEhMTeeGFF3j6\n6advfjCZ2N23TCbYuVMp4do+xGHVBYxr2szgmMt4d6zQFR2tTOhSUrp8MKJdm6mNNXlrOFlpW+/1\n0/vxvQHfIzU81alrCyGE6Nk8mu4EQKfTMWbMGMaMGeP0TW/s+Llz59Dr9dZJHcCQIUNuu1dg/fr1\nDt3nmWeesVbLCA0NZejQodb8Pu3Xltfd8/Vbb711y/EaODCTb76B7OzrryP7k1GyBWPLVhrCwNs7\nSfn5y5dh2DAyn38etFqn+7Nq4yq2X9hOWP8wAIqOFxHhF8H/efr/EOobes///+pOrzt+b7tDf+S1\njF9Pei3jp57X7X8uKirClRyO2LnSjRG73bt3s2jRIio61Od87733+PTTT9mxY0eX7iERO3XLysqy\nfglAiczt3w/btoHRCN6tDfQt2kG/5mP072fB1/f6D3p5wbhxMHYs9qG7rjt95TTfnf2ONpMtkfFD\nsQ8xO202eq3Dvxv1GDeOnVAXGT91k/FTL49H7Fzpxo4HBgZSf0Oy2Lq6OoKCgjzZLdGNdPwPU20t\nfPcdFBUpByOSSveRWLaX1EQD8enXV1jbD0ZMngwu+vfGZDaxtXAr2WXZ1ja9Vs/c9LkM7TXUJfe4\nH8lfKuom46duMn7irhM7i8XChQsX6NOnD3q9a+aBN55mTU9Px2g0kp+fb12OzcnJYdCgQU7dZ/ny\n5WRmZsq/6CplsUBODmzYAG0tZmIvHafvhe2EezfSfxgEBFz/wdRUmD4dYmJcdu+G1ga+Pv01xXXF\n1rYw3zAeH/Q4vQKdO4AhhBBCtMvKyrJbnnXWXZdiLRYLAQEBNDY2dvmwRDuTyYTBYGDFihWUl5fz\n3nvvodfr0el0LF68GI1Gw/vvv8/Ro0eZO3cu2dnZ9O/fv0v3kqVYdcrLK2br1gJyck5gNA7G3y+Z\ndK2BlMItBDRVkpgIiYnXU8/FxNgORrhQcW0xX53+isa2RmtbRkQGC/svxFfve4dPCpClILWT8VM3\nGT/18thSrEajYdiwYeTl5XV5ktXuzTff5I033rC+/uSTT1i+fDm/+c1veOedd1i6dCnR0dFERkby\n7rvvOn0/oS55ecWsXJlPQ8NUjhzRkujTj+SrfyI1tJWIiFD6PwjBwShLrVOmwJAhXU4ufCsWi4Xs\nsmy2Fm61S2Uype8UxvcZL3kThRBCdHsOHZ547bXX+OSTT3jmmWdISEiwzio1Gg1Lly71RD87TSJ2\n6vOHP2xn99be6M+tpW/TaULaLhHg25e0uAZmz+6Lzs9bORgxZozLDka0azW2sipvFaevnLa2BXgF\n8L0B3yM5LNml9xJCCCFu5NHDE3v27CEpKYmdO3fe9F53ndiB7LHrVsxmaGqy/dPYaP2zqb6RghNN\nXPt0K2OvlDIdMxosaDRwgOMYfaPQjXxIORgRGOjyrlU2VfLFqS+oaq6ytsUHx7No4CKCfYJdfj8h\nhBCincf32KmVROw8wGi0m6BZ/3yrtuZmWzbhDmpq4Px5uHYN9uduYJbBD4BjllomhYTSEhDBNxnh\nvPbde255hJOXT7I6bzUGs8HaNqr3KGakzECn1bnlnvc72eOjbjJ+6ibjp14eT3dSVVXFunXruHTp\nEr/85S8pLy/HYrEQHx/vdCdEN2GxQGvrLaNqt/xza2uXb9XaCgUFUFlpawv280VjrCEgIAwdflTG\nDqHRq4a0/rEueDh7JrOJTQWbOFh+0NrmpfVifsZ8Hoh5wOX3E0IIITzBoYjdzp07+d73vsfw4cPZ\nu3cvDQ0NZGVl8Yc//IE1a9Z4op+dJhG76ywWJRzm6GTNaHRPPzQa8PPD7B9I4eUAThQEcE0bSJtX\nAAbvACwBgfg0fck8UzlF5Y0YLTp0Ogt9+4ZxYkA6U37yE5d1pa6ljq9Of0VZfZm1LcIvgscHPU50\nQLTL7iOEEEI4yqO1YocOHcp//Md/MG3aNMLCwqipqaGlpYX/z959xzV19X8A/9ywwooEJMjeskSp\nG22RIeB6XK1Wq22Bum1dbZ/2p0WgVqvtU2nF1lnFhbb6wmr7VFSmYgeKo25FBRTFgYMNgZzfH3mI\nXtkYCMHv+/XipTn33pNzc5JwON8zbGxscO/ZLpd2pEM37Kqr6x2vViscWloqH9/WGgQC+WJyBgby\nfxv6v74+snMF+P13fi8dAHh6ylcteXj7MrJiYxGgo6M4llRRAaeQENi6uCilyNcfXceeC3tQKi1V\npLmbumOUyyjoaOo0cCUhhBDSeto0FJuTk4PBgwfz0rS0tFBdXf3CBWhNajV5QipteIza8+PVWouW\nVv0NtOfThML/bfvQsKIi4PAvwD//8NNNTYFhwwB7e/ljQxcXICQEyUlJ+OfCBXR3d4dTQIBSGnWM\nMaTnpiP5RjIY5B8cASdAoEMg+lv1p6VMlIjG+Kg3qj/1RvWnfpQ9eaJJDTs3NzckJCRgyJAhirSk\npCR4erbvsUiRkZGqe3LGgPLypodAKysbz7OlhMKm9aoZGCh1GRGZDMjIAFJS+MPxtLUBX1+gXz9A\n47n5CbYuLrB1cYFAiV9OZdIy/HLpF1wuuKxIM9A2wDj3cbA1slXKcxBCCCEtUdMBFRUVpZT8mhSK\n/euvvzBixAgMGzYMu3fvxttvv41ff/0V+/btQ9++fZVSEGVrlVCsTNb4eLVn01qrR5PjAD29JodA\noaSt4JojJwf4/Xfg7l1+erdu8rCrqI1WEckvzsdP537Co/JHijTbTrZ4w/0NGOrQXsSEEELahzYd\nYwcAeXl52L59O3JycmBjY4PJkye36xmxHMchafVqOA4e3HAor6qq7vFqdTXaSkvrXLJDKTQ0mh4C\n1dVV6o4LylRcDBw+LN/j9VmdO8vDrg5tuNbv6fzT+O3Kb6iSPZ0QMsB6AALsA2gpE0IIIe1Kmzfs\nAEAmk+HBgwcwNTVt92OSOI4DmzcPSSUlcAoKgq2pad2NtfLy1iuEtnbTQ6A6Ok0ar9Ze1Rd21dKS\nh137968ddm3Ii4wTqZJV4cDVA8i8k6lI09HQwSjXUXA3dW9RnqTpaIyPeqP6U29Uf+qrTSdPPHr0\nCHPmzMHPP/8MqVQKLS0tjBs3DqtWrYKxsfELF6K1RO7dC18jI1zLy4Ntnz7KyVRXt+mNNS0t5Txn\nO5ebC/z3v7XDrh4e8rBrp05tV5bH5Y/x8/mfcbvotiLNVM8Ub3Z7E531OrddQQghhJAmUMnOE6NH\nj4ampiaWLFkCGxsb5ObmYvHixaisrMS+ffuUVhhl4jgObNAgAECqUAjf/v3rPlEgqH+82vNpenrN\n63bq4IqLgcRE4PRpfrqJiTzs6ujYtuW5WnAV8RfjUVb1dNawp8QT/3L5F7Q1lLu3LCGEEKJMbRqK\n7dSpE+7cuQM9PT1FWmlpKczNzfHkyZMXLkRr4DgObMQIQFsbyaam8B83rv7xamocAlUFmQw4cQJI\nTuZHsrW0gEGD5GHXtpyvIWMypGWn4UjOEcVSJhqcBoKdgtHHok+7HzZACCGEtGko1tXVFdnZ2XB3\nfzo+KScnB66uri9cgFbVq5digVsoaYHbl93Nm/Kwa34+P93dHQgOVl7YtanjREqlpYi/GI+sh1mK\nNJGOCOPcx8G6k7VyCkOahcb4qDeqP/VG9Uea1LDz9/dHUFAQ3nnnHVhbWyM3Nxfbt2/H22+/jU2b\nNoExBo7jEBYW1trlbZZkiURpC9y+7EpK5LNd6wq7Dh0KODm1fZnyCvPw8/mf8aTiaa+xvZE93nB/\nA/ra+m1fIEIIIUTFmhSKrWn9PxvSqmnMPSslJUW5pXsBHMchIiJCfXaeaKcaCrv6+ADe3m2/TB5j\nDJl3MnHg6gFUs6drBb5m8xr87P0g4NrnUjCEEELI82omT0RFRbX9cifqpEPvFdtGbt6ULzJ85w4/\n3c1NHnY1Mmr7Mkmrpfjtym84c/fpQnlCTSHGuI6BS2fqmSWEEKKelNVuoa4NUktJCbBvH/Djj/xG\nnbExMGkS8Oabrd+oq2vq98Oyh9h4ciOvUdfFoAum9ZpGjbp2RJnT9knbo/pTb1R/pO33miLtlkwG\nZGYCSUn8sKumpjzsOmCASnYnAwBcenAJey/uRUX109WPvbp4YbjzcGhpvBzrBRJCCCGNoVAsAQDc\nuiWf7fp82NXVFRgyRDVhV0C+lEnyjWSk56Yr0jQ4DQxzHoae5j1pKRNCCCEdQpsud0I6rtJS+SLD\nJ0/y08Vi+WzXrl1VUy4AKKkswZ4Le3Dj8Q1FmpHQCOM9xsPC0EJ1BSOEEELaqSY37C5evIjdu3fj\n7t27+P7773Hp0iVUVlaie/furVk+0kpkMnljLikJKHu6UQM0NYHXXgMGDlRN2PVy1mUkZiYi42QG\nCo0KYWlric4W8q3AnIydMNZtLPS09BrJhagSraOl3qj+1BvVH2nS5Indu3fDx8cHeXl52Lp1KwCg\nqKgICxYsaNXCkdaRlwds3Aj89hu/UefiAsyeLd89QlWNutiUWJzSPYUz3Bk8Mn+E0xdOo+B2AXzt\nfDHJcxI16gghhJAGNGmMnaurK3bt2gUvLy+IxWI8evQIUqkU5ubmePDgQVuUs9loHbvaSkvlPXQn\nTwLP1rpYLB9Hp+p1nL/c9iUytDLwqPyRIk1ToIlXq15FZFik6gpGCCGEtBKVrGNnYmKC+/fvQyAQ\n8Bp2lpaWuHfv3gsXojXQ5ImnGJM35hITa4ddX31VHnbVUuHE0lJpKVKzU7Hqp1Uot3o6HddQ2xAe\nEg90edAF8ybMU10BCSGEkFbWpuvY9ezZE9u2beOl/fTTT+jbt+8LF4C0rtu35WHXX3/lN+qcnYFZ\nswBfX9U16mRMhoy8DMT8HYOMvAwI/vd25MBBK1cLr5i/AqGmENoCbdUUkLQIraOl3qj+1BvVH2nS\nSKqYmBgEBgbixx9/RGlpKYKCgnDlyhUcOnSotctHWqisTB52zczkh12NjJ7OdlXlSiHXH11HQlYC\n7pU87fF1cHBA9o1suPVxw/3H9yHgBKi4WoEAvwDVFZQQQghRI01ex66kpAS//fYbcnJyYGNjg+HD\nh8PQ0LC1y9diL2soljHg1Cl52LW09Gm6hoY87Prqq6oNuz4se4hD1w7h0oNLvHSxUIxgp2DgEZB8\nKhmVskpoC7QR0DMALk60qwQhhJCOTVntFlqguAO5c0e+yPCtW/x0Z2d5L52xsWrKBQAVVRU4mnsU\nf978E9WsWpGuraENH1sf9LfqD00BLatICCHk5dSmCxTn5OQgKioKp06dQnFxMa8QV65ceeFCkBdT\nVgYkJwMnTtQOu9bMdlVV2JUxhjN3zyDxeiKKK4t5x7y6eCHAPgCGOrV7fmktJvVFdafeqP7UG9Uf\naVLDbty4cXBzc8OSJUsgFApbu0ykiRgDTp8GDh+uHXYdOFC+0LAqw643n9zEgawDuF10m5duJbLC\nUKehsBRZqqhkhBBCSMfUpFBsp06d8PDhQ2hoaLRFmZSio4di79wBfv8duHmTn+7kJA+7mpioplwA\nUFhRiMTrifjn7j+8dENtQwQ6BsJT4kl7vBJCCCHPaNNQ7IgRI5CWlgZ/f/8XfsK2FBkZ2eEWKC4v\nl4ddjx/nh107dZKHXV1dVRd2lVZL8eetP3E05yikMqkiXVOgiQHWA/CqzavQ1qClSwghhJAaNQsU\nK0uTeuwePHgAb29vdO3aFRKJ5OnFHIdNmzYprTDK1NF67BgDzpyRh11LSp6ma2gAAwbIw67aKmoz\nMcZw8cFFHLp2CI/LH/OOuZu6I9AhEGJdcbPypHEi6ovqTr1R/ak3qj/11aY9dmFhYdDW1oabmxuE\nQqHiySmc1jby8+Vh19xcfrqjozzs2rmzasoFAPnF+UjISkD242xeupm+GYY4DYG92F41BSOEEEJe\nQk3qsTM0NEReXh5EIlFblEkpOkKPXXk5kJICZGTww64ikTzs6uamurBrSWUJUrJTkHk7EwxPC6en\npQd/e3/0NO8JAdekjU0IIYSQl16b9th1794dBQUFatWwU2eMAf/8Axw6VDvs6u0N+PioLuxaLavG\n8dvHkZqdivKqp/u6CjgB+lr2xSDbQdDV0lVN4QghhJCXXJMadv7+/ggODkZoaCjMzMwAQBGKDQsL\na9UCvmzu3pUvMvx82NXBARg2TLVh16yHWUjISsCD0ge8dEexI4Y4DYGpvqnSnovGiagvqjv1RvWn\n3qj+SJMadkePHoWFhUWde8NSw045ysuB1FR52FUme5ouEgHBwYC7u+rCrgWlBTh47SCuFPAXozbW\nNcYQpyFwNnam8ZaEEEJIO0BbiqkYY8DZs/Kw6zObekAgkIddBw1SXdi1vKocR3KO4O9bf/O2AdPR\n0MEgu0Hoa9mXtgEjhBBClKDVx9g9O+tV9mwX0nMEAhog31J378pnu+bk8NPt7eVhV1PlRTabRcZk\nOJ1/GknXk1AifTrIjwMn3wbMIQAG2gaqKRwhhBBC6lVvw04kEqGoqEh+kmbdp3Ech+rq6jqPkfpV\nVMjDrn//zQ+7GhrKw64eHqoLu+Y+ycWBqwdwp/gOL91aZI2hzkNhYWjRJuWgcSLqi+pOvVH9qTeq\nP1Jvw+78+fOK/1+/fr1NCtPRMQacOwccPFg77Nq/vzzsqqOjmrI9KX+CxOuJOHvvLC9dpCNCoEMg\nukm60Tg6QgghpJ1r0hi7//znP/joo49qpa9cuRILFixolYK9qPY2xu7ePXnYNTubn25nJw+7PrOh\nR5uSVktx7OYxHMs9VmsbsIHWAzHQZiBtA0YIIYS0MmW1W5q8QHFNWPZZYrEYjx49euFCtIb20rCr\nqADS0oC//qoddg0KArp1U03YlTGGC/cv4NC1Q3hS8YR3zMPUA4GOgTASGrV9wQghhJCXUJssUJyc\nnAzGGKqrq5GcnMw7du3atXa/YHFkZCR8fX1VMt6AMeD8eXnY9dk2sUAA9OsH+PqqLux6p+gOErIS\nkPOEP2uji0EXDHUaClsjW9UU7Bk0TkR9Ud2pN6o/9Ub1p35SU1ORmpqqtPwabNiFhYWB4zhUVFTg\nvffeU6RzHAczMzPExMQorSCtITIyUiXPe/++POx64wY/3dYWGD5cdWHXksoSJN9Ixsk7J2ttAxZg\nH4BXzF+hbcAIIYSQNlTTARUVFaWU/JoUin377bexbds2pTxhW1FFKLaiAjhyBPjzT37Y1cBAHnb1\n9FRN2LVaVo2MvAykZqeiorpCkS7gBOhn2Q+D7AZBqCls+4IRQgghBEAbj7FTR23ZsGMMuHBBHnYt\nLHyaLhAAffvKw65CFbWbrhZcRUJWAgrKCnjpzsbOCHYKRmc9Fe5RRgghhBAAbTTGjjTuwQN52PX5\nFWFsbORh1/9trdv25Sp9gINZB3H14VVeuomuiXwbMBNn1RSsiWiciPqiulNvVH/qjeqPUMOuhSor\nn4Zdn12jWV9fHnbt3l01YdfyqnKkZafh77y/IWNP48E6GjrwtfNFX8u+0BBotH3BCCGEENLqKBTb\nTIwBFy8CCQn8sCvHycOufn6qCbvKmAyn7pxC0o0klEpLn5YLHHqa94S/vT/0tfXbvmCEEEIIaRSF\nYlXgwQPgwAHg2jV+uo2NfJHhLl1UU66cxzk4kHUA+cX5vHTbTrYY4jQE5obmqikYIYQQQtoUNeya\noLISOHoU+OOP2mHXwECgRw/VhF0flz/G4WuHcf7+eV56J51OCHIMgrupu9puA0bjRNQX1Z16o/pT\nb1R/hBp2DWAMuHRJHnZ98szmDBwH9OkD+PurJuxaWV2JY7nHcOzmMVTJqhTpWgItvGrzKgZYD4CW\nhlbbF4wQQgghKkVj7OpRUCAPu2Zl8dOtreWzXVURdmWM4dy9czh8/TAKKwp5xzwlnhjsMBidhJ3a\nvmCEEEIIeSE0xq6VSKXy2a7Ph1319ORhVy8v1YRdbxfdRkJWAnKf5PLSzQ3MMdR5KGw62bR9oQgh\nhBDSrlDD7n8aCrv27i0Pu+rqtn25iiuLkXQ9CafzT/O2AdPX0sdgh8Ho0aVHh9wGjMaJqC+qO/VG\n9afeqP4INexQf9jVykoedjVXwaTSKlkV/r71N47kHOFtA6bBaaCfVT8Msh0EHdQ4tIAAACAASURB\nVE2dti8YIYQQQtqtl3qMnVQqn+167FjtsOvgwcArr7R92JUxhisFV3Dw2kE8LHvIO9bVpCuCHYNh\nomfStoUihBBCSKuiMXYvgDHg8mV52PXx46fpqg673i+5j4SsBFx7xF8or7NeZwxxGgInY6e2LxQh\nhBBC1IbaDc7KyMjAgAEDMGjQILz11luoqqpq/KJnPHwIxMUBu3bxG3WWlsDUqfLQa1s36sqkZUjI\nSsCaE2t4jTqhphBDnIZgZu+ZL12jLjU1VdVFIC1EdafeqP7UG9UfUbseOxsbG6SkpEBHRwcLFy7E\nvn378Prrrzd6nVQKpKfLw67PtgX19ICAAKBnz7YPu8qYDJm3M5GSnVJrG7BeFr3gZ+dH24ARQggh\npMnUeoxdREQEXnnlFYwePbrWsWdj1TVh10ePnj0ub8wFBMgbd23txqMbSMhKwN2Su7x0OyM7DHEa\ngi4GKtqfjBBCCCFtTllj7NS2YZeTk4OJEyfi6NGj0NDQqHWc4zisWJEEgcARxcW2vGMWFvKQq6Vl\nW5X2qUdlj3D4+mFcuH+Bl24kNEKQYxDcOrup7TZghBBCCGkZZTXs2nSM3erVq9G7d28IhUKEhoby\njj18+BBjxoyBgYEB7OzssHPnTsWx6Oho+Pn54ZtvvgEAFBYW4p133sGWLVvqbNTVSEjwxy+/ZOHB\ngxwA8rFz//oXMGVK2zfqKqsrkXwjGd8f/57XqNMSaMHf3h+z+8xW671dlY3Giagvqjv1RvWn3qj+\nSJuOsbO0tER4eDgOHjyIsrIy3rHZs2dDKBTi3r17OHXqFIYPH44ePXrA3d0d8+fPx/z58wEAVVVV\nmDBhAiIiIuDs7Nzg88lkgKZmAG7cSEZwsK1Kwq6MMZy9dxaHrx1GUWUR71h3s+4Y7DAYIh1R2xaK\nEEIIIR2SSkKx4eHhuHXrFjZv3gwAKCkpgbGxMc6fPw8nJ/nsz3fffRcWFhb48ssveddu27YN8+fP\nh6enJwBg5syZGD9+fK3n4DgOZmbvQiSyg4VFNkaP9oKXl5diRe6av2pa8/H9kvt4Yv4EtwpvIft0\nNgDAzssOFoYWMLpjBImBpE3LQ4/pcUsfd+rUCYWF/P2JCSGENI9YLEZ8fLzicWpqKrKzswEAW7Zs\nUd8xdp999hny8vIUDbtTp07h1VdfRUlJieKclStXIjU1Ffv372/Rc3Ach6lTGczNATOzZMya5a+U\nsjdFUUURkm7ItwF7loG2gXwbMLMeFHIlakVZYz8IIeRl1tB3qVovUPx8o6a4uBgiET8caWhoiKIi\nfuiyuSwsgIqKJAQEtM0acFWyKvx16y8cyTmCyupKRboGpwFva2+8ZvMabQPWRLTfISGEENJ8KmnY\nPd8iNTAwqBXmefLkCQwNDV/oeSSSZAQEOMHFxbbxk18AYwyXCy7jYNZBPCp/xDvm2tkVQY5BMNY1\nbtUyEEIIIYS0ix67rl27oqqqCllZWYoxdmfOnEG3bt1e6Hnu3TuCO3cErdqwu1dyDwlZCbj+6Dov\n3VTPFEOchsDR2LHVnrsjo946QgghL4PU1FSlzmZu0zF21dXVkEqliIqKQl5eHjZs2ABNTU1oaGhg\n4sSJ4DgOGzduxMmTJzFixAj8+eefcHNza9FztfaYoDJpGVKyU3Di9gnImEyRrqupCz97P/S26A0B\np3Y7thFSJxpjRwghL64txti1actjyZIl0NPTw4oVK7B9+3bo6upi6dKlAIAffvgBZWVlkEgkmDx5\nMtauXdviRl1rkjEZMvIysOrvVcjIy1A06jhw6GvZFx/0+wB9LftSo+4F0VpMRNWys7MhEAjwxx9/\ntNlzCgQCxMXFtUrevr6+mDp1aqvkTVrG3t4ey5YtU3UxlGbMmDH46quvmn1dYGAg1qxZ0wolqltk\nZGSjy6WpszZtfURGRkImk/F+Fi9eDEA+BXjv3r0oLi5GdnY2JkyY0JZFa5Lrj65j7Ym1+P3q7yir\neroOn72RPWb0noFhzsOgp6WC/ckIIfUKCQlRLIguEAhw5MgRFZeofvn5+U3a+7qGQCBAWloaYmNj\nYW9v3+C5HMe1+Wz8L774otFyvcxOnDihWKNV3aWnpyM9PR0ffPABLz03NxczZ86Eg4MDhEIhrKys\nMGTIEOzbt09xTkREBKKiolBa+nTP9Jo/rGp+jIyM0L9//2atlHHr1q12/5lvDSoZY9dWIiMj4evr\n+8LjtR6WPcSha4dw6cElXrpYKEawUzBcTFxo+RIlozF26uXy5RwkJl6DVCqAlpYMgwc7vtDYVmXm\np4oGTUtJJJJmX6Mu96aupFIptLS0WiVvExOTVsm3Nctcn++++w5vvfUWdHV1FWmnT5+Gv78/HBwc\nEB0dDQ8PD1RXVyMpKQnz58+Hn58fRCIRXn31VYhEIvz000+1dqXav38/+vbti4cPH2LFihV4/fXX\ncezYMfTt27fJZWvvw0iUPcauQ8cLaxp2LVVRVYHE64n4PuN7XqNOW0MbAfYBmN13Nlw7u9IXK3mp\nXb6cg9jYLNy/74/Hj31x/74/YmOzcPlyTrvIr6Ev9Xv37iE0NBRdunSBrq4uXF1dFetr1mXRokVw\nd3eHvr4+bGxsMHPmTN6M/sLCQoSGhsLc3BxCoRA2Njb48MMPFcfT09MxcOBAiEQiiEQieHl54dCh\nQ4rjz4dii4uLMW/ePNjY2EAoFMLe3r7Wou0vIiYmBq6urtDV1UXXrl2xbNkyVFdXK47HxcWhX79+\nMDIygqmpKUaMGIGrV6/y8li2bBkcHR0hFAohkUgwZMgQlJeXIzY2FosXL0ZOTo6i1+Xzzz+vsxxS\nqRQLFiyAtbU1hEIhLCwsMHHiRMVxxhjCw8MhkUhgaGiICRMmIDo6mtd4qSu8lp6eDoFAgNzcXADA\n48ePMXnyZNja2kJPTw+urq5YuXIl75qQkBAEBgYiJiYGdnZ2EAqFqKiowN27dxESEgKJRKJojBw9\nerTJ91AXOzs7xXCkmscRERGYO3cuTExM0KVLFyxYsIBXJ8+r6dmKi4vDsGHDYGBgoIiE7dq1C15e\nXtDV1YW9vT0+/PBDXq9YWVkZpk2bBiMjIxgbG2POnDlYuHBhs8OUxcXF2L9/P8aMGaNIY4zh3Xff\nhbW1NTIyMjBq1Cg4OTnBxcUFs2bNwrlz56Cvr684f8yYMdi+fXutvI2NjSGRSODq6ooNGzZAR0cH\n+/btQ1paGjQ0NHDr1i3e+Vu3boWRkRFKS0thY2MDAPDz84NAIICDgwPv3P3798PV1RUGBgbw8/ND\nVlYW7/jvv/+OXr16QSgUwszMDLNnz+a9fjXvlfXr18PW1hadOnXCqFGjcO/evWa9fr6+voiMjGzW\nNQ3p0D12LcUYw5m7Z5B4PRHFlcW8Yz3MemCww2AY6rzYUiykYbSOnfpITLwGHZ0A8P/gDMA//ySj\nT5/m97JlZFxDaWkAL83XNwBJSckt6rWr7w+vsrIyDBo0CPr6+oiLi4OjoyOuXbuGBw8e1JuXnp4e\nNmzYAGtra2RlZWH27NmYM2cOYmNjAcgXXz916hT2798Pc3Nz3Lx5ExcuyPeGrqqqwsiRIxEWFoat\nW7cCAM6dOwe9evY5ZIxhxIgRuHXrFlavXo3u3bsjLy8Ply49/SOz5t5a0isZGRmJ2NhYfPfdd/Dy\n8sKFCxcwY8YMlJeXKxpglZWVWLx4Mdzd3VFYWIjFixdj+PDhOH/+PLS0tBAfH48VK1YgLi4OPXr0\nQEFBAdLS0gAAEyZMwOXLl7Fjxw6cOHECAHi/yJ8VExOD3bt3Y8eOHXBwcEB+fj5vbOOqVasQHR2N\nNWvWwNvbG3v37kVUVFSte27sNaioqICnpyc++ugjiMVipKenY8aMGTA2NkZISIjivIyMDIhEIvz6\n668QCASoqqqCn58fPDw8kJCQACMjI+zatQuBgYE4ffo0XF1dG72HutRVbzExMfj000+RkZGBkydP\nYtKkSejWrRvCwsIazOuTTz7BV199hTVr1oAxhtjYWCxYsAAxMTEYOHAgbt68iffffx/3799XvP8+\n+eQT7N+/H9u3b4eLiws2b96MNWvWwNTUtMHnet4ff/yBqqoq9OnTR5F25swZnD17Ftu3b4dAULsP\n6fn3fb9+/bBq1aoGexs1NDSgoaEBqVSKQYMGoWvXrti0aZOiIQsAGzZswKRJk6Cnp4eTJ0+iZ8+e\niI+Px4ABA3h7y9+5cwdr167Fzp07oaGhgbCwMISFhSnCtv/88w9GjhyJuXPnYufOnbh+/TqmT5+O\noqIixesHAMePH4dEIsGBAwdQWFiIt956Cx999BHvnDbHOqiW3trNJzfZ+hPrWURKBO9nQ+YGdvPJ\nTSWXktQnJSVF1UUgz2jo8xQdncIiIhgbNIj/ExwsT2/uT3BwSq28IiLkz6NMGzduZEKhkOXl5dV5\n/MaNG4zjOHbs2LF684iPj2c6OjqKx6NGjWIhISF1nvvw4UPGcRxLTU2tNz+O49iOHTsYY4wlJiYy\njuNYZmZmU26nUb6+vmzq1KmMMcZKSkqYnp4eO3jwIO+cLVu2MCMjo3rzKCgoYBzHsT/++IMxxtjK\nlStZ165dmVQqrfP8JUuWMDs7u0bLNnfuXObv71/vcUtLS/bZZ5/x0t544w2mpaWleBwREcGcnJx4\n5xw9epRxHMdycnLqzXvOnDksMDBQ8fjdd99lYrGYlZSUKNI2b97MrKysWFVVFe9aPz8/Nm/evCbd\nQ13s7OzY0qVLFY9tbW3ZqFGjeOcMHTqUTZw4sd48at6nX3zxBS/d1taWrVu3jpeWlpbGOI5jjx8/\nZsXFxUxHR4dt2rSJd07//v2Zs7Nzs+4jJiaGmZiY8NJ++uknxnEcO3XqVJPyyMzMZBzHsatXr/Lu\nKz09nTHGWFlZGYuIiGAcxynetytXrmS2trZMJpMxxhi7ePEi4ziOnT59mjHG2M2bNxnHcSwtLY33\nXBEREUxTU5M9ePCAV16BQMAqKioYY4xNnjyZ9evXj3fdvn37mEAgYLm5uYwx+XvFzMyMVVZWKs5Z\nsWIFMzc3r/c+G/ouVVaTrMOHYpsaty6sKET8xXhsPLkReUV5inRDbUOMcR2D9155D1Yiq1YqKXke\n9dapDy0tWZ3pGhp1pzdGIKj7Om3tluVXn8zMTHh4eMDCwqLJ18THx8PHxweWlpYwNDTE5MmTIZVK\nkZ+fDwCYNWsW9uzZA09PT8ybNw8JCQmKULBYLMaUKVMQHByMYcOGYcWKFbhy5UqD5ROLxejZs+eL\n3Wgdzp8/j7KyMowdOxaGhoaKnxkzZqCwsBAFBQUA5GOkxowZAwcHB4hEItjayntMc3LkYfE333wT\nUqkUtra2CA0Nxfbt21FcXFzv89YnNDQUZ8+ehZOTE2bOnIn4+HhIpVIA8vD27du3MWDAAN41AwcO\nbPbYKZlMhuXLl8PLywumpqYwNDTEunXrFKHaGm5ubrwepePHjyM/Px9GRka81ys9PV0RvmvoHpqK\n4zh4eXnx0szNzXH37t1Gr312zNn9+/eRm5uL+fPn88o7bNgwcByHrKwsZGVlobKyEv379+fl079/\n/2a/rnVtKNDcPGp2n3r8+DEvPSgoCIaGhjAwMMAPP/yAb7/9FkFBQQDke8rfu3cPBw8eBABs3LgR\nvXv3Ro8ePRp9PgsLC94YR3NzczDGFGHUCxcuwMfHh3eNj48PGGOKXngAcHV15fUwNrW+npWamkqh\n2KZqygtVJavCnzf/xNHco7xtwDQFmvC28sZrtq9BW0O7FUtJiHobPNgRsbFJ8PV9Gj6tqEhCSIgT\nXFyan9/ly/L8dHT4+bXG1oDN+eXz999/Y/z48Vi4cCG++eYbiMVi/Pnnn3j33XdRWSn/7ggKCkJu\nbi4OHjyI1NRUTJ48GZ6enkhKSoJAIMD69esxd+5cHDp0CIcPH0Z4eDhWr16NadOmKf3eGiKTyRvJ\ne/bsQdeuXWsdF4vFKC0tRVBQEHx8fBAbGwszMzMwxuDh4aG4XwsLC1y6dAkpKSlITk7GkiVL8Mkn\nn+Dvv/+GlVXT/xDu0aMHbty4gcOHDyMlJQVz585FeHg4/vrrrybnIRAIatXn8w2rb775BsuXL8e3\n336LV155BYaGhli5ciX++9//8s57Pkwok8ng5uaGX375pdbz1pzb0D00ZxclbW3+7xuO4xT11ZBn\nw9w1569atQp+fn61zrW0tFSE9JUxRtzIyKjWFqAu//vwnz9/vlZjtS5PnjxR5PWs2NhY9OrVSzEO\n8FnGxsZ44403sGHDBgQEBGDr1q1NXj6mrtcZAO+1bsr3w/Nh45asRVczyTMqKqpZ19WnQ/fYNYQx\nhgv3L2B1xmok3UjiNercOrthdp/ZCHAIoEaditA6durDxcUWISFOkEiSYWSUCokk+X+NupbNYlV2\nfvXp3bs3Lly4gLy8vMZPhnwgfufOnfH555+jT58+cHJyws2bN2udJxaLMWHCBKxduxb//e9/kZaW\nhosXLyqOe3h4YP78+fj999/x3nvvYf369XU+X69evfDo0SNkZma27AYb4OHhAaFQiGvXrsHBwaHW\nj0AgwMWLF/HgwQMsXboUPj4+cHFxwcOHD2v90tLW1kZwcDBWrFiBs2fPorS0VLGUhba2doMD/5+l\nr6+P0aNH47vvvsOJEydw8eJFHDlyBCKRCJaWljh27Bjv/GPHjvEaJRKJBPfu3eP9Yj558iTvmiNH\njmDo0KEICQlBjx494ODggCtXrjTauOnTpw+uX78OQ0PDWq9Vly5dGr2HtmZmZgZra2tcunSpzvrV\n0dGBk5MTtLW1a40D/Ouvv5rd2HN2dsajR494vbVeXl7w9PTEihUr6nwPFBcX89JzcnKgo6OjmPBQ\nw9LSEg4ODrUadTWmT5+OX3/9FWvXrkV5eTlvwkpN462p78FneXh41Kq7tLQ0cBwHDw8PRVp7nDzZ\noXvs6nO3+C4SshJw4/ENXrpEX4KhTkNhL6Z1lwhpDhcXW6U2vJSdX10mTpyIr776CiNHjsRXX30F\nBwcHXL9+HQUFBRg/fnyt811dXXH//n1s2rQJvr6+SE9Pr7Wo6qJFi9C7d2+4u7tDIBBg+/btMDQ0\nhI2NDbKysrBhwwaMHDkSVlZWuH37No4ePYpevXrVWb6AgAC89tprePPNN7Fy5Up4enri9u3buHTp\nEt57771m3y9jTNEoMzAwwMKFC7Fw4UJwHIeAgABUVVXh7NmzOH36NJYvXw5bW1vo6Ohg1apVWLBg\nAbKzs/Hpp5/yfpH9+OOPYIyhT58+MDIyQlJSEoqKiuDu7g5AvgBvfn4+/vrrLzg5OUFfX5+3HEaN\nr7/+GpaWlujRowf09PSwc+dOaGpqKnoTP/zwQ4SHh8PV1RX9+vXD/v37kZSUxMvD398fpaWlWLx4\nMUJDQ3Hy5En88MMPvHNcXV2xbds2pKamwsLCAlu3bkVGRgbEYnGDr92kSZMQHR2N4cOHY+nSpXB2\ndsbdu3eRnJwMd3d3jBo1qtF7qK9OGnr8IpYuXYr33nsPYrEYI0eOhJaWFi5evIiEhASsXbsW+vr6\nmD59Oj777DOYmZnB2dkZW7ZswcWLF2FmZqbIZ+/evfi///s/JCcn1ztswdvbG5qamjh+/DivhzA2\nNhYBAQHo168fwsPD4e7ujurqaqSlpeGrr77CqVOnFCHYv/76C97e3rV60hozcOBAuLi44OOPP8a7\n777L67ns3LkzDAwMcPDgQbi5uUFHR6fRuq7x8ccfo2fPnliwYAGmTZuG7OxsfPDBB5g8eTKvN1qZ\ndaY0Shmp1w7VdWsllSXst8u/sciUSN7EiOVHl7OMWxmsWlatgpIS0v511K+K/Px89s4777DOnTsz\noVDI3Nzc2JYtWxhj8sHbAoGAN3kiPDycmZmZMX19fTZ8+HC2c+dOJhAIFIPzlyxZwrp168YMDAxY\np06dmK+vr+L6O3fusLFjxzIrKyumo6PDLCws2LRp01hhYaEi/2cnTzDGWFFREfvggw+Yubk509bW\nZvb29mzFihUtutdnJ0/U2LhxI/Py8mJCoZCJxWLWv39/tnbtWsXxPXv2MGdnZyYUClnPnj1ZWloa\n09TUVLxG8fHxbMCAAUwsFjM9PT3m6enJG4wvlUrZW2+9xYyNjRnHcSwqKqrOsq1bt4716tWLiUQi\nZmBgwPr27cv279+vOC6TydjChQtZ586dmb6+Phs3bhyLjo5mmpqavHw2bdrEHBwcmK6uLhs2bBjb\ntWsXr36ePHnCxo8fz0QiETMxMWHvv/8+Cw8PZ/b29oo8QkJCeJMpahQUFLCZM2cyS0tLpq2tzSwt\nLdnYsWMVA/Ubu4e6PD954vnHjDE2ZcoU5ufnV28edb1Pa/zyyy/M29ub6enpMZFIxLy8vNiSJUsU\nx8vKyti0adOYSCRiRkZGbNasWWzu3LnM09NTcc7mzZt5r2F9xo0bxz744INa6dnZ2Wz69OnMzs6O\naWtrMwsLCxYUFMR27drFO8/JyYn9+OOPTbqv53377beM4zh24sSJWse2bt3K7O3tmaampqKeIyMj\na00QOXr0aK37/P3331mvXr2Yjo4OMzU1ZbNmzWKlpaWK43W9V7Zt28YEAkG9ZW3ou1RZ37Ntulds\nW+I4DhEREfD19cVrPq/hxO0TSMlOQXlVueIcASdAH4s+8LXzha5W7b8iCSFytFcsaW9iY2MxderU\nZk9QIA3z9/eHiYkJdu/e3azrjh07htGjRyMnJ6feJXzqc/ToUbzxxhvIzs6us0e3Mf/+97+RlJTU\nKsMWlK2u79KaBYqjoqKU8j3boRt2jDFce3gNCVkJuF96n3fcUeyIYKdgSPSbv9I7aX20jl37Qg07\n0t5Qw+7FnTt3DpmZmfD29kZlZSW2bduGr7/+GgkJCYqZp80xduxYeHt74+OPP27WdYGBgXj99dcx\nY8aMZl335MkTXLlyBUFBQYiJicHkyZObdb0qNPRdqqzv2Q49xi40OhT6ZvrobNFZkWasa4xgx2B0\nNenaLgc9EkIIaRr6Dn8xHMdh7dq1mDt3Lm/mb0sadYB8OaCWOHz4cIuuGzVqFDIyMjBx4kS1aNS1\nlQ7dYzdo8yBUZVXBy90LFtYWGGQ7CP2s+kFT0KHbs4QoHfXYEULIi6MeOyXQdNKE9IEUc96YAwNt\nA1UXhxBCCCGk1XTodexEOiL0NO8JN4kbNerUDK1jRwghhDRfh+6xe5LwBA9feQgnC+WvWE8IIYQQ\n8qJqZsUqS4ceYxeREoGKqxUI8QuBi1ML9jYihACgMXaEEKIMNMbuBUnuSRDgF0CNOkIIIYS8FDp0\nj10HvbWXAq1j177Q54kQQl5cW/TYdejJE4QQ0lLZ2dkQCAS1NklvTQKBAHFxca2St6+vL6ZOndoq\neZOWsbe3x7Jly1RdjEa15vuSKB817Ei7RL11RFlCQkIQGhoKQP4L6siRIyouUf3y8/Px+uuvN/l8\ngUCAtLQ0xMbGwt7evsFzOY5r8wV9v/jii0bL9TI7ceIE5s+fr5S8/vzzT4wZMwZdunSBrq4unJyc\n8Pbbb+PUqVNNzmPKlCnw8/NTSnmI6lDDjhDSoamiQdNSEokEOjo6zbpGXe5NXbXmlmUmJiYt2hv1\neZs3b4aPjw+EQiHi4uJw6dIl/PTTT7Czs8PcuXOVUFKiTjp0wy4yMpLWQ1NTVG/q5XLWZXz/0/f4\ndte3+P6n73E563K7ya+hMSv37t1DaGioopfD1dUVmzdvrvf8RYsWwd3dHfr6+rCxscHMmTNRWFio\nOF5YWIjQ0FCYm5tDKBTCxsYGH374oeJ4eno6Bg4cCJFIBJFIBC8vLxw6dEhx/PmQV3FxMebNmwcb\nGxsIhULY29vjyy+/bOlLUUtMTAxcXV2hq6uLrl27YtmyZaiurlYcj4uLQ79+/WBkZARTU1OMGDEC\nV69e5eWxbNkyODo6QigUQiKRYMiQISgvL0dsbCwWL16MnJwcCAQCCAQCfP7553WWQyqVYsGCBbC2\ntoZQKISFhQUmTpyoOM4YQ3h4OCQSCQwNDTFhwgRER0dDS0tLcU5kZCScnZ15+aanp0MgECA3NxcA\n8PjxY0yePBm2trbQ09ODq6srVq5cybsmJCQEgYGBiImJgZ2dHYRCISoqKnD37l2EhIRAIpFAJBLh\n1VdfxdGjR5t8D3Wxs7PD0qVLeY8jIiIwd+5cmJiYoEuXLliwYAGvTp53+/ZtzJw5E1OnTsXOnTvh\n7+8PW1tb9OrVC0uWLMGvv/4KQB4FmT59Ou9axhgcHR3xxRdfICoqCps2bUJaWpqivrZu3ao498mT\nJ3j77bchEolgbW2N5cuX8/IqKirC9OnTIZFIIBQK0adPH95WYTVDG3bv3o0RI0ZAX18fjo6O2LJl\nS4Ov0csgNTUVkZGRSsuvQ8+KVeYLRQip2+Wsy4hNiYWO89OeptiUWISgZcsMKTu/+nq0ysrKMGjQ\nIOjr6yMuLg6Ojo64du0aHjx4UG9eenp62LBhA6ytrZGVlYXZs2djzpw5iI2NBQB89tlnOHXqFPbv\n3w9zc3PcvHkTFy5cAABUVVVh5MiRCAsLU/zCPHfuHPT09Op8LsYYRowYgVu3bmH16tXo3r078vLy\ncOnSpVr31pJeycjISMTGxuK7776Dl5cXLly4gBkzZqC8vFzRAKusrMTixYvh7u6OwsJCLF68GMOH\nD8f58+ehpaWF+Ph4rFixAnFxcejRowcKCgqQlpYGAJgwYQIuX76MHTt24MSJEwAAfX39OssSExOD\n3bt3Y8eOHXBwcEB+fj5vbOOqVasQHR2NNWvWwNvbG3v37kVUVFSte27sNaioqICnpyc++ugjiMVi\npKenY8aMGTA2NkZISIjivIyMDIhEIvz6668QCASoqqqCn58fPDw8kJCQACMjI+zatQuBgYE4ffo0\nXF1dG72HutRVbzExMfj000+RkZGBkydPYtKkSejWrRvCwsLqzOPnn39G893umQAAIABJREFUZWUl\nPvvsszqPd+rUCQAwY8YMTJs2DStXrlTUQ3JyMnJzczFlyhQYGhri6tWryM7OVuz5WnMtAERFRWHp\n0qX4/PPPceDAAbz//vvo27cv/P39AQBhYWHIzMzEjh07YGNjgzVr1mDEiBH4559/4OLy9HP76aef\nYsWKFVi1ahV+/PFHTJkyBQMGDKjVKH+Z+Pr6wtfXF1FRUcrJkHVQHfjWCGlzDX2eVu9azSJSItig\nzYN4P8OWDGMRKRHN/hm6ZGitvCJSItj3P32v1HvauHEjEwqFLC8vr87jN27cYBzHsWPHjtWbR3x8\nPNPR0VE8HjVqFAsJCanz3IcPHzKO41hqamq9+XEcx3bs2MEYYywxMZFxHMcyMzObcjuN8vX1ZVOn\nTmWMMVZSUsL09PTYwYMHeeds2bKFGRkZ1ZtHQUEB4ziO/fHHH4wxxlauXMm6du3KpFJpnecvWbKE\n2dnZNVq2uXPnMn9//3qPW1pass8++4yX9sYbbzAtLS3F44iICObk5MQ75+jRo4zjOJaTk1Nv3nPm\nzGGBgYGKx++++y4Ti8WspKREkbZ582ZmZWXFqqqqeNf6+fmxefPmNeke6mJnZ8eWLl2qeGxra8tG\njRrFO2fo0KFs4sSJ9eYxc+bMBuusRnl5OTM1NWUbN25UpE2YMIGNHj1a8fi9995jvr6+ta7lOI7N\nnTuXl+bm5sb+7//+jzHG2NWrVxnHcezAgQO8c3r27MnCwsIYY08/T9HR0Yrj1dXVzNDQkK1fv77R\n8ncUDX2XKqvd0qFDsYSQ1idldY9Bqkb94aOGyCCrM71SVtmi/OqTmZkJDw8PWFhYNPma+Ph4+Pj4\nwNLSEoaGhpg8eTKkUiny8/MBALNmzcKePXvg6emJefPmISEhQREKFovFmDJlCoKDgzFs2DCsWLEC\nV65cabB8YrEYPXv2fLEbrcP58+dRVlaGsWPHwtDQUPEzY8YMFBYWoqCgAABw+vRpjBkzBg4ODhCJ\nRLC1tQUA5OTkAADefPNNSKVS2NraIjQ0FNu3b0dxcXGzyxMaGoqzZ8/CyckJM2fORHx8vGJsW2Fh\nIW7fvo0BAwbwrhk4cGCzl4aQyWRYvnw5vLy8YGpqCkNDQ6xbt04Rqq3h5ubG60k9fvw48vPzYWRk\nxHu90tPTkZWV1eg9NBXHcfDy8uKlmZub4+7du/Vewxhr0uugo6ODkJAQbNiwAQBQUFCAX375pckz\npZ8vl4WFBe7duwcAil5pHx8f3jk+Pj44f/58vfkIBAJIJJIG7480HzXsSLtEY+zUhxanVWe6BjRa\nlJ+gnq8lbYF2i/JrSHMaBn///TfGjx8PX19f/PLLLzh16hTWrl0LxhgqK+WNzqCgIOTm5mLRokUo\nLy/H5MmT4e/vD5lM3lhdv349MjMzERgYiLS0NHTr1g3r169X+n01pqY8e/bswZkzZxQ/586dw9Wr\nVyEWi1FaWoqgoCBoaGggNjYWx48fx/Hjx8FxnOJ+LSwscOnSJWzatAkSiQRLliyBi4sLbt261azy\n9OjRAzdu3MB//vMfaGtrY+7cufDy8kJRUVGT8xAIBLXq8/mG1TfffIPly5dj3rx5SExMxJkzZzBl\nyhRUVFTwzns+PC6TyeDm5sZ7rc6cOYNLly4pGkrKuAcA0Nbmv885jlPUV11cXV1RWFiIvLy8RvOe\nPn06jh8/jrNnz2Lbtm2QSCQYOnRoi8oFoMFyAXV/vpp7f6T5OvQYO0JI6xvcazBiU2Lh6+yrSKu4\nWoGQCS0cY2dVe4xdxdUKBPgFKKO4Cr1798bmzZuRl5cHS0vLRs9PT09H586deRMAfv7551rnicVi\nTJgwARMmTEBoaCi8vb1x8eJFeHh4AAA8PDzg4eGB+fPnY+bMmVi/fj2mTZtWK59evXrh0aNHyMzM\nRK9evV7gTmvz8PCAUCjEtWvXMGTIkDrPuXjxIh48eIClS5cqxkj98ccftX5Za2trIzg4GMHBwViy\nZAnMzMywb98+zJ49G9ra2g0O/H+Wvr4+Ro8ejdGjR2PhwoUwNzfHkSNHMHz4cFhaWuLYsWO8Rsix\nY8d449MkEgnu3bsHmUwGgUD+x8HJkyd5z3HkyBEMHTqUN57uypUrjY7N69OnD7Zt2wZDQ0OYmpq2\n6B5ay7hx4/Dpp5/iiy++wJo1a2odf/ToEcRiMQDA0dER/v7+2LBhA1JSUhAWFsa79+bU17PX1by3\n09LSeHV05MgRpb93SeOoYUfaJVrHTn24OLkgBCFIOpmESlkltAXaL7SVn7Lzq8/EiRPx1VdfYeTI\nkfjqq6/g4OCA69evo6CgAOPHj691vqurK+7fv49NmzbB19cX6enptX6RLlq0CL1794a7uzsEAgG2\nb98OQ0ND2NjYICsrCxs2bMDIkSNhZWWF27dv4+jRo/X+4gsICMBrr72GN998EytXroSnpydu376N\nS5cu4b333mv2/T4bsjMwMMDChQuxcOFCcByHgIAAVFVV4ezZszh9+jSWL18OW1tb6OjoYNWqVViw\nYAGys7Px6aef8n6h//jjj2CMoU+fPjAyMkJSUhKKiorg7u4OQL4Ab35+Pv766y84OTlBX1+/zuU9\nvv76a1haWqJHjx7Q09PDzp07oampia5duwIAPvzwQ4SHh8PV1RX9+vXD/v37kZSUxMvD398fpaWl\nWLx4MUJDQ3Hy5En88MMPvHNcXV2xbds2pKamwsLCAlu3bkVGRoai4VOfSZMmITo6GsOHD8fSpUvh\n7OyMu3fvIjk5Ge7u7hg1alSj91BfnTT0uCksLCywevVqTJ8+HY8fP8bUqVPh4OCAhw8fYt++fUhN\nTVVMaAHkvXaTJk2CTCbDlClTeHk5ODhgz549uHDhgmL2b109dTVlrSmvo6Mjxo0bh1mzZmHdunWK\nyRMXLlzArl27Gix/S+6ZNEIpI/XaoQ58a4S0uY76ecrPz2fvvPMO69y5MxMKhczNzY1t2bKFMSYf\n7C0QCHiTJ8LDw5mZmRnT19dnw4cPZzt37mQCgUAxOH/JkiWsW7duzMDAgHXq1In5+voqrr9z5w4b\nO3Yss7KyYjo6OszCwoJNmzaNFRYWKvJ/dvIEY4wVFRWxDz74gJmbmzNtbW1mb2/PVqxY0aJ7fXby\nRI2NGzcyLy8vJhQKmVgsZv3792dr165VHN+zZw9zdnZmQqGQ9ezZk6WlpTFNTU3FaxQfH88GDBjA\nxGIx09PTY56enmzTpk2K66VSKXvrrbeYsbEx4ziORUVF1Vm2devWsV69ejGRSMQMDAxY37592f79\n+xXHZTIZW7hwIevcuTPT19dn48aNY9HR0UxTU5OXz6ZNm5iDgwPT1dVlw4YNY7t27eLVz5MnT9j4\n8eOZSCRiJiYm7P3332fh4eHM3t5ekUdISAhvMkWNgoICNnPmTGZpacm0tbWZpaUlGzt2LDt9+nST\n7qEuz0+eeP4xY4xNmTKF+fn5NZgPY4ylp6ez0aNHM4lEwnR0dJiDgwObMGEC+/vvv3nnSaVSJpFI\n2IgRI2rl8fDhQzZs2DDWqVMnxnGcop6ff18yxtjgwYNZaGio4nFhYSGbPn06MzU1ZTo6OqxPnz7s\n8OHDiuN1fZ4YY8zJyane90VH1NB3qbK+Z2mvWNIu0V6x7Qt9nkh7Exsbi6lTp7bqAsIdUUFBAayt\nrfHTTz/hX//6l6qL89KhvWJfEC1QTAghhMjXUczPz8eiRYtgZWVFjbp2RNkLFFOPHSGkUfR5Iu1N\nbGwspk2bppihSxqWmpoKf39/ODg4YNu2bfD29lZ1kV5KbdFjRw07Qkij6PNECCEvjkKx5KVFIXRC\nCCGk+ahhRwghhBDSQVAolhDSKPo8EULIi6NQLCGEEEIIaTJq2JF2icbYEUIIIc1HDTtCCCGEkA6C\nxtgRQhpFnydCCHlxNMaOEEJUJDs7GwKBAH/88UebPadAIEBcXFyr5O3r64upU6e2St6kZezt7bFs\n2TJVF0MpIiMj4ezsrOpiEFDDjrRTNMaOKEtISAhCQ0MByBtOR44cUXGJ6pefn4/XX3+9yecLBAKk\npaUhNjYW9vb2DZ7LcRw4jnvRIjbLF1980Wi5XmYnTpzA/PnzXzgfgUAATU1NnDt3jpdOr//LSVPV\nBSCEqL+cy5dxLTERAqkUMi0tOA4eDFsXl3aRnyoaNC0lkUiafY263Ju6kkql0NLSapW8TUxMlJaX\njo4OPv74Yxw4cEBpeRL11KF77CIjI6nnR035+vqqugikiXIuX0ZWbCz879+H7+PH8L9/H1mxsci5\nfLld5NfQmJV79+4hNDQUXbp0ga6uLlxdXbF58+Z6z1+0aBHc3d2hr68PGxsbzJw5E4WFhYrjhYWF\nCA0Nhbm5OYRCIWxsbPDhhx8qjqenp2PgwIEQiUQQiUTw8vLCoUOHFMefD8UWFxdj3rx5sLGxgVAo\nhL29Pb788ssWvQ51iYmJgaurK3R1ddG1a1csW7YM1dXViuNxcXHo168fjIyMYGpqihEjRuDq1au8\nPJYtWwZHR0cIhUJIJBIMGTIE5eXliI2NxeLFi5GTkwOBQACBQIDPP/+8znJIpVIsWLAA1tbWEAqF\nsLCwwMSJExXHGWMIDw+HRCKBoaEhJkyYgOjoaF6Dq65QYHp6OgQCAXJzcwEAjx8/xuTJk2Fraws9\nPT24urpi5cqVvGtCQkIQGBiImJgY2NnZQSgUoqKiAnfv3kVISAgkEglEIhFeffVVHD16tMn3UBc7\nOzssXbqU9zgiIgJz586FiYkJunTpggULFvDqpD4ffPABDh8+jMTExHrPacprFBsbCy0tLaSmpsLT\n0xN6enrw9/dHfn4+UlJS4OXlBQMDAwQGBuL27du1niMuLg4ODg7Q1dVFUFAQcnJyFMdu3LiBsWPH\nwtLSEvr6+ujevTu2b9/e6L11dKmpqYiMjFRafh26x06ZLxQhpG7XEhMRoKMDPPNHVACA5H/+gW2f\nPs3PLyMDAaWlvLQAX18kJyW1qNeuvh6tsrIyDBo0CPr6+oiLi4OjoyOuXbuGBw8e1JuXnp4eNmzY\nAGtra2RlZWH27NmYM2cOYmNjAQCfffYZTp06hf3798Pc3Bw3b97EhQsXAABVVVUYOXIkwsLCsHXr\nVgDAuXPnoKenV+dzMcYwYsQI3Lp1C6tXr0b37t2Rl5eHS5cu1bq3lvRKRkZGIjY2Ft999x28vLxw\n4cIFzJgxA+Xl5YoGWGVlJRYvXgx3d3cUFhZi8eLFGD58OM6fPw8tLS3Ex8djxYoViIuLQ48ePVBQ\nUIC0tDQAwIQJE3D58mXs2LEDJ06cAADo6+vXWZaYmBjs3r0bO3bsgIODA/Lz83ljG1etWoXo6Gis\nWbMG3t7e2Lt3L6Kiomrdc2OvQUVFBTw9PfHRRx9BLBYjPT0dM2bMgLGxMUJCQhTnZWRkQCQS4ddf\nf4VAIEBVVRX8/Pzg4eGBhIQEGBkZYdeuXQgMDMTp06fh6ura6D3Upa56i4mJwaeffoqMjAycPHkS\nkyZNQrdu3RAWFtZgXp6enggJCcHHH3+MkydP1vtaNOV9IpPJ8Pnnn2PTpk3Q1NTEm2++iXHjxkEg\nEGD9+vXQ0dHBhAkTsGDBAuzatUtx3Z07d7B27Vrs2bMHMpkM77//PsaOHYvMzEwAQElJCQYPHoyo\nqCgYGBjgv//9L0JDQ2FlZfVS/zHv6+sLX19fREVFKSW/Dt2wI+orNTX1pf6gqxOBVFp3ehN6Geq8\nTiarO72yskX5PdsDJ3sm77i4OGRnZ+PatWuwsLAAANja2jaY16JFixT/t7GxwbJlyzBx4kRFwy43\nNxevvPIK+vyvQWtlZQVvb28AQFFRER4/fox//etfcHR0BADFv3VJTk7GkSNHcOLECfTs2ROAvEdn\n4MCBinNqenJ8fHzw7rvvNvxCPKO0tBRff/019u7di6CgIMW9L1myBHPnzlU07J5t7ADy17Jz5844\nceIEvL29kZOTgy5duiA4OBiampqwsrJCjx49FOfr6+tDQ0Oj0RBzbm4uunbtCh8fHwDy1613796K\n419//TXmz5+Pt99+GwDw8ccfIyMjA/v27ePl09iMQjMzM3zyySeKx7a2tsjIyEBcXBzvXjU0NLBt\n2zZFozs2NhZFRUXYtWsXNDQ0AAALFy5EYmIi1q1bh+jo6Ebvoal8fHzw73//G4D8/bF582YkJiY2\n2rDjOA5LliyBs7MztmzZUqvuajRl1iVjDN9++y26d+8OAJg2bRr+/e9/IzMzE6+88goAYPr06bze\nRkD+voqNjYWDgwMAYNu2bXBxcUFycjL8/f3RrVs3dOvWTXH++++/j8TERMTFxdH3vRJ16FAsIaT1\nyeoZfyT73y/AZucnqPtrSaat3aL86pOZmQkPDw9Fo64p4uPj4ePjA0tLSxgaGmLy5MmQSqXIz88H\nAMyaNQt79uyBp6cn5s2bh4SEBMUvUrFYjClTpiA4OBjDhg3DihUrcOXKlQbLJxaLFY06ZTp//jzK\nysowduxYGBoaKn5mzJiBwsJCFBQUAABOnz6NMWPGwMHBASKRSNHwrQmvvfnmm5BKpbC1tUVoaCi2\nb9+O4uLiZpcnNDQUZ8+ehZOTE2bOnIn4+HhI//cHQ2FhIW7fvo0BAwbwrhk4cGCzl4aQyWRYvnw5\nvLy8YGpqCkNDQ6xbt04Rhqzh5ubG60k9fvw48vPzYWRkxHu90tPTkZWV1eg9NBXHcfDy8uKlmZub\n4+7du0263tzcHB9++CHCw8Px/+3deVAUZ/oH8O8gDAPMjI6iyFEKCIoIiwmia0wIikexxotdD7Ie\nsAYsrzVuVkMgoC5SCSagbnklbowoOkazVsqrSi0Vr1JYK0BZEYJoQDciKBgOUQLD+/vDZX4Og3JI\nZmj4fqqmyu5+++2n+3GGZ97unn769Gmbtt00Dl9fX/20g4MDAOgLvcZ5ZWVlBjno27evvqgDAE9P\nT9jb2+tHrWtqahAdHQ0fHx/06dMHKpUKJ06cMDr+9Go4YkedEr+9Sceg8eNxZvduBD+XszO1tfAI\nDwfacep00I8/PuvP2tqwv+DgDojWUFsKg4yMDMyaNQsxMTFITk6GRqPBlStXsGDBAvz6v9HEiRMn\n4s6dOzh58iTS09Mxd+5c+Pr64syZM/rTWCtWrMCpU6dw+vRpxMXFYcuWLYiKiurwfXuZxpHLb7/9\nFoMHDzZartFoUFNTg4kTJyIwMBC7d++Gg4MDhBAYNmyYfn+dnJyQl5eHc+fO4ezZs0hISMCHH36I\njIwMuLi4tDoePz8//PTTTzh9+jTOnTuHFStWIC4uDlevXm11HxYWFkb5bFpYJScn49NPP8WmTZvw\n2muvQaVSISUlBcePHzdo1/T0eENDA4YOHYrvvvvOaLuNbV+2DyqVqtX7IW/yBUYmkxmMNLdk9erV\n2LlzJ5KTk41Ou7bmGDW2e37dxn/3eO7LWuM8IUSrLwNYtWoVjhw5go0bN2LIkCGwtbXFBx98YHCd\nKr06jtgR0SsZOGQIPMLDcbZfP6T36oWz/frBIzy83XexdnR/LzJixAjcuHEDP//8c6vaX7p0Cfb2\n9vjHP/6BgIAAeHh44O7du0btNBoN5syZgx07duD48eM4f/48cnNz9cuHDRuGlStX4sSJE1i4cCG+\n/PLLZrfn7++PR48e6a9P6kjDhg2DQqHArVu34O7ubvSysLBAbm4uHj58iMTERAQGBmLIkCEoLy83\nKgzkcjkmTZqEpKQkXL9+HTU1NfpTpHK5vFUX/gPPTttOnz4dmzdvxrVr15Cbm4sLFy5ArVbD2dkZ\nly9fNmh/+fJlg4KiX79+KC0tNSiCvv/+e4N1Lly4gJCQEISHh8PPzw/u7u7Iz89vsTAJCAjA7du3\noVKpjI5V//79W9wHU7Kzs8O6deuwYcMGo5G+1hyjV/HgwQPcvn1bP52fn4+HDx/C29sbwLPjP3fu\nXPzpT3+Cr68v3Nzc8GM7b4qiF+OIHXVKvMZOWgYOGdKhhVdH99ecsLAwbNiwAVOnTsWGDRvg7u6O\n27dvo6ysDLNmzTJq7+XlhQcPHmDXrl0ICgrCpUuXsH37doM2sbGxGDFiBLy9vWFhYYG0tDSoVCoM\nGDAABQUF2LlzJ6ZOnQoXFxfcu3cPFy9ehL+/f7PxBQcH46233sLs2bORkpICX19f3Lt3D3l5eVi4\ncGGb91cIoS/KlEolYmJiEBMTA5lMhuDgYNTX1+P69evIzs7Gp59+ioEDB8La2hr//Oc/8be//Q2F\nhYWIjo42KIK++uorCCEQEBCAXr164cyZM6iqqtL/IXdzc8P9+/dx9epVeHh4wM7ODjY2NkaxffbZ\nZ3B2doafnx9sbW2h1WphaWmpH01sPL3o5eWFUaNG4ciRIzhz5oxBH+PGjUNNTQ3i4+MRERGB77//\nHtu2bTNo4+Xlhb179yI9PR1OTk7Ys2cPMjMzodFoXnrs/vznP2Pjxo2YPHkyEhMT4enpiZKSEpw9\nexbe3t6YNm1ai/vwopy8bLq9Fi5ciM2bN+Orr74yuL6xNcfoVdja2iIiIgIpKSkQQmD58uV47bXX\nMG7cOADPjv93332H0NBQ2NnZISUlBcXFxXB0dOywGAiA6KK68K51C+fOnTN3CPScrvp+un//vpg/\nf76wt7cXCoVCDB06VKSmpgohhPjpp5+EhYWFuHz5sr59XFyccHBwEHZ2dmLy5MlCq9UKCwsLUVRU\nJIQQIiEhQfj4+AilUil69uwpgoKC9OsXFxeL0NBQ4eLiIqytrYWTk5OIiooSlZWV+v5lMpnYt2+f\nfrqqqkosX75cODo6CrlcLtzc3ERSUlK79jUoKEhERkYazPvXv/4lhg8fLhQKhdBoNOL3v/+92LFj\nh375t99+Kzw9PYVCoRCvv/66OH/+vLC0tNQfo8OHD4s33nhDaDQaYWtrK3x9fcWuXbv069fV1Yl3\n331X9O7dW8hkMrFu3bpmY/viiy+Ev7+/UKvVQqlUipEjR4ojR47olzc0NIiYmBhhb28v7OzsxMyZ\nM8XGjRuFpaWlQT+7du0S7u7uwsbGRvzhD38QBw4cMMhPRUWFmDVrllCr1aJPnz5i2bJlIi4uTri5\nuen7CA8PFxMmTDCKsaysTCxevFg4OzsLuVwunJ2dRWhoqMjOzm7VPjTH1dVVJCYmvnBaCCHee+89\nMXbs2Jf20/T/jRBCHD9+XMhkMoN9a80x+vrrr4WVlZXBOnv37hUWFhYG8xr/7+t0OiGEEGvXrhWe\nnp5i3759wtXVVSgUCjF+/HhRWFioX+fu3bti0qRJws7OTjg6Ooq1a9eKhQsXtrh/XcnLPks76nOW\nz4olohbx/USdze7duxEZGdnmGxSIzInPiiUiIiKiVmNhR50SnxhCRC3h49SIjLGwIyIiyQkPD9f/\n7AoR/T9eY0dELeL7iYjo1fEaOyIiIiJqNRZ21CnxGjsiIqK2Y2FHRERE1EVI7hq7kpIShIaGQi6X\nQy6XY//+/ejTp49RO14TRNRxevfujUePHpk7DCIiSdNoNCgvL292WUfVLZIr7BoaGmBh8WygMTU1\nFcXFxYiOjjZqx8KOiIiIpKLb3jzRWNQBQGVlZYvP+CNp4jV20sXcSRvzJ23MH0musAOAnJwcjBo1\nClu2bEFYWJi5w6HfQHZ2trlDoHZi7qSN+ZM25o9MWtht2bIFI0aMgEKhQEREhMGy8vJyzJgxA0ql\nEq6urtBqtfplGzduxNixY5GcnAwA8PPzQ0ZGBtavX4+EhART7gKZyC+//GLuEKidmDtpY/6kjfkj\nkxZ2zs7OiIuLw1/+8hejZUuXLoVCoUBpaSn27duHxYsX48aNGwCAlStX4ty5c/jggw8MHvisVqtR\nW1trsvjboyOHxdvbV1vWa03bl7Vpz7LOeuqgo+PqivnrrLkDpJe/V83dy5ZL7b0H8LOzpWXdJXev\n0l9H5k9K7z2TFnYzZszAtGnTjO5iffz4MQ4fPoyEhATY2tpizJgxmDZtGvbu3WvUR3Z2Nt5++22M\nGzcOKSkpWL16tanCbxd+OLW8rLn5hYWFLcbxW+uKH04ttemIPy6dIXeA9PLXWQq7rpi/7vLeAzpH\n/qT23mtNWykVdma5K/bjjz/Gzz//jK+//hoAkJWVhTfffBOPHz/Wt0lJSUF6ejqOHDnSrm14eHjg\n1q1bHRIvERER0W9p0KBBKCgoeOV+LDsgljaTyWQG09XV1VCr1QbzVCoVqqqq2r2Njjg4RERERFJi\nlrtimw4SKpVKVFZWGsyrqKiASqUyZVhEREREkmaWwq7piN3gwYNRX19vMMqWk5MDHx8fU4dGRERE\nJFkmLex0Oh2ePn2K+vp66HQ61NbWQqfTwc7ODqGhoYiPj0dNTQ0uXbqEo0ePYt68eaYMj4iIiEjS\nTFrYNd71mpSUhLS0NNjY2CAxMREAsG3bNjx58gT9+vXD3LlzsWPHDgwdOtSU4RERERFJmuSeFfsq\nKisrMX78eOTm5iIjIwPe3t7mDonaIDMzE++//z6srKzg7OyMPXv2wNLSLPf/UBuVlJQgNDQUcrkc\ncrkc+/fvN/rZI+r8tFotVqxYgdLSUnOHQm1QWFiIgIAA+Pj4QCaT4eDBg7C3tzd3WNRK6enpWL9+\nPRoaGvDXv/4V06dPf2n7blXY1dfX45dffsGqVavw97//HcOGDTN3SNQG9+/fh0ajgbW1NWJiYuDv\n748//vGP5g6LWqGhoUH/nOfU1FQUFxcjOjrazFFRW+h0OsycORN37tzBtWvXzB0OtUFhYSFWrVqF\nQ4cOmTsUaqMnT55g9uzZ+Pe//w0rK6tWrSPJZ8W2l6WlJb+lSFj//v1hbW0NALCyskKPHj3MHBG1\nVmNRBzwbOddoNGaMhtpDq9Vi1qxZRje/kTRcvnwZgYGBiI2NNXco1AZXrlyBjY0NpkyZgtDQUJSU\nlLS4Trcq7KhrKCoqwunTpzFlyhRzh0JtkJOTg1GjRmHLli0ICwsdOHdqAAAJYUlEQVQzdzjUBjqd\nDocOHcLs2bPNHQq1g5OTE27duoULFy6gtLQUhw8fNndI1EolJSUoKCjAsWPHEBkZibVr17a4jiQL\nuy1btmDEiBFQKBSIiIgwWFZeXo4ZM2ZAqVTC1dUVWq222T74rdN8XiV/lZWVmD9/PlJTUzliZwav\nkjs/Pz9kZGRg/fr1SEhIMGXY9D/tzV9aWhpH6zqB9uZPLpfDxsYGABAaGoqcnByTxk3tz51Go8GY\nMWNgaWmJcePG4YcffmhxW5K88tzZ2RlxcXE4efIknjx5YrBs6dKlUCgUKC0tRVZWFiZPngw/Pz+j\nGyW60aWFnU5781dfX485c+ZgzZo18PT0NFP03Vt7c1dXV6e/PkStVqO2ttYc4Xd77c1fbm4usrKy\nkJaWhps3b+L999/Hpk2bzLQX3Vd781ddXQ2lUgkAuHDhAq8vN4P25i4gIADJyckAgOzsbAwaNKjl\njQkJ+/jjj0V4eLh+urq6WsjlcnHz5k39vPnz54vo6Gj9dEhIiHBychKjR48Wu3fvNmm8ZKit+duz\nZ4/o06ePCAoKEkFBQeKbb74xecz0TFtzl5GRIQIDA8XYsWPFxIkTxd27d00eM/2/9nx2NgoICDBJ\njPRibc3fiRMnhL+/v3jrrbfEggULhE6nM3nM9Ex73ntbt24VgYGBIigoSNy+fbvFbUhyxK6RaDLq\nlp+fD0tLS3h4eOjn+fn5IT09XT994sQJU4VHLWhr/ubNm8cfre4k2pq7kSNH4vz586YMkV6iPZ+d\njTIzM3/r8KgFbc1fSEgIQkJCTBkivUB73ntLlizBkiVLWr0NSV5j16jp9R7V1dVQq9UG81QqFaqq\nqkwZFrUS8yddzJ20MX/SxvxJlylyJ+nCrmnlq1QqUVlZaTCvoqICKpXKlGFRKzF/0sXcSRvzJ23M\nn3SZIneSLuyaVr6DBw9GfX09CgoK9PNycnLg4+Nj6tCoFZg/6WLupI35kzbmT7pMkTtJFnY6nQ5P\nnz5FfX09dDodamtrodPpYGdnh9DQUMTHx6OmpgaXLl3C0aNHeV1WJ8P8SRdzJ23Mn7Qxf9Jl0ty9\n+j0eprdmzRohk8kMXuvWrRNCCFFeXi6mT58u7OzsxMCBA4VWqzVztNQU8yddzJ20MX/SxvxJlylz\n162eFUtERETUlUnyVCwRERERGWNhR0RERNRFsLAjIiIi6iJY2BERERF1ESzsiIiIiLoIFnZERERE\nXQQLOyIiIqIugoUdERERURfBwo6IqInw8HDExcV1aJ+LFy/G+vXrO7RPIqKmLM0dABFRZyOTyYwe\n1v2qtm/f3qH9ERE1hyN2RETN4NMWiUiKWNgRUaeSlJQEFxcXqNVqeHl54ezZswCAzMxMjB49GhqN\nBk5OTli+fDnq6ur061lYWGD79u3w9PSEWq1GfHw8bt26hdGjR6NXr16YM2eOvn16ejpcXFzwySef\noG/fvnBzc8P+/ftfGNOxY8cwfPhwaDQajBkzBtevX39h25UrV8LBwQE9e/bE7373O9y4cQOA4end\nKVOmQKVS6V89evTAnj17AAB5eXmYMGEC+vTpAy8vLxw6dOiF2woKCkJ8fDzefPNNqNVqTJo0CWVl\nZa080kTUFbGwI6JO48cff8TWrVtx7do1VFZW4tSpU3B1dQUAWFpaYvPmzSgrK8OVK1dw5swZbNu2\nzWD9U6dOISsrC1evXkVSUhIiIyOh1Wpx584dXL9+HVqtVt+2pKQEZWVluHfvHlJTUxEVFYWbN28a\nxZSVlYWFCxdi586dKC8vx6JFizB16lT8+uuvRm1PnjyJixcv4ubNm6ioqMChQ4fQu3dvAIand48e\nPYqqqipUVVXh4MGDcHR0RHBwMB4/fowJEyZg7ty5ePDgAQ4cOIAlS5YgNzf3hcdMq9Vi9+7dKC0t\nxa+//orPP/+8zcediLoOFnZE1Gn06NEDtbW1+OGHH1BXV4cBAwbA3d0dAPD6669j5MiRsLCwwMCB\nAxEVFYXz588brL969WoolUp4e3vD19cXISEhcHV1hVqtRkhICLKysgzaJyQkwMrKCoGBgZg8eTK+\n+eYb/bLGIuzLL7/EokWLEBAQAJlMhvnz58Pa2hpXr141il8ul6Oqqgq5ubloaGjAkCFD0L9/f/3y\npqd38/PzER4ejoMHD8LZ2RnHjh2Dm5sbFixYAAsLCwwfPhyhoaEvHLWTyWSIiIiAh4cHFAoFZs2a\nhezs7DYccSLqaljYEVGn4eHhgU2bNmHt2rVwcHBAWFgYiouLATwrgt555x04OjqiZ8+eiI2NNTrt\n6ODgoP+3jY2NwbRCoUB1dbV+WqPRwMbGRj89cOBA/baeV1RUhOTkZGg0Gv3rv//9b7Ntx44di2XL\nlmHp0qVwcHDAokWLUFVV1ey+VlRUYNq0aUhMTMQbb7yh31ZGRobBtvbv34+SkpIXHrPnC0cbGxuD\nfSSi7oeFHRF1KmFhYbh48SKKioogk8nw4YcfAnj2cyHe3t4oKChARUUFEhMT0dDQ0Op+m97l+ujR\nI9TU1Oini4qK4OTkZLTegAEDEBsbi0ePHulf1dXVmD17drPbWb58Oa5du4YbN24gPz8fn332mVGb\nhoYGvPvuuwgODsZ7771nsK23337bYFtVVVXYunVrq/eTiLo3FnZE1Gnk5+fj7NmzqK2thbW1NRQK\nBXr06AEAqK6uhkqlgq2tLfLy8lr18yHPn/ps7i7XNWvWoK6uDhcvXsTx48cxc+ZMfdvG9pGRkdix\nYwcyMzMhhMDjx49x/PjxZkfGrl27hoyMDNTV1cHW1tYg/ue3Hxsbi5qaGmzatMlg/XfeeQf5+flI\nS0tDXV0d6urq8J///Ad5eXmt2kciIhZ2RNRp1NbW4qOPPkLfvn3h6OiIhw8f4pNPPgEAfP7559i/\nfz/UajWioqIwZ84cg1G45n53runy56f79++vv8N23rx5+OKLLzB48GCjtv7+/ti5cyeWLVuG3r17\nw9PTU38Ha1OVlZWIiopC79694erqCnt7e6xatcqozwMHDuhPuTbeGavVaqFUKnHq1CkcOHAAzs7O\ncHR0xEcffdTsjRqt2Uci6n5kgl/3iKibSU9Px7x583D37l1zh0JE1KE4YkdERETURbCwI6Juiacs\niagr4qlYIiIioi6CI3ZEREREXQQLOyIiIqIugoUdERERURfBwo6IiIioi2BhR0RERNRF/B91bdtd\n40wV6QAAAABJRU5ErkJggg==\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10a5b13d0>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 15
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name='performance2'></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"# Performance growth rates: NumPy and SciPy library functions"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Okay, now that we have seen that Cython improved the performance of our Python code and that the matrix equation (using NumPy) performed even better, let us see how they compare against the in-built NumPy and SciPy library functions. \n",
|
|
"\n",
|
|
"Note that we are now passing `numpy.arrays` to the NumPy, SciPy, and (C)Python matrix functions (not to the Cython implemtation though!), since they are optimized for it."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"funcs = ['cy_classic_lstsqr', 'py_matrix_lstsqr',\n",
|
|
" 'numpy_lstsqr', 'scipy_lstsqr']\n",
|
|
"\n",
|
|
"orders_n = [10**n for n in range(1, 7)]\n",
|
|
"perf2 = {f:[] for f in funcs}\n",
|
|
"\n",
|
|
"for n in orders_n:\n",
|
|
" x_list = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
|
|
" y_list = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
|
|
" x_ary = np.asarray(x_list)\n",
|
|
" y_ary = np.asarray(y_list)\n",
|
|
" for f in funcs:\n",
|
|
" if f != 'cy_classic_lstsqr':\n",
|
|
" perf2[f].append(timeit.Timer('%s(x_ary,y_ary)' %f, \n",
|
|
" 'from __main__ import %s, x_ary, y_ary' %f).timeit(1000))\n",
|
|
" else:\n",
|
|
" perf2[f].append(timeit.Timer('%s(x_list,y_list)' %f, \n",
|
|
" 'from __main__ import %s, x_list, y_list' %f).timeit(1000))\n"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 35
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"labels = [ ('cy_classic_lstsqr', '\"classic\" least squares in Cython (numpy arrays)'),\n",
|
|
" ('py_matrix_lstsqr', '\"matrix\" least squares in (C)Python and NumPy'),\n",
|
|
" ('numpy_lstsqr', 'in NumPy'),\n",
|
|
" ('scipy_lstsqr','in SciPy'),\n",
|
|
" ]\n",
|
|
"\n",
|
|
"plt.rcParams.update({'font.size': 12})\n",
|
|
"\n",
|
|
"fig = plt.figure(figsize=(10,8))\n",
|
|
"for lb in labels:\n",
|
|
" plt.plot(orders_n, perf2[lb[0]], alpha=0.5, label=lb[1], marker='o', lw=3)\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('time per computation in milliseconds [ms]')\n",
|
|
"#plt.xlim([1,max(orders_n) + max(orders_n) * 10])\n",
|
|
"plt.legend(loc=4)\n",
|
|
"plt.grid()\n",
|
|
"plt.xscale('log')\n",
|
|
"plt.yscale('log')\n",
|
|
"plt.title('Performance of least square fit implementations')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAnYAAAIECAYAAACUvmMzAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xdc09f+P/DXJ4RN2ENwgIADQcFtnbj3tgpWW2312nF7\n29723tufrQVrrR3f1ttWe9uqdbYqpe5aN3EvXBUUZCgKArL3SnJ+f3wkgxlJIPnA+/l49PFoTpKT\nk5ykvPv+vM85HGOMgRBCCCGECJ7I0AMghBBCCCH6QYEdIYQQQkgrQYEdIYQQQkgrQYEdIYQQQkgr\nQYEdIYQQQkgrQYEdIYQQQkgrQYEdabVkMhlefvllODs7QyQS4cyZM4YekiD99ttv8PHxgVgsxssv\nv1znYxYtWoSxY8e28MhIzbk5ffo0RCIRHj9+/Mx9de7cGZ9++mkzjLI2Ly8vrF69ukVey1iJRCL8\n+uuvhh4GaYUosCMGtWjRIohEIohEIpiamsLLywuvvfYacnNzde77999/x86dO3Ho0CFkZGTgueee\n08OI2xa5XI6XX34ZISEhePToEb755ps6H8dxHDiOa9Gx7dixAyJR2/1PWF1zM3jwYGRkZMDd3R0A\ncO7cOYhEIjx8+LDR/qKjo/HOO+8097ABGOb7oovU1NQm/8/hmDFjsHjx4lrtGRkZmD17tj6GR4gG\nsaEHQMjw4cMREREBmUyG6OhoLF26FI8ePcKhQ4ea1F9lZSXMzMyQkJCA9u3bY9CgQTqNr7q/tujx\n48coKSnBxIkTlcFCXRhjoL3On51CoQCAJgWo9c2Nq6trrcdqMzdOTk7PPIa2Rp/f8brmiRB9aLv/\nu0uMhqmpKVxdXeHh4YFp06bhrbfewpEjR1BRUQEA2LVrF4KCgmBpaYnOnTvj3XffRWlpqfL5wcHB\nWLJkCVasWAEPDw94enpi5MiR+Oijj5CcnAyRSARvb28AQFVVFd5//3106NAB5ubm8Pf3x86dOzXG\nIxKJ8N1332H+/Pmwt7fHiy++iC1btsDU1BRSqRQ9e/aElZUVRo0ahYyMDERFRSEoKAg2NjYYO3as\nxmWw+/fvY9asWWjfvj2sra3Rq1cv7NixQ+P1goODsXTpUqxatQru7u5wcnLCSy+9hJKSEo3H7d69\nG3379oWlpSWcnZ0xadIk5OfnK+//7rvv0L17d1haWqJr16749NNPIZfLG/zsL126hOHDh8PKygqO\njo544YUXkJWVBQDYsmULPD09AfDB97NmLBqbt+PHjyM4OBhOTk6wt7dHcHAwrl69qtHHxo0b4efn\nB0tLSzg5OWHEiBFIS0uDVCrFiy++CADKjG99l4kB4NNPP4WPjw8sLCzg6uqKCRMmoLy8XOOz69Ch\nA6ytrTFhwgRs27ZN45Jm9fyrqyuLs3TpUvj6+sLKygo+Pj744IMPUFlZqbw/PDwcXbp0QUREBLp3\n7w5zc3MkJCSguLgYb731lnIMffr0wd69e+t9P/XNjVQqVY77wYMHGD58OAD+MqtIJMKoUaPq7bPm\n5VEvLy989NFHeO2112Bvb4927drhf//7H8rLy/HGG2/A0dERHTp0wPr16zX6EYlE+PbbbzF79mzY\n2NigQ4cO+Pbbb+t9XYD/XYaHh8Pb2xuWlpYICAjATz/9VKvfdevWYd68ebCxsYGXlxf27t2LvLw8\nhIaGwtbWFj4+PtizZ4/G8zIzM7Fo0SK4urrC1tYWQ4cOxdmzZ5X3V39mJ06cwPDhw2FtbQ1/f38c\nOXJE+ZhOnToBAEaOHKnx35PGft+LFi3CqVOnsHXrVuX3tPr7UvNSbHp6OkJCQuDg4AArKyuMHDkS\n165de6ZxAo1/10kbwAgxoJdeeomNHTtWo+2rr75iHMex4uJitnnzZubg4MB27NjB7t+/z86cOcN6\n9erFFi5cqHz8iBEjmEQiYa+99hq7e/cui4mJYbm5uey9995jnTt3ZpmZmSw7O5sxxth7773HnJyc\nWGRkJEtISGCffvopE4lE7OTJk8r+OI5jTk5ObP369Sw5OZklJCSwzZs3M5FIxEaOHMmuXLnCrl+/\nzrp06cKGDh3Khg8fzi5fvsxu3rzJunfvzubNm6fs6/bt22z9+vXsr7/+YsnJyey7775jYrGYRUVF\naYzf3t6e/fOf/2Tx8fHs2LFjzNHRka1YsUL5mJ9//pmZmpqyTz75RPke161bp3xfYWFhzNPTk+3b\nt489ePCAHT58mHXq1Emjj5rS09OZRCJhL7zwAouJiWHnzp1jvXr1YsOHD2eMMVZWVsauXr3KOI5j\nBw8eZJmZmayysrLeeRwzZozytjbztnfvXvbbb7+xe/fusTt37rAlS5YwR0dHlpOTwxhjLDo6monF\nYrZ9+3b28OFDdvv2bbZp0yaWmprKKisr2fr16xnHcSwzM5NlZmaywsLCOsf2+++/M1tbW3bo0CH2\n6NEjdvPmTfbNN9+wsrIyxhhj+/btY2KxmK1du5YlJCSwTZs2MVdXVyYSiVhaWpry/YjFYo1+Hz16\nxDiOY6dPn2aMMaZQKNgHH3zArly5wlJSUtiBAweYu7s7CwsLUz4nLCyMWVlZseDgYHblyhWWkJDA\nioqKWHBwMBs5ciQ7f/48u3//Pvvpp5+YmZmZxvdSXX1zExUVxTiOY2lpaUwul7MDBw4wjuNYdHQ0\ny8zMZHl5efV+H7y8vNjq1auVtz09PZm9vT1bu3YtS0pKYp988gkTiURs/PjxyrY1a9YwkUjE7ty5\no3wex3HM0dGRrVu3jiUkJLBvvvmGicVitn///npf66WXXmKBgYHs+PHj7MGDB2z37t3M3t6ebdq0\nSaPfdu3asW3btrGkpCT2+uuvM2trazZu3Di2detWlpSUxN58801mbW2t/A6VlpYyPz8/NmfOHHbt\n2jWWlJTEVq9ezczNzdndu3cZY0z5mQUGBrKjR4+yxMREtnjxYmZra6v8vG7cuME4jmN79+7V+O9J\nY7/vgoICNnz4cBYSEqL8nlb/hjiOY7/88ovyuzNgwADWu3dvdv78eXb79m02b9485uDgoHwtbcbZ\n2HedtA0U2BGDqhkQxMbGMm9vb/bcc88xxvg/Lj/++KPGc06fPs04jmP5+fmMMT4w6tatW62+w8LC\nmK+vr/J2SUkJMzc3Z//73/80Hjdz5kw2atQo5W2O49iSJUs0HrN582bGcRy7deuWsu3LL79kHMex\n69evK9vWrl3LnJ2dG3zP06dPZ0uXLlXeHjFiBAsKCtJ4zGuvvab8DBhjrGPHjuzNN9+ss7+SkhJm\nZWXFjh49qtG+detWZm9vX+84PvzwQ9axY0dWVVWlbLt16xbjOI6dOXOGMcbY/fv3Gcdx7Pz58w2+\np5rzqM281SSXy5mDg4Pyj92ePXuYnZ1dvQHb9u3bGcdxDY6LMca+/vpr1rVrV433qW7IkCFswYIF\nGm3vvfeeMkBiTLvArr7X7tKli/J2WFgYE4lE7NGjR8q2qKgoZmFhwQoKCjSeu3jxYjZjxox6+65r\nbtQDO8YYO3v2LOM4jqWkpNTbT7W6AruZM2cqbysUCmZra8umTZum0ebg4MDWrVunbOM4jr344osa\nfc+fP58NGzasztdKTk5mIpGIxcfHazxn5cqVGr8LjuPYO++8o7ydlZXFOI5j//jHP5RteXl5jOM4\n9scffzDG+Hnr0KEDk8lkGn2PHDmSvf3224wx1We2d+9e5f2ZmZmM4zh27Ngxxph2c12t5u97zJgx\nbPHixbUepx7YnThxgnEcpww2GWOsoqKCubu7s48//ljrcTb2XSdtA12KJQYnlUohkUhgZWWFnj17\nwtfXF7/88guysrLw8OFDvPPOO5BIJMp/Jk2aBI7jkJiYqOyjb9++jb5OYmIiKisrlZenqg0fPhyx\nsbEabQMGDKj1fI7j0LNnT+VtNzc3AECvXr002nJycpS1OKWlpXj//fcREBAAJycnSCQSHD58WKOY\nneM4BAYGaryWu7s7MjMzAQBPnjxBamoqxo0bV+f7io2NRVlZGWbNmqXxOb366qsoLCxETk5Ovc8b\nNGgQxGJVqW2vXr1gZ2eHO3fu1PkcbWg7b/fv38fChQvRpUsX2NnZwc7ODgUFBcrPZty4cfD29kbn\nzp0RGhqKDRs21PteGjJv3jxUVVXB09MTixcvxo4dO1BcXKy8/+7duxg8eLDGc4YMGdKk975hwwYM\nHDgQ7dq1g0QiwfLly2stXHBzc0OHDh2Ut69evYrKykq0b99e4/P65ZdfNL7jLa3m95LjOLi4uGh8\n3zmOg6urq/LyfbWaC5UGDx5c6zdWLTo6Gowx9O3bV+P9r1mzptb7Vx+Ps7MzTExMNMZjb28PMzMz\nPHnyBAD/2WZkZMDe3l6j73PnztXqOygoSPnvrq6uMDExUf4G66PN71sbsbGxcHJyQvfu3ZVtZmZm\nGDhwYK3PraFxNvZdJ20DLZ4gBjdo0CBs3boVYrEYHh4eykCj+j9W3377LUaOHFnree3btwfA/3Gx\ntrbW65jq6k8kEmms5Kv+dxMTk1ptjDFwHId//etfOHDgANauXYtu3brBysoK7777LgoKCjT6rrk4\ng+M4ZWF9Y6ofFxkZia5du9a638HBoc7ncRzXLAseqsfT2LxNmTIFrq6u+P7779GxY0eYmppi6NCh\nypo0a2trREdH4/z58zhx4gR++OEH/Pvf/8bJkyfRp08frcfj4eGBuLg4REVF4dSpU1i1ahX+85//\n4PLlyxoBVkPqWtxQVVWlcfu3337D3//+d3z++ecYMWIEbG1tERERgQ8++EDjcTW/WwqFAnZ2doiO\njq71GoZetFOzrpDjuDrbtP2u1qX6uRcvXoSVlVWtvhsaT31jrO5ToVDAz88P+/btq/W8mq9V12fd\n2PvS9vfdVNX/HdF2nPr4rhPho4wdMTgLCwt4e3ujU6dOGtkjNzc3dOzYEXFxcfD29q71j7m5+TO9\njq+vL8zNzXH69GmN9tOnT2tk4vTp7NmzWLBgAebMmYOePXuic+fOiI+Pf6atHlxdXdGhQwccPXq0\nzvv9/f1hYWGBpKSkOj+n+lZc+vv749KlSxoByq1bt1BQUICAgIBne6NqtJm3nJwc3L17F++//z7G\njh2rXEhQnWmpJhKJMGzYMKxcuRLXrl2Du7u7crFL9R84bYJTMzMzjB8/Hp9//jlu376N0tJS7N+/\nHwDQo0cPnD9/XuPxNW+7urpCLpdrjO/69esajzlz5gx69+6Nt99+G71794aPjw/u37/f6Nj69++P\n/Px8lJWV1fqsdP1jXP0ZNbaIRt8uXryocfvChQvw9/ev87HV2faUlJRa779z5846jaN///5ITk6G\nRCKp1Xe7du207qe+z1Gb37eZmRlkMlmD/fv7+yt/E9UqKipw+fLlZ/4tNvRdJ22D4DJ2mZmZmDVr\nFszMzGBmZoZff/2Vlum3YqtXr8Yrr7wCBwcHTJs2Daamprh79y6OHDmCH374AYD2W21YWVnhH//4\nB1asWKG8pBQZGYkDBw7gxIkTzTL+bt26Yd++fZg1axasra3x9ddfIz09XeOPijbjDwsLw2uvvQY3\nNzfMnj0bCoUCUVFRCA0NhZOTE5YvX47ly5eD4ziMHj0aMpkMt2/fxs2bN/HZZ5/V2eff//53fPPN\nN1i0aBGWL1+OvLw8vP766xg+fHiTL0VWa2zeHBwc4OLigp9++gne3t7Izs7Gv//9b1haWir72L9/\nP+7fv49hw4bBxcUF165dw6NHj9CjRw8AUP7R379/P4YMGQIrK6s6M62bNm0CYwz9+/eHvb09Tp48\niaKiImU/7777Lp5//nkMGDAAEydOxLlz57Bjxw6NP84DBw6ERCLB+++/j//3//4fkpKS8PHHH2u8\nTvfu3fHzzz/jwIED8Pf3x6FDhxpc2Vpt1KhRGDNmDGbNmoUvvvgCPXv2RF5eHi5cuABLS0ssWbLk\n2SfgKU9PT4hEIvzxxx+YO3cuzM3NYWdnV+dja34H6/pOatv2xx9/YP369Rg3bhyOHDmCiIgIREZG\n1vkcX19fvPzyy1i6dCm++OILDBo0CCUlJbh27Zrye9FUL7zwAtauXYvJkydj9erV6NKlCzIzM3Hq\n1Cn06NED06dP16ofZ2dn2NjY4OjRo/Dz84O5uTkcHBy0+n137twZUVFRSE5Ohq2tLezt7TX+BxYA\nRo8ejQEDBmD+/PlYv349bG1tsWrVKlRWVuK1117T+v029l0nbYPgMnYuLi44f/48oqKiMH/+fGzY\nsMHQQyI6aGyj0gULFiAiIgKHDh3CwIEDMWDAAKxcuVIjk1FfH3W1r169GkuXLsXbb7+Nnj174tdf\nf8Uvv/xS5yXDuvp71ra1a9cqt18ZM2YMOnbsiDlz5tS6pFuzn5ptr7zyCrZs2YLIyEj07t0bI0aM\nwNGjR5V/ID788EN8/fXX2LBhA4KCgjBs2DB88803DWY8XF1dcezYMaSmpqJ///6YOnWqMtht7D3W\n9Z7VH9fYvIlEIvz2229ISkpCr1698PLLL+Odd97R2I/N0dERBw8exMSJE9GtWze8//77WLFihXKz\n1/79++Ott97CsmXL4ObmhjfffLPOsTk6OmLz5s0YOXIkevTogf/+97/YsGGDcs5nzJiBr776Cl98\n8QUCAwOxc+dOfP755xrBh4ODA3bu3IlLly4hMDAQq1evxpdffqnxnpctW4aFCxdi8eLF6NOnD65e\nvYrw8PBG5xoADhw4gFmzZuGdd96Bn58fpkyZgj///BO+vr6Nfu4Ntbm5uWHNmjX47LPP4OHhgZkz\nZ2rdV1O+79U++ugjnDhxAkFBQfjss8/w5ZdfagRRNZ/z008/4Z133sHq1avh7++PMWPGYPv27fDx\n8al3vNqoztD369cPixcvRrdu3TB79mxER0fDy8urwfegTiQSYf369YiIiEDHjh2VWUZtft/vvvsu\nnJ2dERgYCFdXV1y4cKHO19i3bx+6d++OyZMnY8CAAXjy5AmOHz8OR0dHrcfZ2HedtA0ca44imxby\n3XffwczMDMuWLTP0UAghrYhUKsWoUaOQmpoKDw8PQw9HUEQiEXbs2IH58+cbeiiEtEmCuxQL8HVA\nf/vb35Cfn19rQ1NCCCGEkLbKYJdi161bh379+sHCwqLWOXq5ubmYOXOmcnfxmicDBAYG4vLly/jk\nk0+watWqlhw2IaSNENJZpoQQUs1gGbv27dtjxYoVOHr0KMrKyjTue+ONN2BhYYEnT57gxo0bmDx5\nMgIDA9GjRw9UVVUpl7fb2toqj50ihBB9CQ4ObvGVpK2FLlufEEJ0Z/AauxUrViA1NRWbN28GAJSU\nlMDR0RGxsbHKwuGXXnoJHh4eWLNmDa5cuYJ//etfMDExgampKTZt2lTnlgDt27fXOLOTEEIIIcRY\n+fj46GVTcoOviq0ZV967dw9isVhjNVhgYKBy9+0BAwbg9OnTOHXqFI4ePVrvPk+PHz9WbiNhyH/C\nwsIM3tezPE+bxzb0mKbcV1e7Pj83Y5i71jp/xjp3Qpw/XeeuofuF9tvT9zjaym/PWOZPaL89bR7b\nEr+9pKQkvcRVBg/sataxFBcXw9bWVqNNIpGgqKioJYelN8HBwQbv61mep81jG3pMU+6rq/3BgweN\njqO56XPudOnPmOfPWOcOEN786Tp3Dd0vtN8eQP/tbOy++h5vDPMntN+eNo9tid+evhj8UuyHH36I\ntLQ05aXYGzduYOjQoSgpKVE+5v/+7/9w5swZHDhwQOt+m+u4JNIyFi1ahC1bthh6GKQJaO6EjeZP\n2Gj+hEtfcYvRZey6du0KmUymcZ351q1bTTriKDw8HFKpVNchEgNYtGiRoYdAmojmTtho/oSN5k94\npFIpwsPD9dafwTJ2crkcVVVVWLlyJdLS0rBhwwaIxWKYmJggNDQUHMdh48aNuH79OqZMmYKLFy/C\nz89P6/4pY0cIIYQQoRB8xm7VqlWwsrLC559/jh07dsDS0hKrV68GAHz//fcoKyuDq6srFixYgB9+\n+OGZgjoifJRpFS6aO2Gj+RM2mj9isH3swsPD6009Ojg4aHV4NiGEEEIIUTH44onmwnEcwsLCEBwc\n3KyrTwghhBBCmkoqlUIqlWLlypV6uRTbqgO7VvrWCCGEENLKCL7GjpCGUJ2IcNHcCRvNn7DR/BEK\n7AghhBBCWolWfSmWauwIIYQQYsyoxk5LVGNHCCGEEKGgGjvSqlGdiHDR3AkbzZ+w0fwRCuwIIYQQ\nQloJuhRLCCGEEGJgdClWC+Hh4ZSWJoQQQojRkkql9Z7E1RSUsSNGSSqV0mpmgaK5EzaaP2Gj+RMu\nytgRQgghhBANlLEjhBBCCDEwytgRQgghhBANFNgRo0SLXoSL5k7YaP6EjeaPtOrAjlbFEkIIIcSY\n0apYLVGNHSGEEEKEgmrsCCGEEEKIBgrsiFGiS+jCRXMnbDR/wkbzRyiwI4QQQghpJajGjhBCCCHE\nwPQVt4j1MBZCCCGEENIE8fEpOHEiSW/9tepLsbTdiXDRvAkXzZ2w0fwJG82fsMTHp2Dlykhs3XpG\nb3226oydPveFIYQQQgjRp8OHkyCXvwsrKwBYqZc+qcaOEEIIIaSF3bsHvPeeFIWFwQCA06epxo4Q\nQgghRFDKyoAjR4BbtwCZTKH3/lt1jR0RLqoTES6aO2Gj+RM2mj/jFh8PfP89H9QBgLe3D0SikwgI\n0N9rUMaOEEIIIaQZqWfp1I0c6YklS4ALF07p7bWoxo4QQgghpJnExwOHDgFFRao2GxtgyhSge3dV\nG+1jRwghhBBipOrL0vXsCUyciKcrYfWPauyIUaI6EeGiuRM2mj9ho/kzDvHxwPr1mkGdjQ0QEgLM\nnt18QR3QyjN24eHhCA4ORnBwsKGHQgghhJBWrqwM+PNP4K+/NNt79QImTKg7oJNKpXoNyKnGjhBC\nCCFER/HxwMGDQHGxqq2uWrr6UI0dIYQQQoiBNZSlmzgRsLRs2fFQjR0xSlQnIlw0d8JG8ydsNH8t\nq7qWTj2oq66lmzWr5YM6gDJ2hBBCCCHPxNiydOqoxo4QQgghREv11dJNnQp069b0fqnGjhBCCCGk\nhRhzlk4d1dgRo0R1IsJFcydsNH/CRvPXPOLi6q6lCw01XC1dfShjRwghhBBSB6Fk6dRRjR0hhBBC\nSA1xcfwZr/qupasP1dgRQgghhOhZaSl/xquQsnTqqMaOGCWqExEumjtho/kTNpo/3cTFAd9/L4xa\nuvpQxo4QQgghbVppKV9Ld/u2ZntgIH/GqxACumqtusYuLCwMwcHBCA4ONvRwCCGEEGKEWrqWriap\nVAqpVIqVK1fqpcauVQd2rfStEUIIIURHxpal01fcQjV2xChRnYhw0dwJG82fsNH8aae6lk49qJNI\n+Fq6mTOFdem1JqqxI4QQQkibYGxZuuZAl2IJIYQQ0urVVUsnkQBTprRMLV1jaB87QgghhJBGtIUs\nnTqqsSNGiepEhIvmTtho/oSN5k/T3bv8Ga81a+nmzxd+LV19KGNHCCGEkFalrWXp1FGNHSGEEEJa\njbt3+Vq6khJVm0TC70vXtavhxtUYqrEjhBBCCHmqtBQ4fBiIidFsDwoCxo9v3Vk6dVRjR4wS1YkI\nF82dsNH8CVtbnb/qWjr1oK66lm7GjLYT1AGUsSOEEEKIQFGWrjaqsSOEEEKI4Ai1lq4+VGNHCCGE\nkDaHsnQNoxo7YpTaap1Ia0BzJ2w0f8LW2uePaukaRxk7QgghhBg1ytJpT3A1dleuXMHbb78NU1NT\ntG/fHtu2bYNYXDs+pRo7QgghRPju3AH++KN2Ld20aUCXLoYbl77pK24RXGCXkZEBBwcHmJubY/ny\n5ejbty9mz55d63EU2BFCCCHC1VCWbsIEwMLCMONqLvqKWwRXY9euXTuYm5sDAExNTWFiYmLgEZHm\n0NrrRFozmjtho/kTttYyf3fu1F1L98ILfC1dawvq9EmwNXYpKSk4fvw4PvroI0MPhRBCCCF6UFLC\nn/FaM0vXuzdfS9caA7qU+HgknTiht/4MlrFbt24d+vXrBwsLCyxevFjjvtzcXMycORM2Njbw8vLC\nzp07Ne4vLCzEiy++iK1bt1LGrpUKDg429BBIE9HcCRvNn7AJef7u3AG+/14zqLO15bN006e33qAu\nccsWjIqN1VufBsvYtW/fHitWrMDRo0dRVlamcd8bb7wBCwsLPHnyBDdu3MDkyZMRGBiIHj16QCaT\nISQkBGFhYejSmqomCSGEkDaopISvpasZ27TmLF21pGPHMDotDXj4UG99GixjN3PmTEyfPh1OTk4a\n7SUlJdizZw9WrVoFKysrDBkyBNOnT8f27dsBADt37sSVK1ewatUqjBw5EhEREYYYPmlmraVOpC2i\nuRM2mj9hE9r8VWfp1IO61p6lUyovh+jyZb0GdYAR1NjVXAFy7949iMVi+Pr6KtsCAwOVX9aFCxdi\n4cKFWvW9aNEieHl5AQDs7e0RFBSkTFNX90e3jfP2zZs3jWo8dJtu0226Tbf1d7usDCguDkZsLPDg\nAX+/l1cwevcGLC2lSEsDunQxnvHq/XZBAXDqFDZfvowtRUXQJ4Nvd7JixQqkpqZi8+bNAICzZ89i\n7ty5SE9PVz5mw4YN+PXXXxEVFaV1v7TdCSGEEGJ86tqXztaWP+O1TVRYJSQAkZFARQVSsrORePMm\nRnt7g9u+vXWcFVvzTdjY2KCwsFCjraCgABKJpCWHRQghhBA9asu1dAAAxoDz54GTJ/l/B+Dp7g6M\nG4dTqanA05IzXYn00osOOI7TuN21a1fIZDIkJiYq227duoWAgIBn7js8PFyZAiXCQvMmXDR3wkbz\nJ2zGOn/11dItWNAGaukAoKoK+P134MQJZVAHOzvg5Zdx39YWZ5480dtLGSxjJ5fLUVVVBZlMBrlc\njoqKCojFYlhbW2PWrFn46KOPsHHjRly/fh0HDx7ExYsXn/k1wsPD9T9wQgghhGilzWfpAL6ebtcu\nQK3EDJ6ewNy5gLU1gt3dERwcjJUrV+rl5QxWYxceHo6PP/64VttHH32EvLw8vPzyyzh+/DicnZ3x\n2WefISRAG3DXAAAgAElEQVQk5Jn6pxo7QgghxHBiY/lautJSVZutLX/Gq9r6yNYtJQWIiNAsKOzf\nnz8TrcY+vG32rFhtUWBHCCGEtDzK0j0VHc1/EAoFf1skAiZNAvr1q/Phbfas2GdBNXbCRfMmXDR3\nwkbzJ2yGnr/YWP6M1zZbSwcAcjlw6BD/T3VQZ20NLFpUZ1AnlUr1Wjpm8FWxzYlq7AghhJDmV1LC\nX3a9c0ezvU8fYNy4NhLQAUBxMX/pVX3TYXd3ICSEXyxRh+Dg4NZRY9fc6FIsIYQQ0vyolu6px4/5\nRRLqW7b17Ml/EKamjT5dX3FLq87YEUIIIaR5UJZOze3bwP79gEzG3+Y4YMwYYPBg/t9bENXYEaNE\n8yZcNHfCRvMnbC01f9W1dOpBXXUt3bRpbSioUyiA48f5PeqqgzoLC/6w2yFDtArqqMbuGVCNHSGE\nEKI/lKVTU1bGB3RqByrA2RkIDQWcnLTuhmrstEQ1doQQQoj+UC2dmqwsvp4uJ0fV1rUrMHs2YG7e\npC6pxo4QQgghzY6ydDXExwN79gAVFaq24cOBkSObVE8XnxiPE9dO6G14rbrGjggX1fkIF82dsNH8\nCZs+54+xumvp7OyAhQvbWC0dwH8gZ8/ymbrqoM7UFHj+eWDUqCYHdVuitiDdJb3xB2upVWfswsPD\nldeuCSGEEKIdytLVUFnJr3pV33nZ3p7fn65duyZ3e+LaCdwvuI/oddF6GCSPauwIIYQQAkCVpTt8\nWLOWzs6Oz9D5+BhubAaTnw/s3AlkZqravLz4TJ21tU5df7DxA1wyvQQ5k+P04tNUY0cIIYQQ/Sgu\n5gO6mlm6vn2BsWPbYJYOAB484E+SUI9yBwzgD701MWlyt4wxnH90HjczbkLeQa77ONVQjR0xSlTn\nI1w0d8JG8ydsTZk/xoCYGOD77+uupZs6tQ0GdYwBV64A27apgjoTEz5tOWmSTkFdlbwKe+7uwYnk\nE+js3RmyRBnMTZq2krYulLEjhBBC2qjiYr6W7u5dzfa+fflauibu3CFsMhmfurx+XdVmYwPMmwd0\n7KhT1wXlBdgVswvpxfxiCWcPZ0ySTIJlkSWO4ZhOfVejGjtCCCGkjaFaunoUFfGXXh89UrV5ePCL\nJGxtder6YcFD7I7ZjZKqEmVbP49+mOg7ESYiE9rHThu0KpYQQgjRRFm6eqSlAbt3A4WFqrbAQGDK\nFH5bEx1ce3wNhxMOQ874ejoRJ8KkLpPQz6MfpFKpXksg6s3YLVy4UKsOzM3NsXHjRr0NSF8oYyds\nUqmUAnKBorkTNpo/YWto/ihL14Bbt4CDB1XnvXIcH+UOGtSk/emqyRVyHE06iitpV5RtVqZWmOs/\nF172XhqPbfaMXUREBJYvX17vi1QP4KuvvjLKwI4QQgghPMrS1UOhAI4fBy5eVLVZWgJz5ugc6ZZW\nlSIiNgIP8h8o29rZtENIQAjsLex16rsh9WbsfHx8kJSU1GgH3bp1Q3x8vN4HpivK2BFCCGnrKEvX\ngLIyIDISUI91XFyA0FDA0VGnrjOKM7ArZhfyy/OVbf4u/pjefTrMTMzqfI6+4hZaPEEIIYS0QpSl\na8CTJ/zRYLm5qrbu3YGZM3X+YO5k3cHeu3tRpahSto3qPArDOg0D18BlXX3FLU3axy45ORkPHjzQ\n+cUJqQ/tpSVcNHfCRvMnbFKpFIwBt2/zZ7yqB3V2dsCLL/L70rXpoC4uDti4UTOoGzGC385Ehw+G\nMYao+1GIiI1QBnXmJuYIDQjFcM/hDQZ1+qTVqtiQkBD84x//wODBg7F582a8/vrr4DgO3377LZYs\nWdLcYySEEEJIA+LjU3DiRBJu3foL27YpYGXlA2dnT+X9lKUDf136zBkgKkrVZmbGZ+n8/HTqukJW\ngb1xexGXHadsc7R0RGhAKFysXRp8bnxyMk6on0GrI60uxbq4uCAtLQ1mZmYICAjAjz/+CHt7e0yf\nPh2JiYl6G4w+cRyHsLAw2u6EEEJIqxYfn4ItWxKRnz8aCQn8wk6Z7CSCgnzh4+OJ6dMBb29Dj9LA\nKiuBvXs1U5gODvz+dG5uOnWdW5aLXTG78KTkibLNx8EHc3rMgaWpZYPPjU9Oxsrt25GQnY3odeta\nrsbO3t4e+fn5SEtLw4ABA5CWlgYAkEgkKCoq0nkQzYFq7AghhLQFX399ChcujEJ2tma7n98p/Pe/\no9p2lg4A8vKAnTv5urpqnTsDzz8PWFnp1HVyXjJ+i/0NZbIyZdtzHZ7DWJ+xEHGNV7t9e+AALvr4\nIL2yEqf79Gm5GrvAwECsWbMGH3/8MSZPngwASE1NhZ2dnc4DIKQuVOcjXDR3wkbzJyyxsUBUlEgZ\n1OXnS2Fuzu+r262biIK65GTgp580g7pBg/hDcHUI6hhjuJR6CTv+2qEM6sQiMWZ0n4HxvuO1Cuqe\nVFbidGEh0isrmzyOumhVY7dp0yasWLECZmZm+OKLLwAAFy9exAsvvKDXwRBCCCGkcaWl/BYmMTGA\nXK5Qtjs5Af37A2IxYGamaKCHVo4x4PJl4Ngxfq86ADAx4VeOBAXp1LVMIcMf9/7AjYwbyjaJmQTz\nAuahg20HLYbGcL24GH/m5KCsekNkPaLtTgghhBABiYvjD0koeXrkaHZ2CuLiEtGjx2jl9msVFSex\naJEvunXzrL+j1komAw4dAm7eVLVJJPyq1w6NB14NKaoowu7Y3UgtTFW2tZe0R0hACCTmkkafXy6X\n42BODmKfTl72o0f4KyEBfkOH4qfu3Vt2H7uzZ8/ixo0bKCoqUgZNHMdh+fLlOg+iOVBgRwghpDUp\nKwP+/BP46y/N9t69gc6dU3DuXBIqK0UwM1Ng9GifthnUFRXx572mqgIvdOjAB3WSxgOvhqQVpmFX\nzC4UVarWFgS6BWJqt6kQixq/AJpaXo7IrCzkq2XpXM3MEFRcjJv37uGNadNaLrB78803ERERgWHD\nhsHSUnOFx/bt23UeRHOgwE7Y6LxK4aK5EzaaP+N07x6fpVNfryiR8KdHdOmiamvT85eaygd16h9S\nUBAwZQp/bVoHf2X+hQPxByBT8EEZBw7jfcdjYPuBje5PxxjDhcJCnMzLg0ItLuknkWC8oyNMRXw9\nXrOfFatux44diI2NhYeHh84vSAghhBDtlJcDR48CN25otgcGAhMm8MeaEvAf0KFDgFzO3xaJgPHj\ngQEDAB02BlYwBU4kn8CFRxeUbZZiS8zpMQc+jo2fx1Ysk2FvdjaSylSrZi1EIkxzdkYPa+smj6sh\nWmXsevXqhVOnTsHZ2blZBtEcKGNHCCFEyJKSgP37gcJCVZu1NV//37274cZlVBQKfoHEpUuqNktL\nfisTHTfvK6sqQ+SdSCTlqc6SdbFyQWjPUDhaNn6WbFJZGfZmZaG4OtgE0MHcHHNcXGBvalrr8S16\nVuzVq1fx6aefYv78+XCrsZHf8OHDdR5Ec6DAjhBCiBBVVADHjwPR0ZrtAQHApEk6b73WepSWAr/9\nBty/r2pzdQVCQ/nNh3WQVZKFXTG7kFOWo2zr5tQNs/xmwVzc8B4ycsYQlZeH84WFGnHIUDs7jHRw\ngEk9GcQWvRR77do1HD58GGfPnq1VY/fo0SOdB9FcwsPD6eQJgWrTdSICR3MnbDR/hnX/Pp+ly89X\ntVlZAZMnA/7+jT+/zcxfZiawaxe/+XA1Pz/+eDAzM526vpdzD7/f+R0V8gpl23DP4RjpNbLRerr8\nqir8np2NR+XlyjZrExPMcnGBTz3XzaVSqV73j9QqsPvggw9w6NAhjB07Vm8v3BLCw8MNPQRCCCGk\nUZWVwIkTwJUrmu1+fnztfzOVYwnTnTvAvn38h1Zt5Ehg+HCd6ukYYzj38BxO3T8FBj5zZioyxYzu\nM+Dv2nhUfaekBAeys1GuUO0f6GNpiZnOzrBpYPFGdQJq5cqVTR67Oq0uxXbq1AmJiYkw0zEKbkl0\nKZYQQogQPHzIxym5uao2S0v+smtAgE6xSuvCGCCVAqdPq9rMzIBZs3QuOqySV2F//H7EPIlRttmZ\n2yG0Zyja2bRr+LkKBY7m5iJabTWuiOMwyt4eQ+zsGs3yVWvRGrstW7bgypUrWLFiRa0aO5FIq1PJ\nWhwFdoQQQoxZVRVw6hRf96/+56prV36BhI7brrUuFRXAnj1AfLyqzdERCAnh6+p0UFBegF0xu5Be\nnK5s87TzxFz/ubA2azhVmlVZicisLGSqZQ/txWLMdnFBRwuLZxpHiwZ29QVvHMdBrrbaw5hQYCds\nbaZOpBWiuRM2mr+WkZoK7N0L5Khq82FhwW9hEhjY9Cxdq5y/3Fxg504gK0vV5uMDzJmj834vKfkp\niIiNQElVibKtv0d/TPCdABORSb3PY4zhRnEx/szNRZXapdce1taY5uQEC5P6n1ufFl08kZycrPML\nEUIIIW2dTMZfTTx/XjNL5+vLbzZsa2uwoRmnpCR+5avaYgQMHgyMGcPvVaeD6MfROJxwGArGB2Yi\nToRJXSahn0e/Bp9XoVDgYHY2YkpUwaCY4zDB0RF9JRKtL702FzorlhBCCGkBjx/zWTr1xJO5Ob+P\nbu/eVEungTH+GvWxY6oIWCzmr1EHBurUtVwhx5HEI7j6+KqyzdrUGnP958LTvuFj2NIqKhCZlYW8\nqiplm4uZGea4uMBNx3UI+opb6g13V6xYoVUHYWFhOg+CEEIIaa3kcr6WbuNGzaCuc2fgtdeAPn0o\nqNNQVcWvJjl6VBXU2doCixfrHNSVVJZg261tGkGdu407/tb3bw0GdYwxXCgowKb0dI2gro9Egr+5\nu+sc1OlTvRk7Gxsb/FXzpOEaGGPo27cv8tU33DESlLETtlZZJ9JG0NwJG82ffmVk8Fm6zExVm6kp\nMG4c0K+f/gM6wc9fYSG/P93jx6q2jh2BefMAGxudus4ozsCumF3IL1fFLAGuAZjebTpMTWqfBFGt\nRC7HvuxsJJSWKtvMRSJMdXJCgI5jUtfsNXalpaXw9fVttANz84Z3YCaEEELaGrkcOHeO35lDrbYe\nnp7AjBk6H4zQOj16BOzeDRQXq9r69OH3fWlgHzhtxD6Jxb64fahS8Nk2DhxGdR6FoZ2GNlgTd7+s\nDHuys1Ekkynb2j89FsyhjmPBjAHV2BFCCCF69OQJfyVRPelkagqMHg0MHEiXXet0/Trwxx98RAzw\nCyMmTAD699d50+GoB1E4k3JG2WZuYo7ZPWajq1PXep+nYAzS/HycLSjQiCUG29lhdAPHgumiRVfF\nEkIIIaRhCgVw4QIQFaWKTwD+SuKMGYCTk+HGZrTkcr6WTv3IDSsrYO5cwMtLp64rZBXYc3cP4nNU\ne985WjoiNCAULtYu9T6vQCbD71lZeFjjWLAZzs7oIoCDeo1zd2HS5unz3DzSsmjuhI3mr2mys4Gf\nf+aPBasO6sRivpZu8eKWC+oENX8lJcD27ZpBnZsb8Le/6RzU5ZblYuP1jRpBnY+DD5b2WdpgUBdX\nUoIfHj/WCOo6W1riVQ8PQQR1QCvP2IWHhyvPYCOEEEL0TaHgd+U4dYrfo65a+/Z8ls6l/hiibcvI\n4BdJqC++9PcHpk/njwnTQVJuEiLvRKJMVqZsG9xxMMZ4j4GIqzufJVMocCwvD1cKC5VtIo5DsL09\nhtrZQdSM18+lUqleA3KqsSOEEEKaICcH2L+fP+u1mokJEBwMDBmi8/65rVdsLF+EWL1tCMcBo0YB\nQ4fqXE93KfUSjiUdAwP/918sEmNq16kIbFf/NinZT48Fy1A7Fszu6bFgnZ7xWDBdtGiN3ZMnT2Bp\naQmJRAKZTIZt27bBxMQECxcuNNqzYgkhhJDmwBh/9fDECVVsAgDu7nyWrsaR6qQaY3xq8+xZVZu5\nOTB7Nn9Arg5kChkO3TuEmxk3lW0SMwlCAkLQ3rZ9PcNhuFVcjMO5uahUW7rs9/RYMMsmHAtmDLSK\nyqZMmYLExEQAwAcffICvvvoKa9euxT//+c9mHRxpuwRVJ0I00NwJG81fw/LygK1bgT//VAV1IhGf\npVuyxPBBndHOX3k5f96relDn5MR/aDoGdUUVRdhyc4tGUNfBtgP+1vdv9QZ1FQoF9mZnY192tjKo\nE3McJjs5Ya6Li2CDOkDLjF1CQgKCgoIAADt27MCFCxcgkUjQo0cP/Pe//23WARJCCCGGxhhw7Rp/\nwpXaFTu4ufFZOnd3w43N6OXk8EFddraqzdcXmDMH0PFSZ2phKnbH7EZRZZGyLahdEKZ0nQKxqO4Q\nJ72iAr9lZSFXLd3qbGqKOS4uaNcK9ubVqsbO2dkZqampSEhIQEhICGJjYyGXy2FnZ4di9Y0EjQjV\n2BFCCNGHggLgwAH+PPpqIhFfEjZ8uM5757ZuiYlAZCSfsas2ZAi/qZ+OpVy3Mm7h4L2DkCn4VSsi\nToRxPuMwsP3AOjcdZozhcmEhjuflQa4WH/SWSDDR0RFmBi4ta9EauwkTJmDu3LnIycnBvHnzAAB3\n7txBhw4ddB4AIYQQYowYA27eBI4cASoqVO0uLnyWrn3dV/kIwH94Fy7whYjVwYpYzK967dlTp64V\nTIHjScdxMfWiss1SbInn/Z+Ht4N3nc8pfXos2D21Y8HMRCJMcXJCLz0eC2YMtMrYlZeXY+vWrTAz\nM8PChQshFoshlUqRkZGBkJCQlhjnM6OMnbAJ/rzDNozmTtho/nhFRXyWLiFB1cZxwODBwMiRxpul\nM4r5q6riP7zbt1VttrZASAjg4aFT12VVZYi8E4mkPFX61NXaFSEBIXC0dKzzOQ/KyvB7jWPB3J8e\nC+ZkRMeCtWjGzsLCAsuWLdNoM/gXhxBCCNEzxvh45PBhzauHTk58lq5jR8ONTRAKCvj96dLTVW2d\nOvEnSeiYGcsqycLOmJ3ILctVtnV37o6Z3WfCXFy7Nk7BGM7k5+N0jWPBnrOzw2h7e4hb6a4e9Wbs\nFi5cqPnAp9erGWMa1663bdvWjMNrOsrYEUIIeRbFxcChQ0BcnGb7oEF8SZgRJXeM08OHwO7d/IkS\n1fr1AyZO5Df400F8djz23N2DCrnqmvgIzxEI9gqus56u8OmxYClq0bnV02PBuhrpCRLNnrHz8fFR\nfljZ2dnYunUrpk6dCk9PT6SkpODQoUN46aWXdB4AIYQQYmgxMXyWTq0ECw4OfEmYjqdbtQ3R0fwe\nMNXnqYlEwKRJfGCnA8YYzj48i6j7UcpNh01FppjpNxM9XHrU+Zz40lLsy85GmdqBvV4WFpjl4gJb\nY72Grkda1diNGzcOK1aswLBhw5Rt586dw8cff4xjx4416wCbijJ2wmYUdSKkSWjuhK2tzV9JCR/Q\nxcZqtvfvD4wdq/PpVi2uxedPLucDuuhoVZu1NX/p1dNTp64r5ZXYH7cfsVmqybG3sEdIQAja2bSr\n9XiZQoETeXm4pHYsGPf0WLBhzXwsmD60aI3dpUuXMGjQII22gQMH4uLFi/U8gxBCCDFud+/yl17V\nrxza2fFZOu+6F1cSdSUlQEQEkJKianN35xdJ2Nnp1HV+eT52xexCRnGGss3L3gtz/efCyrT2pdSc\nqipEZmUhXW35su3TY8E8W/BYMGOgVcZuxIgR6N+/P1atWgVLS0uUlpYiLCwMly9fxpkzZ1pinM+M\nMnaEEELqUlbGZ+nUF20CQJ8+wPjx/ClXpBHp6fwiiYICVVtAAB8V61iMmJKfgt2xu1FapbouPqD9\nAIz3GQ8TUe1avb+Ki3EoJ0fjWLBuVlaY7uwMKwGdINGiGbstW7Zg/vz5sLW1hYODA/Ly8tCvXz/8\n+uuvOg+AEEIIaSn37vE7cajvrW9rC0ybxh+GQLQQEwPs3686U43j+NUlQ4bw/66D6MfROJxwGArG\nB2kmnAkmdZmEvh59az22UqHA4Zwc3FSbTBOOwzhHRwyQSOpcVNEWaJWxq/bw4UM8fvwY7u7u8NTx\n2nlzo4ydsLW1Op/WhOZO2Frr/JWX8xsN37yp2R4UBEyYoPPJVkajWedPoQBOnQLOnVO1WVgAs2cD\nXbro1LVcIcefiX8i+rGqVs/a1BrzAuahk12nWo/PeHosWI7asWBOT48FcxdoyrVFM3bVLCws4Orq\nCrlcjuTkZACAdwsXIhQWFmLMmDG4e/cuLl++jB496l4VQwghhAD8qVYHDgBqNfWwsQGmTgW6dTPc\nuASlvBz4/XfNHZudnfl6OmdnnbouqSxBRGwEUgpUtXruNu4ICQiBnYVmrR5jDFeLinA0N1fjWLBA\nGxtMcnKCeSvdm+5ZaJWxO3LkCF555RWkq284CD66lKstJ24JMpkM+fn5+Ne//oX33nsP/v7+dT6O\nMnaEENK2VVQAx44B165ptvfsyW+tZqTbmRmf7Gxg504gJ0fV1rUrMGuWzqnO9KJ07IrZhYIKVa1e\ngGsApnebDlMTzVq9Mrkc+7OzEVfjWLDJTk4IbAXHgrVoxu7111/HihUr8OKLL8LKwL8EsVgMZx3/\n74AQQkjrlpzMl4Gp1/ZbWwOTJwN0oecZ3LvHZ+rUD8sdNow/V03H7FjMkxjsj9uPKgV/OZUDh9He\nozGk45Ba9XEPy8vxe1YWCtSOBWtnZoY5Li5wFtqeNM1Mq1nJz8/HsmXLDB7UkbZDKpUaegikiWju\nhE3o81dZCfzxB7Btm2ZQ16MH8PrrrT+o09v8MQacPctn6qqDOlNTYM4cfqGEDkEdYwwnk08i8k6k\nMqgzNzFHaM9QDO00VCOoqz4WbHNGhkZQN9DWFkvc3Smoq4NWM/PKK6/g559/1usLr1u3Dv369YOF\nhQUWL16scV9ubi5mzpwJGxsbeHl5YefOnXX20VZXvBBCCKktJQX43/+Aq1dVbZaWfCzy/PN8xo5o\nobKSz9KdPMkHeAC/L90rr/BbmuigQlaBXTG7cPbhWWWbk6UTlvZdiq5OXTUeWySTYXtmJk7l5Skv\nUVqamCDE1RUTnZxa7VmvutKqxm7o0KG4cuUKPD090a6dardnjuOavI/d3r17IRKJcPToUZSVlWHz\n5s3K+0JDQwEAmzZtwo0bNzB58mRcuHBBY6HE4sWLqcaOEEIIqqr4GOTyZVUcAvALI6ZO1fns+bYl\nP5/fny5DtTEwPD35kyR0jIxzSnOwK2YXskqzlG2+jr6Y02MOLMSatXoJpaXYm52NUrU6/k4WFpjt\n4gK7VnosWIvW2C1ZsgRLliypcxBNNXPmTABAdHQ0UlNTle0lJSXYs2cPYmNjYWVlhSFDhmD69OnY\nvn071qxZAwCYNGkSbt26hfj4eCxbtqzeM2sXLVoEr6eH/Nnb2yMoKEi5DLw6XU236Tbdptt0W7i3\nHz0CvvxSisJCwMuLv//xYykGDABCQoLBccY1XqO+7eUFRERAeueO6nb//pBaWABXr+rUf1phGh45\nPkK5rBwPbj4AALww9QWM9h6NM6fPKB8vZwxfHzyI2JISeD098erB5csItLbGoilTIOI44/m8dLxd\n/e8PHjyAPj3TPnbN4cMPP0RaWpoyY3fjxg0MHToUJWpnvHz99deQSqU4cOCA1v1Sxk7YpFKp8kdA\nhIXmTtiEMn8yGRAVBVy4oJml69KFz9LZ2hpubIbUpPljjD/r9c8/+b3qAMDEBJg0Cehbe2PgZ+ua\n4VLqJRxLOgYGfqLEIjGmdZuGXm69NB6b+/RYsMdqCzUkYjFmOTujs6WlTuMQghbN2DHGsHnzZmzf\nvh1paWno0KEDFixYgMWLF+tc51bz+cXFxbCt8YuUSCQoKirS6XUIIYS0DmlpwL59QJbqih7MzfmN\nhoOCdD78oG2Ry/nz1dT3hLGx4S+9dqq9MfCzkClkOBh/ELcybynbbM1tERIQAg+Jh8Zjbz89FqxC\n7ViwLlZWmOHsDGsBHQtmDLQK7D799FNs27YN7777Ljp16oSHDx/iyy+/xOPHj/Hhhx/qNICa0amN\njQ0K1XeRBFBQUACJRKLT6xBhEULGgNSN5k7YjHn+ZDLg9Gng/HlVYgkAvL35I0p1PHe+VXim+Ssu\nBnbvBh49UrV5eADz5un8YRZWFGJ3zG6kFaUp2zradsS8gHmwMVMVPVYqFPgzNxc31JI3JhyHMQ4O\nGGRrS4skm0CrwG7Dhg04ffq0xjFi48ePx7Bhw3QO7GpOWteuXSGTyZCYmAjfpwf33bp1CwFNWIkT\nHh6O4OBgo/4PFSGEkMalp/NZusxMVZuZGTBuHH+1kP7+P6PHj/lFEuqJlF69+OvYpqb1P08LqYWp\n2B2zG0WVqmCtd7vemNx1MsQiVdiRWVmJyKwsZFVWKtscnx4L5iHQY8GaQiqVatTd6UqrGjtXV1fc\nv38f1morYoqLi+Ht7Y0nT5406YXlcjmqqqqwcuVKpKWlYcOGDRCLxTAxMUFoaCg4jsPGjRtx/fp1\nTJkyBRcvXoSfn5/2b4xq7ARNKHU+pDaaO2EztvmTy/nt1M6c0czSeXnxWToHB4MNzShpNX9//cWf\nsVa9LxzHAWPHAs89p3OEfDPjJg7GH4Sc8atZRZwI433GY0D7AcpEDmMM0U+PBZOp/Z3uaWODKW34\nWDB9xS1afXoTJkzAggULEBcXh7KyMty9excvvvgixo8f3+QXXrVqFaysrPD5559jx44dsLS0xOrV\nqwEA33//PcrKyuDq6ooFCxbghx9+eKagjhBCiPBlZgIbNwJSqSqoMzXljwN76SUK6p6ZQsGfsbZn\njyqos7AAXngBGDxYp6BOwRQ4kngE++L2KYM6S7ElFvZaiIEdBiqDujK5HL9lZeGPnBxlUGcqEmG6\nszNmOTu32aBOn7TK2BUUFODNN9/E7t27UVVVBVNTU8ydOxffffcd7O3tW2Kcz4zjOISFhdGlWEII\nERiFgq+jk0r5jF21Tp2AGTMAR0eDDU24ysqAyEggKUnV5uIChIQATk66dV1Vht/u/IbkvGRlm6u1\nK0IDQuFgqYq+Hz09Fixf7QQJNzP+WDAXMzOdxiBk1ZdiV65cqZeM3TNtdyKXy5GdnQ1nZ2eYGPkq\nFbMrdEAAACAASURBVLoUSwghwpOVxdfSpalq7iEW86dYDRyo8/GkbVNWFn80WG6uqq1bN2DWLH45\nsQ6elDzBzts7kVeep2zzc/bDTL+ZMDPhgzXGGM4VFCAqPx8Ktb/L/W1tMc7BAaY0qQBa+FLs1q1b\ncevWLZiYmMDNzQ0mJia4desWtm/frvMACKmLPgtJScuiuRM2Q81fdZbuxx81g7r27YFXX+XLv+jv\nf+NqzV98PLBhg2ZQN2IEn6nTMaiLy47DxusbNYK6YK9gzPWfqwzqip8eC3YyL08Z1FmIRJjn6orJ\nTk4U1DUDrVbFrlixAjdv3tRo69ChA6ZOnYqFCxc2y8AIIYS0DTk5fJZOfdcNExNg5Ei+9Iv+9jcB\nY/yqk1OnVG2mpsDMmYDa8ZxN65rhTMoZRD2IUraZmZhhZveZ8HNR1cMnPj0WrETtenpHCwvMdnaG\nvY4rb0n9tLoU6+DggOzsbI3LrzKZDE5OTigoKGjWATYVXYolhBDjxhh/vuvJk/x5r9Xc3fn4w9XV\ncGMTtMpKPlJ+ejQYAMDeHggNBdzcdOtaXol9cftwJ0vVt4OFA0ICQuBmw/ctZwyn8vJwXi0+4DgO\nQ+3sEGxvDxPam6ZOLXryhJ+fHyIjIzFv3jxl2969e41+pSrtY0cIIcYpL4+PPVJSVG0iEX+VcOhQ\nPmNHmiAvj9+fTn3Dv86dgeefB6ysdOo6vzwfO2/vRGaJqu/O9p3xvP/zsDLl+86rqsLvWVlIVTsW\nzMbEBLNcXODdBo4FawqD7GN37tw5TJo0CWPHjoW3tzeSkpJw4sQJHD58GEOHDtXbYPSJMnbCZmx7\naRHt0dwJW3PPX/WxpMeP84mlam5ufJauXbtme+lWLSU+Hkm7d+OvP/9ELwcH+Hh7w9PZmV9xMm6c\nzpHyg/wHiIiNQGlVqbJtYPuBGOczDiYivu/YkhIcyM7WOBbM19ISM5ydYSPWKo/UprVoxm7o0KG4\nffs2fv31V6SmpmLAgAH45ptv0LFjR50HQAghpG3Iz+f3xU1W7YoBkQgYNgwYPpyydE2VEheHxNWr\nMTo1FaKyMgSbm+PkX38Bb78Nz4kTdeqbMYbox9H4M/FPKBgfsJlwJpjcdTL6uPcBAFQpFDiSm4tr\naseCiTgOox0cMJiOBWtxz7zdSWZmJjw8PBp/sIFRxo4QQowDY8CNG8DRo4DaFTq4uPBZOgH8STFe\n+fk49fe/Y1RqqqrNzAzw98epLl0w6vXXm9y1XCHH4YTDuJZ+TdlmY2aDef7z0NGOT+w8eXos2BO1\n9Ku9WIw5Li7oYGHR5Ndui1o0Y5eXl4c33ngDkZGREIvFKC0txYEDB3DlyhV88sknOg+CEEJI61RY\nyGfpEhNVbRwHDBkCBAfze9SRJmCMPxrs8GGIsrNV7RIJEBAAmJtDpH6t+xkVVxYjIjYCDwseKts8\nJB6Y5z8PdhZ2YIzhenExjuTmokrt0qu/tTWmOjnBgtKvBqPVIvJXX30Vtra2SElJgfnTfW+ee+45\n7Nq1q1kHp6vw8HDaU0ugaN6Ei+ZO2PQ1f4wBN28C33+vGdQ5OwOvvAKMGUNBXZOVlgIREcDevUBF\nBRTV+8F4ekLq4KDcn07RxNMc0ovSseHaBo2grqdrTywOWgw7CzuUy+WIzMrCwexsZVAn5jhMdXbG\nHBcXCuqekVQqRXh4uN760+pndfLkSaSnp8NUbd8ZFxcXPHnyRG8DaQ76/KAIIYRop6gIOHSI3xu3\nGscBgwYBo0bx26mRJkpIAPbvB4qLlU0+vXvjZH4+Rru4AA8eAABOVlTAd/ToZ+4+5kkM9sftR5WC\n33+GA4cx3mMwuONgcByH1PJyRNY4Fsz16bFgrm34WDBdVO/esXLlSr30p1WNna+vL86cOQMPDw84\nODggLy8PDx8+xLhx4xAXF6eXgegb1dgRQkjLYgyIiQEOH+aPJq3m6AhMnw54ehpubIJXWQkcO8Yv\nKVbXrx8wbhxS7t9H0smTEFVWQmFmBp/Ro+HZrZvW3SuYAqfun8K5h+eUbRZiC8z2m40uTl3AGMOF\nwkKNEyQAoK9EggmOjnSChB60aI3dkiVLMGfOHHzyySdQKBS4ePEili9fjmXLluk8AEIIIcJXUsJn\n6e7e1WwfMIC/7ErJHB2kpgJ79mgeC2ZjA0ybBnTtCgDw7NbtmQI5deWycuy5uwf3cu4p25ytnBES\nEAJnK2cUy2TYl52NRLVo3VwkwjRnZ/hbWzftPZFmo1XGjjGGb7/9Fj/++CMePHiATp064dVXX8Vb\nb71ltMuYKWMnbLQXmnDR3AlbU+bvzh0+qCtVbXEGe3s+S9e5s37H16bI5cDp0/zRYOp/z/z8gKlT\n69xw+FnnL6c0BztjdiK7VLUAo4tjF8zuMRsWYgskl5VhT1YWitWOBWtvbo45Li5woGvqetWiGTuO\n4/DWW2/hrbfe0vkFCSGEtA6lpfxl15gYzfZ+/YCxY3U+Y75ty8ris3Tp6ao2c3Ng0iSgVy++aFFH\nibmJiLwTiXJZubJtaKehGNV5FBg4nMzLw7mCAo1gY4idHUY5ONCxYEZMq4zdqVOn4OXlBW9vb6Sn\np+M///kPTExMsGbNGrQz0m3COY5DWFgYHSlGCCHNIC6Oz9Kp1fDD1pbP0vn4GG5cgscYcOUKfzSH\n2gIFeHkBM2bwqVCdX4LhwqMLOJF8Agx8CCAWiTG923T0dOuJ/Koq/J6djUflqoDP2sQEM52d4avj\nsWSktuojxVauXKmXjJ1WgV337t1x7NgxdOrUCaGhoeA4DhYWFsjOzsaBAwd0HkRzoEuxhBCif2Vl\nwJEjwK1bmu29ewPjxwO0J60OCgv5A3TVj+YwMQFGjwaee04vWboqeRUO3juIvzL/UrbZmtsiJCAE\nHhIP3C0pwf7sbJSr7U3nbWmJWXQsWLPTV9yiVWBna2uLwsJCVFVVwc3NTbmfnbu7O3JycnQeRHOg\nwE7YqE5LuGjuhK2h+UtI4DcbVjs5ChIJX+71tIafNEX1cuI//gDUsmRo144/msPNTeuuGpq/wopC\n7IrZhcdFj5Vtnew6Ya7/XJiLrXAsLw9XCwuV94k4DiPt7THUzs5o6+lbkxatsbO1tUVGRgZiY2Ph\n7+8PiUSCiooKVFVV6TwAQgghxq28nN9p4/p1zfZevYCJEwFLS8OMq1UoK+OvacfGqtqa4WiORwWP\nsDt2N4orVdfO+7j3waQuk5AnU2D7/2fvzqOjrtNE/7+/VZXKUklVVkISskACISCLgOwiElQUXMA7\njtraTessp7X9zZ3uvjPn2O2I9u3pO/fO9DinnRlnbFvHdlpbRbRFFBUIO7IKghAIIQshgZClUtlr\n+f7++FKVqpCESlKpJXle53BMPqnlk3yt5KnP53meT20tl3sdC/ZgWhrZsgQbcfz6P+aZZ55h/vz5\ndHV18dJLLwGwd+9eioqKRnRyYuySFZ/IJdcusvW+fuXlWj9cq7VnzGTSVummTg3u3EadsjLth+u9\nBJqUpK3S5eQM6SH7ev0dqz3G5rObcapaZatO0bGqYBXzMuZxvK2NLb2OBSsymbgvJYVYOUEiIvm1\nFQtQWlqKXq+noKAAgLNnz9LV1cWMGTNGdIJDJVuxQggxdP31w73pJq0wU3Loh8Fu14ojDh70HZ8z\nR0tUDFA5sUt1sbVsK1/VfOUZi4uK46HpD5FhzmFzQwPfeFW/GBSFu5KTmZeQIFuvIRDUHLtIJIFd\nZJM8rcgl1y6ylZSUkJe3nA8/hObmnvG4OFi9GqZPD93cRoWaGq2NiXd+usmkNRseYoNhb+7XX7u9\nnfdOvceF5guer6Wb0nn4pofp0MXxfn09jV7pVGnXjgVLl07SITPiOXZTp071HBeWnZ3d7ySqqqr6\n/Fo42LBhg7Q7EUIIP5SWVvLZZ+f54osTuFwuJk3KJzVVOwOsqEgL6uLjQzzJSOZ0ao2Gd+0Cr21P\nCgu1oC6AJzhcabvC29+8TVNnk2esKLWIB6Y+wNG2Tr5sqsXpFUDMuXYsmFGOBQsJd7uTQOl3xW73\n7t3ceuutniftT7gGTbJiJ4QQ/iktreSll8qoqCj2nPHqcGxj4cICvvvdXGbMCEinjbGroUFbpaup\n6RkzGrXKk9mzA/LDLS0r5csjX1Jtq+bby9+SMzGH1MxUAG7Pu525E5bwUUMD57yOB4nW6ViTksIM\nidjDgmzF3oAEdkIIcWNtbfA//+d2zp1b4TOekgKLF2/nxz9e0c89xQ2pqpak+PnnWl6dW06OViCR\nlBSQpyktK+WNHW9Qm1ZLRXMFAI4yB7fcdAt/ufIviTbl8sHVq9i8Gh5nXjsWLFmOBQsbI74V+9xz\nz/X7JO5xRVF48cUXhz0JIXqTPK3IJdcuMqgqHDum5fBXV/dswdlsJdxyy3LS00Gvl625IbPZtIrX\nsrKeMb0ebr8dFi+GAG57fvLVJ5w1n6WhuYHmM80kTk0kfmo8afZ0avXp7Lp82edv+WKLhWI5FmzU\n6jewq66uHrAqxh3YCSGEiCz19fDxx+BOkdbptJyvceMgM1PriwtgNLr6eQQxoFOntN507n1t0H64\n69b1/HAD5FzDOUoqS2jJ7GksnBSTxKS0mXzTmkm3VwVM3LVjwSZLSfOoJluxQggxRtjtWu7+vn1a\nLr9bd3cljY1ljB9f7Bnr6trG+vUFFBbmhmCmEaqzE7ZsgRM9x3WhKNpxYCtWBKzZMGhHg31R/gUH\naw5ycM9B2idouXMTzBOwJM2gVEklus3MLdPmATDx2rFgCXIsWNga8Ry7cu+z6gYwadKkYU9iJEhg\nJ4QQPcrKtBOrmnoKJdHptAMOli2D8vJKtm07T3e3DqPRRXFxvgR1g1Ferp3z6nUkFxaLlkuXlxfQ\np6q11fLB6Q+ob68H4Oqlqxw6dJzo9Em0xYyjxWUkIc7C4ltWkJaS6jkWTCe7bGFtxAM7nR/7/4qi\n4PR+2xdGJLCLbJKnFbnk2oWX1lb47DPtKFJvOTmwZo22Q+hNrt8g2e2wbRscOOA7Pns2rFoFATyS\nS1VV9lXvY/uF7Z5TJADMXSkcPA8n8/NoOnGSuFkzMZeWc8ecOfxg7lxy5ViwiDDixRMul+RWCCFE\npFJVOHIEvvzS91z5mBi44w7tkANZwBmm2lqtjUl9fc9YXJx23lqAj9y0dlrZdGaTp+oVwKBEcfPE\nu3h3dyl1i6aRChgS60hMyyQ1M5fx5eUS1I1Bo3qzXRoURy65ZpFLrl3oXb6sFUdcvOg7PnOmdmLV\nQL1w5fr5weWCPXugpMS32fDkyXD//QHv5Hzyykk2n91Mp0OL0FXAYMojYdwSDjkNXPZqY5I0bx4F\nsbFkRkdL5B4hgtag+K677mLr1q0AnkbF191ZUdi1a1fAJhNIshUrhBhrurth507Yv9833khO1rZd\nwzQlOrI0NsKmTVBd3TMWFaVtuwZ4GbTL0cWWc1s4fvk4AC6gnniikueQGJ/nyZk7uHMn7bNmkRYV\nRV5MDCa9HoBxJ0/y1L33Bmw+YmSN+Fbsd7/7Xc/HTz75ZL+TEGIkSJ5P5JJrFxpnz2oFmd7nu+r1\nsHQp3Hqr/wWZcv36oapw9Chs3apF0G4TJmhtTJKTA/p0VdYqPjj9Ac2dzThRqCWeq4bxTEydjiXa\n4rmdXlFYM2MGZ8+eJXH+fCoOHMC0cCFdR45QPGdOQOckIkO/L/XvfOc7no/Xr18fjLkIIYQYJJsN\nPv0Uvv3WdzwvT1ulS00NybRGl9ZW+OMftejZTaeD5cu1yDmAzYadLic7K3eyu3I33SjUYKEGM8mm\nTG5KLsCg0/5sG3U65iUksNBsxpyXR2lSEttOnuTqhQuMi4+neM4cCmWJdkzyu4/drl27OHbsGG1t\nbUBPg+Jnn312RCc4VLIVK4QYzVwuOHQItm+Hrq6e8bg4uPNOmDVLUqwC4vRpLWHR64xV0tK0NiaZ\nmQF9qob2Bj44/QHltjqqMVNLAopiZErKFMaZ0gCtyfBCs5lbEhKIvbblKkaHEd+K9fbMM8/w7rvv\ncuuttxIbGzvsJxVCCDF0tbVarHHpku/47NlaUCcHCwRAZ6fWJ+brr33HFy6E4mItry5AVFXlaO1R\nNp77kgtqHHVMQEUhMTqRqalTiTFEYzEYWGKxcHN8PFEBXCEUo49fK3ZJSUmcOnWKzAC/OxlJsmIX\n2STPJ3LJtRs5XV2wYwd89ZWW8uWWmqptuwaiD65cP6CiQiuQsFp7xsxmeOCBgFegtNvbeePbzexo\nqqeeOEBBQWFi4kSyLdmkG40stViYbjL5dbarXL/IFdQVu+zsbIxG47CfTAghxNCcOaMVR3gfbGAw\naIURS5YE9LSqscvh0Pa29+/3jZxnzoR77gl4s+EddaX8Z9l+6pwKoPWgiTPEUZRWxDRzKkstFqbE\nxkqhohgUv1bsDh06xN///d/z6KOPkp6e7vO1ZcuWjdjkhkNW7IQQo4HVqhVHnDnjOz5pEqxeDSkp\noZnXqFNXpzUbvnKlZyw2VlsKnT49YE/jUlW+sbXwWvlXnGj23UvPSsjizsxpLE9KISc6WgK6MSao\nK3ZHjhxhy5Yt7N69+7ocu2rvXj5CCCECwuXStlx37PDtrmEyaU2GZ8yQ4oiAcLlg3z7tB+19RGZ+\nvtZs2GwOyNM4XC5OtLXx6ZVq9tWdos3e5vmaUR/FfVkz+B9ZhYyPjg7I84mxy68Vu5SUFN555x3u\nuOOOYMwpIGTFLrJJnkjkkms3fDU1WnFEXZ3v+Ny5sHKltpA0UsbU9Wtq0nLpqqp6xqKitDPXbrkl\nIJFzl8vFUZuNfVYr3zZVUN50ARXtb5MOlXkJFv6/omImxFlu8Ej+GVPXb5QJ6oqdyWTitttuG/aT\nCSGE6F9np5bideiQb4rXuHHajmBOTujmNqqoqlbt+umnvsuhWVlaG5MANP9rczo52NLCQZuN5u52\nzlwtpamzCQA9LnKVdtbnL+DWrHmy5SoCyq8VuzfeeIODBw/y3HPPXZdjpwvTsmtZsRNCRApV1dql\nffqp1nDYLSoKbrsNFi3STpEQAdDWpjUbLi3tGdPpYNkyrRJlmD/oZrud/S0tHG1txe5yUd9eT+nV\nszhUB0acTMDK3PgE/nTaWlLjpHu06BGouMWvwK6/4E1RFJzeOQlhRFEUnn/+eZYvXy7L0kKIsNXc\nDJ98AufO+Y4XFGjFEUlJoZnXqFRaqgV1bT35baSkaEeCZWUN66GvdHez12rlm7Y2XKqKw+WkrLGM\nurY6YrCTQwvjaeW2nKUsz1uOXieRutCUlJRQUlLCCy+8ELzArqKiot+v5QWicdIIkBW7yCZ5IpFL\nrp1/nE44cABKSsBu7xmPj4e774Zp00JTHDEqr19Xl3bG69GjvuPz52v5dMNoNlzd2ckeq5VSr5Mp\nrF0tnK4/jcHZQg5W0mgjMdrCuqJ15CbmDvm5/DEqr98YEdQcu3AN3oQQIhJVV8PmzXD5cs+YosC8\nedqhBgFslyaqqrQCiaamnrGEBK3itaBgSA+pqirnOzrYbbVS2dnZM45KRXMlVmspU7CSRAcKMDN9\nJvdMvocYg1xYMfL8Pis20siKnRAi3HR0wLZtcPiw73h6Otx7L0yYEJp5jUpOp9bCZO9e30qU6dO1\nSpQhlBa7VJVv29rYY7VS5110AXQ4OmhqPIGp4wIWtMN7YwwxrJ68mhnpM4b1rYixIagrdkIIIYZO\nVeHkSe3oUe/0rqgouP12WLBAiiMC6soVrdmwd7+YmBgtafGmmwa9x+1wufi6tZW9LS00ee+bAwoQ\nb7+CvW4nma6e7dhcSy5ri9aSGJM4nO9EiEGTwE6EJckTiVxy7Xw1NmrFEefP+45PmaKdUpUYZn/3\nI/r6qaqWuPjll77NhidN0rZeLYPrFdfpdHLYZuNASwutvQoFo3Q6psdG0VS3h8rGb3Fn6ekUHSsm\nrmBx9mJ0SvC7RkT09RMBIYGdEEKMAKdT2wXctUs7gtTNbNaKI6ZOlZMjAqq5GT78ELyL/QwGraPz\nggWD+mG3OhwcaGnhkM1Gl8vl87VYvZ75CQmkOa+y9ez72Lp7+tOkxqWyrmgdmQmZw/1uhBgyv3Ls\nysvL+elPf8rXX39Na2trz50VhSrvjt1hRHLshBChUlmpFUfU1/eMKYoWX9x+O8ipUQGkqnDiBGzZ\nolW/umVkaG1M0tL8fqhGu519Vitft7bi6PX3w2wwsMhsZpYpll0V2zlw8YDP12/JvIU78+8kSj/0\nClsxtgU1x+7RRx+loKCAX/3qV9edFSuEEELT3q7tAvbuqpGRoRVHZMpCTmC1t2tnr50+3TOmKFqj\n4dtu8ztxsa6ri70tLZxsa7vuD2tqVBRLLBZmxsdzte0K/3Xs91xu6ylnNkWZuH/q/UxJmRKQb0mI\n4fJrxc5sNtPU1IQ+grJ7ZcUuskmeSOQai9fOvWi0dasWa7gZjbBihdYuLUwP6blOxFy/c+fgo4/A\naxeJ5GTtSLDs7BveXVVVqrq62GO1cs77ol2TGR3NrRYLhXFxKMBXNV/xZfmXOFw9++qTkydz/9T7\niTfGB+I7CoiIuX7iOkFdsVu2bBnHjh1j3rx5w35CIYQYTa5e1YojLlzwHS8q0nLpzObQzGvU6u6G\nzz+/vmfMvHlw551aND0AVVU529HBHquVaq8edG75sbEstVjIi4lBURRsXTY+PPMh55t6ql8MOgN3\n5d/FvEw551WEH79W7J5++mn+8Ic/sG7dOp+zYhVF4cUXXxzRCQ6VrNgJIUaSwwF79sDu3b4FmBaL\nVu1aWBi6uY1aFy9qbUwaG3vG4uPhvvu0MuMBOFWVk21t7LVaudKrB52iKBTFxbHUYiHTKwHydP1p\n/lj6RzocHZ6xjPgM1hWtI83kf+6eEP4I6opdW1sba9aswW63c/HiRUB71yPvVIQQY9GFC1pxREND\nz5hOBwsXwvLlN1w0EoPldMLOnVoU7f2Hr6hIazZsMvV7V7vLxdHWVvZZrVi9y5MBvaIwKz6eJRYL\nKV7HinU7u/n03KccqzvmGVNQWJKzhNvzbpdzXkVYk5MnRFiSPJHINZqvXVubtgt4/LjveFaWVhwx\nfnxo5hVIYXf96uu1Vbra2p6x6GhtWXTmzH7bmHQ4nRy02fiqpYX2Xj3ojDod8xISWGg2Yzb4rm9c\nbLnIB6c/oLGjZ1XQEm1hbdFa8hLzAvZtjZSwu37CbyO+YldRUeE5I7a8vLzfB5g0adKwJyGEEOFM\nVeHYMfjiC+1YMLfoaK1N2ty5kVMcETFUFb76Sisz9l5py8uDBx7ot7Nzy7UedIdtNrp79aCL0+tZ\naDZzS0ICsb2KAV2qi92Vu9lZuROX2nO/m8bdxOrJq4mNko4QIjL0u2KXkJCAzaY1XtT18xtLURSc\nvd4JhQtZsRNCBEJ9vbbtWlnpOz59OqxapZ0nLwLMatUqXr0XFfR6KC6GRYv6XKW72t3NvpYWjre2\n4uz1uz/RYGCxxcLN8fFE9fH3rKmjiQ9Of0B1S7VnLFofzeopq5kxboakHYmgCFTcEpFbsX/7t3/L\n/v37ycvL47e//S0Gw/ULjxLYCSGGw27XUrr27vUtjkhM1I4cnTw5dHMbtdyH6n7yCXhXrI4fr7Ux\n8Srec7t0rWXJ6fb2637njzMaWWqxMN1kQt9HcKaqKscvH2fLuS10O3sKKnIsOawrWifnvIqgClTc\nEnGbB8ePH+fSpUvs2rWLqVOn8v7774d6SmIElJSUhHoKYohGw7U7fx7+/d+148DcQZ1OB0uXwtNP\nj+6gLmTXr6MD3n8fNm7sCeoURfuh/9mf+QR1qqpS3tHBm3V1/OelS3zbq7FwdkwMj6an84PMTGbG\nx/cZ1HXYO3jv2/f48MyHnqBOp+gonljM+tnrIzaoGw2vPzE8EXdW7P79+7nrrrsAWLVqFa+//joP\nP/xwiGclhBgNWlu1JsPffOM7np2tFUeMGxeaeY16ZWXa1qut59xVEhO1VbrcXM+QS1U5097OHquV\nS97Hh10z+VrLktyYmAGfrrypnA/PfEhLV4tnLCU2hXVF68gyZw3/+xEihCIusGtqaiIjIwPQTsRo\n9O5nJEYNqeqKXJF47VQVjhzR8vS9dwBjYuCOO2DOnEGdIR/Rgnr97HatIuXgQd/xOXPgrrs8h+o6\nXC5OXOtB12C3+9xUURRuMplYYjYz/gaH8DpcDrZf2M6+6n0+43Mz5nJXwV0Y9ZHfpyYSX38isEIW\n2L388su88cYbnDx5kkceeYTXX3/d87XGxkaefPJJvvjiC1JTU/nlL3/JI488AkBiYiItLdq7LKvV\nSnJyckjmL4QYHS5f1oojqqt9x2fO1A4yiA+f06JGl5oarY2JdzNAk0lbGp06FYAul4ujNhv7W1po\n6dWDzqAo3JyQwGKzmSSvHnT9udJ2hY3fbvQ55zUuKo77Cu9jaurUwHxPQoSBQQd2rl7l4/1VzN5I\nVlYWzz33HFu3bqXDu38A2kkXMTExXLlyhWPHjrF69WpmzZrFtGnTWLx4Mb/61a94/PHH2bp1K0uX\nLh3S84vwJr2YIlekXLvubq3n7f794P1rLTlZK47Izw/d3EJpxK+f06lVpeza5fuDLyzUTpAwmWhz\nOjnY0sJBm42OXp0XonU65pvNLEhIIL6PwrneVFXlYM1Bvij/wuec14LkAh6Y+kBYnfMaCJHy+hMj\nx6/A7siRI/zwhz/k+PHjdHrtUwyn3cnatWsBOHz4sOc0C9BOufjggw84deoUcXFxLFmyhPvvv5/f\n/e53/PKXv2TWrFmkp6ezbNkycnNz+Zu/+ZshPb8QYuw6d04rvGxu7hnT62HJErj1VvBjAUgMxdWr\nsGmTtlrnZjRqh+rOnk2zw8H+hgaOtrZi77WIEK/Xs8hiYW58PDF6/05+sHXZ+Kj0I8oayzxjBp2B\nO/Pv5JbMW6SNiRiV/Arsvve973Hffffx2muvERcXF9AJ9C7tPXv2LAaDgYKCAs/YrFmzfCp95Q/y\nNQAAIABJREFU/u///b9+Pfb69es9TZYTExOZPXu2552M+/Hk8/D83D0WLvORz/3/fPny5WE1H+/P\n585dzqefwpYt2ud5edrXOzpKWLQIVqwIr/mOmuu3YwecOcPyxkaw2ympqNC+vmwZrF3LpsOHOfnR\nR6izZ+NSVSoOHAAgb+FCkqOiiD5xgoKYGJasWOH381dZq6hLraPd3k7F19rzLVy6kHVF6/j20Lfs\nPLczLH7egf48nF9/8rnv5+6PK669HgLFrz52ZrMZq9U6Iu9unnvuOS5evOjJsdu9ezcPPfQQtV7H\nx7z66qv8/ve/Z8eOHX4/rvSxE0K4uVxw+DBs2wbexZSxsVoe3ezZY6c4IuhsNq3itaxn1Qy9Hm6/\nneo5c9hjs1Ha3n7d3cYbtR5000wmdIO4ON3ObraWbeVI7RHPmILCouxFrJi4AoMu4moGxRgx4keK\neVu7di1bt25l1apVw37C3np/E/Hx8Z7iCDer1UqCtHcfU0q8VutEZAm3a1dbqxVHeO/+gRbM3XHH\ngOfHj0kBvX6nTmk/fK88anXcOM6vWcPuqCgqL1++7i55MTEstVjIj40d9GJCTUsNH5z+gIaOnoIM\nc7SZtVPXMjFp4tC/jwgSbq8/EXx+BXYdHR2sXbuWW2+9lXSvJpGKovDmm28OawK9X7hTpkzB4XBQ\nVlbm2Y49fvw4N91006Afe8OGDZ6laSHE2NLdDTt2wIEDWjsTt9RUWLNGO3JUjJDOTtiyBU6c8Ay5\nFIVvFy9mz9Sp1Dkcvsd5AFOv9aCbcIMedH1xqS72VO2hpKLE55zX6WnTWTNljZzzKsJaSUmJz/bs\ncPm1Fbthw4a+76woPP/880N6YqfTid1u54UXXqCmpoZXX30Vg8GAXq/nkUceQVEUfvOb33D06FHW\nrFnD/v37KSoq8vvxZStWiLHrzBktrvBe/DcYtMKIJUu0j8UIKS+HDz/0/PAdisLX6ensXbyYpl47\nLzpFYabJxBKLhTSjcUhP19TRxKYzm6iyVnnGovXR3DP5Hmamz5QCCRExIv6s2A0bNvDiiy9eN/Z3\nf/d3NDU18cQTT3j62P2f//N/Bn26hAR2Qow9Vit8+qkW2HmbOFFbpUtJCc28xgS7XUtivFb40KnT\ncTghgQOFhbROnuwTTUfpdMyNj2eRxYJliFG2qqqcuHyCLee20OXsSZzMNmezrmgdSbFJw/t+hAiy\noAd2O3bs4M0336SmpoYJEybw2GOPseJahVI4ksAuskmeSOQKxbVzueCrr7St1+6es9wxmbQDDGbM\nkOIIfw3p+tXWas2G6+tp1es5YDZzKDmZrsJCSEvz3CxWr2d+QgILzGbi/GxZ0pcOewebz27mVP0p\nz5hO0XFb7m3cmnsrOkU35MeOdPK7M3IFtXjiN7/5Dc8++yx/9md/xoIFC6iqquLRRx/lxRdf5C/+\n4i+GPYmRIjl2Qox+NTVafr5XIT2gnUp1xx1a5asYIS4X7NkDJSU06nTsS0nh6/h4HCkpWsPha9ur\nZoOBRWYzcxMSMOqGF3RdaLrApjObfM55TY5NZl3ROiaYJwzrsYUIhZDk2E2ePJn333+fWbNmecZO\nnDjBunXrKPMuYQ8jsmInxOjW1aXt/B065FsckZamnUqVkxO6uY0JjY3wwQfUXbnCXrOZkyYTql6v\nHdmRmQlAalQUSywWZsbHox/mkqnD5WDHhR3sq96HSs8Fn5Mxh1UFq0bFOa9ibAvqVmxKSgq1tbUY\nvZJbu7q6yMzMpMH7nL8wIoGdEKOTqsLp01ounc3WM24wwG23weLFWps0MUJUFfXwYap27mRPXBzn\n3E3rzWbtjNfYWLKio1lqsVAYFzeoHnT9qW+rZ+PpjdS11nnG4qLiuHfKvRSl+V9UJ0Q4C1Tc4tea\n+JIlS/jRj35EW1sbAK2trfzkJz9h8eLFw57ASPrXjz+mtLw81NMQQxDIZWkRXCN57Zqb4fe/h3ff\n9Q3qCgrgqae0qlcJ6oZnoOun2myUvvsuvz1yhNdTU7WgTlG03jGzZ5OfnMz3xo/nzzIyKBpkY+E+\nn+/aOa//ceQ/fIK6/KR8fjDvBxLU9UF+dwq/cuxeeeUVHn74YSwWC8nJyTQ2NrJ48WLefvvtkZ7f\nsLz35ZfsPXqU5x9/nMJJk0I9HSHEEDmdWrFlSYlWfOkWHw+rVsH06VIcMZKcqsrJb75h79GjXAFw\n95qLi0MpKqIoPZ2lFguZ0dEBe87W7lY+OvMR5xrPecYMOgMrJ61kQdYCaWMiRo2Q5Ni5VVdXc+nS\nJTIzM8nOzg7YJEaCoijc8fXXRCsKaSdP8j/uuguzXo/ZYPD8N0GvJ2qYibxCiJFVXa0VR3gfUqAo\nMG8eFBf3xBgi8OwuF0cbGth3+DDWXqdE6LOymDVjBktSUkiJigro85ZeLeWPpX+kzd7mGUs3pbOu\naB3p8ekD3FOIyDXiVbGqqnreEblcWifvrKwssrKyfMZ0YRwYdbtcdAN2u52DvY4pc4vV668L+Mx6\nPQleH0frdPLuUIgg6+jQiiOOHPEtjkhP14ojJkgBZECVlpfz5alT2AHV5SI1L49aoP3bb30O2DVG\nRTFv9mwWFhZiDnCn525nN5+f/5zDlw77jC+asIjiScVyzqsQfuj3VWI2m7FdS2Ix9PPiVRQFZ69j\nYcKRfoAIuMPppMPp5LJ386tejDqdzypf7yDQbDAQJ8FfQEkvpsg13GunqnDyJGzdCq2tPeNRUXD7\n7bBggeTRBVppeTm/PXwYde5cju3ejWvWLLq++ILZikLqta7OcU4nC1NTuWXlSmJH4IDdS7ZLbPx2\no885rwnGBNYWrWVSkqTS+Et+d4p+A7tTp3oaP5ZHaAHCQrMZ26FD3H3LLaQkJ9PidNLicGC79t8W\npxOXH8ue3S4XV10urnon9/SiV5R+g74Er/8GokJMiNGqsRE++QTOn/cdnzIF7rkHEhNDM69Io6oq\nXS4XbS4X7U4n7S4XbU6n5+N2p9Pna9t27+ZKQQEdZ87QdvEipqgoYnNzufD11xRYLCzu7OTm224j\nasaMgM/VpbrYW7WXHRU7fM55nZY2jTVT1hAXFRfw5xRiNOs3sMvxagL1/vvv85Of/OS62/zqV7/i\nRz/60cjMLAC++dnP+NN772XN9Ol9fl1VVdqcTk/A1+J0+gR97v/aXa4+7+/Nqao0Oxw0Oxz93kZR\nFOK9tn4T+tgGlrw/jbzjjFxDuXZOJ+zbBzt3gvdLKCEB7r4biorGdnGEU1V9gzKvjz1BW6+v+fOm\n1c3a1kZHbS1JDgdJEyaA3U5HaysTGht5ZupU9A89pLUzCbDmzmY2nd5EpbXSM2bUG7m74G5mj58t\nuyBDIL87I09IiicSEhI827LekpKSaGpqCthkAilQSYiqqtLpcvUZ8HkHgx0B3JKO65Xjd93qn+T9\niVGkslIrjqiv7xlTFJg/H1asgAAWWoYFVVXp9grUBlpJc3+t0483l4OcBLS1af1jrFY+3bqVuDlz\niHK5MHV3k9XSQkpnJ82VlfzLa6+NSFR94vIJPjn7ic85rxPME1hXtI7k2OSAP58Q4S4oR4pt374d\nVVVxOp1s377d52vnz5/HPALv4MKNoijE6vXE6vWMM/bf2by7j+Cv9+dtLpdfF6392i9zf/P++sv/\ni+S8P8kTiVz+XruODvjiCzh61Hc8I0Mrjrh2eEHYc6kqHYNYSWt3OnEEoXm6UafDpNcTp9MRB8RZ\nrZjq64mrqyOurg5TRwdxLhdxTifZZ85QVl1N9OzZVFRUkDplCl2XLzM3OzvgQV2no5NPzn7CN1e+\n8YzpFB3LcpexLHfZmD7nNRDkd6cYMLB74oknUBSFrq4unnzySc+4oiikp6fz61//esQnGCmMOh0p\nOt2AZf9OVcU2wJavOxgMZN5ff1u+7v/GS96fCDJVhRMntOKI9vaecaNRW6GbPx9CmY1gd7n8Xklr\nd7no8PMN23AoiqIFaO5ATa/H5PW5Sa/3/djhwHDxopasWFmpHag7QJrIxKgoljY1se3oUa52dDAu\nOppik4ma9MC2FqlormDT6U1Yu6yesaSYJNYVrSPbEt4ttISIFH5txT7++OP87ne/C8Z8AiZSjxTr\nK++vr/w/f/L+/NE776+//D+D5P2JAGho0LZdL1zwHZ86Vculs1gC+3zuVAp/V9LaXK6AvbYGYlCU\n64Mxd8DWR/AWo9MN/AasrQ2qqrR/lZVQW+vbI6YvCQmQmwu5uVR2d1O2eTPFXvve27q6KFi/ntzC\nwmF/v06Xkx0VO9hbtdfnnNebx9/MqoJVRBtG2X67EEMQ1LNiI1GkBnb+cP+x8gn6+lj9C2ReTty1\nQC+hj1U/93+jJfgT/XA4YM8e2L1bK5Rws1i0ald/Ywd3EUHvYKyvlbQ2p5OOQRYRDFWsvytp175m\nHO5rxWrVArjKSi2Y805Q7E9KCuTkeII5EhN9tlkrS0s5v20buu5uXEYj+cXFAQnqrrZfZeO3G6lt\nrfWMxRpiubfwXqalTRv24wsxWgQlx87NarWyYcMGdu7cSUNDg6c5saIoVFVVDXsSI2XDhg0sX758\n1OUbeOf9pQ8y7693MNjqZ9GHO++vbpB5f72DQX/z/iRPJPK4G9ye/uYbimbMYOX06RROmsSFC9oq\nXUNPezJ0Opi/QGXJbSp2vZOLnTdeSWt3OukKwmqaXlH8Xklzfz6i6Qyqqv3wvAO55uaB76MoWifn\n3NyeYC4+fsC75BYWkltYSElJCSsC8NpTVZXDlw7z+fnPsbt6UkYmJU3igakPYI4e/TnaoSC/OyNP\nSKpiH3vsMaqrq/nrv/5rz7bs//t//48HH3wwbNudjOYVu0Dyzvvrr+WLv3l//nDn/fW35VtXVcX+\nM2coPXnSJzgIlL7+n+g90td32vt+fd5mhB6nz8ce6vcxQo9zrrycd77+GuPcuVR+9RUZ8+fTvP8Q\nqd03cdWWg13v1P7pXMSlOJk83YXe5MQZhNdo9CBW0kx6PUZFCW3RkculnZ/mHci1tQ18H71eqzZx\nB3I5OUM+ay0QgUFbdxsflX7E2YazPVNU9KyctJKFExZGbFFXJJDALnIFdSs2LS2N06dPk5qaisVi\nwWq1UlNTw7333svR3iVtYUICu8BxeeX99bXl6/7vcCv9rlZX83VpKYZ583BvVDmOHOHmwkJSe51N\n7HdAJP8PBMXBnTu5OrmQpuZOXC4Fu11FVWOIOVpK1uTbAC32mDRRiz+G+nddpyjE+rmSZtLridXp\nwj8/1OHQihvc+XHV1T5HePUpKgqys3sCuQkTtLEwcLbhLB+d+cjnnNdxpnE8WPSgnPMqxACCuhWr\nqiqWa1nNCQkJNDc3k5GRwblz54Y9ARH+dIpCgsFAgsHQb1OxvvL++sr/Gyjvr7y8HMO8eQC4b6Wb\nO5ey48e1pqkibLW0d1J3uRNVTaS9XcujU9VmFGcnAGlpUFAA0b0yB6J0Or9X0uJ0OmIiuIWPR1eX\nFry5A7kbVKwCEBvrmx83fnzYnatmd9r5/PznHLp0yGd84YSFrJy0Us55FSJI/HqlzZw5k127dlFc\nXMzSpUt5+umnMZlMFAYgsVaMDoPJ+7uu19+1j09FRWFXFOyqSvPhwyReC/KcI/SHvK8AofdIX8/c\n51ivx/LnfsF8HL/vN8THabvchsuSTEc7dJ85jHHyfHTONPRXjvL97yRSmNN38DYmTllxV6y6t1X9\nqVg1m30DubS0oB29MZStvFpbLRtPb+Rq+1XPWLwxnrVT15KfnB/gGYqByFas8Cuwe/XVVz0f/8u/\n/AvPPvssVquVN998c8QmJkYno05HqtFIah9fazSbqbdYcAEXTCbyrq0Sj0tK4ge5uZ7bDTloifSV\nnjBls8HWb7JoOH6OhNlz6WyIIyYhnvjyI6zOyeJ7M5JCPcXgGoGK1XDlUl3sq97Hjgs7cKo9hVhT\nU6dyX+F9cs6rECHgV47dV199xYIFC64bP3jwIPPnzx+RiQ2X5NhFntLyct44epTouXM9Y11HjrB+\nzpyAFlCIwDl9Gv74R9i5czv11jyaY04RZYKMVChKnM60ggqeempFqKc5cnpXrFZWaoHdQIZQsRqO\nrJ1WNp3ZREVzhWfMqDeyqmAVN4+/Wd5ICTFIQc2xW7lyZZ9nxa5atYrGxsZhT2KkjNZ2J6NV4aRJ\nrAe2nTxJN2AEiiWoC0tdXfDZZ3DsmPb5pEn52I6XsTDzXiZO1NqZdHVto7i4ILQTDbQQV6yGi5NX\nTrL57GY6HZ2esayELNYVrSMlLiWEMxMi8gS13Ynr2lE5iYmJWHu9Cz1//jxLlizhypUrAZtMIMmK\nXWSTPJHwVV0NH3wATU09YxYLzJxZSWnpeb799gTTps2kuDifwsLc/h8oEgy3YjU3F7KywqZi1R8D\nvfY6HZ1sObeFE5dPeMYUFM85r3pdeBV0jEXyuzNyBWXFzmAw9PkxgE6n46c//emwJyCEiAxOJ+za\npf3z/t0zYwasXg0xMbkUF+dSUqKL3D8s7opV92rcKKlYDYTK5ko2ndlEc2dPc+SkmCTWFq0lx5IT\nwpkJIbwNuGJXUVEBwLJly9i9e7cnklQUhbS0NOLiwjcxVlbshAichgZtla6mpmcsJkYL6GbMCN28\nhi3CKlZDwelyUlJRwp6qPT7nvM5Kn8U9k++Rc16FCBA5K/YGJLATYvhUFY4e1fLp7D2nQpGXBw88\noBVvRhTvitXKSrh69cb3SUnxLXSIkIrVQGhob2Dj6Y1csl3yjMUYYrh3yr1MHzc9hDMTYvQJavHE\n448/3ucEAGl5IkaE5ImEXlubVvFaWtozptfDihWwaJFWINGXsLl2qqoFbu4VuTFUsTocJSUl3Hbb\nbRytPcpnZZ/5nPM6MXEia4vWyjmvYSxsXn8iZPwK7PLz830iybq6OjZu3Mh3vvOdEZ2cECI0zp2D\njz6C1taesbQ0WLcOMjJCN68BuVxQV+e7tTqYitXcXK3oIcIrVoeqtKyUL498yfETx/mvY/+FKd1E\naqbWcVKv6CmeVMyiCYukjYkQYW7IW7GHDx9mw4YNbN68OdBzCgjZihVi8Ox2+PxzOOR7KhQLFsDK\nlWFW3DmUilWjUTtXNUIrVkdKaVkpb+x4A1uWjbMNZ+l2duMoczB72myKCop4cNqDjI8fH+ppCjGq\nhTzHzuFwkJSU1Gd/u3AggZ0Qg3PpklYg4Z12Fh+v5dIVhEM7OqlYDThbl43zTed5+Z2XqUyu9Nl2\nBZhum85LT71ElF6CXyFGWlBz7LZt2+az/N7W1sY777zD9OmSPCtGhuSJBI/LBXv3wo4d2sduU6fC\nfffBYIvfA3btpGI14BwuB5XNlZxvOs/5xvNcbrsMwMXWi9gTtaCu+Uwz46aPozClkPyYfAnqIoz8\n7hR+BXZPPvmkT2BnMpmYPXs2b7/99ohNLBDk5InIU1layvkvv+TE6dO4Tp0if+VKcgsLQz2tUau5\nWVulq6rqGTMa4e67YfbsIMdEzc2+hQ5SsTpsqqpytf0qZY1lnG86T2Xz9atyADq0SpgoXRTJscnM\ny5yHUW/E2GoM9pSFGHOCevJEJJOt2DDkdGrbad3d2r9eH1eePUvZxx9T7C631OnY5nBQsHo1ufn5\nYDBo22juf4P9XP7ge6gqnDgBW7b4pqVNmKAVSCQnB2ECw6lYdQdzY6xi1R8d9g7Km8o533SessYy\nWrpa+r2tXtGTY8khyhbFgRMHSJqW5HkT33Wui/W3r6ewQN5YCREMQc+xa25u5pNPPuHSpUtkZmZy\nzz33kJSUNOwJjBQJ7IZJVbX8pT4CsBt+3N/XnM4Bn3L7wYOsaG+/ftxkYsUttwz/expOUDjQ54F4\nrCAGnR0dsHkznDrVM6bTwbJl2r/+2pgMi1SsjhiX6uJiy0XON57nfNN5alpqfBoJ95Yal0p+Uj75\nyfnkJeZh1GurcqVlpWw7uo1uVzdGnZHiOcUS1AkRREHNsdu+fTvr1q2jsLCQ3NxcKisreeqpp9i4\ncSMrV64c9iREAKjqjQOrwQRj3d2+CVdBoPN6vpLmZpZf636ru0FA6Den84bBZcjodIEPOPsIQKsv\n6flihx5bmx6LzoCq02NO0nPPvXoycwxg6+O+fkZ63tvoM6dMIf+mm8g1GLQgTipWA6q5s1nbXm08\nz4XmC3Q6Ovu9bYwhhklJkzzBXGJM312lCwsKKSwolBytCCfXT/gV2D399NP853/+Jw899JBn7L33\n3uOHP/whZ86cGbHJjWouV2BXw7q7Q/0d3ZhOp/3xNhohOvq6j111dVjrarnUdJkLaifjXR1kJKXj\nmpAN8+ZpK4ju4Mz7Y38+D9eAzs3l0v7Zr89/CtTDX7igxVeTvMYzMqDABPoPB7izotwwaKysr6ds\n3z6KjUZ0ly+z/NQptr37LsyeTW5qat+PKxWrfut2dlPRXOEJ5ho6Gvq9rYJCljmL/KR8CpILyDJn\noVNGYhlWCBGO/NqKTUxMpKGhAb3XL1273U5aWhrNzc0D3DN0FEVh28svBy753r0tGYgArKvrxm0a\nwoHB0Hcg1k9gdsOP+8hz67B30NTZRFNHE9s/38KZ37zGrala7k+0IZo9DQp3/PUG7rj73uF9L6o6\nuEBwOEHkUD4fQa2tcPq0785nVBQUFkJ/Mddg+bWNbjb7FjpIxWq/VFWlrrXOU71aZa3Cqfb/5sQc\nbaYguYD8pHwmJU0iNio2iLMVQgRC0I8Ue/nll/mrv/orz9i///u/93nUWDhZUVPDtldegQcfJDc7\ne2gBmPvjcF/xAe2vdX+B1VCCsQCsnrhUF7YuG422K54ArrGj0fNxh6PDc9uDFQex3ZVA1bfNRDsd\ndOm7ab49kVNHXuF8Wg1ZCVlkmbPITMhknGnc4FYhFEULVA1+/S8fXKqqLakFOKhUHU5KTzk4fs6J\nGu9EZ3KiczkYn+ZkzmwnsUY/n8uPXzS6vrbtY2PRjR+vNcKTitUbau1u9eTJnW88T5u9/xzEKF0U\neYl55Cfnk5+UT2pcqpwIIYQA/FyxW7JkCQcPHmTcuHFkZWVRU1PDlStXWLBggeeXiaIo7Nq1a8Qn\n7C9FUVBvuw0IYPJ9ICnKjQOrwQRjUVEjlPV+Y3anvc+grbGjkebO5gFXGrwd2HOAzglarlDzmWYS\np2q5QDEXY1i4dKHPbaN0UWQkZJCVoAV6WeYskmKS5I/bNS0t8OGHUF7eM2YwwJ13wi23DDK+cged\nAwSR23/7W1ZcvQqqSsnFiywvKgKjke3jxrHiqacC/v2NBg6Xg2prtacVSV1r3YC3Tzela6tyyfnk\nWHIw6EbmTYrkaEU2uX6RK6grdn/+53/On//5n99wQuEqIMn3Op1/QZa/wVhUVMSsXqiqSru9/bqg\nzf2xrXvop49E6aJIik0iKSaJ+sR6upO7iTZEc6HmAvGmeGzdNhSu/znZXXaqrFVUWXsasMUaYj0r\neu7VvXjj2GuH8e238PHHWvWrW0aG1sYkLW0ID6jTaf8GKGTI/9M/Zdsbb1AcHQ02GxiNbOvqoqC4\neAhPODqpqkpDRwPnG7U2JBXNFX32lHOLi4rzFDzkJ+WTEJ0QxNkKISLV6O5jt3Il6PVsT0xkxR13\nDC8YG+V90JwuJ9Yua5+rbk2dTXQ7h16cYYoykRSbRHJsMkkxST4fxxvjPW8K3OdVRk+O9ty361wX\njyx7hIRxCdTYaqhpqeGS7RLWrhv0PLvGEm3xrOhlJWSRkZBBjGF0tszo6oJPP4Wvv+4ZUxRYsgRu\nv33k6xIqS0s5v20buu5uXEYj+cXFY765dKejU+spd22Ltbmz/5xknaIjx5LjCeYy4jPC+g2zECKw\ngt7HbteuXRw7doy2axnYqqqiKArPPvvssCcxEhRFQX3+eW3VYP36Mf8HBqDL0dXvqpu1y4pLHVp7\nE52iIzEm8bqgzb0SF22IvvGDXONvL63W7lZPkOcO+Lzz9fqjoJASl+JZ0ctKyCI9Pn3EtrWCpaoK\nNm2CpqaeMYtFW6XLzQ3dvMYal+riku2Sp3q1xlYz4OsqOTbZU/SQl5g3qNeKEGJ0CWpg98wzz/Du\nu+9y6623EhvrW231u9/9btiTGAmKorDtX/91TK0aqKqKrdvW76pbu/36qkV/Reuj+111s8RYAt5O\nYbB5Iqqq0tTZpAV6LTXU2GqotdUOuNXlplf0pMen+xRnpMalRkSLCKcTdu6E3bt9axxmzoR77glN\nP9+xluNj7bR6TnkobyofsKdctD6aiUkTPa1IkmLDr8n7WLt+o41cv8gV1By7t956i1OnTpGZmTns\nJwym0Zi07XA5aOpo6nPVramzCYdr6K0zzNHmPlfdkmOTiTXEhvW2kKIoJMcmkxybzE3jbgK01ZP6\ntnrPil6NrYYrbVeuW0Fxqk4u2S5xyXaJQ5cOAWDUG8lMyPTJ17NEW8LqZ9DQABs3wqVLPWMxMbBm\nDdx0U+jmNdrZnXYqmis8wdzV9v7PtFVQyEzI9OTJTTBPQK+TXn1CiJHj14rdzJkz2b59O6mBanoV\nBIqi8Pzzz7N8+fKIeveiqiodjg5PoNbY0ejzsa3LNuBxQQMx6AwkxiT2ueqWGJNIlH70d/m3O+3U\ntdb55OsN1OzVmynK5JOvl5mQicloGuEZX09V4cgR2LrVt5/xxIlaZxGLJehTGtVUVeVK2xVP9Wpl\nc+WAld4JxgRP9eqkpEnERcUFcbZCiEhTUlJCSUkJL7zwQvC2Yg8dOsTf//3f8+ijj5Kenu7ztWXL\nlg17EiMhnM+KdakuWrpargva3B8PtJVzI3FRcf2uuiUYE8JqxSlcdNg7PLl67q1cfyt9E2MSffL1\nMhIyPGdvjoS2NvjoIzh7tmdMr4fiYli0aFTX9wRVW3cb5U3lnmCutbu139sadAZyLbmeYC4tLk1e\nZ0KIQQtqjt0rr7zCX/3VX5GQkHBdjl11dfWwJzESQh3YdTu7+111a+5sHnKhgoKCJcYNNbGAAAAg\nAElEQVRCUsy1wK1XADdaKj5DnSfS0tXiU5xxyXbJr4BbQSHNlOaTr5duSg/I9tvZs1pQ532CxLhx\nWoHE+PHDfviACfW1Gwqny0l1S7WnFUlta+2Atx9nGuepXs215I6q1e5IvH6ih1y/yBXUHLuf/vSn\nbN68mTvuuGPYTzhaqKpKm72t31W3gd7h30iULsoTtHkHcO4tU8nRGXnmaDPmNDNFaUWAdr0bOxp9\n8vXqWuuuy2lU0bbtrrRd4VjdMUBb0RkfP96nmXJKbIrfqzrd3fD553D4sO/4woXaSt0A7eVEP9zF\nNu7q1QvNFwZs6RNriPXkyeUn52OONgdxtkII4T+/VuxycnIoKyvDaBy5LaZAC0Tk63Q5ae5s7nPV\nramjya+Ky/7EG+OvC9rcH5uiTLKVEwGcLidX2q745OtdabviVw5ktD76umbKfW2VX7qkFUg0eKUB\nJiRouXT5+YH+jka3TkcnFc0VnmCuqbOp39vqFB0TzBM8rUgyEjIiokpaCBG5groV+8Ybb3Dw4EGe\ne+6563LsdCE6xupG/P0BdTo6+111s3Zah1yooFf0Wm+3PlbdkmKTRjQPS4ROt7ObWlutT77eQAGE\ntwRjgmdFL8OURcU3mezfHYv3MaxFRXDvvRAn+fg35FJd1NpqPdWrF1suDpgCkRSTRH6y1oYkLzFv\n1KQ1CCEiQ1ADu/6CN0VRcAbiuK4RoCgKL7/zMsVzisnIzuh31c2fprb9iTHE9LvqZo42yzv8YRhN\neSLt9vbrmikPdMB7RwecOQNWK8SSTAJZJBuyuO/2TFYuyMBoCO+911Beu5auFs8pD+VN5QP2bjTq\njUxMnOjZYk2OTZaVckbXa28skusXuYKaY1fufZJ4BPnE8Ql/ePMPzCyaSWrm4Fu1KChab7c+Vt2S\nY5OJMcTIHwJxQ3FRcUxOmczklMmAlt9l7bL6NFO+ZLtEl6Oby5fh3Dmt8TBAB41EmRuxFH3DQTsc\n3qtjnGmcT77eONO4Mfsmwu7Uzgx2V69eabsy4O0z4jM81avZ5mzJVxVCjDqDOivW5XJx+fJl0tPT\nw3YL1k1RFG57/TYATBdN3LL0lj5vZ9AZ+l11S4xJjPijpkRkaG1z8c5HDRw+W0MLNdi4RJtSR06u\nk9zcgduYROmiyEjI8MnXS4pJGpVvOlRVpb693lO9WmmtHLApd7wx3nPKw6SkSSHpOyiEEP4I6opd\nS0sLP/zhD3nnnXdwOBwYDAYefvhhfv3rX2OJgG6oep2eCeYJfQZw3ofQCxEK58/Dhx/qsNnSGE8a\n45lNcjLcv9aBwXLZJ1/vavvV6/I+7S5t1arKWuUZizXEXtdMOSE6IdjfWkC029spbyr3bLG2dLX0\ne1u9oic3MddTvZpuSpfXtxBiTPFrxe573/sera2t/PKXvyQnJ4eqqiqeffZZ4uLiePPNN4Mxz0FT\nFIUfb/0xMYYYMq9m8tRDo+94sdFsLOSJOBzw5Zdw4IDv+Ny5cNdd0FcRepejy3P8mTtfz9pl9ev5\nzNHm65opj0SBwHCvndPlpMZW46levWS7NGARU2pcqqd6NTcxVwqThmksvPZGM7l+kSuoK3afffYZ\n5eXlmEzaNsaUKVN44403mDRp0rAnMJLijfF0neui+PbiUE9FCB+XL2ttTK54pYTFxcH990NhYf/3\nizZoh8hPTJroGWvtbvXJ16tpqemzKKilq4WWrhZOXz3tGUuNS/XJ1xsfPz4k6QdNHU2e6tULTRfo\ncnb1e9sYQwyTkiZ5gjlLTPjvGgghRLD4tWKXl5dHSUkJeXl5nrGKigqWLVtGVVVV/3cMIUVR+Nc/\n/CvFc4opLBjgL6UQQaSq2grdl1/2FEgATJ6sBXXx8YF4DpXmzmafZsq1tlq/+i7qFT3p8ek++Xqp\ncakBL87ocnRR0VzhCeYaOxr7va2CwgTzBE8rksyEzDFbLCKEGL2C2u7kf//v/81//dd/8eMf/5jc\n3FwqKir453/+Zx5//HGee+65YU9iJIT6SDEhemtpgU2b4MKFnrGoKLjzTpg3b2TPeXWpLurb6n2a\nKV9uu+zX0XZGvZGM+AzPFm6WOQtLtGVQuWuqqlLbWuvJk6u2VuNU+2+VZIm2eKpXJyZOJDYqtt/b\nCiHEaBDUwM7lcvHGG2/w3//939TW1pKZmckjjzzCE088EbaJyRLYRbbRlidy6hR8/DF0eh03m5EB\nDz4IqYPvxBMQdqedutY6n3y9ho6GG98RrYWLd75eZkImF6su8uWRLzl96jRF04tYOGMhhmQDZY1l\nlDeVD9i7L0oXRV5inieYG8yRayKwRttrb6yR6xe5gppjp9PpeOKJJ3jiiSeG/YTD1dLSwsqVKzl9\n+jRfffUV06ZNC/WUhOhXZyd8+ikcP94zpiiwdCksXw76ELZRi9JHkW3JJtuS7RnrsHdQ21rrk69n\n67Zdd992ezvnGs9xrvEcAFcvXeXM2TMkTUuiSd/EBccF3v7928yeNrvfHpLj48d7WpFkW7KltZAQ\nQgSAXyt2zzzzDI888giLFy/2jO3bt493332Xl156aUQn2JvD4aC5uZn/9b/+Fz/5yU+YPn16n7eT\nFTsRapWV2tZrc3PPWGIirF0Lubmhm9dgtXS1XNdMudPR6XObg3sO0j7h+lMevHtImqJMnlMe8pPz\niTcGIKFQCCFGiaBuxaamplJTU0N0dLRnrLOzk+zsbOrr64c9iaH4/ve/L4GdCEtOJ5SUwJ49WrGE\n26xZcPfdEBPhR5CqqkpjR6NPvt7GLRuvC+wUFDIaMnjqT54iPymf8fHjZXtVCCH6EfStWJfLN8na\n5XJJ4CRGTKTmiVy9Ch98AJcu9YzFxsKaNdDPe5CIoygKKXEppMSlMDN9JgDtZ9upSKrA1m2j8utK\npsydQmJMIhlxGSzNWRriGYvBiNTXntDI9RN+9QxYunQpP/vZzzzBndPp5Pnnn+fWW28d1JO9/PLL\nzJs3j5iYGL7//e/7fK2xsZG1a9cSHx9PXl4eb7/9tudr//zP/8ztt9/OP/3TP/ncR979i3ChqnDo\nEPzHf/gGdRMnwg9+MHqCuv7cOe9OjFVGMhMyyUjIICUuBcd5B8VzpIekEEIEk19bsdXV1axZs4ba\n2lpyc3OpqqoiIyODjz/+mOzs7Bvd3WPTpk3odDq2bt1KR0cHr7/+uudrjzzyCACvvfYax44dY/Xq\n1ezbt6/f4gjZihXhorUVPvoIzp3rGdPrYeVKWLhwZNuYhJPSslK2Hd1Gt6sbo84oPSSFEGIQgppj\nB9oq3cGDB6muriY7O5sFCxag0w2tSehzzz3HxYsXPYFdW1sbycnJnDp1ioKCAkA7xiwzM5Nf/vKX\n193/nnvu4fjx4+Tm5vKXf/mXfO9737v+G5PATgRBaSn88Y/Q5tXJY9w4rY1Jenro5iWEECKyBDXH\nDkCv17No0SIWLVo07CftPfGzZ89iMBg8QR3ArFmzKCkp6fP+W7Zs8et51q9f7zktIzExkdmzZ3ty\nD9yPLZ+H5+cvvfRSWF+vL74o4dAh6O7WPq+o0L7+yCPLKS6GPXtKOH06fOYbzM+9X7fhMB/5XK7f\nWPpcrl/kfO7+uKKigkDye8UukHqv2O3evZuHHnqI2tpaz21effVVfv/737Njx44hPYes2EW2kpIS\nz4sg3NTUaAUSDV69fBMStDYmYX58clCE87UTNybXL7LJ9YtcQV+xC6TeE4+Pj6elpcVnzGq1kpCQ\nEMxpiTASjr+YXC7YvRt27tQ+dps2De69V6t+FeF57YT/5PpFNrl+4oaBnaqqXLhwgZycHAyGwMSB\nvatZp0yZgsPhoKyszLMde/z4cW666aZhPc+GDRtYvny5/I8uhq2xUWs2XF3dMxYdDffcAzNnjp0C\nCSGEEIFVUlLisz07XDfcilVVFZPJRGtr65CLJdycTid2u50XXniBmpoaXn31VQwGA3q9nkceeQRF\nUfjNb37D0aNHWbNmDfv376eoqGhIzyVbsZEtXLYTVBW+/lo7Fqy7u2c8J0fbek1KCt3cwlW4XDsx\nNHL9Iptcv8gVqLjlhpGaoijcfPPNlJaWDvvJfv7znxMXF8c//MM/8NZbbxEbG8svfvELAP7t3/6N\njo4Oxo0bx2OPPcYrr7wy5KBOiEBob4d339VambiDOp0OVqyA9eslqBNCCBF+/Cqe+NnPfsZbb73F\n+vXryc7O9kSViqLwxBNPBGOegyYrdmI4zp+HDz8Em61nLCUF1q2DrKzQzUsIIcToFNTiiT179pCX\nl8fOnTuv+1q4BnYgOXZi8Ox22LYNDhzwHZ83D+68E4zG0MxLCCHE6BT0HLtIJSt2kS0UeSJ1dVob\nkytXesZMJrj/fpgyJahTiWiS4xPZ5PpFNrl+kSvo7U4aGhr45JNPqKur42/+5m+oqalBVVUmTJgw\n7EkIEUqqCvv3ayt1TmfP+JQpcN99EB8furkJIYQQg+HXit3OnTt58MEHmTdvHnv37sVms1FSUsI/\n/dM/8fHHHwdjnoMmK3bCH1arlkt34ULPWFQU3HUXzJ0rbUyEEEIER1DPip09ezb/+I//yMqVK0lK\nSqKpqYnOzk5ycnK44r1vFUYksBM3cvIkbN4MnZ09Y5mZWoFEamro5iWEEGLsCVq7E4DKykpWrlzp\nMxYVFYXTe98qDG3YsCGgCYkieEbyunV2arl077/fE9QpCixbBk8+KUHdcMlrLrLJ9Ytscv0iT0lJ\nCRs2bAjY4/mVY1dUVMRnn33GqlWrPGPbtm1jxowZAZvISAjkD0qMDhUV2gkSVmvPWGKitkqXkxOy\naQkhhBij3N07XnjhhYA8nl9bsQcOHGDNmjXcc889vPfeezz++ON8/PHHfPTRR8yfPz8gEwk02YoV\n3pxO2LED9u7ViiXcZs+Gu+/WjgcTQgghQiWoOXYANTU1vPXWW1RWVpKTk8Njjz0W1hWxEtgJt/p6\nbeu1trZnLDYW1qyB6dNDNy8hhBDCLeiBHYDL5eLq1aukpaWhhHm5oAR2kS0QvZhUFQ4dgs8/B4ej\nZ3zSJHjgATCbhzdH0TfpoxXZ5PpFNrl+kSuoxRNNTU08/vjjxMbGMn78eGJiYnjsscdobGwc9gRG\nkhRPjF2trfDf/w1btvQEdQYDrFoFjz8uQZ0QQojwEOjiCb9W7B544AEMBgM///nPycnJoaqqir/7\nu7+ju7ubjz76KGCTCSRZsRu7zpyBP/4R2tt7xtLTtQKJ9PTQzUsIIYToT1C3Yi0WC7W1tcTFxXnG\n2tvbycjIwOpdXhhGJLAbe7q74bPP4OhR3/HFi2HFCm3FTgghhAhHQd2KnTp1KhUVFT5jlZWVTJ06\nddgTEKIvg91Cv3gRXnnFN6gzm+G734U775SgLpgk/SGyyfWLbHL9hF9/7lasWMGdd97Jd7/7XbKz\ns6mqquKtt97i8ccf57e//S2qqqIoCk888cRIz1cIHy4X7Nql/XO5esanT9eqXmNjQzc3IYQQItj8\n2op1V9h4V8K6gzlvO3bsCOzshkFRFJ5//nlP4z8x+jQ2am1MLl7sGYuOhtWrYcYMOedVCCFE+Csp\nKaGkpIQXXngh+O1OIonk2I1eqgrHjmn5dN3dPeO5ubB2rXaShBBCCBFJgppjJ0Sw9Zcn0t4O776r\nVb26gzqdDlauhO99T4K6cCA5PpFNrl9kk+snJKVcRIyyMvjwQ61HnVtqqtbGJDMzdPMSQgghwoVs\nxYqwZ7fDl1/CV1/5jt9yi1bxGhUVmnkJIYQQgRKouEVW7ERYq63VCiTq63vGTCbtSLDJk0M3LyGE\nECIc+Z1jd/r0aV588UWefvppAM6cOcOJEydGbGJibNu+vYS9e+E3v/EN6goL4amnJKgLZ5LjE9nk\n+kU2uX7Cr8DuvffeY9myZdTU1PDmm28CYLPZ+NGPfjSikxNjT2lpJf/4j9v5xS++5he/2M7ly5WA\ntt16773w8MPaip0QQgghrudXjt3UqVN55513mD17NklJSTQ1NWG328nIyODq1avBmOegSR+7yHP6\ndCX/8A9lXLxYjMOhjTkc27jrrgKeeiqXlJTQzk8IIYQItJD0sUtJSaG+vh6dTucT2GVlZXHlypVh\nT2IkSPFEZKmshL/92+3U1a3wGc/NhXnztvPMMyv6uacQQggR+YLax27OnDn87ne/8xn7wx/+wPz5\n84c9ATG2tbTAxo3w+uvQ3Nzzv2N7ewk33wwTJ4LTKe0WI4nk+EQ2uX6RTa6f8Ksq9te//jV33HEH\nr732Gu3t7dx5552cPXuWzz//fKTnJ0YphwP279fOeLXbtTGdzoVOBzk54HSCxaKNG42u/h9ICCGE\nEB5+97Fra2tj8+bNVFZWkpOTw+rVq0lISBjp+Q2ZbMWGJ1WFs2e148Camny/lpRUSWVlGWZzsWes\nq2sb69cXUFiYG+SZCiGEEMETqLhFGhSLoLl6VQvoysp8x9PT4e67IS9Pq4rdtu083d06jEYXxcX5\nEtQJIYQY9YIa2FVWVvLCCy9w7NgxWr3Oc1IUhbNnzw57EiNBArvw0dUFO3fCgQPg8tpVjY2F22+H\nefO08169lZSUSDVzhJJrF9nk+kU2uX6RK6gnT/zJn/wJRUVF/PznPycmJmbYTyrGBlWF48e148C8\nz3dVFJg7F1asgLi40M1PCCGEGG38WrGzWCw0Njai1+uDMaeAkBW70KqpgS1btP96y8nRtl0zMkIz\nLyGEECIcBXXFbs2aNf8/e/cdFcXVN3D8u0svi2BZEBQQUBBEsKBGjYBgi71FTDACggV9LLHEQFSs\nT9SIMda4xmDPo0aNSV4rAgZ7jy12xWiwRo2dsu8fG1aW3gQW7+ccz3HvzNy5szPL/vZWEhISaN1a\nu+YSi4qKEhMUl7KnTyE2Fk6c0Ew3M4M2baBePVWNnSAIgiAIbyYoLikFqrG7f/8+7733HnXq1EEu\nl785WCJh+fLlJVaYkiRq7EpXWhocOqTqS/fq1Zt0HR1o0QJatgR9/YLnJ/qJaC9x77SbuH/aTdw/\n7VWqNXYhISHo6+tTt25dDA0N1SeXiKoXAdUo1+3bVaNeM3NxgbZtoXLlsimXIAiCILxrClRjJ5PJ\nuHXrFmZmZqVRphIhauzevocPYccOuHBBM71qVWjfHpycyqZcgiAIgqBtSrXGrn79+jx48ECrAjvh\n7Xn9Gn77DfbvVzXBZjAwAB8faNJE1QQrCIIgCELpKlBg17p1a9q1a0dwcDCWlpYA6qbYkJCQt1pA\nofxQKuHMGdi1S7XGa2YNGoCfH5ialsy5RD8R7SXunXYT90+7ifsnFCiw++2337C2ts5xbVgR2L0b\nkpNV05ckJWmm29iopi+pUaNsyiUIgiAIwhtiSTEhT8+fw549cOyYqsYug4mJavoSDw8xfYkgCIIg\nFNdb72OXedRreuZ1oLKQZl0LSqgQ0tPh6FGIi4MXL96kS6XQrBm0agViERJBEARBKF9yjcoyD5TQ\n1dXN8Z+enl6pFFIoXdevw7ffqppeMwd1Tk4QHq6awuRtB3UlOVmjULrEvdNu4v5pN3H/hFxr7M6e\nPav+/9WrV0ulMELZevwYdu6ETLceAAsL1fQldeqIZldBEARBKM8K1Mfuq6++YsyYMdnSo6Oj+fTT\nT99KwYpL9LEruJQU1dQliYmq/2fQ01M1ub73HugWaJiNIAiCIAhFUVJxS4EnKP7nn3+ypVtYWPD3\n338XuxBvgwjs8qdUwh9/qCYZfvRIc5u7u2pwhJi6UBAEQRDevlKZoHjPnj0olUrS0tLYs2ePxrYr\nV66U+wmLo6Ki8PHxEXP65ODePdi2DbK2sltZqaYvsbMrm3JlKI9zMVWuXLnc/pARBEEQyj8LCwse\nPnyokRYfH1+ifSPzrLGzt7dHIpGQlJSEra3tm4MkEiwtLfn888/p0qVLiRWmJIkau5y9fAnx8XD4\nsGrkawZjY2jdGho2VI18LWvlMbATz5QgCIJQHHl9j5RqU2y/fv1YtWpVsU9WmsSXsKb0dDh5EmJj\n4dmzN+kSCXh5ga8vGBmVXfm0gXimBEEQhOIoN4GdNhJfwm/cvKlqdr19WzPd3l7V7PrvKnFCPsQz\nJQiCIBRHaQR2YqxjBfbPP7B7N5w6pZleqZJqLjpX1/I7fUl5bIoVBEEQhPJOBHYVUGoqHDoECQnw\n+vWbdF1daNECWrZUTWUiCIIgCELFIppiK5hLl2D7dnjwQDO9bl1VLZ2FRdmUqyJ4V58pQRAEoWSU\nRlNsORj/KJSEBw9g7VpYs0YzqKtWDT75BPr0EUGdUHjXr19HKpWyf//+UjunVCpl7dq1byVvHx8f\nwsLC3kreQtHUqlWLGTNmlHUx8vU2n8uCGjVqFOHh4WVaBiFniYmJ2Nvb8+rVq7IuigjstN2rV6p+\ndIsWwcWLb9INDVXLgA0eDA4OZVe+ohLrHZasoKAggoODAdUX1N69e8u4RLlLTk6mZ8+eBd5fKpWS\nkJBATEwMtWrVynNfiUSCpJQ7lk6bNi3fcr3Ljh49yqhRo0okrwMHDtC9e3esrKwwMjLCycmJfv36\nceLEiQLnERoaiq+vb4mUpyRdu3YNhULBF198UdZFEXLQsmVLnJycWLBgQVkXRfSx01ZKJZw+Dbt2\nqQZJZJBIoEED8PMDE5OyK9+76MKFG+zefYWUFCl6eun4+zvi7Fy8mZ5LKs+yCGiKSi6XF/oYbbk2\nbZWSkoLeW+qYW6VKlRLJ5/vvv2fgwIH06tWLtWvX4ujoyP3799myZQsjRowo1z9mCmLRokX4+flh\nbW1d1kUpl16/fo2+vn629Lf57GYVEhJCZGQkn376aZn+TRI1dlro9m1Yvhw2bdIM6mrWhLAw6NJF\n+4M6bRsRe+HCDWJiLnPvXmsePfLh3r3WxMRc5sKFG+Uiz7z6bdy9e5fg4GB1LYeLiwvff/99rvtH\nRkbi6uqKiYkJtra2DBkyhCdPnqi3P3nyhODgYKpXr46hoSG2traMHj1avT0xMZEWLVpgZmaGmZkZ\nnp6e7Ny5U709a5PX06dPGTlyJLa2thgaGlKrVi3++9//Fvo9yM38+fNxcXHByMiIOnXqMGPGDNLS\n0tTb165dS9OmTTE3N6datWp06tSJS5cuaeQxY8YMHB0dMTQ0RC6X0759e16+fElMTAwTJ07kxo0b\nSKVSpFIpU6ZMybEcKSkpfPrpp9SsWRNDQ0Osra3p27evertSqWTChAnI5XJkMhkBAQHMnTtX40sr\nKiqK2rVra+SbmJiIVColKSkJgEePHhEYGIidnR3Gxsa4uLgQHR2tcUxQUBBt2rRh/vz52NvbY2ho\nyKtXr7hz5w5BQUHI5XLMzMxo2bIlv/32W4GvISf29vZMnz5d4/WkSZMYMWIEVapUwcrKik8//VTj\nnmR1+/ZthgwZQlhYGOvWraN169bY2dnRqFEjpk6dys8//wyo/q4MGjRI41ilUomjoyPTpk1j8uTJ\nLF++nISEBPX9WrlypXrfx48f069fP8zMzKhZsyZffvmlRl7//PMPgwYNQi6XY2hoiJeXF7t27VJv\nz+jasGHDBjp16oSJiQmOjo6sWLEiz/cIYM2aNXTv3l0jLaNrwdSpU6levTpVqlShf//+PMs0WWnG\nvcxs9erVSDPNRJ/x3GzYsAEnJydMTEzo2bMnT58+ZcOGDTg7O2NmZkbv3r01PusZec+dOxcbGxtM\nTEz48MMP1Sv0xMfHo6ury59//qlx/pUrV2Jubs6LFy9yvNZr167Ro0cPdZ7169dn9erV2a49NDSU\nCRMmUL16dezt7dWfs7Vr1/LBBx9gamrKxIkTAQgLC8PJyQljY2McHR2JjIzk9b+jC69evYpUKuXA\ngQMa59i7dy+6urrcvHkTgGXLllG3bl2MjIyoUqUK3t7e3Lp1S71/586duXnzJomJiTleV2kRNXZa\n5Nkz2LMHjh9X1dhlkMnA3x/q1y+/05dUdLt3X8HAwA/NFmQ/fv99D15eRau1O3z4Cs+f+2mk+fj4\nERu7p9C1drn9enzx4gXe3t6YmJioazmuXLnC/fv3c83L2NgYhUJBzZo1uXz5MkOHDmX48OHExMQA\n8MUXX3DixAm2bt1K9erVuXnzJufOnQMgNTWVLl26EBISov7CPHPmDMbGxjmeS6lU0qlTJ/78808W\nLFhA/fr1uXXrFn/88Ue2aytKrWRUVBQxMTHMmzcPT09Pzp07x+DBg3n58qU6AHv9+jUTJ07E1dWV\nJ0+eMHHiRDp27MjZs2fR09Nj06ZNzJw5k7Vr1+Lh4cGDBw9ISEgAICAggAsXLrBmzRqOHj0KgEku\nv7rmz5/Phg0bWLNmDQ4ODiQnJ2v0bfzmm2+YO3cuixcv5r333mPz5s1Mnjw52zXn9x68evUKd3d3\nxowZg4WFBYmJiQwePJjKlSsTFBSk3u/w4cOYmZnx888/I5VKSU1NxdfXFzc3N7Zv3465uTk//PAD\nbdq04eTJk7i4uOR7DTnJ6b7Nnz+f8ePHc/jwYY4fP87HH39MvXr1CAkJyTGP9evX8/r161ybKStV\nqgTA4MGDGThwINHR0er7sGfPHpKSkggNDUUmk3Hp0iWuX7/Opk2bNI4FmDx5MtOnT2fKlCls27aN\nYcOG0aRJE1q3bg2oamyOHTvGmjVrsLW1ZfHixXTq1Inff/8dZ2dndT7jx49n5syZfPPNN3z33XeE\nhobSvHnzbEF5hosXL5KcnEzTpk2zbdu4cSMhISEkJCRw48YNAgICsLOzUz+/Bf1c/PXXX6xcuZIt\nW7bw8OFDevXqRY8ePdDT02Pjxo08efKEnj17MmPGDI2A9vDhw5iYmLBz507u379PWFgYAwYMYNOm\nTfj4+FC7dm2WL1+uDrAAFAoFH3/8MUa5zIr/7Nkz/P39mTx5Mqampvz6668EBwdTo0YNjR/969ev\nJzAwkLi4ONLS0tQ/YD/77DNmzZrF4sWLAdXfEUtLS9atW4elpSWnTp1i0KBB6ASL1c8AACAASURB\nVOnpERUVhYODA23btkWhUPDee+9plLNdu3bUrFmTY8eOMWTIEL7//nu8vb15/Pgxhw8f1ii3TCbD\nzc2NPXv28P777+f7nr81ygqqIl1aaqpSeeCAUvnf/yqVkya9+TdlilK5a5dS+fJlGRfwLYiLiyvr\nImST1zM1d26cctIkpdLbW/Nfu3ZxGvesMP/atYvLlt+kSapzlZRly5YpDQ0Nlbdu3cpx+7Vr15QS\niUS5b9++XPPYtGmT0sDAQP26a9euyqCgoBz3ffjwoVIikSjj4+NzzU8ikSjXrFmjVCqVyt27dysl\nEony2LFjBbmcfPn4+CjDwsKUSqVS+ezZM6WxsbFyx44dGvusWLFCaW5unmseDx48UEokEuX+/fuV\nSqVSGR0draxTp44yJSUlx/2nTp2qtLe3z7dsI0aMULZu3TrX7TY2NsovvvhCI61Xr15KPT099etJ\nkyYpnZycNPb57bfflBKJRHnjxo1c8x4+fLiyTZs26tf9+/dXWlhYKJ89e6ZO+/7775U1atRQpqam\nahzr6+urHDlyZIGuISf29vbK6dOnq1/b2dkpu3btqrFPhw4dlH379s01jyFDhuR5zzK8fPlSWa1a\nNeWyZcvUaQEBAcpu3bqpXw8YMEDp4+OT7ViJRKIcMWKERlrdunWVn3/+uVKpVCovXbqklEgkym3b\ntmns07BhQ2VISIhSqXzzeZo7d656e1pamlImkymXLl2aa7l//vlnpUQiUT59+lQj3dvbW+np6amR\nNmTIEOV7772nft2/f3+lv7+/xj6rVq1SSiQS9etJkyYpdXV1lQ8ePFCnDR06VKmjo6O8f/++Om3E\niBHKxo0ba+Qtk8mUT548Uaft3LlTKZFIlFeuXFEqlarPh52dnTI9PV2pVCqV58+fV0okEuXJkydz\nvd6cdO3aVf3Zzbh2Z2dnjX0y3t9p06blm190dLSydu3a6tebNm1SmpiYqK/l77//VhobGyu3bNmi\n3l6pUiWNa81Jly5dlB999FGu2/P6HimpuEU0xZZzV6/CkiWqKUxevnyTXqcOhIerauoMDMqufIKK\nnl56juk6OjmnF4RUmvOx+vpFzzOrY8eO4ebmVqh+O5s2baJVq1bY2Nggk8kIDAwkJSWF5ORkAMLD\nw9m4cSPu7u6MHDmS7du3q39JW1hYEBoaSrt27fjggw+YOXMmFzOP+smhfBYWFjRs2LB4F5qDs2fP\n8uLFC3r06IFMJlP/Gzx4ME+ePOHBv8PLT548Sffu3XFwcMDMzAw7O1Vt6Y0bqibxPn36kJKSgp2d\nHcHBwaxevZqnT58WujzBwcGcPn0aJycnhgwZwqZNm0hJSQFUzdu3b9+mefPmGse0aNGi0NMjpKen\n8+WXX+Lp6Um1atWQyWR8++236qbaDHXr1tWoST1y5AjJycmYm5trvF+JiYlcvnw532soKIlEgqen\np0Za9erVuXPnTq7HKJXKAr0PBgYGBAUFoVAoAHjw4AFbtmwp8EjprOWytrbm7t27AOpa6VatWmns\n06pVK86ePZtrPlKpFLlcnuf1PX78GMhe2yuRSPDw8NBIy++9yo2NjQ2VK1dWv7a0tMTKykqjD6Sl\npaX6ejO4uroik8nUrzOe0Yz345NPPuHu3bvs2LEDUDVnNm7cOFu5M3v+/Dnjx4+nXr16VKlSBZlM\nxv/93/9le0YbNWqU4/FNmjTJlqZQKGjatClWVlbIZDIiIiI08uvcuTOVKlVizZo1gKq52tzcnM6d\nOwPQtm1bHBwcqFWrFn379kWhUKj/RmQmk8l49OhRrtdWGkRTbDn16BHs2AHnz2umV6kC7dqpAruK\nTNv62Pn7OxITE4uPz5um01evYgkKciJTC0yhXLigytPAQDNPPz+n4hZXQ2ECg0OHDvHhhx8SERHB\nnDlzsLCw4MCBA/Tv31/dX6Vt27YkJSWxY8cO4uPjCQwMxN3dndjYWKRSKUuXLmXEiBHs3LmTXbt2\nMWHCBBYsWMDAgQNL9Lryk56uCpA3btxInRw+UBYWFjx//py2bdvSqlUrYmJisLS0RKlU4ubmpr5e\na2tr/vjjD+Li4tizZw9Tp07ls88+49ChQ9SoUaPA5fHw8ODatWvs2rWLuLg4RowYwYQJEzh48GCB\n85BKpdnuZ9bAas6cOXz55Zd8/fXXNGjQAJlMRnR0NL/++qvGflmbx9PT06lbty5btmzJdt6MffO6\nhsxf/vnJ2gleIpGo71dOXFxcePLkCbdu3cLGxibPvAcNGsScOXM4ffo0sbGxyOVyOnToUKRyAXmW\nC3L+fBX2+szNzQFVE2XW4C6/vAryTADZBhhIJJIc07KWM7+/H1WqVKFXr14oFAr8/PxYuXJlvtPb\njB07lq1btzJ37lycnZ0xNjZm9OjR6gA3oyy5dWvImr5hwwaGDRvGzJkz8fb2xszMjPXr1xMZGane\nR1dXlwEDBqBQKBg8eDDLli0jODhY3RfRxMSEo0ePsm/fPnbv3s2SJUsYN24csbGxGj88Hz9+jEUZ\nzy0mauzKmZQUiIuDBQs0gzp9fWjTBoYMqfhBnTZydrYjKMgJuXwP5ubxyOV7/g3qij4q9m3kmVXj\nxo05d+6cRgfgvCQmJlK1alWmTJmCl5cXTk5O6o7FmVlYWBAQEMCSJUv49ddfSUhI4HymB9rNzY1R\no0bxf//3fwwYMIClS5fmeL5GjRrx999/c+zYsaJdYB7c3NwwNDTkypUrODg4ZPsnlUo5f/489+/f\nZ/r06bRq1QpnZ2cePnyY7ctMX1+fdu3aMXPmTE6fPs3z58/56aef1Nvy6vifmYmJCd26dWPevHkc\nPXqU8+fPs3fvXszMzLCxsWHfvn0a++/bt0+j/5RcLufu3bsaX77Hjx/XOGbv3r106NCBoKAgPDw8\ncHBw4OLFi/n2w/Ly8uLq1avIZLJs75WVlVW+1/A29e7dGwMDA6ZNm5bj9ozO/ACOjo60bt0ahULB\nd999R0hIiMa1F+Z+ZT7Ozc0NQN2/MsPevXtxd3cv8LXkJKPvXUYtcWFYWlpyO8tC4VmfieI4f/48\n/2QaxZfRp9LV1VWdNmjQIH7++WeWLFnCy5cv8x1Q89tvvxEYGEivXr1wd3enVq1aXLhwocgjTffu\n3UuDBg0YOXIkDRo0wNHRkWvXrmXLLzQ0lFOnTrFkyRJOnz5NaGioxnapVMr777/P5MmTOXbsGNWr\nV882t+GNGzdy/KFYmrSuxu7w4cOMHDkSPT09bGxsWLlyJbq6WncZ2SiVcO4c7NwJmX6UAODhoWpy\nLcQPXq2njWvFOjvblWjQ9bbyzKxv377MmjWLLl26MGvWLBwcHLh69SoPHjzgww8/zLa/i4sL9+7d\nY/ny5fj4+JCYmKjuoJwhMjKSxo0b4+rqilQqZfXq1chkMmxtbbl8+TIKhYIuXbpQo0YNbt++zW+/\n/ZZrk4qfnx/vv/8+ffr0ITo6Gnd3d27fvs0ff/zBgAEDCn29mZvsTE1NiYiIICIiAolEgp+fH6mp\nqZw+fZqTJ0/y5ZdfYmdnh4GBAd988w2ffvop169fZ/z48RpfCN999x1KpRIvLy/Mzc2JjY3ln3/+\nUX+x1apVi+TkZA4ePKgecZhTp/HZs2djY2ODh4cHxsbGrFu3Dl1dXfWXxOjRo5kwYQIuLi40bdqU\nrVu3Ehsbq5FH69atef78ORMnTiQ4OJjjx4+zaNEijX1cXFxYtWoV8fHxWFtbs3LlSg4fPpxvLcPH\nH3/M3Llz6dixI9OnT6d27drcuXOHPXv24OrqSteuXfO9htzuSV6vC8La2poFCxYwaNAgHj16RFhY\nGA4ODjx8+JCffvqJ+Ph4jYBr0KBBfPzxx6Snp2f78nZwcGDjxo2cO3dOPfo3p5q6jLJmlNfR0ZHe\nvXsTHh7Ot99+qx48ce7cOX744Yc8y5/fNdepUwcrKysOHTqkETAVpAna39+fmTNnsmjRItq1a8ee\nPXvYsGFDnscUhkQi4ZNPPmHatGk8ePCAoUOH0rVrVxwyTaDaokULnJ2dGTt2LP3798+1pi2Ds7Mz\nW7ZsoUePHpiYmBAdHc1ff/2l8QOioM3voHrmly9fztatW3Fzc+OXX35h8+bN2Y63tbWlffv2jBw5\nEn9/f+zt7dXbtm7dytWrV3n//fepVq0ax44d4+bNm+qAHlSjos+dO1fm311aV2Nna2tLXFwcCQkJ\n2Nvbq38Va7M7d2DFCtiwQTOos7aGAQOge/d3K6gTSo+RkREJCQnUq1ePgIAAXF1d+c9//sPLTB06\nMwcxHTt2JDIykoiICOrXr8/69euZPXu2xj5GRkZMnDiRxo0b4+XlxZkzZ9i2bRsymQxTU1MuX75M\nQEAAzs7O9OrVixYtWuQ5qeevv/7KBx98wODBg3FxcaFfv3459m0piKwjBL/44guio6NRKBR4enry\n/vvvM2/ePPWEwlWrVmX16tXs2rWLevXqMW7cOObMmaMxVUTlypX5/vvv8fX1xdXVla+//hqFQqGe\n5LZ79+707t2bjh07IpfLmT17do5lq1SpEtHR0TRv3pz69evz008/8eOPP6pra0aMGMHw4cMZNWoU\nDRo04NChQ0ycOFHjy6lOnTooFArWrVuHu7s7MTExzJgxQ+OaJ0yYgLe3N127dqV58+Y8fvyY4cOH\na+yT00hKAwMDEhISaNy4McHBwTg7O9OzZ0+OHj2q/gLM7xpyuyd5vc6tPFkNGDCAhIQEdY2Qi4sL\nvXv35uLFi9ne827dumFubk779u2zNd0OGDAALy8vmjdvjlwuzzMoy1quZcuW0a5dOwIDA/H09OTA\ngQP88ssvGoFtbteXn8DAQDZv3pzn+XNK8/PzY9q0acyYMQNPT0/i4+OZOHFivve7oGlNmjShZcuW\ntGnThg4dOuDh4cHy5cuzlT80NJTXr18XqMvF3LlzsbOzw9fXF39/f2rWrEmvXr3yLXNGelaDBg2i\nX79+BAcH07BhQ44cOUJUVFSO+4aFheVYTgsLC37++Wc6dOiAs7Mz48ePZ8KECeqJ30EV/NWsWTNb\nP8vSptVrxU6aNIkGDRrQrVu3bNu0YV3PFy9Uza5HjmhOX2JsrKqh8/QEqdaF3hWXNjxTwrslJiaG\nsLCwQg9QeNc9ePCAmjVr8r///U/dOb68u379OvXq1ePChQv59iMsLUFBQdy6dUtjrr7cZPRHexvd\nKkrSokWLmDp1Kjdv3ix0a6Cfnx8dOnRgzJgxue4j1orNw40bN9i1a5fWfCgzS0+Ho0dh/nw4fPhN\nUCeVQrNmMHw4NGwogjpBEISSlJqaSnJyMpGRkdSoUUOrvj/s7e0ZOHCgVqyrm9njx485cuQICoWi\nxJaOexuePXvGH3/8waxZsxg6dGihg7rExESuXr3K8OHD31IJC65UQ4cFCxbQuHFjDA0NNaovAR4+\nfEj37t0xNTXF3t6edevWqbfNnTsXX19f5syZA6iG/n/yySesWLECHR2d0ryEYktKgqVL4Zdf4Pnz\nN+kODqp1Xdu3V63z+q4Ta8UKQsGI5dQKLjExEWtra3bv3l2g1R7Km+joaBYuXFjWxVArSBN5165d\n8fb2pkePHgQGBpZSyQpv6NCheHh44O7uztixYwt9fMuWLbl27Vqu/TFLU6k2xW7evBmpVMqOHTt4\n8eKFxrJFGaNkvvvuO06cOEHHjh3Zv3+/RkdReDNz/ZgxY9SzfeekvDWbPXmiWtf19GnNdHNz1fQl\nLi5i1YjMyuPgifL2TAmCIAjapTSaYsukj92ECRP4888/1YHds2fPqFy5MmfPnsXJSTVHV//+/bG2\nts62JuSqVasYNWqUevj4kCFDchy9J5FI6N+/v7pTr7m5OZ6enupgIaNG6G2/btnShwMHYMWKeFJT\nwd5etf3mzXjc3WHoUB/09EqvPOJ10V/7+vqKwE4QBEEoMolEQlxcnPp1fHw8169fB2DFihXaG9h9\n8cUX3Lp1Sx3YnThxgpYtW2osXBwdHU18fDxbt24t0jnKunZFqYSLF1WTDD98qLnNzQ3atoVMSxAK\nWqCsnylBEARBu5VGjV2ZTACXtU3+6dOnmJmZaaTJZDKNSQ+1yf37qiXA/l1lR83SEjp0gExT4wi5\nKI9NsYIgCIJQ3pVJYJc1IjU1NeXJkycaaY8fPy7UEjTlwatXkJAABw+qRr5mMDICX19o3FiMdBUE\nQRAE4e0pFzV2derUITU1lcuXL6v72J06dYp69eoV6zxRUVH4+Pi89ZofpRJOnYLduyHz2t8SCTRq\nBK1bq+amEwpO1NYJgiAI74L4+PgSnQmiVPvYpaWlkZKSwuTJk7l16xYKhQJdXV10dHTo27cvEomE\nZcuWcfz4cTp16sSBAweoW7dukc5VWv2hbt2Cbdvgzz81021tVc2u1au/9SIIpUT0sRMEQRCKo8JN\nUDx16lSMjY2ZOXMmq1evxsjIiOnTpwOq2Z5fvHiBXC4nMDCQJUuWFDmoKw1Pn8JPP4FCoRnUmZlB\nz54QHCyCuuIQ89i9e2rVqvVWJ1+VSqXZFuwWys7169eRSqXqReOLa9SoUYSHhxf6uNDQUD777LMS\nKUNBxMTEoKenV2rnK01BQUG0adOmrIvxzivVwC4qKor09HSNfxMnTgRU67Bt3ryZp0+fcv36dQIC\nAkqzaAWWlgYHDqhWjThx4k26jg60agXDhoG7u5iTTihfgoKC1JOCS6VS9u7d+9bPOW3aNPWaqwVx\n9OjRQs1MHx8fr16zNfP1lSf+/v7lslzlga2tLcnJyTRp0qTYeV27dg2FQsEXX3yhkf7gwQPGjRuH\ni4sLRkZGWFpa4u3tzapVq0hLSwNU028tWrSIW7duaRwrlUrV/0xNTfH09MxxDdS86OrqsnLlyuJd\nnJbJb8JiqVSKrq4uZ86c0Ugv7N+L4oiJidG4v1ZWVnTu3DlbmbRVmfSxKy0l3cfuyhVVs+v9+5rp\nLi6q6UsqVy6R0whoZx+7C5cvsPvYblKUKehJ9PBv5I+zk3O5yLMgM8SXldevX6Ovr0+VKlWKlU95\nvT5tl3F/SppUKkUul5dIXosWLcLPzw9ra2t12s2bN2nZsiX6+vpMmTKFBg0aoKenx759+/jqq6/w\n8PCgfv362NnZ8d5777F06VImT56ske/ChQvp2bMnT548Yfny5YSGhlKpUiV69uxZoHK9i903CnK9\nBgYGjB07lm3btpVCiXKmo6OjDuavXr3KiBEjaN++PefPny/1gZsl3ceuQo/RzAjsiuvvv+GHH2DV\nKs2grmpVCAyEgAAR1L3rLly+QExcDPcs7/HI6hH3LO8RExfDhcsXykWeuf2xzWgOW7duHe3atcPE\nxARXV1cSExNJSkqiffv2mJqa4ubmRmJiosaxYWFhODk5YWxsjKOjI5GRkbx+/RpQ/SKeOHEiN27c\nUP8qnjJlCqBa83LChAmEh4dTtWpVvL291ekZXTMuX75MpUqV+Prrr9XnO3/+PCYmJixbtqxQ15ib\np0+fMmLECGrUqIGJiQkNGzZk8+bNGvtERkbi6uqKiYkJtra2DBkyRGME/5MnTwgODqZ69eoYGhpi\na2vL6NGjAVUt4p49e1ixYoX6PcitpvTPP/+kZ8+eVKtWDSMjIxwdHfnqq6/U2x8+fEifPn0wNTXF\nysqKCRMm0L9/f41mLx8fH8LCwjTyzVoLcvz4cTp06IClpSUymYwmTZqwY8cOjWNyuz/Hjh2jbdu2\nyGQy5HI5PXv2JCkpqcDXkFXWptiM1xs2bKBTp06YmJjg6OhYoKW/1qxZQ/fu3TXSwsPDSUlJ4fjx\n4/Tt2xcXFxccHR355JNPOH78uHqgHkD37t1ZvXp1tnwrVaqEXC7HycmJGTNmULt2bTZv3sy1a9eQ\nSqUcOHBAY/+9e/eiq6tLUlIS9vb2pKWlERwcjFQqzbb85f79+2nYsCEmJiY0btyYo0ePamw/ePAg\nrVq1wtjYmMqVK/Pxxx9z79499faoqChq167N1q1bcXFxwdTUFF9fXy5nnWcri127duHj40OVKlUw\nNzfHx8eHI0eOaOwjlUpZvHgx/fr1w8zMjJo1a/Lll19q7JPTM1nQz+B//vMfdu3axe7du3PdJ+P6\nMktMTEQqlaqfu4xm7fj4eNzd3TE2NqZ169YkJycTFxeHp6cnpqamtGnThtu3b2c7h1wuRy6X06xZ\nM+bOncvt27c5ePAgUVFRuLi4ZNs/JCQEf3//Al1jYfj4+BAVFVVi+VXoGrviev0aEhNh/35ITX2T\nbmAAPj7QpImqCVYoedo2j93uY7sxqG1A/PX4N4l68PsPv+PV0qtIeR5OPMzzGs/h+ps0n9o+xB6P\nLXStXX61WRMmTCA6OpoFCxbw2WefERAQQO3atRk5ciTz588nIiKCjz76iKtXr6Krq4tSqcTS0pJ1\n69ZhaWnJqVOnGDRoEHp6ekRFRREQEMCFCxdYs2aN+gvL1NRUfb5vvvmG0aNHc/DgQVL//XBlrlV0\ncnJi8eLFhISE4O3tTd26denTpw+dO3cmNDQ023UVtkZSqVTSuXNnJBIJ69evx9raml27dhEQEMC2\nbdvUyxUaGxujUCioWbMmly9fZujQoQwfPpyYmBhANdn6iRMn2Lp1K9WrV+fmzZucO3dOfY3Xrl3D\n2tqaefPmAaouJzkJDw/n5cuXxMbGYm5uztWrV0lOTlZvHzBgAGfPnuWXX35BLpfz3//+l61bt9K0\naVON9yK/9+Cff/6hb9++REdHo6enx4oVK+jSpQtnzpzR+BLNen/OnTuHj48PY8aMYcGCBepBcG3a\ntOH333/HwMAgx2u4c+dOge9JhvHjxzNz5ky++eYbvvvuO0JDQ2nevHm2L/kMFy9eJDk5WeO9ePjw\nIdu2bWPKlCk51r7o6OhgnGmqgqZNm3Lt2jWSkpKwtbXNtWwGBga8fv2aWrVq0bZtWxQKBe+99556\nu0KhoF27dtja2nL06FGqV69OdHQ0ffr00cgnPT2diIgI5s+fT9WqVRk1ahQffvghly5dQkdHh+Tk\nZNq2bUuXLl1YvHgxjx49Ijw8nF69epGQkKDO56+//mLJkiWsW7cOHR0dQkJCCAkJybOrxbNnzxg2\nbBgeHh6kpqYSHR1N+/btuXTpEpUz1VBMnjyZ6dOnM2XKFLZt28awYcNo0qSJ+rNRkGcyN+7u7gQF\nBTF27FiOHz+e63NbkM90eno6U6ZMYfny5ejq6tKnTx969+6NVCpl6dKlGBgYEBAQwKeffsoPP/yQ\naz6G/y7SnpKSQlhYGNOnT2fv3r20atUKUH12NmzYUOjm+LIgArscKJVw9izs3Kla4zWzBg3Azw8y\nfUcJAinKlBzT00grcp7ppOeY/jr9daHzyrwuc3p69nyHDx9Oly5dAIiIiKBJkyaMHj2arl27Aqqa\nq4YNG3Lx4kVcXV2RSCRMmzZNfbytrS2XL19m8eLFREVFYWhoiImJCTo6Ojk2tzVp0kTdvzY3H330\nEbt37yYgIIDmzZvz7NkzFAqFeruPj4+6n1Tm6yuIhIQEDh48yJ07d9STo4eFhXHgwAHmz5+v/vKK\njIzUuMYZM2bQt29fdWCXlJREgwYN8PJSBe81atRQf9GbmZmhr6+PkZFRvk2OSUlJdO/enfr166vP\nleHy5cv89NNP6poWgOXLlxepP1JG7VuGqVOn8vPPP7NhwwYiIiLU6VnvT1BQEJ06dWLSpEnqtFWr\nVlG5cmV27NhBly5d8ryGwvjPf/5Dr1691OWbP38+8fHxeQZ2Wc93+fJl0tPTs601npuMpScvXryo\nkU9GDVRqaioxMTGcOXOGYcOGATBo0CD69evHvHnzkMlkPHr0iE2bNqkH6FStWhV4U+uXmVKp5Ouv\nv8bT0xNQ1U41a9aMq1evUrt2bRYuXIi5uTkxMTHo6qq+pletWoWnpyeJiYm0bNkSgFevXrFq1Sp1\nN4Zx48bRt2/fPJvPu3XrpvH622+/5ccff2T79u189NFH6vSAgAAGDBgAqH54LFiwgN27d9O6deti\nP5MSiYSpU6dSu3ZtVqxYQVBQUI77FaQGMOO9zHjuBg4cyLhx4zh27BgNGjQAVPcqozUgJ/fu3WPS\npEmYmZnRpEkTqlatygcffIBCoVAHdmvXrsXY2DhbzXB5VOGbYgvbbp2cDDExsHGjZlBnYwOhodC1\nqwjqSoM21dYB6ElyHuWmQ9GrdKW5fDz1pSXf38nDw0P9f0tLSwD1H8rMaXfv3lWnKRQKmjZtipWV\nFTKZjIiICI2mudxIJJICd5jPqB1atWoVa9euLbG+L0eOHOH169fY2Nggk8nU/9asWaPRlLVp0yZa\ntWql3i8wMJCUlBR1bVp4eDgbN27E3d2dkSNHsn379iL1qRo5ciQzZsygWbNmjB8/nt9++029LaMG\nsHnz5uo0PT09dTBZGPfu3SM8PJy6detiYWGBTCbj7NmzGvctp/tz5MgRNm/erPFeVa1alVevXnHp\n0qV8r6EwMoIdeNMPL6+av8ePHwNgYmKiTivsPcgI7h89eqSRHhoaikwmw8jIiNGjR/P5558zcOBA\nADp37kylSpVYs2YNAKtXr8bc3JzOnTvnez6JRKLxmav+7xQKGdd59uxZmjVrpg7qQPV5rFSpEmfP\nnlWnWVtba/RNrV69OkqlUuNzmtW1a9fo168ftWvXplKlSlSqVInHjx9n++xmvg8Z58rItySeyerV\nqzN69GgmTJjAy5cvC3xcVhKJRL12POT+9+vBgwcaz0VaWpr6Wba0tOTq1av8+OOP6oB80KBB/Pjj\nj+rnS6FQ0L9/f417UlLi4+NFU2xBFeaNev4c4uLg6FFVjV0GExNo0wY8PMRIVyF3/o38iYmLwae2\njzrt1aVXBAUEFXkAxYUaqj52BrUNNPL08/UrbnGzyTz9QkbzR05pGbV9GzZsYNiwYcycORNvb2/M\nzMxYv369Rg1XXjJ/Cefl0qVL/PXXX0ilUi5dulSgZp6CSE9Pp1KlStn6uH4IfQAAIABJREFUNQHq\nmo5Dhw7x4YcfEhERwZw5c7CwsODAgQP0799f3Zewbdu2JCUlsWPHDuLj4wkMDMTd3Z3Y2Fj1iN2C\nCAoKon379mzfvp24uDg6dOhA9+7dWbVqVa7HZA1epFJptrSUFM2a5KCgIP78809mz55NrVq1MDQ0\nJCAgQH09GbLeH6VSySeffML48eOzlSOj+a4o15CTrDVNEokkx1rmDObm5oCqiTGj3LVr10YqlXL2\n7NlsNVQ5yfjyzsgrw4wZM+jatSumpqbZat10dXUZMGAACoWCwYMHs2zZMnV/uvxIpVKNZsasn6+C\nDrrI6b3KnE9OOnXqhFwuZ9GiRdSsWRM9PT1atmyZ7RnIqcYvr3yh8AH1uHHjUCgUzJkzJ1uza0Ge\n54z9cnovM/dpzEhTKpUa20+dOoVEIkEul2d75tu3b49cLmflypW8//77HD9+nHXr1hXq+goqY5Bn\n1sE7RVWha+wKIj0dDh9WTV9y5MiboE4qhebN4T//AU9PEdSVNm2bx87ZyZkg3yDkd+WYJ5sjvysn\nyLfoQd3byrOk7N27lwYNGjBy5EgaNGiAo6Mj165d09hHX19f3VRaFM+ePSMgIIC+ffsye/Zshg4d\nypUrV4pbdAAaN27Mo0ePePHiBQ4ODhr/atSoAag6aletWpUpU6bg5eWFk5MTN2/ezJaXhYUFAQEB\nLFmyhF9//ZWEhATOnz8PqN6D1MwddPNgZWVFUFAQK1asYNmyZaxZs4anT5+qmxP37dun3vf169fZ\nOrzL5fJsU3Zk7b/022+/ER4eTqdOnXBzc8PKyqpA72njxo05depUtvfKwcFBIxjK7Rrepowm2hs3\nbqjTKleuTIcOHViwYEG25SpBFSA8f/5c/Trj2Dp16mjsZ2lpiYODQ65N6aGhoZw6dYolS5Zw+vRp\njf6fUPTPgJubGwcPHtQIZE6dOsXjx4+LtSLTgwcPOH/+POPHj6dNmza4uLhgYGCQZw1fhszPUUGf\nyfyYmJgwefJkZs2ala1WVi6Xc/fuXY1g8vjx44XKPz8ODg7UqlUrxx+aUqmUsLAwFAoFCoUCb2/v\nXLsDlDcVusYuP9evq6YvyVrL7+ioWjXi3xpZQSgQZyfnEg+63kaeJcHFxYXly5ezdetW3Nzc+OWX\nX7KNKHVwcCA5OZmDBw/i5OSEiYkJRkZGuf6qz5o+fPhwlEolCxYswNjYmN27d9O3b1/2799f7OYQ\nPz8//P396dGjB7NmzcLd3Z2///6b/fv3Y2RkRGhoKC4uLty7d4/ly5fj4+NDYmIiixcv1sgnMjKS\nxo0b4+rqilQqZfXq1chkMnU/rVq1ahEXF8fVq1cxMzPD3Nw8x7IPGzaMjh07UqdOHV6+fMmmTZuw\ntbXF1NQUJycnunTpwtChQ/n222+Ry+V8+eWX2QImf39/hgwZwsaNG/H09GTjxo0kJiZqBF7Ozs6s\nXr2aFi1akJqaysSJE0lPT9d473O6Pxn9LgMDAxkxYgRVq1bl+vXr/PTTT4wYMYJatWrleQ3FkV8t\nUJ06dbCysuLQoUMafeoWLVpEixYtaNSoEVOmTMHDwwN9fX0OHjzIV199xcqVK9XNdQcPHsTe3r7Q\n/QJtbW1p3749I0eOxN/fX91XL0OtWrXYs2cP7du3R09PT93Ml59hw4Yxb948goKCiIiI4O+//yY8\nPJxWrVrRokWLQpUxMwsLC6pVq8bSpUtxcHDg/v37jBs3DiMjo3yPVSqV6ntR0GeyIAYMGMC8efP4\n7rvvNALo1q1b8/z5cyZOnEhwcDDHjx9n0aJFhc6/OAYMGMDkyZO5ePFiofvxlqV3ssbu8WPYsEHV\nly5zUGdhAX37qqYwEUFd2dK2PnbaLKeRZ/mlZXQcDw4OpmHDhhw5coSoqCiNfbp160bv3r3p2LEj\ncrmc2bNn55p31vT169ezdu1afvjhB/XoxZiYGG7fvl3g5t78bN26lR49ejBq1Cjq1q1Lp06d2LZt\nm3oajI4dOxIZGUlERAT169dn/fr1zJ49W6OcRkZGTJw4kcaNG+Pl5cWZM2fYtm2bui/g6NGjqVq1\nKh4eHlhaWua5ysLIkSNxd3fH29ubFy9eaMzxtXz5cjw9PenUqRM+Pj7UrFmT7t27awQ9/fv3Z+jQ\noQwdOhQvLy9u3brF8OHDNcr7/fffk56eTpMmTejRowcffPABXl5eOTZlZebi4sL+/ft5+vQp7dq1\nw83NjYEDB/Ly5UuNkb55XUNOsp6roM9iVoGBgdl+WNSsWZPjx4/TrVs3oqKiaNSoES1atEChUDBk\nyBDc3NzU+27evJnAwMB8z5OTsLAwXr9+re57l9mcOXM4duwY9vb26r5fuV1T5jS5XM7OnTv5888/\n8fLyonPnztSvX5+NGzdq7F/Y9ytjOpkrV65Qv359QkJCGDVqlLqPX16yni+3Z7KwpFIps2bN4sWL\nFxr516lTB4VCwbp163B3dycmJoYZM2YU+ZkpyHFZWVlZ0bFjR2QymXpAjzYo1bViS5NEImHSpEka\nExSnpKimLklMVP0/g56eatWI996Dt9AvUqgg3sXJRoXyKygoiNu3b7Nz586yLkqZu379OvXq1ePC\nhQvY2NiU2rGgqhmcOnUqN2/efCsd64Wy1aRJE95//33mzJlTIvnl9D2SMUHx5MmTS+Q7pkIHdhmX\nplTCH3/Ajh2QZdAT7u6qwRH/DooSyonyOI+dCOyE8iQoKIhbt26xa9eusi5KufDpp5/y6tUrFi5c\nWKjjwsLCqFKlSrYJePPz7Nkzbt68Sfv27QkNDc22nJmg3e7fv88vv/xCWFgYly5dytbMXlR5fY+U\n1HdMhf95ce+eqh/d1aua6VZWqn50dnZlUy5BEITiKM/LxJWF6OjoIh2XeW7Ewhg6dCjr1q2jbdu2\njB07tkh5COWXXC6ncuXKzJ8/v8SCutJSoWvswsNjkUodqVLlTfRmZKSaYLhhQ9XIV0EoKFFjJwiC\nIBSHqLErprNnW5OaGounJ1SrZoeXF/j6qoI7QRAEQRCEiqbC11np6vrx+PEVBg+GDz4QQZ220LZ5\n7ARBEAShPKjQNXY3b0ZRr54PDRtKyTTSXBAEQRAEoVzIGBVbUip0H7svvlCiowNy+R7Cw1uXdZEE\nLSf62AmCIAjFURp97Cp0U6yODrx6FYufn2NZF0UQBEEQBOGtq9CBnVy+h6AgJ5ydxZwm2kb0sRME\nQRCEwqvQfexE86sgqIjJbAVBEN4NFbrGTtBe5W3VCW03f/58jXUmi8rHxwepVMrixYs10hMTE5FK\npSQlJRX7HPm5fv06UqlU/c/c3JxmzZqxdevWt35uQRCE8k4EdoLwDpDJZFSqVKnY+UgkEgwNDZk8\neTJPnz4tgZIV3datW0lOTubgwYPUrVuXnj17cvjw4TItkyAIQlmr0IFdVFSU6KulpbTxvt24cIE9\nCxcS//XX7Fm4kBsXLpSbPIOCgmjTpk2210uXLsXOzo5KlSrRtWtX7t69m29ePXv2xMDAIM+1NePj\n45FKpdy+fVsjXVdXl5UrVwJvat7WrVtHu3btMDExwdXVlcTERJKSkmjfvj2mpqa4ubmRmJiY7RyV\nK1dGLpfj4uKCQqHAwMCAn376iYSEBHR0dPjzzz819l+5ciXm5ua8ePEi32sUBEEoLfHx8URFRZVY\nfhU+sBNNekJpuHHhApdjYmh97x4+jx7R+t49LsfEFCu4K8k8c1pX9MiRIyQkJLBt2zZ27NjB6dOn\nGTNmTL55GRoaMn36dObOncutW7cKXY6sJkyYwNChQzl58iQuLi4EBATQv39/hgwZwokTJ3B1deWj\njz4iNTU113x1dHTQ0dEhJSUFb29v6tSpw/LlyzX2USgUfPzxxxiJWcoFQShHfHx8SjSwq9CDJwTt\npW0B+ZXdu/EzMIBMNY1+wJ7ff8fOy6toeR4+jN/z5xppfj4+7ImNxc7ZuVB5KZXKbPMjGRoaEhMT\ng56eHgCDBw/m66+/zjcviURCYGAgX3/9NZGRkcTExBSqLFkNHz6cLl26ABAREUGTJk0YPXo0Xbt2\nBSAyMpKGDRty8eJFXF1dNa4J4OXLl3z55Zf8888/+Pv7AzBw4EDmzZvHhAkTkEgk/PHHH+zbt48F\nCxYUq6yCIAjlXYWusROE0iJNSck5PS2t6Hmmp+ec/vp1kfPMzMXFRR3UAVSvXp07d+4U+PjZs2ez\nevVqTp06VaxyeHh4qP9v+e8SMfXr18+WlrWZuG3btshkMkxNTVm0aBFff/01bdu2BaB///7cvXuX\nHTt2ALBs2TIaN26scS5BEISKSAR2QrmkbX3s0jMFSBrpOjpFz1Oa88czXV+/yHlmppelzIWd9dzX\n15cOHTowduzYbE2s0n/Lnjm/tLQ00nMIVjOXIyOfnNKyHhsTE8OpU6e4e/cud+/eZfjw4eptlStX\nplevXigUClJSUli5ciUDBw4s8LUJgiBoK9EUKwglwNHfn9iYGPwyNSHHvnqFU1AQFLLZVJ3nhQuq\nPA0MNPP08ytmaVVy6u9WWLNmzaJ+/fp4ZWlulsvlANy6dQsbGxsATp48WaJLstnY2ODg4JDr9kGD\nBuHr68uSJUt4+fIlffv2LbFzC4IglFcisBPKJW3rY2fn7AxBQeyJjUX6+jXp+vo4+fkVui/c284z\ns6IEWVn76tWtW5cBAwYwd+5cjf2cnJyws7MjKiqKuXPncu/ePSIiIkokmCyoFi1a4OzszNixY+nf\nvz8mJialdm5BEISyIgI7QSghds7OJRZ0lXSeWUfF5jRKNiO9MPkATJkyhbVr12qk6+rq8r///Y/w\n8HAaNGiAs7Mz8+fPx9fXN9/zFSStoAFiaGgoo0aNEs2wgiC8MyTKkmwbKUcK219IKF/i4+PLXa2d\neKa0z7hx44iNjeXYsWNlXRRBEIQ8v0dK6jumQtfYZcxjV94CBEEQ3q7Hjx9z8eJFFAoF8+fPL+vi\nCIIg5Co+Pr5EBwyKGjtBKCDxTGkPHx8fDh8+TN++ffnuu+/KujiCIAhA6dTYicBOEApIPFOCIAhC\ncZRGYCfmsRPKJW2bx04QBEEQygMR2AmCIAiCIFQQoilWEApIPFOCIAhCcYimWEEQBEEQBKHARGAn\nlEuij50gCIIgFJ4I7ARBEARBECoI0cdOEApIPFOCIAhCcYg+doIglIigoCDatGlT1sUAVJMHi7Vb\nBUEQ3g4R2AnlkuhjV7Lmz5/Pxo0bi53PgwcPGD58OA4ODhgaGiKXy2nVqhU//PBDgfPYsmUL0dHR\n6tdBQUFIpVKkUil6enrY29szZMgQHj58WOzyCoIgvGsq9FqxglCaLly9yu6zZ0kB9AB/NzecHRzK\nRZ4ymaxY5cjQs2dPnjx5wtKlS3F2dubevXscOnSoUEGYubl5trRWrVqxfv16UlNTOXr0KGFhYdy8\neZNffvmlRMotCILwrqjQNXZRUVGi5kdL+fj4lHURCuXC1avEHD/OvXr1eFSvHvfq1SPm+HEuXL1a\nLvLM2hSb8Xrp0qXY2dlRqVIlunbtyt27d3PN49GjR+zdu5dp06bh7+9PzZo1adiwIUOGDCE8PFxj\n34ULF+Lq6oqhoSGWlpb06tVLvc3Hx4ewsDCN/fX09JDL5VhbW9OlSxdGjBjB9u3befnyJT4+Pgwa\nNEhjf6VSiaOjI9OnTy/0eyEIglCexMfHExUVVWL5Vegau5J8owQhL7vPnsWgUSPiHz16k+joyO97\n9+IlkRQpz8N79/LcwwMy5enTqBGxZ84UutZOIpEgyVKOI0eOIJfL2bZtG0+ePOGjjz5izJgxrFy5\nMsc8TE1NkclkbNmyBR8fH4yNjXPcb9KkSURHRzNz5kzatm3Ls2fP2LZtW55lyfra0NCQ9PR00tLS\nGDx4MAMHDiQ6OhoTExMA9uzZQ1JSEgMGDCjU+yAIglDe+Pj44OPjw+TJk0skvwpdYydoL22raU3J\nJT2tiEEdQHoux74uQl5KpTLbaCtDQ0NiYmJwdXWlWbNmDB48mN27d+eah66uLitWrGDz5s1YWFjg\n5eXFyJEjiYuLU+/z7NkzZs2axeTJkwkPD8fJyQkPDw/Gjx+fb/kynDt3joULF9KsWTNMTEzo3r07\nhoaGGv34li1bRqdOnbCysirsWyEIglChicBOEEqAXi7pOsUYui7N5Vj9IueoycXFBT29NyWvXr06\nd+7cyfOYbt26cevWLbZv307Pnj05d+4cfn5+DBs2DICzZ8/y6tUr2rZtW6iyxMfHI5PJMDY2xt3d\nHScnJ9asWQOAgYEBQUFBKBQKQDWAY8uWLdmacwVBEIQK3hQraC9t62Pn7+ZGzLFj+DRqpE57dewY\nQa1a4VyrVpHyvKBUEnP8OAZZ8vRr2LDY5QU0gjoo+BxK+vr6+Pr64uvry/jx45k+fToTJkxg3Lhx\nRS5Ls2bNWLFiBbq6ulhbW6Orq/mnadCgQcyZM4fTp08TGxuLXC6nQ4cORT6fIAhCRSUCO0EoAc4O\nDgQBsWfO8BpVrZpfw4bFGhX7NvLMLGu/tqJycXEB4N69e+oBEzt27KBevXoFzsPQ0BCHPK7L0dGR\n1q1bo1AoiIuLIyQkpMTKLwiCUJGIwE4ol+Lj47Wu1s7ZwaHEgq63mWeGws5w/uDBA3r27ElISAj1\n69fH3NycM2fO8Pnnn+Pg4ICnpyc6OjqMHj2aqKgojIyM8Pf358WLF2zbtk3dzy6n/n4FMWjQID7+\n+GPS09MJDQ0t9PGCIAjvAhHYCcI7IOtI1JxGpmak50Ymk9GiRQsWLlzI5cuXefHiBdWrV6ddu3ZE\nRkaio6MDwNSpU6lWrRrffPMNo0aNwsLCAm9v70KXJatu3bphbm5OkyZNsLGxKdB1C4IgvGvEWrGC\nUEDimSpbDx48oGbNmvzvf/+jc+fOZV0cQRCEQhNrxQqC8M5LTU0lOTmZyMhIatSoIYI6QRCEPIjA\nTiiXtG0eO+HtSUxMxNramt27d7NixYqyLo4gCEK5JvrYCYJQrvn4+JCenl7WxRAEQdAKoo+dIBSQ\neKYEQRCE4hB97ARBEARBEIQCE4GdUC6JPnaCIAiCUHgisBMEQRAEQaggtK6P3Z07d+jRowf6+vro\n6+uzdu1aqlSpkm0/0R9KKGmVK1fm77//LutiCIIgCFrKwsKChw8f5ritpOIWrQvs0tPTkUpVFY0r\nVqzgr7/+Ui9VlJkI7ARBEARB0Bbv7OCJjKAO4MmTJ1hYWJRhaYS3RfSx017i3mk3cf+0m7h/gtYF\ndgCnTp2iadOmLFiwgL59+5Z1cYS34OTJk2VdBKGIxL3TbuL+aTdx/4RSDewWLFhA48aNMTQ0JDg4\nWGPbw4cP6d69O6amptjb27Nu3Tr1trlz5+Lr68ucOXMA8PDw4NChQ0ybNo2pU6eW5iUIpeTRo0dl\nXQShiMS9027i/mk3cf+EUg3sbGxsmDBhAiEhIdm2DR06FENDQ+7evcuaNWsYMmQI586dA2DUqFHE\nxcUxevRoUlJS1MeYmZnx6tWrUit/UZRktXhR8yrMcQXZN699irKtvDYdlHS5KuL9K6/3DrTv/hX3\n3uW1Xds+eyD+dua37V25d8XJryTvnzZ99ko1sOvevTtdu3bNNor12bNnbNq0ialTp2JsbEyLFi3o\n2rUrq1atypbHyZMn8fb2pnXr1kRHRzNu3LjSKn6RiD9O+W/LKf369ev5luNtq4h/nPLbpyS+XMrD\nvQPtu3/lJbCriPfvXfnsQfm4f9r22SvIvtoU2JXJqNgvvviCW7du8f333wNw4sQJWrZsybNnz9T7\nREdHEx8fz9atW4t0DicnJ65cuVIi5RUEQRAEQXibHB0duXz5crHz0S2BshSaRCLReP306VPMzMw0\n0mQyGf/880+Rz1ESb44gCIIgCII2KZNRsVkrCU1NTXny5IlG2uPHj5HJZKVZLEEQBEEQBK1WJoFd\n1hq7OnXqkJqaqlHLdurUKerVq1faRRMEQRAEQdBapRrYpaWl8fLlS1JTU0lLS+PVq1ekpaVhYmJC\njx49mDhxIs+fPycxMZGff/6Zfv36lWbxBEEQBEEQtFqpBnYZo15nzpzJ6tWrMTIyYvr06QAsWrSI\nFy9eIJfLCQwMZMmSJdStW7c0iycIgiAIgqDVtG6t2OJ48uQJ/v7+nD9/nkOHDuHq6lrWRRIK4fDh\nw4wcORI9PT1sbGxYuXIlurplMv5HKKQ7d+7Qo0cP9PX10dfXZ+3atdmmPRLKv3Xr1jFixAju3r1b\n1kURCuH69et4eXlRr149JBIJ69evp2rVqmVdLKGA4uPjmTZtGunp6QwfPpxu3brluf87Fdilpqby\n6NEjxo4dy5gxY3BzcyvrIgmFkJycjIWFBQYGBkRERNCoUSN69uxZ1sUSCiA9PV29zvOKFSv466+/\nGD9+fBmXSiiMtLQ0evfuTVJSEkePHi3r4giFcP36dcaOHcuGDRvKuihCIb148YI+ffrw448/oqen\nV6BjtHKt2KLS1dUVv1K0mJWVFQYGBgDo6emho6NTxiUSCiojqANVzbmFhUUZlkYoinXr1vHhhx9m\nG/wmaId9+/bRqlUrIiMjy7ooQiEcOHAAIyMjOnfuTI8ePbhz506+x7xTgZ1QMdy4cYNdu3bRuXPn\nsi6KUAinTp2iadOmLFiwgL59+5Z1cYRCSEtLY8OGDfTp06esiyIUgbW1NVeuXGHv3r3cvXuXTZs2\nlXWRhAK6c+cOly9f5pdffiEsLIyoqKh8j9HKwG7BggU0btwYQ0NDgoODNbY9fPiQ7t27Y2pqir29\n/f+3d6chUfx/HMDfq+bt2lrhFamlJVIpiYJZZkX9WLQDodLII0olD6gHHWJqoRFRgT2w80mFuB4P\ntUAh0QxKE9YIj1YLrCisLHRXa111fg/6O//W459a/9VZ3y9YcGZn5vuZeaN8nGMXKpVq0m3wv865\n8yf59ff3IyEhAffu3eMZuznwJ9kFBgaisbERBQUFyM/PN2XZ9B+zza+4uJhn6+aB2eZnbW0NOzs7\nAEBMTAxevHhh0rpp9tkpFAqEh4fDysoK27ZtQ2tr62/HkuSd556ensjJyUF1dTW+f/9u9F56ejps\nbW3x6dMnqNVqREVFITAwcMKDEgvo1sJ5Z7b5DQ8PIzY2Fnl5efDz85uj6he22WZnMBjE+0Pkcjn0\nev1clL/gzTa/9vZ2qNVqFBcXo7OzE8ePH0dhYeEc7cXCNdv8dDodHB0dAQCPHz/m/eVzYLbZhYSE\n4OrVqwCAlpYWrFq16veDCRJ29uxZISkpSZzW6XSCtbW10NnZKc5LSEgQzpw5I04rlUrBw8NDCAsL\nE+7evWvSesnYTPO7f/++sGTJEiEyMlKIjIwUysrKTF4z/TTT7BobG4WIiAhh69atws6dO4V3796Z\nvGb6r9n87RwTEhJikhppajPN7+HDh0JwcLCwefNmITExURgZGTF5zfTTbH73ioqKhIiICCEyMlJ4\n8+bNb8eQ5Bm7McK4s24ajQZWVlbw9fUV5wUGBqKurk6cfvjwoanKo9+YaX7x8fH80Op5YqbZhYaG\nor6+3pQl0v8wm7+dY5qamv7f5dFvzDQ/pVIJpVJpyhJpCrP53UtLS0NaWtq0x5DkPXZjxt/vodPp\nIJfLjeY5OTlBq9WasiyaJuYnXcxO2piftDE/6TJFdpJu7MZ3vo6Ojujv7zea19fXBycnJ1OWRdPE\n/KSL2Ukb85M25iddpshO0o3d+M539erVGB4eRldXlzjvxYsXWLt2ralLo2lgftLF7KSN+Ukb85Mu\nU2QnycZuZGQEP378wPDwMEZGRqDX6zEyMgIHBwfExMQgNzcXg4ODePLkCSorK3lf1jzD/KSL2Ukb\n85M25iddJs3uz5/xML28vDxBJpMZvc6fPy8IgiB8/fpV2Lt3r+Dg4CB4eXkJKpVqjqul8ZifdDE7\naWN+0sb8pMuU2S2o74olIiIiMmeSvBRLRERERBOxsSMiIiIyE2zsiIiIiMwEGzsiIiIiM8HGjoiI\niMhMsLEjIiIiMhNs7IiIiIjMBBs7IiIiIjPBxo6IaJykpCTk5OT81W0eO3YMBQUFf3WbRETjWc11\nAURE841MJpvwZd1/6saNG391e0REk+EZOyKiSfDbFolIitjYEdG8cunSJSxfvhxyuRz+/v6ora0F\nADQ1NSEsLAwKhQIeHh7IzMyEwWAQ17OwsMCNGzfg5+cHuVyO3NxcvH79GmFhYVi8eDFiY2PF5evq\n6rB8+XJcvHgRy5Ytg4+PD0pKSqasqaqqCkFBQVAoFAgPD8fLly+nXPbEiRNwdXWFs7Mz1q9fj7a2\nNgDGl3d37doFJycn8WVpaYn79+8DADo6OrBjxw4sWbIE/v7+qKiomHKsyMhI5ObmYtOmTZDL5fjn\nn3/Q29s7zSNNROaIjR0RzRuvXr1CUVERmpub0d/fj5qaGnh7ewMArKyscO3aNfT29uLp06d49OgR\nrl+/brR+TU0N1Go1nj17hkuXLiE5ORkqlQpv377Fy5cvoVKpxGV7enrQ29uLDx8+4N69e0hJSUFn\nZ+eEmtRqNY4cOYI7d+7g69evSE1Nxe7duzE0NDRh2erqajQ0NKCzsxN9fX2oqKiAi4sLAOPLu5WV\nldBqtdBqtSgvL4e7uzu2b9+OgYEB7NixA4cOHcLnz59RWlqKtLQ0tLe3T3nMVCoV7t69i0+fPmFo\naAhXrlyZ8XEnIvPBxo6I5g1LS0vo9Xq0trbCYDBgxYoVWLlyJQBgw4YNCA0NhYWFBby8vJCSkoL6\n+nqj9U+dOgVHR0cEBARg3bp1UCqV8Pb2hlwuh1KphFqtNlo+Pz8fixYtQkREBKKiolBWVia+N9aE\n3b59G6mpqQgJCYFMJkNCQgJsbGzw7NmzCfVbW1tDq9Wivb0do6OjWLNmDdzc3MT3x1/e1Wg0SEpK\nQnl5OTw9PVFVVQUfHx8kJibCwsICQUFBiImJmfKsnUwmw+HDh+EKxs8YAAAC2UlEQVTr6wtbW1vs\n378fLS0tMzjiRGRu2NgR0bzh6+uLwsJCnDt3Dq6uroiLi8PHjx8B/GyCoqOj4e7uDmdnZ2RnZ0+4\n7Ojq6ir+bGdnZzRta2sLnU4nTisUCtjZ2YnTXl5e4li/6u7uxtWrV6FQKMTX+/fvJ11269atyMjI\nQHp6OlxdXZGamgqtVjvpvvb19WHPnj24cOECNm7cKI7V2NhoNFZJSQl6enqmPGa/No52dnZG+0hE\nCw8bOyKaV+Li4tDQ0IDu7m7IZDKcPn0awM+PCwkICEBXVxf6+vpw4cIFjI6OTnu7459y/fbtGwYH\nB8Xp7u5ueHh4TFhvxYoVyM7Oxrdv38SXTqfDgQMHJh0nMzMTzc3NaGtrg0ajweXLlycsMzo6ioMH\nD2L79u04evSo0VhbtmwxGkur1aKoqGja+0lECxsbOyKaNzQaDWpra6HX62FjYwNbW1tYWloCAHQ6\nHZycnGBvb4+Ojo5pfXzIr5c+J3vKNS8vDwaDAQ0NDXjw4AH27dsnLju2fHJyMm7evImmpiYIgoCB\ngQE8ePBg0jNjzc3NaGxshMFggL29vVH9v46fnZ2NwcFBFBYWGq0fHR0NjUaD4uJiGAwGGAwGPH/+\nHB0dHdPaRyIiNnZENG/o9XpkZWVh2bJlcHd3x5cvX3Dx4kUAwJUrV1BSUgK5XI6UlBTExsYanYWb\n7HPnxr//67Sbm5v4hG18fDxu3bqF1atXT1g2ODgYd+7cQUZGBlxcXODn5yc+wTpef38/UlJS4OLi\nAm9vbyxduhQnT56csM3S0lLxkuvYk7EqlQqOjo6oqalBaWkpPD094e7ujqysrEkf1JjOPhLRwiMT\n+O8eES0wdXV1iI+Px7t37+a6FCKiv4pn7IiIiIjMBBs7IlqQeMmSiMwRL8USERERmQmesSMiIiIy\nE2zsiIiIiMwEGzsiIiIiM8HGjoiIiMhMsLEjIiIiMhP/Ah/1RvhmnkuIAAAAAElFTkSuQmCC\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10a59ce90>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 36
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"cython_bonus\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"# Bonus: How to use Cython without the IPython magic"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"IPython's notebook is really great for explanatory analysis and documentation, but what if we want to compile our Python code via Cython without letting IPython's magic doing all the work? \n",
|
|
"These are the steps you would need."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 1. Creating a .pyx file containing the the desired code or function."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%file ccy_classic_lstsqr.pyx\n",
|
|
"\n",
|
|
"def ccy_classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"Writing ccy_classic_lstsqr.pyx\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 11
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 2. Creating a simple setup file"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%file setup.py\n",
|
|
"\n",
|
|
"from distutils.core import setup\n",
|
|
"from distutils.extension import Extension\n",
|
|
"from Cython.Distutils import build_ext\n",
|
|
"\n",
|
|
"setup(\n",
|
|
" cmdclass = {'build_ext': build_ext},\n",
|
|
" ext_modules = [Extension(\"ccy_classic_lstsqr\", [\"ccy_classic_lstsqr.pyx\"])]\n",
|
|
")"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"Writing setup.py\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 12
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"####3. Building and Compiling"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"!python3 setup.py build_ext --inplace"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"running build_ext\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"cythoning ccy_classic_lstsqr.pyx to ccy_classic_lstsqr.c\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"building 'ccy_classic_lstsqr' extension\r\n",
|
|
"creating build\r\n",
|
|
"creating build/temp.macosx-10.6-intel-3.4\r\n",
|
|
"/usr/bin/clang -fno-strict-aliasing -Werror=declaration-after-statement -fno-common -dynamic -DNDEBUG -g -fwrapv -O3 -Wall -Wstrict-prototypes -arch i386 -arch x86_64 -g -I/Library/Frameworks/Python.framework/Versions/3.4/include/python3.4m -c ccy_classic_lstsqr.c -o build/temp.macosx-10.6-intel-3.4/ccy_classic_lstsqr.o\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\u001b[1mccy_classic_lstsqr.c:2040:28: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_AsString'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE char* __Pyx_PyObject_AsString(PyObject* o) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2037:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function\r\n",
|
|
" '__Pyx_PyUnicode_FromString' [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyUnicode_FromString(char* c_str) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2104:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_IsTrue'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyObject_IsTrue(PyObject* x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2159:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyIndex_AsSsize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE Py_ssize_t __Pyx_PyIndex_AsSsize_t(PyObject* b) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2188:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_FromSize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject * __Pyx_PyInt_FromSize_t(size_t ival) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1584:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_From_long'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyInt_From_long(long value) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1631:27: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_long' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE long __Pyx_PyInt_As_long(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1731:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_int' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyInt_As_int(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"8 warnings generated.\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\u001b[1mccy_classic_lstsqr.c:2040:28: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_AsString'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE char* __Pyx_PyObject_AsString(PyObject* o) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2037:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function\r\n",
|
|
" '__Pyx_PyUnicode_FromString' [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyUnicode_FromString(char* c_str) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2104:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_IsTrue'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyObject_IsTrue(PyObject* x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2159:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyIndex_AsSsize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE Py_ssize_t __Pyx_PyIndex_AsSsize_t(PyObject* b) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2188:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_FromSize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject * __Pyx_PyInt_FromSize_t(size_t ival) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1584:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_From_long'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyInt_From_long(long value) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1631:27: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_long' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE long __Pyx_PyInt_As_long(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1731:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_int' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyInt_As_int(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"8"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
" warnings generated.\r\n",
|
|
"/usr/bin/clang -bundle -undefined dynamic_lookup -arch i386 -arch x86_64 -g build/temp.macosx-10.6-intel-3.4/ccy_classic_lstsqr.o -o /Users/sebastian/Github/python_reference/benchmarks/ccy_classic_lstsqr.so\r\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 13
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 4. Importing and running the code"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import ccy_classic_lstsqr\n",
|
|
"\n",
|
|
"%timeit py_classic_lstsqr(x, y)\n",
|
|
"%timeit cy_classic_lstsqr(x, y)\n",
|
|
"%timeit ccy_classic_lstsqr.ccy_classic_lstsqr(x, y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"100 loops, best of 3: 2.9 ms per loop\n",
|
|
"1000 loops, best of 3: 212 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"1000 loops, best of 3: 207 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 20
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"numba\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
}
|
|
],
|
|
"metadata": {}
|
|
}
|
|
]
|
|
} |