mirror of
https://github.com/rasbt/python_reference.git
synced 2024-11-24 04:21:15 +00:00
1255 lines
183 KiB
Plaintext
1255 lines
183 KiB
Plaintext
{
|
|
"metadata": {
|
|
"name": "",
|
|
"signature": "sha256:14c3265ea9accf7a70bb5032b9e2b881a487f6b81b55999ef8578645edf4e3dd"
|
|
},
|
|
"nbformat": 3,
|
|
"nbformat_minor": 0,
|
|
"worksheets": [
|
|
{
|
|
"cells": [
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[Sebastian Raschka](www.sebastianraschka.com) \n",
|
|
"last updated: 05/04/2014\n",
|
|
"\n",
|
|
"- [Link to this IPython Notebook on GitHub](https://github.com/rasbt/python_reference/blob/master/benchmarks/cython_least_squares.ipynb) \n",
|
|
"- [Link to the GitHub repository](https://github.com/rasbt/python_reference)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### All code was executed in Python 3.4"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<hr>\n",
|
|
"I am really looking forward to your comments and suggestions to improve and \n",
|
|
"extend this little collection! Just send me a quick note \n",
|
|
"via Twitter: [@rasbt](https://twitter.com/rasbt) \n",
|
|
"or Email: [bluewoodtree@gmail.com](mailto:bluewoodtree@gmail.com)\n",
|
|
"<hr>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"# Implementing the least squares fit method for linear regression and speeding it up via Cython"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"sections\"></a>\n",
|
|
"<br>\n",
|
|
"<br>\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#Sections"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"- [Introduction](#introduction)\n",
|
|
"- [Least squares fit implementations](#implementations)\n",
|
|
"- [Generating sample data and benchmarking](#sample_data)\n",
|
|
"- [Compiling the Python code via Cython in the IPython notebook](#cython_nb)\n",
|
|
"- [Bonus: How to use Cython without the IPython magic](#cython_bonus)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"introduction\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Introduction"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Linear regression via the least squares method is the simplest approach to performing a regression analysis of a dependent and a explanatory variable. The objective is to find the best-fitting straight line through a set of points that minimizes the sum of the squared offsets from the line. \n",
|
|
"The offsets come in 2 different flavors: perpendicular and vertical - with respect to the line. \n",
|
|
"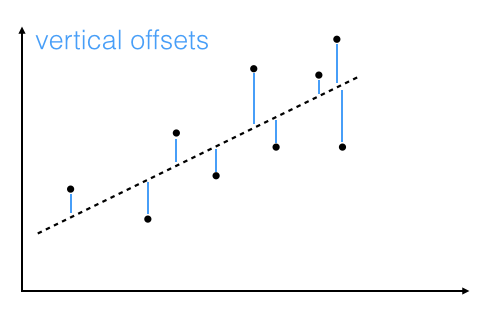 \n",
|
|
"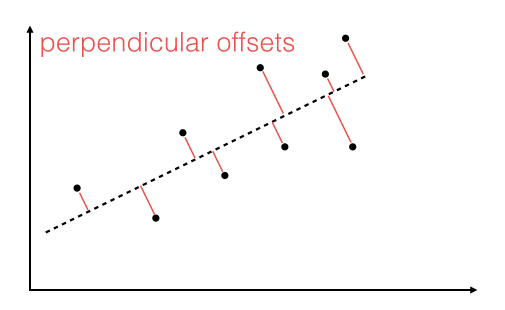 \n",
|
|
"\n",
|
|
"Here, we will use the more common approach: minimizing the sum of the perpendicular offsets.\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In more mathematical terms, our goal is to compute the best fit to *n* points $(x_i, y_i)$ with $i=1,2,...n,$ via linear equation of the form \n",
|
|
"$f(x) = a\\cdot x + b$. \n",
|
|
"Here, we assume that the y-component is functionally dependent on the x-component. \n",
|
|
"In a cartesian coordinate system, $b$ is the intercept of the straight line with the y-axis, and $a$ is the slope of this line."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In order to obtain the parameters for the linear regression line for a set of multiple points, we can re-write the problem as matrix equation \n",
|
|
"$\\pmb X \\; \\pmb a = \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\Rightarrow\\Bigg[ \\begin{array}{cc}\n",
|
|
"x_1 & 1 \\\\\n",
|
|
"... & 1 \\\\\n",
|
|
"x_n & 1 \\end{array} \\Bigg]$\n",
|
|
"$\\bigg[ \\begin{array}{c}\n",
|
|
"a \\\\\n",
|
|
"b \\end{array} \\bigg]$\n",
|
|
"$=\\Bigg[ \\begin{array}{c}\n",
|
|
"y_1 \\\\\n",
|
|
"... \\\\\n",
|
|
"y_n \\end{array} \\Bigg]$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"With a little bit of calculus, we can rearrange the term in order to obtain the parameter vector $\\pmb a = [a\\;b]^T$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\Rightarrow \\pmb a = (\\pmb X^T \\; \\pmb X)^{-1} \\pmb X^T \\; \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"The more classic approach to obtain the slope parameter $a$ and y-axis intercept $b$ would be:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$a = \\frac{S_{x,y}}{\\sigma_{x}^{2}}\\quad$ (slope)\n",
|
|
"\n",
|
|
"\n",
|
|
"$b = \\bar{y} - a\\bar{x}\\quad$ (y-axis intercept)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"where \n",
|
|
"\n",
|
|
"\n",
|
|
"$S_{xy} = \\sum_{i=1}^{n} (x_i - \\bar{x})(y_i - \\bar{y})\\quad$ (covariance)\n",
|
|
"\n",
|
|
"\n",
|
|
"$\\sigma{_x}^{2} = \\sum_{i=1}^{n} (x_i - \\bar{x})^2\\quad$ (variance)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"implementations\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"## Least squares fit implementations"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 1. The matrix approach"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"First, let us implement the equation:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\pmb a = (\\pmb X^T \\; \\pmb X)^{-1} \\pmb X^T \\; \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"which I will refer to as the \"matrix approach\"."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import numpy as np\n",
|
|
"\n",
|
|
"def lin_lstsqr_mat(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 1
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 2. The classic approach"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Next, we will calculate the parameters separately, using only standard library functions in Python, which I will call the \"classic approach\"."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$a = \\frac{S_{x,y}}{\\sigma_{x}^{2}}\\quad$ (slope)\n",
|
|
"\n",
|
|
"\n",
|
|
"$b = \\bar{y} - a\\bar{x}\\quad$ (y-axis intercept)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 4
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 3. Using the lstsq numpy function"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"For our convenience, `numpy` has a function that can also compute the leat squares solution of a linear matrix equation. For more information, please refer to the [documentation](http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.lstsq.html)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def numpy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return np.linalg.lstsq(X,y)[0]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 5
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 4. Using the linregress scipy function"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The last approach is using `scipy.stats.linregress()`, which returns a tuple of 5 different attributes, where the 1st value in the tuple is the slope, and the second value is the y-axis intercept, respectively. The documentation for this function can be found [here](http://docs.scipy.org/doc/scipy-0.13.0/reference/generated/scipy.stats.linregress.html)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import scipy.stats\n",
|
|
"\n",
|
|
"def scipy_lstsqr(x,y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" return scipy.stats.linregress(x, y)[0:2]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 6
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name='sample_data'></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Generating sample data and benchmarking"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In order to test our different least squares fit implementation, we will generate some sample data:\n",
|
|
"- 500 sample points for the x-component within the range [0,500) \n",
|
|
"- 500 sample points for the y-component within the range [100,600) \n",
|
|
"\n",
|
|
"where each sample point is multiplied by a random value within\n",
|
|
"the range [0.8, 12)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"x = [x_i*random.randrange(8,12)/10 for x_i in range(500)]\n",
|
|
"y = [y_i*random.randrange(8,12)/10 for y_i in range(100,600)]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 7
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"#### Visualization"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"To check how our dataset is distributed, and how the straight line, which we obtain via the least square fit method, we will plot it in a scatter plot. \n",
|
|
"Note that we are using our \"matrix approach\" here for simplicity, but after plotting the data, we will check whether all of the four different implementations yield the same parameters."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%pylab inline\n",
|
|
"from matplotlib import pyplot as plt\n",
|
|
"\n",
|
|
"slope, intercept = lin_lstsqr_mat(x, y)\n",
|
|
"\n",
|
|
"line_x = [round(min(x)) - 1, round(max(x)) + 1]\n",
|
|
"line_y = [slope*x_i + intercept for x_i in line_x]\n",
|
|
"\n",
|
|
"plt.figure(figsize=(8,8))\n",
|
|
"plt.scatter(x,y)\n",
|
|
"plt.plot(line_x, line_y, color='red', lw='2')\n",
|
|
"\n",
|
|
"plt.ylabel('y')\n",
|
|
"plt.xlabel('x')\n",
|
|
"plt.title('Linear regression via least squares fit')\n",
|
|
"\n",
|
|
"ftext = 'y = ax + b = {:.3f} + {:.3f}x'\\\n",
|
|
" .format(slope, intercept)\n",
|
|
"plt.figtext(.15,.8, ftext, fontsize=11, ha='left')\n",
|
|
"\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"Populating the interactive namespace from numpy and matplotlib\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stderr",
|
|
"text": [
|
|
"WARNING: pylab import has clobbered these variables: ['random']\n",
|
|
"`%matplotlib` prevents importing * from pylab and numpy\n"
|
|
]
|
|
},
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAfoAAAH4CAYAAACi3S9CAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdUVMfbwPHv0lm6giAgooBRbNi7GCv2EnvXWOPPnhg1\nGksSxRhjoiYaE0SNsb4xEY0Fe+zGmijGLkZARRERFljYnfeP1Y0ELJRlAedzDkf2lpln7q48e++d\nO6MQQggkSZIkSSqSTIwdgCRJkiRJhiMTvSRJkiQVYTLRS5IkSVIRJhO9JEmSJBVhMtFLkiRJUhEm\nE70kSZIkFWEy0UtGd+jQIcqXL2/sMAqtSpUq8fvvv+drnSNHjuTTTz/N0b7e3t7s3bs3jyN6s/3y\nyy+UKlUKe3t7zp07Z5TPhFRwKeRz9FJ+8fb2JiQkhGbNmhk7FMmIypQpQ0hICE2bNjVI+QcOHKBf\nv378888/Bim/IPLx8eGrr76iffv2mdbNnDmT69ev8+OPPxohMqkgkGf0Ur5RKBQoFApjh6Gn0Wjy\nZJvXJYRAfq+Wnsmrz5YQgtu3b+Pv758n5UlFj0z0ktEdOHCAUqVK6V97e3uzYMECqlatiqOjIz17\n9iQ1NVW/ftu2bQQEBODk5ESDBg3466+/9OuCg4Px9fXF3t6eihUr8uuvv+rXrVy5kgYNGjBhwgSc\nnZ2ZNWtWplhmzpxJ165d6devHw4ODqxatYrHjx/z7rvv4u7ujqenJ9OnT0er1QKg1WqZOHEiLi4u\nlC1bliVLlmBiYqJf36RJE6ZNm0aDBg2wsbHh5s2b/P3337Ro0YLixYtTvnx5Nm3apK9/+/btVKxY\nEXt7ezw9PVmwYAEADx48oF27djg5OVG8eHEaN26c4Xg9uxSemprKuHHj8PDwwMPDg/Hjx6NWq/XH\n2dPTky+//BJXV1fc3d1ZuXJllu/Jhg0bqFWrVoZlCxcupGPHjgAMHDiQ6dOnA/Do0SPatWtHiRIl\nKFasGO3btycqKirLcv9LCKF/z5ydnenRowePHj3Sr+/WrRslS5bE0dGRwMBAIiIiXnisvvzyS1Qq\nFa1btyY6Oho7Ozvs7e25e/dupnpfdJwB5s+fr3+vV6xYgYmJCTdu3AB072dISIh+25UrV9KoUSP9\n67Fjx+Ll5YWDgwM1a9bk8OHD+nXZ/Wxdu3aNwMBAHB0dcXFxoWfPnpnakZqaip2dHRqNhqpVq+Ln\n5wf8+5nYuXMnc+fOZcOGDdjZ2VGtWrXXel+kIkZIUj7x9vYWe/fuzbR8//79wtPTM8N2derUETEx\nMSIuLk5UqFBBLFu2TAghxJkzZ0SJEiXEyZMnhVarFatWrRLe3t5CrVYLIYTYtGmTiImJEUIIsWHD\nBmFjYyPu3r0rhBAiNDRUmJmZiSVLlgiNRiOSk5MzxTJjxgxhbm4utmzZIoQQIjk5WXTq1EmMGDFC\nqFQqcf/+fVG7dm3x3XffCSGEWLp0qfD39xdRUVHi0aNHolmzZsLExERoNBohhBCBgYGidOnSIiIi\nQmg0GhEfHy88PT3FypUrhUajEWfPnhXOzs7i0qVLQggh3NzcxOHDh4UQQsTHx4szZ84IIYSYPHmy\nGDFihEhPTxfp6en6bf57XKdPny7q1asnYmNjRWxsrKhfv76YPn26/jibmZmJGTNmiPT0dLF9+3ah\nVCpFfHx8puOgUqmEnZ2duHr1qn5ZzZo1xYYNG4QQQgwcOFBf7sOHD8XmzZtFcnKyePLkiejWrZvo\n1KlT1h+C/8T71VdfiXr16omoqCihVqvF8OHDRa9evfTbhoaGisTERKFWq8W4ceNEQECAft2LjtWB\nAwcyfJ6y8qJ9d+zYIVxdXcXFixdFUlKS6NWrl1AoFOL69etCCCGaNGkiQkJCMsTXsGFD/es1a9aI\nuLg4odFoxIIFC4Sbm5tITU0VQmT/s9WzZ08xZ84cIYQQqamp4siRIy9sz/Mx/vcYz5w5U/Tr1++l\nx0Mq2uQZvVQgjRkzBjc3N5ycnGjfvj3nzp0DYPny5QwfPpxatWqhUCjo378/lpaWHDt2DICuXbvi\n5uYGQPfu3fHz8+PEiRP6ct3d3Rk1ahQmJiZYWVllWXf9+vXp0KEDAI8fP2bHjh0sXLgQa2trXFxc\nGDduHOvXrwdg48aNjBs3Dnd3dxwdHZkyZUqGy/MKhYKBAwdSoUIFTExM2LlzJ2XKlGHAgAGYmJgQ\nEBBAly5d2LhxIwAWFhZcvHiRhIQEHBwc9GdgFhYWxMTEcOvWLUxNTWnQoEGWsa9du5aPP/4YZ2dn\nnJ2dmTFjRoZ7s+bm5nz88ceYmprSunVrbG1tuXz5cqZyrK2t6dixI+vWrQPg6tWrXL58WX9cAH07\nixUrRufOnbGyssLW1papU6dy8ODBrN/Y//juu+/49NNPcXd3x9zcnBkzZvB///d/+rPagQMHYmNj\no193/vx5njx58tJjJV7j9siL9t24cSODBw/G398fpVKZ5VWfl+nTpw9OTk6YmJgwYcIEUlNTMxzf\n7Hy2LCwsuHXrFlFRUVhYWFC/fv1sxfKMkLeM3ngy0UsF0rNkDbqkk5iYCEBkZCQLFizAyclJ/3Pn\nzh1iYmIAWL16NdWqVdOvu3DhAg8fPtSX9fwtghfx9PTU/x4ZGUlaWholS5bUlzlixAhiY2MBiImJ\nyVDm8/tmVWdkZCQnTpzIEP/atWu5d+8eAD///DPbt2/H29ubJk2acPz4cQA++OADfH19admyJT4+\nPsybNy/L2KOjoyldurT+tZeXF9HR0frXxYsXx8Tk3//2SqVSf2z/q3fv3vpEv3btWn0y/y+VSsXw\n4cPx9vbGwcGBwMBAHj9+/FrJ5datW3Tu3Fl/LPz9/TEzM+PevXtoNBomT56Mr68vDg4OlClTBoVC\nwYMHD156rF7Hi/b97/vp5eX12mUCfPHFF/j7++Po6IiTkxOPHz/WxwvZ+2x9/vnnCCGoXbs2lSpV\nIjQ0NFuxSNIzZsYOQJJex7NOfF5eXnz00UdMnTo10zaRkZEMGzaMffv2Ua9ePRQKBdWqVct0hv2q\nep7fplSpUlhaWvLw4cMMCfKZkiVLZujdnVVP7+fL8/LyIjAwkPDw8Czrr1mzJr/++isajYbFixfT\nvXt3bt++ja2tLV988QVffPEFFy9epGnTptSuXZu33347w/7u7u7cunWLChUqAHD79m3c3d1f2uYX\nad68ObGxsZw/f57169fz1VdfZdmuBQsWcOXKFU6ePEmJEiU4d+4c1atXRwjxyuPt5eVFaGgo9erV\ny7Tuxx9/JCwsjL1791K6dGni4+MpVqyY/v180bF6nQ6fL9q3ZMmS3L59W7/d878D2NjYkJSUpH/9\n/P3/Q4cOMX/+fPbt20fFihUBMsT7/DGDV3+2XF1dWb58OQBHjhyhefPmBAYGUrZs2Ve273kFqQOs\nZBzyjF7KV2q1mpSUFP3P6/Y8fvbHcujQoSxbtoyTJ08ihCApKYnffvuNxMREkpKSUCgUODs7o9Vq\nCQ0N5cKFC9mK779noSVLlqRly5ZMmDCBJ0+eoNVquX79uv4Z5e7du/P1118THR1NfHw88+bNy/SH\n9fky27Vrx5UrV1izZg1paWmkpaXxxx9/8Pfff5OWlsZPP/3E48ePMTU1xc7ODlNTU0DXAfHatWsI\nIbC3t8fU1DTL5NCrVy8+/fRTHjx4wIMHD5g9ezb9+vXL1jF4xtzcnG7duvH+++/z6NEjWrRokaFN\nz9qVmJiItbU1Dg4OxMXFZety94gRI5g6dao+ocbGxhIWFqYv19LSkmLFipGUlJThy93LjpWrqysP\nHz4kISEhyzpftm/37t1ZuXIlly5dQqVSZWpLQEAAmzdvJjk5mWvXrhESEqJ/v588eYKZmRnOzs6o\n1Wpmz579whjg1Z+tTZs2cefOHQAcHR1RKBRZvuev4ubmxq1bt+Tl+zeYTPRSvmrTpg1KpVL/M2vW\nrFc+dvf8+ho1avD999/zv//9j2LFiuHn58fq1asB8Pf3Z+LEidSrVw83NzcuXLhAw4YNsyzndep6\nZvXq1ajVavz9/SlWrBjdunXTn8kNHTqUli1bUqVKFWrUqEHbtm0zJeHny7O1tSU8PJz169fj4eFB\nyZIlmTJlir5n/Jo1ayhTpgwODg4sX76cn376CdD1wG7RogV2dnbUr1+fUaNGERgYmCn+adOmUbNm\nTapUqUKVKlWoWbMm06ZNyzKW19G7d2/27t1Lt27dMrXpWVnjxo0jOTkZZ2dn6tevT+vWrV+7nrFj\nx9KhQwdatmyJvb099erV4+TJkwD079+f0qVL4+HhQaVKlfRXaZ550bEqX748vXr1omzZshQrVizL\nXvcv2jcoKIhx48bRtGlTypUrl2nMh/Hjx2NhYYGrqyuDBg2ib9+++nVBQUEEBQVRrlw5vL29sba2\nznDpP7ufrVOnTlG3bl3s7Ozo2LEjixYtwtvbO8vj+LLj3a1bN0B326ZmzZov3E4qugw6YM7ly5cz\nPBJy48YNPvnkE/r27UuPHj2IjIzE29ubjRs34ujoCMDcuXNZsWIFpqamLFq0iJYtWxoqPEnKczt2\n7GDkyJHcunXL2KFIecTExIRr165l+5K5JBUUBj2jf+uttzh79ixnz57l9OnTKJVKOnfuTHBwMC1a\ntODKlSs0a9aM4OBgACIiItiwYQMRERHs3LmT9957T9/7VpIKopSUFLZv3056ejpRUVHMmjWLLl26\nGDssSZIkvXy7dL9nzx58fX0pVaoUYWFhDBgwAIABAwboBzXZsmULvXr1wtzcHG9vb3x9ffWX8SSp\nIBJCMHPmTIoVK0b16tWpWLEis2fPNnZYUh6Sndmkwi7fet2vX7+eXr16AXDv3j1cXV0BXceZZ48W\nRUdHU7duXf0+np6erz3CliQZg7W1tfwyWsTl5TDIkmQM+ZLo1Wo1W7duzfLZ39fpiPU8X19frl+/\nnucxSpIkSVJB5ePjw7Vr13K0b75cut+xYwc1atTAxcUF0J3FP+tZGhMTQ4kSJQDw8PDI8BzynTt3\n8PDwyFDW9evX9Y/2vIk/M2bMMHoMsv2y7bL9sv2y/fn7k5sT3HxJ9OvWrdNftgfo0KEDq1atAmDV\nqlV06tRJv3z9+vWo1Wpu3rzJ1atXqV27dn6EKEmSJElFksEv3SclJbFnzx6+//57/bLJkyfTvXt3\nQkJC9I/Xge456O7du+uHwfz2229lRxhJkiRJygWDJ3obG5sMYz2DbljIPXv2ZLn91KlTsxzeVNJp\n0qSJsUMwqje5/W9y20G2X7a/ibFDKLQMOmCOISgUCgpZyJIkSZKUK7nJfXIIXEmSJEkqwmSilyRJ\nkqQiTCZ6SZIkSSrCZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIkwmekmSJEkqwmSilyRJkqQiTCZ6\nSZIkSSrCZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIkwmekmSJEkqwmSilyRJkqQiTCZ6SZIkSSrC\nZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIszM2AFIkiRJWYuNjWXHjh2YmJjQtm1bnJycjB2SVAgp\nhBDC2EFkh0KhoJCFLEmSlG03btygdu1AUlLqAOnY2p7nzJkjuLu750v9f/75JzNnzichIYn+/bvQ\nv3/ffKlXylpucp88o5ckSSqAJk78mEePRqDVfgRAauqHTJv2KStWfGvwuv/880/q1GlCSso0wINj\nxz7m8eMERo9+z+B1S3lP3qOXJEkqgKKi7qHV1tC/Tk+vwe3bdw1e78OHDwkMbEVKyhBgAtADlWo1\n8+d/Y/C6AU6cOMHIkWMZO/Z9/v7773yps6iTiV6SJKkAatWqMUrlF8Bj4CFK5Ve0bh1o8HqnTp1N\nQoInYPrcUpN8uWW6f/9+mjZtz7JlJVm8WEmtWo25ePGiwest6mSilyRJKoA+/ngy77zjg6lpCczM\nPBgwoA7jx482eL2XLt1Aq+0P/AB8A/yCiUkPxo4dZvC6P/poHirVV8BkhJhNUtJ4Pv98scHrLepk\nopckSSqAzM3NWb36O1JTVaSkJPHttwsxMTH8n+yGDWtgbb0bCAMOYGLyPs2a+TNx4liD152cnAIU\n178WwpnExGSD1qlSqRg+fCzly9chKKgr169fN2h9xiA740mSJBVgpqamr94olx49esSOHTtQKBSM\nHTuSs2ffY//+NoCCRo0aERa2AYVCYfA4hgzpyaRJE1GpbAAVSuVsBg9eZtA6O3fuw++/W5CSspCr\nVw9Tp04Trlw5T7FixQxab36SiV6SJOkN9s8//1CzZiNUqiqAwMZmKqdOHcLc3BwhBK6urvmS5AHe\ne284arWab78dh5mZGR9/PJ+2bdsapK7k5GQ++mgWu3dvR4gngAVabX3U6gMcOHCALl26GKReY5DP\n0UuSJBnZX3/9RUxMDJUrV6ZkyZL5WnfPnoP5v//zRKOZDYCZ2VR69XrI6tXf5Wsc+UkIQZMmbTlx\nwoLU1J3APcABENjZNWbt2g9p166dkaPMKDe5T96jlyRJMqIxYyZRt24Q3bvPw8+vCrt3787X+v/5\n5y4aTS396/T0WkRGRudrDPnt+vXr/PHHeVJTNwHDgCBgBebmg3Fze0KzZs2MHGHekolekiTJSA4f\nPsyKFT+jUl3k8eO9JCX9TNeuffLlquW6devx9q7C+fOnMDObDyQAj1Eqv6Zly0YGr9+YhBAoFKbo\nUuBXQD9MTafRo4eCP/44iLW1tZEjzFsy0UuSJBnJjRs3UCjqAo5PlzRCpUokMTHRoPXu3buXd9+d\nSGTkIpKSdiNEJAqFM6amJejevQKTJ080aP3G5uPjg79/WSwt3wV2Y2FxET8/d0JCluHg4GDs8PKc\nTPSSJElGUqVKFTSafcDNp0vW4eLijq2trUHr3bhxC8nJE4AmQFU0mp/x8ipPcnIioaFL86WnvzGZ\nmJiwb99WBg1yombN+fTuLThyJBwLCwtjh2YQste9JEmSkQQEBDBv3sd88EFVzMycsLaG7du3GLyX\nu4ODLaamd9Boni25g52dHebm5gattyCxs7Nj6dKFxg4jX8he95IkSUaWkJBAbGwspUqVypezyjt3\n7lC1al0SEjqQnl4Ca+tv+eWXH2nVqpXB65ZyJje5TyZ6SZKkN1B0dDQ//BBCUlIyXbt2platWq/e\nSTIameglSZIkqQiTz9FLkiRJkpQlmeglSZIk6UWEgEWLIC7O2JHkmEz0kiRJkpQVrRZGj4axY6FD\nB93rQkg+XidJkiRJ/5WeDkOHwsqVYGEBkyZBPkwTbAgy0UuSJEnS89Rq6NsXNm0CpRK2bIHmzY0d\nVY4Vzq8nkiRJ0hsvKSmJLl36olQ64uzsxY8//pT7QlNS4J13dEne3h7Cwwt1kgf5eJ0kSZJUSPXo\nMYgtW1JITV0M3MTauiPh4Rtp2LBhzgpMTISOHWHfPiheHHbtgho18jTmnJKP10mSJElvnF27dpGa\nOg9wBmqRkjKY3bv35Kyw+Hho2VKX5N3c4ODBApPkc0smekmSJKlQcnAoBlzWv7a0vEzx4sWyX1Bs\nLDRtCseOgZcXHDoEFSvmXaBGJhN9Ieft7U1ERIRBytZoNIwaNQpfX1/8/PwICQl54bZz586lcuXK\nVKhQgYEDB6JWqwG4desWZmZmVKtWTf/z6NEjAI4ePUqDBg2oWLEiFStWZNKkSXkaf58+ffDw8MDE\nxASVSpVh3fHjx6latSpvvfUWrVq1IjY2Vh/T87F6eHhQ4wXf6lUqFT169MDPz48KFSrw22+/6det\nWbOGKlWqYG5uzjfffJPl/gcOHMDU1PSF6yVJermlSz9HqeyDufk4lMqOeHpeYdCgQdkrJDoaAgPh\n7Fnw89MleV9fwwRsLKKQKYQh50hoaKiYOXPmK7fz9vYWFy5cMEgMq1atEq1atRJCCBEbGys8PT3F\nrVu3Mm23a9cuUaVKFaFSqYQQQgwdOlQEBwcLIYS4efOmcHZ2zrL8CxcuiGvXrgkhhEhNTRUNGzYU\nP/744yvjGjBggDhw4MArt9u/f7+4f/++UCgUIikpSb9co9EIHx8fceTIESGEEJ9++qkYPHhwlmV0\n6tRJLFiwIMt1s2bNEsOGDRNCCHH16lXh5uYmEhMT9W2LiIgQ/fv3F998802mfRMSEkSdOnVE+/bt\nxZIlS17ZFkmSsnbu3Dnx+eefi++++048efIkezvfvClE2bJCgBCVKgkRE2OQGPNCbnLfG3VGP3/+\nfP73v//pX9+7dw83NzdSUlJyXfa9e/do2rQpNWvWpFKlSnz44Yf6dUOHDmXChAn67cqWLcuff/75\n0vKyM03lmjVrqFmzJn5+fnl6drhx40aGDRsGgLOzM506dWLTpk2Ztvvzzz9p1KgR1tbWAAQFBfHT\nT6/u/VqxYkV8fHwAsLCwICAggNu3b79yP4VC8VrHp0mTJri4uGRafvr0aaytralfvz4Aw4cPZ+PG\njZm2u3//PuHh4fTr1y/L8jdu3Mjw4cMB8PX1pWbNmuzYsUPftgoVKmBiYpJlB5oJEyYwadIkihcv\nrl+WnJxM1apVCQsLA2Dfvn1UqFCBpKSkV7ZVMr5z584xYMAIevcewsGDB40dzhujatWqfPDBBwwb\nNgxbW9vX3/HyZWjUCG7c0N2LP3BAd2++CHqjnqMfMmQI/v7+fP755yiVSpYvX06fPn2wsrLKtG23\nbt24du1apuUKhYJjx45haWmZYbmjoyNbt27FxsaGtLQ0goKC2LVrF61atWLx4sXUqVOHLVu2sHjx\nYiZNmkSVKlVeGmtWyeFFYmNjOXXqFPfv36datWo0btyYypUrZ9jm0qVL9O7dO8v9W7Zsybx58zIt\nv337NqVLl9a/9vLy4p9//sm0XY0aNfj+++95+PAhDg4ObNy4kcjISP36hIQEatSogUKhoGfPnrz/\n/vuZyrh//z6bN29m+/btr9Xm7Byf//pvu5ydndFqtcTHx+Po6Khfvnr1alq1apXll4WsynnR8fmv\nHTt28OTJE7p06cLWrVv1X1qsra3ZuHEjLVu2xM3NjSFDhvDLL79gY2OT06ZK+eTs2bM0atSSpKQP\nAGu2bOnBzz+vJCgoyNihFXqJiYkMHPgeO3b8hp2dI4sWBdO9e7fcFfrnn9CiBdy/Dw0bwrZt4OCQ\nNwEXQG9UondycqJDhw6sXr2aIUOG8MMPP7Bv374st83qzPVl0tPTef/99zl27BhCCO7evcu5c+do\n1aoVVlZWbNy4kRo1atCmTRtGjBiRZRnbt2/no48+AiAuLg61Ws2vv/4KwOjRoxk8eHCW+7377rsA\nlChRgrZt23LgwIFMib5ChQqcPXs2W216XW+//TajRo2iZcuWWFlZ0axZM3bv3g2Au7s7UVFRODs7\nExsbS4cOHXByctLHDPDkyRM6dOjA+++/T9WqVbOs45NPPmHz5s2ALsEePnxY/+191apVr/zilBOh\noaFZfgHKjfj4eCZPnsyePbqewUKIDF9a3nrrLWbPnk39+vX5+uuvX3g8pILliy++JSnpQ0D3JVal\nKsGsWV/JRJ8HBg0axbZtaaSmXkSlus7Age9QurQXderUyVmBJ09CUBA8eqRL9r/8AkX8y/QblehB\nlzD79OmDi4sL/v7++kvH/9W1a1euX7+e5bpjx45lugrw5ZdfEh8fz8mTJ7GwsGD48OEZbglcvHgR\nBwcH7t69i0ajwdTUNFO5bdq0oU2bNoAueUVGRvLxxx+/sk3PJwohRJaXtSMiIujTp0+W+7do0YLP\nP/8803IvLy9u3bql74wWGRlJmTJlsixjzJgxjBkzBtBd0q74tMeqhYUFzs7OALi4uNCnTx+OHDmi\nT/QqlYp27doRFBTE+PHjX9jG6dOnM336dAAGDRrEoEGDaNy48Qu3f5nSpUtnuOLw4MEDTExMMpzN\nHz9+nEePHunfj6w8Oz7PLr9HRkbStGnTTNs9/35cuHCBu3fvUrt2bX3d27Zt49GjR0ybNg3Q3Vpw\ndXV9rasDUsGQkqIGnr9sbKfvkGoIT5484eHDh3h4eGBubm6wegqCnTt3kJp6DnAD3EhNHUh4+O6c\nJfrff4e2bXXPy3foABs2QBZXdIucPOgjkK/yIuS3335blCpVSmzdujUPItKZOHGiGD9+vBBCiDt3\n7ghXV1cxa9YsIYQQN27cEF5eXuLatWtiwIABYvLkya8s73U745UuXVoMHTpUCCHE/fv3hYeHR551\nzlu5cqVo1aqV0Gq14v79+y/sjCeEEDFPO7HExcWJ6tWriy1btuhjUqvVQgghkpKSRPPmzcWiRYuE\nEEIkJyeLpk2big8//DBbcQ0cOPC1OuMJIYRWqxUKhULfSU6IfzvjHT58WAghxCeffJKpM97QoUNf\nGdfMmTP1x/7KlSvC1dU1Qz1C6DoOvqyz3cCBAzN01tu8ebOoXr26iIuLExUrVhQ7dux4rXZKxhUe\nHi6UypICfhawQyiVviIkJNQgdS1a9K2wsLAVSqWnKFGitPjrr78MUk9B4e5eTsABoZtGTghr6y45\n68C6c6cQ1ta6Qnr1EuLp36XCIje5741M9GvWrBHe3t55EM2/IiMjRe3atUWlSpVEUFCQ6NOnj5g1\na5ZQq9Widu3aYt26dUIIXbLz9/cXO3fufGl5K1eu1H9ReBlvb28xdepUUaNGDeHr65tlD++c0mg0\nYuTIkcLHx0f4+PiI77//Xr9u2bJl4uOPP9a/rly5sqhYsaIoV66cWLx4sX755s2bRaVKlUTVqlWF\nv7+/+PDDD4VWqxVCCLFkyRJhamoqqlWrJgICAkRAQICYM2fOK+MaOHCgOHjw4Cu369y5s/D09BQm\nJibCw8NDBAUF6dcdPXpUVK5cWfj5+YmWLVuK+/fv69epVCrh4OAgLl++nKnMgIAA/ZeapKQk0a1b\nN+Hr6yveeustERYWpt9u7dq1wtPTU9jY2AgnJyfh6ekpLl26lGVbnr1nN2/eFKVKlRJXr14VQuh6\n7nt5eYmoqKhXtlUyvi1btogaNZqKqlUbix9+WGGQOs6cOfP0C8WNp4kvVHh6vmWQugqKX375RVhb\nlxBmZhNF0rhoAAAgAElEQVSFtXUn4etbJfu96zdvFsLcXJfkhwwRIj3dMMEaUG5y3xs5BO6QIUOo\nUKECEydOzKOoJEmSDC80NJTRo/eTlLT66RKBqakVCQmPUCqVeV7ftWvXOH/+PN7e3i8cTyI/nD59\nmt27d+Po6Ejfvn2z17t+zRoYOBA0Gt10swsXQjaeaiooCvQQuPHx8XTt2pUKFSrg7+/PiRMniIuL\no0WLFpQrV46WLVsSHx+v337u3Ln4+flRvnx5wsPD8zSW6Ohoypcvz/Xr1xk1alSeli1JkmRoZcuW\nBY4BCU+X/I6trZP+0da89NNP66hatT6DB/9I48ZdGDducp7X8bpq1KjB5MmTGTFiRPaS/PLl0L+/\nLslPm1Zok3yu5dFVhRfq37+/CAkJEUIIkZaWJuLj48UHH3wg5s2bJ4QQIjg4WH8v9OLFi6Jq1apC\nrVaLmzdvCh8fH6HRaDKUlw8hS5IkFUharVaMGDFOKJWewsGhubCxcRbh4eF5Xk9KSoqwsrIX8OfT\nWwRxQqksJU6fPp3ndRnMggVCf2P/6QBehVlucp9BL90/fvyYatWqcePGjQzLy5cvz8GDB3F1deXu\n3bs0adKEv//+m7lz52JiYqIfbCYoKIiZM2dSt25d/b5y9jpJkt50586dIyYmhqpVq+Lu7p7n5UdH\nR+PrW43k5Hv6Zfb27Vi1agidOnXK8/rylBDwyScwY4bu9ZIlUASu4BbYS/c3b97ExcWFQYMGUb16\ndYYOHUpSUhL37t3D1dUVAFdXV+7d032YoqOj8fT01O/v6elJVFSUIUOUJEkqdAICAmjdurVBkjzo\n/i7b2loB654uOUda2omCP66DEDBpki7Jm5hAaGiRSPK5ZdDn6NPT0zlz5gxLliyhVq1ajBs3juDg\n4AzbvGo406zWzZw5U/97kyZNaNKkSV6FLEmS9Ma7ceMGtrYOxMb2BYZhYSFYuXLlC8fRKBC0Wl1S\nX7YMzMxg7VrolssR9IzowIEDHDhwIE/KMmii9/T0xNPTk1q1agG6QWjmzp2Lm5sbd+/exc3NjZiY\nGEqUKAGAh4dHhkFC7ty5g4eHR6Zyn0/0kiRJUt7RaDQ0bdqOqKhRwHBgDxYWgwgMbGTs0F4sPR0G\nD4YffwRLS/j5Z93AOIXYf09iZ82aleOyDHrp3s3NjVKlSnHlyhUA9uzZQ8WKFWnfvj2rVq0CdCPA\nPbvn06FDB9avX49arebmzZtcvXpVP4KYJEmSZHhRUVHExSUixBjAEmiLqWkAZ86cMXZoWVOroWdP\nXZK3sYHt2wt9ks9rBh8Cd/HixfTp0we1Wo2Pjw+hoaFoNBq6d+9OSEgI3t7e+pnD/P396d69O/7+\n/piZmfHtt99maxY3SZIkKXecnJxIT08A7gCegIr09GsvnNzJqJKT4Z13YMcO3aQ0O3ZAvXrGjqrA\neSMHzJEkSSpo1Go1oaGh3LwZSb16dejYsaPRYgkOXsAnnyxCo2mHuflhOnSoxZo13+fqxCsxMZF3\n3x3Nrl27cHQsztKln9O6deucB/nkCbRvDwcPgrMzhIdDtWo5L6+Ay03uk4lekiTJyDQaDYGBbTh7\nVqBSNcLGZi1jxvRgzpyZRovp0KFDnD17ljJlytCuXbtcX13t0qUv27drSE2dB/yNUtmXY8f25Gzm\nyUePoHVrOHECSpaEPXvA3z9X8RV0MtFLkiQVYlOmTGHevE0IcRkwBe5hbl6Gx48fGmTUO2OwtnYg\nJeU6oJvN0tx8HHPmePL+++9nr6D796FlSzh/HkqXhr174QWzkBYlBfY5ekmSJOnlQkNXEhy8BCHK\noEvyAC4oFBaoVCpjhpanbGwcgFv61+bmN3FwcMheIVFREBioS/LlysGhQ29Eks8tmeglSZKMRKvV\nMm7cdGAl8BewGrgNjMXHx49ixYoZM7w89eWXc1AqO6JQTMfKqhvu7rfo1avX6xdw8yY0agR//w1V\nqujmli9VKttxpKSkkJycnO39CjOZ6CVJkoxk9Oj3SUhQAWWBHcBSoBqwik2bVhapp4769+/Lzp3r\nmTbNhODghpw5c/j1J6j5+29dkr95E2rXhv374enoqq9Lo9HQv/9wbG0dsbNzomvXfqjV6hy0pPCR\n9+glSZKM4NSpU9Sp0wCtdhz/JvkY4F2aN2/E7t3bjBtgQXHunO6efGwsNG4M27aBnV22i5k7dz6f\nfrodlSoMMMXauitjx9Zi7tycD0STn+Q9ekmSpFwKDw/HxyeA4sW96NNnqEHvjx87dozGjYPQagHe\nB7oB/YH3aNKkJjt3bjFY3YXK8ePw9tu6JB8UpHtOPptJPiEhga+++orly39CpXoPsAOUJCePZu/e\nowYJu6CRiV6SpDfeX3/9RadOfbhxYw5xcQfYvDmeAQNGGqy+GTO+IDl5LrohZrsC1VAo+lOsmAUb\nN67H1NT0FSVkX0JCAt26DaREibJUqdKAkydP5nkdeerAAWjeHOLjoXNn+PVXUCqzVURCQgIBAfWZ\nMuUYt25ZAb/r15maHsPbO/MQ60WRwUfGkyRJKuh27dqFRtMbaANASsq3/PZbOYPVp1KlAMWBhcAX\nwExcXBI4fvyQwUag69SpD0ePOpOauovY2D9o2rQtERGn8fLyMkh9ubJ9u27Eu5QU6NMHVq7UTVST\nTatXr+bu3QqkpGwA7gF1USjOYGvrgLX1JRYs+P1VRRQJ8oxekqQ3np2dHWZmt59bchulMvv3gV/X\n0KE9USonA4eBmiiVD1m8+DODzQ6nVqs5eHAXqanfAX5Ab6AF+/fvN0h9ufLzz9Cpky7JDxsGq1fn\nKMmD7oxerX52TF2BXVhaXmDFisFcvnyWUjnotV8YyUQvSdIbr3fv3ri6XsXSshcKxSyUyo588cWn\nBqtvwIB+fPnlB/j5vU+5clNYsmQm3bsbbkpVMzMzzMzM0Z3VAggUiqjX7/WeX1avhu7dIS0NJkzQ\nTTlrkvM01apVKywsVgH7gNtYWX1Ex47v0LVrVxwdHfMs7IJO9rqXJElCd/b3/fffExsbR1BQiwxT\nhBYFc+bM57PPvkelGoyV1Sl8fP7h1KmDWFlZGTs0naVL4b33dL/PmKH7yYPHC8PCwvjf/yaTkBBP\nmzZt+OGHRSizea+/IJBD4EqSJGWDEIL169ezf/9RvL09GDt2NDY2NsYOK0+Fh4czY8YCUlPVjBzZ\nlyFDBrN161b27z+Ep6cbI0aMKDhtnj8fJk369/fsDov7BpCJXpIkKRsmTZrGN9+EoVINxtLyGD4+\nNzl9+veCc3abA7/99htjx07jyZME6tatzu7dv5Oc/DXggFI5ni++mMDIkcOMHWZGQsDMmTB7tu71\nt9/CSMM97VCYyUQvSZL0mtRqNTY29qSn3wZKAAJb24b89NOHdOjQwdjh5cipU6cIDGyLSrUKKIOp\naVs0mlHA+Kdb7KFixRlcuHDEiFH+hxAwcSIsXKi7Dx8aCv37GzuqAis3uU8+XidJ0hslLS0NUABO\nT5coUChKFNrxzyMiIujRoz8q1SAgCACNpgHw/IA/Ksxy2HPdIDQa3f345cvB3BzWrdM9TpcNycnJ\nLF68hCtXImnYsCYDBgwoUkMG56UC9M5LkiQZno2NDQ0aNOX48aGkpk5EoTiGiclxAgOXGju0bLt0\n6RI1azYiObkREAnsBdKAeigU7yOEGeCIUjmbGTOWGDVWvfR0GDgQfvoJrKxg82bd3PLZkJaWRuPG\nrblwwYmUlCasW/cNJ06cZ+nShYaJuZCTl+4lSXrjJCQkMHz4eA4dOoanpwfff/8llStXNnZY2RIT\nE0OFClV5/DgQmI9uMhwPwBa4yOTJ/+POnYekpKgZMqQXrVq1yvMYhBCo1WosLS1fb4fUVOjZUzfK\nna0tbN0KOXi6Yf/+/XToMIHExNPonhKPx9zckwcPorG3t892eYWBHOtekiTpJdLT0zl+/DiHDh0i\nOTkZe3t71q0L4c6dCI4f313okjzA5MmzePKkJqAFQoB26Ka6PY6p6UQuXrzFjz8uZ9OmlTlO8klJ\nSXTu3AdLS1ucnNwJCQnVrwsJCUWpdESptKNmzSbcu3fvJSUBKhV06KBL8o6OsGdPjpK8rigVJibF\n+TeF2WFiYkFKSkqOyivq5KV7SZKKtKSkJBo1CuLq1UcoFFYUK5bM8eN7cXNzM3ZouXLrVjRabS9g\nBnAdGIeu7wFoNM24fj0813UMGTKGHTu0qNX/oFbfZsyYdpQt6421tTVjxkwjJeU4UI7z56fQpUt/\njhzZlXVBCQnQrh0cOgQuLrB7N1StmuO46tevj7n5CBSKrxHibSwsllK5chWDDR9c2MkzekmSirRP\nPgnm0qVSJCb+yZMnfxAd3Y4xYyYbO6wcu3v3LleuXKFp07oolaFAOGCPbprbJCAdS8vvqVevRq7r\nCg/fTWrqHHQdF6uSnDyE3bv3cvToUdLTuwIVAFPS06fzxx+Hsi4kLk43Oc2hQ+DhAb//nqskD+Dk\n5MTRo3tp0GAXnp696NBBRXj4L7Iz3gvIM3pJkoq0ixevk5LSmmfnNWlpbbh06SPjBpUDQgiGDx/L\n6tU/YmbmiIuLDUFBAWzZUhEhBJ6efty9WxKFwoxatWqzcOE3ua7Tyak4cXERQBlAYGkZgYtLXVxd\nXTE3/xW1WgOYAqdwcsriCsm9e9CiBfz1F5QpA3v36v7NA+XKlePQoe15UlZRJxO9JElFWt26Vdm7\ndy3Jyd0AcywtV1GrVu7OKPObEIIRI0YSEvI7Wu0tUlPtSUmZTalSJ0hKSgDA0tKSuLg40tLSKFGi\nRJ6c3S5bNp+OHXuh0fQATmFpGcn9+7707NmTatVWc+5cfYR4CyF2sGrVjxl3/ucf3Zn8lStQvrzu\nnrzHmzEtbEEje91LklSkpaWl0alTb/btO4BCYU7FiuXYuzesUPXOXrbse0aPnkJ6+lhg+tOlkTg5\nNSAu7o5B646IiODTTz/j55/3oVaPw9z8BsWK7ebcuaOcPHmShw8f0rBhQ/z8/P7d6fp1aNYMIiMh\nIAB27YISJQwaZ1EnB8yRJEl6AXNzc7Zt20hUVBTp6el4eXlhkosZ0fLb4cOH+fDDz0hPHwjsBiYB\nlkAYZcv6Grz+GzdusHlzOGr1NqAOaWkQH9+fdevWMX78+Mw7RETozuRjYqBuXd3c8k5OmbeT8o1M\n9JIkFXkKhQJPT09jh5FtBw8epHXrbiQnFwcaA7fRdYBzwtLyFmvWGHZI27Vr1zF06Iekpgp087nr\npKe7kZiYlHmHM2egVSt48ED36FxYGNjZGTRG6dXkpXtJkoqM9PR0fvjhBy5dukbNmlXp27dvoe6J\n3apVV8LD26DrVT8O3aN0F7GyWsnevdupX7++QesvX74Oly9/CmwFLgNfADdQKody9Ohuqj7fe/7o\nUWjTBh4/1v37f/8H1tYGje9NIi/dS5L0xtNqtbRp05UjR56gUrXExmYx+/cfZ8WK3Pc+N5a0tHTA\nHEgGWgHf4uqaxM6dBwgICDB4/enp6YASXYKfCrTGycmMjRvXZkzy+/bpBsNJSoKuXXXD21pYGDw+\n6fUUnhtVkiRJL3HmzBmOHr2ISrUT+JCkpD2sXbuWu3fvGju0HHvvvb6YmIwFlgN2QCRduwYZNMnH\nxsZy7tw5EhIS+N//BmJjMxzYDwSgVKrZuXMjzZs3/3eHbdt0Z/BJSTBggG6CGpnkCxSZ6CVJKhKS\nkpIwNXVBdwYMYIeZmT2JiYnGDCtXTE1NsbDwAQ4CXwFHWbFitcFuX3733Q94eZUjMLAfHh4+VKpU\ngXnz/ke1asE0aLCWbds2ULt27X932LgROnfWjWH/3nuwYgUUpFnyJEBeupckqYioXr06lpbRmJh8\njVbbBjOzlbi7F8Pb29vYoeVYXFwcpqb+/HtO5ktqqoq0tDQs8vis+dq1a4wfP5WUlD9ISfEFDtC5\nczcePLjDqFEjMu8QGgpDhoBWC5MmQXAwFOL+EEWZPKOXJKlIsLOz48iR3dSqtQ1n55YEBl7kwIHf\nCtY87K9p+/btdO8+iB079qHR/IZu+tl4zMwmUbNmozxP8gCXL1/GwqI68OyRvSZotVbExMRk3njJ\nEhg8WJfkZ8+WSb6Ak73uJUmSXiImJoaDBw+iVCpp1arV60/JmkO6R9omoVJ9hEJxHyurL7G1dSIh\n4QF16jRm06ZQShhg8JnLly9TrVpjkpP/ALyAY9jYtOPBgyisrKz+3TA4GKZM0f2+YAFMmJDnsUiZ\n5Sb3yUQvSZL0AufOnSMwMAgh6iPEPcqU0XL8+F6USqXB6ixXrhZXr84FdB3eFIqpTJig5Ysvgg1W\n5zMLFy5m6tSZWFj4kp5+nY0bV9G2bVvdSiFg+nT47DPd2fuyZTBsWLbKT0xMRKPR4ODgYIDoizY5\nH70kSZIBvPvuOBIS5vDkyWYSEw9z9aoHS5YY9nG9tDQ1YKt/LYQtKSlqg9b5zPjxo7ly5Rzbt3/J\nrVuXMib58eN1Sd7UFH78MVtJXqPR0L//MJycSuDi4kGrVp1RqVQGaoX0XzLRS5IkZeH+/fvcvn0b\nqPd0iYKUlLpERkYbtN533+2FldUgdNPPrkOp/Ir+/XsatM7nlSpVigYNGvw7t7tGA0OHwtdf6x6b\n27QJ+vTJVplffbWYn3++THr6PdLS4vj9dzMmTfrYANHn3JEjR+jYsQ9t2/Zk165dxg4nT8lEL0mS\n9B+DB4/A3b0scXGJwGdAOnAPpTKUJk0MNxrd+vUb+eyzYDSaWExNu1Kp0tds3bo+4yNt+SktDfr2\nhZAQ3Sh3YWG6x+myaf/+E6hUQ9GNBWBBSsp7/P77yTwPN6eOHDlCy5adCQtryPbtLenSZRDbtm0z\ndlh5RiZ6SZKk58ycOYvQ0M1oNNfQaq8CEYASMzNvxo3rTteuXQ1S782bNxk8eBQpKQdJS3uARhNK\nTEwUjRs3Nkh9r5SSohvlbv163Xj1O3fqxrHPAV/fUlhY/A7o7jGbmh6ibNlSeRhs7nz55XeoVDOA\nkcBgVKqFBAd/a+yw8kzhe+5EkiTJgBYu/AZoD7g9XfIHYE5CwmOs83Ds9vT0dL7+egknTpynYkUf\n/P3fwty8NsnJz4aWfQeVahT37t3DI7/ncU9Kgk6ddHPIOznpppmtVSvHxc2YMYXffnube/caAdZY\nW19j0aKDeRdvLmm1gn8HWgIwQ6PRGiucPCcTvSRJEnD+/Hl69RpGQkIC8DsQDzgC27C1dcnTJA/Q\nrdsAwsPvolL1JCwsjLJlfyE9/R7wECgO/AmkULx48dcqT6vVcvHiRdLS0qhUqVLOn7V//BjatoUj\nR3RzyO/eDVWq5Kysp5ycnPjzz2Ps37+f9PR0AgMDC1TP+9GjB7FrV2+Sk5WAJUrlRCZM+NLYYeUZ\n+XidJElvvEePHlG2bEXi4+cC+4BjwGOgNHCR0NBvGDhwYJ7VFxUVhY9PFVJTzwG9gb8AFf7+Vbh1\n6y5mZlVJSztJSMgSevXq8cryUlJSaNGiE2fPXsHExIqSJa04fHgXLi4upKen8+TJExwdHV89k9+D\nBxAUBKdPg6cn7N0L5crlRZMLvPDwcObMWUJ6uoZx4wbTtes7xg4pA/kcvSRJUg6lpKTQvXsftm27\nhRCngRTgfWAlJUq4sGhRMD16vDrZZseNGzeoXLkRKlV9wB1YCDzEyqoxn3zyLuXKlaNSpUqULVv2\ntcqbNesz5s07RXLyJsAUc/OJdO78CB8fDz7/fAEKhSleXj7s2fMrZcqUybqQmBho0QIuXgQfH91l\n+0I8fHBRIxO9JElSDnXrNoCwsFuo1beBvwFL4CEWFmWIjr752pfOX8fOnTuZOnUeycnJJCQ8Ijr6\nIXAC8Hm6xVwmTHjEggWfZ6vczp378euvzYCBT5ccpnjxXjx8mPi0fD/gc/z9N3Px4onMBURGQvPm\ncO0a+PvrLte7u+eskZJByAFzJEmSckCr1fLrrxtQq8OAOsDbwFQsLOozevToPE3y69ato3373pw9\n+z/+/juYR4/MsLIyRzcFLIAGa+tDlCnjle2yq1f3x9r6ZyANEJiZrScu7i7QBSgHKICJXLp0Co1G\nk3Hnq1ehUSNdkq9WDQ4elEm+iJFn9JIkvbGEEFhbO5Ca+hfgCazD3PwT3nuvNQsXLnz1Pe3XdObM\nGerUeZv09GnAB0+XHqFUqaEkJDxCiGpotTFUqlScAwd+y/Z4+qmpqbRu3ZUTJ85hYmKFp6c9V678\niVZbEd0ZvSVwCBubLiQmxv6744ULujP5e/egfn347TdwdMyTNhcEp06dYvv2HTg42DNgwAAcC3Hb\ncpP7ZK97SZLeWAqFgqlTpzBvXmtUqlGYm5/HzU3B7Nmz8yzJA0ye/Bnp6XWAhOeWPsbOzpHTpw9y\n9OhRbG1tCQwMzNFse5aWluzdG8aVK1dQq9VUqFCBgIAGXLyYBlRDd1a/h6+//vrfnU6fhpYtIS4O\nmjaFLVvA1vYFNRQ+W7dupWfPIaSkDMLcPIIFC5Zy/vwxnJycjB1a/hOFTCEMWZKkAm79+vWiX79h\nYvLkaeLhw4e5KissLEyUKuUvHBxKiu7dB4rNmzcLX98aApYLcBEwQ8AiYWJSXPz888951ILM7ty5\nI6pXbyxMTEyFnV1xsWLFin9XHjokhL29ECBEu3ZCJCfnef33798Xbdt2E2XLVhOdO/cV0dHReV7H\ny3h7VxYQLnQD9QthadlHzJ8/P19jyEu5yX3y0r0kSW+U06dP8+mnC0lMTGbIkB706NE9z8o+c+YM\nDRsGkZy8FiiJQtEcU1NXTE3TSE3VAPOBdZia7mPixEHMmzc3z+p+ESFExqsTe/ZAx46gUkH37rBm\nDZibv7iAHLh79y7e3pVJTW0LDAF+pXTp7fz995mMU94aUPHiXsTF7edZR0eFYgZTpmj57LNP8qX+\nvCY740mSJL2Gv/76i8DAIH79tTZ79rzD4MGTWbFiZZ6Vv2vXLtTq/uimmN2EEE1JTz9LauoFwAdz\n84G4up5k/vyp2UrySUlJDB06Bj+/mjRt2oHLly+/9r4ZknxYmG4wHJUKBg2CtWvzPMkDDBgwktRU\nE2AF0BCYz927ppw+fTrP63qR9u3bYm09EfgHOIyV1XLatAnKt/oLEnmPXpKkN8by5StJShoNjAFA\npSpJcPAkBg8emCflOzg4YGFxmuRk0CWYQHQ93gFm4OU1kmvXsp/s3nmnHwcPWpCS8g3Xrx+nXr2m\nXL587t8Z5v4jPj6egwcPYm5uzttvv60b1W/9et0ENRoNjB4NX30FJq93rqdSqYiOjsbd3R2lUvnK\n7S9fvg5oADVgBWjRaBIxN8CXihdZuvRLtNpxbNlSCxsbexYu/JoGDRrkW/0FiTyjlyTpjaHVasn4\nZ88kT28F9uvXDze3v7Gy6gncBb5EN8qeCkvLxTRqVCfbZapUKvbs2U5KymqgDkKMJS2tJvv3789y\n+8jISN56K4B+/b6hZ885VKlSD9XixdC7ty7JT5mim3L2NZP8zp07KVHCi4CAFri4eLJlS9gr9wkI\nqIxC4QZ0AlYC7+Dqakn16tVft9m5Zm1tzerV3/H48V2io6/k6S2aQidPegnko0IYsiRJBcTZs2eF\nUuksYJmAn4VS6SuWLv0uT+t4/PixWLBggahQobowMXEU4CbAVtSp87ZISEjIdnmpqanCzMxSwIOn\nHcu0wta2sfjll1+y3L51627C1HS2ftsJpnWFvkfaZ59lq+74+HhhY1NcwKGnRZwQSmVxcf/+/Zfu\nd/fuXeHjU0WYm7sJExMX4e1dQTx69ChbdUsZ5Sb3yUv3kiS9MQICAti7dyszZy4gKSmZIUM+ZsCA\nfnlah729PTY2NkRG2qDVRgNWmJlNw97+EnZ2dtkuz8LCgpEjRxMS0gqVaigWFscpWfIxrf4zZey1\na9do3bor165FAqMAmMJc5miO6zb4+msYMyZbdd+4cQNTU3d099kBamNu7sPVq1dfeNsAwNXVlYiI\nP4iIiMDCwoIKFSrk6eOKUjbl4ReOfFEIQ5Yk6SW++WaZKFmynHBxKSOmTZslNBqNsUPKtWHDRgv4\nUn8iDRdEyZLlclyeVqsV338fInr0GCymTJku4uPjM60vU6aSUCgWChgvoIuYwwdCgNCA2NWjV47q\nvX//vrCychRw+Wk7bggrq2Lizp07OW5Lbh08eFD4+VUXTk6eokuXvuLx48dGiyU/5Sb3FbqsKRO9\nJBUdGzZsFEqlj4CTAi4IpbKmmDv3C2OHlWuLFy8RSmUzASkChDA1/VS8/Xb7XJWp0WiESqXKtDwy\nMlK0a9ddKBSWAoRQ8EQsoowQINQgvm3cTKSnp+e43h9+CBXW1s7CwaGpsLZ2EYsXL815I3Lp6tWr\nwsbGWcAvAm4KS8sBomXLzkaLJz8V6ERfunRpUblyZREQECBq1aolhBDi4cOHonnz5sLPz0+0aNEi\nw72bOXPmCF9fX/HWW2+JXbt2ZQ5YJnpJKjI6deorIOS5M989okqVRsYOK9fS0tJEUFAXYWNTWtjb\nBwhPz3IiMjIyx+X98MMKYWVlJ0xNLUSVKvVFVFSUEEKIuLg44eJSWpiYzBBgI0w4L1YwUAgQKSjE\nqY8/zpP23Lx5U+zatUtcv349T8rLqWXLlglr60HPfV5UwtTUPFdfZAqL3OQ+g9+jVygUHDhwgGLF\niumXBQcH06JFCyZNmsS8efMIDg4mODiYiIgINmzYQEREBFFRUTRv3pwrV65g8pq9QyVJKlyKFbPH\nxOQ2Wu2zJZE4OtobM6Q8YWZmxvbt/8fFixdRqVRUrlxZ94hbDpw8eZIxYz4iJeUPwI+LF2fQuXM/\nTpzYy549e0hJqYhWOxNzyvAjtelBKkkoWNi4BR/NnJkn7fH29sa7AExZa2+v+7yAQPfY4j9YWNjI\nHPEK+XJ0xH8eXwkLC2PAgAEADBgwgF9//RWALVu2/D979xkfVfE1cPy3NduSUNIoodfQQeklgBTp\nHRA/SjQAACAASURBVEUQRaog2MEOSlP0ryKK8AARRDoISBEEDIQivQQQQq8hEAglfct5Xuwag4Ak\n2U1C8H5f6d07M2fWjzl7507h2WefRafTUaJECcqUKcOuXbtyIkSFQpEL3n33dby9v0erfQW1eiRm\n80g+/fR9t+o8efIkn376KV988QWXLl3yUKSZp1KpqFy5MrVr185ykgfYsWMHdnsXoDygxm5/h717\ntwKg0WiAVLxIZilL6EkKt4CDn07kvfBfH7sJcJ06daJYsVsYDF2BjzGZWvLpp+Meu356Wo480T/1\n1FNoNBoGDRrEgAEDiImJITAwEHDOzoyJiQHg8uXL1K1bN61s0aJFc/V/VIVCkb1Kly7NoUO7mD17\nDlarjZ49w6lUqVKW6rJarXTr9hwrV64C+qDRWBk79kn27t1KqVKlPBt4DipUqBBa7QJSUmw4/2Tv\nokCBQgC0aNGCwj6j+C6+LM3kItfR8k27jox+++1cjTm7GI1Gdu8OZ8aMGVy+HEPz5tNp2bJlbof1\nyMv2RL9t2zYKFSrEtWvXaNGiBRUqVLjrc5VK9a+/xu732eh0w1GhoaGEhoZ6KlyFQpHDihUrxgcf\nuPcUD/Dhh2NZtWonzv3kh2K3w61bH/DJJ5MIC5vqdv25pWvXrkybNpddu2oDFbHb1zFnzlwAvO12\nIgv5ort0gut6AyuGDuODSRNzN+BsZjabGTFiRG6Hke3Cw8MJDw/3SF3ZnugLFXL+8vT396dz587s\n2rWLwMBArly5QlBQENHR0QQEBABQpEgRLly4kFb24sWLFClS5J46R3vovZNCoXh8rFq1EYcjACib\ndk2kHNeuncxynadOnaJ37yGcPBlFpUqV+fHHqQQHB3sg2gc7ceIEx44do0yZMlSsWBGNRsP69T8T\nFhbGhx9+xpUrcfTuPZBl076k8bhx6Pbvh+BgCm7cSL+yZR/egCJP+OdD7JgxY7JcV7a+o09MTOTO\nnTuA81CG9evXU6VKFTp06MDs2bMBmD17Np06dQKgQ4cOLFiwgNTUVM6cOcOJEyeoXbt2doaoUCge\nE4GBfkAw8CFwCjiCVjuG7t3bZKm+hIQEGjRowa5drYmN3UhEhC/ly9ehR48X6Nv3JQICyhAcXIkZ\nM2Z5rA/Tps2gWrUG9O49lVq1mjJp0leAc2Tzk0++4MqVlxFJQX99EgHde8L+/VCmDGzdCkqSVzyI\n5yb/3+v06dNSrVo1qVatmlSqVEnGjx8vIs7ldc2bN7/v8rpx48ZJ6dKlpXz58vLrr7/eU2c2h6xQ\nKLLJnTt37rsO3FMiIyPFYvEXjaaGgK+oVBZ5990PxeFwZKm+7du3i49PLdcyrvkCRV1LAasLlBLY\nKbBF9PpgWbx4idvxx8bGujanOeFq84IYDAXl7NmzEh0dLQaDn4BIcc7ISUqJgNwKDhbJ4XPeFbnD\nndynnEevUCiyVUJCAp079+b339ch4qB//8F8993/smVJ1IULF1i1ahVarZYuXbpQsGDBLNcVGRlJ\n3brtSEyMApoCHwFlgDrAj8DTrjt/oHXr1axdu9it2CMjI2nQoCd37hxNu+brW49ffvmMJ554gnz5\n/CmRuoINvEAwF9mn9sK26mdqP/30v9SqeFwo59ErFIpH1uuvv0tEhBc2203s9iv8+OMfTJv2f9nS\nVnBwMEOGDGHAgAFuJXmAypUr06xZXUymlsBV4BjQCNAD0enuvIRO5/6f0pIlSwKxwAbXlR3YbCcp\nX748RqORWa+OIIKWBHOR7WoTkzt05cnWefd8davVypIlS/j+++85evTowwsoskx5olcoFNmqfPna\nREV9DdRzXZlB9+7bWLQoLDfDyhC73U5YWBhhYT+yffte4DvgFZzzmIcBycAU9u6N8MgRrOHh4XTs\n2JPUVCE11Ur+/PmpX78OP7zclwK9ekFcHBcqVODI2LG06tIlz64ft1qtNGnShsjIRByOisBK5s+f\nQYcOHXI7tEeWO7lPOb1OoVBki6SkJL799jsSE+NRqSIQqQcIev02SpUqmtvhZYhGo6F///4EBATQ\ns+fXJCc/D5iBF4H/odNBWNh0j52zHhoaSkTEb9Su3RSH4y2uX29P/JpP8FrdFhwO6NCB4IULCTYY\nPNJeblm0aBGHDqWSkBCBc2B5Ky+99BzXrimJPjsoiV6hUHhcamoqDRq05M8//UhO7gB8gl6/Hi+v\nFIKC4nnnna9yO8RMCQgIQKM5ByQBXYHK6HQ1iI6+8MBXBPHx8fTpM5CtW/8gKKgQ06ZNon79+v/a\nzvXr12ncuAUpKcWBd2nJOn62r8KEg/j27bEsWQI6nae7l+OuXr2K1VqVv98eV+fmzZjcDOmxpryj\nVygUHrdx40ZOnEghOXkpMBHYg822hbCwVzl4cDu+vr65HWKm1KlThzZtGmCx1MfL62VMppaMHz/+\ngUk+KSmJ4sWrsHx5IrGxazh8eDgtWnTk9OnTiAg2m+2+5X755RdSUioBCXRiCb/QHhNJzFLrufPd\nd49Fkgdo1KgRGs1i4CCQilb7IXXrNs3tsB5byhO9QqHwuMTERFSqQP5+liiDRqPnqaeecmvf99yi\nUqlYuPAHfvnlF86dO0fNms/RoEGDB97/4YdjuXHjInAY51B/BVJTV/HRR2NYtmwlycnx1K3blBUr\n5uHn55dWzuFwoFL50YvrzKYHWoSv8GN3zw70K5o3XndkxBNPPMG0aV/w8svNSUy8xRNPhLJ06U+5\nHdY9oqKiWLJkKVqthl69elE0j/43UCbjKRQKj7t69SrlylXj1q2PgYbo9V9Rs+YpduzY8NCyj4PG\njdsTEREO7Me5JE9QqWqg010hNXUjUBad7k0aNjzLpk0r08pdvXqVCSXL80XiTdTAOJUvv9avweYt\nGx/bE9rsdrvrcJ5Hy759+2jcuBXJyc+hVidjMq1g375tuXZugrK8TqFQPFICAgKIiFjPE0/MJyio\nI+3aJbFmjXvrzPOSKlXKotFUBVoBnwI90OlO43D0AioBeqzW0WzfHn5XuYCffuJLV5L/NrgsjjGj\nCN+84bFN8sAjmeQB3nrrYxISxmK3f4XV+j137gxk7NjPczusLFGG7hUKRbaoUqUKu3dvyu0wcsW4\ncR8SHt6SM2fspKRMQKXS4O3ty507ewAHzmes/RQo4DzFExEYOxY+/ND571OmMHTo0FyKPvdYrVaW\nLl3KlStXaNSoEbVq1cq1WOLibgF/P707HKW5du1ErsXjjsf3Z6JCoVBkwu3bt9mxYwcnTrj/xzxf\nvnzs37+VMWOGotNZsNvnc/36bGy2o3h51cNk6ofJ9AyzZn3jTPIjRzqTvFoNYWHwH0zyNpuNpk3b\n0b//t4wadZLGjdvx44+5996+e/e2mEwfAFHAIUym8fTs2S7X4nGLe7vv5rw8GLJCoXjE7du3T/Ln\nLyw+Pk+I0Rgogwe/muU98tPr1Km3wAzX3vUisFJKlqwk06ZNk2PHjonY7SJDhjg/1GpFFi3yQG/y\npiVLlojFUlfA5vquDorFUtAj/x2ywm63y8iRH0j+/EXFz6+4TJr0Za7E8Rd3cp8ydK9QKNyyf/9+\nNm/ejJ+fHz169ECv1+d2SA8VHR3N+PGfEx0dS/v2TzF69GfExU0CegG3+PHH+nTo8CtPu7mPvNls\nQKW6zt9zqG5RpEhxBg4cCDYbvPgizJkDXl6wdCm0betmz/Ku2NhYHI4Q4K939hVJTLyF3W5Hq835\nVKVWq5k48WMmTvw4x9v2NGXWvUKhyLLFi5fQt+9QHI7uaLVHqVDBzvbtvz3Syf7GjRuEhNTi+vVO\n2GyVMZm+JCnpOCK3AefSP73+FSZOLMVrr73mVluRkZHUq9eMhISXASMm0/9YvXoRofXrQ69ezuRu\nNsPKldCsmfudy8OOHj3Kk0+Gkpi4DKiJVvsRNWvuY+fOjbkd2iNBmXWvUChyxeDBr5KUtJKUlCkk\nJGzg2DENixYtyu2w/tWSJUu4c+dJbLYvgZdITFwJmID5rjuuo9Oto3Llym63VaVKFXbt2sywYfEM\nGhTN77+vIrROHejUyZnkfX3ht9/+80keICQkhAULZlKwYC+02gLUrn2IlSvn5XZYjwVl6F6hUGTZ\n7duxOJeLAaix2UK4fv16bob0UFarFYfDku6KNxqNlXz5xpCS8gWpqdEMHjyEFi1aeKS9kJAQvvnm\nC+e/3LkDbdpAeDj4+cH69VCjhkfayYz4+HgiIiJQqVQ0adLkkdnEqH379sTGts/tMB47yhO9QqHI\nsgYNnkKnGwXEAztRqxfTpEmTLNUlIpw/f56oqCjsdrtH40yvffv26HSrgalABEZjL/r0eYHz54+x\ndet8Tp2K5PPPx91TzuFwcODAAXbu3ElKSspdny1YsJDKlRtQsWJdpk+fcf+G4+KgRQsID0cKFeKd\n+k0o3LYX1as3Ztu2bZ7v6ANER0dToUJNevacSI8en1C5cu1H/seZwk2emQ+Yc/JgyArFYys2Nlaa\nNm0nWq1BChQoIosWLc5SPVarVTp2fFYMBn8xm4tLSMiTcu3aNQ9H+7cDBw5IaGh7CQmpJ2+99b6k\npqb+6/1JSUnSsGErMZtLibd3FSlZsrJER0eLiMiKFSvEZAoWWCOwUUymsjJr1g93VxATI1KtmgiI\no3hxaVa8okBtgR0Cc8VgKCCHDx++p90//vhDRo16T8aNGy8xMTEe6fszz/QTrXaka2a7Q3S6oTJo\n0AiP1K3IPu7kvjyXNZVEr1A8fr788msxmZoJJLmSzwjp1u35LNVltVrlzJkzcuvWLRERmTkzTAoX\nLi9+fsXl9dffEZvNluk6P/lkvBgMHQSsAg7RakdKp07PiYhI27bPCMxKt4RuhVSv3kjat39GKldu\nIO88P0Ds5cs7PyxXTtbPnClgETiVrsxwGTt23F1trlq1SozGAIEPRafrLwEBxeXKlStZ+k7Se+KJ\n5gK/pmt7kTRv3tnteh/k9u3bEh4eLnv37s21pXKPA3dynzJ0r1Aoct3u3ZEkJnYHDIAKq7U3e/ce\nynQ9x44do1ixClSq1Ah//yK89NJAXnnlIy5f/oHY2HV8/30EH31077D8wxw6FEVycnuc05pU2Gyd\nOHLkOOBcQgdx6e6+yJEjkaxZE0L84WEM+HEe6uPHkcqV+bxDV/p9NNHVz/RlYvHyunulwquvfkhS\n0g/AGKzW/+PGjdZMnTot07H/U+PGtTEYvgdSgESMxhk0bvyk2/Xez/HjxylVqjIdOoyiceNutGvX\nI1tfyyjuT0n0CoUi11WpUhajcQ3gPL5Vo1lJxYrlMl1P+/bPcOXKmyQmXiA19SizZy8jMfFNoC5Q\nnsTEz1i06JdM11urViWMxiU4k6Og18+jRg3nrPxRo4ZjNk8AxgKfode/g05XgzL27kTwJiUlgd0q\nNcOrPsFH323n4sUhrn52A74FXkWj+YU+ffrc1WZCQjwQnPbvNlsxbt+Oz3Ts/zRu3IeEhqrR6/3R\n6QJo0yaAd9550+16/+n06dN07vw816+/ye3bO0hI+JPw8KuEhYV5vC3FQ3hwZCFH5MGQFQrFQyQn\nJ7vegZcRH5+aEhxcQS5evJipOmw2m6hU6nQ7q4loNDVEpRog0EqgkEBlCQmpnen4UlNTpXXrLmI0\nBomXV4CYTEWkefOOsmXLFhEROXjwoAwc+Ir06/eyfPHFF1LfVF1i8BcBCaeB5NcYRK+3CMS4Yvuf\ngE5UqnxisfhLRETEPW0OH/62mEzNBY4JbBKTqZBs3rw5wzFbrVYZM2a8NGzYVnr3HnDP93njxg2J\ni4vL9HfxMA6HQ4YOfUMMBn8BH4Ez6V4TjJU33xzp8Tb/C9zJfXkuayqJXqF4PNntdtm7d69s375d\nEhMTs1SHv39xgcUCMwW+Er2+uKhU3gIfCZwXmCI+PkFp7+8zw+FwyOTJk8VgKCrwk8B0MZn8Zfv2\n7XfdlxQeLjfVGhGQtVSRgsb60rfvIDEafV0xOJOewdBFJk6c+MA5A6mpqTJs2Bvi719SihevLAsX\nLpJbt27JoUOH5MaNGw+Nt3fv/q55D8tFqx0lgYElsyWxpxcTEyOtW7cXjaaEQJxAW4EPBBwCN8Vs\nrik//fRTtsbwuFISvUKhUIjIzz//LCqVRaCNQE/Ras1iMAS7Eo0zwfr61svUk3F6tWo1E1iR7gn1\nS3n22Zf+vuH330XMZhGQg6XLSpe2PeV///tabDabjBz5gZjNNQV+Eo3mHfHzC5arV69muO21a9eK\n2VxQvL0risGQT+bOnffAe1NSUkSj0QvcTovVYnlaFi5cmKV+Z8SdO3ckOLi8qNWNBYa42r0gUEnA\nT7y88kn//sOUCXlZ5E7uUzbMUSgUj40tW3ag0fTFZpsCgM32GXb7x8BtwBdIwWaLxtvbO1P1bt68\nmd9+20hMTAygSvdJAlFRR5k8eTI9fXwIHDIEkpPhueeo+sMPLE23R/uECWMoXrwoK1euoHBhP8aM\n2Y6/v3+G2o+Pj6dbt94kJKwAGgBHGDCgCU2aNKJo0aIZ7EX2bh++YcMGbt4sisMxEhgG3ACKAq8R\nHDyJnTt/p1ChQtnWvuLBlESvUCgeG5cuXcNmq5fuSkN8fApgs4WSkNAZs/k3mjWrQ/Xq1TNcZ1jY\nbIYNe4/ExJfQar1RqV5C5GvgIjCBw4fbs/2NlQy2ufZkHzgQpk51HjmbjkqlYsiQgQwZMjDT/Tp/\n/jxqdUGcSR6gEnp9CCdOnLhvotfr9fTs2YflyzuTmDgcrXYnZvOftGrVKtNtZ5TzR4QGaAF0AcoB\nFgoUsLFq1Rolyeci5VAbhUKRI5KTk/nyy685fPgkdepUY+jQIWg0mocXzIQff/yJwYMnkJi4CvDF\naOzFoEHVqFu3BgcOHKJ8+bL06dMnU+0WKFCEuLhVQA2cM+6fpFQpDfHxt7l8uR3POaoQxotocLC4\nWGm6nz0BKtXDqs2U27dvExRUnKSk34HqwGmMxtr8+edeihcvft8yNpuNceM+47fftlGiRGE+/XQ0\nRYoU8Whc6d26dYsKFWpy7dqz2O0N8PKaRIMGBlauXIzZbM62dv8r3Ml9SqJXKBTZKiEhgXfeGU1Y\n2HySkqpht7fHZFpAmzbFWLx4jkfbEhHGjBnPZ59Nwmaz0qNHL2bN+tat0/QMBm9SUs4D+QHQ64cx\nblwJtm49QKEVGqbi7MNonmdZ5VMcitz6r/WdPHmSAwcOEBwcTJ06dTIcx8KFi+nXbwg6XTlSU6OY\nNGkcQ4cOynK/3HHgwAFmzvwRtVrFgAEvpB0AdOnSJV5//X3Onr1E06Z1+fjj9x/pkwzzEiXRKxSK\nR5LD4aBGjYYcOWLCbj8LHMc5vJuIwVCMkycPZstT5l9/I1QeeLLu1KkXv/4qpKRMBDagUr0OxDNK\n68V4axIAb/IBU00RvP56Mz755IMH1rVgwSL69RuKTtcQu/0Afft24dtvv8hwLNHR0Zw4cYKSJUsS\nHBz88ALZICIigtatu5CYOBywYzZ/S0TEemrkwuE8/yVu5b6szwHMHXkwZIXiP+vFFwcJFBD4XeDJ\ndLPV7WIyFZVTp07ldogPdefOHenZ80XJl6+waDT5RMX/5CM++KsjMlxnFqMxnwwcOFysVusD60lN\nTRWDwUfggKvoTTGbS8gff/yR6ZhsNpv83//9n7z66psSFhYmdrvdnS5miN1ul8GDX3WtjZ9218qD\nzp17Z3v7/3Xu5D5lZzyFQpHm2rVr7NmzxyOnme3du5f581fi3O61JnATGAPsRasdTqlSRShRooTb\n7TgcDs6ePcvVq1fdrut+LBYLCxbM4tixfWg1KiZxkdF8gh01gww1CF34I4mJcUyb9jVa7YPnN8fF\nxeFc6FTNdcUXjaY658+fz1Q8IkKXLr0ZMWIOX31VkGHDptG794AMlY2MjKRjx140atSOqVOnZ+oJ\nccqU75gzZwdQB0i/WiCA+PikTPVBkcM89nMjh+TBkBWKPOGHH34UozG/+PhUF5OpgCxb9rNb9S1d\nulS8vdsLtBDoKfB/AmVFp/OXLl16S2xsrNsxnzt3ToKCSotG4ydarbf07t0/255ukxMTZbpaKwKS\ngk66ME/M5rKydevWDJW32+0SGFhSYLbrSfigmEz+EhUVlak4Dh8+7DotL8lVT7wYDP5y5syZfy13\n4sQJsVj8RaX6UmCZmExVZOzYTx/a3r59+6Ro0fKug3jCBH4QKCewxbVjX0lZuHBRpvqgyDx3cl+e\ny5pKolcoPO/SpUtiNBYQOOJKHnvEZCqQpZ3Url69Kl269JFixUJEo/EV2CUwSqC2GAwF5fr16x6J\nOSUlRXx8gl2bszgE7ohO94RMn/5/HqlfxHkM78yZM2XmtGmS2K2bCEgiSCevVmKxVJEePV7I1AYw\nBw8elMDAkuLllV8MBh+ZPz/zG9j88ccf4uNTI93QuYjFUk4iIyP/tdyYMR+LRvNqunKHxN+/5L+W\niY+PlwIFigjME3hb4CXXd/29QEkxmQrLjBmzMt0HRea5k/uUdfQKhYJTp06h15cnKSnEdaUWGk0Q\n58+fJ1++fBmux2az0bjx05w61QirNQyVahwqVSMMhnyYzV6sW7eeAgUKuB2vzWajV6++3L6dAAzG\nuYmNBau1D9u27WHAgP5ut3HhwgVq1WqILeEJwlJ2YbRfxGE2c/6LL2glwoBixXj66aczNeGvatWq\nXL58ktjYWPLnz49Op8t0XFWqVMFsvk18/CQcjs5oNPMpWFBDuXL/fgiQM870Q/WOh8Z+4sQJrNZ8\nwLNAK6AxUA+TyQ+DIZWdOzdTpkyZTPdBkbOUd/QKhYJSpUqRmnocOOa6sg+bLZpixYplqp5jx45x\n8eJNrNb/AbURWY7ZXJolS2Zx5cppatas6ZF4R478kF9+OQhYgF9dV+3ASsqWzXjMEyZMxNs7EIPB\nl+7d+5KQkJD22fvvjyPpek/mJSbQ0X6ROAyMrNmAY0FBJCUlYTKZsjSrX61WExAQkKUkD2Aymdi6\ndT11627Ez+8pGjbcSUTEuocuY+vV61mMxnmoVJ8DSzCZnuO114b8a5mAgABSUy8DV4ECwFp0uj+Z\nMKElx48fUJJ8XuG5gYWckQdDVijyhFmzZovBkF98fGqKyVRAFi9emuk6oqKixGAIEkh0DQ+nitlc\nQg4ePOjRWAMDywhsFvATCBKoJ1BSvL0LS3JycobqeP31N10rAvYKXBOttpP06tU/7fP2TdpJOBVF\nQGLwl6p8IwUKlBCLpbro9a+IyVRSPv54okf7ld0OHz4snTv3ltDQDjJt2owMvXZ4//2PxWQqISbT\nS2I2l5Y33ng3ByJV/JM7uU9ZR69QKNLExMRw7tw5SpUqhZ+fX6bKXr16lUaNWhMVFYlzsLAzRmMC\ntWs72LTpF9Rqzw0glixZjbNnvwL8gFeAQ5QoEcSePREULFjwoeXj4uLw9y+C3f42MNp19TT58jUh\nLu4C3LjBlRo1CDp/nosU4imWcc4wFLs9Bqs1CjAB0ej15YiJuZCp1xt50datWzly5Ajly5cnNDQ0\nt8P5T3In9ylD9wqFIk1gYCC1a9fOdJK32WxUqFCHqKgngSTgOGr1Zp55JpB165Z5NMkDfPrp+xiN\nzwFr0GqrUrCgme3bN2YoyYNz4xmt1gxEpbt6DJPJDDExEBpK0PnzxPr40lwXx2ldM0JDi2A0lseZ\n5AEKodXm4+bNmx7t26OoYcOGDBo0SEnyeZQyGU+hULht+fLlxMXFAh/h/LNSAoejH8HBOry8vDze\nXo8e3QkI8GfJkpX4+uZj6NCdmTo0pUSJEuj1KlJSdgKdcZ6yFsbUdz+Fxo0hKgoqVMBvwwaOFS4M\nQGxsLKVLVwaWAy1Rqf6PAgVMnD59mrlz5xIYGEifPn0wGAwe769C4Q4l0SsUCrc5j2/1BXYBnQAH\nsIVChZ7LtjZDQ0Oz/IRpMplYu/Zn2rbtQmLiRlQqGzPfHUmHSZPg3DmoXh3WrYOAgLRDaf39/Vm3\nbjk9e/bj8uUeVKhQkx49nqd9+74kJz+HwbCV77//kR07Nij7u/+DiLBt2zYuXbpEzZo1KVu2bG6H\n9J+ivKNXKBRu279/P/XqNSclRQW0BI5jMkVz48bZbHmivx+bzcbq1auJi4ujUaNGlC5dOu2z3377\njZ9/Xk3+/D4MHz6UwMDAtDJXr17F/9o1dE8/DdHRULcurFkD+fP/a3sigtmcn6SkP4AKgGCxNGHW\nrFfo3r17Nvb0b8uXL2fgwFe5dSuWxo2fYtGiMPI/JO6cJiK8+OLLLFmyAY2mGlbrZubM+Z5u3brm\ndmh5irLXvUKhyHU//TRfjEZfUanUUqpUiJw7dy7H2k5NTZV69Z4Si6WOmM3PicnkJxs2bBARkZde\nGihQUGCSqFSDxN+/mMTExPxdeO9eET8/5y4yoaEit29nqE2r1SpqtVYgJW0TGpPpBZk+fXp2dPEu\nDodDFi9eLF5efgJbBeJErx8kzZt3yPa2M2vz5s1iNpcVuOP6nvaK0eibI/vzP07cyX15LmsqiV6h\neHQ5HA5JTU3N0Tbj4+OlevXaArUF7K5kslaKFq0gGzduFPAV2J6WjNXqPjJp0iRn4W3bRHx9nR88\n/bRYb9+Wd98dLRUq1JEGDVrLrl277mkvJSUlbVlao0atRacbInBFYK2YTH5y/PjxbO2vzWaTdu16\niE6XT2BAup3ubotWa8jWtrNi7ty5YrH0SBenQ3Q6s9y8eTO3Q8tT3Ml9yqx7hULhMSqVKssbwWTV\nwIGvEhmZDDTi74VETxIbe5nVq9cBOiAg7X6HI4iEhETYtAlatoRbt6BrV1i+nFffGc1XX/3OsWOf\ns21bD5o2bcOJEycAuH79Og0btsJotGA0+jBlylSWL/+JZs1iMJsrERz8OitWzH/oDnXumjlzJps2\nxWC1fgGc5u/d7o7h7Z2xVQc5qVatWtjtvwORAKhU0wkKKoqPj0/uBvZf4sEfHDkiD4asUOSq2UZO\nXwAAIABJREFUpKQk6ddvqPj7l5QyZWrKr7/+mtsh3eXOnTsyePCrUr16E3nmmX5y5cqVTJX38ysh\n8JNAUYEoAZuo1cMlNLSdjB8/QdTqqgLNBfYLfCfgI520RklWqZyPmM8/L+I6XtZi8Rc4l/b0qdMN\nk88++0xERFq16iI63csCqQInxGQqJps2bfL49/Eww4e/ITBRIFmgvqtvQ8RoDJQFCzK/d35OmDt3\nnhgMPqLX+0rRouXk6NGjuR1SnuNO7stzWVNJ9ApF5vTuPUAMhg4CxwVWidHoJwcOHMjtsETEOdTf\noEFL8fLqJbBBdLo3pXjxEElMTMxwHRUqPCmwzHXQikVAK8HBFSQmJkZu3LghRYuWE42mskBhAYv0\noLek4jyFboaXSeLSHbKTP38RgcNpid7Lq6989dVXIiJisfgJRKd9plK9I6NHj/H4d/IwYWFhYjLV\nFYgXSBSVqqOULh0ie/bsyfFYMsNqtUpsbGymDgFS/M2d3KcM3SsUj7nly5eTnPwdUA5oi9X6PGvX\nrs3tsAC4dOkSe/fuJyVlNtAcq/Uzbtwws3PnzgzX8f33kzCZBmIw7MNkakSpUhU4cmQXAQEB5M+f\nn8jInXz99WBef/0ZBukNzGMeOmx8xlu84VWNg5GRaXW9995bmEydgeloNG/h7b2JZ599FgA/vyBg\nj+tOB0bjPgoVCvLYd5FRzz//PJ06VcJgKIHFUpXixU8SHr6OWrVqpd1z9epVXnhhCA0btuW998aQ\nmpqa43H+k1arpWDBglk6H0DhHmUdvULxmDOZLMTHXwKKAKDVXsRiKZm7QbloNBpE7ICNv/8cpaLR\naO57v81mY926dWlL6IoXL06TJk3Yv38b69evx2KpR/fu3TGbzWll8uXLx9ChQ7k9fjw+qbEAfMDH\njOV1TLaKdy1He+ONEQQHF2bp0rUEBORn1KgdBAQ43+/PmjWZdu16oFI9jUp1ivLltfTt2zdD/YyO\njmbEiJFcvHiNli0b8t57b2d5LoNareann2Zw/vyHxMfHU7Zs2bvqSkhI4Mknm3D58tPYbIPYt28a\nhw/3ZcWK+VlqT/EY8ODIQo7IgyErFLnqhx/miMlUROAT0eufl6JFy2XpnPns4HA4pG3b7mI0Pi0w\nX7y8XpBKlWpLSkrKPfempKS4ltA9KRZLTzGb/WTz5s0Za2jChLTD20fqA0SjeVvM5lrSs+eLmRpK\nPnnypMycOVOWLl163xjv59ixY6LR/DVDfoloNE2lc+fnMtxmZq1Zs0a8vRulm+WeKDqd+ZH5b67I\nGndyn/JEr1A8hmJjYzl48CBBQUH07duH4sWDWb16HQULhjBo0Fe5eghLREQE3377A2q1ihEjBrBs\n2VwmTvycbduWEhJSijFjvr7vznJz587l4EEHiYk7AA2wkr59h3LmTOQ996YRgQ8+gHHjQKVCpk6l\nYZEi+Bw6RNmyI+nWrVumhpJLly5910Y8GdGlSy/s9jLANECF3d6GlSsLcvPmzfv+d1ixYgVjx36D\n3W5nxIh+9O3bJ1PtyT2bqihD5f95nvu9kTPyYMgKRY7asmWLWCz+4uvbWIzGwjJo0IhHZgLUxo0b\nxWQKEJgs8KWYTH6ybdu2DJX95JNPRK0ele5JNUZMpgIPLuBwiIwY4bxZoxGZO9dDvcgci6WgQMN0\ncSeLWm2SGzdu3HPv2rVrxWgs5JpcuEpMppIyZ07m4o6Pj5dixSqITveawHIxGttK+/Y9PdUdRS5x\nJ/fluaypJHqF4t/5+xcXWO1KKrfEbC4vv/32W6bquHnzphw9elTi4+M9GlvTph0FfkiX9L6Vjh17\nZais80dCcYEzAnbRal+Tpk3b3/9mm02kf39nI3q9yLJlHuxF5tSo0cg14/9tgTUCT0uVKnXue2+H\nDr0E/i/d97Nc6tRpmek2Y2Ji5IUXhkiDBm3k3XdHZ/g1g+LR5U7uU4buFYrHiM1mIzb2AtDadcUH\nkYacOnWKp556KkN1zJu3gP79h6DV+iMSx88/z89w2YexWm2AOd0VM6mptgfca2XBggXExMTQsGFD\nmjVrxtixbzBqVCXsdjvVq9dlwYJF9ysIffvC/PlgNMLPP0OrVh6JPysWLJhB/frNuXXrJ+z2MEqV\nKsSOHdvve69erwMS0l2JR6fL/J/pgIAAwsK+y1rAisePB39w5Ig8GLJCkaNKlKgkMMv1RHhRTKZg\n2b59e4bKXrhwQYzGggKHXOV/F4vFz2NP9gsXLnI9la8UWCYmUxFZtWrVPffdvHlTAgPLiEpVW1Sq\nYWIwBMnMmWEi4twCNiEh4f4NJCWJdOzofBz29hbJ6GS9bHbnzh3Ztm2bREZG/utrlF27donJ5Ccw\nSWCyGI0Bsn79+hyM9G63b98Wm82Wa+0r/uZO7stzWVNJ9ArFv4uMjBR//+JisZQSvd5bxo+flOGy\nGzZsEF/fJumGjkUsltLy559/eiy+efPmS61azeSJJ5rLsvsMqTscDqlS5QmBGvL33vVHxGDw/fe5\nBvHxIi1aOIPOn1/kPvvU5wW7d++W3r0HSM+e/SQ8PDxXYjh37pxUqFBLtFqjeHlZZMaMWbkSh+Jv\n7uQ+5ZhaheIxlJqaytmzZ/Hz86NAgQIZLnf69GkqV65DUtJeoBhwCKOxCVeunMuxvclv3LhBQEBh\n7PZngTDXVRtgICioFCkpifTs2Z3Jkz/7e/34rVvQrh1s3QoBAfDbb1C1ao7E+ziqXr0hhw+3xm5/\nD4jCZGrKli2/3LUpjyJnuZP7sn1nPLvdTo0aNWjfvj3g/J+4RYsWlCtXjpYtW3Lz5s20eydMmEDZ\nsmWpUKEC69evz+7QFIrHll6vp1y5chlO8mfOnCE8PByj0cj48R9hNNbC17cxRmMzZs2alqMHkGg0\nGlQqNbAK+B24BXRDpcrPlSuziYvbwuzZh3nrrQ+cBa5fh+bNnUm+aFGIiFCSvBscDgeRkX9gt4/E\nuTSvPA5He/7444/cDk2RRdme6L/++mtCQkLS1qpOnDiRFi1aEBUVRfPmzZk4cSIAR48eZeHChRw9\nepRff/2Vl19+GYfDkd3hKRT/eV98MZlKlWrTqdMHlClThWLFinDkyC6WLRvNiRMHeeaZHjkaj6+v\nL1279sTLqwjQGwhEowlH5G2gHlCKpKTPWbr0F7hyBUJDYe9eKF3ameSz+fS4nGS1Wvnhhx8YO3Ys\nGzduzJE21Wo1+fIFAX8l9lQ0mr0UKVIkR9pXZAMPvT64rwsXLkjz5s1l06ZN0q5dOxERKV++fNrp\nVNHR0VK+fHkRERk/frxMnDgxrWyrVq1kx44d99SZzSErFHmGw+GQS5cuydmzZ7O8Tj4qKkqMRn+B\n86534XvEaMz34MluOcRqtcqECZOkRo0GUqRIJSlWrLxoNIPTzR34WZqXrSlSpozzQkiIyKVLuRqz\np9lsNmnUqLWYzaGiVo8Uk6mETJr0ZY60vXr1ajGZ/MTbu6dYLFWkTZtuYrfbc6Rtxf25k/uy9Yn+\ntddeY9KkSajVfzcTExNDYGAgAIGBgcTExABw+fJlihYtmnZf0aJFuXTpUnaGp1DkWVarlY4dn6VU\nqSpUrFiXOnWacfv27UzXc/r0afT6qkCw60ot1GpfoqOjPRpvZmm1WkqXLsHx4+e5dOl9zp8fgt3+\nIzpdX9TqUVQx9OOXWxfh5EmoUQM2b4bChXMkth9+mEPBgsEYjb507dqHhISEhxfKgg0bNrB/fwwJ\nCRtwOCaSmLiZd999F6vVmi3tpdemTRsOHfqDqVPbs2zZF/zyy8K7/o4r8pZsW0e/atUqAgICqFGj\nBuHh4fe9R6VS/ev2kw/6bPTo0Wn/HBoaSmhoqBuRKhR5z6BBL7N69RUcjkuAjkOHBvDqq+8wa9a3\nmaqnTJkyJCfvAzYCzYDfUasTH4lh2kmTppGYOBno5LqSRMWKSxnc0Jv+izTorl6F+vVh9WpsFguv\nDnuDOXPmotPpef/9t3jtteEej2nLli28/PI7JCWtBEqwZs1Q+vcfzvz5Mz3eVlxcHCpVKZzb/QIU\nRURFUlJSlg/EyYysbPer8Jzw8PAH5s7MyrZEv337dlauXMmaNWtITk7m9u3b9OnTh8DAQK5cuUJQ\nUBDR0dFpJ0MVKVKECxcupJW/ePHiA//YpE/0CsV/zaZNm5g9+2ccjv8BBgBSUl5g5853MlVPbGws\nHTv2AkxAZzQaA0ajsHz5QgwGg8fjziznD/3083TMtA4IYsiC+XDjBjRrBitWgMXCR++NISxsL4mJ\nu4DbvP9+F4oUKUSPHt09GtO6db+RlNQfcM4+T06eyLp1DT3axl8aNGiAw/EKsBxogFb7OZUqVc/R\niZGK3PPPh9gxY8ZkvTIPvkJ4oPDw8LR39G+99Vbau/gJEybIyJEjRUTkyJEjUq1aNUlJSZHTp09L\nqVKl7vveMYdCVigeWZ069RZoJ9Ar3Trzt6RLlz6Zqqdr1z6i0w0XcAgkisEQKhMnfpZNUWfesmXL\nXKfuzRGYJs298onVbHa+k2/Xzrk5jkv58rUFItK9w58mPXv283hMX375pRgMPdK1s1ZKlKji8Xb+\nEhERISVKVBaTKb80btxGoqOjs60txaPNndyXY1vg/jUMP2rUKHr06MHMmTMpUaIEixY5t7AMCQmh\nR48ehISEoNVq+e677zJ1qpRC8V+h1WqAJjif9KoBWvT6C0yZ8i+nuN3Hvn2RWK3/h3MJlZHk5J4c\nPLgnU3XcunWLCRMmcfbsZZo1q8+AAS957P/bzp07s3ChjsmTf+DJ27F8fDAZTUIy9OgBc+dCuuHr\nggXzAycA59O1VnsCf3/3T+i7du0affu+zO7deyhWrDjfffcpRYrMIjq6I1ZrCbTaeUyd+qPb7TxI\nw4YN//10PoUiIzz4gyNH5MGQFQqP2r59uxiNfgJfC4wUvb6ALFmyJNP1tGnTXTSaD11PplYxGtvL\n+PGfZrj85cuXXSfRPSswXfT66jJs2BuZjuOhVqxwHkwDIi++6Dyw5h927twpZrOfaLWviJdXX/Hz\nC5aLFy+61axzh766rlPgTohKNU3y5y8sZ8+elenTp8vnn38uhw4dEhHnKoFt27bJxo0b5c6dOxlu\nY9euXbJgwQI5cuSIW7EqHn/u5L48lzWVRK9QOJN95869pX37ZzO0F/pfS/H+Wtoq4lz+GhxcXnx8\naorZXEYaNmwpycnJGY6hVq0GArVdQ/8icF00Gq9Mn5RmtVolLi7u/ksE5893HjELIsOGifzLEq/j\nx4/Lp59+Kl9++eVd/cyKixcvysyZM0Wvz5+ufyI+Pi3u2Zs/MTFRnnwyVCyWSuLjU18KFSot586d\ne2gbb7zxrphMxcTbu6uYTIEybdoMt2L+p507d0qtWqESHFxJBgx4RRITEz1avyJnKYleoVA8UHx8\nvDRp0kYMhoLi5ZVf2rbtnpaMExMTZdu2bbJnz55Mr5PW680CbdO9r04RtVqfqTX406fPFL3eLDqd\nRcqUqSZnzpz5+8MZM0RUKmflo0Y5z5fPAb///ruYzX7i7d1KwEvguqt/NrFYKsvmfxyU88kn48Vg\n6CJgExDRaD6RVq26PrD+mJgYadq0jahU+dPVHSVeXj5y+/Ztt+O32WyyYMECMRjyC8wW2C8GQyfp\n2jVzczgUjxYl0SsUigcaNuwNMRh6CqQKJInR2EY++mhslupyOBwyefK3UqlSfdFq8wkECPxP4A+B\nzlKx4hMZrmvPnj1iMhUSOC7gELV6olSq5Dqn/auv/j5VZ9y4LMWaVUFBpQTWupp/Q6CswHgxGltL\ngwYt7znN7dlnXxL4Pt0Pnt1SsmT1+9admpoq5crVELW6q0DoXYcHmc3F5NSpU27FnpqaKo0bPy1e\nXoUEnktX/03Rag1Z3lhJkfvcyX3KDggKxWNux479JCf3A3SAgaSkvmzbti9LdU2ZMpVRo77jyJGP\nsdleBuJRqb5HpepE/vx72bJlbYbr2rlzJyLtgHKACofjDY4e3Y1j7Fh49VXnTV99Be++m6VYs0JE\nuHr1PBDqujIJrbYkTZpsZNKkdmza9AsajeauMvXr18BkmofzHHkHev1Mateucd/6jx8/zuXLd3A4\nvgYOAztcnyzGYHDctWlYZkVFRfHWW2+xe7eVlJSPgfQbKF1Dp8v9JZOKXOK53xs5Iw+GrFDkql69\nXhKt9g3Xk51DvLxekldeeTNLdVWsWFdgU7onxbflyScbyJw5cyQp3XK3jFixYoVYLDUEkl11bZb/\nGSzOilUq59D9v3j//Y/Ez6+UBAaWkQkTJnnsabVq1fqiVk90vZs/KyZTsGzduvWB99tsNnnmmRfF\nyyufGI1BUqNGQ7lx48Z97z1x4oQYjYVcfV4tUEDAKPnzF5E9e/ZkOeZ33hktRmOA6PXFBcYK3Bao\nIPCiwFdiMpWViRM/z3L9itznTu7Lc1lTSfQKxcOlpqbKvn375ODBg3L58mUpXjxEvL3riLd3TalQ\noZbcvHkzS/VWq9ZYYHlaolepxsjAga9kqS673S4dOjwjFkuI+Fi6yndag7hecovMmycizlcFx44d\nk127dt317r9Nm44CRQV2CewTgyFEpkyZmqU4/unMmTNSsmRl8fIqIDqdSb744usMlbty5YqcO3fu\nX+c6OBwOadOmm5hMLQSmisHQWho1uvd1QGbs3r1bTKaiAlcFFgmECMQKXBeVqoEULlxOli5dmuX6\nFY8Gd3Kfch69QvGYuX79Og0btuLixQREUqlSpSSrVy/iwIEDaDQa6tati5eXV5bqXrlyJT169CMl\npSWgwWRay+7dWwgJCQEgNTWVsLAwzp49T/36ddOOp34QEeH3DRsoMXYspbZsAb0eFi2Cjh1xOBz0\n6TOQn39eg04XiMFwk4iIdVy9epUmTbricHwJ9HLV9At1637Ljh2/Zqlf94vr2rVr+Pj4eHyXQKvV\nyjfffMvevUeoXr0CI0a8gl6vz3Q9s2f/SFjYEu7cieX48QASEn4GBHgH+BKDwZfSpUuycePKtPNF\nFHmXW7nPIz81clAeDFmhyFHPPTdAdLqhrqFnmxgM3eTddz/ySN1z5swVLy9/0WieEa22vDRv3i5t\nyNxqtUq9ek+JydRSYLSYTOUePukvJUWkRw/nk7zJJJJuqeC8efPEbH5SIN41ejBZatZsLDNnzhSN\npqLAp+leIUyRp57q7JE+5gVTpkwVk6ms6wn+XQEfgVPy18l++fMXlgsXLiiT7x4j7uS+PJc1lUSv\nUPy7qlUb/eM9+lx5+ukebtdrs9nEYPAWOOyqN1nM5hDZsGGDiIisX7/e9c7d5vr8smi1hgeuzT93\n/LjsLRwsApJsMIhjy5a7Pv/ggw8FPkjXj0vi7R0gf/zxhxgMQQJ+rlnxb4tKZXLrHbenpKamyscf\nj5eWLbvJK6+8KXFxcdnSTokSVQW2pvtu2olGYxKLpbTky1dIdu7cmS3tKnKPO7lPmXWvUDxmqlcP\nQa9fiPNAGCtG41Jq1arkdr2JiYnYbDYgxHXFC5WqStqRtrdu3UKlCubv09YCUat1JCYm3lPXnvBw\nosqHUPPyBa5joYmtKKNWrb/rnkqVQjCbVwN3AFCr51O+fAh16tThww/fQK9PRqebjcHwPTNmfMPG\njRv54IOP2LMnc9v4elL37n2ZMGEz69d3Zfr0OOrVe4qUlBS36xURLl68mPZd37vNcA0GDerPnj2r\niY4+Te3atd1uU/EY8dzvjZyRB0NWKHLUjRs3pHLlOmI2lxKTKVgaNWqd6RnxD1KmTDVRqz8T52E6\nO8Vo9JOoqCgREYmOjhZv7wCBnwTOiU73mtSo0fDeSuLiZKfOuaXtZYKkEpECF0Svt9w11OxwOKRz\n516uYeliAmZ5442RaZ/HxMRIZGSknD17VgICSohe309UqvfEZAqQNWvWeKS/mXH16lXR630FEtNW\nOHh715KNGze6Ve+dO3ekXr2nxGDwFy+vAtKuXQ+ZPPnbdEP334jZ7CeHDx/2UE8UjyJ3cl+ey5pK\nolcoHs5ms8nhw4flzz//dOs9bVxcnPTq1V/KlKklbdp0l4iICKlQ4QlRq7Xi7e0nP//881337969\nWypWrC358hWWFi06y9WrV++u8No1cVSvLgJyDpOUIcqVFK+KRmO8J9ayZWsIfCJwQOCkmEzFJCIi\n4q57PvpojGi1g9INY6+ScuUyvnGPp0RHR4uXV35xbkz015a59TO0RfG/GThwuHh59RawinPDo1by\nyScTZPbsH6Vp047Svv2zj8RrC0X2cif3KbPuFQrFfTkcDmrXbkpkZAVSU/uh0awjIGAOUVEH0Ol0\n6PX6zJ1Ud/kytGgBR49ySq2hqcOHC7wPVAY+oHXrQqxdu/yu9rVaHSLJODf7AYNhMJMmVWbYsGGE\nh4fz3XezOXBgPydO9MQ52xzgMIULd+PSpWMe+ibuz2q18u2333Ho0HFq1Ahh8OBBtGjRiZ07vUlO\n7o9Wu4FChZbz5597MZvNWW6nWrXGHDo0BmjquvITTz+9kjVrFnqkH4q8wZ3cp7yjVygU93Xx4kWO\nHj1OaupUoA52+4ckJASwa9cuvLy8Mpfkz52Dxo3h6FGoVImLP80l1ihotVNQq/sQEuJg5crFAMyd\nOw9//+JYLAXQ6/MB61yVxKPRbKV06dKsX7+etm2fYfHiJzlxogEwCdgCnMRofI2uXTt49Lv4J4fD\nQevWXXj33dWEhVVk1KhldO3ah9WrF/HSS0WpUWMcXbteZefO391K8gDly5dCq/1r2aDg5bWOkJDS\n7ndC8d/hoVGFHJMHQ1Yo8qQrV66Il1e+tOVtYBeLpfI9Q+d/WbFihbRt+4x069ZX9u7d+/cHx4+L\nFC3qHMuuVUskNlZERM6fPy/Lli2Tbdu2pQ3Zb9261bX//U6Ba6LTPSVarbf4+jYVk6mY9O07WBwO\nhzRq1NY1F+Cv4fq+YjQGSsGCxWTIkNckNTU1276Xffv2ScGCRVyz/lNc7SeJ0RgkJ06c8Hh70dHR\nUrx4RfHxqS0WS1WpXLmORw6/UeQt7uQ+bW7/0FAoFI+mwMBAOnbsyKpVbUlMfA6DYT0BASqOHDmC\nv78/5cuXT7t3/vwF9O//NomJHwM3Wbu2Fdu2baCaWu0cro+JgYYNYdUq8PUFIDg4mODg4Lva/O23\nDSQlvQg4Z41brWFYLDVZvPgd/P39qV69uuu6DTCmK9mQFi2srFjxUzZ+IxAWNpt+/V7G+ZpgEfDX\nRjdeaDTeJCUlZbluq9WKTqe753pQUBBHj+5h165daRse3e8+heKBPPiDI0fkwZAVijzLZrPJV19N\nlm7d+krRomXFbK4tJtMLYjL5ydq1a0VEZNGixWI0FhZYk+4Je6yM7dRdJH9+54UWLUTi4x/a3uTJ\nk11Hvv5VzwYJDq54z30//TRPTKYSAisFFovJVEh+/fVXj/c/vf3794uXV0HX1rtJAhUFPhQ4IBrN\n21K6dNUsjSTs379fgoMriEqlloCAErJt27ZsiF6R17mT+/Jc1lQSvUKR8+bMmSNmcxPXsjoR2CRB\nQaVlyZKlYjIFC1QS2JCWoBsxWBJ1Oue/dOggksHlfXfu3JGyZauJydRedLoRYjT6y6pVq+57748/\n/iS1ajWT2rVbyIoVK2TPnj0ybtw4+fbbb+XOnTue7L6IiEydOlUMhucFvAVOClwU6CAqVT5p1Ki1\nXL58OdN1JiYmSsGCRQXmur7bFeLtHSDXr1/3ePyKvM2d3KcM3SsUeYSIMGtWGFu27KJs2WK89toI\ntyd6ZVRMTAypqTX4e/5uTW7cuMKUKbNJTPwM5xGtg4HPaUkEP/M9Rivw7LMwezZkcKjZYrGwf/82\n5s2bx82bN2nZ8jeqVat233t79+5F797Ove6XL19Oo0ZtSE19Hr1+L1988T0HDmzD29vbzZ7/rVCh\nQmi1R4BPgYZAI2Anw4cP4quvJmapzlOnTpGaagGec13pgFo9gSNHjtCoUSOPxK1Q5LnH4zwYskLh\nEYMHvyom0xMCU8Rg6CFVq9aTlJQUt+u1Wq1y+PBhiYqKeuCa+x07driOVz0iYBWt9jVp1OhpadGi\ni8As15P8bOlICUn+67G+f38RN05lywiHwyFjx34qKpWPwO9pIwpGY1f55ptv0u47ePCgPPVUJ6la\ntbF89NFYsVqtmW7LbrdL69ZdxGKpLkZjG9HpLDJx4kS34ndOePQViHbFfkOMxkA5fvy4W/UqHj/u\n5L48lzWVRK/4L4qPjxet1ijOY1nrC+QTtdpfpk+f7la9165dk4oVnxCLpbQYjYWlZctOD/zxMHNm\nmJhM+USt1kqdOs0lJiZGNm3aJEajv8A30os+Yv0r044YIeLGRj0HDhyQl14aKi++OER27Nhx33vs\ndrsMHz5C9PpyrhnwF9MSvVo9Sj7++BMRETl79qx4eweISjVFYKOYTI1lyJBXsxSX3W6XNWvWSFhY\nmBw7dizL/Utv9OjxYjIVF5Opn5jNZWT48Lc9Uq/i8aIkeoXiMXf9+nXR6SwCJQW+Ebgm8J34+ARJ\nfAYmuT1Ijx4viF7/ijhPuksRo/FpGTfu0wfe73A47plwtmXLFvm+Zj2x/5Vl338/Lck7HA5Zs2aN\nfP/997J79+4MxbRnzx4xmfwExgv8P3tnHhZl9b7xe/aZd4YBZFUBE0TEfV9zScP9p7lruaWpaS5l\nkdpimaW2mZq54JqaW6amiAuaqKm57xsiGIobIoIyMMDM/ftjRoKvoCCoYedzXV7F+57znOeckvs9\n2/N8R0ly486dO3OUeTC7Vii8CCwg0J9AdwLXCOyhTufBv/76iyQ5ffp0ajSDsh3wi6MkORdglApP\nVFQUa9duRoPBjdWqvfzQR8LevXs5Z86ch/opEDxACL1A8IJjtVpZrVp9Ar7ZBIt0cKie70xlBw4c\n4IIFC7g7W5a48uXrENiXzeZ8du7ct2DOTZ36j0PZlrKtVit79HiTen1l6nQDKUml+NPG0LK+AAAg\nAElEQVRPcx5rrmvXfgR+yObTYjZr9n85ymzZsoUGQ1UCIwgE2+/69yPgSLW6BJct+4WbN29maGgo\nv//+e+p0vbPZu0gHB7eC9bEQhITMp1xuJPANgWuUyX6km1uZQn2gCf57FEb7xGE8gaAYIJPJsHRp\nCKpXbwyrNQmAI4D7yMy8AWdn58fWnzLle0ycOA0yWXMAX2Hw4B6YOnUSKlUKQEzMWmRk1AdggU63\nETVq1MufUyTw5ZfA+PG2n2fOBN55J+v1/v37ERq6BykpJ2G78x6N996rigED+kGr1eZpNjXVbO/f\nA5yQlpaeo0x8fDyAQABjADQEcA2AAgaDGps2rcHAgSNw86YBMpkGWm00tNpMpKePhcUSCEn6DsHB\n7+Wvj4Vky5YtGDnyY1itngCCAQDkcJjNi3D69GnUq5fPsRYICkMRfnA8E4qhywJBkTF48Ejq9VUp\nl4+hXl+d/fq9/dg6u3btolJpyLaHbTvwdf78ed64cYN+flXp4FCZen1ZNm7cOs/88TmwWsng4Acb\n4uSiRQ8VWbt2LY3G/8uxAqHVuvDGjRuPNL1hwwZKkheBTQTCKUnluGjRzznKREVF2Zf3dxG4Qpms\nHT08vBkdHc3hw9+nWj3Evh1BKpUfs23bLhw8eAQ7dHidCxcuLlSin/xw8OBBVq/emDqdO4FP7WcI\nkuzjcJ+SVIrnzp17qj4IXiwKo32PrTl9+nTeuXPniRsoaoTQC/7LWK1Wrlu3jl9++SXXrFnzWMHa\nsmULtVpn2tK8/iO4jo6NGBERQZJMS0vjoUOHeOLECVoslsc7YbGQQ4fSrqLkqlU5/Nu7dy9/++03\n7tu3zy7GOwlkUiabRh+fCvkS2ZUrV7FKlZdZsWIDzpu3INcyYWFhdHHxolyuYPXqLzM2NpYk2bJl\nVwIrsvU3nNWrN318v4qIv//+mwaDG4GlBN6yby8MI1CdwMeUyyuzV68BT/1jQ/Bi8VSF/qOPPqKf\nnx+7devGzZs3P/f/OYXQC4oLVquV0dHRPHfuHDOf8jWzvPD1rUZgHW3R3JbbZ7mb6eDgztv2mPMF\nIiOD7NvXpqAaDblxY9Yrq9XKnj3fpF5fjkbj/1GSXDlp0iSWKFGaMpmc5cvXfCqx4P/3d9KkSd9Q\nklrY9+3N1Gq7cMSI4CJvNy8WLFhAvf4N+0fGVfvY9yXwGpVKHT/++OPn/ntUUPx4qkJP2k64bt68\nmT169KCfnx/HjRvHqKioJ260MAihFxQH0tPT2bZtV+p0HtTry7By5XpPJqyFxMXFh7YobkcJ+BNQ\nUKcrwV27dhXcmNlMduliE3m9nty+PcfrsLAw6vWVCZjsIhdBZ+dSJPlE99ZJW3jYLVu28Pr16/mu\nk5GRwe7d+1Gl0lOtdmDLlq/RZDI9UftPwooVK2gwvJq1dQAcpFyu4ieffMpjx449Mz8ELxaF0b58\npamVy+Xw9PSEh4cHFAoFEhMT0bVrVwQHBz+towMCQbFm8OCh2Lw5HqmpfyMlJQYXLtTBO+8U7O+L\nxWIptB9t27aGVjsGQGkAy6HTeWDz5rVo0qRJwQylpgKvvQb89pstKc22bUCLFjmKxMbGgqyHf5LN\nvIy7d28gIyMDSmXBzv2SxFtvjUCjRh3Qo8e3KFeuCiIiIvJVV6lUYtWqxYiPj8P165exdes66HS6\nx1V7ItLT07F3717s27cP6em2A4MdOnRAqVIJ0GheB/AdJKk3vvjiS0yc+EVWUh6B4JnyuC+BadOm\nsWbNmgwKCuKqVauy7tBaLBb6+vo+8RfGk5IPlwWC58qOHTuoULgQmJdtn3g//f1r56v+5s2bs5a7\nAwPr8NKlS0/sS0pKCrt3709JcqaLizcXLfqZGRkZDA0N5dKlS3n58uXHG0lOJps1s3XExYXMnoI2\nG9u3b6da7W5fQSBlsuksX77GE/kdHh5Ovb4CgWT7+G2li4vXE9l6Wty5c4cBATXp4FCNDg5VGRhY\nO+s8U3JyMidPnsJhw97lunXrnrOngheBwmjfY2uOHz8+z18GZ86ceeKGnxQh9IJ/O927v0mgA4HX\nCGTYl3A/YMeOrz+2bkxMjP0AWwSBDMrl37Js2cpFtqdrNpvZoMGrNBjq0GDoQb3e9dHL+HfukPXr\n20S+ZEkyj7/zly9fppubD9XqagQ0BAwsXdr/iffk586dS0kakO1DyUKZTEGz2cwJEyaxdOlAvvRS\nVf7889Insl8YrFYrz58/z44de2Q73W+lWj2YQ4aMeub+CP4bPFWh/7chhF7wb6dPn8EEviIQRKAc\ngUpUq13yld1s9erVdHDolE3grFSrjUW2v79gwQJKUnMCmXb7v/OllyrnXvjWLZorViQBXtPoOPO9\n4Dz32jt16k2FYoLdZhoVikEcNGj4E/t54MAB+xW7v+0257Fs2cr8+uvvKUk1CRwhEEFJ8s4zu93T\nIDExkX5+1SiXuxDwoC1N7oP/Vuv58svtnpkvgv8WhdG+fO3RCwSC/PPee29Dr/8BQAsAXaDRXMfK\nlfNQsmTJh8rGxcXh44/HY9SoD7B37164u7uDPAcgzV4iCoAFRqOxwH7Yfjfk5Nq1a0hLqwtAYX9S\nH7duXXu4clwcLI0aQX32LC6gBOqaf8SHcw9h8OCRubYVG3sNFkt9+08aWCwtcPny9QL7/IC6deti\n4sRgqNWVoNf7wMNjEjZuXIklS36DyfQ9gJoAmsJkGodly9Y+cTsFITMzE1Wr1sGlSzJYrbEA+gNY\nBCADQAa02mWoXz/3THsCwfNECL1AUMTUqFEDe/ZsQ+/el9C9+y2Ehf2KTp06PVTu6tWrqFq1Hr7+\nOgkzZiShadM2CAmZh6ZNK8NgqA+dbhAkqSlmzJgGVT7TvALArFlzYTC4QqXSok2brrh3717Wu4YN\nG0KrXQEgBoAVSuUU1KvXKKeBmBigcWMoLl7EabkRTXAWVzEQJtM6LF26MNdDgi1aNIJONw22dLVJ\nkKSZCApq9FC5gjB69EjEx8fh1KlduHLlAipVqgSDQQ/gnw8Imew6jMZnk6r39OnTuHEjEUAnABKA\n8QDuAnCDVuuFevVM+OKLT56JLwJBgSi6hYVnQzF0WSDIlXHjPqFCMdIe3KUkgS8I9Kanpy9/+eUX\nzp49+7GJYK5fv87w8PCsKGvbt2+nJPkQOEvgPjWaPuzaNWfs+qlTZ1CtlqhQaFi7dlPeunXrn5fn\nzpGlS5MA43196a1vk21pOpEKhTrXmABms5nduvWlQqGmQqHmgAHDnkrsgJ07d1KncyXwOeXy0TQa\n3XOcAzhy5Ahff/0tdu3aj9v/5/pfYTl+/Dg1Gg8CtQncs4/JVwwMrMXLly+Lu/GCp0phtE9mN1Bs\nkMlkuS5JCgTFjZEj38ePP7oCWAxgIQDbDFij6YtJk6pj9OjRj6y/detWdOnSG0plZaSnn8eIEYMg\nl1swZYoawGf2Upfh7NwYd+5cyVHXYrHAbDZDkqR/Hp44AQQFAfHxQJMmuPPzzwis1wwJCb1hsdSG\nJE1Dz56VsGDBT3n6ZDabQRK3b9+GwWCAk5NTQYflsRw5cgTLl6+GRqPGoEEDULZsWQDA0aNH0bhx\nK5hMYwDoodN9gV9/nY927doVSbuZmZmoXbspTp1KgtV6A4ADVKoknDt3CH5+fkXShkCQF4XSvqL5\n1nh2FEOXBYJcCQ0NpVzuTEAiEJM1c5bLx/Lzzyc8sm5mZiYNBhcCe+z1blOSfDh69GhqtZ2zBWv5\nneXK5eOK219/kU5ONgdatSJTUkiSsbGxfP31t/jyy+341VffPHaWfu3aNQYG1qZO506VSs/33hv7\n0Ew3IyODP/wwnb16DeSXX05mamrq4/3LB717DyLwbbYViF9Zp86rRWL7AUlJSRw+/H3WqtWMvXr1\ney5BkAT/TQqjfSJ7nUDwHLBarRg16mNYrV1gOxj3NoBpAGKg1S5E+/Zhj6yflJSE9PQMAC/bn7hA\noaiLKlWqoEyZCFy92hpWqw9ksvUICVn9aGciImBt3x7ylBSsgwzBZ2Kw9MQJNGjQAN7e3ggJmQaL\nJX8HAnv3fhsXL76KzMxJAO4gJKQZGjWqjS5dumSV6dHjTWzZEgeTqQd0ui0IDW2PP//cCoVCkbfh\nfGA2Z+CfYD0AICEzM7NQNv8Xo9GIH3/8rkhtCgRPnSL84HgmFEOXBYKHaNiwhf2+eQKBNAKjCLjT\nxaUsN23a9Nj6VquVbm4+BNbYZ6+XqNN58NSpUzSZTFy6dClnzZrFCxcuPNpQWBitWi0JcClqUoEk\nAmvp4ODOa9eusX//t6lUaqlUSmzZstNjQ8k6O5cmcDnbrPoLjhkzLuv9uXPnqNW6ZAuTm0mDIYAH\nDhzI17g9ij/++IM6nQeBVQRCKUl+XLhwcaHtCgT/BgqjfcVONYXQC4o74eHhdpF/ibbMbg/uyzfl\nolzSvebFoUOHWKJEaRoMZanRGDlr1tyCObJmDa0qFQlwDjSUwZIl0EZjczZt2pxKZV3a0quaqdV2\n5bBhox9psmrVRgTm2+2kU5KaMyQkhJcuXWK5ctWoUGgJOBM52qrD3bt3F8z3PAgLC2P9+i1Zq1Zz\nIfKCF4rCaJ84jCcQPGUyMzMxduxnWLVqPQwGA+rWrYAlS34DMBPAh7Bd1zoBb+8kXLx4HBqN5rE2\nSWLlypU4fPgoXFyc8fbbb6NEiRL5d2rpUqB/f8BqxVQ0wPs4CeAigJIAUqFQ+IDUwmr9CkBfe6Vd\nqFz5Y5w69WeeZk+ePImmTVuDrAiLJQ516pTD1q1rUbVqA0RG9oTV+h6AOgBqAxgEhSIMnp6/IDLy\neM6DgXmQkZGBhQsX4tKly6hTpya6du0KmUyW/34LBMWUwmifEHqB4Cnz7rtjMG/eQZhMPwC4ArX6\nDVgsLrBY3AC8DiAcMtkOXL4cCR8fn3zZ7NSpFzZvPgOzuTskKRzNmrkjNHT1Q6IXGxuLS5cuwd/f\nH15eXraHc+YAQ4cCAL7Tl0Bwyh4AGwCEAGgDhWIbyHhYrQMA3LM/l0Eun4i2bc9g48aVj/QtISEB\nBw8ehNFoRIMGDZCZmQmdTg+r1Qxb6I4EKBSN4eycjtq1ayAkZCq8vb0f22er1YpXX+2AAwfSYDI1\ng16/GoMGtcUPP0zJ15jlZk8uF6FEBMUDcepeIHgGWK1Wzp4dwrp1g9i8eUfu27cvX/Xc3X3t99of\n7Ft/Qm/vQKrVXlQofKlQOPHXX3/Ntx/jxo23n9S/mxVyVq/35ZH/STYzZ8486nQudHRsTJ3OxRYX\n/ttvHzjBSSVK0dMzgErlGPsp/U1UqcqwV69eVCq97OcHqhJ4mUAjKpWOjImJKciQkbSNm4ODK4ED\n9qZTaTBU4ebNmwtkZ8+ePTQYAmnLH2C7aaBS6ZmYmFggO7dv32bjxm0olytpMLhy8eIlBaovEDwP\nCqN9xU41hdALnhfffz+dklSRwEYC8ylJrvnKL16mTOVse/GkSjWEX3wxkdu3b+evv/7Kq1ev5tuH\nmzdvUq02EPDJdoWONBjqMyIiIqvc1atXqdOVIHDRXuYMJyo0WSI/TNaBwEGqVK9To3GlXv8SNZoS\nbNu2C5csWUKNxpXAJwROEhhAoASrVGn0RONGkuvXr6dO50qDoTs1mvL09CzP/v3fZnR09GPr/vzz\nUjo6elIuV1KhqJ/tg8lKnc69QONHki1adKBK9Y79EOQJSlJJ/vXXX0/aNYHgmSCEXiB4BpQpU4XA\n/mxC8znfffeDx9ZbsWIlJakUga+pVA6nq6s3r1+/nqPM/fv3+dFHn/G113rz66+/yzN5zKlTp2gw\nBBCoQuAz+/37GXR09GRSUlJWub1799LRsW6WIH6H0SRAi0zGwdqAbH3IpEZTgrt37+bnn0+kJHnS\nwaELlUonymSuBLwJvEyttiK//356ocYvMjKSPXu+QY3Gm8AiyuXj6eRU8pFCvXfvXkpSSQJH7af5\nHQnMJRBDpXIMAwNr02KxFMgPjcaBwJ1sH17v8euvvy5U3wSCp01htE/coxcI8ontnnd61s8yWTqU\nysff/e7Zswc8PNzx228b4ejojOHDD8DT0zPrfWZmJho3bo2zZ71gNrfCtm2/YN++I1i/fvlDtnx9\nfaFS3QPwCYBNAOZALk/Hli1hOe65lytXDhkZlyDDYczCfLyNuUgHcHLMGCyfuRmAFbb9chPIDHh4\neGDy5O9gNp8AUAbATSiV5VGihCNksusYOnQA3ntvxBON2wP8/f0RHr4HZnMYgMqwWgGT6QaWL1+O\n4ODgXOvs3LkTZnMfADXsT9ZDJusEJ6eJqFmzFpYt21jgfXZnZ3fcuHECQDMAVqjVJ+HuXvXJOyYQ\n/Nspwg+OZ0IxdFnwgjBv3gJKUlkCP1Mm+4Z6vWtWjPnCsHfvXhoMlbNdOTNRoymRZ1rbw4cPs2RJ\nP8rlKrq4eOV5NW3NytX8RaEmAZoA/vXZ50xPT2eNGi9Tq+1GYA4lqRH79BnEkydP0sGhQraZPuno\n2CDf197u3r3LJUuWcMGCBYyLi8vx7sSJE2zSpB0DAupSo8m+nUAqlSM5efLkPO3OmTOHktQu2zbF\ndpYuHZAvn/IiNDSUOp0rdbq3aDA0Zu3aTWk2mwtlUyB42hRG+4qdagqhFzxPVq/+lW3b9mCPHm/y\n5MmTD71PTU1ldHT0YwPLZCciIoJGY11mX07X6Tx5+fLlR9YzmUx5J1JJSyM7dSIBZkoSU7IF4UlJ\nSeGECV+yV6+BnDlzFi0WC1NSUujo6Ml/8qtHUK93ZXx8/GP9v3XrFkuX9qde356S1JOOjp48c+YM\nSVsIXQcHdwKzCPxJhaI8FYrqBLYRmE293pWRkZFZthYvXsJSpQLo4uLDkSODmZyczMqV61GvD6JG\nM5SS5FYk+efPnDnDWbNmceXKlULkBcUCIfQCwb+ArVu30mBwoV7vTb2+RL4FKSUlhd7eAVQqPyaw\nhxrNQNau3fTJs6GlpNji1QO2+PX5PGi2b98+OjuXolrtSAcHV4aHh+er3qhRwfbDbbYmZbLpbNGi\nI0ly9uzZ1On6ZfuIuU25XMvq1ZuxRYuOPHr0aJadrVu3UpK8COwlcIGS1JTBwZ8wNTWVS5Ys4fTp\n03nq1KmCj4dA8AIghF4geM7cvXuXBoMrgV12QdtHSXLJ14yYJOPi4vjaa28wMLA++/V7m3fv3s3x\nPj09PX+HzpKSyCZNbKrq5kYeP57jdUZGBkePHsfSpSvQ378WN2zYkOO9xWJhfHx8gVLMdu7cl8CC\nbGK+h4GB9UmSCxYsoCR1zvbub2q1xlw/YgYNGk7g+2xlD/Gll6rl2w+B4EWmMNonokUIBEXApUuX\nIJeXAtDE/qQBVCpfXLx48bF1SSI6Ohp9+nTG1q2rsXjxbDg6OgIAUlJS0LZtN+h0Bmi1BowfPzHv\noBl37gCvvgrs3g2UKmX7Z7VqOYp8+OGnmDNnH+LiVuHixYno0eMt7N+/P+u9XC6Hq6trgRLMtGnT\nFJL0I4DrAO5Bp5uMVq2aAgA6d+4MR8cTUCpHApgPSWqHDz8MzjWanbOzEQpFbLYnf8NodMi3HwKB\nIA+K7HPjGVEMXRb8B7h16xa1WqdsB81iqNWWeOwdb6vVyi5d+lCvL0+jsQP1eldu3749633//kOp\n1fYgkEogjpJUkStXruT69evZunU3duz4hi0hzI0bZJUqtqlw2bLkpUu5tufhUY7A6Wyz5gn84IMx\nheq71Wrlhx9+QpVKR4VCzR49+jMtLS3r/c2bNzlqVDC7devPxYuXZM3mjx07xt9//z0rCE9cXBxd\nXb2pUr1FmWwcJcktx1gIBP9lCqN94nqdQFAEuLm5YejQgZg5szrU6gqwWmMxZcpElC5d+pH1QkND\nsWXLSaSknACgBbAdPXsOQHz83wCAHTt2Iy3tF/u7UjCZhmD27AU4dOg8TKYvASTj7NbWOOnuAG1s\nLBAQAGzfDjwId/s/SJIetpl3JQCAUnkdDg6lCtV3mUwGk+keLBaCJM6cOY+EhASUKmWz6+7ujmnT\nvslR5733xiEkZBmUyqrIzDyIJUvmokuXzjh16iAWL/4ZJlMqOnfehurVqxfKN4FAgOI3PS6GLgv+\nA7z//kfU6/2o1Q6kRlOGgwYNz1e9mTNnUqsdkm2GnU65XJG1H1+3bgv+kw3OSrW6Dz08yhMIJUD6\nIooxcLZVrlaNvHkzh32r1crjx4/zjz/+4J07d7hmzRrqdJ4EvqJS+Q5dXb3zvMaXX954oz+BEgQi\n7dfgxrFu3eZ5lj906BAlyTtb0Joj1OkcmZ6eXig/BIIXmcJo31Pbo09LS0O9evVQvXp1VKxYEePG\njQMA3LlzB0FBQShfvjxatmyJu3fvZtWZPHky/P39UaFCBWzbtu1puSYQFJqzZ8+iceO28PWtjq5d\n38BPP4UgJeUA0tLmw2w+jKVLl+PKlSuPtVO7dm3I5aEAYgAQcvkMVKhQKysIzNy538HB4SPo9b1g\nMAShTJmTcHFxAaBEBZzDbjTBS0hElKs7sHMn4O6eZZsk3njjLTRs2AGvvTYeZctWxEsvvYQtW1Zh\n5Mg7GDfOFdu2/Y5Ro8ahevWmGDZsNFJSUgo0DgkJCVi5cgWAXgD8AcgAfIwjR/bmWefvv/+GUlkT\ngLP9SU1YrQokJiYWqG2BQJBPiu5742FSUlJI2k761qtXj3v27GFwcHBWuMkpU6ZwzBjb/uCZM2dY\nrVo1pqenMyYmhn5+frmeMn7KLgsEj+XmzZt0cipJmWwmgcNUqVpSocgeVpY0Gqvy8OHD+bI3Y8Ys\nqtV6ajQl+NJLlXjpf/bXr169ysWLF3PVqlVMSUnhokU/s4G2FG/BSAKMkKt4IJe97DVr1lCvr0Eg\nxe7Xcvr5/XOK/f79+/TyKk+lchyBHdRqe7Jp07YFutYXFRVFjcaFQH3+k2xmO52cSj9Ubv/+/UxK\nSmJkZCR1OrdsZwVW0s3Np8ChbAWC/xKF0b5nopopKSmsXbs2T58+zYCAAN64cYMkef36dQYE2KJc\nTZo0iVOmTMmq06pVK+7fv/9hh4XQC54zK1eupINDx2zCHk9AR2CVXexW0Nm5FO/du5dvm2lpabx5\n82b+RHbfPpoliQT4l4sHd2/dmmuxr7/+mkrl6Gx+3qVarc96v23bNhqNjXJsG2g0zll/P/NDRkYG\nvb0DCFSz/+lCQM81a9aQtG0dDB/+AXU6dxqNtejkVJJHjhzhkiXLqNUaqdN50tXV+6HMewKBICeF\n0b6ner3OarWievXq8PDwwCuvvIJKlSrh5s2b8PDwAAB4eHjg5s2bAIBr1679ky8bgJeXF+Li4p6m\newLBE6HVakHeAfDPNTeFIhOlS38CmUwDb+8J2L59IwwGQ456UVFRqF79ZWi1RpQvXxPHjh3LeqfR\naODu7p7rtbMc/PEHEBQEtckEdOmCetdi0bhly1yLVqtWDRrNRgDxAACZbBEqVPjnup1CoQBpztaP\nTJCWAl2tUyqV2LVrM2rUMEKlioSHx2GsX/8LunTpAgAIDw/HokUbkZp6AcnJh3H37lR07twHffq8\ngTt3buDChYO4fj0aNWvWzHebAoGgYDzVU/dyuRzHjx9HUlISWrVqhZ07d+Z4L5PJHvmLLa93n3/+\neda/N2vWDM2aNSsKdwWCfNGyZUuULv0FLl/uC7O5PvT6BRg0aDR++GEKLJbchTIjIwPNmrXFtWvD\nQG7ExYub0Lx5O8TEnIWTk1Ou7WzYsAEhISug12sxduxI1Lh2DejSBTCbgb59gQULAGXef4VbtWqF\nESNex9Sp5aBSlYCTkwq//RaW9b5Ro0YoXZqIjn4L6ektIEmL0br1/8HV1bVA41G2bFkcPbo713fn\nz59HZmYLAA/62AlXrvQGSeh0Onh7exeoLYHgv0JERAQiIiKKxljRLSw8mi+++ILffvstAwICslJ0\nXrt2LWvpfvLkyTmSW7Rq1SrXHNHP0GWBIE+SkpI4fvwE9ukzmIsWLX7skvv58+dpMPj+T9KYRty5\nc2eu5W2pbW3pXIGp7K1xoFWptFUcOpQswH52fHw8IyMjcz3VfvfuXb777ods3bobv/xySpGffN++\nfTv1+nIEbtv7/TN9fasUaRsCwX+BwmjfU1PN+Ph4JiYmkrQl32jcuDG3b9/O4ODgrL34yZMnP3QY\nz2w2Mzo6mr6+vrn+8hRCLyiO3Lx5kxqNo30/nwRSKEnePHHiRK7lK1VqSGAzAbIfFjETMpvIBweT\nBYyBb7FYuHbtWk6dOpV79uwpiu4UiA8++JhabQkajZXp4pJ3nwUCQd78K4X+5MmTrFGjBqtVq8Yq\nVarwm2++IUkmJCSwRYsW9Pf3Z1BQUNbHAEl+9dVX9PPzY0BAALds2ZK7w0LoBc+QpKQk9u07hH5+\nNRkU1OmhE/EF4YMPPqZeH0Cl8gPq9TXZq9eAPFcCAgPrE9jBYZiZtQSwtmbdAot8eno6X365JbXa\nalSrh1OSfPjttz88cR+elCtXrvDYsWNZN3EEAkHBKIz2yewGig0ymSzvWN8CQRFCEo0bt8bhwyVh\nNg+DXL4TLi6zEBl5Is999ccRFhaGkydPwt/fH507d87zHEpIyHxcGT4WEzMSAABjVXp02rMD9erV\ny3dbqampqFWrEc6duwUgCrboerFQqQJx9248JEl6oj4IBIJnT2G0T4TAFQjyICEhAYcOHUB6+m0A\nSlitdWE2h2Pv3r1o167dE9ls3bo12rRp8+jT9SQGX/kbyEiAFcAP5auiTciMAok8AEyf/iOiolQA\nqsEm8gDgDYVCQnJyshB6geA/gsheJxDkgVqtBpkBwGR/QpBJUKvVBbaVnJyMRo2CoFJpIUnO+P77\n6bkXJIHRo4EvvwQUCsiXLcP7F06gadOm+W4rLi4OISEh2LhxGzIyOgA4BGCTvR9T4OnpAfdsEfQE\nAsGLjVi6FwgewcCB72DlymMwmfpBo9kFf/9oHDmyO99in5iYiDfffAcbNmwGabfYDeoAACAASURB\nVATwGwBnaLVB+PXXGWjfvv0/hS0W4O23gfnzAbUaWLkS6NSpQP6eOXMGDRu2QGZmS2RmnkJ6uhXA\nFAAjAVyG0eiJ48d3o2zZsgWyKxAIni+F0T4xoxf8J7h8+TIaNWqFEiW8UK9eC0RFReWr3rx5P+Lb\nb/uiV69DGDOmAvbv355vkSeJVq06IzTUAHIvgDEAOgJwQlraEISHR/xTOCMD6NPHJvI6HbBhQ4FF\nHgBGjfoY9+59ApNpCdLTj0AmU0Au7wqtNgk1atTHokXTsXDhIsyaNQtpaWmwWq2YOnUGmjbtgF69\nBiImJqbAbQoEgn83YkYveOExm80oV64qrl0bAKu1J+TytXB3n4lLl0491X1qW6pWP6SnJwB4EESn\nDYC3ASzF5Ml1MHbsGCAtDejZE/j9d8DBAQgNBZo0KVBbW7duxebN27Fixe+4dWs+gAf1F6Ft2y0I\nCZmKwYPfQVjYPgCDIZcfQOXKKWjSpCEWLvwTJtOHUChOw2ici3PnjmZFrxQIBP8OxIxeIHgEFy5c\nQFKSHFbrGABlYLW+B5PJiNOnT+coZzabER8fX2QfklqtFlZrOoAk+xMrgFgA70Ol2gJHRyPSExOB\nDh1sIu/sDOzYUWCRnzVrLjp3HoLp011w+7YeMtl4AHcBXIVePx2dO7fG3r17ERa2BcA+AF/Cat2G\ns2ctmDPnJ5hMawF0hsUyHmlpzbB+/foi6b9AIPh3IIRe8MJjNBqRkZEA4L79SSoyMm7BaDRmlZk9\nOwRGowu8vQPg61sF0dHR+bKdnJyMN94YBB+fymjUqDXOnDmT9U6v12PYsOHQ61sAmArbbD4WQAKs\n1sH44v2VOOtTFggPt6WXjYgA6tQpcP/GjfsMJlMogLGwWg9ALr8GudwTGk0gRo58DQMG9EdY2A4A\nFgA+9loyWCw+sMW5z34DoGhXzKKiojBjxgzMmzcPSUlJj68gEAiKnkLc338uFEOXBc8Rq9VKq9XK\n3r0HUa+vQ+AL6vUN2KVLn6xgNcuXL6dC4UogigApl3/HwMA6+bLftGlbajR9CRynTDaLjo6evHnz\nZo72ly1bxiFDRrJ9+44E1ATOsARu8xBqkQBTXFzICxeeuI8ajYFAQlZoXY1mKKdOncqbN2+yWbP2\n1Omc6ODgTsCPwGACVwisJyCxXr0mlKQGBH6nXP4lnZxKZoWoPnv2LGfOnMlly5YxNTW1wH7t37+f\ner0rNZohlKTOLF3an7dv337ifgoE/2UKo33FTjWF0AvyQ0ZGBgcOfIdqtZ46nSPHjfuMS5cu5Ycf\njuPPP/+clfv8/PnzVKv1BPpni0OfQZlMzszMzEe2ce/ePSqV2mx52ElJasdPP/2USUlJOcpGRUVR\nq3UloKQH/uZJVCYBRskc+MtXXxWqr1279qVW25nAOQJrKEmu3LZtGyXJk8Bwe9jdVQT0BLwJONr/\nfEmt1pnjxn3KRo3asmvXvoyKiiJJbtmyhZLkSq12EPX6FqxcuR5NJlOB/KpZsymBZVljo1IN4scf\njy9UXwWC/ypC6AWC/+Gjjz6nJDW3i1wsJaka581b8FC5Dz8cR6CrPZd6ql2U/qCLi1dWmQMHDvCd\nd97j6NEfMjIykiT5yy/L2aHD65TJVNni11sJVKNOV5FubmWyRJMkw8LC6OgYRG+8zEg4kgBPowzL\napx5/vz5QvXVZDKxf/+h9PAox4oV6zE8PJwlS/oSUBHIzBJarbYzVSpnAnMJXLYn1qnLvXv3PmTT\n2zuQwNasful07Th79uwC+eXjU5nA0WwfUNM4cOA7heqrQPBfpTDaJ/boBS8koaE7YDJ9DMAVgDdM\nptHYuHHHQ+WsVgIIAFAVtghy/weZ7P+wfPkCAMAff/yBV15pj59+csUPPyhQq1YjBAePxaBBE7Bh\nQwuQdQE0APA+gOYAVEhNPYqEhBEYMGBkVjvlypWDd9ph7EEU/JGEo5DjFdzGtNWLERAQUKi+6nQ6\nLFo0CzduXMSZM3/Bw8MD9+4pAagBXH7QUwB/Qy7PBFAFQBkAR5GRcQnlypV7yGZiYry9HADIYDZX\nxa1b8QXyq127IOh04wEkADgPSfoR7du/+iRdFAgEhaEIPzieCcXQZcFzoGXLzpTJpmfNJpXKDzhk\nyMiHyp08eZKS5EpgNoFJVKu9ciwv16/fksDyLDsy2QSq1c4ETtufxdiXwV+yL4s3IHCPwCmWKlWe\nN2/etG0TnDrF+0YjCfAvhZ6lpBIMDd2Uwxer1cpdu3ZxxYoVvHjx4hP3PTY2llqtC4Hv7T59QKA+\nq1VryA0bNlCvd6GDgz8lyZm//bY2Vxvt2nWnWj2QQAqBk5Sk0ty9e3eB/EhNTWWvXgOo0Rjo4ODG\nqVOnP3GfBIL/OoXRvmKnmkLoBfnh9OnTNBo9qNP1oyR1o7t7GcbFxeVa9sCBAwwK6sz69Vtx9uyQ\nHBnlKld+mcD2bMvPs6lUGu0Cn0HAh8Db9mV7C4FuBMZSLg+iXK6lRlOCbT3KMNPJiQSY2qgR/9q+\nnfHx8Tl8sFqt7NnzTer1AXRw6EpJcuX69evz1Ver1cpvvpnKsmWr0d+/Nn/5ZTkHDRpBvb4agT5U\nqUqzbt2XaTabSdrOFpw9e5bJycl52kxMTOSrr3akQqGmg4MbFyxYlC9fBALB06Ew2icC5gheWK5e\nvYrQ0FAolUp06tQJLi4uBbYxdeoMfPrpAphMcwHchyS9iVdfbYDt26/DZOoFYAKAXwA8WJJeBZls\nKGxx8Q+gIeIRhlfhiDSgXTtgzRpAq83RBkn8+OOPGDNmFtLSjgHQATgIvb4NIiK24syZMyhfvjwa\nNGiQq4/Tp8/ERx+FwGQKyfJx9eo5SE1NxalTp1GhQgB69OgBubzgO3UkH52ARyAQPBMKpX1F8qnx\nDCmGLguKMVarlVOmfJdjtpyZmcnPP/+Kvr5VCXjYT+xbCKQTaM369RtTr+/HFgjnfUgkwNWQMS2X\nGbTFYmFQUEcqlS72Q4EPVg6slMlU1OlK0WB4g5JUhsHBn+TqY9WqjQlsy1Z3Drt16/+0h0YgEDxD\nCqN94jCeQPAIZDIZxox5H9HRxxEZeQgdO3ZA1659MWnSJNy+fRMuLhoAuwB4AygJne4oBg7sizaZ\nO7AJ7aCHCYvwCvooHdC991AsXrwk66ucJF55pRXCw08jMzMMwG4AZ+3tzgCpRWrqAdy/vwwm0xHM\nnBmCixcvPuSjXi8B+OegnEwWD4NB97SHRiAQFBOE0AsEBeCtt0Zi82Yr0tOvIDl5K0ymDDRvXhEe\nHnrI5WYolf7YNexdrEiPgwbpmKPywUD8hQzrYGzY8CqGD/8WEydOBgBs2LABf/11DkALAHUBfA+g\nPgAtSpb8CXq9CwAve8suUKvL4fr16w/5VK9eJQCDAUwCMBaSNB3BwSOe/mAIBIJigRB6gSCf3Lhx\nAxs3/g6z+VUAegDVkJY2BIGBfkhKug2r9Ri63huAnzNMUJKI6toVR/u1hEbbEVbrtwD6IyVlHb79\n9gcAQHR0NKzW+gDCAPwNoDeAT+HvH4iLF49DrU4HsAa2MLXhsFguomLFijl8Onz4MEJCVgD4GbZZ\n/UF4epZEYGBgkfX7wIEDCArqjAYNWmPOnHnijIxAUMxQPm8HBILnze7du3HgwAF4eXmhe/fuUCgU\nSEtLQ1paGpycnAAAx44dQ7NmbWAy1QQwG8BiAFuh0ZyFQuEJtdoXg9LCMAOjAABfaDzRdswYVN63\nD+SpbK3pYbFkAgBq1qwJtXoGMjOHAKgEQAOl0opNmw5CkiRs2/Y72rXrhjt3+sDBwRnr1v0KV1dX\nAEBqairOnTuHzZs3g2wPoIv9TyZiYrSwWCxQKBQoLKdOnULz5u1hMn0FwBOnTo2DyZSK0aNHPrau\nQCD4l1BUBwWeFcXQZcFz4sqVK+zUqTerVm3MYcNGMyUl5aEyU6fOoCT5UKV6j3p9Q7Zo0YFjx46n\nUqmlSqVnnTrNePv2bVat2ojAQvthNwuBNlSrK7JcuaqMiYnheJXuwUk4jsQo6vUuTEhI4OXLl2kw\nuBGYSeAPSlJTDh78z33+iROnUKXSU6FwpVZbgrNmzcrhn9Vq5b1793Jc+btw4QI9PMrSwaEy1WpH\nKpWBBNLszUewRInSRTaG778/hsD4bAf9/qKPT+Uisy8QCPJHYbSv2KmmEHpBfkhOTmbJkn5UKD4l\n8AeVynrU671YqVJDLl68hCSZnp5OlUqy34kngXRqtT7UagMI3CSQSaVyAB0dvQkYCERmE7wpbNGi\nNe8lJ5PjxpEALQCHadwoSSW4cWNoli8nTpxg8+Yd6OHhR1/fGhw0aHhW4pvLly/TwcGNMtkIAjMp\nST5cuHDxI/tWo0bjbMGA7lKhKEmt1p8ODp0pSa7cvHlzocbu+vXrPHfuHM1mMz/4YCxlsnHZ+r2H\nL71UtVD2BQJBwRFCLxD8D5s2baKDQzO7OP1KoAyBLQS2UpJe4ooVK5mYmEiVymAPdvMg8UoFApOy\nrrgB9QkMJdCLtsxvmQSuU6+vyDWrV5MjRtgqKhRMXbiQ58+f5/379x/yZ8CAYZSkxgRWUKUaRS+v\n8kxOTuYnn4ynQvFuNiHdzTJlHj1j1utdCFzPVucj9u3bjytXrmR0dPQTj5nVauXo0eOo0TjSYPBj\nqVLluHXrVur1rpTJviWwjJLkyzlzQp64DYFA8GQURvvEYTxBsSIxMRGtW3eBVmuEu3tZrF+/Ptdy\ntv3pNNgOsv0CYDKAVgBawmT6GnPnLoejoyP8/QOhUHwGIAlAGGSyK9Bq/wSQCaAngFMAPgLwE4Bo\nAAbI5WXw7oiu6BwWBvz4I6BW49bs2eixPhzdug3CuHETkJqamuVLeno6fv55PkymjQB6IiNjGpKS\nymDbtm1IT8+AxeKQzXMjMjIyHjkG/v6BkMnW2H+6D71+C9q1a4sePXrA29sbsbGxSElJKeDIAmFh\nYZg7dx3M5ku4fz8KN24Mw4cfTsT+/X+ga9czaN36d8yfPwlDhgwqsG2BQPAcKcIPjmdCMXRZUIQE\nBb1GtXoQbfnX91CS3Hns2LGHyqWmptLfvzrV6rcIvExgVrYZ8Fy2bt2VJHn16lXWq9eCarWeXl4B\n3Lp1K+vUaUat1pdAZQI17CsCtr15na45Z02fTvbo8SAvLe+tXUt39zJUKL4g8Ae12s5s06ZLDl8U\nCrU9brytmoNDO65atYpHjx61x9pfRmAnJak2x4+f+MgxOH/+PN3dX6LRWJU6nQf79h1Cq9XKEydO\n0N29DCWpFDUaB86ZM69AYztp0iQqFMHZximBGo1DgWwIBIKnQ2G0r9ipphD6/y7bt2+nLfXq3Swx\nUquHc+rUqSRtOegvXbrEW7dukbTFax81KpgNGrSgSuVEYAqBrylJrrmmZn1Aeno6hwwZQpVqKIF9\nBNwIdCFQgY3rNKWlXTtb40YjuWcP161bRweHltkEMo1KpS5HLPkuXfpQp2tLYCsVigl0c/PhnTt3\nSJIRERGsX78lK1VqyEmTvrUlwXkMKSkpPHz4cFbyG6vVylKlyhH42e7DRUqSJ0+cOJHv8V29ejX1\n+prZPkh+ZkBArXzXFwgETw8h9IIXnhMnTthnvu4EDmTtoev1QVy8eDFjY2NZtmxl6vXeVKuNHDky\nOMdJ9cOHD3PAgGEcMGAYDx06lGc7sbGxXLduHefOnUtJ8rIf1IulTNadlV+qQEvz5jY1L1GCV9av\nZ/36r1KvL0G5vHa2vf4kKpXaHKf8zWYzg4M/Ya1azdmpU29evny5SMcnKSmJSqWU7WODNBh6ccmS\nJbmWP3jwIEeOfJ8ffDCWUVFRJG0fC716DaAkedHRsQGdnUvx+PHjReqnQCB4MoTQC154Jk78kgrF\nBwRW0RZf/l0CjVm1agOmpqayQYMgKhQT7GKbQL2+Mn/77bcCtbFt2zbq9a40GttTry/HmjUbUaWS\nqFY7skbZykytVcumoJ6eTD10iCVL+lEu/47AOQJeBN4ksJSS1Jj9+g15SiORO1arlQ4OrgT+zDqN\nr9f7cs+ePQ+V3bFjByXJjcBEyuUf0sHBnRcuXMiyc/LkSUZERDAxMfGZ9kEgEOSNEHrBC8/UqVOp\n0fSxi9ghAsNpNLrRZDJx5MhgAjoCcdlmtOP5ySefFqiNEiW8COyw10+hwVCZv//+OxMuXKC1Rg2b\nYW9vMjKShw8fpoNDlRz72TKZKxs2bMXvv5/GzMzMpzQSeRMWFkZJcqWjY0tKkhffeef9XMvVrfsq\ngRVZvstkn3Hw4BHP2FuBQFAQCqN94tS9oFjQt29fODn9CaXybQA7IUnrMW3at1iyZBnmz98JoCps\noWQBwAy9fgfKlfPLl+3Lly8jMLAO7tyJA9DU/lSC2VwDYfPnw7FjR8iOHQPKlQP+/BPw94fRaERG\nRjwAk728BqQFer0ao0ePKpKodAWlTZs2iIw8juXLR2Hv3o2YOfO7rHe0fdQDAFJSTAA8sr3zQHKy\n6X/NCQSCFwSRj15QbIiPj8ePP/6EhIQkvPZaW2i1WrRu3QMm00QA9WC7PlcGMtlltGvXGOvXL89T\ncK1WK06ePImUlBT07DkQcXH9Qf4KoC+AUQCi4YM6+AMm+CEN1sBAyHfsAEqWBABs2bIFr73WG2az\nF4CuAEIBBEAuX4HU1PtQq9WP7IvFYsGKFSsQExODmjVrol27dkU1TA/1c+TIYISEzAYAvPnmIPj5\nlcGECUthMs0FcA+S1B9r1oSgTZs2T8UHgUBQeAqjfULoBcWSK1euIDCwJlJSmgFwBhAC4C6Aj1C3\n7jn89dcfkMlkudZNS0tDUNBrOHo0EqmpySCTAZgBRAHoAOAa/JGGHdDDG4k4Kjfi/LQv8foIW0a4\nEydOoGHDIJhM/QFsstepCKAllMoyuHXrOm7dugUfHx/odA+niyWJ//u/HoiIiIPJ1BSStBYjRvTA\n5MkTiniUgO++m4bPPlsNk+l3AHJIUieMG9cOCoUcc+cuhVqtxuefv4/XX+9V5G0LBIKio1DaV9h9\ng2dNMXRZ8BRYsWIFHRy62O/TVyTwKoEgOjmVzDpYlhcTJ06iTteRwNcEOhBwIHDKvmdtYmV48Doc\nSYC78TJdVQP4ww8/kCSPHDnCN954gwrFaAKJBDwJ6Ak4Uqn04auvtqNWa4ssZzR65HoYbv/+/dTr\n/QmY7W3eolptyPPw25kzZ/jDDz9wwYIFuUbdexTNmnUg8Fu2swQb2aBB6wLZEAgEz5/CaJ/YoxcU\nS5ydnUFeAmAEcBBAZygUEThz5jDKly//yLonT0YiNbU9bKlhW8CWja4FgH6oDX/sQjw8kYRtaIzW\neB/3Fb8jKCgIH374KRo37ojffjsBiyUawI8AygOIBHAEMpkOu3btRlraX7h/PwrJyYvQvn23hyLd\n3b17F0qlD4AHy/uuUCodkJyc/JCv27dvR506TTF27EWMGLEW1as3wv379/M9TqVLu0OhOJ71s1x+\nHKVLu+e7vkAgeAEowg+OZ0IxdFlQhFitVqalpTEzM5NNmrShXt+UCsWHlKQy/O67afmy8fXX31GS\nWhGYS6CuPQDPMTZGVSbZp77r4UUN3CiTGbl27VqePHmSklSKwG37TN6Xtvj5O7LNlhdTqfTNcZdd\nkkoyNjY2R/u3b9+mo6MngaUEblKh+IJ+flVzDZTj61uNwKasuAFabbesAEH54e+//6arqzclqSsl\nqQdLlChdqHj4AoHg+VAY7RP56AXFhvnzF2DEiPdhNqcgIKA6Nm5cgb179yIuLg716y9E8+bN82Xn\nvfdGIiJiP3buHI/MTAsyMz3QEgqsQyokAMuhQj/oYJHdwYYNq9G+fTts2rQJKlUVAC52K4cA+AI4\nC8DWrkJxFuQdADcAeAI4DDIV7u45Z9AuLi7YuTMMr78+GLGxo1C1ak2sXh0KufzhBbbExATY9v8B\nQIa0tIqIj0/I95j5+Pjg3Lmj2LBhAwCgffsZD/kjEAhebMRhPEGxYMWKFXj99cEA/gBQC8DXKF9+\nDS5cOPJE9kgiJiYG6enp+CmoA767GgMNMjEfPhiCVwD5GqxZsxSdOnUCAMTGxiIwsBZMpi329tfA\n0fEdWCxERsZrkMlMMBh2o1+/3pg1awHU6kBkZJzGhAnj4O7uBn9/fzRo0KDAfvbo8SY2bDAjLW0W\ngL8hSe0RGroEr7zyyhP1WyAQFE/EYTzBC4+ra2kC3bMti1spl6sfeTjt3r177Nq1Lw0GN5YqVZ7r\n1q17uNAvv9Ail5MAp6ElZehHlUrPZcuWPVR07dp11OmcqNW60sXFi4cOHWJMTAynT5/On376KSvG\nfmRkJMPDw/nRR59RkkrTYHidklSGY8d+VuB+37t3jx069KJaraeTU0nOn7+wwDYEAkHxpzDaJ2b0\ngmKBWi0hI8MXwBEAGgCnoFTWh9l8L9clbwDo2rUvQkMzYDaPADASQBTq1q2FtWuXoHTp0sC8ecCQ\nIQCJUx06YujtdGh1Ggwc2B1HjpyAyZSG3r27o2HDhlk2MzIykJCQADc3t0cGxbFdrysPs/k0AC8A\nt6HVVsTp0/vh55e/QD4CgUDwgMJon9ijFzx30tPTcePGDXh6euYZaKZmzYY4cOAOgLoAqgH4HcHB\n7+Yp8gCwefMmmM07ALwCYBiARTh48Bf4+FTEaHk6vs1MsxWcPBlVxo7FnwAuXbqEmjUb4f79/rBa\nS2LRotcwadI4+Pn5oXbt2nBxcUF6ejosFstjhV6tLmkPqAMArtBo/HD9+nUh9AKB4NlSRKsKz4xi\n6LLgEWzdupUGgyslqRQNBldu27Yt13JXrlxh+fI1qFTqqVCoOXLk6Mfa9vDwJfCK/YT8gyV/Cz+G\nU9ax+CV1G+WoM3z4aMpkH2VtDwBBlMtL0WhsQ63WmVqtAyWpFB0c3Lhjx448205JSaGTU0kCa+y2\nttHBwZ0JCQkFGyCBQCCgSGojKKbcuXOHer0rgd12MdxFvd41z8AxVquVt27dYmpqar7sr1q1moAT\ngZIE0ghYOQWjSYCZkLM/JtPVtUyOOv36vU3gh6zgMkAlAib7z1sJlLL/+w4aDG5MSkrKs/2DBw/S\n3f0lKpVaOjuXZERERL7HRiAQCLJTGO0TAXMEz42LFy9CofAB0Nj+pAkUCi9ERUXlWl4mk8HNzQ1a\nrTbHc7PZjNjYWJjN5hzPu3fvhm7d2gPQQoY2mIkmGIOpyADQC8uxGFXg5FQiR52+fbtBp/sGwGYA\nuwDUBvAgjO0rsF2dswJoDrncHdHR0Xn2r06dOrhxIxqJifFISIhD06ZN8ywrEAgETwsh9ILnhpeX\nF9LTY2CLUAcAl5Ge/je8vLweVS0H4eHhcHX1QrlytWEwuOLtt4ciMzMz631IyI9Q4CYWYjfewZ9I\nA9AJdfArdkGn64+ffpqSw17z5s2xbNlMVKgwASVL/g6Vaks2/34EUAW2vzaXkJ4eZzvU9whkMhkM\nBkOecfcFAoHgqVOEKwvPhGLosuARTJs2kzqdO43GNtTp3Dljxqx8101MTLQv/e+yL6fvJmBgmzZd\naLVaSZK3rl7lr7Bdn7sHic3xO4FR1GqNPHnyZJ62zWYzZ82axebNW1Gp1FGnc6ejYylqNC52X904\ne3ZIofsvEAgE+aEw2ieu1wmeOxcuXEBkZCTKly+PgICAh95fuXIFy5cvR2amBd27d4O/vz8AYO/e\nvWjS5E1YrZHZSteCWh2NixdPwMfNDezaFbKwMNyFHG1RHvtRA8AGLF78E/r165erP5mZmWjatC2O\nHZMhNfVlSNIyDBz4f5g27RtERkbi4sWLqFChQpYfRUlcXBwSEhLg7++fa+Y7gUDw30QEzBEUezIy\nMhgXF0ez2Zzj+cWLF+no6EmVaigVindpMLjx6NGjJMn33gu2Z46Lts/oYwg4U6crxYtHj5KvvGI7\neOfszA5e5QnIqdMZOW/evEf6Eh4eToOhOoFMu90bVKl0NJlMBeqTxWJhVFQUY2JislYYHsX7/9/e\nnQdEVb0NHP8OMwPMgOAOCCKGIiIIKq65YC6E5p7mXtpiWpbtZmbaT8W0zD1zqUxLLTX33dxywdwV\nLU1REUVxIZEBZmDO+8fQlK9LiwgyPJ+/nLuc+zy3iWfuveee88YQ5eJSQhUrVlWVLu2vjh49+q+O\nJ4RwXPdT++Q9elHg9uzZQ0xMRzIyLICZefO+oGNH29Cz//vfx6Sl9cdqHQbAzZtBvPXWCAYM6M3G\njTuATkAEUBM4ClQnokIagf37Q1wc+Pig3biRZSEhmM1m9Hr93z4vv3HjBk5OfsAf78mXQaPRYzKZ\n/vFV9o0bN2jevB3x8SdRKptHH63LypXf4eLicsft169fz/Tpi8jKOklWVinS0mbRsWPv/zzErxBC\n/EE644kCZTabefzxDly7NpmMjEtkZGykV68XOHfuHABXr/6O1VrxL3s8wu7d+3j66Y85fjwLuAws\nBSyAjvByyWzTmdHExUGFCrB9O4TYJoVxdnb+R53iHn30UWyT1swFzqDXv0lISBglS5b8mz3/9MYb\nQzl8OACT6SwZGefYsUMxevS4W7ZRSvHtt/Pp3PkZPvxwNBZLS/6cNKc7p04d/cfHE0KIu5FCL/LF\nwYMHWbVqFefPn79l+YULF8jKcgI65C6phV5fg/j4eAC6dGmN0TgaOAz8irPzu5jNBm7e/Ins7J+A\n60BX3N1TaFKpLHvdrOiOHoWgIFuR/w+j0Hl5ebF582pCQz+jRIlGPPbYWdav/+Ef/UhYsmQJPXo8\nz9Kla8nK6ontroAzGRnd2L370C3bjh07nuef/5BFixqya1cpzOaVwB9z0i/F3//2/gpCCPGv5d0T\nhPxRCEMu8l5++U1lNPopT89oZTSWVitXrrSvS09PV66uHgric5+Hpyij0cf+fNpqtapx4z5VpUsH\nqBIl/HJ7wb+au+1pBRuVVuuijq1apawVK9pGvAsLUyo5Od/zHDVqjDIa5fUbaAAAIABJREFUKymY\npjSaGgoG5I6ul6NcXHqoN98ccsv2Hh5eCn6xj8Kn1YYqvb6U8vSsrUqUKGfviyCEEPdT+6TXvXig\ndu7cScuWPUlPPwB4Artxc2vNjRsp9nHqv/56Hv37v45OV5fs7AO88spzxMYOv2N7u3fvpmnTDmRm\nhmCb4KYMIU4X2F/KDZeUFKhdG9auhX9xm/1esX/77SKMRlcGDHiBgICAO253/fp1YmKeJC4uDtgN\nhAIpaDRhODuXRK+HSpVKsn37Wtzd3e37ubmVwmQ6DNjexXd27s/rrxenbdu2VKtWDQ8Pj/vOQQjh\nGO6n9kmhFw/Ut99+S79+y7h5c6F9mV5fjKFD38JoNNKlSxf8/f357bffOHLkCBUrViQiIuKebTZs\nGMWOHaeBQ1TnHBtoRFnSuB4WRomffoI8KJCrV6/mySf7kJExCCenqxQr9g0HDuykYsWKt23bsWMv\nVq1yw2xeDOwHygOg0w2gXz8nevfuTc2aNdHpbu372r//a3z99UFMphHAr7i7v8ehQ7t55JFH7jt+\nIYRjkUIvHlrx8fHUqdMMk2k7UBn4Bo2mH1ptL5ycwNX1B37+eRtBQUG37XvlyhUOHDhAqVKlqFGj\nhv0ZucHgQWZmb+rQi7U8TglSWQv0MpYk8WrSbUPk/hfVqzfkyJG3gHYAODm9wyuvKD79dOxt2/r4\nBJGcvAz4HDgCjARO4Ob2Jvv377hjbmB7X/+DD0axdOk6SpcuyYQJ/6NGjRr3HbsQwvHcT+2Tznji\ngapWrRoTJozGxaUWRqMvzs4DUepFsrM/w2z+jLS0QQwdOvq2/fbs2UNgYCidO8fSuHEnunbta/+S\nKwVNWMpGmlOCVJZQk3aUx4SRixcv5knc6ekmwMv+2Wr1Ii3NdMdty5cvj0azDRgHNECjeRJ//4/Z\ntGnlXYs8gE6nY9SoD4iP38nWrSulyAshHggp9OKBe/75vly9epHjx3dRq1YdoLF9nVKVuHIl9bZ9\nunTpy40bk/n99x9JTz/GqlWHWLp0KQAfN3uMNVygGDeZhwdd+AUzA9FoTPj4+ORJzE8/3Rmj8RVg\nL7AOo/FjevTodMdtv/xyEp6eI/DwaI+7+xpq1Ajkl1/2ULdu3TyJRQgh7scDLfSJiYk0bdqUatWq\nERoayqRJkwC4du0aLVq0ICgoiJYtW5Ka+ucf+tjYWCpXrkxwcDDr169/kOGJfDRlynSqVo0gLm4r\nWu0QIB74CaPxf3Tu3Oq27S9cOA08nvvJgNnchFOnTsHixby0YTUGFF+7etAbKy5Gf4zGj1i48Os8\nuW0PMHToO7z1Vjv8/fsQFDSUr7+eTNOmTe+4bbVq1Thx4hBz5jzP4sWj2b17kwxfK4R4eNxfh/97\nu3jxojpw4IBSSqm0tDQVFBSkjh07pt566y310UcfKaWUGjNmjHrnnXeUUkrFx8er8PBwZTabVUJC\nggoMDFQ5OTm3tPmAQxYPwOLFi5XRWFnBSQXXlJNTeQUuCtyVwVBS7d69+7Z9wsLqK41mvH0IWje3\nQHXk7beVcrJNUKNef10pq1UlJiaqHTt2qJSUlALITAgh8sf91L4HekXv7e1t70Ht7u5O1apVSUpK\nYvny5fYJRZ5++mn7Ldlly5bRrVs39Ho9AQEBVKpUiT179jzIEEUeyszM5OjRoyQnJ9+yfOXKTZhM\nLwOVgJtYrWnAFiCNjIzZPP54h9vmkv/hh7n4+n6Om5s/zs6V+bZJCKFjx4LVCh98AB9/DBoNfn5+\nNGjQgNKlS9v3VUqxYsUKJk2axE8//fSg0xZCiIdavj2jP3PmDAcOHKBu3bpcunQJLy9bRycvLy8u\nXboE2EZJ++tc5H5+fiQlJeVXiOI+xMfH4+8fTIMGTxIQUJUhQ0bY1/n6lkGvPwJcAZpjK/j1cte2\nx2JxsQ95+4dHHnmEIUNe5bHHGrDk0Tq0Xb3CtmLcOBg+HO4ySp1Siu7dn6Nbt6G8/favREf34KOP\nxudxtrceLzZ2HKVK+VOypB/vvTcCq9X6wI4nhBD/Vr5ManPz5k06derExIkTKVas2C3rNBrNPYcW\nvdO64cOH2/8dFRVFVFRUXoUq/qN27XqQkvI+8CyQwqRJ9Tlx4hd++eUcZcuWpFSp46Sk1CMnpw6w\nGVvRLw2cIDv7mv2HH9iKZ82ajTh48DrDqEhrNgFgmTQJ/cCB94xj7969rFixmfT0o4AReJdhw6oy\nYMDzt3338sIXX3zFyJFzMJnWAjomTOhOyZLFeeONV/P8WEKIomPLli1s2bIlT9p64IXeYrHQqVMn\nevXqRfv27QHbVXxycjLe3t5cvHiRsmXLAuDr60tiYqJ93/Pnz+Pr63tbm38t9KLgKaVISDgK9Mxd\nUoaMjKYsX74Li2Uax4//jIfHXkqUcOPKlUFAFaAGUB2tdidTpky4ZRS42bO/4ODBOMbxIm8yhRyc\neEFbji5BQUT/TSwpKSlotZWwFXkAP3S6YqSmpnL58mXi4+MJCAigevXqeZL7woWrMJneA2wT55hM\nI/j++0lS6IUQ9+X/X8SOGDHi7hv/jQd6614pxbPPPktISAiDBg2yL2/bti1z5swBYM6cOfYfAG3b\ntmXBggWYzWYSEhI4efIkderUeZAhijyg0Wjw9a0MLMtdcgOrdT0Wy0igMVbrG1gsDShf3gedbjnw\nAbAYZ+fLDBzYl+ee63NLe5s2bGMa8CZTMKPnKRbypdX/tuf4d1KrVi2s1oPASiALjWYipUp5sHnz\nVsLC6tGr1+fUrx/D0KH/y5Pcy5QpjpPT6b+ci1OULOmZJ20LIUSeyJPugHexfft2pdFoVHh4uIqI\niFARERFqzZo16urVq6pZs2aqcuXKqkWLFur69ev2fUaNGqUCAwNVlSpV1Nq1a29r8wGHLP6jPXv2\nKE9Pb+XpWU8ZDN5KozEquJzba14pd/doNW3aNFWhQlVVrFiEcnMLVA0bRqvMzMxbG7JY1P6w6kqB\nMqFVMUxQME7pdB7q6tWr/yiW7du3Kx+fSsrJSadCQuqoQ4cOKVdXTwVHc+O5rAwGb/vEOffjxIkT\nysPDS+n1Lyqd7mXl7l5GHTp06L7bFUKIv7qf2idD4Io8k5qaytGjRylTpgxTp85i9uytmEwD0Ov3\n4u29kfj4n9Hr9Rw8eBAXFxfCw8PtE9sAkJUF3bvDkiWkazS003jxo9Lg5JTF0qVzeOKJJ245XnZ2\nNu+99yHff7+C4sU9+fTTETRp0sS+XimFRqMhISGBsLAmpKf/2eHP07Ml8+e/RkxMzH3nnZiYyIIF\nC7BarXTu3FnGqhdC5DkZ614UOKUU58+fx2w2U7FiRTQaDdOnz2Dduu1UqODD+++/c8srcLcxmaBT\nJ9vMc8WLk7FkCStSUsjMzKR58+aUK1futl1eeeUtZs/+GZNpLHAGo/Eldu3adNvzd7PZjLd3Ra5f\nn4Zt7PoDGI0tOX58H/7+/nl6HoQQ4kGQQi8KVHZ2Np069WL9+o04OblSubI/mzevpESJEv+sgbQ0\naNMGtm6FMmVg/Xr4mxnsAEqWLM/165uxva5nm3hm2DA3Pvhg2G3bxsXFERPTkcxMK5DBl1/OwN+/\nPGazmdq1a2M0Gm/bRwghHhb3U/vy5fU64dg+/XQSGzakkJmZCDhz/PjLDBjwJvPnz/77na9dg5gY\n2LMHypWDTZsgOBj489b73bi4uALX7J+12qsYDKXuuG3dunW5fPksycnJuLm5ER3dkePHL+Pk5I6H\nRyq7dm26ZQwHIYRwFDKpjbgvixYtZvDg/5GR0Q1wBZwwm3uzb9/hv9/50iVo2tRW5CtWhO3bOaXX\n07NnX4oXL49Wq8fLq+Jd3yX93//exWjsDExCq30NT8/19hEX70Sn0+Hn58ekSVM5cqQ0N28e5saN\nOC5e7Er//m/+l/SFEOKhJ1f04h/bv38/n3wyjawsC/369SQgIIDevV/Eau0OrAaeAbTodCuoWrXy\nvRs7fx6aNYMTJ6BKFdi4kdNmMzVqNCAtTQu8BbzE5cubadOmC7/+evC25/TPPdeXcuW8WbRoJaVK\nefLaa7tvGXjnbuLjT5GZGQ1oAcjJieHXX1f/+xMihBCFgBR68Y8cOHCARo2iMZkGA+6sWfM0L73U\nE52uCfAx8ARQDVB4e8Nnn22+a1s5J06gadECp3PnIDzc9ky+bFmmvz2Emzc7AkuA13K3jsbJKZJ9\n+/bdsUNeq1ataNXq9tnv7qVu3XBWrZqPydQDcMHZ+SsiI8P/VRtCCFFYyK178besVisDB76NyfQW\n8AbQD5NpCsuXb8JqPQxYgfXABzg7n+f48TsXZYDvPxxJcpVgnM6d46CrkcS5cyF3ZESTKROlvIF0\n4I9X4TLIyTlhHz3xTrGdPHmSs2fP/uOOKq+++jKPP+6Di4sfBoMf1arFM3XquH9+QoQQohCRQi/+\n1jPP9Gf37l/5c1hZAAOuru507NgUo7EGbm7dMBoH8eWXs3F3d79jO/HffEPUBx/gi2IzUTTJeoMn\ner5oX9+zZxeMxmlAV6AB0Adn55q0bt3ojiMkXr9+nVq1GhMR0Yzg4Dq0bt0Zi8Xyt/nodDoWL57H\n6dNHOHZsJ3v3bv3nbwgIIUQhI4Ve3NP58+f5/vvF5OTMAEYCC4FVuLq+xMCBz+Dq6oLFcgGLZRNl\nypSkadMmd2znzPz5lO/dmzJYWY0frZjPDfU+R4/G2Wd7q1evHkuWfE2NGr/h7+9BmzapfPfdGBYs\n+OKOve8HDnyHY8eqYTKdITPzHFu2pPPxxxP+cW7lypUjICDg1kF7hBDCwcgzenFP6enpaLUeQDTw\nFTAROECDBtVxcdEzb94GLJalQH2SkmLp2fNFNm1adksbv//wA6W798AdxSKa0R1fLDwNvEeJEj63\nFNro6Giio/9u6hqb/fuPYDaPw/Z71YWMjKfYvXsD48aNZ+/eo0REBPP666/i4uJi38dkMpGamoq3\nt7cUeCFEkSAD5oh7ys7OpkqVmpw925acnKexTVwzAReXkmi1lzCZtIA3kAbMolSp3ly5cta+/+/f\nfotrj564oJhDb55lNjkAeGAwGFi8eN5/Hoa2U6feLF/uQ3b2GMCKq2s3ypU7zsWL5cjIeBKDYTl1\n6uTw448rcXJyYvz4Sbz77hCcnIx4eZVm06YVBAYG3ucZEkKIB09GxhMP1IULF2jUKIbTpy9im152\nGvAKcBXYCrgAY4CFREaW4Oeff7Tt+P33ZD/1FDqlmEZZXuYCCi1wDSenchw+vI9q1arZj7N69Wr6\n9h3I9euXqFevCYsWfUWZMmXs681mM5mZmfYpbZOTk6lfvznXrjljtZp45JGSnDiRQGbmmdyYLLi5\nVWHHjh9IT0+nRYuumEzbgQpoNOMJCfmOo0d3P+jTJ4QQ9+1+ap/cuxT3ZLFYGDHiIxITfwM6AOuA\n48Bu4ElsBRWgAxpNAnPnTrN9/Oor6NoVnVKMpQ8v8QiK7sBkNJpGuLuXZuTI8aSmpgLwyy+/0Lnz\n01y6NAuzOYldu4Jo27a7PY7hw0fh5uZJqVI+1K4dxZUrV/D29ub48b2sWTOFzZvnMXfudLRaI+Cc\nu5cOJyd3zGYz+/btw2p9AqgAgFIvcfz4XvnRKIRweFLoxT0NGTKCefPisVh+BH4AXgKeBprnfjYB\nCphD48YNCQ4OhqlToU8fsFqZXq4ig6kNbASqA+NRSs+NGz+wZIkTLVq0RynFtm3bgDZAU8ATi2Us\ne/ZswWw28/jjbRgxYhrZ2afIzk7j0KHq9OzZDwAnJyfq169PZGQkISEhlC9fAr3+dWAPOt0QSpe2\nUr16dSpUqIBWuxPIyM1sM2XK+N9ziF0hhHAEUujFPS1duhaTaSRQF9gGfAs8CrgDQUAAEIhe/znf\nfPM5fPQRvPyybedPPqHR+hUULzGSYsXaA19g+2EQB9TGbJ7O0aPxXLx4kZIlS+Lk9Cu2d/IBTuDq\nWowpUz5j06ZDwPNAOcAJi+VNdu/exaOPRmMwuGM0ejJ16nR0Oh3btq2hbdurBAb2p1Wrs+zcuREX\nFxfatGlDTEw4bm7V8fBojbt7bxYs+CK/TqMQQhQYeUYv7ujKlSssXbqUUaMmc+bMm0AvIAnbVfkJ\noH7uv3XodCvZuGElTTZtgpEjURoN8S+/TNVPP0Wr1XLt2jWGDRvG55/vJDs7GziI7TfmTZydy3Hh\nQgIeHh40avQ4R49aMZsj0Onm0759c/bu/YWTJ6sDF4FVufstwGh8HYulIxbLBCABo7EZq1Z9TVRU\n1F1zUkqxe/duUlJSiIyMvOugPkII8bCRzngiTyUmJlKz5qOYTA3IyUklK2s7tiv649hmizsKlAHm\noNePYP63M+i0YwdMmEA20M+lLt/pzdSu7cuMGZ8ycOC77Nu3h6tXG2C1JgFeQDNgJr161eLrr2cA\nts52CxcuJCEhgalTv+TGjXpkZp7G1gHwJHADKItO9xM6HWRmnshtC5ycBtOqVTyNGzcmJiaG0NDQ\nfD1nQgjxIEmhF3lGKUXr1p1Yt64KVmts7tJ2aDRxKPU9ts54U4EmODsfonePVszUmmHWLLKArgxj\nKSOAbNzcGqPVniQ9fRA5OaFAb+Bd4CRa7Sbq1XuEbds23vY++5gxH/HBB8cwm+cAl4HaQHlcXbPR\n639j3boVdOv2PGfPjgVaAVY0mih0OhPQEL3+G5YvX0CzZs3y45QJIcQDJ73uRZ5QStG9+7OsW7cT\nq/Wvk7yYUCoWaIRtdLzReHruYd3KGczISoVZs8BgoKPWmaX8Md2rjqysWmRleZKT8x7QDtiORvMR\nYWEnGDr0ebZsWX/HQWuuXUvFbP7j/faywFKKFTvBl18OIiHhV+rXr8+XX07GaHwaN7deODvXRamz\nWCw7sFgmYDLN5qWXBj+4EyWEEIWIFHpht27dOlas2IPVOhj4BLgApKDVnsz99x9cqV09gqipU9F8\n+y24u8PatVyNbIRWOwZbL/zf0GoXodXqcz8DVESns7Bt2wqGD3+Po0ePMn/+fPbt23dLHE88EYPR\n+DmwCziPwfABnTt3oWvXrpQqVQqApk2bcvjwbiZPfozoaF/gOf581S+I69evPZiTJIQQhY0qZAph\nyIXG559/rozGvgqsCoYoKKZArzp16qbc3csojeZtBR+oUoZS6lqdOkqBUiVKKBUXp5RSKikpSVWv\nXl/pdK7K2dlNTZ48VYWG1lUuLj0UzFRGY0PVq9cLSimlxo79VBmNPqpYsc7KaPRTw4ePviWWefO+\nUV5egcrDw0v16vWCysjIuGvcGzduVEajn4K9Ci4qg6Gd6tv3pQd3ooQQIp/dT+2TZ/TCbt++fTRq\n1IaMjG1AJWAilSp9xa5dG+jb9yV2744joGRxNrgoPA8ftk0vu2EDVK9+Szvp6em4urqi1Wq5efMm\nY8Z8zIkTZ2nUKJKXXupPSkoKFSoEk5W1H5iObaKcVCZPHsXLL7/0n2KfPftL3nnnAzIy0mnfvgOz\nZk3GYDDc5xkRQoiHg3TGE3li4cLv6dnzmdxX4PR4eXmxadNyOnbsxZkzDXE3N2Wd5gUi1RWUnx+a\njRuhSpV/fZyDBw/SuHEP0tLCsD0SmAEk4+LSlbVrF9zzFTkhhCiKpDOeuG9nz56lT5/+ZGfvxPYa\n21QyM03cuHGDCxeyKGF+ly0MI1Jd4bRGx+mvvvpPRR7Ax8eH9PTz2EbLmwwEA1FkZb3GkiUr8iol\nIYQQSKEXueLj49HrawHh2Dq1PY3FYhvsxs9qYhtNCOMoxwimhUsprP7+/+k4V69e5Z13BuPk9BgQ\nCCTa1+l0iXh6uudBNkIIIf4g89ELACpUqEB29hEgBdtgOEewWm/SxNeXH7Mv4kMW+wmgnUsAJSp7\nYjab/1G7WVlZ6PV6nJyciI+Pp1Gjlty86UJ29kBsV/LPAP2A83h6bmDAgD0PKEMhhCia5IpeAFCt\nWjVef70/RmM4Hh4xGAyPsWjEe7jHxOBjzuJsOT9eqeZNcs5Ozp51p3bt5gwfPvqu7V27do2GDaNx\nc/PAYCjGJ59M5JlnBpKaOgyLZRTwJVAL28Q4S9FolgCQkZFx1zaFEEL8e9IZT9ziyJEjnDlzhppK\n4du3L1y9Sk5UFGtffJEOvfpisWwC6gGXMBgi2Lt3EyEhIbe107p1FzZuLI3ZPAk4j9H4GHq9md9/\n/xGoDAwDxuZuHQV8h5PT50RF7WDTpmX5k6wQQhQS0hlP5JmwsDDalCyJb69ecPUq5pYtCTt7haee\n/RSLpQq2KWovAl7o9WGcOXPmlv1TUlI4fvw4O3b8hNn8LranQwGYTL0oU6Y0ev00bAPoDEKrDQA6\nYxtW1xOrtQWnTiXkY7ZCCOH4pNALAC5cuMCkSZNYMmAA1hYt4MYN6NyZNwKqcCqpIenpu4D92Iay\nHQocxmLZT1BQkL2NESNiKV++EnXrtiMtLQP4OXeNFYNhLy+80IOQkJ9xcSmDXu9PkyaBGAyngTTA\nirPzDGrXrpnPmQshhGOTW/eCU6dOERnZiKY3Q5ifvRkXrPzeoQOe339P8+jObNrUDduVN8A6NJqe\naLUmnJy0ZGdnUKtWI4YOHUS3bq9gMu0GvIF30WgmYzS2RaM5S8WKOUREhJOQkESdOqG8997bWCwW\ngoJqcuPGNcAZd3c3TpzYh4+PT4GdCyGEeBjJrXtxX4YOHc3jvzdiYfZWXLAyhQY8k+MKWi2NG9fG\nYJgFmIAsDIYZtG7dBL3eE7P5J6zW0fz8cwo9e/bDam2IrcgD/A+lTEye3IIZM14mNTWVBQvc+Omn\nZ/nss4O88MKrDBz4DhkZT2F7xe4Q2dm1+OKLOQV1GoQQwiFJoRfUOLifb9T36MkmlsEMpBFLl6/H\n3b08ZcuWICamDHq9F87OZWnUyErDhrXJyekMfA6sAN4nLa0TWVnL+fO9+FX4+DxCnz59KFasGKmp\nPlgs44EOZGQsYcmS7/jxx5+wWDoDpYEAMjM7sm/fsYI5CUII4aDkPfoiJjk5mVGjxpGUlEKbNs14\n5kYqb/9yEIAhvEEs5YHhwFTS0zPo3/8VVq6cz6xZk7FarZQqVYpvvvkGnW4lZvMebPPFewJd0Oni\n0WiqYzCEYLX+xvTpM0lJScm93aT5SxQalNJy/Xo2Gs23KFUPyMZgWEKtWo/m7wkRQggHJ8/oi5Br\n164REhLJ1avtyM4OY5h+CCMslwBY2Tyap3buxWTKwfaOe/vcvabSuPFKtm5dY2/HYrHQpEkrdu3a\nAvwOGAFwd2/D8OFRBAcH8/77Yzh+/Fes1izatGnL7t17SE5uQ05OFLaJbDyAMUAobm4+KJVB3brV\nWbNmMS4uLgghhPiTPKMX/8iSJUtIS6tFdvZ4RvEbIyyXsAJq5kye2LCWs2d/QaPRANa/7GXF2dn5\nlnb0ej3btq2hQYMmODu3B9ah1X6IwXCYPn36MH/+Mo4dCyYz8yJm8wWWLfuNMmVKEBq6A632RSAS\n+Aooh4uLnqVLp7J37zo2blwuRV4IIfKYFHoHdPbsWb766iuWLFlCVlaWfbnFYgGrGxN5lSHEko2W\np7XO8OyzAJQuXZrWraOAF4Cvgc9xchrK8OFv33YMnU7H5s2ref31+kRGjqN9+9/4+edtlCxZkri4\n/WRlPQdoATeys/ty8KCOEyeS8PDQoNOZgR24uj5NnTp1aNasGVWrVsXJSb6OQgiR1+TWvYP57rvv\n6NHjeZRqjk6XRHCwll27NmIwGEg8c4YtlavSKzuTLPT0cg7BrXt9vvzyM/v+SimGDh3KggWrKVbM\njYkTR9GkSZN/FUNMTGc2bKhOTs772O4OdANCgccpVepJmjaN4sSJBOrXr8nHH4/E3V0mshFCiHuR\n+egFYBv0pnz5alits4BOgEKni+HTT5/g5X79oFcvWLiQDCctA/2qUPKpjowaNQy9Xp+ncZw7d456\n9R7j2rWSZGXdwDZJzjogmeLFG3H9elKeHk8IIRydPKMv4qxWKzNnzqRjx6ewWsH2DBxAQ3Z2PX45\neBg6dYKFC8HDA8PWLUw/dQiNRkPlyrUIDW3A+vXr8ywef39/fv31AJMnP4+LSzK22emOYjQ+S48e\nXfPsOEIIIf6eXNE7gF69XmDx4iNkZHgDx4EmwBQgCSN12eSWSb30G1CyJKxfD7Vq8dprg5kxYxcm\n03ggEaPxBbZuXU1kZOQ9j/Vvbdu2jUGDhpGa+judOrUmNnY4Op281SmEEP+G3LovwpKTkylfPojs\n7AvANWzPwgOAX/AAVuFKQ9LA2xs2bIDQUADKln2ElJRVQNXcloYxeLCV2NiRBZCFEEKIe5Fb90XY\nwYMHyc7WA26AP/A2cIVS1OFHytKQNM476ehbKZxt167Z9zMYjECK/bNOdxk3N0M+Ry+EEOJBk0Jf\niMXFxbFs2TI0GmfgFeAIoMObLLayk1okcRItDazj+fKnJ4mJeZKdO3cCEBv7HgZDd+ATtNpX8PRc\nRd++fVi+fDkTJ05k27ZtzJkzl9Kl/TEaS/DUU30wmUwFmK0QQoj/Qm7dF1LDh49m3LjpKBVKRsYu\noBoQjz9l2UQSlUjnpIuBxllTSaZP7l6T6Nr1EPPnz+bKlStERNTj8uV0IIcqVSoSHFyFNWsOk53d\nEFiE1QoWy0rAH1fXAXTuXIqvv/68oFIWQogiS57RFzHnz5+ncuVwMjOPAV7AEGAy1V29WJF5Gn8U\nlurVidF4sunQG9g6580GNtCsmY6NG1fSo8dzfP+9OxbLp4DC2TkGpeKxWE5gG9L2FaAEMCL3qKdw\nc3uUmzeT8z9hIYQo4uQZfRGzf/9+rNay2Io8wGjqGMqwyzkFfxQ8+ij6bdt4YchAXF37ARWBnUAk\n27btYeHC7/j558NYLG2xTTbjhNkcjlIV+GPcetvz/qN/OeoJ0tOzWLVqVT5lKYQQIi/IFX0hc/r0\naSIi6pGWZgbmAm2oxXjWa96kpFLQvDksXQpubmRkZFCqlC8ZGVGNMUnHAAARyUlEQVTAktwWduDm\n1onMTAs5OTGAH/ADcB2NxoRS84EWwKfAqNx/BwDfAB0pU2YDSUm/5PkgO0IIIe5OruiLkPHjp5Ce\n/jywBhhAQ5z5kTcoqRQp9euTk1vkATp37k1GRioQ+JcWKpCefoOcnG3YrvI3A4uAeSiVCbwGFAOW\nYpt+tjRQDtgIOHP9umLevHn5lK0QQoj7JYW+kElLM2G1egH1acEs1mGb8HWRrhxBh9N5rFVnzGYz\nb745hFWrlgDuwBxgA3Aa24Q1Ltg67+mBWUAY0DJ32x8AM7AbF5fywHzgCjAJWIrV2ooLFy7kZ8pC\nCCHugxT6QqZHj44YjWNpx4esoA1GLMyiKU9lnyM1fR87d6YxcOBAPvtsOeAMjARygD5ATeAAtufw\nCwAFXPxL6+FoNM2Akbi4dKN8+QwiIsLRaLYDQcAiXF1X8Oijj+ZnykIIIe6DPKMvhHYNHEjtKVPQ\nARPR8RoJKPxy13bH2XktZvO7wA1gBRCN7db7MWy3/H8BPsQ2YE4x4HXgQu62FwgOrk737h0ZNGgQ\nmZmZtGrVhQMHdqHVahk3biyvvPJS/iYshBBFnLxeV5TMnAn9+oFSxDq5McRqBHoD44CVQA+gA7bh\ncJcC84AvgTNABrY54gOAg0AMtiv6hthG1msFPIZe34OqVQ+zf/92tFotABkZGbi4uMic8UIIUQCk\nM15RMWECvPACKMUQJyNDrNOxzVS3DCgOdAWGAtOB34Ha2Ir8YeAZoCzwG7ZOeDGAN5CK7UdBKaAz\n8B4WyzR+++08p0+fth/aYDBIkRdCiEJI/nIXBkrByJHw2msAvOpkINZaEbgJTARM2Ap+CWy36w3A\nJqAD3t7nqF07HGfnj4HG/Pme/AhsPwJaYrttPxRoCwwGLFitWTg7O+dXhkIIIR6QB1ro+/bti5eX\nF2FhYfZl165do0WLFgQFBdGyZUtSU1Pt62JjY6lcuTLBwcF5Oj96oWexwIYNWDUaXtBVYJK1N9AM\neB9YDvQHdvLqq0/i7j4DjWYkMAuDYTqTJo1lz57NrFixBNu79JdyG90EVAE+o0cPX4KCKuDqegH4\nEoOhHU2bNsLf3z//cxVCCJGnHmih79OnD2vXrr1l2ZgxY2jRogUnTpygWbNmjBkzBoBjx46xcOFC\njh07xtq1axkwYABWq/VBhld4ODszvFYD2mpcmZndE2iH7fn7WGAfWu1sund/igkTJhAXt4U+fS7y\n1FN7+eGHL+jc+UkArly5hu0WfQBQAZgGdMDLqzzz5s3k4MHdvP12OO3b/8j77zdj2bL5aDSaAklX\nCCFEHlIPWEJCggoNDbV/rlKlikpOTlZKKXXx4kVVpUoVpZRSo0ePVmPGjLFvFx0drXbt2nVbe/kQ\n8kPnyJEjymDwUTBTQYSC3xV8ocBHabUe6qWXXldms/mu+1+6dEkZDCUVPKPAT4GbAj+l0birHTt2\n5GMmQggh/ov7qX26/P5hcenSJby8bGO0e3l5cemS7VbyhQsXqFevnn07Pz8/kpKS8ju8h9K5c+dw\ndg4jI+NZ4BDwCOBM8eJWPv10It26dbttSNrt27fz2Wdz0GqdaNasAc7Oj5CRMRvblfw6dLo4Fi/+\nhgYNGuR/QkIIIfJNvhf6v9JoNPe8PXy3dcOHD7f/OyoqiqioqDyO7OESGhqKxbIf2A9MBrzRaGLJ\nyanLK69M56OPphAX9yMeHh4AbNiwgXbtepKRMRTIYvHiN3Ifg/wKvAxEodc3loFvhBDiIbVlyxa2\nbNmSJ23le6H38vIiOTkZb29vLl68SNmyZQHw9fUlMTHRvt358+fx9fW9Yxt/LfRFgb+/P3PnzqBn\nz+YopScnx0pOzmDS0oYCioSEPowePY7Y2A+ZO3ceb701koyM8djeqYeMDD21ay/h6NGGODtXwmz+\njVmzplGqVKkCzUsIIcSd/f+L2BEjRtx947+R76/XtW3bljlz5gAwZ84c2rdvb1++YMECzGYzCQkJ\nnDx5kjp16uR3eA+tjh07kJR0mlGjBlOiREms1qa5azRkZTXmxImzvPPO+wwY8AmXLxuwjVv/B3d8\nfPw4deooq1d/yunT8XTv3rUAshBCCJHfHugVfbdu3di6dStXrlyhfPnyfPjhhwwePJguXbowe/Zs\nAgIC+O677wAICQmhS5cuhISEoNPpmDZtmvT6/oukpCRq147i+vXKmM3uwHigDpCJ0fgVjz7akcGD\nB5OdfQ7bBDavYZu0JgujcRj9+8/Gx8cHHx+fAsxCCCFEfpMhcAuBM2fOEBZWk5s3G2N7re4m0Bw4\njF6voWXLGIKDH2H8+AkolYZtdrq5ODkNpUKFkowf/4H9zokQQojCR4bAdXAvvvgmN2+GAzVyl7gD\n8ylevATLly9m8+atjB/vjFKB2IbB3YdGc5Nixczs3LlGirwQQhRhckVfCFSqVItTp54FYrHNMFcB\nJ6fn6dLFkzNnzrN7dy+gJ5AONKNYsSSqVw9l+vRxhIaGFmToQggh8oBc0Tu4Bg0icXHZCwzHNhmN\nD6GhF5g5cyJpaTfBPkWtG9CHmJgW/PTTGinyQgghpNAXBpMnj6VGjXO4uLyNTvc7tWpFMGDA0wB0\n794eo/Ft4AiwE6Mxlh495Fa9EEIIG7l1X0gopVi0aBFPPz2AnJyn0OkS8fY+zb592/nkk0nMnDkX\nZ2dnhg17g+ee61vQ4QohhMhD91P7pNAXIpUq1eDUqf8BTwDg4tKNUaMieeONNwo2MCGEEA+UPKMv\nIlJTrwFV7Z+zsqpy+fLVggtICCHEQ08KfSESHd0CV9ch2KabPYjROJPHH29R0GEJIYR4iEmhL0Rm\nzJhIq1bOuLgEULx4KyZN+pCmTZv+/Y5CCCGKLHlGL4QQQjzk5Bm9EEIIIe5ICr0QQgjhwKTQCyGE\nEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQ\nCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjh\nwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0Q\nQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5M\nCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGE\nEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA7soSv0a9euJTg4mMqVK/PRRx8VdDgPnS1b\nthR0CAWqKOdflHMHyV/y31LQIRRaD1Whz8nJ4eWXX2bt2rUcO3aM+fPnc/z48YIO66FS1L/sRTn/\nopw7SP6S/5aCDqHQeqgK/Z49e6hUqRIBAQHo9Xq6du3KsmXLCjosIYQQotB6qAp9UlIS5cuXt3/2\n8/MjKSmpACMSQgghCjeNUkoVdBB/WLx4MWvXrmXmzJkAzJs3j7i4OCZPnmzfplKlSpw6daqgQhRC\nCCHyXWBgIL/99tt/2leXx7HcF19fXxITE+2fExMT8fPzu2Wb/5qoEEIIURQ9VLfuIyMjOXnyJGfO\nnMFsNrNw4ULatm1b0GEJIYQQhdZDdUWv0+mYMmUK0dHR5OTk8Oyzz1K1atWCDksIIYQotB6qZ/RC\nCCGEyFsP1a37v/r++++pVq0aWq2W/fv337IuNjaWypUrExwczPr16+3L9+3bR1hYGJUrV+bVV1/N\n75AfqKIwkFDfvn3x8vIiLCzMvuzatWu0aNGCoKAgWrZsSWpqqn3d3b4HhVViYiJNmzalWrVqhIaG\nMmnSJKBonIPMzEzq1q1LREQEISEhvPvuu0DRyP2vcnJyqFGjBm3atAGKVv4BAQFUr16dGjVqUKdO\nHaBo5Z+amsqTTz5J1apVCQkJIS4uLu/yVw+p48ePq19//VVFRUWpffv22ZfHx8er8PBwZTabVUJC\nggoMDFRWq1UppVTt2rVVXFycUkqpmJgYtWbNmgKJPa9lZ2erwMBAlZCQoMxmswoPD1fHjh0r6LDy\n3LZt29T+/ftVaGiofdlbb72lPvroI6WUUmPGjFHvvPOOUurO34OcnJwCiTuvXLx4UR04cEAppVRa\nWpoKCgpSx44dKzLnID09XSmllMViUXXr1lXbt28vMrn/4ZNPPlHdu3dXbdq0UUoVre9/QECAunr1\n6i3LilL+vXv3VrNnz1ZK2f4fSE1NzbP8H9pC/4f/X+hHjx6txowZY/8cHR2tdu3apS5cuKCCg4Pt\ny+fPn6/69euXr7E+KDt37lTR0dH2z7GxsSo2NrYAI3pwEhISbin0VapUUcnJyUopWyGsUqWKUuru\n3wNH0q5dO7Vhw4Yidw7S09NVZGSkOnr0aJHKPTExUTVr1kz9+OOP6oknnlBKFa3vf0BAgLpy5cot\ny4pK/qmpqapixYq3Lc+r/B/aW/d3c+HChVteuftjUJ3/v9zX19dhBtspygMJXbp0CS8vLwC8vLy4\ndOkScPfvgaM4c+YMBw4coG7dukXmHFitViIiIvDy8rI/wigquQO89tprjBs3DienP/8sF6X8NRoN\nzZs3JzIy0j6WSlHJPyEhgTJlytCnTx9q1qzJ888/T3p6ep7lX6C97lu0aEFycvJty0ePHm1/RiVs\n/wMI23m417lwlPN08+ZNOnXqxMSJEylWrNgt6xz5HDg5OXHw4EF+//13oqOj2bx58y3rHTn3lStX\nUrZsWWrUqHHXMd0dOX+AHTt24OPjQ0pKCi1atCA4OPiW9Y6cf3Z2Nvv372fKlCnUrl2bQYMGMWbM\nmFu2uZ/8C7TQb9iw4V/v8/8H1Tl//jx+fn74+vpy/vz5W5b7+vrmSZwF7Z8MJOSovLy8SE5Oxtvb\nm4sXL1K2bFngzt8DR/jvbbFY6NSpE7169aJ9+/ZA0TsHnp6etG7dmn379hWZ3Hfu3Mny5ctZvXo1\nmZmZ3Lhxg169ehWZ/AF8fHwAKFOmDB06dGDPnj1FJn8/Pz/8/PyoXbs2AE8++SSxsbF4e3vnSf6F\n4ta9+ssbgG3btmXBggWYzWYSEhI4efIkderUwdvbGw8PD+Li4lBKMXfuXPsfysKuKA8k1LZtW+bM\nmQPAnDlz7P9N7/Y9KMyUUjz77LOEhIQwaNAg+/KicA6uXLli71GckZHBhg0bqFGjRpHIHWx3MRMT\nE0lISGDBggU89thjzJ07t8jkbzKZSEtLAyA9PZ3169cTFhZWZPL39vamfPnynDhxAoCNGzdSrVo1\n2rRpkzf552WHgry0ZMkS5efnp1xdXZWXl5d6/PHH7etGjRqlAgMDVZUqVdTatWvty/fu3atCQ0NV\nYGCgGjhwYEGE/cCsXr1aBQUFqcDAQDV69OiCDueB6Nq1q/Lx8VF6vV75+fmpL774Ql29elU1a9ZM\nVa5cWbVo0UJdv37dvv3dvgeF1fbt25VGo1Hh4eEqIiJCRUREqDVr1hSJc3D48GFVo0YNFR4ersLC\nwtTYsWOVUqpI5P7/bdmyxd7rvqjkf/r0aRUeHq7Cw8NVtWrV7H/jikr+Sil18OBBFRkZqapXr646\ndOigUlNT8yx/GTBHCCGEcGCF4ta9EEIIIf4bKfRCCCGEA5NCL4QQQjgwKfRCCCGEA5NCL4QQQjgw\nKfRCCCGEA5NCL4QQQjgwKfRCCCGEA5NCL4S4p59//pnw8HCysrJIT08nNDSUY8eOFXRYQoh/SEbG\nE0L8rffff5/MzEwyMjIoX74877zzTkGHJIT4h6TQCyH+lsViITIyEoPBwK5duwr1lKBCFDVy614I\n8beuXLlCeno6N2/eJCMjo6DDEUL8C3JFL4T4W23btqV79+6cPn2aixcvMnny5IIOSQjxD+kKOgAh\nxMPt66+/xsXFha5du2K1WmnQoAFbtmwhKiqqoEMTQvwDckUvhBBCODB5Ri+EEEI4MCn0QgghhAOT\nQi+EEEI4MCn0QgghhAOTQi+EEEI4MCn0QgghhAOTQi+EEEI4sP8Diwf1C+duoqkAAAAASUVORK5C\nYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x105785f60>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 8
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"#### Comparing the results from the different implementations"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"As mentioned above, let us confirm that the different implementation computed the same parameters (i.e., slope and y-axis intercept) as solution for the linear equation."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import prettytable\n",
|
|
"\n",
|
|
"params = [appr(x,y) for appr in [lin_lstsqr_mat, classic_lstsqr, numpy_lstsqr, scipy_lstsqr]]\n",
|
|
"\n",
|
|
"print(params)\n",
|
|
"\n",
|
|
"fit_table = prettytable.PrettyTable([\"\", \"slope\", \"y-intercept\"])\n",
|
|
"fit_table.add_row([\"matrix approach\", params[0][0], params[0][1]])\n",
|
|
"fit_table.add_row([\"classic approach\", params[1][0], params[1][1]])\n",
|
|
"fit_table.add_row([\"numpy function\", params[2][0], params[2][1]])\n",
|
|
"fit_table.add_row([\"scipy function\", params[3][0], params[3][1]])\n",
|
|
"\n",
|
|
"print(fit_table)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"[array([ 0.95181895, 107.01399744]), (0.95181895319126741, 107.01399744459181), array([ 0.95181895, 107.01399744]), (0.95181895319126764, 107.01399744459175)]\n",
|
|
"+------------------+----------------+---------------+\n",
|
|
"| | slope | y-intercept |\n",
|
|
"+------------------+----------------+---------------+\n",
|
|
"| matrix approach | 0.951818953191 | 107.013997445 |\n",
|
|
"| classic approach | 0.951818953191 | 107.013997445 |\n",
|
|
"| numpy function | 0.951818953191 | 107.013997445 |\n",
|
|
"| scipy function | 0.951818953191 | 107.013997445 |\n",
|
|
"+------------------+----------------+---------------+\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 9
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"#### Initial performance comparison"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"For a first impression how the performances of the different least squares implementations compare against each other, let us do a quick benchmark using the `timeit` module via IPython's `%timeit` magic."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"for lab,appr in zip([\"matrix approach\",\"classic approach\",\n",
|
|
" \"numpy function\",\"scipy function\"],\n",
|
|
" [lin_lstsqr_mat, classic_lstsqr, \n",
|
|
" numpy_lstsqr, scipy_lstsqr]):\n",
|
|
" print(\"\\n{}: \".format(lab), end=\"\")\n",
|
|
" %timeit appr(x, y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"matrix approach: 1000 loops, best of 3: 270 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"classic approach: 100 loops, best of 3: 2.83 ms per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"numpy function: 1000 loops, best of 3: 372 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"scipy function: 1000 loops, best of 3: 594 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 10
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"The timing above indicates, that the \"classic\" approach (Python's standard library functions only) is significantly worse in performance than the other implemenations - roughly by a magnitude of 10."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"<a name=\"cython_nb\"></a>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Compiling the Python code via Cython in the IPython notebook"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Maybe we can speed things up a little bit via [Cython's C-extensions for Python](http://cython.org). Cython is basically a hybrid between C and Python and can be pictured as compiled Python code with type declarations. \n",
|
|
"Since we are working in an IPython notebook here, we can make use of the IPython magic: It will automatically convert it to C code, compile it, and load the function. \n",
|
|
"Just to be thorough, let us also compile the other functions, which already use numpy objects."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%load_ext cythonmagic"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 15
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"import numpy as np\n",
|
|
"import scipy.stats\n",
|
|
"cimport numpy as np\n",
|
|
"\n",
|
|
"def cy_lin_lstsqr_mat(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)\n",
|
|
"\n",
|
|
"def cy_classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)\n",
|
|
"\n",
|
|
"def cy_numpy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return np.linalg.lstsq(X,y)[0]\n",
|
|
"\n",
|
|
"def cy_scipy_lstsqr(x,y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" return scipy.stats.linregress(x, y)[0:2]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 16
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### Comparing the compiled Cython code to the original Python code"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"for lab,appr in zip([\"matrix approach\",\"classic approach\",\n",
|
|
" \"numpy function\",\"scipy function\"],\n",
|
|
" [(lin_lstsqr_mat, cy_lin_lstsqr_mat), \n",
|
|
" (classic_lstsqr, cy_classic_lstsqr),\n",
|
|
" (numpy_lstsqr, cy_numpy_lstsqr),\n",
|
|
" (scipy_lstsqr, cy_scipy_lstsqr)]):\n",
|
|
" print(\"\\n\\n{}: \".format(lab))\n",
|
|
" %timeit appr[0](x, y)\n",
|
|
" %timeit appr[1](x, y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"matrix approach: \n",
|
|
"1000 loops, best of 3: 274 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"1000 loops, best of 3: 260 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"\n",
|
|
"classic approach: \n",
|
|
"100 loops, best of 3: 2.82 ms per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"1000 loops, best of 3: 212 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"\n",
|
|
"numpy function: \n",
|
|
"1000 loops, best of 3: 379 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"1000 loops, best of 3: 370 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"\n",
|
|
"scipy function: \n",
|
|
"1000 loops, best of 3: 608 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"100 loops, best of 3: 613 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 17
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"As we've seen before, our \"classic\" implementation of the least square method is pretty slow compared to using numpy's functions. This is not surprising, since numpy is highly optmized and uses compiled C/C++ and Fortran code already. This explains why there is no significant difference if we used Cython to compile the numpy-objects-containing functions. \n",
|
|
"However, we were able to speed up the \"classic approach\" quite significantly, roughly by 1500%.\n",
|
|
"\n",
|
|
"The following 2 code blocks are just to visualize our results in a bar plot."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"funcs = ['classic_lstsqr', 'cy_classic_lstsqr', \n",
|
|
" 'lin_lstsqr_mat', 'numpy_lstsqr', 'scipy_lstsqr']\n",
|
|
"labels = ['classic approach','classic approach (cython)', \n",
|
|
" 'matrix approach', 'numpy function', 'scipy function']\n",
|
|
"\n",
|
|
"times = [timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000)\n",
|
|
" for f in funcs]\n",
|
|
"\n",
|
|
"times_rel = [times[0]/times[i+1] for i in range(len(times[1:]))]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 18
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%pylab inline\n",
|
|
"import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"x_pos = np.arange(len(funcs))\n",
|
|
"plt.bar(x_pos, times, align='center', alpha=0.5)\n",
|
|
"plt.xticks(x_pos, labels, rotation=45)\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.title('Performance of different least square fit implementations')\n",
|
|
"plt.show()\n",
|
|
"\n",
|
|
"x_pos = np.arange(len(funcs[1:]))\n",
|
|
"plt.bar(x_pos, times_rel, align='center', alpha=0.5, color=\"green\")\n",
|
|
"plt.xticks(x_pos, labels[1:], rotation=45)\n",
|
|
"plt.ylabel('relative performance gain')\n",
|
|
"plt.title('Performance gain compared to the classic least square implementation')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"Populating the interactive namespace from numpy and matplotlib\n"
|
|
]
|
|
},
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAFhCAYAAABwNN3iAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdYFGfXB+DfLoiwVAEBXZpYEkBEbNgiS+yoSDS22Msr\nEjQaEyOmKCb2GhMTY4n62n01FkQwxrIalWI3kSCWgIC6ETtFYHfP9wcwH0sRMO4u6Lmvi4udnWdm\nzjPtzDxTVkREBMYYY288sb4DYIwxVj1wQmCMMQaAEwJjjLFCnBAYY4wB4ITAGGOsECcExhhjAF7z\nhKBQKNCpUydYWFhg2rRp+g5H73JyctCnTx9YWVlh0KBBFZaXy+VwcnISups2bYqTJ08CAIgIo0eP\nhrW1Ndq2bQsAWLVqFezt7WFhYYFHjx5ppxIvqWRdWOVdu3YNzZs3h4WFBb7//nuEhIRgzpw5lR6+\nquWrwtXVFUePHtXKuPVp69at6N69u+4nTNWMi4sLmZiYkJmZGdnb29OoUaMoMzPzpcb19ddfU//+\n/V9xhDXXpk2bqE2bNqRSqSpV/vjx4+To6Fhmv5MnT5KjoyNlZ2cTEVFeXh6ZmJjQH3/88crirQoX\nFxc6evRouf1fVJdXZeTIkfTll19qdRr6MGbMGJo6dWqZ/XQxX1/E1dX1hctdHzZs2EAdO3asdPm/\n//6bRCJRpbdLbap2ZwgikQiRkZF49uwZLly4gHPnzlX56IKIoFarkZKSAnd395eKQ6lUvtRw1VlK\nSgqaNGkCsfjfL/aUlBS4urrCxMQEAHDv3j08f/78pee3Wq3+V/GIRCIQP2NZoZdZr1NSUuDh4aGF\naFhx1WL91XNCKqVkxv/000+pd+/eREQUExND7dq1IysrK/L29ia5XC6U8/Pzoy+++II6dOhAJiYm\nNGzYMKpVqxYZGRmRmZkZHT16lHJzc2ny5MlUv359ql+/Pk2ZMoVyc3OJqOBIRyqV0sKFC8nBwYGG\nDx9O4eHh9P7779OwYcPI3NycvLy8KCkpiebNm0d2dnbk7OxMhw8fFmJYv349ubu7k7m5Obm5udHq\n1auFfkXjX7p0KdnZ2VG9evVow4YNQv/s7GyaOnUqubi4kKWlJXXs2JFycnIqrHdJCQkJ5OfnR1ZW\nVuTp6UkRERFERDRz5kwyMjKiWrVqkZmZGa1fv77UsNnZ2TRy5EiqU6cOeXh40KJFizSO/lxcXOjI\nkSO0bt06MjY2JgMDAzIzM6MhQ4aQqakpiUQiMjMzo86dOxMR0V9//UVdunQha2treuutt+h///uf\nMK6RI0fShAkTqGfPnmRqakpHjx6l9PR06tevH9WtW5caNGhA3333nVB+1qxZNGDAABoxYgSZm5uT\np6cnnTt3joiIhg0bRmKxWDizXLx4cam6lTySfdG04uLiqG3btmRlZUX16tWjiRMnUl5entB/ypQp\nZGdnRxYWFuTl5UV//vknrV69WmN9CwwMLHP5lDUsEVFGRgb16dOHLCwsqE2bNvTll18KR5llHUH6\n+fnRunXriIjoxo0b5O/vTzY2NmRra0tDhw6lx48fayy3hQsXkpeXFxkbG5NKpar0OuXv708GBgZk\nbGxM5ubmlJSUJJwJZWVlkbGxMYnFYjIzMyNzc3O6e/duqXEUP3Mq2g4WLVpEdevWpXr16tHevXvp\n4MGD1LhxY7K2tqb58+drLPf+/fvToEGDyNzcnFq0aEGXL18W+hffX6jVapo/fz41bNiQbGxsaODA\ngfTw4UONebhhwwZycnIia2trWrVqFcXHx5OXlxdZWVnRxIkTNeL++eefyd3dnerUqUPdu3enlJQU\noZ9IJKKffvqJGjduTFZWVhQaGkpEBdtf8W2jTp06REQUGRlJzZs3JwsLC3JycqLw8HBhXE5OTsK2\nY25uTjExMaXOMk6fPk2tWrUiS0tLat26NZ05c0ZjXfjqq6+oQ4cOZG5uTt26daOMjAwiIsrJyaGh\nQ4eSjY0NWVlZUevWrUmhUJS5rImIqmVCOHLkCBER3b59mzw9PWnmzJmUlpZGNjY2FB0dTUREv/32\nG9nY2AgV9/PzIxcXF0pISCCVSkX5+fk0atQo+uqrr4Rxf/XVV9SuXTu6f/8+3b9/n9q3by/0P378\nOBkaGlJYWBjl5eVRTk4OzZo1i4yNjenw4cOkVCppxIgR5OLiQvPmzSOlUklr166lBg0aCOM/ePAg\n3bp1i4iITpw4QRKJhC5cuKAx/lmzZpFSqaSoqCiSSCTChvvhhx+Sv78/3blzR9hgc3Nzy633/fv3\nS827vLw8atiwIc2fP5/y8/Pp2LFjZG5uTteuXSMiovDwcBo+fHi583769OnUqVMnevToEaWmppKn\npyc5OTlpLJuijW/jxo0aK2xycrLGTiszM5McHR1p48aNpFKp6OLFi2Rra0sJCQlEVLCTsLS0FFbs\n7OxsatGiBX3zzTeUn59Pt27dIjc3N/r111+JiIRlER0dTWq1mmbMmEFt27YtM7ayFE8IKpXqhdM6\nf/48xcXFkUqlouTkZHJ3d6dvv/2WiIgOHTpELVu2pCdPnhARUWJiorATLLm+lfSiYQcNGkSDBg2i\n7Oxs+vPPP0kqldI777xDRGUnBJlMRj///DMRFSSEI0eOUF5eHt2/f586depEU6ZMEcq6uLiQj48P\npaWl0fPnz6u0TpWcVsl6yuXyCpuMipcv2g6++eYbYRuysbGhDz74gDIzM+nq1atkYmJCycnJRFSw\n3GvVqkW//PILKZVKWrJkCTVo0ICUSiURaS73b7/9ltq1a0fp6emUl5dHwcHBNGTIEI15GBISQrm5\nuXT48GEyMjKioKAgun//PqWnp5OdnR2dOHGCiIj27dtHjRo1osTERFKpVDRnzhxq3769UCeRSER9\n+vShJ0+e0O3bt6lu3bp06NAhIiq9bRTNp6Lkf+XKFbK3t6d9+/YRUelth0iz2enBgwdkZWVFW7Zs\nIZVKRdu3b6c6deoIyc7Pz48aNWpE169fp5ycHJLJZBQWFkZERD/99BP16dOHcnJySK1W04ULF+jp\n06flLqtqlxBcXFzIzMyMrKysyMXFhUJDQyknJ4cWLFhQamfWvXt3+u9//0tEBSvtrFmzNPqPGjVK\no023YcOGwkZARPTrr7+Sq6srERWsqEZGRsIZA1HBytitWzehOyIigszMzEitVhMR0dOnT0kkEgkb\neElBQUG0YsUKYfwmJiYaC93Ozk7Y8ZiYmNCVK1dKjaOiehd38uRJcnBw0PhuyJAhwtHIrFmzaNiw\nYWXGSkQaO0UiojVr1mhs7MU3vpJHMCV3Wjt27BB2aEXGjx9Ps2fPJqKChDBy5EihX2xsLDk7O2uU\nnzdvHo0ePVqIvWvXrkK/oh1HWbGVpXhCqGhaJS1fvpzee+89IiI6evQoNWnShGJjY0u1+ZZc30o6\nduxYmcMqlUqqVauWkLiJiD7//PMXniGU3EkXt3fvXvLx8RG6XV1dNc5Gq7JOFU2r6GykZD0rcw2h\nZHkTE5NS21B8fLxQvmXLlrR//34iKlju7dq1E/qp1WqqV68enTp1Sqhb0XJ3d3fXWAfu3LlDtWrV\nIpVKJczDO3fuCP1tbGw0zlr79+8vbK89evTQmL8qlYokEgndvn2biAoSwunTp4X+AwcOpAULFhBR\n5a4hTJ48mT7++GMiKnv5Fh/Hpk2byNfXV2P4du3a0caNG4moYPnMnTtX6Pfjjz9Sjx49iKig1aJ9\n+/Zl7lvKYqjvJquSRCIR9u/fj3fffVfj+5SUFOzatQsHDhwQvlMqlRrlKrqL5M6dO3BxcRG6nZ2d\ncefOHaG7bt26MDIy0hjGzs5O+GxiYgJbW1uIRCKhGwAyMzNhYWGB6OhozJ49G9evX4darUZ2djaa\nNWsmDG9jY6PRfi+RSJCZmYmMjAw8f/4cDRs2LBVzZepdvH4l54GLiwvS09NfOF/KG97Z2blSw5Ul\nJSUFcXFxqFOnjvCdUqnEiBEjABQsZ6lUqlH+zp07GuVVKhU6deokdNvb2wufJRIJnj9/DrVaXeVr\nIhVNKykpCVOnTsX58+eRnZ0NpVKJVq1aAQDeffddTJw4EaGhoUhJSUG/fv2wZMkSmJubVzhdf3//\nMofNysqCUql86XmvUCgwefJknDp1Cs+ePYNarYa1tbVGmeLjrso6VaRonX8VbGxsSm1DxZetiYkJ\nMjMzhW5HR0eNOBwdHTW22yLJycl47733NNYHQ0NDKBQKobvkdMqbbkpKCiZPnoxPPvlEYxrp6enC\nvHRwcBC+l0gkyMrKKrfOcXFxCAsLw9WrV5GXl4fc3FwMHDiw3PLF3blzp9T64OLiojEPisdSvB7D\nhw9HamoqBg8ejMePH2PYsGGYO3cuDA3L3vVXu4vK5XF2dsbw4cPx6NEj4e/Zs2f47LPPhDIVrbT1\n69dHcnKy0H379m3Ur1+/3OGrshHk5uaif//++Oyzz/DPP//g0aNHCAgIqNSFIltbWxgbG+PGjRul\n+lWm3sXrl5qaqjHNlJQUjQ3qRerVq4fbt28L3cU/V5WzszP8/PxKxf3DDz8IZYrPX2dnZzRo0ECj\n/NOnTxEZGVmqbFmqsqycnJxeOK2QkBB4eHjgxo0bePLkCebOnatx0XvSpEk4d+4cEhISkJSUhMWL\nF1c6hrKGtbOzg6GhYbnz3tTUFACQnZ0tfHfv3j3h8+effw4DAwP8+eefePLkCTZv3lzqIn3JeV3Z\ndao8ReOr7Hz/NwklNTVV+KxWq5GWlqax3RZxdnbGoUOHNOqVnZ2NevXqVXmazs7OWLNmjca4srKy\nhFusX6Ssun7wwQcICgpCWloaHj9+jAkTJgjLqKJ5I5VKkZKSovFdSkqKxgFVeQwNDTFz5kxcvXoV\nZ86cQWRkJDZt2lRu+RqTEIYNG4YDBw7g8OHDUKlUeP78OeRyucbRb8mdb8nuIUOGYM6cOcjIyEBG\nRga+/vprDB8+vNxpVmZnXiQvLw95eXmwtbWFWCxGdHQ0Dh8+XKlhxWIxxowZg6lTp+Lu3btQqVSI\niYlBXl5epepdpG3btpBIJFi0aBHy8/Mhl8sRGRmJwYMHVyqOgQMHYv78+Xj8+DHS0tLw/fffV7r+\nJfXu3RtJSUnYsmUL8vPzkZ+fj7NnzyIxMRFA6Xnbpk0bmJubY9GiRcjJyYFKpcKff/6Jc+fOlVm+\nJHt7e9y8ebNSsVU0rczMTJibm0MikSAxMRGrVq0SNtpz584hLi4O+fn5kEgkMDY2hoGBgRDDrVu3\nyp1uecOKxWL069cP4eHhyMnJQUJCAjZt2iRMs27dupBKpdi8eTNUKhXWr1+vUdfMzEyYmprCwsIC\n6enpQoIqT1XWqSLF5z8VNDULdX7w4AGePn36wmGrsi2VdP78eezduxdKpRLffvstjI2Ny9wxT5gw\nAZ9//rmQTO/fv4+IiIgqTasozgkTJmDevHlISEgAADx58gS7du164XDF50laWhry8/OF/pmZmahT\npw6MjIwQHx+Pbdu2aSxfsVhc7vrbs2dPJCUlYfv27VAqldi5cycSExPRu3fvUnGXdPz4cfzxxx9Q\nqVQwNzdHrVq1hPW1LDUmITg6OmL//v2YN28e7Ozs4OzsjKVLl2rMiLKO8It/9+WXX6JVq1Zo1qwZ\nmjVrhlatWuHLL7+s9PDllQEAc3NzfPfddxg4cCCsra2xfft29O3b94XDFrdkyRJ4eXmhdevWsLGx\nwYwZM6BWq8utd1m3adaqVQsHDhxAdHQ06tati4kTJ2Lz5s1o0qRJufUpbtasWXBxcUGDBg3Qo0cP\njBgxotzyFc0bMzMzHD58GDt27IBUKkW9evUwY8YM5OXllTm8WCxGZGQkLl26BDc3N9StWxfjx48X\ndjQVTW/GjBmYM2cO6tSpg2XLlpUbMwAYGBi8cFpLlizBtm3bYGFhgfHjx2sk1KdPn2L8+PGwtraG\nq6srbG1thYcex44di4SEBNSpUwf9+vUrNf0XDbty5UpkZmbCwcEBY8aMwejRozXW7bVr12Lx4sWw\ntbVFQkICOnToIPSbNWsWLly4AEtLS/Tp0wf9+/d/4XKuyjpV1rwuvizefvttDBkyBG5ubrC2ttY4\ncymrfMlxldVdsl/fvn2xc+dOWFtbY+vWrdizZ0+ZO7XJkycjMDAQ3bp1g4WFBdq1a4f4+PhKTadk\nmaCgIEyfPh2DBw+GpaUlvLy88Ouvv76wDkXfde7cGZ6ennBwcBCanH/88UfMnDkTFhYW+OabbzQe\nDJVIJPjiiy/QoUMHWFtbIy4uTmN8NjY2iIyMxNKlS2Fra4slS5YgMjJSo1mwvOWjUCgwYMAAWFpa\nwsPDAzKZ7IUHwSL6N6m7ElQqFVq1agVHR0eNNkug4OnRvn37ws3NDQDQv39/jR00Y2+qjRs34uef\nf8bvv/+u71D0avbs2bhx4wY2b96s71DeCFq/qLxixQp4eHjg2bNnZfb38/Or8mkdY+zNoOXjVVaC\nVpuM0tLSEBUVhXHjxpW7YHmBM1ZaRc17bwqeD7ql1SajAQMG4PPPP8fTp0+xZMmSUk1GJ06cQL9+\n/eDo6AipVIolS5bwI/KMMaYnWjtDiIyMhJ2dHXx8fMo9C2jRogVSU1Nx+fJlTJo0CUFBQdoKhzHG\nWEUq9fjaS5gxYwY5OjqSq6srOTg4kEQieeFrE4gKnjp88OBBqe+9vb0JAP/xH//xH/9V4c/b27tK\n+22dvLpCLpcLL6gr7t69e8Ij7HFxceTi4lLm8EC1e8PGK1XylRuvm9e5fq9z3Yi4fjVdVfedOnt1\nRdGFodWrVwMAgoODsXv3bqxatQqGhoaQSCTYsWOHrsJhjDFWgk4Sgp+fH/z8/AAUJIIioaGhCA0N\n1UUIjDHGKlBjnlR+nclkMn2HoFWvc/1e57oBXL83jdafVH4V+NewGGOs6qq67+QzBMYYYwA4ITDG\nGCvECYExxhgATgiMMcYKcUJgjDEGgBMCY4yxQpwQGGOMAeCEwBhjrBAnBMYYYwA4ITDGGCvECYEx\nxhgATgiMMcYKcUJgjDEGgBMCY4yxQlpPCCqVCj4+PujTp0+Z/T/66CM0btwY3t7euHjxorbDYYwx\nVg6tJ4QVK1bAw8ND+AnN4qKionDjxg1cv34da9asQUhIiLbDYYwxVg6tJoS0tDRERUVh3LhxZf5I\nQ0REBEaOHAkA8PX1xePHj6FQKLQZEmOMsXJoNSF8/PHHWLx4McTisieTnp4OJycnodvR0RFpaWna\nDIkxxlg5DLU14sjISNjZ2cHHxwdyubzcciXPHMpqWgKA8PBw4bNMJtP5b6GGhS3EvXs5Op3mv+Xg\nYIIFC6brOwzGmI7I5fIX7m8rorWEcObMGURERCAqKgrPnz/H06dPMWLECGzatEkoI5VKkZqaKnSn\npaVBKpWWOb7iCUEf7t3LgaurfmOoquTkcH2HwBjToZIHy7Nnz67S8FprMpo3bx5SU1Px999/Y8eO\nHXj33Xc1kgEABAYGCt/FxsbCysoK9vb22gqJMcbYC2jtDKGkoqag1atXAwCCg4MREBCAqKgoNGrU\nCKamptiwYYOuwmGMMVaCThKCn58f/Pz8ABQkguJWrlypixAYY4xVgJ9UZowxBoATAmOMsUKcEBhj\njAHghMAYY6wQJwTGGGMAOCEwxhgrxAmBMcYYAE4IjDHGCnFCYIwxBoATAmOMsUKcEBhjjAHghMAY\nY6wQJwTGGGMAOCEwxhgrxAmBMcYYAE4IjDHGCmk1ITx//hy+vr5o3rw5PDw8MGPGjFJl5HI5LC0t\n4ePjAx8fH8yZM0ebITHGGCuHVn8xzdjYGMePH4dEIoFSqUTHjh1x6tQpdOzYUaOcn58fIiIitBkK\nY4yxCmi9yUgikQAA8vLyoFKpYG1tXaoMEWk7DMYYYxXQekJQq9Vo3rw57O3t4e/vDw8PD43+IpEI\nZ86cgbe3NwICApCQkKDtkBhjjJVBq01GACAWi3Hp0iU8efIE3bt3h1wuh0wmE/q3aNECqampkEgk\niI6ORlBQEJKSkkqNJzw8XPgsk8k0xsEYY6zgmqxcLn/p4UWkw/aab775BiYmJvj000/LLdOgQQOc\nP39eo2lJJBLpvVlp1KhwuLqG6zWGqkpODsfGjeH6DoMxpidV3XdqtckoIyMDjx8/BgDk5OTgt99+\ng4+Pj0YZhUIhBBwfHw8iKvM6A2OMMe3SapPR3bt3MXLkSKjVaqjVagwfPhydO3fG6tWrAQDBwcHY\nvXs3Vq1aBUNDQ0gkEuzYsUObITHGGCuHTpuMXhY3Gb0cbjJi7M1WrZqMGGOM1RycEBhjjAHghMAY\nY6wQJwTGGGMAOCEwxhgrxAmBMcYYAE4IjDHGCnFCYIwxBoATAmOMsUKcEBhjjAHghMAYY6wQJwTG\nGGMAOCEwxhgrxAmBMcYYAE4IjDHGCnFCYIwxBkCLCeH58+fw9fVF8+bN4eHhgRkzZpRZ7qOPPkLj\nxo3h7e2NixcvaiscxhhjFdDaT2gaGxvj+PHjkEgkUCqV6NixI06dOoWOHTsKZaKionDjxg1cv34d\ncXFxCAkJQWxsrLZCYowx9gJabTKSSCQAgLy8PKhUKlhbW2v0j4iIwMiRIwEAvr6+ePz4MRQKhTZD\nYowxVg6tJgS1Wo3mzZvD3t4e/v7+8PDw0Oifnp4OJycnodvR0RFpaWnaDIkxxlg5tNZkBABisRiX\nLl3CkydP0L17d8jlcshkMo0yJX8AWiQSlTmu8PBw4bNMJis1HsYYe9PJ5XLI5fKXHl6rCaGIpaUl\nevXqhXPnzmnsyKVSKVJTU4XutLQ0SKXSMsdRPCEwxhgrreTB8uzZs6s0vNaajDIyMvD48WMAQE5O\nDn777Tf4+PholAkMDMSmTZsAALGxsbCysoK9vb22QmKMMfYCWjtDuHv3LkaOHAm1Wg21Wo3hw4ej\nc+fOWL16NQAgODgYAQEBiIqKQqNGjWBqaooNGzZoKxzGGGMV0FpC8PLywoULF0p9HxwcrNG9cuVK\nbYXAGGOsCvhJZcYYYwA4ITDGGCvECYExxhgATgiMMcYKcUJgjDEGgBMCY4yxQpwQGGOMAahEQsjM\nzIRKpQIAXLt2DREREcjPz9d6YIwxxnSrwoTQqVMn5ObmIj09Hd27d8fmzZsxatQoHYTGGGNMlypM\nCEQEiUSCPXv24MMPP8SuXbvw559/6iI2xhhjOlSpawgxMTHYunUrevXqBaDgdw4YY4y9XipMCN9+\n+y3mz5+P9957D56enrh58yb8/f11ERtjjDEdqvDldn5+fvDz8xO6GzZsiO+++06rQTHGGNO9ChPC\n2bNnMW/ePCQnJ0OpVAIo+FWzK1euaD04xhhjulNhQhg6dCiWLFmCpk2bQizmxxYYY+x1VeEevm7d\nuggMDISbmxtcXV2Fv8pITU2Fv78/PD090bRp0zKbmuRyOSwtLeHj4wMfHx/MmTOnypVgjDH271V4\nhjBr1iyMHTsWXbp0gZGREYCCJqN+/fpVOPJatWph+fLlaN68OTIzM9GyZUt07doV7u7uGuX8/PwQ\nERHxklVgjDH2KlSYEP773//i2rVrUCqVGk1GlUkIDg4OcHBwAACYmZnB3d0dd+7cKZUQiKiqcTPG\nGHvFKkwI586dQ2JiIkQi0b+aUHJyMi5evAhfX1+N70UiEc6cOQNvb29IpVIsWbIEHh4e/2pajDHG\nqq7Cawjt27dHQkLCv5pIZmYm3n//faxYsQJmZmYa/Vq0aIHU1FRcvnwZkyZNQlBQ0L+aFmOMsZdT\n4RlCTEwMmjdvjgYNGqB27doAqnbbaX5+Pvr3749hw4aVubM3NzcXPvfs2RMffvghHj58CGtra41y\n4eHhwmeZTAaZTFap6TPG2JtCLpdDLpe/9PAVJoRDhw699MiJCGPHjoWHhwemTJlSZhmFQgE7OzuI\nRCLEx8eDiEolA0AzITDGGCut5MHy7NmzqzR8hQmhsreYluX06dPYsmULmjVrBh8fHwDAvHnzcPv2\nbQBAcHAwdu/ejVWrVsHQ0BASiQQ7dux46ekxxhh7eRUmhH+jY8eOFb4ILzQ0FKGhodoMgzHGWCXw\no8eMMcYAcEJgjDFWqMKE8Msvv6Bx48awsLCAubk5zM3NYWFhoYvYGGOM6VCF1xA+++wzREZGlnq6\nmDHG2OulwjMEBwcHTgaMMfYGqPAMoVWrVhg0aBCCgoKq/HI7xhhjNUeFCeHJkycwMTHB4cOHNb7n\nhMAYY6+XChPCxo0bdRAGY4wxfSs3ISxcuBDTp0/HpEmTSvUTiUT8u8qMMfaaKTchFL2CumXLlhqv\nviaif/0qbMYYY9VPuQmhT58+AIBRo0bpKhbGGGN6xE8qM8YYA8AJgTHGWCFOCIwxxgBUIiFcu3YN\nnTt3hqenJwDgypUrmDNnjtYDY4wxplsVJoT//Oc/mDdvnvCUspeXF7Zv3671wBhjjOlWhQkhOzsb\nvr6+QrdIJEKtWrUqNfLU1FT4+/vD09MTTZs2LffZhY8++giNGzeGt7c3Ll68WMnQGWOMvUoVPqlc\nt25d3LhxQ+jevXs36tWrV6mR16pVC8uXL0fz5s2RmZmJli1bomvXrhovy4uKisKNGzdw/fp1xMXF\nISQkBLGxsS9RFcYYY/9GhQlh5cqVGD9+PBITE1G/fn00aNAAW7durdTIHRwc4ODgAAAwMzODu7s7\n7ty5o5EQIiIiMHLkSACAr68vHj9+DIVCAXt7+5epD2OMsZdUYUJo2LAhjh49iqysLKjVapibm7/U\nhJKTk3Hx4kWN5icASE9Ph5OTk9Dt6OiItLQ0TgiMMaZjFSaER48eYdOmTUhOToZSqQRQ9XcZZWZm\n4v3338eKFStgZmZWqj8RaXTzqzEYY0z3KkwIAQEBaNeuHZo1awaxWFzldxnl5+ejf//+GDZsGIKC\ngkr1l0qlSE1NFbrT0tIglUpLlQsPDxc+y2QyyGSySsfAGGNvArlcDrlc/tLDV5gQcnNzsWzZspca\nORFh7Nix8PDwwJQpU8osExgYiJUrV2Lw4MGIjY2FlZVVmc1FxRMCY4yx0koeLM+ePbtKw1eYED74\n4AOsWbNWHLvXAAAgAElEQVQGffr0Qe3atYXvra2tKxz56dOnsWXLFjRr1gw+Pj4AgHnz5uH27dsA\ngODgYAQEBCAqKgqNGjWCqakpNmzYUKUKMMYYezUqTAjGxsaYNm0a5s6dC7G44LEFkUiEW7duVTjy\njh07Qq1WV1hu5cqVlQiVMcaYNlWYEJYuXYqbN2/C1tZWF/EwxhjTkwqfVG7cuDFMTEx0EQtjjDE9\nqvAMQSKRoHnz5vD39xeuIfBPaDLG2OunwoQQFBRU6nZRfk6AMcZePxUmBP4JTcYYezOUmxAGDBiA\nXbt2wcvLq1Q/kUiEK1euaDUwxhhjulVuQlixYgUAIDIykl8twRhjb4By7zKqX78+AODHH3+Eq6ur\nxt+PP/6oswAZY4zpRoW3nR4+fLjUd1FRUVoJhjHGmP6U22S0atUq/Pjjj7h586bGdYRnz56hQ4cO\nOgmOMcaY7pSbED744AP07NkTYWFhWLhwoXAdwdzcHDY2NjoLkDHGmG6UmxAsLS1haWmJHTt26DIe\nxhhjelLhNQTGGGNvBk4IjDHGAHBCYIwxVogTAmOMMQBaTghjxoyBvb19ma+/AAp+/9PS0hI+Pj7w\n8fHBnDlztBkOY4yxF6jw5Xb/xujRozFp0iSMGDGi3DJ+fn6IiIjQZhiMMcYqQatnCO+88w7q1Knz\nwjIl35PEGGNMP/R6DUEkEuHMmTPw9vZGQEAAEhIS9BkOY4y90bTaZFSRFi1aIDU1FRKJBNHR0QgK\nCkJSUlKZZcPDw4XPMpkMMplMN0EyxlgNIZfLIZfLX3p4EWm5zSY5ORl9+vTBH3/8UWHZBg0a4Pz5\n87C2ttb4XiQS6b1padSocLi6hus1hqpKTg7Hxo3h+g6DMaYnVd136rXJSKFQCMHGx8eDiEolA8YY\nY7qh1SajIUOG4MSJE8jIyICTkxNmz56N/Px8AEBwcDB2796NVatWwdDQEBKJhN+bxBhjeqTVhLB9\n+/YX9g8NDUVoaKg2Q2CMMVZJ/KQyY4wxAJwQGGOMFeKEwBhjDAAnBMYYY4U4ITDGGAPACYExxlgh\nTgiMMcYAcEJgjDFWiBMCY4wxAJwQGGOMFeKEwBhjDAAnBMYYY4U4ITDGGAPACYExxlghTgiMMcYA\ncEJgjDFWSKsJYcyYMbC3t4eXl1e5ZT766CM0btwY3t7euHjxojbDYYwx9gJaTQijR4/GoUOHyu0f\nFRWFGzdu4Pr161izZg1CQkK0GQ5jjLEX0GpCeOedd1CnTp1y+0dERGDkyJEAAF9fXzx+/BgKhUKb\nITHGGCuHXq8hpKenw8nJSeh2dHREWlqaHiNijLE3l6G+AyAijW6RSFRmufDwcOGzTCaDTCbTYlSM\nMVbzyOVyyOXylx5erwlBKpUiNTVV6E5LS4NUKi2zbPGEwBhjrLSSB8uzZ8+u0vB6bTIKDAzEpk2b\nAACxsbGwsrKCvb29PkNijLE3llbPEIYMGYITJ04gIyMDTk5OmD17NvLz8wEAwcHBCAgIQFRUFBo1\nagRTU1Ns2LBBm+Ewxhh7Aa0mhO3bt1dYZuXKldoMgTHGWCXxk8qMMcYAcEJgjDFWiBMCY4wxAJwQ\nGGOMFeKEwBhjDAAnBMYYY4U4ITDGGAPACYExxlghTgiMMcYAcEJgjDFWiBMCY4wxAJwQGGOMFeKE\nwBhjDAAnBMYYY4U4ITDGGANQDX5TmTHGKhIWthD37uXoO4xKc3AwwYIF0/UdRpVpPSEcOnQIU6ZM\ngUqlwrhx4zB9uuZMksvl6Nu3L9zc3AAA/fv3x5dffqntsBhjNci9ezlwdQ3XdxiVlpwcru8QXopW\nE4JKpcLEiRNx5MgRSKVStG7dGoGBgXB3d9co5+fnh4iICG2GwhhjrAJavYYQHx+PRo0awdXVFbVq\n1cLgwYOxf//+UuWISJthMMYYqwStJoT09HQ4OTkJ3Y6OjkhPT9coIxKJcObMGXh7eyMgIAAJCQna\nDIkxxlg5tNpkJBKJKizTokULpKamQiKRIDo6GkFBQUhKSipVLjw8XPgsk8kgk8leYaSMMVbzyeVy\nyOXylx5eqwlBKpUiNTVV6E5NTYWjo6NGGXNzc+Fzz5498eGHH+Lhw4ewtrbWKFc8ITDGGCut5MHy\n7NmzqzS8VpuMWrVqhevXryM5ORl5eXnYuXMnAgMDNcooFArhGkJ8fDyIqFQyYIwxpn1aPUMwNDTE\nypUr0b17d6hUKowdOxbu7u5YvXo1ACA4OBi7d+/GqlWrYGhoCIlEgh07dmgzJMYYY+XQ+nMIPXv2\nRM+ePTW+Cw4OFj6HhoYiNDRU22EwxhirAL+6gjHGGAB+dQVjr4Wa9moHoOa+3uF1xgmBsddATXu1\nA1BzX+/wOuMmI8YYYwA4ITDGGCvECYExxhgATgiMMcYK8UVl9kbgu3AYqxgnBPZG4LtwGKsYNxkx\nxhgDwGcIrBA3qTDGOCEwANykwhjjJiPGGGOFOCEwxhgDwAmBMcZYIa0mhEOHDuHtt99G48aNsXDh\nwjLLfPTRR2jcuDG8vb1x8eJFbYbDGGPsBbSWEFQqFSZOnIhDhw4hISEB27dvx19//aVRJioqCjdu\n3MD169exZs0ahISEaCucai05Wa7vELTqda7f61w3gOv3ptFaQoiPj0ejRo3g6uqKWrVqYfDgwdi/\nf79GmYiICIwcORIA4Ovri8ePH0OhUGgrpGrrdV8pX+f6vc51A7h+bxqtJYT09HQ4OTkJ3Y6OjkhP\nT6+wTFpamrZCYowx9gJaSwgikahS5YjopYZjjDH2ipGWxMTEUPfu3YXuefPm0YIFCzTKBAcH0/bt\n24Xut956i+7du1dqXN7e3gSA//iP//iP/6rw5+3tXaX9ttaeVG7VqhWuX7+O5ORk1K9fHzt37sT2\n7ds1ygQGBmLlypUYPHgwYmNjYWVlBXt7+1LjunTpkrbCZIwxVkhrCcHQ0BArV65E9+7doVKpMHbs\nWLi7u2P16tUAgODgYAQEBCAqKgqNGjWCqakpNmzYoK1wGGOMVUBEVKIRnzHG2BuJn1RmjDEGgBMC\ne4PdvXsX06dPx82bN/HgwQMAgFqt1nNU/6/kyfvrcjJPRK9NXYqUVaeaWEdOCK+5oh2cUqnUcyTV\nT7169QAAW7duRWhoKC5dugSxWFwtNmQiEm7BvnPnDh49evRa3ZItEonw66+/YtmyZdi2bZu+w3kl\nRCIRzp49i+joaPz9998QiUTV6gCjMjghvKYePnyI9PR0iMViHDp0CJ9//jmWL1+u77CqjaINdeHC\nhZgwYQJkMhl69uyJkydP6n1DVigU+OmnnwAAv/32G/r27Yt3330Xe/fuxdOnT/UW16tQlOguX76M\nSZMmQaFQIDo6GsHBwfoO7aUV1eno0aPo27cvfvnlF7Ru3RoXL16EWCyuUUmBfyDnNZSVlYWlS5fC\n1NQUXl5eCAsLw5QpU7Bw4ULcu3cPc+fOhaHhm7noi47+xWIx8vLyYGRkBDs7O0yYMAG1a9fGkCFD\n8Msvv6Bt27YaR+m6jO/8+fM4c+YMFAoF4uLisHnzZly5cgXr169HVlYWAgMDYWFhodO4XhWRSIQT\nJ05gy5YtWLFiBXr27IkbN25g3rx5mDBhgpAIaxKRSISEhATs3r0bO3bsQKdOneDt7Y3OnTvj2LFj\naN68OdRqNcTi6n/8bRAeHh6u7yDYq2VkZIQnT57g2rVruHjxIt5//32MHz8egwYNwrJly3D9+nXI\nZLIasYJqQ1FzxYYNG5CQkABfX18AgI+PD6ysrPDZZ5+hR48esLGx0WlcRQlIKpXCxMQEFy9ehEKh\nwKeffgpPT0+YmJhg69atICK4ubnB2NhYp/G9rJKJ9fLly5g7dy5cXFzg5+cHS0tLNGvWDFFRUYiK\nikLfvn31GG3VqFQqqFQqLFiwAGfOnMFbb70FLy8vtG3bFqampujXrx969+6N+vXr6zvUSuGE8Boh\nIuFIxN3dHZaWljh16hRu3ryJli1bwsnJCb169cLs2bNx48YNdOvW7bVql65I0Y4pJiYGoaGh6NGj\nB5YuXQqFQoF33nkHBgYGaNGiBXJzc5GSkoI2bdpApVLpJHEWnbmIRCLcuXMHPj4+MDQ0xNmzZ6FQ\nKNCuXTu4u7vDwMAAW7ZsQUBAAMzNzbUe179VvF4pKSkgIjRv3hwdO3bEV199BTc3N7i7u8PKygo+\nPj5o2bJlmQ+nVifF65SdnQ0TExPIZDL8888/SElJgbW1NaRSKXx9fWFhYQFTU1M0bNhQz1FXUpWe\na2bVmlqtJiKiAwcO0OjRo4mI6MiRIzR58mRaunQp/f3330REdO/ePTpz5oy+wtSrxMREGjlyJK1e\nvZqIiNLT06lDhw70+eefU15eHhEVzLP//Oc/Oo2raNlFRUWRm5sbXbt2jbKzs2nv3r304Ycf0rJl\ny4SyZb3epbpSqVREVLBOtm/fngIDA2ns2LF09epVOnHiBDVq1Ih2796tMUzRvKiuiuKLjo6mLl26\n0KhRo+ibb74hIqLp06fT1KlT6dSpUxr1qO51KsIJ4TXz66+/kqenJx08eFD47uDBgzR16lSaO3cu\n3bp1S/i+pqyk/0bJOkZFRVHv3r1pyJAhwry4c+cOeXt706effiqUCw0Npbt37+o01qtXr5Knpyed\nOHFC+C47O5v27dtHo0aNokWLFhHR/+9kq/Pyy8nJET6npKSQh4cHnT9/nv744w/atGkTBQQE0L17\n92jPnj3k6OhICoWiWteHiCg/P1/4HB8fTx4eHhQZGUnnzp2j5s2b06RJk0itVtOHH35IH3/8MT16\n9EiP0b6cN/PK4mvs3LlzCA8PR0BAAJ4/fw5jY2MEBARALBYjIiJC45bK1725qHhdb926BYlEgs6d\nO0MqlWLt2rXYt28f+vXrBxcXF+FWwSIrV67UebxKpRIdO3ZEp06doFQqoVarYWJigi5dukAkEsHN\nzQ0AhCas6rr8FAoFtm/fjrFjxwrNWk5OTmjRogWAgtt9z58/j8OHD2P48OFo27Yt7Ozs9Blyhf75\n5x/h9mQjIyNkZ2ejS5cu6NWrFwDgwoULaNOmDU6fPo2vv/4aCoUCVlZWeo666t7Mq4qvCSrjfvm7\nd+/il19+AQDhomNcXBxkMhnmz58v7FTeBCKRCCKRCNHR0ejVqxemTp2KVq1awdLSEoMGDUJycjK2\nbduGlJQU1KtXD+3bt9fZQ1NlTUcikeDQoUOIjIyEoaEhjIyM8Ouvv+K///0vAgMD0bRpU63H9SrU\nrl0bPXv2RGZmJs6dOwdnZ2colUp88cUXAAAbGxtYW1sjKSkJAFC3bl0A1ftBrnv37qFPnz548OAB\nUlNTYWFhgaNHjwoPNIpEIvj7++PJkyewsbGBh4eHniN+OZwQaqjiG09ycrLw86SffPIJ6tSpIzxz\nEB8fj1GjRuHy5cuwtLTUS6z6dPv2bcyaNQtr167Ftm3bMGjQIAQGBqJJkybo168f0tPTNe4TL0oi\nulB0C+bixYtx7NgxNGzYEMuXL8eyZcuwcuVKREVFYfr06ZBKpTqJ59/Kz89HdnY2rKys4OTkhPnz\n52PdunW4evUqli5diuTkZAwcOBAHDhzAtm3b0LlzZwAQboGujmc8+fn5AIBmzZrB2toaq1atwoIF\nC9C0aVMMHToUrVu3hlwuR2RkJKKiomrkWUFx/HK7GooK75iJiIhAeHg4pFIppFIpJk+ejL///hur\nVq1CdnY2MjIyMGfOHPTp00ffIesElbjFMTMzEyEhIZg7dy6cnZ0BAJMmTYKBgQG+/fZbKBQKvd3V\nEh0djalTp2LKlClYsmQJxo0bh169eiEjIwNLly6Fg4MD+vbti969e+vlmYiqyMvLg1wuh62tLZKS\nkpCSkoJhw4ZhyZIlMDIyQr9+/eDm5oY5c+bAysoKbdq0Qa9evap1vXJzc/H777/D0dERmZmZSEpK\ngr29PX777TcQEebPn4+1a9cKd4IFBwfXiGX1Qjq/asFemd9//51atmxJCoWC1q5dS2ZmZvTxxx9T\ncnIyqdVqunXrFqWkpBBRwQXI6n7R7lVQKpVERPTs2TPKz8+n3NxcCgoKou+//14os2PHDpo+fbq+\nQiS1Wk2pqakUFBRESUlJdPToUWrYsCENGTKEZs6cSc+ePStVviYsu927d1O7du2oQYMGtG/fPiIi\nun//Pk2aNImmTZtGV65c0Shf3ev19OlTOnDgAMlkMqpfvz4lJiYSEdHp06dp2rRpFBYWRg8fPiSi\ngov/RNW/ThXh5xBqsKysLHTp0gW3bt3CsmXLsH//fqxZswZHjhxBmzZt0KhRI41mohp71FIJt2/f\nRl5eHszMzLBv3z5MmDABf/zxBwwMDDBq1CiEhYUhMTER586dw6pVqzBmzBg0adJEZ/FRsXvXRSIR\nLCws0KFDB2RlZWHSpEmIi4uDvb09PvnkExgZGcHb2xu1a9fWGKY6osJrISKRCM7Ozjhz5gxq166N\nbt26wczMDLa2tmjbti0OHjyIP//8E+3atROubVXXehUtq9q1ayM7Oxvz58+Hr68v2rdvj/r168PJ\nyQkWFha4fPky5HI5/Pz8YGRkBLFYXG3rVFmcEGqI4juUR48eQaVSQSqVwtHREatXr0aXLl0QEBCA\n3NxcxMTE4P3334e1tbUwfE1eSStjzpw5mDlzJlq3bo1Vq1Zh9OjRcHJywg8//ABnZ2d8/vnnePDg\nAZ4+fYrx48eje/fuOj+1F4lEuHLlCs6dOwcDAwPUr18f9+7dw5EjRzB+/Hjk5OTgjz/+wMSJE+Hk\n5KSzuP4tsViM3377DZs3b8aiRYsgFouxb98+GBsbw93dHUqlEl5eXvDx8akx9RKJRPjtt99gbW2N\nUaNGoW7duti9ezcMDQ3RuHFjGBkZwcjICD179oS9vf1r89Q/33Zag4hEIuzfvx8///wznjx5gg8+\n+ACdO3dGq1atsG7dOuTn52Pnzp1YtmwZGjVqpO9wdaLoyezFixdDrVZj0KBBGDZsGAYPHoycnBzY\n2Nhg0aJFyMjIwLhx44ThSMeXzkQiEfbt24eZM2fCzc0NJiYmaNKkCYKDg+Hg4IAuXbogNTUV3377\nLZo2bVpj2qGL7uL65JNPsHz5cpiammL06NHIyclBZGQkzp49i3Xr1uH48eM15i6pojpNnjwZ33//\nPbp37w4LCws8fPgQe/fuRWxsLC5duoQVK1agQYMG+g731dJfaxWrqsTERPL09KRLly7Rnj176Isv\nvqCvv/6a4uPj6ccff6SAgAA6cOAAEdX8tszKyMzMpD///JOIiOLi4ujp06cUFhZG7u7uwtO8ubm5\nFBUVRTKZjJKTk4WHunSh+DJ49uwZDR48mC5cuEBERCdOnKCwsDDatGkT3b9/n7Zt2yY8PV6Tll1e\nXh5NnjyZoqOjiYjo+fPnQr/o6Ghavnw5HTp0SF/hvZTMzEzq1q0bHT16lIj+/wHAv//+m/73v/9R\n7969hWskrxtOCNVc0cp4584dio6Opp49ewr94uLiqHPnzhQXF0dE//90aE3aofwbt2/fpjFjxlBo\naChJpVLhouWECROoffv2pFAoiKggKdy/f1+nsRWf/6dPn6bo6Ghq164dbdu2jYgKnnpdsmQJTZgw\nodRw1XnZlRXb8OHDS12kv3z5ssbTytW5XkVxFf1//PgxyWQy4SJy0QXjjIwMIipYn4rKV9c6vazX\no+HrNaVWqyESiXDmzBkMHToULi4uMDY2xq5duwAAbdq0gaenJ65evQoAqFWrljBsTWhu+DfUajWc\nnJzQrVs3rF+/Hh988AG8vLwAAKtWrYK3tze6du2Kf/75B0ZGRrC1tQWg+6aia9euYdq0aWjWrBk+\n/fRTHDlyBCdOnIChoSFatmyJhw8f4unTp8KzEDXlomRKSgoSEhIAAGPGjEF+fj72798PADh79iwm\nTJiA69evC+VrQr0UCgUAwNLSEh06dEBYWBgePnwIExMTnDx5Er1798Y///yj8dxEda9TVfFF5WpM\nJBLhyJEjWLduHUJCQtCuXTtkZGTg6tWrOHbsGAwMDLB48WKEhITA0dGx2r/S4FUSiUQ4duwYYmNj\n8cUXX2DPnj3Izc2Fq6srTExM0KtXL9y8eRN2dnbC8wdFw+kqvsuXL2PgwIHo3bs3AgMDUbt2bWRl\nZeHrr79GUlISFi5ciLCwMHh5edWIZUaF1zUiIyMxcuRI7Nq1C7dv30afPn1w9+5d7NixAzt27MDP\nP/+M2bNno1OnTvoOuUJFdYqKisJ//vMf/Prrr6hTpw78/f3xzz//YOrUqcjJycHcuXMRHh6OFi1a\n1Ihl9dL0fIbCSih5Crpx40YSiUS0Zs0aIiJSKBTC2zjHjRuncc3gTXPq1Cnq1q0bERW8odTPz4+2\nbt1K27Zto/fff194e6mu5k1ZTQhDhw6lFi1aCM8W5OXl0YULF2jv3r109uxZncb3Kvz111/Up08f\nSkxMpEePHlG7du3o66+/pszMTHrw4AHFxMQITS01pUklLi6O+vbtSzExMbRgwQIKCQmhrVu3UnZ2\nNu3atYt++eUXOnnyJBHVnDq9LE4I1UzRypaeni60wW7fvp1q165Np0+f1ijzujwMU1kl65iRkUEj\nR46kc+fOEVHBm16HDx9O7777Lu3YsUNv8cXExNDOnTvp6tWrREQ0ZswY6tGjh7C8Sg5T3Zdd8bb1\n4OBgatmyJd28eZOICq5tderUiT766KNyh6tuil8z+OeffyggIID69u0r9P/pp58oODiYNm/erPGQ\nYE1YVv8WJ4RqpGhli4yMpDZt2lC3bt3om2++oYcPH9KuXbvIxsZGOFJ5kxTfCM+fP0/9+/env/76\ni5RKJa1bt478/PyE5Pno0SPh4p8uN96iaZ08eZKaNGlCAwcOpEGDBtG0adOIiGj06NEkk8nKTAo1\nwaVLl+jZs2d0/vx5Gjp0KC1evJiSk5OJqCAp+Pr60l9//aXnKKum6KaDrVu3UpMmTWjdunVCv+++\n+47GjBlD6enp+gpPLzghVDOxsbHUs2dPunDhAkVHR9PChQtpwoQJpFar6aeffiKJREKPHj3S6e2T\n+lT8qCwpKYmysrJo4sSJ9Omnn1KfPn3o+PHjNGjQIOEOI33+KMmZM2eoe/fuwhlLYmIihYSE0A8/\n/EBERIGBgUIzUU1QNP9yc3NpypQp1KtXL3r27BnFxMTQxIkTadmyZcJvShTdeVMTKJVKun//PpmY\nmNDOnTuJiGjPnj3Uu3dvWr9+vVCu6LUvbxJOCNXIw4cPaeDAgdSiRQvhuz/++IOGDBlCR44cISIS\njsreFEU7pYMHD5Kvry9du3aNiAreM7Nx40Z67733yMrKisaNG6e32Ips3bqVRCKRcKSZk5ND27dv\np+Dg4BcOV91kZmZq/BgMUUET5qeffkoDBgygZ8+eUWxsLI0dO5YWLVpE2dnZwjukqmvdiq4nEf3/\nDwzt27ePrK2tae/evUREtHfvXvL396e1a9fqJcbqgBOCHpXVJnnkyBFq1qwZzZ49W/hu4sSJNH/+\nfCL6/19tqq4bnjb89ddf9PbbbwvXUIp7/PgxXb16lWQymfDQly4UX3b3798XmoI2bNhAbm5uQgKP\njo6mjh07UkZGhrDTrM6uXr1KISEhpFAo6OTJk7RixQqh3927d+njjz+mESNGUFZWFp0+fVp4MLA6\nu3r1Kn355ZdERJSQkECHDx8WlldUVBTVrl1beNBs9+7dFB8fr7dY9Y0Tgh4V7VCOHDlC8+bNo7Vr\n11JGRgbJ5XLq378/jRo1ik6cOEGenp7CU5NvgtTUVNq8ebPQffLkSRowYIDQXVZSHDFihE7nUdG0\nIyIiyM/Pj9555x1as2YNXbt2jXbu3EkSiYTGjRtHQUFBwhFodZednU1dunQRmk2OHTtG9vb2tHLl\nSiIqaGo5duwYNW3alAYNGlQjmi2fPHlCfn5+dPbsWXr69ClNmTKFxowZQ0ePHqWsrCwiIlq+fDmJ\nRCKKiooShnuTDriK4wfT9IQK73/+/fffMWHCBJiammLt2rX47rvvUKtWLUyaNAmxsbGYMWMG1q1b\nh3fffRdKpVLfYesEEWHz5s24fPkyAMDNzQ0PHjzA4cOHART8oMqxY8ewcOFCEBFu3ryJmzdv6vSH\nZEQiEc6fP4+lS5dixYoVmDRpElJSUrBjxw706tULK1aswO+//46AgAAEBQVBpVJV618EAwATExMM\nHToU69evh1Qqhb+/Pw4ePIjly5fjhx9+gIGBAWrXro3OnTtj+vTpNeKFbiqVCtnZ2di+fTs++ugj\nfPzxx3B2dsYvv/yCmJgYAED79u3Rr18/jfq81s8avIh+89GbLTExkYYMGSI8Y5Cenk5TpkyhsLAw\nIiKSy+U0YsQIWrBggT7D1KmiZpUVK1bQrl27iKjgesGSJUto2rRptGDBApLL5eTp6UmHDx8Whnvw\n4IFO47x79y6NHj2a2rdvL3x3+vRp6tKlC8XGxhJRwTUFqVRKJ06c0GlsL6P4tRpjY2Py8/OjzMxM\nIir4QflmzZrR2LFjyc7OTnhvUXU/ii6Kb+XKlWRoaCi8JiQvL49mzpxJY8eOpbFjx1Ljxo1r5DMh\n2sBPKusQFZ4VFL2S4uTJkzhx4gTS0tLQvn17SKVSeHt7Y+bMmQgMDMTbb78NS0tLHDt2DB07doRE\nItF3FbSu6Cjt7t27+Pbbb+Hv7w97e3s4ODhAIpHg4MGDuH79OkJCQhAQEAClUgmxWAwTExOtxkXF\nXj9e1E1EiImJQXZ2Nnx9feHk5ISYmBioVCq0bt0aXl5eqF+/Pt5++22NV5FXR0X1srGxgUwmg7W1\nNVasWIGWLVvCy8sLPXr0wNtvv43hw4ejU6dONeJtrEXx3b17F127dsXy5ctRu3ZtdOjQAZ06dYJE\nIoGpqSmGDh2Kd955R2OYNxX/hKaOFN+hpKenC80bp0+fxpYtW9C4cWMMHjwYWVlZGDBgAA4ePAip\nVG+AZkAAAB1rSURBVIq8vDwolco3IhmUNGvWLGzYsAHx8fFwcHAQvn/+/DmMjY1L7aS1pfh0Tp06\nhZycHNSuXRudOnXC7t27cfDgQUgkEgwaNAjjxo3D2rVr4efnp9WYXpXiO3aVSgUDAwMABe8qWr9+\nPa5du4Y5c+ZovE5dV/P9VTt37hy6du2Kb775BhMnTtToV1Pr9Mrp5bzkDVT8lLxVq1Y0Y8YM+uKL\nL4QLdUFBQdSqVSvq0qULHTx4UGOYN4larda4WPnZZ5/RW2+9RRcuXNBoFtLHvDlw4AB5enrS6tWr\nqWnTpsLF1z179pC3tzd1796djh07RkRU6rbN6uzy5cvC5+J3Qt2+fZvCwsLovffeo+zs7Bq1Pqam\nptKTJ0+EmIvqdeHCBTIwMNC4e4r9P24y0pGio8spU6Zg27ZtuHTpEvbs2YNLly4hNDQUbm5uuHfv\nHlq1aoURI0a8MS+qK2o+K2r6Kapv0Q/fdO3aFUqlEvv370diYiIUCgWaNm2q8/mSkpKCTz75BP/7\n3/+gUCgQHx+PY8eOgYgwatQo2NraIjMzEwYGBmjVqlWNuOBKhWcHgwcPRlJSEjp37qwRt6WlJZo0\naSI029WEdZGIoFAoMHXqVLRv3x516tSBWq2GgYEBVCoV6tevj169esHU1BQNGzbUd7jVDicEHVGp\nVEhISMC4ceOQnp6OtWvXYvXq1YiKisLx48cRHBwMQ0NDnD59GgqFAs2bNxdO319HDx8+xMOHD2Fp\naYlDhw5h3bp1wm/uikQiiMViqFQqiMVitG3bFu7u7rCxscGmTZvQtWtXrV8zKEkkEqFbt27IyMhA\nWFgYTpw4AScnJ0ycOBHm5uYYOnQoHj16hKtXr6JNmzY6j68qihJB0Q6+WbNmOHv2LHx9fWFsbKyx\n47e0tISNjY2+Qq0ykUgEMzMzHD9+HAcPHkRQUJCwHRWtU1KpFA0bNqwR10F0jROCjojFYjg7Ows/\n6Tht2jR07NgRZ86cQXJyMtq0aYMOHTpALBbj3XffhYWFhb5D1pqsrCwsWrQICQkJePz4MT777DP0\n6tULy5cvR3p6Ovz9/SEWiyEWi4UzCFtbWzRo0AD9+/fX6fWUop2GsbExrK2tcf78eVhaWqJHjx74\n+++/YWtri3feeQeNGzdGw4YN4efnBysrK53F9zKKbnd+/vw5xGIx6v9fe3ca1tSZ9gH8H0CpEZei\nFUG8BJFLKipQFFlUVERxgVarjLhQbBFFBYUyoi1DtVOnrSwK0xYVF1xaWVoVcUGEBKhQUKQjmyyj\nogUFRcGwB5L7/YA5Bev0bWeQJPD8PhHIubjPSXLuPNv96OggIiICY8aMUepvzb/88guqq6sxbNgw\nWFtb49q1azAzM8OgQYO49xGbWvr7FL9dq4TohXF62WN1dXUQEUQiEfLz8yEUCpGXl4fw8HBMmDAB\nAODo6NhlALU3GjhwIMzNzfHkyROcOXMGW7Zswbp165CRkYGffvoJAQEB3JqLF7teeqIrpvPrx+Px\nujyWSqXIzMzE3//+d3h6esLZ2Rlz5syBRCKBhoaGwiZyej4rSkYoFMLf3x9eXl5IS0uDi4sL9u7d\ni2fPnskxyj+n8/mIRCJ89NFH+Oyzz+Dn54e2tjaUlpbi/PnzAHrmfdMbsFlG3Yw6zVYoKCiApqYm\ndHR0ujwnNTUVoaGhaGpqgoeHB5ydnblje/O3FiLi+nMBICsrC2FhYZBIJPjiiy8wduxYPHr0CA4O\nDpg9ezaCg4Pldj1ycnJw7Ngx/POf//zN6xITE4Pa2lro6enBwcFBKV43WYx5eXno168fdHR0uCnN\nn332GQwMDJCQkICrV69i3Lhx3BiOIpOd08OHDzF48GDweDzU19djy5YtmDhxIs6ePQuJRILY2FgY\nGhrKO1zl0IMD2H1C55IGM2bM4PY7lpHNoGloaOBqrfeFOutEv16bhIQEWrt2LRF1lO3YsmULhYSE\n0N27d4mIqKqqittwvid1nt109erV3xSle1ktImV47WTxXb58mbS1tcnV1ZV0dXW5Uh9VVVVUVFRE\nTk5O5OjoKM9Q/5DO1zw+Pp5MTU1p0qRJ9Ne//pXbp+H+/ft0+PBhmj17NreAUdFfJ0XAEsIrUFZW\nRmZmZi8tdfyyG0hfeqNevnyZjI2Nuam1RB1TcX19fWn37t1cOWWinrsunfcoKCsro6ysLCooKKA5\nc+bQ06dPuzxXmaaTdnbz5k3auHEjt2r6+PHjpK+v/5vEu2rVKqqrq5NHiH9aYWEh2dnZUVFREf3y\nyy/cKn+RSMQ957vvvqNFixZRS0uLHCNVHordJlQS5eXl8PLy4h7X1NRg+PDhmDJlCgBw/eGNjY0v\n3Zhb0bsbulNOTg527tyJhQsXoqWlBQCwcOFC2Nvbo6Ki4jf9969aXV0dtm/fjtraWohEIgQFBcHD\nwwPBwcEQCoX44osvEBsbi9TUVEilUm6DdUUnu44SiQRisRg7d+5ESkoKGhoa0N7ejjVr1mDjxo0I\nCwuDVCoFACQlJSErKwttbW3yDP0/qqqqwu7duyGVSlFTU4PQ0FA8evQIQ4cOha6uLvz8/CAUCnHq\n1CnumEGDBqG+vp47R+b3sVlG3WDo0KHQ0tJCS0sLXn/9dWhqaiIpKQmvv/46dHV10a9fP6Snp+Pk\nyZOwsrKCqqpqn0gC9JK+9djYWNy4cQPLli3jbq7Z2dmwtLTErFmzoK2t3aMxtrS0YMqUKWhubsaD\nBw+wbt06eHp6YubMmcjNzYWhoSF+/PFHCAQCjB07FqNHj+7R+P4XPB4PjY2N4PP5mD9/PvLy8lBV\nVQVjY2MMGTIET548QWlpKZYsWQIej4fm5masW7fuN2NeiuLx48cwMjKCWCzGsGHDoKmpibKyMtTV\n1WHMmDEYNWoUWltbUVdXBxsbG0gkElRWVsLFxaXH31dKS84tFKUmlUq7dCFYW1vTjBkziKijOJu3\ntzdt376dzp49S+PGjetSjK2369w1dvfuXSoqKuJ+9vT0pNDQUCLq2ODcyMiIKwjXk/HJ3L9/n06c\nOEEzZ84koVBIRB3jBatXr6aTJ0/+x+MUXUJCAllaWtInn3xCV69epfr6elq2bBnNnz+fAgICaOrU\nqXT69Gl5h/n/6nzNxWIxffDBB7R27Vpqa2uj5ORk8vT0pGXLllFUVBSNGzeOEhMT5RitcmNdRv8l\net4kV1NTQ3FxMYCOukQqKipwdnaGt7c3HB0d0dLSgqSkJISFhcHe3l7hSyB3Jx6Ph3PnzmHp0qXY\ntm0bNmzYgObmZixevBgCgQB2dnZYt24d9uzZg2nTpsklxqSkJHh6esLMzAwuLi4IDg5GWloaVFVV\nMXfuXFRUVMglrv8GdZpaWllZiePHj2Pz5s0YPHgwjh49ioyMDBw/fhxaWlrIzc1FaGgolixZwh2r\niDrHVVhYCBUVFfj4+IDP58PHxwe2trZYuXIlGhsbkZSUhJCQEMyfPx8SiUSOUSsxeWYjZda5NpGB\ngQG3jy4RkY2NDS1dupR7LBvQUoYZKd3pxx9/JHNzc6qurqbIyEjS0NAgHx8fKi8vJ6lUSnfu3OH2\nre3JayP7PyUlJbRw4UJuJlh1dTVFRESQk5MTXb16lXJycrjaRMpAdl45OTl06NAh8vf3J6KOUt1R\nUVHk7u5O8fHx1NTURM7OzrRlyxaqrq5W6PekLLZLly6Rvr4+5eXlUXt7OxUVFdGGDRtoy5YtJBaL\nKSUlhXx8fCg0NJQePXok56iVF0sI/4MbN27Q+PHj6eeffyaijv2OZTNWpk2bRnZ2dkRESrGz1KtQ\nVFREWVlZdPHiRbKwsKC8vDyysbGhBQsWcHsjy/TETamlpYVLzvfv36fAwECaMGECHT58mHvOo0eP\naN++fTRv3jxuRy1FvmHKyGIUCAQ0evRocnNzIz6fT/n5+UTUcV4HDx4kV1dXam5upocPH9KqVauo\nqqpKnmH/ISUlJTRx4kRKT0/nfieVSqmoqIjee+898vT0JCKiEydOkL+/f4/vjdGbsIVpfwJR1xK5\neXl5iI2Nxfjx41FZWYmYmBgYGhpix44dMDMzQ2ZmJqytreUZco/pfG1qa2vRr18/aGhoAAD8/Pxg\naGiI9evXIyIiAlFRUfj222+7lFR+1drb25GRkYG7d+9CQ0MDhYWFWLJkCeLj41FXVwdHR0fMmjUL\nQMfgZVNTE8aMGdNj8XWH4uJi+Pj4ICAgADY2Nvj0008RFxeH6OhoGBsb49GjRxCLxdDV1QXQtdy1\nIqEXJiOUlpbi888/x9GjRyGRSCCRSNC/f3+0t7fj7t27aGpqgomJCQCgvr4egwYNklfoSo/NMvqT\neDwekpKSUFZWBn19faSnp0MoFGLWrFnYvHkzysvLIRaL8dZbb2H06NF9qs46j8dDfHw8AgMDceTI\nEYjFYq6uz8mTJyESiRAdHY2goCCYmpr2aGwqKipoaGhAUFAQoqKisHHjRkyfPh06OjooKSlBSUkJ\niAgGBgYYOHAgF/eLNydF0zk+gUCAhIQEEBHs7e1ha2uL2tpa+Pr6wt7eHvr6+lxpDSJSyJXInT8v\nt27dQmNjIzQ0NBAYGAgtLS1MnjwZqqqqSEpKQmxsLN555x2MHDmSK4Sorq4u5zNQbiwh/AmyG972\n7dsxe/ZsTJkyBba2tlixYgVMTExQVVWFkJAQuLi4QE9PjztGkW8o3YXH46GkpATr16/HV199hfHj\nx6O4uBi3bt2ChYUFhg4diosXL2Lr1q2YO3euXDa3GTJkCE6fPg1dXV3w+XwYGRlBV1cXBgYGuH79\nOu7cuQMzM7MuxfMU/bWTlVWPiYmBh4cHtLW18a9//QsPHz7ElClTMHPmTDx79gwjR47s0uJR5POS\nTUbYvHkz5syZg/Hjx8PAwAARERG4d+8eRCIRPv74Yzg7O8PIyAgAq1XUbeTRT6Wsnj59SrNnz6bi\n4mKSSCSUk5NDJ06coKamJhIIBGRtbU1nzpwhIuXod+4OsvN88OABXbp0iRYsWMD9LTs7m+zs7LhB\n2+bmZu6Ynrg+nf/PgwcPuN8VFBTQxo0b6W9/+xsRdezZHBcXR6Wlpa88plehoKCARo8eTSEhIURE\nFBsbSx4eHrRv374uz1OW92Rubi6ZmJhw40wPHz6k69evU2FhITk7O5OXlxedP3+eiJTnnJSFciy7\nlBN6obugvb0dPB4PcXFxKC4uhqqqKgQCAerq6uDq6orDhw/DyMhIYafwdTdZAbTMzEwEBATg66+/\nxmuvvYa4uDgsX74cFhYWMDY25vYI6NevH3dsT31D5fF4uHDhAnbt2gVra2v0798fe/bswZo1a3Di\nxAksXboUBQUFiIuLU7oCaCKRCHw+H8bGxkhMTMTy5ctBRPjwww/R1taGK1eu4N69e1zLQJFbBZ29\n9tprMDExgUAgQGxsLIRCIQDA398fMTEx3PP6yuesJ7Euo/+AOnU1lJSUQEVFBcOHD4eenh4KCwux\nbNky+Pr6YsKECUhMTMS7774LLS0t7nhl+fD9L3g8HpKTk3Ho0CF4enrCysoKNTU1KCwshEAggKqq\nKoKCguDp6QldXd0e3wWOx+MhLS0NPj4++Pbbb1FRUYGIiAgUFhbCy8sLJiYmaG5uhqurK2xsbHok\npu5ARLh9+zbc3d1haGiIkSNHQktLC7a2tvDz8wMAuLu7Y9q0adwAsjLh8/morq7GyZMn8c4778DN\nzQ18Ph9tbW3c4DHQd7pje5Q8myeKTFbZ8ty5c2Rubk5bt24lb2/vLsXXEhMTacKECV0KtfV2LzbR\no6KiiMfj0cGDB4moYy5/cnIyrVu3jtzd3SkhIeGlx/UEiURCV65cofz8fEpMTCQLCwsqLCykqVOn\n0po1a7o8V9HXiLwsvsDAQHJycqLr169Ta2srERF5enqStrY2lZeXyyPMbiWbInzt2jWaOHEiXbly\nRc4R9X4sIbxAVpKaqKMP3MzMjCoqKujjjz+mSZMm0erVqyknJ4caGhpowYIFcr3hyYPsPCsrK7kx\ngVOnTpG6ujplZGR0eY5sTUZP3mxlaz5aWlq6xLF69WrutfLz8+uyfkQZyM5FKBRSeHg4VwokJCSE\nHB0dKSkpiRISEmjNmjV069YteYbabdrb2+n69es0depUOnv2LBH1nc+ZvLAuo05qa2uxZ88eVFdX\nY9KkSaioqMDSpUtRXl6OiIgIhIeHIzc3F0lJSbCyssL777+PiRMn9pmppfR8TOXChQvYuHEjzp49\ni3v37sHFxQVmZmZYtWoVrKysuD5r2ZhBTzbteTwezpw5g23btiE7Oxt8Ph+GhoZISkrCgAED8ODB\nAyQmJuL48eMwNjZW+GmlwK/XPSsrCx4eHmhqasK1a9fw5MkTbNq0Cc+ePUNKSgqOHTsGT09PzJgx\no8txykpFRQVDhw6Fg4MDrKys+sznTJ7YoHInqqqq4PP5yMnJgYaGBpycnAB0DGbt27cPM2fOxKVL\nl1BdXc3Nj5bpC29SHo+H7OxsfP3119i/fz+qq6uRl5eHjz76CN988w2ePHkCBwcHVFZWYvDgwT02\nFZBeWBR39OhRuLq6QiQSYevWrTh48CDc3Nywf/9+lJaWwtfXV6kGkGXXfefOnYiOjsbkyZNx6tQp\nZGZmIjIyEu7u7lBTU+PKrssSQW94T/L5fIwdO5Z73BvOSaHJr3GiOKRSKTdm0NDQQOHh4eTt7U0/\n/PADERFt2LCB7OzsKCUlhYyNjbm6RX2t+fr06VNydnamt956i/tdfn4+ubi4UHJyMhGRXPquZa9D\nVlYWffXVV7Rz507ub1FRUWRqako//fQTERE9e/aMO0aZXr/Lly+TqqoqBQUFEVHHRj3R0dHk7u5O\ne/fupfb2dq67TJnOi1EsrMvoORUVFQgEAty5cwdLlizB7du3cfPmTaipqcHb2xtpaWnIzs7G5s2b\nYWdnp/TN8T+CXmiiDxgwAJqamrh06RIeP34MW1tbjBgxAqmpqaivr8f06dOhoaEBFRWVHrs+sv+T\nkZGB9957D0+ePMHPP/8MQ0NDjBo1Cubm5lBTU4O/vz9WrFiBIUOGcHEp0+tnYGAAExMTBAcHQ1NT\nEyYmJnjzzTfR2NgIGxsbaGlpKeV5MQpGvvlIcZw7d45MTU3p0qVLRERUV1dHoaGh5OXlRRcvXiSi\nvle1VHaOycnJ9I9//IMiIyOppqaGUlNT6d133yU3NzdKS0sjY2Njbn9eecjKyqK5c+fSzZs3iYgo\nICCANm3aREKhkMRiMRERVVRUyC2+7nT+/HkyMzOjqKgoeYfC9EIsIVDHStW3336b61aQ3UTq6uro\nyy+/pA0bNihFVcjuJEsG6enpNG7cOAoLCyMLCwsKDAykjIwMSk1NJSMjI7K2tuaum7z2G758+TKp\nqKhwK3VbW1spMDCQ3NzcKCUlpUvy7g2J/OzZs/Tmm29SZWUl19XJMN2BFQBBR3dRTU0NRCIRgF+b\n3GKxGL6+vti+fXuXRWd9gWxBXkREBLZt2wZvb2+cOXMGIpEICQkJsLW1xf79+zFu3DikpaUBgNz2\nG543bx5Onz6NQ4cO4bvvvkP//v0REBAAbW1tjBgxoksXSm/oTnn77beRlpYGHR0dhaxWyigvNoYA\noH///mhoaEBpaSlGjBgBLS0tZGRkwNvbG/PmzVPK1Z7/DXreHy+VSsHj8ZCeno60tDRUVFTA2toa\no0aNgomJCQIDA+Hk5AQjIyMMGTIEAoEA06dP71IUrqcZGRlBT08Pu3fvhrq6OszNzTFnzpxem8gH\nDhwIQPmnljKKhe2H8FxlZSUOHDgAoVAIGxsbxMXFITw8HIsWLZJ3aD2COg0gV1ZWYtSoUQA6tgU9\nefIkDA0NsWLFCjQ2NmL58uW4cOECRo0aBbFYjPb2drkmg87i4+OxY8cOJCcnQ0tLi32DZpg/gSWE\nTpqampCdnY3q6mro6enB0tKyzyyGkX3TvHjxIj755BPY29tDRUUFu3btQnp6OsLDw1FRUYGhQ4fC\nx8cHCxcuVNhvp48fP8Ybb7wh7zAYRumwhWmd8Pl8zJ49m3vcV5IB8GtdfX9/f8TGxuLYsWM4ffo0\nHjx4gAMHDmDAgAE4cuQIDAwMMH/+fHmH+7tkyUBRExbDKCo2qPw7estqzz9CIpFwO5pVVFQgOTkZ\nR48eRVVVFTw8PGBubg4nJyeUlpbi0KFDXClwRabo8TGMomEtBAZAR9kOOzs78Hg87N27FyEhIbCy\nsoK+vj7KyspQVlaGxYsXg4gwdepUuc0oYhjm1WGf6j7oxa4U2WN1dXW0trZCJBIhPz8fUqkUeXl5\niIyM5LYqdHR0lFfYDMO8YmxQuY/pPC5SUFAATU1N6OjodHlOamoqQkND0dTUBA8PDzg7O3PHsm4Y\nhum9WELoY2Q39YSEBAQFBSE4OBgWFhbc32XbYjY2NoKIoKGh0acG1xmmL2MJoQ/697//DWdnZxw8\neBBTpkzp8reX3fxZy4Bh+gY2y6gPKC8vh5eXF/dYVjdflgza29sBAI2NjS+dWcWSAcP0DSwh9AF6\nenpwc3PDnTt3AACTJ0+GpqYmUlJSIBaLoaamhvT0dOzZswctLS1gjUaG6ZtYl1EvRkSQSCTcFFEb\nGxuoqqpyK49v374NPp8PS0tL+Pn54ZtvvoG9vb2co2YYRl5YQuilOo8FFBcXc9NGZ82ahREjRiA2\nNhbJycm4cOECxGIxFi1apNDlKBiGefVYQuilOtcm8vb2RkxMDMzNzQEA06dPh5aWFn744QcAQGtr\nK9TV1dlsIobp41hC6MVyc3OxcuVKREdHw9TUFPfu3cOIESMwYMAAWFpaQkNDA8nJydxUU4Zh+ja2\nUrkXefEbvpqaGpYtW4b8/HwkJiYiJiYGhoaG2LFjB7KyspCZmQkALBkwDAOAzTLqdXg8HpKSkpCY\nmIjhw4ejubkZp06dgr6+PqKjo6Gvr4/c3FwAgLW1NahjG1U5R80wjCJgCaEX4fF4iI+Px4cffoi2\ntjbo6Ohg9+7dOHPmDP7yl7+gra0NV65cgYGBQZdj2JgBwzAASwi9Sm1tLcLCwvD9999j0aJFuHHj\nBr7//ntIpVIIhUKsX78egYGBmDVrFmsVMAzzG2wMQYm9OEVUtkdBXFwciouLoaqqCoFAgLq6Ori6\nuuLw4cMwMjJiyYBhmJdiLQQl1fmmXlJSgqdPn+KNN95AYGAg6uvrsXbtWhw7dgyRkZG4du0aBgwY\nwK1FANjUUoZhfotNO1VSEokEqqqqSEhIwK5duzBjxgxIpVJs3boV+vr6AIDLly/D19cXQUFBWLhw\noZwjZhhG0bEWgpJpaGgA0LHD2bVr1/DJJ58gPj4eAwcOhFAoRGBgIG7cuIHGxkaEhYXhyy+/5FYg\nMwzD/B7WQlAitbW1CA4OhrGxMVauXIns7Gz0798fjx8/xvbt27Fv3z5ERkZCJBIhODgY2trabD8D\nhmH+MNZCUCKqqqrg8/nIycnBuXPnMG3aNJiZmSElJQX79u3DzJkzoauri2HDhqGxsREaGhrcsSwZ\nMAzz/2EJQQnIqpYOHjyYGyNISUnB6dOnAQAikQiffvopBAIBEhISsGnTJpiamrKWAcMwfwrrMlIC\nsumlAoEAra2tsLW1xYEDB1BeXo7FixfD3t4eH3zwAZqamrB8+XIsXbqUVS1lGOZPYwlBSSQkJCAw\nMBCff/45HBwc8OzZMxw5cgR3797FggULsGDBAla1lGGY/wnrMlIC9fX1OHz4MCIiIuDg4IC2tjYM\nGTIE77//PnR1dXHu3DlUV1dDXV0dACtHwTDMf4etVFYCKioqqKmpgUgkAvDrN3+xWAxfX19UVlZC\nS0tLniEyDNMLsBaCEhg4cCCcnZ2RmZmJoqIiqKmpISMjA6tWrcLjx48xZswYeYfIMEwvwMYQlERl\nZSUOHDgAoVAIGxsbxMXFITw8HIsWLZJ3aAzD9BIsISiRpqYmZGdno7q6Gnp6erC0tGQDyAzDdBuW\nEJQYSwYMw3QnNqisxFgiYBimO7FBZYZhGAYASwgMwzDMcywhMAzDMABYQmAYhmGeYwmBYRiGAcAS\nAsMwDPMcSwgMwzAMAOD/AFCftMrEW+2BAAAAAElFTkSuQmCC\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x105a7fe10>"
|
|
]
|
|
},
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAbwAAAFhCAYAAAALEB8uAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdYFNfXB/Dv0HvvSBFLbKhoVMQCBAt2xdiiGMXYEo2G\nFImxkGjsxhKNURNrLLEiYo0i6M+GGkuQCDZQkSKCUgV2Oe8fvjthAbvMIns+z+MjW+7cM3fKmTsz\nd1YgIgJjjDFWzWmoOgDGGGNMCpzwGGOMqQVOeIwxxtQCJzzGGGNqgRMeY4wxtcAJjzHGmFqQNOGl\npaWhffv2MDExwddffy1l1e+krl27YuPGjaoOo8pydXXF0aNHJatPQ0MDt27dqtQ6hg0bhqlTp1ba\n9I2NjZGYmPhKZaKiouDk5FQ5AVVzjRo1wvHjx9/6dBMTE6GhoYGSkpK3Pm1VGzt2LGbOnFkp09Z6\n0RdcXV2Rnp4OTU1NGBoaokuXLli2bBkMDQ1fubJVq1bBxsYG2dnZrxWsutm/f7+qQ6jSBEGAIAgV\nfjZs2DA4OTlhxowZrzVtHx8fBAYGYsSIEW8S4it73jy9DTk5OZU27TfxpsurqoqNjVV1CJJ61eW4\nbt06/P777zhx4oT43ooVKyorvBf38ARBQEREBHJycvD333/j/Pnzr5x9iQglJSVISkpC/fr1XytQ\nmUz2WuXYu6GqLd/KTDovws+CqJqq2jrKXgO9gKurKx09elR8/dVXX1H37t2JiOj06dPUunVrMjMz\noyZNmlBUVJT4PW9vb/ruu++oTZs2pK+vT0OGDCFtbW3S0dEhIyMjOnr0KBUWFtKECRPIwcGBHBwc\naOLEiVRYWEhERMeOHSNHR0eaO3cu2dnZUWBgIIWGhtKHH35IQ4YMIWNjY3J3d6eEhASaNWsW2djY\nkLOzMx0+fFiMYc2aNVS/fn0yNjYmNzc3WrlypfiZYvoLFy4kGxsbsre3p7Vr14qf5+fnU3BwMLm4\nuJCpqSm1bduWCgoKXjjfZV24cIGaNm1KxsbG1K9fP+rfvz9NmTKFiIgyMzOpW7duZG1tTebm5tS9\ne3e6d++eUhv+9ttvRES0du1aatOmDX311Vdkbm5ONWvWpAMHDjyz3jt37lCfPn3I2tqaLC0tady4\ncUREJJfLacaMGeTi4kI2NjY0dOhQevz4MRER3b59mwRBoLVr15KTkxNZWFjQihUrKCYmhtzd3cnM\nzEycjiImLy8vGjduHJmamlK9evWU1pWXaX/F8h06dCiVlJTQ7NmzqVatWmRpaUn9+/enzMxMscyG\nDRvI2dmZLC0t6ccffyy3biqsXLlSaV3r2bMnERHFxcWRt7c3mZmZUcOGDSk8PLzCtps8eTJpamqS\nnp4eGRkZ0fjx44mISBAE+vXXX6lOnTpkZmZGn332mVK533//nerXr0/m5ubUuXNnSkpKeubyOXHi\nhLgOOTk50fr164mIaNiwYS+9fqxdu5bc3NzI2NiYatasSZs2bSIiouvXr1P79u3J1NSUrKysaMCA\nAWIZQRDo5s2bRPT8dby0Y8eOUY0aNcTXycnJFBAQQNbW1lSzZk1aunSp+NnZs2fJ09OTzMzMyN7e\nnsaNG0dFRUXi5xMnTiQbGxsyMTEhd3d3io2NfebyKquiskREGRkZ1KNHDzIxMaGWLVvSlClTqG3b\ntkT03zotl8vF6ZTerm7cuEG+vr5kaWlJVlZWNHjwYHr06JH4XRcXF5o7dy65u7uTnp4eyeXyV9r+\nXVxcxHV0+vTpr7T/8vb2ppCQEGrZsiWZmJhQr169xO2h7Hw9evSIgoKCyN7enhwdHWnKlCniZ4rt\n9IsvviAzMzOqVasWnTx5ktasWUNOTk5kY2Mjrn9ERE+ePKEvv/ySnJ2dydbWlsaMGSOuF8/bbz5r\nOSq2aWNjY2rQoAHt3r2biJ5uj3p6eqSpqUlGRkZkbm5OREQff/yxuA0QEa1atYpq165NFhYW1LNn\nT7p//7742Yu2ybJeKuEdOXKEiJ7uRBs2bEjTpk2je/fukaWlpbjT/euvv8jS0pIyMjLEheXi4kJx\ncXEkl8upuLiYhg0bRlOnThWnPXXqVGrdujU9ePCAHjx4QF5eXuLnx44dIy0tLQoJCaGioiIqKCig\n6dOnk56eHh0+fJhkMhkNHTqUXFxcaNasWSSTyWj16tVUs2ZNcfr79u2jW7duERFRdHQ0GRgY0N9/\n/600/enTp5NMJqP9+/eTgYGBuLJ/+umn5OvrS/fv3xdX8sLCwmfO94MHD8q1XWFhITk7O9PSpUtJ\nJpPRrl27SEdHR5zHhw8f0q5du6igoIBycnKoX79+1Lt3b7G8j48P/f7770T0dKXV1tam3377jUpK\nSmjFihXk4OBQ4TKTyWTUuHFjCg4Opvz8fHry5AmdPHmSiJ7ulGvXrk23b9+m3NxcCggIoMDAQCL6\nbyMaO3YsFRYW0uHDh0lHR4d69+5NDx48oOTkZLKxsaHo6GgxJi0tLVq8eDHJZDL6888/ydTUVNwo\nX6b9Sy/fxYsXU+vWrSk5OZmKiopo9OjRNGjQICIiunr1KhkZGdGJEyeosLCQgoODSUtLq8KER0Tl\n1rWioiKqVasWzZ49m4qLiykyMpKMjY0pPj6+wvKl215BEATq0aMHPX78mO7cuUPW1tZ08OBBIiIK\nCwuj2rVr07Vr10gul9PMmTPJy8urwmknJiaSsbExbd26lWQyGT18+JAuXbokxq3Y2J+3fuTm5pKJ\niQklJCQQEVFqaipdvXqViIgGDhxIs2bNIqKn66Bi2SvmQZHwnrWOl1U64cnlcmrWrBnNmDGDiouL\n6datW+Tm5kaHDh0ioqcHeGfPniW5XE6JiYlUv359Wrx4MRERHTx4kJo3by4eYF27do1SUlIqXF5l\nPa/sgAEDaMCAAZSfn0+xsbHk6OhI7dq1I6KKE17pZXvjxg06cuQIFRUV0YMHD6h9+/Y0ceJE8bsu\nLi7k4eFB9+7doydPnrzS9k+k3GF41f2Xt7c3OTo60tWrVykvL4/69u1LQ4YMqXC+evfuTWPGjKH8\n/HxKT0+nli1bigeYiu103bp1VFJSQlOmTCFHR0fxYOTw4cNkbGxMeXl5RPT0wKJXr16UlZVFOTk5\n1KNHD/r222/FdeF5+82KluP27dvFZfXnn3+SoaEhpaamEhHRunXrxIMThdLTOHr0KFlZWdHFixep\nsLCQxo8fT+3btxe/+7xtsiIvTHguLi5kZGREZmZm5OLiQp999hkVFBTQnDlzxB2lQufOncUjBR8f\nH5o+fXq5GSmduWvVqqXUSzl06BC5uroS0dOG1dHRUdoAp0+fTp06dRJfh4eHk5GREZWUlBARUXZ2\nNgmCIG4UZfXu3ZuWLFkiTl9fX19pQ7CxsRE3Vn19fbpy5Uq5abxovkuLjo4mR0dHpffatm37zA37\n4sWL4lEOUfmEV7t2bfGzvLw8EgSB0tLSyk3n1KlTZG1trTRvCh988AGtWLFCfB0fH0/a2tokl8vF\njaj0EZSlpSVt27ZNfN23b19xB7Z27dpySbdly5a0cePGCuevbPuXXb7169dXSmD3798nbW1tkslk\n9P3334vJTzH/Ojo6z014pde148ePk52dndJ3Bg0aRKGhoRWW9/HxEXsBCoIgKCWP/v3709y5c4mI\nyN/fXylByuVyMjAwoDt37pSb9qxZsyggIOCl4i6t9PqRm5tLZmZmtHPnTsrPz1f63tChQ2nUqFFK\nvcHS83Dz5s3nruNllU54Z86cIWdn53LzM3z48ArLLlq0iPr06UNET3dedevWpTNnzpRbN58330RE\nkZGRFZaVyWSkra2tdOAyefLk5/bwKjqYUdi9ezd5eHiIr11dXZXO/LzK9q8oXzrhvcr+y8fHR0w0\nRE97RDo6OlRSUqI0X6mpqaSrq6vUO9+8eTP5+voS0dPttE6dOuJnV65cIUEQKD09XXzP0tKSLl++\nTCUlJWRoaCgeFBE93Z8oEvHz9ptEL16ORERNmzalPXv2iLE9L+EFBQXRpEmTxM9yc3NJW1tbPHtS\n0TY5Z86cZ9b9Utfw9uzZg6ysLCQmJmLZsmXQ09NDUlIStm/fDnNzc/HfyZMnkZqaKpZ90Z1d9+/f\nh4uLi/ja2dkZ9+/fF19bW1tDR0dHqYyNjY34t76+PqysrMTrLfr6+gCA3NxcAMCBAwfg6ekJS0tL\nmJubY//+/Xj48KFY3tLSEhoa/zWBgYEBcnNzkZGRgSdPnqBWrVrlYn6Z+S49f46OjkrvOTk5iddo\n8vPzMXr0aLi6usLU1BTe3t54/PjxM6/h2NnZKcVael5Lu3v3LlxcXJTmTSElJaVcm8tkMqSlpYnv\n2drain/r6+uXe52Xlye+Ljt/Li4uSElJAfDi9i+7fBMTE9GnTx+xXRs0aAAtLS2kpaUhJSUFNWrU\nUJp/S0vLipqpQvfv3y+3Prq4uCA5OfmZZSq6jld2GSjaPykpCRMmTBBjV8RW0fTv3bsHNze3F8b8\nvPXD0NAQf/75J3799Vc4ODige/fuiI+PBwDMmzcPRISWLVuiUaNGWLt2bblpP28df56kpCTcv39f\naf2fPXs20tPTAQAJCQno3r077O3tYWpqiu+++05c5h988AHGjRuHzz77DLa2thg9evRL30Tj6+tb\nYdkHDx5AJpMpLVtnZ+eXnp+0tDQMHDgQNWrUgKmpKQIDA5XWUUB5P/Yq239FXmX/VbZuZ2dnFBcX\nIyMjQ2maSUlJKC4uhr29vRjTmDFj8ODBA/E7Zbdh4On2V/q93NxcPHjwAPn5+WjevLk4rS5duijV\n+az95rNs2LABHh4e4vRiY2PLtfGzlN1fGRoawtLSUmm7etY2WZHXHpbg7OyMwMBAZGVlif9ycnLw\nzTffiN950YV/BwcHpVuk79y5AwcHh2eWf5UbCQoLC9G3b1988803SE9PR1ZWFrp27fpSNwRYWVlB\nT08PN27cKPfZy8y3gr29fbkd3p07d8T5WLhwIRISEhATE4PHjx8jOjoa9LTX/dLzWREnJyfcuXMH\ncrm83GcVtbmWlpbSBvEqys5fUlISHBwcXqr9yy5PZ2dnHDx4UKlt8/Pz4eDgAHt7e9y9e1f8bn5+\n/nM3mrLTdnBwwN27d5XqT0pKUkqizyv/Is7Ozli1apVS7Hl5efD09Cz3XScnJ9y8efOFsb9o/ejU\nqRMOHz6M1NRU1KtXDyNHjgTwdOe2atUqJCcnY+XKlfj000/LDad43jr+PE5OTqhZs6bSfGZnZyMi\nIgLA01vKGzRogBs3buDx48f48ccflW6dHz9+PM6fP4+4uDgkJCRg/vz5SvP8PBWVtbGxgZaWFu7c\nuSN+r/TfirvJ8/PzxfdKJ6fJkydDU1MTsbGxePz4MTZu3FjuVv/Ssb3K9v82lJ0vbW1tWFlZKX3H\nyckJurq6ePjwoRjT48eP8c8//7xyfVZWVtDX10dcXJw4rUePHr30nfVll2NSUhJGjRqF5cuXIzMz\nE1lZWWjUqJG4Dr9qjsjLy8PDhw/LHWi/rNdOeEOGDMHevXtx+PBhyOVyPHnyBFFRUUo7wLI77rKv\nBw0ahJkzZyIjIwMZGRn44YcfEBgY+Mw6XyURFBUVoaioCFZWVtDQ0MCBAwdw+PDhlyqroaGBoKAg\nBAcHIyUlBXK5HKdPn0ZRUdFLzbeCl5cXNDU1sWzZMshkMuzZswfnzp0TP8/NzYW+vj5MTU2RmZmJ\n77///qXn73latWoFe3t7hISEID8/H0+ePMGpU6cAPG3zRYsWITExEbm5uZg8eTIGDhxYYW/wWUov\nh/T0dCxduhTFxcXYvn07rl27hq5du75W+48ZMwaTJ08WN/IHDx4gPDwcAPDhhx8iIiICJ0+eRFFR\nEaZNm/bcMUi2trZKO3lPT08YGBhg3rx5KC4uRlRUFCIiIjBw4MBnln9eUlK0g6ItxowZg1mzZiEu\nLg4A8PjxY2zfvr3CcoMHD8aRI0ewfft2yGQyPHz4EJcvXy43zeetH+np6dizZw/y8vKgra0NQ0ND\naGpqAgC2b9+Oe/fuAQDMzMwgCEK55fu8dfx5WrZsCWNjY8ybNw8FBQWQy+WIjY3F+fPnxZiNjY1h\nYGCAa9euYcWKFeJO7fz58zh79iyKi4thYGAAPT09Meayy6usZ5XV0NBAQEAAQkNDUVBQgLi4OGzY\nsEGs09raGo6Ojti4cSPkcjnWrFmjtFxzc3NhaGgIExMTJCcniwn4WV5l+39TRIQ//vgD//77L/Lz\n8zFt2jT069evXJKwt7dHp06dEBwcjJycHJSUlODmzZuvNf5PQ0MDI0eOxMSJE8UeYnJy8kvvO8su\nx7y8PAiCACsrK5SUlGDt2rVKQzVsbW1x7949FBcXK823YhsYNGgQ1q5di8uXL6OwsBCTJ0+Gp6fn\nM3vxL8oRr53watSogT179mDWrFmwsbGBs7MzFi5c+Nwj+LJjjKZMmYL3338fjRs3RuPGjfH+++9j\nypQpL13+Wd8Bng6wXbp0Kfr37w8LCwts2bIFvXr1em7Z0hYsWAB3d3e0aNEClpaW+Pbbb1FSUvLM\n+a5o56utrY1du3bh999/h7m5OTZt2oTu3buLp/EmTpyIgoICWFlZwcvLC126dHlmTC8z7woaGhrY\nu3cvbty4AWdnZzg5OWHbtm0AgKCgIAQGBqJ9+/Zwc3ODgYEBfv7555dqk4q+06pVK1y/fh3W1taY\nOnUqdu7cCXNz89dq/wkTJqBnz57o1KkTTExM0Lp1a8TExAAAGjRogOXLl+Ojjz6Cg4MDLCwsnnvK\nfMSIEYiLi4O5uTkCAgKgra2NvXv34sCBA7C2tsa4ceOwceNG1K1bt8LyEyZMwI4dO2BhYYGJEyc+\nsx0U89C7d29MmjQJAwcOhKmpKdzd3XHo0KEKyzk5OWH//v1YuHAhLC0t4eHhgStXrpSb5vPWj5KS\nEixatAiOjo6wtLTEiRMnxPFL58+fh6enJ4yNjdGrVy8sXboUrq6u5dr8Wev4s+YVADQ1NREREYFL\nly7Bzc0N1tbWGDVqlNgDWLBgATZv3gwTExOMGjVK6YAiOzsbo0aNgoWFBVxdXWFlZSU+gKLs8irr\neWWXLVuG3Nxc2NnZISgoCMOHD1faD61evRrz58+HlZUV4uLi0KZNG/Gz6dOn4++//4apqSl69OiB\nvn37PncbeJXtv6I2fNn9l+LvwMBADBs2DPb29igqKsLSpUsr/O6GDRtQVFSEBg0awMLCAv369RN7\nsq+y7wCAuXPnonbt2vD09ISpqSk6duyIhISElypbdjk2aNAAX375JVq3bg07OzvExsaibdu24vf9\n/PzQsGFD2NnZiad7S8fr5+eHGTNmoG/fvnBwcMDt27exdevW57bf8+IT6E3Pn1Wyu3fvYujQoUhP\nT4cgCBg1ahQ+//xzZGZmYsCAAUhKSoKrqyu2bdsGMzMzVYf7Qq1atcKnn36Kjz/+WNWhvLGKBo0y\npmrVZb309fVFYGAggoKCVB1KtVHln6Wpra2NRYsW4erVqzhz5gyWL1+Of//9F3PmzBGPPPz8/DBn\nzhxVh1qh48ePIzU1FTKZDOvXr0dsbCz8/f1VHRZj7B1Qxfsj75wqn/Ds7OzQtGlTAICRkRHq16+P\n5ORkhIeHi72kjz/+GGFhYaoM85ni4+PRtGlTmJubY9GiRdixY8dr3yBS1VT2Y7AYex3Vab2sLvNR\nVVT5U5qlJSYmwtvbG7GxsXB2dkZWVhaAp0dBFhYW4mvGGGOsrCrfw1PIzc1F3759sWTJEhgbGyt9\nVp2O6BhjjFWOF/5aQlVQXFyMvn37IjAwEL179wbw9HbW1NRU2NnZISUlRWlAp0LTpk3F270ZY4y9\nnCZNmuDSpUuqDuOtq/I9PCLCiBEj0KBBA6Xbw3v27In169cDANavXy8mwtIuX74sjumoyv+mT5+u\n8hiq0z9uT27LqvrvXWnP6tpRqPI9vJMnT+KPP/5A48aN4eHhAQCYPXs2QkJC0L9/f/z+++/isATG\nGGPsWap8wmvbtu0zB3UeOXJE4mgYY4y9q6r8KU114OPjo+oQqhVuz7eH2/Lt4vZUrXdqWMKrEgQB\n1Xj2GGOsUlTXfSf38BhjjKkFTniMMcbUAic8xhhjaqHK36VZmUJCQ5D66OV+qbi6szOzw5zQqvkA\nbsYYexvUOuGlPkqFa29XVYdRJSSGJao6BMYYq1R8SpMxxpha4ITHGGNMLXDCY4wxphY44THGGFML\nnPAYY4ypBU54jDHG1AInPMYYY2qBEx5jjDG1wAmPMcaYWuCExxhjTC1wwmOMMaYWOOExxhhTC5zw\nGGOMqQVOeIwxxtQCJzzGGGNqgRMeY4wxtcAJjzHGmFrghMcYY0wtcMJjjDGmFjjhMcYYUwuc8Bhj\njKkFTniMMcbUAic8xhhjaoETHmOMMbXACY8xxpha4ITHGGNMLXDCY4wxphY44THGGFMLnPAYY4yp\nBU54jDHG1AInPMYYY2qBEx5jjDG1wAmPMcaYWuCExxhjTC1wwmOMMaYWOOExxhhTC5zwGGOMqQUt\nqSqKj4/HggULkJiYCJlMBgAQBAGRkZFShcAYY0yNSZbw+vXrh7Fjx+KTTz6BpqYmgKcJjzHGGJOC\nZAlPW1sbY8eOlao6xhhjTIlk1/B69OiB5cuXIyUlBZmZmeK/FwkKCoKtrS3c3d3F90JDQ1GjRg14\neHjAw8MDBw8erMzQGWOMVQOS9fDWrVsHQRCwYMECpfdv37793HLDhw/H+PHjMXToUPE9QRAQHByM\n4ODgSomVMcZY9SNZwktMTHytcu3atauwLBG9WUCMMcbUSqUnvKNHj8LPzw87d+6s8CaVgICA15ru\nzz//jA0bNuD999/HwoULYWZm9qahMsYYq8YqPeEdP34cfn5+2Lt371tLeGPHjsW0adMAAFOnTsWX\nX36J33//vcLvhoaGin/7+PjAx8fnletjjLHqLCoqClFRUaoOo9IJ9A6cG0xMTESPHj3wzz//vNJn\ngiA899TnsInD4Nrb9W2G+s5KDEvEusXr3mgaIaEhSH2U+nYCesfZmdlhTugcVYfB2Gt50b7zXSXZ\nNTwAiIiIQFxcHJ48eSK+p+ipvYqUlBTY29sDAHbv3q10BydTndRHqXwA8f8SwxJVHQJjrAzJEt7o\n0aNRUFCAyMhIjBw5Etu3b0erVq1eWG7QoEGIjo5GRkYGnJyc8P333yMqKgqXLl2CIAioWbMmVq5c\nKcEcMMYYe5dJlvBOnTqFf/75B40bN8b06dPx5Zdfwt/f/4XltmzZUu69oKCgygiRMcZYNSbZwHN9\nfX0AgIGBAZKTk6GlpYXUVL7ewxhjTBqS9fC6d++OrKwsfP3112jevDkAYOTIkVJVzxhjTM1JlvAU\nN6f07dsX3bp1w5MnT3jsHGOMMclIlvAqGnhuamoKd3d32NjYSBUGY4wxNSVZwluzZg1Onz4NX19f\nAE8HOjZr1gy3b9/GtGnTlJ6VyRhjjL1tkiW84uJi/Pvvv7C1tQUApKWlITAwEGfPnkX79u054THG\nGKtUkt2leffuXTHZAYCNjQ3u3r0LS0tL6OjoSBUGY4wxNSVZD8/X1xfdunVD//79QUTYuXMnfHx8\nkJeXxzevMMYYq3SSJbzly5dj586dOHnyJADg448/Rt++fSEIAo4dOyZVGIwxxtSUZAlPEAR8+OGH\n+PDDD6WqkjHGGBNJdg2PMcYYUyVOeIwxxtSCpAkvPz8f8fHxUlbJGGOMAZAw4YWHh8PDwwOdO3cG\nAFy8eBE9e/aUqnrGGGNqTrKEFxoairNnz8Lc3BwA4OHhgVu3bklVPWOMMTUnWcLT1tYuN95OQ4Mv\nITLGGJOGZBmnYcOG2LRpE2QyGa5fv47x48fDy8tLquoZY4ypOckS3s8//4yrV69CV1cXgwYNgomJ\nCRYvXixV9YwxxtScZAPPDQ0NMWvWLMyaNUuqKhljjDGRZD28Dh064NGjR+LrzMxM8Y5NxhhjrLJJ\nlvAyMjKUblqxsLBAWlqaVNUzxhhTc5IlPE1NTSQlJYmvExMT+S5NxhhjkpHsGt6PP/6Idu3aoX37\n9gCA48ePY9WqVVJVzxhjTM1JlvD8/f1x4cIFnDlzBoIgYPHixbCyspKqesYYY2pOsoQHAEVFRbCw\nsIBMJkNcXBwAiD0+xhhjrDJJlvAmTZqEP//8Ew0aNICmpqb4Pic8xhhjUpAs4e3evRvx8fHQ1dWV\nqkrGGGNMJNltkrVq1UJRUZFU1THGGGNKJOvh6evro2nTpvDz8xN7eYIgYOnSpVKFwBhjTI1JlvB6\n9uxZ7vfvBEGQqnrGGGNqTrKEN2zYMKmqYowxxsqRLOElJCRg8uTJiIuLQ0FBAYCnPTz+EVjGGGNS\nkOymleHDh2PMmDHQ0tJCVFQUPv74YwwePFiq6hljjKk5yRJeQUEBOnToACKCi4sLQkNDsW/fPqmq\nZ4wxpuYkO6Wpp6cHuVyO2rVrY9myZXBwcEBeXp5U1TPGGFNzkiW8xYsXIz8/H0uXLsXUqVORnZ2N\n9evXS1U9Y4wxNSdZwmvZsiUAwNjYGOvWrZOqWsYYYwyAhAnv3LlzmDVrFhITEyGTyQA8vUvzypUr\nUoXAGGNMjUmW8AYPHowFCxagUaNG/MOvjDHGJCdZwrO2ti73pBXGGGNMKpIlvOnTp2PEiBHo0KED\ndHR0ADw9pRkQECBVCIwxxtSYZAlv/fr1iI+Ph0wmUzqlyQmPMcaYFCRLeOfPn8e1a9f4gdGMMcZU\nQrKE5+Xlhbi4ODRs2FCqKhl7p4WEhiD1Uaqqw6gS7MzsMCd0jqrDYO84yRLe6dOn0bRpU9SsWVPp\n9/B4WAJjFUt9lArX3q6qDqNKSAxLVHUIrBqQJOEREVatWgVnZ2cpqmOMMcbKkayH9+mnnyI2Nlaq\n6hhjjDElkowAFwQBzZs3R0xMzCuXDQoKgq2tLdzd3cX3MjMz0bFjR9StWxedOnXCo0eP3ma4jDHG\nqiHJHnly5swZtG7dGm5ubnB3d4e7uzsaN278wnLDhw/HwYMHld6bM2cOOnbsiISEBPj5+WHOHL6Y\nzRhj7Pl1TnejAAAgAElEQVQkO6V56NAhABCHJRDRS5Vr164dEhMTld4LDw9HdHQ0AODjjz+Gj48P\nJz3GGGPPJVkPz9XVFY8ePUJ4eDj27t2Lx48fw9XV9bWmlZaWBltbWwCAra0t0tLS3mKkjDHGqiPJ\nenhLlizB6tWrERAQACLCkCFDMHLkSHz++edvNF1BEJ47mD00NFT828fHBz4+Pm9UH2OMVTdRUVGI\niopSdRiVTrKE99tvv+Hs2bMwNDQEAISEhMDT0/O1Ep6trS1SU1NhZ2eHlJQU2NjYPPO7pRMeY4yx\n8sp2Br7//nvVBVOJJP2dntLP0HyTnwjq2bOn+Gvp69evR+/evd84NsYYY9WbZD284cOHo1WrVuIp\nzbCwMAQFBb2w3KBBgxAdHY2MjAw4OTnhhx9+QEhICPr374/ff/8drq6u2LZtmwRzwBhj7F1W6Qnv\n1q1bcHNzQ3BwMLy9vfG///0PgiBg3bp18PDweGH5LVu2VPj+kSNH3naojDHGqrFKT3j9+vXDhQsX\n4Ofnh6NHj6J58+aVXSVjjDFWTqUnPLlcjh9//BHx8fH46aeflMbfCYKA4ODgyg6BMcYYq/ybVrZu\n3QpNTU3I5XLk5OQgNzdX/JeTk1PZ1TPGGGMAJOjh1atXD19//TVcXFwwaNCgyq6OMcYYq5AkwxI0\nNTWxYMECKapijDHGKiTZOLyOHTtiwYIFuHv3LjIzM8V/jDHGmBQkG4e3detWCIKA5cuXK71/+/Zt\nqUJgjDGmxiRLeGV/8YAxxhiTkmSnNPPy8jBjxgyMHDkSAHD9+nVERERIVT1jjDE1J1nCGz58OHR0\ndHDq1CkAgIODA7777jupqmeMMabmJEt4N2/exKRJk6CjowMA4q8mMMYYY1KQLOHp6uqioKBAfH3z\n5k3o6upKVT1jjDE1J9lNK6GhofD398e9e/fw0Ucf4eTJk1i3bp1U1TPGGFNzkiW8Tp06oVmzZjh7\n9iyICEuXLoWVlZVU1TPGGFNzkiU8IkJ0dLT480DFxcXo06ePVNUzxhhTc5Jdw/v000+xcuVKNG7c\nGI0aNcLKlSvx6aefSlU9Y4wxNSdZD+/YsWOIi4uDhsbTHDts2DA0aNBAquoZY4ypOcl6eLVr18ad\nO3fE13fu3EHt2rWlqp4xxpiak6yHl52djfr166Nly5YQBAExMTFo0aIFevToAUEQEB4eLlUojDHG\n1JBkCe+HH34o954gCCAiCIIgVRiMMcbUlGQJz8fHR6qqGGOMsXIku4bHGGOMqRInPMYYY2pB0oSX\nn5+P+Ph4KatkjDHGAEiY8MLDw+Hh4YHOnTsDAC5evIiePXtKVT1jjDE1J1nCCw0NxdmzZ2Fubg4A\n8PDwwK1bt6SqnjHGmJqTLOFpa2vDzMxMuXINvoTIGGNMGpJlnIYNG2LTpk2QyWS4fv06xo8fDy8v\nL6mqZ4wxpuYkS3g///wzrl69Cl1dXQwaNAgmJiZYvHixVNUzxhhTc5INPI+Pj8esWbMwa9Ysqapk\njDHGRJL18IKDg1GvXj1MnToVsbGxUlXLGGOMAZAw4UVFReHYsWOwsrLC6NGj4e7ujhkzZkhVPWOM\nMTUn6W2S9vb2mDBhAn799Vc0adKkwgdKM8YYY5VBsmt4cXFx2LZtG3bs2AFLS0sMGDAAP/30k1TV\nM8bUXEhoCFIfpao6DJWzM7PDnNA5qg5DJSRLeEFBQRg4cCAOHToER0dHqapljDEAQOqjVLj2dlV1\nGCqXGJao6hBURrKEd+bMGamqYowxxsqp9ITXr18/bN++He7u7uU+EwQBV65cqewQGGOMscpPeEuW\nLAEAREREgIiUPuNfOmeMMSaVSr9L08HBAQDwyy+/wNXVVenfL7/8UtnVM8YYYwAkHJZw+PDhcu/t\n379fquoZY4ypuUo/pblixQr88ssvuHnzptJ1vJycHLRp06ayq2eMMcYASJDwPvroI3Tp0gUhISGY\nO3eueB3P2NgYlpaWlV09Y4wxBkCChGdqagpTU1Ns3boVAJCeno4nT54gLy8PeXl5cHZ2ruwQGGOM\nMemu4YWHh6NOnTqoWbMmvL294erqii5dukhVPWOMMTUnWcKbMmUKTp8+jbp16+L27ds4evQoWrVq\nJVX1jDHG1JxkCU9bWxtWVlYoKSmBXC6Hr68vzp8/L1X1jDHG1JxkjxYzNzdHTk4O2rVrh8GDB8PG\nxgZGRkZSVc8YY0zNSZbwwsLCoK+vj0WLFmHTpk3Izs7G9OnT32iarq6uMDExgaamJrS1tRETE/OW\nomWMMVbdSJbwFL05TU1NDBs27K1MUxAEREVFwcLC4q1MjzHGWPVV6QnPyMjomc/MFAQB2dnZbzT9\nss/nZIwxxipS6QkvNze30qYtCAI6dOgATU1NjB49GiNHjqy0uhhjjL3bJDulCQAnTpzAjRs3MHz4\ncDx48AC5ubmoWbPma0/v5MmTsLe3x4MHD9CxY0fUq1cP7dq1U/pOaGio+LePjw98fHxeuz7GGKuO\noqKiEBUVpeowKp1kCS80NBTnz59HQkIChg8fjqKiIgwePBinTp167Wna29sDAKytrdGnTx/ExMQ8\nN+Exxhgrr2xn4Pvvv1ddMJVIsnF4u3fvRnh4OAwNDQEAjo6Ob3S6Mz8/Hzk5OQCAvLw8HD58uMIf\nmWWMMcYACXt4urq60ND4L7/m5eW90fTS0tLQp08fAIBMJsPgwYPRqVOnN5omY4yx6kuyhNevXz+M\nHj0ajx49wqpVq7BmzRp88sknrz29mjVr4tKlS28xQsYYY9WZJAmPiDBgwABcu3YNxsbGSEhIwIwZ\nM9CxY0cpqmeMMcak6+F17doVsbGxfNqRMcaYSkhy04ogCGjevDk/+osxxpjKSNbDO3PmDP744w+4\nuLiId2oKgoArV65IFQJjjDE1JlnCO3TokFRVMcYYY+VIlvBcXV2lqooxxhgrR7KB54wxxpgqccJj\njDGmFjjhMcYYUwuc8BhjjKkFTniMMcbUAic8xhhjaoETHmOMMbXACY8xxpha4ITHGGNMLXDCY4wx\nphY44THGGFMLnPAYY4ypBU54jDHG1AInPMYYY2qBEx5jjDG1wAmPMcaYWuCExxhjTC1wwmOMMaYW\nOOExxhhTC5zwGGOMqQVOeIwxxtQCJzzGGGNqgRMeY4wxtcAJjzHGmFrghMcYY0wtcMJjjDGmFjjh\nMcYYUwuc8BhjjKkFTniMMcbUAic8xhhjaoETHmOMMbXACY8xxpha4ITHGGNMLXDCY4wxphY44THG\nGFMLnPAYY4ypBU54jDHG1AInPMYYY2qBEx5jjDG1wAmPMcaYWninE97BgwdRr1491KlTB3PnzlV1\nOIwxxqqwdzbhyeVyjBs3DgcPHkRcXBy2bNmCf//9V9VhvZbES4mqDqFa4fZ8e7gt3y5uT9V6ZxNe\nTEwMateuDVdXV2hra2PgwIHYs2ePqsN6LbwRvF3cnm8Pt+Xbxe2pWu9swktOToaTk5P4ukaNGkhO\nTlZhRIwxxqqydzbhCYKg6hAYY4y9QwQiIlUH8TrOnDmD0NBQHDx4EAAwe/ZsaGhoYNKkSeJ3mjZt\nisuXL6sqRMYYeyc1adIEly5dUnUYb907m/BkMhnee+89HD16FA4ODmjZsiW2bNmC+vXrqzo0xhhj\nVZCWqgN4XVpaWli2bBk6d+4MuVyOESNGcLJjjDH2TO9sD48xxhh7Fe/sTSuMMcbYq+CEx54rJSUF\nkyZNws2bN/Hw4UMAQElJiYqjUo2yJ0P45MjrISJuuzdUURtym74YJzz2XPb29gCATZs24bPPPsOl\nS5egoaGhdhsXEYlDYe7fv4+srCweGvMGBEHAoUOH8NNPP2Hz5s2qDuedJAgCzp07hwMHDuD27dsQ\nBEFtD0ZfFic89kyKjWfu3LkYM2YMfHx80KVLFxw/flytNq60tDT8+uuvAIC//voLvXr1wgcffIDd\nu3cjOztbxdG9WxQHDpcvX8b48eORlpaGAwcOYPTo0aoO7Z2haMOjR4+iV69e2LlzJ1q0aIGLFy9C\nQ0NDbbbL1/HO3qXJKo+i96ahoYGioiLo6OjAxsYGY8aMga6uLgYNGoSdO3fC09NTqedTHRERLly4\ngFOnTiEtLQ1nz57Fxo0bceXKFaxZswZ5eXno2bMnTExMVB3qO0EQBERHR+OPP/7AkiVL0KVLF9y4\ncQOzZs3CmDFjxAML9myCICAuLg47duzA1q1b0b59ezRp0gR+fn6IjIxE06ZNUVJSAg0N7s+UpRka\nGhqq6iBY1aM45bR27VrExcWhVatWAAAPDw+YmZnhm2++gb+/PywtLVUcaeVRJHNHR0fo6+vj4sWL\nSEtLw1dffYWGDRtCX18fmzZtAhHBzc0Nenp6qg65Sip7UHT58mX8+OOPcHFxgbe3N0xNTdG4cWPs\n378f+/fvR69evVQYbdUml8shl8sxZ84cnDp1Cu+99x7c3d3h6ekJQ0NDBAQEoHv37nBwcFB1qFUS\nJzymRLFzOn36ND777DP4+/tj4cKFSEtLQ7t27aCpqYlmzZqhsLAQSUlJaNmyJeRyebU7mlT0cgVB\nwP379+Hh4QEtLS2cO3cOaWlpaN26NerXrw9NTU388ccf6Nq1K4yNjVUcddVTuh2TkpJARGjatCna\ntm2LqVOnws3NDfXr14eZmRk8PDzQvHlz2NraqjjqqqV0G+bn50NfXx8+Pj5IT09HUlISLCws4Ojo\niFatWsHExASGhoaoVauWiqOumngcHisnPj4es2fPhpeXF0aNGoX79++jf//+8Pb2RmhoKLS1tXH0\n6FH8+eefWLVqlarDrRSKxH/gwAGMGzcOBw4cgJOTEw4dOoS//voLtWvXxhdffAHg6TU+3klXTHFq\nLSIiArNnz4aVlRWsra0RHByMjIwMjBgxAnPmzEHfvn3FMtX9NPmrUrTHwYMHsXDhQtSoUQO1atXC\nlClTEBISguLiYgQEBMDLy0tsN27DZyCm9kpKSpRe79+/n7p3706DBg2iW7duERHR/fv3qUmTJvTV\nV1+J3/vss88oJSVF0lildPXqVWrYsCFFR0eL7+Xn51NYWBgNGzaM5s2bR0REcrmciMq3ozorKCgQ\n/05KSqIGDRrQhQsX6J9//qENGzZQ165dKTU1lXbt2kU1atSgtLQ0br8yiouLxb9jYmKoQYMGFBER\nQefPn6emTZvS+PHjqaSkhD799FP64osvKCsrS4XRvhv4phU1R6U6+Ldu3YKBgQH8/Pzg6OiI1atX\nIywsDAEBAXBxcRFvf1ZYtmyZKkKWjEwmQ9u2bdG+fXvIZDKUlJRAX18fHTp0gCAIcHNzAwDxdC4f\nUT+VlpaGLVu2YMSIEeJpXicnJzRr1gzA06EuFy5cwOHDhxEYGAhPT0/Y2NioMuQqJz09XRwKpKOj\ng/z8fHTo0AHdunUDAPz9999o2bIlTp48iR9++AFpaWkwMzNTcdRVX/W68MJemSAI4qm7bt26ITg4\nGO+//z5MTU0xYMAAJCYmYvPmzUhKSoK9vT28vLyq5cDhiubJwMAABw8eREREBLS0tKCjo4NDhw5h\n/fr16NmzJxo1aqSiaKs2XV1ddOnSBbm5uTh//jycnZ0hk8nw3XffAQAsLS1hYWGBhIQEAIC1tTUA\nHjhdWmpqKnr06IGHDx/i7t27MDExwdGjR8WHPwiCAF9fXzx+/BiWlpZo0KCBiiN+N3DCY7hz5w6m\nT5+O1atXY/PmzRgwYAB69uyJunXrIiAgAMnJyUpjexRJsrpR3DI/f/58REZGolatWli0aBF++ukn\nLFu2DPv378ekSZPg6Oio6lCrpOLiYuTn58PMzAxOTk6YPXs2fvvtN1y9ehULFy5EYmIi+vfvj717\n92Lz5s3w8/MD8PRB8AD3kIGnbQgAjRs3hoWFBVasWIE5c+agUaNGGDx4MFq0aIGoqChERERg//79\n3Kt7RXzTihqiMhe0c3NzMXbsWPz4449wdnYGAIwfPx6amppYvHix2tyUceDAAQQHB2PixIlYsGAB\nPvnkE3Tr1g0ZGRlYuHAh7Ozs0KtXL3Tv3p1vCiijqKgIUVFRsLKyQkJCApKSkjBkyBAsWLAAOjo6\nCAgIgJubG2bOnAkzMzO0bNkS3bp143YspbCwECdOnECNGjWQm5uLhIQE2Nra4q+//gIRYfbs2Vi9\nerV4p/Do0aN5XXxFfA1PDZWUlEBTUxO5ubnQ09ODjo4OcnNzER4ejnHjxgEA2rZti4sXLwJAtU92\nRITk5GSsWrUK4eHhuHv3LogIly9fRn5+Pr7++mvs3btX6ftMmY6ODnJychAaGorU1FQsWrQIjo6O\n+O677/DDDz9g586dCAwMxJIlS8Qy3I7KioqK8OTJE4wdOxYJCQmIjIzEe++9B319fYSFheG7777D\nN998g9GjR6OgoAD6+vrchq+Ix+GpkTt37qCoqAhGRkYICwvDmDFj8M8//0BTUxPDhg1DSEgIrl27\nhvPnz2PFihUICgpC3bp1VR12paBSY5sEQYCJiQnatGmDvLw8jB8/HmfPnoWtrS2+/PJL6OjooEmT\nJtDV1VUqw/679ikIApydnXHq1Cno6uqiU6dOMDIygpWVFTw9PbFv3z7ExsaidevW4gB9bsenFOui\nrq4u8vPzMXv2bLRq1QpeXl5wcHCAk5MTTExMcPnyZURFRcHb2xs6OjrQ0NDgNnxFnPDUyMyZMzFt\n2jS0aNECK1aswPDhw+Hk5ITly5fD2dkZkydPxsOHD5GdnY1Ro0ahc+fO1fp0iSAIuHLlCs6fPw9N\nTU04ODggNTUVR44cwahRo1BQUIB//vkH48aNg5OTk6rDrbI0NDTw119/YePGjZg3bx40NDQQFhYG\nPT091K9fHzKZDO7u7vDw8OB2fAZBEPDXX3/BwsICw4YNg7W1NXbs2AEtLS3UqVMHOjo60NHRQZcu\nXWBra1vtHvQgFT6lqQYUg3/nz5+PkpISDBgwAEOGDMHAgQNRUFAAS0tLzJs3DxkZGfjkk0/EctX5\ndIkgCAgLC8O0adPg5uYGfX191K1bF6NHj4adnR06dOiAu3fvYvHixWjUqFG1TvxvQnGH75dffolF\nixbB0NAQw4cPR0FBASIiInDu3Dn89ttvOHbsGN/V+gyKNpwwYQJ+/vlndO7cGSYmJsjMzMTu3btx\n5swZXLp0CUuWLEHNmjVVHe67TbIRf0wlcnNzKTY2loiIzp49S9nZ2RQSEkL169en1NRUIiIqLCyk\n/fv3k4+PDyUmJooDqaubkpIScXBzTk4ODRw4kP7++28iIoqOjqaQkBDasGEDPXjwgDZv3kynTp0q\nV44pKyoqogkTJtCBAweIiOjJkyfiZwcOHKBFixbRwYMHVRXeOyE3N5c6depER48eJaL/HmBw+/Zt\n2rZtG3Xv3p3CwsJUGWK1wT28ai4zMxM//fSTeOH7wIEDmD17Nh49eoSAgADs3r0bNjY28PPzQ4sW\nLWBlZaXqkCsFleqhnTp1CtnZ2UhKSsK1a9fg4eEBLy8vnDt3DqdOnUJgYCAGDRoklgP4lnkFKtPT\n1dbWRmZmJqKiouDv7y9e57xy5Qp8fHzg7+8vlgO4HYH/2lDxv0wmQ1FRkTjc5cmTJ9DX14exsTH6\n9euHXr16QUdHh9vwLeATwdVYSUkJnJyc0KlTJ6xZswYfffQR3N3dAQArVqxAkyZN0LFjR6Snp0NH\nR0dMdlSNT2XGx8fj66+/RuPGjfHVV1/hyJEjiI6OhpaWFpo3b47MzExkZ2eL4w75poCKJSUlIS4u\nDgAQFBSE4uJi7NmzBwBw7tw5jBkzBtevXxe/z+1YXlpaGgDA1NQUbdq0QUhICDIzM6Gvr4/jx4+j\ne/fuSE9PVxqnyG34ZjjhVWMaGhqIjIzElStXsHfvXly+fBm//fYbMjMzAQC//PILOnbsqLRjAqrn\nEaTiR0cDAgLQoUMHODg4oGnTpmjWrBnGjRuHiRMnYvjw4QgMDISJiQnfFFABRY8kIiIC/v7++PDD\nDzFp0iTUq1cPNWvWxMqVK9GjRw8MHToUISEh4sEV+4+iDffv34/u3bujb9++OHz4MIYNG4YmTZqg\nTZs2mD9/PsaOHYtvv/0WNjY2vC6+RTzwvJpTPGvv0KFDOHr0KGbMmIFRo0ZBEATs2rULmzdvhra2\ndrW8KaOiU0BDhgzBv//+i+joaBgZGaG4uBixsbFISkpCjRo18P7771fLtnhbrl27hm+++Qbz58+H\nra0tunbtii5duiA4OBiFhYVISEiAubk53nvvPT4F9wwxMTGYNWsWQkJCEB0djaSkJLRt2xZ9+vTB\nvn37oKGhAWtra7Rr147b8C3ja3jVTNmddb169cSH9fr5+UEul+OPP/5AcnIyRo0aBW1tbQDVd4MS\nBAFnzpzBnTt30KhRI/zxxx8YMWIE+vXrh127dkFfXx8eHh7w8PAAUL1P574uxTr1+PFjLF68GPfv\n34e2tjbMzMywc+dODBw4EBkZGViyZAk8PT2VylbX9epVlL5ml5GRge+//x7a2trw9PSEp6cnVq5c\niePHj6OkpAS9e/eGkZGRWA7gNnybeBxeNaHYqARBwN9//43x48ejcePGcHR0RFZWFubPn4+BAwfi\nvffeg6+vLz788EO0aNGi2vZmFPN14sQJBAUFISsrC8ePH0dMTAyWLVuGyMhILF++HAMGDBCTPsDX\nSSqiOB1saWkJV1dXXL9+HVlZWXB0dESNGjXEHwlu27at0k1P3I5PKdrhwYMHsLGxgSAI2LFjBwwM\nDNCsWTO8//77uH37Ns6cOYM2bdqIvzDB6+LbxwmvGih9JHj9+nW4ubnhzJkz+Oeff7B8+XJ069YN\n165dQ8OGDWFrawtdXV0YGBiI5avjRqX41fYZM2bgl19+weeffw53d3ecOHECSUlJmDlzJnbv3o36\n9evDwcFB1eFWSYqDhqKiIixYsACrVq3C6NGj4erqihMnTiA1NRV2dnZwcnLC0KFDq/0j6F6XXC5H\nZmYmXFxcUKdOHQwcOBA1atTAli1bUFhYCA8PD7Rq1QoeHh6oUaOGqsOt1jjhVROKC+ETJ06En58f\nAgMD0bp1awiCgA0bNuDIkSPIyclBz549lRJcdUp2ZXurJ06cwPz589GyZUs0a9YMRkZGKCgowNmz\nZ9G9e3cMGjQIDg4O1baX+7ry8vKgoaEBTU1NAICmpiYaN26MGzduYMOGDRg5ciTs7e1x8OBBpKen\no1mzZtDW1oaGhga35f8rLi4W2w8ADA0N0ahRI4waNQrvvfce+vTpAwMDA6xevRrFxcVo1qwZTE1N\nVRixmpBgrB+TwL///kv16tWjkydPlvvs0aNHdPXqVfLx8REHWlc3pQeHP3jwgPLz84mIaO3ateTm\n5kZHjhwhoqeDodu2bUsZGRkkk8lUFm9VdfXqVRo7diylpaXR8ePHacmSJeJnKSkp9MUXX9DQoUMp\nLy+PTp48KT7UgP3n6tWrNGXKFCIiiouLo8OHD4vr4/79+0lXV1ccSL5jxw6KiYlRWazqhhPeO+ru\n3bu0ceNG8fXx48epX79+4uvi4mIiIqUnhAwdOlR8mkN1o5jP8PBw8vb2pnbt2tGqVasoPj6e/vzz\nTzIwMKBPPvmEevfuTbt371ZxtFVTfn4+dejQgdasWUNERJGRkWRra0vLli0jIiKZTEaRkZHUqFEj\nGjBgQLV9Is+bePz4MXl7e9O5c+coOzubJk6cSEFBQXT06FHKy8sjIqJFixaRIAi0f/9+sRw/yUca\nPMDjHUVE2LhxIy5fvgwAcHNzw8OHD3H48GEAT39UMzIyEnPnzgUR4ebNm7h582a1/fFSQRBw4cIF\nLFy4EEuWLMH48eORlJSErVu3olu3bliyZAlOnDiBrl27onfv3pDL5XxHZhn6+voYPHgw1qxZA0dH\nR/j6+mLfvn1YtGgRli9fDk1NTejq6sLPzw+TJk3i8WEVkMvlyM/Px5YtW/D555/jiy++gLOzM3bu\n3InTp08DALy8vBAQEKDUfnwaWCIqTrjsNShOxS1ZsoS2b99ORETZ2dm0YMEC+vrrr2nOnDkUFRVF\nDRs2pMOHD4vlHj58qJJ4pZCSkkLDhw8nLy8v8b2TJ09Shw4d6MyZM0REtGnTJnJ0dKTo6GhVhVll\nKXoY+/btIz09PfL29qbc3FwiIoqJiaHGjRvTiBEjyMbGRnxuJvdKlCnaY9myZaSlpUVjxowhoqfP\nG502bRqNGDGCRowYQXXq1KFz584plWHS4JtW3kGKI8OUlBQsXrwYvr6+sLW1hZ2dHQwMDLBv3z5c\nv34dY8eORdeuXSGTyaChoQF9fX0VR/72UJkxSvT/v8t2+vRp5Ofno1WrVnBycsLp06chl8vRokUL\nuLu7w8HBAfXq1YOFhYUqw69yFO1oaWkJHx8fWFhYYMmSJWjevDnc3d3h7++PevXqITAwEO3bt+eb\nUyqgaI+UlBR07NgRixYtgq6uLtq0aYP27dvDwMAAhoaGGDx4MNq1a6dUhkmDn7Tyjps+fTrWrl2L\nmJgY2NnZie8/efIEenp61XLwaul5+t///oeCggLo6uqiffv22LFjB/bt2wcDAwMMGDAAn3zyCVav\nXg1vb28VR101lU5ccrlcvLMwKSkJa9asQXx8PGbOnInatWsrlQGq1zpVGc6fP4+OHTtixowZGDdu\nnNJn3IaqwT28d5CiNyMIAnx9fZGamopvv/0Wbdq0ga6uLvT19aGlpaU0GL06UcxTREQEJk6ciPfe\new/Tp08Xr0HR/1/fvHjxIubMmQMfHx+xl8uUKX4EV/GjonK5HBoaGjAzM0Pt2rVx48YNbN26FT17\n9oSWlpbY9tVtnXpT9+7dAwDo6OhAEATI5XLUqFEDnTt3Rt++fWFmZoZWrVqJ3+c2VA1OeO+AkpIS\n8WdENDQ0xA1F8cOuHTt2hEwmw549e3Dt2jWkpaWhUaNG1XqDSkpKwpdffolt27YhLS0NMTExiIyM\nBCAVHDkAABfkSURBVBFh2LBhsLKyQm5uLjQ1NfH+++9zsquA4oBo4MCBSEhIgJ+fn1I7mZqaom7d\nuuIp8+q8Pr0uIkJaWhqCg4Ph5eUFc3NzlJSUQFNTE3K5HA4ODujWrRsMDQ1Rq1YtVYer9jjhVWGZ\nmZnIzMyEqakpDh48iN9++w2xsbHigPLSR+Senp6oX78+LC0tsWHDBnTs2LFaXbMrSxAEdOrUCRkZ\nGeJDeJ2cnDBu3DgYGxtj8ODByMrKwtWrV9GyZctq3RavqmzPv3Hjxjh37hxatWoFPT09pcRmamoK\nS0tLVYVa5QmCACMjIxw7dgz79u1D7969xdPCiu3T0dERtWrV4uueVQAnvCoqLy8P8+bNQ1xcHB49\neoRvvvkG3bp1w6JFi5CcnAxfX19oaGhAQ0ND7AFaWVmhZs2a6Nu3r9Kjw6oTxU5DT08PFhYWuHDh\nAkxNTeHv74/bt2/DysoK7dq1Q506dVCrVi14e3vDzMxM1WFXKYpnjD558gQaGhpwcHDAihUr4OLi\nwr2QV3D37l2kpaXB0tISXl5eiImJgYeHB4yNjcVtkoceVC1800oVtmvXLpw8eRJZWVnw9PTEqFGj\nkJaWhn79+sHLywszZ84UfxyytOp2JFl2fkq/3r17N3755Re0b98eK1euxI4dO+Dp6al0AwYrf5PE\nDz/8gL///huGhoYYOnQo0tPTsWXLFmzZsoUfcfUMpde77OxsfPbZZxAEATY2Nvjmm28wdOhQBAQE\nYNSoUSqOlD0LJ7wqhojEawAAcObMGSxZsgRyuRxz5syBm5sb0tPT4e/vD19fXyxYsKBaJbdnOX/+\nPNavX4+ff/65XAL8888/kZWVBVdXV/j7+1e7hP82KNrkypUr0NbWhoODA0xNTREZGYmZM2eiVq1a\n2Lt3L/73v/+hdu3a4vVh9h9FG6akpMDExASCICAnJwcTJkxAo0aNEBYWBrlcjm3btqFOnTqqDpdV\ngH8PrwrS1NREREQEdu3ahTVr1iAvLw979+5FWFgYAgIC4OrqigMHDuDWrVvVesdeeqdbWFiI4uJi\nAP/1UhS9uAEDBohl+PitPMWOWvHL2h07dkRkZCTWr1+PDz74AA0bNkRmZibS09MRHByM8PBwTnal\nlO4dh4eHY/r06ZDL5fD398eYMf/X3r1HVVmlDxz/HkERRGUwQfFksZAlLh3IVBQxdTQVMafRAcfx\nTjkYFl6I8bJSSFdmeWGUJi+hJiMqSKnIoIhc1IQ83moEvGboKCipIYdA5QD790edEzj2K1fagcPz\n+UvgvGvts9fr+7x772c/+zXi4+O5evUqLi4uxMXFcfnyZdzd3eXFqx6Su7qeMT6Y5s2bR0BAAACD\nBw9m6NChFBYWsm3bNgoKCnB2dsbHx8ciH/B3794Fvl/0/+qrr9DpdDg4OJjOYTOysrKiqqqqzrWS\n7v2/jCO7pKQk4uPjiY2N5d1332Xq1Kl8/vnnODs706VLF5KSkmjVqhWlpaXmbnK9Yrynzpw5Q3R0\nNNu2bWPv3r0YDAZiYmIoKyvj6aef5pVXXuFvf/sbq1ev5v79+3If1kMS8OqhEydO8Pbbb+Pv78+9\ne/cA8Pf3Z8iQIVy7dq1OkLO0/1R37txh3rx5lJSUoNfrWb58OcHBwaxYsYKsrCzee+89duzYwcGD\nB6mpqXnoGqb4cVRSXV1NZWUlb7/9NhkZGXz33XdUVVUxceJEpk+fzurVq6mpqQEgLS2No0ePmkbS\njd2NGzdYsmQJNTU13Lp1i6ioKL755hscHBzQarWEh4eTlZXF9u3bTde0bNmSsrIyU5+K+kWeFmb2\nsGmP69evk5ubS0BAAM2bNwdAp9MxcOBAfHx8LD6pIDw8nNLSUkpKSli/fj3w/RaNwsJC7O3t2bVr\nF6WlpTRr1oy+ffuaubX1W0VFBS1btmTTpk3MmDGD9PR0unXrRseOHencuTO5ubmm+8/FxYWMjIw6\np5Y3Znfv3iUwMJAbN27g5OTEpEmTKCkpYdu2bYwdO5YOHTowceJEbt++TU1NDTU1Ndja2rJu3TrZ\nBlNfPaEaneIXqH2GW0FBgTpz5ozp3yEhISoqKkoppZROp1MeHh6mIsiWqHYR3f/+979qy5Ytqn//\n/iorK0sp9X3B7AkTJqi4uLifvE7UlZycrPr06aMiIyPVkSNHVFlZmQoICFDDhg1TCxYsUL169VI7\nd+40dzPrndr3VGVlpXr11VdVUFCQMhgMKj09XYWEhKiAgAC1efNm1alTJ5WammrG1opHIfvwzMy4\nEB4SEoJOp+Pw4cP06NEDJycnEhMT2bhxIwkJCSxdupRBgwaZu7lPlHH9MiIigokTJ9KqVSs2b95M\nhw4dcHV1paysjKKiIvr16/c/14m6yRWFhYUsW7aMSZMmUVVVxYEDB2jZsiWzZs3i4MGDXLp0iXfe\neYdhw4aZrpV+rNuH+fn5tG3bFnd3d/7zn/+wf/9+pk2bxu9+9zsyMzMpKioiLCyMESNGmApAiPpN\nAp4ZGYsfz58/n3379qHRaFi+fDkAI0eO5LXXXqN///6MHz8eb29viy04a3zYXrhwgUWLFhEZGUn3\n7t3p2LEj1dXVbNmyhY4dO+Li4mLaXG9kaX3xaxnPBTxy5AhKKcLCwnB1dcVgMJCamoq1tTUzZ85k\n7969XL16leeffx47Ozvpx1o0Gg2pqalMmDCBF198kS5duuDm5sbnn39OZmYmQUFBaLVaioqKqK6u\nplOnTtjb25u72eIXkFcSM2vTpg0ffvghJ0+eJCYmhpycHI4dO0ZISAgXL17E1dWVjh07mj5vSQ+m\n+/fvm7LZrl69ytatW7l8+TJ5eXkAODk58ec//5lBgwaxePFiunTpwh/+8AeLzEz9tYwvDVlZWYwa\nNYojR47wwQcfkJeXR7t27fD398fb25tPP/0UjUbD6tWruXXrlozsHmB88fr73/9ObGwsv//977Gy\nssLDw4MZM2Zw584dZs6cyaBBg3j++ecpLi6WAgcNiGw8/w3VHqGVlJTQtGlT05theHg47u7uTJs2\njbVr17J582a2bt1a51gWS1JVVUV2djYFBQXY29uTn5/PqFGjSEpK4s6dO4wcOZKBAwcCcPPmTSoq\nKnjmmWfM2+h67ty5c8yePZsFCxbg6+vL4sWLSUxMJD4+nq5du/LNN99QWVmJVqsFkGo0P3gw6F+4\ncIGlS5fy8ccfU11dTXV1Nc2aNaOqqoqCggIqKirw8vICoKysjJYtW5qr6eIRSZbmb0yj0ZCUlMTG\njRspLS1l3LhxDB48mJ49e7JhwwYMBgMJCQlERUVZbLADsLa2pk2bNrzzzjvk5uayadMmPD09sbW1\nZevWrezfvx+DwcCQIUNo27at6ToZkdRVuz9Onz7N1atX2bNnD76+vkRERGBlZYW/vz8pKSl069at\nznUS7OoWKjh79iy2tra0bt2aw4cPEx8fz9ixY7GysiItLY3jx4/z1ltvAT++LEiwa1hkDe83pNFo\nOH/+PNOmTeOf//wnnTt35ty5c5w9exZvb28cHBzYu3cvs2bN4sUXX7TINbva36l169bs3LkTrVaL\nnZ0dHh4eaLVa3NzcOH78OF9//TXdu3evUwjbkvricTCuAyckJBAcHEz79u358ssvuX79Oj179qR/\n//6UlpbSrl27OiNk6ccfGRPH3njjDQYNGkTnzp1xc3Nj7dq1XLlyBb1ez1tvvcWYMWPw8PAAkASV\nhuo3zgptlIxpzkVFRWrfvn1q+PDhpr/pdDo1ePBgpdPplFJK3b1713SNpaXc1/5ORUVFpt/l5eWp\n6dOnq4ULFyqllNLr9SoxMVFduHDBbG1tSPLy8tTTTz+tVq5cqZRSaseOHSo4OFitWrWqzucs7X56\nXE6dOqW8vLzU+fPnlVJKXb9+XR0/flzl5+erMWPGqNDQUPXvf/9bKSV92NDJlOYTZqwHmZOTw4IF\nC/jwww9p3rw5iYmJBAYG4u3tTdeuXU3ntjVt2tR0rSW+hWs0GlJSUli0aBF9+/alWbNmLFu2jIkT\nJ7JlyxZGjx5NXl4eiYmJUoD3Z+j1euzs7OjatSupqakEBgailOLNN9/EYDBw4MABrly5YhrZWeL9\n9Dg0b94cLy8vMjMz2bFjB1lZWQDMnTuXhIQE0+eUpDs0eDKl+YRpNBrS09PZsGEDISEh+Pj4cOvW\nLfLz88nMzMTKyorly5cTEhKCVqs1TZVY4sNJo9Fw6NAhZs+ezdatW7l27Rpr164lPz+f0NBQvLy8\nuHv3LpMmTcLX19fcza23lFJcunSJqVOn4u7uTrt27XB2dmbAgAGEh4cDMHXqVHr37m1KUBE/zc7O\njuLiYuLi4vjTn/7ElClTsLOzw2AwmJJTQOq0WgKZiH4CHnwTLCwsZOvWrVy9ehWAwMBA/Pz8+Pbb\nb9m2bRvR0dH07t3b4t8ga2pqMBgMpuryu3fv5tChQ5w9e5ZJkyah1WqZMWMGQ4cORSll8f3xKGr3\nh0ajoVOnTvTs2ZOlS5fy5ZdfUllZSbdu3Rg6dCjvvfceV65coX379mZudcPQokULQkNDOXjwIKNH\nj6asrIw1a9ZI/1kis02mWjDjPH9hYaFpTW779u3KxsZGZWdn1/lMRUWF6WdLXB+orq5WSil17969\nOt95woQJKjk5WSmlVHh4uOrcubP64osvzNbO+s7Yd1lZWSo6OtpUhm7lypVq5MiRKi0tTSUnJ6uJ\nEyeqs2fPmrOpDVZVVZU6fvy46tWrl9q9e7dSStbsLI1MaT5m6oc08ZSUFKZPn87u3bu5cuUKf/3r\nX+nevTvjx4/Hx8fHtK5iXLOz1OkSjUbDrl27mDNnDjqdDjs7O9zd3UlLS8PW1paioiJSU1P517/+\nRdeuXWXbwUMY++To0aMEBwdTUVHBsWPHuH37Nq+//jqlpaVkZGQQGxtLSEgIL7zwQp3rxC/TpEkT\nHBwc8PPzq3P0lvSh5ZCN50+ATqdj0aJFLFmyhOLiYk6fPk1BQQFr1qzho48+IiwsjMLCQlq1amWR\n6c3qgQ32kydPZty4cej1elMf1NTUsG7dOi5cuEBYWJjp7D95SD+cTqcjMjKSZcuW4enpyfbt28nJ\nycHT05OgoCCsra25desWTz31lPThYyL9aHkkS/MxKykpISoqiuLiYrp37w6AVqvl3XffJTMzk2nT\npuHn54eDg4OZW/pkaTQadDodJ06coEePHowdOxYAGxubOtVk9Ho9rVq1krfpn1FaWkp6ejppaWl4\nenoSGBhIkyZNSE9Pp7y8nNDQUBwdHc3dTIsi96LlkSnNX+nBB7WtrS2Ojo7s27ePmzdvMmDAAJyc\nnDh48CBlZWX069cPe3t7mjRpYpFvkMbvlJ2dzeTJk7l9+zZffPEF7u7udOjQgR49emBtbc3cuXMZ\nO3YsrVu3NvWBpfXF4+Tm5oaXlxcrVqzA0dERLy8vunTpQnl5Ob6+vjg7O0s/CvEzZErzVzI+4DMy\nMjh27Bht27Zl1KhR5OXl8cEHH9CyZUuCgoKYPn060dHRFn/ED3w//bZgwQJWrlyJp6cnCxcupKSk\nhICAAHx9fWnatCmFhYV06NDB3E1tcFJSUli4cCEzZ85k8uTJ5m6OEA2K5S0g/YaMwe6zzz7jtdde\no0WLFsTExBAdHU3Tpk0JDQ3l6NGjzJ8/nw0bNjBo0CCqqqrM3ewnrrS0lMzMTNLT0wFYuHAhbdq0\nITY2ls8++wyllCnYyfvWoxkxYgSRkZG8//77puNphBC/jAS8X8FYG3Pt2rXMmTOHGTNmsGvXLvR6\nPcnJyQwYMIB169bRqVMnDh06BHxfNNnSDR06lJ07d7Jhwwa2bdtGs2bNWLBgAe3bt8fJyanOlJtM\nvz26l19+mUOHDuHi4iIFoIV4BJb/9H3MjKM6Y8mw/Px8bt68yf79+xk+fDharZY5c+YwbNgw3njj\nDfr27YvBYCAuLs6URdcYvPzyy1hbW7Nw4UIqKyuZMmUKS5YskQD3mBhPkLDEdWAhnhRZw3sEtRNU\naq9BZWdnExcXh7u7O2PHjqW8vJzAwEBSUlLo0KEDlZWVVFVV1an631gkJSUxf/580tPTcXZ2lhGJ\nEMJsJOA9AuPb9N69e4mMjGTIkCE0adKERYsWcfjwYaKjo7l27RoODg7Mnj0bf39/eQPn+wNca59p\nJ4QQ5iBTmo/AePbY3Llz2bFjB7GxsezcuZOioiLWr1+Pra0tmzZtws3NjWHDhpm7ufWGTL8JIeoD\nSVp5BNXV1ej1euLj47l27Rrp6el8/PHH3Lhxg+DgYHr06MEf//hHLly4wIYNG6iqqpIHfC3SF0II\nc5IR3iOwsrJi8ODBaDQa/vGPf7By5Up8fHxwdXXl4sWLXLx4kZdeegmlFL169WoUGZlCCNFQyBP5\nJzw4/Wb82cbGhvv376PX68nNzaWmpobTp08TExODh4cHACNHjjRXs4UQQvwESVp5iNrZmHl5eTg6\nOuLi4lLnMwcPHiQqKoqKigqCg4MZM2aM6VqZuhNCiPpHAt5DGINWcnIyy5cvZ8WKFXh7e5v+btyD\nV15ejlIKe3t7KX4shBD1nAS8n/DVV18xZswYPvroI3r27Fnnbw8LbjKyE0KI+k2yNH9w+fJlQkND\nTT8bq6IYg52xBmZ5eflDD2uVYCeEEPWbBLwfPPvss0yZMoWvv/4aAE9PTxwdHcnIyKCyshJra2sO\nHz7MsmXLuHfvnhQ9FkKIBqbRT2kqpaiurjZtIfD19cXKyspUOeXSpUvY2dnRp08fwsPDWbNmDUOG\nDDFzq4UQQjyqRh3waq/FnTt3zrStYODAgTg5ObFjxw7S09NJSUmhsrKSESNGSLkwIYRooBp9wDPW\nxpwxYwYJCQn06NEDgH79+uHs7Mynn34KwP3797GxsZFsTCGEaKAadcADOHXqFOPGjSM+Pp7nnnuO\nK1eu4OTkhK2tLX369MHe3p709HTTVgQhhBANU6OrtPLgCM3a2pqAgAByc3NJTU0lISEBd3d35s+f\nz9GjR8nJyQGQYCeEEA1co3yKazQa0tLSSE1N5amnnuLu3bts374dV1dX4uPjcXV15dSpUwD07dsX\npZRkZQohRAPX6AKeRqMhKSmJN998E4PBgIuLC0uWLGHXrl385S9/wWAwcODAAdzc3OpcI2t2QgjR\nsDW6gFdSUsLq1av55JNPGDFiBCdPnuSTTz6hpqaGrKwspk2bRkREBAMHDpRRnRBCWBCLX8N7cAuB\n8Yy6xMREzp07h5WVFZmZmdy5c4dJkyaxceNGPDw8JNgJIYSFsegRXu2gdf78eb799lvatm1LREQE\nZWVlBAUFERsbS0xMDMeOHcPW1ta0Fw9k64EQQlgSi96WUF1djZWVFcnJySxatIgXXniBmpoaZs2a\nhaurKwD79+8nLCyM5cuX4+/vb+YWCyGEeFIscoT33XffAd+fUH7s2DEiIyNJSkqiRYsWZGVlERER\nwcmTJykvL2f16tW8//77pgoqQgghLJPFjfBKSkpYsWIFXbt2Zdy4ceh0Opo1a8bNmzeZN28eq1at\nIiYmBr1ez4oVK2jfvr2cZyeEEI2AxY3wrKyssLOz48SJE+zZs4fevXvTvXt3MjIyWLVqFf3790er\n1dKmTRvKy8uxt7c3XSvBTgghLJfFBDzjqQetWrUyrdFlZGSwc+dOAPR6PYsXLyYzM5Pk5GRef/11\nnnvuORnZCSFEI2ExU5rG7QeZmZncv3+fAQMGsH79ei5fvsxLL73EkCFDePXVV6moqCAwMJDRo0fL\nqQdCCNGIWEzAA0hOTiYiIoKlS5fi5+dHaWkpmzZtoqCggOHDhzN8+HA59UAIIRopi5nSLCsrY+PG\njaxduxY/Pz8MBgOtW7fmlVdeQavVsmfPHoqLi7GxsQGkXJgQQjQ2FlNppUmTJty6dQu9Xg/8OHKr\nrKwkLCyMwsJCnJ2dzdlEIYQQZmQxI7wWLVowZswYcnJyOHPmDNbW1mRnZzN+/Hhu3rzJM888Y+4m\nCiGEMCOLWsMrLCxk/fr1ZGVl4evrS2JiItHR0YwYMcLcTRNCCGFmFhXwACoqKtDpdBQXF/Pss8/S\np08fSVARQghheQHvQRLshBBCgAUlrfwUCXRCCCHAgpJWhBBCiP+PBDwhhBCNggQ8IYQQjYIEPCGE\nEI2CBDwhhBCNggQ8IYQQjYIEPCGEEI3C/wElANR3gSZd6QAAAABJRU5ErkJggg==\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x1066dcef0>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 19
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"cython_bonus\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Bonus: How to use Cython without the IPython magic"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"IPython's notebook is really great for explanatory analysis and documentation, but what if we want to compile our Python code via Cython without letting IPython's magic doing all the work? \n",
|
|
"These are the steps you would need."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 1. Creating a .pyx file containing the the desired code or function."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%file ccy_classic_lstsqr.pyx\n",
|
|
"\n",
|
|
"def ccy_classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"Writing ccy_classic_lstsqr.pyx\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 11
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 2. Creating a simple setup file"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%file setup.py\n",
|
|
"\n",
|
|
"from distutils.core import setup\n",
|
|
"from distutils.extension import Extension\n",
|
|
"from Cython.Distutils import build_ext\n",
|
|
"\n",
|
|
"setup(\n",
|
|
" cmdclass = {'build_ext': build_ext},\n",
|
|
" ext_modules = [Extension(\"ccy_classic_lstsqr\", [\"ccy_classic_lstsqr.pyx\"])]\n",
|
|
")"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"Writing setup.py\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 12
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"####3. Building and Compiling"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"!python3 setup.py build_ext --inplace"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"running build_ext\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"cythoning ccy_classic_lstsqr.pyx to ccy_classic_lstsqr.c\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"building 'ccy_classic_lstsqr' extension\r\n",
|
|
"creating build\r\n",
|
|
"creating build/temp.macosx-10.6-intel-3.4\r\n",
|
|
"/usr/bin/clang -fno-strict-aliasing -Werror=declaration-after-statement -fno-common -dynamic -DNDEBUG -g -fwrapv -O3 -Wall -Wstrict-prototypes -arch i386 -arch x86_64 -g -I/Library/Frameworks/Python.framework/Versions/3.4/include/python3.4m -c ccy_classic_lstsqr.c -o build/temp.macosx-10.6-intel-3.4/ccy_classic_lstsqr.o\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\u001b[1mccy_classic_lstsqr.c:2040:28: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_AsString'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE char* __Pyx_PyObject_AsString(PyObject* o) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2037:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function\r\n",
|
|
" '__Pyx_PyUnicode_FromString' [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyUnicode_FromString(char* c_str) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2104:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_IsTrue'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyObject_IsTrue(PyObject* x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2159:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyIndex_AsSsize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE Py_ssize_t __Pyx_PyIndex_AsSsize_t(PyObject* b) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2188:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_FromSize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject * __Pyx_PyInt_FromSize_t(size_t ival) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1584:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_From_long'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyInt_From_long(long value) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1631:27: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_long' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE long __Pyx_PyInt_As_long(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1731:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_int' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyInt_As_int(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"8 warnings generated.\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\u001b[1mccy_classic_lstsqr.c:2040:28: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_AsString'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE char* __Pyx_PyObject_AsString(PyObject* o) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2037:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function\r\n",
|
|
" '__Pyx_PyUnicode_FromString' [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyUnicode_FromString(char* c_str) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2104:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_IsTrue'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyObject_IsTrue(PyObject* x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2159:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyIndex_AsSsize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE Py_ssize_t __Pyx_PyIndex_AsSsize_t(PyObject* b) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2188:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_FromSize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject * __Pyx_PyInt_FromSize_t(size_t ival) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1584:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_From_long'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyInt_From_long(long value) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1631:27: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_long' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE long __Pyx_PyInt_As_long(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1731:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_int' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyInt_As_int(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"8"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
" warnings generated.\r\n",
|
|
"/usr/bin/clang -bundle -undefined dynamic_lookup -arch i386 -arch x86_64 -g build/temp.macosx-10.6-intel-3.4/ccy_classic_lstsqr.o -o /Users/sebastian/Github/python_reference/benchmarks/ccy_classic_lstsqr.so\r\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 13
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 4. Importing and running the code"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import ccy_classic_lstsqr\n",
|
|
"\n",
|
|
"%timeit classic_lstsqr(x, y)\n",
|
|
"%timeit cy_classic_lstsqr(x, y)\n",
|
|
"%timeit ccy_classic_lstsqr.ccy_classic_lstsqr(x, y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"100 loops, best of 3: 2.9 ms per loop\n",
|
|
"1000 loops, best of 3: 212 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"1000 loops, best of 3: 207 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 20
|
|
}
|
|
],
|
|
"metadata": {}
|
|
}
|
|
]
|
|
} |