mirror of
https://github.com/rasbt/python_reference.git
synced 2024-11-24 04:21:15 +00:00
1035 lines
116 KiB
Plaintext
1035 lines
116 KiB
Plaintext
{
|
|
"metadata": {
|
|
"name": "",
|
|
"signature": "sha256:4324cc9b055392dcbb5813ce3a18ba58a848b9da045d6c60188030f257582522"
|
|
},
|
|
"nbformat": 3,
|
|
"nbformat_minor": 0,
|
|
"worksheets": [
|
|
{
|
|
"cells": [
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[Sebastian Raschka](http://sebastianraschka.com) \n",
|
|
"\n",
|
|
"- [Open in IPython nbviewer](http://nbviewer.ipython.org/github/rasbt/python_reference/blob/master/tutorials/multiprocessing_intro.ipynb?create=1) \n",
|
|
"\n",
|
|
"- [Link to this IPython notebook on Github](https://github.com/rasbt/python_reference/blob/master/tutorials/multiprocessing_intro.ipynb) \n",
|
|
"\n",
|
|
"- [Link to the GitHub Repository python_reference](https://github.com/rasbt/python_reference)\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import time\n",
|
|
"print('Last updated: %s' %time.strftime('%d/%m/%Y'))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"Last updated: 19/06/2014\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 21
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<hr>\n",
|
|
"I would be happy to hear your comments and suggestions. \n",
|
|
"Please feel free to drop me a note via\n",
|
|
"[twitter](https://twitter.com/rasbt), [email](mailto:bluewoodtree@gmail.com), or [google+](https://plus.google.com/+SebastianRaschka).\n",
|
|
"<hr>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 1,
|
|
"metadata": {},
|
|
"source": [
|
|
"Parallel processing via the `multiprocessing` module"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
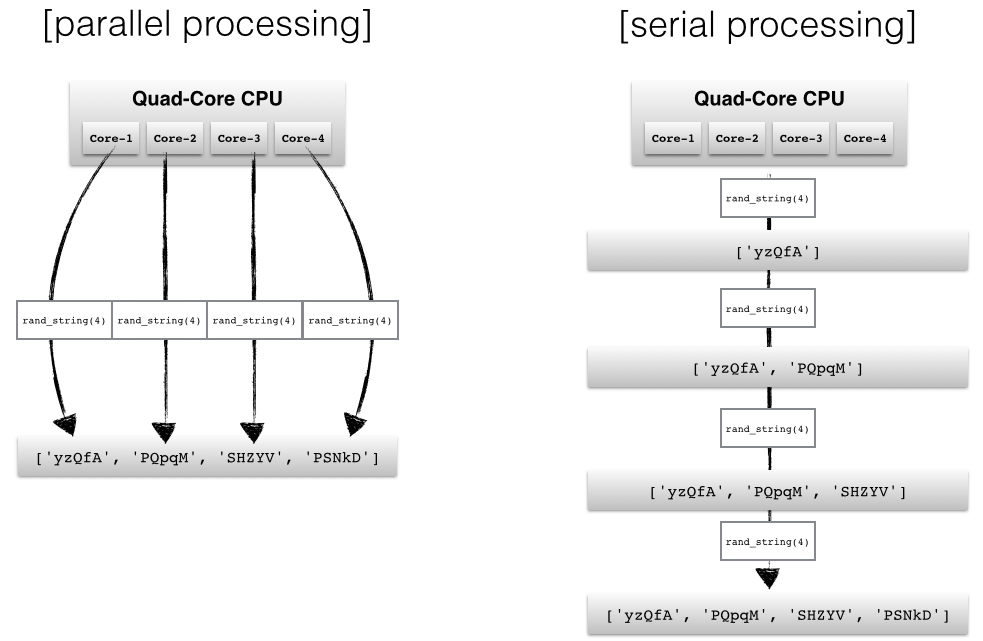
"CPUs with multiple cores have become the standard in the recent development of modern computer architectures, whether it is our desktop machine at home, our laptop, and especially supercomputer facilities. \n",
|
|
"\n",
|
|
"However, the default Python interpreter's GIL (Global Interpreter Lock) is designed for simplicity, and in order to prevent conflicts between threads, it executes only one statement at a time (so-called serial processing).\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 3,
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"Multi-Threading vs. Multi-Processesing\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Depending on the application, two different approaches in parallel programming are either to run code via threads or multiple processes, respectively. If we submit \"jobs\" to different threads, those jobs can be pictured as \"sub-task\" of a single process and those threads will usually have access to the same memory areas (i.e., shared memory). This approach can easily lead to conflicts in case of improper synchronization, for example, if processes are writing to the same memory location at the same time. \n",
|
|
"\n",
|
|
"A safer approach (although less efficient due to the communication overhead between separate processes) is to submit multiple processes to completely separate memory locations (i.e., distributed memory): Every process will run completely independent from each other.\n",
|
|
"\n",
|
|
"Here, we will take a look at Python's [`multiprocessing`](https://docs.python.org/dev/library/multiprocessing.html) module and how we can use it to submit multiple processes that can run independently from each other in order to make best use of our CPU cores."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
""
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 2,
|
|
"metadata": {},
|
|
"source": [
|
|
"Sections"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"- [Introduction to the multiprocessing module](#Introduction-to-the-multiprocessing-module)\n",
|
|
"\n",
|
|
" - [The Process class](#The-Process-class)\n",
|
|
" \n",
|
|
" - [Defining an own Process class](#Defining-an-own-Process-class)\n",
|
|
" \n",
|
|
" - [The Pool class](#The-Pool-class)\n",
|
|
" \n",
|
|
"- [Parzen kernel density estimation as benchmarking function](#Parzen-kernel-density-estimation-as-benchmarking-function)\n",
|
|
" \n",
|
|
" - [The Parzen-window method in a nutshell](#The-Parzen-window-method-in-a-nutshell)\n",
|
|
" \n",
|
|
" - [Sample data and timeit benchmarks](#Sample-data-and-timeit-benchmarks)\n",
|
|
" \n",
|
|
" - [Benchmarking functions](#Benchmarking-functions)\n",
|
|
" \n",
|
|
" - [Preparing the plotting of the results](#Preparing-the-plotting-of-the-results)\n",
|
|
"\n",
|
|
"- [Results](#Results)\n",
|
|
"\n",
|
|
"- [Conclusion](#Conclusion)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 1,
|
|
"metadata": {},
|
|
"source": [
|
|
"Introduction to the `multiprocessing` module"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The [multiprocessing](https://docs.python.org/dev/library/multiprocessing.html) module in Python's Standard Libarary has a lot of powerful features. If you want to read about all the nitty-gritty tips, tricks, and details, I would recommend to use the [official documentation](https://docs.python.org/dev/library/multiprocessing.html) as an entry point. \n",
|
|
"\n",
|
|
"In the following sections, I want to provide a brief overview of different approaches to show how the `multiprocessing` module can be used for prallel programming."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 3,
|
|
"metadata": {},
|
|
"source": [
|
|
"The `Process` class"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The most basic approach is probably to use the `Process` class from the `multiprocessing` module. \n",
|
|
"Here, we will use a simple queue function to compute the cubes for the 6 numbers 1, 2, 3, 4, 5, and 6 in 6 parallel processes."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import multiprocessing as mp\n",
|
|
"\n",
|
|
"# Define an output queue\n",
|
|
"output = mp.Queue()\n",
|
|
"\n",
|
|
"# define a example function\n",
|
|
"def cube(x, output):\n",
|
|
" output.put(x**3)\n",
|
|
"\n",
|
|
"# Setup a list of processes that we want to run\n",
|
|
"processes = [mp.Process(target=cube, args=(x, output)) for x in range(1,7)]\n",
|
|
"\n",
|
|
"# Run processes\n",
|
|
"for p in processes:\n",
|
|
" p.start()\n",
|
|
"\n",
|
|
"# Exit the completed processes\n",
|
|
"for p in processes:\n",
|
|
" p.join()\n",
|
|
"\n",
|
|
"# Get process results from the output queue\n",
|
|
"results = [output.get() for p in processes]\n",
|
|
"\n",
|
|
"print(results)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"[1, 8, 27, 64, 125, 216]\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 1
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 3,
|
|
"metadata": {},
|
|
"source": [
|
|
"Defining an own `Process` class"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"We can also define our own `Process` classes based on the `multiprocessing.Process` parent-class. Note that we will define a `run` method, which will be automatically executed when we start a process-instance via `.start()`."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"class CubeProcess(mp.Process):\n",
|
|
" def __init__(self, x, output):\n",
|
|
" super(mp.Process, self).__init__()\n",
|
|
" self.x = x\n",
|
|
" self.queue = output\n",
|
|
" def run(self):\n",
|
|
" self.queue.put(self.x**3)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 2
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"# Define an output queue\n",
|
|
"output = mp.Queue()\n",
|
|
"\n",
|
|
"# Setup a list of processes that we want to run\n",
|
|
"processes = [CubeProcess(x, output) for x in range(1,7)]\n",
|
|
"\n",
|
|
"# Run processes\n",
|
|
"for p in processes:\n",
|
|
" p.start()\n",
|
|
"\n",
|
|
"# Exit the completed processes\n",
|
|
"for p in processes:\n",
|
|
" p.join()\n",
|
|
"\n",
|
|
"# Get process results from the output queue\n",
|
|
"results = [output.get() for p in processes]\n",
|
|
"\n",
|
|
"print(results)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"[1, 8, 27, 64, 125, 216]\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 3
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 3,
|
|
"metadata": {},
|
|
"source": [
|
|
"The `Pool` class"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Another and more convenient approach for simple parallel processing tasks is provided by the `Pool` class. \n",
|
|
"\n",
|
|
"There are four methods that are particularly interesing:\n",
|
|
"\n",
|
|
" - Pool.apply\n",
|
|
" \n",
|
|
" - Pool.map\n",
|
|
" \n",
|
|
" - Pool.apply_async\n",
|
|
" \n",
|
|
" - Pool.map_async\n",
|
|
" \n",
|
|
"The `Pool.apply` and `Pool.map` methods are basically equivalents to Python's in-built [`apply`](https://docs.python.org/2/library/functions.html#apply) and [`map`](https://docs.python.org/2/library/functions.html#map) functions."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Before we come to the `async` variants of the `Pool` methods, let us take a look at a simple example using `Pool.apply` and `Pool.map`. Here, we will set the number of processes to 4, which means that the `Pool` class will only allow 4 processes running at the same time."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def cube(x):\n",
|
|
" return x**3"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 4
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"pool = mp.Pool(processes=4)\n",
|
|
"results = [pool.apply(cube, args=(x,)) for x in range(1,7)]\n",
|
|
"print(results)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"[1, 8, 27, 64, 125, 216]\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 6
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"pool = mp.Pool(processes=4)\n",
|
|
"results = pool.map(cube, range(1,7))\n",
|
|
"print(results)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"[1, 8, 27, 64, 125, 216]\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 7
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The `Pool.map` and `Pool.apply` will lock the main program until all processes are finished and return the results. The `async` variants, in contrast, will submit the processes to be run in the background without locking the main program, which can be quite useful for certain applications. \n",
|
|
"However, if we use this asynchronous approach, we need to use the `get` method in order to obtain the `return` values."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"pool = mp.Pool(processes=4)\n",
|
|
"results = [pool.apply_async(cube, args=(x,)) for x in range(1,7)]\n",
|
|
"output = [p.get() for p in results]\n",
|
|
"print(output)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"[1, 8, 27, 64, 125, 216]\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 8
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 1,
|
|
"metadata": {},
|
|
"source": [
|
|
"Parzen kernel density estimation as benchmarking function"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In the following approach, I want to do a simple comparison of a serial vs. multiprocessing approach where I will use a slightly more complex function than the `cube` example, which he have been using above. \n",
|
|
"\n",
|
|
"Here, I define a function for performing a Kernel density estimation for probability density functions using the Parzen-window technique. \n",
|
|
"I don't want to go into much detail about the theory of this technique, since we are mostly interested to see how `multiprocessing` can be used for performance improvements, but you are welcome to read my more detailed article about the [Parzen-window method here](http://sebastianraschka.com/Articles/2014_parzen_density_est.html). "
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import numpy as np\n",
|
|
"\n",
|
|
"def parzen_estimation(x_samples, point_x, h):\n",
|
|
" \"\"\"\n",
|
|
" Implementation of a hypercube kernel for Parzen-window estimation.\n",
|
|
"\n",
|
|
" Keyword arguments:\n",
|
|
" x_sample:training sample, 'd x 1'-dimensional numpy array\n",
|
|
" x: point x for density estimation, 'd x 1'-dimensional numpy array\n",
|
|
" h: window width\n",
|
|
" \n",
|
|
" Returns the predicted pdf as float.\n",
|
|
"\n",
|
|
" \"\"\"\n",
|
|
" k_n = 0\n",
|
|
" for row in x_samples:\n",
|
|
" x_i = (point_x - row[:,np.newaxis]) / (h)\n",
|
|
" for row in x_i:\n",
|
|
" if np.abs(row) > (1/2):\n",
|
|
" break\n",
|
|
" else: # \"completion-else\"*\n",
|
|
" k_n += 1\n",
|
|
" return (k_n / len(x_samples)) / (h**point_x.shape[1])"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 9
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<hr>\n",
|
|
"**A quick note about the \"completion else**\n",
|
|
"\n",
|
|
"Sometimes I receive comments about whether I used this for-else combination intentionally or if it happened by mistake. That is a legitimate question, since this \"completion-else\" is rarely used (that's what I call it, I am not aware if there is an \"official\" name for this, if so, please let me know). \n",
|
|
"I have a more detailed explanation [here](http://sebastianraschka.com/Articles/2014_deep_python.html#else_clauses) in one of my blog-posts, but in a nutshell: In contrast to a conditional else (in combination with if-statements), the \"completion else\" is only executed if the preceding code block (here the `for`-loop) has finished.\n",
|
|
"<hr>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 3,
|
|
"metadata": {},
|
|
"source": [
|
|
"The Parzen-window method in a nutshell"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"So what this function does in a nutshell: It counts points in a defined region (the so-called window), and divides the number of those points inside by the number of total points to estimate the probability of a single point being in a certain region.\n",
|
|
"\n",
|
|
"Below is a simple example where our window is represented by a hypercube centered at the origin, and we want to get an estimate of the probability for a point being in the center of the plot based on the hypercube."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%matplotlib inline"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 10
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"from mpl_toolkits.mplot3d import Axes3D\n",
|
|
"import matplotlib.pyplot as plt\n",
|
|
"import numpy as np\n",
|
|
"from itertools import product, combinations\n",
|
|
"fig = plt.figure(figsize=(7,7))\n",
|
|
"ax = fig.gca(projection='3d')\n",
|
|
"ax.set_aspect(\"equal\")\n",
|
|
"\n",
|
|
"# Plot Points\n",
|
|
"\n",
|
|
"# samples within the cube\n",
|
|
"X_inside = np.array([[0,0,0],[0.2,0.2,0.2],[0.1, -0.1, -0.3]])\n",
|
|
"\n",
|
|
"X_outside = np.array([[-1.2,0.3,-0.3],[0.8,-0.82,-0.9],[1, 0.6, -0.7],\n",
|
|
" [0.8,0.7,0.2],[0.7,-0.8,-0.45],[-0.3, 0.6, 0.9],\n",
|
|
" [0.7,-0.6,-0.8]])\n",
|
|
"\n",
|
|
"for row in X_inside:\n",
|
|
" ax.scatter(row[0], row[1], row[2], color=\"r\", s=50, marker='^')\n",
|
|
"\n",
|
|
"for row in X_outside: \n",
|
|
" ax.scatter(row[0], row[1], row[2], color=\"k\", s=50)\n",
|
|
"\n",
|
|
"# Plot Cube\n",
|
|
"h = [-0.5, 0.5]\n",
|
|
"for s, e in combinations(np.array(list(product(h,h,h))), 2):\n",
|
|
" if np.sum(np.abs(s-e)) == h[1]-h[0]:\n",
|
|
" ax.plot3D(*zip(s,e), color=\"g\")\n",
|
|
" \n",
|
|
"ax.set_xlim(-1.5, 1.5)\n",
|
|
"ax.set_ylim(-1.5, 1.5)\n",
|
|
"ax.set_zlim(-1.5, 1.5)\n",
|
|
"\n",
|
|
"plt.show()\n"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAZQAAAGUCAYAAAASxdSgAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXeUVOX9/9/3Tp/ZQpG6LCxNQUXEgCJIEVgWUIkRCwqK\nDdFEjTExNiwYG/zUX+QY2/fYYn5BiFEhAZYOFiKgIUG/iqgUkaZI2d2pt/3+WJ/rnbv3ztyZuW1m\nn9c5niO7s3eeO+V5P5/OSJIkgUKhUCiUAmGdXgCFQqFQSgMqKBQKhUIxBSooFAqFQjEFKigUCoVC\nMQUqKBQKhUIxBSooFAqFQjEFKigUCoVCMQUqKBQKhUIxBSooFAqFQjEFKigUCoVCMQUqKBQKhUIx\nBSooFAqFQjEFKigUCoVCMQUqKBQKhUIxBSooFAqFQjEFKigUCoVCMQUqKBQKhUIxBSooFAqFQjEF\nKigUCoVCMQUqKBQKhUIxBSooFAqFQjEFKigUCoVCMQUqKBQKhUIxBSooFAqFQjEFKigUCoVCMQUq\nKBQKhUIxBSooFAqFQjEFKigUCoVCMQUqKBQKhUIxBSooFAqFQjEFr9MLoFD0kCQJqVQKPM/D7/fD\n4/GAYRgwDOP00igUigaMJEmS04ugUNSIogiO4+T/iIiIoohAICALDMtSI5tCcQvUQqG4CkmSIAgC\nGhoa4Pf7wbKs/J8kSYjH42AYBhzHAQBYloXX64XP56MCQ6E4DBUUimuQJAkcx0EQBNnNpYRYKcT1\nRYzrVCqFVCoFgAoMheIkVFAorkAURaRSKUiSJMdJRFFEPB6HIAjwer3weDxpf6MUGKBZkEjchQoM\nhWI/NIZCcRTi4iJxEiISx44dgyRJspVCHicIAliWhcfjkf/TC9ITgVF+xFmWhc/nkwWKCgyFYh5U\nUCiOQawJURRlMSFxkkQigVAoBL/fD47j5I2/qakJgUCACgyF4kKoy4viCFouLkEQ0NTUlCYQahiG\nSdv4lcJCxElPYNQpx0RckskkkskkACowFEohUEGh2IokSeB5HjzPg2EYecNOpVKIRqMIBoMIBoNo\namoydD2GYeD1euH1euXrmykwHo9Hjr94vV5aA0OhZIAKCsU2SG2J2sUVi8XAcRzKy8tlYSDkuoEb\nFRilBZJJYERRRGNjIwDIwqK0YKjAUCg/QQWFYjnKwDvw08bN8zyi0Sg8Hg8qKyst2ZwzCUwymYQo\nimnWi5bAkP9YloUoikgkEvL1qcBQKD9BBYViKWoXF7FKEokE4vE4wuEw/H6/bRtxPgKj/FstC4YK\nDIXSDBUUimXo1ZZEo1GIooiKigrNwDvBjgREIwJDrBOSUZbNRUYFhtJaoYJCMR11bQk55XMch2g0\nCp/Ph7Kysoyba6bfWSk0WgKTSCTkYL0RF5lynVRgKK0JKigUU9GrLUkkEkgkEohEIi1aquSC3Rsw\nEUSGYeD3+yGKIkRRBM/z4DgOkiTlLDCkHxlABYZSWlBBoZgGyYiSJAnBYFB2cZEU4MrKyqKv6yCN\nKokFI4qi7CIzKjDKGhoqMJRSggoKpWCUgXdRFAE0b57q2pJS3ByJwPh8PgAtBYY8RikQRgVGEAT4\nfD74/X4qMJSigAoKpSC0XFyiKCIWiyGVSqGsrEzebPO5drGRSWBIw0p1kaWewKRSKVlYyGNIfIcK\nDMWNUEGh5A2JIwBIE5NUKgWv14uKioq8XVylslEWIjDAT0kCQMtkBwBpnZSpwFCchgoKJWe0aksA\nyC1LvF5v1iyu1opSYEirFz2BUVtoWi4yMjuGQATG6/WmxW8oFDuggkLJCb32KdFoFDzPIxgMynUn\nZlGqm6JSILQERhRFJJNJ8DxvuNCSCIwkSXIPMyowFLuggkIxhLp9CtnYeJ5HU1MTvF4vKisrkUwm\nIQiCk0stWtQCE4vF5IaUPM8jmUzK3ZZzFRjye2UMhgoMxWyooFCyohzNq7RKksmk3D4lEAjYup7W\nABEX4sYiWWBEJPIRGHXciwoMxUyooFAykmv7FCI2haJ3nda84SnFA0BGgdHKAqMCQ7EaKigUTfTm\nlpD2KX6/nwbeLSabMGcSGI7jkEgkMk6z1BOYeDwOAHLshQoMxShUUCgtyDSaN5lMFtw+JZ/1tNaN\nLJf7NktgyPvNMAw4jmthwZA0ZSowFDVUUChpaNWWCIKAaDQKIHv7FLNcXsrr0U0rP8wQGKU7k8TS\nqMBQ9KCCQgGgX1vSGtqnGKEUEgGMCgx5rNoyNCIwyj5kVGBaH1RQKHIDR5JRRDaTTKN5rcZsS4fS\nEj2BIW36o9FozhZMKpWSkwOUAkM+V1RgShsqKK0YZW1JKpWSJycKgoCmpiZ4PJ6C2qdQigulwBAx\nUFbxi6KYt8AAkOtrqMCULlRQWimZaktisRhCoRACgUDOX/hStCxK8Z6MoEwjBtKnWRYqMEoLhsRg\nqMAUP1RQWiFatSUA5JOkEy6uTLTmLC83YURg9GbBkL9XuteA5hgd6WGmbhVDBab4cM+uQbEcvdoS\nnuflDsHl5eWu+xKrN6XWaC24kUwCY2RcMoAWAkPa+JDHq7PIKO6GCkorIdtoXq/XK8dQCsHMSnky\nrItSHJghMADSxENtwVCBcTdUUFoByvG06vYpkiShoqICyWTSlSd/0t2YbiD2QToVF0o+AqP8W6Cl\nBUMFxt1QQSlhMrVPaWpqQiAQQCgUcp2LiyAIAhoaGsCyrFzrQKBB3OIjk8AkEglZNEh35GwuMmJ1\nKwVGXQdDsRcqKCWK3twS0j6lkNG8VkM2Cp7nUV5eLt+DKIpIJBLy3HUAuidcivtRCkwgEJBHRxNX\nrCRJGV1k6j5kJEtRK02Zfj7sgQpKiaGeW6Jsn0KKF7Xap1jdJdgopM2LKIrw+/3wer1pJ1CSCeT1\netMsMJKKSjYPOg63+CCC4ff7wbJs2rhk4rKlAuNuqKCUEFq1JUDxtE9RrpNhmLTRtmrI/ZEmlbn2\nqSoGWnu6tHJcMoAWAgOgxfubi8CQFGVq4ZoHFZQSQau2JNf2KU4F5bVcceRLbxS9NiIkJZoU4dE+\nU9lxMjkjk4hmEhhixeYiMMSFSlAWWpI6GEpuUEEpcjLVlkSjUXg8HlRWVmb9cjj15SF9xIDsnYxz\nQUtgjKawUopjkJlSYIgFUojAJBIJcBwnH7yURZbFaOE6ARWUIkavtkQ5mteM2pJcyCWGko8rLt8Y\njZEMI7Lx0Crt4oO8X7kIjF6assfj0bRgqMBkhwpKkSIIAmKxmOwmUtaWaI3mzYadFehuyDbTyjAi\nm486g8yN9TmliBVzdHIRGK2/V66NCkx2qKAUGUoXF/k3wzDyaF6fz+fq0by5uLjs3MgzuU+Ur7XS\ngqFYgxWvrZbAkEMEyRIkkPdZbcFQgckOFZQiIlNtSSKRsH00rxaZLB1SUGnExeXkl1G9+ZAuAizL\nyptPsWeQtXa0YmyxWCztPVY+hgqMMaigFAF6tSXKnxca0LbS5eUGF1chkI2glFOUlbRGFx/5TpHN\nX8uCydaqX0tg4vF4Wnym1AWGCorLyTaal2EYV3YIJliVxeUkmTLIjLRxLwacWK+b6m700tCNHiKU\nVq7y70tdYKiguBi92pJ4PI5UKoVwOJz2AXUTRAiLoWdYoWTKIKMpysVDJkGzWmDIcweDwaIWGCoo\nLkTpylJ+CJXtUyoqKkzPijGr9QoAU1xcxep6UQtMtgrvUrDaWhtmC4yyjxl53Pz583H//ffbf3MF\nQD/JLoPUlhAxIR+uZDKJhoYGBAIBlJWVyadct226ZIYJz/OorKzMW0wync7cds/ZIMH9YDCISCSC\nUCgEj8cjpyhHo1G5qI7OgHGOQlxuRGD8fj9CoRAikYg8QptkYJI0f57nNT/DyhgOy7JYuXJlobdk\nO9RCcRF6Lq5oNCp33rVyNG+hGzXJ4gIgi54ZqE92xSYoatQpynrBX5K+3FpwUwylUIzE2ZQWjPq+\nBUEoSsuVCooLyNQ+hYxE1WqfYubmWsgXWTn5MRKJIBqNmrKm1kAm1wnQ7Dq0O4OslDZ2o1gt3Jni\nbERggGZPxM6dO9G+fXuEQiFL12QFxSeBJYZy9ofSKkkkEmhsbEQoFCqKQkWSuux0HUyxo3SdAJDb\n5wA/ZfaRpAxBEFqVBWMHdn3PiMAEAgGEw+G0uqyHHnoIp512GrZv346HHnoI7777bsZmqddeey06\ndeqEAQMGaP5+/fr1qKysxKBBgzBo0CA8/PDDltwTQAXFMYhVQgZGETEhG3QymURFRQUCgYChaxVK\nPtYOx3FoaGiAx+NBeXm56SY63SxbbjyRSER2lSWTSSowJQTLsggEAliwYAFWrVqFvn37oqmpCb/9\n7W/RvXt32WpVc80116C+vj7jtUeNGoWtW7di69atmD17thXLB0BdXo6gV1tCgnd+v9+QVeKU1aJ2\ncVlhlbjVInMaPdcJz/PyECr1kLFieS1bo6tND5Zl0bNnT8ybNw9As+tTrzffiBEjsHv37ozXs+ug\nQS0UmyG1CWoXVywWQ1NTE8LhMMLhsGu/WEoXV0VFhaaYmB04p6dufYjAkAyycDiclkEWi8VoBpkB\nnBYz9fPHYjGEw2H534XEUxiGwcaNGzFw4EBMmjQJn332WUFrzQS1UGyCnCRJxlZZWRmAn0beAvlV\nkiuLogrBiAgoLahSLlQsZvSaXKr7UxVz8VxrIB6PIxKJmHKtM844A3v37kU4HMby5ctx4YUXYseO\nHaZcWw21UGxAXVtCSKVSaGhogM/nsyQGYRakOr8YLCjKTygbXJLaiGAwCJZlM9ZGOH1adwKn71n9\n/NFoNM1CKYTy8nL5WhMnTgTHcThy5Igp11ZDLRSL0aotIXNLOI4ruFmi1XUZhcxYobiLTCnKytoI\noNlyttuCcXpTdxNkQJ4ZHDp0CB07dgTDMNi8eTMkSUK7du1MubYaKigWoVdbQuack/YpbrFKtISJ\n1MEYTRLIdK1816OMMykFmVI4SoHx+/2yeyyRSJRMk8tiQf19ycXldfnll2PDhg04fPgwqqurMWfO\nHLnFz6xZs/Dmm2/iueeeg9frRTgcxhtvvGH6+glUUCxAbzRvKpWSC9UikYgpX04rLBQ7srgo7oME\n+IGfgsCtZUyyG6wjtcurU6dOhv5uwYIFGX//q1/9Cr/61a8KWptRqKCYDEnfBJB2oo7FYhAEAeFw\nGIlEwvEPrx5ktDB1cVGUKcrZxiSb0eTSDZu6W4jH40VZKU8FxST0akuI28jn86GiokK3OKnQ5y4U\nst7GxsaCxwiXQr+t1kqm9y3TmGT1jHY6Jjk3yERQQiwWkzNBiwkqKCagN5pXy21k9mZrxpeWVF0D\nza4OI9X5lNLGSFGtMoss1wmHbsNt1pGZQXk7oYJSAOrRvMrAezQahSRJtriNChEoZRYXANeM5yXC\nS2JPSv9+a4C8p27a5DJR6HyQ1k62wsZiofV8Q01GkiRwHAdBEFq0T8k0pdBNForSHVdWVoZjx46Z\nti4zkCQJDQ0N8v+TwjyGYeT23nRTcidG2rer4y9OWgluc9FSC6UVkWk0b6FTCu2AbM4kNdHsLC4z\nRJNYfWRIEYF0ZlaP1i21rKNSI1P7dvJeEheaU4cFNxU20hhKK0CvtkQ5mjdb+xQrLJRcrqfMOFO7\n49wQTFcKMwAEg8E08SZuk2AwaHnWEcU61AIjiiKSyaQcewTQwj3Wmg4L1OVV4mjVlgDNA3FisRiC\nwWDaTAMj17P7C6LOOHPbF5Q0ngSa20U0Nja2eIxS9LSyjojgF1tQuLVD3kuGYeD3+9MOC+oMMisO\nC04H5dXPb2YvLzuhgmIAskmpXVyxWAwcx+U0mtfsD60Rq0Lp4gqHw5ZnceVj6Sir8kn+fS7XIO8L\ncd9ptRWhVd/ZcTqOQYSitR8WOI4ryoJiKigZIB/iY8eOpc1I53ke0WgUHo9HczSv0Wvb8SUgM+m1\nXFxqnHB56cVzzGjdotVWROmzV3fdLbVNqVTIdFgolQwyrf2g2O4BoIKii7K2hBQjqk/6fr8/rzfd\nzA9KJhFwu4srF7ErFC2fPS3KK070UpR5nk9rckkOC0asUXVhodM4HcvMFyooKjLVlsTjcVNaklht\nCRTi4rLrg0wSGTweT1axs+L1ysWlUqxf7mIjX6s9U4qyOhvQje5O9eermD9vVFAU6NWWAM0tSXLt\numsH6s22kFO/WfeVTQBSqRSi0ahcle/066nnUlGeeMlj3LghUdLRS1FWjkl245Ax5TqK1QVLBeVH\n9GpLSJfVUChkWrM2qyyUYnBxxeNxpFIpw4kMTpzW1CdecspVfh6Uc9vd5CoplGI+HethxN1JHqec\nCWMXWpZZsb4PrV5QMs0tISmsxDXiVkgOP8ldzzeLy0pXHHk9GYYxNAfGTWJIPheBQKBF111l/MVt\nJ958Kfb1Z0PL3RmPx2VXNzlQOPV+8jxftF2+W7Wg6NWWEJcMqS1pbGx0tBgxGzzP2xLYzhfSjibX\nWh23ot6QSi3jyCmcSFkm33uGYRAIBMCyrO3vp3oviMViRVmDArRiQSEfGL3aEmX7FDdUkGvB87w8\nW8VNLi7yelkxqMtt74WRjKN8AsJOF9q1VvTeT/WYZGLBmBVPU7ddKcYqeaAVCoqR9ilWj+Y1Y1Mk\nLi6l6LlhXQRJktDU1NTqBnVlyjjSailSSvGXUsRoPZOZGWTFOlwLaGWCojW3BPhpc9bLOnLTqZhk\ncfE8j/Ly8rQUZ7dAXmc3ZsXZjTIg3BriL8WKUYtQL4NMS2CMNizVagxJXV4uRl1bonRxKTdnvawj\nswUl3+spazdIhT7JPnILyWQSqVQKPp+v4C+Fm4TcLIzGX0g7d7tx8vUuRjdfpgyyfBuWUpeXi9Gr\nLSEptl6vN+/2KfmSz0apzOLKt0LfinURlPEnN9SWFAOZ3GPk8BOPx20vyKPvXf4oDwxA5o4MenNg\nqKC4FL3aklyryJ08KWdrQumGU7w6/kTakFNyQ3naJWMGfD6fXJAH0PiLVVhlHelZpMqODMokFoZh\nilpQSvITSQLvZKYGedNILUQymURFRYVjLUmMioAgCGhoaIAkSaisrLRlBG6u98lxHBoaGuR4SWvb\n5FauXIna2lrU1NTgzDPPxOuvvy6PUy4UIjDBYBCRSAShUAgejweCICAWiyEajSKZTMqdsCnuhlik\npKN2JBKR9yBJkvD9999j3LhxWLp0KQ4cOCC7zPS49tpr0alTJwwYMED3Mbfeeiv69u2LgQMHYuvW\nrabejxYl9+0XRRGJREIuUCKnDrLxkd5RTrQkyYVkMomGhgYEAgFEIhHdNZhpoeRyn6QYrKmpCWVl\nZWnjjq2IOTmN1v3Mnz8fV111FTZt2oQjR45g+/btuOOOO3DttddassGTky4RGFLTw3EcotEoYrEY\nkskkBEEoSoFxKobi1GuldHl6vV60adMG9957LwRBwLJly9ChQweMHTsWr7zyiubfX3PNNaivr9e9\n/rJly/DVV1/hyy+/xIsvvoibbrrJqluRKSmXF6kYP3bsGNq2bStvbGQCYL61EMS6MYtMG26+c1bs\nRBRFRKNR2XKyyipxgzuPrEPNDz/8gIcfflhOBSbEYjHU19fjww8/xNlnn23pmoq5IaIbcer1IULq\n9/tx7rnnYseOHZg0aRIuuOACvPvuu3K3czUjRozA7t27da+7ZMkSzJgxAwBw1lln4dixYzh06BA6\ndepkxW0AKCFBUfflIT+LRqMAUPDGZ8fGppXFZSdGNnD1ICw3rtEOli1bpvt5isfjWLBggaWCoiZb\nQ0TAWPylGDOtSg0S362oqMD555+f93X27duH6upq+d/dunXDt99+SwXFCOQEpmyfks9oXi3M/oJp\nWTzZamEyXcuODVZvEJaTa3ISMspAC5KO7iR66axunXjYmtOV1bNYzKxDUb+uVt9nyQgKkL6RxePx\ntPYpZl3XbIrBxWXnIKxiYcSIEbpfzrKyMowfP97mFWXGSP2L1+uVs42cwmlhcwNmZXlVVVVh7969\n8r+//fZbVFVVFXzdTJRUUJ5kRQEwTUysgAgUWS9pT5KPmJgdlFdfS/maOikmbrN4+vfvj5EjRyIY\nDKb93OfzoX379rjwwgsdWll2tLKNSFsR0miUjBlwW+FsKaK2kIjLq1AmT56MP//5zwCADz/8EG3a\ntLHU3QWUkIUiSRIaGhoQCoUQj8dNPelYYaGQjdotQ6a0cHoQlttdZ6+//jp+//vf44033oDX6wXH\ncRg5ciSee+65vEcIEOx0wyjdYyzLgud5eL3egqq9iwmnXV5qiFs5G5dffjk2bNiAw4cPo7q6GnPm\nzJHjZbNmzcKkSZOwbNky9OnTB5FIRDdbzExKRlBYlkWbNm3AMIzphXVmN01MpVKy+6hQF5cVm65y\nEFY+lp7bhcAsgsEg5s+fj0cffRT79u3DCSecgPbt2zu9rIJhGAY+ny9tXojV8Re3bep2ov6uRKNR\nQ4KyYMGCrI955pln8l5XPpSMoABIa2Pgxg2NZHERl4Pb4iUkWaCxsREALO+6XCqUlZXhpJNOcnoZ\npqDe2Emii1b8RdnOnTS3pOnJ+WGFy8sJ3LWjmYRbmjkqUbqPWJZtUb9QKGac8EiQNhgMOpISrIfT\ngWLKTxht567snuyWz5EebrOOjLq83EhJCorZmNU0kWRxmdkqwyx3QzKZRDKZhMfjMeV0ZNb9ET++\nJEmOduGlaJOp265eM0RKOmpB4zjOtQlF2SgpQSEbv1tcXnYN7VLed64oU4JDoZAps1XMOu0RMSYB\nbrJZAc2plWZPzaMUjta8djLQLlP8xUkrwW0WClC86dMlJSgEN7i81HPp1X5ptwheY2MjvF4vKioq\nXDOoS5KaRweLoohwOAyfzweO4+Q6iWg0Cr/fr+tmoadgd0DcXaQIViv+ohQWN3wnnMCNgpYvVFBy\nwMgbr8yQsrNQsZD5KsQCcMOXWtknTNmrSk02NwsRFzdUgVOayRR/4ThO/u60poOB+vumHLVRjJSk\noJiN0TfXqIvLyW68dlTm53t/xGLy+XwIh8Nytlk2jFaB0yyk7DhV/+LxeJBMJuX6F3X8hYzTtQI3\nWAjK53f6UFcIJSUoVrVPV15T74OXycXlFsg8GIZhXJcSTF4/o0PP9DDShVdpvbjpNWjtkENBpmFU\nbuo/RmlJSQkKwex28wQtkcqnCNCJGA/HcWhqasooeE64vLK5CAtdT6YspGQyKf+eblLuQutgIIoi\neJ5vEX8pZsuzlDK8gBIWFCssFDWkPX6+J347TG0S4E4kEq7rb6aMl2i9fla8NnrusVLapEqRTJZn\nIpGAJEl5W55ucHkRiJVerJSUoFj5oVCLVCEuLiva4WsJKNmwSfNJuxo7FsNcFSBzkJgUnio3MIp1\n5LqpKy3PQCCgW/+iLLB0I1qNIUOhkIMrKoySEhSC1e3mC+lzRSikdsQIZMP2+XwoKysz9Dx2uby0\nMszcgN4mxXEcRFGUa1/scI9RAcsNI4kZxRB/KeYqeYAKSk7XFAQBsVjMdUFt9f26dcM2I6XazkI4\nskkBzQJNal/sco85semphz0VI7nGX0iihhOoP8dmzUJxCiooBiHptmZlcVm5xnxTgs1ak9Z18s0w\nc8tJXc89pjVi18oUV0ruGIm/kM+Z05l/NIbiIqz4EpNTNWlN4kb/JrGe4vE4WJZ1ZB59JvKNl7jp\nHtQo3WN2tXgvZZyqfwkEAojFYmBZ1pHCWKuGazlFSQkKwayTNjlVA82T+Mw8uZhpoYiiKHcJdlsN\nDHG/ZZtDX8yQyma1D1/LxUKsFze9R60d9eFAL/5iR984M+fJOwEVFB3UdRuxWMw17hcCSQnmeR6B\nQKBg68lMkSM9tziOKzjDrNg2Xy0Xi3K0LlAcGUitESOFsWbGzmgMpQgoZGMkLq5kMmlp3Uahm7ey\nhsPv9zs2610Lcl8kXbnYg7yFwjAtJyCS2IvdJ+BsuO3QZAeZ3G3qwthMsTMz4i9UUFyE+kORq19W\n6eKqrKxM+3BYFUTPB3VMIhaLmb6ufDc1YtkBMJyunG0tdvDRgY8Q42IY2X2kpc+j1YFX6wTsZKNO\np7LLisFSs7rzQjweL+ox0iUlKIR8PphkIySuI/U1nGzoSCCDsEiuOtmUzMzOyhfl2sLhsNxBwKn1\n5MLOYzvx87//HDEuhtM6noaxNWMxrsc4DOkyBD6PtZ0F9DYoUvsSjUape8zFGK1/0bM+aWFjkWC0\ncNCp1iS5ioByEJadVe9GIOnKPM/LLi7ijnP7Brjhmw24btl1GNV9FKrLq3F+n/OxZvca3LX+Luw6\nvgvndDsHo6tHY1TVKPQL9rN8PWSDYhgGqVQKgUCAdk62GLM+p7nEX/RSy2lQ3kVoqX8mMrm4tK5t\nRcNJI5C2+B6PBxUVFZZbT/msjbTst2ODM6PLgCRJ+J///g/mfTgPL096Gf/57j84GD2IEdUjMKJ6\nBB4c8SC+j32PtXvWYtXOVZi3aR7KA+UY22MsxtWMw4jqESjzl5l4Vy0xskGVSufkUiioVKMVf1En\nZwCQiytZli36GEppvYMKsm02HMfh+PHj8Hq9KC8vN/RhtrtDMNDcM6yhoQGBQACRSMTyDTsXceI4\nDg0NDfD7/abES+wiJaRw2+rb8PJ/X8aqqaswsvtIMGh53x3CHXBZ/8vw3Pjn8MnVn+DP5/8Z1RXV\nePbfz+LEF07EpEWT8OTmJ/GfQ/+BKFl/2CAbVCAQQDgcRjgchsfjkTs4RKNRJJNJ8DzfKoPr+WKX\nJU2SM4LBIMLhsOxaF0URy5cvx+DBg7Fjxw58/PHHhmYB1dfXo1+/fujbty/mzp3b4vfr169HZWUl\nBg0ahEGDBuHhhx+24rbSKCkLBcg+V17p4sqlNsLuzTKXNiV2W0/KeInbOhhn43DsMKb/YzraBNtg\n1eWrUO4vB/Dj5wb6mzDLsDit42k4reNpuG3IbYhyUby39z2s2b0G1y67FseTx3Fu93MxtmYsxvQY\ng06RTpbfSzb/fT7prVSI7IEkZxCRqaurQ8eOHTF37lz89a9/xT333INBgwZhzpw5GDNmTIu/FwQB\nN998M1YioTvAAAAgAElEQVSvXo2qqioMGTIEkydPRv/+/dMeN2rUKCxZssSu2yo9QSHotf8gvv1s\nLi4j1zN7fQSlK87utNts92k0lmOGW8rs1/yT7z/BFYuvwCX9L8HsYbPBMumvay7PFfFFMKHXBEzo\nNQEAsOf4HqzdsxZLv1qKO9fdieqKaoztMRZja8ZiaNehCHit7amWrb0IYDy9tVgszVLC6/ViyJAh\niEQiePnll9G2bVu899576Natm+bjN2/ejD59+qCmpgYAMHXqVCxevLiFoNh9QChZQQHSX0yO4xCN\nRgtql27Hm5Mt20wLu2Io2WI5bmbxjsW4bc1teGLME5hy0pQWv89moWSjR2UPXHPaNbjmtGvAizw+\nOvARVu9ejQfffxA7juzA2VVny/GXPm37GEoWKVSM9dq7u7E1jFMJHE5bZFqFjZFIBOFwGHV1dbp/\nt2/fPlRXV8v/7tatGzZt2pT2GIZhsHHjRgwcOBBVVVV44okncPLJJ5t/EwpKVlDIm5Svi0vvemah\nFgG9lGC3QIQuFAohEAjY/uXP9/lEScTcD+fi9U9fx1sXvYVBnQZpX18jhpIvXtaLoVVDMbRqKGYP\nn40j8SNY/816rNm9Bk9/9DS8rFe2XkZ1H4XKQKUpz5sJo4PFlI0SWxNOCyrBaFDeyHrPOOMM7N27\nF+FwGMuXL8eFF16IHTt2mLFMXUpOUJSuFuI6kiTJlPYfVs5YKTQl2Ky1aQmdWyc+ZqMp1YSbVtyE\nA00HsO6KdRnjGgys21DahdrhopMuwkUnXQRJkrD9h+1Ys2cNXt72Mm6svxGndDhFFpgzOp0BD2tt\nSrjSPabunEze71LJHnM7agtFEARDXcKrqqqwd+9e+d979+5t4R4rLy+X/3/ixIn45S9/iSNHjqBd\nu3YmrFybkhMUAglq5+I6shMieIIgoLGxET6fL283klX3VojQOZnKDDTHNC5ffDkGdhqIpZcsNRTD\nKMTlZRSGYdD/hP7of0J/3PyzmxHn4ti4byPW7FmDm1fejIPRgzi3+7kYXT0aI6tGolewly1rIu6x\nWCwmHxpaQ+dkt9VKGW0cOnjwYHz55ZfYvXs3unbtioULF2LBggVpjzl06BA6duwIhmGwefNmSJJk\nqZgAJSgoREg4joPf7zctp9uKDVIQBDQ0NLhuEBbgjnhJvq/5xm83YsbSGbhtyG345aBfuioOpSbk\nC2FsTbN1glHA/sb9zbUvu1bhwQ8eRMdIR9l6GV41HCGftVXUkiTJVomdnZPdtrHbhfK+c/n8eb1e\nPPPMM6irq4MgCLjuuuvQv39/vPDCCwCAWbNm4c0338Rzzz0Hr9eLcDiMN954w5J7UMJIJeYwPXr0\nKDiOk1sdmNXGQBRFHD9+HG3bti34WpIkobGxUa4sL3RaHMdxiMfjqKioKHhtDQ0N8Pl8SCQSBcVL\njh07hvLy8oLcjPF4HJIkIRgMguM4eR2xWAyBQEDz2q9uexV/2PgHvDjhxeZN2iAvbH0BXxz5Ak+N\nfarF7ziOgyAICAaDed9LrnAchxSXwufHP8eaPWuwZvcafPr9pziz65kYVzMOY3qMQf/2/U3fhKPR\nKEKhkK6bS+keEwQBgDmDxTK9p1ZCsuCcqk5vamqS68skScLEiRPxwQcfOLIWMyg5C4UMwSKT2NyG\nMq6jrKJ1A+Q0aka8xKwTP2nrkkqlZL++1nU5gcPdG+7Guj3rUH9ZPfq27Zv7em1weeWCh/VgcJfB\nGNxlMO4ceieOJ4/j3W/exZo9a/DC1hfAiRzG9BiDsTVjMbr7aLQPWd9UUOkeU3ZOVrvH3NA52ShO\nrdGN+1OhuGc3Mwmv1wtBEEwv9jNjg1TOWGFZVp4O54a1kRodURQRDoddEXyXJEkWklAoJLtelIFj\nr9eLY8ljuHrp1fB7/Fh7xdq8sqYYMHCZnrSgMlCJC/pegAv6XgBJkvDVsa+wZvcavPHZG7h11a3o\n27Zvc2PLmubGll7W2q+30c7JRtxjrdXlBaQLWrG/BiUnKFaTzwdfK1OK4zjXnFCUiQHkZOk0yhNv\nJBIBx3HweDzw+XyIRqOyf/+/B/6LGctn4Pze5+OB4Q/A78s/LdxtFkomGIZB37Z90bdtX9w46EYk\n+SQ27d+ENXvW4I61d+Cbhm8wonpEc3ymx1j0qOxhy5qy9a5yW+dkNwlZKpVyxUGuEEpOUMiHww3t\n5oHCqvONUsi9plIpRKNROTHASA8hqyFjg30+n+aplqS9rty9Er9c+Us8MvIRXHLiJXJPq3yyksys\nQ3GCgDeAkd1HYmT3kZgzYg4ORQ9h7Z61WLtnLR7Z+Agq/BVy8H9EN+sbWwItB4tptXbP5MYsddRi\nRr6HxUzJCQrBiqydXNuJkEFYPp8P4XC4hWnr5JdIr1eYWevK5zrqNSkDv+rHPbXlKby07SUsunAR\nhnQZAgBZi/YyWV9uOaWaRadIJ1x+8uW4/OTLIUoiPvn+E6zZvQbPfPQMrlt6Hc7ofAZ6VPTA0Kqh\nuPLUK+W/s+rEnq1zMtB8kFC25m9tkFlCxQwVlBwxek1yyrYjJTjXe1VaTW4Z0au1Jp7nWzwuxsVw\n05qbsKdhD9ZevhZdy7um/V6raE/tdtGbqFdMLq9cYBkWAzsOxMCOA3H7mbejKdWEl7e9jAffexD/\ne/h/0wTFLtTuMZKiTg4CgP77ZCZOurzUz00FpZVhtFtrLBYDx3GGmifaTSarySmUMZxMa9rXuA9X\nLLkCvSp6YeklS1EWyO62yeZ2kVuOiJItLejdwLo96/B/t/xfnNfnPAzsONDp5cgQF2c291ixZI/l\nCnV5uRCrYihGrqksBqysrLT1Q2/kXo1YTWa+bkbnvZDah0x1Hpv3b8ZV/7wKN51xE2aePBNBb+41\nIXpuF5L2yvN8WtsRJzctq07Of/r3nzB/y3y8ddFbeOuLtyzPBMuHbJ2TScp9sbeG0WoMSQXFpdjt\n8lJujEaKAc1cn5HOtUZnq5iFkTVl6xFGXqPXP3kd96y7B8/WPYsJvSbIBY9mrFHuyOsPgPU0N1BU\nn4pLoWGiIAq4e8PdWP/Neqy6fBW6V3THos8XwcO4Z5S0HlZ2TnZTlhdpDFvMUEHJ8ZpqlJt1LsWA\nVqxP68vh5GwVPYz2CONFHrPfm41V36zCskuWod8J1s10J7NRtGoqlLUvhVaEO0GMi+G6ZdehMdWI\nlZetRJtgGwCAIAlpnwenRJM8r9HX1GjnZLe7x2iWVytHLQJu2az1vjAkXpLLDBirYzuiKKKxsTFr\nj7CjiaOY9s40CKKAd698F2Ue6+e3K4PyylMxSRDweDxFVxH+XfQ7XPrOpTip/Ul47fzX4Pf8VKcj\niAK8TMstwK33ooVe52Sjg8XcZHmWQlDe+eOqyVgZQ1HC8zwaGhpymkmvhVVrTCaTaGxslGeP271J\naL3+HMfh+PHj8Pv9cv8iLXb8sAMj/zwSJ7U7CQsvWIh2IWs7pALZ29eT4H4oFEIkEpFjUMlkEtFo\nVG5Iauco5mx88cMXGPfGOIzvOR7P1z2fJiZAs4Vidat8uyEHgUAggEgkglAoJB8EYrEYYrEYksmk\nbHWSv3ECrRgKdXm5FGUHT7M+MKSdSyKRKHgQltkfYuUGTrLM8o2XWCFyRl+zFV+vwPVLr8dDox7C\nFf2uAMdxpq9FD6P3rQ4au3Ea4vt738eMpTPw0IiHMO2UaZqPEUShKGIohaDlHlN2TmYYBizLQhAE\nxy3NeDyODh06OPb8ZlCyggKYM9dcDSnCKnRgF2D++kRRRCwWA8MwebvgzLbsjKZRS5KEpzc/jae3\nPI2FFy3EsG7DkEwmbXNJFNJ6JdumZaSw0kwWfb4Id62/Cy+f9zJGdx+t+zhBElyR5WVXYFwre4wk\neKjdY3bEybQsFLO6ozuF858mk7HqQ0By4lmWde089cbGRlcNFCNt+rMJXIJP4Ff1v8Kn332KDVdu\nQPfK7gDsd0WYlTmm3rSMFlYWiiRJeGLzE3h126v45yX/xMknZJ4fzou8nIzQGiHWCREQpzsnx+Nx\nlJVZ3xLHSkpOUJSYddomKcFmn1zMWh/JzQ+HwwXP7CBuvUIhp79sAneg6QAue+syVFdUY+30tYj4\nnfEhZ7NQ8n2fjBZWFpqRxAkcfrPmN9j23Tasvnw1upR1yfo3glT6Li+jkJ5xyiw/Ymnm2jnZKJIk\npR2yaB2KS1G6kgrZsNX1G27qEAyku5NIzYQbSKVShiZmfnTgI1z21mW4/vTrcdewuxy1qjI1hzTz\nAKFXWEliRcrTslEakg246p9Xwct6sezSZYYbP6pdXk7VZLip/QnBiKVpdudkKigupxBBISnBSneN\n2QHiQtfX2NgIlmVRWVmJhoYGU9eWD0oBJq3w9Zj+znQs3rEYdw+7G78b+rucvpCW1BjB/vb1ytRk\nUjxJxIXM9CEbm571sq9xHy5++2IM7ToU/2fM/8kpJiKIpZflZRVqS1P5XpEi2FzdY7SXVytBOQgr\nGAympSK7IS1Ub31OdQkmz00mUVZUVGStZi/3l+Ok9idh6VdL8fSWpzG6x2jU9a5DXa86VJVXpV3X\nDpzqraZ8fqXLhbhZMgWMt323DZe9cxluHHQjbh18a86nZKuzvARBwBdffAGGYXDSSSe5oqhWTT7v\nuZZ7TGuwWK6dk2kMxeXkukko24Fopbeavenks75kMqmZfuuku4j0MPN6vXLNS7b1nNzhZIR9YTxZ\n+yS+i36HVbtWof7resxeNxtdy7tiQu8JGNt9LE5re5ot95CtDsVuSMA4EAiktRshPv0N+zbglrW3\nYN7oeZjSb0pe77+VWV6LFi3CnXfeKYthJBLBU089hcmTJ1vyfIVQ6HdHaWkC6WnkmTonq7/7tFLe\npeQTQyEnbFEUTUkJNkKu6zPSrsRuiLVktIcZwct6wUvN7ek7Rjpi2qnTMO3U5sr4LQe2oP7retyz\n4R58ffRrnFtzLsb1GIfamtoW7erNxE3t69XuEGVq8ivbXsEjGx/BqxNfxeCOgxGNRvNqlmhVltey\nZctwyy23yLEGoHmznDlzJsrKyjBmzJi0x7upn5YZ6LWG0eoRp6QUXF7us0FNxOiGzfM8jh8/LqcE\nu63lvCAIcoxEb31mrc3odYg119TUhLKysjTXmxE8jAeC2HJ4lof1YGjVUDw48kG8O/1dbLxiIy7o\newHW7VmHs18/G8P+PAx/+NcfsHHfRnCCeTGtQupQ7EKURMx5fw6e/uhp1F9Wj5E1I+VOCGSWiF41\nuBbqLC+zPtv33XdfmpgQ4vE4HnjgAVOewyysFjMSAyPtj4hngcRhEokE1qxZg1deeQXBYNDQQbG+\nvh79+vVD3759MXfuXM3H3Hrrrejbty8GDhyIrVu3mn1bupSkhZILuQ7CstvlpRcvcRKSXcbzfN4C\n52E9EKSWgqKmY7jZernkxEsgSAI+Pvgxln+5HLPfm409DXswqvsojO85HuNqxhlKldWDAQM360mS\nT+KmFTfhm4ZvsHrqapwQPkH+nZHCSi1/viiJLVxehX6+4vE4du7cqfv7bdu2lZxFkgtK9xjP8wgE\nAvB4PFi/fj02btyIU045BXV1dRg/fjzGjBnTogxAEATcfPPNWL16NaqqqjBkyBBMnjwZ/fv3lx+z\nbNkyfPXVV/jyyy+xadMm3HTTTfjwww9tub+StFCM9PMiLqR4PI7y8nJDYmLnl4BkTBELIFuxopnW\nU6brkOyyQl2DHsYDXmw5kTHTWrysF2d1PQt3nXUX1k5diy1Xb8GEXhOwZvcanPXaWRj++nA8+N6D\n2PjtRkPXVuK0hcJu2QLPu+9q/u5I/Ah+/vefgxd5/OPif6SJiRpyIg4EAgiHw4hEIvB6vXK6azQa\nla0XXuRND8qTIVl6+P3+VismWrAsi9GjR+PVV1/FwIED8frrr6NTp06YN28evvvuuxaP37x5M/r0\n6YOamhr4fD5MnToVixcvTnvMkiVLMGPGDADAWWedhWPHjuHQoUO23E9JWyh6mywJIhMXl1Gfs11B\neSfjJZm+7KR7cSAQKNha8rDaLi+jawGa56ZPO2Uapp0yDbzI46MDH2Hl7pW4c/2d2HN8D0Z3H43a\nnrWGrJdMdSiWI4oIXXMNEIsh+sUXgGIEwq5ju3Dx2xdjYq+JeGjkQznHPPQKK1OpFFJ8CjzXbMnk\nWvuih9frRW1tLVasWNEiI9Lj8eDnP/95i79xYx2KE8/NMAwGDx6MwYMH4+6779b8m3379qG6ulr+\nd7du3bBp06asj/n222/RqVMnk++gJSVpoSjR6njb0NAAv9+PsrIy16UyGomXaGF1fEfZvdhoa5dM\n6/GyXkMuL0K25/OyXgytGor7h9+P96a/hy1Xb0FdrzrZejnn9XMw5/05+Ne+f2laL05aKN4lS8D8\n8AOYeBy+v/5V/vnHBz9G3cI63DjoRjw86uGCA+hKf344HAYYIOBvziCLx+Nyymu22Es25s6dizZt\n2qRlIfr9frRr1w4PPfRQQfdQKmi9vka+U0bFT319u0Sz5C0UgjIlOJdBWOrrWWmh5Dr10QrUa1J3\nC9AqVvzmm2+wcuVKSJKE8ePHo0ePHlnXrheUz2eNWqitly0HtmDVrlX4/brfY8/xPTi3x7morWm2\nXjqXdXYubVgUEZg9G0w0CgDwz5kD7oorsHTnUvx23W/x7IRnMbHXREuemhd5+L1+BINBuVCPdDko\nZI57TU0N/vWvf2H+/PlYvHgxGIbBlClTcMstt7iqm64bul7kWkNWVVWFvXv3yv/eu3cvunXrlvEx\n3377LaqqqmAHJSko6hiKKIqIRqOQJAmVlZV5WyVWWQFuFDsAaa+blmtQkiTcfvvteOWVV+Takzvu\nuANXXXUVHn/88YzXztVCKQQv68XZVWfj7Kqzcf859+Ng00Gs3r0aq3avwj0b7kGPyh7oXtEdRxJH\nwIu8rR14iXVCYOJxvPfYTNzVaSMWTl6IM7udadlzi5Iox1DI+8cwDEKhUFqxXj6deLt06YLHHnsM\njz32WNZ1OB2kd0NMJ5VKGRqFMXjwYHz55ZfYvXs3unbtioULF2LBggVpj5k8eTKeeeYZTJ06FR9+\n+CHatGlji7sLKFFBIZDKduLicksXXgJZH6l/KUTszEYQBDQ2NsLn8+kO6Hr++efx2muvyRsO4S9/\n+Qtqamowa9Ys3esbDcoDP/VRItlMhdK5rDOmnzod00+dDl7ksXn/Zvzp33/CJ999gl7P9cKYHmPk\n2EuniIVfRJV1AgBMNIqznl+MZR9tRPcTelv33NAubFQexrTmuBfbxEq3otW63shwLa/Xi2eeeQZ1\ndXUQBAHXXXcd+vfvjxdeeAEAMGvWLEyaNAnLli1Dnz59EIlE8Morr1h2Hy3WZ9sz2YwkSeA4DjzP\no6ysLO9BWErMtgJEUZRPJmVlZaZ0Ly0UpQhnS6WeN28eYrFYi5/HYjH88Y9/xMyZM3X/1mhQXim4\n5P5IFbkZJ1sv68WwbsNwOH4YkiThybFPYvXu1VixcwXuXn83aiprMLbHWIyuGo3hNcNNtV7U1gmh\nrRSAf/lGpK60VlByyfJSpyarW43kU1jpNE5bRkpymYUyceJETJyY7gZVH96eeeYZ09aWCyUpKCRL\niswBN0NM1Ncv9IOYSqWQTCbh9XpNGftphtiR1i6SJKG8vDyj643neRw8eFD394cPH5bbTmhhxOUl\nCAIkSZLfQyIwyWQSgiCkjRQodCMjzSG7lHXBladeiStPvRKcwGHzgc1Y8fUK3PXeXdhfv1+OvdTW\n1KJjpGPezwcAgQceAGIxSCwLUWrOiGIZFkwsjsgjjyA1fXpB189GviOAM7UaccvESrejZaEUe5U8\nUKKCQjaySCSieYLOFzO+GMogdzAYNLXZZKGt+kmqMkk1zYTH40FZWRkaGxs1fx8KhTIKeTaXF0lQ\nYBgG4XAYqVRKzlIim5TP55Nbihe6kWllefk8PgzvNhxndT4Ld595N47yR7F692rU76zH3evvRs82\nPTGupnlm++DOg3PenFO3347D33yOv372V5zWYSBGdx8lr5kLBgGLN2Kzug3nW1hJcJOl4BRUUFxM\nMBgEy7JpbhKzUPYJyxV1kJvjONMEpZAvJKnLISJhpBU+wzCYOXMmnn322RYxlGAwiKuvvjrjmvQq\n5ZUNMMPhsGYLD+Ua1DUWuWxkadcyUIfStbwrrhpwFa4acBU4gcOm/Zuwavcq/Gb1b7Cvad9PsZce\n4wxZL+vG9MaMpQ/hodmPYfgp06BsJJNMJi3PO7NiwJZS9IH0OSKZGiU6gZtqUIzGUNxOSQoKkHs6\nXi7XzeeapChQGeR2qjeYEnVrl1zWc99992Hjxo349NNP0dTUBAAoKytD//79cd9992VuvaJhoahb\nuuSCeiPTc8PoBZFzrUPxeXw4p/ocnFN9DuaMmIP9jfuxevdqLPtqGe5cdyd6tenV7BrrWatpvSz8\nfCHuXn+37tx3SZIsj0Wo29dbscFmKqwkok/cmq3ZUqEWiotRZqq4gVz7heVDPuKUSCQ0W+EbvU4o\nFMKaNWuwatUqvPnmmxBFERdffLGcgZJMJnX/Vm2hqAeakXiJcpPJZcPRc8PoBZELrUPRsl5W7lqJ\n21bfhgNNB2TrZWyPsXjt09fw2ievGZr7biVWtq/XQin6pEEiEReSQGP2FES3ov4sl0KnYaBEBYVg\nhQWQyzWzFQU6ZaEQS4DjuIJbu3g8HkyYMAETJkxI+7kgZA64e1mv7O4jKcqZUruVr1Wur5ue9aJM\ngSXuRzNOyUrr5aGRD2Ff4z6s3r0a//zqn/jVil8h5Avh46s/RueyzgU9T6FY0csrF0hwn+f5tIaJ\nhRZWGsVNFhF1eRURZn9wjGxm5MQNIKd+YflidJPVGm3sxHqIy4sE36203tRopcAyDANBFNJmixgp\n4DNCVXkVZgyYgRkDZuAP7/8BxxLHHBcTIP8sLysgqeBaUxDzKawsNqLRKMrLy51eRsGUtKBY8aEz\nck0SL8lWTGm3hWJ0XYD1pzcP4wEncIhGo3l3BzADckr2+XxgWRbhcLiF9UJqXsx4TYK+ICqQW3zI\nKqweAVwIpV5Yqf4sJRIJdO7s/CGjUEpSUNQdPM3cHLOJgB3xknzWZdQSsOOLKUkSuCQHTijc5WYW\npA5Fy3oh7rBYLJZ2Sg7eeSe4Sy+FOHiw4eeRJMk144bdZKFkw4rCSre5vGgMpQiwywpQxiX0mig6\nsTYjzR3tRHa5gQEYZBQTOy04recip2RCIBBoniPC8xA++gjlL7wAZtMmRNeuNXxKliDBJXpiS5aX\nEXJ93lIorNQKytMYiotRWiZWzzApJC5h5trU15IkCU1NTbrNHfUww6rTep2UwfeKsgrbmkMagVgo\nmVD6+IM/Nj30fvEFhLVrkRg2zFCGktssFDuzvKwi38JKaqGYT/F/mgxgpaDkEpfQupaZ61JCihW9\nXq9uc0c7IfUuxOXmTXhznqpoJbm8Pux//wvvpk1gJAlSLIbKRx5BdO3atAwldQBZTn2GewTF6Swv\nK8ilsNLJGjB1nREVlCLByo2UxEvUdRxGscqlQzZvJ+eqKCH1Lsrgu9GZ8nZitLAxcN99wI+ZRwwA\nz/bt8G3cCPacc5qv86OPn+d5udKfiIubTsVuiaFY+ZpkK6wkYq8WfruhLi+XY6XLi7RQMaOOw+x1\naW3e+VzLjNdM2aRT/Trl0r7eDhgwMKIn7H//C8+P1olMLIbA7NmIrV/ffC2Fj1+5iXEch2QqCQ/r\nkcfuOrWJiZIIBkzBUyCLCXVhJUlHJhMrARhyW5oBbb1SpFhhBZAuwZWVlaY1jCz0OiStNZlMukbk\nRFGEKIpy5bsSD+uRO+xmQytYbmZTTXJNIxaK0jqR/xYAu307PO+/D+FHK0V5XaULxufzgQGTtok5\n0duKF3lXWCdOQsScVO0T95hdhZVKqMurFUI+aF6v15T5JWZ9QInFBEBz886VQkWYxG8A6L5OXtZr\naB6KXRhpDsns2gXv+vWQysshqnuBJRLwP/kk4ipBUSNBgpf1yn3TtHpb2eHf16pBcZM7zm6U4gJY\nX1ipVYdCBaUIMMNCUXbAJTUcZte15Hs9ZVIAqfh2EmWzyWQyqbse17m8DFgoUnU1YsuXA7z2ukXV\nbG/Na+Cn91qrtxUJIAuCIFt4VlgvbsrwcjJdWS/z0e7CSjuagdqBOz5RFqD80po1J6SiokI2id2A\nMinA5/O1aCNvN8r4jcfjybieXIPyVtekiKKIpKDfzBIA4PVCGD7csjUoA8ixWEyus8inHX82SjHD\ny0rMLqxUi2ipWIclKyiEQjYi5ZwQ4kridU6ndq5Pq1jR6lqbbOtRN5vMFuPwMu5JGxYlEX/c8kds\n3r8ZV/7jSozvOR61NbXW9NuSYChtmPS28nq9LawXM4r3BEloVQF5LfLdxM0urHR6hIWZlLyg5It6\nTohZFk+hqId0qU9Ddp908i3qdEvacJyL48YVNyIhJLBpxiZ8fPBjrNy1EvduuBc1lTUY33M8xnYf\niwHtBpjyfEqXVy5opb/mO0wMaBZRt7i8ip18CivV31MnU5bNpOQ/UblmBEmShEQigUQioZt665Q1\nQCrNlUO6lNexm0zryYaRoDxgrYAfjh3G1MVT0b2iO5ZcvARBbxD92vfDtFOmpc00+fWaX+P72PcY\n13Mc6nrWYUyPMWgXapfXc5pRKa/OHMt1mBjgriyvUnH3AMYLK8nv5ILXErFSSlZQ8rEo1PESrdRb\nKz74RtZntLmjGV9OI6+ZsngyGAzmfA2ng/JfHvkSU96egov7XYzZw2a3cP8oZ5rcP+x+7DyyE+8e\neBeLti/Cr1f/Gqd2OBXje45HXc86nHLCKYZf83wtlEzkOkwM0B7/WyqBYaPYIWR6liXQnCr8yiuv\nQBRF2a1pdD1HjhzBZZddhj179qCmpgaLFi1CmzZtWjyupqZG3st8Ph82b95s6v2pKflPj1FBEQRB\nnjZC2BQAACAASURBVKWeqY7DikLJTJB4CWnz7nSnYKA5+N7U1ISysjJNMTECy7CQIBmuRTGT9/e+\njwmLJuCOs+7A/cPvNxRLqC6vxvUDr8eiCxfhq1lf4Xdn/g4Hmg7giiVX4OT/ORm/XvVrLP1qKZpS\nTRmvY3UvL3JCDgQCCIfDCIfD8Hg84HkesVgMsVgMyWQSHM9Rl5fNkPeGpCZHIhH069cPX3zxBT76\n6CPU1NRg1qxZePvtt7N6VR5//HHU1tZix44dGDt2LB5//HHd51y/fj22bt1quZgAJWyh5AI5/TvR\nqiSTQCktpsrKSsdPj1rB93xhGAYexgNBFMB6cruvQkT9jc/ewD0b7sFLk17CuT3OzesaIV8ItT2b\n58VLkoQvj36JlbtW4vmtz2Pm8pkY0nUI6nrWYXzP8ejTtk/a39rdy0svOymWiIGRGLnvmFNdqEvF\n1ZMPDMOgtrYWgwYNwrFjxzBv3jzU19fj7bffxoUXXpjxb5csWYINGzYAAGbMmIHRo0frioqdr3HJ\nCooRl5eReInWde14g7QyzOxam9Z18p1AmcmMJ4F5H6wfriVJEuZ+OBd/+d+/YOklS9H/hP6mXJdh\nGJzY7kSc2O5E3Pyzm9GQbMD6b9Zj5a6V+OOWPyLiizS7xnrVYXjVcEfjBcrsJH/AD6/HK1svyWRz\nyjRxe9k9tMqpOhQ3PC+pku/fvz/69zf2uTx06BA6deoEAOjUqRMOHTqk+TiGYTBu3Dh4PB7MmjUL\nM2fOLPwGMlCygkLQ22RJa3dRFHM6/Vvh8lJfTy/DzCnyCb4beYzRavlCX++UkMKtq27F5z98jjWX\nr0GnSKeCrpeJikAFJvedjMl9J0OSJGz7fhtW7FyBRzc+iu0/bEf7UHsM6DAA+xr3oaq8yrJ1ZIMU\nNir9+6QVTGsYuesm9BpD1tbW4uDBgy1+/sgjj6T9O1OG2AcffIAuXbrg+++/R21tLfr164cRI0aY\ns3ANWqWgKFu7m9FCxUxIcWA+HYytsFCyBd8LIZfAvCiKeZ0ojyaOYvqS6agIVGDZpcsQ8dnXgI9h\nGAzsOBADOw7E74f+Hj/Ef8ANy2/AruO7MOz1YehW3k0O7A/uMtjWmIa6sJFsSmQcMgkeKyvD7epr\nZRdOudv0LBQ1q1at0r1Gp06dcPDgQXTu3BkHDhxAx44dNR/XpUsXAECHDh3wi1/8Aps3b7ZUUEo+\nKK8mlUqhoaEBgUAAkUgk5y+GVRYKiZckEglUVFTk1Q7fbMwIvmfCwxirRSExLhJU5nlefs0ysevY\nLtS+UYsBHQfgLxf8xVYx0aJ9qD1ObHcipvafiq9v/BpPjnkSDBj8du1v0fv53rhm6TV447M38EP8\nB8vXote6nnwfyDCxUCgkH26IizgWiyGRSMjvQyE4nTLsBmEk2Zu5MHnyZLz22msAgNdee00z5hKL\nxdDY2Cg/x8qVKzFggDn1VHqUrIWijqEQkz6ZTBbU2p1g5hdBkiQ0NjbmXByoxiyxkyRJLsoqJPie\nrU+Zl/VmFBSSZqlsnCeKYosZ71rtxrcc2IIrllyB3535O8waNCuv9VsBSRv2sl4MrRqKoVVDcf85\n92N/436s3LUSS75cgt+t/R36tu2L8T3HY2LviRjYcaDpG58gGu/llRZ7UVTtZxsmRtFG/Z2Ix+M5\nC8pdd92FSy+9FC+99JKcNgwA+/fvx8yZM7F06VIcPHgQF110EYDmnn/Tpk3D+PHjzbsRDUpWUAhk\nUyOjcAvNljL7y0JOfYFAIOeJj1agzJMvRNyM4GH1XV7EYgN+6lgsCEJaUVgwGNSsSP7nzn/i9rW3\n49m6ZzGx10TL1p8PeoLftbwrrj7talx92tVI8kms27kOa79di2uXXYumVBNqa2pR16sOo7uPRkWg\nouB18CKfV+sVIhjqrrxaw8TcOs8dcFd2WT7Dtdq1a4fVq1e3+HnXrl2xdOlSAECvXr3wn//8x5Q1\nGqXkBUUQmk/ALMuaNgo328nbKKlUCqlUSg52m7WufCHBd1KMZXWasl5QXhRFNDY2pvnriT+ftHYn\nva78fr98auY4DvM/mo8Xt72IBZMWYFDnQRAEwXU+/2xrCXgDGNltJGp712KeZx6+Pvo1Vu5aiZe3\nvYwb62/EGZ3PkNOST2x3Yl73JkqiKc0hldaL1kwRt1svbsjyysfl5VZKWlCI7x2AqXPVC924lc0d\n3TCiF0gPvpPRqFbDMmwLC4WIGvHfNzQ0yKJAxIS0dud5Xk5xFSQBd757Jz7c/yFWX74aXSNdNavF\nrchYYvbvh//pp5F8/HEgW6GqwTHDSnq37Y2b2t6Em864CVEuig3fbMDKXStx4d8vhM/jk62XEd1G\nIOQLGbqmFe3rjVgv6mFiTsdQ3EAsFkNlZaXTyzCFkhUUsmmXl5ejsbHRNR9cpfutoqICqVRKtqLM\nun6uqMcGx+Nxy+pZlKiD8kTUSHsZ8rfxeFxOb+U4DoIgwO/3y26wo7GjmLliJiRIWH7JcrQJNbeg\nUPe6UmcsmXVq9j/8MHx/+Qv4sWMhZPFRF1opH/FFMKn3JEzqPQmSJOGzw59hxa4VeGrzU7hm6TUY\nVjUMdb2arZfuFd11r6PVvt5sN5DaetEaJsayrCPuJyf3A/VzJxIJVFU5l0JuJiUrKCzLygWBdtSO\nGEGZrmymxaRcVy6YWfmeD17WK7deUYsacZ2EQiHZnUUKK5XWxrcN3+Lity7Gzzr/DHNHzoXP40Mq\nlZItF+V/ymrxTKfmXGC+/Ra+N98EAzTPla+tzWilmFkpzzAMTulwCk7pcApuP/N2HE0cxdo9a7Fi\n5wo8svERdAh3kF1jQ7sOhc/zUyJKtiwvs1E2TSQuSkEQwHGcHC9zYhSyG4jFYgiFjFmWbqdkBQWA\nfPqxoro91+vp1XPYVXmvRm0pabXBtxoP6wEncIjFYkilUrKoEZcWiZNIkiRbFqFQSO6qu+mbTbhm\nxTW44fQbcPtZt8tzWMjfkzYjANLiMdlOzbm0gfc/+ijwY98ldu9eeFatymilWHkybhtsiyknTcGU\nk6ZAEAX8+9C/sXLXSsx+dzZ2HduF0d1Ho65XHWprajVHANsJeR8Yprn9SzAYLOh9KCa06lByDcq7\nlZIWFKvIZUMgm6Hy9G3luow2wsxkKdkVa/IyXjRGG8EHeNmaVIoJwzByejDLsnK2l9frxbp963DD\n8hvwxLlP4Pye5yMajcrJBMr0VjJGVykuRFiUg5AyDbHSuw/ZOvmxLTkTjWa1Uuzq5eVhPRjSZQiG\ndBmCe4fdi0PRQ1i1axVW7FyBu9ffjTJfGTjJ+cmjpNWLkffBTOvFLS5wIL+0YbfSKgTFKZeXsrlj\npnb4dlooVla+54IoioDU7HopLy+Xf6bMyhIEAdFoFH6/Py154cWtL+Lxfz2Ov/3ibzir6iwALQPA\nkiTJlghxdSktEqBZWImwkOfUajVO3DKJRCItHVZpnRCyWSlWtK83QqdIJ0w/dTqmnzod7+99H5ct\nvgwjq0favg4j6L0PpWK9EBElUAulSFBmkdjtViKpr8pYjtVku08ygz6bpWT168XzfLOF5GluUgg0\nb+7ki8YwDDiOQzweRzAYlLOGBFHAvRvuxYqdK7DmijXo2aZn2pqJgASDQbkAklyHzINQurvIc2az\nXjwejxyXIemwvoMHUaawTuR1ZLNSDI4AtorlO5fjlyt+iT+f/2eMrRnr2DqMooy9APkNE9PCTXUo\neq1XipGSFhQldlooPM+jsbHRUHNHO8ROmabsRPBdiXJQmN/jhyAJ8sZO3FypVEqujieFjDEuhuuW\nXoejiaNYc8WarBMTWZZFIBCQs8VIHQtxjRHLRVk/QdxtAFrUr6jTYf0vvgjwPMSyMvz4AFkmPNu3\nw7NxI4Thw1usyykLBQD+3//+Pzzw3gNYdOEiDOkypMXvnXAD5fqc+QwT08NNLi9qoRQRVmRT6YkA\nsQLyae5oxbqyBd/tXI86k4tlWCS5pGyZEOHjeR6RSEQWvkPRQ7j07UvRt21fvHr+qwh49YeM6a2D\nuFCU1ksikZCr74m4sCybFtgn/082L7nQcuZMSMOHt3ClkXsR+vWD58fHKyk0bThf5n80Hy9sfQFL\nL1mKk9qfZPvzW4Ge9aJMD8/HerEaGpQvcuy2AsrLyw0PLLJybfmmKZu9Jq30ZEFozjISJVEWk1gs\nBkmSEIlE5I3488OfY8pbUzDtlGm4Z9g9BW8KWpsQiZMQ15hSYIjvnqyZiIanVy8IvXunCYYH6TPE\nkz8mEyg3NbstFEmScP9796N+Zz1WTF2BbuXdbHtuu9EbJqZV3OqmoHwikaBpw8WA0l1hpcsr3+FT\nZkOyooD04LuT1fhqC0mZyUUGbCkzuZTCt27POlz9z6vx6KhHMe3UaZasT92+hdRGEHGTJAl+vx/B\nYFDXNZYpsE82NTJjhOf5vFvx5wov8rhl1S3YcWQH6i+rR/tQe0ufz00oY2pAS+uFuFedaM2jfu/d\nJG6FUtKCosQqQcln+JTetczCSbebmlgsJs+dAdIzuTxMcx1KU1NTi0yu1z99HfdtuA+vX/A6Rna3\nJxtJuQklk0kkEgn4/X4IgoCGhoa0rDG1a0xd8wIgrSI/EAg0CwkjQRRERKPRtD5XZh9C4lwcVy+9\nGpzIYcnFSxxv3a+HXZup2npJpVLged41w8SooBQRVrmVlAHmQCA3vz7B7LWRzCYz2s4XAgmC+/1+\n2T+szuTyMB5EY9G0TC5JkvCHD/6AhZ8tRP3UevRr36+gdeQK2WzImAPyGpJqfeUJN1PNC9kolVlj\nLMvCw3oQ8DfP4slUsV/IRns0cRRTF09FdXk1nqt7Lq1CnpI+TIwIvZ3DxJTvbSlZJ0ArEhTiojAL\njuOQTCZzipdYCSmglKTCW/QXChFaUqgGQDOTCxLg9XvlxyT5JG6svxG7ju3Cumnr0DGiPYXOKkit\nCc/zKCsrS3sNSZaX0jWWT80LaTWTrWIfaBblXK2XA00HcNFbF2Fk9Ug8NvqxnFrUl9rmZhTi9gSg\n6aa0uh1/Kb3uzu+EFmJFDIWcYHOdRa+HGWsjwXeySZkhJvmsSdkVoLy8XN5seZ5Pa6OSSCTAcRwC\nvgBIwtMP8R9w+TuXo0O4A5Zfttxw11yzUCYFZBsLXUjNi1I4yAalrhQnMSXyOKMn5q+OfoWL3roI\nMwbMwO1Dbi+ZTcoK9D7fyvdWab2o2/EXYr2UkoCoKWlBUWKGoFixcReKMvgun/wLJN8vCRnPq3S3\nkRb9yrRgURQRiUTgZb3gRR5fH/0aU/4+Bef1OQ9/GPWHvAY/FYJeUoBRcql5YVgGPq9P7jsGQJ7z\nog7uk5iSkRPzfw79B5e+cynuHXYvZgyYYe4LZCFObq5GnlfLeiECAxRuvair5oudViEoZnxgycYd\nDAbBsqwpGzfw09ry+WKpg+9mrSlXlJlc5eXl8ibo8/lk9xexxDweD8LhsByU//yHz/Gb1b/BvcPv\nxfWnX2/72kWxOUDu8/lMyYbLVvPC8zwkUcpY86K+XrYT8wcHPsANK27A/Nr5OL/P+QWtn6KP2k1J\nDg+5DBNTH2xJN4hSoaQFxSyXFynIU27cTrZu0Kt8N8u1l8t11LUuwE+ZXORkzvO8bAGQFGufz4dP\nv/8Uy3cux6vnv4oL+l5Q8LpzhayLWBdmo1XzwrBM2kRKdcW+KIry50vpKlRaL8oT89tfvI3frfsd\nXhj3AoZ1GYZkMum6Qj43UqhlQAQjl2Fi6r8HSqvtClDigkLId6PVKsgj17NifUau62Tluxp1ixmg\nZSYX2bRJJpeyXUbXSFcwEoPrl16PYVXDcF6f8zCpzyR0Le9q+dpJvCMUClnaAVqJ0pVVUVHRouaF\nrIPjOIRCobR2/EDLmpdXPnkFc/81F+9MeQcDOgzQbUNiJBXWiQPSwYMH8f777yMcDmPMmDFFfVLP\nlmShF3ehgtJKICdphmFQWVmZ9iGwo/JeCyNt5+1aF3FlEatNGXhWZnKpe3IpT+3LLl8GURTxQ/QH\nrNy5Est3LseD7z2I7hXdMbH3RJzX5zwM6jzIdAHXWpddkPb16sI7EiPh+eaRyKTDMXGfKdOReZ7H\nk1uexILPF2DpxUvRq20vQ21IjAT27bBqeJ7HbbfdhoULF8Ln88mf26effhqXXHKJ5c9vNcr3Qp0V\nSNzSyWQSX3zxBQDkLCh/+9vf8OCDD2L79u3YsmULzjjjDM3H1dfX47bbboMgCLj++utx5513FnZj\nBmgVgpLrRku64ZK55lZ/yYysz87K90zrIVlaiURCTpnWy+RKpVJpPbm0YFkWHco7YNrAabjitCuQ\n5JJ4/5v3sXznclz9j6sR5aOY0HMCzut7Hs7tcW5B2V8kC43juKzrsgotS5TUuIiiKMegiG9eXfPC\neljcteEubNy3EfWX1qNDqIOua0yrDYldqbCZeOCBB/C3v/0NyWQSyWRS/vnNN9+M6upqDB061PI1\n2JkMoDw8KOuY5syZgw8//BBdu3bF888/j0mTJqF7d/2xzYQBAwbg7bffxqxZs3QfIwgCbr75Zqxe\nvRpVVVUYMmQIJk+ejP79+5t5ay0onfQCDfKJoaRSKTQ2NiIUCulm/JhtCWS7XjKZRFNTEyKRSMbu\nxVZbKMQFSGI3Xq9XPnkRq4TEd0gtRy6bNsMwCPqDGNdnHJ6ofQJbr9uKxb9YjJryGjz14VOo+VMN\nprw5BS/95yUcaDqQ89q1Gk/ajXrAlnpdyvYt4XAY5eXlcp+n403HcdU7V2Hbd9vwjyn/QLc23eQO\nA6QYkrjRSIsX4KcNLRAIIBwOIxQKya34o9Eo4vG4nLVkNbFYDC+99JIcZ1ASj8fx+OOP27IOp1DG\nXv7+97/jpZdewoknnogPPvgAP/vZzzB9+vSs1+jXrx9OPPHEjI/ZvHkz+vTpg5qaGvh8PkydOhWL\nFy826zZ0oRbKjygD3dmKFe1yLeWyJqtRugArKioAQHe6IsMwiEQiBZ0Aidvg1C6n4tQup+K3w36L\n75u+x4qvV6B+Zz3uf/d+1FTWYFLvSTivz3kY2Gmg7vMRIQRQ8LoKRdkc0si6iBgkxASuWXUNQt4Q\n/n7h3+GFFw0NDYbmvJDsOqUVowwmk2aWQPOGb2WH3j179mSM+23bts3U53Mb6n2DZVkMHjwY999/\nPwRBwHfffWfK8+zbtw/V1dXyv7t164ZNmzaZcu1MtApBIeiZuU4HurUEKp81WZXllSmTSzldkfTt\nyjYDJh9YlkWnik64atBVuPL0KxFPxvH+3vex/OvlmL54OpJiUnaNje4xGkFvUF5nNBq1bF25IknN\nFookNU/zZFk2q1v1cOwwprw1BaeccArmj58PL+uVr5XrnBee59NcYkp3Gs/zCAQCeQf2jdC2bduM\n1lDbtm0Lfg4juKX+RRmU93g86NKlCwCgtrYWBw8ebPG3jz76KC64IHtGpFP31ioEJdOLm0+Ld6st\nFLImj8eTtWrbakgmFxkZrDwB62VyWQ3DMAgHwxjfdzxq+9RCEAR89t1nWP71cszbOA9X//NqjOg2\nAhN7T8TIziPRrU03Rzsut0CC/JnLJnJ7G/bi53/7OS7oewEeHPFgi+SQfOe8qJtZks+zGYH9THTu\n3Bmnn346tmzZ0qIdUigUwg033JDzNYsZvSyvVatWFXTdqqoq7N27V/733r170a2b9aMLSlpQtDKz\nlD8rdL66WaccpUApCyjzOVGbKXTqwslMmVx2pt8qIafy07qehtO6noY7ht+B7xq/Q/3X9aj/uh6z\nN8xG77a9ZdfYgI4DHBUWURKRTCYNFVJ+fvhzXPjmhbhl8C24efDNGa+rleVFrBetOS/qZpZ67fgz\nBfYz1Vlk4oUXXsDYsWMRi8XkWEokEsHPfvYzXHvttYavUwhOWSjq543FYmjXLvP00WzX02Lw4MH4\n8ssvsXv3bnTt2hULFy7EggUL8n4eo5S0oChRbtrKnlPZ5qvrXcsKCm07b/a6YrGYKZlcdsKyLNqF\n2uGiPhdh2oBpSAkpvP/N+1j29TJMfWcqeJGXU5JHdh8pu8bsgOd58BwvWxSZ2LRvE6a+MxWPnfsY\npp48NefnyjbnhYiLz+eT3ZUkPRnQnvNC4jSk35i6zkJpvWSiV69e+Pe//43XXnsNy5YtQ3l5Oa66\n6iqcd955rmi0aickfT0X3n77bdx66604fPgwzjvvPAwaNAjLly/H/v37MXPmTCxduhRerxfPPPMM\n6urqIAgCrrvuOsszvACAkZws+bYBUnV87NgxlJeXg2VZRKNRCIKQcxaSkqNHj5rW1bexsREA5DXl\n+6WSJAlHjx5F27Zt8xYX4ttPpVLy/ZGTrDqTSxRFuY2KGyCNO5PJZAuRI5vqp999iuVfL8eKXSuw\n/eh2jKoehUl9JmFi74mWdjcmhZQ3rb0Jv+j3C1zc72Ldx67YuQI3LL8BL058EXW96kxfi7IfFXF7\neb1eOftLPfYYQIvAvhJlYJ/EaIwG9kmnArsPJNFoVL5fOyH7EenMMHfuXAwbNgyTJk2ydR1W0WqO\nAyRwTGITZHpgIdczQ4uVJ/9CEwIKtVCUmVzKn6nFhASAnc6YUkIsJq3W88BPrrHTu56O07uejjuH\n34lDjYew/KvlWLZjGe5adxdObHciJvWehEl9JuHUDqeadm/KQkqGYTLOlH/jszdw97q7sejCRTir\n6ixTnl+NsucUqbciSSDKIL1eYF+ZjPH/2zvz6KiqdO0/VZlIJZUAgmkI+RjES6AbIQFJd2OYp5AR\nQQkgImCMtBr0gihLWxBtnJDlvYJcR4aFBklCBiEJU0tkSoKCCkhE8KabQSIIZK6qVKW+P3L38eTk\nnKpTVWeq1P6t1auXUNTZOTlnP3vv932fl69LJbtinwiRms2r+FAzKM+mubmZVsp7K42NjW7HJuSA\n7V5MHHnVHAu78+Tt27fb1TGQtGAtZUwRSPqt3e7cep6g1+vRK7wXFo1YhIWxC9FkbsJX//oKJT+X\n4IFdbdXa5GgsPioeQf7ueX2R4j2yY3LUU37D1xvw7tfvYs/sPRjSY4hb1xMLSaQwGAzMkS/Xj4oc\njZHjMfIMsM0syWKIHah3FNjXorgoCVfIqKB4GTqdjsl66dKlC1MkJsX3erJDYftgkfNqKcflyvdx\nkxPIz2UymdqllMpppOgunlrPA233LKRLCBIGJWDaf0yDzWbD6ZrTKL5YjFcOv4Lzt85j3P8bh8SB\niZh611T0NPR0+p1COyaSNsz97OrDq1H0UxEOzD2AqLAovq+UDCEfM3acRGyfF3bGGDk+c1axzzZQ\nJN+hpJmllk75Scy0s9DpBaWxsZFxYJU64Ofug8kNvpPVtRoIZXIZDAam5zbZqZAgr1aQ2noe+H1S\njYmMQUxkDFbetxK/1P2C0oulKKwqxPJ/LsfgOwa3ZY3dnYjBdwzucF12jIlUvzN/x6mUt7ZakbUv\nC2eun8H+OfvRw9DD45/BEa74mInp88Jugcx3NCYU2CdCQqr0ye5FbGBfCtTK8mL/bNQc0ssglhNS\nT9ruPIxCle9S1rWI/S6ygma3MWbHc8iLDbSJTlBQEGw2G+rq6todg6h1TKfUjkmv1yOyayQWj1iM\nRbGL0GhqRNm/ylDycwnSctLgr/dHwoAEJN6diPui7kOAPsBh9Tt792iymtr8yloaUTy7GKGBobL9\nHEDH4zdXEKp5IQsSsTUv7N0LCfKT41MS2Cc1L3JW7GsFkmnaWej0gkKaEkldjOjq96ldjc8dC8l0\nI8kJXBsVIn42m43JjiP/lm1cSIrdiLgo8eKrYT0PtP3OQ4NDkRidiOmDpsNms+G7a9+h+EIxVpWt\nwsXaixgTOQZT+09FcnQyQnQdjzLIDqXWXIvZ+bMRERKBbSnbEOgn785PyhRvd2pe2LsXIqok/Zw8\nc3yBfS2YWUoJXx0KPfLyIsgvT47qdrHfx26oxBc0JsFOKXD2c/J5cjnK5OKOl/vi8/X0IDsYOV58\nNa3n2ZBd3Ig+IzCizwistK7Ev278CwcuHcDui7ux8vBK/LHHH5mjsUHdB7XdW9hRa67F1OypGN1n\nNN6a+JasLY+dZb9JgSs1L0RciGAAbQsErh0MESxHfd3dbcOtlQwvoE3otRST9JROX4dCttHEtFCq\noDzpOujsYeA2oeJ7kEnSgBQrldra2rZ+7TyTLcnkIrb8QEcxcTeTi0wSxOmWtABmZwh5AilGbWlp\ngcFg0EwhJdB2XxsbG9vFGxpMDfiy+kuU/lyK/f/ajyD/ICQMSMCRK0dQ01CDx2Iew3N/eU7WiU0L\n9ULcmhf2YoNMpmSnQnYvABzWvJDvZNfQuFKxT2I3auwMuHU3CQkJOHz4sGYEzlM6/Q6FoMaRl9jK\nd6nHxvddfJlcXBsVT+ISQscg3Awhd+IujoLcasPnY6bT6WAMNiJlcAqSo5NhtVrx7bVvUXyxGD/e\n+BET+k7AsnuXyTou7j1Ta8Ji7zTIcanFYmFideT5c8XM0llnRGeBfS3tUDobPiUoUh0rOUMo+K4E\nfC8KETZiM8MnJlLHJbjHIEINo5ytKkmNCaC+9TwXMfeM/Kz3Rt2Le6PuxQvxL8BmbZsASTBb6gQH\nrd4zMg6SRUgWMWJqXrhmltyjMbYdjJRmllLDFjMioJ2JTi8ocsVQhL6PxB9aW1sVt53nGwsRtrCw\nMMZVlpxdk6MGT7J/xMAXd+FOJERguFX6WiykBNyP5fj7+cPfz7/dit0doRWCPH9ibPGVhggw+565\nWvPiKGtMbJdKraGl35GnaO/uegl8IsAOvpNWrmqNiytsQplccgds+cbHLp5jryjZ6ad6vR5NTU1M\nR0KtvHREgKXImHJXaIXwBgEWumdia164gX0iLI5qXriBffJvLBaL24F9d+Eet2npdyQFPiMocu0C\nCGKC70qNjQibXq+H0Whk/owrJuRYRM2eK3zZPBaLpZ1fFDkbVxs5BVioSl3s0ZgcRZ5S4UxMV40U\noQAAIABJREFUuLhS80IckrldKoGOuxcS4yI7IRKcB9y34vcE4hDQmej0giLnkReJyXhqOw9IawfR\n3NyMoKAgyTO55Ia8XCQrCQBvN0I1ahHYQW4lBJhvxS50NEZ+n1qzxQE8K6YEXKt5IUe4YswsSUEl\nO4WZBPal7lJJ4L7jzc3NbvVh0jKdXlDYyCEozc3N7arN3f0uKSArr8DAQBgMBt7gOzvFNTAwUDNi\nYrfzW89zV6nuHgd5OjYpg9y1tbX4+eefERERgd69ezv9vKOjMa3a4gBgjgal3M25UvPCDewT4WDP\nA3yCJXdgn3xHZytqBHxIUKSedNirICls5z0VO5PJhObm5nbVyXJnckmFs6Mk9kvvznGQJxDzSXJt\nT54jk8mEZ555Bjt37kRgYCDMZjNGjBiBTz75BFFR4gwh2Udj/v7+zDFXa2urZmxx2DVDcqZ5s+8F\nAN54HFtgiFg0NzdDr9ejpaUFdnv7Pi9iA/tS7JKbmpokq4vTCj4lKFLtUFpbW2EymWC32xEeHq7q\nKp+byUXGJZTJpXaFORey+rfbXbOeZx8HkWJKqa1gpI5LPPzwwzh48CBMJhMzQVVUVGDcuHH4/vvv\nXVqtksUBu4hVjqwxV2EvDpSuGeKreWHfC+KaTQL1AESbWXLT392p2OezXelMxpCADwiK1DEUq9WK\nhoYG+Pv7S2Y77+7YuP5g5HssFku7YjGlM7nEIpX1PN8RSGNjIwAwq1NXJ1Ru9bunnD9/nhET7nXq\n6+uxY8cOLF68WNR3CaUs8x2NKXlMSJ414vqg5rPGvRdsy3yy2BJT88KNvZBjRfKdxIXDHTPLztYL\nBfABQSFIISgWiwWNjY3MOTp5QNWA6w9G/owcZZGdCvB//T40VmEup/U8N1OKTHJirWBI9buUR4PH\njx8XvP+NjY3Yu3evKEERG+R25ThIiudCK5X5QpjNZiYex95pOKt54ZpZsv9fqEulUGCfu0Mhc0ln\nwmcEheCO7QJZebGD79zgnie4KnZklxQUFMRkiZCHnzzEbBNInU6H+vr6DgFLtVDCel4oO8iZFQxf\n8Z0UOPLS0ul+N+oUgh2XcGenyT0OYh8Teno0pmUxIfVY7BgYd1fLrnkB0G7hIbbmRUxgn/ue0yMv\nL4R95OUO5IEkVu/tmiVJXNciRuzILslgMDCTg5hMLim9tTxBrcQAMVYw5LgwNDRU8rqXqVOnMkct\nXIKDg/HQQw8J/lup4xJCx4TuHI1p1eYFEFfo6WnNC/mdignskyQAk8mEiooK1NfXuywoOTk5WL16\nNaqqqnDixAnExsbyfq5fv36MO0ZAQAAqKytdv4Fu0OkFhQ1ZIYh96NnHSiRGwf4uKcclBpLJ5Y4n\nl5gJVe6eJlqynueer5vNZmblSSqopYw1hIWFYf369Vi+fDkzAQNtO5dp06Zh7NixvP9O7voXMUdj\n7MZZ3LGRn8XdGJhcuFNrJUXNi9VqbScu7PtLMsssFgvWrl2LM2fOoH///ggNDUViYiL69OnjdIxD\nhw5Ffn4+MjMznf4shw4dQvfu3UXcLenwCUFhbzXF7iq4x0rcB1LqQklHkBe3paVF0JMLgOhMLqHg\nLbuniZQFhNw0Ui1UvbMhx5dGo7GdwDibUF1lwYIFGDhwIN58802cOXMGEREReOKJJzBnzhze+6zG\n6l/oaMxkMrXLoNPpdEwwWmueYVLF5zyteeGaWZLvDAsLw969e/Hee+/h3//+N44cOYIXXngBzzzz\nDF544QWHY4qOjhY9fqXmJzY+ISgEsQ8WO/iuVLGY0O6JL5NLSk8u9gqKnBWTQDYJLnqSGcQ9X9dS\nYoBQyjJfYydu8NZdURw9ejQKCwtFjY04BKi1+hc6GmtqamJsQ7SUgg7IZ0EjtJPjq4UiR2PsjDHy\nP/KO6fV6WK1WjB8/HrNmzYLNZkNDQ4MkYyXjnTRpEvz8/JCZmYmMjAzJvtsR2noaZMbZroIv+O7u\nd0kxNqFMLj5PLlfqOByNgbvl5xYQurJa1/L5OpmwHaUs8x0TKmEFw06n1srqn/y85NiGHPtYLBY0\nNzdLupNzFyX9zMTUvAQEBLQTY4vFAj8/P0ZcfvvtNyapxs/PD+Hh4QCAyZMn49q1ax2uuXbtWiQn\nJ4sa39GjR9GrVy9cv34dkydPRnR0NOLj46W7AQJQQfk/HAXfHeFO1pgYHGVyETEhL5Cfn58sq1ih\nAkIxq3Wt+oUB7p+v8wVvpa7x8Ib7xnWAdhZrUOJnYIuJ0v5YfEfIbNdoIiKBgYHMs/Prr79i9+7d\nmDBhQofv279/v8dj6tWrFwCgZ8+emDFjBiorK6mgSIWzGIqj4Luj75RrjNwjN0eZXErZuztKteSm\nnQpNPFpAivvG3skJWcG4s1rXsmOwownbWayBXeMhx8+kpphw4dZCkRR5nU6H27dv45FHHkF8fDz2\n7t2LDz74AOPGjXP7WkKL46amJthsNhiNRjQ2NmLfvn1YtWqV29dxBe0caCsA38NstVpRV1eHwMBA\nl49l5AjMm0wmNDY2wmg0CooJqQR3xypfCoiABAcHw2g0Mn5Ezc3NqK+vR0NDgyYnRSKAUt83spML\nCQlBWFgYAgICmB1mQ0MDU1jp6FkhZ+hkFaul+8YdmyPIhBocHIzQ0FAmbmY2m1FXV4fGxkbG1VcK\ntCQmXIh5bGBgIIxGI7p3746MjAwcOXIEly5dwqJFi5CVlYWTJ0+K/s78/HxERUWhvLwciYmJSEhI\nAABcvXoViYmJAIBr164hPj4ew4cPR1xcHJKSkjBlyhRZfkYuOrsaqQAKQ3ofsCc6wPPg++3bt2E0\nGiXJWqqtrYVer2fSQz3N5FIDcp7OztcXW50uN2rUv7BX6y0tLQD4rWD4+tJrBbKjk2Js7CQHkl7r\nydEYdyesJfh2m7W1tUhPT8cLL7yAyZMn48yZM9i9ezf+9Kc/iY6NaB2fEhQSbwgKCmKC76GhoW5P\nzFIJit1ux+3bt5mGWCQ+IpTJZTAYNJV6SwoCuZYg3AlELSdcLdS/sDPorFYrk0FHVu+k3cAXX3yB\nH3/8EZGRkZgxY4bTCno5kVJMuLCPTdliK/ZojCwQtdgDhmRmssWkvr4ec+bMwfLlyzF9+nS1hygb\nPiEoxMSNZPWQLAuj0ejRxFZbW9vO7dUdyHGC3W5HcHAwAgMDHWZyObLwUAOxVdzsTBir1SqpK7Aj\nPG3wJBetra1MvxAAuHDhAu6//36YTCY0NDQwHk+ffvopJk+erPj45PAzE4IrtjabzWEcSutiwrV6\naWxsRHp6OrKyspCamqr2EGXF5wTFYrEgICBAkjTWuro6j144dtvglpYWBAUFMT5c7EwuraWQEthC\n58r95B4FyZGCyy2m1JIIA+3b4ra2tmLQoEGoqanp8DmDwcAUQSqFkmLCh6OjMQCa7U7JJyZNTU2Y\nO3cuMjMzMXPmTLWHKDvaestkhBQh6fV6TdREWCwW1NfXIyQkBMHBwczOiS0mZPdCgpxqj5kNOULU\n6XRuJTOQn8loNDIpzySoT1wB3F3rkGJKNXpyiMFsNrfrsX7w4MF2dixsbDYbPv74Y4/uhyuQ7CyD\nwaBaEzaSNUaSHEjaemNjIxoaGhireC2thfnEpLm5GfPnz8fixYt9QkwAH0kbJpM3CQxLWT3r6kNN\njohMJhNTPGm326HX65mjI7YFvRYDtVKmtwql4LprfaL1Yko+x+ALFy4wR19czGYzqqqqZLGC4SKX\n07InkIxCUkRJdiXclgRqFlTyiYnZbMaCBQvw0EMPYfbs2aqMSw208dTIjE6ng9FoZI6+pMQVQSGT\nndVq7eDJRfL4ST2DzWZjDOiIVYMWkNt6nl1M6ar1idaPB4ViTX379mVaAnMJCgpCdHQ0QkNDZbGC\nIWghcUEIclxNYowER/dDqYJKtuMCEROLxYJHHnkEs2bNwty5c2Ufg5bwiRgK20GVrA6lgJuG7Ah2\nfxJHNipkjMHBwe2q09nVuEq9LFzU7EnPDepziynJi63FCnOunxl3bC0tLbjrrrvw22+/dfi3wcHB\n+P7779G7d+8O38nOkvIkDsWO52gpcQEQn2km5f0QC1tMyAKmpaUFixYtwrRp0/Doo49q6jlUAm0t\nRWRGCf8tPtixENL/wFEmF3sFy3UElttHSgi1V7DO7C1IRbYWxcTZEVxAQAAKCwuRmJjYrvhSp9Ph\n448/7iAmQEcrGO79EGsFo9UsOMC1tGUhaxy2yamU9VDk98oWE6vVioyMDEyYMMEnxQTwkR0KebjI\nCluq3H72uakQJJMrODiYaT/K58kl9qiGnWJJArVy9gpn75q0Vv8C/F79TmJRWiqm5FvBOqKxsRG5\nubk4ffo0+vbti/T0dPTs2dPl67KfD0cpuJ1FTJzBlzXmyVEhEROdTtdOTB5//HHExcUhKyvLJ8UE\noILiEeyHig8lPLnIypRMHlJOpuyjGq3VvwD8R3BaKaYkiwR2oFYN2MemLS0t7VpEu9PuQAmULKh0\ndbfP3nGS7ESbzYYnn3wSQ4cOxbJly3xWTAAfExSymiU20Z5Cjhe4bTzZNvikEp8tJuQFltpyg28y\ndTcjiO/F0RJijuDUKqbUqskjuR/s7pRSN1PzFHYAXsmCSvZuX2hBxvdOtLa2YunSpRg4cCCef/55\nTdxDNaExFInhs8EnL7JOp2MmdjliElzXVz67eTErdS1bqJMjOIvF4vSohi/uInccikyIWiy8A37v\nTkkSQ+SMM7iKkmICCKesC2WNNTc3A2gvJsuWLUPfvn2pmPwfPrFDIV5Tra2tqK2tRbdu3ST5XpIL\nT2wyXM3kUiomIZQhxbdSV9oW3xXE2ryI+R454lByHtV4irNMM/YuXo2jQrWr87lw3xlyTM1Omnn+\n+efRtWtXvPLKKx69J4sWLcKePXtw55134vTp0x3+/tChQ0hNTcWAAQMAADNnzsSLL77o9vXkxKd2\nKFLD3vHYbDameNJRJpca7XDFrtTJ+LQ+IUrZmVKKYkpAexMiG2diAnRspsbtQChnyroW7x07LZ1k\nX/r5+WHz5s147bXXMGTIEHTv3h2vvvqqx/dj4cKFeOqpp/Dwww8Lfmbs2LEoKiry6DpK4FOCIteR\nV0tLCxoaGkRncqlZwU0EhBxnkcmUvDRkhU5WZFpA7up3McWUjlbqatbnOMOdeye0AJGjYZYWxYRA\nhJjtVbdkyRL88ssv+Omnn2A2mxEVFYW4uDhs2bIFffr0ces68fHxqK6udjoWb8AnBIU89OT/pZos\n2X5bzjK5mpqaNBekJTEdMh6DwcC44JLxqp1+q3T1O18feUcrdaliYS0tLfjmm29gt9sRGxsrSfxF\nisQK9gIEaF8k7KkVjDeICXtXZ7fb8dprr8FsNqOgoAB6vR4NDQ3Yv38/7rzzTtnGotPpcOzYMQwb\nNgyRkZFYt24dhgwZItv1PMEnBIWNVKtvEpchwXelMrmkhB2TYKeP8q3U5fSQEkLtbClnK3Vi6Olp\nC4NPP/0Uzz77LLOjtdvtWLNmDR577DG3v9PVGhixkKNCd6xx2GhdTEiiAltM1q1bh+vXr2PTpk3M\nOxAaGooZM2bIOp7Y2FhcunQJBoMBJSUlSEtLw/nz52W9prv4RFAeaMuqstvtuHXrFsLDwz2aFMnL\nSgLc4eHhTIdCsish19SqPxK3Mt9ZMSW3lkFsxpi7aDlbikw4xL3ak6B+aWkpHnroISaDiBAcHIz3\n3nsPDz74oFvjk0NMnF2TW9/BFhf2GIiYaPW9YCfbEDH57//+b1y4cAEffPCBLIk01dXVSE5O5g3K\nc+nfvz+++eYbdO/eXfJxeIq2KpoUwNM4SmtrK+rr65mJGADTsIsdfCeOwp6uXuXAVet5nU6HwMBA\nGAwGxk6cHPXV19eL6pnuCqReKDg4WJNiYjabYbVaYTQaYTQamZbNFovF5b7pq1at6iAmQFuN06pV\nq1y+p+zOpEoaZBIBIS0JSLEvtyUB2x5fa++FkJi89957OHfunGxi4oyamhrmOaisrITdbtekmAA+\nfOTlDiSTKzAwEMHBwcwkSpyBuZlcWqxC9vQYSe7aDi1aqBO4Ew753XIzpLj1P+x7wv2+s2fPCl7v\nypUraGpqYhYuzlD7iJAglPhBjpH8/PyYpBWtvB/c41/yLn/00Uf49ttvsXXrVtnEZM6cOSgrK8ON\nGzcQFRWFl19+mWmLnJmZidzcXGzatInxAtyxY4cs45ACnzvyqq2tdat5EF8mFzmWIX5J/v7+zDGI\nFqvL5bSel6K2Q8veUmJSb/n+jTObj549ewo21woICMD169dFPataERMh2Jlw7GQHtuCq5aLNrg0j\nCwW73Y7Nmzfj8OHD2L59u+biPFpFW0tAGfEkGE8yWkJDQ9utzMmxFwnQm0wmAG0r1paWFlWb/nCR\nO7WVW9vBzQZylDHGfaG1KCbupC2zd3NCjsCzZs1CdnY2syIl+Pn5ISkpSbSYaLXHOsC/62Rn0ZEj\nTrncC5zBJybbt2/Hl19+iezsbComLuAzO5SWlhYm/hEUFCQq44qsSi0WC4xGI9N3QyiTi3wvWaWz\nnU2VNidko3ZygCOPMZ1OJ0n1u1zIFeAm4vLLL79gypQp+O2335gFSVBQEMLDw3H06FFe63ru92g1\neQEQf4TJ3uFarVbGCkYuF22CyWTqICY7duxAUVERdu7cqcl7qmV8TlDENsVie3IZjUbo9XqHmVx8\nK38+c0KpOuyJQQ2bFzFjYmeMAWCSA7QwPjZKeZrdunULH374IXbu3AmbzYbU1FRkZmYiIiLCocBq\n2eoF8CwepoQVDFdMACA3Nxeff/458vLyHLaloPDjM4JC2v+K6WFChIdUtZM/4/PkEmNSCAinVcp1\ndsw+89ei9bzdbmd8z/R6vWa6UhLUikmI9V3Tcn0TIG1yhStedGJhv7vk3SgoKMC2bduQn58v2JKC\n4hgqKBy4mVyAY08udyZrdnaUs5x9d5CiQlpO+Fb+fPdEjfN0QDvHSOx7QgwKySRKjjC1eL5PxESO\nXafQPXHFCoZPTHbv3o0PP/wQBQUForPqKB3xOUFx1BSLZHIZDAYmBZRPTEgAUYrJmrwgZAVGXhB3\nJ1ItW88D4tyMpcgY83R8Wlv5k3tCjjABMM+J3PfEFeQUEy7knvA1mBNKiCGZhOyU/r1792LDhg0o\nKCiA0WiUdcydHZ8TFKGmWI4yudgGj3JO1p5OpFq2ngfcP6aRsysl3/i0aAcCtD9GIpmE7BiD0tY4\nXEg8Ua14mLNWv3xicvDgQbz99tsoLCyUrPGeL+MzgsJO2SS1BIB7mVxKHYNwe4M7WpF6y5m6p5O1\nlF0p+canxYJKwPH4hKxxlEr+ANQXEy7cuAv5sy5dujD3paysDK+99hoKCws97pHkrKcJAGRlZaGk\npAQGgwFbtmxBTEyMR9fUIj4nKOxKZxIYttvtzKrF1UwupeCKC5lIAwICmCpkrU6GcqUtS+UxpnZa\ntTNcmaxd8dRSY3xqYDabYTKZEBAQgFOnTmHevHm47777cO7cOezfv99t23k2hw8fRmhoKB5++GFe\nQSkuLsaGDRtQXFyMiooKLF26FOXl5R5fV2toK/VHAUgcpLW1FXV1ddDpdDAajYzNvCNPLjWPQYi9\nR2hoKIxGIyMkdXV1aG5uRmBgoOYyuYDfX2Y5PM2k8BiTc3xS4Opk7cxTq7m5mTlOVWN8SmOxWJhj\nLoPBgNGjR+O//uu/cOPGDfTo0QNDhgxBamoqjh8/7tF14uPjHe5yioqKsGDBAgBAXFwcbt++jZqa\nGo+uqUW09wbJDImF1NXVISgoiMn2EsrkstlsmvPkIvUsRPzIRFpfX6+JQkqgfQ2MEvfPVY8xpcfn\nDp5a0XA9tVxxLxCDN4gJd3wnTpzAu+++i/z8fERERODWrVsoLi7uEFOVmitXriAqKor57z59+uDy\n5cuIiIiQ9bpK4zOCws7fJ1XZYjK5PG03Kwds63myuyJ/zm4IpXQhJXt8arQ6JgiZE7ItT4joaFVM\nSNGdlONz1MvE1cJBrYsJOQZmj+/kyZN4/vnnsWvXLmYi79atG+bNm6fImLi7Qq3NK1LgM4ICtL2k\nZrOZeanUyOTyFHYHQ27asrNVuhJFg+76XskFn8dYU1MTYy1vMplU70rJhs+oUA4cdabU6/UODRu1\nbOIJ8Kcuf/fdd1i2bBl27dqFXr16KT6myMhIXLp0ifnvy5cvIzIyUvFxyI32lmYywV5RAeiQyaXT\n6WC1WtHQ0MAUNWphgmHDFjtn4yOrdPZZOtl5NTQ0oLm5mSkMk3p8UtXoSA2Jien1eoSFhcFoNMLf\n35+JRbnSx0TO8cktJlzIYsNgMMBoNDJu2o2NjUzchTwr7NRbbxGTs2fPYunSpdi5c6dqk3hKSgq2\nbdsGACgvL0fXrl073XEX4ENZXq2trcxkUV9fz6yeyaQntxuvp0iVtsxX6+JJISVB6zs7Z+4BUmWM\neTI+bnMnteE+K0RoSWq6FsbIhi+1+ty5c1iyZAk+//xz9O/fX7Zrs3uaREREdOhpAgBPPvkkSktL\nERISgs2bNyM2Nla28aiFzwgKWV2R4DU7vkAClVrfwsshdmy7E3cr0rViVSKEq47BcnhHObueq71W\nlIZkwwUFBTFFwloopiTwicn58+eRkZGB7OxsDBw4UNXx+Qo+Iyitra1MxzigbRK0WCxM0ROxnlf7\nxeCiZI2EK4WUBK0XVHq6c5LbY4yICXFv0KqYcL2vyI5OqCpdSfh61F+8eBGLFi3C9u3bMWjQIEXH\n48toa/aUkS+++AIpKSn46KOP8Ouvv6KxsRHLli1DfX09goODGYfhhoYGmM1m1c7RCeQIhOyclKiR\n4Na68PVJZ68/SH/w4OBgTYsJaXDlzmTNjUWRSZ/bK92ddRk7W0+rYmIymTqICfB7DVBISAhTA0Tu\nN6kBkjpGxwefmFRXV2PRokXYunUrFROF8Zkdit1ux40bN5Cfn4/s7GxUVVVh1KhReO2119C3b18m\nXZjbv0SoH7jcY9WS9Tyf3YlOp2OCx1osCFTiGM4TjzEiJsSoVKti4mqCgJDZqStuwGLhE5NLly5h\n/vz5+PjjjzF06FDJrkURh88ICuGbb75BSkoKHn/8cURGRiI/Px/19fWYOnUqUlNT24kLn8W83OLi\nDdbzZKIBoJlCSjZqHMO54jEmVxdIKZEq20wuY08+I8+rV69i7ty5+OCDDzB8+HC3v5viPj4lKHa7\nHcnJyVi8eDFmzJjB/HltbS2++OIL5OXl4caNG5gyZQpSU1Nx1113ORUXKYO03pApxW7XS1Kt1d7R\nsdGCY7CjjDEAaGpqYupitPg7lqsOhk903enCyPc7vnbtGubMmYP33nsPI0aMkGzMFNfwKUEBwBQx\nClFfX489e/YgLy8PV69excSJE5GWloZBgwY5FBdPzfe0bj3vLBNJKdF1hBYdg7nHqHa7nRETpRuH\nOUOpokpyLaHFiKPnhbwnbDH59ddfkZ6ejnfeeQd//vOfZRszxTk+Jyiu0NjYiJKSEuTl5aG6uhrj\nxo3DjBkzMGTIEOj1eslqOrSeKeXqMZxQVz05uy9q3QqEJH2w409qdqXkoqSY8F1bTCYdn5jcuHED\n6enpeOuttzB69GjFxkzhhwqKSJqbm7Fv3z7k5eXhxx9/xJgxYzBjxgzcc889HomL1q3T2VYv7pz3\ny1VIyUbrViDkKJPsPgF1u1Jy4R5lqm0qyndf/Pz8OrQ9vnnzJmbPno21a9di7Nixqo2Z8jtUUNzA\nYrHg4MGDyM3NxenTpzF69GikpaVhxIgRzMvILRjkTqJ2u52x1tb6RBgQECDZMRx759La2urRJKrm\nqlosYrPNlOpKyUVLYsIHaXtssVgAABcuXMDp06cxZswYLFmyBKtXr8bEiRMluVZpaSmefvpp2Gw2\nPProo3juuefa/f2hQ4eQmpqKAQMGAABmzpyJF198UZJrdxaooHhIS0sLysrKkJOTg1OnTmHUqFFI\nS0tDXFwcIxLsyYJMolp3u1Ui7ZavkNKVtFstT4SA+/3p5epKyUWLdi9c2PfQ398fX3/9Nd566y18\n+eWXGDhwIBYuXNhukvfkOoMGDcKBAwcQGRmJe++9F9nZ2Rg8eDDzmUOHDmH9+vUoKiry9MfqtGjv\nLfQyAgICMGnSJLz//vs4duwYZs2ahYKCAkyYMAHLli3DV199BbvdzhQMkt7WJLZA0jO1pOtWq5V5\nieW0UuEWUoo1atRyrxqCu2IC/O4ETIoGAwICYLVaUV9fL1nhrbeJCXGxGDx4MJqamrB9+3asXbsW\nZ8+exV/+8hccOHDAo2tVVlZi4MCB6NevHwICApCeno7CwsIOn9PSe6pFtHdo78X4+/tj3LhxGDdu\nHGw2G44fP47c3Fy89NJLuOeeezB58mS8/fbbmDVrFp544gkmvZTd8EiNM3Q2amVKce3Uyc6lubm5\nXdqtTqfTlD0+H1KmLpOKdD6beXcz6bxRTIC2JJm5c+di6dKlSEtLAwAkJSU57copBr4GWBUVFe0+\no9PpcOzYMQwbNgyRkZFYt24dhgwZ4tF1OxtUUGTCz88P9913H+677z60traisLAQjz76KAYPHowf\nfvgB+/btw7hx45gjJXL8Y7FY0NTU1K5nvFIvvFYypYQmUZPJBAC8vWC0gpx1MK52peTDG4woSeyO\nLSZNTU2YN28elixZwogJQYpnVcx9iI2NxaVLl2AwGFBSUoK0tDScP3/e42t3JrR3VtAJOXXqFJ54\n4gmsWbMGX331FZYuXYoTJ04gISEBGRkZ2L17N8xmM4KCghASEtKhZzyfj5aUcH3DtJQgQCbRLl26\nMLUKfn5+7TyjpFihSgHxNmNnIsmFOx5j3iImDQ0NjFkr0JZhOX/+fCxevBizZs2S5brcBliXLl1C\nnz592n2G3GcASEhIQEtLC27evCnLeLwVGpRXgLNnz+LChQtITU1t9+d2ux1nzpxBTk7Dwr5tAAAY\nl0lEQVQODhw4gD59+iAtLQ1TpkxhHlyuq6vUAVpvCG7zZZtpoZCSjZaKKoUyxojAaFlMuOnVZrMZ\n8+fPR3p6Oh566CHZrm21WjFo0CAcPHgQvXv3xqhRozoE5WtqanDnnXdCp9OhsrISDz74IKqrq2Ub\nkzdCBUUj2O12VFVVITc3F3v37sWdd96J1NRUTJs2DUajkfkMV1zcsa5gX5O43Wp1khGTbSZkSKhU\nwaBWjgr5IEepZrO5Q62LlhYPfGJisVjwyCOPIDU1FY888ojsv8eSkhImbXjx4sVYuXIl3n//fQBt\nTbI2btyITZs2wd/fHwaDAevXr6eV+RyooGgQu92OCxcuIC8vD8XFxejWrRuSk5Mxffp0dO3alfkM\nmUDd6TBIDAq12q4XcC9TSqiQUg63W0DbYgJ0dK62Wq2qdaUUgk9MWlpasGjRIkydOhUZGRmafD4p\nHaGConHsdjuqq6uRl5eHPXv2wGAwIDk5GUlJSejWrZug7b6jiULrJpSAdHY0fDVAUmXSab1C31Hz\nLqW7UgrB7VkDtP3uMzIyMGbMGPztb3/T5PNJ4YcKihdht9tx+fJl7Nq1C0VFRfD390dycjKSk5PR\no0cPUT1dbDYbk6KsRRNKQL6Wx9xCSk8y6YiYaLUOxpVOkHJ3pRSCT0xsNhsef/xxjBo1CllZWZp8\nPinCUEHxUux2O2pqarBr1y4UFhbCZrMhKSkJKSkpiIiIEAxct7a2IigoiHmBtYZSwW13q9G9we7F\nk546SnmM8SVa2Gw2PPnkk/jTn/6E5cuXUzHxQjqdoOTk5GD16tWoqqrCiRMnEBsby/u5fv36ISws\njDlHrqysVHik0sHuRllQUACTyYTp06cjJSUFkZGR0Ol0OH78OO666y6EhITAZrOpnhXFh1rxCG6y\ng1BswRsy4qRu0CaHx5jdbmecl8mRa2trK55++mkMGDAAK1eu1MTzSHGdTicoVVVV0Ov1yMzMxNtv\nvy0oKP3798c333yD7t27KzxC+bl58yYKCwuxa9cu1NXVITo6Gnl5eSgoKEBsbKzmUm4B7cQjhOJR\n/v7+sFgssNlsmmjLzIfc3T6l8BgjySDsBmOtra1Yvnw5evXqhZdeeomKiRfT6QSFMH78eKeC8vXX\nX+OOO+5QeGTK8uabb+L111/HxIkTce3aNcFulGql3Gr5CImbSQcAQUFBmtrVEeQWE77rCXWlFPod\nConJypUrERYWhldffVVT95TiOj5rvaLT6TBp0iT4+fkhMzMTGRkZag9JctavX4+PP/4YJ0+eRL9+\n/ZhulK+88gquXLmCSZMmMd0o/f3921nAkICunOLC9ZTSkpgAv1ejt7S0QK/Xo0uXLoxxplSdOqWA\niIlOp1OsR72rHmNCYvLSSy8hODgYr7zyChWTToBX7lAmT56Ma9eudfjztWvXIjk5GYDzHcovv/yC\nXr164fr165g8eTLeffddxMfHyzpupblw4QLCw8PRs2fPDn/X2NiI0tJS5Obm4n//938xfvz4dt0o\nAec9XTzBG2xAhFb9SjQNc3WMSoqJs/HwZYyR40NyH+12O9asWQOz2Yz169dLsphw1s8EALKyslBS\nUgKDwYAtW7YgJibG4+tSfscrBUUMzgSFzcsvv4zQ0FAsW7ZMgZFpD75ulGlpaRg2bFgHcZGqMZaS\nxzPuIHaManZeJKt+d7tpyg0RF+LGoNPpsG7dOsTFxeHUqVOora3Fu+++K4mYiOlnUlxcjA0bNqC4\nuBgVFRVYunQpysvLPb425Xe0dcYgMUJa2dTUhPr6egBtK/V9+/Zh6NChSg5NUwQHByM1NRXbtm3D\n4cOHMWHCBHzyySeYMGECXnjhBZw4cQI6nQ5dunRBaGhou74uQkaEQnhDhb4rY9TpdMwxjtFobHdv\n6urqXLo37oxRq2JCMJlM8Pf3R1hYGLp06YLw8HCsXbsW69evx40bN5CTk8O8i54gpp9JUVERFixY\nAACIi4vD7du3UVNT4/G1Kb/T6QQlPz8fUVFRKC8vR2JiIhISEgAAV69eRWJiIgDg2rVriI+Px/Dh\nwxEXF4ekpCRMmTJFzWFrhsDAQCQkJODjjz/G0aNHkZiYiM8++wzjx4/HihUrcOzYsXYNw1yZQImT\nrJ+fn2YnQU8nam7TMPa9kco12hvEhOzw2GMku7bhw4fj4sWLmDhxIrZu3YoHHnjA4+vx9TO5cuWK\n089cvnzZ42tTfqfTBeVnzJiBGTNmdPjz3r17Y8+ePQCAAQMG4Ntvv1V6aF4H6UY5adIkWK1WHDly\nBLm5uVi5ciVGjhyJ1NRU/PWvf+3Q04U0DGNXopNJUMsV+lJb0hBxIfeGBK6bm5vdNmn0JjFhx3Xs\ndjs2bdqEH374AVu2bIGfnx8ee+wxPPbYYx53nwTE9TMhY3Pn31HE0el2KGqQk5ODP/7xj/Dz88PJ\nkycFP1daWoro6GjcfffdeOONNxQcoeeQbpQbNmxAeXk55s2bh9LSUkycOBFZWVn45z//CZvN1m51\nzu7pUl9fDz8/P82LCbEBkXqMUrT19SYxAdBOTD766COcPHkSmzdv7lBnJEUMRUw/E+5nLl++jMjI\nSI+vTfkdKigSMHToUOTn52PMmDGCnyG2EqWlpfjhhx+QnZ2Nc+fOKThK6SDdKN955x1UVFQgIyMD\nZWVlmDx5MpYsWYK9e/eipaUFgYGBqKqqwrlz55hdirN+8Wogt5hwISm3BoMBYWFhCAoKgs1mQ0ND\nAxoaGphUajbstFtvEBN2NteWLVtw9OhRbN26VTY7nZEjR+Knn35CdXU1LBYLPv/8c6SkpLT7TEpK\nCrZt2wYAKC8vR9euXRERESHLeHyVTnfkpQbR0dFOP8MOGgJggobsLBRvRK/XIy4uDnFxcWhtbcV3\n332HnJwcvPHGG7jjjjtQUVHRrm8Et1+8pz1dPEVMvxU5cdbWlxyLkXulVXdokgYOtBeTTz/9FAcP\nHsSOHTtk7WLp7++PDRs2YOrUqUw/k8GDB7frZzJ9+nQUFxdj4MCBCAkJwebNm2Ubj69CBUUh+AKC\nFRUVKo5IevR6PWJiYhATE4M9e/Zg/vz5uP/++/E///M/2L17N9LS0jB58mSEhITw9otXuj+H2mLC\nhdRsEOFgiwvBZrOpXkjJRcjZeMeOHdi9ezdycnI8akEgloSEBCYJh5CZmdnuvzds2CD7OHwZKigi\nEVNM6QgtTQByc/ToUSxevBglJSWIi4tr141y48aNiIiIaNeNkqzO2dXWznq6eIo7zbuURKfTQa/X\nw2q1IiAgAIGBgbBarYo4GLiCkJjk5uZi165dyMvL04RYU5SBCopI9u/f79G/FxM07CyMGjUKR48e\nxV133QWgbXIcPHgw/v73v+PFF19kulE+8MADHbpROhIXYnPiKaR5l9T9VqSEL+OMu3MxmUySNw1z\nBSG3g4KCAnz22WfIz8/XbJsEijx02kp5NRg/fjzWrVuHESNGdPg7q9WKQYMG4eDBg+jduzdGjRrV\noZLX1xDbjVLIGdkdcfEmMRGTYs1tGkbujRJV+nxisnv3bnz44YcoKChASEiIbNenaBMqKBKQn5+P\nrKws3LhxA+Hh4YiJiUFJSQmuXr2KjIwMpv6lpKSE8RpavHgxVq5cqfLItYPYbpSe2O4r1bzLE1wR\nE75/S+xx2PbynvQu4YNr6km+e+/evXj33XdRWFgIo9Eo2fUo3gMVFIrm4OtGmZiYiNTUVIfdKB2J\nS2cXEy7cpmFSZdMJicnBgwfx9ttvo7CwEOHh4W5/P8W7oYJC0TRiulE66+lC4g3eIiZSxx24fV3c\nzaYTEpOysjKsXbsWRUVF6Natm6Rjp3gXVFC8mJs3b2L27Nn417/+hX79+mHnzp3o2rVrh891pnbH\n3G6U06ZNQ2pqKvr27cuICzuuQIonScxEi9l2cooJF76OlGTn4igmxW5/HBoaytzHI0eOYM2aNSgs\nLOz0zeoozqGC4sWsWLECPXr0wIoVK/DGG2/g1q1beP311zt8rrO2O66trcUXX3yBvLw8XL9+nelG\nOXDgQOh0OuTn52P06NEwGo2wWq2aSrclKCkmXMQeGwp11Tx+/Dj+/ve/o7CwkLfnDsX3oILixURH\nR6OsrAwRERG4du0axo0bh6qqqg6f84V2x6QbZV5eHlNEevz4cZSWljLuBFL2dJECIiaBgYGq12qw\nxYUrvuTP2GJy4sQJPP/88ygoKJDcvsQXd96dBSooXky3bt1w69YtAG0TQvfu3Zn/ZjNgwACEh4d3\n6nbHbF566SV89NFHGD9+PC5evMjbjZJ7LKa0uGhJTLiwjw2J3X5AQADOnTuHoUOH4uzZs1i2bBny\n8/PRq1cvya/v6ztvb0abEUoKg1CF/j/+8Y92/63T6QQnwqNHj7ZrdxwdHd3p2h0T3nrrLezatQsn\nT57EH/7wB6Yb5YYNGzp0oxSy3Ze7loP0hdGK5QsX0jSMHIMZDAa0tLTg2WefxY8//gij0YjVq1fL\nFoAvKipCWVkZAGDBggUYN24cr6AAwk30KOpAdyheTHR0NA4dOoQ//OEP+OWXXzB+/HjeIy82nb3d\n8YULF9C1a1f06NGjw99ZLBYcPHgQubm5OH36NEaPHo3U1FSMHDmSd+dis9kkr+XQupgQzGYzLBZL\nu2Ous2fPYsWKFRg7diwOHTqEb7/9FvPmzcPGjRslvTbdeXsvdIfixaSkpGDr1q147rnnsHXrVqSl\npXX4TFNTE2w2G4xGI9PueNWqVSqMVhkGDhwo+HekG2VCQgJaWlpQVlaG7OxsPPvss4iLi0NaWhri\n4uKcNsVyV1y0ZkYpBJ+YnDt3Dn/729/w+eefY8CAAQCAX3/91ekCRgi68+6c0B2KF3Pz5k08+OCD\n+Pe//90ueMmu0P/5559x//33A2izHZk3bx6t0OfA7kZZUVGBESNGIC0tDX/961+ZuhW+QkFXOi5q\n3YySYDabYTabERoayvxc58+fR0ZGBj777DPcfffdso+B7ry9FyooFAoLm82G48ePIzc3F0ePHsU9\n99yDtLQ0jBkzhvH+crUK3ZvF5OLFi1i0aBG2b9+OQYMGKTKOFStW4I477sBzzz2H119/Hbdv3+4Q\nQ+HuvKdMmYJVq1ZhypQpioyRwg8VFApFgNbWVpw4cQK5ubkoKyvD4MGDkZaWhnHjxjFHVs6q0L1F\nTCwWC0wmE0JCQpgCx+rqaixYsABbt27FkCFDFBsL3Xl7L1RQKKIpLS1lzC0fffRRPPfccx0+k5WV\nhZKSEhgMBmzZsgUxMTEqjFR62N0o//nPf2LAgAFIS0vDxIkTERwcDKCjuOj1erS2tiIoKEjTNu58\nYnL58mXMmzcPn3zyCYYOHaryCCneAhUUiihsNhsGDRqEAwcOIDIyEvfee28H+/3i4mJs2LABxcXF\nqKiowNKlS1FeXq7iqOXBbrfjzJkzyMnJwYEDB9CnTx+kpqZiypQpjGX7+fPncccddzDBfal7ukgF\nn5hcvXoVc+fOxfvvv99pFgQUZVC+iTfFK6msrMTAgQPRr18/BAQEID09HYWFhe0+U1RUhAULFgAA\n4uLicPv2bdTU1KgxXFnR6XQYOnQo1qxZg6NHj+Lll1/Gzz//jLS0NDz00EPYuHEjpk6diu+//x6h\noaEwGo3o0qULU8xYX1/PmCyqCZ+YXLt2DfPmzcN7771HxYTiMlRQKKIgdiaEPn364MqVK04/c/ny\nZcXGqAbsbpRHjhzBggULsGbNGgwfPhzvv/8+PvvsM9TW1sLf3x/BwcEwGo0IDg6G3W7vIC5KHhYQ\nB2a2mPz666+YO3cu3nnnHYwcOVKxsVA6D7QOhSIKsXUX3ElRCwaMSnHq1ClkZmZiy5YtuP/++5lu\nlPPmzWO6USYmJqJ79+4d2vk2Nja63DDMXUhdDVtMbty4gblz52LdunX4y1/+Ist1KZ0fKigUUURG\nRuLSpUvMf1+6dAl9+vRx+JnLly8jMjJSsTGqTVBQED744AOkpKQAaPOaWr58OZYtW8Z0o3zkkUeY\nbpRJSUno2bNnB3FpamqSzRmZT0xu3ryJuXPnYu3atbjvvvskuQ7FN6FBeYoorFYrBg0ahIMHD6J3\n794YNWqUw6B8eXk5nn766U4ZlPcEdjfKgoIC2Gw2JCUldehGybaAkUpc+LpW3r59G7Nnz8aqVasw\nadIkKX9Uig9CBYUimpKSEiZtePHixVi5ciXef/99AEBmZiYA4Mknn0RpaSlCQkKwefNmxMbGqjlk\nTcPXjTIhIQEpKSno06cPIxzsniXuigufmNTV1SE9PR3PP/88pk2bJtvPSfEdqKBQKBrBWTdKwL2e\nLlarFU1NTe3EpKGhAenp6fjP//xPJCUlKfYzUjo3VFAoFA3irBslIK6nC5+YNDY2Ys6cOXjiiScw\nY8YM1X5GSueDCgqFonG43SgnTpyItLQ0REdH84qLzWZjMsXMZjNCQkIYMWlqasLcuXORkZGBBx54\nQPKx5uTkYPXq1aiqqsKJEycEjzzFuC5QvA9ah0LxCkpLSxEdHY27774bb7zxRoe/P3ToEMLDwxET\nE4OYmBi8+uqrKoxSHoxGI9LT05GTk4P9+/dj+PDhWLduHSZOnIhXXnkFZ86cAdCWZUYKKYE2s0eg\nrY/Jjh07cP36dcyfPx8LFy6URUwAYOjQocjPz8eYMWMEP2Oz2ZhY2w8//IDs7GycO3dOlvFQlIWm\nDVM0D5mA2LYvKSkp7TLMAGDs2LEoKipSaZTKEBISgpkzZ2LmzJmC3SjNZjNWrFiBvXv3IigoCE1N\nTdi+fTueeuopDB48GDabDbW1tQgPD5d8fNHR0U4/w3ZdAMC4LnB/nxTvg+5QKJpHjO0L4HvtYIOD\ng5Gamopt27bh8OHDmDBhAt58802mC+Xp06cBACNGjEBYWBhef/11PPXUU9i5cyeioqKQnZ2tyrjF\nuC5QvBO6Q6FoHr4JqKKiot1ndDodjh07hmHDhiEyMhLr1q1T1HJdbQIDA9GrVy9UVFRgy5YtCA8P\nR3Z2NpYvX46GhgY888wzeOyxx6DT6bBgwQLU1dW57SUm1G1x7dq1SE5Odvrvfck9wdeggkLRPGIm\noNjYWFy6dAkGgwElJSVIS0vD+fPnFRiddvjHP/6BjRs3YubMmQCASZMmwWq1orS0FImJie3uY1hY\nmNvX2b9/v0fjFOO6QPFO6JEXRfOImYCMRiMMBgMAMD3jb968qeg41Wbnzp2MmBD8/f2RlJSkyq5A\n6Ahy5MiR+Omnn1BdXQ2LxYLPP/+csauheDdUUCiaR8wEVFNTw0xglZWVsNvt6N69uxrDVQ0tHCXl\n5+cjKioK5eXlSExMREJCAoC2HiuJiYkA2kRuw4YNmDp1KoYMGYLZs2fTgHwngdahULwCZ7YvGzdu\nxKZNm+Dv7w+DwYD169fjz3/+s8qjplB8CyooFAqFQpEEeuRFoVAoFEmggkKhOGHRokWIiIjA0KFD\nBT+TlZWFu+++G8OGDcOpU6cUHB2Foh2ooFAoTli4cCFKS0sF/764uBgXLlzATz/9hA8++ABLlixR\ncHQUinaggkKhOCE+Ph7dunUT/PuioiIsWLAAABAXF4fbt2+jpqZGqeFRKJqBCgqF4iF8lfyXL19W\ncUQUijpQQaFQJICbLKmFmhAKRWmooFAoHsKt5L98+TIiIyNVHBGFog5UUCgUD0lJScG2bdsAAOXl\n5ejatSsiIiJUHhWFojzUHJJCccKcOXNQVlaGGzduICoqCi+//DJaWloAtFXpT58+HcXFxRg4cCBC\nQkKwefNmlUfsHmK7Lfbr1w9hYWHw8/NDQEAAKisrFR4pRavQSnkKhQIAqKqqgl6vR2ZmJt5++21B\nQenfvz+++eYbn/NKoziH7lAoFAoAcd0WCXQdSuGDxlAoFA3jrEr/0KFDCA8PR0xMDGJiYvDqq6/K\nPiadTodJkyZh5MiR+PDDD2W/HsV7oDsUCkXDLFy4EE899RQefvhhwc+MHTsWRUVFor7P026LAHD0\n6FH06tUL169fx+TJkxEdHY34+HhR/5bSuaGCQqFomPj4eFRXVzv8jCvHT552WwSAXr16AQB69uyJ\nGTNmoLKykgoKBQA98qJQvBqdTodjx45h2LBhmD59On744QdJvldIpJqamlBfXw8AaGxsxL59+xya\nZlJ8CyooFIoXExsbi0uXLuG7777DU089hbS0NLe/S0y3xWvXriE+Ph7Dhw9HXFwckpKSMGXKFEl+\nFor3Q9OGKRSNU11djeTkZJw+fdrpZ2lKL0VN6A6FQvFiampqmOOpyspK2O12KiYU1aBBeQpFwzir\n0s/NzcWmTZvg7+8Pg8GAHTt2qDxiii9Dj7woFAqFIgn0yItCoVAokkAFhUKhUCiSQAWFQqFQKJJA\nBYVCoVAokkAFhUKhUCiSQAWFQqFQKJLw/wG01aU/LOMn1wAAAABJRU5ErkJggg==\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x109e81f60>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 11
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"point_x = np.array([[0],[0],[0]])\n",
|
|
"X_all = np.vstack((X_inside,X_outside))\n",
|
|
"\n",
|
|
"print('p(x) =', parzen_estimation(X_all, point_x, h=1))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"p(x) = 0.3\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 12
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 2,
|
|
"metadata": {},
|
|
"source": [
|
|
"Sample data and `timeit` benchmarks"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In the section below, we will create a random dataset from a bivariate Gaussian distribution with a mean vector centered at the origin and a identity matrix as covariance matrix. "
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import numpy as np\n",
|
|
"\n",
|
|
"np.random.seed(123)\n",
|
|
"\n",
|
|
"# Generate random 2D-patterns\n",
|
|
"mu_vec = np.array([0,0])\n",
|
|
"cov_mat = np.array([[1,0],[0,1]])\n",
|
|
"x_2Dgauss = np.random.multivariate_normal(mu_vec, cov_mat, 10000)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 13
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The expected probability of a point at the center of the distribution is ~ 0.15915 as we can see below. \n",
|
|
"And our goal is here to use the Parzen-window approach to predict this density based on the sample data set that we have created above. \n",
|
|
"\n",
|
|
"\n",
|
|
"In order to make a \"good\" prediction via the Parzen-window technique, it is - among other things - crucial to select an appropriate window with. Here, we will use multiple processes to predict the density at the center of the bivariate Gaussian distribution using different window widths."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"from scipy.stats import multivariate_normal\n",
|
|
"var = multivariate_normal(mean=[0,0], cov=[[1,0],[0,1]])\n",
|
|
"print('actual probability density:', var.pdf([0,0]))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"actual probability density: 0.159154943092\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 14
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 2,
|
|
"metadata": {},
|
|
"source": [
|
|
"Benchmarking functions"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Below, we will set up a benchmarking functions for our serial and multiprocessig approach that we can pass to our `timeit` benchmark function."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def serial(samples, x, widths):\n",
|
|
" return [parzen_estimation(samples, x, w) for w in widths]\n",
|
|
"\n",
|
|
"def multiprocess(processes, samples, x, widths):\n",
|
|
" pool = mp.Pool(processes=processes)\n",
|
|
" return [pool.apply(parzen_estimation, args=(samples, x, w)) for w in widths]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 15
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Just to get an idea what the results would look like (i.e., the predicted densities for different window widths):"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"widths = np.arange(0.1, 1.3, 0.1)\n",
|
|
"point_x = np.array([[0],[0]])\n",
|
|
"results = []\n",
|
|
"\n",
|
|
"results = multiprocess(4, x_2Dgauss, point_x, widths)\n",
|
|
"for w,r in zip(widths, results):\n",
|
|
" print('h = %s, p(x) = %s' %(w, r))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"h = 0.1, p(x) = 0.016\n",
|
|
"h = 0.2, p(x) = 0.0305\n",
|
|
"h = 0.3, p(x) = 0.045\n",
|
|
"h = 0.4, p(x) = 0.06175\n",
|
|
"h = 0.5, p(x) = 0.078\n",
|
|
"h = 0.6, p(x) = 0.0911666666667\n",
|
|
"h = 0.7, p(x) = 0.106\n",
|
|
"h = 0.8, p(x) = 0.117375\n",
|
|
"h = 0.9, p(x) = 0.132666666667\n",
|
|
"h = 1.0, p(x) = 0.1445\n",
|
|
"h = 1.1, p(x) = 0.157090909091\n",
|
|
"h = 1.2, p(x) = 0.1685\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 16
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Based on the results, we can say that the best window-width would be h=1.1, since the estimated result is close to the actual result ~0.15915."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"mu_vec = np.array([0,0])\n",
|
|
"cov_mat = np.array([[1,0],[0,1]])\n",
|
|
"n = 100000\n",
|
|
"\n",
|
|
"x_2Dgauss = np.random.multivariate_normal(mu_vec, cov_mat, n)\n",
|
|
"\n",
|
|
"benchmarks = []\n",
|
|
"\n",
|
|
"benchmarks.append(timeit.Timer('serial(x_2Dgauss, point_x, widths)', \n",
|
|
" 'from __main__ import serial, x_2Dgauss, point_x, widths').timeit(number=1))\n",
|
|
"\n",
|
|
"benchmarks.append(timeit.Timer('multiprocess(2, x_2Dgauss, point_x, widths)', \n",
|
|
" 'from __main__ import multiprocess, x_2Dgauss, point_x, widths').timeit(number=1))\n",
|
|
"\n",
|
|
"benchmarks.append(timeit.Timer('multiprocess(3, x_2Dgauss, point_x, widths)', \n",
|
|
" 'from __main__ import multiprocess, x_2Dgauss, point_x, widths').timeit(number=1))\n",
|
|
"\n",
|
|
"benchmarks.append(timeit.Timer('multiprocess(4, x_2Dgauss, point_x, widths)', \n",
|
|
" 'from __main__ import multiprocess, x_2Dgauss, point_x, widths').timeit(number=1))\n",
|
|
"\n",
|
|
"benchmarks.append(timeit.Timer('multiprocess(6, x_2Dgauss, point_x, widths)', \n",
|
|
" 'from __main__ import multiprocess, x_2Dgauss, point_x, widths').timeit(number=1))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 17
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 2,
|
|
"metadata": {},
|
|
"source": [
|
|
"Preparing the plotting of the results"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import platform\n",
|
|
"\n",
|
|
"def print_sysinfo():\n",
|
|
" \n",
|
|
" print('\\nPython version :', platform.python_version())\n",
|
|
" print('compiler :', platform.python_compiler())\n",
|
|
" \n",
|
|
" print('\\nsystem :', platform.system())\n",
|
|
" print('release :', platform.release())\n",
|
|
" print('machine :', platform.machine())\n",
|
|
" print('processor :', platform.processor())\n",
|
|
" print('CPU count :', mp.cpu_count())\n",
|
|
" print('interpreter:', platform.architecture()[0])\n",
|
|
" print('\\n\\n')"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 18
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"from matplotlib import pyplot as plt\n",
|
|
"import numpy as np\n",
|
|
"\n",
|
|
"def plot_results():\n",
|
|
" bar_labels = ['serial', '2', '3', '4', '6']\n",
|
|
"\n",
|
|
" fig = plt.figure(figsize=(10,8))\n",
|
|
"\n",
|
|
" # plot bars\n",
|
|
" y_pos = np.arange(len(benchmarks))\n",
|
|
" y_pos = [x for x in y_pos]\n",
|
|
" plt.yticks(y_pos, bar_labels, fontsize=16)\n",
|
|
" plt.barh(y_pos, benchmarks,\n",
|
|
" align='center', alpha=0.4, color='g')\n",
|
|
"\n",
|
|
" # annotation and labels\n",
|
|
" plt.xlabel('time in seconds for n=%s' %n, fontsize=14)\n",
|
|
" plt.ylabel('number of processes', fontsize=14)\n",
|
|
" t = plt.title('Serial vs. Multiprocessing via Parzen-window estimation', fontsize=18)\n",
|
|
" plt.ylim([-1,len(benchmarks)+0.5])\n",
|
|
" plt.grid()\n",
|
|
"\n",
|
|
" plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 19
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 1,
|
|
"metadata": {},
|
|
"source": [
|
|
"Results"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"plot_results()\n",
|
|
"print_sysinfo()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAoIAAAIACAYAAAAWiA3GAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XuczPX////7a5Y9srK71inW+VQrtCqKtSuHkFKpVI4R\nobd376R3vD9R76SipJS3nCl9oxx6o5w3x9690UFCjiuHSE67rIjX7w+/nbcxy85q5zmvNbfr5bIX\n5jWvnXnMfQ77mNfrMa+xbNu2BQAAgKDjCnQBAAAACAwaQQAAgCBFIwgAABCkaAQBAACCFI0gAABA\nkKIRBAAACFI0gpAkpaWlyeVyacqUKVd9GS6XS127ds3Hqgq+Jk2aqGLFij6v36VLF7lcPC1zs3v3\nbrlcLr344ouBLsVnFSpUUEpKSqDLwGX46/WrID5W81NBuP2TJ0+Wy+XSl19+GehSAoK/OA60c+dO\nPfHEE6pRo4aioqIUExOjWrVqqUuXLkpLS/Pb9VqWJcuy/vRlOF12s+VyubR+/foc1xk5cqR7nT/T\nHEvemUyePFmjRo267LoFIUOnKEhZ+eu+rVChgvux6nK5FBYWpooVK6pHjx7au3dvvl/ftcyfj6eC\n9FjNq927d2vIkCH67rvvLrtOoG9/WlqaXnzxRR0/ftzrvOznZqBrDJRCgS4AntatW6fk5GSFhYWp\nU6dOuuGGG5SVlaWffvpJixYtUnR0tJo0aZLv15ucnKysrCwVKhQ8D4nw8HBNmjRJN998s9d5kyZN\nUnh4uE6fPp3vLw6TJ09Wenq6+vXr53XeuHHjNHbs2Hy9vmtRhQoVdPr0aYWEhAS6FJ/99NNPfvtD\nU65cOQ0bNkySlJGRoeXLl2vixIlasGCBvv/+e8XGxvrleq8lBe3x5CS7d+/WSy+9pEqVKummm27y\nOM8pz9W0tDS99NJL6tq1q4oVK+ZxXseOHdWhQwcVLlw4QNUFVvD81S8gXnzxRZ0+fVpfffWVEhMT\nvc4/ePBgvl5fRkaGihYtKsuyFBoamq+X7XTt2rXTRx99pDfffNPjtv/3v//VDz/8oEceeUTTp0/3\ny3VfriHwVyOemZmpIkWK+OWyA6WgPV79+UemWLFieuSRR9yne/bsqfj4eI0ePVqTJk1S//79//R1\nZL9WXKsK2uPJiS73RWVOyjanGl0ul6NqNI1dww6zbds2xcbG5tgESlLJkiW9li1ZskTNmzdX8eLF\nFRERoZtuuinHrUrZM0rffPONWrRooeuuu8797i2nGUHbtjV06FA1btxYpUuXVlhYmBISEtS7d28d\nOXLkqm7f5s2b5XK59Mwzz+R4focOHRQWFqbffvtNkvTzzz+rW7duSkhIUHh4uEqWLKnbb79dU6dO\nvarrv1jXrl119OhRzZkzx2P5pEmTFB8frzZt2nj9TvYsyYoVK7zO82UesEKFClqxYoV7bib7J/vy\ncpoRzF52+PBhderUSXFxcSpSpIjuvPNOffPNNx7rXjyP8/HHH+vmm29WZGSknnrqKfc648ePV716\n9RQZGanrrrtOLVq00OrVq3Osd/ny5WrdurViY2MVERGhypUrq3v37u77J9vHH3+sO+64Q9HR0YqK\nitJtt92mTz/91Ovy5s+fr+TkZJUoUUKRkZFKSEjQ/fffr23btrnX8eU+z2nu6OJl8+bNU/369RUR\nEaEyZcpowIABOnfunFc9n376qW666SZFREQoISFBL730kpYsWeLTSMBzzz0nl8uljRs3ep13/Phx\nRUREqF27du5lOc0ILlq0SA899JAqVaqkyMhIFS9eXC1atMjx8ZVXzZs3lyTt2LEjz9eV/VjetWuX\nHnjgAcXExLi3oly6K/rin0tv37p169SuXTuVKFFC4eHhqlGjhl555RWv+yL7+g4cOKAOHTooJiZG\nUVFRatmypcdj40q6du2qiIgI/f777+5la9eulcvlUmxsrEcD8Pnnn8vlcmnmzJnuZTnNCGYvW7t2\nrZKTk1WkSBHFxcWpR48eOnnypFcNq1at0u23367IyEiVKlVKTz31lDIzM3Os9+TJk3r++edVuXJl\nhYeHq3Tp0urcubP27NnjXuf3339XRESEunTp4vG7PXv2lMvl0l//+leP5Q899JCKFSum8+fP55rX\ntm3b1LFjR/dre8WKFTVgwACdOnXKY73cno+TJ09WamqqpAv3waWPhdyeq5988onq1KmjyMhIValS\nRePHj5ckpaen64EHHlBsbKyio6PVsWNHryy3bNmi3r1764YbbnC/9iQlJWnChAke63Xp0kUvvfSS\nJKlixYruGrOXXe51/fDhw+rTp4/KlSunsLAwlS9fXn379vX6+5f9+8uXL9eIESPc92n16tXz5W+V\nv7FF0GGqVKmiBQsWaPbs2R5/RC7n/fffV69evdSwYUP94x//UFRUlBYtWqQnn3xSO3bs0Ouvv+5e\n17Is7dmzR02bNtWDDz6o9u3bez2xLt5S9fvvv2vEiBF64IEH1K5dO0VFRenrr7/WhAkTtGrVKq1f\nvz7PWzlq1qyp+vXra/r06Ro+fLhH03PixAnNnTtXrVq1UmxsrP744w81a9ZM+/fvV58+fVStWjUd\nP35c3333nVatWqVOnTrl6bovvZ1169ZVnTp1NHHiRD344IOSLuwe+uijj/T4449f1Rac3Hb9jRo1\nSs8//7wOHz6st956y728Zs2auV5Gy5YtFRsbqxdffFEHDhzQ6NGjlZycrLVr1+qGG27wWHfOnDna\ns2ePevfurd69eys6OlrSheZl+PDhuvXWWzVs2DCdOHFC77//vlJSUjR37lzddddd7ssYO3asnnzy\nSZUrV059+vRRQkKC0tPTNW/ePO3bt8+9u/Ef//iHXnnlFd111116+eWX5XK5NGvWLLVv316jR49W\n7969JUlffvml2rZtq9q1a2vgwIG67rrrtG/fPi1dulQ7duxQ1apV83yf55TVggUL9N577+nJJ59U\n9+7dNWfOHI0YMULFixfX888/717v448/VocOHVS1alUNGTJEISEhmjJliv7973/7dF926dJFw4cP\n19SpUzV8+HCP82bMmKHff//d4w94TjNIU6ZM0bFjx9SlSxddf/312rt3r8aPH6+mTZtq+fLluuOO\nO65Yw5VkN1BxcXF5vi7LspSZmank5GTdcccdGjZsmA4dOiTpwmP40iboq6++0ujRo1WqVCn3svnz\n5+u+++5TtWrV1L9/f8XExGjNmjV64YUX9O2332rGjBke13fy5Ek1btxYDRo00LBhw7Rz506NGjVK\n99xzj3744YdcP0TVtGlTTZkyRatXr3Y3JkuXLpXL5dKxY8f0zTffqF69epKkZcuW5di45nSff/vt\nt7r77rvVrVs3PfbYY1q+fLkmTJggl8vl8Yb7P//5j+68804VK1ZMf//731WsWDH9v//3/3J8k3X2\n7Fm1aNFCa9asUfv27fXss8/qp59+0pgxY7Ro0SKtW7dOZcuWVVhYmG6//XYtX77c4/ezb9eyZcvc\ny2zbVlpamho3bpxrVuvXr1dqaqpiYmL05JNPqmzZsvr222/19ttva/Xq1fryyy9VqFAhn56PycnJ\nGjhwoF555RX17NlTjRo1kuS90SKnbOfNm6d//etf6tOnj2JiYjR+/Hg98cQTCgkJ0eDBg9WsWTMN\nGzZMX3/9tSZOnKjw8HCNGzfO/ftffvmlVq5cqbZt26pixYo6efKkZsyYoR49eujXX3/V3//+d0lS\nr169lJGRodmzZ+utt95yPydq16592YyOHz+uhg0baseOHXr88cdVr149bdiwQWPGjNGyZcv09ddf\ne+1lGThwoE6fPq0nn3xSoaGhGjNmjLp06aIqVaqoYcOGV7xPAsqGo6xdu9YODQ21Lcuyq1atanft\n2tUeM2aMvXnzZq919+/fb4eFhdmPPvqo13n9+vWzQ0JC7J07d7qXJSQk2JZl2RMmTPBaf/ny5bZl\nWfaUKVM8lp8+fdpr3QkTJtiWZdkzZszwWG5Zlt21a9dcb+O7775rW5ZlL1iwwGP5+PHjbcuy7Nmz\nZ9u2bdvfffedbVmWPXz48FwvMy86d+5sW5ZlHz582H7nnXfskJAQe+/evbZt2/aHH35oW5Zlb9q0\nyZ45c6ZXJpMmTbIty7K//PJLr8tNTk62K1aseFXLLq0tp2X333+/x/L169fbLpfLbtmypXvZrl27\nbMuy7NDQUHvLli0e62/ZssW2LMtu1KiRffbsWffy/fv329ddd51doUIF+9y5c7Zt2/bPP/9sh4aG\n2jfccIN9/PhxrzrPnz/vrsGyLHvQoEFe69x77712dHS0nZmZadu2bT/99NO2ZVn2r7/+muNtt23f\n7/Ps2/niiy96LStSpIidnp7usf6NN95oly5d2n367NmzdpkyZexSpUrZx44dcy/PzMy0K1WqlONz\nISf169e3y5Qp484t2x133GGXKFHCI+eEhAQ7JSXFY72TJ096XebBgwftuLg4u1WrVrlef/bl1qxZ\n0z58+LD966+/2jt37rQnTpxoFytWzA4NDbU3bdqU5+tKTk62Lcuy/+///i/X69+1a5cdHx9vV61a\n1T5y5Iht27adlZVllyxZ0k5OTvbKZuTIkbZlWXZaWprX9V16vw8fPty2LMteuHBhrnXs3bvX67GY\nkpJi33PPPXZ0dLT9+uuvu5fXq1fPrl27tsfv5/T6ZVmWHRISYn/99dcey1u3bm0XLlzYI9MGDRrY\nYWFh9rZt29zLzpw5Y99yyy1ej9X333/ftizLfu655zwud/78+bZlWXbHjh3dy15++WXbsiz35aan\np7vXsSzLPnjwoG3btv3999/blmXZb775Zq5Z1a5d265Zs6b7uZlt9uzZtmVZ9uTJk23b9v35eLm/\nH7ad+3N1z5497uW//vqrHR4ebluWZY8cOdLjcu677z47NDTUI/OcHtPnz5+3mzRpYhcrVszj+Td4\n8GDbsiyv1wbbzvl1feDAgbZlWfaYMWM81s3++3XxcyP79+vVq+dxnfv27bPDwsLsDh06eF2nk7Br\n2GFuu+02rV+/Xp07d9aJEyc0efJk9e7dW7Vq1VJycrJ27drlXveTTz7RmTNn1K1bNx0+fNjjp02b\nNjp//ryWLFnicfmxsbF5OkRCWFiYJOncuXM6duyYDh8+7H4X/fXXX1/VbezQoYNCQ0O9NplPnTpV\nsbGx7l2y2buili1bpl9//fWqrutKLMvSI488osKFC7t3A06aNEm33HKLatWqle/X92cNGDDA43S9\nevXUrFkzLVmyxGt3TuvWrVW9enWPZXPnznVfzsWziKVLl1bXrl2Vnp6ub7/9VpI0c+ZMnT17VoMH\nD3ZvTbxY9rv7Dz/8UJZlqVOnTl6PwbvvvlsZGRlau3atJOm6666TdOFx+8cff+R4G/PjPr/33ntV\nvnx5j2VNmjTRL7/84s5p/fr1OnDggLp06eIxOB4VFaVevXr5fF2dO3fWgQMHtHjxYveyXbt2ac2a\nNerQoUOuM5+RkZHu/2dmZuq3336Ty+XSLbfcov/85z8+17FlyxaVKFFC8fHxqly5sh5//HHFx8dr\n7ty57sdyXq/LsqxcZwuPHz+uNm3a6I8//tD8+fNVvHhxSdLixYt16NAhdenSRUeOHPF4XGRvdV60\naJHHZYWEhOgvf/mLx7Ls15rt27fnmkHZsmVVrVo191ay7Fnrli1bKjk5WUuXLpUkHTt2TN999517\nq2FuGjRooPr163vV9ccff2j37t2SpEOHDumrr77SPffcoypVqrjXK1y4sJ5++mmvy5w9e7ZCQkI8\ntlBLUqtWrXTTTTe5n6vShS2dkty3a9myZSpUqJCGDBkiy7LcWwuz/83tdm3cuFEbN25Uhw4dlJWV\n5XHfZO/Wzr5v/P0afO+996pcuXLu03FxcapWrZoKFSqkPn36eKx7xx136OzZs+7MJc/H9OnTp/Xb\nb7/pt99+U7NmzXTixAlt3br1qmubPXu24uPj9cQTT3gs79mzp0qUKKHZs2d7/U7v3r09nvNlypRR\ntWrVfHr8BhKNoAPdeOONmjRpkn755Rft3r1bU6ZMUaNGjbRy5Urdc889Onv2rKQL83aSdOeddyo+\nPt7jp3nz5rIsy707J1vlypXz9MnFGTNm6NZbb1VkZKRiYmLcf2gk6ejRo1d1+4oXL642bdpo7ty5\nysjIkHRhZmTVqlV6+OGH3U+khIQEDRo0SIsWLVLp0qWVlJSk5557TuvWrbuq681JTEyM2rZt6/4k\n7/Llyx17LMSLdx9fvOzcuXNKT0/3WF6tWjWvdbPfRFy6G1mSu1nYuXOnpP/tVqxbt+4Va9q8ebNs\n21aNGjW8HoPdu3eXZVnuDzj17dtXdevWVe/evRUbG6vWrVvrnXfe0eHDh92Xlx/3eaVKlbyWZe/G\nzp5tzM7i0mZZyjm7y8npTc3UqVNl27ZPows7duzQww8/rOLFiys6OtrdzH3++ec6duyYz3VUrFhR\nS5Ys0ZIlS7RixQpt375dP/30k1q2bHnV11WiRIkc3wRk++OPP9S+fXtt375dn376qapWreo+L/u1\nqVu3bl6Pi5o1a+b42lSmTBmvgf1L77fz58/rl19+8fg5ceKEe/2UlBStW7dOmZmZWrNmjU6fPq3U\n1FSlpKRo1apVOnv2rNLS0nT+/HmfG0FfHk/Zz5saNWp4rZvT83bXrl0qU6aM16dXpQvPz4yMDPfz\nIikpSUWLFnU3esuWLVNSUpIqVaqkxMREd4O7bNkyxcbGen1q91LZ983gwYO97puSJUvq1KlT7vvG\n36/BOWVbvHhxlS5d2ms0J/tNxsXzyZmZmerfv7/Kly+vyMhI92P6H//4h6Sr/xslXbiPqlev7rWb\nPSQkRFWrVvXYKHOl2xMTE+M1U+00zAg6XPny5dWxY0d17NhRjRo10urVq/Xf//5XDRs2dA8/T5s2\nTaVLl87x9y/98MLF76ByM2vWLD388MO69dZb9fbbb6tcuXIKDw/XH3/8oZYtW/o0kHw5nTp10qxZ\nszRjxgw9/vjjmjZtmmzbVufOnT3W++c//6lu3bpp/vz5WrlypcaPH6/hw4drwIABevXVV6/6+i/W\nrVs33XXXXerRo4fCwsLUoUOHy657pSb6clu5AiEv9/OfYdu2LMvSF198cdnDQ2Q3mTExMfrvf/+r\nlStXavHixVqxYoWefvppDR48WAsWLNBtt90m6c/f51c6TIV9mU81Xq2YmBi1atVKc+bM0cmTJxUV\nFaVp06apVq1aOR6W6GKZmZlq3LixsrKy9PTTTysxMVFFixaVy+XSK6+84jUXdiVRUVFXbGyu5rpy\newz17t1bS5Ys0YQJE7wOaZWd84gRI1SnTp0cf79MmTIep3253/bs2eP1x7ZLly6aOHGipAtbz8aO\nHasVK1ZozZo17q2EWVlZeuaZZ/TVV19p2bJlCgkJUXJy8hVvX17q8qdChQqpUaNGHo1g9uxpSkqK\nPvvsM9m2rS+//FJ33nlnrpeXXXP//v093ihcLLvpkvz7Gny5bH3N/JFHHtH8+fPVs2dPNW7cWLGx\nsQoJCdH8+fM1cuTIP/U36mpcrm4Tj5M/g0awALnlllu0evVq7du3T9L/tlzExsb6/O42L6ZNm6aI\niAgtX75c4eHh7uVbtmz505fdqlUrxcXFadq0ae5GsGbNmkpKSvJat2LFiurbt6/69u2r33//XS1a\ntNDrr7+u/v37u4d+/4zmzZvr+uuv15IlS/Too49ecStITEyMJOX4qeldu3a5d6VfydUeS+7HH3/U\nrbfe6rWsUKFCSkhIyPX3s7fk/vDDD15vEH788UdJ/3tHm72l7JtvvvHY1XWpatWqaeHChSpXrlyO\nW0Mu5XK5lJyc7P4jvHHjRt188816+eWXNW/ePPd6/r7PK1SoICnnx3Jedyd17txZc+bM0YwZM1St\nWjXt3LlTr732Wq6/t3TpUh04cECTJk3yegM0cODAPNVg+rqGDx+u8ePH67nnnstxC3r2a1NkZGS+\nvjaVLl3aa9zl4oaySZMmsixLS5cu1dq1a93XXbt2bcXFxWnp0qVavny56tWrd8XneV5lP5+yt7Zd\nLPu5dbFKlSpp4cKFOn78uNdWwR9//FHFihXzeJynpqZqwYIFmjlzpvbv3+/eXdy0aVONGjVKn376\nqY4fP+5T1tn3jcvl8vm+ye35GIgDMR87dkzz5s1T586d9d5773mcd+nYgZT3191KlSppy5YtOnfu\nnEeD98cff+inn37KcetfQcWuYYdZvHhxjoe5yMrK0qJFi2RZlnsLy4MPPqiwsDANHjxYp0+f9vqd\n48eP68yZM1ddS/aD/+J6bNvWyy+/fNWXma1QoUJ65JFHtHLlSk2fPl3bt2/3+gN14sQJ927wbGFh\nYe6G4+LN/lu2bHHvnskry7L07rvvasiQIXruueeuuG72i+jFM2GS9NFHH+nAgQM+XV+RIkWuePid\ny71gXfwJcEnasGGDlixZoqZNm/q0BbBt27ayLEvDhw/32HqZ3SBUqFDBvSv4gQceUGhoqF588UX3\n7vucdOzYUdKFZiKnd98XH/cyp90j1atXV3h4uPu+zMt9/mfUr19fpUuX1uTJkz12i2ZmZupf//pX\nni6rdevWiouL09SpUzV16lS5XC499thjuf5e9vPr0twWLVp01fO3Jq5r9uzZ+vvf/6777rvPfRDr\nS7Vo0ULx8fF69dVXc7zPsrKyLntYlSsJCwtTamqqx8/Fb0Di4uKUmJioefPmad26de5Gx7IspaSk\naObMmfrxxx/z/Y1zyZIlddttt2nu3Lkeh7s5c+aMRo4c6bV+u3btdP78ea8tap9//rm+/fZbtW3b\n1mN5dr1DhgxReHi4br/9dklS48aNFRISoiFDhnisdyV169bVjTfeqH/961857t78448/8vx8zP70\nrMldoCEhIbIsy+sxfeDAAY0fP97rdTSvNbZr106//vqr+3A22caNG6fDhw/7dFSPgoItgg7z9NNP\n68iRI2rbtq1uvPFGRUZG6ueff9b06dO1bds2de7c2T3jVbZsWY0ZM0bdu3dXzZo11bFjR5UvX16/\n/vqrNm7cqLlz52rz5s1eg/O+at++vWbNmqXU1FR17NhRZ8+e1Zw5c5SVlZUvt7Vz5856++239eST\nTyokJMTrj+eyZcv0xBNP6IEHHlC1atVUpEgRrV+/XhMmTNBtt93mMZNUq1YtJSQk5PjC5ou7775b\nd999d67rVa9eXXfeeafGjh0r27Z100036dtvv9WcOXNUpUoVrxdNyXu3QIMGDTR//nz17dtXDRo0\nUEhIiJo2baoSJUrkuH62PXv2qEWLFrr77rvdh4+JioryOnTJ5VSrVk3PPvusXn/9dTVu3FgPPvig\nMjIy9P777+vUqVP66KOP3C+eZcuW1VtvvaU+ffooMTFRnTp1Uvny5bVv3z599tlnmjhxom666SYl\nJSVpyJAhGjJkiOrUqaP27durdOnSOnDggNavX6/PP//cfVy37t27a9++fWrevLnKly+vrKwsffzx\nxzp58qR7ni4v9/mfERISohEjRujRRx/VLbfcoscff1whISGaPHmyYmNjtXv3bp+3IBQqVEgdOnTQ\n6NGjtX79ejVr1uyyoxoXa9SokUqVKqVnnnlGu3fvdh/C44MPPlBiYmKOxye8WldzXTk9Dn/77Tc9\n9thjioyMVIsWLfTBBx94nF+qVCndeeedioyM1NSpU3XvvfeqevXq6tatmypXrqxjx45py5Ytmj17\ntubMmaPGjRtf8fquRmpqqt566y1ZluXRGKWmprqPG+iPPShvvvmmmjRpottvv119+vRxHz4mpzf2\nXbp00ZQpU/Taa69p9+7datSokbZv36733ntPpUqV0iuvvOKxfp06dVS8eHFt3rxZKSkp7lnK6Oho\nJSUl6T//+Y/KlCmT48xrTqZNm6bU1FTVrl1b3bp1U61atXTq1Clt375ds2fP1quvvqpOnTr5/Hy8\n4YYbVLRoUb333nuKjIxUsWLFVLJkyav+bm1fHgtFixZV8+bN9cEHHygiIkJJSUlKT0/X+++/r0qV\nKnnNMTZo0EDShUNoPfLIIwoPD1diYmKOM9PShQ/VzZw5U3369NGGDRtUp04dffPNN5o4caJq1Kjh\n9eG9P3t7AsroZ5SRq0WLFtl9+vSxb7rpJjsuLs4uVKiQHRcXZ6emptqTJk3K8XdWr15tt2vXzo6P\nj7dDQ0PtMmXK2Kmpqfabb77pcfiXChUqeB2+Itvy5cttl8vl9fH/cePG2bVq1bLDw8Pt0qVL2z17\n9rSPHDly2UMt+HL4mIslJibaLpfLbt68udd5u3btsnv16mXXrFnTjo6OtqOiouxatWrZgwcPtk+c\nOOF13Zc7JMulunTpYrtcLvu333674nozZ87MMZNffvnFbt++vR0dHW0XKVLEbtWqlb1lyxa7SZMm\nXjXktOzUqVP2448/bpcsWdIOCQmxXS6X+7AF2bVdrHPnzrbL5bIPHz5sd+zY0Y6NjbUjIyPtpk2b\n2hs2bPBYN6dDNVxq3Lhxdt26de3w8HA7Ojrabt68ub1q1aoc1120aJHdrFkzu1ixYnZ4eLhduXJl\n+4knnvDKbv78+XaLFi3smJgYOywszC5fvrzdqlUre+zYse51Zs2aZbdt29a+/vrr7bCwMLtEiRJ2\nkyZN7FmzZnnU78t9fqVDUuR024cMGWK7XC6vQ0fMnDnTrl27trvmwYMHuw+hMXPmzMtmeKnsw+i4\nXC57+vTpOa6T0/Pv+++/t1u2bGkXL17cLlq0qJ2SkmKvWrUqx8fB5VSoUMFOTEzMdb28XFdOj1vb\n/l/GLpfLtizL6+fS2/fDDz/Yjz32mF22bFk7NDTULlmypH377bfbL7/8svtQM75c35Uez5f697//\nbVuWZVepUsVj+bZt22zLsuywsDA7KyvL6/fy8po2adIkj+dtthUrVtgNGza0w8PD7VKlStl9+/a1\nf/jhhxxvw8mTJ+3nn3/erlSpkjubTp06eRxO5WL333+/7XK57Jdfftlj+aBBg2yXy2U/9thjlw8l\nB+np6XaLiutTAAAgAElEQVSvXr3sChUq2KGhoXZsbKydlJRkDxw40H04rby8Bi9YsMCuV6+e+/Av\n2Y+FvD5XL/dYyCnzw4cP2927d7fLlCljh4eH27Vr17bHjx9vT548Ocf75/XXX7crVapkFy5c2Ha5\nXO7rv9z9+euvv9q9e/e2r7/+ertw4cJ2uXLl7L59+3q9/l3u9690e5zEsm2nt6pAcOvSpYumTp1q\nfPA5WL3xxht69tln9dVXX+mWW24JdDkA4FfMCAIFQCCGsa91Z8+e9dptl5mZqXfffVdxcXHub6EA\ngGsZM4JAAcCG+/y3Y8cO3XXXXerQoYMqVKigAwcOaMqUKUpPT9eYMWNyPRg0AFwLeKUDHC6n76jF\nnxcfH68GDRroww8/1KFDh1SoUCHVrl1br7/+uh544IFAlwcARjAjmIs6derou+++C3QZAAAAuco+\nmoWvmBHMxXfffSfbtvkx+DN48OCA1xBsP2RO5sHwQ+ZkHgw/ed14RSMIx7n4S8VhBpmbR+bmkbl5\nZO58NIIAAABBikYQjpP9heowh8zNI3PzyNw8Mnc+PiySC8uyREQAAKAgyGvfwhZBOE5aWlqgSwg6\nZG4emZtH5uaRufPRCAIAAAQpdg3ngl3DAACgoGDXMAAAAHxCIwjHYabEPDI3j8zNI3PzyNz5aAQB\nAACCFDOCuWBGEAAAFBTMCAIAAMAnNIJwHGZKzCNz88jcPDI3j8ydj0YQAAAgSDEjmAtmBAEAQEHB\njCAAAAB8QiMIx2GmxDwyN4/MzSNz88jc+WgEAQAAghQzgrlgRhAAABQUzAgCAADAJzSCcBxmSswj\nc/PI3DwyN4/MnY9GEAAAIEgxI5gLZgQBAEBBwYwgAAAAfEIjCMdhpsQ8MjePzM0jc/PI3PloBAEA\nAIIUM4K5YEYQAAAUFMwIAgAAwCc0gnAcZkrMI3PzyNw8MjePzJ2PRhAAACBIMSOYC2YEAQBAQcGM\nIAAAAHxCIwjHYabEPDI3j8zNI3PzyNz5aAQBAACCFDOCuWBGEAAAFBTMCAIAAMAnNIJwHGZKzCNz\n88jcPDI3j8ydj0YQAAAgSDEjmAtmBAEAQEHBjCAAAAB8QiMIx2GmxDwyN4/MzSNz88jc+WgEAQAA\nghQzgrlgRhAAABQUzAgCAADAJzSCcBxmSswjc/PI3DwyN4/MnY9GEAAAIEgxI5gLZgQBAEBBwYwg\nAAAAfEIjCMdhpsQ8MjePzM0jc/PI3PloBAEAAIIUM4K5YEYQAAAUFMwIAgAAwCc0gnAcZkrMI3Pz\nyNw8MjePzJ2PRhAAACBIMSOYC2YEAQBAQcGMIAAAAHxCIwjHYabEPDI3j8zNI3PzyNz5aAQBAACC\nFDOCuWBGEAAAFBTMCAIAAMAnNIJwHGZKzCNz88jcPDI3j8ydj0YQAAAgSDEjmAtmBAEAQEHBjCAA\nAAB8QiMIx2GmxDwyN4/MzSNz88jc+WgEAQAAghQzgrlgRhAAABQUzAgCAADAJzSCcBxmSswjc/PI\n3DwyN4/MnY9GEAAAIEgxI5gLZgQBAEBBwYwgAAAAfEIjCMdhpsQ8MjePzM0jc/PI3PloBAEAAIIU\nM4K5sCxLA18bGOgyAADIF/HR8erXq1+gy4Cf5HVGsJAfa7lmJDRNCHQJAADki/Sl6YEuAQ7CrmE4\nztZ1WwNdQtAhc/PI3DwyN48ZQeejEQQAAAhSNIJwnOpJ1QNdQtAhc/PI3DwyN69JkyaBLgG5oBEE\nAAAIUjSCcBzmeMwjc/PI3DwyN48ZQeejEQQAAAhSNIJwHOZ4zCNz88jcPDI3jxlB56MRBAAACFI0\ngnAc5njMI3PzyNw8MjePGUHnoxEEAAAIUjSCcBzmeMwjc/PI3DwyN48ZQeejEQQAAAhSNIJwHOZ4\nzCNz88jcPDI3jxlB56MRBAAACFI0gnAc5njMI3PzyNw8MjePGUHnoxEEAAAIUjSCcBzmeMwjc/PI\n3DwyN48ZQeejEQQAAAhSNIJwHOZ4zCNz88jcPDI3jxlB5wvaRnDBggVq3LixihYtqmLFiql+/fpa\nvnx5oMsCAAAwJigbwbFjx+ree+9V/fr1NWfOHM2cOVMPPvigsrKyAl0axBxPIJC5eWRuHpmbx4yg\n8xUKdAGm7d69W3/96181YsQI/eUvf3Evb968eQCrAgAAMC/otghOnDhRhQoVUq9evQJdCi6DOR7z\nyNw8MjePzM1jRtD5gq4RXLVqlapXr67p06ercuXKKly4sKpWrar33nsv0KUBAAAYFXSN4P79+7Vt\n2zYNGDBAAwcO1OLFi9WsWTP17dtXb7/9dqDLg5jjCQQyN4/MzSNz85gRdL6gmxE8f/68MjIyNGXK\nFN17772SLmy63r17t4YNG+YxN5ht0uBJiisTJ0mKKBKhctXLuXcxZL+wcDr/Tv+89WdH1RMMp7M5\npR5Oc9ofp3/e+rOj6gnU6XCFS/pfk5a9+9Yfp7/99lu/Xj6n5f7/7t27dTUs27btq/rNAqpBgwb6\n+uuvdeLECUVFRbmXjxw5Us8884wOHDigkiVLupdblqWx68YGolQAAPJd+tJ0DR0wNNBlwE8sy1Je\nWrug2zV8ww035CkgAACAa1XQNYL33XefJOmLL77wWP7FF1+oXLlyHlsDERjM8ZhH5uaRuXlkbh4z\ngs4XdDOCrVq1UkpKinr27KnDhw+rYsWKmjlzphYvXqzJkycHujwAAABjgm5GUJIyMjL0/PPP65NP\nPtHRo0dVs2ZN/f3vf9fDDz/stS4zggCAawkzgte2vM4IBt0WQUkqWrSoRo8erdGjRwe6FAAAgIAJ\nuhlBOB9zPOaRuXlkbh6Zm8eMoPPRCAIAAAQpGkE4Dt8Hah6Zm0fm5pG5eXzXsPPRCAIAAAQpGkE4\nDnM85pG5eWRuHpmbx4yg89EIAgAABCkaQTgOczzmkbl5ZG4emZvHjKDz0QgCAAAEKRpBOA5zPOaR\nuXlkbh6Zm8eMoPPRCAIAAAQpGkE4DnM85pG5eWRuHpmbx4yg89EIAgAABCkaQTgOczzmkbl5ZG4e\nmZvHjKDz0QgCAAAEKRpBOA5zPOaRuXlkbh6Zm8eMoPPRCAIAAAQpGkE4DnM85pG5eWRuHpmbx4yg\n89EIAgAABCkaQTgOczzmkbl5ZG4emZvHjKDz0QgCAAAEKRpBOA5zPOaRuXlkbh6Zm8eMoPMVCnQB\nBUH60vRAlxBUDu44qPDj4YEuI6iQuXlkbh6ZXxAfHR/oEuAglm3bdqCLcDLLskREAACgIMhr38Ku\nYQAAgCBFIwjHYabEPDI3j8zNI3PzyNz5aAQBAACCFDOCuWBGEAAAFBTMCAIAAMAnNIJwHGZKzCNz\n88jcPDI3j8ydj0YQAAAgSDEjmAtmBAEAQEHBjCAAAAB8QiMIx2GmxDwyN4/MzSNz88jc+WgEAQAA\nghQzgrlgRhAAABQUee1bCvmxlmvGoNcHBboEAADyRXx0vPr16hfoMuAQNII+SGiaEOgSgsrWdVtV\nPal6oMsIKmRuHpmbR+YXpC9NN3ZdaWlpatKkibHrQ94xIwgAABCkaAThOLxjN4/MzSNz88jcPLYG\nOh+NIAAAQJCiEYTjbF23NdAlBB0yN4/MzSNz8ziOoPPRCAIAAAQpnxrBc+fO6dy5c+7TBw4c0Pjx\n47V69Wq/FYbgxRyPeWRuHpmbR+bmMSPofD41gq1bt9bo0aMlSZmZmapfv76effZZJScna8qUKX4t\nEAAAAP7hUyO4fv16paSkSJJmzZqlokWL6tChQxo/frzeeOMNvxaI4MMcj3lkbh6Zm0fm5jEj6Hw+\nNYKZmZkqXry4JGnRokVq166dChcurJSUFG3fvt2vBQIAAMA/fGoEy5Urp1WrVikzM1MLFy5Us2bN\nJElHjhxRZGSkXwtE8GGOxzwyN4/MzSNz85gRdD6fvmLumWeeUadOnRQVFaWEhAQ1btxYkrRixQrV\nrl3brwUCAADAP3zaItizZ0+tXbtWEydO1OrVqxUSEiJJqly5sv75z3/6tUAEH+Z4zCNz88jcPDI3\njxlB5/Npi6AkJSUlKSkpyWNZmzZt8r0gAAAAmOHTFkHbtvXuu+/qhhtuUEREhHbu3ClJevXVVzVj\nxgy/FojgwxyPeWRuHpmbR+bmMSPofD41gqNGjdLLL7+sHj16eCwvU6aM+/iCAAAAKFh8agTHjBmj\ncePG6a9//asKFfrf3uR69erphx9+8FtxCE7M8ZhH5uaRuXlkbh4zgs7nUyO4Z88eJSYmei0vXLiw\nsrKy8r0oAAAA+J9PjWDFihW1fv16r+Wff/65atWqle9FIbgxx2MemZtH5uaRuXnMCDqfT43gs88+\nq759++rDDz/U+fPntWbNGg0ZMkQDBw7Us88+6+8a/aply5ZyuVz6v//7v0CXAgAAYJRPjWDXrl31\n4osv6vnnn1dWVpY6deqk8ePH65133tHDDz/s7xr95qOPPtL3338vSbIsK8DVIBtzPOaRuXlkbh6Z\nm8eMoPP51AhKUo8ePbRnzx4dPHhQBw4c0N69e/X444/7sza/Onr0qP72t79p5MiRgS4FAAAgIHxq\nBM+dO6dz585JkkqUKKHz589r/PjxWr16tV+L86fnnntOiYmJeuihhwJdCi7BHI95ZG4emZtH5uYx\nI+h8Pn2zSOvWrXXXXXepX79+yszMVP369XXy5EllZGRowoQJ6ty5s7/rzFerVq3StGnT3LuFAQAA\ngpFPWwTXr1+vlJQUSdKsWbNUtGhRHTp0SOPHj9cbb7zh1wLz25kzZ9SzZ089++yzqlq1aqDLQQ6Y\n4zGPzM0jc/PI3DxmBJ3Pp0YwMzNTxYsXlyQtWrRI7dq1U+HChZWSkqLt27f7tcD89vrrr+v333/X\noEGDAl0KAABAQPm0a7hcuXJatWqV7r77bi1cuND9/cJHjhxRZGSkXwvMT3v27NHQoUM1YcIEZWVl\neRwM+/Tp0zp+/LiKFi0ql8uzP540eJLiysRJkiKKRKhc9XLuWZPsd5iczt/T2ZxSD6c5nd+nqydV\nd1Q9wXA6e5lT6gnU6XCFS/rf1rrsOT5/nc5m6vqC7XT2/3fv3q2rYdm2bee20tixY9W3b19FRUUp\nISFBGzZsUEhIiEaNGqW5c+dq2bJlV3XlpqWlpSk1NfWK63z77beqXbu2+7RlWRq7bqy/SwMAwIj0\npekaOmBooMuAn1iWJR9aOzefdg337NlTa9eu1cSJE7V69WqFhIRIkipXrqx//vOfV1dpANStW1dp\naWkeP8uXL5ckdezYUWlpaapcuXKAqwRzPOaRuXlkbh6Zm8eMoPP5tGtYkpKSkpSUlOQ+ffbsWbVp\n08YvRflLsWLF1Lhx4xzPS0hIuOx5AAAA1yKftgiOGjVKn376qft0t27dFB4ermrVqmnrVt5hIX9x\nrC/zyNw8MjePzM3jOILO51Mj+Pbbbysu7sKHJVasWKGZM2dq+vTpqlu3rp555hm/FmjC+fPn9dJL\nLwW6DAAAAKN8agT379+vSpUqSZL+/e9/64EHHtBDDz2kIUOGaO3atX4tEMGHOR7zyNw8MjePzM1j\nRtD5fGoEo6OjdfDgQUnS4sWL1bRpU0lSoUKFdPr0af9VBwAAAL/x6cMizZs3V48ePVSvXj1t375d\nd911lyTpxx9/VMWKFf1aIIIPczzmkbl5ZG4emZvHjKDz+bRFcPTo0brjjjt0+PBhffLJJ4qNjZV0\n4avnHnnkEb8WCAAAAP/waYtgsWLF9M4773gt5wMW8IeLj/wPM8jcPDI3j8zNS0tLY6ugw/m0RVCS\nfvnlFw0fPlxPPvmkDh8+LElatWqVdu3a5bfiAAAA4D8+NYLr169X9erVNX36dI0fP14nTpyQdOGD\nI4MGDfJrgQg+vGM3j8zNI3PzyNw8tgY6n0+N4DPPPKN+/frpm2++UXh4uHt5y5YttWrVKr8VBwAA\nAP/xqRHcsGGDunTp4rW8VKlS7sPKAPmFY32ZR+bmkbl5ZG4exxF0Pp8awYiICB05csRr+datWxUf\nH5/vRQEAAMD/fGoE77nnHr344oseB4/etWuXBgwYoPvvv99vxSE4McdjHpmbR+bmkbl5zAg6n0+N\n4PDhw3X06FGVKFFCp06d0h133KEqVarouuuu08svv+zvGgEAAOAHPjWCxYoV08qVKzV37ly9+uqr\n6tevnxYuXKgVK1aoSJEi/q4RQYY5HvPI3DwyN4/MzWNG0Pl8OqC0JFmWpdTUVKWmpvqzHgAAABji\n0xbBLl26aOTIkV7L33zzTXXv3j3fi0JwY47HPDI3j8zNI3PzmBF0Pp8awS+++EIpKSley1NTUzV/\n/vx8LwoAAAD+51MjeOzYsRxnASMjI3M8rAzwZzDHYx6Zm0fm5pG5ecwIOp9PjWDVqlU1b948r+UL\nFixQlSpV8r0oAAAA+J9PHxbp37+/evXqpUOHDqlp06aSpCVLluitt97Su+++69cCEXyY4zGPzM0j\nc/PI3DxmBJ3Pp0awc+fOOn36tP75z3/q1VdflSSVLVtWI0eOVLdu3fxaIAAAAPzDp13DktSzZ0/t\n3btXv/zyi3755Rf9/PPP6tWrlz9rQ5Bijsc8MjePzM0jc/OYEXQ+n48jKEk7d+7Ujz/+KMuyVLNm\nTVWqVMlfdQEAAMDPLNu27dxWOnHihLp166ZZs2bJ5bqwEfH8+fO6//77NXHiRBUtWtTvhQaKZVka\n+NrAQJcBAEC+iI+OV79e/QJdBvzEsiz50Nr9b31fGsGuXbtqzZo1ev/999WgQQNJ0po1a9SzZ0/d\nfvvtmjhx4tVX7HB5DRQAACBQ8tq3+DQj+Nlnn2ncuHFKTk5WaGioQkND1aRJE40bN05z5sy56mKB\nnDBTYh6Zm0fm5pG5eWTufD41gllZWYqNjfVaHhMTo9OnT+d7UQAAAPA/n3YN33nnnYqOjta0adMU\nFRUlScrMzFSnTp104sQJLVmyxO+FBgq7hgEAQEHhlxnBjRs3qkWLFjp16pRuuukm2batjRs3KjIy\nUgsXLtSNN974p4p2MhpBAABQUPhlRjAxMVHbtm3T8OHDdfPNNyspKUnDhw/X9u3br+kmEIHBTIl5\nZG4emZtH5uaRufPlehzBM2fOqHz58lq6dKl69OhhoiYAAAAY4NOu4euvv16LFi1SrVq1TNTkKOwa\nBgAABYVfdg0/9dRTGjZsmM6ePXvVhQEAAMBZfGoEV61apblz5+r6669X06ZNdffdd7t/2rZt6+8a\nEWSYKTGPzM0jc/PI3Dwydz6fvms4NjZW9913X47nWZaVrwUBAADADJ9mBIMZM4IAAKCgyGvf4tMW\nwWw7duzQ5s2bJUk1a9ZU5cqV81ZdATXo9UGBLgEAgHwTHx2vfr36BboMOIBPjeBvv/2mbt266d//\n/rdcrgtjhefPn1ebNm00adKkHL9+7lqS0DQh0CUEla3rtqp6UvVAlxFUyNw8MjePzP8nfWm6ketJ\nS0tTkyZNjFwXro5PHxbp3r27duzYoZUrVyorK0tZWVlauXKldu3ape7du/u7RgAAAPiBTzOCkZGR\nWrJkiRo2bOixfO3atWratKlOnTrltwIDzbIsjV03NtBlAACQb9KXpmvogKGBLgN+4JfjCMbFxSkq\nKspreWRkpOLi4nyvDgAAAI7hUyP4wgsv6Omnn9bevXvdy/bu3au//e1veuGFF/xWHILT1nVbA11C\n0CFz88jcPDI3j+MIOp9PHxYZNWqUdu/erQoVKqhs2bKSpH379ikiIkKHDh3SqFGjJF3YHPn999/7\nr1oAAADkG58awfvvv9+nC+Pg0sgPfKrPPDI3j8zNI3Pz+MSw8/nUCA4ZMsTPZQAAAMA0n2YEAZOY\n4zGPzM0jc/PI3DxmBJ2PRhAAACBI0QjCcZjjMY/MzSNz88jcPGYEnY9GEAAAIEhdthEMCQnRoUOH\nJEndunXTiRMnjBWF4MYcj3lkbh6Zm0fm5jEj6HyXbQQjIiKUkZEhSZo8ebJOnz5trCgAAAD432UP\nH9OwYUO1a9dO9erVkyT169dPERERHuvYti3LsjRx4kT/VomgwhyPeWRuHpmbR+bmMSPofJdtBKdO\nnaoRI0Zo+/btkqTffvtNoaGhHgeNzm4EAQAAUPBcthEsVaqURowYIUmqUKGCpk+frri4OGOFIXht\nXbeVd+6Gkbl5ZG4emZuXlpbGVkGH8+mbRXbv3u3nMgAAAGCaz4ePmTdvnho1aqTY2FjFxcUpOTlZ\n8+fP92dtCFK8YzePzM0jc/PI3Dy2BjqfT43g+PHjdd9996lKlSp67bXX9Oqrr6pixYpq166dJkyY\n4O8aAQAA4Ac+NYKvvfaa3nzzTU2aNEndu3dX9+7dNXnyZL3xxht67bXX/F1jvlq4cKFSU1NVunRp\nhYeHq1y5cnrooYe0efPmQJeG/x/H+jKPzM0jc/PI3DyOI+h8PjWCe/bsUcuWLb2Wt2zZssDNDx49\nelT169fXu+++q8WLF2vYsGHatGmTbrvtNv3888+BLg8AAMAYnz4sUq5cOS1atEhVqlTxWL548WIl\nJCT4pTB/efjhh/Xwww+7Tzdq1Ei33HKLatSooU8++URPP/10AKuDxBxPIJC5eWRuHpmbx4yg8/nU\nCD777LN66qmntGHDBt1+++2SpFWrVmnatGl65513/FqgCTExMZIufK0eAABAsPBp13DPnj318ccf\na/Pmzerfv7/69++vrVu3aubMmerZs6e/a/SLc+fO6cyZM9q2bZt69uypkiVLemwpROAwx2MemZtH\n5uaRuXnMCDqfT1sEJaldu3Zq166dP2sx6tZbb9WGDRskSQkJCVq6dKni4+MDXBUAAIA5lm3bdqCL\nCIQtW7YoIyNDO3bs0IgRI3Tw4EGtWrXKa+bRsiyNXTc2QFUCAJD/0pema+iAoYEuA35gWZby0toF\nbSN4sePHj6tChQp6+OGHNWbMGI/zLMvSba1vU1yZC1+vF1EkQuWql3MPHWfvauA0pznNaU5zuqCc\nTl+arma3NJP0vw90ZO/G5XTBOp39/+yjuEyZMoVG8GokJSUpJiZGixYt8ljOFkHz+D5Q88jcPDI3\nj8z/x9QWQb5r2Ly8bhH0+SvmrmUHDx7Uli1bVLly5UCXAgAAYEyuHxY5c+aMGjVqpKlTp6p69YL/\nTqpdu3a6+eablZiYqOjoaP30008aOXKkQkND9cwzzwS6PIhjfQUCmZtH5uaRuXlsDXS+XBvB0NBQ\n7dq1S5ZlmajH7xo0aKAZM2bojTfe0JkzZ1SuXDmlpKTo+eefV/ny5QNdHgAAgDE+7Rru1KmTxo0b\n5+9ajBgwYIDWrVuno0eP6uTJk9qyZYvGjBlDE+ggHOvLPDI3j8zNI3PzOI6g8/l0HMFTp07pgw8+\n0OLFi3XzzTcrKipKkmTbtizL0ttvv+3XIgEAAJD/fGoEf/zxR9WrV0+StGPHDvdu4uxGEMhPzPGY\nR+bmkbl5ZG4eM4LO51MjyKZdAACAa0+eDh9z+PBh/ec//9Hp06f9VQ/AHE8AkLl5ZG4emZvHhiTn\n86kRzMjIUPv27RUfH6+GDRtq//79kqRevXppyJAh/qwPAAAAfuJTI/jcc89p37592rBhgyIiItzL\n27Rpo1mzZvmtOAQn5njMI3PzyNw8MjePGUHn82lG8LPPPtOsWbNUp04djw+H1KhRQzt37vRbcQAA\nAPAfn7YIHj16VLGxsV7LMzIyFBISku9FIbgxx2MemZtH5uaRuXnMCDqfT41gUlKSPvvsM6/l77//\nvho2bJjvRQEAAMD/fNo1PGzYMLVo0UKbNm3S2bNnNXLkSP3www/6+uuvtWLFCn/XiCDDHI95ZG4e\nmZtH5uYxI+h8Pm0RbNiwodasWaMzZ86ocuXKWrp0qcqWLauvvvpKN998s79rBAAAgB/4fBzBxMRE\nTZ06VZs2bdKPP/6oDz74QImJif6sDUGKOR7zyNw8MjePzM1jRtD5fNo1LElZWVmaPn26Nm/eLEmq\nWbOmHnnkEY/DyQAAAKDgsGzbtnNbacOGDWrTpo2ysrKUmJgo27a1adMmhYWFad68edf07mHLsjR2\n3dhAlwEAQL5JX5quoQOGBroM+IFlWfKhtXPzadfwE088oTvuuEN79+7VihUrtHLlSv38889q3Lix\nevbsedXFAgAAIHB8agQ3bdqkwYMHKyoqyr0sKipKL7zwgn744Qe/FYfgxByPeWRuHpmbR+bmMSPo\nfD41gtWrV3d/v/DFDhw4oOrV+Tg+AABAQXTZD4scOXLE/f+hQ4fqL3/5i1544QU1aNBAkrR27VoN\nHTpUr776qv+rRFDhWF/mkbl5ZG4emZvHcQSd77KNYFxcnNeyRx991GvZPffco3PnzuVvVQAAAPC7\nyzaCy5YtM1kH4LZ13VbeuRtG5uaRuXlkbl5aWhpbBR3uso0gdxwAAMC1zafjCErS77//rk2bNunQ\noUM6f/68x3mtWrXyS3FOYFmWBr42MNBlAACQb+Kj49WvV79AlwE/yOtxBH1qBJctW6ZHH31UBw8e\nzPH8SxvDa0leAwUAAAgUvxxQ+sknn1Tr1q21a9cunTx5UqdOnfL4AfITx50yj8zNI3PzyNw8Mnc+\nn75reP/+/Ro4cKASEhL8XQ8AAAAM8WnX8IMPPqi2bdvqscceM1GTo7BrGAAAFBR+mRE8evSoOnTo\noBo1aigxMVGFCxf2OL9Tp055r7SAoBEEAAAFhV8awRkzZqhLly46ffq0IiMjZVmWx/kZGRl5r7SA\noBE0j+NOmUfm5pG5eWRuHpmb55cPi/Tv31+9e/dWRkaGMjMzlZGR4fEDAACAgsenLYLR0dH65ptv\nVLlyZRM1OQpbBAEAQEHhly2C9913nxYvXnzVRQEAAMB5fDp8TOXKlTVo0CCtXLlStWvX9vqwyN/+\n9je/FIfgxEyJeWRuHpmbR+bmkbnz+dQITpgwQUWLFtXq1au1Zs0ar/NpBAEAAAoen79rOFgxIwgA\nAItophEAACAASURBVAoKv8wIAgAA4Nrj067hp556yuvYgRd7++23860gJxr0+qBAlxBU0nekK6Ey\nX2doEpmbR+bmBXPm8dHx6tern/HrZUbQ+XxqBDdu3OjRCJ45c0ZbtmzRuXPnVLduXb8V5xQJTYPz\nhSNQThc7rYQkMjeJzM0jc/OCOfP0pemBLgEO5VMjmJaW5rXs9OnT6tatmxo3bpzfNSHIVU+qHugS\ngg6Zm0fm5pG5eWwNdL6rnhEMDw/XoEGDNHTo0PysBwAAAIb8qQ+LHD58mK+YQ77bum5roEsIOmRu\nHpmbR+bm5bRHEc7i067hN954w2NG0LZt7d+/Xx9++KFatWrlt+IAAADgPz4dR7BChQoejaDL5VKJ\nEiWUmpqq559/XkWLFvVrkYFkWZbGrhsb6DIAALhq6UvTNXQAo1zBIK/HEfRpi+Du3buvth4AAAA4\nFAeUhuMwx2MemZtH5uaRuXnMCDqfT1sEbdvWxx9/rKVLl+rQoUM6f/68+zzLsvTZZ5/5rUAAAAD4\nh0+N4IABA/TWW28pJSVFpUuX9pgXvNI3jgBXg2N9mUfm5pG5eWRuHscRdD6fGsGpU6dq+vTpat++\nvb/rAQAAgCE+zQieP38+KL5KDs7AHI95ZG4emZtH5uYxI+h8PjWCPXr00AcffODvWgAAAGCQT7uG\njx8/rg8//FCLFy9W7dq1VbhwYUkXPkRiWZbefvttvxaJ4MIcj3lkbh6Zm0fm5jEj6Hw+NYKbNm1S\nnTp1JElbtmxxL89uBAEAAFDw+NQIso8fJm1dt5V37oaRuXlkbh6Zm5eWlsZWQYfjgNIAAABBikYQ\njsM7dvPI3DwyN4/MzWNroPPRCAIAAAQpGkE4Dsf6Mo/MzSNz88jcPD5j4HxB1wh+8sknuvfee1W+\nfHlFRkaqRo0aGjhwoDIzMwNdGgAAgFGWbdt2oIswqUGDBrr++uvVrl07XX/99frmm280ZMgQ1ahR\nQ2vWrPE6HI5lWRq7bmyAqgUA4M9LX5quoQOGBroMGGBZlvLS2vl0+Jhrybx58xQbG+s+3bhxY8XE\nxKhz585KS0tTSkpKAKsDAAAwJ+h2DV/cBGZLSkqSJO3fv990OcgBczzmkbl5ZG4emZvHjKDzBV0j\nmJMvv/xSklSzZs0AVwIAAGBO0M0IXmrfvn2qW7eu6tatq4ULF3qdz4wgAKCgY0YweDAjmAeZmZm6\n5557FBoaqkmTJl12vUmDJymuTJwkKaJIhMpVL+c+MGn2rgZOc5rTnOY0p518Ons3bfZBnjl9bZzO\n/v/u3bt1NYJ2i2BWVpZatWqljRs36ssvv9QNN9yQ43psETSP7wM1j8zNI3PzgjnzQG0R5LuGzWOL\noA/Onj2rBx54QBs2bNDixYsv2wQCAABcy4KuETx//rweffRRpaWlad68ebrlllsCXRIuEazv2AOJ\nzM0jc/PI3Dy2Bjpf0DWCffr00SeffKJBgwYpIiJCX331lfu8cuXKqWzZsgGsDgAAwJygO3zMF198\nIcuyNHToUDVs2NDjZ8KECYEuD+JYX4FA5uaRuXlkbh7HEXS+oNsiuGvXrkCXAAAA4AhBt0UQzscc\nj3lkbh6Zm0fm5jEj6Hw0ggAAAEGKRhCOwxyPeWRuHpmbR+bmMSPofDSCAAAAQYpGEI7DHI95ZG4e\nmZtH5uYxI+h8NIIAAABBikYQjsMcj3lkbh6Zm0fm5jEj6Hw0ggAAAEGKRhCOwxyPeWRuHpmbR+bm\nMSPofDSCAAAAQYpGEI7DHI95ZG4emZtH5uYxI+h8NIIAAABBikYQjsMcj3lkbh6Zm0fm5jEj6Hw0\nggAAAEGKRhCOwxyPeWRuHpmbR+bmMSPofDSCAAAAQYpGEI7DHI95ZG4emZtH5uYxI+h8NIIAAABB\nikYQjsMcj3lkbh6Zm0fm5jEj6Hw0ggAAAEGKRhCOwxyPeWRuHpmbR+bmMSPofIUCXUBBkL40PdAl\nAABw1eKj4wNdAhzKsm3bDnQRTmZZlojIrLS0NN5FGkbm5pG5eWRuHpmbl9e+hV3DAAAAQYotgrlg\niyAAACgo2CIIAAAAn9AIwnE47pR5ZG4emZtH5uaRufPRCAIAAAQpZgRzwYwgAAAoKJgRBAAAgE9o\nBOE4zJSYR+bmkbl5ZG4emTsfjSAAAECQYkYwF8wIAgCAgoIZQQAAAPiERhCOw0yJeWRuHpmbR+bm\nkbnzsWs4F5ZlaeBrAwNdRlBJ35GuhMoJgS4jqJC5eWRuHpmbR+a+iY+OV79e/fLlsvK6a5hGMBeW\nZWnsurGBLgMAAFyj0pema+iAoflyWcwIAgAAwCc0gnCcreu2BrqEoEPm5pG5eWRuHpk7H40gAABA\nkKIRhONUT6oe6BKCDpmbR+bmkbl5ZO58NIIAAABBikYQjsNMiXlkbh6Zm0fm5pG589EIAgAABCka\nQTgOMyXmkbl5ZG4emZtH5s5HIwgAABCkaAThOMyUmEfm5pG5eWRuHpk7H40gAABAkKIRhOMwU2Ie\nmZtH5uaRuXlk7nw0ggAAAEGKRhCOw0yJeWRuHpmbR+bmkbnz0QgCAAAEKRpBOA4zJeaRuXlkbh6Z\nm0fmzkcjCAAAEKRoBOE4zJSYR+bmkbl5ZG4emTvfNdUIdunSRRUrVszz76WlpcnlcmnFihV+qAoA\nAMCZCgW6gPz0wgsvKCMjI9Bl4E9ipsQ8MjePzM0jc/PI3PmuiUbw999////au/OgqK60DeDPbWUR\nW4QoIgK2gBJBlMXdqINGibtxjIxiEKLGZSqOZoxOTGZGSOI2cQkuKdeIpcbouGsUd4y44a7RKEqB\ngBNQ1Ki4IfB+f0x5P1tAICO3G/r5VVFyb5++5/TDEV+630bY2NjA09PT1EshIiIiqjA0fWk4KSkJ\n/fr1g7OzM6pVqwaDwYDQ0FDk5+cDAG7duoVRo0bBzc0Ntra28PHxwZIlS4yuERsbC51Oh0OHDmHA\ngAFwdHRE27ZtART90vDkyZMRFBSEmjVrwsnJCW+//TaOHz+uzQOm34U9Jdpj5tpj5tpj5tpj5uZP\n02cEe/bsiVq1amHhwoWoXbs2MjIysHPnTogI7t+/j/bt2+Pp06eIjo6Gh4cH4uLiMHr0aDx9+hQf\nffSR0bUGDx6MsLAwjB49Gnl5eep5RVGMxt24cQPjxo2DwWDAw4cPsXLlSnTs2BGnTp2Cn5+fJo+b\niIiIyBxpVghmZ2cjOTkZc+bMQa9evdTzgwYNAgDExMQgLS0NP//8M7y8vAAAnTt3xm+//Ybo6Gj8\n+c9/hk73/09gDhgwANOnTy80j4gYHS9dulT9PD8/HyEhIThz5gyWLl2Kb7755rU+Rno92FOiPWau\nPWauPWauPWZu/jR7abh27drw9PTE3/72NyxduhRXr141uj0uLg5t2rRBgwYNkJeXp36EhITg9u3b\nuHTpktH4fv36lWrevXv3olOnTqhduzasrKxgbW2NpKQkJCUlvbbHRkRERFQRafrS8J49exAVFYVJ\nkybh9u3b8PDwwIQJEzBq1CjcvHkTycnJsLKyKnQ/RVFw+/Zto3MuLi4lznf69Gn06NED3bt3x3ff\nfQcXFxfodDoMHz4cT548KfW6l09ejtr1agMAqumrwf1Nd/WnnOf9Dzx+fcfpV9LRZXAXs1mPJRw/\nP2cu67GE45ezN/V6LOF47+q9/P6t8TG/n5f+OD4+HgAQHBxcpuPnn6empuL3UOTl11I1cu7cOcyf\nPx/Lli3Djh07EB0djapVqyImJqbI8d7e3tDr9YiNjcXQoUNx7dq1Qu8SjoyMxMGDB5GSkgIA+Pzz\nzxETE4N79+6hSpUq6jiDwQAvLy/s378fwH8D7Ny5M+Lj49GxY0ejayqKgkUnF73Oh04luHLyivoX\ng7TBzLXHzLXHzLXHzEvn+r7rmDJxymu5lqIohdrkXsVkvz7G398fs2bNwrJly3Dx4kV069YN8+bN\ng7u7O5ycnF7LHI8ePTLqKwSA/fv3Iz09Xe1DJPPDbxraY+baY+baY+baY+bmT7NC8Pz58xg7diwG\nDhwILy8v5OfnIzY2FlZWVujcuTO8vLywdu1adOjQAR9//DG8vb3x8OFDXL58GQkJCdi8eXOZ5+ze\nvTtiYmIQGRmJyMhIJCUl4auvvoKrq2uZqmUiIiKiykizN4u4uLjAYDBg9uzZ6Nu3L8LCwpCZmYnt\n27cjMDAQ9vb2OHLkCHr06IEZM2agW7duGDZsGLZt24bOnTsbXevlXxHz4vkXbwsJCcHcuXNx+PBh\n9O7dG7GxsVi5ciUaNmxY6BrFXZO092LvFGmDmWuPmWuPmWuPmZs/k/UIVhTsEdQee0q0x8y1x8y1\nx8y1x8xLx5Q9gpr+zyJEpcFvGtpj5tpj5tpj5tpj5uaPhSARERGRhWIhSGaHPSXaY+baY+baY+ba\nY+bmj4UgERERkYViIUhmhz0l2mPm2mPm2mPm2mPm5o+FIBEREZGFYiFIZoc9Jdpj5tpj5tpj5tpj\n5uaPhSARERGRhWIhSGaHPSXaY+baY+baY+baY+bmj4UgERERkYViIUhmhz0l2mPm2mPm2mPm2mPm\n5o+FIBEREZGFYiFIZoc9Jdpj5tpj5tpj5tpj5uaPhSARERGRhWIhSGaHPSXaY+baY+baY+baY+bm\nj4UgERERkYViIUhmhz0l2mPm2mPm2mPm2mPm5o+FIBEREZGFYiFIZoc9Jdpj5tpj5tpj5tpj5uaP\nhSARERGRhWIhSGaHPSXaY+baY+baY+baY+bmj4UgERERkYWqauoFVATX91039RIsyvXk6zB4GUy9\nDIvCzLXHzLXHzLXHzEunjn0dk82tiIiYbPYKQFEUMCJtxcfHIzg42NTLsCjMXHvMXHvMXHvMXHtl\nrVtYCJaAhSARERFVFGWtW9gjSERERGShWAiS2YmPjzf1EiwOM9ceM9ceM9ceMzd/LASJiIiILBR7\nBEvAHkEiIiKqKNgjSERERESlwkKQzA57SrTHzLXHzLXHzLXHzM0fC0EiIiIiC8UewRKwR5CIiIgq\nCvYIEhEREVGpsBAks8OeEu0xc+0xc+0xc+0xc/PHQpCIiIjIQrFHsATsESQiIqKKgj2CRERERFQq\nLATJ7LCnRHvMXHvMXHvMXHvM3PyxECQiIiKyUOwRLAF7BImIiKiiYI8gEREREZUKC0EyO+wp0R4z\n1x4z1x4z1x4zN38sBImIiIgsFHsES8AeQSIiIqoo2CNIRERERKXCQpDMDntKtMfMtcfMtcfMtcfM\nzR8LQSIiIiILxR7BErBHkIiIiCoK9ggSERERUamwECSzw54S7TFz7TFz7TFz7TFz88dCkIiIiMhC\nsUewBOwRJCIiooqCPYJEREREVCosBMnssKdEe8xce8xce8xce8zc/LEQJCIiIrJQ7BEsAXsEiYiI\nqKJgjyARERERlQoLQTI77CnRHjPXHjPXHjPXHjM3fywEyeycPXvW1EuwOMxce8xce8xce8zc/LEQ\nJLPz22+/mXoJFoeZa4+Za4+Za4+Zmz8WgkREREQWioUgmZ3U1FRTL8HiMHPtMXPtMXPtMXPzx18f\nU4KAgACcO3fO1MsgIiIiKpG/v3+ZejNZCBIRERFZKL40TERERGShWAgSERERWSgWgkREREQWioVg\nMeLi4tC4cWM0atQIM2bMMPVyLEKDBg3QrFkzBAYGolWrVqZeTqU0dOhQODs7o2nTpuq5O3fuoGvX\nrvD29kZISAh/79drVlTmUVFRcHNzQ2BgIAIDAxEXF2fCFVY+6enp6NSpE5o0aQI/Pz/MnTsXAPd6\neSouc+718vPkyRO0bt0aAQEB8PX1xaRJkwCUfZ/zzSJFyM/Px5tvvom9e/fC1dUVLVu2xJo1a+Dj\n42PqpVVqHh4eOHXqFN544w1TL6XSOnToEPR6PYYMGYILFy4AACZOnIjatWtj4sSJmDFjBu7evYvp\n06ebeKWVR1GZR0dHo0aNGvjrX/9q4tVVTpmZmcjMzERAQABycnLQvHlzbN68GcuXL+deLyfFZb5u\n3Tru9XL06NEj2NnZIS8vD+3bt8fMmTOxdevWMu1zPiNYhMTERDRs2BANGjSAlZUVBg4ciC1btph6\nWRaBP5eUrw4dOsDR0dHo3NatWxEREQEAiIiIwObNm02xtEqrqMwB7vXyVLduXQQEBAAA9Ho9fHx8\ncOPGDe71clRc5gD3enmys7MDAOTm5iI/Px+Ojo5l3ucsBItw48YNuLu7q8dubm7qhqbyoygKunTp\nghYtWmDJkiWmXo7FyMrKgrOzMwDA2dkZWVlZJl6RZZg3bx78/f0xbNgwvkRZjlJTU3HmzBm0bt2a\ne10jzzNv06YNAO718lRQUICAgAA4OzurL82XdZ+zECyCoiimXoJFOnz4MM6cOYOdO3diwYIFOHTo\nkKmXZHEUReH+18Do0aORkpKCs2fPwsXFBePHjzf1kiqlnJwc9O/fHzExMahRo4bRbdzr5SMnJwfv\nvfceYmJioNfrudfLmU6nw9mzZ5GRkYGffvoJBw4cMLq9NPuchWARXF1dkZ6erh6np6fDzc3NhCuy\nDC4uLgAAJycn9OvXD4mJiSZekWVwdnZGZmYmAODXX39FnTp1TLyiyq9OnTrqN+jhw4dzr5eDZ8+e\noX///ggPD8e7774LgHu9vD3P/P3331cz517XRs2aNdGzZ0+cOnWqzPuchWARWrRogatXryI1NRW5\nublYu3Yt+vTpY+plVWqPHj3CgwcPAAAPHz7E7t27jd5lSeWnT58+WLFiBQBgxYoV6jdwKj+//vqr\n+vmmTZu4118zEcGwYcPg6+uLcePGqee518tPcZlzr5ef7Oxs9aX2x48fY8+ePQgMDCzzPue7houx\nc+dOjBs3Dvn5+Rg2bJj6tmwqHykpKejXrx8AIC8vD4MHD2bm5WDQoEE4ePAgsrOz4ezsjC+++AJ9\n+/ZFaGgo0tLS0KBBA6xbtw4ODg6mXmql8XLm0dHRiI+Px9mzZ6EoCjw8PLBo0SK1p4f+dwkJCejY\nsSOaNWumviw2bdo0tGrVinu9nBSV+dSpU7FmzRru9XJy4cIFREREoKCgAAUFBQgPD8eECRNw586d\nMu1zFoJEREREFoovDRMRERFZKBaCRERERBaKhSARERGRhWIhSERERGShWAgSERERWSgWgkREREQW\nioUgkYVITU2FTqfD6dOnNZ87Nja20H/xZSmys7Oh0+nw008//e5rbNmyBY0aNYKVlRWGDh36GldH\nRJaOhSBRJRQcHIwxY8YYnatfvz4yMzPh7++v+XoGDhyIlJQUzeetLIYNG4YBAwYgLS0NMTExpl5O\niRYvXoxOnTrBwcEBOp0OaWlphcbcvXsX4eHhcHBwgIODA4YMGYJ79+4ZjUlLS0Pv3r2h1+vh5OSE\nsWPH4tmzZ0ZjLly4gD/84Q+ws7ODm5sbvvzyy0JzHTx4EM2bN0e1atXg5eWFRYsWFRqzYcMG+Pr6\nwtbWFk2aNMHmzZv/xxSIKgYWgkQWQqfToU6dOqhSpYrmc9va2qJ27dqaz1sZ3L17F3fu3EFISAhc\nXFx+9zOrubm5r3llxXv8+DG6deuG6OjoYseEhYXh7Nmz2LVrF+Li4nD69GmEh4ert+fn56Nnz554\n+PAhEhISsGbNGqxfvx7jx49Xx9y/fx9du3aFi4sLTp48iZiYGHz99deYPXu2OiYlJQU9evRA+/bt\ncfbsWUyaNAljxozBxo0b1TFHjx7FwIEDER4ejnPnzmHw4MEYMGAA/19csgxCRJVKRESEKIpi9HH9\n+nVJSUkRRVHk1KlTIiJy4MABURRFdu7cKYGBgVKtWjXp0KGDZGRkyL59+6Rp06ai1+uld+/ecufO\nHaM5vvvuO/Hx8RFbW1vx9vaWOXPmSEFBQbFrWr58uej1evV48uTJ4ufnJ2vWrBFPT0+pUaOGvPvu\nu5Kdnf3KxxYdHS0Gg0FsbGykbt26MmTIEKPbZ8yYIV5eXlKtWjVp2rSprFq1yuj2GzduSFhYmNSq\nVUvs7OwkICBADhw4oN6+cOFC8fLyEmtra2nYsKEsWbLE6P6KosjixYvlvffek+rVq4unp2ehORIT\nEyUoKEhsbW0lMDBQtm/fLoqiyMGDB0VEJDc3V8aMGSP16tUTGxsbcXd3l08//bTIx/v8a/Tix/Pr\nbNiwQfz8/NRrTJkyxei+BoNBoqKi5IMPPhAHBwcJDQ0tco6IiAjp1auXfPPNN+Lq6iqOjo7ywQcf\nyKNHj4r5KpTeiRMn1P33okuXLomiKHLkyBH1XEJCgiiKIklJSSIismPHDtHpdJKRkaGOWbVqldja\n2sqDBw9EROTbb7+VmjVrypMnT9QxX331lbi6uqrHEydOFG9vb6P5hw8fLm3btlWPQ0NDJSQkxGhM\nly5dZNCgQb/3oRNVGCwEiSqZe/fuSbt27WTYsGGSlZUlWVlZkp+fX2wh2Lp1a0lISJDz58+Ln5+f\ntGvXTjp16iSJiYly8uRJ8fDwkLFjx6rXX7x4sbi4uMiGDRskNTVVtm3bJnXr1pX58+cXu6aiCkG9\nXi9//OMf5cKFC3L06FExGAwycuTIYq+xfv16sbe3lx07dkh6erqcPHlSFixYoN7+2WefSePGjWXX\nrl2Smpoq33//vVSvXl1+/PFHERHJycmRhg0bSvv27SUhIUFSUlJky5YtaiG4ceNGsbKykgULFsjV\nq1dl3rx5YmVlJdu2bVPnUBRF3NzcZPXq1ZKcnCyTJk0Sa2trSUtLExGRBw8eiJOTk4SGhsrFixdl\n165d0rhxY6MCbubMmeLu7i6HDh2S9PR0OXLkiMTGxhb5mHNzc9WiadOmTZKVlSW5ubly8uRJqVKl\nikRFRcnVq1dl9erVotfrZd68eep9DQaD2Nvby9dffy3Jycly7dq1IueIiIiQmjVryogRI+Ty5cuy\ne/ducXBwkGnTpqljpkyZInq9/pUfCQkJha5dXCG4bNkyqVGjhtG5goIC0ev1ahb/+Mc/xM/Pz2jM\nzZs3RVEUiY+PFxGR8PBw6dWrl9GYxMREURRFUlNTRUSkQ4cO8tFHHxmNWbdunVhZWUleXp6IiNSv\nX19mzpxpNOZf//qXGAyGIjMjqkxYCBJVQsHBwTJmzBijc8UVgrt371bHzJ8/XxRFkTNnzqjnoqKi\njP5Bdnd3L/Qs2Jw5c8TX17fY9RRVCNra2sr9+/fVc1OmTJGGDRsWe41Zs2bJm2++Kc+ePSt0W05O\njlSrVq1QMTJ27Fjp0aOHiPy3gK1Ro4bcvn27yOs/L55fFBkZKe3bt1ePFUWRzz77TD3Oy8sTOzs7\nWb16tYiILFq0SBwcHOThw4fqmFWrVhkVgn/5y1/k7bffLvZxvuzWrVtG9xcRCQsLK3SNqKgocXNz\nU48NBoP06dOnxOtHRERI/fr1jZ7R/fDDD6VLly7q8Z07dyQ5OfmVH48fPy507eIKwSlTpoinp2eh\n8Z6enjJ9+nR1DS8/xoKCAqlatar88MMPIiLStWvXQl+z69evi6IocuzYMRER8fb2li+//NJozMGD\nB0VRFMnMzBQREWtra1m5cqXRmBUrVoiNjU0RiRFVLlVN/dI0EZlWs2bN1M/r1KkDAGjatKnRuZs3\nbwIAbt26hYyMDIwYMQKjRo1Sx+Tl5ZV5XoPBYNTv5uLios5TlNDQUMydOxceHh5455130K1bN/Tp\n0wfW1ta4dOkSnjx5gnfeeQeKoqj3efbsGTw8PAAAZ86cgb+/P954440ir3/58mUMHz7c6Nxbb72F\nrVu3Gp17Ma8qVarAyclJXfcvv/wCf39/2NnZqWPatGljdP/IyEh07doV3t7eCAkJQY8ePdC9e3ej\ndZfk8uXL6NWrV6G1RkdHIycnB3q9HoqioEWLFqW6nq+vr9H8Li4uOH78uHrs6OgIR0fHUq/vdRGR\nV95elsyIqGgsBIksnJWVlfr5839YX3xDiaIoKCgoAAD1z0WLFqFdu3avbd6X5ymKm5sbrly5gn37\n9mHv3r0YP348oqOjcfz4cfV+27dvR/369Yudp6TCoigvFxslrbukOQIDA5Gamopdu3Zh3759iIiI\ngL+/P/bs2VOmwqa4eV68RvXq1Ut1rapVjf8pePkxTZ06FdOmTXvlNeLi4vDWW2+Var66devi1q1b\nRudEBDdv3kTdunXVMUeOHDEak52djfz8fKMxmZmZRmOysrLU2141pmrVquobmIob8/waRJUZ3zVM\nVAlZW1v/rmfpSuLs7Ix69erh2rVr8PT0LPRR3mxsbNCjRw/Mnj0bJ06cwMWLF3HkyBE0adIENjY2\nSE1NLbQmd3d3AEBQUBDOnz+P27dvF3ltHx8fJCQkGJ1LSEhAkyZNSr0+X19fXLhwAY8ePVLPHTt2\nrNA4vV6P/v3749tvv8WPP/6I/fv3Izk5udTz+Pj44PDhw4XW6u7uXuri70UlFaCjR4/GuXPnXvnR\nvHnzUs/Xtm1b5OTk4OjRo+q5o0eP4uHDh+oPGO3atcMvv/yCGzduqGP27NkDGxsbda62bdvi0KFD\nePr0qdEYV1dXGAwGdcyePXuM5t+zZw9atmyp/sBT3JjSFrZEFRmfESSqhBo0aIDExERcv34d1atX\nR61atV7btaOjozFmzBg4ODige/fuePbsGU6fPo3//Oc/+PTTT1/bPC+LjY1Ffn4+WrVqBb1ej7Vr\n18La2hqNGjWCXq/HJ598gk8++QQigg4dOiAnJwfHjh1DlSpV8OGHHyIsLAzTp09H3759MX36dNSr\nVw8///wz7O3tERwcjAkTJmDAgAFo3rw5unbtiri4OHz//ffYtGlTqdcYFhaGzz//HEOHDsU///lP\n3LhxA1OmTDEaM3v2bNSrVw/+/v6wsrLC6tWrUbNmTbi5uZV6nvHjx6Nly5aIjo7GoEGDcOLECcye\nPbvEZ+2KU9KzmGV9aTgzMxOZmZlISkoCAFy8eBF37tyBwWCAo6MjfHx80K1bN4wcORKLFy+GEOHE\nAQAAAmtJREFUiGDkyJHo3bs3GjVqBAAICQlBkyZNMGTIEMyaNQvZ2dmYOHEiRowYAb1eD+C/eUdH\nRyMyMhJ///vfceXKFcyYMQNRUVHqWkaNGoX58+fj448/xogRI3D48GGsWLECP/zwgzpm7Nix6Nix\nI2bMmIG+ffti06ZNiI+PL1RsE1VKpmtPJKLykpSUJG3bthU7OzvR6XTqr4/R6XRGbxbR6XRGb574\n97//LTqdzuhaCxcuFCcnJ6Nza9asUX9FiqOjo3To0EHWrl1b7HqWL19u9C7RqKgoadq06SvHvGzz\n5s3Stm1bcXBwkOrVq0urVq3UdwQ/N2/ePPH19RUbGxtxcnKSkJAQ2bt3r3p7RkaG/OlPfxIHBwex\ns7OToKAgozdhLFy4UBo2bChWVlbSqFEjWbp0qdH1FUWRDRs2GJ1r0KCBzJo1Sz0+fvy4BAUFiY2N\njQQEBMi2bdtEp9Op8yxZskSCgoKkRo0aYm9vL8HBwXL06NFiH/etW7eM7v/cxo0bpWnTpmJtbS31\n69eXqVOnvnJdxYmMjJTevXsbnSvq61MWkydPVn/djU6nU/9csWKFOubu3bvy/vvvi729vdjb20t4\neLjcu3fP6DppaWnSq1cvsbOzk1q1asnYsWMlNzfXaMyFCxekY8eOYmtrK/Xq1ZMvvvii0HoOHjyo\nfk08PT1l0aJFhcasX79eGjduLNbW1uLr6yubNm363Y+fqCJRRH5H0wwRERERVXjsESQiIiKyUCwE\niYiIiCwUC0EiIiIiC8VCkIiIiMhCsRAkIiIislAsBImIiIgsFAtBIiIiIgvFQpCIiIjIQv0fbRXV\nznewV8UAAAAASUVORK5CYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10b49e438>"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"Python version : 3.4.1\n",
|
|
"compiler : GCC 4.2.1 (Apple Inc. build 5577)\n",
|
|
"\n",
|
|
"system : Darwin\n",
|
|
"release : 13.2.0\n",
|
|
"machine : x86_64\n",
|
|
"processor : i386\n",
|
|
"CPU count : 4\n",
|
|
"interpreter: 64bit\n",
|
|
"\n",
|
|
"\n",
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 20
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "heading",
|
|
"level": 2,
|
|
"metadata": {},
|
|
"source": [
|
|
"Conclusion"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#Sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"We can see that we could speed up the density estimations for our Parzen-window function if we submitted them in parallel.\n",
|
|
"However, on my particular machine it didn't make any differences if we submitted 2, 3, 4, or 6 processes in parallel. \n",
|
|
"\n",
|
|
"In practice, it doesn't make much sense to submit more processes than the CPU supports (e.g., here 6 processes for a 4-core CPU). For larger benchmarks, this would to a slower performace, because of an additional overhead for communicating between the additional processes."
|
|
]
|
|
}
|
|
],
|
|
"metadata": {}
|
|
}
|
|
]
|
|
} |