mirror of
https://github.com/rasbt/python_reference.git
synced 2024-12-18 08:10:24 +00:00
1745 lines
344 KiB
Plaintext
1745 lines
344 KiB
Plaintext
{
|
|
"metadata": {
|
|
"name": "",
|
|
"signature": "sha256:3b47add80317bb8ad369eacd5528c941bb1a2cbd92ae5b33aae66d56ae35c741"
|
|
},
|
|
"nbformat": 3,
|
|
"nbformat_minor": 0,
|
|
"worksheets": [
|
|
{
|
|
"cells": [
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[Sebastian Raschka](http://www.sebastianraschka.com) \n",
|
|
"last updated: 05/04/2014\n",
|
|
"\n",
|
|
"- [Link to this IPython Notebook on GitHub](https://github.com/rasbt/python_reference/blob/master/benchmarks/cython_least_squares.ipynb) \n",
|
|
"- [Link to the GitHub repository](https://github.com/rasbt/python_reference)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### The code in this notebook was executed in Python 3.4.0"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<hr>\n",
|
|
"I am really looking forward to your comments and suggestions to improve and \n",
|
|
"extend this little collection! Just send me a quick note \n",
|
|
"via Twitter: [@rasbt](https://twitter.com/rasbt) \n",
|
|
"or Email: [bluewoodtree@gmail.com](mailto:bluewoodtree@gmail.com)\n",
|
|
"<hr>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"# Implementing the least squares fit method for linear regression and speeding it up via Cython"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"sections\"></a>\n",
|
|
"<br>\n",
|
|
"<br>\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#Sections"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"- [Introduction](#introduction)\n",
|
|
"- [Least squares fit implementations](#implementations)\n",
|
|
"- [Generating sample data and benchmarking](#sample_data)\n",
|
|
"- [Compiling the Python code via Cython in the IPython notebook](#cython_nb)\n",
|
|
"- [Performance growth rates for different sample sizes](#sample_sizes)\n",
|
|
"- [Bonus: How to use Cython without the IPython magic](#cython_bonus)\n",
|
|
"- [Appendix I: Cython vs. Numba](#numba)\n",
|
|
"- [Appendix II: Cython with and without type declarations](#type_declarations)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"introduction\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
" \n",
|
|
"(Note that this chart just reflects my rather objective thoughts after experimenting with Cython, and it is not based on real numbers or benchmarks.)\n",
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Introduction"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Linear regression via the least squares method is the simplest approach to performing a regression analysis of a dependent and a explanatory variable. The objective is to find the best-fitting straight line through a set of points that minimizes the sum of the squared offsets from the line. \n",
|
|
"The offsets come in 2 different flavors: perpendicular and vertical - with respect to the line. \n",
|
|
"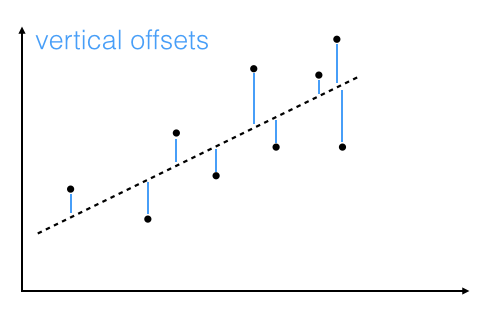 \n",
|
|
"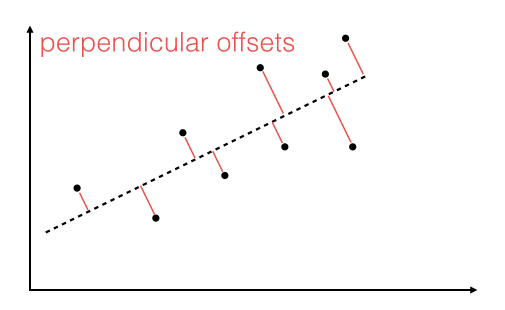 \n",
|
|
"\n",
|
|
"As Michael Burger summarizes it nicely in his article \"[Problems of Linear Least Square Regression - And Approaches to Handle Them](http://www.arsa-conf.com/archive/?vid=1&aid=2&kid=60101-220)\": \"the perpendicular offset method delivers a more precise result but is are more complicated to handle. Therefore normally the vertical offsets are used.\" \n",
|
|
"Here, we will also use the method of computing the vertical offsets.\n",
|
|
"\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In more mathematical terms, our goal is to compute the best fit to *n* points $(x_i, y_i)$ with $i=1,2,...n,$ via linear equation of the form \n",
|
|
"$f(x) = a\\cdot x + b$. \n",
|
|
"Here, we assume that the y-component is functionally dependent on the x-component. \n",
|
|
"In a cartesian coordinate system, $b$ is the intercept of the straight line with the y-axis, and $a$ is the slope of this line."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In order to obtain the parameters for the linear regression line for a set of multiple points, we can re-write the problem as matrix equation \n",
|
|
"$\\pmb X \\; \\pmb a = \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\Rightarrow\\Bigg[ \\begin{array}{cc}\n",
|
|
"x_1 & 1 \\\\\n",
|
|
"... & 1 \\\\\n",
|
|
"x_n & 1 \\end{array} \\Bigg]$\n",
|
|
"$\\bigg[ \\begin{array}{c}\n",
|
|
"a \\\\\n",
|
|
"b \\end{array} \\bigg]$\n",
|
|
"$=\\Bigg[ \\begin{array}{c}\n",
|
|
"y_1 \\\\\n",
|
|
"... \\\\\n",
|
|
"y_n \\end{array} \\Bigg]$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"With a little bit of calculus, we can rearrange the term in order to obtain the parameter vector $\\pmb a = [a\\;b]^T$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\Rightarrow \\pmb a = (\\pmb X^T \\; \\pmb X)^{-1} \\pmb X^T \\; \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"The more classic approach to obtain the slope parameter $a$ and y-axis intercept $b$ would be:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$a = \\frac{S_{x,y}}{\\sigma_{x}^{2}}\\quad$ (slope)\n",
|
|
"\n",
|
|
"\n",
|
|
"$b = \\bar{y} - a\\bar{x}\\quad$ (y-axis intercept)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"where \n",
|
|
"\n",
|
|
"\n",
|
|
"$S_{xy} = \\sum_{i=1}^{n} (x_i - \\bar{x})(y_i - \\bar{y})\\quad$ (covariance)\n",
|
|
"\n",
|
|
"\n",
|
|
"$\\sigma{_x}^{2} = \\sum_{i=1}^{n} (x_i - \\bar{x})^2\\quad$ (variance)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"implementations\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"## Least squares fit implementations"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 1. The matrix approach"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"First, let us implement the equation:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$\\pmb a = (\\pmb X^T \\; \\pmb X)^{-1} \\pmb X^T \\; \\pmb y$"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"which I will refer to as the \"matrix approach\"."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import numpy as np\n",
|
|
"\n",
|
|
"def lin_lstsqr_mat(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 36
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 2. The classic approach"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Next, we will calculate the parameters separately, using only standard library functions in Python, which I will call the \"classic approach\"."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"$a = \\frac{S_{x,y}}{\\sigma_{x}^{2}}\\quad$ (slope)\n",
|
|
"\n",
|
|
"\n",
|
|
"$b = \\bar{y} - a\\bar{x}\\quad$ (y-axis intercept)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 37
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 3. Using the lstsq numpy function"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"For our convenience, `numpy` has a function that can also compute the leat squares solution of a linear matrix equation. For more information, please refer to the [documentation](http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.lstsq.html)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def numpy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return np.linalg.lstsq(X,y)[0]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 38
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"### 4. Using the linregress scipy function"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"The last approach is using `scipy.stats.linregress()`, which returns a tuple of 5 different attributes, where the 1st value in the tuple is the slope, and the second value is the y-axis intercept, respectively. The documentation for this function can be found [here](http://docs.scipy.org/doc/scipy-0.13.0/reference/generated/scipy.stats.linregress.html)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import scipy.stats\n",
|
|
"\n",
|
|
"def scipy_lstsqr(x,y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" return scipy.stats.linregress(x, y)[0:2]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 39
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name='sample_data'></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Generating sample data and benchmarking"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In order to test our different least squares fit implementation, we will generate some sample data: \n",
|
|
"- 500 sample points for the x-component within the range [0,500) \n",
|
|
"- 500 sample points for the y-component within the range [100,600) \n",
|
|
"\n",
|
|
"where each sample point is multiplied by a random value within\n",
|
|
"the range [0.8, 12)."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"x = [x_i*random.randrange(8,12)/10 for x_i in range(500)]\n",
|
|
"y = [y_i*random.randrange(8,12)/10 for y_i in range(100,600)]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 40
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"#### Visualization"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"To check how our dataset is distributed, and how the straight line, which we obtain via the least square fit method, we will plot it in a scatter plot. \n",
|
|
"Note that we are using our \"matrix approach\" here for simplicity, but after plotting the data, we will check whether all of the four different implementations yield the same parameters."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%pylab inline\n",
|
|
"from matplotlib import pyplot as plt\n",
|
|
"\n",
|
|
"slope, intercept = lin_lstsqr_mat(x, y)\n",
|
|
"\n",
|
|
"line_x = [round(min(x)) - 1, round(max(x)) + 1]\n",
|
|
"line_y = [slope*x_i + intercept for x_i in line_x]\n",
|
|
"\n",
|
|
"plt.figure(figsize=(8,8))\n",
|
|
"plt.scatter(x,y)\n",
|
|
"plt.plot(line_x, line_y, color='red', lw='2')\n",
|
|
"\n",
|
|
"plt.ylabel('y')\n",
|
|
"plt.xlabel('x')\n",
|
|
"plt.title('Linear regression via least squares fit')\n",
|
|
"\n",
|
|
"ftext = 'y = ax + b = {:.3f} + {:.3f}x'\\\n",
|
|
" .format(slope, intercept)\n",
|
|
"plt.figtext(.15,.8, ftext, fontsize=11, ha='left')\n",
|
|
"\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAfoAAAH4CAYAAACi3S9CAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdUVMfbwPHv0lm6giAgooBRbNi7GCv2EnvXWOPPnhg1\nGksSxRhjoiYaE0SNsb4xEY0Fe+zGmijGLkZARRERFljYnfeP1Y0ELJRlAedzDkf2lpln7q48e++d\nO6MQQggkSZIkSSqSTIwdgCRJkiRJhiMTvSRJkiQVYTLRS5IkSVIRJhO9JEmSJBVhMtFLkiRJUhEm\nE70kSZIkFWEy0UtGd+jQIcqXL2/sMAqtSpUq8fvvv+drnSNHjuTTTz/N0b7e3t7s3bs3jyN6s/3y\nyy+UKlUKe3t7zp07Z5TPhFRwKeRz9FJ+8fb2JiQkhGbNmhk7FMmIypQpQ0hICE2bNjVI+QcOHKBf\nv378888/Bim/IPLx8eGrr76iffv2mdbNnDmT69ev8+OPPxohMqkgkGf0Ur5RKBQoFApjh6Gn0Wjy\nZJvXJYRAfq+Wnsmrz5YQgtu3b+Pv758n5UlFj0z0ktEdOHCAUqVK6V97e3uzYMECqlatiqOjIz17\n9iQ1NVW/ftu2bQQEBODk5ESDBg3466+/9OuCg4Px9fXF3t6eihUr8uuvv+rXrVy5kgYNGjBhwgSc\nnZ2ZNWtWplhmzpxJ165d6devHw4ODqxatYrHjx/z7rvv4u7ujqenJ9OnT0er1QKg1WqZOHEiLi4u\nlC1bliVLlmBiYqJf36RJE6ZNm0aDBg2wsbHh5s2b/P3337Ro0YLixYtTvnx5Nm3apK9/+/btVKxY\nEXt7ezw9PVmwYAEADx48oF27djg5OVG8eHEaN26c4Xg9uxSemprKuHHj8PDwwMPDg/Hjx6NWq/XH\n2dPTky+//BJXV1fc3d1ZuXJllu/Jhg0bqFWrVoZlCxcupGPHjgAMHDiQ6dOnA/Do0SPatWtHiRIl\nKFasGO3btycqKirLcv9LCKF/z5ydnenRowePHj3Sr+/WrRslS5bE0dGRwMBAIiIiXnisvvzyS1Qq\nFa1btyY6Oho7Ozvs7e25e/dupnpfdJwB5s+fr3+vV6xYgYmJCTdu3AB072dISIh+25UrV9KoUSP9\n67Fjx+Ll5YWDgwM1a9bk8OHD+nXZ/Wxdu3aNwMBAHB0dcXFxoWfPnpnakZqaip2dHRqNhqpVq+Ln\n5wf8+5nYuXMnc+fOZcOGDdjZ2VGtWrXXel+kIkZIUj7x9vYWe/fuzbR8//79wtPTM8N2derUETEx\nMSIuLk5UqFBBLFu2TAghxJkzZ0SJEiXEyZMnhVarFatWrRLe3t5CrVYLIYTYtGmTiImJEUIIsWHD\nBmFjYyPu3r0rhBAiNDRUmJmZiSVLlgiNRiOSk5MzxTJjxgxhbm4utmzZIoQQIjk5WXTq1EmMGDFC\nqFQqcf/+fVG7dm3x3XffCSGEWLp0qfD39xdRUVHi0aNHolmzZsLExERoNBohhBCBgYGidOnSIiIi\nQmg0GhEfHy88PT3FypUrhUajEWfPnhXOzs7i0qVLQggh3NzcxOHDh4UQQsTHx4szZ84IIYSYPHmy\nGDFihEhPTxfp6en6bf57XKdPny7q1asnYmNjRWxsrKhfv76YPn26/jibmZmJGTNmiPT0dLF9+3ah\nVCpFfHx8puOgUqmEnZ2duHr1qn5ZzZo1xYYNG4QQQgwcOFBf7sOHD8XmzZtFcnKyePLkiejWrZvo\n1KlT1h+C/8T71VdfiXr16omoqCihVqvF8OHDRa9evfTbhoaGisTERKFWq8W4ceNEQECAft2LjtWB\nAwcyfJ6y8qJ9d+zYIVxdXcXFixdFUlKS6NWrl1AoFOL69etCCCGaNGkiQkJCMsTXsGFD/es1a9aI\nuLg4odFoxIIFC4Sbm5tITU0VQmT/s9WzZ08xZ84cIYQQqamp4siRIy9sz/Mx/vcYz5w5U/Tr1++l\nx0Mq2uQZvVQgjRkzBjc3N5ycnGjfvj3nzp0DYPny5QwfPpxatWqhUCjo378/lpaWHDt2DICuXbvi\n5uYGQPfu3fHz8+PEiRP6ct3d3Rk1ahQmJiZYWVllWXf9+vXp0KEDAI8fP2bHjh0sXLgQa2trXFxc\nGDduHOvXrwdg48aNjBs3Dnd3dxwdHZkyZUqGy/MKhYKBAwdSoUIFTExM2LlzJ2XKlGHAgAGYmJgQ\nEBBAly5d2LhxIwAWFhZcvHiRhIQEHBwc9GdgFhYWxMTEcOvWLUxNTWnQoEGWsa9du5aPP/4YZ2dn\nnJ2dmTFjRoZ7s+bm5nz88ceYmprSunVrbG1tuXz5cqZyrK2t6dixI+vWrQPg6tWrXL58WX9cAH07\nixUrRufOnbGyssLW1papU6dy8ODBrN/Y//juu+/49NNPcXd3x9zcnBkzZvB///d/+rPagQMHYmNj\no193/vx5njx58tJjJV7j9siL9t24cSODBw/G398fpVKZ5VWfl+nTpw9OTk6YmJgwYcIEUlNTMxzf\n7Hy2LCwsuHXrFlFRUVhYWFC/fv1sxfKMkLeM3ngy0UsF0rNkDbqkk5iYCEBkZCQLFizAyclJ/3Pn\nzh1iYmIAWL16NdWqVdOvu3DhAg8fPtSX9fwtghfx9PTU/x4ZGUlaWholS5bUlzlixAhiY2MBiImJ\nyVDm8/tmVWdkZCQnTpzIEP/atWu5d+8eAD///DPbt2/H29ubJk2acPz4cQA++OADfH19admyJT4+\nPsybNy/L2KOjoyldurT+tZeXF9HR0frXxYsXx8Tk3//2SqVSf2z/q3fv3vpEv3btWn0y/y+VSsXw\n4cPx9vbGwcGBwMBAHj9+/FrJ5datW3Tu3Fl/LPz9/TEzM+PevXtoNBomT56Mr68vDg4OlClTBoVC\nwYMHD156rF7Hi/b97/vp5eX12mUCfPHFF/j7++Po6IiTkxOPHz/WxwvZ+2x9/vnnCCGoXbs2lSpV\nIjQ0NFuxSNIzZsYOQJJex7NOfF5eXnz00UdMnTo10zaRkZEMGzaMffv2Ua9ePRQKBdWqVct0hv2q\nep7fplSpUlhaWvLw4cMMCfKZkiVLZujdnVVP7+fL8/LyIjAwkPDw8Czrr1mzJr/++isajYbFixfT\nvXt3bt++ja2tLV988QVffPEFFy9epGnTptSuXZu33347w/7u7u7cunWLChUqAHD79m3c3d1f2uYX\nad68ObGxsZw/f57169fz1VdfZdmuBQsWcOXKFU6ePEmJEiU4d+4c1atXRwjxyuPt5eVFaGgo9erV\ny7Tuxx9/JCwsjL1791K6dGni4+MpVqyY/v180bF6nQ6fL9q3ZMmS3L59W7/d878D2NjYkJSUpH/9\n/P3/Q4cOMX/+fPbt20fFihUBMsT7/DGDV3+2XF1dWb58OQBHjhyhefPmBAYGUrZs2Ve273kFqQOs\nZBzyjF7KV2q1mpSUFP3P6/Y8fvbHcujQoSxbtoyTJ08ihCApKYnffvuNxMREkpKSUCgUODs7o9Vq\nCQ0N5cKFC9mK779noSVLlqRly5ZMmDCBJ0+eoNVquX79uv4Z5e7du/P1118THR1NfHw88+bNy/SH\n9fky27Vrx5UrV1izZg1paWmkpaXxxx9/8Pfff5OWlsZPP/3E48ePMTU1xc7ODlNTU0DXAfHatWsI\nIbC3t8fU1DTL5NCrVy8+/fRTHjx4wIMHD5g9ezb9+vXL1jF4xtzcnG7duvH+++/z6NEjWrRokaFN\nz9qVmJiItbU1Dg4OxMXFZety94gRI5g6dao+ocbGxhIWFqYv19LSkmLFipGUlJThy93LjpWrqysP\nHz4kISEhyzpftm/37t1ZuXIlly5dQqVSZWpLQEAAmzdvJjk5mWvXrhESEqJ/v588eYKZmRnOzs6o\n1Wpmz579whjg1Z+tTZs2cefOHQAcHR1RKBRZvuev4ubmxq1bt+Tl+zeYTPRSvmrTpg1KpVL/M2vW\nrFc+dvf8+ho1avD999/zv//9j2LFiuHn58fq1asB8Pf3Z+LEidSrVw83NzcuXLhAw4YNsyzndep6\nZvXq1ajVavz9/SlWrBjdunXTn8kNHTqUli1bUqVKFWrUqEHbtm0zJeHny7O1tSU8PJz169fj4eFB\nyZIlmTJlir5n/Jo1ayhTpgwODg4sX76cn376CdD1wG7RogV2dnbUr1+fUaNGERgYmCn+adOmUbNm\nTapUqUKVKlWoWbMm06ZNyzKW19G7d2/27t1Lt27dMrXpWVnjxo0jOTkZZ2dn6tevT+vWrV+7nrFj\nx9KhQwdatmyJvb099erV4+TJkwD079+f0qVL4+HhQaVKlfRXaZ550bEqX748vXr1omzZshQrVizL\nXvcv2jcoKIhx48bRtGlTypUrl2nMh/Hjx2NhYYGrqyuDBg2ib9+++nVBQUEEBQVRrlw5vL29sba2\nznDpP7ufrVOnTlG3bl3s7Ozo2LEjixYtwtvbO8vj+LLj3a1bN0B326ZmzZov3E4qugw6YM7ly5cz\nPBJy48YNPvnkE/r27UuPHj2IjIzE29ubjRs34ujoCMDcuXNZsWIFpqamLFq0iJYtWxoqPEnKczt2\n7GDkyJHcunXL2KFIecTExIRr165l+5K5JBUUBj2jf+uttzh79ixnz57l9OnTKJVKOnfuTHBwMC1a\ntODKlSs0a9aM4OBgACIiItiwYQMRERHs3LmT9957T9/7VpIKopSUFLZv3056ejpRUVHMmjWLLl26\nGDssSZIkvXy7dL9nzx58fX0pVaoUYWFhDBgwAIABAwboBzXZsmULvXr1wtzcHG9vb3x9ffWX8SSp\nIBJCMHPmTIoVK0b16tWpWLEis2fPNnZYUh6Sndmkwi7fet2vX7+eXr16AXDv3j1cXV0BXceZZ48W\nRUdHU7duXf0+np6erz3CliQZg7W1tfwyWsTl5TDIkmQM+ZLo1Wo1W7duzfLZ39fpiPU8X19frl+/\nnucxSpIkSVJB5ePjw7Vr13K0b75cut+xYwc1atTAxcUF0J3FP+tZGhMTQ4kSJQDw8PDI8BzynTt3\n8PDwyFDW9evX9Y/2vIk/M2bMMHoMsv2y7bL9sv2y/fn7k5sT3HxJ9OvWrdNftgfo0KEDq1atAmDV\nqlV06tRJv3z9+vWo1Wpu3rzJ1atXqV27dn6EKEmSJElFksEv3SclJbFnzx6+//57/bLJkyfTvXt3\nQkJC9I/Xge456O7du+uHwfz2229lRxhJkiRJygWDJ3obG5sMYz2DbljIPXv2ZLn91KlTsxzeVNJp\n0qSJsUMwqje5/W9y20G2X7a/ibFDKLQMOmCOISgUCgpZyJIkSZKUK7nJfXIIXEmSJEkqwmSilyRJ\nkqQiTCZ6SZIkSSrCZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIkwmekmSJEkqwmSilyRJkqQiTCZ6\nSZIkSSrCZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIkwmekmSJEkqwmSilyRJkqQiTCZ6SZIkSSrC\nZKKXJEmSpCJMJnpJkiRJKsJkopckSZKkIszM2AFIkiRJWYuNjWXHjh2YmJjQtm1bnJycjB2SVAgp\nhBDC2EFkh0KhoJCFLEmSlG03btygdu1AUlLqAOnY2p7nzJkjuLu750v9f/75JzNnzichIYn+/bvQ\nv3/ffKlXylpucp88o5ckSSqAJk78mEePRqDVfgRAauqHTJv2KStWfGvwuv/880/q1GlCSso0wINj\nxz7m8eMERo9+z+B1S3lP3qOXJEkqgKKi7qHV1tC/Tk+vwe3bdw1e78OHDwkMbEVKyhBgAtADlWo1\n8+d/Y/C6AU6cOMHIkWMZO/Z9/v7773yps6iTiV6SJKkAatWqMUrlF8Bj4CFK5Ve0bh1o8HqnTp1N\nQoInYPrcUpN8uWW6f/9+mjZtz7JlJVm8WEmtWo25ePGiwest6mSilyRJKoA+/ngy77zjg6lpCczM\nPBgwoA7jx482eL2XLt1Aq+0P/AB8A/yCiUkPxo4dZvC6P/poHirVV8BkhJhNUtJ4Pv98scHrLepk\nopckSSqAzM3NWb36O1JTVaSkJPHttwsxMTH8n+yGDWtgbb0bCAMOYGLyPs2a+TNx4liD152cnAIU\n178WwpnExGSD1qlSqRg+fCzly9chKKgr169fN2h9xiA740mSJBVgpqamr94olx49esSOHTtQKBSM\nHTuSs2ffY//+NoCCRo0aERa2AYVCYfA4hgzpyaRJE1GpbAAVSuVsBg9eZtA6O3fuw++/W5CSspCr\nVw9Tp04Trlw5T7FixQxab36SiV6SJOkN9s8//1CzZiNUqiqAwMZmKqdOHcLc3BwhBK6urvmS5AHe\ne284arWab78dh5mZGR9/PJ+2bdsapK7k5GQ++mgWu3dvR4gngAVabX3U6gMcOHCALl26GKReY5DP\n0UuSJBnZX3/9RUxMDJUrV6ZkyZL5WnfPnoP5v//zRKOZDYCZ2VR69XrI6tXf5Wsc+UkIQZMmbTlx\nwoLU1J3APcABENjZNWbt2g9p166dkaPMKDe5T96jlyRJMqIxYyZRt24Q3bvPw8+vCrt3787X+v/5\n5y4aTS396/T0WkRGRudrDPnt+vXr/PHHeVJTNwHDgCBgBebmg3Fze0KzZs2MHGHekolekiTJSA4f\nPsyKFT+jUl3k8eO9JCX9TNeuffLlquW6devx9q7C+fOnMDObDyQAj1Eqv6Zly0YGr9+YhBAoFKbo\nUuBXQD9MTafRo4eCP/44iLW1tZEjzFsy0UuSJBnJjRs3UCjqAo5PlzRCpUokMTHRoPXu3buXd9+d\nSGTkIpKSdiNEJAqFM6amJejevQKTJ080aP3G5uPjg79/WSwt3wV2Y2FxET8/d0JCluHg4GDs8PKc\nTPSSJElGUqVKFTSafcDNp0vW4eLijq2trUHr3bhxC8nJE4AmQFU0mp/x8ipPcnIioaFL86WnvzGZ\nmJiwb99WBg1yombN+fTuLThyJBwLCwtjh2YQste9JEmSkQQEBDBv3sd88EFVzMycsLaG7du3GLyX\nu4ODLaamd9Boni25g52dHebm5gattyCxs7Nj6dKFxg4jX8he95IkSUaWkJBAbGwspUqVypezyjt3\n7lC1al0SEjqQnl4Ca+tv+eWXH2nVqpXB65ZyJje5TyZ6SZKkN1B0dDQ//BBCUlIyXbt2platWq/e\nSTIameglSZIkqQiTz9FLkiRJkpQlmeglSZIk6UWEgEWLIC7O2JHkmEz0kiRJkpQVrRZGj4axY6FD\nB93rQkg+XidJkiRJ/5WeDkOHwsqVYGEBkyZBPkwTbAgy0UuSJEnS89Rq6NsXNm0CpRK2bIHmzY0d\nVY4Vzq8nkiRJ0hsvKSmJLl36olQ64uzsxY8//pT7QlNS4J13dEne3h7Cwwt1kgf5eJ0kSZJUSPXo\nMYgtW1JITV0M3MTauiPh4Rtp2LBhzgpMTISOHWHfPiheHHbtgho18jTmnJKP10mSJElvnF27dpGa\nOg9wBmqRkjKY3bv35Kyw+Hho2VKX5N3c4ODBApPkc0smekmSJKlQcnAoBlzWv7a0vEzx4sWyX1Bs\nLDRtCseOgZcXHDoEFSvmXaBGJhN9Ieft7U1ERIRBytZoNIwaNQpfX1/8/PwICQl54bZz586lcuXK\nVKhQgYEDB6JWqwG4desWZmZmVKtWTf/z6NEjAI4ePUqDBg2oWLEiFStWZNKkSXkaf58+ffDw8MDE\nxASVSpVh3fHjx6latSpvvfUWrVq1IjY2Vh/T87F6eHhQ4wXf6lUqFT169MDPz48KFSrw22+/6det\nWbOGKlWqYG5uzjfffJPl/gcOHMDU1PSF6yVJermlSz9HqeyDufk4lMqOeHpeYdCgQdkrJDoaAgPh\n7Fnw89MleV9fwwRsLKKQKYQh50hoaKiYOXPmK7fz9vYWFy5cMEgMq1atEq1atRJCCBEbGys8PT3F\nrVu3Mm23a9cuUaVKFaFSqYQQQgwdOlQEBwcLIYS4efOmcHZ2zrL8CxcuiGvXrgkhhEhNTRUNGzYU\nP/744yvjGjBggDhw4MArt9u/f7+4f/++UCgUIikpSb9co9EIHx8fceTIESGEEJ9++qkYPHhwlmV0\n6tRJLFiwIMt1s2bNEsOGDRNCCHH16lXh5uYmEhMT9W2LiIgQ/fv3F998802mfRMSEkSdOnVE+/bt\nxZIlS17ZFkmSsnbu3Dnx+eefi++++048efIkezvfvClE2bJCgBCVKgkRE2OQGPNCbnLfG3VGP3/+\nfP73v//pX9+7dw83NzdSUlJyXfa9e/do2rQpNWvWpFKlSnz44Yf6dUOHDmXChAn67cqWLcuff/75\n0vKyM03lmjVrqFmzJn5+fnl6drhx40aGDRsGgLOzM506dWLTpk2Ztvvzzz9p1KgR1tbWAAQFBfHT\nT6/u/VqxYkV8fHwAsLCwICAggNu3b79yP4VC8VrHp0mTJri4uGRafvr0aaytralfvz4Aw4cPZ+PG\njZm2u3//PuHh4fTr1y/L8jdu3Mjw4cMB8PX1pWbNmuzYsUPftgoVKmBiYpJlB5oJEyYwadIkihcv\nrl+WnJxM1apVCQsLA2Dfvn1UqFCBpKSkV7ZVMr5z584xYMAIevcewsGDB40dzhujatWqfPDBBwwb\nNgxbW9vX3/HyZWjUCG7c0N2LP3BAd2++CHqjnqMfMmQI/v7+fP755yiVSpYvX06fPn2wsrLKtG23\nbt24du1apuUKhYJjx45haWmZYbmjoyNbt27FxsaGtLQ0goKC2LVrF61atWLx4sXUqVOHLVu2sHjx\nYiZNmkSVKlVeGmtWyeFFYmNjOXXqFPfv36datWo0btyYypUrZ9jm0qVL9O7dO8v9W7Zsybx58zIt\nv337NqVLl9a/9vLy4p9//sm0XY0aNfj+++95+PAhDg4ObNy4kcjISP36hIQEatSogUKhoGfPnrz/\n/vuZyrh//z6bN29m+/btr9Xm7Byf//pvu5ydndFqtcTHx+Po6Khfvnr1alq1apXll4WsynnR8fmv\nHTt28OTJE7p06cLWrVv1X1qsra3ZuHEjLVu2xM3NjSFDhvDLL79gY2OT06ZK+eTs2bM0atSSpKQP\nAGu2bOnBzz+vJCgoyNihFXqJiYkMHPgeO3b8hp2dI4sWBdO9e7fcFfrnn9CiBdy/Dw0bwrZt4OCQ\nNwEXQG9UondycqJDhw6sXr2aIUOG8MMPP7Bv374st83qzPVl0tPTef/99zl27BhCCO7evcu5c+do\n1aoVVlZWbNy4kRo1atCmTRtGjBiRZRnbt2/no48+AiAuLg61Ws2vv/4KwOjRoxk8eHCW+7377rsA\nlChRgrZt23LgwIFMib5ChQqcPXs2W216XW+//TajRo2iZcuWWFlZ0axZM3bv3g2Au7s7UVFRODs7\nExsbS4cOHXByctLHDPDkyRM6dOjA+++/T9WqVbOs45NPPmHz5s2ALsEePnxY/+191apVr/zilBOh\noaFZfgHKjfj4eCZPnsyePbqewUKIDF9a3nrrLWbPnk39+vX5+uuvX3g8pILliy++JSnpQ0D3JVal\nKsGsWV/JRJ8HBg0axbZtaaSmXkSlus7Age9QurQXderUyVmBJ09CUBA8eqRL9r/8AkX8y/QblehB\nlzD79OmDi4sL/v7++kvH/9W1a1euX7+e5bpjx45lugrw5ZdfEh8fz8mTJ7GwsGD48OEZbglcvHgR\nBwcH7t69i0ajwdTUNFO5bdq0oU2bNoAueUVGRvLxxx+/sk3PJwohRJaXtSMiIujTp0+W+7do0YLP\nP/8803IvLy9u3bql74wWGRlJmTJlsixjzJgxjBkzBtBd0q74tMeqhYUFzs7OALi4uNCnTx+OHDmi\nT/QqlYp27doRFBTE+PHjX9jG6dOnM336dAAGDRrEoEGDaNy48Qu3f5nSpUtnuOLw4MEDTExMMpzN\nHz9+nEePHunfj6w8Oz7PLr9HRkbStGnTTNs9/35cuHCBu3fvUrt2bX3d27Zt49GjR0ybNg3Q3Vpw\ndXV9rasDUsGQkqIGnr9sbKfvkGoIT5484eHDh3h4eGBubm6wegqCnTt3kJp6DnAD3EhNHUh4+O6c\nJfrff4e2bXXPy3foABs2QBZXdIucPOgjkK/yIuS3335blCpVSmzdujUPItKZOHGiGD9+vBBCiDt3\n7ghXV1cxa9YsIYQQN27cEF5eXuLatWtiwIABYvLkya8s73U745UuXVoMHTpUCCHE/fv3hYeHR551\nzlu5cqVo1aqV0Gq14v79+y/sjCeEEDFPO7HExcWJ6tWriy1btuhjUqvVQgghkpKSRPPmzcWiRYuE\nEEIkJyeLpk2big8//DBbcQ0cOPC1OuMJIYRWqxUKhULfSU6IfzvjHT58WAghxCeffJKpM97QoUNf\nGdfMmTP1x/7KlSvC1dU1Qz1C6DoOvqyz3cCBAzN01tu8ebOoXr26iIuLExUrVhQ7dux4rXZKxhUe\nHi6UypICfhawQyiVviIkJNQgdS1a9K2wsLAVSqWnKFGitPjrr78MUk9B4e5eTsABoZtGTghr6y45\n68C6c6cQ1ta6Qnr1EuLp36XCIje5741M9GvWrBHe3t55EM2/IiMjRe3atUWlSpVEUFCQ6NOnj5g1\na5ZQq9Widu3aYt26dUIIXbLz9/cXO3fufGl5K1eu1H9ReBlvb28xdepUUaNGDeHr65tlD++c0mg0\nYuTIkcLHx0f4+PiI77//Xr9u2bJl4uOPP9a/rly5sqhYsaIoV66cWLx4sX755s2bRaVKlUTVqlWF\nv7+/+PDDD4VWqxVCCLFkyRJhamoqqlWrJgICAkRAQICYM2fOK+MaOHCgOHjw4Cu369y5s/D09BQm\nJibCw8NDBAUF6dcdPXpUVK5cWfj5+YmWLVuK+/fv69epVCrh4OAgLl++nKnMgIAA/ZeapKQk0a1b\nN+Hr6yveeustERYWpt9u7dq1wtPTU9jY2AgnJyfh6ekpLl26lGVbnr1nN2/eFKVKlRJXr14VQuh6\n7nt5eYmoqKhXtlUyvi1btogaNZqKqlUbix9+WGGQOs6cOfP0C8WNp4kvVHh6vmWQugqKX375RVhb\nlxBmZhNF0rhoAAAgAElEQVSFtXUn4etbJfu96zdvFsLcXJfkhwwRIj3dMMEaUG5y3xs5BO6QIUOo\nUKECEydOzKOoJEmSDC80NJTRo/eTlLT66RKBqakVCQmPUCqVeV7ftWvXOH/+PN7e3i8cTyI/nD59\nmt27d+Po6Ejfvn2z17t+zRoYOBA0Gt10swsXQjaeaiooCvQQuPHx8XTt2pUKFSrg7+/PiRMniIuL\no0WLFpQrV46WLVsSHx+v337u3Ln4+flRvnx5wsPD8zSW6Ohoypcvz/Xr1xk1alSeli1JkmRoZcuW\nBY4BCU+X/I6trZP+0da89NNP66hatT6DB/9I48ZdGDducp7X8bpq1KjB5MmTGTFiRPaS/PLl0L+/\nLslPm1Zok3yu5dFVhRfq37+/CAkJEUIIkZaWJuLj48UHH3wg5s2bJ4QQIjg4WH8v9OLFi6Jq1apC\nrVaLmzdvCh8fH6HRaDKUlw8hS5IkFUharVaMGDFOKJWewsGhubCxcRbh4eF5Xk9KSoqwsrIX8OfT\nWwRxQqksJU6fPp3ndRnMggVCf2P/6QBehVlucp9BL90/fvyYatWqcePGjQzLy5cvz8GDB3F1deXu\n3bs0adKEv//+m7lz52JiYqIfbCYoKIiZM2dSt25d/b5y9jpJkt50586dIyYmhqpVq+Lu7p7n5UdH\nR+PrW43k5Hv6Zfb27Vi1agidOnXK8/rylBDwyScwY4bu9ZIlUASu4BbYS/c3b97ExcWFQYMGUb16\ndYYOHUpSUhL37t3D1dUVAFdXV+7d032YoqOj8fT01O/v6elJVFSUIUOUJEkqdAICAmjdurVBkjzo\n/i7b2loB654uOUda2omCP66DEDBpki7Jm5hAaGiRSPK5ZdDn6NPT0zlz5gxLliyhVq1ajBs3juDg\n4AzbvGo406zWzZw5U/97kyZNaNKkSV6FLEmS9Ma7ceMGtrYOxMb2BYZhYSFYuXLlC8fRKBC0Wl1S\nX7YMzMxg7VrolssR9IzowIEDHDhwIE/KMmii9/T0xNPTk1q1agG6QWjmzp2Lm5sbd+/exc3NjZiY\nGEqUKAGAh4dHhkFC7ty5g4eHR6Zyn0/0kiRJUt7RaDQ0bdqOqKhRwHBgDxYWgwgMbGTs0F4sPR0G\nD4YffwRLS/j5Z93AOIXYf09iZ82aleOyDHrp3s3NjVKlSnHlyhUA9uzZQ8WKFWnfvj2rVq0CdCPA\nPbvn06FDB9avX49arebmzZtcvXpVP4KYJEmSZHhRUVHExSUixBjAEmiLqWkAZ86cMXZoWVOroWdP\nXZK3sYHt2wt9ks9rBh8Cd/HixfTp0we1Wo2Pjw+hoaFoNBq6d+9OSEgI3t7e+pnD/P396d69O/7+\n/piZmfHtt99maxY3SZIkKXecnJxIT08A7gCegIr09GsvnNzJqJKT4Z13YMcO3aQ0O3ZAvXrGjqrA\neSMHzJEkSSpo1Go1oaGh3LwZSb16dejYsaPRYgkOXsAnnyxCo2mHuflhOnSoxZo13+fqxCsxMZF3\n3x3Nrl27cHQsztKln9O6deucB/nkCbRvDwcPgrMzhIdDtWo5L6+Ay03uk4lekiTJyDQaDYGBbTh7\nVqBSNcLGZi1jxvRgzpyZRovp0KFDnD17ljJlytCuXbtcX13t0qUv27drSE2dB/yNUtmXY8f25Gzm\nyUePoHVrOHECSpaEPXvA3z9X8RV0MtFLkiQVYlOmTGHevE0IcRkwBe5hbl6Gx48fGmTUO2OwtnYg\nJeU6oJvN0tx8HHPmePL+++9nr6D796FlSzh/HkqXhr174QWzkBYlBfY5ekmSJOnlQkNXEhy8BCHK\noEvyAC4oFBaoVCpjhpanbGwcgFv61+bmN3FwcMheIVFREBioS/LlysGhQ29Eks8tmeglSZKMRKvV\nMm7cdGAl8BewGrgNjMXHx49ixYoZM7w89eWXc1AqO6JQTMfKqhvu7rfo1avX6xdw8yY0agR//w1V\nqujmli9VKttxpKSkkJycnO39CjOZ6CVJkoxk9Oj3SUhQAWWBHcBSoBqwik2bVhapp4769+/Lzp3r\nmTbNhODghpw5c/j1J6j5+29dkr95E2rXhv374enoqq9Lo9HQv/9wbG0dsbNzomvXfqjV6hy0pPCR\n9+glSZKM4NSpU9Sp0wCtdhz/JvkY4F2aN2/E7t3bjBtgQXHunO6efGwsNG4M27aBnV22i5k7dz6f\nfrodlSoMMMXauitjx9Zi7tycD0STn+Q9ekmSpFwKDw/HxyeA4sW96NNnqEHvjx87dozGjYPQagHe\nB7oB/YH3aNKkJjt3bjFY3YXK8ePw9tu6JB8UpHtOPptJPiEhga+++orly39CpXoPsAOUJCePZu/e\nowYJu6CRiV6SpDfeX3/9RadOfbhxYw5xcQfYvDmeAQNGGqy+GTO+IDl5LrohZrsC1VAo+lOsmAUb\nN67H1NT0FSVkX0JCAt26DaREibJUqdKAkydP5nkdeerAAWjeHOLjoXNn+PVXUCqzVURCQgIBAfWZ\nMuUYt25ZAb/r15maHsPbO/MQ60WRwUfGkyRJKuh27dqFRtMbaANASsq3/PZbOYPVp1KlAMWBhcAX\nwExcXBI4fvyQwUag69SpD0ePOpOauovY2D9o2rQtERGn8fLyMkh9ubJ9u27Eu5QU6NMHVq7UTVST\nTatXr+bu3QqkpGwA7gF1USjOYGvrgLX1JRYs+P1VRRQJ8oxekqQ3np2dHWZmt59bchulMvv3gV/X\n0KE9USonA4eBmiiVD1m8+DODzQ6nVqs5eHAXqanfAX5Ab6AF+/fvN0h9ufLzz9Cpky7JDxsGq1fn\nKMmD7oxerX52TF2BXVhaXmDFisFcvnyWUjnotV8YyUQvSdIbr3fv3ri6XsXSshcKxSyUyo588cWn\nBqtvwIB+fPnlB/j5vU+5clNYsmQm3bsbbkpVMzMzzMzM0Z3VAggUiqjX7/WeX1avhu7dIS0NJkzQ\nTTlrkvM01apVKywsVgH7gNtYWX1Ex47v0LVrVxwdHfMs7IJO9rqXJElCd/b3/fffExsbR1BQiwxT\nhBYFc+bM57PPvkelGoyV1Sl8fP7h1KmDWFlZGTs0naVL4b33dL/PmKH7yYPHC8PCwvjf/yaTkBBP\nmzZt+OGHRSizea+/IJBD4EqSJGWDEIL169ezf/9RvL09GDt2NDY2NsYOK0+Fh4czY8YCUlPVjBzZ\nlyFDBrN161b27z+Ep6cbI0aMKDhtnj8fJk369/fsDov7BpCJXpIkKRsmTZrGN9+EoVINxtLyGD4+\nNzl9+veCc3abA7/99htjx07jyZME6tatzu7dv5Oc/DXggFI5ni++mMDIkcOMHWZGQsDMmTB7tu71\nt9/CSMM97VCYyUQvSZL0mtRqNTY29qSn3wZKAAJb24b89NOHdOjQwdjh5cipU6cIDGyLSrUKKIOp\naVs0mlHA+Kdb7KFixRlcuHDEiFH+hxAwcSIsXKi7Dx8aCv37GzuqAis3uU8+XidJ0hslLS0NUABO\nT5coUChKFNrxzyMiIujRoz8q1SAgCACNpgHw/IA/Ksxy2HPdIDQa3f345cvB3BzWrdM9TpcNycnJ\nLF68hCtXImnYsCYDBgwoUkMG56UC9M5LkiQZno2NDQ0aNOX48aGkpk5EoTiGiclxAgOXGju0bLt0\n6RI1azYiObkREAnsBdKAeigU7yOEGeCIUjmbGTOWGDVWvfR0GDgQfvoJrKxg82bd3PLZkJaWRuPG\nrblwwYmUlCasW/cNJ06cZ+nShYaJuZCTl+4lSXrjJCQkMHz4eA4dOoanpwfff/8llStXNnZY2RIT\nE0OFClV5/DgQmI9uMhwPwBa4yOTJ/+POnYekpKgZMqQXrVq1yvMYhBCo1WosLS1fb4fUVOjZUzfK\nna0tbN0KOXi6Yf/+/XToMIHExNPonhKPx9zckwcPorG3t892eYWBHOtekiTpJdLT0zl+/DiHDh0i\nOTkZe3t71q0L4c6dCI4f313okjzA5MmzePKkJqAFQoB26Ka6PY6p6UQuXrzFjz8uZ9OmlTlO8klJ\nSXTu3AdLS1ucnNwJCQnVrwsJCUWpdESptKNmzSbcu3fvJSUBKhV06KBL8o6OsGdPjpK8rigVJibF\n+TeF2WFiYkFKSkqOyivq5KV7SZKKtKSkJBo1CuLq1UcoFFYUK5bM8eN7cXNzM3ZouXLrVjRabS9g\nBnAdGIeu7wFoNM24fj0813UMGTKGHTu0qNX/oFbfZsyYdpQt6421tTVjxkwjJeU4UI7z56fQpUt/\njhzZlXVBCQnQrh0cOgQuLrB7N1StmuO46tevj7n5CBSKrxHibSwsllK5chWDDR9c2MkzekmSirRP\nPgnm0qVSJCb+yZMnfxAd3Y4xYyYbO6wcu3v3LleuXKFp07oolaFAOGCPbprbJCAdS8vvqVevRq7r\nCg/fTWrqHHQdF6uSnDyE3bv3cvToUdLTuwIVAFPS06fzxx+Hsi4kLk43Oc2hQ+DhAb//nqskD+Dk\n5MTRo3tp0GAXnp696NBBRXj4L7Iz3gvIM3pJkoq0ixevk5LSmmfnNWlpbbh06SPjBpUDQgiGDx/L\n6tU/YmbmiIuLDUFBAWzZUhEhBJ6efty9WxKFwoxatWqzcOE3ua7Tyak4cXERQBlAYGkZgYtLXVxd\nXTE3/xW1WgOYAqdwcsriCsm9e9CiBfz1F5QpA3v36v7NA+XKlePQoe15UlZRJxO9JElFWt26Vdm7\ndy3Jyd0AcywtV1GrVu7OKPObEIIRI0YSEvI7Wu0tUlPtSUmZTalSJ0hKSgDA0tKSuLg40tLSKFGi\nRJ6c3S5bNp+OHXuh0fQATmFpGcn9+7707NmTatVWc+5cfYR4CyF2sGrVjxl3/ucf3Zn8lStQvrzu\nnrzHmzEtbEEje91LklSkpaWl0alTb/btO4BCYU7FiuXYuzesUPXOXrbse0aPnkJ6+lhg+tOlkTg5\nNSAu7o5B646IiODTTz/j55/3oVaPw9z8BsWK7ebcuaOcPHmShw8f0rBhQ/z8/P7d6fp1aNYMIiMh\nIAB27YISJQwaZ1EnB8yRJEl6AXNzc7Zt20hUVBTp6el4eXlhkosZ0fLb4cOH+fDDz0hPHwjsBiYB\nlkAYZcv6Grz+GzdusHlzOGr1NqAOaWkQH9+fdevWMX78+Mw7RETozuRjYqBuXd3c8k5OmbeT8o1M\n9JIkFXkKhQJPT09jh5FtBw8epHXrbiQnFwcaA7fRdYBzwtLyFmvWGHZI27Vr1zF06Iekpgp087nr\npKe7kZiYlHmHM2egVSt48ED36FxYGNjZGTRG6dXkpXtJkoqM9PR0fvjhBy5dukbNmlXp27dvoe6J\n3apVV8LD26DrVT8O3aN0F7GyWsnevdupX7++QesvX74Oly9/CmwFLgNfADdQKody9Ohuqj7fe/7o\nUWjTBh4/1v37f/8H1tYGje9NIi/dS5L0xtNqtbRp05UjR56gUrXExmYx+/cfZ8WK3Pc+N5a0tHTA\nHEgGWgHf4uqaxM6dBwgICDB4/enp6YASXYKfCrTGycmMjRvXZkzy+/bpBsNJSoKuXXXD21pYGDw+\n6fUUnhtVkiRJL3HmzBmOHr2ISrUT+JCkpD2sXbuWu3fvGju0HHvvvb6YmIwFlgN2QCRduwYZNMnH\nxsZy7tw5EhIS+N//BmJjMxzYDwSgVKrZuXMjzZs3/3eHbdt0Z/BJSTBggG6CGpnkCxSZ6CVJKhKS\nkpIwNXVBdwYMYIeZmT2JiYnGDCtXTE1NsbDwAQ4CXwFHWbFitcFuX3733Q94eZUjMLAfHh4+VKpU\ngXnz/ke1asE0aLCWbds2ULt27X932LgROnfWjWH/3nuwYgUUpFnyJEBeupckqYioXr06lpbRmJh8\njVbbBjOzlbi7F8Pb29vYoeVYXFwcpqb+/HtO5ktqqoq0tDQs8vis+dq1a4wfP5WUlD9ISfEFDtC5\nczcePLjDqFEjMu8QGgpDhoBWC5MmQXAwFOL+EEWZPKOXJKlIsLOz48iR3dSqtQ1n55YEBl7kwIHf\nCtY87K9p+/btdO8+iB079qHR/IZu+tl4zMwmUbNmozxP8gCXL1/GwqI68OyRvSZotVbExMRk3njJ\nEhg8WJfkZ8+WSb6Ak73uJUmSXiImJoaDBw+iVCpp1arV60/JmkO6R9omoVJ9hEJxHyurL7G1dSIh\n4QF16jRm06ZQShhg8JnLly9TrVpjkpP/ALyAY9jYtOPBgyisrKz+3TA4GKZM0f2+YAFMmJDnsUiZ\n5Sb3yUQvSZL0AufOnSMwMAgh6iPEPcqU0XL8+F6USqXB6ixXrhZXr84FdB3eFIqpTJig5Ysvgg1W\n5zMLFy5m6tSZWFj4kp5+nY0bV9G2bVvdSiFg+nT47DPd2fuyZTBsWLbKT0xMRKPR4ODgYIDoizY5\nH70kSZIBvPvuOBIS5vDkyWYSEw9z9aoHS5YY9nG9tDQ1YKt/LYQtKSlqg9b5zPjxo7ly5Rzbt3/J\nrVuXMib58eN1Sd7UFH78MVtJXqPR0L//MJycSuDi4kGrVp1RqVQGaoX0XzLRS5IkZeH+/fvcvn0b\nqPd0iYKUlLpERkYbtN533+2FldUgdNPPrkOp/Ir+/XsatM7nlSpVigYNGvw7t7tGA0OHwtdf6x6b\n27QJ+vTJVplffbWYn3++THr6PdLS4vj9dzMmTfrYANHn3JEjR+jYsQ9t2/Zk165dxg4nT8lEL0mS\n9B+DB4/A3b0scXGJwGdAOnAPpTKUJk0MNxrd+vUb+eyzYDSaWExNu1Kp0tds3bo+4yNt+SktDfr2\nhZAQ3Sh3YWG6x+myaf/+E6hUQ9GNBWBBSsp7/P77yTwPN6eOHDlCy5adCQtryPbtLenSZRDbtm0z\ndlh5RiZ6SZKk58ycOYvQ0M1oNNfQaq8CEYASMzNvxo3rTteuXQ1S782bNxk8eBQpKQdJS3uARhNK\nTEwUjRs3Nkh9r5SSohvlbv163Xj1O3fqxrHPAV/fUlhY/A7o7jGbmh6ibNlSeRhs7nz55XeoVDOA\nkcBgVKqFBAd/a+yw8kzhe+5EkiTJgBYu/AZoD7g9XfIHYE5CwmOs83Ds9vT0dL7+egknTpynYkUf\n/P3fwty8NsnJz4aWfQeVahT37t3DI7/ncU9Kgk6ddHPIOznpppmtVSvHxc2YMYXffnube/caAdZY\nW19j0aKDeRdvLmm1gn8HWgIwQ6PRGiucPCcTvSRJEnD+/Hl69RpGQkIC8DsQDzgC27C1dcnTJA/Q\nrdsAwsPvolL1JCwsjLJlfyE9/R7wECgO/AmkULx48dcqT6vVcvHiRdLS0qhUqVLOn7V//BjatoUj\nR3RzyO/eDVWq5Kysp5ycnPjzz2Ps37+f9PR0AgMDC1TP+9GjB7FrV2+Sk5WAJUrlRCZM+NLYYeUZ\n+XidJElvvEePHlG2bEXi4+cC+4BjwGOgNHCR0NBvGDhwYJ7VFxUVhY9PFVJTzwG9gb8AFf7+Vbh1\n6y5mZlVJSztJSMgSevXq8cryUlJSaNGiE2fPXsHExIqSJa04fHgXLi4upKen8+TJExwdHV89k9+D\nBxAUBKdPg6cn7N0L5crlRZMLvPDwcObMWUJ6uoZx4wbTtes7xg4pA/kcvSRJUg6lpKTQvXsftm27\nhRCngRTgfWAlJUq4sGhRMD16vDrZZseNGzeoXLkRKlV9wB1YCDzEyqoxn3zyLuXKlaNSpUqULVv2\ntcqbNesz5s07RXLyJsAUc/OJdO78CB8fDz7/fAEKhSleXj7s2fMrZcqUybqQmBho0QIuXgQfH91l\n+0I8fHBRIxO9JElSDnXrNoCwsFuo1beBvwFL4CEWFmWIjr752pfOX8fOnTuZOnUeycnJJCQ8Ijr6\nIXAC8Hm6xVwmTHjEggWfZ6vczp378euvzYCBT5ccpnjxXjx8mPi0fD/gc/z9N3Px4onMBURGQvPm\ncO0a+PvrLte7u+eskZJByAFzJEmSckCr1fLrrxtQq8OAOsDbwFQsLOozevToPE3y69ato3373pw9\n+z/+/juYR4/MsLIyRzcFLIAGa+tDlCnjle2yq1f3x9r6ZyANEJiZrScu7i7QBSgHKICJXLp0Co1G\nk3Hnq1ehUSNdkq9WDQ4elEm+iJFn9JIkvbGEEFhbO5Ca+hfgCazD3PwT3nuvNQsXLnz1Pe3XdObM\nGerUeZv09GnAB0+XHqFUqaEkJDxCiGpotTFUqlScAwd+y/Z4+qmpqbRu3ZUTJ85hYmKFp6c9V678\niVZbEd0ZvSVwCBubLiQmxv6744ULujP5e/egfn347TdwdMyTNhcEp06dYvv2HTg42DNgwAAcC3Hb\ncpP7ZK97SZLeWAqFgqlTpzBvXmtUqlGYm5/HzU3B7Nmz8yzJA0ye/Bnp6XWAhOeWPsbOzpHTpw9y\n9OhRbG1tCQwMzNFse5aWluzdG8aVK1dQq9VUqFCBgIAGXLyYBlRDd1a/h6+//vrfnU6fhpYtIS4O\nmjaFLVvA1vYFNRQ+W7dupWfPIaSkDMLcPIIFC5Zy/vwxnJycjB1a/hOFTCEMWZKkAm79+vWiX79h\nYvLkaeLhw4e5KissLEyUKuUvHBxKiu7dB4rNmzcLX98aApYLcBEwQ8AiYWJSXPz888951ILM7ty5\nI6pXbyxMTEyFnV1xsWLFin9XHjokhL29ECBEu3ZCJCfnef33798Xbdt2E2XLVhOdO/cV0dHReV7H\ny3h7VxYQLnQD9QthadlHzJ8/P19jyEu5yX3y0r0kSW+U06dP8+mnC0lMTGbIkB706NE9z8o+c+YM\nDRsGkZy8FiiJQtEcU1NXTE3TSE3VAPOBdZia7mPixEHMmzc3z+p+ESFExqsTe/ZAx46gUkH37rBm\nDZibv7iAHLh79y7e3pVJTW0LDAF+pXTp7fz995mMU94aUPHiXsTF7edZR0eFYgZTpmj57LNP8qX+\nvCY740mSJL2Gv/76i8DAIH79tTZ79rzD4MGTWbFiZZ6Vv2vXLtTq/uimmN2EEE1JTz9LauoFwAdz\n84G4up5k/vyp2UrySUlJDB06Bj+/mjRt2oHLly+/9r4ZknxYmG4wHJUKBg2CtWvzPMkDDBgwktRU\nE2AF0BCYz927ppw+fTrP63qR9u3bYm09EfgHOIyV1XLatAnKt/oLEnmPXpKkN8by5StJShoNjAFA\npSpJcPAkBg8emCflOzg4YGFxmuRk0CWYQHQ93gFm4OU1kmvXsp/s3nmnHwcPWpCS8g3Xrx+nXr2m\nXL587t8Z5v4jPj6egwcPYm5uzttvv60b1W/9et0ENRoNjB4NX30FJq93rqdSqYiOjsbd3R2lUvnK\n7S9fvg5oADVgBWjRaBIxN8CXihdZuvRLtNpxbNlSCxsbexYu/JoGDRrkW/0FiTyjlyTpjaHVasn4\nZ88kT28F9uvXDze3v7Gy6gncBb5EN8qeCkvLxTRqVCfbZapUKvbs2U5KymqgDkKMJS2tJvv3789y\n+8jISN56K4B+/b6hZ885VKlSD9XixdC7ty7JT5mim3L2NZP8zp07KVHCi4CAFri4eLJlS9gr9wkI\nqIxC4QZ0AlYC7+Dqakn16tVft9m5Zm1tzerV3/H48V2io6/k6S2aQidPegnko0IYsiRJBcTZs2eF\nUuksYJmAn4VS6SuWLv0uT+t4/PixWLBggahQobowMXEU4CbAVtSp87ZISEjIdnmpqanCzMxSwIOn\nHcu0wta2sfjll1+y3L51627C1HS2ftsJpnWFvkfaZ59lq+74+HhhY1NcwKGnRZwQSmVxcf/+/Zfu\nd/fuXeHjU0WYm7sJExMX4e1dQTx69ChbdUsZ5Sb3yUv3kiS9MQICAti7dyszZy4gKSmZIUM+ZsCA\nfnlah729PTY2NkRG2qDVRgNWmJlNw97+EnZ2dtkuz8LCgpEjRxMS0gqVaigWFscpWfIxrf4zZey1\na9do3bor165FAqMAmMJc5miO6zb4+msYMyZbdd+4cQNTU3d099kBamNu7sPVq1dfeNsAwNXVlYiI\nP4iIiMDCwoIKFSrk6eOKUjbl4ReOfFEIQ5Yk6SW++WaZKFmynHBxKSOmTZslNBqNsUPKtWHDRgv4\nUn8iDRdEyZLlclyeVqsV338fInr0GCymTJku4uPjM60vU6aSUCgWChgvoIuYwwdCgNCA2NWjV47q\nvX//vrCychRw+Wk7bggrq2Lizp07OW5Lbh08eFD4+VUXTk6eokuXvuLx48dGiyU/5Sb3FbqsKRO9\nJBUdGzZsFEqlj4CTAi4IpbKmmDv3C2OHlWuLFy8RSmUzASkChDA1/VS8/Xb7XJWp0WiESqXKtDwy\nMlK0a9ddKBSWAoRQ8EQsoowQINQgvm3cTKSnp+e43h9+CBXW1s7CwaGpsLZ2EYsXL815I3Lp6tWr\nwsbGWcAvAm4KS8sBomXLzkaLJz8V6ERfunRpUblyZREQECBq1aolhBDi4cOHonnz5sLPz0+0aNEi\nw72bOXPmCF9fX/HWW2+JXbt2ZQ5YJnpJKjI6deorIOS5M989okqVRsYOK9fS0tJEUFAXYWNTWtjb\nBwhPz3IiMjIyx+X98MMKYWVlJ0xNLUSVKvVFVFSUEEKIuLg44eJSWpiYzBBgI0w4L1YwUAgQKSjE\nqY8/zpP23Lx5U+zatUtcv349T8rLqWXLlglr60HPfV5UwtTUPFdfZAqL3OQ+g9+jVygUHDhwgGLF\niumXBQcH06JFCyZNmsS8efMIDg4mODiYiIgINmzYQEREBFFRUTRv3pwrV65g8pq9QyVJKlyKFbPH\nxOQ2Wu2zJZE4OtobM6Q8YWZmxvbt/8fFixdRqVRUrlxZ94hbDpw8eZIxYz4iJeUPwI+LF2fQuXM/\nTpzYy549e0hJqYhWOxNzyvAjtelBKkkoWNi4BR/NnJkn7fH29sa7AExZa2+v+7yAQPfY4j9YWNjI\nHPEK+XJ0xH8eXwkLC2PAgAEADBgwgF9//RWALVu2/D979xkfVfE1cPy3NduSUNIoodfQQeklgBTp\nHRA/SjQAACAASURBVEUQRaog2MEOSlP0ryKK8AARRDoISBEEDIQivQQQQq8hEAglfct5Xuwag4Ak\n2U1C8H5f6d07M2fWjzl7507h2WefRafTUaJECcqUKcOuXbtyIkSFQpEL3n33dby9v0erfQW1eiRm\n80g+/fR9t+o8efIkn376KV988QWXLl3yUKSZp1KpqFy5MrVr185ykgfYsWMHdnsXoDygxm5/h717\ntwKg0WiAVLxIZilL6EkKt4CDn07kvfBfH7sJcJ06daJYsVsYDF2BjzGZWvLpp+Meu356Wo480T/1\n1FNoNBoGDRrEgAEDiImJITAwEHDOzoyJiQHg8uXL1K1bN61s0aJFc/V/VIVCkb1Kly7NoUO7mD17\nDlarjZ49w6lUqVKW6rJarXTr9hwrV64C+qDRWBk79kn27t1KqVKlPBt4DipUqBBa7QJSUmw4/2Tv\nokCBQgC0aNGCwj6j+C6+LM3kItfR8k27jox+++1cjTm7GI1Gdu8OZ8aMGVy+HEPz5tNp2bJlbof1\nyMv2RL9t2zYKFSrEtWvXaNGiBRUqVLjrc5VK9a+/xu732eh0w1GhoaGEhoZ6KlyFQpHDihUrxgcf\nuPcUD/Dhh2NZtWonzv3kh2K3w61bH/DJJ5MIC5vqdv25pWvXrkybNpddu2oDFbHb1zFnzlwAvO12\nIgv5ort0gut6AyuGDuODSRNzN+BsZjabGTFiRG6Hke3Cw8MJDw/3SF3ZnugLFXL+8vT396dz587s\n2rWLwMBArly5QlBQENHR0QQEBABQpEgRLly4kFb24sWLFClS5J46R3vovZNCoXh8rFq1EYcjACib\ndk2kHNeuncxynadOnaJ37yGcPBlFpUqV+fHHqQQHB3sg2gc7ceIEx44do0yZMlSsWBGNRsP69T8T\nFhbGhx9+xpUrcfTuPZBl076k8bhx6Pbvh+BgCm7cSL+yZR/egCJP+OdD7JgxY7JcV7a+o09MTOTO\nnTuA81CG9evXU6VKFTp06MDs2bMBmD17Np06dQKgQ4cOLFiwgNTUVM6cOcOJEyeoXbt2doaoUCge\nE4GBfkAw8CFwCjiCVjuG7t3bZKm+hIQEGjRowa5drYmN3UhEhC/ly9ehR48X6Nv3JQICyhAcXIkZ\nM2Z5rA/Tps2gWrUG9O49lVq1mjJp0leAc2Tzk0++4MqVlxFJQX99EgHde8L+/VCmDGzdCkqSVzyI\n5yb/3+v06dNSrVo1qVatmlSqVEnGjx8vIs7ldc2bN7/v8rpx48ZJ6dKlpXz58vLrr7/eU2c2h6xQ\nKLLJnTt37rsO3FMiIyPFYvEXjaaGgK+oVBZ5990PxeFwZKm+7du3i49PLdcyrvkCRV1LAasLlBLY\nKbBF9PpgWbx4idvxx8bGujanOeFq84IYDAXl7NmzEh0dLQaDn4BIcc7ISUqJgNwKDhbJ4XPeFbnD\nndynnEevUCiyVUJCAp079+b339ch4qB//8F8993/smVJ1IULF1i1ahVarZYuXbpQsGDBLNcVGRlJ\n3brtSEyMApoCHwFlgDrAj8DTrjt/oHXr1axdu9it2CMjI2nQoCd37hxNu+brW49ffvmMJ554gnz5\n/CmRuoINvEAwF9mn9sK26mdqP/30v9SqeFwo59ErFIpH1uuvv0tEhBc2203s9iv8+OMfTJv2f9nS\nVnBwMEOGDGHAgAFuJXmAypUr06xZXUymlsBV4BjQCNAD0enuvIRO5/6f0pIlSwKxwAbXlR3YbCcp\nX748RqORWa+OIIKWBHOR7WoTkzt05cnWefd8davVypIlS/j+++85evTowwsoskx5olcoFNmqfPna\nREV9DdRzXZlB9+7bWLQoLDfDyhC73U5YWBhhYT+yffte4DvgFZzzmIcBycAU9u6N8MgRrOHh4XTs\n2JPUVCE11Ur+/PmpX78OP7zclwK9ekFcHBcqVODI2LG06tIlz64ft1qtNGnShsjIRByOisBK5s+f\nQYcOHXI7tEeWO7lPOb1OoVBki6SkJL799jsSE+NRqSIQqQcIev02SpUqmtvhZYhGo6F///4EBATQ\ns+fXJCc/D5iBF4H/odNBWNh0j52zHhoaSkTEb9Su3RSH4y2uX29P/JpP8FrdFhwO6NCB4IULCTYY\nPNJeblm0aBGHDqWSkBCBc2B5Ky+99BzXrimJPjsoiV6hUHhcamoqDRq05M8//UhO7gB8gl6/Hi+v\nFIKC4nnnna9yO8RMCQgIQKM5ByQBXYHK6HQ1iI6+8MBXBPHx8fTpM5CtW/8gKKgQ06ZNon79+v/a\nzvXr12ncuAUpKcWBd2nJOn62r8KEg/j27bEsWQI6nae7l+OuXr2K1VqVv98eV+fmzZjcDOmxpryj\nVygUHrdx40ZOnEghOXkpMBHYg822hbCwVzl4cDu+vr65HWKm1KlThzZtGmCx1MfL62VMppaMHz/+\ngUk+KSmJ4sWrsHx5IrGxazh8eDgtWnTk9OnTiAg2m+2+5X755RdSUioBCXRiCb/QHhNJzFLrufPd\nd49Fkgdo1KgRGs1i4CCQilb7IXXrNs3tsB5byhO9QqHwuMTERFSqQP5+liiDRqPnqaeecmvf99yi\nUqlYuPAHfvnlF86dO0fNms/RoEGDB97/4YdjuXHjInAY51B/BVJTV/HRR2NYtmwlycnx1K3blBUr\n5uHn55dWzuFwoFL50YvrzKYHWoSv8GN3zw70K5o3XndkxBNPPMG0aV/w8svNSUy8xRNPhLJ06U+5\nHdY9oqKiWLJkKVqthl69elE0j/43UCbjKRQKj7t69SrlylXj1q2PgYbo9V9Rs+YpduzY8NCyj4PG\njdsTEREO7Me5JE9QqWqg010hNXUjUBad7k0aNjzLpk0r08pdvXqVCSXL80XiTdTAOJUvv9avweYt\nGx/bE9rsdrvrcJ5Hy759+2jcuBXJyc+hVidjMq1g375tuXZugrK8TqFQPFICAgKIiFjPE0/MJyio\nI+3aJbFmjXvrzPOSKlXKotFUBVoBnwI90OlO43D0AioBeqzW0WzfHn5XuYCffuJLV5L/NrgsjjGj\nCN+84bFN8sAjmeQB3nrrYxISxmK3f4XV+j137gxk7NjPczusLFGG7hUKRbaoUqUKu3dvyu0wcsW4\ncR8SHt6SM2fspKRMQKXS4O3ty507ewAHzmes/RQo4DzFExEYOxY+/ND571OmMHTo0FyKPvdYrVaW\nLl3KlStXaNSoEbVq1cq1WOLibgF/P707HKW5du1ErsXjjsf3Z6JCoVBkwu3bt9mxYwcnTrj/xzxf\nvnzs37+VMWOGotNZsNvnc/36bGy2o3h51cNk6ofJ9AyzZn3jTPIjRzqTvFoNYWHwH0zyNpuNpk3b\n0b//t4wadZLGjdvx44+5996+e/e2mEwfAFHAIUym8fTs2S7X4nGLe7vv5rw8GLJCoXjE7du3T/Ln\nLyw+Pk+I0Rgogwe/muU98tPr1Km3wAzX3vUisFJKlqwk06ZNk2PHjonY7SJDhjg/1GpFFi3yQG/y\npiVLlojFUlfA5vquDorFUtAj/x2ywm63y8iRH0j+/EXFz6+4TJr0Za7E8Rd3cp8ydK9QKNyyf/9+\nNm/ejJ+fHz169ECv1+d2SA8VHR3N+PGfEx0dS/v2TzF69GfExU0CegG3+PHH+nTo8CtPu7mPvNls\nQKW6zt9zqG5RpEhxBg4cCDYbvPgizJkDXl6wdCm0betmz/Ku2NhYHI4Q4K939hVJTLyF3W5Hq835\nVKVWq5k48WMmTvw4x9v2NGXWvUKhyLLFi5fQt+9QHI7uaLVHqVDBzvbtvz3Syf7GjRuEhNTi+vVO\n2GyVMZm+JCnpOCK3AefSP73+FSZOLMVrr73mVluRkZHUq9eMhISXASMm0/9YvXoRofXrQ69ezuRu\nNsPKldCsmfudy8OOHj3Kk0+Gkpi4DKiJVvsRNWvuY+fOjbkd2iNBmXWvUChyxeDBr5KUtJKUlCkk\nJGzg2DENixYtyu2w/tWSJUu4c+dJbLYvgZdITFwJmID5rjuuo9Oto3Llym63VaVKFXbt2sywYfEM\nGhTN77+vIrROHejUyZnkfX3ht9/+80keICQkhAULZlKwYC+02gLUrn2IlSvn5XZYjwVl6F6hUGTZ\n7duxOJeLAaix2UK4fv16bob0UFarFYfDku6KNxqNlXz5xpCS8gWpqdEMHjyEFi1aeKS9kJAQvvnm\nC+e/3LkDbdpAeDj4+cH69VCjhkfayYz4+HgiIiJQqVQ0adLkkdnEqH379sTGts/tMB47yhO9QqHI\nsgYNnkKnGwXEAztRqxfTpEmTLNUlIpw/f56oqCjsdrtH40yvffv26HSrgalABEZjL/r0eYHz54+x\ndet8Tp2K5PPPx91TzuFwcODAAXbu3ElKSspdny1YsJDKlRtQsWJdpk+fcf+G4+KgRQsID0cKFeKd\n+k0o3LYX1as3Ztu2bZ7v6ANER0dToUJNevacSI8en1C5cu1H/seZwk2emQ+Yc/JgyArFYys2Nlaa\nNm0nWq1BChQoIosWLc5SPVarVTp2fFYMBn8xm4tLSMiTcu3aNQ9H+7cDBw5IaGh7CQmpJ2+99b6k\npqb+6/1JSUnSsGErMZtLibd3FSlZsrJER0eLiMiKFSvEZAoWWCOwUUymsjJr1g93VxATI1KtmgiI\no3hxaVa8okBtgR0Cc8VgKCCHDx++p90//vhDRo16T8aNGy8xMTEe6fszz/QTrXaka2a7Q3S6oTJo\n0AiP1K3IPu7kvjyXNZVEr1A8fr788msxmZoJJLmSzwjp1u35LNVltVrlzJkzcuvWLRERmTkzTAoX\nLi9+fsXl9dffEZvNluk6P/lkvBgMHQSsAg7RakdKp07PiYhI27bPCMxKt4RuhVSv3kjat39GKldu\nIO88P0Ds5cs7PyxXTtbPnClgETiVrsxwGTt23F1trlq1SozGAIEPRafrLwEBxeXKlStZ+k7Se+KJ\n5gK/pmt7kTRv3tnteh/k9u3bEh4eLnv37s21pXKPA3dynzJ0r1Aoct3u3ZEkJnYHDIAKq7U3e/ce\nynQ9x44do1ixClSq1Ah//yK89NJAXnnlIy5f/oHY2HV8/30EH31077D8wxw6FEVycnuc05pU2Gyd\nOHLkOOBcQgdx6e6+yJEjkaxZE0L84WEM+HEe6uPHkcqV+bxDV/p9NNHVz/RlYvHyunulwquvfkhS\n0g/AGKzW/+PGjdZMnTot07H/U+PGtTEYvgdSgESMxhk0bvyk2/Xez/HjxylVqjIdOoyiceNutGvX\nI1tfyyjuT0n0CoUi11WpUhajcQ3gPL5Vo1lJxYrlMl1P+/bPcOXKmyQmXiA19SizZy8jMfFNoC5Q\nnsTEz1i06JdM11urViWMxiU4k6Og18+jRg3nrPxRo4ZjNk8AxgKfode/g05XgzL27kTwJiUlgd0q\nNcOrPsFH323n4sUhrn52A74FXkWj+YU+ffrc1WZCQjwQnPbvNlsxbt+Oz3Ts/zRu3IeEhqrR6/3R\n6QJo0yaAd9550+16/+n06dN07vw816+/ye3bO0hI+JPw8KuEhYV5vC3FQ3hwZCFH5MGQFQrFQyQn\nJ7vegZcRH5+aEhxcQS5evJipOmw2m6hU6nQ7q4loNDVEpRog0EqgkEBlCQmpnen4UlNTpXXrLmI0\nBomXV4CYTEWkefOOsmXLFhEROXjwoAwc+Ir06/eyfPHFF1LfVF1i8BcBCaeB5NcYRK+3CMS4Yvuf\ngE5UqnxisfhLRETEPW0OH/62mEzNBY4JbBKTqZBs3rw5wzFbrVYZM2a8NGzYVnr3HnDP93njxg2J\ni4vL9HfxMA6HQ4YOfUMMBn8BH4Ez6V4TjJU33xzp8Tb/C9zJfXkuayqJXqF4PNntdtm7d69s375d\nEhMTs1SHv39xgcUCMwW+Er2+uKhU3gIfCZwXmCI+PkFp7+8zw+FwyOTJk8VgKCrwk8B0MZn8Zfv2\n7XfdlxQeLjfVGhGQtVSRgsb60rfvIDEafV0xOJOewdBFJk6c+MA5A6mpqTJs2Bvi719SihevLAsX\nLpJbt27JoUOH5MaNGw+Nt3fv/q55D8tFqx0lgYElsyWxpxcTEyOtW7cXjaaEQJxAW4EPBBwCN8Vs\nrik//fRTtsbwuFISvUKhUIjIzz//LCqVRaCNQE/Ras1iMAS7Eo0zwfr61svUk3F6tWo1E1iR7gn1\nS3n22Zf+vuH330XMZhGQg6XLSpe2PeV///tabDabjBz5gZjNNQV+Eo3mHfHzC5arV69muO21a9eK\n2VxQvL0risGQT+bOnffAe1NSUkSj0QvcTovVYnlaFi5cmKV+Z8SdO3ckOLi8qNWNBYa42r0gUEnA\nT7y88kn//sOUCXlZ5E7uUzbMUSgUj40tW3ag0fTFZpsCgM32GXb7x8BtwBdIwWaLxtvbO1P1bt68\nmd9+20hMTAygSvdJAlFRR5k8eTI9fXwIHDIEkpPhueeo+sMPLE23R/uECWMoXrwoK1euoHBhP8aM\n2Y6/v3+G2o+Pj6dbt94kJKwAGgBHGDCgCU2aNKJo0aIZ7EX2bh++YcMGbt4sisMxEhgG3ACKAq8R\nHDyJnTt/p1ChQtnWvuLBlESvUCgeG5cuXcNmq5fuSkN8fApgs4WSkNAZs/k3mjWrQ/Xq1TNcZ1jY\nbIYNe4/ExJfQar1RqV5C5GvgIjCBw4fbs/2NlQy2ufZkHzgQpk51HjmbjkqlYsiQgQwZMjDT/Tp/\n/jxqdUGcSR6gEnp9CCdOnLhvotfr9fTs2YflyzuTmDgcrXYnZvOftGrVKtNtZ5TzR4QGaAF0AcoB\nFgoUsLFq1Rolyeci5VAbhUKRI5KTk/nyy685fPgkdepUY+jQIWg0mocXzIQff/yJwYMnkJi4CvDF\naOzFoEHVqFu3BgcOHKJ8+bL06dMnU+0WKFCEuLhVQA2cM+6fpFQpDfHxt7l8uR3POaoQxotocLC4\nWGm6nz0BKtXDqs2U27dvExRUnKSk34HqwGmMxtr8+edeihcvft8yNpuNceM+47fftlGiRGE+/XQ0\nRYoU8Whc6d26dYsKFWpy7dqz2O0N8PKaRIMGBlauXIzZbM62dv8r3Ml9SqJXKBTZKiEhgXfeGU1Y\n2HySkqpht7fHZFpAmzbFWLx4jkfbEhHGjBnPZ59Nwmaz0qNHL2bN+tat0/QMBm9SUs4D+QHQ64cx\nblwJtm49QKEVGqbi7MNonmdZ5VMcitz6r/WdPHmSAwcOEBwcTJ06dTIcx8KFi+nXbwg6XTlSU6OY\nNGkcQ4cOynK/3HHgwAFmzvwRtVrFgAEvpB0AdOnSJV5//X3Onr1E06Z1+fjj9x/pkwzzEiXRKxSK\nR5LD4aBGjYYcOWLCbj8LHMc5vJuIwVCMkycPZstT5l9/I1QeeLLu1KkXv/4qpKRMBDagUr0OxDNK\n68V4axIAb/IBU00RvP56Mz755IMH1rVgwSL69RuKTtcQu/0Afft24dtvv8hwLNHR0Zw4cYKSJUsS\nHBz88ALZICIigtatu5CYOBywYzZ/S0TEemrkwuE8/yVu5b6szwHMHXkwZIXiP+vFFwcJFBD4XeDJ\ndLPV7WIyFZVTp07ldogPdefOHenZ80XJl6+waDT5RMX/5CM++KsjMlxnFqMxnwwcOFysVusD60lN\nTRWDwUfggKvoTTGbS8gff/yR6ZhsNpv83//9n7z66psSFhYmdrvdnS5miN1ul8GDX3WtjZ9218qD\nzp17Z3v7/3Xu5D5lZzyFQpHm2rVr7NmzxyOnme3du5f581fi3O61JnATGAPsRasdTqlSRShRooTb\n7TgcDs6ePcvVq1fdrut+LBYLCxbM4tixfWg1KiZxkdF8gh01gww1CF34I4mJcUyb9jVa7YPnN8fF\nxeFc6FTNdcUXjaY658+fz1Q8IkKXLr0ZMWIOX31VkGHDptG794AMlY2MjKRjx140atSOqVOnZ+oJ\nccqU75gzZwdQB0i/WiCA+PikTPVBkcM89nMjh+TBkBWKPOGHH34UozG/+PhUF5OpgCxb9rNb9S1d\nulS8vdsLtBDoKfB/AmVFp/OXLl16S2xsrNsxnzt3ToKCSotG4ydarbf07t0/255ukxMTZbpaKwKS\ngk66ME/M5rKydevWDJW32+0SGFhSYLbrSfigmEz+EhUVlak4Dh8+7DotL8lVT7wYDP5y5syZfy13\n4sQJsVj8RaX6UmCZmExVZOzYTx/a3r59+6Ro0fKug3jCBH4QKCewxbVjX0lZuHBRpvqgyDx3cl+e\ny5pKolcoPO/SpUtiNBYQOOJKHnvEZCqQpZ3Url69Kl269JFixUJEo/EV2CUwSqC2GAwF5fr16x6J\nOSUlRXx8gl2bszgE7ohO94RMn/5/HqlfxHkM78yZM2XmtGmS2K2bCEgiSCevVmKxVJEePV7I1AYw\nBw8elMDAkuLllV8MBh+ZPz/zG9j88ccf4uNTI93QuYjFUk4iIyP/tdyYMR+LRvNqunKHxN+/5L+W\niY+PlwIFigjME3hb4CXXd/29QEkxmQrLjBmzMt0HRea5k/uUdfQKhYJTp06h15cnKSnEdaUWGk0Q\n58+fJ1++fBmux2az0bjx05w61QirNQyVahwqVSMMhnyYzV6sW7eeAgUKuB2vzWajV6++3L6dAAzG\nuYmNBau1D9u27WHAgP5ut3HhwgVq1WqILeEJwlJ2YbRfxGE2c/6LL2glwoBixXj66aczNeGvatWq\nXL58ktjYWPLnz49Op8t0XFWqVMFsvk18/CQcjs5oNPMpWFBDuXL/fgiQM870Q/WOh8Z+4sQJrNZ8\nwLNAK6AxUA+TyQ+DIZWdOzdTpkyZTPdBkbOUd/QKhYJSpUqRmnocOOa6sg+bLZpixYplqp5jx45x\n8eJNrNb/AbURWY7ZXJolS2Zx5cppatas6ZF4R478kF9+OQhYgF9dV+3ASsqWzXjMEyZMxNs7EIPB\nl+7d+5KQkJD22fvvjyPpek/mJSbQ0X6ROAyMrNmAY0FBJCUlYTKZsjSrX61WExAQkKUkD2Aymdi6\ndT11627Ez+8pGjbcSUTEuocuY+vV61mMxnmoVJ8DSzCZnuO114b8a5mAgABSUy8DV4ECwFp0uj+Z\nMKElx48fUJJ8XuG5gYWckQdDVijyhFmzZovBkF98fGqKyVRAFi9emuk6oqKixGAIEkh0DQ+nitlc\nQg4ePOjRWAMDywhsFvATCBKoJ1BSvL0LS3JycobqeP31N10rAvYKXBOttpP06tU/7fP2TdpJOBVF\nQGLwl6p8IwUKlBCLpbro9a+IyVRSPv54okf7ld0OHz4snTv3ltDQDjJt2owMvXZ4//2PxWQqISbT\nS2I2l5Y33ng3ByJV/JM7uU9ZR69QKNLExMRw7tw5SpUqhZ+fX6bKXr16lUaNWhMVFYlzsLAzRmMC\ntWs72LTpF9Rqzw0glixZjbNnvwL8gFeAQ5QoEcSePREULFjwoeXj4uLw9y+C3f42MNp19TT58jUh\nLu4C3LjBlRo1CDp/nosU4imWcc4wFLs9Bqs1CjAB0ej15YiJuZCp1xt50datWzly5Ajly5cnNDQ0\nt8P5T3In9ylD9wqFIk1gYCC1a9fOdJK32WxUqFCHqKgngSTgOGr1Zp55JpB165Z5NMkDfPrp+xiN\nzwFr0GqrUrCgme3bN2YoyYNz4xmt1gxEpbt6DJPJDDExEBpK0PnzxPr40lwXx2ldM0JDi2A0lseZ\n5AEKodXm4+bNmx7t26OoYcOGDBo0SEnyeZQyGU+hULht+fLlxMXFAh/h/LNSAoejH8HBOry8vDze\nXo8e3QkI8GfJkpX4+uZj6NCdmTo0pUSJEuj1KlJSdgKdcZ6yFsbUdz+Fxo0hKgoqVMBvwwaOFS4M\nQGxsLKVLVwaWAy1Rqf6PAgVMnD59mrlz5xIYGEifPn0wGAwe769C4Q4l0SsUCrc5j2/1BXYBnQAH\nsIVChZ7LtjZDQ0Oz/IRpMplYu/Zn2rbtQmLiRlQqGzPfHUmHSZPg3DmoXh3WrYOAgLRDaf39/Vm3\nbjk9e/bj8uUeVKhQkx49nqd9+74kJz+HwbCV77//kR07Nij7u/+DiLBt2zYuXbpEzZo1KVu2bG6H\n9J+ivKNXKBRu279/P/XqNSclRQW0BI5jMkVz48bZbHmivx+bzcbq1auJi4ujUaNGlC5dOu2z3377\njZ9/Xk3+/D4MHz6UwMDAtDJXr17F/9o1dE8/DdHRULcurFkD+fP/a3sigtmcn6SkP4AKgGCxNGHW\nrFfo3r17Nvb0b8uXL2fgwFe5dSuWxo2fYtGiMPI/JO6cJiK8+OLLLFmyAY2mGlbrZubM+Z5u3brm\ndmh5irLXvUKhyHU//TRfjEZfUanUUqpUiJw7dy7H2k5NTZV69Z4Si6WOmM3PicnkJxs2bBARkZde\nGihQUGCSqFSDxN+/mMTExPxdeO9eET8/5y4yoaEit29nqE2r1SpqtVYgJW0TGpPpBZk+fXp2dPEu\nDodDFi9eLF5efgJbBeJErx8kzZt3yPa2M2vz5s1iNpcVuOP6nvaK0eibI/vzP07cyX15LmsqiV6h\neHQ5HA5JTU3N0Tbj4+OlevXaArUF7K5kslaKFq0gGzduFPAV2J6WjNXqPjJp0iRn4W3bRHx9nR88\n/bRYb9+Wd98dLRUq1JEGDVrLrl277mkvJSUlbVlao0atRacbInBFYK2YTH5y/PjxbO2vzWaTdu16\niE6XT2BAup3ubotWa8jWtrNi7ty5YrH0SBenQ3Q6s9y8eTO3Q8tT3Ml9yqx7hULhMSqVKssbwWTV\nwIGvEhmZDDTi74VETxIbe5nVq9cBOiAg7X6HI4iEhETYtAlatoRbt6BrV1i+nFffGc1XX/3OsWOf\ns21bD5o2bcOJEycAuH79Og0btsJotGA0+jBlylSWL/+JZs1iMJsrERz8OitWzH/oDnXumjlzJps2\nxWC1fgGc5u/d7o7h7Z2xVQc5qVatWtjtvwORAKhU0wkKKoqPj0/uBvZf4sEfHDkiD4asUOSq2UZO\nXwAAIABJREFUpKQk6ddvqPj7l5QyZWrKr7/+mtsh3eXOnTsyePCrUr16E3nmmX5y5cqVTJX38ysh\n8JNAUYEoAZuo1cMlNLSdjB8/QdTqqgLNBfYLfCfgI520RklWqZyPmM8/L+I6XtZi8Rc4l/b0qdMN\nk88++0xERFq16iI63csCqQInxGQqJps2bfL49/Eww4e/ITBRIFmgvqtvQ8RoDJQFCzK/d35OmDt3\nnhgMPqLX+0rRouXk6NGjuR1SnuNO7stzWVNJ9ApF5vTuPUAMhg4CxwVWidHoJwcOHMjtsETEOdTf\noEFL8fLqJbBBdLo3pXjxEElMTMxwHRUqPCmwzHXQikVAK8HBFSQmJkZu3LghRYuWE42mskBhAYv0\noLek4jyFboaXSeLSHbKTP38RgcNpid7Lq6989dVXIiJisfgJRKd9plK9I6NHj/H4d/IwYWFhYjLV\nFYgXSBSVqqOULh0ie/bsyfFYMsNqtUpsbGymDgFS/M2d3KcM3SsUj7nly5eTnPwdUA5oi9X6PGvX\nrs3tsAC4dOkSe/fuJyVlNtAcq/Uzbtwws3PnzgzX8f33kzCZBmIw7MNkakSpUhU4cmQXAQEB5M+f\nn8jInXz99WBef/0ZBukNzGMeOmx8xlu84VWNg5GRaXW9995bmEydgeloNG/h7b2JZ599FgA/vyBg\nj+tOB0bjPgoVCvLYd5FRzz//PJ06VcJgKIHFUpXixU8SHr6OWrVqpd1z9epVXnhhCA0btuW998aQ\nmpqa43H+k1arpWDBglk6H0DhHmUdvULxmDOZLMTHXwKKAKDVXsRiKZm7QbloNBpE7ICNv/8cpaLR\naO57v81mY926dWlL6IoXL06TJk3Yv38b69evx2KpR/fu3TGbzWll8uXLx9ChQ7k9fjw+qbEAfMDH\njOV1TLaKdy1He+ONEQQHF2bp0rUEBORn1KgdBAQ43+/PmjWZdu16oFI9jUp1ivLltfTt2zdD/YyO\njmbEiJFcvHiNli0b8t57b2d5LoNareann2Zw/vyHxMfHU7Zs2bvqSkhI4Mknm3D58tPYbIPYt28a\nhw/3ZcWK+VlqT/EY8ODIQo7IgyErFLnqhx/miMlUROAT0eufl6JFy2XpnPns4HA4pG3b7mI0Pi0w\nX7y8XpBKlWpLSkrKPfempKS4ltA9KRZLTzGb/WTz5s0Za2jChLTD20fqA0SjeVvM5lrSs+eLmRpK\nPnnypMycOVOWLl163xjv59ixY6LR/DVDfoloNE2lc+fnMtxmZq1Zs0a8vRulm+WeKDqd+ZH5b67I\nGndyn/JEr1A8hmJjYzl48CBBQUH07duH4sWDWb16HQULhjBo0Fe5eghLREQE3377A2q1ihEjBrBs\n2VwmTvycbduWEhJSijFjvr7vznJz587l4EEHiYk7AA2wkr59h3LmTOQ996YRgQ8+gHHjQKVCpk6l\nYZEi+Bw6RNmyI+nWrVumhpJLly5910Y8GdGlSy/s9jLANECF3d6GlSsLcvPmzfv+d1ixYgVjx36D\n3W5nxIh+9O3bJ1PtyT2bqihD5f95nvu9kTPyYMgKRY7asmWLWCz+4uvbWIzGwjJo0IhHZgLUxo0b\nxWQKEJgs8KWYTH6ybdu2DJX95JNPRK0ele5JNUZMpgIPLuBwiIwY4bxZoxGZO9dDvcgci6WgQMN0\ncSeLWm2SGzdu3HPv2rVrxWgs5JpcuEpMppIyZ07m4o6Pj5dixSqITveawHIxGttK+/Y9PdUdRS5x\nJ/fluaypJHqF4t/5+xcXWO1KKrfEbC4vv/32W6bquHnzphw9elTi4+M9GlvTph0FfkiX9L6Vjh17\nZais80dCcYEzAnbRal+Tpk3b3/9mm02kf39nI3q9yLJlHuxF5tSo0cg14/9tgTUCT0uVKnXue2+H\nDr0E/i/d97Nc6tRpmek2Y2Ji5IUXhkiDBm3k3XdHZ/g1g+LR5U7uU4buFYrHiM1mIzb2AtDadcUH\nkYacOnWKp556KkN1zJu3gP79h6DV+iMSx88/z89w2YexWm2AOd0VM6mptgfca2XBggXExMTQsGFD\nmjVrxtixbzBqVCXsdjvVq9dlwYJF9ysIffvC/PlgNMLPP0OrVh6JPysWLJhB/frNuXXrJ+z2MEqV\nKsSOHdvve69erwMS0l2JR6fL/J/pgIAAwsK+y1rAisePB39w5Ig8GLJCkaNKlKgkMMv1RHhRTKZg\n2b59e4bKXrhwQYzGggKHXOV/F4vFz2NP9gsXLnI9la8UWCYmUxFZtWrVPffdvHlTAgPLiEpVW1Sq\nYWIwBMnMmWEi4twCNiEh4f4NJCWJdOzofBz29hbJ6GS9bHbnzh3Ztm2bREZG/utrlF27donJ5Ccw\nSWCyGI0Bsn79+hyM9G63b98Wm82Wa+0r/uZO7stzWVNJ9ArFv4uMjBR//+JisZQSvd5bxo+flOGy\nGzZsEF/fJumGjkUsltLy559/eiy+efPmS61azeSJJ5rLsvsMqTscDqlS5QmBGvL33vVHxGDw/fe5\nBvHxIi1aOIPOn1/kPvvU5wW7d++W3r0HSM+e/SQ8PDxXYjh37pxUqFBLtFqjeHlZZMaMWbkSh+Jv\n7uQ+5ZhaheIxlJqaytmzZ/Hz86NAgQIZLnf69GkqV65DUtJeoBhwCKOxCVeunMuxvclv3LhBQEBh\n7PZngTDXVRtgICioFCkpifTs2Z3Jkz/7e/34rVvQrh1s3QoBAfDbb1C1ao7E+ziqXr0hhw+3xm5/\nD4jCZGrKli2/3LUpjyJnuZP7sn1nPLvdTo0aNWjfvj3g/J+4RYsWlCtXjpYtW3Lz5s20eydMmEDZ\nsmWpUKEC69evz+7QFIrHll6vp1y5chlO8mfOnCE8PByj0cj48R9hNNbC17cxRmMzZs2alqMHkGg0\nGlQqNbAK+B24BXRDpcrPlSuziYvbwuzZh3nrrQ+cBa5fh+bNnUm+aFGIiFCSvBscDgeRkX9gt4/E\nuTSvPA5He/7444/cDk2RRdme6L/++mtCQkLS1qpOnDiRFi1aEBUVRfPmzZk4cSIAR48eZeHChRw9\nepRff/2Vl19+GYfDkd3hKRT/eV98MZlKlWrTqdMHlClThWLFinDkyC6WLRvNiRMHeeaZHjkaj6+v\nL1279sTLqwjQGwhEowlH5G2gHlCKpKTPWbr0F7hyBUJDYe9eKF3ameSz+fS4nGS1Wvnhhx8YO3Ys\nGzduzJE21Wo1+fIFAX8l9lQ0mr0UKVIkR9pXZAMPvT64rwsXLkjz5s1l06ZN0q5dOxERKV++fNrp\nVNHR0VK+fHkRERk/frxMnDgxrWyrVq1kx44d99SZzSErFHmGw+GQS5cuydmzZ7O8Tj4qKkqMRn+B\n86534XvEaMz34MluOcRqtcqECZOkRo0GUqRIJSlWrLxoNIPTzR34WZqXrSlSpozzQkiIyKVLuRqz\np9lsNmnUqLWYzaGiVo8Uk6mETJr0ZY60vXr1ajGZ/MTbu6dYLFWkTZtuYrfbc6Rtxf25k/uy9Yn+\ntddeY9KkSajVfzcTExNDYGAgAIGBgcTExABw+fJlihYtmnZf0aJFuXTpUnaGp1DkWVarlY4dn6VU\nqSpUrFiXOnWacfv27UzXc/r0afT6qkCw60ot1GpfoqOjPRpvZmm1WkqXLsHx4+e5dOl9zp8fgt3+\nIzpdX9TqUVQx9OOXWxfh5EmoUQM2b4bChXMkth9+mEPBgsEYjb507dqHhISEhxfKgg0bNrB/fwwJ\nCRtwOCaSmLiZd999F6vVmi3tpdemTRsOHfqDqVPbs2zZF/zyy8K7/o4r8pZsW0e/atUqAgICqFGj\nBuHh4fe9R6VS/ev2kw/6bPTo0Wn/HBoaSmhoqBuRKhR5z6BBL7N69RUcjkuAjkOHBvDqq+8wa9a3\nmaqnTJkyJCfvAzYCzYDfUasTH4lh2kmTppGYOBno5LqSRMWKSxnc0Jv+izTorl6F+vVh9WpsFguv\nDnuDOXPmotPpef/9t3jtteEej2nLli28/PI7JCWtBEqwZs1Q+vcfzvz5Mz3eVlxcHCpVKZzb/QIU\nRURFUlJSlg/EyYysbPer8Jzw8PAH5s7MyrZEv337dlauXMmaNWtITk7m9u3b9OnTh8DAQK5cuUJQ\nUBDR0dFpJ0MVKVKECxcupJW/ePHiA//YpE/0CsV/zaZNm5g9+2ccjv8BBgBSUl5g5853MlVPbGws\nHTv2AkxAZzQaA0ajsHz5QgwGg8fjziznD/3083TMtA4IYsiC+XDjBjRrBitWgMXCR++NISxsL4mJ\nu4DbvP9+F4oUKUSPHt09GtO6db+RlNQfcM4+T06eyLp1DT3axl8aNGiAw/EKsBxogFb7OZUqVc/R\niZGK3PPPh9gxY8ZkvTIPvkJ4oPDw8LR39G+99Vbau/gJEybIyJEjRUTkyJEjUq1aNUlJSZHTp09L\nqVKl7vveMYdCVigeWZ069RZoJ9Ar3Trzt6RLlz6Zqqdr1z6i0w0XcAgkisEQKhMnfpZNUWfesmXL\nXKfuzRGYJs298onVbHa+k2/Xzrk5jkv58rUFItK9w58mPXv283hMX375pRgMPdK1s1ZKlKji8Xb+\nEhERISVKVBaTKb80btxGoqOjs60txaPNndyXY1vg/jUMP2rUKHr06MHMmTMpUaIEixY5t7AMCQmh\nR48ehISEoNVq+e677zJ1qpRC8V+h1WqAJjif9KoBWvT6C0yZ8i+nuN3Hvn2RWK3/h3MJlZHk5J4c\nPLgnU3XcunWLCRMmcfbsZZo1q8+AAS957P/bzp07s3ChjsmTf+DJ27F8fDAZTUIy9OgBc+dCuuHr\nggXzAycA59O1VnsCf3/3T+i7du0affu+zO7deyhWrDjfffcpRYrMIjq6I1ZrCbTaeUyd+qPb7TxI\nw4YN//10PoUiIzz4gyNH5MGQFQqP2r59uxiNfgJfC4wUvb6ALFmyJNP1tGnTXTSaD11PplYxGtvL\n+PGfZrj85cuXXSfRPSswXfT66jJs2BuZjuOhVqxwHkwDIi++6Dyw5h927twpZrOfaLWviJdXX/Hz\nC5aLFy+61axzh766rlPgTohKNU3y5y8sZ8+elenTp8vnn38uhw4dEhHnKoFt27bJxo0b5c6dOxlu\nY9euXbJgwQI5cuSIW7EqHn/u5L48lzWVRK9QOJN95869pX37ZzO0F/pfS/H+Wtoq4lz+GhxcXnx8\naorZXEYaNmwpycnJGY6hVq0GArVdQ/8icF00Gq9Mn5RmtVolLi7u/ksE5893HjELIsOGifzLEq/j\nx4/Lp59+Kl9++eVd/cyKixcvysyZM0Wvz5+ufyI+Pi3u2Zs/MTFRnnwyVCyWSuLjU18KFSot586d\ne2gbb7zxrphMxcTbu6uYTIEybdoMt2L+p507d0qtWqESHFxJBgx4RRITEz1avyJnKYleoVA8UHx8\nvDRp0kYMhoLi5ZVf2rbtnpaMExMTZdu2bbJnz55Mr5PW680CbdO9r04RtVqfqTX406fPFL3eLDqd\nRcqUqSZnzpz5+8MZM0RUKmflo0Y5z5fPAb///ruYzX7i7d1KwEvguqt/NrFYKsvmfxyU88kn48Vg\n6CJgExDRaD6RVq26PrD+mJgYadq0jahU+dPVHSVeXj5y+/Ztt+O32WyyYMECMRjyC8wW2C8GQyfp\n2jVzczgUjxYl0SsUigcaNuwNMRh6CqQKJInR2EY++mhslupyOBwyefK3UqlSfdFq8wkECPxP4A+B\nzlKx4hMZrmvPnj1iMhUSOC7gELV6olSq5Dqn/auv/j5VZ9y4LMWaVUFBpQTWupp/Q6CswHgxGltL\ngwYt7znN7dlnXxL4Pt0Pnt1SsmT1+9admpoq5crVELW6q0DoXYcHmc3F5NSpU27FnpqaKo0bPy1e\nXoUEnktX/03Rag1Z3lhJkfvcyX3KDggKxWNux479JCf3A3SAgaSkvmzbti9LdU2ZMpVRo77jyJGP\nsdleBuJRqb5HpepE/vx72bJlbYbr2rlzJyLtgHKACofjDY4e3Y1j7Fh49VXnTV99Be++m6VYs0JE\nuHr1PBDqujIJrbYkTZpsZNKkdmza9AsajeauMvXr18BkmofzHHkHev1Mateucd/6jx8/zuXLd3A4\nvgYOAztcnyzGYHDctWlYZkVFRfHWW2+xe7eVlJSPgfQbKF1Dp8v9JZOKXOK53xs5Iw+GrFDkql69\nXhKt9g3Xk51DvLxekldeeTNLdVWsWFdgU7onxbflyScbyJw5cyQp3XK3jFixYoVYLDUEkl11bZb/\nGSzOilUq59D9v3j//Y/Ez6+UBAaWkQkTJnnsabVq1fqiVk90vZs/KyZTsGzduvWB99tsNnnmmRfF\nyyufGI1BUqNGQ7lx48Z97z1x4oQYjYVcfV4tUEDAKPnzF5E9e/ZkOeZ33hktRmOA6PXFBcYK3Bao\nIPCiwFdiMpWViRM/z3L9itznTu7Lc1lTSfQKxcOlpqbKvn375ODBg3L58mUpXjxEvL3riLd3TalQ\noZbcvHkzS/VWq9ZYYHlaolepxsjAga9kqS673S4dOjwjFkuI+Fi6yndag7hecovMmycizlcFx44d\nk127dt317r9Nm44CRQV2CewTgyFEpkyZmqU4/unMmTNSsmRl8fIqIDqdSb744usMlbty5YqcO3fu\nX+c6OBwOadOmm5hMLQSmisHQWho1uvd1QGbs3r1bTKaiAlcFFgmECMQKXBeVqoEULlxOli5dmuX6\nFY8Gd3Kfch69QvGYuX79Og0btuLixQREUqlSpSSrVy/iwIEDaDQa6tati5eXV5bqXrlyJT169CMl\npSWgwWRay+7dWwgJCQEgNTWVsLAwzp49T/36ddOOp34QEeH3DRsoMXYspbZsAb0eFi2Cjh1xOBz0\n6TOQn39eg04XiMFwk4iIdVy9epUmTbricHwJ9HLV9At1637Ljh2/Zqlf94vr2rVr+Pj4eHyXQKvV\nyjfffMvevUeoXr0CI0a8gl6vz3Q9s2f/SFjYEu7cieX48QASEn4GBHgH+BKDwZfSpUuycePKtPNF\nFHmXW7nPIz81clAeDFmhyFHPPTdAdLqhrqFnmxgM3eTddz/ySN1z5swVLy9/0WieEa22vDRv3i5t\nyNxqtUq9ek+JydRSYLSYTOUePukvJUWkRw/nk7zJJJJuqeC8efPEbH5SIN41ejBZatZsLDNnzhSN\npqLAp+leIUyRp57q7JE+5gVTpkwVk6ms6wn+XQEfgVPy18l++fMXlgsXLiiT7x4j7uS+PJc1lUSv\nUPy7qlUb/eM9+lx5+ukebtdrs9nEYPAWOOyqN1nM5hDZsGGDiIisX7/e9c7d5vr8smi1hgeuzT93\n/LjsLRwsApJsMIhjy5a7Pv/ggw8FPkjXj0vi7R0gf/zxhxgMQQJ+rlnxb4tKZXLrHbenpKamyscf\nj5eWLbvJK6+8KXFxcdnSTokSVQW2pvtu2olGYxKLpbTky1dIdu7cmS3tKnKPO7lPmXWvUDxmqlcP\nQa9fiPNAGCtG41Jq1arkdr2JiYnYbDYgxHXFC5WqStqRtrdu3UKlCubv09YCUat1JCYm3lPXnvBw\nosqHUPPyBa5joYmtKKNWrb/rnkqVQjCbVwN3AFCr51O+fAh16tThww/fQK9PRqebjcHwPTNmfMPG\njRv54IOP2LMnc9v4elL37n2ZMGEz69d3Zfr0OOrVe4qUlBS36xURLl68mPZd37vNcA0GDerPnj2r\niY4+Te3atd1uU/EY8dzvjZyRB0NWKHLUjRs3pHLlOmI2lxKTKVgaNWqd6RnxD1KmTDVRqz8T52E6\nO8Vo9JOoqCgREYmOjhZv7wCBnwTOiU73mtSo0fDeSuLiZKfOuaXtZYKkEpECF0Svt9w11OxwOKRz\n516uYeliAmZ5442RaZ/HxMRIZGSknD17VgICSohe309UqvfEZAqQNWvWeKS/mXH16lXR630FEtNW\nOHh715KNGze6Ve+dO3ekXr2nxGDwFy+vAtKuXQ+ZPPnbdEP334jZ7CeHDx/2UE8UjyJ3cl+ey5pK\nolcoHs5ms8nhw4flzz//dOs9bVxcnPTq1V/KlKklbdp0l4iICKlQ4QlRq7Xi7e0nP//881337969\nWypWrC358hWWFi06y9WrV++u8No1cVSvLgJyDpOUIcqVFK+KRmO8J9ayZWsIfCJwQOCkmEzFJCIi\n4q57PvpojGi1g9INY6+ScuUyvnGPp0RHR4uXV35xbkz015a59TO0RfG/GThwuHh59RawinPDo1by\nyScTZPbsH6Vp047Svv2zj8RrC0X2cif3KbPuFQrFfTkcDmrXbkpkZAVSU/uh0awjIGAOUVEH0Ol0\n6PX6zJ1Ud/kytGgBR49ySq2hqcOHC7wPVAY+oHXrQqxdu/yu9rVaHSLJODf7AYNhMJMmVWbYsGGE\nh4fz3XezOXBgPydO9MQ52xzgMIULd+PSpWMe+ibuz2q18u2333Ho0HFq1Ahh8OBBtGjRiZ07vUlO\n7o9Wu4FChZbz5597MZvNWW6nWrXGHDo0BmjquvITTz+9kjVrFnqkH4q8wZ3cp7yjVygU93Xx4kWO\nHj1OaupUoA52+4ckJASwa9cuvLy8Mpfkz52Dxo3h6FGoVImLP80l1ihotVNQq/sQEuJg5crFAMyd\nOw9//+JYLAXQ6/MB61yVxKPRbKV06dKsX7+etm2fYfHiJzlxogEwCdgCnMRofI2uXTt49Lv4J4fD\nQevWXXj33dWEhVVk1KhldO3ah9WrF/HSS0WpUWMcXbteZefO391K8gDly5dCq/1r2aDg5bWOkJDS\n7ndC8d/hoVGFHJMHQ1Yo8qQrV66Il1e+tOVtYBeLpfI9Q+d/WbFihbRt+4x069ZX9u7d+/cHx4+L\nFC3qHMuuVUskNlZERM6fPy/Lli2Tbdu2pQ3Zb9261bX//U6Ba6LTPSVarbf4+jYVk6mY9O07WBwO\nhzRq1NY1F+Cv4fq+YjQGSsGCxWTIkNckNTU1276Xffv2ScGCRVyz/lNc7SeJ0RgkJ06c8Hh70dHR\nUrx4RfHxqS0WS1WpXLmORw6/UeQt7uQ+bW7/0FAoFI+mwMBAOnbsyKpVbUlMfA6DYT0BASqOHDmC\nv78/5cuXT7t3/vwF9O//NomJHwM3Wbu2Fdu2baCaWu0cro+JgYYNYdUq8PUFIDg4mODg4Lva/O23\nDSQlvQg4Z41brWFYLDVZvPgd/P39qV69uuu6DTCmK9mQFi2srFjxUzZ+IxAWNpt+/V7G+ZpgEfDX\nRjdeaDTeJCUlZbluq9WKTqe753pQUBBHj+5h165daRse3e8+heKBPPiDI0fkwZAVijzLZrPJV19N\nlm7d+krRomXFbK4tJtMLYjL5ydq1a0VEZNGixWI0FhZYk+4Je6yM7dRdJH9+54UWLUTi4x/a3uTJ\nk11Hvv5VzwYJDq54z30//TRPTKYSAisFFovJVEh+/fVXj/c/vf3794uXV0HX1rtJAhUFPhQ4IBrN\n21K6dNUsjSTs379fgoMriEqlloCAErJt27ZsiF6R17mT+/Jc1lQSvUKR8+bMmSNmcxPXsjoR2CRB\nQaVlyZKlYjIFC1QS2JCWoBsxWBJ1Oue/dOggksHlfXfu3JGyZauJydRedLoRYjT6y6pVq+57748/\n/iS1ajWT2rVbyIoVK2TPnj0ybtw4+fbbb+XOnTue7L6IiEydOlUMhucFvAVOClwU6CAqVT5p1Ki1\nXL58OdN1JiYmSsGCRQXmur7bFeLtHSDXr1/3ePyKvM2d3KcM3SsUeYSIMGtWGFu27KJs2WK89toI\ntyd6ZVRMTAypqTX4e/5uTW7cuMKUKbNJTPwM5xGtg4HPaUkEP/M9Rivw7LMwezZkcKjZYrGwf/82\n5s2bx82bN2nZ8jeqVat233t79+5F797Ove6XL19Oo0ZtSE19Hr1+L1988T0HDmzD29vbzZ7/rVCh\nQmi1R4BPgYZAI2Anw4cP4quvJmapzlOnTpGaagGec13pgFo9gSNHjtCoUSOPxK1Q5LnH4zwYskLh\nEYMHvyom0xMCU8Rg6CFVq9aTlJQUt+u1Wq1y+PBhiYqKeuCa+x07driOVz0iYBWt9jVp1OhpadGi\ni8As15P8bOlICUn+67G+f38RN05lywiHwyFjx34qKpWPwO9pIwpGY1f55ptv0u47ePCgPPVUJ6la\ntbF89NFYsVqtmW7LbrdL69ZdxGKpLkZjG9HpLDJx4kS34ndOePQViHbFfkOMxkA5fvy4W/UqHj/u\n5L48lzWVRK/4L4qPjxet1ijOY1nrC+QTtdpfpk+f7la9165dk4oVnxCLpbQYjYWlZctOD/zxMHNm\nmJhM+USt1kqdOs0lJiZGNm3aJEajv8A30os+Yv0r044YIeLGRj0HDhyQl14aKi++OER27Nhx33vs\ndrsMHz5C9PpyrhnwF9MSvVo9Sj7++BMRETl79qx4eweISjVFYKOYTI1lyJBXsxSX3W6XNWvWSFhY\nmBw7dizL/Utv9OjxYjIVF5Opn5jNZWT48Lc9Uq/i8aIkeoXiMXf9+nXR6SwCJQW+Ebgm8J34+ARJ\nfAYmuT1Ijx4viF7/ijhPuksRo/FpGTfu0wfe73A47plwtmXLFvm+Zj2x/5Vl338/Lck7HA5Zs2aN\nfP/997J79+4MxbRnzx4xmfwExgv8P3tnHhZl9b7xe/aZd4YBZFUBE0TEfV9zScP9p7lruaWpaS5l\nkdpimaW2mZq54JqaW6amiAuaqKm57xsiGIobIoIyMMDM/ftjRoKvoCCoYedzXV7F+57znOeckvs9\n2/N8R0ly486dO3OUeTC7Vii8CCwg0J9AdwLXCOyhTufBv/76iyQ5ffp0ajSDsh3wi6MkORdglApP\nVFQUa9duRoPBjdWqvfzQR8LevXs5Z86ch/opEDxACL1A8IJjtVpZrVp9Ar7ZBIt0cKie70xlBw4c\n4IIFC7g7W5a48uXrENiXzeZ8du7ct2DOTZ36j0PZlrKtVit79HiTen1l6nQDKUml+NPG0LK+AAAg\nAElEQVRPcx5rrmvXfgR+yObTYjZr9n85ymzZsoUGQ1UCIwgE2+/69yPgSLW6BJct+4WbN29maGgo\nv//+e+p0vbPZu0gHB7eC9bEQhITMp1xuJPANgWuUyX6km1uZQn2gCf57FEb7xGE8gaAYIJPJsHRp\nCKpXbwyrNQmAI4D7yMy8AWdn58fWnzLle0ycOA0yWXMAX2Hw4B6YOnUSKlUKQEzMWmRk1AdggU63\nETVq1MufUyTw5ZfA+PG2n2fOBN55J+v1/v37ERq6BykpJ2G78x6N996rigED+kGr1eZpNjXVbO/f\nA5yQlpaeo0x8fDyAQABjADQEcA2AAgaDGps2rcHAgSNw86YBMpkGWm00tNpMpKePhcUSCEn6DsHB\n7+Wvj4Vky5YtGDnyY1itngCCAQDkcJjNi3D69GnUq5fPsRYICkMRfnA8E4qhywJBkTF48Ejq9VUp\nl4+hXl+d/fq9/dg6u3btolJpyLaHbTvwdf78ed64cYN+flXp4FCZen1ZNm7cOs/88TmwWsng4Acb\n4uSiRQ8VWbt2LY3G/8uxAqHVuvDGjRuPNL1hwwZKkheBTQTCKUnluGjRzznKREVF2Zf3dxG4Qpms\nHT08vBkdHc3hw9+nWj3Evh1BKpUfs23bLhw8eAQ7dHidCxcuLlSin/xw8OBBVq/emDqdO4FP7WcI\nkuzjcJ+SVIrnzp17qj4IXiwKo32PrTl9+nTeuXPniRsoaoTQC/7LWK1Wrlu3jl9++SXXrFnzWMHa\nsmULtVpn2tK8/iO4jo6NGBERQZJMS0vjoUOHeOLECVoslsc7YbGQQ4fSrqLkqlU5/Nu7dy9/++03\n7tu3zy7GOwlkUiabRh+fCvkS2ZUrV7FKlZdZsWIDzpu3INcyYWFhdHHxolyuYPXqLzM2NpYk2bJl\nVwIrsvU3nNWrN318v4qIv//+mwaDG4GlBN6yby8MI1CdwMeUyyuzV68BT/1jQ/Bi8VSF/qOPPqKf\nnx+7devGzZs3P/f/OYXQC4oLVquV0dHRPHfuHDOf8jWzvPD1rUZgHW3R3JbbZ7mb6eDgztv2mPMF\nIiOD7NvXpqAaDblxY9Yrq9XKnj3fpF5fjkbj/1GSXDlp0iSWKFGaMpmc5cvXfCqx4P/3d9KkSd9Q\nklrY9+3N1Gq7cMSI4CJvNy8WLFhAvf4N+0fGVfvY9yXwGpVKHT/++OPn/ntUUPx4qkJP2k64bt68\nmT169KCfnx/HjRvHqKioJ260MAihFxQH0tPT2bZtV+p0HtTry7By5XpPJqyFxMXFh7YobkcJ+BNQ\nUKcrwV27dhXcmNlMduliE3m9nty+PcfrsLAw6vWVCZjsIhdBZ+dSJPlE99ZJW3jYLVu28Pr16/mu\nk5GRwe7d+1Gl0lOtdmDLlq/RZDI9UftPwooVK2gwvJq1dQAcpFyu4ieffMpjx449Mz8ELxaF0b58\npamVy+Xw9PSEh4cHFAoFEhMT0bVrVwQHBz+towMCQbFm8OCh2Lw5HqmpfyMlJQYXLtTBO+8U7O+L\nxWIptB9t27aGVjsGQGkAy6HTeWDz5rVo0qRJwQylpgKvvQb89pstKc22bUCLFjmKxMbGgqyHf5LN\nvIy7d28gIyMDSmXBzv2SxFtvjUCjRh3Qo8e3KFeuCiIiIvJVV6lUYtWqxYiPj8P165exdes66HS6\nx1V7ItLT07F3717s27cP6em2A4MdOnRAqVIJ0GheB/AdJKk3vvjiS0yc+EVWUh6B4JnyuC+BadOm\nsWbNmgwKCuKqVauy7tBaLBb6+vo+8RfGk5IPlwWC58qOHTuoULgQmJdtn3g//f1r56v+5s2bs5a7\nAwPr8NKlS0/sS0pKCrt3709JcqaLizcXLfqZGRkZDA0N5dKlS3n58uXHG0lOJps1s3XExYXMnoI2\nG9u3b6da7W5fQSBlsuksX77GE/kdHh5Ovb4CgWT7+G2li4vXE9l6Wty5c4cBATXp4FCNDg5VGRhY\nO+s8U3JyMidPnsJhw97lunXrnrOngheBwmjfY2uOHz8+z18GZ86ceeKGnxQh9IJ/O927v0mgA4HX\nCGTYl3A/YMeOrz+2bkxMjP0AWwSBDMrl37Js2cpFtqdrNpvZoMGrNBjq0GDoQb3e9dHL+HfukPXr\n20S+ZEkyj7/zly9fppubD9XqagQ0BAwsXdr/iffk586dS0kakO1DyUKZTEGz2cwJEyaxdOlAvvRS\nVf7889Insl8YrFYrz58/z44de2Q73W+lWj2YQ4aMeub+CP4bPFWh/7chhF7wb6dPn8EEviIQRKAc\ngUpUq13yld1s9erVdHDolE3grFSrjUW2v79gwQJKUnMCmXb7v/OllyrnXvjWLZorViQBXtPoOPO9\n4Dz32jt16k2FYoLdZhoVikEcNGj4E/t54MAB+xW7v+0257Fs2cr8+uvvKUk1CRwhEEFJ8s4zu93T\nIDExkX5+1SiXuxDwoC1N7oP/Vuv58svtnpkvgv8WhdG+fO3RCwSC/PPee29Dr/8BQAsAXaDRXMfK\nlfNQsmTJh8rGxcXh44/HY9SoD7B37164u7uDPAcgzV4iCoAFRqOxwH7Yfjfk5Nq1a0hLqwtAYX9S\nH7duXXu4clwcLI0aQX32LC6gBOqaf8SHcw9h8OCRubYVG3sNFkt9+08aWCwtcPny9QL7/IC6deti\n4sRgqNWVoNf7wMNjEjZuXIklS36DyfQ9gJoAmsJkGodly9Y+cTsFITMzE1Wr1sGlSzJYrbEA+gNY\nBCADQAa02mWoXz/3THsCwfNECL1AUMTUqFEDe/ZsQ+/el9C9+y2Ehf2KTp06PVTu6tWrqFq1Hr7+\nOgkzZiShadM2CAmZh6ZNK8NgqA+dbhAkqSlmzJgGVT7TvALArFlzYTC4QqXSok2brrh3717Wu4YN\nG0KrXQEgBoAVSuUU1KvXKKeBmBigcWMoLl7EabkRTXAWVzEQJtM6LF26MNdDgi1aNIJONw22dLVJ\nkKSZCApq9FC5gjB69EjEx8fh1KlduHLlAipVqgSDQQ/gnw8Imew6jMZnk6r39OnTuHEjEUAnABKA\n8QDuAnCDVuuFevVM+OKLT56JLwJBgSi6hYVnQzF0WSDIlXHjPqFCMdIe3KUkgS8I9Kanpy9/+eUX\nzp49+7GJYK5fv87w8PCsKGvbt2+nJPkQOEvgPjWaPuzaNWfs+qlTZ1CtlqhQaFi7dlPeunXrn5fn\nzpGlS5MA43196a1vk21pOpEKhTrXmABms5nduvWlQqGmQqHmgAHDnkrsgJ07d1KncyXwOeXy0TQa\n3XOcAzhy5Ahff/0tdu3aj9v/5/pfYTl+/Dg1Gg8CtQncs4/JVwwMrMXLly+Lu/GCp0phtE9mN1Bs\nkMlkuS5JCgTFjZEj38ePP7oCWAxgIQDbDFij6YtJk6pj9OjRj6y/detWdOnSG0plZaSnn8eIEYMg\nl1swZYoawGf2Upfh7NwYd+5cyVHXYrHAbDZDkqR/Hp44AQQFAfHxQJMmuPPzzwis1wwJCb1hsdSG\nJE1Dz56VsGDBT3n6ZDabQRK3b9+GwWCAk5NTQYflsRw5cgTLl6+GRqPGoEEDULZsWQDA0aNH0bhx\nK5hMYwDoodN9gV9/nY927doVSbuZmZmoXbspTp1KgtV6A4ADVKoknDt3CH5+fkXShkCQF4XSvqL5\n1nh2FEOXBYJcCQ0NpVzuTEAiEJM1c5bLx/Lzzyc8sm5mZiYNBhcCe+z1blOSfDh69GhqtZ2zBWv5\nneXK5eOK219/kU5ONgdatSJTUkiSsbGxfP31t/jyy+341VffPHaWfu3aNQYG1qZO506VSs/33hv7\n0Ew3IyODP/wwnb16DeSXX05mamrq4/3LB717DyLwbbYViF9Zp86rRWL7AUlJSRw+/H3WqtWMvXr1\ney5BkAT/TQqjfSJ7nUDwHLBarRg16mNYrV1gOxj3NoBpAGKg1S5E+/Zhj6yflJSE9PQMAC/bn7hA\noaiLKlWqoEyZCFy92hpWqw9ksvUICVn9aGciImBt3x7ylBSsgwzBZ2Kw9MQJNGjQAN7e3ggJmQaL\nJX8HAnv3fhsXL76KzMxJAO4gJKQZGjWqjS5dumSV6dHjTWzZEgeTqQd0ui0IDW2PP//cCoVCkbfh\nfGA2Z+CfYD0AICEzM7NQNv8Xo9GIH3/8rkhtCgRPnSL84HgmFEOXBYKHaNiwhf2+eQKBNAKjCLjT\nxaUsN23a9Nj6VquVbm4+BNbYZ6+XqNN58NSpUzSZTFy6dClnzZrFCxcuPNpQWBitWi0JcClqUoEk\nAmvp4ODOa9eusX//t6lUaqlUSmzZstNjQ8k6O5cmcDnbrPoLjhkzLuv9uXPnqNW6ZAuTm0mDIYAH\nDhzI17g9ij/++IM6nQeBVQRCKUl+XLhwcaHtCgT/BgqjfcVONYXQC4o74eHhdpF/ibbMbg/uyzfl\nolzSvebFoUOHWKJEaRoMZanRGDlr1tyCObJmDa0qFQlwDjSUwZIl0EZjczZt2pxKZV3a0quaqdV2\n5bBhox9psmrVRgTm2+2kU5KaMyQkhJcuXWK5ctWoUGgJOBM52qrD3bt3F8z3PAgLC2P9+i1Zq1Zz\nIfKCF4rCaJ84jCcQPGUyMzMxduxnWLVqPQwGA+rWrYAlS34DMBPAh7Bd1zoBb+8kXLx4HBqN5rE2\nSWLlypU4fPgoXFyc8fbbb6NEiRL5d2rpUqB/f8BqxVQ0wPs4CeAigJIAUqFQ+IDUwmr9CkBfe6Vd\nqFz5Y5w69WeeZk+ePImmTVuDrAiLJQ516pTD1q1rUbVqA0RG9oTV+h6AOgBqAxgEhSIMnp6/IDLy\neM6DgXmQkZGBhQsX4tKly6hTpya6du0KmUyW/34LBMWUwmifEHqB4Cnz7rtjMG/eQZhMPwC4ArX6\nDVgsLrBY3AC8DiAcMtkOXL4cCR8fn3zZ7NSpFzZvPgOzuTskKRzNmrkjNHT1Q6IXGxuLS5cuwd/f\nH15eXraHc+YAQ4cCAL7Tl0Bwyh4AGwCEAGgDhWIbyHhYrQMA3LM/l0Eun4i2bc9g48aVj/QtISEB\nBw8ehNFoRIMGDZCZmQmdTg+r1Qxb6I4EKBSN4eycjtq1ayAkZCq8vb0f22er1YpXX+2AAwfSYDI1\ng16/GoMGtcUPP0zJ15jlZk8uF6FEBMUDcepeIHgGWK1Wzp4dwrp1g9i8eUfu27cvX/Xc3X3t99of\n7Ft/Qm/vQKrVXlQofKlQOPHXX3/Ntx/jxo23n9S/mxVyVq/35ZH/STYzZ8486nQudHRsTJ3OxRYX\n/ttvHzjBSSVK0dMzgErlGPsp/U1UqcqwV69eVCq97OcHqhJ4mUAjKpWOjImJKciQkbSNm4ODK4ED\n9qZTaTBU4ebNmwtkZ8+ePTQYAmnLH2C7aaBS6ZmYmFggO7dv32bjxm0olytpMLhy8eIlBaovEDwP\nCqN9xU41hdALnhfffz+dklSRwEYC8ylJrvnKL16mTOVse/GkSjWEX3wxkdu3b+evv/7Kq1ev5tuH\nmzdvUq02EPDJdoWONBjqMyIiIqvc1atXqdOVIHDRXuYMJyo0WSI/TNaBwEGqVK9To3GlXv8SNZoS\nbNu2C5csWUKNxpXAJwROEhhAoASrVGn0RONGkuvXr6dO50qDoTs1mvL09CzP/v3fZnR09GPr/vzz\nUjo6elIuV1KhqJ/tg8lKnc69QONHki1adKBK9Y79EOQJSlJJ/vXXX0/aNYHgmSCEXiB4BpQpU4XA\n/mxC8znfffeDx9ZbsWIlJakUga+pVA6nq6s3r1+/nqPM/fv3+dFHn/G113rz66+/yzN5zKlTp2gw\nBBCoQuAz+/37GXR09GRSUlJWub1799LRsW6WIH6H0SRAi0zGwdqAbH3IpEZTgrt37+bnn0+kJHnS\nwaELlUonymSuBLwJvEyttiK//356ocYvMjKSPXu+QY3Gm8AiyuXj6eRU8pFCvXfvXkpSSQJH7af5\nHQnMJRBDpXIMAwNr02KxFMgPjcaBwJ1sH17v8euvvy5U3wSCp01htE/coxcI8ontnnd61s8yWTqU\nysff/e7Zswc8PNzx228b4ejojOHDD8DT0zPrfWZmJho3bo2zZ71gNrfCtm2/YN++I1i/fvlDtnx9\nfaFS3QPwCYBNAOZALk/Hli1hOe65lytXDhkZlyDDYczCfLyNuUgHcHLMGCyfuRmAFbb9chPIDHh4\neGDy5O9gNp8AUAbATSiV5VGihCNksusYOnQA3ntvxBON2wP8/f0RHr4HZnMYgMqwWgGT6QaWL1+O\n4ODgXOvs3LkTZnMfADXsT9ZDJusEJ6eJqFmzFpYt21jgfXZnZ3fcuHECQDMAVqjVJ+HuXvXJOyYQ\n/Nspwg+OZ0IxdFnwgjBv3gJKUlkCP1Mm+4Z6vWtWjPnCsHfvXhoMlbNdOTNRoymRZ1rbw4cPs2RJ\nP8rlKrq4eOV5NW3NytX8RaEmAZoA/vXZ50xPT2eNGi9Tq+1GYA4lqRH79BnEkydP0sGhQraZPuno\n2CDf197u3r3LJUuWcMGCBYyLi8vx7sSJE2zSpB0DAupSo8m+nUAqlSM5efLkPO3OmTOHktQu2zbF\ndpYuHZAvn/IiNDSUOp0rdbq3aDA0Zu3aTWk2mwtlUyB42hRG+4qdagqhFzxPVq/+lW3b9mCPHm/y\n5MmTD71PTU1ldHT0YwPLZCciIoJGY11mX07X6Tx5+fLlR9YzmUx5J1JJSyM7dSIBZkoSU7IF4UlJ\nSeGECV+yV6+BnDlzFi0WC1NSUujo6Ml/8qtHUK93ZXx8/GP9v3XrFkuX9qde356S1JOOjp48c+YM\nSVsIXQcHdwKzCPxJhaI8FYrqBLYRmE293pWRkZFZthYvXsJSpQLo4uLDkSODmZyczMqV61GvD6JG\nM5SS5FYk+efPnDnDWbNmceXKlULkBcUCIfQCwb+ArVu30mBwoV7vTb2+RL4FKSUlhd7eAVQqPyaw\nhxrNQNau3fTJs6GlpNji1QO2+PX5PGi2b98+OjuXolrtSAcHV4aHh+er3qhRwfbDbbYmZbLpbNGi\nI0ly9uzZ1On6ZfuIuU25XMvq1ZuxRYuOPHr0aJadrVu3UpK8COwlcIGS1JTBwZ8wNTWVS5Ys4fTp\n03nq1KmCj4dA8AIghF4geM7cvXuXBoMrgV12QdtHSXLJ14yYJOPi4vjaa28wMLA++/V7m3fv3s3x\nPj09PX+HzpKSyCZNbKrq5kYeP57jdUZGBkePHsfSpSvQ378WN2zYkOO9xWJhfHx8gVLMdu7cl8CC\nbGK+h4GB9UmSCxYsoCR1zvbub2q1xlw/YgYNGk7g+2xlD/Gll6rl2w+B4EWmMNonokUIBEXApUuX\nIJeXAtDE/qQBVCpfXLx48bF1SSI6Ohp9+nTG1q2rsXjxbDg6OgIAUlJS0LZtN+h0Bmi1BowfPzHv\noBl37gCvvgrs3g2UKmX7Z7VqOYp8+OGnmDNnH+LiVuHixYno0eMt7N+/P+u9XC6Hq6trgRLMtGnT\nFJL0I4DrAO5Bp5uMVq2aAgA6d+4MR8cTUCpHApgPSWqHDz8MzjWanbOzEQpFbLYnf8NodMi3HwKB\nIA+K7HPjGVEMXRb8B7h16xa1WqdsB81iqNWWeOwdb6vVyi5d+lCvL0+jsQP1eldu3749633//kOp\n1fYgkEogjpJUkStXruT69evZunU3duz4hi0hzI0bZJUqtqlw2bLkpUu5tufhUY7A6Wyz5gn84IMx\nheq71Wrlhx9+QpVKR4VCzR49+jMtLS3r/c2bNzlqVDC7devPxYuXZM3mjx07xt9//z0rCE9cXBxd\nXb2pUr1FmWwcJcktx1gIBP9lCqN94nqdQFAEuLm5YejQgZg5szrU6gqwWmMxZcpElC5d+pH1QkND\nsWXLSaSknACgBbAdPXsOQHz83wCAHTt2Iy3tF/u7UjCZhmD27AU4dOg8TKYvASTj7NbWOOnuAG1s\nLBAQAGzfDjwId/s/SJIetpl3JQCAUnkdDg6lCtV3mUwGk+keLBaCJM6cOY+EhASUKmWz6+7ujmnT\nvslR5733xiEkZBmUyqrIzDyIJUvmokuXzjh16iAWL/4ZJlMqOnfehurVqxfKN4FAgOI3PS6GLgv+\nA7z//kfU6/2o1Q6kRlOGgwYNz1e9mTNnUqsdkm2GnU65XJG1H1+3bgv+kw3OSrW6Dz08yhMIJUD6\nIooxcLZVrlaNvHkzh32r1crjx4/zjz/+4J07d7hmzRrqdJ4EvqJS+Q5dXb3zvMaXX954oz+BEgQi\n7dfgxrFu3eZ5lj906BAlyTtb0Joj1OkcmZ6eXig/BIIXmcJo31Pbo09LS0O9evVQvXp1VKxYEePG\njQMA3LlzB0FBQShfvjxatmyJu3fvZtWZPHky/P39UaFCBWzbtu1puSYQFJqzZ8+iceO28PWtjq5d\n38BPP4UgJeUA0tLmw2w+jKVLl+PKlSuPtVO7dm3I5aEAYgAQcvkMVKhQKysIzNy538HB4SPo9b1g\nMAShTJmTcHFxAaBEBZzDbjTBS0hElKs7sHMn4O6eZZsk3njjLTRs2AGvvTYeZctWxEsvvYQtW1Zh\n5Mg7GDfOFdu2/Y5Ro8ahevWmGDZsNFJSUgo0DgkJCVi5cgWAXgD8AcgAfIwjR/bmWefvv/+GUlkT\ngLP9SU1YrQokJiYWqG2BQJBPiu5742FSUlJI2k761qtXj3v27GFwcHBWuMkpU6ZwzBjb/uCZM2dY\nrVo1pqenMyYmhn5+frmeMn7KLgsEj+XmzZt0cipJmWwmgcNUqVpSocgeVpY0Gqvy8OHD+bI3Y8Ys\nqtV6ajQl+NJLlXjpf/bXr169ysWLF3PVqlVMSUnhokU/s4G2FG/BSAKMkKt4IJe97DVr1lCvr0Eg\nxe7Xcvr5/XOK/f79+/TyKk+lchyBHdRqe7Jp07YFutYXFRVFjcaFQH3+k2xmO52cSj9Ubv/+/UxK\nSmJkZCR1OrdsZwVW0s3Np8ChbAWC/xKF0b5nopopKSmsXbs2T58+zYCAAN64cYMkef36dQYE2KJc\nTZo0iVOmTMmq06pVK+7fv/9hh4XQC54zK1eupINDx2zCHk9AR2CVXexW0Nm5FO/du5dvm2lpabx5\n82b+RHbfPpoliQT4l4sHd2/dmmuxr7/+mkrl6Gx+3qVarc96v23bNhqNjXJsG2g0zll/P/NDRkYG\nvb0DCFSz/+lCQM81a9aQtG0dDB/+AXU6dxqNtejkVJJHjhzhkiXLqNUaqdN50tXV+6HMewKBICeF\n0b6ner3OarWievXq8PDwwCuvvIJKlSrh5s2b8PDwAAB4eHjg5s2bAIBr1679ky8bgJeXF+Li4p6m\newLBE6HVakHeAfDPNTeFIhOlS38CmUwDb+8J2L59IwwGQ456UVFRqF79ZWi1RpQvXxPHjh3LeqfR\naODu7p7rtbMc/PEHEBQEtckEdOmCetdi0bhly1yLVqtWDRrNRgDxAACZbBEqVPjnup1CoQBpztaP\nTJCWAl2tUyqV2LVrM2rUMEKlioSHx2GsX/8LunTpAgAIDw/HokUbkZp6AcnJh3H37lR07twHffq8\ngTt3buDChYO4fj0aNWvWzHebAoGgYDzVU/dyuRzHjx9HUlISWrVqhZ07d+Z4L5PJHvmLLa93n3/+\neda/N2vWDM2aNSsKdwWCfNGyZUuULv0FLl/uC7O5PvT6BRg0aDR++GEKLJbchTIjIwPNmrXFtWvD\nQG7ExYub0Lx5O8TEnIWTk1Ou7WzYsAEhISug12sxduxI1Lh2DejSBTCbgb59gQULAGXef4VbtWqF\nESNex9Sp5aBSlYCTkwq//RaW9b5Ro0YoXZqIjn4L6ektIEmL0br1/8HV1bVA41G2bFkcPbo713fn\nz59HZmYLAA/62AlXrvQGSeh0Onh7exeoLYHgv0JERAQiIiKKxljRLSw8mi+++ILffvstAwICslJ0\nXrt2LWvpfvLkyTmSW7Rq1SrXHNHP0GWBIE+SkpI4fvwE9ukzmIsWLX7skvv58+dpMPj+T9KYRty5\nc2eu5W2pbW3pXIGp7K1xoFWptFUcOpQswH52fHw8IyMjcz3VfvfuXb777ods3bobv/xySpGffN++\nfTv1+nIEbtv7/TN9fasUaRsCwX+BwmjfU1PN+Ph4JiYmkrQl32jcuDG3b9/O4ODgrL34yZMnP3QY\nz2w2Mzo6mr6+vrn+8hRCLyiO3Lx5kxqNo30/nwRSKEnePHHiRK7lK1VqSGAzAbIfFjETMpvIBweT\nBYyBb7FYuHbtWk6dOpV79uwpiu4UiA8++JhabQkajZXp4pJ3nwUCQd78K4X+5MmTrFGjBqtVq8Yq\nVarwm2++IUkmJCSwRYsW9Pf3Z1BQUNbHAEl+9dVX9PPzY0BAALds2ZK7w0LoBc+QpKQk9u07hH5+\nNRkU1OmhE/EF4YMPPqZeH0Cl8gPq9TXZq9eAPFcCAgPrE9jBYZiZtQSwtmbdAot8eno6X365JbXa\nalSrh1OSfPjttz88cR+elCtXrvDYsWNZN3EEAkHBKIz2yewGig0ymSzvWN8CQRFCEo0bt8bhwyVh\nNg+DXL4TLi6zEBl5Is999ccRFhaGkydPwt/fH507d87zHEpIyHxcGT4WEzMSAABjVXp02rMD9erV\ny3dbqampqFWrEc6duwUgCrboerFQqQJx9248JEl6oj4IBIJnT2G0T4TAFQjyICEhAYcOHUB6+m0A\nSlitdWE2h2Pv3r1o167dE9ls3bo12rRp8+jT9SQGX/kbyEiAFcAP5auiTciMAok8AEyf/iOiolQA\nqsEm8gDgDYVCQnJyshB6geA/gsheJxDkgVqtBpkBwGR/QpBJUKvVBbaVnJyMRo2CoFJpIUnO+P77\n6bkXJIHRo4EvvwQUCsiXLcP7F06gadOm+W4rLi4OISEh2LhxGzIyOgA4BGCTvR9T4OnpAfdsEfQE\nAsGLjVi6FwgewcCB72DlymMwmfpBo9kFf/9oHDmyO99in5iYiDfffAcbNmwGabfYDeoAACAASURB\nVATwGwBnaLVB+PXXGWjfvv0/hS0W4O23gfnzAbUaWLkS6NSpQP6eOXMGDRu2QGZmS2RmnkJ6uhXA\nFAAjAVyG0eiJ48d3o2zZsgWyKxAIni+F0T4xoxf8J7h8+TIaNWqFEiW8UK9eC0RFReWr3rx5P+Lb\nb/uiV69DGDOmAvbv355vkSeJVq06IzTUAHIvgDEAOgJwQlraEISHR/xTOCMD6NPHJvI6HbBhQ4FF\nHgBGjfoY9+59ApNpCdLTj0AmU0Au7wqtNgk1atTHokXTsXDhIsyaNQtpaWmwWq2YOnUGmjbtgF69\nBiImJqbAbQoEgn83YkYveOExm80oV64qrl0bAKu1J+TytXB3n4lLl0491X1qW6pWP6SnJwB4EESn\nDYC3ASzF5Ml1MHbsGCAtDejZE/j9d8DBAQgNBZo0KVBbW7duxebN27Fixe+4dWs+gAf1F6Ft2y0I\nCZmKwYPfQVjYPgCDIZcfQOXKKWjSpCEWLvwTJtOHUChOw2ici3PnjmZFrxQIBP8OxIxeIHgEFy5c\nQFKSHFbrGABlYLW+B5PJiNOnT+coZzabER8fX2QfklqtFlZrOoAk+xMrgFgA70Ol2gJHRyPSExOB\nDh1sIu/sDOzYUWCRnzVrLjp3HoLp011w+7YeMtl4AHcBXIVePx2dO7fG3r17ERa2BcA+AF/Cat2G\ns2ctmDPnJ5hMawF0hsUyHmlpzbB+/foi6b9AIPh3IIRe8MJjNBqRkZEA4L79SSoyMm7BaDRmlZk9\nOwRGowu8vQPg61sF0dHR+bKdnJyMN94YBB+fymjUqDXOnDmT9U6v12PYsOHQ61sAmArbbD4WQAKs\n1sH44v2VOOtTFggPt6WXjYgA6tQpcP/GjfsMJlMogLGwWg9ALr8GudwTGk0gRo58DQMG9EdY2A4A\nFgA+9loyWCw+sMW5z34DoGhXzKKiojBjxgzMmzcPSUlJj68gEAiKnkLc338uFEOXBc8Rq9VKq9XK\n3r0HUa+vQ+AL6vUN2KVLn6xgNcuXL6dC4UogigApl3/HwMA6+bLftGlbajR9CRynTDaLjo6evHnz\nZo72ly1bxiFDRrJ9+44E1ATOsARu8xBqkQBTXFzICxeeuI8ajYFAQlZoXY1mKKdOncqbN2+yWbP2\n1Omc6ODgTsCPwGACVwisJyCxXr0mlKQGBH6nXP4lnZxKZoWoPnv2LGfOnMlly5YxNTW1wH7t37+f\ner0rNZohlKTOLF3an7dv337ifgoE/2UKo33FTjWF0AvyQ0ZGBgcOfIdqtZ46nSPHjfuMS5cu5Ycf\njuPPP/+clfv8/PnzVKv1BPpni0OfQZlMzszMzEe2ce/ePSqV2mx52ElJasdPP/2USUlJOcpGRUVR\nq3UloKQH/uZJVCYBRskc+MtXXxWqr1279qVW25nAOQJrKEmu3LZtGyXJk8Bwe9jdVQT0BLwJONr/\nfEmt1pnjxn3KRo3asmvXvoyKiiJJbtmyhZLkSq12EPX6FqxcuR5NJlOB/KpZsymBZVljo1IN4scf\njy9UXwWC/ypC6AWC/+Gjjz6nJDW3i1wsJaka581b8FC5Dz8cR6CrPZd6ql2U/qCLi1dWmQMHDvCd\nd97j6NEfMjIykiT5yy/L2aHD65TJVNni11sJVKNOV5FubmWyRJMkw8LC6OgYRG+8zEg4kgBPowzL\napx5/vz5QvXVZDKxf/+h9PAox4oV6zE8PJwlS/oSUBHIzBJarbYzVSpnAnMJXLYn1qnLvXv3PmTT\n2zuQwNasful07Th79uwC+eXjU5nA0WwfUNM4cOA7heqrQPBfpTDaJ/boBS8koaE7YDJ9DMAVgDdM\nptHYuHHHQ+WsVgIIAFAVtghy/weZ7P+wfPkCAMAff/yBV15pj59+csUPPyhQq1YjBAePxaBBE7Bh\nQwuQdQE0APA+gOYAVEhNPYqEhBEYMGBkVjvlypWDd9ph7EEU/JGEo5DjFdzGtNWLERAQUKi+6nQ6\nLFo0CzduXMSZM3/Bw8MD9+4pAagBXH7QUwB/Qy7PBFAFQBkAR5GRcQnlypV7yGZiYry9HADIYDZX\nxa1b8QXyq127IOh04wEkADgPSfoR7du/+iRdFAgEhaEIPzieCcXQZcFzoGXLzpTJpmfNJpXKDzhk\nyMiHyp08eZKS5EpgNoFJVKu9ciwv16/fksDyLDsy2QSq1c4ETtufxdiXwV+yL4s3IHCPwCmWKlWe\nN2/etG0TnDrF+0YjCfAvhZ6lpBIMDd2Uwxer1cpdu3ZxxYoVvHjx4hP3PTY2llqtC4Hv7T59QKA+\nq1VryA0bNlCvd6GDgz8lyZm//bY2Vxvt2nWnWj2QQAqBk5Sk0ty9e3eB/EhNTWWvXgOo0Rjo4ODG\nqVOnP3GfBIL/OoXRvmKnmkLoBfnh9OnTNBo9qNP1oyR1o7t7GcbFxeVa9sCBAwwK6sz69Vtx9uyQ\nHBnlKld+mcD2bMvPs6lUGu0Cn0HAh8Db9mV7C4FuBMZSLg+iXK6lRlOCbT3KMNPJiQSY2qgR/9q+\nnfHx8Tl8sFqt7NnzTer1AXRw6EpJcuX69evz1Ver1cpvvpnKsmWr0d+/Nn/5ZTkHDRpBvb4agT5U\nqUqzbt2XaTabSdrOFpw9e5bJycl52kxMTOSrr3akQqGmg4MbFyxYlC9fBALB06Ew2icC5gheWK5e\nvYrQ0FAolUp06tQJLi4uBbYxdeoMfPrpAphMcwHchyS9iVdfbYDt26/DZOoFYAKAXwA8WJJeBZls\nKGxx8Q+gIeIRhlfhiDSgXTtgzRpAq83RBkn8+OOPGDNmFtLSjgHQATgIvb4NIiK24syZMyhfvjwa\nNGiQq4/Tp8/ERx+FwGQKyfJx9eo5SE1NxalTp1GhQgB69OgBubzgO3UkH52ARyAQPBMKpX1F8qnx\nDCmGLguKMVarlVOmfJdjtpyZmcnPP/+Kvr5VCXjYT+xbCKQTaM369RtTr+/HFgjnfUgkwNWQMS2X\nGbTFYmFQUEcqlS72Q4EPVg6slMlU1OlK0WB4g5JUhsHBn+TqY9WqjQlsy1Z3Drt16/+0h0YgEDxD\nCqN94jCeQPAIZDIZxox5H9HRxxEZeQgdO3ZA1659MWnSJNy+fRMuLhoAuwB4AygJne4oBg7sizaZ\nO7AJ7aCHCYvwCvooHdC991AsXrwk66ucJF55pRXCw08jMzMMwG4AZ+3tzgCpRWrqAdy/vwwm0xHM\nnBmCixcvPuSjXi8B+OegnEwWD4NB97SHRiAQFBOE0AsEBeCtt0Zi82Yr0tOvIDl5K0ymDDRvXhEe\nHnrI5WYolf7YNexdrEiPgwbpmKPywUD8hQzrYGzY8CqGD/8WEydOBgBs2LABf/11DkALAHUBfA+g\nPgAtSpb8CXq9CwAve8suUKvL4fr16w/5VK9eJQCDAUwCMBaSNB3BwSOe/mAIBIJigRB6gSCf3Lhx\nAxs3/g6z+VUAegDVkJY2BIGBfkhKug2r9Ri63huAnzNMUJKI6toVR/u1hEbbEVbrtwD6IyVlHb79\n9gcAQHR0NKzW+gDCAPwNoDeAT+HvH4iLF49DrU4HsAa2MLXhsFguomLFijl8Onz4MEJCVgD4GbZZ\n/UF4epZEYGBgkfX7wIEDCArqjAYNWmPOnHnijIxAUMxQPm8HBILnze7du3HgwAF4eXmhe/fuUCgU\nSEtLQ1paGpycnAAAx44dQ7NmbWAy1QQwG8BiAFuh0ZyFQuEJtdoXg9LCMAOjAABfaDzRdswYVN63\nD+SpbK3pYbFkAgBq1qwJtXoGMjOHAKgEQAOl0opNmw5CkiRs2/Y72rXrhjt3+sDBwRnr1v0KV1dX\nAEBqairOnTuHzZs3g2wPoIv9TyZiYrSwWCxQKBQoLKdOnULz5u1hMn0FwBOnTo2DyZSK0aNHPrau\nQCD4l1BUBwWeFcXQZcFz4sqVK+zUqTerVm3MYcNGMyUl5aEyU6fOoCT5UKV6j3p9Q7Zo0YFjx46n\nUqmlSqVnnTrNePv2bVat2ojAQvthNwuBNlSrK7JcuaqMiYnheJXuwUk4jsQo6vUuTEhI4OXLl2kw\nuBGYSeAPSlJTDh78z33+iROnUKXSU6FwpVZbgrNmzcrhn9Vq5b1793Jc+btw4QI9PMrSwaEy1WpH\nKpWBBNLszUewRInSRTaG778/hsD4bAf9/qKPT+Uisy8QCPJHYbSv2KmmEHpBfkhOTmbJkn5UKD4l\n8AeVynrU671YqVJDLl68hCSZnp5OlUqy34kngXRqtT7UagMI3CSQSaVyAB0dvQkYCERmE7wpbNGi\nNe8lJ5PjxpEALQCHadwoSSW4cWNoli8nTpxg8+Yd6OHhR1/fGhw0aHhW4pvLly/TwcGNMtkIAjMp\nST5cuHDxI/tWo0bjbMGA7lKhKEmt1p8ODp0pSa7cvHlzocbu+vXrPHfuHM1mMz/4YCxlsnHZ+r2H\nL71UtVD2BQJBwRFCLxD8D5s2baKDQzO7OP1KoAyBLQS2UpJe4ooVK5mYmEiVymAPdvMg8UoFApOy\nrrgB9QkMJdCLtsxvmQSuU6+vyDWrV5MjRtgqKhRMXbiQ58+f5/379x/yZ8CAYZSkxgRWUKUaRS+v\n8kxOTuYnn4ynQvFuNiHdzTJlHj1j1utdCFzPVucj9u3bjytXrmR0dPQTj5nVauXo0eOo0TjSYPBj\nqVLluHXrVur1rpTJviWwjJLkyzlzQp64DYFA8GQURvvEYTxBsSIxMRGtW3eBVmuEu3tZrF+/Ptdy\ntv3pNNgOsv0CYDKAVgBawmT6GnPnLoejoyP8/QOhUHwGIAlAGGSyK9Bq/wSQCaAngFMAPgLwE4Bo\nAAbI5WXw7oiu6BwWBvz4I6BW49bs2eixPhzdug3CuHETkJqamuVLeno6fv55PkymjQB6IiNjGpKS\nymDbtm1IT8+AxeKQzXMjMjIyHjkG/v6BkMnW2H+6D71+C9q1a4sePXrA29sbsbGxSElJKeDIAmFh\nYZg7dx3M5ku4fz8KN24Mw4cfTsT+/X+ga9czaN36d8yfPwlDhgwqsG2BQPAcKcIPjmdCMXRZUIQE\nBb1GtXoQbfnX91CS3Hns2LGHyqWmptLfvzrV6rcIvExgVrYZ8Fy2bt2VJHn16lXWq9eCarWeXl4B\n3Lp1K+vUaUat1pdAZQI17CsCtr15na45Z02fTvbo8SAvLe+tXUt39zJUKL4g8Ae12s5s06ZLDl8U\nCrU9brytmoNDO65atYpHjx61x9pfRmAnJak2x4+f+MgxOH/+PN3dX6LRWJU6nQf79h1Cq9XKEydO\n0N29DCWpFDUaB86ZM69AYztp0iQqFMHZximBGo1DgWwIBIKnQ2G0r9ipphD6/y7bt2+nLfXq3Swx\nUquHc+rUqSRtOegvXbrEW7dukbTFax81KpgNGrSgSuVEYAqBrylJrrmmZn1Aeno6hwwZQpVqKIF9\nBNwIdCFQgY3rNKWlXTtb40YjuWcP161bRweHltkEMo1KpS5HLPkuXfpQp2tLYCsVigl0c/PhnTt3\nSJIRERGsX78lK1VqyEmTvrUlwXkMKSkpPHz4cFbyG6vVylKlyhH42e7DRUqSJ0+cOJHv8V29ejX1\n+prZPkh+ZkBArXzXFwgETw8h9IIXnhMnTthnvu4EDmTtoev1QVy8eDFjY2NZtmxl6vXeVKuNHDky\nOMdJ9cOHD3PAgGEcMGAYDx06lGc7sbGxXLduHefOnUtJ8rIf1IulTNadlV+qQEvz5jY1L1GCV9av\nZ/36r1KvL0G5vHa2vf4kKpXaHKf8zWYzg4M/Ya1azdmpU29evny5SMcnKSmJSqWU7WODNBh6ccmS\nJbmWP3jwIEeOfJ8ffDCWUVFRJG0fC716DaAkedHRsQGdnUvx+PHjReqnQCB4MoTQC154Jk78kgrF\nBwRW0RZf/l0CjVm1agOmpqayQYMgKhQT7GKbQL2+Mn/77bcCtbFt2zbq9a40GttTry/HmjUbUaWS\nqFY7skbZykytVcumoJ6eTD10iCVL+lEu/47AOQJeBN4ksJSS1Jj9+g15SiORO1arlQ4OrgT+zDqN\nr9f7cs+ePQ+V3bFjByXJjcBEyuUf0sHBnRcuXMiyc/LkSUZERDAxMfGZ9kEgEOSNEHrBC8/UqVOp\n0fSxi9ghAsNpNLrRZDJx5MhgAjoCcdlmtOP5ySefFqiNEiW8COyw10+hwVCZv//+OxMuXKC1Rg2b\nYW9vMjKShw8fpoNDlRz72TKZKxs2bMXvv5/GzMzMpzQSeRMWFkZJcqWjY0tKkhffeef9XMvVrfsq\ngRVZvstkn3Hw4BHP2FuBQFAQCqN94tS9oFjQt29fODn9CaXybQA7IUnrMW3at1iyZBnmz98JoCps\noWQBwAy9fgfKlfPLl+3Lly8jMLAO7tyJA9DU/lSC2VwDYfPnw7FjR8iOHQPKlQP+/BPw94fRaERG\nRjwAk728BqQFer0ao0ePKpKodAWlTZs2iIw8juXLR2Hv3o2YOfO7rHe0fdQDAFJSTAA8sr3zQHKy\n6X/NCQSCFwSRj15QbIiPj8ePP/6EhIQkvPZaW2i1WrRu3QMm00QA9WC7PlcGMtlltGvXGOvXL89T\ncK1WK06ePImUlBT07DkQcXH9Qf4KoC+AUQCi4YM6+AMm+CEN1sBAyHfsAEqWBABs2bIFr73WG2az\nF4CuAEIBBEAuX4HU1PtQq9WP7IvFYsGKFSsQExODmjVrol27dkU1TA/1c+TIYISEzAYAvPnmIPj5\nlcGECUthMs0FcA+S1B9r1oSgTZs2T8UHgUBQeAqjfULoBcWSK1euIDCwJlJSmgFwBhAC4C6Aj1C3\n7jn89dcfkMlkudZNS0tDUNBrOHo0EqmpySCTAZgBRAHoAOAa/JGGHdDDG4k4Kjfi/LQv8foIW0a4\nEydOoGHDIJhM/QFsstepCKAllMoyuHXrOm7dugUfHx/odA+niyWJ//u/HoiIiIPJ1BSStBYjRvTA\n5MkTiniUgO++m4bPPlsNk+l3AHJIUieMG9cOCoUcc+cuhVqtxuefv4/XX+9V5G0LBIKio1DaV9h9\ng2dNMXRZ8BRYsWIFHRy62O/TVyTwKoEgOjmVzDpYlhcTJ06iTteRwNcEOhBwIHDKvmdtYmV48Doc\nSYC78TJdVQP4ww8/kCSPHDnCN954gwrFaAKJBDwJ6Ak4Uqn04auvtqNWa4ssZzR65HoYbv/+/dTr\n/QmY7W3eolptyPPw25kzZ/jDDz9wwYIFuUbdexTNmnUg8Fu2swQb2aBB6wLZEAgEz5/CaJ/YoxcU\nS5ydnUFeAmAEcBBAZygUEThz5jDKly//yLonT0YiNbU9bKlhW8CWja4FgH6oDX/sQjw8kYRtaIzW\neB/3Fb8jKCgIH374KRo37ojffjsBiyUawI8AygOIBHAEMpkOu3btRlraX7h/PwrJyYvQvn23hyLd\n3b17F0qlD4AHy/uuUCodkJyc/JCv27dvR506TTF27EWMGLEW1as3wv379/M9TqVLu0OhOJ71s1x+\nHKVLu+e7vkAgeAEowg+OZ0IxdFlQhFitVqalpTEzM5NNmrShXt+UCsWHlKQy/O67afmy8fXX31GS\nWhGYS6CuPQDPMTZGVSbZp77r4UUN3CiTGbl27VqePHmSklSKwG37TN6Xtvj5O7LNlhdTqfTNcZdd\nkkoyNjY2R/u3b9+mo6MngaUEblKh+IJ+flVzDZTj61uNwKasuAFabbesAEH54e+//6arqzclqSsl\nqQdLlChdqHj4AoHg+VAY7RP56AXFhvnzF2DEiPdhNqcgIKA6Nm5cgb179yIuLg716y9E8+bN82Xn\nvfdGIiJiP3buHI/MTAsyMz3QEgqsQyokAMuhQj/oYJHdwYYNq9G+fTts2rQJKlUVAC52K4cA+AI4\nC8DWrkJxFuQdADcAeAI4DDIV7u45Z9AuLi7YuTMMr78+GLGxo1C1ak2sXh0KufzhBbbExATY9v8B\nQIa0tIqIj0/I95j5+Pjg3Lmj2LBhAwCgffsZD/kjEAhebMRhPEGxYMWKFXj99cEA/gBQC8DXKF9+\nDS5cOPJE9kgiJiYG6enp+CmoA767GgMNMjEfPhiCVwD5GqxZsxSdOnUCAMTGxiIwsBZMpi329tfA\n0fEdWCxERsZrkMlMMBh2o1+/3pg1awHU6kBkZJzGhAnj4O7uBn9/fzRo0KDAfvbo8SY2bDAjLW0W\ngL8hSe0RGroEr7zyyhP1WyAQFE/EYTzBC4+ra2kC3bMti1spl6sfeTjt3r177Nq1Lw0GN5YqVZ7r\n1q17uNAvv9Ail5MAp6ElZehHlUrPZcuWPVR07dp11OmcqNW60sXFi4cOHWJMTAynT5/On376KSvG\nfmRkJMPDw/nRR59RkkrTYHidklSGY8d+VuB+37t3jx069KJaraeTU0nOn7+wwDYEAkHxpzDaJ2b0\ngmKBWi0hI8MXwBEAGgCnoFTWh9l8L9clbwDo2rUvQkMzYDaPADASQBTq1q2FtWuXoHTp0sC8ecCQ\nIQCJUx06YujtdGh1Ggwc2B1HjpyAyZSG3r27o2HDhlk2MzIykJCQADc3t0cGxbFdrysPs/k0AC8A\nt6HVVsTp0/vh55e/QD4CgUDwgMJon9ijFzx30tPTcePGDXh6euYZaKZmzYY4cOAOgLoAqgH4HcHB\n7+Yp8gCwefMmmM07ALwCYBiARTh48Bf4+FTEaHk6vs1MsxWcPBlVxo7FnwAuXbqEmjUb4f79/rBa\nS2LRotcwadI4+Pn5oXbt2nBxcUF6ejosFstjhV6tLmkPqAMArtBo/HD9+nUh9AKB4NlSRKsKz4xi\n6LLgEWzdupUGgyslqRQNBldu27Yt13JXrlxh+fI1qFTqqVCoOXLk6Mfa9vDwJfCK/YT8gyV/Cz+G\nU9ax+CV1G+WoM3z4aMpkH2VtDwBBlMtL0WhsQ63WmVqtAyWpFB0c3Lhjx448205JSaGTU0kCa+y2\nttHBwZ0JCQkFGyCBQCCgSGojKKbcuXOHer0rgd12MdxFvd41z8AxVquVt27dYmpqar7sr1q1moAT\ngZIE0ghYOQWjSYCZkLM/JtPVtUyOOv36vU3gh6zgMkAlAib7z1sJlLL/+w4aDG5MSkrKs/2DBw/S\n3f0lKpVaOjuXZERERL7HRiAQCLJTGO0TAXMEz42LFy9CofAB0Nj+pAkUCi9ERUXlWl4mk8HNzQ1a\nrTbHc7PZjNjYWJjN5hzPu3fvhm7d2gPQQoY2mIkmGIOpyADQC8uxGFXg5FQiR52+fbtBp/sGwGYA\nuwDUBvAgjO0rsF2dswJoDrncHdHR0Xn2r06dOrhxIxqJifFISIhD06ZN8ywrEAgETwsh9ILnhpeX\nF9LTY2CLUAcAl5Ge/je8vLweVS0H4eHhcHX1QrlytWEwuOLtt4ciMzMz631IyI9Q4CYWYjfewZ9I\nA9AJdfArdkGn64+ffpqSw17z5s2xbNlMVKgwASVL/g6Vaks2/34EUAW2vzaXkJ4eZzvU9whkMhkM\nBkOecfcFAoHgqVOEKwvPhGLosuARTJs2kzqdO43GNtTp3Dljxqx8101MTLQv/e+yL6fvJmBgmzZd\naLVaSZK3rl7lr7Bdn7sHic3xO4FR1GqNPHnyZJ62zWYzZ82axebNW1Gp1FGnc6ejYylqNC52X904\ne3ZIofsvEAgE+aEw2ieu1wmeOxcuXEBkZCTKly+PgICAh95fuXIFy5cvR2amBd27d4O/vz8AYO/e\nvWjS5E1YrZHZSteCWh2NixdPwMfNDezaFbKwMNyFHG1RHvtRA8AGLF78E/r165erP5mZmWjatC2O\nHZMhNfVlSNIyDBz4f5g27RtERkbi4sWLqFChQpYfRUlcXBwSEhLg7++fa+Y7gUDw30QEzBEUezIy\nMhgXF0ez2Zzj+cWLF+no6EmVaigVindpMLjx6NGjJMn33gu2Z46Lts/oYwg4U6crxYtHj5KvvGI7\neOfszA5e5QnIqdMZOW/evEf6Eh4eToOhOoFMu90bVKl0NJlMBeqTxWJhVFQUY2JislYYHsX7/9/e\nnQdEVb0NHP8OMwPMgOAOCCKGIiIIKq65YC6E5p7mXtpiWpbtZmbaT8W0zD1zqUxLLTX33dxywdwV\nLU1REUVxIZEBZmDO+8fQlK9LiwgyPJ+/nLuc+zy3iWfuveee88YQ5eJSQhUrVlWVLu2vjh49+q+O\nJ4RwXPdT++Q9elHg9uzZQ0xMRzIyLICZefO+oGNH29Cz//vfx6Sl9cdqHQbAzZtBvPXWCAYM6M3G\njTuATkAEUBM4ClQnokIagf37Q1wc+Pig3biRZSEhmM1m9Hr93z4vv3HjBk5OfsAf78mXQaPRYzKZ\n/vFV9o0bN2jevB3x8SdRKptHH63LypXf4eLicsft169fz/Tpi8jKOklWVinS0mbRsWPv/zzErxBC\n/EE644kCZTabefzxDly7NpmMjEtkZGykV68XOHfuHABXr/6O1VrxL3s8wu7d+3j66Y85fjwLuAws\nBSyAjvByyWzTmdHExUGFCrB9O4TYJoVxdnb+R53iHn30UWyT1swFzqDXv0lISBglS5b8mz3/9MYb\nQzl8OACT6SwZGefYsUMxevS4W7ZRSvHtt/Pp3PkZPvxwNBZLS/6cNKc7p04d/cfHE0KIu5FCL/LF\nwYMHWbVqFefPn79l+YULF8jKcgI65C6phV5fg/j4eAC6dGmN0TgaOAz8irPzu5jNBm7e/Ins7J+A\n60BX3N1TaFKpLHvdrOiOHoWgIFuR/w+j0Hl5ebF582pCQz+jRIlGPPbYWdav/+Ef/UhYsmQJPXo8\nz9Kla8nK6ontroAzGRnd2L370C3bjh07nuef/5BFixqya1cpzOaVwB9z0i/F3//2/gpCCPGv5d0T\nhPxRCEMu8l5++U1lNPopT89oZTSWVitXrrSvS09PV66uHgric5+Hpyij0cf+fNpqtapx4z5VpUsH\nqBIl/HJ7wb+au+1pBRuVVuuijq1apawVK9pGvAsLUyo5Od/zHDVqjDIa5fUbaAAAIABJREFUKymY\npjSaGgoG5I6ul6NcXHqoN98ccsv2Hh5eCn6xj8Kn1YYqvb6U8vSsrUqUKGfviyCEEPdT+6TXvXig\ndu7cScuWPUlPPwB4Artxc2vNjRsp9nHqv/56Hv37v45OV5fs7AO88spzxMYOv2N7u3fvpmnTDmRm\nhmCb4KYMIU4X2F/KDZeUFKhdG9auhX9xm/1esX/77SKMRlcGDHiBgICAO253/fp1YmKeJC4uDtgN\nhAIpaDRhODuXRK+HSpVKsn37Wtzd3e37ubmVwmQ6DNjexXd27s/rrxenbdu2VKtWDQ8Pj/vOQQjh\nGO6n9kmhFw/Ut99+S79+y7h5c6F9mV5fjKFD38JoNNKlSxf8/f357bffOHLkCBUrViQiIuKebTZs\nGMWOHaeBQ1TnHBtoRFnSuB4WRomffoI8KJCrV6/mySf7kJExCCenqxQr9g0HDuykYsWKt23bsWMv\nVq1yw2xeDOwHygOg0w2gXz8nevfuTc2aNdHpbu372r//a3z99UFMphHAr7i7v8ehQ7t55JFH7jt+\nIYRjkUIvHlrx8fHUqdMMk2k7UBn4Bo2mH1ptL5ycwNX1B37+eRtBQUG37XvlyhUOHDhAqVKlqFGj\nhv0ZucHgQWZmb+rQi7U8TglSWQv0MpYk8WrSbUPk/hfVqzfkyJG3gHYAODm9wyuvKD79dOxt2/r4\nBJGcvAz4HDgCjARO4Ob2Jvv377hjbmB7X/+DD0axdOk6SpcuyYQJ/6NGjRr3HbsQwvHcT+2Tznji\ngapWrRoTJozGxaUWRqMvzs4DUepFsrM/w2z+jLS0QQwdOvq2/fbs2UNgYCidO8fSuHEnunbta/+S\nKwVNWMpGmlOCVJZQk3aUx4SRixcv5knc6ekmwMv+2Wr1Ii3NdMdty5cvj0azDRgHNECjeRJ//4/Z\ntGnlXYs8gE6nY9SoD4iP38nWrSulyAshHggp9OKBe/75vly9epHjx3dRq1YdoLF9nVKVuHIl9bZ9\nunTpy40bk/n99x9JTz/GqlWHWLp0KQAfN3uMNVygGDeZhwdd+AUzA9FoTPj4+ORJzE8/3Rmj8RVg\nL7AOo/FjevTodMdtv/xyEp6eI/DwaI+7+xpq1Ajkl1/2ULdu3TyJRQgh7scDLfSJiYk0bdqUatWq\nERoayqRJkwC4du0aLVq0ICgoiJYtW5Ka+ucf+tjYWCpXrkxwcDDr169/kOGJfDRlynSqVo0gLm4r\nWu0QIB74CaPxf3Tu3Oq27S9cOA08nvvJgNnchFOnTsHixby0YTUGFF+7etAbKy5Gf4zGj1i48Os8\nuW0PMHToO7z1Vjv8/fsQFDSUr7+eTNOmTe+4bbVq1Thx4hBz5jzP4sWj2b17kwxfK4R4eNxfh/97\nu3jxojpw4IBSSqm0tDQVFBSkjh07pt566y310UcfKaWUGjNmjHrnnXeUUkrFx8er8PBwZTabVUJC\nggoMDFQ5OTm3tPmAQxYPwOLFi5XRWFnBSQXXlJNTeQUuCtyVwVBS7d69+7Z9wsLqK41mvH0IWje3\nQHXk7beVcrJNUKNef10pq1UlJiaqHTt2qJSUlALITAgh8sf91L4HekXv7e1t70Ht7u5O1apVSUpK\nYvny5fYJRZ5++mn7Ldlly5bRrVs39Ho9AQEBVKpUiT179jzIEEUeyszM5OjRoyQnJ9+yfOXKTZhM\nLwOVgJtYrWnAFiCNjIzZPP54h9vmkv/hh7n4+n6Om5s/zs6V+bZJCKFjx4LVCh98AB9/DBoNfn5+\nNGjQgNKlS9v3VUqxYsUKJk2axE8//fSg0xZCiIdavj2jP3PmDAcOHKBu3bpcunQJLy9bRycvLy8u\nXboE2EZJ++tc5H5+fiQlJeVXiOI+xMfH4+8fTIMGTxIQUJUhQ0bY1/n6lkGvPwJcAZpjK/j1cte2\nx2JxsQ95+4dHHnmEIUNe5bHHGrDk0Tq0Xb3CtmLcOBg+HO4ySp1Siu7dn6Nbt6G8/favREf34KOP\nxudxtrceLzZ2HKVK+VOypB/vvTcCq9X6wI4nhBD/Vr5ManPz5k06derExIkTKVas2C3rNBrNPYcW\nvdO64cOH2/8dFRVFVFRUXoUq/qN27XqQkvI+8CyQwqRJ9Tlx4hd++eUcZcuWpFSp46Sk1CMnpw6w\nGVvRLw2cIDv7mv2HH9iKZ82ajTh48DrDqEhrNgFgmTQJ/cCB94xj7969rFixmfT0o4AReJdhw6oy\nYMDzt3338sIXX3zFyJFzMJnWAjomTOhOyZLFeeONV/P8WEKIomPLli1s2bIlT9p64IXeYrHQqVMn\nevXqRfv27QHbVXxycjLe3t5cvHiRsmXLAuDr60tiYqJ93/Pnz+Pr63tbm38t9KLgKaVISDgK9Mxd\nUoaMjKYsX74Li2Uax4//jIfHXkqUcOPKlUFAFaAGUB2tdidTpky4ZRS42bO/4ODBOMbxIm8yhRyc\neEFbji5BQUT/TSwpKSlotZWwFXkAP3S6YqSmpnL58mXi4+MJCAigevXqeZL7woWrMJneA2wT55hM\nI/j++0lS6IUQ9+X/X8SOGDHi7hv/jQd6614pxbPPPktISAiDBg2yL2/bti1z5swBYM6cOfYfAG3b\ntmXBggWYzWYSEhI4efIkderUeZAhijyg0Wjw9a0MLMtdcgOrdT0Wy0igMVbrG1gsDShf3gedbjnw\nAbAYZ+fLDBzYl+ee63NLe5s2bGMa8CZTMKPnKRbypdX/tuf4d1KrVi2s1oPASiALjWYipUp5sHnz\nVsLC6tGr1+fUrx/D0KH/y5Pcy5QpjpPT6b+ci1OULOmZJ20LIUSeyJPugHexfft2pdFoVHh4uIqI\niFARERFqzZo16urVq6pZs2aqcuXKqkWLFur69ev2fUaNGqUCAwNVlSpV1Nq1a29r8wGHLP6jPXv2\nKE9Pb+XpWU8ZDN5KozEquJzba14pd/doNW3aNFWhQlVVrFiEcnMLVA0bRqvMzMxbG7JY1P6w6kqB\nMqFVMUxQME7pdB7q6tWr/yiW7du3Kx+fSsrJSadCQuqoQ4cOKVdXTwVHc+O5rAwGb/vEOffjxIkT\nysPDS+n1Lyqd7mXl7l5GHTp06L7bFUKIv7qf2idD4Io8k5qaytGjRylTpgxTp85i9uytmEwD0Ov3\n4u29kfj4n9Hr9Rw8eBAXFxfCw8PtE9sAkJUF3bvDkiWkazS003jxo9Lg5JTF0qVzeOKJJ245XnZ2\nNu+99yHff7+C4sU9+fTTETRp0sS+XimFRqMhISGBsLAmpKf/2eHP07Ml8+e/RkxMzH3nnZiYyIIF\nC7BarXTu3FnGqhdC5DkZ614UOKUU58+fx2w2U7FiRTQaDdOnz2Dduu1UqODD+++/c8srcLcxmaBT\nJ9vMc8WLk7FkCStSUsjMzKR58+aUK1futl1eeeUtZs/+GZNpLHAGo/Eldu3adNvzd7PZjLd3Ra5f\nn4Zt7PoDGI0tOX58H/7+/nl6HoQQ4kGQQi8KVHZ2Np069WL9+o04OblSubI/mzevpESJEv+sgbQ0\naNMGtm6FMmVg/Xr4mxnsAEqWLM/165uxva5nm3hm2DA3Pvhg2G3bxsXFERPTkcxMK5DBl1/OwN+/\nPGazmdq1a2M0Gm/bRwghHhb3U/vy5fU64dg+/XQSGzakkJmZCDhz/PjLDBjwJvPnz/77na9dg5gY\n2LMHypWDTZsgOBj489b73bi4uALX7J+12qsYDKXuuG3dunW5fPksycnJuLm5ER3dkePHL+Pk5I6H\nRyq7dm26ZQwHIYRwFDKpjbgvixYtZvDg/5GR0Q1wBZwwm3uzb9/hv9/50iVo2tRW5CtWhO3bOaXX\n07NnX4oXL49Wq8fLq+Jd3yX93//exWjsDExCq30NT8/19hEX70Sn0+Hn58ekSVM5cqQ0N28e5saN\nOC5e7Er//m/+l/SFEOKhJ1f04h/bv38/n3wyjawsC/369SQgIIDevV/Eau0OrAaeAbTodCuoWrXy\nvRs7fx6aNYMTJ6BKFdi4kdNmMzVqNCAtTQu8BbzE5cubadOmC7/+evC25/TPPdeXcuW8WbRoJaVK\nefLaa7tvGXjnbuLjT5GZGQ1oAcjJieHXX1f/+xMihBCFgBR68Y8cOHCARo2iMZkGA+6sWfM0L73U\nE52uCfAx8ARQDVB4e8Nnn22+a1s5J06gadECp3PnIDzc9ky+bFmmvz2Emzc7AkuA13K3jsbJKZJ9\n+/bdsUNeq1ataNXq9tnv7qVu3XBWrZqPydQDcMHZ+SsiI8P/VRtCCFFYyK178besVisDB76NyfQW\n8AbQD5NpCsuXb8JqPQxYgfXABzg7n+f48TsXZYDvPxxJcpVgnM6d46CrkcS5cyF3ZESTKROlvIF0\n4I9X4TLIyTlhHz3xTrGdPHmSs2fP/uOOKq+++jKPP+6Di4sfBoMf1arFM3XquH9+QoQQohCRQi/+\n1jPP9Gf37l/5c1hZAAOuru507NgUo7EGbm7dMBoH8eWXs3F3d79jO/HffEPUBx/gi2IzUTTJeoMn\ner5oX9+zZxeMxmlAV6AB0Adn55q0bt3ojiMkXr9+nVq1GhMR0Yzg4Dq0bt0Zi8Xyt/nodDoWL57H\n6dNHOHZsJ3v3bv3nbwgIIUQhI4Ve3NP58+f5/vvF5OTMAEYCC4FVuLq+xMCBz+Dq6oLFcgGLZRNl\nypSkadMmd2znzPz5lO/dmzJYWY0frZjPDfU+R4/G2Wd7q1evHkuWfE2NGr/h7+9BmzapfPfdGBYs\n+OKOve8HDnyHY8eqYTKdITPzHFu2pPPxxxP+cW7lypUjICDg1kF7hBDCwcgzenFP6enpaLUeQDTw\nFTAROECDBtVxcdEzb94GLJalQH2SkmLp2fNFNm1adksbv//wA6W798AdxSKa0R1fLDwNvEeJEj63\nFNro6Giio/9u6hqb/fuPYDaPw/Z71YWMjKfYvXsD48aNZ+/eo0REBPP666/i4uJi38dkMpGamoq3\nt7cUeCFEkSAD5oh7ys7OpkqVmpw925acnKexTVwzAReXkmi1lzCZtIA3kAbMolSp3ly5cta+/+/f\nfotrj564oJhDb55lNjkAeGAwGFi8eN5/Hoa2U6feLF/uQ3b2GMCKq2s3ypU7zsWL5cjIeBKDYTl1\n6uTw448rcXJyYvz4Sbz77hCcnIx4eZVm06YVBAYG3ucZEkKIB09GxhMP1IULF2jUKIbTpy9im152\nGvAKcBXYCrgAY4CFREaW4Oeff7Tt+P33ZD/1FDqlmEZZXuYCCi1wDSenchw+vI9q1arZj7N69Wr6\n9h3I9euXqFevCYsWfUWZMmXs681mM5mZmfYpbZOTk6lfvznXrjljtZp45JGSnDiRQGbmmdyYLLi5\nVWHHjh9IT0+nRYuumEzbgQpoNOMJCfmOo0d3P+jTJ4QQ9+1+ap/cuxT3ZLFYGDHiIxITfwM6AOuA\n48Bu4ElsBRWgAxpNAnPnTrN9/Oor6NoVnVKMpQ8v8QiK7sBkNJpGuLuXZuTI8aSmpgLwyy+/0Lnz\n01y6NAuzOYldu4Jo27a7PY7hw0fh5uZJqVI+1K4dxZUrV/D29ub48b2sWTOFzZvnMXfudLRaI+Cc\nu5cOJyd3zGYz+/btw2p9AqgAgFIvcfz4XvnRKIRweFLoxT0NGTKCefPisVh+BH4AXgKeBprnfjYB\nCphD48YNCQ4OhqlToU8fsFqZXq4ig6kNbASqA+NRSs+NGz+wZIkTLVq0RynFtm3bgDZAU8ATi2Us\ne/ZswWw28/jjbRgxYhrZ2afIzk7j0KHq9OzZDwAnJyfq169PZGQkISEhlC9fAr3+dWAPOt0QSpe2\nUr16dSpUqIBWuxPIyM1sM2XK+N9ziF0hhHAEUujFPS1duhaTaSRQF9gGfAs8CrgDQUAAEIhe/znf\nfPM5fPQRvPyybedPPqHR+hUULzGSYsXaA19g+2EQB9TGbJ7O0aPxXLx4kZIlS+Lk9Cu2d/IBTuDq\nWowpUz5j06ZDwPNAOcAJi+VNdu/exaOPRmMwuGM0ejJ16nR0Oh3btq2hbdurBAb2p1Wrs+zcuREX\nFxfatGlDTEw4bm7V8fBojbt7bxYs+CK/TqMQQhQYeUYv7ujKlSssXbqUUaMmc+bMm0AvIAnbVfkJ\noH7uv3XodCvZuGElTTZtgpEjURoN8S+/TNVPP0Wr1XLt2jWGDRvG55/vJDs7GziI7TfmTZydy3Hh\nQgIeHh40avQ4R49aMZsj0Onm0759c/bu/YWTJ6sDF4FVufstwGh8HYulIxbLBCABo7EZq1Z9TVRU\n1F1zUkqxe/duUlJSiIyMvOugPkII8bCRzngiTyUmJlKz5qOYTA3IyUklK2s7tiv649hmizsKlAHm\noNePYP63M+i0YwdMmEA20M+lLt/pzdSu7cuMGZ8ycOC77Nu3h6tXG2C1JgFeQDNgJr161eLrr2cA\nts52CxcuJCEhgalTv+TGjXpkZp7G1gHwJHADKItO9xM6HWRmnshtC5ycBtOqVTyNGzcmJiaG0NDQ\nfD1nQgjxIEmhF3lGKUXr1p1Yt64KVmts7tJ2aDRxKPU9ts54U4EmODsfonePVszUmmHWLLKArgxj\nKSOAbNzcGqPVniQ9fRA5OaFAb+Bd4CRa7Sbq1XuEbds23vY++5gxH/HBB8cwm+cAl4HaQHlcXbPR\n639j3boVdOv2PGfPjgVaAVY0mih0OhPQEL3+G5YvX0CzZs3y45QJIcQDJ73uRZ5QStG9+7OsW7cT\nq/Wvk7yYUCoWaIRtdLzReHruYd3KGczISoVZs8BgoKPWmaX8Md2rjqysWmRleZKT8x7QDtiORvMR\nYWEnGDr0ebZsWX/HQWuuXUvFbP7j/faywFKKFTvBl18OIiHhV+rXr8+XX07GaHwaN7deODvXRamz\nWCw7sFgmYDLN5qWXBj+4EyWEEIWIFHpht27dOlas2IPVOhj4BLgApKDVnsz99x9cqV09gqipU9F8\n+y24u8PatVyNbIRWOwZbL/zf0GoXodXqcz8DVESns7Bt2wqGD3+Po0ePMn/+fPbt23dLHE88EYPR\n+DmwCziPwfABnTt3oWvXrpQqVQqApk2bcvjwbiZPfozoaF/gOf581S+I69evPZiTJIQQhY0qZAph\nyIXG559/rozGvgqsCoYoKKZArzp16qbc3csojeZtBR+oUoZS6lqdOkqBUiVKKBUXp5RSKikpSVWv\nXl/pdK7K2dlNTZ48VYWG1lUuLj0UzFRGY0PVq9cLSimlxo79VBmNPqpYsc7KaPRTw4ePviWWefO+\nUV5egcrDw0v16vWCysjIuGvcGzduVEajn4K9Ci4qg6Gd6tv3pQd3ooQQIp/dT+2TZ/TCbt++fTRq\n1IaMjG1AJWAilSp9xa5dG+jb9yV2744joGRxNrgoPA8ftk0vu2EDVK9+Szvp6em4urqi1Wq5efMm\nY8Z8zIkTZ2nUKJKXXupPSkoKFSoEk5W1H5iObaKcVCZPHsXLL7/0n2KfPftL3nnnAzIy0mnfvgOz\nZk3GYDDc5xkRQoiHg3TGE3li4cLv6dnzmdxX4PR4eXmxadNyOnbsxZkzDXE3N2Wd5gUi1RWUnx+a\njRuhSpV/fZyDBw/SuHEP0tLCsD0SmAEk4+LSlbVrF9zzFTkhhCiKpDOeuG9nz56lT5/+ZGfvxPYa\n21QyM03cuHGDCxeyKGF+ly0MI1Jd4bRGx+mvvvpPRR7Ax8eH9PTz2EbLmwwEA1FkZb3GkiUr8iol\nIYQQSKEXueLj49HrawHh2Dq1PY3FYhvsxs9qYhtNCOMoxwimhUsprP7+/+k4V69e5Z13BuPk9BgQ\nCCTa1+l0iXh6uudBNkIIIf4g89ELACpUqEB29hEgBdtgOEewWm/SxNeXH7Mv4kMW+wmgnUsAJSp7\nYjab/1G7WVlZ6PV6nJyciI+Pp1Gjlty86UJ29kBsV/LPAP2A83h6bmDAgD0PKEMhhCia5IpeAFCt\nWjVef70/RmM4Hh4xGAyPsWjEe7jHxOBjzuJsOT9eqeZNcs5Ozp51p3bt5gwfPvqu7V27do2GDaNx\nc/PAYCjGJ59M5JlnBpKaOgyLZRTwJVAL28Q4S9FolgCQkZFx1zaFEEL8e9IZT9ziyJEjnDlzhppK\n4du3L1y9Sk5UFGtffJEOvfpisWwC6gGXMBgi2Lt3EyEhIbe107p1FzZuLI3ZPAk4j9H4GHq9md9/\n/xGoDAwDxuZuHQV8h5PT50RF7WDTpmX5k6wQQhQS0hlP5JmwsDDalCyJb69ecPUq5pYtCTt7haee\n/RSLpQq2KWovAl7o9WGcOXPmlv1TUlI4fvw4O3b8hNn8LranQwGYTL0oU6Y0ev00bAPoDEKrDQA6\nYxtW1xOrtQWnTiXkY7ZCCOH4pNALAC5cuMCkSZNYMmAA1hYt4MYN6NyZNwKqcCqpIenpu4D92Iay\nHQocxmLZT1BQkL2NESNiKV++EnXrtiMtLQP4OXeNFYNhLy+80IOQkJ9xcSmDXu9PkyaBGAyngTTA\nirPzDGrXrpnPmQshhGOTW/eCU6dOERnZiKY3Q5ifvRkXrPzeoQOe339P8+jObNrUDduVN8A6NJqe\naLUmnJy0ZGdnUKtWI4YOHUS3bq9gMu0GvIF30WgmYzS2RaM5S8WKOUREhJOQkESdOqG8997bWCwW\ngoJqcuPGNcAZd3c3TpzYh4+PT4GdCyGEeBjJrXtxX4YOHc3jvzdiYfZWXLAyhQY8k+MKWi2NG9fG\nYJgFmIAsDIYZtG7dBL3eE7P5J6zW0fz8cwo9e/bDam2IrcgD/A+lTEye3IIZM14mNTWVBQvc+Omn\nZ/nss4O88MKrDBz4DhkZT2F7xe4Q2dm1+OKLOQV1GoQQwiFJoRfUOLifb9T36MkmlsEMpBFLl6/H\n3b08ZcuWICamDHq9F87OZWnUyErDhrXJyekMfA6sAN4nLa0TWVnL+fO9+FX4+DxCnz59KFasGKmp\nPlgs44EOZGQsYcmS7/jxx5+wWDoDpYEAMjM7sm/fsYI5CUII4aDkPfoiJjk5mVGjxpGUlEKbNs14\n5kYqb/9yEIAhvEEs5YHhwFTS0zPo3/8VVq6cz6xZk7FarZQqVYpvvvkGnW4lZvMebPPFewJd0Oni\n0WiqYzCEYLX+xvTpM0lJScm93aT5SxQalNJy/Xo2Gs23KFUPyMZgWEKtWo/m7wkRQggHJ8/oi5Br\n164REhLJ1avtyM4OY5h+CCMslwBY2Tyap3buxWTKwfaOe/vcvabSuPFKtm5dY2/HYrHQpEkrdu3a\nAvwOGAFwd2/D8OFRBAcH8/77Yzh+/Fes1izatGnL7t17SE5uQ05OFLaJbDyAMUAobm4+KJVB3brV\nWbNmMS4uLgghhPiTPKMX/8iSJUtIS6tFdvZ4RvEbIyyXsAJq5kye2LCWs2d/QaPRANa/7GXF2dn5\nlnb0ej3btq2hQYMmODu3B9ah1X6IwXCYPn36MH/+Mo4dCyYz8yJm8wWWLfuNMmVKEBq6A632RSAS\n+Aooh4uLnqVLp7J37zo2blwuRV4IIfKYFHoHdPbsWb766iuWLFlCVlaWfbnFYgGrGxN5lSHEko2W\np7XO8OyzAJQuXZrWraOAF4Cvgc9xchrK8OFv33YMnU7H5s2ref31+kRGjqN9+9/4+edtlCxZkri4\n/WRlPQdoATeys/ty8KCOEyeS8PDQoNOZgR24uj5NnTp1aNasGVWrVsXJSb6OQgiR1+TWvYP57rvv\n6NHjeZRqjk6XRHCwll27NmIwGEg8c4YtlavSKzuTLPT0cg7BrXt9vvzyM/v+SimGDh3KggWrKVbM\njYkTR9GkSZN/FUNMTGc2bKhOTs772O4OdANCgccpVepJmjaN4sSJBOrXr8nHH4/E3V0mshFCiHuR\n+egFYBv0pnz5alits4BOgEKni+HTT5/g5X79oFcvWLiQDCctA/2qUPKpjowaNQy9Xp+ncZw7d456\n9R7j2rWSZGXdwDZJzjogmeLFG3H9elKeHk8IIRydPKMv4qxWKzNnzqRjx6ewWsH2DBxAQ3Z2PX45\neBg6dYKFC8HDA8PWLUw/dQiNRkPlyrUIDW3A+vXr8ywef39/fv31AJMnP4+LSzK22emOYjQ+S48e\nXfPsOEIIIf6eXNE7gF69XmDx4iNkZHgDx4EmwBQgCSN12eSWSb30G1CyJKxfD7Vq8dprg5kxYxcm\n03ggEaPxBbZuXU1kZOQ9j/Vvbdu2jUGDhpGa+judOrUmNnY4Op281SmEEP+G3LovwpKTkylfPojs\n7AvANWzPwgOAX/AAVuFKQ9LA2xs2bIDQUADKln2ElJRVQNXcloYxeLCV2NiRBZCFEEKIe5Fb90XY\nwYMHyc7WA26AP/A2cIVS1OFHytKQNM476ehbKZxt167Z9zMYjECK/bNOdxk3N0M+Ry+EEOJBk0Jf\niMXFxbFs2TI0GmfgFeAIoMObLLayk1okcRItDazj+fKnJ4mJeZKdO3cCEBv7HgZDd+ATtNpX8PRc\nRd++fVi+fDkTJ05k27ZtzJkzl9Kl/TEaS/DUU30wmUwFmK0QQoj/Qm7dF1LDh49m3LjpKBVKRsYu\noBoQjz9l2UQSlUjnpIuBxllTSaZP7l6T6Nr1EPPnz+bKlStERNTj8uV0IIcqVSoSHFyFNWsOk53d\nEFiE1QoWy0rAH1fXAXTuXIqvv/68oFIWQogiS57RFzHnz5+ncuVwMjOPAV7AEGAy1V29WJF5Gn8U\nlurVidF4sunQG9g6580GNtCsmY6NG1fSo8dzfP+9OxbLp4DC2TkGpeKxWE5gG9L2FaAEMCL3qKdw\nc3uUmzeT8z9hIYQo4uQZfRGzf/9+rNay2Io8wGjqGMqwyzkFfxQ8+ij6bdt4YchAXF37ARWBnUAk\n27btYeHC7/j558NYLG2xTTbjhNkcjlIV+GPcetvz/qN/OeoJ0tOzWLVqVT5lKYQQIi/IFX0hc/r0\naSIi6pGWZgbmAm2oxXjWa96kpFLQvDksXQpubmRkZFCqlC8ZGVGNMUnHAAARyUlEQVTAktwWduDm\n1onMTAs5OTGAH/ADcB2NxoRS84EWwKfAqNx/BwDfAB0pU2YDSUm/5PkgO0IIIe5OruiLkPHjp5Ce\n/jywBhhAQ5z5kTcoqRQp9euTk1vkATp37k1GRioQ+JcWKpCefoOcnG3YrvI3A4uAeSiVCbwGFAOW\nYpt+tjRQDtgIOHP9umLevHn5lK0QQoj7JYW+kElLM2G1egH1acEs1mGb8HWRrhxBh9N5rFVnzGYz\nb745hFWrlgDuwBxgA3Aa24Q1Ltg67+mBWUAY0DJ32x8AM7AbF5fywHzgCjAJWIrV2ooLFy7kZ8pC\nCCHugxT6QqZHj44YjWNpx4esoA1GLMyiKU9lnyM1fR87d6YxcOBAPvtsOeAMjARygD5ATeAAtufw\nCwAFXPxL6+FoNM2Akbi4dKN8+QwiIsLRaLYDQcAiXF1X8Oijj+ZnykIIIe6DPKMvhHYNHEjtKVPQ\nARPR8RoJKPxy13bH2XktZvO7wA1gBRCN7db7MWy3/H8BPsQ2YE4x4HXgQu62FwgOrk737h0ZNGgQ\nmZmZtGrVhQMHdqHVahk3biyvvPJS/iYshBBFnLxeV5TMnAn9+oFSxDq5McRqBHoD44CVQA+gA7bh\ncJcC84AvgTNABrY54gOAg0AMtiv6hthG1msFPIZe34OqVQ+zf/92tFotABkZGbi4uMic8UIIUQCk\nM15RMWECvPACKMUQJyNDrNOxzVS3DCgOdAWGAtOB34Ha2Ir8YeAZoCzwG7ZOeDGAN5CK7UdBKaAz\n8B4WyzR+++08p0+fth/aYDBIkRdCiEJI/nIXBkrByJHw2msAvOpkINZaEbgJTARM2Ap+CWy36w3A\nJqAD3t7nqF07HGfnj4HG/Pme/AhsPwJaYrttPxRoCwwGLFitWTg7O+dXhkIIIR6QB1ro+/bti5eX\nF2FhYfZl165do0WLFgQFBdGyZUtSU1Pt62JjY6lcuTLBwcF5Oj96oWexwIYNWDUaXtBVYJK1N9AM\neB9YDvQHdvLqq0/i7j4DjWYkMAuDYTqTJo1lz57NrFixBNu79JdyG90EVAE+o0cPX4KCKuDqegH4\nEoOhHU2bNsLf3z//cxVCCJGnHmih79OnD2vXrr1l2ZgxY2jRogUnTpygWbNmjBkzBoBjx46xcOFC\njh07xtq1axkwYABWq/VBhld4ODszvFYD2mpcmZndE2iH7fn7WGAfWu1sund/igkTJhAXt4U+fS7y\n1FN7+eGHL+jc+UkArly5hu0WfQBQAZgGdMDLqzzz5s3k4MHdvP12OO3b/8j77zdj2bL5aDSaAklX\nCCFEHlIPWEJCggoNDbV/rlKlikpOTlZKKXXx4kVVpUoVpZRSo0ePVmPGjLFvFx0drXbt2nVbe/kQ\n8kPnyJEjymDwUTBTQYSC3xV8ocBHabUe6qWXXldms/mu+1+6dEkZDCUVPKPAT4GbAj+l0birHTt2\n5GMmQggh/ov7qX26/P5hcenSJby8bGO0e3l5cemS7VbyhQsXqFevnn07Pz8/kpKS8ju8h9K5c+dw\ndg4jI+NZ4BDwCOBM8eJWPv10It26dbttSNrt27fz2Wdz0GqdaNasAc7Oj5CRMRvblfw6dLo4Fi/+\nhgYNGuR/QkIIIfJNvhf6v9JoNPe8PXy3dcOHD7f/OyoqiqioqDyO7OESGhqKxbIf2A9MBrzRaGLJ\nyanLK69M56OPphAX9yMeHh4AbNiwgXbtepKRMRTIYvHiN3Ifg/wKvAxEodc3loFvhBDiIbVlyxa2\nbNmSJ23le6H38vIiOTkZb29vLl68SNmyZQHw9fUlMTHRvt358+fx9fW9Yxt/LfRFgb+/P3PnzqBn\nz+YopScnx0pOzmDS0oYCioSEPowePY7Y2A+ZO3ceb701koyM8djeqYeMDD21ay/h6NGGODtXwmz+\njVmzplGqVKkCzUsIIcSd/f+L2BEjRtx947+R76/XtW3bljlz5gAwZ84c2rdvb1++YMECzGYzCQkJ\nnDx5kjp16uR3eA+tjh07kJR0mlGjBlOiREms1qa5azRkZTXmxImzvPPO+wwY8AmXLxuwjVv/B3d8\nfPw4deooq1d/yunT8XTv3rUAshBCCJHfHugVfbdu3di6dStXrlyhfPnyfPjhhwwePJguXbowe/Zs\nAgIC+O677wAICQmhS5cuhISEoNPpmDZtmvT6/oukpCRq147i+vXKmM3uwHigDpCJ0fgVjz7akcGD\nB5OdfQ7bBDavYZu0JgujcRj9+8/Gx8cHHx+fAsxCCCFEfpMhcAuBM2fOEBZWk5s3G2N7re4m0Bw4\njF6voWXLGIKDH2H8+AkolYZtdrq5ODkNpUKFkowf/4H9zokQQojCR4bAdXAvvvgmN2+GAzVyl7gD\n8ylevATLly9m8+atjB/vjFKB2IbB3YdGc5Nixczs3LlGirwQQhRhckVfCFSqVItTp54FYrHNMFcB\nJ6fn6dLFkzNnzrN7dy+gJ5AONKNYsSSqVw9l+vRxhIaGFmToQggh8oBc0Tu4Bg0icXHZCwzHNhmN\nD6GhF5g5cyJpaTfBPkWtG9CHmJgW/PTTGinyQgghpNAXBpMnj6VGjXO4uLyNTvc7tWpFMGDA0wB0\n794eo/Ft4AiwE6Mxlh495Fa9EEIIG7l1X0gopVi0aBFPPz2AnJyn0OkS8fY+zb592/nkk0nMnDkX\nZ2dnhg17g+ee61vQ4QohhMhD91P7pNAXIpUq1eDUqf8BTwDg4tKNUaMieeONNwo2MCGEEA+UPKMv\nIlJTrwFV7Z+zsqpy+fLVggtICCHEQ08KfSESHd0CV9ch2KabPYjROJPHH29R0GEJIYR4iEmhL0Rm\nzJhIq1bOuLgEULx4KyZN+pCmTZv+/Y5CCCGKLHlGL4QQQjzk5Bm9EEIIIe5ICr0QQgjhwKTQCyGE\nEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQ\nCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjh\nwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0Q\nQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5M\nCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGE\nEA5MCr0QQgjhwKTQCyGEEA5MCr0QQgjhwKTQCyGEEA7soSv0a9euJTg4mMqVK/PRRx8VdDgPnS1b\nthR0CAWqKOdflHMHyV/y31LQIRRaD1Whz8nJ4eWXX2bt2rUcO3aM+fPnc/z48YIO66FS1L/sRTn/\nopw7SP6S/5aCDqHQeqgK/Z49e6hUqRIBAQHo9Xq6du3KsmXLCjosIYQQotB6qAp9UlIS5cuXt3/2\n8/MjKSmpACMSQgghCjeNUkoVdBB/WLx4MWvXrmXmzJkAzJs3j7i4OCZPnmzfplKlSpw6daqgQhRC\nCCHyXWBgIL/99tt/2leXx7HcF19fXxITE+2fExMT8fPzu2Wb/5qoEEIIURQ9VLfuIyMjOXnyJGfO\nnMFsNrNw4ULatm1b0GEJIYQQhdZDdUWv0+mYMmUK0dHR5OTk8Oyzz1K1atWCDksIIYQotB6qZ/RC\nCCGEyFsP1a37v/r++++pVq0aWq2W/fv337IuNjaWypUrExwczPr16+3L9+3bR1hYGJUrV+bVV1/N\n75AfqKIwkFDfvn3x8vIiLCzMvuzatWu0aNGCoKAgWrZsSWpqqn3d3b4HhVViYiJNmzalWrVqhIaG\nMmnSJKBonIPMzEzq1q1LREQEISEhvPvuu0DRyP2vcnJyqFGjBm3atAGKVv4BAQFUr16dGjVqUKdO\nHaBo5Z+amsqTTz5J1apVCQkJIS4uLu/yVw+p48ePq19//VVFRUWpffv22ZfHx8er8PBwZTabVUJC\nggoMDFRWq1UppVTt2rVVXFycUkqpmJgYtWbNmgKJPa9lZ2erwMBAlZCQoMxmswoPD1fHjh0r6LDy\n3LZt29T+/ftVaGiofdlbb72lPvroI6WUUmPGjFHvvPOOUurO34OcnJwCiTuvXLx4UR04cEAppVRa\nWpoKCgpSx44dKzLnID09XSmllMViUXXr1lXbt28vMrn/4ZNPPlHdu3dXbdq0UUoVre9/QECAunr1\n6i3LilL+vXv3VrNnz1ZK2f4fSE1NzbP8H9pC/4f/X+hHjx6txowZY/8cHR2tdu3apS5cuKCCg4Pt\ny+fPn6/69euXr7E+KDt37lTR0dH2z7GxsSo2NrYAI3pwEhISbin0VapUUcnJyUopWyGsUqWKUuru\n3wNH0q5dO7Vhw4Yidw7S09NVZGSkOnr0aJHKPTExUTVr1kz9+OOP6oknnlBKFa3vf0BAgLpy5cot\ny4pK/qmpqapixYq3Lc+r/B/aW/d3c+HChVteuftjUJ3/v9zX19dhBtspygMJXbp0CS8vLwC8vLy4\ndOkScPfvgaM4c+YMBw4coG7dukXmHFitViIiIvDy8rI/wigquQO89tprjBs3DienP/8sF6X8NRoN\nzZs3JzIy0j6WSlHJPyEhgTJlytCnTx9q1qzJ888/T3p6ep7lX6C97lu0aEFycvJty0ePHm1/RiVs\n/wMI23m417lwlPN08+ZNOnXqxMSJEylWrNgt6xz5HDg5OXHw4EF+//13oqOj2bx58y3rHTn3lStX\nUrZsWWrUqHHXMd0dOX+AHTt24OPjQ0pKCi1atCA4OPiW9Y6cf3Z2Nvv372fKlCnUrl2bQYMGMWbM\nmFu2uZ/8C7TQb9iw4V/v8/8H1Tl//jx+fn74+vpy/vz5W5b7+vrmSZwF7Z8MJOSovLy8SE5Oxtvb\nm4sXL1K2bFngzt8DR/jvbbFY6NSpE7169aJ9+/ZA0TsHnp6etG7dmn379hWZ3Hfu3Mny5ctZvXo1\nmZmZ3Lhxg169ehWZ/AF8fHwAKFOmDB06dGDPnj1FJn8/Pz/8/PyoXbs2AE8++SSxsbF4e3vnSf6F\n4ta9+ssbgG3btmXBggWYzWYSEhI4efIkderUwdvbGw8PD+Li4lBKMXfuXPsfysKuKA8k1LZtW+bM\nmQPAnDlz7P9N7/Y9KMyUUjz77LOEhIQwaNAg+/KicA6uXLli71GckZHBhg0bqFGjRpHIHWx3MRMT\nE0lISGDBggU89thjzJ07t8jkbzKZSEtLAyA9PZ3169cTFhZWZPL39vamfPnynDhxAoCNGzdSrVo1\n2rRpkzf552WHgry0ZMkS5efnp1xdXZWXl5d6/PHH7etGjRqlAgMDVZUqVdTatWvty/fu3atCQ0NV\nYGCgGjhwYEGE/cCsXr1aBQUFqcDAQDV69OiCDueB6Nq1q/Lx8VF6vV75+fmpL774Ql29elU1a9ZM\nVa5cWbVo0UJdv37dvv3dvgeF1fbt25VGo1Hh4eEqIiJCRUREqDVr1hSJc3D48GFVo0YNFR4ersLC\nwtTYsWOVUqpI5P7/bdmyxd7rvqjkf/r0aRUeHq7Cw8NVtWrV7H/jikr+Sil18OBBFRkZqapXr646\ndOigUlNT8yx/GTBHCCGEcGCF4ta9EEIIIf4bKfRCCCGEA5NCL4QQQjgwKfRCCCGEA5NCL4QQQjgw\nKfRCCCGEA5NCL4QQQjgwKfRCCCGEA5NCL4S4p59//pnw8HCysrJIT08nNDSUY8eOFXRYQoh/SEbG\nE0L8rffff5/MzEwyMjIoX74877zzTkGHJIT4h6TQCyH+lsViITIyEoPBwK5duwr1lKBCFDVy614I\n8beuXLlCeno6N2/eJCMjo6DDEUL8C3JFL4T4W23btqV79+6cPn2aixcvMnny5IIOSQjxD+kKOgAh\nxMPt66+/xsXFha5du2K1WmnQoAFbtmwhKiqqoEMTQvwDckUvhBBCODB5Ri+EEEI4MCn0QgghhAOT\nQi+EEEI4MCn0QgghhAOTQi+EEEI4MCn0QgghhAOTQi+EEEI4sP8Diwf1C+duoqkAAAAASUVORK5C\nYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10f9e8a50>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 42
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"#### Comparing the results from the different implementations"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"As mentioned above, let us confirm that the different implementation computed the same parameters (i.e., slope and y-axis intercept) as solution for the linear equation."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import prettytable\n",
|
|
"\n",
|
|
"params = [appr(x,y) for appr in [lin_lstsqr_mat, classic_lstsqr, numpy_lstsqr, scipy_lstsqr]]\n",
|
|
"\n",
|
|
"print(params)\n",
|
|
"\n",
|
|
"fit_table = prettytable.PrettyTable([\"\", \"slope\", \"y-intercept\"])\n",
|
|
"fit_table.add_row([\"matrix approach\", params[0][0], params[0][1]])\n",
|
|
"fit_table.add_row([\"classic approach\", params[1][0], params[1][1]])\n",
|
|
"fit_table.add_row([\"numpy function\", params[2][0], params[2][1]])\n",
|
|
"fit_table.add_row([\"scipy function\", params[3][0], params[3][1]])\n",
|
|
"\n",
|
|
"print(fit_table)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"[array([ 0.95181895, 107.01399744]), (0.95181895319126741, 107.01399744459181), array([ 0.95181895, 107.01399744]), (0.95181895319126764, 107.01399744459175)]\n",
|
|
"+------------------+----------------+---------------+\n",
|
|
"| | slope | y-intercept |\n",
|
|
"+------------------+----------------+---------------+\n",
|
|
"| matrix approach | 0.951818953191 | 107.013997445 |\n",
|
|
"| classic approach | 0.951818953191 | 107.013997445 |\n",
|
|
"| numpy function | 0.951818953191 | 107.013997445 |\n",
|
|
"| scipy function | 0.951818953191 | 107.013997445 |\n",
|
|
"+------------------+----------------+---------------+\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 43
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"\n",
|
|
"#### Initial performance comparison"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"For a first impression how the performances of the different least squares implementations compare against each other, let us do a quick benchmark using the `timeit` module via IPython's `%timeit` magic."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"for lab,appr in zip([\"matrix approach\",\"classic approach\",\n",
|
|
" \"numpy function\",\"scipy function\"],\n",
|
|
" [lin_lstsqr_mat, classic_lstsqr, \n",
|
|
" numpy_lstsqr, scipy_lstsqr]):\n",
|
|
" print(\"\\n{}: \".format(lab), end=\"\")\n",
|
|
" %timeit appr(x, y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"matrix approach: 10000 loops, best of 3: 163 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"classic approach: 1000 loops, best of 3: 1.55 ms per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"numpy function: 1000 loops, best of 3: 221 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"scipy function: 1000 loops, best of 3: 362 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 44
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"The timing above indicates, that the \"classic\" approach (Python's standard library functions only) is significantly worse in performance than the other implemenations - roughly by a magnitude of 10."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"<a name=\"cython_nb\"></a>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Compiling the Python code via Cython in the IPython notebook"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Maybe we can speed things up a little bit via [Cython's C-extensions for Python](http://cython.org). Cython is basically a hybrid between C and Python and can be pictured as compiled Python code with type declarations. \n",
|
|
"Since we are working in an IPython notebook here, we can make use of the IPython magic: It will automatically convert it to C code, compile it, and load the function. \n",
|
|
"Just to be thorough, let us also compile the other functions, which already use numpy objects.\n",
|
|
"\n",
|
|
"**Note** \n",
|
|
"Of course Cython has much more horsepower under its hood - more than I am showing in this article (for example, I am not using Cython's type definitions via `cdef` here). Here, I want to focus on how to speed up existing Python code by making only minimal changes to it. \n",
|
|
"[In a later section - Appendix II](#type_declarations) We will see how static type declarations can further improve the performance via Cython."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%load_ext cythonmagic"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"The cythonmagic extension is already loaded. To reload it, use:\n",
|
|
" %reload_ext cythonmagic\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 45
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"import numpy as np\n",
|
|
"import scipy.stats\n",
|
|
"cimport numpy as np\n",
|
|
"\n",
|
|
"def cy_lin_lstsqr_mat(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)\n",
|
|
"\n",
|
|
"def cy_classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)\n",
|
|
"\n",
|
|
"def cy_numpy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" X = np.vstack([x, np.ones(len(x))]).T\n",
|
|
" return np.linalg.lstsq(X,y)[0]\n",
|
|
"\n",
|
|
"def cy_scipy_lstsqr(x,y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" return scipy.stats.linregress(x, y)[0:2]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 46
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### Comparing the compiled Cython code to the original Python code"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"for lab,appr in zip([\"matrix approach\",\"classic approach\",\n",
|
|
" \"numpy function\",\"scipy function\"],\n",
|
|
" [(lin_lstsqr_mat, cy_lin_lstsqr_mat), \n",
|
|
" (classic_lstsqr, cy_classic_lstsqr),\n",
|
|
" (numpy_lstsqr, cy_numpy_lstsqr),\n",
|
|
" (scipy_lstsqr, cy_scipy_lstsqr)]):\n",
|
|
" print(\"\\n\\n{}: \".format(lab))\n",
|
|
" %timeit appr[0](x, y)\n",
|
|
" %timeit appr[1](x, y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"matrix approach: \n",
|
|
"10000 loops, best of 3: 165 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"10000 loops, best of 3: 166 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"\n",
|
|
"classic approach: \n",
|
|
"1000 loops, best of 3: 1.59 ms per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"10000 loops, best of 3: 127 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"\n",
|
|
"numpy function: \n",
|
|
"1000 loops, best of 3: 220 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"1000 loops, best of 3: 221 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"\n",
|
|
"\n",
|
|
"scipy function: \n",
|
|
"1000 loops, best of 3: 361 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"1000 loops, best of 3: 367 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 47
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"As we've seen before, our \"classic\" implementation of the least square method is pretty slow compared to using numpy's functions. This is not surprising, since numpy is highly optmized and uses compiled C/C++ and Fortran code already. This explains why there is no significant difference if we used Cython to compile the numpy-objects-containing functions. \n",
|
|
"However, we were able to speed up the \"classic approach\" quite significantly, roughly by 1500%.\n",
|
|
"\n",
|
|
"The following 2 code blocks are just to visualize our results in a bar plot."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"funcs = ['classic_lstsqr', 'cy_classic_lstsqr', \n",
|
|
" 'lin_lstsqr_mat', 'numpy_lstsqr', 'scipy_lstsqr']\n",
|
|
"labels = ['classic approach','classic approach (cython)', \n",
|
|
" 'matrix approach', 'numpy function', 'scipy function']\n",
|
|
"\n",
|
|
"times = [timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000)\n",
|
|
" for f in funcs]\n",
|
|
"\n",
|
|
"times_rel = [times[0]/times[i+1] for i in range(len(times[1:]))]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 50
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"#%pylab inline\n",
|
|
"#import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"x_pos = np.arange(len(funcs))\n",
|
|
"plt.bar(x_pos, times, align='center', alpha=0.5)\n",
|
|
"plt.xticks(x_pos, labels, rotation=45)\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.title('Performance of different least square fit implementations')\n",
|
|
"plt.grid()\n",
|
|
"plt.show()\n",
|
|
"\n",
|
|
"x_pos = np.arange(len(funcs[1:]))\n",
|
|
"plt.bar(x_pos, times_rel, align='center', alpha=0.5, color=\"green\")\n",
|
|
"plt.xticks(x_pos, labels[1:], rotation=45)\n",
|
|
"plt.ylabel('relative performance gain')\n",
|
|
"plt.title('Performance gain compared to the classic least square implementation')\n",
|
|
"plt.grid()\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAFhCAYAAABwNN3iAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XlcFPX/B/DXIiCgHAJeHIIIJiKCigeagmkqKGhqKnnh\nkWhqmh2alqJ5YZ5FmWnKN1M0yxMBTW0xD8Ajj0TwalFRSLwQQWGX9+8P2vmxHALmsruz7+fj4UNm\nZ3bm/Z6ZnffO5zMzKyEiAmOMMb1noOkAGGOMaQcuCIwxxgBwQWCMMfYvLgiMMcYAcEFgjDH2Ly4I\njDHGAIi8IGRlZaFbt26wsLDAxx9/rOlwNC4/Px9BQUGwsrLC0KFDK51eKpXC0dFRGG7VqhWOHj0K\nACAijBkzBtbW1ujUqRMAYO3atWjYsCEsLCzw8OFD9STxkkrnwqouLS0N3t7esLCwwNdff41JkyZh\n4cKFVX5/daevDmdnZxw+fFgt89akLVu2oHfv3jW/YNIyTk5OZGpqSnXr1qWGDRtSaGgo5ebmvtS8\nFixYQIMGDXrFEequH3/8kTp06EAKhaJK0//+++/k4OBQ7rijR4+Sg4MD5eXlERFRQUEBmZqa0sWL\nF19ZvNXh5OREhw8frnD8i3J5VUaPHk2fffaZWpehCWPHjqUZM2aUO64m1uuLODs7v3C7a8KmTZvo\n9ddfr/L0f//9N0kkkip/LtVJ684QJBIJYmJi8OTJE5w9exanT5+u9rcLIkJRURHS09Ph7u7+UnHI\n5fKXep82S09PR/PmzWFg8N83e3p6OpydnWFqagoAyMzMxLNnz156fRcVFf2neCQSCYjvsazUy+zX\n6enpaNmypRqiYSVpxf6r4YJURumK/9FHH1G/fv2IiOjkyZPk6+tLVlZW5OXlRVKpVJjOz8+P5syZ\nQ126dCFTU1MaMWIEGRkZkbGxMdWtW5cOHz5Mz58/p2nTppGdnR3Z2dnR9OnT6fnz50RU/E3H3t6e\nIiIiqFGjRjRy5EgKDw+nwYMH04gRI8jc3Jw8PT3pypUrtHjxYmrQoAE1adKEDh48KMSwceNGcnd3\nJ3Nzc3JxcaF169YJ45TzX7FiBTVo0IAaN25MmzZtEsbn5eXRjBkzyMnJiSwtLen111+n/Pz8SvMu\nLSUlhfz8/MjKyoo8PDxo7969REQ0d+5cMjY2JiMjI6pbty5t3LixzHvz8vJo9OjRVK9ePWrZsiUt\nW7ZM5dufk5MTHTp0iDZs2EAmJiZUq1Ytqlu3LoWEhFCdOnVIIpFQ3bp1qUePHkREdPnyZerZsydZ\nW1vTa6+9Rj///LMwr9GjR9PEiRMpICCA6tSpQ4cPH6aMjAwaOHAg1a9fn5o2bUpfffWVMP28efPo\n7bffplGjRpG5uTl5eHjQ6dOniYhoxIgRZGBgIJxZfvnll2VyK/1N9kXLSkpKok6dOpGVlRU1btyY\npkyZQgUFBcL46dOnU4MGDcjCwoI8PT3pr7/+onXr1qnsb8HBweVun/LeS0SUnZ1NQUFBZGFhQR06\ndKDPPvtM+JZZ3jdIPz8/2rBhAxERXbt2jbp37042NjZka2tLw4cPp0ePHqlst4iICPL09CQTExNS\nKBRV3qe6d+9OtWrVIhMTEzI3N6crV64IZ0JPnz4lExMTMjAwoLp165K5uTndvXu3zDxKnjkpPwfL\nli2j+vXrU+PGjWnXrl20f/9+cnNzI2tra1qyZInKdh80aBANHTqUzM3NqW3btnT+/HlhfMnjRVFR\nES1ZsoSaNWtGNjY2NGTIEHrw4IHKOty0aRM5OjqStbU1rV27lpKTk8nT05OsrKxoypQpKnH/8MMP\n5O7uTvXq1aPevXtTenq6ME4ikdB3331Hbm5uZGVlRZMnTyai4s9fyc9GvXr1iIgoJiaGvL29ycLC\nghwdHSk8PFyYl6Ojo/DZMTc3p5MnT5Y5yzh+/Dj5+PiQpaUltW/fnk6cOKGyL3z++efUpUsXMjc3\np169elF2djYREeXn59Pw4cPJxsaGrKysqH379pSVlVXutiYi0sqCcOjQISIiunnzJnl4eNDcuXPp\n9u3bZGNjQ3FxcURE9Ntvv5GNjY2QuJ+fHzk5OVFKSgopFAoqLCyk0NBQ+vzzz4V5f/755+Tr60v3\n7t2je/fuUefOnYXxv//+OxkaGtKsWbOooKCA8vPzad68eWRiYkIHDx4kuVxOo0aNIicnJ1q8eDHJ\n5XJav349NW3aVJj//v376caNG0RElJCQQGZmZnT27FmV+c+bN4/kcjnFxsaSmZmZ8MF97733qHv3\n7nTnzh3hA/v8+fMK8753716ZdVdQUEDNmjWjJUuWUGFhIR05coTMzc0pLS2NiIjCw8Np5MiRFa77\nmTNnUrdu3ejhw4d069Yt8vDwIEdHR5Vto/zwRUVFqeywMplM5aCVm5tLDg4OFBUVRQqFgv7880+y\ntbWllJQUIio+SFhaWgo7dl5eHrVt25a++OILKiwspBs3bpCLiwsdOHCAiEjYFnFxcVRUVESffvop\nderUqdzYylOyICgUihcu68yZM5SUlEQKhYJkMhm5u7vT6tWriYgoPj6e2rVrR48fPyYiotTUVOEg\nWHp/K+1F7x06dCgNHTqU8vLy6K+//iJ7e3vq2rUrEZVfEPz9/emHH34gouKCcOjQISooKKB79+5R\nt27daPr06cK0Tk5O1KZNG7p9+zY9e/asWvtU6WWVzlMqlVbaZFRyeuXn4IsvvhA+QzY2NvTOO+9Q\nbm4uXbp0iUxNTUkmkxFR8XY3MjKiX3/9leRyOS1fvpyaNm1KcrmciFS3++rVq8nX15cyMjKooKCA\nwsLCKCQkRGUdTpo0iZ4/f04HDx4kY2NjGjBgAN27d48yMjKoQYMGlJCQQEREu3fvJldXV0pNTSWF\nQkELFy6kzp07CzlJJBIKCgqix48f082bN6l+/foUHx9PRGU/G8r1pCz+Fy5coIYNG9Lu3buJqOxn\nh0i12en+/ftkZWVFP/30EykUCoqOjqZ69eoJxc7Pz49cXV3p6tWrlJ+fT/7+/jRr1iwiIvruu+8o\nKCiI8vPzqaioiM6ePUs5OTkVbiutKwhOTk5Ut25dsrKyIicnJ5o8eTLl5+fT0qVLyxzMevfuTf/7\n3/+IqHinnTdvnsr40NBQlTbdZs2aCR8CIqIDBw6Qs7MzERXvqMbGxsIZA1HxztirVy9heO/evVS3\nbl0qKioiIqKcnBySSCTCB7y0AQMG0Jo1a4T5m5qaqmz0Bg0aCAceU1NTunDhQpl5VJZ3SUePHqVG\njRqpvBYSEiJ8G5k3bx6NGDGi3FiJSOWgSET0/fffq3zYS374Sn+DKX3Q2rZtm3BAU5owYQLNnz+f\niIoLwujRo4VxiYmJ1KRJE5XpFy9eTGPGjBFif/PNN4VxygNHebGVp2RBqGxZpa1atYreeustIiI6\nfPgwNW/enBITE8u0+Zbe30o7cuRIue+Vy+VkZGQkFG4iotmzZ7/wDKH0QbqkXbt2UZs2bYRhZ2dn\nlbPR6uxTymUpz0ZK51mVPoTS05uampb5DCUnJwvTt2vXjvbs2UNExdvd19dXGFdUVESNGzemY8eO\nCbkpt7u7u7vKPnDnzh0yMjIihUIhrMM7d+4I421sbFTOWgcNGiR8Xvv06aOyfhUKBZmZmdHNmzeJ\nqLggHD9+XBg/ZMgQWrp0KRFVrQ9h2rRp9MEHHxBR+du35Dx+/PFH6tixo8r7fX19KSoqioiKt8+i\nRYuEcd9++y316dOHiIpbLTp37lzusaU8hppusipNIpFgz549eOONN1ReT09Px44dO7Bv3z7hNblc\nrjJdZVeR3LlzB05OTsJwkyZNcOfOHWG4fv36MDY2VnlPgwYNhL9NTU1ha2sLiUQiDANAbm4uLCws\nEBcXh/nz5+Pq1asoKipCXl4eWrduLbzfxsZGpf3ezMwMubm5yM7OxrNnz9CsWbMyMVcl75L5lV4H\nTk5OyMjIeOF6qej9TZo0qdL7ypOeno6kpCTUq1dPeE0ul2PUqFEAirezvb29yvR37txRmV6hUKBb\nt27CcMOGDYW/zczM8OzZMxQVFVW7T6SyZV25cgUzZszAmTNnkJeXB7lcDh8fHwDAG2+8gSlTpmDy\n5MlIT0/HwIEDsXz5cpibm1e63O7du5f73qdPn0Iul7/0us/KysK0adNw7NgxPHnyBEVFRbC2tlaZ\npuS8q7NPKSn3+VfBxsamzGeo5LY1NTVFbm6uMOzg4KASh4ODg8rnVkkmk+Gtt95S2R8MDQ2RlZUl\nDJdeTkXLTU9Px7Rp0/Dhhx+qLCMjI0NYl40aNRJeNzMzw9OnTyvMOSkpCbNmzcKlS5dQUFCA58+f\nY8iQIRVOX9KdO3fK7A9OTk4q66BkLCXzGDlyJG7duoVhw4bh0aNHGDFiBBYtWgRDw/IP/VrXqVyR\nJk2aYOTIkXj48KHw78mTJ/jkk0+EaSrbae3s7CCTyYThmzdvws7OrsL3V+dD8Pz5cwwaNAiffPIJ\n/vnnHzx8+BCBgYFV6iiytbWFiYkJrl27VmZcVfIumd+tW7dUlpmenq7ygXqRxo0b4+bNm8Jwyb+r\nq0mTJvDz8ysT9zfffCNMU3L9NmnSBE2bNlWZPicnBzExMWWmLU91tpWjo+MLlzVp0iS0bNkS165d\nw+PHj7Fo0SKVTu+pU6fi9OnTSElJwZUrV/Dll19WOYby3tugQQMYGhpWuO7r1KkDAMjLyxNey8zM\nFP6ePXs2atWqhb/++guPHz/G5s2by3TSl17XVd2nKqKcX1XX+38pKLdu3RL+Lioqwu3bt1U+t0pN\nmjRBfHy8Sl55eXlo3LhxtZfZpEkTfP/99yrzevr0qXCJ9YuUl+s777yDAQMG4Pbt23j06BEmTpwo\nbKPK1o29vT3S09NVXktPT1f5QlURQ0NDzJ07F5cuXcKJEycQExODH3/8scLpdaYgjBgxAvv27cPB\ngwehUCjw7NkzSKVSlW+/pQ++pYdDQkKwcOFCZGdnIzs7GwsWLMDIkSMrXGZVDuZKBQUFKCgogK2t\nLQwMDBAXF4eDBw9W6b0GBgYYO3YsZsyYgbt370KhUODkyZMoKCioUt5KnTp1gpmZGZYtW4bCwkJI\npVLExMRg2LBhVYpjyJAhWLJkCR49eoTbt2/j66+/rnL+pfXr1w9XrlzBTz/9hMLCQhQWFuLUqVNI\nTU0FUHbddujQAebm5li2bBny8/OhUCjw119/4fTp0+VOX1rDhg1x/fr1KsVW2bJyc3Nhbm4OMzMz\npKamYu3atcKH9vTp00hKSkJhYSHMzMxgYmKCWrVqCTHcuHGjwuVW9F4DAwMMHDgQ4eHhyM/PR0pK\nCn788UdhmfXr14e9vT02b94MhUKBjRs3quSam5uLOnXqwMLCAhkZGUKBqkh19imlkuufipuahZzv\n37+PnJycF763Op+l0s6cOYNdu3ZBLpdj9erVMDExKffAPHHiRMyePVsopvfu3cPevXurtSxlnBMn\nTsTixYuRkpICAHj8+DF27NjxwveVXCe3b99GYWGhMD43Nxf16tWDsbExkpOTsXXrVpXta2BgUOH+\nGxAQgCtXriA6OhpyuRzbt29Hamoq+vXrVybu0n7//XdcvHgRCoUC5ubmMDIyEvbX8uhMQXBwcMCe\nPXuwePFiNGjQAE2aNMGKFStUVkR53/BLvvbZZ5/Bx8cHrVu3RuvWreHj44PPPvusyu+vaBoAMDc3\nx1dffYUhQ4bA2toa0dHR6N+//wvfW9Ly5cvh6emJ9u3bw8bGBp9++imKiooqzLu8yzSNjIywb98+\nxMXFoX79+pgyZQo2b96M5s2bV5hPSfPmzYOTkxOaNm2KPn36YNSoURVOX9m6qVu3Lg4ePIht27bB\n3t4ejRs3xqeffoqCgoJy329gYICYmBicO3cOLi4uqF+/PiZMmCAcaCpb3qeffoqFCxeiXr16WLly\nZYUxA0CtWrVeuKzly5dj69atsLCwwIQJE1QKak5ODiZMmABra2s4OzvD1tZWuOlx3LhxSElJQb16\n9TBw4MAyy3/ReyMjI5Gbm4tGjRph7NixGDNmjMq+vX79enz55ZewtbVFSkoKunTpIoybN28ezp49\nC0tLSwQFBWHQoEEv3M7V2afKW9clt0WLFi0QEhICFxcXWFtbq5y5lDd96XmVN1x6XP/+/bF9+3ZY\nW1tjy5Yt2LlzZ7kHtWnTpiE4OBi9evWChYUFfH19kZycXKXllJ5mwIABmDlzJoYNGwZLS0t4enri\nwIEDL8xB+VqPHj3g4eGBRo0aCU3O3377LebOnQsLCwt88cUXKjeGmpmZYc6cOejSpQusra2RlJSk\nMj8bGxvExMRgxYoVsLW1xfLlyxETE6PSLFjR9snKysLbb78NS0tLtGzZEv7+/i/8Eiyh/1K6KzF2\n7Fjs378fDRo0wMWLF8uMz87OxogRI5CZmQm5XI6PPvoIoaGh6gqHMZ0RFRWFH374AX/88YemQ9Go\n+fPn49q1a9i8ebOmQ9ELaj1DGDNmDOLj4yscHxkZiTZt2uDcuXOQSqX48MMPRXlDGGPs5ajx+yor\nh1oLQteuXVWu5CitcePGwml6Tk4ObGxsKuz9ZkyfVNa8py94PdQstTYZAcWXggUFBZXbZFRUVIQ3\n3ngDV65cwZMnT/Dzzz8jICBAneEwxhirgEY7lRcvXgxvb2/cuXMH586dw+TJk/HkyRNNhsQYY3pL\no+0zJ06cwJw5cwAAzZo1Q9OmTZGWlibcBKTk6upa5UsKGWOMFfPy8sK5c+eqPL1GzxBatGiBQ4cO\nASi+PCotLQ0uLi5lprt+/bpwna8Y/82bN0/jMXB+nBvnJ75/58+fr9YxWa1nCCEhIUhISEB2djYc\nHR0xf/584WaNsLAwzJ49G2PGjIGXlxeKioqwbNmyMrfc64OSd0+LkZjzE3NuAOenb9RaEKKjo184\n3tbWVuV5KowxxjRHZ+5UFjOx34wn5vzEnBvA+ekbtV92+irwr2Exxlj1VffYyWcIWkAqlWo6BLUS\nc35izg3g/PQNFwTGGGMAuMmIMcZEi5uMGGOMvRQuCFpA7O2YYs5PzLkBnJ++4YLAGGMMAPchMMaY\naHEfAmOMsZfCBUELiL0dU8z5iTk3gPPTN1wQGGOMAeA+BMYYEy3uQ2CMMfZSuCBoAbG3Y4o5PzHn\nBnB++oYLAmOMMQBq7kMYO3Ys9u/fjwYNGuDixYvlTiOVSvHBBx+gsLAQtra25VZs7kNgjLHqq+6x\nU60F4Y8//kDdunUxatSocgvCo0eP0KVLFxw4cAAODg7Izs6Gra1t2SC1oCDMmhWBzMx8jcZQXY0a\nmWLp0pmaDoMxpiHVPXaq9Sc0u3bt+sLfLN26dSsGDRoEBwcHACi3GGiLzMx8ODuHq2XeMpkUzs7+\naphv+Cuf58uQSqXw9/fXdBhqIebcAM5P32i0D+Hq1at48OABunfvDh8fH2zevFmT4TDGmF5T6xlC\nZQoLC3H27FkcPnwYeXl58PX1RadOneDm5lZm2tDQUDg7OwMArKys4O3tLVR2Zb+DOoczM2X4d/GQ\nyYrHK7/V/9dh5Wuvan7KYaWaWD8vGla+pqnlq3PY399fq+Lh/PQ7P6lUiqioKAAQjpfVofYb02Qy\nGYKCgsrtQ4iIiEB+fj7Cw8MBAOPHj0efPn0wePBg1SC1oA8hNDRcbU1G6iKThSMqKlzTYTDGNESn\nbkzr378/jh07BoVCgby8PCQlJaFly5aaDEkjSn+jFxvlNxgxEnNuAOenb9TaZBQSEoKEhARkZ2fD\n0dER8+fPR2FhIQAgLCwMLVq0QJ8+fdC6dWsYGBjg3Xff1cuCwBhj2oCfZVRF3GTEGNM1OtVkxBhj\nTHtwQdAC3Iegu8ScG8D56RsuCIwxxgBwQdAK6rhLWZuUvB9BbMScG8D56RsuCIwxxgBwQdAK3Ieg\nu8ScG8D56RsuCIwxxgBwQdAK3Iegu8ScG8D56RsuCIwxxgBwQdAK3Iegu8ScG8D56RsuCIwxxgBw\nQdAK3Iegu8ScG8D56RsuCIwxxgBwQdAK3Iegu8ScG8D56RsuCIwxxgBwQdAK3Iegu8ScG8D56Ru1\nFoSxY8eiYcOG8PT0fOF0p06dgqGhIXbu3KnOcBhjjL2AWgvCmDFjEB8f/8JpFAoFZs6ciT59+mj8\nV9E0hfsQdJeYcwM4P32j1oLQtWtX1KtX74XTfP311xg8eDDq16+vzlAYY4xVQqN9CBkZGdizZw8m\nTZoEoPj3P/UR9yHoLjHnBnB++sZQkwufPn06li5dKvwQ9IuajEJDQ+Hs7AwAsLKygre3t7Axlad9\n6hzOzJTh38ULTTzKA7m2DivVxPrhYR7mYc0PS6VSREVFAYBwvKwOCam54V4mkyEoKAgXL14sM87F\nxUUoAtnZ2TAzM8P69esRHBysGuS/BUOTQkPD4ewcrpZ5y2RStZwlyGThiIoKf+XzrS6pVCrsvGIj\n5twAzk/XVffYqdEzhBs3bgh/jxkzBkFBQWWKAWOMsZqh1oIQEhKChIQEZGdnw9HREfPnz0dhYSEA\nICwsTJ2L1inch6C7xJwbwPnpG7UWhOjo6CpPu2nTJjVGwhhjrDJ8p7IW4PsQdJeYcwM4P33DBYEx\nxhgALghagfsQdJeYcwM4P33DBYExxhgALghagfsQdJeYcwM4P33DBYExxhgALghagfsQdJeYcwM4\nP33DBYExxhgALghagfsQdJeYcwM4P33DBYExxhgALghagfsQdJeYcwM4P33DBYExxhgALghagfsQ\ndJeYcwM4P33DBYExxhgALghagfsQdJeYcwM4P33DBYExxhgANReEsWPHomHDhvD09Cx3/JYtW+Dl\n5YXWrVujS5cuuHDhgjrD0Vrch6C7xJwbwPnpG7UWhDFjxiA+Pr7C8S4uLjh69CguXLiAzz//HBMm\nTFBnOIwxxl5ArQWha9euqFevXoXjfX19YWlpCQDo2LEjbt++rc5wtBb3IeguMecGcH76Rmv6EH74\n4QcEBgZqOgzGGNNbhpoOAAB+//13bNy4EcePH69wmtDQUDg7OwMArKys4O3tLVR3ZTugOoczM2X4\nd/FCm7/ym/1/HU5MXI1Gjbxf2fxK90nUxPp50fDq1atrfHvV1HDJNmhtiIfz0+/8pFIpoqKiAEA4\nXlaHhIio2u+qBplMhqCgIFy8eLHc8RcuXMDAgQMRHx8PV1fX8oOUSKDmMCsVGhoOZ+dwtcxbJpOq\npdlIJgtHVFT4K59vdUmlUmHnFRsx5wZwfrquusdOjTYZ3bx5EwMHDsRPP/1UYTHQB9yHoLvEnBvA\n+ekbtTYZhYSEICEhAdnZ2XB0dMT8+fNRWFgIAAgLC8OCBQvw8OFDTJo0CQBgZGSE5ORkdYbEGGOs\nAmotCNHR0S8cv2HDBmzYsEGdIegEdTUZaQsxn5aLOTeA89M3WnOVEWOMMc3igqAFxHx2AIi7nVbM\nuQGcn77hgsAYYwwAFwStwM8y0l1izg3g/PQNFwTGGGMAuCBoBe5D0F1izg3g/PQNFwTGGGMAqlAQ\ncnNzoVAoAABpaWnYu3evcHMZezW4D0F3iTk3gPPTN5UWhG7duuH58+fIyMhA7969sXnzZoSGhtZA\naIwxxmpSpQWBiGBmZoadO3fivffew44dO/DXX3/VRGx6g/sQdJeYcwM4P31TpT6EkydPYsuWLejb\nty8AoKioSK1BMcYYq3mVFoTVq1djyZIleOutt+Dh4YHr16+je/fuNRGb3uA+BN0l5twAzk/fVPpw\nOz8/P/j5+QnDzZo1w1dffaXWoBhjjNW8SgvCqVOnsHjxYshkMsjlcgDFP7pw4cIFtQenL7gPQXeJ\nOTeA89M3lRaE4cOHY/ny5WjVqhUMDPi2BcYYE6tKj/D169dHcHAwXFxc4OzsLPyrirFjx6Jhw4bw\n9PSscJr3338fbm5u8PLywp9//lnlwMWE+xB0l5hzAzg/fVPpGcK8efMwbtw49OzZE8bGxgCKm4wG\nDhxY6czHjBmDqVOnYtSoUeWOj42NxbVr13D16lUkJSVh0qRJSExMrGYKjDHGXoVKC8L//vc/pKWl\nQS6XqzQZVaUgdO3aFTKZrMLxe/fuxejRowEAHTt2xKNHj5CVlYWGDRtWIXTx4D4E3SXm3ADOT99U\nWhBOnz6N1NRUSCSSV77wjIwMODo6CsMODg64ffu23hUExhjTBpX2IXTu3BkpKSlqC4CIVIbVUXi0\nHfch6C4x5wZwfvqm0jOEkydPwtvbG02bNkXt2rUBvLrLTu3t7XHr1i1h+Pbt27C3ty932tDQUKEz\n28rKCt7e3sLpnnKjqnM4M1MGZV+68gCubOr5r8OZmede6fxKF5iaWD8vGj537pxGl8/DPKwvw1Kp\nFFFRUQBQ5Yt/SpJQ6a/opVTUB1DVhclkMgQFBeHixYtlxsXGxiIyMhKxsbFITEzE9OnTy+1Ulkgk\nZc4kalpoaDicncM1GkN1yWThiIoK13QYjDENqe6xs9IzhJepMkohISFISEhAdnY2HB0dMX/+fOHR\n2WFhYQgMDERsbCxcXV1Rp04dbNq06aWXxRhj7L+ptCD8F9HR0ZVOExkZqc4QdIJMJhX1lUZSqVQ4\nvRUbMecGcH76hm89ZowxBoALglYQ89kBIO5rvcWcG8D56ZtKC8Kvv/4KNzc3WFhYwNzcHObm5rCw\nsKiJ2BhjjNWgSgvCJ598gr179yInJwdPnjzBkydPkJOTUxOx6Q2+D0F3iTk3gPPTN5UWhEaNGsHd\n3b0mYmGMMaZBlV5l5OPjg6FDh2LAgAHVfrgdqxruQ9BdYs4N4Pz0TaUF4fHjxzA1NcXBgwdVXueC\nwBhj4lJpQVDeBs3Uh+9D0F1izg3g/PRNhQUhIiICM2fOxNSpU8uMk0gk/LvKjDEmMhUWhJYtWwIA\n2rVrp/IEUiLSyyeSqpOYzw4AcbfTijk3gPPTNxUWhKCgIADFTxlljDEmfnynshbg+xB0l5hzAzg/\nfcMFgTHGGAAuCFqB+xB0l5hzAzg/fVNpQUhLS0OPHj3g4eEBALhw4QIWLlyo9sAYY4zVrEoLwrvv\nvovFixdHMEfbAAAgAElEQVQLdyl7enpW6XcOWNVxH4LuEnNuAOenbyotCHl5eejYsaMwLJFIYGRk\nVKWZx8fHo0WLFnBzc0NERESZ8dnZ2ejTpw+8vb3RqlUrvgmOMcY0qNKCUL9+fVy7dk0Y/uWXX9C4\nceNKZ6xQKDBlyhTEx8cjJSUF0dHRuHz5sso0kZGRaNOmDc6dOwepVIoPP/wQcrn8JdLQbdyHoLvE\nnBvA+embSh9dERkZiQkTJiA1NRV2dnZo2rQptmzZUumMk5OT4erqKvwm87Bhw7Bnzx6VJ6c2btwY\nFy5cAADk5OTAxsYGhoZq/VVPxhhjFaj0DKFZs2Y4fPgwsrOzkZaWhuPHjwsH+RfJyMiAo6OjMOzg\n4ICMjAyVad59911cunQJdnZ28PLywpo1a6qfgQhwH4LuEnNuAOenbyr9Ov7w4UP8+OOPkMlkQnNO\nVZ5lVJXHWyxevBje3t6QSqW4fv063nzzTZw/fx7m5uZVDJ8xxtirUmlBCAwMhK+vL1q3bg0DA4Mq\nP8vI3t4et27dEoZv3boFBwcHlWlOnDiBOXPmACg+E2natCnS0tLg4+NTZn6hoaHCmYmVlRW8vb2F\n9j9llVfncGamDMoTI+U3emXb/38dVr72quZX+oyjJtbPi4aVr2lq+eoc9vf316p4OD/9zk8qlQoX\n51SlJac0CRHRiyZo27Ytzp49W+0Zy+VyvPbaazh8+DDs7OzQoUMHREdHq/QhzJgxA5aWlpg3bx6y\nsrLQrl07XLhwAdbW1qpBSiSoJEy1Cw0Nh7NzuEZjqC6ZLBxRUeGaDoMxpiHVPXZW2ofwzjvv4Pvv\nv8fdu3fx4MED4V9lDA0NERkZid69e6Nly5YYOnQo3N3dsW7dOqxbtw4AMHv2bJw+fRpeXl7o2bMn\nli1bVqYY6APuQ9BdYs4N4Pz0TaVNRiYmJvj444+xaNEiGBgU1w+JRIIbN25UOvOAgAAEBASovBYW\nFib8bWtri3379lU3ZsYYY2pQaZNR06ZNcerUKdja2tZUTGVwk9HL4SYjxvTbK28ycnNzg6mp6X8K\nijHGmPartCCYmZnB29sbEyZMwNSpUzF16lS8//77NRGb3uA+BN0l5twAzk/fVNqHMGDAAAwYMEDl\nNf4JTcYYE59K+xC0AfchvBzuQ2BMv1X32FnhGcLbb7+NHTt2wNPTs9yFKJ9BxBhjTBwqLAjK5wrF\nxMSUqTDcZPRqlbxLWYxK3qUsNmLODeD89E2Fncp2dnYAgG+//RbOzs4q/7799tsaC5AxxljNqPQq\no4MHD5Z5LTY2Vi3B6Csxnx0A4n7mvJhzAzg/fVNhk9HatWvx7bff4vr16yr9CE+ePEGXLl1qJDjG\nGGM1p8IzhHfeeQf79u1DcHAwYmJisG/fPuzbtw9nzpyp0g/ksKrj+xB0l5hzAzg/fVPhGYKlpSUs\nLS2xbdu2moyHMcaYhlTah8DUj/sQdJeYcwM4P33DBYExxhgALghagfsQdJeYcwM4P33DBYExxhgA\nNReE+Ph4tGjRAm5uboiIiCh3GqlUijZt2qBVq1Z6257HfQi6S8y5AZyfvqn0aacvS6FQYMqUKTh0\n6BDs7e3Rvn17BAcHq/ym8qNHjzB58mQcOHAADg4OyM7OVlc4jDHGKqG2M4Tk5GS4urrC2dkZRkZG\nGDZsGPbs2aMyzdatWzFo0CA4ODgAgEZ/lU2TuA9Bd4k5N4Dz0zdqKwgZGRlwdHQUhh0cHJCRkaEy\nzdWrV/HgwQN0794dPj4+2Lx5s7rCYYwxVgm1NRlV5YmohYWFOHv2LA4fPoy8vDz4+vqiU6dOcHNz\nKzNtaGgonJ2dAQBWVlbw9vYW2v+UVV6dw5mZMvy7eOEbvbLt/78OK197VfMrfcZRE+vnRcPK1zS1\nfHUO+/v7a1U8nJ9+5yeVShEVFQUAwvGyOtT2AzmJiYkIDw9HfHw8AGDJkiUwMDDAzJkzhWkiIiKQ\nn5+P8PBwAMD48ePRp08fDB48WDVI/oGcl8I/kMOYfqvusVNtTUY+Pj64evUqZDIZCgoKsH37dgQH\nB6tM079/fxw7dgwKhQJ5eXlISkpCy5Yt1RWS1uI+BN0l5twAzk/fqK3JyNDQEJGRkejduzcUCgXG\njRsHd3d3rFu3DgAQFhaGFi1aoE+fPmjdujUMDAzw7rvv6mVBYIwxbcC/qVxF3GTEGNM1WtNkxBhj\nTLdwQdAC3Iegu8ScG8D56RsuCIwxxgBwQdAK/Cwj3SXm3ADOT99wQWCMMQaAC4JW4D4E3SXm3ADO\nT99wQWCMMQaAC4JW4D4E3SXm3ADOT99wQWCMMQaAC4JW4D4E3SXm3ADOT99wQWCMMQaAC4JW4D4E\n3SXm3ADOT99wQWCMMQaAC4JW4D4E3SXm3ADOT99wQWCMMQaAC4JW4D4E3SXm3ADOT9+otSDEx8ej\nRYsWcHNzQ0RERIXTnTp1CoaGhti5c6c6w2GMMfYCaisICoUCU6ZMQXx8PFJSUhAdHY3Lly+XO93M\nmTPRp08fjf8qmqZwH4LuEnNuAOenb9RWEJKTk+Hq6gpnZ2cYGRlh2LBh2LNnT5npvv76awwePBj1\n69dXVyiMMcaqQG0FISMjA46OjsKwg4MDMjIyykyzZ88eTJo0CUDx73/qI+5D0F1izg3g/PSNobpm\nXJWD+/Tp07F06VLhh6Bf1GQUGhoKZ2dnAICVlRW8vb2Fjak87VPncGamDP8uXmjiUR7ItXVYqSbW\nDw/zMA9rflgqlSIqKgoAhONldUhITQ33iYmJCA8PR3x8PABgyZIlMDAwwMyZM4VpXFxchCKQnZ0N\nMzMzrF+/HsHBwapB/lswNCk0NBzOzuFqmbdMJlXLWYJMFo6oqPBXPt/qkkqlws4rNmLODeD8dF11\nj51qO0Pw8fHB1atXIZPJYGdnh+3btyM6Olplmhs3bgh/jxkzBkFBQWWKAWOMsZqhtoJgaGiIyMhI\n9O7dGwqFAuPGjYO7uzvWrVsHAAgLC1PXonUO9yHoLjHnBnB++kZtBQEAAgICEBAQoPJaRYVg06ZN\n6gyFMabDZs2KQGZmvqbDqLJGjUyxdOnMyifUMmotCKxq1NWHoC3E3E4r5twA7ckvMzNfLX146uy/\n00X86ArGGGMAuCBoBTGfHQDibqcVc26A+PMT+2evurggMMYYA8AFQSvws4x0l5hzA8Sfn9g/e9XF\nBYExxhgALghaQeztmGJuhxZzboD48xP7Z6+6uCAwxhgDwAVBK4i9HVPM7dBizg0Qf35i/+xVFxcE\nxhhjALggaAWxt2OKuR1azLkB4s9P7J+96uKCwBhjDAAXBK0g9nZMMbdDizk3QPz5if2zV11cEBhj\njAHggqAVxN6OKeZ2aDHnBog/P7F/9qqLCwJjjDEANVAQ4uPj0aJFC7i5uSEiIqLM+C1btsDLywut\nW7dGly5dcOHCBXWHpHXE3o4p5nZoMecGiD8/sX/2qkutP5CjUCgwZcoUHDp0CPb29mjfvj2Cg4Ph\n7u4uTOPi4oKjR4/C0tIS8fHxmDBhAhITE9UZFmOio65fFMvMlCEqSvrK56urvygmdmotCMnJyXB1\ndYWzszMAYNiwYdizZ49KQfD19RX+7tixI27fvq3OkLSS2NsxxdwOrS25qesXxf796L5y2vKLYmL/\n7FWXWpuMMjIy4OjoKAw7ODggIyOjwul/+OEHBAYGqjMkxhhjFVDrGYJEIqnytL///js2btyI48eP\nlzs+NDRUONOwsrKCt7e38O1M2c6pzuHMTJnwbUnZ7qj8dvFfhxMTV6NRI+9XNr/S7aI1sX5eNLx6\n9eoa3141NVyyjV2T8ahr/yy5L73K/TMzUybMl/N7dcNSqRRRUVH/xuOM6pIQEVX7XVWUmJiI8PBw\nxMfHAwCWLFkCAwMDzJyp2nZ44cIFDBw4EPHx8XB1dS0bpEQCNYZZJaGh4Wo5JQfU+0PfUVHhr3y+\n1aUtP9SuDtqSm7r2T23ZN8Wen7pU99ip1iYjHx8fXL16FTKZDAUFBdi+fTuCg4NVprl58yYGDhyI\nn376qdxioA/E3o6pDQdMdRFzboD4902x51ddam0yMjQ0RGRkJHr37g2FQoFx48bB3d0d69atAwCE\nhYVhwYIFePjwISZNmgQAMDIyQnJysjrDYowxVg61FgQACAgIQEBAgMprYWFhwt8bNmzAhg0b1B2G\nVlPXaau20JZmFXUQc26A+PdNsedXXWovCIxpA127Th/ga/VZzeOCoAXE/g1FG75B69p1+oB2XKsv\n9n1T7PlVFz/LiDHGGAAuCFpB7M9TEfPzcMS+7Tg//cIFgTHGGADuQ9AK2tCOqa5OVyWxPiBNG7ad\nOnF++oULAgOgvk5XddKGTlfGxISbjLSA2NsxxZyfmHMDOD99wwWBMcYYAC4IWkHs7Zhizk/MuQGc\nn77hgsAYYwwAFwStIPZ2TDHnJ+bcAM5P33BBYIwxBoALglYQezummPMTc24A56dvuCAwxhgDoOaC\nEB8fjxYtWsDNzQ0RERHlTvP+++/Dzc0NXl5e+PPPP9UZjtYSezummPMTc24A56dv1FYQFAoFpkyZ\ngvj4eKSkpCA6OhqXL19WmSY2NhbXrl3D1atX8f333wu/mqZvMjPPaToEtRJzfmLODeD89I3aCkJy\ncjJcXV3h7OwMIyMjDBs2DHv27FGZZu/evRg9ejQAoGPHjnj06BGysrLUFZLWevbskaZDUCsx5yfm\n3ADOT9+orSBkZGTA0dFRGHZwcEBGRkal09y+fVtdITHGGHsBtRUEiURSpemI6KXeJyaPHsk0HYJa\niTk/MecGcH56h9Tk5MmT1Lt3b2F48eLFtHTpUpVpwsLCKDo6Whh+7bXXKDMzs8y8vLy8CAD/43/8\nj//xv2r88/LyqtZxW22Pv/bx8cHVq1chk8lgZ2eH7du3Izo6WmWa4OBgREZGYtiwYUhMTISVlRUa\nNmxYZl7nznHHD2OMqZvaCoKhoSEiIyPRu3dvKBQKjBs3Du7u7li3bh0AICwsDIGBgYiNjYWrqyvq\n1KmDTZs2qSscxhhjlZAQlWrEZ4wxppf4TmXGGGMAuCAwPXb37l3MnDkT169fx/379wEARUVFGo7q\n/5U+eRfLyTwRiSYXpfJy0sUcuSCInPIAJ5fLNRyJ9mncuDEAYMuWLZg8eTLOnTsHAwMDrfggE5Fw\nCfadO3fw8OFDUV2SLZFIcODAAaxcuRJbt27VdDivhEQiwalTpxAXF4e///4bEolEq75gVAUXBJF6\n8OABMjIyYGBggPj4eMyePRurVq3SdFhaQ/lBjYiIwMSJE+Hv74+AgAAcPXpU4x/krKwsfPfddwCA\n3377Df3798cbb7yBXbt2IScnR2NxvQrKQnf+/HlMnToVWVlZiIuLQ1hYmKZDe2nKnA4fPoz+/fvj\n119/Rfv27fHnn3/CwMBAp4qC2q4yYprz9OlTrFixAnXq1IGnpydmzZqF6dOnIyIiApmZmVi0aBEM\nDfVz0yu//RsYGKCgoADGxsZo0KABJk6ciNq1ayMkJAS//vorOnXqpPItvSbjO3PmDE6cOIGsrCwk\nJSVh8+bNuHDhAjZu3IinT58iODgYFhYWNRrXqyKRSJCQkICffvoJa9asQUBAAK5du4bFixdj4sSJ\nQiHUJRKJBCkpKfjll1+wbds2dOvWDV5eXujRoweOHDkCb29vFBUVwcBA+79/1woPDw/XdBDs1TI2\nNsbjx4+RlpaGP//8E4MHD8aECRMwdOhQrFy5ElevXoW/v79O7KDqoGyu2LRpE1JSUtCxY0cAQJs2\nbWBlZYVPPvkEffr0gY2NTY3GpSxA9vb2MDU1xZ9//omsrCx89NFH8PDwgKmpKbZs2QIigouLC0xM\nTGo0vpdVurCeP38eixYtgpOTE/z8/GBpaYnWrVsjNjYWsbGx6N+/vwajrR6FQgGFQoGlS5fixIkT\neO211+Dp6YlOnTqhTp06GDhwIPr16wc7OztNh1olXBBEhIiEbyLu7u6wtLTEsWPHcP36dbRr1w6O\njo7o27cv5s+fj2vXrqFXr16iapeujPLAdPLkSUyePBl9+vTBihUrkJWVha5du6JWrVpo27Ytnj9/\njvT0dHTo0AEKhaJGCqfyzEUikeDOnTto06YNDA0NcerUKWRlZcHX1xfu7u6oVasWfvrpJwQGBsLc\n3Fztcf1XJfNKT08HEcHb2xuvv/46Pv/8c7i4uMDd3R1WVlZo06YN2rVrV+7NqdqkZE55eXkwNTWF\nv78//vnnH6Snp8Pa2hr29vbo2LEjLCwsUKdOHTRr1kzDUVdRte5rZlqtqKiIiIj27dtHY8aMISKi\nQ4cO0bRp02jFihX0999/ExFRZmYmnThxQlNhalRqaiqNHj2a1q1bR0REGRkZ1KVLF5o9ezYVFBQQ\nUfE6e/fdd2s0LuW2i42NJRcXF0pLS6O8vDzatWsXvffee7Ry5Uph2vIe76KtFAoFERXvk507d6bg\n4GAaN24cXbp0iRISEsjV1ZV++eUXlfco14W2UsYXFxdHPXv2pNDQUPriiy+IiGjmzJk0Y8YMOnbs\nmEoe2p6TEhcEkTlw4AB5eHjQ/v37hdf2799PM2bMoEWLFtGNGzeE13VlJ/0vSucYGxtL/fr1o5CQ\nEGFd3Llzh7y8vOijjz4Spps8eTLdvXu3RmO9dOkSeXh4UEJCgvBaXl4e7d69m0JDQ2nZsmVE9P8H\nWW3efvn5+cLf6enp1LJlSzpz5gxdvHiRfvzxRwoMDKTMzEzauXMnOTg4UFZWllbnQ0RUWFgo/J2c\nnEwtW7akmJgYOn36NHl7e9PUqVOpqKiI3nvvPfrggw/o4cOHGoz25ehnz6KInT59GuHh4QgMDMSz\nZ89gYmKCwMBAGBgYYO/evSqXVIq9uahkrjdu3ICZmRl69OgBe3t7rF+/Hrt378bAgQPh5OQkXCqo\nFBkZWePxyuVyvP766+jWrRvkcjmKiopgamqKnj17QiKRwMXFBQCEJixt3X5ZWVmIjo7GuHHjhGYt\nR0dHtG3bFkDx5b5nzpzBwYMHMXLkSHTq1AkNGjTQZMiV+ueff4TLk42NjZGXl4eePXuib9++AICz\nZ8+iQ4cOOH78OBYsWICsrCxYWVlpOOrq089eRZGgcq6Xv3v3Ln799VcAEDodk5KS4O/vjyVLlggH\nFX0gkUggkUgQFxeHvn37YsaMGfDx8YGlpSWGDh0KmUyGrVu3Ij09HY0bN0bnzp1r7Kap8pZjZmaG\n+Ph4xMTEwNDQEMbGxjhw4AD+97//ITg4GK1atVJ7XK9C7dq1ERAQgNzcXJw+fRpNmjSBXC7HnDlz\nAAA2NjawtrbGlStXAAD169cHoN03cmVmZiIoKAj379/HrVu3YGFhgcOHDws3NEokEnTv3h2PHz+G\njY0NWrZsqeGIXw4XBB1V8sMjk8mEnyf98MMPUa9ePeGeg+TkZISGhuL8+fOwtLTUSKyadPPmTcyb\nNw/r16/H1q1bMXToUAQHB6N58+YYOHAgMjIyVK4TVxaRmqC8BPPLL7/EkSNH0KxZM6xatQorV65E\nZGQkYmNjMXPmTNjb29dIPP9VYWEh8vLyYGVlBUdHRyxZsgQbNmzApUuXsGLFCshkMgwZMgT79u3D\n1q1b0aNHDwAQLoHWxjOewsJCAEDr1q1hbW2NtWvXYunSpWjVqhWGDx+O9u3bQyqVIiYmBrGxsTp5\nVlASP9xOR9G/V8zs3bsX4eHhsLe3h729PaZNm4a///4ba9euRV5eHrKzs7Fw4UIEBQVpOuQaQaUu\ncczNzcWkSZOwaNEiNGnSBAAwdepU1KpVC6tXr0ZWVpbGrmqJi4vDjBkzMH36dCxfvhzjx49H3759\nkZ2djRUrVqBRo0bo378/+vXrp5F7IqqjoKAAUqkUtra2uHLlCtLT0zFixAgsX74cxsbGGDhwIFxc\nXLBw4UJYWVmhQ4cO6Nu3r1bn9fz5c/zxxx9wcHBAbm4urly5goYNG+K3334DEWHJkiVYv369cCVY\nWFiYTmyrF6rxXgv2yvzxxx/Url07ysrKovXr11PdunXpgw8+IJlMRkVFRXTjxg1KT08nouIOSG3v\ntHsV5HI5ERE9efKECgsL6fnz5zRgwAD6+uuvhWm2bdtGM2fO1FSIVFRURLdu3aIBAwbQlStX6PDh\nw9SsWTMKCQmhuXPn0pMnT8pMrwvb7pdffiFfX19q2rQp7d69m4iI7t27R1OnTqWPP/6YLly4oDK9\ntueVk5ND+/btI39/f7Kzs6PU1FQiIjp+/Dh9/PHHNGvWLHrw4AERFXf+E2l/TpXh+xB02NOnT9Gz\nZ0/cuHEDK1euxJ49e/D999/j0KFD6NChA1xdXVWaiXT2W0sV3Lx5EwUFBahbty52796NiRMn4uLF\ni6hVqxZCQ0Mxa9YspKam4vTp01i7di3Gjh2L5s2b11h8VOLadYlEAgsLC3Tp0gVPnz7F1KlTkZSU\nhIYNG+LDDz+EsbExvLy8ULt2bZX3aCP6ty9EIpGgSZMmOHHiBGrXro1evXqhbt26sLW1RadOnbB/\n/3789ddf8PX1Ffq2tDUv5baqXbs28vLysGTJEnTs2BGdO3eGnZ0dHB0dYWFhgfPnz0MqlcLPzw/G\nxsYwMDDQ2pyqiguCjih5QHn48CEUCgXs7e3h4OCAdevWoWfPnggMDMTz589x8uRJDB48GNbW1sL7\ndXknrYqFCxdi7ty5aN++PdauXYsxY8bA0dER33zzDZo0aYLZs2fj/v37yMnJwYQJE9C7d+8aP7WX\nSCS4cOECTp8+jVq1asHOzg6ZmZk4dOgQJkyYgPz8fFy8eBFTpkyBo6NjjcX1XxkYGOC3337D5s2b\nsWzZMhgYGGD37t0wMTGBu7s75HI5PD090aZNG53JSyKR4LfffoO1tTVCQ0NRv359/PLLLzA0NISb\nmxuMjY1hbGyMgIAANGzYUDR3/fNlpzpEIpFgz549+OGHH/D48WO888476NGjB3x8fLBhwwYUFhZi\n+/btWLlyJVxdXTUdbo1Q3pn95ZdfoqioCEOHDsWIESMwbNgw5Ofnw8bGBsuWLUN2djbGjx8vvI9q\nuOtMIpFg9+7dmDt3LlxcXGBqaormzZsjLCwMjRo1Qs+ePXHr1i2sXr0arVq10pl2aOVVXB9++CFW\nrVqFOnXqYMyYMcjPz0dMTAxOnTqFDRs24Pfff9eZq6SUOU2bNg1ff/01evfuDQsLCzx48AC7du1C\nYmIizp07hzVr1qBp06aaDvfV0lxrFauu1NRU8vDwoHPnztHOnTtpzpw5tGDBAkpOTqZvv/2WAgMD\nad++fUSk+22ZVZGbm0t//fUXERElJSVRTk4OzZo1i9zd3YW7eZ8/f06xsbHk7+9PMplMuKmrJpTc\nBk+ePKFhw4bR2bNniYgoISGBZs2aRT/++CPdu3ePtm7dKtw9rkvbrqCggKZNm0ZxcXFERPTs2TNh\nXFxcHK1atYri4+M1Fd5Lyc3NpV69etHhw4eJ6P9vAPz777/p559/pn79+gl9JGLDBUHLKXfGO3fu\nUFxcHAUEBAjjkpKSqEePHpSUlERE/393qC4dUP6Lmzdv0tixY2ny5Mlkb28vdFpOnDiROnfuTFlZ\nWURUXBTu3btXo7GVXP/Hjx+nuLg48vX1pa1btxJR8V2vy5cvp4kTJ5Z5nzZvu/JiGzlyZJlO+vPn\nz6vcrazNeSnjUv7/6NEj8vf3FzqRlR3G2dnZRFS8Pymn19acXpY4Gr5EqqioCBKJBCdOnMDw4cPh\n5OQEExMT7NixAwDQoUMHeHh44NKlSwAAIyMj4b260NzwXxQVFcHR0RG9evXCxo0b8c4778DT0xMA\nsHbtWnh5eeHNN9/EP//8A2NjY9ja2gKo+aaitLQ0fPzxx2jdujU++ugjHDp0CAkJCTA0NES7du3w\n4MED5OTkCPdC6EqnZHp6OlJSUgAAY8eORWFhIfbs2QMAOHXqFCZOnIirV68K0+tCXllZWQAAS0tL\ndOnSBbNmzcKDBw9gamqKo0ePol+/fvjnn39U7pvQ9pyqizuVtZhEIsGhQ4ewYcMGTJo0Cb6+vsjO\nzsalS5dw5MgR1KpVC19++SUmTZoEBwcHrX+kwaskkUhw5MgRJCYmYs6cOdi5cyeeP38OZ2dnmJqa\nom/fvrh+/ToaNGgg3H+gfF9NxXf+/HkMGTIE/fr1Q3BwMGrXro2nT59iwYIFuHLlCiIiIjBr1ix4\nenrqxDajf/s1YmJiMHr0aOzYsQM3b95EUFAQ7t69i23btmHbtm344YcfMH/+fHTr1k3TIVdKmVNs\nbCzeffddHDhwAPXq1UP37t3xzz//YMaMGcjPz8eiRYsQHh6Otm3b6sS2emkaPkNhpZQ+BY2KiiKJ\nRELff/89ERFlZWUJT+McP368Sp+Bvjl27Bj16tWLiIqfUOrn50dbtmyhrVu30uDBg4Wnl9bUuimv\nCWH48OHUtm1b4d6CgoICOnv2LO3atYtOnTpVo/G9CpcvX6agoCBKTU2lhw8fkq+vLy1YsIByc3Pp\n/v37dPLkSaGpRVeaVJKSkqh///508uRJWrp0KU2aNIm2bNlCeXl5tGPHDvr111/p6NGjRKQ7Ob0s\nLghaRrmzZWRkCG2w0dHRVLt2bTp+/LjKNGK5GaaqSueYnZ1No0ePptOnTxNR8ZNeR44cSW+88QZt\n27ZNY/GdPHmStm/fTpcuXSIiorFjx1KfPn2E7VX6Pdq+7Uq2rYeFhVG7du3o+vXrRFTct9WtWzd6\n//33K3yftinZZ/DPP/9QYGAg9e/fXxj/3XffUVhYGG3evFnlJkFd2Fb/FRcELaLc2WJiYqhDhw7U\nq1cv+uKLL+jBgwe0Y8cOsrGxEb6p6JOSH8IzZ87QoEGD6PLlyySXy2nDhg3k5+cnFM+HDx8KnX81\n+eFVLuvo0aPUvHlzGjJkCA0dOpQ+/vhjIiIaM2YM+fv7l1sUdMG5c+foyZMndObMGRo+fDh9+eWX\nJO9I+x8AACAASURBVJPJiKi4KHTs2JEuX76s4SirR3nRwZYtW6h58+a0YcMGYdxXX31FY8eOpYyM\nDE2FpxFcELRMYmIiBQQE0NmzZykuLo4iIiJo4sSJVFRURN999x2ZmZnRw4cPa/TySU0q+a3sypUr\n9PTpU5oyZQp99NFHFBQURL///jsNHTpUuMJIkz9KcuLECerdu7dwxpKamkqTJk2ib775hoiIgoOD\nhWYiXaBcf8+fP6fp06dT37596cmTJ3Ty5EmaMmUKrVy5UvhNCeWVN7pALpfTvXv3yNTUlLZv305E\nRDt37qR+/frRxo0bhemUj33RJ1wQtMiDBw9oyJAh1LZtW+G1ixcvUkhICB06dIiISPhWpi+UB6X9\n+/dTx44dKS0tjYiKnzMTFRVFb731FllZWdH48eM1FpvSli1bSCKRCN808/PzKTo6msLCwl74Pm2T\nm5ur8mMwRMVNmB999BG9/fbb9OTJE0pMTKRx48bRsmXLKC8vT3iGlLbmpuxPIvr/HxjavXs3WVtb\n065du4iIaNeuXdS9e3dav369RmLUBlwQNKi8NslDhw5R69ataf78+cJrU6ZMoSVLlhDR//9qk7Z+\n8NTh8uXL1KJFC6EPpaRHjx7RpUuXyN/fX7jpqyaU3Hb37t0TmoI2bdpELi4uQgGPi4uj119/nbKz\ns4WDpja7dOkSTZo0ibKysujo0aO0Zs0aYdzdu3fpgw8+oFGjRtHTp0/p+PHjwo2B2uzSpUv02Wef\nERFRSkoKHTx4UNhesbGxVLt2beFGs19++YWSk5M1FqumcUHQIOUB5dChQ7R48WJav349ZWdnk1Qq\npUGDBlFoaCglJCSQh4eHcNekPrh16xZt3rxZGD569Ci9/fbbwnB5RXHUqFE1uo6Uy967dy/5+flR\n165d6fvvv6e0tDTavn07mZmZ0fjx42nAgAHCN1Btl5eXRz179hSaTY4cOUINGzakyMhIIipuajly\n5Ai1atWKhg4dqhPNlo8fPyY/Pz86deoU5eTk0PTp02ns2LF0+PBhevr0KRERrVq1iiQSCcXGxgrv\n06cvXCXxjWkaQv9e//zHH39g4sSJqFOnDtavX4+vvvoKRkZGmDp1KhITE/Hpp59iw4YNeOONNyCX\nyzUddo0gImzevBnnz58HALi4uOD+/fs4ePAggOIfVDly5AgiIiJARLh+/TquX79eoz8kI5FIcObM\nGaxYsQJr1qzB1KlTkZ6ejm3btqFv375Ys2YN/vjjDwQGBmLAgAFQKBRa/YtgAGBqaorhw4dj48aN\nsLe3R/fu3bF//36sWrUK33zzDWrVqoXatWujR48emDlzpk480E2hUCAvLw/R0dF4//338cEHH6BJ\nkyb49ddfcfLkSQBA586dMXDgQJV8RH2vwYtoth7pt9TUVAoJCRHuMcjIyKDp06fTrFmziIhIKpXS\nqFGjaOnSpZoMs0Ypm1XWrFlDO3bsIKLi/oLly5fTxx9/TEuXLiWpVEoeHh508OBB4X3379+v0Tjv\n3r1LY8aMoc6dOwuvHT9+nHr27EmJiYlEVNynYG9vTwkJCTUa28so2VdjYmJCfn5+lJubS0TFPyjf\nunVrGjduHDVo0EB4bpG2f4tWxhcZGUmGhobCY0IKCgpo7ty5NG7cOBo3bhy5ubnp5D0h6sB3Ktcg\n+vesQPlIiqNHjyIhIQG3b99G586dYW9vDy8vL8ydOxfBwcFo0aIFLC0tceTIEbz++uswMzPTdApq\np/yWdvfuXaxevRrdu3dHw4YN0ahRI5iZmWH//v24evUqJk2ahMDAQMjlchgYGMDU1FStcVGJx48r\nh4kIJ0+eRF5eHjp27AhHR0ecPHkSCoUC7du3h6enJ+zs7NCiRQuVR5FrI2VeNjY28Pf3h7W1Ndas\nWYN27drB09MTffr0QYsWLTBy5Eh069ZNJ57Gqozv7t27ePPNN7Fq1SrUrl0bXbp0Qbdu3WBmZoY6\ndepg+PDh6Nq1q8p79BX/hGYNKXlAycjIEJo3jh8/jp9++glubm4YNmwYnj59irfffhv79++Hvb09\nCgoKIJfL9aIYlDZv3jxs2rQJycnJaNSokfD6s2fPYGJiUuYgrS4ll3Ps2DHk5+ejdu3a6NatG375\n5Rfs378fZmZmGDp0KMaPH4/169fDz89PrTG9KiUP7AqFArVq1QJQ/KyijRs3Ii0tDQsXLlR5nHpN\nrfdX7fTp03jzzTfxxRdfYMqUKSrjdDWnV04j5yV6qOQpuY+PD3366ac0Z84coaNuwIAB5OPjQz17\n9qT9+/ervEefFBUVqXRWfvLJJ/Taa6/R2bNnVZqFNLFu9u3bRx4eHrRu3Tpq1aqV0Pm6c+dO8vLy\not69e9ORI0eIiMpctqnNzp8/L/xd8kqomzdv0qxZs+itt96ivLw8ndofb926RY8fPxZiVuZ19uxZ\nqlWrlsrVU+z/cZNRDVF+u5w+fTq2bt2Kc+fOYefOnTh37hwmT54MFxcXZGZmwsfHB6NGjdKbB9Up\nm8+UTT/KfJU/fPPmm29CLpdjz549SE1NRVZWFlq1alXj6yU9PR0ffvghfv75Z2Rl/V979x4Xc77/\nAfw1MxFTRFopOUo6IlQbSSEkIqxrR26b3UQuUWuxu07Ys87uKqGzuyGXXHapdpFckppRq7aS9ohS\nORRbNESZrqZm3r8/Mt8t6+xv7UkzU5/nX03N99H7+52Z73s+t/dHgoyMDIhEIhARvLy8YGBggKqq\nKggEAgwbNkwjBlzpRetg3rx5KCgogIuLS7O49fT08Ne//pXrttOE9yIRQSKRICAgAI6OjujevTsU\nCgUEAgHkcjmMjY3h7u4OHR0dmJubqzpctcMSQiuRy+XIzc2Ft7c3SkpKEB4ejr179+L8+fMQi8VY\ntmwZtLS0kJKSAolEAhsbG6753hY9ffoUT58+hZ6eHuLi4rB//35uz10ejwc+nw+5XA4+nw8HBwcM\nHDgQPXr0wJEjR+Dq6vrGxwxexuPxMHHiRJSVlWHjxo1ISkpCnz59sGrVKnTp0gULFixAeXk5cnJy\nYG9v3+rxvQ5lIlDe4IcOHYqrV69ixIgR6NSpU7Mbv56eHnr06KGqUF8bj8eDrq4uxGIxzp07hxkz\nZnCfI+V7qnfv3jA3N9eIcZDWxhJCK+Hz+fjLX/7Cben44YcfYtSoUUhNTUVRURHs7e3h5OQEPp+P\n8ePHo2vXrqoO+Y2prq7G9u3bkZubi4qKCqxfvx7u7u7YuXMnSkpKMG7cOPD5fPD5fK4FYWBgADMz\nM8yePbtVx1OUN41OnTpBX18f165dg56eHtzc3FBYWAgDAwOMHj0aFhYWMDc3h7OzM7p169Zq8f0Z\nyunOdXV14PP5MDY2RlhYGPr27avR35p/+eUXSCQS9OjRA46OjsjIyICtrS26dOnCvY/Y1NLfp/7t\nWg1EL43TKx9ra2uDiCCVSnHjxg2IxWJkZ2cjNDQUgwYNAgBMmzat2QBqW6SjowM7Ozs8efIEp06d\nwpo1a7B06VKkpKTgp59+wqZNm7g1Fy93vbRGV0zT14/H4zV7rFAokJqain/84x/w9fWFh4cHxo8f\nD7lcDl1dXbVN5PRiVpSSWCzGhg0bsHr1aiQlJcHT0xM7d+7Es2fPVBjl62l6PlKpFB9//DE+++wz\nrFu3DvX19SgoKMDZs2cBtM77pi1gs4xaGDWZrXDz5k3o6+vD2Ni42XMuX76MkJAQ1NTUwMfHBx4e\nHtyxbflbCxFx/bkAkJaWht27d0Mul+OLL75Av3798OjRI7i5uWHcuHEIDg5W2fXIzMzE4cOH8a9/\n/es3r0tkZCTKy8thamoKNzc3jXjdlDFmZ2ejQ4cOMDY25qY0f/bZZzA3N0dsbCyuXLmC/v37c2M4\n6kx5Tg8fPkTXrl3B4/FQWVmJNWvWYPDgwTh9+jTkcjmioqJgYWGh6nA1QysOYLcLTUsajB49mtvv\nWEk5g6aqqoqrtd4e6qwT/XptYmNjacmSJUTUWLZjzZo1tGPHDiosLCQiotLSUm7D+dbUdHbTlStX\nflOU7lW1iDThtVPGd/HiRTIyMqLFixeTiYkJV+qjtLSUcnNzafr06TRt2jRVhvqHNL3mMTExZGNj\nQ0OGDKEPP/yQ26fh/v37dODAARo3bhy3gFHdXyd1wBLCG3D79m2ytbV9ZanjV91A2tMb9eLFi2Rl\nZcVNrSVqnIobEBBA27Zt48opE7XedWm6R8Ht27cpLS2Nbt68SePHj6enT582e64mTSdt6vr167Ri\nxQpu1fSRI0fIzMzsN4l3wYIFVFFRoYoQX1tOTg65uLhQbm4u/fLLL9wqf6lUyj3nu+++I3d3d6qr\nq1NhpJpDvduEGqKoqAirV6/mHpeVlcHAwADDhg0DAK4/vLq6+pUbc6t7d0NLyszMxJYtWzBlyhTU\n1dUBAKZMmQJXV1cUFxf/pv/+TauoqMDGjRtRXl4OqVSKoKAg+Pj4IDg4GGKxGF988QWioqJw+fJl\nKBQKboN1dae8jnK5HDKZDFu2bEFiYiKqqqrQ0NCARYsWYcWKFdi9ezcUCgUAID4+Hmlpaaivr1dl\n6P9VaWkptm3bBoVCgbKyMoSEhODRo0fo1q0bTExMsG7dOojFYhw/fpw7pkuXLqisrOTOkfl9bJZR\nC+jWrRsMDQ1RV1eH7t27Q19fH/Hx8ejevTtMTEzQoUMHJCcn49ixYxg5ciQEAkG7SAL0ir71qKgo\nXLt2DXPmzOFurunp6XBwcMDYsWNhZGTUqjHW1dVh2LBhqK2txYMHD7B06VL4+vpizJgxyMrKgoWF\nBX788UeIRCL069cPffr0adX4/hc8Hg/V1dUQCoWYNGkSsrOzUVpaCisrK+jp6eHJkycoKCjAzJkz\nwePxUFtbi6VLl/5mzEtdPH78GJaWlpDJZOjRowf09fVx+/ZtVFRUoG/fvujduzeeP3+OiooKODk5\nQS6Xo6SkBJ6enq3+vtJYKm6haDSFQtGsC8HR0ZFGjx5NRI3F2fz8/Gjjxo10+vRp6t+/f7NibG1d\n066xwsJCys3N5X729fWlkJAQImrc4NzS0pIrCNea8Sndv3+fjh49SmPGjCGxWExEjeMFCxcupGPH\njv3X49RdbGwsOTg40ObNm+nKlStUWVlJc+bMoUmTJtGmTZto+PDhdPLkSVWH+f9qes1lMhm9//77\ntGTJEqqvr6eEhATy9fWlOXPmUEREBPXv35/i4uJUGK1mY11GfxK9aJJraWkhLy8PQGNdIj6fDw8P\nD/j5+WHatGmoq6tDfHw8du/eDVdXV7UvgdySeDwezpw5g1mzZmH9+vVYvnw5amtrMXXqVIhEIri4\nuGDp0qXYvn07RowYoZIY4+Pj4evrC1tbW3h6eiI4OBhJSUkQCASYMGECiouLVRLXn0FNppaWlJTg\nyJEjWLVqFbp27YpDhw4hJSUFR44cgaGhIbKyshASEoKZM2dyx6qjpnHl5OSAz+fD398fQqEQ/v7+\ncHZ2xvz581FdXY34+Hjs2LEDkyZNglwuV2HUGkyV2UiTNa1NZG5uzu2jS0Tk5OREs2bN4h4rB7Q0\nYUZKS/rxxx/Jzs6OJBIJhYeHk66uLvn7+1NRUREpFAq6e/cut29ta14b5f/Jz8+nKVOmcDPBJBIJ\nhYWF0fTp0+nKlSuUmZnJ1SbSBMrzyszMpP3799OGDRuIqLFUd0REBHl7e1NMTAzV1NSQh4cHrVmz\nhiQSiVq/J5WxXbhwgczMzCg7O5saGhooNzeXli9fTmvWrCGZTEaJiYnk7+9PISEh9OjRIxVHrblY\nQvgfXLt2jQYMGEA///wzETXud6ycsTJixAhycXEhItKInaXehNzcXEpLS6Pz58+Tvb09ZWdnk5OT\nE02ePJnbG1mpNW5KdXV1XHK+f/8+BQYG0qBBg+jAgQPccx49ekS7du2iiRMncjtqqfMNU0kZo0gk\noj59+pCXlxcJhUK6ceMGETWe1759+2jx4sVUW1tLDx8+pAULFlBpaakqw/5D8vPzafDgwZScnMz9\nTqFQUG5uLr377rvk6+tLRERHjx6lDRs2tPreGG0JW5j2Goial8jNzs5GVFQUBgwYgJKSEkRGRsLC\nwgIfffQRbG1tkZqaCkdHR1WG3GqaXpvy8nJ06NABurq6AIB169bBwsICy5YtQ1hYGCIiIvDtt982\nK6n8pjU0NCAlJQWFhYXQ1dVFTk4OZs6ciZiYGFRUVGDatGkYO3YsgMbBy5qaGvTt27fV4msJeXl5\n8Pf3x6ZNm+Dk5IRPP/0U0dHROHHiBKysrPDo0SPIZDKYmJgAaF7uWp3QS5MRCgoK8Pnnn+PQoUOQ\ny+WQy+Xo2LEjGhoaUFhYiJqaGlhbWwMAKisr0aVLF1WFrvHYLKPXxOPxEB8fj9u3b8PMzAzJyckQ\ni8UYO3YsVq1ahaKiIshkMrz99tvo06dPu6qzzuPxEBMTg8DAQBw8eBAymYyr63Ps2DFIpVKcOHEC\nQUFBsLGxadXY+Hw+qqqqEBQUhIiICKxYsQKjRo2CsbEx8vPzkZ+fDyKCubk5dHR0uLhfvjmpm6bx\niUQixMbGgojg6uoKZ2dnlJeXIyAgAK6urjAzM+NKaxCRWq5Ebvp5uXXrFqqrq6Grq4vAwEAYGhpi\n6NChEAgEiI+PR1RUFGbMmIFevXpxhRC1tbVVfAaajSWE16C84W3cuBHjxo3DsGHD4OzsjHnz5sHa\n2hqlpaXYsWMHPD09YWpqyh2jzjeUlsLj8ZCfn49ly5bhq6++woABA5CXl4dbt27B3t4e3bp1w/nz\n57F27VpMmDBBJZvb6Onp4eTJkzAxMYFQKISlpSVMTExgbm6Oq1ev4u7du7C1tW1WPE/dXztlWfXI\nyEj4+PjAyMgI//73v/Hw4UMMGzYMY8aMwbNnz9CrV69mLR51Pi/lZIRVq1Zh/PjxGDBgAMzNzREW\nFoZ79+5BKpXik08+gYeHBywtLQGwWkUtRhX9VJrq6dOnNG7cOMrLyyO5XE6ZmZl09OhRqqmpIZFI\nRI6OjnTq1Cki0ox+55agPM8HDx7QhQsXaPLkydzf0tPTycXFhRu0ra2t5Y5pjevT9P88ePCA+93N\nmzdpxYoV9Pe//52IGvdsjo6OpoKCgjce05tw8+ZN6tOnD+3YsYOIiKKiosjHx4d27drV7Hma8p7M\nysoia2trbpzp4cOHdPXqVcrJySEPDw9avXo1nT17log055w0hWYsu1QReqm7oKGhATweD9HR0cjL\ny4NAIIBIJEJFRQUWL16MAwcOwNLSUm2n8LU0ZQG01NRUbNq0CV9//TU6deqE6OhozJ07F/b29rCy\nsuL2COjQoQN3bGt9Q+XxeDh37hy2bt0KR0dHdOzYEdu3b8eiRYtw9OhRzJo1Czdv3kR0dLTGFUCT\nSqUQCoWwsrJCXFwc5s6dCyLCBx98gPr6ely6dAn37t3jWgbq3CpoqlOnTrC2toZIJEJUVBTEYjEA\nYMOGDYiMjOSe114+Z62JdRn9F9SkqyE/Px98Ph8GBgYwNTVFTk4O5syZg4CAAAwaNAhxcXGYPXs2\nDA0NueM15cP3v+DxeEhISMD+/fvh6+uLkSNHoqysDDk5ORCJRBAIBAgKCoKvry9MTExafRc4Ho+H\npKQk+Pv749tvv0VxcTHCwsKQk5OD1atXw9raGrW1tVi8eDGcnJxaJaaWQES4c+cOvL29YWFhgV69\nesHQ0BDOzs5Yt24dAMDb2xsjRozgBpA1iVAohEQiwbFjxzBjxgx4eXlBKBSivr6eGzwG2k93bKtS\nZfNEnSkrW545c4bs7Oxo7dq15Ofn16z4WlxcHA0aNKhZoba27uUmekREBPF4PNq3bx8RNc7lT0hI\noKVLl5K3tzfFxsa+8rjWIJfL6dKlS3Tjxg2Ki4sje3t7ysnJoeHDh9OiRYuaPVfd14i8Kr7AwECa\nPn06Xb16lZ4/f05ERL6+vmRkZERFRUWqCLNFKacIZ2Rk0ODBg+nSpUsqjqjtYwnhJcqS1ESNfeC2\ntrZUXFxMn3zyCQ0ZMoQWLlxImZmZVFVVRZMnT1bpDU8VlOdZUlLCjQkcP36ctLW1KSUlpdlzlGsy\nWvNmq1zzUVdX1yyOhQsXcq/VunXrmq0f0QTKcxGLxRQaGsqVAtmxYwdNmzaN4uPjKTY2lhYtWkS3\nbt1SZagtpqGhga5evUrDhw+n06dPE1H7+ZypCusyaqK8vBzbt2+HRCLBkCFDUFxcjFmzZqGoqAhh\nYWEIDQ1FVlYW4uPjMXLkSLz33nsYPHhwu5laSi/GVM6dO4cVK1bg9OnTuHfvHjw9PWFra4sFCxZg\n5MiRXJ+1csygNZv2PB4Pp06dwvr165Geng6hUAgLCwvEx8ejc+fOePDgAeLi4nDkyBFYWVmp/bRS\n4NfrnpaWBh8fH9TU1CAjIwNPnjzBypUr8ezZMyQmJuLw4cPw9fXF6NGjmx2nqfh8Prp16wY3NzeM\nHDmy3XzOVIkNKjchEAggFAqRmZkJXV1dTJ8+HUDjYNauXbswZswYXLhwARKJhJsfrdQe3qQ8Hg/p\n6en4+uuvsWfPHkgkEmRnZ+Pjjz/GN998gydPnsDNzQ0lJSXo2rVrq00FpJcWxR06dAiLFy+GVCrF\n2rVrsW/fPnh5eWHPnj0oKChAQECARg0gK6/7li1bcOLECQwdOhTHjx9HamoqwsPD4e3tDS0tLa7s\nujIRtIX3pFAoRL9+/bjHbeGc1JrqGifqQ6FQcGMGVVVVFBoaSn5+fvTDDz8QEdHy5cvJxcWFEhMT\nycrKiqtb1N6ar0+fPiUPDw96++23ud/duHGDPD09KSEhgYhIJX3XytchLS2NvvrqK9qyZQv3t4iI\nCLKxsaGffvqJiIiePXvGHaNJr9/FixdJIBBQUFAQETVu1HPixAny9vamnTt3UkNDA9ddpknnxagX\n1mX0Ap/Ph0gkwt27dzFz5kzcuXMH169fh5aWFvz8/JCUlIT09HSsWrUKLi4uGt8c/yPopSZ6586d\noa+vjwsXLuDx48dwdnZGz549cfnyZVRWVmLUqFHQ1dUFn89vteuj/D8pKSl499138eTJE/z888+w\nsLBA7969YWdnBy0tLWzYsAHz5s2Dnp4eF5cmvX7m5uawtrZGcHAw9PX1YW1tjYEDB6K6uhpOTk4w\nNDTUyPNi1Ixq85H6OHPmDNnY2NCFCxeIiKiiooJCQkJo9erVdP78eSJqf1VLleeYkJBA//znPyk8\nPJzKysro8uXLNHv2bPLy8qKkpCSysrLi9udVhbS0NJowYQJdv36diIg2bdpEK1euJLFYTDKZjIiI\niouLVRZfSzp79izZ2tpSRESEqkNh2iCWEKhxpeo777zDdSsobyIVFRX05Zdf0vLlyzWiKmRLUiaD\n5ORk6t+/P+3evZvs7e0pMDCQUlJS6PLly2RpaUmOjo7cdVPVfsMXL14kPp/PrdR9/vw5BQYGkpeX\nFyUmJjZL3m0hkZ8+fZoGDhxIJSUlXFcnw7QEVgAEjd1FZWVlkEqlAH5tcstkMgQEBGDjxo3NFp21\nB8oFeWFhYVi/fj38/Pxw6tQpSKVSxMbGwtnZGXv27EH//v2RlJQEACrbb3jixIk4efIk9u/fj+++\n+w4dO3bEpk2bYGRkhJ49ezbrQmkL3SnvvPMOkpKSYGxsrJbVShnNxcYQAHTs2BFVVVUoKChAz549\nYWhoiJSUFPj5+WHixIkaudrzz6AX/fEKhQI8Hg/JyclISkpCcXExHB0d0bt3b1hbWyMwMBDTp0+H\npaUl9PT0IBKJMGrUqGZF4VqbpaUlTE1NsW3bNmhra8POzg7jx49vs4lcR0cHgOZPLWXUC9sP4YWS\nkhLs3bsXYrEYTk5OiI6ORmhoKNzd3VUdWqugJgPIJSUl6N27N4DGbUGPHTsGCwsLzJs3D9XV1Zg7\ndy7OnTuH3r17QyaToaGhQaXJoKmYmBh89NFHSEhIgKGhIfsGzTCvgSWEJmpqapCeng6JRAJTU1M4\nODi0m8Uwym+a58+fx+bNm+Hq6go+n4+tW7ciOTkZoaGhKC4uRrdu3eDv748pU6ao7bfTx48f4623\n3lJ1GAyjcdjCtCaEQiHGjRvHPW4vyQD4ta7+hg0bEBUVhcOHD+PkyZN48OAB9u7di86dO+PgwYMw\nNzfHpEmTVB3u71ImA3VNWAyjrtig8u9oK6s9/wi5XM7taFZcXIyEhAQcOnQIpaWl8PHxgZ2dHaZP\nn46CggLs37+fKwWuztQ9PoZRN6yFwABoLNvh4uICHo+HnTt3YseOHRg5ciTMzMxw+/Zt3L59G1On\nTgURYfjw4SqbUcQwzJvDPtXt0MtdKcrH2traeP78OaRSKW7cuAGFQoHs7GyEh4dzWxVOmzZNVWEz\nDPOGsUHldqbpuMjNmzehr68PY2PjZs+5fPkyQkJCUFNTAx8fH3h4eHDHsm4Yhmm7WEJoZ5Q39djY\nWAQFBSE4OBj29vbc35XbYlZXV4OIoKur264G1xmmPWMJoR36z3/+Aw8PD+zbtw/Dhg1r9rdX3fxZ\ny4Bh2gc2y6gdKCoqwurVq7nHyrr5ymTQ0NAAAKiurn7lzCqWDBimfWAJoR0wNTWFl5cX7t69CwAY\nOnQo9PX1kZiYCJlMBi0tLSQnJ2P79u2oq6sDazQyTPvEuozaMCKCXC7npog6OTlBIBBwK4/v3LkD\noVAIBwcHrFu3Dt988w1cXV1VHDXDMKrCEkIb1XQsIC8vj5s2OnbsWPTs2RNRUVFISEjAuXPnIJPJ\n4O7urtblKBiGefNYQmijmtYm8vPzQ2RkJOzs7AAAo0aNgqGhIX744QcAwPPnz6Gtrc1mEzFMO8cS\nQhuWlZWF+fPn48SJE7CxscG9e/fQs2dPdO7cGQ4ODtDV1UVCQgI31ZRhmPaNrVRuQ17+hq+lpYU5\nc+bgxo0biIuLQ2RkJCwsLPDRRx8hLS0NqampAMCSAcMwANgsozaHx+MhPj4ecXFxMDAwQG1tW/uv\nOwAAA19JREFULY4fPw4zMzOcOHECZmZmyMrKAgA4OjqCGrdRVXHUDMOoA5YQ2hAej4eYmBh88MEH\nqK+vh7GxMbZt24ZTp07hb3/7G+rr63Hp0iWYm5s3O4aNGTAMA7CE0KaUl5dj9+7d+P777+Hu7o5r\n167h+++/h0KhgFgsxrJlyxAYGIixY8eyVgHDML/BxhA02MtTRJV7FERHRyMvLw8CgQAikQgVFRVY\nvHgxDhw4AEtLS5YMGIZ5JdZC0FBNb+r5+fl4+vQp3nrrLQQGBqKyshJLlizB4cOHER4ejoyMDHTu\n3JlbiwCwqaUMw/wWm3aqoeRyOQQCAWJjY7F161aMHj0aCoUCa9euhZmZGQDg4sWLCAgIQFBQEKZM\nmaLiiBmGUXeshaBhqqqqADTucJaRkYHNmzcjJiYGOjo6EIvFCAwMxLVr11BdXY3du3fjyy+/5FYg\nMwzD/B7WQtAg5eXlCA4OhpWVFebPn4/09HR07NgRjx8/xsaNG7Fr1y6Eh4dDKpUiODgYRkZGbD8D\nhmH+MNZC0CACgQBCoRCZmZk4c+YMRowYAVtbWyQmJmLXrl0YM2YMTExM0KNHD1RXV0NXV5c7liUD\nhmH+PywhaABl1dKuXbtyYwSJiYk4efIkAEAqleLTTz+FSCRCbGwsVq5cCRsbG9YyYBjmtbAuIw2g\nnF4qEonw/PlzODs7Y+/evSgqKsLUqVPh6uqK999/HzU1NZg7dy5mzZrFqpYyDPPaWELQELGxsQgM\nDMTnn38ONzc3PHv2DAcPHkRhYSEmT56MyZMns6qlDMP8T1iXkQaorKzEgQMHEBYWBjc3N9TX10NP\nTw/vvfceTExMcObMGUgkEmhrawNg5SgYhvlz2EplDcDn81FWVgapVArg12/+MpkMAQEBKCkpgaGh\noSpDZBimDWAtBA2go6MDDw8PpKamIjc3F1paWkhJScGCBQvw+PFj9O3bV9UhMgzTBrAxBA1RUlKC\nvXv3QiwWw8nJCdHR0QgNDYW7u7uqQ2MYpo1gCUGD1NTUID09HRKJBKampnBwcGADyAzDtBiWEDQY\nSwYMw7QkNqiswVgiYBimJbFBZYZhGAYASwgMwzDMCywhMAzDMABYQmAYhmFeYAmBYRiGAcASAsMw\nDPMCSwgMwzAMAOD/ANLifp9XPWcHAAAAAElFTkSuQmCC\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10eeafd50>"
|
|
]
|
|
},
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAbwAAAFhCAYAAAALEB8uAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdYFGfXBvB7qNJ7EaSIxgiKghWxYVBj16BGiSWoiSXR\naEyR1xjljbFrLNGYmESJPTHGGuyK+tl7I4JtsYIFlSqwy/n+8N2JC4iKw8yynN91eSWz7Mw8c+/O\nnJ3nmdkViIjAGGOMGTgjpRvAGGOMyYELHmOMsQqBCx5jjLEKgQseY4yxCoELHmOMsQqBCx5jjLEK\nQdaCl5qaihYtWsDW1hZffPGFnKsulzp06IBly5Yp3Qy95evri127dsm2PiMjI1y9erVM1xEVFYWv\nv/66zJZvY2MDlUr1SvPEx8fDy8urbBpk4GrXro19+/ZJvlyVSgUjIyMUFBRIvmylDRs2DN9++22Z\nLNvkRU/w9fXF3bt3YWxsDCsrK7Rv3x7z58+HlZXVK69s0aJFcHV1RXp6eqkaW9HExcUp3QS9JggC\nBEEo9m9RUVHw8vLCxIkTS7XssLAw9OvXD4MGDXqdJr6ykrZJChkZGWW27Nfxuq+Xvjp//rzSTZDV\nq76OsbGx+PXXX7F//37xsYULF5ZV8158hicIAjZv3oyMjAycPHkSx48ff+XqS0QoKChAcnIy/P39\nS9VQtVpdqvlY+aBvr29ZFp0X4e+C0E/69h5lpUAv4OvrS7t27RKnP//8c+rUqRMRER06dIiaNGlC\n9vb2VLduXYqPjxef17JlS/rqq6+oadOmZGFhQX379iVTU1MyMzMja2tr2rVrF+Xm5tLIkSPJw8OD\nPDw8aNSoUZSbm0tERHv27CFPT0+aNm0aubu7U79+/SgmJoZ69OhBffv2JRsbGwoMDKSkpCSaPHky\nubq6kre3N23fvl1sw+LFi8nf359sbGzIz8+PfvrpJ/Fv2uXPmjWLXF1dqXLlyrRkyRLx79nZ2TR6\n9Gjy8fEhOzs7atasGeXk5Lxwuws7ceIEBQUFkY2NDfXs2ZPeffddGjduHBERpaWlUceOHcnFxYUc\nHByoU6dOdPPmTZ0Mf/nlFyIiWrJkCTVt2pQ+//xzcnBwoKpVq9KWLVueu97r16/TO++8Qy4uLuTk\n5ETDhw8nIiKNRkMTJ04kHx8fcnV1pf79+9Pjx4+JiOjatWskCAItWbKEvLy8yNHRkRYuXEhHjx6l\nwMBAsre3F5ejbVNoaCgNHz6c7OzsqGbNmjrvlZfJX/v69u/fnwoKCmjKlClUrVo1cnJyonfffZfS\n0tLEeZYuXUre3t7k5OREkyZNKvLe1Prpp5903mtdunQhIqKEhARq2bIl2dvbU61atWjjxo3FZjd2\n7FgyNjamSpUqkbW1NY0YMYKIiARBoB9//JHeeOMNsre3p48//lhnvl9//ZX8/f3JwcGB3n77bUpO\nTn7u67N//37xPeTl5UW//fYbERFFRUW99PtjyZIl5OfnRzY2NlS1alVasWIFERFdunSJWrRoQXZ2\nduTs7Ey9evUS5xEEga5cuUJEJb/Hn7Vnzx6qUqWKOH3r1i2KiIggFxcXqlq1Ks2bN0/825EjRygk\nJITs7e2pcuXKNHz4cMrLyxP/PmrUKHJ1dSVbW1sKDAyk8+fPP/f1Kqy4eYmI7t+/T507dyZbW1tq\n1KgRjRs3jpo1a0ZE/76nNRqNuJxn96vLly9Tq1atyMnJiZydnalPnz706NEj8bk+Pj40bdo0CgwM\npEqVKpFGo3ml/d/Hx0d8j06YMOGVjl8tW7ak6OhoatSoEdna2lLXrl3F/aHwdj169IgGDhxIlStX\nJk9PTxo3bpz4N+1++umnn5K9vT1Vq1aNDhw4QIsXLyYvLy9ydXUV339ERE+ePKHPPvuMvL29yc3N\njYYOHSq+L0o6bj7vddTu0zY2NhQQEEDr1q0joqf7Y6VKlcjY2Jisra3JwcGBiIjef/99cR8gIlq0\naBFVr16dHB0dqUuXLnT79m3xby/aJwt7qYK3c+dOInp6EK1VqxaNHz+ebt68SU5OTuJBd8eOHeTk\n5ET3798XXywfHx9KSEggjUZD+fn5FBUVRV9//bW47K+//pqaNGlC9+7do3v37lFoaKj49z179pCJ\niQlFR0dTXl4e5eTk0IQJE6hSpUq0fft2UqvV1L9/f/Lx8aHJkyeTWq2mn3/+mapWrSou/++//6ar\nV68SEdHevXvJ0tKSTp48qbP8CRMmkFqtpri4OLK0tBTf7B999BG1atWKbt++Lb7Jc3Nzn7vd9+7d\nK5Jdbm4ueXt707x580itVtNff/1FZmZm4jY+ePCA/vrrL8rJyaGMjAzq2bMndevWTZw/LCyMfv31\nVyJ6+qY1NTWlX375hQoKCmjhwoXk4eFR7GumVqupTp06NHr0aMrOzqYnT57QgQMHiOjpQbl69ep0\n7do1yszMpIiICOrXrx8R/bsTDRs2jHJzc2n79u1kZmZG3bp1o3v37tGtW7fI1dWV9u7dK7bJxMSE\n5syZQ2q1mn7//Xeys7MTd8qXyf/Z13fOnDnUpEkTunXrFuXl5dGQIUMoMjKSiIguXLhA1tbWtH//\nfsrNzaXRo0eTiYlJsQWPiIq81/Ly8qhatWo0ZcoUys/Pp927d5ONjQ0lJiYWO/+z2WsJgkCdO3em\nx48f0/Xr18nFxYW2bt1KRETr16+n6tWr08WLF0mj0dC3335LoaGhxS5bpVKRjY0NrV69mtRqNT14\n8IBOnz4ttlu7s5f0/sjMzCRbW1tKSkoiIqKUlBS6cOECERH17t2bJk+eTERP34Pa1167DdqC97z3\neGHPFjyNRkP16tWjiRMnUn5+Pl29epX8/Pxo27ZtRPT0A96RI0dIo9GQSqUif39/mjNnDhERbd26\nlerXry9+wLp48SLduXOn2NersJLm7dWrF/Xq1Yuys7Pp/Pnz5OnpSc2bNyei4gves6/t5cuXaefO\nnZSXl0f37t2jFi1a0KhRo8Tn+vj4UHBwMN28eZOePHnySvs/ke4Jw6sev1q2bEmenp504cIFysrK\nou7du1Pfvn2L3a5u3brR0KFDKTs7m+7evUuNGjUSP2Bq99PY2FgqKCigcePGkaenp/hhZPv27WRj\nY0NZWVlE9PSDRdeuXenhw4eUkZFBnTt3pv/85z/ie6Gk42Zxr+OaNWvE1+r3338nKysrSklJISKi\n2NhY8cOJ1rPL2LVrFzk7O9OpU6coNzeXRowYQS1atBCfW9I+WZwXFjwfHx+ytrYme3t78vHxoY8/\n/phycnJo6tSp4oFS6+233xY/KYSFhdGECROKbMizlbtatWo6Zynbtm0jX19fInoarJmZmc4OOGHC\nBGrbtq04vXHjRrK2tqaCggIiIkpPTydBEMSdorBu3brR3LlzxeVbWFjo7Aiurq7izmphYUFnz54t\nsowXbfez9u7dS56enjqPNWvW7Lk79qlTp8RPOURFC1716tXFv2VlZZEgCJSamlpkOQcPHiQXFxed\nbdN66623aOHCheJ0YmIimZqakkajEXeiZz9BOTk50R9//CFOd+/eXTyALVmypEjRbdSoES1btqzY\n7Sucf+HX19/fX6eA3b59m0xNTUmtVtN///tfsfhpt9/MzKzEgvfse23fvn3k7u6u85zIyEiKiYkp\ndv6wsDDxLEBLEASd4vHuu+/StGnTiIioXbt2OgVSo9GQpaUlXb9+vciyJ0+eTBERES/V7mc9+/7I\nzMwke3t7Wrt2LWVnZ+s8r3///jR48GCds8Fnt+HKlSslvscLe7bgHT58mLy9vYtsz4ABA4qdd/bs\n2fTOO+8Q0dODV40aNejw4cNF3pslbTcR0e7du4udV61Wk6mpqc4Hl7Fjx5Z4hlfchxmtdevWUXBw\nsDjt6+ur0/PzKvu/dv5nC96rHL/CwsLEQkP09IzIzMyMCgoKdLYrJSWFzM3Ndc7OV65cSa1atSKi\np/vpG2+8If7t7NmzJAgC3b17V3zMycmJzpw5QwUFBWRlZSV+KCJ6ejzRFuKSjptEL34diYiCgoJo\nw4YNYttKKngDBw6kMWPGiH/LzMwkU1NTsfekuH1y6tSpz133S43hbdiwAQ8fPoRKpcL8+fNRqVIl\nJCcnY82aNXBwcBD/HThwACkpKeK8L7qy6/bt2/Dx8RGnvb29cfv2bXHaxcUFZmZmOvO4urqK/29h\nYQFnZ2dxvMXCwgIAkJmZCQDYsmULQkJC4OTkBAcHB8TFxeHBgwfi/E5OTjAy+jcCS0tLZGZm4v79\n+3jy5AmqVatWpM0vs93Pbp+np6fOY15eXuIYTXZ2NoYMGQJfX1/Y2dmhZcuWePz48XPHcNzd3XXa\n+uy2PuvGjRvw8fHR2TatO3fuFMlcrVYjNTVVfMzNzU38fwsLiyLTWVlZ4nTh7fPx8cGdO3cAvDj/\nwq+vSqXCO++8I+YaEBAAExMTpKam4s6dO6hSpYrO9js5ORUXU7Fu375d5P3o4+ODW7duPXee4sbx\nCr8G2vyTk5MxcuRIse3athW3/Js3b8LPz++FbS7p/WFlZYXff/8dP/74Izw8PNCpUyckJiYCAKZP\nnw4iQqNGjVC7dm0sWbKkyLJLeo+XJDk5Gbdv39Z5/0+ZMgV3794FACQlJaFTp06oXLky7Ozs8NVX\nX4mv+VtvvYXhw4fj448/hpubG4YMGfLSF9G0atWq2Hnv3bsHtVqt89p6e3u/9Pakpqaid+/eqFKl\nCuzs7NCvXz+d9yigexx7lf2/OK9y/Cq8bm9vb+Tn5+P+/fs6y0xOTkZ+fj4qV64stmno0KG4d++e\n+JzC+zDwdP979rHMzEzcu3cP2dnZqF+/vris9u3b66zzecfN51m6dCmCg4PF5Z0/f75Ixs9T+Hhl\nZWUFJycnnf3qeftkcUp9W4K3tzf69euHhw8fiv8yMjLw5Zdfis950cC/h4eHziXS169fh4eHx3Pn\nf5ULCXJzc9G9e3d8+eWXuHv3Lh4+fIgOHTq81AUBzs7OqFSpEi5fvlzkby+z3VqVK1cucsC7fv26\nuB2zZs1CUlISjh49isePH2Pv3r2gp2fdL72dxfHy8sL169eh0WiK/K24zE1MTHR2iFdRePuSk5Ph\n4eHxUvkXfj29vb2xdetWnWyzs7Ph4eGBypUr48aNG+Jzs7OzS9xpCi/bw8MDN27c0Fl/cnKyThEt\naf4X8fb2xqJFi3TanpWVhZCQkCLP9fLywpUrV17Y9he9P9q2bYvt27cjJSUFNWvWxIcffgjg6cFt\n0aJFuHXrFn766Sd89NFHRW6nKOk9XhIvLy9UrVpVZzvT09OxefNmAE8vKQ8ICMDly5fx+PFjTJo0\nSefS+REjRuD48eNISEhAUlISZsyYobPNJSluXldXV5iYmOD69evi8579f+3V5NnZ2eJjzxansWPH\nwtjYGOfPn8fjx4+xbNmyIpf6P9u2V9n/pVB4u0xNTeHs7KzzHC8vL5ibm+PBgwdimx4/foxz5869\n8vqcnZ1hYWGBhIQEcVmPHj166SvrC7+OycnJGDx4MBYsWIC0tDQ8fPgQtWvXFt/Dr1ojsrKy8ODB\ngyIftF9WqQte3759sWnTJmzfvh0ajQZPnjxBfHy8zgGw8IG78HRkZCS+/fZb3L9/H/fv38c333yD\nfv36PXedr1II8vLykJeXB2dnZxgZGWHLli3Yvn37S81rZGSEgQMHYvTo0bhz5w40Gg0OHTqEvLy8\nl9purdDQUBgbG2P+/PlQq9XYsGEDjh07Jv49MzMTFhYWsLOzQ1paGv773/++9PaVpHHjxqhcuTKi\no6ORnZ2NJ0+e4ODBgwCeZj579myoVCpkZmZi7Nix6N27d7Fng8/z7Otw9+5dzJs3D/n5+VizZg0u\nXryIDh06lCr/oUOHYuzYseJOfu/ePWzcuBEA0KNHD2zevBkHDhxAXl4exo8fX+I9SG5ubjoH+ZCQ\nEFhaWmL69OnIz89HfHw8Nm/ejN69ez93/pKKkjYHbRZDhw7F5MmTkZCQAAB4/Pgx1qxZU+x8ffr0\nwc6dO7FmzRqo1Wo8ePAAZ86cKbLMkt4fd+/exYYNG5CVlQVTU1NYWVnB2NgYALBmzRrcvHkTAGBv\nbw9BEIq8viW9x0vSqFEj2NjYYPr06cjJyYFGo8H58+dx/Phxsc02NjawtLTExYsXsXDhQvGgdvz4\ncRw5cgT5+fmwtLREpUqVxDYXfr0Ke968RkZGiIiIQExMDHJycpCQkIClS5eK63RxcYGnpyeWLVsG\njUaDxYsX67yumZmZsLKygq2tLW7duiUW4Od5lf3/dRERli9fjn/++QfZ2dkYP348evbsWaRIVK5c\nGW3btsXo0aORkZGBgoICXLlypVT3/xkZGeHDDz/EqFGjxDPEW7duvfSxs/DrmJWVBUEQ4OzsjIKC\nAixZskTnVg03NzfcvHkT+fn5Otut3QciIyOxZMkSnDlzBrm5uRg7dixCQkKeexb/ohpR6oJXpUoV\nbNiwAZMnT4arqyu8vb0xa9asEj/BF77HaNy4cWjQoAHq1KmDOnXqoEGDBhg3btxLz/+85wBPb7Cd\nN28e3n33XTg6OmLVqlXo2rVrifM+a+bMmQgMDETDhg3h5OSE//znPygoKHjudhd38DU1NcVff/2F\nX3/9FQ4ODlixYgU6deokduONGjUKOTk5cHZ2RmhoKNq3b//cNr3MtmsZGRlh06ZNuHz5Mry9veHl\n5YU//vgDADBw4ED069cPLVq0gJ+fHywtLfH999+/VCbFPadx48a4dOkSXFxc8PXXX2Pt2rVwcHAo\nVf4jR45Ely5d0LZtW9ja2qJJkyY4evQoACAgIAALFizAe++9Bw8PDzg6OpbYZT5o0CAkJCTAwcEB\nERERMDU1xaZNm7Blyxa4uLhg+PDhWLZsGWrUqFHs/CNHjsSff/4JR0dHjBo16rk5aLehW7duGDNm\nDHr37g07OzsEBgZi27Ztxc7n5eWFuLg4zJo1C05OTggODsbZs2eLLLOk90dBQQFmz54NT09PODk5\nYf/+/eL9S8ePH0dISAhsbGzQtWtXzJs3D76+vkUyf957/HnbCgDGxsbYvHkzTp8+DT8/P7i4uGDw\n4MHiGcDMmTOxcuVK2NraYvDgwTofKNLT0zF48GA4OjrC19cXzs7O4hdQFH69Citp3vnz5yMzMxPu\n7u4YOHAgBgwYoHMc+vnnnzFjxgw4OzsjISEBTZs2Ff82YcIEnDx5EnZ2dujcuTO6d+9e4j7wKvt/\ncRm+7PFL+//9+vVDVFQUKleujLy8PMybN6/Y5y5duhR5eXkICAiAo6MjevbsKZ7JvsqxAwCmTZuG\n6tWrIyQkBHZ2dmjTpg2SkpJeat7Cr2NAQAA+++wzNGnSBO7u7jh//jyaNWsmPj88PBy1atWCu7u7\n2N37bHvDw8MxceJEdO/eHR4eHrh27RpWr15dYn4lHsNKHF3UAwMGDCBXV1eqXbt2kb/NnDmTBEGg\nBw8eKNCy0mnUqBHFxsYq3QxJFDfgzJjSDOV9WdLFNax09P67NAcMGICtW7cWefzGjRvYsWOHzoCm\nPtq3bx9SUlKgVqvx22+/4fz582jXrp3SzWKMlQPEX0IgKb0veM2bN4eDg0ORx0ePHo3p06cr0KJX\nk5iYiKCgIDg4OGD27Nn4888/S32BiL4p66/BYqw0DOl9aSjboS8EKgcfIVQqFTp37ixedbRhwwbE\nx8dj9uzZqFq1Kk6cOAFHR0eFW8kYY0yfvfDLo/VNdnY2Jk+ejB07doiPlYOazRhjTGHlruBduXIF\nKpUKdevWBfD0Jt769evj6NGjOjd1AkD16tVfeGk5Y4wxXXXr1sXp06eVbobk9H4Mr7DAwECkpqbi\n2rVruHbtGqpUqYKTJ08WKXbA0+JI/7unQ5//TZgwQfE2GNI/zpOz1Nd/5SVP7X2hhkbvC15kZCRC\nQ0ORlJQELy+vIl+TZAiDuq/6g5ysZJyndDhLaXGeytL7Ls1Vq1aV+Pey/gVqxhhjhkHvz/Aqgqio\nKKWbYFA4T+lwltLiPJVVLm5LKC1BEGDAm8cYY2XCUI+dfIanB+Lj45VugkHhPKXDWUqL81QWFzzG\nGGMVAndpMsYY02Gox04+w2OMMVYhcMHTA9yvLy3OUzqcpbQ4T2VxwWOMMVYhVOgxvOiYaKQ8SpGx\nRfrL3d4dU2OmKt0MxpgeMNQxPL3/ppWylPIoBb7dfJVuhl5QrVcp3QTGGCtT3KWpB1SnVUo3waDw\nOIl0OEtpcZ7K4oLHGGOsQuCCpwd8g3yVboJBCQsLU7oJBoOzlBbnqSwueIwxxioELnh6gMfwpMXj\nJNLhLKXFeSqLCx5jjLEKgQueHuAxPGnxOIl0OEtpcZ7K4oLHGGOsQuCCpwd4DE9aPE4iHc5SWpyn\nsrjgMcYYqxC44OkBHsOTFo+TSIezlBbnqSwueIwxxioELnh6gMfwpMXjJNLhLKXFeSpL7wvewIED\n4ebmhsDAQPGxL774Av7+/qhbty4iIiLw+PFjBVvIGGOsPND7gjdgwABs3bpV57G2bdviwoULOHPm\nDGrUqIEpU6Yo1Dpp8BietHicRDqcpbQ4T2XpfcFr3rw5HBwcdB5r06YNjIyeNr1x48a4efOmEk1j\njDFWjuh9wXuRxYsXo0OHDko347XwGJ60eJxEOpyltDhPZZXrgjdp0iSYmZnhvffeU7opjDHG9JyJ\n0g0ordjYWMTFxWHXrl0lPi8qKgq+vr4AAHt7ewQFBYn96Ck3U4DT/46hac+0Kuq09tOnNh+e5uln\n6Ut7yvu0lr60JywsDPHx8YiNjQUA8XhpiAQiIqUb8SIqlQqdO3fGuXPnAABbt27FZ599hr1798LZ\n2fm58wmCgJI2L2pUFHy7+Urd3HJJtV6F2DmxSjeDMaYHXnTsLK/0vkszMjISoaGhSExMhJeXFxYv\nXowRI0YgMzMTbdq0QXBwMD766COlm/laeAxPWoU/SbPS4yylxXkqS++7NFetWlXksYEDByrQEsYY\nY+WZ3p/hVQR8H560tGMU7PVxltLiPJXFBY8xxliFwAVPD/AYnrR4nEQ6nKW0OE9lccFjjDFWIXDB\n0wM8hictHieRDmcpLc5TWVzwGGOMVQhc8PQAj+FJi8dJpMNZSovzVBYXPMYYYxUCFzw9wGN40uJx\nEulwltLiPJXFBY8xxliFwAVPD/AYnrR4nEQ6nKW0OE9lccFjjDFWIcj25dGJiYmYOXMmVCoV1Go1\ngKc/QbF79265mqC3eAxPWjxOIh3OUlqcp7JkK3g9e/bEsGHD8MEHH8DY2BjA04LHGGOMyUG2Lk1T\nU1MMGzYMjRs3RoMGDdCgQQPUr19frtXrNR7DkxaPk0iHs5QW56ks2Qpe586dsWDBAty5cwdpaWni\nP8YYY0wOAsn0O+6+vr7FdmFeu3atzNb5op+pjxoVBd9uvmW2/vJEtV6F2DmxSjeDMaYHXnTsLK9k\nG8NTqVRyrYoxxhgroswL3q5duxAeHo61a9cWe4YXERFR1k3Qe6rTKr5SU0Lx8fF8NZxEOEtpcZ7K\nKvOCt2/fPoSHh2PTpk1c8BhjjClGtjE8JfAY3svjMTzGmBaP4Ulg8+bNSEhIwJMnT8THxo8fL2cT\nGGOMVVCy3ZYwZMgQ/PHHH5g3bx6ICH/88QeSk5PlWr1e4/vwpMX3OkmHs5QW56ks2QrewYMHsXTp\nUjg6OmLChAk4fPgwEhMTXzjfwIED4ebmhsDAQPGxtLQ0tGnTBjVq1EDbtm3x6NGjsmw6Y4wxAyBb\nwbOwsAAAWFpa4tatWzAxMUFKSsoL5xswYAC2bt2q89jUqVPRpk0bJCUlITw8HFOnTi2TNsuFr9CU\nFl8FJx3OUlqcp7JkK3idOnXCw4cP8cUXX6B+/frw9fVFZGTkC+dr3rw5HBwcdB7buHEj3n//fQDA\n+++/j/Xr15dJmxljjBkO2Qre+PHj4eDggO7du0OlUuHixYuYOHFiqZaVmpoKNzc3AICbmxtSU1Ol\nbKrseAxPWjxOIh3OUlqcp7Jku0qzuBvP7ezsEBgYCFdX11IvVxCEEn91ISoqCr6+vgAAe3t7BAUF\nid0KKTdTgNP/dilqC4/c01pKrV87rd0ZtfmU12ktfWlPeZ4+ffq0XrWnvE/ra57x8fGIjY0FAPF4\naYhkuw+vY8eOOHToEFq1agXgadj16tXDtWvXMH78ePTv3/+586pUKnTu3Bnnzp0DANSsWRPx8fFw\nd3fHnTt30KpVK1y8eLHIfHwf3suT4j686JhopDx68bhsReBu746pMeV7bJlVXHwf3mvKz8/HP//8\nI3ZFpqamol+/fjhy5AhatGhRYsErrEuXLvjtt98wZswY/Pbbb+jWrVtZNZu9gpRHKfwB4n9U61VK\nN4ExVohsY3g3btwQix0AuLq64saNG3BycoKZmdlz54uMjERoaCgSExPh5eWFJUuWIDo6Gjt27ECN\nGjWwe/duREdHy7EJZYbH8KTFeUqncDcxez2cp7JkO8Nr1aoVOnbsiHfffRdEhLVr1yIsLAxZWVmw\nt7d/7nyrVq0q9vGdO3eWVVMZY4wZINkK3oIFC7B27VocOHAAwNPbCbp37w5BELBnzx65mqGX+D48\naXGe0tFe4MCkwXkqS7aCJwgCevTogR49esi1SsYYY0wk2xgeez4ec5IW5ykdHnOSFuepLC54jDHG\nKgRZC152dvZLfWF0RcNjTtLiPKXDY07S4jyVJVvB27hxI4KDg/H2228DAE6dOoUuXbrItXrGGGMV\nnGwFLyYmBkeOHBG/CDo4OBhXr16Va/V6jcecpMV5SofHnKTFeSpLtoJnampa5H47IyMeQmSMMSYP\n2SpOrVq1sGLFCqjValy6dAkjRoxAaGioXKvXazzmJC3OUzo85iQtzlNZshW877//HhcuXIC5uTki\nIyNha2uLOXPmyLV6xhhjFZxsBc/KygqTJ0/G8ePHcfz4cUyaNAmVKlWSa/V6jcecpMV5SofHnKTF\neSpLtoLXunVrPHr0SJxOS0sTr9hkjDHGyppsBe/+/fs6F604OjqW+18qlwqPOUmL85QOjzlJi/NU\nlmwFz9hOClWnAAAgAElEQVTYGMnJyeK0SqXiqzQZY4zJRraKM2nSJDRv3hx9+/ZF37590aJFC0ye\nPFmu1es1HnOSFucpHR5zkhbnqSzZfi2hXbt2OHHiBA4fPgxBEDBnzhw4OzvLtXrGGGMVnGwFDwDy\n8vLg6OgItVqNhIQEAECLFi3kbIJe4jEnaXGe0uExJ2lxnsqSreCNGTMGv//+OwICAmBsbCw+zgWP\nMcaYHGQreOvWrUNiYiLMzc3lWmW5oTqt4rMSCXGe0omPj+ezEglxnsqS7aKVatWqIS8vT67VMcYY\nYzpkO8OzsLBAUFAQwsPDxbM8QRAwb948uZqgt/hsRFqcp3T4bERanKeyZCt4Xbp0KfL7d4IgyLV6\nxhhjFZxsBS8qKkquVZU7POYkLc5TOjzmJC3OU1myjeElJSWhR48eCAgIQNWqVVG1alX4+fm91jKn\nTJmCWrVqITAwEO+99x5yc3Mlai1jjDFDI1vBGzBgAIYOHQoTExPEx8fj/fffR58+fUq9PJVKhZ9/\n/hknT57EuXPnoNFosHr1aglbLB8+G5EW5ykdPhuRFuepLNkKXk5ODlq3bg0igo+PD2JiYvD333+X\nenm2trYwNTVFdnY21Go1srOz4enpKWGLGWOMGRLZCl6lSpWg0WhQvXp1zJ8/H3/99ReysrJKvTxH\nR0d89tln8Pb2hoeHB+zt7dG6dWsJWywf/u5HaXGe0uHvfpQW56ks2S5amTNnDrKzszFv3jx8/fXX\nSE9Px2+//Vbq5V25cgVz5syBSqWCnZ0devbsiRUrVhTpJo2KioKvry8AwN7eHkFBQWK3QsrNFOD0\nv11g2gOl3NNaSq1fO63dGbX5vOo056k7/bp56sP06dOn9ao95X1aX/OMj49HbGwsAIjHS0MkEBEp\n3YjS+P3337Fjxw788ssvAIBly5bh8OHDWLBggfgcQRBQ0uZFjYqCbzffsm5quaBar0LsnNjXWgbn\n+S8p8mRMKS86dpZXsnVpHjt2DO+88w6Cg4MRGBiIwMBA1KlTp9TLq1mzJg4fPoycnBwQEXbu3ImA\ngAAJW8wYY8yQyNal2adPH8ycORO1a9eW5Idf69ati/79+6NBgwYwMjJCvXr1MHjwYAlaKj++b0xa\nnKd0+L4xaXGeypKt4Lm4uBT5ppXX9eWXX+LLL7+UdJmMMcYMk2wFb8KECRg0aBBat24NMzMzAE/7\niSMiIuRqgt7isxFpcZ7S4bMRaXGeypKt4P32229ITEyEWq3W6dLkgscYY0wOshW848eP4+LFi/yF\n0cXgMSdpcZ7S4TEnaXGeypLtKs3Q0FAkJCTItTrGGGNMh2xneIcOHUJQUBCqVq2q83t4Z8+elasJ\neovPRqTFeUqHz0akxXkqS5aCR0RYtGgRvL295VgdY4wxVoRsZ3gfffQRzp8/L9fqyhUec5KWoeQZ\nHRONlEcpirYh5WYK3Ku4K9oGAHC3d8fUmKlKN+O18RiesmQpeIIgoH79+jh69CgaNWokxyoZK/dS\nHqUo/1Vtp/Wji1i1XqV0E5gBkO0M7/Dhw1i+fDl8fHxgZWUFgMfwtPThgGJIOE/pcJbS4rM7ZclW\n8LZt2wYA4m0JhvjFpIwxxvSXbLcl+Pr64tGjR9i4cSM2bdqEx48fG/TPULwK/v02aXGe0uEspcW/\nh6cs2Qre3Llz0bdvX9y7dw+pqano27cv5s2bJ9fqGWOMVXCydWn+8ssvOHLkiDh+Fx0djZCQEHzy\nySdyNUFv8TiJtDhP6XCW0uIxPGXJdoYHQOc7NKX4iSDGGGPsZclWdQYMGIDGjRsjJiYGEyZMQEhI\nCAYOHCjX6vUaj5NIi/OUDmcpLR7DU1aZd2levXoVfn5+GD16NFq2bIn/+7//gyAIiI2NRXBwcFmv\nnjHGGAMgQ8Hr2bMnTpw4gfDwcOzatQv169cv61WWOzxOIi3OUzqcpbR4DE9ZZV7wNBoNJk2ahMTE\nRHz33Xc6998JgoDRo0eXdRMYY4yxsh/DW716NYyNjaHRaJCRkYHMzEzxX0ZGRlmvvlzgcRJpcZ7S\n4SylxWN4yirzM7yaNWviiy++gI+PDyIjI8t6dYwxxlixZLlK09jYGDNnzpRjVeUSj5NIi/OUDmcp\nLR7DU5ZstyW0adMGM2fOxI0bN5CWlib+Y4wxxuQg2zetrF69GoIgYMGCBTqPX7t2Ta4m6C1D+f02\nfcF5SoezlBb/Hp6yZCt4KpVK8mU+evQIH3zwAS5cuABBELB48WKEhIRIvh7GGGPln2xdmllZWZg4\ncSI+/PBDAMClS5ewefPm11rmyJEj0aFDB/zzzz84e/Ys/P39pWiq7PgTtLQ4T+lwltLisztlyfrV\nYmZmZjh48CAAwMPDA1999VWpl/f48WPs379f/HoyExMT2NnZSdJWxhhjhke2gnflyhWMGTMGZmZm\nACD+akJpXbt2DS4uLhgwYADq1auHDz/8ENnZ2VI0VXZ8r5O0OE/pcJbS4vvwlCXbGJ65uTlycnLE\n6StXrsDc3LzUy1Or1Th58iTmz5+Phg0bYtSoUZg6dSq++eYbnedFRUWJPzRrb2+PoKAgsVsh5WYK\ncPrfbhvtzi33tJZS69dOa3dGbT6vOs156k4bQp4pl1MUfz2lylMfpk+fPq1X7dFOx8fHIzY2FgAM\n+oe5BXr2u77K0Pbt2zFp0iQkJCSgTZs2OHDgAGJjY9GqVatSLS8lJQVNmjQRr/L8v//7P0ydOlVn\nXFAQBJS0eVGjouDbzbdU6zc0qvUqxM6Jfa1lcJ7/4jylJUWe7OW96NhZXsl2hte2bVvUq1cPR44c\nARFh3rx5cHZ2LvXy3N3d4eXlhaSkJNSoUQM7d+5ErVq1JGwxY4wxQyLbGB4RYe/evdi5cyd2796N\n/fv3v/Yyv//+e/Tp0wd169bF2bNnMXbsWAlaKj8eJ5EW5ykdzlJaPIanLNnO8D766CNcuXIFkZGR\nICL89NNP2LFjB3744YdSL7Nu3bo4duyYhK1kjDFmqGQreHv27EFCQgKMjJ6eVEZFRSEgIECu1es1\nvtdJWpyndDhLafF9eMqSrUuzevXquH79ujh9/fp1VK9eXa7VM8YYq+BkK3jp6enw9/dHy5YtERYW\nhoCAAGRkZKBz587o0qWLXM3QSzxOIi3OUzqcpbR4DE9ZsnVpFr4/Dvj30ldBEORqBmOMsQpKtoLH\nfdfPx+Mk0uI8pcNZSouPg8qSrUuTMcYYUxIXPD3A4yTS4jylw1lKi8fwlCVrwcvOzkZiYqKcq2SM\nMcYAyFjwNm7ciODgYLz99tsAgFOnTlX4qzO1eJxEWpyndDhLafEYnrJkK3gxMTE4cuQIHBwcAADB\nwcG4evWqXKtnjDFWwclW8ExNTWFvb6+7ciMeQgR4nERqnKd0OEtp8RiesmSrOLVq1cKKFSugVqtx\n6dIljBgxAqGhoXKtnjHGWAUnW8H7/vvvceHCBZibmyMyMhK2traYM2eOXKvXazxOIi3OUzqcpbR4\nDE9Zst14npiYiMmTJ2Py5MlyrZIxxhgTyXaGN3r0aNSsWRNff/01zp8/L9dqywUeJ5EW5ykdzlJa\nPIanLNkKXnx8PPbs2QNnZ2cMGTIEgYGBmDhxolyrZ4wxVsHJeplk5cqVMXLkSPz444+oW7dusV8o\nXRHxOIm0OE/pcJbS4jE8ZclW8BISEhATE4PatWtj+PDhCA0Nxa1bt+RaPWOMsQpOtoI3cOBA2Nvb\nY9u2bdi7dy8++ugjuLq6yrV6vcbjJNLiPKXDWUqLx/CUJdtVmocPH5ZrVYwxxlgRZV7wevbsiTVr\n1iAwMLDI3wRBwNmzZ8u6CXqPx0mkxXlKx5CyjI6JRsqjFKWbgdj1sYqu393eHVNjpiraBqWUecGb\nO3cuAGDz5s0gIp2/8S+dM8bkkvIoBb7dfJVuhuJU61VKN0ExZT6G5+HhAQD44Ycf4Ovrq/Pvhx9+\nKOvVlws8TiItzlM6nKW0OE9lyXbRyvbt24s8FhcX99rL1Wg0CA4ORufOnV97WYwxxgxXmXdpLly4\nED/88AOuXLmiM46XkZGBpk2bvvby586di4CAAGRkZLz2spRiSOMk+oDzlA5nKS3OU1llXvDee+89\ntG/fHtHR0Zg2bZo4jmdjYwMnJ6fXWvbNmzcRFxeHr776Ct99950UzWWMMWagyrxL087ODr6+vli9\nejV8fHxgaWkJIyMjZGVl4fr166+17E8//RQzZswo97+rx/360uI8pcNZSovzVJZs9+Ft3LgRn332\nGW7fvg1XV1ckJyfD398fFy5cKNXyNm/eDFdXVwQHB5d4M2dUVBR8fX0BAPb29ggKChK/3iflZgpw\n+t9uBu2bUe5pLaXWr53W5qjN51WnOU/daUPIM+VyiuKvJ+cp7bTWs/nEx8cjNjb26fP/d7w0RAIV\nvlegjNSpUwe7d+9GmzZtcOrUKezZswfLli3D4sWLS7W8sWPHYtmyZTAxMcGTJ0+Qnp6O7t27Y+nS\npeJzBEEocivEs6JGRfFlyv+jWq9C7JzY11oG5/kvzlNanKd0XibLFx07yyvZ+gJNTU3h7OyMgoIC\naDQatGrVCsePHy/18iZPnowbN27g2rVrWL16Nd566y2dYscYY4w9S7aC5+DggIyMDDRv3hx9+vTB\nJ598Amtra8mWX55vYud+fWlxntLhLKXFeSpLtoK3fv16WFpaYvbs2WjXrh2qV6+OTZs2SbLsli1b\nYuPGjZIsizHGmGGS7aIV7dmcsbExoqKi5FptucD35kiL85QOZyktzlNZZV7wrK2tn9vdKAgC0tPT\ny7oJjDHGWNl3aWZmZiIjI6PYf1zsnuJ+fWlxntLhLKXFeSpL1ju29+/fjyVLlgAA7t27h2vXrsm5\nesYYYxWYbAUvJiYG06ZNw5QpUwAAeXl56NOnj1yr12vcry8tzlM6nKW0OE9lyVbw1q1bh40bN8LK\nygoA4OnpiczMTLlWzxhjrIKTreCZm5vrfOdlVlaWXKvWe9yvLy3OUzqcpbQ4T2XJVvB69uyJIUOG\n4NGjR1i0aBHCw8PxwQcfyLV6xhhjFZws9+EREXr16oWLFy/CxsYGSUlJmDhxItq0aSPH6vUe9+tL\ni/OUDmcpLc5TWbLdeN6hQwecP38ebdu2lWuVjDHGmEiWLk1BEFC/fn0cPXpUjtWVO9yvLy3OUzqc\npbQ4T2XJdoZ3+PBhLF++HD4+PuKVmoIg4OzZs3I1gTHGWAUmW8Hbtm2bXKsqd7hfX1qcp3Q4S2lx\nnsqSreAZ8q/oMsYY03+yfrUYKx7360uL85QOZyktzlNZXPAYY4xVCFzw9AD360uL85QOZyktzlNZ\nXPAYY4xVCFzw9AD360uL85QOZyktzlNZXPAYY4xVCFzw9AD360uL85QOZyktzlNZXPAYY4xVCFzw\n9AD360uL85QOZyktzlNZ5bbg3bhxA61atUKtWrVQu3ZtzJs3T+kmMcYY02OyfbWY1ExNTTF79mwE\nBQUhMzMT9evXR5s2beDv7690014Z9+tLi/OUDmcpLc5TWeX2DM/d3R1BQUEAAGtra/j7++P27dsK\nt4oxxpi+KrcF71kqlQqnTp1C48aNlW5KqXC/vrQ4T+lwltLiPJVVbrs0tTIzM9GjRw/MnTsX1tbW\nRf4eFRUl/lKDvb09goKCEBYWBgBIuZkCnP63m0H7ZpR7Wkup9Wun4+PjAUDM51WnOU/daUPIM+Vy\niuKvJ+cp7bTWs/nEx8cjNjb26fMN+JdtBCIipRtRWvn5+ejUqRPat2+PUaNGFfm7IAgoafOiRkXB\nt5tvGbaw/FCtVyF2TuxrLYPz/BfnKS3OUzovk+WLjp3lVbnt0iQiDBo0CAEBAcUWO8YYY+xZ5bbg\nHThwAMuXL8eePXsQHByM4OBgbN26VelmlQr360uL85QOZyktzlNZ5XYMr1mzZigoKFC6GYwxxsqJ\ncnuGZ0j43hxpcZ7S4SylxXkqiwseY4yxCoELnh7gfn1pcZ7S4SylxXkqiwseY4yxCoELnh7gfn1p\ncZ7S4SylxXkqiwseY4yxCoELnh7gfn1pcZ7S4SylxXkqiwseY4yxCoELnh7gfn1pcZ7S4SylxXkq\niwseY4yxCoELnh7gfn1pcZ7S4SylxXkqiwseY4yxCoELnh7gfn1pcZ7S4SylxXkqiwseY4yxCoEL\nnh7gfn1pcZ7S4SylxXkqiwseY4yxCoELnh7gfn1pcZ7S4SylxXkqiwseY4yxCoELnh7gfn1pcZ7S\n4SylxXkqiwseY4yxCoELnh7gfn1pcZ7S4SylxXkqiwseY4yxCqFcF7ytW7eiZs2aeOONNzBt2jSl\nm1Nq3K8vLc5TOpyltDhPZZXbgqfRaDB8+HBs3boVCQkJWLVqFf755x+lm1UqKZdTlG6CQeE8pcNZ\nSovzVFa5LXhHjx5F9erV4evrC1NTU/Tu3RsbNmxQulml8iTzidJNMCicp3Q4S2lxnsoqtwXv1q1b\n8PLyEqerVKmCW7duKdgixhhj+qzcFjxBEJRugmQepTxSugkGhfOUDmcpLc5TWQIRkdKNKI3Dhw8j\nJiYGW7duBQBMmTIFRkZGGDNmjPicoKAgnDlzRqkmMsZYuVS3bl2cPn1a6WZIrtwWPLVajTfffBO7\ndu2Ch4cHGjVqhFWrVsHf31/ppjHGGNNDJko3oLRMTEwwf/58vP3229BoNBg0aBAXO8YYY89Vbs/w\nGGOMsVdRbi9aYYwxxl4FFzxWojt37mDMmDG4cuUKHjx4AAAoKChQuFXKKNwZwp0jpUNEnN1rKi5D\nzvTFuOCxElWuXBkAsGLFCnz88cc4ffo0jIyMKtzORUTirTC3b9/Gw4cPDerWGLkJgoBt27bhu+++\nw8qVK5VuTrkkCAKOHTuGLVu24Nq1axAEocJ+GH1ZXPDYc2l3nmnTpmHo0KEICwtD+/btsW/fvgq1\nc6WmpuLHH38EAOzYsQNdu3bFW2+9hXXr1iE9PV3h1pUv2g8OZ86cwYgRI5CamootW7ZgyJAhSjet\n3NBmuGvXLnTt2hVr165Fw4YNcerUKRgZGVWY/bI0yu1VmqzsaM/ejIyMkJeXBzMzM7i6umLo0KEw\nNzdHZGQk1q5di5CQEJ0zH0NERDhx4gQOHjyI1NRUHDlyBMuWLcPZs2exePFiZGVloUuXLrC1tVW6\nqeWCIAjYu3cvli9fjrlz56J9+/a4fPkyJk+ejKFDh4ofLNjzCYKAhIQE/Pnnn1i9ejVatGiBunXr\nIjw8HLt370ZQUBAKCgpgZMTnM4UZx8TExCjdCKZ/tF1OS5YsQUJCAho3bgwACA4Ohr29Pb788ku0\na9cOTk5OCre07GiLuaenJywsLHDq1Cmkpqbi888/R61atWBhYYEVK1aAiODn54dKlSop3WS9VPhD\n0ZkzZzBp0iT4+PigZcuWsLOzQ506dRAXF4e4uDh07dpVwdbqN41GA41Gg6lTp+LgwYN48803ERgY\niJCQEFhZWSEiIgKdOnWCh4eH0k3VS1zwmA7twenQoUP4+OOP0a5dO8yaNQupqalo3rw5jI2NUa9e\nPeTm5iI5ORmNGjWCRqMxuE+T2rNcQRBw+/ZtBAcHw8TEBMeOHUNqaiqaNGkCf39/GBsbY/ny5ejQ\noQNsbGwUbrX+eTbH5ORkEBGCgoLQrFkzfP311/Dz84O/vz/s7e0RHByM+vXrw83NTeFW65dnM8zO\nzoaFhQXCwsJw9+5dJCcnw9HREZ6enmjcuDFsbW1hZWWFatWqKdxq/cT34bEiEhMTMWXKFISGhmLw\n4MG4ffs23n33XbRs2RIxMTEwNTXFrl278Pvvv2PRokVKN7dMaAv/li1bMHz4cGzZsgVeXl7Ytm0b\nduzYgerVq+PTTz8F8HSMjw/SxdN2rW3evBlTpkyBs7MzXFxcMHr0aNy/fx+DBg3C1KlT0b17d3Ee\nQ+8mf1XaPLZu3YpZs2ahSpUqqFatGsaNG4fo6Gjk5+cjIiICoaGhYm6c4XMQq/AKCgp0puPi4qhT\np04UGRlJV69eJSKi27dvU926denzzz8Xn/fxxx/TnTt3ZG2rnC5cuEC1atWivXv3io9lZ2fT+vXr\nKSoqiqZPn05ERBqNhoiK5liR5eTkiP+fnJxMAQEBdOLECTp37hwtXbqUOnToQCkpKfTXX39RlSpV\nKDU1lfMrJD8/X/z/o0ePUkBAAG3evJmOHz9OQUFBNGLECCooKKCPPvqIPv30U3r48KGCrS0f+KKV\nCo6eOcG/evUqLC0tER4eDk9PT/z8889Yv349IiIi4OPjI17+rDV//nwlmiwbtVqNZs2aoUWLFlCr\n1SgoKICFhQVat24NQRDg5+cHAGJ3Ln+ifio1NRWrVq3CoEGDxG5eLy8v1KtXD8DTW11OnDiB7du3\no1+/fggJCYGrq6uSTdY7d+/eFW8FMjMzQ3Z2Nlq3bo2OHTsCAE6ePIlGjRrhwIED+Oabb5Camgp7\ne3uFW63/DGvghb0yQRDErruOHTti9OjRaNCgAezs7NCrVy+oVCqsXLkSycnJqFy5MkJDQw3yxuHi\ntsnS0hJbt27F5s2bYWJiAjMzM2zbtg2//fYbunTpgtq1ayvUWv1mbm6O9u3bIzMzE8ePH4e3tzfU\najW++uorAICTkxMcHR2RlJQEAHBxcQHAN04/KyUlBZ07d8aDBw9w48YN2NraYteuXeKXPwiCgFat\nWuHx48dwcnJCQECAwi0uH7jgMVy/fh0TJkzAzz//jJUrV6JXr17o0qULatSogYiICNy6dUvn3h5t\nkTQ02kvmZ8yYgd27d6NatWqYPXs2vvvuO8yfPx9xcXEYM2YMPD09lW6qXsrPz0d2djbs7e3h5eWF\nKVOm4JdffsGFCxcwa9YsqFQqvPvuu9i0aRNWrlyJ8PBwAE+/CB7gM2TgaYYAUKdOHTg6OmLhwoWY\nOnUqateujT59+qBhw4aIj4/H5s2bERcXx2d1r4gvWqmAqNCAdmZmJoYNG4ZJkybB29sbADBixAgY\nGxtjzpw5FeaijC1btmD06NEYNWoUZs6ciQ8++AAdO3bE/fv3MWvWLLi7u6Nr167o1KkTXxRQSF5e\nHuLj4+Hs7IykpCQkJyejb9++mDlzJszMzBAREQE/Pz98++23sLe3R6NGjdCxY0fO8Rm5ubnYv38/\nqlSpgszMTCQlJcHNzQ07duwAEWHKlCn4+eefxSuFhwwZwu/FV8RjeBVQQUEBjI2NkZmZiUqVKsHM\nzAyZmZnYuHEjhg8fDgBo1qwZTp06BQAGX+yICLdu3cKiRYuwceNG3LhxA0SEM2fOIDs7G1988QU2\nbdqk83ymy8zMDBkZGYiJiUFKSgpmz54NT09PfPXVV/jmm2+wdu1a9OvXD3PnzhXn4Rx15eXl4cmT\nJxg2bBiSkpKwe/duvPnmm7CwsMD69evx1Vdf4csvv8SQIUOQk5MDCwsLzvAV8X14Fcj169eRl5cH\na2trrF+/HkOHDsW5c+dgbGyMqKgoREdH4+LFizh+/DgWLlyIgQMHokaNGko3u0zQM/c2CYIAW1tb\nNG3aFFlZWRgxYgSOHDkCNzc3fPbZZzAzM0PdunVhbm6uMw/7d+xTEAR4e3vj4MGDMDc3R9u2bWFt\nbQ1nZ2eEhITg77//xvnz59GkSRPxBn3O8Snte9Hc3BzZ2dmYMmUKGjdujNDQUHh4eMDLywu2trY4\nc+YM4uPj0bJlS5iZmcHIyIgzfEVc8CqQb7/9FuPHj0fDhg2xcOFCDBgwAF5eXliwYAG8vb0xduxY\nPHjwAOnp6Rg8eDDefvttg+4uEQQBZ8+exfHjx2FsbAwPDw+kpKRg586dGDx4MHJycnDu3DkMHz4c\nXl5eSjdXbxkZGWHHjh1YtmwZpk+fDiMjI6xfvx6VKlWCv78/1Go1AgMDERwczDk+hyAI2LFjBxwd\nHREVFQUXFxf8+eefMDExwRtvvAEzMzOYmZmhffv2cHNzM7gvepALd2lWANqbf2fMmIGCggL06tUL\nffv2Re/evZGTkwMnJydMnz4d9+/fxwcffCDOZ8jdJYIgYP369Rg/fjz8/PxgYWGBGjVqYMiQIXB3\nd0fr1q1x48YNzJkzB7Vr1zbowv86tFf4fvbZZ5g9ezasrKwwYMAA5OTkYPPmzTh27Bh++eUX7Nmz\nh69qfQ5thiNHjsT333+Pt99+G7a2tkhLS8O6detw+PBhnD59GnPnzkXVqlWVbm75Jtsdf0wRmZmZ\ndP78eSIiOnLkCKWnp1N0dDT5+/tTSkoKERHl5uZSXFwchYWFkUqlEm+kNjQFBQXizc0ZGRnUu3dv\nOnnyJBER7d27l6Kjo2np0qV07949WrlyJR08eLDIfExXXl4ejRw5krZs2UJERE+ePBH/tmXLFpo9\nezZt3bpVqeaVC5mZmdS2bVvatWsXEf37BQbXrl2jP/74gzp16kTr169XsokGg8/wDFxaWhq+++47\nceB7y5YtmDJlCh49eoSIiAisW7cOrq6uCA8PR8OGDeHs7Kx0k8sEPXOGdvDgQaSnpyM5ORkXL15E\ncHAwQkNDcezYMRw8eBD9+vVDZGSkOB/Al8xrUaEzXVNTU6SlpSE+Ph7t2rUTxznPnj2LsLAwtGvX\nTpwP4ByBfzPU/letViMvL0+83eXJkyewsLCAjY0Nevbsia5du8LMzIwzlAB3BBuwgoICeHl5oW3b\ntli8eDHee+89BAYGAgAWLlyIunXrok2bNrh79y7MzMzEYkcG3JWZmJiIL774AnXq1MHnn3+OnTt3\nYu/evTAxMUH9+vWRlpaG9PR08b5DviigeMnJyUhISAAADBw4EPn5+diwYQMA4NixYxg6dCguXbok\nPp9zLCo1NRUAYGdnh6ZNmyI6OhppaWmwsLDAvn370KlTJ9y9e1fnPkXO8PVwwTNgRkZG2L17N86e\nPYtNmzbhzJkz+OWXX5CWlgYA+OGHH9CmTRudAxNgmJ8gtT86GhERgdatW8PDwwNBQUGoV68ehg8f\njowINqMAACAASURBVFGjRmHAgAHo168fbG1t+aKAYmjPSDZv3ox27dqhR48eGDNmDGrWrImqVavi\np59+QufOndG/f39ER0eLH67Yv7QZxsXFoVOnTujevTu2b9+OqKgo1K1bF02bNsWMGTMwbNgw/Oc/\n/4Grqyu/FyXEN54bOO137W3btg27du3CxIkTMXjwYAiCgL/++gsrV66EqampQV6UUVwXUN++ffHP\nP/9g7969sLa2Rn5+Ps6fP4/k5GRUqVIFDRo0MMgspHLx4kV8+eWXmDFjBtzc3NChQwe0b98eo0eP\nRm5uLpKSkuDg4IA333yTu+Ce4+jRo5g8eTKio6Oxd+9eJCcno1mzZnjnnXfw999/w8jICC4uLmje\nvDlnKDEewzMwhQ/WNWvWFL+sNzw8HBqNBsuXL8etW7cwePBgmJqaAjDcHUoQBBw+fBjXr19H7dq1\nsXz5cgwaNAg9e/bEX3/9BQsLCwQHByM4OBiAYXfnlpb2PfX48WPMmTMHt2/fhqmpKezt7bF27Vr0\n7t0b9+/fx9y5cxESEqIzr6G+r17Fs2N29+/fx3//+1+YmpoiJCQEISEh+Omnn7Bv3z4UFBSgW7du\nsLa2FucDOEMp8X14BkK7UwmCgJMnT2LEiBGoU6cOPD098fDhQ8yYMQO9e/fGm2++iVatWqFHjx5o\n2LChwZ7NaLdr//79GDhwIB4+fIh9+/bh6NGjmD9/Pnbv3o0FCxagV69eYtEHeJykONruYCcnJ/j6\n+uLSpUt4+PAhPD09UaVKFfFHgps1a6Zz0RPn+JQ2h3v37sHV1RWCIODPP/+EpaUl6tWrhwYNGuDa\ntWs4fPgwmjZtKv7CBL8XpccFzwA8+0nw0qVL8PPzw+HDh3Hu3DksWLAAHTt2xMWLF1GrVi24ubnB\n3NwclpaW4vyGuFNpf7V94sSJ+OGHH/DJJ58gMDAQ+/fvR3JyMr799lusW7cO/v7+8PDwULq5ekn7\noSEvLw8zZ87EokWLMGTIEPj6+mL//v1ISUmBu7s7vLy80L9/f4P/CrrS0mg0SEtLg4+PD9544w30\n7t0bVapUwapVq5Cbm4vg4GA0btwYwcHBqFKlitLNNWhc8AyEdiB81KhRCA8PR79+/dCkSRMIgoCl\nS5di586dyMjIQJcuXXQKnCEVu8Jnq/v378eMGTPQqFEj1KtXD9bW1sjJycGRI0fQqVMnREZGwsPD\nw2DPcksrKysLRkZGMDY2BgAYGxujTp06uHz5MpYuXYoPP/wQlStXxtatW3H37l3Uq1cPpqamMDIy\n4iz/Jz8/X8wPAKysrFC7dm0MHjwYb775Jt555x1YWlri559/Rn5+PurVqwc7OzsFW1xByHCvH5PB\nP//8QzVr1qQDBw4U+dujR4/owoULFBYWJt5obWievTn83r17lJ2dTURES5YsIT8/P9q5cycRPb0Z\nulmzZnT//n1Sq9WKtVdfXbhwgYYNG0apqam0b98+mjt3rvi3O3fu0Keffkr9+/enrKwsOnDggPil\nBuxfFy5coHHjxhERUUJCAm3fvl18P8bFxZG5ubl4I/mff/5JR48eVaytFQ0XvHLqxo0btGzZMnF6\n37591LNnT3E6Pz+fiEjnG0L69+8vfpuDodFu58aNG6lly5bUvHlzWrRoESUmJtLvv/9OlpaW9MEH\nH1C3bt1o3bp1CrdWP2VnZ1Pr1q1p8eLFRES0e/ducnNzo/nz5xMRkVqtpt27d1Pt2rWpV69eBvuN\nPK/j8ePH1LJlSzp27Bilp6fTqFGjaODAgbRr1y7KysoiIqLZs2eTIAgUFxcnzsff5CMPvsGjnCIi\nLFu2DGfOnAEA+Pn54cGDB9i+fTuApz+quXv3bkybNg1EhCtXruDKlSsG++OlgiDgxIkTmDVrFubO\nnYsRI0YgOTkZq1evRseOHTF37lzs378fHTp0QLdu3aDRaPiKzEIsLCzQp08fLF68GJ6enmjVqhX+\n/vtvzJ49GwsWLICxsTHMzc0RHh6OMWPG8P1hxdBoNMjOzsaqVavwySef4NNPP4W3tzfWrl2LQ4cO\nAQBCQ0MRERGhkx93A8tE4YLLSkHbFTd37lxas2YNERGlp6fTzJkz6YsvvqCpU6dSfHw81apVi7Zv\n3y7O9+DBA0XaK4c7d+7QgAEDKDQ0VHzswIED1Lp1azp8+DAREa1YsYI8PT1p7969SjVTb2nPMP7+\n+2+qVKkStWzZkjIzM4mI6OjRo1SnTh0aNGgQubq6it+byWclurR5zJ8/n0xMTGjo0KFE9PT7RseP\nH0+DBg2iQYMG0RtvvEHHjh3TmYfJgy9aKYe0nwzv3LmDOXPmoFWrVnBzc4O7uzssLS3x999/49Kl\nSxg2bBg6dOgAtVoNIyMjWFhYKNxy6VChe5Tof7/LdujQIWRnZ6Nx48bw8vLCoUOHoNFo0LBhQwQG\nBsLDwwM1a9aEo6Ojks3XO9ocnZycEBYWBkdHR8ydOxf169dHYGAg2rVrh5o1a6Jfv35o0aIFX5xS\nDG0ed+7cQZs2bTB79myYm5ujadOmaNGiBSwtLWFlZYU+ffqgefPmOvMwefA3rZRzEyZMwJIlS3D0\n6FG4u7uLjz958gSVKlUyyJtX/7+9e4/r+e4fP/749ImUUhNFGrqqCzeuzJxS5riIZptDuJjG5soy\nx7gcbkPjYsxp5JrDwjSnDhZpEeuAYcppF+VMuihySp8U+vTp/ftj+3xWxvea39inPj3vf0mf9+32\n+rxu717P1/H5KvudDh48yMOHD7GwsKBTp05s27aN+Ph4rKysGDRoECNHjiQsLIzOnTsbudQVU9nA\npdPpDDsLs7KyWL9+PefPn2fu3Lm4ubmVewZM6516GY4dO4aPjw//+te/GDNmTLnfSR0ah4zwKiH9\naEalUtG1a1du3rzJ9OnT8fb2xsLCAktLS8zNzcsdRjcl+u/03XffMWHCBJo0aUJISIhhDUr5ZX3z\n5MmTLFiwgC5duhhGuaI8/SW4+ktFdTodZmZm2NnZ4ebmxqVLl4iIiODtt9/G3NzcUPem9k79Udev\nXwegevXqqFQqdDodzs7O9OzZk/79+2NnZ0f79u0Nn5c6NA4JeJVAaWmp4RoRMzMzwx+K/mJXHx8f\nSkpKiI2N5dy5c+Tm5tKiRQuT/oPKyspi0qRJREVFkZubS1paGsnJySiKwvDhw6lTpw4PHjxArVbT\npk0bCXZPoe8QDR48mAsXLtC9e/dy9WRra8tf//pXw5S5Kb9P/78URSE3N5fg4GC8vLx45ZVXKC0t\nRa1Wo9PpcHJyws/Pj5o1a+Lq6mrs4lZ5EvAqsHv37nHv3j1sbW1JSEhg7dq1pKenGw6Ul+2Re3p6\n0qxZM+zt7fnmm2/w8fExqTW7J6lUKnr06MGdO3cMSXhfffVVxowZg42NDUOHDiUvL4+MjAzatWtn\n0nXxvJ4c+Xt4eHD06FHat29PjRo1ygU2W1tb7O3tjVXUCk+lUmFtbU1KSgrx8fG8++67hmlh/d9n\ngwYNcHV1lXXPCkACXgVVWFjIwoULOXPmDPfv32fKlCn4+fnxxRdfkJ2dTdeuXTEzM8PMzMwwAqxT\npw4uLi7079+/XOowU6JvNGrUqEHt2rU5fvw4tra2+Pr6kpmZSZ06dXjjjTdwd3fH1dWVzp07Y2dn\nZ+xiVyj6HKOPHj3CzMwMJycnVq1aRaNGjWQU8hyuXbtGbm4u9vb2eHl5kZaWRqtWrbCxsTH8TcrR\ng4pFNq1UYDExMRw6dIi8vDw8PT0JDAwkNzcXf39/vLy8mDt3ruFyyLJMrSf55Pcp+/P27dtZuXIl\nnTp1Ys2aNWzbtg1PT89yGzDEbzdJzJkzhxMnTlCzZk0CAgK4desWW7duZevWrZLi6hnKvncajYaP\nP/4YlUqFg4MDU6ZMISAggH79+hEYGGjkkopnkYBXwSiKYlgDADhy5AjLly9Hp9OxYMEC/vKXv3Dr\n1i18fX3p2rUrixcvNqng9izHjh0jPDycFStW/CYARkZGkpeXR+PGjfH19TW5gP8i6Ovk1KlTVKtW\nDScnJ2xtbUlOTmbu3Lm4uroSFxfHwYMHcXNzM6wPi1/p6/DGjRvUqlULlUpFQUEB48ePp0WLFuzY\nsQOdTkdUVBTu7u7GLq54CrkPrwJSq9V89913xMTEsH79egoLC4mLi2PHjh3069ePxo0bs3v3bq5c\nuWLSDXvZRvfx48dotVrg11GKfhQ3aNAgwzPSf/stfUOtv1nbx8eH5ORkwsPD6datG82bN+fevXvc\nunWL4OBgdu7cKcGujLKj4507dxISEoJOp8PX15ePPvqIiIgIrl27hpOTE5s2beLq1au4u7tLx6sC\nkre6gtE3TNOmTWPAgAEAdO/enR49epCdnc2WLVvIzMzE0dGRDh06mGQD//DhQ+DnRf9Lly6RmpqK\nnZ2d4R42PbVaTUlJSblnZbv3b+lHdrGxsURERBAeHs5nn33GyJEj+fHHH3F0dKRZs2bExsZSq1Yt\n8vPzjV3kCkX/Tp05c4bQ0FC2bNnCrl270Gq1hIWFUVBQwKuvvsoHH3zAP/7xD5YvX87jx4/lPayA\nJOBVQMeOHePTTz+ld+/ePHr0CIDevXvj4+PD9evXywU5U/ujun//PtOmTSMvLw+NRsOiRYsIDAxk\n8eLFpKSksGDBAqKioti3bx+lpaVPXcMUv45KdDodxcXFfPrppyQlJfHgwQNKSkoYNmwYo0ePZvny\n5ZSWlgKwd+9ejhw5YhhJV3U3b95k3rx5lJaWcufOHZYuXcqtW7ews7PD2dmZyZMnk5KSwtatWw3P\n2NjYUFBQYKhTUbFIa2FkT5v2uHHjBqdPn2bAgAHUqFEDgNTUVLp06UKHDh1MflPB5MmTyc/PJy8v\njzVr1gA/H9HIzs7G2tqa7du3k5+fT/Xq1fHy8jJyaSu2oqIibGxsWL9+PePGjSMxMZEWLVrQsGFD\nmjRpwunTpw3vn5OTE0lJSeVuLa/KHj58iL+/Pzdv3sTBwYGAgADy8vLYsmULgwcPpkGDBgwbNoy7\nd+9SWlpKaWkplpaWrF69Wo7BVFQvKUen+B3K3uGWmZmpnDlzxvDvoKAgZenSpYqiKEpqaqrStGlT\nQxJkU1Q2ie5///tfZePGjUqnTp2UlJQURVF+Tpj93nvvKZs2bXrmc6K8uLg4xdPTUwkJCVEOHjyo\nFBQUKAMGDFB69uypzJgxQ2nbtq0SExNj7GJWOGXfqeLiYuXDDz9URowYoWi1WiUxMVEJCgpSBgwY\noGzYsEFxc3NTEhISjFha8TzkHJ6R6RfCg4KCSE1N5cCBA7Ru3RoHBweio6NZt24dkZGRzJ8/n27d\nuhm7uC+Vfv1y1qxZDBs2jFq1arFhwwYaNGiAi4sLBQUF5OTk0LFjx988J8pvrsjOzmbhwoUEBARQ\nUlLC999/j42NDRMmTGDfvn1cvnyZuXPn0rNnT8OzUo/l6zAjI4O6devi7u7Of/7zH/bs2cOoUaN4\n5ZVXSE5OJicnh+DgYPz8/AwJIETFJgHPiPTJj6dPn87u3btRqVQsWrQIgD59+vDRRx/RqVMnhg4d\nSrt27Uw24ay+sb1w4QKzZ88mJCSEVq1a0bBhQ3Q6HRs3bqRhw4Y4OTkZDtfrmVpd/FH6ewEPHjyI\noigEBwfj4uKCVqslISEBc3Nzxo8fz65du7h27Rqvv/46VlZWUo9lqFQqEhISeO+993jzzTdp1qwZ\nrq6u/PjjjyQnJzNixAicnZ3JyclBp9Ph5uaGtbW1sYstfgfpkhiZvb09X375JcePHycsLIzDhw+T\nlpZGUFAQFy9exMXFhYYNGxo+b0oN0+PHjw272a5du8bmzZu5evUq6enpADg4ONC/f3+6devGnDlz\naNasGV27djXJnal/lL7TkJKSQt++fTl48CArVqwgPT2devXq0bt3b9q1a8e3336LSqVi+fLl3Llz\nR0Z2T9B3vP75z38SHh7O3/72N9RqNU2bNmXcuHHcv3+f8ePH061bN15//XVyc3MlwUElIgfP/0Rl\nR2h5eXlUq1bN0DOcPHky7u7ujBo1ilWrVrFhwwY2b95c7loWU1JSUsKhQ4fIzMzE2tqajIwM+vbt\nS2xsLPfv36dPnz506dIFgNu3b1NUVESjRo2MW+gK7ty5c0ycOJEZM2bg7e3NnDlziI6OJiIigubN\nm3Pr1i2Ki4txdnYGkGw0v3gy6F+4cIH58+fz9ddfo9Pp0Ol0VK9enZKSEjIzMykqKqJly5YAFBQU\nYGNjY6yii+ckuzT/ZCqVitjYWNatW0d+fj5Dhgyhe/futGnThrVr16LVaomMjGTp0qUmG+wAzM3N\nsbe3Z+7cuZw+fZr169fj4eGBpaUlmzdvZs+ePWi1Wnx8fKhbt67hORmRlFe2Pk6dOsW1a9fYuXMn\n3t7ezJo1C7VaTe/evYmPj6dFixblnpNgVz5RwdmzZ7G0tMTW1pYDBw4QERHB4MGDUavV7N27l6NH\nj/LJJ58Av3YWJNhVLrKG9ydSqVScP3+eUaNG8e9//5smTZpw7tw5zp49S7t27bCzs2PXrl1MmDCB\nN9980yTX7Mp+J1tbW2JiYnB2dsbKyoqmTZvi7OyMq6srR48e5cqVK7Rq1apcImxTqosXQb8OHBkZ\nSWBgIPXr1+enn37ixo0btGnThk6dOpGfn0+9evXKjZClHn+l3zg2ZswYunXrRpMmTXB1dWXVqlVk\nZWWh0Wj45JNPGDhwIE2bNgWQDSqV1Z+8K7RK0m9zzsnJUXbv3q306tXL8LvU1FSle/fuSmpqqqIo\nivLw4UPDM6a25b7sd8rJyTH8X3p6ujJ69Ghl5syZiqIoikajUaKjo5ULFy4YrayVSXp6uvLqq68q\nS5YsURRFUaKiopTAwEBl2bJl5T5nau/Ti3LixAmlZcuWyvnz5xVFUZQbN24oR48eVTIyMpSBAwcq\nY8eOVb777jtFUaQOKzuZ0nzJ9PkgDx8+zIwZM/jyyy+pUaMG0dHR+Pv7065dO5o3b264t61atWqG\nZ02xF65SqYiPj2f27Nl4eXlRvXp1Fi5cyLBhw9i4cSP9+vUjPT2d6OhoScD7P2g0GqysrGjevDkJ\nCQn4+/ujKAqTJk1Cq9Xy/fffk5WVZRjZmeL79CLUqFGDli1bkpycTFRUFCkpKQBMnTqVyMhIw+cU\n2e5Q6cmU5kumUqlITExk7dq1BAUF0aFDB+7cuUNGRgbJycmo1WoWLVpEUFAQzs7OhqkSU2ycVCoV\n+/fvZ+LEiWzevJnr16+zatUqMjIyGDt2LC1btuThw4cEBATg7e1t7OJWWIqicPnyZUaOHIm7uzv1\n6tXD0dGRzp07M3nyZABGjhxJ+/btDRtUxLNZWVmRm5vLpk2bePfddxk+fDhWVlZotVrD5hSQPK2m\nQCaiX4Ine4LZ2dls3ryZa9euAeDv74+vry/37t1jy5YthIaG0r59e5PvQZaWlqLVag3Z5Xfs2MH+\n/fs5e/YsAQEBODs7M27cOHr06IGiKCZfH8+jbH2oVCrc3Nxo06YN8+fP56effqK4uJgWLVrQo0cP\nFixYQFZWFvXr1zdyqSuHmjVrMnbsWPbt20e/fv0oKChg5cqVUn+myGiTqSZMP8+fnZ1tWJPbunWr\nYmFhoRw6dKjcZ4qKigw/m+L6gE6nUxRFUR49elTuO7/33ntKXFycoiiKMnnyZKVJkybKyZMnjVbO\nik5fdykpKUpoaKghDd2SJUuUPn36KHv37lXi4uKUYcOGKWfPnjVmUSutkpIS5ejRo0rbtm2VHTt2\nKIoia3amRqY0XzDll23i8fHxjB49mh07dpCVlcXf//53WrVqxdChQ+nQoYNhXUW/Zmeq0yUqlYrt\n27czZcoUUlNTsbKywt3dnb1792JpaUlOTg4JCQl88803NG/eXI4dPIW+To4cOUJgYCBFRUWkpaVx\n9+5dPv74Y/Lz80lKSiI8PJygoCDeeOONcs+J38fMzAw7Ozt8fX3LXb0ldWg65OD5S5Camsrs2bOZ\nN28eubm5nDp1iszMTFauXMlXX31FcHAw2dnZ1KpVyyS3NytPHLB///33GTJkCBqNxlAHpaWlrF69\nmgsXLhAcHGy4+08a6adLTU0lJCSEhQsX4uHhwdatWzl8+DAeHh6MGDECc3Nz7ty5Q506daQOXxCp\nR9MjuzRfsLy8PJYuXUpubi6tWrUCwNnZmc8++4zk5GRGjRqFr68vdnZ2Ri7py6VSqUhNTeXYsWO0\nbt2awYMHA2BhYVEum4xGo6FWrVrSm/4f8vPzSUxMZO/evXh4eODv74+ZmRmJiYkUFhYyduxYateu\nbeximhR5F02PTGn+QU821JaWltSuXZvdu3dz+/ZtOnfujIODA/v27aOgoICOHTtibW2NmZmZSfYg\n9d/p0KFDvP/++9y9e5eTJ0/i7u5OgwYNaN26Nebm5kydOpXBgwdja2trqANTq4sXydXVlZYtW7J4\n8WJq165Ny5YtadasGYWFhXh7e+Po6Cj1KMT/IFOaf5C+gU9KSiItLY26devSt29f0tPTWbFiBTY2\nNowYMYLRo0cTGhpq8lf8wM/TbzNmzGDJkiV4eHgwc+ZM8vLyGDBgAN7e3lSrVo3s7GwaNGhg7KJW\nOvHx8cycOZPx48fz/vvvG7s4QlQqpreA9CfSB7sffviBjz76iJo1axIWFkZoaCjVqlVj7NixHDly\nhOnTp7N27Vq6detGSUmJsYv90uXn55OcnExiYiIAM2fOxN7envDwcH744QcURTEEO+lvPR8/Pz9C\nQkL4/PPPDdfTCCF+Hwl4f4A+N+aqVauYMmUK48aNY/v27Wg0GuLi4ujcuTOrV6/Gzc2N/fv3Az8n\nTTZ1PXr0ICYmhrVr17JlyxaqV6/OjBkzqF+/Pg4ODuWm3GT67fm988477N+/HycnJ0kALcRzMP3W\n9wXTj+r0KcMyMjK4ffs2e/bsoVevXjg7OzNlyhR69uzJmDFj8PLyQqvVsmnTJsMuuqrgnXfewdzc\nnJkzZ1JcXMzw4cOZN2+eBLgXRH+DhCmuAwvxssga3nMou0Gl7BrUoUOH2LRpE+7u7gwePJjCwkL8\n/f2Jj4+nQYMGFBcXU1JSUi7rf1URGxvL9OnTSUxMxNHRUUYkQgijkYD3HPS96V27dhESEoKPjw9m\nZmbMnj2bAwcOEBoayvXr17Gzs2PixIn07t1beuD8fIFr2TvthBDCGGRK8zno7x6bOnUqUVFRhIeH\nExMTQ05ODmvWrMHS0pL169fj6upKz549jV3cCkOm34QQFYFsWnkOOp0OjUZDREQE169fJzExka+/\n/pqbN28SGBhI69atefvtt7lw4QJr166lpKREGvgypC6EEMYkI7znoFar6d69OyqVii+++IIlS5bQ\noUMHXFxcuHjxIhcvXuStt95CURTatm1bJXZkCiFEZSEt8jM8Of2m/9nCwoLHjx+j0Wg4ffo0paWl\nnDp1irCwMJo2bQpAnz59jFVsIYQQzyCbVp6i7G7M9PR0ateujZOTU7nP7Nu3j6VLl1JUVERgYCAD\nBw40PCtTd0IIUfFIwHsKfdCKi4tj0aJFLF68mHbt2hl+rz+DV1hYiKIoWFtbS/JjIYSo4CTgPcOl\nS5cYOHAgX331FW3atCn3u6cFNxnZCSFExSa7NH9x9epVxo4da/hZnxVFH+z0OTALCwufelmrBDsh\nhKjYJOD9onHjxgwfPpwrV64A4OHhQe3atUlKSqK4uBhzc3MOHDjAwoULefTokSQ9FkKISqbKT2kq\nioJOpzMcIfD29katVhsyp1y+fBkrKys8PT2ZPHkyK1euxMfHx8ilFkII8byqdMAruxZ37tw5w7GC\nLl264ODgQFRUFImJicTHx1NcXIyfn5+kCxNCiEqqygc8fW7McePGERkZSevWrQHo2LEjjo6OfPvt\ntwA8fvwYCwsL2Y0phBCVVJUOeAAnTpxgyJAhRERE8Nprr5GVlYWDgwOWlpZ4enpibW1NYmKi4SiC\nEEKIyqnKZVp5coRmbm7OgAEDOH36NAkJCURGRuLu7s706dM5cuQIhw8fBpBgJ4QQlVyVbMVVKhV7\n9+4lISGBOnXq8PDhQ7Zu3YqLiwsRERG4uLhw4sQJALy8vFAURXZlCiFEJVflAp5KpSI2NpZJkyah\n1WpxcnJi3rx5bN++nUGDBqHVavn+++9xdXUt94ys2QkhROVW5QJeXl4ey5cvZ9u2bfj5+XH8+HG2\nbdtGaWkpKSkpjBo1ilmzZtGlSxcZ1QkhhAkx+TW8J48Q6O+oi46O5ty5c6jVapKTk7l//z4BAQGs\nW7eOpk2bSrATQggTY9IjvLJB6/z589y7d4+6desya9YsCgoKGDFiBOHh4YSFhZGWloalpaXhLB7I\n0QMhhDAlJn0sQafToVariYuLY/bs2bzxxhuUlpYyYcIEXFxcANizZw/BwcEsWrSI3r17G7nEQggh\nXhaTHOE9ePAA+PmG8rS0NEJCQoiNjaVmzZqkpKQwa9Ysjh8/TmFhIcuXL+fzzz83ZFARQghhmkxu\nhJeXl8fixYtp3rw5Q4YMITU1lerVq3P79m2mTZvGsmXLCAsLQ6PRsHjxYurXry/32QkhRBVgciM8\ntVqNlZUVx44dY+fOnbRv355WrVqRlJTEsmXL6NSpE87Oztjb21NYWIi1tbXhWQl2Qghhukwm4Olv\nPahVq5ZhjS4pKYmYmBgANBoNc+bMITk5mbi4OD7++GNee+01GdkJIUQVYTJTmvrjB8nJyTx+/JjO\nnTuzZs0arl69yltvvYWPjw8ffvghRUVF+Pv7069fP7n1QAghqhCTCXgAcXFxzJo1i/nz5+Pr60t+\nfj7r168nMzOTXr160atXL7n1QAghqiiTmdIsKChg3bp1rFq1Cl9fX7RaLba2tnzwwQc4Ozuzc+dO\ncnNzsbCwACRdmBBCVDUmk2nFzMyMO3fuoNFogF9HbsXFxQQHB5OdnY2jo6MxiyiEEMKITGaEj5ET\naQAAALJJREFUV7NmTQYOHMjhw4c5c+YM5ubmHDp0iKFDh3L79m0aNWpk7CIKIYQwIpNaw8vOzmbN\nmjWkpKTg7e1NdHQ0oaGh+Pn5GbtoQgghjMykAh5AUVERqamp5Obm0rhxYzw9PWWDihBCCNMLeE+S\nYCeEEAJMaNPKs0igE0IIASa0aUUIIYT4v0jAE0IIUSVIwBNCCFElSMATQghRJUjAE0IIUSVIwBNC\nCFElSMATQghRJfw/5a9/wr1GWjoAAAAASUVORK5CYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10eeac310>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 51
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"sample_sizes\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Performance growth rates for different sample sizes"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In the plot above, we've seen how the different implemantations perform for a fixed sample size n=500. Now, let us take a look at the effect of the sample size on the relative performances for each approach. We will consider the sample sizes 10, 100, 1000, 10000, 100000, and 1000000."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"funcs = ['cy_classic_lstsqr', \n",
|
|
" 'lin_lstsqr_mat', 'numpy_lstsqr', 'scipy_lstsqr']\n",
|
|
"labels = ['classic approach (cython)', 'matrix approach', \n",
|
|
" 'numpy function', 'scipy function']\n",
|
|
"orders_n = [10**n for n in range(1, 7)]\n",
|
|
"times_n = {f:[] for f in funcs}\n",
|
|
"\n",
|
|
"for n in orders_n:\n",
|
|
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
|
|
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
|
|
" for f in funcs:\n",
|
|
" times_n[f].append(timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 22
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"#%pylab inline\n",
|
|
"#import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"plt.figure(figsize=(10,8))\n",
|
|
"\n",
|
|
"for f in times_n.keys():\n",
|
|
" plt.plot(orders_n, times_n[f], alpha=0.5, label=f, marker='o', lw=2)\n",
|
|
"\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
|
|
"plt.legend(loc=2)\n",
|
|
"plt.grid()\n",
|
|
"\n",
|
|
"plt.title('Performance of least square fit implementations for different sample sizes')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAmEAAAH4CAYAAAACdDpdAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XlcVOX+B/DPDLIz7JvsCl4VV9IQxQWFXCqXXFBLBDW9\nppZbtyxTKXOrvLef3bxXCyXF3VLLJU2QUivJzA0MFQUUUFAUZZEZZr6/P+YyMayDMMyZme/79fIl\nZ+ac5zznfM+c+c5znvMcERERGGOMMcZYixLrugKMMcYYY8aIkzDGGGOMMR3gJIwxxhhjTAc4CWOM\nMcYY0wFOwhhjjDHGdICTMMYYY4wxHeAkzIDdvXsX/fv3h62tLf7xj3/oujo6V1ZWhuHDh8Pe3h7j\nx4+v8X5sbCyioqJ0UDP9t2/fPnh7e8PW1hbnz59H586d8dNPP2m8fGPn11RmZibEYjEUCkWzl61r\nr732Gj788MMWXWdlnCUSCS5cuNDs5Vf9DGZnZ0MikaByFKXazmdTpkyBo6MjQkJCmr0uhiA5ORne\n3t7NWubJkyfRoUOHZi3TmLXSdQWYOj8/P+Tn58PExATW1tYYNmwY/v3vf8Pa2rrRZW3cuBGurq54\n9OiRFmqqf/bu3Yv8/HwUFhZCLK75+0MkEmm9Dn5+fti0aRMGDRqk9XW1pDfffBPr16/H8OHDAQCX\nL19WvRcbG4uMjAxs3bq1zuWrzm8MYmJi4O3tjeXLl2s0f3x8POLi4nDy5EnVa//5z3+0Vb06VY9z\nc6v6GfTx8cHjx49V09XPZydPnsTx48eRm5sLCwsLrdSnLpmZmWjbti0qKipqPZcYsn79+uHPP//U\ndTUMhnEdPXpAJBLh4MGDePz4Mc6dO4ezZ882+tcuEUGhUCArKwsdO3Z8qnpUVFQ81XJClpWVhb/9\n7W91njRbYtxikUjUIutpisbGnoiQnZ2NwMBALdWICUFT49zU1sjq57OsrCz4+fk9VQLWXOc3oX+W\nmR4gJih+fn6UmJiomn7zzTfpxRdfJCKiX375hXr37k329vbUrVs3Sk5OVs03YMAAWrx4MYWGhpKl\npSVNmjSJTE1NyczMjGxsbCgxMZHKy8tp7ty55OHhQR4eHjRv3jwqLy8nIqITJ06Qp6cnrVmzhtzd\n3SkqKopiY2Np7NixNGnSJJJIJNSlSxe6evUqrVy5klxdXcnHx4eOHTumqsOmTZuoY8eOJJFIqG3b\ntrRhwwbVe5Xlr127llxdXal169a0efNm1fulpaW0YMEC8vX1JTs7O+rbty+VlZU1uN3VpaWl0YAB\nA8je3p46depE3377LRERLV26lMzMzMjU1JRsbGxo06ZNNZZdtmwZTZo0STVd33rr29aCggJ64YUX\nyN7enhwdHalfv36kUCho0qRJJBaLydLSkmxsbOjjjz+uUYe6liUiOnfuHAUFBZFEIqHx48fT+PHj\n6b333iMios2bN1Pfvn3VyhKJRJSRkUFERAcPHqTu3buTra0teXt7U2xsrGq+mzdvkkgkori4OPLx\n8aEBAwYQEVFcXBx17NiRHBwcaMiQIZSVlVWjvk+ePCFra2sSiURkbW1NAQEBRETk6+tLx48fpyNH\njqjt9+7du9caN19fX9Vxv2zZskYddwMGDKBFixZRcHAw2dra0siRI6mwsFBt2+RyORERPXz4kKZO\nnUqtW7cmT09Peu+991Tvbd68mfr06UPz588ne3t78vf3p9OnT9OmTZvI29ubXF1d6auvvlLb9oUL\nF5KPjw+5ubnRzJkzVcdsfcf7hg0b1D6bI0aMICKiVatWkb+/P0kkEgoMDKR9+/YRkfKYtrCwIBMT\nE7KxsSEHBwciIoqOjlbFn4ho48aNFBAQQI6OjjRixAjKzc1VOxb++9//Urt27cje3p5mz56teu/a\ntWvUv39/srOzI2dnZxo/frzGca7r81ZZv5kzZ9KwYcPI2tpa7bxW6caNG9S/f3+SSCT03HPP0Zw5\nc1SfwcrYVVRUUHR0tNo+27Bhg9o+qTyev/vuO+rWrRvZ29tTnz596OLFi2rH2Jo1a6hLly5kYWFB\ncrm8wXPqkiVLKDQ0lCQSCQ0ePJju3btHRETe3t4kEonIxsaGbGxs6Ndff62xbWfOnKEePXqQra0t\nubm50YIFC1TvjR07ltzd3cnOzo769+9Pqampavvttddeo2HDhpGNjQ317duX8vLy6I033iB7e3vq\n0KED/fHHH2rbtWrVKgoMDCQHBweaMmUKPXnyhIiUx6GXl5dq3pycHBo9ejS5uLhQmzZtaN26dTXq\nXenQoUMUGBhIEomEPD096ZNPPqlR5s6dO1X7wMbGhszMzCgsLEx1zNT1+ajvPGdsOAkTGD8/Pzp+\n/DgREWVnZ1OnTp1o6dKldPv2bXJycqIjR44QEdEPP/xATk5OqpPCgAEDyNfXl9LS0kgul5NMJqOY\nmBhasmSJquwlS5ZQ7969qaCggAoKCqhPnz6q90+cOEGtWrWiRYsWkVQqpbKyMlq2bBlZWFjQsWPH\nqKKigiZPnky+vr60cuVKqqiooC+++ILatGmjKv/QoUN048YNIiL68ccfycrKis6dO6dW/rJly6ii\nooIOHz5MVlZW9PDhQyIimjVrFg0cOJByc3NVJ8fy8vI6t7ugoKDGvpNKpeTv70+rVq0imUxGSUlJ\nJJFIKD09nYiIYmNjKSoqqs59XzUJa2h/17atlSfGRYsW0cyZM6miooIqKiro1KlTavGt7cuoUl3L\nlpeXk4+PD3366adUUVFBe/fuJVNTU1X8GkrCkpOT6fLly0REdPHiRXJzc6P9+/cT0V9fdtHR0VRa\nWkplZWW0f/9+CggIoD///JPkcjl9+OGH1KdPnzrrXXVd1bezof1eff7GHncDBgwgT09PSk1NpZKS\nEhozZkyNL/LKRGvUqFE0c+ZMKi0tpfz8fAoODlYl0Js3b6ZWrVpRfHw8KRQKeu+998jT05PmzJlD\nUqmUjh07RhKJhEpKSoiIaN68eTRy5Eh68OABPX78mIYPH07vvPMOETV8vFf/bBIR7dmzh/Ly8oiI\naNeuXWRtbU137twhIqL4+Pga8a1aRmJiIjk7O9Mff/xB5eXl9Prrr1P//v3V4jN8+HAqKiqi7Oxs\ncnFxoaNHjxIR0YQJE2jlypVEpDzOTp8+XWecqsa5oc9bdHQ02dnZ0c8//0xEpEoMqgoJCaGFCxeS\nVCqln376iSQSiepYqR676vus+j45d+4cubq6UkpKCikUCvrqq6/Iz8+PpFIpESmTlaCgILp9+zY9\nefJEo3NqQEAAXbt2jcrKyigsLIwWLVpERESZmZlqdatNSEgIJSQkEBFRSUmJWqK2efNmKi4uJqlU\nSvPmzVP7cRIdHU3Ozs507tw5evLkCQ0aNIh8fX1p69atquNy4MCBqvl9fX2pS5cudPv2bSosLKTQ\n0FBVcl41YZLL5fTMM8/Q8uXLSSaT0Y0bN6ht27aq46A6d3d31fnn4cOHaufyqoldpUePHlHHjh1p\n48aNRFT/56O+c6Sx4SRMYHx9fcnGxobs7e3J19eXZs+eTWVlZbR69eoaX2RDhgxR/TIPCwujZcuW\nqb0fExOj9kvZ399fdcIhIjp69Cj5+fkRkfKDZWZmpmoZI1J+GQ4ePFg1/e2335KNjY3qF8ujR49I\nJBJRUVFRrdsyatQo+r//+z9V+ZaWlmonLVdXVzpz5gzJ5XKytLRU+9VaqaHtruqnn34id3d3tdcm\nTpyo+pVcvaWruqrvN2a91bd16dKlNHLkSLp+/XqN+RpKwupa9scffyQPDw+116om0Q0lYdXNnTuX\n5s+fT0R/fdndvHlT9f7QoUMpLi5ONS2Xy8nKyoqys7NrLa++JKyh/V7b/I057sLCwlQndyJl64yZ\nmRkpFAq1L/I7d+6Qubm56tc4EdH27dtVX2ibN2+mdu3aqd67ePEiiUQiys/PV73m5OREFy5cIIVC\nQdbW1mrb/PPPP6uSw/qOd6Kan83adO/enQ4cOKCqW31J2NSpU+ntt99WvVdcXEympqaq1kuRSKSW\nXEVGRtKaNWuIiGjy5Mk0Y8YMun37dr31qSyncpsb+rxFR0dTdHR0nWVlZWVRq1atqLS0VPXayy+/\nXGcCXX2fVd8nM2fOrJHYtm/fnn766SciUh5jVVvfNTmnrlixQvXe+vXraejQobXWrTb9+/enZcuW\n1fqDsaoHDx6QSCSiR48eqbZzxowZqvc/++wzCgwMVE1fvHiR7O3tVdN+fn5qLfGHDx8mf39/IlJP\nmH799Vfy8fFRW/fKlStpypQptdbLx8eHNmzYUOP8XlsSJpfL6YUXXqBZs2YRETX4+ajvHGlsuE+Y\nwIhEIhw4cAAPHjxAZmYm/v3vf8PCwgJZWVnYs2cPHBwcVP9Onz6NO3fuqJZt6C6Y3Nxc+Pr6qqZ9\nfHyQm5urmnZxcYGZmZnaMq6urqq/LS0t4ezsrOo8a2lpCQAoLi4GABw5cgQhISFwcnKCg4MDDh8+\njPv376uWd3JyUuuPZWVlheLiYty7dw9PnjyBv79/jTprst1Vt6/6PvD19UVOTk69+6U2Da23vm39\nxz/+gYCAAAwePBj+/v5Ys2aNxuuta9nc3Fx4enrW2DZNnTlzBgMHDoSrqyvs7e2xYcMGtdgA6sdP\nVlYW5s6dq9p2JycnAHiqffk0GnPcAep19/HxgUwmw71799TKzMrKgkwmQ+vWrVXbNXPmTBQUFKjm\ncXNzU1svoPxcVH2tuLgYBQUFKC0tRY8ePVRlDRs2TG2ddR3vddmyZQuCgoJU5V2+fLlGjOqSl5en\ndjxYW1vDyclJLV7u7u5qdans9P7RRx+BiBAcHIzOnTtj8+bNGq2zrs9b5TlFJBLVe07Kzc2Fg4OD\naj9XLv+0srKysHbtWrXP7O3bt9XOcdWP8YbOLVX3WWXsNRUXF4erV6+iY8eOCA4OxqFDhwAAcrkc\nixYtQkBAAOzs7NCmTRsAUDt2qh7/FhYWNT4P1etR/fivus1Vt7dyn1f+W7VqFfLz82ut/9dff43D\nhw/Dz88PYWFh+PXXX+vc1sWLF6OkpATr1q0DgAY/H005RxoavjtST/j4+CAqKgobN26sc56G7u7z\n8PBAZmamqnNrdnY2PDw86ly+MXcLlpeXY8yYMUhISMDIkSNhYmKCl156SaOOq87OzrCwsMD169fR\ntWtXtfc02e5KHh4euHXrFohIVfesrKynup26vvU2tK02Njb45JNP8MknnyA1NRWDBg1CcHAwBg4c\n2OA+rW3ZZ599Fh4eHjUSoKysLAQEBABQfumWlpaq3quepL788st44403cPToUZiZmWH+/Pk1kpTq\nd6YtWbIEEydO1GBv1a8l7jrNzs5W+9vU1BTOzs4oKSlRve7t7Q1zc3Pcv3+/yXe0OTs7w9LSEmlp\naWjdunWjl6++T7KysjBjxgwkJSWhd+/eEIlECAoKUh1Tmn62K5WUlOD+/fs1EvfauLm5qY7z06dP\nIyIiAgMGDEDbtm0bXGdTPm+tW7fGgwcPUFpaCisrK9XyJiYmGi1fnY+PDxYvXox33323znmqH+Oa\nnlvqK6cuAQEB2L59OwBlQjN27FgUFhZi7969+Pbbb5GYmAhfX188fPgQjo6OTerkX/34r3per+Tt\n7Y02bdrg6tWrGpXZs2dP7N+/H3K5HJ999hkiIyPV1lNp586d2LVrF3777TdV7Br6fNR1njO0u8Y1\nwS1hemLSpEn47rvvcOzYMcjlcjx58gTJyclqX8zVP8TVpydOnIgPP/wQ9+7dw7179/DBBx/UOy5W\nY04KUqkUUqkUzs7OEIvFOHLkCI4dO6bRsmKxGFOnTsWCBQuQl5cHuVyOX375BVKpVKPtrhQSEgIr\nKyt89NFHkMlkSE5OxsGDBzFhwgSNt6NSfettaFsPHjyI69evg4hga2sLExMT1Ze+m5sbMjIy6lzv\noUOHaixrYmKC3r17o1WrVli3bh1kMhm++eYb/Pbbb6rlunXrhtTUVFy4cAFPnjxBbGysWrnFxcVw\ncHCAmZkZUlJSsH379nq/SGbOnImVK1ciLS0NAFBUVIQ9e/Y0ej8CytaEzMxMrd1JRkRISEjAlStX\nUFpaiqVLl2LcuHE1tq9169YYPHgwFixYgMePH0OhUCAjI+OpxicTi8WYPn065s2bp2pJy8nJ0fiY\nd3Nzw40bN1TTJSUlEIlEcHZ2hkKhwObNm9WG7XBzc8Pt27chk8nUtrtyn06cOBGbN2/GhQsXUF5e\njnfffRchISHw8fGpdf1VY7Fnzx7cvn0bAGBvbw+RSKRRktrQ562hePv6+qJnz55YtmwZZDIZTp06\nhYMHD9Y5f0PlTZ8+Hf/973+RkpICIkJJSQkOHTpUZ+vV05xTK7m4uEAsFtf7WU5ISFAdG3Z2dqr9\nWlxcDHNzczg6OqKkpKRG0tjYzwkRYf369cjJyUFhYSFWrFhR6zkvODgYEokEH330EcrKyiCXy3H5\n8mWcPXu2xrwymQzbtm1DUVERTExMIJFIak2O//jjD7z++uvYt2+fqrUcaPjzUdd5zhhxEqYnvLy8\ncODAAaxcuRKurq7w8fHB2rVr1T6wtbVkVX3tvffeQ8+ePdG1a1d07doVPXv2xHvvvafx8nXNAwAS\niQTr1q1DZGQkHB0dsWPHDowcObLeZav65JNP0KVLFzz77LNwcnLCO++8A4VCUed213a7u6mpKb77\n7jscOXIELi4umDNnDrZu3Yq//e1vdW5PXdtb3/5uaFuvX7+O5557DhKJBH369MHs2bMxYMAAAMA7\n77yDDz/8EA4ODvjnP/9Zow7Xrl2rdVlTU1N88803iI+Ph5OTE3bv3o3Ro0er4v+3v/0NS5cuRURE\nBNq3b49+/fqpbev69euxdOlS2NraYvny5TUGq62+X0aNGoW3334bEyZMgJ2dHbp06YKjR4/Wu+/q\nMm7cOADKy3M9e/asc76qZWl63FX+HRUVhZiYGLRu3RpSqVR1WaT6vFu2bIFUKkVgYCAcHR0xbtw4\nVauhJuutas2aNQgICEBISAjs7Ozw3HPPqbUy1LfstGnTkJaWBgcHB4wePRqBgYFYuHAhevfuDXd3\nd1y+fBl9+/ZVzR8eHo5OnTrB3d1ddWmqan3Dw8OxfPlyjBkzBh4eHrh58yZ27txZ7/6rfO3s2bMI\nCQmBRCLByJEjsW7dOvj5+dVa76rlNPXzBgDbt2/HmTNn4OjoiA8++ADR0dF1rq96edWne/TogS++\n+AJz5syBo6Mj2rVrhy1bttRZh8aeU6uuz8rKCosXL0ZoaCgcHByQkpJSo/yjR4+ic+fOkEgkmD9/\nPnbu3Alzc3NMnjwZvr6+8PT0ROfOnVUtn5puZ231evnll1WX9tq1a1fred3ExAQHDx7E+fPn0bZt\nW7i4uGDGjBl1jiOZkJCANm3awM7ODhs3bsS2bdtqlHngwAE8fPgQffv2hUQigUQiwQsvvACg/s9H\nXec5YyQiLf08ffLkCQYMGIDy8nJIpVKMHDkSq1atQmxsLL788ktVP4uVK1di2LBhAIBVq1Zh06ZN\nMDExwbp16zB48GBtVI0xgzBlyhR4eXlpPOCnoRo4cCCioqIwdepUXVeFsRbXpk0bxMXFGeWlPEOg\ntT5hFhYWOHHiBKysrFBRUYG+ffvi1KlTEIlEWLBgARYsWKA2f1paGnbt2oW0tDTk5OQgIiICV69e\nNbrRiBnTlLYu7+kj3heMMX2k1QynsrOlVCqFXC6Hg4MDgNpPmAcOHMDEiRNhamoKPz8/BAQE1NrE\nyxhT0uRyj7Hg/cAY00davTtSoVDgmWeeQUZGBl577TV06tQJe/fuxWeffYYtW7agZ8+eWLt2Lezt\n7ZGbm6v2EFYvL68Wux2eMX2k6VAChu7EiRO6rgJjOnPz5k1dV4E1gVaTMLFYjPPnz6OoqAhDhgxB\ncnIyXnvtNSxduhQAsGTJEixcuBBxcXG1Ll/br1tPT89ax0BhjDHGGBOabt264fz587W+1yIdruzs\n7PDCCy/g7NmzcHV1VV1GefXVV1WXHD09PXHr1i3VMrdv3651jJvc3FzVrdn8Txj/li1bpvM68D+O\niz7845gI8x/HRXj/DCkmFy5cqDM/0loSdu/ePTx8+BAAUFZWhh9++AFBQUFqg0ju27cPXbp0AQCM\nGDECO3fuhFQqxc2bN3Ht2jUEBwdrq3qsGVUdJJIJB8dFeDgmwsRxER5jiYnWLkfm5eUhOjoaCoUC\nCoUCUVFRCA8Px+TJk3H+/HmIRCK0adMGGzZsAAAEBgYiMjISgYGBaNWqFdavX8+dbRljjDFmsLQ2\nTpi2iEQi6FmVDV5ycjLCwsJ0XQ1WDcdFeDgmwsRxER5Dikl9eQsnYYwxxhhjWlJf3mIwI6E6Ojqq\nOvzzP/6n6T9HR0ddH7pak5ycrOsqsGo4JsLEcREeY4mJVoeoaEkPHjzgFjLWaCIR9ztkjDGmGwZz\nObKu1xmrDx83jDHGtKm+7xmDuRzJGGOMMaZPOAljzEAZS58KfcIxESaOi/AYS0w4CWOMMcYY0wHu\nE2YgwsLCEBUVhWnTpjV72dnZ2ejUqRMePXr0VB3Zk5OTERUVpfZYKqEw9uOGMcaYdnGfMCNQOeSC\nNvj4+ODx48dav5MwNjYWUVFRWl0HY4wxJhQGM0RFXdLTs3D8eAZkMjFMTRWIiPBH+/a+LV4G053K\nXyDGNhyFIY04bSg4JsLEcREeY4mJQbeEpadnIT7+OgoKBuHhwzAUFAxCfPx1pKdntWgZt27dwujR\no+Hq6gpnZ2fMnj0bTk5OuHz5smqe/Px8WFtb4/79+/WWdeDAAXTv3h12dnYICAjAsWPHasyTkZGB\nQYMGwdnZGS4uLpg0aRKKiopU769ZswZeXl6wtbVFhw4dkJSUBABISUlBz549YWdnB3d3dyxcuBCA\n8kGqYrEYCoUCAFBYWIgpU6bA09MTjo6OeOmllzTeF3Wt//vvv8eqVauwa9cuSCQSBAUFAQDi4+Ph\n7+8PW1tbtG3bFtu3bwcAyOVyvPnmm3BxcYG/vz8+//xztTqGhYXhvffeQ2hoKKytrXHz5s1G1ZEx\nxhjTNoNuCTt+PAPm5uFQv8kiHBcvJuHZZzVryUpJyUBpabhqOiwMMDcPR2JikkatYXK5HC+++CIi\nIiKwbds2mJiY4LfffgMAJCQkYPXq1QCAHTt2ICIiAk5OTvXUJQXR0dH4+uuvER4ejtzcXDx+/LjW\neRcvXoz+/fujqKgIY8aMQWxsLP71r38hPT0dn3/+Oc6ePQt3d3dkZ2ejoqICADB37lzMnz8fr7zy\nCkpLS3Hp0qVay46KioKtrS3S0tJgbW2NX375pcH9UKmu9bdt2xbvvvsuMjIysGXLFgBASUkJ5s6d\ni7Nnz6Jdu3a4e/euKkn94osvcOjQIZw/fx5WVlYYPXp0jZauhIQEHDlyBO3bt1clZ8bEGH5F6huO\niTBxXITHWGJi0EmYTFZ7Q59crnkDoEJR+7xSqWZlpKSkIC8vDx9//DHEYuUyoaGhaNWqFSIjI1VJ\n2NatW7Fo0aJ6y4qLi8O0adMQHq5MCj08PGqdz9/fH/7+/gAAZ2dnzJ8/Hx988AEAwMTEBOXl5UhN\nTYWTkxN8fHxUy5mZmeHatWu4d+8enJ2d0atXrxpl5+Xl4fvvv0dhYSHs7OwAAP369dNoXzS0fiKq\n0XlRLBbj0qVL8PLygpubG9zc3AAAu3fvxvz58+Hp6QkAePfdd/Hjjz+qlhOJRIiJiUHHjh1V5TDG\nGGNCYtBJmKlp5aUp9dddXRWYNUuzMj7/XIGCgpqvm5lp1rJy69Yt+Pr61kgCevXqBUtLSyQnJ8Pd\n3R0ZGRkYMWJEvWXdvn0bL7zwQoPrvHv3LubOnYtTp07h8ePHUCgUqmckBgQE4NNPP0VsbCxSU1Mx\nZMgQ/POf/0Tr1q0RFxeHpUuXomPHjmjTpg2WLVtWY323bt2Co6OjKgFrrPrWX521tTV27dqFTz75\nBNOmTUNoaCjWrl2L9u3bIy8vD97e3qp5qyZzlaq+b4yMpU+FPuGYCBPHRXiMJSYG3TwQEeGP8vJE\ntdfKyxMRHu7fYmV4e3sjOzsbcrm8xnvR0dFISEjA1q1bMW7cOJiZmTVY1vXr1xtc57vvvgsTExNc\nvnwZRUVF2Lp1q9rluIkTJ+LkyZPIysqCSCTC22+/DUCZIG3fvh0FBQV4++23MXbsWJSVldWoQ2Fh\noVofs8aqa/21dZwfPHgwjh07hjt37qBDhw6YPn06AKB169bIzs5WzVf170rG1hGfMcaYfjHoJKx9\ne1/ExATA1TUJ9vbJcHVNQkxMQKPubGxqGb169ULr1q2xaNEilJaW4smTJ/j5558BAJMmTcI333yD\nbdu2YfLkyQ2WNW3aNGzevBlJSUlQKBTIyclBenp6jfmKi4thbW0NW1tb5OTk4OOPP1a9d/XqVSQl\nJaG8vBzm5uawsLCAiYkJAGUfqoL/NfvZ2dlBJBLVaMFr3bo1hg0bhlmzZuHhw4eQyWT46aefNNoX\nDa3f3d0dmZmZqkuS+fn5OHDgAEpKSmBqagpra2vVvJGRkVi3bh1ycnLw4MEDrF69ukbSZezjfxnD\nr0h9wzERJo6L8BhNTEjP1FVlIW9KdnY2jRo1ipycnMjZ2Znmzp2rei88PJzatGmjcVn79u2jrl27\nkkQioYCAADp27BgREYWFhVFcXBwREaWmplKPHj3IxsaGgoKCaO3ateTt7U1ERBcvXqTg4GCSSCTk\n6OhIw4cPp7y8PCIimjRpErm6upKNjQ117tyZDhw4QEREN2/eJLFYTHK5nIiICgsLKTo6mtzc3MjB\nwYHGjBlTb51PnDih0frv379Pffv2JQcHB+rRowfl5eXRgAEDyM7Ojuzt7WngwIF05coVIiKqqKig\n+fPnk5OTE7Vt25Y+//xzEolEqjpW3R/1EfJxwxhjTP/V9z3DI+br2LRp0+Dp6anqOM+eTmZmJtq2\nbYuKiopGdcLX1+NGE8bSp0KfcEyEieMiPIYUk/q+Zwy6Y77QZWZm4ptvvsH58+d1XRXGGGOMtTCD\n7hMmZEvHNwwaAAAgAElEQVSWLEGXLl3w1ltvwdf3r/5lK1euhEQiqfFPk7sidUkI9eaO+OoM5Vek\nIeGYCBPHRXiMJSZ8OZIZNT5uGGOMaRM/wJsxI5Ss/qgIJgAcE2HiuAiPscSEkzDGGGOMMR3gy5HM\nqPFxwxhjTJv4ciRjjDHGmMBwEsaYgTKWPhX6hGMiTBwX4TGWmHASxmqVmZkJsVis9sxJxhhjjDUf\n7hPGaqXpCPTx8fGIi4vDyZMnW7B2zYePG8YYY9pk1CPmp19Px/Hfj0NGMpiKTBHRIwLtA9q3eBms\n8RQKRaMeQcQYY4zpE4P+hku/no74E/EocCvAQ/eHKHArQPyJeKRfT2+xMvz8/LB27Vp069YN9vb2\nmDBhAsrLyxEfH49+/fqpzSsWi3Hjxg0AQExMDGbNmoXnn38eEokE/fr1w507dzB37lw4ODigY8eO\nao878vPzw+rVq9GpUyc4Ojpi6tSpKC8vBwB07twZBw8eVM0rk8ng7OyMCxcuaLwf4uPj4e/vD1tb\nW7Rt2xbbt2/Hn3/+iZkzZ+KXX36BRCKBo6MjAODw4cPo1KkTbG1t4eXlhbVr16rK+fjjj+Hh4QEv\nLy9s2rSpxja/9tpreP7552FjY2M0fQK0hfef8HBMhInjIjzGEhODbgk7/vtxmLczR3Jm8l8vmgIX\nd17Es32f1aiMlFMpKPUqBTKV02F+YTBvZ47Ec4katYaJRCLs2bMHR48ehbm5OUJDQxEfHw8LC4sG\nl92zZw+OHTuGwMBAPP/88wgJCcGHH36ITz/9FEuXLsWCBQuQlJSkmn/79u04duwYrKysMHz4cHz4\n4YdYvnw5oqOjkZCQgBdffBGAMkny9PREt27dNNoHJSUlmDt3Ls6ePYt27drh7t27uH//Pjp06IAN\nGzbgyy+/VLscOW3aNOzduxehoaEoKipSJVnff/891q5di6SkJPj5+eHVV1+tsa4dO3bgyJEj6N27\ntyqJZIwxxgyRQbeEyUhW6+tyyDUuQ4HaO6ZLFVKNy3jjjTfg7u4OBwcHDB8+XKMHdotEIowePRpB\nQUEwNzfHSy+9BGtra0yaNAkikQiRkZH4448/1OafM2cOPD094eDggMWLF2PHjh0AgFdeeQWHDh1C\ncXExAGDr1q2IiorSuP6AspXu0qVLKCsrg5ubGwIDAwGg1uvcZmZmSE1NxaNHj2BnZ4egoCAAwO7d\nuzF16lQEBgbCysoK77//fo1lR40ahd69ewMAzM3NG1VHps5Ynr2mTzgmwsRxER5jiYlBt4SZikwB\nKFuvqnK1csWssFkalfH53c9R4FZQ43UzsZnG9XB3d1f9bWVlhdzcXI2Wc3V1Vf1tYWGhNm1paalK\nqip5e3ur/vbx8VGtx8PDA6Ghodi7dy9GjRqF77//Hp999pnG9be2tsauXbvwySefYNq0aQgNDcXa\ntWvRvn3tLYFff/01PvzwQyxatAhdu3bF6tWrERISgry8PDz77F8tkD4+PmrLiUQieHl5aVwvxhhj\nTJ8ZdEtYRI8IlF9Tv6RVfq0c4c+Et2gZtbG2tkZpaalq+s6dO00qDwCys7PV/vbw8FBNV16S3LNn\nD/r06YPWrVs3quzBgwfj2LFjuHPnDjp06IDp06cDUCZO1fXs2RP79+9HQUEBRo0ahcjISABA69at\na9SRaY+x9KnQJxwTYeK4CI+xxMSgk7D2Ae0RMzAGrvmusL9jD9d8V8QMjGnUnY3NUUZVlZfvunXr\nhtTUVFy4cAFPnjxBbGxsrfM1ptz169cjJycHhYWFWLFiBSZMmKB6/6WXXsK5c+ewbt06TJ48uVFl\n5+fn48CBAygpKYGpqSmsra1hYmICAHBzc8Pt27chkykv/cpkMmzbtg1FRUUwMTGBRCJRzRsZGYn4\n+HhcuXIFpaWlNS5H8lARjDHGjIlBX44ElElUU4eTaI4yKolEIohEIrRr1w5Lly5FREQErKyssHLl\nSnzxxRc15qtruvK1qn+//PLLGDx4MHJzczFq1Ci89957qvctLCwwevRo7Nq1C6NHj9a4roByqIh/\n/etfiI6OhkgkQlBQEP7zn/8AAMLDw9GpUye4u7vDxMQEOTk5SEhIwOuvvw65XI4OHTpg27ZtAICh\nQ4di3rx5GDRoEExMTLB8+XJs37693m1kT89Y+lToE46JMHFchMdYYsKDtRqINm3aIC4uDoMGDapz\nnuXLl+PatWvYsmVLC9asfmKxGNevX0fbtm11sn5jP24YY4xpFz/Am6GwsBCbNm3CjBkzdF0V1kKM\npU+FPuGYCBPHRXiMJSachBmBL774Aj4+Phg2bBj69u2ren3btm2QSCQ1/nXp0qXF6saXHxljjBkr\nvhzJjBofN4wxxrSJL0cyxhhjjAkMJ2GMGShj6VOhTzgmwsRxER5jiQknYYwxxhhjOsB9wphR4+OG\nMcaYNnGfMMYYY4wxgeEkTMv8/PyQmJiIVatWqZ63+LRiY2MRFRXVTDVjhs5Y+lToE46JMHFchMdY\nYsJJmJZVPornnXfeUXss0dOWpYmwsDDExcU1aV26ZgjbwBhjjNXH4J8dmZWejozjxyGWyaAwNYV/\nRAR82zfuOZDNUUZz0LTvkrYGQK2oqECrVi1zyPAgrk1nLM9e0yccE2HiuAiPscTEoFvCstLTcT0+\nHoMKChD28CEGFRTgenw8stLTW7QMIlK7lJiZmQmxWIwtW7bA19cXLi4uWLlyZaO27cmTJ5g0aRKc\nnZ3h4OCA4OBg5OfnY/HixTh58iTmzJkDiUSCN954AwAwf/58uLm5wc7ODl27dkVqaioA4P79+xgx\nYgTs7OzQq1cvLFmyBP369VOtRywWY/369WjXrh3aN5B4isVi/Oc//0G7du1ga2uLpUuXIiMjA717\n94a9vT0mTJgAmUwGAHj48CFefPFFuLq6wtHREcOHD0dOTg4A1LkNjDHGmCEx6JawjOPHEW5uDlS5\nthwOIOniRfg++6xmZaSkILy09K8XwsIQbm6OpMTERrWG1dayc/r0aVy9ehXp6ekIDg7G6NGj0aFD\nB43K++qrr/Do0SPcvn0b5ubmOH/+PCwtLbFixQr8/PPPiIqKwtSpUwEAR48excmTJ3Ht2jXY2toi\nPT0ddnZ2AIDZs2fDysoKd+7cwY0bNzBkyJAaD9M+cOAAfvvtN1haWjZYr2PHjuGPP/5AdnY2goKC\ncOrUKezYsQOOjo7o3bs3duzYgcmTJ0OhUGDatGnYu3cvKioqMHXqVMyZMwf79u2rdRtY4yUnJxvN\nr0l9wTERJo6LcKSnZ+H48QxcuXIRHTt2RUSEP9q399V1tbTGoFvCxP9rdanxulyueRkKRe2vS6VP\nVaeqli1bBnNzc3Tt2hXdunXDhQsXNF7WzMwM9+/fx7Vr1yASiRAUFASJRKJ6v+qlSzMzMzx+/BhX\nrlyBQqFA+/bt4e7uDrlcjm+++QYffPABLC0t0alTJ0RHR9e47PnOO+/A3t4e5ubmDdbrrbfego2N\nDQIDA9GlSxcMGzYMfn5+sLW1xbBhw/DHH38AABwdHfHSSy/BwsICNjY2ePfdd/Hjjz+qlcVDRzDG\nmPFIT89CfPx15OcPQmFhdxQUDEJ8/HWkp2fpumpaY9AtYQpTU+Uf1X7hKFxdgVmzNCvj88+BgoKa\nr5uZNbV6cHd3V/1tZWWFkpISjZeNiorCrVu3MGHCBDx8+BCTJk3CihUrVH22qra8DRw4EHPmzMHs\n2bORlZWF0aNH45NPPkFJSQkqKirg7e2tmtfHx6fGuqq+3xA3NzfV35aWljWm79y5AwAoLS3F/Pnz\ncfToUTx48AAAUFxcDCJS1Z37hTUN/7IXHo6JMHFchOH48QyIxeG4dAkoLQ2DTAaYm4cjMTHJYFvD\nDLolzD8iAonl5WqvJZaXwz88vEXLaC5Vk5JWrVph6dKlSE1Nxc8//4yDBw9iy5YtNear9Prrr+Ps\n2bNIS0vD1atX8fHHH8PV1RWtWrVCdna2ar6qf9e23uaydu1aXL16FSkpKSgqKsKPP/4IIlK1fnEC\nxhhjxuXePTF+/x0oLATkcqCsTPm6VGq4qYrhbhkA3/btERATgyRXVyTb2yPJ1RUBMTGN6svVHGUA\nml1aa2iequ8nJyfj0qVLkMvlkEgkMDU1hYmJCQBla1RGRoZq3rNnz+LMmTOQyWSwsrKChYUFTExM\nIBaLMXr0aMTGxqKsrAxpaWnYsmVLsyZAVetc9e/i4mJYWlrCzs4OhYWFeP/999WWq74NrPGMZZwd\nfcIxESaOi24RAb//DqSkKPDkCSCRAC4uybC1Vb5vZlZ7tyBDYNBJGKBMogbNmoWwefMwaNaspxpa\noqllVI4VVjW5qS3RaSj5qVrGnTt3MG7cONjZ2SEwMBBhYWGquy/nzp2LvXv3wtHREfPmzcOjR48w\nY8YMODo6ws/PD87OzvjHP/4BAPj3v/+N4uJiuLu7Y+rUqZgyZYpastSYhKyhbapa/3nz5qGsrAzO\nzs7o06cPhg0bpjZv9W1gjDFmeGQy4Ntvge++A9q08YeLSyKCgoDKHj/l5YkID/fXbSW1SGvPjnzy\n5AkGDBiA8vJySKVSjBw5EqtWrUJhYSHGjx+PrKws+Pn5Yffu3bC3twcArFq1Cps2bYKJiQnWrVuH\nwYMH16wwPztSq+Lj4xEXF4eTJ0/quiotgo8bxhjTjQcPgN27gbw8wNQUePFFwMIiC4mJGZBKxTAz\nUyA8XP/vjqzve0ZrHfMtLCxw4sQJWFlZoaKiAn379sWpU6fw7bff4rnnnsNbb72FNWvWYPXq1Vi9\nejXS0tKwa9cupKWlIScnBxEREbh69SrEYoNvrGOMMcaMytWrwDffAE+eAI6OwPjxgPI+Ll+9T7oa\nQ6sZjpWVFQBAKpVCLpfDwcEB3377LaKjowEA0dHR2L9/PwDlWFQTJ06Eqakp/Pz8EBAQgJSUFG1W\nT5CGDRsGiURS49/q1atbZP3VL5tWdfLkyVrrZlt54Z4JCvdzER6OiTBxXFqOQgGcOAFs365MwNq3\nB2bMqEzA/mIsMdHqEBUKhQLPPPMMMjIy8Nprr6FTp064e/euatgCNzc33L17FwCQm5uLkJAQ1bJe\nXl6qEdSNyZEjR3S6/ujoaFWSXF2/fv3w+PHjFq4RY4wxQ1BaCnz9NZCRAYhEwKBBQN++yr+NlVaT\nMLFYjPPnz6OoqAhDhgzBiRMn1N6vr9Wl8v3axMTEwM/PDwBgb2+P7t27N1udmfGpOlp25a8vQ5gO\nCwsTVH14GqrXhFIfnubplprOzQVWrEhGSQkQGBiGsWOB7Oxk/Pij4Z2/Kv/OzMxEQ7TWMb+65cuX\nw9LSEl9++SWSk5Ph7u6OvLw8DBw4EH/++afqctuiRYsAAEOHDsX777+PXr16qVeYO+azZsTHDWOM\naQ8RcO4ccPiwcuwvLy9g3Djgf0/OMwr1fc9orU/YvXv38PDhQwBAWVkZfvjhBwQFBWHEiBH46quv\nACiffzhq1CgAwIgRI7Bz505IpVLcvHkT165dQ3BwsLaqx5jBq/qrjAkDx0SYOC7aIZMBBw4oh5+Q\ny4FnnwViYjRLwIwlJlq7HJmXl4fo6GgoFAooFApERUUhPDwcQUFBiIyMRFxcnGqICgAIDAxEZGQk\nAgMD0apVK6xfv55HTWeMMcb00IMHwK5dwJ07fw0/0a2brmslPC12ObK58OVI1pz4uGGMseZV9/AT\nxkknlyPZ05NIJBp16Htafn5+SExM1Fr5jDHGjI9CASQl/TX8RIcOtQ8/wf7CSZgAPX78WHX3pzY0\ndFcqAGRmZkIsFkOhMNxndhk6Y+lToU84JsLEcWm60lJg2zbgp5+UQ06EhytbwCwsnq48Y4mJVoeo\nEIL0GzdwPDUVMgCmACI6dUL7tm1bvAx9pY1LdXK5XPWwccYYY/otJ0f5+KGiIsDaGhgzBjCSr8gm\nM+iWsPQbNxB/7hwKOnfGw86dUdC5M+LPnUP6jRstWsaaNWvg5eUFW1tbdOjQAUlJSVAoFFi5ciUC\nAgJga2uLnj17qganFYvFuPG/8mNiYjBz5kwMHjwYtra2CAsLQ3Z2NgBg9uzZePPNN9XWNWLECHz6\n6aca1y0lJQU9e/aEnZ0d3N3dVeX1798fgHIcNolEgjNnzuD69esYMGAA7O3t4eLiggkTJqjK+eGH\nH9ChQwfY29vj9ddfx4ABAxAXFwdA+TzK0NBQLFiwAM7Oznj//fc1rh97epVj1zDh4JgIE8fl6RAB\nv/8ObNqkTMC8vIC//715EjBjiYlBt4QdT02FeY8eSP7fUBkAAH9/XPzpJzyr4Z2XKT/9hNJu3YD/\nlRFmbw/zHj2QePmyRq1h6enp+Pzzz3H27Fm4u7sjOzsbFRUVWLt2LXbu3IkjR46gXbt2uHjxIiwt\nLWstY/v27Th8+DCCg4Px1ltv4ZVXXsHJkycRExODUaNG4eOPP4ZIJMK9e/eQmJioSn40MXfuXMyf\nPx+vvPIKSktLcenSJQDKRxS1adMGRUVFqud3Tpw4EUOHDsWPP/4IqVSKs2fPAlAORzJmzBjEx8dj\n5MiR+Oyzz/Df//5XbeT9lJQUvPzyy8jPz4dUKtW4fowxxoRHJgMOHQLOn1dOP/ssMGQI0Mqgs4rm\nZ9AtYbI6Xpc3YugLRR3zappGmJiYoLy8HKmpqZDJZPDx8UHbtm0RFxeHFStWoF27dgCArl27wtHR\nsdYyXnzxRfTt2xdmZmZYsWIFfvnlF+Tk5ODZZ5+FnZ2dqpP9zp07MXDgQLi4uGi8fWZmZrh27Rru\n3bsHKysr1eC4tV2GNDMzQ2ZmJnJycmBmZoY+ffoAAA4fPozOnTtj9OjRMDExwbx58+Du7q62rIeH\nB2bPng2xWAyLp+0kwBrFWPpU6BOOiTBxXBrnwQMgLk6ZgJmaAqNHAy+80LwJmLHExKBzVtP//R9m\nb6/2uqujI2a1aaNRGZ9fvoyCassDgJmGdQgICMCnn36K2NhYpKamYsiQIVi7di1u3boFf3//BpcX\niUTw8vJSTVtbW8PR0RG5ubnw9PTE5MmTkZCQgIiICCQkJGD+/Pka1kwpLi4OS5cuRceOHdGmTRss\nW7YML7zwQq3zfvTRR1iyZAmCg4Ph4OCAhQsXYsqUKcjNzVWrIwB4e3vXO80YY0z/8PATzcugW8Ii\nOnVC+e+/q71W/vvvCO/UqUXLmDhxIk6ePImsrCyIRCK8/fbb8Pb2xvXr1xtclohw69Yt1XRxcTEK\nCwvh4eEBAJg0aRIOHDiACxcu4M8//1Q9gUBTAQEB2L59OwoKCvD2229j7NixKCsrq/XuSTc3N2zc\nuBE5OTnYsGEDZs2ahYyMDHh4eKjVsXqdgbqfA8q0x1j6VOgTjokwcVwa1tLDTxhLTAw6CWvfti1i\nnnkGrpcvw/7yZbhevoyYZ55p1J2NTS3j6tWrSEpKQnl5OczNzWFhYYFWrVrh1VdfxZIlS3D9+nUQ\nES5evIjCwsJayzh8+DBOnz4NqVSKJUuWoHfv3vD09AQAeHl5oWfPnpg8eTLGjh0Lc3NzjbcNABIS\nElBQUAAAsLOzg0gkglgshouLC8RiMTIyMlTz7tmzB7dv3wag7LAvEolgYmKC559/Hqmpqdi3bx8q\nKiqwbt063Llzp1H1YIwxJkzVh5+IiGja8BPsLwZ9ORJQJlFNHU6iKWWUl5fjnXfewZUrV2BqaorQ\n0FBs3LgRrq6uKC8vx+DBg3Hv3j107NgR+/btA6DeaiQSifDyyy/j/fffxy+//IIePXogISFBbR3R\n0dGYPHky1q1b1+j6HT16FAsXLkRpaSn8/Pywc+dOVSK3ePFihIaGoqKiAkeOHMHZs2cxf/58FBUV\nwc3NDevWrVONZ7Znzx688cYbmDJlCqKiohAaGqq2DdwS1vKSk5ON5tekvuCYCBPHpW66Gn7CWGLC\njy0SuClTpsDLywvLly+vc56TJ09i0qRJyMrKasGa1W/gwIGIiorC1KlTdV2VehnqcQMYz0lMn3BM\nhInjUlPl8BNHjigfvu3lBURGAra2LbN+Q4pJfd8zBt8Spu8aShBkMhk+/fRTTJ8+vYVqpDlDTW70\nhaGcwAwJx0SYOC7qqg8/ERysHH6iJcfYNpaYGHSfMENQ36W8K1euwMHBAXfv3sW8efNUr2dnZ0Mi\nkdT4Z2trq+rT1RL4EiRjjOmXwsKaw088/3zLJmDGhC9HMqNmyMeNITXnGwqOiTBxXJSENPyEIcWE\nL0cyxhhjrFYKBZCcrLz7EVAOPzFqFN/92BK4JYwZNT5uGGPGrLQU+PprICNDOfxEeDgQGqr8mzUP\nbgljjDHGmJrqw0+MHQto+DAZ1kwMpmO+g4ODqhM7/+N/mv5zcHDQ9aGrNcby7DV9wjERJmOLCxFw\n9iywaZMyAfPyAv7+d0BICZixxMRgWsLqGm2eaZ8hdaBkjDFDJpMBBw8CFy4op3Ux/AT7i8H0CWOM\nMcZY3QoLgV27gLt3lcNPDB8OdO2q61oZvvryFoNpCWOMMcZY7dLTgX37hDH8BPuLwfQJY7pjLNfu\n9Q3HRXg4JsJkyHFRKICkJGDHDmUC1qEDMGOG8BMwQ45JVdwSxhhjjBmgkhLl8BM3biiHnIiIAPr0\n4eEnhIT7hDHGGGMGhoefEA7uE8YYY4wZASLg99+BI0cAuVw5/ERkJGBrq+uasdpwnzDWZMZy7V7f\ncFyEh2MiTIYSF5kM2L9fOQSFXA706gVMmaKfCZihxKQh3BLGGGOM6bnqw0+MGAF06aLrWrGGcJ8w\nxhhjTI9VHX7CyUk5/ISrq65rxSpxnzDGGGPMwCgUwIkTwMmTyumOHYGRIwELC93Wi2mO+4SxJjOW\na/f6huMiPBwTYdLHuJSUAAkJygRMJAKee07ZAd9QEjB9jMnT4JYwxhhjTI/cvg3s2cPDTxgC7hPG\nGGOM6QEi4OxZ4PvvlXc/ensD48bp592PxoT7hDHGGGN6TCZTDj1x4YJyulcvYPBgwMREt/ViTcN9\nwliTGcu1e33DcREejokwCT0uhYXAl18qEzBTU2DMGGDYMMNOwIQek+bCLWGMMcaYQPHwE4aN+4Qx\nxhhjAlPb8BOjRgHm5rqtF2s87hPGGGOM6YmSEuDrr4EbN5TDT0REAH36KP9mhoX7hLEmM5Zr9/qG\n4yI8HBNhElJcbt8GNmxQJmDW1kB0NBAaanwJmJBiok3cEsYYY4zpGA8/YZy4TxhjjDGmQzIZ8N13\nwMWLymkefsKwcJ8wxhhjTIAKC4Fdu4C7d5XDT4wYAXTpoutasZbCfcJYkxnLtXt9w3ERHo6JMOkq\nLn/+qez/dfeucviJ6dM5AatkLJ8VbgljjDHGWpBCASQlAadOKad5+AnjxX3CGGOMsRZSUgLs3Qvc\nvMnDTxgL7hPGGGOM6djt28Du3cCjR8rhJ8aNA/z8dF0rpkvcJ4w1mbFcu9c3HBfh4ZgIk7bjQgT8\n9huwebMyAfP2BmbO5ASsPsbyWeGWMMYYY0xLpFLg4EEefoLVjvuEMcYYY1pw/77y8iMPP2HcuE8Y\nY4wx1oL+/BPYtw8oL1cOPzF+PODqqutaMaHhPmGsyYzl2r2+4bgID8dEmJozLgoFcPw4sHOnMgHr\n2BGYMYMTsMYyls8Kt4QxxhhjzaDq8BNisXL4id69efgJVjfuE8YYY4w1EQ8/werCfcIYY4wxLagc\nfuLoUUAuB3x8lAmYRKLrmjF9wH3CWJMZy7V7fcNxER6OiTA9bVykUmXn+8OHlQlYSAgQHc0JWHMw\nls8Kt4QxxhhjjXT/PrBrF5CfD5iZKYef6NxZ17Vi+kZrfcJu3bqFyZMnIz8/HyKRCDNmzMAbb7yB\n2NhYfPnll3BxcQEArFy5EsOGDQMArFq1Cps2bYKJiQnWrVuHwYMH16ww9wljjDGmQ1WHn3B2BiIj\n+e5HVrf68hatJWF37tzBnTt30L17dxQXF6NHjx7Yv38/du/eDYlEggULFqjNn5aWhpdffhm//fYb\ncnJyEBERgatXr0IsVr9iykkYY4wxXVAogKQk4NQp5XRgIDByJGBurtt6MWGrL2/RWp8wd3d3dO/e\nHQBgY2ODjh07IicnBwBqrcyBAwcwceJEmJqaws/PDwEBAUhJSdFW9VgzMpZr9/qG4yI8HBNh0iQu\nJSXA1q3KBEwsVj56aNw4TsC0xVg+Ky3SMT8zMxN//PEHQkJCAACfffYZunXrhmnTpuHhw4cAgNzc\nXHh5eamW8fLyUiVtjDHGmK7cugVs2KAc/8vGBpg8GejTh8f/Yk2n9Y75xcXFGDt2LP7v//4PNjY2\neO2117B06VIAwJIlS7Bw4ULExcXVuqyojiM8JiYGfv8bgMXe3h7du3dHWFgYgL+yZ55u2elKQqkP\nT4chLCxMUPXhaaheE0p9eLr+6RMnkvHnn8C9e2GQy4HS0mQEBwN+fsKonyFPh+nx+avy78zMTDRE\nq4O1ymQyvPjiixg2bBjmzZtX4/3MzEwMHz4cly5dwurVqwEAixYtAgAMHToU77//Pnr16qVeYe4T\nxhhjTMukUuDgQeDiReV0SAjw3HOAiYlu68X0j076hBERpk2bhsDAQLUELC8vT/X3vn370OV/j5Qf\nMWIEdu7cCalUips3b+LatWsIDg7WVvVYM6qa/TPh4LgID8dEmKrH5f594MsvlQmYmRkwdiwwdCgn\nYC3JWD4rWrscefr0aSQkJKBr164ICgoCoByOYseOHTh//jxEIhHatGmDDRs2AAACAwMRGRmJwMBA\ntGrVCuvXr6/zciRjjDGmDVeuAPv3/zX8xPjxwP9GVGKs2fGzIxljjBk9Hn6CaQs/O5IxxhirQ3Ex\n8PXXyrsfxWJl36+QEL77kWmf1vqEMeNhLNfu9Q3HRXg4JsJz6xbwj38kq4afiI4GevfmBEzXjOWz\nwi1hjDHGjA4R8NtvwNGjQFkZ4OOjHHyVH77NWhL3CWOMMWZUpFLgu++AS5eU0zz8BNMm7hPGGGOM\nQaOxlSQAACAASURBVDn8xK5dQH6+cviJkSOBTp10XStmrLhPGGsyY7l2r284LsLDMdGtK1eAjRuV\nCZizMzB9ujIB47gIj7HEhFvCGGOMGTSFAkhMBE6fVk7z8BNMKLhPGGOMMYPFw08wXeM+YYwxxozO\nrVvA7t3A48fK4SfGjQN8fXVdK8b+wn3CWJMZy7V7fcNxER6OScsgAs6cATZvViZgPj7A3/9edwLG\ncREeY4kJt4QxxhgzGNWHn+jdG4iI4OEnmDBxnzDGGGMGgYefYELEfcIYY4wZtCtXgP37gfJy5fAT\n48cDLi66rhVj9eM+YazJjOXavb7huAgPx6T5KRTADz8oW8DKy5UtX9OnNy4B47gIj7HEhFvCGGOM\n6aXiYmDvXiAzk4efYPqJ+4QxxhjTOzz8BNMX3CeMMcaYQSACUlKAo0eVlyJ9fYGxYwGJRNc1Y6zx\nuE8YazJjuXavbzguwsMxaRqpFPjmG+DIEWUC1rs3MHly0xMwjovwGEtMuCWMMcaY4PHwE8wQcZ8w\nxhhjglZ1+AkXFyAykoefYPqD+4QxxhjTOwoFcPw48PPPyulOnYARIwBzc93Wi7Hmwn3CWJMZy7V7\nfcNxER6OieaKi4EtW5QJmFgMDBmi7ICvjQSM4yI8xhITbgljjDEmKDz8BDMW3CeMMcaYIPDwE8wQ\ncZ8wxhhjgiaVAt9+C1y+rJzu3RuIiABMTHRbL8a0ifuEsSYzlmv3+objIjwck9rduwd88YUyATMz\nU15+HDKk5RIwjovwGEtMuCWMMcaYzqSlAQcO8PATzDhxnzDGGGMtrrbhJ0aOVLaEMWZIuE8YY4wx\nwSguBvbuBTIzlcNPDB4M9OoFiES6rhnTtaz0dGQcPw6xTAaFqSn8IyLg2769rqulNdwnjDWZsVy7\n1zccF+HhmADZ2cCGDcoEzMYGiIkBQkJ0m4BxXIQhKz0d1+PjMSg/H0hJwaCCAlyPj0dWerquq6Y1\nnIQxxhjTOiLg11+B+Hjl+F++vsDMmYCPj65rxoQi4/hxhJeXA+fPA+npQEUFws3NkZGYqOuqaQ33\nCWOMMaZV1Yef6NMHCA/n4SdYFQ8fInnePIRlZiqnTU2BLl0AW1sk29sjbN48nVavKbhPGGOMMZ24\ndw/YtQsoKFB2uh81CggM1HWtmGA8eQKcPAn8+isU+fnKToJeXsom0lbKFEVhwHdr8OVI1mTcn0KY\nOC7CY2wxSUsDNm5UJmAuLsCMGcJMwIwtLoIglysfj7BuHXD6NCCXw3/oUCR27w60bYvk27cBAInl\n5fAPD9dxZbWHW8IYY4w1q+rDT3TuDIwYwcNPMCg7B169Cvzwg7KZFFB2EBw8GL6enkB6OpISE3Hx\n3j0oXF0REB5u0HdHcp8wxhhjzaa4GNizB8jK4uEnWDW5ucCxY8pbYwHAyQl47jmgfXuDPkC4Txhj\njDGty85WJmCPHysfuj1uHN/9yAAUFQFJScCFC8ppKytgwACgZ0+jvzuD+4SxJuP+FMLEcREeQ41J\nbcNP/P3v+pOAGWpcdK68HEhMBD77TJmAmZgob4194w1l82g9CZixxIRbwhhjjD01Hn6C1aBQAOfO\nASdOACUlytc6d1YeGA4Ouq2bwHCfMMYYY0+Fh59gaoiA69eV/b4KCpSveXsDQ4Yoh50wUtwnjDHG\nWLNKSwP271e2hLm4AOPHA87Ouq4V05k7d5TJ140bymkHByAiQpmVG3Cn+6biPmGsyYzl2r2+4bgI\njyHERKFQftfu3q1MwDp3BqZP1+8EzBDiojOPHwMHDigfCHrjBmBhoWz5mj0b6NTpqRMwY4kJt4Qx\nxhjTSPXhJ4YMAYKDuaHDKEmlyoHgTp8GZDLlAdGrF9C/v/LuR6YR7hPGGGOsQdnZytav4mIefsKo\nKRTKOx2TkpStYADQsaPy0qOTk27rJlDcJ4wxxthTIQLOnFFeglQoAD8/YOxYwMZG1zVjLS4jQ3kg\n3L2rnPb0VI7G6+ur23rpMe4TxprMWK7d6xuOi/DoW0ykUuDrr4Hvv1cmYH36AJMnG14Cpm9xaXH5\n+cC2bcDWrcoEzM4OGDMGePVVrSVgxhITbgljjDFWQ9XhJ8zNgZEjefgJo1NcrBzr69w5ZZOouTnQ\nrx8QEgK04vShOXCfMMYYY2p4+AkjJ5MBv/wCnDqlPAjE/8/enQe3fd93/n/i4AXgC1ESRYoUL12W\nRF0UKZKSKB625SuNvUnd2j97d2NPuslus9NuJzvjeLLHrPdo7Gk702Qz7iSts3Emma6dpHHceFvb\nsk2Qog5S92Xd4iGSIkXxwBcgCeL4/v74QLQs6yZAfAG8HzOZ6AvbxIf8CMCbn8/7+/pYoboampvB\n6Uz06JKO9IQJIYS4o3AYdu5Un7+g4ieeekoFsYo0YBhw9Kg6asjrVY+tWqWa7hctSuzYUpT0hIlZ\nS5e9+2Qj82I+Zp4Tnw9+9jNVgFmt8MQTqu0nHQowM8/LnOnqgh//GH7zG1WAFRbCCy/Ac88lpABL\nlzmRlTAhhEhz3d0q/0viJ9LQ8DB8+CGcPq2u3W51xuOGDRIANwekJ0wIIdKUYcDeveozWOIn0ozf\nDx4P7N+vJj8zE7Zvh61bISMj0aNLKdITJoQQ4nMCAXj3XThxQl3X16sFEKs0qaS2UEgFv7W2qr8E\nFotqun/wQam+E0BebmLW0mXvPtnIvJiPWebkyhX4u79TBVhWlrr78ZFH0rcAM8u8xJVhwPHj8MMf\nqqXPQABWrIA//mN48knTFWBpMSfISpgQQqSVEyfUecvT05CfD888I/ETKa+nB95/H/r61HVBgUq6\nX748seMS8esJ6+3t5Wtf+xpDQ0NYLBa++c1v8qd/+qeMjIzw7LPP0t3dTXl5OW+//Ta5ubkAfO97\n3+MnP/kJNpuNH/zgBzz66KNfHLD0hAkhxD27MX5i/Xq1AJIOdz+mrZERter16afq2uWChx6Cysr0\nXfZMgNvVLXErwi5fvszly5eprKzE5/NRXV3NO++8w//5P/+HvLw8XnrpJV577TVGR0d59dVXOXny\nJM8//zydnZ309fWxY8cOzpw5g/WGvyhShAkhxL3RdfjVr9RdkFYrPPYY1NbKzW8pa3JSNd13dqrq\nOyNDnTlVXy9VdwLcrm6JWym8ePFiKisrAXC5XKxZs4a+vj7effddXnjhBQBeeOEF3nnnHQB++9vf\n8txzz5GRkUF5eTkrVqygo6MjXsMTMZQue/fJRubFfBIxJ93d8KMfqf/XNHjxRairkwLseinzWgmF\n1FLn97+vbnuNRGDTJviTP1GN90lUgKXMnNzBnPSEdXV1cejQIerq6hgcHKSgoACAgoICBqOnsff3\n97Nly5aZ/6a4uJi+a/vXQggh7onET6QRw1Bbjh9+CKOj6rFly1Tf1+LFiR2buK24F2E+n4+nn36a\n73//+2ia9rl/ZrFYsNzm17Fb/bMXX3yR8vJyAHJzc6msrKS5uRn4rHqW67m9vsYs45HrZpqbm001\nHrlm5rF4P9/Wrc28+y689566/pf/spmHH4bWVnP9POQ6BtdXrtCs69DTQ0tXF8ybR/O///ewciUt\nHg+cOmWu8d7ldXMSv39d+3NXVxd3Etew1mAwyJe//GWeeOIJ/uzP/gyA1atX09LSwuLFixkYGODB\nBx/k1KlTvPrqqwC8/PLLADz++OO88sor1NXVfX7A0hMmhBC3dOUKvPWWCkLPyoKvfAXWrEn0qETM\njY6qMx6PH1fXTqfacqyqSuqm+9PnTrPzwE6CRpAMSwY7qnewasWqRA9rVhLSE2YYBn/0R39ERUXF\nTAEG8NRTT/Hmm28C8Oabb/KVr3xl5vH/+3//L9PT01y8eJGzZ89SW1sbr+GJGLq++hfmIfNiPvGe\nkxMn4G//VhVg+fnwjW9IAXY3kuq1MjWlth1/+ENVgNnt0NAAf/qnsHlz0hdgP/3kp5ybd45/PvfP\nXCm4wk8/+Smnz51O9NDiJm7bke3t7fz85z9nw4YNbNq0CVARFC+//DLPPPMMb7zxxkxEBUBFRQXP\nPPMMFRUV2O12Xn/99dtuVQohhFDCYfW5vHevupb4iRQUDqsjhjwemJhQj23YoI45mDcvsWOLkbd2\nvcWn2qeMXR5jzDeGHtDRVmp8dPCjpF8NuxU5O1IIIZKYrqvDt3t6JH4iJRmGOlz7ww/h6lX1WFmZ\nmuiiosSOLQYMw+Di2EU8XR7eeu8tpoqnsFvtLNGWUOwuJsOWQe7lXP7s//uzO38xk5KzI4UQIgV1\nd6sCzOdT8RPPPAMlJYkelYiZ/n744AO41uC9cKE6X2rVqqSvsg3D4PzoeTxdHnq9vQBkWbNYnLuY\nYncxdutn5UmmNXWXdJN381iYRlL1U6QRmRfzidWcGIaKg3rzTVWAlZfDv/23UoDdL9O9VsbH4R/+\nAX78Y1WAORzwxBPwrW/B6tVJXYAZhsHZq2d549Ab/Pzoz+n19pJjz+HhpQ/zP57+HxReKcRutdN1\nuAuAwNkAD1c9nNhBx9EdV8J8Ph85OTnYbDZOnz7N6dOneeKJJ8jIyJiL8QkhhLhOIKDOfjx5Ul3X\n16u2oCTuxxbXBAKwa5eqsEMhsNlgyxbVeJ+dnejRzYphGJy5egZPt4d+vR8AR4aDbSXbqCmqIcue\nBUCWLYuPDn7E8Mgw+UP5PPzgwynbDwZ30RNWVVXFrl27GB0dpb6+npqaGjIzM/nFL34xV2P8HOkJ\nE0KkK4mfSFGRCBw8CJ98An6/emzdOlVdz5+f2LHNkmEYnBo+hafbw2XfZQCcGU7qS+vZXLSZTFvq\nbjVeM6ueMMMwcDgcvPHGG3zrW9/ipZdeYuPGjTEfpBBCiFs7cUKtgE1Pq/iJZ59VLUIiiRkGnD2r\nmu6vXFGPlZSopvvi4sSObZYMw+DT4U/xdHkY9KuTcVyZLraXbqe6sJoMm+ymwV025u/Zs4df/OIX\nvPHGGwBEIpG4Dkokl5brEsCFeci8mM/9zInET8RfQl4rly+rpvsLF9T1/Pmq6X7NmqTu+YoYEU5e\nOUlrdytD/iEA3FlutpduZ9PiTXddfKXL+9cdi7C//uu/5nvf+x5f/epXWbt2LefPn+fBBx+ci7EJ\nIURauzF+4vHHoaYmqT+jha7Dxx/D4cNqJSw7G5qa1MTakzewIGJEOD50nNbuVoYnhgGYlzVPFV+F\nmz53t6P4jOSECSGECUn8RIqZnob2dti9G4JB1XRfU6MKsJycRI/uvkWMCMcGj9Ha3crVSZVjlpud\nS0NpA5WLK7FZbQkeYeLNqiess7OTP//zP6erq4tQKDTzBY8ePRrbUQohhJiJn9i5U/VrL10Kf/AH\n6mhAkYQiEbXq9cknahUM1JbjI4/AggWJHdsshCNhjg4epbW7ldGpUQDmZ8+nsayRDQUbpPi6S3dc\nCXvggQf4y7/8S9atW4f1unugy8vL4z22m5KVMPNJl737ZCPzYj53mpMb4ye2b4eHHpL4iXiL22vl\n/HnV9zWoGtNZsgQefVQl3iepcCTM4cuHaetpY2xqDICFOQtpLGtkfcF6rJbY/GVNpfevWa2ELVq0\niKeeeirmgxJCCPGZG+MnvvpVlcspktDQkCq+zp1T17m5Km5i3bqkbegLRUIcGjjErp5djAfGAchz\n5NFY1si6/HUxK77SzR1Xwj744APeeustduzYQWb0dhyLxcLv//7vz8kAbyQrYUKIVHP8OLz7rsRP\nJD2fT207Hjyo9pWzsqCxEerqkrbpPhQJcXDgILt6duENeAHId+bTWNZIxaIKKb7uwqxWwt58801O\nnz5NKBT63HZkooowIYRIFRI/kSKCQdXIt2uXqqSt1s+a7pO0mS8YDnJg4ADtPe3o06qXrcBZQFN5\nE2vy1mBJ0hU9s7njStiqVas4deqUaX7gshJmPqm0d59KZF7M5/o5uT5+wmZT+ZwSP5EY9/1aMQw4\nehQ++gi8apWIVatU031eXkzHOFemw9Ps79/P7t7d+KZ9ACx2LaaprInVeavnrBZIpfevWa2Ebdu2\njZMnT7J27dqYD0wIIdJRVxf86ldq98rthj/8Q4mfSDpdXfD++zAwoK4LC1XT/dKlCR3W/ZoOT9PR\n18Hu3t1MBCcAKNKKaCpr4oGFD5hmISbV3HElbPXq1Zw/f56lS5eSlaUO2ExkRIWshAkhkpXET6SA\n4WG1h3z6tLp2u1XT/YYNSbmMGQgF6OjrYM+lPTPF1xJtCc3lzaxYsEKKrxi4Xd1yxyKsq6vrpo9L\nRIUQQtw9iZ9Icn4/eDywf7+qoDMz1SRu3QoZyXcO4lRoin2X9rH30l4mQ5MAlLhLaCpvYvn85VJ8\nxdCsijCzkSLMfFJp7z6VyLyYx9AQvP027N/fwqpVzRI/YTK3fa2EQurOibY2VUlbLFBVBQ8+CC7X\nnI4zFiaDk+y9tJd9ffuYCk0BUDavjKbyJpbmLjVN8ZVK71+z6gkTQghx/66Pn8jNhW9+U+InkoJh\nqMnbuRPGVS4WK1eqpvv8/MSO7T5MBCdU8XVpH4FwAICluUtpKm+iPLc8sYNLY7ISJoQQcXBj/MSG\nDfDlL0v8RFLo6VFN93196rqgQDXdL1+e2HHdB/+0nz2X9tDR18F0eBqAZfOX0VTWRFlu8ib3JxNZ\nCRNCiDkk8RNJamREVc6ffqquXS7VuFdZmXTNe75pH7t7d9PZ10kwEgRgxYIVNJU1UTJPbsU1izsW\nYb/+9a95+eWXGRwcnKnkLBYL3muZKCLtpdLefSqReUmMG+MnnnkGiovVP5M5MaeW99+n2TCgs1Mt\nYWZkQH09bNuWdEuXekCnvbedA/0HZoqvBxY+QFNZE0vcSxI8uruXLq+VOxZhL730Er/73e9Ys2bN\nXIxHCCGSksRPJKFQSBVev/41FBWppcpNm1TTvdud6NHdE2/AS3tPOwcGDhCKhABYnbeaxrJGirSi\nBI9O3Mode8Lq6+tpb2+fq/HckfSECSHMRuInkoxhqMnauRNGR9Vjy5apvq/FixM7tns0PjXOrp5d\nHBw4SNgIA7Ambw1N5U0sdiXX95KqZtUTtnnzZp599lm+8pWvmOIAbyGEMJNr8RPDw+q8ZomfMLlL\nl1TTfW+vul60SBVfK1YkVdPe2NQYbd1tHL58mLARxoKFtYvW0ljWSIGrINHDE3fpjkXY+Pg4OTk5\nfPDBB597XIowcU267N0nG5mX+Dt+XK2ABYPqBrpnnrl9/ITMSQKNjqozHo8fV9dOp9p2rKqipbWV\n5pUrEzu+uzQ6OUpbjyq+IkYECxbW56+noayBfGfyRWfcSrq8Vu5YhP30pz+dg2EIIUTyCIfhgw9g\n3z51LfETJjY1Ba2tarLCYbDbVcr99u1q6TJJXJ24SltPG0cHj84UXxsLNtJQ1kCeIzkPCxe36Ql7\n7bXX+M53vsOf/MmffPE/slj4wQ9+EPfB3Yz0hAkhEknX1fZjb6+Kn3j8cdi8Oal2stJDOKyOGPJ4\nYEKdicjGjapZb968xI7tHgxPDNPa3cqxwWMYGFgtVjYUbKChtIGFDkn9TQb31RNWUVEBQHV19eeO\nMTAMwzTHGgghxFzq6lL5X37/F+MnhEkYhjpc+8MP4epV9Vh5uer7KkqeuwSv+K/Q2t3K8aHjM8XX\npsWbaChtYH7O/EQPT8SIJOaLWUuXvftkI/MSO4YBu3erlqLZxE/InMRZf7/aJ+7qUtcLF6pjhlat\nuu1SpZnmZdA3SGt3KyevnMTAwGaxsalwE9tLt5ObnZvo4c0ZM83JbElivhBC3KdAAN5557MQdYmf\nMKHxcVUhHz2qrh0OaG6G6mq1Z5wELvsu4+ny8Omw+otms9ioKqxie+l25mUnz/apuDeyEiaEELcw\nNARvvaV2tSR+woQCAdi1S6XkhkKq4NqyBRoaIDs70aO7K/16P54uD6evngbAbrVTXVhNfWk97qzk\nCowVNycrYUIIcY+OHYN33/0sfuLZZ2HBgkSPSgBqT/jAAWhpUQ16AOvWwY4dkJscW3Z93j483R7O\nXD0DQIY1g81Fm9lWsg0tS0vw6BLn9IUL7DxxgiCQAexYu5ZVy5Ylelhxc8cF9dOnT/Pwww+zdu1a\nAI4ePcr//J//M+4DE8mjpaUl0UMQNyHzcn/CYfinf1In2QSDKn7i3/yb2BRgMiezZBhw5gz8zd/A\ne++pAqykRE3QH/zBfRdgczkvveO9/Pzoz/nbg3/LmatnyLBmUF9Sz3/Y8h94bMVjaV+A/fTgQYbW\nrWOv18uVdev46cGDnL5wIdFDi5s7roR94xvf4C/+4i/4d//u3wGwfv16nnvuOf7zf/7PcR+cEELM\nJa9X3f0o8RMmdPmyarq/9oE8f75qul+zJikmqHusG0+3hwujavyZtkxql9SytXgrzkw5YBTgn44f\n58q6dfR7vVyenGSFYZBVXc1Hx4+n7GrYHYuwiYkJ6urqZq4tFgsZGRlxHZRILqlyB0uqkXm5Nxcv\nwq9+Fd/4CZmT++D1wscfw5EjaiUsJwcaG6GmRgWvxkC85sUwDLrHu2npaqFrrAuALFsWdcV1bCne\ngiPDEZfnTTZXpqfp0HU+HBvDPzkJwKKaGiYjETSbjekEjy+e7vg3eNGiRZw7d27m+le/+hWFhYVx\nHZQQQsyVa/ETO3eqPy9bBk8/fe/xEyLGpqehvV1NTjColiZra1UBlpOT6NHdlmEYXBy7iKfLQ/d4\nNwDZ9my2FG+hbkkdORnmHv9ciBgGZyYm2KfrXIwWXkYkQq7dzpKsLPIyMri2vpnKB1Hc8e7I8+fP\n881vfpPdu3czf/58li5dyi9+8QvKy8vnaIifJ3dHmk8q5bmkEpmXO7sxfqKhQR0nGK/4CZmTuxCJ\nwOHDavXL51OPVVSopvs43RkRq3kxDIPzo+fxdHno9aoDwnPsOar4Kq4j254cd2zG00Q4zEFdp1PX\nGQ+FAMi0WtnocpE7PMzvjh0jq7qarr17Kd+yhcCBA7xYVZXU25Gzujty+fLlfPTRR/j9fiKRCJqW\nvk2DQojUIfETJnT+vOr7GhxU18XFKum+tDSx47oDwzA4O3IWT5eHPr0PAEeGg63FW6ldUkuWPXnO\nqIyX/kCADq+X434/oWhBsjAjgxpNo9LlIttmg4ULycvI4KPjxxm+eJF8l4uHk7wAu5M7roSNjo7y\ns5/9jK6uLkLRqlXOjhRCJDOJnzCZoSFVfF1rfcnNVStfa9eauuneMAzOXD2Dp9tDv94PgDPDybaS\nbWwu2pz2xVcoEuHkxAQdXi+XAgFAfYavzMmhVtNYnpOTFscgzmol7Etf+hJbt25lw4YNWK1WOTtS\nCJG0wmH1Wb9vn7reuBG+/GWQe40SxOeDTz6BgwdVQ15Wlur5qquLWdN9PBiGwanhU3i6PVz2XQbA\nlemaKb4ybancxXRn3lCI/brOAV3HHw4DkGOzscnlokbTmC8vuBl3XAmrqqri4MGDczWeO5KVMPOR\nPhdzknn5PDPET8icRAWDKuV+1y7VgG+1qsloblZHDs2xu50XwzA4eeUkrd2tDPrVlqmWqVFfWk91\nYTUZtvQtLgzDoHtqig5d59TEBJHo5/TizExq3W7WO51k3EOzZSq9Vma1Evb888/z4x//mCeffJKs\nrM+WVhfI2r0QIknMRfyEuAuGoaImPv5YVcWgDtd+5BHIy0vs2G4jYkQ4eeUkni4PVyauAODOcrO9\ndDtVhVXYreZdtYu36UiEoz4fHbrO0LQKk7BaLKxzOql1uynJypLds9u440rYD3/4Q/7Tf/pP5Obm\nYo1WsRaLhQsJSrCVlTAhxN2S+AkTuXgR3n9fha4CFBbCY49Bgu60vxsRI8LxoeO0drcyPDEMwLys\neTSUNVC5uDKti6+rwSCdXi+HfT6mIhEAXDYbmzWNak1DM/F28ly7Xd1yxyJs6dKldHZ2kmeS31Kk\nCBNC3I2pKfjtb+cufkLcwvCwasQ7o85IxO2Ghx9W50GZdIUkYkQ4OniUtu42rk5eBSA3O5eGUlV8\n2ay2BI8wMQzD4NzkJPu8Xs5Fs70ASrOzqdU01jid2Ew6p4k0q+3IlStXkmPyYDyRWKm0d59K0nle\nro+fyM5W8ROrViV6VGk2J36/OmD7wAGV/ZWZCdu3w9atprsT4tq8hCNhjgweoa27jdGpUQAW5Cyg\nobSBDQUb0rb4mgyHORzdchwNBgGwWyxsiDbaF2bF/i7QdHmt3LEIczgcVFZW8uCDD870hCUyokII\nIW5H4icSLBSCvXuhrU2l4VosnzXdu1yJHt1NhSNhDvQfoK2njbGpMQAW5iyksayR9QXrsVrSc/n0\nciBAp65z1O8nGN1yzLXbqXG72eRy4bClZ1EaS3fcjvzpT3/6xf/IYuGFF16I15huS7YjhRA3Ew6r\nlqOODnUt8RNzzDDg+HHVgDc+rh5buVI13efnJ3ZstxCKhDg0cIhdPbsYD6gx5znyaCprYm3+2rQs\nvsKGwalotlf31NTM48tzcqh1u1mZk4NVthzvyax6wsxGijAhxI1ujJ944gmorjZty1Hq6e5WfV99\nKi2eggKVdL98eWLHdQuhSIgD/Qdo723HG1B3aeY782ksa6RiUUVaFl++UIgDPh/7dR09GsyeZbVS\nGd1yzMtM7+yz2bivnrA//MM/5Je//CXr16+/6Rc8evRo7EYoklq67N0nm3SZl2SKn0i5Obl6Va18\nXbv7QdPgoYfUMqQJ74AIhoMcGDhAe087+rQOQIGzgJy+HF5oeiHtohQMw+BSIECHrnPS7yccLRQW\nZWZSq2lscLnIStA8ptxr5RZuWYR9//vfB+B3v/vdFyq4dPuLKoQwH4mfSKCJCWhtVXu/kYja862v\nh23bVAO+yUyHp9nfv5/2nnb8QT8Aha5CmsqbWLVwFR6/J60+14KRCMf9fjp0nYHrjhNa43RSq2mU\nZ2en1c8jke64Hfmd73yH11577Y6PzRXZjhRCTE3BO+/AqVPqurFR9X2bcPEltYRCqvBqbVWTc7EH\nDwAAIABJREFUYLFAZaVa/dK0RI/uCwKhAJ39nezu3c1EcAKAIq2IprImHlj4QNoVGmPBIJ26zkGf\nj8nocUIOm41qTWOzpjFPsr3iYlY9YZs2beLQoUOfe2z9+vUcO3YsdiO8B1KECZHeBgfh7bfNFz+R\n0gwDTp5Uy46jKrqB5ctV31dBQWLHdhOBUICOvg529+5mMqTyrIrdxTSVNbFiwYq0Kr4Mw+DC1BQd\nXi9nJidnPj+LsrKoc7tZ63Bgl99e4uq+esL+5m/+htdff53z589/ri9M13Xq6+tjP0qRtNJl7z7Z\npOK8HD0K//iPyRs/kZRz0turmu57e9X1okWq+FqxwnR3PkyFpth3aR97Lu1hKqTu7Ctxl9Bc3syy\n+ctuWXwl5bzcQSAS4YjPR4fXy3A028tmsbDO5aLW7WZJHLK9YikV5+RmblmEPf/88zzxxBO8/PLL\nvPbaazNVnKZpLFy48K6++Ne//nXee+898vPzZ1bO/tt/+2/83d/9HYsWLQLgz//8z3niiScA+N73\nvsdPfvITbDYbP/jBD3j00Udn9c0JIVKDxE8kwOioWvk6cUJdO53qyIGqKtPt+04GJ9l7aS/7+vbN\nFF9l88poLm+mPLc8rVa+rkxP06nrHPb5mI5me7nt9pnjhJyS7WUqcY2oaGtrw+Vy8bWvfW2mCHvl\nlVfQNI1vf/vbn/t3T548yfPPP09nZyd9fX3s2LGDM2fOzJxXOTNg2Y4UIq14vWr78dIliZ+YE5OT\nKmh13z5V/drtquG+vh5MtnoyEZxgT+8eOvo6CIRVg/nS3KU0lTdRnlue2MHNoYhhcGZigg5d58J1\nxwmVZ2dT63az2uGQbK8EmtWxRbPR0NBAV1fXFx6/2WB++9vf8txzz5GRkUF5eTkrVqygo6ODLVu2\nxHOIQggTuz5+Yt48FT+xZEmiR5WiwmHYv18dNXTtg3zjRtV0P29eQod2I/+0nz2XVPE1HZ4GYPn8\n5TSVN1E6rzTBo5s7E+EwB3WdTl1nPJrtlWG1stHppNbtJt+Ed6qKz0vIrRD/+3//b372s5+xefNm\n/uqv/orc3Fz6+/s/V3AVFxfTdy34T5hauuzdJ5tknhfDgPZ2+Oijz+In/uAPwOFI9Mhmx5RzYhjq\nNtOdO9XdDgDl5fDYY1BYmNCh3cg37WN37246+zoJRlSf04oFK2gqa6JkXsl9f11Tzstt9AcCdHi9\nHPf7CUUXNRZmZFCjaVS6XGSnwJZjss3J/ZrzIuyP//iP+a//9b8C8F/+y3/hP/7H/8gbb7xx03/3\nVvv4L774IuXl5QDk5uZSWVk5M1ktLS0Acj2H14cPHzbVeOQ6ua+np2FkpJlTp6Crq4UNG+Bf/atm\nrFZzjG8214cPHzbVeFp+9Svo7KQ5J0ddj4zA5s00/+t/DRZL4scXva7eWk17bzu/fO+XhI0w5ZXl\nPLDwATJ6MljEIko2lMzq619jlu/3ZtehSIQ333+fU34/zupqALr27aM4M5MXH3+c5Tk5eDwe9ppk\nvOl8fe3PN9sJvFHcjy3q6uriySefvGmkxfX/7NVXXwXg5ZdfBuDxxx/nlVdeoa6u7vMDlp4wIVLW\n4CC89RaMjEj8RFyNj6tlxmsnnzgc0Nysmu1MtIriDXjZ1bOLgwMHCUXUdtvqvNU0ljVSpBUleHRz\nwxsKsV/XOaDr+KPZXtlWK1XRbK8FcneK6SWsJ+xmBgYGKIwucf/mN7+Zib946qmneP755/n2t79N\nX18fZ8+epba2dq6HJ4RIkOvjJxYvVv1fyRQ/kRQCAdV0v3evCl612WDLFmhoUFWvSYxPjc8UX2FD\nFR4ViypoLGtksWtxgkcXf4Zh0D01RYeuc2pigkj0A3xxZia1bjfrnU4yrNYEj1LEQlyLsOeeew6P\nx8Pw8DAlJSW88sortES3rywWC0uXLuVHP/oRABUVFTzzzDNUVFRgt9t5/fXX0+q24mTW0pIee/fJ\nJlnm5cb4icpK+L3fS834iYTNSSQCBw5AS4u6ywFg3TrYsQNyc+d+PLcwNjVGW3cbhy8fJmyEsWBh\n7aK1NJY1UuCKXyisWV4r05EIx/x+OrxeBqfVDQdWi4V10Ub7kqystPlcNMucxFtci7C///u//8Jj\nX//612/573/3u9/lu9/9bjyHJIQwEYmfiDPDgLNnVdjq8LB6rLRUha2a6JTzkckR2rrbODJ4hIgR\nwYKF9fnraSxrZJFzUaKHF3cj0eOEDuk6U9FsL5fNNpPtpclxQikr7j1hsSY9YUKkBomfiLPLl9US\n48WL6nrBAnjkEVi92jRV7tWJq7T1tHF08OhM8bWhYAMNZQ3kOfISPby4MgyDc5OTdOg6ZycmZh4v\nyc6mVtOocDqxmWSexOyYqidMCJHeboyfWL4cnn46+eMnTMPrhY8/hiNH1A84JweamqCmxjRN91f8\nV2jraePY4DEMDKwWK5sWb6KhrIEFOandCDgZDnPY56NT1xmJHidkt1hY73JRq2kUmiwQV8SXFGFi\n1tJl7z7ZmHFepqbgnXdULBVAY6O6KS9deozjOifT06q63b1b3d1gs0FtrfohRyMoEm3IP0Rrdysn\nhk58vvgqbWB+zvyEjWsuXiuD09N0eL0c9fsJRrccc+12atxuNrlcOExSIJuFGd+/4kGKMCHEnLgx\nfuL3fx8eeCDRo0oBkQgcPqxWv3w+9VhFhWq6N8ntpYO+QTzdHk5eOQmAzWJjU+EmtpduJzfbPDcG\nxFrYMDg1MUGH10v31NTM48tzcqh1u1mZkyPHCaU56QkTQsTdjfETzz4L8xO38JE6zp1TTfdDQ+q6\nuFg13Zea4+ieAX2A1u5WPh3+FFDFV3VRNfUl9czLNtdRSLHkC4U44POxX9fRo8cJZVmtVLpc1Gga\neZmZCR6hmEvSEyaESIhwGP75n6GzU12ncvzEnBochA8/VEUYqJiJHTtg7VpTNN336/14ujycvnoa\nALvVTnVhNfWl9biz3AkeXXwYhsGlQIAOXeek3084+qG7KDOTWk1jg8tFVrrsu4u7JkWYmLV02btP\nNomeF4mf+KJZz4nPp7YdDx1STffZ2Spota4OTBBjcMl7CU+Xh7MjZwHIsGawuWgz20q2oWVpCR7d\nrc1mXoKRCCf8fvbpOgOBAKBWPtY4ndRqGuXZ2WmT7RVLiX7/miuJf9UKIVLOhQsqfmJiQuInYiIY\nVA337e2qAd9qVXc7Njeb4rbS3vFePN0ezo2olbkMawa1S2rZVrINZ6YzwaOLj7FgkP26zkGfj4no\ncUIOm43q6HFC80xQFAvzk54wIUTMGAbs2qUWayR+IgYMQ0VNfPQR6Lp6bPVqtfWYl/gcre6xbjzd\nHi6MXgAg05ZJ3ZI6thRvScniyzAMLk5N0eH1cnpycuazqCgri1pNY53TiV22HMUNpCdMCBF3U1Pw\nm9/AadUGlHbxEzF38aIKW718WV0XFsJjj0F5eUKHZRgGXWNdeLo9dI11AZBly6KuWBVfjozUq7gD\nkQhHfD46vF6Go9leNouFtdFsryVpdJyQiC0pwsSspcvefbKZy3mR+Im7c1dzcuWKaro/c0Zdu91q\n5Wv9+oQ21BmGwcWxi3i6PHSPdwOQbc9mS/EW6pbUkZNhjiyy+3GreRmenqZD1zns8zEdzfZy2+1s\n1jSqXC5csuUYN+nyuSJ/g4QQsyLxEzHi96sDtg8cUNlfmZmq6X7LloTeTmoYBudHz+Pp8tDr7QUg\nx57D1pKt1C6pJduenbCxxUPEMDgzMUGHrnNhcnLm8fLsbGrdblY7HJLtJWJGesKEEPclFFK7ZRI/\nMUvBIOzbB21tEAio1a7qarWX63IlbFiGYXB25CyeLg99eh8AjgwH20q2UVNUQ5Y9tY7XmQiHOajr\ndOo649FsrwyrlY1OJzVuNwWS7SXuk/SECSFianwcfvnLz+InvvQlqKpK7/iJe2YYcOyYarofH1eP\nrVypwlYXLUrgsAxOXz2Np8vDgG8AAGeGUxVfS2rItKVWMdIfCNDh9XLc7ycU/aBckJFBraZR6XKR\nLccJiTiSIkzMWrrs3SebeM2LxE/cv5k56e5WSfd9aoWJxYtV8bVsWcLGZhgGp4ZP4en2cNmnbgZw\nZbqoL6mnuqg6pYqvsGFwwu+nw+vlUiBA1969LN26lQccDmo1jeU5OdJon2Dp8rkiRZgQ4q5I/EQM\njI+rOxg+Vcf4oGnw0EOwcWPCbiM1DIOTV07S2t3KoH9QDStTY3vpdqoKq8iwpc7+sjcU4oCuc0DX\n8UWzvbKtVtY6nfzRkiUskL10McekJ0wIcUc3xk80Nan/SfzEXZqYAI9HNdBFIqpxbvt22LpVNeAn\nQMSIcGLoBK3drVyZuAKAO8s9U3zZranxO7phGPREtxw/nZggEv38KMjMpNbtZoPTSYb8RRZxJD1h\nQoj7JvETsxAKQUcHtLaqStZiUc1zDz6oVsESIGJEOD50nNbuVoYnhgGYlzWPhrIGKhdXpkzxNR2J\ncCy65Tg4PQ2A1WJhrdNJrdtNqWR7CRNIjVebSKh02btPNrGYlyNH4He/k/iJe2YYcPIk7NwJo6Pq\nseXLaXE6aX7qqYQMKRwJc2zoGK3drYxMjgCQm51LY1kjGws2YrOmRgP6SDBIp65zSNeZimZ7uaLH\nCVVrGu6bZHvJe5j5pMucSBEmhPiCG+MnNm1Sd0BKy8xd6O1VP7xLl9R1fr5qul++XG1JzrFwJMyR\nwSO0dbcxOqUKwgU5C2gobWBDwYaUKL4Mw+Dc5CQdus65644TKsnOplbTqHA6scmqlzAh6QkTQnzO\n+Di8/ba6cU/iJ+7B6Kha+TpxQl07narpftOmhDTPhSIhDl8+zK6eXYxNjQGwMGchjWWNrC9Yj9WS\n/H1Qk+Ewh30+OnWdkehxQnaLhfXR44QKs1Iry0wkJ+kJE0LclRvjJ559FoqKEj0qk5ucVEGr+/ZB\nOAx2O2zbBvX1kIAiIBQJcWjgELt6djEeUPljeY48msqaWJu/NiWKr8HpaTq8Xo76/QSjW465djs1\nbjebXC4cku0lkoQUYWLW0mXvPtncy7zcGD+xYoVqwJf4idsIh9V+rcejCjFQURMPP6zOe7yJeL5W\nguEgBwcOsqtnF/q0DkC+M5+msibWLFqT9MVX2DA4NTFBh9dL99TUzOPLc3KodbtZmZNz38cJyXuY\n+aTLnEgRJkSak/iJe2QYcOqUOmR7RDW4U14Ojz0GhYVzPpxgOMj+/v2097bjm/YBUOAsoKm8iTV5\na5L+DkBfKMRBn4/9uo43epxQltVKpctFjaaRJ8cJiSQmPWFCpLHLl1X/17X4iaefVifniFvo61NJ\n993d6jovDx55RGV2zHGxMx2eprOvk929u/EH/QAUugppKm9i1cJVSV18GYZBXyBAh65zwu8nHH3P\nX5SZSa2mscHlIkt+SxBJQnrChBBfIPET92BsTJ3xeOyYunY41AHb1dXq7oU5FAgF6OxXxddEcAKA\nIq2I5vJmVi5YmdTFVzASUccJ6Tr9gQCgPsBWOxzUut0szc5O6u9PiBtJESZmLV327pPNreYlFIJ/\n/mfYv19dS/zEbUxNqWa5vXvVD85uhy1bVNp9dvY9f7nZvFamQlN09HWwp3cPkyHVg1bsLqaprIkV\nC1YkdXEyFgyyX9c56PMxET1OyGGzUeVysVnTyI3zX055DzOfdJkTKcKESCPXx0/Y7Z/FT4gbRCJw\n4AC0tIBfbfWxfr1qus/NndOhTIWm2HdpH3su7WEqpBrSS+eV0lTWxLL5y5K2+DIMg4tTU3R4vZy+\nLturKCuLWk1jndOJXbYcRYqTnjAh0sT18RO5ufDMMxI/8QWGAWfPqr6vYXWkD6Wlqul+yZI5Hcpk\ncJK9l/ay99JeAmG1NVeeW05TWRPlueVJW3wFIhGO+Hx0eL0MR7O9bNeOE9I0lshxQiLFSE+YEGlM\n4ifu0sCAKr4uXlTXCxaopvvVq+e06X4iOMGe3j109HXMFF9Lc5fSVK6Kr2Q1PD1Nh65zxOcjEM32\nctvtbNY0qlwuXDc5TkiIVCd/68WspcvefbJpaWlhy5ZmiZ+4E69XVahHjqgqNSdH/ZBqamLedH+7\n14p/2s/u3t109ncyHVYHTi+fv5ym8iZK55XGdBxzJWIYnJmYoEPXuXAtSw0oz86m1u1mlcNhiuOE\n5D3MfNJlTqQIEyJFjYzAj36kTtPJyVGrXxI/cZ1AANrbYc8edYuozQa1tdDYqH5gc8Q37VPFV18n\nwYjanlu5YCVN5U0Uu4vnbByxNBEOc8jno9PrZSya7ZVhtbLR6aTG7aZAsr2EAKQnTIiUdOQI/OM/\nqhv6CgtV/5fET0RFInDoEHzyCfhUuCkVFbBjh9qCnCN6QKe9t539/fsJRVShsmrhKhrLGlnintv+\ns1gZiGZ7HfP5CEXfpxdkZFCraVS6XGTLcUIiDUlPmBBpQuIn7uDcOdX3NTSkrouLVdN9ScmcDcEb\n8LKrZxcHBw7OFF+r81bTVNZEoTb3ifuzFTYMTkazvXqjxwlZLBZWOhzUahorcnKk0V6IW5AiTMxa\nuuzdm92N8RP5+S38i3/RnOhhmcPgoCq+zp9X17m5auVr7do5a7ofnxrn9V++Tqg0RNhQWVgViypo\nLGtksWvxnIwhlryhEAd0nQO6ji+a7ZVttbJJ06jRNBYkUeUv72Hmky5zIkWYECng/Hn49a8/Hz9x\n5kyiR2UCuq62HQ8dUk332dmq56u2VlWqc2B0cpRdPbs4fPkw56+eZ2nJUtblr6OxrJF8Z/6cjCFW\nDMOgJxCgw+vl04kJItEtloLMTGrdbtY7nWTKXR9C3DXpCRMiiRkGtLWpOkPiJ64zPa0a7tvb1Z+t\nVnW3Y1PTnP1wRiZHaOtu48jgESJGBAsW1hesp6G0gUXORXMyhliZjkQ45vfT4fUyOK3u3LRaLKyJ\nHidUKtleQtyS9IQJkYImJ+Gdd1T8hMWijjJsbEzz+IlIBI4eVec86rp6bPVqlfe1cOGcDOHqxFVa\nu1s5NnRspvjaWLCRhrIG8hx5czKGWBkJBunUdQ7pOlPRbC+nzcZmTaNa03BLtpcQsyKvIDFr6bJ3\nbyaXL8Nbb90+fiLt5uXCBdX3dfmyui4qgkcfhfLyOXn6K/4rtPW0cWzwGAYGVouVTYs30VDWwIIc\ndddlMsyJYRicm5ykQ9c5d91xQiXZ2dRqGmscjpQ7TigZ5iXdpMucSBEmRJI5fBh+9zuJn5hx5Qp8\n+OFnTXDz5qkzHtevn5Om+yH/EK3drZwYOvH54qu0gfk5yTMxU9eyvXSdkehxQnaLhfXRRvuirKwE\nj1CI1CM9YUIkiRvjJ6qqVPxE2u4I+f3qgO0DB9Q2ZFYWbN8OW7bMSSbHoG8QT7eHk1dOAmCz2NhU\nuIntpdvJzZ7bQ75nY3B6mk6vlyN+P8HolmOu3U6N280mlwuHZHsJMSvSEyZEkrsxfuJLX1JFWFoK\nBmHvXnUgZiDwWdN9czM4nXF/+gF9AE+3h1PDpwBVfFUXVVNfUs+87Hlxf/5YCBsGpycm6PB66Ypm\newEsy8mhVtN4wOHAKo32QsSdFGFi1tJl7z5RbhY/UVR05/8u5ebFMODYMdV0Pz6uHnvgAdV0vyj+\ndxv2efto7W7l9FV1EKfdamdz0Wa2lWzDneW+q6+R6DnxhUIc9PnYr+t4o8cJZVqtVLpc1Ggai9L0\nOKFEz4v4onSZEynChDCpm8VPPP30nB5raB7d3fD++9Dfr64XL1ZN98uWxf2pL3kv4enycHbkLAAZ\n1gw2F22mvrQeV6Yr7s8/W4Zh0Bc9TuiE3084ui2Sl5FBrdvNRpeLrBRrtBciWUhPmBAmNDkJv/mN\n6jW3WFS8VVPTnIW7m8fVq6rp/pTa+kPTVNP9hg1xz+LoGe/B0+Xh/KhK2c+0ZVJTVMO2km04M+O/\n7TlboUiE49HjhPoDAUC9f67KyaHW7WZpdrZkewkxB6QnTIgkcjfxEylvYgI8HujsVE33mZlQXw9b\nt6o/x1H3WDctXS1cHLsIqOKrbkkdW0u24sgwfwruWDDIfl3noM/HRPQ4IYfNRpXLxWZNIzeJjhMS\nItVJESZmLV327ufCjfETzz6r+sDuR1LOSygEHR3Q2gpTU2rpr6oKHnxQrYLFiWEYdI114en20DXW\nBUCWLYstxVvYUryFnIzY7AHHa04Mw+Di1BQdXi+nr8v2KszKok7TWOt0kiFbjreUlK+VFJcucyJF\nmBAmEArBP/2TSluANIyfMAw4cQJ27oSxMfXY8uWq76ugII5Pa3Bh9AKebg894z0AZNuz2VK8hbol\ndTErvuIlEIlwJJrtdSV6nJDNYmGty0WtprFEjhMSwtSkJ0yIBEv7+IneXtV0f+mSus7PV8XXihVx\ne0rDMDg/eh5Pl4deby8AOfYctpZspXZJLdn27Lg9dywMT0/Tqesc9vkIRLO9NLudGk2jyuXClTbV\nuxDmJz1hQpjU/cZPpISRERU3ceKEuna51Lbjpk1xa7o3DIOzI2fxdHno0/sAcGQ42FayjZqiGrLs\n5k2FjxgGZycn6fB6OT85OfN4WXY2dW43qxwObLLqJURSkSJMzFq67N3HkmGotqeWFvXnlStVA34s\n4ydMOy+Tk+qb7+iAcFil22/dqhrv43Q0jmEYnL56Gk+XhwHfAADODKcqvpbUkGmbm3ys+5mTiWvH\nCXm9jEWzvTKsVjY4ndS63RSkabZXLJn2tZLG0mVOpAgTYo7dGD/R3Jwm8RPhsLrb0eNRPwSLBSor\n4aGHwH13Yaf3yjAMPh3+lNbuVi771MHerkwX9SX1bC7aTIbNvHcKDkSzvY75fISiWxkLMjKo0TQq\nXS5y5DghIZKe9IQJMYdujJ94+um4tj6Zg2GonK8PP1RbkABLl6q+r8LCuDxlxIjw6ZVP8XR7GPIP\nAaBlamwv3U5VYZVpi6+wYXAymu3Ve91xQisdDmo1jRU5OdJoL0SSkZ4wIUzg+viJoiLV/3W/8RNJ\no68PPvhAJd4D5OWp4mvlyrgs/UWMCCeGTtDa3cqViSsAuLPcNJQ2sKlwE3arOd/y9FCI/brOAV3H\nF832yrZa2aRp1GgaCyTbS4iUZM53JJFU0mXv/n4lKn4iofMyNqaa7o8dU9cOh2q6r6qCOGyjRYwI\nxwaP0drdytXJqwDMy5pHQ1kDlYsrTVN8XT8nhmHQEwjQ4fXy6cQEkehvygWZmdS63ax3OsmUbK85\nIe9h5pMucxLXd6avf/3rvPfee+Tn53Ms+mY8MjLCs88+S3d3N+Xl5bz99tvkRpcDvve97/GTn/wE\nm83GD37wAx599NF4Dk+IuBsbU/ET/f2q6Pq931M3/6WsqSnYtQv27lXVp90OW7bA9u2QHfvYh3Ak\nzLEhVXyNTKqtzvnZ82koa2BjwUZsVvP1TU1HIhzz++nwehmMZntZLRbWRhvtSyXbS4i0EdeesLa2\nNlwuF1/72tdmirCXXnqJvLw8XnrpJV577TVGR0d59dVXOXnyJM8//zydnZ309fWxY8cOzpw5g/WG\n3wSlJ0wki3PnVPzE5KTadnz22bi1QCVeOKyW+lpaVN4GwPr16pzHOOy5hiNhjgweoa27jdGpUQAW\n5CygsayR9fnrTVl8jQSDdOo6h3SdqWi2l9NmY7OmUa1puCXbS4iUlLCesIaGBrq6uj732LvvvovH\n4wHghRdeoLm5mVdffZXf/va3PPfcc2RkZFBeXs6KFSvo6Ohgy5Yt8RyiEDE3F/ETpmEY6jbPDz+E\n4WH1WGkpPPYYLFkS86cLRUIcvnyYXT27GJtSyfp5jjwayxpZl78Oq8Vc23eGYXB+cpJ9us65644T\nKs7Kos7tZo3DgV22HIVIW3P+q9fg4CAF0WNICgoKGBwcBKC/v/9zBVdxcTF9fX1zPTxxH9Jl7/5u\n3Bg/8eCD0NiYmPiJuM/LwIBqur+oDrpmwQJ45BFYvTrm33AoEuLgwEF29ezCG/ACsMixiMayRtbm\nrzVd8TUVDnPY56ND1xkJBgGwWyxw5Ahff+IJiuKUhybuj7yHmU+6zElC178tFsttex9u9c9efPFF\nysvLAcjNzaWysnJmslpaWgDkeg6vDx8+bKrxJOp6YAD+1/9qweeDNWuaefppuHSpBY/HHOOL2bXf\nT/P0NBw9SsvFi5CZSfPXvw41NbS0tcHgYMyeb+dHOzkzcobJJZPo0zpdh7vIzc7lG7//DdYsWkOr\np5XWT1tN8/P5hw8/5PTEBJHKSoKRCF179+K02Xju0Uep0jR+/M47nNmzhyKTjFeu1fU1ZhmPXCf3\n9bU/37gTeDNxzwnr6uriySefnOkJW716NS0tLSxevJiBgQEefPBBTp06xauvvgrAyy+/DMDjjz/O\nK6+8Ql1d3ecHLD1hwoQOHYL33kvx+IlAANrbYc8eCAbVXY51ddDQEPO91mA4yP7+/bT3tuOb9gFQ\n4CygqbyJNXlrTNW4HjYMTk9M0OH10nVdtteynBxqNY0HHA6sJhqvEGJumSon7KmnnuLNN9/kO9/5\nDm+++SZf+cpXZh5//vnn+fa3v01fXx9nz56ltrZ2rocnxD25MX6iuhqeeCL+8RNzKhJRVeYnn4BP\nFUSsXQs7dsD8+TF9qunwNJ19nezu3Y0/6Aeg0FVIU3kTqxauMlXx5Q+HOaDr7Nd1vNHjhDKtVipd\nLmo0jUWZmQkeoRDC7OL6UfHcc8/h8XgYHh6mpKSE//7f/zsvv/wyzzzzDG+88cZMRAVARUUFzzzz\nDBUVFdjtdl5//XVTveGKW2tpSY+9+xuZPX4iJvNy7pzq+xpSqfMUF6um+5KSWY/veoFQgM5+VXxN\nBNXdlUu0JTSVN7FywUrTvBcYhkFf9DihE34/4ehvt3kZGdS63Wx0uciyWm/536fra8XsZF7MJ13m\nJK5F2N///d/f9PGdO3fe9PHvfve7fPe7343nkISIiZSPnxgcVMXX+fPqev58tfJVURHRw9evAAAg\nAElEQVTTpvup0BQdfR3s6d3DZGgSgGJ3Mc3lzSyfv9w0xVcoEuF49Dih/kAAUFsMqx0Oat1ulmZn\nm2asQojkIWdHCnEPUj5+QtfVtuOhQ+obzM5Wt3fW1sZ0j3UyOMm+vn3svbSXqZDqoyqdV0pTWRPL\n5i8zTUEzFgyyX9c56PMxET1OKMdmo9rlYrOmkSvHCQkh7sBUPWFCJKvJSfiHf4CzZxMfPxFz09Oq\n4b69Xf3ZalWFV1OTOnIoRiaCE+y9tJd9l/YRCKsVpfLccprKmijPLTdF8WUYBl1TU+zzejl9XbZX\nYVYWdZrGWqeTjNtsOQohxN2SIkzMWjrs3Q8MwFtvqT6wnBx4+mlYsSLRo7q9u5qXSASOHIGPP1ar\nYABr1qitx4ULYzaWieAEe3r3sK9vH9NhdVTPsvnLaCxrpDy3PGbPMxuBSISj0WyvK9HjhGwWCxUu\nF7WaRnEMjhNKh9dKMpJ5MZ90mRMpwoS4g5SNn7hwQfV9Xb6srouKVNN9WVnMnsI/7Wd37246+ztn\niq/l85fTVN5E6bzSmD3PbAxPT9Op6xz2+QhEjxPS7HZ1nJDLhSulbnUVQpiJ9IQJcQspGz9x5Yo6\nZujMGXU9b54643H9+pjtrfqmfbT3tLO/fz/BiEqMX7lgJU3lTRS7i2PyHLMRMQzOTk7S4fVyfnJy\n5vGy7Gxq3W5WOxzYTLA1KoRIftITJsQ9Mnv8xH3x+dQdBQcPqm3IrCwVtFpXBzFqMNcDOu29qvgK\nRVR21qqFq2gqb6JIK4rJc8zGRDjMIZ+PTq+XsWi2V4bVygank1q3mwLJ9hJCzCEpwsSspdre/fXx\nE/Pnq+3HZIyfmJmXYBD27oVdu1TqvdUKNTXQ3AxOZ0yeyxvwsqtnFwcHDs4UX2vy1tBY1kihlvgf\n3kA02+uYz0co+hvp/IwMajWNSpeLHJttTsaRaq+VVCHzYj7pMidShAkRlXLxE4YBR4/CRx/B+Lh6\n7IEH1CHbixbF5CnGpsbY1bOLQwOHCBsqwqFiUQWNZY0sdi2OyXPcr7BhcDKa7dV73XFCKx0OajWN\nFTk5prgbUwiRvqQnTAi+GD/R3Jzk8RNdXarpvr9fXS9eDI8+CsuWxeTLj06O0tbTxuHLh4kYESxY\nWJu/lsayRvKd+TF5jvulh0Ls13UO6Dq+aLZXttXKJk1js6axULK9hBBzSHrChLiNZIyfuKWrV1XT\n/alT6lrTVNP9hg1qG3KWRiZHaOtu48jgkZnia0PBBhpKG1jkjM3q2v0wDIPeQIAOr5eTExNEom94\n+ZmZ1LndrHc6yZRsLyGEyUgRJmYtmffuUyZ+YmICPB7o7FRN95mZtDgcNH/rWxCDZvOrE1dp7W7l\n2NAxIkYEq8VK5eJKGkobWOiIXZ7YvQpGIhzz++nwerkczfayWixUOJ3UahplJjtOKJlfK6lM5sV8\n0mVOpAgTaSkUgv/3/9SNgpDE8ROhEOzbB21tMDWl9k+rqlSc/4EDsy7Arviv0NrdyvGh4xgYWC1W\nNi3eRENZAwtyFsTom7h3o8EgnbrOQV1nKprt5bTZqI5uObqTbiKFEOlIesJE2hkbU9uPAwOq6Pry\nl6GyMtGjukeGASdOwM6d6hsCtYf6yCNQUDDrLz/kH6K1u5UTQycwMLBZbFQurmR76Xbm58yf9de/\nH4ZhcH5ykg5d5+x1xwkVZ2VR63ZT4XBgly1HIYTJSE+YEFE3xk88+6zqWU8qvb3w/vtw6ZK6zs9X\nTfcxaGS77LtMa3crJ6+cBMBmsVFVWEV9aT252YnZp50Khzns89Gp61wNquBXu8XCOpeLWreboqys\nhIxLCCFmS4owMWvJsHdvGKplyuNRf37gAfjqV5MsfmJkRK18nVQFEi4XPPSQWsa7yQrQvczLgD6A\np9vDqWHV0G+32qkqrGJ76XbcWe5YfQf3ZGh6mg6vl6N+P9PRLcd5djs1mkaVpuGYo2yvWEqG10o6\nknkxn3SZEynCRMq7MX7ioYdUULyJ+rVvb3JSBZh1dEA4rNLtt22D+vpZ93z1efvwdHs4c1UdYWS3\n2tlctJn6knq0LC0Wo78nEcPg1MQEHV4vXddley3LyaFW03jA4cCaNBMnhBC3Jz1hIqVdHz/hcKj4\nieXLEz2quxQOq7sdPR5ViFkssHGjqiLds1uduuS9hKfLw9mRswBkWDOoWVLDtpJtuDJdsRj9PfGH\nwxzQdfbrOt7ocUKZViuVLhc1msYiOU5ICJGkpCdMpKWDB9UdkEkXP2EY8OmnautxZEQ9tnSp6vua\n5flJPeM9eLo8nB89D0CmLZOaIlV8OTNjc4TRveiLZnsd9/sJR9+k8jIyqHW72ehykSWN9kKIFCZF\nmJg1s+3d3xg/sXkzPP54ksRP9PWppvueHnWdl6eKr5Ur73n/9Pp56RrrwtPl4eLYRQCybFnULqll\na8lWHBmOWH4HdxSKRDgR3XLsCwQA9ZviKoeDOrebpSbL9ools71WhCLzYj7pMifJ8LEkxF0bHYW3\n307C+ImxMbXydfy4unY61dlJVVVwnw3ohmFwcfQiLV0tdI93A6r42lK8hS3FW8jJmNu7EsavO05o\nInqcUI7NRlV0yzFXjhMSQqQZ6QkTKePsWdWAn1TxE1NTKmh13z61hGe3w5YtsH07ZGff15c0DIML\noxfwdHvoGVcratn2bLYWb6WuuI5s+/193fsdS9fUFB26zqmJiZnXbmFWFrWaxjqnkwzZchRCpDDp\nCRMpLSnjJ8JhlWjf0qKOHAJ1vuNDD91345phGJwbOYen28Mlr8oQy7HnsLVkK7VLaue0+ApEIhz1\n+ejQda5EjxOyWSxUuFzUahrFWVkpu+UohBB3S4owMWuJ3LufnFThq+fOJUn8hGHAmTPqkO3hYfVY\nWZnq+1qy5D6/pMGZq2fwdHvo1/sBcGQ4yLmUwzef/iZZ9rkLMx2enqZT1zns8xGIZntpdjubNY1q\nlwtXUjTmxU+69LkkG5kX80mXOUnvd0SR1Pr7Vf9X0sRPDAyopvuuLnW9YIE6Zmj16vuqGg3D4PTV\n03i6PAz4BgBwZjipL61nc9FmdrftnpMCLGIYnJ2cpMPr5fzk5MzjZdnZ1LrdrHY4sJm2KhZCiMSR\nnjCRlK6Pn1iyRMVPzJuX6FHdwvg4fPwxHDmirnNyVNP95s331XRvGAafDn+Kp8vDoH8QAFemi/oS\nVXxl2OamwX0iHOaQz0en18tYNNsrw2plg9NJjaaxWI4TEkII6QkTqSMYVMXXoUPq2tTxE4EAtLfD\n7t2qWrTZoK5O7ZfeR8NaxIhw8spJWrtbGfIPAaBlamwv3U5VYdWcFV8DgQAdus4xn49Q9I1lfkYG\ntZpGpctFThIeJySEEIlgxo8ukWTmau8+aeInIhFVJX7yCfh86rG1a2HHDnXb5r1+OSPCiaETtHa3\ncmXiCgDuLDcNpQ1sKtyE3Xrzl3Es5yVsGHzq97NP1+m97jihlQ4HtZrGipwcabS/C+nS55JsZF7M\nJ13mRIowkRSSIn7CMNQdAh9+CENqpYqSEtV0X1Jyz18uYkQ4NniM1u5Wrk5eBSA3O5eG0gY2Lt54\ny+IrlvRQaOY4IV802yv72nFCbjcLJdtLCCHum/SECVOLRFT0RGuryeMnBgfhgw/gvDoOiPnz1cpX\nRcU9N92HI2GODh6lraeNkUl1bNH87Pk0lDWwsWAjNmt8t/sMw6A3epzQyYkJItHXW35mJrWaxgaX\ni0zJ9hJCiLsiPWEiKU1MqNUvU8dP6Lradjx0SFWJ2dnQ2Ai1tffcqBaOhDkyeIS27jZGp0YBWJCz\ngMayRtbnr4978RWMRDjm99Ph9XI5mu1ltViocDqp1TTKUvg4ISGESAQpwsSsxWPv3vTxE9PTquG+\nvV3dLWC1qqb7xkY14HsQioQ4fPkwbd1tjAfGAchz5NFY1si6/HVYLfe36nS38zIaDNKp6xzy+ZiM\nbjk6bTaqNY3NmobblHc9JKd06XNJNjIv5pMucyLvrsJ0Dh6E995TofKmi5+IRFTUxMcfq1UwgDVr\n1NbjwoX39KVCkRAHBw6yq2cX3oAXgEWORTSVN1GxqOK+i6+7YRgG5ycn6dB1zk5OziyVF2dlUet2\nU+FwYJctRyGEiCvpCROmYfr4iQsXVNjqoMrmoqgIHntMJd7fg2A4yIGBA7T3tKNPq0Iu35lPU5kq\nvuK55TcVDnPY56NT17kaDAJgt1hY53RS43azRLK9hBAipqQnTJjejfETTz4JGzcmelRRQ0Pqjsez\nZ9X1vHlq5WvduntqUJsOT3Og/wDtve34plV0xWLXYprKmlidtzquxdfQ9DQdXi9H/X6mo8cJzbPb\nqdE0NmkaTsn2Ev9/e3ceHPV1JXr8291qrd2tFUlIAu0SiwAJUItdODJmMmO8xMZ2HNuVOM/PcTKu\nZBY7MzWTSiX1HEOlMm/iSWZcWTw4ydhx8pyZeIkxtrEQi4RAILOIXRsSQoDW7pbUUnff98dtd8Bs\nAiS6JZ1Plav4/fTrX9/WkdHh3vM7Vwhx20kSJm7Zra7dh2z7CadTb7BdV6eL7iMi9JMBZWVwA60Z\nhr3D7Gnfw67Tu3CNuABIs6ZRnllOQWLBuCVfWz/+mFS7ndr+fpov6u2VExWF3WqlIDoaoxTa31ZT\npc5lopG4hJ6pEhNJwkTQfNp+Yts2fVxYqNtPREYGd1yMjEBNDWzfrgvwjUa9Nrp6NcTEjPo2bo+b\n2vZaqtuqGRgZACDdmk55Vjn5Cfnjlny5vF72ORz8v/PnSfb3Kws3GllgsWC3WpkWHj4u7yuEEOLG\nSE2YCIortZ9YsSLI7SeUggMH4KOPoF8XylNQoDfZnjZt1LcZ8gzp5Ot0NYMevaH1DNsMyrPKyY3P\nHbfkq93f2+uQy4XX//9IotmM3WZjQUwMkbLkKIQQt53UhImQ8tn2Ew8+CDk5QR5Uc7NutnrmjD6e\nPl13us/OHvUtBkcG2d2+m5q2GoY8evlvZuxMVmetJjsue1ySL4/Px+GBAWr7+2l3uwH9P3xhdDR2\nm40c6e0lhBAhS5IwcctGu3avlG4/8ac/hVD7iQsXdNH9sWP62GbT03ILFox6Wm5gZICathp2t+3G\n7dWJUFZcFuWZ5WTFZY1LEtTn8bDX4aDO4WDA39srymRiocXCYquVeLOZyspKcqdATcVEMlXqXCYa\niUvomSoxkSRM3BafbT9RWqq7OwSt/cTAgC6637tXF6eFh+v10KVLR1107xp2Ud1WTW17LcNe3WE+\nJz6H8sxyMuNurG3FaCilaB4aotbh4OjAQGB6OzU8nDKbjaKYGMzS20sIISYMqQkT4+7i9hNmM9x9\ndxDbT3g8sHu3LrofGtKzXQsXwh13gMUyqls4h51Un65mz5k9geQrLyGPVZmrmBk7c8yHPOzz8YnT\nSa3DwfmLthOa699OKCMiQpYchRAiRElNmAiaEyfgzTd1vpOQoJcfg9J+Qik4fBg+/FAXowHk5em6\nr+TkUd3C4Xaw6/Qu9p7Zy4hPNzrNT8inPKucDFvGmA/5wvAwexwO6p1O3P7eXtawMBZbrSy0WLCG\nTBdbIYQQN0P+Fhe37Epr9yHVfqK1VRfdt7Xp45QUnXyNcjPKfnc/O1t3UtdRh8fnAaAwsZDyrHLS\nrGljOlSfUpwYHKS2v59Tg4OB85mRkdhtNmZFR2Ma5azXVKmpmEgkJqFJ4hJ6pkpMJAkTY25gQM9+\nnToV5PYT3d165quhQR9bLHowxcW699d19A31saN1B/s69uFVuvh9dtJsVmWuYrp1+pgOddDrZb9/\nO6Ee/3ZCZqORef4lx1TZTkgIISYdqQkTY+rMGXjjDejrC2L7icFBPQW3Z49+DNNshmXLYPlyXYB/\nHb1Dvexo3cH+jv14lRcDBuZMm8OqzFWkWFLGdKhn3W5qHQ4OOJ14/D/X8Waz3k7IYiFKensJIcSE\nJjVhYtyFRPsJrxdqa6GqSidiBoOe9frc53TrievoGexhe+t26s/W41M+DBgoSi5iVeYqkmNGVzc2\nqmEqxRGXi1qHg9aLthPKi4rCbrORFxUl2wkJIcQUIEmYuGUffliJy7U6eO0nlIIjR/TSY3e3Pped\nrQcxiqcAuge7qWqp4kDngUDyNT9lPqsyV5EUnTRmw3R4PNQ5HOx1OHD6e3tFGI2UWCyU2mwk3sB+\nlKMxVWoqJhKJSWiSuISeqRITScLELenp0bNfNluQ2k+0temi+9ZWfTxtmt5mKD//ukVoFwYusL1l\nOwc6D6BQGA1GilOLWTlzJYnRiWMyPKUUp/3bCTUMDODzT0knh4djt1qZb7EQLr29hBBiSpKaMHHT\njh/X+z9+2n7i4Yf1g4e3RW+vnvk6dEgfx8ToDbYXLbpu0f1513mqWqo4dO7QJcnXipkrSIhKGJPh\njfh8HHS5qO3v5+xFvb1mRUdjt1rJlO2EhBBiSpCaMDGmgtp+YmhIN1qtqdE1YGFhusv9ihVwnScI\nO52dVLVU0XC+AYXCZDAFkq/4qPgxGV7PyAh7HA72O50M+pccY0wmFlmtLLJaiZXeXkIIIfzkN4K4\nIVdqP+HxVBIZuXp839jrhbo6vdXQwIA+N38+VFRct/r/rPNsIPkCMBlMLJy+kBUzVxAbeetPDiil\nODU4SK3DwYnBwcC/eDIiIrDbbMyJjiYsCEuOU6WmYiKRmIQmiUvomSoxkSRMjFp7u95+6LPtJyor\nx/FNldLrnh98oDfbBsjM1EX3addulNrh6GBbyzaOXjgKQJgxjEXTF7F85nJsEdd/WvJ6hrxePvEv\nOXb5e3uZDAaKLBbsNhvp0ttLCCHENUhNmLiuz7afyMiA9etvQ/uJM2d00X1zsz5OTNRF94WF1yy6\nb+9vZ1vLNo53HQd08rU4bTHLZyzHGmG95WGd828n9InTybB/O6HYT7cTslqJkd5eQggh/KQmTNy0\nkRF4912or9fHt6X9RF8fbN0Kn3yij6OjobwcFi+GayQ4p/tOs61lGye7TwJgNpopTS9l2YxlWMJH\ntzn31fiU4tjAALUOB00XbSeUHRWF3WqlMDpaensJIYS4IZKEiavq6dHd78+evXb7iTFbu3e7YccO\nqK4Gj0cnXGVlsGrVNav+W/ta2da8jVM9pwAIN4VjT7ezNGMpMeExtzQkl9fLPoeDPQ4H/R69b2S4\n0cgCi4VSq5XkUXTgD5apUlMxkUhMQpPEJfRMlZgELQnLysrCZrNhMpkwm83U1tbS3d3Nww8/TEtL\nC1lZWfzud78jLi4uWEOc0m5r+wmfT693fvwxuFz6XFGRLrqPv/pTi829zWxr3kZTbxMAEaYIyjLK\nWJKxhGhz9C0Nqd3f2+uQy4XXP42caDZjt9lYEBNDpCw5CiGEuEVBqwnLzs6mrq6OhIQ/92V6/vnn\nSUpK4vnnn2fjxo309PSwYcOGS14nNWHjy+fThfZVVfp41iy4775xaj+hFJw8qeu+zp/X52bM0Oud\nGRlXeYmiqbeJbc3baOlrASAyLJKydJ18RZmjbno4Hp+PwwMD1Pb30+52A/rnrcC/nVCO9PYSQghx\ng66VtwQ1Cdu7dy+JiX/uTD5r1iy2bdtGSkoKZ8+eZfXq1Rw9evSS10kSNn6u1H5ixYrrNp6/OWfP\n6uSrsVEfx8fDnXfCnDlXfEOlFI09jWxr2UZrn+6OHxUWxZKMJZRllBEZdvNZYp/Hw16Hg30OBy5/\nb68ok4mFFguLrVbix3g7ISGEEFNHSCZhOTk5xMbGYjKZePrpp3nqqaeIj4+np6cH0L90ExISAseB\nAUsSNi4ubj8REwMPPKDbT4zGDa3dOxy66L6+Xs+ERUbqovvS0itW+yulONl9km0t22jrbwN08rVs\nxjLs6XYiwm6uDYRSiuahIWodDo4ODAR+plLDwymz2SiKicE8wbcTmio1FROJxCQ0SVxCz2SKSUg+\nHblz506mT5/O+fPnWbNmDbNmzbrk6waD4apLP1/+8pfJysoCIC4ujuLi4kCwKv1Nq+R4dMcff1zJ\n8eNw7txqvF5wuSopLYWcnNHfr76+/vrvt2wZ7NpF5a9/DV4vq3NyoKyMSgC3m9X+BOzT68vLyzne\ndZyfvfkzuga7yCrOItocTVRbFIVJhazMXHlTn/eDrVtpHBzEW1zMueFhmmtqMBgM3F1Rgd1q5WR1\nNX0GA+YQiY8cT67jev9jxqEyHjnWx58KlfHI8cQ+/vTPzZ+2V7qGkOgT9r3vfQ+LxcLPf/5zKisr\nSU1NpaOjgzvuuEOWI8fRbWk/4fPpVhNbt+pZMIDZs/XSY+Llm2QrpTh64ShVLVV0ODsAiDHHsHzm\nchanLSbcFH5Tw+gaGWFPfz/7nU7c/t5eFpOJxf7thKyynZAQQohxEHIzYQMDA3i9XqxWKy6Xiy1b\ntvDd736Xe+65h1dffZVvf/vbvPrqq9x3333BGN6U0N2tlx8/bT+xbp3eBWhMnTql6746O/Vxejrc\ndZfueP8ZSimOXDjCtuZtdLr09ZZwCytmrmDR9EWYTTdel+VTipODg9T293Pyot5eMyMjsVutzI6J\nwSSF9kIIIYIkKDNhTU1N3H///QB4PB6+9KUv8Y//+I90d3fz0EMP0draetUWFTITduvGuv1EZeVn\n1u7PndPbDJ04oY9jY/XMV1HRZUX3PuWj4XwDVS1VnHOdA8AabmXFzBUsnL7wppKvQa+X/U4nexwO\nevzbCZmNRubFxGC3WkmdItsJXRYXEXQSk9AkcQk9kykmITcTlp2dHaiNuFhCQgIffvhhEEY0NYx7\n+wmnU/f62rdPF91HRMDKlbBkyWVrnD7l49C5Q1S1VHFhQO8JGRsRy4qZKyiZXkKY8cZ/NM+63dQ6\nHBxwOvH4f+DjzWZKrVZKLBaipLeXEEKIEBISNWE3QmbCbs5n209UVMDy5WPUfmJkRHe537EDhofB\naNRbDJWX60ctL+JTPg52HqSqpYquwS4A4iLjWDlzJcWpxZiMN5YoeZXiiMtFrcNB69BQ4Hyev7dX\nXlSUbCckhBAiaEJuJkzcXrfSfuKalIIDB+Cjj6C/X58rLNSbbCclXXKp1+flQOcBqlqq6BnSbUfi\nI+NZlbmK+Snzbzj5cng81Dkc1DmdOPzbCUUYjZRYLJTabCRKby8hhBAhTpKwSUwpqKuD994Dr1c3\noX/oIbDZxuDmzc3w/vvQ0UFlczOrly7VRffZ2Zdc5vV5qT9bz/bW7fQO9QKQEJXAqsxVzEued0PJ\nl1KK0/7thBoGBvD5/2WRHB6O3WplvsVCuNE4Bh9ucphMNRWThcQkNElcQs9UiYkkYZPUZ9tP2O26\n/cQtl0VduKCL7o8d08c2m26r/9WvXrK26fF52N+xnx2tO+hz9wGQFJ3EqsxVFCUXYTSMPlka8fk4\n6HJR29/P2eFhAIwGA3P8hfaZsp2QEEKICUhqwiahcWk/4XLBtm2wd6+u8A8P18nX0qX6Tfw8Pg/7\nOvaxo3UH/W69RDktehrlWeXMmTbnhpKvnpERvZ2Q08mgfzuhaJOJRVYri61WYqW3lxBCiBAnNWFT\nyLFj8N//PXbtJ/B4oKYGtm8Ht1vPdi1aBHfcARZL4LIR7wh1HXXsbN2JY1g3ZU2JSaE8q5zZSbNH\nPVOllKJxaIja/n6ODw4GfnDTIyKw22zMjY4mTJYchRBCTAKShE0SY95+Qik4dEgX3ffqWi7y8nTd\nV3Jy4LJh7zA/e/NnDGUM4Rx2ApBqSaU8s5xZSbNGnXwNeb184l9y7PL39jIZDBRZLNhtNtKnSG+v\nsTRVaiomEolJaJK4hJ6pEhNJwiaBMW8/0dqqi+7b2/VxSopOvnJzA5cMe4fZ076HXad3cfjMYbKS\ns0izplGeWU5BYsGok69zw8PscTj4xOlk2L+dUGxYGIutVhZarcRIby8hhBCTlNSETXCfbT/x4IOX\nPaA4et3duuj+yBF9bLHA5z4HxcW69xfg9ripba+luq2agZEBANKt6azOWk1eQt6oki+fUhwbGKDW\n4aDpou2EsqOisFutFEZHS28vIYQQk4LUhE1CY9p+YnBQF93v2aNvZjbDsmV6Oi1cb5g95Blid9tu\natpqGPToxGmGbQblWeXkxueOKvlyeb3sczjY63DQ5+/tFW40ssBiodRqJTn85jbnFkIIISYiScIm\noJEReOcd+OQTfXzT7Sc8Hp14bdumK/kNBigp0UX3/mxucGSQ3e06+Rry6I70mbGZlGeVkx2XjcFg\nuO7afbu/t9chlwuv/18DiWYzdpuNBTExRMqS47iYKjUVE4nEJDRJXELPVImJJGETTHc3vPEGdHbe\nQvsJpfSS4wcfQI/uXk9Ojq77Sk0FYGBkgJq2Gna37cbtdQOQHZdNeVY5WXFZ130Lj8/H4YEBavv7\naXfr1xsMBgqjo7HbbORIby8hhBBTnNSETSBj0n6irQ22bNHF9wDTpunkKy8PDAZcwy6q26qpba9l\n2Ksbo+bE51CeWU5mXOZ1b9/36XZCDgcuf2+vKJNJbydktRIv2wkJIYSYQqQmbILz+eDjj3WrLrjJ\n9hM9PbrdxKFD+jgmRi87LlwIRiPOYSe7Tu9iT/seRny6RUReQh7lmeXMiJ1xzVsrpWgZGqLW4eDo\nRdsJpYaHY7fZmBcTg1l6ewkhhBCXkCQsxLlcuv1EY6Mu2brzTl0zP+qVvKEhnb3V1Oii+7Aw3eV+\nxQqIiMDhdrDr9C72ntkbSL4KEgsozywn3ZZ+zVsP+3wccDr5zfvvE7d4MaC3EyqKicFuszEjIkKW\nHINoqtRUTCQSk9AkcQk9UyUmkoSFsFtqP+H16i2Gtm3TjcRAF49VVEBsLP3ufnae2EpdRx0en35S\ncVbSLFZlriLNmnbNW3eNjLCnv5/9Tidun49ej4cMk4nFViuLrFassp2QEEIIcV1SExaClNL50+bN\nN9F+QildPPbBB9DVpc9lZurHJ9PS6BvqY0frDvZ17MOrdM3W7KTZlGeVk2pJvfCfGkwAABnASURB\nVOptfUpxcnCQ2v5+Tl7U22tmZCR2q5XZMTGYZNZLCCGEuMS18hZJwkLMZ9tPlJXpuvlRdXE4c0YX\n3Tc36+PERFizBgoL6XX3sb1lO/Vn6/EqLwYMzJk2h1WZq0ixXL26f9DrZb/TyR6Hgx7/dkJhBgPz\n/YX202U7ISGEEOKqJAmbID7bfuKee2DevFG8sK9PF90fOKCPo6OhvBwWL6ZnuJ/trTr58ikfBgwU\nJRexMnMlyTHJV73lWbebWoeDgy4XI/7thOLCwrDbbJRYLERdlBVOlbX7iUbiEnokJqFJ4hJ6JlNM\n5OnICeDi9hOJibr9RPLVcyTN7YYdO6C6WjdeNZlgyRJYuZIun4vtJ97mQOeBQPI1P2U+qzJXkRSd\ndMXbeZXiiMtFrcNB69BQ4HxeVBR2m428qCjZTkgIIYQYIzITFmSfbT8xezbce+912k/4fLBvn36h\ny6XPFRVBRQUXIrxUtVRxsPMgCoXRYGR+ynxWzlxJYnTiFW/n9HioczrZ63Dg8G8nFGE06t5eNhuJ\n0ttLCCGEuCkyExZijh1r4cMPT+F0Gjl82IfNlsu0aZnXbz+hFJw4oYvuz5/X52bMgLVrOR8fQVXL\nVg6dOxRIvkpSS1gxcwUJUQlXuJWizb/k2HDRdkLTwsOxW63Mt1iIkN5eQgghxLiRJOw2O3ashU2b\nTuJ2V3D4sF5RNBg+4p/+CZYvv0ZH+rNnddF9Y6M+jo+HNWvonJFAVet2Gk42oFCYDCaKU4tZmbmS\nuMi4y24z4vNxyL/k2HHRdkKzY2KwW61k3cR2QpNp7X4ykbiEHolJaJK4hJ6pEhNJwm6zLVtOce5c\nBY2NemLLZoO5cys4fnwrd955hSTM4YCtW6G+Xr8gMhLKyzk7ewbb2nZypO4IACaDiYXTF7Ji5gpi\nI2Mvu03PyAh7HQ72OZ0M+rcTijaZWGS1sthqJVZ6ewkhhBC3ldSE3UY9PfD1r1fS0bEagPR0yM0F\noxHi4ir51rdW//ni4WHYuRN27dJ9K0wmKC3lzMJ8tnXWcqzrGABhxjAWTV/E8pnLsUVc2khMKUXj\n0BC1/f0cHxwMfN/SIyKw22zMjY4mTJYchRBCiHEjNWFBppSeyHrvPejr8xEeDoWF+inIT4WH6zYQ\n+Hz64o8/1rNgAHPmcMY+h0rHAY43/BoAs9HM4rTFLJuxDGuE9ZL3c/t81Dud7Onv54K/t5fJYKDI\nYsFus5Euvb2EEEKIoJOZsHHmcsHbb8PRo/o4Lq6FtraTWCwVgWvc7o/48pfzKAzz6Lqvzk79hfR0\nziydx1bfSU52nwR08lWaXsqyGcuwhFsuea/zw8PUOhx84nQy7O/tZQsLo9RqZaHVSsyoOr7euKmy\ndj/RSFxCj8QkNElcQs9kionMhAXJ0aM6AXO5dCnXX/4lzJuXyfHj8NFHWxkeNhIe7uOu4jjy9myH\nkzrRIi6ODvscPojuoPHCZgDCTeHY0+0szVhKTHhM4D18SnFsYIBah4Omi7YTyo6Kwm61UhgdLb29\nhBBCiBAkM2HjwO3WS4/19fo4Oxvuuw9i/fXyLceOcerDDzE6nfiamsg1m8lMTISICDpK8vkgqZ9G\nZysAEaYIyjLKWJKxhGhzdOA9XF4v+xwO9joc9Pl7e4UbjSzwbyeUHB5+Wz+zEEIIIS4n2xbdRs3N\n8D//A729EBYGd96p93/8dDKq5dgxTr7yChXnzkFrK3i9fOj1EvvAWo7akzg1fBaAyLBIlmQsoSy9\njChzVOD+Z9xuavv7OeRy4fF/HxLNZkqtVootFiLHaclRCCGEEDdOliNvA49Hb99YU6ML8dPS4P77\nYdq0iy7y+Ti1aRNLdu2kvasTn/LRHx1OdGYiv22uxlpcSlRYlE6+MsqIDNNt8z0+Hw0DA9T299N2\nUW+vguho7FYruVFRN9zbayxNprX7yUTiEnokJqFJ4hJ6pkpMJAkbAx0det/Hc+d0u4lVq/R/l0xK\nNTbCli0M7NhOZ2crA3FGGhOMdEcO4rvQis+aS0V2BfZ0OxFh+unFfo+HvQ4HdQ4HLn9vryiTSW8n\nZLUSL9sJCSGEEBOWLEfeAp9Pt/KqrASvV7ec+MIXdP+vgHPn9DZDJ06glOKn7/6O3LhBOmMUGAwY\nDUZiI2LZE5XL//nP/4dSipahIWodDo4ODODzf9bU8HDsNhvzYmIwS28vIYQQYkKQ5chx0N2tZ79O\nn9bHdjusWQOBySmHQ2dn+/aBUvSqQXZlmXh7aTxpTS7uMIYRGxGLNcLKthEfhvkF7O3vp9bh4Nzw\nMABGg4GimBjsNhszIiKCuuQohBBCiLElSdgNUgrq6uD993Uje5sN7r1Xd74HdKf76mo9RTY8jGPE\nxd402JVjZiQqnIiOJDqTY/nPkwqjIYxho5EoewHRmQswdXUBYDGZWGy1sshqxToBthOaKmv3E43E\nJfRITEKTxCX0TJWYhP5v+BDicMAf//jndl7z5uneX1FRXNbp3jXs4kD8MNsLIhiIjSbcFE55xlJK\nvGVs+PgdvF9ZioMIBjHj2bGX8plRzIyMxG61MjsmBpPMegkhhBCTmtSEjdLhw/DOOzA4qJOuu++G\nuXP9Xzx5Utd9dXYyODLIkYh+qgoi6U2NJcwYhj3dzvIZyzGZIvmnN9+kdkYGZx09KBRGDOTHJrLi\nTAf/eP/9t/1zCSGEEGL8SE3YLRgchD/9CQ4e1Md5eXr50WpFby+0ZQucOsWQZ4iTvgvsyI/gbFYy\nJmMYpdMXsipzFUOGCCodDj5xXuDw4CCmyChyo2NIi4hgeng4ZoOBqHPng/o5hRBCCHF7SRJ2DadO\n6eXH/n5dcL92LSxaBAanA/64FerrGfa4aRrsYFd2GKdnpaFMJkpSi1mZuYrzKoL/7umncfBC4J7J\nYWHYYmJINJu5eMFxIve3nypr9xONxCX0SExCk8Ql9EyVmEgSdgUjI3p1sbZWH2dk6MaridZhqNwJ\nu3YxMjRAq7ON2jRoXJ7BSKSZouQiymau4rQ3gl93OegZ6QXAbDSywP+UY8/SpWzatw/DokWB93PX\n1VGxcGEwPqoQQgghgkRqwj6jvR3+8Afo6tKNV++4A5Yv9WH8ZD98/DGe/l7a+tvYH+/mePEMBmOj\nmZU0i6L0lTR5IzjgcjHi8wEQbzZj928nFHVR59ZjjY18dPgww+gZsIq5cynMyRm3zySEEEKI4JC9\nI0fB64WqKti+XT/oOG0afOF+xXTXSdiyBW/nWdod7TRE9HOkZAZ9KbFkx+WSOX0FLSqKpsHBwL1y\no6Ios9nIi4rCKE85CiGEEFOWJGHXcf68brx65ozeaHvJEqiYe5awrVvwnTpJh6ODY75zHFmQzvms\naaTEZpGcvIzTKppejweAcKORBRYLdquVaeETucLrxk2VtfuJRuISeiQmoUniEnomU0zk6cirUAp2\n74YPP9QbcMfFwf0V/WSe2orvF/V0ODo4NdDO0aIUzsxaQJQtk+lJds4ZrHSOKMBDwkVLjpGXbBYp\nhBBCCHF1U3YmrK9PP/nY2KiPF8518xfWnZj37ORc3xmaHK2cyI2naUEmI3HZRCUsxB0WH3iiMe+i\nJUfZTkgIIYQQVyLLkRdRCg4cgPfeg6EhiI708VBuHZlNH9N1oZWmniaa0qM5tjCPrqQ8wuPmERWV\nhAEDEUYjxRYLpVYrSVNsyVEIIYQQN06SML+BAd31vqEBUIrFtuPcqbYwcP4ETT1NtMUa2F82h9Op\nBUTEzWZaTAoGDCSazdhtNootFiKMxrH9QJPAZFq7n0wkLqFHYhKaJC6hZzLFRGrCgOPH4a23wOmE\nhKEz3Bu1hdhz9RzpbaI9fISa8gUcn1lAbGw+6ZbpGA1G8qOjKbNayZUlRyGEEEKMsUk/EzY8DO+/\nD3V1EDHUR5nzI4rMO+gYbKLFOMR2ewlHsgpIjssh3ZZOtCmMEosFu81Ggtk8jp9ECCGEEJPdlF2O\nbG3VrScc54fIatvBYuOHjESc5IjRzY6SBRzNziMtIYsMWwapEZGU2WzMlyVHIYQQQoyRKZeEeTxQ\nWQm7tnuZfqaOggvvEp14lIMWxe7Zs2nKziQ1KYuZsTOYa7Fht9nIiYyUJcebNJnW7icTiUvokZiE\nJolL6JlMMZlSNWGdnfCHNxXehmMUN76FOe4A+/PD+CR7Dh2Z00lMyWZ5fBZL4hKxW63Ey5KjEEII\nIYJg0syE+XxQXQ17/qedjONv4TTVcWqWmeaMNLrSE4lNy2XRtFxWJyQz32IhXJYchRBCCDHOJu1y\n5MYf/ojfv/cnfBgZ6fewwjeD/Pw4TuSacUyPpS81jpjMXO5Mm01F4nSyZMlRCCGEELfRtZKwCTsd\ntPGHP+LXH24hbelyshaVknHPat6fD39IdXO2KAMWL+CJ5Xfzcsld/K+MHLKlzcS4qaysDPYQxBVI\nXEKPxCQ0SVxCz1SJScglYZs3b2bWrFnk5+ezcePGK14Tf9dd/N83XifTvhSHNYqm7OmcnZZI9LIy\nGnv7efpz9/KfZetYn5ZDnNR8jbv6+vpgD0FcgcQl9EhMQpPEJfRMlZiEVBLm9Xr567/+azZv3kxD\nQwOvv/46R44cuew69fT/5nxuLvXRZnpjrXhNBkyeIVK7e5jefoG/SM3BLDVft01vb2+whyCuQOIS\neiQmoUniEnqmSkxCKlOpra0lLy+PrKwszGYzjzzyCH/84x8vu05FRGIsLqbbBzED/aSdO096lwPL\nkAeDzxeEkQshhBBC3JiQSsLa29uZMWNG4DgjI4P29vbLrjP6vMTEx6Hq6khyDBPpNWDAwMnqatZ/\n/i9v55AF0NzcHOwhiCuQuIQeiUlokriEnqkSk5B6OvLNN99k8+bN/PznPwfgN7/5Dbt37+bf/u3f\nAteYUlLwnTsXrCEKIYQQQozaggULrlrjFlLNWtPT0zl9+nTg+PTp02RkZFxyjbez83YPSwghhBBi\nzIXUcuTixYs5ceIEzc3NDA8P88Ybb3DPPfcEe1hCCCGEEGMupGbCwsLC+MlPfsLatWvxer189atf\nZfbs2cEelhBCCCHEmAupmjAhhBBCiKkipJYjr2U0TVzFjTl9+jR33HEHc+fOpaioiJdeegmA7u5u\n1qxZQ0FBAXfdddcl/VpefPFF8vPzmTVrFlu2bAmcr6urY968eeTn5/PNb34zcN7tdvPwww+Tn5/P\nkiVLaGlpCXzt1VdfpaCggIKCAn71q1/dhk88cXi9XkpKSli3bh0gMQkFvb29PPjgg8yePZs5c+aw\ne/duiUuQvfjii8ydO5d58+bx6KOP4na7JSZB8OSTT5KSksK8efMC54Idh6amJsrKysjPz+eRRx5h\nZGRkvD7+rVETgMfjUbm5uaqpqUkNDw+rBQsWqIaGhmAPa8Lr6OhQ+/fvV0op5XA4VEFBgWpoaFDP\nPfec2rhxo1JKqQ0bNqhvf/vbSimlDh8+rBYsWKCGh4dVU1OTys3NVT6fTymlVGlpqdq9e7dSSqnP\nf/7z6r333lNKKfXTn/5UPfPMM0oppX7729+qhx9+WCmlVFdXl8rJyVE9PT2qp6cn8Geh/ehHP1KP\nPvqoWrdunVJKSUxCwBNPPKF++ctfKqWUGhkZUb29vRKXIGpqalLZ2dlqaGhIKaXUQw89pDZt2iQx\nCYKqqiq1b98+VVRUFDgXrDj09vYqpZRav369euONN5RSSn3ta19T//Ef/zHe34abMiGSsF27dqm1\na9cGjl988UX14osvBnFEk9O9996rPvjgA1VYWKjOnj2rlNKJWmFhoVJKqR/84Adqw4YNgevXrl2r\nqqur1ZkzZ9SsWbMC519//XX19NNPB66pqalRSulfXElJSUoppV577TX1ta99LfCap59+Wr3++uvj\n+wEniNOnT6uKigq1detWdffddyullMQkyHp7e1V2dvZl5yUuwdPV1aUKCgpUd3e3GhkZUXfffbfa\nsmWLxCRImpqaLknCghkHn8+nkpKSlNfrVUopVV1dfUkOEUomxHLkaJu4ipvX3NzM/v37KSsro7Oz\nk5SUFABSUlLo9LcFOXPmzCUtQz6Nw2fPp6enB+JzcezCwsKIjY2lq6vrqvcS8Dd/8zf88Ic/xHjR\n1lsSk+Bqampi2rRpfOUrX2HhwoU89dRTuFwuiUsQJSQk8Hd/93fMnDmTtLQ04uLiWLNmjcQkRAQz\nDt3d3cTFxQX+Dr34XqFmQiRhBoMh2EOY1JxOJw888AA//vGPsVqtl3zNYDDI9/82euedd0hOTqak\npAR1lWdmJCa3n8fjYd++fXz9619n3759xMTEsGHDhkuukbjcXqdOneJf//VfaW5u5syZMzidTn7z\nm99cco3EJDTczjhMtHhPiCRsNE1cxc0ZGRnhgQce4PHHH+e+++4D9L9azp49C0BHRwfJycnA5XFo\na2sjIyOD9PR02traLjv/6WtaW1sB/Yusr6+PxMREielV7Nq1i7feeovs7Gy++MUvsnXrVh5//HGJ\nSZBlZGSQkZFBaWkpAA8++CD79u0jNTVV4hIke/fuZdmyZSQmJhIWFsYXvvAFqqurJSYhIlh/Z6Wn\np5OQkEBvby8+/17SbW1tpKenj+8HvlnBXg8djZGREZWTk6OampqU2+2Wwvwx4vP51OOPP66+9a1v\nXXL+ueeeC6zZv/jii5cVVLrdbtXY2KhycnICBZV2u13V1NQon893WUHlp2v2r7/++iUFldnZ2aqn\np0d1d3cH/iz+rLKyMlATJjEJvpUrV6pjx44ppZT67ne/q5577jmJSxDV19eruXPnqoGBAeXz+dQT\nTzyhfvKTn0hMguSzNWHBjsP69evVb3/7W6WUrhWTwvxb9Kc//UkVFBSo3Nxc9YMf/CDYw5kUtm/f\nrgwGg1qwYIEqLi5WxcXF6r333lNdXV2qoqJC5efnqzVr1lzyl8sLL7ygcnNzVWFhodq8eXPg/N69\ne1VRUZHKzc1Vzz77bOD80NCQWr9+vcrLy1NlZWWqqakp8LVXXnlF5eXlqby8PLVp06bb8pknksrK\nysDTkRKT4Kuvr1eLFy9W8+fPV/fff7/q7e2VuATZxo0b1Zw5c1RRUZF64okn1PDwsMQkCB555BE1\nffp0ZTabVUZGhnrllVeCHofGxkZlt9tVXl6eeuihh9Tw8PD4fhNukjRrFUIIIYQIgglREyaEEEII\nMdlIEiaEEEIIEQSShAkhhBBCBIEkYUIIIYQQQSBJmBBCCCFEEEgSJoQQQggRBJKECSGmlNWrV1NX\nV3dL93j77bfZuHHjGI1ICDFVhQV7AEIIcTuNxT5269atY926dWM0IiHEVCUzYUKIoHK5XPzVX/0V\nxcXFzJs3j9///vcAfP/738dutzNv3jyefvrpwPWrV6/mb//2byktLWX27Nns2bOH+++/n4KCAr7z\nne8A0NzczKxZs3jssceYM2cO69evZ3Bw8LL33rJlC8uWLWPRokU89NBDuFyuy6556aWXmDt3LgsW\nLODRRx8FYNOmTTz77LMAFBcXU1JSQklJCdHR0Wzfvh2Xy8WTTz5JWVkZCxcu5K233rrsvpWVlaxe\nvZr169cze/ZsHnvssVv/ZgohJhRJwoQQQbV582bS09Opr6/n4MGDrF27FoBnn32W2tpaDh48yODg\nIO+88w6gZ7IiIiLYs2cPzzzzDPfeey8vv/wyhw4dYtOmTfT09ABw/PhxvvGNb9DQ0IDNZuPf//3f\nL3nfCxcu8MILL/DRRx9RV1fHokWL+Jd/+ZfLxrdx40bq6+v55JNPePnllwNj+FR9fT379+/n+9//\nPqWlpSxdupQXXniBiooKdu/ezdatW3nuuecYGBi47N719fX8+Mc/pqGhgcbGRnbu3Dk231QhxIQg\nSZgQIqjmz5/PBx98wD/8wz+wY8cObDYbAFu3bmXJkiXMnz+frVu30tDQEHjNPffcA0BRURFFRUWk\npKQQHh5OTk4Op0+fBmDGjBksXboUgMcee4wdO3YEXq+UoqamhoaGBpYtW0ZJSQm/+tWvaG1tveL4\nHn30Uf7rv/4Lk8l0xc9w4sQJnn/+eX73u98RFhbGli1b2LBhAyUlJdxxxx243e7AuC5mt9tJS0vD\nYDBQXFxMc3PzzX0ThRATktSECSGCKj8/n/379/Puu+/yz//8z1RUVPD888/zjW98g7q6OtLT0/ne\n977H0NBQ4DUREREAGI3GwJ8/PfZ4PMCls1VKqSvWga1Zs4bXXnvtmuN79913qaqq4u233+aFF17g\n4MGDXLzlrtPp5OGHH+YXv/gFKSkpgfN/+MMfyM/Pv+a9Lx67yWQKjF0IMTXITJgQIqg6OjqIjIzk\nS1/6En//93/P/v37AwlXYmIiTqczUCd2I1pbW6mpqQHgtddeY+XKlYGvGQwGlixZws6dOzl16hSg\na9NOnDhxyT2UUrS2trJ69Wo2bNhAX18fTqfzkmuefPJJvvKVr7B8+fLAubVr1/LSSy8Fjvfv33/D\n4xdCTH4yEyaECKqDBw/y3HPPYTQaMZvNvPzyy8TGxvLUU09RVFREamoqZWVlV3zttZ50LCws5Kc/\n/SlPPvkkc+fO5Zlnnrnk60lJSWzatIkvfvGLuN1uAF544YVLZq+8Xi+PP/44fX19KKX45je/SWxs\nbOB9W1tbefPNNzlx4gSvvPIKAL/85S/5zne+w7e+9S3mz5+Pz+cjJyfnsuL8K439Vp/aFEJMLAZ1\n8by6EEJMAs3Nzaxbt46DBw8GeyhCCHFVshwphJiUZFZJCBHqZCZMCCGEECIIZCZMCCGEECIIJAkT\nQgghhAgCScKEEEIIIYJAkjAhhBBCiCCQJEwIIYQQIgj+P2WGO4pdoAcIAAAAAElFTkSuQmCC\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10f9e1050>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 34
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"cython_bonus\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Bonus: How to use Cython without the IPython magic"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"IPython's notebook is really great for explanatory analysis and documentation, but what if we want to compile our Python code via Cython without letting IPython's magic doing all the work? \n",
|
|
"These are the steps you would need."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 1. Creating a .pyx file containing the the desired code or function."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%file ccy_classic_lstsqr.pyx\n",
|
|
"\n",
|
|
"def ccy_classic_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"Writing ccy_classic_lstsqr.pyx\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 11
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 2. Creating a simple setup file"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%file setup.py\n",
|
|
"\n",
|
|
"from distutils.core import setup\n",
|
|
"from distutils.extension import Extension\n",
|
|
"from Cython.Distutils import build_ext\n",
|
|
"\n",
|
|
"setup(\n",
|
|
" cmdclass = {'build_ext': build_ext},\n",
|
|
" ext_modules = [Extension(\"ccy_classic_lstsqr\", [\"ccy_classic_lstsqr.pyx\"])]\n",
|
|
")"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"Writing setup.py\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 12
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"####3. Building and Compiling"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"!python3 setup.py build_ext --inplace"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"running build_ext\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"cythoning ccy_classic_lstsqr.pyx to ccy_classic_lstsqr.c\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"building 'ccy_classic_lstsqr' extension\r\n",
|
|
"creating build\r\n",
|
|
"creating build/temp.macosx-10.6-intel-3.4\r\n",
|
|
"/usr/bin/clang -fno-strict-aliasing -Werror=declaration-after-statement -fno-common -dynamic -DNDEBUG -g -fwrapv -O3 -Wall -Wstrict-prototypes -arch i386 -arch x86_64 -g -I/Library/Frameworks/Python.framework/Versions/3.4/include/python3.4m -c ccy_classic_lstsqr.c -o build/temp.macosx-10.6-intel-3.4/ccy_classic_lstsqr.o\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\u001b[1mccy_classic_lstsqr.c:2040:28: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_AsString'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE char* __Pyx_PyObject_AsString(PyObject* o) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2037:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function\r\n",
|
|
" '__Pyx_PyUnicode_FromString' [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyUnicode_FromString(char* c_str) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2104:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_IsTrue'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyObject_IsTrue(PyObject* x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2159:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyIndex_AsSsize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE Py_ssize_t __Pyx_PyIndex_AsSsize_t(PyObject* b) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2188:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_FromSize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject * __Pyx_PyInt_FromSize_t(size_t ival) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1584:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_From_long'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyInt_From_long(long value) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1631:27: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_long' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE long __Pyx_PyInt_As_long(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1731:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_int' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyInt_As_int(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"8 warnings generated.\r\n"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\u001b[1mccy_classic_lstsqr.c:2040:28: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_AsString'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE char* __Pyx_PyObject_AsString(PyObject* o) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2037:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function\r\n",
|
|
" '__Pyx_PyUnicode_FromString' [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyUnicode_FromString(char* c_str) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2104:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_IsTrue'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyObject_IsTrue(PyObject* x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2159:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyIndex_AsSsize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE Py_ssize_t __Pyx_PyIndex_AsSsize_t(PyObject* b) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2188:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_FromSize_t'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject * __Pyx_PyInt_FromSize_t(size_t ival) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1584:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_From_long'\r\n",
|
|
" [-Wunused-function]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE PyObject* __Pyx_PyInt_From_long(long value) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1631:27: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_long' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE long __Pyx_PyInt_As_long(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1731:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_int' is not\r\n",
|
|
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
|
|
"static CYTHON_INLINE int __Pyx_PyInt_As_int(PyObject *x) {\r\n",
|
|
"\u001b[0;1;32m ^\r\n",
|
|
"\u001b[0m"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"8"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
" warnings generated.\r\n",
|
|
"/usr/bin/clang -bundle -undefined dynamic_lookup -arch i386 -arch x86_64 -g build/temp.macosx-10.6-intel-3.4/ccy_classic_lstsqr.o -o /Users/sebastian/Github/python_reference/benchmarks/ccy_classic_lstsqr.so\r\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 13
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### 4. Importing and running the code"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import ccy_classic_lstsqr\n",
|
|
"\n",
|
|
"%timeit classic_lstsqr(x, y)\n",
|
|
"%timeit cy_classic_lstsqr(x, y)\n",
|
|
"%timeit ccy_classic_lstsqr.ccy_classic_lstsqr(x, y)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"100 loops, best of 3: 2.9 ms per loop\n",
|
|
"1000 loops, best of 3: 212 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n",
|
|
"1000 loops, best of 3: 207 \u00b5s per loop"
|
|
]
|
|
},
|
|
{
|
|
"output_type": "stream",
|
|
"stream": "stdout",
|
|
"text": [
|
|
"\n"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 20
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"numba\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Appendix I: Cython vs. Numba"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"Like we did with Cython before, we will use the minimalist approach to Numba and see how they compare against each other. \n",
|
|
"\n",
|
|
"Numba is using the [LLVM compiler infrastructure](http://llvm.org) for compiling Python code to machine code. Its strength is to work with NumPy arrays to speed-up code. If you want to read more about Numba, see the original [website and documentation](http://numba.pydata.org/numba-doc/0.13/index.html)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"def lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 1
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%load_ext cythonmagic"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 2
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"\n",
|
|
"def cy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 3
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"from numba import jit\n",
|
|
"\n",
|
|
"@jit\n",
|
|
"def nmb_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"ename": "ImportError",
|
|
"evalue": "No module named 'llvm'",
|
|
"output_type": "pyerr",
|
|
"traceback": [
|
|
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m\n\u001b[0;31mImportError\u001b[0m Traceback (most recent call last)",
|
|
"\u001b[0;32m<ipython-input-4-505a644bdc72>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[0;32m----> 1\u001b[0;31m \u001b[0;32mfrom\u001b[0m \u001b[0mnumba\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mjit\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 2\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 3\u001b[0m \u001b[0;34m@\u001b[0m\u001b[0mjit\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 4\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0mnmb_lstsqr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mx\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0my\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 5\u001b[0m \u001b[0;34m\"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
|
|
"\u001b[0;32m/Library/Frameworks/Python.framework/Versions/3.3/lib/python3.3/site-packages/numba/__init__.py\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 3\u001b[0m \"\"\"\n\u001b[1;32m 4\u001b[0m \u001b[0;32mfrom\u001b[0m \u001b[0m__future__\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mprint_function\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mdivision\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mabsolute_import\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 5\u001b[0;31m \u001b[0;32mfrom\u001b[0m \u001b[0;34m.\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mtesting\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mdecorators\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 6\u001b[0m \u001b[0;32mfrom\u001b[0m \u001b[0;34m.\u001b[0m\u001b[0m_version\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mget_versions\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 7\u001b[0m \u001b[0;31m# Re-export typeof\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
|
|
"\u001b[0;32m/Library/Frameworks/Python.framework/Versions/3.3/lib/python3.3/site-packages/numba/decorators.py\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 5\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mwarnings\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 6\u001b[0m \u001b[0;32mfrom\u001b[0m \u001b[0mnumba\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0msigutils\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 7\u001b[0;31m \u001b[0;32mfrom\u001b[0m \u001b[0mnumba\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mtargets\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mregistry\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 8\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 9\u001b[0m \u001b[0;31m# -----------------------------------------------------------------------------\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
|
|
"\u001b[0;32m/Library/Frameworks/Python.framework/Versions/3.3/lib/python3.3/site-packages/numba/targets/registry.py\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 1\u001b[0m \u001b[0;32mfrom\u001b[0m \u001b[0m__future__\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mprint_function\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mdivision\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mabsolute_import\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 2\u001b[0m \u001b[0;32mfrom\u001b[0m \u001b[0mnumba\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mutils\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mtyping\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 3\u001b[0;31m \u001b[0;32mfrom\u001b[0m \u001b[0mnumba\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mtargets\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mcpu\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 4\u001b[0m \u001b[0;32mfrom\u001b[0m \u001b[0mnumba\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mtargets\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mdescriptors\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mTargetDescriptor\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 5\u001b[0m \u001b[0;32mfrom\u001b[0m \u001b[0mnumba\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mdispatcher\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
|
|
"\u001b[0;32m/Library/Frameworks/Python.framework/Versions/3.3/lib/python3.3/site-packages/numba/targets/cpu.py\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 2\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 3\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0msys\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 4\u001b[0;31m \u001b[0;32mimport\u001b[0m \u001b[0mllvm\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcore\u001b[0m \u001b[0;32mas\u001b[0m \u001b[0mlc\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 5\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mllvm\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mpasses\u001b[0m \u001b[0;32mas\u001b[0m \u001b[0mlp\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 6\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mllvm\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mee\u001b[0m \u001b[0;32mas\u001b[0m \u001b[0mle\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
|
|
"\u001b[0;31mImportError\u001b[0m: No module named 'llvm'"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 4
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"# ... this section is still in progress"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<a name=\"type_declarations\"></a>\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Appendix II: Cython with and without type declarations"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"[[back to top](#sections)]"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"In the sections above, we have been using the simplest approach to Cython without using static type declarations and thereby neglecting one of its major strengths. \n",
|
|
"Let us now see how we can further improve the Cython implementation of our \"classic least squares approach\" by adding those type declarations."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"First, our \"simple\" approach using Cython from the previous section:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"def cy_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 54
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"And now, the same code with static type declarations:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"%%cython\n",
|
|
"def static_type_lstsqr(x, y):\n",
|
|
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
|
|
" cdef double x_avg, y_avg, var_x, cov_xy, slope, y_interc, x_i, y_i\n",
|
|
" x_avg = sum(x)/len(x)\n",
|
|
" y_avg = sum(y)/len(y)\n",
|
|
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
|
|
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
|
|
" slope = cov_xy / var_x\n",
|
|
" y_interc = y_avg - slope*x_avg\n",
|
|
" return (slope, y_interc)"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 55
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"Now, let us see how the two functions (with and without static type declarations) compare against each other for different sample sizes."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"funcs = ['cy_lstsqr', 'static_type_lstsqr'] \n",
|
|
"labels = ['simple Cython', 'Cython w. type declarations']\n",
|
|
"orders_n = [10**n for n in range(1, 7)]\n",
|
|
"times_n = {f:[] for f in funcs}\n",
|
|
"\n",
|
|
"for n in orders_n:\n",
|
|
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
|
|
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
|
|
" for f in funcs:\n",
|
|
" times_n[f].append(timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000))"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 58
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"#%pylab inline\n",
|
|
"#import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"plt.figure(figsize=(10,8))\n",
|
|
"\n",
|
|
"for f in times_n.keys():\n",
|
|
" plt.plot(orders_n, times_n[f], alpha=0.5, label=f, marker='o', lw=2)\n",
|
|
"\n",
|
|
"plt.xlabel('sample size n')\n",
|
|
"plt.ylabel('time in ms')\n",
|
|
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
|
|
"plt.legend(loc=2)\n",
|
|
"plt.grid()\n",
|
|
"\n",
|
|
"plt.title('Performance of a simple least square fit implementation')\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAmEAAAH4CAYAAAACdDpdAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdYVGf6N/Dv0KQN0osComhUXBVs2BJRsUaxYzCiJkZT\nNm3NrtFsVEyylrzJpq1J1KhYY4sNW4gFW1xL1JiIgqKAAqIoFqQMwzzvH+fnLChNYZgzc76f6+K6\n5szMOdwz9wxz8zz3PEclhBAgIiIiojplYewAiIiIiJSIRRgRERGREbAIIyIiIjICFmFERERERsAi\njIiIiMgIWIQRERERGQGLMDI52dnZeO655+Dk5IR//OMfxg7H6AoKCjB48GA4Oztj9OjRBvs9AwcO\nxMqVKw1ybAsLC1y+fPmJ94uNjcWzzz5rgIjM35EjR9CsWTM4OTlh69atGDhwIFasWFHt/eX4epC7\nuXPnYtKkScYOg2TEytgBkDIEBATgxo0bsLS0hIODAwYMGID//Oc/cHBweOJjLVq0CJ6enrh3754B\nIjU9GzduxI0bN3D79m1YWBju/6qdO3ca7NhyFhYWhujoaEycONHYodSqmTNn4u2338Zbb70FABgy\nZIj+ttjYWCxZsgSHDh2qcH+lvR5iYmKQkpJS7cIzISEB0dHRuHr1qv666dOnGyo8MlEcCaM6oVKp\nsH37dty/fx+nTp3CyZMn8cknnzzRMYQQ0Ol0SEtLQ8uWLZ8qDq1W+1T7yVlaWhqeeeYZgxZgSqZS\nqYwdQpWe5nWdnp6OoKAgA0RDRNUmiOpAQECA2Lt3r37773//uxg0aJAQQoijR4+KLl26CGdnZ9G2\nbVuRkJCgv1+PHj3EP//5T9GtWzdhZ2cnxo4dK6ytrYWNjY1wdHQUe/fuFUVFReKdd94RDRo0EA0a\nNBDvvvuuKCoqEkIIsX//ftGwYUMxf/584e3tLaKjo0VMTIwYOXKkGDt2rFCr1aJ169YiOTlZzJkz\nR3h6egp/f38RHx+vj2Hp0qWiZcuWQq1WiyZNmoiFCxfqb3t4/M8//1x4enoKHx8fsWzZMv3t+fn5\nYsqUKaJRo0aifv36onv37qKgoKDKx/2oxMRE0aNHD+Hs7CxatWoltm3bJoQQYubMmcLGxkZYW1sL\nR0dHsXTp0sf2PXbsmOjcubNwdnYWPj4+4s033xQajabc31NQUCBefPFF4ebmJpydnUXHjh3FjRs3\n9Ln44YcfhBBCLFu2THTt2lX87W9/E87OziIwMFAcOXJELF26VPj5+QlPT0+xfPly/XHHjx8vXn31\nVdGnTx+hVqtFjx49RFpamv52lUolUlJShBBCFBYWivfee0/4+/sLLy8v8dprr+mfs0ctW7ZMdO/e\nXb99/vx5ER4eLlxdXUXz5s3F+vXr9bdt375dBAcHCycnJ+Hn5ydiYmIqfdzZ2dnigw8+EJaWlsLW\n1lY4OjqKt956q1rPWXZ2thBCiMuXL4vnnntOqNVq0adPH/HXv/5VjB07VgghvXZ8fX3LHKtRo0b6\n90lVeVOpVGLBggWiadOmokmTJkIIIeLi4kTbtm2Fs7Oz6Nq1qzh79my5z1uTJk2EhYWFsLOzE2q1\nWhQVFenze/78eVGvXj1haWkpHB0dhYuLS7nHkMPr4eH779NPPxUeHh7Cx8dHbN68WezYsUM0a9ZM\nuLq6irlz5+qPq9PpxNy5c0VgYKBwc3MTkZGR4vbt20IIIa5cuSJUKpVYvny58Pf3F+7u7uJf//qX\nEEKIXbt2lXmfBQcHCyEq/tuQl5cnbG1thYWFhXB0dBRqtVpkZmaKWbNm6fMvhBBbt24VQUFBwtnZ\nWYSFhYnz58+XeS189tlnok2bNqJ+/fpi9OjRorCwsNxckOliEUZ1IiAgQOzZs0cIIUR6erpo1aqV\nmDlzprh27Zpwc3MTu3btEkII8csvvwg3NzeRk5MjhJD+0Ddq1EgkJiaKkpISUVxcLCZMmCBmzJih\nP/aMGTNEly5dxM2bN8XNmzdF165d9bfv379fWFlZiWnTpgmNRiMKCgrErFmzhK2trYiPjxdarVaM\nGzdONGrUSMyZM0dotVqxePFi0bhxY/3xd+zYIS5fviyEEOLAgQPC3t5enDp1qszxZ82aJbRardi5\nc6ewt7cXd+7cEUII8cYbb4iePXuKzMxMUVJSIo4ePSqKiooqfNw3b9587LnTaDQiMDBQzJ07VxQX\nF4t9+/YJtVotkpKShBBCxMTEiOjo6Aqf+99++00cO3ZMlJSUiNTUVNGyZUvx5Zdflnvf77//Xgwe\nPFgUFBQInU4nTp06Je7duyeEECIsLEwsWbJECCF96FpZWYnY2Fih0+nEhx9+KBo2bKgvFOLj44Va\nrRYPHjwQQkgfumq1Whw6dEhfNJcunkp/6L777rtiyJAhIjc3V9y/f18MHjxYTJ8+vdx4SxdheXl5\nwtfXV8TGxoqSkhJx+vRp4e7uLhITE4UQQiQkJIg///xTCCHE2bNnhZeXl9iyZcsTPe4nfc46d+4s\n3nvvPaHRaMTBgweFWq3W56q8Iqz0PytV5U2lUom+ffuK3NxcUVhYKE6dOiU8PT3F8ePHhU6nE8uX\nLxcBAQH6f0ge9eg/RqUfZ2xsbJn8lEcOr4eH77+PP/5Y/951c3MTY8aMEXl5eeLcuXPCzs5OpKam\nCiGE+PLLL0WXLl1ERkaG0Gg04tVXXxVRUVFCiP8VYZMnTxaFhYXi999/F/Xq1RMXLlwQQpT/Pqvs\nb0NCQsJj+Y2JidEXYUlJScLBwUHs2bNHaLVa8emnn4qmTZuK4uJifX5CQ0NFVlaWuH37tmjZsqX4\n/vvvK80JmR4WYVQnGjVqJBwdHYWzs7No1KiR+Otf/yoKCgrEvHnzHvvD1q9fP/1/zWFhYWLWrFll\nbp8wYYL48MMP9duBgYH6YkYIIX7++WcREBAghJD+SNvY2JT5IJo1a5bo27evfnvbtm3C0dFR6HQ6\nIYQQ9+7dEyqVSty9e7fcxzJ06FDx1Vdf6Y9vZ2cnSkpK9Ld7enrqPzzt7OzKHY2o6nGXdvDgQeHt\n7V3muqioKP1IzqP/XVfliy++EMOGDSv3tqVLl1Y4gvLoh26zZs30t509e1aoVCr9qJkQQri5uYnf\nf/9dCCF96D78sBNCKpgsLS3FtWvXhBD/+9DV6XTCwcFB/wEshBC//vprmaK4tNJF2Nq1a8Wzzz5b\n5vbJkyeL2bNnl7vvO++8I/72t79V63E/HPEpT0X7pqWlCSsrK5Gfn6+/bsyYMdUuwh71aN5UKpXY\nv3+/fvu1114r88+JEEI0b95cHDhwoNzjVVaEPTrCWB45vB4evv8efe8eP35cf//27duLrVu3CiGE\naNGiRZnHnJmZKaytrUVJSYm+CMvIyNDf3qlTJ7Fu3TohRPXeZ4/+bXg0v6WP8dFHH4nRo0frb9Pp\ndKJhw4b6fAUEBIjVq1frb586dap47bXXKv39ZHrYmE91QqVSYevWrejVq1eZ69PS0rBhwwbExcXp\nr9NqtWXu5+fnV+mxMzMz0ahRI/22v78/MjMz9dseHh6wsbEps4+np6f+sp2dHdzd3fW9P3Z2dgCA\nvLw8ODk5YdeuXZg9ezYuXrwInU6H/Px8tGnTRr+/m5tbmX4se3t75OXlIScnB4WFhQgMDHws5uo8\n7tKP79HnoFGjRsjIyKj0eXkoOTkZU6ZMwW+//Yb8/HxotVp06NCh3Ps+bCR+4YUXcOfOHYwdOxb/\n+te/YGX1+J8KLy8v/eWHz5mHh0eZ6/Ly8gBI+ff19dXf5uDgAFdXV2RmZqJhw4b662/evIn8/Hy0\nb99ef534v17AqqSlpeHYsWNwcXHRX6fVajFu3DgAwLFjxzBt2jScO3cOGo0GRUVFiIyMrNbjrqwv\nrKJ9MzMz4eLion9uAClvpRu1K1OdvJV+XaSlpWHFihX45ptv9NcVFxcjKyurWr+vpoz1enBzc3vs\nvftoLA9/b1paGoYNG1bm/WplZYXs7Gz9tre3t/7yw/dyRar621CZzMxM+Pv767dVKhX8/PzKvK9L\nx2JnZ1fm7xqZB3byklH5+/sjOjoaubm5+p/79+9j6tSp+vtU1RjdoEEDpKam6rfT09PRoEGDCvd/\nkkbroqIijBgxAlOnTsWNGzeQm5uLgQMHQghR5b7u7u6wtbXFpUuXHrutOo+79OO7evVqmd+ZlpZW\n5kOsMq+//jqCgoJw6dIl3L17F//6178qLGqsrKwwc+ZMnDt3Dr/++iu2b9/+RMsWVEQIUab4yMvL\nw+3bt8vkCZCeMzs7OyQmJuqflzt37lTrm7D+/v7o0aPHY8/pggULAABjxozB0KFDce3aNdy5cwev\nvfaa/nmo7HFX9XqpaN8GDRogNzcX+fn5+vumpaXpj+fg4FDmtpKSEty8eVO/XZ28lY7N398f//zn\nP8s8/ry8vKdatsTQX0aoi9dDefz9/bF79+4yz1F+fj58fHyq3PfR56Sqvw1VPYcNGzZEWlqafvvh\nc1K6CK3s95N5YBFGRjV27FjExcUhPj4eJSUlKCwsREJCQpn/Bh8teB7djoqKwieffIKcnBzk5OTg\no48+QnR0dIW/szoF1EMajQYajQbu7u6wsLDArl27EB8fX619LSws8PLLL2PKlCnIyspCSUkJjh49\nCo1GU63H/VDnzp1hb2+PTz/9FMXFxUhISMD27dvxwgsvVCuOvLw8qNVq2Nvb48KFC/juu+8qvG9C\nQgL++OMPlJSUQK1Ww9raGpaWltX6PVXZuXMnjhw5Ao1GgxkzZqBLly6PfeBYWFhg0qRJePfdd/UF\nSUZGRrWe8+effx7JyclYtWoViouLUVxcjBMnTuDChQsApOfBxcUFNjY2OH78ONasWaP/YKvscXt5\neSElJaXC31vRvv7+/ujQoQNmzZqF4uJiHD58GNu3b9fv98wzz6CwsBA7d+5EcXExPvnkExQVFelv\nf5K8AcCkSZPw/fff4/jx4xBC4MGDB9ixY0elIzkV8fLywrVr11BcXPzE+1aXoV8P5XnttdfwwQcf\nID09HYA00rZt27Zq7evt7Y3U1FT934+q/jZ4eXnh1q1bFRaMo0aNwo4dO7Bv3z4UFxfj888/h62t\nLbp27Vru/Z/k7xaZDhZhZFS+vr7YunUr5syZA09PT/j7++Pzzz8v8wenvJGs0td9+OGH6NChA9q0\naYM2bdqgQ4cO+PDDD6u9f0X3AQC1Wo2vv/4akZGRcHV1xY8//lhmPaXy9i3ts88+Q+vWrdGxY0e4\nublh+vTp0Ol0FT7u8kaorK2tERcXh127dsHDwwNvvvkmVq5ciWeeeabCx/NoDGvWrIGTkxMmT56M\nF154ocL7X79+HaNGjUL9+vURFBSkXyPrUdV5Dh+9bcyYMZg9ezbc3Nxw+vRprFq1qtx958+fj6ZN\nm6Jz586oX78++vTpg+Tk5AqPWzpX8fHxWLt2LRo2bAgfHx9Mnz4dGo0GAPDtt99i5syZcHJywscf\nf1xmhKiyx/3OO+9g48aNcHV1xbvvvvtEz9maNWtw7NgxuLq64qOPPsK4ceP0r+369evj22+/xSuv\nvAJfX184OjqWmV6sKm+PPt/t27fH4sWL8eabb8LV1RXNmjV76lHM3r17o1WrVvD29i4zdV8RY74e\nnuT3vvPOO4iIiEDfvn3h5OSELl264Pjx49Xad9SoUQCk6c8OHTpU+behRYsWiIqKQpMmTeDq6oqs\nrKwyz1Pz5s2xatUqvPXWW/Dw8MCOHTsQFxdX7tT/w9g4GmZ+VMJA5XVhYSF69OiBoqIiaDQaDBky\nBHPnzkVMTAx++OEHfa/AnDlzMGDAAADSasJLly6FpaUlvv76a/Tt29cQoRFRHXvppZfg6+uLjz/+\n2NihGNXs2bNx6dIlg600byr4eiCSGKwx39bWFvv374e9vT20Wi26d++Ow4cPQ6VSYcqUKZgyZUqZ\n+ycmJmLdunVITExERkYGwsPDkZyczAUoicwAp1IkfB4kfB6IJAatcOzt7QFIc+clJSX6by2V9wbc\nunUroqKiYG1tjYCAADRt2rTMMDERmS5OpUj4PEj4PBBJDLpEhU6nQ7t27ZCSkoLXX38drVq1wsaN\nG/HNN99gxYoV6NChAz7//HM4OzsjMzMTnTt31u/r6+tb7a/gE5G8LVu2zNghyMKsWbOMHYIs8PVA\nJDFoEWZhYYEzZ87g7t276NevHxISEvD6669j5syZAIAZM2bgvffew5IlS8rdv7z/lBo2bMi1UoiI\niMgktG3bFmfOnCn3tjppuKpfvz6ef/55nDx5Ep6envqh6FdeeUU/5diwYcMy68Zcu3at3PVSMjMz\nIaSV/vkjk59Zs2YZPQb+MC+m8MOcyPOHeZHfjznl5Pfff6+wPjJYEZaTk4M7d+4AAAoKCvDLL78g\nJCQE169f199n8+bNaN26NQAgIiICa9euhUajwZUrV3Dx4kV06tTJUOFRLSq9UCrJB/MiP8yJPDEv\n8qOUnBhsOjIrKwvjx4+HTqeDTqdDdHQ0evfujXHjxuHMmTNQqVRo3LgxFi5cCAAICgpCZGQkgoKC\nYGVlhW+//ZaNm0RERGS2DLZOmKGoVCqYWMhmLyEhAWFhYcYOgx7BvMgPcyJPzIv8mFNOKqtbWIQR\nERERGUhldYvZrITq6uqqb/jnD39q+uPq6mrsl3SNJSQkGDsEegRzIk/Mi/woJScGXaKiLuXm5nKE\njGqNSsV+RCIiMiyzmY6s6Hqip8HXExER1YbKPk/MZjqSiIiIyJSwCCMyU0rpqTAlzIk8MS/yo5Sc\nsAgjIiIiMgL2hJmQhIQEREdHlzm9ExmGEl5PRERkeOwJU5iYmBhER0cbOwwiIiKqhNksUVGRpKQ0\n7NmTguJiC1hb6xAeHojmzRvV+THMwcNKnss3mAZzWnHaXDAn8sS8yI9ScmLWI2FJSWmIjb2Emzd7\n4c6dMNy82QuxsZeQlJRWp8e4evUqhg8fDk9PT7i7u+Ovf/0r3Nzc8Oeff+rvc+PGDTg4OODWrVvV\nPu78+fPh6+sLJycntGjRAvv27cPu3bsxd+5crFu3Dmq1GiEhIQCA2NhYBAYGwsnJCU2aNMGaNWsA\nACUlJfj73/8ODw8PBAYGYsGCBbCwsIBOpwMAhIWF4cMPP0S3bt3g4OCAK1euVDs+IiIiqphZj4Tt\n2ZOCevV6o+yXLHrj7Nl96NixeiNZx4+nID+/t347LAyoV6839u7dV63RsJKSEgwaNAjh4eFYvXo1\nLC0tceLECQDAqlWrMG/ePADAjz/+iPDwcLi5uVUrrqSkJCxYsAAnT56Et7c30tPTodVq0aRJE3zw\nwQdISUnBihUrAAAPHjzAO++8g5MnT6JZs2bIzs7WF3uLFy/Gjh07cObMGdjb22P48OGPjXStWrUK\nu3btQvPmzfXFGcmfEv6LNDXMiTwxL/KjlJyY9UhYcXH5D6+kpPoPW6cr/74aTfWOcfz4cWRlZeH/\n/b//Bzs7O9jY2KBbt24YN24cfvzxR/39Vq5c+UR9XJaWligqKsK5c+dQXFwMf39/NGnSBIA0bfho\nE6CFhQX++OMPFBQUwMvLC0FBQQCA9evX429/+xsaNmwIFxcXfPDBB2X2ValUmDBhAlq2bAkLCwtY\nWZl13U5ERFRnzPoT1dr64ZRa2es9PXV4443qHWPBAh1u3nz8ehub6o0IXb16FY0aNYKFRdmiLTQ0\nFHZ2dkhISIC3tzdSUlIQERFRvaAANG3aFF9++SViYmJw7tw59OvXD//+97/h4+Pz2H0dHBywbt06\nfPbZZ5g4cSK6deuGzz//HM2bN0dWVhb8/Pz09/X3939s/9K3k+lQSk+FKWFO5Il5kR+l5MSsR8LC\nwwNRVLS3zHVFRXvRu3dgnR3Dz88P6enpKCkpeey28ePHY9WqVVi5ciVGjRoFGxubascFAFFRUTh0\n6BDS0tKgUqnw/vvvAyi/cb5v376Ij4/H9evX0aJFC0yaNAkA4OPjg/T0dP39Sl9+iI34REREtc+s\ni7DmzRthwoSm8PTcB2fnBHh67sOECU2f6JuNNT1GaGgofHx8MG3aNOTn56OwsBC//vorAGDs2LHY\ntGkTVq9ejXHjxj3RY0tOTsa+fftQVFSEevXqwdbWFpaWlgAAb29vpKam6qcVb9y4ga1bt+LBgwew\ntraGg4OD/r6RkZH4+uuvkZGRgdzcXMybN++xoovrZZkmJfwXaWqYE3liXuRHKTkx6+lIQCqiarqc\nRE2OYWFhgbi4OLz99tvw9/eHSqXCiy++iK5du8LPzw/t2rXD5cuX0b1792od72GBVFRUhOnTp+P8\n+fOwtrZGt27dsGjRIgDAqFGjsGrVKri5uaFJkybYvn07vvjiC4wfPx4qlQohISH47rvvAACTJk1C\ncnIy2rZti/r16+O9997D/v37y/2dREREVHu4Yr6RTZw4EQ0bNsRHH31k7FAAAKmpqWjSpAm0Wu1j\nfWxKYqqvp9KU0lNhSpgTeWJe5MecclLZ54nZj4TJWWpqKjZt2oQzZ84YOxQiIiKqY8od6jCyGTNm\noHXr1pg6dSoaNfrfVOecOXOgVqsf+3n++efrLDZOP5oHc/kv0pwwJ/LEvMiPUnLC6UiicvD1RERE\ntYEn8CZSoISyp4ogGWBO5Il5kR+l5IRFGBEREZERcDqSqBx8PRERUW3gdCQRERGRzLAIIzJTSump\nMCXMiTwxL/KjlJywCDNhc+fO1Z8D0lSFhYVhyZIlxg6DiIiozrEnzEhiYmKQkpKClStXVuv+CQkJ\niI6OxtWrV2sthgkTJsDPzw8ff/xxrR3zSfXs2RPR0dF4+eWXK72fhYUFLl26hCZNmtRJXKb2eiIi\nInlS9Ir5SZeSsOe3PSgWxbBWWSO8fTiaN21e58egmjNEUaTVamFlZfZvAyIikiGzno5MupSE2P2x\nuOl1E3e87+Cm103E7o9F0qWkOj3G/Pnz4evrCycnJ7Ro0QI7d+7E3LlzsW7dOqjVaoSEhAAAli1b\nhqCgIDg5OSEwMFB/Qu4HDx5gwIAByMzMhFqthpOTE7KyshATE4Po6Gj97zl8+DC6du0KFxcX+Pv7\nY/ny5RXGtGjRIqxZswaffvop1Go1IiIi8Nlnn2HkyJFl7vf222/j3XffBSBNHU6fPh2hoaGoX78+\nhg4ditzcXP19//vf/+p/f3BwMA4cOFDt5wgALl26hB49esDZ2RkeHh6IiooCADz33HMAgLZt20Kt\nVmPDhg3IycnBoEGD4OLiAjc3Nzz33HP6Iu306dNo164dnJyc8MILL+CFF17AjBkzAEgjir6+vvj0\n00/h4+ODiRMnPlGMpkQpPRWmhDmRJ+ZFfpSSE7MeAtjz2x7Ua1YPCakJ/7vSGji79iw6du9YrWMc\nP3wc+b75QKq0HRYQhnrN6mHvqb3VGg1LSkrCggULcPLkSXh7eyM9PR1arRYffPABUlJSsGLFCv19\nvby8sGPHDjRu3BgHDx7EgAED0LFjR4SEhGD37t0YO3ZsmenI0qcXSktLw8CBA7F48WKMHDkSd+/e\nrXTqcvLkyTh69Cj8/Pz0Jw+/fv06YmJicPfuXdSvXx9arRbr1q3D7t279futXLkS8fHxCAgIwLhx\n4/D2229j5cqVyMjIwKBBg7Bq1Sr0798fe/bswYgRI3DhwgW4u7tX67meMWMG+vfvjwMHDkCj0eDk\nyZMAgIMHD8LCwgJnz57VT0dOnz4dfn5+yMnJASAVgCqVChqNBkOHDsWUKVPw5ptvYsuWLYiKisK0\nadP0vyc7Oxu5ublIT09HSUlJtWIjIiKqbWY9ElYsisu9vgTV/+DVQVfu9Rqdplr7W1paoqioCOfO\nnUNxcTH8/f3RpEkTCCEem14bOHAgGjduDEAa/enbty8OHToEoPypuNLXrVmzBn369MHo0aNhaWkJ\nV1dXtG3btsr4Sh/D29sbzz77LDZs2AAA2L17N9zd3fUjdSqVCuPGjUNQUBDs7e3x8ccfY/369dDp\ndFi1ahUGDhyI/v37AwDCw8PRoUMH7Ny5s1rPEwDY2NggNTUVGRkZsLGxQdeuXSu9b1ZWFlJTU2Fp\naYlu3boBkIoxrVaLd955B5aWlhgxYgQ6dixbcFtYWGD27NmwtraGra1tteMzNUo595opYU7kiXmR\nH6XkxKxHwqxV1gCk0avSPO098UbYG9U6xoLsBbjpdfOx620sbKq1f9OmTfHll18iJiYG586dQ79+\n/fDvf/+73Pvu2rULs2fPxsWLF6HT6ZCfn482bdpU6/dcvXq1VprWx48fj++//x6vvPIKVq1ahXHj\nxpW53c/PT3/Z398fxcXFyMnJQVpaGjZs2IC4uDj97VqtFr169ar27/70008xY8YMdOrUCS4uLnjv\nvffw0ksvlXvff/zjH4iJiUHfvn0BSCN777//PjIzM9GwYcMy9y19gnQA8PDwgI1N9fJHRERkKGY9\nEhbePhxFF4vKXFd0sQi92/Wu02NERUXh0KFDSEtLg0qlwvvvvw8Li7JPfVFREUaMGIGpU6fixo0b\nyM3NxcCBA/UjVaWnHsvj7++PlJSUasdU0TGHDBmCs2fP4s8//8SOHTvw4osvlrk9PT29zGVra2t4\neHjA398f0dHRyM3N1f/cv38fU6dOrXY8Xl5eWLRoETIyMrBw4UK88cYbuHz5crn3dXR0xGeffYaU\nlBRs27YN//73v7Fv3z40aNAAGRkZZe6blpZW5eM2R0rpqTAlzIk8MS/yo5ScmHUR1rxpc0zoOQGe\nNzzhfN0Znjc8MaHnhCf6ZmNNj5GcnIx9+/ahqKgI9erVg62tLSwtLeHl5YXU1FR9kaXRaKDRaODu\n7g4LCwvs2rUL8fHx+uN4eXnh1q1buHfvXrm/Z8yYMdizZw82bNgArVaLW7du4ffff680Ni8vr8eK\nHDs7O4wYMQJjxoxBaGgofH199bcJIbBq1SqcP38e+fn5mDlzJkaNGgWVSoWxY8ciLi4O8fHxKCkp\nQWFhIRISEh4riCqzYcMGXLt2DQDg7OwMlUqlL1a9vLzKFJk7duzApUuXIISAk5MTLC0tYWlpiS5d\nusDKygogt9nSAAAgAElEQVRff/01iouLsWnTJpw4caLaMRAREdUZYWIqClmuD+Xs2bOiU6dOQq1W\nC1dXVzF48GCRlZUlbt26Jbp37y5cXFxE+/bthRBCLFiwQHh5eQlnZ2cRHR0toqKixIwZM/THevnl\nl4Wbm5twcXERmZmZIiYmRkRHR+tvP3TokAgNDRVOTk7Cz89PrFixotLYLl68KIKDg4Wzs7MYNmxY\nmeOoVCoRGxtb5v5hYWFi+vTpolOnTsLJyUlERESIW7du6W8/duyY6NGjh3B1dRUeHh5i0KBBIj09\nvdIYwsLCxJIlS4QQQkydOlU0bNhQODo6isDAQLF48WL9/b7//nvh4+MjnJ2dxfr168UXX3whAgIC\nhIODg/D19RWffPKJ/r4nT54UISEhQq1Wi9GjR4vRo0eLDz/8UAghxP79+4Wfn1+lMQkh39cTERGZ\nlso+T7hYKz3m6tWraNGiBbKzs+Ho6Ki/vroLq8rNSy+9BF9f3ydalJavJyIiqg08gTdVm06nw+ef\nf46oqKgyBdhDpliYmGLMtUEpPRWmhDmRJ+ZFfpSSE7P+diQBrVq1KtNM/9CiRYv0i6E+9ODBA3h5\neaFx48Zl1gYr7Wma2h0dHcvdb/fu3fqlJQxJpVIpphmfiIhMB6cjicrB1xMREdUGTkcSERERyQyL\nMCIzpZSeClPCnMgT8yI/SskJizAiIiIiIzCbnjBXV1fk5uYaISIyRy4uLrh9+7axwyAiIhNXWU+Y\n2RRhRERERHLDxnwyKKXM3Zsa5kV+mBN5Yl7kRyk5YRFGREREZAScjiQiIiIyEE5HEhEREckMizCq\nMaXM3Zsa5kV+mBN5Yl7kRyk5YRFGREREZATsCSMiIiIyEPaEEREREckMizCqMaXM3Zsa5kV+mBN5\nYl7kIykpDQsW7MObb36JBQv2ISkpzdghGRSLMCIiIjK6pKQ0xMZeQkZGL2RkBOPmzV6Ijb1k1oWY\nwYqwwsJChIaGIjg4GEFBQZg+fToA4Pbt2+jTpw+eeeYZ9O3bF3fu3NHvM3fuXDRr1gwtWrRAfHy8\noUKjWhYWFmbsEKgczIv8MCfyxLzIw549KSgo6I2TJ4G7d8OQlwfUq9cbe/emGDs0gzFYEWZra4v9\n+/fjzJkzOHv2LPbv34/Dhw9j3rx56NOnD5KTk9G7d2/MmzcPAJCYmIh169YhMTERu3fvxhtvvAGd\nTmeo8IiIiEgmhACSky3w+++ARgM4OQE2NtJtGo35TtoZ9JHZ29sDADQaDUpKSuDi4oJt27Zh/Pjx\nAIDx48djy5YtAICtW7ciKioK1tbWCAgIQNOmTXH8+HFDhke1hP0U8sS8yA9zIk/Mi3EVFgLr1wMX\nL+ogBODvD9Svn6AvwmxszHdAxqBFmE6nQ3BwMLy8vNCzZ0+0atUK2dnZ8PLyAgB4eXkhOzsbAJCZ\nmQlfX1/9vr6+vsjIyDBkeERERGRE2dnA4sXA+fNAixaBeOaZvWjSBFCppNuLivaid+9A4wZpQFaG\nPLiFhQXOnDmDu3fvol+/fti/f3+Z21UqFVQPn+lyVHTbhAkTEBAQAABwdnZGcHCwfk7/4X803K7b\n7YfkEg+3wxAWFiareLgN/XVyiYfb3Dbm9g8/JODoUcDPLwxeXkC7dldw585N5OXtg7OzBVJT/412\n7RqgefPesoi3utsPL6empqIqdbZY68cffww7Ozv88MMPSEhIgLe3N7KystCzZ09cuHBB3xs2bdo0\nAED//v0xe/ZshIaGlg2Yi7USERGZLK0W2L0bOHlS2g4OBp5/HrC2Nm5chmKUxVpzcnL033wsKCjA\nL7/8gpCQEERERGD58uUAgOXLl2Po0KEAgIiICKxduxYajQZXrlzBxYsX0alTJ0OFR7WodPVP8sG8\nyA9zIk/MS925cwdYtkwqwCwtgcGDgSFDHi/AlJITg01HZmVlYfz48dDpdNDpdIiOjkbv3r0REhKC\nyMhILFmyBAEBAVi/fj0AICgoCJGRkQgKCoKVlRW+/fbbSqcqiYiIyHRcugT89BNQUAA4OwORkUCD\nBsaOyrh47kgiIiIyGJ0OOHgQOHBAWoqiWTNg+HDAzs7YkdWNyuoWgzbmExERkXLl50ujXykp0jce\ne/UCnn32f99+VDqD9YSRcihl7t7UMC/yw5zIE/NiGBkZwMKFUgFmbw+MHQs891z1CjCl5IQjYURE\nRFRrhJAa73fvBkpKAF9fYNQooH59Y0cmP+wJIyIiolqh0QDbtwNnz0rboaFA377SNyGVij1hRERE\nZFA5OdLph27ckJaciIgAWrc2dlTyxp4wqjGlzN2bGuZFfpgTeWJeai4xUTr90I0bgLs7MHlyzQow\npeSEI2FERET0VEpKgD17gKNHpe1WraQRsHr1jBuXqWBPGBERET2x+/eBDRuA9HTAwkLq/QoN5fIT\nj2JPGBEREdWa1FSpAHvwAFCrpdXv/fyMHZXpYU8Y1ZhS5u5NDfMiP8yJPDEv1ScEcPgwsHy5VIA1\nbgy89lrtF2BKyQlHwoiIiKhKhYXAli3AhQvS9rPPAj17SlOR9HTYE0ZERESVun5dWn7i9m3A1hYY\nNgxo3tzYUZkG9oQRERHRUzlzRlqAVasFfHyk/i8XF2NHZR44iEg1ppS5e1PDvMgPcyJPzEv5tFog\nLk6agtRqgXbtgJdfrpsCTCk54UgYERERlZGbK00/ZmUBVlbA888DISHGjsr8sCeMiIiI9JKTgU2b\npEZ8Fxdp+tHHx9hRmS72hBEREVGldDogIQE4eFDabt4cGDoUsLMzalhmjT1hVGNKmbs3NcyL/DAn\n8sS8SGt+rVolFWAqFRAeDrzwgvEKMKXkhCNhRERECnb1qrT6/b17gIMDMHKktAgrGR57woiIiBRI\nCOD4ceDnn6WpSD8/YNQowMnJ2JGZF/aEERERkZ5GA2zbBvz5p7TduTPQpw9gaWncuJSGPWFUY0qZ\nuzc1zIv8MCfypLS83LwJLF4sFWA2NtLoV//+8irAlJITjoQREREpxJ9/SiNgGg3g4QGMHg24uxs7\nKuViTxgREZGZKykB4uOBY8ek7datgcGDpZEwMiz2hBERESnUvXvStx+vXpWmHPv1Azp2lJaiIONi\nTxjVmFLm7k0N8yI/zIk8mXNeLl8GFi6UCjAnJ+Cll4BOneRfgJlzTkrjSBgREZGZEQI4fBjYt0+6\nHBgIDB8urQNG8sGeMCIiIjNSUABs3iydAxIAevSQfiw492UU7AkjIiJSgKwsYP16IDdXOuXQ8OFA\ns2bGjooqwrqYakwpc/emhnmRH+ZEnswlL6dOAUuWSAVYgwbAq6+abgFmLjmpCkfCiIiITFhxMbBz\nJ3D6tLTdoYO0+KoVP+Fljz1hREREJur2bWn68fp1qegaNAgIDjZ2VFQae8KIiIjMzIULwJYtQGEh\n4OoqrX7v5WXsqOhJsCeMakwpc/emhnmRH+ZEnkwtLzodsGcPsHatVIC1aAFMnmxeBZip5eRpcSSM\niIjIROTlAT/9BFy5Ii05ER4OdOki/8VXqXzsCSMiIjIB6enS6Yfu3wccHYGRI4GAAGNHRVVhTxgR\nEZGJEgL473+BX36RpiIbNZIKMLXa2JFRTbEnjGpMKXP3poZ5kR/mRJ7knJeiImn06+efpQKsa1dg\n3DjzL8DknJPaxJEwIiIiGbpxQ1p+IicHqFcPGDoUaNnS2FFRbWJPGBERkcycPQvExUkLsXp6SstP\nuLkZOyp6GuwJIyIiMgFaLRAfDxw/Lm23aSMtwGpjY9y4yDDYE0Y1ppS5e1PDvMgPcyJPcsnL3bvA\nsmVSAWZpKRVfw4YpswCTS04MjSNhRERERpaSIq3/lZ8P1K8PREYCDRsaOyoyNPaEERERGYkQwMGD\nQEKCdLlpU2D4cMDe3tiRUW1hTxgREZHM5OcDmzcDFy9KK9737Ak89xxXv1cS9oRRjSll7t7UMC/y\nw5zIkzHykpkJLFokFWB2dsCLLwI9erAAe0gp7xWOhBEREdURIYDffgN27QJKSqS+r8hIqQ+MlIc9\nYURERHWguBjYvh34/Xdpu2NHoF8/wIrDIWaNPWFERERGdOuWtPp9djZgbQ0MHiytAUbKxp4wqjGl\nzN2bGuZFfpgTeTJ0Xs6fl/q/srOlVe8nTWIBVhWlvFc4EkZERGQAOh2wZw/w66/SdlAQMGSIdB5I\nIoA9YURERLXu/n1g40YgLQ2wsAD69AE6d+a3H5WIPWFERER1JC0N2LAByMsD1Gpg1CjA39/YUZEc\nsSeMakwpc/emhnmRH+ZEnmorL0JIU4/Ll0sFWEAA8OqrLMCehlLeKxwJIyIiqqHCQmDrVqkJHwC6\ndwd69ZKmIokqYrCesKtXr2LcuHG4ceMGVCoVJk+ejLfffhsxMTH44Ycf4OHhAQCYM2cOBgwYAACY\nO3culi5dCktLS3z99dfo27fv4wGzJ4yIiGQkOxtYtw64fRuwtQWGDgVatDB2VCQXldUtBivCrl+/\njuvXryM4OBh5eXlo3749tmzZgvXr10OtVmPKlCll7p+YmIgxY8bgxIkTyMjIQHh4OJKTk2HxyL8R\nLMKIiEgufv9dWoC1uBjw8gJGjwZcXY0dFclJZXWLwQZKvb29ERwcDABwdHREy5YtkZGRAQDlBrN1\n61ZERUXB2toaAQEBaNq0KY4fP26o8KgWKWXu3tQwL/LDnMjT0+RFq5WKr82bpQIsOBh45RUWYLVF\nKe+VOpmtTk1NxenTp9G5c2cAwDfffIO2bdti4sSJuHPnDgAgMzMTvr6++n18fX31RRsREZFc3LkD\nLF0KnDwpnXIoIkJa/8va2tiRkakxeGN+Xl4eRo4cia+++gqOjo54/fXXMXPmTADAjBkz8N5772HJ\nkiXl7quqYEGVCRMmICAgAADg7OyM4OBghIWFAfhf9cztut1+SC7xcDsMYWFhsoqH29BfJ5d4uP3k\n29euARkZYSgoAHJyEtCzJ9CunXziM5ftMBP++/XwcmpqKqpi0MVai4uLMWjQIAwYMADvvvvuY7en\npqZi8ODB+OOPPzBv3jwAwLRp0wAA/fv3x+zZsxEaGlo2YPaEERFRHdPpgAMHgIMHpaUonnkGGDYM\nsLMzdmQkd0bpCRNCYOLEiQgKCipTgGVlZekvb968Ga1btwYAREREYO3atdBoNLhy5QouXryITp06\nGSo8qkWlq3+SD+ZFfpgTeaoqL/n5wOrVUhEGAL17A1FRLMAMSSnvFYNNRx45cgSrVq1CmzZtEBIS\nAkBajuLHH3/EmTNnoFKp0LhxYyxcuBAAEBQUhMjISAQFBcHKygrffvtthdORREREdeHaNWn1+7t3\nAXt7YORIoEkTY0dF5oLnjiQiInqEEFLj/e7dQEkJ4OsLREYCTk7GjoxMDc8dSUREVE0aDRAXB/zx\nh7QdGgr07QtYWho3LjI/BusJI+VQyty9qWFe5Ic5kafSecnJAX74QSrAbGyk6ccBA1iA1TWlvFc4\nEkZERAQgMRHYskUaCXN3l1a//78z7BEZBHvCiIhI0UpKgD17gKNHpe2//AUYPBioV8+4cZF5YE8Y\nERFROe7dAzZuBNLTAQsLoF8/oFMngF/Op7rAnjCqMaXM3Zsa5kV+mBN5uXIFWLgQOHgwAU5OwEsv\nSU34LMCMTynvFY6EERGRoggBHDkC7N0rXfb2Bl59FXBwMHZkpDTsCSMiIsUoLAQ2bwaSkqTt554D\nwsKkqUgiQ2BPGBERKd7168C6dUBuLmBrCwwfLp0DkshYWPtTjSll7t7UMC/yw5wYz+nT0vpfubmA\nj480/fiwAGNe5EcpOeFIGBERmS2tFti5Ezh1Stpu1w4YOBCw4qcfyQB7woiIyCzl5gLr1wNZWVLR\n9fzzQEiIsaMipWFPGBERKUpyMrBpk9SI7+IirX7v7W3sqIjKYk8Y1ZhS5u5NDfMiP8yJ4el00tIT\na9ZIBVjz5lL/V2UFGPMiP0rJCUfCiIjILDx4APz0E3D5srTgau/eQLduXHyV5Is9YUREZPKuXgU2\nbJBOQ+TgAIwcCTRubOyoiNgTRkREZkoI4Phx4OefpalIf3+pAHNyMnZkRFVjTxjVmFLm7k0N8yI/\nzEnt0mik6cddu6QCrEsXYPz4Jy/AmBf5UUpOOBJGREQm5+ZNafX7nBzAxgYYMgRo1crYURE9GfaE\nERGRSfnzT2DbNmkkzNMTiIwE3N2NHRVR+dgTRkREJq+kBIiPB44dk7ZbtwYGD5ZGwohMEXvCqMaU\nMndvapgX+WFOnt69e8CyZVIBZmkprX4/fHjtFGDMi/woJSccCSMiIlm7fBnYuBHIzwfq1wdGjQJ8\nfY0dFVHNsSeMiIhkSQjg0CFg/37pcmAgMGIEYG9v7MiIqo89YUREZFIKCoDNm6VzQAJAjx7SjwWb\naMiM8OVMNaaUuXtTw7zID3NSPZmZwMKFUgFmZwe8+CLQs6fhCjDmRX6UkhOOhBERkSwIAZw+Dezc\nCWi1QIMG0vITzs7GjozIMNgTRkRERldcDOzYAZw5I2136AD07w9YcaiATBx7woiISLZu3wbWrweu\nXwesrYFBg4C2bY0dFZHhsSeMakwpc/emhnmRH+bkcRcuSP1f168Drq7AK6/UfQHGvMiPUnLCkTAi\nIqpzOh2wdy9w5Ii03bKldP5HW1vjxkVUl9gTRkREdSovT1p8NTVV+sZjeDjQpQugUhk7MqLax54w\nIiKShfR0YMMG4P59wNFRWv2+USNjR0VkHOwJoxpTyty9qWFe5EfJORECOHoUiI2VCrBGjYBXX5VH\nAabkvMiVUnLCkTAiIjKooiJg61YgMVHa7toV6N1bOhE3kZKxJ4yIiAzmxg1g3Trg1i2gXj1g6FCp\nCZ9IKdgTRkREde7sWSAuTlqI1ctLWv3ezc3YURHJB3vCqMaUMndvapgX+VFKTrRaafX7TZukAqxt\nW2n9L7kWYErJiylRSk44EkZERLXm7l1p9fuMDKnna+BAoF07Lj9BVB72hBERUa24dEka/crPl066\nHRkpnYSbSMnYE0ZERAYjBHDggPQjBNC0KTB8OGBvb+zIiOSNPWFUY0qZuzc1zIv8mGNO8vOB1auB\nhw+tZ0/gxRdNqwAzx7yYOqXkhCNhRET0VDIypP6vu3elomvECCAw0NhREZkO9oQREdETEQL47Tdg\n1y6gpARo2FDq/6pf39iREckPe8KIiKhWaDTA9u3SGmAA0KkT0LcvYMVPE6Inxp4wqjGlzN2bGuZF\nfkw9J7duAT/8IBVg1tbS9OPAgaZfgJl6XsyRUnJi4m8dIiKqC+fPA1u2SOeBdHeXph89PY0dFZFp\nY08YERFVqKQE2LsX+PVXaTsoCBgyRDoPJBFVjT1hRET0xO7fBzZuBNLSAAsLqfcrNJSr3xPVFvaE\nUY0pZe7e1DAv8mNKOUlNBRYulAowtRqYMAHo3Nk8CzBTyotSKCUnHAkjIiI9IaSpx717AZ0OaNxY\nasB3dDR2ZETmhz1hREQEACgslJrvL1yQtrt3B3r1kqYiiejpsCeMiIgqlZ0NrFsH3L4N2NoCw4YB\nzZsbOyoi88b/b6jGlDJ3b2qYF/mRa07OnJHW/7p9G/D2BiZPVlYBJte8KJlScsKRMCIihdJqpVMP\n/fabtB0SIi2+am1t3LiIlMJgPWFXr17FuHHjcOPGDahUKkyePBlvv/02bt++jdGjRyMtLQ0BAQFY\nv349nJ2dAQBz587F0qVLYWlpia+//hp9+/Z9PGD2hBER1didO9LJtzMzpRXvBw4E2rUzdlRE5qey\nusVgRdj169dx/fp1BAcHIy8vD+3bt8eWLVuwbNkyuLu7Y+rUqZg/fz5yc3Mxb948JCYmYsyYMThx\n4gQyMjIQHh6O5ORkWDzSEcoijIioZi5eBDZtAgoKABcXafV7Hx9jR0VkniqrWwzWE+bt7Y3g4GAA\ngKOjI1q2bImMjAxs27YN48ePBwCMHz8eW7ZsAQBs3boVUVFRsLa2RkBAAJo2bYrjx48bKjyqRUqZ\nuzc1zIv8GDsnOh2wfz+werVUgD3zjNT/pfQCzNh5occpJSd10hOWmpqK06dPIzQ0FNnZ2fDy8gIA\neHl5ITs7GwCQmZmJzp076/fx9fVFRkZGXYRHRGT2HjyQRr9SUqQFV3v1kpagMMfFV4lMhcGLsLy8\nPIwYMQJfffUV1Gp1mdtUKhVUlfwFqOi2CRMmICAgAADg7OyM4OBghIWFAfhf9cztut1+SC7xcDsM\nYWFhsoqH29BfV9e/v2nTMKxfD5w9mwBbW2Dq1DA0aWL854Pb3K5oO8yE/349vJyamoqqGHSx1uLi\nYgwaNAgDBgzAu+++CwBo0aIFEhIS4O3tjaysLPTs2RMXLlzAvHnzAADTpk0DAPTv3x+zZ89GaGho\n2YDZE0ZEVC1CACdOAD//LJ2I288PGDUKcHIydmREymGUnjAhBCZOnIigoCB9AQYAERERWL58OQBg\n+fLlGDp0qP76tWvXQqPR4MqVK7h48SI6depkqPCoFpWu/kk+mBf5qcucaDTS9OPOnVIB1rmzdP5H\nFmCP43tFfpSSE4NNRx45cgSrVq1CmzZtEBISAkBagmLatGmIjIzEkiVL9EtUAEBQUBAiIyMRFBQE\nKysrfPvtt5VOVRIRUflycqTV72/eBGxsgIgI4C9/MXZURPQonjuSiMiMnDsHbN0qjYR5eEjLT3h4\nGDsqIuXiuSOJiMxcSQnwyy/Af/8rbf/lL9IImI2NceMioooZrCeMlEMpc/emhnmRH0Pl5N49IDZW\nKsAsLIABA4ARI1iAVRffK/KjlJxUORKWl5cHOzs7WFpaIikpCUlJSRgwYACseXIxIiKju3IF2LhR\nWgfMyUn69qOfn7GjIqLqqLInrF27djh8+DByc3PRrVs3dOzYETY2Nli9enVdxVgGe8KIiKTlJw4f\nBvbtky43aSKNfjk4GDsyIiqtRktUCCFgb2+PTZs24Y033sCGDRvw559/1nqQRERUPQUFwNq1wN69\nUgH23HPA2LEswIhMTbV6wo4ePYrVq1fj+eefBwDodDqDBkWmRSlz96aGeZGf2shJVhawaBGQlATY\n2QFjxkinILJgh+9T43tFfpSSkyp7wr788kvMnTsXw4YNQ6tWrZCSkoKePXvWRWxERFTK6dPAjh2A\nViuddDsyEnBxMXZURPS0uE4YEZHMFRdLK9+fPi1tt28vfQPSiosMEclejdYJO3HiBObMmYPU1FRo\ntVr9Ac+ePVu7URIR0WNyc6XV769fl4quQYOA4GBjR0VEtaHKLoIXX3wRL730En766SfExcUhLi4O\n27Ztq4vYyEQoZe7e1DAv8vOkOUlKAhYulAowV1fglVdYgBkC3yvyo5ScVDkS5uHhgYiIiLqIhYiI\nAOh0wP79wKFD0nbz5sCwYYCtrXHjIqLaVWVPWHx8PNatW4fw8HDY/N/yyyqVCsOHD6+TAB/FnjAi\nMmcPHkiLr165AqhUQO/eQLdu0mUiMj016glbvnw5kpKSoNVqYVHqO9DGKsKIiMxVejqwYQNw/z7g\n6AiMHAkEBBg7KiIylCpHwpo3b44LFy5AJZN/wzgSJj8JCQkICwszdhj0COZFfirKiRDAsWNAfLw0\nFenvL51+SK2u+xiViO8V+TGnnNRoJKxr165ITExEq1ataj0wIiKlKyoCtm0Dzp2Ttrt0AcLDAUtL\n48ZFRIZX5UhYixYtkJKSgsaNG6NevXrSTkZcooIjYURkLm7elJafyMkB6tUDhgwBgoKMHRUR1abK\n6pYqi7DU1NRyrw8wUqMCizAiMgd//AHExQEaDeDpKa1+7+5u7KiIqLbV6ATeAQEB5f4QPaSU9VxM\nDfMiPwkJCSgpkVa//+knqQBr00Za/4sFmPHwvSI/SskJT3pBRFRH8vKAZcuAa9eknq/+/YEOHbj8\nBJFS8dyRRER1ICVFGv3Kzwfq15emHxs2NHZURGRoNfp2JBERPT0hpJXv9++XLgcGAiNGAPb2xo6M\niIytyp6wn376Cc2aNYOTkxPUajXUajWcnJzqIjYyEUqZuzc1zIvxFRQAa9YA+/ZJ287OCXjxRRZg\ncsP3ivwoJSdVjoRNnToV27dvR8uWLesiHiIis5CZCaxfD9y5A9jZSaNf164BFlX+60tESlFlT1i3\nbt1w5MiRuoqnSuwJIyI5EwI4dUr6BmRJCdCggdT/5exs7MiIyBhq1BPWoUMHjB49GkOHDpXFCbyJ\niOSquBjYsQM4c0ba7tgR6NcPsGL3LRGVo8qB8bt378LOzg7x8fHYvn07tm/fjri4uLqIjUyEUubu\nTQ3zUrdu3QJ++EEqwKytgWHDgOefL1uAMSfyxLzIj1JyUuX/Z7GxsXUQBhGR6bpwAdi8WToPpJub\nNP3o5WXsqIhI7irsCZs/fz7ef/99vPXWW4/vpFLh66+/Nnhw5WFPGBHJhU4H7N0LPGybbdlSOv+j\nra1x4yIi+XiqnrCg/zuLbPv27aEqtZyzEKLMNhGREuXlARs3Aqmp0jcew8OBLl24+j0RVR9XzKca\nS0hIQFhYmLHDoEcwL4aTlgZs2CAVYo6OwKhRQKNGVe/HnMgT8yI/5pQTrphPRFQLhACOHgX27JGm\nIhs1kgowR0djR0ZEpogjYURE1VBUBGzZApw/L2136wb07s3FV4mochwJIyKqgexsafX7W7eAevWA\noUOlJnwiopqo8n+4pKQk9O7dG61atQIAnD17Fp988onBAyPToZT1XEwN81I7fv9dWv/r1i1p2YnJ\nk5++AGNO5Il5kR+l5KTKImzSpEmYM2eOfrX81q1b48cffzR4YERExqTVAtu3S+t/FRcDbdsCr7wi\nrQNGRFQbquwJ69ChA06ePImQkBCcPn0aABAcHIwzD8/LUcfYE0ZEhnbnjvTtx4wMwNISGDgQaNeO\ny08Q0ZOrUU+Yh4cHLl26pN/euHEjfHx8ai86IiIZuXQJ+OknoKBAOul2ZKR0Em4iotpW5XTkf/7z\nHzFBi0sAACAASURBVLz66qu4cOECGjRogC+++ALfffddXcRGJkIpc/emhnl5MjodkJAArF4tFWDN\nmgGvvlq7BRhzIk/Mi/woJSdVjoQFBgZi7969ePDgAXQ6HdRqdV3ERURUZ/LzgU2bpFEwlQro1Qt4\n9llOPxKRYVXZE5abm4sVK1YgNTUVWq1W2onnjiQiM5GRIS0/cfcuYG8PjBgBBAYaOyoiMhc16gkb\nOHAgunTpgjZt2sDCwoLnjiQisyAEcPIksHs3UFIC+PpKq9/Xr2/syIhIKaocCWvXrh1OnTpVV/FU\niSNh8mNO5/gyJ8xLxTQaafmJs2el7U6dgH79pG9CGhJzIk/Mi/yYU05qNBI2ZswYLFq0CIMHD0a9\nevX017u6utZehEREdSQnR5p+vHEDsLYGIiKA1q2NHRURKVGVI2H/+c9/8M9//hPOzs6w+L+TpKlU\nKly+fLlOAnwUR8KI6GklJgJbt0rngXR3l5af8PQ0dlREZM4qq1uqLMIaN26MEydOwN3d3SDBPSkW\nYUT0pEpKgD17gKNHpe1WraQRsFKD+0REBlFZ3VLlOmHNmjWDnZ1drQdF5kMp67mYGuZFcv8+sHy5\nVIBZWAD9+wMjRxqnAGNO5Il5kR+l5KTKnjB7e3sEBwejZ8+e+p4wYy5RQURUXampwMaNQF4eoFZL\n33709zd2VEREkiqnI2NjYx/fSaXC+PHjDRVTpTgdSURVEQI4cgTYu1e63LixNPrl4GDsyIhIaWrU\nEyY3LMKIqDKFhcCWLcCFC9L2s88CPXtKU5FERHXtqXrCRo0aBQBo3br1Yz9t2rQxTKRkkpQyd29q\nlJiX69eBRYukAszWFoiKAnr3lk8BpsScmALmRX6UkpMKe8K++uorAMD27dsfq+C4Yj4Ryc2ZM9IC\nrFot4O0tLT/B5QyJSM6qnI58//33MX/+/CqvqyucjiSi0rRaYNcu4LffpO2QEGDgQGkhViIiY6tR\nT1hISAhOnz5d5rrWrVvjjz/+qL0InwCLMCJ6KDdXWv0+KwuwspKKr3btjB0VEdH/PFVP2HfffYfW\nrVsjKSmpTD9YQEAAe8KoDKXM3Zsac89LcrLU/5WVBbi4ABMnyr8AM/ecmCrmRX6UkpMKi7AxY8Yg\nLi4OERER2L59O+Li4hAXF4fffvsNq1evrtbBX375ZXh5eaF1qROzxcTEwNfXFyEhIQgJCcGuXbv0\nt82dOxfNmjVDixYtEB8fX4OHRUTmSqcD9u0D1qwBCgqA5s2ByZMBHx9jR0ZE9GQMukTFoUOH4Ojo\niHHjxumnL2fPng21Wo0pU6aUuW9iYiLGjBmDEydOICMjA+Hh4UhOTtafr1IfMKcjiRTrwQPgp5+A\ny5cBlQro1Qvo3l26TEQkRzU6bVFNPPvss3BxcXns+vKC2bp1K6KiomBtbY2AgAA0bdoUx48fN2R4\nRGRCrl4FFi6UCjAHB2DcOGkNMBZgRGSqjLJ6zjfffIO2bdti4sSJuHPnDgAgMzMTvr6++vv4+voi\nIyPDGOHRE1LK3L2pMZe8CAEcOwYsWwbcuwf4+QGvviqtgm9qzCUn5oZ5kR+l5KTKc0fWttdffx0z\nZ84EAMyYMQPvvfcelixZUu59K1qPbMKECQgICAAAODs7Izg4GGFhYQD+lzhu1932mTNnZBUPt81n\n+5dfEvDrr4AQ0ra9fQICAgAnJ3nE96TbZ86ckVU83Ja2H5JLPNw27e2Hl1NTU1EVg5+2KDU1FYMH\nDy53SYvSt82bNw8AMG3aNABA//79MXv2bISGhpYNmD1hRIpw86a0/MTNm4CNDTBkCNCqlbGjIiJ6\nMkbrCStPVlaW/vLmzZv135yMiIjA2rVrodFocOXKFVy8eBGdOnWq6/CISAb+/BNYvFgqwDw8gEmT\nWIARkfkxaBEWFRWFrl27IikpCX5+fli6dCnef/99tGnTBm3btsWBAwfwxRdfAACCgoIQGRmJoKAg\nDBgwAN9+++3/b+/eg6K87/2Bv7mLiiCXBQWVOwi73hKviQaDl6aJd8FokzS1zS9NezJN26PJyZxO\nJ5mx4vScM6c5TU/O5MQxmZ7YRE28xMQYMKgx3pV0FxS5LSgiK1e577L7/f3xLRsRxQssz7P7vF8z\nnfHZBfzip5iP3+/neT98PJKbuHVLn9TBHetitwMHDgA7dwJWK2AwyAYsIkLplQ0Od6yJFrAu6qOV\nmrh0Jmz79u19Xlu/fv0dP/7111/H66+/7solEZFK3bgB7Ngh74L08QEWLwamT+fdj0TkuVw+EzbY\nOBNG5HnKy2X+V1sbMGqUfPj2TTdLExG5rf76liG/O5KIqIcQwDffyAR8IYD4eGDVKpkDRkTk6YZ8\nMJ88j1bO7t2N2uvS0QFs3w7k5ckG7LHHgGee8ewGTO010SrWRX20UhPuhBHRkKupkfETjY1AYCCw\nYgWQnKz0qoiIhhZnwohoSJ07B3z+OdDdDYwdK+e/QkKUXhURkWtwJoyIFGezyebr/Hl5/dBDwBNP\nAL78W4iINIozYTRgWjm7dzdqqktDA/Dee7IB8/UFli8HlizRXgOmpprQ91gX9dFKTTT2VyARDbWL\nF4Hdu4HOTiA0VB4/RkUpvSoiIuVxJoyIXMLhkNET33wjr1NT5Q7YsGHKrouIaChxJoyIhlRrqwxf\nraiQifcLFgBz5jD9nojoZpwJowHTytm9u1GqLlVVwP/8j2zARo4Efvxj4JFH2IAB/FlRK9ZFfbRS\nE+6EEdGgEAI4cQL46it5FDl+PJCVBQQFKb0yInIXxaXFyD2biwuFF1BYW4gFDy1ASmKK0styGc6E\nEdGAdXUBe/YARUXyes4cIDNTPoibiOheFJcWY2veVtyIvoEbXTeQFJaErpIuPD//ebduxDgTRkQu\nY7HI9Pu6OiAgAFi2DEhLU3pVROQu7A47ShtK8cfP/ojy0eVw1DkAAGODxmJE0gjknctz6yasP5wJ\nowHTytm9uxmKuhiNwLvvygZMpwP+3/9jA9Yf/qyoE+sy9BzCgYrGCuwt3ot/+/bfsN20HVdar8Ah\nHBgVMAojqkfA38cfAGB1WBVeretwJ4yI7lt3N3DwIHDqlLyeNAl46inA31/ZdRGRegkhUN1SDZPF\nhEJLIVqsLc73IkdEYmLYRPhH+yPQLxDmWjP8fPwAAP7envsXC2fCiOi+NDfL48fqajnz9cQT8hFE\nvPuRiG7H0maBsdYIk8WExs5G5+ujh42GIdIAvU4P3QgdikuLse3rbQhICnB+jKfPhLEJI6J7VlYm\n87/a24HgYJl+Hx2t9KqISG0aOxphsphgtBhhabM4Xw/yD0K6Lh0GnQFjg8bC65Z/vRWXFiPvXB6s\nDiv8vf2ROS3TrRswgE0YuVh+fj4yMjKUXgbdYjDrIgRw5AiQny9/nZgIrFwJDB8+KF9eM/izok6s\ny+Bo6WpB4fVCmCwmXLlxxfl6oG8g0iLSoNfpMSFkAry97j6O7kk14d2RRPTA2tuBTz8FSkrkkWNG\nBjBvHuDN23qINK/D1oELdRdgrDXC3GSGgGw2/H38kRKWAkOkAQmjE+Djzbya2+FOGBHd0dWrcv6r\nqQkIDARWrZK7YESkXVa7FcV1xTBZTChtKIVd2AEAPl4+SApLgl6nR3JYsvPuRq3jThgR3RchgLNn\ngS++AOx2OfeVlQWEhCi9MiJSQk+Wl9FiRHFdMWwOGwDAC16IHx0Pg86A1PBUBPoFKrxS98ImjAbM\nk87uPcmD1sVmAz77DPjuO3k9fTqweDHgy78tBow/K+rEutyeQzhgbjLDZDGh6HoROrs7ne/FjIqB\nQWdAui4dI/1HDvrvrZWa8K9VInKqr5fHj7W1gJ8fsGSJzAAjIm3oyfIy1hpReL0QrdZW53uRIyJh\niDQgPSIdowNHK7hKz8GZMCICAFy4AOzeLZ8DGRYGrFkjU/CJyPPdLcvLoDMgYkSEgit0X5wJI6I7\ncjiA3Fzg22/ldVqafP5jQED/n0dE7q2xoxFGi2y87ifLiwYPmzAaMK2c3bube6lLSwuwcydQWSkj\nJxYuBGbNYvq9q/BnRZ20VJeeLC9jrRHVLdXO1x8ky8uVtFITNmFEGlVZCezYAbS2AkFBwOrVwIQJ\nSq+KiAYbs7zUizNhRBojBHD8uDyCdDiA2FjZgI0c/BuciEghzPJSD86EEREAoLMT2LNHDuEDwKOP\nAo8/zvR7Ik/Q7ehGWUNZv1leEyMmYpjvMIVXSj3YhNGAaeXs3t3cWpfaWuCjj4CGBjl0v2IFkJqq\n3Pq0iD8r6uTOdekvy2vcqHHQ6/Quy/JyJXeuyf1gE0akAd99JwNYbTYgMlLGT4SGKr0qInoQ95Ll\npdfpETKMj7hQO86EEXmw7m7gwAHgzBl5PWUK8OSTMoiViNxLbWstTBZTnyyv0MBQ6HV6ZnmpFGfC\niDSoqUmm31+9Kh859MQTwLRpjJ8gcif9ZXnpdXrodXpmebkxNmE0YFo5u3cnJSXAH/+Yj7FjMxAS\nAmRnA2PHKr0q4s+KOqmtLnfL8jJEGjA+eLziWV6upLaauAqbMCIP4nAAhw8DR44AViuQlASsXAkE\nBiq9MiLqT4etA0XXi2CymJjlpSGcCSPyEO3twK5dQFmZPHKcPx+YO5fHj0Rq1ZPlZbQYUdZQdtss\nr5SwFPj5cIjTnXEmjMjDXbki0++bm4Hhw4FVq4CEBKVXRUS36nZ0o7ShFCaLiVlexCaMBk4rZ/dq\nJIS88/HAAcBuB2JigKwsIDiYdVEj1kSdXF0XT83yciWt/KywCSNyU1YrsG8fYDTK65kzgUWLAB+O\njBApjlledC84E0bkhurqZPyExQL4+wNLlwJ6vdKrIiJmedGtOBNG5EGKioDdu+VOWHi4TL+P4N/p\nRIphlhc9KDZhNGBaObtXmt0O5OYCx4/L6/R0uQMWEHD7j2dd1Ic1UacHqQuzvFxLKz8rbMKI3MCN\nG8DOnUBVFeDtDSxeDMyYwfgJoqHUX5ZXangq9Do9s7zovnAmjEjlKipkA9bWBgQFyfT7ceOUXhWR\nNtwty8ugMyA5LJlZXnRHnAkjckNCAMeOAXl58tdxccDq1cCIEUqvjMiz9ZfllTA6AXqdnlleNCjY\nhNGAaeXsfih1dgKffgoUF8vruXNlAr73fYyXsC7qw5qoU35+PuY9Ng/mJjOMtUZcqLvALC+FaeVn\nhU0YkcpcuwZ89BHQ2AgMGwasWAGkpCi9KiLPI4TAlRtXcPLKSZw5fqZXllfUyCjnnY3M8iJX4UwY\nkYqcPw/s3w90dwNjxsj5r9GjlV4VkWepba11Rko0dTY5Xw8NDIVBJ0NUmeVFg4UzYUQq190NfP45\ncO6cvJ42DXjiCcCPs75Eg6Kho8EZososL1ILNmE0YFo5u3eVxkaZfl9TA/j6Ak8+CUydOvCvy7qo\nD2sytO41y+vI4SOIToxWcKV0K638rLAJI1LQpUvAJ5/IQfzRo+Xx45gxSq+KyH31ZHkZLUZUNlUy\ny4tUjTNhRApwOICvvwaOHpXXKSlyAH8Y73gnum/M8iI140wYkYq0tQG7dgHl5TLxPjMTeOQRpt8T\n3Q9meZEnYBNGA6aVs/vBcPkysGOHfAzRiBEyfDUuzjW/F+uiPqzJwDiEo98sL0OkAWkRafed5cW6\nqI9WauLSJmz9+vXYv38/dDodjEYjAKChoQFr1qxBZWUlYmNj8fHHHyMkRGawbN68GVu3boWPjw/e\neustLFq0yJXLIxoyQgCnTgFffimPIseNA7KygFGjlF4Zkbr1ZHmZLCYUXi9klhd5FJfOhB09ehQj\nR47Ec88952zCNm7ciPDwcGzcuBFbtmxBY2MjcnJyUFRUhHXr1uH06dOorq7GggULcOnSJXjfEhHO\nmTByN1YrsHcvYDLJ69mzgQULAB/OBRPdlhACljYLs7zIIyg2EzZ37lyYzeZer+3duxeHDx8GAPz4\nxz9GRkYGcnJysGfPHqxduxZ+fn6IjY1FYmIiTp06hVmzZrlyiUQudf26TL+vqwP8/YFly4D0dKVX\nRaROPVlexlojrrdfd74+KmAU0iPSYYg0YMzIMczyIo8x5DNhtbW1iIyMBABERkaitrYWAHD16tVe\nDVdMTAyqq6tv+zVIXbRydn+/TCa5A2a1AhERwJo1QHj40P3+rIv6sCZ9tXS1OENUb83yStelQ6/T\nY0LwBJc2XqyL+milJooO5nt5efX7g3Wn955//nnExsYCAEJCQjBlyhRnsfLz8wGA10N4XVBQoKr1\nKH1ttwNWawZOngTM5nzExQEvvJABf391rI/Xyl0XFBSoaj1KXc94ZAYuXL+AHZ/vwLXWa4idEgsA\nuPL3KxgfPB5rn1qL+NHxOHrkKMxXzYjNiHXpenqo5c+H1+593fPrW08Cb8flOWFmsxlLlixxzoSl\npqYiPz8fUVFRqKmpwfz583Hx4kXk5OQAAF577TUAwA9+8AO88cYbmDlzZu8FcyaMVOzGDZl+f+WK\nnPlavBiYPp3xE0RWuxUX6y7CZDGhtKEUDuEAwCwv8nyqyglbunQp3n//fbz66qt4//33sXz5cufr\n69atw29+8xtUV1ejpKQEM2bMGOrlET2w8nJg506gvV3e9ZidDcTEKL0qIuX0ZHkZa424VH+JWV5E\nt3BpE7Z27VocPnwYdXV1GDduHN5880289tpryM7OxnvvveeMqACAtLQ0ZGdnIy0tDb6+vvjLX/7C\n4Us3kZ+f79yO1SIhZPL911/LXyckACtXyhwwJWm9LmqkhZq4KsvLlbRQF3ejlZq4tAnbvn37bV/P\nzc297euvv/46Xn/9dVcuiWhQdXQAn34qnwEJAI89Jv/n7a3suoiGErO8iB4Mnx1J9ICuXpXzX01N\nQGCg3P1KSlJ6VURDg1leRPdGVTNhRO5OCOD8eeDzz4HubmDsWDn/FcJ/5JMGMMuLaPCwCaMB08rZ\nPQDYbMD+/cA/kgbw8MPAD34A+KrwJ0lLdXEX7lqTO2V5DfcbjrSItCHJ8nIld62LJ9NKTVT4nw4i\ndWpokMeP164Bfn7AU08BkycrvSoi12i3tePC9QswWoyobKqEgDxO8ffxR2p4Kgw6A+JHx8PHm8/f\nInpQnAkjugcXLwK7dwOdnUBoqEy//8eDH4g8Rn9ZXslhydDr9MzyIrpPnAkjekAOB5CXBxw7Jq9T\nU4Hly4FhjDUiD3G3LC9DpAGp4anM8iJyATZhNGCeenbf2irDV81mGTmxYAEwe7b7pN97al3cmVpq\n4hAOVDRWwGQx3THLKz0iHSP8FQ67GyJqqQt9Tys1YRNGdBtVVcCOHUBLCzByJLB6NfCPx5USuaWe\nLC+jxYhCSyHabG3O95jlRaQMzoQR3UQI4MQJ4Kuv5FHkhAmyAQsKUnplRPdPCIHatlrnnY3M8iIa\nepwJI7oHXV3Anj1AUZG8njMHyMyUD+ImcifM8iJyD2zCaMA84ezeYgE++giorwcCAuTw/cSJSq9q\nYDyhLp7GlTXx9CwvV+LPivpopSZswkjz/v53YN8+GcSq08n4ibAwpVdFdHfM8iJyb5wJI83q7ga+\n/BI4fVpeT54MPPkk4O+v7LqI+nOnLC9fb18khSYxy4tIZTgTRnSL5maZfl9dLWe+nngCeOgh94mf\nIG25U5aXt5c3s7yI3BibMBowdzu7Ly0FPvkEaG8HgoPlw7ejo5Ve1eBzt7powf3UpL8sr/HB46HX\n6TWV5eVK/FlRH63UhE0YaYYQwOHD8n9CAImJwMqVwPDhSq+MSLpblpdBZ0C6Lp1ZXkQegjNhpAnt\n7XL3q7RUHjlmZADz5vH4kZTXX5ZXWGCYM0SVWV5E7okzYaRp1dVy/qu5We56rVwpd8GIlNTQ0QBj\nrREmi6lPlldP48UsLyLPxiaMBkytZ/dCAGfPAl98Adjtcu4rO1vOgWmBWuuiZfsP7kfoxFAYLUZc\nbbnqfL0ny8ugM2B88Hg2XkOMPyvqo5WasAkjj2SzAZ99Bnz3nbyePh1YvBjw5f/jaYi129pRdL0I\nJosJ+UX5iPWPBSCzvCaGT4Rep2eWF5FGcSaMPE59vUy/t1gAPz9gyRJg0iSlV0Va0tXdheL6Yhhr\njShrLGOWF5GGcSaMNOPCBWD3bvkcyLAwmX6v0ym9KtKCbkc3SupLYLKYmOVFRPeETRgNmBrO7u12\nIC8P+PZbeZ2WBixbJp8DqVVqqIun68nyMlqMuFh38a5ZXqyJOrEu6qOVmrAJI7fX0gLs3AlUVgLe\n3sDChcCsWYyfINdglhcRDRbOhJFbM5tlA9baCgQFAVlZwPjxSq+KPM29ZHkZIg0IHx6u4CqJSI04\nE0YeRwh59JiXBzgcQGwssHo1MHKk0isjT8IsLyJyJTZhNGBDfXbf2SmH7y9elNePPgo8/rg8iqTv\naWWmYrDd6LqBQkuhS7K8WBN1Yl3URys1YRNGbqW2VsZPNDQAw4YBy5cDqalKr4rc3c1ZXpVNlRCQ\nRwfM8iIiV+JMGLmNggJg/34ZxBoVJdPvQ0OVXhW5q7tleRkiDUgKTWKWFxENCGfCyK11d8tHD509\nK6+nTAGefFIGsRLdj/6yvBJDE6HX6ZnlRURDhk0YDZgrz+6bmuTDt69elY8c+uEPgalTGT9xL7Qy\nU3E3N2d5Xbh+AV32Lud744PHw6AzIC0izZnl5UqsiTqxLuqjlZqwCSPVKikBPvkE6OgAQkJk+v2Y\nMUqvityBEAKXb1yGyWK6Y5aXXqdH8DCNPM2diFSJM2GkOg4HcPiw/B8AJCcDK1YAgYHKrovUrSfL\nqydSormr2fleWGAYDJGy8WKWFxENJc6Ekdtobwd27QLKyuSR4+OPywgKHj/SnfRkeRktRtS11zlf\n78nyMugMiBoZxSwvIlIdNmE0YIN1dn/lipz/unEDGD5chq/Gxw98fVrlyTMVrszyciVProk7Y13U\nRys1YRNGihMCOH0a+PJL+SDucePk44dGjVJ6ZaQmzPIiIk/DmTBSlNUK7NsHGI3yeuZMYNEiwIf/\nHSUwy4uI3B9nwkiV6upk+v3164C/P7B0KaDXK70qUhqzvIhIK9iE0YA9yNl9YSGwZ4/cCQsPl/ET\nERGuWZ9WudNMhZqyvFzJnWqiJayL+milJmzCaEjZ7cBXXwEnTshrvR5YsgQICFB2XTT0+svyGjNy\nDPQ6PbO8iMijcSaMhsyNG8COHcDly4C3N7B4MTBjBuMntIRZXkSkNZwJI8VVVAA7dwJtbfKux6ws\neRckaUN9ez1MFhOzvIiIbsImjAasv7N7IYBjx4C8PPnr+Hhg1SpghHuP9rgFpWcqbnTdgMligsli\n6pPllR6RDr1Or8osL1dSuiZ0e6yL+milJmzCyGU6OoDdu4HiYnk9bx6QkSGPIskz9WR5GWuNqGqu\ncmZ5BfgEIDU8FYZIA+JC4pjlRUQEzoSRi9TUyPT7xkZg2DBg5Ur5DEjyPMzyIiK6M86E0ZA6fx7Y\nvx/o7gbGjAGys4HRo5VeFQ2mm7O8iuuL0e3oBsAsLyKi+8EmjAas5+zeZgM+/1w2YQAwbRrwwx8C\nvvx/mSIGe6bCIRwobyyHyWLy6CwvV9LKnIu7YV3URys14X8eaVA0Nsr0+2vXZNP15JPA1KlKr4oG\nilleRESuw5kwGrDiYuDTT4HOTnnsuGYNEBWl9KroQTHLi4ho8HAmjFzC4QC+/ho4elRep6QAK1bI\nQXxyP8zyIiIaWmzC6IG0tcnw1YoKwGzOx89+loFHHmH6vZrcy0wFs7yGllbmXNwN66I+WqkJmzC6\nb1VV8vFDLS0ydHXxYuDRR5VeFd0rZnkREakDZ8LongkBnDwJHDwojyLHj5ePHwoKUnpldDdd3V24\nWHcRJoupT5ZXclgy9Do9s7yIiFyAM2E0YF1dwN69QGGhvJ49G1iwAPDhZolq9WR5GS1GXKq/1CfL\ny6AzIDU8FQG+AQqvlIhIm9iE0V1dvy7jJ+rqAH9/YPlyIC3t+/e1cnbvDm7O8tp/cD+iJ0U735sQ\nPAF6nZ5ZXgriz4o6sS7qo5WaKNaExcbGYtSoUfDx8YGfnx9OnTqFhoYGrFmzBpWVlYiNjcXHH3+M\nkJAQpZZIAIxGYN8+wGoFdDqZfh/OZAJV6cnyMtYaUXS9yJnlZXPYmOVFRKRiis2ExcXF4ezZswgN\nDXW+tnHjRoSHh2Pjxo3YsmULGhsbkZOT0+vzOBM2NOx24MsvgVOn5LXBACxZInfCSHlCCFxrvea8\ns5FZXkRE6tRf36JoE3bmzBmEhYU5X0tNTcXhw4cRGRmJa9euISMjAxcvXuz1eWzCXK+5Wd79eOWK\nnPn6wQ+Ahx9m/IQa1LfXw2iRIarM8iIiUj9VNmHx8fEIDg6Gj48PXnzxRbzwwgsYPXo0GhsbAch/\n6YeGhjqvnQtmE+ZSZWXArl1AezsQHCzvfoyJ6f9ztHJ2r5QHzfJiXdSHNVEn1kV9PKkmqrw78tix\nYxgzZgyuX7+OhQsXIjU1tdf7Xl5ed/zX/PPPP4/Y2FgAQEhICKZMmeIsVn5+PgDw+j6vH3ssA0eP\nAlu3yuvMzAysWgWcOpWP0tL+P7+goEDx9Xva9YxHZqDoehF27N+B2rZaxE6JBQBU/70a44PHY+2S\ntYgLicPRI0dRcbUCEzImqGr9vL79dUFBgarWw2t53UMt6+G1e1/3/NpsNuNuVJET9sYbb2DkyJF4\n9913kZ+fj6ioKNTU1GD+/Pk8jhwCHR3AJ58AJSXyyHHePOCxxwBvb6VXpi3M8iIi8jyqO45sb2+H\n3W5HUFAQ2trasGjRIvz+979Hbm4uwsLC8OqrryInJwdNTU0czHexq1eBjz8GmpqAwEBg5UogKUnp\nVWlHf1le8aPjmeVFROTmVNeEVVRUYMWKFQCA7u5u/OhHP8K//Mu/oKGhAdnZ2aiqqrpjRAWbsMEh\nBHDuHPD55/JOyLFjZfzEgySC5OfnO7dj6e5uzvK6cP0CuuxdzvcGM8uLdVEf1kSdWBf18aSaElba\nYwAAGBNJREFUqG4mLC4uzjkbcbPQ0FDk5uYqsCJtsdmA/fuBnhI8/LC8A9KX0b0uc6csLwAYM3IM\nDJEGpEekM8uLiEhDVDETdj+4EzYwDQ0y/b62FvDzA556Cpg8WelVeab+srzCh4c7Q1SZ5UVE5LlU\ntxNGyrh4Efj0U/kcyNBQYM0aIDJS6VV5njtleQUHBDsbL2Z5ERERmzANcDiAvDzg2DF5PXEisGwZ\nMGzY4Hx9Tzq7f1DNnc0ovF4IY60RNa01ztdH+I1AWkQaDJEGjBs1bkgbL9ZFfVgTdWJd1EcrNWET\n5uFaW4GdOwGzWUZOLFgAzJ7N9PvB0G5rR6GlECaLCZXNlc7XA3wCMDFiIvQ6PeJHx8Pbi1kfRETU\nF2fCPFhlpXz8UGsrMHKkTL+fMEHpVbm3niwvo8WI8sbyPlleBp0BSWFJ8PXmv2+IiIgzYZojBHD8\nOJCbK48iJ0wAVq8GgoKUXpl76i/LKzE0kVleRET0QNiEeZiuLmD3buDCBXn9yCNAZqZr0+898ex+\nqLK8XMkT6+LuWBN1Yl3URys1YRPmQWprZfp9fT0QEAAsXy6H8One3JzlVXi9EO22dud7zPIiIqLB\nxpkwD/H3vwP79skg1shImX4fFqb0qtTvXrK8DDoDwobzD5OIiO4fZ8I8WHc38OWXwOnT8nryZBnA\n6sdnPPeLWV5ERKQ0NmFurKlJ3v1YXQ34+AA//CEwbdrQx0+4y9m9GrO8XMld6qIlrIk6sS7qo5Wa\nsAlzU6WlwK5dQEeHfOh2drZ8CDf11mZtQ9H1ImZ5ERGR6nAmzM04HMCRI8DhwzKKIikJWLECGD5c\n6ZWpB7O8iIhILTgT5iHa24FPPpG7YF5ewPz5wLx5TL8HZJbXpfpLMFlMfbK8kkKToNfpmeVFRESq\nwibMTVRXy/iJ5ma567VqFZCQoPSqJKXO7nuyvIy1Rlysu9gny8sQaUBaRBqG+2lzm1ArMxXuhDVR\nJ9ZFfbRSEzZhKicEcOYMcOAAYLcD0dFy/itYo1FVQghUNVfBZDHdMctLr9NjVMAoBVdJRER0d5wJ\nUzGrFfjsM5kBBgAzZgCLFgG+Gmude7K8jBYjCi2FzPIiIiK3wZkwN1RXJ48fLRaZ+bV0KWAwKL2q\noVXXXucMUWWWFxEReRo2YSpUVATs2SOfAxkeLo8fdTqlV3Vng3l2r7UsL1fSykyFO2FN1Il1UR+t\n1IRNmIrY7UBuLnD8uLxOT5c7YAEefkMfs7yIiEiLOBOmEi0tMv2+qgrw9pazXzNnem78BLO8iIhI\nCzgTpnJmM7BzJ9DaCgQFAVlZwPjxSq9q8NnsNpQ0lDDLi4iICGzCFFFcXInc3DJYrd64fNkBmy0B\nYWETEBcn879GjlR6hfenv7N7u8OOiqYKZnkpQCszFe6ENVEn1kV9tFITNmFDrLi4Etu2lcLHJxMX\nL8q7ILu78/DTnwLPPjsB3h4w9tRfltfYoLHOOxuZ5UVERFrGmbAh9vbbh1BW9jguXJAP3/b1BVJT\ngbS0Q/jFLx5XenkP7G5ZXgadDFFllhcREWkJZ8JUorsbMJm8ceGCvB45Ut4BGRgIWK3uuQXWk+Vl\nrDWivqPe+XpPlpch0oDIEZGMlCAiIroFm7AhcuUKsHs3UFkp7wIcNw6IjQV8fOT7/v4O5RZ3n5o7\nm50hqjWtNTAXmBE7JRYj/EYgXZcOvU7PLC8V0MpMhTthTdSJdVEfrdSETZiL2WzA11/L7C8hgGnT\nEtDYmIeIiEznx3R15SEzM1HBVd5dT5aX0WJEVXOV8/UAnwAkhiZi7aS1iBsdxywvIiKie8SZMBe6\nfFkm39fVybyvOXOAjAygvLwSeXny7kh/fwcyMxOQkjJB6eX20dXdhQt1F2CymPpkeaWEpUCv0zPL\ni4iIqB/99S1swlzAZgMOHQJOnJC7XxERwLJlQEyM0iu7u/6yvBJGJzDLi4iI6D5wMH8IVVXJ3a/6\nern79eijcvfLV8V/0nfK8vKC1z1leWnl7N7dsC7qw5qoE+uiPlqpiYpbA/diswF5ecDJk9/vfi1f\nDkRHK72y22OWFxERkbJ4HDkIKivl7ldDg3zu4yOPAI89pr7dr5uzvEwWE2503XC+xywvIiKiwcfj\nSBexWuXsV8/ul04nd7/GjlV6Zb0xy4uIiEh92IQ9oFt3v+bOBebNU8/u161ZXj1ckeWllbN7d8O6\nqA9rok6si/popSYqaRnch9X6/ewXAERGyjsf1bD71V+W18SIiTDoDMzyIiIiUgnOhN0Hs1nufjU2\n9t796km9VwKzvIiIiNSLM2EDZLUCubnAqVPyOipK7n6NGaPMenqyvIy1RpQ0lPTK8koKTYIh0oCU\nsBRmeREREakYm7C7qKiQu19NTXL3a948uQM21Ltfdocd5Y3lMFlMfbK8YkNiodfp+83yciWtnN27\nG9ZFfVgTdWJd1EcrNWETdgddXXL36/RpeR0VJe98jIoaujX0ZHkZLUYUXS/qk+Vl0BmQrktnlhcR\nEZEb4kzYbZSXA3v3yt0vHx+5+/Xoo0Oz+yWEQE1rjfPORmZ5ERERuS/OhN2jri7gq6+AM2fk9Zgx\ncvcrMnJwf5/i0mLkns2FTdjg5+WHBQ8tQNjYMBhrZYgqs7yIiIg8H3fC/qGsTO5+NTfLHa/HHpPJ\n94O9+1VcWoxtX29DQFIAOrs7YWmz4Op3V5GYmIjwseEAXJPl5UpaObt3N6yL+rAm6sS6qI8n1YQ7\nYf3o6gIOHgTOnpXXY8fKOx8He/cLkEeNnx7/FLW6WtTX1KO5q1m+MR6oMldhwbQFzPIiIiLSCE3v\nhJWWAvv2fb/7lZEhd7+8B7H/sdltMDeZUdJQgkv1l3Ag9wA6YzoByEiJsMAw6EboEN8cj9+u++3g\n/cZERESkOO6E3aKzU+5+nTsnr6Oj5e6XTjc4X7+5sxmX6i+hpKEEFY0VsDlszveG+QxD8IhghA0P\nQ2hgqDNENbAtcHB+cyIiInILmmvCSkrk7teNG3L3a/58YM6cge1+OYQDl5svO3e7LG2WXu+PGTkG\nyWHJSApLQkt0Cz7I/wABEd8HqXaVdCFzfuaDL0BhnnR270lYF/VhTdSJdVEfrdREM01YZyfw5ZfA\n+fPyOjpa3vkYEfFgX6/d1o7ShlJcqr+EsoYydHR3ON/z9/FHwugEJIUlISk0CUEBQd9/4ijgea/n\nkXcuD1aHFf7e/sicn4mUxJQBfHdERETkbjQxE3bpktz9amkBfH3l7tfs2fe3+yWEwLXWayhpKEFJ\nfQmu3LgCge/XERYY5tztGh88ns9qJCIiIu3OhHV0yN2vggJ5HRMjd7/Cw+/t8612K8oby+V8V30J\nWqwtzvd8vHwQGxKLpLAkJIclIzQw1AXfAREREXkqj23Cbt39evxxYNasu+9+NXQ0OJsuc5MZdmF3\nvhfkH+RsuuJHx8Pfx9/F34V70MrZvbthXdSHNVEn1kV9tFITj2vCOjqAAweA776T1+PGyTsf77T7\nZXfYUdlc6Wy8bk6r94IXxo0a55ztihoZpfrgVCIiInIPHjUTVlwsd79aW+XuV2YmMHNm392vlq4W\n52xXWWMZrHar871hvsOQGJqI5LBkJIYmYrjfcFd+O0REROTBPHYmrLi4Erm5ZWhr80ZJiQMBAQkI\nD5+A8ePl7lfYP55xLYRAdUs1SuplhERNa02vrxM5ItK52zUueBzT6omIiMjl3LYJKy6uxLZtpbhx\nIxMlJYDVCjgcefjFL4Ds7AmwOjpRaCnDpfpLKG0oRZutzfm5ft5+iBsdJ+9mDE1C8LBgBb8T96eV\ns3t3w7qoD2uiTqyL+milJqprwg4cOIBXXnkFdrsdP/vZz/Dqq6/2+Zi33z6Eysp6fGeahPKmtyG8\nbQj098Wk1Kk4XbsHHd8F4fKNy3AIh/NzQoaFOJuu2JBY+Pn4DeW35dEKCgo08cPiblgX9WFN1Il1\nUR+t1ERVTZjdbsc//dM/ITc3F9HR0Zg+fTqWLl2KiRMn9vq4X7/zEnxrx2FU8kT46gUCQhrQPrwB\nR8v/hvHV4QhqngJvL2/EhsQ6G6/w4eEcqneRpqYmpZdAt8G6qA9rok6si/popSaqasJOnTqFxMRE\nxMbGAgCefvpp7Nmzp08TZvthI2yHy2GNu4SxY+Jh/0dv5RsfCFyzISstCwmhCRjmO2yIvwMiIiKi\ne6OqJqy6uhrjxo1zXsfExODkyZN9P9DHCiR6w26/hkCvqRiGEAxHGHzsdZg7MRbpuvQhXDWZzWal\nl0C3wbqoD2uiTqyL+milJqqKqNi1axcOHDiAd999FwDw17/+FSdPnsR//dd/OT/GK8QXaLbf6UsQ\nERERqcbkyZNR0PPonluoaicsOjoaly9fdl5fvnwZMTExvT5GNHUP9bKIiIiIBp2qArEefvhhlJSU\nwGw2w2q14qOPPsLSpUuVXhYRERHRoFPVTpivry/+/Oc/Y/HixbDb7fjpT3/aZyifiIiIyBOoaiaM\niIiISCtUdRzZnwMHDiA1NRVJSUnYsmWL0svxCJcvX8b8+fORnp4OvV6Pt956CwDQ0NCAhQsXIjk5\nGYsWLeqV17J582YkJSUhNTUVBw8edL5+9uxZGAwGJCUl4Ve/+pXz9a6uLqxZswZJSUmYNWsWKisr\nne+9//77SE5ORnJyMj744IMh+I7dh91ux9SpU7FkyRIArIkaNDU1YfXq1Zg4cSLS0tJw8uRJ1kVh\nmzdvRnp6OgwGA9atW4euri7WRAHr169HZGQkDAaD8zWl61BRUYGZM2ciKSkJTz/9NGw2m6u+/YER\nbqC7u1skJCSIiooKYbVaxeTJk0VRUZHSy3J7NTU14vz580IIIVpaWkRycrIoKioSGzZsEFu2bBFC\nCJGTkyNeffVVIYQQhYWFYvLkycJqtYqKigqRkJAgHA6HEEKI6dOni5MnTwohhHjiiSfEF198IYQQ\n4u233xYvvfSSEEKIv/3tb2LNmjVCCCHq6+tFfHy8aGxsFI2Njc5fk/Tv//7vYt26dWLJkiVCCMGa\nqMBzzz0n3nvvPSGEEDabTTQ1NbEuCqqoqBBxcXGis7NTCCFEdna22LZtG2uigCNHjohz584JvV7v\nfE2pOjQ1NQkhhMjKyhIfffSREEKIn//85+K///u/Xf3H8EDcogn79ttvxeLFi53XmzdvFps3b1Zw\nRZ5p2bJl4quvvhIpKSni2rVrQgjZqKWkpAghhPjDH/4gcnJynB+/ePFicfz4cXH16lWRmprqfH37\n9u3ixRdfdH7MiRMnhBDyP1zh4eFCCCE+/PBD8fOf/9z5OS+++KLYvn27a79BN3H58mWRmZkpDh06\nJJ566ikhhGBNFNbU1CTi4uL6vM66KKe+vl4kJyeLhoYGYbPZxFNPPSUOHjzImiikoqKiVxOmZB0c\nDocIDw8XdrtdCCHE8ePHe/UQauIWx5G3C3Gtrq5WcEWex2w24/z585g5cyZqa2sRGRkJAIiMjERt\nbS0A4OrVq70iQ3rqcOvr0dHRzvrcXDtfX18EBwejvr7+jl+LgF//+tf44x//CG/v7388WRNlVVRU\nICIiAj/5yU8wbdo0vPDCC2hra2NdFBQaGorf/va3GD9+PMaOHYuQkBAsXLiQNVEJJevQ0NCAkJAQ\n59+hN38ttXGLJozPfHSt1tZWrFq1Cn/6058QFBTU6z0vLy/++Q+hzz77DDqdDlOnToW4wz0zrMnQ\n6+7uxrlz5/CLX/wC586dw4gRI5CTk9PrY1iXoVVWVob//M//hNlsxtWrV9Ha2oq//vWvvT6GNVGH\noayDu9XbLZqwewlxpQdjs9mwatUqPPvss1i+fDkA+a+Wa9euAQBqamqg0+kA9K3DlStXEBMTg+jo\naFy5cqXP6z2fU1VVBUD+h6y5uRlhYWGs6R18++232Lt3L+Li4rB27VocOnQIzz77LGuisJiYGMTE\nxGD69OkAgNWrV+PcuXOIiopiXRRy5swZzJkzB2FhYfD19cXKlStx/Phx1kQllPo7Kzo6GqGhoWhq\naoLD4XB+rejoaNd+ww9K6fPQe2Gz2UR8fLyoqKgQXV1dHMwfJA6HQzz77LPilVde6fX6hg0bnGf2\nmzdv7jNQ2dXVJcrLy0V8fLxzoHLGjBnixIkTwuFw9Bmo7Dmz3759e6+Byri4ONHY2CgaGhqcv6bv\n5efnO2fCWBPlzZ07VxQXFwshhPj9738vNmzYwLooqKCgQKSnp4v29nbhcDjEc889J/785z+zJgq5\ndSZM6TpkZWWJv/3tb0IIOSvGwfwB+vzzz0VycrJISEgQf/jDH5Rejkc4evSo8PLyEpMnTxZTpkwR\nU6ZMEV988YWor68XmZmZIikpSSxcuLDXXy6bNm0SCQkJIiUlRRw4cMD5+pkzZ4RerxcJCQni5Zdf\ndr7e2dkpsrKyRGJiopg5c6aoqKhwvrd161aRmJgoEhMTxbZt24bke3Yn+fn5zrsjWRPlFRQUiIcf\nflhMmjRJrFixQjQ1NbEuCtuyZYtIS0sTer1ePPfcc8JqtbImCnj66afFmDFjhJ+fn4iJiRFbt25V\nvA7l5eVixowZIjExUWRnZwur1eraP4QHxLBWIiIiIgW4xUwYERERkadhE0ZERESkADZhRERERApg\nE0ZERESkADZhRERERApgE0ZERESkADZhRKQpGRkZOHv27IC+xr59+7Bly5ZBWhERaZWv0gsgIhpK\ng/EcuyVLlmDJkiWDtCIi0iruhBGRotra2vDkk09iypQpMBgM2LFjBwDgzTffxIwZM2AwGPDiiy86\nPz4jIwO/+c1vMH36dEycOBGnT5/GihUrkJycjN/97ncAALPZjNTUVDzzzDNIS0tDVlYWOjo6+vze\nBw8exJw5c/DQQw8hOzsbbW1tfT7mrbfeQnp6OiZPnox169YBALZt24aXX34ZADBlyhRMnToVU6dO\nxfDhw3H06FG0tbVh/fr1mDlzJqZNm4a9e/f2+br5+fnIyMhAVlYWJk6ciGeeeWbgf5hE5FbYhBGR\nog4cOIDo6GgUFBTAaDRi8eLFAICXX34Zp06dgtFoREdHBz777DMAcicrICAAp0+fxksvvYRly5bh\nnXfegclkwrZt29DY2AgAuHTpEn75y1+iqKgIo0aNwl/+8pdev29dXR02bdqEvLw8nD17Fg899BD+\n4z/+o8/6tmzZgoKCAnz33Xd45513nGvoUVBQgPPnz+PNN9/E9OnTMXv2bGzatAmZmZk4efIkDh06\nhA0bNqC9vb3P1y4oKMCf/vQnFBUVoby8HMeOHRucP1QicgtswohIUZMmTcJXX32F1157Dd988w1G\njRoFADh06BBmzZqFSZMm4dChQygqKnJ+ztKlSwEAer0eer0ekZGR8Pf3R3x8PC5fvgwAGDduHGbP\nng0AeOaZZ/DNN984P18IgRMnTqCoqAhz5szB1KlT8cEHH6Cqquq261u3bh3+7//+Dz4+Prf9HkpK\nSrBx40Z8/PHH8PX1xcGDB5GTk4OpU6di/vz56Orqcq7rZjNmzMDYsWPh5eWFKVOmwGw2P9gfIhG5\nJc6EEZGikpKScP78eezfvx//+q//iszMTGzcuBG//OUvcfbsWURHR+ONN95AZ2en83MCAgIAAN7e\n3s5f91x3d3cD6L1bJYS47RzYwoUL8eGHH/a7vv379+PIkSPYt28fNm3aBKPRiJsfudva2oo1a9bg\nf//3fxEZGel8/ZNPPkFSUlK/X/vmtfv4+DjXTkTawJ0wIlJUTU0Nhg0bhh/96Ef453/+Z5w/f97Z\ncIWFhaG1tdU5J3Y/qqqqcOLECQDAhx9+iLlz5zrf8/LywqxZs3Ds2DGUlZUBkLNpJSUlvb6GEAJV\nVVXIyMhATk4Ompub0dra2utj1q9fj5/85Cd45JFHnK8tXrwYb731lvP6/Pnz971+IvJ83AkjIkUZ\njUZs2LAB3t7e8PPzwzvvvIPg4GC88MIL0Ov1iIqKwsyZM2/7uf3d6ZiSkoK3334b69evR3p6Ol56\n6aVe74eHh2Pbtm1Yu3Yturq6AACbNm3qtXtlt9vx7LPPorm5GUII/OpXv0JwcLDz962qqsKuXbtQ\nUlKCrVu3AgDee+89/O53v8Mrr7yCSZMmweFwID4+vs9w/u3WPtC7NonIvXiJm/fViYg8gNlsxpIl\nS2A0GpVeChHRHfE4kog8EneViEjtuBNGREREpADuhBEREREpgE0YERERkQLYhBEREREpgE0YERER\nkQLYhBEREREp4P8DGaETtWbn1E4AAAAASUVORK5CYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x10eea0790>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 59
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"<br>\n",
|
|
"<br>\n",
|
|
"The improvement is pretty significant when static type declarations are used. One more experiment to see by how much we could improve our \"classic least squares\" code via Cython compared to the initial Python implementation.\n",
|
|
"<br>\n",
|
|
"<br>"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import random\n",
|
|
"random.seed(12345)\n",
|
|
"\n",
|
|
"x = [x_i*random.randrange(8,12)/10 for x_i in range(500)]\n",
|
|
"y = [y_i*random.randrange(8,12)/10 for y_i in range(100,600)]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 60
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"import timeit\n",
|
|
"\n",
|
|
"funcs = ['classic_lstsqr', 'cy_lstsqr', 'static_type_lstsqr', \n",
|
|
" 'lin_lstsqr_mat', 'numpy_lstsqr', 'scipy_lstsqr']\n",
|
|
"labels = ['classic approach','classic approach (cython)', \n",
|
|
" 'classic approach (cython + type decl.)',\n",
|
|
" 'matrix approach', 'numpy function', 'scipy function']\n",
|
|
"\n",
|
|
"times = [timeit.Timer('%s(x,y)' %f, \n",
|
|
" 'from __main__ import %s, x, y' %f).timeit(1000)\n",
|
|
" for f in funcs]\n",
|
|
"\n",
|
|
"times_rel = [times[0]/times[i+1] for i in range(len(times[1:]))]"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"prompt_number": 61
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"collapsed": false,
|
|
"input": [
|
|
"#%pylab inline\n",
|
|
"#import matplotlib.pyplot as plt\n",
|
|
"\n",
|
|
"x_pos = np.arange(len(funcs[1:]))\n",
|
|
"plt.bar(x_pos, times_rel, align='center', alpha=0.5, color=\"green\")\n",
|
|
"plt.xticks(x_pos, labels[1:], rotation=90)\n",
|
|
"plt.ylabel('relative performance gain')\n",
|
|
"plt.title('Performance gain compared to the classic least square implementation')\n",
|
|
"plt.grid()\n",
|
|
"plt.show()"
|
|
],
|
|
"language": "python",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"metadata": {},
|
|
"output_type": "display_data",
|
|
"png": "iVBORw0KGgoAAAANSUhEUgAAAbwAAAG/CAYAAAAjJGJxAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl8Dff3P/DXJGLLLhFJSHIRSgiJKLEmqb3WWoLakqBo\naX3ThSoV9aH0Ux+EVmk1UdUWpYSiisYeEhVbKrFdSyQRImSP3Lx/f+SXaa5ESNw7c+d9z/PxyOOR\nu82cc+/cOXfmzLxHYIwxEEIIIZwzkTsAQgghRApU8AghhBgFKniEEEKMAhU8QgghRoEKHiGEEKNA\nBY8QQohRkLTgpaWloXv37rCyssKHH34o5awV6fXXX8fGjRvlDsNgqVQqHDx4ULL5mZiY4Pr163qd\nR1BQEObNm6e36VtaWkKtVlfpNdHR0XBxcdFPQJxr3bo1jhw5ovPpqtVqmJiYoLi4WOfTltu0adPw\nn//8Ry/TrvG8J6hUKty7dw+mpqYwNzdHv379sHr1apibm1d5ZuvWrYODgwMeP35crWCNzZ49e+QO\nwaAJggBBECp8LCgoCC4uLli4cGG1pu3v749x48Zh4sSJLxNilVWWky5kZWXpbdov42U/L0N18eJF\nuUOQVFU/x8jISKxfvx5Hjx4V71uzZo2+wnv+Fp4gCNi9ezeysrLw999/Iy4ursrVlzGG4uJi3Lx5\nEy1btqxWoEVFRdV6HVEGQ/t89Vl0nofGgjBMhraMkmpgz6FSqdjBgwfF2x988AEbMGAAY4yxkydP\nsk6dOjEbGxvWtm1bFh0dLT7Pz8+PffLJJ6xLly6sTp06bOzYsczMzIzVrFmTWVhYsIMHD7KCggL2\n3nvvMWdnZ+bs7MxmzpzJCgoKGGOM/fXXX6xhw4Zs6dKlzNHRkY0bN46FhYWx4cOHs7FjxzJLS0vm\n6enJkpKS2OLFi5mDgwNzdXVl+/fvF2P4/vvvWcuWLZmlpSVr0qQJW7t2rfhY6fSXLVvGHBwcmJOT\nE4uIiBAfz83NZaGhoczNzY1ZW1uzrl27sry8vOfm/bQzZ84wLy8vZmlpyUaMGMECAwPZ3LlzGWOM\nZWRksP79+7P69eszW1tbNmDAAHbnzh2t9/C7775jjDEWERHBunTpwj744ANma2vLGjduzPbu3fvM\n+d66dYu98cYbrH79+szOzo5Nnz6dMcaYRqNhCxcuZG5ubszBwYGNHz+ePXr0iDHG2I0bN5ggCCwi\nIoK5uLiwevXqsTVr1rDTp08zT09PZmNjI06nNKbOnTuz6dOnM2tra9aiRQutZeVF3v/Sz3f8+PGs\nuLiYff7556xp06bMzs6OBQYGsoyMDPE1P/zwA3N1dWV2dnZs0aJF5ZbNUmvXrtVa1gYNGsQYYywh\nIYH5+fkxGxsb1qpVKxYVFVXhezdnzhxmamrKateuzSwsLNiMGTMYY4wJgsC++eYb1qxZM2ZjY8Pe\neecdrdetX7+etWzZktna2rI+ffqwmzdvPvPzOXr0qLgMubi4sA0bNjDGGAsKCnrh5SMiIoI1adKE\nWVpassaNG7NNmzYxxhi7cuUK6969O7O2tmb29vZs5MiR4msEQWDXrl1jjFW+jJf1119/sUaNGom3\nk5OT2dChQ1n9+vVZ48aNWXh4uPjYqVOnmK+vL7OxsWFOTk5s+vTprLCwUHx85syZzMHBgVlZWTFP\nT0928eLFZ35eT6votYwxdv/+fTZw4EBmZWXFOnTowObOncu6du3KGPt3mdZoNOJ0yn6vrl69ygIC\nApidnR2zt7dnY8aMYZmZmeJz3dzc2NKlS5mnpyerXbs202g0Vfr+u7m5icvo/Pnzq7T+8vPzY7Nn\nz2YdOnRgVlZWbPDgweL34em8MjMzWUhICHNycmINGzZkc+fOFR8r/Z7+3//9H7OxsWFNmzZlx48f\nZ99//z1zcXFhDg4O4vLHGGP5+fns/fffZ66urqxBgwZs6tSp4nJR2XrzWZ9j6Xfa0tKSeXh4sN9+\n+40xVvJ9rF27NjM1NWUWFhbM1taWMcbYhAkTxO8AY4ytW7eOubu7s3r16rFBgwaxu3fvio897zv5\ntBcqeAcOHGCMlaxEW7VqxT799FN2584dZmdnJ650//zzT2ZnZ8fu378vflhubm4sISGBaTQa9uTJ\nExYUFMTmzZsnTnvevHmsU6dOLD09naWnp7POnTuLj//111+sRo0abPbs2aywsJDl5eWx+fPns9q1\na7P9+/ezoqIiNn78eObm5sYWL17MioqK2LfffssaN24sTv/3339n169fZ4wxdvjwYVa3bl32999/\na01//vz5rKioiO3Zs4fVrVtXXNjffvttFhAQwO7evSsu5AUFBc/MOz09vdx7V1BQwFxdXVl4eDgr\nKipi27dvZzVr1hRzfPDgAdu+fTvLy8tjWVlZbMSIEWzIkCHi6/39/dn69esZYyULrZmZGfvuu+9Y\ncXExW7NmDXN2dq7wMysqKmJt2rRhoaGhLDc3l+Xn57Pjx48zxkpWyu7u7uzGjRssOzubDR06lI0b\nN44x9u+XaNq0aaygoIDt37+f1axZkw0ZMoSlp6ez5ORk5uDgwA4fPizGVKNGDbZixQpWVFTENm/e\nzKytrcUv5Yu8/2U/3xUrVrBOnTqx5ORkVlhYyKZMmcJGjx7NGGPs0qVLzMLCgh09epQVFBSw0NBQ\nVqNGjQoLHmOs3LJWWFjImjZtyj7//HP25MkTdujQIWZpackSExMrfH3Z976UIAhs4MCB7NGjR+zW\nrVusfv36bN++fYwxxnbs2MHc3d3Z5cuXmUajYf/5z39Y586dK5y2Wq1mlpaW7JdffmFFRUXswYMH\nLD4+Xoy79Mte2fKRnZ3NrKysWFJSEmOMsdTUVHbp0iXGGGOjRo1iixcvZoyVLIOln31pDqUF71nL\n+NPKFjyNRsPatWvHFi5cyJ48ecKuX7/OmjRpwv744w/GWMkPvFOnTjGNRsPUajVr2bIlW7FiBWOM\nsX379jEfHx/xB9bly5dZSkpKhZ/X0yp77ciRI9nIkSNZbm4uu3jxImvYsCHr1q0bY6ziglf2s716\n9So7cOAAKywsZOnp6ax79+5s5syZ4nPd3NyYt7c3u3PnDsvPz6/S958x7Q2Gqq6//Pz8WMOGDdml\nS5dYTk4OGzZsGBs7dmyFeQ0ZMoRNnTqV5ebmsnv37rEOHTqIPzBLv6eRkZGsuLiYzZ07lzVs2FD8\nMbJ//35maWnJcnJyGGMlPywGDx7MHj58yLKystjAgQPZxx9/LC4Lla03K/oct27dKn5WmzdvZubm\n5iw1NZUxxlhkZKT446RU2WkcPHiQ2dvbs7Nnz7KCggI2Y8YM1r17d/G5lX0nK/Lcgufm5sYsLCyY\njY0Nc3NzY++88w7Ly8tjS5YsEVeUpfr06SP+UvD392fz588vl0jZyt20aVOtrZQ//viDqVQqxljJ\nG1uzZk2tL+D8+fNZ7969xdtRUVHMwsKCFRcXM8YYe/z4MRMEQfxSPG3IkCFs5cqV4vTr1Kmj9UVw\ncHAQv6x16tRh58+fLzeN5+Vd1uHDh1nDhg217uvateszv9hnz54Vf+UwVr7gubu7i4/l5OQwQRBY\nWlpauemcOHGC1a9fXyu3Uq+99hpbs2aNeDsxMZGZmZkxjUYjfonK/oKys7NjW7ZsEW8PGzZMXIFF\nRESUK7odOnRgGzdurDC/p9//pz/fli1bahWwu3fvMjMzM1ZUVMQWLFggFr/S/GvWrFlpwSu7rB05\ncoQ5OjpqPWf06NEsLCyswtf7+/uLWwGlBEHQKh6BgYFs6dKljDHG+vbtq1UgNRoNq1u3Lrt161a5\naS9evJgNHTr0heIuq+zykZ2dzWxsbNi2bdtYbm6u1vPGjx/P3nrrLa2twbI5XLt2rdJl/GllC15M\nTAxzdXUtl09wcHCFr12+fDl74403GGMlK6/mzZuzmJiYcstmZXkzxtihQ4cqfG1RUREzMzPT+uEy\nZ86cSrfwKvoxU+q3335j3t7e4m2VSqW156cq3//S15cteFVZf/n7+4uFhrGSLaKaNWuy4uJirbxS\nU1NZrVq1tLbOf/rpJxYQEMAYK/meNmvWTHzs/PnzTBAEdu/ePfE+Ozs7du7cOVZcXMzMzc3FH0WM\nlaxPSgtxZetNxp7/OTLGmJeXF9u5c6cYW2UFLyQkhM2aNUt8LDs7m5mZmYl7Tyr6Ti5ZsuSZ836h\nHt7OnTvx8OFDqNVqrF69GrVr18bNmzexdetW2Nrain/Hjx9Hamqq+NrnHdl19+5duLm5ibddXV1x\n9+5d8Xb9+vVRs2ZNrdc4ODiI/9epUwf29vZiv6VOnToAgOzsbADA3r174evrCzs7O9ja2mLPnj14\n8OCB+Ho7OzuYmPz7FtStWxfZ2dm4f/8+8vPz0bRp03Ixv0jeZfNr2LCh1n0uLi5ijyY3NxdTpkyB\nSqWCtbU1/Pz88OjRo2f2cBwdHbViLZtrWbdv34abm5tWbqVSUlLKvedFRUVIS0sT72vQoIH4f506\ndcrdzsnJEW8/nZ+bmxtSUlIAPP/9f/rzVavVeOONN8T31cPDAzVq1EBaWhpSUlLQqFEjrfzt7Owq\nepsqdPfu3XLLo5ubG5KTk5/5mor6eE9/BqXv/82bN/Hee++JsZfGVtH079y5gyZNmjw35sqWD3Nz\nc2zevBnffPMNnJ2dMWDAACQmJgIAvvjiCzDG0KFDB7Ru3RoRERHlpl3ZMl6Zmzdv4u7du1rL/+ef\nf4579+4BAJKSkjBgwAA4OTnB2toan3zyifiZv/baa5g+fTreeecdNGjQAFOmTHnhg2gCAgIqfG16\nejqKioq0PltXV9cXzictLQ2jRo1Co0aNYG1tjXHjxmkto4D2eqwq3/+KVGX99fS8XV1d8eTJE9y/\nf19rmjdv3sSTJ0/g5OQkxjR16lSkp6eLz3n6OwyUfP/K3pednY309HTk5ubCx8dHnFa/fv205vms\n9eaz/PDDD/D29hand/HixXLv8bM8vb4yNzeHnZ2d1vfqWd/JilT7tARXV1eMGzcODx8+FP+ysrLw\n0Ucfic95XuPf2dlZ6xDpW7duwdnZ+Zmvr8qBBAUFBRg2bBg++ugj3Lt3Dw8fPsTrr7/+QgcE2Nvb\no3bt2rh69Wq5x14k71JOTk7lVni3bt0S81i2bBmSkpJw+vRpPHr0CIcPHwYr2ep+4Twr4uLiglu3\nbkGj0ZR7rKL3vEaNGlpfiKp4Or+bN2/C2dn5hd7/pz9PV1dX7Nu3T+u9zc3NhbOzM5ycnHD79m3x\nubm5uZV+aZ6etrOzM27fvq01/5s3b2oV0cpe/zyurq5Yt26dVuw5OTnw9fUt91wXFxdcu3btubE/\nb/no3bs39u/fj9TUVLRo0QKTJ08GULJyW7duHZKTk7F27Vq8/fbb5U6nqGwZr4yLiwsaN26slefj\nx4+xe/duACWHlHt4eODq1at49OgRFi1apHXo/IwZMxAXF4eEhAQkJSXhv//9r1bOlanotQ4ODqhR\nowZu3bolPq/s/6VHk+fm5or3lS1Oc+bMgampKS5evIhHjx5h48aN5Q71LxtbVb7/uvB0XmZmZrC3\nt9d6jouLC2rVqoUHDx6IMT169AgXLlyo8vzs7e1Rp04dJCQkiNPKzMx84SPrn/4cb968ibfeegtf\nffUVMjIy8PDhQ7Ru3VpchqtaI3JycvDgwYNyP7RfVLUL3tixY7Fr1y7s378fGo0G+fn5iI6O1loB\nPr3ifvr26NGj8Z///Af379/H/fv38dlnn2HcuHHPnGdVCkFhYSEKCwthb28PExMT7N27F/v373+h\n15qYmCAkJAShoaFISUmBRqPByZMnUVhY+EJ5l+rcuTNMTU2xevVqFBUVYefOnYiNjRUfz87ORp06\ndWBtbY2MjAwsWLDghfOrTMeOHeHk5ITZs2cjNzcX+fn5OHHiBICS93z58uVQq9XIzs7GnDlzMGrU\nqAq3Bp+l7Odw7949hIeH48mTJ9i6dSsuX76M119/vVrv/9SpUzFnzhzxS56eno6oqCgAwPDhw7F7\n924cP34chYWF+PTTTys9B6lBgwZaK3lfX1/UrVsXX3zxBZ48eYLo6Gjs3r0bo0aNeubrKytKpe9D\n6XsxdepULF68GAkJCQCAR48eYevWrRW+bsyYMThw4AC2bt2KoqIiPHjwAOfOnSs3zcqWj3v37mHn\nzp3IycmBmZkZzM3NYWpqCgDYunUr7ty5AwCwsbGBIAjlPt/KlvHKdOjQAZaWlvjiiy+Ql5cHjUaD\nixcvIi4uTozZ0tISdevWxeXLl7FmzRpxpRYXF4dTp07hyZMnqFu3LmrXri3G/PTn9bRnvdbExARD\nhw5FWFgY8vLykJCQgB9++EGcZ/369dGwYUNs3LgRGo0G33//vdbnmp2dDXNzc1hZWSE5OVkswM9S\nle//y2KM4ccff8Q///yD3NxcfPrppxgxYkS5IuHk5ITevXsjNDQUWVlZKC4uxrVr16p1/p+JiQkm\nT56MmTNniluIycnJL7zufPpzzMnJgSAIsLe3R3FxMSIiIrRO1WjQoAHu3LmDJ0+eaOVd+h0YPXo0\nIiIicO7cORQUFGDOnDnw9fV95lb882pEtQteo0aNsHPnTixevBgODg5wdXXFsmXLKv0F//Q5RnPn\nzkX79u3Rpk0btGnTBu3bt8fcuXNf+PXPeg5QcoJteHg4AgMDUa9ePfz8888YPHhwpa8t68svv4Sn\npydeffVV2NnZ4eOPP0ZxcfEz865o5WtmZobt27dj/fr1sLW1xaZNmzBgwABxN97MmTORl5cHe3t7\ndO7cGf369XtmTC+SeykTExPs2rULV69ehaurK1xcXLBlyxYAQEhICMaNG4fu3bujSZMmqFu3Llat\nWvVC70lFz+nYsSOuXLmC+vXrY968edi2bRtsbW2r9f6/9957GDRoEHr37g0rKyt06tQJp0+fBgB4\neHjgq6++wptvvglnZ2fUq1ev0l3mEydOREJCAmxtbTF06FCYmZlh165d2Lt3L+rXr4/p06dj48aN\naN68eYWvf++99/Drr7+iXr16mDlz5jPfh9IchgwZglmzZmHUqFGwtraGp6cn/vjjjwpf5+Ligj17\n9mDZsmWws7ODt7c3zp8/X26alS0fxcXFWL58ORo2bAg7OzscPXpUPH8pLi4Ovr6+sLS0xODBgxEe\nHg6VSlXuPX/WMv6sXAHA1NQUu3fvRnx8PJo0aYL69evjrbfeErcAvvzyS/z000+wsrLCW2+9pfWD\n4vHjx3jrrbdQr149qFQq2NvbiwNQPP15Pa2y165evRrZ2dlwdHRESEgIgoODtdZD3377Lf773//C\n3t4eCQkJ6NKli/jY/Pnz8ffff8Pa2hoDBw7EsGHDKv0OVOX7X9F7+KLrr9L/x40bh6CgIDg5OaGw\nsBDh4eEVPveHH35AYWEhPDw8UK9ePYwYMULckq3KugMAli5dCnd3d/j6+sLa2hq9evVCUlLSC732\n6c/Rw8MD77//Pjp16gRHR0dcvHgRXbt2FZ/fo0cPtGrVCo6OjuLu3rLx9ujRAwsXLsSwYcPg7OyM\nGzdu4Jdffqn0/at0HVZpd9EA3Lp1i/n7+zMPDw/WqlUr8aCH+fPns4YNGzIvLy/m5eVV6SH6hqRD\nhw4sMjJS7jB0oqKGMyFy42W5rOzgGlI9zx1pRW5mZmZYvnw5vLy8kJ2dDR8fH/Tq1QuCICA0NBSh\noaFyh1ipI0eOoHnz5rC3t8emTZtw8eJF9O3bV+6wCCEKwGgQAp0y+ILn6OgoHoVjYWGBli1bivvL\nlbAwJCYmIjAwEDk5OWjatCl+/fXXah8gYmj0PQwWIdXB03LJSx6GQmBKqBr/n1qthp+fHy5duoRl\ny5YhIiIC1tbWaN++PZYtWwYbGxu5QySEEGKgFHN5oOzsbAwfPhwrV66EhYUFpk2bhhs3biA+Ph5O\nTk54//335Q6REEKIAVPEFt6TJ08wYMAA9OvXr8Ij5tRqNQYOHFjuvBN3d/fnHlpOCCFEW9u2bREf\nHy93GDpn8D08xhgmTpwIDw8PrWKXkpICJycnAMBvv/0GT0/Pcq+9du2aIvp81RUWFoawsDBZY5gd\nNhupmS82ykRVxcfEw8vXS+fTdbRxxJKwJTqfblUYwmenT5SfsvHaOzT4gnf8+HH8+OOPaNOmDby9\nvQEAixcvxs8//4z4+HgIgoDGjRtj7dq1MkcqvapeyFMfUjNToRqi0su04y/H62Xa6h1qnU+zyjEY\nwGenT5QfMUQGX/C6du1a4Umd/fr1kyEaQgghSqWYg1ZIeUFBQXKHoFdefXW/O9NQ8P7ZUX7EEFHB\nUzB/f3+5Q9ArlZdK7hD0hvfPjvIjhogKnoJFR0fLHYJeqePVcoegN7x/dpQfMURU8AghhBgFKngK\nxvtuFdqlqVyUHzFEVPAIIYQYBSp4CsZ7H4F6eMpF+RFDRAWPEEKIUaCCp2C89xGoh6dclB8xRFTw\nCCGEGAUqeArGex+BenjKRfkRQ0QFjxBCiFGggqdgvPcRqIenXJQfMURU8AghhBgFKngKxnsfgXp4\nykX5EUNEBY8QQohRoIKnYLz3EaiHp1yUHzFEVPAIIYQYBSp4CsZ7H4F6eMpF+RFDRAWPEEKIUaCC\np2C89xGoh6dclB8xRFTwCCGEGAUqeArGex+BenjKRfkRQ0QFjxBCiFGggqdgvPcRqIenXJQfMURU\n8AghhBgFKngKxnsfgXp4ykX5EUNEBY8QQohRoIKnYLz3EaiHp1yUHzFEVPAIIYQYBSp4CsZ7H4F6\neMpF+RFDRAWPEEKIUaCCp2C89xGoh6dclB8xRFTwCCGEGAUqeArGex+BenjKRfkRQ0QFjxBCiFEw\n+IJ3+/ZtBAQEoFWrVmjdujXCw8MBABkZGejVqxeaN2+O3r17IzMzU+ZIpcd7H4F6eMpF+RFDZPAF\nz8zMDMuXL8elS5cQExODr776Cv/88w+WLFmCXr16ISkpCT169MCSJUvkDpUQQogBM/iC5+joCC8v\nLwCAhYUFWrZsieTkZERFRWHChAkAgAkTJmDHjh1yhikL3vsI1MNTLsqPGCKDL3hlqdVqnD17Fh07\ndkRaWhoaNGgAAGjQoAHS0tJkjo4QQoghqyF3AC8qOzsbw4YNw8qVK2Fpaan1mCAIEAShwtcFBQVB\npVIBAGxsbODl5SXufy/9labU26X3yRlP6p1UqKAC8O8WWWnv7WVvl96nq+k9vcUo5+fn7+8v+/JD\n+VF+pbejo6MRGRkJAOL6kkcCY4zJHcTzPHnyBAMGDEC/fv0wc+ZMAECLFi0QHR0NR0dHpKSkICAg\nAJcvX9Z6nSAIUEB6ihY0MwiqISq5w6gS9Q41IldEyh0GIQaL13Wnwe/SZIxh4sSJ8PDwEIsdAAwa\nNAgbNmwAAGzYsAFDhgyRK0TZlP5C4xX18JSL8iOGyOB3aR4/fhw//vgj2rRpA29vbwDA559/jtmz\nZyMwMBDr16+HSqXCli1bZI6UEEKIIZNsl2ZiYiK+/PJLqNVqFBUVlcxcEHDo0CG9zZPXzXJDQrs0\nCeEPr+tOybbwRowYgWnTpmHSpEkwNTUFgGceaEIIIYTommQ9PDMzM0ybNg0dO3ZE+/bt0b59e/j4\n+Eg1ey7x3kegHp5yUX7EEElW8AYOHIivvvoKKSkpyMjIEP8IIYQQKUjWw1OpVBXuwrxx44be5snr\nfmhDQj08QvjD67pTsh6eWq2WalaEEEJIOXrfpXnw4EEAwLZt27B9+/Zyf6T6eO8jUA9PuSg/Yoj0\nvoV35MgR9OjRA7t27apwl+bQoUP1HQIhhBCijKHFqovX/dCGhHp4hPCH13WnpCOt7N69GwkJCcjP\nzxfv+/TTT6UMgRBCiJGS7LSEKVOmYMuWLQgPDwdjDFu2bMHNmzelmj2XeO8jUA9PuSg/YogkK3gn\nTpzADz/8gHr16mH+/PmIiYlBYmKiVLMnhBBi5CQreHXq1AEA1K1bF8nJyahRowZSU1Olmj2Xyl4X\nj0dlr4vHG94/O8qPGCLJengDBgzAw4cP8eGHH4pDik2ePFmq2RNCCDFykm3hffrpp7C1tcWwYcOg\nVqtx+fJlLFy4UKrZc4n3PgL18JSL8iOGSLItvG3btpU7D8/a2hqenp5wcHCQKgxCCCFGSrLz8Pr3\n74+TJ08iICAAQMkvpHbt2uHGjRv49NNPMX78eJ3Pk9dzSQwJnYdHCH94XXdKtoX35MkT/PPPP2jQ\noAEAIC0tDePGjcOpU6fQvXt3vRQ8QgghpJRkPbzbt2+LxQ4AHBwccPv2bdjZ2aFmzZpShcEV3vsI\n1MNTLsqPGCLJtvACAgLQv39/BAYGgjGGbdu2wd/fHzk5ObCxsZEqDEIIIUZKsh5eaZE7fvw4AKBL\nly4YNmxYhQNK6wqv+6ENCfXwCOEPr+tOybbwBEHA8OHDMXz4cKlmSQghhIgk6+ER3eO9j0A9POWi\n/IghooJHCCHEKEha8HJzc2nAaB3ifTw/GktTuSg/YogkK3hRUVHw9vZGnz59AABnz57FoEGDpJo9\nIYQQIydZwQsLC8OpU6dga2sLAPD29sb169elmj2XeO8jUA9PuSg/YogkK3hmZmblzrczMaEWIiGE\nEGlIVnFatWqFTZs2oaioCFeuXMGMGTPQuXNnqWbPJd77CNTDUy7KjxgiyQreqlWrcOnSJdSqVQuj\nR4+GlZUVVqxYIdXsCSGEGDnJCp65uTkWL16MuLg4xMXFYdGiRahdu7ZUs+cS730E6uEpF+VHDJFk\nBa9nz57IzMwUb2dkZIhHbBJCCCH6JlnBu3//vtZBK/Xq1UNaWppUs+cS730E6uEpF+VHDJFkBc/U\n1BQ3b94Ub6vVajpKkxBCiGQkqziLFi1Ct27dMHbsWIwdOxbdu3fH4sWLpZo9l3jvI1APT7koP2KI\nJLtaQt++fXHmzBnExMRAEASsWLEC9vb2Us2eEEKIkZN0n2JhYSHq1asHS0tLJCQk4MiRI899TUhI\nCBo0aABPT0/xvrCwMDRq1Aje3t7w9vbGvn379Bm2weK9j0A9POWi/IghkmwLb9asWdi8eTM8PDxg\namoq3t+TNxc5AAAgAElEQVS9e/dKXxccHIwZM2Zg/Pjx4n2CICA0NBShoaF6i5cQQghfJNvC++23\n35CYmIg9e/Zg165d4t/zdOvWTRx/sywer8ZbVbz3EaiHp1yUHzFEkhW8pk2borCwUGfTW7VqFdq2\nbYuJEydqnd9HCCGEVERgEm0qDR06FOfOnUOPHj1Qq1atkpkLAsLDw5/7WrVajYEDB+LChQsAgHv3\n7qF+/foAgHnz5iElJQXr168v9zpBEGhLUM+CZgZBNUQldxhVot6hRuSKSLnDIMRg8brulKyHN2jQ\noHLXvxMEoVrTcnBwEP+fNGkSBg4c+MznBgUFQaVSAQBsbGzg5eUlNpxLd0vQ7erfTr2TChVUAP7d\nBVl6sImh3i5lCO8f3abbhnA7OjoakZGRACCuL3kk2Rbey3h6Cy8lJQVOTk4AgOXLlyM2NhY//fRT\nudfx+iulVHR0tLjwykWfW3jqeLVejtQ0hC08Q/js9InyUzZe152SbeElJSVhzpw5SEhIQF5eHoCS\nN/V5F4EdPXo0Dh8+jPv378PFxQULFixAdHQ04uPjIQgCGjdujLVr10qRAiGEEAWTbAuvS5cuWLBg\nAUJDQ7Fr1y5ERERAo9Fg4cKFepsnr79SDAn18AjhD6/rTsmO0szLy0PPnj3BGIObmxvCwsLw+++/\nSzV7QgghRk6ygle7dm1oNBq4u7tj9erV2L59O3JycqSaPZdKm868ovPwlIvyI4ZIsh7eihUrkJub\ni/DwcMybNw+PHz/Ghg0bpJo9IYQQI6eIozSri9f90IaEeniE8IfXdadkW3ixsbFYvHgx1Go1ioqK\nAJS8qefPn5cqBEIIIUZMsh7emDFjEBwcjG3btonjaEZFRUk1ey7x3kegHp5yUX7EEEm2hVe/fv1y\nI60QQgghUpGsh7d//35s3rwZPXv2RM2aNUtmLggYOnSo3ubJ635oQ0I9PEL4w+u6U7ItvA0bNiAx\nMRFFRUUwMfl3T6o+Cx4hhBBSSrKCFxcXh8uXL1d7wGhSHu/j+elrLE1DwPtnR/kRQyTZQSudO3dG\nQkKCVLMjhBBCtEjWw2vRogWuXbuGxo0ba10PT5+nJfC6H9qQUA+PEP7wuu6UZJcmYwzr1q2Dq6ur\nFLMjhBBCypFsl+bbb78NlUpV7o9UH+/nAtF5eMpF+RFDJEnBEwQBPj4+OH36tBSzI4QQQsqRrIf3\nyiuv4OrVq3Bzc4O5uXnJzKmHp3jUwyOEP7yuOyU7LeGPP/4AAPG0BB7fTEIIIYZLsh6eSqVCZmYm\noqKisGvXLjx69Ih6eC+J9z4C9fCUi/Ijhkiygrdy5UqMHTsW6enpSEtLw9ixYxEeHi7V7AkhhBg5\nyXp4np6eiImJEft3OTk58PX1xYULF/Q2T0PZDz07bDZSM1PlDuOFOdo4YknYkhd6LvXwCOGPoaw7\ndU2yHh4ArTE0y/7Pu9TMVEUVBfUOtdwhEEKIzklWdYKDg9GxY0eEhYVh/vz58PX1RUhIiFSz5xLP\nPS6A7/x47wFRfsQQ6X0L7/r162jSpAlCQ0Ph5+eHY8eOQRAEREZGwtvbW9+zJ4QQQgBIUPBGjBiB\nM2fOoEePHjh48CB8fHz0PUujweuVBErxnB/vI+1TfsQQ6b3gaTQaLFq0CImJifjf//6n1QgVBAGh\noaH6DoEQQgjRfw/vl19+gampKTQaDbKyspCdnS3+ZWVl6Xv2XOO5xwXwnR/vPSDKjxgivW/htWjR\nAh9++CHc3NwwevRofc+OEEIIqZAkR2mampriyy+/lGJWRoXnHhfAd36894AoP2KIJDstoVevXvjy\nyy9x+/ZtZGRkiH+EEEKIFCQreL/88gu++uordO/eHT4+PuIfqT6ee1wA3/nx3gOi/IghkmykFbVa\nLdWsCCGEkHIk28LLycnBwoULMXnyZADAlStXsHv3bqlmzyWee1wA3/nx3gOi/IghknRosZo1a+LE\niRMAAGdnZ3zyySdSzZ4QQoiRk6zgXbt2DbNmzULNmjUBQLxqAqk+nntcAN/58d4DovyIIZKs4NWq\nVQt5eXni7WvXrqFWrVpSzZ4QQoiRk+yglbCwMPTt2xd37tzBm2++iePHjyMyMlKq2XOJ5x4XwHd+\nvPeAKD9iiCQreL1790a7du1w6tQpMMYQHh4Oe3v7574uJCQEv//+OxwcHMSLxWZkZGDkyJG4efMm\nVCoVtmzZAhsbG32nQAghRMEk26XJGMPhw4dx4MABHDp0CEePHn2h1wUHB2Pfvn1a9y1ZsgS9evVC\nUlISevTogSVLXuzq3LzhuccF8J0f7z0gyo8YIskK3ttvv421a9eiTZs2aN26NdauXYu33377ua/r\n1q0bbG1tte6LiorChAkTAAATJkzAjh079BIzIYQQfki2S/Ovv/5CQkICTExKamxQUBA8PDyqNa20\ntDQ0aNAAANCgQQOkpaXpLE4l4bnHBfCdH+89IMqPGCLJCp67uztu3boFlUoFALh16xbc3d1ferqC\nIEAQhGc+HhQUJM7TxsYGXl5e4sJaultC37dLle6iK12RG+rtUi+SX+qdVKhgWPHrMj+6TbeN4XZ0\ndLR4EGHp+pJHAit7RVY96t69O2JjY9GhQwcIgoDTp0/j1VdfhZWVFQRBQFRU1DNfq1arMXDgQPGg\nlRYtWiA6OhqOjo5ISUlBQEAALl++XO51giBAovQqFTQzCKohKp1PVx2v1stWkHqHGpErIl/oufrK\nDTCM/PQlOjqa660Eyk/ZDGXdqWuSbeF99tln5e4rfVMr20KryKBBg7BhwwbMmjULGzZswJAhQ3QV\nJiGEEE5JVvCq+2to9OjROHz4MO7fvw8XFxd89tlnmD17NgIDA7F+/XrxtARjxHOPC+A7P563DgDK\njxgmyQpedf38888V3n/gwAGJIyGEEKJkkp2WQHSP5/PUAL7ze/qAJt5QfsQQSVrwcnNzkZiYKOUs\nCSGEEAAS7tKMiorChx9+iIKCAqjVapw9exbz58+v9OhMUjmee1yAYeQ3O2w2UjNT9TLtyB2Repmu\no40jloTJO/oQ7z0u3vPjlaSDR586dQoBAQEAAG9vb1y/fl2q2RNSLamZqXo77UJf1DvUcodAiEGS\nbJemmZlZuQGeS0ddIdXDc48L4Ds/nnMD+O9x8Z4frySrOK1atcKmTZtQVFSEK1euYMaMGejcubNU\nsyeEEGLkJCt4q1atwqVLl1CrVi2MHj0aVlZWWLFihVSz55Ih9Lj0ief8eM4N4L/HxXt+vJKsh5eY\nmIjFixdj8eLFUs2SEEIIEUm2hRcaGooWLVpg3rx5uHjxolSz5RrvfSCe8+M5N4D/Hhfv+fFKsoIX\nHR2Nv/76C/b29pgyZQo8PT2xcOFCqWZPCCHEyEl6mKSTkxPee+89fPPNN2jbtm2FA0qTF8d7H4jn\n/HjODeC/x8V7frySrOAlJCQgLCwMrVu3xvTp09G5c2ckJydLNXtCCCFGTrKCFxISAhsbG/zxxx84\nfPgw3n77bTg4OEg1ey7x3gfiOT+ecwP473Hxnh+vJDtKMyYmRqpZEUIIIeXoveCNGDECW7duhaen\nZ7nHBEHA+fPn9R0Ct3jvA/GcH8+5Afz3uHjPj1d6L3grV64EAOzevbvcJeOreqVzQgghpLr03sNz\ndnYGAHz99ddQqVRaf19//bW+Z8813vtAPOfHc24A/z0u3vPjlWQHrezfv7/cfXv27JFq9oQQQoyc\n3ndprlmzBl9//TWuXbum1cfLyspCly5d9D17rvHeB+I5P55zA/jvcfGeH6/0XvDefPNN9OvXD7Nn\nz8bSpUvFPp6lpSXs7Oz0PXtCCCEEgAS7NK2traFSqfDLL7/Azc0NdevWhYmJCXJycnDr1i19z55r\nvPeBeM6P59wA/ntcvOfHK8l6eFFRUWjWrBkaN24MPz8/qFQq9OvXT6rZE0IIMXKSFby5c+fi5MmT\naN68OW7cuIGDBw+iY8eOUs2eS7z3gXjOj+fcAP57XLznxyvJCp6ZmRns7e1RXFwMjUaDgIAAxMXF\nSTV7QgghRk6ygmdra4usrCx069YNY8aMwbvvvgsLCwupZs8l3vtAPOfHc24A/z0u3vPjlWQFb8eO\nHahbty6WL1+Ovn37wt3dHbt27ZJq9oQQQoycZINHl27NmZqaIigoSKrZco33PhDP+fGcG8B/j4v3\n/Hil94JnYWHxzDEzBUHA48eP9R0CIYQQov9dmtnZ2cjKyqrwj4rdy+G9D8RzfjznBvDf4+I9P15J\n1sMDgKNHjyIiIgIAkJ6ejhs3bkg5e0IIIUZMsh5eWFgY4uLikJSUhODgYBQWFmLMmDE4ceKEVCFw\nh/c+EM/5GUpus8NmIzUzVS/TjtwRqZfpOto4YknYEr1M+0VRD0+ZJCt4v/32G86ePQsfHx8AQMOG\nDZGdnS3V7AkhFUjNTIVqiEruMKpEvUMtdwhEoSTbpVmrVi2YmPw7u5ycHKlmzS3e+0A858dzbgD/\n+VEPT5kkK3gjRozAlClTkJmZiXXr1qFHjx6YNGmSVLMnhBBi5CTZpckYw8iRI3H58mVYWloiKSkJ\nCxcuRK9evaSYPbcMpQ+kLzznx3NuAP/5UQ9PmSTr4b3++uu4ePEievfuLdUsCSGEEJEkuzQFQYCP\njw9Onz6t0+mqVCq0adMG3t7e6NChg06nrQS890l4zo/n3AD+86MenjJJtoUXExODH3/8EW5ubjA3\nNwdQUgjPnz9f7WkKgoDo6GjUq1dPV2ESQgjhlGQF748//tDLdBljepmuEvDeJ+E5P55zA/jPj3p4\nyiRZwVOpVDqfpiAI6NmzJ0xNTTFlyhRMnjxZ5/MghBDCB8kKnj4cP34cTk5OSE9PR69evdCiRQt0\n69ZN6zlBQUFisbWxsYGXl5f466x0P7y+b5cq7WuU/vp92dsxv8bA0d1RZ9N7uu/yIvml3kmFCrqd\nvzHkVzYWyk9/+enrdtnvthzz10c+kZGRAPSzcWIoBMbJPsEFCxbAwsIC77//vnifIAgGscszaGaQ\nXkazUMer9bLrSL1DjcgVkS/0XH3lBvCdn75yAyg/KURHR3O9W9NQ1p26Jung0bqUm5uLrKwsACWj\ntuzfvx+enp4yRyUt3vskPOfHc24A//nxXOx4pthdmmlpaXjjjTcAAEVFRRgzZgyd40cIIeSZFLuF\n17hxY8THxyM+Ph4XL17Exx9/LHdIkuP9XCee8+M5N4D//Og8PGVSbMEjhBBCqoIKnoLx3ifhOT+e\ncwP4z496eMpEBY8QQohRoIKnYLz3SXjOj+fcAP7zox6eMlHBI4QQYhSo4CkY730SnvPjOTeA//yo\nh6dMij0PjxBCnmd22GykZqbKHcYLc7RxxJKwJXKHwS0qeAqmz+GbDAHP+fGcG2A4+aVmpipq6DT1\nDrXOp0n+Rbs0CSGEGAUqeApmCL+g9Ynn/HjODaD8iGGigkcIIcQoUMFTMN7PdeI5P55zAyg/Ypio\n4BFCCDEKVPAUjPc+As/58ZwbQPkRw0QFjxBCiFGggqdgvPcReM6P59wAyo8YJip4hBBCjAIVPAXj\nvY/Ac3485wZQfsQwUcEjhBBiFKjgKRjvfQSe8+M5N4DyI4aJCh4hhBCjQAVPwXjvI/CcH8+5AZQf\nMUxU8AghhBgFKngKxnsfgef8eM4NoPyIYaKCRwghxChQwVMw3vsIPOfHc24A5UcMExU8QgghRoEK\nnoLx3kfgOT+ecwMoP2KYqOARQggxClTwFIz3PgLP+fGcG0D5EcNEBY8QQohRoIKnYLz3EXjOj+fc\nAMqPGCYqeIQQQowCFTwF472PwHN+POcGUH7EMFHBI4QQYhQUXfD27duHFi1aoFmzZli6dKnc4UiO\n9z4Cz/nxnBtA+RHDpNiCp9FoMH36dOzbtw8JCQn4+eef8c8//8gdlqRSr6bKHYJe8Zwfz7kBlB8x\nTIoteKdPn4a7uztUKhXMzMwwatQo7Ny5U+6wJJWfnS93CHrFc3485wZQfsQwKbbgJScnw8XFRbzd\nqFEjJCcnyxgRIYQQQ6bYgicIgtwhyC4zNVPuEPSK5/x4zg2g/IhhEhhjTO4gqiMmJgZhYWHYt28f\nAODzzz+HiYkJZs2aJT7Hy8sL586dkytEQghRpLZt2yI+Pl7uMHROsQWvqKgIr7zyCg4ePAhnZ2d0\n6NABP//8M1q2bCl3aIQQQgxQDbkDqK4aNWpg9erV6NOnDzQaDSZOnEjFjhBCyDMpdguPEEIIqQrF\nHrRizPLz81FQUCB3GHrDe36EEHkodpemMSkuLsaOHTvw888/48SJEyguLgZjDKampujUqRPGjBmD\nIUOGKPbIVd7zK5WcnAy1Wg2NRgPGGARBQPfu3eUOSycSExPx5ZdfQq1Wo6ioCEDJkdSHDh2SOTLd\n2LZtG2bPno20tDSU7hQTBAGPHz+WOTJSFbRLUwG6d++Obt26YdCgQfDy8kKtWrUAAAUFBTh79iyi\noqJw7NgxHDlyROZIq4f3/ABg1qxZ2Lx5Mzw8PGBqairev2vXLhmj0p02bdpg2rRpaNeunZifIAjw\n8fGROTLdaNq0KXbv3k3HCSgcFTwFKCgoEIvAyzzHUPGeHwA0b94cFy5cUHQOlfHx8cGZM2fkDkNv\nunTpguPHj8sdBnlJtEtTAcquJDUaDdLS0sTdRgDg6uqq6BXpi8Su5PyAki2EwsJCxefxLAMHDsRX\nX32FoUOHauVYr149GaPSnfbt22PkyJEYMmQIatasCaBkC3bo0KEyR0aqgrbwFGTVqlVYsGABHBwc\ntHaLXbhwQcao9Kt///74/fff5Q6j2mbMmAEAuHv3LuLj49GjRw+xIAiCgPDwcDnD0xmVSlWuxyoI\nAq5fvy5TRLoVFBQEoPwITxERETJEQ6qLCp6CNG3aFKdPn4adnZ3coUjm7t27cHZ2ljuMaouMjBRX\nkqUHqpT9f8KECXKGR4hRoYKnIAEBAdi/fz/MzMzkDoVUUXZ2NurUqSNumWs0GuTn58Pc3FzmyHSj\nsLAQa9aswZEjRyAIAvz8/DB16lRultXbt2/j3XffxbFjxwCUHGi1cuVKNGrUSObISFVQwVOQkJAQ\nJCUloX///lp9hNDQUJkjezmenp7PfEwQBJw/f17CaPTD19cXBw4cgIWFBQAgKysLffr0wYkTJ2SO\nTDcmTpyIoqIiTJgwAYwxbNy4ETVq1MB3330nd2g60bNnT4wZMwZjx44FAGzatAmbNm3Cn3/+KXNk\npCrooBUFcXV1haurKwoLC1FYWKi1i0zJeDk0vzL5+flisQMAS0tL5ObmyhiRbsXGxmr9MOnRowfa\ntGkjY0S6lZ6ejuDgYPF2UFAQli9fLmNEpDqo4ClIWFgYgJKtA6BkpckDlUoFALhx4wYcHR1Rp04d\nAEBeXh7S0tJkjEx3zM3NcebMGfG8tLi4ODFPHtSoUQNXr16Fu7s7AODatWuoUYOf1YudnR02btyI\nN998E4wx/PLLL7C3t5c7LFJFtEtTQS5cuIDx48fjwYMHAID69etjw4YNaN26tcyR6YaPjw9Onjwp\n7q4tKChAly5dEBcXJ3NkLy82NhajRo2Ck5MTACAlJQWbN29G+/btZY5MNw4ePIjg4GA0btwYAKBW\nqxEREYHXXntN5sh0Q61WY8aMGYiJiQEAdO7cGatWrYKrq6vMkZGqoIKnIJ06dcLixYsREBAAAIiO\njsacOXO46QN5eXmVuwZX27ZtubmmYWFhIRITEyEIAl555RVuDugolZ+fr5Ufr+ccEuXiZ5+DEcjN\nzRWLHQD4+/sjJydHxoh0y97eHjt37sTgwYMBADt37uRqt1FiYiISEhKQn5+Pv//+GwAwfvx4maN6\nOQcPHkSPHj2wbds2CIIgjjN59epVAFD8idlLly7FrFmzxPMpy+LpPEpjQQVPQRo3boyFCxdi3Lhx\nYIxh06ZNaNKkidxh6cw333yDMWPGYPr06QCARo0aYePGjTJHpRthYWE4fPgwLl26hP79+2Pv3r3o\n2rWr4gvekSNH0KNHD+zatavCA6iUXvA8PDwAlOxuL5sfLweMGRvapakgGRkZmD9/vjimX7du3RAW\nFgZbW1uZI9Ot7OxsMMa4OSgHAFq3bo1z586hXbt2OHfuHNLS0jBmzBgcOHBA7tB04vr16+V+fFV0\nn1Jt2bIFgYGBz72PGDYqeMRgpKam4pNPPkFycjL27duHhIQEnDx5EhMnTpQ7tJf26quvIjY2Fj4+\nPjh06BCsrKzQokULJCYmyh2aTrRr107cTVuKpwGlvb29cfbs2efeRwwb7dJUEN6vORYUFITg4GAs\nWrQIANCsWTMEBgZyU/AePnyIyZMno3379jA3N0fnzp3lDuul/fPPP0hISEBmZia2b98u7up7/Pgx\n8vPz5Q7vpe3duxd79uxBcnIy3n33XbFHmZWVxd1BR8aACp6CjBgxAtOmTcOkSZO0rjnGi/v372Pk\nyJFYsmQJAMDMzIybc7m+/vprAMDUqVPRt29fPH78mIsTs5OSkrBr1y48evRIawABS0tLfPvttzJG\nphvOzs7w8fHBzp074ePjIxZ0S0tLOvFcgfhYmxgJMzMzTJs2Te4w9MbCwkI8xxAAYmJiYG1tLWNE\nurVz506tsSZ5KHiDBw/G4MGDcfLkSXTq1EnucHSubdu2aNu2LYYOHQpzc3OtsVALCgpkjo5UlYnc\nAZDny8jIwIMHD8RrjqWkpCAjI0P848WyZcswcOBAXL9+HZ07d8a4ceO4Oex79uzZCA8PR6tWrdCy\nZUuEh4fj448/ljssnVmzZg0yMzPF2w8fPkRISIiMEelW7969kZeXJ97Ozc1Fz549ZYyIVAcdtKIA\nFV1rrKwbN25IGI1+PXnyRDyQg6eTsz09PREfH6+1heDl5cXNtQwrGjSgovuUivf8jAXt0lQAtVoN\noGQki9q1a2s9xsOBAWVPWi5b2JOSkgAo/1wuoKTXmpmZKV7LMDMzk6v+K2MMGRkZ4hXOMzIyoNFo\nZI5Kd3gfC9VYUMFTkM6dO5c79Lui+5Sm9KTle/fu4cSJE+L4i3/99Rc6d+7MRcH7+OOP0a5dOwQE\nBIAxhsOHD4sH5/Dg/fffR6dOnRAYGAjGGLZu3YpPPvlE7rB0ZsWKFQgMDCw3FipRFip4CpCSkoK7\nd+8iNzcXf//9t9ah3zxcYiYyMhIA0KtXLyQkJGitVHi4InhxcTFMTExw8uRJxMbGQhAELFmyRMyT\nB+PHjxfPMRQEAb/99ps4SgkPXn31Vfzzzz9cj4VqDKiHpwAbNmxAZGQk4uLitEbXt7S0RFBQEBdb\nQADQokUL/PPPP+KuvuLiYnh4eODy5csyR/byeDoJ+1k0Gg1SU1NRVFQkfoY8XU3gxIkTuHHjhlZ+\nSh8azthQwVOQX3/9FcOHD5c7DL2ZPn06kpKSxGuObd68Gc2aNcOqVavkDu2lzZ49G/b29hg5ciTM\nzc3F+0t7Xkq3atUqLFiwAA4ODuKBOQC4OShn7NixuH79Ory8vLTy42HZNCZU8BSkSZMmGDZsGIKD\ng7naXVTW9u3bcfToUQBA9+7d8cYbb8gckW5UdKStIAi4fv26TBHpVtOmTXH69GnxoBzetGzZEgkJ\nCVwdaGSMqOApyOPHj/HLL78gMjISGo0GISEhGD16NKysrOQOjRi5gIAA7N+/n9u+1ogRI7By5Uo4\nOzvLHQp5CVTwFCo6OhpjxozBw4cPMWLECMybNw/u7u5yh0WeIS8vD19//TWOHTsGQRDQrVs3TJs2\nrdxpJkoVEhKCpKQk9O/fX7xivSAICA0NlTky3fD390d8fDw6dOggXthWEARERUXJHBmpCjpKU0GK\niorw+++/IyIiAmq1Gu+//z7efPNNHDt2DK+//rp43hoxPOPHj4eVlZU4APFPP/2EcePGYevWrXKH\nphOurq5wdXVFYWEhCgsLubteXFhYmNwhEB2gLTwFadKkCfz9/TFp0qRyI+3PmDGDiwZ6bm4ubt++\njVdeeUXuUHTKw8MDCQkJz72PEKI/tIWnIOfPn4eFhUWFj/FQ7KKiovDhhx+ioKAAarUaZ8+exfz5\n87nYbdSuXTutAZZjYmLEUTt4EBAQUO4+ni5dZWFhIW6xFhYW4smTJ7CwsMDjx49ljoxUBRU8BXnn\nnXewcuVK2NjYACgZvumDDz7A999/L3NkuhEWFoZTp06JK09vb29ujmKMi4tDly5d4OLiAkEQcOvW\nLbzyyivw9PSEIAg4f/683CG+lP/+97/i//n5+di2bRs3l3YCgOzsbPH/4uJiREVFISYmRsaISHXw\ns0QagXPnzonFDig5h0vpw4qVZWZmppUfAJiY8HFBj3379gH49/qFvHUSyg6IAABdu3bFq6++KlM0\n+mViYoIhQ4YgLCyMq+HhjAEVPAXhfYDeVq1aYdOmTSgqKsKVK1cQHh7OxVXBgZLz8M6cOYNjx47B\nxMQEXbp0Qbt27eQOS2fKXqaquLgYcXFxXO3u27Ztm/h/cXExzpw5Q4NHKxAVPAXhfYDeVatWYdGi\nRahVqxZGjx6NPn36YN68eXKHpROfffYZtm7diqFDh4IxhuDgYAwfPpyb/Nq1ayduvdaoUQMqlQrr\n16+XOSrd2b17t/h/aX47d+6UMSJSHXSUpsJcunRJHKD3tdde43LElUePHkEQBK5OqG/evDnOnz8v\nnneXl5eHtm3bKv5Ukq1bt2LEiBG4fv06mjRpInc4Ojdr1iwsXboUW7ZsQWBgoNzhkJfER4OEc1lZ\nWeL/rVq1wowZMzB9+nStYlf2OUoVGxsLT09PtGnTBp6enmjbti3i4uLkDksnGjZsqHXF7Pz8fDRq\n1EjGiHRj8eLFAMDtGK+///47GGP4/PPP5Q6F6ADt0lSAN954A6+88goGDx6M9u3ba/XwYmNjsWPH\nDly5cgUHDhyQOdKXExISgq+//hrdunUDABw7dgwhISGKP4IRAKysrNCqVSv07t0bAPDnn3+iQ4cO\nmKWd018AABrKSURBVDFjBgRBQHh4uMwRVo+dnR169eqF69evY+DAgVqP8TASSb9+/WBra4vs7GxY\nWlpqPVZ6iS6iHLRLUyEOHTqEn376CcePH8fdu3cBAM7OzujatSvGjBkDf39/eQPUAW9vb5w9e1br\nvnbt2nFxJGrpNf8qIgiCYq/7V1hYiL///hvjxo3Dd999p3X0qSAI8PPzkzE63Rk0aJDiizehgkcM\nyMyZM5GXl4fRo0cDADZv3ozatWtj3LhxAMDVUY28uXfvHhwcHOQOg5BKUcEjBsPf37/S8Rf/+usv\nCaPRraSkJMyZMwcJCQliL4+nywMRogTUwyMG48CBA1yNzlFWcHAwFixYgNDQUERHRyMiIoKrcygJ\nUQI6SpMYjObNm+PDDz/kckDlvLw89OzZE4wxuLm5ISwsDL///rvcYenMgwcP5A5Br6KiolBcXCx3\nGOQlUcFTGI1Gg7t37+LWrVviHy/i4+PRrFkzTJo0CR07dsTatWu5OQqudu3a0Gg0cHd3x+rVq7F9\n+3bk5OTIHZbO+Pr6YsSIEdizZw93w6YBJf1kd3d3fPTRR7h8+bLc4ZBqoh6egqxatQoLFiyAg4MD\nTE1NxfsvXLggY1T6wdsFbk+fPo2WLVsiMzMT8+bNw+PHj/HRRx/B19dX7tB0ori4GAcOHMD333+P\n2NhYBAYGIjg4GM2bN5c7NJ159OgRfv75Z0RGRkIQBAQHB2P06NHlTlcghosKnoI0bdoUp0+fhp2d\nndyh6MXTF7gdP368eIHbOXPmKH5UEmNx6NAhjB07Fjk5OfDy8sLnn3/OzZio9+/fx8aNG7FixQp4\neHjgypUrePfdd/Huu+/KHRp5AXweIcApV1dXrobbelrz5s3h7++Pjz76SGsFOXz4cBw+fFjGyMjz\n3L9/H5s2bcIPP/yABg0aYPXq1Rg4cCDOnTuH4cOHQ61Wyx3iS9m5cyciIyNx5coVjB8/HrGxsXBw\ncEBubi48PDyo4CkEbeEpwLJlywAACQkJuHz5MgYMGICaNWsCKDm0PTQ0VM7wdObYsWPo2rXrc+8j\nhqd58+YYO3YsQkJCyg2ZtmTJEsyePVumyHRjwoQJmDhxIrp3717usQMHDqBnz54yREWqigqeAoSF\nhWldR+3pc9Xmz58vR1g6V9GoKhWNvsKLwsJC8YeL0hUXF8PExASPHz+GIAhc9rVSUlJw+vRpmJiY\n4NVXX4Wjo6PcIZEqol2aChAWFiZ3CHp18uRJnDhxAvfu3cP//vc/8Si/rKwsbg4F9/PzQ2RkJBo3\nbgyg5CCWSZMmcTFOKACcOXMGISEh4lG1NjY2WL9+fbkLwyrVd999h88++wwBAQFgjGH69On49NNP\nMXHiRLlDI1VABU9BevXqha1bt4pXBc/IyMDo0aPxxx9/yBzZyyksLERWVhY0Go3WVR+srKzw66+/\nyhiZ7syZMwf9+vXDjBkzkJycjL1791Y6vqbS8DzwNwB88cUXOHv2rHjA2IMHD9CpUycqeApDBU9B\n0tPTxWIHAPXq1UNaWpqMEemGn58f/Pz8EBQUBJVKJXc4etGnTx+sWbMGvXr1Qv369XH27FmudonV\nqFFDLHYA0LVrV65GzbG3t4eFhYV428LCAvb29jJGRKqDnyXSCJiamuLmzZtwc3MDAKjVapiY8DN2\nAK/FDgAWLlyIzZs34+jRozh//jz8/PywbNkyDBgwQO7QdMLPzw9TpkzRGvjbz89P7MkqfeDvpk2b\nwtfXF4MHDwZQctRmmzZtsGzZMq4OHOMdFTwFWbRoEbp16yYeKXbkyBGsW7dO5qjIi3jw4AFiY2NR\np04ddOrUCX379sWkSZO4KXjx8fEQBAELFiwA8O/BVfHx8QCUPfA3UFLwmjZtKh4wNnjwYAiCgOzs\nbJkjI1VBR2kqTHp6OmJiYiAIAnx9fWm3CiGEvCAqeArz8OFDJCUlIT8/X/y1WdG5QUq2YcMGxV4Q\n9WnvvfceVq5cWe5q4AAfVwQv9fDhQ/zwww9Qq9UoKioCAEVfyb2UsXx+xoJ2aSrIt99+i/DwcNy5\ncwdeXl6IiYlBp06dcOjQIblD06kVK1ZwU/DGjx8PAPjggw/KDapc2bX/lOb1119Hp06d0KZNG5iY\nmFR4vqgSlX5+77//frnHeMjP2NAWnoK0bt0asbGx6NSpE+Lj43H58mV8/PHH+O233+QOTad4O9m8\nqKgI48ePx08//SR3KHpT0aABPMnOzkadOnXEQds1Gg3y8/Nhbm4uc2SkKmgLT0Fq166NOnXqAADy\n8/PRokULJCYmyhyVbgQEBIj/X716VbwtCILit2Br1KiBW7duoaCgALVq1ZI7HL148803sW7dOgwc\nOFArx3r16skYle706NEDBw8eFE9NyM3NRZ8+fXDixAmZIyNVQQVPQVxcXPDw4UMMGTIEvXr1gq2t\nLTeH8kdEREAQBDDG0L9/f0RGRnJ1XbXGjRuja9euGDRoEOrWrQuAr3FQa9eujQ8//BCLFi0ST5UR\nBAHXr1+XOTLdKCgo0DoPz9LSErm5uTJGRKqDCp6ClO66DAsLg7+/Px4/foy+ffvKHJVulC3cNWvW\nFM815EXpYe3FxcVcHsq+bNkyXLt2jdujhs3NzXHmzBn4+PgAAOLi4sS9LUQ5qOApTHx8PI4ePQqg\n5OhMXgYfLqt0vEmeeHh4IDAwUOu+LVu2yBSN7jVr1ozrArBixQoEBgbCyckJQMlA0ps3b5Y5KlJV\ndNCKgqxcuRLffvsthg4dCsYYduzYgcmTJ9O1uBSgogNxeDo4Z8iQIbh06RICAgLEHh4PpyWUVVhY\niMTERAiCgFdeeQVmZmZyh0SqiAqegnh6eiImJkY8MiwnJwe+vr64cOGCzJGRZ9m7dy/27NmDzZs3\nY9SoUVpXgkhISMDp06dljlA3KhoIWxAEbk4v2bJlC/r27QsrKyssXLgQZ8+exdy5cxU/ZJqxoV2a\nClN27EyextHklbOzM3x8fLBz5074+PiIBc/KygrLly+XOTrdCQoKkjsEvVq4cCECAwNx7NgxHDx4\nEB988AGmTp3KzQ8WY0EFT0GCg4PRsWNHrV2aISEhcodFKtG2bVu0bdsWb775Jpf91lIV9V15Okqz\n9Py73bt3Y/LkyRgwYADmzZsnc1SkqqjgKURxcTE6duwIPz8/HDt2DIIgIDIyEt7e3nKHplMajQZp\naWni8FQA4OrqKmNEuqFWqzFnzhwkJCQgLy8PAF8FITY2Vvw/Pz8fv/76Kx48eCBjRLrVsGFDvPXW\nW/jzzz8xe/Zs5Ofnc3NxYmNCPTwF8fLyEkef59GqVauwYMECODg4iL+oAXDRo+zSpQsWLFiA0NBQ\n7Nq1CxEREdBoNFi4cKHcoekNT6Ov5OTkYN++fWjTpg2aNWuGlJQUXLhwAb1795Y7NFIFVPAU5IMP\nPoCvry+GDRvG5Th+TZs2xenTp8WrSvOkdOXv6ekpFnCeCsKZM2f+X3v3FhPV1b4B/NlACKYjAqIh\nJFJwkALVEYuAKIrxEIwnhKqJJWCkaEMMTYuNjUERjxfWQ6WtPahYSTXxUFLUqjUGTasRUZGDEDBi\nKVKJEvfggEKQYf8viPMvsV/7pUy/tffi+SVe7B0vnkTiy7v2u9Zy/Ez29vbi5s2b+PLLL1FZWSk4\nGdH/45KmgXz11VfYvXs3XF1d4eHhAaBvWcxmswlO5hwBAQHw9PQUHeNf4eHhAbvdjuDgYHz++efw\n9/fHs2fPRMdymjVr1jgKnpubGwIDA6XaZ0hyYIdHupGeno67d+9i3rx5jgEPWY7fKisrQ1hYGNra\n2rBhwwbYbDasXbsWkyZNEh2NaNBgh2cgmqahqKgIV65cgYuLC+Li4pCUlCQ6ltMEBAQgICAA3d3d\n6O7uluaKGQCIjo4G0HcG45/tWTO6rq4ufP/992hsbITdbnf82+Xm5oqORuTADs9AMjMz0dDQgGXL\nlkHTNBw7dgxmsxn79u0THc2p2tvbAfQVB1ncuHED27dvf+WC1KqqKsHJnCMhIQFeXl6IjIzsN3D0\nZ/fIEYnCgmcgoaGhqK2tdWw47+3tRXh4OOrq6gQnc47q6mqkpaU5xtlHjBiBw4cPY+zYsYKTDVxI\nSAh27tyJsWPH9jswQJbbLsaOHYs7d+6IjkH0l7ikaSDBwcFoampy/CfZ1NSE4OBgsaGcaNWqVdi9\ne7fjLrzLly9j1apVUtw5NmLECCxcuFB0jH/N5MmTUVVVBYvFIjoK0X/EDs9Apk2bhhs3biA6OhqK\noqCsrAxRUVHw9PSEoig4deqU6IgDMn78+FfG2P/snRFduHABx44dw6xZs/oN5CQnJwtO5hxhYWG4\nd+8egoKC+h0eLcuSLcmBHZ6BbN68GQAcgxx//F1FhuGOoKAgbNmyBampqdA0DUeOHMHo0aNFx3KK\nw4cPo76+Hj09Pf2WNGUpeOfOnRMdgehvscMzmJaWFpSVlcHFxQVRUVHw8/MTHclpVFXFxo0bcfXq\nVQDA1KlTkZeXB29vb8HJBu6NN95AXV2dFL+YEBkVC56BHDhwAJs3b+73jSs3Nxfvvvuu4GT0d1as\nWIGPPvoIb775pugoRIMWC56BhISE4Nq1a46jt548eYLY2FjcvXtXcDLnqK+vx86dO18Z3S8pKRGc\nbOBCQ0PR0NDAb1xEAvEbnoH4+vrCZDI5nk0mE3x9fQUmcq4lS5YgMzMTGRkZjr1csiwBnj9/XnQE\nokGPHZ6BpKam4s6dO0hMTAQAFBcXw2KxwGKxSHEEV2RkJG7duiU6BhFJih2egZjNZpjNZkfXk5iY\nCEVR0NHRITjZwKiqCk3TsGDBAnzxxRdITk52LPsBgI+Pj8B0RCQLdngkXGBg4F8uXf7666//wzRE\nJCsWPAN5/PgxduzY8cqt2TIMdQB9BxC/vPbor94REf0TLn//V0gvUlJSEBoaivv37yMvLw+BgYGY\nOHGi6FhOM3ny5P/qHRHRP8FveAby5MkTZGRkID8/H/Hx8YiPj5ei4LW0tODhw4d4/vw5ysvLHVfL\n2Gw2PH/+XHQ8IpIEC56BvDyD0c/PD2fOnIG/vz+sVqvgVAN34cIFfPvtt/j999/7XSczdOhQbN++\nXWAyIpIJv+EZyOnTpzF16lQ8ePAAWVlZsNlsyMvLk+YU/pMnT2Lx4sWiYxCRpFjwSDdGjx6Nt99+\nGytWrEB4eLjoOEQkGQ6tkG5UVFRgzJgxyMjIQExMDL7++mvYbDbRsYhIEuzwSJcuX76MlJQUWK1W\nLFmyBBs2bJDqslsi+t9jh0e60dPTg+LiYixatAgffPAB1qxZg/v372PBggWYO3eu6HhEZHAseAay\nbt26flOZVqsV69evF5jIuUJCQlBcXIy1a9eioqIC2dnZ8PPzw+LFi5GQkCA6HhEZHJc0DSQiIgIV\nFRX93k2YMAG3b98WlMi5Ojo6+t0GQUTkTOzwDKS3txddXV2O587OTnR3dwtM5FyrV69GW1ub41lV\nVaSnpwtMREQy4cZzA0lJScHMmTORnp4OTdNw6NAhpKWliY7lNJWVlfDy8nI8+/j4oLy8XGAiIpIJ\nC56BfPzxx7BYLLh48SIURUFubq5U37Y0TYOqqo7rgFRVhd1uF5yKiGTBb3ikG4WFhdi2bRuWLl0K\nTdNw4sQJ5OTkSNXFEpE4LHgGMGXKFFy9ehUmk+mVe+NeHrIsi5qaGpSUlEBRFMyYMYMnrhCR07Dg\nkXDt7e0YOnTogP8OEdFf4ZSmgTQ0NDimNC9duoT8/Px+U41GlZSUhNWrV+PChQtQVdXxXlVV/PTT\nT8jMzERSUpLAhEQkA3Z4BjJ+/HjcunULjY2NmDt3LhITE1FTU4OzZ8+KjjZgJSUlOHr0KK5evYqH\nDx8CAPz9/REXF4eUlBRMnz5dbEAiMjwWPAN5ucl8x44dGDJkCLKysqTaeE5E9G/ikqaBuLu74+jR\noygsLMT8+fOhaRpevHghOhYRkSGw4BlIQUEBSktLkZOTg6CgIDQ2NiI1NVV0LCIiQ+CSpkGpqorm\n5mZYLBbRUYiIDIEnrRhIfHw8Tp8+jZ6eHkRGRmLEiBGYMmUK9uzZIzqa09jtdjx69Ag9PT2OdwEB\nAQITEZEsWPAM5OnTp/D09MSBAweQlpaGTZs2Ydy4caJjOc1nn32GTZs2YeTIkXB1dXW8r66uFpiK\niGTBgmcgdrsdLS0tOH78OLZu3QoAr5y8YmSffvop6uvrMXz4cNFRiEhCHFoxkJeHRZvNZkRHR6Oh\noQFjxowRHctpAgIC4OnpKToGEUmKQysk3K5duwAAtbW1qKurw/z58+Hu7g6gr4PNzs4WGY+IJMEl\nTQPp7OzEwYMHUVtbi87OTgB9BaGgoEBwsoFpb2+HoigICAjAqFGj0N3dLdXFtkSkD+zwDGTx4sUI\nCwvDkSNHsHHjRnz33XcICwtDfn6+6GhERLrHb3gGcu/ePWzZsgUmkwnLly/H2bNncf36ddGxnGb2\n7Nn9DsNWVVWqC26JSCwWPAN5+V1r2LBhqK6uRltbG1pbWwWncp7W1lZ4eXk5nn18fPDo0SOBiYhI\nJix4BrJy5UqoqoqtW7di4cKFCA8Px9q1a0XHchpXV1f89ttvjufGxka4uPBHlIicg9/wSDfOnz+P\nVatWYdq0aQCAn3/+Gd988w3mzJkjOBkRyYAFzwBeju3/kaIo0DRNurH91tZWlJaWQlEUTJo0Cb6+\nvqIjEZEkuC3BAF6O7Q8Gbm5uGDlyJLq6ulBbWwsAjo6PiGgg2OGRbuzfvx/5+flobm5GREQESktL\nERsbi5KSEtHRiEgCnAgwkOXLl/cb27darUhPTxeYyLn27t2LsrIyvP7667h06RJu376NYcOGiY5F\nRJJgwTOQysrKfmP73t7eKC8vF5jIuTw8PDBkyBAAQFdXF0JDQ1FfXy84FRHJgt/wDETTNKiqCh8f\nHwB9G7PtdrvgVM4zatQoWK1WLFq0CLNnz4a3tzcCAwNFxyIiSfAbnoEUFhZi27ZtWLp0KTRNw4kT\nJ5CTk4O0tDTR0Zzu8uXLsNlsmDNnjmPDPRHRQLDgGUxNTQ1KSkqgKApmzJiB8PBw0ZGcqqKiAr/8\n8guAvunM8ePHC05ERLJgwSPd2Lt3L/bv34/k5GRomoYffvgBK1euxPvvvy86GhFJgAWPdGPcuHEo\nLS3Fa6+9BgB49uwZJk2ahOrqasHJiEgGnNIkXfnj2Zk8R5OInIlTmqQbK1asQExMTL8lTZn2GRKR\nWFzSJF3o7e3FtWvX4OHhgStXrkBRFEydOhUTJkwQHY2IJMGCR7oRERGBiooK0TGISFL8SEK6MWvW\nLJw8eRL8HYyI/g3s8Eg3TCYTnj9/DldXV3h4eADouwbJZrMJTkZEMmDBIyKiQYFTmqQbmqahqKgI\nV65cgYuLC+Li4pCUlCQ6FhFJgh0e6UZmZiYaGhqwbNkyaJqGY8eOwWw2Y9++faKjEZEEWPBIN0JD\nQ1FbW+vYcN7b24vw8HDU1dUJTkZEMuCUJulGcHAwmpqaHM9NTU0IDg4WmIiIZMIOj3Rj2rRpuHHj\nBqKjo6EoCsrKyhAVFQVPT08oioJTp06JjkhEBsahFdKNzZs3A+jbigCg3368l++IiP4pdnikKy0t\nLSgrK4OLiwuioqLg5+cnOhIRSYLf8Eg3Dhw4gJiYGBQVFeHkyZOIiYnBwYMHRcciIkmwwyPdCAkJ\nwbVr1zB8+HAAwJMnTxAbG4u7d+8KTkZEMmCHR7rh6+sLk8nkeDaZTPD19RWYiIhkwg6PdCM1NRV3\n7txBYmIiAKC4uBgWiwUWiwWKoiA7O1twQiIyMk5pkm6YzWaYzWbHRGZiYiIURUFHR4fgZEQkA3Z4\nREQ0KLDDI914/PgxduzYgdraWnR2dgLo239XUlIiOBkRyYBDK6QbKSkpCA0Nxf3795GXl4fAwEBM\nnDhRdCwikgSXNEk33nrrLZSXl8NisaCqqgoAMHHiRNy8eVNwMiKSAZc0STfc3d0BAH5+fjhz5gz8\n/f1htVoFpyIiWbDgkW7k5OSgra0Nu3btQlZWFmw2G/bs2SM6FhFJgkuaREQ0KHBohYiIBgUWPCIi\nGhRY8IiIaFBgwSPdWLduXb+pTKvVivXr1wtMREQyYcEj3Th37hy8vb0dz97e3vjxxx8FJiIimbDg\nkW709vaiq6vL8dzZ2Ynu7m6BiYhIJtyHR7qRkpKCmTNnIj09HZqm4dChQ0hLSxMdi4gkwX14pCvn\nzp3DxYsXoSgKZs+ejYSEBNGRiEgSLHhERDQo8BseCTdlyhQAgMlkwtChQ/v98fT0FJyOiGTBDo+I\niAYFdnikGw0NDY4pzUuXLiE/Px9tbW2CUxGRLFjwSDeSk5Ph5uaGe/fu4b333sODBw/wzjvviI5F\nRJJgwSPdcHFxgZubG4qKipCVlYVPPvkELS0tomMRkSRY8Eg33N3dcfToURQWFmL+/PnQNA0vXrwQ\nHYuIJMGCR7pRUFCA0tJS5OTkICgoCI2NjUhNTRUdi4gkwSlN0iVVVdHc3AyLxSI6ChFJgh0e6UZ8\nfDxsNhtUVUVkZCQyMjLw4Ycfio5FRJJgwSPdePr0KTw9PVFUVIS0tDSUlZXh4sWLomMRkSRY8Eg3\n7HY7WlpacPz4ccybNw8AoCiK4FREJAsWPNKN3NxcJCQkwGw2Izo6Gg0NDRgzZozoWEQkCQ6tEBHR\noMD78Eg3Ojs7cfDgQdTW1qKzsxNA35JmQUGB4GREJAMuaZJupKam4tGjRzh//jymT5+O5uZmmEwm\n0bGISBJc0iTdiIiIQEVFBSwWC6qqqvDixQvExcXh+vXroqMRkQTY4ZFuuLu7AwCGDRuG6upqtLW1\nobW1VXAqIpIFv+GRbqxcuRKqqmLr1q1YuHAhOjo6sGXLFtGxiEgSXNIkIqJBgR0eCbdr165X3imK\nAk3ToCgKsrOzBaQiItmw4JFw7e3tPFGFiP51XNIkIqJBgVOapBvLly9HW1ub49lqtSI9PV1gIiKS\nCQse6UZlZSW8vLwcz97e3igvLxeYiIhkwoJHuqFpGlRVdTyrqgq73S4wERHJhEMrpBtr1qxBbGws\nli5dCk3TcOLECeTk5IiORUSS4NAK6UpNTQ1KSkqgKApmzJiB8PBw0ZGISBIseERENCjwGx4REQ0K\nLHhERDQosOAREdGgwIJHRESDAgseERENCv8HW+pAuTxU0ZIAAAAASUVORK5CYII=\n",
|
|
"text": [
|
|
"<matplotlib.figure.Figure at 0x106418090>"
|
|
]
|
|
}
|
|
],
|
|
"prompt_number": 63
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"metadata": {},
|
|
"source": [
|
|
"This is a pretty significant performance gain. The \"Cython + type declarations\" approach sped up our initial Python code 25 times."
|
|
]
|
|
}
|
|
],
|
|
"metadata": {}
|
|
}
|
|
]
|
|
} |