mathdatech/Python
1
0
Fork 0
mirror of https://github.com/TheAlgorithms/Python.git synced 2024-11-24 05:21:09 +00:00
Code Issues Packages Projects Releases Wiki Activity

Added Dequeue in Python

Browse Source
This commit is contained in:
97arushisharma 2017-10-25 01:37:11 +05:30
commit 9bc80eac2d
105 changed files with 295341 additions and 0 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

91
.gitignore vendored Normal file
View File

@ -0,0 +1,91 @@
# Byte-compiled / optimized / DLL files
__pycache__/
*.py[cod]
*$py.class
# C extensions
*.so
# Distribution / packaging
.Python
env/
build/
develop-eggs/
dist/
downloads/
eggs/
.eggs/
lib/
lib64/
parts/
sdist/
var/
*.egg-info/
.installed.cfg
*.egg
# PyInstaller
# Usually these files are written by a python script from a template
# before PyInstaller builds the exe, so as to inject date/other infos into it.
*.manifest
*.spec
# Installer logs
pip-log.txt
pip-delete-this-directory.txt
# Unit test / coverage reports
htmlcov/
.tox/
.coverage
.coverage.*
.cache
nosetests.xml
coverage.xml
*,cover
.hypothesis/
# Translations
*.mo
*.pot
# Django stuff:
*.log
local_settings.py
# Flask stuff:
instance/
.webassets-cache
# Scrapy stuff:
.scrapy
# Sphinx documentation
docs/_build/
# PyBuilder
target/
# IPython Notebook
.ipynb_checkpoints
# pyenv
.python-version
# celery beat schedule file
celerybeat-schedule
# dotenv
.env
# virtualenv
venv/
ENV/
# Spyder project settings
.spyderproject
# Rope project settings
.ropeproject
.idea
.DS_Store

101
Graphs/a_star.py Normal file
View File

@ -0,0 +1,101 @@
grid = [[0, 1, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0],#0 are free path whereas 1's are obstacles
[0, 1, 0, 0, 0, 0],
[0, 1, 0, 0, 1, 0],
[0, 0, 0, 0, 1, 0]]
'''
heuristic = [[9, 8, 7, 6, 5, 4],
[8, 7, 6, 5, 4, 3],
[7, 6, 5, 4, 3, 2],
[6, 5, 4, 3, 2, 1],
[5, 4, 3, 2, 1, 0]]'''
init = [0, 0]
goal = [len(grid)-1, len(grid[0])-1] #all coordinates are given in format [y,x]
cost = 1
#the cost map which pushes the path closer to the goal
heuristic = [[0 for row in range(len(grid[0]))] for col in range(len(grid))]
for i in range(len(grid)):
for j in range(len(grid[0])):
heuristic[i][j] = abs(i - goal[0]) + abs(j - goal[1])
if grid[i][j] == 1:
heuristic[i][j] = 99 #added extra penalty in the heuristic map
#the actions we can take
delta = [[-1, 0 ], # go up
[ 0, -1], # go left
[ 1, 0 ], # go down
[ 0, 1 ]] # go right
#function to search the path
def search(grid,init,goal,cost,heuristic):
closed = [[0 for col in range(len(grid[0]))] for row in range(len(grid))]# the referrence grid
closed[init[0]][init[1]] = 1
action = [[0 for col in range(len(grid[0]))] for row in range(len(grid))]#the action grid
x = init[0]
y = init[1]
g = 0
f = g + heuristic[init[0]][init[0]]
cell = [[f, g, x, y]]
found = False # flag that is set when search is complete
resign = False # flag set if we can't find expand
while not found and not resign:
if len(cell) == 0:
resign = True
return "FAIL"
else:
cell.sort()#to choose the least costliest action so as to move closer to the goal
cell.reverse()
next = cell.pop()
x = next[2]
y = next[3]
g = next[1]
f = next[0]
if x == goal[0] and y == goal[1]:
found = True
else:
for i in range(len(delta)):#to try out different valid actions
x2 = x + delta[i][0]
y2 = y + delta[i][1]
if x2 >= 0 and x2 < len(grid) and y2 >=0 and y2 < len(grid[0]):
if closed[x2][y2] == 0 and grid[x2][y2] == 0:
g2 = g + cost
f2 = g2 + heuristic[x2][y2]
cell.append([f2, g2, x2, y2])
closed[x2][y2] = 1
action[x2][y2] = i
invpath = []
x = goal[0]
y = goal[1]
invpath.append([x, y])#we get the reverse path from here
while x != init[0] or y != init[1]:
x2 = x - delta[action[x][y]][0]
y2 = y - delta[action[x][y]][1]
x = x2
y = y2
invpath.append([x, y])
path = []
for i in range(len(invpath)):
path.append(invpath[len(invpath) - 1 - i])
print "ACTION MAP"
for i in range(len(action)):
print action[i]
return path
a = search(grid,init,goal,cost,heuristic)
for i in range(len(a)):
print a[i]

267
Graphs/basic-graphs.py Normal file
View File

@ -0,0 +1,267 @@
# Accept No. of Nodes and edges
n, m = map(int, raw_input().split(" "))
# Initialising Dictionary of edges
g = {}
for i in xrange(n):
g[i + 1] = []
"""
--------------------------------------------------------------------------------
Accepting edges of Unweighted Directed Graphs
--------------------------------------------------------------------------------
"""
for _ in xrange(m):
x, y = map(int, raw_input().split(" "))
g[x].append(y)
"""
--------------------------------------------------------------------------------
Accepting edges of Unweighted Undirected Graphs
--------------------------------------------------------------------------------
"""
for _ in xrange(m):
x, y = map(int, raw_input().split(" "))
g[x].append(y)
g[y].append(x)
"""
--------------------------------------------------------------------------------
Accepting edges of Weighted Undirected Graphs
--------------------------------------------------------------------------------
"""
for _ in xrange(m):
x, y, r = map(int, raw_input().split(" "))
g[x].append([y, r])
g[y].append([x, r])
"""
--------------------------------------------------------------------------------
Depth First Search.
Args : G - Dictionary of edges
s - Starting Node
Vars : vis - Set of visited nodes
S - Traversal Stack
--------------------------------------------------------------------------------
"""
def dfs(G, s):
vis, S = set([s]), [s]
print s
while S:
flag = 0
for i in G[S[-1]]:
if i not in vis:
S.append(i)
vis.add(i)
flag = 1
print i
break
if not flag:
S.pop()
"""
--------------------------------------------------------------------------------
Breadth First Search.
Args : G - Dictionary of edges
s - Starting Node
Vars : vis - Set of visited nodes
Q - Traveral Stack
--------------------------------------------------------------------------------
"""
from collections import deque
def bfs(G, s):
vis, Q = set([s]), deque([s])
print s
while Q:
u = Q.popleft()
for v in G[u]:
if v not in vis:
vis.add(v)
Q.append(v)
print v
"""
--------------------------------------------------------------------------------
Dijkstra's shortest path Algorithm
Args : G - Dictionary of edges
s - Starting Node
Vars : dist - Dictionary storing shortest distance from s to every other node
known - Set of knows nodes
path - Preceding node in path
--------------------------------------------------------------------------------
"""
def dijk(G, s):
dist, known, path = {s: 0}, set(), {s: 0}
while True:
if len(known) == len(G) - 1:
break
mini = 100000
for i in dist:
if i not in known and dist[i] < mini:
mini = dist[i]
u = i
known.add(u)
for v in G[u]:
if v[0] not in known:
if dist[u] + v[1] < dist.get(v[0], 100000):
dist[v[0]] = dist[u] + v[1]
path[v[0]] = u
for i in dist:
if i != s:
print dist[i]
"""
--------------------------------------------------------------------------------
Topological Sort
--------------------------------------------------------------------------------
"""
from collections import deque
def topo(G, ind=None, Q=[1]):
if ind == None:
ind = [0] * (len(G) + 1) # SInce oth Index is ignored
for u in G:
for v in G[u]:
ind[v] += 1
Q = deque()
for i in G:
if ind[i] == 0:
Q.append(i)
if len(Q) == 0:
return
v = Q.popleft()
print v
for w in G[v]:
ind[w] -= 1
if ind[w] == 0:
Q.append(w)
topo(G, ind, Q)
"""
--------------------------------------------------------------------------------
Reading an Adjacency matrix
--------------------------------------------------------------------------------
"""
def adjm():
n, a = input(), []
for i in xrange(n):
a.append(map(int, raw_input().split()))
return a, n
"""
--------------------------------------------------------------------------------
Floyd Warshall's algorithm
Args : G - Dictionary of edges
s - Starting Node
Vars : dist - Dictionary storing shortest distance from s to every other node
known - Set of knows nodes
path - Preceding node in path
--------------------------------------------------------------------------------
"""
def floy((A, n)):
dist = list(A)
path = [[0] * n for i in xrange(n)]
for k in xrange(n):
for i in xrange(n):
for j in xrange(n):
if dist[i][j] > dist[i][k] + dist[k][j]:
dist[i][j] = dist[i][k] + dist[k][j]
path[i][k] = k
print dist
"""
--------------------------------------------------------------------------------
Prim's MST Algorithm
Args : G - Dictionary of edges
s - Starting Node
Vars : dist - Dictionary storing shortest distance from s to nearest node
known - Set of knows nodes
path - Preceding node in path
--------------------------------------------------------------------------------
"""
def prim(G, s):
dist, known, path = {s: 0}, set(), {s: 0}
while True:
if len(known) == len(G) - 1:
break
mini = 100000
for i in dist:
if i not in known and dist[i] < mini:
mini = dist[i]
u = i
known.add(u)
for v in G[u]:
if v[0] not in known:
if v[1] < dist.get(v[0], 100000):
dist[v[0]] = v[1]
path[v[0]] = u
"""
--------------------------------------------------------------------------------
Accepting Edge list
Vars : n - Number of nodes
m - Number of edges
Returns : l - Edge list
n - Number of Nodes
--------------------------------------------------------------------------------
"""
def edglist():
n, m = map(int, raw_input().split(" "))
l = []
for i in xrange(m):
l.append(map(int, raw_input().split(' ')))
return l, n
"""
--------------------------------------------------------------------------------
Kruskal's MST Algorithm
Args : E - Edge list
n - Number of Nodes
Vars : s - Set of all nodes as unique disjoint sets (initially)
--------------------------------------------------------------------------------
"""
def krusk((E, n)):
# Sort edges on the basis of distance
E.sort(reverse=True, key=lambda x: x[2])
s = [set([i]) for i in range(1, n + 1)]
while True:
if len(s) == 1:
break
print s
x = E.pop()
for i in xrange(len(s)):
if x[0] in s[i]:
break
for j in xrange(len(s)):
if x[1] in s[j]:
if i == j:
break
s[j].update(s[i])
s.pop(i)
break

21
License Normal file
View File

@ -0,0 +1,21 @@
MIT License
Copyright (c) 2016 The Algorithms
Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files (the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.

305
Neural_Network/convolution_neural_network.py Normal file
View File

@ -0,0 +1,305 @@
#-*- coding: utf-8 -*-
'''
- - - - - -- - - - - - - - - - - - - - - - - - - - - - -
Name - - CNN - Convolution Neural Network For Photo Recognizing
Goal - - Recognize Handing Writting Word Photo
Detail：Total 5 layers neural network
* Convolution layer
* Pooling layer
* Input layer layer of BP
* Hiden layer of BP
* Output layer of BP
Author: Stephen Lee
Github: 245885195@qq.com
Date: 2017.9.20
- - - - - -- - - - - - - - - - - - - - - - - - - - - - -
'''
import numpy as np
import matplotlib.pyplot as plt
class CNN():
def __init__(self,conv1_get,size_p1,bp_num1,bp_num2,bp_num3,rate_w=0.2,rate_t=0.2):
'''
:param conv1_get: [a,c,d]，size, number, step of convolution kernel
:param size_p1: pooling size
:param bp_num1: units number of flatten layer
:param bp_num2: units number of hidden layer
:param bp_num3: units number of output layer
:param rate_w: rate of weight learning
:param rate_t: rate of threshold learning
'''
self.num_bp1 = bp_num1
self.num_bp2 = bp_num2
self.num_bp3 = bp_num3
self.conv1 = conv1_get[:2]
self.step_conv1 = conv1_get[2]
self.size_pooling1 = size_p1
self.rate_weight = rate_w
self.rate_thre = rate_t
self.w_conv1 = [np.mat(-1*np.random.rand(self.conv1[0],self.conv1[0])+0.5) for i in range(self.conv1[1])]
self.wkj = np.mat(-1 * np.random.rand(self.num_bp3, self.num_bp2) + 0.5)
self.vji = np.mat(-1*np.random.rand(self.num_bp2, self.num_bp1)+0.5)
self.thre_conv1 = -2*np.random.rand(self.conv1[1])+1
self.thre_bp2 = -2*np.random.rand(self.num_bp2)+1
self.thre_bp3 = -2*np.random.rand(self.num_bp3)+1
def save_model(self,save_path):
#save model dict with pickle
import pickle
model_dic = {'num_bp1':self.num_bp1,
'num_bp2':self.num_bp2,
'num_bp3':self.num_bp3,
'conv1':self.conv1,
'step_conv1':self.step_conv1,
'size_pooling1':self.size_pooling1,
'rate_weight':self.rate_weight,
'rate_thre':self.rate_thre,
'w_conv1':self.w_conv1,
'wkj':self.wkj,
'vji':self.vji,
'thre_conv1':self.thre_conv1,
'thre_bp2':self.thre_bp2,
'thre_bp3':self.thre_bp3}
with open(save_path, 'wb') as f:
pickle.dump(model_dic, f)
print('Model saved： %s'% save_path)
@classmethod
def ReadModel(cls,model_path):
#read saved model
import pickle
with open(model_path, 'rb') as f:
model_dic = pickle.load(f)
conv_get= model_dic.get('conv1')
conv_get.append(model_dic.get('step_conv1'))
size_p1 = model_dic.get('size_pooling1')
bp1 = model_dic.get('num_bp1')
bp2 = model_dic.get('num_bp2')
bp3 = model_dic.get('num_bp3')
r_w = model_dic.get('rate_weight')
r_t = model_dic.get('rate_thre')
#create model instance
conv_ins = CNN(conv_get,size_p1,bp1,bp2,bp3,r_w,r_t)
#modify model parameter
conv_ins.w_conv1 = model_dic.get('w_conv1')
conv_ins.wkj = model_dic.get('wkj')
conv_ins.vji = model_dic.get('vji')
conv_ins.thre_conv1 = model_dic.get('thre_conv1')
conv_ins.thre_bp2 = model_dic.get('thre_bp2')
conv_ins.thre_bp3 = model_dic.get('thre_bp3')
return conv_ins
def sig(self,x):
return 1 / (1 + np.exp(-1*x))
def do_round(self,x):
return round(x, 3)
def convolute(self,data,convs,w_convs,thre_convs,conv_step):
#convolution process
size_conv = convs[0]
num_conv =convs[1]
size_data = np.shape(data)[0]
#get the data slice of original image data, data_focus
data_focus = []
for i_focus in range(0, size_data - size_conv + 1, conv_step):
for j_focus in range(0, size_data - size_conv + 1, conv_step):
focus = data[i_focus:i_focus + size_conv, j_focus:j_focus + size_conv]
data_focus.append(focus)
#caculate the feature map of every single kernel, and saved as list of matrix
data_featuremap = []
Size_FeatureMap = int((size_data - size_conv) / conv_step + 1)
for i_map in range(num_conv):
featuremap = []
for i_focus in range(len(data_focus)):
net_focus = np.sum(np.multiply(data_focus[i_focus], w_convs[i_map])) - thre_convs[i_map]
featuremap.append(self.sig(net_focus))
featuremap = np.asmatrix(featuremap).reshape(Size_FeatureMap, Size_FeatureMap)
data_featuremap.append(featuremap)
#expanding the data slice to One dimenssion
focus1_list = []
for each_focus in data_focus:
focus1_list.extend(self.Expand_Mat(each_focus))
focus_list = np.asarray(focus1_list)
return focus_list,data_featuremap
def pooling(self,featuremaps,size_pooling,type='average_pool'):
#pooling process
size_map = len(featuremaps[0])
size_pooled = int(size_map/size_pooling)
featuremap_pooled = []
for i_map in range(len(featuremaps)):
map = featuremaps[i_map]
map_pooled = []
for i_focus in range(0,size_map,size_pooling):
for j_focus in range(0, size_map, size_pooling):
focus = map[i_focus:i_focus + size_pooling, j_focus:j_focus + size_pooling]
if type == 'average_pool':
#average pooling
map_pooled.append(np.average(focus))
elif type == 'max_pooling':
#max pooling
map_pooled.append(np.max(focus))
map_pooled = np.asmatrix(map_pooled).reshape(size_pooled,size_pooled)
featuremap_pooled.append(map_pooled)
return featuremap_pooled
def _expand(self,datas):
#expanding three dimension data to one dimension list
data_expanded = []
for i in range(len(datas)):
shapes = np.shape(datas[i])
data_listed = datas[i].reshape(1,shapes[0]*shapes[1])
data_listed = data_listed.getA().tolist()[0]
data_expanded.extend(data_listed)
data_expanded = np.asarray(data_expanded)
return data_expanded
def _expand_mat(self,data_mat):
#expanding matrix to one dimension list
data_mat = np.asarray(data_mat)
shapes = np.shape(data_mat)
data_expanded = data_mat.reshape(1,shapes[0]*shapes[1])
return data_expanded
def _calculate_gradient_from_pool(self,out_map,pd_pool,num_map,size_map,size_pooling):
'''
calcluate the gradient from the data slice of pool layer
pd_pool: list of matrix
out_map: the shape of data slice(size_map*size_map)
return: pd_all: list of matrix, [num, size_map, size_map]
'''
pd_all = []
i_pool = 0
for i_map in range(num_map):
pd_conv1 = np.ones((size_map, size_map))
for i in range(0, size_map, size_pooling):
for j in range(0, size_map, size_pooling):
pd_conv1[i:i + size_pooling, j:j + size_pooling] = pd_pool[i_pool]
i_pool = i_pool + 1
pd_conv2 = np.multiply(pd_conv1,np.multiply(out_map[i_map],(1-out_map[i_map])))
pd_all.append(pd_conv2)
return pd_all
def trian(self,patterns,datas_train, datas_teach, n_repeat, error_accuracy,draw_e = bool):
#model traning
print('----------------------Start Training-------------------------')
print(' - - Shape: Train_Data ',np.shape(datas_train))
print(' - - Shape: Teach_Data ',np.shape(datas_teach))
rp = 0
all_mse = []
mse = 10000
while rp < n_repeat and mse >= error_accuracy:
alle = 0
print('-------------Learning Time %d--------------'%rp)
for p in range(len(datas_train)):
#print('------------Learning Image: %d--------------'%p)
data_train = np.asmatrix(datas_train[p])
data_teach = np.asarray(datas_teach[p])
data_focus1,data_conved1 = self.convolute(data_train,self.conv1,self.w_conv1,
self.thre_conv1,conv_step=self.step_conv1)
data_pooled1 = self.pooling(data_conved1,self.size_pooling1)
shape_featuremap1 = np.shape(data_conved1)
'''
print(' -----original shape ', np.shape(data_train))
print(' ---- after convolution ',np.shape(data_conv1))
print(' -----after pooling ',np.shape(data_pooled1))
'''
data_bp_input = self._expand(data_pooled1)
bp_out1 = data_bp_input
bp_net_j = np.dot(bp_out1,self.vji.T) - self.thre_bp2
bp_out2 = self.sig(bp_net_j)
bp_net_k = np.dot(bp_out2 ,self.wkj.T) - self.thre_bp3
bp_out3 = self.sig(bp_net_k)
#--------------Model Leaning ------------------------
# calcluate error and gradient---------------
pd_k_all = np.multiply((data_teach - bp_out3), np.multiply(bp_out3, (1 - bp_out3)))
pd_j_all = np.multiply(np.dot(pd_k_all,self.wkj), np.multiply(bp_out2, (1 - bp_out2)))
pd_i_all = np.dot(pd_j_all,self.vji)
pd_conv1_pooled = pd_i_all / (self.size_pooling1*self.size_pooling1)
pd_conv1_pooled = pd_conv1_pooled.T.getA().tolist()
pd_conv1_all = self._calculate_gradient_from_pool(data_conved1,pd_conv1_pooled,shape_featuremap1[0],
shape_featuremap1[1],self.size_pooling1)
#weight and threshold learning process---------
#convolution layer
for k_conv in range(self.conv1[1]):
pd_conv_list = self._expand_mat(pd_conv1_all[k_conv])
delta_w = self.rate_weight * np.dot(pd_conv_list,data_focus1)
self.w_conv1[k_conv] = self.w_conv1[k_conv] + delta_w.reshape((self.conv1[0],self.conv1[0]))
self.thre_conv1[k_conv] = self.thre_conv1[k_conv] - np.sum(pd_conv1_all[k_conv]) * self.rate_thre
#all connected layer
self.wkj = self.wkj + pd_k_all.T * bp_out2 * self.rate_weight
self.vji = self.vji + pd_j_all.T * bp_out1 * self.rate_weight
self.thre_bp3 = self.thre_bp3 - pd_k_all * self.rate_thre
self.thre_bp2 = self.thre_bp2 - pd_j_all * self.rate_thre
# calculate the sum error of all single image
errors = np.sum(abs((data_teach - bp_out3)))
alle = alle + errors
#print(' ----Teach ',data_teach)
#print(' ----BP_output ',bp_out3)
rp = rp + 1
mse = alle/patterns
all_mse.append(mse)
def draw_error():
yplot = [error_accuracy for i in range(int(n_repeat * 1.2))]
plt.plot(all_mse, '+-')
plt.plot(yplot, 'r--')
plt.xlabel('Learning Times')
plt.ylabel('All_mse')
plt.grid(True, alpha=0.5)
plt.show()
print('------------------Training Complished---------------------')
print(' - - Training epoch: ', rp, ' - - Mse: %.6f' % mse)
if draw_e:
draw_error()
return mse
def predict(self,datas_test):
#model predict
produce_out = []
print('-------------------Start Testing-------------------------')
print(' - - Shape: Test_Data ',np.shape(datas_test))
for p in range(len(datas_test)):
data_test = np.asmatrix(datas_test[p])
data_focus1, data_conved1 = self.convolute(data_test, self.conv1, self.w_conv1,
self.thre_conv1, conv_step=self.step_conv1)
data_pooled1 = self.pooling(data_conved1, self.size_pooling1)
data_bp_input = self._expand(data_pooled1)
bp_out1 = data_bp_input
bp_net_j = bp_out1 * self.vji.T - self.thre_bp2
bp_out2 = self.sig(bp_net_j)
bp_net_k = bp_out2 * self.wkj.T - self.thre_bp3
bp_out3 = self.sig(bp_net_k)
produce_out.extend(bp_out3.getA().tolist())
res = [list(map(self.do_round,each)) for each in produce_out]
return np.asarray(res)
def convolution(self,data):
#return the data of image after convoluting process so we can check it out
data_test = np.asmatrix(data)
data_focus1, data_conved1 = self.convolute(data_test, self.conv1, self.w_conv1,
self.thre_conv1, conv_step=self.step_conv1)
data_pooled1 = self.pooling(data_conved1, self.size_pooling1)
return data_conved1,data_pooled1
if __name__ == '__main__':
pass
'''
I will put the example on other file
'''

152
Neural_Network/neuralnetwork_bp3.py Normal file
View File

@ -0,0 +1,152 @@
#-*- coding:utf-8 -*-
'''
Author: Stephen Lee
Date: 2017.9.21
BP neural network with three layers
'''
import numpy as np
import matplotlib.pyplot as plt
class Bpnn():
def __init__(self,n_layer1,n_layer2,n_layer3,rate_w=0.3,rate_t=0.3):
'''
:param n_layer1: number of input layer
:param n_layer2: number of hiden layer
:param n_layer3: number of output layer
:param rate_w: rate of weight learning
:param rate_t: rate of threshold learning
'''
self.num1 = n_layer1
self.num2 = n_layer2
self.num3 = n_layer3
self.rate_weight = rate_w
self.rate_thre = rate_t
self.thre2 = -2*np.random.rand(self.num2)+1
self.thre3 = -2*np.random.rand(self.num3)+1
self.vji = np.mat(-2*np.random.rand(self.num2, self.num1)+1)
self.wkj = np.mat(-2*np.random.rand(self.num3, self.num2)+1)
def sig(self,x):
return 1 / (1 + np.exp(-1*x))
def sig_plain(self,x):
return 1 / (1 + np.exp(-1*x))
def do_round(self,x):
return round(x, 3)
def trian(self,patterns,data_train, data_teach, n_repeat, error_accuracy, draw_e=False):
'''
:param patterns: the number of patterns
:param data_train: training data x; numpy.ndarray
:param data_teach: training data y; numpy.ndarray
:param n_repeat: echoes
:param error_accuracy: error accuracy
:return: None
'''
data_train = np.asarray(data_train)
data_teach = np.asarray(data_teach)
# print('-------------------Start Training-------------------------')
# print(' - - Shape: Train_Data ',np.shape(data_train))
# print(' - - Shape: Teach_Data ',np.shape(data_teach))
rp = 0
all_mse = []
mse = 10000
while rp < n_repeat and mse >= error_accuracy:
alle = 0
final_out = []
for g in range(np.shape(data_train)[0]):
net_i = data_train[g]
out1 = net_i
net_j = out1 * self.vji.T - self.thre2
out2=self.sig(net_j)
net_k = out2 * self.wkj.T - self.thre3
out3 = self.sig(net_k)
# learning process
pd_k_all = np.multiply(np.multiply(out3,(1 - out3)),(data_teach[g]-out3))
pd_j_all = np.multiply(pd_k_all * self.wkj,np.multiply(out2,1-out2))
#upgrade weight
self.wkj = self.wkj + pd_k_all.T * out2 *self.rate_weight
self.vji = self.vji + pd_j_all.T * out1 * self.rate_weight
#upgrade threshold
self.thre3 = self.thre3 - pd_k_all * self.rate_thre
self.thre2 = self.thre2 - pd_j_all * self.rate_thre
#calculate sum of error
errors = np.sum(abs((data_teach[g] - out3)))
alle = alle + errors
final_out.extend(out3.getA().tolist())
final_out3 = [list(map(self.do_round,each)) for each in final_out]
rp = rp + 1
mse = alle/patterns
all_mse.append(mse)
def draw_error():
yplot = [error_accuracy for i in range(int(n_repeat * 1.2))]
plt.plot(all_mse, '+-')
plt.plot(yplot, 'r--')
plt.xlabel('Learning Times')
plt.ylabel('All_mse')
plt.grid(True,alpha = 0.7)
plt.show()
# print('------------------Training Complished---------------------')
# print(' - - Training epoch: ', rp, ' - - Mse: %.6f'%mse)
# print(' - - Last Output: ', final_out3)
if draw_e:
draw_error()
def predict(self,data_test):
'''
:param data_test: data test, numpy.ndarray
:return: predict output data
'''
data_test = np.asarray(data_test)
produce_out = []
# print('-------------------Start Testing-------------------------')
# print(' - - Shape: Test_Data ',np.shape(data_test))
# print(np.shape(data_test))
for g in range(np.shape(data_test)[0]):
net_i = data_test[g]
out1 = net_i
net_j = out1 * self.vji.T - self.thre2
out2 = self.sig(net_j)
net_k = out2 * self.wkj.T - self.thre3
out3 = self.sig(net_k)
produce_out.extend(out3.getA().tolist())
res = [list(map(self.do_round,each)) for each in produce_out]
return np.asarray(res)
def main():
#example data
data_x = [[1,2,3,4],
[5,6,7,8],
[2,2,3,4],
[7,7,8,8]]
data_y = [[1,0,0,0],
[0,1,0,0],
[0,0,1,0],
[0,0,0,1]]
test_x = [[1,2,3,4],
[3,2,3,4]]
#building network model
model = Bpnn(4,10,4)
#training the model
model.trian(patterns=4,data_train=data_x,data_teach=data_y,
n_repeat=100,error_accuracy=0.1,draw_e=True)
#predicting data
model.predict(test_x)
if __name__ == '__main__':
main()

123
Neural_Network/perceptron.py Normal file
View File

@ -0,0 +1,123 @@
'''
Perceptron
w = w + N * (d(k) - y) * x(k)
Using perceptron network for oil analysis,
with Measuring of 3 parameters that represent chemical characteristics we can classify the oil, in p1 or p2
p1 = -1
p2 = 1
'''
import random
class Perceptron:
def __init__(self, sample, exit, learn_rate=0.01, epoch_number=1000, bias=-1):
self.sample = sample
self.exit = exit
self.learn_rate = learn_rate
self.epoch_number = epoch_number
self.bias = bias
self.number_sample = len(sample)
self.col_sample = len(sample[0])
self.weight = []
def trannig(self):
for sample in self.sample:
sample.insert(0, self.bias)
for i in range(self.col_sample):
self.weight.append(random.random())
self.weight.insert(0, self.bias)
epoch_count = 0
while True:
erro = False
for i in range(self.number_sample):
u = 0
for j in range(self.col_sample + 1):
u = u + self.weight[j] * self.sample[i][j]
y = self.sign(u)
if y != self.exit[i]:
for j in range(self.col_sample + 1):
self.weight[j] = self.weight[j] + self.learn_rate * (self.exit[i] - y) * self.sample[i][j]
erro = True
#print('Epoch: \n',epoch_count)
epoch_count = epoch_count + 1
# if you want controle the epoch or just by erro
if erro == False:
print('\nEpoch:\n',epoch_count)
print('------------------------\n')
#if epoch_count > self.epoch_number or not erro:
break
def sort(self, sample):
sample.insert(0, self.bias)
u = 0
for i in range(self.col_sample + 1):
u = u + self.weight[i] * sample[i]
y = self.sign(u)
if y == -1:
print('Sample: ', sample)
print('classification: P1')
else:
print('Sample: ', sample)
print('classification: P2')
def sign(self, u):
return 1 if u >= 0 else -1
samples = [
[-0.6508, 0.1097, 4.0009],
[-1.4492, 0.8896, 4.4005],
[2.0850, 0.6876, 12.0710],
[0.2626, 1.1476, 7.7985],
[0.6418, 1.0234, 7.0427],
[0.2569, 0.6730, 8.3265],
[1.1155, 0.6043, 7.4446],
[0.0914, 0.3399, 7.0677],
[0.0121, 0.5256, 4.6316],
[-0.0429, 0.4660, 5.4323],
[0.4340, 0.6870, 8.2287],
[0.2735, 1.0287, 7.1934],
[0.4839, 0.4851, 7.4850],
[0.4089, -0.1267, 5.5019],
[1.4391, 0.1614, 8.5843],
[-0.9115, -0.1973, 2.1962],
[0.3654, 1.0475, 7.4858],
[0.2144, 0.7515, 7.1699],
[0.2013, 1.0014, 6.5489],
[0.6483, 0.2183, 5.8991],
[-0.1147, 0.2242, 7.2435],
[-0.7970, 0.8795, 3.8762],
[-1.0625, 0.6366, 2.4707],
[0.5307, 0.1285, 5.6883],
[-1.2200, 0.7777, 1.7252],
[0.3957, 0.1076, 5.6623],
[-0.1013, 0.5989, 7.1812],
[2.4482, 0.9455, 11.2095],
[2.0149, 0.6192, 10.9263],
[0.2012, 0.2611, 5.4631]
]
exit = [-1, -1, -1, 1, 1, -1, 1, -1, 1, 1, -1, 1, -1, -1, -1, -1, 1, 1, 1, 1, -1, 1, 1, 1, 1, -1, -1, 1, -1, 1]
network = Perceptron(sample=samples, exit = exit, learn_rate=0.01, epoch_number=1000, bias=-1)
network.trannig()
while True:
sample = []
for i in range(3):
sample.insert(i, float(input('value: ')))
network.sort(sample)

174
README.md Normal file
View File

@ -0,0 +1,174 @@
# The Algorithms - Python <!-- [![Build Status](https://travis-ci.org/TheAlgorithms/Python.svg)](https://travis-ci.org/TheAlgorithms/Python) -->
### All algorithms implemented in Python (for education)
These are for demonstration purposes only. There are many implementations of sorts in the Python standard library that are much better for performance reasons.
## Sort Algorithms
### Bubble
![alt text][bubble-image]
From [Wikipedia][bubble-wiki]: Bubble sort, sometimes referred to as sinking sort, is a simple sorting algorithm that repeatedly steps through the list to be sorted, compares each pair of adjacent items and swaps them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which indicates that the list is sorted.
__Properties__
* Worst case performance O(n^2)
* Best case performance O(n)
* Average case performance O(n^2)
###### View the algorithm in [action][bubble-toptal]
### Insertion
![alt text][insertion-image]
From [Wikipedia][insertion-wiki]: Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort.
__Properties__
* Worst case performance O(n^2)
* Best case performance O(n)
* Average case performance O(n^2)
###### View the algorithm in [action][insertion-toptal]
### Merge
![alt text][merge-image]
From [Wikipedia][merge-wiki]: In computer science, merge sort (also commonly spelled mergesort) is an efficient, general-purpose, comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the implementation preserves the input order of equal elements in the sorted output. Mergesort is a divide and conquer algorithm that was invented by John von Neumann in 1945.
__Properties__
* Worst case performance O(n log n)
* Best case performance O(n)
* Average case performance O(n)
###### View the algorithm in [action][merge-toptal]
### Quick
![alt text][quick-image]
From [Wikipedia][quick-wiki]: Quicksort (sometimes called partition-exchange sort) is an efficient sorting algorithm, serving as a systematic method for placing the elements of an array in order.
__Properties__
* Worst case performance O(n^2)
* Best case performance O(n log n) or O(n) with three-way partition
* Average case performance O(n^2)
###### View the algorithm in [action][quick-toptal]
### Selection
![alt text][selection-image]
From [Wikipedia][selection-wiki]: The algorithm divides the input list into two parts: the sublist of items already sorted, which is built up from left to right at the front (left) of the list, and the sublist of items remaining to be sorted that occupy the rest of the list. Initially, the sorted sublist is empty and the unsorted sublist is the entire input list. The algorithm proceeds by finding the smallest (or largest, depending on sorting order) element in the unsorted sublist, exchanging (swapping) it with the leftmost unsorted element (putting it in sorted order), and moving the sublist boundaries one element to the right.
__Properties__
* Worst case performance O(n^2)
* Best case performance O(n^2)
* Average case performance O(n^2)
###### View the algorithm in [action][selection-toptal]
### Shell
![alt text][shell-image]
From [Wikipedia][shell-wiki]: Shellsort is a generalization of insertion sort that allows the exchange of items that are far apart. The idea is to arrange the list of elements so that, starting anywhere, considering every nth element gives a sorted list. Such a list is said to be h-sorted. Equivalently, it can be thought of as h interleaved lists, each individually sorted.
__Properties__
* Worst case performance O(nlog2 2n)
* Best case performance O(n log n)
* Average case performance depends on gap sequence
###### View the algorithm in [action][shell-toptal]
### Time-Compexity Graphs
Comparing the complexity of sorting algorithms (Bubble Sort, Insertion Sort, Selection Sort)
[Complexity Graphs](https://github.com/prateekiiest/Python/blob/master/sorts/sortinggraphs.png)
----------------------------------------------------------------------------------
## Search Algorithms
### Linear
![alt text][linear-image]
From [Wikipedia][linear-wiki]: linear search or sequential search is a method for finding a target value within a list. It sequentially checks each element of the list for the target value until a match is found or until all the elements have been searched.
Linear search runs in at worst linear time and makes at most n comparisons, where n is the length of the list.
__Properties__
* Worst case performance O(n)
* Best case performance O(1)
* Average case performance O(n)
* Worst case space complexity O(1) iterative
### Binary
![alt text][binary-image]
From [Wikipedia][binary-wiki]: Binary search, also known as half-interval search or logarithmic search, is a search algorithm that finds the position of a target value within a sorted array. It compares the target value to the middle element of the array; if they are unequal, the half in which the target cannot lie is eliminated and the search continues on the remaining half until it is successful.
__Properties__
* Worst case performance O(log n)
* Best case performance O(1)
* Average case performance O(log n)
* Worst case space complexity O(1)
----------------------------------------------------------------------------------------------------------------------
## Ciphers
### Caesar
![alt text][caesar]<br>
In cryptography, a **Caesar cipher**, also known as Caesar's cipher, the shift cipher, Caesar's code or Caesar shift, is one of the simplest and most widely known encryption techniques.<br>
It is **a type of substitution cipher** in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet. For example, with a left shift of 3, D would be replaced by A, E would become B, and so on. <br>
The method is named after **Julius Caesar**, who used it in his private correspondence.<br>
The encryption step performed by a Caesar cipher is often incorporated as part of more complex schemes, such as the Vigenère cipher, and still has modern application in the ROT13 system. As with all single-alphabet substitution ciphers, the Caesar cipher is easily broken and in modern practice offers essentially no communication security.
###### Source: [Wikipedia](https://en.wikipedia.org/wiki/Caesar_cipher)
### Vigenère
The **Vigenère cipher** is a method of encrypting alphabetic text by using a series of **interwoven Caesar ciphers** based on the letters of a keyword. It is **a form of polyalphabetic substitution**.<br>
The Vigenère cipher has been reinvented many times. The method was originally described by Giovan Battista Bellaso in his 1553 book La cifra del. Sig. Giovan Battista Bellaso; however, the scheme was later misattributed to Blaise de Vigenère in the 19th century, and is now widely known as the "Vigenère cipher".<br>
Though the cipher is easy to understand and implement, for three centuries it resisted all attempts to break it; this earned it the description **le chiffre indéchiffrable**(French for 'the indecipherable cipher').
Many people have tried to implement encryption schemes that are essentially Vigenère ciphers. Friedrich Kasiski was the first to publish a general method of deciphering a Vigenère cipher in 1863.
###### Source: [Wikipedia](https://en.wikipedia.org/wiki/Vigen%C3%A8re_cipher)
### Transposition
In cryptography, a **transposition cipher** is a method of encryption by which the positions held by units of plaintext (which are commonly characters or groups of characters) are shifted according to a regular system, so that the ciphertext constitutes a permutation of the plaintext. That is, the order of the units is changed (the plaintext is reordered).<br>
Mathematically a bijective function is used on the characters' positions to encrypt and an inverse function to decrypt.
###### Source: [Wikipedia](https://en.wikipedia.org/wiki/Transposition_cipher)
[bubble-toptal]: https://www.toptal.com/developers/sorting-algorithms/bubble-sort
[bubble-wiki]: https://en.wikipedia.org/wiki/Bubble_sort
[bubble-image]: https://upload.wikimedia.org/wikipedia/commons/thumb/8/83/Bubblesort-edited-color.svg/220px-Bubblesort-edited-color.svg.png "Bubble Sort"
[insertion-toptal]: https://www.toptal.com/developers/sorting-algorithms/insertion-sort
[insertion-wiki]: https://en.wikipedia.org/wiki/Insertion_sort
[insertion-image]: https://upload.wikimedia.org/wikipedia/commons/7/7e/Insertionsort-edited.png "Insertion Sort"
[quick-toptal]: https://www.toptal.com/developers/sorting-algorithms/quick-sort
[quick-wiki]: https://en.wikipedia.org/wiki/Quicksort
[quick-image]: https://upload.wikimedia.org/wikipedia/commons/6/6a/Sorting_quicksort_anim.gif "Quick Sort"
[merge-toptal]: https://www.toptal.com/developers/sorting-algorithms/merge-sort
[merge-wiki]: https://en.wikipedia.org/wiki/Merge_sort
[merge-image]: https://upload.wikimedia.org/wikipedia/commons/c/cc/Merge-sort-example-300px.gif "Merge Sort"
[selection-toptal]: https://www.toptal.com/developers/sorting-algorithms/selection-sort
[selection-wiki]: https://en.wikipedia.org/wiki/Selection_sort
[selection-image]: https://upload.wikimedia.org/wikipedia/commons/thumb/b/b0/Selection_sort_animation.gif/250px-Selection_sort_animation.gif "Selection Sort Sort"
[shell-toptal]: https://www.toptal.com/developers/sorting-algorithms/shell-sort
[shell-wiki]: https://en.wikipedia.org/wiki/Shellsort
[shell-image]: https://upload.wikimedia.org/wikipedia/commons/d/d8/Sorting_shellsort_anim.gif "Shell Sort"
[linear-wiki]: https://en.wikipedia.org/wiki/Linear_search
[linear-image]: http://www.tutorialspoint.com/data_structures_algorithms/images/linear_search.gif
[binary-wiki]: https://en.wikipedia.org/wiki/Binary_search_algorithm
[binary-image]: https://upload.wikimedia.org/wikipedia/commons/f/f7/Binary_search_into_array.png
[caesar]: https://upload.wikimedia.org/wikipedia/commons/4/4a/Caesar_cipher_left_shift_of_3.svg

7193
ciphers/Prehistoric Men.txt Normal file
View File

File diff suppressed because it is too large Load Diff

76
ciphers/affine_cipher.py Normal file
View File

@ -0,0 +1,76 @@
import sys, random, cryptomath_module as cryptoMath
SYMBOLS = """ !"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~"""
def main():
message = input('Enter message: ')
key = int(input('Enter key [2000 - 9000]: '))
mode = input('Encrypt/Decrypt [E/D]: ')
if mode.lower().startswith('e'):
mode = 'encrypt'
translated = encryptMessage(key, message)
elif mode.lower().startswith('d'):
mode = 'decrypt'
translated = decryptMessage(key, message)
print('\n%sed text: \n%s' % (mode.title(), translated))
def getKeyParts(key):
keyA = key // len(SYMBOLS)
keyB = key % len(SYMBOLS)
return (keyA, keyB)
def checkKeys(keyA, keyB, mode):
if keyA == 1 and mode == 'encrypt':
sys.exit('The affine cipher becomes weak when key A is set to 1. Choose different key')
if keyB == 0 and mode == 'encrypt':
sys.exit('The affine cipher becomes weak when key A is set to 1. Choose different key')
if keyA < 0 or keyB < 0 or keyB > len(SYMBOLS) - 1:
sys.exit('Key A must be greater than 0 and key B must be between 0 and %s.' % (len(SYMBOLS) - 1))
if cryptoMath.gcd(keyA, len(SYMBOLS)) != 1:
sys.exit('Key A %s and the symbol set size %s are not relatively prime. Choose a different key.' % (keyA, len(SYMBOLS)))
def encryptMessage(key, message):
'''
>>> encryptMessage(4545, 'The affine cipher is a type of monoalphabetic substitution cipher.')
'VL}p MM{I}p~{HL}Gp{vp pFsH}pxMpyxIx JHL O}F{~pvuOvF{FuF{xIp~{HL}Gi'
'''
keyA, keyB = getKeyParts(key)
checkKeys(keyA, keyB, 'encrypt')
cipherText = ''
for symbol in message:
if symbol in SYMBOLS:
symIndex = SYMBOLS.find(symbol)
cipherText += SYMBOLS[(symIndex * keyA + keyB) % len(SYMBOLS)]
else:
cipherText += symbol
return cipherText
def decryptMessage(key, message):
'''
>>> decryptMessage(4545, 'VL}p MM{I}p~{HL}Gp{vp pFsH}pxMpyxIx JHL O}F{~pvuOvF{FuF{xIp~{HL}Gi')
'The affine cipher is a type of monoalphabetic substitution cipher.'
'''
keyA, keyB = getKeyParts(key)
checkKeys(keyA, keyB, 'decrypt')
plainText = ''
modInverseOfkeyA = cryptoMath.findModInverse(keyA, len(SYMBOLS))
for symbol in message:
if symbol in SYMBOLS:
symIndex = SYMBOLS.find(symbol)
plainText += SYMBOLS[(symIndex - keyB) * modInverseOfkeyA % len(SYMBOLS)]
else:
plainText += symbol
return plainText
def getRandomKey():
while True:
keyA = random.randint(2, len(SYMBOLS))
keyB = random.randint(2, len(SYMBOLS))
if cryptoMath.gcd(keyA, len(SYMBOLS)) == 1:
return keyA * len(SYMBOLS) + keyB
if __name__ == '__main__':
import doctest
doctest.testmod()
main()

53
ciphers/brute-force_caesar_cipher.py Normal file
View File

@ -0,0 +1,53 @@
def decrypt(message):
"""
>>> decrypt('TMDETUX PMDVU')
Decryption using Key #0: TMDETUX PMDVU
Decryption using Key #1: SLCDSTW OLCUT
Decryption using Key #2: RKBCRSV NKBTS
Decryption using Key #3: QJABQRU MJASR
Decryption using Key #4: PIZAPQT LIZRQ
Decryption using Key #5: OHYZOPS KHYQP
Decryption using Key #6: NGXYNOR JGXPO
Decryption using Key #7: MFWXMNQ IFWON
Decryption using Key #8: LEVWLMP HEVNM
Decryption using Key #9: KDUVKLO GDUML
Decryption using Key #10: JCTUJKN FCTLK
Decryption using Key #11: IBSTIJM EBSKJ
Decryption using Key #12: HARSHIL DARJI
Decryption using Key #13: GZQRGHK CZQIH
Decryption using Key #14: FYPQFGJ BYPHG
Decryption using Key #15: EXOPEFI AXOGF
Decryption using Key #16: DWNODEH ZWNFE
Decryption using Key #17: CVMNCDG YVMED
Decryption using Key #18: BULMBCF XULDC
Decryption using Key #19: ATKLABE WTKCB
Decryption using Key #20: ZSJKZAD VSJBA
Decryption using Key #21: YRIJYZC URIAZ
Decryption using Key #22: XQHIXYB TQHZY
Decryption using Key #23: WPGHWXA SPGYX
Decryption using Key #24: VOFGVWZ ROFXW
Decryption using Key #25: UNEFUVY QNEWV
"""
LETTERS = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
for key in range(len(LETTERS)):
translated = ""
for symbol in message:
if symbol in LETTERS:
num = LETTERS.find(symbol)
num = num - key
if num < 0:
num = num + len(LETTERS)
translated = translated + LETTERS[num]
else:
translated = translated + symbol
print("Decryption using Key #%s: %s" % (key, translated))
def main():
message = input("Encrypted message: ")
message = message.upper()
decrypt(message)
if __name__ == '__main__':
import doctest
doctest.testmod()
main()

44
ciphers/caesar_cipher.py Normal file
View File

@ -0,0 +1,44 @@
# The Caesar Cipher Algorithm
def main():
message = input("Enter message: ")
key = int(input("Key [1-26]: "))
mode = input("Encrypt or Decrypt [e/d]: ")
if mode.lower().startswith('e'):
mode = "encrypt"
elif mode.lower().startswith('d'):
mode = "decrypt"
translated = encdec(message, key, mode)
if mode == "encrypt":
print("Encryption:", translated)
elif mode == "decrypt":
print("Decryption:", translated)
def encdec(message, key, mode):
message = message.upper()
translated = ""
LETTERS = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
for symbol in message:
if symbol in LETTERS:
num = LETTERS.find(symbol)
if mode == "encrypt":
num = num + key
elif mode == "decrypt":
num = num - key
if num >= len(LETTERS):
num -= len(LETTERS)
elif num < 0:
num += len(LETTERS)
translated += LETTERS[num]
else:
translated += symbol
return translated
if __name__ == '__main__':
import doctest
doctest.testmod()
main()

14
ciphers/cryptomath_module.py Normal file
View File

@ -0,0 +1,14 @@
def gcd(a, b):
while a != 0:
a, b = b % a, a
return b
def findModInverse(a, m):
if gcd(a, m) != 1:
return None
u1, u2, u3 = 1, 0, a
v1, v2, v3 = 0, 1, m
while v3 != 0:
q = u3 // v3
v1, v2, v3, u1, u2, u3 = (u1 - q * v1), (u2 - q * v2), (u3 - q *v3), v1, v2, v3
return u1 % m

102
ciphers/playfair_cipher.py Normal file
View File

@ -0,0 +1,102 @@
import string
import itertools
def chunker(seq, size):
it = iter(seq)
while True:
chunk = tuple(itertools.islice(it, size))
if not chunk:
return
yield chunk
def prepare_input(dirty):
"""
Prepare the plaintext by uppcasing it
and seperating repeated letters with X's
"""
dirty = ''.join([c.upper() for c in dirty if c in string.ascii_letters])
clean = ""
if len(dirty) < 2:
return dirty
for i in range(len(dirty)-1):
clean += dirty[i]
if dirty[i] == dirty[i+1]:
clean += 'X'
clean += dirty[-1]
if len(clean) & 1:
clean += 'X'
return clean
def generate_table(key):
# I and J are used interchangably to allow
# us to use a 5x5 table (25 letters)
alphabet = "ABCDEFGHIKLMNOPQRSTUVWXYZ"
# we're using a list instead of a '2d' array because it makes the math
# for setting up the table and doing the actual encoding/decoding simpler
table = []
# copy key chars into the table if they are in `alphabet` ignoring duplicates
for char in key.upper():
if char not in table and char in alphabet:
table.append(char)
# fill the rest of the table in with the remaining alphabet chars
for char in alphabet:
if char not in table:
table.append(char)
return table
def encode(plaintext, key):
table = generate_table(key)
plaintext = prepare_input(plaintext)
ciphertext = ""
# https://en.wikipedia.org/wiki/Playfair_cipher#Description
for char1, char2 in chunker(plaintext, 2):
row1, col1 = divmod(table.index(char1), 5)
row2, col2 = divmod(table.index(char2), 5)
if row1 == row2:
ciphertext += table[row1*5+(col1+1)%5]
ciphertext += table[row2*5+(col2+1)%5]
elif col1 == col2:
ciphertext += table[((row1+1)%5)*5+col1]
ciphertext += table[((row2+1)%5)*5+col2]
else: # rectangle
ciphertext += table[row1*5+col2]
ciphertext += table[row2*5+col1]
return ciphertext
def decode(ciphertext, key):
table = generate_table(key)
plaintext = ""
# https://en.wikipedia.org/wiki/Playfair_cipher#Description
for char1, char2 in chunk(ciphertext, 2):
row1, col1 = divmod(table.index(char1), 5)
row2, col2 = divmod(table.index(char2), 5)
if row1 == row2:
plaintext += table[row1*5+(col1-1)%5]
plaintext += table[row2*5+(col2-1)%5]
elif col1 == col2:
plaintext += table[((row1-1)%5)*5+col1]
plaintext += table[((row2-1)%5)*5+col2]
else: # rectangle
plaintext += table[row1*5+col2]
plaintext += table[row2*5+col1]
return plaintext

63
ciphers/rabin_miller.py Normal file
View File

@ -0,0 +1,63 @@
# Primality Testing with the Rabin-Miller Algorithm
import random
def rabinMiller(num):
s = num - 1
t = 0
while s % 2 == 0:
s = s // 2
t += 1
for trials in range(5):
a = random.randrange(2, num - 1)
v = pow(a, s, num)
if v != 1:
i = 0
while v != (num - 1):
if i == t - 1:
return False
else:
i = i + 1
v = (v ** 2) % num
return True
def isPrime(num):
if (num < 2):
return False
lowPrimes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59,
61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127,
131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191,
193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257,
263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331,
337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401,
409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467,
479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563,
569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631,
641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709,
719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797,
809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877,
881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967,
971, 977, 983, 991, 997]
if num in lowPrimes:
return True
for prime in lowPrimes:
if (num % prime) == 0:
return False
return rabinMiller(num)
def generateLargePrime(keysize = 1024):
while True:
num = random.randrange(2 ** (keysize - 1), 2 ** (keysize))
if isPrime(num):
return num
if __name__ == '__main__':
num = generateLargePrime()
print('Prime number:', num)
print('isPrime:', isPrime(num))

124
ciphers/rsa_cipher.py Normal file
View File

@ -0,0 +1,124 @@
import sys, rsa_key_generator as rkg, os
DEFAULT_BLOCK_SIZE = 128
BYTE_SIZE = 256
def main():
filename = 'encrypted_file.txt'
response = input('Encrypte\Decrypt [e\d]: ')
if response.lower().startswith('e'):
mode = 'encrypt'
elif response.lower().startswith('d'):
mode = 'decrypt'
if mode == 'encrypt':
if not os.path.exists('rsa_pubkey.txt'):
rkg.makeKeyFiles('rsa', 1024)
message = input('\nEnter message: ')
pubKeyFilename = 'rsa_pubkey.txt'
print('Encrypting and writing to %s...' % (filename))
encryptedText = encryptAndWriteToFile(filename, pubKeyFilename, message)
print('\nEncrypted text:')
print(encryptedText)
elif mode == 'decrypt':
privKeyFilename = 'rsa_privkey.txt'
print('Reading from %s and decrypting...' % (filename))
decryptedText = readFromFileAndDecrypt(filename, privKeyFilename)
print('writing decryption to rsa_decryption.txt...')
with open('rsa_decryption.txt', 'w') as dec:
dec.write(decryptedText)
print('\nDecryption:')
print(decryptedText)
def getBlocksFromText(message, blockSize=DEFAULT_BLOCK_SIZE):
messageBytes = message.encode('ascii')
blockInts = []
for blockStart in range(0, len(messageBytes), blockSize):
blockInt = 0
for i in range(blockStart, min(blockStart + blockSize, len(messageBytes))):
blockInt += messageBytes[i] * (BYTE_SIZE ** (i % blockSize))
blockInts.append(blockInt)
return blockInts
def getTextFromBlocks(blockInts, messageLength, blockSize=DEFAULT_BLOCK_SIZE):
message = []
for blockInt in blockInts:
blockMessage = []
for i in range(blockSize - 1, -1, -1):
if len(message) + i < messageLength:
asciiNumber = blockInt // (BYTE_SIZE ** i)
blockInt = blockInt % (BYTE_SIZE ** i)
blockMessage.insert(0, chr(asciiNumber))
message.extend(blockMessage)
return ''.join(message)
def encryptMessage(message, key, blockSize=DEFAULT_BLOCK_SIZE):
encryptedBlocks = []
n, e = key
for block in getBlocksFromText(message, blockSize):
encryptedBlocks.append(pow(block, e, n))
return encryptedBlocks
def decryptMessage(encryptedBlocks, messageLength, key, blockSize=DEFAULT_BLOCK_SIZE):
decryptedBlocks = []
n, d = key
for block in encryptedBlocks:
decryptedBlocks.append(pow(block, d, n))
return getTextFromBlocks(decryptedBlocks, messageLength, blockSize)
def readKeyFile(keyFilename):
fo = open(keyFilename)
content = fo.read()
fo.close()
keySize, n, EorD = content.split(',')
return (int(keySize), int(n), int(EorD))
def encryptAndWriteToFile(messageFilename, keyFilename, message, blockSize=DEFAULT_BLOCK_SIZE):
keySize, n, e = readKeyFile(keyFilename)
if keySize < blockSize * 8:
sys.exit('ERROR: Block size is %s bits and key size is %s bits. The RSA cipher requires the block size to be equal to or greater than the key size. Either decrease the block size or use different keys.' % (blockSize * 8, keySize))
encryptedBlocks = encryptMessage(message, (n, e), blockSize)
for i in range(len(encryptedBlocks)):
encryptedBlocks[i] = str(encryptedBlocks[i])
encryptedContent = ','.join(encryptedBlocks)
encryptedContent = '%s_%s_%s' % (len(message), blockSize, encryptedContent)
fo = open(messageFilename, 'w')
fo.write(encryptedContent)
fo.close()
return encryptedContent
def readFromFileAndDecrypt(messageFilename, keyFilename):
keySize, n, d = readKeyFile(keyFilename)
fo = open(messageFilename)
content = fo.read()
messageLength, blockSize, encryptedMessage = content.split('_')
messageLength = int(messageLength)
blockSize = int(blockSize)
if keySize < blockSize * 8:
sys.exit('ERROR: Block size is %s bits and key size is %s bits. The RSA cipher requires the block size to be equal to or greater than the key size. Did you specify the correct key file and encrypted file?' % (blockSize * 8, keySize))
encryptedBlocks = []
for block in encryptedMessage.split(','):
encryptedBlocks.append(int(block))
return decryptMessage(encryptedBlocks, messageLength, (n, d), blockSize)
if __name__ == '__main__':
main()

45
ciphers/rsa_key_generator.py Normal file
View File

@ -0,0 +1,45 @@
import random, sys, os
import rabin_miller as rabinMiller, cryptomath_module as cryptoMath
def main():
print('Making key files...')
makeKeyFiles('rsa', 1024)
print('Key files generation successful.')
def generateKey(keySize):
print('Generating prime p...')
p = rabinMiller.generateLargePrime(keySize)
print('Generating prime q...')
q = rabinMiller.generateLargePrime(keySize)
n = p * q
print('Generating e that is relatively prime to (p - 1) * (q - 1)...')
while True:
e = random.randrange(2 ** (keySize - 1), 2 ** (keySize))
if cryptoMath.gcd(e, (p - 1) * (q - 1)) == 1:
break
print('Calculating d that is mod inverse of e...')
d = cryptoMath.findModInverse(e, (p - 1) * (q - 1))
publicKey = (n, e)
privateKey = (n, d)
return (publicKey, privateKey)
def makeKeyFiles(name, keySize):
if os.path.exists('%s_pubkey.txt' % (name)) or os.path.exists('%s_privkey.txt' % (name)):
print('\nWARNING:')
print('"%s_pubkey.txt" or "%s_privkey.txt" already exists. \nUse a different name or delete these files and re-run this program.' % (name, name))
sys.exit()
publicKey, privateKey = generateKey(keySize)
print('\nWriting public key to file %s_pubkey.txt...' % name)
with open('%s_pubkey.txt' % name, 'w') as fo:
fo.write('%s,%s,%s' % (keySize, publicKey[0], publicKey[1]))
print('Writing private key to file %s_privkey.txt...' % name)
with open('%s_privkey.txt' % name, 'w') as fo:
fo.write('%s,%s,%s' % (keySize, privateKey[0], privateKey[1]))
if __name__ == '__main__':
main()

70
ciphers/simple_substitution_cipher.py Normal file
View File

@ -0,0 +1,70 @@
import sys, random
LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
def main():
message = input('Enter message: ')
key = 'LFWOAYUISVKMNXPBDCRJTQEGHZ'
resp = input('Encrypt/Decrypt [e/d]: ')
checkValidKey(key)
if resp.lower().startswith('e'):
mode = 'encrypt'
translated = encryptMessage(key, message)
elif resp.lower().startswith('d'):
mode = 'decrypt'
translated = decryptMessage(key, message)
print('\n%sion: \n%s' % (mode.title(), translated))
def checkValidKey(key):
keyList = list(key)
lettersList = list(LETTERS)
keyList.sort()
lettersList.sort()
if keyList != lettersList:
sys.exit('Error in the key or symbol set.')
def encryptMessage(key, message):
"""
>>> encryptMessage('LFWOAYUISVKMNXPBDCRJTQEGHZ', 'Harshil Darji')
'Ilcrism Olcvs'
"""
return translateMessage(key, message, 'encrypt')
def decryptMessage(key, message):
"""
>>> decryptMessage('LFWOAYUISVKMNXPBDCRJTQEGHZ', 'Ilcrism Olcvs')
'Harshil Darji'
"""
return translateMessage(key, message, 'decrypt')
def translateMessage(key, message, mode):
translated = ''
charsA = LETTERS
charsB = key
if mode == 'decrypt':
charsA, charsB = charsB, charsA
for symbol in message:
if symbol.upper() in charsA:
symIndex = charsA.find(symbol.upper())
if symbol.isupper():
translated += charsB[symIndex].upper()
else:
translated += charsB[symIndex].lower()
else:
translated += symbol
return translated
def getRandomKey():
key = list(LETTERS)
random.shuffle(key)
return ''.join(key)
if __name__ == '__main__':
main()

53
ciphers/transposition_cipher.py Normal file
View File

@ -0,0 +1,53 @@
import math
def main():
message = input('Enter message: ')
key = int(input('Enter key [2-%s]: ' % (len(message) - 1)))
mode = input('Encryption/Decryption [e/d]: ')
if mode.lower().startswith('e'):
text = encryptMessage(key, message)
elif mode.lower().startswith('d'):
text = decryptMessage(key, message)
# Append pipe symbol (vertical bar) to identify spaces at the end.
print('Output:\n%s' %(text + '|'))
def encryptMessage(key, message):
"""
>>> encryptMessage(6, 'Harshil Darji')
'Hlia rDsahrij'
"""
cipherText = [''] * key
for col in range(key):
pointer = col
while pointer < len(message):
cipherText[col] += message[pointer]
pointer += key
return ''.join(cipherText)
def decryptMessage(key, message):
"""
>>> decryptMessage(6, 'Hlia rDsahrij')
'Harshil Darji'
"""
numCols = math.ceil(len(message) / key)
numRows = key
numShadedBoxes = (numCols * numRows) - len(message)
plainText = [""] * numCols
col = 0; row = 0;
for symbol in message:
plainText[col] += symbol
col += 1
if (col == numCols) or (col == numCols - 1) and (row >= numRows - numShadedBoxes):
col = 0
row += 1
return "".join(plainText)
if __name__ == '__main__':
import doctest
doctest.testmod()
main()

35
ciphers/transposition_cipher_encrypt-decrypt_file.py Normal file
View File

@ -0,0 +1,35 @@
import time, os, sys
import transposition_cipher as transCipher
def main():
inputFile = 'Prehistoric Men.txt'
outputFile = 'Output.txt'
key = int(input('Enter key: '))
mode = input('Encrypt/Decrypt [e/d]: ')
if not os.path.exists(inputFile):
print('File %s does not exist. Quitting...' % inputFile)
sys.exit()
if os.path.exists(outputFile):
print('Overwrite %s? [y/n]' % outputFile)
response = input('> ')
if not response.lower().startswith('y'):
sys.exit()
startTime = time.time()
if mode.lower().startswith('e'):
content = open(inputFile).read()
translated = transCipher.encryptMessage(key, content)
elif mode.lower().startswith('d'):
content = open(outputFile).read()
translated =transCipher .decryptMessage(key, content)
outputObj = open(outputFile, 'w')
outputObj.write(translated)
outputObj.close()
totalTime = round(time.time() - startTime, 2)
print('Done (', totalTime, 'seconds )')
if __name__ == '__main__':
main()

60
ciphers/vigenere_cipher.py Normal file
View File

@ -0,0 +1,60 @@
LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
def main():
message = input('Enter message: ')
key = input('Enter key [alphanumeric]: ')
mode = input('Encrypt/Decrypt [e/d]: ')
if mode.lower().startswith('e'):
mode = 'encrypt'
translated = encryptMessage(key, message)
elif mode.lower().startswith('d'):
mode = 'decrypt'
translated = decryptMessage(key, message)
print('\n%sed message:' % mode.title())
print(translated)
def encryptMessage(key, message):
'''
>>> encryptMessage('HDarji', 'This is Harshil Darji from Dharmaj.')
'Akij ra Odrjqqs Gaisq muod Mphumrs.'
'''
return translateMessage(key, message, 'encrypt')
def decryptMessage(key, message):
'''
>>> decryptMessage('HDarji', 'Akij ra Odrjqqs Gaisq muod Mphumrs.')
'This is Harshil Darji from Dharmaj.'
'''
return translateMessage(key, message, 'decrypt')
def translateMessage(key, message, mode):
translated = []
keyIndex = 0
key = key.upper()
for symbol in message:
num = LETTERS.find(symbol.upper())
if num != -1:
if mode == 'encrypt':
num += LETTERS.find(key[keyIndex])
elif mode == 'decrypt':
num -= LETTERS.find(key[keyIndex])
num %= len(LETTERS)
if symbol.isupper():
translated.append(LETTERS[num])
elif symbol.islower():
translated.append(LETTERS[num].lower())
keyIndex += 1
if keyIndex == len(key):
keyIndex = 0
else:
translated.append(symbol)
return ''.join(translated)
if __name__ == '__main__':
main()

180
data_structures/AVL/AVL.py Normal file
View File

@ -0,0 +1,180 @@
'''
A AVL tree
'''
class Node:
def __init__(self, label):
self.label = label
self._parent = None
self._left = None
self._right = None
self.height = 0
@property
def right(self):
return self._right
@right.setter
def right(self, node):
if node is not None:
node._parent = self
self._right = node
@property
def left(self):
return self._left
@left.setter
def left(self, node):
if node is not None:
node._parent = self
self._left = node
@property
def parent(self):
return self._parent
@parent.setter
def parent(self, node):
if node is not None:
self._parent = node
self.height = self.parent.height + 1
else:
self.height = 0
class AVL:
def __init__(self):
self.root = None
self.size = 0
def insert(self, value):
node = Node(value)
if self.root is None:
self.root = node
self.root.height = 0
self.size = 1
else:
# Same as Binary Tree
dad_node = None
curr_node = self.root
while True:
if curr_node is not None:
dad_node = curr_node
if node.label < curr_node.label:
curr_node = curr_node.left
else:
curr_node = curr_node.right
else:
node.height = dad_node.height
dad_node.height += 1
if node.label < dad_node.label:
dad_node.left = node
else:
dad_node.right = node
self.rebalance(node)
self.size += 1
break
def rebalance(self, node):
n = node
while n is not None:
height_right = n.height
height_left = n.height
if n.right is not None:
height_right = n.right.height
if n.left is not None:
height_left = n.left.height
if abs(height_left - height_right) > 1:
if height_left > height_right:
left_child = n.left
if left_child is not None:
h_right = (right_child.right.height
if (right_child.right is not None) else 0)
h_left = (right_child.left.height
if (right_child.left is not None) else 0)
if (h_left > h_right):
self.rotate_left(n)
break
else:
self.double_rotate_right(n)
break
else:
right_child = n.right
if right_child is not None:
h_right = (right_child.right.height
if (right_child.right is not None) else 0)
h_left = (right_child.left.height
if (right_child.left is not None) else 0)
if (h_left > h_right):
self.double_rotate_left(n)
break
else:
self.rotate_right(n)
break
n = n.parent
def rotate_left(self, node):
aux = node.parent.label
node.parent.label = node.label
node.parent.right = Node(aux)
node.parent.right.height = node.parent.height + 1
node.parent.left = node.right
def rotate_right(self, node):
aux = node.parent.label
node.parent.label = node.label
node.parent.left = Node(aux)
node.parent.left.height = node.parent.height + 1
node.parent.right = node.right
def double_rotate_left(self, node):
self.rotate_right(node.getRight().getRight())
self.rotate_left(node)
def double_rotate_right(self, node):
self.rotate_left(node.getLeft().getLeft())
self.rotate_right(node)
def empty(self):
if self.root is None:
return True
return False
def preShow(self, curr_node):
if curr_node is not None:
self.preShow(curr_node.left)
print(curr_node.label, end=" ")
self.preShow(curr_node.right)
def preorder(self, curr_node):
if curr_node is not None:
self.preShow(curr_node.left)
self.preShow(curr_node.right)
print(curr_node.label, end=" ")
def getRoot(self):
return self.root
t = AVL()
t.insert(1)
t.insert(2)
t.insert(3)
# t.preShow(t.root)
# print("\n")
# t.insert(4)
# t.insert(5)
# t.preShow(t.root)
# t.preorden(t.root)

1
data_structures/Arrays Normal file
View File

@ -0,0 +1 @@
Arrays implimentation using python programming.

28
data_structures/Binary Tree/FenwickTree.py Normal file
View File

@ -0,0 +1,28 @@
class FenwickTree:
def __init__(self, SIZE): # create fenwick tree with size SIZE
self.Size = SIZE
self.ft = [0 for i in range (0,SIZE)]
def update(self, i, val): # update data (adding) in index i in O(lg N)
while (i < self.Size):
self.ft[i] += val
i += i & (-i)
def query(self, i): # query cumulative data from index 0 to i in O(lg N)
ret = 0
while (i > 0):
ret += self.ft[i]
i -= i & (-i)
return ret
if __name__ == '__main__':
f = FenwickTree(100)
f.update(1,20)
f.update(4,4)
print (f.query(1))
print (f.query(3))
print (f.query(4))
f.update(2,-5)
print (f.query(1))
print (f.query(3))

90
data_structures/Binary Tree/LazySegmentTree.py Normal file
View File

@ -0,0 +1,90 @@
import math
class SegmentTree:
def __init__(self, N):
self.N = N
self.st = [0 for i in range(0,4*N)] # approximate the overall size of segment tree with array N
self.lazy = [0 for i in range(0,4*N)] # create array to store lazy update
self.flag = [0 for i in range(0,4*N)] # flag for lazy update
def left(self, idx):
return idx*2
def right(self, idx):
return idx*2 + 1
def build(self, idx, l, r, A):
if l==r:
self.st[idx] = A[l-1]
else :
mid = (l+r)//2
self.build(self.left(idx),l,mid, A)
self.build(self.right(idx),mid+1,r, A)
self.st[idx] = max(self.st[self.left(idx)] , self.st[self.right(idx)])
# update with O(lg N) (Normal segment tree without lazy update will take O(Nlg N) for each update)
def update(self, idx, l, r, a, b, val): # update(1, 1, N, a, b, v) for update val v to [a,b]
if self.flag[idx] == True:
self.st[idx] = self.lazy[idx]
self.flag[idx] = False
if l!=r:
self.lazy[self.left(idx)] = self.lazy[idx]
self.lazy[self.right(idx)] = self.lazy[idx]
self.flag[self.left(idx)] = True
self.flag[self.right(idx)] = True
if r < a or l > b:
return True
if l >= a and r <= b :
self.st[idx] = val
if l!=r:
self.lazy[self.left(idx)] = val
self.lazy[self.right(idx)] = val
self.flag[self.left(idx)] = True
self.flag[self.right(idx)] = True
return True
mid = (l+r)//2
self.update(self.left(idx),l,mid,a,b,val)
self.update(self.right(idx),mid+1,r,a,b,val)
self.st[idx] = max(self.st[self.left(idx)] , self.st[self.right(idx)])
return True
# query with O(lg N)
def query(self, idx, l, r, a, b): #query(1, 1, N, a, b) for query max of [a,b]
if self.flag[idx] == True:
self.st[idx] = self.lazy[idx]
self.flag[idx] = False
if l != r:
self.lazy[self.left(idx)] = self.lazy[idx]
self.lazy[self.right(idx)] = self.lazy[idx]
self.flag[self.left(idx)] = True
self.flag[self.right(idx)] = True
if r < a or l > b:
return -math.inf
if l >= a and r <= b:
return self.st[idx]
mid = (l+r)//2
q1 = self.query(self.left(idx),l,mid,a,b)
q2 = self.query(self.right(idx),mid+1,r,a,b)
return max(q1,q2)
def showData(self):
showList = []
for i in range(1,N+1):
showList += [self.query(1, 1, self.N, i, i)]
print (showList)
if __name__ == '__main__':
A = [1,2,-4,7,3,-5,6,11,-20,9,14,15,5,2,-8]
N = 15
segt = SegmentTree(N)
segt.build(1,1,N,A)
print (segt.query(1,1,N,4,6))
print (segt.query(1,1,N,7,11))
print (segt.query(1,1,N,7,12))
segt.update(1,1,N,1,3,111)
print (segt.query(1,1,N,1,15))
segt.update(1,1,N,7,8,235)
segt.showData()

64
data_structures/Binary Tree/SegmentTree.py Normal file
View File

@ -0,0 +1,64 @@
import math
class SegmentTree:
def __init__(self, N):
self.N = N
self.st = [0 for i in range(0,4*N)] # approximate the overall size of segment tree with array N
def left(self, idx):
return idx*2
def right(self, idx):
return idx*2 + 1
def build(self, idx, l, r, A):
if l==r:
self.st[idx] = A[l-1]
else :
mid = (l+r)//2
self.build(self.left(idx),l,mid, A)
self.build(self.right(idx),mid+1,r, A)
self.st[idx] = max(self.st[self.left(idx)] , self.st[self.right(idx)])
def update(self, idx, l, r, a, b, val): # update(1, 1, N, a, b, v) for update val v to [a,b]
if r < a or l > b:
return True
if l == r :
self.st[idx] = val
return True
mid = (l+r)//2
self.update(self.left(idx),l,mid,a,b,val)
self.update(self.right(idx),mid+1,r,a,b,val)
self.st[idx] = max(self.st[self.left(idx)] , self.st[self.right(idx)])
return True
def query(self, idx, l, r, a, b): #query(1, 1, N, a, b) for query max of [a,b]
if r < a or l > b:
return -math.inf
if l >= a and r <= b:
return self.st[idx]
mid = (l+r)//2
q1 = self.query(self.left(idx),l,mid,a,b)
q2 = self.query(self.right(idx),mid+1,r,a,b)
return max(q1,q2)
def showData(self):
showList = []
for i in range(1,N+1):
showList += [self.query(1, 1, self.N, i, i)]
print (showList)
if __name__ == '__main__':
A = [1,2,-4,7,3,-5,6,11,-20,9,14,15,5,2,-8]
N = 15
segt = SegmentTree(N)
segt.build(1,1,N,A)
print (segt.query(1,1,N,4,6))
print (segt.query(1,1,N,7,11))
print (segt.query(1,1,N,7,12))
segt.update(1,1,N,1,3,111)
print (segt.query(1,1,N,1,15))
segt.update(1,1,N,7,8,235)
segt.showData()

103
data_structures/Binary Tree/binary_seach_tree.py Normal file
View File

@ -0,0 +1,103 @@
'''
A binary search Tree
'''
class Node:
def __init__(self, label):
self.label = label
self.left = None
self.right = None
def getLabel(self):
return self.label
def setLabel(self, label):
self.label = label
def getLeft(self):
return self.left
def setLeft(self, left):
self.left = left
def getRight(self):
return self.right
def setRight(self, right):
self.right = right
class BinarySearchTree:
def __init__(self):
self.root = None
def insert(self, label):
# Create a new Node
node = Node(label)
if self.empty():
self.root = node
else:
dad_node = None
curr_node = self.root
while True:
if curr_node is not None:
dad_node = curr_node
if node.getLabel() < curr_node.getLabel():
curr_node = curr_node.getLeft()
else:
curr_node = curr_node.getRight()
else:
if node.getLabel() < dad_node.getLabel():
dad_node.setLeft(node)
else:
dad_node.setRight(node)
break
def empty(self):
if self.root is None:
return True
return False
def preShow(self, curr_node):
if curr_node is not None:
print(curr_node.getLabel(), end=" ")
self.preShow(curr_node.getLeft())
self.preShow(curr_node.getRight())
def getRoot(self):
return self.root
'''
Example
8
/ \
3 10
/ \ \
1 6 14
/ \ /
4 7 13
'''
t = BinarySearchTree()
t.insert(8)
t.insert(3)
t.insert(1)
t.insert(6)
t.insert(4)
t.insert(7)
t.insert(10)
t.insert(14)
t.insert(13)
t.preShow(t.getRoot())

61
data_structures/Graph/BreadthFirstSearch.py Normal file
View File

@ -0,0 +1,61 @@
# Author: OMKAR PATHAK
class Graph():
def __init__(self):
self.vertex = {}
# for printing the Graph vertexes
def printGraph(self):
for i in self.vertex.keys():
print(i,' -> ', ' -> '.join([str(j) for j in self.vertex[i]]))
# for adding the edge beween two vertexes
def addEdge(self, fromVertex, toVertex):
# check if vertex is already present,
if fromVertex in self.vertex.keys():
self.vertex[fromVertex].append(toVertex)
else:
# else make a new vertex
self.vertex[fromVertex] = [toVertex]
def BFS(self, startVertex):
# Take a list for stoting already visited vertexes
visited = [False] * len(self.vertex)
# create a list to store all the vertexes for BFS
queue = []
# mark the source node as visited and enqueue it
visited[startVertex] = True
queue.append(startVertex)
while queue:
startVertex = queue.pop(0)
print(startVertex, end = ' ')
# mark all adjacent nodes as visited and print them
for i in self.vertex[startVertex]:
if visited[i] == False:
queue.append(i)
visited[i] = True
if __name__ == '__main__':
g = Graph()
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
g.printGraph()
print('BFS:')
g.BFS(2)
# OUTPUT:
# 0  ->  1 -> 2
# 1  ->  2
# 2  ->  0 -> 3
# 3  ->  3
# BFS:
# 2 0 3 1

61
data_structures/Graph/DepthFirstSearch.py Normal file
View File

@ -0,0 +1,61 @@
# Author: OMKAR PATHAK
class Graph():
def __init__(self):
self.vertex = {}
# for printing the Graph vertexes
def printGraph(self):
print(self.vertex)
for i in self.vertex.keys():
print(i,' -> ', ' -> '.join([str(j) for j in self.vertex[i]]))
# for adding the edge beween two vertexes
def addEdge(self, fromVertex, toVertex):
# check if vertex is already present,
if fromVertex in self.vertex.keys():
self.vertex[fromVertex].append(toVertex)
else:
# else make a new vertex
self.vertex[fromVertex] = [toVertex]
def DFS(self):
# visited array for storing already visited nodes
visited = [False] * len(self.vertex)
# call the recursive helper function
for i in range(len(self.vertex)):
if visited[i] == False:
self.DFSRec(i, visited)
def DFSRec(self, startVertex, visited):
# mark start vertex as visited
visited[startVertex] = True
print(startVertex, end = ' ')
# Recur for all the vertexes that are adjacent to this node
for i in self.vertex.keys():
if visited[i] == False:
self.DFSRec(i, visited)
if __name__ == '__main__':
g = Graph()
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
g.printGraph()
print('DFS:')
g.DFS()
# OUTPUT:
# 0  ->  1 -> 2
# 1  ->  2
# 2  ->  0 -> 3
# 3  ->  3
# DFS:
# 0 1 2 3

40
data_structures/Graph/Graph.py Normal file
View File

@ -0,0 +1,40 @@
# Author: OMKAR PATHAK
# We can use Python's dictionary for constructing the graph
class AdjacencyList(object):
def __init__(self):
self.List = {}
def addEdge(self, fromVertex, toVertex):
# check if vertex is already present
if fromVertex in self.List.keys():
self.List[fromVertex].append(toVertex)
else:
self.List[fromVertex] = [toVertex]
def printList(self):
for i in self.List:
print(i,'->',' -> '.join([str(j) for j in self.List[i]]))
if __name__ == '__main__':
al = AdjacencyList()
al.addEdge(0, 1)
al.addEdge(0, 4)
al.addEdge(4, 1)
al.addEdge(4, 3)
al.addEdge(1, 0)
al.addEdge(1, 4)
al.addEdge(1, 3)
al.addEdge(1, 2)
al.addEdge(2, 3)
al.addEdge(3, 4)
al.printList()
# OUTPUT:
# 0 -> 1 -> 4
# 1 -> 0 -> 4 -> 3 -> 2
# 2 -> 3
# 3 -> 4
# 4 -> 1 -> 3

28
data_structures/Graph/Graph_list.py Normal file
View File

@ -0,0 +1,28 @@
class Graph:
def __init__(self, vertex):
self.vertex = vertex
self.graph = [[0] for i in range(vertex)]
def add_edge(self, u, v):
self.graph[u - 1].append(v - 1)
def show(self):
for i in range(self.vertex):
print('%d: '% (i + 1), end=' ')
for j in self.graph[i]:
print('%d-> '% (j + 1), end=' ')
print(' ')
g = Graph(100)
g.add_edge(1,3)
g.add_edge(2,3)
g.add_edge(3,4)
g.add_edge(3,5)
g.add_edge(4,5)
g.show()

29
data_structures/Graph/Graph_matrix.py Normal file
View File

@ -0,0 +1,29 @@
class Graph:
def __init__(self, vertex):
self.vertex = vertex
self.graph = [[0] * vertex for i in range(vertex) ]
def add_edge(self, u, v):
self.graph[u - 1][v - 1] = 1
self.graph[v - 1][u - 1] = 1
def show(self):
for i in self.graph:
for j in i:
print(j, end=' ')
print(' ')
g = Graph(100)
g.add_edge(1,4)
g.add_edge(4,2)
g.add_edge(4,5)
g.add_edge(2,5)
g.add_edge(5,3)
g.show()

211
data_structures/Graph/dijkstra_algorithm.py Normal file
View File

@ -0,0 +1,211 @@
# Title: Dijkstra's Algorithm for finding single source shortest path from scratch
# Author: Shubham Malik
# References: https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm
import math
import sys
# For storing the vertex set to retreive node with the lowest distance
class PriorityQueue:
# Based on Min Heap
def __init__(self):
self.cur_size = 0
self.array = []
self.pos = {} # To store the pos of node in array
def isEmpty(self):
return self.cur_size == 0
def min_heapify(self, idx):
lc = self.left(idx)
rc = self.right(idx)
if lc < self.cur_size and self.array(lc)[0] < self.array(idx)[0]:
smallest = lc
else:
smallest = idx
if rc < self.cur_size and self.array(rc)[0] < self.array(smallest)[0]:
smallest = rc
if smallest != idx:
self.swap(idx, smallest)
self.min_heapify(smallest)
def insert(self, tup):
# Inserts a node into the Priority Queue
self.pos[tup[1]] = self.cur_size
self.cur_size += 1
self.array.append((sys.maxsize, tup[1]))
self.decrease_key((sys.maxsize, tup[1]), tup[0])
def extract_min(self):
# Removes and returns the min element at top of priority queue
min_node = self.array[0][1]
self.array[0] = self.array[self.cur_size - 1]
self.cur_size -= 1
self.min_heapify(1)
del self.pos[min_node]
return min_node
def left(self, i):
# returns the index of left child
return 2 * i + 1
def right(self, i):
# returns the index of right child
return 2 * i + 2
def par(self, i):
# returns the index of parent
return math.floor(i / 2)
def swap(self, i, j):
# swaps array elements at indices i and j
# update the pos{}
self.pos[self.array[i][1]] = j
self.pos[self.array[j][1]] = i
temp = self.array[i]
self.array[i] = self.array[j]
self.array[j] = temp
def decrease_key(self, tup, new_d):
idx = self.pos[tup[1]]
# assuming the new_d is atmost old_d
self.array[idx] = (new_d, tup[1])
while idx > 0 and self.array[self.par(idx)][0] > self.array[idx][0]:
self.swap(idx, self.par(idx))
idx = self.par(idx)
class Graph:
def __init__(self, num):
self.adjList = {} # To store graph: u -> (v,w)
self.num_nodes = num # Number of nodes in graph
# To store the distance from source vertex
self.dist = [0] * self.num_nodes
self.par = [-1] * self.num_nodes # To store the path
def add_edge(self, u, v, w):
# Edge going from node u to v and v to u with weight w
# u (w)-> v, v (w) -> u
# Check if u already in graph
if u in self.adjList.keys():
self.adjList[u].append((v, w))
else:
self.adjList[u] = [(v, w)]
# Assuming undirected graph
if v in self.adjList.keys():
self.adjList[v].append((u, w))
else:
self.adjList[v] = [(u, w)]
def show_graph(self):
# u -> v(w)
for u in self.adjList:
print(u, '->', ' -> '.join(str("{}({})".format(v, w))
for v, w in self.adjList[u]))
def dijkstra(self, src):
# Flush old junk values in par[]
self.par = [-1] * self.num_nodes
# src is the source node
self.dist[src] = 0
Q = PriorityQueue()
Q.insert((0, src)) # (dist from src, node)
for u in self.adjList.keys():
if u != src:
self.dist[u] = sys.maxsize # Infinity
self.par[u] = -1
while not Q.isEmpty():
u = Q.extract_min() # Returns node with the min dist from source
# Update the distance of all the neighbours of u and
# if their prev dist was INFINITY then push them in Q
for v, w in self.adjList[u]:
new_dist = self.dist[u] + w
if self.dist[v] > new_dist:
if self.dist[v] == sys.maxsize:
Q.insert((new_dist, v))
else:
Q.decrease_key((self.dist[v], v), new_dist)
self.dist[v] = new_dist
self.par[v] = u
# Show the shortest distances from src
self.show_distances(src)
def show_distances(self, src):
print("Distance from node: {}".format(src))
for u in range(self.num_nodes):
print('Node {} has distance: {}'.format(u, self.dist[u]))
def show_path(self, src, dest):
# To show the shortest path from src to dest
# WARNING: Use it *after* calling dijkstra
path = []
cost = 0
temp = dest
# Backtracking from dest to src
while self.par[temp] != -1:
path.append(temp)
if temp != src:
for v, w in self.adjList[temp]:
if v == self.par[temp]:
cost += w
break
temp = self.par[temp]
path.append(src)
path.reverse()
print('----Path to reach {} from {}----'.format(dest, src))
for u in path:
print('{}'.format(u), end=' ')
if u != dest:
print('-> ', end='')
print('\nTotal cost of path: ', cost)
if __name__ == '__main__':
graph = Graph(9)
graph.add_edge(0, 1, 4)
graph.add_edge(0, 7, 8)
graph.add_edge(1, 2, 8)
graph.add_edge(1, 7, 11)
graph.add_edge(2, 3, 7)
graph.add_edge(2, 8, 2)
graph.add_edge(2, 5, 4)
graph.add_edge(3, 4, 9)
graph.add_edge(3, 5, 14)
graph.add_edge(4, 5, 10)
graph.add_edge(5, 6, 2)
graph.add_edge(6, 7, 1)
graph.add_edge(6, 8, 6)
graph.add_edge(7, 8, 7)
graph.show_graph()
graph.dijkstra(0)
graph.show_path(0, 4)
# OUTPUT
# 0 -> 1(4) -> 7(8)
# 1 -> 0(4) -> 2(8) -> 7(11)
# 7 -> 0(8) -> 1(11) -> 6(1) -> 8(7)
# 2 -> 1(8) -> 3(7) -> 8(2) -> 5(4)
# 3 -> 2(7) -> 4(9) -> 5(14)
# 8 -> 2(2) -> 6(6) -> 7(7)
# 5 -> 2(4) -> 3(14) -> 4(10) -> 6(2)
# 4 -> 3(9) -> 5(10)
# 6 -> 5(2) -> 7(1) -> 8(6)
# Distance from node: 0
# Node 0 has distance: 0
# Node 1 has distance: 4
# Node 2 has distance: 12
# Node 3 has distance: 19
# Node 4 has distance: 21
# Node 5 has distance: 11
# Node 6 has distance: 9
# Node 7 has distance: 8
# Node 8 has distance: 14
# ----Path to reach 4 from 0----
# 0 -> 7 -> 6 -> 5 -> 4
# Total cost of path: 21

83
data_structures/Heap/heap.py Normal file
View File

@ -0,0 +1,83 @@
#!/usr/bin/python
class Heap:
def __init__(self):
self.h = []
self.currsize = 0
def leftChild(self,i):
if 2*i+1 < self.currsize:
return 2*i+1
return None
def rightChild(self,i):
if 2*i+2 < self.currsize:
return 2*i+2
return None
def maxHeapify(self,node):
if node < self.currsize:
m = node
lc = self.leftChild(node)
rc = self.rightChild(node)
if lc is not None and self.h[lc] > self.h[m]:
m = lc
if rc is not None and self.h[rc] > self.h[m]:
m = rc
if m!=node:
temp = self.h[node]
self.h[node] = self.h[m]
self.h[m] = temp
self.maxHeapify(m)
def buildHeap(self,a):
self.currsize = len(a)
self.h = list(a)
for i in range(self.currsize/2,-1,-1):
self.maxHeapify(i)
def getMax(self):
if self.currsize >= 1:
me = self.h[0]
temp = self.h[0]
self.h[0] = self.h[self.currsize-1]
self.h[self.currsize-1] = temp
self.currsize -= 1
self.maxHeapify(0)
return me
return None
def heapSort(self):
size = self.currsize
while self.currsize-1 >= 0:
temp = self.h[0]
self.h[0] = self.h[self.currsize-1]
self.h[self.currsize-1] = temp
self.currsize -= 1
self.maxHeapify(0)
self.currsize = size
def insert(self,data):
self.h.append(data)
curr = self.currsize
self.currsize+=1
while self.h[curr] > self.h[curr/2]:
temp = self.h[curr/2]
self.h[curr/2] = self.h[curr]
self.h[curr] = temp
curr = curr/2
def display(self):
print (self.h)
def main():
l = list(map(int,raw_input().split()))
h = Heap()
h.buildHeap(l)
h.heapSort()
h.display()
if __name__=='__main__':
main()

73
data_structures/LinkedList/DoublyLinkedList.py Normal file
View File

@ -0,0 +1,73 @@
'''
- A linked list is similar to an array, it holds values. However, links in a linked list do not have indexes.
- This is an example of a double ended, doubly linked list.
- Each link references the next link and the previous one.
'''
class LinkedList:
def __init__(self):
self.head = None
self.tail = None
def insertHead(self, x):
newLink = Link(x) #Create a new link with a value attached to it
if(self.isEmpty() == True): #Set the first element added to be the tail
self.tail = newLink
else:
self.head.previous = newLink # newLink <-- currenthead(head)
newLink.next = self.head # newLink <--> currenthead(head)
self.head = newLink # newLink(head) <--> oldhead
def deleteHead(self):
temp = self.head
self.head = self.head.next # oldHead <--> 2ndElement(head)
self.head.previous = None # oldHead --> 2ndElement(head) nothing pointing at it so the old head will be removed
if(self.head == None):
self.tail = None
return temp
def insertTail(self, x):
newLink = Link(x)
newLink.next = None # currentTail(tail) newLink -->
self.tail.next = newLink # currentTail(tail) --> newLink -->
newLink.previous = self.tail #currentTail(tail) <--> newLink -->
self.tail = newLink # oldTail <--> newLink(tail) -->
def deleteTail(self):
temp = self.tail
self.tail = self.tail.previous # 2ndLast(tail) <--> oldTail --> None
self.tail.next = None # 2ndlast(tail) --> None
return temp
def delete(self, x):
current = self.head
while(current.value != x): # Find the position to delete
current = current.next
if(current == self.head):
self.deleteHead()
elif(current == self.tail):
self.deleteTail()
else: #Before: 1 <--> 2(current) <--> 3
current.previous.next = current.next # 1 --> 3
current.next.previous = current.previous # 1 <--> 3
def isEmpty(self): #Will return True if the list is empty
return(self.head == None)
def display(self): #Prints contents of the list
current = self.head
while(current != None):
current.displayLink()
current = current.next
print()
class Link:
next = None #This points to the link in front of the new link
previous = None #This points to the link behind the new link
def __init__(self, x):
self.value = x
def displayLink(self):
print("{}".format(self.value), end=" ")

22
data_structures/LinkedList/__init__.py Normal file
View File

@ -0,0 +1,22 @@
class Node:
def __init__(self, item, next):
self.item = item
self.next = next
class LinkedList:
def __init__(self):
self.head = None
def add(self, item):
self.head = Node(item, self.head)
def remove(self):
if self.is_empty():
return None
else:
item = self.head.item
self.head = self.head.next
return item
def is_empty(self):
return self.head == None

50
data_structures/LinkedList/singly_LinkedList.py Normal file
View File

@ -0,0 +1,50 @@
class Node:#create a Node
def __int__(self,data):
self.data=data#given data
self.next=None#given next to None
class Linked_List:
pass
def insert_tail(Head,data):
if(Head.next is None):
Head.next = Node(data)
else:
insert_tail(Head.next, data)
def insert_head(Head,data):
tamp = Head
if (tamp == None):
newNod = Node()#create a new Node
newNod.data = data
newNod.next = None
Head = newNod#make new node to Head
else:
newNod = Node()
newNod.data = data
newNod.next = Head#put the Head at NewNode Next
Head=newNod#make a NewNode to Head
return Head
def printList(Head):#print every node data
tamp=Head
while tamp!=None:
print(tamp.data)
tamp=tamp.next
def delete_head(Head):#delete from head
if Head!=None:
Head=Head.next
return Head#return new Head
def delete_tail(Head):#delete from tail
if Head!=None:
tamp = Node()
tamp = Head
while (tamp.next).next!= None:#find the 2nd last element
tamp = tamp.next
tamp.next=None#delete the last element by give next None to 2nd last Element
return Head
def isEmpty(Head):
return Head is None #Return if Head is none

39
data_structures/Queue/DeQueue.py Normal file
View File

@ -0,0 +1,39 @@
# Python code to demonstrate working of
# extend(), extendleft(), rotate(), reverse()
# importing "collections" for deque operations
import collections
# initializing deque
de = collections.deque([1, 2, 3,])
# using extend() to add numbers to right end
# adds 4,5,6 to right end
de.extend([4,5,6])
# printing modified deque
print ("The deque after extending deque at end is : ")
print (de)
# using extendleft() to add numbers to left end
# adds 7,8,9 to right end
de.extendleft([7,8,9])
# printing modified deque
print ("The deque after extending deque at beginning is : ")
print (de)
# using rotate() to rotate the deque
# rotates by 3 to left
de.rotate(-3)
# printing modified deque
print ("The deque after rotating deque is : ")
print (de)
# using reverse() to reverse the deque
de.reverse()
# printing modified deque
print ("The deque after reversing deque is : ")
print (de)

45
data_structures/Queue/QueueOnList.py Normal file
View File

@ -0,0 +1,45 @@
"""Queue represented by a python list"""
class Queue():
def __init__(self):
self.entries = []
self.length = 0
self.front=0
def __str__(self):
printed = '<' + str(self.entries)[1:-1] + '>'
return printed
"""Enqueues {@code item}
@param item
item to enqueue"""
def put(self, item):
self.entries.append(item)
self.length = self.length + 1
"""Dequeues {@code item}
@requirement: |self.length| > 0
@return dequeued
item that was dequeued"""
def get(self):
self.length = self.length - 1
dequeued = self.entries[self.front]
self.front-=1
self.entries = self.entries[self.front:]
return dequeued
"""Rotates the queue {@code rotation} times
@param rotation
number of times to rotate queue"""
def rotate(self, rotation):
for i in range(rotation):
self.put(self.get())
"""Enqueues {@code item}
@return item at front of self.entries"""
def front(self):
return self.entries[0]
"""Returns the length of this.entries"""
def size(self):
return self.length

50
data_structures/Queue/QueueOnPseudoStack.py Normal file
View File

@ -0,0 +1,50 @@
"""Queue represented by a pseudo stack (represented by a list with pop and append)"""
class Queue():
def __init__(self):
self.stack = []
self.length = 0
def __str__(self):
printed = '<' + str(self.stack)[1:-1] + '>'
return printed
"""Enqueues {@code item}
@param item
item to enqueue"""
def put(self, item):
self.stack.append(item)
self.length = self.length + 1
"""Dequeues {@code item}
@requirement: |self.length| > 0
@return dequeued
item that was dequeued"""
def get(self):
self.rotate(1)
dequeued = self.stack[self.length-1]
self.stack = self.stack[:-1]
self.rotate(self.length-1)
self.length = self.length -1
return dequeued
"""Rotates the queue {@code rotation} times
@param rotation
number of times to rotate queue"""
def rotate(self, rotation):
for i in range(rotation):
temp = self.stack[0]
self.stack = self.stack[1:]
self.put(temp)
self.length = self.length - 1
"""Reports item at the front of self
@return item at front of self.stack"""
def front(self):
front = self.get()
self.put(front)
self.rotate(self.length-1)
return front
"""Returns the length of this.stack"""
def size(self):
return self.length

0
data_structures/Queue/__init__.py Normal file
View File

23
data_structures/Stacks/__init__.py Normal file
View File

@ -0,0 +1,23 @@
class Stack:
def __init__(self):
self.stack = []
self.top = 0
def is_empty(self):
return (self.top == 0)
def push(self, item):
if self.top < len(self.stack):
self.stack[self.top] = item
else:
self.stack.append(item)
self.top += 1
def pop(self):
if self.is_empty():
return None
else:
self.top -= 1
return self.stack[self.top]

21
data_structures/Stacks/balanced_parentheses.py Normal file
View File

@ -0,0 +1,21 @@
from Stack import Stack
__author__ = 'Omkar Pathak'
def balanced_parentheses(parentheses):
""" Use a stack to check if a string of parentheses are balanced."""
stack = Stack(len(parentheses))
for parenthesis in parentheses:
if parenthesis == '(':
stack.push(parenthesis)
elif parenthesis == ')':
stack.pop()
return not stack.is_empty()
if __name__ == '__main__':
examples = ['((()))', '((())']
print('Balanced parentheses demonstration:\n')
for example in examples:
print(example + ': ' + str(balanced_parentheses(example)))

62
data_structures/Stacks/infix_to_postfix_conversion.py Normal file
View File

@ -0,0 +1,62 @@
import string
from Stack import Stack
__author__ = 'Omkar Pathak'
def is_operand(char):
return char in string.ascii_letters or char in string.digits
def precedence(char):
""" Return integer value representing an operator's precedence, or
order of operation.
https://en.wikipedia.org/wiki/Order_of_operations
"""
dictionary = {'+': 1, '-': 1,
'*': 2, '/': 2,
'^': 3}
return dictionary.get(char, -1)
def infix_to_postfix(expression):
""" Convert infix notation to postfix notation using the Shunting-yard
algorithm.
https://en.wikipedia.org/wiki/Shunting-yard_algorithm
https://en.wikipedia.org/wiki/Infix_notation
https://en.wikipedia.org/wiki/Reverse_Polish_notation
"""
stack = Stack(len(expression))
postfix = []
for char in expression:
if is_operand(char):
postfix.append(char)
elif char not in {'(', ')'}:
while (not stack.is_empty()
and precedence(char) <= precedence(stack.peek())):
postfix.append(stack.pop())
stack.push(char)
elif char == '(':
stack.push(char)
elif char == ')':
while not stack.is_empty() and stack.peek() != '(':
postfix.append(stack.pop())
# Pop '(' from stack. If there is no '(', there is a mismatched
# parentheses.
if stack.peek() != '(':
raise ValueError('Mismatched parentheses')
stack.pop()
while not stack.is_empty():
postfix.append(stack.pop())
return ' '.join(postfix)
if __name__ == '__main__':
expression = 'a+b*(c^d-e)^(f+g*h)-i'
print('Infix to Postfix Notation demonstration:\n')
print('Infix notation: ' + expression)
print('Postfix notation: ' + infix_to_postfix(expression))

16
data_structures/Stacks/next.py Normal file
View File

@ -0,0 +1,16 @@
# Function to print element and NGE pair for all elements of list
def printNGE(arr):
for i in range(0, len(arr), 1):
next = -1
for j in range(i+1, len(arr), 1):
if arr[i] < arr[j]:
next = arr[j]
break
print(str(arr[i]) + " -- " + str(next))
# Driver program to test above function
arr = [11,13,21,3]
printNGE(arr)

68
data_structures/Stacks/stack.py Normal file
View File

@ -0,0 +1,68 @@
__author__ = 'Omkar Pathak'
class Stack(object):
""" A stack is an abstract data type that serves as a collection of
elements with two principal operations: push() and pop(). push() adds an
element to the top of the stack, and pop() removes an element from the top
of a stack. The order in which elements come off of a stack are
Last In, First Out (LIFO).
https://en.wikipedia.org/wiki/Stack_(abstract_data_type)
"""
def __init__(self, limit=10):
self.stack = []
self.limit = limit
def __bool__(self):
return not bool(self.stack)
def __str__(self):
return str(self.stack)
def push(self, data):
""" Push an element to the top of the stack."""
if len(self.stack) >= self.limit:
raise StackOverflowError
self.stack.append(data)
def pop(self):
""" Pop an element off of the top of the stack."""
if self.stack:
return self.stack.pop()
else:
raise IndexError('pop from an empty stack')
def peek(self):
""" Peek at the top-most element of the stack."""
if self.stack:
return self.stack[-1]
def is_empty(self):
""" Check if a stack is empty."""
return not bool(self.stack)
def size(self):
""" Return the size of the stack."""
return len(self.stack)
class StackOverflowError(BaseException):
pass
if __name__ == '__main__':
stack = Stack()
for i in range(10):
stack.push(i)
print('Stack demonstration:\n')
print('Initial stack: ' + str(stack))
print('pop(): ' + str(stack.pop()))
print('After pop(), the stack is now: ' + str(stack))
print('peek(): ' + str(stack.peek()))
stack.push(100)
print('After push(100), the stack is now: ' + str(stack))
print('is_empty(): ' + str(stack.is_empty()))
print('size(): ' + str(stack.size()))

75
data_structures/Trie/Trie.py Normal file
View File

@ -0,0 +1,75 @@
"""
A Trie/Prefix Tree is a kind of search tree used to provide quick lookup
of words/patterns in a set of words. A basic Trie however has O(n^2) space complexity
making it impractical in practice. It however provides O(max(search_string, length of longest word)) lookup
time making it an optimal approach when space is not an issue.
"""
class TrieNode:
def __init__(self):
self.nodes = dict() # Mapping from char to TrieNode
self.is_leaf = False
def insert_many(self, words: [str]):
"""
Inserts a list of words into the Trie
:param words: list of string words
:return: None
"""
for word in words:
self.insert(word)
def insert(self, word: str):
"""
Inserts a word into the Trie
:param word: word to be inserted
:return: None
"""
curr = self
for char in word:
if char not in curr.nodes:
curr.nodes[char] = TrieNode()
curr = curr.nodes[char]
curr.is_leaf = True
def find(self, word: str) -> bool:
"""
Tries to find word in a Trie
:param word: word to look for
:return: Returns True if word is found, False otherwise
"""
curr = self
for char in word:
if char not in curr.nodes:
return False
curr = curr.nodes[char]
return curr.is_leaf
def print_words(node: TrieNode, word: str):
"""
Prints all the words in a Trie
:param node: root node of Trie
:param word: Word variable should be empty at start
:return: None
"""
if node.is_leaf:
print(word, end=' ')
for key, value in node.nodes.items():
print_words(value, word + key)
def test():
words = ['banana', 'bananas', 'bandana', 'band', 'apple', 'all', 'beast']
root = TrieNode()
root.insert_many(words)
# print_words(root, '')
assert root.find('banana')
assert not root.find('bandanas')
assert not root.find('apps')
assert root.find('apple')
test()

0
data_structures/__init__.py Normal file
View File

37
dynamic_programming/FloydWarshall.py Normal file
View File

@ -0,0 +1,37 @@
import math
class Graph:
def __init__(self, N = 0): # a graph with Node 0,1,...,N-1
self.N = N
self.W = [[math.inf for j in range(0,N)] for i in range(0,N)] # adjacency matrix for weight
self.dp = [[math.inf for j in range(0,N)] for i in range(0,N)] # dp[i][j] stores minimum distance from i to j
def addEdge(self, u, v, w):
self.dp[u][v] = w;
def floyd_warshall(self):
for k in range(0,self.N):
for i in range(0,self.N):
for j in range(0,self.N):
self.dp[i][j] = min(self.dp[i][j], self.dp[i][k] + self.dp[k][j])
def showMin(self, u, v):
return self.dp[u][v]
if __name__ == '__main__':
graph = Graph(5)
graph.addEdge(0,2,9)
graph.addEdge(0,4,10)
graph.addEdge(1,3,5)
graph.addEdge(2,3,7)
graph.addEdge(3,0,10)
graph.addEdge(3,1,2)
graph.addEdge(3,2,1)
graph.addEdge(3,4,6)
graph.addEdge(4,1,3)
graph.addEdge(4,2,4)
graph.addEdge(4,3,9)
graph.floyd_warshall()
graph.showMin(1,4)
graph.showMin(0,3)

74
dynamic_programming/edit_distance.py Normal file
View File

@ -0,0 +1,74 @@
"""
Author : Turfa Auliarachman
Date : October 12, 2016
This is a pure Python implementation of Dynamic Programming solution to the edit distance problem.
The problem is :
Given two strings A and B. Find the minimum number of operations to string B such that A = B. The permitted operations are removal, insertion, and substitution.
"""
class EditDistance:
"""
Use :
solver = EditDistance()
editDistanceResult = solver.solve(firstString, secondString)
"""
def __init__(self):
self.__prepare__()
def __prepare__(self, N = 0, M = 0):
self.dp = [[-1 for y in range(0,M)] for x in range(0,N)]
def __solveDP(self, x, y):
if (x==-1):
return y+1
elif (y==-1):
return x+1
elif (self.dp[x][y]>-1):
return self.dp[x][y]
else:
if (self.A[x]==self.B[y]):
self.dp[x][y] = self.__solveDP(x-1,y-1)
else:
self.dp[x][y] = 1+min(self.__solveDP(x,y-1), self.__solveDP(x-1,y), self.__solveDP(x-1,y-1))
return self.dp[x][y]
def solve(self, A, B):
if isinstance(A,bytes):
A = A.decode('ascii')
if isinstance(B,bytes):
B = B.decode('ascii')
self.A = str(A)
self.B = str(B)
self.__prepare__(len(A), len(B))
return self.__solveDP(len(A)-1, len(B)-1)
if __name__ == '__main__':
import sys
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
solver = EditDistance()
print("****************** Testing Edit Distance DP Algorithm ******************")
print()
print("Enter the first string: ", end="")
S1 = input_function()
print("Enter the second string: ", end="")
S2 = input_function()
print()
print("The minimum Edit Distance is: %d" % (solver.solve(S1, S2)))
print()
print("*************** End of Testing Edit Distance DP Algorithm ***************")

42
dynamic_programming/fastfibonacci.py Normal file
View File

@ -0,0 +1,42 @@
"""
This program calculates the nth Fibonacci number in O(log(n)).
It's possible to calculate F(1000000) in less than a second.
"""
import sys
# returns F(n)
def fibonacci(n: int):
if n < 0:
raise ValueError("Negative arguments are not supported")
return _fib(n)[0]
# returns (F(n), F(n-1))
def _fib(n: int):
if n == 0:
# (F(0), F(1))
return (0, 1)
else:
# F(2n) = F(n)[2F(n+1) − F(n)]
# F(2n+1) = F(n+1)^2+F(n)^2
a, b = _fib(n // 2)
c = a * (b * 2 - a)
d = a * a + b * b
if n % 2 == 0:
return (c, d)
else:
return (d, c + d)
if __name__ == "__main__":
args = sys.argv[1:]
if len(args) != 1:
print("Too few or too much parameters given.")
exit(1)
try:
n = int(args[0])
except ValueError:
print("Could not convert data to an integer.")
exit(1)
print("F(%d) = %d" % (n, fibonacci(n)))

57
dynamic_programming/fibonacci.py Normal file
View File

@ -0,0 +1,57 @@
"""
This is a pure Python implementation of Dynamic Programming solution to the fibonacci sequence problem.
"""
class Fibonacci:
def __init__(self, N=None):
self.fib_array = []
if N:
N = int(N)
self.fib_array.append(0)
self.fib_array.append(1)
for i in range(2, N + 1):
self.fib_array.append(self.fib_array[i - 1] + self.fib_array[i - 2])
elif N == 0:
self.fib_array.append(0)
def get(self, sequence_no=None):
if sequence_no != None:
if sequence_no < len(self.fib_array):
return print(self.fib_array[:sequence_no + 1])
else:
print("Out of bound.")
else:
print("Please specify a value")
if __name__ == '__main__':
import sys
print("\n********* Fibonacci Series Using Dynamic Programming ************\n")
# For python 2.x and 3.x compatibility: 3.x has no raw_input builtin
# otherwise 2.x's input builtin function is too "smart"
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
print("\n Enter the upper limit for the fibonacci sequence: ", end="")
try:
N = eval(input())
fib = Fibonacci(N)
print(
"\n********* Enter different values to get the corresponding fibonacci sequence, enter any negative number to exit. ************\n")
while True:
print("Enter value: ", end=" ")
try:
i = eval(input())
if i < 0:
print("\n********* Good Bye!! ************\n")
break
fib.get(i)
except NameError:
print("\nInvalid input, please try again.")
except NameError:
print("\n********* Invalid input, good bye!! ************\n")

141
dynamic_programming/k_means_clustering_tensorflow.py Normal file
View File

@ -0,0 +1,141 @@
import tensorflow as tf
from random import choice, shuffle
from numpy import array
def TFKMeansCluster(vectors, noofclusters):
"""
K-Means Clustering using TensorFlow.
'vectors' should be a n*k 2-D NumPy array, where n is the number
of vectors of dimensionality k.
'noofclusters' should be an integer.
"""
noofclusters = int(noofclusters)
assert noofclusters < len(vectors)
#Find out the dimensionality
dim = len(vectors[0])
#Will help select random centroids from among the available vectors
vector_indices = list(range(len(vectors)))
shuffle(vector_indices)
#GRAPH OF COMPUTATION
#We initialize a new graph and set it as the default during each run
#of this algorithm. This ensures that as this function is called
#multiple times, the default graph doesn't keep getting crowded with
#unused ops and Variables from previous function calls.
graph = tf.Graph()
with graph.as_default():
#SESSION OF COMPUTATION
sess = tf.Session()
##CONSTRUCTING THE ELEMENTS OF COMPUTATION
##First lets ensure we have a Variable vector for each centroid,
##initialized to one of the vectors from the available data points
centroids = [tf.Variable((vectors[vector_indices[i]]))
for i in range(noofclusters)]
##These nodes will assign the centroid Variables the appropriate
##values
centroid_value = tf.placeholder("float64", [dim])
cent_assigns = []
for centroid in centroids:
cent_assigns.append(tf.assign(centroid, centroid_value))
##Variables for cluster assignments of individual vectors(initialized
##to 0 at first)
assignments = [tf.Variable(0) for i in range(len(vectors))]
##These nodes will assign an assignment Variable the appropriate
##value
assignment_value = tf.placeholder("int32")
cluster_assigns = []
for assignment in assignments:
cluster_assigns.append(tf.assign(assignment,
assignment_value))
##Now lets construct the node that will compute the mean
#The placeholder for the input
mean_input = tf.placeholder("float", [None, dim])
#The Node/op takes the input and computes a mean along the 0th
#dimension, i.e. the list of input vectors
mean_op = tf.reduce_mean(mean_input, 0)
##Node for computing Euclidean distances
#Placeholders for input
v1 = tf.placeholder("float", [dim])
v2 = tf.placeholder("float", [dim])
euclid_dist = tf.sqrt(tf.reduce_sum(tf.pow(tf.sub(
v1, v2), 2)))
##This node will figure out which cluster to assign a vector to,
##based on Euclidean distances of the vector from the centroids.
#Placeholder for input
centroid_distances = tf.placeholder("float", [noofclusters])
cluster_assignment = tf.argmin(centroid_distances, 0)
##INITIALIZING STATE VARIABLES
##This will help initialization of all Variables defined with respect
##to the graph. The Variable-initializer should be defined after
##all the Variables have been constructed, so that each of them
##will be included in the initialization.
init_op = tf.initialize_all_variables()
#Initialize all variables
sess.run(init_op)
##CLUSTERING ITERATIONS
#Now perform the Expectation-Maximization steps of K-Means clustering
#iterations. To keep things simple, we will only do a set number of
#iterations, instead of using a Stopping Criterion.
noofiterations = 100
for iteration_n in range(noofiterations):
##EXPECTATION STEP
##Based on the centroid locations till last iteration, compute
##the _expected_ centroid assignments.
#Iterate over each vector
for vector_n in range(len(vectors)):
vect = vectors[vector_n]
#Compute Euclidean distance between this vector and each
#centroid. Remember that this list cannot be named
#'centroid_distances', since that is the input to the
#cluster assignment node.
distances = [sess.run(euclid_dist, feed_dict={
v1: vect, v2: sess.run(centroid)})
for centroid in centroids]
#Now use the cluster assignment node, with the distances
#as the input
assignment = sess.run(cluster_assignment, feed_dict = {
centroid_distances: distances})
#Now assign the value to the appropriate state variable
sess.run(cluster_assigns[vector_n], feed_dict={
assignment_value: assignment})
##MAXIMIZATION STEP
#Based on the expected state computed from the Expectation Step,
#compute the locations of the centroids so as to maximize the
#overall objective of minimizing within-cluster Sum-of-Squares
for cluster_n in range(noofclusters):
#Collect all the vectors assigned to this cluster
assigned_vects = [vectors[i] for i in range(len(vectors))
if sess.run(assignments[i]) == cluster_n]
#Compute new centroid location
new_location = sess.run(mean_op, feed_dict={
mean_input: array(assigned_vects)})
#Assign value to appropriate variable
sess.run(cent_assigns[cluster_n], feed_dict={
centroid_value: new_location})
#Return centroids and assignments
centroids = sess.run(centroids)
assignments = sess.run(assignments)
return centroids, assignments

14
dynamic_programming/knapsack.py Normal file
View File

@ -0,0 +1,14 @@
"""
Given weights and values of n items, put these items in a knapsack of capacity W to get the maximum total value in the knapsack.
"""
def knapsack(W, wt, val, n):
dp = [[0 for i in range(W+1)]for j in range(n+1)]
for i in range(1,n+1):
for w in range(1,W+1):
if(wt[i-1]<=w):
dp[i][w] = max(val[i-1]+dp[i-1][w-wt[i-1]],dp[i-1][w])
else:
dp[i][w] = dp[i-1][w]
return dp[n][w]

48
dynamic_programming/longest common subsequence.py Normal file
View File

@ -0,0 +1,48 @@
"""
LCS Problem Statement: Given two sequences, find the length of longest subsequence present in both of them.
A subsequence is a sequence that appears in the same relative order, but not necessarily continious.
Example:"abc", "abg" are subsequences of "abcdefgh".
"""
def LCS(x,y):
b=[[] for j in range(len(x)+1)]
c=[[] for i in range(len(x))]
for i in range(len(x)+1):
b[i].append(0)
for i in range(1,len(y)+1):
b[0].append(0)
for i in range(len(x)):
for j in range(len(y)):
if x[i]==y[j]:
b[i+1].append(b[i][j]+1)
c[i].append('/')
elif b[i][j+1]>=b[i+1][j]:
b[i+1].append(b[i][j+1])
c[i].append('|')
else :
b[i+1].append(b[i+1][j])
c[i].append('-')
return b,c
def print_lcs(x,c,n,m):
n,m=n-1,m-1
ans=[]
while n>=0 and m>=0:
if c[n][m]=='/':
ans.append(x[n])
n,m=n-1,m-1
elif c[n][m]=='|':
n=n-1
else:
m=m-1
ans=ans[::-1]
return ans
if __name__=='__main__':
x=['a','b','c','b','d','a','b']
y=['b','d','c','a','b','a']
b,c=LCS(x,y)
print('Given \nX : ',x)
print('Y : ',y)
print('LCS : ',print_lcs(x,c,len(x),len(y)))

41
dynamic_programming/longest_increasing_subsequence.py Normal file
View File

@ -0,0 +1,41 @@
'''
Author : Mehdi ALAOUI
This is a pure Python implementation of Dynamic Programming solution to the longest increasing subsequence of a given sequence.
The problem is :
Given an ARRAY, to find the longest and increasing sub ARRAY in that given ARRAY and return it.
Example: [10, 22, 9, 33, 21, 50, 41, 60, 80] as input will return [10, 22, 33, 41, 60, 80] as output
'''
def longestSub(ARRAY): #This function is recursive
ARRAY_LENGTH = len(ARRAY)
if(ARRAY_LENGTH <= 1): #If the array contains only one element, we return it (it's the stop condition of recursion)
return ARRAY
#Else
PIVOT=ARRAY[0]
isFound=False
i=1
LONGEST_SUB=[]
while(not isFound and i<ARRAY_LENGTH):
if (ARRAY[i] < PIVOT):
isFound=True
TEMPORARY_ARRAY = [ element for element in ARRAY[i:] if element >= ARRAY[i] ]
TEMPORARY_ARRAY = longestSub(TEMPORARY_ARRAY)
if ( len(TEMPORARY_ARRAY) > len(LONGEST_SUB) ):
LONGEST_SUB = TEMPORARY_ARRAY
else:
i+=1
TEMPORARY_ARRAY = [ element for element in ARRAY[1:] if element >= PIVOT ]
TEMPORARY_ARRAY = [PIVOT] + longestSub(TEMPORARY_ARRAY)
if ( len(TEMPORARY_ARRAY) > len(LONGEST_SUB) ):
return TEMPORARY_ARRAY
else:
return LONGEST_SUB
#Some examples
print(longestSub([4,8,7,5,1,12,2,3,9]))
print(longestSub([9,8,7,6,5,7]))

40
dynamic_programming/longest_increasing_subsequence_O(nlogn).py Normal file
View File

@ -0,0 +1,40 @@
#############################
# Author: Aravind Kashyap
# File: lis.py
# comments: This programme outputs the Longest Strictly Increasing Subsequence in O(NLogN)
# Where N is the Number of elements in the list
#############################
def CeilIndex(v,l,r,key):
while r-l > 1:
m = (l + r)/2
if v[m] >= key:
r = m
else:
l = m
return r
def LongestIncreasingSubsequenceLength(v):
if(len(v) == 0):
return 0
tail = [0]*len(v)
length = 1
tail[0] = v[0]
for i in range(1,len(v)):
if v[i] < tail[0]:
tail[0] = v[i]
elif v[i] > tail[length-1]:
tail[length] = v[i]
length += 1
else:
tail[CeilIndex(tail,-1,length-1,v[i])] = v[i]
return length
v = [2, 5, 3, 7, 11, 8, 10, 13, 6]
print LongestIncreasingSubsequenceLength(v)

32
dynamic_programming/longest_sub_array.py Normal file
View File

@ -0,0 +1,32 @@
'''
Auther : Yvonne
This is a pure Python implementation of Dynamic Programming solution to the longest_sub_array problem.
The problem is :
Given an array, to find the longest and continuous sub array and get the max sum of the sub array in the given array.
'''
class SubArray:
def __init__(self, arr):
# we need a list not a string, so do something to change the type
self.array = arr.split(',')
print("the input array is:", self.array)
def solve_sub_array(self):
rear = [int(self.array[0])]*len(self.array)
sum_value = [int(self.array[0])]*len(self.array)
for i in range(1, len(self.array)):
sum_value[i] = max(int(self.array[i]) + sum_value[i-1], int(self.array[i]))
rear[i] = max(sum_value[i], rear[i-1])
return rear[len(self.array)-1]
if __name__ == '__main__':
whole_array = input("please input some numbers:")
array = SubArray(whole_array)
re = array.solve_sub_array()
print("the results is:", re)

59
dynamic_programming/max_sub_array.py Normal file
View File

@ -0,0 +1,59 @@
"""
author : Mayank Kumar Jha (mk9440)
"""
import time
import matplotlib.pyplot as plt
from random import randint
def find_max_sub_array(A,low,high):
if low==high:
return low,high,A[low]
else :
mid=(low+high)//2
left_low,left_high,left_sum=find_max_sub_array(A,low,mid)
right_low,right_high,right_sum=find_max_sub_array(A,mid+1,high)
cross_left,cross_right,cross_sum=find_max_cross_sum(A,low,mid,high)
if left_sum>=right_sum and left_sum>=cross_sum:
return left_low,left_high,left_sum
elif right_sum>=left_sum and right_sum>=cross_sum :
return right_low,right_high,right_sum
else:
return cross_left,cross_right,cross_sum
def find_max_cross_sum(A,low,mid,high):
left_sum,max_left=-999999999,-1
right_sum,max_right=-999999999,-1
summ=0
for i in range(mid,low-1,-1):
summ+=A[i]
if summ > left_sum:
left_sum=summ
max_left=i
summ=0
for i in range(mid+1,high+1):
summ+=A[i]
if summ > right_sum:
right_sum=summ
max_right=i
return max_left,max_right,(left_sum+right_sum)
if __name__=='__main__':
inputs=[10,100,1000,10000,50000,100000,200000,300000,400000,500000]
tim=[]
for i in inputs:
li=[randint(1,i) for j in range(i)]
strt=time.time()
(find_max_sub_array(li,0,len(li)-1))
end=time.time()
tim.append(end-strt)
print("No of Inputs Time Taken")
for i in range(len(inputs)):
print(inputs[i],'\t\t',tim[i])
plt.plot(inputs,tim)
plt.xlabel("Number of Inputs");plt.ylabel("Time taken in seconds ")
plt.show()

28
dynamic_programming/minimum_partition.py Normal file
View File

@ -0,0 +1,28 @@
"""
Partition a set into two subsets such that the difference of subset sums is minimum
"""
def findMin(arr):
n = len(arr)
s = sum(arr)
dp = [[False for x in range(s+1)]for y in range(n+1)]
for i in range(1, n+1):
dp[i][0] = True
for i in range(1, s+1):
dp[0][i] = False
for i in range(1, n+1):
for j in range(1, s+1):
dp[i][j]= dp[i][j-1]
if (arr[i-1] <= j):
dp[i][j] = dp[i][j] or dp[i-1][j-arr[i-1]]
for j in range(s/2, -1, -1):
if dp[n][j] == True:
diff = s-2*j
break;
return diff

107
hashes/md5.py Normal file
View File

@ -0,0 +1,107 @@
import math
def rearrange(bitString32):
if len(bitString32) != 32:
raise ValueError("Need length 32")
newString = ""
for i in [3,2,1,0]:
newString += bitString32[8*i:8*i+8]
return newString
def reformatHex(i):
hexrep = format(i,'08x')
thing = ""
for i in [3,2,1,0]:
thing += hexrep[2*i:2*i+2]
return thing
def pad(bitString):
startLength = len(bitString)
bitString += '1'
while len(bitString) % 512 != 448:
bitString += '0'
lastPart = format(startLength,'064b')
bitString += rearrange(lastPart[32:]) + rearrange(lastPart[:32])
return bitString
def getBlock(bitString):
currPos = 0
while currPos < len(bitString):
currPart = bitString[currPos:currPos+512]
mySplits = []
for i in range(16):
mySplits.append(int(rearrange(currPart[32*i:32*i+32]),2))
yield mySplits
currPos += 512
def not32(i):
i_str = format(i,'032b')
new_str = ''
for c in i_str:
new_str += '1' if c=='0' else '0'
return int(new_str,2)
def sum32(a,b):
return (a + b) % 2**32
def leftrot32(i,s):
return (i << s) ^ (i >> (32-s))
def md5me(testString):
bs =''
for i in testString:
bs += format(ord(i),'08b')
bs = pad(bs)
tvals = [int(2**32 * abs(math.sin(i+1))) for i in range(64)]
a0 = 0x67452301
b0 = 0xefcdab89
c0 = 0x98badcfe
d0 = 0x10325476
s = [7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, \
5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, \
4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, \
6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21 ]
for m in getBlock(bs):
A = a0
B = b0
C = c0
D = d0
for i in range(64):
if i <= 15:
#f = (B & C) | (not32(B) & D)
f = D ^ (B & (C ^ D))
g = i
elif i<= 31:
#f = (D & B) | (not32(D) & C)
f = C ^ (D & (B ^ C))
g = (5*i+1) % 16
elif i <= 47:
f = B ^ C ^ D
g = (3*i+5) % 16
else:
f = C ^ (B | not32(D))
g = (7*i) % 16
dtemp = D
D = C
C = B
B = sum32(B,leftrot32((A + f + tvals[i] + m[g]) % 2**32, s[i]))
A = dtemp
a0 = sum32(a0, A)
b0 = sum32(b0, B)
c0 = sum32(c0, C)
d0 = sum32(d0, D)
digest = reformatHex(a0) + reformatHex(b0) + reformatHex(c0) + reformatHex(d0)
return digest
def test():
assert md5me("") == "d41d8cd98f00b204e9800998ecf8427e"
assert md5me("The quick brown fox jumps over the lazy dog") == "9e107d9d372bb6826bd81d3542a419d6"
print("Success.")
if __name__ == "__main__":
test()

139
machine_learning/decision_tree.py Normal file
View File

@ -0,0 +1,139 @@
"""
Implementation of a basic regression decision tree.
Input data set: The input data set must be 1-dimensional with continuous labels.
Output: The decision tree maps a real number input to a real number output.
"""
import numpy as np
class Decision_Tree:
def __init__(self, depth = 5, min_leaf_size = 5):
self.depth = depth
self.decision_boundary = 0
self.left = None
self.right = None
self.min_leaf_size = min_leaf_size
self.prediction = None
def mean_squared_error(self, labels, prediction):
"""
mean_squared_error:
@param labels: a one dimensional numpy array
@param prediction: a floating point value
return value: mean_squared_error calculates the error if prediction is used to estimate the labels
"""
if labels.ndim != 1:
print("Error: Input labels must be one dimensional")
return np.mean((labels - prediction) ** 2)
def train(self, X, y):
"""
train:
@param X: a one dimensional numpy array
@param y: a one dimensional numpy array.
The contents of y are the labels for the corresponding X values
train does not have a return value
"""
"""
this section is to check that the inputs conform to our dimensionality constraints
"""
if X.ndim != 1:
print("Error: Input data set must be one dimensional")
return
if len(X) != len(y):
print("Error: X and y have different lengths")
return
if y.ndim != 1:
print("Error: Data set labels must be one dimensional")
return
if len(X) < 2 * self.min_leaf_size:
self.prediction = np.mean(y)
return
if self.depth == 1:
self.prediction = np.mean(y)
return
best_split = 0
min_error = self.mean_squared_error(X,np.mean(y)) * 2
"""
loop over all possible splits for the decision tree. find the best split.
if no split exists that is less than 2 * error for the entire array
then the data set is not split and the average for the entire array is used as the predictor
"""
for i in range(len(X)):
if len(X[:i]) < self.min_leaf_size:
continue
elif len(X[i:]) < self.min_leaf_size:
continue
else:
error_left = self.mean_squared_error(X[:i], np.mean(y[:i]))
error_right = self.mean_squared_error(X[i:], np.mean(y[i:]))
error = error_left + error_right
if error < min_error:
best_split = i
min_error = error
if best_split != 0:
left_X = X[:best_split]
left_y = y[:best_split]
right_X = X[best_split:]
right_y = y[best_split:]
self.decision_boundary = X[best_split]
self.left = Decision_Tree(depth = self.depth - 1, min_leaf_size = self.min_leaf_size)
self.right = Decision_Tree(depth = self.depth - 1, min_leaf_size = self.min_leaf_size)
self.left.train(left_X, left_y)
self.right.train(right_X, right_y)
else:
self.prediction = np.mean(y)
return
def predict(self, x):
"""
predict:
@param x: a floating point value to predict the label of
the prediction function works by recursively calling the predict function
of the appropriate subtrees based on the tree's decision boundary
"""
if self.prediction is not None:
return self.prediction
elif self.left or self.right is not None:
if x >= self.decision_boundary:
return self.right.predict(x)
else:
return self.left.predict(x)
else:
print("Error: Decision tree not yet trained")
return None
def main():
"""
In this demonstration we're generating a sample data set from the sin function in numpy.
We then train a decision tree on the data set and use the decision tree to predict the
label of 10 different test values. Then the mean squared error over this test is displayed.
"""
X = np.arange(-1., 1., 0.005)
y = np.sin(X)
tree = Decision_Tree(depth = 10, min_leaf_size = 10)
tree.train(X,y)
test_cases = (np.random.rand(10) * 2) - 1
predictions = np.array([tree.predict(x) for x in test_cases])
avg_error = np.mean((predictions - test_cases) ** 2)
print("Test values: " + str(test_cases))
print("Predictions: " + str(predictions))
print("Average error: " + str(avg_error))
if __name__ == '__main__':
main()

121
machine_learning/gradient_descent.py Normal file
View File

@ -0,0 +1,121 @@
"""
Implementation of gradient descent algorithm for minimizing cost of a linear hypothesis function.
"""
import numpy
# List of input, output pairs
train_data = (((5, 2, 3), 15), ((6, 5, 9), 25),
((11, 12, 13), 41), ((1, 1, 1), 8), ((11, 12, 13), 41))
test_data = (((515, 22, 13), 555), ((61, 35, 49), 150))
parameter_vector = [2, 4, 1, 5]
m = len(train_data)
LEARNING_RATE = 0.009
def _error(example_no, data_set='train'):
"""
:param data_set: train data or test data
:param example_no: example number whose error has to be checked
:return: error in example pointed by example number.
"""
return calculate_hypothesis_value(example_no, data_set) - output(example_no, data_set)
def _hypothesis_value(data_input_tuple):
"""
Calculates hypothesis function value for a given input
:param data_input_tuple: Input tuple of a particular example
:return: Value of hypothesis function at that point.
Note that there is an 'biased input' whose value is fixed as 1.
It is not explicitly mentioned in input data.. But, ML hypothesis functions use it.
So, we have to take care of it separately. Line 36 takes care of it.
"""
hyp_val = 0
for i in range(len(parameter_vector) - 1):
hyp_val += data_input_tuple[i]*parameter_vector[i+1]
hyp_val += parameter_vector[0]
return hyp_val
def output(example_no, data_set):
"""
:param data_set: test data or train data
:param example_no: example whose output is to be fetched
:return: output for that example
"""
if data_set == 'train':
return train_data[example_no][1]
elif data_set == 'test':
return test_data[example_no][1]
def calculate_hypothesis_value(example_no, data_set):
"""
Calculates hypothesis value for a given example
:param data_set: test data or train_data
:param example_no: example whose hypothesis value is to be calculated
:return: hypothesis value for that example
"""
if data_set == "train":
return _hypothesis_value(train_data[example_no][0])
elif data_set == "test":
return _hypothesis_value(test_data[example_no][0])
def summation_of_cost_derivative(index, end=m):
"""
Calculates the sum of cost function derivative
:param index: index wrt derivative is being calculated
:param end: value where summation ends, default is m, number of examples
:return: Returns the summation of cost derivative
Note: If index is -1, this means we are calculating summation wrt to biased parameter.
"""
summation_value = 0
for i in range(end):
if index == -1:
summation_value += _error(i)
else:
summation_value += _error(i)*train_data[i][0][index]
return summation_value
def get_cost_derivative(index):
"""
:param index: index of the parameter vector wrt to derivative is to be calculated
:return: derivative wrt to that index
Note: If index is -1, this means we are calculating summation wrt to biased parameter.
"""
cost_derivative_value = summation_of_cost_derivative(index, m)/m
return cost_derivative_value
def run_gradient_descent():
global parameter_vector
# Tune these values to set a tolerance value for predicted output
absolute_error_limit = 0.000002
relative_error_limit = 0
j = 0
while True:
j += 1
temp_parameter_vector = [0, 0, 0, 0]
for i in range(0, len(parameter_vector)):
cost_derivative = get_cost_derivative(i-1)
temp_parameter_vector[i] = parameter_vector[i] - \
LEARNING_RATE*cost_derivative
if numpy.allclose(parameter_vector, temp_parameter_vector,
atol=absolute_error_limit, rtol=relative_error_limit):
break
parameter_vector = temp_parameter_vector
print("Number of iterations:", j)
def test_gradient_descent():
for i in range(len(test_data)):
print("Actual output value:", output(i, 'test'))
print("Hypothesis output:", calculate_hypothesis_value(i, 'test'))
if __name__ == '__main__':
run_gradient_descent()
print("\nTesting gradient descent for a linear hypothesis function.\n")
test_gradient_descent()

172
machine_learning/k_means_clust.py Normal file
View File

@ -0,0 +1,172 @@
'''README, Author - Anurag Kumar(mailto:anuragkumarak95@gmail.com)
Requirements:
- sklearn
- numpy
- matplotlib
Python:
- 3.5
Inputs:
- X , a 2D numpy array of features.
- k , number of clusters to create.
- initial_centroids , initial centroid values generated by utility function(mentioned in usage).
- maxiter , maximum number of iterations to process.
- heterogeneity , empty list that will be filled with hetrogeneity values if passed to kmeans func.
Usage:
1. define 'k' value, 'X' features array and 'hetrogeneity' empty list
2. create initial_centroids,
initial_centroids = get_initial_centroids(
X,
k,
seed=0 # seed value for initial centroid generation, None for randomness(default=None)
)
3. find centroids and clusters using kmeans function.
centroids, cluster_assignment = kmeans(
X,
k,
initial_centroids,
maxiter=400,
record_heterogeneity=heterogeneity,
verbose=True # whether to print logs in console or not.(default=False)
)
4. Plot the loss function, hetrogeneity values for every iteration saved in hetrogeneity list.
plot_heterogeneity(
heterogeneity,
k
)
5. Have fun..
'''
from sklearn.metrics import pairwise_distances
import numpy as np
TAG = 'K-MEANS-CLUST/ '
def get_initial_centroids(data, k, seed=None):
'''Randomly choose k data points as initial centroids'''
if seed is not None: # useful for obtaining consistent results
np.random.seed(seed)
n = data.shape[0] # number of data points
# Pick K indices from range [0, N).
rand_indices = np.random.randint(0, n, k)
# Keep centroids as dense format, as many entries will be nonzero due to averaging.
# As long as at least one document in a cluster contains a word,
# it will carry a nonzero weight in the TF-IDF vector of the centroid.
centroids = data[rand_indices,:]
return centroids
def centroid_pairwise_dist(X,centroids):
return pairwise_distances(X,centroids,metric='euclidean')
def assign_clusters(data, centroids):
# Compute distances between each data point and the set of centroids:
# Fill in the blank (RHS only)
distances_from_centroids = centroid_pairwise_dist(data,centroids)
# Compute cluster assignments for each data point:
# Fill in the blank (RHS only)
cluster_assignment = np.argmin(distances_from_centroids,axis=1)
return cluster_assignment
def revise_centroids(data, k, cluster_assignment):
new_centroids = []
for i in range(k):
# Select all data points that belong to cluster i. Fill in the blank (RHS only)
member_data_points = data[cluster_assignment==i]
# Compute the mean of the data points. Fill in the blank (RHS only)
centroid = member_data_points.mean(axis=0)
new_centroids.append(centroid)
new_centroids = np.array(new_centroids)
return new_centroids
def compute_heterogeneity(data, k, centroids, cluster_assignment):
heterogeneity = 0.0
for i in range(k):
# Select all data points that belong to cluster i. Fill in the blank (RHS only)
member_data_points = data[cluster_assignment==i, :]
if member_data_points.shape[0] > 0: # check if i-th cluster is non-empty
# Compute distances from centroid to data points (RHS only)
distances = pairwise_distances(member_data_points, [centroids[i]], metric='euclidean')
squared_distances = distances**2
heterogeneity += np.sum(squared_distances)
return heterogeneity
from matplotlib import pyplot as plt
def plot_heterogeneity(heterogeneity, k):
plt.figure(figsize=(7,4))
plt.plot(heterogeneity, linewidth=4)
plt.xlabel('# Iterations')
plt.ylabel('Heterogeneity')
plt.title('Heterogeneity of clustering over time, K={0:d}'.format(k))
plt.rcParams.update({'font.size': 16})
plt.show()
def kmeans(data, k, initial_centroids, maxiter=500, record_heterogeneity=None, verbose=False):
'''This function runs k-means on given data and initial set of centroids.
maxiter: maximum number of iterations to run.(default=500)
record_heterogeneity: (optional) a list, to store the history of heterogeneity as function of iterations
if None, do not store the history.
verbose: if True, print how many data points changed their cluster labels in each iteration'''
centroids = initial_centroids[:]
prev_cluster_assignment = None
for itr in range(maxiter):
if verbose:
print(itr, end='')
# 1. Make cluster assignments using nearest centroids
cluster_assignment = assign_clusters(data,centroids)
# 2. Compute a new centroid for each of the k clusters, averaging all data points assigned to that cluster.
centroids = revise_centroids(data,k, cluster_assignment)
# Check for convergence: if none of the assignments changed, stop
if prev_cluster_assignment is not None and \
(prev_cluster_assignment==cluster_assignment).all():
break
# Print number of new assignments
if prev_cluster_assignment is not None:
num_changed = np.sum(prev_cluster_assignment!=cluster_assignment)
if verbose:
print(' {0:5d} elements changed their cluster assignment.'.format(num_changed))
# Record heterogeneity convergence metric
if record_heterogeneity is not None:
# YOUR CODE HERE
score = compute_heterogeneity(data,k,centroids,cluster_assignment)
record_heterogeneity.append(score)
prev_cluster_assignment = cluster_assignment[:]
return centroids, cluster_assignment
# Mock test below
if False: # change to true to run this test case.
import sklearn.datasets as ds
dataset = ds.load_iris()
k = 3
heterogeneity = []
initial_centroids = get_initial_centroids(dataset['data'], k, seed=0)
centroids, cluster_assignment = kmeans(dataset['data'], k, initial_centroids, maxiter=400,
record_heterogeneity=heterogeneity, verbose=True)
plot_heterogeneity(heterogeneity, k)

108
machine_learning/linear_regression.py Normal file
View File

@ -0,0 +1,108 @@
"""
Linear regression is the most basic type of regression commonly used for
predictive analysis. The idea is preety simple, we have a dataset and we have
a feature's associated with it. The Features should be choose very cautiously
as they determine, how much our model will be able to make future predictions.
We try to set these Feature weights, over many iterations, so that they best
fits our dataset. In this particular code, i had used a CSGO dataset (ADR vs
Rating). We try to best fit a line through dataset and estimate the parameters.
"""
import requests
import numpy as np
def collect_dataset():
""" Collect dataset of CSGO
The dataset contains ADR vs Rating of a Player
:return : dataset obtained from the link, as matrix
"""
response = requests.get('https://raw.githubusercontent.com/yashLadha/' +
'The_Math_of_Intelligence/master/Week1/ADRvs' +
'Rating.csv')
lines = response.text.splitlines()
data = []
for item in lines:
item = item.split(',')
data.append(item)
data.pop(0) # This is for removing the labels from the list
dataset = np.matrix(data)
return dataset
def run_steep_gradient_descent(data_x, data_y,
len_data, alpha, theta):
""" Run steep gradient descent and updates the Feature vector accordingly_
:param data_x : contains the dataset
:param data_y : contains the output associated with each data-entry
:param len_data : length of the data_
:param alpha : Learning rate of the model
:param theta : Feature vector (weight's for our model)
;param return : Updated Feature's, using
curr_features - alpha_ * gradient(w.r.t. feature)
"""
n = len_data
prod = np.dot(theta, data_x.transpose())
prod -= data_y.transpose()
sum_grad = np.dot(prod, data_x)
theta = theta - (alpha / n) * sum_grad
return theta
def sum_of_square_error(data_x, data_y, len_data, theta):
""" Return sum of square error for error calculation
:param data_x : contains our dataset
:param data_y : contains the output (result vector)
:param len_data : len of the dataset
:param theta : contains the feature vector
:return : sum of square error computed from given feature's
"""
error = 0.0
prod = np.dot(theta, data_x.transpose())
prod -= data_y.transpose()
sum_elem = np.sum(np.square(prod))
error = sum_elem / (2 * len_data)
return error
def run_linear_regression(data_x, data_y):
""" Implement Linear regression over the dataset
:param data_x : contains our dataset
:param data_y : contains the output (result vector)
:return : feature for line of best fit (Feature vector)
"""
iterations = 100000
alpha = 0.0001550
no_features = data_x.shape[1]
len_data = data_x.shape[0] - 1
theta = np.zeros((1, no_features))
for i in range(0, iterations):
theta = run_steep_gradient_descent(data_x, data_y,
len_data, alpha, theta)
error = sum_of_square_error(data_x, data_y, len_data, theta)
print('At Iteration %d - Error is %.5f ' % (i + 1, error))
return theta
def main():
""" Driver function """
data = collect_dataset()
len_data = data.shape[0]
data_x = np.c_[np.ones(len_data), data[:, :-1]].astype(float)
data_y = data[:, -1].astype(float)
theta = run_linear_regression(data_x, data_y)
len_result = theta.shape[1]
print('Resultant Feature vector : ')
for i in range(0, len_result):
print('%.5f' % (theta[0, i]))
if __name__ == '__main__':
main()

123
machine_learning/perceptron.py Normal file
View File

@ -0,0 +1,123 @@
'''
Perceptron
w = w + N * (d(k) - y) * x(k)
Using perceptron network for oil analysis,
with Measuring of 3 parameters that represent chemical characteristics we can classify the oil, in p1 or p2
p1 = -1
p2 = 1
'''
import random
class Perceptron:
def __init__(self, sample, exit, learn_rate=0.01, epoch_number=1000, bias=-1):
self.sample = sample
self.exit = exit
self.learn_rate = learn_rate
self.epoch_number = epoch_number
self.bias = bias
self.number_sample = len(sample)
self.col_sample = len(sample[0])
self.weight = []
def trannig(self):
for sample in self.sample:
sample.insert(0, self.bias)
for i in range(self.col_sample):
self.weight.append(random.random())
self.weight.insert(0, self.bias)
epoch_count = 0
while True:
erro = False
for i in range(self.number_sample):
u = 0
for j in range(self.col_sample + 1):
u = u + self.weight[j] * self.sample[i][j]
y = self.sign(u)
if y != self.exit[i]:
for j in range(self.col_sample + 1):
self.weight[j] = self.weight[j] + self.learn_rate * (self.exit[i] - y) * self.sample[i][j]
erro = True
#print('Epoch: \n',epoch_count)
epoch_count = epoch_count + 1
# if you want controle the epoch or just by erro
if erro == False:
print('\nEpoch:\n',epoch_count)
print('------------------------\n')
#if epoch_count > self.epoch_number or not erro:
break
def sort(self, sample):
sample.insert(0, self.bias)
u = 0
for i in range(self.col_sample + 1):
u = u + self.weight[i] * sample[i]
y = self.sign(u)
if y == -1:
print('Sample: ', sample)
print('classification: P1')
else:
print('Sample: ', sample)
print('classification: P2')
def sign(self, u):
return 1 if u >= 0 else -1
samples = [
[-0.6508, 0.1097, 4.0009],
[-1.4492, 0.8896, 4.4005],
[2.0850, 0.6876, 12.0710],
[0.2626, 1.1476, 7.7985],
[0.6418, 1.0234, 7.0427],
[0.2569, 0.6730, 8.3265],
[1.1155, 0.6043, 7.4446],
[0.0914, 0.3399, 7.0677],
[0.0121, 0.5256, 4.6316],
[-0.0429, 0.4660, 5.4323],
[0.4340, 0.6870, 8.2287],
[0.2735, 1.0287, 7.1934],
[0.4839, 0.4851, 7.4850],
[0.4089, -0.1267, 5.5019],
[1.4391, 0.1614, 8.5843],
[-0.9115, -0.1973, 2.1962],
[0.3654, 1.0475, 7.4858],
[0.2144, 0.7515, 7.1699],
[0.2013, 1.0014, 6.5489],
[0.6483, 0.2183, 5.8991],
[-0.1147, 0.2242, 7.2435],
[-0.7970, 0.8795, 3.8762],
[-1.0625, 0.6366, 2.4707],
[0.5307, 0.1285, 5.6883],
[-1.2200, 0.7777, 1.7252],
[0.3957, 0.1076, 5.6623],
[-0.1013, 0.5989, 7.1812],
[2.4482, 0.9455, 11.2095],
[2.0149, 0.6192, 10.9263],
[0.2012, 0.2611, 5.4631]
]
exit = [-1, -1, -1, 1, 1, -1, 1, -1, 1, 1, -1, 1, -1, -1, -1, -1, 1, 1, 1, 1, -1, 1, 1, 1, 1, -1, -1, 1, -1, 1]
network = Perceptron(sample=samples, exit = exit, learn_rate=0.01, epoch_number=1000, bias=-1)
network.trannig()
while True:
sample = []
for i in range(3):
sample.insert(i, float(input('value: ')))
network.sort(sample)

63
machine_learning/scoring_functions.py Normal file
View File

@ -0,0 +1,63 @@
import numpy
""" Here I implemented the scoring functions.
MAE, MSE, RMSE, RMSLE are included.
Those are used for calculating differences between
predicted values and actual values.
Metrics are slightly differentiated. Sometimes squared, rooted,
even log is used.
Using log and roots can be perceived as tools for penalizing big
erors. However, using appropriate metrics depends on the situations,
and types of data
"""
#Mean Absolute Error
def mae(predict, actual):
predict = np.array(predict)
actual = np.array(actual)
difference = abs(predict - actual)
score = difference.mean()
return score
#Mean Squared Error
def mse(predict, actual):
predict = np.array(predict)
actual = np.array(actual)
difference = predict - actual
square_diff = np.square(difference)
score = square_diff.mean()
return score
#Root Mean Squared Error
def rmse(predict, actual):
predict = np.array(predict)
actual = np.array(actual)
difference = predict - actual
square_diff = np.square(dfference)
mean_square_diff = square_diff.mean()
score = np.sqrt(mean_square_diff)
return score
#Root Mean Square Logarithmic Error
def rmsle(predict, actual):
predict = np.array(predict)
actual = np.array(actual)
log_predict = np.log(predict+1)
log_actual = np.log(actual+1)
difference = log_predict - log_actual
square_diff = np.square(difference)
mean_square_diff = square_diff.mean()
score = np.sqrt(mean_square_diff)
return score

45333
other/Dictionary.txt Normal file
View File

File diff suppressed because it is too large Load Diff

18
other/FindingPrimes.py Normal file
View File

@ -0,0 +1,18 @@
'''
-The sieve of Eratosthenes is an algorithm used to find prime numbers, less than or equal to a given value.
-Illustration: https://upload.wikimedia.org/wikipedia/commons/b/b9/Sieve_of_Eratosthenes_animation.gif
'''
from math import sqrt
def SOE(n):
check = round(sqrt(n)) #Need not check for multiples past the square root of n
sieve = [False if i <2 else True for i in range(n+1)] #Set every index to False except for index 0 and 1
for i in range(2, check):
if(sieve[i] == True): #If i is a prime
for j in range(i+i, n+1, i): #Step through the list in increments of i(the multiples of the prime)
sieve[j] = False #Sets every multiple of i to False
for i in range(n+1):
if(sieve[i] == True):
print(i, end=" ")

34
other/LinearCongruentialGenerator.py Normal file
View File

@ -0,0 +1,34 @@
__author__ = "Tobias Carryer"
from time import time
class LinearCongruentialGenerator(object):
"""
A pseudorandom number generator.
"""
def __init__( self, multiplier, increment, modulo, seed=int(time()) ):
"""
These parameters are saved and used when nextNumber() is called.
modulo is the largest number that can be generated (exclusive). The most
efficent values are powers of 2. 2^32 is a common value.
"""
self.multiplier = multiplier
self.increment = increment
self.modulo = modulo
self.seed = seed
def next_number( self ):
"""
The smallest number that can be generated is zero.
The largest number that can be generated is modulo-1. modulo is set in the constructor.
"""
self.seed = (self.multiplier * self.seed + self.increment) % self.modulo
return self.seed
if __name__ == "__main__":
# Show the LCG in action.
lcg = LinearCongruentialGenerator(1664525, 1013904223, 2<<31)
while True :
print lcg.next_number()

28
other/anagrams.py Normal file
View File

@ -0,0 +1,28 @@
import collections, pprint, time, os
start_time = time.time()
print('creating word list...')
path = os.path.split(os.path.realpath(__file__))
word_list = sorted(list(set([word.strip().lower() for word in open(path[0] + '/words')])))
def signature(word):
return ''.join(sorted(word))
word_bysig = collections.defaultdict(list)
for word in word_list:
word_bysig[signature(word)].append(word)
def anagram(myword):
return word_bysig[signature(myword)]
print('finding anagrams...')
all_anagrams = {word: anagram(word)
for word in word_list if len(anagram(word)) > 1}
print('writing anagrams to file...')
with open('anagrams.txt', 'w') as file:
file.write('all_anagrams = ')
file.write(pprint.pformat(all_anagrams))
total_time = round(time.time() - start_time, 2)
print('Done [', total_time, 'seconds ]')

49
other/binary_exponentiation.py Normal file
View File

@ -0,0 +1,49 @@
"""
* Binary Exponentiation for Powers
* This is a method to find a^b in a time complexity of O(log b)
* This is one of the most commonly used methods of finding powers.
* Also useful in cases where solution to (a^b)%c is required,
* where a,b,c can be numbers over the computers calculation limits.
* Done using iteration, can also be done using recursion
* @author chinmoy159
* @version 1.0 dated 10/08/2017
"""
def b_expo(a, b):
res = 1
while b > 0:
if b&1:
res *= a
a *= a
b >>= 1
return res
def b_expo_mod(a, b, c):
res = 1
while b > 0:
if b&1:
res = ((res%c) * (a%c)) % c
a *= a
b >>= 1
return res
"""
* Wondering how this method works !
* It's pretty simple.
* Let's say you need to calculate a ^ b
* RULE 1 : a ^ b = (a*a) ^ (b/2) ---- example : 4 ^ 4 = (4*4) ^ (4/2) = 16 ^ 2
* RULE 2 : IF b is ODD, then ---- a ^ b = a * (a ^ (b - 1)) :: where (b - 1) is even.
* Once b is even, repeat the process to get a ^ b
* Repeat the process till b = 1 OR b = 0, because a^1 = a AND a^0 = 1
*
* As far as the modulo is concerned,
* the fact : (a*b) % c = ((a%c) * (b%c)) % c
* Now apply RULE 1 OR 2 whichever is required.
"""

50
other/binary_exponentiation_2.py Normal file
View File

@ -0,0 +1,50 @@
"""
* Binary Exponentiation with Multiplication
* This is a method to find a*b in a time complexity of O(log b)
* This is one of the most commonly used methods of finding result of multiplication.
* Also useful in cases where solution to (a*b)%c is required,
* where a,b,c can be numbers over the computers calculation limits.
* Done using iteration, can also be done using recursion
* @author chinmoy159
* @version 1.0 dated 10/08/2017
"""
def b_expo(a, b):
res = 0
while b > 0:
if b&1:
res += a
a += a
b >>= 1
return res
def b_expo_mod(a, b, c):
res = 0
while b > 0:
if b&1:
res = ((res%c) + (a%c)) % c
a += a
b >>= 1
return res
"""
* Wondering how this method works !
* It's pretty simple.
* Let's say you need to calculate a ^ b
* RULE 1 : a * b = (a+a) * (b/2) ---- example : 4 * 4 = (4+4) * (4/2) = 8 * 2
* RULE 2 : IF b is ODD, then ---- a * b = a + (a * (b - 1)) :: where (b - 1) is even.
* Once b is even, repeat the process to get a * b
* Repeat the process till b = 1 OR b = 0, because a*1 = a AND a*0 = 0
*
* As far as the modulo is concerned,
* the fact : (a+b) % c = ((a%c) + (b%c)) % c
* Now apply RULE 1 OR 2, whichever is required.
"""

55
other/detecting_english_programmatically.py Normal file
View File

@ -0,0 +1,55 @@
import os
UPPERLETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
LETTERS_AND_SPACE = UPPERLETTERS + UPPERLETTERS.lower() + ' \t\n'
def loadDictionary():
path = os.path.split(os.path.realpath(__file__))
dictionaryFile = open(path[0] + '/Dictionary.txt')
englishWords = {}
for word in dictionaryFile.read().split('\n'):
englishWords[word] = None
dictionaryFile.close()
return englishWords
ENGLISH_WORDS = loadDictionary()
def getEnglishCount(message):
message = message.upper()
message = removeNonLetters(message)
possibleWords = message.split()
if possibleWords == []:
return 0.0
matches = 0
for word in possibleWords:
if word in ENGLISH_WORDS:
matches += 1
return float(matches) / len(possibleWords)
def removeNonLetters(message):
lettersOnly = []
for symbol in message:
if symbol in LETTERS_AND_SPACE:
lettersOnly.append(symbol)
return ''.join(lettersOnly)
def isEnglish(message, wordPercentage = 20, letterPercentage = 85):
"""
>>> isEnglish('Hello World')
True
>>> isEnglish('llold HorWd')
False
"""
wordsMatch = getEnglishCount(message) * 100 >= wordPercentage
numLetters = len(removeNonLetters(message))
messageLettersPercentage = (float(numLetters) / len(message)) * 100
lettersMatch = messageLettersPercentage >= letterPercentage
return wordsMatch and lettersMatch
import doctest
doctest.testmod()

18
other/euclidean_gcd.py Normal file
View File

@ -0,0 +1,18 @@
# https://en.wikipedia.org/wiki/Euclidean_algorithm
def euclidean_gcd(a, b):
while b:
t = b
b = a % b
a = t
return a
def main():
print("GCD(3, 5) = " + str(euclidean_gcd(3, 5)))
print("GCD(5, 3) = " + str(euclidean_gcd(5, 3)))
print("GCD(1, 3) = " + str(euclidean_gcd(1, 3)))
print("GCD(3, 6) = " + str(euclidean_gcd(3, 6)))
print("GCD(6, 3) = " + str(euclidean_gcd(6, 3)))
if __name__ == '__main__':
main()

68
other/frequency_finder.py Normal file
View File

@ -0,0 +1,68 @@
# Frequency Finder
# frequency taken from http://en.wikipedia.org/wiki/Letter_frequency
englishLetterFreq = {'E': 12.70, 'T': 9.06, 'A': 8.17, 'O': 7.51, 'I': 6.97,
'N': 6.75, 'S': 6.33, 'H': 6.09, 'R': 5.99, 'D': 4.25,
'L': 4.03, 'C': 2.78, 'U': 2.76, 'M': 2.41, 'W': 2.36,
'F': 2.23, 'G': 2.02, 'Y': 1.97, 'P': 1.93, 'B': 1.29,
'V': 0.98, 'K': 0.77, 'J': 0.15, 'X': 0.15, 'Q': 0.10,
'Z': 0.07}
ETAOIN = 'ETAOINSHRDLCUMWFGYPBVKJXQZ'
LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
def getLetterCount(message):
letterCount = {'A': 0, 'B': 0, 'C': 0, 'D': 0, 'E': 0, 'F': 0, 'G': 0, 'H': 0,
'I': 0, 'J': 0, 'K': 0, 'L': 0, 'M': 0, 'N': 0, 'O': 0, 'P': 0,
'Q': 0, 'R': 0, 'S': 0, 'T': 0, 'U': 0, 'V': 0, 'W': 0, 'X': 0,
'Y': 0, 'Z': 0}
for letter in message.upper():
if letter in LETTERS:
letterCount[letter] += 1
return letterCount
def getItemAtIndexZero(x):
return x[0]
def getFrequencyOrder(message):
letterToFreq = getLetterCount(message)
freqToLetter = {}
for letter in LETTERS:
if letterToFreq[letter] not in freqToLetter:
freqToLetter[letterToFreq[letter]] = [letter]
else:
freqToLetter[letterToFreq[letter]].append(letter)
for freq in freqToLetter:
freqToLetter[freq].sort(key = ETAOIN.find, reverse = True)
freqToLetter[freq] = ''.join(freqToLetter[freq])
freqPairs = list(freqToLetter.items())
freqPairs.sort(key = getItemAtIndexZero, reverse = True)
freqOrder = []
for freqPair in freqPairs:
freqOrder.append(freqPair[1])
return ''.join(freqOrder)
def englishFreqMatchScore(message):
'''
>>> englishFreqMatchScore('Hello World')
1
'''
freqOrder = getFrequencyOrder(message)
matchScore = 0
for commonLetter in ETAOIN[:6]:
if commonLetter in freqOrder[:6]:
matchScore += 1
for uncommonLetter in ETAOIN[-6:]:
if uncommonLetter in freqOrder[-6:]:
matchScore += 1
return matchScore
if __name__ == '__main__':
import doctest
doctest.testmod()

49
other/nested_brackets.py Normal file
View File

@ -0,0 +1,49 @@
'''
The nested brackets problem is a problem that determines if a sequence of
brackets are properly nested. A sequence of brackets s is considered properly nested
if any of the following conditions are true:
- s is empty
- s has the form (U) or [U] or {U} where U is a properly nested string
- s has the form VW where V and W are properly nested strings
For example, the string "()()[()]" is properly nested but "[(()]" is not.
The function called is_balanced takes as input a string S which is a sequence of brackets and
returns true if S is nested and false otherwise.
'''
def is_balanced(S):
stack = []
open_brackets = set({'(', '[', '{'})
closed_brackets = set({')', ']', '}'})
open_to_closed = dict({'{':'}', '[':']', '(':')'})
for i in range(len(S)):
if S[i] in open_brackets:
stack.append(S[i])
elif S[i] in closed_brackets:
if len(stack) == 0 or (len(stack) > 0 and open_to_closed[stack.pop()] != S[i]):
return False
return len(stack) == 0
def main():
S = input("Enter sequence of brackets: ")
if is_balanced(S):
print(S, "is balanced")
else:
print(S, "is not balanced")
if __name__ == "__main__":
main()

14
other/password_generator.py Normal file
View File

@ -0,0 +1,14 @@
import string
import random
letters = [letter for letter in string.ascii_letters]
digits = [digit for digit in string.digits]
symbols = [symbol for symbol in string.punctuation]
chars = letters + digits + symbols
random.shuffle(chars)
min_length = 8
max_length = 16
password = ''.join(random.choice(chars) for x in range(random.randint(min_length, max_length)))
print('Password: ' + password)
print('[ If you are thinking of using this passsword, You better save it. ]')

25
other/tower_of_hanoi.py Normal file
View File

@ -0,0 +1,25 @@
def moveTower(height, fromPole, toPole, withPole):
'''
>>> moveTower(3, 'A', 'B', 'C')
moving disk from A to B
moving disk from A to C
moving disk from B to C
moving disk from A to B
moving disk from C to A
moving disk from C to B
moving disk from A to B
'''
if height >= 1:
moveTower(height-1, fromPole, withPole, toPole)
moveDisk(fromPole, toPole)
moveTower(height-1, withPole, toPole, fromPole)
def moveDisk(fp,tp):
print('moving disk from', fp, 'to', tp)
def main():
height = int(input('Height of hanoi: '))
moveTower(height, 'A', 'B', 'C')
if __name__ == '__main__':
main()

38
other/word_patterns.py Normal file
View File

@ -0,0 +1,38 @@
import pprint, time
def getWordPattern(word):
word = word.upper()
nextNum = 0
letterNums = {}
wordPattern = []
for letter in word:
if letter not in letterNums:
letterNums[letter] = str(nextNum)
nextNum += 1
wordPattern.append(letterNums[letter])
return '.'.join(wordPattern)
def main():
startTime = time.time()
allPatterns = {}
with open('Dictionary.txt') as fo:
wordList = fo.read().split('\n')
for word in wordList:
pattern = getWordPattern(word)
if pattern not in allPatterns:
allPatterns[pattern] = [word]
else:
allPatterns[pattern].append(word)
with open('Word Patterns.txt', 'w') as fo:
fo.write(pprint.pformat(allPatterns))
totalTime = round(time.time() - startTime, 2)
print('Done! [', totalTime, 'seconds ]')
if __name__ == '__main__':
main()

235886
other/words Normal file
View File

File diff suppressed because it is too large Load Diff

162
searches/binary_search.py Normal file
View File

@ -0,0 +1,162 @@
"""
This is pure python implementation of binary search algorithm
For doctests run following command:
python -m doctest -v binary_search.py
or
python3 -m doctest -v binary_search.py
For manual testing run:
python binary_search.py
"""
from __future__ import print_function
import bisect
def binary_search(sorted_collection, item):
"""Pure implementation of binary search algorithm in Python
Be careful collection must be sorted, otherwise result will be
unpredictable
:param sorted_collection: some sorted collection with comparable items
:param item: item value to search
:return: index of found item or None if item is not found
Examples:
>>> binary_search([0, 5, 7, 10, 15], 0)
0
>>> binary_search([0, 5, 7, 10, 15], 15)
4
>>> binary_search([0, 5, 7, 10, 15], 5)
1
>>> binary_search([0, 5, 7, 10, 15], 6)
"""
left = 0
right = len(sorted_collection) - 1
while left <= right:
midpoint = (left + right) // 2
current_item = sorted_collection[midpoint]
if current_item == item:
return midpoint
else:
if item < current_item:
right = midpoint - 1
else:
left = midpoint + 1
return None
def binary_search_std_lib(sorted_collection, item):
"""Pure implementation of binary search algorithm in Python using stdlib
Be careful collection must be sorted, otherwise result will be
unpredictable
:param sorted_collection: some sorted collection with comparable items
:param item: item value to search
:return: index of found item or None if item is not found
Examples:
>>> binary_search_std_lib([0, 5, 7, 10, 15], 0)
0
>>> binary_search_std_lib([0, 5, 7, 10, 15], 15)
4
>>> binary_search_std_lib([0, 5, 7, 10, 15], 5)
1
>>> binary_search_std_lib([0, 5, 7, 10, 15], 6)
"""
index = bisect.bisect_left(sorted_collection, item)
if index != len(sorted_collection) and sorted_collection[index] == item:
return index
return None
def binary_search_by_recursion(sorted_collection, item, left, right):
"""Pure implementation of binary search algorithm in Python by recursion
Be careful collection must be sorted, otherwise result will be
unpredictable
First recursion should be started with left=0 and right=(len(sorted_collection)-1)
:param sorted_collection: some sorted collection with comparable items
:param item: item value to search
:return: index of found item or None if item is not found
Examples:
>>> binary_search_std_lib([0, 5, 7, 10, 15], 0)
0
>>> binary_search_std_lib([0, 5, 7, 10, 15], 15)
4
>>> binary_search_std_lib([0, 5, 7, 10, 15], 5)
1
>>> binary_search_std_lib([0, 5, 7, 10, 15], 6)
"""
midpoint = left + (right - left) // 2
if sorted_collection[midpoint] == item:
return midpoint
elif sorted_collection[midpoint] > item:
return binary_search_by_recursion(sorted_collection, item, left, midpoint-1)
else:
return binary_search_by_recursion(sorted_collection, item, midpoint+1, right)
def __assert_sorted(collection):
"""Check if collection is sorted, if not - raises :py:class:`ValueError`
:param collection: collection
:return: True if collection is sorted
:raise: :py:class:`ValueError` if collection is not sorted
Examples:
>>> __assert_sorted([0, 1, 2, 4])
True
>>> __assert_sorted([10, -1, 5])
Traceback (most recent call last):
...
ValueError: Collection must be sorted
"""
if collection != sorted(collection):
raise ValueError('Collection must be sorted')
return True
if __name__ == '__main__':
import sys
# For python 2.x and 3.x compatibility: 3.x has no raw_input builtin
# otherwise 2.x's input builtin function is too "smart"
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
user_input = input_function('Enter numbers separated by comma:\n')
collection = [int(item) for item in user_input.split(',')]
try:
__assert_sorted(collection)
except ValueError:
sys.exit('Sequence must be sorted to apply binary search')
target_input = input_function(
'Enter a single number to be found in the list:\n'
)
target = int(target_input)
result = binary_search(collection, target)
if result is not None:
print('{} found at positions: {}'.format(target, result))
else:
print('Not found')

102
searches/interpolation_search.py Normal file
View File

@ -0,0 +1,102 @@
"""
This is pure python implementation of interpolation search algorithm
"""
from __future__ import print_function
import bisect
def interpolation_search(sorted_collection, item):
"""Pure implementation of interpolation search algorithm in Python
Be careful collection must be sorted, otherwise result will be
unpredictable
:param sorted_collection: some sorted collection with comparable items
:param item: item value to search
:return: index of found item or None if item is not found
"""
left = 0
right = len(sorted_collection) - 1
while left <= right:
point = left + ((item - sorted_collection[left]) * (right - left)) // (sorted_collection[right] - sorted_collection[left])
#out of range check
if point<0 or point>=len(sorted_collection):
return None
current_item = sorted_collection[point]
if current_item == item:
return point
else:
if item < current_item:
right = point - 1
else:
left = point + 1
return None
def interpolation_search_by_recursion(sorted_collection, item, left, right):
"""Pure implementation of interpolation search algorithm in Python by recursion
Be careful collection must be sorted, otherwise result will be
unpredictable
First recursion should be started with left=0 and right=(len(sorted_collection)-1)
:param sorted_collection: some sorted collection with comparable items
:param item: item value to search
:return: index of found item or None if item is not found
"""
point = left + ((item - sorted_collection[left]) * (right - left)) // (sorted_collection[right] - sorted_collection[left])
#out of range check
if point<0 or point>=len(sorted_collection):
return None
if sorted_collection[point] == item:
return point
elif sorted_collection[point] > item:
return interpolation_search_by_recursion(sorted_collection, item, left, point-1)
else:
return interpolation_search_by_recursion(sorted_collection, item, point+1, right)
def __assert_sorted(collection):
"""Check if collection is sorted, if not - raises :py:class:`ValueError`
:param collection: collection
:return: True if collection is sorted
:raise: :py:class:`ValueError` if collection is not sorted
Examples:
>>> __assert_sorted([0, 1, 2, 4])
True
>>> __assert_sorted([10, -1, 5])
Traceback (most recent call last):
...
ValueError: Collection must be sorted
"""
if collection != sorted(collection):
raise ValueError('Collection must be sorted')
return True
if __name__ == '__main__':
import sys
# For python 2.x and 3.x compatibility: 3.x has no raw_input builtin
# otherwise 2.x's input builtin function is too "smart"
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
user_input = input_function('Enter numbers separated by comma:\n')
collection = [int(item) for item in user_input.split(',')]
try:
__assert_sorted(collection)
except ValueError:
sys.exit('Sequence must be sorted to apply interpolation search')
target_input = input_function(
'Enter a single number to be found in the list:\n'
)
target = int(target_input)
result = interpolation_search(collection, target)
if result is not None:
print('{} found at positions: {}'.format(target, result))
else:
print('Not found')

62
searches/linear_search.py Normal file
View File

@ -0,0 +1,62 @@
"""
This is pure python implementation of linear search algorithm
For doctests run following command:
python -m doctest -v linear_search.py
or
python3 -m doctest -v linear_search.py
For manual testing run:
python linear_search.py
"""
from __future__ import print_function
def linear_search(sequence, target):
"""Pure implementation of linear search algorithm in Python
:param sequence: some sorted collection with comparable items
:param target: item value to search
:return: index of found item or None if item is not found
Examples:
>>> linear_search([0, 5, 7, 10, 15], 0)
0
>>> linear_search([0, 5, 7, 10, 15], 15)
4
>>> linear_search([0, 5, 7, 10, 15], 5)
1
>>> linear_search([0, 5, 7, 10, 15], 6)
"""
for index, item in enumerate(sequence):
if item == target:
return index
return None
if __name__ == '__main__':
import sys
# For python 2.x and 3.x compatibility: 3.x has no raw_input builtin
# otherwise 2.x's input builtin function is too "smart"
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
user_input = input_function('Enter numbers separated by coma:\n')
sequence = [int(item) for item in user_input.split(',')]
target_input = input_function(
'Enter a single number to be found in the list:\n'
)
target = int(target_input)
result = linear_search(sequence, target)
if result is not None:
print('{} found at positions: {}'.format(target, result))
else:
print('Not found')

47
searches/quick_select.py Normal file
View File

@ -0,0 +1,47 @@
import collections
import sys
import random
import time
import math
"""
A python implementation of the quick select algorithm, which is efficient for calculating the value that would appear in the index of a list if it would be sorted, even if it is not already sorted
https://en.wikipedia.org/wiki/Quickselect
"""
def _partition(data, pivot):
"""
Three way partition the data into smaller, equal and greater lists,
in relationship to the pivot
:param data: The data to be sorted (a list)
:param pivot: The value to partition the data on
:return: Three list: smaller, equal and greater
"""
less, equal, greater = [], [], []
for element in data:
if element.address < pivot.address:
less.append(element)
elif element.address > pivot.address:
greater.append(element)
else:
equal.append(element)
return less, equal, greater
def quickSelect(list, k):
#k = len(list) // 2 when trying to find the median (index that value would be when list is sorted)
smaller = []
larger = []
pivot = random.randint(0, len(list) - 1)
pivot = list[pivot]
count = 0
smaller, equal, larger =_partition(list, pivot)
count = len(equal)
m = len(smaller)
#k is the pivot
if m <= k < m + count:
return pivot
# must be in smaller
elif m > k:
return quickSelect(smaller, k)
#must be in larger
else:
return quickSelect(larger, k - (m + count))

112
searches/ternary_search.py Normal file
View File

@ -0,0 +1,112 @@
'''
This is a type of divide and conquer algorithm which divides the search space into
3 parts and finds the target value based on the property of the array or list
(usually monotonic property).
Time Complexity : O(log3 N)
Space Complexity : O(1)
'''
import sys
# This is the precision for this function which can be altered.
# It is recommended for users to keep this number greater than or equal to 10.
precision = 10
# This is the linear search that will occur after the search space has become smaller.
def lin_search(left, right, A, target):
for i in range(left, right+1):
if(A[i] == target):
return i
# This is the iterative method of the ternary search algorithm.
def ite_ternary_search(A, target):
left = 0
right = len(A) - 1;
while(True):
if(left<right):
if(right-left < precision):
return lin_search(left,right,A,target)
oneThird = (left+right)/3+1;
twoThird = 2*(left+right)/3+1;
if(A[oneThird] == target):
return oneThird
elif(A[twoThird] == target):
return twoThird
elif(target < A[oneThird]):
right = oneThird-1
elif(A[twoThird] < target):
left = twoThird+1
else:
left = oneThird+1
right = twoThird-1
else:
return None
# This is the recursive method of the ternary search algorithm.
def rec_ternary_search(left, right, A, target):
if(left<right):
if(right-left < precision):
return lin_search(left,right,A,target)
oneThird = (left+right)/3+1;
twoThird = 2*(left+right)/3+1;
if(A[oneThird] == target):
return oneThird
elif(A[twoThird] == target):
return twoThird
elif(target < A[oneThird]):
return rec_ternary_search(left, oneThird-1, A, target)
elif(A[twoThird] < target):
return rec_ternary_search(twoThird+1, right, A, target)
else:
return rec_ternary_search(oneThird+1, twoThird-1, A, target)
else:
return None
# This function is to check if the array is sorted.
def __assert_sorted(collection):
if collection != sorted(collection):
raise ValueError('Collection must be sorted')
return True
if __name__ == '__main__':
# For python 2.x and 3.x compatibility: 3.x has not raw_input builtin
# otherwise 2.x's input builtin function is too "smart"
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
user_input = input_function('Enter numbers separated by coma:\n')
collection = [int(item) for item in user_input.split(',')]
try:
__assert_sorted(collection)
except ValueError:
sys.exit('Sequence must be sorted to apply the ternary search')
target_input = input_function(
'Enter a single number to be found in the list:\n'
)
target = int(target_input)
result1 = ite_ternary_search(collection, target)
result2 = rec_ternary_search(0, len(collection)-1, collection, target)
if result2 is not None:
print('Iterative search: {} found at positions: {}'.format(target, result1))
print('Recursive search: {} found at positions: {}'.format(target, result2))
else:
print('Not found')

53
sorts/bogosort.py Normal file
View File

@ -0,0 +1,53 @@
"""
This is a pure python implementation of the bogosort algorithm
For doctests run following command:
python -m doctest -v bogosort.py
or
python3 -m doctest -v bogosort.py
For manual testing run:
python bogosort.py
"""
from __future__ import print_function
import random
def bogosort(collection):
"""Pure implementation of the bogosort algorithm in Python
:param collection: some mutable ordered collection with heterogeneous
comparable items inside
:return: the same collection ordered by ascending
Examples:
>>> bogosort([0, 5, 3, 2, 2])
[0, 2, 2, 3, 5]
>>> bogosort([])
[]
>>> bogosort([-2, -5, -45])
[-45, -5, -2]
"""
def isSorted(collection):
if len(collection) < 2:
return True
for i in range(len(collection) - 1):
if collection[i] > collection[i + 1]:
return False
return True
while not isSorted(collection):
random.shuffle(collection)
return collection
if __name__ == '__main__':
import sys
# For python 2.x and 3.x compatibility: 3.x has no raw_input builtin
# otherwise 2.x's input builtin function is too "smart"
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
user_input = input_function('Enter numbers separated by a comma:\n')
unsorted = [int(item) for item in user_input.split(',')]
print(bogosort(unsorted))

53
sorts/bubble_sort.py Normal file
View File

@ -0,0 +1,53 @@
"""
This is pure python implementation of bubble sort algorithm
For doctests run following command:
python -m doctest -v bubble_sort.py
or
python3 -m doctest -v bubble_sort.py
For manual testing run:
python bubble_sort.py
"""
from __future__ import print_function
def bubble_sort(collection):
"""Pure implementation of bubble sort algorithm in Python
:param collection: some mutable ordered collection with heterogeneous
comparable items inside
:return: the same collection ordered by ascending
Examples:
>>> bubble_sort([0, 5, 3, 2, 2])
[0, 2, 2, 3, 5]
>>> bubble_sort([])
[]
>>> bubble_sort([-2, -5, -45])
[-45, -5, -2]
"""
length = len(collection)
for i in range(length-1, -1, -1):#range(length-1, -1, -1)
for j in range(i):#range(1, i)
if collection[j] > collection[j+1]:
collection[j], collection[j+1] = collection[j+1], collection[j]
return collection
if __name__ == '__main__':
import sys
# For python 2.x and 3.x compatibility: 3.x has no raw_input builtin
# otherwise 2.x's input builtin function is too "smart"
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
user_input = input_function('Enter numbers separated by a comma:\n')
unsorted = [int(item) for item in user_input.split(',')]
print(bubble_sort(unsorted))

56
sorts/bucket_sort.py Normal file
View File

@ -0,0 +1,56 @@
#!/usr/bin/env python
# Author: OMKAR PATHAK
# This program will illustrate how to implement bucket sort algorithm
# Wikipedia says: Bucket sort, or bin sort, is a sorting algorithm that works by distributing the
# elements of an array into a number of buckets. Each bucket is then sorted individually, either using
# a different sorting algorithm, or by recursively applying the bucket sorting algorithm. It is a
# distribution sort, and is a cousin of radix sort in the most to least significant digit flavour.
# Bucket sort is a generalization of pigeonhole sort. Bucket sort can be implemented with comparisons
# and therefore can also be considered a comparison sort algorithm. The computational complexity estimates
# involve the number of buckets.
# Time Complexity of Solution:
# Best Case O(n); Average Case O(n); Worst Case O(n)
from P26_InsertionSort import insertionSort
import math
DEFAULT_BUCKET_SIZE = 5
def bucketSort(myList, bucketSize=DEFAULT_BUCKET_SIZE):
if(len(myList) == 0):
print('You don\'t have any elements in array!')
minValue = myList[0]
maxValue = myList[0]
# For finding minimum and maximum values
for i in range(0, len(myList)):
if myList[i] < minValue:
minValue = myList[i]
elif myList[i] > maxValue:
maxValue = myList[i]
# Initialize buckets
bucketCount = math.floor((maxValue - minValue) / bucketSize) + 1
buckets = []
for i in range(0, bucketCount):
buckets.append([])
# For putting values in buckets
for i in range(0, len(myList)):
buckets[math.floor((myList[i] - minValue) / bucketSize)].append(myList[i])
# Sort buckets and place back into input array
sortedArray = []
for i in range(0, len(buckets)):
insertionSort(buckets[i])
for j in range(0, len(buckets[i])):
sortedArray.append(buckets[i][j])
return sortedArray
if __name__ == '__main__':
sortedArray = bucketSort([12, 23, 4, 5, 3, 2, 12, 81, 56, 95])
print(sortedArray)

36
sorts/cocktail_shaker_sort.py Normal file
View File

@ -0,0 +1,36 @@
from __future__ import print_function
def cocktail_shaker_sort(unsorted):
"""
Pure implementation of the cocktail shaker sort algorithm in Python.
"""
for i in range(len(unsorted)-1, 0, -1):
swapped = False
for j in range(i, 0, -1):
if unsorted[j] < unsorted[j-1]:
unsorted[j], unsorted[j-1] = unsorted[j-1], unsorted[j]
swapped = True
for j in range(i):
if unsorted[j] > unsorted[j+1]:
unsorted[j], unsorted[j+1] = unsorted[j+1], unsorted[j]
swapped = True
if not swapped:
return unsorted
if __name__ == '__main__':
import sys
# For python 2.x and 3.x compatibility: 3.x has no raw_input builtin
# otherwise 2.x's input builtin function is too "smart"
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
user_input = input_function('Enter numbers separated by a comma:\n')
unsorted = [int(item) for item in user_input.split(',')]
cocktail_shaker_sort(unsorted)
print(unsorted)

72
sorts/counting_sort.py Normal file
View File

@ -0,0 +1,72 @@
"""
This is pure python implementation of counting sort algorithm
For doctests run following command:
python -m doctest -v counting_sort.py
or
python3 -m doctest -v counting_sort.py
For manual testing run:
python counting_sort.py
"""
from __future__ import print_function
def counting_sort(collection):
"""Pure implementation of counting sort algorithm in Python
:param collection: some mutable ordered collection with heterogeneous
comparable items inside
:return: the same collection ordered by ascending
Examples:
>>> counting_sort([0, 5, 3, 2, 2])
[0, 2, 2, 3, 5]
>>> counting_sort([])
[]
>>> counting_sort([-2, -5, -45])
[-45, -5, -2]
"""
# if the collection is empty, returns empty
if collection == []:
return []
# get some information about the collection
coll_len = len(collection)
coll_max = max(collection)
coll_min = min(collection)
# create the counting array
counting_arr_length = coll_max + 1 - coll_min
counting_arr = [0] * counting_arr_length
# count how much a number appears in the collection
for number in collection:
counting_arr[number - coll_min] += 1
# sum each position with it's predecessors. now, counting_arr[i] tells
# us how many elements <= i has in the collection
for i in range(1, counting_arr_length):
counting_arr[i] = counting_arr[i] + counting_arr[i-1]
# create the output collection
ordered = [0] * coll_len
# place the elements in the output, respecting the original order (stable
# sort) from end to begin, updating counting_arr
for i in reversed(range(0, coll_len)):
ordered[counting_arr[collection[i] - coll_min]-1] = collection[i]
counting_arr[collection[i] - coll_min] -= 1
return ordered
if __name__ == '__main__':
import sys
# For python 2.x and 3.x compatibility: 3.x has not raw_input builtin
# otherwise 2.x's input builtin function is too "smart"
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
user_input = input_function('Enter numbers separated by a comma:\n')
unsorted = [int(item) for item in user_input.split(',')]
print(counting_sort(unsorted))

34
sorts/gnome_sort.py Normal file
View File

@ -0,0 +1,34 @@
from __future__ import print_function
def gnome_sort(unsorted):
"""
Pure implementation of the gnome sort algorithm in Python.
"""
if len(unsorted) <= 1:
return unsorted
i = 1
while i < len(unsorted):
if unsorted[i-1] <= unsorted[i]:
i += 1
else:
unsorted[i-1], unsorted[i] = unsorted[i], unsorted[i-1]
i -= 1
if (i == 0):
i = 1
if __name__ == '__main__':
import sys
# For python 2.x and 3.x compatibility: 3.x has no raw_input builtin
# otherwise 2.x's input builtin function is too "smart"
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
user_input = input_function('Enter numbers separated by a comma:\n')
unsorted = [int(item) for item in user_input.split(',')]
gnome_sort(unsorted)
print(unsorted)

65
sorts/heap_sort.py Normal file
View File

@ -0,0 +1,65 @@
'''
This is a pure python implementation of the heap sort algorithm.
For doctests run following command:
python -m doctest -v heap_sort.py
or
python3 -m doctest -v heap_sort.py
For manual testing run:
python heap_sort.py
'''
from __future__ import print_function
def heapify(unsorted, index, heap_size):
largest = index
left_index = 2 * index + 1
right_index = 2 * index + 2
if left_index < heap_size and unsorted[left_index] > unsorted[largest]:
largest = left_index
if right_index < heap_size and unsorted[right_index] > unsorted[largest]:
largest = right_index
if largest != index:
unsorted[largest], unsorted[index] = unsorted[index], unsorted[largest]
heapify(unsorted, largest, heap_size)
def heap_sort(unsorted):
'''
Pure implementation of the heap sort algorithm in Python
:param collection: some mutable ordered collection with heterogeneous
comparable items inside
:return: the same collection ordered by ascending
Examples:
>>> heap_sort([0, 5, 3, 2, 2])
[0, 2, 2, 3, 5]
>>> heap_sort([])
[]
>>> heap_sort([-2, -5, -45])
[-45, -5, -2]
'''
n = len(unsorted)
for i in range(n // 2 - 1, -1, -1):
heapify(unsorted, i, n)
for i in range(n - 1, 0, -1):
unsorted[0], unsorted[i] = unsorted[i], unsorted[0]
heapify(unsorted, 0, i)
return unsorted
if __name__ == '__main__':
import sys
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
user_input = input_function('Enter numbers separated by a comma:\n')
unsorted = [int(item) for item in user_input.split(',')]
print(heap_sort(unsorted))

53
sorts/insertion_sort.py Normal file
View File

@ -0,0 +1,53 @@
"""
This is a pure python implementation of the insertion sort algorithm
For doctests run following command:
python -m doctest -v insertion_sort.py
or
python3 -m doctest -v insertion_sort.py
For manual testing run:
python insertion_sort.py
"""
from __future__ import print_function
def insertion_sort(collection):
"""Pure implementation of the insertion sort algorithm in Python
:param collection: some mutable ordered collection with heterogeneous
comparable items inside
:return: the same collection ordered by ascending
Examples:
>>> insertion_sort([0, 5, 3, 2, 2])
[0, 2, 2, 3, 5]
>>> insertion_sort([])
[]
>>> insertion_sort([-2, -5, -45])
[-45, -5, -2]
"""
for index in range(1, len(collection)):
while 0 < index and collection[index] < collection[index - 1]:
collection[index], collection[
index - 1] = collection[index - 1], collection[index]
index -= 1
return collection
if __name__ == '__main__':
import sys
# For python 2.x and 3.x compatibility: 3.x has no raw_input builtin
# otherwise 2.x's input builtin function is too "smart"
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
user_input = input_function('Enter numbers separated by a comma:\n')
unsorted = [int(item) for item in user_input.split(',')]
print(insertion_sort(unsorted))

76
sorts/merge_sort.py Normal file
View File

@ -0,0 +1,76 @@
"""
This is a pure python implementation of the merge sort algorithm
For doctests run following command:
python -m doctest -v merge_sort.py
or
python3 -m doctest -v merge_sort.py
For manual testing run:
python merge_sort.py
"""
from __future__ import print_function
def merge_sort(collection):
"""Pure implementation of the merge sort algorithm in Python
:param collection: some mutable ordered collection with heterogeneous
comparable items inside
:return: the same collection ordered by ascending
Examples:
>>> merge_sort([0, 5, 3, 2, 2])
[0, 2, 2, 3, 5]
>>> merge_sort([])
[]
>>> merge_sort([-2, -5, -45])
[-45, -5, -2]
"""
length = len(collection)
if length > 1:
midpoint = length // 2
left_half = merge_sort(collection[:midpoint])
right_half = merge_sort(collection[midpoint:])
i = 0
j = 0
k = 0
left_length = len(left_half)
right_length = len(right_half)
while i < left_length and j < right_length:
if left_half[i] < right_half[j]:
collection[k] = left_half[i]
i += 1
else:
collection[k] = right_half[j]
j += 1
k += 1
while i < left_length:
collection[k] = left_half[i]
i += 1
k += 1
while j < right_length:
collection[k] = right_half[j]
j += 1
k += 1
return collection
if __name__ == '__main__':
import sys
# For python 2.x and 3.x compatibility: 3.x has no raw_input builtin
# otherwise 2.x's input builtin function is too "smart"
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
user_input = input_function('Enter numbers separated by a comma:\n')
unsorted = [int(item) for item in user_input.split(',')]
print(merge_sort(unsorted))

76
sorts/normal_distribution_QuickSort_README.md Normal file
View File

@ -0,0 +1,76 @@
#Normal Distribution QuickSort
Algorithm implementing QuickSort Algorithm where the pivot element is chosen randomly between first and last elements of the array and the array elements are taken from a Standard Normal Distribution.
This is different from the ordinary quicksort in the sense, that it applies more to real life problems , where elements usually follow a normal distribution. Also the pivot is randomized to make it a more generic one.
##Array Elements
The array elements are taken from a Standard Normal Distribution , having mean = 0 and standard deviation 1.
####The code
```python
>>> import numpy as np
>>> from tempfile import TemporaryFile
>>> outfile = TemporaryFile()
>>> p = 100 # 100 elements are to be sorted
>>> mu, sigma = 0, 1 # mean and standard deviation
>>> X = np.random.normal(mu, sigma, p)
>>> np.save(outfile, X)
>>> print('The array is')
>>> print(X)
```
------
#### The Distribution of the Array elements.
```python
>>> mu, sigma = 0, 1 # mean and standard deviation
>>> s = np.random.normal(mu, sigma, p)
>>> count, bins, ignored = plt.hist(s, 30, normed=True)
>>> plt.plot(bins , 1/(sigma * np.sqrt(2 * np.pi)) *np.exp( - (bins - mu)**2 / (2 * sigma**2) ),linewidth=2, color='r')
>>> plt.show()
```
-----
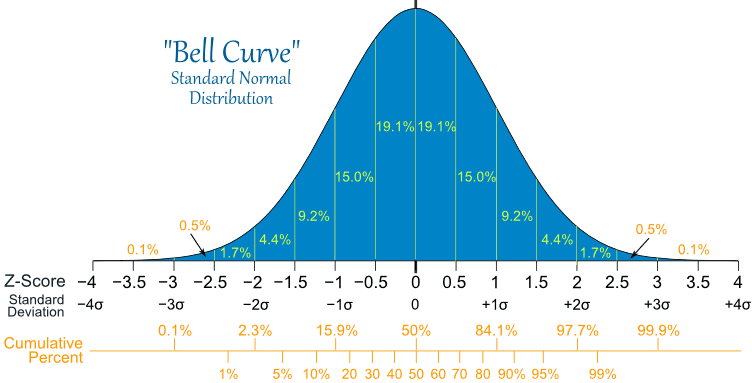
![](https://www.mathsisfun.com/data/images/normal-distrubution-large.gif)
---
---------------------
--
##Plotting the function for Checking 'The Number of Comparisons' taking place between Normal Distribution QuickSort and Ordinary QuickSort
```python
>>>import matplotlib.pyplot as plt
# Normal Disrtibution QuickSort is red
>>> plt.plot([1,2,4,16,32,64,128,256,512,1024,2048],[1,1,6,15,43,136,340,800,2156,6821,16325],linewidth=2, color='r')
#Ordinary QuickSort is green
>>> plt.plot([1,2,4,16,32,64,128,256,512,1024,2048],[1,1,4,16,67,122,362,949,2131,5086,12866],linewidth=2, color='g')
>>> plt.show()
```
----
------------------

54
sorts/quick_sort.py Normal file
View File

@ -0,0 +1,54 @@
"""
This is a pure python implementation of the quick sort algorithm
For doctests run following command:
python -m doctest -v quick_sort.py
or
python3 -m doctest -v quick_sort.py
For manual testing run:
python quick_sort.py
"""
from __future__ import print_function
def quick_sort(ARRAY):
"""Pure implementation of quick sort algorithm in Python
:param collection: some mutable ordered collection with heterogeneous
comparable items inside
:return: the same collection ordered by ascending
Examples:
>>> quick_sort([0, 5, 3, 2, 2])
[0, 2, 2, 3, 5]
>>> quick_sort([])
[]
>>> quick_sort([-2, -5, -45])
[-45, -5, -2]
"""
ARRAY_LENGTH = len(ARRAY)
if( ARRAY_LENGTH <= 1):
return ARRAY
else:
PIVOT = ARRAY[0]
GREATER = [ element for element in ARRAY[1:] if element > PIVOT ]
LESSER = [ element for element in ARRAY[1:] if element <= PIVOT ]
return quick_sort(LESSER) + [PIVOT] + quick_sort(GREATER)
if __name__ == '__main__':
import sys
# For python 2.x and 3.x compatibility: 3.x has no raw_input builtin
# otherwise 2.x's input builtin function is too "smart"
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
user_input = input_function('Enter numbers separated by a comma:\n')
unsorted = [ int(item) for item in user_input.split(',') ]
print( quick_sort(unsorted) )

27
sorts/radix_sort.py Normal file
View File

@ -0,0 +1,27 @@
def radixsort(lst):
RADIX = 10
maxLength = False
tmp , placement = -1, 1
while not maxLength:
maxLength = True
# declare and initialize buckets
buckets = [list() for _ in range( RADIX )]
# split lst between lists
for i in lst:
tmp = i // placement
buckets[tmp % RADIX].append( i )
if maxLength and tmp > 0:
maxLength = False
# empty lists into lst array
a = 0
for b in range( RADIX ):
buck = buckets[b]
for i in buck:
lst[a] = i
a += 1
# move to next
placement *= RADIX

66
sorts/random_normaldistribution_quicksort.py Normal file
View File

@ -0,0 +1,66 @@
from random import randint
from tempfile import TemporaryFile
import numpy as np
import math
def _inPlaceQuickSort(A,start,end):
count = 0
if start<end:
pivot=randint(start,end)
temp=A[end]
A[end]=A[pivot]
A[pivot]=temp
p,count= _inPlacePartition(A,start,end)
count += _inPlaceQuickSort(A,start,p-1)
count += _inPlaceQuickSort(A,p+1,end)
return count
def _inPlacePartition(A,start,end):
count = 0
pivot= randint(start,end)
temp=A[end]
A[end]=A[pivot]
A[pivot]=temp
newPivotIndex=start-1
for index in range(start,end):
count += 1
if A[index]<A[end]:#check if current val is less than pivot value
newPivotIndex=newPivotIndex+1
temp=A[newPivotIndex]
A[newPivotIndex]=A[index]
A[index]=temp
temp=A[newPivotIndex+1]
A[newPivotIndex+1]=A[end]
A[end]=temp
return newPivotIndex+1,count
outfile = TemporaryFile()
p = 100 # 1000 elements are to be sorted
mu, sigma = 0, 1 # mean and standard deviation
X = np.random.normal(mu, sigma, p)
np.save(outfile, X)
print('The array is')
print(X)
outfile.seek(0) # using the same array
M = np.load(outfile)
r = (len(M)-1)
z = _inPlaceQuickSort(M,0,r)
print("No of Comparisons for 100 elements selected from a standard normal distribution is :")
print(z)

56
sorts/selection_sort.py Normal file
View File

@ -0,0 +1,56 @@
"""
This is a pure python implementation of the selection sort algorithm
For doctests run following command:
python -m doctest -v selection_sort.py
or
python3 -m doctest -v selection_sort.py
For manual testing run:
python selection_sort.py
"""
from __future__ import print_function
def selection_sort(collection):
"""Pure implementation of the selection sort algorithm in Python
:param collection: some mutable ordered collection with heterogeneous
comparable items inside
:return: the same collection ordered by ascending
Examples:
>>> selection_sort([0, 5, 3, 2, 2])
[0, 2, 2, 3, 5]
>>> selection_sort([])
[]
>>> selection_sort([-2, -5, -45])
[-45, -5, -2]
"""
length = len(collection)
for i in range(length):
least = i
for k in range(i + 1, length):
if collection[k] < collection[least]:
least = k
collection[least], collection[i] = (
collection[i], collection[least]
)
return collection
if __name__ == '__main__':
import sys
# For python 2.x and 3.x compatibility: 3.x has no raw_input builtin
# otherwise 2.x's input builtin function is too "smart"
if sys.version_info.major < 3:
input_function = raw_input
else:
input_function = input
user_input = input_function('Enter numbers separated by a comma:\n')
unsorted = [int(item) for item in user_input.split(',')]
print(selection_sort(unsorted))

Some files were not shown because too many files have changed in this diff Show More