2014-05-04 22:57:02 +00:00
{
"metadata": {
"name": "",
2014-05-06 18:38:02 +00:00
"signature": "sha256:90a74ceed4e3dca395013883669de508e2ef94573e58cf24ce3ba49686ca5fe0"
2014-05-04 22:57:02 +00:00
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-05 00:16:02 +00:00
"[Sebastian Raschka](http://www.sebastianraschka.com) \n",
2014-05-06 05:08:11 +00:00
"last updated: 05/06/2014\n",
2014-05-04 22:57:02 +00:00
"\n",
2014-05-04 23:11:16 +00:00
"- [Link to this IPython Notebook on GitHub](https://github.com/rasbt/python_reference/blob/master/benchmarks/cython_least_squares.ipynb) \n",
2014-05-04 22:57:02 +00:00
"- [Link to the GitHub repository](https://github.com/rasbt/python_reference)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-05 19:34:22 +00:00
"#### The code in this notebook was executed in Python 3.4.0"
2014-05-04 22:57:02 +00:00
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<hr>\n",
"I am really looking forward to your comments and suggestions to improve and \n",
"extend this little collection! Just send me a quick note \n",
"via Twitter: [@rasbt](https://twitter.com/rasbt) \n",
"or Email: [bluewoodtree@gmail.com](mailto:bluewoodtree@gmail.com)\n",
"<hr>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Implementing the least squares fit method for linear regression and speeding it up via Cython"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a name=\"sections\"></a>\n",
"<br>\n",
"<br>\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#Sections"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- [Introduction](#introduction)\n",
"- [Least squares fit implementations](#implementations)\n",
"- [Generating sample data and benchmarking](#sample_data)\n",
"- [Compiling the Python code via Cython in the IPython notebook](#cython_nb)\n",
2014-05-05 05:44:10 +00:00
"- [Performance growth rates for different sample sizes](#sample_sizes)\n",
2014-05-05 19:34:22 +00:00
"- [Bonus: How to use Cython without the IPython magic](#cython_bonus)\n",
"- [Appendix I: Cython vs. Numba](#numba)\n",
2014-05-05 23:31:23 +00:00
"- [Appendix II: Cython with and without type declarations](#type_declarations)\n",
2014-05-06 05:08:11 +00:00
"- [Appendix III: Cython performance after replacing list comprehensions by explicit for loops](#explicit_loops)\n",
"- [Final Comparison: Cython vs. NumPy vs. SciPy for least squares fitting](#showdown)"
2014-05-04 22:57:02 +00:00
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a name=\"introduction\"></a>\n",
"<br>\n",
"<br>"
]
},
2014-05-05 19:34:22 +00:00
{
"cell_type": "markdown",
"metadata": {},
"source": [
" \n",
"(Note that this chart just reflects my rather objective thoughts after experimenting with Cython, and it is not based on real numbers or benchmarks.)\n",
"<br>\n",
"<br>\n",
"<br>\n",
"<br>"
]
},
2014-05-04 22:57:02 +00:00
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Introduction"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[[back to top](#sections)]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
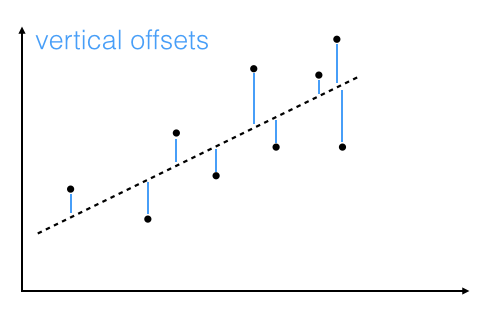
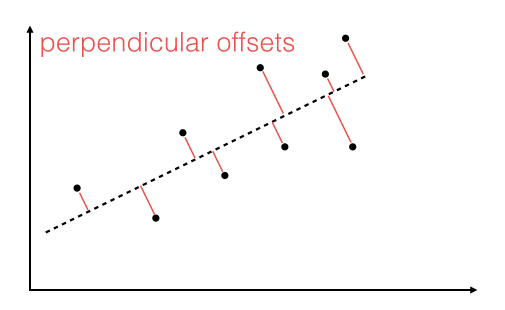
"Linear regression via the least squares method is the simplest approach to performing a regression analysis of a dependent and a explanatory variable. The objective is to find the best-fitting straight line through a set of points that minimizes the sum of the squared offsets from the line. \n",
"The offsets come in 2 different flavors: perpendicular and vertical - with respect to the line. \n",
" \n",
" \n",
"\n",
2014-05-05 02:17:27 +00:00
"As Michael Burger summarizes it nicely in his article \"[Problems of Linear Least Square Regression - And Approaches to Handle Them](http://www.arsa-conf.com/archive/?vid=1&aid=2&kid=60101-220)\": \"the perpendicular offset method delivers a more precise result but is are more complicated to handle. Therefore normally the vertical offsets are used.\" \n",
"Here, we will also use the method of computing the vertical offsets.\n",
"\n"
2014-05-04 22:57:02 +00:00
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In more mathematical terms, our goal is to compute the best fit to *n* points $(x_i, y_i)$ with $i=1,2,...n,$ via linear equation of the form \n",
"$f(x) = a\\cdot x + b$. \n",
2014-05-06 18:38:02 +00:00
"We further have to assume that the y-component is functionally dependent on the x-component. \n",
2014-05-04 22:57:02 +00:00
"In a cartesian coordinate system, $b$ is the intercept of the straight line with the y-axis, and $a$ is the slope of this line."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In order to obtain the parameters for the linear regression line for a set of multiple points, we can re-write the problem as matrix equation \n",
"$\\pmb X \\; \\pmb a = \\pmb y$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$\\Rightarrow\\Bigg[ \\begin{array}{cc}\n",
"x_1 & 1 \\\\\n",
"... & 1 \\\\\n",
"x_n & 1 \\end{array} \\Bigg]$\n",
"$\\bigg[ \\begin{array}{c}\n",
"a \\\\\n",
"b \\end{array} \\bigg]$\n",
"$=\\Bigg[ \\begin{array}{c}\n",
"y_1 \\\\\n",
"... \\\\\n",
"y_n \\end{array} \\Bigg]$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With a little bit of calculus, we can rearrange the term in order to obtain the parameter vector $\\pmb a = [a\\;b]^T$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$\\Rightarrow \\pmb a = (\\pmb X^T \\; \\pmb X)^{-1} \\pmb X^T \\; \\pmb y$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"The more classic approach to obtain the slope parameter $a$ and y-axis intercept $b$ would be:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$a = \\frac{S_{x,y}}{\\sigma_{x}^{2}}\\quad$ (slope)\n",
"\n",
"\n",
"$b = \\bar{y} - a\\bar{x}\\quad$ (y-axis intercept)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"where \n",
"\n",
"\n",
"$S_{xy} = \\sum_{i=1}^{n} (x_i - \\bar{x})(y_i - \\bar{y})\\quad$ (covariance)\n",
"\n",
"\n",
"$\\sigma{_x}^{2} = \\sum_{i=1}^{n} (x_i - \\bar{x})^2\\quad$ (variance)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a name=\"implementations\"></a>\n",
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"## Least squares fit implementations"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[[back to top](#sections)]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 1. The matrix approach"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First, let us implement the equation:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$\\pmb a = (\\pmb X^T \\; \\pmb X)^{-1} \\pmb X^T \\; \\pmb y$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"which I will refer to as the \"matrix approach\"."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import numpy as np\n",
"\n",
"def lin_lstsqr_mat(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" X = np.vstack([x, np.ones(len(x))]).T\n",
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-06 18:38:02 +00:00
"prompt_number": 1
2014-05-04 22:57:02 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 2. The classic approach"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-06 18:38:02 +00:00
"Next, we will calculate the parameters separately, using standard library functions in Python only, which I will call the \"classic approach\"."
2014-05-04 22:57:02 +00:00
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"$a = \\frac{S_{x,y}}{\\sigma_{x}^{2}}\\quad$ (slope)\n",
"\n",
"\n",
"$b = \\bar{y} - a\\bar{x}\\quad$ (y-axis intercept)"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def classic_lstsqr(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" x_avg = sum(x)/len(x)\n",
" y_avg = sum(y)/len(y)\n",
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
" slope = cov_xy / var_x\n",
" y_interc = y_avg - slope*x_avg\n",
" return (slope, y_interc)"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-06 18:38:02 +00:00
"prompt_number": 2
2014-05-04 22:57:02 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 3. Using the lstsq numpy function"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-06 18:38:02 +00:00
"For our convenience, `numpy` has a function that can computes the least squares solution of a linear matrix equation. For more information, please refer to the [documentation](http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.lstsq.html)."
2014-05-04 22:57:02 +00:00
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def numpy_lstsqr(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" X = np.vstack([x, np.ones(len(x))]).T\n",
" return np.linalg.lstsq(X,y)[0]"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-06 18:38:02 +00:00
"prompt_number": 3
2014-05-04 22:57:02 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 4. Using the linregress scipy function"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-06 18:38:02 +00:00
"Also scipy has a least squares function, `scipy.stats.linregress()`, which returns a tuple of 5 different attributes, where the 1st value in the tuple is the slope, and the second value is the y-axis intercept, respectively. \n",
"The documentation for this function can be found [here](http://docs.scipy.org/doc/scipy-0.13.0/reference/generated/scipy.stats.linregress.html)."
2014-05-04 22:57:02 +00:00
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import scipy.stats\n",
"\n",
"def scipy_lstsqr(x,y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" return scipy.stats.linregress(x, y)[0:2]"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-06 18:38:02 +00:00
"prompt_number": 4
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Teaser"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"The following plot below should give you an impression of how the performance of the 4 different approaches will compare to each other at the end of this article."
]
2014-05-04 22:57:02 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a name='sample_data'></a>\n",
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generating sample data and benchmarking"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[[back to top](#sections)]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-06 18:38:02 +00:00
"In order to test our different least squares fit implementations, we will generate some sample data: \n",
2014-05-04 22:57:02 +00:00
"- 500 sample points for the x-component within the range [0,500) \n",
"- 500 sample points for the y-component within the range [100,600) \n",
"\n",
"where each sample point is multiplied by a random value within\n",
2014-05-06 18:38:02 +00:00
"the range [0.8, 12) to simulate some scatter in our dataset."
2014-05-04 22:57:02 +00:00
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import random\n",
"random.seed(12345)\n",
"\n",
"x = [x_i*random.randrange(8,12)/10 for x_i in range(500)]\n",
"y = [y_i*random.randrange(8,12)/10 for y_i in range(100,600)]"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-06 18:38:02 +00:00
"prompt_number": 5
2014-05-04 22:57:02 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
2014-05-04 23:21:25 +00:00
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
2014-05-04 22:57:02 +00:00
"#### Visualization"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-06 18:38:02 +00:00
"To check how our dataset is distributed, and how the least squares regression line looks like, we will plot the results in a scatter plot. \n",
"Note that we are only using our \"matrix approach\" to visualize the results - for simplicity. We expect all 4 approaches to produce similar results, which we will confirm after visualizing the data."
2014-05-04 22:57:02 +00:00
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
2014-05-06 18:38:02 +00:00
"%pylab inline"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 7
},
{
"cell_type": "code",
"collapsed": false,
"input": [
2014-05-04 22:57:02 +00:00
"from matplotlib import pyplot as plt\n",
"\n",
"slope, intercept = lin_lstsqr_mat(x, y)\n",
"\n",
"line_x = [round(min(x)) - 1, round(max(x)) + 1]\n",
"line_y = [slope*x_i + intercept for x_i in line_x]\n",
"\n",
"plt.figure(figsize=(8,8))\n",
"plt.scatter(x,y)\n",
"plt.plot(line_x, line_y, color='red', lw='2')\n",
"\n",
"plt.ylabel('y')\n",
"plt.xlabel('x')\n",
"plt.title('Linear regression via least squares fit')\n",
"\n",
"ftext = 'y = ax + b = {:.3f} + {:.3f}x'\\\n",
" .format(slope, intercept)\n",
"plt.figtext(.15,.8, ftext, fontsize=11, ha='left')\n",
"\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAfoAAAH4CAYAAACi3S9CAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdUVMfbwPHv0lm6giAgooBRbNi7GCv2EnvXWOPPnhg1\nGksSxRhjoiYaE0SNsb4xEY0Fe+zGmijGLkZARRERFljYnfeP1Y0ELJRlAedzDkf2lpln7q48e++d\nO6MQQggkSZIkSSqSTIwdgCRJkiRJhiMTvSRJkiQVYTLRS5IkSVIRJhO9JEmSJBVhMtFLkiRJUhEm\nE70kSZIkFWEy0UtGd+jQIcqXL2/sMAqtSpUq8fvvv+drnSNHjuTTTz/N0b7e3t7s3bs3jyN6s/3y\nyy+UKlUKe3t7zp07Z5TPhFRwKeRz9FJ+8fb2JiQkhGbNmhk7FMmIypQpQ0hICE2bNjVI+QcOHKBf\nv378888/Bim/IPLx8eGrr76iffv2mdbNnDmT69ev8+OPPxohMqkgkGf0Ur5RKBQoFApjh6Gn0Wjy\nZJvXJYRAfq+Wnsmrz5YQgtu3b+Pv758n5UlFj0z0ktEdOHCAUqVK6V97e3uzYMECqlatiqOjIz17\n9iQ1NVW/ftu2bQQEBODk5ESDBg3466+/9OuCg4Px9fXF3t6eihUr8uuvv+rXrVy5kgYNGjBhwgSc\nnZ2ZNWtWplhmzpxJ165d6devHw4ODqxatYrHjx/z7rvv4u7ujqenJ9OnT0er1QKg1WqZOHEiLi4u\nlC1bliVLlmBiYqJf36RJE6ZNm0aDBg2wsbHh5s2b/P3337Ro0YLixYtTvnx5Nm3apK9/+/btVKxY\nEXt7ezw9PVmwYAEADx48oF27djg5OVG8eHEaN26c4Xg9uxSemprKuHHj8PDwwMPDg/Hjx6NWq/XH\n2dPTky+//BJXV1fc3d1ZuXJllu/Jhg0bqFWrVoZlCxcupGPHjgAMHDiQ6dOnA/Do0SPatWtHiRIl\nKFasGO3btycqKirLcv9LCKF/z5ydnenRowePHj3Sr+/WrRslS5bE0dGRwMBAIiIiXnisvvzyS1Qq\nFa1btyY6Oho7Ozvs7e25e/dupnpfdJwB5s+fr3+vV6xYgYmJCTdu3AB072dISIh+25UrV9KoUSP9\n67Fjx+Ll5YWDgwM1a9bk8OHD+nXZ/Wxdu3aNwMBAHB0dcXFxoWfPnpnakZqaip2dHRqNhqpVq+Ln\n5wf8+5nYuXMnc+fOZcOGDdjZ2VGtWrXXel+kIkZIUj7x9vYWe/fuzbR8//79wtPTM8N2derUETEx\nMSIuLk5UqFBBLFu2TAghxJkzZ0SJEiXEyZMnhVarFatWrRLe3t5CrVYLIYTYtGmTiImJEUIIsWHD\nBmFjYyPu3r0rhBAiNDRUmJmZiSVLlgiNRiOSk5MzxTJjxgxhbm4utmzZIoQQIjk5WXTq1EmMGDFC\nqFQqcf/+fVG7dm3x3XffCSGEWLp0qfD39xdRUVHi0aNHolmzZsLExERoNBohhBCBgYGidOnSIiIi\nQmg0GhEfHy88PT3FypUrhUajEWfPnhXOzs7i0qVLQggh3NzcxOHDh4UQQsTHx4szZ84IIYSYPHmy\nGDFihEhPTxfp6en6bf57XKdPny7q1asnYmNjRWxsrKhfv76YPn26/jibmZmJGTNmiPT0dLF9+3ah\nVCpFfHx8puOgUqmEnZ2duHr1qn5ZzZo1xYYNG4QQQgwcOFBf7sOHD8XmzZtFcnKyePLkiejWrZvo\n1KlT1h+C/8T71VdfiXr16omoqCihVqvF8OHDRa9evfTbhoaGisTERKFWq8W4ceNEQECAft2LjtWB\nAwcyfJ6y8qJ9d+zYIVxdXcXFixdFUlKS6NWrl1AoFOL69etCCCGaNGkiQkJCMsTXsGFD/es1a9aI\nuLg4odFoxIIFC4Sbm5tITU0VQmT/s9WzZ08xZ84cIYQQqamp4siRIy9sz/Mx/vcYz5w5U/Tr1++l\nx0Mq2uQZvVQgjRkzBjc3N5ycnGjfvj3nzp0DYPny5QwfPpxatWqhUCjo378/lpaWHDt2DICuXbvi\n5uYGQPfu3fHz8+PEiRP6ct3d3Rk1ahQmJiZYWVllWXf9+vXp0KEDAI8fP2bHjh0sXLgQa2trXFxc\nGDduHOvXrwdg48aNjBs3Dnd3dxwdHZkyZUqGy/MKhYKBAwdSoUIFTExM2LlzJ2XKlGHAgAGYmJgQ\nEBBAly5d2LhxIwAWFhZcvHiRhIQEHBwc9GdgFhYWxMTEcOvWLUxNTWnQoEGWsa9du5aPP/4YZ2dn\nnJ2dmTFjRoZ7s+bm5nz88ceYmprSunVrbG1tuXz5cqZyrK2t6dixI+vWrQPg6tWrXL58WX9cAH07\nixUrRufOnbGyssLW1papU6dy8ODBrN/Y//juu+/49NNPcXd3x9zcnBkzZvB///d/+rPagQMHYmNj\no193/vx5njx58tJjJV7j9siL9t24cSODBw/G398fpVKZ5VWfl+nTpw9OTk6YmJgwYcIEUlNTMxzf\n7Hy2LCwsuHXrFlFRUVhYWFC/fv1sxfKMkLeM3ngy0UsF0rNkDbqkk5iYCEBkZCQLFizAyclJ/3Pn\nzh1iYmIAWL16NdWqVdOvu3DhAg8fPtSX9fwtghfx9PTU/x4ZGUlaWholS5bUlzlixAhiY2MBiImJ\nyVDm8/tmVWdkZCQnTpzIEP/atWu5d+8eAD///DPbt2/H29ubJk2acPz4cQA++OADfH19admyJT4+\nPsybNy/L2KOjoyldurT+tZeXF9HR0frXxYsXx8Tk3//2SqVSf2z/q3fv3vpEv3btWn0y/y+VSsXw\n4cPx9vbGwcGBwMBAHj9+/FrJ5datW3Tu3Fl/LPz9/TEzM+PevXtoNBomT56Mr68vDg4OlClTBoVC\nwYMHD156rF7Hi/b97/vp5eX12mUCfPHFF/j7++Po6IiTkxOPHz/WxwvZ+2x9/vnnCCGoXbs2lSpV\nIjQ0NFuxSNIzZsYOQJJex7NOfF5eXnz00UdMnTo10zaRkZEMGzaMffv2Ua9ePRQKBdWqVct0hv2q\nep7fplSpUlhaWvLw4cMMCfKZkiVLZujdnVVP7+fL8/LyIjAwkPDw8Czrr1mzJr/++isajYbFixfT\nvXt3bt++ja2tLV988QVffPEFFy9epGnTptSuXZu33347w/7u7u7cunWLChUqAHD79m3c3d1f2uYX\nad68ObGxsZw/f57169fz1VdfZdmuBQsWcOXKFU6ePEmJEiU4d+4c1atXRwjxyuPt5eVFaGgo9erV\ny7Tuxx9/JCwsjL1791K6dGni4+MpVqyY/v180bF6nQ6fL9q3ZMmS3L59W7/d878D2NjYkJSUpH/9\n/P3/Q4cOMX/+fPbt20fFihUBMsT7/DGDV3+2XF1dWb58OQBHjhyhefPmBAYGUrZs2Ve273kFqQOs\nZBzyjF7KV2q1mpSUFP3P6/Y8fvbHcujQoSxbtoyTJ08ihCApKYnffvuNxMREkpKSUCgUODs7o9Vq\nCQ0N5cKFC9mK779noSVLlqRly5ZMmDCBJ0+eoNVquX79uv4Z5e7du/P1118THR1NfHw88+bNy/SH\n9fky27Vrx5UrV1izZg1paWmkpaXxxx9/8Pfff5OWlsZPP/3E48ePMTU1xc7ODlNTU0DXAfHatWsI\nIbC3t8fU1DTL5NCrVy8+/fRTHjx4wIMHD5g9ezb9+vXL1jF4xtzcnG7duvH+++/z6NEjWrRokaFN\nz9qVmJiItbU1Dg4OxMXFZety94gRI5g6dao+ocbGxhIWFqYv19LSkmLFipGUlJThy93LjpWrqysP\nHz4kISEhyzpftm/37t1ZuXIlly5dQqVSZWpLQEAAmzdvJjk5mWvXrhESEqJ/v588eYKZmRnOzs6o\n1Wpmz579whjg1Z+tTZs2cefOHQAcHR1RKBRZvuev4ubmxq1bt+Tl+zeYTPRSvmrTpg1KpVL/M2vW\nrFc+dvf8+ho1avD999/zv//9
"text": [
2014-05-06 18:38:02 +00:00
"<matplotlib.figure.Figure at 0x107806610>"
2014-05-04 22:57:02 +00:00
]
}
],
2014-05-06 18:38:02 +00:00
"prompt_number": 8
2014-05-04 22:57:02 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
2014-05-04 23:21:25 +00:00
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
2014-05-04 22:57:02 +00:00
"#### Comparing the results from the different implementations"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-06 18:38:02 +00:00
"As mentioned above, let us now confirm that the different implementations computed the same parameters (i.e., slope and y-axis intercept) as solution of the linear equation."
2014-05-04 22:57:02 +00:00
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import prettytable\n",
"\n",
"params = [appr(x,y) for appr in [lin_lstsqr_mat, classic_lstsqr, numpy_lstsqr, scipy_lstsqr]]\n",
"\n",
"print(params)\n",
"\n",
"fit_table = prettytable.PrettyTable([\"\", \"slope\", \"y-intercept\"])\n",
"fit_table.add_row([\"matrix approach\", params[0][0], params[0][1]])\n",
"fit_table.add_row([\"classic approach\", params[1][0], params[1][1]])\n",
"fit_table.add_row([\"numpy function\", params[2][0], params[2][1]])\n",
"fit_table.add_row([\"scipy function\", params[3][0], params[3][1]])\n",
"\n",
"print(fit_table)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[array([ 0.95181895, 107.01399744]), (0.95181895319126741, 107.01399744459181), array([ 0.95181895, 107.01399744]), (0.95181895319126764, 107.01399744459175)]\n",
"+------------------+----------------+---------------+\n",
"| | slope | y-intercept |\n",
"+------------------+----------------+---------------+\n",
"| matrix approach | 0.951818953191 | 107.013997445 |\n",
"| classic approach | 0.951818953191 | 107.013997445 |\n",
"| numpy function | 0.951818953191 | 107.013997445 |\n",
"| scipy function | 0.951818953191 | 107.013997445 |\n",
"+------------------+----------------+---------------+\n"
]
}
],
2014-05-06 18:38:02 +00:00
"prompt_number": 9
2014-05-04 22:57:02 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
2014-05-04 23:21:25 +00:00
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
2014-05-04 22:57:02 +00:00
"#### Initial performance comparison"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-06 18:38:02 +00:00
"To get an initial impression of how the performances of the different least squares implementations compare against each other, let us do a quick benchmark using the `timeit` module via IPython's `%timeit` magic."
2014-05-04 22:57:02 +00:00
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import timeit\n",
"\n",
"for lab,appr in zip([\"matrix approach\",\"classic approach\",\n",
" \"numpy function\",\"scipy function\"],\n",
" [lin_lstsqr_mat, classic_lstsqr, \n",
" numpy_lstsqr, scipy_lstsqr]):\n",
" print(\"\\n{}: \".format(lab), end=\"\")\n",
" %timeit appr(x, y)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
2014-05-06 18:38:02 +00:00
"matrix approach: 10000 loops, best of 3: 158 \u00b5s per loop"
2014-05-04 22:57:02 +00:00
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"\n",
2014-05-06 18:38:02 +00:00
"classic approach: 1000 loops, best of 3: 1.6 ms per loop"
2014-05-04 22:57:02 +00:00
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"\n",
2014-05-06 18:38:02 +00:00
"numpy function: 1000 loops, best of 3: 217 \u00b5s per loop"
2014-05-04 22:57:02 +00:00
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"\n",
2014-05-06 18:38:02 +00:00
"scipy function: 1000 loops, best of 3: 366 \u00b5s per loop"
2014-05-04 22:57:02 +00:00
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n"
]
}
],
2014-05-06 18:38:02 +00:00
"prompt_number": 10
2014-05-04 22:57:02 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
2014-05-06 18:38:02 +00:00
"The timing above indicates that the \"classic\" approach (Python's standard library functions only) is significantly worse in performance than the other implemenations - roughly by a magnitude of 10. However, we should keep in mind that this experiment was done for a fixed sample size n=500."
2014-05-04 22:57:02 +00:00
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<br>\n",
"<a name=\"cython_nb\"></a>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Compiling the Python code via Cython in the IPython notebook"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[[back to top](#sections)]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Maybe we can speed things up a little bit via [Cython's C-extensions for Python](http://cython.org). Cython is basically a hybrid between C and Python and can be pictured as compiled Python code with type declarations. \n",
2014-05-06 18:38:02 +00:00
"Since we are working in an IPython notebook here, we can make use of the very convenient *IPython magic*: It will take care of the conversion to C code, the compilation, and eventually the loading of the function. \n",
"Let us also compile the functions for the other 3 least squares approaches - those already use numpy objects and therefore we don't expect any performance gain here, but it is good to be thorough.\n",
2014-05-05 19:34:22 +00:00
"\n",
"**Note** \n",
2014-05-06 18:38:02 +00:00
"Of course Cython has much more horsepower under its hood - more than I am showing in this section of this article (for example, I am not using Cython's type definitions via `cdef` here, but we will get to it [in a later section - Appendix II](#type_declarations)). \n",
"The focus of this section should be on how to speed up existing Python code by making only minimal changes to it. "
2014-05-04 22:57:02 +00:00
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%load_ext cythonmagic"
],
"language": "python",
"metadata": {},
2014-05-06 18:38:02 +00:00
"outputs": [],
"prompt_number": 11
2014-05-04 22:57:02 +00:00
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%cython\n",
"import numpy as np\n",
"import scipy.stats\n",
"cimport numpy as np\n",
"\n",
"def cy_lin_lstsqr_mat(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" X = np.vstack([x, np.ones(len(x))]).T\n",
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)\n",
"\n",
"def cy_classic_lstsqr(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" x_avg = sum(x)/len(x)\n",
" y_avg = sum(y)/len(y)\n",
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
" slope = cov_xy / var_x\n",
" y_interc = y_avg - slope*x_avg\n",
" return (slope, y_interc)\n",
"\n",
"def cy_numpy_lstsqr(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" X = np.vstack([x, np.ones(len(x))]).T\n",
" return np.linalg.lstsq(X,y)[0]\n",
"\n",
"def cy_scipy_lstsqr(x,y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" return scipy.stats.linregress(x, y)[0:2]"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-06 18:38:02 +00:00
"prompt_number": 12
2014-05-04 22:57:02 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Comparing the compiled Cython code to the original Python code"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import timeit\n",
"\n",
"for lab,appr in zip([\"matrix approach\",\"classic approach\",\n",
" \"numpy function\",\"scipy function\"],\n",
" [(lin_lstsqr_mat, cy_lin_lstsqr_mat), \n",
" (classic_lstsqr, cy_classic_lstsqr),\n",
" (numpy_lstsqr, cy_numpy_lstsqr),\n",
" (scipy_lstsqr, cy_scipy_lstsqr)]):\n",
" print(\"\\n\\n{}: \".format(lab))\n",
" %timeit appr[0](x, y)\n",
" %timeit appr[1](x, y)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"\n",
"matrix approach: \n",
2014-05-06 18:38:02 +00:00
"10000 loops, best of 3: 159 \u00b5s per loop"
2014-05-04 22:57:02 +00:00
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
2014-05-06 18:38:02 +00:00
"10000 loops, best of 3: 159 \u00b5s per loop"
2014-05-04 22:57:02 +00:00
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"\n",
"\n",
"classic approach: \n",
2014-05-06 18:38:02 +00:00
"1000 loops, best of 3: 1.62 ms per loop"
2014-05-04 22:57:02 +00:00
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
2014-05-06 18:38:02 +00:00
"10000 loops, best of 3: 126 \u00b5s per loop"
2014-05-04 22:57:02 +00:00
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"\n",
"\n",
"numpy function: \n",
2014-05-06 18:38:02 +00:00
"1000 loops, best of 3: 218 \u00b5s per loop"
2014-05-04 22:57:02 +00:00
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
2014-05-06 18:38:02 +00:00
"1000 loops, best of 3: 220 \u00b5s per loop"
2014-05-04 22:57:02 +00:00
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"\n",
"\n",
"scipy function: \n",
2014-05-06 18:38:02 +00:00
"1000 loops, best of 3: 372 \u00b5s per loop"
2014-05-04 22:57:02 +00:00
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
2014-05-06 18:38:02 +00:00
"1000 loops, best of 3: 354 \u00b5s per loop"
2014-05-04 22:57:02 +00:00
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n"
]
}
],
2014-05-06 18:38:02 +00:00
"prompt_number": 13
2014-05-04 22:57:02 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<br>\n",
2014-05-06 18:38:02 +00:00
"As we've seen before, our \"classic\" implementation of the least square method is pretty slow compared to the other approaches which use Numpy objects. This is not surprising, since Numpy is highly optimized and uses compiled C/C++ and Fortran code already. This explains why there is no significant difference if we used Cython to compile the numpy-objects-containing functions. \n",
"However, we were able to speed up the \"classic approach\" quite significantly via Cython, roughly by 1500%.\n",
2014-05-04 22:57:02 +00:00
"\n",
"The following 2 code blocks are just to visualize our results in a bar plot."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import timeit\n",
"\n",
"funcs = ['classic_lstsqr', 'cy_classic_lstsqr', \n",
" 'lin_lstsqr_mat', 'numpy_lstsqr', 'scipy_lstsqr']\n",
"labels = ['classic approach','classic approach (cython)', \n",
" 'matrix approach', 'numpy function', 'scipy function']\n",
"\n",
"times = [timeit.Timer('%s(x,y)' %f, \n",
" 'from __main__ import %s, x, y' %f).timeit(1000)\n",
" for f in funcs]\n",
"\n",
"times_rel = [times[0]/times[i+1] for i in range(len(times[1:]))]"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-06 18:38:02 +00:00
"prompt_number": 14
2014-05-04 22:57:02 +00:00
},
{
"cell_type": "code",
"collapsed": false,
"input": [
2014-05-06 18:38:02 +00:00
"import matplotlib.pyplot as plt\n",
2014-05-04 22:57:02 +00:00
"\n",
"x_pos = np.arange(len(funcs))\n",
"plt.bar(x_pos, times, align='center', alpha=0.5)\n",
"plt.xticks(x_pos, labels, rotation=45)\n",
"plt.ylabel('time in ms')\n",
"plt.title('Performance of different least square fit implementations')\n",
2014-05-05 19:34:22 +00:00
"plt.grid()\n",
2014-05-04 22:57:02 +00:00
"plt.show()\n",
"\n",
"x_pos = np.arange(len(funcs[1:]))\n",
"plt.bar(x_pos, times_rel, align='center', alpha=0.5, color=\"green\")\n",
"plt.xticks(x_pos, labels[1:], rotation=45)\n",
"plt.ylabel('relative performance gain')\n",
"plt.title('Performance gain compared to the classic least square implementation')\n",
2014-05-05 19:34:22 +00:00
"plt.grid()\n",
2014-05-04 22:57:02 +00:00
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
2014-05-06 18:38:02 +00:00
"png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAFhCAYAAABwNN3iAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3X1cjff/B/DXSaWiG4XQrciEFHITo4yhKIahuStMGsbs\nhrERc5e53drMGG1GfJnbVAw7GbpxM7eRu50QNblLiur0/v3RzvXrdKOyTuec67yfj4eHrnNd57re\n7+u6zvU+1+dzXeeSEBGBMcaYztNTdwCMMcY0AxcExhhjALggMMYY+xcXBMYYYwC4IDDGGPsXFwTG\nGGMARF4QMjIy0KNHD5iZmeHTTz9Vdzhql5ubCz8/P1hYWGD48OEVTi+VSmFnZycMt2nTBseOHQMA\nEBGCgoJgaWmJLl26AADWrl0La2trmJmZ4fHjx6pJ4jWVzIVVXkpKCtzd3WFmZoZvv/0WISEhWLhw\nYaXfX9Xpq8LR0RFHjhxRybzVacuWLejbt2/NL5g0jIODAxkbG1PdunXJ2tqaAgMDKTs7+7XmtWDB\nAhoyZEg1R6i9fvnlF+rUqRPJ5fJKTf/HH3+Qra1tmeOOHTtGtra2lJOTQ0REeXl5ZGxsTBcvXqy2\neKvCwcGBjhw5Uu74V+VSXcaOHUtffPGFSpehDuPGjaMZM2aUOa4m1uurODo6vnK7q8OmTZvozTff\nrPT0f//9N0kkkkp/LlVJ484QJBIJoqKi8OzZM5w9exanT5+u8rcLIkJhYSFSU1Ph4uLyWnEUFBS8\n1vs0WWpqKlq0aAE9vf++2VNTU+Ho6AhjY2MAQHp6Ol68ePHa67uwsPA/xSORSEB8j2WFXme/Tk1N\nRatWrVQQDStOI/ZfNRekUkpW/E8++YQGDBhARETx8fHk6elJFhYW5ObmRlKpVJjOy8uL5syZQ926\ndSNjY2MaNWoUGRgYkKGhIdWtW5eOHDlCL1++pGnTplGTJk2oSZMmNH36dHr58iURFX3TsbGxobCw\nMGrUqBGNHj2aQkNDaejQoTRq1CgyNTUlV1dXunbtGi1evJgaNmxI9vb2dOjQISGGjRs3kouLC5ma\nmpKTkxOtW7dOGKeY/4oVK6hhw4bUuHFj2rRpkzA+JyeHZsyYQQ4ODmRubk5vvvkm5ebmVph3ScnJ\nyeTl5UUWFhbUunVr2rdvHxERzZ07lwwNDcnAwIDq1q1LGzduLPXenJwcGjt2LNWrV49atWpFy5Yt\nU/r25+DgQIcPH6YNGzaQkZER1apVi+rWrUsBAQFUp04dkkgkVLduXerVqxcREV25coV69+5NlpaW\n9MYbb9D//vc/YV5jx46lSZMmkY+PD9WpU4eOHDlCaWlpNHjwYGrQoAE1bdqUvvnmG2H6efPm0bvv\nvktjxowhU1NTat26NZ0+fZqIiEaNGkV6enrCmeXXX39dKreS32RftazExETq0qULWVhYUOPGjWnK\nlCmUl5cnjJ8+fTo1bNiQzMzMyNXVlS5dukTr1q1T2t/8/f3L3D5lvZeIKDMzk/z8/MjMzIw6depE\nX3zxhfAts6xvkF5eXrRhwwYiIrpx4wb17NmTrKysqH79+jRy5Eh68uSJ0nYLCwsjV1dXMjIyIrlc\nXul9qmfPnlSrVi0yMjIiU1NTunbtmnAm9Pz5czIyMiI9PT2qW7cumZqa0v3790vNo/iZk+JzsGzZ\nMmrQoAE1btyYdu/eTQcOHCBnZ2eytLSkJUuWKG33IUOG0PDhw8nU1JTat29P58+fF8YXP14UFhbS\nkiVLqFmzZmRlZUXDhg2jR48eKa3DTZs2kZ2dHVlaWtLatWspKSmJXF1dycLCgqZMmaIU908//UQu\nLi5Ur1496tu3L6WmpgrjJBIJ/fDDD+Ts7EwWFhY0efJkIir6/BX/bNSrV4+IiKKiosjd3Z3MzMzI\nzs6OQkNDhXnZ2dkJnx1TU1OKj48vdZZx4sQJ8vDwIHNzc+rYsSOdPHlSaV/48ssvqVu3bmRqakp9\n+vShzMxMIiLKzc2lkSNHkpWVFVlYWFDHjh0pIyOjzG1NRKSRBeHw4cNERHT79m1q3bo1zZ07l+7e\nvUtWVlYUExNDRES///47WVlZCYl7eXmRg4MDJScnk1wup/z8fAoMDKQvv/xSmPeXX35Jnp6e9ODB\nA3rw4AF17dpVGP/HH3+Qvr4+zZo1i/Ly8ig3N5fmzZtHRkZGdOjQISooKKAxY8aQg4MDLV68mAoK\nCmj9+vXUtGlTYf4HDhygW7duERFRXFwcmZiY0NmzZ5XmP2/ePCooKKDo6GgyMTERPrgffPAB9ezZ\nk+7duyd8YF++fFlu3g8ePCi17vLy8qhZs2a0ZMkSys/Pp6NHj5KpqSmlpKQQEVFoaCiNHj263HU/\nc+ZM6tGjBz1+/Jju3LlDrVu3Jjs7O6Vto/jwRUREKO2wMplM6aCVnZ1Ntra2FBERQXK5nP766y+q\nX78+JScnE1HRQcLc3FzYsXNycqh9+/b01VdfUX5+Pt26dYucnJzo4MGDRETCtoiJiaHCwkL6/PPP\nqUuXLmXGVpbiBUEul79yWWfOnKHExESSy+Ukk8nIxcWFVq9eTUREsbGx1KFDB3r69CkREV29elU4\nCJbc30p61XuHDx9Ow4cPp5ycHLp06RLZ2NhQ9+7diajsguDt7U0//fQTERUVhMOHD1NeXh49ePCA\nevToQdOnTxemdXBwoHbt2tHdu3fpxYsXVdqnSi6rZJ5SqbTCJqPi0ys+B1999ZXwGbKysqL33nuP\nsrOz6fLly2RsbEwymYyIira7gYEB/fbbb1RQUEDLly+npk2bUkFBAREpb/fVq1eTp6cnpaWlUV5e\nHgUHB1NAQIDSOgwJCaGXL1/SoUOHyNDQkAYNGkQPHjygtLQ0atiwIcXFxRER0Z49e6h58+Z09epV\nksvltHDhQuratauQk0QiIT8/P3r69Cndvn2bGjRoQLGxsURU+rOhWE+K4n/hwgWytramPXv2EFHp\nzw6RcrPTw4cPycLCgn799VeSy+UUGRlJ9erVE4qdl5cXNW/enK5fv065ubnk7e1Ns2bNIiKiH374\ngfz8/Cg3N5cKCwvp7NmzlJWVVe620riC4ODgQHXr1iULCwtycHCgyZMnU25uLi1durTUwaxv3770\n888/E1HRTjtv3jyl8YGBgUptus2aNRM+BEREBw8eJEdHRyIq2lENDQ2FMwaiop2xT58+wvC+ffuo\nbt26VFhYSEREWVlZJJFIhA94SYMGDaI1a9YI8zc2Nlba6A0bNhQOPMbGxnThwoVS86go7+KOHTtG\njRo1UnotICBA+DYyb948GjVqVJmxEpHSQZGI6Mcff1T6sBf/8JX8BlPyoLVt2zbhgKYwceJEmj9/\nPhEVFYSxY8cK4xISEsje3l5p+sWLF1NQUJAQ+9tvvy2MUxw4yoqtLMULQkXLKmnVqlX0zjvvEBHR\nkSNHqEWLFpSQkFCqzbfk/lbS0aNHy3xvQUEBGRgYCIWbiGj27NmvPEMoeZAubvfu3dSuXTth2NHR\nUelstCr7lGJZirORknlWpg+h5PTGxsalPkNJSUnC9B06dKC9e/cSUdF29/T0FMYVFhZS48aN6fjx\n40Juiu3u4uKitA/cu3ePDAwMSC6XC+vw3r17wngrKyuls9YhQ4YIn9d+/foprV+5XE4mJiZ0+/Zt\nIioqCCdOnBDGDxs2jJYuXUpEletDmDZtGn300UdEVPb2LT6PX375hTp37qz0fk9PT4qIiCCiou2z\naNEiYdz3339P/fr1I6KiVouuXbuWeWwpi766m6xKkkgk2Lt3L9566y2l11NTU7Fjxw7s379feK2g\noEBpuoquIrl37x4cHByEYXt7e9y7d08YbtCgAQwNDZXe07BhQ+FvY2Nj1K9fHxKJRBgGgOzsbJiZ\nmSEmJgbz58/H9evXUVhYiJycHLRt21Z4v5WVlVL7vYmJCbKzs5GZmYkXL16gWbNmpWKuTN7F8yu5\nDhwcHJCWlvbK9VLe++3t7Sv1
2014-05-04 22:57:02 +00:00
"text": [
2014-05-06 18:38:02 +00:00
"<matplotlib.figure.Figure at 0x1079680d0>"
2014-05-04 22:57:02 +00:00
]
},
{
"metadata": {},
"output_type": "display_data",
2014-05-06 18:38:02 +00:00
"png": "iVBORw0KGgoAAAANSUhEUgAAAbwAAAFhCAYAAAALEB8uAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdYFOfaBvB7qALSqyBFNEZQFKyIDWOJXYMaJZagJpZE\nj8YUOcYoJ8YWNZZoTEyixJ5jjI0gNkQ9KvZOBNtiBbtUhV2e7w+/nbCAqDjMLMvzuy6vZJadmXfu\n3Zln531ndgUiIjDGGGMGzkjpBjDGGGNy4ILHGGOsUuCCxxhjrFLggscYY6xS4ILHGGOsUuCCxxhj\nrFKQteClp6ejdevWsLGxweeffy7nqiukLl26YOXKlUo3Q2/5+Phg9+7dsq3PyMgIV65cKdd1RERE\n4Kuvviq35VtbW0OlUr3SPAkJCfD09CyfBhm4evXqYd++fZIvV6VSwcjICAUFBZIvW2mjRo3CN998\nUy7LNnnRE3x8fHDnzh0YGxvDysoKnTt3xqJFi2BlZfXKK1u6dClcXFyQkZFRpsZWNrGxsUo3Qa8J\nggBBEEr8W0REBDw9PTF16tQyLTs0NBSDBg3CsGHDXqeJr6y0bZJCZmZmuS37dbzu66Wvzp07p3QT\nZPWqr2N0dDR+/fVX7N+/X3xsyZIl5dW8F5/hCYKAmJgYZGZm4sSJEzh27NgrV18iQkFBAVJTU+Hn\n51emhqrV6jLNxyoGfXt9y7PovAh/F4R+0rf3KCsDegEfHx/avXu3OP3ZZ59Rt27diIjo0KFD1Lx5\nc7Kzs6MGDRpQQkKC+Lw2bdrQl19+SS1atCALCwsaOHAgmZqakpmZGVWtWpV2795NT58+pbFjx5K7\nuzu5u7vTuHHj6OnTp0REtGfPHvLw8KBZs2aRm5sbDRo0iKKioqhPnz40cOBAsra2poCAAEpJSaHp\n06eTi4sLeXl50Y4dO8Q2LFu2jPz8/Mja2pp8fX3pp59+Ev+mXf7cuXPJxcWFqlWrRsuXLxf/npOT\nQ+PHjydvb2+ytbWlli1bUm5u7gu3u6jjx49TYGAgWVtbU9++fendd9+lSZMmERHRgwcPqGvXruTs\n7Ez29vbUrVs3unHjhk6Gv/zyCxERLV++nFq0aEGfffYZ2dvbU40aNWjbtm3PXe+1a9fonXfeIWdn\nZ3J0dKTRo0cTEZFGo6GpU6eSt7c3ubi40ODBg+nx48dERHT16lUSBIGWL19Onp6e5ODgQEuWLKEj\nR45QQEAA2dnZicvRtikkJIRGjx5Ntra2VKdOHZ33ysvkr319Bw8eTAUFBTRjxgyqWbMmOTo60rvv\nvksPHjwQ51mxYgV5eXmRo6MjTZs2rdh7U+unn37Sea/16NGDiIiSkpKoTZs2ZGdnR3Xr1qUtW7aU\nmN3EiRPJ2NiYqlSpQlWrVqUxY8YQEZEgCPTjjz/SG2+8QXZ2dvTxxx/rzPfrr7+Sn58f2dvb09tv\nv02pqanPfX32798vvoc8PT3pt99+IyKiiIiIl35/LF++nHx9fcna2ppq1KhBq1evJiKiixcvUuvW\nrcnW1pacnJyoX79+4jyCINDly5eJqPT3eGF79uyh6tWri9M3b96ksLAwcnZ2pho1atDChQvFvx0+\nfJiCg4PJzs6OqlWrRqNHj6a8vDzx7+PGjSMXFxeysbGhgIAAOnfu3HNfr6JKmpeI6N69e9S9e3ey\nsbGhpk2b0qRJk6hly5ZE9M97WqPRiMspvF9dunSJ2rZtS46OjuTk5EQDBgygR48eic/19vamWbNm\nUUBAAFWpUoU0Gs0r7f/e3t7ie3TKlCmvdPxq06YNRUZGUtOmTcnGxoZ69uwp7g9Ft+vRo0c0dOhQ\nqlatGnl4eNCkSZPEv2n3008++YTs7OyoZs2adODAAVq2bBl5enqSi4uL+P4jInry5Al9+umn5OXl\nRa6urjRy5EjxfVHacfN5r6N2n7a2tiZ/f3/auHEjET3bH6tUqULGxsZUtWpVsre3JyKi999/X9wH\niIiWLl1KtWrVIgcHB+rRowfdunVL/NuL9smiXqrg7dq1i4ieHUTr1q1LkydPphs3bpCjo6N40N25\ncyc5OjrSvXv3xBfL29ubkpKSSKPRUH5+PkVERNBXX30lLvurr76i5s2b0927d+nu3bsUEhIi/n3P\nnj1kYmJCkZGRlJeXR7m5uTRlyhSqUqUK7dixg9RqNQ0ePJi8vb1p+vTppFar6eeff6YaNWqIy//r\nr7/oypUrRES0d+9esrS0pBMnTugsf8qUKaRWqyk2NpYsLS3FN/tHH31Ebdu2pVu3bolv8qdPnz53\nu+/evVssu6dPn5KXlxctXLiQ1Go1/fnnn2RmZiZu4/379+nPP/+k3NxcyszMpL59+1KvXr3E+UND\nQ+nXX38lomdvWlNTU/rll1+ooKCAlixZQu7u7iW+Zmq1murXr0/jx4+nnJwcevLkCR04cICInh2U\na9WqRVevXqWsrCwKCwujQYMGEdE/O9GoUaPo6dOntGPHDjIzM6NevXrR3bt36ebNm+Ti4kJ79+4V\n22RiYkLz588ntVpNv//+O9na2oo75cvkX/j1nT9/PjVv3pxu3rxJeXl5NGLECAoPDyciovPnz1PV\nqlVp//799PTpUxo/fjyZmJiUWPCIqNh7LS8vj2rWrEkzZsyg/Px8io+PJ2tra0pOTi5x/sLZawmC\nQN27d6fHjx/TtWvXyNnZmeLi4oiIaNOmTVSrVi26cOECaTQa+uabbygkJKTEZatUKrK2tqZ169aR\nWq2m+/fv06lTp8R2a3f20t4fWVlZZGNjQykpKURElJaWRufPnyciov79+9P06dOJ6Nl7UPvaa7dB\nW/Ce9x4vqnDB02g01LBhQ5o6dSrl5+fTlStXyNfXl7Zv305Ezz7gHT58mDQaDalUKvLz86P58+cT\nEVFcXBw1atRI/IB14cIFun37domvV1GlzduvXz/q168f5eTk0Llz58jDw4NatWpFRCUXvMKv7aVL\nl2jXrl2Ul5dHd+/epdatW9O4cePE53p7e1NQUBDduHGDnjx58kr7P5HuCcOrHr/atGlDHh4edP78\necrOzqbevXvTwIEDS9yuXr160ciRIyknJ4fu3LlDTZs2FT9gavfT6OhoKigooEmTJpGHh4f4YWTH\njh1kbW1N2dnZRPTsg0XPnj3p4cOHlJmZSd27d6d///vf4nuhtONmSa/j+vXrxdfq999/JysrK0pL\nSyMioujoaPHDiVbhZezevZucnJzo5MmT9PTpUxozZgy1bt1afG5p+2RJXljwvL29qWrVqmRnZ0fe\n3t708ccfU25uLs2cOVM8UGq9/fbb4ieF0NBQmjJlSrENKVy5a9asqXOWsn37dvLx8SGiZ8GamZnp\n7IBTpkyhjh07itNbtmyhqlWrUkFBARERZWRkkCAI4k5RVK9evWjBggXi8i0sLHR2BBcXF3FntbCw\noDNnzhRbxou2u7C9e/eSh4eHzmMtW7Z87o598uRJ8VMOUfGCV6tWLfFv2dnZJAgCpaenF1vOwYMH\nydnZWWfbtN566y1asmSJOJ2cnEympqak0WjEnajwJyhHR0f673//K0737t1bPIAtX768WNFt2rQp\nrVy5ssTtK5p/0dfXz89Pp4DdunWLTE1NSa1W03/+8x+x+Gm338zMrNSCV/i9tm/fPnJzc9N5Tnh4\nOEVFRZU4f2hoqHgWoCUIgk7xePfdd2nWrFlERNSpUyedAqnRaMjS0pKuXbtWbNnTp0+nsLCwl2p3\nYYXfH1lZWWRnZ0cbNmygnJwcnecNHjyYhg8frnM2WHgbLl++XOp7vKjCBS8xMZG8vLyKbc+QIUNK\nnHfevHn0zjvvENGzg1ft2rUpMTGx2HuztO0mIoqPjy9xXrVaTaampjofXCZOnFjqGV5JH2a0Nm7c\nSEFBQeK0j4+PTs/Pq+z/2vkLF7xXOX6FhoaKhYbo2RmRmZkZFRQU6GxXWloamZub65ydr1mzhtq2\nbUtEz/bTN954Q/zbmTNnSBAE
2014-05-04 22:57:02 +00:00
"text": [
2014-05-06 18:38:02 +00:00
"<matplotlib.figure.Figure at 0x1078eeb10>"
2014-05-04 22:57:02 +00:00
]
}
],
2014-05-06 18:38:02 +00:00
"prompt_number": 16
2014-05-04 22:57:02 +00:00
},
2014-05-05 05:44:10 +00:00
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a name=\"sample_sizes\"></a>\n",
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Performance growth rates for different sample sizes"
]
},
2014-05-05 19:34:22 +00:00
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[[back to top](#sections)]"
]
},
2014-05-05 05:44:10 +00:00
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-06 18:38:02 +00:00
"In the previous section, we have seen how the different implemantations perform for a fixed sample size n=500. Now, let us take a look at the effect of different sample sizes on the relative performances for each approach. We will consider the sample sizes 10, 100, 1000, 10000, 100000, and 1000000."
2014-05-05 05:44:10 +00:00
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import timeit\n",
2014-05-05 19:34:22 +00:00
"import random\n",
"random.seed(12345)\n",
2014-05-05 05:44:10 +00:00
"\n",
"funcs = ['cy_classic_lstsqr', \n",
" 'lin_lstsqr_mat', 'numpy_lstsqr', 'scipy_lstsqr']\n",
2014-05-06 05:08:11 +00:00
"\n",
2014-05-05 05:44:10 +00:00
"orders_n = [10**n for n in range(1, 7)]\n",
"times_n = {f:[] for f in funcs}\n",
"\n",
"for n in orders_n:\n",
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
" for f in funcs:\n",
" times_n[f].append(timeit.Timer('%s(x,y)' %f, \n",
" 'from __main__ import %s, x, y' %f).timeit(1000))"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-06 18:38:02 +00:00
"prompt_number": 17
2014-05-05 05:44:10 +00:00
},
{
"cell_type": "code",
"collapsed": false,
"input": [
2014-05-06 18:38:02 +00:00
"import matplotlib.pyplot as plt\n",
2014-05-05 05:44:10 +00:00
"\n",
2014-05-06 18:38:02 +00:00
"labels = [('cy_classic_lstsqr', 'Cython implementation'), \n",
" ('lin_lstsqr_mat', 'numpy matrix equation'),\n",
" ('numpy_lstsqr', 'numpy.linalg.lstsq()'), \n",
" ('scipy_lstsqr', 'scipy.stats.linregress()')] \n",
2014-05-05 05:44:10 +00:00
"\n",
2014-05-06 18:38:02 +00:00
"matplotlib.rcParams.update({'font.size': 12})\n",
2014-05-05 05:44:10 +00:00
"\n",
2014-05-06 18:38:02 +00:00
"fig = plt.figure(figsize=(10,8))\n",
"for lb in labels:\n",
" plt.plot(orders_n, times_n[lb[0]], alpha=0.5, label=lb[1], marker='o', lw=3)\n",
2014-05-05 05:44:10 +00:00
"plt.xlabel('sample size n')\n",
2014-05-06 18:38:02 +00:00
"plt.ylabel('performance gain relative to the slowest approach')\n",
"plt.xlim([1,max(orders_n) + max(orders_n) * 10])\n",
2014-05-05 05:44:10 +00:00
"plt.legend(loc=2)\n",
2014-05-05 19:34:22 +00:00
"plt.grid()\n",
2014-05-06 18:38:02 +00:00
"plt.xscale('log')\n",
"plt.yscale('log')\n",
2014-05-05 05:44:10 +00:00
"plt.title('Performance of least square fit implementations for different sample sizes')\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
2014-05-06 18:38:02 +00:00
"png": "iVBORw0KGgoAAAANSUhEUgAAAnMAAAIECAYAAAByl6h3AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXdYFcfXx7+79N7kAqLSBUHFih1BUGM0MVGjYAVrRM2r\nMVFjA3tJ1BjF+JNYKGrsaDSRKAIqmihYoogo1UazYUNAOO8fhA0LF7hcQBTn8zw8Dzs7c+bM2ZnZ\nc6ctR0QEBoPBYDAYDMZ7CV/fCjAYDAaDwWAw5Ic5cwwGg8FgMBjvMcyZYzAYDAaDwXiPYc4cg8Fg\nMBgMxnsMc+YYDAaDwWAw3mOYM8dgMBgMBoPxHsOcubfEmzdvMHbsWDRq1Ag8z+P06dP1rdJ7yb59\n+2BlZQVFRUWMHTtWahwvLy/07t37LWvGKPtsoqKiwPM8Hjx4UG1ZFhYWWL58eR1oWR5zc3MsW7bs\nreT1rsLzPHbt2lXfatRLPxkZGSmqp2WvAeDatWtwcnKCmpoaLC0tAQB3796Fm5sbNDU1oaCgUOd6\nfki8jfro4uKCiRMn1mkebxPmzJXCy8sLPM+D53koKSnB3NwckydPxuPHj2ss+8CBA9i9ezeOHj2K\njIwMdOnSpRY0/rAoLCzE2LFj4eHhgbt372L9+vVS43EcB47j3qpuISEh4PkPtzlJezZdu3ZFRkYG\nTExMAABnz54Fz/O4c+dOlfJiYmIwY8aMulYbQP3Ul5pw7949uR0dd3d3eHt7lwvPyMjA4MGDa0O9\nGvEu9JPdunUT1VsAmDVrFnR1dZGQkICLFy8CAJYvX46HDx/i6tWrSE9Pf+t6SmP8+PFwdXWtbzXe\nC0JDQ7F27dr6VqPWUKxvBd41nJ2dsXfvXrx58wYxMTGYMGEC7t69i6NHj8olLz8/H8rKyrh9+zZM\nTU3RuXPnGulXIu9D5MGDB3j58iX69esn6mjLQkRgZ2FXn6KiIgCQyymt6NlIJJJycWV5NgYGBtXW\n4UOjNuu4tOdUH7wL/aSSklI5eyQmJmLMmDFo1qyZSNeOHTvCysqqRroWFBRASUmpRjIY1UdXV7e+\nVahdiCEwZswYcnd3F4UtW7aMFBQU6PXr10REtHv3bnJ0dCRVVVUyNzenr7/+ml6+fCnE79mzJ40b\nN47mz59PJiYmZGxsTC4uLsRxnPBnYWFBRET5+fk0e/ZsMjU1JWVlZbK3t6ddu3aJ8uc4jn766Sfy\n9PQkHR0dGjZsGG3fvp0UFRUpIiKCWrZsSWpqauTq6krp6el06tQpcnR0JA0NDXJ3d6f79+8LspKT\nk+nzzz+nxo0bk7q6OrVq1YqCg4NF+fXs2ZPGjx9PixcvJmNjY9LX16fRo0fTixcvRPF+/fVXateu\nHamqqpKBgQH169ePnjx5Itz/6aefyNbWllRVVcnGxoaWLVtGb968qdT+58+fpx49epCamhrp6enR\n8OHDKSsri4iItm/fLrIhx3EUFRUl83Os6rn9+eef1LNnT9LX1ycdHR3q2bMnXbhwQSQjICCA7Ozs\nSFVVlfT19cnZ2Znu3btHERER5XTz9vausJzLli0jS0tLUlFRIUNDQ+rbty/l5uaKbGdqakrq6urU\nt29fCgwMJI7jhGdZ8vxLc/fu3XI2GT9+PFlZWZGamhpZWlrS3LlzKS8vT7jv6+tL1tbWtGfPHrK1\ntSVFRUW6efMmPX/+nL766itBh7Zt29LBgwcrLE9Fz6bELvfv36eUlJRycVxdXSuUaWZmRkuXLhVd\nL1iwgL788kvS0dEhIyMj2rRpE+Xm5pKPjw/p6emRqakpbdy4USSH4zhav349DRo0iDQ0NMjU1JTW\nr18vimNubk7Lli0TrvPz88nX15csLCxIVVWVHBwc6H//+185uRs2bKChQ4eShoYGmZmZ0cGDB+nx\n48fk4eFBWlpaZGlpSQcOHBCly8jIoDFjxpChoSFpaWlRt27d6PTp08L9EpudOHGCevToQerq6mRv\nb09//PGHKG9p/UlV7XvMmDEVtiGO42jnzp1C3AcPHtCwYcNIV1eX1NTUyMXFhWJiYqqlJ1HVdb00\nPXv2rLV+0sPDQ2oeRFW3r6rqrZ+fX4Xtvaq2UyJv586d1K9fP9LQ0KA5c+YQkWzvlsr6Zl9f33J6\nBQYGSrVBTk4OeXl5kbGxMamoqFDTpk3p66+/Fu7L0h/K0wZKyh8SEkK9evUS+qZff/21nOzS9bG6\nfRJRcZ84aNAgatSoEamqqpKlpSV9//335exZ+pmX/TM3Nxfi3759mwYNGkS6urqkp6dHffr0oWvX\nrsls07qGOXOlGDNmDPXu3VsUtmbNGuI4jl68eEHbt28nPT09CgkJoZSUFDp9+jS1bt2aRo0aJcTv\n2bMnaWlp0eTJkyk+Pp6uX79Ojx8/pm+++YYsLCwoMzOTHj58SERE33zzDRkYGND+/fvp9u3btHz5\ncuJ5nsLDwwV5HMeRgYEB+fv7U3JyMt2+fZu2b99OPM+Tq6srXbhwgS5dukQ2NjbUvXt3cnZ2pr//\n/puuXLlCdnZ2NGzYMEHWtWvXyN/fn/755x9KTk6mDRs2CE5haf11dXXp66+/poSEBPrzzz9JX1+f\nFixYIMTZtm0bKSkp0dKlS4Uybty4USiXr68vmZmZUWhoKKWmptLvv/9OzZo1E8koS3p6OmlpadGI\nESPo+vXrdPbsWWrdujU5OzsTEVFubi5dvHiROI6j3377jTIzMyk/P7/C51jamZPluR06dIj27dtH\nt27dohs3btD48eNJX1+fHj16REREMTExpKioSMHBwXTnzh26du0abd26le7du0f5+fnk7+9PHMdR\nZmYmZWZm0rNnz6TqduDAAdLW1qajR4/S3bt36cqVK7R+/XrhBRcaGkqKioq0bt06un37Nm3dupUk\nEgnxPF8tZ66oqIjmzZtHFy5coLS0NDpy5AiZmJiQr6+vkMbX15fU1dXJxcWFLly4QLdv36bnz5+T\ni4sLubq6UnR0NKWkpNCWLVtIWVlZVC9LU9GzKf1SLCwspCNHjhDHcRQTE0OZmZki578sZR0sMzMz\n0tXVpXXr1lFSUhItXbqUeJ6nvn37CmErVqwgnufpxo0bQjqO40hfX582btxIt2/fpvXr15OioiId\nPny4wrzGjBlDjo6OdOLECUpNTaU9e/aQrq4ubd26VSTX2NiYgoKCKCkpiXx8fEhDQ4P69OlDgYGB\nlJSURNOmTSMNDQ2hDr169YpatGhBQ4YModjYWEpKSqJly5aRiooKxcfHE9F/LxVHR0cKCwujxMRE\n8vb2Jm1tbcFely9fJo7j6NChQ6L+pKr2nZOTQ87OzuTh4SHU05I2VPrlWVRURE5OTtS2bVuKjo6m\na9eu0bBhw0hPT0/ISxY9q6rrZanNfjIxMVFqHrK0r7L1NiMjg5o2bUrfffcdZWZm0osXLygjI4O6\ndu1KI0eOFNp7UVFRlW2nxJlp0qQJ7dq1i1JTUyklJUXmd0tlffOLFy9oxIgR1K1bN+H5VmTradOm\nkaOjI124cIHu3r1L586do19++UW4X1V/KG8bKCl/48aNadeuXXTr1i2aP38+KSgo0OXLl0WyS9fH\n6vZJRESffPIJ9e7dm65evUppaWkUERFBu3fvFu67uLjQhAkTiKj4B0OJzTIzM+nGjRtkampKY8eO\nJaLiH2FGRkbk4+ND169fp1u3btG0adPIwMCAsrOzZbJpXcOcuVKUdQLi4uLI0tKSunTpQkTFL5Sy\nv9CjoqKI4zh6+vQpERU3OFtb23KyS0ZBSnj58iWpqKjQzz//LIr3+eefU69evYRrjuOEXw8llIyE\nXL16VQj7/vvvieM4unTpkhC2bt06atSoUaVlHjhwoFChS/Rv06aNKM7kyZMFGxARNW3alKZNmyZV\n3suXL0ldXZ3CwsJE4YGBgaSrq1uhHvPnz6emTZtSQUGBEHb16lXiOE4YuSjpCKKjoystU9nnKMtz\nK0thYSHp6ekJHcrBgwdJR0en
2014-05-05 05:44:10 +00:00
"text": [
2014-05-06 18:38:02 +00:00
"<matplotlib.figure.Figure at 0x10846f5d0>"
2014-05-05 05:44:10 +00:00
]
}
],
2014-05-06 18:38:02 +00:00
"prompt_number": 19
2014-05-05 05:44:10 +00:00
},
2014-05-06 05:08:11 +00:00
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
2014-05-06 18:38:02 +00:00
"In this performance comparison using different sample sizes, we can see that our Cython approach is actually not so fast anymore. However, this is just the simplest approach to using Cython. \n",
"There are a lot of improvements that can be made. In a [later section](#showdown) we will come back to this comparison and see how the Cython version of our simple least squares implementation holds up against the other approaches, after we tweaked it a little bit.\n",
2014-05-06 05:08:11 +00:00
"<br>"
]
},
2014-05-04 22:57:02 +00:00
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a name=\"cython_bonus\"></a>\n",
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Bonus: How to use Cython without the IPython magic"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[[back to top](#sections)]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"IPython's notebook is really great for explanatory analysis and documentation, but what if we want to compile our Python code via Cython without letting IPython's magic doing all the work? \n",
"These are the steps you would need."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 1. Creating a .pyx file containing the the desired code or function."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%file ccy_classic_lstsqr.pyx\n",
"\n",
"def ccy_classic_lstsqr(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" x_avg = sum(x)/len(x)\n",
" y_avg = sum(y)/len(y)\n",
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
" slope = cov_xy / var_x\n",
" y_interc = y_avg - slope*x_avg\n",
" return (slope, y_interc)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Writing ccy_classic_lstsqr.pyx\n"
]
}
],
"prompt_number": 11
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2. Creating a simple setup file"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%file setup.py\n",
"\n",
"from distutils.core import setup\n",
"from distutils.extension import Extension\n",
"from Cython.Distutils import build_ext\n",
"\n",
"setup(\n",
" cmdclass = {'build_ext': build_ext},\n",
" ext_modules = [Extension(\"ccy_classic_lstsqr\", [\"ccy_classic_lstsqr.pyx\"])]\n",
")"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Writing setup.py\n"
]
}
],
"prompt_number": 12
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<br>\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"####3. Building and Compiling"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"!python3 setup.py build_ext --inplace"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"running build_ext\r\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"cythoning ccy_classic_lstsqr.pyx to ccy_classic_lstsqr.c\r\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"building 'ccy_classic_lstsqr' extension\r\n",
"creating build\r\n",
"creating build/temp.macosx-10.6-intel-3.4\r\n",
"/usr/bin/clang -fno-strict-aliasing -Werror=declaration-after-statement -fno-common -dynamic -DNDEBUG -g -fwrapv -O3 -Wall -Wstrict-prototypes -arch i386 -arch x86_64 -g -I/Library/Frameworks/Python.framework/Versions/3.4/include/python3.4m -c ccy_classic_lstsqr.c -o build/temp.macosx-10.6-intel-3.4/ccy_classic_lstsqr.o\r\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\u001b[1mccy_classic_lstsqr.c:2040:28: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_AsString'\r\n",
" [-Wunused-function]\u001b[0m\r\n",
"static CYTHON_INLINE char* __Pyx_PyObject_AsString(PyObject* o) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2037:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function\r\n",
" '__Pyx_PyUnicode_FromString' [-Wunused-function]\u001b[0m\r\n",
"static CYTHON_INLINE PyObject* __Pyx_PyUnicode_FromString(char* c_str) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2104:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_IsTrue'\r\n",
" [-Wunused-function]\u001b[0m\r\n",
"static CYTHON_INLINE int __Pyx_PyObject_IsTrue(PyObject* x) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2159:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyIndex_AsSsize_t'\r\n",
" [-Wunused-function]\u001b[0m\r\n",
"static CYTHON_INLINE Py_ssize_t __Pyx_PyIndex_AsSsize_t(PyObject* b) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2188:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_FromSize_t'\r\n",
" [-Wunused-function]\u001b[0m\r\n",
"static CYTHON_INLINE PyObject * __Pyx_PyInt_FromSize_t(size_t ival) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1584:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_From_long'\r\n",
" [-Wunused-function]\u001b[0m\r\n",
"static CYTHON_INLINE PyObject* __Pyx_PyInt_From_long(long value) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1631:27: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_long' is not\r\n",
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
"static CYTHON_INLINE long __Pyx_PyInt_As_long(PyObject *x) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1731:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_int' is not\r\n",
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
"static CYTHON_INLINE int __Pyx_PyInt_As_int(PyObject *x) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"8 warnings generated.\r\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\u001b[1mccy_classic_lstsqr.c:2040:28: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_AsString'\r\n",
" [-Wunused-function]\u001b[0m\r\n",
"static CYTHON_INLINE char* __Pyx_PyObject_AsString(PyObject* o) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2037:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function\r\n",
" '__Pyx_PyUnicode_FromString' [-Wunused-function]\u001b[0m\r\n",
"static CYTHON_INLINE PyObject* __Pyx_PyUnicode_FromString(char* c_str) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2104:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyObject_IsTrue'\r\n",
" [-Wunused-function]\u001b[0m\r\n",
"static CYTHON_INLINE int __Pyx_PyObject_IsTrue(PyObject* x) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2159:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyIndex_AsSsize_t'\r\n",
" [-Wunused-function]\u001b[0m\r\n",
"static CYTHON_INLINE Py_ssize_t __Pyx_PyIndex_AsSsize_t(PyObject* b) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:2188:33: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_FromSize_t'\r\n",
" [-Wunused-function]\u001b[0m\r\n",
"static CYTHON_INLINE PyObject * __Pyx_PyInt_FromSize_t(size_t ival) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1584:32: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1munused function '__Pyx_PyInt_From_long'\r\n",
" [-Wunused-function]\u001b[0m\r\n",
"static CYTHON_INLINE PyObject* __Pyx_PyInt_From_long(long value) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1631:27: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_long' is not\r\n",
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
"static CYTHON_INLINE long __Pyx_PyInt_As_long(PyObject *x) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m\u001b[1mccy_classic_lstsqr.c:1731:26: \u001b[0m\u001b[0;1;35mwarning: \u001b[0m\u001b[1mfunction '__Pyx_PyInt_As_int' is not\r\n",
" needed and will not be emitted [-Wunneeded-internal-declaration]\u001b[0m\r\n",
"static CYTHON_INLINE int __Pyx_PyInt_As_int(PyObject *x) {\r\n",
"\u001b[0;1;32m ^\r\n",
"\u001b[0m"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"8"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" warnings generated.\r\n",
"/usr/bin/clang -bundle -undefined dynamic_lookup -arch i386 -arch x86_64 -g build/temp.macosx-10.6-intel-3.4/ccy_classic_lstsqr.o -o /Users/sebastian/Github/python_reference/benchmarks/ccy_classic_lstsqr.so\r\n"
]
}
],
"prompt_number": 13
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 4. Importing and running the code"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import ccy_classic_lstsqr\n",
"\n",
"%timeit classic_lstsqr(x, y)\n",
"%timeit cy_classic_lstsqr(x, y)\n",
"%timeit ccy_classic_lstsqr.ccy_classic_lstsqr(x, y)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"100 loops, best of 3: 2.9 ms per loop\n",
"1000 loops, best of 3: 212 \u00b5s per loop"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"1000 loops, best of 3: 207 \u00b5s per loop"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n"
]
}
],
"prompt_number": 20
2014-05-05 19:34:22 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a name=\"numba\"></a>\n",
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Appendix I: Cython vs. Numba"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[[back to top](#sections)]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-06 18:38:02 +00:00
"Like we did with Cython before, we will use the minimalist approach to Numba and see how the two - Cython and Numba - compare against each other. \n",
2014-05-05 19:34:22 +00:00
"\n",
2014-05-06 18:38:02 +00:00
"Numba is using the [LLVM compiler infrastructure](http://llvm.org) for compiling Python code to machine code. Its strength is to work with NumPy arrays to speed-up the code. If you want to read more about Numba, please see refer to the original [website and documentation](http://numba.pydata.org/numba-doc/0.13/index.html)."
2014-05-05 23:31:23 +00:00
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-06 18:38:02 +00:00
"<br>\n",
2014-05-05 23:31:23 +00:00
"Here is our \"classic\" approach in Python, where I removed the list comprehensions, since they caused errors in the Numba compilation."
2014-05-05 19:34:22 +00:00
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def lstsqr(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" x_avg = sum(x)/len(x)\n",
" y_avg = sum(y)/len(y)\n",
2014-05-05 23:31:23 +00:00
" var_x = 0\n",
" for x_i in x:\n",
" var_x += (x_i - x_avg)**2\n",
" cov_xy = 0\n",
" for x_i, y_i in zip(x,y):\n",
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
2014-05-05 19:34:22 +00:00
" slope = cov_xy / var_x\n",
" y_interc = y_avg - slope*x_avg\n",
" return (slope, y_interc)"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-05 23:31:23 +00:00
"prompt_number": 22
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The Cython-compiled version of it:"
]
2014-05-05 19:34:22 +00:00
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%load_ext cythonmagic"
],
"language": "python",
"metadata": {},
2014-05-05 23:31:23 +00:00
"outputs": []
2014-05-05 19:34:22 +00:00
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%cython\n",
"\n",
"def cy_lstsqr(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" x_avg = sum(x)/len(x)\n",
" y_avg = sum(y)/len(y)\n",
2014-05-05 23:31:23 +00:00
" var_x = 0\n",
" for x_i in x:\n",
" var_x += (x_i - x_avg)**2\n",
" cov_xy = 0\n",
" for x_i, y_i in zip(x,y):\n",
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
2014-05-05 19:34:22 +00:00
" slope = cov_xy / var_x\n",
" y_interc = y_avg - slope*x_avg\n",
" return (slope, y_interc)"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-05 23:31:23 +00:00
"prompt_number": 26
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"And now the Numba-compiled version:"
]
2014-05-05 19:34:22 +00:00
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from numba import jit\n",
"\n",
"@jit\n",
"def nmb_lstsqr(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" x_avg = sum(x)/len(x)\n",
" y_avg = sum(y)/len(y)\n",
2014-05-05 23:31:23 +00:00
" var_x = 0\n",
" for x_i in x:\n",
" var_x += (x_i - x_avg)**2\n",
" cov_xy = 0\n",
" for x_i, y_i in zip(x,y):\n",
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
" \n",
2014-05-05 19:34:22 +00:00
" slope = cov_xy / var_x\n",
" y_interc = y_avg - slope*x_avg\n",
" return (slope, y_interc)"
],
"language": "python",
"metadata": {},
2014-05-05 23:31:23 +00:00
"outputs": [],
"prompt_number": 27
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<br>\n",
"Now, let us see how the different approaches compare against each other for different sample sizes."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import timeit\n",
"import random\n",
"random.seed(12345)\n",
"\n",
"funcs = ['lstsqr', 'cy_lstsqr', 'nmb_lstsqr'] \n",
"orders_n = [10**n for n in range(1, 7)]\n",
"times_n = {f:[] for f in funcs}\n",
"\n",
"for n in orders_n:\n",
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
" for f in funcs:\n",
" times_n[f].append(timeit.Timer('%s(x,y)' %f, \n",
" 'from __main__ import %s, x, y' %f).timeit(1000))"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 28
},
{
"cell_type": "code",
"collapsed": false,
"input": [
2014-05-06 18:38:02 +00:00
"%pylab inline"
],
"language": "python",
"metadata": {},
"outputs": []
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import matplotlib.pyplot as plt\n",
2014-05-05 23:31:23 +00:00
"\n",
"plt.figure(figsize=(10,8))\n",
"\n",
"for f in times_n.keys():\n",
" plt.plot(orders_n, times_n[f], alpha=0.5, label=f, marker='o', lw=2)\n",
"\n",
"plt.xlabel('sample size n')\n",
"plt.ylabel('time in ms')\n",
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
"plt.legend(loc=2)\n",
"plt.grid()\n",
"\n",
"plt.title('Performance of a simple least square fit implementation')\n",
"plt.show()"
],
"language": "python",
"metadata": {},
2014-05-05 19:34:22 +00:00
"outputs": [
{
2014-05-05 23:31:23 +00:00
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAmEAAAH4CAYAAAACdDpdAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl4k2XW+PFv0n1vKV2A0gUKhULZBRSQQhFwYRlBliKL\nivO6jCvzc3RUFp0RxhnfcfB1m2GpClhABWRHliqiUtmkUKC00AJtKS2lQOmSNrl/fzxDpFCgSNts\n53Ndva4+SZ7kJCdPcnLfd050SimFEEIIIYRoVHpLByCEEEII4YikCBNCCCGEsAApwoQQQgghLECK\nMCGEEEIIC5AiTAghhBDCAqQIE0IIIYSwACnChM0pKCjg7rvvxtfXl//3//6fpcOxuPLycoYNG4a/\nvz9jx45tsNu57777+OyzzxrkuvV6PceOHbvl/ZKSkujXr18DRGT/duzYQZs2bfD19WXVqlXcd999\nfPrpp3Xe3xqfD9Zu9uzZPP7445YOQ1gRZ0sHIBxDZGQkZ86cwcnJCS8vL+69917+7//+Dy8vr1u+\nrn//+98EBwdz4cKFBojU9nzxxRecOXOG4uJi9PqG+1y1bt26BrtuaxYfH8/EiRN57LHHLB1KvZo+\nfTrPPvsszzzzDAAjRowwn5eUlMT8+fPZvn37dfd3tOfDzJkzycrKqnPhmZKSwsSJEzl58qT5tFde\neaWhwhM2SkbCRKPQ6XSsWbOGixcvsmfPHnbt2sVf/vKXW7oOpRQmk4mcnBzat2//m+Korq7+TftZ\ns5ycHNq2bdugBZgj0+l0lg7hpn7L8/rEiRPExsY2QDRCiDpTQjSCyMhItWXLFvP2H//4R/XAAw8o\npZT68ccf1Z133qn8/f1V586dVUpKivly/fv3V6+++qrq06eP8vDwUA8//LBycXFRrq6uytvbW23Z\nskVVVlaq5557TjVv3lw1b95cPf/886qyslIppdS2bdtUixYt1N/+9jcVGhqqJk6cqGbOnKlGjx6t\nHn74YeXj46Pi4uJURkaGeuutt1RwcLAKDw9XmzZtMsewYMEC1b59e+Xj46NatWqlPv74Y/N5l6//\nnXfeUcHBwapZs2Zq4cKF5vPLysrUiy++qCIiIpSfn5/q27evKi8vv+n9vlp6errq37+/8vf3Vx06\ndFBff/21Ukqp6dOnK1dXV+Xi4qK8vb3VggULrtl3586dqnfv3srf3181a9ZM/eEPf1AGg6HW2ykv\nL1cTJkxQgYGByt/fX91xxx3qzJkz5lzMmzdPKaXUwoUL1V133aVeeOEF5e/vr1q3bq127NihFixY\noFq2bKmCg4PVJ598Yr7eyZMnq//5n/9R99xzj/Lx8VH9+/dXOTk55vN1Op3KyspSSilVUVGhpk2b\npsLDw1VISIh64oknzI/Z1RYuXKj69u1r3j506JAaNGiQatKkiYqJiVHLli0zn7dmzRrVpUsX5evr\nq1q2bKlmzpx5w/tdUFCg/vznPysnJyfl7u6uvL291TPPPFOnx6ygoEAppdSxY8fU3XffrXx8fNQ9\n99yjnn76afXwww8rpbTnTlhYWI3rioiIMB8nN8ubTqdT77//voqOjlatWrVSSim1evVq1blzZ+Xv\n76/uuusutX///loft1atWim9Xq88PDyUj4+PqqysNOf30KFDys3NTTk5OSlvb28VEBBQ63VYw/Ph\n8vH39ttvq6CgINWsWTO1YsUKtXbtWtWmTRvVpEkTNXv2bPP1mkwmNXv2bNW6dWsVGBioxowZo4qL\ni5VSSh0/flzpdDr1ySefqPDwcNW0aVP117/+VSml1Pr162scZ126dFFKXf+1obS0VLm7uyu9Xq+8\nvb2Vj4+PysvLUzNmzDDnXymlVq1apWJjY5W/v7+Kj49Xhw4dqvFc+Mc//qE6deqk/Pz81NixY1VF\nRUWtuRC2S4ow0SgiIyPV5s2blVJKnThxQnXo0EFNnz5dnTp1SgUGBqr169crpZT65ptvVGBgoCoq\nKlJKaS/0ERERKj09XRmNRlVVVaWmTJmiXn/9dfN1v/766+rOO+9UhYWFqrCwUN11113m87dt26ac\nnZ3Vyy+/rAwGgyovL1czZsxQ7u7uatOmTaq6ulpNmjRJRUREqLfeektVV1er//znPyoqKsp8/WvX\nrlXHjh1TSin17bffKk9PT7Vnz54a1z9jxgxVXV2t1q1bpzw9PVVJSYlSSqmnnnpKDRgwQOXl5Smj\n0ah+/PFHVVlZed37XVhYeM1jZzAYVOvWrdXs2bNVVVWV2rp1q/Lx8VFHjhxRSik1c+ZMNXHixOs+\n9rt371Y7d+5URqNRZWdnq/bt26t333231st+9NFHatiwYaq8vFyZTCa1Z88edeHCBaWUUvHx8Wr+\n/PlKKe1N19nZWSUlJSmTyaRee+011aJFC3OhsGnTJuXj46MuXbqklNLedH18fNT27dvNRfOVxdOV\nb7rPP/+8GjFihDp37py6ePGiGjZsmHrllVdqjffKIqy0tFSFhYWppKQkZTQa1d69e1XTpk1Venq6\nUkqplJQUdeDAAaWUUvv371chISFq5cqVt3S/b/Ux6927t5o2bZoyGAzqu+++Uz4+PuZc1VaEXflh\n5WZ50+l0avDgwercuXOqoqJC7dmzRwUHB6vU1FRlMpnUJ598oiIjI80fSK529QejK+9nUlJSjfzU\nxhqeD5ePvzfffNN87AYGBqrExERVWlqqDh48qDw8PFR2drZSSql3331X3XnnnSo3N1cZDAb1P//z\nP2r8+PFKqV+LsN///veqoqJC/fLLL8rNzU0dPnxYKVX7cXaj14aUlJRr8jtz5kxzEXbkyBHl5eWl\nNm/erKqrq9Xbb7+toqOjVVVVlTk/vXr1Uvn5+aq4uFi1b99effTRRzfMibA9UoSJRhEREaG8vb2V\nv7+/ioiIUE8//bQqLy9Xc+bMueaFbciQIeZPzfHx8WrGjBk1zp8yZYp67bXXzNutW7c2FzNKKbVx\n40YVGRmplNJepF1dXWu8Ec2YMUMNHjzYvP31118rb29vZTKZlFJKXbhwQel0OnX+/Pla78vIkSPV\nv/71L/P1e3h4KKPRaD4/ODjY/Obp4eFR62jEze73lb777jsVGhpa47Tx48ebR3Ku/nR9M//85z/V\n7373u1rPW7BgwXVHUK5+023Tpo35vP379yudTmceNVNKqcDAQPXLL78opbQ33ctvdkppBZOTk5M6\ndeqUUurXN12TyaS8vLzMb8BKKfXDDz/UKIqvdGURlpycrPr161fj/N///vdq1qxZte773HPPqRde\neKFO9/vyiE9trrdvTk6OcnZ2VmVlZebTEhMT61yEXe3qvOl0OrVt2zbz9hNPPFHjw4lSSsXExKhv\nv/221uu7URF29Qhjbazh+XD5+Lv62E1NTTVfvnv37mrVqlVKKaXatWtX4z7n5eUpFxcXZTQazUVY\nbm6u+fyePXuqpUuXKqXqdpxd/dpwdX6vvI433nhDjR071nyeyWRSLVq0MOcrMjJSLV682Hz+Sy+9\npJ544okb3r6wPbIwXzQKnU7HqlWrGDhwYI3Tc3JyWL58OatXrzafVl1dXeNyLVu2vOF15+XlERER\nYd4ODw8nLy/PvB0UFISrq2uNfYKDg83/e3h40LRpU/PaHw8PDwBKS0vx9fVl/fr1zJo1i6NHj2Iy\nmSgrK6NTp07m/QMDA2usx/L09KS0tJSioiIqKipo3br1NTHX5X5fef+ufgwiIiLIzc294eNyWUZG\nBi+++CK7d++mrKyM6upqevToUetlLy8kHjduHCUlJTz88MP89a9/xdn52peKkJAQ8/+XH7OgoKAa\np5WWlgJa/sPCwszneXl50aRJE/Ly8mjRooX59MLCQsrKyujevbv5NPXftYA3k5OTw86dOwkICDCf\nVl1dzaRJkwDYuXMnL7/8MgcPHsRgMFBZWcmYMWPqdL9vtC7sevvm5eUREBBgfmxAy9uVC7VvpC55\nu/J5kZOTw6effsp7771nPq2q
"text": [
"<matplotlib.figure.Figure at 0x1031a8710>"
2014-05-05 19:34:22 +00:00
]
}
],
2014-05-05 23:31:23 +00:00
"prompt_number": 32
2014-05-05 19:34:22 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-06 18:38:02 +00:00
"Without making any modifications to the original Python code - thereby we are not accounting for the particular strengths of Numba (Numpy) and Cython (static type declarations), we see that Cython performs significantly better than Numba."
2014-05-05 19:34:22 +00:00
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a name=\"type_declarations\"></a>\n",
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Appendix II: Cython with and without type declarations"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[[back to top](#sections)]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In the sections above, we have been using the simplest approach to Cython without using static type declarations and thereby neglecting one of its major strengths. \n",
2014-05-06 18:38:02 +00:00
"Now, let us see how and if we can further improve the Cython implementation of our \"classic least squares approach\" by adding those type declarations."
2014-05-05 19:34:22 +00:00
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-05 23:31:23 +00:00
"Here is our \"classic\" approach in Python:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def lstsqr(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" x_avg = sum(x)/len(x)\n",
" y_avg = sum(y)/len(y)\n",
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
" slope = cov_xy / var_x\n",
" y_interc = y_avg - slope*x_avg\n",
" return (slope, y_interc)"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-06 18:38:02 +00:00
"prompt_number": 21
2014-05-05 23:31:23 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The Cython-compiled version of it:"
2014-05-05 19:34:22 +00:00
]
},
2014-05-05 23:31:23 +00:00
{
"cell_type": "code",
"collapsed": false,
"input": [
"%load_ext cythonmagic"
],
"language": "python",
"metadata": {},
2014-05-06 18:38:02 +00:00
"outputs": [],
"prompt_number": 23
2014-05-05 23:31:23 +00:00
},
2014-05-05 19:34:22 +00:00
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%cython\n",
"def cy_lstsqr(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" x_avg = sum(x)/len(x)\n",
" y_avg = sum(y)/len(y)\n",
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
" slope = cov_xy / var_x\n",
" y_interc = y_avg - slope*x_avg\n",
" return (slope, y_interc)"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-06 18:38:02 +00:00
"prompt_number": 24
2014-05-05 19:34:22 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"And now, the same code with static type declarations:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%cython\n",
"def static_type_lstsqr(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" cdef double x_avg, y_avg, var_x, cov_xy, slope, y_interc, x_i, y_i\n",
" x_avg = sum(x)/len(x)\n",
" y_avg = sum(y)/len(y)\n",
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
" slope = cov_xy / var_x\n",
" y_interc = y_avg - slope*x_avg\n",
" return (slope, y_interc)"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-06 18:38:02 +00:00
"prompt_number": 25
2014-05-05 19:34:22 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<br>\n",
"Now, let us see how the two functions (with and without static type declarations) compare against each other for different sample sizes."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import timeit\n",
"import random\n",
"random.seed(12345)\n",
"\n",
"funcs = ['cy_lstsqr', 'static_type_lstsqr'] \n",
"labels = ['simple Cython', 'Cython w. type declarations']\n",
"orders_n = [10**n for n in range(1, 7)]\n",
"times_n = {f:[] for f in funcs}\n",
"\n",
"for n in orders_n:\n",
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
" for f in funcs:\n",
" times_n[f].append(timeit.Timer('%s(x,y)' %f, \n",
" 'from __main__ import %s, x, y' %f).timeit(1000))"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-06 18:38:02 +00:00
"prompt_number": 26
2014-05-05 19:34:22 +00:00
},
{
"cell_type": "code",
"collapsed": false,
"input": [
2014-05-06 18:38:02 +00:00
"%pylab inline"
],
"language": "python",
"metadata": {},
"outputs": []
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import matplotlib.pyplot as plt\n",
2014-05-05 19:34:22 +00:00
"\n",
"plt.figure(figsize=(10,8))\n",
"\n",
"for f in times_n.keys():\n",
" plt.plot(orders_n, times_n[f], alpha=0.5, label=f, marker='o', lw=2)\n",
"\n",
"plt.xlabel('sample size n')\n",
"plt.ylabel('time in ms')\n",
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
"plt.legend(loc=2)\n",
"plt.grid()\n",
"\n",
"plt.title('Performance of a simple least square fit implementation')\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
2014-05-06 18:38:02 +00:00
"png": "iVBORw0KGgoAAAANSUhEUgAAAmcAAAH/CAYAAAASb3qiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdYFGf3N/DvotKLKIKooNgwImDvCkYsWKIYCyrqqmCL\nKUYTjfGx5JFcyeNPkxiNsaKJLdZoYktEERXfSDSigCAigopYiIKgSNn7/WPCxpUiILCz7PdzXVwy\nuzszZ+fsrId7zswohBACRERERCQLBtoOgIiIiIj+xeKMiIiISEZYnBERERHJCIszIiIiIhlhcUZE\nREQkIyzOiIiIiGSExRlVmNzcXEyaNAk2NjYwMDBAaGiotkPSSbt370aTJk1QvXp1TJo0qdLWq1Qq\n0adPH51al4GBAbZv314OEVFJvbyfnzp1qsz5DAkJgYGBAZKTkysgUu2tS642b96MGjVqaDsMKgSL\nMz2nVCphYGAAAwMD1KhRA40aNcL06dPx999/v/ay9+7dix07duDXX39FSkoKunTpUg4R65e8vDxM\nmjQJvr6+uHXrFr755ptKW/e3336LPXv2VMq6FAoFFApFpayrvHl5eWHixInaDkNrXt7Pu3btWuCz\n4+/vj169er1yWd26dUNKSgrs7e0rMmSdtXTpUjg5OZV6vtu3bxf6B7Kvr69eF6dyVl3bAZD29ezZ\nE7t27UJubi7+/PNPBAQE4NatW/j111/LtLzs7GwYGhoiLi4O9evXR+fOnV8rvvzl6aPk5GRkZmbC\n29u70v/DsrCwqLR1CSHA62Frz+vsY4Xt52UdjalRowZsbW3LNC+92sv7mLGxMYyNjbUUDRVLkF6b\nMGGC8PLy0ngsMDBQVKtWTWRlZQkhhNixY4dwd3cXxsbGolGjRuLDDz8UmZmZ6td7eHiIyZMniwUL\nFgh7e3tRt25d4enpKRQKhfrHyclJCCFEdna2mDt3rqhfv74wNDQULVu2FNu3b9dYv0KhECtXrhSj\nR48WVlZWYtSoUSIoKEhUr15dnDx5UrRq1UqYmJiIXr16ibt374oTJ04Id3d3YWZmJry8vMSdO3fU\ny7px44bw8fER9erVE6ampsLV1VX8+OOPGuvz8PAQ/v7+4rPPPhN169YVtWrVEuPHjxcZGRkar9u5\nc6do27atMDY2FrVr1xbe3t7i0aNH6udXrlwpnJ2dhbGxsWjWrJkIDAwUubm5xW7/c+fOiR49eggT\nExNhbW0txowZI+7fvy+EECIoKEhjGyoUCnHq1KlCl/Pbb78JDw8PUatWLWFlZSU8PDzE+fPni113\nWlqaUCqVom7dusLIyEg4ODiIDz/8UP38y5+N/OmVK1eK+vXrC3NzczF16lSRm5srvv32W+Ho6Cis\nra3FlClTRHZ2tsb2nTRpkpg7d66wsbERlpaWYsqUKerPV2HrEuLVn7vCKBQKsW3bNvX0kydPxHvv\nvSfq168vTE1NRZs2bcS+ffs05pk/f7544403hKmpqXBwcBDTpk0TaWlpJdpOEyZMKHGObt26JYYN\nGyZsbGyEsbGxaNy4sVi2bJn6+dTUVDFy5EhhZmYm7OzsxIIFC8T48eM1tkv+Z/VF//3vf0WjRo3U\n0xcuXBD9+/cXtra2wtzcXHTo0EEcPXpUY56GDRuKBQsWiOnTp4vatWuLzp07CyGE+PPPP0WfPn2E\nubm5qFOnjhg2bJhITEwscnt7eHgUup+/mM9FixYV2EZbtmwpdHknT54UCoVCvQ/nTx8+fFh07txZ\nmJiYiPbt24vo6GgREREhunbtKkxNTUXHjh1FdHS0ejn53xfHjx8XLVu2FMbGxqJTp07i0qVLRa5L\nCCHi4uLEsGHDRM2aNYW1tbXo27evuHLlSoHllvZ7SAhpH+3ataswMTER9evXFxMnThSpqanq5/O3\n2dq1a4Wjo6OwtLQUb731lrh375563S9vxyVLlgghhNi2bZvo2LGjsLKyEjY2NmLgwIHi2rVr6mW/\nPF9+nvLfz4sOHTok2rZtK4yMjIStra2YMWOGxn73qjipfLA403MTJkwQffr00Xhs+fLlQqFQiIyM\nDBEUFCSsra3F1q1bRUJCgggNDRVubm5i3Lhx6td7eHgICwsLMX36dHH16lURGRkp/v77bzFnzhzh\n5OQk7t27Jx4+fCiEEGLOnDmidu3aYs+ePSIuLk58/vnnwsDAQAQHB6uXp1AoRO3atcXq1avFjRs3\nRFxcnAgKChIGBgaiV69e4vz58+LixYuiWbNmonv37qJnz57ijz/+EJcuXRItWrQQo0aNUi/rypUr\nYvXq1eLy5cvixo0b4ttvv1V/ub4Yf82aNcWHH34oYmNjxW+//SZq1aol/vOf/6hfs2nTJlGjRg2x\ndOlS9XtctWqV+n0tWrRINGzYUPz888/i5s2b4vDhw8LR0VFjGS+7e/eusLCwEGPHjhWRkZHizJkz\nws3NTfTs2VMIIcSzZ89EeHi4UCgU4pdffhH37t3TKHpetH//frF7925x7do1ER0dLfz9/UWtWrU0\nvvxf9u677wp3d3dx/vx5cevWLREWFiY2bNigfl6pVGp8NiZMmCAsLS2FUqkUMTEx4pdffhHGxsai\nX79+YsKECSImJkYcOnRImJiYiDVr1mhs3/yCLH8+W1tbMWvWLI1lv1iElORzV5gXizOVSiU8PT1F\nr169xNmzZ0VCQoJYt26dMDQ01Pi8LV26VJw5c0YkJiaK4OBg0aJFCzFhwoQSbae0tDTRs2dP4evr\nK+7du1dsjgYPHiz69OkjIiIiRGJiojh58qTYsWOH+vmhQ4eKZs2aiZMnT4qoqCjh5+cnLC0tNXLg\n6ekpAgICNJb7cnEWEhIitmzZIqKjo0VcXJxYsGCBMDQ01PjPumHDhsLS0lIsWbJExMXFiatXr4qo\nqChhbm4uFi9eLGJjY0VkZKQYMWKEaN68uUYh/aKi9vMXv1cyMjLE2LFjRbdu3dTb6NmzZ4Uur6ji\nrG3btuLkyZMiOjpadOnSRbi5uYlu3bqJEydOiKtXr4ru3buLTp06qZeT/33Rrl07ERoaKi5fviwG\nDRok6tevr173y+tKSUkRdnZ2YsaMGSIyMlJcu3ZNvPvuu6J27driwYMHGsst7fdQcHCwMDU1FatW\nrRLXr18X4eHholevXsLDw0P9mgkTJggrKysxZswYERUVJc6dOyecnJzUn/lnz56JefPmCQcHB/V2\nzP8DMigoSPz666/ixo0b4tKlS+Ktt94SzZo1U38W//rrL6FQKMT+/fs18vRycRYRESGqVaum/i48\ncuSIcHR01NjvXhUnlQ8WZ3ru5f8Uo6KiROPGjUWXLl2EENKX+Nq1azXmOXXqlFAoFOLx48dCCOk/\nX2dn5wLLXrRokWjatKl6OjMzUxgZGWn8xy2EED4+PuLNN99UTysUigKjA/l/NUZERKgfW7ZsmVAo\nFOLixYvqx7766ithY2NT7HseMmSIxn9wHh4eonXr1hqvmT59unobCCGEg4ODePfddwtdXmZmpjA1\nNRXHjh3TeHzLli2iZs2aRcaxYMEC4eDgIHJyctSPRURECIVCIUJDQ4UQQiQkJAiFQiHOnj1b7Ht6\nWV5enrC2ttYYRXrZkCFDhFKpLPL5wkbO7OzsNOIdOHCgqFOnjkZBMmTIEDF8+HD1tIeHh3BychIq\nlUr92Lp164SxsbF4+vRpoesqyeeuMC8WZydPnhTGxsYao2BCCDFx4kQxdOjQIpexb98+YWRkpPF+\nittOXl5eYuLEiUU+n8/d3V0sXry40Ofi4uKEQqEQx48fVz+WnZ0t6tevX+rirKh1BwYGqqcbNmxY\nYKRywoQJwtfXV+OxrKwsYWpqKn7++ecil/3yfp6/rBeXP3nyZOHp6VlsjEIUXZwdOHBA/Zrdu3cL\nhUKhMQK6f/9+oVAo1CM8+d8XJ06cUL/m0aNHwtzcXGzcuLHQdS1atEg9gphPpVKJJk2aiK+//lpj\nuaX9HvLw8BCffPKJxrITExM1
2014-05-05 19:34:22 +00:00
"text": [
2014-05-06 18:38:02 +00:00
"<matplotlib.figure.Figure at 0x10ed0dd90>"
2014-05-05 19:34:22 +00:00
]
}
],
2014-05-06 18:38:02 +00:00
"prompt_number": 27
2014-05-05 19:34:22 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<br>\n",
2014-05-06 18:38:02 +00:00
"The improvement is pretty significant when static type declarations are used. \n",
"One more experiment to see by how much we could improve our \"classic least squares\" code via Cython compared to the initial Python implementation:\n",
2014-05-05 19:34:22 +00:00
"<br>\n",
"<br>"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import random\n",
"random.seed(12345)\n",
"\n",
"x = [x_i*random.randrange(8,12)/10 for x_i in range(500)]\n",
"y = [y_i*random.randrange(8,12)/10 for y_i in range(100,600)]"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-06 18:38:02 +00:00
"prompt_number": 30
2014-05-05 19:34:22 +00:00
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import timeit\n",
"\n",
"funcs = ['classic_lstsqr', 'cy_lstsqr', 'static_type_lstsqr', \n",
" 'lin_lstsqr_mat', 'numpy_lstsqr', 'scipy_lstsqr']\n",
"labels = ['classic approach','classic approach (cython)', \n",
" 'classic approach (cython + type decl.)',\n",
" 'matrix approach', 'numpy function', 'scipy function']\n",
"\n",
"times = [timeit.Timer('%s(x,y)' %f, \n",
" 'from __main__ import %s, x, y' %f).timeit(1000)\n",
" for f in funcs]\n",
"\n",
"times_rel = [times[0]/times[i+1] for i in range(len(times[1:]))]"
],
"language": "python",
"metadata": {},
"outputs": [],
2014-05-06 18:38:02 +00:00
"prompt_number": 31
2014-05-05 19:34:22 +00:00
},
{
"cell_type": "code",
"collapsed": false,
"input": [
2014-05-06 18:38:02 +00:00
"%pylab inline"
],
"language": "python",
"metadata": {},
"outputs": []
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import matplotlib.pyplot as plt\n",
2014-05-05 19:34:22 +00:00
"\n",
"x_pos = np.arange(len(funcs[1:]))\n",
"plt.bar(x_pos, times_rel, align='center', alpha=0.5, color=\"green\")\n",
"plt.xticks(x_pos, labels[1:], rotation=90)\n",
2014-05-06 18:38:02 +00:00
"plt.ylabel('rel. performance gain')\n",
"plt.title('Performance gain compared to the classic least square'\\\n",
" '(n={})'.format(len(x)))\n",
2014-05-05 19:34:22 +00:00
"plt.grid()\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
2014-05-06 18:38:02 +00:00
"png": "iVBORw0KGgoAAAANSUhEUgAAAdUAAAHnCAYAAADuC8dRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdUFPcWB/DvIEhHepGuIGAJaNBn1NhiLyHYY8WWRJNn\nNM0WItanSSwxaiwxYkQxsUejGGM3MZYoJCoqlgUsoKCiokjxvj88zDICiro4uz/u5xzOYX87O3vv\nlrk7c6dIRERgjDHG2AszUjsAxhhjTBRcVBljjDEd4aLKGGOM6QgXVcYYY0xHuKgyxhhjOsJFlTHG\nGNMRVYtqfn4+Bg0aBEdHRxgZGWHfvn1qhiOsPXv2wMjICFeuXFE7FKFERESgdevWqsYQFRUFf39/\nVZ7bx8cHU6dOfWnP17x5c7zzzjvP/XiNRgMjIyP8+eefOoyKPY6I8Oqrr2LNmjVqh6IzMTExaNiw\nYZmmfWpRjYiIgJGREYyMjGBiYgIfHx8MGzYMN27ceOFA161bh9jYWGzZsgVpaWl47bXXXnierLjG\njRsjLS0Nbm5uaociHEmSSr3v0qVLOvuxqMt56YokSU/MX9c2btyIWbNmvbTn0xU/Pz9MnDhR7TBe\nmlWrVuHBgwfo3r17uT5P0dpU+FepUiU8fPhQMd3WrVsREhICMzMz+Pr6Yvbs2cXmdejQITRq1Ajm\n5uaoWrUqxo0bp5hP7969cfPmTaxbt+6pcZVpTbVp06ZIS0tDcnIy5s6di/Xr16N///5leWiJcnNz\nAQBJSUlwd3dHw4YN4ezsDBMTkxeaHyuZiYkJnJ2dX+oC0FDk5+e/0OPLcu4UXZ5fpSKfq8XW1hZW\nVlZqh/HMRPjePcsyds6cORg8eHA5RvOIJElybSr8u3r1KoyMtGXt6NGjCAsLQ8eOHZGQkICoqCiM\nGzcOixYtkqdJTU1F69atERQUhGPHjuG7777DokWLMH78eHkaIyMjDBgwAHPnzn16YPQUAwYMoFat\nWinGpk6dSpUqVaKcnBwiIoqNjaXg4GAyMzMjHx8f+uijjyg7O1uevlmzZjR48GD6/PPPyc3NjVxd\nXal58+YkSZL85+vrS0REubm5NHr0aHJ3d6fKlStTzZo1adWqVYrnlySJ5s6dS2+//TZVqVKFevbs\nScuWLSNjY2PavXs31a5dm8zNzalFixZ09epV2rVrFwUHB5OlpSW1atWKLl++LM/rwoULFB4eTlWr\nViULCwuqU6cOrVixQvF8zZo1oyFDhtCkSZPI1dWV7O3tqX///nT37l3FdKtXr6Z69eqRmZkZOTg4\nUPv27enmzZvy/XPnzqWAgAAyMzMjf39/mjp1KuXn5z/x9f/999+pdu3aZGZmRiEhIbRv3z6SJIli\nYmLkacaNG0dBQUFkYWFBnp6e9N5771FWVpZ8/+7du0mSJDnvwts7duyg119/nSwsLKhmzZq0bdu2\nJ8ZCRLRjxw5q0qQJWVhYUJUqVahZs2Z0/vx5+f6vvvqKfH19qXLlylS9enWaM2eO4vHe3t4UGRlJ\n7733HlWpUoVcXFxowYIFdP/+fRo+fDjZ2dmRu7s7zZs3T/E4SZLom2++oS5dupClpSW5u7vTN998\no5hmzpw5FBISQlZWVuTq6kq9evWiq1evFnsdfv31V2rcuDGZmZnRwoULy/TeZGZmUo8ePcjS0pJc\nXFzo888/p/79+xf7bjwec0mfcSKi6OhoCgoKosqVK5OHhwd9/vnnT/wslDavCRMmkJ+fH23atIkC\nAgLI0tKSmjdvTklJSYrHHz16lFq3bk1WVlbk5OREXbp0oeTk5FKfj4goLy+PoqKiqFq1amRqakru\n7u703//+V77fx8eHpk6dKt9euXIlNWjQgKpUqUKOjo7UsWNHOnv2rGKeU6dOlefn5OREbdu2pfv3\n7xMRUWpqKnXp0oUcHR3JzMyMqlWrRl999ZX82MLvYVHz5s2joKAgMjU1JWdnZ+ratWup+Vy8eJEk\nSaI//vhDHktLS6MBAwaQk5MTWVtbU+PGjWnfvn2Kxw0ZMoSqV69O5ubmVK1aNRo3bhw9ePBAvv9J\ncTdr1qzYe1fa637ixAlq06YN2drakqWlJQUFBSmWRRqNhtq2bUvm5ubk6elJc+fOLfaaeHt705Qp\nUxTzHTx4MDVv3ly+/dtvv1GzZs3I3t5e/g4fPnxY8ZjHl7G9evWSH9uoUSMyNzcnd3d3GjhwIGVm\nZsqPO3PmDEmSRBcvXiw2vwULFlDfvn3J2tqaPDw86H//+1+Jr0NZlVSbHvf2229T48aNFWOffvop\n+fj4yLfHjh1Lnp6eimnmz59PlpaWdO/ePXns5MmTJEkSpaSkPPE5y1RUW7durRibOXMmSZJEd+/e\npWXLlpGdnR3FxMTQxYsXad++ffTKK69Qv3795OmbNWtG1tbWNGzYMEpMTKQTJ07QjRs36JNPPiFf\nX19KT0+njIwMIiL65JNPyMHBgdauXUtJSUk0bdo0MjIyop07d8rzkySJHBwcaP78+XThwgVKSkqi\nZcuWkZGREbVo0YIOHz5Mx44dI39/f2rSpAk1bdqUDh06RPHx8RQYGEg9e/aU5/Xvv//S/Pnz6Z9/\n/qELFy7Qt99+KxfnovHb2trSRx99RGfOnKHffvuN7O3tKTIyUp7mhx9+IBMTE5oyZYqc47x58+S8\nJkyYQN7e3rRx40bSaDS0detW8vLyUszjcZcuXSJzc3MaOnQoJSYm0s6dO6levXokSRKtXLlSnm7K\nlCl04MABSk5Opp07d1JgYCANGDBAvr+0ohocHEzbt2+nc+fO0cCBA8nGxkbxI+BxO3bsoEqVKtGo\nUaPon3/+oTNnzlB0dDSdOXOGiB4t4MzNzWnJkiV07tw5WrhwIZmZmdHSpUvleXh7e5OtrS3Nnj2b\nzp8/T1OmTCEjIyNq27atPPa///2PjIyM6NSpU4r33N7enubNm0dJSUn0zTffkLGxMW3atEme5ptv\nvqGdO3eSRqOhgwcPUqNGjahZs2bFXofAwEDasmULaTQaunTpUpnem7feeov8/f1p9+7ddPLkSerb\nty/Z2NgU+24Udfz4cZIkiTZs2KD4jG/ZsoUqVapE06dPp6SkJPrpp5/Izs7uiZ+F0uY1YcIEsrS0\npPbt29OxY8coISGBXn31VXr99dflx548eZKsrKwoKiqKzpw5QydOnKDu3btTjRo15B/GJenfvz85\nOztTTEwMXbhwgY4cOaL4IfN4UV22bBlt2bKFLly4QPHx8fTmm2+Sv78/5ebmEhHRunXryMbGhrZs\n2UKpqakUHx9P33zzjVxUO3fuTK1bt6aEhARKTk6m3bt3U2xsrDz/5s2b09ChQ+XbX3zxBVlZWdH8\n+fMpKSmJ4uPjn7igfryo3rt3j4KCgqhbt270999/0/nz52nq1KlkampKiYmJRET08OFDGj9+PB0+\nfJiSk5Ppl19+ITc3N5owYYI83yfFfePGDfL19aVPP/2U0tPTKT09nQoKCkqMr06dOtSnTx9KTEyk\nixcv0rZt22jLli1yHHXr1qUGDRrQ4cOHKT4+nlq3bk02NjaK1+Tx94ToUVFt0aKFfHvDhg20Zs0a\nOnv2LJ06dYqGDBlC9vb2iuL4+DL23LlztHPnTrKwsKB58+bRuXPn6MiRI9SiRQvFd2zRokXk5ORU\nLDdJksjFxYW+//57unDhAs2fP58kSVIs1999912ysrJ64l/RFayIiAiysbEhV1dX8vX1pa5du9LJ\nkycVz+vl5UWTJ09WjP3++++K5WHTpk1p8ODBimnOnTtX7AfYw4cPydbWlqKjo4vlV9Qzr6mePHmS\nqlWrRq+99hoRPVpILlq0SPGYvXv3kiRJdOvWLSJ6VJQCAgKKzbvwV3ah7OxsMjU1pe+++04xXXh4\nOLVs2VK+LUlSsV+sy5YtI0mSKCEhQR776quvSJIkOnbsmDw2e/ZscnR0fGLOYWFhig9qs2bNKCQk\nRDHNsGHD5NeAiMjT01PxK76o
2014-05-05 19:34:22 +00:00
"text": [
2014-05-06 18:38:02 +00:00
"<matplotlib.figure.Figure at 0x10ed1da90>"
2014-05-05 19:34:22 +00:00
]
}
],
2014-05-06 18:38:02 +00:00
"prompt_number": 35
2014-05-05 19:34:22 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This is a pretty significant performance gain. The \"Cython + type declarations\" approach sped up our initial Python code 25 times."
]
2014-05-05 23:31:23 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a name=\"explicit_loops\"></a>\n",
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Appendix III: Cython performance after replacing list comprehensions by explicit for loops"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[[back to top](#sections)]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
2014-05-06 18:38:02 +00:00
"In Python, we have those wonderful list, set, and dictionary comprehensions, which do not only look prettier and are easier to read (at least most of the time) than nested loop structures, but they also additionally come with some small performance benefits. \n",
2014-05-05 23:31:23 +00:00
"Does this also apply in Cython? Let's check it out."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"This is the code for our \"classic\" least squares approach that we have been using in the previous sections:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def lstsqr_comprehensions(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" x_avg = sum(x)/len(x)\n",
" y_avg = sum(y)/len(y)\n",
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
" slope = cov_xy / var_x\n",
" y_interc = y_avg - slope*x_avg\n",
" return (slope, y_interc)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 46
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"And here is a version where I replaced the list comprehensions by for-loops:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def lstsqr_loops(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" x_avg = sum(x)/len(x)\n",
" y_avg = sum(y)/len(y)\n",
" var_x = 0\n",
" for x_i in x:\n",
" var_x += (x_i - x_avg)**2\n",
" cov_xy = 0\n",
" for x_i, y_i in zip(x,y):\n",
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
" slope = cov_xy / var_x\n",
" y_interc = y_avg - slope*x_avg\n",
" return (slope, y_interc)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 48
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"Finally, the Cython versions of the two functions (with and without using list comprehensions) that we have defined above:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%load_ext cythonmagic"
],
"language": "python",
"metadata": {},
"outputs": []
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%cython\n",
"\n",
"def cy_lstsqr_comprehensions(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" cdef double x_avg, y_avg, var_x, cov_xy, slope, y_interc, x_i, y_i\n",
" x_avg = sum(x)/len(x)\n",
" y_avg = sum(y)/len(y)\n",
" var_x = sum([(x_i - x_avg)**2 for x_i in x])\n",
" cov_xy = sum([(x_i - x_avg)*(y_i - y_avg) for x_i,y_i in zip(x,y)])\n",
" slope = cov_xy / var_x\n",
" y_interc = y_avg - slope*x_avg\n",
" return (slope, y_interc)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 49
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%cython\n",
"\n",
"def cy_lstsqr_loops(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" cdef double x_avg, y_avg, var_x, cov_xy, slope, y_interc, x_i, y_i\n",
" x_avg = sum(x)/len(x)\n",
" y_avg = sum(y)/len(y)\n",
" var_x = 0\n",
" for x_i in x:\n",
" var_x += (x_i - x_avg)**2\n",
" cov_xy = 0\n",
" for x_i, y_i in zip(x,y):\n",
" cov_xy += (x_i - x_avg)*(y_i - y_avg)\n",
" slope = cov_xy / var_x\n",
" y_interc = y_avg - slope*x_avg\n",
" return (slope, y_interc)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 50
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<br>\n",
"We will generate some sample data for different sample sizes and take a look at the results for the regular Python functions, and the Cython code separately."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import timeit\n",
"import random\n",
"random.seed(12345)\n",
"\n",
"funcs = ['lstsqr_comprehensions', 'lstsqr_loops',\n",
" 'cy_lstsqr_comprehensions', 'cy_lstsqr_loops'] \n",
"\n",
"orders_n = [10**n for n in range(1, 6)]\n",
"times_n = {f:[] for f in funcs}\n",
"\n",
"for n in orders_n:\n",
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
" for f in funcs:\n",
" times_n[f].append(timeit.Timer('%s(x,y)' %f, \n",
" 'from __main__ import %s, x, y' %f).timeit(1000))"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 52
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"plt.figure(figsize=(8,6))\n",
"plt.plot(orders_n, times_n['lstsqr_comprehensions'], alpha=0.5, \n",
" label='list comprehensions', marker='o', lw=2)\n",
"plt.plot(orders_n, times_n['lstsqr_loops'], alpha=0.5, \n",
" label='for-loops', marker='o', lw=2)\n",
"plt.xlabel('sample size n')\n",
"plt.ylabel('time in ms')\n",
"plt.legend(loc=2)\n",
"plt.grid()\n",
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
"plt.title('Performance comparison list comprehensions and for-loops')\n",
"plt.show()\n",
"\n",
"plt.figure(figsize=(8,6))\n",
"plt.plot(orders_n, times_n['cy_lstsqr_comprehensions'], alpha=0.5, \n",
" label='list comprehensions (Cython', marker='o', lw=2)\n",
"plt.plot(orders_n, times_n['cy_lstsqr_loops'], alpha=0.5, \n",
" label='for-loops (Cython)', marker='o', lw=2)\n",
"plt.xlabel('sample size n')\n",
"plt.ylabel('time in ms')\n",
"plt.legend(loc=2)\n",
"plt.grid()\n",
"plt.xlim([0,max(orders_n) + max(orders_n) * 0.1])\n",
"plt.title('Performance comparison list comprehensions and for-loops in Cython')\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAfEAAAGJCAYAAACaQwrRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd4VFX++PH3pBHSG0kIaZDQEkoQBKSGLh1pCwiC4FdZ\nle+6+lt1UcEO+oW1rS7qIqjoioB0WJASpIgBaUpIIJCENEJCgCSkTDJzfn/cZTaBVFIn+byeJ8+T\nOzPnzLmfuclnzj3nnqtTSimEEEIIYXYs6rsBQgghhLg3ksSFEEIIMyVJXAghhDBTksSFEEIIMyVJ\nXAghhDBTksSFEEIIMyVJ3AylpaUxYMAAnJyc+Mtf/lLfzRFlOHjwIB06dKjT9wwPD2flypUAfPPN\nN4wYMaJO378hKR6LujJq1Ci+/vrrOn3PmhQYGMjevXtLfS4vL4+xY8fi4uLCH/7wh2q/16uvvsqs\nWbOqXU9TZ1XfDWgqAgMDuXr1KpaWltjb2zNy5Ej+/ve/Y29vX+W6PvvsMzw9PcnKyqqFloqa0r9/\nf6Kjo+v0PXU6HTqdDoCHH36Yhx9+uMIyc+bMwc/PjzfeeKO2m1eniseiruzYsaNO36+mlRez9evX\nc/XqVTIzM7GwqH7/r64/m8ZKeuJ1RKfTsW3bNrKzszlx4gTHjx/nzTffrFIdSimMRiMJCQl07Njx\nntpRVFR0T+VE1Uica5fEt+4lJCTQrl27e0rgpX1ess5YzZAkXg98fHx48MEH+f333wE4evQoffr0\nwdXVlbCwMA4cOGB6bXh4OC+//DL9+vXD3t6e2bNn89VXX/Huu+/i6OjIvn370Ov1PPPMM7Rq1YpW\nrVrx5z//Gb1eD0BERAS+vr68++67tGzZkrlz5/Laa68xZcoUZs2ahZOTE126dOHChQssWbIELy8v\nAgIC+PHHH01tWLVqFSEhITg5OREUFMRnn31meu52/X/729/w8vLCx8eH1atXm57Py8vjueeeIzAw\nEBcXF/r3709+fn6F+32nxMREJk6ciKenJx4eHixYsAAAo9HIm2++SWBgIF5eXsyePdt0hiI+Ph4L\nCwtWr16Nv78/7u7urFixgmPHjtGlSxdcXV1N9QCsXr2avn37smDBAlxcXOjYsSP79u2rUhxux3ne\nvHlERETg5+dnes0777yDr68vTk5OdOjQwVR3QUFBhZ9fWfEtz+rVq+nfvz+g/cP885//jJeXF87O\nznTp0oWzZ8/y2Wef8e2335qOp/Hjx5da19mzZxk2bBju7u54e3uzZMmSSrf9//7v//D09MTHx4dN\nmzaxY8cO2rVrh7u7O0uXLjW9x6uvvsrkyZOZNm0aTk5OdO/enTNnzpieDwwM5N1336VLly44Ojpi\nNBorPIbi4+Pp168fTk5OjBgxgmvXrpmeq+jvbtGiRaWWzc/PZ+bMmXh4eODq6krPnj1JT083lbt9\nCl8pVeGx+dVXXxEQEECLFi14++23Te8fGRlJjx49cHZ2xtvbm+eee67Uz+XGjRuMGTMGT09P3Nzc\nGDt2LMnJyZXaD4Cvv/6agIAAPDw8Srz/nRYvXswbb7zB2rVrcXR0ZNWqVZXavy+++IKAgACGDh1a\nZt23bdmyhdDQUFxdXRk0aFCJs1jnzp0jPDwcV1dXOnXqxNatW03PzZkzh/nz5zN8+HCcnJwIDw/n\n8uXLpudLO+4bFSXqRGBgoNqzZ49SSqnLly+r0NBQtWjRIpWUlKTc3d3Vzp07lVJK/fjjj8rd3V1l\nZGQopZQaOHCgCggIUFFRUcpgMKjCwkI1Z84c9corr5jqfuWVV9QDDzyg0tPTVXp6uurTp4/p+f37\n9ysrKyv14osvKr1er/Ly8tTixYuVra2t2r17tyoqKlKPPPKICggIUG+//bYqKipSn3/+uWrdurWp\n/u3bt6tLly4ppZQ6cOCAsrOzUydOnChR/+LFi1VRUZHasWOHsrOzUzdu3FBKKfXkk0+qQYMGqZSU\nFGUwGNTPP/+sCgoKytzv9PT0u2JXVFSkunTpop599lmVm5ur8vPz1eHDh5VSSq1cuVIFBweruLg4\nlZOToyZOnKhmzZqllFIqLi5O6XQ69cc//lEVFBSo3bt3KxsbGzVhwgSVnp6ukpOTlaenpzpw4IBS\nSqlVq1YpKysr9f7776uioiK1du1a5ezsrDIzMysdh+Jx3r9/v/L19VVKKRUdHa38/PxUamqqUkqp\nhIQEdfHixUp/fmXF907h4eFq5cqVpv3p16+fUkqpf//736p79+7q5s2bpvbcbsudx9OdsrKylLe3\nt/rb3/6mCgoKVHZ2tvrll18q3fY33njDdFy5u7urGTNmqJycHHX27FnVvHlzFR8fr5RSavHixcra\n2lpt2LBBFRUVqWXLlqnWrVuroqIipZRSAQEBqlu3biopKUnl5+dX6m8nKChIXbhwQeXl5anw8HD1\n4osvKqVUpcoGBweXWnbFihVq7NixKi8vTxmNRnXixAmVlZV1V/wrc2w+/vjjKj8/X50+fVo1a9ZM\nRUdHK6WU6t27t1qzZo1SSqlbt26po0ePlvrZXLt2Tf3www8qLy9PZWdnqylTpqgJEyaYni9vP86e\nPascHBzUwYMHVUFBgXr22WeVlZWV2rt3b6nv9eqrr5raX9n9mz17tulv9k6LFy9WM2fOVEopFRMT\no+zt7dWePXtUUVGRevfdd1VwcLAqLCxUer1eBQUFqSVLlqjCwkK1b98+5ejoqGJiYpRSSs2ePVs5\nOjqa9uNPf/pTpY77xkKSeB0JCAhQDg4OysXFRQUEBKinnnpK5eXlqaVLl5b4w1BKqREjRqgvv/xS\nKaX9U1i8eHGJ5+fMmaNefvll03ZQUJDpn5FSSu3atUsFBgYqpbR/pDY2NqqgoMD0/OLFi9Xw4cNN\n21u2bFEODg7KaDQqpbR/2jqdznTg32nChAnqgw8+MNXfvHlzZTAYTM97enqqX375RRkMBtW8eXN1\n5syZu+qoaL+LO3LkiGrRokWJ97ht8ODB6h//+IdpOyYmRllbWyuDwWD6R5KSkmJ63t3dXX3//fem\n7UmTJqn3339fKaUlPR8fnxL19+zZU3399deVisOdcS6exC9cuKA8PT3Vnj17lF6vL1FPRZ9fWfEt\nTVlJfO/evapdu3bq6NGjd8XxzuPpTt9++6267777Sn2uMm2/87iKjIw0vb579+5q8+bNSintuHzg\ngQdMzxmNRtWyZUt16NAhpZT2RXjVqlWm5yvzt/PWW2+Znvvkk0/Ugw8+WO2yX3zxherTp0+px3Xx\n+Ffm2ExOTjY937NnT7V27VqllFIDBgxQixcvLvVLbXlOnjypXF1dS7SnrP147bXX1PTp003P3bp1\nS9nY2JSZxIsn3cruX1xcXJltLV7f66+/rv7whz+YnjMajapVq1YqIiJC/fTTT8rb27tE2enTp6tX\nX31VKaUl8eL7kZOToywtLVVSUpLat29fmcd9YyGn0+uITqdj8+bNXL9+nfj4eP7+979ja2tLQkIC\n69atw9XV1fRz+PBhrly5Yipb/JRsaVJSUggICDBt+/v7k5KSYtpu0aIFNjY2Jcp4enqafm/evDke\nHh6miSbNmzcHICcnB4CdO3fSu3dv3N3dcXV1ZceOHSVOybm7u5cYJ7OzsyMnJ4eMjAzy8/MJCgq6\nq82V2e/bEhMTCQgIKHUsLjU19a59LyoqIi0tzfSYl5dXiX29c/vWrVum7VatWpWoPyAggNTU1ErF\nobQ43xYcHMz777/Pq6++ipeXF9OnTzfVW9HnV1Z8q2Lw4ME8/fTTPPXUU3h5efHEE0+QnZ1dqbKJ\niYm0adOm1Ocq0/Y7j6s74198X3x9fU2/63Q6fH19S9RX/G+hMseQt7d3qe9VnbKzZs1ixIgRTJs2\njVatWvHCCy+UOuZbmWOz+HsU/1xXrlzJ+fPn6dixIz179mT79u131Q+Qm5vLE088QWBgIM7Ozgwc\nOJCbN2+WGG8uaz9SUlJKxNvO
"text": [
"<matplotlib.figure.Figure at 0x10e8f8610>"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAeoAAAGJCAYAAABFDXDOAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl8TXf++PFXQoJE9kgiO0ntgtZSFLG2lNYoKtagqr/B\nTKtT7bSKKqodVBedfnVUSmyli30pGqNUaRGqxJpYEksESSSyfn5/nMltQja5N7n3JO/n4+Eh5957\nznmf9z03n5zz/tzPx0oppRBCCCGERbI2dwBCCCGEKJo01EIIIYQFk4ZaCCGEsGDSUAshhBAWTBpq\nIYQQwoJJQy2EEEJYMGmoi3Ht2jU6d+6Mo6Mjr732mrnDEUXYu3cvjRo1qtB9hoaGsmTJEgBWrFjB\nk08+WaH7tyT5c1FR+vTpw/Llyyt0n6YUGBjIrl27Cn0uPT2dfv364ezszPPPP2/0vmbMmMGIESOM\n3o6pWNJ7Fx4ezttvv23uMEpU6RrqwMBA7OzscHBwwMvLi9GjR3P37t0ybWvx4sV4eHiQnJzMv/71\nLxNHKkylU6dOnDp1qkL3aWVlhZWVFQDDhg1j+/btJa6jl18KDyt/LirKli1bLKrxeVjF5WzdunVc\nv36dpKQk1qxZY5J9WRJj37uVK1fSunVrHBwc8Pb2pk+fPuzbt6/E9SIiIujUqVOBx8xx7pZFpWuo\nrays2LRpEykpKRw+fJhff/2VWbNmPdQ2lFLk5uYSFxdH48aNyxRHdnZ2mdYTD0fyXL4kvxUvLi6O\nBg0aYG398L+eC3u/KtOYVgsWLOCVV15h6tSpXL9+nUuXLjFhwgQ2bNhg7tDKVaVrqPPz9vbmqaee\n4vfffwfgwIEDdOjQARcXF1q2bMmePXsMrw0NDWXq1Kk88cQT2NvbM2rUKJYtW8YHH3yAg4MDu3fv\nJjMzk5dffhkfHx98fHx45ZVXyMzMBCAqKgpfX18++OAD6taty5gxY3jnnXcYNGgQI0aMwNHRkZCQ\nEM6cOcN7772Hp6cnAQEB/PDDD4YYli5dSpMmTXB0dCQoKIjFixcbnsvb/oIFC/D09MTb25uIiAjD\n8+np6bz66qsEBgbi7OxMp06duHfvXonHfb9Lly4xYMAAPDw8cHd3Z9KkSQDk5uYya9YsAgMD8fT0\nZNSoUSQnJwMQGxuLtbU1ERER+Pv74+bmxueff86hQ4cICQnBxcXFsB3Q/rLt2LEjkyZNwtnZmcaN\nG7N79+6HykNenseOHUtUVBR+fn6G17z//vv4+vri6OhIo0aNDNvOyMgo8f0rKr/Fyf+XulKKV155\nBU9PT5ycnAgJCeHEiRMsXryYlStXGs6nZ599ttBtnThxgp49e+Lm5oaXlxfvvfdeqWP/17/+hYeH\nB97e3nz//fds2bKFBg0a4Obmxty5cw37mDFjBgMHDmTIkCE4Ojry2GOPcezYMcPzgYGBfPDBB4SE\nhODg4EBubm6J51BsbCxPPPEEjo6OPPnkk9y8edPwXEmfu2nTphW67r179xg+fDju7u64uLjQtm1b\nbty4YVgv73a7UqrEc3PZsmUEBARQp04d5syZY9j/wYMHad26NU5OTnh5efHqq68W+r7cvn2bvn37\n4uHhgaurK/369ePKlSulOg6A5cuXExAQgLu7e4H932/69Om8++67rFmzBgcHB5YuXVqq4/vyyy8J\nCAigR48eRW47z4YNG2jatCkuLi507dq1wN2okydPEhoaiouLC82aNWPjxo2G58LDw3nppZfo1asX\njo6OhIaGcvHiRcPzhZ33hcn/3kVERPDEE0/w2muv4erqSv369dm2bVuh6925c4fp06fz2Wef0b9/\nf2rVqkW1atV4+umnef/997l69Sr29vYkJSUZ1jl8+DAeHh78/vvvvPTSS/z88884ODjg6upqeE1S\nUhJ9+/bF0dGRxx9/nPPnzxue279/P23atMHZ2Zm2bdvy888/FziO4t5zk1KVTGBgoNq5c6dSSqmL\nFy+qpk2bqmnTpqnLly8rNzc3tXXrVqWUUj/88INyc3NTiYmJSimlunTpogICAtQff/yhcnJyVFZW\nlgoPD1dvv/22Ydtvv/22at++vbpx44a6ceOG6tChg+H5H3/8UVWvXl298cYbKjMzU6Wnp6vp06er\nmjVrqh07dqjs7Gw1cuRIFRAQoObMmaOys7PVF198oerVq2fY/ubNm9X58+eVUkrt2bNH2dnZqcOH\nDxfY/vTp01V2drbasmWLsrOzU7dv31ZKKfXXv/5Vde3aVcXHx6ucnBz1888/q4yMjCKP+8aNGw/k\nLjs7W4WEhKjJkyertLQ0de/ePbVv3z6llFJLlixRwcHB6sKFCyo1NVUNGDBAjRgxQiml1IULF5SV\nlZX6f//v/6mMjAy1Y8cOZWtrq/r3769u3Lihrly5ojw8PNSePXuUUkotXbpUVa9eXS1cuFBlZ2er\nNWvWKCcnJ5WUlFTqPOTP848//qh8fX2VUkqdOnVK+fn5qYSEBKWUUnFxcercuXOlfv+Kyu/9QkND\n1ZIlSwzH88QTTyillNq2bZt67LHH1J07dwzx5MVy//l0v+TkZOXl5aUWLFigMjIyVEpKivrll19K\nHfu7775rOK/c3NzU0KFDVWpqqjpx4oSqVauWio2NVUopNX36dGVjY6O++eYblZ2drebNm6fq1aun\nsrOzlVJKBQQEqFatWqnLly+re/fuleqzExQUpM6cOaPS09NVaGioeuONN5RSqlTrBgcHF7ru559/\nrvr166fS09NVbm6uOnz4sEpOTn4g/6U5N1988UV17949FR0drWrUqKFOnTqllFLq8ccfV5GRkUop\npe7evasOHDhQ6Htz8+ZN9e2336r09HSVkpKiBg0apPr37294vrjjOHHihKpdu7bau3evysjIUJMn\nT1bVq1dXu3btKnRfM2bMMMRf2uMbNWqU4TN7v+nTp6vhw4crpZSKiYlR9vb2aufOnSo7O1t98MEH\nKjg4WGVlZanMzEwVFBSk3nvvPZWVlaV2796tHBwcVExMjFJKqVGjRikHBwfDcfz9738v1Xl/v/s/\nOzY2Nuo///mPys3NVf/+97+Vt7d3oett3bpVVa9eXeXk5BT6vFJK9enTR/373/82LL/88svqb3/7\nm1JKqYiICEO8eUaNGqXc3NzUoUOHVHZ2tho2bJgaMmSIUkp7z52dnVVkZKTKyclRq1atUi4uLobf\nU8W956ZW6RrqgIAAVbt2beXs7KwCAgLUhAkTVHp6upo7d26Bk18ppZ588kn11VdfKaW0k2f69OkF\nng8PD1dTp041LAcFBRl+4Sil1Pbt21VgYKBSSvtlaWtrqzIyMgzPT58+XfXq1cuwvGHDBlW7dm2V\nm5urlNJ+MVtZWRlO7vv1799fffTRR4bt16pVq8BJ6uHhoX755ReVk5OjatWqpY4dO/bANko67vz2\n79+v6tSpU+gHoVu3bgU+ADExMcrGxkbl5OQYflnEx8cbnndzc1Nff/21Yfm5555TCxcuVEppH877\nP4xt27ZVy5cvL1Ue7s9z/ob6zJkzysPDQ+3cuVNlZmYW2E5J719R+S1MUQ31rl27VIMGDdSBAwce\nyOP959P9Vq5cqR599NFCnytN7PefVwcPHjS8/rHHHlPr169XSmnnZfv27Q3P5ebmqrp166qffvpJ\nKaX9sbt06VLD86X57MyePdvw3Geffaaeeuopo9f98ssvVYcOHQo9r/PnvzTn5pUrVwzPt23bVq1Z\ns0YppVTnzp3V9OnTC/3DtThHjhxRLi4uBeIp6jjeeecdFRYWZnju7t27ytbWtsiGOn/DWtrju3Dh\nQpGx5t/ezJkz1fPPP294Ljc3V/n4+KioqCj13//+V3l5eRVYNywsTM2YMUMppTVq+Y8jNTVVVatW\nTV2+fFnt3r27yPP+fvd/doKDgwvkxsrKSl27du2B9SIjIx+I736rV69WHTt2VEppFx5eXl7q0KFD\nhn3d31CHh4ercePGGZa3bNmi
"text": [
"<matplotlib.figure.Figure at 0x10565c6d0>"
]
}
],
"prompt_number": 71
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"As we can see in the first plot, the list comprehensions lead to a slightly increased performance in regular Python code. \n",
"But the second plot is quite interesting: List comprehensions in Cython are significantly slower than the regular for-loop structures.\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"Let us do a quick comparison by how much we were able to improve the performance of the simple least square implementation using Cython so far:\n",
"<br>"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import random\n",
"random.seed(12345)\n",
"\n",
"x = [x_i*random.randrange(8,12)/10 for x_i in range(500)]\n",
"y = [y_i*random.randrange(8,12)/10 for y_i in range(100,600)]"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 72
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import timeit\n",
"\n",
"funcs = ['lstsqr_comprehensions', 'cy_lstsqr_comprehensions', \n",
" 'cy_lstsqr_loops'] \n",
"labels = ['list comprehensions', 'list comprehensions (Cython)', \n",
" 'for-loops (Cython)']\n",
"\n",
"times = [timeit.Timer('%s(x,y)' %f, \n",
" 'from __main__ import %s, x, y' %f).timeit(1000)\n",
" for f in funcs]\n",
"\n",
"times_rel = [times[0]/times[i+1] for i in range(len(times[1:]))]"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 73
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"#%pylab inline\n",
"#import matplotlib.pyplot as plt\n",
"\n",
"plt.figure(figsize=(8,6))\n",
"x_pos = np.arange(len(funcs[1:]))\n",
"plt.bar(x_pos, times_rel, align='center', alpha=0.5, color=\"green\")\n",
"plt.xticks(x_pos, labels[1:], rotation=90)\n",
"plt.ylabel('relative performance gain')\n",
"plt.title('Performance gain compared to the classic least square implementation')\n",
"ftext = 'For-loops in Cython are {:.2f}x faster then list comprehensions'\\\n",
" .format(times[1]/times[2],1)\n",
"plt.figtext(.15,.8, ftext, fontsize=11, ha='left')\n",
"plt.xlim([-1,len(funcs[1:])])\n",
"plt.ylim([0,max(times_rel)*1.2])\n",
"plt.grid()\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAesAAAIBCAYAAABpxJfYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl4DXf7P/D3SSSWJJLIIoLkWC9LgqCoIomdqiq11Rba\n0qqiSqlS6VdrKS1NaUurYntqeRShqmpXtVQpJZLYYk+sQRKRnJP790d+mScn2wnmTA7n/bou12Uy\nZ2bumfnM3Ocz98wcnYgIiIiIyGrZFXcAREREVDgmayIiIivHZE1ERGTlmKyJiIisHJM1ERGRlWOy\nJiIisnJM1v9fYmIiWrVqhbJly2LcuHHFHY7V69y5M5YtW1bcYVgtvV6P7du3a7Y8Ozs7nDt3zqLL\nCAsLw+TJky02fxcXF8THxz/SNLt27ULlypUtE9AzLiAgAHv27FF9vvHx8bCzs0NmZqbq8y5ub7/9\nNj799NNiWXaJYlmqSvR6Pa5fvw57e3s4OTmhU6dOmDdvHpycnB55XgsXLoS3tzfu3btngUifPZs3\nby7uEKyaTqeDTqfLd1xYWBgqV66MqVOnPta8Q0JCMGDAALz++utPEuIjK2yd1HD//n2LzftJPOn+\nslYnTpwo7hA09aj7MTIyEosWLcLevXuVv3377beWCs+sp7pnrdPpsGnTJty/fx9HjhzB4cOHH/lb\nj4ggMzMTFy5cQO3atR8rDoPB8FjT0dPB2vavJROmOXyHknWytjZKFiBPMb1eL9u3b1eGx44dK126\ndBERkf3798vzzz8vbm5uUr9+fdm1a5fyueDgYPnoo4/khRdekNKlS0v//v3FwcFBHB0dxdnZWbZv\n3y4PHz6UUaNGia+vr/j6+sro0aPl4cOHIiKyc+dOqVixosycOVN8fHxkwIABEh4eLq+++qr0799f\nXFxcJDAwUOLi4mTatGni7e0tfn5+snXrViWGH3/8UWrXri0uLi5StWpVWbBggTIue/5ffPGFeHt7\nS4UKFWTx4sXK+NTUVBkzZoz4+/uLq6urtGjRQh48eGB2vXP7+++/pUGDBuLi4iI9e/aUXr16yaRJ\nk0RE5Pbt2/Liiy+Kl5eXuLu7S5cuXeTy5csm2/CHH34QEZHFixfLCy+8IGPHjhV3d3epUqWK/Prr\nrwUu9+LFi/LKK6+Il5eXeHh4yIgRI0RExGg0ytSpU8Xf31+8vb1l4MCBcvfuXREROX/+vOh0Olm8\neLFUrlxZypUrJ99++60cOnRIAgMDxc3NTZlPdkzNmzeXESNGiKurq9SqVcukrRRl+2fv34EDB0pm\nZqZMnz5dqlWrJh4eHtKrVy+5ffu2Ms3SpUvFz89PPDw85LPPPsvTNrMtWLDApK117dpVRESio6Ml\nODhY3NzcpG7duhIVFZXvtps4caLY29tLqVKlxNnZWd59910REdHpdPLdd99JjRo1xM3NTd555x2T\n6RYtWiS1a9cWd3d36dChg1y4cKHA/bN3716lDVWuXFmWLFkiIiJhYWFFbh+LFy+WqlWriouLi1Sp\nUkVWrFghIiKnT5+WVq1aiaurq3h6ekrv3r2VaXQ6nZw9e1ZECm/jOe3cuVMqVaqkDF+5ckW6d+8u\nXl5eUqVKFYmIiFDGHTx4UJo1ayZubm5SoUIFGTFihKSnpyvjR48eLd7e3lK2bFkJDAyUEydOFLi/\ncstvWhGRmzdvyksvvSRly5aVJk2ayKRJk6RFixYi8r82bTQalfnkPK7OnDkjoaGh4uHhIZ6entKv\nXz9JSkpSPuvv7y8zZ86UwMBAKVWqlBiNxkc6/v39/ZU2OmXKlEc6fwUHB8uECROkSZMmUrZsWXn5\n5ZeV4yH3eiUlJcmQIUOkQoUKUrFiRZk0aZIyLvs4fe+998TNzU2qVasm+/btkx9//FEqV64s3t7e\nSvsTEUlLS5P3339f/Pz8pHz58vLWW28p7aKw82ZB+zH7mHZxcZE6derIunXrRCTreCxVqpTY29uL\ns7OzuLu7i4jIoEGDlGNARGThwoVSvXp1KVeunHTt2lWuXr2qjDN3TD6qpz5Zb9u2TUSyEkDdunXl\n448/lsuXL4uHh4eSMH7//Xfx8PCQmzdvikhWQ/P395fo6GgxGo2SkZEhYWFhMnnyZGXekydPluef\nf15u3LghN27ckObNmyvjd+7cKSVKlJAJEyZIenq6PHjwQKZMmSKlSpWSrVu3isFgkIEDB4q/v79M\nmzZNDAaDfP/991KlShVl/r/88oucO3dORER2794tZcqUkSNHjpjMf8qUKWIwGGTz5s1SpkwZ5UAd\nPny4hIaGytWrV5UD9OHDhwWu940bN/Jsu4cPH4qfn59ERESIwWCQn3/+WRwdHZV1vHXrlvz888/y\n4MEDuX//vvTs2VO6deumTB8SEiKLFi0SkawDzsHBQX744QfJzMyUb7/9Vnx9ffPdZwaDQerVqydj\nxoyR1NRUSUtLk3379olIVkKpXr26nD9/XpKTk6V79+4yYMAAEfnfCeDtt9+Whw8fytatW8XR0VG6\ndesmN27ckCtXroi3t7fs3r1bialEiRIyd+5cMRgMsmrVKnF1dVVOKEXZ/jn379y5c+X555+XK1eu\nSHp6ugwbNkz69u0rIiInT54UZ2dn2bt3rzx8+FDGjBkjJUqUyDdZi0ietpaeni7VqlWT6dOnS0ZG\nhuzYsUNcXFwkNjY23+lzbvtsOp1OXnrpJbl7965cvHhRvLy8ZMuWLSIisn79eqlevbrExMSI0WiU\nTz/9VJo3b57vvOPj48XFxUVWrlwpBoNBbt26Jf/8848Sd/aJqrD2kZycLGXLlpW4uDgREUlISJCT\nJ0+KiEifPn1k2rRpIpLVBrP3ffY6ZCfrgtp4bjmTtdFolIYNG8rUqVMlIyNDzp07J1WrVpXffvtN\nRLK+nB48eFCMRqPEx8dL7dq1Ze7cuSIismXLFmnUqJHy5TAmJkauXbuW7/7KrbBpe/fuLb1795bU\n1FQ5ceKEVKxYUVq2bCki+SfrnPv2zJkzsm3bNklPT5cbN25Iq1atZPTo0cpn/f39JSgoSC5fvixp\naWmPdPyLmHZ2HvX8FRwcLBUrVpSTJ09KSkqK9OjRQ/r375/venXr1k3eeustSU1NlevXr0uTJk2U\nL8fZx2lkZKRkZmbKpEmTpGLFisoXqa1bt4qLi4ukpKSISNaXopdfflnu3Lkj9+/fl5deekk+/PBD\npS0Udt7Mbz+uWbNG2VerVq0SJycnSUhIEBGRyMhI5YtVtpzz2L59u3h6esrRo0fl4cOH8u6770qr\nVq2UzxZ2TD6OpzpZ+/v7i7Ozs7i5uYm/v7+888478uDBA5kxY4Zyks/WoUMH5RtaSEiITJkyxWR8\nzhORiEi1atVMeoe//fab6PV6EclqFI6OjiYnjylTpkj79u2V4aioKHF2dpbMzEwREbl3757odDrl\ngM6tW7du8tVXXynzL126tMlB7O3trZxoSpcuLcePH88zD3PrndPu3bulYsWKJn9r0aJFgSelo0eP\nKt8uRfIm6+rVqyvjUlJSRKfTSWJiYp75/Pnnn+Ll5WWybtlat24t3377rTIcGxsrDg4OYjQalRNA\nzm+uHh4esnr1amW4R48eysl38eLFeb4wNGnSRJYtW5bv+uXe/rn3b+3atU2S79WrV8XBwUEMBoN8\n8sknSuLOXn9HR8dCk3XOtrZnzx7x8fEx+Uzfvn0lPDw83+lDQkKU3lc2nU5nkvh69eolM2fOFBGR\njh07miR3o9EoZcqUkYsXL+aZ97Rp06R79+5FijunnO0jOTlZ3NzcZO3atZKammryuYEDB8rQoUNN\neuE51+Hs2bOFtvHccibrAwcOiJ+fX571GTx4cL7TzpkzR1555RURyTrx1qxZUw4cOJCnbRa23iIi\nO3bsyHdag8EgDg4OJl+6Jk6cWGjPOr8vYtnWrVsnQUFByrBerze54vYox3/29DmT9aOcv0JCQpQk\nKZLVE3V0dJTMzEyT9UpISJCS
"text": [
"<matplotlib.figure.Figure at 0x10e919d10>"
]
}
],
"prompt_number": 88
2014-05-06 05:08:11 +00:00
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a name=\"showdown\"></a>\n",
"<br>\n",
"<br>\n",
"<br>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Final Comparison: Cython vs. NumPy vs. SciPy for least squares fitting"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To wrap it up, let us compare the Cython code of our simple least squares fit implementation to the Numpy and Scipy functions - after we made some improvements by adding static type declarations and explicit for loops."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%load_ext cythonmagic"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 1
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%cython\n",
"\n",
"def cy_lstsqr(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" cdef double x_avg, y_avg, temp, var_x, cov_xy, slope, y_interc, x_i, y_i\n",
" x_avg = sum(x)/len(x)\n",
" y_avg = sum(y)/len(y)\n",
" var_x = 0\n",
" for x_i, y_i in zip(x,y):\n",
" temp = (x_i - x_avg)\n",
" var_x += temp**2\n",
" cov_xy += temp*(y_i - y_avg)\n",
" slope = cov_xy / var_x\n",
" y_interc = y_avg - slope*x_avg\n",
" return (slope, y_interc)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 2
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import numpy as np\n",
"import scipy.stats"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 3
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def lin_lstsqr_mat(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" X = np.vstack([x, np.ones(len(x))]).T\n",
" return (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(y)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 4
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def numpy_lstsqr(x, y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" X = np.vstack([x, np.ones(len(x))]).T\n",
" return np.linalg.lstsq(X,y)[0]"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 5
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def scipy_lstsqr(x,y):\n",
" \"\"\" Computes the least-squares solution to a linear matrix equation. \"\"\"\n",
" return scipy.stats.linregress(x, y)[0:2]"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 6
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import timeit\n",
"import random\n",
"random.seed(12345)\n",
"\n",
"funcs = ['cy_lstsqr', 'lin_lstsqr_mat',\n",
" 'numpy_lstsqr', 'scipy_lstsqr'] \n",
"\n",
"orders_n = [10**n for n in range(1, 6)]\n",
"times_n = {f:[] for f in funcs}\n",
"\n",
"for n in orders_n:\n",
" x = [x_i*random.randrange(8,12)/10 for x_i in range(n)]\n",
" y = [y_i*random.randrange(10,14)/10 for y_i in range(n)]\n",
" for f in funcs:\n",
" times_n[f].append(min(timeit.Timer('%s(x,y)' %f, \n",
" 'from __main__ import %s, x, y' %f)\n",
" .repeat(repeat=3, number=1000)))"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 26
},
{
"cell_type": "code",
"collapsed": false,
"input": [
2014-05-06 18:38:02 +00:00
"%pylab inline"
],
"language": "python",
"metadata": {},
"outputs": []
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import matplotlib.pyplot as plt\n",
2014-05-06 05:08:11 +00:00
"\n",
"labels = [('cy_lstsqr', 'Cython implementation'), \n",
" ('lin_lstsqr_mat', 'numpy matrix equation'),\n",
" ('numpy_lstsqr', 'numpy.linalg.lstsq()'), \n",
" ('scipy_lstsqr', 'scipy.stats.linregress()')] \n",
"\n",
"matplotlib.rcParams.update({'font.size': 12})\n",
"\n",
"fig = plt.figure(figsize=(10,8))\n",
"for lb in labels:\n",
" plt.plot(orders_n, times_n[lb[0]], alpha=0.5, label=lb[1], marker='o', lw=3)\n",
"plt.xlabel('sample size n')\n",
"plt.ylabel('performance gain relative to the slowest approach')\n",
"plt.xlim([1,max(orders_n) + max(orders_n) * 10])\n",
"plt.legend(loc=2)\n",
"plt.grid()\n",
"plt.xscale('log')\n",
"plt.yscale('log')\n",
"plt.title('Performance of least square fit implementations for different sample sizes')\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAnIAAAIECAYAAACdVcNJAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXdYVMfXx7/30vsuZQFR6YKgYtdYEBQ1RBNjiYIVLDG2\nvBrzsytg10SNUYyRqDQ1ligxmkgsgDVRsCuioCAqxYqKCAjn/QO54cICC8Jimc/z7PPszp05c+bc\nO3PPTuWIiMBgMBgMBoPBeOfg61oBBoPBYDAYDEb1YI4cg8FgMBgMxjsKc+QYDAaDwWAw3lGYI8dg\nMBgMBoPxjsIcOQaDwWAwGIx3FObIMRgMBoPBYLyjMEdOSbx69QojR46EsbExeJ7H0aNH61qld5Kd\nO3fC1tYWqqqqGDlypNw4Pj4+6N69u5I1Y5S+NzExMeB5Hvfu3auyLGtrayxevLgWtCyLlZUVFi1a\npJS83lZ4nsfWrVvrWo06aSejo6NFz2np3wBw6dIltG3bFlpaWrCxsQEApKamolu3btDV1YWKikqt\n6/khoYzn0c3NDV9++WWt5qEsmCNXAh8fH/A8D57noaamBisrK4wbNw6PHj16Y9m//fYbtm3bhn37\n9iE9PR0fffRRDWj8YVFQUICRI0fCy8sLqampWL16tdx4HMeB4zil6hYeHg6e/3Crk7x706FDB6Sn\np8Pc3BwAcPz4cfA8j9u3b1cqLzY2FlOmTKlttQHUzfPyJty5c6faTo6Hhwd8fX3LhKenp6N///41\nod4b8Ta0kx07dhQ9twAwbdo0SCQSJCQk4MyZMwCAxYsX48GDB7hw4QLS0tKUrqc8Ro8eDXd397pW\n450gIiICK1eurGs1agTVulbgbcPV1RU7duzAq1evEBsbizFjxiA1NRX79u2rlry8vDyoq6vjxo0b\nsLCwQPv27d9Iv2J5HyL37t1DdnY2PD09RY1saYgIbJ/rqlNYWAgA1XJIy7s3MpmsTFxF7o2RkVGV\ndfjQqMlnXN59qgvehnZSTU2tjD0SExMxYsQINGzYUKRrmzZtYGtr+0a65ufnQ01N7Y1kMKqORCKp\naxVqDmIIjBgxgjw8PERhixYtIhUVFXr58iUREW3bto1cXFxIU1OTrKys6JtvvqHs7GwhfpcuXWjU\nqFE0Z84cMjc3JzMzM3JzcyOO44SPtbU1ERHl5eXR9OnTycLCgtTV1cnJyYm2bt0qyp/jOPrxxx/J\n29ubDAwMaNCgQbR582ZSVVWlqKgoatKkCWlpaZG7uzulpaXRkSNHyMXFhXR0dMjDw4Pu3r0ryLp5\n8yb17duX6tWrR9ra2tS0aVMKCwsT5delSxcaPXo0zZ8/n8zMzMjQ0JCGDx9Oz58/F8X79ddfqWXL\nlqSpqUlGRkbk6elJjx8/Fq7/+OOP5ODgQJqammRvb0+LFi2iV69eVWj/U6dOUefOnUlLS4ukUikN\nHjyYMjMziYho8+bNIhtyHEcxMTEK38fK7tvff/9NXbp0IUNDQzIwMKAuXbrQ6dOnRTKCgoLI0dGR\nNDU1ydDQkFxdXenOnTsUFRVVRjdfX99yy7lo0SKysbEhDQ0NMjExoZ49e1JOTo7IdhYWFqStrU09\ne/akkJAQ4jhOuJfF978kqampZWwyevRosrW1JS0tLbKxsaFZs2ZRbm6ucN3Pz4/s7Oxo+/bt5ODg\nQKqqqnTt2jV69uwZff3114IOLVq0oN27d5dbnvLuTbFd7t69S7du3SoTx93dvVyZlpaWtHDhQtHv\nuXPn0ldffUUGBgZkampK69ato5ycHBo/fjxJpVKysLCgtWvXiuRwHEerV6+mfv36kY6ODllYWNDq\n1atFcaysrGjRokXC77y8PPLz8yNra2vS1NQkZ2dn+vnnn8vIXbNmDQ0cOJB0dHTI0tKSdu/eTY8e\nPSIvLy/S09MjGxsb+u2330Tp0tPTacSIEWRiYkJ6enrUsWNHOnr0qHC92GYHDx6kzp07k7a2Njk5\nOdFff/0lyltee1JZ/R4xYkS5dYjjONqyZYsQ9969ezRo0CCSSCSkpaVFbm5uFBsbWyU9iSp/1kvS\npUuXGmsnvby85OZBVHn9quy59ff3L7e+V1Z3iuVt2bKFPD09SUdHh2bMmEFEir1bKmqb/fz8yugV\nEhIi1wZZWVnk4+NDZmZmpKGhQQ0aNKBvvvlGuK5Ie1idOlBc/vDwcOratavQNv36669lZJd8Hqva\nJhEVtYn9+vUjY2Nj0tTUJBsbG/ruu+/K2LPkPS/9sbKyEuLfuHGD+vXrRxKJhKRSKfXo0YMuXbqk\nsE1rE+bIlWDEiBHUvXt3UdiKFSuI4zh6/vw5bd68maRSKYWHh9OtW7fo6NGj1KxZMxo2bJgQv0uX\nLqSnp0fjxo2j+Ph4unz5Mj169Ii+/fZbsra2poyMDHrw4AEREX377bdkZGREu3btohs3btDixYuJ\n53k6fPiwII/jODIyMqLAwEC6efMm3bhxgzZv3kw8z5O7uzudPn2azp49S/b29tSpUydydXWlf//9\nl86fP0+Ojo40aNAgQdalS5coMDCQLl68SDdv3qQ1a9YIDmFJ/SUSCX3zzTeUkJBAf//9NxkaGtLc\nuXOFOJs2bSI1NTVauHChUMa1a9cK5fLz8yNLS0uKiIig5ORk+vPPP6lhw4YiGaVJS0sjPT09GjJk\nCF2+fJmOHz9OzZo1I1dXVyIiysnJoTNnzhDHcfTHH39QRkYG5eXllXsfSzpyity3PXv20M6dO+n6\n9et09epVGj16NBkaGtLDhw+JiCg2NpZUVVUpLCyMbt++TZcuXaKNGzfSnTt3KC8vjwIDA4njOMrI\nyKCMjAx6+vSpXN1+++030tfXp3379lFqaiqdP3+eVq9eLbzcIiIiSFVVlVatWkU3btygjRs3kkwm\nI57nq+TIFRYW0uzZs+n06dOUkpJCe/fuJXNzc/Lz8xPS+Pn5kba2Nrm5udHp06fpxo0b9OzZM3Jz\ncyN3d3c6ceIE3bp1izZs2EDq6uqi57Ik5d2bki/EgoIC2rt3L3EcR7GxsZSRkSFy/EtT2rmytLQk\niURCq1atoqSkJFq4cCHxPE89e/YUwpYsWUI8z9PVq1eFdBzHkaGhIa1du5Zu3LhBq1evJlVVVfr9\n99/LzWvEiBHk4uJCBw8epOTkZNq+fTtJJBLauHGjSK6ZmRmFhoZSUlISjR8/nnR0dKhHjx4UEhJC\nSUlJNGnSJNLR0RGeoRcvXlDjxo1pwIABFBcXR0lJSbRo0SLS0NCg+Ph4IvrvheLi4kKRkZGUmJhI\nvr6+pK+vL9jr3LlzxHEc7dmzR9SeVFa/s7KyyNXVlby8vITntLgOlXxxFhYWUtu2balFixZ04sQJ\nunTpEg0aNIikUqmQlyJ6Vvasl6Ym28nExES5eShSv0o/t+np6dSgQQOaOXMmZWRk0PPnzyk9PZ06\ndOhAQ4cOFep7YWFhpXWn2JGpX78+bd26lZKTk+nWrVsKv1sqapufP39OQ4YMoY4dOwr3tzxbT5o0\niVxcXOj06dOUmppKJ0+epF9++UW4Xll7WN06UFz+evXq0datW+n69es0Z84cUlFRoXPnzolkl3we\nq9omERF9+umn1L17d7pw4QKlpKRQVFQUbdu2Tbju5uZGY8aMIaKiPwvFNsvIyKCrV6+ShYUFjRw5\nkoiK/oCZmprS+PHj6fLly3T9+nWaNGkSGRkZ0f379xWyaW3CHLkSlHYArly5QjY2NvTRRx8RUdHL\npPQ/85iYGOI4jp48eUJERZXNwcGhjOzi3o9isrOzSUNDg3766SdRvL59+1LXrl2F3xzHCf8aiinu\nAblw4YIQ9t133xHHcXT27FkhbNWqVWRsbFxhmfv06SM8zMX6N2/eXBRn3Lhxgg2IiBo0aECTJk2S\nKy87O5u0tbUpMjJSFB4SEkISiaRcPebMmUMNGjSg/Px8IezChQvEcZzQY1HcCJw4caLCMpW+j4rc\nt9IUFBSQVCoVGpPdu3eTgYFB
"text": [
"<matplotlib.figure.Figure at 0x111098fd0>"
]
}
],
"prompt_number": 70
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"So, using a few tweaks, such as static type declarations and explicit for-loops instead of list comprehensions, we managed to increase the performance of our least squares fit implementation quite significantly - it outperforms the alternative functions in Numpy and Scipy now."
]
2014-05-04 22:57:02 +00:00
}
],
"metadata": {}
}
]
}